直线一级倒立摆的牛顿—欧拉方法建模
倒立摆实验报告(PID控制)

专业实验报告直线单级倒立摆控制系统硬件结构框图如图1所示,包括计算机、I/O设备、伺服系统、倒立摆本体和光电码盘反馈测量元件等几大部分,组成了一个闭环系统。
图1 一级倒立摆实验硬件结构图对于倒立摆本体而言,可以根据光电码盘的反馈通过换算获得小车的位移,小车的速度信号可以通过差分法得到。
摆杆的角度由光电码盘检测并直接反馈到I/O设备,速度信号可以通过差分法得到。
计算机从I/O设备中实时读取数据,确定控制策略(实际上是电机的输出力矩),并发送给I/O设备,I/O设备产生相应的控制量,交与伺服驱动器处理,然后使电机转动,带动小车运动,保持摆杆平衡。
图2是一个典型的倒立摆装置。
铝制小车由6V的直流电机通过齿轮和齿条机构来驱动。
小车可以沿不锈钢导轨做往复运动。
小车位移通过一个额外的与电机齿轮啮合的齿轮测得。
小车上面通过轴关节安装一个摆杆,摆杆可以绕轴做旋转运动。
系统的参数可以改变以使用户能够研究运动特性变化的影响,同时结合系统详尽的参数说明和建模过程,我们能够方便地设计自己的控制系统。
图2 一级倒立摆实验装置图上面的倒立摆控制系统的主体包括摆杆、小车、便携支架、导轨、直流伺服电机等。
主体、驱动器、电源和数据采集卡都置于实验箱内,实验箱通过一条USB数据线与上位机进行数从上图可以看出,系统在1.5秒后达到平衡,但是存在一定的稳态误差。
为消除稳态误差,我们增加积分参数Ki,令Kp=40,Ki=60,Kd=2,得到以下仿真结果:图8 直线一级倒立摆PID控制仿真结果图从上面仿真结果可以看出,系统可以较好的稳定,但由于积分因素的影响,稳定时间明显增大。
双击“Scope1”,得到小车的位置输出曲线为:图9 施加PID控制器后小车位置输出曲线图由于PID 控制器为单输入单输出系统,所以只能控制摆杆的角度,并不能控制小车的位置,所以小车会往一个方向运动,PID控制分析中的最后一段,若是想控制电机的位置,使得倒立摆系统稳定在固定位置附近,那么还需要设计位置PID闭环。
电气系统综合设计实验报告直线一级倒立摆控制系统设计

电气控制系统设计——直线一级倒立摆控制系统设计学院轮机工程学院班级电气1111姓名李杰学号 36姓名韩学建学号 35成绩指导老师肖龙海2014 年 12 月 25 日小组成员与分工:韩学建主要任务:二阶系统建模与性能分析,二阶控制器的设计,二阶系统的数字仿真与调试,二阶系统的实物仿真与调试;二阶状态观测器的数字仿真与调试,二阶状态观测器的实物仿真与调试;李杰主要任务:四阶系统建模与性能分析,四阶控制器的设计,四阶系统的数字仿真与调试,四阶系统的实物仿真与调试;四阶状态观测器的数字仿真与调试,四阶状态观测器的实物仿真与调试;前言倒立摆系统是非线性、强耦合、多变量和自然不稳定的系统,倒立摆是机器人技术、控制理论、计算机控制等多个领域、多种技术的有机结合,其被控系统本身又是一个绝对不稳定、高阶次、多变量、强耦合的非线性系统,可以作为一个典型的控制对象对其进行研究;倒立摆系统作为控制理论研究中的一种比较理想的实验手段,为自动控制理论的教学、实验和科研构建一个良好的实验平台,以用来检验某种控制理论或方法的典型方案,促进了控制系统新理论、新思想的发展;本报告通过设计二阶、四阶两种倒立摆控制器来加深对实际系统进行建模方法的了解和掌握随动控制系统设计的一般步骤及方法;熟悉倒立摆系统的组成及基本结构并利用MATLAB对系统模型进行仿真,利用学习的控制理论对系统进行控制器的设计,并对系统进行实际控制实验,对实验结果进行观察和分析,研究调节器参数对系统动态性能的影响,非常直观的了解控制器的控制作用;目录第一章设计的目的、任务及要求倒立摆系统的基本结构 (4)设计的目的 (4)设计的基本任务 (4)设计的要求 (4)设计的步骤 (5)第二章一级倒立摆建模及性能分析微分方程的推导 (5)系统的稳定性和能控能观性分析 (11)二阶的能观性、能控性分析 (13)四阶的能观性、能控性分析 (18)第三章倒立摆系统二阶控制器、状态观测器的设计与调试设计的要求 (22)极点配置 (22)控制器仿真设计与调试 (23)状态观测器仿真设计与调试 (28)第四章倒立摆系统四阶控制器、状态观测器的设计与调试设计的要求 (26)极点配置 (26)控制器仿真设计与调试 (27)状态观测器仿真设计与调试 (28)心得体会 (31)参考文献 (31)第一章设计的目的、任务及要求倒立摆系统的基本结构与工作原理图倒立摆系统硬件框图图倒立摆系统工作原理框图倒立摆系统通过计算机、I/O卡、伺服系统、倒立摆本体和光电码盘反馈测量元件组成一个闭环系统;以直线一级倒立摆为例,其工作原理框图如图所示;图中光电码盘1由伺服电机自带,小车的位移可以根据该码盘的反馈通过换算获得,速度信号可以通过对位移的差分得到;各个摆杆的角度由光电码盘2测量并直接反馈到I/O卡,而角速度信号可以通过对角度的差分得到;计算机从I/O卡实时读取数据,确定控制决策电机的输出力矩,并发给I/O卡;I/O卡经过电控箱内部电路产生相应的控制量,驱动电机转动,使小车按控制要求进行运动,以达到控制目的;实验过程中需要了解倒立摆装置基本结构;了解编码盘、行程开关等的基本工作原理;进行行程开关、编码盘和电机基本测试;设计的目的本设计要求我们针对设计要求,利用课堂所学知识及实验室实测来的系统数据采用工程设计法进行一级直线倒立摆控制系统设计;绘制原理图,同时在实验室进行实验检验设计结果,分析数据,编写设计报告;目的是使学生掌握随动控制系统设计的一般步骤及方法;设计的基本任务本课程设计的被控对象采用固高科技生产的GLIP2001一级直线倒立摆;通过设计与调试使学生能够:1熟悉倒立摆系统的组成及其基本结构;2掌握通过解析法建立系统数学模型及进行工作点附近线性化的方法;3掌握系统性能的计算机辅助分析;4掌握系统控制器的设计与仿真;5研究调节器参数对系统动态性能的影响;设计的要求1.熟悉倒立摆系统结构,熟悉倒立摆装置的基本使用方法;2.建立系统的数学模型,并在工作点附近线性化;3.分析系统的稳定性、频域性能、能控性与能观性;4.采用状态空间的极点配置法设计控制器,要求系统调节时间ts<=3s,阻尼比ξ>= and ξ<=1;实验步骤1.倒立摆系统基本结构分析2.对象的建模3..系统性能分析4.控制器设计与调试5.设计报告的撰写第二章一级倒立摆建模及性能分析系统建模可以分为两种:机理建模和实验建模;实验建模就是通过在研究对象上加上一系列的研究者事先确定的输入信号,激励研究对象并通过传感器检测其可观测的输出, 应用数学手段建立起系统的输入-输出关系;这里面包括输入信号的设计选取,输出信号的精确检测,数学算法的研究等等内容;机理建模就是在了解研究对象的运动规律基础上,通过物理、化学的知识和数学手段建立起系统内部的输入-状态关系;对于倒立摆系统,由于其本身是自不稳定的系统,实验建模存在一定的困难;但是忽略掉一些次要的因素后,倒立摆系统就是一个典型的运动的刚体系统,可以在惯性坐标系内应用经典力学理论建立系统的动力学方程;下面采用牛顿-欧拉方法建立直线型一级倒立摆系统的数学模型;微分方程的推导在忽略了空气阻力和各种摩擦之后,可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统,如图所示;我们不妨做以下假设:M 小车质量m 摆杆质量b 小车摩擦系数l 摆杆转动轴心到杆质心的长度I 摆杆惯量 F 加在小车上的力x 小车位置φ摆杆与垂直向上方向的夹角θ摆杆与垂直向下方向的夹角考虑到摆杆初始位置为竖直向下图是系统中小车和摆杆的受力分析图;其中,N 和P 为小车与摆杆相互作用力的水平和垂直方向的分量;注意:在实际倒立摆系统中检测和执行装置的正负方向已经完全确定,因而矢量方向定义如图所示,图示方向为矢量正方向;分析小车水平方向所受的合力,可以得到以下方程:①由摆杆水平方向的受力进行分析可以得到下面等式:②即:③把这个等式代入①式中,就得到系统的第一个运动方程④为了推出系统的第二个运动方程,对摆杆垂直方向上的合力进行分析,可以得到下面方程:⑤⑥力矩平衡方程如下:⑦注意:此方程中力矩的方向,由于θ= π+φ,cosφ= -cosθ,sinφ= -sinθ,故等式前面有负号; 合并这两个方程,约去P 和N ,得到第二个运动方程:⑧设θ=π+φφ是摆杆与垂直向上方向之间的夹角,假设φ与1单位是弧度相比很小,即φ<<1,则可以进行近似处理:用u 来代表被控对象的输入力F ,线性化后两个运动方程如下:⑨对式3-9进行拉普拉斯变换,得到⑩注意:推导传递函数时假设初始条件为0;由于输出为角度φ,求解方程组的第一个方程,可以得到:⑾⑿如果令则有⒀把上式代入方程组的第二个方程,得到:⒁整理后得到传递函数:⒂其中,该系统状态空间方程为:⒃方程组对解代数方程,得到解如下:⒄整理后得到系统状态空间方程:⒅由9的第一个方程为对于质量均匀分布的摆杆有:于是可以得到:化简得到:⒆⒇以小车加速度为输入的系统状态空间方程:稳定性分析P=polyA;r=rootsP;ii=findrealr>0;n=lengthii;ifn>0disp'不稳定';elsedisp'稳定';end不稳定由此得到系统在未加控制器之前是发散的,不稳定的能控能观性分析A= 0 1 0 0;0 0 0 0;0 0 0 1;0 0 0;B= 0 1 0 3';C= 1 0 0 0;0 0 1 0;D= 0 0 ';>> n=4;Uc=ctrbA,B;Vo=obsvA,C;>> ifrankUc==nifrankVo==ndisp'系统状态即能控又能观'else disp'系统状态即能控,但不能观'endelse ifrankVo==ndisp'系统状态能观,但不能控'else disp'系统状态不能控,但也不能观' endend系统状态即能控又能观二阶的能观性、能控性分析>> A=0 1; 0;>> B=0 3';>> C=0 0 ;1 0;>> D=0;二阶能控性分析:>> M=ctrbA,BM =0 33 0>> rankMans =2说明系统是能控的二阶能观性分析:>> N=obsvA,CN =0 11 0>> rankNans =2说明系统是能观的四阶的能观性、能控性>> A=0 1 0 0; 0 0 0 0;0 0 0 1;0 0 0;;>> B=0 1 0 3';>> C= 1 0 0 0;0 0 1 0;>> D=0 0';四阶能控性分析:>> M=ctrbA,BM =0 0 00 0 00 00 0>> rankMans =4说明系统是能控的四阶能观性分析:>> N=obsvA,CN =0 0 00 0 00 0 00 0 00 0 0 00 0 00 0 0 00 0 0>> rankNans =4说明系统是能观的第三章倒立摆系统二阶控制器的设计设计的要求建立以X’’为输入,Φ与Φ’为状态变量,y为输出的模型分析系统的稳定性,能控能观性设计状态反馈控制器进行极点配置,是系统ξ>= ts<=3s极点配置取ξ=,Ts=;则Wn=,极点为±利用MATLAB进行计算:clear;T=input'T=';zeta=input'zeta=';Wn=4/Tzeta;A=0 1; 0;B=0;3;S1=-zetaWn-Wnsqrtzeta^2-1;S2=-zetaWn+Wnsqrtzeta^2-1;P=S1,S2;K=placeA,B,P则:K0=,K1=;控制器的仿真测试与调试图二阶系统结构图以小车加速度为输入,摆杆偏移角度和角速度为状态变量的模型,K值为反馈矩阵,输出为角度的波形图仿真波形图:取 &= 极点为:Wn=则 K0= K1= 图仿真结果波形图有次图可得加入控制器之后系统可以稳定,可见控制器的设计是合理的硬件调试硬件调试结构图以小车加速度为输入,摆杆偏移角度和角速度为状态变量的模型,加入Л模块纠正反馈角度符号通过调试K值,当K取的时候,可使仿真结果较稳定;从摆杆的角度可以看出,角度可以稳定下来,施加一干扰后,摆杆可以很快恢复稳定;状态观测器的仿真测试与调试图二阶状态观测器数字仿真图以小车加速度为输入,摆杆偏移角度和角速度为状态变量的模型,K值为反馈矩阵,输出为角度的波形图仿真波形图:取 &= 极点为:Wn=则 K0= K1= 图仿真结果波形图反馈矩阵G的求法T=input'T=';zeta=input'zeta=';Wn=4/Tzeta;A=0 1; 0;B=0;3;C=1 0;S1=-zetaWn-Wnsqrtzeta^2-1;S2=-zetaWn+Wnsqrtzeta^2-1;P=S1,S2;OP=5P;G=placeA',C',OPG=实物调试由图可知,施加扰动后摆杆能很快恢复,符合系统要求;第四章倒立摆系统四阶控制器的设计设计要求根据设计要求,确定系统闭环极点,设计状态反馈控制器,并进行仿真、调试验证;极点配置取 &= T= Wn= 极点为:±;-20±利用MATLAB进行计算:T=input'T=';zeta=input'zeta=';Wn=4/Tzeta;A=0 1 0 0;0 0 0 0;0 0 0 1;0 0 0;B=0;1;0;3;S1=-zetaWn-Wnsqrtzeta^2-1;S2=-zetaWn+Wnsqrtzeta^2-1;P=,-20+,S1,S2;K=placeA,B,Pk0=,k1=,k2= ,k3=;则K=控制器的仿真测试与调试图四阶系统仿真结构图以小车加速度为输入,摆杆角度、角速度、小车位移、加速度为状态变量,上半部分为位移输出,下半部分为角度输出仿真结果:位移:角度:实物调试:图硬件调试结构图将K1、K2、K3、K4合并后反馈作用系统,系统为单输入双输出四阶一级倒立摆状态空间极点配置实时控制结果平衡时上为位移,下位角度直线一级倒立摆状态空间极点配置实时控制结果施加干扰上为位移,下位角度状态观测器仿真设计与调试图四阶状态观测器数字仿真图四阶系统仿真结构图以小车加速度为输入,摆杆角度、角速度、小车位移、加速度为状态变量,上半部分为位移输出,下半部分为角度输出反馈矩阵G的求法T=input'T=';zeta=input'zeta=';Wn=4/Tzeta;A=0 1 0 0;0 0 0 0;0 0 0 1;0 0 0;B=0;1;0;3;C=1 0 0 0;0 0 1 0;S1=-zetaWn-Wnsqrtzeta^2-1;S2=-zetaWn+Wnsqrtzeta^2-1;P=,-10+,S1,S2;OP=3P;G=placeA',C',OP'G =实物调试反馈矩阵G和增益矩阵K分别调用matlab程序即可实物仿真与结果心得体会通过此次课程设计,使我更加扎实的掌握了有关MATLAB方面的知识,在设计过程中虽然遇到了一些问题,但经过一次又一次的思考,一遍又一遍的检查终于找出了原因所在,也暴露出了前期我在这方面的知识欠缺和经验不足;实践出真知,通过亲自动手制作,使我们掌握的知识不再是纸上谈兵;课程设计诚然是一门专业课,给我很多专业知识以及专业技能上的提升,同时又是一门讲道课,一门辩思课,给了我许多道,给了我很多思,给了我莫大的空间;同时,设计让我感触很深;使我对抽象的理论有了具体的认识;通过这次课程设计,我掌握了倒立摆装置的识别和测试;熟悉了控制系统的设计原理;了解了现代控制理论的设计方法;以及如何提高倒立摆系统的性能等等,掌握了MATLAB、simulink的使用方法和技术,通过查询资料,对所学知识有了很多新的认识;自己写主要参考文献:1.夏德玲、翁贻方,自动控制理论.北京,北京工业大学出版社,2006年1月2.刘豹、唐万生,现代控制理论.北京,机械工业出版社,2006年6月3.李国勇、谢克明,计算机仿真技术与CAD.北京,电子工业出版社,2009年1月4.Googol Technology直线倒立摆系统GLIP系列安装与使用手册固高科技。
一级倒立摆数学模型建立

一、直线一级倒立摆系统的数学模型1、倒立摆系统是一种复杂的非线性系统,为了简化对系统的反洗,在建立数学模型的过程中,作以下假设:1.)小车、摆杆在运动过程中都是不变得刚体;2.)皮带轮与传动带之间没有相对滑动,皮带不能拉伸变长,传动带没有抖振以及伸长的现象;3.)交流伺服电机的输入和输出之间是纯线性的关系;而且忽略不计电机的电枢绕组中的电感等动态特性;4.)将整个系统运行中的摩擦、各种阻力及机械传动间隙等不确定性忽略不计。
通过上述假设,则可以将直线一级倒立摆系统抽象成小车和均质敢组成的系统,如图1.1所示。
图1.1倒立摆系统2、各参数符号含义如下:符号含义单位数值M 小车质量kg 1.096m 摆杆质量kg 0,109b 小车摩擦系数N/m/sec 0.1l 摆杆转动轴心到杆质心的长度m 0.25I 摆杆转动惯性Kg*m²0.0034g 重力加速度N/kg 9.8x 小车的水平位置mθ摆角大小radN 小车对摆杆水平方向作用力NP 小车对摆杆竖直方向作用力NF 电动机经传动机构给小车的力Nφ摆杆与垂直向上方向的夹角rad3、采用牛顿--欧拉方法建立直线型一级倒立摆系统的数学模型。
图1.2是系统中小车和摆杆的受力分析图。
(a)小车的受力分析 (b)摆杆受力分析图1.2小车与摆杆的受力分析对小车水平方向所受的力进行受力分析,可以得到方程:N x b F x M --=⋅⋅⋅ 式(1.1)对摆杆水平方向所受的力进行受力分析并化简整理,可以得到等式:θθθθsin cos 2⋅⋅⋅⋅⋅-==ml ml x m N 式(1.2)将式(1.2)带入式(1.1)中,可以得到系统的第一个运动方程:θθθθsin cos )(2⋅⋅⋅⋅⋅⋅-+++=ml ml x b x m M F 式(1.3)对摆杆垂直方向所受的力进行受力分析并化简整理,可以得到下面等式:θθθθcos sin 2⋅⋅⋅--=ml ml mg P 式(1.4)力矩平衡方程如下:⋅⋅=--θθθI Nl Pl cos sin 式(1.5)将有关P 和N 的等式代入式(1.5)中,得到系统的第二个运动方程:θθθcos sin )(2⋅⋅⋅⋅-=++x ml mgl ml I 式(1.6)假设φ与1(单位弧度)相比很小,即φ<<1,并设θ=π+φ(φ是摆杆与垂直向上方向的夹角),可以作近似处理:φθθθ-=-==⎪⎭⎫⎝⎛s i n ,1c o s,02dt d 式(1.7)将被控对象的输入力F 用u 来表示,可以得到两个线性化后运动方程,如下 所示:⎪⎩⎪⎨⎧=-++=-+⋅⋅⋅⋅⋅⋅⋅⋅⋅u m l x b x m M x m l m glm l I φφφ)()(2式(1.8)对方程组式(1.8)进行拉氏变换,得到:⎪⎩⎪⎨⎧=Φ-++=Φ-Φ+)()()()()()()()()(22222s U s s ml s bX s s X m M s s mlX s mgl s s ml I 式(1.9)假设初始条件为零,对上述方程组的第一个方程求解,可得:)()()(22s s g ml ml I s X Φ⎥⎦⎤⎢⎣⎡-+= 式(1.10)将式(1.10)代入方程组式(1.9)中的第二个方程,可得:222222)()()()()()()(s s ml s s s g ml ml I b s s s g ml ml I m M s U Φ-Φ⎥⎦⎤⎢⎣⎡-++Φ⎥⎦⎤⎢⎣⎡-++= 式(1.11)整理,可以得到摆角的传递函数为:sq bm gl s q m gl m M s q m l I b s sqm l s U s -+-++=Φ23242)()()()( 式(1.12)式中:]))([(222l m ml I m M q -++=将倒立摆的实际参数值代入上式,得到摆角的传递函数为:ss s s s s U s 3141.28853.270883.03566.2)()(2342-++=Φ 式(1.13)同理,可以得到小车位置的传递函数:sq bm gl s q m gl m M s q m l I b s qm gls q m l I s U s X -+-++-+=23242)()()()()( 式(1.14)将实际的参数值代入,得到小车位置的传递函数为:s s s s s s U s X 3141.28853.270883.01413.238832.0)()(2342--+-= 式(1.15)在方程组(1.8)中对⋅⋅x 、⋅⋅φ求解代数方程,得到解如下:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+++++++++-==++++++++++-==⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅u Mm l m M I m l Mm l m M I m M m gl x Mm l m M I m lb u Mm l m M I m l I Mm l m M I gl m x Mm l m M I b m l I x xx 2222222222)()()()()()()()()(φφφφφ 式(1.16)设系统状态空间方程为:⎪⎩⎪⎨⎧+=+=⋅Du Cx y Bu Ax x 式(1.17)整理式(1.16),得到系统状态空间方程:u Mml m M I ml Mml m M I ml I x x Mml m M I m M mgl Mml m M I mlb Mml m M I gl m Mml m M I bml I x x ⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡++++++⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡+++++-+++++-=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡⋅⋅⋅⋅⋅⋅⋅⋅2222222222)(0)()(00)()()(010000)()()(00010φφφφ 式(1.18)u x x x y ⎥⎦⎤⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⋅⋅0001000001φφφ 式(1.19)将已知的M 、m 、b 、g 、l 、I 代入式(1.18)可得状态方程u x x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡⋅⋅⋅⋅⋅⋅⋅⋅3566.208832.0008285.272357.00100006293.00883.000010φφφφ 式(1.20)输出方程u x x x y ⎥⎦⎤⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⋅⋅0001000001φφφ 式(1.21)。
直线一级倒立摆的建模及性能分析

直线一级倒立摆的建模及性能分析1 直线一级倒立摆数学模型的建立 (1)2 直线一级倒立摆系统的实际模型 (5)3 直线一级倒立摆系统的性能分析 (6)相关理论的介绍 (6)倒立摆系统的性能分析 (7)1 直线一级倒立摆数学模型的建立所谓系统的数学模型,是指利用数学结构来反映实际系统内部之间、系统内部与外部某些主要相关因素之间的精确的定量表示。
数学模型是分析、设计、预测以及控制一个系统的理论基础。
因此,对于实际系统的数学模型的建立就显得尤为重要。
系统数学模型的构建可以分为两种:实验建模和机理建模。
实验建模就是通过在研究对象上加上一系列的研究者事先确定的输入信号,激励研究对像并通过传感器检测其可观测的输出,应用数学手段建立起系统的输入-输出关系。
机理建模就是在了解研究对象的运动规律的基础上,通过物理、化学的知识和数学手段建立起系统内部的输入-状态关系。
对于倒立摆系统,由于其本身是不稳定的系统,无法通过测量频率特性的方法获取其数学模型,实验建模存在一定的困难。
但是经过小心的假设忽略掉一些次要的因素后,倒立摆系统是一个典型的机电一体化系统,其机械部分遵守牛顿运动定律,其电子部分遵守电磁学的基本定律,因此可以通过机理建模得到系统较为精确的数学模型。
为了简单起见,在建模时忽略系统中的一些次要的难以建模的因素,例如空气阻力、伺服电机由于安装而产生的静摩擦力、系统连接处的松弛程度、摆杆连接处质量分布不均匀、传动皮带的弹性、传动齿轮的间隙等。
将小车抽象为质点,摆杆抽象为匀质刚体,摆杆绕转轴转动,这样就可以通过力学原理建立较为精确的数学模型。
我们可以应用牛顿力学的分析方法或者欧拉-拉格朗日原理建立系统的动力学模型。
对于直线一级倒立摆这样比较简单的系统,我们采用通俗易懂的牛顿力学分析法建模。
为了建立直线一级倒立摆的数学模型,采用如下的坐标系:图1直线一级倒立摆的物理模型其中,F 为加在小车上的力,M 为小车质量,m 为摆杆质量,I 为摆杆惯量, l 为摆杆转动轴心到杆质心的长度,x 为小车位移,φ为摆杆与垂直向上方向的夹角,b 为小车在滑轨上所受的摩擦力,N 和P 为摆杆相互作用力的水平和垂直方向的分量。
直线一级倒立摆的牛顿—欧拉方法建模

直线一级倒立摆的牛顿—欧拉方法建模首先,我们需要定义系统的坐标和状态变量。
在这个问题中,我们可以选择将质点的位置和角度作为系统的状态。
令x表示质点的水平位置,θ表示摆杆与竖直方向的夹角。
其次,我们需要确定系统的动力学方程。
根据牛顿第二定律和欧拉定理,可以得到如下的动力学方程:m * x'' = -m * g * sin(θ) - c * x';I * θ'' = m * g * cos(θ) * L - J * θ'其中,m是质点的质量,g是重力加速度,c是摩擦系数,L是摆杆的长度,I是质点关于摆杆固定点的转动惯量,J是摆杆的转动惯量。
最后,我们可以采用数值方法来求解这个动力学方程。
牛顿-欧拉方法是一种常用的数值方法,它基于一阶泰勒级数展开近似,并使用离散时间步长来进行数值计算。
具体步骤如下:1.将时间t离散化为n个时间步长Δt的序列:t_0,t_1,...,t_n。
2.初始化系统的状态变量:x(0),θ(0),x'(0),θ'(0)。
3.对于每个时间步长i,计算状态变量的更新:a. 计算加速度:x''(i) = (1/m) * (-m * g * sin(θ(i)) - c * x'(i))θ''(i) = (1/I) * (m * g * cos(θ(i)) * L - J * θ'(i))b.使用泰勒级数展开逼近位置和速度:x(i+1)=x(i)+Δt*x'(i)+0.5*Δt^2*x''(i)θ(i+1)=θ(i)+Δt*θ'(i)+0.5*Δt^2*θ''(i)c.使用泰勒级数展开逼近速度和加速度:x'(i+1)=x'(i)+Δt*x''(i)θ'(i+1)=θ'(i)+Δt*θ''(i)d.根据实际情况对状态进行调整,如质点位置不能超过摆杆范围等。
直线一级倒立摆系统的PID控制算法设计

摘要直线一级倒立摆由直线运动模块和一级摆体组件组成,是最常见的倒立摆之一。
设计直线一级倒立摆前,首先要应清楚直线一级倒立摆的定义及它的特性,其次用数学建模的方法建立直线一级倒立摆模型。
再次PID控制器的结构与参数设计,将直线一级倒立摆当作简单的单输入单输出系统(忽略了小车位移的控制),采用了 PID控制器设计方法进行了控制器结构设计和参数设计。
确定PID控制器主要参数KP、KI、KD,通过改变这三个参数的值,使直线一级倒立摆由开环不稳定系统变为闭环稳定系统。
直线一级倒立摆系统在PID控制器下用MATLAB进行仿真,通过改变控制器PID主要参数,使得仿真曲线更接近理论曲线。
这些便是直线一级倒立摆系统的PID控制算法设计的主要内容。
关键词:直线一级倒立摆;Matlab仿真;PID控制ABSTRACTInverted pendulum linear 1-stage stands upside down suspends is composed by the translation module and the level pendulum mass module, is most common stands upside down suspends one Front the design straight line level stands upside down suspends, first must be supposed the clear straight line level to stand upside down the definition and its characteristic which suspends, next stands upside down with mathematics modelling method establishment straight line level suspends the model. Once more the PID controller structure and the parameter design, stood upside down Inverted pendulum linear 1-stage suspends the regard simple single input list output system (to neglect car displacement control), used the PID controller design method to carry on the controller structural design and the parameter design. Determined PID controller main parameter KP, KI, KD, through change these three parameters the value, causes the straight line level to stand upside down suspends becomes the closed loop stable system by the split-ring unstable system. Inverted pendulum linear 1-stage stands upside down suspends the system to carry on the simulation under the PID controller with MATLAB, through the change controller PID main parameter, causes the simulation curve closer theoretical curve.These then are the straight line level stands upside down suspends the system the PID control algorithm design primary coverage.Keywords:Inverted pendulum linear;Matlab Simulation; PID control目录第1章绪论 (1)第2章倒立摆系统 (2)2.1 系统的组成 (3)2.1.1 倒立摆本体 (3)2.1.2 电控箱 (4)2.1.3 电机 (4)2.1.4 编码器 (4)2.1.5 控制卡 (5)2.2 系统使用说明 (5)2.2.1 直线一级摆硬件操作系统 (5)2.2.2 一级摆软件操作说明 (5)第3章自动控制及MATLAB软件介绍 (7)3.1自动控制概念 (7)3.2 自动控制系统的类型 (8)3.2.1 随机系统与自动调整系统 (8)3.2.2 线性系统和非线性系统 (9)3.2.3 连续系统和离散系统 (9)3.2.4 单输入单输出系统和多输入多输出系统 (9)3.2.5 确定系统与不确定系统 (9)3.2.6 集中参数系统和分布参数系统 (9)3.3 自动控制理论概要 (10)3.3.1 自动控制系统所要分析的问题 (10)3.3.2 自动控制系统的设计问题 (10)3.4 MATLAB实验软件 (10)3.5.1 MATLAB的基本介绍 (11)3.5.2 MATLAB程序设计基础 (12)第4章 PID控制 (13)4.1 PID控制原理 (13)4.2 数字PID控制 (14)4.2.1 位置式PID控制算法 (14)4.2.2 增量式PID控制算法 (15)4.3 常见的PID控制系统 (15)4.3.1 串级PID控制 (15)4.3.2 纯滞后系统的大林控制算法 (16)4.3.3 纯滞后系统的smith控制算法 (17)第5章直线一级倒立摆的牛顿—欧拉方法建模 (19)5.1 微分方程的推导 (19)5.2 传递函数 (21)5.3 状态方程 (21)5.4 实际系统模型 (23)5.5 采用MATLAB语句形式进行仿真 (24)第6章直线一级倒立摆控制器设计及仿真 (27)6.1 PID参数的调整 (28)6.2 PID控制回路运行 (28)6.3直线一级倒立摆PID控制器设计 (29)6.4直线一级倒立摆PID控制器设计MATLAB仿真 (32)结论 (37)参考文献 (38)致谢 (39)附录 (40)第1章绪论计算机的诞生和发展给自动控制增添了先进的工具,现代控制理论的发展,又给自动控制提供了新的理论支柱。
直线一级倒立摆控制方法设计

直线一级倒立摆控制方法设计倒立摆的数学模型设计倒立摆系统是一个典型的非线性、强耦合、多变量和不稳定系统,作为控制系统的被控对象,许多抽象的控制概念都可以通过倒立摆直观地表现出来。
本设计是以一阶倒立摆为被控对象来进行设计的。
状态空间法:状态空间法可以进行单输入多输出系统设计,因此在这个实验中,我们将尝试同时对摆杆角度和小车位置进行控制。
根据设计要求,给小车加一个阶跃输入信号。
此次用Matlab 求出系统的状态空间方程各矩阵,并仿真系统的开环阶跃响应。
在这里给出一个state.m 文件,执行这个文件,Matlab 将会给出系统状态空间方程的A,B,C 和D 矩阵,并绘出在给定输入为一个0.2m 的阶跃信号时系统的响应曲线。
直线一级倒立摆系统数学建模 在忽略了空气阻力、各种摩擦之后,可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统。
如图所示:系统状态方程为:XAX Bu Y CX Du=+=+假设系统内部各相关参数为:M 小车质量 0.5kg m 摆杆质量 0.2kgb 小车摩擦系数 0.1N/m/sec l 摆杆转动轴心到杆质心的长度 0.3mI 摆杆惯量 0.006kg*m*m T 采样时间 0.005s x 小车位置φ 摆杆与垂直向上方向的夹角θ 摆杆与垂直向下方向的夹角(考虑到摆杆初始位置为竖直向下) 应用牛顿-欧拉方法,可得到系统状态空间方程为:222222201()0()()0()0()()x I ml b m gl x I M m Mml I M m Mml lb mgl M m I M m Mml I M m Mml φφ⎡⎤⎢⎥⎡⎤-+⎢⎥⎢⎥⎢⎥++++⎢⎥=⎢⎢⎥⎢⎢⎥⎢-+⎢⎥⎣⎦⎢++++⎣⎦ 0 0 0 0 0 0m 0 2220()0()x I ml x I M m Mml u ml I M m Mml φφ⎡⎤⎢⎥⎡⎤+⎢⎥⎢⎥⎢⎥++⎢⎥+⎥⎢⎥⎢⎥⎥⎢⎥⎢⎥⎥⎢⎥⎢⎥⎣⎦⎥⎢⎥++⎣⎦1000000100x x x Y u φφφ⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥==+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦ 以上就是一阶倒车摆系统的状态空间表达式。
倒立摆实验
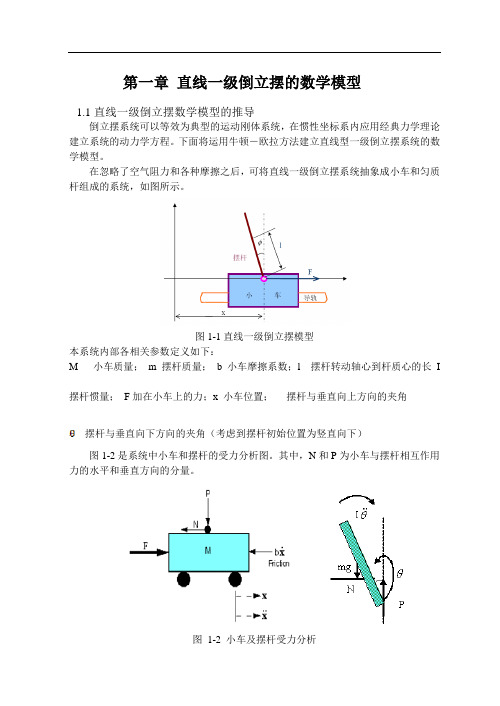
第一章直线一级倒立摆的数学模型1.1直线一级倒立摆数学模型的推导倒立摆系统可以等效为典型的运动刚体系统,在惯性坐标系内应用经典力学理论建立系统的动力学方程。
下面将运用牛顿-欧拉方法建立直线型一级倒立摆系统的数学模型。
在忽略了空气阻力和各种摩擦之后,可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统,如图所示。
图1-1直线一级倒立摆模型本系统内部各相关参数定义如下:M 小车质量;m 摆杆质量;b 小车摩擦系数;l 摆杆转动轴心到杆质心的长I 摆杆惯量;F加在小车上的力;x 小车位置;摆杆与垂直向上方向的夹角摆杆与垂直向下方向的夹角(考虑到摆杆初始位置为竖直向下)图1-2是系统中小车和摆杆的受力分析图。
其中,N和P为小车与摆杆相互作用力的水平和垂直方向的分量。
图1-2 小车及摆杆受力分析应用Newton方法来建立系统的动力学方程过程如下:分析小车水平方向所受的合力,可以得到以下方程:M+m x+bx+mlθcosθ−mlθsinθ=FI+ml2θ+mgl sinθ=−mlx cosθ1.微分方程模型设θ=π+Φ,当摆杆与垂直向上方向之间的夹角与1(单位是弧度)相比很小,即Φ≪1时,则可以进行近似处理:cosθ=−1,sinθ=−Φ,(dθdt)2=0。
为了与控制理论的表达习惯相统一,即u一般表示控制量,用u来代表被控对象的输入力F,线性化后得到该系统数学模型的微分方程表达式:M+m x+bx−mlΦ=uI+ml2Φ+mglΦ=−mlx2.传递函数模型对以上的方程组进行拉普拉斯变换,得到M+m X(s)s2+bX(s)s−mlΦ(s)s2=U(s)I+ml2Φ(s)s2+mglΦ(s)=−mlX(s)s2注意:推导传递函数时假设初始条件为0。
对上述方程组进行化简,可得到以摆杆摆角为输出量的传递函数:Φ(s)=mlq s2s4+b(I+ml2)q s3−(M+m)mglq s2−bmglq s其中,q=[M+m I+ml2−(ml)2]3.状态空间数学模型由现代控制理论原理可知,控制系统的状态空间方程可写成如下形式:X=AX+BuY=CX+Du对于本系统,可得状态方程为:xx ΦΦ=0100−(I+ml2)bI M+m+Mml2m2gl2I M+m+Mml20001−mlb mgl(M+m)xxΦΦ+I+ml2I M+m+Mml2ml2u4.实际系统参数小车质量M=1.096 Kg;摆杆质量m= 0.109 Kg;小车摩擦系数b=0 .1N/m/sec;摆杆转动轴心到杆质心的长度l=0.25m;摆杆惯量I=0.0034 kg m2。
直线一级倒立摆建模

一、直线一级倒立摆建模根据自控原理实验书上相关资料,直线一级倒立摆在建模时,一般忽略掉系统中的一些次要因素.例如空气阻力、伺服电机的静摩擦力、系统连接处的松弛程度等,之后可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统,如下图所示:倒立摆系统是典型的机电一体化系统,其机械部分遵循牛顿的力学定律,其电气部分遵守电磁学的基本定理.因此,可以通过机理建模方法得到较为准确的系统数学模型,通过实际测量和实验来获取系统模型参数.无论哪种类型的倒立摆系统,都具有3个特性,即:不确定性、耦合性、开环不稳定性. 直线型倒立摆系统,是由沿直线导轨运动的小车以及一端固定于小车上的匀质长杆组成的系统. 小车可以通过传动装置由交流伺服电机驱动. 小车导轨一般有固定的行程,因而小车的运动范围是受到限制的。
虽然倒立摆的形式和结构各异,但所有的倒立摆都具有以下的特性:1) 非线性倒立摆是一个典型的非线性复杂系统,实际中可以通过线性化得到系统的近似模型,线性化处理后再进行控制。
也可以利用非线性控制理论对其进行控制。
倒立摆的非线性控制正成为一个研究的热点。
2) 不确定性主要是模型误差以及机械传动间隙,各种阻力等,实际控制中一般通过减少各种误差来降低不确定性,如通过施加预紧力减少皮带或齿轮的传动误差,利用滚珠轴承减少摩擦阻力等不确定因素。
3) 耦合性倒立摆的各级摆杆之间,以及和运动模块之间都有很强的耦合关系,在倒立摆的控制中一般都在平衡点附近进行解耦计算,忽略一些次要的耦合量。
4) 开环不稳定性倒立摆的平衡状态只有两个,即在垂直向上的状态和垂直向下的状态,其中垂直向上为绝对不稳定的平衡点,垂直向下为稳定的平衡点。
由于机构的限制,如运动模块行程限制,电机力矩限制等。
为了制造方便和降低成本,倒立摆的结构尺寸和电机功率都尽量要求最小,行程限制对倒立摆的摆起影响尤为突出,容易出现小车的撞边现象。
由此,约束限制直线型一级倒立摆系统的实际控制要求可归结为3点:(1)倒立摆小车控制过程的最大位移量不能超过小车轨道的长度;(2)为保证倒立摆能顺利起立,要求初始偏角小于20°;(3)为保证倒立摆保持倒立的平衡态,要求控制系统响应速度足够快。
直线一级倒立摆的数学建模和根轨迹控制

直线一级倒立摆的数学建模和根轨迹控制直线一级倒立摆是一种基于控制理论的研究对象,它可以通过数学建模来进行分析和控制。
数学建模的过程中,需要将倒立摆的动力学方程、控制器以及传感器等元器件进行建模。
根据建模结果可以分析系统的稳定性、响应速度等特征,并为设计控制策略提供参考。
根轨迹控制是一种常用于控制系统设计的方法,它通过分析控制系统的传递函数,绘制根轨迹图来评估控制系统的稳定性和性能。
对于直线一级倒立摆,可以根据其数学模型进行传递函数分析,得出控制系统的传递函数,并绘制根轨迹图。
在根轨迹图上,可以根据根轨迹的位置来判断系统的稳定性和响应速度,从而确定控制策略并调整控制参数,以实现目标控制效果。
因此,直线一级倒立摆的数学建模和根轨迹控制在控制理论研究和工程应用中具有重要意义,可以为控制系统设计提供有效的方法和手段。
(完整版)倒立摆实验报告(PID控制)

专业实验报告3. 实验装置直线单级倒立摆控制系统硬件结构框图如图1所示,包括计算机、I/O设备、伺服系统、倒立摆本体和光电码盘反馈测量元件等几大部分,组成了一个闭环系统。
图1 一级倒立摆实验硬件结构图对于倒立摆本体而言,可以根据光电码盘的反馈通过换算获得小车的位移,小车的速度信号可以通过差分法得到。
摆杆的角度由光电码盘检测并直接反馈到I/O设备,速度信号可以通过差分法得到。
计算机从I/O设备中实时读取数据,确定控制策略(实际上是电机的输出力矩),并发送给I/O设备,I/O设备产生相应的控制量,交与伺服驱动器处理,然后使电机转动,带动小车运动,保持摆杆平衡。
图2是一个典型的倒立摆装置。
铝制小车由6V的直流电机通过齿轮和齿条机构来驱动。
小车可以沿不锈钢导轨做往复运动。
小车位移通过一个额外的与电机齿轮啮合的齿轮测得。
小车上面通过轴关节安装一个摆杆,摆杆可以绕轴做旋转运动。
系统的参数可以改变以使用户能够研究运动特性变化的影响,同时结合系统详尽的参数说明和建模过程,我们能够方便地设计自己的控制系统。
图2 一级倒立摆实验装置图上面的倒立摆控制系统的主体包括摆杆、小车、便携支架、导轨、直流伺服电机等。
主图7 直线一级倒立摆PD控制仿真结果图从上图可以看出,系统在1.5秒后达到平衡,但是存在一定的稳态误差。
为消除稳态误差,我们增加积分参数Ki,令Kp=40,Ki=60,Kd=2,得到以下仿真结果:图8 直线一级倒立摆PID控制仿真结果图从上面仿真结果可以看出,系统可以较好的稳定,但由于积分因素的影响,稳定时间明显增大。
双击“Scope1”,得到小车的位置输出曲线为:图9 施加PID控制器后小车位置输出曲线图由于PID 控制器为单输入单输出系统,所以只能控制摆杆的角度,并不能控制小车的位置,所以小车会往一个方向运动,PID控制分析中的最后一段,若是想控制电机的位置,使得倒立摆系统稳定在固定位置附近,那么还需要设计位置PID闭环。
直线一级倒立摆实验教程

声明
固高科技保留在没有预先通知的情况下修改产品或其特性的权利。 固高科技并不承担由于使用产品不当而产生的直接或是间接的伤害或损坏的责任。
商标
Windows 和 Microsoft 是 Microsoft 的注册商标。 IPM 和 IPM Motion Studio 是 Technosoft 公司的商标。 MATLAB 是 MathWorks 公司的商标。 LabVIEW 是美国国家仪器(NI)公司的商标。
1
直线一级倒立摆实验教程 V1.00
固高科技 (深圳) 有限公司
目
录
版权声明 ........................................................................................................................................................... 1 声明 ................................................................................................................................................................... 1 商标 ................................................................................................................................................................... 1 联系我们 ..........................
一阶倒立摆的数学模型

一阶倒立摆的数学模型好啦,今天咱们来聊聊一阶倒立摆。
听起来挺复杂的,其实就是一个小摆子,站在一根杆子上面,像个小丫头在平衡木上玩儿。
你有没有想过,为什么这个简单的东西能让科学家们绞尽脑汁?这就像你和朋友一起玩平衡游戏,谁摔倒谁就得请客,呵呵。
想象一下,那个小摆子,就像一颗苹果,静静地待在杆子的顶端。
它看起来很稳,但其实它随时可能倾倒。
风一吹,或者你稍微碰一下,它就可能开始摇晃。
这就是一阶倒立摆的魅力所在:看似简单,实则深奥。
其实啊,倒立摆的运动就像生活,有时候一不小心就会摔得四脚朝天,嘿嘿。
在物理学里,这种摆动其实可以用一组方程来描述。
别怕,听起来复杂,但实际上就像做数学题时,那些公式就像调皮的孩子,让你既爱又恨。
摆子的运动可以用牛顿第二定律来解释,就是说,力等于质量乘以加速度。
这里面有个小秘密哦,那就是摆子的质量和重力都影响它的运动。
如果摆子太重了,或者你施加的力不够,嘿嘿,它就没法保持平衡了。
说到平衡,真是个难题。
生活中也一样,工作和休息、家庭和朋友,所有的东西都得拿捏得当。
就像那个倒立摆,要时刻保持平衡,稍不留神就可能倾斜。
想象一下,当你走在悬崖边缘,心里一定咯噔一下吧?其实倒立摆也是一样,重力就像那无形的悬崖,随时准备让它掉下去。
那要怎么才能让这个小摆子不倒呢?聪明的科学家们可不止是站着想。
他们设计了一些控制器,像小小的守护者,时刻监测着摆子的倾斜角度。
只要一发现不对劲,就会迅速调整力的方向,帮助摆子重新找回平衡。
这就好比你在街上遇到突如其来的风,立马稳住自己的身子,别让自己摔倒,哈哈。
说到底,一阶倒立摆不仅仅是物理上的问题,更是一种哲学。
它教会我们,生活中有很多不确定的因素。
我们永远无法预料下一秒会发生什么,但只要我们能及时调整自己的状态,就能保持在“平衡”的位置上,过上更精彩的生活。
这种灵活应对的智慧,就像古人说的“应变随时”,我们在面对挑战时总能找到办法。
当然了,搞定这个倒立摆的过程并不是一帆风顺的。
牛顿欧拉动力学方程建模

牛顿欧拉动力学方程建模牛顿-欧拉动力学方程是描述刚体运动的基本方程之一、它在刚体力学中起着重要的作用,能够揭示物体运动的规律和动力学特性。
牛顿-欧拉动力学方程是由牛顿第二定律和刚体动力学平衡方程组成,可以描述刚体在运动过程中的力和加速度之间的关系。
下面将详细介绍牛顿-欧拉动力学方程的建模过程。
首先,我们需要了解刚体的基本概念。
刚体是一个几何形状不变的物体,可以看作是由许多质点组成的。
每个质点都有其质量和位置,质点与质点之间的相对位置在运动过程中保持不变。
然后,我们需要定义刚体的运动学和动力学参数。
刚体的运动学参数包括线速度、角速度和加速度,而动力学参数则包括质量、惯性矩阵和力矩。
其中,质量是描述刚体惯性的物理量,惯性矩阵则描述了刚体绕各个坐标轴转动的难易程度,力矩则描述了刚体受到的外力作用。
然后,我们将刚体的动力学平衡方程考虑进来,以描述刚体的转动。
刚体的动力学平衡方程可以表示为τ=Iα,其中τ是刚体所受合外力矩,I是刚体的惯性矩阵,α是刚体的角加速度。
这个方程描述了刚体的转动。
最后,通过将平动和转动的方程组合起来,我们可以得到牛顿-欧拉动力学方程。
具体来说,欧拉动力学方程可以表示为:m*v̇=FI*ω̇=τ其中,m是刚体的质量,v̇是刚体的线加速度,F是刚体所受合外力,I是刚体的惯性矩阵,ω̇是刚体的角加速度,τ是刚体所受合外力矩。
这两个方程描述了刚体在运动过程中的力和加速度之间的关系,提供了一种建模刚体运动的方法。
利用它们,我们可以分析刚体的运动特性,例如刚体的轨迹、速度和力矩分布等。
总结起来,牛顿-欧拉动力学方程是用来描述刚体运动的重要方程。
它基于牛顿第二定律和刚体动力学平衡方程,可以揭示物体运动的规律和动力学特性。
通过对质点的运动学和动力学参数的定义和分析,我们可以将牛顿-欧拉动力学方程应用于刚体运动的建模和分析,从而进一步研究刚体的行为和性质。
直线一级倒立摆系统建模

内蒙古科技大学本科生课程设计论文题目:直线一级倒立摆系统建模仿真实验学生姓名:赵永明学号:1067112225专业:测控技术与仪器班级:10-2班指导教师:梁丽2013年12 月 5 日摘要本文主要研究的是一级倒立摆的PID控制问题,并对其PID的参数进行了优化,优化算法是遗传算法。
倒立摆是典型的快速、多变量、非线性、强耦合、自然不稳定系统。
由于在实际中有很多这样的系统,因此对它的研究在理论上和方法论上均有深远的意义。
本文首先简单的介绍了一下倒立摆以及倒立摆的控制方法,并对其参数优化算法做了分类介绍。
然后,介绍了本文选用的优化参数的算法遗传算法的基本理论和操作方法。
接着建立了一级倒立摆的数学模型,并求出其状态空间描述。
本文着重讲述的是利用遗传算法来对PID的参数进行优化的实现方法。
最后,用Simulink 对系统进行了仿真,得出遗传算法在实际控制中是一种较为理想的PID参数优化方法的结论。
关键词:PID控制器;一级倒立摆;仿真目录摘要................................................................................................ 错误!未定义书签。
第一章前言.................................................................................. 错误!未定义书签。
1.1 设计背景.......................................................................... 错误!未定义书签。
1.2 设计意义.......................................................................... 错误!未定义书签。
第二章被控对象的分析与建模. (1)第三章设计理论及仿真过程...................................................... 错误!未定义书签。
二阶系统的阶跃响应与线性系统的稳定性和稳态误差分析.
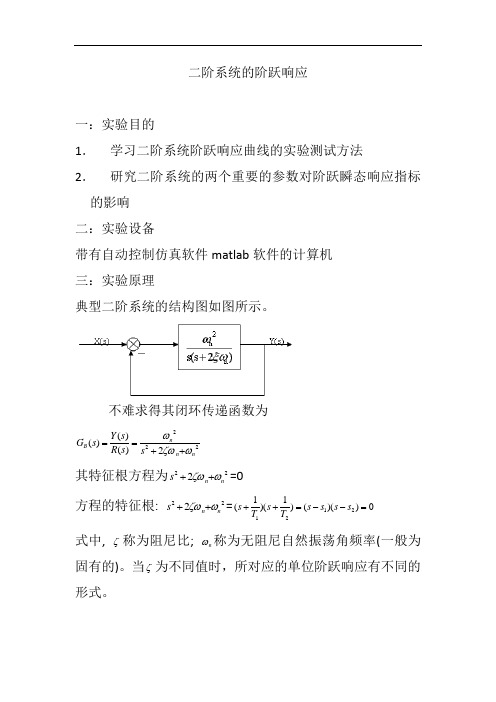
二阶系统的阶跃响应一:实验目的1. 学习二阶系统阶跃响应曲线的实验测试方法2. 研究二阶系统的两个重要的参数对阶跃瞬态响应指标的影响 二:实验设备带有自动控制仿真软件matlab 软件的计算机 三:实验原理典型二阶系统的结构图如图所示。
不难求得其闭环传递函数为2222)()()(n n n B s s R s Y s G ωζωω++==其特征根方程为222n n s ωζω++=0 方程的特征根: 222nn s ωζω++=0))(()1)(1(2121=--=++s s s s T s T s 式中,ζ称为阻尼比;n ω称为无阻尼自然振荡角频率(一般为固有的)。
当ζ为不同值时,所对应的单位阶跃响应有不同的形式。
四:实验内容研究特征参量ζ和n ω对二阶系统性能的影响标准二阶系统的闭环传递函数为:2222)()(nn n s s s R s C ωζωω++=二阶系统的单位阶跃响应在不同的特征参量下有不同的响应曲线。
我们研究ζ对二阶系统性能的影响,设定无阻尼自然振荡频率)/(1s rad n =ω,考虑3种不同的ζ值:ζ=0.2,0.4,1,利用MATLAB 对每一种ζ求取单位阶跃响应曲线,分析参数ζ对系统的影响。
五:仿真程序和结果图1、二阶系统阶跃响应曲线 程序 for j=1:1:3kais=[0.2,0.4,1]; w=[1/0.47,1/1,1/1.47]; subplot(3,1,j) hold on for i=1:3 num=w(j)^2;den=[1,2*kais(i)*w(j),w(j)^2]step(num,den);grid on end hold off end 结果图σ%n ω0.2 0.4 11/0.47 1/1 1/1.47ζζ2、变换ζ和ω的值:nfor j=1:1:3kais=[0.2,0.4,1];w=[1/0.47,1/1,1/1.47];subplot(3,1,j)hold onfor i=1:3num=w(i)^2;den=[1,2*kais(j)*w(i),w(i)^2]step(num,den);grid onendhold offend3、增加一组ζ值:for j=1:1:3kais=[0,0.2,0.4,1];w=[1/0.47,1/1,1/1.47];subplot(3,1,j)hold onfor i=1:4num=w(j)^2;den=[1,2*kais(i)*w(j),w(j)^2]step(num,den);grid onendhold offend结果图:分析: σ%n ω0.2 0.4 11/0.47 1/1 1/1.47六:结论与收获 结论: (1) 当0=ζ时,输出响应为等幅振荡。
一阶倒立摆动力学方程推导

x
J ml2 M m m2l2 cos2
ml cos.F m2l2 sin cos. 2 M m m lg sin m2l2 cos2 M m J ml2
式中 J 为摆杆的转动惯量:
J ml2 3
梅科尔工作室
若取小车质量 M=2kg,摆杆质量 m=1kg,摆杆长度 2 l =1m,重力加速度取 g= 10m / s2 ,则可以得 一阶倒立摆简化模型:
..
x
0.44F
3.33
..
0.4F 12
拉氏变换
(s) F (s)
0.4 s2 12
x(s)
(s)
1.1s2 s2
10
(3) 简单的二阶动力学方程如何化为传递函数
y
Jy
ku
x y
Ax Cx
Bu Du
x 为 n 维状态向量; y 为 m 维输出向量; u 为 r 维输入向量; A 为
n n 维系统矩阵,由系统参数决定;B 为 n r 维输入矩阵;C 为 m n
维输出矩阵; D 为 m r 维矩阵,直接联系输入量、输出量的前向传递
(前馈)系数,又称前馈系数
x1 x2
y y
x2
x1 x2 Jx2
ku
x
x1 x2
y y
,
u
为标量;
A
0 0
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图1 直线一级倒立摆系统
系统模型
m I
l
•
我们不妨做以下假设:
• •
F
M
•
b
X
• •
图1 直线一级倒立摆系统
• •
M m b l I F x a
小车质量 摆杆质量 小车摩擦系数 摆杆转动轴心到杆质心的长度 摆杆惯量 加在小车上的力 小车位置 摆杆与垂直向上中小车和摆杆的受力分析图。其 中,N和P为小车和摆杆相互作用力的水平和垂 直的分量。注意:图示方向为矢量正方向。
2
0 0 2 x I ml 0 2 x I ( M m ) Mm l u 1 0 m l 0 2 I ( M m) Mm l
x 0 x 1 0 0 0 x y u 0 0 1 0 0
P N F
I
M
bX
P
X
mg
N
l
X
图2 小车隔离受力图
图3 摆杆隔离受力图
微分方程的推导
P
•
N F
分析小车水平方向所受的合 力,可以得到以下方程: F bx N M x
M
bX
X
X
图2 小车隔离受力图
微分方程的推导
•
I
分析小车水平方向所受的合力, 可以得到以下方程:
•
用 来代表被控对象的输入力 F ,线性化后两个运 动方程如下:
m gl m l ( I m l2 ) x u ( M m ) x b x m l
(1.3)
传递函数 对方程组(1.3)进行拉普拉斯变换,得到
( I m l2 )( s) s 2 m gl( s) m lX( s) s 2 2 2 ( M m ) X ( s ) s bX ( s ) s m l ( s ) s U ( s) (1.4)
•
代入上式中,得到系统的第一个 运动方程:
(1.1)
微分方程的推导
•
I
分析摆杆垂直方向所受的合 力,可以得到以下方程:
d2 P m g m 2 (l cos ) dt
P
mg
N
sin ml 2 cos 即:P mg ml
•
力矩平衡方程如下:
图3 摆杆隔离受力图
P
F bx N M x
•
N
mg
摆杆水平方向的受力进行分析, 可以得到下面等式:
d2 N m 2 ( x l sin ) dt
图3 摆杆隔离受力图
cos ml 2 sin F bx ml (M m) x
l
cos ml 2 sin ml 即: N m x
建模方法 对于倒立摆系统,由于其本身是自 不稳定的系统,实验建模存在一定的困 难。但经过小心的假设忽略掉一些次要 的因素后,倒立摆系统就是一个典型的 运动的刚体系统,可以在惯性坐标系内 应用经典力学理论建立系统的动力学方 程。
系统模型
m I
l
F
M
b
X
在忽略了空气阻 力,各种摩擦之后, 可将直线一级倒立摆 系统抽象成小车和匀 质杆组成的系统,如 图所示。
状态空间方程 整理后得到系统状态空间方程:
0 x 0 x 0 0 1 ( I m l2 )b I ( M m) Mm l2 0 m lb I ( M m) Mm l2 0 m gl 2 I ( M m) Mm l2 0 m gl( M m) I ( M m) Mm l2
直线一级倒立摆的牛顿—欧拉方法建模
概述
系统建模可以分为两种:实验建模和机理建模。 实验建模就是通过在研究对象上加上一系列的 研究者事先确定的输入信号,激励研究对象并 通过传感器检测其可观测的输出,应用数学手 段建立起系统的输入— 输出关系; 机理建模就是在了解研究对象的运动规律基础 上,通过物理、化学的知识和数学手段建立起 系统内部的输入— 状态关系。
整理消去X(s)后得到传递函数:(假设初始 ml 2 条件为0) s
( s) U ( s) q 2 b ( I m l ) 3 ( M m)m gl 2 bm gl 4 s s s s q q q 2 2 q [( M m )( I ml ) ( ml )] 其中:
开环系统仿真 实际系统的模型参数如下:
M m b l I T 小车质量 1.096Kg 摆杆质量 0.109Kg 0.1N / m / sec 小车摩擦系数 0.25m 摆杆转动轴心到杆质心的长度 摆杆惯量 0.0034 kg m 2 采样频率 0.005 sec
•
l
Pl sin Nl cos I
合并这两个方程,约去P和N,得 到系统的第二个运动方程:
mglsin ml cos ( I ml ) x
2
(1.2)
微分方程的推导
假设 很小,即 0 ,则可以进行近似处理:
0 cos 1, sin ,
状态空间方程 系统状态空间方程为:
AX Bu X y CX Du
解代数方程,得到解如下: x , 方程组(1.3)对
x x ( I m l2 )b m 2 gl 2 ( I m l2 ) x x u 2 2 2 I ( M m) Mm l I ( M m) Mm l I ( M m) Mm l m lb m gl( M m) ml x u 2 2 2 I ( M m) Mm l I ( M m) Mm l I ( M m) Mm l
