新高三月质量检测试题目数学7页

合集下载

八年级数学第二学期3月份质量检测测试卷含答案

八年级数学第二学期3月份质量检测测试卷含答案一、选择题1．下列计算，正确的是（）A ． 235+=B ． 2323+=C ． 8220-=D ． 510-=2．下列根式是最简二次根式的是（）A ．4B ．21x +C ．12D ．40.5 3．计算32782-⨯的结果是（） A ．3 B ．3- C ．23 D ．534．下列二次根式中是最简二次根式的为（）A ．12B ．30C ．8D ．125．下列计算正确的是（）A ．42=±B ．()233-=-C ．()255-=D ．()233-=-6．化简二次根式 22a a a +-的结果是（） A ．2a -- B ．－2a --C ．2a -D ．－2a - 7．下列计算不正确的是（）A ．35525-=B ．236⨯=C 774=D 363693=+==8．下列运算正确的是（）A x 2x 3xB ．2﹣2=1C ．55D ．x ﹣x （a ﹣b x9．如果2a a 2a 1-+，那么a 的取值范围是（）A ．a 0=B ．a 1=C ．a 1≤D ．a=0a=1或 10．下列计算正确的是（） A 235=B 623=C 23(3)86-=-D 321= 11．下列运算正确的是（）A 235=B ．(228-=C 112222=D ．()21313-=- 12．下列计算正确的是（） A ．235+= B ．2332-= C ．()222= D ．393=二、填空题13．设42-的整数部分为 a,小数部分为 b.则1a b-= __________________________. 14．能力拓展： 11:2121A -=+；21:3232A -=+；31:4343A -=+；4:54A -=________．…n A ：________．()1请观察1A ，2A ，3A 的规律，按照规律完成填空．()2比较大小1A 和2A∵32+________21+ ∴132+________121+ ∴32-________21-()3同理，我们可以比较出以下代数式的大小：43-________32-；76-________54-；1n n +-________1n n --15．对于任何实数a ，可用[a]表示不超过a 的最大整数，如[4]=4，[3]=1．现对72进行如下操作：72 [72]=8 [8]=2 2]=1，类似地，只需进行3次操作后变为1的所有正整数中，最大的是________．16．把31a-根号外的因式移入根号内，得________ 17．若613x ，小数部分为y ，则(213)x y 的值是___.18．若0xy >，则二次根式2y x -________． 19．下列各式：2521+n 2b 0.1y 是最简二次根式的是:_____（填序号）20．4x -x 的取值范围是_____ 三、解答题21．计算及解方程组：（1-1-）（2)2+ （3）解方程组：251032x y x y x y -=⎧⎪+-⎨=⎪⎩ 【答案】（1）2）7；（3）102x y =⎧⎨=⎩．【分析】（1）首先化简绝对值，然后根据二次根式乘法、加减法法则运算即可；（2）首先根据完全平方公式化简，然后根据二次根式加减法法则运算即可；（3）首先将第二个方程化简，然后利用加减消元法即可求解．【详解】（11-1+（11=1 （22+）=34-=7-=7-（3）251032x y x y x y -=⎧⎪⎨+-=⎪⎩①② 由②得：50x y -= ③②-③得： 10x =把x=10代入①得：y=2∴原方程组的解是：102x y =⎧⎨=⎩【点睛】本题考查了二次根式的混合运算，加减消元法解二元一次方程，熟练掌握二次根式的运算法则是本题的关键．22．观察下列各式子，并回答下面问题．（1）试写出第n 个式子（用含n 的表达式表示），这个式子一定是二次根式吗？为什么？（2）你估计第16个式子的值在哪两个相邻整数之间？试说明理由．【答案】（1，该式子一定是二次根式，理由见解析；（215和16之间．理由见解析．【分析】（1）依据规律可写出第n 个式子，然后判断被开方数的正负情况，从而可做出判断；（2）将16n =代入，得出第16，再判断即可．【详解】解：（1该式子一定是二次根式，因为n 为正整数，2(1)0n n n n -=-≥，所以该式子一定是二次根式（215=16=，∴1516<<.15和16之间．【点睛】本题考查的知识点是二次根式的定义以及估计无理数的大小，掌握用“逼近法”估算无理数的大小的方法是解此题的关键．23．先阅读下列解答过程，然后再解答：,a b ，使a b m +=，ab n =，使得22m +==)a b ==>7,12m n ==，由于437,4312+=⨯=，+=，=即：227===+。

【新结构】华大新高考联盟2024届高三下学期3月教学质量测评数学试卷+答案解析

【新结构】华大新高考联盟2024届高三下学期3月教学质量测评数学试卷❖一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.若，则z的虚部为()A. B. C. D.12.已知集合，，则图中阴影部分表示的集合为()A. B. C. D.3.对A，B两地国企员工的上班迟到情况进行统计，可知两地国企员工的上班迟到时间均符合正态分布，其中A地员工的上班迟到时间为单位：，，对应的曲线为，B地员工的上班迟到时间为单位：，，对应的曲线为，则下列图象正确的是()A. B.C. D.4.已知，，若，则()A. B. C. D.5.若，则()A. B. C. D.6.已知抛物线的焦点为F，准线l与x轴的交点为P，过点F的直线与C交于M，N两点，若，且，则()A. B. C. D.7.已知实数a，b满足，则的最小值与最大值之和为()A.4B.5C.6D.78.已知正方体的边长为4，其中点E为线段的中点，点F，G分别在线段，上运动，若恒成立，则实数的取值范围为()A. B. C. D.二、多选题：本题共3小题，共18分。

在每小题给出的选项中，有多项符合题目要求。

全部选对的得6分，部分选对的得2分，有选错的得0分。

9.已知正数m，n满足，则()A.B.C.D.，，10.六氟化硫，化学式为，在常压下是一种无色、无臭、无毒、不燃的稳定气体，有良好的绝缘性，在电器工业方面具有广泛用途.六氟化硫结构为正八面体结构，如图所示，硫原子位于正八面体的中心，6个氟原子分别位于正八面体的6个顶点，若相邻两个氟原子之间的距离为m，则()A.该正八面体结构的表面积为B.该正八面体结构的体积为C.该正八面体结构的外接球表面积为D.该正八面体结构的内切球表面积为11.若关于x的不等式在上恒成立，则实数a的值可以是()A. B. C. D.2三、填空题：本题共3小题，每小题5分，共15分。

12.若函数的图象关于原点对称，则__________.13.已知平面凸四边形ABCD的对角线分别为AC，BD，其中，，则__________;若，则四边形ABCD 的面积的最大值为__________.14.已知双曲线的左、右焦点分别为，，点P在双曲线C上，且，，若点Q也在双曲线C上，则双曲线C的离心率为__________.四、解答题：本题共5小题，共77分。

江苏常熟中学2024届高三第二学期3月高考诊断性测试数学试题

江苏常熟中学2024届高三第二学期3月高考诊断性测试数学试题注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知函数2,0()2,0x xx f x e x x x ⎧>⎪=⎨⎪--≤⎩若函数1()()()2g x f x k x =-+在R 上零点最多，则实数k 的取值范围是（）A ．2(0,)3eB ．2(,0)3e-C ．1(,0)2e-D ．1(0,)2e2．双曲线的渐近线与圆(x －3)2＋y 2＝r 2(r ＞0)相切，则r 等于( )A ．B ．2C ．3D ．63．若双曲线()22210x y a a-=>的一条渐近线与圆()2222x y +-=至多有一个交点，则双曲线的离心率的取值范围是（） A ．)2,⎡+∞⎣B ．[)2,+∞C ．(2D ．(]1,24．已知函数2()sin 3cos444f x x x x πππ=，则(1)(2)...(2020)f f f +++的值等于（）A ．2018B ．1009C ．1010D ．20205．已知13313711log ,(),log 245a b c ===，则,,a b c 的大小关系为A ．a b c >>B ．b a c >>C ．c b a >>D ．c a b >>6．已知集合{}{}22(,)4,(,)2xA x y x yB x y y =+===，则AB 元素个数为( )A ．1B ．2C ．3D ．47．己知函数sin ,2,2(),2223sin ,2,2(),222x x k k k z y x x k k k z ππππππππππ⎧⎛⎫⎡⎫+∈-+∈ ⎪⎪⎪⎢⎪⎝⎭⎣⎭=⎨⎛⎫⎡⎫⎪-+∈++∈ ⎪⎪⎢⎪⎝⎭⎣⎭⎩的图象与直线(2)(0)y m x m =+>恰有四个公共点()()()()11123344,,,,.,,,A x y B x y C x y D x y ，其中1234x x x x <<<，则()442tan x x +=（） A ．1-B ．0C ．1D ．222+ 8．一个超级斐波那契数列是一列具有以下性质的正整数:从第三项起，每一项都等于前面所有项之和(例如:1，3，4，8，16…).则首项为2，某一项为2020的超级斐波那契数列的个数为（） A ．3B ．4C ．5D ．69．如图，在正方体1111ABCD A B C D -中，已知E 、F 、G 分别是线段11A C 上的点，且11A E EF FG GC ===.则下列直线与平面1A BD 平行的是（）A ．CEB ．CFC ．CGD ．1CC10．已知命题:0p x ∀>,ln(1)0x +>；命题:q 若a b >，则22a b >，下列命题为真命题的是（） A ．p q ∧ B ．p q ∧⌝ C ．p q ⌝∧ D ．p q ⌝∧⌝11．在复平面内，31ii+-复数（i 为虚数单位）的共轭复数对应的点位于（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限12．8x x ⎛ ⎝的二项展开式中，2x 的系数是（）A ．70B ．-70C ．28D ．-28二、填空题：本题共4小题，每小题5分，共20分。

高三数学3月复习质量监测卷六文扫描版,含答案

12.图37・函数 y = sin 2x + — =sin2[x+— !6丿 \ 12丿的图象向左平移醫个单位得到严S 叫吨+创 12 8. 9.・/> 兀 • c 兀sin 2 x + — =sin 2x + — ・ 3,故选B.如图1所示，球心O 到下底而的距离OO == = G 所以其外选 A.A，所以其外接球的表而积为4nR 2=2\n,故zsi 咱+si 吟+・..+sin*=O,故选C.图丄1.5P10.如图2,曲线y = J" + 2x 的轨迹是以（h 0）为圆心，1为半径的上半圆. 兀由几何概型得P = | =故选C ・2 40.5：-0.511. "）吕況+*" +X + 1有极值点” O“f （X ）" +心+ 1有两个不同的零点”O“u< 0或^ > 4" O “a W 0或(2 4” ,故选 B ・如图3,取线段町的中点M,贝I J|O/； + CZ ：I =I2OM ・| = 8,参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 DABCADBACCBD1. A = {-h 0,1,2}, 3 = {-2, -1, 0, 1},所以 Ap|B = {-l, 0, 1},故选 D ・2. g = a_i)(2_i )=j^ + Mj,所以加+ i = 2_“，即6/ = 1,故选 A.2 + i 5 5 533. 由 1厶 + 2/；1=5, 1。

一2厶 1=3 得(；+4“・/； + 4^=25 ①，才一4“•厶+ 4/； =9 ②，①一②得8a •万=16 ,所以u • b = 2 ,故选B.5. {%}是等差数列，S 5=S^ 9得均二。

，所以S l3 =13a 7 =0 ＞故选A ・6. 抛物线ar+ y 2 = 0可化为），=_©，其准线方程为x = -,即- = -1, “ = -4,故选D ・4 44.110 +H5=6x4+6，故选C. 一 110 + n接球的半径R = jAO f2+ OO 92=15・令/ = 由/（0 = 0> 得f=0 或/ = 2,再由/（A）=0.解得x = 0, x = 2:由f（x） = 2,解得*5,即函数y = f（.f（x））的所有零点所构成的集合为｛0, 2, 5）.1-75116・由题意得Q4丄〃，设点O到直线3x-4v-25 = 0的距离为〃，则" =5,则V32 + 42 SpQB =1OAW PA 1=1 PA 1= JpO「-oA = yjpo2 -1 N Jd"= 2岳■三、解答题（共70分.解答应写出文字说明，证明过程或演算步骤）17・（本小题满分12分）解：（I ）在ZVIBC中，由4我遊=屈疋一川一戻），得2"sinC =苗3-川一戻）即S in C = EH )=一血cos C ,2ab即tanC = ->/3, C =—・...........................................................................................3I [ 1 1 /(II ) sin2 A + sin2 B = - (1 - cos 2A) + -仆一cos 2B) = l --cos 2 A - - cos 2 —-A2' 2' 2 2 1.3在△ABC中, （5分）= -^sin2A-lcos2A + l = -lsin (2A + #+l,(8分) 二、填空题（本大题共4小题，每小题5分，共20分）所以牡（0,导2胃0，¥）, 2A +討自¥（10 分）1 '所以寸n 2A +13] 24丿文档从网络中收集，已重新整理排版.word版本可编辑:•欢迎下载支持. 所以sin2 A+sin2B的取值范囤为［斗， ........................................................... （12分）18.（本小题满分12分）解：（I）愿意不愿意总计男生15 45 60女生20 20 40总计35 65 100.............................................................................................................................. （2 分）计算Q =—叱四一=毗“山-心斯〜6 59<6 635 ,（a + b）（c + d）（a + c）（b + d）60x40x35x65所以没有99%的把握认为愿意参与志愿活动与性别有关. ....................... （6分）（II）用分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者，则女生4人，男生3人，分別编号为{1, 2, 3, 4}, {“，b, c},从中任取两人的所有基本事件如下：共有21种情况，其中满足两人中至少有一人是女生的基本事件数有18个.因为E为PD边上的中点，所以EF//AD,且EF =、AD，2因为AD〃BC, BC = -AD.2所以EF//BG 且EF = BC,所以四边形3VF 是平行四边形，所以CE 〃貯，又CE （Z 平而PAB , BFu 平而,所以CE 〃平面必3. .......................................................................................................... （4分）（ID UE 明：在直角梯形ABCD 中，AB = BC = -AD = 2.2所以AC = 2妃CD = 2近,所以AD 2=AC 2+CD\所以CQ 丄AC,① 又Q4丄平而ABCD,所以〃丄CQ,② 又P4p|AC = A ，所以CD 丄平而E4C, 因为CQu 平而PCD,所以平而Q4C 丄平面PCD. ............................................................................................. （8分）（III ）解：因为E 为PD 边上的中点，PA 丄平而所以 '$_XC £ = ^D-ACE = 2^-ACD 因为S,心=卜2迈・2近=4, PA = 2,4所以Vp^cE =-・ ................................ 20・（本小题满分12分）解：（I ）设椭圆c 的方程为4+7^ = IG />/7>O ）, / lr故椭圆C 的方程为- + y 2=l. ............................................................................................. (4分)4(II)直线OP 的方程为y = ^x,2设直线 AB 方程为 y = ^-x + m , A (X], yj, B(x 2, y 2).将直线AB 的方程代入椭圆C 的方程并整理得x 2 + E +用-1 = 0, 由△ = 3m 2 一 4(加‘ 一 1) > 0 ,得 nr < 4 ,x x + x 2 = -*m, x x x 2 = nt 2 一 L• PA,（12 分）由题意可得13 7+丽儿解得 a 2 = 4,h 2= L （6分）综上所述，—2e 》W“Wl. ............................................................................................. （12分）22.（本小题满分10分）【选修4-4：坐标系与参数方程】解：（I ）由 C ；的参数方程得（x-l ）2 + y 2 =l （y^0）,化简得 x 2 + y 2-2x = 0（y^0）,由 OA 丄 OB 得•B =o 到直线加的距离〃=胆二二慣・ .................V 42所以S®显肋=绘=应皿 2 2 2V? 10T（8分）（10分）21・（本小题满分12分）f (x)" 2x + “ JXX(x-a)(2x + a)X1° 当">0时，xe(0, a), f\x)>0: xe(a, +oo), ,f(x)<0：f （x ）（0, “）上单调递增，f （x ） {£ （a. +8）上单调递减; 2°当d=o 时，此时y （x ）在（0,+8）上单调递减:3° 当"<0 时，*（0, —*j, f\x ） > 0 :制—号,+ooj, f （x ）<0：念）在0,—打.上单调递增，./Xx ）在-牛+J.上单调递减. ..................... （6分）（1【）由（I ）可知1°当“>0时, /(X )max = f (")= “'in ci 一 + a 1 = In “WO,解得 0 v “ W1 ：2°当“ =0时, /(x) = -x 2^0,在(0, +oo)上恒成立; 3°当"<0时,即 ln^-U-2；(a}3a 2 '"2>,解得一2dW"vO ・4又 L4BI=召 + x 2 )2 - 4X ,X 2 =丄?・ ^4-nr 解：(I ) f(x) = a 2\nx-x 2 +ax ,定义域为(0, +oo),/(X )max a 2 In工工"in4 2（II ）当点P 到左点M （4, 3的）的距离最小时，PM 的延长线过（1，0）,此时PM 所在直线的倾斜角为即由数形结合可知，弔,丰23・（本小题满分10分）【选修4-5：不等式选讲】解：（I ）函数 f （x ）=l;r + "l-l;i-〃lW|" + b|,所以|“ + b|=4, 因为">0, Z?>0 ,所以“ + b = 4. ................................................................................................................ （5 分）（ID=—G/+2/?+2z/+/?）; 1^—（1+i ）2 = 1,a + 2h 2a+b 12 \a + 2b 2a+ h ） 12 3当且仅当“ + ” = % + » 即“ = b = 2时，—!—+ —^取得最小值二a + 2b 2a+b3................................................................................................................................. （10 分）（5分）（10 分）（2分）。

高三数学下学期3月质量检测试题文含解析试题

创作；朱本晓 2022年元月元日2021届高三数学下学期3月质量检测试题文〔含解析〕一、选择题：此题一共12小题，每一小题5分，一共60分．在每一小题给出的四个选项里面，只有一项是哪一项符合题目要求的．z ＝〔1+2i 〕〔1+ai 〕〔a ∈R 〕，假设z ∈R ，那么实数a ＝〔〕A.12B. 12-C. 2D. ﹣2【答案】D 【解析】【分析】化简z ＝〔1+2i 〕〔1+ai 〕=()()122a a i -++，再根据z ∈R 求解. 【详解】因为z ＝〔1+2i 〕〔1+ai 〕=()()122a a i -++，又因为z ∈R ，所以20a +=，解得a ＝-2. 应选：D【点睛】此题主要考察复数的运算及概念，还考察了运算求解的才能，属于根底题.M ＝{x |﹣1＜x ＜2}，N ＝{x |x 〔x +3〕≤0}，那么M ∩N ＝〔〕A. [﹣3，2〕B. 〔﹣3，2〕C. 〔﹣1，0]D. 〔﹣1，0〕【答案】C 【解析】【分析】先化简N ＝{x |x 〔x +3〕≤0}={x |-3≤x ≤0}，再根据M ＝{x |﹣1＜x ＜2}，求两集合的交集. 【详解】因为N ＝{x |x 〔x +3〕≤0}={x |-3≤x ≤0}，又因为M ＝{x |﹣1＜x ＜2}，所以M ∩N ＝{x |﹣1＜x ≤0}. 应选：C【点睛】此题主要考察集合的根本运算，还考察了运算求解的才能，属于根底题. 3.同时抛掷两个质地均匀的骰子，向上的点数之和小于5的概率为〔〕创作；朱本晓 2022年元月元日 A.19B. 16C. 118D. 512【答案】B 【解析】【分析】先列举算出抛掷两个质地均匀的骰子一共有根本领件的总数，再找出向上的点数之和小于5的事件的根本领件的个数，然后通过古典概型的概率公式求解. 【详解】抛掷两个质地均匀的骰子，一共有6636⨯=种可能，向上的点数之和小于5的有()()()()()()1112132122,3,1，，，，，，，，，有6种，所以向上的点数之和小于5的概率为16. 应选：B【点睛】此题主要考察古典概型的概率求法，还考察了运算求解的才能，属于根底题. 4.执行如下图的程序框图，输出的s 的值是〔〕A.53B.85C.138D.2113【答案】C 【解析】【分析】根据循环构造依次进展，直至不符合4i ≤，终止循环，输出s . 【详解】第一次循环，2,1s i ==，第二次循环，3,22s i ==，第三次循环，5,33s i ==，第四次循环，8,45s i ==，第四次循环，13,58s i ==，此时不满足4i ≤，输出138s =.应选：C【点睛】此题主要考察程序框图中的循环构造，还考察了逻辑推理的才能，属于根底题. 5.数列{a n }的前n 项之和S n ＝n 2+1，那么a 1+a 3＝〔〕 A. 6 B. 7 C. 8 D. 9【答案】B 【解析】【分析】根据数列{a n }的前n 项之和S n ＝n 2+1，求出123,,a a a ，再求解. 【详解】数列{a n }的前n 项之和S n ＝n 2+1，所以112S a ==，所以21225,3S a a a =+=∴=，所以3123310,5S a a a a =++=∴=，所以a 1+a 3＝7. 应选：B【点睛】此题主要考察数列的前n 项和与项的关系，还考察了运算求解的才能，属于根底题.C 1：x 2+y 2＝4与圆C 2：x 2+y 2﹣4x +4y ﹣12＝0的公一共弦的长为〔〕C. D. 【答案】C 【解析】【分析】两圆方程相减，得到公一共弦所在的直线方程，然后利用其中一个圆，结合弦长公式求解.【详解】因为圆C 1：x 2+y 2＝4与圆C 2：x 2+y 2﹣4x +4y ﹣12＝0，两式相减得20x y --=，即公一共弦所在的直线方程. 圆C1：x 2+y 2＝4，圆心到公一共弦的间隔为d =，所以公一共弦长为：l ==. 应选：C【点睛】此题主要考察直线与圆，圆与圆的位置关系，还考察了运算求解的才能，属于根底题. 7.tan 〔4πα+〕＝7，且32ππα＜＜，那么sinα＝〔〕 A.35B. 35-C. 45D. 45-【答案】B 【解析】【分析】先利用两角和的正切转化tan 〔4πα+〕＝1tan 7,1tan αβ+=-求得3tan 4α=，再结合平方关系22sin cos 1αα+=求解.【详解】因为tan 〔4πα+〕＝1tan 7,1tan αα+=-所以3tan 4α=，即sin 3cos 4αα=，又因为22sin cos 1αα+=且32ππα＜＜，所以sinα＝35. 应选：B【点睛】此题主要考察两角和的正切及同角三角函数根本关系式化简求值，还考察了运算求解的才能，属于根底题.1e ，2e 是夹角为60°的两个单位向量，而a =212e e +，b =-31e +22e ，那么向量a 和b夹角为〔〕 A.6π B.3π C.23π D.56π 【答案】C 【解析】【分析】先根据1e ，2e 是夹角为60°的两个单位向量，且a =212e e +，b =-31e +22e ，求得a b ⋅，a ，b ，再代入夹角公式cos ,a b a b a b⋅=求解.【详解】因为1e ，2e 是夹角为60°的两个单位向量，且a =212e e +，b =-31e +22e ，所以()()121272322a b e e e e ⋅⋅-+=-=+，所以()21227a e e =+=，()212327b e e =-+=所以1cos ,2a ba b a b⋅==-，，又因为[],0,a b π∈ 所以向量a 和b 夹角为23π. 应选：C【点睛】此题主要考察平面向量的数量积运算，还考察了运算求解的才能，属于中档题.f 〔x 〕＝sin 2x +sin 2〔x 3π+〕，那么f 〔x 〕的最小值为〔〕A.12 B.14【答案】A 【解析】【分析】先通过降幂公式和辅助角法将函数转化为()11cos 223f x x π⎛⎫=-+ ⎪⎝⎭，再求最值.【详解】函数f 〔x 〕＝sin 2x +sin 2〔x 3π+〕，=21cos 21cos 2322x x π⎛⎫-+⎪-⎝⎭+， =1cos 23sin 2111cos 222223x x x π⎛⎫⎛⎫--=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭，因为[]cos 21,13x π⎛⎫+∈- ⎪⎝⎭，所以f 〔x 〕的最小值为12. 应选：A【点睛】此题主要考察倍角公式及两角和与差的三角函数的逆用，还考察了运算求解的才能，属于中档题.SG 1G 2G 3中，E 、F 分别是G 1G 2及G 2G 3的中点，D 是EF 的中点，如今沿SE 、SF 及EF 把这个正方形折成一个四面体，使G 1、G 2、G 3三点重合，重合后的点记为G ，那么，在四面体S ﹣EFG 中必有〔〕A. SG ⊥△EFG 所在平面B. SD ⊥△EFG 所在平面C. GF ⊥△SEF 所在平面D. GD ⊥△SEF 所在平面【答案】A 【解析】【分析】在正方形SG 1G 2G 3中，有S G 1⊥G 1E ，在折叠后其垂直关系不变，所以有SG ⊥EG.同理有有SG ⊥FG ，再由线面垂直的断定定理证明.【详解】在正方形SG 1G 2G 3中，因为S G 1⊥G 1E ，所以在四面体中有SG ⊥EG.又因为S G 3⊥G 3F ，所以在四面体中有SG ⊥FG ，且GE GF G =，所以 SG ⊥△EFG 所在平面. 应选：A【点睛】此题主要考察折叠问题及线面垂直的断定定理，还考察了推理论证的才能，属于中档题.x 的不等式x 3﹣ax 2+1≥0在[﹣1，1]恒成立，那么实数a 的取值范围是〔〕A. a ≤0B. a ≤lC. a ≤2D.a 2≤【答案】A 【解析】【分析】当0x =时，不等式成立，当0x ≠时将不等式x 3﹣ax 2+1≥0在[)(]1,00,1x ∈-恒成立，转化为21a x x≤+在[)(]1,00,1x ∈-恒成立，最后求解即可.【详解】当0x =时，不等式成立，a R ∈当0x ≠时关于x 的不等式x 3﹣ax 2+1≥0在[)(]1,00,1x ∈-恒成立，即21a x x≤+在[)(]1,00,1x ∈-恒成立，令()21g x x x =+，()1332102g x x x'=-=⇒=，当[)1,0x ∈-时，()0g x '>，当(]0,1x ∈时，()0g x '<. 所以()g x 在[)1,0-递增，在(]0,1递减当[)1,0x ∈-时，()()min 10g x g =-= 当(]0,1x ∈时，()()min 12g x g == 所以()g x 的最小值为0. 所以0a ≤【点睛】此题主要考察不等式恒成立问题及导数求最值，还考察了转化化归的思想和运算求解的才能，属于中档题.12.△ABC 的三边分别为a ，b ，c ，假设满足a 2+b 2+2c 2＝8，那么△ABC 面积的最大值为〔〕【答案】B 【解析】【分析】根据a 2+b 2+2c 2＝8，得到22282a b c +=-，由余弦定理得到22cos 83ab C c =-，由正弦定理得到2sin 4ab C S =，两式平方相加得()()()22224834ab c S =-+，而222822a b c ab +=-≥，两式结合有()()()()222222248283165S c c c c≤---=-，再用根本不等式求解.【详解】因为a 2+b 2+2c 2＝8，所以22282a b c +=-，由余弦定理得222283cos 22a b c c C ab ab+--==，即22cos 83ab C c =-① 由正弦定理得in 12s S ab C =，即2sin 4ab C S =②由①，②平方相加得()()()()()222222222483482ab c S abc =-+≤+=-，所以()()()()2222222222116556448283165525c c S cc c c ⎛⎫-+≤---=-≤= ⎪⎝⎭，即245S ≤，所以S ≤，当且仅当22a b =且221655c c -=即222128,55a b c ===时，取等号.【点睛】此题主要考察了正弦定理和余弦定理及根本不等式的应用，还考察了运算求解的才能，属于中档题.二、填空题：此题一共4小题，每一小题5分，一共20分．f 〔x 〕＝xlnx +1在点〔e ，e +l 〕处的切线方程为___．【答案】2x ﹣y ﹣e +1＝0．【解析】【分析】根据函数f 〔x 〕＝xlnx +1，求导得()1ln f x x '=+，再分别求得()f e '，()f e ，用点斜式写出切线方程.【详解】因为函数f 〔x 〕＝xlnx +1，所以()1ln f x x '=+，所以()1ln 2f e e '=+=，()ln 11f e e e e =+=+，所以切线方程为：()()12y e x e -+=-，即210x y e --+=. 故答案为：210x y e --+=【点睛】此题主要考察了导数的几何意义，还考察了运算求解的才能，属于根底题.f 〔x 〕cosx a sinx +=在〔0，2π〕上单调递减，那么实数a 的取值范围为___．【答案】a ≥﹣1．【解析】【分析】将函数f 〔x 〕cosx a sinx +=在〔0，2π〕上单调递减，转化()21cos 0sin a xf x x --'=≤在〔0，2π〕上恒成立即1cos a x ≥-在〔0，2π〕上恒成立再求1cos x -最大值即可.【详解】因为函数f 〔x 〕cosx asinx +=在〔0，2π〕上单调递减，所以()21cos 0sin a xf x x --'=≤在〔0，2π〕上恒成立，即1cos a x ≥-在〔0，2π〕上恒成立，因为0,2x π⎛⎫∈ ⎪⎝⎭，所以()cos 0,1x ∈，所以1(,1]cos x-∈-∞-，所以1a ≥-. 故答案为：1a ≥-【点睛】此题主要考察了导数与函数的单调性，还考察了转化化归的思想和运算求解的才能，属于中档题.15.M =M 的最大值为___．【答案】1. 【解析】【分析】利用柯西不等式求解. 【详解】由柯西不等式得：22221x y ⎡⎤⎡⎤≤++=⎢⎥⎢⎥⎣⎦⎣⎦，=221x y +=取等号. 故M 的最大值为1 故答案为：1【点睛】此题主要考察了柯西不等式的应用，还考察了运算求解的才能，属于中档题. 16.根据气象部门预报，在间隔某个码头A 南偏东45°方向的600km 处的热带风暴中心B 正以30km /h 的速度向正北方向挪动，间隔风暴中心450km 以内的地区都将受到影响，从如今起经过___小时后该码头A 将受到热带风暴的影响〔准确到0.01〕．h.【解析】【分析】先建立坐标系，设风暴中心最初在B处，经th后到达C处．自B向x轴作垂线，垂足为D．假设在点C处受到热带风暴的影响，那么AC＝450，那么有22+=450，即AD DC22cos sin t︒+︒-=450；两边平方并化简、整理求解.(60045)(6004530)【详解】建立如下图直角坐标系：设风暴中心最初在B处，经th后到达C处．自B向x轴作垂线，垂足为D．假设在点C处受到热带风暴的影响，那么OC＝450，22AD DC+=450，22cos sin t︒+︒-=450；(60045)(6004530)两边平方并化简、整理得t2﹣2t+175＝0∴t1025=或者1025，≈159.0241所以9.14时后码头将受到热带风暴的影响．【点睛】此题主要考察了三角函数的实际应用，还考察了运算求解的才能，属于中档题.三、解答题：一共70分．解容许写出文字说明、证明过程或者演算步骤．第17-21题为必考题，每个试题考生都必须答题．第22、23题为选考题，考生根据要求答题．〔一〕必考题：一共60分．17.假设等比数列{a n}的前n项和为S n，满足a4﹣a1＝S3，a5﹣a1＝15．〔1〕求数列{a n}的首项a1和公比q；〔2〕假设a n＞n+100，求n的取值范围．【答案】〔1〕q＝2，a1＝1；〔2〕n≥7.【解析】【分析】〔1〕根据a 4﹣a 1＝S 3，a 5﹣a 1＝15，利用“q ，a 1〞法求解.〔2〕由〔1〕建立不等式12n -＞n +100，通过估值法求解. 【详解】〔1〕∵a 4﹣a 1＝S 3，a 5﹣a 1＝15．显然公比q ≠1，∴()()()3131********a q a q q a q ⎧-⎪-=⎪-⎨⎪-=⎪⎩，解可得q ＝2，a 1＝1，〔2〕由〔1〕可得a n ＝12n -， ∵a n ＞n +100，即12n -＞n +100，解可得，n ≥7．【点睛】此题主要考察了等比数列的通项公式及其应用，还考察了运算求解的才能，属于中档题.18.如图，在棱长为a 的正方体ABCD ﹣A 1B 1C 1D 1中，P ，Q ，L 分别为棱A 1D 1，C 1D 1，BC 的中点．〔1〕求证：AC ⊥QL ；〔2〕求四面体DPQL 的体积．【答案】〔1〕见解析；〔2〕318a . 【解析】【分析】〔1〕取CD 的中点H ，根据正方体的几何性质，有QH ⊥AC ，AC ⊥HL ，再利用线面垂直的断定定理证明.〔2〕连接PB 1，B 1L ，四边形LDPB 1是平行四边形，根据等体积法，那么有11Q PDL Q PB L L QPB V V V ---==，然后通过1L QPB V -求解.【详解】〔1〕证明：如下图：H 为CD 的中点，连接QH ，HL ，P ，Q ，L 分别为棱A 1D 1，C 1D 1，BC 的中点．所以QH ⊥AC ，AC ⊥HL ，QH ∩HL ＝H ，所以AC ⊥平面QHL ， ∵QL ⊂平面QHL ， ∴AC ⊥QL ；〔2〕解：如下图：连接PB 1，B 1L ，四边形LDPB 1是平行四边形，那么11Q PDL Q PB L L QPB V V V ---==1121111111111332222222L QPB PQB V S AA a a a a a a a a -∆⎛⎫=⨯⨯=⨯-⨯⨯-⨯⨯-⨯⨯⨯ ⎪⎝⎭318a =．【点睛】此题主要考察了正方体的几何特征和线面垂直的断定定理，以及三棱锥的体积，还考察了空间想象，推理论证，运算求解的才能，属于中档题.19.一个小商店从一家食品购进10袋白糖，每袋白糖的HY 重量是500g ，为了理解这些白糖的实际重量，称量出各袋白糖的实际重量〔单位：g 〕如下：503，502，496，499，491，498，506，504，501，510〔1〕求这10袋白糖的平均重量x和HY差s；〔2〕从这10袋中任取2袋白糖，那么其中恰有一袋的重量不在〔x-s，x+s〕的概率是≈5.08≈16.06≈5.09≈16.09〕【答案】〔1〕501，5.08；〔2〕16 45.【解析】【分析】〔1〕根据提供的数据，利用平均数和方差公式求解.〔2〕根据〔1〕的结合，算出重量在〔x-s，x+s〕内的袋数和不在内的袋数，然后得出从10袋中选2袋的方法数和恰有一袋的方法数，再利用古典概型的概率公式求解.【详解】〔1〕根据题意，10袋白糖的实际重量如下：503，502，496，499，491，498，506，504，501，510，那么其平均重量110x=〔503+502+496+499+491+498+506+504+501+510〕＝500110+〔3+2﹣4﹣1﹣9﹣2+6+4+1+10〕＝501，其方差S2110=[〔503﹣501〕2+〔502﹣501〕2+〔496﹣501〕2+〔499﹣501〕2+〔491﹣501〕2+〔498﹣501〕2+〔506﹣501〕2+〔504﹣501〕2+〔501﹣501〕2+〔510﹣501〕2]＝25.8；那么其HY差s=≈5.08；〔2〕根据题意，由〔1〕的结论，10袋白糖在〔x-s，x+s〕之间的有503，502，496，499，498，506，504，501，一共8袋，从10袋白糖中任取两袋，有C102＝45种取法，其中恰有一袋的重量不在〔x-s，x+s〕的情况有8×2＝16种，那么恰有一袋的重量不在〔x-s，x+s〕的概率P16 45 =．【点睛】此题主要考察了平均数，方差及古典概型的概率，还考察了运算求解的才能，属于中档题.20.抛物线Γ：y2＝2px〔p＞0〕的焦点为F，P是抛物线Γ上一点，且在第一象限，满足FP=〔2，〕〔1〕求抛物线Γ的方程；〔2〕经过点A 〔3，﹣2〕的直线交抛物线Γ于M ，N 两点，经过定点B 〔3，﹣6〕和M 的直线与抛物线Γ交于另一点L ，问直线NL 是否恒过定点，假如过定点，求出该定点，否那么说明理由．【答案】〔1〕y 2＝4x ；；〔2〕直线NL 恒过定点〔﹣3，0〕，理由见解析. 【解析】【分析】〔1〕根据抛物线的方程，求得焦点F 〔2p，0〕，利用FP =〔2，，表示点P 的坐标，再代入抛物线方程求解.〔2〕设M 〔x 0，y 0〕，N 〔x 1，y 1〕，L 〔x 2，y 2〕，表示出MN 的方程y 01014x y y y y +=+和ML 的方程y 02024x y y y y +=+，因为A 〔3，﹣2〕，B 〔3，﹣6〕在这两条直线上，分别代入两直线的方程可得y 1y 2＝12，然后表示直线NL 的方程为：y ﹣y 1124y y =+〔x 214y-〕，代入化简求解.【详解】〔1〕由抛物线的方程可得焦点F 〔2p，0〕，满足FP =〔2，P 的坐标为〔22p+，，P 在抛物线上，所以〔2＝2p 〔22p +〕，即p 2+4p ﹣12＝0，p ＞0，解得p ＝2，所以抛物线的方程为：y 2＝4x ；〔2〕设M 〔x 0，y 0〕，N 〔x 1，y 1〕，L 〔x 2，y 2〕，那么y 12＝4x 1，y 22＝4x 2，直线MN 的斜率k MN10102210101044y y y y y y x x y y --===--+，那么直线MN 的方程为：y ﹣y 0104y y =+〔x 204y -〕，即y 01014x y y y y +=+①，同理可得直线ML 的方程整理可得y 02024x y y y y +=+②，将A 〔3，﹣2〕，B 〔3，﹣6〕分别代入①，②的方程可得01010202122126y y y y y y y y +⎧-=⎪+⎪⎨+⎪-=⎪+⎩，消y 0可得y 1y 2＝12，易知直线k NL 124y y =+，那么直线NL 的方程为：y ﹣y 1124y y =+〔x 214y -〕，即y 124y y =+x 1212y y y y ++，故y 124y y =+x 1212y y ++，所以y 124y y =+〔x +3〕，因此直线NL 恒过定点〔﹣3，0〕．【点睛】此题主要考察了抛物线的方程及直线与抛物线的位置关系，直线过定点问题，还考察了转化化归的思想和运算求解的才能，属于中档题. 21.〔1〕研究函数f 〔x 〕sinxx=在〔0，π〕上的单调性；〔2〕求函数g 〔x 〕＝x 2+πcos x 的最小值．【答案】〔1〕f 〔x 〕在〔0，π 〕递减；〔2〕24π.【解析】【分析】〔1〕根据()sinx f x x =，求导得()2'xcosx sinxf x x -=，设m 〔x 〕＝x cos x ﹣sin x ，x ∈〔0，π〕，通过求导来判断其正负，从而得到f ′〔x 〕的正负，进而研究f 〔x 〕的单调性.〔2〕易知g 〔x 〕是偶函数，故只需求x ∈[0，+∞〕时g 〔x 〕的最小值，求导得g ′〔x 〕＝2x ﹣πsin x ，根据sinx 的特点，分x ∈〔0，2π〕和2x π⎛⎫∈+∞ ⎪⎝⎭，时两种情况讨论g 〔x 〕单调性，进而求其最小值.【详解】〔1〕因为()sinx f x x =，所以()2'xcosx sinxf x x-=，设m 〔x 〕＝x cos x ﹣sin x ，x ∈〔0，π〕，m ′〔x 〕＝﹣x sin x ＜0，所以m 〔x 〕在〔0，π 〕递减，那么m 〔x 〕＜m 〔0〕＝0 故f ′〔x 〕＜0，所以f 〔x 〕在〔0，π 〕递减；〔2〕观察知g 〔x 〕为偶函数，故只需求x ∈[0，+∞〕时g 〔x 〕的最小值，由g ′〔x 〕＝2x ﹣πsin x ，当x ∈〔0，2π〕时，设n 〔x 〕＝2x ﹣π sin x ，那么n ′〔x 〕＝2﹣π cos x ，显然 n ′〔x 〕递增，而n ′〔0〕＝2﹣π＜0，'202n π⎛⎫=⎪⎝⎭＞，由零点存在定理，存在唯一的002x π⎛⎫∈ ⎪⎝⎭，，使得n ′〔x 0〕＝0当x ∈〔0，x 0〕时，n ′〔x 〕＜0，n 〔x 〕递减，当02x x π⎛⎫∈ ⎪⎝⎭，时，n ′〔x 〕＞0，n 〔x 〕递增，而n 〔0〕＝0，02n π⎛⎫=⎪⎝⎭，故02x π⎛⎫∈ ⎪⎝⎭，时，n 〔x 〕＜0，即02x π⎛⎫∈ ⎪⎝⎭，时，g ′〔x 〕＜0，那么g 〔x 〕递减；又当2x π⎛⎫∈+∞⎪⎝⎭，时，2x ＞π＞π sin x ，g ′〔x 〕＞0，g 〔x 〕递增；所以2()24ming x g ππ⎛⎫== ⎪⎝⎭．【点睛】此题主要考察了导数与函数的单调性及最值，还考察了转化化归的思想和运算求解的才能，属于难题.〔二〕选考题：一共10分，请考生在第22、23题中任选一题答题，假如多做，那么按所做的第一题计分．[选修4-4：坐标系与参数方程]xOy 中，曲线C 1的参数方程为54x cos y sin αα=⎧⎨=⎩〔α为参数〕，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，曲线C 2：ρ2﹣4ρcosθ+3＝0．〔1〕求曲线C 1的一般方程和曲线C 2的直角坐标方程；〔2〕假设点P 在曲线C 1上，点Q 曲线C 2上，求|PQ |的最小值．【答案】〔1〕2212516x y +=，〔x ﹣2〕2+y 2＝1；〔2〕2.【解析】【分析】〔1〕由C 1的参数方程为5(4x cos y sin ααα=⎧⎨=⎩为参数〕，消去参数即可转换为直角坐标方程，根据曲线C 2：ρ2﹣4ρcosθ+3＝0．利用cos ,sin x y ρθρθ==转换为直角坐标方程.〔2〕设点P 〔5cos θ，4sinθ〕，根据点Q 在圆上，先求点P 到圆心的间隔，然后减去半径即为最小值.【详解】〔1〕曲线C 1的参数方程为5(4x cos y sin ααα=⎧⎨=⎩为参数〕，两式平方相加整理得2212516x y +=．将cos ,sin x y ρθρθ==代入ρ2﹣4ρcosθ+3＝0．得x 2+y 2﹣4x +3＝0，整理得〔x ﹣2〕2+y 2＝1．〔2〕设点P 〔5cosθ，4sinθ〕在曲线C 1上，圆心O 〔2，0〕，所以：PO ===，当cosθ＝1时，|PO |min ＝3，所以|PQ |的最小值3﹣1＝2．【点睛】此题主要考察了参数方程，普通方程，极坐标方程间的互化及点与圆的位置关系，还考察了转化化归的思想和运算求解的才能，属于中档题.[选修4-5：不等式选讲]f〔x〕＝|2x﹣a|+|x﹣a+1|．〔1〕当a＝4时，求解不等式f〔x〕≥8；〔2〕关于x的不等式f〔x〕22a≥在R上恒成立，求参数a的取值范围．【答案】〔1〕[5，+∞〕∪〔∞，13-]；〔2〕[﹣2，1].【解析】【分析】〔1〕根据a＝4时，有f〔x〕＝|2x﹣4|+|x﹣3|，然后利用绝对值的几何意义，去绝对值求解.〔2〕根据绝对值的零点有a﹣1和12a，分a﹣112a=，a﹣112a＞和a﹣112a＜时三种情况分类讨论求解.【详解】〔1〕当a＝4时，f〔x〕＝|2x﹣4|+|x﹣3|，〔i〕当x≥3时，原不等式可化为3x﹣7≥8，解可得x≥5，此时不等式的解集[5，+∞〕；〔ii〕当2＜x＜3时，原不等式可化为2x﹣4+3﹣x≥8，解可得x≥9此时不等式的解集∅；〔iii〕当x≤2时，原不等式可化为﹣3x+7≥8，解可得x13≤-，此时不等式的解集〔∞，13 -]，综上可得，不等式的解集[5，+∞〕∪〔∞，13 -]，〔2〕〔i〕当a﹣112a=即a＝2时，f〔x〕＝3|x﹣1|22a≥=2显然不恒成立，〔ii〕当a﹣112a＞即a＞2时，()1321211123211x a x af x x a x ax a x a⎧-+-≤⎪⎪⎪=--⎨⎪-+≥-⎪⎪⎩，，＜＜，，结合函数的单调性可知，当x12a=时，函数获得最小值f〔12a〕112a=-，假设f〔x〕22a≥在R上恒成立，那么211122a a-≥，此时a不存在，〔iii〕当a﹣112a＜即a＜2时，f〔x〕3211111213212x a x ax a x ax a x a⎧⎪-+-≤-⎪⎪=-+-⎨⎪⎪-+≥⎪⎩，，＜＜，假设f〔x〕22a≥在R上恒成立，那么121122a a-≥，解得﹣2≤a≤1，此时a的范围[﹣2，1]，综上可得，a的范围围[﹣2，1]．【点睛】此题主要考察了绝对值不等式的解法及含有绝对值的不等式恒成立问题，还考察了分类讨论的思想和运算求解的才能，属于中档题.励志赠言经典语录精选句；挥动**，放飞梦想。

人教版八年级数学上学期3月份质量检测测试卷含答案

人教版八年级数学上学期3月份质量检测测试卷含答案一、选择题1．,a==ba 、b 可以表示为（）A ．10a b+ B ．10-b aC ．10ab D ．ba2．下列各式成立的是（）A3= B3= C．22(3=- D．2-=3．已知5x =-，则2101x x -+的值为（） A．-B．C．2- D ．0 4．m 能取的最小整数值是（） A ．m = 0B ．m = 1C ．m = 2D ．m = 35．下列式子中，为最简二次根式的是（） ABCD6．已知m 、nm ，n ）为（） A ．（2，5）B ．（8，20）C ．（2，5），（8，20）D ．以上都不是7．已知226a b ab +=，且a>b>0，则a ba b+-的值为( ) ABC ．2D ．±28．下列计算正确的是（） A．+=B ．()322326a ba b -=-C ．222()a b a b -=-D ．2422a ab a a b a -+⋅=-++9．当4x =-的值为（）A ．1BC ．2D ．310．已知0xy <，化简二次根式） ABC．D．11．若式子2(1)m -有意义，则实数m 的取值范围是（）A ．m ＞﹣2B ．m ＞﹣2且m ≠1C ．m ≥﹣2D ．m ≥﹣2且m ≠112．如果实数x ，y =-(),x y 在（） A ．第一象限 B ．第二象限C ．第一象限或坐标轴上D ．第二象限或坐标轴上二、填空题13．已知x =()21142221x x x x -⎛⎫+⋅= ⎪-+-⎝⎭_________14．已知实数,x y 满足(2008x y =，则2232332007x y x y -+--的值为______.15．当x x 2﹣4x +2017=________． 16．已知x =，a 是x 的整数部分，b 是x 的小数部分，则a-b=_______17．+的形式(,,a b c 为正整数)，则abc =______.18．下面是一个按某种规律排列的数阵：根据数阵排列的规律，第 5 行从左向右数第 3 个数是，第 n （n 3≥ 且 n 是整数）行从左向右数第 n 2- 个数是（用含 n 的代数式表示）．19．mn ＝________． 20．古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式，称为海伦—秦九韶公式：如果一个三角形的三边长分别是a ，b ，c ，记2a b cp ++=，那么三角形的面积S =ABC 中，A ∠，B ，C ∠所对的边分别记为a ，b ，c ，若4a =，5b =，7c =，则ABC 面积是_______．三、解答题21．先阅读下列解答过程，然后再解答：,a b，使a b m=，使得+=，ab n22m+==a b==>)+=⨯=，==，由于437,4312m n7,12+=，=即：227===+。

人教版八年级数学上学期3月份质量检测测试卷

人教版八年级数学上学期3月份质量检测测试卷一、选择题1．若有意义，则 x 的取值范围是（）A ．3x >B ．3x ≥C ．3x ≤D ．x 是非负数2．已知2a =，2b =的值为（） A ．4B ．5C ．6D ．73．下列计算正确的是（）A 3=±B 0-=C =D 5=-4．下列方程中，有实数根的方程是（）A 0=B 10=C 2=D 1=．5．下列运算正确的是（）A ．3=B =C ．=D =6的倒数是（）A B ．2C ．D ．2-7．若a ，b ＝，则a b 的值为（）A ．12B ．14C ．321+D8．已知a 满足2018a -a ，则a －2 0182＝( ) A ．0B ．1C ．2 018D ．2 0199．给出下列化简①（）2=2=2=12=，其中正确的是（） A ．①②③④B ．①②③C ．①②D ．③④10．下列运算中正确的是（）A ．=B()23===C 3===D 1==11．下列根式中是最简二次根式的是（）A ．23B ．10C ．9D ．3a12．估计（12+6）3÷的值应在（） A ．1和2之间B ．3和4之间C ．4和5之间D ．5和6之间二、填空题13．设42-的整数部分为 a,小数部分为 b.则1a b-= __________________________. 14．若a ，b ，c 是实数，且21416210a b c a b c ++=-+-+--，则2b c +=________．15．若x +y =5+3，xy =15-3，则x+y=_______．16．将一组数2，2，6，22，10，…，251按图中的方法排列：若2的位置记为（2，3），7的位置记为（3，2），则这组数中最大数的位置记为______．171262_____．18．2m 1-1343m --mn ＝________． 19．下列各式：2521+n ③24b 0.1y 是最简二次根式的是:_____（填序号）20．2a ·8a (a ≥0)的结果是_________.三、解答题21．计算： 22(31)(233)(33)63--【答案】3. 【解析】【分析】先运用完全平方公式、平方差公式进行化简，然后进行计算. 【详解】解：原式3232626 3232]-4 3【点睛】本题主要考查了二次根式的化简；特别是灵活运用全平方公式、平方差公式是解答本题的关键.22．计算：（1﹣（2）（3）244x -﹣12x -．【答案】（1）2（3）-12x + 【解析】分析：（1）根据二次根式的运算，先把各二次根式化为最简二次根式，再合并同类二次根式即可；（2）根据乘法的分配律以及二次根式的性质进行计算即可；（3）根据异分母的分式的加减，先因式分解，再通分，然后按同分母的分式进行加减计算，再约分即可.详解：（1（2）（3）24142x x --- =41(2)(2)2x x x -+--= 42(2)(2)(2)(2)x x x x x +-+-+-=2(2)(2)xx x -+-=12x -+ 点睛：此题主要考查了二次根式的运算和分式的加减运算，熟练应用运算法则和运算律以及二次根式的性质进行计算是解题关键.23．）÷）（a ≠b ）．【答案】【解析】试题分析：先计算括号内的，然后把除法转化为乘法，约分即可得出结论．试题解析：解：原式＝()()a b a b --+-24．阅读下列材料，然后回答问题：1==. 以上这种化简过程叫做分母有理化.221===. （1）请用其中一种方法化简；（2+99+【答案】(2) 3 1. 【分析】(1)运用了第二种方法求解，即将4（2）先把每一个加数进行分母有理化，再找出规律，即后面的第二项可以和前面的第一项抵消，然后即可得出答案.【详解】（1）原式==；（2）原式=+++…=﹣1+﹣+﹣+…﹣=﹣1=3﹣1【点睛】本题主要考查了分母有理化，找准有理化的因式是解题的关键.25．先化简再求值：321943x y x y x x x x y ⎛- ⎝，其中340x y --=．【答案】(25x x xy -3 【分析】先根据二次根式的混合运算顺序和运算法则化简原式，再利用非负数的性质得出x ，y 的值，继而将x 、y 的值代入计算可得答案．【详解】解：321943x y x y x x x x y ⎛- ⎝ ()()24x xy x x xy =-(25x x xy =-∵ 340x y -- ∴ 3,4x y == 当3,4x y ==时原式(233512310393=-=-=【点睛】本题主要考查了二次根式的化简求值，解题的关键是掌握非负数的性质和二次根式的混合运算顺序和法则．26．观察下列一组等式，然后解答后面的问题21)(21)1=，(32)(32)1=， (43)(43)1=， (54)(54)1=⋯⋯（1）观察以上规律，请写出第n 个等式： (n 为正整数）．（2（3【答案】（1）1=；（2）9；（3【分析】(1)根据规律直接写出,(2)先找出规律，分母有理化，再化简计算.(3)先对两个式子变形，分子有理化，变为分子为1，再比大小. 【详解】解：（1）根据题意得：第n 个等式为1=；故答案为1=；（2）原式111019==-=；（3-==，<∴>．【点睛】本题是一道利用规律进行求解的题目，解题的关键是掌握平方差公式.27．已知x y ==求下列各式的值： (1)22x xy y -+；(2).y xx y+ 【答案】(1) 72;(2)8. 【分析】计算出xy=12，（1）把x 2-xy+y 2变形为（x+y ）2-3xy ，然后利用整体代入的方法计算；（2）把原式变形为2()2x y xyxy+-，然后利用整体代入的方法计算.【详解】∵x =，y ==32∴xy=12,(1)22x xy y -+ =（x+y ）2-3xy,=2132-⨯ =72; (2)y x x y +=2212()22812x y xyxy-⨯+-==.【点睛】本题考查了二次根式的化简求值：二次根式的化简求值，一定要先化简再代入求值．二次根式运算的最后，注意结果要化到最简二次根式，二次根式的乘除运算要与加减运算区分，避免互相干扰．28．计算：0(3)|1|π-+．【答案】【分析】根据二次根式的意义和性质以及零次幂的定义可以得到解答．【详解】解：原式11=+=【点睛】本题考查实数的运算，熟练掌握二次根式的运算和零次幂的意义是解题关键．29．已知长方形的长a =b =. (1)求长方形的周长；(2)求与长方形等面积的正方形的周长，并比较其与长方形周长的大小关系．【答案】（1）2）长方形的周长大. 【解析】试题分析：（1）代入周长计算公式解决问题；（2）求得长方形的面积，开方得出正方形的边长，进一步求得周长比较即可．试题解析： (1)()11222223a b ⎛+=⨯=⨯⨯⨯=⨯= ⎝∴长方形的周长为 .(2)114.23=⨯⨯=正方形的面积也为4. 2.= 周长为：428.⨯=8.>∴长方形的周长大于正方形的周长．30．先阅读下面的解题过程，然后再解答.a ，b ，使a b m +=，ab n =，即22m +==0)a b ==±>.这里7m =，12n =，由于437+=，4312⨯=，所以22+==，2===.. 【答案】见解析【分析】应先找到哪两个数的和为13，积为42．再判断是选择加法，还是减法．【详解】根据题意，可知13m =，42n =，由于7613+=，7642⨯=，所以2213+=，====【点睛】此题考查二次根式的性质与化简，解题关键在于求得13m =，42n =.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】直接利用二次根式有意义的条件进而分析得出答案．【详解】有意义的x 的取值范围是：x ≥3．故选：B ．【点睛】本题考查二次根式有意义的条件，解题关键是正确掌握定义和二次根式有意义的条件．2．B解析：B 【分析】根据二次根式的混合运算和完全平方公式进行计算，即可得到结果．【详解】解：∵2a =，2b =， ∴227a b ++2252527 55454745425=∴255故选：B ．【点睛】本题主要考查了二次根式的混合运算和完全平方公式，熟悉相关运算法则是解题的关键3．B解析：B 【分析】直接利用二次根式的性质化简得出答案．【详解】3=，故此选项错误；0=，正确；D. 5=，故此选项错误；故选：B【点睛】此题主要考查了二次根式的加减，正确掌握二次根式的性质是解题关键．4．C解析：C【分析】k=的形式，再根据二次根式成立的条件逐个进行判断即可．【详解】解：A、x2+4=0，此时方程无解，故本选项错误；B10=，-，1∵算术平方根是非负数，∴此时方程无解，故本选项错误；C2=，∴x+1=4，∴x=3，故本选项正确；D1=，∴x-3≥0且3-x≥0，解得：x=3，代入得：0+0=1，此时不成立，故本选项错误；故选：C．【点睛】本题考查了二次根式的意义，能根据二次根式成立的条件进行判断是解此题的关键．5．A解析：A【分析】根据各个选项中的式子，可以计算出正确的结果，从而可以解答本题．【详解】A、3=，故选项A正确；B B错误；C、18=，故选项C错误；D=D错误；故选：A．【点睛】本题考查了二次根式的混合运算，解答本题的关键是明确二次根式混合运算的计算方法．6．B解析：B【分析】根据倒数的定义，即可得到答案.【详解】2，；故选：B.【点睛】本题考查了倒数的定义和化为最简二次根式，解题的关键是熟记倒数的定义进行解题. 7．B解析：B【解析】【分析】将a可化简为关于b的式子，从而得到a和b的关系，继而能得出ab 的值．【详解】a=b44=．∴14ab=．故选：B．【点睛】本题考查二次根式的乘除法，有一定难度，关键是在分母有理化时要观察b的形式．8．D解析：D【解析】【分析】根据二次根式的被开数的非负性，求的a的范围，然后再化简绝对值，最后，依据二次根式的定义进行变形即可．【详解】解：等式2018a-＝a成立，则a≥2019，∴，，∴a-2019=20182，∴a-20182=2019．故选D．【点睛】本题主要考查的是二次根式有意义的条件，求得a的取值范围是解题的关键．9．C解析：C【分析】根据二次根式的性质逐一进行计算即可求出答案．【详解】①原式=2，故①正确；②原式=2，故②正确；③原式==④原式==，故④错误，故选C．【点睛】本题考查二次根式的性质和化简，熟练掌握二次根式的性质是解题的关键.10．B解析：B【分析】根据二次根式的乘除法则求出每个式子的值，再判断即可．【详解】=⨯=＝42，故本选项不符合题意；解: A. 67===，故本选项，符合题意；===，故本选项不符合题意；D. ==3，故本选项不符合题意；故选B．【点睛】本题考查二次根式的性质和二次根式的乘除法则，能灵活运用二次根式的乘除法则进行计算是解题关键．11．B解析：B【分析】根据最简二次根式的条件：①根号下不含能开得尽方的因数或因式；②根号下不含分母，据此逐项判断即可．【详解】解：A、被开方数含分母，故A不符合题意；B、被开方数不含分母；被开方数不含能开得尽方的因数或因式．，故B符合题意；C被开方数含能开得尽方的因数或因式，故C不符合题意；D、被开方数含能开得尽方的因数或因式，故D不符合题意；故选：B．【点睛】本题考查了最简二次根式，解题的关键是掌握最简二次根式的两个条件．12．B解析：B【分析】原式利用多项式除以单项式法则计算，估算确定出范围即可．【详解】＝∵1＜2＜4，∴1＜2，即3＜＜4，则原式的值应在3和4之间．故选：B．【点睛】本题考查了二次根式的混合运算，以及无理数的估算，解题的关键是熟练掌握运算法则进行解题．二、填空题13．【分析】根据实数的估算求出a,b，再代入即可求解.【详解】∵1＜＜2，∴-2＜-＜-1，∴2＜＜3∴整数部分a=2,小数部分为-2=2-，∴==故填：.此题主要考查无理解析：1 【分析】根据实数的估算求出a,b ，再代入1a b -即可求解. 【详解】∵1＜2，∴-2＜＜-1，∴2＜43∴整数部分a=2,小数部分为4，∴1ab -=2222=-=12-故填：12-. 【点睛】此题主要考查无理数的估算，分母有理化等，解题的关键熟知实数的性质.14．21【分析】结合态，根据完全平方公式的性质，将代数式变形，即可计算得，，的值，从而得到答案．【详解】∵∴∴∴∴∴∴∴．【点睛】本题考查了二次根式、完全平方公式的知识；解题的解析：21【分析】结合态，根据完全平方公式的性质，将代数式变形，即可计算得a ，b ，c 的值，从而得【详解】∵10a b c ++=∴100a b c ---=∴2221490⎡⎤⎡⎤⎡⎤-+-+-=⎣⎦⎣⎦⎣⎦∴2221)2)3)0++=∴123===∴111429a b c -=⎧⎪-=⎨⎪-=⎩∴2511a b c =⎧⎪=⎨⎪=⎩∴2251121b c +=⨯+=．【点睛】本题考查了二次根式、完全平方公式的知识；解题的关键是熟练掌握二次根式、完全平方公式、一元一次方程的性质，从而完成求解．15．8+2【解析】根据配方法，由完全平方公式可知x+y==（）2-2，然后把+=+，=-整体代入可得原式=（+）2-2（-）=5+3+2-2+2=8+2.故答案为：8+2.解析：【解析】根据配方法，由完全平方公式可知x+y=2222+=+-）2整体代入可得原式=2-2）故答案为：16．（17,6）【解析】观察、分析这组数据可发现：第一个数是的积；第二个数是的积；第三个数是的积，的积.∵这组数据中最大的数：，∴是这组数据中的第102个数.∵每一行排列了6个数，而∴是第1解析：（17,6）【解析】的积，.∵这组数据中最大的数：∴102个数.∵每一行排列了6个数，而1026=17÷ ∴17行第6个数，∴这组数据中最大的一个数应记为（17，6）.点睛：（1）这组数据组中的第n 2）该组数据是按从左到右，从小到大，每行6个数进行排列的；（3）6n ÷6n ÷的余数是所在的列数.17．6【分析】利用二次根式乘除法法则进行计算即可．【详解】＝＝＝6，故答案为6．【点睛】本题考查了二次根式的乘除法，熟练运用二次根式的乘除法法则是解题的关键．解析：6【分析】==进行计算即可．【详解】＝6，故答案为6．【点睛】本题考查了二次根式的乘除法，熟练运用二次根式的乘除法法则是解题的关键．18．21【分析】根据二次根式及同类二次根式的定义列出方程组即可求出答案.【详解】∵最简二次根式与是同类二次根式，∴ ，解得，，∴故答案为21.解析：21【分析】根据二次根式及同类二次根式的定义列出方程组即可求出答案.【详解】∴1221343nm m-=⎧⎨-=-⎩，解得，73mn=⎧⎨=⎩，∴7321.mn=⨯=故答案为21.19．②③【分析】根据最简二次根式的被开方数不含分母；被开方数不含能开得尽方的因数或因式，可得答案．【详解】②③是最简二次根式，故答案为②③．【点睛】本题考查最简二次根式的定义，解析：②③【分析】根据最简二次根式的被开方数不含分母；被开方数不含能开得尽方的因数或因式，可得答案．【详解】是最简二次根式，故答案为②③．【点睛】本题考查最简二次根式的定义，最简二次根式必须满足两个条件：被开方数不含分母；被开方数不含能开得尽方的因数或因式．20．4a【解析】【分析】根据二次根式乘法法则进行计算即可得.【详解】===4a，故答案为4a.【点睛】本题考查了二次根式的乘法，熟练掌握二次根式乘法法则是解题的关键.解析：4a【解析】【分析】根据二次根式乘法法则进行计算即可得.)0a≥===4a，故答案为4a.【点睛】本题考查了二次根式的乘法，熟练掌握二次根式乘法法则是解题的关键.三、解答题21．无22．无23．无24．无25．无26．无27．无28．无29．无30．无。

新高三月质量检测试题目数学共5页文档

济南外国语学校2019-2019学年度第一学期高三质量检测数学试题（2019.9）（时间120分钟，满分120分）第Ⅰ卷一．选择题（本题共12个小题，每题4分，共48分）1．全集U ＝{1,2,3,4,5,6},集合M ＝{2,3,5},N ＝{4,5},则∁U (M ∪N )= ( )A ．{1,3,5}B ．{2,4,6}C ．{1,5}D ．{1,6}2. 若0cos 02sin <>αα且，则α是 ( ) A.第二象限角 B.第三象限角C.第一或第三象限角D.第二或第三象限角3．已知54sin ),2,2(-=-∈αππα，则αtan 等于 ( )A.43-B.34- C.53- D.344. 下列函数中，在其定义域内既是奇函数又是增函数的是（）A.2+5()y x x R =-∈ B.3-()y x x x R =+∈ C. )(3R x x y ∈=D. )0,(1≠∈-=x R x xy 5. 已知奇函数)(x f 的图象是两条直线的一部分（如图所示），其定义域为]1,0()0,1[⋃-，则不等式1)()(->--x f x f 的解集是（） A.{}011|≠≤≤-x x x 且 B.⎭⎬⎫⎩⎨⎧≤<-<≤-10211|x x x 或 C.{}01|<≤-x x D.⎭⎬⎫⎩⎨⎧≤<<≤-12101|x x x 或6. 设 1.50.90.4812314,8,2y y y -⎛⎫=== ⎪⎝⎭，则（）A. 312y y y >>B. 213y y y >>C. 132y y y >>D. 123y y y >> 7.若等差数列{}n a 的前3项和3191S a ==且，则2a 等于 ( ) A 、3 B 、4 C 、5 D 、68.各项都为正项的等比数列{}n a 中，首项13a =，前三项和为21，则345a a a ++=（） A 、33 B 、72 C 、84 D 、1899 .已知平面上三点A 、B 、C 满足3AB =，4BC =，5CA =，则ABB C B CC A C AA B ⋅+⋅+⋅的值等于 ( )A.25B.24C.－25D.－24 10.已知b a b a k b a 3),2,3(),2,1(-+-==与垂直时k 值为 ( )A.17B.18C.19D.2011.已知)(x f '是函数)(x f 的导数，y=)(x f '的图象如图所示，则y=)(x f 的图象最有可能是下图中（）12.设x ，y 满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x ，若目标函数z=ax+by （a>0，b>0）的是最大值为12，则23a b +的最小值为( ). A.625 B. 38 C. 311 D. 4第Ⅱ卷二．填空题（本题共4个小题，每题4分，共16分）13.已知△ABC 的周长为9，且4:2:3sin :sin :sin =C B A ，则cos C ＝ . 14. 已知βα,⎪⎭⎫⎝⎛∈ππ,43，sin(βα+)=－,53 sin ,13124=⎪⎭⎫ ⎝⎛-πβ则cos ⎪⎭⎫⎝⎛+4πα= _______ . 15．设的最小值，求且yx y x y x 11120,0+=+>>． 16．等比数列｝｛n a 的公比为q ，前n 项的积为n T ，并且满足()01)1(,01,120102009201020091<-->-⋅>a a a a a ，给出下列结论①10<<q ；②120112009<⋅a a ；③2010T 是n T 中最大的；④使得1>n T 成立的最大的自然数n 是4018.其中正确结论的序号为（将你认为正确的全部填上）.三．解答题（本题共六个小题，共56分）17.（8分）已知(s i n ,c o s ),o s ,3c o s )a x x b x =-=，函数3()f x a b =⋅+（1）求)(x f 的最小正周期，并求其图象对称中心的坐标；（2）当02x π≤≤时，求函数f (x )的值域.18. （8分）二次函数)(x f 满足x x f x f 2)()1(=-+，且1)0(=f . （1）求)(x f 的解析式；（2）在区间[]1,1-上，)(x f y =图象恒在直线m x y +=2上方，试确定实数m 取值范围.19. （8分）已知函数21()21x x f x -=+，（1）判断函数()f x 的奇偶性；（2）求证：()f x 在R 上为增函数；20．（ 10分）学校要建一个面积为2392m 的长方形游泳池，并且在四周要修建出宽为2m 和4m 的小路（如图所示）。

2021年高一3月质量检测数学试题(实验班)含答案

实用文档2021年高一3月质量检测数学试题（实验班）含答案一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的) 1．下列说法正确的是( )A ．共线向量的方向相同B ．零向量是C ．长度相等的向量叫做相等向量D ．共线向量是在一条直线上的向量 2．已知cos(π2＋φ)＝32，且|φ|<π2，则tan φ＝( )A ．－33 B.33C ．－ 3 D.3 3．已知A 、B 、D 三点共线，存在点C ，满足CD →＝43CA →＋λCB→，则λ＝( )A.23 B ．13 C ．－13 D ．－234．已知函数在区间[，b ]上是增函数，且，，则的值为( )A ．0B ．22C ．－1D ．1 5.已知函数)(),2,0)(tan()(x f y x A x f =<>+=πφωφω的部分图像如图，则＝ ( )A ．2＋ 3 B. 3 C.33D ．2－ 3 6．下列函数中，最小正周期为π，且图象关于直线x ＝π3对称的是( ) A ．y ＝sin(2x －π6) B ．y ＝sin(x 2＋π6)C ． y ＝sin(2x ＋π6) D ．y ＝sin(2x －π3)实用文档7．如图所示，点P 在∠AOB 的对角区域MON 的阴影内，满足OP →＝xOA →＋yOB →，则实数对(x ，y )可以是( )A.⎝ ⎛⎭⎪⎫12，－13B.⎝ ⎛⎭⎪⎫14，12C.⎝ ⎛⎭⎪⎫－23，－13D.⎝ ⎛⎭⎪⎫－34，25 8．将函数f (x )＝2sin(ωx ＋φ)的图像向左平移π2个单位长度，若所得图像与原图像重合，则ω的值不可能为( )A ．4B ．6C ．8D ．12 9．设a ＝sin5π7，b ＝cos 2π7，c ＝tan 2π7，则a ，b ，c 的大小关系为（） A.b<a<c B.b<c<a C.c<b<a D.a<b<c 10．为得到函数y ＝cos 的图象，只需将函数y ＝sin x 的图象( )A ．向左平移π6个单位长度B ．向右平移π6个单位长度C ．向右平移5π6个单位长度D 向左平移5π6个单位长度11．已知某海滨浴场的海浪高度y (米)是时间t (0≤t ≤24，单位：小时)的函数，记作y ＝f (t )．下表是某日各时的浪高数据：t (小时) 0 3 6 9 12 15 18 21 24 y (米)1.51.00.51.01.510.50.991.5经长期观测，y ＝f (t )的曲线可近似地看成是函数y ＝A cos ωt ＋b 的图像．根据以上数据，你认为一日(持续24小时)内，该海滨浴场的海浪高度超过1.25米的时间为( )A ．10小时B ．8小时C ．6小时D ．4小时12．在△ABC 所在平面内有一点P ，如果PA →＋PB →＋PC →＝AB →，则△PAB 与△ABC的面积之比是( )A.13B.12C.23D.34二、填空题(本大题共4小题，每小题5分，共20分．)13、已知向量＝(2，3)，＝(－1，2)，若与共线，则的值为________．14．函数的定义域为_______.15．函数(x ∈[－π，0])的递减区间是________．16．给出下列命题：①函数y ＝tan x 的图像关于点（，0）(k ∈Z )对称；②函数f (x )＝sin |x |是最小正周期为π的周期函数；③函数y ＝cos 2x ＋sin x 最小值为－1；④设θ为第二象限的角，则tan实用文档θ2>cosθ2，且sinθ2>cosθ2.其中正确的命题序号是________．三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分) (1)计算3sin （－1 200°）tan 113π－cos 585°·tan(2)化简18．(本小题满分12分)设M ，N ，P 是△ABC 三边上的点，它们使BM →＝13BC →，CN →＝13CA →，AP →＝13AB →，若AB →＝，AC →＝，试用，将MN →，NP →，PM →表示出来．19．(本小题满分12分)已知A ，B ，C 三点坐标分别为(－1,0)，(3，－1)，(1,2)，AE →＝13AC →，BF →＝13BC →.(1)求点E ，F 及向量EF →的坐标；2)求证：EF//AB20．(本题满分12分）某同学用“五点法”画函数f (x )＝A sin(ωx ＋φ)(ω>0，|φ|<π2)在某一个周实用文档期内的图象时，列表并填入部分数据，如下表：ωx ＋φ 0π2 π3π2 2π xπ3 5π6 A sin(ωx ＋φ)5－5(1)请将上表数据补充完整，并直接写出函数f (x )的解析式；(2)将y ＝f (x )图象上所有点向左平移π6个单位长度，得到y ＝g (x )图象，求y ＝g (x )的图象离原点O 最近的对称中心．21.(本小题满分12分) 如右图所示，函数y ＝2cos(ωx ＋θ)(x ∈R ，ω>0,0≤θ≤π2)的图象与y 轴交于点(0，3)，且该函数的最小正周期为π.(1)求θ和ω的值； (2)已知点A (π2，0)，点P 是该函数图象上一点，点Q (x 0，y 0)是PA 的中点，当y 0＝32， x 0∈[π2，π]时，求x 0的值．22．(本小题满分12分)已知是函数图像上的任意两点，且角的终边经过点P (1，－3)，若时，的最小值为π3.(1)求函数的解析式； (2)求函数的递增区间；(3)当时，不等式恒成立，求实数的取值范围．实用文档高一年级第一阶段检测（A ）数学答案 xx.3一、选择题 BCCDB,ACBAD,BA 二、填空题13、-2 14、 15、 16、①③ 三、解答题 17、（1）原式＝3sin （－120°－3×360°）tan ⎝ ⎛⎭⎪⎫3π＋2π3－cos(225°＋360°)·tan ⎝⎛⎭⎪⎫－9π－14π ＝－3sin 120°tan 2π3＋cos 225°tan π4＝－3sin 60°－tanπ3＋(－cos 45°)·tan π4＝3·323＋⎝ ⎛⎭⎪⎫－22×1＝32－22.（2）18、解如图所示，MN →＝CN →－CM →＝－13AC →－23CB →＝－13AC →－23(AB →－AC →)＝13AC →－23AB →＝13b －23a . 同理可得NP →＝13a －23b ，PM →＝－MP →＝－(MN →＋NP →)＝13a ＋13b .实用文档19、解 (1)设O (0,0)，则OE →＝OA →＋AE →＝OA →＋13AC →＝(－1,0)＋13(2,2)＝⎝ ⎛⎭⎪⎫－13，23，OF →＝OB →＋BF →＝OB →＋13BC →＝(3，－1)＋13(－2,3)＝⎝⎛⎭⎪⎫73，0， ∴E ⎝ ⎛⎭⎪⎫－13，23，F ⎝ ⎛⎭⎪⎫73，0.∴EF →＝OF →－OE →＝⎝ ⎛⎭⎪⎫83，－23.(2)证明：∵AB →＝OB →－OA →＝(4，－1)， EF →＝⎝ ⎛⎭⎪⎫83，－23∴AB →＝32⎝ ⎛⎭⎪⎫83，－23＝32EF →.∴EF →∥AB →.因为EF 与AB 没有公共点 ∴EF//AB20、[解析] (1)根据表中已知数据，解得A ＝5，ω＝2，φ＝－π6，数据补全如下表：实用文档且函数表达式为f (x )＝5sin(2x －6)． (2)由(1)知f (x )＝5sin(2x －π6)，因此g (x )＝5sin[2(x ＋π6)－π6]＝5sin(2x ＋π6) 因为y ＝sin x 的对称中心为(k π，0)，k ∈Z . 令2x ＋π6＝k π，k ∈Z ，解得x ＝k π2－π12，k ∈Z . 即y ＝g (x )图象的对称中心为(k π2－π12，0)，k ∈Z ，其中离原点O 最近的对称中心为(－π12，0)． 21解：解 (1)将x ＝0，y ＝3代入函数y ＝2cos(ωx ＋θ)中，得cos θ＝32，因为0≤θ≤π2，所以θ＝π6. 由已知T ＝π，且ω>0，得ω＝2πT＝2ππ＝2.(2)因为点A (π2，0)，Q (x 0，y 0)是PA 的中点，y 0＝32，所以点P 的坐标为(2x 0－π2，3)．又因为点P 在y ＝2cos(2x ＋π6)的图象上，且π2≤x 0≤π，所以cos(4x 0－5π6)＝32，且7π6≤4x 0－5π6≤19π6，从而得4x 0－5π6＝11π6，或4x 0－5π6＝13π6，即x 0＝2π3，或x 0＝3π4.22解：(1)因为角φ的终边经过点P (1，－3)，实用文档所以tan φ＝－3，且－π2＜φ＜0，得φ＝－π3. 函数f (x )的最大值为2，又|f (x 1)－f (x 2)|＝4时，|x 1－x 2|的最小值为π3，得周期T ＝2π3，即2πω＝2π3，所以ω＝3.所以f (x )＝2sin ⎝⎛⎭⎪⎫3x －π3.(2)令－π2＋2k π ≤3x －π3≤π2＋2k π，k ∈Z ，得－π18＋2k π3≤x ≤5π18＋2k π3，k ∈Z . 所以函数f (x )的递增区间为⎣⎢⎡⎦⎥⎤－π18＋2k π3，5π18＋2k π3，k ∈Z . (3)当x ∈⎣⎢⎡⎦⎥⎤0，π6时，－π3≤3x －π3≤π6，得－3≤f (x )≤1，所以2＋f (x )＞0，则mf (x )＋2m ≥f (x )恒成立等价于m ≥f （x ）2＋f （x ）＝1－22＋f （x ）恒成立．因为2－3≤2＋f (x )≤3，所以1－22＋f （x ）最大值为13，所以实数m 的取值范围是⎣⎢⎡⎭⎪⎫13，＋∞.31293 7A3D 稽-23787 5CEB 峫3:38521 9679 陹28614 6FC6 濆37097 90E9 郩35396 8A44 詄S27890 6CF2 泲Zz349498885 袅32717 7FCD 翍。

2021年高一下学期3月质检数学试卷(重点班)含解析

2021年高一下学期3月质检数学试卷（重点班）含解析一.选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．方程x2+y2+2ax﹣by+c=0表示圆心为C（2，2），半径为2的圆，则a，b，c的值依次为（）A．2，4，4 B．﹣2，4，4 C．2，﹣4，4 D．2，﹣4，﹣42．直线3x﹣4y﹣4=0被圆（x﹣3）2+y2=9截得的弦长为（）A．B．4 C．D．23．两个圆C1：x2+y2+2x+2y﹣2=0与C2：x2+y2﹣4x﹣2y+1=0的位置关系是（）A．外切B．内切C．相交D．外离4．若直线（1+a）x+y+1=0与圆x2+y2﹣2x=0相切，则a的值为（）A．﹣1，1 B．﹣2，2 C．1 D．﹣15．以点（﹣3，4）为圆心，且与x轴相切的圆的方程是（）A．（x﹣3）2+（y+4）2=16 B．（x+3）2+（y﹣4）2=16 C．（x﹣3）2+（y+4）2=9 D．（x+3）2+（y﹣4）2=96．过点A （1，﹣1）、B （﹣1，1）且圆心在直线x+y﹣2=0上的圆的方程是（）A．（x﹣3）2+（y+1）2=4 B．（x+3）2+（y﹣1）2=4 C．（x﹣1）2+（y﹣1）2=4 D．（x+1）2+（y+1）2=47．空间直角坐标系中，点A（﹣3，4，0）和点B（2，﹣1，6）的距离是（）A． B． C．9 D．8．sin（﹣1560°）=（）A． B． C． D．9．如果cos（π+A）=﹣，那么sin（+A）的值是（）A． B． C． D．10．函数y=cos（﹣x）的最小正周期是（）A． B．πC．2πD．5π11．函数y=2sin（﹣2x），x∈[0，π]）为增函数的区间是（）A．[0，]B．[，] C．[，] D．[，π]12．要得到函数y=cos（2x+1）的图象，只要将函数y=cos2x的图象（）A．向左平移1个单位 B．向右平移1个单位C．向左平移个单位D．向右平移个单位二.填空题（本大题共4小题，每小题5分，满分20分，把答案填在题中横线上）13．圆x2+y2=1上的点到直线3x+4y﹣25=0距离的最小值为______．14．以点A（1，4）、B（3，﹣2）为直径的两个端点的圆的方程为______．15．若cosα=﹣，且α∈（π，），则tanα=______．16．函数f（x）=3sin（2x﹣）的图象为C，如下结论中正确的是______①图象C关于直线x=π对称；②图象C关于点（，0）对称；③函数即f（x）在区间（﹣，）内是增函数；④由y=3sin2x的图角向右平移个单位长度可以得到图象C．三.解答题（本大题共6小题，共70分．解答时应写出必要的文字说明.证明过程或演算步骤）17．已知cosα=﹣，求sinα，tanα18．已知函数（1）求函数的单调区间（2）求使函数取得最大值、最小值时的自变量x的值，并分别写出最大值、最小值．19．已知．（1）求sinx﹣cosx的值；（2）求的值．20．求过点M（3，1），且与圆（x﹣1）2+y2=4相切的直线l的方程．21．已知f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）图象的一部分如图所示：（1）求f（x）的解析式；（2）写出f（x）的单调区间．22．已知圆C：（x﹣1）2+（y﹣2）2=25，直线l：（2m+1）x+（m+1）y﹣7m﹣4=0（m∈R）（Ⅰ）证明：无论m取什么实数，l与圆恒交于两点；（Ⅱ）求直线被圆C截得的弦长最小时l的方程．xx学年山东省济宁市微山一中高一（下）3月质检数学试卷（重点班）参考答案与试题解析一.选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．方程x2+y2+2ax﹣by+c=0表示圆心为C（2，2），半径为2的圆，则a，b，c的值依次为（）A．2，4，4 B．﹣2，4，4 C．2，﹣4，4 D．2，﹣4，﹣4【考点】二元二次方程表示圆的条件．【分析】先根据方程求出用a、b和c表示的圆心坐标和圆的半径，再由题意代入对应的式子求出a、b和c的值．【解答】解：由x2+y2+2ax﹣by+c=0得，圆心坐标是（﹣a，），半径为r2=，因圆心为C（2，2），半径为2，解得a=﹣2，b=4，c=4，故选B．2．直线3x﹣4y﹣4=0被圆（x﹣3）2+y2=9截得的弦长为（）A． B．4 C． D．2【考点】直线与圆相交的性质．【分析】先根据圆的方程求得圆的圆心坐标和半径，进而利用点到直线的距离求得圆心到直线的距离，进而利用勾股定理求得被截的弦的一半，则弦长可求．【解答】解：根据圆的方程可得圆心为（3，0），半径为3则圆心到直线的距离为=1∴弦长为2×=4故选C3．两个圆C1：x2+y2+2x+2y﹣2=0与C2：x2+y2﹣4x﹣2y+1=0的位置关系是（）A．外切 B．内切 C．相交 D．外离【考点】圆与圆的位置关系及其判定．【分析】把两圆的方程化为标准形式，求出圆心和半径，求得|C1C2|的值，根据2﹣2＜|C1C2|＜2+2，得到两圆相交．【解答】解：圆C1：x2+y2+2x+2y﹣2=0 即（x+1）2+（y+1）2=4，表示以C1（﹣1，﹣1）为圆心，以2为半径的圆．C2：x2+y2﹣4x﹣2y+1=0 即（x﹣2）2+（y﹣1）2=4，表示以C2（2，1）为圆心，以2为半径的圆．两圆的圆心距|C1C2|==，2﹣2＜|C1C2|＜2+2，故两圆相交，故选C．4．若直线（1+a）x+y+1=0与圆x2+y2﹣2x=0相切，则a的值为（）A．﹣1，1 B．﹣2，2 C．1 D．﹣1【考点】圆的切线方程．【分析】把圆的方程化为标准形式，根据圆心到直线（1+a）x+y+1=0的距离等于半径，求得a的值．【解答】解：圆x2+y2﹣2x=0 即（x﹣1）2+y2 =1，表示以（1，0）为圆心、半径等于1的圆，再根据圆心到直线（1+a）x+y+1=0的距离d==1，求得a=﹣1，故选：D．5．以点（﹣3，4）为圆心，且与x轴相切的圆的方程是（）A．（x﹣3）2+（y+4）2=16 B．（x+3）2+（y﹣4）2=16 C．（x﹣3）2+（y+4）2=9 D．（x+3）2+（y﹣4）2=9【考点】直线与圆的位置关系．【分析】直接求出圆的半径，即可得到满足题意的圆的方程．【解答】解：以点（﹣3，4）为圆心，且与x轴相切的圆的半径为：4；所以所求圆的方程为：（x+3）2+（y﹣4）2=16．故选：B．6．过点A （1，﹣1）、B （﹣1，1）且圆心在直线x+y﹣2=0上的圆的方程是（）A．（x﹣3）2+（y+1）2=4 B．（x+3）2+（y﹣1）2=4 C．（x﹣1）2+（y﹣1）2=4 D．（x+1）2+（y+1）2=4【考点】圆的标准方程．【分析】先求AB的中垂线方程，它和直线x+y﹣2=0的交点是圆心坐标，再求半径，可得方程．【解答】解：圆心一定在AB的中垂线上，AB的中垂线方程是y=x，排除A，B选项；圆心在直线x+y﹣2=0上验证D选项，不成立．故选C．7．空间直角坐标系中，点A（﹣3，4，0）和点B（2，﹣1，6）的距离是（）A． B． C．9 D．【考点】空间两点间的距离公式．【分析】根据题目中所给的两个点的坐标，把点的坐标代入求两点之间的距离的公式，进行式子的加减和平方运算，得到结果．【解答】解：∵A（﹣3，4，0），B（2，﹣1，6）∴代入两点间的距离公式可得：|AB|==故选D．8．sin（﹣1560°）=（）A． B． C． D．【考点】运用诱导公式化简求值．【分析】把所求式子中的角﹣1560°变为﹣1800°+240°后，利用诱导公式及特殊角的三角函数值即可求出值．【解答】解：因为sin（﹣1560°）=sin（﹣1800°+240°）=sin=﹣sin60°=﹣．故选C．9．如果cos（π+A）=﹣，那么sin（+A）的值是（）A． B． C． D．【考点】运用诱导公式化简求值．【分析】根据题意结合诱导公式先对条件进行化简，然后对所求化简，进而可以得到答案．【解答】解：由题意可得：，根据诱导公式可得cosA=，所以=cosA=，故选B．10．函数y=cos（﹣x）的最小正周期是（）A． B．πC．2πD．5π【考点】三角函数的周期性及其求法．【分析】直接利用复合三角函数的周期性与求法，求得所给函数的最小正周期．【解答】解：函数y=cos（﹣x）=cos（x﹣）的最小正周期T==5π，故选D．11．函数y=2sin（﹣2x），x∈[0，π]）为增函数的区间是（）A．[0，]B．[，] C．[，] D．[，π]【考点】正弦函数的单调性；函数y=Asin（ωx+φ）的图象变换．【分析】先根据诱导公式进行化简，再由复合函数的单调性可知y=﹣2sin（2x﹣）的增区间可由y=2sin（2x﹣）的减区间得到，再由正弦函数的单调性可求出x的范围，最后结合函数的定义域可求得答案．【解答】解：由y=2sin（﹣2x）=﹣2sin（2x﹣）其增区间可由y=2sin（2x﹣）的减区间得到，即2kπ+≤2x﹣≤2kπ+，k∈Z∴kπ+≤x≤kπ+，k∈Z．令k=0，≤x≤，故选C．12．要得到函数y=cos（2x+1）的图象，只要将函数y=cos2x的图象（）A．向左平移1个单位 B．向右平移1个单位C．向左平移个单位D．向右平移个单位【考点】函数y=Asin（ωx+φ）的图象变换．【分析】化简函数y=cos（2x+1），然后直接利用平移原则，推出平移的单位与方向即可．【解答】解：因为函数y=cos（2x+1）=cos[2（x+）]，所以要得到函数y=cos（2x+1）的图象，只要将函数y=cos2x 的图象向左平移个单位．故选C．二.填空题（本大题共4小题，每小题5分，满分20分，把答案填在题中横线上）13．圆x2+y2=1上的点到直线3x+4y﹣25=0距离的最小值为4．【考点】直线与圆的位置关系．【分析】圆心（0，0）到直线3x+4y﹣25=0的距离d=，圆x2+y2=1上的点到直线3x+4y﹣25=0距离的最小值是AC=5﹣r，从而可求【解答】解：∵圆心（0，0）到直线3x+4y﹣25=0的距离d=∴圆x2+y2=1上的点到直线3x+4y﹣25=0距离的最小值是AC=5﹣r=5﹣1=4故答案为：414．以点A（1，4）、B（3，﹣2）为直径的两个端点的圆的方程为（x﹣2）2+（y﹣1）2=10．【考点】圆的标准方程．【分析】根据中点坐标公式求出线段AB的中点坐标即为圆心的坐标，然后根据两点间的距离公式求出圆心到A的距离即为圆的半径，根据求出的圆心坐标和圆的半径写出圆的标准方程即可．【解答】解：设线段AB的中点为O，所以O的坐标为（，），即（2，1），则所求圆的圆心坐标为（2，1）；由|AO|==，得到所求圆的半径为，所以所求圆的方程为：（x﹣2）2+（y﹣1）2=10．故答案为：（x﹣2）2+（y﹣1）2=1015．若cosα=﹣，且α∈（π，），则tanα=．【考点】任意角的三角函数的定义．【分析】根据α∈（π，），cosα=﹣，求出sinα，然后求出tanα，即可．【解答】解：因为α∈（π，），cosα=﹣，所以sinα=﹣，所以tanα==故答案为：16．函数f（x）=3sin（2x﹣）的图象为C，如下结论中正确的是①②③①图象C关于直线x=π对称；②图象C关于点（，0）对称；③函数即f（x）在区间（﹣，）内是增函数；④由y=3sin2x的图角向右平移个单位长度可以得到图象C．【考点】函数y=Asin（ωx+φ）的图象变换；正弦函数的单调性；正弦函数的对称性．【分析】把代入求值，只要是的奇数倍，则①正确，把横坐标代入求值，只要是π的倍数，则②对；同理由x的范围求出的范围，根据正弦函数的单调区间判断③是否对，因为向右平移故把x=x﹣代入进行化简，再比较判断④是否正确．【解答】解：①、把代入得，，故①正确；②、把x=代入得，，故②正确；③、当时，求得，故③正确；④、有条件得，，故④不正确．故答案为：①②③．三.解答题（本大题共6小题，共70分．解答时应写出必要的文字说明.证明过程或演算步骤）17．已知cosα=﹣，求sinα，tanα【考点】同角三角函数基本关系的运用．【分析】由已知中cosα=﹣，我们可得α为第II象限或第III象限的角，根据同角三角函数关系，分类讨论后，即可得到答案．【解答】解：∵cosα=﹣，∴α为第II或第III象限的角①当为第II象限的角时sinα==，tanα=﹣②为第III象限的角时sinα=﹣=﹣，tanα=．18．已知函数（1）求函数的单调区间（2）求使函数取得最大值、最小值时的自变量x的值，并分别写出最大值、最小值．【考点】正弦函数的单调性；三角函数的最值．【分析】（1）由条件利用正弦函数的单调性，求得函数的单调区间．（2）利用正弦函数的定义域和值域，求得函数取得最大值、最小值，以及此时的自变量x的值．【解答】解：（1）对于函数y=3sin（2x+），令2kπ﹣≤2x+≤2kπ+，求得kπ﹣≤x≤kπ+，可得函数的增区间为[kπ﹣，kπ+]，k∈Z；再结合x∈[0，π]，可得函数的增区间为[0，]、[，π]．令2kπ+≤2x+≤2kπ+，求得kπ+≤x≤kπ+，可得函数的减区间为[kπ+，kπ+]，k∈Z；再结合x∈[0，π]，可得函数的减区间为[，]．（2）∵函数y=3sin（2x+），x∈[0，π]，∴2x+∈[，]，令2x+=，求得x=，可得函数的最大值为3；令2x+=，求得x=，可得函数的最小值为﹣3．19．已知．（1）求sinx﹣cosx的值；（2）求的值．【考点】运用诱导公式化简求值；同角三角函数间的基本关系．【分析】（1）利用同角三角函数基本关系式直接求出sinx和cosx的值，进而求出结果．（2）先利用诱导公式化简所求的式子，将原式分子分母同除以cos2x，转化成tanx的表达式去解．【解答】解：∵sinx=﹣2cosx，又sin2x+cos2x=1，∴5cos2x=1，∴（1）（2）原式==…20．求过点M（3，1），且与圆（x﹣1）2+y2=4相切的直线l的方程．【考点】圆的切线方程．【分析】设出切线方程，求出圆的圆心与半径，利用圆心到直线的距离等于半径，求出k，写出切线方程即可．【解答】解：设切线方程为y﹣1=k（x﹣3），即kx﹣y﹣3k+1=0，∵圆心（1，0）到切线l的距离等于半径2，∴，解得k=﹣，∴切线方程为y﹣1=﹣（x﹣3），即3x+4y﹣13=0，当过点M的直线的斜率不存在时，其方程为x=3，圆心（1，0）到此直线的距离等于半径2，故直线x=3也适合题意．所以，所求的直线l的方程是3x+4y﹣13=0或x=3．21．已知f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）图象的一部分如图所示：（1）求f（x）的解析式；（2）写出f（x）的单调区间．【考点】由y=Asin（ωx+φ）的部分图象确定其解析式；正弦函数的单调性．【分析】（1）由图象直接求出A和T，可求ω，根据特殊点（，2）求出φ，即可求函数f（x）的解析式；（2）根据正弦函数的单调性直接求出函数的单调增区间和单调减区间即可．【解答】解：（1）由图可知A=2T=π∴ω=2当时f（x）取最大值∴φ=∴φ=符合条件∴f（x）=2sin（2x+）（2）f（x）的单调递增区间为f（x）的单调递减区间为22．已知圆C：（x﹣1）2+（y﹣2）2=25，直线l：（2m+1）x+（m+1）y﹣7m﹣4=0（m∈R）（Ⅰ）证明：无论m取什么实数，l与圆恒交于两点；（Ⅱ）求直线被圆C截得的弦长最小时l的方程．【考点】直线与圆相交的性质．【分析】（Ⅰ）求得所给的直线经过x+y﹣4=0 和2x+y﹣7=0的交点M（3，1），而点M在圆C：（x﹣1）2+（y﹣2）2=25的内部，从而得到l与圆恒交于两点．（Ⅱ）弦长最小时，MC和弦垂直，再利用点斜式求得弦所在的直线的方程．【解答】解：（Ⅰ）证明：直线l：（2m+1）x+（m+1）y﹣7m﹣4=0，即x+y﹣4+m（2x+y﹣7）=0，恒经过直线x+y﹣4=0 和2x+y﹣7=0的交点M（3，1），而点M到圆心C（1，2）的距离为MC==＜半径5，故点M在圆C：（x﹣1）2+（y﹣2）2=25的内部，故l与圆恒交于两点．（Ⅱ）弦长最小时，MC和弦垂直，故弦所在的直线l的斜率为==2，故直线l的方程为y﹣1=2（x﹣3），即2x﹣y﹣5=0．xx年10月6日33161 8189 膉?31736 7BF8 篸30035 7553 畓K28080 6DB0 涰g27187 6A33 樳29589 7395 玕27356 6ADC 櫜28164 6E04 渄39689 9B09 鬉G39604 9AB4 骴。

高三数学3月第一次质量普查调研考试试题理含解析试题

卜人入州八九几市潮王学校内蒙古2021届高三3月第一次质量普查调研考试数学〔理〕试题一、选择题〔本大题一一共12小题〕1.设全集为R，集合，，那么〔〕A. B.C. D.【答案】B【解析】【分析】解一元二次不等式求得求得集合B，再根据补集、交集的定义即可求出．【详解】解：，或者，，．应选：B．【点睛】此题考察了集合的化简与运算问题，是根底题目．2.假设复数为虚数单位在复平面内所对应的点在虚轴上，那么实数a为〔〕A. B.2 C. D.【答案】D【解析】【分析】利用复数代数形式的乘除运算化简，再由实部为求得值．【详解】解：在复平面内所对应的点在虚轴上，，即．应选：D．【点睛】此题考察复数代数形式的乘除运算，考察复数的代数表示法及其几何意义，是根底题．3.正方形ABCD的边长为2，以AB中点O为圆心，1为半径画圆，从正方形ABCD中任取一点P，那么点P 落在该圆中的概率为A. B. C. D.【答案】B【解析】【分析】先求出圆落在正方形中的面积为，正方形的面积为4，再由几何概型的概率公式可得点落在该圆中的概率为。

【详解】解：如下列图，因为，圆的半径为1所以，圆落在正方形中〔阴影局部〕的面积为，而正方形的面积为4，由几何概型的概率公式可得点落在该圆中的概率为。

【点睛】此题考察几何概型的概念与概率公式，几何概型有两大特征：1.无限性，2.等可能性，几何概型的概率公式为〔构成事件的区域长度〔面积、体积〕〕÷〔试验的全部结果所构成的区域长度〔面积、体积〕〕。

4.函数的大致图象为A. B.C. D.【答案】A【解析】【分析】判断函数的奇偶性和图象的对称性，利用特殊值进展排除即可．【详解】函数，那么函数是奇函数，图象关于原点对称，排除C，D，，排除B，应选：A．【点睛】此题主要考察函数图象的识别和判断，利用函数奇偶性和对称性的关系以及特殊值，结合排除法是解决此题的关键．5.在等比数列中，，且为和的等差中项，那么为A.9B.27C.54D.81【答案】B【解析】【分析】根据题意，设等比数列的公比为q，由为和的等差中项，可得，利用等比数列的通项公式代入化简为，解得q，又，即，，分析可得、q的值，可得数列的通项公式，将代入计算可得答案．【详解】解：根据题意，设等比数列的公比为q，假设为和的等差中项，那么有，变形可得，即，解得或者3；又，即，那么，，那么，那么有；应选：B．【点睛】此题考察等比数列的性质以及通项公式，关键是掌握等比数列通项公式的形式，属于根底题．6.政府为了调查民对A、B两效劳部门的效劳满意度情况，随机访问了50位民，根据这50位民对两部门的评分评分越高说明民的满意度越高绘制的茎叶图如图：那么以下说法正确的选项是A.这50位民对A、B两部门评分的方差，A部门的评分方差大B.估计民对A、B两部门的评分高于90的概率一样C.这50位民对A部门的评分其众数大于中位数D.该的民对B部门评分中位数的估计值是67【答案】D【解析】【分析】根据茎叶图的知识以及样本来估计总体，进展合理的评价，恰当的描绘即可．【详解】由茎叶图知，民对甲部门的评分的中位数高于乙部门的评分的中位数，而且由茎叶图可以大致看出对甲部门的评分HY差要小于乙部门的HY差，说明该民对甲部门的评价较高、评价较为一致，对乙部门的评价较低、评价差异较大，由茎叶图知，50位民对甲、乙部门的评分高于90的比率分别为，，故该的民对甲、乙两部门的评分高于90的概率得估计值分别为，，故A，B，C错误；由茎叶图知，50位民对甲部门的评分有小到大顺序，排在第25，26位的是75，75，故样本的中位数是75，所以该的民对甲部门的评分的中位数的估计值是75．50位民对乙部门的评分有小到大顺序，排在第25，26位的是66，68，故样本的中位数是，所以该的民对乙部门的评分的中位数的估计值是67，故D正确；应选：D．【点睛】此题主要考察了茎叶图的知识，以及中位数，用样本来估计总体的统计知识，属于根底题．7.函数〔其中，，〕的图象如下列图，为了得到的图象，只需将的图象上所有点A.向右平移个单位长度B.向左平移个单位长度C.向右平移个单位长度D.向左平移个单位长度【答案】A【解析】【分析】由函数的图象的顶点坐标求出A，由周期求出，由五点法作图求出的值，可得得解析式，再利用函数的图象变换规律，得出结论．【详解】解：根据函数〔其中，，〕的图象，可得，，．再利用五点法作图可得，求得，为了得到的图象，只需将的图象上所有点向右平移个单位长度，即可，应选：A．【点睛】此题主要考察由函数的局部图象求解析式，由函数的图象的顶点坐标求出A，由周期求出，由五点法作图求出的值，函数的图象变换规律，属于根底题．8.九章算术是我国古代的数学名著，表达了古代劳动人民的数学智慧，其中第六章“均输〞中，有一竹节容量问题，某老师根据这一问题的思想设计了如下列图的程序框图，假设输出m的值是67，那么输入a的值是A.7B.4C.5D.11【答案】C【解析】模拟程序框图的运行过程，如下：输入，，，；，；，；，；输出，完毕；令，解得.应选C.9.圆柱被一个平面截去一局部后与半径为1的半球组成一个几何体该几何体三视图中的正视图和俯视图如下列图假设该几何体的外表积为A. B. C. D.【答案】C【解析】【分析】该几何体是由半个圆柱对接半个球而形成的，利用三视图的数据求解几何体的外表积，然后推出结果．【详解】该几何体是由半个圆柱对接半个球而形成的，视图表示的是几何体程度放置时的情形，其外表积．应选：C．【点睛】此题考察三视图求解几何体的外表积，考察空间想象才能以及计算才能．10.甲：相交直线l、m都在平面内，并且都不在平面内；乙：直线l、m中至少有一条与平面相交；丙：平面与平面相交．当甲成立时A.乙是丙的充分而不必要条件B.乙是丙的必要而不充分条件C.乙是丙的充分且必要条件D.乙既不是丙的充分条件又不是丙的必要条件【答案】C【解析】【分析】判断乙是丙的什么条件，即看乙丙、丙乙是否成立当乙成立时，直线l、m中至少有一条与平面相交，那么平面与平面至少有一个公一共点，故相交相交反之丙成立时，假设l、m中至少有一条与平面相交，那么，由矛盾，故乙成立．【详解】解：当甲成立，即“相交直线l、m都在平面内，并且都不在平面内〞时，假设“l、m中至少有一条与平面相交〞，那么“平面与平面相交〞成立；假设“平面与平面相交〞，那么“l、m中至少有一条与平面相交〞也成立应选：C．【点睛】此题考察空间两条直线、两个平面的位置关系判断、充要条件的判断，考察逻辑推理才能．11.函数与的零点分别为，，且，那么，，的大小关系为A. B.C. D.【答案】B【解析】【分析】利用函数与方程的关系，分别转化为与的图象，和的图象，和的图象，利用数形结合研究，，的范围即可得到结论．【详解】解：由得，即，作出函数与的图象如图，黑色图象，由图象知两个图象交点的横坐标满足，由得，作出和的图象如图红色图象由图象知两个图象交点的横坐标满足，作出和，的图象如图蓝色图象由图象知两个图象交点的横坐标满足，综上，，的大小关系为，应选：B．【点睛】此题主要考察函数与方程的应用，根据条件转化为两个函数图象交点问题，利用数形结合求出对应究，，的范围是解决此题的关键．12.双曲线的上、下焦点分别为，，过且倾斜角为锐角的直线1与圆相切，与双曲线的上支交于点假设线段的垂直平分线过点，那么该双曲线的渐近线的方程为A. B.C. D.【答案】B【解析】【分析】先设与圆相切于点E，利用，及直线与圆相切，可得几何量之间的关系，从而可求双曲线的渐近线方程．【详解】解：设与圆相切于点E，因为，所以为等腰三角形，N为的中点，所以，又因为在直角中，，所以又，由可得，即为，即，，那么双曲线的渐近线方程为，即为应选：B．【点睛】此题考察直线与圆相切，考察双曲线的定义，考察双曲线的几何性质，注意运用平面几何的性质，考察运算才能，属于中档题．二、填空题〔本大题一一共4小题〕13.，是单位向量，且与夹角为，那么等于______．【答案】3【解析】14.在的展开式中，的系数为______．【答案】80【解析】【分析】利用二项式展开式的通项公式，化简后求得的值，进而求得结论．【详解】解：的展开式中，通项公式，令，解得．的系数．故答案为：80．【点睛】此题考察了二项式定理的通项公式，考察了推理才能与计算才能，属于根底题．15.设抛物线的焦点为F，准线为L，P为抛物线上一点，，A为垂足假设直线AF的斜率为，那么以PF为直径的圆的HY方程为______．【答案】【解析】【分析】利用抛物线的定义，，设F在l上的射影为，依题意，可求得，，从而可求得点P的纵坐标，代入抛物线方程可求得点P的横坐标，从而可求得．进而求得圆的方程【详解】解：抛物线的焦点为F，准线为l，P为抛物线上一点，，，准线l的方程为：；设F在l上的射影为，又，依题意，，，，轴，点P的纵坐标为，设点P的横坐标为，，，．故以PF为直径的圆的圆心为，半径为2．以PF为直径的圆的HY方程为.故答案为：．【点睛】此题考察抛物线的简单性质，考察转化思想，考察解三角形的才能，属于中档题．16.等差数列的公差为2，前n项和为，且，，成等比数列令，那么数列的前100的项和为______．【答案】【解析】【分析】首项利用条件求出数列的通项公式，进一步利用裂项相消法求出数列的和．【详解】解：设等差数列的首项为，公差为2，前n项和为，且，，成等比数列．那么：，解得：，所以：，所以：，所以：，，故答案为：【点睛】此题考察的知识要点：数列的通项公式的求法及应用，裂项相消法在数列求和中的应用，主要考察学生的运算才能和转化才能，属于根底题型．三、解答题〔本大题一一共7小题〕17.如图，D是直角斜边BC上一点，．Ⅰ假设，求的大小；Ⅱ假设，且，求AD的长．【答案】Ⅰ，或者Ⅱ【解析】【分析】Ⅰ由可求，在中，由正弦定理可得，即可解得．Ⅱ由在中，由勾股定理可得，，，令，由余弦定理，即可解得AD的值．【详解】Ⅰ，，，在中，由正弦定理可得：，，，或者，又，Ⅱ，，在中，由勾股定理可得：，可得：，，，，令，由余弦定理：在中，，在中，，可得：，解得：，可得：【点睛】此题主要考察了正弦定理，余弦定理，勾股定理在解三角形中的应用，考察了计算才能和转化思想，属于中档题．18.如图，平面四边形ABCD，，，，将沿BD翻折到与面BCD垂直的位置．Ⅰ证明：面ABC；Ⅱ假设E为AD中点，求二面角的大小．【答案】〔1〕见证明；〔2〕【解析】【分析】推导出面BCD，从而，再求出，，，由此能证明平面ABC．以B为原点，在平面BCD中，过B作BD的垂线为x轴，以BD为y轴，以BA为z轴，建立空间直角坐标系，利用向量法能求出二面角的大小．【详解】证明：平面四边形ABCD，，，，面面BCD，，面平面，面BCD，，又，，，，，，，平面ABC．解：面BCD，如图以B为原点，在平面BCD中，过B作BD的垂线为x轴，以BD为y轴，以BA为z轴，建立空间直角坐标系，那么0，，0，，，，是AD的中点，，，，令平面BCE的一个法向量为y，，那么，取，得，面ABC，平面ABC的一个法向量为，，，二面角的大小为．【点睛】此题考察线面垂直的证明，考察二面角的求法，考察空间中线线、线面、面面间的位置关系等根底知识，考察空间想象才能、运算求解才能，考察化归与转化思想、数形结合思想，是中档题．19.某超方案按月订购一种饮料，每天进货量一样，进货本钱每瓶3元，售价每瓶5元，每天未售出的饮料最后打4折当天全部处理完根据往年销售经历，每天需求量与当天最高气温单位：有关假设最高气温不低于25，需求量为500瓶；假设最高气温位于区间，需求量为300瓶；假设最高气温低于20，需求量为100瓶为了确定六月份的订购方案，统计了前三年六月份各天的最高气温数据，得到下面的频数分布表：最高气温天数 2 16 36 25 7 4以最高气温位于各区间的频率代替最高气温位于该区间的概率．Ⅰ求六月份这种饮料一天的需求量单位：瓶的分布列，并求出期望EX；Ⅱ设六月份一天销售这种饮料的利润为单位：元，且六月份这种饮料一天的进货量为单位：瓶，请判断Y的数学期望是否在时获得最大值？【答案】〔1〕见解析〔2〕见解析【解析】【分析】Ⅰ由题意知X的可能取值为100，300，500，分别求出相应的概率，由此能求出X的分布列和．Ⅱ六月份这种饮料的进货量n，当时，求出，故当时，Y的数学期望到达最大值，最大值为520元；当时，，故当时，Y的数学期望到达最大值，最大值为480元由此能求出时，y的数学期望到达最大值，最大值为520元．【详解】解：Ⅰ由题意知X的可能取值为100，300，500，，，，的分布列为：X 100 300 500P．Ⅱ由题意知六月份这种饮料的进货量n满足，当时，假设最高气温不低于25，那么，假设最高气温位于，那么，假设最高气温低于20，那么，，此时，时，Y的数学期望到达最大值，最大值为520元，当时，假设最高气温不低于25，那么，假设最高气温位于，那么，假设最高气温低于20，那么，，此时，时，Y的数学期望到达最大值，最大值为480元，时，Y的数学期望值为：不是最大值，时，y的数学期望到达最大值，最大值为520元．【点睛】此题考察离散型随机变量的分布列、数学期望的求法，考察互斥事件概率加法公式等根底知识，考察运算求解才能，是中档题．20.椭圆C：过点，其左右焦点分别为，，三角形的面积为．Ⅰ求椭圆C的方程；ⅡA，B是椭圆C上的两个动点且不与坐标原点O一共线，假设的角平分线总垂直于x轴，求证：直线AB与两坐标轴围成的三角形一定是等腰三角形．【答案】ⅠⅡ见解析【解析】【分析】Ⅰ由题意可得，解得，，那么椭圆方程可求；Ⅱ设直线PA的方程为，联立直线方程和椭圆方程，求得A的横坐标，同理求得B的横坐标，进一步求得A、B的纵坐标的差，代入斜率公式得答案．【详解】Ⅰ由题意可得，解得，，故椭圆C的方程为，证明Ⅱ：设直线AP的斜率为k，那么直线BP的斜率为，设，，直线PA的方程为，即联立，得．，即设直线PB的方程为，同理求得，直线AB的斜率，易知l与在两坐标轴的截距绝对值相等且都不为0，直线AB与两坐标轴围成的三角形一定是等腰三角形.【点睛】此题考察椭圆HY方程的求法，考察了直线与椭圆位置关系的应用，考察计算才能，属中档题．21.函数，．Ⅰ当时，讨论函数的单调性；Ⅱ假设函数有两个极值点，，且，求证．【答案】〔1〕函数在上单调递减；在和上单调递增．〔2〕见证明【解析】【分析】首先求得导函数，然后分类讨论确定函数的单调性即可；首先确定，的范围，化简的表达式为．构造函数，利用导数求得函数的最小值，并由极限证得，由此证得不等式成立.【详解】解：，，令，，，令那么，当，即时，令那么；令那么．此时函数在上单调递减；在上单调递增．当，即时，令，那么；令那么，此时函数在上单调递减；在和上单调递增．由知，假设有两个极值点，那么且，又，是的两个根，那么，，令，那么，令，那么，令，那么，所以在上单调递减；在上单调递增．，，，得证．【点睛】此题主要考察导函数研究函数的单调性，导函数研究函数的极值，利用导数证明不等式的方法等知识，属于中等题．22.在直角坐标系xoy中，以坐标原点为极点，x轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为，曲线的极坐标方程为，不与坐标轴重合的直线1的极坐标方程为，设1与曲线，异于极点的交点分别为A，B．Ⅰ当时，求；Ⅱ求AB中点轨迹的直角坐标方程．【答案】ⅠⅡ，去掉，【解析】【分析】Ⅰ用直线l的极坐标方程分别代入，的极坐标方程，再根据极径的几何意义可得；Ⅱ先求出AB的中点的轨迹的极坐标方程，再化成直角坐标方程．【详解】Ⅰ当时，联立得；同理得，由极径的几何意义有．Ⅱ由令，，，，，P为AB的中点，，即，所以P点的轨迹的直角坐标方程为，因为直线l不与坐标轴重合，所以需去掉，【点睛】此题考察了简单曲线的极坐标方程，考察轨迹方程的求法，意在考察学生对这些知识的理解掌握程度和分析推理才能.23.函数．Ⅰ在给出的直角坐标系中画出函数的图象；Ⅱ假设关于x的不等式的解集包含，求m的取值范围．【答案】ⅠⅡ【解析】【分析】，画图即可；关于x的不等式的解集包含，可得在上恒成立，解得即可.【详解】，其图象为关于x的不等式的解集包含，即在上恒成立，，即，，上恒成立，，故．【点睛】此题考察绝对值函数的图像的画法，考察绝对值不等式问题，考察分类讨论思想，转化思想，数形结合思想，意在考察学生对这些知识的理解掌握程度和分析推理才能.。

人教版八年级数学上学期3月份质量检测测试卷含答案

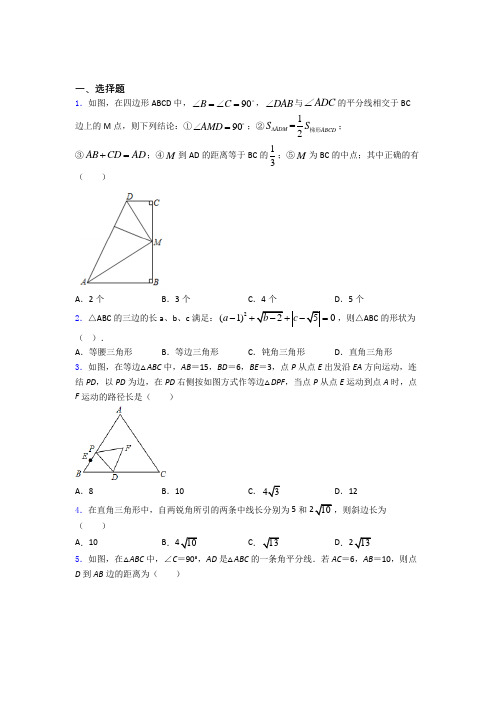
一、选择题1．如图，在四边形ABCD 中，90B C ∠=∠=，DAB ∠与ADC ∠的平分线相交于BC 边上的M 点，则下列结论：①90AMD ∠=；②1=2ADM ABCD S S ∆梯形；③AB CD AD +=；④M 到AD 的距离等于BC 的13；⑤M 为BC 的中点；其中正确的有（）A ．2个B ．3个C ．4个D ．5个 2．△ABC 的三边的长a 、b 、c 满足：2(1)250a b c -+-+-=，则△ABC 的形状为（）．A ．等腰三角形B ．等边三角形C ．钝角三角形D ．直角三角形3．如图，在等边△ABC 中，AB ＝15，BD ＝6，BE ＝3，点P 从点E 出发沿EA 方向运动，连结PD ，以PD 为边，在PD 右侧按如图方式作等边△DPF ，当点P 从点E 运动到点A 时，点F 运动的路径长是（）A ．8B ．10C ．43D ．124．在直角三角形中，自两锐角所引的两条中线长分别为5和10，则斜边长为（）A ．10B ．10C 13D ．135．如图，在△ABC 中，∠C ＝90°，AD 是△ABC 的一条角平分线．若AC ＝6，AB ＝10，则点D 到AB 边的距离为（）A ．2B ．2.5C ．3D ．46．如图，小红想用一条彩带缠绕易拉罐，正好从A 点绕到正上方B 点共四圈，已知易拉罐底面周长是12 cm ，高是20 cm ，那么所需彩带最短的是( )A ．13 cmB ．4cmC ．4cmD ．52 cm7．下列说法不能得到直角三角形的（）A ．三个角度之比为 1：2：3 的三角形B ．三个边长之比为 3：4：5 的三角形C ．三个边长之比为 8：16：17 的三角形D ．三个角度之比为 1：1：2 的三角形8．如图，透明的圆柱形玻璃容器（容器厚度忽略不计）的高为16cm ，在容器内壁离容器底部4cm 的点B 处有一滴蜂蜜，此时一只蚂蚁正好在容器外壁，位于离容器上沿4cm 的点A 处，若蚂蚁吃到蜂蜜需爬行的最短路径为20cm ，则该圆柱底面周长为（）A ．12cmB ．14cmC ．20cmD ．24cm 9．在下列以线段a 、b 、c 的长为边，能构成直角三角形的是（）A ．a =3，b =4，c =6B ．a =5，b =6，c =7C ．a =6，b =8，c =9D ．a =7，b =24，c =25 10．将一根 24cm 的筷子，置于底面直径为 15cm ，高 8cm 的装满水的无盖圆柱形水杯中，设筷子浸没在杯子里面的长度为 hcm ，则 h 的取值范围是（）A ．h≤15cmB ．h≥8cmC ．8cm≤h≤17cmD ．7cm≤h≤16cm二、填空题11．如图，点E 在DBC △边DB 上，点A 在DBC △内部，∠DAE ＝∠BAC ＝90°，AD ＝AE ，AB ＝AC ，给出下列结论，其中正确的是_____（填序号）①BD ＝CE ；②∠DCB ＝∠ABD ＝45°；③BD ⊥CE ；④BE 2＝2（AD 2+AB 2）．12．如图，在Rt ABC 中，90ACB ∠=︒，4AC =，2BC =，以AB 为边向外作等腰直角三角形ABD ，则CD 的长可以是__________．13．已知，如图：在平面直角坐标系中，O 为坐标原点，四边形OABC 是矩形，点A 、C 的坐标分别为A （10，0）、C （0，4），点D 是OA 的中点，点P 在BC 边上运动，当△ODP 是腰长为5的等腰三角形时，点P 的坐标为_____．14．如图，有一个圆柱，它的高等于12厘米，底面半径等于3厘米．在圆柱的下底面A 点有一只蚂蚁，它想吃到上底面上与A 点相对的C 点处的食物，需要爬行的最短路程是___________________（π的值取3）．15．在ABC ∆中，90BAC ∠=︒，以BC 为斜边作等腰直角BCD ∆，连接DA ，若22AB =，42AC =，则DA 的长为______．16．如图，在ABC △中8,4,AB AC BC AD BC ===⊥于点D ，点P 是线段AD 上一个动点，过点P 作PE AB ⊥于点E ，连接PB ，则PB PE +的最小值为________.17．如图，在四边形ABCD 中，AC 平分∠BAD ，BC=CD=10，AC=17，AD=9，则AB=_____.18．如图，E为等腰直角△ABC的边AB上的一点，要使AE＝3，BE＝1，P为AC上的动点，则PB＋PE的最小值为____________．19．四个全等的直角三角形按图示方式围成正方行ABCD，过各较长直角边的中点作垂线，围成面积为4的小正方形EFGH,已知AM为Rt△ABM的较长直角边，AM＝7EF，则正方形ABCD的面积为_______.20．如图，在等腰△ABC中，AB＝AC，底边BC上的高AD＝6cm，腰AC上的高BE＝4m，则△ABC的面积为_____cm2．三、解答题21．如图，△ABC和△ADE都是等腰三角形，其中AB＝AC，AD＝AE，且∠BAC＝∠DAE．（1）如图①，连接BE、CD，求证：BE＝CD；（2）如图②，连接BE、CD，若∠BAC＝∠DAE＝60°，CD⊥AE，AD＝3，CD＝4，求BD的长；（3）如图③，若∠BAC ＝∠DAE ＝90°，且C 点恰好落在DE 上，试探究CD 2、CE 2和BC 2之间的数量关系，并加以说明．22．我们规定，三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差．如图1，在ABC ∆中，AO 是BC 边上的中线，AB 与AC 的“广益值”就等于22AO BO -的值，可记为22AB AC OA BO ∇=-（1）在ABC ∆中，若90ACB ∠=︒，81AB AC ∇=，求AC 的值．（2）如图2，在ABC ∆中，12AB AC ==，120BAC ∠=︒，求AB AC ∇，BA BC ∇的值．（3）如图3，在ABC ∆中，AO 是BC 边上的中线，24ABC S ∆=，8AC =，64AB AC ∇=-，求BC 和AB 的长．23．如图，将一长方形纸片OABC 放在平面直角坐标系中，(0,0)O ，(6,0)A ，(0,3)C ，动点F 从点O 出发以每秒1个单位长度的速度沿OC 向终点C 运动，运动23秒时，动点E 从点A 出发以相同的速度沿AO 向终点O 运动，当点E 、F 其中一点到达终点时，另一点也停止运动．设点E 的运动时间为t :（秒）（1）OE =_________，OF =___________（用含t 的代数式表示）（2）当1t =时，将OEF ∆沿EF 翻折，点O 恰好落在CB 边上的点D 处，求点D 的坐标及直线DE 的解析式；（3）在（2）的条件下，点M 是射线DB 上的任意一点，过点M 作直线DE 的平行线，与x 轴交于N 点，设直线MN 的解析式为y kx b =+，当点M 与点B 不重合时，设MBN ∆的面积为S ，求S 与b 之间的函数关系式．24．如果一个三角形的两条边的和是第三边的两倍，则称这个三角形是“优三角形”，这两条边的比称为“优比”（若这两边不等，则优比为较大边与较小边的比），记为k . （1）命题：“等边三角形为优三角形，其优比为1”，是真命题还是假命题？（2）已知ABC 为优三角形，AB c =，AC b =，BC a =，①如图1，若90ACB ∠=︒，b a ≥，6b =，求a 的值.②如图2，若c b a ≥≥，求优比k 的取值范围.（3）已知ABC 是优三角形，且120ABC ∠=︒，4BC =，求ABC 的面积.25．如图1，在平面直角坐标系中，直线AB 经过点C （a ，a ），且交x 轴于点A （m ，0），交y 轴于点B （0，n ），且m ，n 满足6m -＋（n ﹣12）2＝0．（1）求直线AB 的解析式及C 点坐标；（2）过点C 作CD ⊥AB 交x 轴于点D ，请在图1中画出图形，并求D 点的坐标；（3）如图2，点E （0，﹣2），点P 为射线AB 上一点，且∠CEP ＝45°，求点P 的坐标．26．如图，在平面直角坐标系中，点O 是坐标原点，ABC ∆，ADE ∆，AFO ∆均为等边三角形，A 在y 轴正半轴上，点0()6,B -，点(6,0)C ，点D 在ABC ∆内部，点E 在ABC ∆的外部，32=AD 30DOE ∠=︒，OF 与AB 交于点G ，连接DF ，DG ，DO ，OE .（1）求点A 的坐标；（2）判断DF 与OE 的数量关系，并说明理由；（3）直接写出ADG ∆的周长.27．（知识背景）据我国古代《周髀算经》记载，公元前1120年商高对周公说，将一根直尺折成一个直角，两端连接得到一个直角三角形，如果勾是3，股是4，那么弦就等于5，后人概括为“勾三、股四、弦五”．像3、4、5这样为三边长能构成直角三角形的三个正整数，称为勾股数．（应用举例）观察3，4，5；5，12，13；7，24，25；…可以发现这些勾股数的勾都是奇数，且从3起就没有间断过，并且勾为3时，股14(91)2=-，弦15(91)2=+；勾为5时，股112(251)2=-，弦113(251)2=+；请仿照上面两组样例，用发现的规律填空：（1）如果勾为7，则股24＝弦25＝（2）如果勾用n （3n ≥，且n 为奇数）表示时，请用含有n 的式子表示股和弦，则股＝，弦＝．（解决问题）观察4，3，5；6，8，10；8，15，17；…根据应用举例获得的经验进行填空：（3）如果,,a b c 是符合同样规律的一组勾股数，2a m =（m 表示大于1的整数），则b = ，c = ，这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式．（4）请你利用柏拉图公式，补全下面两组勾股数（数据从小到大排列）第一组：、24、：第二组：、、37．28．如图1，在正方形ABCD 中，点E ，F 分别是AC ，BC 上的点，且满足DE ⊥EF ，垂足为点E ，连接DF ．（1）求∠EDF= （填度数）；（2）延长DE 交AB 于点G ，连接FG ，如图2，猜想AG ，GF ，FC 三者的数量关系，并给出证明；（3）①若AB=6，G 是AB 的中点，求△BFG 的面积；②设AG=a ，CF=b ，△BFG 的面积记为S ，试确定S 与a ，b 的关系，并说明理由．29．阅读下列材料，并解答其后的问题：我国古代南宋数学家秦九韶在其所著书《数学九章》中，利用“三斜求积术”十分巧妙的解决了已知三角形三边求其面积的问题，这与西方著名的“海伦公式”是完全等价的．我们也称这个公式为“海伦•秦九韶公式”，该公式是：设△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，△ABC的面积为S＝()()()()4a b c a b c a c b b c a+++-+-+-．（1）（举例应用）已知△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，且a＝4，b ＝5，c＝7，则△ABC的面积为；（2）（实际应用）有一块四边形的草地如图所示，现测得AB＝（26+42）m，BC＝5m，CD＝7m，AD＝46m，∠A＝60°，求该块草地的面积．30．在平面直角坐标系中，点A（0，4），B（m，0）在坐标轴上，点C，O关于直线AB 对称，点D在线段AB上．（1）如图1，若m＝8，求AB的长；（2）如图2，若m＝4，连接OD，在y轴上取一点E，使OD＝DE，求证：CE＝2DE；（3）如图3，若m＝43，在射线AO上裁取AF，使AF＝BD，当CD+CF的值最小时，请在图中画出点D的位置，并直接写出这个最小值．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】过M 作ME AD ⊥于E ，得出12MDE CDA ∠=∠，12MAD BAD ∠=∠，求出1()902MDA MAD CDA BAD ∠+∠=∠+∠=︒，根据三角形内角和定理求出AMD ∠，即可判断①；根据角平分线性质求出MC ME =，ME MB =，即可判断④和⑤；由勾股定理求出DC DE =，AB AE =，即可判断③；根据SSS 证DEM DCM ∆≅∆，推出DEM DCM S S =三角形三角形，同理得出AEM ABM S S =三角形三角形，即可判断②．【详解】解：过M 作ME AD ⊥于E ，DAB ∠与ADC ∠的平分线相交于BC 边上的M 点，12MDE CDA ∴∠=∠，12MAD BAD ∠=∠， //DC AB ，180CDA BAD ∴∠+∠=︒，11()1809022MDA MAD CDA BAD ∴∠+∠=∠+∠=⨯︒=︒， 1809090AMD ∴∠=︒-︒=︒，故①正确； DM 平分CDE ∠，90()C MC DC ∠=︒⊥，ME DA ⊥，MC ME ，同理ME MB =，12MC MB ME BC ∴===，故⑤正确； M ∴到AD 的距离等于BC 的一半，故④错误；由勾股定理得：222DC MD MC =-，222DE MD ME =-，又ME MC =，MD MD =，DC DE ∴=，同理AB AE =， AD AE DE AB DC ∴=+=+，故③正确；在DEM ∆和DCM ∆中DE DC DM DM ME MC =⎧⎪=⎨⎪=⎩， ()DEM DCM SSS ∴∆≅∆，DEM DCM S S ∴=三角形三角形同理AEM ABM S S =三角形三角形，12AMD ABCD S S ∴=三角形梯形，故②正确；故选：C ．【点睛】本题考查了角平分线性质，垂直定义，直角梯形，勾股定理，全等三角形的性质和判定等知识点的应用，主要考查学生运用定理进行推理的能力．2．D解析：D【分析】由等式可分别得到关于a 、b 、c 的等式，从而分别计算得到a 、b 、c 的值，再由222+=a b c 的关系，可推导得到△ABC 为直角三角形．【详解】 ∵2(1)250a b c --= 又∵()2102050a b c ⎧-≥-≥-≥⎪⎩∴()21=02=05a b c ⎧-⎪⎪-⎨⎪⎪⎩∴125a b c ⎧=⎪=⎨⎪=⎩ ∴222+=a b c∴△ABC 为直角三角形故选：D ．【点睛】本题考察了平方、二次根式、绝对值和勾股定理逆定理的知识；求解的关键是熟练掌握二次根式、绝对值和勾股定理逆定理，从而完成求解．3．D解析：D【分析】首先利用等边三角形的性质和含30°直角三角形的运用，判定△DPE≌△FDH，△DF2Q≌△ADE，然后利用全等三角形的性质，得出点F运动的路径长.【详解】∵△ABC为等边三角形，∴∠B=60°，过D点作DE′⊥AB，过点F作FH⊥BC于H，如图所示：则BE′=12BD=3，∴点E′与点E重合，∴∠BDE=30°，DE3BE3，∵△DPF为等边三角形，∴∠PDF=60°，DP=DF，∴∠EDP+∠HDF=90°∵∠HDF+∠DFH=90°，∴∠EDP=∠DFH，在△DPE和△FDH中，90PED DHFEDP DFHDP FD︒⎧∠=∠=⎪∠=∠⎨⎪=⎩，∴△DPE≌△FDH（AAS），∴FH=DE3∴点P从点E运动到点A时，点F运动的路径为一条线段，此线段到BC的距离为3当点P在E点时，作等边三角形DEF1，∠BDF1=30°+60°=90°，则DF1⊥BC，当点P在A点时，作等边三角形DAF2，作F2Q⊥BC于Q，则四边形DF1F2Q是矩形，∵∠BDE=30°，∠ADF2=60°，∴∠ADE+∠F2DQ=180°﹣30°﹣60°=90°，∵∠ADE+∠DAE=90°，∴∠F2DQ=∠DAE，在△DF2Q和△ADE中，222F QD DEA90F DQ DAEDF AD︒⎧∠=∠=⎪∠=∠⎨⎪=⎩，∴△DF2Q≌△ADE（AAS），∴DQ=AE=AB﹣BE=15﹣3=12，∴F1F2=DQ=12，∴当点P从点E运动到点A时，点F运动的路径长为12，故选：D．【点睛】此题主要考查等边三角形的性质以及全等三角形的判定与性质，解题关键是作好辅助线. 4．D解析：D【分析】根据已知设AC＝x，BC＝y，在Rt△ACD和Rt△BCE中，根据勾股定理分别列等式，从而求得AC，BC的长，最后根据勾股定理即可求得AB的长．【详解】如图，在△ABC中，∠C＝90°，AD、BE为△ABC的两条中线，且AD＝210，BE＝5，求AB的长．设AC＝x，BC＝y，根据勾股定理得：在Rt△ACD中，x2+（12y）2＝（210）2，在Rt△BCE中，（12x）2+y2＝52，解之得，x＝6，y＝4，∴在Rt△ABC中，2264213AB=+=，故选：D．【点睛】此题考查勾股定理的运用，在直角三角形中，已知两条边长时，可利用勾股定理求第三条边的长度.5．C解析：C【分析】作DE⊥AB于E，由勾股定理计算出可求BC=8，再利用角平分线的性质得到DE=DC，设DE=DC=x，利用等等面积法列方程、解方程即可解答.【详解】解：作DE⊥AB于E，如图，在Rt△ABC中，BC＝22106＝8，∵AD是△ABC的一条角平分线，DC⊥AC，DE⊥AB，∴DE＝DC，设DE＝DC＝x，S△ABD＝12DE•AB＝12AC•BD，即10x＝6（8﹣x），解得x＝3，即点D到AB边的距离为3．故答案为C．【点睛】本题考查了角平分线的性质和勾股定理的相关知识，理解角的平分线上的点到角的两边的距离相等是解答本题的关键..6．D解析：D【解析】【分析】本题就是把圆柱的侧面展开成矩形，“化曲面为平面”，用勾股定理解决..要求彩带的长，需将圆柱的侧面展开，进而根据“两点之间线段最短”得出结果，在求线段长时，借助于勾股定理．【详解】如图，由图可知，彩带从易拉罐底端的A处绕易拉罐4圈后到达顶端的B处，将易拉罐表面切开展开呈长方形，则螺旋线长为四个长方形并排后的长方形的对角线长，设彩带最短长度为xcm，∵∵易拉罐底面周长是12cm，高是20cm，∴x2=(12×4)2+202∴x2=(12×4)2+202，所以彩带最短是52cm．故选D ．【点睛】本题考查了平面展开−−最短路径问题，圆柱的侧面展开图是一个矩形，此矩形的长等于圆柱底面周长，高等于圆柱的高，7．C解析：C【分析】三角形内角和180°，根据比例判断A 、D 选项中是否有90°的角，根据勾股定理的逆定理判断B 、C 选项中边长是否符合直角三角形的关系.【详解】A 中，三个角之比为1:2:3，则这三个角分别为：30°、60°、90°，是直角三角形； D 中，三个角之比为1:1:2，则这三个角分别为：45°、45°、90°，是直角三角形；B 中，三边之比为3:4:5，设这三条边长为：3x 、4x 、5x ，满足：()()()222345x x x +=，是直角三角形；C 中，三边之比为8:16:17，设这三条边长为：8x 、16x 、17x ，()()()22281617x x x +≠，不满足勾股定理逆定理，不是直角三角形故选：C【点睛】本题考查直角三角形的判定，常见方法有2种；（1）有一个角是直角的三角形；（2）三边长满足勾股定理逆定理. 8．D解析：D【分析】将容器侧面展开，建立A 关于EG 的对称点A ′，根据两点之间线段最短可知A ′B 的长度即为所求．【详解】解：如图：将圆柱展开，EG 为上底面圆周长的一半，作A 关于E 的对称点A'，连接A'B 交EG 于F ，则蚂蚁吃到蜂蜜需爬行的最短路径为AF+BF 的长，即AF+BF=A'B=20cm ，延长BG，过A'作A'D⊥BG于D，∵AE=A'E=DG=4cm，∴BD=16cm，Rt△A'DB中，由勾股定理得：A'D=22201612-=cm∴则该圆柱底面周长为24cm．故选：D．【点睛】本题考查了平面展开---最短路径问题，将图形展开，利用轴对称的性质和勾股定理进行计算是解题的关键．同时也考查了同学们的创造性思维能力．9．D解析：D【解析】A选项：32+42≠62，故不符合勾股定理的逆定理，不能组成直角三角形，故错误；B选项：52+62≠72，故不符合勾股定理的逆定理，不能组成直角三角形，故错误；C选项：62+82≠92，故不符合勾股定理的逆定理，不能组成直角三角形，故错误；D选项：72+242=252，故符合勾股定理的逆定理，能组成直角三角形，故正确．故选D．10．C解析：C【分析】筷子浸没在水中的最短距离为水杯高度，最长距离如下图，是筷子斜卧于杯中时，利用勾股定理可求得.【详解】当筷子笔直竖立在杯中时，筷子浸没水中距离最短，为杯高=8cmAD是筷子，AB长是杯子直径，BC是杯子高，当筷子如下图斜卧于杯中时，浸没在水中的距离最长由题意得：AB=15cm，BC=8cm，△ABC是直角三角形∴在Rt△ABC中，根据勾股定理，AC=17cm∴8cm≤h≤17cm故选：C【点睛】本题考查勾股定理在实际生活中的应用，解题关键是将题干中生活实例抽象成数学模型，然后再利用相关知识求解.二、填空题11．①③【分析】①由已知条件证明DAB ≌EAC 即可；②由①可得∠ABD=∠ACE<45°，∠DCB>45°；③由∠ECB+∠EBC=∠ABD+∠ECB+∠ABC=∠ACE+∠ECB+∠ABC =45°+45°=90°可判断③； ④由BE 2＝BC 2－EC 2＝2AB 2－（CD 2﹣DE 2）＝2AB 2－CD 2+2AD 2＝2（AD 2+AB 2）－CD 2可判断④．【详解】解：∵∠DAE ＝∠BAC ＝90°，∴∠DAB ＝∠EAC ，∵AD ＝AE ，AB ＝AC ，∴∠AED=∠ADE=∠ABC=∠ACB=45°， ∵在DAB 和EAC 中，AD AE DAB EAC AB AC ⎧⎪⎨⎪⎩＝＝＝， ∴DAB ≌EAC ，∴BD ＝CE ，∠ABD ＝∠ECA ，故①正确；由①可得∠ABD=∠ACE<45°，∠DCB>45°故②错误；∵∠ECB+∠EBC=∠ABD+∠ECB+∠ABC=∠ACE+∠ECB+∠ABC =45°+45°=90°，∴∠CEB ＝90°，即CE ⊥BD ，故③正确；∴BE 2＝BC 2－EC 2＝2AB 2－（CD 2﹣DE 2）＝2AB 2－CD 2+2AD 2＝2（AD 2+AB 2）－CD 2． ∴BE 2＝2（AD 2+AB 2）－CD 2，故④错误．故答案为：①③．【点睛】本题主要考查全等三角形判定与性质以及勾股定理的应用，熟记全等三角形的判定与性质定理以及勾股定理公式是解题关键．12．【分析】在ABC 中计算AB ，情况一：作AE CE ⊥于E ，计算AE ，DE ，CE ，可得CD ；情况二：作BE CE ⊥于E ，计算BE ，CE ，DE ，可得CD ；情况三：作DE CE ''⊥，计算,,DF DE CE ''，可得CD ．【详解】∵90ACB ︒∠=，4,2AC BC ==，∴25AB =，情况一：当25AD AB ==时，作AE CE ⊥于E∴ 1122BC AC AB AE ⋅=⋅，即455AE =，1455DE = ∴22855CE AC AE =-= ∴22213CD CE DE =+=情况二：当25BD AB ==时，作BE CE ⊥于E ，∴1122BC AC AB BE ⋅=⋅，即45BE =，145DE = ∴2225CE BC BE =-= ∴22210CD CE DE =+=情况三：当AD BD =时，作DE CE ''⊥，作BE CE ⊥于E∴1122BC AC AB BE ⋅=⋅， ∴45BE =355CE ∴= ∵ABD △为等腰直角三角形 ∴152BF DF AB === ∴95DE DF E F DF BE ''=+=+= 25355CE EE CE BF CE ''=-=-=-= ∴2232CD CE E D ''=+=故答案为：1021332【点睛】本题考查了等腰直角三角形的探索，勾股定理的计算等，熟知以上知识是解题的关键．13．．（3，4）或（2，4）或（8，4）．【分析】题中没有指明△ODP 的腰长与底分别是哪个边，故应该分情况进行分析，从而求得点P 的坐标．【详解】解：（1）OD 是等腰三角形的底边时，P 就是OD 的垂直平分线与CB 的交点，此时OP ＝PD ≠5；（2）OD 是等腰三角形的一条腰时：①若点O 是顶角顶点时，P 点就是以点O 为圆心，以5为半径的弧与CB 的交点，在直角△OPC 中，CP 22OP OC -2254-3，则P 的坐标是（3，4）． ②若D 是顶角顶点时，P 点就是以点D 为圆心，以5为半径的弧与CB 的交点，过D 作DM ⊥BC 于点M ，在直角△PDM 中，PM 22PD DM -3，当P 在M 的左边时，CP ＝5﹣3＝2，则P 的坐标是（2，4）；当P 在M 的右侧时，CP ＝5+3＝8，则P 的坐标是（8，4）．故P 的坐标为：（3，4）或（2，4）或（8，4）．故答案为：（3，4）或（2，4）或（8，4）．【点睛】本题考查了等腰三角形的性质和勾股定理的运用等知识,注意正确地进行分类，考虑到所有可能的情况并进行分析求解是解题的关键.14．15厘米【分析】要想求得最短路程，首先要画出圆柱的侧面展开图，把A和C展开到一个平面内．根据两点之间，线段最短，结合勾股定理即可求出蚂蚁爬行的最短路程．【详解】解：如图，展开圆柱的半个侧面是矩形，π=厘米，矩形的宽BC=12厘米．∴矩形的长是圆柱的底面周长的一半，即AB=39∴蚂蚁需要爬行最短路程2222=+=+=厘米．AC BC AB12915故答案为：15厘米【点睛】求两个不在同一平面内的两点之间的最短距离时，一定要展开到一个平面内，根据两点之间，线段最短．15．6或2.【分析】由于已知没有图形，当Rt△ABC固定后，根据“以BC为斜边作等腰直角△BCD”可知分两种情况讨论：①当D点在BC上方时，如图1，把△ABD绕点D逆时针旋转90°得到△DCE，证明A、C、E三点共线，在等腰Rt△ADE中，利用勾股定理可求AD长；②当D点在BC下方时，如图2，把△BAD绕点D顺时针旋转90°得到△CED，证明过程类似于①求解．【详解】解：分两种情况讨论：①当D点在BC上方时，如图1所示，把△ABD绕点D逆时针旋转90°，得到△DCE，则∠ABD=∠ECD，CE=AB=22，AD=DE，且∠ADE=90°在四边形ACDB中，∠BAC+∠BDC=90°+90°=180°，∴∠ABD+∠ACD=360°-180°=180°，∴∠ACD+∠ECD=180°，∴A、C、E三点共线．∴AE=AC+CE=42+22=62在等腰Rt△ADE中，AD2+DE2=AE2，即2AD2=（62）2，解得AD=6②当D点在BC下方时，如图2所示，把△BAD绕点D顺时针旋转90°得到△CED，则CE=AB=22，∠BAD=∠CED，AD=AE且∠ADE=90°，所以∠EAD=∠AED=45°，∴∠BAD=90°+45°=135°，即∠CED=135°，∴∠CED+∠AED=180°，即A、E、C三点共线．∴AE=AC-CE=42-22=22在等腰Rt△ADE中，2AD2=AE2=8，解得AD=2．故答案为：6或2.【点睛】本题主要考查了旋转的性质、勾股定理，解决这类等边（或共边）的两个三角形问题，一般是通过旋转的方式作辅助线，转化线段使得已知线段于一个特殊三角形中进行求解． 16．15 【分析】根据题意点B 与点C 关于AD 对称，所以过点C 作AB 的垂线，与AD 的交点即点P ，求出CE 即可得到答案【详解】∵8,AB AC AD BC ==⊥∴点B 与点C 关于AD 对称过点C 作CE ⊥AB 于一点即为点P ，此时PB PE +最小∵8,4,AB AC BC AD BC ===⊥∴BD=2在Rt △A BC 中， 222282215AD AB BD =-=-= ∵S △ABC=1122BC AD AB CE ⋅⋅=⋅⋅ ∴42158CE ⨯=得15CE =故此题填15【点睛】此题考察最短路径，根据题意找到对称点，作直角三角形，利用勾股定理解决问题 17．21【分析】在AB 上截取AE=AD ，连接CE ，过点C 作CF ⊥AB 于点F ，先证明△ADC ≌△AEC ，得出AE=AD=9，CE=CD=BC ＝10的长度，再设EF=BF=x ，在Rt △CFB 和Rt △CFA 中，由勾股定理求出x ，再根据AB=AE+EF+FB 求得AB 的长度．【详解】如图所示，在AB 上截取AE=AD ，连接CE ，过点C 作CF ⊥AB 于点F ，∵AC 平分∠BAD ，∴∠DAC=∠EAC ．在△AEC 和△ADC 中，AE AD DAC EACAC AC ⎧⎪∠∠⎨⎪⎩＝＝＝∴△ADC ≌△AEC （SAS ），∴AE=AD=9，CE=CD=BC =10，又∵CF ⊥AB ，∴EF=BF ，设EF=BF=x ．∵在Rt △CFB 中，∠CFB=90°，∴CF 2=CB 2-BF 2=102-x 2，∵在Rt △CFA 中，∠CFA=90°，∴CF 2=AC 2-AF 2=172-（9+x ）2，即102-x 2=172-（9+x ）2，∴x=6，∴AB=AE+EF+FB=9+6+6=21，∴AB 的长为21．故答案是：21.【点睛】考查全等三角形的判定和性质、勾股定理和一元二次方程等知识，解题的关键是作辅助线，构造全等三角形，再运用用方程的思想解决问题．18．5【解析】试题分析：作点B 关于AC 的对称点F ，构建直角三角形，根据最短路径可知：此时PB +PE 的值最小，接下来要求出这个最小值，即求EF 的长即可，因此要先求AF 的长，证明△ADF ≌△CDB ，可以解决这个问题，从而得出EF =5，则PB +PE 的最小值为5．解：如图，过B 作BD ⊥AC ，垂足为D ，并截取DF =BD ，连接EF 交AC 于P ，连接PB 、AF ，则此时PB +PE 的值最小，∵△ABC 是等腰直角三角形，∴AB =CB ,∠ABC =90°，AD =DC ，∴∠BAC =∠C =45°，∵∠ADF =∠CDB ，∴△ADF ≌△CDB ，∴AF =BC ,∠FAD =∠C =45°，∵AE =3，BE =1，∴AB =BC =4，∴AF =4，∵∠BAF =∠BAC +∠FAD =45°+45°=90°,∴由勾股定理得：EF ，∵AC 是BF 的垂直平分线，∴BP =PF ，∴PB +PE =PF +PE =EF =5，故答案为5.点睛：本题主要考查最短路径问题.解题的关键在于要利用轴对称知识，结合两点之间线段最短来求解.19．32【分析】由题意设AM=2a ，BM=b ，则正方形ABCD 的面积=224a b ＋，由题意可知EF=(2a-b)-2（a-b)=2a-b-2a ＋2b=b ，由此分析即可．【详解】解：设AM=2a ．BM=b ．则正方形ABCD 的面积=224a b ＋由题意可知EF=（2a-b)-2（a-b)=2a-b-2a ＋2b=b ，∵AM EF ，2,,a a ∴== ∵正方形EFGH 的面积为4，∴24b =，∴正方形ABCD 的面积=2224+832.a b b ==故答案为32.【点睛】本题考查正方形的性质、勾股定理以及线段的垂直平分线的定义等知识，解题的关键是灵活运用所学知识解决问题.20．【分析】根据三角形等面积法求出32AC BC = ，在Rt△ACD 中根据勾股定理得出AC 2=14BC 2+36，依据这两个式子求出AC 、BC 的值.【详解】∵AD 是BC 边上的高，BE 是AC 边上的高， ∴12AC•BE＝12BC•AD， ∵AD＝6，BE ＝4， ∴AC BC ＝32， ∴22AC BC ＝94， ∵AB＝AC ，AD⊥BC，∴BD＝DC ＝12BC ， ∵AC 2﹣CD 2＝AD 2，∴AC 2＝14BC 2+36， ∴221364BC BC +＝94，整理得，BC 2＝3648⨯，解得：BC＝∴△ABC 的面积为12×cm 2故答案为：【点睛】本题考查了三角形的等面积法以及勾股定理的应用，找出AC 与BC 的数量关系是解答此题的关键．三、解答题21．（1）证明见解析；（2）5；（3）CD 2+CE 2＝BC 2，证明见解析．【分析】（1）先判断出∠BAE=∠CAD ，进而得出△ACD ≌△ABE ，即可得出结论．（2）先求出∠CDA=12∠ADE=30°，进而求出∠BED=90°，最后用勾股定理即可得出结论．（3）方法1、同（2）的方法即可得出结论；方法2、先判断出CD 2+CE 2=2（AP 2+CP 2），再判断出CD 2+CE 2=2AC 2．即可得出结论．【详解】解：∵∠BAC ＝∠DAE ，∴∠BAC +∠CAE ＝∠DAE +∠CAE ，即∠BAE ＝∠CAD ．又∵AB ＝AC ，AD ＝AE ，∴△ACD≌△ABE（SAS），∴CD＝BE．（2）如图2，连结BE，∵AD＝AE，∠DAE＝60°，∴△ADE是等边三角形，∴DE＝AD＝3，∠ADE＝∠AED＝60°，∵CD⊥AE，∴∠CDA＝12∠ADE＝12×60°＝30°，∵由（1）得△ACD≌△ABE，∴BE＝CD＝4，∠BEA＝∠CDA＝30°，∴∠BED＝∠BEA+∠AED＝30°+60°＝90°，即BE⊥DE，∴BD5．（3）CD2、CE2、BC2之间的数量关系为：CD2+CE2＝BC2，理由如下：解法一：如图3，连结BE．∵AD＝AE，∠DAE＝90°，∴∠D＝∠AED＝45°，∵由（1）得△ACD≌△ABE，∴BE＝CD，∠BEA＝∠CDA＝45°，∴∠BEC＝∠BEA+∠AED＝45°+45°＝90°，即BE⊥DE，在Rt△BEC中，由勾股定理可知：BC2＝BE2+CE2．∴BC2＝CD2+CE2．解法二：如图4，过点A作AP⊥DE于点P．∵△ADE为等腰直角三角形，AP⊥DE，∴AP＝EP＝DP．∵CD2＝（CP+PD）2＝（CP+AP）2＝CP2+2CP•AP+AP2，CE2＝（EP﹣CP）2＝（AP﹣CP）2＝AP2﹣2AP•CP+CP2，∴CD2+CE2＝2AP2+2CP2＝2（AP2+CP2），∵在Rt△APC中，由勾股定理可知：AC2＝AP2+CP2，∴CD2+CE2＝2AC2．∵△ABC为等腰直角三角形，由勾股定理可知：∴AB2+AC2＝BC2，即2AC2＝BC2，∴CD2+CE2＝BC2．【点睛】本题是几何变换综合题，主要考查了全等三角形的判定和性质，勾股定理，等边三角形的判定和性质，等腰直角三角形的判定和性质，解（1）的关键是判断出∠BAE=∠CAD，解（2）（3）的关键是判断出BE⊥DE，是一道中等难度的中考常考题．22．(1)AC=9;(2)AB∇AC=-72,BA∇BC=73【分析】(1)在Rt AOC∆中,根据勾股定理和新定义可得AO2-OC2=81=AC2;(2)①先利用含30°的直角三角形的性质求出AO=2,OB=23再用新定义即可得出结论;②先构造直角三角形求出BE,AE,再用勾股定理求出BD,最后用新定义即可得出结论;(3)作BD⊥CD,构造直角三角形BCD,根据三角形面积关系求出BD,根据新定义和勾股定理逆定理得出三角形AOD是直角三角形,根据中线性质得出OA的长度,根据勾股定理求出OC,从而得出BC,再根据勾股定理求出CD,再求出AD,再运用勾股定理求出AB.【详解】(1)已知如图:AO为BC上的中线,在Rt AOC ∆中,AO 2-OC 2=AC 2因为81AB AC ∇=所以AO 2-OC 2=81所以AC 2=81所以AC=9.(2)①如图2,取BC 的中点D ,连接AO ,∵AB =AC ,∴AO ⊥BC ,在△ABC 中,AB =AC ,∠BAC =120°,∴∠ABC =30°,在Rt △AOB 中,AB =12,∠ABC =30°,∴AO =6,OB =2222126AB AO -=-=63,∴AB ∇AC =AO 2﹣BO 2=36﹣108=﹣72, ②取AC 的中点D ,连接BD ,∴AD =CD =12AC =6,过点B 作BE ⊥AC 交CA 的延长线于E ,在Rt △ABE 中,∠BAE =180°﹣∠BAC =60°,∴∠ABE =30°, ∵AB =12,∴AE =6,BE =222212663AB AE -=-=, ∴DE =AD +AE =12,在Rt △BED 中,根据勾股定理得,BD =()2222631267BE DE +=+=∴BA ∇BC =BD 2﹣CD 2=216;(3)作BD ⊥CD,因为24ABC S ∆=,8AC =,所以BD=26ABC S AC ∆÷=,因为64AB AC ∇=-,AO 是BC 边上的中线,所以AO 2-OC 2=-64,所以OC2-AO2=64,由因为AC2=82=64,所以OC2-AO2= AC2所以∠OAC=90°所以OA=242283 22ABCSAC∆⨯÷=⨯÷=所以OC=22228373AC OA+=+=所以BC=2OC=273,在Rt△BCD中,CD=()2222276163BC BD-=-=所以AD=CD-AC=16-8=8所以AB=22228610AD BD+=+=【点睛】考核知识点:勾股定理逆定理,含30°直角三角形性质.借助辅助线构造直角三角形,运用勾股定理等直角三角形性质解决问题是关键.23．（1）6-t，t+23；（2）D(1，3)，y=34-x+154；（3）1515215()4215215()2b bSb b⎧-+≤<⎪⎪=⎨⎪->⎪⎩【分析】（1）根据点E，F的运动轨迹和速度，即可得到答案；（2）由题意得：DF=OF=53，DE=OE=5，过点E作EG⊥BC于点G，根据勾股定理得DG=4，进而得D(1，3)，根据待定系数法，即可得到答案；（3）根据题意得直线直线MN的解析式为：34y x b=-+，从而得M(443b-，3)，分2种情况：①当点M在线段DB上时，②当点M在DB的延长线上时，分别求出S与b之间的函数关系式，即可．【详解】∵(0,0)O，(6,0)A，(0,3)C，∴OA=6，OC=3，∵AE=t×1= t ， ∴OE =6-t ，OF =(t+23)×1=t+23，故答案是：6-t ，t+23；（2）当1t =时，OE =6-t=5，OF =t+23=53， ∵将OEF ∆沿EF 翻折，点O 恰好落在CB 边上的点D 处，∴DF=OF=53，DE=OE=5，过点E 作EG ⊥BC 于点G ，则EG=OC=3，CG=OE=5，∴4=，∴CD=CG-DG=5-4=1，∴D(1，3)，设直线DE 的解析式为：y=kx+b ，把D(1，3)，E(5，0)代入y=kx+b ，得350k b k b +=⎧⎨+=⎩ ，解得：34154k b ⎧=-⎪⎪⎨⎪=⎪⎩， ∴直线DE 的解析式为：y=34-x+154；（3）∵MN ∥DE ，∴直线直线MN 的解析式为：34y x b =-+，令y=3，代入34y x b =-+，解得：x=443b -， ∴M(443b -，3)． ①当点M 在线段DB 上时，BM=6-(443b -)=4103b -+， ∴1143(10)223S BM AB b =⋅=⨯⨯-+=215b -+， ②当点M 在DB 的延长线上时，BM=443b --6=4103b -， ∴1143(10)223S BM AB b =⋅=⨯⨯-=215b -，综上所述：1515215()4215215()2b b S b b ⎧-+≤<⎪⎪=⎨⎪->⎪⎩．【点睛】本题主要考查一次函数与几何图形的综合，掌握勾股定理与一次函数的待定系数法，是解题的关键．24．（1）该命题是真命题，理由见解析；（2）①a 的值为92；②k 的取值范围为13k ≤<；（3）ABC ∆203123．【分析】（1）根据等边三角形的性质、优三角形和优比的定义即可判断；（2）①先利用勾股定理求出c 的值，再根据优三角形的定义列出,,a b c 的等式，然后求解即可；②类似①分三种情况分析，再根据三角形的三边关系定理得出每种情况下,,a b c 之间的关系，然后根据优比的定义求解即可；（3）如图（见解析），设BD x =，先利用直角三角形的性质、勾股定理求出AC 、AB 的长及ABC ∆面积的表达式，再类似（2），根据优三角形的定义分三种情况分别列出等式，然后解出x 的值，即可得出ABC ∆的面积．【详解】（1）该命题是真命题，理由如下：设等边三角形的三边边长为a则其中两条边的和为2a ，恰好是第三边a 的2倍，满足优三角形的定义，即等边三角形为优三角形又因该两条边相等，则这两条边的比为1，即其优比为1故该命题是真命题；（2）①90,6CB b A ∠=︒=22236c a b a ∴=++根据优三角形的定义，分以下三种情况：当2a b c +=时，26236a a +=+，整理得24360a a -+=，此方程没有实数根。

高三数学3月质量检测试题含解析试题

卜人入州八九几市潮王学校一中2021届高三数学3月质量检测试题〔含解析〕一、单项选择题：此题一共8小题，每一小题5分，一共40分.在每一小题给出的四个选项里面，只有一项符合题目要求.{}|2,0xA y y x -==<，集合12|B x y x ⎧⎫==⎨⎬⎩⎭，那么A B ⋂=〔〕A.[)1,+∞B.()1,+∞C.()0,+∞D.[)0,+∞【答案】B 【解析】因为，，所以A B ⋂=()1,+∞.应选B.2.设()()()2i 3i 35i x y +-=++(i 为虚数单位〕，其中,x y 是实数，那么i x y +等于() A.5 13 C.22 D.2【答案】A 【解析】由()()()2i 3i 35i x y +-=++，得()()632i 35i x x y ++-=++，∴63325x x y +=⎧⎨-=+⎩，解得34x y =-⎧⎨=⎩，∴i 34i 5x y +=-+=．应选A ．3.已设,a b 都是正数，那么“33a b log log ＜〞是“333a b ＞＞〞的〔〕 A.充分不必要条件 B.必要不充分条件 C.充分且必要条件 D.既不充分也不必要条件【答案】B 【解析】【分析】由33a b log log ＜和333a b ＞＞分别求出a ，b 的关系，然后利用必要条件、充分条件及充分必要条件的判断方法得答案．【详解】由33a b log log ＜，得01b a ＜＜＜或者01a b ＜＜＜或者1a b ＞＞，由333a b ＞＞，得1a b ＞＞，“33a b log log ＜〞是“333a b ＞＞〞的必要不充分条件．应选：B ．【点睛】此题主要考察了必要条件、充分条件及充分必要条件的判断方法，考察了不等式的性质，属于中档题．4.甲、乙、丙三位同学获得某项竞赛活动的前三名，但详细名次未知．3人作出如下预测：甲说：我不是第三名；乙说：我是第三名；丙说：我不是第一名．假设甲、乙、丙3人的预测结果有且只有一个正确，由此判断获得第三名的是 A.甲 B.乙C.丙D.无法预测【答案】A 【解析】【分析】假设甲的预测正确，那么乙、丙的预测错误，推出矛盾！假设乙的预测正确，甲、丙的预测错误，推出矛盾！假设丙的预测正确，甲、乙的预测错误，可推出三个人的名次．【详解】假设甲的预测正确，乙、丙的预测错误，那么丙是第一名，甲不是第三名，那么甲是第二名，乙是第三名，矛盾！假设乙的预测正确，甲、丙的预测错误，那么乙是第三名，甲的预测错误，那么甲是第三名，矛盾！假设丙的预测正确，那么甲、乙的预测错误，那么甲是第三名，乙不是第三名，丙是第一名，那么乙是第二名．因此，第三名是甲，应选A ．【点睛】此题考察合情推理，突出假设法在推理中的应用，通过不断试错来推出结论，考察推理分析才能，属于中等题．5.九章算术是我国古代数学名著，其中有这样一个问题:“今有宛田，下周三十步，径十六步，问为田几何？〞意思说：现有扇形田，弧长三十步，直径十六步，问面积多少？书中给出计算方法：以径乘周，四而一，即扇形的面积等于直径乘以弧长再除以4.在此问题中，扇形的圆心角的弧度数是〔〕A.415B.158C.154D.120【答案】C 【解析】【分析】由题意，根据给出计算方法：扇形的面积等于直径乘以弧长再除以4，再由扇形的弧长公式列出方程，即可求解.【详解】由题意，根据给出计算方法：以径乘周，四而一，即扇形的面积等于直径乘以弧长再除以4，再由扇形的弧长公式，可得扇形的圆心角301584l r α===〔弧度〕，应选C. 【点睛】此题主要考察了扇形的弧长公式的实际应用问题，其中解答中认真审题，正确理解题意，合理利用扇形的弧长公式求解是解答的关键，着重考察了分析问题和解答问题的才能，属于根底题.6.假设22nx ⎫⎪⎭的展开式中只有第六项的二项式系数最大，那么展开式中的常数项是〔〕A.210B.180C.160D.175【答案】B 【解析】【分析】根据题意，得出二项式的指数n 的值，再利用展开式的通项公式求出常数项是多少．【详解】解：22nx ⎫⎪⎭展开式中只有第六项的二项式系数最大，∴展开式中一共有11项，n ＝10；∴展开式的通项公式为551021101022()(1)2rr rr r r rr T C C x x--+=⋅-=-⋅⋅令5502r-=，得2r ，∴常数项是2221102180T C +=⋅=，应选B ．【点睛】此题考察了二项式定理的应用问题，也考察了逻辑推理与运算才能，是根底题目．7.泉城上矗立着的“泉标〞，成为泉城的标志和象征.为了测量“泉标〞高度，某同学在“泉标〞的正西方向的点A 处测得“泉标〞顶端的仰角为45°，沿点A 向北偏东30°前进100m 到达点B ，在点B 处测得“泉标〞顶端的仰角为30°，那么“泉标〞的高度为〔〕 A.50m B.100mC.120mD.150m【答案】A 【解析】【分析】先设DC ＝x ，然后在△ABC 中，利用余弦定理可得2221)10021002x x =+-⨯⨯⨯，再求解即可. 【详解】解:根据题意，作出图形如下列图：所以AB ＝100，∠BAC ＝60°，∠DBC ＝30°，设DC ＝x ，所以AC ＝x ，BC =，在△ABC 中，利用余弦定理的应用得2221)10021002x x =+-⨯⨯⨯，得25050000x x -=+，又0x>，解得50x =，应选:A【点睛】此题考察了余弦定理的应用，重点考察了运算才能，属根底题. 8.函数()f x 满足(2)(2)6f x f x -++=，31()2x g x x -=-，且()f x 与()g x 的图像交点为()11,x y ，()22,x y ，…，()88,x y ，那么128128x x x y y y +++++++的值是()A.20B.24C.36D.40【答案】D 【解析】【分析】根据条件判断()f x 和()g x 都关于()2,3中心对称，由此求得128128x x x y y y +++++++的值.【详解】由于()f x 满足(2)(2)6f x f x -++=，当0x =时，()23f =，所以()f x 关于()2,3中心对称.由于()325315()3222x x g x x x x -+-===+---，所以()g x 关于()2,3中心对称.故()f x 和()g x 都关于()2,3中心对称.所以()f x 与()g x 的图像交点()11,x y ，()22,x y ，…，()88,x y ，两两关于()2,3对称.所以128128x x x y y y +++++++828340=⨯+⨯=.应选D.【点睛】本小题主要考察函数图像的对称性，考察化归与转化的数学思想方法，属于根底题.二、多项选择题：此题一共4小题，联盟每一小题5分，一共20分.在每一小题给出的选项里面，有多项符合题目要求.全部选对的得5分，局部选对的得3分，有选错的得0分.9.某颗人造地球卫星的运行轨道是以地球的中心F 为一个焦点的椭圆，如下列图，它的近地点A 〔离地面最近的点〕距地面m 千米，远地点B 〔离地面最远的点〕距地面n 千米，并且F A B 、、三点在同一直线上，地球半径约为R 千米，设该椭圈的长轴长、短轴长、焦距分别为222a b c 、、，那么〔〕A.a c m R -=+B.a c n R +=+C.2a m n=+D.b =【答案】ABD 【解析】【分析】根据条件数形结合可知m a c Rn a c R =--⎧⎨=+-⎩，然后变形后，逐一分析选项，得到正确答案.【详解】因为地球的中心是椭圆的一个焦点，并且根据图象可得m a c Rn a c R=--⎧⎨=+-⎩，〔*〕a c m R ∴-=+，故A 正确； a c n R +=+，故B 正确；〔*〕两式相加22m n a R +=-，可得22a m n R =++，故C 不正确；由〔*〕可得m R a c n R a c+=-⎧⎨+=+⎩，两式相乘可得()()22m R n R a c ++=-222a c b -=，()()2b m R n R b ∴=++⇒=，故D 正确.应选ABD【点睛】此题考察圆锥曲线的实际应用问题，意在考察抽象，概括，化简和计算才能，此题的关键是写出近地点和远地点的方程，然后变形化简.10.甲罐中有5个红球，2个白球和3个黑球，乙罐中有4个红球，3个白球和3个黑球．先从甲罐中随机取出一球放入乙罐，分别以1A ，2A 和3A 表示由甲罐取出的球是红球，白球和黑球的事件；再从乙罐中随机取出一球，以B 表示由乙罐取出的球是红球的事件，那么以下结论中正确的选项是〔〕A.()25P B =B.()15|11PB A =C.事件B 与事件1A 互相HYD.1A ，2A ，3A 是两两互斥的事件【答案】BD 【解析】【分析】由题意1A ，2A ，3A 是两两互斥的事件，由条件概率公式求出1(|)P B A ，()()()()123P B P B A P B A P B A =⋅+⋅+⋅对照四个选项判断即可.【详解】由题意1A ，2A ，3A 是两两互斥的事件，12351213(),(),()10210510P A P A P A =====， ()11115()52111()112|P P BA P A B A ⨯===，故B 正确；()()()()123552434910111011101122P B P B A P B A P B A =⋅+⋅+⋅=⨯+⨯+⨯=，故A ，C 不正确；1A ，2A ，3A 是两两互斥的事件，故D 正确.应选：BD ．【点睛】此题考察了互斥事件和条件概率，考察了学生实际应用，转化划归，数学运算的才能，属于中档题.11.点P 是双曲线E ：221169x y -=的右支上一点，1F ，2F 为双曲线E 的左、右焦点，12PF F ∆的面积为20，那么以下说法正确的选项是〔〕A.点P 的横坐标为203 B.12PF F ∆的周长为803C.12F PF ∠小于3π D.12PF F ∆的内切圆半径为34【答案】ABC 【解析】【分析】设12F PF ∆的内心为I ，连接22IP IF IF 、、，设()P m n ，,利用12PF F ∆的面积为20，可求得P 点坐标；12PF F ∆的周长为2121|+|||||F P F F F P +，借助P 点坐标，可得解；利用1PF k ，2PF k 可求得12tan F PF ，可研究12F PF ∠范围；()12121212PF FS r PF PF F F ∆=++可求得内切圆半径r .【详解】设12F PF ∆的内心为I ，连接22IP IF IF 、、，双曲线E ：221169x y -=中的4a =，3b =，5c =，不妨设()Pm n ，，0m >，0n >，由12PF F ∆的面积为20，可得1215202F F n cn n ===，即4n =，由2161169m -=，可得203m =，故A 符合题意；由2043P ⎛⎫⎪⎝⎭，，且()150F -，，()250F ，，可得11235PFk =，2125PF k =，那么(121212360535tan 012123191535F PF -==∈⨯+⨯，那么123F PF π<∠，故C 符合题意；由12371350333PF PF +==+=，那么12PF F ∆的周长为50801033+=，故B 符合题意；设12PF F ∆的内切圆半径为r ，可得()12121211422r PF PF F F F F ++=⋅⋅，可得80403r =，解得32r =，故D 不符合题意．应选：ABC ．【点睛】此题考察了双曲线的性质综合，考察了学生综合分析，转化化归，数学运算的才能，属于中档题. 12.正四棱柱1111ABCD A B C D -的底面边长为2，侧棱11AA =，P 为上底面1111D C B A 上的动点，给出以下四个结论中正确结论为〔〕A.假设3PD =，那么满足条件的P 点有且只有一个B.假设PD=P 的轨迹是一段圆弧C.假设PD ∥平面1ACB ，那么DP 长的最小值为2D.假设PD ∥平面1ACB ，且PD=，那么平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形的面积为94π【答案】ABD 【解析】【分析】假设3PD =，由于P 与1B 重合时3PD =，此时P 点唯一；()13PD =，，那么1PD =即点P 的轨迹是一段圆弧；当P 为11A C 中点时，DP 有最小值为=C ；平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆，其半径为32=，可得D . 【详解】如图： ∵正四棱柱1111ABCD A B C D -的底面边长为2，∴11B D =11AA =，∴13DB==，那么P 与1B 重合时3PD =，此时P 点唯一，故A 正确；∵()13PD ，，11DD =，那么1PD =P 的轨迹是一段圆弧，故B 正确；连接1DA ，1DC ，可得平面11//A DC 平面1ACB ，那么当P 为11A C 中点时，DP 有最小值为=，故C 错误；由C 知，平面BDP 即为平面11BDD B ，平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面32=，面积为94π，故D 正确．应选：ABD ．【点睛】此题考察了立体几何综合，考察了学生空间想象，逻辑推理，转化划归，数学运算的才能，属于较难题.三、填空题：此题一共4小题，每一小题5分，一共20分. 13.向量(1,1)ax =+，(,2)b x =，假设满足a b ，且方向一样，那么x =__________．【答案】1 【解析】【分析】由向量平行坐标表示计算．注意验证两向量方向是否一样．【详解】∵ab ，∴(1)20x x +-=，解得1x =或者2x =-，1x =时，(1,2),(1,2)a b ==满足题意，2x =-时，(1,1),(2,2)a b =-=-，方向相反，不合题意，舍去．∴1x =．故答案为：1．【点睛】此题考察向量平行的坐标运算，解题时要注意验证方向一样这个条件，否那么会出错．14.m 是2与8的等比中项，那么圆锥曲线221yx m-=的离心率是_____．2【解析】【分析】由m 是2与8的等比中项算出4m =±,再分两种情况计算圆锥曲线221yx m-=的离心率即可.【详解】由m 是2与8的等比中项有22816m ,故4m =±.当4m =时圆锥曲线方程2214y x -=,为焦点在x 轴的双曲线,其中1,a c ==此时离心率e =当4m =-时圆锥曲线方程2214y x +=,,为焦点在y 轴的椭圆,其中2,a c ==此时离心率e =2【点睛】此题主要考察椭圆与双曲线方程运用,属于根底题型. 15.对于函数()f x ，假设在定义域内存在实数0x 满足()()00f x f x -=-，那么称函数()f x 为“倒戈函数〞．设()321x f x m =+-〔m R ∈，且0m ≠〕是定义在[﹣1，1]上的“倒戈函数〞，那么实数m的取值范围是_____．【答案】103⎡⎫-⎪⎢⎣⎭，【解析】【分析】()()00f x f x -=-即004332x x m -=--+，构造函数00332x x y -=--+，[]011x ∈-，，利用换元法求函数值域，即得解. 【详解】∵()321x f x m =+-是定义在[﹣1，1]上的“倒戈函数，∴存在[]011x ∈-，满足()()00f x f x -=-，∴00321321x x m m -+-=--+，∴004332x x m -=--+，构造函数00332x x y -=--+，[]011x ∈-，，令03x t =，133t ⎡⎤∈⎢⎥⎣⎦，， 12y t t =--+，403y ⎡⎤∈-⎢⎥⎣⎦，， ∴4403m -≤<， ∴103m -≤<，故答案为：103⎡⎫-⎪⎢⎣⎭，. 【点睛】此题考察了函数综合，考察了学生，综合分析，转化划归，数学运算的才能，属于较难题.16.函数(),()f x x g x x ωω=，其中0>ω，,,A B C 是这两个函数图像的交点，且不一共线.①当1ω=时，ABC ∆面积的最小值为___________；②假设存在ABC ∆是等腰直角三角形，那么ω的最小值为__________. 【答案】(1).2π(2).2π【解析】【分析】①利用函数的图象和性质的应用求出三角形的底和高，进一步求出三角形的面积； ②利用等腰直角三角形的性质的应用求出ω的最小值．【详解】函数(),()f x x g x x ωω==，其中0>ω，,,A B C 是这两个函数图象的交点，当1ω=时，(),()f x x g x x ωω==．所以函数的交点间的间隔为一个周期2π，高为2=．所以：()121122ABC S ππ∆⋅⋅+＝＝．如下列图：①当1ω=时，ABC ∆面积的最小值为2π；②假设存在ABC ∆是等腰直角三角形，利用直角三角形斜边的中线等于斜边的一半，那么2222πω⎭⋅＝，解得ω的最小值为 2π．故答案为：2π， 2π．【点睛】此题主要考察了三角函数的图象和性质的应用，主要考察学生的运算才能和转换才能及思维才能，属于根底题型．四、解答题：本大题一一共6小题，一共70分.解容许写出必要的文字说明、证明过程或者演算步骤. 17.数列{}n a 满足：123a a a +++()1312nn a +=- 〔1〕求{}n a 的通项公式；〔2〕假设数列{}n b 满足3n na bn a =，求{}n b 的前n 项和nT.【答案】〔1〕13-=n n a ;〔2〕13211()()443nn n T .【解析】【分析】〔1〕利用2n ≥时，1n n n a S S -=-求解；检验11a =成立即可求解〔2〕由3n n a b na =，得11(1)()3nnb n ，利用错位相减求和即可【详解】〔1〕令123S n n a a a a1n =时，11a =2n ≥时，113nnn na S S ，11a =满足所以13-=n n a ；〔2〕由3n n a b na =，11(1)()3n nb n12n n T b b b 2112()3311(1)()3n n ①23111()2()333n T 11(2)()3n n 1(1)()3n n ②①-②得【点睛】此题考察利用前n 项和求通项公式，考察错位相减求和，准确利用前n 项和求出通项公式是关键，是中档题18.在锐角ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c .sinsin 3b A a B π⎛⎫=+ ⎪⎝⎭．〔1〕求角B 的大小；〔2〕求ca的取值范围【答案】〔1〕3B π=；〔2〕1,22⎛⎫⎪⎝⎭【解析】【分析】〔1〕根据正弦定理边化角，与两角和的正弦公式求得B 的值；〔2〕根据正弦定理边化角，再利用同角的三角函数关系结合角的范围求得取值范围．【详解】〔1〕由sinsin 3b A a B π⎛⎫=+ ⎪⎝⎭，根据正弦定理，有sin sinsin sin 3B A A B π⎛⎫=+ ⎪⎝⎭即有1sin sin sin 32π⎛⎫=+=+ ⎪⎝⎭BB B B那么有tan B=0B π<<，所以，3B π=〔2〕由〔1〕，3B π=，那么23A C π+=，又ABC ∆为锐角三角形，所以，02A π<<且2032A <-<ππ，所以62A ππ<<，于是tan3>A那么21sin sin sin 13222sin sin sin 2π⎛⎫-+ ⎪⎝⎭====+<A A A c C a A A A又112tan 22+>A所以，c a 的取值范围是1,22⎛⎫ ⎪⎝⎭【点睛】此题主要考察了正弦定理、同角的三角函数关系以及两角和差的正弦公式，正确求得角的范围是解题的关键．19.如图，三棱柱111ABC A B C -中，CA CB =，145BAA ∠=︒，平面11AA C C ⊥平面11AA B B .〔1〕求证：1AA BC ⊥；〔2〕假设12BB ==，直线BC 与平面11ABB A 所成角为45︒，D 为1CC 的中点，求二面角111B A D C --的余弦值.【答案】〔1〕见解析〔2〕2【解析】【分析】〔1〕过点C 作CO ⊥AA 1，那么CO ⊥平面AA 1B 1B ，CO ⊥OB ，推导出Rt△AOC ≌Rt△BOC ，从而AA 1⊥OB ，再由AA 1⊥CO ，得AA 1⊥平面BOC ，由此能证明AA 1⊥BC ．〔2〕以O 为坐标原点，OA ，OB ，OC 所在直线分别为x ，y ，z 轴，建立空间直角坐标系，利用向量法能求出二面角B 1﹣A 1D ﹣C 1的余弦值．【详解】〔1〕过点C 作1CO AA ⊥，垂足为O ，因为平面11AA C C ⊥平面11AA B B ，所以CO ⊥平面11AA B B ，故CO OB ⊥，又因为CA CB =，CO CO =，90COA COB ∠=∠=︒，所以Rt AOC Rt BOC ∆≅∆，故OA OB =，因为145A AB ∠=︒，所以1AA OB ⊥，又因为1AA CO ⊥，所以1AA ⊥平面BOC ，故1AA BC ⊥.〔2〕以O 为坐标原点，OA ，OB ，OC 所在直线为x ，y ，z 轴，建立空间直角坐标系O xyz -，因为CO ⊥平面11AA B B ，所以CBO ∠是直线BC 与平面11AA B B 所成角，故45CBO ∠=︒，所以AB =1AO BO CO ===，()1,0,0A ，()0,1,0B ，()0,0,1C ，()11,0,0A -，()12,1,0B -，()1,0,1D -，设平面11A B D 的法向量为()111,,n x y z =，那么1100n A D n B D ⎧⋅=⎪⎨⋅=⎪⎩，所以111100z x y z =⎧⎨-+=⎩，令11x =，得()1,1,0n =，因为OB ⊥平面11AAC C ，所以OB 为平面11AC D 的一条法向量，()0,1,0OB =， 2cos ,2n OB n OB n OB⋅==⋅，所以二面角111B A D C --.【点睛】此题考察线线垂直的证明，考察二面角的余弦值的求法，考察空间中线线、线面、面面间的位置关系等根底知识，考察运算求解才能，考察数形结合思想，是中档题．20.为进步城居民生活幸福感，某城公交公司大力确保公交车的准点率，减少居民乘车候车时间是为此，该公司对某站台乘客的候车时间是进展统计乘客候车时间是受公交车准点率、交通拥堵情况、节假日人流量增大等情况影响在公交车准点率正常、交通拥堵情况正常、非节假日的情况下，乘客候车时间是随机变量X满足正态分布()2,Nμσ在公交车准点率正常、交通拥堵情况正常、非节假日的情况下，调查了大量乘客的候车时间是，经过统计得到如图频率分布直方图.〔1〕在直方图各组中，以该组区间的中点值代表该组中的各个值，试估计2,μσ的值；〔2〕在统计学中，发生概率低于千分之三的事件叫小概率事件，一般认为，在正常情况下，一次试验中，小概率事件是不能发生的在交通拥堵情况正常、非节假日的某天，随机调查了该站的10名乘客的候车时间是，发现其中有3名乘客候车时间是超过15分钟，试判断该天公交车准点率是否正常，说明理由.5.16≈≈≈，76340.84130.2898,0.84130.3546,0.15870.0040,0.15870.0006≈≈≈≈，()0.6826P X μσμσ-<<+=，(22)0.9544P X μσμσ-<<+=，(33)0.9973P X μσμσ-<<+=〕【答案】〔1〕10μ=，219.2σ=〔2〕准点率正常，详见解析【解析】【分析】〔1〕由频率分布直方图结合均值和方差公式可求出μ和σ；〔2〕由正态分布求得(14.38)P x >再根据n 次HY 重复试验中事件发生k 次的概率公式求有3名乘客候车时间是超过15分钟的概率从而得出结论.【详解】〔1〕0.120.260.4100.2140.11810μ=⨯+⨯+⨯+⨯+⨯=，〔2〕10 4.3814.38μσ+=+=，设3名乘客候车时间是超过15分钟的事件为A ，1()(14.38)0.15872p X P x μσμσ--<<+>==，33710()(0.1587)(0.8413)0.1390.003P A C =≈>，准点率正常【点睛】考察正态分布，考察数学建模，数据分析，数学运算的数学素养. 21.椭圆2:2(0)C y px p =>，点F 为抛物线的焦点，焦点F 到直线3x-4y+3=0的间隔为d 1，焦点F 到抛物线C 的准线的间隔为d 2，且1235d d =． (1)抛物线C 的HY 方程;(2)假设在x 轴上存在点M ，过点M 的直线l 分别与抛物线C 相交于P 、Q 两点，且2211PMQM+为定值，求点M 的坐标. 【答案】〔1〕24y x =；〔2〕()2,0M 【解析】【分析】〔1〕根据点到直线的间隔公式以及抛物线的性质可求得1d 和2d ，再结合1235d d =解出p 即可得抛物线的方程；〔2〕设点M 的坐标为(),0t ，设点P ，Q 的坐标分别为()11,x y ，()22,x y ，设直线l 的方程为x my t=+，与抛物线方程联立可得PM，QM，把根与系数的关系代入可得()2222211221t m m t PMQM++=+，由其为定值可得2t =，即得结果.代入同理可得结论．【详解】〔1〕由题意知，焦点F 的坐标为,02p ⎛⎫ ⎪⎝⎭，那么133362510pp d ++==，2d p =，又363105p p +=，解得：2p =.故抛物线C 的HY 方程为24y x =. 〔2〕设点M 的坐标为(),0t ，设点P ，Q 的坐标分别为()11,x y ，()22,x y ，显然直线ll 的方程为x my t =+.联立方程2,4,x my t y x =+⎧⎨=⎩消去x ，并整理得2440y my t --=，那么()2160mt ∆=+>且124y y m +=，124y y t .由1PM ==，2QM ==.有()()()221222222222212121111111y y m ym ym y y PMQM ++=+=+++.假设2211PMQM +为定值，必有2t =.所以当2211PMQM+为定值时，点M 的坐标为()2,0.【点睛】此题考察了抛物线的HY 方程及其性质、一元二次方程的根与系数的关系、定点问题，考察了推理才能与计算才能，属于中档题． 22.函数()()20f x lnx ax x a =--+≥．()1讨论函数()f x 的极值点的个数；()2假设函数()f x 有两个极值点1x ，2x ，证明：()()12322f x f x ln +>-．【答案】(1)见解析(2)见解析【解析】【分析】()1先求出函数的导函数，通过讨论a 的范围确定导函数的符号，从而得出函数的单调区间，进而判断函数极值点个数；()2由()1可知当且仅当10,8a ⎛⎫∈ ⎪⎝⎭时()f x 有极小值1x 和极大值2x ，且1x ，2x 是方程的两个正根，那么1212x x a +=，121.2x x a=根据函数()2f x lnx ax x =--+表示出()()121214f x f x lna ln a +=+++，令()1214g a lna ln a=+++，通过对()g a 求导即可证明结论．【详解】解：()1函数()()20f x lnx ax x a =--+≥，()()2212121210ax x ax x f x ax x x x x-+-+-∴=--+>=-'=，0x > 0a ≥，∴当0a=时，()1x f x x'-=，0x >，当()0,1x ∈时，()0f x '<，()f x 单调递减；当()1,x ∈+∞时，()0f x '>，()f x 单调递增；∴当1x =时，()f x 有极小值；当18a≥时，0≤，故()0f x '≤， ()f x ∴在()0,+∞上单调递减，故此时()f x 无极值；当108a <<时，0>，方程()0f x '=有两个不等的正根1x ，2x ．可得1x =2x=那么当10,4x a ⎛⎫∈ ⎪ ⎪⎝⎭及14x a ⎛⎫+∈+∞ ⎪ ⎪⎝⎭时， ()0f x '<，()f x 单调递减；当1144x a a ⎛⎫-∈ ⎪ ⎪⎝⎭时，()0f x '>；()f x 单调递增； ()f x ∴在1x x =处有极小值，在2x x =处有极大值．综上所述：当0a=时，()f x 有1个极值点；当18a ≥时，()f x 没有极值点；当108a <<时，()f x 有2个极值点． ()2由()1可知当且仅当10,8a ⎛⎫∈ ⎪⎝⎭时()f x 有极小值点1x 和极大值点2x ，且1x ，2x 是方程的两个正根，那么1212x x a +=，1212x x a=． ()()()(()()2121212121211[)2ln 212144f x f x x x a x x x x lnx lnx a lna ln a a ⎤∴+=+-+--+=++=+++⎦；令()1214g a lna ln a=+++， 108a <<；()24104a g x a -'=<， ()g a ∴在10,8⎛⎫ ⎪⎝⎭上单调递减，故()13228g a g ln ⎛⎫>=- ⎪⎝⎭， ()()12322f x f x ln ∴+>-．【点睛】此题考察了利用导数研究函数的单调性和极值，注意分类讨论思想的运用，属于难题．。

华大新高考联盟2022届高三3月教学质量测评(新高考卷)数学试题及答案

华大新高考联盟2022届高三3月教学质量测评数学一、选择题：每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知复数()2i i z m n =+-，其中,m n ∈R ，若z 为纯虚数，则（）．A ．0m ≠，2n =-B ．2m ≠-，0n =C ．0m =，2n =-D ．2m =-，0n ≠2．设集合()(){}350A x x x =--<，{}7B x m x =<<，若{}37A B x x ⋃=<<，则实数m 的取值范围为（）．A ．(]3,5B ．[]3,5D ．()3,5D ．[)3,53．某大学开设选修课，要求学生根据自己的专业方向以及自身兴趣从6个科目中选择3个科目进行研修，已知某班级a 名学生对科目的选择如下所示，则a 、b 的一组值可以是（）．科目国际金融统计学市场管理二战历史市场营销会计学人数2428141519bA ．40a =，10b =B ．40a =，30b =C ．37a =，21b =D ．37a =，11b =4．已知圆锥的表面积为90π，母线与底面所成角为θ，若2cos 3θ=，则圆锥的体积为（）．A ．108πB ．365πC ．363πD ．72π5．函数()244xf x x =-的零点个数为（）．A ．0B ．1C ．2D ．36．“黄金三角形”是几何历史上的瑰宝，它有两种类型，其中一种是顶角为36°的等股三角形，暂且称为“黄金三角形A ”．如图所示，已知五角星是由5个“黄金三角形A ”与1个正五边形组成，其中51sin184-︒=，则阴影部分面积与五角形面积的比值为（）．A ．514-B ．55C ．516+D ．35207．已知下表所示的数据的回归直线为ˆˆˆybx a =+，则ˆb =（）．i 12345i x 357911iy 1y 2y 3y 4y 5y A ．3.15B ．4.15C ．2.25D ．1.25参考公式：在线性回归方程ˆˆˆybx a =+中，()()()121ˆniii ni i x x y y b x x ==--=-∑∑，ˆˆay bx =-．参考数据：51686iii x y==∑，5180i i y ==∑．8．已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F ，2F ，点M ，N 均在双曲线C 的右支上，其中点M 在第一象限，M ，N ，2F 三点共线，且211cos 4MF F ∠=-，若11MF N MNF ∠=∠，则双曲线C 的渐近线方程为（）．A ．5y =B ．y x=±C ．3y x=D ．2y x=二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．已知l ，m ，n 是空间中三条不同的直线，α，β是空间中两个不同的平面，则下列说法错误的是（）．A ．若l α⊂，m α⊂，l n ⊥，m n ⊥，则n α⊥B ．若αβ∥，l α⊥，l m ⊥，m α⊄，则m β∥C ．若αβ⊥，l αβ⋂=，m α⊂，n β∥，m l ⊥，则m n ⊥D ．若l α⊥，m β⊥，αβ⊥，n l ∥，则m n∥10．十二平均律是我国明代音乐理论家和数学家朱载堉发明的．明万历十二年(公元1584年)．他写成《律学新说》，提出了十二平均律的理论．十二平均律的数学意义是：在1和2之间插入11个数，使包含1和2的这13个数依次成递增的等比数列，记插入的11个数之和为M ，插入11个数后这13个数之和为N ，则依此规则，下列说法正确的是（）．A ．插入的第82B ．插入的第5个数是插入的第12倍C ．3M >D ．7N <11．已知函数()()sin cos cos f x x x =+，则下列说法正确的是（）．A ．直线πx =为函数()f x 图象的一条对称轴B ．函数()f x 在[]0,π上单调递增C ．函数()f x 在[]π,2π上单调递增D ．x ∃∈R ，()6214f x +≥+12．已知三棱锥S ABC -中，SA ⊥平面ABC ，2SA AB BC ===，2AC =，点E ，F 分别是线段AB ，BC 的中点，直线AF ，CE 相交于点G ，则过点G 的平面α与截三棱锥S ABC -的外接球O 所得截面面积可以是（）．A ．2π3B ．8π9C ．πD ．3π2三、填空题：本题共4小题，每小题5分，共20分．13．85312x x ⎛⎫ ⎝的展开式中32x -项的系数为______．14．已知平面向量a ，b ，c 满足，b c ⊥ ，2b c == ，若8a b a c ⋅=⋅=，则a = ______．15．抛物线具有以下光学性质：从焦点出发的光线经抛物线反射后平行于抛物线的对称轴．该性质在实际生产中应用非常广泛．如图所示，从抛物线()2:20C y px p =>的焦点F 向y 轴正方向发出的两条光线a ，b 分别经抛物线上的A ，B 两点反射，已知两条入射光线与x 轴所成锐角均为60°，且323FA FB +=，则p =______．16．已知函数()f x 的定义域为R ，图象关于原点对称，其导函数为()f x '，若当0x >时()()ln 0x x f x f x +⋅'<，则不等式()()44xf x f x ⋅>的解集为______．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．(10分)已知首项为13的数列{}n a 的前n 项和为n S ，且()1123n n n n n S n a a a S ++++=+．(1)记111n n nb a a +=-，求证：数列{}n b 为等差数列；(2)求98S 的值．18．(12分)2021年11月7日，在《英雄联盟》S11的总决赛中，中国电子竞技俱乐部EDG 完成逆转，斩获冠军，掀起了新一波电子竞技在中国的热潮．为了调查A 地25岁以下的年轻人的性别与对电子竞技的爱好程度是否具有相关性，研究人员随机抽取了500人作出调查，所得数据统计如下表所示：热爱电子竞技对电子竞技无感男性20050女性100(1)判断是否有99.9％的把握认为A 地25岁以下的年轻人的性别与对电子竞技的爱好程度有关？(2)若按照性别进行分层抽样的方法，从被调查的热爱电子竞技的年轻人中随机抽取15人，再从这15人中任取3人，记抽到的男性人数为X ，求X 的分布列以及数学期望()E X ．附：()()()()()22n ad bc K a b c d a c b d -=++++，其中n a b c d =+++．()20P K k ≥0.100.050.0250.0100.0050.0010k 2.7063.8415.0246.6357.87910.82819．(12分)如图所示，四棱锥S ABCD -中，底面ABCD 为矩形，AC 与BD 交于点O ，点E 在线段SD 上，且OE ∥平面SAB ，二面角S AB C --，S AD C --均为直二面角．(1)求证：SE DE =；(2)若2SA AD ==，且钝二面角A BE C --的余弦值为32020-，求AB 的值．20．(12分)已知ABC △中，角A ，B ，C 所对的边分别为a ，b ，c ，且sin 2C B=2C A =，2c =．(1)求证：ABC △是等腰直角三角形；(2)已知点P 在ABC △的内部，且PB PC =，PA AC =，求cos PAB ∠．21．(12分)已知椭圆()2222:10x y C a b a b +=>>的离心率为12，且过点31,2⎛⎫- ⎪⎝⎭．(1)求椭圆C 的标准方程；(2)过点()0,1且斜率为k 的直线l 与椭圆C 交于M ，N 两点，且()(,3G G x t t >，若NG x ⊥轴，求证：存在实数t ，使得直线MG 过y 轴上的定点．22．(12分)完成下列问题：(1)已知函数()2cos sin x f x e x x x =--，[]0,πx ∈，求函数()f x 的最小值；(2)若关于x 的方程[]()sin 10,πxmx x x e x +=-∈有两个实数根，求实数m 的取值范围．华大新高考联盟2022届高三3月教学质量测评数学参考答案和评分标准一、选择题1．【答案】A【命题意图】本题考查复数的四则运算、复数的基本概念，考查数学运算、逻辑推理的核心素养．【解析】依题意，()()2i i 2i z m n n m =+-=++，故0m ≠，2n =-，故选A ．2．【答案】D【命题意图】本题考查集合的运算、一元二次不等式的解法，考查数学运算、逻辑推理的核心素养．【解析】依题意，()(){}{}35035A x x x x x =--<=<<；而{}37A B x x ⋃=<<，结合数轴可知，35m ≤<，故选D ．3．【答案】D【命题意图】本题考查数学文化、推理与证明，考查数学建模、数学运算、逻辑推理的核心素养．【解析】依题意，32428141519a b =+++++，故3100a b =+；观察可知，故选D ．4．【答案】B【命题意图】本题考查空间角、空间几何体的结构特征、空间几何体的表面积与体积，考查直观想象、数学运算、逻辑推理的核心素养．【解析】依题意，2cos 3r l θ==，故23r l =；而2210πππ90π9rl r l +==，解得9l =，则263r l ==，故圆锥的体积211π681365π33V Sh ==⨯⨯⨯-=，故选B ．5．【答案】D【命题意图】本题考查函数的图象与性质、函数的零点，考查直观想象、数学运算、逻辑推理的核心素养．【解析】令()0f x =，得124x x -=；在同一直角坐标系中分别作出14x y -=，2y x =的大致图象如图所示；观察可知，两个函数的图象有3个交点(其中1个交点的横坐标介于1-到0之间，另外两个交点分别为()1,1，()2,4，故函数()244x f x x =-的零点个数为3，故选D ．6．【答案】B【命题意图】本题考查数学文化、几何概型，考查直观想象、数学建模、数学运算、逻辑推理的核心素养．【解析】依题意，512sin184BCAC -︒==，故512BC AC =；设ABC △的面积为x ，则BCD △和CEF △的面积均为512x -，CDE △的面积为x，512252551262x xx x-+⋅=-⋅+，故选B ．7．【答案】A【命题意图】本题考查线性回归方程及其应用，考查直观想象、数学运算、逻辑推理的核心素养．【解析】()()()()()522222137579711740ii x x =-=-+-+-+-=∑，而()()55115686780126iii ii i x x y y x y xy ==--=-=-⨯=∑∑，故126ˆ 3.1540b==，故选A ．8．【答案】C【命题意图】本题考查双曲线的方程与性质，考查直观想象、数学运算、逻辑推理的核心素养．【解析】因为11MF N MNF ∠=∠，故1MF MN =．设1MF x =，则22MF x a =-，则222NF MN MF a =-=，则14NF a =．在12NF F △中，由余弦定理，2221122122212cos NF F F NF F F NF NF F =+-∠，化简可得22260c ac a --=，即2260e e --=，解得2212b e a=+=，则3ba=C 的渐近线方程为3y x =，故选C ．二、选择题9．【答案】ABD【命题意图】本题考查空间线面的位置关系，考查直观想象、逻辑推理的核心素养．【解析】A 中，若l m ∥，则n α⊥未必成立；B 中，可能有m β⊂；因为αβ⊥，l αβ⋂=，m α⊂，m l ⊥，则m β⊥，而n β∥，故l n ⊥，故C 正确；D 中，m n ⊥．故选ABD ．10．【答案】BC【命题意图】本题考查数学文化、等比数列的通项公式与前n 项和公式，考查数学建模、数学运算、逻辑推理的核心素养．【解析】依题意，11a =，132a =，故122q =，故812839124a a q ===A 错误；因为43622a q a ==，故B 正确；()112111212121112112122121211111121212a q M q----===------，要证3M >，即证11211312-->-，即证1121421>-，即证112524>，即证12524⎛⎫> ⎪⎝⎭，而()1265 1.524⎛⎫>> ⎪⎝⎭，故C 正确；而3N M =+，要证7N >，即证4M >，即证11211412-->-，即证1121521>-，即证112625>，即证12625⎛⎫> ⎪⎝⎭，而()()12636 1.4 1.925⎛⎫>>> ⎪⎝⎭，故7N >，D 错误，故选BC ．11．【答案】AC【命题意图】本题考查三角函数的图象与性质，考查直观想象、数学运算、逻辑推理的核心素养．【解析】依题意，()()()2πsin cos 2πcos 2πf x x x -=-+-⎡⎤⎣⎦()()sin cos cos x x f x =+=，故A 正确；易知()()2πf x f x +=，故2π为函数()f x 的一个周期；当[]0,πx ∈时，[]cos 1,1x ∈-，故()sin cos y x =，cos y x =在[]0,π上单调递减，即()()sin cos cos f x x x =+在[]0,π上单调递减，由对称性可知，函数()f x 在[]π,2π上单调递增，故B 错误，C 正确；结合单调性以及函数的奇偶性可知，函数()f x 的最大值为()5π620sin111sin 1124f =+<+=+，故D 错误．故选AC ．12．【答案】BCD【命题意图】本题考查空间线面的位置关系、空间几何体的表面积与体积，考查直观想象、数学运算、逻辑推理的核心素养．【解析】因为222AB BC AC +=，故AB BC ⊥，故三棱锥S ABC -的外接球O 的半径222622R ++==；取AC 的中点D ，连接BD 必过点G ，因为2AB BC ==，故1133DG BD ==，因为22OD =，故22221112318OG ⎛⎫⎛⎫=+= ⎪ ⎪ ⎪⎝⎭⎝⎭，则过点G 的平面截球O 所得截面圆的最小半径2261182189r ⎛⎫=-= ⎪ ⎪⎝⎭，故截面面积的最小值为8π9，最大值为23ππ2R =，故选BCD ．三、填空题13．【答案】448-【命题意图】本题考查二项式定理，考查数学运算、逻辑推理的核心素养．【解析】853x x ⎛⎫⎝的展开式的通项公式为()()()31115102848188221rrrr rr r r T C xxC x----+=⋅⋅-=⋅⋅-⋅．令1134102r -=-，解得5r =，故所求系数为()553821448C ⋅⋅-=-．14．【答案】2【命题意图】本题考查平面向量的数量积及其应用，考查直观想象、数学运算、逻辑推理的核心素养．【解析】依题意，()0a b a c a b c ⋅-⋅=⋅-=；而b c ⊥ ，8a b a c ⋅=⋅=，2b c == ，故45a b a c ⋅=⋅=︒，故cos 458a b a b ⋅=︒= ，解得2a =．15．【答案】4【命题意图】本题考查抛物线的方程、直线与抛物线综合性问题，考查直观想象、数学运算、逻辑推理的核心素养．【解析】如图所示，延长BF 交抛物线C 于点A '，则23223sin 60pFA FB A B '+===︒，解得4p =．16．【答案】()(),10,1-∞-⋃【命题意图】本题考查函数的图象与性质、导数的几何意义，考查数学运算、逻辑推理的核心素养．【解析】当0x >时，()()()()()ln 0ln 0ln 0f x f x x x f x x f x x f x x'''+⋅<⇔+⋅<⇔⋅<⎡⎤⎣⎦，故函数()()ln g x x f x =⋅在()0,+∞上单调递减，易知()10g =，故当()0,1x ∈时，()0g x >，()0f x <，当()1,x ∈+∞时，()0g x <，()0f x <；而()()()44440xxf x f x f x ⎡⎤⋅>⇔⋅->⎣⎦，而()()44xh x f x ⎡⎤=⋅-⎣⎦为奇函数，则当0x >时，当()440xf x ⎡⎤⋅->⎣⎦的解为01x <<，故当x ∈R 时，()440xf x ⎡⎤⋅->⎣⎦的解为1x <-或01x <<，故不等式()()44xf x f x ⋅>的解集为()(),10,1-∞-⋃．四、解答题17．【命题意图】本题考查数列的递推公式、数列求和，考查数学运算、逻辑推理的核心素养．【解析】（1）依题意，()1123n n n n n a a a a +++=-，则1123n n n n a a n a a ++-+=，故11123n n nn b a a +-=+=．故125232n n b b n n +-=+--=，故数列{}n b 是公差为2的等差数列．（2）由（1）可知11121n n n a a --=+，121121n n n a a ---=-，…，21115a a -=，累加可得，()()12151112n n n a a ++--=．故()1111222n a n n n n ⎛⎫==- ⎪++⎝⎭，981111111131114651110023243598229910019800S ⎛⎫⎛⎫=-+-+-++-=--=⎪ ⎪⎝⎭⎝⎭L ．18．【命题意图】本题考查独立性检验、超几何分布、离散型随机变量的分布列以及数学期望，考查数学运算、数学建模、逻辑推理的核心素养．【解析】（1）完善表格如下所示：热爱电子竞技对电子竞技无感总计男性20050250女性100150250总计300200500则2K 的观测值()25002001501005025083.33310.8282502503002003k ⨯⨯-⨯==≈>⨯⨯⨯．有99.9％的把握认为A 地25岁以下的年轻人的性别与对电子竞技的爱好程度有关．（2）依题意，这15人中男生有10人，女生有5人，则X 的可能取值为0，1，2，3，故()353155432015141391C P X C ⨯⨯====⨯⨯，()215103155210201571391C C P X C ⨯⨯====⨯⨯，()12510315559452571391C C P X C ⨯⨯====⨯⨯，()310315109824315141391C P X C ⨯⨯====⨯⨯，故X 的分布列为：X 0123P291209145912491则()2045241232919191E X =⨯+⨯+⨯=．19．【命题意图】本题考查空间线面的位置关系、向量法求二面角，考查直观想象、数学运算、逻辑推理的核心素养．【解析】（1）因为OE ∥平面SAB ，OE ⊂平面SBD ，平面SAB ⋂平面SBD SB =，故OE SB ∥．因为四边形ABCD 为矩形，故BO DO =，则SE DE =．（2）∵四边形ABCD 为矩形，∴AB AD ⊥．∵平面SAD ⊥平面ABCD ，平面SAD ⋂平面ABCD AD =，AB ⊂平面ABCD ，∴AB ⊥平面SAD ．∵SA ⊂平面SAD ，∴AB SA ⊥．同理AD SA ⊥．又AB AD A ⋂=，AB ⊂平面ABCD ，AD ⊂平面ABCD ，∴SA ⊥平面ABCD ．设AB a =，以A 为坐标原点，AB ，AD ，AS 所在直线分别为x ，y ，z 轴，建立如图所示的空间直角坐标系，则()0,0,0A ，(),0,0B a ，(),2,0C a ，()0,2,0D ，()0,1,1E ，()0,0,2S ．设(),,m x y z =为平面ABE 的法向量，∵00m AB m AE ⎧⋅=⎪⎨⋅=⎪⎩，∴00x y z =⎧⎨+=⎩，令1y =，则1z =-．∵平面ABE 的一个法向量()0,1,1m =-．设(),,n x y z =为平面CBE 的法向量，∵00n CB n CE ⎧⋅=⎪⎨⋅=⎪⎩，∴200y ax y z -=⎧⎨--+=⎩，令1x =，则z a =．∴平面CBE 的一个法向量()1,0,n a =．∴2320cos ,2021m n m n m na ⋅==-⋅+，解得3a AB ==．20．【命题意图】本题考查正弦定理、余弦定理、三角恒等变换，考查直观想象、逻辑推理、数学运算的核心素养．【解析】（2）依题意，sin sin 22sin cos C A A A ==，即22222b c a c a bc+-=⋅，而sin 2C B =，故2c b =，故32262a a -=-即()(222262a aa a -++=-，化简可得((2220a a +=，因为0a >，故2a b ==．而222a b c +=，故ABC △是等腰直角三角形．（2）由（1）可知，π2C =，设PAC α∠=，其中π0,4α⎛⎫∈ ⎪⎝⎭，而PA AC =，则π22PCA α∠=-，π2PCB ∠=．取BC 的中点D ，则PD BC ⊥，故22cos2PC α=．又2AP AC ==，在APC △中，由正弦定理，22cos22πsin sin 22ααα=⎛⎫- ⎪⎝⎭．化简可得，1sin 2α=．因为π0,4α⎛⎫∈ ⎪⎝⎭，即π6α=，故ππ62cos cos 464PAB +⎛⎫∠=-=⎪⎝⎭．21．【命题意图】本题考查椭圆的方程、直线与椭圆综合性问题，考查直观想象、逻辑推理、数学运算的核心素养．【解析】（1）依题意，22222121914c a ab a bc ⎧=⎪⎪⎪+=⎨⎪⎪-=⎪⎩，解得24a =，23b =，故椭圆C 的方程为22143x y +=．（2）当()2,0M -，31,2N ⎛⎫⎪⎝⎭，()1,G t 时，直线MG 的方程为()23t y x =+，交y 轴于点20,3t ⎛⎫⎪⎝⎭；当31,2M ⎛⎫⎪⎝⎭，()2,0N -，()2,G t -时，直线MG 的方程为()332123t y x --=--，交y 轴于点30,3t +⎛⎫ ⎪⎝⎭．若直线MG 经过y 轴上定点，则2333t t +=，即3t =，直线MG 交y 轴于点()0,2．下面证明存在实数3t =，使得直线MG 经过y 轴上定点()0,2．联立221143y kx x y =+⎧⎪⎨+=⎪⎩，消y 整理，得()2243880k x kx ++-=，设()11,M x y ，()22,N x y ，则122843k x x k -+=+，122843x x k -=+．设点()2,3G x ，所以直线MG 的方程：()121233y y x x x x --=--．令0x =，得()121212121121212121212313333x x kx x y x x x yx x kx x y x x x x x x x x -+-+---=+===----．因为1212kx x x x =+，所以()12121212123222x x x x x x y x x x x --+-===--．所以直线MG 过定点()0,2．综上所述，存在实数3t =，使得直线MG 经过y 轴上定点()0,2．22．【命题意图】本题考查利用导数研究函数的性质，考查数学运算、逻辑推理、直观想象的核心素养．【解析】（1）依题意，()2sin 2cos x f x e x x x '=+-．因为[]0,πx ∈，所以1xe ≥，sin 0x x ≥，因此()22cos 0f x x '≥-≥，所以()f x 在[]0,π上单调递增，于是()()02f x f ≥=，故函数()f x 的最小值为2．（2）令()1sin xg x e mx x x =---，()()sin cos 1xg x e m x x x '=-+-，当12m ≤时，()1sin 12xg x e x x x ≥---，由（1）可知，当(]0,πx ∈时，1sin 102xe x x x --->，∴当(]0,πx ∈时，()0g x >．而()00g =，∴当[]0,πx ∈时，()g x 仅有1个零点，舍去．当12m >时，()()cos sin 1x g x e m x x x '=-+-，()()sin 2cos xg x e m x x x ''=+-．当π,π2x ⎡⎤∈⎢⎥⎣⎦时，()0g x ''>，所以()g x '单调递增．当π0,2x ⎡⎤∈⎢⎥⎣⎦时，()()3sin cos x g x e m x x x '''=++．因为0xe >，()3sin cos 0m x x x +≥，所以()0g x '''>，所以()g x ''单调递增．又()0120g m ''=-<，π2ππ022g e m ⎛⎫''=+>⎪⎝⎭，因此()g x ''在π0,2⎡⎤⎢⎥⎣⎦上存在唯一的零点0x ，且0π0,2x ⎛⎫∈ ⎪⎝⎭．当()00,x x ∈时，()0g x ''<，所以()g x '单调递减；当0π,2x x ⎛⎫∈ ⎪⎝⎭时，()0g x ''>，所以()g x '单调递增．又()00g '=，()()000g x g ''<=，()πππ10g e m '=+->，因此()g x '在[]0,π上存在唯一的零点1x ，且()10,πx x ∈．当()10,x x ∈时，()0g x '<，所以()g x 单调递减；当()1,πx x ∈时，()0g x '>，所以()g x 单调递增．又()00g =，()()100g x g <=，()πππ10g e =-->，所以()g x 在()1,πx 上存在唯一零点，因此()g x 在[]0,π上有两个零点．综上所述，实数m 的取值范围是1,2⎛⎫+∞⎪⎝⎭．。

高中数学毕业班3月质量检查考试试题

2021届高中数学毕业班3月质量检查考试试题一、选择题〔50分〕1．设复数z 满足〔1＋i 〕＝2〔i 为虚数单位〕，那么z ＝ A.1一i B.1＋i C ．一1一i D.一1＋i 2.某程序框图如下图，那么输出的S 的值是A.11B. 19C. 26D. 573．设集合A ＝｛x ｜x ＜a ｝，B ＝｛x ｜x ＜3｝，那么“a ＜3”是“A ⊆C B 〞的4.如图，函数f(x)＝()sin(2)(0,||)2f x A x A πϕϕ=+><的图象过点(0，3〕，那么 f(x)的图象的一个对称中心是A 、〔－3π，0〕 B 、〔－6π，0〕 C 、〔6π，0〕 D 、〔4π，0〕 5．高三年上学期期末考试中，某班级数学成绩的频率分布直方图如下图，数据分组依次如下：［70，90〕，［90，110〕，［110，130〕，［130，150］．估计该班级数学成绩的平均分等于A. 112 B ．114 C ．1161B 1C 1D 1中，AA 1＝2AB ＝2AD ，G 为CC 1中点，那么直线A 1C 1与 BG 所成角的大小是A. 30°B. 45°C. 60°D. 120° 7、数列{n a ｝满足11111,1(*)211n n a n N a a +==-∈--学科网，那么10a ＝ A.910 B. 109 C, 1011 D. 11108.如图，正六边形ABCDEF 中，AB ＝2，那么()()BC BA AF BC -+＝A. -6B. －3 3 D. 69.f(x)是定义在R 上的奇函数，且f 〔x －2〕＝f 〔x ＋2〕，当0＜x ＜2时,f(x)＝1一log 2(x ＋1〕，那么当0 <x <4时，不等式〔x 一2〕f 〔x 〕＞0的解集是 A. (0，1〕 (2,3〕 B. (0，1〕〔3,4〕C.〔1,2〕〔3,4〕 D 〔1,2〕〔2，3〕10.函数f (x)＝321(23)()3x mx m x m R +++∈存在两个极值点12,x x ，直线l 经过点211(,)A x x ，222(,)B x x ，记圆221(1)5x y ++=上的点到直线l 的最短间隔为g 〔m 〕，g 〔m 〕的取值范围是A. [0,2]B. [0,3]C. [0，5 D 、[0，5〕第II 卷〔非选择题一共100分〕二、填空题：本大题一一共5小题，每一小题4分，一共20分． 11、62()x x-的展开式中的常数项是〔用数字答题〕．,x y 满足约束条件260240x y y x +-≥⎧⎪≤⎨⎪-≤⎩学科网，那么y x 的最小值为＿＿＿ {n a ｝的前n 项和为Sn ，S 3二a 1十3a 2，那么公比q ＝＿＿＿．a 和b ，在a ＋b 为偶数的条件下｜a －b ｜＞2发生的概率是＿．15.如图，在平面直角坐标系xoy 中，将直线2xy =与直线x ＝1及x 轴所围成的图形绕x 轴旋转一周得到一个圆锥，圆锥的体积据此类比：将曲线y＝x2与直线y＝4所围成的图形绕y轴旋转一周得到一个旋转体，该旋转体的体积V＝＿＿＿三、解答题：本大题一一共6小题：一共80分．解容许写出必要文字说明、证明过程或者演算步骤．16．〔本小题满分是13分〕在2021-2021赛季CB A常规赛中，某篮球运发动在最近5场比赛中的投篮次数及投中次数如下表所示：〔I)分别求该运发动在这5场比赛中2分球的平均命中率和3分球的平均命中率；〔II〕视这5场比赛中2分球和3分球的平均命中率为相应的概率，假设该运发动在第6场比赛终场前一分钟分别获得1次2分球和1次3分球的投篮时机，求该运动员在最后一分钟内得分的分布列和数学期望．17．〔本小题满分是13分〕在平面直角坐标系xoy 中，点P 〔x ，y 〕满足a ·b =3，其中向量a ＝〔2x +3，y 〕，b ＝〔2x －3，y 〕．〔I 〕求点P 的轨迹方程；〔II 〕过点F 〔0,1〕的直线l 交点P 的轨迹于A ，B 两点，假设｜AB ｜＝165，求直线l 的方程．18．〔本小题满分是13分〕如图，在Rt △ABC 中，∠ACB ＝2π，AC=3，BC ＝2，P 是△ABC 内的一点．〔I)假设P 是等腰直角三角形PBC 的直角顶点，求PA 的长；〔II 〕假设∠BPC ＝23π，设∠PCB ＝θ，求△PB C 的面积S 〔θ〕的解析式，并求S(θ)的最大值·19．〔本小题满分是13分〕等边三角形PAB 的边长为2，四边形ABCD 为矩形，AD =4,平面PAB ⊥平面ABCD, E ，F ，G 分别是线段AB ，CD ，OD 上的点·〔I 〕如图〔〔1〕，假设G 为线段PD 的中点，BE ＝DF ＝23，证明：PB ∥平面EFG; 〔II 〕如图(2〕，假设E, F 分别为线段AB ，CD 的中点，DG = 2 GP ，试问：矩形ABCD 内〔包括边界〕能否找到点H ，使之同时满足以下两个条件，并说明理由．〔i 〕点H 到点F 的间隔与点H 到直线AB 的间隔之差大于4；〔ii 〕GH ⊥PD ．20．〔本小题满分是14分〕函数2411()(,())222x f x f x m =+在处的切线方程为8x －9y ＋t ＝0.〔,m N t R ∈∈) 〔I 〕求m 和t 的值；〔II 〕假设关于x 的不等式f(x) 89ax ≤+在［1,2+∞〕恒成立，务实数a 的取值范围，21．此题有〔1〕、〔2〕、〔3)三个选答题，每一小题7分，请考生任选2题答题，满分是14分，假如多做，那么按所做的前两题计分．答题时，先需要用2B 铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填人括号中．(1〕〔本小题满分是7分〕选修4-2：矩阵与变换矩阵M ＝11a b ⎛⎫ ⎪⎝⎭ 的一个属于特征值3的特征向量11α⎛⎫⎪⎝⎭＝，正方形区域OABC 在矩阵N对应的变换作用下得到矩形区域OA'B'C’，如下图．〔I〕求矩阵M;〔II〕求矩阵N及矩阵〔MN〕－1．(2〕〔本小题满分是7分〕选修4-4：坐标系与参数方程平面直角坐标系xoy中，圆C1的参数方程为22cos(y=2sinϕϕϕ⎧⎨⎩x=＋为参数〕，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，圆C2的极坐标方程为ρ＝4sin9.〔I〕写出圆C1的普通方程及圆C2的直角坐标方程；〔II)圆C1与圆C2是否相交，假设相交，恳求出公一共弦的长；假设不相交，请说明理由．(3〕〔本小题满分是7分〕选修4一5：不等式选讲函数f(x)＝｜x一m｜，关于x的不等式f(x) ≤3的解集为［一1,5］．〔I〕务实数m的值；〔B〕a，b，c∈R，且a－2b＋2c＝m，求a2＋b2＋c2的最小值．励志赠言经典语录精选句；挥动**，放飞梦想。

高三数学三月质量检测试卷

一、选择题（每题5分，共50分）1. 已知函数f(x) = 2x^3 - 3x^2 + 4x + 1，则f(x)的零点个数是（）A. 1B. 2C. 3D. 42. 若向量a = (1, 2, 3)，向量b = (2, 1, 0)，则向量a与向量b的夹角余弦值是（）A. 1/3B. 2/3C. 1D. 03. 已知数列{an}是等差数列，且a1 = 3，a5 = 15，则公差d等于（）A. 2B. 3C. 4D. 54. 下列函数中，在区间（0，+∞）上单调递增的是（）A. y = x^2 - 4x + 3B. y = 2x - 1C. y = x^3 - 3x^2 + 4x - 1D. y = 1/x5. 已知等比数列{an}的前三项分别为a1，a2，a3，且a1 + a2 + a3 = 14，a1 a3 = 36，则该数列的公比q等于（）A. 2B. 3C. 4D. 66. 已知函数f(x) = |x - 2| + |x + 1|，则f(x)的图像是（）A. 单调递增B. 单调递减C. 先递增后递减D. 先递减后递增7. 若函数f(x) = x^2 - 4x + 5在区间[1，3]上的最大值为m，最小值为n，则m + n等于（）A. 8B. 9C. 10D. 118. 已知向量a = (2, 3)，向量b = (-1, 2)，则向量a与向量b的叉积等于（）A. 1B. 2C. 3D. 49. 若等差数列{an}的前n项和为Sn，且a1 = 3，公差d = 2，则S10等于（）A. 110B. 120C. 130D. 14010. 已知函数f(x) = x^3 - 6x^2 + 9x - 1，则f(x)的图像是（）A. 单调递增B. 单调递减C. 先递增后递减D. 先递减后递增二、填空题（每题5分，共50分）11. 若函数f(x) = x^2 - 4x + 3的图像的对称轴为x = ，则f(x)的图像与x轴的交点坐标为______。

2021-2022年高三数学3月教学质量检测试题

2021-2022年高三数学3月教学质量检测试题一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若集合，，则（）A． B． C． D．2.已知复数满足，则复数的虚部等于（）A．1 B．-1 C． 2 D．-23.在等差数列中，已知是函数的两个零点，则的前9项和等于（）A．-18 B．9 C．18 D．364.下列关于命题的说法错误的是（）A．函数的最小值为2B．命题“”的否定是“”；C．“”是“”的充要条件；D．，5.阅读下边的程序框图，运行相应的程序，输出的结果为（）A． B． C． D．36.已知是R上的偶函数,且满足,当时, ,则A．-2 B．2 C．-4 D．47.在区间上随机取一个x,则y=sinx在0到之间的概率为A． B． C． D．8.中国古代数学著《九章算术》中记载了公元前344年商鞅督造一种标准量器——商鞅铜方升，其三视图如图所示（单位：寸），若取3，其体积为13.5（立方寸），则图中的为（）A．2.4 B．1.8 C．1.6 D．1.29.设不等式组104x x y x y ≥⎧⎪-≤⎨⎪+≤⎩，表示的平面区域为，若直线上存在内的点，则实数的取值范围是（）A ．B ．C ．D ．10.已知三棱锥的四个顶点均在同一球面上，其中是正三角形，平面，，则该球的表面积为（） A ． B ． C ． D ．11.已知离心率为的双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为，是双曲线的一条渐近线上的点，且，为坐标原点，若，则双曲线的实轴长是（） A ．32 B ．16 C ．8 D ．412.已知21()[(3)](2)2x f x x a x b =----，当x<0时，，则a 的取值范围为 A ． B ． C ． D ．第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每小题5分，共20分）13.平面内有三点(03),(33),(x -1A B C -，，，），且，则x 为．14.过抛物线的焦点作直线交抛物线于，若，则线段AB 中点的纵坐标为． 15.已知为数列的前项的和，对都有，若，则．16.若实数满足，则的最小值为．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17. 已知23()3sin cos f x x x x =+-（1）求的单调增区间；（2）已知中，为锐角且，，求周长的最大值. 18（本小题满分12分）如图，菱形ABCD 的边长为12，∠BAD=60°，．将菱形ABCD 沿对角线AC 折起，得到三棱锥B-ACD ，点M 是棱Bc 的中点，DM=6． (I)求证：OD ⊥平面ABC ；(Ⅱ)求三棱锥M -ABD 的体积，19．（本小题满分12分）某市为鼓励居民节约用水，将实行阶梯式计量水价，该市每户居民每月用水量划分为三档，水价实行分档递增第一级水量：用水量不超过20吨，水价标准为1.60元／吨；第二级水量：用水量超过20吨但不超过40吨，超出第一级水量的部分，水价标准比第一级水价提高0 80元／吨；第=三级水量：用水量超过40吨，超出第二级水量的部分，水价标准比第一级水价提高1.60元／吨随机调查了该市500户居民，获得了他们某月的用水量数据，整理得到如下的频率分布表：(I)根据频率分布表中的数据，写出a ，b ，c 的值；(Ⅱ)从该市调查的500户居民中随机抽取一户居民，求该户居民用水量不超过36吨的概率；(Ⅲ)假设同组中的每个数据用该组区间的中点值代替，试估计该市每户居民该月的平均水费。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

济南外国语学校2011-2012学年度第一学期高三质量检测数学试题（2011.9）（时间120分钟，满分120分）第Ⅰ卷一．选择题（本题共12个小题，每题4分，共48分）1．全集U ＝{1,2,3,4,5,6},集合M ＝{2,3,5},N ＝{4,5},则∁U (M ∪N )= ( )A ．{1,3,5}B ．{2,4,6}C ．{1,5}D ．{1,6}2. 若0cos 02sin <>αα且，则α是 ( ) A.第二象限角 B.第三象限角 C.第一或第三象限角 D.第二或第三象限角 3．已知54sin ),2,2(-=-∈αππα，则αtan 等于 ( )A.43-B.34- C.53- D.344. 下列函数中，在其定义域内既是奇函数又是增函数的是（）A.2+5()y x x R =-∈B.3-()y x x x R =+∈C. )(3R x x y ∈=D. )0,(1≠∈-=x R x xy5. 已知奇函数)(x f 的图象是两条直线的一部分（如图所示），其定义域为]1,0()0,1[⋃-，则不等式1)()(->--x f x f 的解集是（） A.{}011|≠≤≤-x x x 且 B.⎭⎬⎫⎩⎨⎧≤<-<≤-10211|x x x 或 C.{}01|<≤-x x D.⎭⎬⎫⎩⎨⎧≤<<≤-12101|x x x 或 6. 设 1.50.90.4812314,8,2y y y -⎛⎫=== ⎪⎝⎭，则（）A. 312y y y >>B. 213y y y >>C. 132y y y >>D.123y y y >>7.若等差数列{}n a 的前3项和3191S a ==且，则2a 等于 ( )A 、3B 、4C 、5D 、68.各项都为正项的等比数列{}n a 中，首项13a =，前三项和为21，则345a a a ++=（）A 、33B 、72C 、84D 、1899 .已知平面上三点A 、B 、C 满足3AB =u u u r ，4BC =u u u r ，5CA =u u u r，则AB BC BC CA CA AB ⋅+⋅+⋅u u u r u u u r u u u r u u u r u u u r u u u r的值等于 ( )A.25B.24C.－25D.－24 10.已知b a b a k b a 3),2,3(),2,1(-+-==与垂直时k 值为 ( ) A.17 B.18 C.19 D.2011.已知)(x f '是函数)(x f 的导数，y=)(x f '的图象如图所示，则y=)(x f 的图象最有可能是下图中（）12.设x ，y 满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x ，若目标函数z=ax+by （a>0，b>0）的是最大值为12，则23ab +的最小值为 ( ).A.625B. 38C. 311D. 4第Ⅱ卷题号二1819202122总分合分人复核人得分二．填空题（本题共4个小题，每题4分，共16分）得分13.已知△ABC 的周长为9，且4:2:3sin :sin :sin =C B A ，则cos C ＝ . 14. 已知βα,⎪⎭⎫⎝⎛∈ππ,43，sin(βα+)=－,53 sin ,13124=⎪⎭⎫ ⎝⎛-πβ则cos ⎪⎭⎫⎝⎛+4πα= _______ . 15．设的最小值，求且yxy x y x 11120,0+=+>> ．16．等比数列｝｛n a 的公比为q ，前n 项的积为n T ，并且满足()01)1(,01,120102009201020091<-->-⋅>a a a a a ，给出下列结论①10<<q ；②120112009<⋅a a ；③2010T 是n T 中最大的；④使得1>n T 成立的最大的自然数n 是4018.其中正确结论的序号为（将你认为正确的全部填上）.三．解答题（本题共六个小题，共56分）17.（8分）已知(sin ,cos ),(cos )a x x b x x =-=r v，函数()f x a b =⋅rr （1）求)(x f 的最小正周期，并求其图象对称中心的坐标；（2）当02x π≤≤时，求函数f (x )的值域.18. （8分）二次函数)(x f 满足x x f x f 2)()1(=-+，且1)0(=f .（1）求)(x f 的解析式；（2）在区间[]1,1-上，)(x f y =图象恒在直线m x y +=2上方，试确定实数m 取值范围.19. （8分）已知函数21()21x x f x -=+，（1）判断函数()f x 的奇偶性；（2）求证：()f x 在R 上为增函数；20．（ 10分）学校要建一个面积为2392m 的长方形游泳池，并且在四周要修建出宽为2m 和4m 的小路（如图所示）。

问游泳池的长和宽分别为多少米时，占地面积最小？并求出占地面积的最小值。

21. （10分）已知：数列}{n a 的前n 项和为n S ，,31=a 且当n 2≥,*∈N n 满足 1n S -是n a 与-3的等差中项.(1)求432,,a a a ；(2) 求数列}{n a 的通项公式.22．（12分）已知函数f (x )＝x 3－ax 2－3x .(1)若f (x )在区间[1，＋∞)上是增函数，求实数a 的取值范围；(2)若x ＝－13是f (x )的极值点，求f (x )在[1，a ]上的最大值；(3)在(2)的条件下，是否存在实数b ，使得函数g (x )＝bx 的图象与函数f (x )的图象恰有3个交点？若存在，请求出实数b 的取值范围；若不存在，试说明理由．高三数学参考答案一．选择题1. D2. B3. B4. C5. B6. C7.A8. C9. C 10. C 11. B 12.A二．填空题13.14- 14.－655615.223+ 16.①②④ 三．解答题17.解：（1）2()sin cos f x x x x =sin(2)3x π=- ………2分所以)(x f 的最小正周期为π令sin(2)03x π-=，得2,,.326k x k x k Z ππππ-=∴=+∈．故所求对称中心的坐标为(,0),().26k k Z ππ+∈- ………4分（2）0.2x π≤≤Q 22.333x πππ∴-<-≤………6分即)(x f的值域为.⎡⎤⎢⎥⎣⎦- ………8分18. 解：（1）由1)0(=f ，可设)0(1)(2≠++=a bx ax x f故)1(1)1()1()()1(22++-++++=-+bx ax x b x a x f x f b a ax ++=2由题意得，⎩⎨⎧=+=022b a a ，解得⎩⎨⎧-==11b a ；故1)(2+-=x x x f ………4分（2）由题意得，m x x x +>+-212 即m x x >+-132 对[]1,1-∈x 恒成立设13)(2+-=x x x g ，则问题可转化为m x g mim >)(又)(x g 在[]1,1-上递减，故1)1()(-==g x g mim ，故1-<m ………8分19．证明：（1）函数()f x 的定义域为R ，且212()12121x x x f x -==-++，所以2222()()(1)(1)2()21212121x x x x f x f x ---+=-+-=-+++++即()()f x f x -=-，所以()f x 是奇函数. ………4分（2）R x x ∈21、设，21x x <有()()()121212121222221212121(21)(21)x x x x x x x x f x f x ----=-=++++，所以，函数()f x 在R 上是增函数. ………8分 20．解：设游泳池的长为xm ，则游泳池的宽为392m x, 又设占地面积为2ym ，……2分依题意，得392784(8)(4)4244()424224y x x x x=++=++≥+=当且仅当784x x=,即28x =时,取“=”. 答：游泳池的长为28m ,宽为737m ………10分21.解：（1）由题知，1n S -是n a 与-3的等差中项.∴123n n S a -=- 即123n n a S -=+（n 2≥,*∈N n ） ………………………2分()81323232134=+++=+=a a a S a ………………………………………5分（2）由题知321+=-n n S a （n 2≥,*∈N n ） ①②—①得n n n n n a S S a a 2)(211=-=--+ 即n n a a 31=+（n 2≥,*∈N n ）③ ………8分 Q 123a a =也满足③式即 n n a a 31=+（*∈N n ） ∴ }{n a 是以3为首项，3为公比的等比数列.∴ n a =n 3（*∈N n ） ……………10分22.【解】 (1)f ′(x )＝3x 2－2ax －3. ∵f (x )在[1，＋∞)是增函数，∴f ′(x )在[1，＋∞)上恒有f ′(x )≥0，即 3x 2－2ax －3≥0在[1，＋∞)上恒成立，则必有a3≤1且f ′(1)＝－2a ≥0.∴a ≤0. ………4分(2)依题意，f ′(－13)＝0，即13＋23a －3＝0. ∴a ＝4，∴f (x )＝x 3－4x 2－3x . 令f ′(x )＝3x 2－8x －3＝0，得x 1＝－13，x 2＝3.则当x 变化时，f ′(x )与f (x )变化情况如下表∴f (x )在[1,4]上的最大值是f (1)＝－6. ………8分(3)函数g (x )＝bx 的图象与函数f (x )的图象恰有3个交点，即方程x 3－4x 2－3x ＝bx 恰有3个不等实根． ∴x 3－4x 2－3x －bx ＝0， ∴x ＝0是其中一个根，∴方程x 2－4x －3－b ＝0有两个非零不等实根．∴⎩⎨⎧Δ＝16＋4(3＋b)＞0－3－b ≠0∴b ＞－7且b ≠－3.∴存在满足条件的b 值，b 的取值范围是b >－7且b ≠－3. ………12分希望以上资料对你有所帮助，附励志名3条：1、积金遗于子孙，子孙未必能守；积书于子孙，子孙未必能读。

不如积阴德于冥冥之中，此乃万世传家之宝训也。

2、积德为产业，强胜于美宅良田。

新高三月质量检测试题目数学7页

八年级数学第二学期3月份 质量检测测试卷含答案

【新结构】华大新高考联盟2024届高三下学期3月教学质量测评数学试卷+答案解析

江苏常熟中学2024届高三第二学期3月高考诊断性测试数学试题

高三数学3月复习质量监测卷六文扫描版,含答案

高三数学下学期3月质量检测试题文含解析试题

人教版八年级数学上学期3月份质量检测测试卷含答案

人教版八年级数学上学期3月份质量检测测试卷

新高三月质量检测试题目数学共5页文档

2021年高一3月质量检测数学试题(实验班)含答案

2021年高一下学期3月质检数学试卷(重点班)含解析

高三数学3月第一次质量普查调研考试试题 理含解析 试题

人教版八年级数学上学期3月份质量检测测试卷含答案

高三数学3月质量检测试题含解析 试题

华大新高考联盟2022届高三3月教学质量测评(新高考卷)数学试题及答案

高中数学毕业班3月质量检查考试试题

高三数学三月质量检测试卷

2021-2022年高三数学3月教学质量检测试题

八年级数学第二学期3月份质量检测测试卷含答案

高三数学3月第一次质量普查调研考试试题理含解析试题

高三数学3月质量检测试题含解析试题