微观经济学-清华大学课件Ch5Choice消费者最优选择
合集下载
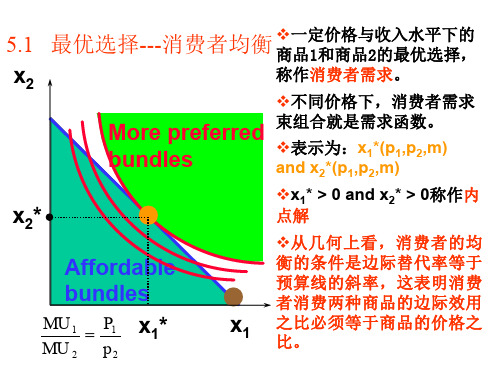
消费者最优选择

可以得到一个新的包含约束条件的目标效用函数,即
u( x) x1a x2b
求这一效用函数的一阶导数并令其为零得:
x*1
(a
am b)p1
.
x*2
(a
bm b)p2
.
❖ 3.约束条件极值求解法--根据目标函数和约束条 件p1x1 + p2x2 = m建立拉格朗日函数,即:
u( x) x1a x2b
x1*
x1*
a
a
b
m p1
Engel curve for good 1
x
* 2
b a
b
m p2
x1*
恩格尔曲线
m
m
(a
b) b
p2
x2*
Engel
curve
for good 2
x2*
m
a
a
b
p1 x1*
m
b
b
p2 x2*
不同偏好条件下的收入提供曲线和恩格尔曲线
(二)完全替代 ❖ 当边际替代率的绝对值大于预算线的斜率的绝对值时,收入提供曲线
x2
称作消费者需求。
❖不同价格下,消费者需求
束组合就是需求函数。
More preferred
bundles
❖表示为:x1*(p1,p2,m) and x2*(p1,p2,m)
❖x1* > 0 and x2* > 0称作内
x2*
点解
❖从几何上看,消费者的均
Affordable bundles
衡的条件是边际替代率等于 预算线的斜率,这表明消费 者消费两种商品的边际效用
p1 p2
MRS12
p1 p2
MRS12
u( x) x1a x2b
求这一效用函数的一阶导数并令其为零得:
x*1
(a
am b)p1
.
x*2
(a
bm b)p2
.
❖ 3.约束条件极值求解法--根据目标函数和约束条 件p1x1 + p2x2 = m建立拉格朗日函数,即:
u( x) x1a x2b
x1*
x1*
a
a
b
m p1
Engel curve for good 1
x
* 2
b a
b
m p2
x1*
恩格尔曲线
m
m
(a
b) b
p2
x2*
Engel
curve
for good 2
x2*
m
a
a
b
p1 x1*
m
b
b
p2 x2*
不同偏好条件下的收入提供曲线和恩格尔曲线
(二)完全替代 ❖ 当边际替代率的绝对值大于预算线的斜率的绝对值时,收入提供曲线
x2
称作消费者需求。
❖不同价格下,消费者需求
束组合就是需求函数。
More preferred
bundles
❖表示为:x1*(p1,p2,m) and x2*(p1,p2,m)
❖x1* > 0 and x2* > 0称作内
x2*
点解
❖从几何上看,消费者的均
Affordable bundles
衡的条件是边际替代率等于 预算线的斜率,这表明消费 者消费两种商品的边际效用
p1 p2
MRS12
p1 p2
MRS12
微观经济学消费者选择ppt课件

随着消费者对该商品消费量的增加,总效用也在增加, 但总效用的增加会呈现出递减的趋势。西方经济学家把边 际效用的这种变化趋势称为边际效用递减规律。
边际效用递减规律表明:在其他商品的消费保持不变 的情况下,随着消费者对某种商品的消费量的增加,其边 际效用最终将趋向下降。
边际效用为什么 会递减呢?
解释: 1) 生理或心理上的原因 2) 物品用途上的原因
14
货币存在边际效用递减的规律吗?
如若存在,将意味着什么呢?
本书将货币的边际效用看做是一个常数。
15
三、消费者均衡分析
此部分内容是要告诉你 消费者如何做才能实现效用 的最大化。
1.消费者均衡的含义:是指单个消费者追求效用最大 化时所采取的购买行为。(考虑三个因素:欲望、货币收 入和商品价格)
消费者均衡是研究消费者如何把全部的货币收入分 配在购买各种商品中以获得最大的效用。此时,消费 者既不想再增加也不想再减少任何商品的购买数量。
第三章 消费者选择(效用论)
1
•教学目的及要求:通过本章的学
习,要求学生掌握无差异曲线和
预算线的含义及特点、消费者均
衡的约束条件和均衡条件、需求
曲线的推导方Βιβλιοθήκη 、替代效应和收入效应的含义,并能对不同物品
的价格效应进行正确分解。
•教学重点:基数效用论和边际效
用分析方法,序数效用论和无差
异曲线分析方法
2
效用论概述
知识结构
替代效应 收入效应
基数 序数 不确定性
边际效用递减 消费者均衡
无差异曲线 预算线
消费者均衡 单个需求曲线
价格变化 收入变化
市场需求曲线
3
消费者行为是指在一定的收入和价格下消费 者为获得最大满足而对各种商品所作出的选择活 动。本章就是考察决定需求的消费者行为理论, 首先研究消费者的个人效用,其次考察消费者的 预算约束,在此基础上,进一步阐明消费者的选 择问题。
《微观经济学》清华大学-Tsinghua Micro Ch14 021025.ppt

Only in one special circumstance do these three measures coincide.
$ Equivalent Utility Gains
Suppose rice can be bought only in lumps of one kilogram.
Consumer’s Surplus
p1 p1(x1), the inverse ordinary demand curve for commodity 1
Q: What is the most you would pay to enter the market?
Monetary Measures of Gains-toTrade
A: You would pay up to the dollar value of the gains-to-trade you would enjoy once in the market.
Use r1 to denote the most a single consumer would pay for a 1st kilogram -- call this her reservation price for the 1st kilogram.
r1 is the dollar equivalent of the marginal utility of the 1st kilogram.
so, as an approximation, the reservation-price curve is replaced with the consumer’s ordinary demand curve.
Consumer’s Surplus
$ Equivalent Utility Gains
Suppose rice can be bought only in lumps of one kilogram.
Consumer’s Surplus
p1 p1(x1), the inverse ordinary demand curve for commodity 1
Q: What is the most you would pay to enter the market?
Monetary Measures of Gains-toTrade
A: You would pay up to the dollar value of the gains-to-trade you would enjoy once in the market.
Use r1 to denote the most a single consumer would pay for a 1st kilogram -- call this her reservation price for the 1st kilogram.
r1 is the dollar equivalent of the marginal utility of the 1st kilogram.
so, as an approximation, the reservation-price curve is replaced with the consumer’s ordinary demand curve.
Consumer’s Surplus
中级微观经济学课件-Chapter5_Choice

p1x1 p1 • a • m a m m a b p1 a b
u ( x1 ,
x2 )
x1a
x1a 2
Optimizing Mathematically
In trying to “do the best she can given her circumstances”, a consumer choosesa bundle (x1,x2)
那么计算一般需求以柯布道格拉斯函数为例因此mrsmrsdxdxaxbx计算一般需求以柯布道格拉斯函数为例因此mrs因此mrsdxdxaxbx计算一般需求以柯布道格拉斯函数为例因此mrs因此mrsdxdxaxbxaxbxbpap计算一般需求以柯布道格拉斯函数为例计算一般需求以柯布道格拉斯函数为例因此可知bpap计算一般需求以柯布道格拉斯函数为例因此可知bpap代入计算一般需求以柯布道格拉斯函数为例因此可知bpapbpap代入可得可简化为计算一般需求以柯布道格拉斯函数为例计算一般需求以柯布道格拉斯函数为例计算一般需求以柯布道格拉斯函数为例我们得到了柯布道格拉斯效用函数的消费者最优可行消费束
在最优选择点上,
无差异曲线不穿过预算线。
x2*
x1*
x1
x2
消费束(x1,x2)是无差异曲
线和预算线的交点
x2
x1
x1
x2
消费束(x1,x2)是无差异曲线
和预算线的交点,则在红色
x2
线段上总能够找到比(x1,x2) 更好的点
x1
x1
❖ 无差异曲线不穿过预算线是否就意味着 相切呢?
❖ 大多数情况下是如此,但存在例外。
This is an example of a constrained optimization problem.
北大微观经济学(英文版)ch5 ChoicePPT课件

Affordable
bundles
2020/8/3
x1
中级微观经济学
6
Rational Constrained Choice
x2
x2*
2020/8/3
x1*
x1
中级微观经济学
7
Rational Constrained Choice
x2
(x1*,x2*) is the most
preferred affordable
(b) The slope of the indiff.
curve at (x1*,x2*) equals the slope of the budget
constraint. x2*
2020/8/3
x1*
x1
中级微观经济学
13
Rational Constrained Choice
(x1*,x2*) satisfies two conditions:
(x1, x2) is not optimal choice
She can be better off increasing her
2020c/8/o3 nsumption of x . 中级 1 微观经济学
15
x2
2020/8/3
x1
x1
中级微观经济学
16
Computing Ordinary Demands
bundle.
x2*
2020/8/3
x1*
x1
中级微观经济学
8
Rational Constrained Choice
The most preferred affordable bundle is called the consumer’s ORDINARY DEMAND (一般需求)at the given prices and budget. Ordinary demands will be denoted by x1*(p1,p2,m) and x2*(p1,p2,m).
微观经济学第五章 消费者选择

其时显示性偏好强相对于偏好弱只是多了 一个不存在间接显示偏好,即排除了在偏 好弱公理上可能发生的传递性悖论,而性 状良好偏好的无差异曲线正好可以满足传 递性,所以在此基础上最优化的行为对应 的就是显示性偏好强,或者说我们观察到 的最优化行为一定满足显示性偏好强公理。
三、利用显示偏好理论导出无差异曲线
一、预算线与消费者生活水平的比较
利用预算线以及预算限值下消费者实际购买选择可以进行 这种生活状况的比较。
x2
p1
p0
1 X
X0
o
p1
p0
x1
图5-18 消费者1期生活水平高于0期
x2
p
0
0 X
x2
p1
1 X
p1
p0
X1
X0
o
p0
p1
x1
o
p1
p0
x1
图5-19 消费者0期生活水平好 于 1期
萨缪尔森(Samuelson,1938年)最先提出显示偏 好公理,可以概括为:如果消费者的行为是追求 效用最大化,那么消费者在市场上所能购买的商 品组合就是他所能购买的最优商品组合,这些实 际购买的商品组合优于那些消费者有能力购买而 没有购买的商品组合。 显示偏好弱公理,如果组合A直接显示出比B更被 消费者所偏好,而且,A和B不同,则不可能有直 接显示出B比A更被消费者偏好。 显示偏好强公理,如果A(直接或间接地)显示 比B更被消费者所偏好,而且A和B不同,则不可 能有组合B(直接或间接地)显示比A更被消费者 所偏好。
E2
E1
U1
E
S
U2
o
q0
q1
j0
清华大学讲义——微观经济学课程PPT

历年考题 名词解释 资本的边际替代率(2002年) 论述及计算 (2008年)已知某厂商的生产函数为Q=L2/5K3/5, 劳动的价格为PL=2,资本的价格为PK=3。试问: ①产量为10时,最低成本支出的大小和L与K的使 用数量; ②总成本为60元时,厂商的均衡产量和L与K的使 用数量; ③什么是边际收益递减规律?该生产函数的要素报 酬是否受该规律支配,为什么?
p D3 p2 E p1 p3 D E3 D1
D2 E2 E1
S
pE
O p S3 p3 p1 p2 D O x3 x1 x2 E3 E1 E2 S1 S2
xE p p2 D3 p1 p3 D1 D2
x, y S1
O p S2 E2 p2 p1 p3
x3
x1 D2 D1
x2 S1 E2 E1
x, y
D3
rL RTS L, K = rK r L + r K = c K L (等)成本方程 MPL MPK = rK 或 rL r L + r K = c K L
K A B E
K
y3 y2 y1 O
L
L
既定产量下的成本最小化
rL RTS L , K = rK f ( L, K ) = y MPL MPK = rK 或 rL f ( L, K ) = y ⇒ 成本函数: c = c( y )
STC3
LTC
O c SAC1
y1
y2
y3 SMC3
y LMC SAC3 LAC
SMC1
短期成本曲线 与长期成本 曲线之间的 关系
O
b
SAC2 SMC2
c e y1
g
y2
Ch5Choice选择

(p1+t)x1*+p2x2*=m
B
初始选择 税收R*=tx1*
A
x1
对x1征收从量税后,消费者的情况变得糟糕,因为位 于更低的无差异曲线上(傻瓜都知道这一结论). 34
现在考虑政府征收同量所得税的情形:
x2
预算约束变为
p1x1+p2x2=m-R*=m-tx1*.
这条预算线(红线)与初始预算线(白 线)是平行的(为什么?)
变换,从而构造一个新的效用函数V V=F(U)=F[U(x1,x2)],F(U)是U的单调递增函 数。 可以证明:单调变换不会改变原最优消费束。 因为,我们在上一章已证明,单调变换不会改 变边际替代率MRS12;而效用极大时
︱MRS12︱=p1/p2。
14
5.1最优选择:一阶条件
练习:
无差异曲线比预算线陡峭或平缓无法相凹偏好无差异曲线不是凸向原点而是凹向原点完全替代与完全互补两商品中其中一种为厌恶品或中性商品20521凹偏好?商品1和2都是好商品左图满足偏好的单调性但不满足凸性是凹偏好
Chapter Five
Choice 消费者最优选择
1
引言
这一章将预算约束和偏好理论(效用函数)结合
预算线
5.2.3两商品完全替代的情形
x2 无差异曲线MRS = -1
假设两种商品可以1: 1完全替代,即 MRS=-1,则最优解 取决于两种商品价格 的大小。
预算线斜率 -p1/p2 x1
X1=0, 若p1>p2; x1=m/p1, 若p1<p2 X1=0到m/p1之间的任何数量,若p1=p2
26
11
5.1 最优选择:一阶条件的解释
MU1/P1=MU2/P2=入
消费者最优选择
(一)效用函数U(x1, x2)为C-D效用函数
预算约束为:p1x1 + p2x2= m,消费者具有良好性状偏好
p1变化,p2 和m不变
x2
U ( x1 , x2 )
x1a
x
b 2
p1
价格提供曲线 p1’’’
x1* x2*
a ab
b ab
m p1 m p2
x2*
(a
bm b)
x1*
x1
m p1 ap2 x2*
a
不同偏好条件下的收入提供曲线和恩格尔曲线
(四)相似(位似)偏好
对于任意两个消费束 (x1,x2), (y1,y2)如果当(x1,x2) f(y1,y2)时一 定有(kx1,kx2) f (ky1,ky2) ,那么这种性质的偏好就称作相似
偏好。 以上三种偏好都是相似偏好。
随着收入m变化一 商品束需求量的变 动轨迹称为恩格尔 曲线。
X2
A3
I收C入C 提供曲线
A2
x2Y’3 ’’
E3
xAY21’2 ’ xY2’1
E2 E1
U1
U3 U2
O
xX11’B1xX12’Xx’31’B’2 ’ B3 X1
m
m3
EC
E3
正常品
m2 m1
E2
E1
O
X1 X2 X3
X1
不同偏好条件下的收入提供曲线和恩格尔曲线
p1
p1x1 + p2x2 = m
价格提供曲线 p1’’’
x2 = ax1 p1’’
需求曲线
x1*
p1
m ap2
x2*
消费者最优选择课件

跨期消费选择与储蓄决策
跨期消费
01
消费者的消费选择不仅限于当期,还可能涉及未来多期的消费
决策,例如购买房贷、汽车等大额商品。
储蓄动机
02
储蓄是跨期消费选择的重要方面,消费者可能出于预防性储蓄
、平滑消费等动机而进行储蓄。
跨期替代效应
03
在跨期消费选择中,消费者需要考虑不同时期的替代效应,即
当前时期的消费可能会减少未来时期的消费能力。
预算约束原则
消费者的消费行为受到预算约束,即在不同产品或服务的 组合中,每种产品或服务的价格乘以数量不能超过消费者 的预算。
最优组合原则
在满足预算约束和边际替代原则的前提下,消费者应当选 择能够使其效用或满足度最大化的产品或服务组合。
02
消费者最优选择模型
效用函数与偏好关系
01
02
03
效用函数
描述消费者从消费某种商 品或服务中所获得的满足 程度。
偏好关系
消费者对不同商品或服务 的偏好,反映在消费选择 上。
偏好公理
消费者对商品或服务的偏 好应满足传递性、完全性 、单调性和连续性等公理 。
预算约束与消费选择
预算约束
消费者在一定收入水平下 所能承受的消费成本。
消费选择
在预算约束下,消费者根 据效用最大化原则选择商 品或服务。
消费者最优选择
在预算约束下,选择能够 最大化效用的商品或服务 组合。
06
消费者最优选择的应用 案例
个人储蓄与投资组合选择
总结词
个人储蓄与投资组合选择是消费者最优 选择的重要应用之一,它可以帮助人们 有效地管理自己的财富并追求更高的收 益。
VS
详细描述
在个人储蓄方面,消费者应该考虑自己的 短期和长期需求,以及未来的不确定性, 通过权衡取舍来确定最优的储蓄计划。在 投资组合选择方面,消费者应该根据自身 的风险承受能力和投资目标,合理分配资 产,以降低风险并追求更高的收益。
微观经济学-清华大学课件Ch5Choice消费者最优选择

(x1*,x2*) also exhausts the budget so
p1x* 1p2x* 2m . (B)
Computing Ordinary Demands a Cobb-Douglas Example.
So we have discovered that the most preferred affordable bundle for a consumer with Cobb-Douglas preferences
In mathematical terms, this is a constrained maximization problem;
In economics, this is a rational choice problem.
Rational Constrained Choice
x2
More preferred bundles
Affordable bundles
x1
Rational Constrained Choice
The most preferred affordable bundle is called the consumer’s ORDINARY DEMAND at the given prices and budget. Ordinary demands will be denoted by x1*(p1,p2,m) and x2*(p1,p2,m).
U (x1,x2)x1 axb 2
is
( ) (x * 1 ,x * 2 )(a a m b )p 1 ,(a b m b )p 2.
Computing Ordinary Demands -
a Cobb-Douglas Example.
p1x* 1p2x* 2m . (B)
Computing Ordinary Demands a Cobb-Douglas Example.
So we have discovered that the most preferred affordable bundle for a consumer with Cobb-Douglas preferences
In mathematical terms, this is a constrained maximization problem;
In economics, this is a rational choice problem.
Rational Constrained Choice
x2
More preferred bundles
Affordable bundles
x1
Rational Constrained Choice
The most preferred affordable bundle is called the consumer’s ORDINARY DEMAND at the given prices and budget. Ordinary demands will be denoted by x1*(p1,p2,m) and x2*(p1,p2,m).
U (x1,x2)x1 axb 2
is
( ) (x * 1 ,x * 2 )(a a m b )p 1 ,(a b m b )p 2.
Computing Ordinary Demands -
a Cobb-Douglas Example.
微观经济学第五章-选择

•
E0
•
•
0
• •
1
•
E1: 为需求1单位的最优 选择。
B
• • •
2
x1
5.3 最优选择---实例
5. 凹形偏好-消费者不认为平均消费束比极端消费束更好
x2
最优选择永远是边界选择。
A
•
0
Ux1x2
• B
E
x1
5.3 最优选择---实例
6. 柯布-道格拉斯偏好
U(x1,x2) = x1a x2b ( a>0 ,b>0 )
x* 2 bm . ( a b )p 2
最优选择:
x* 1 am . ( a b )p1
消费者在商品1上的花费占其收入的比重: p 1x 1 p1 a am = • = m (a+b)p1 m ( a+b ) 消费者在商品2上的花费占其收入的比重: p 2x 2 b = m ( a+b )
5.1 最优选择---消费者均衡
x2
最优选择(x1*,x2*)满足
全部收入都用于消费 能给其带来最高效用水 平的消费束。
Maxu u ( x1 , x2 )
x2*
s.t. p1 x1 p2 x2 m
x1*
x1
5.1 最优选择---消费者均衡
2. 折拗的嗜好 无差异曲线在最优消费点 上没有切点。 x2 3. 边界最优 无差异曲线与预算线不相切。
3. 中性物品和厌恶品 假设商品1是嗜好品,商品2是厌恶品 x1 = m/p1 x2 = 0
5.3 最优选择---实例
4. 离散商品 假设商品1是只能以整数单位获得的商品,而商品2是支 付一切的货币。 如果消费者选择1,2,3, …..n 单位商品1, 那他就 选择了消费束 (1,m-p1), (2, m-2p1) , (3, m3p1),……( n, m-np1) 。 E0: 为需求零单位的最优 选择。 x2(m)
微观经济学第三讲-消费者选择理论PPT课件

MU X MUY
PX
PY
20
第三节 消费者均衡
三、消费者特殊选择行为:角点解(P41)
边际替代率等于相对价格,即无差异曲线的斜率=预算线的斜率 (主客观评价一致)的均衡条件不一定总能满足。如不满足就可 能出现角点解。
至少有两类情况下出现角点解: 一种是选择行为受到约束,不得不选择MRS不等于相对价格之
MUxΔX +MUy ΔY = 0 因此 MRSxy=-ΔY/ΔX =MUx / MUy 所以,无差异曲线的斜率可以用 MUx / MUy来表 示,即横轴上商品X的相对边际效用。
14
2.商品的边际替代率递减规律:
第二节 消费者偏好
在维持效用水平不变的前提下,随着一种商品 的消费数量的连续增加,消费者为了得到每一 单位的这种商品所需要放弃的另一种商品的消 费数量是递减的。
二、基数效用和序数效用
在对效用的“度量”的问题上,西方经济学家先后提出了基 数效用和序数效用的概念,并在此基础上,形成了分析消费 者行为的两种方法,它们分别是: ◎基数效用论者的边际效用分析方法 ◎序数效用论者的无差异曲线的分析方法
➢(在19世纪和20世纪初期,西方经济学家普遍使用基数效用的概念。认 为效用可以具体衡量并加总求和。)
2
dMU(Q)/dQ=d2U(Q)/d2Q O 1 2 3 4 5 6 5Q
第一节 基数效用论
(3)边际效用递减规律的内容
在一定时间内,在其他商品的消费数量 保持不变 的条件下,随着消费者对某种商品 消费量的增加,消费者从该商品连续增加的 每一消费单位中所得到的效用增量即边际效 用是递减的。
6
3.消费者均衡
11
2.无差异曲线及其特征
(3)无差异曲线不相交
微观经济学-现代观点课件-5 选择 Choice汇编

管理学院 刘大为
10
完全互补
消费必须满足下列预算约束
由于两种商品总是被一起消费,可以把它们视为一
种整体商品,消费者将全部资金用于购买这种商品,
它的价格为 p1+ p2。
10/29/2020
管理学院 刘大为
11
5.3 一些例子——中性商品和厌恶商品
商品束中含有中性商品(neutral good),消费者将会 把全部资金用于购买他喜欢的商品,购买中性商品数量 为零。对于厌恶品(bad),上述结论仍然成立。 如果商品1是消费者喜欢的商品(good),商品2 为厌恶 品,则它们的需求函数分别为:
因 此,使用变量的指数之和为1 的柯布-道格拉 斯函数比较方便。如果u(x1, x2 ) = x1ax21-a , 则我们立即可将a解释为花费在商品1上的收入 比例。
10/29/2020
管理学院 刘大为
16
5.4 估计效用函数
观察需求行为可知道相应的潜在偏好的一些重 要信息。如果我们能获得足够多的消费者选择 行为的观察资料,通常就能够估计出产生这些 行为的效用函数。
如果无差异曲线为严 格凸,即无差异曲线 上不含有直线段,那 么每条预算线上仅有 唯一的最优点。
10/29/2020
管理学院 刘大为
5
MRS
MRS 的其中一种解释是,消费者恰好不愿买也 不愿意卖时两种商品的交换比率。
市场提供给消费者的交换比率是-p1/p2,即: 如果放弃一单位商品1,可以购买p1/p2单位商
人们必须对商品的交换率达成一致:为了多得到一 单位的一种商品,他们愿意放弃多少单位另外一种 商品。
10/29/2020
管理学院 刘大为
19
MRS 条件的意义
[北大微观经济学课件]ch5Choice
![[北大微观经济学课件]ch5Choice](https://img.taocdn.com/s3/m/cbc41d35650e52ea551898b5.png)
x2
x2*
x1*
x1
Rational Constrained Choice
x2 (x1*,x2*) is the most preferred affordable bundle.
x2*
x1*
x1
Rational Constrained Choice
The
most preferred affordable bundle is called the consumer’s ORDINARY DEMAND (一般需求)at the given prices and budget. Ordinary demands will be denoted by x1*(p1,p2,m) and x2*(p1,p2,m).
(x1*,x2*)
also exhausts the budget so
* * p x p x m . 11 22
(B)
Computing Ordinary Demands a Cobb-Douglas Example.
So
now we know that * bp * 1 x2 x1 ap2
Examples of Corner Solutions -the Perfect Substitutes Case
x2 MRS = -1
Slope = -p1/p2 with p1 > p2. x1
Examples of Corner Solutions -the Perfect Substitutes Case
Chapter Five
Choice 选择
Structure
Rational
constrained choice Computing ordinary demands – Interior solution (内在解) – Corner solution (角点解) – “Kinky” solution Example: Choosing taxes
x2*
x1*
x1
Rational Constrained Choice
x2 (x1*,x2*) is the most preferred affordable bundle.
x2*
x1*
x1
Rational Constrained Choice
The
most preferred affordable bundle is called the consumer’s ORDINARY DEMAND (一般需求)at the given prices and budget. Ordinary demands will be denoted by x1*(p1,p2,m) and x2*(p1,p2,m).
(x1*,x2*)
also exhausts the budget so
* * p x p x m . 11 22
(B)
Computing Ordinary Demands a Cobb-Douglas Example.
So
now we know that * bp * 1 x2 x1 ap2
Examples of Corner Solutions -the Perfect Substitutes Case
x2 MRS = -1
Slope = -p1/p2 with p1 > p2. x1
Examples of Corner Solutions -the Perfect Substitutes Case
Chapter Five
Choice 选择
Structure
Rational
constrained choice Computing ordinary demands – Interior solution (内在解) – Corner solution (角点解) – “Kinky” solution Example: Choosing taxes
消费者选择课件(微观经济学)

60 4
边际效用MU 0 30 20 10 0
总效用TU
面包的消费量从一个 增加到两个,满足程 度从30个效用单位增 加到50个,即增加了 20个效用单位。
边际效用递减:随着对某商品消费量的增加, 人们从该商品连续增加的每个因:兴奋度递减。 心理原因:人性。 物品本身用途的多样性。
时候,消费品价格指数提高多少?为了使他保持原有的效用水平
,他的收入必须提高多少百分率?
(4)消费品价格指数提高百分率=原 价有 格价 指格 数指 增数 量
(30 2.88 20 3) (30 2 20 3) 22% 30 2 203
收入提高的百分率=24 /120 20%
里昂·瓦尔拉斯(1834--1910),法国经济学家,被公认为数 理经济学的奠基者之一。他是洛桑学派的创始人,是最早积 极倡导方法论个人主义的经济学家。瓦尔拉斯对经济学的贡 献主要在两个方面:一是独立发展了价值理论中的边际效用 概念;二是创立了一般均衡理论。瓦尔拉斯父亲也是经济学 家,他因数学基础较差未考上著名的理工大学,不得不到矿 学院去学习工程。其间,他受到古诺著作的启发,决心要把 经济学发展成为数理经济学,他不断地学习数学,并刻苦钻 研,终于在学术上取得了巨大的进步。瓦尔拉斯与杰文斯、 门格尔等人各自独立地发现了边际效用的概念。
是消费者的主观心理感受。
效用 萨缪尔森提出:幸福= ———
欲望
增加幸福的方法: (1)欲望不变而提高效用 (2)清心寡欲
《最好吃的东西》
免子和猫争论,世界上什么东西最好吃。 免子说,“世界上萝卜最好吃。萝卜又甜又 脆又解渴,我一想起萝卜就要流口水。” 猫不同意,说,“世界上最好吃的东西是老鼠。 老鼠的肉非常嫩,嚼起来又酥又松,味道美极了!” 免子和猫争论不休、相持不下,跑去请猴子评理。 猴子听了,不由得大笑起来:“瞧你们这两个傻瓜蛋,连这点儿
边际效用MU 0 30 20 10 0
总效用TU
面包的消费量从一个 增加到两个,满足程 度从30个效用单位增 加到50个,即增加了 20个效用单位。
边际效用递减:随着对某商品消费量的增加, 人们从该商品连续增加的每个因:兴奋度递减。 心理原因:人性。 物品本身用途的多样性。
时候,消费品价格指数提高多少?为了使他保持原有的效用水平
,他的收入必须提高多少百分率?
(4)消费品价格指数提高百分率=原 价有 格价 指格 数指 增数 量
(30 2.88 20 3) (30 2 20 3) 22% 30 2 203
收入提高的百分率=24 /120 20%
里昂·瓦尔拉斯(1834--1910),法国经济学家,被公认为数 理经济学的奠基者之一。他是洛桑学派的创始人,是最早积 极倡导方法论个人主义的经济学家。瓦尔拉斯对经济学的贡 献主要在两个方面:一是独立发展了价值理论中的边际效用 概念;二是创立了一般均衡理论。瓦尔拉斯父亲也是经济学 家,他因数学基础较差未考上著名的理工大学,不得不到矿 学院去学习工程。其间,他受到古诺著作的启发,决心要把 经济学发展成为数理经济学,他不断地学习数学,并刻苦钻 研,终于在学术上取得了巨大的进步。瓦尔拉斯与杰文斯、 门格尔等人各自独立地发现了边际效用的概念。
是消费者的主观心理感受。
效用 萨缪尔森提出:幸福= ———
欲望
增加幸福的方法: (1)欲望不变而提高效用 (2)清心寡欲
《最好吃的东西》
免子和猫争论,世界上什么东西最好吃。 免子说,“世界上萝卜最好吃。萝卜又甜又 脆又解渴,我一想起萝卜就要流口水。” 猫不同意,说,“世界上最好吃的东西是老鼠。 老鼠的肉非常嫩,嚼起来又酥又松,味道美极了!” 免子和猫争论不休、相持不下,跑去请猴子评理。 猴子听了,不由得大笑起来:“瞧你们这两个傻瓜蛋,连这点儿
《微观经济学》第四讲选择

范里安《微观经济学:现代观点》
第四讲 选 择
一、最优选择 1.最优选择的条件 最优选择是指消费者预算集中处在最高无差异曲线上的商品 束。一般情况下,在最优选择处,无差异曲线和预算线是相切的。
ቤተ መጻሕፍቲ ባይዱ图4-1 最优选择
只有在良性偏好情况下,无差异曲线与预算线相切,切点才 为最优选择。 无差异曲线与预算线相切并不是最优选择的充分和必要条件。 最优选择下,边际替代率等于预算线斜率,即边际效用之比 等于价格之比,为 MU P 。
1 2
m p1 t x1 p2 x2
政府此时征得的税收为 R tx1 。
如果政府征收相同数量的所得税,此时的预算约束为:
p1 x1 p2 x2 m R m tx1
可以发现此预算线的斜率与不征税时的预算线斜率相同,并 且此预算线经过点 x1,x2 。
P c 1 x1 在此基础上可推导出:m c d
三、税收类型的选择——从量税Vs所得税 原来的预算约束为:
p1 x1 p2 x2 m
如果按税率t 对商品1的消费课税,预算约束就变为:
p1 t x1 p2 x2 m
假定消费者在新的预算约束下的最优选择为 x ,x ,则必满 足:
对商品1来说,需求函数为:
2.完全互补 完全互补情况下的最优选择必然总是出现在对角线上。
图4-3 完全互补情况下的最优选择 U x1,x2 min ax1, bx2 ,则关于商品1和商品2的 效用函数为: 最优选择为:
x1 bm am ,x2 bP bP 1 aP 2 1 aP 2
3.凹偏好 凹形偏好的选择永远是边界选择,即存在角点解。
图4-4 凹偏好情况下的最优选择
第四讲 选 择
一、最优选择 1.最优选择的条件 最优选择是指消费者预算集中处在最高无差异曲线上的商品 束。一般情况下,在最优选择处,无差异曲线和预算线是相切的。
ቤተ መጻሕፍቲ ባይዱ图4-1 最优选择
只有在良性偏好情况下,无差异曲线与预算线相切,切点才 为最优选择。 无差异曲线与预算线相切并不是最优选择的充分和必要条件。 最优选择下,边际替代率等于预算线斜率,即边际效用之比 等于价格之比,为 MU P 。
1 2
m p1 t x1 p2 x2
政府此时征得的税收为 R tx1 。
如果政府征收相同数量的所得税,此时的预算约束为:
p1 x1 p2 x2 m R m tx1
可以发现此预算线的斜率与不征税时的预算线斜率相同,并 且此预算线经过点 x1,x2 。
P c 1 x1 在此基础上可推导出:m c d
三、税收类型的选择——从量税Vs所得税 原来的预算约束为:
p1 x1 p2 x2 m
如果按税率t 对商品1的消费课税,预算约束就变为:
p1 t x1 p2 x2 m
假定消费者在新的预算约束下的最优选择为 x ,x ,则必满 足:
对商品1来说,需求函数为:
2.完全互补 完全互补情况下的最优选择必然总是出现在对角线上。
图4-3 完全互补情况下的最优选择 U x1,x2 min ax1, bx2 ,则关于商品1和商品2的 效用函数为: 最优选择为:
x1 bm am ,x2 bP bP 1 aP 2 1 aP 2
3.凹偏好 凹形偏好的选择永远是边界选择,即存在角点解。
图4-4 凹偏好情况下的最优选择
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x2*
x1*
x1
Rational Constrained Choice
x2
(x1*,x2*) is interior .
(b) The slope of the indiff.
curve at (x1*,x2*) equals the slope of the budget
constraint. x2*
x2
The most preferred affordable bundle
x1
Examples of Corner Solutions --
the Non-Convex Preferences Case
x2
Notice that the “tangency solution” is not the most preferred affordable
Affordable bundles
x1
Rational Constrained Choice
The most preferred affordable bundle is called the consumer’s ORDINARY DEMAND at the given prices and budget.
At
(x1*,x2*),
a b
MRpS1=x-1p*1/p2
p
2
x
* 2
so
(A)
Computing Ordinary Demands a Cobb-Douglas Example.
(x1*,x2*) also exhausts the budget so
p1x* 1p2x* 2m . (B)
bm
(a b )p 2
x*1
am (ab)p1
x1
Rational Constrained Choice
When x1* > 0 and x2* > 0 and (x1*,x2*) exhausts the budget, and indifference curves have no ‘kinks’, the ordinary demands are obtained by solving:
x1*
x1
Rational Constrained Choice
(x1*,x2*) satisfies two conditions: (a) the budget is exhausted;
p1x1* + p2x2* = m (b) the slope of the budget constraint,
Computing Ordinary Demands a Cobb-Douglas Example.
So we have discovered that the most preferred affordable bundle for a consumer with Cobb-Douglas preferences
Computing Ordinary Demands a Cobb-Douglas Example.
So the MRS is
M R S d d x x 1 2 U U / /x x 1 2 b a x x 1 1 a a x 1 b 2 x b 2 1 a b x x 1 2 .
M U2x U 2bx1 axb 21
Computing Ordinary Demands a Cobb-Douglas Example.
So the MRS is
M R S d d x x 1 2 U U / /x x 1 2 b a x x 1 1 a a x 1 b 2 x b 2 1 a b x x 1 2 .
-p1/p2, and the slope of the indifference curve containing (x1*,x2*) are equal at (x1*,x2*).
Computing Ordinary Demands a Cobb-Douglas Example.
Suppose that the consumer has Cobb-Douglas preferences. U (x1,x2)x1 axb 2
x2 = ax1
x1
Examples of ‘Kinky’ Solutions -the Perfect Complements Case
x2
U(x1,x2) = min{ax1,x2}
(a) p1x1* + p2x2* = m (b) x2* = ax1*
x2 = ax1
x2*
x1*
x1
Summary: Three Steps to Find the Optimal
(a) p1x1* + p2x2* = y
(b) the slopes of the budget constraint, -p1/p2, and of the indifference curve containing (x1*,x2*) are equal at (x1*,x2*).
Rational Constrained Choice
x2
y
MRS = -1
p2
Slope = -p1/p2 with p1 = p2.
y
x1
p1
Examples of Corner Solutions -the Perfect Substitutes Case
x2
y
All the bundles in the
p2
constraint are equally the
bundle.
The most preferred affordable bundle
x1
Examples of ‘Kinky’ Solutions -the Perfect Complements Case
x2
U(x1,x2) = min{ax1,x2}
x2 = ax1 x1
Examples of ‘Kinky’ Solutions -the Perfect Complements Case
U (x1,x2)x1 axb 2
is
( ) (x * 1 ,x * 2 )(a a m b )p 1 ,(a b m b )p 2.
Computing Ordinary Demands -
a Cobb-Douglas Example.
x2
U (x1,x2)x1 axb 2
x
* 2
x2
x1
Examples of Corner Solutions -the Non-Convex Preferences Case
x2 Which is the most preferred affordable bundle?
x1
Examples of Corner Solutions -the Non-Convex Preferences Case
x2
U(x1,x2) = min{ax1,x2}
x2 = ax1 x1
Examples of ‘Kinky’ Solutions -the Perfect Complements Case
x2
U(x1,x2) = min{ax1,x2}
The most preferred affordable bundle
Ordinary demands will be denoted by x1*(p1,p2,m) and x2*(p1,p2,m).
Rational Constrained Choice
When x1* > 0 and x2* > 0 the demanded bundle is INTERIOR.
Computing Ordinary Demands a Cobb-Douglas Example.
Suppose that the consumer has Cobb-Douglas preferences.
Then
U (x1,x2)x1 axb 2
M U1x U 1ax1 a1xb 2
x2 MRS = -1
x*2 0
Slope = -p1/p2 with p1 < p2.
x
* 1
y p1
x1
Examples of Corner Solutions --
the Perfect Substitutes Case
ቤተ መጻሕፍቲ ባይዱ
So when U(x1,x2) = x1 + x2, the most
In mathematical terms, this is a constrained maximization problem;
In economics, this is a rational choice problem.
Rational Constrained Choice
x2
More preferred bundles
x1
Examples of ‘Kinky’ Solutions -the Perfect Complements Case
x2
U(x1,x2) = min{ax1,x2}
MRS = -
MRS is undefined
x2 = ax1 MRS = 0
x1
Examples of ‘Kinky’ Solutions -the Perfect Complements Case
x2
U(x1,x2) = min{ax1,x2}
x2 = ax1 MRS = 0
