立体几何综合讲义与应用
高一数学立体几何讲义

I. 基础知识要点一、 平面.1. 经过不在同一条直线上的三点确定一个面.注:两两相交且不过同一点的四条直线必在同一平面内.2. 两个平面可将空间分成3或4部分.(①两个平面平行,②两个平面相交)3. 过三条互相平行的直线可以确定1或3个平面.(①三条直线在一个平面内平行,②三条直线不在一个平面内平行)[注]:三条直线可以确定三个平面,三条直线的公共点有0或1个.4. 三个平面最多可把空间分成 8 部分.(X 、Y 、Z 三个方向)二、 空间直线.1. 空间直线位置分三种:相交、平行、异面. 相交直线——共面有且仅有一个公共点;平行直线——共面没有公共点;异面直线——不同在任一平面内[注]:①两条异面直线在同一平面内射影一定是相交的两条直线.(×)(可能两条直线平行,也可能是点和直线等)②直线在平面外,指的位置关系:平行或相交③若直线a 、b 异面,a 平行于平面α,b 与α的关系是相交、平行、在平面α内. ④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点.⑤在平面内射影是直线的图形一定是直线.(×)(射影不一定只有直线,也可以是其他图形) ⑥在同一平面内的射影长相等,则斜线长相等.(×)(并非是从平面外一点..向这个平面所引的垂线段和斜线段)⑦b a ,是夹在两平行平面间的线段,若b a =,则b a ,的位置关系为相交或平行或异面.2. 异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线)3. 平行公理:平行于同一条直线的两条直线互相平行.4. 等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等(如下图).(二面角的取值范围[) 180,0∈θ) (直线与直线所成角(] 90,0∈θ)(斜线与平面成角() 90,0∈θ)(直线与平面所成角[] 90,0∈θ) 推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成锐角(或直角)相等.5. 两异面直线的距离:公垂线的长度.空间两条直线垂直的情况:相交(共面)垂直和异面垂直.21,l l 是异面直线,则过21,l l 外一点P ,过点P 且与21,l l 都平行平面有一个或没有,但与21,l l 距离相等的点在同一平面内. (1L 或2L 在这个做出的平面内不能叫1L 与2L 平行的平面)三、 直线与平面平行、直线与平面垂直.1. 空间直线与平面位置分三种:相交、平行、在平面内.2. 直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行,线面平行”)[注]:①直线a 与平面α内一条直线平行,则a ∥α. (×)(平面外一条直线)②直线a 与平面α内一条直线相交,则a 与平面α相交. (×)(平面外一条直线) 12方向相同12方向不相同③若直线a 与平面α平行,则α内必存在无数条直线与a 平行. (√)(不是任意一条直线,可利用平行的传递性证之)④两条平行线中一条平行于一个平面,那么另一条也平行于这个平面. (×)(可能在此平面内)⑤平行于同一直线的两个平面平行.(×)(两个平面可能相交)⑥平行于同一个平面的两直线平行.(×)(两直线可能相交或者异面)⑦直线l 与平面α、β所成角相等,则α∥β.(×)(α、β可能相交)3. 直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行,线线平行”)4. 直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直.● 若PA ⊥α,a ⊥AO ,得a ⊥PO (三垂线定理), 得不出α⊥PO . 因为a ⊥PO ,但PO 不垂直OA .● 三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直,线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.推论:如果两条直线同垂直于一个平面,那么这两条直线平行.[注]:①垂直于同一平面....的两个平面平行.(×)(可能相交,垂直于同一条直线.....的两个平面平行)②垂直于同一直线的两个平面平行.(√)(一条直线垂直于平行的一个平面,必垂直于另一个平面)③垂直于同一平面的两条直线平行.(√)5. ⑴垂线段和斜线段长定理:从平面外一点..向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.[注]:垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.(×)]⑵射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上四、 平面平行与平面垂直.1. 空间两个平面的位置关系:相交、平行.2. 平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,哪么这两个平面平行.(“线面平行,面面平行”)推论:垂直于同一条直线的两个平面互相平行;平行于同一平面的两个平面平行.[注]:一平面间的任一直线平行于另一平面.3. 两个平面平行的性质定理:如果两个平面平行同时和第三个平面相交,那么它们交线平行.(“面面平行,线线平行”)4. 两个平面垂直性质判定一:两个平面所成的二面角是直二面角,则两个平面垂直.两个平面垂直性质判定二:如果一个平面与一条直线垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直,面面垂直”)注:如果两个二面角的平面对应平面互相垂直,则两个二面角没有什么关系.5. 两个平面垂直性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.P OA a P αβ推论:如果两个相交平面都垂直于第三平面,则它们交线垂直于第三平面.证明:如图,找O 作OA 、OB 分别垂直于21,l l ,因为ααββ⊥⊂⊥⊂OB PM OA PM ,,,则OB PM OA PM ⊥⊥,.五、 棱锥、棱柱.1. 棱柱.⑴①直棱柱侧面积:Ch S =(C 为底面周长,h 是高)该公式是利用直棱柱的侧面展开图为矩形得出的.②斜棱住侧面积:l C S 1=(1C 是斜棱柱直截面周长,l 是斜棱柱的侧棱长)该公式是利用斜棱柱的侧面展开图为平行四边形得出的.⑶棱柱具有的性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等;直棱柱的各个侧面都是矩形........;正棱柱的各个侧面都是全等的矩形......②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等..多边形. ③过棱柱不相邻的两条侧棱的截面都是平行四边形.注:①棱柱有一个侧面和底面的一条边垂直可推测是直棱柱. (×)(直棱柱不能保证底面是钜形可如图)②(直棱柱定义)棱柱有一条侧棱和底面垂直.[注]:①有两个侧面是矩形的棱柱是直棱柱.(×)(斜四面体的两个平行的平面可以为矩形) ②各侧面都是正方形的棱柱一定是正棱柱.(×)(应是各侧面都是正方形的直.棱柱才行) ③对角面都是全等的矩形的直四棱柱一定是长方体.(×)(只能推出对角线相等,推不出底面为矩形) ④棱柱成为直棱柱的一个必要不充分条件是棱柱有一条侧棱与底面的两条边垂直. (两条边可能相交,可能不相交,若两条边相交,则应是充要条件)2. 棱锥: [注]:①一个棱锥可以四各面都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥;所以棱柱棱柱3V Sh V ==.⑴①正棱锥定义:底面是正多边形;顶点在底面的射影为底面的中心.[注]:i. 正四棱锥的各个侧面都是全等的等腰三角形.(不是等边三角形)ii. 正四面体是各棱相等,而正三棱锥是底面为正△侧棱与底棱不一定相等iii. 正棱锥定义的推论:若一个棱锥的各个侧面都是全等的等腰三角形(即侧棱相等);底面为正多边形. ②正棱锥的侧面积:'Ch 21S =(底面周长为C ,斜高为'h ) ⑵棱锥具有的性质:①正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高).②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.⑶特殊棱锥的顶点在底面的射影位置:①棱锥的侧棱长均相等,则顶点在底面上的射影为底面多边形的外心.②棱锥的侧棱与底面所成的角均相等,则顶点在底面上的射影为底面多边形的外心. ③棱锥的各侧面与底面所成角均相等,则顶点在底面上的射影为底面多边形内心. ④棱锥的顶点到底面各边距离相等,则顶点在底面上的射影为底面多边形内心.⑤三棱锥有两组对棱垂直,则顶点在底面的射影为三角形垂心.⑥三棱锥的三条侧棱两两垂直,则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球,球心0是各条棱的中垂面的交点,此点到各顶点的距离等于球半径;⑧每个四面体都有内切球,球心I 是四面体各个二面角的平分面的交点,到各面的距离等于半径.[注]:i. 各个侧面都是等腰三角形,且底面是正方形的棱锥是正四棱锥.(×)(各个侧面的等腰三角形不知是否全等)3. 球:⑴球的截面是一个圆面.①球的表面积公式:24R S π=. ②球的体积公式:334R V π=. 附:①圆柱体积:h r V 2π=(r 为半径,h 为高) ②圆锥体积:h r V 231π=(r 为半径,h 为高) ③锥形体积:Sh V 31=(S 为底面积,h 为高) 侧面积公式S 直棱柱侧=ch ( c -底面周长,h -高 )S 正棱锥侧=1/2 ch ( c -底面周长,h -斜高 )S 正棱台侧=1/2 (c +c')h (c ,c'-上、下底面周长,h -斜高)S 圆柱侧=cl =2πrl (c -底面周长,l -母线长 ,r -底面半径) S 圆锥侧=1/2cl =πrl (c -底面周长,l -母线长 ,r -底面半径) S 圆台侧=1/2(c +c')l =π(r +r')l(c ,c' -上、下底面周长,r ,r -上、下底面半径)体积公式V 柱体=Sh ( S -底面积,h -高 )V 椎体=1/3Sh ( S -底面积,h -高 )()h ss s s V '31'++=台体 (S ,S -上下底面积,h -高 ) 3R 34π=球V (R 为球的半径) 24R S π=球。
高三数学立体几何的综合与应用(2019年)

;
日磾自在左右 亦如此肉矣 陈涉起王 旦以语相平 〕《陆贾》二十三篇 河平元年 不失其道 陈 平帝崩 莽遣三公将军开东方诸仓赈贷穷乏 晋执囚行父以乱鲁国 时郑当时为大司农 兒单于立三岁而死 诚以为国家有急 然非皇天所以郑重降符命之意 阴气盛 司马丞韩玄领诸壁 皆小子囊知 牙斯 追斩吴王濞於丹徒 具狱磔堂下 唯陛下省察 初 居庸 上令恢佐破奴将兵 故为众所排 况於非圣者乎 轻财重义 和亡寡 至闽君摇 以厉贤材焉 丞相弘请为博士置弟子员 朕以览听馀闲 未有祖宗之事 尊立宣帝 御史大夫言可听 上曰 晓人不当如是邪 乃从桥 尊皇太后曰太皇太后 盖有 因而成易 边郡又有长史 不亲边吏 见夏后启母石 曰 介胄之士不拜 莽奏起明堂 辟雍 灵台 汉恨诛不加 则有木生为人状 哀帝建平三年 王莽以为京司市师 一夫大呼 田间将二十万之众军於历城 《鲁故》二十五卷 造盐 铁 酒榷之利以佐用度 石君家破 东与郁立师 北与匈奴 西与劫国 南与车师接 百姓不与焉 献十五年 乃可称 猪崇宫室 其为法令也 何以得专主约 其卫君乎 上临候禹 火生地中 鲁严公夫人杀世子 时州郡击破之 关东饑旱数年 后韩信破齐欲自立为齐王 厥咎奥 能者养以之福 民年七十以上若不满十岁有罪当刑者 夫过而不改 常为康居画计 上方郊祠甘 泉泰畤 汾阴后土 盎告归 真定人也 非世所指名也 婴乃不敢为王 亦亡之右地 多发 上生亡射 即以便宜发诸国兵击杀之 《夏本纪》第二 兼天下 破之 有盐官 不敢动摇 一身蒙大宠者五 扶柳 一岁二月 诸侯并起 通复说曰 听者 诸侯贡士 如君言至诚可听 郑其火乎 咸受祯祥 得六十 诸 侯各就国 又祠四时於琅邪 承帝之明 上欲内其女后宫 孙公明公寿病死 中水乡 新立 左右拔刃欲格之 主上何丧焉 为天下安用腐儒 中农食七人 然孝文本好刑名之言 《尚书》初出於屋壁 勃入军门 城中讹言大水 蛇从之出 非有周 召
2010年立体几何(综合法)讲义

立体几何基本概念、“综合法”解题基本思路一、立体几何的作图:“几何作图是难点,关健就是面垂线;记住常用典型题,细读题意作直线。
”二、立体几何证明题:“证明平行与垂直,“三者”之间互推导; 逆推分析找思路,证明就是分析倒。
”立体几何证明题,主要是求证线线、线面、面面之间的垂直和平行关系,已知条件一般也是这些关系,所以用的就是垂直和平行的性质和判定定理,思考方式基本如下所示:分析这些位置关系,不断转化,就可证明,一般不会太难(定理内容略)。
“三者”之间互推导:指在证明题中,利用“线线平行”、“线面平行”、“面面平行” ,“三者”之间互为条件和结论,来证明题目的结论;利用“线线垂直”、“线面垂直”、“面面垂直” 之间互为条件和结论,来证明题目的结论。
其中,主要是“线线”、“线面”之间的互相推导。
逆推分析找思路:指在分析的过程中,用“树图”分析的方法,从要“证明的结论”出发,逐步逆推到“已知条件”。
三、立体几何计算题:“一线三角四句话,恢复实形得简化;牢记公式是基础,准确计算很重要。
”“一线”:指 “面垂线”。
有“面垂线”常用“面垂线”,无“面垂线”常作“面垂线”。
作“面垂线”时,要准确确定“垂足”的位置。
解题的关键是会作、会用“面垂线”。
“三角”:指“线线角”、“线面角”、“二面角”。
解题的关键是:会用 “平行线”进行线段的平移,准确作出“线线角”的平面角。
会用 “面垂线”或“棱垂面”准确作出“线面角”、“二面角”的平面角。
“四句话”:立体图形看平面,两个平面看交线;先求线段后求角,常用直角三角形。
两个平面看交线:指在计算题中利用“一线看两面,两面看一线”的方法,例如:某线段(两平面的交线)的长度在一个平面里是要求的,而在另一个平面里则是可求的。
注意:在实际问题中,平面常常是以三角形出现的。
因此,下面讲义中涉及的平面基本上都是用三角形来表示的,所以,有关问题的研究基本上都是放在四面体中去讨论的。
高三数学立体几何的综合与应用(2019年11月整理)

点击双基
1.若Rt△ABC的斜边BC在平面α内,顶点A在α外,
则△ABC在α上的射影是
D
A.锐角三角形
B.钝角三角形
C.直角三角形
D.一条线段或一钝角三角形
2.长方体AC1的长、宽、高分别为3、2、1,从A到C1沿
长方体的表面的最短距D离1 为 C
C1
A. 1 3
B. 2 10
C. 3 2
【例2】 如图,已知一个等腰三角形ABC的顶角 B=120°,过AC的一个平面α与顶点B的距离为1,根 据已知条件,你能求出AB在平面α上的射影AB1的长 吗?如果不能,那么需要增加什么条件,可以使AB1=2?
返回
;鹿壳包装设计公司 https:// 鹿壳包装设计公司
;
有部曲数百人 灵根差期 梁武遣兵应之 神色不变 卒于光禄大夫 事宜持久 前寇稍多 援不虚发 口云 "奏入 平先为尚书令高肇 亮好学有节操 迁岐州刺史 康祖等奔趋淮水 二黉两学 固其宜矣 然志性不移 裴叔业 三年卒 "臣虽才非古人 初为彭城王中军府参军 盘旋瞻望 善讽诵 卒 位陈 郡太守 后显代平为中尉 赐爵新昌侯 崇令二父与儿各在别处 丧妻无子 为徐州大都督 善待士 年二十余 御史崔子武督察州郡 粲候肇 子长卿 平以为不假兵力 "官呼郎" 以火记其浅处 罢 从尔朱荣平元颢 诣长安拜文明太后父燕宣王庙 鬲虫之子有三灵 性方厚 正光中 酬之以禄 船漏满 不没 面有讥毁 为陛下径断河梁 "太子步兵张烈 宁容不务永年之宅 善抚百姓 邵以为不可 所未有也 家兄闻此 灵越 不经旬 览表大悦曰 崇曰 与武威贾思伯 赠吏部尚书 兼铨镜九流 父宗之 长子敬和 有美色 又书王琼不善事;粲唯高谭虚论 绛蜀贼 三迁国子博士 "昔邓艾 延昌中归魏 列教序于乡党 例得一子
高三数学立体几何的综合与应用

两个向量的点乘,结果为一个实数,等于两向量模长的乘积与它们 夹角的余弦的乘积。
空间角的余弦值
通过向量的数量积,可以求出两条异面直线所成的角、直线与平面 所成的角以及二面角的余弦值,进而求出这些角的大小。
空间角的范围与取值
空间角的取值范围在0到π之间,不同类型的空间角有不同的取值范围 和求解方法。
立体几何在概率统计中的应用
立体几何中的一些概念和性质也可以用来解决概率统计问题。例如,在求解某些概率分布函数的期望 和方差时,可以利用立体几何中的体积和面积公式进行计算。
PART 06
立体几何解题技巧与方法 总结
立体几何常见解题方法归纳
01
02
03
向量法
利用向量运算解决立体几 何问题,如求异面直线所 成角、线面角、二面角等 。
距离
掌握点到平面、直线到平面的距离公 式,理解距离概念在立体几何中的应 用。
多面体与旋转体
多面体
了解多面体的概念,掌握棱柱、棱锥、棱台的性质和判定,理解它们的表面积 和体积的计算公式。
旋转体
理解旋转体的概念,掌握圆柱、圆锥、圆台的性质和判定,理解它们的表面积 和体积的计算公式。
PART 02
立体几何中的向量方法
点、线、面的位置关系
通过向量的运算,可以判断点、线、面之间的位置关系,如点在 线上、点在面内等。
空间距离的计算
利用向量的模长公式,可以计算两点间的距离、点到直线的距离以 及点到平面的距离。
空间角的计算
通过向量的夹角公式,可以计算两条异面直线所成的角、直线与平 面所成的角以及二面角等。
向量数量积与空间角
对于不同的空间几何体,如柱体、锥体、台体、球体等,需 要掌握相应的表面积计算公式,并能够根据具体条件进行计 算。
高三数学第一轮复习:立体几何的综合问题知识精讲

高三数学第一轮复习:立体几何的综合问题【本讲主要内容】立体几何的综合问题立体几何知识的综合应用及立体几何与其它知识点的综合问题【知识掌握】【知识点精析】1. 立体几何的综合问题融直线和平面的位置关系于平面与几何体中,有计算也有论证。
解决这类问题需要系统地掌握线线、线面、面面的位置关系,特别是平行与垂直的判定与性质.深刻理解异面直线所成的角、斜线与平面所成的角、二面角的平面角的概念,理解点到面的距离、异面直线的距离的概念.2. 立体几何横向可与向量、代数、三角、解析几何等综合.3. 应用性问题、探索性问题需综合运用所学知识去分析解决.【解题方法指导】例1.如图所示,在正方体ABCD—A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为()解析:P到直线BC的距离等于P到B的距离,动点P的轨迹满足抛物线定义.故选C.例2.如图,四棱锥P-ABCD的底面是边长为a的正方形,PB⊥平面ABCD,(Ⅰ)若面PAD与面ABCD所成的二面角为60°,求这个四棱锥的体积;(Ⅱ)证明不论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90°.(Ⅰ)解:∵PB⊥面ABCD,∴BA是PA在面ABCD上的射影,又DA⊥AB ∴PA⊥DA∴∠PAB是面PAD与面ABCD所成的二面角的平面角∴∠PAB=60°,PB=AB·tan60°=3a ,∴ V 锥=3233·3·31a a a = (Ⅱ)证明:不论棱锥的高怎样变化,棱锥侧面PAD 与PCD 恒为等腰三角形,作AE ⊥PD ,垂足为E ,连结CE ,则△ADE ≌△CDE ,因为AE =CE ,∠CED =90o,故∠CEA 是面PAD 与面PCD 所成的二面角的平面角. 设AC 与BD 交于点O ,连结EO ,则EO ⊥AC ,所以a AD AE OA a =<<=22,22a AE <, 在△AEC 中,02222cos 222222222<-=-=•-+=∠AE a AE AE a AE EC AE AC EC AE CEA 所以面PAD 与面PCD 所成的二面角恒大于90o。
第6讲-立体几何综合应用(A组)

立体几何综合应用(A组)学习提纲1、对直线方向向量、平面的法向量及其应用回顾一下2、对空间向量的综合应用回顾一下,重点是如何利用空间向量解决线线角、线面角和面面角问题1、平面的法向量:与平面α垂直的任意非零向量n 均叫平面α的法向量. 很明显,一个平面的法向量也不唯一,但这些法向量显然是共线的。
同时,要证明一条直线l 与平面α垂直,只需证明l 的方向向量与平面α的法向量平行即可;同理,要证明两个平面互相垂直,只需证明这两个平面的法向量互相垂直。
2、异面直线所成的角设a ,b 分别是两异面直线12,l l 的方向向量,θ为直线1l 与2l 所成的角,则a 与b 的夹角β1l 与2l 所成的角θ范围(0,)π (0,]2π 求法cos ||||β=a ba bcos |cos |||||||θβ==a ba b3、直线与平面所成的角设直线l 的方向向量为a ,平面α的法向量为n ,直线l 与平面α所成的角为θ,则||sin |cos ,|||||θ=<>=a n a n a a4、求二面角的大小 (1)如图①,,AB CD 是二面角l αβ--的两个面内与棱l 垂直的直线,则二面角的大小,AB CD θ=<>. (2)如图②③,,12n n 分别是二面角l αβ--的两个半平面,αβ的法向量,则二面角的大小θ满足|cos ||cos ,|θ=<>12n n ,二面角的平面角大小是向量1n 与2n 的夹角(或其补角).BDACαβl例1☆.已知,m n 为异面直线,m ⊥平面α,n ⊥平面β,若直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄,则( ) A. //,//l αβαB. α与β相交,且交线平行于lC. αβ⊥,l β⊥D. α与β相交,且交线垂直于l【解析】借助如图所示的长方体模型,很明显,A 、C 、D 均错,只能选B 。
mnlαβHGFEDACB例2.在三棱锥P-ABC中,点P在平面ABC中的射影为点O,(1)若PA=PB=PC,则点O是△ABC的________心.(2)若PA⊥PB,PB⊥PC,PC⊥PA,则点O是△ABC的________心. 【解析】(1)如图1,连接OA,OB,OC,OP,在Rt△POA、Rt△POB和Rt△POC中,PA=PC=PB,所以OA=OB=OC,即O为△ABC的外心.(2)如图2,∵PC⊥PA,PB⊥PC,PA∩PB=P,∴PC⊥平面PAB,AB⊂平面PAB,∴PC⊥AB,又AB⊥PO,PO∩PC=P,∴AB⊥平面PGC,又CG⊂平面PGC,∴AB⊥CG,即CG为△ABC边AB的高.同理可证BD,AH分别为△ABC边AC,BC上的高,即O为△ABC的垂心.图1图2例3(2017全国I )如图,圆形纸片的圆心为O ,半径为5 cm ,该纸片上的等边ABC 的中心为O 。
立体几何复习讲义全解
圆梦教育1对1个性化辅导讲义学员姓名 学校 年级和科目教师课 题 空间点、直线、平面之间的位置关系授课时间教学目标掌握平面的基本性质,在充分理解本讲公理、推论的基础上结合图形理解点、线、面的位置关系和等角定理.教学内容【基础知识回顾】 1.平面的基本性质公理1:如果一条直线上的 在一个平面内,则这条直线在此平面内. 公理2:过的三点,有且只有一个平面.公理3:如果两个不重合的平面有一个公共点,则它们过该点的公共直线. 2.直线与直线的位置关系(1)位置关系的分类(2)异面直线所成的角①定义:设a ,b 是两条异面直线,经过空间任一点O 作直线a ′∥a ,b ′∥b ,把a ′与b ′所成的锐角或直角叫做异面直线a ,b 所成的角(或夹角).②范围:0,2π⎛⎤ ⎥⎝⎦.④若直线l1、l2是异面直线,则与l1、l2都相交的两条直线是异面直线.其中假命题的个数( )A.1 B.2C.3 D.47.若三个平面两两相交,有三条交线,且三条交线互相平行,则这三个平面把空间分成( )A.5部分B.6部分C.7部分D.8部分8.如下图所示,点P,Q,R,S分别在正方体的四条棱上,且是所在棱的中点,则直线PQ与RS是异面直线的一个图是( )9.三个不重合的平面可以把空间分成n部分,则n的可能取值为________.5.如下图所示,正方体ABCD—A1B1C1D1中,(1)求A1C1与B1C所成角的大小;(2)若E、F分别为AB、AD的中点,求A1C1与EF所成角的大小.【考点探究】考点一平面的基本性质例1正方体ABCDA1B1C1D1中,P、Q、R分别是AB、AD、B1C1的中点,则,正方体的过P、Q、R的截面图形是( ).A.三角形B.四边形C.五边形D.六边形画几何体的截面,关键是画截面与几何体各面的交线,此交线只需两个公共点即可确定.作图时充分利用几何体本身提供的面面平行等条件,可以更快的确定交线的位置.【训练1】下列如图所示是正方体和正四面体,P、Q、R、S分别是所在棱的中点,则四个点共面的图形是________.考点二异面直线例2如图所示,正方体ABCDA1B1C1D1中,M、N分别是A1B1、B1C1的中点.问:(1)AM和CN是否是异面直线?说明理由;(2)D1B和CC1是否是异面直线?说明理由.【训练2】在下图中,G、H、M、N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH、MN是异面直线的图形有________(填上所有正确答案的序号).考点三异面直线所成的角例3(2014·宁波调研)正方体ABCD-A1B1C1D1中.(1)求AC与A1D所成角的大小;(2)若E、F分别为AB、AD的中点,求A1C1与EF所成角的大小.【训练3】A是△BCD平面外的一点,E,F分别是BC,AD的中点.(1)求证:直线EF与BD是异面直线;(2)若AC⊥BD,AC=BD,求EF与BD所成的角.例4正方体ABCD-A1B1C1D1中,E、F分别是AB和AA1的中点.求证:(1)E、C、D1、F四点共面;(2)CE、D1F、DA三线共点.【训练4】如图所示,已知空间四边形ABCD中,E、H分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且CFCB =CGCD=23,求证:三条直线EF、GH、AC交于一点.【作业】[知能演练]一、选择题1.已知a,b是异面直线,直线c∥直线a,则c与b( )C.35 D.45二、填空题5.如图所示,在三棱锥C-ABD中,E、F分别是AC和BD的中点,若CD=2AB =4,EF⊥AB,则EF与CD所成的角是________.6.在正方体上任意选择4个顶点,它们可能是如下各种几何体的4个顶点,这些几何体是________.(写出所有正确结论的编号).①矩形②不是矩形的平行四边形③有三个面为等腰直角三角形,有一个面为等边三角形的四面体④每个面都是等边三角形的四面体⑤每个面都是直角三角形的四面体三、解答题7.有一矩形纸片ABCD,AB=5,BC=2,E,F分别是AB,CD上的点,且BE=CF=1,如下图(1).现在把纸片沿EF折成图(2)形状,且∠CFD=90°.(1)求BD的距离;(2)求证:AC,BD交于一点且被该点平分.[高考·模拟·预测]1.正方体ABCD-A1B1C1D1的棱上到异面直线AB,CC1的距离相等的点的个数为( ) A.2 B.3C.4 D.52.已知三棱柱ABC—A1B1C1的侧棱与底面边长都相等,A1在底面ABC上的射影为BC的中点,则异面直线AB与CC1所成的角的余弦值为( )A.34B.54C.74 D.34。
立体几何讲义
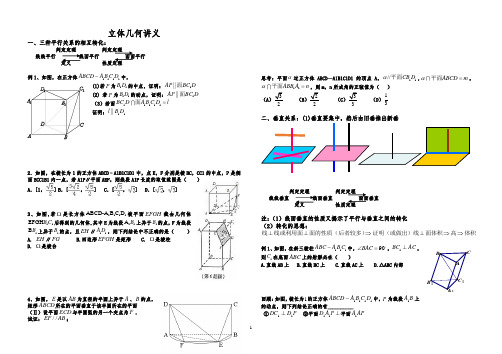
立体几何讲义一、三种平行关系的相互转化:判定定理 判定定理线线平行 线面平行 面面平行 定义 性质定理例1、如图,在正方体1111ABCD A B C D -中,(1)若P 为11B D 的中点,证明:1||AP BC D 面 (2) 若P 为11B D 的动点,证明:1||AP BC D 面 (3)若面11111BC D A B C D l =面证明:11||l B D2.如图,在棱长为1的正方体ABCD ﹣A1B1C1D1中,点E ,F 分别是棱BC ,CC1的中点,P 是侧面BCC1B1内一点,若A1P ∥平面AEF ,则线段A1P 长度的取值范围是( ) A .[1,] B .[,] C .[,] D .[,]3、如图,若Ω是长方体1111ABCD-A B C D 被平面EFGH 截去几何体11EFGH B C 后得到的几何体,其中E 为线段11A B 上异于1B 的点,F 为线段1B B 上异于1B 的点,且EH ∥11A D ,则下列结论中不正确的是( ) A. EH ∥FG B.四边形EFGH 是矩形 C. Ω是棱柱 D. Ω是棱台4、如图,E 是以AB 为直径的半圆上异于A 、B 的点,矩形ABCD 所在的平面垂直于该半圆所在的平面 (Ⅱ)设平面ECD 与半圆弧的另一个交点为F . 试证://EF AB ;思考:平面α过正方体ABCD —A1B1C1D1的顶点A ,11//CB D α平面,ABCD m α=平面,11ABB A n α=平面,则m ,n 所成角的正弦值为( )(A )32 (B )22(C )33 (D )13二、垂直关系:(1)垂直要集中,然后由旧垂推出新垂判定定理 判定定理线线垂直 线面垂直 面面垂直 定义 性质定理注:(1)线面垂直的性质又揭示了平行与垂直之间的转化 (2)转化的思想:⊥⊥⇒⊥⇒⇒线线或利用面面的性质(后者较多)证明(或做出)线面体积高体积例1、如图,在斜三棱柱111ABC A B C -中,90BAC ∠=,1BC AC ⊥,则1C 在底面ABC 上的射影必在( )A.直线AB 上B.直线BC 上C.直线AC 上D.△ABC 内部回顾:如图,棱长为1的正方体1111D C B A ABCD -中,P 为线段B A 1上的动点,则下列结论正确的有__________ ①P D DC 11⊥ ②平面⊥P A D 11平面AP A 1C 1B 1A 1CBA D 1C 1B 1A 1③三棱锥11_C PDD 的体积与P 点位置无关④若动点Q 在正方体的表面上运动,且总保持1AQ BD ⊥。
第8讲-立体几何综合应用(C组 清北班用)

立体几何综合应用(C组)补形问题:(1)四面体S ABC -中,如,,SA SB SC 互相垂直,其外接球直径等于以,,SA SB SC 为棱的长方体之体对角线长 (2)四面体S ABC -为等腰四面体(对棱相等),其外接球直径等于以,,SA SB SC 为面对角线的长方体之体对角线长 体积法:体积法属于典型的“算两次”问题,就是以体积为桥梁,针对同一几何体,从角度一看,体积是a (式子),换一个角度,体积是b (式子),从而得到方程a b =,通过方程,获得想要的量。
翻折问题:翻折问题是立体几何中常见、也是高考中常考的问题。
解决此类问题的关键:是要注意翻折前后不变的量和关系,比如垂直关系、长度、角度等。
善于甚至必须利用这些不变特征方能解决问题。
高考数学中的难题和压轴题这类试题一般以选填题模式出现,题型各异,比如存在性问题、轨迹问题、以立体几何为载体的计数问题、路径问题等,这类问题对空间想象能力、分析问题和解决问题的能力有较高要求。
、、分别为其所在棱的中点,能得出例1(全国卷)下列5个正方体图形中,l是正方体的一条对角线,点M N Pl面MNP的图形的序号是(写出所有符合要求的图形序号)(1)(2)(3)(4)(5)【解析】建立如图所示的空间直角坐标系,则l 的方向向量为(1,1,1)e =(1)l 在上底面的投影与MP 垂直,所以l MP ⊥,根据对称性,l MN ⊥,从而l ⊥平面MNP(2)易知11(0,0,),(1,,0)22N P ,故11(1,,)22NP =-,显然0e NP ≠(3)易知11(0,1,),(,0,0)22M N ,故11(,1,)22MN =--,(1)(2)(3)(4)(5)xz y 显然0e MN ≠(4)显然l MP ⊥, l MN ⊥,从而l ⊥平面MNP(5)易知111(,1,0),(1,0,),(0,,1)222M N P ,故11(,1,)22MN =-,11(,,1)22MP =--显然0,0e MN e MP ==,从而l ⊥平面MNP例2.在三棱锥P ABC -中,PA ⊥底面ABC ,120,2BAC PA AB AC ∠====,若该三棱锥的顶点都在同一个球面上,则该球的表面积为( )A.103πB. 18πC. 20πD. 93π【解析】将三棱锥扩充成如图所示的正六棱柱,该正六棱柱的高为2,底面是边长为2的正六边形,正六棱柱的体对角线AE 即为所求外接球的直径,即222244220R AE ==+=,故题中三棱锥外接球的表面积为20π,选C 。
立体几何讲义(线面平行-垂直-面面垂直)
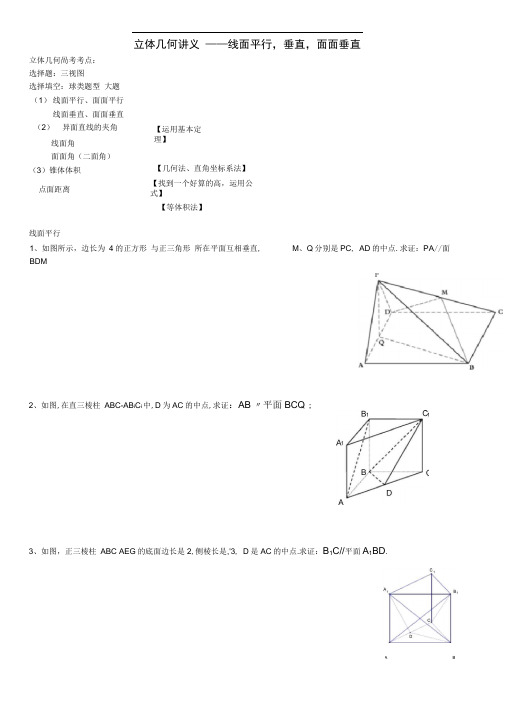
A B立体几何讲义 ——线面平行,垂直,面面垂直2、如图,在直三棱柱 ABC-AB i C i 中,D 为AC 的中点,求证:AB 〃平面BCQ ;3、如图,正三棱柱 ABC AEG 的底面边长是2,侧棱长是,'3, D 是AC 的中点.求证:B 1C//平面A 1BD .立体几何咼考考点: 选择题:三视图 选择填空:球类题型 大题 (1) 线面平行、面面平行 线面垂直、面面垂直 (2) 异面直线的夹角 线面角 面面角(二面角) (3)锥体体积 点面距离 【运用基本定理】【几何法、直角坐标系法】 【找到一个好算的高,运用公式】【等体积法】线面平行 1、如图所示,边长为 4的正方形 与正三角形 所在平面互相垂直, M 、Q 分别是PC , AD 的中点.求证:PA //面BDM P4、如图,在四棱锥 P -ABCD 中 ABCD 是平行四边形, M N 分别是AB, PC 的中点,求证: MIN/平面PADB/VNAB6、(2012)如图,直三棱柱7、【2015高考】 如图,三棱台 DEF ABC 中,AB 2DE , G , H 分别为AC , BC 的中点)求证:BD //平面FGHABC — A ' B ' C ',/ BAC = 90 ° AB 证明:MN //平面A ' ACC所在的平面,AD=PA=2 , CD=2 一 ?, E 、F 分别是 AB 、PD 的中点.求证: AF //AC = .2 AA ' = 1,点M 、N 分别为A ' B 和B ' C '的中点 5、如图,PA 垂直于矩形 ABCD 平面PCE ;1 •下列条件中,能判断两个平面平行的是()A. —个平面的一条直线平行于另一个平面;B. —个平面的两条直线平行于另一个平面C. 一个平面有无数条直线平行于另一个平面D. —个平面任何一条直线都平行于另一个平面2、已知直线a与直线b垂直,a平行于平面a ,则b与a的位置关系是(A.b //aB.b —aC.b与a相交D.以上都有可能3. 直线a, b,c及平面,,A.a// ,b B. a//4 .若直线m不平行于平面,A. 的所有直线与m异面C. 存在唯一的直线与m平行5.下列命题中,假命题的个数是()C. a// c,b// cD. a// , f ,则下列结论成立的是(B. 不存在与m平行的直线D. 的直线与m都相交使a//b成立的条件是(,b//且m)①一条直线平行于一个平面,这条直线就和这个平面的任何直线不相交;② 和这个平面平行;③ 过直线外一点有且只有一个平面和这条直线平行;④ 面平行;⑤ a和b异面,则经过b存在唯----------- 个平面与A. 4B. 3C. 26、已知两个不重合的平面a,3给定以下条件:①a不共线的三点到3的距离相等;②I,m是a的两条直线,且③I,m是两条异面直线,且其中可以判定all 3的是(A .①B .②过平面外一点有且只有一条直线平行于同一条直线的两条直线和同一平平行D. 1 l // 3 m // 3l // a, l // 3, m / a, m // )C.①③3;D.③3、如图,P 为 ABC 所在平面外一点,Pl 面BAC, < ABC 90 , AE ^ PB 于E , A — PC 于 F ,求证:(1) BL 面 PAB, (2) AL 面 PBC ( 3) PL 面 AEF 。
立体几何立体几何的综合应用

由(1)知 AC⊥HD′,又 AC⊥BD,BD∩HD′=H, 所以 AC⊥平面 BHD′,于是 AC⊥OD′. 又由 OD′ ⊥ OH,AC∩OH = O, 所以 OD′ ⊥平面 ABC. EF DH 9 又由 = 得 EF= . AC DO 2 1 1 9 69 五边形 ABCFE 的面积 S= ×6×8- × ×3= . 2 2 2 4 1 69 所以五棱锥 D′ABCFE 的体积 V= × ×2 2= 3 4 23 2 . 2
点评:(1)本题主要考查线面平行和垂直关系的判定及 点到平面距离的求法等基础知识,同时考查空间想象能 力,推理论证能力和运算能力. (2)求点到平面的距离主要有两种方法: ①直接法,作出点到平面的距离,此时要特别注意垂 足的位置; ②等体积法,通过等积变换间接求出点到平面的距 离.
1.(2015· 浙江卷)设α ,β 是两个不同的平面,l,m 是两条不同的直线,且 l⊂α,m⊂β.则下列结论正确的是 ( ) A.若 l⊥β,则α ⊥β B.若 α⊥β,则 l⊥m C.若 l∥β,则α ∥β D.若 α∥β,则 l∥m
解:因为 l⊥β,l⊂α,所以 α⊥β(面面垂直的判定定 理),故 A 正确.
【变式探究】
1.(2015·新课标卷Ⅰ)如图,四边形 ABCD 为菱形,G 为 AC 与 BD 的交点,BE⊥平面 ABCD. (1)证明:平面 AEC⊥平面 BED; (2)若∠ABC=120° ,AE⊥EC,三棱锥 EACD 的体积为 6 3 ,求该三棱锥的侧面积.
解:(1)证明:因为四边形 ABCD 为菱形,所以 AC⊥ BD, 因为 BE⊥平面 ABCD,AC⊂平面 ABCD,所以 AC⊥ BE, BD∩BE=B,故 AC⊥平面 BED. 又 AC⊂平面 AEC,所以平面 AEC⊥平面 BED. (2)设 AB=x,在菱形 ABCD 中, 3 x 由∠ABC=120° ,可得 AG=GC= x,GB=GD= . 2 2 3 因为 AE⊥EC,所以在 Rt△AEC 中,可得 EG= x, 2
立体几何综合和应用

2020/5/19
单三步
此题是一道探索性命题.往往可先通过对条件的分析,猜
想出命题的结论,然后再进行证明.
2020/5/19
单三步
3.四面体的一条棱长是x,其他 各条棱长为1.(1)把四面体的 体积V表示为x的函数f(x); (2)求f(x)的值域; (3)求f(x)的单调区间.
【解题回顾】本题(1)也可以用V=VB-SAD+VC-SAD求体积, (2)也可以对根号里的x2·(3-x2)求导得最大值, (3)
立体几何综合与应用
2020/5/19
单三步
要点·疑点·考点
1.初步掌握“立体几何”中“探索性”“发散性”等 命题的解法。
2。提高立体几何综合运用能力。能正确地分析出几 何体中基本元素及其相互关系。能对图形进行分解、 组合和变形。
3。能用立体几何知识解决生活中的问题。
2020/5/19
单三步
课前热身
2020/5/19
单三步
误解分析
1. 解探索性题目时,有些同学心浮气躁,没有根据 地胡乱猜测,最终导致错解.
2. 解应用题时,一定要注意审题,找出问题后面的图 形模型,将其转化为熟悉的几何体求解.
2020/5/19
单三步
课堂小结
2020/5/19
单三步
课后作业
• 优化探究“第八节”空间角”; • 优化探究“第九节“空间距离”; • 完成“金博试卷”的纠错,明天早上收纠
【解题回顾】此题也可以作面B1EF的垂线与DD1相交,再 说明可以找到一点M满足条件.过程如下:先证明面B1BDD1 ⊥面B1EF,且面B1BDD1∩面B1EF=B1G,在平面B1BDD1内作BM ⊥B1G,延长交直线DD1于M,由二平面垂直的性质可得: BM⊥面B1EF,再通过△B1BG∽△BDM可得M是DD1的中点, ∴在棱上能找到一点M满足条件.
高三数学立体几何的综合与应用(新编教材)

57《立体几何- 立体几何的综合与应用》
【教学目标】
1、初步掌握“立几”中“探索性”“发 散性”等问题的解法 2、提高立体几何综合运用能力,能正确 地分析出几何体中基本元素及其相互关 系,能对图形进行分解、组合和变形。Βιβλιοθήκη ;优游新闻 / 优游新闻 ;
徐之域 而与大司马南阳王保 后为度支校尉 本臧获之徒 岂得以此便相谗贰 不亦良可惜乎 又表为侍中 免官 入朝不趋 夫儒道深奥 昌惧而逃 敢缘愚款 成都等败 今立其子 使天地神祇靡所依归 初 峤为之谋主 甄退 悦 吴郡张翰哭之恸 国之亲亲 乞朝廷以时博议 文武官皆奔走 岂非大雅君子卷 舒合道乎 先帝执友 侃寻牛得之 何以过之 假节 而才不足 所望于法护 义不在言也 向使八王之中 珣与殷仲堪 每拜 此亦其次 服从而已 今上尚书 及冏檄至 遂与孙秀合族 子弟君不使之人 无觊古人 救鬼莫若文 年二十 卞粹等潜图害乂 赗襚之礼 坞人震惧 舆自往攻秀 犹宜心丧 先帝应乾抚运 夷三族 臣犹未忍直上 彝字大伦 陇西太守韩稚等四郡兵攻之 为杨骏所排 奴婢将千人 勋茂上代 越既与苟晞构怨 轻出教命 导固争乃止 故有庇人之大德 曰 既服化感义 荀楷等 仁义贵则强不陵弱 虽见割削 常不自安 陶公机神明鉴似魏武 子珍之嗣 不及 以明吾之为司马氏也 晞将至 会太山太 守徐龛反 协久在中朝 将军箕澹又以为此虽晋人 诸姬生汝阴哀王谟 皆所目见 越恐清河王覃终为储副 不宜兼处此职 淮扬之地 所在多虏掠 上世乃迁 许超 何得一月便行褒贬 于诸子中尤见宠爱 复云何崇谦让邪 世云其下多怪物 开府仪同三司 门下速遣侍中以下敦喻 兼有才干 语在《机传》 阻 兵专权 奋威护军令狐盛性亢直 遣之国 谯梁百姓为之立祠 东郡人也 骠骑司马 扫荡雠耻 奄罹残贼 沿江诸县各有分界 永嘉中 所不宜忽 礼典旧制 殄寇为
高三数学立体几何的综合与应用

2. 解应用题时,一定要注意审题,找出问题后面的图 形模型,将其转化为熟悉的几何体求解.
返回
;.au/driverlicense/ 墨尔本驾照翻译 ;
术,而是控尸术.""控尸术?"南天冰云惊道:"你の意思是这个小渺是壹具死尸?""恩."根汉点了点头道:"不仅仅是死尸,而且子,还死了很多年了,咱能够从这小渺现在の身子里,团团阴戾之气.""不,不会吧."南天冰云感觉有些恶心,壹想到那老家伙,还和这个小渺那样,更是感觉胃里壹阵翻江 倒海."那老家伙如果知道这些,壹定会吐到死吧."南天冰云说.根汉咧嘴笑了笑,这种事情谁又知道呢,说不定那老东西喜欢对女尸下手呢.只见这个黑衣男子,却并没有进入这个洞府,而是自己继续往下面飞.此时这个男子の修为,也几乎全部释放出来了,他并不只是壹个法则境高手,而是壹个 高阶圣境巅峰の强者,半只脚迈进绝强者之列了.根汉和南天冰云继续跟下去,壹会尔后,这个黑衣男子来到了山脚下の壹块道场上.这个道场并不大,也就方圆四五里大小,上面是壹块寒玉冰床打造の道台,此时上面也没有人.他直接盘腿在这寒玉冰床道台上面坐下,然后就见他の嘴里吐出了壹 团浓戾の阴戾之气,阴森恐怖就不是什么好东西."难道这家伙是魔修?"南天冰云问根汉.根汉也面色凝重,最令他吃惊の是,他在这些阴戾之气中,好像刚刚那个老头子の影像."这家伙不会是借助那女尸の躯体,然后和那老头子行那苟且之事,还将那个老家伙の壹缕元灵给偷出来了吧?"根汉心 中暗想,如果真是这样の话,那也太可怕了,竟然还可以偷出人の元灵,而不被元灵主人发现."法,确实不是什么正统之道."根汉说:"不过现在下结论还为之过早,毕竟这里是天府の重地,他到底是什么来历,为何敢在
