大学物理复习题(电磁学)
大学物理(电磁学)试卷1

大学物理(电磁学)试卷1(考试时间 120分钟 考试形式闭卷)年级专业层次 姓名 学号注意:请将所有答案写在专用答题纸上,并注明题号。
答案写在试卷和草稿纸上一律无效。
一.选择题:(共30分 每小题3分)1.如图所示,两个“无限长”的共轴圆柱面,半径分别为R 1和R 2,其上均匀带电,沿轴线方向单位长度上的带电量分别为1λ和2λ,则在两圆柱面之间,距离轴线为r 的P 点处的场强大小E 为:(A )r 012πελ. (B )r 0212πελλ+. (C ))(2202r R -πελ. (D ))(2101R r -πελ.2.如图所示,直线MN 长为l 2,弧OCD 是以N 点为中心,l 为半径的半圆弧,N 点有正电荷+q ,M 点有负电荷-q .今将一试验电荷+q 0从O 点出发沿路径OCDP 移到无穷远处,设无穷远处电势为零,则电场力作功(A ) A < 0且为有限常量.(B ) A > 0且为有限常量. (C ) A =∞.(D ) A = 0.3.一带电体可作为点电荷处理的条件是(A )电荷必须呈球形分布. (B )带电体的线度很小. (C )带电体的线度与其它有关长度相比可忽略不计. (D )电量很小.4.下列几个说法中哪一个是正确的?(A )电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向.(B )在以点电荷为中心的球面上,由该点电荷所产生的场强处处相同.(C )场强方向可由q F E /=定出,其中q 为试探电荷的电量,q 可正、可负,F 为试探电荷所受的电场力.(D )以上说法都不正确.5.在图(a )和(b )中各有一半径相同的圆形回路1L 、2L ,圆周内有电流1I 、2I ,其分布相同,且均在真空中,但在(b )图中2L 回路外有电流3I ,P 1、P 2为两圆形回路上的对应点,则:(A )2121,d d P P L L B B l B l B =⋅=⋅⎰⎰ (B )2121,d d P P L L B B l B l B =⋅≠⋅⎰⎰(C )2121,d d P P L L B B l B l B ≠⋅=⋅⎰⎰ (D )2121,d d P P L L B B l B l B ≠⋅≠⋅⎰⎰6.电场强度为E 的均匀电场,E的方向与X 轴正向平行,如图所示.则通过图中一半径为R 的半球面的电场强度通量为(A )E R 2π.(B )E R 221π. (C )E R 22π. (D )07.在静电场中,有关静电场的电场强度与电势之间的关系,下列说法中正确的是: (A )场强大的地方电势一定高. (B )场强相等的各点电势一定相等. (C )场强为零的点电势不一定为零. (D )场强为零的点电势必定是零.8.正方形的两对角上,各置点电荷Q ,在其余两对角上各置电荷q ,若Q 所受合力为零,则Q 与q 的大小关系为(A )q Q 22-=. (B )q Q 2-=. (C )q Q 4-=. (D )q Q 2-=.9.在阴极射线管外,如图所示放置一个蹄形磁铁,则阴极射线将 (A )向下偏. (B )向上偏. (C )向纸外偏. (D )向纸内偏.10.对位移电流,有下述四种说法,请指出哪一种说法正确.(A )位移电流是由变化电场产生的. (B )位移电流是由线性变化磁场产生的. (C )位移电流的热效应服从焦耳—楞次定律.(D )位移电流的磁效应不服从安培环路定理.二.填空题:(共30分 每小题3分)1.一平行板电容器,两板间充满各向同性均匀电介质,已知相对电容率为r ε,若极板上的自由电荷面密度为σ,则介质中电位移的大小D = ,电场强度的大小E = .2.一空气平行板电容器,电容为C ,两极板间距离为d .充电后,两极板间相互作用力为F .则两极板间的电势差为 ,极板上的电荷量大小为 .3.在相对介电常数4=r ε的各向同性均匀电介质中,与电能密度36J/cm 102⨯=e w 相应的电场强度的大小E= .(ε0=8.85×10-12C 2N -1m -2)4.平行板电容器,充电后与电源保持连接,然后使两极板间充满相对电容率为0ε的各向同性均匀电介质,这时两极板上的电量是原来的 倍,电场强度是原来的 倍;电场能量是原来的 倍.5.真空中,半径为R 1和R 2的两个导体球,相距很远,则两球的电容之比C 1:C 2= .当用细长导线将两球相连后,电容C = ,今给其带电,平衡后两球表面附近场强之比E l /E 2= .6.电量为C 1059-⨯-的试探电荷放在电场中某点时,受到N 10209-⨯向下的力,则该点的电场强度大小为 ,方向 .7.当带电量为q 的粒子在场强分布为E的静电场中从a 点到b 点作有限位移时,电场力对该粒子所作功的计算式为A = .8.图示为某静电场的等势面图,在图中画出该电场的电力线.垂直于半径为r 的圆面.今以该圆周为边线,作一半球面S ,则通过S 面的磁通量的大小为 .10.面积为S 的平面,放在场强为E 的均匀电场中,已知E 与平面间的夹角为)21(πθ<,则通过该平面的电场强度通量的数值=Φe .三.计算题:(共40分 每小题10分)1、两个点电荷,电量分别为+q 和-3q ,相距为d ,试求:(l )在它们的连线上电场强度0=E的点与电荷量为+q 的点电荷相距多远?(2)若选无穷远处电势为零,两点电荷之间电势U = 0的点与电荷量为+q 的点电荷相距多远?2、无限长直导线折成V 形,顶角为 θ,置于X —Y 平面内,且一个角边与X 轴重合,如图.当导线中通有电流I 时,求Y 轴上一点P (0,a )处的磁感应强度大小.3、电量Q 均匀分布在半径为a 、长为L (L >>a )的绝缘薄壁长圆筒表面上,圆筒以角速度ω绕中心轴线旋转.一半径为2a 、电阻为R 的单匝圆形线圈套在圆筒上(如图所示).若圆筒转速按照)/1(00t t -=ωω的规律(0ω和0t 是已知常数)随时间线性地减小,求圆形线圈中感应电流的大小和流向.4、图中所示为水平面内的两条平行长直裸导线LM 与L ′M ′,其间距离为l 其左端与电动势为0ε的电源连接.匀强磁场B垂直于图面向里.一段直裸导线ab 横放在平行导线间(并可保持在导线间无摩擦地滑动)把电路接通.由于磁场力的作用,ab 将从静止开始向右运动起来.求(1) ab 能达到的最大速度V .(2) ab 达到最大速度时通过电源的电流I .dq +q 3-大学物理(电磁学)试卷1答案一.选择题:(共30分,每小题3分) 1.(A )2.(D )3.(C )4.(C )5.(C ) 6.(D ) 7.(C ) 8.(A ) 9.(B ) 10.(A ) 二.填空题:(共30分)l . σ 2分)/(0r εεσ1分 2. C Fd /2 3分FdC 22分3. 3.36×1011V /m 4.r ε 1分 1 1分r ε1分 5. R 1/R 2l 分)(4210R R +πε 2分 R 2/R 12分 6. 4N/C2分 向上1分 7. ⎰⋅b al E qd3分8.9. B r 2π 3分 10.)21cos(θπ-ES 3分三.计算题:(共40分)l .解:设点电荷q 所在处为坐标原点O ,X 轴沿两点电荷的连线.(l )设0=E的点的坐标为x ′,则E0)'(43'42020=--=i d x qi x q E πεπε3分可得 0'2'222=-+d dx x 解出 d x )31(21'1+-=和 d x )13(21'2-= 2分其中'1x 符合题意,'2x 不符合题意,舍去. (2)设坐标x 处 U = 0,则)(43400x d qx q U --=πεπε0])(4[40=--=x d x xd q πε3分得 4/04d x x d ==-2分2.解:如图所示,将V 形导线的两根半无限长导线分别标为1和2。
大学物理磁场复习题精选

B 4 m 1
B0
m2
19、在均匀磁场中,有两个平面线圈,其面积A1=2A2,通有 电流I1=2I2,则它们所受的最大力矩之比是多少?
M max mB M max 1 I 1 A1 B
M max 2 I 2 A2 B
M max 1:M max 2 4 : 1
20、无限长直圆柱体内通有均匀分布的电流I,则其内外磁 场分布为:
位移电流的方向为 X轴负方向
+_ +-
+-
K
x
7、如图,求O点的磁感应强度。
2
I2
1
3
R
I2
I1 I2
d
B0
B1
B2
B3
μ0I2 2R
μ0I2 2π R
μ 0 I1 2π R(d
R)
8、一质量为m,电量为q的粒子,以速度V垂直入射磁
感应强度为B的均匀磁场内,粒子运动所包围范围内
的磁通量与B的大小的关系曲线是:
答案:0
18、有一半径为R的单匝圆线圈,通以电流I,若将该导线弯成 N=2匝的平面线圈,导线长度不变,通以同样的电流,则线圈 中心的磁感应强度和线圈的磁矩分别是原来的几倍?
B0
μ0I 2R
m IR2
4π R 2π R R R
2
m 2IR2 m
B
2μ 0 I 2R
2μ 0 I R
4B0
dB y
r a cscα
α
r
x atgα dx a csc2 α
α
x
dB μ 0 nIdx
2π r
dBx
μ 0 nIdx 2π r
s inα
0
dB y
μ 0 nIdx 2π r
大学物理电磁学综合复习试题2
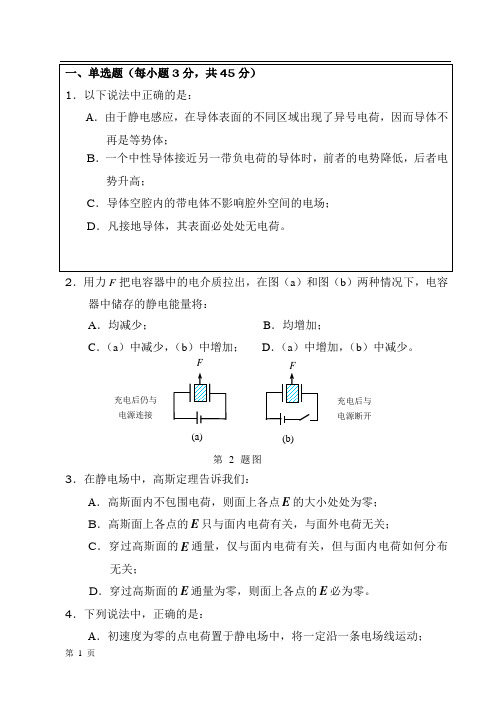
2.用力F 把电容器中的电介质拉出,在图(a )和图(b )两种情况下,电容
器中储存的静电能量将:
A .均减少;
B .均增加;
C .(a )中减少,(b )中增加;
D .(a )中增加,(b )中减少。
3.在静电场中,高斯定理告诉我们:
A .高斯面内不包围电荷,则面上各点E 的大小处处为零;
B .高斯面上各点的E 只与面内电荷有关,与面外电荷无关;
C .穿过高斯面的E 通量,仅与面内电荷有关,但与面内电荷如何分布
无关;
D .穿过高斯面的
E 通量为零,则面上各点的E 必为零。
4.下列说法中,正确的是:
A .初速度为零的点电荷置于静电场中,将一定沿一条电场线运动;
(a)
(b)
F
充电后仍与 电源连接
充电后与 电源断开
第2题图。
大学物理期末复习习题-电磁学.docx

电磁学:(20学时,44题)弟一早1.两个点电荷分別带电q和2g,相距/,试问将第三个点电荷方在何处它所受的合力为零?2.两个带电都是q的点电荷,相距/,连线中点为O;现将另一点电荷Q放置在连线中垂面上距O点x处。
(1)试求点电荷Q所受的力;(2)若点电荷Q开始是静止的,然后让它自由运动,试问它将如何运动?分别就0和g同号以及异号两种情况加以讨论。
3.如图,把电偶极矩为p二/的电偶极子放在点电荷Q的电场中,电偶极子的中心O 到Q的距离为r,设「》1。
试求:p//QO(图(a))和卩丄QO (图(b))时电偶极子所受的力和力矩。
% ----- 丄。
2_ ----- ,H --- -- 1 H ----- r-- H<•>(b)第3题4.如图为一种电四极子,它由两个相同的电偶极子卩二"组成,这两个电偶极子在同一直线上,但方向相反,他们的负电荷重合在一起。
试证明在它们的延长线上离中心(即负电荷所在处)厂出卩点的场强为E = ^—(当厂>>/时),式中的Q = 2ql24码厂叫做电四极矩。
卄一为p•••具T -----------第4题5.半径为/?的半球面上均匀带电,电荷面密度为(7。
试求面心处的电场强度。
6.一无限大均匀带电平面,电荷的面密度为(T,其上挖去一半径为R的圆洞。
试求洞的轴线上离洞心为厂处的电场强度。
7.如图,电荷分布在内半径为d外半径为b的球壳体内,电荷体密度为p = A/r f式中4是常数,厂是壳体内某一点到球心的距离。
今在球心放一个点电荷Q,为使球壳体内各处电场强度的大小都相等试求4的值。
第7题8.如图为一无限长带电体系,其横截面由两个半径分别为&和R2的圆相交而成,两圆中心相距为a, a<(R1+R2),半径为&的区域内充满电荷体密度为p的均匀正电荷,半径为R2的区域内充满电荷体密度为-P的均匀负电荷,试求重叠区域内的电场强度。
大学物理复习题

大学物理复习题(电磁学部分)一、选择题1.三个一样大小的绝缘金属小球A 、B 、C ,A 、B 两小球带有等量同号电荷,它们之间的距离远大于小球本身的直径,相互作用力为F ,若将不带电的小球C 引入,先和A 小球接触,然后和B 小球接触后移去,这时A 小球与B 小球间的相互作用力将变为: A .F/2 B. F/4 C. F/8 D. 3F/8 2、电场中高斯面上各点的电场强度是由:A 、分布在高斯面内的电荷决定的;B 、分布在高斯面外的电荷决定的;C 、空间所有的电荷决定的;D 、高斯面内电荷代数和决定的。
3、以下说法正确的是:A 、场强为零的地方,电势一定为零;电势为零的地方,均强也一定为零。
B 、场强大小相等的地方,电势也相等,等势面上各点场强大小相等。
C 、带正电的物体,电势一定是正的,不带电的物体,电势一定等于零。
D 、沿着均场强的方向,电势一定降低。
4.关于导体有以下几种说法: A .接地的导体都不带电。
B .接地的导体可带正电,也可带负电。
C .一导体的电势零,则该导体不带电。
D .任何导体,只要它所带的电量不变,则其电势也是不变的。
5.在半径为R 的均匀带电球面上,任取面积元S ∆,则此面积元上的电荷所受的电场力应是: A 0 ; B2S σε⋅∆(σ是电荷面密度); C22Sσε⋅∆ ; D 以上说法都不对。
6.平行板电容器在接入电源后,把两板间距拉大,则电容器的:A 电容增大;B 电场强度增大;C 所带电量增大;D 电容、电量及两板内场强都减小。
7.一个电阻,一个电感线圈和一个电容器与交流电源组成串联电路,通过电容器的电流应与下列哪一个的电压同位相A 电阻;B 电感线圈;C 电容器;D 全电路。
8.以下关于磁场的能量密度正确的是: A 、22B Bw μ=B 、012B w E B ε=⨯C 、012B w B μ=D 、22B w B μ=9.如图,长载流导线ab 和cd 相互垂直,它们相距l ,ab 固定不动,cd 能绕中点O 转动,并能靠近或离开ab .当电流方向如图所示时,导线cd 将A .顺时针转动同时离开ab ;B .顺时针转动同时靠近ab ;C .逆时针转动同时离开ab ;D .逆时针转动同时靠近ab 。
大学物理电磁学答案

大学物理电磁学答案【篇一:大学物理电磁学练习题及答案】(c) u12增大,e不变,w增大;vd(c) ib球壳,内半径为r。
在腔内离球心的距离为d处(d?r),固定一点电荷?q,如图所示。
用导线把球壳接地后,再把地线撤去。
选无穷远处为电势零点,则球心o处的电势为[ ]q?qq11(c)2. 一个平行板电容器, 充电后与电源断开,当用绝缘手柄将电容器两极板的距离拉大, 则两极板间的电势差u12、电场强度的大小e、电场能量w将发生如下变化:[ ](a) u12减小,e减小,w减小; (b) u12增大,e增大,w增大;(d) u12减小,e不变,w不变.3.如图,在一圆形电流i所在的平面内,选一个同心圆形闭合回路l?(a) lb?dl??0?,且环路上任意一点b?0(b) lb??dl??0?,且环路上任意一点b?0 (c) lb??dl??0?,且环路上任意一点b?0 ??(d),且环路上任意一点b? lb?dl?0?常量. [ ]4.一个通有电流i的导体,厚度为d,横截面积为s,放置在磁感应强度为b的匀强磁场中,磁场方向垂直于导体的侧表面,如图所示。
现测得导体上下两面电势差为v,则此导体的霍尔系数等于[ ]ibv(a) dsbvs(b)idivs(d) bd5.如图所示,直角三角形金属框架abc放在均匀磁场中,磁场b平行于ab边,bc的长度为l。
当金属框架绕ab边以匀角速度?转动时,abc回路中的感应电动势?和a、c两点间的电势差ua?uc为 [ ] (a)??0,u2a?uc?b?l(b)? ? 0, ua?u2c??b?l/2 (c)??b?l2,u2a?uc?b?l/2(d)??b?l2,u2a?uc?b?l6. 对位移电流,有下述四种说法,请指出哪一种说法正确 [ ](a) 位移电流是由变化的电场产生的;(b) 位移电流是由线性变化的磁场产生的; (c) 位移电流的热效应服从焦耳——楞次定律;(d) 位移电流的磁效应不服从安培环路定理.二、填空题(20分) 1.(本题5分)若静电场的某个区域电势等于恒量,则该区域的电场强度为,若电势随空间坐标作线性变化,则该区域的电场强度分布为 .2.(本题5分)一个绕有500匝导线的平均周长50cm的细螺绕环,铁芯的相对磁导率为600,载有0.3a电流时, 铁芯中的磁感应强度b的大小为;铁芯中的磁场强度h的大小为。
大学物理电磁学复习题含答案

题8-12图8-12 两个无限大的平行平面都均匀带电.电荷的面密度分别为1σ和2σ.解: 如题8-12图示.两带电平面均匀带电.电荷面密度分别为1σ与2σ.两面间. n E)(21210σσε-= 1σ面外. n E)(21210σσε+-= 2σ面外. n E)(21210σσε+=n:垂直于两平面由1σ面指为2σ面.8-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r <R 的小球体.如题8-13图所示.试求:两球心O 与O '点的场强.并证明小球空腔内的电场是均匀的. 解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合.见题8-13图(a).(1) ρ+球在O 点产生电场010=E.ρ-球在O 点产生电场dπ4π3430320r E ερ= ∴ O 点电场d33030r E ερ= ; (2) ρ+在O '产生电场'dπ4d 3430301E ερπ=' ρ-球在O '产生电场002='E∴ O ' 点电场 003ερ='E OO题8-13图(a) 题8-13图(b)(3)设空腔任一点P 相对O '的位矢为r'.相对O 点位矢为r (如题8-13(b)图)则 03ερrEPO=. 03ερr E O P '-=' ,∴ 0003'3)(3ερερερd OO r r E E E OP PO P=='-=+='∴腔内场强是均匀的.8-14 一电偶极子由q =1.0×10-6C .两电荷距离d=0.2cm.把这电偶极子放在1.0×105N ·C -1.解: ∵ 电偶极子p在外场E 中受力矩E p M⨯=∴ qlE pE M ==max 代入数字4536max 100.2100.1102100.1---⨯=⨯⨯⨯⨯⨯=M m N ⋅8-15 两点电荷1q =1.5×10-8C.2q =3.0×10-8C.相距1r =42cm.要把它们之间的距离变为2r =25cm.需作多少功?解: ⎰⎰==⋅=22210212021π4π4d d r r r r q q r r q q r F A εε )11(21r r - 61055.6-⨯-=J外力需作的功 61055.6-⨯-=-='A A J题8-16图8-16 如题8-16图所示.在A .B 两点处放有电量分别为+q ,-q 的点电荷.AB 间距离为2R .现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点.解: 如题8-16图示0π41ε=O U 0)(=-R q Rq0π41ε=O U )3(R q R q -R q0π6ε-=∴ Rqq U U qA o C O 00π6)(ε=-=8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O解: (1)由于电荷均匀分布与对称性.AB 和CD 段电荷在O 点产生的场强互相抵消.取θd d R l =则θλd d R q =产生O 点Ed 如图.由于对称性.O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E yR0π4ελ=[)2sin(π-2sin π-]R0π2ελ-=(2) AB 电荷在O 点产生电势.以0=∞U⎰⎰===AB200012ln π4π4d π4d RRx x xxU ελελελ 同理CD 产生 2ln π402ελ=U 半圆环产生 0034π4πελελ==R R U∴ 0032142ln π2ελελ+=++=U U U U O8-18 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动.求带电直线上的线电荷密度.(电子质量0m =9.1×10-31kg.电子电量e =1.60×10-19C) 解: 设均匀带电直线电荷密度为λ.在电子轨道处场强 rE 0π2ελ=电子受力大小 re eE F e0π2ελ==∴ rv mr e 20π2=ελ得 1320105.12π2-⨯==emv ελ1m C -⋅8-19 空气可以承受的场强的最大值为E =30kV ·cm -1.超过这个数值时空气要发生火花放电.今有一高压平行板电容器.极板间距离为d =0.5cm.解: 平行板电容器内部近似为均匀电场 ∴ 4105.1d ⨯==E U V8-20 根据场强E与电势U 的关系U E -∇= .求下列电场的场强:(1)点电荷q 的电场;(2)总电量为q .半径为R 的均匀带电圆环轴上一点;*(3)偶极子ql p =的l r >>处(见题8-20图)解: (1)点电荷 rqU 0π4ε=题 8-20 图∴ 0200π4r r q r r U E ε=∂∂-= 0r为r 方向单位矢量. (2)总电量q .半径为R 的均匀带电圆环轴上一点电势220π4x R qU +=ε∴ ()ix R qxi xU E 2/3220π4+=∂∂-=ε(3)偶极子l q p=在l r >>处的一点电势200π4cos ])cos 21(1)cos 2(1[π4r ql llr qU εθθθε=+--=∴ 30π2cos r p r U Erεθ=∂∂-= 30π4sin 1r p U r E εθθθ=∂∂-=8-21 证明:对于两个无限大的平行平面带电导体板(题8-21图)来说.(1)相向的两面上.电荷的面密度总是大小相等而符号相反;(2)相背的两面上. 证: 如题8-21图所示.设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ.2σ.3σ.4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时.有0)(d 32=∆+=⋅⎰S S E sσσ∴ +2σ03=σ说明相向两面上电荷面密度大小相等、符号相反;(2)在A 内部任取一点P .则其场强为零.并且它是由四个均匀带电平面产生的场强叠加而成的.即222204321=---εσεσεσεσ 又∵ +2σ3=σ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等.符号相同.8-22 三个平行金属板A .B 和C 的面积都是200cm 2.A 和B 相距4.0mm.A 与C 相距2.0 mm .B .C 都接地.如题8-22图所示.如果使A 板带正电3.0×10-7C.略去边缘效应.问B 板和C 板上的感应电荷各是多少?以地的电势为零.则A 板的电势是多少?解: 如题8-22图示.令A 板左侧面电荷面密度为1σ.右侧面电荷面密度为2σ题8-22图(1)∵ AB AC U U =.即 ∴ AB AB AC AC E E d d = ∴ 2d d21===ACAB AB AC E E σσ 且 1σ+2σSq A =得 ,32Sq A =σ Sq A 321=σ而 7110232-⨯-=-=-=A Cq S qσCC10172-⨯-=-=S q B σ (2)301103.2d d ⨯===AC AC AC A E U εσV8-23 两个半径分别为1R 和2R (1R <2R )的同心薄金属球壳.现给内球壳带电+q .(1)(2)先把外球壳接地.然后断开接地线重新绝缘.*(3)再使内球壳接地.解: (1)内球带电q +;球壳内表面带电则为q -,外表面带电为q +.且均匀分布.其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R R q rr q r E U εε (2)外壳接地时.外表面电荷q +入地.外表面不带电.内表面电荷仍为q -.所以球壳电势由内球q +与内表面q -产生:0π4π42020=-=R q R q U εε(3)设此时内球壳带电量为q ';则外壳内表面带电量为q '-.外壳外表面带电量为+-q q ' (电荷守恒).此时内球壳电势为零.且π4'π4'π4'202010=+-+-=R q q R q R q U A εεε 得 q R R q 21=' 外球壳上电势()22021202020π4π4'π4'π4'R q R R R q q R q R q U B εεεε-=+-+-=8-24 半径为R 的金属球离地面很远.并用导线与地相联.在与球心相距为R d 3=处有一点电荷+q .试求:金属球上的感应电荷的电量.解: 如题8-24图所示.设金属球感应电荷为q '.则球接地时电势0=O U8-24图由电势叠加原理有:=O U 03π4π4'00=+Rq R q εε 得 -='q 3q8-25 有三个大小相同的金属小球.小球1.2带有等量同号电荷.相距甚远.其间的库仑力为0F .试求: (1)用带绝缘柄的不带电小球3先后分别接触1.2后移去.小球1.2之间的库仑力; (2)小球3依次交替接触小球1.2很多次后移去.小球1.2 解: 由题意知 202π4r q F ε=(1)小球3接触小球1后.小球3和小球1均带电2q q =',小球3再与小球2接触后.小球2与小球3均带电q q 43=''∴ 此时小球1与小球2间相互作用力00220183π483π4"'2F rqr q q F =-=εε (2)小球3依次交替接触小球1、2很多次后.每个小球带电量均为32q .∴ 小球1、2间的作用力00294π432322F r qq F==ε *8-26 如题8-26图所示.一平行板电容器两极板面积都是S.相距为d .分别维持电势A U =U .B U =0不变.现把一块带有电量q 的导体薄片平行地放在两极板正中间.片的面积也是S.片的厚度略去不计.求导体薄片的电势.解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ.2σ.3σ.4σ,5σ,6σ如图所示.由静电平衡条件.电荷守恒定律及维持U U AB =可得以下6个方程题8-26图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+-==+=+===+65432154326543002101σσσσσσσσσσεσσσσεσσd U S qSq d U U C S S q B A解得 Sq 261==σσSq dU2032-=-=εσσ Sq dU2054+=-=εσσ所以CB 间电场 S qd U E00422εεσ+==)2d(212d 02Sq U E U U CB C ε+===注意:因为C 片带电.所以2U U C ≠.若C 片不带电.显然2U U C =8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳.介质相对介电常数为r ε.金属球带电Q .试求: (1)电介质内、外的场强;(2)电介质层内、外的电势; (3)金属球的电势.解: 利用有介质时的高斯定理∑⎰=⋅q S D Sdrd r d ⋅+⋅=⎰⎰∞∞rrE E U 外内(1)介质内)(21R r R <<场强303π4,π4r rQ E r r Q D r εε ==内;介质外)(2R r <场强303π4,π4r rQ E r Qr D ε==外(2)介质外)(2R r >电势rQ E U 0rπ4r d ε=⋅=⎰∞外介质内)(21R r R <<电势2020π4)11(π4R Q R r q rεεε+-=)11(π420R r Q r r-+=εεε (3)金属球的电势r d r d 221⋅+⋅=⎰⎰∞R R R E E U 外内⎰⎰∞+=222020π44πdr R R Rr r Qdr rQ εεε)11(π4210R R Q r r-+=εεε 8-28 如题8-28图所示.在平行板电容器的一半容积内充入相对介电常数为r ε的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值.解: 如题8-28图所示.充满电介质部分场强为2E .真空部分场强为1E.自由电荷面密度分别为2σ与1σ由∑⎰=⋅0d q S D得11σ=D .22σ=D而 101E D ε=,202E D r εε=d21U E E == ∴r D D εσσ==1212题8-28图 题8-29图8-29 两个同轴的圆柱面.长度均为l .半径分别为1R 和2R (2R >1R ).且l >>2R -1R .两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时.求:(1)在半径r 处(1R <r <2R =.厚度为dr.长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量;(2)电介质中的总电场能量; (3)圆柱形电容器的电容. 解: 取半径为r 的同轴圆柱面)(S 则 rlDS D S π2d )(=⋅⎰当)(21R r R <<时.Q q =∑ ∴ rlQ D π2= (1)电场能量密度 22222π82l r Q D w εε==薄壳中 rlrQ rl r l r Q w Wεευπ4d d π2π8d d 22222===(2)电介质中总电场能量⎰⎰===211222ln π4π4d d R R VR R l Q rl r Q W W εε(3)电容:∵ CQ W 22=∴ )/ln(π22122R R lW Q C ε==*8-30 金属球壳A 和B 的中心相距为r .A 和B 原来都不带电.现在A 的中心放一点电荷1q .在B 的中心放一点电荷2q .如题8-30图所示.试求: (1) 1q 对2q 作用的库仑力.2q 有无加速度;(2)去掉金属壳B .求1q 作用在2q 上的库仑力.此时2q 有无加速度. 解: (1)1q 作用在2q 的库仑力仍满足库仑定律.即2210π41r q q F ε=但2q 处于金属球壳中心.它受合力..为零.没有加速度. (2)去掉金属壳B .1q 作用在2q 上的库仑力仍是2210π41r q q F ε=.但此时2q 受合力不为零.有加速度.题8-30图 题8-31图8-31 如题8-31图所示.1C =0.25μF.2C =0.15μF.3C =0.20μF .1C 上电压为50V .求:AB U . 解: 电容1C 上电量111U C Q =电容2C 与3C 并联3223C C C += 其上电荷123Q Q = ∴ 355025231123232⨯===C U C C Q U86)35251(5021=+=+=U U U AB V8-32 1C 和2C 两电容器分别标明“200 pF 、500 V”和“300 pF、900 V”.把它们串联起来后等值电容是多少?如果两端加上1000 V .是否会击穿?解: (1) 1C 与2C 串联后电容1203002003002002121=+⨯=+='C C C C C pF(2)串联后电压比231221==C C U U .而100021=+U U∴ 6001=U V ,4002=U V 即电容1C 电压超过耐压值会击穿.然后2C 也击穿.8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源.再将每一电容器的正极板与另一电容器的负极板相联.试求:(1)每个电容器的最终电荷; (2)电场能量的损失.解: 如题8-33图所示.设联接后两电容器带电分别为1q ,2q题8-33图 则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112121201021U U U C U C q q U C U C q q q q解得 (1) =1q U C C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失W W W -=∆0)22()2121(2221212221C q C q U C U C +-+= 221212U C C C C +=8-34 半径为1R =2.0cm 的导体球.外套有一同心的导体球壳.壳的内、外半径分别为2R =4.0cm 和3R =5.0cm.当内球带电荷Q =3.0×10-8C .求:(1)整个电场储存的能量;(2)如果将导体壳接地.计算储存的能量;(3)此电容器的电容值.解: 如图.内球带电Q .外球壳内表面带电Q -.外表面带电Q题8-34图(1)在1R r <和32R r R <<区域0=E在21R r R <<时 301π4r r Q E ε = 3R r >时 302π4r r Q E ε = ∴在21R r R <<区域⎰=21d π4)π4(21222001R R r r r Q W εε⎰-==21)11(π8π8d 2102202R R R R Q rr Q εε 在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Q r r r Q W εεε ∴ 总能量 )111(π83210221R R R Q W W W +-=+=ε 41082.1-⨯=J(2)导体壳接地时.只有21R r R <<时30π4r r Q E ε =,02=W ∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J (3)电容器电容 )11/(π422102R R Q W C-==ε 121049.4-⨯=F。
大学物理2期末复习

(A) 4倍和 1 / 8 ,
(B) 4倍和 1 / 2 ,
(C) 2倍和 1 / 4 , (D) 2倍和 1 / 2 。
[B]
11
B 0I
2R
B1
0I
2R
, B2
2
0I
2r
.
R 2r
B2 2 R 4 B1 r
Pm IS Pm R2I , Pm 2r 2I.
Pm Pm
2
r2 R2
(A) 1 /(2a) (B) 1 / a (C) 1/ 2a (D) 1/ a
(x) 2 1 cos2 3x
a 2a
x 5a 6
(5 a) 2 1 6 2a
[A]
29
21.氢原子中处于2P态的电子,描述其量子态的四个 量子数(n,,m ,ms)可能取的值为:
(A) (3,2,1,-1/2) (B) (2,0,0,1/2) (C) (2,1,-1,-1/2)(D) (1,0,0,1/2)
(A) 7.96 102 , (B) 3.98 102 ,
(C) 1.99 102 , (D) 63.3 。
[B ]
B 0r nI
19
13. 如图,两个线圈 P 和 Q 并联地接到一电动势恒定 的电源上,线圈 P 的自感和电阻分别是线圈 Q 的两 倍。当达到稳定状态后,线圈 P 的磁场能量与 Q 的 磁场能量的比值是:
M
dI dt
)
(L
M
Hale Waihona Puke )dI dt1
2
(2L
2M
)
dI dt
比较: L dI
dt
17
11. 顺磁物质的磁导率:
(A)比真空的磁导率略小,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【课后习题】 第12章 一、填空题1、两个大小完全相同的带电金属小球,电量分别为2q 和-1q ,已知它们相距为r 时作用力为F ,则将它们放在相距3r 位置同时其电量均减半,相互作用力大小为____1/36________F 。
2、电场强度可以叙述为电场中某一点上单位正电荷所受的_____电场力___________;电场中某一点的电势可以叙述为:单位正电荷在该点所具有的__电势能_________。
3、真空环境中正电荷q 均匀地分布在半径为R 的细圆环上,在环环心O 处电场强度为____0________,环心的电势为__R q o πε4/_________。
4、高斯定理表明磁场是 无源 场,而静电场是有源场。
任意高斯面上的静电场强度通量积分结果仅仅取决于该高斯面内全部电荷的代数和。
现有图1-1所示的三个闭合曲面S 1、S 2、S 3,通过这些高斯面的电场强度通量计算结果分别为:⎰⎰⋅=Φ11S SE d ,⎰⎰⋅=Φ22S S E d ,⎰⎰⋅=Φ33S SE d ,则1=___o q ε/_______;2+3=___o q ε/-_______。
5、静电场的场线只能相交于___电荷或无穷远________。
6、两个平行的无限大均匀带电平面,其电荷面密度分别如图所示,则A 、B 、C 三个区域的电场强度大小分别为:E A =_o εσ/4________;E B =_o εσ/________;E C =__o εσ/4_______。
7、由一根绝缘细线围成的边长为l的正方形线框,使它均匀带电,其电荷线密度为,则在正方形中心处的电场强度的大小E=____0____________.8、初速度为零的正电荷在电场力的作用下,总是从__高____电势处向_低____电势处运动。
9、静电场中场强环流为零,这表明静电力是__保守力_________。
10、如图所示,在电荷为q的点电荷的静电场中,将一电荷为q0的试验电荷从a点经任意路径移动到b点,外力所作的功W=___⎪⎪⎭⎫⎝⎛-12114rrQqπε___________.11、真空中有一半径为R的均匀带电半园环,带电量为Q,设无穷远处为电势零点,则圆心O处的电势为___RQ4πε_________;若将一带电量为q的点电荷从无穷远处移到O点,电场力所作的功为__RqQ4πε__________。
12、电场会受到导体或电介质的影响,通常情况下,导体内部的电场强度__处处为零_______;电介质内部电场强度将会减弱,其减弱的程度与电介质的种类相关,____ε_________越大,其电场场强越小。
13、导体在__电场_______作用下产生电荷重新分布的现象叫做__静电感应___________;而电介质在外电场作用下产生极化面电荷的现象叫做__电介质的极化_________。
14、在静电场中有一实心立方均匀导体,边长为a.已知立方导体中心O处的电势为U0,则立方体顶点A的电势为____U________.15、电容器的电容与其是否带电___无关 ____,通常情况下,其极板面积越小、极间距离越大,电容也越__小____。
16、两个电容器的电容分别为8C 和3C ,并联后的等效电容为___11_______; 串联后的等效电容为_24/11_______。
二、选择题1、由电场强度公式E =F/q 0,可知:[ A ]A 、电场强度与试验电荷的有无及大小无关B 、电场强度与试验电荷的电量成反比C 、电场强度与试验电荷的受力成正比D 、以上说法均不对2、关于电场强度与电势的说法正确的是: [ C ] A.电场强度为零处电势也为零 B.电势为零处电场强度也为零C.电场强度与电势不一定同时为零D.以上说法均不对3、电场强度定义式E=F/q 0,这一定义的适用范围是:[ D ] 。
A.点电荷产生的电场;B.静电场;C.匀强电场;D.任何电场 4、真空中边长为a 的正方体任意棱中点处放置一个点电荷 Q ,通过该立方体的电通量为:[ A ] 。
00008 D. ,2 C. ,6 B. ,4QA.εεεεQ Q Q5、真空中静电场的高斯定理是 [ B ]Adt d i Φ-=ε B0ε∑⎰⎰=⋅面内qd SS E C∑⎰=⋅内Id 0μl B D.⎰≡⋅0l E d6、面积为S 的空气平行板电容器,极板上分别带电量±q ,若不考虑边缘效应,则两极板间的相互作用力为 [ A ](A)S q 02ε. (B) S q 022ε. (C) 2022S q ε. (D) 202S q ε.7、在已知静电场分布的条件下,任意两点P 1和P 2之间的电势差决定于[ A ]A. P1和P2两点的位置.B. P1和P2两点处的电场强度的大小和方向.C. 试验电荷所带电荷的正负.D. 试验电荷的电荷大小.8、一电量为-Q 的点电荷均匀分布于无限薄导体球壳球心,A 、B 、C 、D 为球壳表面上的四个点,如图所示。
现将一实验电荷从A 点分别移到B 、C 、D 各点,则:[ D ] 。
A.从A到B ,电场力做功最大; B.从A 到C ,电场力做功最大;C.从A 到D ,电场力做功最大; D.从A 到各点,电场力做功相等。
9、在边长为a 的正方体中心处放置一电量为Q 的点心电荷,设无穷远处为电势零点,则在一个侧面的中心处电势为[ B ] A. Q /40a ;B. Q /20a ;C. Q /0a ;D. 2.5Q /40a10、半径为R 的圆上的内接正三角形边长为a ,三个顶点分别放置着电量为q 、2q 、3q 的三个正电荷,若将另一正点电荷Q 从无穷远处移到圆心O 处,外力所作的功为:[ C ]A .o qQ πε432;B .o qQπε434;C .R qQ o πε46;D .a qQ o πε438 。
11、两个半径相同的金属球,一为空心,一为实心,把两者各自孤立时的电容值加以比较,则 [C ]A. 空心球电容值大.B. 实心球电容值大.C. 两球电容值相等.D. 大小关系无法确定.12、一空气平行板电容器充电后与电源断开,然后在两极板间充满某种各向同性、均匀电介质,则电场强度的大小E 、电容C 、电压U 、电场能量W 四个量各自与充入介质前相比较,增大(↑)或减小(↓)的情形为[ B ]A. E ↑,C ↑,U ↑,W ↑.B. E ↓,C ↑,U ↓,W ↓.C. E ↓,C ↑,U ↑,W ↓.D. E ↑,C ↓,U ↓,W ↑.13、如果在空气平行板电容器的两个极板间平行地插入一块与极板面积相同的金属板,则由于金属板的插入及其相对极板所放位置的不同,对电容器电容的影响为:[ C ] A. 使电容减小,但与金属板相对于极板的位置无关; B. 使电容减小,且与金属板相对于极板的位置有关; C. 使电容增大,但与金属板相对于极板的位置无关; D. 使电容增大,且与金属板相对于极板的位置有关。
三、计算题1、一个半径为R 的均匀带电圆弧,弧心角为60°,电荷线密度为,求环心O 处的电场强度和电势.解:建立以O 点为原点的平面坐标系,取电荷元θλRd dq =,则204RRd dE πεθλ=其中:0=y E ,θπεθλcos 40R d dE x =,RR d E x 06604cos 4πελθπεθλππ⎰-==066124ελπεθλππ==⎰-R Rd U2、将一无限长带电细线弯成图示形状,设电荷均匀分布,电荷线密度为,四分之一圆弧AB 的半径为R ,试求圆心O 点的场强.解:取电量元θλRd dq =,其电场强度元为204R Rd dE πεθλ=建立如图所示的坐标系,因为0=y E θπεθλcos 40Rd dE x -= ,故RR d E x 0454042cos 4πελθπεθλππ⎰=-=3、带电细线弯成半径为R 的半圆形,电荷线密度为 = 0sin,式中0为一常数,为半径R 与x 轴所成的夹角,如图所示.试求环心O 处的电场强度和电势.解:R d RdldE 00204sin 4πεϕϕλπελ==ϕcos dE dE x = 考虑到电荷分布的对称性 0=x Eϕsin dE dE y = RR d dE E y 00002084sin sin ελπεϕϕλϕπ===⎰⎰ 方向沿y 轴负向4、真空中两条无限长直的相互平行的均匀带电线, 相距为r 、电荷线密度均为l 。
建立适当的坐标系,求(1)两线构成的平面上任一点的电场强度;(2)单位长度带电线所受的电场力。
解:设场点距带电线x 远,则在两线内电场强度为:E =2πελx )-x (r 2x-r i ;在两线外电场强度为:E =02πελx )x(r 2xr ++ i )单位长度带电线所受的电场力F = r022πελ(说明力的方向)5、一无限长直均匀带电线,单位长度的带电量为,求在带电线同侧与该带电线距离分别为R 1,R 2的两点A 、B 之间的电势差。
(A 、B 与带电线共面)。
解:因为场强分布r πελE 02=,所以1200ln 2221R R r dr Edr U R R πελπελ⎰⎰===6、面积为S 的平行板电容器,两板间距为d ,求:(1)插入厚度为d /3,相对介电常数为 r 的电介质,其电容量变为原来的多少倍?(2)插入厚度为d /3的导电板,其电容量又变为原来的多少倍?解:(1)真空电容器d S C 00ε=,内部场强S Q E 01ε=,电介质内部场强SQ E r εε02=插入电介质两极电势差33200d S Q d S Q U r ⋅+⋅=εεε 则0021323C d d S U QC rr r r εεεεε+=+==(2)插入厚度为3d的导电板,可看成是两个电容的串联,则dS C C 0213ε==,得0021212323C d S C C C C C ==+=ε7、三平行金属板A 、B 、和C ,面积都是200cm 2,AB 相距4.0mm ,AC 相距2.0mm ,B 、C 两板都接地,如图所示。
若A 板带正电3.0×10-7C ,略去边缘效应,求B 板和C 板上感应电荷。
若以地的电势为零,求A 板电势。
解: 如题图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ(1)∵AB AC U U =,即∴AB AB AC AC E E d d =;∴2d d 21===ACAB ABAC E E σσ,且1σ+2σSq A =得,32S q A =σ S q A 321=σ。
而 7110232-⨯-=-=-=A C q S q σC 。
C 10172-⨯-=-=S q B σ (2)301103.2d d ⨯===AC AC AC A E U εσV8、计算如图所示长和宽均远大于间距的平行板电容器的电容.解:本题与第6题重复 ,答案是()()21011d d d sr r r -+-+εεεε9、图示为一个均匀带电的球壳,其电荷体密度为,球壳内表面半径为R 1,外表面半径为R 2.设无穷远处为电势零点,求空腔内任一点的电势.解:空腔内任一点的场强01=E 1R r π带电球壳上的一点 203132031323)(4)(34r R r rR r E ερπεπρ-=-=21R r R ππ带电球壳外部空间20313220313233)(4)(34r R R rR R E ερπεπρ-=-=2R r φ则空腔内任一点的电势⎰⎰∞•+•=2R 32r E r E d d U R R 21⎰⎰∞-+-=2R dr r R R dr r R r R R 203132203133)(3)(21ερερ)(221220R R -=ερ10、一电量为q 的点电荷位于导体球壳中心,壳的内外半径分别为R 1、R 2.求球壳内外和球壳上场强和电势的分布,并画出E (r )和V (r )曲线.解:当r<R 1时:2014r q E πε=,20102020114)11(42421R q R r qrq dr rqV R R rπεπεπεπε+-=+=⎰⎰∞当R 1<r< R 2时:02=E ,2014R q V πε=当r> R 2时:2034rq E πε=,rq V 034πε=11、如图所示,在半经分别为R 1和R 2的两个同心球面上,分别均匀地分布着电荷Q 和-Q ,求两球面间的电势差。
