运筹学在企业投资中的应用
运筹学应用例题
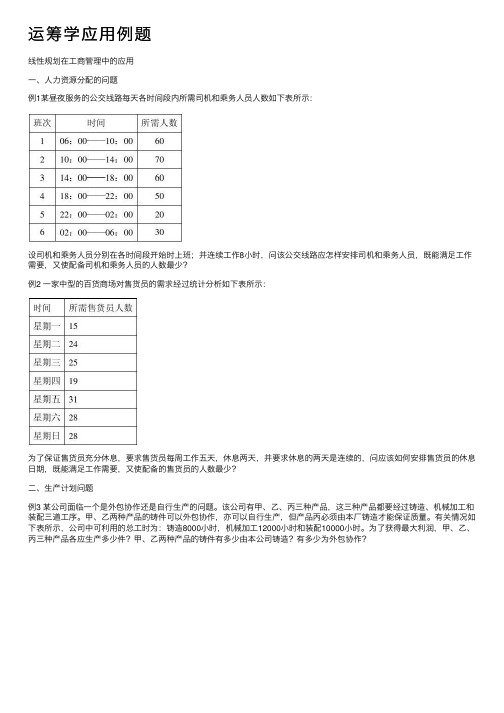
运筹学应⽤例题线性规划在⼯商管理中的应⽤⼀、⼈⼒资源分配的问题例1某昼夜服务的公交线路每天各时间段内所需司机和乘务⼈员⼈数如下表所⽰:设司机和乘务⼈员分别在各时间段开始时上班;并连续⼯作8⼩时,问该公交线路应怎样安排司机和乘务⼈员,既能满⾜⼯作需要,⼜使配备司机和乘务⼈员的⼈数最少?例2 ⼀家中型的百货商场对售货员的需求经过统计分析如下表所⽰:为了保证售货员充分休息,要求售货员每周⼯作五天,休息两天,并要求休息的两天是连续的,问应该如何安排售货员的休息⽇期,既能满⾜⼯作需要,⼜使配备的售货员的⼈数最少?⼆、⽣产计划问题例3 某公司⾯临⼀个是外包协作还是⾃⾏⽣产的问题。
该公司有甲、⼄、丙三种产品,这三种产品都要经过铸造、机械加⼯和装配三道⼯序。
甲、⼄两种产品的铸件可以外包协作,亦可以⾃⾏⽣产,但产品丙必须由本⼚铸造才能保证质量。
有关情况如下表所⽰,公司中可利⽤的总⼯时为:铸造8000⼩时,机械加⼯12000⼩时和装配10000⼩时。
为了获得最⼤利润,甲、⼄、丙三种产品各应⽣产多少件?甲、⼄两种产品的铸件有多少由本公司铸造?有多少为外包协作?三、套裁下料问题例4 某⼯⼚要做100套钢架,每套钢架需要长度分别为2.9⽶、2.1⽶、和1.5⽶的圆钢各⼀根。
已知原料每根长7.4⽶,问应如何下料,可使所⽤原料最省?四、配料问题例5某⼯⼚要⽤三种原料1、2、3混合调配出三种不同规格的产品甲、⼄、丙,产品的规格要求、产品的单价、每天能供应的原材料数量及原材料单价如下表所⽰:问该⼚应如何安排⽣产,才能使利润最⼤?五、投资问题例6 某部门现有资⾦200万元,今后五年内考虑给以下的项⽬投资:项⽬A :从第⼀年到第五年每年年初都可以投资,当年末能收回本利110%;项⽬B :从第⼀年到第四年每年年初都可以投资,次年末能收回本利125%,但规定每年最⼤投资额不能超过30万元;项⽬C :第三年初需要投资,到第五年末能收回本利140%,但规定每年最⼤投资额不能超过80万元;项⽬D :第⼆年初需要投资,到第五年末能收回本利155%,但规定每年最⼤投资额不能超过100万元。
运筹学案例七:投资决策问题(2)

运筹学案例七: 投资决策问题(2)一.问题的提出某投资开发公司拥有总资金100万元,今有4个项目可供选择投资.投入资金及预计收 益如下表所示:项 目 一 二 三 四 投入资金 预计收益 40 30 50 40 35 25 40 35应如何决策投资方案.二.构造数学模型一个好的投资方案应是投资少,收益大的方案.设{1,2,3,4)(i 不投资第i项目0,决定投资第i项目1,==x i数学模型:⎩⎨⎧==-≤+++++++++4,3,2,1,0)1(10040355040)35254030max()40355040(min 432143214321i x x x x x x x x x x x x x x ii改写上述模型为分式规划模型:x x x x x x x x z 432143214035504035254030max ++++++=⎩⎨⎧==-≤+++4,3,2,1,0)1(100403550404321i x x x x x x ii 令τy x jj =,得⎪⎩⎪⎨⎧=≥≤-+++=++++++==)4,3,2,1(0,001004035504014035504035254030max 4321432143211j y y y y y y y y y y y y y z j 或τττ 简化之,得⎪⎩⎪⎨⎧=≥=++++++==)4,3,2,1(0100114035504035254030max 432143211j y y y y y y y y y z jττ或三.求解针对上述特殊模型,采用隐枚举算法思想进行求解.计算表格:),,,(4321y y y y(1)→τ (2) Z 1 (0, 0, 0,τ) (0, 0,τ, 0) (0, 0,τ,τ) (0,τ, 0, 0) (0,τ, 0,τ) (0,τ,τ, 0) (0,τ,τ,τ) (τ,0, 0, 0) (τ,0, 0,τ) (τ,0,τ, 0) (τ,0,τ,τ) (τ,τ,0, 0) (τ,τ,0,τ) (τ,τ,τ,0) (τ,τ,τ,τ)1/40 √ 1/35 √ 1/75 √ 1/50 √ 1/90 √ 1/85 √ 1/125 × 1/40 √ 1/80 √ 1/75 √ 1/115 × 1/90 √ 1/130 × 1/125 × 1/165 ×0.875 0.714 0.8 0.8 0.833 0.765 0.75 0.8125 0.733 0.777X * =( 0, 0, 0, 1 )T max Z=0.875讨论:上述模型最优解对实际投资决策问题显然无法运用.分析其原因构模时缺少考虑总投资应尽量使用条件,例如,至少应把不低于总投资百分之一定比例的资金投入相应项目.本题中应追加: x 1+x 2+x 3+x 4>1 约束条件,于是,模型为:x x x x x x x x z 432143214035504035254030max ++++++=⎪⎩⎪⎨⎧==-=+++≤+++4,3,2,1,0)1(21004035504043214321i x x x x x x x x x x i i令τy x jj =,得⎪⎪⎩⎪⎪⎨⎧=≥≥=+++=++++++==)4,3,2,1(0,0)2(10012)1(14035504035254030max 4321432143211j y y y y y y y y y y y y y z j 或ττττ 计算表格),,,(4321y y y y(1)→τ (2)Z 1( 0, 0,τ,τ) ( 0,τ, 0,τ) ( 0,τ,τ, 0) (τ, 0, 0,τ) (τ,0 ,τ, 0) (τ,τ, 0, 0) 1/75 √ 1/90 √ 1/85 √ 1/80 √ 1/75 √ 1/90 √ 0.8 0.833 0.765 0.8125 0.733 0.777X * = ( 0,1,0,1 )T即公司应投资第二和第四项目,总投资金额为90万元,最大总收益为75万元.另解: 以单位投资所获收益和最大构造模型如下4,3,2,114,3,2,10)1(1004035504087755443max 43214321=-=⎪⎩⎪⎨⎧==-≤++++++=j y x j x x x x x x x x x x z j j j j 令化为标准型:⎪⎪⎪⎩⎪⎪⎪⎨⎧==-≥++++-≥----+++=4,3,2,10)1()1(0354*******)0(075435487284175435487min 312431243124j y y y y y y y y y y y y y y f j j计算表格:),,,(3124y y y y (0) (1)满足否? f ( 0, 0, 0, 0 ) ( 1, 0, 0, 0 ) ( 1, 1, 0, 0 ) ( 1, 0, 1, 0 ) ( 1, 0, 0, 1 ) ( 0, 1, 0, 0 ) ( 0, 1, 1, 0 ) ( 0, 1, 0, 1 ) ( 0, 0, 1, 0 ) ( 0, 0, 1, 1 ) 1.4643 -65 0.5893 -25 -0.2107 -0.1607 -0.1250 0.6643 -15 -0.0857 -0.0500 0.7143 -25 0 10 × × × × × × × × × √28/41X* = ( 0,1,0,1 )T。
运筹学案例集

运筹学案例集常州宝菱重工机械有限公司孔念荣收集整理运筹学的一些典型性应用•合理利用材料问题:如何在保证生产的条件下,下料最少•配料问题:在原料供应量的限制下,如何获取最大收益•投资问题:从投资项目中选取最佳组合,使投资回报最大•产品生产计划:合理利用人力、物力、财力等,使获利最大•劳动力安排:用最少的劳动力来满足工作的需要•运输问题:如何制定最佳调运方案,使总运费最少一、生产计划问题案例1(2-4)、某工厂用A、B、C、D四种原料生产甲、乙两种产品,生产甲和乙所需各种原料的数量以及在一个计划期内各种原料的现有数量见下表所示。
又已知每单位产品甲、乙的售价分别为400元和600元,问应如何安排生产才能获得最大收益?已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制,如下表:问题:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多?案例3(2-25)、某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量,数据如下表所示。
问题:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?案例4(2-28)、永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序;有三种规格的设备B1、B2、B3能完成 B 工序。
Ⅰ可在A、B的任何规格的设备上加工;Ⅱ可在任意规格的A设备上加工,但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工,数据如下表所示。
问题:为使该厂获得最大利润,应如何制定产品加工方案?案例5、某造纸厂用原材料白坯纸生产原稿纸、笔记本和练习本三种产品。
该厂现有工人100人,每月白坯纸供应量为3万公斤。
已知工人的劳动生产率为:每人每月生产原稿纸30捆,或生产日记本30打,或练习本30箱。
运筹学案例六:投资决策问题(1)

运筹学案例六: 投资决策问题(1)一. 问题的提出某公司有五项工程可进行投资.公司决定在前二年中,每年投资10万元;在后二年中, 每年投资8万元.五个项目的投资需要量及其相应的得利情况如下表所示(单位:万元)项目 年度1 2 3 4 51 2 3 42 23 34 1 -2 3 05 4 5 3 3 4 0 2 -2 2 2四年净收入 14 17 15 11 14表中的负数表示当年的收益返回.试问如何投资能使总收益最高.二.构造数学模型设)5,,2,1i (i 0,i ,1y i =⎩⎨⎧=不投资对项目投资对项目,则问题的数学模型为:⎪⎪⎩⎪⎪⎨⎧==≤+++≤+++-≤-+++≤+++++++=5,,2,1,1082533824423102352102342.1411151714max 53215432154321542154321 i y y y y y y y y y y y y y y y y y y y t s y y y y y z i 或二.求解先化成极小化标准型,再对负系数的变量作变量代换)5,,2,1(1 =-=i y x i i 目标函数的系数按递减次序排列,于是,0-1规划模型为: x x x x x f 451321114141517min ++++=⎪⎪⎩⎪⎪⎨⎧==≥++++-≥++++--≥+-+++≥++++-5,,2,110)4(023535)3(0423423)2(032251)1(032241.513245132451324512j x x x x x x x x x x x x x x x x x x x t s j 或这里,目标函数中已把常数-71省去.先通过试探法找出一个可行解,容易看出 )0,1,1,0,0(),,,,(45132=x x x x x是可行解,相应目标值为28.在最小化问题中,目标值大于28,显然不可能是最优值.因此,增加一个过滤性约束:28111414151745132≤++++x x x x x 即为)0(011141415172845132≥-----x x x x x计算表格:),,,,(45132x x x x x约 束 条 件满足条件 目标值(0) (1) (2) (3) (4) (0,0,0,0,0) (1,0,0,0,0) (1,1,0,0,0) (1,0,1,0,0) (1,0,0,1,0) (1,0,0,0,1) (0,1,0,0,0) (0,1,1,0,0) (0,1,0,1,0) (0,1,0,0,1) (0,0,1,0,0) (0,0,1,1,0) (0,0,1,0,1) (0,0,0,1,0) (0,0,0,1,1) (0,0,0,0,1) 28 11 -4 -3 -3 0 13 -1 -1 2 14 0 3 14 3 17 -1 3 6 -1 2 1 4 1 4 2 2 5 9 3 6 -1 2 4 -5 -1 5 0 4 3 1 0 -2 -2 -3 -5× × × × × × × × × √ × × × × × × 26最优解: X=( 0,0,1,1,0 )T, f=26原问题最优解: Y=( 1,1,0,0,1)T , Z=45公司对工程1,2,5进行投资,最高总收益为45万元.[附注]迭代过程中,一旦过滤性条件(0)值为负数,则1右边增加出现1的数均不需检查,显见,这些数对应的(0)值都为负数,且绝对值比前者大.。
2.6-运筹学应用实例汇总
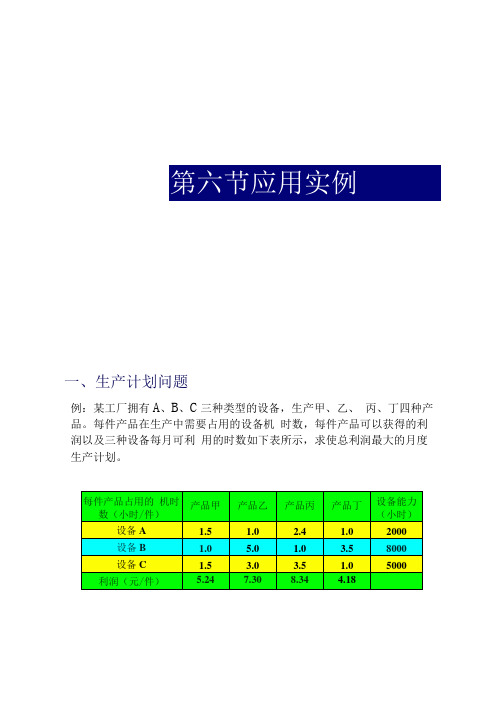
一、生产计划问题例:某工厂拥有A、B、C三种类型的设备,生产甲、乙、丙、丁四种产品。
每件产品在生产中需要占用的设备机时数,每件产品可以获得的利润以及三种设备每月可利用的时数如下表所示,求使总利润最大的月度生产计划。
建模思路■用线性规划制订使总利润最大的生产计划。
■设变量X1为第i种产品的生产件数(i=1, 2, 3, 4),目标函数z为相应的生产计划可以获得的总利润。
在加工时间以及利润与产品产量成线性关系的假设下,可以建立如下的线性规划模型:建模max z= 5.24X1 +7.30x2 +8.34x3 +4.18x4目标函数1.5Xj +1.0x2+2.4X3+1.0X4<2000LOX1 +5.0X2+1.0X3+3.5X4<8000 约束条件1・5X] +3.0X2+3.5X3+1.0X4<5000Xp X2, X3, X4 >0 变量非负约束练习:某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量。
数据如下表。
问:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?甲 .乙丙资源限制铸造工时(小时/件)51078000机加工工时(小时/件)64812000装配工时(小时/件)32210000自产铸件成本(兀/件)354外协铸件成本(兀/件)56一机加工成本(元/件)213装配成本(元/件)322产品售价(元/件)231816解:设孙孙寺分别为三道工序都由本公司加工的甲、乙、丙三种产品的件数,同,幅分别为由外协铸造再由本公司加工和装配的甲、乙两种产品的件数。
求占的利润:利润二售价-各成本之和产品甲全部自制的利润产品甲铸造外协,其余自制的利润产品乙全部自制的利润产品乙铸造外协,其余自制的利润产品丙的利润可得到毛(i = 1,2, 3,4,5)的利润分别为15、10、7、13、9=23-(3+2+3)=15 =23-(5+2+3)=13 =18-(5+1+2)=10 =18-(6+1+2)=9 =16-(4+3+2)=7通过以上分析,可建立如下的数学模型:目标函数:Max 15百+ 10电+ 7两+ 13题+ 9不约束条件:5为+ 10西+ 7玛<80006为+ 4出+ 8^ + 6々+ 4不3百+ 2X2 + 2均+ 3局+ 2不毛,演,传,演,与12000 10000二、混合配料问题例:某工厂要用四种合金T1, T2, T3和T4为原料,经熔炼成为一种新的不锈钢G。
运筹学应用与解决方法

运筹学应用与解决方法
运筹学是运用数学、统计学和经济学等方法研究和解决实际问题的学科。
在许多领域中,特别是在供应链管理、生产计划、物流、市场营销和金融等方面,运筹学的应用非常广泛。
以下是一些常见的运筹学应用和解决方法:
1. 供应链管理:运筹学可以应用于优化供应链网络设计、库存管理、物流运输路线规划、订单分配等问题。
例如,通过数学模型和算法,可以减少库存成本、运输费用,提高物流效率,优化供应链的整体性能。
2. 生产计划:运筹学可以帮助企业优化生产计划,减少生产成本,提高生产效率。
通过数学模型和优化算法,可以制定最佳的生产计划,考虑到产能、设备利用率、订单交付时间等因素。
3. 资源分配:运筹学可以帮助决策者在有限的资源下进行最优的分配。
例如,分配有限的人力资源、货物、资金等,以最大化效益或实现特定目标。
4. 市场营销:运筹学可以用于优化市场营销策略,帮助企业制定最佳的产品定价、广告投放方案、渠道管理策略等。
通过数学模型和数据分析,可以预测市场需求、分析竞争对手行为,以及确定最佳的市场推广策略。
5. 金融风险管理:运筹学可以应用于金融领域,帮助金融机构进行风险管理和投资决策。
通过建立数学模型和使用统计方法,可以评估风险,制定投资组合,
优化资产配置,降低投资风险。
在解决这些问题时,运筹学通常使用数学优化、线性规划、整数规划、动态规划、模拟等方法。
这些方法可以帮助分析问题、建立数学模型,然后使用算法和计算工具进行求解,得到最优或接近最优的解决方案。
同时,运筹学也需要充分考虑实际情况和限制条件,确保解决方案在实际操作中可行和可实施。
运筹学在财务管理中的应用

运筹学在财务管理中的应用运筹学在财务管理中的应用运筹学是一门研究如何寻找最优解决方案的学科,它包括线性规划、整数规划、动态规划、图论等多种方法。
在财务管理中,我们可以运用运筹学的理论和方法,解决诸如投资决策、资金流量规划等问题,从而优化企业的利益和经济效益。
以下就介绍一些运筹学在财务管理中的应用。
1. 投资决策投资决策是管理者必须面对的问题之一。
在投资过程中,不仅需要考虑投资金额和预期收益,还需要考虑风险和收益之间的平衡。
使用运筹学的线性规划和整数规划模型,可以帮助管理者确定最佳的投资方案,优化投资组合,获取最大化的经济效益。
2. 资金流量规划资金流量规划是企业日常经营中不可或缺的一部分。
合理的资金流量规划可以确保企业获得足够的资金支持,并能有效地避免财务风险。
在资金流量规划中,运筹学可以帮助管理者做出最优决策,优化流动资金的配置和使用,以及制定合适的资金管理策略。
3. 风险管理企业面临的风险往往十分复杂和多样化,例如市场风险、信用风险、汇率风险等。
运筹学的方法可以将风险量化和评估,在制定风险管理策略时提供有力的支持。
例如,使用运筹学的风险模型可以帮助管理者确定最佳的风险规避策略,控制风险并最大限度地提高收益。
4. 资产负债管理资产负债管理是指企业在财务管理中根据不同的经济环境条件和市场需求,优化资产和负债之间的关系,从而达到风险控制和回报最大化。
在资产负债管理中,运筹学的方法可以帮助企业制定最佳的投资组合和融资方案,降低财务风险和资金成本。
总之,运筹学在财务管理中的应用非常广泛,可以帮助企业制定最佳的财务策略和决策,提高企业的效益和竞争力。
因此,我们需要深入研究和应用运筹学的理论和方法,为企业的发展和成长提供有力的支持。
运筹学应用领域

运筹学的应用1、市场销售在广告预算和媒介选择、竞争性定价、新产品开发、销售计划的制定等方面。
如美国杜邦公司在五十年代起就非常重视将运筹学用于研究如何做好广告工作,产品定价和新产品的引入。
通用电力公司对某些市场进行模拟研究。
2、生产计划在总体计划方面主要是从总体确定生产、存贮和劳动力的配合等计划以适应波动的需求计划,主要劳动力的配合等计划以适应波动的需求计划,主要用线性规划和模拟方法等。
如某一重型制造厂用线性规划安排生产计划,节省10%生产费用。
此外还可用于生产作业计划、日程表的编排等。
此外,还有在合理下料、配料问题、物料管理等方面的应用。
3、库存管理主要应用于多种物资库存量的管理,确定某些设备的能力或容量,如停车场的大小、新增发电设备容量大小、电子计算机的内存量、合理的水库容量等。
美国国某机器制造公司应用存贮论后,节省18%的费用。
目前国外新动向是:将库存理论与计算机的物资管理信息系统相结合。
如美国西电公司,从1971年起用五年时间建立了“西电物资管理系统”,使公司节省了大量物资存贮费用和运输费用,而且减少了管理人员。
4、运输问题涉及空运、水运、公路运输、铁路运输、管道运输、厂内运输。
空运问题涉及飞行航斑和飞行机组人员服务时间安排等。
为此在国际运筹学协会中设有航空组,专门研究空运中的运筹学问题。
水运有船舶航运计划、港口装卸设备的配置和船到港后的运行安排。
公路运输除了汽车调度计划外,还有公路网的设计和分析,市内公共汽车路线的选择和行车时刻表的安排,出租汽车的调度和停车场的设立。
铁路运输方面的应用就更多了。
5、财政和会计这里涉及预算、贷款、成本分析、定价、投资、证券管理、现金管理等。
用得较多方法是:统计分析、数学规划、决策分析。
此外还有盈亏点分析法、价值分析法等。
6、人事管理这里涉及六个方面。
首先是人员的获得和需求估计;第二是人才的开发,即进行教育和训练;第三是人员的分配,主要是各种指派问题;第四是各类人员的合理利用问题;第五是人才的评价,其中有如何测定一个人对组织、社会的贡献;第六是工资和津贴的确定等。
运筹学方法

运筹学方法运筹学是一门研究如何在有限资源下,做出最优决策的学科。
它涉及到数学、统计学、计算机科学等多个领域,是一种综合性的学科。
运筹学方法可以应用于各种领域,如工业、交通、金融、医疗等,以提高效率、降低成本、优化资源利用等方面。
运筹学方法的基本思想是将问题抽象成数学模型,通过数学方法求解最优解。
这种方法可以帮助人们在复杂的决策问题中做出正确的决策。
下面我们来看几个运筹学方法的应用案例。
1. 生产调度在工业生产中,如何合理地安排生产计划,是一个非常重要的问题。
运筹学方法可以帮助企业制定最优的生产计划,以提高生产效率和降低成本。
例如,一家工厂需要生产两种产品,每种产品需要不同的原材料和生产时间。
如何安排生产计划,使得生产成本最低?这个问题可以通过运筹学方法建立数学模型,然后通过计算机程序求解最优解。
2. 物流配送在物流配送中,如何合理地安排运输路线,是一个非常重要的问题。
运筹学方法可以帮助物流公司制定最优的运输路线,以提高配送效率和降低成本。
例如,一家物流公司需要将货物从多个仓库配送到多个客户,如何安排运输路线,使得总运输成本最低?这个问题可以通过运筹学方法建立数学模型,然后通过计算机程序求解最优解。
3. 股票投资在股票投资中,如何选择最优的投资组合,是一个非常重要的问题。
运筹学方法可以帮助投资者制定最优的投资策略,以提高收益和降低风险。
例如,一位投资者需要选择多个股票组成投资组合,如何选择最优的投资组合,使得收益最高,风险最小?这个问题可以通过运筹学方法建立数学模型,然后通过计算机程序求解最优解。
4. 医疗资源分配在医疗领域中,如何合理地分配医疗资源,是一个非常重要的问题。
运筹学方法可以帮助医疗机构制定最优的资源分配方案,以提高医疗效率和降低成本。
例如,一家医院需要合理地分配医生和护士的工作时间,如何安排工作时间,使得医疗效率最高,成本最低?这个问题可以通过运筹学方法建立数学模型,然后通过计算机程序求解最优解。
运筹学案例集(最新整理)

运筹学案例集常州宝菱重工机械有限公司孔念荣收集整理运筹学的一些典型性应用•合理利用材料问题:如何在保证生产的条件下,下料最少•配料问题:在原料供应量的限制下,如何获取最大收益•投资问题:从投资项目中选取最佳组合,使投资回报最大•产品生产计划:合理利用人力、物力、财力等,使获利最大•劳动力安排:用最少的劳动力来满足工作的需要•运输问题:如何制定最佳调运方案,使总运费最少一、生产计划问题案例1(2-4)、某工厂用A、B、C、D四种原料生产甲、乙两种产品,生产甲和乙所需各种原料的数量以及在一个计划期内各种原料的现有数量见下表所示。
又已知每单位产品甲、乙的售价分别为400元和600元,问应如何安排生产才能获得最大收益?所需原料产品A B C D甲乙4442824现有原料数量28203224案例2(2-6)、某工厂在计划期内要安排Ⅰ、Ⅱ两种产品的生产,已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制,如下表:问题:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多?案例3(2-25)、某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量,数据如下表所示。
问题:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?案例4(2-28)、永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序;有三种规格的设备B1、B2、B3能完成 B 工序。
Ⅰ可在A、B的任何规格的设备上加工;Ⅱ可在任意规格的A设备上加工,但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工,数据如下表所示。
问题:为使该厂获得最大利润,应如何制定产品加工方案?案例5、某造纸厂用原材料白坯纸生产原稿纸、笔记本和练习本三种产品。
你能够列举一些常见的运筹帷幄之中的例子吗?

你能够列举一些常见的运筹帷幄之中的例子吗?运筹帷幄,字面上是指指挥军队在帷幄中制定战术战略,实际上它有更广泛的含义。
它是指在任何复杂的情境下,通过精心策划和高效决策来达到最佳结果的能力。
在现代社会,运筹帷幄的原则不仅仅应用于战争,也被广泛应用于管理、工程、运输、供应链、金融等领域。
下面是一些常见的运筹帷幄的例子:一、交通运输方面的运筹帷幄交通运输领域是一个复杂而庞大的系统,而运筹帷幄在其中起到了关键作用。
举个例子,城市交通拥堵是一个世界性难题,为了解决这个问题,运筹学家运用模型和算法来优化交通信号灯时间、调整交通流量分配以及推出交通违规惩罚等策略,以期缓解拥堵。
这样的例子还包括公共交通线路优化、物流配送路径规划等。
二、供应链管理中的运筹帷幄供应链管理是一个涉及多个环节和参与方的复杂系统。
在供应链管理中,运筹学的原理被用来最大限度地减少成本、提高效率和降低风险。
例如,通过运筹学模型和算法,可以确定最佳的库存管理策略,以避免库存过高或过低,同时满足需求;在供应链网络设计中,可以运用运筹学的方法来确定最佳的仓储和分销中心的位置和数量。
三、金融领域的运筹帷幄在金融领域,运筹学的原理广泛应用于风险管理、资产配置、投资组合优化等方面。
例如,在投资组合优化中,运筹学方法可以帮助投资者找到最佳的资产组合,以在给定风险水平下获得最大的回报。
此外,运筹学还可以用于优化金融衍生品的定价、设计最优的套利策略等。
四、生产和运作管理中的运筹帷幄在生产和运作管理中,运筹学的原理被广泛用于提高效率、降低成本和优化资源利用。
例如,运筹学方法可以用于优化生产计划和排程,确定最佳的生产线配置和生产批量,以最大限度地提高产能和生产效率。
此外,运筹学方法还可以用于供应链和物流管理,以优化仓储和配送的效率。
五、医疗卫生领域的运筹帷幄在医疗卫生领域,运筹学的原理被用来优化医疗资源配置和调度,提高医疗效率和质量。
例如,在医院资源管理中,可以利用运筹学模型来合理分配医疗设备、床位和医护人员,以满足患者的需求,提高床位利用率和医疗质量。
关于运筹学在企业管理中的应用(一)

关于运筹学在企业管理中的应用(一)
运筹学作为一门利用数学、统计学和优化理论等手段解决实际问题的领域,发展至今已经广泛应用于企业管理中,对企业决策、生产过程和人员管理等方面均有重要作用。
一、决策方面
企业在制定决策方案时,需要综合考虑各种因素的权衡,运筹学通过数学建模和仿真等方法,为决策者提供科学的决策支持。
例如,企业制定投资决策时可以应用投资决策分析模型,去评估方案的风险与收益;在制定营销策略时可以应用市场预测模型和营销决策模型去确定合适的销售渠道和营销手段。
二、生产过程方面
运筹学还可以协助企业优化生产流程,提高生产效率。
例如,在物流运输中,运筹学可以帮助企业规划最优的货物运输方案和调度计划;在生产中,可以应用生产计划模型和生产控制模型去调整生产计划和控制生产进度;在库存管理中,可以应用库存模型和采购模型去最小化库存成本和提高库存周转率。
三、人员管理方面
运筹学可以帮助企业更好地管理人力资源,提高人员效能。
例如,在人力资源管理中,可以应用人力资源决策模型去应用科学的方法制定人员的招聘计划和晋升计划;在生产调度中,可以应用人员调度模型和排班模型去合理分配工人的工作时间,提高劳动效率;在绩效考核中,可以建立绩效评价模型去全面评估员工的表现和贡献,从而更好
地激励员工的工作积极性。
总之,运筹学在企业管理中具有广泛的应用,尤其在当今竞争激烈的市场环境下,利用优化手段对企业进行决策支持和流程优化,能有效帮助企业提高效率、降低成本并获得更大的利润空间。
运筹学应用与解决方法

运筹学应用与解决方法
运筹学是一种管理和决策科学,主要用于优化资源的分配和决策的制定。
它可以应用于各种不同的领域,包括生产、物流、交通运输、供应链管理、金融和医疗等。
以下是运筹学在实际应用中常见的问题和解决方法:
1. 生产规划和调度:通过运筹学方法,可以优化生产线的安排和产品的调度,以最大程度地提高生产效率和降低成本。
2. 库存管理:利用运筹学方法,可以确定最优的库存水平和再订货点,以最大限度地减少库存成本和避免缺货。
3. 供应链优化:通过运筹学模型,可以优化供应链中的各个环节,例如供应商选择、运输方式、仓储和配送策略等,以最大程度地提高供应链的效率和降低成本。
4. 路径规划和交通流优化:利用运筹学方法,可以确定最短路径和最优交通流分配,以最小化交通拥堵和降低交通成本。
5. 金融投资组合优化:通过运筹学模型,可以优化投资组合的配置,以最大程度地提高收益和降低风险。
6. 医院排班和资源分配:利用运筹学方法,可以优化医院的医生排班和资源分配,以提高医院的效率和病人的满意度。
在解决这些问题时,通常会使用运筹学中的一些常见方法,例如线性规划、整数规划、动态规划、网络流、模拟、启发式方法等。
通过建立数学模型和利用计算机算法,可以在大量可能的解决方案中找到最优解决方案。
运筹学在经济领域中的应用

运筹学在经济领域中的应用一、引言运筹学是一门研究在复杂环境下进行决策的数学学科,它尝试通过建立数学模型、分析和优化方法来解决实际问题。
在经济领域中,运筹学的应用可以帮助企业和决策者做出最佳决策,提高效益和资源利用率,减少成本和风险。
二、市场定价2.1 价格弹性通过运筹学的方法,可以帮助企业确定产品的最佳价格。
首先需要分析市场上的价格弹性,即价格变化对需求量的影响程度。
运筹学可以通过建立经济模型,使用回归分析等方法来量化价格弹性,并根据市场需求量和竞争情况来调整价格。
2.2 优惠策略在市场竞争激烈的情况下,企业可以利用运筹学的方法来制定优惠策略,以吸引更多的消费者。
通过分析消费者的购买行为和偏好,可以确定最适宜的优惠幅度和销售方式,从而提高产品的销售量和市场份额。
三、供应链管理3.1 生产规划与调度供应链管理是企业运营中非常重要的一环,它涉及到原材料的采购、生产的安排和产品的配送。
运筹学可以帮助企业建立供应链模型,优化生产规划和调度安排,以达到最佳效益和满足客户需求。
3.2 库存管理企业在供应链中需要合理管理库存,以避免库存过高或过低带来的问题。
运筹学可以通过建立库存模型和优化算法,帮助企业确定最佳的库存水平和补货策略,以减少库存成本和避免商品积压或断货的情况。
3.3 运输路线优化供应链中的物流运输是一个重要的环节,它直接影响到产品的及时到达和成本效益。
运筹学可以通过建立运输网络模型和优化算法,帮助企业确定最佳的运输路线,以降低成本、提高运输效率和服务质量。
3.4 供应商选择与评价运筹学可以帮助企业在供应链中选择最合适的供应商,并对供应商进行绩效评价。
通过建立供应商评价指标和模型,可以有效地评估供应商的质量、交货能力和成本等方面的表现,以保证供应链的稳定和高效运行。
四、投资组合优化投资组合优化是运筹学在金融领域的一项重要应用。
通过建立数学模型,可以帮助投资者确定最佳的投资组合,以实现风险与收益的平衡。
运筹学就业方向

运筹学就业方向
运筹学是一门广泛应用于各种领域的学科,包括物流,制造业,金融等等。
因此,运筹学的就业方向也非常广泛。
1. 物流领域:运筹学可以帮助物流公司进行调度和路线优化,提高效率和降低成本。
因此,物流领域是运筹学专业毕业生的最主要就业方向之一。
毕业生可以担任调度员,路线规划师,物流策划师等职位。
2. 制造业:运筹学可以帮助制造企业优化生产计划,提高生产效率和降低成本。
因此,制造企业也是运筹学专业毕业生的一个就业方向。
毕业生可以担任生产调度师,生产计划师,供应链管理师等职位。
3. 金融领域:运筹学在金融领域也有广泛的应用。
毕业生可以在银行,保险公司,证券公司等机构中工作。
他们可以担任风险管理师,投资分析师,量化交易员等职位。
4. 政府部门:运筹学在政府部门中也有广泛的应用,如公共交通部门,城市规划部门等。
毕业生可以担任调度员,规划师,交通运输专家等职位。
总之,运筹学是一个非常实用的学科,毕业生可以在各种领域中找到自己的就业方向。
需要注意的是,运筹学是一门高度数学化的学科,毕业生需要具备扎实的数学功底和分析能力。
- 1 -。
运筹学的起源与发展

运筹学的起源与发展运筹学是一门研究优化资源配置、提高系统效率的学科。
从古代的军事思想和管理哲学中起源,运筹学经过多个阶段的发展,已成为解决现实问题不可或缺的工具。
1、运筹学的起源运筹学的思想可以追溯到古代。
例如,古代的军事家在策划战役时,会考虑兵力、战略和战术等因素,力求以最小的代价取得最大的胜利。
这种对资源优化配置的追求,正是运筹学的核心思想。
在管理哲学中,运筹学也得到了应用,如古代的皇帝在治理国家时,会考虑各种资源、政策和社会稳定等因素,以制定出最优的政策。
2、运筹学的发展运筹学真正的发展是在20世纪初。
当时,由于工业革命的出现,人们开始面对更加复杂的大规模问题,如生产计划、物资管理和交通运输等。
这些问题的出现促进了运筹学的诞生。
2.1产生阶段20世纪初,一些科学家开始运用数学和统计学方法来解决实际问题。
例如,亨利·福特在生产线上采用流水线生产方式,大大提高了汽车的生产效率。
这个阶段的主要成果是确定了运筹学的基本研究方法和应用领域。
2.2发展阶段在20世纪中叶,运筹学得到了进一步发展。
随着计算机技术的进步,运筹学开始采用更加高效的算法和优化技术,以解决更加复杂的问题。
例如,兰德公司在这个时期为美国军方提供了一系列重要的优化方案,为美国在冷战中的胜利做出了贡献。
2.3成熟阶段进入21世纪,运筹学已经发展成为一门成熟的学科。
随着大数据和人工智能等新技术的出现,运筹学开始与这些领域深度融合,形成了诸多新的研究方向和应用领域。
例如,机器学习和人工智能技术在运筹学中的应用,为解决实际问题提供了更加强大的支持。
3、运筹学的应用运筹学在各个领域都有广泛的应用。
在商业领域,运筹学被用来制定供应链管理、生产计划和库存管理等策略,以提高企业的效率和竞争力。
例如,亚马逊通过运用运筹学算法来优化其物流和仓储系统,从而实现了高效的商品配送和服务。
在工业领域,运筹学被应用于生产过程优化、设备维护和能源管理等方面。
实用运筹学

实用运筹学实用运筹学运筹学是一门综合性的学科,旨在通过系统地分析和解决现实生活中遇到的各种决策问题。
实用运筹学是运筹学理论与方法在实践中的应用,涵盖了广泛的领域,如生产与运输管理、物流优化、项目管理、决策分析等。
本文旨在介绍实用运筹学的基本概念、方法以及在现实生活中的应用。
一、实用运筹学的基本概念实用运筹学是一门以数理模型和方法为基础的决策科学,主要是通过建立数学模型来描述和分析复杂的实际问题,从而寻求最优或较优的解决方案。
实用运筹学综合了数学、统计学、计算机科学、经济学等多个学科的理论和方法,具有广泛的应用价值。
实用运筹学的研究过程包括问题建模、模型求解和方案评价三个主要步骤。
首先,需要将实际问题抽象为数学模型,明确问题的目标、约束和决策变量。
然后,运用数学和计算机的方法求解模型,得到一个或多个解,并进行方案评价和灵敏度分析,以确定最优解或帮助决策者做出有理性的决策。
实用运筹学主要利用线性规划、整数规划、动态规划、图论、概率统计等方法来解决问题。
线性规划用于求解线性目标函数和线性约束条件下的最优解;整数规划则考虑决策变量的整数限制;动态规划适用于具有最优子结构的问题;图论用于描述和分析网络结构等问题;概率统计可以用于描述和分析不确定性和风险等问题。
二、实用运筹学的应用领域1. 生产与运输管理实用运筹学在生产与运输管理中的应用主要包括生产调度、库存管理、供应链优化等方面。
通过建立数学模型,可以优化生产调度,使生产效率最大化,减少生产成本。
同时,在物流中,也可以使用实用运筹学的方法,对运输路径、仓储规划等进行优化,提高运输效率和降低物流成本。
2. 物流优化物流是现代社会经济活动中不可或缺的一环,物流优化是实用运筹学的一个重要应用领域。
通过运用实用运筹学的方法,可以对供应链网络进行规划,确定最佳的物流路径和配送策略,实现库存的合理化管理,提高物流效率和降低物流成本。
3. 项目管理实用运筹学在项目管理中的应用主要包括项目时间调度、资源分配等方面。
运筹学基础及应用
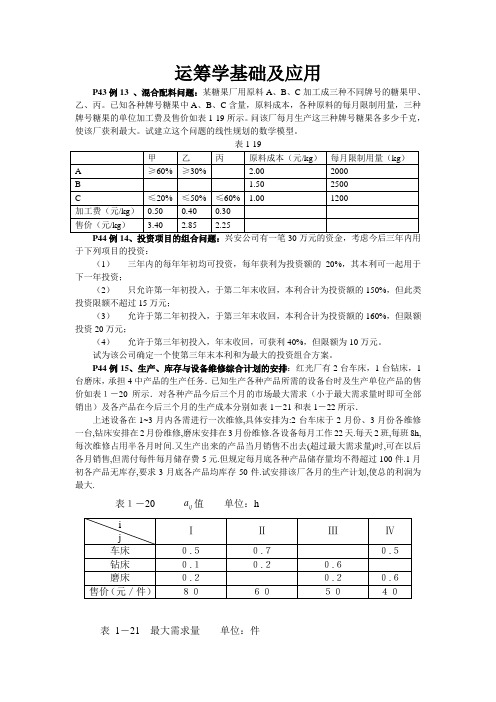
运筹学基础及应用P43例13 、混合配料问题:某糖果厂用原料A、B、C加工成三种不同牌号的糖果甲、乙、丙。
已知各种牌号糖果中A、B、C含量,原料成本,各种原料的每月限制用量,三种牌号糖果的单位加工费及售价如表1-19所示。
问该厂每月生产这三种牌号糖果各多少千克,使该厂获利最大。
试建立这个问题的线性规划的数学模型。
表1-19P44例14、投资项目的组合问题:兴安公司有一笔30万元的资金,考虑今后三年内用于下列项目的投资:(1)三年内的每年年初均可投资,每年获利为投资额的20%,其本利可一起用于下一年投资;(2)只允许第一年初投入,于第二年末收回,本利合计为投资额的150%,但此类投资限额不超过15万元;(3)允许于第二年初投入,于第三年末收回,本利合计为投资额的160%,但限额投资20万元;(4)允许于第三年初投入,年末收回,可获利40%,但限额为10万元。
试为该公司确定一个使第三年末本利和为最大的投资组合方案。
P44例15、生产、库存与设备维修综合计划的安排:红光厂有2台车床,1台钻床,1台磨床,承担4中产品的生产任务.已知生产各种产品所需的设备台时及生产单位产品的售价如表1-20所示.对各种产品今后三个月的市场最大需求(小于最大需求量时即可全部销出)及各产品在今后三个月的生产成本分别如表1-21和表1-22所示.上述设备在1~3月内各需进行一次维修,具体安排为:2台车床于2月份、3月份各维修一台,钻床安排在2月份维修,磨床安排在3月份维修.各设备每月工作22天.每天2班,每班8h,每次维修占用半各月时间.又生产出来的产品当月销售不出去(超过最大需求量)时,可在以后各月销售,但需付每件每月储存费5元.但规定每月底各种产品储存量均不得超过100件.1月初各产品无库存,要求3月底各产品均库存50件.试安排该厂各月的生产计划,使总的利润为最大.表1-20a值单位:h表1-21 最大需求量单位:件P81例1、某食品公司经销的主要产品之一是糖果。
运筹学研究生就业前景

运筹学研究生就业前景运筹学作为一门综合性学科,对于解决实际问题具有重要意义,因此运筹学研究生的就业前景也十分广阔。
首先,运筹学研究生可在企事业单位从事决策咨询和规划工作。
随着经济的发展和市场的竞争,企业越来越重视决策过程的科学化和规划的有效性。
运筹学研究生可以运用数理统计、线性规划、决策分析等方法,帮助企业优化生产计划、仓储运营、配送方案等,提高生产效率和降低成本,因此在企业中具有很高的就业竞争力。
其次,运筹学研究生还可在金融领域从事量化分析和投资决策。
随着金融市场的不断发展和创新,对于高效的量化分析和风险控制能力的需求也越来越大。
运筹学研究生具备数理统计、金融工程、投资组合管理等方面的知识和技能,可以在投资银行、基金公司、保险公司等金融机构从事量化研究、风险管理、资产配置等工作。
此外,运筹学研究生还可在交通运输领域从事运输规划和智能交通管理。
随着城市化进程的加快和人口的快速增长,交通问题日益突出。
运筹学研究生可以运用交通运输经济学和运筹学的方法,分析交通需求、优化交通网络布局、设计智能交通控制系统等,为城市交通提供科学的解决方案。
此外,运筹学研究生还可在电子商务、物流、供应链管理等领域从事相关工作。
随着互联网的快速发展和电子商务的兴起,运筹学在物流配送、供应链管理等方面的应用也越来越广泛。
运筹学研究生可以运用优化算法、模拟仿真等技术,解决电子商务和物流领域的实际问题。
综上所述,运筹学研究生的就业前景非常广阔。
无论是在企事业单位的咨询决策、金融领域的量化分析、交通运输领域的规划管理,还是在电子商务、物流、供应链管理等领域的实际应用,运筹学研究生都可以发挥他们的专业知识和技能,为社会经济发展做出积极贡献。
因此,选择运筹学作为研究生专业是非常有前途的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LUOYANG NORMAL UNIVERSITY2013届本科毕业论文运筹学在企业投资中的应用院(系)名称数学科学学院专业名称数学与应用数学学生姓名郭雅坤学号110412006指导教师张玉兰副教授完成时间2013.5运筹学在企业投资中的应用郭雅坤数学科学学院数学与应用数学学号:110412006指导老师:张玉兰摘要:投资决策是企业发展战略的主要组成部分.如何将有限的资本配置到市场需求的无限投资中去,满足项目投资配置的要求并取得最大的经济效益,是每个企业投资决策者必须要解决的问题.运筹学以数学为工具,寻找各种问题的最优方案,它的许多知识,例如线性规划模型、目标规划模型、动态规划模型等,在企业的投资运行中有着越来越广泛的应用.关键词:投资决策;线性规划;动态规划;目标规划1 现代企业投资问题分析企业投资是指企业的决策者们为了获取更多的资产或权益,以自有的资产投入,并自愿承担相应的风险,所进行的一种很正常的经济活动.1.1企业投资的特点[]1(1) 投资时机的选择性投资不是随便进行的,只有在客观上存在投资的有利条件时,企业才会根据自身的具体情况,制定合适的投资方案.(2) 投资目的的多样性从根本上讲,企业投资的目的都是为了获得投资收益,从而实现自己的财务目标.但是企业在投资时总是各个相对独立的项目进行的,具体投资业务的直接目的也是有区别的.总的来说,可以分为以下几种类型:①扩充企业的规模;②控制相关子企业;③维持现有规模效益;④提高产品质量,降低生产成本;⑤承担社会义务;⑥应对经营风险.(3) 投资收益的不确定性投资的目标收益需要未来才能实现,最终能够收益多少,在进行投资之初是很难准确把握的.正因为如此,每项投资都存在一定的风险. (4) 投资回收的时限性任何投资都需要有回报,但由于资金时间价值的客观存在,投资必须要及时的收回并有收益.1.2企业投资需要考虑的因素[]2 (1) 投资风险投资风险表现为未来收益和增值的不确定性. (2) 投资弹性投资弹性涉及两个方面:规模弹性和结构弹性. (3) 投资管理和经营控制能力对外投资管理与对内投资管理比较,涉及因素多、关系复杂、管理难度大. (4) 筹资能力和投资环境 (5) 投资收益投资中考虑投资收益,要求在投资方案的选择上必须以投资收益的大小来取舍,要以投资收益具有的确定性的方案为选择对象,要分析影响投资收益的因素,并针对这些因素及其投资方案作用的方向、程度,寻求提高投资收益的有效途径. 2 运筹学应用模型介绍及案例研究 2.1 线性规划模型及案例研究[]3线性规划模型是目前应用最广泛的一种优化方法,被广泛的应用于生产计划、物资调用、企业投资优化、资源优化配置等问题.所谓的线性规划问题即在一组线性不等式或不等式的约束之下,求一个线性函数的最大值或最小值的问题,它的一般形式为[]4:⎪⎩⎪⎨⎧+==≥+=≥+++==+++++=),...,1(,...,1,0,...,1,...,...,1,........min 2211221111n q j x q j x m p i b x a x a x a p i b x a x a x a t s x c x c z j jin in i i i n in i i nn 为自由未知量,其中,1,j x j n =⋯为待定的决策变量,我们把这个已知的系数ij a 组成的矩阵1111n m mn a a A a a ⎛⎫ ⎪=⎪ ⎪⎝⎭称为约束矩阵.A 的列向量记为,1,;j A j n =⋯,A 的行向量记为.,,2,1,m i A T i =.称1122n n c x c x c x ++⋯+为目标函数.企业投资决策必然要受到资源有限的约束.由于资金分配问题的影响,许多传统的选择标准将不再有效.有时企业需要考虑独立型资金分配.独立型资金分配问题运用线性规划模型进行分析,力求使投资有较好的结果.独立投资方案的特点是各方案的投资和收益具有可加性.在多个投资方案可供选择时,企业或公司在自有资金额的限定下,必须科学的确定各方案的投入比例,实现最佳的投放组合.企业在选择独立型资金分配时需要考虑以下三个方面[]5: (1) 决策变量假设投资公司对各独立投资方案各期投入资金的百分比相同,现设投资公司对n 个独立投资方案的投资百分比分别为12,,n x x x ⋯. (2) 目标函数在理想的资本市场,净现值NPV 最大等价于财富最大,净现值能比较全面的反映投资项目的经济效益情况.因此,选择n 个独立投资方案总的净现值最大作为目标函数:.max 1i ni i NPV x NPV ∑==(3) 约束条件为达到投资各期投入资金的百分比相同,须对各方案各期所需资金及公司可用于投资的资金累计处理,对于每期投资后拥有资金的余额,留作下期投资使用,资金约束的一般形式为:m k b p x p x p x kt t kt tn n kt t kt t ,...,2,1,. (1)1122111=≤+++∑∑∑∑====综合以上几点,得到独立型投资方案的线性规划模型[]6为:⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=≥≤+++≤+++≤+++≤++++++=∑∑∑∑∑∑∑∑∑∑∑∑============),...,2,1(,0...............,........max 11122111313131223111212121222111111221112211n i x b p x p x p x b p x p x p x b p x p x p x b p x p x p x t s NPV x NPV x NPV x NPV i mt tm t tn n m t t mt t t t t tn n t t t t t t t tn n t t t t n n n n案例分析一:某房地产公司利用自有资金对三个可行投资方案进行组合投资,由于受到工程工期的和资金额的限制,只能按一定的百分比对各方案进行投资,投资分四期进行,各方案所需资金和企业各期可用于的投资资金、各方案预计净现值等资料. 如下表所示:企业投资原始数据表(百万元)方案要求各期的投资百分比相同,方案运行后的净现值按所投资金百分比.设对三个方案的投资百分比分别为 1,2,3x x x ,从而得到该问题的线性规划模型为:⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤++≤++≤++≤++++=)3,2,1(01018232181519156912113576..8109max 321321321321321i x x x x x x x x x x x x x t s x x x NPV i利用单纯形法求解,得到该投资方案的最优解为:%33.131521≈=x ,,02=x %40523==x ,此时4.4max =NPV ,即投资公司每期把资金的13.33%投入方案一,40%投入方案三,方案二不投资金,这是可取得最大的净现值440万元. 2.2 动态规划模型及案例研究动态规划是一种研究多阶段决策问题的理论和方法.我们所说的多阶段决策问题是指,一个系统,可以分成若干个阶段,任意一个阶段k ,系统的状态可以用k x 表示(k x 可以是数量、向量、集合等).在每一阶段k 的每一状态k x 都有一个决策集合)(k k x Q ,在)(k k x Q 中选定一个决策)(k k k x Q q ∈,状态k x 就转移到新的状态),(1k k k k q x T x =+,并且得到效益),(k k k q x R .我们的目的就是在每一个阶段都在他的决策集合中选择一个决策,使所有阶段的总效益),(k k kk q x R ∑达到最优,即就是要在所有可能的策略中选取一个最优的策略,使得在预定的标准下得到最好的效果.一般的多阶段决策问题具有这样的递推关系是:设()1n k k f x -+表示第k 个阶段的状态为k x 经过1+-k n 个阶段的最优目标函数值,则有:{}(){}n n n Q q n k k n k k k Q q k k n q x R x f x f q x R x f kk kk ,max )()(),(max )(111∈+-∈+-=+=根据该递推关系,从后面开始分别求出()()()1211,,n n n f x f x f x -,⋯,其中()1n f x 就是该多阶段决策问题的最优目标函数值.我们把这种递推关系式称为动态规划的基本方程[]7.我们从多阶段决策问题的数学模型可以得到,动态规划最优化原理:对于多阶段决策问题的最优策略,如果用它的前i步策略产生的情况(加上原有的约束条件)来形成一个前i步问题,那么所给最优策略的前i阶段的策略构成这前i步问题的一个最优策略.资源分配问题是属于线性规划、非线性规划这一类的静态问题,其主要作用是将数量一定的资源(如原材料、资金、机器设备、劳动力等)恰当的分配给若干个使用者,使总的目标函数值最优.这类问题通常与时间无关.但是,我们人为的引入时间因素,把它看做按阶段进行的一个多阶段决策问题,这就使得动态规划模型成为求解这类静态问题的有效方法[]8.这里我们给出某总公司对子公司进行投资分配的问题.案例分析二:某总公司要投入600万的资金给下属的4个子公司,各个子公司所得到的利润与投资额大小的关系如下表:表1分析:此表表明,把600万元投入到第一、第二、第三、第四个子公司所得的利润分别为170万元、130万元、230万元、140万元;投入500万元所得的利润分别为170万元、120万元、220万元、130万元.为简化计算,本例中投资额以百万元为分配单位,并引入下面符号:s:总公司投入的资金总量.n :选定的可进行投资的子公司总数.i x :分配给第i 个子公司的资金数量.()i i g X :第i 个子公司接受数量为i X 的资金后所提供的利润. ()k f X :以数量为x 的资金跟配给K 个子公司所得的最大的总利润. 如果()i i g X 中有非线性函数,我们可以利用动态规划方法进行求解,这时我们把整个问题分成n 个阶段,构造动态模型,建立基本的方程,第一阶段讨论把资金分配给第一个子公司是的情况;第二个阶段讨论把资金分配给第一、第二个子公司时的最优分配方案,及所提供的最大利润;第K 个阶段是把资金分配给前K 个子公司时的最优方案以及提供的最大利润.根据动态规划的最优化原理,我们得到:{}),,3,2()()(max )()()(1011n k z X f z g X f X g X f k k xz k =-+==-≤≤ (1)这里假设:各子公司之间进行分配时可以确定投资金额的最小分配单位,这个最小单位可以根据实际情况来确定.例如以百万元为分配单位,而X 就是按这个单位计量.这时z 仅取非负整数,即x ,...,2,1,0. {}),,3,2()()(max)(1,,2,1,0n k z X f z g X f k k Xz k =-+=-= (2)解 下面我们把整个问题进行分阶段求解第一阶段,这时第一个子公司是唯一的投资对象,显然()()11(0,1,2,3,4,5,6)f X g X X ==其结果可列成下表:表2第二阶段,这时要研究如何在第一个子公司、第二个子公司之间进行投资的最优方案,使得利润为最大,根据公式(2),当投资总额为600万元时,得:()()(){}2210,1,66max 6z f g z f z =⋯=+-即24001304012010011013010016080170401700max )0()6()1()5()2()4()3()3()4()2()5()1()6()0(max )6(121212*********=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+++++++=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+++++++=f g f g f g f g f g f g f g f最优策略为(4,2)即对第一个子公司投资400万元,第二个子公司投资200万元.这时两个子公司提供的利润总额最高为240万元.当对这两个子公司的投资额为500万元时,所能得到的最大利润为:()()(){}2210,1,55max 5z f g z f z =⋯=+-即21001204011010010013080160401700max )0()5()1()4()2()3()3()2()4()1()5()0(max )5(1212121212122=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧++++++=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧++++++=f g f g f g f g f g f g f最优策略为(3,2),即第一个子公司投资300万元,第二个子公司投资200万元. 当对这两个子公司的投资额为400万元时,所得的最大利润为:()()(){}2210,1,4max 4z f g z f z =⋯4=+-即18001104010010080130401600max )0()4()1()3()2()2()3()1()4()0(max )4(12121212122=⎪⎪⎪⎩⎪⎪⎪⎨⎧+++++=⎪⎪⎪⎩⎪⎪⎪⎨⎧+++++=f g f g f g f g f g f 最优策略为)2,2(,即第一个子公司投资200万元,第二个子公司投资200万元.当对这两个子公司的投资额为300万元时,所能创造的最大利润为:()()(){}2210,1,3max 3z f g z f z =⋯3=+-即14001004080100401300max )0()3()1()2()2()1()3()0(max )3(121212122=⎪⎪⎩⎪⎪⎨⎧++++=⎪⎪⎩⎪⎪⎨⎧++++=f g f g f g f g f最优策略为)1,2(,第一个子公司投资200万元,第二个子公司投资100万元.当对这两个子公司的投资额为200万元时,所能创造的最大利润为:()()(){}2210,1,22max 2z f g z f z ==+-即1008040401000max )0()2()1()1()2()0(max )2(1212122=⎪⎩⎪⎨⎧+++=⎪⎩⎪⎨⎧+++=f g f g f g f 最优策略为)0,2(即第一个子公司的投资额为200万元,第二个子公司的投资额为0. 当对这两个子公司的投资总额为100万元时,所能创造的最大利润为:⎩⎨⎧=++=⎩⎨⎧++=40040400max )0()1()1()0(max )1(12122f g f g f最优策略为)0,1(或)1,0(,即只对其中的任意一家投入100万元,另一家投入0万元. 很明显的我们可以得到,0)0(2=f . 上述计算结果可以汇总成下表:表3第三阶段,这时要在第二阶段的基础上研究在第一、第二、第三个子公司之间进行投资的最优方案,根据公式(2)()()(){}3320,1,,max z X f X g z f X z =⋯=+- 当6X =时,所能创造的最大利润为:()()(){}3320,1,,66max 6z f g z f z =⋯=+- 即310023040220100200140170180120210502400max )0()6()1()5()2()4()3()3()4()2()5()1()6()0(max )6(232323232323233=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+++++++=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+++++++=f g f g f g f g f g f g f g f最优策略为)3,1,2(,即对第一个子公司投资200万元,第二个子公司投资100万元,第三个子公司投资300万元.依照第二阶段的方法,当对这三家子公司的投资额分别为500万元,400万元,300万元,200万元,100万元,0万元时,所能创造的最大利润分别为:270万元,220万元,170万元,120万元,50万元,0万元.综合本阶段的计算,最终的结果如下表:表4第四阶段,这时应该在第三阶段所得到的结果的基础上研究在这四个子公司之间进行投资的最优分配问题.已知能够对这四个子公司进行投资的总金额为600万元,所以,()()(){}4430,1,,66max 6z f g z f z =⋯=+-即32001405013012012017010022080210503100max )0()6()1()5()2()4()3()3()4()2()5()1()6()0(max )6(343434343434344=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+++++++=+++++++=f g f g f g f g f g f g f g f 此时可以明显的看出,最优策略为(2,0,3,1).这样我们就得到整个问题的最优解,即向第一个公司投资200万元,第三个公司投资300万元,第四个公司投资100万元,第二个公司不进行投资.投资600万元后该公司所能得到的最大总利润为320万元.当投资的目标很多或者投资分配的单位较小时,计算的工作量就很大,这时必须借助Lingo,Matlab 等计算机软件来帮助完成.2.3 目标规划模型及案例研究目标规划是一种解决多准则问题的方法,是线性规划的特殊应用能够处理单个主目标与多个目标并存,以及多个主目标与多个次目标并存的问题.它对众多的目标分别确定一个希望实现的目标值,然后按目标的重要程度依次进行考虑与计算,以求得最接近各目标预定数值的方案.在投资决策时,我们常常面临着几个方案,这些方案在技术上都是可行的,经济上也是合理的,以往的技术经济分析方法是通过对某一个经济技术指标的确定和比较来决定方案的取舍,例如通常取净现值最大的方案或者内部收益率最高的方案为最优方案,即将决策问题归结为目标问题.然而在投资选择过程中逐渐开始要求几个目标同时达到优化,既要求投资回收期短,还要求内部收益率高,又要求净现值大于零等等众多的经济指标优化.这些问题都要借助于目标规划.一般的目标规划的模型如下[]9:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥=≥==-+=≤+=+-+-==++-=-=∑∑∑∑),...,2,1(,0,),...,2,1(,0),...,2,1(,),...,2,1(,..)(min 1111L l d d n j x m l g d d x c m i b x a t s d w d w p z l l j i l l jn j l nj i j ij i ki i Li ki K k k其中:k p 为第k 级优先因子),..,2,1(K k =,且123p p p ≥≥≥⋯;d +表示超出目标的差值,正偏差量; d -表示未达到目标的差值,负偏差量.式中:(1) 当实际值为超出目标值时:0,0>=+-d d ;(2) 当实际值未达到目标值时:0,0=>+-d d ;(3) 当实际值等于目标值时: 0,0==+-d d ;(4)+-kiki w w ,为赋予第l 个目标约束的正负偏差变量权系数; (5) l g 为第l 个目标的预期值,L l ,,2,1 =.案例分析三:深圳某电子科技公司计划开发三种新的产品A,B,C.公司计划在这三种产品退出市场前的总利润为450万元,根据调查这三种产品的单位长期利润分别是7元,5元,15元且分别在2年,2.5年,1年后退出市场.另外,单位产品分别需要消耗0.06人,0.04人,0.1人,且公司能够维持的目标人数为100人.由于资金紧缺,公司至多能够投入66万元来开发生产这三种产品,其中,固定成本为20万元,三种新产品的变动成本为1元,0.5元,3.6元.为了使各种目标达到最优,试提出解决方案. 解 根据目标的重要性,我们将总目标利润分配权数设为5,资金限制的权数为4,员工数限制分配权数可以分为两个部分,避免裁员和避免增加员工的权数分别为3和2.在企业的实际运行目标中,最优先考虑的应该是总利润,其次是投资成本,最后考虑员工的增减和员工的士气.所以综合题目及以上分析,我们可得下表:表5第一层次的目标是最小化偏差1y -,其优先级为1p ;第二层的目标是最小化偏差2y +,其优先级为2p ,第三层次的目标是最小化偏差量33,y y +-,其优先级为3p . 设决策变量1x ,2x ,3x 分别代表公司产品,A,B,C 的平均每天的生产水平.由此我们可得数学模型为⎪⎪⎩⎪⎪⎨⎧=≥=-+++=-+⨯+⨯⨯+⨯⨯+=-+⨯+⨯⨯+⨯⨯+++=+-+-+-+-+-3,2,1,01001.004.006.0660*******.33655.25.036521204500000365153655.2536527..)23()4()5(min 3332122331113213332211j x y y x x x y y x x x y y x x x t s y y p y p y p z j运用Lingo 软件直接对模型进行求解,可得结果为:,219177.1008,021==x x 0,67123.59,100000,03221313=======-+--y y y y y y x .因此,我们可以建议产品B 每天平均生产1008件,推迟产品A,C 的生产,需要进一步调研,视情况再定是否要对产品A,C 进行生产.3y =59.6712说明公司如果采取以上决策,则会多出员工59人.一种情况是进行裁员减小公司规模,另一种是保留现有员工,以待公司有以后更好的发展,也可以考虑把他们安排到其他的老的产品生产线.1y =100000,说明在公司实现450万元目标之后还能再多盈利10万元.12230y y y y --+-====,说明在此方案下,目标资金限制和员工目标问题都得到了解决.结束语运筹学在是通过实际的分析运算考解决实际问题的科学,它与实际结合的非常紧密,在问题的解决中起到了非常重要的作用,深刻在实际的投资优化中,我们可以把投资行为中的各种问题模型化、数据化,帮助投资者进行分析,但运筹学本身不做决策,只提供各种有效可行地方案,最终的决策权还是在决策者手中.由于自己的知识面相对狭窄,因此对于某些问题的研究还不够全面,不够深入,需要在以后的工作和学习中不断完善.致谢本文是在指导老师张老讲师悉心指导下完成的.从论文的选题,文献查询、开题以及论文研究的每个细节上,导师都倾注了很大的心血.在这几个月里,老师严谨的治学态度、渊博的学识以及缜密的逻辑思维都深深的影响着我,从老师那里学到了许多的东西!会让我在以后的生活中更加拼搏!请允许我向我的指导老师表示衷心的感谢!此外,除了老师的悉心教导,同学之间的帮助对我也起了很大帮助,在此也对他们表示感谢!同学们“谢谢”!参考文献[1] 胡运权.郭耀煌.运筹学教程[M].清华大学出版社,2003.[2] 刁在筠.刘桂真.宿洁.马建华.运筹学[M].高等教育出版社,2007.[3] 厉以宁等.中国企业投资分析报告[M].经济科学出版社,2009.[4] 胡运权.运筹学基础及应用[M].哈尔滨工业大学出版社,2006.[5] 甘应爱.运筹学[M].清华大学出版社.[6] 孙威武.投资方案中规划理论的应用[J].中南财经政法大学学报,2006,159(6),69.[7] 邓成望.运筹学的原理及方法[M].华中理工大学出版社,1998.[8] 谭跃进.定量分析方法[M].中国人民大学出版社,2009.[9] 马钧.毛瑛.投资项目决策[M].中国经济出版社.Application of operations research in business investmentGUO Ya-kunCollege of Mathematics Science NO:110412006Tutor:ZHANG Yu-lanAbstract: The investment decision is a major component of enterprise development strategies. How to configure a limited amount of capital to the market demand unlimited investment to meet the configuration requirements of the project investment and achieve maximum economic benefits is the question which enterprises decision-maker must solve. In capital limited within a certain range, how to use the scientific method to determine a reasonable portfolio according to different kinds of investment programs has an extremely important function for companies to fully rational use of funds and to get the best investment results. Operations research, which uses mathematical tools to find the optimal solution of various problems, many of its knowledge, such as linear programming model, multi-objective programming model, dynamic programming model, are widely used in the investment and operation of the enterprise .Keywords: investment decisions; linear programming; dynamic programming; multi-objective planning。
