八上综合测试题2015.12.26

合集下载

八年级上册综合测试题(共6套,含答案)

八年级上册综合测试题(共6套)一、选择题（共20题，每题2分，共40分）1、血吸虫是扁形动物，能寄生在人、畜的血管内，引起肠炎，肝硬化等疾病。

我国科研工作者通过长期调查研究总结出预防血吸虫病的有效方法是（ A ）A 消灭钉螺B 避免下水作业C 不吃草鱼、鲫鱼等淡水鱼以及虾类D 不吃猪肉2、在生活中，有很多平时叫鱼的动物却不是真正的鱼类，下列都属于鱼类的一组是（ C ）A 比目鱼、带鱼、鲍鱼B 鲳鱼、娃娃鱼、草鱼C 鳙鱼、金钱鱼、草鱼D 鳙鱼、鳄鱼、青鱼解析：A项中鲍鱼属于软休动物，B 项中娃娃鱼属于两栖动物，D项中鳄鱼属于爬行动物。

3、美丽的工艺品珊瑚属于（ D ）A 一种具有优美造型的天然矿物质B 一种植物的化石C 一种原生动物分泌的石灰质物质D 一种腔肠动物分泌的石灰质物质4、人很可能感染蛔虫病的生活习惯是（ B）①喝白开水②喝生水③睡懒觉④随地大便⑤不勤洗手⑥不勤濑口A ①②④B ②④⑤C ①②③④D ①②③⑥5、把甲蚯蚓的尾部切去，把乙蚯蚓的头部切去，过一段时间，结果是（ C ）A 甲不能长出尾部，乙能长出头部B 甲和乙均不能长出失去的部分C 甲和乙均能长出失去的部分D 甲能长出失去的尾部，乙不能长出头部。

6、世界上许多国家成立了蚯蚓养殖厂，并把蚯蚓养殖厂称为“环境净化装置”。

蚯蚓能用来净化环境的主要原因是（ D ）A 能在湿润土壤的深层生活B 身体柔软软，能在垃圾中钻洞C 身体分节，运动灵活自如D 能分解枯叶、配根等中的有机物7、有关河蚌体内的珍珠的形成，下列叙述正确的是（ A ）A 由外套膜分泌的珍珠质包被异物形成的B 由闭壳肌的分泌物包被异物形成的C 由斧足上的细胞分泌的黏液形成的D 由贝壳外层细胞分裂形成的8、到海边去游玩时，我们喜欢在沙滩上拾贝壳、捉螃蟹，具有贝壳的动物和螃蟹分别属于（ B）A 软体动物和环节动物B 软体动物和节肢动物C 无脊椎动物和脊椎动物D 环节动物和爬行动物9、如果你想了解蜜蜂的结构特点和生活习性，应从下列哪本书中查找比较方便（ B ）A 《生物学》B 《昆虫学》C 《软体动物学》D 《脊椎动物学》10、你有过捉鱼的经历吗？下河摸鱼时，已经捉到手的鱼往往又会让它挣脱，这是由于其体表生有很滑的黏液。

八年级上册全册全套试卷综合测试卷(word含答案)

八年级上册全册全套试卷综合测试卷（word含答案）一、初二物理声现象实验易错压轴题（难）1．在探究声音的产生和传播的条件时，同学们做了以下实验．(1)小华同学将一只通电的小电铃放在连通了抽气机的玻璃罩内，如图1所示，用抽气机把玻璃罩内的空气逐渐抽出，会发现声音的响度逐渐减小。

如果把空气又逐渐通入玻璃罩内，将会发现_________，此实验说明_______。

(2)小丽等同学利用如图2所示的实验装置进行探究，将系在细线上的乒乓球靠近音叉。

①当小丽同学用小锤敲击音叉的时候，既能听到音叉发出的声音，又能观察到________，通过实验现象得到的结论是__________。

②乒乓球在实验中起到什么作用？_________。

③在实验操作过程中，小丽同学采用：先将音叉离开乒乓球一定距离后敲击音叉，然后再靠近乒乓球，观察现象；小刚同学采用：先将音叉贴紧乒乓球，然后再敲击音叉，观察现象。

你认为哪位同学的操作合理？________。

理由是______。

【答案】声音的响度逐渐增大声音的传播需要介质乒乓球被弹起跳动发声的音叉在振动将不易观察到的音叉的振动转化为乒乓球的弹起小丽小刚的做法分不清是音叉振动让乒乓球跳动起来，还是敲击音叉的人的动作让乒乓球跳动起来【解析】【分析】【详解】(1)[1][2]随着玻璃罩内空气的逐渐减少，声音响度逐渐减小，如果把空气逐渐通入玻璃罩，声音响度会逐渐增大。

说明声音的传播需要介质；(2)[3][4]用小锤敲击音叉时，既能听到声音又能观察到乒乓球被弹起跳动，说明发声的音叉在振动；[5]实验中利用乒乓球把音叉不易观察的微小振动转化为乒乓球的明显振动；[6][7]小丽同学先敲击音叉，然后将音叉再靠近乒乓球，若乒乓球振动，则能证明发声的音叉在振动；小刚先将音叉贴紧乒乓球，然后敲击音叉，若乒乓球振动，则分不清是因为人敲击使球振动，还是音叉引起球的振动。

所以小刚的操作不合理。

2．大海同学为了探究琴弦的音调与音弦的材料、张紧程度、横截面积、长短的关系，设计了如图所示的实验，采用了表一所列各种规格的琴弦、几个钩码和一个能够测量振动频率的仪器．编号材料长度/cm 横截面积/mm2A 铜60 0.76B 铜60 0.89C 铜60 1.02D 铜80 0.76E 铜F 铜100 0.76G 钢80 1.02H 尼龙80 1.02I 尼龙100 1.02实验步骤：（1）在大木板的两边立起两块小木板，在大木板的一端牢牢钉人一根大钉子，把弦的一端绑在钉子上，另一端垂在桌边，把钩码绑在垂下的弦上．（如图）（2）为了验证“琴弦发出声音的音调高低，可能与琴弦的粗细有关”这一猜想，应选用编号为A、____ 、____ 的琴弦进行实验．（如表）（3）为了验证“琴弦发出声音的音调高低，可能与琴弦的长短有关”这一猜想，应选用编号为____ 、____ 、____ 的琴弦进行实验．（如表）（4）表一中有的材料规格还没填全，为了验证“琴弦发出声音的音调高低．可能与琴弦的材料有关”这一猜想，必须知道该项内容．请在表中填上所缺数据．（如表）______、______【答案】B C A D F80 1.02【解析】【详解】(2)在探究“琴弦发出声音的音调高低，可能与琴弦的粗细有关”时，要控制琴弦的材料和长度相同，故选A. B. C的琴弦进行实验；(3)探究“琴弦发出声音的音调高低，可能与琴弦的长短有关”时，应控制琴弦的材料和横截面积相同，所以选A. D. F的琴弦进行实验；(4)为了验证“琴弦发出声音的音调高低。

八年级上册全册全套试卷综合测试(Word版含答案)

八年级上册全册全套试卷综合测试（Word版含答案）一、八年级数学三角形填空题（难）∠=，边AB的垂直平分线交边BC于点D，边AC的垂直平分线1．在ABC中，BACα∠的度数为______.(用含α的代数式表示)交边BC于点E，连结AD，AE，则DAE【答案】2α﹣180°或180°﹣2α【解析】分两种情况进行讨论，先根据线段垂直平分线的性质，得到∠B=∠BAD，∠C=∠CAE，进而得到∠BAD+∠CAE=∠B+∠C=180°－a，再根据角的和差关系进行计算即可．解：有两种情况：①如图所示,当∠BAC⩾90°时，∵DM垂直平分AB，∴DA=DB，∴∠B=∠BAD，同理可得，∠C=∠CAE，∴∠BAD+∠CAE=∠B+∠C=180°−α，∴∠DAE=∠BAC−(∠BAD+∠CAE)=α−(180°−α)=2α−180°；②如图所示,当∠BAC<90°时，∵DM垂直平分AB，∴DA=DB，∴∠B=∠BAD，同理可得，∠C=∠CAE，∴∠BAD+∠CAE=∠B+∠C=180°−α，∴∠DAE=∠BAD+∠CAE−∠BAC=180°−α−α=180°−2α.故答案为2α−180°或180°−2α.点睛：本题主要考查垂直平分线的性质.根据题意准确画出符合题意的两种图形是解题的关键.2．如图，△ABC中，BD、BE分别是高和角平分线，点F在CA的延长线上，FH⊥BE，交BD于点G，交BC于点H．下列结论：①∠DBE＝∠F；②2∠BEF＝∠BAF＋∠C；③∠F＝∠BAC－∠C；④∠BGH＝∠ABE＋∠C．其中正确个数是( )A．4个B．3个C．2个D．1个【答案】B【解析】解：①∵BD⊥FD，∴∠FGD+∠F=90°，∵FH⊥BE，∴∠BGH+∠DBE=90°，∵∠FGD=∠BGH，∴∠DBE=∠F，①正确；②∵BE平分∠ABC，∴∠ABE=∠CBE，∠BEF=∠CBE+∠C，∴2∠BEF=∠ABC+2∠C，∠BAF=∠ABC+∠C，∴2∠BEF=∠BAF+∠C，②正确；③∠ABD=90°﹣∠BAC，∠DBE=∠ABE﹣∠ABD=∠ABE﹣90°+∠BAC=∠CBD﹣∠DBE﹣90°+∠BAC，∵∠CBD=90°﹣∠C，∴∠DBE=∠BAC﹣∠C﹣∠DBE，由①得，∠DBE=∠F，∴∠F=∠BAC﹣∠C﹣∠DBE，③错误；④∵∠AEB=∠EBC+∠C，∵∠ABE=∠CBE，∴∠AEB=∠ABE+∠C，∵BD⊥FC，FH⊥BE，∴∠FGD=∠FEB，∴∠BGH=∠ABE+∠C，④正确．故答案为①②④．点睛：本题考查的是三角形内角和定理，正确运用三角形的高、中线和角平分线的概念以及三角形外角的性质是解题的关键．3．将等边三角形、正方形、正五边形按如图所示的位置摆放，如果∠1=40°，∠2=50°，那么∠ 3的度数等于______________．【答案】12°【解析】等边三角形的内角的度数是60°，正方形的内角度数是90°，正五边形的内角的度数是108°，则∠3=360°-60°-90°-108°-∠1-∠2=12°．点睛：本题考查的是多边形的内角，熟知正三角形、正四边形、正五边形各内角的度数是解答此题的关键．4．一个多边形的内角和与外角和的差是180°，则这个多边形的边数为_____．【答案】5【解析】【分析】根据多边形的内角和公式（n﹣2）•180°与外角和定理列式求解即可【详解】解：设这个多边形的边数是n，则（n﹣2）•180°﹣360°＝180°，解得n＝5．故答案为5．【点睛】本题考查了多边形的内角和与外角和定理，任意多边形的外角和都是360°，与边数无关．5．如图，B处在A处的南偏西45°方向，C处在A处的南偏东15°方向，C处在B处的北偏东80°方向，则∠ACB= ．【答案】85°.【解析】试题分析：令A→南的方向为线段AE，B→北的方向为线段BD，根据题意可知，AE，DB 是正南，正北的方向BD//AE=45°+15°=60°又=180°-60°-35°=85°.考点：1、方向角. 2、三角形内角和.6．如图，在△ABC中，∠ABC、∠ACB的平分线BE、CD相交于点F，∠A=60°，则∠BFC=______．【答案】120【解析】【分析】根据角平分线的定义可得出∠CBF=12∠ABC、∠BCF=12∠ACB，再根据内角和定理结合∠A=60°即可求出∠BFC的度数．【详解】∵∠ABC、∠ACB的平分线BE、CD相交于点F，∴∠CBF=12∠ABC，∠BCF=12∠ACB．∵∠A=60°，∴∠ABC+∠ACB=180°﹣∠A=120°，∴∠BFC=180°﹣（∠CBF+BCF）=180°﹣12（∠ABC+∠ACB）=120°．故答案为120°．【点睛】本题考查了三角形内角和定理，根据角平分线的定义结合三角形内角和定理求出角的度数是解题的关键．二、八年级数学三角形选择题（难）7．如图，小明从A点出发，沿直线前进10米后向左转10°再沿直线前进10米后向左转20°再沿直线前进10米后向左转30°……照这样下去，他第一次回到出发地A点时，一共走了（）A．80米B．160米C．300米D．640米【答案】A【解析】【分析】利用多边形的外角和得出小明回到出发地A点时左转的次数，即可求出多边形的边数，即可解决问题．【详解】解：由题意可知，小明第一次回到出发地A点时，他一共转了360 ，由题意得10°+20° +30°+40°+50°+60°+70°+80°=360°，所以共转了8次，每次沿直线前进10米，所以一共走了80米．故选：A．【点睛】本题考查根据多边形的外角和解决实际问题，注意多边形的外角和是360︒，要注意第一次转了10°，第二次转了20°，第三次转了30°……，利用好规律解题．8．如图，四边形ABCD 中，E 、F 、G 、H 依次是各边中点，O 是四边形ABCD 内一点，若四边形AEOH 、四边形BFOE 、四边形CGOF 的面积分别为7、9、10，则四边形DHOG 的面积为（）A ．7B ．8C ．9D ．10【答案】B【解析】分析：连接OC ，OB ，OA ，OD ，易证S △OBF =S △OCF ，S △ODG =S △OCG ，S △ODH =S △OAH ，S △OAE =S △OBE ，所以S 四边形AEOH +S 四边形CGOF =S 四边形DHOG +S 四边形BFOE ，所以可以求出S 四边形DHOG ．详解：连接OC ，OB ，OA ，OD ，∵E、F 、G 、H 依次是各边中点，∴△AOE 和△BOE 等底等高，∴S △OAE =S △OBE ，同理可证，S △OBF =S △OCF ，S △ODG =S △OCG ，S △ODH =S △OAH ，∴S 四边形AEOH +S 四边形CGOF =S 四边形DHOG +S 四边形BFOE ，∵S 四边形AEOH =7，S 四边形BFOE =9，S 四边形CGOF =10，∴7+10=9+S 四边形DHOG ，解得，S 四边形DHOG =8．故选B.点睛：本题考查了三角形的面积．解决本题的关键将各个四边形划分，充分利用给出的中点这个条件，证得三角形的面积相等，进而证得结论．9．已知直线m n ，将一块含45︒角的直角三角板ABC 按如图方式放置，其中斜边BC 与直线n 交于点D .若125∠=︒，则2∠的度数为（）A ．60︒B ．65︒C ．70︒D ．75︒【答案】C【解析】【分析】先求出∠AED=∠1+∠B=25°+45°=70°，再根据平行线的性质可知∠2=∠AED=70°．【详解】设直线n 与AB 的交点为E 。

度八年级上综合能力测试题

度八年级上综合能力测试题口试局部(85分〕第一卷选择题(60分〕I.词汇测试〔15分〕i.从下面每题的A、B、C三个选项中选出可以交流划线局部的最正确选项。

〔共8小题，每小题1分〕()1. — Do you have trouble finishing this task on your own?—Yes. I require someone to help me.A. funB. timeC. difficulty()2. — Your company is developing a new kind of camera, isn’t it?—Yes, it is. Customers can buy it in March next year.A.producingB. introducingC. reducing()3. —It’s stupid of you to make such a mistake. You should be careful enough.—I was too careless at th at time. I won’t make it a gain.A. awfulB. foolishC. wrong()4. 一In our group, he is the most special because he always has different opinions from others. —That’s true. Almost no one doesn’t know him.A. unusualB. popularC. successful()5. — In order to control the machine well, these workers need to be trained for weeks.—We’ve made a training plan. It w ill be carried out next Monday.A. challengeB. improveC. operate()6. — He is unaware of the problem between his parents and him.—So he cannot get on well with them.A. doesn’t mentionB. doesn’t realizeC. doesn’t memorize()7. —I can’t find out the situation here, so I am not able to give you any advice.—Well... I want you to read these materials.A. know aboutB. think aboutC. worry about()8. — Look out! There is a hole in front of you.—Thank you for reminding me.A. Get downB. Rush outC. Be carefulii.依据句子意思，从下面每题的A、B、C三个选项中选出恰当的词语完成句子。

八年级上册全册全套试卷综合测试(Word版含答案)

∴PC⊥PQ．
（3）如图（2），分两种情况讨论：
当AC=BP，AP=BQ时，△ACP≌△BPQ，则
，
解得，
当AC=BQ，AP=BP时，△ACP≌△BQP，则，
解得
综上所述，存在或使得△ACP与△BPQ全等．
【点睛】
本题主要考查了全等三角形的判定与性质的综合应用，能熟练进行全等的分析判断以及运用分类讨论思想是解题关键．
2．如图，在中，，点是边上的动点，连接，以为斜边在的下方作等腰直角三角形．
（1）填空：的面积等于；
（2）连接，求证：是的平分线；
（3）点在边上，且，当从点出发运动至点停止时，求点相应的运动路程．
【答案】（1）；（2）证明见解析；（3）
【解பைடு நூலகம்】
【分析】
（1）根据直角三角形的面积计算公式直接计算可得；
（3）将绕点逆时针旋转一定的角度，如图3所示，（1）中的“ 为等腰直角三角形”成立吗？请说明理由.
【答案】（1）详见解析；（2）是，证明详见解析；（3）成立，证明详见解析.
【解析】
【分析】
根据等腰直角三角形的性质得出，，推出，，，推出，，求出即可．
延长ED交AC于F，求出，，，根据ASA推出 ≌ ，推出即可．
，
，
，
为EC中点，
，
，，
，
，，
，
，
在和中
≌ ，
，
，
是等腰直角三角形．
是等腰直角三角形，
理由是：过点C作，与DM的延长线交于点F，连接BF，
可证得 ≌ ，
，，
，
作于点N，
由已知，，

八年级上册全册全套试卷综合测试卷(word含答案)

八年级上册全册全套试卷综合测试卷（word 含答案）一、八年级数学三角形填空题（难）1．如图，将一副直角三角板，按如图所示叠放在一起，则图中∠COB =____．【答案】105°．【解析】【分析】先根据直角三角形的特殊角可知：∠ECD=45°，∠BDC=60°，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．【详解】如图，∠ECD =45°，∠BDC =60°，∴∠COB =∠ECD +∠BDC =45°+60°=105°．故答案为：105°．【点睛】此题考查三角形外角的性质，掌握三角形的一个外角等于与它不相邻的两个内角的和的性质是解题的关键．2．等腰三角形的三边长分别为：x +1，2x +3，9，则x =________.【答案】3【解析】①当x+1=2x+3时，解得x=−2(不合题意,舍去)；②当x+1=9时，解得x=8，则等腰三角形的三边为:9、19、9，因为9+9=18<19，不能构成三角形，故舍去；③当2x+3=9时，解得x=3，则等腰三角形的三边为:4、9、9，能构成三角形。

所以x 的值是3.故填3.3．如图，七边形ABCDEFG 中，AB ，ED 的延长线交于点O ，若l ∠，2∠，3∠，4∠的外角和等于210，则BOD ∠的度数为______．【答案】30【解析】【分析】由外角和内角的关系可求得∠1、∠2、∠3、∠4的和，由五边形内角和可求得五边形OAGFE 的内角和，则可求得∠BOD ．【详解】1∠、2∠、3∠、4∠的外角的角度和为210，12342104180∠∠∠∠∴++++=⨯，1234510∠∠∠∠∴+++=，五边形OAGFE 内角和()52180540=-⨯=，1234BOD 540∠∠∠∠∠∴++++=，BOD 54051030∠∴=-=．故答案为：30【点睛】本题主要考查多边形的内角和，利用内角和外角的关系求得∠1、∠2、∠3、∠4的和是解题的关键．4．如图，在ABC ∆中，B 与C ∠的平分线交于点P .若130BPC ∠=︒，则A ∠=______．【答案】80°【解析】【分析】根据三角形内角和可以求得∠PBC+∠PCB 的度数，再根据角平分线的定义，求出∠ABC+∠ACB ，最后利用三角形内角和定理解答即可.【详解】解：在△PBC 中，∠BPC=130°，∴∠PBC+∠PCB=180°-130°=50°.∵PB 、PC 分别是∠ABC 和∠ACB 的角平分线，∴∠ABC+∠ACB=2（∠PBC+∠PCB ）=2×50°=100°，在△ABC 中，∠A=180°-（∠ABC+∠ACB ）=180°-100°=80°.故答案为80°.【点睛】本题主要考查了三角形的内角和定理和角平分线的定义，掌握三角形的内角和定理和角平分线的定义是解题的关键.5．如果一个n 边形的内角和是1440°，那么n=__．【答案】10【解析】∵n 边形的内角和是1440°，∴(n−2)×180°=1440°，解得：n=10.故答案为：10.6．如图所示，请将12A ∠∠∠、、用“＞”排列__________________.【答案】21A ∠∠∠＞＞【解析】【分析】根据三角形的外角的性质判断即可．【详解】解：根据三角形的外角的性质得，∠2＞∠1，∠1＞∠A∴∠2＞∠1＞∠A ，故答案为：∠2＞∠1＞∠A ．【点睛】本题考查了三角形的外角的性质，掌握三角形的一个外角大于和它不相邻的任何一个内角是解题的关键．二、八年级数学三角形选择题（难）7．如图，在△ABC 中，点D 是BC 边上的一点，E ，F 分别是AD ，BE 的中点，连结CE ，CF ，若S △CEF ＝5，则△ABC 的面积为（）A．15 B．20 C．25 D．30【答案】B【解析】【分析】根据题意，利用中线分的三角形的两个图形面积相等，便可找到答案【详解】解：根据等底同高的三角形面积相等，可得∵F是BE的中点，S△CFE＝S△CFB＝5，∴S△CEB＝S△CEF+S△CBF＝10，∵E是AD的中点，∴S△AEB＝S△DBE，S△AEC＝S△DEC，∵S△CEB＝S△BDE+S△CDE∴S△BDE+S△CDE＝10∴S△AEB+S△AEC＝10∴S△ABC＝S△BDE+S△CDE+S△AEB+S△AEC＝20故选：B．【点睛】熟悉三角形中线的拓展性质：分其两个三角形的面积是相等的，这样便可在实际问题当中家以应用.8．已知，如图，AB∥CD，则图中α、β、γ三个角之间的数量关系为（）A．α-β＋γ=180°B．α＋β－γ=180° C．α＋β＋γ=360° D．α－β－γ=90°【答案】B【解析】【分析】延长CD交AE于点F，利用平行证得β=∠AFD；再利用三角形外角定理及平角定义即可得到答案.【详解】如图，延长CD交AE于点F∵AB∥CD∴β=∠AFD∵∠FDE+α=180°∴∠FDE=180°-α∵γ+∠FDE=∠ADF∴γ+180°-α=β∴α＋β－γ=180°故选B【点睛】本题考查平行线的性质以及三角形外角定理的应用，熟练掌握相关性质定理是解题关键.9．如图，三角形ABC中，AB=AC，D，E分别为边AB，AC上的点，DM平分∠BDE，EN平分∠DEC，若∠DMN=110°，则∠DEA=（）A．40°B．50°C．60°D．70°【答案】A【解析】【分析】由等腰三角形的性质得到∠B=∠C，由角平分线的定义得到∠BDM=∠EDM，∠CEN=∠DEN，根据外角的性质得∠B=∠DMN－∠BDM，∠C=∠ENM－∠CEN，整理可得∠DMN+∠DEN=∠EDM+∠ENM，再根据四边形的内角和可得∠DMN+∠DEN=∠EDM+∠ENM=180°，则∠DEN=70°，故∠DEA=40°．【详解】解：∵AB=AC，∴∠B=∠C，又∵DM平分∠BDE，EN平分∠DEC，∴∠BDM=∠EDM，∠CEN=∠DEN，∵∠B=∠DMN－∠BDM=∠DMN－∠EDM，∠C=∠ENM－∠CEN=∠ENM－∠DEN，∴∠DMN－∠EDM=∠ENM－∠DEN，即∠DMN+∠DEN=∠EDM+∠ENM，∵四边形DMNE内角和为360°，∴∠DMN+∠DEN=∠EDM+∠ENM=180°，∴∠DEN=70°，则∠DEA=180°－2∠DEN=40°.故选A．10．一个多边形的内角和是外角和的3倍，则这个多边形是（）A．六边形B．七边形C．八边形D．九边形【答案】C【解析】解：设多边形的边数是n，根据题意得，（n﹣2）•180°=3×360°，解得n=8，∴这个多边形为八边形．故选C．【点评】本题主要考查了多边形的内角和公式与外角和定理，根据题意列出方程是解题的关键，要注意“八”不能用阿拉伯数字写．11．如图，将一张含有30角的三角形纸片的两个顶点叠放在矩形的两条对边上，若∠的大小为（）∠=，则1244α-A．14B．16C．90α-D．44【答案】A【解析】分析：依据平行线的性质，即可得到∠2=∠3=44°，再根据三角形外角性质，可得∠3=∠1+30°，进而得出结论．详解：如图，∵矩形的对边平行，∴∠2=∠3=44°，根据三角形外角性质，可得：∠3=∠1+30°，∴∠1=44°﹣30°=14°．故选A．点睛：本题主要考查了平行线的性质以及三角形外角性质的运用，解题时注意：两直线平行，同位角相等．12．长度分别为2，7，x的三条线段能组成一个三角形，的值可以是（）A．4B．5C．6D．9【答案】C【解析】【分析】根据三角形的三边关系可判断x的取值范围，进而可得答案.【详解】解：由三角形三边关系定理得7－2＜x＜7+2，即5＜x＜9．因此，本题的第三边应满足5＜x＜9，把各项代入不等式符合的即为答案．4，5，9都不符合不等式5＜x＜9，只有6符合不等式，故选C．【点睛】本题考查的是三角形的三边关系，属于基础题型，掌握三角形的三边关系是解题的关键.三、八年级数学全等三角形填空题（难）13．如图，△ABC中，AC＝BC＝5，∠ACB＝80°，O为△ABC中一点，∠OAB＝10°，∠OBA ＝30°，则线段AO的长是_____．【答案】5【解析】【分析】作∠CAO的平分线AD，交BO的延长线于点D，连接CD，由等边对等角得到∠CAB＝∠CBA＝50°，再推出∠DAB＝∠DBA，得到AD＝BD，然后可证△ACD≌△BCD，最后证△ACD≌△AOD，即可得AO＝AC＝5．【详解】解：如图，作∠CAO的平分线AD，交BO的延长线于点D，连接CD，∵AC ＝BC ＝5，∴∠CAB ＝∠CBA ＝50°，∵∠OAB ＝10°，∴∠CAD ＝∠OAD ＝1(CAB OAB)2∠-∠＝()150102︒︒-＝20°， ∵∠DAB ＝∠OAD+∠OAB ＝20°+10°＝30°，∴∠DAB ＝30°＝∠DBA ，∴AD ＝BD ，∠ADB ＝120°，在△ACD 与△BCD 中AC BC AD BD CD CD =⎧⎪=⎨⎪=⎩∴△ACD ≌△BCD （SSS ）∴∠CDA ＝∠CDB ，∴∠CDA ＝∠CDB ＝()1360ADB 2︒-∠＝()13601202︒︒-＝120°，在△ACD 与△AOD 中CDA ADO 120AD ADCAD OAD ︒⎧∠=∠=⎪=⎨⎪∠=∠⎩∴△ACD ≌△AOD （ASA ）∴AO ＝AC=5，故答案为5．【点睛】本题考查全等三角形的判定和性质，作辅助线构造全等三角形是解决本题的关键.14．如图，C 为线段AE 上一动点（不与点A ，E 重合），在AE 同侧分别作正△ABC 和正△CDE ，AD 与BE 交于点O ，AD 与BC 交于点P ，BE 与CD 交于点Q ，连接PQ ．以下五个结论：①AD=BE ；②PQ ∥AE ；③AP=BQ ；④CO 平分∠AOE ；⑤∠AOB=60°．恒成立的结论有__．（把你认为正确的序号都填上）【答案】①②③④⑤【解析】【分析】根据等边三角形的性质及SAS即可证明△ACD≌△BCE即可求解.【详解】①△ABC和△DCE均是等边三角形，点A，C，E在同一条直线上，∴AC=BC，EC=DC，∠BCE=∠ACD=120°∴△ACD≌△ECB∴AD=BE，故本选项正确；②∵△ACD≌△ECB∴∠CBQ=∠CAP，又∵∠PCQ=∠ACB=60°，CB=AC，∴△BCQ≌△ACP，∴CQ=CP，又∠PCQ=60°，∴△PCQ为等边三角形，∴∠QPC=60°=∠ACB，∴PQ∥AE，故本选项正确；③∵∠ACB=∠DCE=60°，∴∠BCD=60°，∴∠ACP=∠BCQ，∵AC=BC，∠DAC=∠QBC，∴△ACP≌△BCQ（ASA），∴CP=CQ，AP=BQ，故本选项正确；④∵BC∥DE，∴∠CBE=∠BED，∵∠CBE=∠DAE，∴∠AOB=∠OAE+∠AEO=60°，同理可得出∠AOE=120°，∵D，O，C，E四点共圆，∴∠OCD=∠OED，∴∠OAC=∠OCD，∴∠DCE=∠AOC=60°，∴OC平分∠AOE，故④正确；⑤∵△ABC、△DCE为正三角形，∴∠ACB=∠DCE=60°，AC=BC，DC=EC，∴∠ACB+∠BCD=∠DCE+∠BCD，∴∠ACD=∠BCE，∴△ACD≌△BCE（SAS），∴∠CAD=∠CBE，∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB，∵∠ACB=∠CBE+∠CEB=60°，∴∠AOB=60°，故本选项正确．综上所述，正确的结论是①②③④⑤．【点睛】本题考查等边三角形的性质、全等三角形的判定与性质，利用旋转不变性，找到不变量，是解题关键．15．如图，在△ABD中，∠BAD＝80°，C为BD延长线上一点，∠BAC＝130°，△ABD的角平分线BE与AC交于点E，连接DE，则∠DEB＝_____．【答案】40°【解析】【分析】做辅助线，构建角平分线的距离，根据角平分线的性质和逆定理可得：EF=EG=EH，设∠DEG=y，∠GEB=x，根据三角形内角和定理可得：∠GEA=∠FEA=40°，∠FEB=∠HEB，列方程为2y+x=80-x,y+x=40,可得结论：∠DEB＝40°.【详解】如图，过E作EF⊥AB于F，EG⊥AD于G，EH⊥BC于H，∵BE平分∠ABD∴EH=EF∵∠BAC＝130°，∠BAD＝80°∴∠FAE=∠CAD=50°∴EF=EG∴EG=EH ∴ED 平分∠CDG∴∠HED=∠DEG设∠DEG=y ，∠GEB=x ，∵∠EFA=∠EGA=90°∴∠GEA=∠FEA=40°∵∠EFB=∠EHB=90°，∠EBH=∠EBF∴∠FEB=∠HEB∴2y+x=80-x,2y+2x=80y+x=40即∠DEB ＝40°.故答案为：40°.【点睛】本题考查三角形内角和定理和角平分线的性质，正确作辅助线是解题的关键.16．如图，在△ABC 中， ∠BAC=90°， AB=AC=22，点D ，E 均在边BC 上，且∠DAE=45°，若BD=1，则DE=__________．【答案】53【解析】分析：根据等腰直角三角形的性质得45B ACB ∠=∠=，把△ABD 绕点A 逆时针旋转90得到△ACF ,连接,EF 如图，根据旋转的性质得,,AD AF BAD CAF =∠=∠45,ABD ACF ∠=∠=接着证明45,EAF ∠=然后根据“SAS”可判断△ADE ≌△AFE ，得到DE =FE ，由于90ECF ACB ACF ∠=∠+∠=，根据勾股定理得222CE CF EF +=，设,DE EF x == 则3CE x =-，则()22231,x x -+=由此即可解决问题．详解：90BAC AB AC ∠==，，∴45B ACB ∠=∠=，把△ABD 绕点A 逆时针旋转90得到△ACF ,连接,EF 如图,则△ABD ≌△ACF ,,,45,AD AF BAD CAF ABD ACF =∠=∠∠=∠=∵45DAE ∠=，∴45BAD CAE ∠+∠=，∴45,CAF CAE ∠+∠=即45,EAF ∠=∴∠EAD =∠EAF ，在△ADE 和△AFE 中AE AE EAD EAF AD AF =⎧⎪∠=∠⎨⎪=⎩， ∴△ADE ≌△AFE ，∴DE =FE ，∵90ECF ACB ACF ∠=∠+∠=，∴222CE CF EF +=，Rt △ABC 中，∵22AB AC ==， ∴224BC AB AC +=，∵1BD =，设,DE EF x == 则3CE x =-，则有()22231,x x -+=解得：5.3x =∴5.3DE = 故答案为5.3点睛：本题属于全等三角形的综合题，涉及三角形旋转，全等三角形的判定与性质，勾股定理等知识点，综合性较强，难度较大.17．如图，在△ABC 中，∠C =90°，AC =BC ，AD 是△ABC 的角平分线，DE ⊥AB ，垂足为点E ．已知AB =12，则△DEB 的周长为_______．【答案】12【解析】根据角平分线的性质，由AD是∠CAB的平分线，DE⊥AB，∠C=90°，可得到CD=ED，然后根据直角三角形的全等判定HL证得Rt△ACD≌Rt△AED，再由全等的性质得到AC=AE，然后根据AC=BC，因此可得△DEB的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB=12.故答案为：12.点睛：此题主要考查了全等三角形的性质和角平分线的性质，解题时根据全等三角形的性质和角平分线的性质得到相等的线段，然后再代还求解即可.18．如图，AD=AB,∠C=∠E,AB=2，AE=8，则DE=_________.【答案】6【解析】根据三角形全等的判定“AAS”可得△ADC≌△ABE，可得AD=AB=2，由AE=8可得DE=AE-AD=6.故答案为：6.点睛：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、SSA、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．四、八年级数学全等三角形选择题（难）19．如图，在△ABC中，AB=AC，高BD，CE交于点O，AO交BC于点F，则图中共有全等三角形（）A ．8对B ．7对C ．6对D ．5对【答案】B【解析】【分析】易证△ABC 是关于AF 对称的图形，其中的小三角形也关于AF 对称，共可找出7对三角形.【详解】全等的三角形有：①△AFB≌△AFC；②△CEB≌△BDC；③△AEO≌△ADO；④△EOB≌△DOC；⑤△OBF≌△OFC；⑥△AOB≌△AOC；⑦△AEC≌△ADB证明①△AFB≌△AFC∵AB=AC，CE⊥AB，BD⊥AC 又∵1122ABC S AB CE AC BD == ∴CE=BD∴在Rt△BCE 和Rt△CBD 中BC BC CE BD=⎧⎨=⎩ ∴△BCE≌△CBD∴BE=CD，∴AE=AD在Rt△AEO 和Rt△ADO 中AE AD AO AO =⎧⎨=⎩∴△AEO≌△ADO∴∠EOD=∠DOA在△BAF 和△CAF 中AB AC BAF CAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴△BAF≌△CAF，得证其余全等证明过程类似故选：B【点睛】本题考查全等的证明，解题关键是利用等腰三角形的性质，推导出图形中边的关系，为证全等作准备20．如图，△ABC 是等边三角形，AQ =PQ ，PR ⊥AB 于点R ，PS ⊥AC 于点S ，PR =PS .下列结论：①点P 在∠A 的角平分线上；②AS =AR ；③QP ∥AR ；④△BRP ≌△QSP ．其中，正确的有（）A．1个 B．2个 C．3个 D．4个【答案】D【解析】∵△ABC是等边三角形，PR⊥AB，PS⊥AC，且PR=PS，∴P在∠A的平分线上，故①正确；由①可知，PB=PC，∠B=∠C，PS=PR，∴△BPR≌△CPS，∴AS=AR，故②正确；∵AQ=PQ，∴∠PQC=2∠PAC=60°=∠BAC，∴PQ∥AR，故③正确；由③得，△PQC是等边三角形，∴△PQS≌△PCS，又由②可知，④△BRP≌△QSP，故④也正确，∵①②③④都正确，故选D．点睛：本题考查了角平分线的性质与全等三角形的判定与性质，准确识图并熟练掌握全等三角形的判定方法与性质是解题的关键．21．如图，点 D 是等腰直角△ABC 腰 BC 上的中点，点B 、B′ 关于 AD 对称，且BB′ 交AD 于 F，交 AC 于 E，连接 FC 、 AB′，下列说法：① ∠BAD=30°； ② ∠BFC=135°；③ AF=2B′ C；正确的个数是（）A．1 B．2 C．3 D．4【答案】B【解析】【分析】依据点D是等腰直角△ABC腰BC上的中点，可得tan∠BAD=12，即可得到∠BAD≠30°；连接B'D，即可得到∠BB'C=∠BB'D+∠DB'C=90°，进而得出△ABF≌△BCB'，判定△FCB'是等腰直角三角形，即可得到∠CFB'=45°，即∠BFC=135°；由△ABF≌△BCB'，可得AF=BB'=2BF=2B'C；依据△AEF与△CEB'不全等，即可得到S△AFE≠S△FCE．【详解】∵点D是等腰直角△ABC腰BC上的中点，∴BD=12BC=12AB，∴tan∠BAD=12，∴∠BAD≠30°，故①错误；如图，连接B'D，∵B、B′关于AD对称，∴AD垂直平分BB'，∴∠AFB=90°，BD=B'D=CD，∴∠DBB'=∠BB'D，∠DCB'=∠DB'C，∴∠BB'C=∠BB'D+∠DB'C=90°，∴∠AFB=∠BB'C，又∵∠BAF+∠ABF=90°=∠CBB'+∠ABF，∴∠BAF=∠CBB'，∴△ABF≌△BCB'，∴BF=CB'=B'F，∴△FCB'是等腰直角三角形，∴∠CFB'=45°，即∠BFC=135°，故②正确；由△ABF≌△BCB'，可得AF=BB'=2BF=2B'C，故③正确；∵AF＞BF=B'C，∴△AEF与△CEB'不全等，∴AE≠CE，∴S△AFE≠S△FCE，故④错误；故选B．【点睛】本题主要考查了轴对称的性质以及全等三角形的判定与性质的运用，如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．22．如图，AD是△ABC的外角平分线，下列一定结论正确的是（）A ．AD+BC=AB+CD ，B ．AB+AC=DB+DC,C ．AD+BC ＜AB+CD ，D ．AB+AC ＜DB+DC【答案】D【解析】【分析】在BA 的延长线上取点E,使AE=AC,连接ED,证△ACD ≌△AED,推出DE=DC,根据三角形中任意两边之和大于第三边即可得到AB+AC ＜DB+DC.【详解】解: 在BA 的延长线上取点E, 使AE=AC,连接ED,∵AD 是△ABC 的外角平分线，∴∠EAD=∠CAD,在△ACD 和△AED 中,AD AD EAD CAD AC AE =⎧⎪∠=∠⎨⎪=⎩∴△ACD ≌△AED(SAS)∴DE=DC,在△EBD 中,BE ＜BD+DE,∴AB+AC ＜DB+DC故选:D.【点睛】本题主要考查三角形全等的证明,全等三角形的性质,三角形的三边关系,作辅助线构造以AB 、AC 、DB 、DC 的长度为边的三角形是解题的关键，也是解本题的难点.23．如图，已知等腰Rt △ABC 和等腰Rt △ADE ，AB=AC=4，∠BAC=∠EAD=90°，D 是射线BC上任意一点，连接EC ．下列结论：①△AEC △ADB ；② EC ⊥BC ； ③以A 、C 、D 、E 为顶点的四边形面积为8；④当BD=时，四边形AECB 的周长为10524++;⑤ 当BD=32B 时,ED=5AB ；其中正确的有（）A ．5个B ．4个C ．3 个D ．2个【答案】B【解析】解：∵∠BAC =∠EAD =90°，∴∠BAD =∠CAE ，∵AB =AC ，AD =AE ，∴△AEC ≌△ADB ，故①正确； ∵△AEC ≌△ADB ，∴∠ACE =∠ABD =45°，∵∠ACB =45°，∴J IAO ECB =90°，∴EC ⊥BC ，故②正确；∵四边形ADCE 的面积=△ADC 的面积+△ACE 的面积=△ADC 的面积+△ABD 的面积=△ABC 的面积=4×4÷2=8．故③正确；∵BD =2，∴EC =2，DC =BC -BD =422=32，∴DE 2=DC 2+EC 2，=(2222+=20，∴DE =25，∴AD =AE =252=10.∴AECB 的周长=AB +DC +CE +AE =442210+45210+，故④正确；当BD =32BC 时，CD =12BC ，∴DE 221322BC BC ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭10BC 5．故⑤错误．故选B ．点睛：此题是全等三角形的判定与性质的综合运用，熟练掌握等腰直角三角形的性质是解答此题的关键．24．下列条件中，不能判定两个直角三角形全等的是( )A ．两条直角边对应相等B ．有两条边对应相等C ．斜边和一锐角对应相等D ．一条直角边和斜边对应相等【答案】B【解析】根据全等三角形的判定SAS ，可知两条直角边对应相等的两个直角三角形全等，故A 不正确；根据一条直角边和斜边对应相等的两个直角三角形，符合全等三角形的判定定理HL ，能判定全等；若两条直角边对应相等的两个直角三角形，符合全等三角形的判定定理SAS ，也能判全等，但是有两边对应相等，没说明是什么边对应，故不能判定，故B正确．根据全等三角形的判定AAS，可知斜边和一锐角对应相等的两直角三角形全等，故C不正确；根据直角三角形的判定HL，可知一条直角边和斜边对应相等两直角三角形全等，故D不正确.故选B.点睛：此题主要考查了直角三角形全等的判定，解题时利用三角形全等的判定SSS，SAS，ASA，AAS，HL，直接判断即可.五、八年级数学轴对称三角形填空题（难）25．如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α．以OC为一边作等边三角形OCD，连接AC、AD，当△AOD是等腰三角形时，求α的角度为______【答案】110°、125°、140°【解析】【分析】先求出∠DAO=50°，分三种情况讨论：①AO=AD，则∠AOD=∠ADO，②OA=OD，则∠OAD=∠ADO，③OD=AD，则∠OAD=∠AOD，分别求出α的角度即可.【详解】解：∵设∠CBO=∠CAD=a，∠ABO=b，∠BAO=c，∠CAO=d，则a+b=60°，b+c=180°﹣110°=70°，c+d=60°，∴b﹣d=10°，∴（60°﹣a）﹣d=10°，∴a+d=50°，即∠DAO=50°，分三种情况讨论：①AO=AD，则∠AOD=∠ADO，∴190°﹣α=α﹣60°，∴α=125°；②OA=OD，则∠OAD=∠ADO，∴α﹣60°=50°，∴α=110°；③OD=AD，则∠OAD=∠AOD，∴190°﹣α=50°，∴α=140°；所以当α为110°、125°、140°时，三角形AOD是等腰三角形，故答案为：110°、125°、140°.【点睛】本题是对等边三角形的考查，熟练掌握等边三角形的性质定理及分类讨论是解决本题的关键.26．如图，△ABC中，AB＝8，AC＝6，∠ABC与∠ACB的平分线交于点F，过点F作DE∥BC，分别交AB、AC于点D、E，则△ADE的周长为_____．【答案】14．【解析】【分析】先根据角平分线的定义及平行线的性质得BD＝DF，CE＝EF，则△ADE的周长＝AB+AC＝14．【详解】∵BF平分∠ABC，∴∠DBF＝∠CBF，∵DE∥BC，∴∠CBF＝∠DFB，∴∠DBF＝∠DFB，∴BD＝DF，同理FE＝EC，∴△AED的周长＝AD+AE+ED＝AB+AC＝8+6＝14．故答案为：14．【点睛】此题考查角平分线的性质，平行线的性质，等腰三角形的等角对等边的性质.27．如图，在△ABC中，AB=AC，∠BAC=120°，D为BC上一点，DA⊥AC，AD=24 cm，则BC的长________cm．【答案】72【解析】【分析】按照等腰三角形的性质、角的和差以及含30°直角三角形的性质进行解答即可.【详解】解：∵AB=AC ，∠BAC=120°∴∠B=∠C=30°∵DA ⊥AC ，AD=24 cm∴DC=2AD=48cm ，∵∠BAC=120°，DA ⊥AC∴∠BAD=∠BAC-90°=30°∴∠B=∠BAD∴BD=AD=24cm∴BC=BD+DC=72cm故答案为72.【点睛】本题考查了腰三角形的性质、角的和差以及含30°直角三角形的性质，其中灵活运用含30°直角三角形的性质是解答本题的关键.28．如图，已知AB=A 1B ，A 1B 1=A 1A 2，A 2B 2=A 2A 3，A 3B 3=A 3A 4，…若∠A=70°，则锐角∠A n 的度数为______.【答案】1702n -︒ 【解析】【分析】根据等腰三角形的性质以及三角形的内角和定理和外角的性质即可得出答案.【详解】在△1ABA 中，AB=A 1B ，∠A=70°可得：∠1BAA =∠1BA A =70°在△112B A A 中，A 1B 1=A 1A 2可得：∠112A B A =∠121A A B根据外角和定理可得：∠1BA A =∠112A B A +∠121A A B∴∠112A B A =∠121A A B =702︒ 同理可得：∠232A A B =2702︒ ∠343A A B =3702︒ …….以此类推：∠A n =1702n -︒ 故答案为：1702n -︒. 【点睛】本题主要考查等腰三角形、三角形的基本概念以及规律的探索，准确识图，熟练掌握和灵活运用相关知识是解题的关键..29．如图，△ABC 中，AC ＝DC ＝3，BD 垂直∠BAC 的角平分线于D ，E 为AC 的中点，则图中两个阴影部分面积之差的最大值为________．【答案】92【解析】【分析】首先证明两个阴影部分面积之差＝S △ADC ，当CD ⊥AC 时，△ACD 的面积最大．【详解】延长BD 交AC 于点H ．设AD 交BE 于点O ．∵AD⊥BH，∴∠ADB＝∠ADH＝90°，∴∠ABD＋∠BAD＝90°，∠H＋∠HAD＝90°，∵∠BAD＝∠HAD，∴∠ABD＝∠H，∴AB＝AH，∵AD⊥BH，∴BD＝DH，∵DC＝CA，∴∠CDA＝∠CAD，∵∠CAD＋∠H＝90°，∠CDA＋∠CDH＝90°，∴∠CDH＝∠H，∴CD＝CH＝AC，∵AE＝EC，∴S△ABE＝14S△ABH，S△CDH＝14S△ABH，∵S△OBD−S△AOE＝S△ADB−S△ABE＝S△ADH−S△CDH＝S△ACD，∵AC＝CD＝3，∴当DC⊥AC时，△ACD的面积最大，最大面积为12×3×3＝92．故填：92．【点睛】本题考查等腰三角形的判定和性质，三角形中线的性质等知识，解题的关键是学会用转化的思想思考问题．30．如图，在第1个△A1BC中，∠B＝20°，A1B＝CB；在边A1B上任取一点D，延长CA1到A2，使A1A2＝A1D，得到第2个△A1A2D；在边A2D上任取一点E，延长A1A2到A3，使A2A3＝A2E，得到第3个△A2A3E，按此做法继续下去，第2019个等腰三角形的底角度数是______________．【答案】20181802⎛⎫⨯ ⎪⎝⎭【解析】【分析】根据等腰三角形的性质求出∠BA 1C 的度数，再根据三角形外角的性质及等腰三角形的性质分别求出∠DA 2A 1，∠EA 3A 2及∠FA 4A 3的度数，找出规律即可得出第2019个三角形中以A 2019为顶点的内角度数．【详解】解：∵在△CBA 1中，∠B=20°，A 1B=CB ，∴∠BA 1C=°180-2B ∠=80°， ∵A 1A 2=A 1D ，∠BA 1C 是△A 1A 2D 的外角，∴∠DA 2A 1=12∠BA 1C=12×80°；同理可得∠EA 3A 2=（12）2×80°，∠FA 4A 3=（12）3×80°， ∴第n 个三角形中以A n 为顶点的底角度数是（12） n-1×80°． ∴第2017个三角形中以A 2019为顶点的底角度数是（12）2018×80°，故答案为：（12） 2018×80°．【点睛】本题考查的是等腰三角形的性质及三角形外角的性质，根据题意得出∠DA 2A 1，∠EA 3A 2及∠FA 4A 3的度数，找出规律是解答此题的关键．六、八年级数学轴对称三角形选择题（难）31．如图，120AOB ∠=︒，OP 平分AOB ∠，且2OP =，若点M N 、分别在OA OB 、上，且PMN ∆为等边三角形，则满足上述条件的PMN ∆有（）A ．1个B ．2个C ．3个D ．无数个【答案】D【解析】【分析】根据题意在OA、OB上截取OE=OF=OP，作∠MPN=60°，只要证明△PEM≌△PON即可反推出△PMN是等边三角形满足条件，以此进行分析即可得出结论.【详解】解：如图在OA、OB上截取OE=OF=OP，作∠MPN=60°．∵OP平分∠AOB，120AOB∠=︒，∴∠EOP=∠POF=60°，∵OE=OF=OP，∴△OPE，△OPF是等边三角形，∴EP=OP，∠EPO=∠OEP=∠PON=∠MPN=60°，∴∠EPM=∠OPN，在△PEM和△PON中，PEM PONPE POEPM OPN∠⎪∠⎧⎩∠⎪∠⎨＝＝＝∴△PEM≌△PON（ASA）．∴PM=PN，∵∠MPN=60°，∴△PNM是等边三角形，∴只要∠MPN=60°，△PMN就是等边三角形，故这样的三角形有无数个．故选：D．【点睛】本题考查等边三角形的判定和性质、全等三角形的判定和性质、角平分线的定义等知识，解题的关键是正确添加辅助线并构造全等三角形.32．等边△ABC，在平面内找一点P，使△PBC、△PAB、△PAC均为等腰三角形，具备这样条件的P点有多少个？（）A．1个B．4个C．7个D．10个【答案】D【解析】试题分析：根据点P在等边△ABC内，而且△PBC、△PAB、△PAC均为等腰三角形，可知P点为等边△ABC的垂心；由此可得分别以三角形各顶点为圆心，边长为半径，交垂直平分线的交点就是满足要求的．解：由点P在等边△ABC内，而且△PBC、△PAB、△PAC均为等腰三角形，可知P点为等边△ABC的垂心；因为△ABC是等边三角形，所以分别以三角形各顶点为圆心，边长为半径画弧，交垂直平分线的交点就是满足要求的，每条垂直平分线上得3个交点，再加三角形的垂心，一共10个．故选D．点评：此题主要考查等腰三角形的性质和等边三角形的性质，有一定的拔高难度，属于中档题．33．如图，在等边三角形ABC中，在AC边上取两点M、N，使∠MBN＝30°．若AM＝m，MN＝x，CN＝n，则以x，m，n为边长的三角形的形状为（）A．锐角三角形B．直角三角形C．钝角三角形D．随x，m，n的值而定【答案】C【解析】【分析】将△ABM绕点B顺时针旋转60°得到△CBH．连接HN．想办法证明∠HCN=120°HN=MN=x即可解决问题．【详解】将△ABM绕点B顺时针旋转60°得到△CBH．连接HN．∵△ABC是等边三角形，∴∠ABC=∠ACB=∠A=60°．∵∠MON=30°，∴∠CBH+∠CBN=∠ABM+∠CBN=30°，∴∠NBM=∠NBH．∵BM=BH，BN=BN，∴△NBM≌△NBH，∴MN=NH=x．∵∠BCH=∠A=60°，CH=AM=n，∴∠NCH=120°，∴x，m，n为边长的三角形△NCH是钝角三角形．故选C．【点睛】本题考查了等边三角形的性质、全等三角形的判定和性质、旋转的性质等知识，解题的关键是学会利用旋转法添加辅助线，构造全等三角形解决问题，属于中考常考题型．34．如图，P为∠AOB内一定点，M、N分别是射线OA、OB上一点，当△PMN周长最小时，∠MPN=110°，则∠AOB=（）A．35°B．40°C．45°D．50°【答案】A【解析】【分析】作P关于OA，OB的对称点P1，P2．连接OP1，OP2．则当M，N是P1P2与OA，OB的交点时，△PMN的周长最短，根据对称的性质可以证得：∠OP1M=∠OPM=50°，OP1=OP2=OP，根据等腰三角形的性质求解．【详解】作P关于OA，OB的对称点P1，P2．连接OP1，OP2．则当M，N是P1P2与OA，OB的交点时，△PMN的周长最短，连接P1O、P2O，∵PP1关于OA对称，∠MPN=110°∴∠P1OP=2∠MOP，OP1=OP，P1M=PM，∠OP1M=∠OPM，同理可得：∠P2OP=2∠NOP，OP=OP2，∴∠P1OP2=∠P1OP+∠P2OP=2（∠MOP+∠NOP）=2∠AOB，OP1=OP2=OP，∴△P1OP2是等腰三角形．∴∠OP2N=∠OP1M，∴∠P1OP2=180°-110°=70°，∴∠AOB=35°，故选A．【点睛】考查了对称的性质，解题关键是正确作出图形和证明△P1OP2是等腰三角形是．35．如图，在△ABC中，BI，CI分别平分∠ABC，∠ACB，过I点作DE∥BC，交AB于D，交AC于E，给出下列结论：①△DBI是等腰三角形；②△ACI是等腰三角形；③AI平分∠BAC；④△ADE周长等于AB＋AC．其中正确的是( )A．①②③B．②③④C．①③④D．①②④【答案】C【解析】【分析】根据角平分线的性质、平行线的性质、等腰三角形的判定与性质分别对各选项分析判断后利用排除法求解．【详解】①∵IB平分∠ABC，∴∠DBI=∠CBI．∵DE∥BC，∴∠DIB=∠CBI，∴∠DBI=∠DIB，∴BD=DI，∴△DBI是等腰三角形．故本选项正确；②∵∠BAC不一定等于∠ACB，∴∠IAC不一定等于∠ICA，∴△ACI不一定是等腰三角形．故本选项错误；③∵三角形角平分线相交于一点，BI，CI分别是∠ABC和∠ACB的平分线，∴AI平分∠BAC．故本选项正确；④∵BD=DI，同理可得EI=EC，∴△ADE的周长=AD+DI+EI+AE=AD+BD+EC+AE=AB+AC．故本选项正确；其中正确的是①③④．故选C．【点睛】本题考查了等腰三角形的判定与性质，熟记三角形的角平分线相交于一点是解题的关键．36．如图，O是正三角形ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；②点O与O′的距离为4；③∠AOB=150°；④S四边形AOBO′=6+33；⑤S△AOC+S△AOB=6+934．其中正确的结论是（）A．①②③⑤B．①③④C．②③④⑤D．①②⑤【答案】A【解析】试题解析：由题意可知，∠1+∠2=∠3+∠2=60°，∴∠1=∠3，又∵OB=O′B，AB=BC，∴△BO′A≌△BOC，又∵∠OBO′=60°，∴△BO′A可以由△BOC绕点B逆时针旋转60°得到，故结论①正确；如图①，连接OO′，∵OB=O′B，且∠OBO′=60°，∴△OBO′是等边三角形，∴OO′=OB=4．故结论②正确；∵△BO′A≌△BOC，∴O′A=5．在△AOO′中，三边长为3，4，5，这是一组勾股数，∴△AOO′是直角三角形，∠AOO′=90°，∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°，故结论③正确；S四边形AOBO′=S△AOO′+S△OBO′=12×3×4+34×42=6+43，故结论④错误；如图②所示，将△AOB绕点A逆时针旋转60°，使得AB与AC重合，点O旋转至O″点．易知△AOO″是边长为3的等边三角形，△COO″是边长为3、4、5的直角三角形，则S△AOC+S△AOB=S四边形AOCO″=S△COO″+S△AOO″=123293，故结论⑤正确．综上所述，正确的结论为：①②③⑤．故选A ．七、八年级数学整式的乘法与因式分解选择题压轴题（难）37．下列计算正确的是（）A ．224a a a +=B ．352()a a =C ．527a a a ⋅=D ．2222a a -= 【答案】C【解析】【详解】解：A. 222a a 2a +=，故A 错误；B. ()326a a =，故B 错误；C. 527a a a ⋅=，正确；D. 2222a a a -=，故D 错误；故选C38．若x 2+2(m+1)x+25是一个完全平方式，那么m 的值（）A ．4 或-6B ．4C ．6 或4D ．-6【答案】A【解析】【详解】解：∵x 2+2（m+1）x+25是一个完全平方式，∴△=b 2-4ac=0，即：[2（m+1）]2-4×25=0整理得，m 2+2m-24=0，解得m 1=4，m 2=-6，所以m 的值为4或-6．故选A.39．已知a ，b ，c 是△ABC 的三条边的长度，且满足a 2－b 2=c （a －b ），则△ABC 是（）A ．锐角三角形B ．钝角三角形C ．等腰三角形D ．等边三角形【答案】C【解析】【分析】已知等式左边分解因式后，利用两数相乘积为0两因式中至少有一个为0得到a=b ，即可确定出三角形形状．【详解】已知等式变形得：（a+b ）（a-b ）-c （a-b ）=0，即（a-b ）（a+b-c ）=0，∵a+b-c≠0，∴a-b=0，即a=b ，则△ABC 为等腰三角形．故选C ．【点睛】此题考查了因式分解的应用，熟练掌握因式分解的方法是解本题的关键．40．下列各式从左边到右边的变形是因式分解的是（）A ．(a ＋1)(a －1)＝a 2－1B ．a 2－6a ＋9＝(a －3)2C ．x 2＋2x ＋1＝x (x ＋2x )＋1D ．－18x 4y 3＝－6x 2y 2·3x 2y【答案】B【解析】【分析】分解因式就是把一个多项式化为几个整式的积的形式．因此，要确定从左到右的变形中是否为分解因式，只需根据定义来确定．【详解】A 、是多项式乘法，不是因式分解，错误；B 、是因式分解，正确．C 、右边不是积的形式，错误；D 、左边是单项式，不是因式分解，错误．故选B ．【点睛】本题的关键是理解因式分解的定义：把一个多项式化为几个最简整式的积的形式，这种变形叫做把这个多项式因式分解，然后进行正确的因式分解．41．若2149x kx ++是完全平方式，则实数k 的值为（） A ．43 B ．13 C ．43± D ．13± 【答案】C【解析】【分析】本题是已知平方项求乘积项，根据完全平方式的形式可得出k 的值．【详解】由完全平方式的形式（a±b ）2=a 2±2ab+b 2可得： kx=±2•2x•13，解得k=±43．故选：C 【点睛】本题关键是有平方项求乘积项，掌握完全平方式的形式（a±b ）2=a 2±2ab+b 2是关键．42．下列各运算中，计算正确的是（）A ．a 12÷a 3=a 4B ．（3a 2）3=9a 6C ．（a ﹣b ）2=a 2﹣ab+b 2D ．2a•3a=6a 2【答案】D【解析】【分析】根据同底数幂的除法、积的乘方、完全平方公式、单项式乘法的法则逐项计算即可得.【详解】A 、原式=a 9，故A 选项错误，不符合题意；B 、原式=27a 6，故B 选项错误，不符合题意；C 、原式=a 2﹣2ab+b 2，故C 选项错误，不符合题意；D 、原式=6a 2，故D 选项正确，符合题意，故选D ．【点睛】本题考查了同底数幂的除法、积的乘方、完全平方公式、单项式乘法等运算，熟练掌握各运算的运算法则是解本题的关键．八、八年级数学整式的乘法与因式分解填空题压轴题（难）43．分解因式212x 123y xy y -+-=___________【答案】()232x 1y --【解析】根据因式分解的方法，先提公因式-3y ，再根据完全平方公式分解因式为：()()22212x 12334x 41321y xy y y x y x -+-=--+=--. 故答案为()232x 1y --.44．若22(3)16x m x +-+是关于x 的完全平方式，则m =__________．【答案】7或-1【解析】【分析】直接利用完全平方公式的定义得出2（m-3）=±8，进而求出答案．详解：∵x 2+2（m-3）x+16是关于x 的完全平方式，∴2（m-3）=±8，解得：m=-1或7，故答案为-1或7．。

八年级上级综合测试题

八年级上级综合测试题一、选择题（每题2分，共12分）1、下列几种估测最符合实际情况的是（ B ）A．人步行的速度约为5m/s B．全新的2B铅笔长约18cmC．人体感觉最舒适的温度约为37℃D．一张试卷厚度的大约1mm2、下列现象不能说明光的直线传播的是（ D ）3、魔术师把手伸进一锅沸腾的“油”，1分钟、2分钟……再把手拿出来——没事！对这个现象的分析准确的是（ B）A、魔术师有特异功能B、是因为“油”的沸点低C、“油”在沸腾时的温度持续升高D、是因为手上沾有水吸收了“油”中的热4、下列关于声音的说法中准确的是（ B ）A.只要物体振动，我们就能听到声音B.一切正在发声的物体都在振动C.物体的振动停止后还会发出很弱的声音D.没有听到发出声音的物体一定没振动5、小明同学用放大镜看自己的指纹时，觉得指纹的像太小。

为了使指纹的像能大一些，以下做法，准确的是（ A ）A．眼睛和手指不动，让放大镜离手指稍远些B．眼睛和手指不动，让放大镜离手指稍近些C．放大镜和手指不动，让眼睛离放大镜稍远些D．放大镜和手指不动，让眼睛离放大镜稍近些6、、用质量相等铜、铁、铝制成等体积的三个空心球，比较它们空心部分的体积，则（ C ）A.铜的最大B.铁的最大C.铝的最大D.无法判定二、填空题（每空1分，共18分）1.根据图示，写出被测物体的长度是_____厘米。

2. 远处传来美妙动听的钢琴声，小刚同学寻声而去，其_____不变，但______ 越来越大，琴声是通过____________传入人耳的．3．2011年11月3日1时23分，“神舟八号”到达“天宫一号”30米停泊点，开始以0.2米／秒的相对速度向“天宫一号”缓缓靠拢对接。

从30米的停泊点到相互接触共耗时________秒。

对接完成后，若以“天宫一号”为参照物，“神舟八号”是________的。

4、在电冰箱的冷凝器内，从压缩机送来的氟利昂的蒸气变成了液态，这是用______________的方法使气体液化并__________（吸收/放出）热量；在电冰箱的蒸发器内，液态氟利昂迅速汽化，__________（吸收/放出）热量，使冷冻室内的温度降低。

八年级上综合测试卷学生版

八年级上综合测试卷时间：45分钟满分：100分一、选择题（以下每题各只有一个正确答案，每题3分，共45分）1．随着经济实力的增强，我国的国防事业得到了飞速的发展。

如图所示为我国空军战机空中加油时的情景，以下说法正确的是（）A．以地面为参照物，加油机是静止的B．以加油机为参照物，受油机是运动的C．以地面为参照物，加油机和受油机都是静止的D．以受油机为参照物，加油机是静止的2．以下是同学们的一些估测数据，你认为数据符合实际的是（）A．人体感到舒适的温度是37℃B．人步行的速度约是1.2m/sC．教室地面到天花板的高度大约为300mm D．一节课的时间大约27000s3．下列现象中，是由光的直线传播形成的是（）A．水中的荷花B．“折断”的筷子C．镜中的人D．墙上的手影4．下列事例中，物体的质量发生变化的是（）A．被太阳晒热的砖块B．烧杯中正在沸腾的水C．铁球被压成铁饼D．从地球带到太空的食品5．在“用托盘天平测物体质量时”，某同学用已调好的天平在测物体质量过程中，通过增、减砝码后，发现指针指在分度盘的中央刻度线左边一点，这时他应该（）A．把横梁右端螺母向右旋出一些B．把横梁右端螺母向左旋出一些C．把天平右盘的砝码减少一些D．向右移动游码6．如图所示是我国自行研制即将首飞的C919大型喷气客机，它的机身和机翼均采用了极轻的碳纤维材料。

这种材料的优点是（）A．密度小B．弹性小C．体积小D．硬度小7．如图所示是某物质熔化时温度随时间变化的图象，根据图象中的信息，判断下列说法，正确的是（）A．该物质为非晶体，熔点为80℃B．在第10min时物质处于液态C．物质从开始熔化到安全熔化完，持续了6minD．该物质在熔化过程中温度一直升高8．如图所示，有经验的渔民都知道，只有瞄准鱼的下方才能叉到鱼，产生这一结论的原因是（）A．光的折射B．光的反射C．光的直线传播D．光的色散9．如图，一束光在空气和玻璃的分界面上发生了反射和折射。

初二上册综合练习题

初二上册综合练习题综合练习题是初二上册各科知识的综合测试，旨在检查学生对上册所学内容的掌握情况，提高学生的学习能力和解决问题的能力。

以下是一组综合练习题，帮助学生巩固和复习初二上册所学的各科知识。

语文1.下面一段文字中有几处错别字，请找出并改正：学年伊始，全班全体同学朝气蓬勃，满腔热血。

同学们主动参与了各项社团活动，并积极参与学校的各类竞赛中。

在模拟考试中，班里不少同学都取得了优异的成绩。

2.下面一段文字是描述一位同学的，请提取关键词并组成一个副标题：李明同学是我们班的一名优秀学生。

他学习勤奋，乐于助人，兴趣广泛，特别擅长数学和英语两科。

数学1.已知a = 3，b = 5，c = 7，请计算 a² + b² + c²的值。

2.首项是2，公差是4的等差数列的前10项之和是多少？英语阅读理解Read the passage and answer the questions accordingly.Dogs are known for their incredible sense of smell. They can sniff out people, drugs, and even some diseases. But who knew they could sniff out a bee that had been to another country?Honey bees from Brazil and a type of honey bee from the United Kingdom (UK) are almost exactly the same, so it can be very hard to tell them apart. The only difference is that Brazilian honey bees have yellow and black stripes on their bodies, while UK honey bees have black and yellow stripes.In 2010, scientists from the UK wanted to find out whether bees could travel from Brazil to the UK and mate with the local bees. They decided to put a special mark on the bees that came from Brazil so that they could identify them.The scientists traveled to Brazil and captured a group of honey bees. They took them back to the UK and released them so they could fly around and mate with the local bees. After a while, the scientists noticed something very interesting. The bees that had come from Brazil were mating a lot more than the local bees. In fact, they were mating with almost all of the available female bees. How did they do it? Did they just find the locals more attractive? Or was there something else going on?The scientists finally figured it out. The bees had been using their sense of smell to find the female bees. But how had they managed to find so many so quickly? Maybe the answer lay in the fact that honey bees can recognize a friend or family member just by smell. By sniffing out familiar smells, the bees were able to find and mate with the female bees.3. What was the difference between Brazilian honey bees and UK honey bees?4. Why did the scientists put a special mark on the bees that came from Brazil?5. How did the Brazilian bees manage to find and mate with so many female bees in the UK?6. What can honey bees recognize just by smell?科学1.请判断下列各项在科学研究中是否属于可靠的证据，是的话写“√”，否则写“×”：(1)有实验证明，酸性物质会腐蚀金属。

哈尔滨2015年12月八年级上质量检查数学试卷含答案解析

哈尔滨2015年12月八年级上质量检查数学试卷含答案解析一、选择题1．目前，哈尔滨市区正在进行道路的全面改造，有关部门要求司机开车时遵章行驶，在下列交通标志中，不是轴对称图形的是（）A．B．C．D．2．PM2.5是指大气中直径小于或等于2.5微米的颗粒物，2.5微米等于0.000 002 5米，把0.000 002 5用科学记数法表示为（）A．2.5×106 B．0.25×10﹣5 C．2.5×10﹣6 D．25×10﹣73．下列运算正确的是（）A．×=B．=9C．=4+3=7 D．4．将分式中的x、y的值同时扩大2倍，则分式的值（）A．扩大2倍B．缩小到原先的C．保持不变D．无法确定5．下列等式成立的是（）A．（﹣3）﹣2=﹣9 B．（﹣3）﹣2=C．a﹣2×b﹣2=a2×b2 D．6．下列根式中，属于最简二次根式的是（）A．B．C．D．7．如图在直角△ABC中，∠BAC=90°，AB=8，AC=6，DE是AB边的垂直平分线，垂足为D，交边BC于点E，连接AE，则△ACE的周长为（）A．16 B．15 C．14 D．138．某工程队预备修建一条长1200m的道路，由于采纳新的施工方式，实际每天修建道路的速度比原打算快20%，结果提早2天完成任务．若设原打算每天修建道路x m，则按照题意可列方程为（）A．﹣=2 B．﹣=2C．﹣=2 D．﹣=29．若m+n=3，则2m2+4mn+2n2﹣6的值为（）A．12 B．6 C．3 D．010．下列讲法中，错误的是（）A．分式方程的解等于0，就讲明那个分式方程无解B．解分式方程的差不多思路是把分式方程转化为整式方程C．检验是解分式方程必不可少的步骤D．能使分式方程的最简公分母等于零的未知数的值不是原分式方程的解二.填空题11．运算：÷=．12．若分式的值为0，则x的值为．13．把多项式ab3﹣4ab分解因式的结果为．14．若有意义，则m的取值范畴是．15．观看下列各式：1×3=22﹣1，3×5=42﹣1，5×7=62﹣1，…请你把发觉的规律用含n（n为正整数）的等式表示为．16．已知关于x的方程的解是正数，则m的取值范畴是．17．等边三角形两角平分线所夹的锐角的度数是．18．已知等腰△ABC，AB=AC，∠ABC=20°，P为直线BC上一点，BP=AB，则∠PAC的度数为．19．△ABC的三边分不为a，b，c，有b+c=8，bc=a2﹣12a+52，按边分类，则△ABC是三角形．20．在△ABC中，D为AB的中点，∠CDA=45°，E在AC上，连接BE交CD于F，满足EF=EC，△CBF的面积为8，则CF=．三.解答题21．先化简，再求值：，其中a=+122．解分式方程：（1）；（2）﹣2．23．已知，求的值．24．若﹣4y+4=0，求xy的值．25．甲、乙两人预备整理一批新到的实验器材．若甲单独整理需要40分钟完工：若甲、乙共同整理20分钟后，乙需再单独整理20分钟才能完工．（1）咨询乙单独整理多少分钟完工？（2）若乙因工作需要，他的整理时刻不超过30分钟，则甲至少整理多少分钟才能完工？26．如图1，在等边△ABC中，D是BC边上一点，连接AD，将△A BD沿AD翻折至△AED，F为CD上一点，∠AEF=∠AED．（1）求证：AE=BF+EF；（2）如图2，M为AE上一点，连接MD、MF，MD=MF，若CD=4，CF=1，求线段AM的长．27．已知：如图，在平面直角坐标系中，△ABC为直角三角形，∠B= 90°，∠A=30°，点C的坐标为（1，0），点B的坐标为（0，），EF垂直平分AC，交AB于点E，交x轴于点F．（1）求点E的坐标；（2）点P从点C动身沿射线CB以每秒1个单位的速度运动，设点P 运动的时刻为t秒，设△PBE的面积为S，用含t的代数式表示S，并直截了当写出t的取值范畴；（3）在（2）的条件下，过点F作直线m∥BC，在直线m上是否存在点Q，使得△PFQ为等腰直角三角形？若存在，求满足条件t的值，并直截了当写出Q的坐标；若不存在，请讲明理由．2015-2016学年黑龙江省哈尔八年级（上）质检数学试卷（12月份）参考答案与试题解析一、选择题1．目前，哈尔滨市区正在进行道路的全面改造，有关部门要求司机开车时遵章行驶，在下列交通标志中，不是轴对称图形的是（）A．B．C．D．【考点】轴对称图形．【分析】按照轴对称图形的概念求解．【解答】解：A、是轴对称图形，故本选项错误；B、是轴对称图形，故本选项错误；C、不是轴对称图形，故本选项正确；D、是轴对称图形，故本选项错误．故选C．【点评】本题考查了轴对称图形的概念：轴对称图形的关键是查找对称轴，图形两部分沿对称轴折叠后可重合．2．PM2.5是指大气中直径小于或等于2.5微米的颗粒物，2.5微米等于0.000 002 5米，把0.000 002 5用科学记数法表示为（）A．2.5×106 B．0.25×10﹣5 C．2.5×10﹣6 D．25×10﹣7【考点】科学记数法—表示较大的数．【分析】科学记数法确实是将一个数字表示成（a×10的n次幂的形式），其中1≤|a|＜10，n表示整数．n为整数位数减1，即从左边第一位开始，在首位非零的后面加上小数点，再乘以10的n次幂．此题n＜0，n=﹣6．【解答】解：将0.000 002 5用科学记数法表示为：2.5×10﹣6．故选：C．【点评】此题考查了科学记数法的表示方法．用科学记数法表示一个数的方法是：（1）确定a：a是只有一位整数的数；（2）确定n：当原数的绝对值≥10时，n为正整数，n等于原数的整数位数减1；当原数的绝对值＜1时，n 为负整数，n的绝对值等于原数中左起第一个非零数前零的个数（含整数位数上的零）．3．下列运算正确的是（）A．×=B．=9C．=4+3=7 D．【考点】二次根式的混合运算．【分析】按照二次根式的除法、乘法以及二次根式的化简进行运算即可．【解答】解：A、×=，故本选项错误；B、÷=3，故本选项错误；C、==5，故本选项错误；D、=，故本选项正确；故选D．【点评】本题考查了二次根式的混合运算，把握二次根式的化简求值是解题的关键．4．将分式中的x、y的值同时扩大2倍，则分式的值（）A．扩大2倍B．缩小到原先的C．保持不变D．无法确定【考点】分式的差不多性质．【分析】按照已知得出=，求出后判定即可．【解答】解：将分式中的x、y的值同时扩大2倍为=，即分式的值扩大2倍，故选A．【点评】本题考查了分式的差不多性质的应用，要紧考查学生的明白得能力和辨析能力．5．下列等式成立的是（）A．（﹣3）﹣2=﹣9 B．（﹣3）﹣2=C．a﹣2×b﹣2=a2×b2 D．【考点】负整数指数幂；分式的差不多性质．【分析】分不按照负整数指数幂、分式的差不多性质分不进行运算．【解答】解：A、错误，（﹣3）﹣2=；B、正确；C、错误，a﹣2×b﹣2=；D、错误，．故选B．【点评】本题要紧考查了负整数指数幂的意义，注意a﹣n=，而不是﹣an．6．下列根式中，属于最简二次根式的是（）A．B．C．D．【考点】最简二次根式．【分析】按照最简二次根式的定义分不对每一项进行分析即可．【解答】解：A、=2，不是最简二次根式；B、是最简二次根式；C、=|a|，不是最简二次根式；D、=，不是最简二次根式；故选B．【点评】此题考查了最简二次根式，在判定最简二次根式的过程中要注意：（1）在二次根式的被开方数中，只要含有分数或小数，就不是最简二次根式；（2）在二次根式的被开方数中的每一个因式（或因数），如果幂的指数等于或大于2，也不是最简二次根式．7．如图在直角△ABC中，∠BAC=90°，AB=8，AC=6，DE是AB边的垂直平分线，垂足为D，交边BC于点E，连接AE，则△ACE的周长为（）A．16 B．15 C．14 D．13【考点】线段垂直平分线的性质；勾股定理．【分析】第一连接AE，由在直角△ABC中，∠BAC=90°，AB=8，A C=6，利用勾股定理即可求得BC的长，又由DE是AB边的垂直平分线，按照线段垂直平分线的性质，即可得AE=BE，继而可得△ACE的周长为：BC+AC．【解答】解：连接AE，∵在Rt△ABC中，∠BAC=90°，AB=8，AC=6，∴BC==10，∵DE是AB边的垂直平分线，∴AE=BE，∴△ACE的周长为：AE+EC+AC=BE+CE+AC=BC+AC=10+6=16．故选A．【点评】此题考查了线段垂直平分线的性质与勾股定理．此题难度不大，注意把握数形结合思想与转化思想的应用，注意垂直平分线上任意一点，到线段两端点的距离相等定理的应用．8．某工程队预备修建一条长1200m的道路，由于采纳新的施工方式，实际每天修建道路的速度比原打算快20%，结果提早2天完成任务．若设原打算每天修建道路x m，则按照题意可列方程为（）A．﹣=2 B．﹣=2C．﹣=2 D．﹣=2【考点】由实际咨询题抽象出分式方程．【专题】工程咨询题．【分析】设原打算每天修建道路x m，则实际每天修建道路为（1+20%）x m，按照采纳新的施工方式，提早2天完成任务，列出方程即可．【解答】解：设原打算每天修建道路x m，则实际每天修建道路为（1 +20%）x m，由题意得，﹣=2．故选：D．【点评】本题考查了由实际咨询题抽象出分式方程，关键是读明白题意，设出未知数，找出合适的等量关系，列出方程．9．若m+n=3，则2m2+4mn+2n2﹣6的值为（）A．12 B．6 C．3 D．0【考点】完全平方公式．【分析】按照完全平方公式的逆用，先整理出完全平方公式的形式，再代入数据运算即可．【解答】解：原式=2（m2+2mn+n2）﹣6，=2（m+n）2﹣6，=2×9﹣6，=12．故选A．【点评】本题利用了完全平方公式求解：（a±b）2=a2±2ab+b2，要注意把m+n看成一个整体．10．下列讲法中，错误的是（）A．分式方程的解等于0，就讲明那个分式方程无解B．解分式方程的差不多思路是把分式方程转化为整式方程C．检验是解分式方程必不可少的步骤D．能使分式方程的最简公分母等于零的未知数的值不是原分式方程的解【考点】解分式方程．【分析】本题考查对解分式方程差不多思想的明白得．去分母，转化为整式方程求解，检验是解分式方程的常规方法．而分式方程的解有可能是0．【解答】解：A、方程的解为0，不等于分母为0，因此讲法是错误的．而B、C、D都围绕解分式的差不多思想和步骤来讲明的，因此是正确的．故选A．【点评】分式方程时是一种专门的方程，其与整式方程的区不在于分母中是否含有未知数，为此应从概念，解分式方程的差不多思想，确定最简公分母，去分母检验几个方面去认识明白得．二.填空题11．运算：÷=3．【考点】二次根式的乘除法．【分析】直截了当利用二次根式的除法运算法则得出即可．【解答】解：÷==3．故答案为：3．【点评】此题要紧考查了二次根式的除法运算，按照二次根式的运算法则得出是解题关键．12．若分式的值为0，则x的值为﹣1．【考点】分式的值为零的条件．【专题】运算题．【分析】分式的值为0的条件是：（1）分子=0；（2）分母≠0．两个条件需同时具备，缺一不可．据此能够解答本题．【解答】解：由题意可得x2﹣1=0且x﹣1≠0，解得x=﹣1．故答案为﹣1．【点评】由于该类型的题易忽略分母不为0那个条件，因此常以那个知识点来命题．13．把多项式ab3﹣4ab分解因式的结果为ab（b+2）（b﹣2）．【考点】提公因式法与公式法的综合运用．【分析】利用公式法以及提取公因式法分解因式得出即可．【解答】解：ab3﹣4ab=ab（b2﹣4）=ab（b+2）（b﹣2）．故答案为：ab（b+2）（b﹣2）．【点评】此题要紧考查了提取公因式法以及公式法分解因式，熟练应用乘法公式分解因式是解题关键．14．若有意义，则m的取值范畴是m≤0，且m≠﹣1．【考点】二次根式有意义的条件；分式有意义的条件．【分析】第一按照二次根式有意义的条件可知﹣m≥0，再按照分母≠0，可知m+1≠0，再解出解集即可．【解答】解：∵若有意义，∴﹣m≥0，m+1≠0，解得：m≤0，且m≠﹣1，故答案为：m≤0，且m≠﹣1．【点评】此题要紧考查了二次根式有意义的条件，关键把握被开方数为非负数，分母≠0．15．观看下列各式：1×3=22﹣1，3×5=42﹣1，5×7=62﹣1，…请你把发觉的规律用含n（n为正整数）的等式表示为（2n﹣1）（2n+1）=（2 n）2﹣1．【考点】平方差公式．【专题】规律型．【分析】分析可得：发觉的规律为相邻两个奇数的积等于它们平均数的平方减1，故（2n﹣1）（2n+1）=（2n）2﹣1．【解答】解：按照题意可得：规律为（2n﹣1）（2n+1）=（2n）2﹣1，故答案为（2n﹣1）（2n+1）=（2n）2﹣1．【点评】本题考查学生通过观看、归纳、抽象出数列的规律的能力，要求学生第一分析题意，找到规律，并进行推导得出答案，关键规律为：相邻两个奇数的积等于它们平均数的平方减1．16．已知关于x的方程的解是正数，则m的取值范畴是m＞﹣6且m≠﹣4．【考点】分式方程的解．【分析】第一求出关于x的方程的解，然后按照解是正数，再解不等式求出m的取值范畴．【解答】解：解关于x的方程得x=m+6，∵方程的解是正数，∴m+6＞0且m+6≠2，解那个不等式得m＞﹣6且m≠﹣4．故答案为：m＞﹣6且m≠﹣4．【点评】本题考查了分式方程的解，是一个方程与不等式的综合题目，解关于x的方程是关键，解关于x的不等式是本题的一个难点．17．等边三角形两角平分线所夹的锐角的度数是60°．【考点】等边三角形的性质．【分析】按照已知条件和等边三角形的性质可知∠1=∠2=∠ABC=3 0°，因此∠3=∠1+∠2=60°．【解答】解：如图，∵等边三角形ABC中，AD，BE分不是∠BAC，∠ABC的角的平分线，交于点F，∴∠1=∠2=∠ABC=30°，∴∠3=∠1+∠2=60°．故答案为：60°．【点评】本题考查的是等边三角形的性质，熟知等边三角形的三个内角差不多上60°是解答此题的关键．18．已知等腰△ABC，AB=AC，∠ABC=20°，P为直线BC上一点，BP=AB，则∠PAC的度数为60°或150°．【考点】等腰三角形的性质．【分析】如图1，按照等腰三角形的性质和三角形的内角和得到∠C=∠B=20°，∠BAC=140°，由等腰三角形的性质得到∠BAP== 80°，因此求得∠PAC=60°，如图2，同理求得∠P=∠PAB=ABC=10°，因此求得∠PAC=150°．【解答】解：如图1，∵AB=AC，∠ABC=20°，∴∠C=∠B=20°，∴∠BAC=140°，∵BP=AB，∴∠BAP==80°，∴∠PAC=60°，如图2，∵AB=AC，∠ABC=20°，∴∠C=∠B=20°，∴∠BAC=140°，∵BP=AB，∴∠P=∠PAB=ABC=10°，∴∠PAC=150°．综上所述：∠PAC的度数为60°或150°，故答案为：60°或150°．【点评】本题考查了等腰三角形的性质，三角形的外角的性质，三角形的内角和，正确的画出图形是解题的关键．19．△ABC的三边分不为a，b，c，有b+c=8，bc=a2﹣12a+52，按边分类，则△ABC是等腰三角形．【考点】配方法的应用；非负数的性质：偶次方．【分析】将b=8﹣c，代入bc中得到关系式，利用完全平方公式变形后，按照非负数的性质求出a与c的值，进而求出b的值，即可确定出三角形形状．【解答】解：∵b+c=8∴b=8﹣c，∴bc=（8﹣c）c=﹣c2+8c，∴bc=a2﹣12a+52=﹣c2+8c，即a2﹣12a+36+16+c2﹣8c=0，整理得：（a﹣6）2+（c﹣4）2=0，∵（a﹣6）2≥0，（c﹣4）2≥0，∴a﹣6=0，即a=6；c﹣4=0，即c=4，∴b=8﹣4=4，则△ABC为等腰三角形．故答案是：等腰．【点评】此题考查了配方法的应用，非负数的性质，以及等腰三角形的判定，熟练把握完全平方公式是解本题的关键．20．在△ABC中，D为AB的中点，∠CDA=45°，E在AC上，连接BE交CD于F，满足EF=EC，△CBF的面积为8，则CF=4．【考点】三角形的面积．【分析】延长CD到G，使DG=CD，过B作BH⊥DG于H，按照全等三角形的性质得到∠G=∠ACD，S△ACD=S△BDG=S△CBD，按照等腰三角形的性质得到GH=FH，得到S△BHG=S△BFH，设△BDH的面积=x，△BFD的面积=y，则△BHG的面积=x+y，列方程得到S△BDH=4，按照等腰直角三角形的性质得到BH=2，因此得到结论．【解答】解：延长CD到G，使DG=CD，过B作BH⊥DG于H，∵D为AB的中点，∴AD=DB，在△ACD与△BGD中，，∴△ACD≌△BGD，∴∠G=∠ACD，S△ACD=S△BDG=S△CBD，∵EF=EC，∴∠CFE=∠ECF，∵∠EFB=∠EFC，∴∠G=∠BFD，∴BG=BF，∴GH=FH，∴S△BHG=S△BFH，设△BDH的面积=x，△BFD的面积=y，则△BHG的面积=x+y，∴x+x+y=y+8，∴x=4，∴S△BDH=4，∵∠BDH=∠ADC=45°，∴BH=DH，∴BH=2，∵△CBF的面积为8，∴CF=4．故答案为：4．【点评】本题考查了三角形的面积，全等三角形的判定和性质，正确的作出辅助线是解题的关键．三.解答题21．先化简，再求值：，其中a=+1【考点】分式的化简求值；分母有理化．【专题】运算题．【分析】要紧考查了分式的化简求值，其关键步骤是分式的化简．要熟悉混合运算的顺序，正确解题．注意最后结果要分母有理化．【解答】解：原式=，当a=+1时，原式=．【点评】解答本题的关键是对分式进行化简，代值运算要认真．22．解分式方程：（1）；（2）﹣2．【考点】解分式方程．【专题】运算题；分式方程及应用．【分析】两分式方程去分母转化为整式方程，求出整式方程的解得到未知数的值，经检验即可得到分式方程的解．【解答】解：（1）去分母得：4a﹣2=5a，解得：a=﹣2，经检验a=﹣2是分式方程的解；（2）去分母得：1﹣x=﹣1﹣2x+4，解得：x=2，经检验x=2是增根，分式方程无解．【点评】此题考查了解分式方程，解分式方程的差不多思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．23．已知，求的值．【考点】分式的值．【专题】运算题．【分析】我们可将前面式子变式为x2+1=3x，再将后面式子的分母变式为的形式从而求出值．【解答】解：将两边同时乘以x，得x2+1=3x，===．【点评】本题考查的是分式的值，解题关键是用到了整体代入的思想．24．若﹣4y+4=0，求xy的值．【考点】因式分解-运用公式法；非负数的性质：偶次方；非负数的性质：算术平方根．【专题】运算题．【分析】第一把等式变为+（y﹣2）2=0，再按照非负数的性质可得x﹣y=0，y﹣2=0，解出x、y的值，再求出xy即可．【解答】解：+（y﹣2）2=0，∵≥0，（y﹣2）2≥0，∴x﹣y=0，y﹣2=0，解得：y=2，x=2，∴xy=4．【点评】此题要紧考查了公式法分解因式，以及非负数的性质，关键是把握算术平方根和偶次幂都具有非负性．25．甲、乙两人预备整理一批新到的实验器材．若甲单独整理需要40分钟完工：若甲、乙共同整理20分钟后，乙需再单独整理20分钟才能完工．（1）咨询乙单独整理多少分钟完工？（2）若乙因工作需要，他的整理时刻不超过30分钟，则甲至少整理多少分钟才能完工？【考点】分式方程的应用；一元一次不等式的应用．【专题】应用题．【分析】（1）将总的工作量看作单位1，按照本工作分两段时刻完成列出分式方程解之即可；（2）设甲整理y分钟完工，按照整理时刻不超过30分钟，列出一次不等式解之即可．【解答】解：（1）设乙单独整理x分钟完工，按照题意得：，解得x=80，经检验x=80是原分式方程的解．答：乙单独整理80分钟完工．（2）设甲整理y分钟完工，按照题意，得，解得：y≥25，答：甲至少整理25分钟完工．【点评】分析题意，找到关键描述语，找到合适的等量关系是解决咨询题的关键．此题等量关系比较多，要紧用到公式：工作总量=工作效率×工作时刻．26．（2015秋•哈尔滨校级月考）如图1，在等边△ABC中，D是BC 边上一点，连接AD，将△ABD沿AD翻折至△AED，F为CD上一点，∠AEF=∠AED．（1）求证：AE=BF+EF；（2）如图2，M为AE上一点，连接MD、MF，MD=MF，若CD=4，CF=1，求线段AM的长．【考点】全等三角形的判定与性质；等边三角形的性质；翻折变换（折叠咨询题）．【分析】（1）连接AF，按照三角形中已知两边和夹角求第三边即可求得EF=FC，即可解题；（2）按照余弦定理能够求得DE，EM的大小关系，按照DE，EM的大小关系，能够求得AM的长，即可解题．【解答】（1）证明：连接AF，∵AF2=AC2+CF2﹣2AC•CF•cosC，AF2=AE2+EF2﹣2AE•EF•cos∠AEF，AE=AB=AC，∠AEF=∠AED=∠C=60°∴EF=CF，∴AE=AB=BC=BF+FC=BF+EF．（2）解：∵DM2=DE2+EM2﹣2DE•EM•cos60°，FM2=EF2+EM2﹣2EF•EM•cos60°，设DE=x，EM=y，则x2+y2﹣xy=1+y2﹣y，x2﹣1﹣（x﹣1）y=0，（x﹣1）（x+1﹣y）=0，∴x=1（舍去），y=x+1，AM=AE﹣EM=BC﹣y=BD+4﹣y=x+4﹣（x+1）=3．【点评】本题考查了三角形中余弦定理的使用，考查了折叠咨询题的求证，本题中求得DE，EM的大小关系是解题的关键．27．已知：如图，在平面直角坐标系中，△ABC为直角三角形，∠B= 90°，∠A=30°，点C的坐标为（1，0），点B的坐标为（0，），EF垂直平分AC，交AB于点E，交x轴于点F．（1）求点E的坐标；（2）点P从点C动身沿射线CB以每秒1个单位的速度运动，设点P 运动的时刻为t秒，设△PBE的面积为S，用含t的代数式表示S，并直截了当写出t的取值范畴；（3）在（2）的条件下，过点F作直线m∥BC，在直线m上是否存在点Q，使得△PFQ为等腰直角三角形？若存在，求满足条件t的值，并直截了当写出Q的坐标；若不存在，请讲明理由．【考点】一次函数综合题．【分析】（1）第一求得AC的长，则F的横坐标即可求得，然后利用待定系数法求得AB的解析式，则E的坐标即可求得；（2）分成P在线段BC上和在CB的延长线上两种情形讨论，然后按照三角形面积公式求解；（3）△PFQ为等腰直角三角形，则F和Q可能是直角顶点，现在直角边长是m和BC之间的距离，求得两线之间的距离，然后利用三角函数即可求解；当P是直角顶点时，FQ等于m和BC之间距离的2倍，据此即可求解．【解答】解：（1）在直角△ABC中，BC===2，∵直角△ABC中∠A=30°，∴AC=2BC=4，∴OA=3，即A的坐标是（﹣3，0）．则F的坐标是（﹣1，0）．设AB的解析式是y=kx+b，则，解得：，则AB的解析式是y=x+，当x=﹣1时，y=﹣+=，则E的坐标是（﹣1，）；（2）直角△AOB中，AB=2BC=2，在直角△AEF中，AE===，则BE=2﹣=．当0＜t≤2时，P在线段BC上，BP=2﹣t，则S=×（2﹣t）=﹣t+；当t＞2时，P在CB的延长线上，BP=t﹣2，则S=×（t﹣2）=t﹣；（3）作FK⊥BC于点K．在直角△CFK中，FK=FC•sin∠ACK=2×sin60°=2×=，当P于K重合，且Q在Q1的位置时，作Q1R⊥x轴于点R．则FQ1= FK=，∠Q1FR=60°，在直角△Q1RF中，RF=Q1F=，Q1R=Q1F•sin60°=×=，则OR=1+=，则Q1的坐标是（﹣，）；同理，当P于K重合，且Q在Q2的位置时，Q2的坐标是（，﹣）．当∠QPF=90°时，FQ=2FK=，则Q的坐标是（﹣5，）或（1，﹣）．总之，Q的坐标是（﹣，）或（，﹣）或（﹣5，）或（1，﹣）．【点评】本题考查了待定系数法求函数的解析式以及等腰直角三角形的讨论，正确求得FK的长，对△PFQ进行讨论是关键．。

八年级上册全册全套试卷综合测试卷(word含答案)

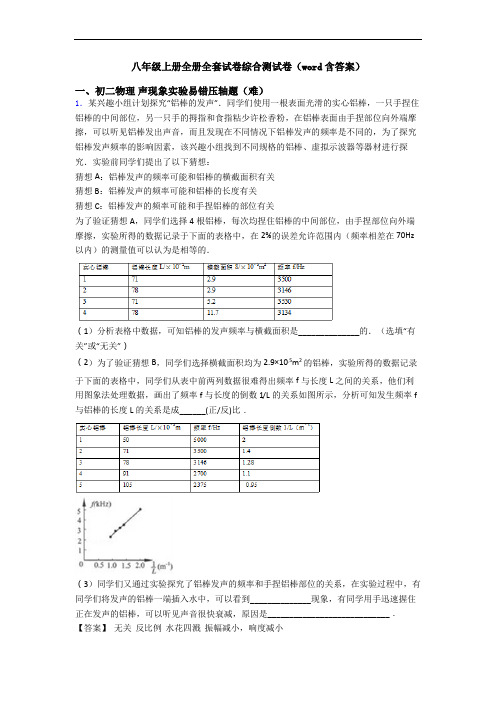
八年级上册全册全套试卷综合测试卷（word含答案）一、初二物理声现象实验易错压轴题（难）1．某兴趣小组计划探究“铝棒的发声”．同学们使用一根表面光滑的实心铝棒，一只手捏住铝棒的中间部位，另一只手的拇指和食指粘少许松香粉，在铝棒表面由手捏部位向外端摩擦，可以听见铝棒发出声音，而且发现在不同情况下铝棒发声的频率是不同的，为了探究铝棒发声频率的影响因素，该兴趣小组找到不同规格的铝棒、虚拟示波器等器材进行探究．实验前同学们提出了以下猜想：猜想A：铝棒发声的频率可能和铝棒的横截面积有关猜想B：铝棒发声的频率可能和铝棒的长度有关猜想C：铝棒发声的频率可能和手捏铝棒的部位有关为了验证猜想A，同学们选择4根铝棒，每次均捏住铝棒的中间部位，由手捏部位向外端摩擦，实验所得的数据记录于下面的表格中，在2%的误差允许范围内（频率相差在70Hz 以内）的测量值可以认为是相等的．（1）分析表格中数据，可知铝棒的发声频率与横截面积是______________的．（选填“有关”或“无关”）（2）为了验证猜想B，同学们选择横截面积均为2.9×10﹣5m2的铝棒，实验所得的数据记录于下面的表格中，同学们从表中前两列数据很难得出频率f与长度L之间的关系，他们利用图象法处理数据，画出了频率f与长度的倒数1/L的关系如图所示，分析可知发生频率f 与铝棒的长度L的关系是成______(正/反)比．（3）同学们又通过实验探究了铝棒发声的频率和手捏铝棒部位的关系，在实验过程中，有同学们将发声的铝棒一端插入水中，可以看到______________现象，有同学用手迅速握住正在发声的铝棒，可以听见声音很快衰减，原因是____________________________．【答案】无关反比例水花四溅振幅减小，响度减小【解析】（1)通过比较表格中的1和3（或者2和4）可知，,当铝棒长度都为0.71m时,横截面积不同,频率为3500hHz和3530Hz,由于这两个频率在2%的误差允许范围内(频率相差在70Hz以内)，故频率是相同的，故结论为：铝棒的发声频率与横截面积是无关的；(2)由图象可知,频率f与长度的倒数1L的关系是一条直线，即成正比，故发生频率f与铝棒的长度L的关系是成反比； (3)有同学们将发声的铝棒一端插入水中，铝棒振动，引起水的振动，故可以看到水花四溅；有同学用手迅速握住正在发声的铝棒，可以听见声音很快衰减，原因是铝棒的振幅减小，响度减小。

八年级上册全册全套试卷综合测试(Word版含答案)

八年级上册全册全套试卷综合测试（Word版含答案）一、初二物理机械运动实验易错压轴题（难）1．小明同学测小车的平均速度，请帮助他完成下列问题：(1)测平均速度需要的测量工具是______和______；该实验依据的原理是___________；(2)小车所放的斜面应保持较____（填“大”或“小”）的坡度，这样小车在斜面上运动时间会____（填“长”或“短”）些，便于测量时间；(3)如图所示，斜面长1.6 m，测得小车从斜面顶端运动到底端所用的时间是5 s。

如果在斜面的中点装上金属片，测得小车从斜面顶端运动到金属片的时间为2.8 s。

请计算出小车通过上半段的平均速度v2为___________m/s；（保留两位小数）(4)小车从斜面顶端运动到底端过程中，小车做的是_________（填“匀速”或“变速”）直线运动。

【来源】甘肃省定西市临洮县2019-2020学年八年级（上）期中考试物理试题【答案】刻度尺停表svt小长 0.29 变速【解析】【分析】【详解】(1)[1][2][3]测小车平均速度的实验原理就是速度的计算公式=svt测量路程和时间需要的仪器是刻度尺和钟表；(2)[4][5]在小车能下滑的情况下，使用的斜面的坡度较小，小车下滑的速度变化较慢，在斜面上运动的时间较长，这样便于测量时间；(3)[6]如图所示，斜面长1.6 m，测得小车从斜面顶端运动到底端所用的时间是5 s。

如果在斜面的中点装上金属片，测得小车从斜面顶端运动到金属片的时间为2.8 s。

请计算出小车通过上半段的平均速度v2为20.8m===0.29m/s2.8ssvt(4)[7]小车从斜面顶端运动到底端过程中，在前一半路程和后一半路程需要的时间不同，所以，小车做的是变速直线运动。

2．小明在“测小车的平均速度”的实验中，设计了如图所示的实验装置：小车从带刻度（分度值为1cm）的斜面项端由静止下滑，图中的圆圈是小车到达A、B、C三处时电子表的显示。

八年级上册全册全套试卷综合测试卷(word含答案)

八年级上册全册全套试卷综合测试卷（word含答案）一、初二物理声现象实验易错压轴题（难）1．噪声是一种严重的环境污染，李明想制作一个防噪声的耳罩，他通过比较几种材料（衣服、锡箔纸、泡沫塑料）的隔音性能，来选择一种隔音性能好的材料做耳罩的填充物。

实验器材除了待检测的材料外，还有：音叉、机械闹钟、鞋盒。

（1）在本实验中适合作声源的是_____，另一个仪器不适合作声源的理由是___（2）李明将声源放入鞋盒内，在其四周塞满待测填充材料，他设想了以下A、B两种实验方案．你认为最佳的是________方案。

A．让人站在距鞋盒一定的距离处，比较所听见声音的响度B．让人一边听声音，一边向后退，直至听不见声音为止，比较此处距鞋盒的距离实验中测得的数据如下表所示，则待测材料中隔音性能最好的是____________。

（3）实验过程中应将声源响度________（选填“调大”或“调小”），因为铃声响度越大时，人要听不到声音时与声源的距离将越_____（选填大或小），导致实验在教室中难以进行．同时在比较不同材料时铃声响度应____（选填“随材料而改变”或“保持不变”），这种物理方法叫_______。

（4）小红从家中也找出下列一些材料开始探究：一张报纸、一件羽绒服、一个薄塑料袋、一些泡沫板，李明认为小红选择这些材料直接进行实验存在一个明显问题，不能有效地说明这些材料的隔声性能，请指出这个明显的问题：_______。

（5）对材料进行科学调整后，他们通过探究得到如下实验数据：由此数据可将这些材料隔声性能最好的是____________。

【答案】机械闹钟音叉发出的声音不稳定，不能持续发声B泡沫塑料调小大保持不变控制变量法没有控制材料厚度相同羽绒服【解析】【分析】【详解】(1)[1][2]机械闹钟，发出的声音稳定，能持续发声，所以选用机械闹钟，而音叉发出的声音不稳定，不能持续发声，所以不选用音叉。

(2)[3]A方案中，由于人耳听到的响度无法测量，只能凭感觉判断，没有可靠的实验数据；在B方案中，通过比较到鞋盒的距离判断隔音效果，因为距离可以测量，有可靠地实验数据，能够较好的判断隔音效果。

八年级上册全册全套试卷综合测试(Word版含答案)

八年级上册全册全套试卷综合测试（Word版含答案）一、八年级数学三角形填空题（难）1．如图，△ABC中，点D、E、F分别在三边上，E是AC的中点，AD、BE、CF交于一点G，BD=2DC，S△GEC=3，S△GDC=4，则△ABC的面积是_____．【答案】30【解析】【分析】由于BD=2DC，那么结合三角形面积公式可得S△ABD=2S△ACD，而S△ABC=S△ABD+S△ACD，可得出S△ABC=3S△ACD，而E是AC中点，故有S△AGE=S△CGE，于是可求S△ACD，从而易求S△ABC．【详解】解：∵BD=2DC，∴S△ABD=2S△ACD，∴S△ABC=3S△ACD．∵E是AC的中点，∴S△AGE=S△CGE．又∵S△GEC=3，S△GDC=4，∴S△ACD=S△AGE+S△CGE+S△CGD=3+3+4=10，∴S△ABC=3S△ACD=3×10=30．故答案为30．【点睛】本题考查了三角形的面积公式、三角形之间的面积加减计算．注意同底等高的三角形面积相等，面积相等、同高的三角形底相等．2．等腰三角形的三边长分别为：x+1，2x+3，9，则x=________.【答案】3【解析】①当x+1=2x+3时，解得x=−2(不合题意,舍去)；②当x+1=9时，解得x=8，则等腰三角形的三边为:9、19、9，因为9+9=18<19，不能构成三角形，故舍去；③当2x+3=9时，解得x=3，则等腰三角形的三边为:4、9、9，能构成三角形。

所以x的值是3.故填3.3．已知a、b、c为△ABC的三边，化简：|a+b﹣c|-|a﹣b﹣c|+|a﹣b+c|=______．--【答案】3a b c【解析】【分析】根据三角形的三边关系判断绝对值内式子的正负，然后利用绝对值的性质去掉绝对值，再去括号合并同类项即可．【详解】解：∵a、b、c为△ABC的三边，∴a+b＞c，a-b＜c，a+c＞b，∴a+b-c＞0，a-b-c＜0，a-b+c＞0，∴|a+b-c|-|a-b-c|+|a-b+c|=(a+b-c)+(a-b- c)+(a-b+c)=a+b-c+a-b- c+a-b+c=3a-b-c．故答案为：3a-b-c．【点睛】本题主要考查了三角形的三边关系定理和利用绝对值的性质进行化简，利用三角形的三边关系得出绝对值内式子的正负是解决此题的关键．4．已知一个三角形的三边长为3、8、a，则a的取值范围是_____________．【答案】5＜a＜11【解析】【分析】根据三角形的三边关系定理：三角形两边之和大于第三边，三角形的两边差小于第三边可得8-3＜a＜8+3，再解即可．【详解】解：根据三角形的三边关系可得：8-3＜a＜8+3，解得：5＜a ＜11，故答案为：5＜a＜11．【点睛】此题主要考查了三角形的三边关系，关键是掌握第三边的范围是：大于已知的两边的差，而小于两边的和．5．如图，△ABC中，∠BAC＝70°，∠ABC的平分线与∠ACB的外角平分线交于点O，则∠BOC＝_____度．【答案】35【解析】【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAC+∠ABC＝∠ACE，∠BOC+∠OBC＝∠OCE，再根据角平分线的定义可得∠OBC＝12∠ABC，∠OCE＝1 2∠ACE，然后整理可得∠BOC＝12∠BAC．【详解】解：由三角形的外角性质，∠BAC+∠ABC＝∠ACE，∠BOC+∠OBC＝∠OCE，∵∠ABC的平分线与∠ACB的外角平分线交于点O，∴∠OBC＝12∠ABC，∠OCE＝12∠ACE，∴12（∠BAC+∠ABC）＝∠BOC+12∠ABC，∴∠BOC＝12∠BAC，∵∠BAC＝70°，∴∠BOC＝35°，故答案为：35°．【点睛】本题考查了三角形的内角和定理、三角形的外角性质，掌握三角形的一个外角等于与它不相邻的两个内角的和的性质，要注意整体思想的利用．6．如图，直线a∥b，∠l＝60°，∠2＝40°，则∠3＝______．【答案】80°．【解析】【分析】根据平行线的性质求出∠4，再根据三角形内角和定理计算即可．【详解】∵a ∥b ，∴∠4=∠l=60°，∴∠3=180°-∠4-∠2=80°，故答案为80°．【点睛】本题考查了平行线的性质、三角形内角和定理，掌握两直线平行，同位角相等是解题的关键．二、八年级数学三角形选择题（难）7．如图：在△ABC 中，G 是它的重心，AG ⊥CD ，如果32BG AC ⋅=，则△AGC 的面积的最大值是（）A ．3B ．8C ．43D ．6 【答案】B【解析】分析：延长BG 交AC 于D ．由重心的性质得到 BG =2GD ，D 为AC 的中点，再由直角三角形斜边上的中线等于斜边的一半，得到AC =2GD ，即有BG =AC ，从而得到AC 、GD 的长．当GD ⊥AC 时，△AGC 的面积的最大，最大值为：12AC •GD ，即可得出结论．详解：延长BG 交AC 于D ．∵G 是△ABC 的重心，∴BG =2GD ，D 为AC 的中点．∵AG ⊥CG ，∴△AGC 是直角三角形，∴AC =2GD ，∴BG =AC ．∵BG•AC=32，∴AC=32=42，GD=22．当GD⊥AC时，．△AGC的面积的最大，最大值为：12AC•GD=142222⨯⨯=8．故选B．点睛：本题考查了重心的性质．解题的关键是熟知三角形的重心到顶点的距离等于它到对边中点距离的2倍．8．如图，在△ABC中，点M、N是∠ABC与∠ACB三等分线的交点．若∠A＝60°，则∠BMN的度数为( )A．45°B．50°C．60°D．65°【答案】B【解析】分析：过点N作NG⊥BC于G，NE⊥BM于E，NF⊥CM于F，根据角平分线上的点到角的两边的距离相等可得NE=NG=NF，再根据到角的两边距离相等的点在角的平分线上判断出MN平分∠BMC，然后根据三角形内角和等于180°求出∠ABC+∠ACB，再根据角的三等分求出∠MBC+∠MCB的度数，然后利用三角形内角和定理求出∠BMC的度数，从而得解．详解：如图，过点N作NG⊥BC于G，NE⊥BM于E，NF⊥CM于F，∵∠ABC的三等分线与∠ACB的三等分线分别交于点M、N，∴BN平分∠MBC，CN平分∠MCB，∴NE=NG，NF=NG，∴NE=NF，∴MN平分∠BMC，∴∠BMN=12∠BMC，∵∠A=60°，∴∠ABC+∠ACB=180°−∠A=180°−60°=120°，根据三等分,∠MBC+∠MCB=23 (∠ABC+∠ACB)=2 3×120°=80°. 在△BMC 中,∠BMC=180°−(∠MBC+∠MCB)=180°−80°=100°. ∴∠BMN=12×100°=50°；故选：B.点睛：本题考查了三角形的内角和定理：三角形内角和为180°；角平分线的性质：角平分线上的点到角两边的距离相等.熟记性质和定理是解本题的关键.9．如图，将一张三角形纸片ABC 的一角折叠，使点A 落在ABC ∆处的'A 处，折痕为DE .如果A α∠=，'CEA β∠=，'BDA γ∠=，那么下列式子中正确的是（）A ．2γαβ=+B ．2γαβ=+C ．γαβ=+D ．180γαβ=--【答案】A【解析】【分析】【详解】分析:根据三角形的外角得：∠BDA'=∠A+∠AFD ，∠AFD=∠A'+∠CEA'，代入已知可得结论. 详解:由折叠得：∠A=∠A'，∵∠BDA'=∠A+∠AFD ，∠AFD=∠A'+∠CEA'，∵∠A=α，∠CEA′=β，∠BDA'=γ，∴∠BDA'=γ=α+α+β=2α+β，故选A.点睛：本题考查了三角形外角的性质，熟练掌握三角形的外角等于与它不相邻的两个内角的和是关键.10．长度分别为2，7，x的三条线段能组成一个三角形，的值可以是（）A．4B．5C．6D．9【答案】C【解析】【分析】根据三角形的三边关系可判断x的取值范围，进而可得答案.【详解】解：由三角形三边关系定理得7－2＜x＜7+2，即5＜x＜9．因此，本题的第三边应满足5＜x＜9，把各项代入不等式符合的即为答案．4，5，9都不符合不等式5＜x＜9，只有6符合不等式，故选C．【点睛】本题考查的是三角形的三边关系，属于基础题型，掌握三角形的三边关系是解题的关键.11．如果一个多边形的内角和是1800°，这个多边形是（）A．八边形B．十四边形C．十边形D．十二边形【答案】D【解析】【分析】n边形的内角和可以表示成（n﹣2）•180°，设这个正多边形的边数是n，就得到方程，从而求出边数．【详解】这个正多边形的边数是n，根据题意得：（n﹣2）•180°=1800°解得：n=12．故选D．【点睛】本题考查了多边形的内角和定理．注意多边形的内角和为：（n﹣2）×180°．的高的是（）12．如下图，线段BE是ABCA．B．C．D．【答案】D【解析】【分析】根据高的画法知，过点B作AC边上的高，垂足为E，其中线段BE是△ABC的高．【详解】解：由图可得，线段BE是△ABC的高的图是D选项；故选：D．【点睛】本题主要考查了三角形的高线的画法，掌握三角形的高的画法是解题的关键．三、八年级数学全等三角形填空题（难）13．已知：如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒，当t的值为_____秒时，△ABP和△DCE全等．【答案】1或7【解析】【分析】分点P在线段BC上和点P在线段AD上两种情况解答即可．【详解】设点P的运动时间为t秒，则BP=2t，当点P在线段BC上时，∵四边形ABCD为长方形，∴AB=CD，∠B=∠DCE=90°，此时有△ABP≌△DCE，∴BP=CE，即2t=2，解得t=1；当点P在线段AD上时，∵AB=4，AD=6，∴BC=6，CD=4，∴AP=BC+CD+DA=6+4+6=16，∴AP=16-2t，此时有△ABP≌△CDE，∴AP=CE ，即16-2t=2，解得t=7；综上可知当t 为1秒或7秒时，△ABP 和△CDE 全等．故答案为1或7．【点睛】本题考查了全等三角形的判定，判定三角形全等方法有：ASA 、SAS 、AAS 、SSS 、HL ．解决本题时注意分情况讨论，不要漏解.14．如图，在等腰三角形ABC 中，90ABC ∠=，D 为AD 边上中点，多D 点作DE DF ⊥，交AB 于E ，交BC 于F ，若3AE =，2CF =，则ABC ∆的面积为______．【答案】252【解析】【分析】利用等腰直角三角形斜边中点D 证明AD=BD ，∠DBC=∠A=45︒，再利用DE DF ⊥证得∠ADE=∠BDF ，由此证明△ADE ≌△BDF ，得到BC 的长度，即可求出三角形的面积.【详解】∵90ABC ∠=︒，AB=BC,∴∠A=45︒，∵D 为AC 边上中点，∴AD=CD=BD ，∠DBC=∠A=45︒，∠ADB=90︒，∵DE DF ⊥,∴∠EDB+∠BDF=∠EDB+∠ADE=90︒，∴∠ADE=∠BDF,∴△ADE ≌△BDF,∴BF==AE=3，∵CF=2，∴AB=BC=BF+CF=5，∴ABC ∆的面积为212BC ⋅=252, 故答案为：252. 【点睛】此题考查等腰直角三角形的性质，三角形全等的判定及性质.15．如图，52A ∠=︒，O 是ABC ∠、ACB ∠的角平分线交点，P 是ABC ∠、ACB ∠外角平分线交点，则BOC ∠=______︒，BPC ∠=_____︒，联结AP ，则PAB ∠=______︒，点O ____（选填“在”、“不在”或“不一定在”）直线AP 上．【答案】116 64 26 在【解析】【分析】∠ABC+∠ACB=180°-∠A ，∠OBC+∠OCB= 12（∠ABC+∠ACB ）, ∠BOC=180°-（∠OBC+∠OCB ），据此可求∠BOC 的度数；∠BCP= 12∠BCE= 12（∠A+∠ABC ），∠PBC= 12∠CBF= 12（∠A+∠ACB ），由三角形内角和定理得：∠BPC=180°-∠BCP-∠PBC ，据此可求∠BPC 的度数；作PG ⊥AB 于G ，PH ⊥AC 于H ，PK ⊥BC 于K ，利用角平分线的性质定理可证明PG=PH ，于是可证得AP 平分∠BAC ，据此可求∠PAB 的度数；同理可证OA 平分∠BAC ，故点O 在直线AP 上．【详解】解：∵O 点是∠ABC 和∠ACB 的角平分线的交点，∴∠OBC+∠OCB=12（∠ABC+∠ACB ） = 12（180°-∠A ） =90°- 12∠A ， ∴∠BOC=180°-（∠OBC+∠OCB ） =180°-90°+12∠A =90°+ 12∠A =90°+26°=116°；如图，∵BP、CP为△ABC两外角的平分线，∴∠BCP= 12∠BCE=12（∠A+∠ABC），∠PBC= 12∠CBF=12（∠A+∠ACB），由三角形内角和定理得：∠BPC=180°-∠BCP-∠PBC=180°- 12[∠A+（∠A+∠ABC+∠ACB）]=180°- 12（∠A+180°）=90°- 12∠A=90°-26°=64°．如图，作PG⊥AB于G，PH⊥AC于H，PK⊥BC于K，连接AP，∵BP、CP为△ABC两外角的平分线，PG⊥AB，PH⊥AC，PK⊥BC，∴PG=PK，PK=PH，∴PG=PH，∴AP平分∠BAC，∴PAB∠=26°同理可证OA平分∠BAC，点O在直线AP上．故答案是：(1) 116 ；(2) 64；(3) 26；(4) 在.【点睛】此题主要考查了角平分线的性质定理和判定定理及三角形内角和定理，熟知定理并正确作出辅助线是解题关键．16．如图：已知△ABC 中，AB =AC ，∠BAC =90°，直角∠EPF 的顶点P 是BC 边上的中点，两边PE ，PF 分别交AB ，AC 于点E ，F ，给出以下四个结论：①AE =CF ；②EF =AP ；③2S 四边形AEPF =S △ABC ；④当∠EPF 在△ABC 内绕顶点P 旋转时（点E 不与A ，B 重合）有BE +CF =EF ；上述结论中始终正确的序号有__________．【答案】①③【解析】【分析】根据题意，容易证明△AEP ≌△CFP ，然后能推理得到①③都是正确．【详解】∵AB=AC ，∠BAC=90°，点P 是BC 的中点，∴∠EAP=12∠BAC=45°，AP=12BC=CP ． ①在△AEP 与△CFP 中， ∵∠EAP=∠C=45°，AP=CP ，∠APE=∠CPF=90°-∠APF ，∴△AEP ≌△CFP ，∴AE=CF ．正确；②只有当F 在AC 中点时EF=AP ，故不能得出EF=AP ，错误；③∵△AEP ≌△CFP ，同理可证△APF ≌△BPE ．∴S 四边形AEPF =S △AEP +S △APF =S △CPF +S △BPE =12S △ABC ，即2S 四边形AEPF =S △ABC ；正确； ④根据等腰直角三角形的性质，2PE ，所以，EF 随着点E 的变化而变化，只有当点E 为AB 的中点时，2PE=AP ，在其它位置时EF≠AP ，故④错误；故答案为：①③．【点睛】本题考查了全等三角形的判定与性质，等腰直角三角形的判定与性质，证得△AEP 和△CFP 全等是解题的关键，也是本题的突破点．17．已知∠ABC=60°，点D 是其角平分线上一点，BD=CD=6，DE//AB 交BC 于点E.若在射线BA 上存在点F ，使DCF BDE S S ∆∆=，请写出相应的BF 的长：BF ＝_________【答案】23或43.【解析】【分析】过点D作DF1∥BE，求出四边形BEDF1是菱形，根据菱形的对边相等可得BE=DF1，然后根据等底等高的三角形的面积相等可知点F1为所求的点，过点D作DF2⊥BD，求出∠F1DF2=60°，从而得到△DF1F2是等边三角形，然后求出DF1=DF2，再求出∠CDF1=∠CDF2，利用“边角边”证明△CDF1和△CDF2全等，根据全等三角形的面积相等可得点F2也是所求的点，然后在等腰△BDE中求出BE的长，即可得解．【详解】如图，过点D作DF1∥BE，易求四边形BEDF1是菱形，所以BE=DF1，且BE、DF1上的高相等，此时S△DCF1=S△BDE；过点D作DF2⊥BD，∵∠ABC=60°，F1D∥BE，∴∠F2F1D=∠ABC=60°，∵BF1=DF1，∠F1BD=12∠ABC=30°，∠F2DB=90°，∴∠F1DF2=∠ABC=60°，∴△DF1F2是等边三角形，∴DF1=DF2，∵BD=CD，∠ABC=60°，点D是角平分线上一点，∴∠DBC=∠DCB=12×60°=30°，∴∠CDF1=180°-∠BCD=180°-30°=150°，∠CDF2=360°-150°-60°=150°，∴∠CDF1=∠CDF2，∵在△CDF1和△CDF2中，1212DF DFCDF CDFCD CD⎧⎪∠∠⎨⎪⎩＝＝＝，∴△CDF1≌△CDF2（SAS），∴点F2也是所求的点，∵∠ABC=60°，点D是角平分线上一点，DE∥AB，∴∠DBC=∠BDE=∠ABD=12×60°=30°，又∵BD=6，∴BE=12×6÷cos30°=3÷32=23，∴BF1=BF2=BF1+F1F2=23+23=43，故BF的长为23或43.故答案为：23或43.【点睛】本题考查全等三角形的判定与性质，三角形的面积，等边三角形的判定与性质，直角三角形30°角所对的直角边等于斜边的一半的性质，熟练掌握等底等高的三角形的面积相等，以及全等三角形的面积相等是解题关键，（3）要注意符合条件的点F有两个．18．已知△ABC中，AB=BC≠AC，作与△ABC只有一条公共边，且与△ABC全等的三角形，这样的三角形一共能作出_____个．【答案】7【解析】只要满足三边对应相等就能保证作出的三角形与原三角形全等，以腰为公共边时有6个，以底为公共边时有一个，答案可得．解：以AB为公共边有三个，以CB为公共边有三个，以AC为公共边有一个，所以一共能作出7个．四、八年级数学全等三角形选择题（难）19．如图是由4个相同的小正方形组成的网格图，其中∠1+∠2等于（）A ．150°B ．180°C ．210°D ．225°【答案】B【解析】【分析】根据SAS 可证得ABC ≌EDC ，可得出BAC DEC ∠∠=，继而可得出答案，再根据邻补角的定义求解. 【详解】由题意得：AB ED =，BC DC =，D B 90∠∠==，ABC ∴≌EDC ，BAC DEC ∠∠∴=，12180∠∠+=．故选B ．【点睛】本题考查全等图形的知识，比较简单，解答本题的关键是判断出ABC ≌EDC ．.20．如图所示，△ABP 与△CDP 是两个全等的等边三角形，且PA ⊥PD ，有下列四个结论：①∠PBC ＝15°，②AD ∥BC ，③PC ⊥AB ，④四边形ABCD 是轴对称图形，其中正确的个数为（）A ．1个B ．2个C ．3个D ．4个【答案】D【分析】根据周角的定义先求出∠BPC 的度数，再根据对称性得到△BPC 为等腰三角形，∠PBC 即可求出；根据题意：有△APD 是等腰直角三角形；△PBC 是等腰三角形；结合轴对称图形的定义与判定，可得四边形ABCD 是轴对称图形，进而可得②③④正确．【详解】根据题意，BPC 36060290150∠=-⨯-= ，BP PC =，()PBC 180150215∠∴=-÷=，①正确；根据题意可得四边形ABCD 是轴对称图形，④正确；∵∠DAB+∠ABC=45°+60°+60°+15°=180°，∴AD//BC ，②正确；∵∠ABC+∠BCP=60°+15°+15°=90°，∴PC ⊥AB ，③正确，所以四个命题都正确，故选D ．【点睛】本题考查了等边三角形的性质、等腰直角三角形的性质、等腰三角形的判定与性质、轴对称图形的定义与判定等，熟练掌握各相关性质与定理是解题的关键.21．如图，点P 是AB 上任意一点，∠ABC=∠ABD ，还应补充一个条件，才能推出△APC ≌△APD ．从下列条件中补充一个条件，不一定能推出△APC ≌△APD 的是( )A ．BC=BD ；B ．AC=AD ；C ．∠ACB=∠ADB ；D ．∠CAB=∠DAB【答案】B【解析】根据题意，∠ABC=∠ABD ，AB 是公共边，结合选项，逐个验证得出：A 、补充BC=BD ，先证出△BPC ≌△BPD ，后能推出△APC ≌△APD ，故正确；B 、补充AC=AD ，不能推出△APC ≌△APD ，故错误；C 、补充∠ACB=∠ADB ，先证出△ABC ≌△ABD ，后能推出△APC ≌△APD ，故正确； D 、补充∠CAB=∠DAB ，先证出△ABC ≌△ABD ，后能推出△APC ≌△APD ，故正确．故选B ．点睛：本题考查了三角形全等判定，三角形全等的判定定理：有AAS ，SSS ，ASA ，SAS ．注意SSA 是不能证明三角形全等的，做题时要逐个验证，排除错误的选项．22．如图，∠C＝∠D＝90°，若添加一个条件，可使用“HL”判定Rt△ABC与Rt△ABD全等，则以下给出的条件适合的是( )A．AC＝AD B．AB＝AB C．∠ABC＝∠ABD D．∠BAC＝∠BAD 【答案】A【解析】根据题意可知∠C=∠D=90°，AB=AB，然后由AC=AD，可根据HL判定两直角三角形全等，故符合条件；而B答案只知道一边一角，不能够判定两三角形全等，故不正确；C答案符合AAS，证明两三角形全等，故不正确；D答案是符合AAS，能证明两三角形全等，故不正确.故选A.23．已知OD平分∠MON，点A、B、C分别在OM、OD、ON上(点A、B、C都不与点O重合)，且AB=BC, 则∠OAB与∠BCO的数量关系为（）A．∠OAB+∠BCO=180°B．∠OAB=∠BCOC．∠OAB+∠BCO=180°或∠OAB=∠BCO D．无法确定【答案】C【解析】根据题意画图，可知当C处在C1的位置时，两三角形全等，可知∠OAB=∠BCO；当点C处在C2的位置时，根据等腰三角形的性质和三角形的外角的性质，∠OAB+∠BCO=180°.故选C.24．在△ABC中，∠C=90°，D为AB的中点，ED⊥AB,∠DAE=∠CAE，则∠CAB＝（）A．30°B．60°C．80 °D．50°【答案】B【解析】试题解析：∵D为AB的中点，ED⊥AB，∴DE为线段AB的垂直平分线，∴AE=BE，∴∠DAE=∠DBE，∴∠DAE=∠DBE=∠CAE，在Rt△ABC中，∵∠CAB+∠DBE=90°，∴∠CAE+∠DAE+∠DBE=90°，∴3∠DBE=90°，∴∠DBE=30°，∴∠CAB=90°-∠DBE=90°-30°=60°．故选B．五、八年级数学轴对称三角形填空题（难）∥，25．如图所示，ABC为等边三角形，P是ABC内任一点，PD AB，PE BC++=____cm．∥，若ABC的周长为12cm，则PD PE PFPF AC【答案】4【解析】【分析】先说明四边形HBDP是平行四边形，△AHE和△AHE是等边三角形，然后得到一系列长度相等的线段,最后求替换求和即可．【详解】∥解：∵PD AB，PE BC∴四边形HBDP是平行四边形∴PD=HB∵ABC为等边三角形,周长为12cm∴∠B=∠A=60°,AB=4∵PE BC∥∴∠AHE=∠B=60°∴∠AHE=∠A=60°∴△AHE是等边三角形∴HE=AH∵∠HFP=∠A=60°∴∠HFP=∠AHE=60°∴△AHE是等边三角形，∴FP=PH∴PD+PE+PF=BH+(HP+PE)=BH+HE=BH+AH=AB=4cm故答案为4cm．【点睛】本题考查了平行四边形的判定和性质以及等边三角形的性质，掌握等边三角形的性质是解答本题的关键．26．如图，已知△ABC和△ADE都是正三角形，连接CE、BD、AF，BF=4,CF=7,求AF的长_________ .【答案】3【解析】【分析】过点A作AF⊥CE交于I，AG⊥BD交于J,证明CAE≅BAD，再证明CAI≅BAJ，求出°7830∠=∠=，然后求出12IF FJ AF==，，通过设FJ x=求出x，即可求出AF的长.【详解】解：过点A作AF⊥CE交于I，AG⊥BD交于J在CAE 和BAD 中 AC AB CAE BADAE AD =⎧⎪∠=∠⎨⎪=⎩∴CAE ≅BAD∴ICA ABJ ∠=∠ ∴BFE CAB ∠=∠（8字形） ∴°120CFD ∠= 在CAI 和BAJ 中 °90ICA ABJ CAI BJA CA BA ∠=∠⎧⎪∠=∠=⎨⎪=⎩ ∴CAI ≅BAJ,AI AJ CI BJ ==∴°60CFA AFJ ∠=∠= ∴°30FAI FAE ∠=∠= 在RtAIF 和RtAJF 中 °30FAI FAE ∠=∠=∴12IF FJ AF ==设FJ x = 7,4CF BF ==则47x x +=-32x ∴=2AF FJ =AF ∴=3【点睛】此题主要考查了通过做辅助线证明三角形全等，得出相关的边相等，学会合理添加辅助线求解是解决本题的重点.27．如图，将ABC ∆沿着过AB 中点D 的直线折叠，使点A 落在BC 边上的1A 处，称为第1次操作，折痕DE 到BC 的距离记为1h ，还原纸片后，再将ADE ∆沿着过AD 中点1D 的直线折叠，使点A 落在DE 边上的2A 处，称为第2次操作，折痕11D E 到BC 的距离记为2h ，按上述方法不断操作下去…经过第2020次操作后得到的折痕20192019D E 到BC 的距离记为2020h ，若11h =，则2020h 的值为______．【答案】2019122-【解析】【分析】根据中点的性质及折叠的性质可得DA=DA ₁=DB,从而可得∠ADA ₁=2∠B,结合折叠的性质可得.，∠ADA ₁=2∠ADE,可得∠ADE=∠B,继而判断DE// BC,得出DE 是△ABC 的中位线，证得AA ₁⊥BC,AA ₁=2，由此发现规律：012122h =-=-₁同理21122h =-3211122222h =-⨯=-…于是经过第n 次操作后得到的折痕Dn-1 En-1到BC 的距离1122n n h -=-，据此求得2020h 的值．【详解】解：如图连接AA ₁,由折叠的性质可得：AA ₁⊥DE, DA= DA ₁ ,A ₂、A ₃…均在AA ₁上又∵ D 是AB 中点，∴DA= DB ,∵DB= DA ₁ ,∴∠BA ₁D=∠B ,∴∠ADA ₁=∠B +∠BA ₁D=2∠B,又∵∠ADA ₁ =2∠ADE ,∴∠ADE=∠B∵DE//BC,∴AA ₁⊥BC ,∵h ₁=1∴AA ₁ =2,∴012122h =-=-₁ 同理：21122h =-； 3211122222h =-⨯=-； …∴经过n 次操作后得到的折痕D n-1E n-1到BC 的距离1122n n h -=-∴20202019122h =-【点睛】本题考查了中点性质和折叠的性质，本题难度较大，要从每次折叠发现规律，求得规律的过程是难点．28．如图，∠BOC=60°，点A 是BO 延长线上的一点，OA=10cm ，动点P 从点A 出发沿AB 以2cm/s 的速度移动，动点Q 从点O 出发沿OC 以1cm/s 的速度移动，如果点P 、Q 同时出发，用t(s)表示移动的时间，当t=_____s 时，△POQ 是等腰三角形.【答案】103或10【解析】【分析】根据△POQ是等腰三角形，分两种情况进行讨论：点P在AO上，点P在BO上，分别计算，即可得解.【详解】当PO=QO时，△POQ是等腰三角形，如图1所示当点P在AO上时，∵PO=AO-AP=10-2t，OQ=t当PO=QO时，102t t-=解得103 t=当PO=QO时，△POQ是等腰三角形，如图2所示当点P在BO上时∵PO=AP-AO=2t-10，OQ=t当PO=QO时，210t t-=解得10t =故答案为：103或10 【点睛】本题考查等腰三角形的性质及动点问题，熟练掌握等腰三角形的性质以及分类讨论思想是解题关键.29．如图，正五边形ABCDE 中，对角线AC 与BE 相交于点F ，则AFE ∠=_______度．【答案】72．【解析】【分析】根据五边形的内角和公式求出EAB ∠，根据等腰三角形的性质，三角形外角的性质计算即可．【详解】解：∵五边形ABCDE 是正五边形，(52)1801085EAB ABC ︒︒-⨯∴∠=∠==，BA BC =，36BAC BCA ︒∴∠=∠=，同理36ABE ∠︒＝，363672AFE ABF BAF ∴∠∠+∠︒+︒︒＝＝＝．故答案为：72【点睛】本题考查的是正多边形的内角与外角，掌握正多边形的内角的计算公式、等腰三角形的性质是解题的关键．30．已知，∠MON =30°，点A 1、A 2、A 3在射线ON 上，点B 1、B 2、B 3…在射线OM 上，△A 1B 1A 2、△A 2B 2A 3、△A 3B 3A 4…均为等边三角形，若OA 1=a ，则△A 7B 7A 8的边长为______．【答案】64a【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3，根据30°角所对直角边等于斜边的一半得到A2B2=2B1A2，进而得出A3B3=4B1A2=4a，A4B4=8B1A2=8a，A5B5=16B1A2…从而得到答案．【详解】∵△A1B1A2是等边三角形，∴A1B1=A2B1，∠3=∠4=∠12=60°，∴∠2=120°．∵∠MON=30°，∴∠1=180°﹣120°﹣30°=30°．又∵∠3=60°，∴∠5=180°﹣60°﹣30°=90°．∵∠MON=∠1=30°，∴OA1=A1B1=a，∴A2B1=a．∵△A2B2A3、△A3B3A4是等边三角形，∴∠11=∠10=60°，∠13=60°．∵∠4=∠12=60°，∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，∴∠1=∠6=∠7=30°，∠5=∠8=90°，∴A2B2=2B1A2，B3A3=2B2A3，∴A3B3=4B1A2=4a，A4B4=8B1A2=8a，A5B5=16B1A2=16a，以此类推：A7B7=64B1A2=64a．故答案为：64a．【点睛】本题考查了等边三角形的性质、等腰三角形的性质以及含30°角的直角三角形的性质，根据已知得出A3B3=4B1A2，A4B4=8B1A2，A5B5=16B1A2进而发现规律是解题的关键．六、八年级数学轴对称三角形选择题（难）31．如图，在△ABC中，∠B=32°，将△ABC沿直线m翻折，点B落在点D的位置，则∠1-∠2的度数是（）A ．32°B ．64°C ．65°D ．70°【答案】B【解析】【分析】此题涉及的知识点是三角形的翻折问题，根据翻折后的图形相等关系，利用三角形全等的性质得到角的关系，然后利用等量代换思想就可以得到答案【详解】如图，在△ABC 中，∠B=32°，将△ABC 沿直线m 翻折，点B 落在点D 的位置∠B=∠D=32° ∠BEH=∠DEH∠1=180︒-∠BEH -∠DEH=180︒-2∠DEH∠2=180︒-∠D -∠DEH -∠EHF=180︒-∠B -∠DEH -(∠B+∠BEH)=180︒-∠B -∠DEH -（∠B+∠DEH）=180︒-32°-∠DEH -32°-∠DEH=180︒-64°-2∠DEH∴∠1-∠2=180︒-2∠DEH -(180︒-64°-2∠DEH)=180︒-2∠DEH -180︒+64°+2∠DEH=64°故选B【点睛】此题重点考察学生对图形翻折问题的实际应用能力，等量代换是解本题的关键32．如图，已知：30MON ∠=︒，点1A 、2A 、3A …在射线ON 上，点1B 、2B 、3B …在射线OM 上，112A B A △、223A B A △、334A B A △…均为等边三角形，若112OA ，则667A B A 的边长为( )A ．6B ．12C ．16D ．32【答案】C【解析】【分析】先根据等边三角形的各边相等且各角为60°得：∠B 1A 1A 2=60°，A 1B 1=A 1A 2，再利用外角定理求∠OB 1A 1=30°，则∠MON=∠OB 1A 1，由等角对等边得：B 1A 1=OA 1=12，得出△A 1B 1A 2的边长为12，再依次同理得出：△A 2B 2A 3的边长为1，△A 3B 3A 4的边长为2，△A 4B 4A 5的边长为：22=4，△A 5B 5A 6的边长为：23=8，则△A 6B 6A 7的边长为：24=16．【详解】解：∵△A 1B 1A 2为等边三角形，∴∠B 1A 1A 2=60°，A 1B 1=A 1A 2，∵∠MON=30°，∴∠OB 1A 1=60°-30°=30°，∴∠MON=∠OB 1A 1，∴B 1A 1=OA 1=12， ∴△A 1B 1A 2的边长为12，同理得：∠OB 2A 2=30°， ∴OA 2=A 2B 2=OA 1+A 1A 2=12+12=1， ∴△A 2B 2A 3的边长为1，同理可得：△A 3B 3A 4的边长为2，△A 4B 4A 5的边长为：22=4，△A 5B 5A 6的边长为：23=8，则△A 6B 6A 7的边长为：24=16．故选：C ．【点睛】本题考查等边三角形的性质和外角定理，运用类比的思想，依次求出各等边三角形的边长，解题关键是总结规律，得出结论．33．如图，在△ABC中，BC的垂直平分线分别交AC，BC于点D，E,若△ABC的周长为24，CE＝4，则△ABD的周长为（）A．16 B．18 C．20 D．24【答案】A【解析】【分析】根据线段的垂直平分线的性质和三角形的周长公式进行解答即可.【详解】解：∵DE是BC的垂直平分线，∴DB=DC，BC=2CE=8又∵AABC的周长为24，∴AB+BC+AC=24∴AB+AC=24-BC=24-8=16∴△ABD的周长=AD+BD+AB=AD+CD+AB=AB+AC=16，故答案为A【点睛】本题考查的是线段的垂直平分线的性质，理解并应用线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.34．如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，在直线AC上取一点P，使得△PAB为等腰三角形，则符合条件的点P共有()A．6个B．5个C．4个D．3个【答案】C【解析】【分析】根据等腰三角形的判定定理即可得到结论．【详解】解：根据题意，∵△PAB为等腰三角形，∴可分为：PA=PB，PA=AB，PB=AB三种情况，如图所示：∴符合条件的点P共有4个；故选择：C.【点睛】本题考查了等腰三角形的判定来解决实际问题，其关键是根据等腰三角形的判定定理解答．35．如图，P为∠AOB内一定点，M、N分别是射线OA、OB上一点，当△PMN周长最小时，∠MPN=110°，则∠AOB=（）A．35°B．40°C．45°D．50°【答案】A【解析】【分析】作P关于OA，OB的对称点P1，P2．连接OP1，OP2．则当M，N是P1P2与OA，OB的交点时，△PMN的周长最短，根据对称的性质可以证得：∠OP1M=∠OPM=50°，OP1=OP2=OP，根据等腰三角形的性质求解．【详解】作P关于OA，OB的对称点P1，P2．连接OP1，OP2．则当M，N是P1P2与OA，OB的交点时，△PMN的周长最短，连接P1O、P2O，∵PP1关于OA对称，∠MPN=110°∴∠P1OP=2∠MOP，OP1=OP，P1M=PM，∠OP1M=∠OPM，同理可得：∠P2OP=2∠NOP，OP=OP2，∴∠P1OP2=∠P1OP+∠P2OP=2（∠MOP+∠NOP）=2∠AOB，OP1=OP2=OP，∴△P1OP2是等腰三角形．∴∠OP 2N=∠OP 1M ，∴∠P 1OP 2=180°-110°=70°，∴∠AOB=35°，故选A ．【点睛】考查了对称的性质，解题关键是正确作出图形和证明△P 1OP 2是等腰三角形是．36．如图，∠AOB ＝30º，∠AOB 内有一定点 P ，且 OP ＝12，在 OA 上有一动点 Q ，OB 上有一动点 R 。

八年级上册全册全套试卷综合测试(Word版含答案)

八年级上册全册全套试卷综合测试（Word 版含答案）一、八年级数学三角形填空题（难）1．如图，ABC 中，点D 在AC 的延长线上，E 、F 分别在边AC 和AB 上，BFE ∠与BCD ∠的平分线相交于点P ，若ABC ∠=70°FEC ∠=80°，则P ∠=______．【答案】85°【解析】【分析】根据四边形内角和等于360°，在四边形FECB 中∠B +∠BFE +∠FEC +∠BCE =360°，结合角平分线的定义计算即可得∠1-∠2=15°；再在四边形EFPC 中求出∠1-∠2+∠P =110°即可解答．【详解】解：∵∠BFE =2∠1，∠BCD =2∠2，又∵∠BFE +∠ABC +∠FEC +∠BCE =360°，ABC ∠=70°，FEC ∠=80°，∴2∠1+（180°-2∠2）+70°+80°=360°，∴∠1-∠2=15°；∵在四边形EFPC 中，∠PFE +∠FEC +∠P +∠PCE =360°，∴∠1+80°+（180°-∠2）+∠P =360°，∴∠1-∠2+∠P =100°，∴∠P =85°，故答案为：85°．【点睛】本题考查的是三角形内角和定理和四边形内角和定理的应用，掌握三角形内角和等于180°和四边形内角和等于360°是解题的关键．2．如图,在平面直角坐标系xOy 中,点A 、B 分别在x 轴的正半轴、y 轴的正半轴上移动,点M 在第二象限，且MA 平分∠BAO ，做射线MB ，若∠1=∠2，则∠M 的度数是_______。

【答案】45︒【解析】【分析】根据三角形内角与外角的关系可得2M MAB ∠∠∠=+由角平分线的性质可得MAB MAO ∠∠=根据三角形内角和定理可得OBA OAB BOA 180∠∠∠++=︒易得∠M 的度数。

2015年秋季八年级上册数学期末综合练习二

八上H-12015年秋季八年级上册数学期末综合练习二（考试时间：120分钟；满分：150分）一、选择题（单项选择，每小题3分，共21分）． 1．4的平方根是（）．A ．±2B ．-2C ． 2D ．2 2．下列各数中，有理数是（）．A ．5B ．3π C ．12D ．3.03003000300003⋅⋅⋅ 3．下列计算结果正确的是（）．A ．22x x x ⋅= B ． 333()ab a b = C ．（538)x x = D ．623a a a ÷= 4．下列命题中，属于假命题的是（）．A ．等角的余角相等B ．在同一平面内垂直于同一条直线的两直线平行C ．相等的角是对顶角D ．有一个角是60°的等腰三角形是等边三角形 5．如图，△ABC ≌△DCB ，若∠A =75°，∠ACB =45°，则∠BCD 等于（）．A ．80°B ．60°C ．40°D ．20°6．若三角形三边的长为下列各组数，则其中是直角三角形的是（）．A ．3，3，3B ．5，6，8C ．4，5，6D ．5，12，137．已知△ABC 中，AC =BC ，点D ，Ｅ分别在边AB ,AC 上，把△BDE 沿直线DE 翻折，使点B 落在点Ｂ＇处，DB ＇，EB ＇分别交AC 于点F ，G ，若∠ADF =80°，则∠EGC 的大小为（）． A ．60° B ．70° C ．80° D ． 90°二、填空题（每小题4分，共40分）．8．计算：38- = ． 9．计算：3(2)a = ． 10．比较大小：23． 11．计算：2(2)x xy x -÷= ．12．若(),0322=-++b a 则ab = ． 13．用反证法证明“a b <”时，应假设．14．在投掷一枚硬币的试验中，共投掷了100次，其中“正面朝上”的频数为52，则“正面朝上”的频率为． 15．如图，OC 平分∠AOB ，点P 是OC 上一点，PM ⊥OB 于点M ，点N 是射线OA 上的一个动点，若PM=5，则PN 的最小值为．16．如图，△ABC 是等边三角形，D 点是AC 的中点，延长BC 使CE=CD ，若BD=3,则DE= ． 17．如图，在Rt △ABC 中，两直角边长分别为a 、b ,斜边长为c . 若Rt △ABC 的面积为3，且a +b =5．则（1）ab = ； (2)c = ．三、解答题（共89分）． 18．(1)计算()20153912712---+-． 19．化简求值()()()2222-+-+x x x ，其中2-=x ．20．因式分解：（1）24ax a - ．（2）221218pm pm p -+．21．如图，在△ABC 中，点D 是BC 边的中点，分别过点B 、C 作BE ⊥AD 于点E ，CF ⊥AD 交AD的延长线于点F ，求证：DE=DF ．22．“先学后教”课题组对学生参与小组合作的深度和广度进行评价，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．课题组随机抽取了若干名初中学生的参与情况，绘制了如图两幅不完整的统计图，请根据图中所给信息解答下列问题：（1）在这次评价中，一共抽查了______名学生；（2）请将条形统计图补充完整；（3）求出扇形统计图中，“主动质疑”所对应扇形的圆心角的度数.（第17题图）（第16题图）（第15题图）（第7题图）（第5题图）八上H-223．我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释，例如：图A 可以用来解释a 2 +2ab+ b 2 ＝(a +b )2，实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.（1）图B 可以解释的代数恒等式是；（2）现有足够多的正方形和矩形卡片(如图C)，试在下面的虚线方框中画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形（每两块纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使该矩形的面积为a 2 +5a b +4b 2，并利用你所画的图形面积对 a 2 +5ab +4b 2进行因式分解.：a 2 +5ab +4b 2 = .25.如图,在△ABC 中，AB =AC =6cm ，BC =4cm ，点D 为AB 的中点. 如果点P 在线段BC 上以1 cm ／s 的速度由点B 向点C 运动，同时，点Q 在线段CA 上由点C 向点A 运动．（1）若点Q 的运动速度与点P 的运动速度相等，经过_____s 后，△BPD ≌CQP ；（2）若点Q 的运动速度与点P 的运动速度不相等.①当点Q 的运动速度为多少时，能够使△BPD 与△CQP 全等?②若点Q 以①中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿△ABC 三边运动，求经过多长时间后，点P 与点Q 第一次．．．相遇,并求出相遇的具体位置.24．如图，△ABC 中，∠C =90°．（1）用尺规作图作AB 边上的垂直平分线DE ，交AC 于点D ，交AB 于点E ．（保留作图痕迹，不要求写作法和证明）；（2）在（1）条件下，连结BD ，当BC =3cm ，AB =5cm 时，求△BCD 的周长.26．如图，将两块腰长相等的三角尺（△ABC 和△DEF ,其中∠ACB =∠DFE =90°）置于水平面上，直角边BC =EF =1cm ，且始终紧贴在水平直线l 上.（1）在图①中，当边DF 与边AC 重合时，AB 与AE 的大小关系是__________；（2）将三角板ABC 以1cm/s 的速度从图①的位置沿直线l 向右平移，设平移的时间为t (s),如图②所示.当0＜t ＜1时，DE 分别交AC 、AB 于点G 、H ，DF 分别交AB 、BG 于点P 、Q , 连结BG 、AE. ①求证：BG =AE ；②在平移过程中，是否存在某时刻t ，使得以点D 、G 、Q 为顶点的三角形是等腰三角形？若存在，请求出t 的值；若不存在，请说明理由.ll B C (F ) EA (D )①D A B F C EH P GQ②。

2015-2016八年级数学上册期末综合训练题(新人教附答案)

2015-2016八年级数学上册期末综合训练题（新人教附答案）说明：1.本训练卷是2014～2015上学期对自贡市八年级期末统一检测数学试题的两套模拟训练的合卷.训练题是按新教材、新课标的要求从纸制资料上选编和改编的，具有较强的应试针对性，题型结构与统考题型结构接轨；两套卷分别安排在每道大题的前后两半部分，共48道小题，200分的题量.2.本合卷的每大题的后半部分共24道题组成一套模拟试题，设计有该部分题的答题卡（答题卡上有题号）；考试时间120分钟，满分100分；考试结束后将答题卡收回，由老师批阅.一、选择题（本大题共16道小题，每小题3分）1、在分式+2xx y中，若将、x y 都扩大为原来的2倍，则所得分式的值（）A.不变B.扩大为原来的2倍C.扩大为原来的4倍D.缩小为原来的122、如果一个等腰三角形的两边长分别是5cm 和6cm ，则此三角形的周长是（） A.15cm B.16cm C.17cm D.16cm 或17cm3、一个多边形的内角和为540°，则它的对角线共有（） A.3条 B.5条 C.6条 D.12条4、已知a b 2+=，则22a b 4b -+的值是（） A.2 B.3 C.4 D.65、如图，,DA AB CB AB ⊥⊥,垂足分别为A B 、，BD AC =,根据这些条件，不能推出的结论是（）A.AD BCB.AD BC =C.AC 平分DAB ∠D.C D ∠=∠6、化简()21x 1x 3x 3x 1+⎛⎫-⋅- ⎪--⎝⎭的结果是（） A.2 B.2x 1- C.2x 3- D.-x 47、如图，用尺规作图法作出OBF AOB ∠=∠,作图痕迹弧 MN 是（）A.以点B 为圆心，OD 长为半径的圆弧；B.以点B 为圆心，DC 长为半径的圆弧；C.以点E 为圆心，OD长为半径的圆弧；D.以点E 为圆心，DC 长为半径的圆弧.8、在ABC中，,AB ACA 120BC 6cm =∠== ，，AB 的垂直平分线交BC 于点N ,交AC 于点F ,则MN 的长为（）A.2cmB.5cm 2C.3cmD.7cm 29、计算()32a -的结果是（）A.6a -B.6aC.5a -D.5a10、已知-=-111a b 2，则-aba b 的值是（）A.12B.2C.-12D.-2 11、如图，已知,AE CF AFD CEB =∠=∠,则添加下列一个条件后，仍无法判定ADF≌CBE的是） A.A C ∠=∠ B.AD CB = C.BE DF = D.AD BC12、一个n 边形除了一个内角外，其余内角之和是2570） A.90° B.15° C.120° D.130°13、一艘海轮位于灯塔P 的南偏东70°方向的M 处，它以40海里/时的速度向正北方向航行，2小时后到达位于灯塔P 的北偏东40°的N 处，则N 处与灯塔P 的距离为（） A.40海里 B.60海里 C.70海里 D.80海里 14、如图，在ABC,ADE中，,,BAC DAE 90AB AC ∠=∠==三点在同一直线上，连接BD BE 、，以下四个结论：①.BD CE =;②.BD CE ⊥;③.ACE DBC 45∠+∠= ；④.DA 平分其中正确的是A.1 B.2 C.3 D.4 15、将正方形OABC 放在平面直角坐标系中，点O 是原点，点 A 的坐标为(1，则点C 的坐标为（）A.()1 B.(1- C.)1 D.()1-16、某早点店的某种食品的售价开始n 根/元，第一次涨价后售价(为b ；从开始到第二次涨价后的涨价增长率为c ，则下列判断中，错误的是（） A.a b c << B.2a c < C.a b c += D.2b c =二、填空题（本大题共12道小题，每小题3分）N 北17、化简：22a 4a 4a 4-++= .18、某电子元件的面积大约为.200000007mm ，用科学记数法表示为 2mm .19、分解因式：()222a 3b b +-= .20、已知点A B 、的坐标分别为()(),,2024，，点O 是原点，以点A B P 、、为顶点的三角形与ABO 全等，写出一个符合条件的点P 的坐标为 .21、如图，△ABC 中，CD 是AB 边上的高，若2ACB 3B 6A ∠=∠=∠:BC AD = .22、如图，ABC中，C 90BAC 30AB 8∠=∠== ，，,AD平分BAC ∠,点P Q 、分别是AB AD 、上的动点，则()PQ BQ + 的最小值是 .23、若()-2x 3x 2-的值为负数，则x 24、若22x x m -+是完全平方式，则m25、如图，在ABC中，DE 垂直平分AC 交AB 于点E , A 30ACB 80∠=∠= ，,则BCE ∠= .26、如图，ABE和ADC 是ABC分别沿AB AC 、边翻折180°形成的；若BAC 130∠= ,则DAE ∠的度数为 .27、将4个数a b c d 、、、排成两行两列，两边各加一条竖线记成a b c d ，定义a bad bc c d=-，上述符号就叫二阶列式；若x 11x81x x 1+-=-+，则x = . 28、甲计划用若干天完成某项工作，在甲独立工作2天后，乙加入此项工作，且甲、乙两人工效相同，结果提前2天完成任务，设甲计划完成此项工作的天数是x ，则x 的值为 .三、解答题（本大题共10道小题，每小题5分）29、已知点()-P 31，关于y 轴对称点Q 的坐标是(),a b 1b +-，求b a 的值.30、如图，在ABC，点D E 、分别在AB AC 、上，CF AB 交DE 的延长线于点F ,,DE EF = AB 8CF 5==，,求BD 的长度.31、若,a b 7ab 12+==，求22a 3ab b ++ 的值？32、一个正多边形的每个内角都比相邻的外角的3倍还多20°，求这个正多边形的边数？33、若关于x 的分式分式方程2m x 21x 3x+-=-无解，求m 的值.34、若多项式2x ax a 3++-分解因式的结果为()()x b x 1+-，分别求a b 、的值？35()()320142015112013828π-⎛⎫⎛⎫---+- ⎪ ⎪⎝⎭⎝⎭36、如图，在ABC中，B 47∠= ,三角形的外角DAC ∠和ACF ∠的平分线交于点E ,求AEC ∠F37、先化简，再求值：()()()()22x 32x 34x x 1x 2+---+-，其中x 是3x 31x 22x-+=--的解.38、作图题：（不要求写作法）如图，ABC在平面直角坐标系中，其中点A B C 、、的坐标分别为()()(),,,,,A 21B 45C 52---.⑴.作ABC 关于直线:l x 1=-的对称的111A B C ；⑵.写出点111A B C 、、的坐标.四、解答题（本大题共6道小题，每小题6分）39、先化简，再求值:y 20+=，求代数式()()()-2x y x y x y 2x ⎡⎤++-÷⎣⎦的值.40、先化简，再求代数式23x 11x 2x 2-⎛⎫-÷ ⎪++⎝⎭的值，其中x 是不等式组x 302x 96+≥⎧⎨+<⎩的整数解.41、四边形ABCD 是正方形，对角线AC BD 、相较于点O ,CDE 是等边三角形，连接AE 交BD 于点E .求证：⑴.AF 2OF =;⑵.FE FB =.42、先化简：-⎛⎫÷-+ ⎪⎝⎭a 11a 2aa ，然后任选一个你喜欢的a 的值代入求值.43、在直角坐标系中，点B 的坐标为()a b ，，且满足2a 4a 40-+=.⑴.求点B 的坐标；⑵.点A 为y 轴上一动点，过点B 作BC AB ⊥交x 轴正半轴于点C . 求证：BA BC =44、一轮船在顺水中航行46km 与在逆水中航行34km 所用的时间和恰好等于该船在静水中航行80km 所用的时间，已知水流速度是/3km h ，求该船在静水中航行的速度.五、解答题（本大题共4道小题，45、47题各7分，46、48题各8分）45、某市在道路改造过程中，需要铺设一条长为1000米的管道，决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米，且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同. ⑴.甲、乙工程队每天各能铺设多少米？⑵.如果要求完成该项工程的工期不超过10天，那么为两个工程队分配工程量（以百米为单位）的方案有几种？请你帮助设计.46、研究几何图形，我们往往先给出这类图形的定义，再研究它的性质和判定．定义：六个内角相等的六边形叫等角六边形． ⑴.研究性质：①.等角六边形的每个内角是多少度？②.如图①，等角六边形ABCDEF 中，三组正对边AB 与DE ，BC 与EF ，CD 与AF 分别有什么位置关系？证明你的结论③.如图②，等角六边形ABCDEF 中，如果有AB=DE ，则其余两组正对边BC 与EF ，CD 与AF 相等吗？证明你的结论 ⑵.探索判定：如图③所示，三组正对边分别平行的六边形ABCDEF 中，A C 120∠=∠= ,该六边形一定是等角六边形吗？为什么？47、⑴.如图①，点B C 、分别在MAN ∠的边AM AN 、上，点E F 、在MAN ∠内部的射线AD上，12∠∠、分别是ABE ❒、CAF ❒的外角.已知,AB AC 12BAC =∠=∠=∠.求证：ABE ❒≌CAF ❒.⑵. 如图②，在等腰三角形ABC 中，,AB AC AB BC =>;点D 在边BC 上，CD 2BD =.点E F 、在线段AD 上，12BAC ∠=∠=∠；若ABC ❒的面积为9，求ABE ❒的面积与CDF❒的面积之和.48、阅读下面的解题过程：已知2x 13x 1=+，求24x x 1+的值. 解：由2x 13x 1=+，知x 0≠，所以2x 13x +=，即1x 3x +=.所以242222x 111x x 2327x x x +⎛⎫=+=+-=-= ⎪⎝⎭所以24x x 1+的值为7的倒数，即17.以上解法中先将已知等式的两边取“倒数”，然后求出待式子倒数值，我们把此题的这种解法叫做“倒数法”。

人教版八年级上册全册综合测试考试试题

总复习八年级上册综合测试试题第Ⅰ卷一、积累与运用（1——4小题，每小题3分,共12分）1、下列加点的字词注音正确的一项是（）（3分）A、两栖（qī）吊唁（yàn）藩篱（fán）褶皱（zhě）B、差使（chāi）轩榭（xiè）额枋（fǎng）匀称（chèng）C、嶙峋（líng）伧俗（cāng）逾时（yú）狼藉（jiè）D、尴尬（ɡān）孕育（yùn）百舸（ɡě）罗绮（qǐ）2、选出有错别字的一项。

（）（3分）A、镂空斟酌交卸重峦叠嶂B、鳌头惶急繁衍销声匿迹C、推崇颓废驻足惟妙惟肖D、脊椎褶皱取缔无动于中3、下列句子中没有语病的一项是（）（ 3分）A、在人生道路上，挫折和失败在所难免，但只有不气馁，坚持下去，总会有成功的一天。

B、全世界每天至少有5万人死于由水污染引起的各种疾病。

C、在交通管理部门的大力宣传下，使我们贵港市的酒后驾车现象大为减少。

D、为了做好食品安全工作，我们每一个人都应该发挥自己的充分作用。

4、下面句子中加点的成语使用得不恰当的一项是( )。

（3分）A、老妇人还没有满意，她要做一个名副其实的坟堆。

B、赵州桥的设计完全合乎科学原理，施工技术更是巧妙绝伦。

C、大致说来，那些门和窗尽量工细而决不庸俗，即使简朴而别有用心。

D、这里没有棕树蛇的天敌，一旦它在夏威夷安家落户，该岛的鸟类将在劫难逃。

二．阅读说明文，完成5—8小题。

（每小题3分，共12分）①手，这个词听起来极其普通，我们几乎随时随地都可以接触到。

然而，你是否知道：手是万物之灵的人类特有的一部分肢体，是其他任何生物所不拥有的。

通常我们把手腕以下部分称为手。

手可分为手掌、手指两部分，由手腕与臂相连，在关节允许范围内可以伸曲自如。

具体来说，手掌由掌心、掌背、掌侧和掌根组成，手指则由指节、指肚、指甲和指尖组成，皮下布满了神经末梢和毛细血管，以指尖处最为丰富。

八上综合测试题2015.12.26

八年级上册综合测试题(共6套,含答案)

八年级上册全册全套试卷综合测试卷(word含答案)

八年级上册全册全套试卷综合测试(Word版 含答案)

度八年级上综合能力测试题

八年级上册全册全套试卷综合测试(Word版 含答案)

八年级上册全册全套试卷综合测试卷(word含答案)

八年级上级综合测试题

八年级上综合测试卷 学生版

初二上册综合练习题

哈尔滨2015年12月八年级上质量检查数学试卷含答案解析

八年级上册全册全套试卷综合测试卷(word含答案)

八年级上册全册全套试卷综合测试(Word版 含答案)

八年级上册全册全套试卷综合测试卷(word含答案)

八年级上册全册全套试卷综合测试(Word版 含答案)

八年级上册全册全套试卷综合测试(Word版 含答案)

2015年秋季八年级上册数学期末综合练习二

2015-2016八年级数学上册期末综合训练题(新人教附答案)

人教版八年级上册全册综合测试考试试题

八年级上册全册全套试卷综合测试(Word版含答案)

八年级上册全册全套试卷综合测试(Word版含答案)

八年级上综合测试卷学生版

八年级上册全册全套试卷综合测试(Word版含答案)

八年级上册全册全套试卷综合测试(Word版含答案)

八年级上册全册全套试卷综合测试(Word版含答案)