(新)高中数学立体几何三视图练习题

合集下载

高三数学空间几何体的三视图与直观图试题答案及解析

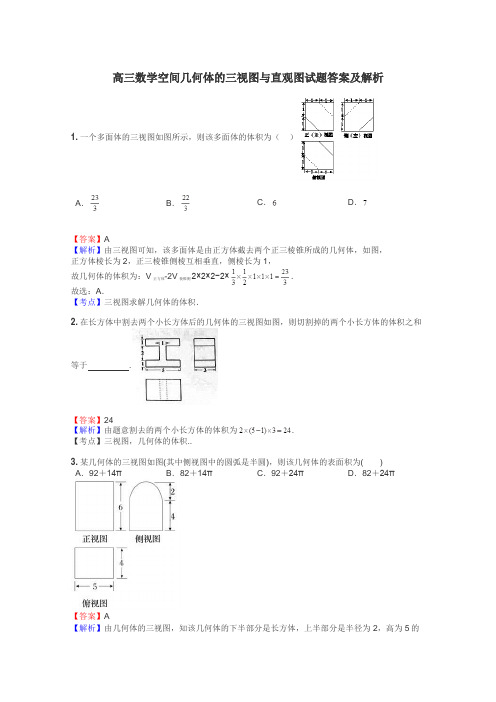
高三数学空间几何体的三视图与直观图试题答案及解析1.一个多面体的三视图如图所示，则该多面体的体积为（）A．B．C．D．【答案】A【解析】由三视图可知，该多面体是由正方体截去两个正三棱锥所成的几何体，如图，正方体棱长为2，正三棱锥侧棱互相垂直，侧棱长为1，故几何体的体积为：V正方体-2V棱锥侧2×2×2−2×．故选：A．【考点】三视图求解几何体的体积．2.在长方体中割去两个小长方体后的几何体的三视图如图，则切割掉的两个小长方体的体积之和等于.【答案】24【解析】由题意割去的两个小长方体的体积为.【考点】三视图，几何体的体积..3.某几何体的三视图如图(其中侧视图中的圆弧是半圆)，则该几何体的表面积为()A．92＋14πB．82＋14πC．92＋24πD．82＋24π【答案】A【解析】由几何体的三视图，知该几何体的下半部分是长方体，上半部分是半径为2，高为5的圆柱的一半．长方体中EH＝4，HG＝4，GK＝5，所以长方体的表面积为(去掉一个上底面)2(4×4＋4×5)＋4×5＝92．半圆柱的两个底面积为π×22＝4π，半圆柱的侧面积为π×2×5＝10π，所以整个组合体的表面积为92＋4π＋10π＝92＋14π，选A．4.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图，可知该几何体为半圆锥和三棱锥的组合体，如图所示，可知左视图为等腰三角形，且轮廓线为实线，故选D．5.一个正方体截去两个角后所得几何体的正视图、侧视图如图所示，则其俯视图为()【答案】C【解析】依题意可知该几何体的直观图如图所示，故其俯视图应为C．6.某几何体的三视图如图所示，则该几何体的体积为A．12B．18C．24D．30【答案】C【解析】由三视图可知该几何体是一个底面为直角三角形的直三棱柱的一部分，其直观图如上图所示，其中,侧面是矩形，其余两个侧面是直角梯形，由于,平面平面,所以平面,所以几何体的体积为：故选C.【考点】1、空间几何体的三视图；2、空间几何体的体积.7.一块石材表示的几何体的三视图如图2所示，将石材切削、打磨、加工成球，则能得到的最大球的半径等于（）A．1B．2C．3D．4【答案】B【解析】由图可得该几何体为三棱柱,因为正视图,侧视图,俯视图的内切圆半径最小的是正视图(直角三角形)所对应的内切圆,所以最大球的半径为正视图直角三角形内切圆的半径,则,故选B.【考点】三视图内切圆球三棱柱8. [2013·四川高考]一个几何体的三视图如图所示，则该几何体可以是()A．棱柱B．棱台C．圆柱D．圆台【答案】D【解析】由正视图和侧视图可知，该几何体不可能是圆柱，排除选项C；又由俯视图可知，该几何体不可能是棱柱或棱台，排除选项A、B.故选D.9.[2013·宁波质检]如图，水平放置的三棱柱的侧棱长和底边长均为2，且侧棱AA1⊥平面A1B1C1，正视图是正方形，俯视图是正三角形，该三棱柱的侧视图面积为()A．2B．C．2D．4【答案】A【解析】由题意可知，该三棱柱的侧视图应为矩形，如图所示．在该矩形中，MM1＝CC1＝2，CM＝C1M1＝·AB＝.所以侧视图的面积为S＝2.10.某几何体的三视图如图所示,则该几何体的体积的最大值为 .【答案】【解析】该几何体是类似墙角的三棱锥，假设一条直角的棱长为x，则三条直角棱长分别为.所以体积为.当且仅当时取等号.【考点】1.三视图.2.函数最值问题.3.空间想象能力.11.（2012•广东）某几何体的三视图如图所示，它的体积为（）A．12πB．45πC．57πD．81π【答案】C【解析】由三视图可知，此组合体上部是一个母线长为5，底面圆半径是3的圆锥，下部是一个高为5，底面半径是3的圆柱故它的体积是5×π×32+π×32×=57π故选C12. (2014·咸宁模拟)某几何体的三视图如图所示(其中侧视图中的圆弧是半圆),则该几何体的表面积为( )A．92+14πB．82+14πC．92+24πD．82+24π【答案】A【解析】由几何体的三视图知该几何体的下半部分是长方体,上半部分是半径为2,高为5的圆柱的一半.所以长方体的表面积为(去掉一个上底面)2(4×4+4×5)+4×5=92.半圆柱的两个底面积为π×22=4π,半圆柱的侧面积为π×2×5=10π,所以整个组合体的表面积为92+4π+10π=92+14π. 13.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为【答案】D【解析】条件对应的几何体是由底面棱长为r的正四棱锥沿底面对角线截出的部分与底面为半径为r的圆锥沿对称轴截出的部分构成的。

高三数学空间几何体的三视图与直观图试题答案及解析

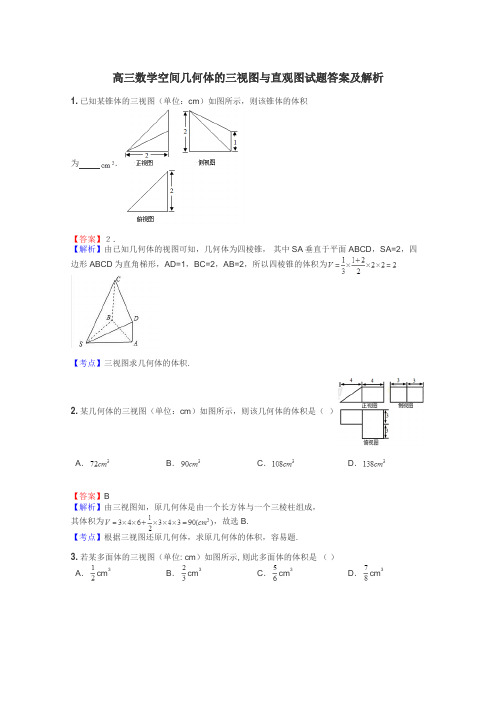
高三数学空间几何体的三视图与直观图试题答案及解析1.已知某锥体的三视图（单位：cm）如图所示，则该锥体的体积为．【答案】２．【解析】由已知几何体的视图可知，几何体为四棱锥，其中SA垂直于平面ABCD，SA=2，四边形ABCD为直角梯形，AD=1，BC=2，AB=2，所以四棱锥的体积为【考点】三视图求几何体的体积.2.某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（）A．B．C．D．【答案】B【解析】由三视图知，原几何体是由一个长方体与一个三棱柱组成，其体积为，故选B.【考点】根据三视图还原几何体，求原几何体的体积，容易题.3.若某多面体的三视图（单位: cm）如图所示, 则此多面体的体积是（）A．cm3B．cm3C．cm3D．cm3【答案】C【解析】由三视图可得，该几何体相当于一个正方体切去一个三个侧棱长为1的三棱锥.所以该几何体的体积为.故选C.【考点】1.三视图.2.空间想象力.3.几何体的体积.4. (2014·孝感模拟)一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )A．16πB．14πC．12πD．8π【答案】A【解析】由三视图可知,该几何体是球挖去半球.其中两个半圆的面积为π×22=4π.个球的表面积为×4π×22=12π,所以这个几何体的表面积是12π+4π=16π.5.如图，某几何体的三视图都是等腰直角三角形，则几何体的体积是（）A．8B．7C．9D．6【答案】C【解析】由三视图可知,几何体是底面为等腰直角三角形,有一侧棱与底面垂直(垂足在非直角处)的三棱锥,其底面面积为×6×3=9,三棱锥的高为3,所以三棱锥的体积=×9×3=9．6.已知某几何体的三视图(如图),正视图和侧视图均为两个相等的等边三角形,府视图为正方形,则几何体的体积为（）A．B．4C．9D．9【答案】C【解析】由三视图可知,几何体由两个同底之正四棱锥组成所以其体积为V=2××32×3×=9 7.一空间几何体的三视图如图所示，该几何体的体积为12π＋，则正视图中x的值为( )A．5B．4C．3D．2【答案】C【解析】三视图，由正四棱锥和圆柱组成，故选C．8.如图，一个四棱锥的底面为正方形，其三视图如图所示，则这个四棱锥的体积为（）A．1B．2C．3D．4【答案】B【解析】由题意，棱锥的高为，底面面积为，∴.【考点】三视图，体积．9.某几何体的三视图如题（6）所示，其侧视图是一个边长为1的等边三角形，俯视图是两个正三角形拼成的菱形，则这个几何体的体积为（）A．1B．C．D．【答案】C【解析】这是由两个三棱锥拼成的几何体，其体积为.选C.【考点】三视图及几何体的体积.10.―个几何体的三视图如图所示(单位：)，则该几何体的体积为．【答案】18+9【解析】由三视图可知，此几何体为两个相切的球上方放了一个长方体组成的组合体，所以其体积为：V=3×6×1+2××=18+911.一个空间几何体的三视图如图所示，该几何体的表面积为__________.【答案】152【解析】几何体为一个三棱柱，底面为一个等腰三角形，底边长为6，底边上高为4，腰长为５.棱柱的高为8.因此表面积为【考点】三视图12.某三棱锥的三视图如图所示，则这个三棱锥的体积为；表面积为．【答案】；．【解析】由三视图知几何体如下图，为一个三棱锥，且三棱锥的一个侧面与底面垂直，底面三角形的一条边长为，该边上的高为，∴几何体的体积．它的表面积为．【考点】由三视图求面积、体积．13.已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是_______.【答案】【解析】由题意可得该几何体是一个三棱锥，体积.【考点】1.三视图的知识.2.立几中的线面关系.3.三棱锥的体积公式.14.一个空间几何体的三视图如图所示，其正视图、侧视图、俯视图均为等腰直角三角形，且直角边长都为1，则这个几何体的体积是【答案】【解析】由三视图，可知该几何体是三棱锥，并且侧棱，，，则该三棱锥的高是，底面三角形是直角三角形，所以这个几何体的体积＝＝．【考点】由三视图求几何体的体积．15.一个几何体的三视图如图所示,则该机合体的体积为( )A．B．C．D．【答案】B【解析】分析可得该几何体是底面为菱形的四棱锥,则高底面面积,所以.故选B【考点】三视图四棱锥体积16.一个几何体的三视图如图所示，则该几何体的体积是【答案】【解析】通过三视图的观察可得，该几何体是一个四棱柱，底面是一个直角梯形，其上下底分别为2,3，梯形的高为2.四棱柱的高为2.所以几何体的体积为.【考点】1.三视图的知识.2.几何体的体积.3.空间想象力.17.某长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为()A．4B．4C．6D．8【答案】D【解析】割补可得其体积为2×2×2＝8.18.某几何体的三视图如图所示，则该几何体的体积是________．【答案】16π－16【解析】由三视图知，该几何体是由一个底面半径为2，高为4的圆柱内挖去一个底面边长为2，高为4的正四棱柱后剩下的部分，∴V＝(π×22－22)×4＝16π－16.19.已知正方体ABCD-A1B1C1D1，M为棱A1B1的中点，N为棱A1D1的中点．如图是该正方体被M，N，A所确定的平面和N，D，C1所确定的平面截去两个角后所得的几何体，则这个几何体的正视图为()．【答案】B【解析】对于选项A，由于只是截去了两个角，此切割不可能使得正视图成为梯形．故A不对；对于B，正视图是正方形符合题意，线段AM的影子是一个实线段，相对面上的线段DC1的投影是正方形的对角线，由于从正面看不到，故应作成虚线，故选项B正确；对于C，正视图是正方形，符合题意，有两条实线存在于正面不符合实物图的结构，故不对；对于D，正视图是正方形，符合题意，其中的两条实线符合俯视图的特征，故D不对．20.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示，则该棱柱的体积为（）A．B．C．D．6【答案】B【解析】由三视图知该直三棱柱高为4，底面正三角形的高为3，所以正三角形边长为6，所以V＝×36×4＝36.故选B.【考点】1.三视图；2.柱体体积计算.21.某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为的扇形,则该几何体的体积为（）A．B．C．D．【答案】D【解析】由题意知道，该几何体体积是圆柱体积的，即.【考点】1、三视图；2、几何体体积.22.右图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为2和4，腰长为4的等腰梯形，则该几何体的侧面积是( )A．B．C．D．【答案】B【解析】由三视图可得该几何体是一个圆台，其两底直径分别为2和4，母线长为4，所以该几何体的侧面积是，选B..【考点】三视图，圆台的侧面积.23.如图是一个组合几何体的三视图，则该几何体的体积是 .A．B．C．D．【答案】A【解析】由三视图还原可知该几何体是一个组合体，下面是一个半径为4，高为8的圆柱，，上面是一个三棱柱，故所求体积为.【考点】三视图，圆柱、三棱柱的体积公式.24.已知一个几何体的三视图如图所示，则该几何体的体积为___________【答案】【解析】该几何体为圆柱中挖去半个球而得的组合体，其体积为.【考点】三视图.25.一个几何体的三视图如图所示（单位长度：），俯视图中圆与四边形相切，且该几何体的体积为，则该几何体的高为 .【答案】【解析】由如图所示的几何体的三视图知：这个几何体是一个半径为的球和一个直四棱柱的结合体，且这个直四棱柱的底面是对角线分别为和的棱形，这个直四棱柱的高为，∴这个几何体的体积：V=，解得h=.【考点】1.三视图；2.几何体的面积和体积26.一个几何体的三视图如图所示，则该几何体的直观图可以是（）【答案】D【解析】通过三视图的俯视图可知，该几何体是由两个旋转体组成，故选D.【考点】1.三视图的应用.27.如图为一个几何体的三视图正视图和侧视图均为矩形，俯视图中曲线部分为半圆，尺寸如图所示，则该几何体的表面积为（）A．B．C．D．【答案】D【解析】由三视图可知，这是一个由半个圆柱和一个三棱柱构成的组合体，这个组合体仍为一个柱体。

高中数学第一章立体几何初步 1.3 三视图练习北师大版必修2-北师大版高一必修2数学试题

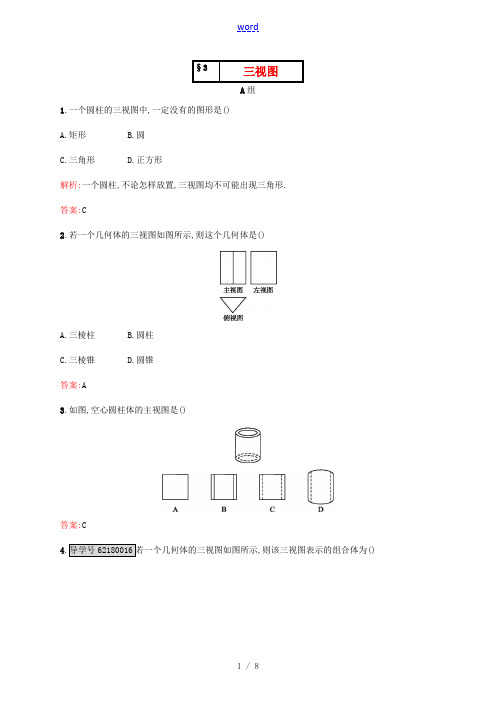
§3三视图A组1.一个圆柱的三视图中,一定没有的图形是()A.矩形B.圆C.三角形D.正方形解析:一个圆柱,不论怎样放置,三视图均不可能出现三角形.答案:C2.若一个几何体的三视图如图所示,则这个几何体是()A.三棱柱B.圆柱C.三棱锥D.圆锥答案:A3.如图,空心圆柱体的主视图是()答案:C4.导学号62180016若一个几何体的三视图如图所示,则该三视图表示的组合体为()A.圆柱与圆锥B.圆柱与三棱锥C.圆柱与四棱锥D.四棱柱与圆锥答案:C5.一个几何体的三视图如图所示,则该几何体的直观图可以是()解析:由俯视图易知,只有选项D符合题意.故选D.答案:D6.如图所示的立体图形,都是由相同的小正方体拼成的.(1)图①的主视图与图②的图相同;(2)图③的主视图与图④的主视图.(填“相同”或“不同”)答案:(1)俯视(2)不同7.如图所示是一个圆锥的三视图,则该圆锥的高为 cm.解析:由三视图知,圆锥的母线长为3 cm,底面圆的直径为3 cm,所以圆锥的轴截面是边长为3 cm 的等边三角形,所以圆锥的高为(cm).答案:8.已知某组合体的主视图与左视图相同(如图1所示,其中AB=AC,四边形BCDE为正方形),则该组合体的俯视图可以是如图2所示的.(把你认为正确的图的序号都填上)图1图2解析:由主视图与左视图可得该几何体可以是由正方体与底面边长相同的四棱锥组合而成的,则其俯视图为图①;可以是由正方体与底面直径与底面正方形边长相同的圆锥组合而成的,则其俯视图为图④;可以是由圆柱与底面相同的圆锥组合而成的,则其俯视图为图③;可以是由圆柱与底面正方形边长等于圆柱底面直径的四棱锥组合而成的,则其俯视图为图②.答案:①②③④9.一个几何体的三视图如图所示,请画出它的实物图.解:由三视图可知,该几何体由正方体和四棱柱组成,如图所示.10.导学号62180017如图所示是一个零件的实物图,画出这个几何体的三视图.解:该零件由一个长方体和一个半圆柱拼接而成,并挖去了一个小圆柱(形成圆孔).主视图反映了长方体的侧面和半圆的底面、小圆柱的底面,左视图反映了长方体的侧面、半圆柱的侧面、小圆柱的侧面,俯视图反映了长方体的底面、半圆柱的侧面和小圆柱的侧面投影后的形状.它的三视图如图所示.B组1.如图①②③分别为三个几何体的三视图,根据三视图可以判断这三个几何体依次分别为()图①图②图③A.三棱台、三棱柱、圆锥B.三棱台、三棱锥、圆锥C.三棱柱、正四棱锥、圆锥D.三棱柱、三棱台、圆锥解析:图①②③对应的原几何体分别是三棱柱、正四棱锥、圆锥,故选C.答案:C2.导学号62180018将正方体(如图1-(1)所示)截去两个三棱锥,得到图1-(2)中的几何体,则该几何体的左视图为(如图2所示)()图1图2解析:左侧被截去的三棱锥的底面三条边中,有两条与正方体的棱重合,另一条应为正方形自左上到右下的对角线,是可见的;右侧被截去的三棱锥的底面的三条边中,有两条与正方体的棱重合,另一条应为正方形自右上到左下(从左面看)的对角线,是不可见的.故选B.答案:B3.如图所示,已知正三棱柱ABC-A1B1C1的底面边长为2,高为3,则其左视图的面积为()A.6B.3C.3D.6解析:由三视图的画法可知,该几何体的左视图是一个矩形,其宽为2sin 60°=,长为3,故面积S=3.答案:C4.已知一几何体的主视图与左视图如图所示,则下列图形中,可以是该几何体的俯视图的图形有()A.①②③⑤B.②③④⑤C.①②④⑤D.①②③④解析:可以结合实物想象,对于①,可认为该几何体的最下部为棱柱,上部为两个圆柱;对于②,可认为该几何体的上部为两个棱柱,下部为圆柱;对于③,可认为该几何体的上部为圆柱,下部为两个棱柱;对于④,可认为该几何体的上部是底面为等腰直角三角形的棱柱,中间为一圆柱,底部为四棱柱;对于⑤,由原几何体最下部的两个视图可知,其俯视图不可能是一个三角形.答案:D5.如图所示,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为.解析:根据三视图还原成实物图,即四棱锥P-ABCD,所以最长的一条棱的长为PB=2.答案:26.已知三棱锥的直观图及其俯视图与左视图如图所示,俯视图是边长为2的正三角形,左视图是有一直角边长为2的直角三角形,则该三棱锥的主视图面积为.解析:三棱锥的主视图如图所示,故主视图的面积为×2×2=2.答案:27.下图是一个几何体的三视图,试画出其实物图.解:由几何体的三视图容易想到该几何体可以由正方体切割而得到,如图所示.俯视图8.导学号62180019一个棱长均为6的正三棱锥,其俯视图如图所示,求其主视图的面积和左视图的面积.解:作出正三棱锥的直观图如图所示,E为BD的中点,AO为三棱锥的高,由三棱锥的放置方式知,其主视图为三角形,底面边长为BD=6,其高等于AO,其左视图为三角形,底面边长等于CE(中线)的长,其高等于AO.在Rt△BCE中,BC=6,BE=3,得CE=3,CO=×CE=2.在Rt△ACO中,AC=6,CO=2,则AO==2,故主视图面积为×6×2=6,左视图的面积为×3×2=9.。

高中立体几何三视图试题精选

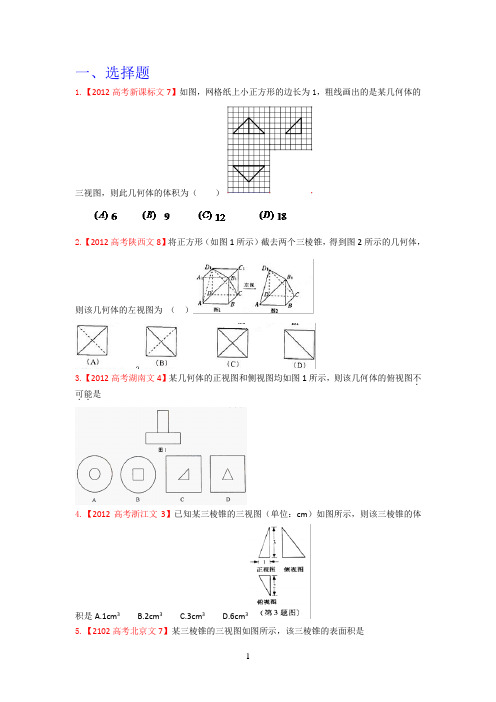
一、选择题1.【2012高考新课标文7】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（）2.【2012高考陕西文8】将正方形（如图1所示）截去两个三棱锥，得到图2所示的几何体，则该几何体的左视图为（）3.【2012高考湖南文4】某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不．可能．．是4.【2012高考浙江文3】已知某三棱锥的三视图（单位：cm）如图所示，则该三棱锥的体积是A.1cm3 B.2cm3 C.3cm3 D.6cm35.【2102高考北京文7】某三棱锥的三视图如图所示，该三棱锥的表面积是（A）28+（B）30+（C）56+（D）60+6．（2010年高考福建卷文科3）若一个底面是正三角形的三棱柱的正视图如图所示,则其侧．面积．．等于( )A. B.2 C. D.67．(2010年高考北京卷文科5)一个长方体去掉一个小长方体，所得几何体的正视图与侧（左）视图分别如右图所示，则该几何体的俯视图为：8．(2010年高考安徽卷文科9)一个几何体的三视图如图，该几何体的表面积是（A）372 （B）360 （C）292 （D）2809．（2010年高考陕西卷文科8）若某空间几何体的三视图如图所示，则该几何体的体积是（A）2 （B）1（C）（D）二、填空题10.【2012高考湖北文15】已知某几何体的三视图如图所示，则该几何体的体积为______11.【2012高考辽宁文13】一个几何体的三视图如图所示，则该几何体的体积为___________.12．（2010年高考天津卷文科12）一个几何体的三视图如图所示，则这个几何体的体积为。

三、解答题13.【2012高考全国文19】（本小题满分12分）如图，四棱锥中，底面为菱形，底面，，，是上的一点，。

（Ⅰ）证明：平面；（Ⅱ）设二面角为，求与平面所成角的大小。

14.【2012高考四川文19】(本小题满分12分)如图，在三棱锥中，，，，点在平面内的射影在上。

高三数学空间几何体的三视图与直观图试题

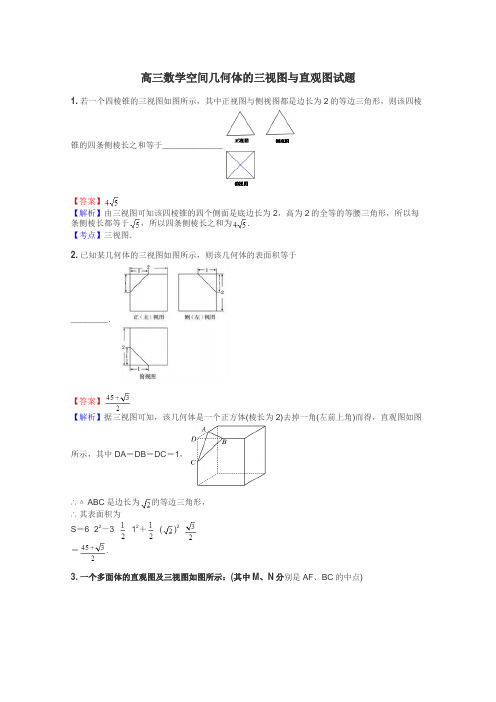
高三数学空间几何体的三视图与直观图试题1.若一个四棱锥的三视图如图所示，其中正视图与侧视图都是边长为2的等边三角形，则该四棱锥的四条侧棱长之和等于_____________【答案】【解析】由三视图可知该四棱锥的四个侧面是底边长为2，高为2的全等的等腰三角形，所以每条侧棱长都等于，所以四条侧棱长之和为．【考点】三视图．2.已知某几何体的三视图如图所示，则该几何体的表面积等于________．【答案】【解析】据三视图可知，该几何体是一个正方体(棱长为2)去掉一角(左前上角)而得，直观图如图所示，其中DA＝DB＝DC＝1，∴△ABC是边长为的等边三角形，∴其表面积为S＝6×22－3××12＋×()2×＝．3.一个多面体的直观图及三视图如图所示：(其中M、N分别是AF、BC的中点)(1)求证：MN∥平面CDEF；(2)求多面体A－CDEF的体积．【答案】（1）见解析（2）【解析】解：由三视图可知，AB＝BC＝BF＝2，DE＝CF＝2，∠CBF＝．(1)证明：取BF的中点G，连接MG、NG，由M、N分别为AF、BC的中点可得，NG∥CF，MG∥EF，∴平面MNG∥平面CDEF，又MN⊂平面MNG，∴MN∥平面CDEF．(2)取DE的中点H．∵AD＝AE，∴AH⊥DE，在直三棱柱ADE－BCF中，平面ADE⊥平面CDEF，平面ADE∩平面CDEF＝DE．∴AH⊥平面CDEF．∴多面体A－CDEF是以AH为高，以矩形CDEF为底面的棱锥，在△ADE中，AH＝．S矩形＝DE·EF＝4，CDEF∴棱锥A－CDEF的体积为V＝·S·AH＝×4×＝．矩形CDEF4.一个几何体的主视图和俯视图如图所示，主视图是边长为的正三角形，俯视图是边长为的正六边形，则该几何体左视图的面积是【答案】【解析】左视图的面积为.【考点】三视图.5.一空间几何体的三视图如图所示，该几何体的体积为12π＋，则正视图中x的值为( )A．5B．4C．3D．2【答案】C【解析】三视图，由正四棱锥和圆柱组成，故选C．6.三棱柱的直观图和三视图如下图所示，其侧视图为正三角形（单位cm）⑴当x=4时，求几何体的侧面积和体积⑵当x取何值时，直线AB1与平面BB1C1C和平面A1B1C1所成角大小相等。

高三数学空间几何体的三视图与直观图试题答案及解析

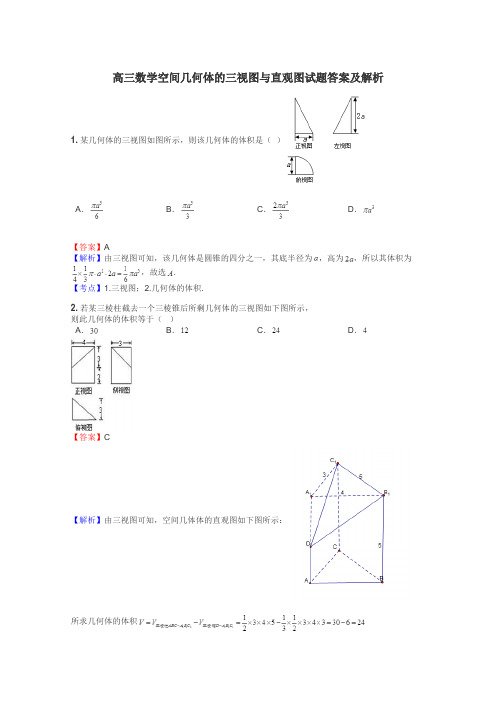
高三数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图如图所示，则该几何体的体积是（）A．B．C．D．【答案】A【解析】由三视图可知，该几何体是圆锥的四分之一，其底半径为，高为，所以其体积为，故选.【考点】1.三视图；2.几何体的体积.2.若某三棱柱截去一个三棱锥后所剩几何体的三视图如下图所示，则此几何体的体积等于（）A．B．C．D．【答案】C【解析】由三视图可知，空间几体体的直观图如下图所示：所求几何体的体积故选C.【考点】1、三视图；2、空间几何体的体积.3.如图，一个几何体的三视图（正视图、侧视图和俯视图）为两个等腰直角三角形和一个边长为1的正方形，则其外接球的表面积为A．πB．2πC．3πD．4π【答案】C【解析】原几何体为有一条侧棱垂直于底面的四棱锥，且底面是边长为1的正方形，垂直于底面的侧棱长也为1，因此，该几何体可以补形为一个棱长为1的正方体，其外接球就是这个正方体的外接球，直径为正方体的对角线长，即2R＝，故R＝故外接球表面积为：4πR2＝3π.【考点】三视图，几何体的外接球及其表面积4.如图所示，一个三棱锥的三视图是三个直角三角形(单位： cm)，则该三棱锥的外接球的表面积为________cm2．【答案】29π【解析】从三棱锥的三视图可知，三棱锥有两侧面与底面垂直，把三棱锥补成长，宽，高分别为4,2,3的长方体，设外接球的半径为R，由42＋22＋32＝4R2得，S＝4πR2＝29π(cm2)．球5.某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为()A．4B．2C．D．8【答案】D【解析】由三视图可知，该几何体如图所示，其底面为正方形，正方形的边长为2．HD＝3，BF ＝1，将相同的两个几何体放在一起，构成一个高为4的长方体，所以该几何体的体积为×2×2×4＝8．6.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图，可知该几何体为半圆锥和三棱锥的组合体，如图所示，可知左视图为等腰三角形，且轮廓线为实线，故选D．7.一个几何体的三视图如图所示，已知这个几何体的体积为，= .【答案】【解析】由三视图知，原几何体是一个四棱锥，底面是面积为的矩形，高为，所以，解得.【考点】三视图，空间几何体的体积.8.如图，水平放置的正三棱柱的主视图是一边长为2的正方形，则该三棱柱的左视图的面积为．【答案】【解析】左视图为一个矩形，长宽分别为，因此面积为.【考点】三视图9.若一个正三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为() A．B．C．D．【答案】B【解析】依题意得，该正三棱柱的底面正三角形的边长为2，侧棱长为1．设该正三棱柱的外接球半径为R，易知该正三棱柱的底面正三角形的外接圆半径是2sin 60°×＝，所以R2＝＋＝，则该球的表面积为4πR2＝．10.图中的网格是边长为1的小正方形，在其上用粗线画出了某多面体的三视图，则该多面体的体积为________．【答案】16【解析】从三视图可知，这是一个四棱锥，.【考点】三视图.11.如图所示，一个空间几何体的正视图和左视图都是边长为的正方形，俯视图是一个直径为的圆，那么这个几何体的体积为 ( )A．B．C．D．【答案】B【解析】几何体是圆柱，.【考点】三视图，圆柱的体积.12.一个几何体的三视图如图所示，其中正视图是一个正三角形，则该几何体的体积为( )A．1B．C．D．【答案】B【解析】由三视图可知，此几何体为三棱锥，如图，其中正视图为，是边长为2的正三角形，，且，底面为等腰直角三角形，，所以体积为，故选B.13.已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的正视图的面积不可能等于（）A．1B．C．D．【答案】C【解析】由题意知，正视图的最大面积为对角面的面积，最小面积为，而，故选C．【考点】三视图.14.已知某几何体的三视图如右图所示，其中俯视图是圆，且该几何体的体积为；直径为2的球的体积为．则()A．B．C．D．【答案】C【解析】由题意，该几何体是一个圆柱挖去一个圆锥得到的几何体，，，∴.选B.【考点】三视图，体积.15.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为（）A．B．C．D．【答案】B【解析】过B作BD⊥AC于点D，则BD=2，CD=2，所以BC=,因为SC⊥平面ABC，所以SC⊥BC，所以SB=,故选B.【考点】三视图、直线与平面垂直的性质.16.一个几何体的三视图如图，则该几何体的体积为（）A．B．C．D．【答案】A【解析】由三视图可知，该几何体是由一个半圆柱和一个三棱锥拼接而成，且半圆柱的底面是半径为的半圆，高为，其底面积为，故其体积为，三棱锥的底面是一个直角三角形，三棱锥的高也为，其底面积为，故其体积为，所以该几何体的体积为，故选A.【考点】1.三视图；2.组合体的体积17.右图为某几何体的三视图，则该几何体的体积为 .【答案】【解析】所求几何体为一个底面半径为1，高为1的圆柱与半径为1的四分之一的球的组合体，所以体积为【考点】三视图18.一个空间几何体的三视图如图所示，该几何体的体积为______.【答案】96【解析】几何体为一个三棱柱，底面为一个等腰三角形，底边长为6，底边上高为4，棱柱的高为8.因此所求体积为【考点】三视图19.把边长为1的正方形ABCD沿对角线BD折起，形成三棱锥C－ABD，它的主视图与俯视图如右上图所示，则二面角 C－AB－D的正切值为．【答案】【解析】如图所示,做BD,AB的中点分别为点E,F.则有CE面ABD,由于EF为等腰直角三角形ABD的中位线,故EF AB,则为二面角 C－AB－D的代表角,所以,故填.【考点】二面角三视图20.已知水平放置的△ABC的直观图△A′B′C′(斜二测画法)是边长为a的正三角形，则原△ABC 的面积为()A．a2B．a2C．a2D．a2【答案】D【解析】斜二测画法中原图面积与直观图面积之比为1∶，则易知S＝ ( a)2，∴S＝a2.21.一个空间几何体的三视图如图所示,则该几何体的体积为()A．πcm3B．3πcm3C．πcm3D．πcm3【答案】D【解析】由三视图可知,此几何体为底面半径为1cm、高为3cm的圆柱上部去掉一个半径为1cm的半球,所以其体积为V=3π-π=π(cm 3).22. 右图为一简单组合体，其底面ABCD 为正方形，PD ⊥平面ABCD ，EC ∥PD ，且PD ＝AD ＝2EC ＝2.(1)请画出该几何体的三视图； (2)求四棱锥B-CEPD 的体积．【答案】(1)见解析 (2)2【解析】解：(1)该组合体的三视图如图所示．(2)∵PD ⊥平面ABCD ， PD ⊂平面PDCE ，∴平面PDCE ⊥平面ABCD. ∵四边形ABCD 为正方形，∴BC ⊥CD ，且BC ＝DC ＝AD ＝2. 又∵平面PDCE∩平面ABCD ＝CD ， BC ⊂平面ABCD. ∴BC ⊥平面PDCE.∵PD ⊥平面ABCD ，DC ⊂平面ABCD ， ∴PD ⊥DC.又∵EC ∥PD ，PD ＝2，EC ＝1，∴四边形PDCE 为一个直角梯形，其面积： S 梯形PDCE ＝ (PD ＋EC)·DC ＝×3×2＝3， ∴四棱锥B-CEPD 的体积V B-CEPD ＝S 梯形PDCE ·BC ＝×3×2＝2.23. 某几何体的三视图如图所示，则该几何体的体积为( )．A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π【答案】A【解析】将三视图还原成直观图为：上面是一个正四棱柱，下面是半个圆柱体．所以V＝2×2×4＋×22×π×4＝16＋8π.24.某几何体的三视图如图所示，则其体积为________．【答案】【解析】由三视图还原几何体为半个圆锥，高为2，底面半圆的半径r＝1.∴体积V＝×(π×12×2)＝.25.如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形，俯视图为正方形，侧视图为直角三角形)．(1)求四棱锥P-ABCD的体积；(2)若G为BC上的动点，求证：AE⊥PG.【答案】（1）（2）见解析【解析】(1)由几何体的三视图可知，底面ABCD是边长为4的正方形，PA⊥平面ABCD，PA∥EB，且PA＝4 ，BE＝2 ，AB＝4.∴VP-ABCD ＝PA·S四边形ABCD＝×4 ×4×4＝.(2)∵＝，∠EBA＝∠BAP＝90°，∴△EBA∽△BAP，∴∠BEA＝∠PBA.∴∠BEA＋∠BAE＝∠PBA＋∠BAE＝90°，∴PB⊥AE又∵BC⊥平面APEB，∴BC⊥AE.∵BC∩PB＝B，∴AE⊥平面PBC.∵PG⊂平面PBC，∴AE⊥PG.26.如图所示，网格上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为________．【答案】9【解析】由题意知，此几何体是三棱锥，其高h＝3，相应底面面积为S＝×6×3＝9，∴V＝Sh＝×9×3＝9.27.某几何体的三视图如图所示，主视图和侧视图为全等的直角梯形，俯视图为直角三角形.则该几何体的表面积为( )A. B. C. D【答案】B【解析】此几何体直观图如图所示。

2022年高考数学空间几何体的直观图与三视图知识点专项练习含答案

专题28 空间几何体的直观图与三视图一、单选题（本大题共12小题，共60分）1.已知一个几何体的正视图和侧视图如图(1)所示，其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图(2)所示)，则此几何体的体积为()A. 1B. √2C. 2D. 2√22.正方形O′A′B′C′的边长为1cm，它是水平放置的一个平面图形的直观图(如图)，则原图形的周长是()A. 6cmB. 8cmC. (2+3√2)cmD. (2+2√3)cm3.一个几何体的三视图如图所示，则该几何体的表面积为()A. 3π2+1+√32B. 3π+12+√32C. 3π+1+√32D. 3π+1+√324.某几何体的三视图如图所示，则该几何体的表面积为()A. 3π+4+√3B. 3π+5+√3C. 52π+6+√3 D. 52π+4+√35.已知某几何体的一条棱长为l，该棱在正视图中的投影长为√2020，在侧视图与俯视图中的投影长为a与b，且a+b=2√1011，则l的最小值为()A. √20212B. √40422C. √2021D. 20216.已知一几何体的三视图如图所示，则该几何体的表面积为()A. √24π+72B. √24π+4 C. 1+√24π+72D. 1+√24π+47.某圆柱的正视图是如图所示的边长为2的正方形，圆柱表面上的点A，B，C，D，F在正视图中分别对应点A，B，C，E，F.其中E，F分别为AB，BC的中点，则异面直线AC与DF所成角的余弦值为()A. 13B. √23C. √33D. √638.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为()A. 22π3B. 28π3C. 34π3D. 40π39.如图，网络纸上小正方形的边长为1，粗实线画出的某几何体的三视图，则该几何体的体积是()A. 18πB. 21πC. 27πD. 36π10.如图所是某一容器三视图，现容中匀速注水，容器中的度h随时间变可能图象是()A. B. C. D.11.如图是一个四棱锥的三视图，则该几何体的体积为()A. 403B. 323C. 163D. 28312.如图所示，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为A. 64−8√2π3B. 64−4√2π3C. 64−8π3D. 64−4π3二、单空题（本大题共4小题，共20分）13.某组合体的正视图和侧视图如图(1)所示，它的俯视图的直观图是图(2)中粗线所表示的平面图形，其中四边形O′A′B′C′为平行四边形，D′为C′B′的中点，则图(2)中平行四边形O′A′B′C′的面积为___________．14.以图①为正视图，在图②③④⑤中选两个分别作为侧视图和附视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为_____________(写出符合求的一组答案即可)．15.在棱长为1的正方体ABCD−A1B1C1D1中，点M，N分别是棱B1C1，C1D1的中点，过A，M，N三点作正方体的截面，将截面多边形向平面ADD1A1作投影，则投影图形的面积为．16.把平面图形α上的所有点在另一个平面上的射影所构成的图形β称为图形α在这个平面上的射影，如图所示，在三棱锥A−BCD中，BC⊥DC，AD⊥DC，BC⊥AB，BC= CD=4，AC=4√3，则△ADB在平面ABC上的射影的面积是________．三、解答题（本大题共2小题，共20分）13．设某几何体的三视图如图(尺寸的长度单位为cm)，（1）用斜二测画法画出该几何体的直观图(不写画法)；（2）求该几何体最长的棱长.14．设一正方形纸片ABCD边长为4厘米，切去阴影部分所示的四个全等的等腰三角形，剩余为一正方形纸片和四个全等的等腰三角形，沿虚线折起，恰好能做成一个正四棱锥，O为正四棱锥底面中心．，（粘接损耗不计），图中AH PQ（1）若正四棱锥的棱长都相等，请求出它的棱长并画出它的直观图示意图；（2）设等腰三角形APQ的底角为x，试把正四棱锥的侧面积表示为x的函数，并求S范围．专题28 空间几何体的直观图与三视图一、单选题（本大题共12小题，共60分）17.已知一个几何体的正视图和侧视图如图(1)所示，其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图(2)所示)，则此几何体的体积为()A. 1B. √2C. 2D. 2√2【答案】B【解析】解：根据直观图可得该几何体的俯视图是一个直角边长分别是2和√2的直角三角形，根据三视图可知该几何体是一个三棱锥，且三棱锥的高为3，所以体积V=13×(12×2×√2)×3=√2．故选B．18.正方形O′A′B′C′的边长为1cm，它是水平放置的一个平面图形的直观图(如图)，则原图形的周长是()A. 6cmB. 8cmC. (2+3√2)cmD. (2+2√3)cm【答案】B【解析】解：如图，OA=1cm，在Rt△OAB中，OB=2√2 cm，∴AB=√OA2+OB2=3cm．∴四边形OABC的周长为8cm．故选B．19.一个几何体的三视图如图所示，则该几何体的表面积为()A. 3π2+1+√32B. 3π+12+√32C. 3π+1+√32D. 3π+1+√32【答案】C【解析】解：由三视图可知几何体上部为三棱锥，下部为半球，三棱锥的底面和2个侧面均为等腰直角三角形，直角边为1，另一个侧面为边长为√2的等边三角形，半球的直径2r=√2，故r=√22．∴S表面积=12×1×1×2+√34×(√2)2+12×4π×(√22)2+π×(√22)2−12×1×1=12+√32+3π2．故选：C．20.某几何体的三视图如图所示，则该几何体的表面积为()A. 3π+4+√3B. 3π+5+√3C. 52π+6+√3 D. 52π+4+√3【答案】A【解析】解：由已知中的三视图可得：该几何体是一个半圆柱和三棱锥的组合体半圆柱的半径为1高2，所以该组合体的面积故选A．21.已知某几何体的一条棱长为l，该棱在正视图中的投影长为√2020，在侧视图与俯视图中的投影长为a与b，且a+b=2√1011，则l的最小值为()A. √20212B. √40422C. √2021D. 2021【答案】C【解析】解：如图所示：设长方体中AB=m，BD为正投影，BE为侧投影，AC为俯视图的投影．故：BD=√2020，BE=a，AC=b，设AE=x，CE=y，BC=z，则：x2+y2+z2=l2，x2+y2=b2，y2+z2=a2，x2+z2=2020，所以2(x2+y2+z2)=a2+b2+2020，故：2l2=a2+b2+2020，因为a2+b2≥(a+b)22=2022，所以2l2≥2022+2020，则l≥√2021．故l的最小值为√2021．故选C．22.已知一几何体的三视图如图所示，则该几何体的表面积为()A. √24π+72B. √24π+4 C. 1+√24π+72D. 1+√24π+4【答案】D【解析】解：几何体左边为四分之一圆锥，圆锥的半径为1，高为1，右边为三棱锥，三棱锥底面是直角边长为1和2的直角三角形，高为1，所以几何体的表面积为：+12×(2+1)×1+12×√2×√(√5)2−(√22)2，故选D．23.某圆柱的正视图是如图所示的边长为2的正方形，圆柱表面上的点A，B，C，D，F在正视图中分别对应点A，B，C，E，F.其中E，F分别为AB，BC的中点，则异面直线AC与DF所成角的余弦值为()A. 13B. √23C. √33D. √63【答案】D【解析】解：如图所示，连结DE，EF，易知EF//AC，所以异面直线AC与DF所成角为∠DFE，由正视图可知，DE⊥平面ABC，所以DE⊥EF．由于AB=BC=2，所以EF=√2，又DE=1，所以DF=√3，在RtΔEFM中，cos∠DFE=√2√3=√63，故选D．24.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为()A. 22π3B. 28π3C. 34π3D. 40π3【答案】C【解析】解：根据几何体得三视图转换为几何体为：该几何体是由一个底面半径为2，高为3的半圆柱和一个半径为2的半球组成，故：V=12⋅π×22×3+12×43×π×23=34π3．故选C．25.如图，网络纸上小正方形的边长为1，粗实线画出的某几何体的三视图，则该几何体的体积是()A. 18πB. 21πC. 27πD. 36π【答案】A【解析】解：该几何体是一个四分之一的圆和圆锥的组合体，如图：有题意知该圆的直径为6cm，圆锥的高为3cm，则该几何体的体积为13×π×32×3+1 4×43π×33=18π，故选A．26.如图所是某一容器三视图，现容中匀速注水，容器中的度h随时间变可能图象是()A. B. C. D.【答案】B【解析】解：三视图表示的容器倒的圆锥，下细，上面，刚开始度增加的相快些．曲越竖直”，后，高度增加来越慢，图越平稳．故B．27.如图是一个四棱锥的三视图，则该几何体的体积为()A. 403B. 323C. 163D. 283【答案】A【解析】解：由三视图得到其直观图(下图所示)，则体积为：13×[12(1+4)×4]×4=403，故选A ．28.如图所示，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为A. 64−8√2π3B. 64−4√2π3C. 64−8π3D. 64−4π3【答案】A【解析】解：这是一个有一条侧棱垂直于底面的四棱锥内部挖去了一个八分之一的球，四棱锥的底面边长和高都等于4，八分之一球的半径为2√2，，故选A ．二、单空题（本大题共4小题，共20分）29. 某组合体的正视图和侧视图如图(1)所示，它的俯视图的直观图是图(2)中粗线所表示的平面图形，其中四边形O ′A ′B ′C ′为平行四边形，D ′为C ′B ′的中点，则图(2)中平行四边形O ′A ′B ′C ′的面积为___________．【答案】3√2【解析】解：由正视图和侧视图可得俯视图如下：∴|O′A′|=4，|O′C′|=32，∠A′O′C′=45°，∴S ΔA′O′C′=12|O′A′|·|O′C′|·sin∠A′O′C′ =12×4×32×√22=3√22， ∴S ▱O′A′B′C′=2S △A′O′C′=3√2，故答案为3√2．30.以图①为正视图，在图②③④⑤中选两个分别作为侧视图和附视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为_____________(写出符合求的一组答案即可)．【答案】②⑤或③④【解析】解：由高度可知，侧视图只能为②或③，侧视图为②，如图(1)平面PAC⊥平面ABC，PA=PC=√2，BA=BC=√5,AC=2，俯视图为⑤；侧视图为③，如图(2)，PA⊥平面ABC，PA=1,AC=AB=√5,BC=2，俯视图为④．故答案为②⑤或③④．31.在棱长为1的正方体ABCD−A1B1C1D1中，点M，N分别是棱B1C1，C1D1的中点，过A，M，N三点作正方体的截面，将截面多边形向平面ADD1A1作投影，则投影图形的面积为．【答案】712【解析】解：直线MN分别与直线A1D1，A1B1交于E，F两点，连接AE，AF，分别与棱DD1，BB1交于G，H两点，连接GN，MH，得到截面五边形AGNMH，向平面ADD1A1作投影，得到五边形AH1M1D1G，由点M，N分别是棱B1C1，C1D1的中点，可得D1E=D1N=12，由△D1EG∽△DAG，可得DG=2D1G=23，同理BH=2B1H=23，则AH1=2A1H1=23，A1M1=D1M1=12，则S AH1M1D1G =1−S A1H1M1−S ADG=1−12×12×13−12×1×23=712，故答案为：712．32.把平面图形α上的所有点在另一个平面上的射影所构成的图形β称为图形α在这个平面上的射影，如图所示，在三棱锥A−BCD中，BC⊥DC，AD⊥DC，BC⊥AB，BC= CD=4，AC=4√3，则△ADB在平面ABC上的射影的面积是________．【答案】8√2【解析】解：因为BC⊥DC，AD⊥DC，BC⊥AB，BC=CD=4，AC=4√3，把三棱锥A−BCD放入如图所示的棱长为4的正方体中，过点D作CE的垂线DF，垂足为F，连接AF，BF，因为BC⊥平面CE，DF⊂平面CE，故BC⊥DF又BC∩CE=C，BC，CE⊂平面ABC则DF⊥平面ABC，故△ADB在平面ABC上的射影为△AFB，因为AB=√42+42=4√2，×4×4√2=8√2，所以△AFB的面积为12即△ADB在平面ABC上的射影的面积为8√2．故答案为8√2．三、解答题（本大题共2小题，共20分）13．设某几何体的三视图如图(尺寸的长度单位为cm)，（1）用斜二测画法画出该几何体的直观图(不写画法)；（2）求该几何体最长的棱长.【答案】（1）答案见解析；（2）4cm.【解析】（1）（2）如下图，SE⊥面ABC，线段AC中点为D2,3,1,4,2,=1======，BD AC SE cm AE cm CE cm AC cm AD DC cm DE cm⊥，=，3BD cm在等腰ABC中，AB AC=在Rt SEA△中，SA=在Rt SEC△中，SC△中，BE==在Rt BDE∴⊥SE⊥面ABC，SE BE在Rt SEB△中，SB=<==<<，在三梭锥S-ABC中，SC AB AC SA SB AC所以最长的棱为AC ，长为4cm14．设一正方形纸片ABCD 边长为4厘米，切去阴影部分所示的四个全等的等腰三角形，剩余为一正方形纸片和四个全等的等腰三角形，沿虚线折起，恰好能做成一个正四棱锥（粘接损耗不计），图中AH PQ ⊥，O 为正四棱锥底面中心．，（1）若正四棱锥的棱长都相等，请求出它的棱长并画出它的直观图示意图；（2）设等腰三角形APQ 的底角为x ，试把正四棱锥的侧面积表示为x 的函数，并求S 范围．【答案】（1），画图见解析；（2）161tan 2tan S x x=++，()0,4.【解析】（1）由题意，设正四棱锥的棱长为a，则AH =，2a AC a +===（2）设PH b =，则tan AH b x =，由2tan 2a x a ⋅+=a =，从而22116tan 442tan 2(tan 1)APQ x S S PQ AH a x x ==⋅⋅⋅==+△，其中(tan 1),x ∈+∞，∴16(0,4)1tan 2tan S x x=∈++。

新课标高考立体几何专题

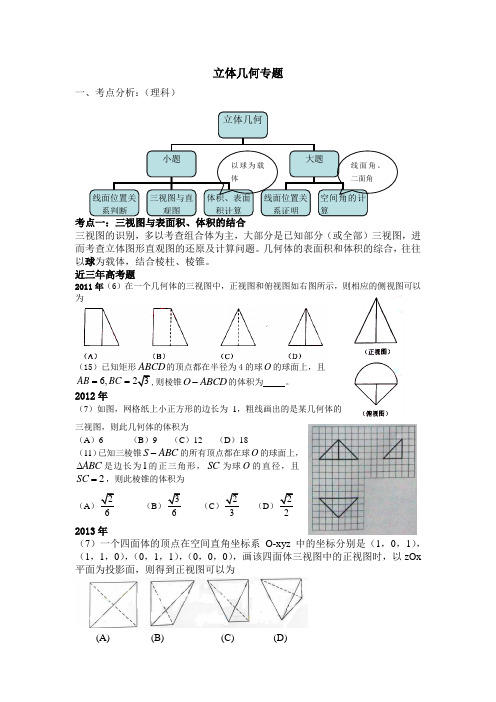
立体几何专题一、考点分析：（理科）三视图的识别，多以考查组合体为主，大部分是已知部分（或全部）三视图，进而考查立体图形直观图的还原及计算问题。

几何体的表面积和体积的综合，往往以球为载体，结合棱柱、棱锥。

近三年高考题2011年（6）在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（15）已知矩形ABCD 的顶点都在半径为4的球O 的球面上，且6,AB BC ==,则棱锥O ABCD -的体积为。

2012年（7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（A ）6 （B）9 （C ）12 （D ）18 （11）已知三棱锥S ABC -的所有顶点都在球O 的球面上，ABC ∆是边长为1的正三角形，SC 为球O的直径，且2SC =，则此棱锥的体积为（A）6 （B ）6 （C ）3 （D ）22013年（7）一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到正视图可以为(A) (B) (C) (D)考点二：空间线面关系的判断该部分的基础是平面的性质、空间直线与直线的位置关系，重点是空间线面平行和垂直关系的判定和性质，面面平行和垂直关系的判定和性质．在复习中要牢牢掌握四个公理和八个定理及其应用，重点掌握好平行关系和垂直关系的证明方法．考点三：求空间角考查空间角的计算为主，解决这类问题往往有两种方法：传统几何法和向量法，这两种方法各有所长，传统几何法的主要思想是把立体问题转化为平面问题，难点在逻辑推理、空间想象能力；向量法在建立空间坐标系后把问题转化成坐标运算，其难点在代数运算。

近三年高考题 2011年(18)如图，四棱锥P-ABCD 中，底面ABCD 为平行四边形，∠DAB=60°,AB=2AD ,PD ⊥底面ABCD . (Ⅰ)证明：PA ⊥BD ；(Ⅱ)若PD =AD ，求二面角A-PB-C 的余弦值。

立体几何三视图高考题集

2012高考题立体几何一、选择题1.【2012高考新课标文7】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（）()A 6 ()B 9 ()C 12 ()D 182.【2012高考新课标文8】平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π3.【2012高考全国文8】已知正四棱柱1111ABCD A B C D -中，2AB =，1CC =E 为1CC 的中点，则直线1AC 与平面BED 的距离为（A ）2 （B （C （D ）14【2012高考湖南文4】某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不．可能．．是5.【2012高考广东文7】某几何体的三视图如图1所示，它的体积为A. 72πB. 48πC. 30πD. 24π6.【2102高考福建文4】一个几何体的三视图形状都相同，大小均等，那么这个几何体不可以是A 球B 三棱锥C 正方体D 圆柱7.【2012高考浙江文5】设l 是直线，a ，β是两个不同的平面A. 若l ∥a ，l ∥β，则a ∥βB. 若l ∥a ，l ⊥β，则a ⊥βC. 若a ⊥β，l ⊥a ，则l ⊥βD. 若a ⊥β, l ∥a ，则l ⊥β 8.【2012高考四川文6】下列命题正确的是（）A 、若两条直线和同一个平面所成的角相等，则这两条直线平行B 、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C 、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D 、若两个平面都垂直于第三个平面，则这两个平面平行二、填空题9.【2012高考四川文14】如图，在正方体1111ABCD A B C D -中，M 、N 分别是CD 、1CC 的中点，则异面直线1A M 与DN 所成的角的大小是____________。

高三数学立体几何试题答案及解析

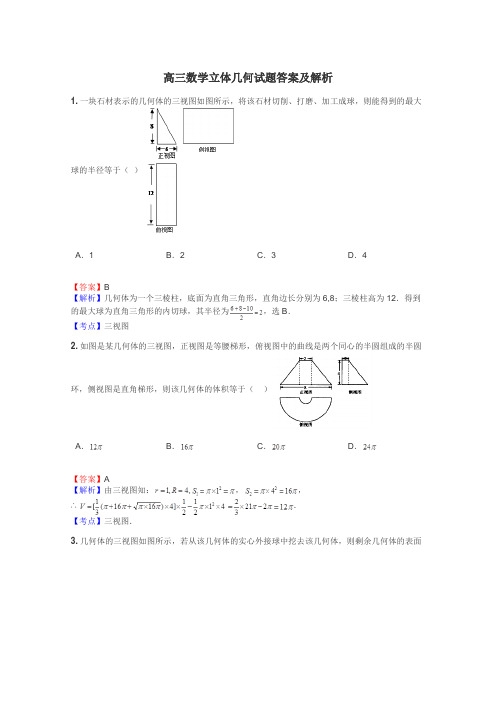
高三数学立体几何试题答案及解析1.一块石材表示的几何体的三视图如图所示，将该石材切削、打磨、加工成球，则能得到的最大球的半径等于（）A．1B．2C．3D．4【答案】B【解析】几何体为一个三棱柱，底面为直角三角形，直角边长分别为6,8；三棱柱高为12．得到的最大球为直角三角形的内切球，其半径为，选B．【考点】三视图2.如图是某几何体的三视图，正视图是等腰梯形，俯视图中的曲线是两个同心的半圆组成的半圆环，侧视图是直角梯形，则该几何体的体积等于（）A．B．C．D．【答案】A【解析】由三视图知：，，∴．【考点】三视图．3.几何体的三视图如图所示，若从该几何体的实心外接球中挖去该几何体，则剩余几何体的表面积是（注：包括外表面积和内表面积）（）A．133B．100C．66D．166【答案】D【解析】由三视图知，该几何体为底面半径为3，搞为8的圆柱．其外接球时半径为5的球．则剩余几何体的表面积是球的表面积与该圆柱表面积的和，即．故选D．【考点】多面体及与其外接球的关系及几何体表面积计算问题．4.（本小题满分12分）如图，已知五面体，其中内接于圆，是圆的直径，四边形为平行四边形，且平面．（1）证明：；（2）若，，且二面角所成角的正切值是，试求该几何体的体积．【答案】（1）见解析；（2）8．【解析】（1）将问题转化为证明平面，再转化为证明（由直径可证）与（由平面可证）；（2）考虑建立空间直角坐标系，通过求两个法向量的夹角来确定二面角所成角的正切值，并确定的长，进而可求得几何体的体积．试题解析：（1）证明：是圆的直径，，又平面，又平面，且，平面又平面，（2）设，以所在直线分别为轴，轴，轴，如图所示则，，，由（Ⅰ）可得，平面，平面的一个法向量是设为平面的一个法向量由条件得，，即不妨令，则，，．又二面角所成角的正切值是，，得该几何体的体积是【考点】1、空间直线与直线、直线与平面的垂直的判定与性质；2、二面角；3、空间几何体的体积．【方法点睛】用空间向量处理某些立体几何问题时，除要有应用空间向量的意识外，关键是根据空间图形的特点建立恰当的空间直角坐标系．若坐标系选取不当，计算量就会增大．总之树立用数解形的观念，即用数形结合的思想解决问题，而建立空间直角坐标系通常考虑以特殊点为坐标原点（如中点、正方体的顶点），特殊直线（如有两两垂直的直线）为坐标轴来建立．5.如图，在多面体中，为菱形，，平面，平面，为的中点，若平面．（1）求证：平面；（2）若，求二面角的余弦值．【答案】（1）见解析；（2）．【解析】（1）证明线面垂直，只要证明这条直线与平面内两条相交直线垂直即可，取中点，连接，可证，先证，即可证明，即可证明结论成立；（2）建立空间直角坐标系，求出平面与平面的法向量，由空间向量公式直接计算即可．试题解析：（1）取AB的中点M，连结GM，MC，G为BF的中点，所以GM //FA，又EC面ABCD， FA面ABCD，∵CE//AF，∴CE//GM，∵面CEGM面ABCD=CM，EG// 面ABCD，∴EG//CM，∵在正三角形ABC中，CM AB，又AF CM∴EG AB， EG AF，∴EG面ABF．（2）建立如图所示的坐标系，设AB=2，则B（）E（0，1，1） F（0，-1，2）=（0，-2，1），=（，-1，-1），=（，1， 1），设平面BEF的法向量=（）则令，则，∴=（）同理，可求平面DEF的法向量 =（-）设所求二面角的平面角为，则=．【考点】1．线面垂直的判定与性质；2．空间向量的应用．【方法点睛】本题主要考查线面垂直的判定与性质、空间向量的应用，属中档题．解答空间几何体中的平行、垂直关系时，一般要根据已知条件把空间中的线线、线面、面面之间的平行、垂直关系进行转化，转化时要正确运用有关的定理，找出足够的条件进行推理；求二面角，则通过求两个半平面的法向量的夹角间接求解．此时建立恰当的空间直角坐标系以及正确求出各点的坐标是解题的关键所在．6.三棱锥及其三视图中的正视图和侧视图如下图所示,，则棱的长为．【答案】．【解析】由已知三视图可知，平面，且底面为等腰三角形．在中，，边上的高为，所以．在中，由可得，故应填．【考点】1、三视图．【易错点晴】本题主要考查了空间几何体的三视图及其空间几何体的面积、体积的计算，考查学生空间想象能力和计算能力，属中档题．其解题过程中容易出现以下错误：其一是不能准确利用已知条件的三视图得出原几何体的空间形状，即不能准确找出该几何体中线线关系、线面关系，导致出现错误；其二是计算不仔细，导致结果出现错误．解决这类问题的关键是正确地处理三视图与原几何体之间的关系．7.在三棱锥中，平面为侧棱上的一点，它的正视图和侧视图如图所示，则下列命题正确的是（）A．平面且三棱锥的体积为B．平面且三棱锥的体积为C．平面且三棱锥的体积为D．平面且三棱锥的体积为【答案】C【解析】∵平面，∴，又，∴平面，∴，又由三视图可得在中，为的中点，∴平面．又平面．故．故选：C．【考点】1．直线与平面垂直的判定；2．命题的真假判断与应用；3．简单空间图形的三视图．8.已知某几何体的三视图的侧视图是一个正三角形，如图所示，则该几何体的体积等于（）A．B．C．D．【答案】C【解析】题设三视图是下图中几何体的三视图，由三视图中的尺寸，知其体积为，故选C．【考点】三视图与几何体的体积．9.如图，在三棱柱ABC A1B1C1中，D，E分别为A1C1，BB1的中点，B1C⊥AB，侧面BCC1B1为菱形．求证：（Ⅰ）DE∥平面ABC1；（Ⅱ）B1C⊥DE．【答案】（Ⅰ）证明见解析；（Ⅱ）证明见解析．【解析】（Ⅰ）取AA1的中点F，连DF，FE，根据中点易证线线平行，从而平面DEF∥平面ABC1，又因为DE平面DEF，所以B1C⊥DE；（Ⅱ）在菱形中B1C⊥BC1，又B1C⊥AB，易证B1C⊥平面ABC1，再根据面面平行的性质，得：B1C⊥平面DEF，从而证明B1C⊥DE．试题解析：（Ⅰ）如图，取AA1的中点F，连DF，FE．又因为D，E分别为A1C1，BB1的中点，所以DF∥AC1，EF∥AB．因为DF平面ABC1，AC1平面ABC1，故DF∥平面ABC1．同理，EF∥平面ABC1．因为DF，EF为平面DEF内的两条相交直线，所以平面DEF∥平面ABC1．因为DE平面DEF，所以DE∥平面ABC1．（Ⅱ）因为三棱柱ABC A1B1C1的侧面BCC1B1为菱形，故B1C⊥BC1．……9分又B1C⊥AB，且AB，BC1为平面ABC1内的两条相交直线，所以B1C⊥平面ABC1．而平面DEF∥平面ABC1，所以B1C⊥平面DEF，因为DE平面DEF，所以B1C⊥DE．【考点】1、线面平行；2、面面平行；3、线面垂直；4、三角形中位线．【方法点晴】本题主要考查的是线面平行、线线平行、线线垂直和线面垂直，属于中档题．解题时一定要注意得线线平行的常用证明方法，构造中位线和平行四边形是最常用方法．证明线面垂直的关键是证明线线垂直，证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的对角线．10.已知，是两个不同的平面，，是两条不同的直线，则下列正确的是（）A．若，，则B．若，，，则C．若，，，则D．若，，，则【答案】C．【解析】A：或者，异面，故A错误；B：根据面面垂直的判定可知B错误；C：正确；D：或，故D错误，故选C．【考点】空间中直线平面的位置关系．11.已知三条不重合的直线和两个不重合的平面，下列命题正确的是（）A．若，，则B．若，，且，则C．若，，则D．若，，且，则【答案】D【解析】A．若，，则,错，有可能；B．若，，且，则，错，有可能；C．若，，则，错，有可能，或异面；D．若，，且，则，正确【考点】空间直线与平面，平面与平面的位置关系12.如图，三角形是边长为4的正三角形，底面，，点是的中点，点在上，且．（1）证明：平面平面；（2）求直线和平面所成角的正弦值．【答案】（1）证明见解析；（2）．【解析】（1）由底面，可得，又，可证的平面，问题得证；（2）在第一问证明的基础上，应用面面垂直的性质定理容易作出平面的垂线，即得斜线的射影，找出角，解直角三角形可得线面角的正弦．试题解析：（1）证明∵底面，底面，∴，又，，∴平面．又平面，∴平面平面．（2）解：过点作，连结．平面平面，平面平面，平面，∴平面，∴为直线和平面所成角．∵是边长为的正三角形，∴，．又∵，∴，，∴．即直线和平面所成角的正弦值为．【考点】空间垂直关系的应用和证明，直线与平面所成的角．【方法点晴】证明面面垂直只能证明线面垂直，而要证明线面垂直就得证明线线垂直，结合题中已知的垂直条件，分析容易找到哪个平面的垂线，逐步完成证明，组织步骤时一定要思路条理；对于直线与平面所成的角遵循作—证（指）—求—答的解题步骤，应当结合条件和前面证明的结论找到平面的垂线是解题的关键，本题中在第一问证明的基础上有了平面的垂面，利用面面垂直的性质定理过直线上一点作交线的垂线即为平面的垂线，连接垂足和斜足即得射影，找到线面角后解直角三角形得解．13.一个几何体的三视图如图所示，则这个几何体的外接球表面积为（）A．B．C．D．【答案】A【解析】几何体为一个三棱锥S-ABC，其中D为AC中点，且SD垂直平面ABC，BD垂直AC，则球心在SD上，设球半径为R，则外接球表面积为，选A.【考点】三视图【方法点睛】1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图．2．三视图中“正侧一样高、正俯一样长、俯侧一样宽”，因此，可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据．14.已知正三角形的三个顶点都在半径为的球面上，球心到平面的距离为，点是线段的中点，过点作球的截面，则截面面积的最小值是_________．【答案】【解析】因为过作球的截面，当截面与垂直时，截面圆的半径最小，所以当截面与垂直时，截面圆的面积有最小值．设正三角形的外接圆圆心为，在中，，所以．在中，，所以，所以截面面积为【考点】1、多面体的外接球；2、球的截面圆性质．【方法点睛】“切”“接”问题的处理规律：①“切”的处理：解决与球的内切问题主要是指球内切多面体与旋转体，解答时首先要找准切点，通过作截面来解决；②“接”的处理：把一个多面体的几个顶点放在球面上即为球的外接问题．解决这类问题的关键是抓住外接的特点，即球心到多面体的顶点的距离等于球的半径．15.（2015•金家庄区校级模拟）如图正方形BCDE的边长为a，已知AB=BC，将△ABE沿BE边折起，折起后A点在平面BCDE上的射影为D点，则翻折后的几何体中有如下描述：①AB与DE所成角的正切值是；②AB∥CE；③VB﹣ACE的体积是a2；④平面ABC⊥平面ADC；⑤直线EA与平面ADB所成角为30°．其中正确的有．（填写你认为正确的序号）【答案】①③④⑤【解析】①由于BC∥DE，则∠ABC（或其补角）为AB与DE所成角；②AB和CE是异面直线；③根据三棱锥的体积公式即可求VB ﹣ACE的体积；④根据面面垂直的判定定理即可证明；⑤根据直线和平面所成角的定义进行求解即可．解：由题意，AB=BC，AE=a，AD⊥平面BCDE，AD=a，AC= a①由于BC∥DE，∴∠ABC（或其补角）为AB与DE所成角∵AB=a，BC=a，AC=a，∴BC⊥AC，∴tan∠ABC=，故①正确；②由图象可知AB与CE是异面直线，故②错误．③VB﹣ACE的体积是S△BCE×AD=×a3=，故③正确；（4）∵AD⊥平面BCDE，BC⊂平面BCDE，∴AD⊥BC，∵BC⊥CD，AD∩CD=D，∴BC⊥平面ADC，∵BC⊂平面ABC，∴平面ABC⊥平面ADC，故④正确；⑤连接CE交BD于F，则EF⊥BD，∵平面ABD⊥平面BDE，∴EF⊥平面ABD，连接F，则∠EAF为直线AE与平面ABD所成角，在△AFE中，EF=，AE=a，∴sin∠EAF==，则∠EAF=30°，故⑤正确，故正确的是①③④⑤故答案为：①③④⑤【考点】命题的真假判断与应用；空间中直线与直线之间的位置关系；平面与平面之间的位置关系．16.已知某几何体的三视图，则该几何体的体积是_______．【答案】．【解析】该几何体是一个四棱锥，底面是边长为2的正方形，高为，所以．【考点】1．空间几何体的表面积与体积；2．空间几何体的三视图与直观图．17.设三棱柱的侧棱垂直于底面，，且三棱柱的所有顶点都在同一球面上，则该球的表面积是．【答案】【解析】由题意可得：把三棱柱补成底面以2为边长的正方形，以为高的长方体，长方体的体对角线就是球的直径，所以，所以该球的表面积是；故填．【考点】空间几何体的表面积．18.某几何体的正视图与侧视图都是等腰梯形，则该几何体可以是下列几何体中的（）①三棱台，②四棱台，③五棱台，④圆台．A．①②B．③④C．①③D．②④【答案】D【解析】由题意得，几何体的正视图和侧视图都是等腰梯形，则根据几何体的三视图的规则可知，该几何体可能为四棱台或圆台，故选D．【考点】空间几何体的三视图．【方法点晴】本题主要考查了空间几何体的三视图的应用，着重考查了推理和运算能力及空间想象能力，属于中档试题，解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则，还原出原几何体的形状，本题的解答中，只是给出了几何体的正视图和侧视图都是等腰梯形，从而可得这个几何体可能是四棱台或圆台．19.在直三棱柱中，，，且异面直线与所成的角等于，设.(1) 求的值；(2) 求三棱锥的体积．【答案】(1)； (2)【解析】(1)由BC ∥B 1C 1可得∠A 1BC 就是异面直线A 1B 与B 1C 1所成的角，从而∠A 1BC =60°，再由AA 1⊥平面ABC ，AB=AC ，则A 1B=A 1C ，△A 1BC 为等边三角形，由已知可得，即可求得 (2)连接B 1C ，则三棱锥B 1–A 1BC 的体积等于三棱锥C –A 1B 1B 的体积，△的面积，又可得平面，利用三棱锥的体积公式可求得．试题解析：(1)∵BC ∥B 1C 1，∴∠A 1BC 就是异面直线A 1B 与B 1C 1所成的角，即∠A 1BC =60°，又AA 1⊥平面ABC ，AB=AC ，则A 1B=A 1C ，∴△A 1BC 为等边三角形，由，， ∴； (2)连接B 1C ，则三棱锥B 1–A 1BC 的体积等于三棱锥C –A 1B 1B 的体积，即：， △的面积，又平面，所以，所以．【考点】异面直线所成的角及三棱锥的体积的求法.20. 如图，在四棱锥中，已知棱，，两两垂直，长度分别为1，2，2.若（），且向量与夹角的余弦值为.（1）求的值；（2）求直线与平面所成角的正弦值.【答案】（1）；（2）.【解析】（1）以为坐标原点，、、分别为、、轴建立空间直角坐标系，写出，的坐标，根据空间向量夹角余弦公式列出关于的方程可求；（2）设岀平面的法向量为，根据，进而得到，从而求出，向量的坐标可以求出，从而可根据向量夹角余弦的公式求出，从而得和平面所成角的正弦值.试题解析：（1）依题意，以为坐标原点，、、分别为、、轴建立空间直角坐标系，因为，所以，从而，则由，解得（舍去）或. （2）易得，，设平面的法向量，则，，即，且，所以，不妨取，则平面的一个法向量，又易得，故，所以直线与平面所成角的正弦值为.考点: 1、空间两向量夹角余弦公式；2、利用向量求直线和平面说成角的正弦.21.如图，在四棱锥中，平面，分别是棱的中点.（1）求证：平面；（2）求证：平面平面.【答案】（1）详见解析（2）详见解析【解析】（1）证明线面平行，一般利用线面平行判定定理，即从线线平行出发给予证明，而线线平行的寻找与证明，往往需结合平面几何条件，如本题利用三角形中位线性质定理得（2）证明面面垂直，一般利用面面垂直判定定理，即从线面垂直出发给予证明，而线面垂直的证明，需多次利用线面垂直的判定与性质定理：先由平行四边形为菱形得，再由平面得，即，从而得平面试题解析：（1）设，连结，因为，为的中点，所以，所以四边形为平行四边形，所以为的中点，所以又因为平面，平面，所以平面.（2）（方法一）因为平面，平面所以，由（1）同理可得，四边形为平行四边形，所以，所以因为，所以平行四边形为菱形，所以，因为平面，平面，所以平面因为平面，所以平面平面.（方法二）连结，因为平面，平面，所以因为，所以，因为平面，平面，所以因为为的中点，所以，由（1），所以又因为为的中点，所以因为，平面，平面所以平面，因为平面，所以平面平面.【考点】线面平行判定定理，面面垂直判定定理22.如图，网格纸上小正方形的边长为1，粗线画出的是某个几何体的三视图，则该几何体的体积为（）A．B．C．D．【答案】A【解析】因为网格纸上小正方形的边长为,有三视图可知，该几何体是下面为底面半径为高为的圆柱体的一半、上面是底面半径为高为的圆锥体的一半，所以体积为，故选A.【考点】1、几何体的三视图；2、圆柱及圆锥的体积公式.【方法点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力，属于难题.三视图问题是考查学生空间想象能力最常见题型，也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键，不但要注意三视图的三要素“高平齐，长对正，宽相等”，还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响.23.已知如图所示的三棱锥的四个顶点均在球的球面上，和所在的平面互相垂直，，，，则球的体积为（）A．B．C．D．【答案】C【解析】因为，，，所以的中点为的外心，连接，则，又和所在的平面互相垂直，所以平面，上的每一点到距离相等，因此正三角形的中心即是外接球球心，其半径也是外接球半径，所以球半径，求体积为，故选C.【考点】1、外接球的性质及勾股定理；2、面面垂直及球的体积公式.【方法点睛】本题主要考查外接球的性质及勾股定理、面面垂直及三棱锥外接球体积的求法，属于难题.要求外接球的表面积和体积，关键是求出求的半径，求外接球半径的常见方法有：①若三条棱两垂直则用（为三棱的长）；②若面（），则（为外接圆半径）；③可以转化为长方体的外接球；④特殊几何体可以直接找出球心和半径.本题是根据方法④直接找出球心并求出半径进而得到求体积的.24.四棱锥的底面是正方形，，分别是的中点（1）求证：；（2）设与交于点，求点到平面的距离【答案】（1）证明见解析；（2）．【解析】（1）要证明线面垂直，一般先证明线线垂直，本题中，由于是中点，因此有，而与垂直，从而与平面垂直，结论得证；（2）要求点到平面的距离，考虑三棱锥，的面积易求（为面积的一半），另外由（1）的结论，此三棱锥以为底时，是高，体积易求，从而所求距离易得．试题解析：（1）证明：连接，由于分别是的中点，所以，又，平面，故，又为正方形，故故，故（2）连接交于点，连接，则交线为，又，故，由于分别是的中点，故为的中点，又，故为三棱锥的高又故，又设点到平面的距离为，，所以【考点】线面垂直的判断，点到平面的距离．25.某几何体的三视图如图，则该几何体的体积为（）A．B．C．D．【答案】C【解析】由题意得，由几何体的三视图，知该几何体是上下底面为梯形的直棱柱，所以该几何体的体积为，故选C.【考点】几何体的三视图及几何体的体积.【方法点晴】本题主要考查了空间几何体的三视图的应用，着重考查了推理和运算能力及空间想象能力，属于中档试题，解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则，还原出原几何体的形状，本题的解答中，该几何体是上下底面为梯形的直棱柱是解答本题的关键，属于基础题.26.一个几何体的三视图如图，则这个几何体的表面积是（）A．B．C．D．【答案】C【解析】由题意得，根据给定的几何体的三视图，可知，原几何体为正方体的一部分，如图所示的红线部分，是一个棱长为的正四面体，所以此几何体的表面积为，故选C．【考点】几何体的三视图与表面积．27.某几何体的三视图如图所示（单位：cm），则该几何体的表面积是______cm2，体积是______cm3.【答案】80，40【解析】由三视图知该组合体是一个长方体上面放置了一个小正方体，，．【考点】三视图.【方法点睛】解决由三视图求空间几何体的表面积与体积问题，一般是先根据三视图确定该几何体的结构特征，再准确利用几何体的表面积与体积公式计算该几何体的表面积与体积．28.如图，在四棱锥中，平面平面，，，，，，.（Ⅰ）求证：平面；（Ⅱ）求直线PB与平面PCD所成角的正弦值；（Ⅲ）在棱PA上是否存在点M，使得BM∥平面PCD?若存在，求的值；若不存在，说明理由.【答案】（Ⅰ）见解析；（Ⅱ）；（Ⅲ）存在，.【解析】（Ⅰ）由面面垂直的性质定理知AB⊥平面，根据线面垂直的性质定理可知，再由线面垂直的判定定理可知平面；（Ⅱ）取的中点，连结，以O为坐标原点建立空间直角坐标系O-xyz，利用向量法可求出直线PB与平面PCD所成角的正弦值；（Ⅲ）假设存在，根据A，P，M三点共线，设，根据BM∥平面PCD，即（为平面PCD的法向量），求出的值，从而求出的值.试题解析：（Ⅰ）因为平面平面，，所以平面.所以.又因为，所以平面.（Ⅱ）取的中点，连结.因为，所以.又因为平面，平面平面，所以平面.因为平面，所以.因为，所以.如图建立空间直角坐标系.由题意得，.设平面的法向量为，则即令，则.所以.又，所以.所以直线与平面所成角的正弦值为.（Ⅲ）设是棱上一点，则存在使得.因此点.因为平面，所以平面当且仅当，即，解得.所以在棱上存在点使得平面，此时.【考点】空间线面垂直的判定定理与性质定理；线面角的计算；空间想象能力，推理论证能力【名师】平面与平面垂直的性质定理的应用：当两个平面垂直时，常作的辅助线是在其中一个平面内作交线的垂线，把面面垂直转化为线面垂直，进而可以证明线线垂直(必要时可以通过平面几何的知识证明垂直关系)，构造(寻找)二面角的平面角或得到点到面的距离等.29.如图，在四棱锥中，底面是菱形，，平面，，点分别为和中点.（1）求证：直线平面；（2）求三棱锥的表面积.【答案】（1）证明见解析；（2）．【解析】（1）要证线面平行，一般先证线线平行，考虑到，是中点，因此取的中点，可证得且，从而得平行四边形，因此有，最终得线面平行；（2）要求三棱锥的表面积，必须求得它的各个面的面积，由平面，得，三角形和的面积可求，由题设又可证，这样就有，另两个面的面积又可求得．试题解析：（1）证明：作FM∥CD交PC于M.∵点F为PD中点，∴. ∴，∴AEMF为平行四边形，∴AF∥EM，∵，∴直线AF平面PEC.（2）连结可知，，由此；；；；因此三棱锥的表面积.【考点】线面平行的判断，多面体的表面积．30.在棱长为3的正方体中，在线段上，且，为线段上的动点，则三棱锥的体积为（）A．1B．C．D．与点的位置有关【答案】B【解析】由于是定值,点到平面的距离是,因此点平面的距离是.所以三棱锥的体积,应选B.【考点】三棱锥体积的运算．31.如图，在多面体中，底面是边长为2的正方形，四边形是矩形，且平面平面，，和分别是和的中点.（1）求证：平面；（2）求.【答案】（1）证明见解析；（2）.【解析】（1）运用线面平行的判定定理求证；（2）借助题设条件及转化化归的思想求解即可. 试题解析:（1）证明：设，连接，在中，因为，，所以，又因为平面，平面，所以平面.（2）因为四边形是正方形，所以，又因为平面平面，平面平面，且平面，所以平面，则到平面的距离为的一半，又因为，所以，所以.【考点】直线与平面的位置关系及棱锥公式的运用．32.如图，在三棱柱中，，，，在底面的射影为的中点，是的中点.（1）证明：平面；（2）求二面角的平面角的余弦值.【答案】（1）证明见解析；（2）.【解析】（1）设为的中点，连接，依题意有，，故平面.根据分析有，故平面；（2）以的中点为原点，分别以射线为轴的正半轴，建立空间直角坐标系，利用向量法求得余弦值为.试题解析：（1）设为的中点，连接.由题意得：平面，所以.因为，所以，，故平面.由分别为的中点，得且，从而且，所以为平行四边形，故，又因为平面，所以平面.（2）方法一：作，且，连结.由，，得，由，，得与全等.由，得，因此为二面角的平面角.由，，，得，，由余弦定理得.方法二：以的中点为原点，分别以射线为轴的正半轴，建立空间直角坐标系，如图所示，由题意知各点坐标如下：，因此，，，设平面的法向量为，平面的法向量为，由，即，可取.由，即，可取，于是.由题意可知，所求二面角的平面角是钝角，故二面角的平面角的余弦值为.【考点】空间向量与立体几何.33.某几何体的三视图如图所示，则该几何体的体积为（）A．B．C．D．【答案】A【解析】由三视图可知，从左往右为半个圆锥，一个圆柱，一个半圆，故体积为.【考点】三视图.34.如图，在四棱柱中，底面，为线段上的任意一点（不包括两点），平面与平面交于.（1）证明：；（2）证明：平面.【答案】（1）证明见解析；（2）证明见解析．【解析】（1）要证线线垂直，一般可证线面垂直，观察题中垂直条件，平面，则有，题中又有，从而有平面，因此结论得证；（2）要证线面平行，就是要证线线平行，直线是平面与平面的交线，因此要得平行，就要有线面平行，而这由可得平面，从而，结论得证．试题解析：（1）证明：因为平面，平面，所以.又，所以平面，而平面，所以.（2）在四棱柱中，，平面，平面，所以平面，又平面，平面与平面交于，所以，因为，所以，而平面，平面，所以平面.【考点】线面垂直的判定与性质，线面平行的判定与性质．【名师】证明线面（面面）平行（垂直）时要注意以下几点：（1）由已知想性质，由求证想判定，即分析法与综合法相结合寻找证题思路。

高三数学空间几何体的三视图与直观图试题答案及解析

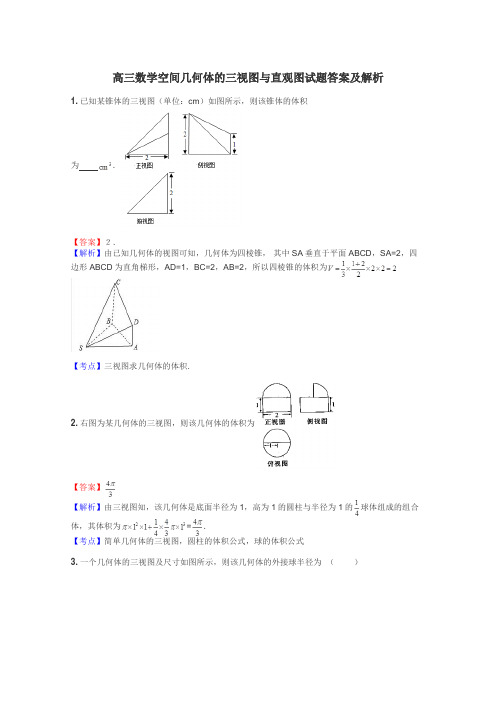
高三数学空间几何体的三视图与直观图试题答案及解析1.已知某锥体的三视图（单位：cm）如图所示，则该锥体的体积为．【答案】２．【解析】由已知几何体的视图可知，几何体为四棱锥，其中SA垂直于平面ABCD，SA=2，四边形ABCD为直角梯形，AD=1，BC=2，AB=2，所以四棱锥的体积为【考点】三视图求几何体的体积.2.右图为某几何体的三视图，则该几何体的体积为【答案】【解析】由三视图知，该几何体是底面半径为1，高为1的圆柱与半径为1的球体组成的组合体，其体积为=．【考点】简单几何体的三视图，圆柱的体积公式，球的体积公式3.一个几何体的三视图及尺寸如图所示，则该几何体的外接球半径为（）A．B．C．D．【答案】C【解析】由三视图可知：该几何体是一个如图所示的三棱锥P-ABC，它是一个正四棱锥P-ABCD 的一半，其中底面是一个两直角边都为6的直角三角形，高PE=4．设其外接球的球心为O，O点必在高线PE上，外接球半径为R，则在直角三角形BOE中，BO2=OE2+BE2=（PE-EO）2+BE2，即R2=（4-R）2+（3）2，解得：R=，故选C.【考点】三视图，球与多面体的切接问题，空间想象能力4.如图是一个几何体的三视图，则该几何体的表面积是____________【答案】28＋12【解析】这是一个侧放的直三棱柱，底面是等腰直角三角形，侧棱长为6故表面积为2×(×2×2)＋(2＋2＋2)×6＝28＋12.【考点】三视图，几何体的表面积.5.在长方体中割去两个小长方体后的几何体的三视图如图，则切割掉的两个小长方体的体积之和等于.【答案】24【解析】由题意割去的两个小长方体的体积为.【考点】三视图，几何体的体积..6.某空间几何体的正视图是三角形，则该几何体不可能是（）圆柱圆锥四面体三棱柱【答案】A【解析】由于圆柱的三视图不可能是三角形所以选A.【考点】三视图.7.某几何体的三视图如图所示，其中正视图是腰长为2的等腰三角形，侧视图是半径为1的半圆，则该几何体的表面积是________．【答案】2(π＋)【解析】由三视图可知此几何体的表面积分为两部分：底面积即俯视图的面积为2；侧面积为一个完整的圆锥的侧面积，且圆锥的母线长为2，底面半径为1，所以侧面积为2π．两部分加起来即为几何体的表面积，为2(π＋)．8.一个锥体的主(正)视图和左(侧)视图如图所示，下面选项中，不可能是该锥体的俯视图的是()【答案】C【解析】俯视图是选项C的锥体的正视图不可能是直角三角形．另外直观图如图1的三棱锥(OP⊥面OEF，OE⊥EF，OP＝OE＝EF＝1)的俯视图是选项A，直观图如图2的三棱锥(其中OP，OE，OF两两垂直，且长度都是1)的俯视图是选项B，直观图如图3的四棱锥(其中OP⊥平面OEGF，底面是边长为1的正方形，OP＝1)的俯视图是选项D．9.如图所示，正方形O′A′B′C′的边长为1，它是水平放置的一个平面图形的直观图，则原图形的周长是()A．6B．8C．2＋3D．2＋2【答案】B【解析】如图，OB＝2，OA＝1，则AB＝3．∴周长为8．10.某几何体的三视图如图所示，且该几何体的体积是2，则正(主)视图的面积等于()A．2B．C．D．3【答案】A【解析】由三视图可知该几何体是一个四棱锥，其底面积就是俯视图的面积S＝(1＋2)×2＝3，其高就是正(主)视图以及侧(左)视图的高x，因此有×3×x＝2，解得x＝2，于是正(主)视图的面积S＝×2×2＝2．11.如图，三棱柱的侧棱长和底边长均为2，且侧棱AA1⊥底面A1B1C1，正视图是边长为2的正方形，俯视图为一个等边三角形，则该三棱柱的侧视图的面积为( )A. C.4 D.【答案】A【解析】侧视图也为矩形，底宽为原底等边三角形的高，侧视图的高为侧棱长，所以侧视图的面积为,故选B.【考点】三视图12.一个几何体的三视图如图所示，则该几何体内切球的体积为 .【答案】【解析】依题意可得该几何体是一个正三棱柱，底面边长为2，高为.由球的对称性可得内切球的半径为.由已知计算得底面内切圆的半径也为.所以内切球的体积为.【考点】1.三视图.2.几何体内切球的对称性.3.球的体积公式.4.空间想象力.13.已知一个正三棱柱的所有棱长均等于2，它的俯视图是一个边长为2的正三角形，那么它的左视图面积的最小值是________．【答案】【解析】如图，正三棱柱中，分别是的中点，则当面与侧面平行时，左视图面积最小，且面积为.【考点】三视图.14.某几何体的三视图如图3所示，则其体积为________．【答案】【解析】原几何体可视为圆锥的一半，其底面半径为1，高为2，∴其体积为×π×12×2×＝.15.已知正△ABC的边长为2，那么用斜二测画法得到的△ABC的直观图△A′B′C′的面积为（）A．B．C．D．【答案】D【解析】∵正△ABC的边长为2，故正△ABC的面积S==设△ABC的直观图△A′B′C′的面积为S′则S′=S=•=故选D16.一个体积为12的正三棱柱的三视图如图所示，则这个三棱柱的侧视图的面积为（）A．B．C．D．【答案】A【解析】依题意可得三棱柱的底面是边长为4正三角形.又由体积为.所以可得三棱柱的高为3.所以侧面积为.故选A.【考点】1.三视图的知识.2.棱柱的体积公式.3.空间想象力.17.某几何体的三视图如题（6）所示，其侧视图是一个边长为1的等边三角形，俯视图是两个正三角形拼成的菱形，则这个几何体的体积为（）A．1B．C．D．【答案】C【解析】这是由两个三棱锥拼成的几何体，其体积为.选C.【考点】三视图及几何体的体积.18.一个四面体的顶点在空间直角坐系O－xyz中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx平面为投影面，则得到的正视图可以为（）A．B．C．D．【答案】A【解析】设O(0，0，0)，A(1，0，1)，B(1，1，0)，C(0，1，1)，将以O，A，B，C为顶点的四面体补成一正方体后，因为OA⊥BC，所以补成的几何体以zOx平面为投影面的正视图为A．19.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几体的体积为（）A．6B．9C．12D．18【答案】B【解析】由三视图可知，此几何体为如图所示的三棱锥，其底面△ABC为等腰三角形且AB=BC，AC=6，AC边上的高为3，SB⊥底面ABC，且SB=3，因此此几体的体积为V=××6×3×3=920.如图所示，一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的表面积为 .【答案】【解析】由三视图知，该几何体是一个圆柱，其表面积为.【考点】三视图及几何体的表面积.21.在三棱锥中，，平面ABC,.若其主视图，俯视图如图所示，则其左视图的面积为【答案】【解析】左视图是一个直角三角形，其直角边分别是2与.所以面积为.【考点】1.三视图知识.2.三角形面积的计算.22.一个几何体的三视图如图所示,则这个几何体的体积是_________.【答案】【解析】由三视图还原几何体，该几何体为底面半径为，高为的圆柱，去掉底面半径为，高为的圆锥的剩余部分，则其体积为．【考点】1、三视图；2、几何体的体积.23.棱长为2的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是( ).A．B．4C．D．3【答案】B【解析】如图，红色虚线表示截面，可见这个截面将正方体分为完全相同的两个几何体，则所求几何体的体积即是原正方体的体积的一半，.【考点】1.三视图；2.正方体的体积24.如图，一个四棱锥的底面为正方形，其三视图如图所示，则这个四棱锥的体积为（）A．1B．2C．3D．4【答案】Ｂ【解析】由题设及图知，此几何体为一个四棱锥，其底面为一个对角线长为的正方形，故其底面积为，由三视图知其中一个侧棱为棱锥的高，其相对的侧棱与高及底面正方形的对角线组成一个直角三角形，由于此侧棱长为，对角线长为，故棱锥的高为，此棱锥的体积为，故选B．【考点】由三视图求面积、体积．25.已知某几何体的三视图如右图所示，其中，正视图，侧视图均是由三角形与半圆构成，俯视图由圆与内接三角形构成，根据图中的数据可得此几何体的体积为（）A．B．C．D．【答案】C【解析】由已知的三视图可知原几何体是上方是三棱锥,下方是半球,∴，故选C.【考点】1.三视图；2.几何体的体积.26.如图是一个组合几何体的三视图,则该几何体的体积是.【答案】36+128π【解析】由三视图还原可知该几何体是一个组合体,下面是一个圆柱,上面是一个三棱柱,故所求体积为V=×3×4×6+16π×8=36+128π.27.某几何体的三视图如图所示，其中俯视图为扇形，则该几何体的体积为（）A．B．C．D．【答案】D【解析】由三视图可知，该几何体是三分之一个圆锥，其体积为.【考点】三视图及几何体的体积.28.某几何体的三视图(图中单位：cm)如图所示，则此几何体的体积是()A．36 cm3B．48 cm3C．60 cm3D．72 cm3【答案】B【解析】由三视图可知几何体上方是一长方体，下方是一放倒的直四棱柱，且四棱柱底面是等腰梯形，上底长为2 cm，下底长为6 cm，高为2 cm，故几何体的体积是2×2×4＋×(2＋6)×2×4＝48(cm3)，故选B.29.如图是某三棱柱被削去一个底面后的直观图、侧(左)视图与俯视图．已知CF＝2AD，侧视图是边长为2的等边三角形，俯视图是直角梯形，有关数据如图所示．求该几何体的体积．【答案】3【解析】解：取CF中点P，过P作PQ∥CB交BE于Q，连接PD，QD，则AD∥CP，且AD＝CP.所以四边形ACPD为平行四边形，所以AC∥PD.所以平面PDQ∥平面ABC.该几何体可分割成三棱柱PDQ－CAB和四棱锥D－PQEF，所以V＝V－CAB＋V D－PQEFPDQ＝×22sin 60°×2＋××＝3.30.一个几何体的三视图如图所示，则该几何体的表面积是()A．6＋8B．12＋7C．12＋8D．18＋2【答案】C【解析】该空间几何体是一个三棱柱．底面为等腰三角形且底面三角形的高是1，底边长是2 ，两个底面三角形的面积之和是2，侧面积是(2＋2＋2)×3＝12＋6，故其表面积是12＋8.31. 已知四棱锥P-ABCD 的三视图如右图所示，则四棱锥P-ABCD 的四个侧面中的最大面积是( )．A ．6B ．8C ．2D ．3【答案】A【解析】四棱锥如图所示：PM ＝3，S △PDC ＝×4×＝2，S △PBC ＝S △PAD ＝×2×3＝3，S △PAB ＝×4×3＝6，所以四棱锥P-ABCD 的四个侧面中的最大面积是6.32. 若某几何体的三视图如图所示，则这个几何体的直观图可以是( )．【答案】B【解析】分别从三视图中去验证、排除．由正视图可知，A 不正确；由俯视图可知，C ，D 不正确，所以选B.33. 一个几何体的三视图如图所示，已知这个几何体的体积为，则h________.【答案】【解析】依题意可得四棱锥的体积为.所以可得.解得.故填.本小题的是常见的立几中的三视图的题型，这类题型关键是要能还原几何体的直观图形.所以培养空间的思想很重要.【考点】1.三视图的识别.2.空间几何体的直观图.34.图中的网格纸是边长为的小正方形，在其上用粗线画出了一四棱锥的三视图，则该四棱锥的体积为（）A．B．C．D．【答案】C【解析】由三视图知，该几何体是一个四棱锥，且其底面为一个矩形，底面积，高为，故该几何体的体积，故选C.【考点】1.三视图；2.锥体的体积35.已知某几何体的三视图如图，其中主视图中半圆直径为2，则该几何体的体积____________【答案】24-【解析】由三视图可知，该几何体是有长方体里面挖了一个半圆柱体，可知，长方体的长为4，宽为3，高为2，那么圆柱体的高位3，底面的半径为1，则可知该几何体的体积为，故答案为．【考点】由三视图求面积、体积．36.把边长为的正方形沿对角线折起，连结，得到三棱锥，其正视图、俯视图均为全等的等腰直角三角形（如图所示），则其侧视图的面积为（）A．B．C．D．【答案】B【解析】在三棱锥中，在平面上的射影为的中点，∵正方形边长为，∴，∴侧视图的面积为.【考点】1.三视图；2.三角形的面积.37.一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的（）A．外接球的半径为B．体积为C．表面积为D．外接球的表面积为【答案】D．【解析】由题意设外接球半径为，则，A错误；外接球的表面积为，D正确；此几何体的体积为，故B错误；此几何体的表面积为，C错误．【考点】三视图及球的表面积公式.38.一个几何体的三视图如图所示，则该几何体的体积为( )A．4B．8C．D．【答案】B【解析】有三视图可以看出，该几何体是一个三棱锥，它的体积为．【考点】三视图，几何体的体积．39.如图，直三棱柱的侧棱长和底面边长均为2，正视图和俯视图如图所示，则其侧视图的面积为（）A．B．C．4D．2【答案】A【解析】由题意易知，直三棱柱的底面是边长为2的正三角形.其侧视图为矩形，矩形的高为2，宽为底面正三角形的高.易知边长为2的正三角形的高为.所以面积为.【考点】三视图40.如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是( )A．B．21C．D．24【答案】A【解析】还原几何体，得棱长为2的正方体和高为1的正四棱锥构成的简单组合体，如图所示，=，选A.【考点】1、几何体的表面积；2、三视图.41.某几何体的三视图如图所示，则它的表面积为（）A．B．C．D．【答案】A【解析】易知该三视图的直观图是倒立的半个三棱锥，其表面积由底面半圆，侧面三角形和侧面扇形，所以，故选A.【考点】1.立体几何三视图；2.表面积和体积的求法.42.一几何体的三视图如图所示，则该几何体的体积为（）A．200＋9πB．200＋18πC．140＋9πD．140＋18π【答案】A【解析】通过观察三视图，易知该几何体是由半个圆柱和长方体组成的，则半个圆柱体积；长方体的体积为,所以该几何体的最终体积，故选A.【考点】1.三视图的应用；2.简单几何体体积的求解.43.一个几何体的三视图如图所示，其中主视图和左视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为( )A．B．C．D．【解析】把原来的几何体补成以为长、宽、高的长方体，原几何体四棱锥与长方体是同一个外接球，，，.【考点】1.补体法；2.几何体与外接球之间的元素换算.44.一个几何体的三视图如图所示，其中府视图为正三角形，则侧视图的面积为（）A．8B．C．D．4【答案】B【解析】由三视图可知：该几何体是一个正三棱柱，高为4，底面是一个边长为2的正三角形．因此，侧视图是一个长为４，宽为的矩形，．【考点】三视图与几何体的关系、几何体的侧面积的求法能力．45.某几何体的三视图如图所示，则它的侧面积为（）A．B．C．24D．【答案】A【解析】由三视图得,这是一个正四棱台,由条件，侧面积.【考点】1.三视图；2.正棱台侧面积的求法.46.一个几何体的三视图如图所示，其中正视图与侧视图都是底边长为6、腰长为5的等腰三角形，则这个几何体的全面积为（）A．B．C．D．【解析】由三视图知，该几何体是一个圆锥，且圆锥的底面直径为，母线长为，用表示圆锥的底面半径，表示圆锥的母线长，则，，故该圆锥的全面积为.【考点】三视图、圆锥的表面积47.一个空间几何体的三视图如右图所示，其中主视图和侧视图都是半径为的圆，且这个几何体是球体的一部分，则这个几何体的表面积为( )A．3πB．4πC．6πD．8π【答案】B【解析】此空间几何体是球体切去四分之一的体积，表面积是四分之三的球表面积加上切面面积，切面面积是两个半圆面面积.故这个几何体的表面积是.【考点】1、几何体的三视图; 2、球的表面积公式.48.右图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为和，腰长为的等腰梯形，则该几何体的表面积是．【答案】【解析】从三视图可以看出：几何体是一个圆台，上底面是一个直径为4的圆，下底面是一个直径为2的圆，侧棱长为4．上底面积，下底面积，侧面是一个扇环形，面积为，所以表面积为．【考点】空间几何体的三视图、表面积的计算．49.某零件的正（主）视图与侧（左）视图均是如图所示的图形（实线组成半径为的半圆，虚线是等腰三角形的两腰），俯视图是一个半径为的圆（包括圆心），则该零件的体积是 ( )A．B．C．D．【解析】由题意易知该几何体为一半球内部挖去一圆锥所成，故体积为.故选C.【考点】1.体积； 2.三视图.50.某四棱台的三视图如图所示,则该四棱台的体积是 ( )A．B．C．D．【答案】B【解析】由三视图可知,该四棱台的上下底面边长分别为和的正方形,高为,故,故选B．【考点】三视图与四棱台的体积51.若一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为（）A．B．C．D．【答案】B【解析】由已知底面是正三角形的三棱柱的正视图,我们可得该三棱柱的底面棱长为2，高为1,则底面外接圆半径，球心到底面的球心距,则球半径,则该球的表面积，故选B.【考点】由三视图求面积、体积．点评：本题考查的知识点是由三视图求表面积，其中根据截面圆半径、球心距、球半径满足勾股定理计算球的半径，是解答本题的关键．52.如图所示是某一容器的三视图，现向容器中匀速注水，容器中水面的高度随时间变化的可能图像是（）A． B． C． D．【答案】B【解析】由三视图可知该几何体是圆锥，顶点在下，底面圆在上，在匀速注水过程中水面高度随着时间的增大而增大，且刚开始时截面积较小，所以高度变化较快，随着水面的升高，截面圆面积增大，高度变化速度减缓，因此函数的瞬时变化率逐渐减小，导数减小，图像为B项【考点】函数导数的定义点评：本题通过高度的瞬时变化率的变化情况得到函数的导数的大小，从而通过做出的切线斜率的变化得出正确图像53.已知一个三棱锥的主视图与俯视图如图所示，则该三棱锥的侧视图面积为（）A．B．C．D．【答案】B【解析】根据题意，由于三棱锥的俯视图为直角三角形，正视图为直角三角形，且斜边长为2，直角边长为，那么结合图像可知其侧视图为底面边长为1，高为的三角形，因此其面积为，故选B.【考点】三棱锥点评：解决的关键是根据三棱锥的三视图来得到底面积和高进而求解侧视图，属于基础题。

三视图立体几何高一数学总结练习含答案解析

§3三视图1.三视图的特点:主、俯视图①;主、左视图②;俯、左视图③,前后对应.2.在绘制三视图时,应注意:若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,分界线和可见轮廓线都用④画出,不可见轮廓线,用⑤画出.一、解决有关三视图的问题1.(2014福建,2,★☆☆)某空间几何体的正视图是三角形,则该几何体不可能是( )A.圆柱B.圆锥C.四面体D.三棱柱思路点拨逐个分析各选项.圆柱的任何视图都不可能为三角形.2.(2014江西,5,★☆☆)一几何体的直观图如图,下列给出的四个俯视图中正确的是( )思路点拨认清直观图是解题关键.3.(2014广东汕头期末,★☆☆)下列几何体各自的三视图中,有且仅有两个视图相同的是( )A.①②B.①③C.①④D.②④思路点拨正确画出三视图是解题的关键.4.(2013四川理,3,★☆☆)一个几何体的三视图如图所示,则该几何体的直观图可以是( )思路点拨综合三个视图,先看轮廓线,再考虑细节.5.(2013湖南理,7,★★☆)已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的主视图的面积不可能等于( )A.1B.√2C.√2-12D.√2+12思路点拨俯视图是正方形,而主视图的视角不固定,从不同角度观察正方体,主视图也不同.6.(2012辽宁理改编,13,★★☆)一个几何体的三视图如图所示,试画出该几何体的直观图.思路点拨整个长方体,挖去一个圆柱.二、空间几何体的直观图与三视图的关系7.(2014浙江改编,3,★☆☆)某几何体的三视图如图所示,则此几何体为( )A.长方体与三棱锥的组合体B.正方体与三棱柱的组合体C.长方体与三棱柱的组合体D.正方体与三棱锥的组合体思路点拨先画出直观图的草图,再加以判断.8.(2014山东高密统测,★★☆)如图所示,甲、乙、丙是三个几何体的三视图,则下列甲、乙、丙对应的标号正确的是( )①长方体②圆锥③三棱锥④圆柱A.④③②B.②①③C.①②③D.③②④思路点拨仔细考量各个视图.以某一个视图为基准,其他两个视图辅助,画出直观图草图.9.(2014河北沧州阶段考试,★★☆)根据如图所示的三视图,想象对应的几何体,并画出草图(尺寸不作严格要求).思路点拨从视图可看出上部为正六棱锥,下部为正六棱柱.一、选择题1.下列说法正确的是( )A.任何几何体的三视图都与其摆放的位置有关B.任何几何体的三视图都与其摆放的位置无关C.有的几何体的三视图与其摆放的位置无关D.正方体的三视图一定是三个全等的正方形2.如果一个空间几何体的主视图与左视图均为全等的等边三角形,俯视图为一个圆及其圆心,那么这个几何体为( )A.棱锥B.棱柱C.圆锥D.圆柱3.如图,空心圆柱体的主视图是( )4.将正三棱柱截去三个角(如图①所示,A,B,C分别是△GHI三边的中点)得到如图②所示的几何体,则该几何体按图②所示方向的左视图为( )5.四个正方体按如图所示的方式放置,其中阴影部分为我们观察的正面,则该组合体的三视图是( )6.如图所示的正方体ABCD-A1B1C1D1是一个用铁丝围成的模型框架,E、F分别是A1D1、CC1的中点,G为正方形ABCD的中心,用铁丝将AE、EF、FG、GA连接起来得到一组合体框架,则该组合体的主视图、左视图和俯视图分别是( )A.①④②B.①②④C.①④③D.②④③7.若某几何体的三视图如图所示,则这个几何体的直观图可能是( )二、填空题8.对几何体的三视图,下列说法正确的是.①主视图反映物体的长和宽;②俯视图反映物体的长和高;③左视图反映物体的高和宽;④主视图反映物体的高和宽.三、解答题9.一个几何体的三视图及其尺寸如图所示(单位:cm),请问该几何体是什么?写出该几何体的母线长,底面半径,高的大小.10.根据如图所示的三视图画出相应空间图形的直观图(尺寸自定).11.一个几何体是由若干个相同的小正方体组成的,其主视图和左视图如图所示,则组成这个几何体的小正方体的个数最多是多少?一、选择题1.(2015山东聊城测试,★☆☆)如图(1)、(2)、(3)、(4)为四个几何体的三视图,根据三视图可以判断这四个几何体分别为( )A.三棱台、三棱柱、圆锥、圆台B.三棱台、三棱锥、圆锥、圆台C.三棱柱、正四棱锥、圆锥、圆台D.三棱柱、三棱台、圆锥、圆台2.(2015河南内黄月考,★☆☆)如下图,三棱柱的侧棱长和底面边长均为2,且侧棱AA1⊥底面A1B1C1,正视图是边长为2的正方形,俯视图为一个等边三角形,则该三棱柱的侧视图的面积为( )A.√3B.2√3C.4D.4√33.(2014湖北黄石模拟,★★☆)如图,水平放置的三棱柱的侧棱长为2,底面是边长为2的等边三角形,侧棱AA1⊥平面A1B1C1,且其主视图是边长为2的正方形,则该三棱柱左视图的面积为( )A.4B.2√C.2√3D.2√24.(2014安徽宿州检测,★★☆)如图所示的直三棱柱的主视图的面积为2a2,则左视图的面积为( )A.2a2B.a2a2C.√3a2D.√345.(2013北京西城一模改编,★☆☆)如图为某几何体的三视图,则此几何体为( )A.球与三棱柱的组合体B.半球与圆柱的组合体C.半球与圆锥的组合体D.半球与三棱柱的组合体二、填空题6.(2014山西太原模拟,★★★)已知正三棱锥V-ABC的主视图、俯视图如图所示,其中VA=4,AC=2√3,则该三棱锥的左视图的面积为.知识清单①长对正②高平齐③宽相等④实线⑤虚线链接高考1.A 由三视图知识可知,圆柱的正视图是矩形,不可能为三角形.故选A.2.B 由几何体的直观图知,该几何体最上面的棱横放且在中间的位置上,因此它的俯视图应排除A、C、D,经验证B符合题意,故选B.3.D 正方体的三个视图都是正方形,不合题意;圆锥的主视图和左视图都是等腰三角形,俯视图是圆(含圆心),符合题意;三棱台的主视图、左视图和俯视图各不相同,不合题意;正四棱锥的主视图和左视图都是三角形,俯视图是正方形(含两条对角线),符合题意,所以②④符合题意.故选D.4.D 由俯视图易知,只有选项D符合题意.故选D.5.C 若该正方体的放置方式如图所示,当主视图的方向与正方体的任一侧面垂直时,主视图的面积最小,其值为1,当主视图的方向与正方体的对角面BDD1B1或ACC1A1垂直时,主视图的面积最大,其值为√2,因为主视图的方向不同,所以主视图的面积S∈[1,√2].故选C.6.解析如图所示:该几何体是长为4,宽为3,高为1的长方体内部挖去一个底面半径为1,高为1的圆柱.7.C 画直观图如图,可见几何体是长方体与三棱柱的组合体.8.A 甲中俯视图是圆,则该几何体是旋转体,又其主视图和左视图均是矩形,则甲是圆柱;乙中俯视图是三角形,则该几何体是多面体,又其主视图和左视图均是三角形,则该多面体的各个面都是三角形,因此,乙是三棱锥;丙中俯视图是圆(含圆心),则该几何体是旋转体,又其主视图和左视图均是三角形,故丙是圆锥.9.解析由主视图和俯视图可知该几何体的下半部分为柱体,上半部分为锥体,因为俯视图为一个正六边形,所以该几何体是由一个正六棱锥和一个正六棱柱组合而成的.它的实物草图如图所示.基础过关一、选择题1.C 球的三视图与其摆放位置无关.2.C 棱锥、棱柱的俯视图不是圆,圆柱的主视图和左视图都是矩形,故选C.3.C 根据三视图的画法可知选C.4.A 左视图一定为直角梯形.5.B 由三视图的定义,可得其对应三视图应为选项B中的相应图形,故选B.6.A 主视图是从前向后观察,易知为①,左视图是从左向右观察,应为④,俯视图为②.7.D A、B的主视图不符合要求,C的俯视图不符合要求.二、填空题8.答案③解析根据三视图定义,主视图反映的是物体的长和高,左视图反映的是物体的宽和高,俯视图反映的是物体的长和宽.三、解答题9.解析主视图与左视图相同,说明它是均匀的对称体,又俯视图为圆(含圆心),根据学过的知识可知该几何体是圆锥.从主视图可知圆锥的底面直径为6 cm,母线长是5 cm,所以该几何体的底面半径为3 cm,母线长为5 cm,高为4 cm.10.解析直观图如图:11.解析由主视图和左视图可知该几何体底部这一层最多摆放9个小正方体,上面一层最多摆放4个小正方体,所以组成这个几何体的小正方体的个数最多是13个.三年模拟一、选择题1.C 仔细观察三视图,先确定大致图形,再细化处理.2.B 侧视图是宽为√3,长为2的矩形,故侧视图的面积为2√3.3.C 三棱柱的左视图为一个矩形,且其一边为三棱柱的高,与这一边相邻的一边为底面三角形的高,故其面积为2×√3=2√3.4.C 由主视图的面积为2a 2得三棱柱的高为2a.左视图为矩形,长为2a,宽为底面图形(三角形)的高√32a,∴左视图的面积为2a×√32a=√3a 2.5.C 显然是半球与圆锥的组合体.二、填空题6.答案 6解析此正三棱锥的侧棱长是4,底面正三角形的边长是2√3,而其左视图是等腰三角形,底边长是2√3,高是三棱锥的高,即为2√3,所以左视图的面积是6.。

高一数学空间几何体的三视图与直观图试题答案及解析

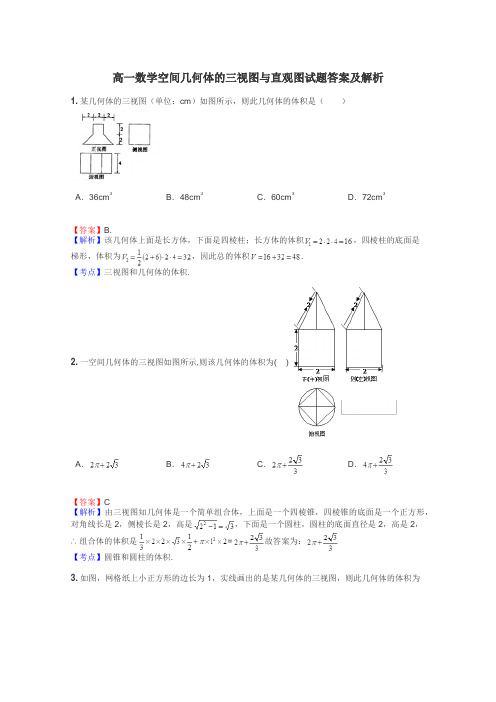
高一数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（）A．36cm3B．48cm3C．60cm3D．72cm3【答案】B.【解析】该几何体上面是长方体，下面是四棱柱；长方体的体积，四棱柱的底面是梯形，体积为，因此总的体积.【考点】三视图和几何体的体积.2.一空间几何体的三视图如图所示,则该几何体的体积为( )A．B．C．D．【答案】C【解析】由三视图知几何体是一个简单组合体，上面是一个四棱锥，四棱锥的底面是一个正方形，对角线长是2，侧棱长是2，高是，下面是一个圆柱，圆柱的底面直径是2，高是2，∴组合体的体积是=故答案为：【考点】圆锥和圆柱的体积.3.如图，网格纸上小正方形的边长为1，实线画出的是某几何体的三视图，则此几何体的体积为（）A．6B．9C．12D．18【答案】C【解析】该几何体是三棱锥，底面是俯视图，三棱锥的高为4；底面三角形是斜边长为6，高为3的等腰直角三角形，此几何体的体积为.故选C.【考点】三视图与几何体的关系；几何体的体积的求法.4.某向何体的三视图如图所示，则该几何体的体积为（）A．B．C．D．【答案】A【解析】由三视图可知,该几何体是一个长方体和一个半圆柱组成的几何体,所以体积为。

【考点】（1）根据三视图确定几何体的构成，（2）圆柱及长方体的体积公式的应用。

5.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为 .【答案】11【解析】由图可知切去的是直淩柱的一角，先算直棱柱的体积，再算切去部分的体积，所以.【考点】1、立体图形的三视图；2、体积的计算.6.右图中的三个直角三角形是一个体积为的几何体的三视图，则（）A．B．C．D．【答案】B【解析】由三视图可知该几何体为三棱锥，其中一侧棱垂直底面，且底面为直角三角形，∴三棱锥的体积为，解得，故选B．【考点】由几何体的三视图求体积．7.已知四棱锥的三视图如图所示,则四棱锥的四个侧面中面积最大的是（）A．3B．C．6D．8【答案】C【解析】通过三视图可作出该几何体的直观图，如图所示．其中底面为矩形，面面，且，，．易得，，，故侧面中面积最大值为6．【考点】几何体的三视图与直观图．8.右图是水平放置的的直观图，轴，，则是（）A．等边三角形B．等腰三角形C．直角三角形D．等腰直角三角形【答案】C【解析】直观图为斜二测画法，原图的画为，因此原为直角三角形.【考点】斜二测画法.9.如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A．B．C．D．【答案】D【解析】主要考查三视图与实物图之间的关系，用三视图中的数据还原出实物图的数据，再根据相关的公式求表面积与体积，本题求的是球和圆柱的表面积．三视图的投影规则是：“主视、俯视长对正；主视、左视高平齐，左视、俯视宽相等”.由三视图可知几何体是半径为1的球和底面半径为1，高为3的圆柱，故其表面积应为球的表面积与圆柱的表面积面积之和减去圆柱一个底面积，即．故选D．【考点】本题考点是由三视图求几何体的面积、体积，考查对三视图的理解与应用10.如图是一个简单的组合体的直观图与三视图，一个棱长为4的正方体，正上面中心放一个球，且球的一部分嵌入正方体中，则球的半径是（）A．B．1C．D．2【答案】B【解析】由已知题中三视图中的俯视图中圆上的点到正方形边长的最小距离为1，已知中的正方体的棱长为4，可得球的半径为1，故选B．【考点】由三视图还原实物图．11.一个几何体的三视图如图所示,则该几何体可以是（）A．棱柱B．棱台C．圆柱D．圆台【答案】D【解析】由正视图和左视图可知此几何体为台体，结合俯视图可知此几何体为圆台。

(完整版)高中数学3三视图课后习题(带答案)

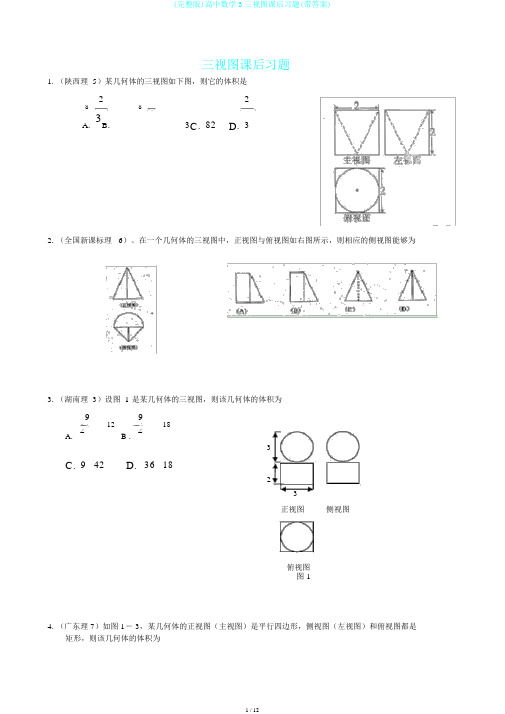
三视图课后习题1. （陕西理 5）某几何体的三视图如下图，则它的体积是2288A ．3B ．3C ．82D ．32. （全国新课标理 6）。

在一个几何体的三视图中，正视图与俯视图如右图所示，则相应的侧视图能够为3. （湖南理 3）设图 1 是某几何体的三视图，则该几何体的体积为991218A ．2B ．23C ．9 42D ． 36 1823 正视图侧视图俯视图图 14. （广东理 7）如图 1－ 3，某几何体的正视图（主视图）是平行四边形，侧视图（左视图）和俯视图都是矩形，则该几何体的体积为A．6 3B．9 3C．12 3D．18 3 5.（北京理 7）某四周体的三视图如下图，该四周体四个面的面积中，最大的是A．8B．62C．10D．826.（安徽理 6）一个空间几何体的三视图如下图，则该几何体的表面积为（A） 48（B） 32+8（C） 48+8（D） 807. （辽宁理 15）一个正三棱柱的侧棱长和底面边长相等，体积为2 3，它的三视图中的俯视图如右图所示，左视图是一个矩形，则这个矩形的面积是．8.（天津理 10）一个几何体的三视图如右图所示（单位：m），则该几何体的体积为__________ m39.（ 2010 湖南文数） 13. 图 2 中的三个直角三角形是一个体积为2的几何体的三视图，则 h=cm 20cm10．（2010 浙江理数）（ 12）若某几何体的三视图（单位：cm）如下图，则此几何体的体积是___________ cm3 .11．（ 2010 辽宁文数）（ 16）如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为.12. （ 2010辽宁理数）（ 15）如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.13. （ 2010 天津文数）（ 12）一个几何体的三视图如下图，则这个几何体的体积为。

高中数学立体几何试题及答案[1]

立体几何专题训练一、选择题（每题5分，共60分）1.在一个几何体的三视图中，正视图和俯视图如右图，则相应的侧视图可以为（）2.将长方体截去一个四棱锥，得到的几何体如右图所示，则该几何体的左视图为（）3.（2011年高考湖南卷文科4)设图１是某几何体的三视图，则该几何体的体积为( )A ．942π+ Ｂ．3618π+ Ｃ．9122π+ Ｄ．9182π+4.某几何体的三视图如图所示，则它的体积是（）（A ）283π-（B ）83π- （C ）82π- （D ）23π5.一个正三棱柱的侧棱长和底面边长相等，体积为的三视图中的俯视图如右图所示．左视图是一个矩形．则这个矩形的面积是( )(A)4 (B)6.1l ，2l ，3l 是空间三条不同的直线，则下列命题正确的是( )（A ）1223,l l l l ⊥⊥⇒1l //2l （B ）12l l ⊥,1l //3l ⇒32l l ⊥ （C ）1l //2l //3l ⇒ 1l ，2l ，3l 共面（D ）1l ，2l ，3l 共点⇒1l ，2l ，3l 共面7.若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积．．．等于 ( )B.2C.D.68.在空间，下列命题正确的是( ) A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行正视图侧视图俯视图图19.一个几何体的三视图如图，该几何体的表面积是()（A）372 （B）360（C）292 （D）28010.设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上，则该球的表面积为( ) （A）3πa2 （B）6πa2（C）12πa2 （D）24πa211.设球的体积为V1,它的内接正方体的体积为V2，下列说法中最合适的是( )A. V1比V2大约多一半B. V1比V2大约多两倍半C. V1比V2大约多一倍D. V1比V2大约多一倍半12.下图是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱，其正(主)视图、俯视图如下图；②存在四棱柱，其正(主)视图、俯视图如下图；③存在圆柱，其正(主)视图、俯视图如下图．其中真命题的个数是( )(A)3 (B)2 (C)1 (D)0二、填空题（每题4分，共16分）13.如图，正方体ABCD-A1B1C1D1中，AB=2，点E为AD的中点，点F在CD上，若EF∥平面AB1C，则线段EF的长度等于_____________.14．一个几何体的三视图如图所示，则这个几何体的体积为.15．已知四棱椎P ABCD-的底面是边长为6 的正方形，侧棱PA⊥底面ABCD，且8PA=，则该四棱椎的体积是。

立体几何三视图练习题

8.1空间几何体的三视图、直观图、表面积与体积练习题（1）1．(2014·福建，2，)某空间几何体的正视图是三角形，则该几何体不可能是( )A ．圆柱B ．圆锥C ．四面体D ．三棱柱2．(2013·四川)一个几何体的三视图如下图，则该几何体的直观图能够是( )3．(2016·课标Ⅰ，6)如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径，若该几何体的体积是28π3，则它的表面积是( )A ．17πB ．18πC ．20πD ．28π4．(2016·山东，5)一个由半球和四棱锥组成的几何体，其三视图如下图，则该几何体的体积为( )A.13＋23πB.13＋23πC.13＋26π D ．1＋26π5．(2016·课标Ⅱ，6)如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为( )A ．20πB ．24πC ．28πD ．32π6．(2016·课标Ⅲ，9)如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为( )A ．18＋36 5B ．54＋185C ．90D ．817．(2015·浙江)某几何体的三视图如下图(单位：cm)，则该几何体的体积是( )A ．8 cm 3B ．12 cm 3C.323 cm 3D.403 cm 3 8．(2014·安徽，7)一个多面体的三视图如下图，则该多面体的表面积为( )A ．21＋ 3B ．18＋ 3C ．21D ．189．(2015·北京，5)某三棱锥的三视图如下左图所示，则该三棱锥的表面积是( )A ．2＋ 5B ．4＋ 5C ．2＋2 5D ．510．(2016·北京房山区一模，5)某四棱锥的三视图如上右图所示，则最长的一条侧棱的长度为( )A. 2B. 3C. 5D.611．(2016·课标Ⅲ，10)在封闭的直三棱柱ABC A 1B 1C 1内有一个体积为V 的球．若AB ⊥BC ，AB ＝6，BC ＝8，AA 1＝3，则V 的最大值是( )A．4π B.9π2C．6π D.32π312．(2015·课标Ⅱ，9)已知A，B是球O的球面上两点，∠AOB＝90°，C为该球面上的动点．若三棱锥OABC体积的最大值为36，则球O的表面积为( )A．36πB．64πC．144πD．256π8.1空间几何体的三视图、直观图、表面积与体积练习题（2）1．(2015·江苏，9)现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个．若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为________．2．(2013·课标Ⅰ，6)如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，假如不计容器的厚度，则球的体积为()A.500π3cm3 B.866π3cm3 C.1 372π3cm3 D.2 048π3cm33．(2016·四川，13)已知三棱锥的四个面都是腰长为2的等腰三角形，该三棱锥的正视图如上右图所示，则该三棱锥的体积是________．4．(2016·天津，11)已知一个四棱锥的底面是平行四边形，该四棱锥的三视图如下左图图所示(单位：m)，则该四棱锥的体积为________m3.5．(2014·课标Ⅰ，12)如上右图所示，网络纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为()A．6 2 B．4 2 C．6 D．46．一个四面体的三视图如下图，则该四面体的表面积是()A．1＋ 3 B．2＋ 3 C．1＋2 2 D．227．(2014·课标Ⅱ)正三棱柱ABCA1B1C1的底面边长为2，侧棱长为3，D为BC中点，则三棱锥AB1DC1的体积为()A ．3 B.32 C ．1 D.328．(2015·河北石家庄调研，8)已知球O ，过其球面上A ，B ，C 三点作截面，若O 点到该截面的距离是球半径的一半，且AB ＝BC ＝2，∠B ＝120°，则球O 的表面积为( )A.64π3B.8π3 C ．4π D.16π99．正四棱锥的顶点都在同一球面上．若该棱锥的高为4，底面边长为2，则该球的表面积为( )A.81π4 B ．16π C ．9π D.27π410．(2015·山东淄博模拟，4)把边长为1的正方形ABCD 沿对角线BD 折起，形成的三棱锥A BCD 的正(主)视图与俯视图如下图，则其侧(左)视图的面积为( )A.22B.12C.24D.1411．一个几何体的三视图如下图，则该几何体的体积为( )A.163B.203C.152D.13212．(2016·江西南昌，6)一个几何体的三视图及尺寸如下图，则该几何体的外接球半径为( )A.12B.316C.174D.174由三视图还原直观图的方法(1)还原后的几何体一般为较熟悉的柱、锥、台、球的组合体．(2)注意图中实、虚线，实际是原几何体中的可视线与被遮挡线．(3)想象原形，并画出草图后实行三视图还原，把握三视图和几何体之间的关系，与所给三视图比较，通过调整准确画出原几何体．根据几何体的三视图判断几何体的结构特征(1)三视图为三个三角形，对应三棱锥；(2)三视图为两个三角形，一个四边形，对应四棱锥；(3)三视图为两个三角形，一个圆，对应圆锥；(4)三视图为一个三角形，两个四边形，对应三棱柱；(5)三视图为两个四边形，一个圆，对应圆柱．求解空间几何体表面积的方法(1)已知几何体的三视图求其表面积，一般是先根据三视图判断空间几何体的形状，再根据题目所给数据与几何体的表面积公式，求其表面积．(2)多面体的表面积是各个面的面积之和，组合体的表面积应注意重合局部的处理．(3)圆柱、圆锥、圆台的侧面是曲面，计算侧面积时需要将这个曲面展开成平面图形计算，而表面积是侧面积与底面圆的面积之和．(4)解决关于外接球的问题的关键是抓住外接的特点，即球心到多面体的顶点的距离都等于球的半径，同时要作一圆面起衬托作用．求体积的常用方法(1)分割求和法：把不规则图形分割成规则图形，然后实行体积计算．(2)补形法：把不规则几何体补成规则几何体，不熟悉的几何体补成熟悉的几何体，便于计算其体积．(3)等积法：选择适当的底面图形求几何体的体积，常用于三棱锥的体积.。

(必考题)高中数学必修二第一章《立体几何初步》测试卷(有答案解析)(3)

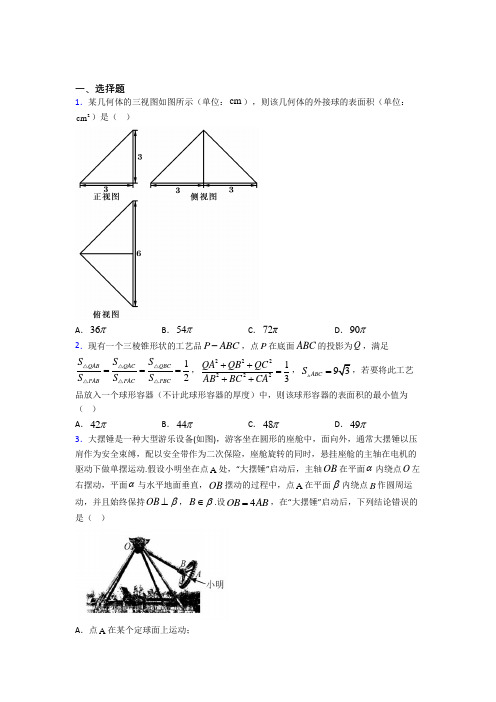
一、选择题1．某几何体的三视图如图所示（单位：cm ），则该几何体的外接球的表面积（单位：2cm ）是（）A ．36πB ．54πC ．72πD ．90π2．现有一个三棱锥形状的工艺品P ABC -，点P 在底面ABC 的投影为Q ，满足12QABQAC QBC PABPACPBCS S S S S S ===△△△△△△，22222213QA QB QC AB BC CA ++=++，93ABCS =，若要将此工艺品放入一个球形容器（不计此球形容器的厚度）中，则该球形容器的表面积的最小值为（）A ．42πB ．44πC ．48πD ．49π3．大摆锤是一种大型游乐设备(如图)，游客坐在圆形的座舱中，面向外，通常大摆锤以压肩作为安全束缚，配以安全带作为二次保险，座舱旋转的同时，悬挂座舱的主轴在电机的驱动下做单摆运动.假设小明坐在点A 处，“大摆锤”启动后，主轴OB 在平面α内绕点O 左右摆动，平面α与水平地面垂直，OB 摆动的过程中，点A 在平面β内绕点B 作圆周运动，并且始终保持OB β⊥，B β∈.设4OB AB =，在“大摆锤”启动后，下列结论错误的是（）A ．点A 在某个定球面上运动；B ．β与水平地面所成锐角记为θ，直线OB 与水平地面所成角记为δ，则θδ+为定值；C ．可能在某个时刻，AB//α；D ．直线OA 与平面α所成角的正弦值的最大值为17. 4．已知三棱锥A BCD -的各棱长都相等，E 为BC 中点，则异面直线AB 与DE 所成角的余弦值为（） A ．13 B ．36C ．33 D ．1165．一个几何体的三视图如图所示，则该几何体的外接球的表面积是（）A ．2πB ．3πC ．4πD ．16π6．如图，在四棱锥P ABCD -中，底面ABCD 是矩形.其中3AB =，2AD =，PAD △是以A ∠为直角的等腰直角三角形，若60PAB ∠=︒，则异面直线PC 与AD 所成角的余弦值是（）A ．2211B ．2211-C 27D ．11117．如图，正方形ABCD 的边长为4，点E ，F 分别是AB ，B C 的中点，将ADE ，EBF △，FCD 分别沿DE ，EF ，FD 折起，使得A ，B ，C 三点重合于点A '，若点G 及四面体A DEF '的四个顶点都在同一个球面上，则以FDE 为底面的三棱锥G -DEF 的高h 的最大值为（）A．263+B．463+C．4263-D．2263-8．某几何体的三视图如图所示，该几何体的体积为V，该几何体所有棱的棱长之和为L，则（）A．8,14253V L==+B．8,1425V L==+C．8,16253V L==+D．8,1625V L==+9．某三棱锥的三视图如图所示，则该三棱锥的体积为（）A．16B．13C．23D．210．在四棱锥P -ABCD 中，//AD BC ，2AD BC =，E 为PD 中点，平面ABE 交PC 于F ，则PFFC=（） A ．1B ．32C ．2D ．311．平行六面体1111ABCD A B C D -的六个面都是菱形，那么点1A 在面11AB D 上的射影一定是11AB D 的________心，点1A 在面1BC D 上的射影一定是1BC D 的________心（）A ．外心、重心B ．内心、垂心C ．外心、垂心D ．内心、重心12．如图（1），Rt ABC ，1,3,2AC AB BC ===，D 为BC 的中点，沿AD 将ACD △折起到AC D '，使得C '在平面ABD 上的射影H 落在AB 上，如图（2），则以下结论正确的是（）A ．AC BD '⊥B ．AD BC '⊥ C ．BD C D ⊥' D ．AB C D ⊥'二、填空题13．已知直三棱柱111ABC A B C -，14AB BC AA ===，42AC =，若点P 是上底面111 A B C 所在平面内一动点，若三棱锥P ABC -的外接球表面积恰为41π，则此时点P 构成的图形面积为________．14．如图所示，Rt A B C '''∆为水平放置的ABC ∆的直观图，其中A C B C ''''⊥，2B O O C ''''==，则ABC ∆的面积是________________.15．已知正四棱锥的体积为18，侧棱与底面所成的角为45，则该正四棱锥外接球的表面积为___________.16．已知一个几何体的三视图如图所示，俯视图为等腰三角形，则该几何体的外接球表面积为_________.17．在三棱锥D ABC -中，AD ⊥平面ABC ，3AC =，17BC =，1cos 3BAC ∠=，若三棱锥D ABC -的体积为27，则此三棱锥的外接球的表面积为______18．已知棱长为4的正方体ABCD -A 1B 1C 1D 1中，点M 是棱AD 的中点，点N 是棱AA 1的中点，P 是侧面四边形ADD 1A 1内一动点（含边界），若C 1P ∥平面CMN ，则线段C 1P 长度的取值范围是________.19．如图，在直角梯形ABCD 中，//,,2,3,60AB CD AB AD CD AB ABC ⊥==∠=°，将此梯形以AD 所在直线为轴旋转一周，所得几何体的表面积是_________________．20．将底面直径为8，高为23为______.三、解答题21．如图，在直三棱柱111ABC A B C -中，1,2AC BC AC BC CC ⊥===.（1）求三棱柱111ABC A B C -的体积；（2）求异面直线1CB 与1AC 所成角的大小；（3）求二面角1B AC C --的平面角的余弦值.22．如图，四棱锥P ABCD -的底面ABCD 是边长为2的菱形，60BCD ∠=，已知2PB PD ==，6PA =，E 为PA 的中点.（1）求证：PC BD ⊥；（2）求二面角B PC E --的余弦值；（3）求三棱锥P BCE -的体积.23．如图，在多面体ABCDEF 中，底面ABCD 为菱形，且∠DAB =π3，AB =2，EF //AC ，EA =ED =3，BE =5.（1）求证：平面EAD ⊥平面ABCD ；（2）求三棱锥F -BCD 的体积.24．如图，四棱锥E ABCD -中，底面ABCD 是边长为2的正方形，平面AEB ⊥平面ABCD ，4EBA π∠=，2EB =F 为CE 上的点，BF CE ⊥.（1）求证：BF ⊥平面ACE ；（2）求点D 到平面ACE 的距离.25．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，四边形ABCD 为梯形，//AD BC ，6BC =，2PA AD CD ===，E 是BC 上一点且23BE BC =，PB AE ⊥.（1）求证：AB ⊥平面PAE ；（2）求点C 到平面PDE 的距离.26．如图，在直角梯形ABED 中，//BE AD ，DE AD ⊥，BC AD ⊥，4AB =，23BE =.将矩形BEDC 沿BC 翻折，使得平面ABC ⊥平面BCDE .（1）若BC BE =，证明：平面ABD ⊥平面ACE ；（2）当三棱锥A BCE -的体积最大时，求平面ADE 与平面ABC 所成的锐二面角的余弦值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】由三视图知该几何体是底面为等腰直角三角形，且侧面垂直于底面的三棱锥，由题意画出图形，结合图形求出外接球的半径，再计算外接球的表面积．【详解】解：由几何体的三视图知，该几何体是三棱锥P ABC -，底面为等腰ABC ∆，且侧面PAB ⊥底面ABC ，如图所示；设D 为AB 的中点，又3DA DB DC DP ====，且PD ⊥平面ABC ，∴三棱锥P ABC -的外接球的球心O 在PD 上，设OP R =，则OA R =，3OD R =-，222(3)3R R ∴=-+，解得3R =，∴该几何体外接球的表面积是32436R cm ππ=．故选：A ．【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.2．D解析：D 【分析】作QM AB ⊥，连接PM ，易证AB PM ⊥，由112122QAB PABAB QMS S AB PM ⨯⨯==⨯⨯△△,得到2PM QM=，再根据12 QAB QACQBCPAB PAC PBCS S SS S S===△△△△△△，由对称性得到AB BC AC==，然后根据22222213QA QB QCAB BC CA++=++，93ABCS=，求得6,23AB AQ==，在AOQ△中，由222AO OQ AQ=+求解半径即可.【详解】如图所示：作QM AB⊥与M，连接PM，因为PQ⊥平面ABC，所以PQ AB⊥，又QM PQ Q⋂=，所以AB⊥平面PQM，所以AB PM⊥，所以112122QABPABAB QMSS AB PM⨯⨯==⨯⨯△△,2PM QM=,因为12QAB QAC QBCPAB PAC PBCS S SS S S===△△△△△△，由对称性得AB BC AC==,又因为22222213QA QB QCAB BC CA++=++，93ABCS=所以21sin60932ABCS AB=⨯⨯=解得6,3AB AQ==所以3,23,3QM PM PQ===，设外接球的半径为r，在AOQ △中，222AO OQ AQ =+，即()()222323r r =-+，解得72r =，所以外接球的表面积为2449S r ππ==，即该球形容器的表面积的最小值为49π. 故选：D 【点睛】关键点点睛：本题关键是由12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△得到三棱锥是正棱锥，从而找到外接球球心的位置而得解..3．C解析：C 【分析】利用已知条件确定OA 是定值，即得A 选项正确；作模型的简图，即得B 正确；依题意点B 在平面α内，不可能AB//α，得C 错误；设AB a ，结合题意知AB α⊥时，直线OA 与平面α所成角最大，计算此时正弦值，即得D 正确. 【详解】因为点A 在平面β内绕点B 作圆周运动，并且始终保持OB β⊥，所22OA OB AB =+，又因为OB ，AB 为定值，所以OA 也是定值，所以点A 在某个定球面上运动，故A 正确；作出简图如下，OB l ⊥，所以2πδθ+=，故B 正确；因为B α∈，所以不可能有AB//α，故C 不正确；设AB a ，则4OB a =，2217OA AB OB a =+，当AB α⊥时，直线OA 与平面α所成角最大，此时直线OA 与平面α1717a=，故D 正确. 故选:C. 【点睛】本题解题关键在于认真读题、通过直观想象，以实际问题为背景构建立体几何关系，再运用立体几何知识突破难点.4．B解析：B 【分析】取AC 中点F ，连接,EF DF ，证明FED ∠是异面直线AB 与DE 所成角（或其补角），然后在三角形中求得其余弦值即可得．【详解】取AC 中点F ，连接,EF DF ，∵E 是BC 中点，∴//EF AB ，12EF AB =，则FED ∠是异面直线AB 与DE 所成角（或其补角），设1AB =，则12EF =，32DE DF ==， ∴在等腰三角形DEF 中，11324cos 63EF FED DE ∠===．所以异面直线AB 与DE 所成角的余弦值为36．故选：B ．【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．5．C解析：C 【分析】由三视图还原出原几何体，确定其结构，再求出外接球的半径得球的表面积．【详解】由三视图，知原几何体是一个四棱锥P ABCD -，如图，底面ABCD 是边长为1的正方形，PB ⊥底面ABCD ，由PB ⊥底面ABCD ，AD ⊂面ABCD ，得PB AD ⊥，又AD AB ⊥，AB PB B ⋂=，,AB PB ⊂平面PAB ，所以AD ⊥平面PAB ，而PA ⊂平面PAB ，所以AD PA ⊥，同理DC PC ⊥，同样由PB ⊥底面ABCD 得PB BD ⊥，所以PD 中点O 到四棱锥各顶点距离相等，即为其外接球球心，PD 为球直径，222222PD PB BD PA AD AB =+=++=，∴外接球半径为12ADr ==，表面积为2414S ππ=⨯=．故选：C ．【点睛】关键点点睛：本题考查由三视图还原几何体，考查棱锥的外接球表面积．解题关键是确定外接球的球心．棱锥的外接球球心在过各面外心（外接圆圆心）且与该面垂直的直线上．6．D解析：D 【分析】在图形中找到（并证明）异面直线所成的角，然后在三角形中计算．【详解】因为//AD BC ，所以PCB ∠是异面直线PC 与AD 所成角（或其补角），又PA AD ⊥，所以PA BC ⊥，因为AB BC ⊥，AB PA A ⋂=，,AB PA ⊂平面PAB ，所以BC ⊥平面PAB ，又PB ⊂平面PAB ，所以PB BC ⊥．由已知2PA AD ==，所以22222cos 23223cos607PB PA AB PA AB PAB =+-⋅∠=+-⨯⨯︒=22211cos 11(7)2BC PCB PC ∠===+，所以异面直线PC 与AD 所成角的余弦值为21111．故选：D ．【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．7．A解析：A 【分析】先求出'A FDE -外接球的半径和外接圆的半径，再利用勾股定理求出外接球的球心到外接圆的圆心的距离，可得高h 的最大值. 【详解】因为A ，B ，C 三点重合于点A '，原来A B C ∠∠∠、、都是直角，所以折起后三条棱'''A F A D A E 、、互相垂直，所以三棱锥'A FDE -可以看作一个长方体的一个角，它们有相同的外接球，外接球的直径就是长方体的体对角线，即为'2'2'22441626R AF AD AE =++=++6R =2241625DE DF AD AE ==++=2222EF BE BF =+= 在DFE △中，22210cos 222522DE EF DF DEF DE EF +-∠===⨯⨯⨯，所以DEF ∠为锐角，所以2310sin 1cos DEF DEF ∠=-∠=，DEF的外接圆的半径为552 2sin310DFrDEF===∠，则球心到DEF外心的距离为2223R r-=，以FDE为底面的三棱锥G-DEF的高h的最大值为1R OO+的距离为263+.故选：A.【点睛】本题考查了翻折问题和外接球的问题，关键点翻折前后量的变化及理解外接球和三棱锥的关系，考查了学生的空间想象力和计算能力.8．A解析：A【分析】由三视图还原几何体，由棱锥的体积公式可得选项.【详解】在如图所示的正方体1111ABCD A B C D-中，P，E分别为11,B C BC的中点，该几何体为四棱锥P ABCD-，且PE⊥平面ABCD．由三视图可知2AB=，则5,3PC PB PD PA====，则21825681425,2233L V=++=+=⨯⨯=．故选：A.【点睛】方法点睛：三视图问题的常见类型及解题策略：(1)由几何体的直观图求三视图．注意正视图、侧视图和俯视图的观察方向，注意看到的部分用实线表示，不能看到的部分用虚线表示．(2)由几何体的部分视图画出剩余的部分视图．先根据已知的一部分三视图，还原、推测直观图的可能形式，然后再找其剩下部分三视图的可能形式．当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是否符合．(3)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图．9．C解析：C【分析】根据题中所给的几何体的三视图还原几何体，得到相应的三棱锥，之后利用椎体体积公式求得结果.【详解】根据题中所给的几何体的三视图还原几何体如图所示：该三棱锥满足底面BCD△是等腰三角形，且底边和底边上的高线都是2；且侧棱AD⊥底面BCD，1AD=，所以112 =221=323V⨯⨯⨯⨯，故选：C.【点睛】方法点睛：该题考查的是有关根据所给几何体三视图求几何体体积的问题，解题方法如下：（1）应注意把握三个视图的尺寸关系：主视图与俯视图长应对正（简称长对正），主视图与左视图高度保持平齐（简称高平齐），左视图与俯视图宽度应相等（简称宽相等），若不按顺序放置和不全时，则应注意三个视图名称；（2）根据三视图还原几何体；（3）利用椎体体积公式求解即可.10．C解析：C【分析】首先通过延长直线,DC AB，交于点G，平面BAE变为GAE，连结PG，EG交于点F，再根据三角形中线的性质，求PFFC的值.【详解】延长,DC AB，交于点G，连结PG，EG交PC于点F，//AD BC ，且2AD BC =，可得点,B C 分别是,AG DG 的中点，又点E 是PD 的中点，PC ∴和GE 是△PGD 的中线，∴点F 是重心，得2PFFC=故选：C 【点睛】关键点点睛：本题的关键是找到PC 与平面BAE 的交点，即将平面BAE 转化为平面GAE 是关键. 11．C解析：C 【分析】将三棱锥111A AB D -、三棱锥11A BC D -分离出来单独分析，根据线段长度以及线线关系证明1A 的射影点分别是11AB D 和1BC D 的哪一种心. 【详解】三棱锥111A AB D -如下图所示：记1A 在面11AB D 上的射影点为O ，连接11,,AO B O D O ，因为11111AA A D A B ==，又1A O ⊥平面11AB D ，所以222222*********1,,AA AO AO A D AO OD A B AO OB =+=+=+ 所以11AO OB OD ==，所以O 为11AB D 的外心；三棱锥11A BC D -如下图所示：记1A 在面1BC D 上的射影点为1O ，连接1111,,BO C O DO ，因为11//BC AD ，且四边形11ADD A 是菱形，所以11AD A D ⊥，所以11BC A D ⊥，又因为11A O ⊥平面1BC D ，所以1111111,AO BC AO A D A ⊥=，所以1BC ⊥平面11AO D ，又因为1DO ⊂平面11AO D ，所以11DO BC ⊥，同理可知：1111,BO DC C O DB ⊥⊥，所以1O 为1BC D 的垂心，故选：C. 【点睛】关键点点睛：解答本题的关键是通过1A 的射影点去证明线段长度的关系、线段位置的关系，借助线面垂直的定义和判定定理去分析解答问题.12．C解析：C 【分析】设AH a =，则3BH a =，由线面垂直的性质和勾股定理可求得DH a AH ==，由等腰三角形的性质可证得BD ⊥DH ，再根据线面垂直的判定和性质可得选项. 【详解】设AH a =，则3BH a =，因为'C H ⊥面ABD ，AB 面ABD ，DH ⊂面ABD ，所以'C H ⊥AB ，'C H ⊥DH ，'C H ⊥DB ，又Rt ABC ，1,3,2AC AB BC ===，D 为BC 的中点，所以'1,6C D BD B DAB π==∠=∠=，所以在'Rt AC H 中，()2''221C H AC AHa =-=-Rt C HD ’中，()2'222'211DH C D C H a a =-=--=，所以DH a AH ==，所以6ADH DAB π∠=∠=，又23ADB π∠=，所以2HDB π∠=，所以BD ⊥DH ，又'C HDH H =，所以BD ⊥面'C DH ，又'C D ⊂面'C DH ，所以BD ⊥'C D ，故选：C. 【点睛】关键点点睛：在解决折叠问题时，关键在于得出折叠的前后中，线线、线面、面面之间的位置关系的不变和变化，以及其中的边的长度、角度中的不变量和变化的量.二、填空题13．【分析】确定是等腰直角三角形的中点分别是和的外心由直棱柱性质得的外接球的球心在上外接球面与平面的交线是圆是以为圆心为半径的圆求出可得面积【详解】则设分别是的中点则分别是和的外心由直三棱柱的性质得平面解析：4π【分析】确定ABC 是等腰直角三角形，11,AC A C 的中点1,D D 分别是ABC 和111A B C △的外心，由直棱柱性质得P ABC -的外接球的球心O 在1DD 上，外接球面与平面111A B C 的交线是圆，是以1D 为圆心，1D P 为半径的圆，求出1PD 可得面积．【详解】4,AB BC AC ===90ABC ∠=︒，设1,D D 分别是11,AC A C 的中点，则1,D D 分别是ABC 和111A B C △的外心，由直三棱柱的性质得1DD ⊥平面ABC ，所以P ABC -的外接球的球心O 在1DD 上，如图，24()41OA ππ=，则2OP OA ==，32OD ===，所以11135422OD DD OD AA OD =-=-=-=，12PD ===， P ABC -的外接球面与平面111A B C 的交线是圆，是以1D 为圆心，1D P 为半径的圆，其面积为224S ππ=⨯=．故答案为：4π．【点睛】关键点点睛：本题考查立体几何中动点轨迹问题的求解，重点考查了几何体的外接球的有关问题的求解，关键是根据外接球的性质确定球心位置，结合勾股定理得出动点所满足的具体条件，结论：三棱锥的外接球的球心在过各面外心且与此面垂直的直线上．14．【分析】根据直观图和原图的之间的关系由直观图画法规则将还原为如图所示是一个等腰三角形直接求解其面积即可【详解】由直观图画法规则将还原为如图所示是一个等腰三角形则有所以故答案为：【点睛】关键点点睛：根解析：82【分析】根据直观图和原图的之间的关系，由直观图画法规则将Rt A B C '''还原为ABC ，如图所示，ABC 是一个等腰三角形，直接求解其面积即可．【详解】由直观图画法规则将Rt A B C '''还原为ABC ，如图所示，ABC 是一个等腰三角形,则有2BO OC B O O C ''''====，242AO A O ''==所以114428222ABCSBC AO =⋅=⨯⨯= 故答案为：2【点睛】关键点点睛：根据斜二测画法的规则，可得出三角形的直观图，并求出对应边长，根据面积公式求解．15．【分析】作出图形计算出正四棱锥的高与底面边长设底面的中心为计算得出为正四棱锥的外接球球心可求得该正四棱锥的外接球半径即可得解【详解】如下图所示设正四棱锥的底面的中心为连接设正四棱锥的底面边长为则由于解析：36π【分析】作出图形，计算出正四棱锥P ABCD -的高与底面边长，设底面ABCD 的中心为E ，计算得出E 为正四棱锥P ABCD -的外接球球心，可求得该正四棱锥的外接球半径，即可得解. 【详解】如下图所示，设正四棱锥P ABCD -的底面ABCD 的中心为E ，连接PE 、AC 、BD ，设正四棱锥P ABCD -的底面边长为a ，则2AC BD a ==，由于E 为正四棱锥P ABCD -的底面ABCD 的中心，则PE ⊥平面ABCD ，由于正四棱锥P ABCD -的侧棱与底面所成的角为45，则45PAC PCA ∠=∠=，所以，PAC △是以APC ∠为直角的等腰直角三角形，同理可知，PBD △是以BPD ∠为直角的等腰直角三角形，E 为AC 的中点，1222PE AC a ==，2ABCD S a =正方形， 231122183326P ABCD ABCD V S PE a a a -=⋅=⨯⨯==正方形，解得32a =，232PE a ==，由直角三角形的性质可得1122PE AC BD ==，即PE AE BE CE DE ====，所以，E 为正四棱锥P ABCD -外接球的球心，球E 的半径为3r PE ==，该球的表面积为2436r ππ=. 故答案为：36π. 【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.16．【分析】首先把三视图转换为直观图进一步求出几何体的外接球的半径最后求出球的表面积【详解】根据几何体的三视图可知该几何体是底面为等腰三角形高为2的三棱锥体如图所示:设底面外接圆的半径为t 圆心为H 则解得解析：414π 【分析】首先把三视图转换为直观图，进一步求出几何体的外接球的半径，最后求出球的表面积.【详解】根据几何体的三视图可知该几何体是底面为等腰三角形，高为2的三棱锥体．如图所示:设底面外接圆的半径为t ,圆心为H ，则2221(2)t t =+-，解得54t =，设外接球的半径r ，球心为O ，则OH ⊥底面，且1OH =，则22541()144r =+=所以41414().164S ππ=⨯⨯= 故答案为：414π 【点睛】关键点点睛：球心与底面外接圆圆心连线垂直底面，且OH 等于棱锥高的一半，利用勾股定理求出球的半径，由面积公式计算即可.17．【分析】设出外接球的半径球心的外心半径r 连接过作的平行线交于连接如图所示在中运用正弦定理求得的外接圆的半径r 再利用的关系求得外接球的半径运用球的表面积公式可得答案【详解】设三棱锥外接球的半径为球心为解析：20π【分析】设出外接球的半径R 、球心O ，ABC 的外心1O 、半径 r , 连接1AO ，过O 作的平行线OE 交AD 于 E ，连接OA ，OD ，如图所示，在ABC 中，运用正弦定理求得 ABC的外接圆的半径r ,再利用1,,R r OO 的关系求得外接球的半径，运用球的表面积公式可得答案.【详解】设三棱锥外接球的半径为R 、球心为O ，ABC 的外心为1O 、外接圆的半径为r ，连接1AO ，过O 作平行线OE 交AD 于E ，连接OA ，OD ，如图所示，则OA OD R ==，1O A r =，OE AD ⊥，所以E 为AD 的中点.在ABC 中，由正弦定理得172sin 22BC r BAC ==∠，解得334r =. 在ABC 中，由余弦定理2222cos BC AB AC AB AC BAC =+-⋅⋅∠，可得2117963AB AB =+-⋅⋅，得4AB =. 所以1122sin 3442223ABC S AB AC BAC =⋅⋅∠=⨯⨯⨯=△. 因为112742333D ABC ABC V S AD AD -=⋅⋅=⨯⨯=△，所以144AD =.连接1OO ，又1//OO AD ，所以四边形1EAO O 为平行四边形，111428EA OO AD ===，所以22221114324588R OO AO ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭. 所以该三棱锥的外接球的表面积()224π4π520πS R ===.故答案为：20π.【点睛】本题考查三棱锥的外接球，及球的表面积计算公式，解决问题的关键在于利用线面关系求得外接球的球心和球半径，属于中档题.18．【分析】分别取棱的中点连接易证平面平面由题意知点必在线段上由此可判断在或处时最长位于线段中点处时最短通过解直角三角形即可求得【详解】如下图所示连分别为所在棱的中点则又平面平面平面四边形为平行四边形又解析：[32,25]【分析】分别取棱1BB 、11B C 的中点M 、N ，连接MN ，易证平面1//A MN 平面AEF ，由题意知点P 必在线段MN 上，由此可判断P 在M 或N 处时1A P 最长，位于线段MN 中点处时最短，通过解直角三角形即可求得．【详解】如下图所示，连MN ，EF ，1A D ，EMM ，N ，E ，F 分别为所在棱的中点，则1//MN A D ，1//EF A D ，//EF MN ∴，又MN ⊂平面1C EF ，EF ⊂平面1C EF ，//MN ∴平面1C EF ．11//,C C EM C C EM =，∴四边形1C CME 为平行四边形，1//C E CM ，又CM ⊄平面1C EF ，1C E ⊂平面1C EF ，//CM ∴平面1C EF ，又NM CM M =， ∴平面//NMC 平面1C EF ．P 是侧面四边形ADD 1A 1内一动点，且C 1P ∥平面CMN ，∴点P 必在线段EF 上．在Rt △11C D E 中，222211114225C E C D D E =+=+=同理，在Rt △11C D F 中，可得125C F =， ∴△1C EF 为等腰三角形．当点P 为EF 中点O 时，1C P EF ⊥，此时1C P 最短；点P 位于,E F 处时，1C P 最长． ()222211(25)232C O C E OE =-=-=1125C E C F ==∴线段1C P长度的取值范围是．故答案为：【点睛】本题考查点、线、面间的距离问题，考查学生的运算能力及推理转化能力，属中档题，解决本题的关键是通过构造平行平面寻找P点位置．19．【分析】此梯形以AD所在直线为轴旋转一周得到的是圆台然后根据圆台的侧面积和表面积公式进行计算【详解】将此梯形以AD所在直线为轴旋转一周得到的是圆台其中圆台的上底半径为r＝CD＝2下底半径为R＝AB＝解析：23π【分析】此梯形以AD所在直线为轴旋转一周，得到的是圆台，然后根据圆台的侧面积和表面积公式进行计算．【详解】将此梯形以AD所在直线为轴旋转一周，得到的是圆台，其中圆台的上底半径为r＝CD＝2，下底半径为R＝AB＝3，母线BC＝2，∴圆台的上底面积为πr2＝4π，下底面积为πR2＝9π，圆台的侧面积为（πr+πR）•BC＝π（2+3）×2＝10π，∴圆台的表面积为4π+9π+10π＝23π，故答案为23π．【点睛】本题考查圆台表面积的计算，利用旋转体的定义确定该几何体是圆台是解决本题的关键．20．【分析】欲使圆柱侧面积最大需使圆柱内接于圆锥设圆柱的高为h底面半径为r用r表示h从而求出圆柱侧面积的最大值【详解】欲使圆柱侧面积最大需使圆柱内接于圆锥；设圆柱的高为h底面半径为r则解得；所以；当时取解析：【分析】欲使圆柱侧面积最大，需使圆柱内接于圆锥，设圆柱的高为h，底面半径为r，用r表示h，从而求出圆柱侧面积的最大值.【详解】欲使圆柱侧面积最大，需使圆柱内接于圆锥；设圆柱的高为h ，底面半径为r ， 23423r =，解得33h r =；所以()23222334S rh r r r πππ⎛⎫===- ⎪ ⎪⎝⎭圆柱侧；当2r 时，S 圆柱侧取得最大值为43π 故答案为：3π.【点睛】本题考查了求圆柱侧面积的最值，考查空间想象能力，将问题转化为函数求最值，属于中档题.三、解答题21．（1）4；（2）60︒；（3）33. 【分析】（1）根据棱锥的体积公式求解即可；（2）作辅助线，利用平行得出异面直线1CB 与1AC 所成角就是COE ∠，再结合等边三角形的性质得出夹角；（3）过C 作1CF AC ⊥于点F ，连接,CF BF ，由11,CF AC BF AC ⊥⊥结合定义得出二面角1B AC C --的平面角，再由直角三角形的边角关系得出平面角的余弦值.【详解】（1）三棱柱111ABC A B C -的体积1122242ABC V S CC ⎛⎫=⋅=⨯⨯⨯= ⎪⎝⎭（2）记1BC 与1B C 的交点为O ，作AB 的中点E ，连接,OE CE ，异面直线1CB 与1AC 所成角就是COE ∠2CO OE CE ===60COE ︒∴∠=（3）过C 作1CF AC ⊥于点F ，连接,CF BF11,CF AC BF AC BFC ⊥⊥⇒∠为所求角 3tan 2,cos 2BC BFC BFC FC ∠===∠=【点睛】关键点睛：在求异面直线的夹角时，关键是利用中位线定理得出平行，从而得出异面直线的夹角.22．（1）证明见解析；（2）155；（3）12. 【分析】（1）连接AC 交BD 于点O ，连接PO ，推导出BD ⊥平面PAC ，进而可得出PC BD ⊥；（2）过点O 在平面PAC 内作OF PC ⊥，垂足为点F ，连接BF ，推导出OFB ∠为二面角B PC E --的平面角，计算出OF 、BF ，可计算出cos OFB ∠，即可得解；（3）计算出PCE 的面积，利用锥体的体积公式可得出13P BCE B PCE PCE V V S OB --==⋅△，即可得解. 【详解】证明：（1）连接AC 交BD 于O 点，连接PO ，∵四边形ABCD 是菱形，AC BD ∴⊥，则O 是BD 的中点，PB PD =，PO BD ∴⊥，又AC PO O =，AC 、OP ⊂平面PAC ，BD ∴⊥平面PAC ，又PC ⊂平面PAC ，PC BD ∴⊥；（2）由（1）知BO ⊥平面PAC ，PC ⊂平面PAC ，则OB PC ⊥，过O 在平面PAC 内作OF PC ⊥于F ，连接BF ，由OB OF O ⋂=，则PC ⊥平面OBF ，BF ⊂平面OBF ，得BF PC ⊥，故OFB ∠为二面角B PC E --的平面角，四边形ABCD 是菱形，60BAD ∠=，ABD ∴为等边三角形，2BD AB AD ∴===，112OB BD ∴==，223OC OA AB OB ==-= OB ⊥平面PAC ，OP ⊂平面PAC ，OP OB ∴⊥，223OP PB OB ∴-= 3OA =3OP =6PA =222OP PA OA +∴=，即OA OP ⊥，即PO AC ⊥，3366PO OC OF PC ⋅⨯∴===，222261012BF BO OF ⎛⎫=+=+= ⎪ ⎪⎝⎭，故615cos 510OF OFB BF ∠===，即二面角B PC E --的余弦值是155；（3）E 为PA 的中点，11333222PCE PAC POA S S S ∴====△△△，又OB ⊥平面PAC ，113113322P BCE B PCE PCE V V S OB --∴==⋅=⨯⨯=△. 【点睛】方法点睛：求二面角常用的方法：（1）几何法：二面角的大小常用它的平面角来度量，平面角的作法常见的有： ①定义法；②垂面法，注意利用等腰三角形的性质；（2）空间向量法：分别求出两个平面的法向量，然后通过两个平面法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求二面角是锐角还是钝角.。

高中数学立体几何点线面位置关系精选题目(附答案)

(2)求不规则几何体的表面积时，通常将所给几何体分割成基本的柱、锥、台体，先求这些柱、锥、台体的表面积，再通过求和或作差求得几何体的表面积．
2．下列说法正确的是()
A．用一平面去截圆台，截面一定是圆面
B．在圆台的上、下底面圆周上各取一点，则两点的连线就是圆台的母线
C．圆台的任意两条母线延长后相交于同一点
A．36πB．64π
C．100πD．144π
解析：选A三棱锥ABCD的三条侧棱两两互相垂直，所以把它扩展为长方体，它和三棱锥ABCD的外接球是同一个，且体对角线的长为球的直径，若设球的半径为R，则2R＝＝6，故R＝3，∴外接球的表面积S＝4πR2＝36π，故选A.
三、空间点、线、面位置关系的判断与证明
(3)(2017·山东高考)由一个长方体和两个圆柱体构成的几何体的三视图如图，则该几何体的体积为________．
[解析]
(1)如图所示，该几何体的表面积S＝1×1＋ ×1×1×2＋2× ×(1＋2)×1＋ × × ＝5＋，故选A.
(2)①正确，正四面体是每个面都是等边三角形的四面体，如正方体ABCDA1B1C1D1中的四面体ACB1D1；②错误，因为球的直径必过球心；③错误，必须是相邻的两个侧面．
4．一个几何体的三视图如图所示，则该几何体的表面积S为________．
解析：根据三视图，可知题中的几何体是由一个长方体挖去一个圆柱得到的，所以S＝2×(4×1＋3×1＋4×3)＋2π－2π＝38.
答案：38
二、与球有关的问题
球的表面积与体积
(1)球的表面积公式S球＝4πR2.
(2)球的体积公式V球＝ πR3.
(2)旋转体的表面积：
①S圆柱＝2πrl＋2πr2；
②S圆锥＝πrl＋πr2；

(新)高中数学立体几何三视图练习题

高三数学空间几何体的三视图与直观图试题答案及解析

高三数学空间几何体的三视图与直观图试题答案及解析

高中数学 第一章立体几何初步 1.3 三视图练习 北师大版必修2-北师大版高一必修2数学试题

高中立体几何 三视图试题精选

高三数学空间几何体的三视图与直观图试题

高三数学空间几何体的三视图与直观图试题答案及解析

2022年高考数学空间几何体的直观图与三视图知识点专项练习含答案

新课标高考立体几何专题

立体几何三视图高考题集

高三数学立体几何试题答案及解析

高三数学空间几何体的三视图与直观图试题答案及解析

三视图立体几何高一数学总结练习含答案解析

高一数学空间几何体的三视图与直观图试题答案及解析

(完整版)高中数学3三视图课后习题(带答案)

高中数学立体几何试题及答案[1]

立体几何三视图练习题

(必考题)高中数学必修二第一章《立体几何初步》测试卷(有答案解析)(3)

高中数学立体几何点线面位置关系精选题目(附答案)

高中数学第一章立体几何初步 1.3 三视图练习北师大版必修2-北师大版高一必修2数学试题

高中立体几何三视图试题精选