高中数学专题——立体几何专题.docx
高考数学立体几何专项知识点精选全文完整版

可编辑修改精选全文完整版高考数学立体几何专项知识点高中数学平面几何不时是数学的一大难点,下面是小编整理的数学平面几何专项知识点,对提高数学效果会有很大的协助。
(1)空间几何体① 看法柱、锥、台、球及其复杂组合体的结构特征.② 能画出复杂空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述的三视图所表示的平面模型,会用斜二侧法画出它们的直观图.③ 了解球、棱柱、棱锥、台的外表积和体积的计算公式(不要求记忆公式).(2)点、直线、平面之间的位置关系① 了解空间直线、平面位置关系的定义,并了解如下可以作为推理依据的公理和定理.◆公理1:假设一条直线上的两点在一个平面内,那么这条直线上一切的点在此平面内.◆公理2:过不在同一条直线上的三点,有且只要一个平面.◆公理3:假设两个不重合的平面有一个公共点,那么它们有且只要一条过该点的公共直线.◆公理4:平行于同一条直线的两条直线相互平行◆定理:空间中假设一个角的两边与另一个角的两边区分平行,那么这两个角相等或互补.② 以平面几何的上述定义、公理和定理为动身点,看法和了解空间中线面平行、垂直的有关性质与判定.了解以下判定定理:◆假设平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.◆假设一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行.◆假设一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.◆假设一个平面经过另一个平面的垂线,那么这两个平面相互垂直.了解以下性质定理,并可以证明:◆假设一条直线与一个平面平行,经过该直线的任一个平面与此平面相交,那么这条直线就和交线平行.◆假设两个平行平面同时和第三个平面相交,那么它们的交线相互平行◆垂直于同一个平面的两条直线平行◆假设两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直.③ 能运用公理、定理和已取得的结论证明一些空间位置关系的复杂命题.温习关注:平面几何试题着重考察空间点、线、面的位置关系的判别及几何体的外表积与体积的计算,关注画图、识图、用图的才干,关注对平行、垂直的探求,关注对条件或结论不完备情形下的开放性效果的探求小编为大家提供的2021-2021高考数学平面几何专项知识点大家细心阅读了吗?最后祝考生们学习提高。
(word完整版)高三数学立体几何经典例题

厦门一中立体几何专题一、选择题(10 X 5' =50 ')1•如图,设0是正三棱锥 P-ABC 底面三角形 ABC 的中心, 过0的动平面与P-ABC 的三条侧棱或其延长线的交点分别记 为 Q 、R 、S ,则-11 1( )PQ PR PSA. 有最大值而无最小值B. 有最小值而无最大值C. 既有最大值又有最小值,且最大值与最小值不等D. 是一个与平面QRS 位置无关的常量2•在正n 棱锥中,相邻两侧面所成的二面角的取值范围是 (A., B., C. 0,D.nn2n的面积的取值范围是()若B €a ,C €3 ,则厶ABC 的周长的最小值是( )B.2 .75.如图,正四面体 A-BCD 中,E 在棱AB 上,F 在棱CD 上,使得詈 Cy =入(0<入<+m ),记f (入)=a x+ 3入,其中a 入表示EF 与AC 所成的角,3入表示EF 与BD 所成的角,贝U( )A. f (入)在(0,+ g )单调增加B. f (入)在(0,+ g )单调减少C. f (入)在(0,1)单调增加,在(1,+ g )单调减少D. f (入)在(0,+ g )为常数合是 ()A. 一条直线B. —个平面C.两条平行直线D.两个平面7.正四棱锥底面积为 Q ,侧面积为S ,则它的体积为 ()A. 1 Q (S2Q 2)B. 1 Q (S2Q 2)6 •3 'C. 1 -Q(S2Q 2)23•正三棱锥P-ABC 的底面边长为 2a,点E 、F 、G 、H 分别是 PA 、PB 、BC 、AC 的中点,则四边形 EFGHA.(0,+ g )B.C.D. ^a 2, 24.已知二面角a -a-3为60°,点A 在此二面角内,且点A 到平面a 、3的距离分别是AE=4, AF=2,6.直线a //平面3,直线a 到平面3的距离为 1,则到直线a 的距离与平面3的距离都等于7的点的集第5题图D.f QS第1题图8. 已知球O的半径为R, A、B是球面上任意两点,则弦长|AB|的取值范围为()B.(0,2R]C. ( 0,2R )D. : R,2R ]9•已知平面aQ 平面B =l,m 是平面a 内的一条直线,则在平面B 内A. .—定存在直线与直线 m 平行,也一定存在直线与直线B. —定存在直线与直线 m 平行,但不一定存在直线与直线C. 不一定存在直线与直线 m 平行,但一定存在直线与直 线m 垂直D. 不一定存在直线与直线 m 平行,也不一定存在直线与 直线m 垂直10. 如图为一个简单多面体的表面展开图(沿图中虚线折11. ______________________________________________________________________ 边长为a 的等边三角形内任一点到三边距离之和为定值,这个定值为 __________________________ ;推广到空间,棱长为a 的正四面体内任一点到各面距离之和为 ______________12. 在厶ABC 中,AB=9, AC=15,/ BAC=120°,其所在平面外一点 P 到A 、B 、C 三个顶点的距离都是14,贝U P 点到直线 BC 的距离为 _____________ . 13. 已知将给定的两个全等的正三棱锥的底面粘在一起, 恰得到一个所有二面角都相等的六面体, 并且该六面体的最短棱的长为 2,则最远的两顶点间的距离是 _______________ .14. ___________________________________________________________________ 有120个等球密布在正四面体 A-BCD 内,问此正四面体的底部放有 ___________________________ 个球. 三、解答题(4X 10' +14' =54')15. 定直线11丄平面a ,垂足为M ,动直线12在平面a 内过定点 N ,但不过定点 M.MN=a 为定值,在11、12上分别有动线段 AB=b,CD = c.b 、c 为定值.问在什么情况下四面体 ABCD 的体积最大?最大值是多少?AC 的中点,求:(1) PM 与FQ 所成的角; (2) P 点到平面 EFB 的距离; (3 )异面直线PM 与FQ 的距离.16.如图所示,已知四边形 ABCD 、EADM 和MDCF 都是边长为 a 的正方形,点 P 、Q 分别是ED 和A. : 0,2 R ] m 垂直A.6B.7C.8D.9、填空题 (4X 4 ' =16')叠即可还原),则这个多面体的顶点数为 (第16题图连结人丘‘将厶DAE 沿AE 折起到△ D 1AE 的位置,使得/(1)试用基向量 AB , AE , AD 1表示向量OD 117.如图,在梯形 ABCD 中,AB // CD ,/ ADC = 90° ,3AD=DC=3,AB=2,E 是 CD 上一点,满足 DE = 1 ,D 1AB = 60° ,设AC 与BE 的交点为O.(2) 求异面直线OD i与AE所成的角.(3) 判断平面D i AE与平面ABCE是否垂直,并说明理由第17题图18. 如图,在斜棱柱ABC —A i B i C i中,底面为正三角形,侧棱长等于底面边长,且侧棱与底面所成的角为60°顶点B i在底面ABC上的射影O恰好是AB的中点.(i)求证:B i C± C i A;(2 )求二面角C i-AB-C的大小.第i8题图i9.如图所示,在三棱锥P-ABC中,PA=PB=PC , BC=2a,AC=a,AB=、3 a,点P到平面ABC的距离为 | a.(i )求二面角P-AC-B的大小;(2)求点B到平面FAC的距离.第i9题图立体几何练习参考答案一、选择题 1.D 设正三棱锥P-ABC 中,各棱之间的夹角为a,棱与底面夹角为B ,h 为点S 到平面PQR 的距离,1 11则 V S -PQR = 3S ^PQR • h= — ( — PQ • PR • sin a ) • PS • sin B ,另一方面,记 O 到各平面的距离为 d,则有33 211 1 dV S -PQR =V O -PQR +V O -PRS +V O -PQS =S ^PQR °d+ S ^PRS ,d+S^PQS -d=3333a + d • - -PQ -PS-sin a •故有 PQ -PR -PS-sin B =d(PQ -PR+PR -PS+PQ -PS),即旦—-PQ -PR -sin a +— •丄 PS ・PR ・sin2321 1 _ sinPR PS d3 2 PQ 常量.2.B 设正n 棱锥的高为h,相邻两侧面所成二面角为B .当h f 0时,正n 棱锥的极限为正n 边形,这时 相邻两侧面所成二面角为平面角,即二面角Qfn.当h fg 时,正n 棱锥的极限为正n 棱柱,这时相邻两侧面所成二面角为正n 边形的内角,nEFGH 为矩形,当 P f 底面△ ABC 的中心O 时,矩形EFGH f 矩形E i F i GH.3a=_Aa 23 34. C 如图,I a 丄AE,a 丄AF,「. a 丄平面 AEF.设a 交平面 AEF 于点G ,则/ EGF 是二面角a -a-3的平面角,/ EGF=60° ,/ EAF=120。
高中数学立体几何判定定理与性质.docx
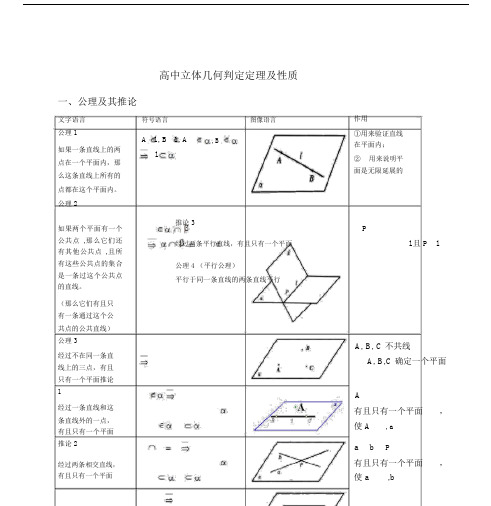
高中立体几何判定定理及性质一、公理及其推论文字语言符号语言图像语言公理 1A l ,B l , A, B如果一条直线上的两l点在一个平面内,那么这条直线上所有的点都在这个平面内。
公理 2作用①用来验证直线在平面内;②用来说明平面是无限延展的如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
(那么它们有且只有一条通过这个公共点的公共直线)公理 3经过不在同一条直线上的三点,有且只有一个平面推论1经过一条直线和这条直线外的一点,有且只有一个平面推论 2经过两条相交直线,有且只有一个平面推论 3经过两条平行直线,有且只有一个平面公理 4 (平行公理)平行于同一条直线的两条直线平行Pl 且 P lA, B, C 不共线A, B,C 确定一个平面A有且只有一个平面,使 A, aa b P有且只有一个平面,使 a,ba ∥ b有且只有一个平面,使 a,ba ∥ ba ∥ cb ∥c ①用来证明两个平面是相交关系;②用来证明多点共线,多线共点。
用来证明多点共面,多线共面用来证明线线平行二、平行关系文字语言(1)公理 4 (平行公理)平行于同一条直线的两条直线平行(2)线面平行的判定定理如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
(3)线面平行的性质定理如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
(4)面面平行的判定定理如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行 .符号语言图像语言作用a ∥ ba ∥ cb ∥ ca ∥ ba a ∥bb∥b a ∥ baa ∥b ∥a b O∥ab(5)面面平行的判定如果两个平面垂直于同一条直线,那么这两个平面平行。
OOOO∥(6)面面平行的性质定理如果两个∥a a ∥ b平行平面同时和第三b个平面相交 ,那么它们的交线平行。
( 7)面面平行的性∥质如果两个平面平行 , a ∥那么其中一个平面内a的直线平行于另一个平面。
高一数学立体几何练习题及部分答案大全.docx

立体几何试题一.选择题(每题 4 分,共 40 分)1. 已知 AB3003001500空间,下列命题正确的个数为()(1)有两组对边相等的四边形是平行四边形, (2)四边相等的四边形是菱形(4)有两边及其夹角对应相等的两个三角(3)平行于同一条直线的两条直线平行 ;形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是()A平行B相交C在平面内D平行或在平面内4. 已知直线 m过平面外一点,作与平行的平面,则这样的平面可作()A 1 个或 2 个B 0个或1个C1个 D 0个6.如图 , 如果 MC 菱形 ABCD 所在平面 , 那么 MA与 BD的位置关系是 ( )A平行B垂直相交C异面D相交但不垂直7. 经过平面外一点和平面内一点与平面垂直的平面有()A 0 个B 1个C无数个 D 1个或无数个8.下列条件中 , 能判断两个平面平行的是 ( )B一个平面内的两条直线平行于另一个平面C一个平面内有无数条直线平行于另一个平面D一个平面内任何一条直线都平行于另一个平面9. 对于直线m ,n 和平面,, 使成立的一个条件是 ( )A m // n, n, mB m // n, n,mC m n,I m, nD m n, m //, n //)10 . 已知四棱锥 , 则中 , 直角三角形最多可以有 (A 1个B2个 C 3个D4个二.填空题(每题 4 分,共16 分)11. 已知ABC的两边 AC,BC分别交平面于点M,N,设直线AB与平面交于点O,则点 O与直线 MN的位置关系为 _________12.过直线外一点与该直线平行的平面有 ___________个,过平面外一点与该平面平行的直线有_____________条13. 一块西瓜切 3 刀最多能切 _________块14.将边长是 a 的正方形 ABCD沿对角线 AC 折起 , 使得折起后 BD得长为 a, 则三棱锥D-ABC的体积为 ___________三、解答题15(10 分)如图,已知 E,F 分别是正方形ABCD A1B1C1 D1的棱 AA1和棱 CC1上的点,且 AE C1 F 。
高中数学立体几何(解析版)

立体几何立体几何一直在高中数学中占有很大的分值,未来的高考中立体几何也会持续成为高考的一个热点,文科高考中立体几何主要考查三视图的相关性质利用,简单几何体的体积,表面积以及外接圆问题.另外选择部分主要考查在点线面位置关系,简单几何体三视图.选择题主要还是以几何体的基本性质为主,解答题部分主要考查平行,垂直关系以及简单几何体的变面积以及体积.本专题针对高考高频知识点以及题型进行总结,希望通过本专题的学习,能够掌握高考数学中的立体几何的题型,将高考有关的立体几何所有分数拿到.【满分技巧】基础知识点考查:一般来说遵循三短一长选最长.要学会抽象问题具体会,将题目中的直线转化成显示中的具体事务,例如立体坐标系可以看做是一个教室的墙角有关外接圆问题:一般图形可以采用补形法,将几何体补成正方体或者是长方体,再利用不在同一个平面的四点确定一个立体平面原理,从而去求.内切圆问题:转化成正方体的内切圆去求.求点到平面的距离问题:采用等体积法.求几何体的表面积体积问题:应注意巧妙选取底面积与高.【考查题型】选择,填空,解答题【限时检测】(建议用时:90分钟)一、单选题AA是1.(2018·上海高考真题)《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马,设1AA为底面矩形的一边,则这样的阳正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点、以1马的个数是()A.4 B.8 C.12 D.16【答案】D【分析】根据新定义和正六边形的性质可得答案.【详解】根据正六边形的性质,则D1﹣A1ABB1,D1﹣A1AFF1满足题意,而C1,E1,C,D,E,和D1一样,有2×4=8,当A1ACC1为底面矩形,有4个满足题意,当A1AEE1为底面矩形,有4个满足题意,故有8+4+4=16故选D.【点睛】本题考查了新定义,以及排除组合的问题,考查了棱柱的特征,属于中档题.2.(2020·上海虹口区·高三一模)在空间,已知直线l及不在l上两个不重合的点A、B,过直线l做平面α,使得点A、B到平面α的距离相等,则这样的平面α的个数不可能是()A.1个B.2个C.3个D.无数个【答案】C【分析】分情况讨论可得出.【详解】(1)如图,当直线AB与l异面时,则只有一种情况;(2)当直线AB与l平行时,则有无数种情况,平面α可以绕着l转动;(3)如图,当l过线段AB的中垂面时,有两种情况.故选:C.3.(2020·上海高三一模)如图,在正四棱柱1111ABCD A B C D -中,底面边长2AB =,高14A A =,E 为棱1A A 的中点.设BAD ∠=α、BED θ∠=、1B ED γ∠=,则α、β、γ之间的关系正确的是( ).A .αγθ=>B .γαθ>>C .θγα>>D .αθγ>>【答案】B 【分析】求出α、β、γ的大小即可求解. 【详解】由题意可得2BAD πα∠==,连接BD ,则BDE 为等边三角形,所以3BED πθ∠==, 连接1B D ,则222122426B D =++=22222BE DE ==+=取1B D 的中点O ,连接EO ,则16BO 862EO =-=所以16tan 32B EO ∠==, 所以13B EO π∠=,即123B ED πγ∠==,所以γαθ>>.故选:B4.已知长方体1111ABCD A B C D -,下列向量的数量积一定不为0的是( )A .1AD AB ⋅B .11AD BC ⋅ C .1BD BC ⋅ D .1BD AC ⋅【答案】C【分析】利用正方体几何性质计算出数量积为零的选项,根据长方体的性质证明数量积一定不为零的选项.【详解】当长方体1111ABCD A B C D -为正方体时,根据正方体的性质可知: 1111,,AB AD AD B C BD AC ⊥⊥⊥,所以10AB AD ⋅=、110AD B C ⋅=、10BD AC ⋅=.根据长方体的性质可知:1BC CD ⊥,所以1BD 与BC 不垂直,即1BD BC ⋅一定不为0.故选:C5.(2020·上海高三一模)已知正方体1111ABCD A B C D -,点P 是棱1CC 的中点,设直线AB 为a ,直线11A D 为b .对于下列两个命题:①过点P 有且只有一条直线l 与a 、b 都相交;②过点P 有且只有一条直线l 与a 、b 都成45︒角.以下判断正确的是( )A .①为真命题,②为真命题B .①为真命题,②为假命题C .①为假命题,②为真命题D .①为假命题,②为假命题【答案】B 【分析】作出过P 与两直线相交的直线l 判断①;通过平移直线a ,b ,结合异面直线所成角的概念判断②.【详解】解:直线AB 与A 1D 1 是两条互相垂直的异面直线,点P 不在这两异面直线中的任何一条上,如图所示:取BB 1的中点Q ,则PQ ∥A 1D 1,且 PQ =A 1D 1,设A 1Q 与AB 交于E ,则点A 1、D 1、Q 、E 、P 共面, 直线EP 必与A 1D 1 相交于某点F ,则过P 点有且只有一条直线EF 与a 、b 都相交,故①为真命题; 分别平移a ,b ,使a 与b 均经过P ,则有两条互相垂直的直线与a ,b 都成45°角,故②为假命题. ∴①为真命题,②为假命题.故选:B .【点睛】本题考查立体几何图形中直线和平面的相交、平行、垂直的性质,体现了数形结合的数学思想,是中档题.二、填空题6.(2020·上海青浦区·高三一模)圆锥底面半径为1cm ,母线长为2cm ,则其侧面展开图扇形的圆心角θ=___________.【答案】π;【分析】根据圆的周长公式易得圆锥底面周长,也就是圆锥侧面展开图的弧长,利用弧长公式可得圆锥侧面展开图扇形的圆心角的大小.【详解】因为圆锥底面半径为1cm ,所以圆锥的底面周长为2cm π, 则其侧面展开图扇形的圆心角22πθπ==, 故答案为:π.【点睛】思路点睛:该题考查的是有关圆锥侧面展开图的问题,解题思路如下:(1)首先根据底面半径求得底面圆的周长;(2)根据圆锥侧面展开图扇形的弧长就是底面圆的周长,结合母线长,利用弧长公式求得圆心角的大小. 7.(2020·上海闵行区·高三一模)如图,已知正四棱柱1111ABCD A B C D -的底面边长为2,高为3,则异面直线1AA 与1BD 所成角的大小是_______.【答案】22;【分析】根据11//AA DD ,得到1DD B ∠异面直线1AA 与1BD 所成的角,然后在1Rt DD B △,利用正切函数求解.【详解】因为11//AA DD ,所以1DD B ∠异面直线1AA 与1BD 所成的角,在正四棱柱1111ABCD A B C D -的底面边长为2,高为3, 所以1122tan 3BD DD B DD ∠==, 因为1(0,)2DD B π∠∈, 所以122arctan3DD B ∠=, 故答案为:22arctan 38.(2019·上海市建平中学高三月考)某几何体由一个半圆锥和一个三棱锥组合而成,其三视图如图所示(单位:厘米),则该几何体的体积(单位:立方厘米)是________.【答案】12π+2,高为3;半圆锥的底面是半径为1的半圆,高为3;据此计算出该几何体的体积.【详解】由三视图可知,三棱锥的体积:1223132V ⎛=⨯⨯= ⎝⎭;半圆锥体积:()11113232V ππ=⨯⨯⨯⨯⨯=,所以总体积为:12π+. 故答案为12π+.【点睛】本题考查空间几何体的体积计算,难度较易.计算组合体的体积时,可将几何体拆分为几个容易求解的常见几何体,然后根据体积公式完成求解.9.(2020·上海高三其他模拟)如图直三棱柱ABB 1-DCC 1中, BB 1⊥AB ,AB=4,BC=2,CC 1=1,DC 上有一动点P ,则△APC 1周长的最小值是 .【答案】521+试题分析:要求周长的最小值,因边为定值,只要求另两边之和的最小值,因两点直线线段最短,所以的最小值为因此△APC 1周长的最小值是521考点:棱柱的相关知识.10.(2020·上海高三一模)已知母线长为6cm 的圆锥的侧面积是底面积的3倍,则该圆锥的底面半径为________cm .【答案】2【分析】设底面半径为r ,由两个面积的关系可得底面半径的值.【详解】解:设底面半径为r ,则由题意,可得213262r r ππ=⨯⨯,解得2r , 故答案为:2.【点睛】本题考查圆锥的侧面积及圆的面积公式,属于基础题.11.(2020·上海高三其他模拟)已知圆锥的母线长为l ,过圆锥顶点的最大截面三角形的面积为212l ,则此圆锥底面半径r 与母线长l 的比r l的取值范围是____________. 【答案】22【分析】先判断两条母线的夹角=90θ时最大截面三角形的面积为212l 22l r ≤和r l <,最后求出r l 的取值范围即可. 【详解】解:过圆锥顶点的截面三角形的面积:1sin 2S l l θ=⋅⋅(θ为两母线的夹角), 因为过圆锥顶点的最大截面三角形的面积为212l ,即两条母线的夹角=90θ时的截面面积,此时底面弦长为2l ,所以22l r ≤,又r l <,所以212r l≤<, 故答案为:2[,1)2【点睛】本题考查空间几何体,是基础题.12.(2020·上海青浦区·高三二模)用一平面去截球所得截面的面积为23cm π,已知球心到该截面的距离为1cm ,则该球的表面积是___________2cm .【答案】16π【分析】由已知求出小圆的半径,然后利用勾股定理求出球的半径,即可求出球的表面积【详解】解:因为用一平面去截球所得截面的面积为23cm π,所以小圆的半径为3cm ,因为球心到该截面的距离为1cm ,所以球的半径为221(3)2+=cm ,所以球的表面积为24216S ππ=⨯=2cm ,故答案为:16π【点睛】此题考查球的截面的半径、球心到截面的距离与球的半径间的关系,属于基础题13.(2020·上海普陀区·高三月考)已知一个半圆柱的高为4,其俯视图如图所示,其左视图的面积为8,则该半圆柱的表面积为______.【答案】1612+π【分析】由圆柱的主视图和左视图知该圆柱的底面直径为4,高为3,由此能求出该几何体的表面积,得到答案.【详解】由题意,其左视图为矩形,其左视图的面积为8,半圆柱的高h 为4,可得半圆的半径r 为2,由于半圆柱的表面积为两个底面半圆面积加侧面展开图形的面积, 即2211222224224161222S r rh rh πππππ=⨯⨯++=⨯⨯⨯+⨯⨯+⨯⨯=+.故答案为:1612+π.【点睛】本题主要考查了空间几何体的三视图的应用,以及圆柱的表面积的计算问题,同时考查了圆柱的结构特征的应用,属于基础题.三、解答题14.(2020·上海虹口区·高三一模)如图在三棱锥P ABC -中,棱AB 、AC 、AP 两两垂直,3AB AC AP ===,点M 在AP 上,且1AM =.(1)求异面直线BM 和PC 所成的角的大小;(2)求三棱锥P BMC -的体积.【答案】(1)5(2)3. 【分析】(1)以点A 为坐标原点,AB 、AC 、AP 所在直线分别为x 、y 、z 轴建立空间直角坐标系A xyz -,利用空间向量法可求得异面直线BM 和PC 所成的角的大小;(2)计算出PMC △的面积,并推导出AB ⊥平面PMC ,利用锥体的体积公式可求得三棱锥P BMC -的体积.【详解】(1)由于AB 、AC 、AP 两两垂直,以点A 为坐标原点,AB 、AC 、AP 所在直线分别为x 、y 、z 轴建立空间直角坐标系A xyz -,如下图所示:则()3,0,0B 、()0,0,0A 、()0,3,0C 、()0,0,3P 、()0,0,1M ,()3,0,1BM =-,()0,3,3PC =-,5cos ,101032BM PC BM PC BM PC⋅<>===-⨯⋅,因此,异面直线BM 和PC 所成的角的大小为5arccos 10; (2)AB AC ⊥,AB AP ⊥,AC AP A =,AB ∴⊥平面APC ,AC AP ⊥,1AM =,2PM AP AM ∴=-=,132PMC S PM AC ∴=⋅=△, 1133333B PMC PMC V S AB -=⋅=⨯⨯=△.【点睛】方法点睛:求空间角的常用方法:(1)定义法:由异面直线所成角、线面角、二面角的定义,结合图形,作出所求空间角,再结合题中条件,解对应的三角形,即可求出结果;(2)向量法:建立适当的空间直角坐标系,通过计算向量的夹角(两直线的方向向量、直线的方向向量与平面的法向量、两平面的法向量)的余弦值,即可求得结果.15.(2020·上海青浦区·高三一模)如图,在长方体1111ABCD A B C D -中,1AB AD ==,12AA =,点P 为棱1DD 的中点.(1)证明:1//BD 平面P AC ;(2)求异面直线1BD 与AP 所成角的大小. 【答案】(1)证明见解析;(2)30.【分析】(1)AC 和BD 交于点O ,则O 为BD 的中点.推导出1//PO BD .由此能证明直线1//BD 平面PAC ;(2)由1//PO BD ,得APO ∠即为异面直线1BD 与AP 所成的角或其补角.由此能求出异面直线1BD 与AP 所成角的大小.【详解】(1)证明:设AC 和BD 交于点O ,则O 为BD 的中点. 连结PO ,又因为P 是1DD 的中点,所以1//PO BD . 又因为PO ⊂平面P AC ,1BD ⊄平面P AC 所以直线1//BD 平面P AC.(2)解:由(1)知,1//PO BD ,所以APO ∠即为异面直线1BD 与AP 所成的角或其补角.因为2PA PC ==,2122AO AC ==且PO AO ⊥, 所以212sin 22AO APO AP ∠===. 又(0,90APO ︒︒⎤∠∈⎦,所以30APO ∠=︒ 故异面直线1BD 与AP 所成角的大小为30. 【点睛】方法点睛:异面直线所成的角的求法方法一:(几何法)找→作(平移法、补形法)→证(定义)→指→求(解三角形) 方法二:(向量法)cos m n m nα=,其中α是异面直线,m n 所成的角,,m n 分别是直线,m n 的方向向量.16.(2020·上海长宁区·高三一模)如图,已知圆锥的顶点为P ,底面圆心为O ,高为23,底面半径为2.(1)求该圆锥的侧面积;(2)设OA 、OB 为该圆锥的底面半径,且90AOB ∠=︒,M 为线段AB 的中点,求直线PM 与直线OB 所成的角的正切值.【答案】(1)8π;(213【分析】(1)利用圆锥侧面积公式即可;(2)通过中点作辅助线即可. 【详解】解:(1)OP ⊥底面OAB 由题意高3h =2r ,所以母线4l圆锥的侧面积S =12lr 12242π=⨯⨯⨯8π= (2)取OA 的中点为N ,因为M 为AB 的中点所以//MN OB ,PMN ∠就是直线PM 与直线OB 所成的角. 因为OB OA ⊥,OB OP ⊥,所以OB ⊥平面POA ,MN ⊥平面POA ,MN PN ⊥ 在Rt △PNM 中,22()132rPN h =+=,112MN OB ==.所以PMN ∠的正切值为13.即直线PM 与直线OB 所成的角正切值为13.17.(2020·上海徐汇区·高三一模)如图:在直三棱柱111ABC A B C -中,2AC BC ==,14CC =,90ACB ∠=,E 、F 分别为棱1AA 、AB 的中点.(1)求异面直线1A C 与EF 所成的角的大小(结果用反三角函数值表示); (2)求五棱锥11C EFBB A -的体积11C EFBB A V -. 【答案】(1)5arctan (2)143.【分析】(1)连接1A B ,利用中位线的性质可得出1//A B EF ,由此可得出1BA C ∠(或其补角)就是异面直线1A C 与EF 所成的角,利用解三角形的知识求出1BA C ∠的正切值,即可得解;(2)计算出五边形1EFBB A 的面积,并推导出CF ⊥平面11AA B B ,再利用锥体的体积公式可计算出五棱锥11C EFBB A -的体积11C EFBB A V -. 【详解】 (1)连接1A B ,E 、F 分别为1AA 、AB 的中点,所以,1//A B EF ,于是1BA C ∠(或其补角)就是异面直线1A C 与EF 所成的角, 在1A BC 中,2BC =,221125AC AA AC =+=,221126A B AA AB =+=,22211A C BC A B ∴+=,所以1BC A C ⊥,所以,1125tan 525BC BAC AC ∠===. 所以,异面直线1A C 与EF 所成角的大小为5arctan5;(2)由于111111822722AEFEFBB A ABB A S S S AB AA AE AF =-=⋅-⋅==五边形矩形 连接CF ,2AC BC ==,F 为AB 的中点,90ACB ∠=,CF AB ∴⊥,且122CF AB == 1AA ⊥平面ABC ,CF ⊂平面ABC ,1CF AA ∴⊥,1AB AA A ⋂=,CF ∴⊥平面11AA B B ,所以11111114722333C EFBB A EFBB A V S CF -=⋅=⨯⨯=五边形. 【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:(1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.18.(2020·上海大学附属中学高三三模)如图,正四棱锥P ABCD -中.(1)求证:BD ⊥平面PAC ; (2)若2AB =,423P ABCD V -=,求二面角A PB C --的余弦值. 【答案】(1)证明见解析;(2)1arccos 3⎛⎫- ⎪⎝⎭【分析】(1)先证明PO BD ⊥,结合,BD AC ⊥利用线面垂直的判定定理可得结论;(2)由423P ABCD V -=求出棱锥的高,可求得侧棱长,判定侧面的形状后可得二面角的平面角,利用余弦定理可得答案. 【详解】(1)因为P ABCD -是正棱锥,P ∴在面ABCD 内射影是AC 与BD 的交点O ,即PO ⊥面ABCD ,PO BD ∴⊥,又,BD AC PO ⊥与AC 在面PAC 内相交,BD ∴⊥面PAC ;(2)2142233P ABCD V PO -=⨯⨯=, 2PO ∴=,222PB =+=,则PAB △与PBC 为边长是2的正三角形,取PB 的中点E ,连,AE CE , 则AE PB ⊥,CE PB ⊥,AEC ∠是二面角的平面角,3381cos 3233AEC +-∠==-⨯⨯,1cos 3AEC arc ⎛⎫∠=- ⎪⎝⎭【点睛】本题主要考查线面垂直的证明以及二面角的求解,考查了正四棱锥的性质,属于中档题.19.(2019·上海市建平中学高三月考)如图:四面体ABCD 的底面ABC 是直角三角形,AC BC ⊥,3AC =,4BC =,DA ⊥平面ABC ,5DA =,E 是BD 上的动点(不包括端点).(1)求证:AE 与BC 不垂直;(2)当AE DC ⊥时,求DEEB的值. 【答案】(1)证明见解析;(2)259.【分析】(1)利用反证法,先假设AE 与BC 垂直,然后根据条件推出与题设矛盾的结论,即可证明出AE与BC 不垂直;(2)先作辅助线//EF BC ,利用AE DC ⊥以及BC ⊥平面DAC 得到DC ⊥平面AEF ,由此得到AF DC ⊥,从而确定出F 点位置,再由DE DFEB FC=得到结果. 【详解】(1)假设AE BC ⊥,因为DA ⊥平面ABC ,所以DA BC ⊥,且DA AE A =,所以BC ⊥平面DAE ,又因为AB平面DAE ,所以BC AB ⊥,又因为由条件可知BC AC ⊥,所以BC AB ⊥不成立, 故假设不成立,所以AE 与BC 不垂直;(2)过E 作//EF BC ,交DC 于F ,连接AF ,因为AC BC ⊥,DA BC ⊥且DA AC A =,所以BC ⊥平面DAC ,因为//EF BC ,所以EF ⊥平面DAC ,所以EF DC ⊥, 又因为AE DC ⊥,EF DC ⊥,EF AE E =,所以DC ⊥平面AEF ,所以DC AF ⊥,又cos 25934AD ADC DC ∠===+,所以cos cos 34DF ADF ADC AD ∠=∠==, 所以34DF =,所以34FC =,所以259DF FC =,所以由相似可知259DE DF EB FC ==. 【点睛】本题考查空间中的垂直关系的判断与证明,难度一般.空间中的不平行、不垂直关系的证明,如果正面证明比较麻烦,可采用反证法去证明.20.(2020·上海市七宝中学高三其他模拟)如图,四边形11ABB A 是圆柱1OO 的轴载面,4AB =,12OO =,以圆柱上底面为底面作高为2的圆锥1PO ,C 、1C 分别在AB 、11A B 上,2AOC π∠=,1113AO C π∠=.(1)求这个几何体的表面积和体积; (2)求二面角111O AC C --的余弦值. 【答案】(1)表面积为(1242π+,体积为323π;(23823-. 【分析】(1)计算出圆锥的母线长,利用圆锥的侧面积公式和圆柱的侧面积、底面积公式可计算出几何体的表面积,结合柱体和锥体的体积公式可求得几何体的体积;(2)以点O 为坐标原点,OA 、OC 、OP 所在直线分别为x 、y 、z 轴建立空间直角坐标系O xyz -,利用空间向量法可求得二面角111O AC C --的余弦值. 【详解】(1)由题意可知,圆柱的底面半径为22ABr ==, 因为1PO 为圆锥的高,且12PO =,所以,圆锥的母线长为221122PA PO r =+=,又12OO =,因此,该几何体的表面积为(22+2222221242S ππππ=⨯⨯⨯+⨯=+.该几何体的体积为22132222233V πππ=⨯⨯+⨯⨯⨯=; (2)以点O 为坐标原点,OA 、OC 、OP 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系O xyz -,则点()10,0,2O ,()12,0,2A ,()13,2C ,()0,2,0C ,设平面11A CC 的一个法向量为(),,m x y z =,()113,0AC =-,()12,2,2AC =--, 由11100m AC m AC ⎧⋅=⎪⎨⋅=⎪⎩,得302220x x y z ⎧-=⎪⎨-+-=⎪⎩,令3x =1y =,13z =所以,平面11A CC 的一个法向量为(3,1,13m =,易知平面111O AC 的一个法向量为()0,0,1n =,()()22233cos ,82331131m n m n m n⋅<>===⋅-++-⨯,由图象可知,二面角111O AC C --31823--【点睛】本题考查组合体的表面积与体积的计算,同时也考查了利用空间向量法计算二面角的余弦值,考查计算能力,属于中等题.21.(2020·上海高三其他模拟)如图,已知⊙O 的直径AB=3,点C 为⊙O 上异于A ,B 的一点,VC ⊥平面ABC ,且VC=2,点M 为线段VB 的中点.(1)求证:BC ⊥平面VAC ;(2)若直线AM 与平面V AC 所成角为4π.求三棱锥B-ACM 的体积. 【答案】(1))祥见解析;(2)试题分析:(1)由线面垂直得VC ⊥BC ,由直径性质得AC ⊥BC ,由此能证明BC ⊥平面V AC .(2)首先由(1)作出直线AM 与平面V AC 所成的角:取VC 的中点N ,连接MN ,AN ,则MN ∥BC ,由(I )得BC ⊥平面VAC ,所以MN ⊥平面V AC ,则∠MAN 为直线AM 与平面V AC 所成的角.即∠MAN=4π,所以MN=AN ;这样就可求出AC 的长,且而求得体积.试题解析:(1)证明:因为VC ⊥平面ABC ,BC ABC ⊂平面,所以VC ⊥BC ,又因为点C 为圆O 上一点,且AB 为直径,所以AC ⊥BC ,又因为VC ,AC ⊂平面V AC ,VC∩AC=C ,所以BC ⊥平面V AC.(2)如图,取VC 的中点N ,连接MN ,AN ,则MN ∥BC ,由(I )得BC ⊥平面V AC ,所以MN ⊥平面V AC ,则∠MAN 为直线AM 与平面V AC 所成的角.即∠MAN=4π,所以MN=AN ;令AC=a,则29-a ,MN=292a -;因为VC=2,M 为VC 中点,所以21a + 所以,292a -=21a +,解得a=1 因为MN ∥BC,所以考点:1.直线与平面垂直的判定;2. 棱柱、棱锥、棱台的体积;3. 直线与平面所成的角.22.(2020·上海高三其他模拟)已知正方体1111ABCD A B C D -,12AA =,E 为棱1CC 的中点.(1)求异面直线AE 与1DD 所成角的大小(结果用反三角表示);(2)求C 点到平面ABE 的距离,并求出三锥C ADE -的体积.【答案】(1)1arccos 3;(2)C 点到平面ABE 25,三锥C ADE -的体积为23. 【分析】(1)由已知得AEC ∠(或补角)是异面直线AE 与1DD 所成角,求解AEC 可得答案;(2)利用等体积E ABC C ABE V V --=,可求得设C 点到平面ABE 的距离,利用C ADE A CDE V V --=,可求得三锥C ADE -的体积.【详解】解:(1)连接AC ,因为11//CC DD ,所以AEC ∠(或补角)是异面直线AE 与1DD 所成角, 在AEC 中,()22221cos 3221EC AEC AE AC EC ∠====++, 所以异面直线AE 与1DD 所成角是1arccos 3;(2)设C 点到平面ABE 的距离为h ,因为E ABC C ABE V V --=,即1133ABC ABE S EC S h ⋅=⋅△△, 又正方体1111ABCD A B C D -中,AB ⊥面11BB C C ,所以ABE △是Rt ABE △,又2222215BE BC EC =+=+=, 所以1111221253232h ⨯⨯⨯⨯=⨯⨯⨯⋅,解得255h =, 所以C ADE A CDE V V --=111212332DCE S AD ⎛⎫=⋅=⨯⨯⨯⨯ ⎪⎝⎭△23=.【点睛】本题考查空间中异面直线所成的角,运用等体积法求点到面的距离以及三棱锥的体积,属于中档题.。
高中空间立体几何经典例题精选全文完整版

可编辑修改精选全文完整版立体几何一、选择题1.(20XX 年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是 ( )A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥【答案】D2 2.(20XX 年上海市春季高考数学试卷(含答案))若两个球的表面积之比为1:4,则这两个球的体积之比为( )A .1:2B .1:4C .1:8D .1:16【答案】C 【答案】A3 3.(20XX 年高考新课标1(理))某几何体的三视图如图所示,则该几何体的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A4 4.(20XX 年高考湖南卷(理))已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 ( )A .1B .2C .2-12D .2+12【答案】C5.(20XX 年普通高等学校招生统一考试山东数学(理)试题(含答案))已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94,底面是边长为3.若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为( )A.512πB .3πC.4πD.6π【答案】B6.(20XX年普通高等学校招生统一考试重庆数学(理)试题(含答案))某几何体的三视图如题()5图所示,则该几何体的体积为()A.5603B.5803C.200D.240【答案】C7.(20XX年高考江西卷(理))如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为,m n,那么m n+=()A.8 B.9 C.10 D.11【答案】A二、填空题8.(20XX年高考北京卷(理))如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为__________.1D1BPD1CCEBA1A【答案】2559.(20XX 年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V ____________.【答案】1:2410.(20XX 年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))某几何体的三视图如图所示,则该几何体的体积是____________.【答案】1616π-11.(20XX 年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________【答案】12π12.(20XX 年上海市春季高考数学试卷(含答案))在如图所示的正方体1111ABCD A B C D -中,异面直线1A B 与1B C 所成角的大小为_______AB C1A D EF1B 1C【答案】3π三、解答题13.(20XX 年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))如图,AB是圆的直径,PA 垂直圆所在的平面,C 是圆上的点. (I)求证:PAC PBC ⊥平面平面;(II)2.AB AC PA C PB A ===--若,1,1,求证:二面角的余弦值D 1 C 1 B 1A 1D C AB14.(20XX 年上海市春季高考数学试卷(含答案))如图,在正三棱锥111ABC A B C -中,16AA =,异面直线1BC 与1AA 所成角的大小为6π,求该三棱柱的体积.【答案】[解]因为1CC 1AA .所以1BC C ∠为异面直线1BC 与1AA .所成的角,即1BC C ∠=6π. 在Rt 1BC C ∆中,113tan 6233BC CC BC C =⋅∠==从而2333ABC S BC ∆==因此该三棱柱的体积为1336183ABC V S AA ∆=⋅==15.(20XX 年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))B 1 A 1C 1ACB如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点.求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.【答案】证明:(1)∵AB AS =,SB AF ⊥∴F 分别是SB 的中点 ∵E.F 分别是SA.SB 的中点 ∴EF ∥AB又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF ∥平面ABC 同理:FG ∥平面ABC又∵EF FG=F, EF.FG ⊆平面ABC ∴平面//EFG 平面ABC (2)∵平面⊥SAB 平面SBC 平面SAB 平面SBC =BC AF ⊆平面SAB AF ⊥SB∴AF ⊥平面SBC 又∵BC ⊆平面SBC ∴AF ⊥BC又∵BC AB ⊥, AB AF=A, AB.AF ⊆平面SAB ∴BC ⊥平面SAB 又∵SA ⊆平面SAB ∴BC ⊥SA16.(20XX 年高考上海卷(理))如图,在长方体ABCD-A 1B 1C 1D 1中,AB=2,AD=1,A 1A=1,证明直线BC 1平行于平面DA 1C,并求直线BC 1到平面D 1AC 的距离.C 11A【答案】因为ABCD-A 1B 1C 1D 1为长方体,故1111//,AB C D AB C D =,故ABC 1D 1为平行四边形,故11//BC AD ,显然B 不在平面D 1AC 上,于是直线BC 1平行于平面DA 1C; 直线BC 1到平面D 1AC 的距离即为点B 到平面D 1AC 的距离设为h考虑三棱锥ABCD 1的体积,以ABC 为底面,可得111(12)1323V =⨯⨯⨯⨯=而1AD C ∆中,11AC DC AD ==故132AD C S ∆= AB CSGFE所以,13123233V h h =⨯⨯=⇒=,即直线BC 1到平面D 1AC 的距离为23.17.(20XX 年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))如图1,在等腰直角三角形ABC中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE =O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '(Ⅰ) 证明:A O '⊥平面BCDE ; (Ⅱ) 求二面角A CD B '--的平面角的余弦值.【答案】(Ⅰ) 在图1中,易得3,OC AC AD ===连结,OD OE,在OCD ∆中,由余弦定理可得OD=由翻折不变性可知A D '=,所以222A O OD A D ''+=,所以A O OD '⊥,理可证A O OE '⊥, 又OD OE O =,所以A O '⊥平面BCDE . (Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角. 结合图1可知,H 为AC 中点,故2OH =,从而2A H '== 所以cos OH A HO A H '∠=='所以二面角ACD B '--向量法:以O 点为原点,建立空间直角坐标系O -.CO BDEA CDOBE'A图1图2C DO BE'AH则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=- 设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y ⎧+=⎪⎨-++=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,1,n =- 由(Ⅰ)知,(OA '=为平面CDB 的一个法向量,所以3cos ,3n OA n OA n OA'⋅'===',即二面角A CD B '--的平面角的余弦值为5.18.(20XX年普通高等学校招生统一考试天津数学(理)试题(含答案))如图, 四棱柱ABCD-A1B1C1D1中, 侧棱A1A⊥底面ABCD, AB//DC, AB⊥AD, AD = CD = 1, AA1 = AB = 2, E为棱AA1的中点.(Ⅰ) 证明B1C1⊥CE;(Ⅱ) 求二面角B1-CE-C1的正弦值.(Ⅲ) 设点M在线段C1E上, 且直线AM与平面ADD1A1所成角的正弦值为2, 求线段AM的长.6【答案】19.(20XX年高考陕西卷(理))如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,12AB AA==(Ⅰ) 证明: A1C⊥平面BB1D1D;(Ⅱ) 求平面OCB1与平面BB1D1D的夹角θ的大小.1A【答案】解:(Ⅰ) BDOAABCDBDABCDOA⊥∴⊂⊥11,,面且面;又因为,在正方形AB CD 中,BDCAACACAACABDAACOABDAC⊥⊂⊥=⋂⊥11111,,故面且面所以;且.在正方形AB CD中,AO = 1 . .111=∆OAOAART中,在OECAOCEAEDB1111111⊥为正方形,所以,则四边形的中点为设.,所以由以上三点得且,面面又OOBDDDBBODDBBBD=⋂⊂⊂111111E.E,DDBBCA111面⊥.(证毕)(Ⅱ) 建立直角坐标系统,使用向量解题.以O为原点,以OC为X轴正方向,以OB为Y轴正方向.则)1,0,1()1,1,1(),10(),1(,0,1,0111-=⇒CABACB,,,,)(.由(Ⅰ)知, 平面BB1D1D的一个法向量.0,0,1),1,1,1(),1,0,1(111)(==-==OCOBCAn设平面OCB1的法向量为,则0,0,2122=⋅=⋅OCnOBnn).1-,1,0(法向量2=n为解得其中一个21221||||||,cos|cos212111=⋅=⋅=><=nnnnnnθ.所以,平面OCB1与平面BB1D1D的夹角θ为3π1A。
(完整word版)高中数学立体几何专项练习

立体几何简答题练习1、正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q,且AP=DQ。
求证:PQ∥平面BCE.(用两种方法证明)2、如图所示,P是平行四边形ABCD所在平面外一点,E、F分别在PA、BD上,且PE:EA=BF:FD,求证:EF∥平面PBC.3、如图,E,F,G,H分别是正方体ABCD-A1B1C1D1的棱BC,CC1,C1D1,AA1的中点。
求证:(1)EG∥平面BB1D1 D;(2)平面BDF∥平面B1D1 H.4、如图所示,已知P 是平行四边形ABCD 所在平面外一点,M 、N 分别为AB 、PC 的中点,平面PAD ∩平面PBC =l. (1)求证:l ∥BC ;(2)MN 与平面PAD 是否平行?试证明你的结论。
5、如图,在四棱锥S-ABCD 中,底面ABCD 是正方形,SA ⊥底面ABCD ,SA=SB ,点M 是SD 的中点,AN ⊥SC ,且交SC 于点N 。
(1)求证:SB ∥平面ACM ;(2)求证:平面SAC ⊥平面AMN ; (3)求二面角D-AC-M 的余弦值。
6、如图,在四棱锥P-ABCD 中,底面ABCD 是边长为2的正方形,侧面PAD ⊥底面ABCD,且PA=PD=22AD,E 、F 分别为PC 、BD 的中点. 求证:(1) 求证:EF ∥平面PAD; (2) 求证:平面PAB ⊥平面PDC;(3) 在线段AB 上是否存在点G,使得二面角C-PD-G 的余弦值为31?说明理由.7、如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点。
(1)求证:C1M∥平面A1ADD1;(2)若CD1垂直于平面ABCD且CD1=3,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值。
8、如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点.(1)证明:PA∥平面EDB;(2)证明:BC⊥DE.9、三棱柱ABC﹣A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.(Ⅰ)求证:MN||平面BCC1B1;(Ⅰ)求证:平面AMN⊥平面A1B1C.10、如图,在三棱锥P﹣ABC中,PA⊥PC,AB=PB,E,F分别是PA,AC的中点.求证:(1)EF∥平面PBC;(2)平面BEF⊥平面PAB.11、如图所示,四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,点M,N分别是AB,PC的中点,且PA=AD(1)求证:MN∥平面PAD(2)求证:平面PMC⊥平面PCD.12、如图,在直三棱柱ABC﹣A1B1C1中,BC⊥AC,D,E分别是AB,AC的中点.(1)求证:B1C1∥平面A1DE;(2)求证:平面A1DE⊥平面ACC1A1.8、如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.△PAD为正三角形,其所在平面垂直于底面ABCD.若G为AD 边的中点,求证:平面PBG⊥平面PAD;9、如图所示,在四棱柱P-ABCD中,底面ABCD是边长为a菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD。
高中数学立体几何专题

高中课程复习专题——数学立体几何一 空间几何体 ㈠ 空间几何体的类型1 多面体:由若干个平面多边形围成的几何体.围成多面体的各个多边形叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点.2 旋转体:把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。
其中,这条直线称为旋转体的轴。
㈡ 几种空间几何体的结构特征 1 棱柱的结构特征1.1 棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1。
2 棱柱的分类1。
3 棱柱的性质⑴ 侧棱都相等,侧面是平行四边形;⑵ 两个底面与平行于底面的截面是全等的多边形; ⑶ 过不相邻的两条侧棱的截面是平行四边形; ⑷ 直棱柱的侧棱长与高相等,侧面的对角面是矩形。
1.4 长方体的性质⑴ 长方体的一条对角线的长的平方等于一个顶点上三 条棱的平方和:AC 12 = AB 2 + AC 2 + AA 12⑵ 长方体的一条对角线AC 1与过定点A 的三条棱所成 的角分别是α、β、γ,那么:cos 2α + cos 2β + cos 2γ = 1 sin 2α + sin 2β + sin 2γ = 2⑶ 长方体的一条对角线AC 1与过定点A 的相邻三个面所组成的角分别为α、β、γ,则:cos 2α + cos 2β + cos 2γ = 2 sin 2α + sin 2β + sin 2γ = 11。
5 棱柱的侧面展开图:正n 棱柱的侧面展开图是由n 个全等矩形组成的以底面周长和侧棱为邻边的矩形。
图1-1 棱柱图1-2 长方体图1-1 棱柱1。
6 棱柱的面积和体积公式S 直棱柱侧面 = c ·h (c 为底面周长,h 为棱柱的高) S 直棱柱全 = c ·h+ 2S 底 V 棱柱 = S 底 ·h 2 圆柱的结构特征2—1 圆柱的定义:以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱. 2-2 圆柱的性质⑴ 上、下底及平行于底面的截面都是等圆; ⑵ 过轴的截面(轴截面)是全等的矩形.2—3 圆柱的侧面展开图:圆柱的侧面展开图是以底面周长和母线长为邻边的矩形. 2—4 圆柱的面积和体积公式S 圆柱侧面 = 2π·r ·h (r 为底面半径,h 为圆柱的高) S 圆柱全 = 2π r h + 2π r 2 V 圆柱 = S 底h = πr 2h 3 棱锥的结构特征 3—1 棱锥的定义⑴ 棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题三立体几何专题【命题趋向】高考对空间想象能力的考查集中体现在立体几何试题上,着重考查空间点、线、面的位置关系的判断及空间角等几何量的计算.既有以选择题、填空题形式出现的试题,也有以解答题形式出现的试题.选择题、填空题大多考查概念辨析、位置关系探究、空间几何量的简单计算求解,考查画图、识图、用图的能力;解答题一般以简单几何体为载体,考查直线与直线、直线与平面、平面与平面的位置关系,以及空间几何量的求解问题,综合考查空间想象能力、推理论证能力和运算求解能力.试题在突出对空间想象能力考查的同时,关注对平行、垂直关系的探究,关注对条件或结论不完备情形下的开放性问题的探究.【考点透析】立体几何主要考点是柱、锥、台、球及其简单组合体的结构特征、三视图、直观图,表面积体积的计算,空间点、直线、平面的位置关系判断与证明,(理科)空间向量在平行、垂直关系证明中的应用,空间向量在计算空间角中的应用等.【例题解析】题型 1 空间几何体的三视图以及面积和体积计算例 1( 2008 高考海南宁夏卷)某几何体的一条棱长为7 ,在该几何体的正视图中,这条棱的投影是长为 6 的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为 a 和b的线段,则a b 的最大值为A.22B.23C. 4D.25分析:想像投影方式,将问题归结到一个具体的空间几何体中解决.解析:结合长方体的对角线在三个面的投影来理解计算,如图设长方体的高宽高分别为m, n, k ,由题意得m2n2k27 ,m2k26n 1 ,1 k2 a , 1m2 b ,所以( a21)(b21)6a2b28,∴ (a b)2a22ab b282ab8 a2b216 a b 4当且仅当 a b 2时取等号.点评 :本题是课标高考中考查三视图的试题中难度最大的一个,我们通过移动三个试图把问题归结为长方体的一条体对角线在三个面上的射影,使问题获得了圆满的解决.例 2 ( 2008 高考山东卷、 2009 年福建省理科数学高考样卷第 3 题)下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是 A . 9πB . 10πC . 11πD . 12π分析:想像、还原这个空间几何体的构成,利用有关的计算公式解答. 解析: 这个空间几何体是由球和圆柱组成的,圆柱的底面半径是 1 3,球的,母线长是 半径是 1,故其表面积是 213212 4 1212,答案 D .点评:由三视图还原空间几何体的真实形状时要注意 “高平齐、 宽相等、 长对正 ”的规则.例 3(江苏省苏州市 2009 届高三教学调研测试第12 题)已知一个正三棱锥 PABC 的主视图如图所示,若ACBC3,2PC 6 ,则此正三棱锥的全面积为 _________ .分析 :正三棱锥是顶点在底面上的射影是底面正三角形的中心的三棱锥,根据这个主试图知道,主试图的投影方向是面对着这个正三棱锥的一条侧棱,并且和底面三角形的一条边垂直,这样就知道了这个三棱锥的各个棱长.解析:这个正三棱锥的底面边长是3、高是 6 ,故底面正三角形的中心到一个顶点的距离是233 3 ,故这个正三棱锥的侧棱长是22 3 ,由此知道这个3632正三棱锥的侧面也是边长为 3 的正三角形,故其全面积是43329 3,答案9 3 .4点评:由空间几何体的一个视图再加上其他条件下给出的问题,对给出的这“一个视图”要仔细辨别投影方向,这是三视图问题的核心.题型 2 空间点、线、面位置关系的判断42009届高三教学调研测试7m,n是两条不同的直线,,为例(江苏苏州市)已知两个不同的平面,有下列四个命题:①若 m, n, m n ,则;②若 m //, n //, m n ,则//;③若 m,n //, m n ,则//;④若 m,n //, //,则m n .其中正确的命题是(填上所有正确命题的序号)_______________ .分析:根据空间线面位置关系的判定定理和性质定理逐个作出判断.解析:我们借助于长方体模型解决.①中过直线m,n 作平面,可以得到平面,所成的二面角为直二面角,如图(1),故①正确;②的反例如图(2);③的反例如图( 3);④中由m,P可得m,过n 作平面可得n 与交线g 平行,由于m g ,故m n.答案①④.点评:新课标的教材对立体几何处理的基本出发点之一就是使用长方体模型,本题就是通过这个模型中提供的空间线面位置关系解决的,在解答立体几何的选择题、填空题时合理地使用这个模型是很有帮助的.例 5(浙江省2009 年高考省教研室第一次抽样测试理科第 5 题)设m, n是两条不同的直线,,是两个不同的平面,下列命题正确的是A .若m n, m, n //,则C.若m, n // , //,则//B.若m n D.若m // , n // , // , 则m // n m //n,m // , n // , 则 //分析:借助模型、根据线面位置关系的有关定理逐个进行分析判断.解析:对于//,结合 m, n // , 则可推得m n.答案C.点评:从上面几个例子可以看出,这类空间线面位置关系的判断类试题虽然形式上各异,但本质上都是以空间想象、空间线面位置关系的判定和性质定理为目标设计的,主要是考查考生的空间想象能力和对线面位置关系的判定和性质定理掌握的程度.题型 3 空间平行与垂直关系的证明、空间几何体的有关计算(文科解答题的主要题型)例 6.(2009江苏泰州期末 16)如图所示,在棱长为2的正方体ABCD A1B1C1D1中,E、F 分别为DD1、 DB 的中点.( 1)求证:EF //平面ABC1D1;( 2)求证:EF B1C ;( 3)求三棱锥V B1EFC 的体积.分析:第一问就是找平行线,最明显的就是EF PBD1;第二问转化为线面垂直进行证明;第三问采用三棱锥的等积变换解决.解析:( 1)连结BD1,如图,在DD1B 中,E 、F 分别为 D1D , DB 的中点,则EF / /D1BD1 B平面ABC1D1EF / / 平面ABC1D1.EF 平面 ABC1D1(2)B 1C ABB 1C BC 1B 1C 平面 ABC 1D 1 B 1C BD 1EFB 1CAB,B 1C平面 ABC 1D 1BD 1平面 ABC 1D 1EF / /BD 1AB I BC 1B( 3)Q CF平面BDD 1B 1 ,CF 平面 EFB 1 且 CF BF2 ,Q EF1BD 13,B 1FBF 2BB 12( 2)2 226 ,2B 1EB 1 D 12 D 1E 2 12 (2 2)23 ∴ EF 2B 1F 2 B 1E 2即 EFB 190o ,V BEFCV C B EF1 S B EF CF = 11EF B 1F CF = 1 1362 1113 13 23 2.点评 :这个题目也属于文科解答题的传统题型.空间线面位置关系证明的基本思想是转化,根据线面平行、垂直关系的判定和性质,进行相互之间的转化,如本题第二问是证明线线垂直,但问题不能只局限在线上,要把相关的线归结到某个平面上(或是把与这些线平行的直线归结到某个平面上,通过证明线面的垂直达到证明线线垂直的目的,但证明线面垂直又得借助于线线垂直,在不断的相互转化中达到最终目的.立体几何中的三棱柱类似于平面几何中的三角形,可以通过 “换顶点 ”实行等体积变换,这也是求点面距离的基本方法之一.例 7.(江苏省苏州市 2009 届高三教学调研测试第 17 题) 在四棱锥 P ABCD 中,ABCACD90o , BACCAD60o , PA 平面 ABCD , E 为 PD 的中点, PA2AB 2.( 1)求四棱锥 P ABCD 的体积 V ;( 2)若 F 为 PC 的中点,求证 PC 平面 AEF ; ( 3)求证 CE ∥平面 PAB .分析 :第一问只要求出底面积和高即可;第二问的线面垂直通过线线垂直进行证明;第三问的线面平行即可以通过证明线线平行、利用线面平行的判定定理解决,也可以通过证明面面平行解决,即通过证明直线CE 所在的一个平面和平面PAB 的平行解决.解析:( 1)在Rt ABC中, AB1, BAC60o,∴BC3,AC 2.在 Rt ACD 中,AC2, ACD60o,∴ CD 2 3,AD4.∴ S11AC CD1153 .AB BC 1 3 2 2 3ABCD22222则 V15 3 253 .323( 2)∵PA CA , F 为 PC 的中点,∴ AF PC .∵ PA平面 ABCD ,∴ PA CD ,∵ AC CD , PAI AC A,∴ CD平面PAC ,∴ CD PC .∵ E为PD中点, F 为PC中点,∴ EF ∥CD ,则 EF CD,∵ AFI EF F ,∴PC 平面 AEF .( 3)证法一:取 AD中点 M ,连EM,CM.则 EM ∥ PA,∵ EM平面PAB,PA平面PAB ,∴EM ∥平面 PAB .在 Rt ACD 中,CAD 60o,AC AM 2 ,∴ACM 60o.而BAC60o,∴MC ∥ AB.∵ MC平面PAB,AB平面PAB,∴MC ∥平面 PAB .∵EMI MC M ,∴平面 EMC ∥平面 PAB .∵ EC平面 EMC ,∴ EC ∥平面 PAB .证法二:延长DC , AB ,设它们交于点N,连PN.∵NAC DAC60o,AC CD ,∴ C为 ND的中点.∵E为PD中点,∴ EC∥PN.∵ EC平面 PAB , PN平面 PAB ,∴EC ∥平面 PAB .点评:新课标高考对文科的立体几何与大纲的高考有了诸多的变化.一个方面增加了空间几何体的三视图、表面积和体积计算,拓展了命题空间;另一方面删除了三垂线定理、删除了凸多面体的概念、正多面体的概念与性质、球的性质与球面距离,删除了空间向量,这就给立体几何的试题加了诸多的枷锁,由于这个原因课标高考文科的立体几何解答题一般就是空间几何体的体积和表面积的计算、空间线面位置关系的证明(主要是平行与垂直).题型 4 空间向量在立体几何中的应用(理科立体几何解答题的主要题型)例8 .( 2009 年福建省理科数学高考样卷第18 题)如图,在棱长为 2 的正方体ABCD A1B1C1D1中,E、F分别为 A1D1和 CC1的中点.(1)求证:EF∥平面ACD1;(2)求异面直线EF与AB所成的角的余弦值;(3)在棱BB1上是否存在一点P,使得二面角P AC P的大小为30o ?若存在,求出BP 的长;若不存在,请说明理由.【解析】解法一:如图分别以DA, DC , DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系D xyz ,由已知得D 0,0,0、A 2,0,0 、 B 2,2,0、 C 0,2,0、 B1 2,2,2、D10,0,2E 1,0,2、、 F0,2,1.( 1)取AD1中点G,则G 1,0,1,uuur uuur1,2, 1 ,CG1, 2,1 ,又 EFuuur uuur由 EF CG ,uuur uuur∴ EF 与CG共线.从而EF∥CG,∵ CG平面 ACD1,EF平面 ACD1,∴EF∥平面 ACD1.uuur0,2,0 ( 2)∵ AB,uuur uuuruuur uuur 4 6cosEF AB,EF, ABuuuruuur2 63|EF | |AB|∴异面直线 EF 与 AB 所成角的余弦值为6 .3( 3)假设满足条件的点P 存在,可设点 P 2,2, t ( 0 t2 ),平面 ACP 的一个法向rx, y, z 量为 n,r uuur uuuruuur2x 2y 0, nAC 0, 0,2, t2,2,0 则 ruuur0. ∵ AP AC ,∴ 2 y tz0,n APr(1,1, 2取 n) .tuuur易知平面 ABC 的一个法向量BB 1 (0,0,2) ,uuur r 30o 或 150o , 依题意知,BB 1, nuuur uur| 4 |34 3 46∴ cos BB 1 , Nt42,即t 2 (22 ) ,解得 t.24t32t 2∵6 (0, 2] ,∴在棱 BB 1 上存在一点 P ,当 BP 的长为 6 时,二面角 P AC B 的3 3大小为 30o .解法二:uuuruuuur uuur(1)同解法一知 EF1,2, 1 , AD 1 2,0,2 ,AC2,2,0 ,uuur uuur 1 uuuur uuur uuur uuuur 共面.又∵ EF平面 ACD 1 ,∴ EF ∥∴ EF AC AD 1 ,∴ EF 、 AC 、 AD 1 2平面 ACD 1 .( 2)、( 3)同解法一.uuuur uuur解法三:易知平面 ACD1的一个法向量是 DB12,2,2 .又∵ EF1,2, 1 ,由uuur uuuurEF DB10 ·,uuur uuuur平面 ACD 1,∴EF∥平面 ACD1.∴ EF DB ,而 EF1( 2)、( 3)同解法一.点评:本题主要考查直线与直线、直线与平面的位置关系、二面角的概念等基础知识;考查空间想像能力、推理论证能力和探索问题、解决问题的能力.利用空间向量证明线面平行的方法基本上就是本题给出的三种,一是证明直线的方向向量和平面内的一条直线的方向向量共线,二是证明直线的方向向量和平面内的两个不共线的向量共面、根据共面向量定理作出结论;三是证明直线的方向向量与平面的一个法向量垂直.例 9(浙江宁波市2008 学年度第一学期期末理科第20 题)已知几何体A BCED 的三视图如图所示,其中俯视图和侧视图都是腰长为 4 的等腰直角三角形,正视图为直角梯形.(1)求异面直线DE与AB所成角的余弦值;(2)求二面角A ED B的正弦值;(3)求此几何体的体积V的大小.【解析】( 1)取EC的中点是 F ,连结 BF ,则BF PDE,∴FBA 或其补角即为异面直线DE与AB所成的角.在BAF中,AB 4 2,BF AF2 5 .∴ cos ABF10 .5∴异面直线 DE 与 AB 所成的角的余弦值为10 .5(2) AC 平面 BCE ,过C 作CG DE 交 DE 于G ,连结 AG .可得 DE 平面 ACG ,从而 AG DE ,∴ AGC 为二面角 A ED B 的平面角.在 RtACG 中, ACG 90o , AC4 ,CG8 5AGC5,∴ tan.52∴ sin 5 .AGC3∴二面角 A EDB 的的正弦值为5 .3(3)V1S BCED AC 16 ,∴几何体的体积 V 为16.3方法二:(坐标法)(1)以 C 为原点,以 CA,CB, CE 所在直线为 x, y, z 轴建立空间直角坐标系.则 A 4,0,0 , B(0,4,0) , D (0,4,2) , E 0,0,4,uuur(0, uuur4, 4,0) , DE4,2), AB (∴ cosuuur uuur 10 DE,AB5∴异面直线 DE 与 AB 所成的角的余弦值为10 .5uuur (4,0,0)( 2)平面 BDE 的一个法向量为 CA ,r设平面 ADE 的一个法向量为 n (x, y, z) ,r uuur r uuur uuur uuur4,2) n AD , n DE , AD( 4,4, 2), DE (0,r uuur r uuur∴ ngAD0, ngDE从而 4 x 4 y 2z 0, 4 y 2z 0 ,r uuur r2令 y 1 ,则 n (2,1,2), cos CA, n3∴二面角 A ED B 的的正弦值为 5 .3(3)V 1S BCED AC16 ,∴几何体的体积V 为16.3点评:本题考查异面直线所成角的求法、考查二面角的求法和多面体体积的求法.空间向量对解决三类角(异面直线角、线面角、面面角)的计算有一定的优势.对理科考生来说除了要在空间向量解决立体几何问题上达到非常熟练的程度外,不要忽视了传统的方法,有些试题开始部分的证明就没有办法使用空间向量.【专题训练与高考预测】说明:文科以选择题、填空题和解答题前三题为主.理科以选择题、填空题和解答题后三题为主.一、选择题1.如图为一个几何体的三视图,尺寸如图所示,则该几何体的表面积为(不考虑接触点)()A.63B.18 3 4C.1823D.322.某几何体的三视图如图所示,根据图中数据,可得该几何体的体积是()A .323B .23 3C .2 23 3D . 3 22 33.已知一个几何体的主视图及左视图均是边长为2 的正三角形, 俯视图是直径为 2的圆,则此几何体的外接球的表面积为( )4B .8A .33C .16D . 32334.一个水平放置的平面图形的斜二测直观图是一个底角为45o ,腰和上底长均为 1的等腰梯形,则这个平面图形的面积是()A .12 B . 12 C . 12D . 222225. 一个盛满水的三棱锥容器 SABC ,不久发现三条侧棱上各有一个小洞D, E,F ,且知SD: DA SE: EBCF :FS2:1 ,若仍用这个容器盛水,则最多可盛原来水的()23193023A .B .C .D .292731276. 点 P 在直径为 2 的球面上,过 P 作两两垂直的三条弦,若其中一条弦长是另一条弦长的2 倍,则这三条弦长之和为最大值是()2703 704156 15A .B .C .D .55557.正方体 ABCD A' B 'C 'D ' 中, AB 的中点为 M ,DD ' 的中点为 N ,异面直线 B 'M 与 CN所成的角是( ) A . 30oB . 90oC . 45oD . 60o.已知异面直线 a 和b 所成的角为o ,P 为空间一定点, 则过点 P 且与 a,b 所成角都是 30o850的直线有且仅有()A . 1条B . 2条C . 3条D . 4条9.如图所示,四边形ABCD 中, AD / / BC, ADAB, BCD45o , BAD 90 o ,将△ ABD 沿 BD 折起,使平面 ABD平面 BCD ,构成三棱锥A BCD ,则在三棱锥A BCD 中,下列命题正确的是()A .平面 ABD 平面 ABCB .平面 ADC 平面 BDC C .平面 ABC 平面 BDCD .平面 ADC平面 ABC10.设 x 、 y 、 z 是空间不同的直线或平面,对下列四种情形:①x 、 y 、 z 均为直线;② x 、 y 是直线, z 是平面;③ z 是直线, x 、 y 是平面;④ x 、 y 、 z 均为平面.其中使 “x ⊥ z 且 y ⊥ z x ∥ y ”为真命题的是()A . ③④B . ①③C . ②③D . ①②11m 、 n 、 l 两个不重合的平面、 ,有下列命题.已知三条不重合的直线①若 m / / n, n,则 m / / ;②若③若l, m且l Pm,则P;m, m,m P, n P,则P;④若,I m , n, n m ,则 n.中正确的命题个数是()A .1B .2C.3D.412.直线AB与直二面角l的两个面分别交于A, B 两点,且 A, B 都不在棱上,设直线 AB 与平面,所成的角分别为 ,,则的取值范围是()A.(0,)B. 0,C.(, )D.{}2222二、填空题13.在三棱锥P ABC 中, PA PB PC 2,APB BPC CPA30o,一只蚂蚁从 A 点出发沿三棱锥的侧面绕一周,再回到 A 点,则蚂蚁经过的最短路程是.14.四面体的一条棱长为x ,其它各棱长为1V表示成 x 的函数 f x ,,若把四面体的体积则 f x 的增区间为,减区间为.15.如图,是正方体平面展开图,在这个正方体中:①BM 与 ED 平行;②CN 与BE 是异面直线;③ CN与 BM 成60o角;④ DM与 BN 垂直.以上四个说法中,正确说法的序号依次是.16.已知棱长为1的正方体ABCD A1B1C1D1中,E是 A1B1的中点,则直线AE 与平面ABC1D1所成的角的正弦值是.三、解答题17.已知,如图是一个空间几何体的三视图.(1)该空间几何体是如何构成的;(2)画出该几何体的直观图;(3)求该几何体的表面积和体积.18.如图,已知等腰直角三角形RBC ,其中RBC90o,RB BC2.点A, D分别是RB ,RC的中点,现将RAD 沿着边 AD 折起到PAD 位置,使 PA AB ,连结 PB 、PC .( 1)求证:BC PB ;( 2)求二面角A CD P 的平面角的余弦值.19.如下图,在正四棱柱ABCD A1B1C1 D1中,AA11 AB,点E,M分别为2A1B,CC1的中点,过点A1, B, M 三点的平面A1 BMN交 C1D1于点N.( 1)求证:EM P平面A1B1C1D1;( 2)求二面角B A1N B1的正切值;( 3)设截面A1BMN把该正四棱柱截成的两个几何体的体积分别为V1,V2( V1V2),求V1 : V2的值.20.如图,在四棱锥P 直于底面 ABCD ,ABCD 中,底面为直角梯形,AD // BC , BAD 90 ,PA AD AB 2BC 2,M ,N 分别为 PC , PB的中点.PA 垂( 1)求证:PB DM;( 2)求BD 与平面ADMN所成的角;( 3)求截面ADMN的面积.21.如图,正方形ACDE所在的平面与平面ABC 垂直,M 是 CE 和 AD 的交点, AC BC ,且 AC BC.( 1)求证:AM平面EBC;(2)求直线AB与平面EBC所成的角的大小;(3)求二面角A EB C的大小.22.已知斜三棱柱ABC A1B1C1,BCA 90o,AC BC 2 ,A1在底面 ABC 上的射影恰为 AC 的中点 D ,又知BA1AC1.( 1)求证:AC1平面A1BC;(2)求CC1到平面A1AB的距离;( 3)求二面角 A A1B C 的一个三角函数值.【参考答案】1.解析: C 该几何体是正三棱柱上叠放一个球.故其表面积为31232322241823.422.解析: B这个空间几何体的是一个底面边长为 3 的正方形、高为 3 的四棱柱,上半部分是一个底面边长为3的正方形、高为 2的四棱锥,故其体积为333 1 3323 32 .33.解析:C由三视图知该几何体是底面半径为1,高为3 的圆锥,其外接球的直径为4 3 .3 4.解析: D 如图设直观图为O ' A ' B ' C ',建立如图所示的坐标系,按照斜二测画法的规则,在原来的平面图形中OCOA ,且 OC 2, BC1,OA 1 22 2 ,故12其面积为11 2 22 2225.解析: D当平面 EFD 处于水平位置时,容器盛水最多1VF SDES 3 VC SAB1S3SDEh 11SD SE sin DSE h 13 SD SE h 1 2 2 14SABh 21SA SB sin ASB h 2SA SB h 23 3 3 273最多可盛原来水得 14 23 .27 276.解析: A 设三边长为x,2 x, y ,则 5x 2 y 24 ,4 4 2 70 .令 x cos , y 2sin , 3x y 3 cos 2sin5557.解析: B 如图,取 AA '的中点 P ,连结 BP ,在正方形 ABB' A'中易证 BP B'M .8B 过点 P 作 a Pa , b Pb ,若 P a ,则取 a 为 a ,若 P b ,则取 b 为 b .这时.解析: a, 相交于P 点,它们的两组对顶角分别为50o 和 130o. 记 a ,b 所确定的平面为 ,b那么在平面 内,不存在与 a , b 都成 30o 的直线. 过点 P 与 a , b 都成 30o角的直线必在平面外,这直线在平面的射影是 a ,b 所成对顶角的平分线. 其中射影是 50o对顶角平分线的直线有两条l 和 l ,射影是 130o 对顶角平分线的直线不存在.故答案选B .9.解析:D 如图,在平面图形中 CDBD ,折起后仍然这样, 由于平面 ABD 平面 BCD ,故 CD平面 ABDCD AB,又 AB AD,故 AB平面 ADC,所以平面 ADC,平面 ABC .10.解析: C x 、 y 、 z 均为直线,显然不行;由于垂直于同一个平面的两条直线平行,故②, 可以使 “x ⊥ z 且 y ⊥ z x ∥ y ”为真命题; 又由于垂直于同一条直线的两个平面 平行,故③可以使 “ ⊥ z 且 y⊥ z x ∥ y”为真命题;当 x 、 y、 z 均为平面时,也x不能使 “x ⊥ z 且 y ⊥ z x ∥ y ”为真命题.11.解析: B ①中有 m的可能; l Pm 且 l,可得 m,又 m ,故 P,②正确;③中当m Pn 时,结论不成立;④就是面面垂直的性质定理,④正确.故两个正确的.12.解析: B如图,在Rt ADC 中,AD AB cos , AC AB sin,而AD AC ,即cos sin cos,故,即,而当AB l时,.222213.解析:22将如图⑴三棱锥P ABC ,沿棱PA 展开得图⑵,蚂蚁经过的最短路程应是AA ,又∵APB BPC CPA30o,APA '90o,∴AA=2 2.66, f ( x)x 3 x2,利用不等式或导数即可判断.14.解析: 0,,342215.解析:③④如图,逐个判断即可.16.解析:10取 CD 的中点 F ,连接 EF 交平面ABC1D1于 O ,连 AO .由已知正方体,5易知 EO平面 ABC1 D1,所以EAO为所求.在 Rt EOA 中,EO1EF1A1 D 2 ,222AE(1)2125, sin EAOEO 10.所以直线 AE 与平面 ABC 1 D 1 所成的角22AE5的正弦值为10 .517.解析:(1)这个空间几何体的下半部分是一个底面边长为上半部分是一个底面边长为2 的正方形高为 1的四棱锥.( 2)按照斜二测的规则得到其直观图,如图.2 的正方形高为1的长方体,( 3)由题意可知, 该几何体是由长方体 ABCD A'B 'C 'D ' 与正四棱锥 PA'B'C'D '构成的简单几何体.由图易得: ABAD2, AA'1, PO'1,取 A'B'中点Q ,连接PQ ,从而PQ PO '2 O 'Q 2 12122 ,所以该几何体表面积S1 B'C' C'D' D'A' PQA'B'B'C'C'D' D'A' AA' AB AD4212.A'B'2体积V 221122116 .3318.解析:( 1)∵点A、D分别是RB、RC的中点,∴AD // BC , AD 1 BC.2∴ PAD RAD RBC90o,∴PA AD.∴ PA BC ,∵ BC AB, PA AB A,∴BC平面 PAB .∵ PB平面 PAB ,∴BC PB.( 2)取RD的中点F,连结 AF、PF.∵RA AD 1,∴AF RC .∵ AP AR, AP AD ,∴ AP 平面RBC.∵ RC平面 RBC ,∴ RC AP .∵ AF AP A,∴RC平面 PAF .∵ PF平面 PAF ,∴ RC PF .∴AFP 是二面角 A CD P 的平面角.在 Rt RAD 中,AF 1RD1RA2AD22,222在 Rt PAF 中,PF PA2AF2 6 ,2AF 23cos AFP2PF6.32∴二面角A CD P 的平面角的余弦值是 3 .3 19.解析:( 1)设A1B1的中点为F,连结EF , FC1.∵ E 为A1B的中点,∴ EF 1BB1.2又 C1M 1BB1,∴ EF MC1.∴四边形 EMC 1F 为平行四边形.2∴EM PFC1.∵EM平面 A1B1C1D1, FC1平面 A1B1C1D1,∴EM P平面 A1B1C1D1.( 2)作B1H A1N 于H,连结BH ,∵BB1⊥平面 A1 B1C1 D1,∴ BH A1N .∴BHB1为二面角 B A1N B1的平面角.∵EM ∥平面A1B1C1D1,EM平面A1BMN,平面 A1BMNI平面A1B1C1D1A1N,∴EM PA1N .又∵ EM PFC1,∴ A1N PFC1.又∵ A1F PNC1,∴四边形 A1FC1N 是平行四边形.∴NC1A1F .设 AA1 a ,则 A1B12a , D N a .1在Rt A1D1N中,A1 N A1D12D1N 25a,∴ sin ∠A1ND1= sinA1D12.A1ND15A1 N在 Rt A1B1H 中, B1H A1B1 sin HA1B124a 2a.55在Rt BB1H 中,tan BHB1BB1a5.B1H4a45( 3)延长A1N与B1C1交于P,则P平面A1BMN,且P平面 BB1C1C .又∵平面 A1BMN I平面 BB1C1C BM,∴ P BM ,即直线A1N , B1C1, BM交于一点 P .又∵平面 MNC 1 P∥平面 BA1B1,∴几何体M NC1BA1B1为棱台.∵S ABB12a a a2, S MNC11a1a 1 a2,112224棱台 MNC 1 BA 1 B 1 的高为 B 1C 1 2a ,故V 1 1 a 2a 2 1 a 21 a2 2a 7 a3 ,34 46V 2 2a 2a7 a 3 17 a 3,.∴V 1 7a6 V 2 .61720.解析:( 1)因为 N 是 PB 的中点, PAAB ,所以 AN PB . 由 PA 底面 ABCD ,得PA AD ,又BAD 90 ,即 BAAD ,AD 平面 PAB ,所以 ADPB ,PB 平面 ADMN ,PB DM .( 2)连结 DN , 因为 BP 平面 ADMN ,即 BN平面 ADMN ,所以 BDN 是 BD与平面 ADMN 所成的角. 在 RtABD 中, BDBA 2 AD 22 2 ,在 Rt PAB中 ,PB PA2AB 22 2 , 故 BN1PB2 , 在 Rt BDN中 ,BN 12sinBDNBDN,故 BD 与平面 ADMN 所成的角是.BD ,又 0226(3)由 M ,N 分别为 PC,PB 的中点,得MN//BC ,且MN1BC1, 又22AD // BC ,故 MN // AD ,由( 1)得 AD 平面 PAB ,又 AN 平面 PAB ,故 ADAN , 四边形 ADMN 是直角梯形,在 RtPAB 中, PBPA 2AB 22 2 , AN1PB2 ,截面 ADMN 的2面积 S1(MN AD) AN1 ( 1 2)25 2 .22 24法二: (1)以 A 点为坐标原点建立空间直角坐标系A xyz ,如图所示(图略)由PA AD AB 2BC 2,得A(0,0,0),P(0,0,2), B(2,0,0), M (1,1,1), D(0,2,0) uuur uuuur23,1)(2,0, 2)(1, 0,所以 PB DM .因为 PB DMuuur uuur2(2,0,2) (0, 2,0)0 ,所以 PB AD ,又 PB DM( 2)因为 PB AD ,故 PBuuur(2, 0, 2) 是平面 ADMN 的法向量.平面 ADMN ,即 PB 设 BD 与平面 ADMN 所成的角为uuur2,2,0).,又BD (uuur uuur uuuur uuuur| 4 | 1 则 sin| cos| BD PB |BD,PB |uuuruuuur4 444 ,|BD||PB| 2又[0 , ],故 ,即 BD 与平面 ADMN 所成的角是 .2 66 因此 BD 与平面 ADMN 所成的角为 .6( 3)同法一.21.解析:法一: ( 1)∵四边形 ACDE 是正方形,EA AC, AM EC .∵平面 ACDE平面 ABC ,又∵ BCAC , BC 平面 EAC . AM平面 EAC , BCAM .AM 平面 EBC . ( 2)连结 BM , AM平面 EBC ,ABM 是直线 AB 与平面 EBC 所成的角.设 EAAC BC 2a ,则 AM2a , AB22a ,sinAM 1ABM,AB2ABM 30 . 即直线 AB 与平面 EBC 所成的角为 30(3)过A作AH EB于 H ,连结 HM .AM平面 EBC , AM EB. EB 平面 AHM .AHM 是二面角 A EB C 的平面角.∵平面 ACDE平面 ABC ,EA平面A BC .EA AB .在 Rt EAB 中,AH EB ,有 AE AB EB AH.由 (2)所设EA AC BC2a可得AB22a,EB 23a ,AHAEAB 22aEB .3sin AHM AM3AHM60 .∴二面角 A EB C等于 60.AH.2法二 : ∵四边形ACDE 是正方形,EA AC, AM EC ,∵平面ACDE平面ABC , EA平面 ABC ,∴可以以点 A 为原点,以过 A 点平行于BC 的直线为x 轴,分别以直线AC和 AE为y 轴和z轴,建立如图所示的空间直角坐标系A xyz .设 EA AC BC 2,则A(0,0,0), B(2,2,0), C(0,2,0), E(0,0,2),M是正方形 ACDE 的对角线的交点,M (0,1,1) .(1)AM(0,1,1),EC(0,2,0) (0,0,2) (0,2, 2),CB(2,2,0)(0,2,0)(2,0,0) ,AM EC0, AM CB0 ,AM EC, AM CB AM平面 EBC .( 2)AM平面 EBC ,AM 为平面EBC的一个法向量,AM(0,1,1), AB ( 2,2,0) , cos AB, AM AB AM1AB AM.2AB, AM60 .∴直线 AB 与平面 EBC 所成的角为 30 .( 3)设平面 EAB 的法向量为 n( x, y, z) ,则 nAE 且 nAB ,n AE 0 且 n AB 0 .(0,0,2) ( x, y, z) 0,z 0,,取 y1 ,则 x 1 , 则 n (1, 1,0) .(2,2,0) ( x, y, z) 0.即xy 0.又∵ AM 为平面 EBC 的一个法向量,且AM (0,1,1),cos n, AMn AM1 ,设二面角 A EB C 的平面角为, 则n AM2cos cos n, AM160 .∴二面角 AEB C 等于 60 .,222.解析:法一:( 1)因为 A 1D平面 ABC ,所以平面 AA 1C 1C 平面 ABC ,又 BC AC ,所以 BC平面1 1,得1 ,又11 ,所以1平面1;AAC CBC ACBAACACA BC( 2)因为 AC 1 A 1C ,所以四边形 AAC 1 1C 为 菱形,故 AA 1 AC2,又D 为 AC中点,知A 1 AC 60o .取 AA 1 中点 F ,则 AA 1 平面 BCF ,从而面 A 1 AB 面BCF ,过C 作CH BF 于H ,则CH面 A 1AB .在 RtBCF 中, BC 2, CF 3,故CH2 21,7即 CC 1 到平面 A 1 AB 的距离为 CH2 21 .7(3)过H作HG A1B于G,连CG,则 CG A1B ,从而CGH 为二面角A A1B C 的平面角,在Rt A1BC 中,A1C BC2,所以CG 2 ,在Rt CGH中,sinCH42 CGH,CG7故二面角 A A1B C 的正弦值为42 .7法二:( 1)如图,取AB的中点E,则 DE // BC ,因为 BC AC ,所以 DE AC ,又A1D平面 ABC ,以DE , DC , DA1为 x, y, z 轴建立空间坐标系,则 A 0, 1,0 , C 0,1,0 , B 2,1,0 , A1 0,0, t , C1 0,2, t ,uuuur uuur uuurAC10,3,t, BA12,1,t, CB2,0,0 ,uuur uuur由 AC CB0 ,知A1C CB ,1又 BA1AC1,从而 AC1平面 A1BC ;uuuur uuur3 t20 ,得t 3 .( 2)由AC1BA1r uuur uuur设平面 A1 AB 的法向量为n x, y, z, AA10,1, 3, AB2,2,0 ,r uuury3z0 n AA所以r uuur12x 2 y ,n AB0设 zr3, 3,11,则nuuuur r所以点 C1到平面 A1 AB 的距离dAC1n221 .rn7ur uuur uuur( 3)再设平面A1BC的法向量为m x, y, z, CA10,1,3, CB2,0,0 ,所以uuururm CA1y3z0,设 z1,ur uuur2x 0m CBur0,3,1 ,则 mur r ur r7故 cosm nA A1BC 的余弦m, n ur r,根据法向量的方向,可知二面角m n7值为7 .7。
