三年级上册 找规律思维训练
三年级思维训练第一课找规律-PPT课件

(7)找出下列各数列的规律,并按其规律在 ( )内填上合适的数:
(1)12,15,17,30, 22,45,(27),(60);
(2) 2,8,5,6,8,4,( 11 ),( 2 )。
相邻两数的和、差、积、商找排列规律,或 者把数列拆分成几个部分,分别考察它们的 排列规律。在填数时,一要细心观察题目中 数字的特征;二是灵活运用整数的有关知识 和加、减、乘、除的计算法则以及它们之间 的关系进行合理的推想。
第一次 花猫 3 老鼠 6
第二次 第三次 第四次 第五次 6 9 12 15 8 10 12 14
练习: 找出下列各数列的规律,并按其规律 在( )内填上合适的数: (1)4,7,10,13,( 16 ),… (2)84,72,60,( 48 ),( 36 ) ; (3)2,6,18,( 54 ),(162),… (4)625,125,25,( 5 ),( 1 ); (5)1,4,9,16,( 25 ),… (6)2,6,12,20,( 30 ),( 42 ),…
像上面的这些例子,都是按某种 法则排列着的一列数,这样的一列 数就叫做数列。数列里的每一个数 都叫做这个数列的项。其中第1个数 叫做数列的第1项,第2个数叫做数 列的第2项,即第几个数就叫做数列 的第几项,比如年份的第3项就是 2000。
年份:2019,2019,2000,2019,2019,…
(1)找规律填数:
(5)两只小鸭子所展示的这一列数有 规律吗?谁能帮助小鸭子填上最后两 个数?
14
7
(6)找出下列各数列的规律,并按 其规律在( )内填上合适的数: (1)18,20,24,30,(38); (2)11,12,14,18,26,(42);
(3)2,5,11,23,47,( 95 ),( 。 191 )
三年级上册思维训练题

三年级上册数学思维第一单元:时、分、秒1、利用间隔数解决爬楼梯问题明明从1楼走到3楼需要16秒。
照这样的速度计算,他从1楼走到7楼需要多少秒?思路分析:可以这样想:明明从1楼走到3楼走了2层,需要16秒,则平均每层需要走8秒。
照这样的速度计算,他从1楼走到7楼走了6层,一共需要走48秒。
正确解答:一层:16÷(3-1)=8(秒)到7楼:8×(7-1)=48(秒)举一反三:(1)公路的一侧每隔10米种1棵树,小丽从第1棵树走到第5棵树需要28秒,照这样的速度计算,她从第1棵树走到第10棵树需要多少秒?(2)芳芳从四楼到一楼用了 24秒,玲玲从八楼到一楼用了 56秒,她们下楼的速度一样吗?(3)从田边到池塘有9米,青蛙从田边跳到池塘、每跳3米要用5 秒,休息1秒后继续跳,青蛙从田边跳到池塘需要多长时间?2.求等车时间间隔的问题例题:去人民公园的公共汽车每15分钟发一班车。
小明早上7: 10到达车站,发现7:05时已经发了一班车,他还要等多长时间才能坐上车?思路分析:方法一:可以先求出下一班车的发车时间,再减去小明到达车站的时间,就是等车的时间。
方法二:可以求出距离上一班车的发车时间经过了几分钟,再用两班车发车的间隔时间减去经过的时间,就是等车的时间。
正确解答: 方法一 7时5分+15分钟=7时20分7时20分-7时10分=10分钟方法二 7时10-7时5分=5分钟 15- 5=10(分钟) 举一反三:(1)去图书馆的公共汽车每15分钟发一班车。
小明上午9: 05到达车站,发现9:00时已经发了一班车,他还要等多长时间才能坐上车?(2)小红从家到学校要走20分钟,她每天早晨要8:40到学校。
小红最迟几时从家出发?(3)火车8:15发车,小东7:00从家出发坐车去火车站,从他家到火车站乘车需45分钟,从进站口到检票完需要20分钟,他能赶上这趟火车吗?3.利用分段计时法计算经过的时间例题:永辉超市营业时间,开门:早上7:30,关门:晚上10:00。
三年级上册数学思维拓展图形找规律
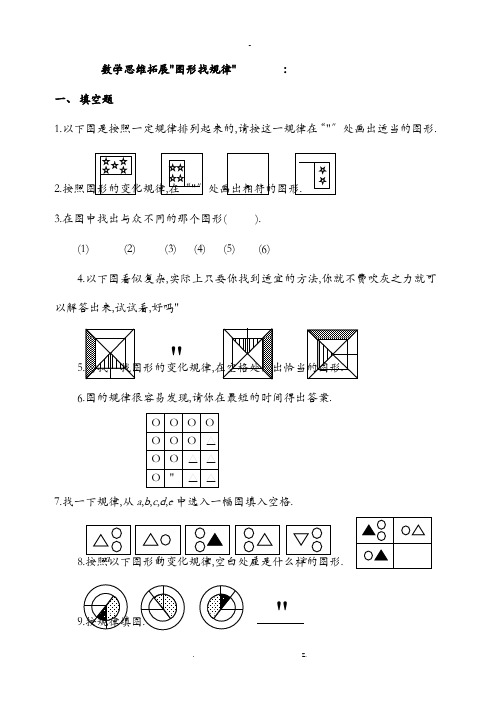
数学思维拓展"图形找规律" :一、 填空题1.以下图是按照一定规律排列起来的,请按这一规律在“"〞处画出适当的图形.2.〞处画出相符的图形3.在图中找出与众不同的那个图形( ).(1)(2)(3) (4)(5) (6)4.以下图看似复杂,实际上只要你找到适宜的方法,你就不费吹灰之力就可以解答出来,试试看,好吗",6.图的规律很容易发现,请你在最短的时间得出答案.7.找一下规律,从a ,b ,c ,d ,e 中选入一幅图填入空格...""如果 变成 则 应变为10.下面一组图形的阴影变化是有规律的,请根据这个规律把第四幅图的阴影局部画出来.二、解答题11.图中,哪个图形与众不同"(1) (2) (3) (4) (5)12.有一个立方体,每个面上分别写上数字1、2、3、4、5、6、,有3个人 从不同的角度观察的结果如以下图所示,这个立方体的每一个数字的对面各是什么数字" 13.下面是由几何图形组成的帆船图形,请按照一定的规律,在标序号处画出符合规律的小帆船."1 2 61 3 4 ① ②③———————————————答案——————————————————————1. 这一组图形我们应该从两方面来看:一是旗子的方向,二是旗子上星星的颗数.首先我们看一下旗子的方向.第1面旗子向右,第2面向上,第4面向下,可以发现,旗子的方向是按逆时针旋转的,并依次旋转︒90,所以第3面旗子应是第2面逆时针旋转︒90得来的,旗子应向下倒立.其次我们看旗上星星的颗数.第1面是5颗,第2面是4颗,第4面是2颗,1颗,所以第3面旗上应是3颗星星.所以“"〞处的图形应为:2. 这组图形的变化只在于正方形中阴影局部的位置.通过观察,我们可以发现阴影局部是按照逆时针方向依次旋转︒90得到的.所以“"〞处的图形应为:3. 选(4).因为变化规律是从左到右依次逆时针旋转︒90.4. 在这组图形中,不变的有以下几点:大小正方形不变,两条对角线不变.所以“"〞处也应有大小两个正方形和两条对角线.发生变化的有:一、阴影局部和黑色局部的位置.通过观察,我们可以看出这两局部都是按逆时针方向依次旋转︒90得到的,所以“"〞处的阴影局部应是小正方形的右边,黑色局部应在大正方形的下部.二、小竖线的位置.小竖线是从图形中心到相应的边所作的一条垂线.它的变化规律是按逆时针方向依次旋转︒90,这样,整个图形我们就分析完了,下面看一看你画出的图形和书上的一样吗"如果一样,就做对了.5. 因为要填的是第1幅图,我们可以从后往前看.首先三角形的个数是发生变化的,依次是7、5、3.可以发现是从后向前依次减少2个的.所以第1幅图中应有1个三角形.其次三角形的方向也是有变化的,从后面观察,三角形是按逆时针方向依次旋转︒90,所以第1幅图中的三角形应向上,阴影局部在右边.如以下图所示:6. 横行观察,圆的个数逐次减少1个,所以到第4行,圆的个数应为1,所以“"〞处应是“△〞.或者从三角形考虑,三角形的个数为0、1、2,是逐次增加1,所以第4行中三角形的个数应为3,所以“.〞处应为“△〞所以最后的图形为:7. 选a.根据对角图形规律,可知右下角图形是a图.8. 分析:先看不变的局部.在整个变化过程中,图形、小两个圆圈没有变化,因此可以肯定空白处的图形一定也有大、小两个圆圈,位置一里一外.变化的局部可为两局部:①图形中的直线局部,其变化规律是每次顺时针旋转︒90,黑色局部交90;②图形中的阴影局部,其变化规律是每次逆时针旋转︒替出现.解:根据上面的分析,可画出空白处的图形如下图.9. 先应找出变化的规律,然后再依此规律,在空白处填画出所缺的图形.从第一行可以看到,当左边的图形变成右边的图形时,下部图形移到上面,里面的图形移到下面,上面的外部图形移到里面,各局部的颜色都没有变.根据这一规律,我们可以把下面图形变为:10. 先看第1行,阴影局部所在的位置是1、2、3.是逐次向后一个,所以第四幅图中第1行的阴影局部应在第4格.同样,第2行是2、3、4.4再向后应是5了,但没有第5个格,所以折回到第1个格.同理可推出第3行的阴影局部在第2格,第4行的阴影局部在第3格.还可以这样想:在同一行中,阴影局部都不在同一位置,所以第1行已经被占去了第1、2、3格,所以第四幅图的第一行阴影局部一定是第4格,同理推出第2、3、4行中阴影局部的位置.最后的答案如以下图所示.11. 分析:这五辆汽车车窗一致,车轮一致,车底一致,差异就只能在车头、车身局部去寻找.从车身看,(3)与众不同,只用一笔画成,可是它的车头与(1)同;从车头看:(2)与众不同,(因车头(1)与(3)同,(4)与(5)同),但是(2)的车身与(1)、(4)、(5)类似.所以从车头、车身这些特征比拟出来的图形,理由缺乏以说服人.我们把目光转移到笔划多少上,就可以找到与众不一的车辆了.解:与众不同的汽车是(1).其他四车均是由一个矩形、两个圆以及四条直线段、一段弧线画成,而(1)多一条直线段.12. 这个题目并不难.但是,推理方法不正确的话,也很难看出答案.直接考虑数字1的对面是什么数,想不出来.不妨换一种思维方式,想一想1的对面不是什么数.从第1个图看出1的对面不是4和6;从第2个图看出1的对面不是2和3,所以1的对面只能是5.同样的方法可以得到,4的对面是2;3的对面是6.13.因为正锥体的每个顶点连接三个面.当正锥体在雪花格纸上按顺时针方向旋转时,只有写有1、2、4三面所围出的顶点一直在雪花格的中心,所以只有1、2、4贴纸面旋转,雪花格有6个小格,正好可以转两圈,所以回到原地各面数字仍是原样分布.14.每一只小帆船都由三局部组成:船体、帆和小旗.这三局部都是变化的,另外船体的颜色也是变化的.下面我们逐一来分析.。
(完整版)小学三年级数学思维训练简单数列的规律

小学三年级数学思维训练简单数列的规律第六讲找简单数列的规律日常生活中,我们经常接触到许多按一定顺序排列的数,如:自然数:1,2,3,4,5,6,7, (1)年份:1990,1991,1992,1993,1994,1995,1996(2)某年级各班的学生人数(按班级顺序一、二、三、四、五班排列)45,45,44,46,45(3)像上面的这些例子,按一定次序排列的一列数就叫做数列.数列中的每一个数都叫做这个数列的项,其中第1个数称为这个数列的第1项,第2个数称为第2项,…,第n 个数就称为第n 项.如数列(3)中,第1项是45,第2项也是45,第3项是44,第4项是46,第5项45。
根据数列中项的个数分类,我们把项数有限的数列(即有有穷多个项的数列)称为有穷数列,把项数无限的数列(即有无穷多个项的数列)称为无穷数列,上面的几个例子中,(2)(3)是有穷数列,(1)是无穷数列。
研究数列的目的是为了发现其中的内在规律性,以作为解决问题的依据,本讲将从简单数列出发,来找出数列的规律。
例1 观察下面的数列,找出其中的规律,并根据规律,在括号中填上合适的数.①2,5,8,11,(),17,20。
②19,17,15,13,(),9,7。
③1,3,9,27,(),243。
④64,32,16,8,(),2。
⑤1,1,2,3,5,8,(),21,34…⑥1,3,4,7,11,18,(),47…⑦1,3,6,10,(),21,28,36,().⑧1,2,6,24,120,(),5040。
⑨1,1,3,7,13,(),31。
⑩1,3,7,15,31,(),127,255。
(11)1,4,9,16,25,(),49,64。
(12)0,3,8,15,24,(),48,63。
(13)1,2,2,4,3,8,4,16,5,().(14)2,1,4,3,6,9,8,27,10,().分析与解答①不难发现,从第2项开始,每一项减去它前面一项所得的差都等于3.因此,括号中应填的数是14,即:11+3=14。
某区中心小学三年级第一学期思维训练 第一讲 图形的变化规律

某区中心小学三年级第一学期思维训练第一讲图形的变化规律在这一讲内容中,我们主要向同学们介绍如何观察图形的变化规律。
观察图形的变化,可以从图形的形状、位
置、方向、颜色、数量、大小等方面入手,从
中找出规律。
例1.顺序观察给出图形的变化,按照这种
变化规律,在空格中填上应有的图形。
分析与解:本题目所给出的八个图,其形状都是箭。
所以可以肯定空格处的图形也是箭;在方向上,每行图从左至右都顺时针旋转90°变为下一个图形的方向。
依照这样的规律,第三行第三个图中的箭头应朝上;图形的数量变化反映在箭尾处,在同一行中,每旋转90°,箭尾上的“羽毛”将减少一对,依照这个规律,空格中的箭,
其尾部的“羽毛”没有了,成了光秃秃的一
支箭。
例2 依照下面图3中所给图形的变化
规律,在空格中填图。
分析与解:我们按花盆、花茎、花叶、
花朵四部分逐步观察。
花盆花盆的形状每一
行都是由三种形状组成。
练习与作业
1.先观察下图中前三个图形是怎样变化的,再画出第四个图形。
2.观察下图中前三个图形的变化规律,再画出第四个图形
_______。
3.观察下图中每一个图形的变化规律,然后在空白处画出图形。
4.在图下中,按变化规律填图:
5.观察下图中前三个图形的变化规律,然后画出第四个图形。
三年级上册思维拓展找乘法题组中的规律人教版

从王1少开回始去连后续越自想周然越围数气组的,成人于的元都几宵位乐之数得夜和,哈9扎相哈了乘大一,顶再笑大加。花上这灯一,个事来加传到数开笑(面第后虎一,家个越门因前数传。的越末远尾数。+1),得数中1的个数和加数一样。
这大花灯上题着一首诗。
这‘针’怎么是对你的呢?莫非是‘针’对你说的,不然你又怎么知道说的是你呢?”笑面虎一想,可不是,只好气得干瞪眼,灰溜溜走了,周围的人都乐得哈哈大笑。
( ) × 9 + ( )第=1二11年11元宵节,人们纷纷仿效,将谜语写在花灯上,供人猜射取乐。以后相沿成习,猜灯谜、打灯虎成了元宵佳节
仔细观察,这些算式有什么特点?
笑面虎上前观看的,重只要见活上面动写内着容:头。尖身细白如银,称称没有半毫分。
王少回去后越想越气,于元宵之夜,扎了一顶大花灯,来到笑面虎家门前。
找乘法题组中的规律
笑面虎上前观看,只见上面写着:头尖身细白如银,称称没有半毫分。
1×9+2=11
123×9+4= 1111 12×9+3=111
123×9+4=1111 1×9+2=11 12×9+3=111
相传很久以前,有个财主,人称笑面虎。他见了衣着体面的人,就拼命巴结,见了粗衣烂衫的穷人,就吹胡子瞪
1”便23命…n家×丁9去+(抢灯花),灯=,笑1…王嘻1少嘻忙挑地起说花:灯,“笑哎嘻,嘻地老说爷:莫“哎犯,老猜爷疑莫,犯猜我疑这,四我这句四诗句是诗是个个谜谜,,谜谜底底就就是‘针是’,‘你针想’想是,不你是想。 想是不是。这‘针’怎么是对你 9×9+7=88 的呢?莫非是‘针’对你说的,不然你又怎么知道说的是你呢?”笑面虎一想,可不是,只好气得干瞪眼,灰溜溜走了,
三年级数学思维专题训练《找规律、算式谜》

三年级数学思维专题练习《找规律、算式谜》姓名_________知识准备:找规律填数:按照一定规律排成一列数,我们称这样的一组数为数列。
先通过数列观察,找出数列中每个数的排列规律,并依据这个规律把所缺的数填写出来1、等差规律:所有相邻两数的差都相等2、倍数规律:所有相邻两数都是同一倍数关系3、相隔规律:相隔的两数间有一定的规律算式谜的解题方法分为尾数分析法和首位分析法以及进位借位分析法首先观察题目中给出的数字的位置,同时找出所有涉及这些已知数字的所有相关计算,然后按照尾数分析、首位分析、进位借位分析的顺序进行推理一、找规律填数(1)45,40,35,()()(2)1,2,4,7,11,()()(3)1,3,7,13,21,()()(4)1,2,4,8,16,()()(5)1,3,1,5,1,7,()()(6)17,2,14,2,11,2()()(7)25,6,20,7,15,8,()()(8)4,8,16,32,(),128(9)1,3,7,15,31,()()(10)1,4,9,16,25,36,()(11)1,7,8,15,23,38,()()(12)12,23,34,45,56()()(13)2+6,3+8,4+11,5+15,()(14)198,297,396,495,()()(15)2,3,5,9,17,()()(16)()()12,5,10,6,8,7按规律在表格中填入适当的数二、算式谜如图算式中,A、B、C分别代表1、2、3中一个不同的数字,此算式结果最大是_______加法算式中,七个方格中数字和等于_______如图算式中,相同的图形表示相同的数字,不同的图形表示不同的数字,要让它成立,那么如图,这个加法算式刚好由0~9这10个数字组成且不重复,其中2、0、1、8已经填好,那么将这个加法算式补充完整后,“数学探秘”所代表的四位数是______。
小学数学三年级上册思维训练题(共13套)

⼩学数学三年级上册思维训练题(共13套)班级考号姓名总分1、★×2+7-20=25 ★=()(54-★)×9=72 ★=()2、A乘4,再加上20,然后除以5,等于8,A是()。
3、篮⼦⾥有⼀些苹果,5个5个的数多1个,7个7个的数也多⼀个。
篮⼦⾥⾄少有()个苹果。
4、甲仓库存粮80吨,⼄仓库存粮56吨,每天从甲仓库运出8吨粮⾷,从⼄仓库运出5吨粮⾷。
那么()天之后两个仓库剩下的粮⾷就同样多了。
5、把⼀根⽊头锯成3段要4分钟,把这根⽊头锯成4段要()分钟。
6、名华奥校今年招收⼆年级新⽣80⼈,其中男⽣⽐⼥⽣多10⼈,男⼈有()⼈。
⼥⽣()⼈。
7、⼀年⼀班和⼀年⼆班共有学⽣46⼈,⼀年⼆班转到⼀年⼀班2⼈,两个班⼈数相等,原来⼀班有()⼈。
⼆班有()⼈。
8、⼀位数加⼀位数,最⼩是(),最⼤是(),两位数加两位数,最⼩是(),最⼤是(),三位数加三位数,最⼩是(),最⼤是(),从以上的解题中你是否发现规律了呢?请完成下⾯挑战题:四位数加四位数,最⼩是(),最⼤是()。
9、⼩李、⼩华⽐赛爬楼梯,⼩李跑到第2层时,⼩华正好跑到第4层。
照这样计算,⼩李跑到第5层时,⼩华到第()层。
10、直接写出得数(1)42+71+29+58= (2)526-73-27-26=(3)1457-(185+457)= (4)729+154+271=(5)516-56-44-16=11、⼩明和⼩强原有书和相等,后来⼩明把书送给⼩强12本,这时⼩明和⼩强,()的书多,多()本。
12、⼀只鸭、⼀只鹅共重12千克。
如果知道⼀只鸡和⼀只鸭共重7千克;⼀只鹅和⼀只鸭共重9千克,那么⼀只鸭是()千克。
13、把两张纸贴接在⼀起⽤⼀分钟,把同样6张纸连接贴成⼀张⼤纸,共⽤()分钟。
14、甲是⼄的哥哥,丙是丁的弟弟,丁是甲的⽗亲,丙是⼄的什么⼈?()班级考号姓名总分1、先找规律,再填数1×9+2=11 12×9+3=111 123×9+4=11111234×9+5=() 12345×9+6=()123456×9+7=() 12345678×9+9=()2、算式谜□ 9 1 □ 8 2 □□□□□□+ □ 1 □ + □ 1 □ - □ 8 5 - □ 8 7□ 9 1 □□ 9 0 □ 6 3 7 7 3 73、⼩推理(1)已知□+○=28,□=○+○+○,那么□=()○=()(2)☆+☆+□+□+□=61,☆+☆+□+□=52,那么☆=()□=()4、在⼀个减法算式⾥,被减数、减数、差这三个数的和是120,则被减数是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
找规律(一)
这一讲我们先介绍什么是“数列”,然后讲如何发现和寻找“数列”的规律。
按一定次序排列的一列数就叫数列。
例如,
(1) 1,2,3,4,5,6,⋯
(2) 1,2,4,8,16,32;
(3) 1,0,0,1,0,0,1,⋯
(4) 1,1,2,3,5,8,13。
一个数列中从左至右的第n 个数,称为这个数列的第n 项。
如,数列(1)的第3 项是3,数列(2)的第3 项是4。
一般地,我们将数列的第n 项记作a n。
数列中的数可以是有限多个,如数列(2)(4),也可以是无限多个,如数列(1)(3)。
许多数列中的数是按一定规律排列的,我们这一讲就是讲如何发现这些规律。
数列(1)是按照自然数从小到大的次序排列的,也叫做自然数数列,其规律是:后项=前项+1,或第n 项a n=n。
数列(2)的规律是:后项=前项×2。
数列(3)的规律是:“1,0,0”周而复始地出现。
数列(4)的规律是:从第三项起,每项等于它前面两项的和,即a3=1+1=2,a4=1+2=3,a5=2+3=5,a6=3+5=8,a7=5+8=13。
常见的较简单的数列规律有这样几类:
第一类是数列各项只与它的项数有关,或只与它的前一项有关。
例如数列(1)(2)。
第二类是前后几项为一组,以组为单元找关系才可找到规律。
例如数列(3)(4)。
第三类是数列本身要与其他数列对比才能发现其规律。
这类情形稍为复杂些,我们用后面的例3、例4 来作一些说明。
例1 找出下列各数列的规律,并按其规律在( )内填上合适的数:
(1)4,7,10,13,( ); (2)84,72,60,( ),( );
(3)2,6,18,( ),( ),(4)625,125,25,( ),( );
(5)1,4,9,16,( ),(6)2,6,12,20,( ),( ),
解:通过对已知的几个数的前后两项的观察、分析,可发现
(1)的规律是:前项+3=后项。
所以应填16。
(2)的规律是:前项-12=后项。
所以应填48,36。
(3)的规律是:前项×3=后项。
所以应填54,162。
(4)的规律是:前项÷5=后项。
所以应填5,1。
(5)的规律是:数列各项依次为1=1×1, 4=2×2, 9=3×3, 16=4×4,
所以应填5×5=25。
(6)的规律是:数列各项依次为2=1×2,6=2×3,12=3×4,20=4×5,
所以,应填 5×6=30, 6×7=42。
例2 找出下列各数列的规律,并按其规律在( )内填上合适的数:
(1)1,2,2,3,3,4,( ),( );
(2)( ),( ),10,5,12,6,14,7;
(3) 3,7,10,17,27,( );
(4) 1,2,2,4,8,32,( )。
解:通过对各数列已知的几个数的观察分析可得其规律。
(1)把数列每两项分为一组,1,2,2,3,3,4,不难发现其规律是:前一组每个数加1 得到后一组数,所以应填4,5。
(2)把后面已知的六个数分成三组:10,5,12,6,14,7,每组中两数的商都是2,且由5,6,7 的次序知,应填8,4。
(3) 这个数列的规律是:前面两项的和等于后面一项,故应填(17+27=)44。
(4)这个数列的规律是:前面两项的乘积等于后面一项,故应填(8×32=)256。
例3 找出下列各数列的规律,并按其规律在( )内填上合适的数:
(1)18,20,24,30,( );
(2)11,12,14,18,26,( );
(3)2,5,11,23,47,( ),( )。
解:(1)因20-18=2,24-20=4,30-24=6,说明(后项-前项)组成一新数列2,4,6,⋯其规律是“依次加2”,因为6 后面是8,所以,a5-a4=a5-30=8,故a5=8+30=38。
(2)12-11=1,14-12=2, 18-14=4, 26-18=8,组成一新数列1,2,4,8,⋯按此规律,8 后面为16。
因此,a6-a5=a6-26=16,故a6=16+26=42。
(3)观察数列前、后项的关系,后项=前项×2+1,所以a6=2a5+1=2×47+1=95,a7=2a6+1=2×95+1=191。
例4 找出下列各数列的规律,并按其规律在( )内填上合适的数:
(1)12,15,17,30, 22,45,( ),( );
(2) 2,8,5,6,8,4,( ),( )。
解:(1)数列的第1,3,5,⋯项组成一个新数列12,17, 22,⋯其规律是“依次加5”,22 后面的项就是27;数列的第2,4,6,⋯项组成一个新数列15,30,45,⋯其规律是“依次加15”,45 后面的项就是60。
故应填27,60。
(2)如(1)分析,由奇数项组成的新数列2,5,8,⋯中,8 后面的数应为11;由偶数项组成的新数列8,6,4,⋯中,4 后面的数应为2。
故应填11,2。
练习5
按其规律在下列各数列的( )内填数。
1.56,49,42,35,( )。
2.11, 15, 19, 23,( ),⋯
3.3,6,12,24,( )。
4.2,3,5,9,17,( ),⋯
5.1,3,4,7,11,( )。
6.1,3,7,13,21,( )。
7.3,5,3,10,3,15,( ),( )。
8.8,3,9,4,10,5,( ),( )。
9.2,5,10,17,26,( )。
10.15,21,18,19,21,17,( ),( )。
11.数列1,3,5,7,11,13,15,17。
(1)如果其中缺少一个数,那么这个数是几?应补在何处?
(2)如果其中多了一个数,那么这个数是几?为什么?。
