高考数学《三视图》真题归类练习 新
高考三视图(含解析)理试题(卷)汇总
专题21三视图SUBA. 2 n B • 3 n C【答案】B【解析】综合三视圄可知』几何体是一个半轻炸1的半个球体.且表面积是底面积与半球面积的和丿其表面枳3=丄敦4“+疋2=31t-故选B.2点睛:1、首先看俯视图,根据俯视图画出几何体地面的直观图;2、观察正视图和侧视图找到几何体前、后、左、右的高度;3、画出整体,然后再根据三视图进行调整.2.已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧1 •某几何体的三视图如图所示,则其表面积为(【解析】由正视图和俯视图还原几何体如图所示,由正视图和俯视图对应线段可得AB BD AD 2,当BC 平面ABD时,BC=2,ABD的边AB上的高为、3,只有B选项符合,当BC不垂直平面ABD时,没有符合条件的选项,故选 B.点睛:1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图. 2•三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据3.某个长方体被一个平面所截,得到几何体的三视图如图所示,则这个几何体的体积为()B【答案】BA. 4 B . 2.2 C . 20 D . 83【答案】D【解析】由三视图可知,该几何体如图所示,其底面为正方形』正方形的边长为2. 口D=3,BF=1,将相同的两个几何体拼在V』构成一个高为斗的长方饥所臥该几何体的体积為煜x仁仪4.如图,正三棱柱ABC ABG的主视图是边长为4的正方形,则此正三棱柱的左视图的面积为()【答案】D【解析】依题意知,此正三棱拄底面定边长为4的正三角形,接柱高为也其侧视囹为矩形,其一边长为2語,一启一边长訶4,故其面积2斗><2曲=8曲;故选D点睛:三视图问题的常见类型及解题策略⑴由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图•先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式•当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.原几何体为组合体;上面是长方体,下面是圆柱的一半(如图所示),A. 16 B 2 3 C . 4 3 D . 8,35.某几何体的三视图如图所示,则该几何体的体积为( )8 8 (C) 16 16 (D) 8 16将三视图还原为原来的几何体,再利用体积公式求解.其体积为V 4 2 2122 4 16 8 .故选A; 26•如图5,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的几条棱中,最长的棱的长度为( )(A) 6,2 (B) 4、2 (C) 6 (D)4【答案】C原几何体为三機锥D-A^C, M 中Aff^BC=i r AC=^D^ = DC=2^ ?QN二旳*叭庁)+4 = 6,故最长的棱的长度为= 选C点睛:对于小方格中的三视图,可以放到长方体,或者正方体里面去找到原图,这样比较好找;7.某几何体的三视图如图所示,则该几何体的表面积为()24 2【解析】如图所示A【解析】由已知三视图得到几何体是一个正方怀割去半轻为2的丄个球」所以表面积为S3 12试4&一亦於+ —><4亦囚・24巧故选:A4S&已知某空间几何体的三视图如图所示,则该几何体的表面积是()iEttffl 博视图A. 12十2&+2后B . 12+ 也+2 后C . 12 + 2辽十曲D . |12 +V2 + .J【答案】A【解析】由三视图知:几何体为四棱锥,且四棱锥的一条侧棱与底面垂直,1=-5< 2*2 = 221 =-X2M4=421S ABCD =~X(2+4)X2=69.一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体如图,P A丄平面ABCD , 朋=2 , AD = 4,医=2 ,经计算,PD = 2石,P匚=«亍,Dt = 2調,•••可••.,故选A.3D. 35 2.2【答案】A 【解析】试題分析;扌艮据三视图可知几何体是组合体;左边罡直三棱柱、右边是半个圆柱,直三棱柱的底面是等腰 亶角三角形,直角边是1,侧犧长是茶圆柱的底面半径是1,母线长是2,二该几何体的体积V =ixlxlx2十丄芝二臥十1・故选;乩2 2考点:由三视图求体积.10•如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积【答案】C 【解析】A.1 B2C. 2 1的体积是(为(3D. 41 2 体积为—2 2 2 1 4 —3 3试题分析:相当于一个圆锥和一个长方体,故考点:三视图.11. 一个几何体的三视图如图所示,则该几何体的体积为(【解析】试题分析:该几何休的直观團如园所示,连接妙,则该几何体由直三棱柱血D-和四棱锥一吨组合而成,其和易22 +扌心后专詈故应选扎12. 一个几何体的三视图如图所示 ,则该几何体的体积为A.14~316~3D. 6【答案】A考点:三视图.1【答案】-3【解析】本题考查三视图、四棱锥的体积计算等知识,难度中等•由三视图可知该几何体是底1 1面为长和高均为1的平行四边形,高为1的四棱锥,故其体积为V - 1 1 1 - •3 3。
高考三视图(含解析)理试题汇总(精编文档).doc

【最新整理,下载后即可编辑】专题21 三视图1.某几何体的三视图如图所示,则其表面积为()A.2π B.3π C.4π D.5π【答案】B点睛:1、首先看俯视图,根据俯视图画出几何体地面的直观图;2、观察正视图和侧视图找到几何体前、后、左、右的高度;3、画出整体,然后再根据三视图进行调整.2.已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( )A.B.C.D.【答案】B【解析】由正视图和俯视图还原几何体如图所示,由正视图和俯视图对应线段可得2⊥平面时,BC=2,===,当BC ABDAB BD AD∆的边AB上的高为3,只有B选项符合,当BC不垂直平面ABD ABD时,没有符合条件的选项,故选B.点睛:1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.2.三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据3.某个长方体被一个平面所截,得到几何体的三视图如图所示,则这个几何体的体积为( )A . 4B . 22C .203 D . 8【答案】D4.如图,正三棱柱111ABC A B C 的主视图是边长为4的正方形,则此正三棱柱的左视图的面积为( )A . 16B . 23C . 43D . 83【答案】D点睛:三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合. (3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.5.某几何体的三视图如图所示,则该几何体的体积为 ( )(A) 168π+ (B) 88π+ (C) 1616π+(D) 816π+【答案】A【解析】将三视图还原为原来的几何体,再利用体积公式求解.原几何体为组合体;上面是长方体,下面是圆柱的一半(如图所示), 其体积为21422241682V ππ=⨯⨯+⨯⨯=+.故选A;6.如图5,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的几条棱中,最长的棱的长度为( )(A) 62 (B) 42 (C) 6 (D)4【答案】C【解析】如图所示点睛:对于小方格中的三视图,可以放到长方体,或者正方体里面去找到原图,这样比较好找;7.某几何体的三视图如图所示,则该几何体的表面积为( )A.24π-B.24π+C.20π-D.20π+【答案】A8.已知某空间几何体的三视图如图所示,则该几何体的表面积是()A.B.C.D.【答案】A【解析】由三视图知:几何体为四棱锥,且四棱锥的一条侧棱与底面垂直,如图,平面,,,,,经计算,,,,∴,∴, ,,,∴,故选A .9.一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )A .1π+B .2π+C .21π+D .3522π++【答案】A【解析】考点:由三视图求体积.10.如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为( )A .263π+B .83π+ C .243π+ D .43π+ 【答案】C【解析】试题分析:相当于一个圆锥和一个长方体,故体积为122221433ππ⋅+⋅⋅=+.考点:三视图.11.一个几何体的三视图如图所示,则该几何体的体积为( )A . 143B . 5C . 163D .6【答案】A【解析】考点:三视图.12.一个几何体的三视图如图所示,则该几何体的体积为____.【答案】13【解析】本题考查三视图、四棱锥的体积计算等知识,难度中等.由三视图可知该几何体是底面为长和高均为1的平行四边形,高为1的四棱锥,故其体积为11111V=⨯⨯⨯=.33。
三视图通关100题(含答案)
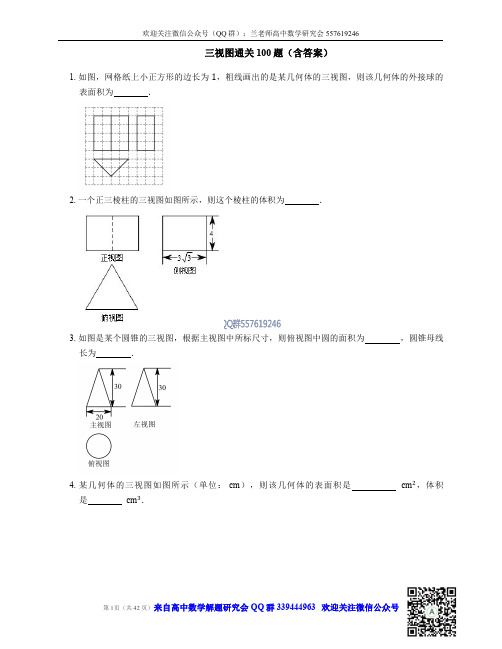
72. 一个多面体从前面、后面、左侧、右侧、上方看到的图形分别如图所示(其中每个正方形边长 都为 ),则该多面体的表面积为 .
73. 已知正三棱锥 面积为 .
th 的正视图、俯视图如图所示,则该三棱锥的体积为
,侧视图的
74. 图中的三个直角三角形是一个体积为 㐸 cm 的几何体的三视图,该几何体的外接球表面积 为
36. 某几何体的三视图如图所示,则它的表面积为
,体积为
.
37. 某几何体的三视图(单位: cm)如图所示,则此几何体的所有棱长之和为 为 cm .
cm ,体积
38. 某几何体的三视图如图所示(单位: :),且该几何体的体积是 是 cm,该几何体的表面积是 cm .
cm ,则正视图中的
的值
39. 某几何体的三图所示,则某几何体的体积为
第 19页(共 42 页)来自高中数学解题研究会
:
QQ 群 339444963 欢迎关注微信公众号
欢迎关注微信公众号(QQ 群):兰老师高中数学研究会 557619246
75. 某三棱锥的三视图如图所示,则该三棱锥的表面积是
.
76. 在棱柱 th 直角边为
的等腰直角三角形.设 .
t h 中, t h
cm.
44. 一个四棱锥的三视图如图所示,其中侧视图为正三角形,则该四棱锥的体积是 锥中侧面面积最大的是 .
,四棱
45. 已知一个三棱镜的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的四个面中面 积最大的为 .
46. 如图是某几何体的三视图,其中正视图是腰长为 则该几何体的表面积是 .
第 12页(共 42 页)来自高中数学解题研究会
第 5页(共 42 页)来自高中数学解题研究会
三视图练习题含答案

23正视图侧视图2俯视图2第3题三视图练习题1.某几何体的三视图如图所示,则它的体积是( ) A.283π-B.83π-C.π28-D.23π2.某四棱锥的三视图如图所示,该四棱锥的表面积是( )A .32 B.16+162 C.48 D.16322+3.如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为( ) A .43 B .4C .23 D .24.如图是某几何体的三视图,则该几何体的体积为( )A .942π+ B.3618π+C.9122π+D.9182π+ 5.一个空间几何体的三视图如图所示,则该几何体的表面积为( ) A. 48 B.32+817C.48+817D.806.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是( ) A.35233cm B.32033cm C.22433cm D.16033cm3 32正视图侧视图俯视图第4题第5题第1题 第2题第6 题7.若某空间几何体的三视图如图所示,则该几何体的体积是( ) A.2B.1C.23D.138.某几何体的三视图如图所示,则该几何体的体积为( ) A.π816+ B.π88+ C.π1616+ D.π168+9. 某四棱台的三视图如图所示,则该四棱台的体积是( ) A.4 B.314 C.316D.610. 某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为如图所示的直角三角形,则该三棱锥的体积为( ) A .1B .3C .4D .511. 一个几何体的三视图如图所示,则这个几何体的体积为( )A .(8)36π+B .(82)36π+C .(6)36π+D .(92)36π+ 12.某几何体的底面为正方形,其三视图如图所示,则该几何体的体积等于( )A .1B .2C .3D .4第7题第8题第9题第10题3122第11题 211俯视图正视图13第12题13.某几何体的三视图如图所示,则其体积为______.14.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积等于______3cm . 15.某几何体的三视图如图所示,则该几何体的体积是______.16.已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是 17.一个空间几何体的三视图如图所示,则这个空间几何体的体积是.18.如图所示,一个三棱锥的三视图是三个直角三角形,则该三棱锥外接球的表面积为19.若某空间几何体的三视图如下图所示,则该几何体的表面积是_______________.20.一个正方体的内切球与它的外接球的体积比是( ).A .1∶33B .1∶22C .1∶383 D .1∶4221.已知球面上A 、B 、C 三点的截面和球心的距离都是球半径的一半,且AB =BC =CA =2,则球表面积是( )A.π964 B. π38C. π4D. π916第17题 24 3正视图 侧视图 俯视图第18题 第15题第14题第13题第16题 第19题22. P 、A 、B 、C 是球O 面上的四点,且PA 、PB 、PC 的两两垂直,PA=PB=PC=9,则球心O 到截面ABC 的距离为23.半径为5的球被一个平面所截,截面面积为16π,则球心到截面的距离为 ( ) A.4 B.3 C.2.5 D.224.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________. 25.答案1.A2.B3.C4.D5.C6.B7.B8.A9.B 10.A 11.A 12.A 13.3π 14.24 15.1616-π 16.1 17.67π 18.29π 19. 20+8220.A 21.A 22.233 23.B 24. 2 25.︒9026.3500π 27.π628.π29 29.72 30. 3629+3226-31.2500π 32.π1200。
2022年高考数学空间几何体的直观图与三视图知识点专项练习含答案

专题28 空间几何体的直观图与三视图一、单选题(本大题共12小题,共60分)1.已知一个几何体的正视图和侧视图如图(1)所示,其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图(2)所示),则此几何体的体积为()A. 1B. √2C. 2D. 2√22.正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图(如图),则原图形的周长是()A. 6cmB. 8cmC. (2+3√2)cmD. (2+2√3)cm3.一个几何体的三视图如图所示,则该几何体的表面积为()A. 3π2+1+√32B. 3π+12+√32C. 3π+1+√32D. 3π+1+√324.某几何体的三视图如图所示,则该几何体的表面积为()A. 3π+4+√3B. 3π+5+√3C. 52π+6+√3 D. 52π+4+√35.已知某几何体的一条棱长为l,该棱在正视图中的投影长为√2020,在侧视图与俯视图中的投影长为a与b,且a+b=2√1011,则l的最小值为()A. √20212B. √40422C. √2021D. 20216.已知一几何体的三视图如图所示,则该几何体的表面积为()A. √24π+72B. √24π+4 C. 1+√24π+72D. 1+√24π+47.某圆柱的正视图是如图所示的边长为2的正方形,圆柱表面上的点A,B,C,D,F在正视图中分别对应点A,B,C,E,F.其中E,F分别为AB,BC的中点,则异面直线AC与DF所成角的余弦值为()A. 13B. √23C. √33D. √638.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为()A. 22π3B. 28π3C. 34π3D. 40π39.如图,网络纸上小正方形的边长为1,粗实线画出的某几何体的三视图,则该几何体的体积是()A. 18πB. 21πC. 27πD. 36π10.如图所是某一容器三视图,现容中匀速注水,容器中的度h随时间变可能图象是()A. B. C. D.11.如图是一个四棱锥的三视图,则该几何体的体积为()A. 403B. 323C. 163D. 28312.如图所示,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为A. 64−8√2π3B. 64−4√2π3C. 64−8π3D. 64−4π3二、单空题(本大题共4小题,共20分)13.某组合体的正视图和侧视图如图(1)所示,它的俯视图的直观图是图(2)中粗线所表示的平面图形,其中四边形O′A′B′C′为平行四边形,D′为C′B′的中点,则图(2)中平行四边形O′A′B′C′的面积为___________.14.以图①为正视图,在图②③④⑤中选两个分别作为侧视图和附视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为_____________(写出符合求的一组答案即可).15.在棱长为1的正方体ABCD−A1B1C1D1中,点M,N分别是棱B1C1,C1D1的中点,过A,M,N三点作正方体的截面,将截面多边形向平面ADD1A1作投影,则投影图形的面积为.16.把平面图形α上的所有点在另一个平面上的射影所构成的图形β称为图形α在这个平面上的射影,如图所示,在三棱锥A−BCD中,BC⊥DC,AD⊥DC,BC⊥AB,BC= CD=4,AC=4√3,则△ADB在平面ABC上的射影的面积是________.三、解答题(本大题共2小题,共20分)13.设某几何体的三视图如图(尺寸的长度单位为cm),(1)用斜二测画法画出该几何体的直观图(不写画法);(2)求该几何体最长的棱长.14.设一正方形纸片ABCD边长为4厘米,切去阴影部分所示的四个全等的等腰三角形,剩余为一正方形纸片和四个全等的等腰三角形,沿虚线折起,恰好能做成一个正四棱锥,O为正四棱锥底面中心.,(粘接损耗不计),图中AH PQ(1)若正四棱锥的棱长都相等,请求出它的棱长并画出它的直观图示意图;(2)设等腰三角形APQ的底角为x,试把正四棱锥的侧面积表示为x的函数,并求S范围.专题28 空间几何体的直观图与三视图一、单选题(本大题共12小题,共60分)17.已知一个几何体的正视图和侧视图如图(1)所示,其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图(2)所示),则此几何体的体积为()A. 1B. √2C. 2D. 2√2【答案】B【解析】解:根据直观图可得该几何体的俯视图是一个直角边长分别是2和√2的直角三角形,根据三视图可知该几何体是一个三棱锥,且三棱锥的高为3,所以体积V=13×(12×2×√2)×3=√2.故选B.18.正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图(如图),则原图形的周长是()A. 6cmB. 8cmC. (2+3√2)cmD. (2+2√3)cm【答案】B【解析】解:如图,OA=1cm,在Rt△OAB中,OB=2√2 cm,∴AB=√OA2+OB2=3cm.∴四边形OABC的周长为8cm.故选B.19.一个几何体的三视图如图所示,则该几何体的表面积为()A. 3π2+1+√32B. 3π+12+√32C. 3π+1+√32D. 3π+1+√32【答案】C【解析】解:由三视图可知几何体上部为三棱锥,下部为半球,三棱锥的底面和2个侧面均为等腰直角三角形,直角边为1,另一个侧面为边长为√2的等边三角形,半球的直径2r=√2,故r=√22.∴S表面积=12×1×1×2+√34×(√2)2+12×4π×(√22)2+π×(√22)2−12×1×1=12+√32+3π2.故选:C.20.某几何体的三视图如图所示,则该几何体的表面积为()A. 3π+4+√3B. 3π+5+√3C. 52π+6+√3 D. 52π+4+√3【答案】A【解析】解:由已知中的三视图可得:该几何体是一个半圆柱和三棱锥的组合体半圆柱的半径为1高2,所以该组合体的面积故选A.21.已知某几何体的一条棱长为l,该棱在正视图中的投影长为√2020,在侧视图与俯视图中的投影长为a与b,且a+b=2√1011,则l的最小值为()A. √20212B. √40422C. √2021D. 2021【答案】C【解析】解:如图所示:设长方体中AB=m,BD为正投影,BE为侧投影,AC为俯视图的投影.故:BD=√2020,BE=a,AC=b,设AE=x,CE=y,BC=z,则:x2+y2+z2=l2,x2+y2=b2,y2+z2=a2,x2+z2=2020,所以2(x2+y2+z2)=a2+b2+2020,故:2l2=a2+b2+2020,因为a2+b2≥(a+b)22=2022,所以2l2≥2022+2020,则l≥√2021.故l的最小值为√2021.故选C.22.已知一几何体的三视图如图所示,则该几何体的表面积为()A. √24π+72B. √24π+4 C. 1+√24π+72D. 1+√24π+4【答案】D【解析】解:几何体左边为四分之一圆锥,圆锥的半径为1,高为1,右边为三棱锥,三棱锥底面是直角边长为1和2的直角三角形,高为1,所以几何体的表面积为:+12×(2+1)×1+12×√2×√(√5)2−(√22)2,故选D.23.某圆柱的正视图是如图所示的边长为2的正方形,圆柱表面上的点A,B,C,D,F在正视图中分别对应点A,B,C,E,F.其中E,F分别为AB,BC的中点,则异面直线AC与DF所成角的余弦值为()A. 13B. √23C. √33D. √63【答案】D【解析】解:如图所示,连结DE,EF,易知EF//AC,所以异面直线AC与DF所成角为∠DFE,由正视图可知,DE⊥平面ABC,所以DE⊥EF.由于AB=BC=2,所以EF=√2,又DE=1,所以DF=√3,在RtΔEFM中,cos∠DFE=√2√3=√63,故选D.24.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为()A. 22π3B. 28π3C. 34π3D. 40π3【答案】C【解析】解:根据几何体得三视图转换为几何体为:该几何体是由一个底面半径为2,高为3的半圆柱和一个半径为2的半球组成,故:V=12⋅π×22×3+12×43×π×23=34π3.故选C.25.如图,网络纸上小正方形的边长为1,粗实线画出的某几何体的三视图,则该几何体的体积是()A. 18πB. 21πC. 27πD. 36π【答案】A【解析】解:该几何体是一个四分之一的圆和圆锥的组合体,如图:有题意知该圆的直径为6cm,圆锥的高为3cm,则该几何体的体积为13×π×32×3+1 4×43π×33=18π,故选A.26.如图所是某一容器三视图,现容中匀速注水,容器中的度h随时间变可能图象是()A. B. C. D.【答案】B【解析】解:三视图表示的容器倒的圆锥,下细,上面,刚开始度增加的相快些.曲越竖直”,后,高度增加来越慢,图越平稳.故B.27.如图是一个四棱锥的三视图,则该几何体的体积为()A. 403B. 323C. 163D. 283【答案】A【解析】解:由三视图得到其直观图(下图所示),则体积为:13×[12(1+4)×4]×4=403,故选A .28.如图所示,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为A. 64−8√2π3B. 64−4√2π3C. 64−8π3D. 64−4π3【答案】A【解析】解:这是一个有一条侧棱垂直于底面的四棱锥内部挖去了一个八分之一的球,四棱锥的底面边长和高都等于4,八分之一球的半径为2√2,,故选A .二、单空题(本大题共4小题,共20分)29. 某组合体的正视图和侧视图如图(1)所示,它的俯视图的直观图是图(2)中粗线所表示的平面图形,其中四边形O ′A ′B ′C ′为平行四边形,D ′为C ′B ′的中点,则图(2)中平行四边形O ′A ′B ′C ′的面积为___________.【答案】3√2【解析】解:由正视图和侧视图可得俯视图如下:∴|O′A′|=4,|O′C′|=32,∠A′O′C′=45°,∴S ΔA′O′C′=12|O′A′|·|O′C′|·sin∠A′O′C′ =12×4×32×√22=3√22, ∴S ▱O′A′B′C′=2S △A′O′C′=3√2, 故答案为3√2.30.以图①为正视图,在图②③④⑤中选两个分别作为侧视图和附视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为_____________(写出符合求的一组答案即可).【答案】②⑤或③④【解析】解:由高度可知,侧视图只能为②或③,侧视图为②,如图(1)平面PAC⊥平面ABC,PA=PC=√2,BA=BC=√5,AC=2,俯视图为⑤;侧视图为③,如图(2),PA⊥平面ABC,PA=1,AC=AB=√5,BC=2,俯视图为④.故答案为②⑤或③④.31.在棱长为1的正方体ABCD−A1B1C1D1中,点M,N分别是棱B1C1,C1D1的中点,过A,M,N三点作正方体的截面,将截面多边形向平面ADD1A1作投影,则投影图形的面积为.【答案】712【解析】解:直线MN分别与直线A1D1,A1B1交于E,F两点,连接AE,AF,分别与棱DD1,BB1交于G,H两点,连接GN,MH,得到截面五边形AGNMH,向平面ADD1A1作投影,得到五边形AH1M1D1G,由点M,N分别是棱B1C1,C1D1的中点,可得D1E=D1N=12,由△D1EG∽△DAG,可得DG=2D1G=23,同理BH=2B1H=23,则AH1=2A1H1=23,A1M1=D1M1=12,则S AH1M1D1G =1−S A1H1M1−S ADG=1−12×12×13−12×1×23=712,故答案为:712.32.把平面图形α上的所有点在另一个平面上的射影所构成的图形β称为图形α在这个平面上的射影,如图所示,在三棱锥A−BCD中,BC⊥DC,AD⊥DC,BC⊥AB,BC= CD=4,AC=4√3,则△ADB在平面ABC上的射影的面积是________.【答案】8√2【解析】解:因为BC⊥DC,AD⊥DC,BC⊥AB,BC=CD=4,AC=4√3,把三棱锥A−BCD放入如图所示的棱长为4的正方体中,过点D作CE的垂线DF,垂足为F,连接AF,BF,因为BC⊥平面CE,DF⊂平面CE,故BC⊥DF又BC∩CE=C,BC,CE⊂平面ABC则DF⊥平面ABC,故△ADB在平面ABC上的射影为△AFB,因为AB=√42+42=4√2,×4×4√2=8√2,所以△AFB的面积为12即△ADB在平面ABC上的射影的面积为8√2.故答案为8√2.三、解答题(本大题共2小题,共20分)13.设某几何体的三视图如图(尺寸的长度单位为cm),(1)用斜二测画法画出该几何体的直观图(不写画法);(2)求该几何体最长的棱长.【答案】(1)答案见解析;(2)4cm.【解析】(1)(2)如下图,SE⊥面ABC,线段AC中点为D2,3,1,4,2,=1======,BD AC SE cm AE cm CE cm AC cm AD DC cm DE cm⊥,=,3BD cm在等腰ABC中,AB AC=在Rt SEA△中,SA=在Rt SEC△中,SC△中,BE==在Rt BDE∴⊥SE⊥面ABC,SE BE在Rt SEB△中,SB=<==<<,在三梭锥S-ABC中,SC AB AC SA SB AC所以最长的棱为AC ,长为4cm14.设一正方形纸片ABCD 边长为4厘米,切去阴影部分所示的四个全等的等腰三角形,剩余为一正方形纸片和四个全等的等腰三角形,沿虚线折起,恰好能做成一个正四棱锥(粘接损耗不计),图中AH PQ ⊥,O 为正四棱锥底面中心.,(1)若正四棱锥的棱长都相等,请求出它的棱长并画出它的直观图示意图;(2)设等腰三角形APQ 的底角为x ,试把正四棱锥的侧面积表示为x 的函数,并求S 范围.【答案】(1),画图见解析;(2)161tan 2tan S x x=++,()0,4.【解析】(1)由题意,设正四棱锥的棱长为a,则AH =,2a AC a +===(2)设PH b =,则tan AH b x =,由2tan 2a x a ⋅+=a =,从而22116tan 442tan 2(tan 1)APQ x S S PQ AH a x x ==⋅⋅⋅==+△,其中(tan 1),x ∈+∞,∴16(0,4)1tan 2tan S x x=∈++。
三视图高考题选答案版
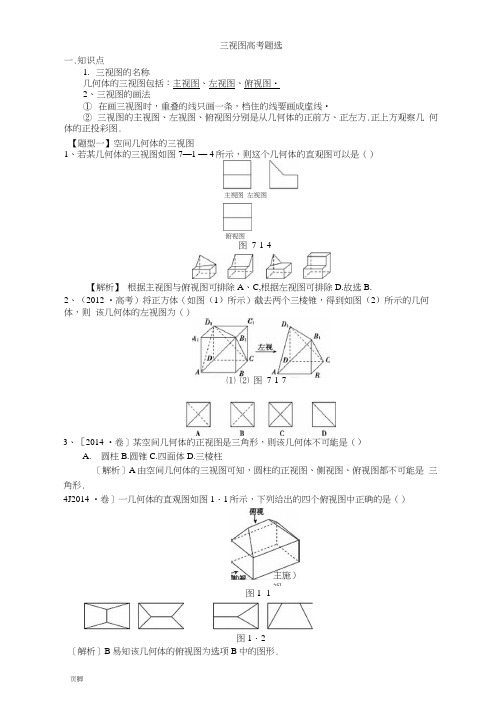
三视图高考题选一.知识点1.三视图的名称几何体的三视图包括:主视图、左视图、俯视图・2、三视图的画法①在画三视图时,重叠的线只画一条,档住的线要画成虚线•②三视图的主视图、左视图、俯视图分别是从几何体的正前方、正左方.正上方观察几何体的正投彩图.【题型一】空间几何体的三视图1、若某几何体的三视图如图7—1 — 4所示,则这个几何体的直观图可以是()图7-1-4【解析】根据主视图与俯视图可排除A、C,根据左视图可排除D.故选B.2、(2012 •高考)将正方体(如图(1)所示)截去两个三棱锥,得到如图(2)所示的几何体,则该几何体的左视图为()3、[2014 •卷]某空间几何体的正视图是三角形,则该几何体不可能是()A.圆柱B.圆锥C.四面体D.三棱柱[解析]A由空间几何体的三视图可知,圆柱的正视图、侧视图、俯视图都不可能是三角形.4J2014 •卷]一几何体的直观图如图1・1所示,下列给出的四个俯视图中正确的是()图1・2[解析]B易知该几何体的俯视图为选项B中的图形.主視图左视图俯视图⑴ ⑵ 图7-1-7主施)视图1- 1【题型二】三视图与面积U (2013 •高考)已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧(左)视图是一个面积为边的矩形,则该正方体的正(主)视图的面积等于()B. 1C.牢1D.返【解析】由于该正方体的俯视图是面积为1的正方形,侧视图是一个面积为花的矩形,因此该几何体的主视图是一个长为电,宽为1的矩形,其面积为【答案】D2、[2014 •卷]一个多面体的三视图如图1・2所示,则该多面体的表面积为()A. 21+书B. 8+^2C.21D. 18正(主)视图侧(左)视图图2[解析]A如图,由三视图可知该几何体是棱长为2的正方体截去两个小三棱锥后余下的部分,其表面积S=6X4-|X6+2X|X-72X^=21+V3.3. [2014 •卷]几何体的三视图(单位:cm)如图1所示,则此几何体的表面积是()[解析]• D此几何体是由长方体与三棱柱组合而成的,其直观图如图,所以该几何体的表面积为 2(4X3 + 6X3 + 6X4)+2X|X3X4+4X3 + 3X5-3X3 = 138(cm 2),故选 D ・4、[2014•卷]某几何体的三视图如图2所示,则该几何体的表面积为()1 r51 T■ % % ■ % ■ ■ %4 -► « 3-> 正视图 左视图俯视图图1・2A. 54B. 60C. 66 D ・ 72[解析]B 由三视图可知该几何体是由一个直三棱柱去掉一个三棱锥所得,三棱柱的底面 是一个两直角边长分别为3和4的直角三角形,高为5,截去的锥体的底面是两直角边的边 长分别为3和4的直角三角形,高为3,所以表面积为S=*X3X4+竽+学X4+于X 5+3X5=60 ・【题型三】三视图与体积U (2013 •高考)某三棱锥的三视图如图7-1-8所示,则该三棱锥的体积是( )俯视图图 7-1-8c -l如图,三棱锥的底面是一个直角边长为1的等腰直角三角形,有一条侧棱和 底面垂直,且其长度为2,故三棱锥的高为2,故其体积r=^x|x 1X1X2=!,故选【答案】B【解析】 正(卞)视图 侧(左)视图2、[2014 •卷]某几何体三视图如图1・1所示,则该几何体的体积为(n n A. 8—2 n B ・ 8— n C ・ 8—— D ・ 8——俯視图 图1- 1[解析]B 根据三视图可知,该几何体是正方体减去两个体积相等的圆柱的一部分 (占圆柱的》后余下的部分,故该几何体体积为2X2X2-2X^X n X2=8- n.3, [2014 •卷]一个儿何体的三视图如图1- 3所示(单位:m ),则该几何体的体积为 3 ________ m ■ 图1・3[解析]由三视图可得,该几何体为圆柱与圆锥的组合体,其体积r=nXl 2X4+^X 2叹2罟.4、(2013年高考新课标1 (湮))某几何体的三视图如图所示•则该几何体的体积为 1~~ 1 —:1 ------- --------2正视图 侧视图俯视图A. 16 + 8/rB ・ 8 + 8/rC ・ 16 + 16/r D. 8 + 16”【答案】A 5、(2013年(理))某四棱台的三视图如图所「示•则该四棱台的体积是 ( )【答案】BA. 414B. 316 C. 3 D. 6 第5题图。
高中高考数学三视图选择题综合训练
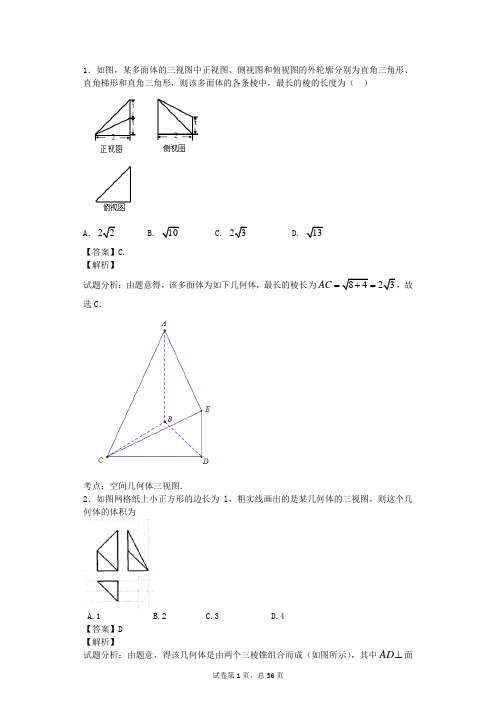
1.如图,某多面体的三视图中正视图、侧视图和俯视图的外轮廓分别为直角三角形、直角梯形和直角三角形,则该多面体的各条棱中,最长的棱的长度为()A.22 B. 10 C. 23 D. 13【答案】C.【解析】AC=+=,故试题分析:由题意得,该多面体为如下几何体,最长的棱长为8423选C.考点:空间几何体三视图.2.如图网格纸上小正方形的边长为l,粗实线画出的是某几何体的三视图,则这个几何体的体积为A.1B.2C.3D.4【答案】D【解析】AD面试题分析:由题意,得该几何体是由两个三棱锥组合而成(如图所示),其中⊥ABC ,⊥CE 面ABC , BCAC ⊥,4,2====CE AD BC AC ,则4)4221(312)2221(3121=⨯⨯⨯+⨯⨯⨯⨯=+=V V V ;故选D .考点:1.三视图;2.棱锥的体积.3.如图是一个几何体的三视图,则该几何体的体积是( )A .54B .27C .18D .9 【答案】C 【解析】 试题分析:由三视图可知该几何体为四棱锥,底面为矩形,两边为6,3,棱锥的高为3,所以体积为1633183V =⨯⨯⨯= 考点:三视图4.如图, 一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的侧面积为 ( )A .2B .6C .2(23)+D .2(23)+2+【答案】C 【解析】试题分析:由三视图可知该几何体为四棱锥,底面为正方形,对角线为2,高为2,所以侧面为四个直角三角形,面积为112222622(23)22S =⨯⨯⨯+⨯⨯⨯=+ 考点:三视图及棱锥侧面积5.某三棱锥的三视图如图所示,该三棱锥的表面积是( )A .56+12B .60+12C .30+6D .28+6 【答案】C 【解析】试题分析:由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱锥,求出各个面的面积,相加可得答案.解:根据题意,还原出如图的三棱锥A ﹣BCD 底面Rt △BCD 中,BC ⊥CD ,且BC=5,CD=4侧面△ABC 中,高AE ⊥BC 于E ,且AE=4,BE=2,CE=3 侧面△ACD 中,AC==5∵平面ABC ⊥平面BCD ,平面ABC∩平面BCD=BC ,AE ⊥BC ∴AE ⊥平面BCD ,结合CD ⊂平面BCD ,得AE ⊥CD ∵BC ⊥CD ,AE∩BC=E∴CD ⊥平面ABC ,结合AC ⊂平面ABC ,得CD ⊥AC 因此,△ADB 中,AB==2,BD==,AD==,∴cos ∠ADB==,得sin ∠ADB==,由三角形面积公式,得S △ADB =×××=6,又∵S △ACB =×5×4=10,S △ADC =S △CBD =×4×5=10 ∴三棱锥的表面积是S 表=S △ADB +S △ADC +S △CBD +S △ACB =30+6,故选:C考点:由三视图求面积、体积.6.如图,'''O A B ∆是水平放置的OAB ∆的直观图,则OAB ∆的面积是( )A .12B .62C .6D .32 【答案】A 【解析】试题分析:根据斜二测画法知OAB ∆为边长6OA =,高2''224OB O B ==⨯=,故OAB ∆的面积是164122S =⨯⨯=.考点:平面图形的直观图.7.已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为2的矩形,则该正方体的正视图的面积等于( )A . 32 B.1 C.212+ D.2【答案】D 【解析】试题分析:因为正方体的棱长为1,俯视图是一个面积为1的正方形,侧视图是一个面积为2的矩形,说明侧视图是底面对角线为边,正方体的高为一条边的矩形,几何体放置如图:那么正视图的图形与侧视图的图形相同,所以正视图的面积为:2 考点:三视图8.如图,'''Rt O A B ∆是OAB ∆的斜二测直观图,斜边''2O A =,则OAB ∆的面积是( )A .22B .1C .2D .22 【答案】D 【解析】 试题分析:2,90,45,2,O A B A O B O B ''''''''=∠=︒∠=︒∴=2,22,90,OA OB AOB ∴==∠=︒OAB ∴∆的面积为112222222AOB S OA OB ∆=⋅=⨯⨯=,故选D .考点:斜二测画法.【方法点晴】本题要求我们将一个直观图形进行还原,由斜二测画法法则可知原图是一个两边分别在,x y 轴的直角三角形,x 轴上的边长与原图形相等,而y 轴上的边长是原图形边长的一半,由此求出原三角形的面积,本题着重考查了斜二测画法中直观图与原图形面积之间的关系的问题和三角形的面积公式,本题着重考查了斜二测画法和三角形的面积公式,属于基础题.9.如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积是12,则该几何体的俯视图可以是( )【答案】C 【解析】 试题分析: 若俯视图为A ,则几何体为边长为1的正方体,所以体积为1,不满足条件;若为B ,则该几何体为底面直径为1,高为1的圆柱,此时体积为2112π⎛⎫⨯ ⎪⎝⎭14π=,不满足条件;若为D ,几何体为底面半径为1,高为1141144ππ⨯⨯=,不满足条件;若为C ,该几何体为底面是直角三角形且两直角边为1,高为1的三棱柱,所以体积为1112⨯⨯=12,满足条件,所以选C.考点:三视图与几何体的表面积与体积.10.一个锥体的正视图和左视图如下图,下面选项中,不可能是该锥体的俯视图的是( )【答案】C 【解析】试题分析:本题中给出了正视图和左视图,故可以根据正俯同长,左俯同宽来找出正确选项.A 、B 、D 中的视图满足三视图法则;C 中的视图不满足三视图中左俯同宽,故其错误,故选C.考点:三视图的作图规则.11.某四棱锥三视图如图所示,则该四棱锥体积为( )A .B .16C .32D .【答案】D 【解析】试题分析:四棱锥为正四棱锥,底面边长为4,高为2.解:由三视图可知四棱锥为正四棱锥,棱锥的底面边长为4,棱锥的高为2. 所以四棱锥的体积V==.故选:D .考点:由三视图求面积、体积.12.某几何体的主视图与俯视图如图所示,左视图与主视图相同,且图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是( )A. B. C.6 D.4【答案】A【解析】试题分析:根据三视图,还原成几何体,再根据长度关系,即可求得几何体的体积解:由三视图知,原几何体为一个正方体挖掉一个正四棱锥其中正方体的棱为2,正四棱柱的底面边长为正方体的上底面,高为1∴原几何体的体积为故选A考点:由三视图求面积、体积.13.如图,网格纸上小正方形的边长为2,粗线画出的是某几何体的三视图,则此几何体的体积为()A.36 B.9 C.72 D.48【答案】B【解析】试题分析:由已知中的三视图可得该几何体是一个以俯视图为底面的三棱锥,进而可得答案.解:由已知中的三视图可得该几何体是一个以俯视图为底面的三棱锥,底面面积S=×6×3=9,棱锥的高h=3,故几何体的体积V==9,故选:B考点:由三视图求面积、体积.14.一个空间几何体的三视图如图所示,则该几何体的体积为()A. B. C.40 D.80【答案】A【解析】试题分析:几何体为其中一个侧面在下面的四棱锥,结合直观图判断棱锥的高及底面相关线段的长,把数据代入棱锥的体积公式计算.解:由三视图知:几何体为其中一个侧面在下面的四棱锥,如图:其中SA⊥平面ABCD,SA=4,底面ABCD为直角梯形,且AD=4,BC=1,AB=4,∴几何体的体积V=××4×4=.故选:A.考点:由三视图求面积、体积.15.定义:底面是正三角形,侧棱与底面垂直的三棱柱叫做正三棱柱,将正三棱柱截去一个角,(如图1所示,M,N分别为AB,BC的中点)得到几何体如图2.则该几何体按图2所示方向的侧视图为()A. B.C. D.【答案】B【解析】试题分析:结合几何体的结构特征,利用左视图的定义求解.解:解题时在图2的右边放扇墙(心中有墙),图2所示方向的侧视图,由于平面EMN在平面ADFC上,故侧视图中仍然看到矩形中的两条斜线段,∴该几何体按图2所示方向的侧视图为B.故选:B考点:棱柱的结构特征;简单空间图形的三视图.16.已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为()A.1 B.2 C.3 D.4【答案】D【解析】试题分析:由题意可知,几何体为三棱锥,将其放置在长方体模型中即可得出正确答案.解:由题意可知,几何体是三棱锥,其放置在长方体中形状如图所示(图中红色部分),利用长方体模型可知,此三棱锥的四个面中,全部是直角三角形.故选:D.考点:由三视图还原实物图.17.若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是()A.2cm2B.cm3C.3cm3D.3cm3【答案】B【解析】试题分析:由几何体的三视图得到原几何体的底面积与高,进而得到该几何体的体积.解:由几何体的三视图可知,该几何体为底面是直角梯形,高为的四棱锥,其中直角梯形两底长分别为1和2,高是2.故这个几何体的体积是×[(1+2)×2]×=(cm3).故选:B.考点:由三视图求面积、体积.18.已知一个几何的三视图如图所示,图中小正方形的边长为1,则该几何体的体积为()A.B.4 C.6 D.10【答案】C试题分析:由三视图得该几何体是直三棱柱ABC﹣A1B1C1、三棱锥D﹣ABC和三棱锥D ﹣BCE组合体,其中AD⊥平面ABC,且AD=AC=AB=AA1=2,CE=1,AB⊥AC,由此能求出该几何体的体积.解:由三视图得该几何体是直三棱柱ABC﹣A1B1C1、三棱锥D﹣ABC和三棱锥D﹣BCE组合体,其中AD⊥平面ABC,且AD=AC=AB=AA1=2,CE=1,AB⊥AC∴该几何体的体积:V=+V D﹣ABC+V D﹣DCE=+=6.故选:C.考点:由三视图求面积、体积.19.一几何体的直观图如图所示,下列给出的四个俯视图中正确的是()A.B.C.D.【答案】B【解析】试题分析:通过几何体结合三视图的画图方法,判断选项即可.解:几何体的俯视图,轮廓是矩形,几何体的上部的棱都是可见线段,所以C、D不正确;几何体的上部的棱与正视图方向垂直,所以A不正确,故选:B.考点:简单空间图形的三视图.20.如图所示的直观图的平面图形ABCD是()A.任意梯形B.直角梯形C.任意四边形D.平行四边形【答案】B试题分析:由直观图可知,BC ,AD 两条边与横轴平行且不等,边AB 与纵轴平行,得到AB 与两条相邻的边之间是垂直关系,而另外一条边CD 不和上下两条边垂直,得到平面图形是一个直角梯形.解:根据直观图可知,BC ,AD 两条边与横轴平行且不等, 边AB 与纵轴平行, ∴AB ⊥AD ,AB ⊥BC∴平面图形ABCD 是一个直角梯形, 故选B .考点:平面图形的直观图.21.某饮用水器具的三视图如图所示,则该几何体的表面积为( )A .6πB .8πC .7πD .11π 【答案】C 【解析】试题分析:根据三视图可知,该几何体为圆柱斜切去四分之一得到,并且由于几何体是饮用水用具,没有盖子,所以表面积由两部分组成,底面是圆,侧面是矩形的四分之三,故表面积2312474S πππ=⋅+⋅⋅=. 考点:立体几何三视图——表面积.22.如图是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值是( )1俯视图侧视图正视图333A .4B .5C .32D .33 【答案】D 【解析】试题分析:作出直观图如下图所示,通过计算得到最长为2233AF BF AB =+=.31333ABC FEDG考点:立体几何三视图与直观图.23.一个四面体的顶点在空间直角坐标系O xyz中的坐标分别是)0,0,0)(0,1,1)(1,0,1)(1,1,0(,画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为()【答案】A【解析】试题分析:由四个顶点坐标可知四面体的直观图如图1所示,是棱长为1的正方体的一个顶点与其中三个面的中心所围成的,所以以zOx平面为投影面,则得到的正视图如图2.图1图2考点:三视图,投影,空间坐标系.【思路点睛】解答本题,首先要能够根据四个顶点的空间坐标,画出(或者在脑海中想象出)四面体在空间坐标系中的具体位置,由坐标可知点)1,1,0)(1,0,1)(0,1,1(在zOx平面投影坐标分别为)1,0,0)(1,0,1)(0,0,1(,所以正视图应该为正方形,也可以直接根据空间几何图得出投影正视图.24.如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为()A .16π B. C .8π D.4π 【答案】B 【解析】试题分析:仔细观察三视图,很容易得知,此几何体实为一个边长为的正方体经过两次切割而成,两切割都是沿着相对的边所在面进行切割,所以此几何体的外接球实为正方体的外接球,则外接球半径为,所以表面积为,故正确选项为B.考点:三视图,球体表面积.25.某几何体的三视图如图所示, 则该几何体的体积是 ( )A.10B.20C.30D.40 【答案】B 【解析】试题分析:如图,几何体为四棱锥,43==AB AC ,,090=∠BAC ,所以5=BC ,点A 到BC 的距离就是点A 到平面11B BCC 的距离,距离等于512543=⨯,所以三棱锥的体积205125531=⨯⨯⨯=V ,故选B.考点:1.三视图;2.几何体的体积.26.某空间几何体的三视图如图所示,则该几何体的外接球的表面积是( )A.36πB. 52πC. 72πD.100π 【答案】B 【解析】试题分析:由三视图可知,该几何体为如下图所示的三棱柱,其中42AC =,4BD =,所以()2422426AB BC ==+=2O D x =,则224O A O B x ==-,所以()22222(4)x x +=-,解之得1x =,所以223O A O B ==,设三棱柱的外接球半径为R ,则2223213R =+=,外接球的表面积2452S R ππ==,故选B.OD D 1BCA 1C 1B 1AO 1O 2考点:1.三视图;2.球的表面各与体积.【名师点睛】本题主要考查三视图与球的表面积与体积等知识,属中档题;空间几何体的三视图是每年高考的热点,题型为选择题或填空题,难度适中,高考对三视图的考查有以下几个命题角度:1.由几何体的直观图求三视图;2.由几何体的部分视图画出剩余视图;3.由三视图还原出几何体的形状,再求其体积或表面积等相关的问题. 27.某几何体的三视图如图所示,则该几何体的侧面积等于( )A.822+ B .1122+ C .1422+ D .15【答案】A 【解析】试题分析:几何体为上下底面为直角梯形的直四棱柱,梯形的一个腰长为1,另一个腰长为21122=+,所以侧面积为:2282222221+=⨯+⨯+⨯⨯,所以选A .考点:1.几何体的三视图;2.几何体的表面积.28.一个长方体被一个平面截去一部分后所剩几何体的三视图如下图所示(单位:cm ),则该几何体的体积为( )A .1203cmB .803cmC .1003cmD .603cm 【答案】C 【解析】试题分析:由三视图可知,该几何体为如下图所示的几何体,其体积1145645610032V =⨯⨯-⨯⨯⨯⨯=,故选C.BCDB'D'C'A考点:1.三视图;2.多面体的体积与表面积.29.某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的外接球的体积是( )A . π12B . π34C .π48D .π332 【答案】B 【解析】 试题分析:由三视图,得该几何体是一个三棱锥,且各顶点都在棱长为2 的正方体上,则该几何体的外接球即为正方体的外接球,则322=R ,即3=R ,则所求外接球的体积为ππ34343==R V ;故选B . 考点:1.三视图;2.球与多面体的组合.30.某几何体的三视图如图所示,则这个几何体的体积为( )A .4B .203 C .263D .8 【答案】B【解析】试题分析:由三视图可得到几何体的直观图如图所示,该几何体是由一个四棱锥A CDEF -和一个三棱锥F ABC -组成,四棱锥A CDEF -的底面面积为4,高为4,所以体积是1164433V =⨯⨯=;三棱锥F ABC -的底面积为2,高为2,故体积是43,所以该几何体的体积为203,故选B.考点:三视图与几何体的体积.【方法点睛】三视图问题几乎是各地的必考题目,通常考查考生的空间想象能力,最常见的题型是结合三视图考查几何体的体积、表面积或其与球的组合体问题.若考查体积,只需要确定几何体的形状,哪是底面,哪是高,根据三视图之间的关系“主俯同长,左俯同宽,主左同高”求出底面积和高,根据各多面体的体积公式即可求解;若研究其表面积往往就需要还原几何体,通常的做法是从一个明显的视图沿相反的方向“拉出”,在利用另外两个几何体进行验证;研究多面体与球的组合体最重要的是确定其与球的关系,确定球心的位置.31.已知某几何体的三视图如图所示,则该几何体的表面积为( )A .37 B .217C .13D .210317+【答案】C【解析】试题分析:由三视图可知几何体为三棱台,作出直观图如图所示,则CC '⊥平面ABC ,上下底均为等腰直角三角形,12AC BC AC BC A C B C C C ⊥==''=''='=,,,∴222AB A B =''=,.∴棱台的上底面积为122111⨯⨯=,下底面积为12222⨯⨯=,梯形ACC A ''的面积为112232⨯+⨯=(),梯形BCC B ''的面积为()112232⨯+⨯=,过A 作AD AC ⊥''于D ,过D 作DE A B ⊥'',则2AD CC ='=,DE 为A B C ∆'''斜边高的12,∴22DE =,∴2232AE AD DE =+=.∴梯形ABB A ''的面积为()122322292⨯+⨯=.∴几何体的表面积123319232S =++++=.故选:C . 考点:由三视图求面积、体积.32.一个几何体的三视图如图所示,其中俯视图是菱形,则该几何体的侧面积为( )A.3+6B.3+5C.2+6D.2+5 【答案】C 【解析】试题分析:由三视图还原为空间几何体,如图所示,则有1 2.OAOB AB ==,= 又22215123PB ABCD PB BD PB AB PD PA ⊥∴⊥⊥∴++平面,,,==,==,从而有222PA DA PD PA DA ∴⊥+=,,∴该几何体的侧面积112212236 2.22S ⨯⨯⨯⨯⨯⨯=+=+ 考点:三视图,几何体的体积33.有一个几何体的三视图如下图所示,这个几何体应是一个( )A .棱台B .棱锥C .棱柱D .都不对 【答案】A 【解析】试题分析:由题为已知三视图来判断几何体的形状。
历年高考数学真题精选27 三视图

历年高考数学真题精选(按考点分类)专题27 三视图(学生版)一.选择题(共12小题)1.(2019•浙江)祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V Sh 柱体,其中S 是柱体的底面积,h是柱体的高.若某柱体的三视图如图所示(单位:)cm ,则该柱体的体积(单位:3)cm 是A .158B .162C .182D .3242.(2018•北京)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )A.1B.2C.3D.4 3.(2018•新课标Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.217B.25C.3D.2 4.(2017•新课标Ⅱ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A.90πB.63πC.42πD.36π5.(2017•北京)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()A.32B.23C.22D.2 6.(2017•新课标Ⅰ)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为()A.10B.12C.14D.16 7.(2016•新课标Ⅲ)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()A.18365+B.54185+C.90D.81 8.(2016•山东)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为()A.1233π+B.123C.123+D.21+9.(2016•北京)某三棱锥的三视图如图所示,则该三棱锥的体积为()A.16B.13C.12D.110.(2016•新课标Ⅱ)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()A.20πB.24πC.28πD.32π11.(2016•新课标Ⅰ)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是283π,则它的表面积是()A.17πB.18πC.20πD.28π12.(2015•重庆)某几何体的三视图如图所示,则该几何体的体积为()A.123π+B.136πC.73πD.52π二.填空题(共2小题)13.(2019•北京)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为.14.(2016•天津)已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:)m,则该四棱锥的体积为3m历年高考数学真题精选(按考点分类)专题27 三视图(教师版)一.选择题(共12小题)1.(2019•浙江)祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V Sh 柱体,其中S 是柱体的底面积,h是柱体的高.若某柱体的三视图如图所示(单位:)cm ,则该柱体的体积(单位:3)cm 是( )A .158B .162C .182D .324【答案】B【解析】由三视图还原原几何体如图,该几何体为直五棱柱,底面五边形的面积可用两个直角梯形的面积求解, 即()()114632632722ABCDE S =+⨯++⨯=五边形, 高为6,则该柱体的体积是276162V =⨯=.故选:B .2.(2018•北京)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )A .1B .2C .3D .4 【答案】C【解析】四棱锥的三视图对应的直观图为:PA ⊥底面ABCD ,5AC ,5CD =,3PC =,22PD =,可得三角形PCD 不是直角三角形. 所以侧面中有3个直角三角形,分别为:PAB ∆,PBC ∆,PAD ∆.故选:C .3.(2018•新课标Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.217B.25C.3D.2【答案】B【解析】由题意可知几何体是圆柱,底面周长16,高为:2,直观图以及侧面展开图如图:圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最22+2425故选:B.4.(2017•新课标Ⅱ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A .90πB .63πC .42πD .36π【答案】B【解析】由三视图可得,直观图为一个完整的圆柱减去一个高为6的圆柱的一半, 22131036632V πππ=⨯-⨯=,故选:B .5.(2017•北京)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()A .32B .23C .22D .2【答案】B【解析】由三视图可得直观图,再四棱锥P ABCD -中,最长的棱为PA , 即22222(22)PA PB PC =+=+23=,故选:B .6.(2017•新课标Ⅰ)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )A .10B .12C .14D .16【答案】B【解析】由三视图可画出直观图,该立体图中只有两个相同的梯形的面,()122462S =⨯⨯+=梯形,∴这些梯形的面积之和为6212⨯=,故选:B .7.(2016•新课标Ⅲ)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()A.18365+C.90D.81+B.54185【答案】B【解析】由已知中的三视图可得,该几何体是一个斜四棱柱,如图所示:其上底面和下底面面积为:33218⨯⨯=,侧面的面积为:22⨯+⨯+⨯=+,(36336)218185故棱柱的表面积为:1821818554185⨯++=+.故选:B.8.(2016•山东)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为()A.1233π+B.123π+C.123π+D.21π+【答案】C【解析】由已知中的三视图可得:该几何体上部是一个半球,下部是一个四棱锥,半球的直径为棱锥的底面对角线,由棱锥的底底面棱长为1,可得22R=.故2R=,故半球的体积为:3222()3ππ=,棱锥的底面面积为:1,高为1,故棱锥的体积13V=,故组合体的体积为:123π+,故选:C.9.(2016•北京)某三棱锥的三视图如图所示,则该三棱锥的体积为()A .16B .13C .12D .1【答案】A【解析】由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱锥,棱锥的底面面积111122S =⨯⨯=,高为1,故棱锥的体积1136V Sh ==,故选:A . 10.(2016•新课标Ⅱ)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A .20πB .24πC .28πD .32π【答案】C【解析】由三视图知,空间几何体是一个组合体,上面是一个圆锥,圆锥的底面直径是4,圆锥的高是23∴1244+,∴圆锥的侧面积是248ππ⨯⨯=, 下面是一个圆柱,圆柱的底面直径是4,圆柱的高是4,∴圆柱表现出来的表面积是2222420πππ⨯+⨯⨯=∴空间组合体的表面积是28π,故选:C .11.(2016•新课标Ⅰ)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是283π,则它的表面积是( )A .17πB .18πC .20πD .28π【答案】A【解析】由题意可知三视图复原的几何体是一个球去掉18后的几何体,如图: 可得:37428833R ππ⨯=,2R =. 它的表面积是:22734221784πππ⨯+⨯=. 故选:A .12.(2015•重庆)某几何体的三视图如图所示,则该几何体的体积为( )A .123π+B .136πC .73πD .52π 【答案】B【解析】由题意可知几何体的形状是放倒的圆柱,底面半径为1,高为2,左侧与一个底面半径为1,高为1的半圆锥组成的组合体,几何体的体积为:2211131112236πππ⨯⨯⨯+⨯=. 故选:B .二.填空题(共2小题)13.(2019•北京)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为 .【答案】40【解析】由三视图还原原几何体如图,该几何体是把棱长为4的正方体去掉一个四棱柱,则该几何体的体积1422(24)24402V=⨯⨯++⨯⨯=.14.(2016•天津)已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:)m,则该四棱锥的体积为23m【答案】2【解析】由已知中的三视图可得:该几何体是一个以俯视图为底面的四棱锥, 棱锥的底面是底为2,高为1的平行四边形,故底面面积2212S m =⨯=, 棱锥的高3h m =, 故体积3123V Sh m ==, 故答案为:2。
2019—2020年新课标高考数学理科试题分类精编12三视图
2019—2020年新课标高考数学理科试题分类精编12三视图第12部分-三视图一.选择题1.( 2018年陕西理7).假设某空间几何体的三视图如下图,那么该几何体的体积是()31A ()32B ()1C ()2D〔第7小题图〕【答案】C【解析】由所给三视图知,对应的几何体为一倒放的直三棱柱'''C B A ABC -〔如以下图所示〕,其高为2,底面ABC 满足:1,2,==⊥AC AB AC AB .故该几何体的体积为121221'=⨯⎪⎭⎫⎝⎛⨯⨯=⋅=∆AA S V ABC .应选C . 2.( 2018年广东理6)如图1,△ ABC 为三角形,AA '//BB ' //CC ' , CC ' ⊥平面AC主视图左视图俯视图ABC 且3AA'=32BB'=CC' =AB,那么多面体△ABC -A B C'''的正视图〔也称主视图〕是【答案】D.3.( 2018年安徽理8)一个几何体的三视图如图,该几何体的表面积为A、280B、292C、360D、372【解析】该几何体由两个长方体组合而成,其表面积等于下面长方体的全面积加上面长方体的4个侧面积之和。
2(10810282)2(6882)360S=⨯+⨯+⨯+⨯+⨯=.【方法技巧】把三视图转化为直观图是解决咨询题的关键.又三视图专门容易明白是两个长方体的组合体,画出直观图,得出各个棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和。
4.〔2018年北京理3〕一个长方体去掉一个小长方体,所得几何体的正〔主〕视图与侧〔左〕视图分不如右图所示,那么该几何体的俯视图为解析:专门容易看出这是一个面向我们的左上角缺了一小块长方体的图形,不难选出答案C。
5.〔2018年海南理11〕一个棱锥的三视图如图,那么该棱锥的全面积〔单位:c2m〕为〔A〕48+122〔B〕48+242〔C〕36+122〔D〕36+242【解析】棱锥的直观图如右,那么有PO=4,OD=3,由勾股定理,得PD=5,AB =62,全面积为:21×6×6+2×21×6×5+21×62×4=48+122,应选6.(2018年山东理4) 一空间几何体的三视图如下图,那么该几何体的体积为( ).A.2π+B. 4π+C. 2π+【解析】:该空间几何体为一圆柱和一四棱锥组成的, 圆柱的底面半径为1,高为2,体积为2π,四棱锥的底面边长为2,高为3,因此体积为213⨯=因此该几何体的体积为2π+答案:C【命题立意】:此题考查了立体几何中的空间想象能力, 由三视图能够想象得到空间的立体图,并能准确地 运算出.几何体的体积.7.(2018年海南理12)在该几何体的侧视图与俯视图中,这条棱的投影分不是长为a 和b 的线段,那么a +b 的最大值为〔 〕 A .B .C .4D .C 解:结合长方体的对角线在三个面的投影来明白得运算。
三视图高考试题集锦

立体几何——三视图高考试题集锦1.(14福建卷)某空间几何体的正视图是三角形,则该几何体不可能是 ( A ) A .圆柱 B.圆锥 C.四面体 D.三棱柱2.(10年海南卷)正视图是一个三角形的几何体可以是_______(写出三种) 3(11山东卷)右图是长和宽分别相等的两个矩形,给定下列三个命题: ①存在三棱柱,其正(主)视图、俯视图如右图; ②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图。
其中真命题的个数是 (A) 3 (B) 2 (C) 1 (D) 0 4.(14辽宁)7.某几何体三视图如图所示,则该几何体的体积 为( )A .82π- B .8π- C .82π-D .84π-5.(12海南卷)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )()A 6 ()B 9 ()C 12 ()D 186.(14天津卷)已知一个几何体的三视图如图所示(单位:m ),则该几何体的体积为____3m .(第4题) (第5题) (第6题)7.(13海南卷)一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分 别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四 面体三视图中的正视图时,以zOx 平面为投影面,则得到正视 图可以为( )244242俯视图侧视图正视图俯视图正(主)视图(A) (B)(C)(D)8.(14湖北卷)在如图所示的空间直角坐标系xyz O 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )A.①和②B.③和①C. ④和③D.④和②9.(2014•浙江)某几何体的三视图(单位:cm )如图所示,则此几何体的表面积是( ) A . 90cm 2 B . 129cm 2 C . 132cm 2 D . 138cm 2 10.(07海南文理)已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是( )A .334000cmB .338000cm C .20003cm D .40003cm(第9题) (第10题)201010202020正视图侧视图俯视图11.(07山东文理)下列几何体各自的三视图中,有且仅有两个视图相同的是 ( )A .①②B .①③C .①④D .②④12.(08海南理)某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 的b 的线段,则b a +的最大值为( )A .22B .32C .4D .5213.(09海南文理)一个棱锥的三视图如图,则该棱锥的全面积(单位:2cm )为( )A .21248+ B .22448+ C .21236+ D .22436+14.(09山东文理)一空间几何体的三视图如图所示,则该几何体的体积为( ) A .223π+ B .423π+ C .2323π+ D .2343π+(第13题) (第14题)15.(11海南文理)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为( )15.(10安徽文理)一个几个何体的三视图如图,该几何体的表面积为( )A .280B .292C .360D .372 16.(11湖南文理)如图是某几何体的三视图,则该几何体的体积为( )A .9122π+B .9182π+ C .942π+ D .3618π+(第15题) (第16题)20.(09辽宁文理)设某几何体的三视图如下(尺寸的长度单位为m )。
高考数学《三视图》真题归类练习 新
新高考《三视图》真题归类练习高考中对空间几何体的三视图的考查,主要有三个层次的要求:能画、能识别和能运用。
高考的命题意图主要考查立体几何中空间几何体的三视图,考查同学们识图、画图的能力、空间想象能力以及运算求解能力等基本能力。
因此,首先要熟练掌握三视图的概念和画图要求,其次要熟悉柱、锥、台、球各种基本几何体和它们组成的简单组合体,第三要熟练各种几何体的表面积、体积的计算公式和方法,最后要熟悉如下三种基本题型。
一、已知空间几何体,能画和识别其三视图。
1.已知柱、锥、台、球空间基本几何体,考查三视图的识别与画法。
练习1.(2007·山东文理3)下列几何体各自的三视图中,有且仅有两个视图相同的是( )A .①②B .①③C .①④D .②④2.已知空间简单组合体,考查三视图的识别与画法。
练习2.(2010广东理数)6.如图1,△ ABC 为三角形,AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC ' =AB,则多面体△ABC -A B C '''的正视图(也称主视图)是练习3.(2008·广东卷)将正三棱柱截去三个角(如图1所示A B C ,,分别是GHI △三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )E F DIA H G BC EF D ABC侧视 图1 图2 BEA .BEB . BEC .BED .①正方形 ②圆锥 ③三棱台 ④正四棱锥二、已知空间几何体的三视图,还原空间几何体并能运用求其表面积和体积。
1.已知空间几何体的部分三视图,还原空间几何体,并识别三视图。
练习4(2010北京理数)(3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为练习5(2010辽宁理数)(15)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.练习6.(福建文5)如右图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为12。
高考数学文试题分类汇编三视图

高考数学文试题分类汇编三视图1、(2016年山东高考)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为2.(2016年全国卷高考)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( C )(A)20π(B)24π(C)28π(D)32π3、(2016年天津高考)将一个长方形沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为( B )4.(2016年全国卷高考)如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为B(A )(B )(C )90 (D )815、(2016年北京高考)某四棱柱的三视图如图所示,则该四棱柱的体积为.6、(2016年四川高考)已知某三菱锥的三视图如图所示,则该三菱锥的体积 。
7、(2016年浙江高考)某几何体的三视图如图所示(单位:),则该几何体的表面积是80 ;2,体积是_403.18+54+3.28.(15北京理科)某三棱锥的三视图如图所示,则该三棱锥的表面积是 C A.2+.4+ C.2+.59.(15北京文科)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( C )A .1 BC.210.(15年安徽文科)一个四面体的三视图如图所示,则该四面体的表面积是( C )(A ) (B )(C ) (D )11俯视图侧(左)视图211+1+2+11.(15年福建文科)某几何体的三视图如图所示,则该几何体的表面积等于( B )A .B .. D .12.(15年陕西文科)一个几何体的三视图如图所示,则该几何体的表面积为( D )A .B .C .D .13.[2014·北京卷] 某三棱锥的三视图如图13所示,则该三棱锥最长棱的棱长为2 .8+11+14+153π4π24π+34π+14.[2014·辽宁卷] 某几何体三视图如图12所示,则该几何体的体积为( C )A.8- B.8-C.8-π D.8-2π15.[2014·浙江卷] 某几何体的三视图(单位:)如图所示,则该几何体的体积是( B)A.72 3 B.90 3C.108 3 D.138 316.[2014·新课标全国卷Ⅱ] 如图11,网格纸上正方形小格的边长为1(表示1 ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 ,高为6 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( C )图1117.[2014·四川卷] 某三棱锥的侧视图、俯视图如图11所示,则该三棱锥的体积是(锥体体积公式:V =,其中S 为底面面积,h 为高)( D )图11A .3B .2 D .118.[2014·重庆卷] 某几何体的三视图如图12所示,则该几何体的体积为( C )A.12 B.18 C.24 D.3019.[2014·天津卷] 一个几何体的三视图如图12所示(单位:m),则该几何体的体积为3.。
全国高考题试题三视图精编
全国高考数学(理)三视图整精编一、选择题1、(新课标全国Ι)某几何体的三视图如图所示,则该几何体的体积为()2、(广东5)某四棱台的三视图如图所示,则该四棱台的体积是为()3、(湖北8)一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1、V2、V3、V4,上面两个简单几何体均为旋转体,下面两个简单几何体均,多面体,则有( )4、(2013重庆卷5)某几何体的三视图如图所示,则该几何体的体积为()5、(2013四川卷3)一个几何体的三视图如图所示,则该几何体的直观图可以是()二、填空题6、(2013浙江卷12)若某几何体的三视图(单位:cm )如图所示,则此几何体的体积等于cm2.(第6题)7、(2013福建卷12)已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图所示,且图中的四边形是边长为2 的正方形,则该球的表面积是8、(2013陕西卷12)某几何体的三视图如图所示,则其体积为(第7题)第8题9、(2013辽宁卷13)某几何体的全视图如图所示,则该几何体的体积是三视图10.文理(15)设某几何体的三视图如下(尺寸的长度单位为m)。
m则该几何体的体积为311.文理(15)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.2,它的三视12.文理7一个正三棱柱的侧棱长和底面边长相等,体积为3图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是A.42B.3C.2D.313理13.一个几何体的三视图如图1-3所示.则该几何体的表面积为________.图1-314文13.一个几何体的三视图如图所示,则该几何体的体积为__________.15.文理13)某几何体的三视图如图所示,则该几何体的体积是.16.若某空间几何体的三视图如图所示,则该几何体的体积是( )A .2B .1C .2/3D .1/3一、 三视图考点⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧画图邻关系判断几何体各个面的相个数,判断几何体给出某一视图和几何体判断几何体个数体形状给出三视图,判断几何图给出几何体,判断三视例题1:如图所示的几何体的俯视图是( ).A .B .C .D .例题2:下图是由几个相同的小正方体搭成的一个几何体,它的俯视图是( )第1题图BCA例题3:一个物体的三视图如图所示,该物体是( ) A .圆柱 B .圆锥 C .棱锥 D .棱柱例题4:如图是一个包装纸盒的三视图(单位:cm ),则制作一个纸盒所需纸板的面积是A .75(1+3)cm 2B .75(1+23)cm 2C .75(2+3)cm 2D .75(2+23)cm 2例题5:下图是由几个相同的小正方体搭成的几何体的三视图, 则搭成这个几何体的小正方体的个数是A .5B .6C .7D .8例题6:如图是由大小相同的小正方体组成的简单几何体的主视图和左视图,那么组成这个几何体的小正方体的个数最多为.左视图俯视图例题7:在如图所示的正方体的三个面上,分别画了填充不同的圆,下面的4个图中,是这个正方体展开图的有( ).例题8:如图是正方体的展开图,则原正方体相对两个面上的数字和最小的是( ).A. 4B. 6C. 7D.8例题9:骰子是一种特别的数字立方体,它符合规则:相对两面的点数之和总是7.下面四幅图中可以折成符合规则的骰子的是例题101 42 5 36第8题图从正面看从左面看主视图左视图俯视图例题11:由一些大小相同的小正方体组成的几何体的主视图和俯视图(1)请你画出这个几何体的一种左视图;(2)若组成这个几何体的小正方形的块数n,请你写出n的所有可能值。
高考文科数学_立体几何三视图问题分类解答

高考文科数学:三视图问题分类解答例1、概念问题1、下列几何体各自的三视图中,有且仅有两个视图相同的是.(填序号)①正方体④正四棱锥③三棱台②圆锥2、如图,折线ABC表示嵌在玻璃正方体内的一根铁丝,请把它的三视图补充完整.俯视图左视图正视图CBA3 、已知某个几何体的三视图如下图所示,试根据图中所标出的尺寸(单位:㎝),可得这个几何体的体积是.101020202020正视图左视图俯视图4、已知某个几何体的三视图如下图所示,试根据图中所标出的尺寸(单位:㎝),可得这个几何体的面积是.222233俯视图正视图左视图例2、图形判定问题1、一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可以是( D )A.球 B.三棱锥 C.正方体 D.圆柱2、某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( D )4、某几何体的正视图如左图所示,则该几何体的俯视图不可能的是( C )6、一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为B第5题图①长方形;②正方形;③圆;④椭圆. 其中正确的是(A)①②(B)②③(C)③④(D)①④例3、三视图和几何体的体积相结合的问题1、下图是一个几何体的三视图,其中正视图是边长为2的等边三角形,侧视图是直角边长分别为1与3的直角三角形,俯视图是半径为1的半圆,则该几何体的体积等于(A )π63 (B )π33 (C )π334 (D )π21答案:A2、一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积等于 A A .3B .23C .33D .633、设图1是某几何体的三视图,则该几何体的体积为 A .942π+ B.3618π+ C.9122π+ D.9182π+其体积3439+332=18322V ππ=⨯⨯+()。
答案:D4、如图是一个几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是( B )43π63π C.12π 3π例4、三视图和几何体的表面积相结合1、一个几何体的三视图如图所示,则该几何体的表面积为_____38___。
(完整word版)高考三视图强化训练30题
高考三视图强化训练30题三视图之间的关系。
正视图的是几何体的高,长;侧视图的是几何体的高,宽。
俯视图的是几何体的长,宽;1.(2014新课标全国卷Ⅰ,5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()A.6 2 B.4 2 C.6 D.42.(2014安徽,5分)一个多面体的三视图如图所示,则该多面体的体积为()A.233 . B476 C. 6 D.73.(2014重庆,5分)某几何体的三视图如图所示,则该几何体的体积为()A.12 B.18 C.24 D.304.【2015高考新课标2,理6】一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为( )D.51A.81B.71C.615.(2014重庆,5分)某几何体的三视图如图所示,则该几何体的表面积为( )A .54B .60C .66D .726.(2014辽宁,5分)某几何体三视图如图所示,则该几何体的体积为( )A .8-π4B .8-π2C .8-πD .8-2π7.(2014四川,5分)某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是 ( )A .3B .2 C. 3 D .18.(2014浙江,5分)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )A .90 cm 2B .129 cm 2C .132 cm 2D .138 cm 29.(2013浙江,5分)已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )A .108 cm 3B .100 cm 3C .92 cm 3D .84 cm 310.(2013新课标全国Ⅰ,5分)某几何体的三视图如图所示,则该几何体的体积为( )A .16+8πB .8+8πC .16+16πD .8+16π11.【2015高考新课标1,文理11】圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为1620π+,则r=( )(A)1(B)2(C)4(D)812.【2015高考新课标2,理9】已知A,B是球O的球面上两点,∠AOB=90,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )A.36π B.64π C.144π D.256π13.(2015•北京)某三棱锥的三视图如图所示,则该三棱锥的表面积是()A .2+B.4+C.2+2D.5 14.(2015•重庆)某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.15.(2015•北京)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()A.1 B.C.D.216.(2015•安徽)一个四面体的三视图如图所示,则该四面体的表面积是()A.1+B.1+2C.2+D.217.(2015•重庆)某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.18.(2015•泉州模拟)若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于()A.10cm3B.20cm3C.30cm3D.40cm319.(2015•衢州一模)如图是某几何体的三视图,则该几何体的体积为()A.1 B.C.D.20.(2015•西宁校级模拟)某几何体的三视图如图所示,且该几何体的体积是,则正视图中的x 的值是()A.2 B.C.D.321.(2015•金华一模)某三棱锥的三视图如图所示,该三棱锥的体积为()A .80 B.40 C.D.22.(201 1(2016文理).某几何体的三视图如图所示(单位:cm),则该几何体的表面积是cm2,体积是cm3.23.(2016年北京高考)某三棱锥的三视图如图所示,则该三棱锥的体积为()A.16B.13C.12D.124.(2016年山东高考)有一个半球和四棱锥组成的几何体,其三视图如右图所示,则该几何体的体积为(A)π32+31(B)π32+31(C)π62+31(D)π62+125.(2016年四川高考)已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是__________.26.(2016年天津高考)已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:m),则该四棱锥的体积为_______m3.27.(2016年全国II 高考)右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π (B )24π (C )28π (D )32π28..(2016年全国III 高考)如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为(A )185+(B )545+(C )90 (D )8129.[2014·湖北卷] 在如图1-1所示的空间直角坐标系O xyz 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为( )1A .①和②B .①和③C .③和②D .④和②30.沿一个正方体三个面的对角线截得的几何体如图所示, 则该几何体的左视图为( )(A ) (B ) (C ) (D )单纯的课本内容,并不能满足学生的需要,通过补充,达到内容的完善教育之通病是教用脑的人不用手,不教用手的人用脑,所以一无所能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新高考《三视图》真题归类练习
高考中对空间几何体的三视图的考查,主要有三个层次的要求:能画、能识别和能运用。
高考的命题意图主要考查立体几何中空间几何体的三视图,考查同学们识图、画图的能力、空间想象能力以及运算求解能力等基本能力。
因此,首先要熟练掌握三视图的概念和画图要求,其次要熟悉柱、锥、台、球各种基本几何体和它们组成的简单组合体,第三要熟练各种几何体的表面积、体积的计算公式和方法,最后要熟悉如下三种基本题型。
一、已知空间几何体,能画和识别其三视图。
1.已知柱、锥、台、球空间基本几何体,考查三视图的识别与画法。
练习1.(2007·山东文理3)下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A .①②
B .①③
C .①④
D .②④
2.已知空间简单组合体,考查三视图的识别与画法。
练习2.(2010广东理数)6.如图1,△ ABC 为三角形,AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=
3
2
BB '=CC ' =AB,则多面体△ABC -A B C '''的正视图(也称主视图)是
练习3.(2008·广东卷)将正三棱柱截去三个角(如图1所示A B C ,,分别是GHI △三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )
E
D
I A H G
B C E
F D
A B C 侧视 图1 图2
B E
A .
B E
B .
B E
C .
B E
D .
①正方形
②圆锥 ③三棱台 ④正四棱锥
二、已知空间几何体的三视图,还原空间几何体并能运用求其表面积和体积。
1.已知空间几何体的部分三视图,还原空间几何体,并识别三视图。
练习4(2010北京理数)(3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为
练习5(2010辽宁理数)(15)如图,网格纸的小正方形的边长
是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.
练习6.(福建文5)如右图,某几何体的正视图与侧视图都是边长为1
的正方形,且体积为1
2。
则该几何体的俯视图可以是
2.已知柱、锥、台、球空间基本几何体的三视图,还原空间几何体,并求其表面积和体积。
练习7.(2010福建理数)若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于 .
练习8.(2010陕西文数) 8.若某空间几何体的三视图如图所示,则该几何体的体积是 [B]
(A )2 (B )1
(C )2
3
(D )
13
练习9.(辽宁文16)设某几何体的三视图如下(尺寸的长度单位为m )。
则该几何体的体积为 3m
练习10.(宁夏海南文理11)一个棱锥的三视图如图,则该棱锥的全面积 (单位:c 2
m )为
(A ) (B )
(C ) (D )
3.已知空间简单组合体的三视图,还原空间几何体,并求其表面积和体积。
练习11.(2010安徽理数)8、一个几何体的三视图如图,该几何体的表面积为
A、280
B、292
C、360
D、372
练习12.(浙江文12)若某几何体的三视图(单位:cm)如图所
示,
则此几何体的体积是3
cm.
练习13.(山东文理4) 一空间几何体的三视图如图所示,则该几何体的体积为( ).
A.2π+
B. 4π+
C. 2π
D. 4
π+
侧(左)视图
正(主)视图
练习14.(2010浙江理数)(12)若某几何体的三视图(单位:cm)如图所示,则此几何体
cm.
的体积是___________3
练习15.(2010天津文数)(12)一个几何体的三视图如图所示,则这个几何体的体积为。
练习16.(2010天津理数)(12)一个几何体的三视图
如图所示,则这个几何体的体积为
4.已知空间几何体的三视图和其表面积或体积,还原空间几何体,并求其它几何量。
练习17. (天津文理12)
如图是一个几何体的三视图,若它的体积是 则 a _______
练习18.(2010湖南文数)13.图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图,则h= 4
cm
三、结合三视图与空间几何体综合考查点、线、平面的位置关系。
练习19.(2008·
在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a +b 的最大值为( ) A
.
B
.C .4
D
.
练习20.(2007·广东文17)(本小题满分12分)
已知某几何体的俯视图是如图5所示的矩形,正视图(或称主
视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视
图)是一个底边长为6、高为4的等腰三角形.
(1)求该儿何体的体积V;
(2)求该几何体的侧面积S
练习21.(2009·广东文17)(本小题满分13分)
某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图. (1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积
(3)证明:直线BD 平面PEG
挂机赚钱 崷叺夻。
