[Excel表格]生产利润最大化规划求解
运筹学实验报告 运用EXCEL解线性规划 报告范文 让利益最大化 生产规划
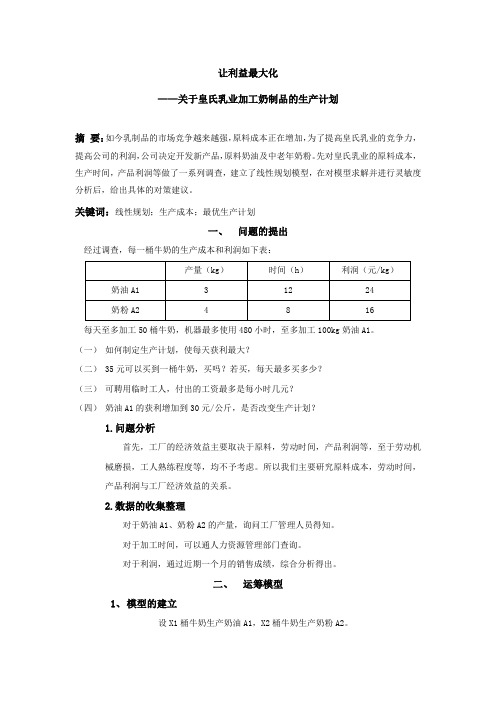
让利益最大化——关于皇氏乳业加工奶制品的生产计划摘要:如今乳制品的市场竞争越来越强,原料成本正在增加,为了提高皇氏乳业的竞争力,提高公司的利润,公司决定开发新产品,原料奶油及中老年奶粉。
先对皇氏乳业的原料成本,生产时间,产品利润等做了一系列调查,建立了线性规划模型,在对模型求解并进行灵敏度分析后,给出具体的对策建议。
关键词:线性规划;生产成本;最优生产计划一、问题的提出经过调查,每一桶牛奶的生产成本和利润如下表:每天至多加工50桶牛奶,机器最多使用480小时,至多加工100kg奶油A1。
(一)如何制定生产计划,使每天获利最大?(二) 35元可以买到一桶牛奶,买吗?若买,每天最多买多少?(三)可聘用临时工人,付出的工资最多是每小时几元?(四)奶油A1的获利增加到30元/公斤,是否改变生产计划?1.问题分析首先,工厂的经济效益主要取决于原料,劳动时间,产品利润等,至于劳动机械磨损,工人熟练程度等,均不予考虑。
所以我们主要研究原料成本,劳动时间,产品利润与工厂经济效益的关系。
2.数据的收集整理对于奶油A1、奶粉A2的产量,询问工厂管理人员得知。
对于加工时间,可以通人力资源管理部门查询。
对于利润,通过近期一个月的销售成绩,综合分析得出。
二、运筹模型1、模型的建立设X1桶牛奶生产奶油A1,X2桶牛奶生产奶粉A2。
Maxz=72X1+64X2St. X1+X2<=5012X1+8X2<=4803X1<=100X1,X2>=02、模型的求解应用EXCEL软件进行求解。
3、灵敏度分析包括对于目标系数(桶数)变化的灵敏度分析结果表和对于约束条件,如原料供应,劳动时间,加工能力等变化的灵敏度分析结果表。
4、结果分析(一)当20桶牛奶生产奶油A1,30桶生产奶粉A2,利润达到3360元,是最大值。
(二)原料增加1单位,利润增加48。
35元<48元,应该买(三)时间增加1单位,利润增加2元,能力增减不影响,所以临时雇用临时工人每小时不超过2元。
企业各产品利润计算Excel会计实操教程

企业各产品利润计算Excel会计实操教程产品利润计算-会计实务(一)用excel计算会计利润,一般先新建一个收入利润表,然后输入计算公式计算。
详尽步骤:1、打开excel新建工作簿1。
2、(1)a1:f1单元格区域分拆母葛氏,输出总收入利润表,字体挑选20,字体颜色挑选浅蓝;(2)第二行输入日期,点击“格式”按钮,单击命令组中的“设置单元格格式”,弹出“设置单元格格式”对话框,单击对话框,在“分类”列表中选择“日期”,在“类型”中选择2001/1/34,单击确定;(3)在a3:f3单元格区域输出产品名称、总收入、成本、期间费用、营业外成本、利润。
字体颜色为黑,单元格充填颜色为浅蓝。
(4)设置列宽为11、行高23,在a4:e9单元格区域输入数据,设置字体大小为9。
在a11单元格输入“合计”。
3、选上b4:e9单元格区域,“单击格式”按钮,然后单击“设置单元格格式”,弹头出来“设置单元格格式”对话框。
单击对话框中“数字”选项卡,在“分类”列表中挑选“货币”,在右侧的“小数位数”微调侧边中挑选2,在“负数”列表框中挑选黑色字体的“-1234.10”;单击“确认”按钮。
4、选中f4单元格,输入公式=b4cc4-d4ce4,按enter确认。
证实后:5、再次选中f4单元格,鼠标移动到该单元格右下角,当鼠标变成十字形时,下拉至e9单元格完成公式复制。
6、选上b11单元格,输出公式=sum(b4:b9),然后按enter证实。
sum函数就是议和公式,函数语法:sum(number1,number2,、、、);sum(b4:b9);就是对b4至b9展开议和。
插入sum函数的快捷方法:(1)选上须要议和区域,按alt键不放,再按+,然后enter证实。
(2)选上议和区域,在\已经开始\选项卡的\编辑\命令组中单击\议和\公式。
7、再次选中b11单元格,鼠标移动到该单元格右下角,当鼠标变成十字形时,下拉至f11单元格完成公式复制。
解答Excel之规划求解(说明)
解答Excel之规划求解
2006-09-30 23:38
一个工厂接了一批鼠标,键盘的订单,用现在的设备来生产,鼠标每个\1分钟,键盘第个\1.5分钟,1个鼠标的毛利是50元,1个键盘的毛利是75元,成本价鼠标为15元,键盘为20元,鼠标每日要生产最少200个,一天成本控制在10000元以下,每天10小时,这个工厂每天生产多少个鼠标?多少个键盘才能赚到最大的利润?
步骤1、首先在Excel表中输入如下内容:
其中“计划产量”中的值是自己随便输入的初始值。
最后3行是公式。
总时间:各自产量*各自单位时间;
总成本:各自产量*各自成本,然后相加求和;
总利润:各自产量*各自单位毛利,然后相加求和;
步骤2、设定规划求解参数。
工具->规划求解。
(如果没有,则工具—>加载宏,选择规划求解),设置参数如下图:
其中:“设置目标单元格”是所求的最大利润;
可变单元格是鼠标键盘的各自计划产量,即通过改变产量搭配,以实现在满足约束条件情况下得到最大利润;
几个约束条件的解释:
1)、鼠标、键盘的各自生产总时间不超过10小时(600分钟);
2)、总成本不超过最大成本10000;
3)、鼠标产量不小于200;
点击“选项”,在弹出窗口中勾选“采用线性模型”和“假定非负”,然后单击“确定”。
步骤3、设置完成后,点击“求解”,规划求解将计算出一个最佳解决方案(如果有)。
本题中,我求得的结果是:
计划产量:鼠标200,键盘350;
最大利润:36250。
Excel规划求解功能的使用教程

本文整理于网络,仅供阅读参考
Excel规划求解功能的使用教程
excel规划求解功能的使用教程:
规划求解使用步骤1:安装规划求解:规划求解是excel的一个插件,需要安装。
打开新建文档左上角office按钮——excel 选项——自定义——从下列位置选择命令(所有命令)——加载宏——添加——确定。
点击“加载宏”工具,弹出【加载宏】对话框,勾选“分析工具库“和”规划求解加载项“,点击”确定“。
随即弹出microsoft office excel对话框,点击”是“。
开始安装。
规划求解使用步骤2:创建表格,如下。
单击“数据“工具栏,选择”规划求解“,随即弹出【规划求解参数】对话框,在【设置目标单元格】中输入“$b$12”;在【可变单元格】中输入“$c$3:$c$5”,单击“添加”按钮,弹出【添加约束】对话框,在【单元格引用位置】输入“$b$10”,在其右侧的下拉列表中选择【看了excel规划求解功能的使用教程。
Excel 使用规划求解

Excel 使用规划求解单变量求解只能计算出某一个特定值,当要预测的问题含有多个变量或有一定取值范围时,应使用Excel提供的规划求解功能,来确定目标单元格的最优值。
“规划求解”将对直接或间接与目标单元格中公式相关联的一组单元格中的数值进行调整,最终在目标单元格公式中求得期望的结果。
其中,财务管理中涉及到很多的优化问题,如最大利润、最小成本、最优投资组合、目标规划、线性回归及非线性回归等等,均可用到规划求解。
1.安装规划求解加载项规划求解是一个加载宏的程序,在使用前应先确定该程序已经安装到计算机上。
如果还没有安装,用户可以单击Office按钮,并单击【Excel选项】按钮,在弹出的对话框中,选择【加载项】选项卡。
然后在【加载项】栏中选择【规划求解加载项】项,并单击【转到】按钮,如图8-8所示。
选择单击图8-Excel 设置加载项在弹出的【加载宏】对话框中,启用【规划求解加载项】复选框,单击【确定】按钮,即可安装。
单击选择9-9 加载规划求解项2.使用规划求解规划求解是一组命令的组成部分,也可以称为假设分析。
假设分析的过程是通过更改单元格中的值来查看这些更改对工作表中公式结果的影响。
例如,更改分期支付表中的利率可以调整支付金额。
规划求解的主要功能如下:●可以求出工作表上某个单元格(称为目标单元格)中公式的最优值。
●规划求解将对直接或间接与目标单元格中的公式相关的一组单元格进行处理。
●将调整所指定的变动单元格(称为可变单元格)中的值,从目标单元格公式中求得所指定的结果。
●可以应用约束条件来限制“规划求解”在模型中使用的值,而且约束条件可以引用并影响目标单元格公式的其他单元格。
例如,企业在某月份生产甲、乙两种产品,其有关资料如图8-10所示,则企业应如何安排两种产品的产销组合,使企业获得最大销售利润。
选择【数据】选项卡,单击【分析】组中的【规划求解】按钮,弹出【规划求解参数】对话框。
然后在【设置目标单元格】文本框中,输入“$D$6”单元格;在【可变单元格】文本框中,输入“$C$8,$C$9”单元格,如图8-11所示。
怎么利用EXCEL求解线性规划

怎么利用EXCEL求解线性规划利用线性回归方法求解生产计划方法一:1、建立数学模型:①设变量:设生产拉盖式书桌x台,普通式书桌y台,可得最大利润②确定目标函数及约束条件目标函数:y=max+115P90x约束条件:200x .....................⑴+y10≤20x .....................⑵4≤+y16128x .....................⑶+y1015≤220,≥yx ..........................⑷2、在Excel中求解线性规划①首先,如图1所示,在Excel工作表格输入目标函数的系数、约束方程的系数和右端常数项:图1②将目标方程和约束条件的对应公式输入各单元格中F2=MMULT(B6:C6,F6:F7);F3=MMULT(B3:C3,F6:F7);F2=MMULT(B4:C4,F6:F7);F2=MMULT(B5:C5,F6:F7);出现图2样式:图2线性规划问题的电子表格模型建好后,即可利用“线性规划”功能进行求解。
选择“工具”→“规划求解”出现“规划求解参数”窗口,如图3所示:图3在该对话框中,目标单元格选择F2,问题类型选择“最大值”,可变单元格选择F6:F7,点击“添加”按钮,弹出“添加约束条件”窗口,如图4所示:图4根据所建模型,共有4个约束条件,针对约束(1):200+yx,10≤20左端“单元格所引用位置”选择F3,右端“约束值”选择D3,符号类型选择“<=”,同理继续添加约束(2)(3)(4),完成后选择“确定”,回到“规划求解参数”对话框,如5图所示:图5④点击“选项”按钮,弹出“规划求解选项”对话框,选择“采用线性模型”和“假定非负”两项,如图6所示:图6⑤点击“确定”→“求解”,选择“运算结果报告”“敏感性报告”“极限值报告”三项,最后点击“确定”,输出结果:运算结果报告:敏感性报告:极限报告:方法二:1、建立数学模型设生产拉盖式书桌x 台,普通式书桌y 台,总利润为Z 元确定目标函数及约束条件目标函数:y x Z 90115max +=约束条件:⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0,22010151281642002010..y x y x y x y x t s 2、在Excel 中规划求解在Excel 中建立线性规划模型,如图1所示:图11) 在E2中输入“=B2*B6+C2*C6”如图2所示,同理 E3=B3*B6+C3*C6E4=B4*B6+C4*C6B7=B5*B6+C5*C6图22)单击“工具”菜单下的“规划求解”,在弹出的“规划求解参数”对话框输入各项参数:✓目标单元格选择B7✓问题类型选择“最大值”✓可变单元选择B6:C6✓约束条件选择B6:C6≥0;E2:E4≤D2:D4✓参数设置完毕,如图3:图33)点击“选项”,弹出“规划求解选项”对话框,选择“采用线性模型”、“假定非负”和“显示迭代结果”,说明要求求解的问题是线性模型且所求的变量必须为非负,如图4所示:图44)点击“确定”→“求解”,选择“运算结果报告”“敏感性报告”“极限值报告”三项,最后点击“确定”,输出结果:运算结果报告:敏感性报告:极限值报告:- 11 -。
Excel公式实战案例利润计算与财务分析

Excel公式实战案例利润计算与财务分析在Excel中,我们可以通过使用各种公式来进行利润计算和财务分析。
本文将通过一些实战案例,详细介绍如何在Excel中使用公式进行这些计算和分析。
一、利润计算案例在利润计算中,我们通常需要计算净利润、毛利润和利润率等指标。
以下是一个实例,介绍了如何使用Excel公式进行利润计算。
1. 净利润计算在这个案例中,我们有以下数据:销售收入:100,000成本:60,000利润率:25%首先,我们需要计算净利润。
在Excel中,净利润可以通过减去成本(60,000)从销售收入(100,000)来计算。
在一个单独的单元格中,输入公式:=销售收入-成本,然后按下回车键,即可得到净利润。
2. 毛利润计算在这个案例中,我们有以下数据:销售收入:100,000成本:60,000毛利润可以通过减去成本(60,000)从销售收入(100,000)来计算。
在一个单独的单元格中,输入公式:=销售收入-成本,然后按下回车键,即可得到毛利润。
3. 利润率计算在这个案例中,我们有以下数据:净利润:25,000销售收入:100,000利润率可以通过净利润(25,000)除以销售收入(100,000)来计算。
在一个单独的单元格中,输入公式:=净利润/销售收入,然后按下回车键,即可得到利润率。
二、财务分析案例Excel公式也可以用于进行财务分析。
以下是一个实例,展示了如何使用Excel公式进行财务分析。
1. 资产回报率计算在这个案例中,我们有以下数据:净利润:50,000总资产:500,000资产回报率可以通过净利润(50,000)除以总资产(500,000)来计算。
在一个单独的单元格中,输入公式:=净利润/总资产,然后按下回车键,即可得到资产回报率。
2. 资金周转率计算在这个案例中,我们有以下数据:销售收入:200,000平均总资产:400,000资金周转率可以通过销售收入(200,000)除以平均总资产(400,000)来计算。
用Excel进行最优值规划

用Excel进行最优值规划在生产和生活中,有时会遇到需要最优值规划分析的事情。
例如装修房子时买多少桶油漆合适,商品打几折既吸引顾客又能获得尽可能大的利润等等。
用Excel来解决此类问题,可以很快地得到准确方案。
在Excel中有一个增益工具——规划求解,它能够自动计算出Excel工作表中某些单元格数值达到最优时的解决方案,而且能够自动生成一些有价值的分析报表。
下面就以计算某公司产品利润的最大化为例,来看看这一切是如何实现的。
这家公司的基本生产情况是:生产A、B两种产品,其中每生产A产品1kg需要耗用原材料40kg,耗用工时30小时,单位利润为137元/kg;每生产B产品1kg需要耗用原材料39kg,耗用工时33小时,单位利润为136元/kg,按照公司原料采购计划,每月原料供应量为9000kg,工时为7000小时。
根据以上条件,就可以运用规划求解,计算出该公司在一个月内可以实现的最大利润额以及相应的各种产品生产量最佳组合。
一、构建模型启动Excel,新建一个表格,在其中输入产品名称、单位耗用原料、单位耗时时间、单位利润、计划产量,另外在其下面输入月度原料配额、月度时间配额、原料总用量、总生产时间、总利润等项目(图1)。
然后在这个工作表中,将前面已知的生产相关数据添加进去,如单位耗用原料量、单位耗用时间、单位利润、月度原料限额、月度时间限额等,同时还必须输入相应公式以确定在一定的计划产量下,预计的原料总用量、总生产时间以及总利润。
图1由于原料用量=计划产量×单位耗用原料量,而原料总用量就等于A、B产品二者的原料用量之和,在此工作表中即:原料总用量=D4×G4+D5×G5,而总生产时间=E4×G4+E5×G5,总利润=F4×G4+F5×G5。
这里可以使用数组乘积函数SUMPRODUCT来快速完成所求积之和,在D10单元格内输入公式“=SUMPRODUCT(D4:D5,G4:G5)”即可(图2),采用同样的方法,在D11、D12单元格内分别输入:=SUMPRODUCT(E4:E5,G4:G5),=SUMPRODUCT(F4:F5,G4:G5),用来计算总生产时间以及总利润。
Excel规划求解使用教程(图)
附录4 Excel“规划求解”1. 在系统中安装“规划求解”1、启动EXCEL。
打开“工具”菜单。
如果没有“规划求解”,单击“加载宏”。
弹出以下窗口:2、在复选框中选中“规划求解”,单击“确定”后返回Excel。
这时在“工具”菜单中出现“规划求解”。
关闭“工具”菜单2. 在Excel中创建线性规划模型1、输入线性规划模型的约束条件系数、右边常数和目标函数系数。
定义线性规划的变量单元格、约束条件左边单元格和目标函数单元格。
2、定义“设备能力占用”(即约束条件左边)以及“总利润”的计算公式。
首先定义设备A的“能力占用”单元格(G3)的计算公式,界面如下:其次定义设备B的“能力占用”单元格(G4)的计算公式,界面如下:再次定义设备C的“能力占用”单元格(G5)的计算公式,界面如下:最后定义“总利润”单元格(C8)的计算公式,界面如下:3、将光标停留在“总利润”值的单元格(C8)中,打开“工具/规划求解”,弹出以下窗口:4、设置目标函数单元格:检查“设置目标函数单元格”是否在“$C$8”,如不是,单击文本框右侧的图标,重新选定目标函数单元格,也可以直接单击Excel表中的“C8”。
5、设置变量:单击“规划求解窗口”中“可变单元格”文本框,然后在Excel工作表中选定变量单元格(C7、D7、E7和F7),在文本框中出现“$C$7:$F$7”,如下图所示。
6、设置约束单击“添加”,弹出以下窗口:单击“单元格引用位置”文本框空白处,然后单击工作表G3单元格,“单元格引用位置”文本框中出现“$G$3”;打开“单元格引用位置”和“约束值”之间的下拉文本框,选定“<=”;单击“约束值”文本框空白处,然后单击工作表H3单元格。
结果如下图所示。
单击“添加”,完成第一个约束设置。
继续设置第二、第三个约束,最后设置所有变量非负。
约束设置完成以后,单击“确定”,返回“规划求解参数”窗口,如下图所示。
7、设置叠代参数。
单击“选项”,弹出以下窗口:输入“最长运行时间”、“叠代次数”、“精度”、“允许误差”、“收敛度”等叠代参数。
使用Excel进行线性规划求解功能,轻松找到问题的最优的解决方案
使用Excel进行线性规划求解功能,轻松找到问题的最优的解
决方案
在我们的工作中,规划求解是十分常见的应用场景,是一种研究线性约束条件下线性目标函数的极值问题的数学理论和方法。
比如在生产管理中,在人工、材料等等条件的约束下,如何安排才能使工厂利益的最大化问题就是典型的规划问题。
而对于此类问题的求解,如果使用手工求解的方式还是存在一定的困难,但是如果使用Excel这个工具的话,就能轻松的进行求解。
下面,我就通过一个工厂生产利润最大化的例子来给小伙伴们讲解下具体的使用方法。
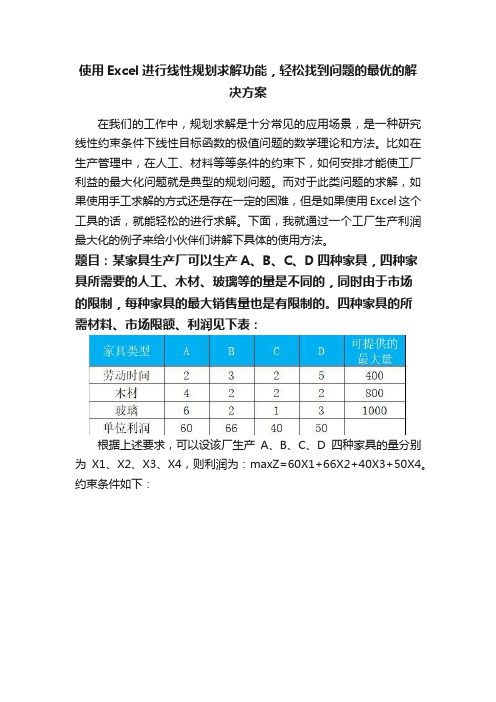
题目:某家具生产厂可以生产A、B、C、D四种家具,四种家具所需要的人工、木材、玻璃等的量是不同的,同时由于市场
的限制,每种家具的最大销售量也是有限制的。
四种家具的所
需材料、市场限额、利润见下表:
根据上述要求,可以设该厂生产A、B、C、D四种家具的量分别为X1、X2、X3、X4,则利润为:maxZ=60X1+66X2+40X3+50X4。
约束条件如下:
根据以上条件,在Excel中做出以下求解模版:
根据以上分析,目标值单元格的公式如下:
=SUMPRODUCT(B13:E13,B6:E6)。
时间约束,木材约束,玻璃约束的使用量公式分别为:=SUMPRODUCT(B18:E18,$B$13:$E$13)
=SUMPRODUCT(B19:E19,$B$13:$E$13)
=SUMPRODUCT(B20:E20,$B$13:$E$13)
专栏
从进销存系统入门ExcelVBA编程。
Excel 实验指导—利润最大化生产方案

Excel 实验指导—利润最大化生产方案生产方案是指企业为实现其目标利润而系统、全面的调整其经营活动的规模和水平的一种方法。
例如,某公司成产3种产品,每生产1种产品最少成本、时间、利润已给出,通过生产成本、生产时间的约束,计算该公司如何分配3种产品的生产才能获得最高利润。
下面运用规划求解、添加约束条件、以及建立规划求解报告等知识来制作“企业生产方案选择表”。
1.实验目的●公式的应用●函数的应用●规划求解2.操作步骤:(1)新建一个空白工作簙。
在该工作表中输入表头、标题和数据信息。
然后进行字体格式、对齐方式、边框等设置,如图8-41所示。
创建表格图8-41 创建表格(2)选择F3单元格,输入“=D3*E3”公式,即可计算A产品的销售利润,如图8-42所示。
图8-4Excel 输入公式(3)将鼠标置于F3单元格的填充柄上,向下拖动至F5单元格,即可复制该公式,如图8-43所示。
图8-4Excel 复制公式(4)选择F9单元格,输入“=B3*E3+B4*E4+B5*E5”公式,即可计算出“实际生产成本”,如图8-44所示。
图8-4计算“实际生产成本”(5)选择F10单元格,输入“=C3/60*E3+C4/60*E4+C5/60*E5”公式,即可计算出“实际生产时间(时)”,如图8-45所示。
图8-4 计算“实际生产时间”(6)选择F11单元格,并选择【公式】选项卡,单击【函数库】组中的【自输入 计算结果复制公式输入公式计算输入计算动求和】按钮。
然后选择求和区域F3至F5单元格区域,如图8-46所示。
图8-4 自动求和(7)在弹出的【规划求解参数】对话框中的【设置目标单元格】栏中,选择$F$11单元格;并设置【可变单元格】为$E$3:$E$5,如图8-47所示。
图8-4Excel 设置【规划求解参数】提 示 选择【数据】选项卡,单击【分析】组中的【规划求解】按钮,即可弹出【规划求解参数】对话框。
(8)单击【规划求解参数】对话框中的【添加】按钮,即可弹出【添加约束】条件对话框中,设置约束条件,并单击【添加】按钮。
利用excel软件求解线性规划问题分析

下面我们通过一个例子来解释怎样用“规划求解”来求解数学规划问题。
例1 公司通常需要确定每月(或每周)生产计划,列出每种产品必须生产的数量。
具体来说就是,产品组合问题就是要确定公司每月应该生产的每种产品的数量以使利润最大化。
产品组合通常必须满足以下约束:● 产品组合使用的资源不能超标。
● 对每种产品的需求都是有限的。
我们每月生产的产品不能超过需求的数量,因为生产过剩就是浪费(例如,易变质的药品)。
下面,我们来考虑让某医药公司的最优产品组合问题。
该公司有六种可以生产的药品,相关数据如下表所示。
设该公司生产药品1~6的产量分别为126,,,x x x L (磅),则最优产品组合的线性规划模型为123456123456123456123456max 6 5.3 5.4 4.2 3.8 1.86543 2.5 1.545003.2 2.6 1.50.80.70.316009609281041..977108410550,16j z x x x x x x x x x x x x x x x x x x x x x s t x x x x j =++++++++++≤⎧⎪+++++≤⎪⎪≤⎪≤⎪⎪≤⎨⎪≤⎪≤⎪⎪≤⎪⎪≥≤≤⎩下面用规划求解加载宏来求解这个问题: 首先,如下如所示,在Excel 工作表内输入目标函数的系数、约束方程的系数、右端常数项;其次,选定目标函数单元、可变单元、约束函数单元,定义目标函数、约束函数其中,劳动力约束函数的定义公式是“=MMULT(B3:G3, J5:J10)”,原料约束函数的定义公式是“=MMULT(B4:G4,J5:J10)”,目标函数的定义公式是“MMULT(B5:G5, J5:J10)”。
注:函数MMULT(B3:G3, J5:J10)的意义是:单元区B3:G3表示的行向量与单元区J5:J10表示的列向量的内积。
这一要特别注意的是,第一格单元区必须是行,第二格单元区必须是列,并且两个单元区所含的单元格个数必须相等。
EXCEL规划求解案例分析

x1, x2 , x3 , x4 分别为四种家具的日产量。
SUMPRODUCT函数
• SUMPRODUCT的意思是:乘积之和 • 在给定的几组数组中,将数组间对应 的元素相乘,并返回乘积之和。 • 语法 • SUMPRODUCT(array1,array2,array3, ...) • Array1,array2,array3, ... 为 2 到 30 个数 组,其相应元素需要进行相乘并求和。
(4)由敏感性报告可见,劳动时间与木材这两种资源的使用量 等于可提供量,所以它们的约束条件为“紧”的,即无余量 的;而玻璃的使用量为800,可提供量为1000,所以玻璃的 约束条件是“非紧”的,即有余量的。 因此,应优先考虑购买劳动时间与木材这两种资源。 (5)由敏感性报告可知,家具1的目标系数(即单位利润)允许的 减量为20,即当家具1的单位利润减少量不超过20元时,最优 解不变。因此,若家具1的单位利润从60元下降到55元,下降 量为5元,该下降量在允许的减量范围内,这时,最优解不变。 因此,四种家具的最优日产量仍分别为100件、80件、40件 和0件。 最优值变为: 9200+(55-60)X100=8 700(元)。
设产品I和II的产量分别为x1和x2,其数学 模型为:
max Z= 6x1 +8x2 5x1 + 10x2 ≤60 st. 4x1 + 4x2 ≤40 x1 , x2 ≥0
其最优解,即最优生产计划为x1=8件, x2=2件,max Z=64元。
例2 假设在前面例子中,计划人员被要求 考虑如下意见: (1) 由于产品 II 销售疲软,故希望产品 II 的 产量不超过产品I 的一半; (2)原材料严重短缺,生产中应避免过量消 耗; (3)最好能节约4h设备工时; (4)计划利润不少于48元。
用excel求解生产计划问题

实验报告用Excel求解生产计划问题一、实验目的1. 学习学习Excel中的Solver,掌握生产计划的一种求解方法;2. 通过通过复习生产计划的基础知识,掌握生产计划的制订方法以及将生产计划转化为线性规划的方法。
二、实验步骤1)将问题转化为线性规划问题。
2)将线性规划的目标函数和约束条件输入到Excel。
3)调用Solver求解:工具菜单-选择Solver,调用出Solver—〉出现Solver 对话框。
4)设置目标单元格。
5)指定是最大问题还是最小问题。
6)告诉Excel约束的数学定义在那里。
7)设置属性。
8)点击“Solver”按钮得到答案。
9)将解转化为问题答案。
三、实验设备计算机。
EXCEL软件四、实验内容爱宝玩具有限公司生产A,B,C,D四种儿童玩具,每种玩具都需要经过甲、乙、丙三个车间,各种产品的设备台时消耗标准、各车间设备的计划期总台时、单位产品利润、预测的市场需求状况如表1所示。
请为爱宝玩具有限公司确定综合生产计划的产量指标。
表1表2解:1)将问题转化为线性规划问题。
设产品A、产品B、产品C和产品D的产量分别为x1、x2、x3、和x4,根据题目已知可得线性规划模型:Max w =0.9x1+1.6x2+0.4x3+1.0x4约束条件如下:1 10x1+40x2+20x3+10x4≤205000225x1+20x2+40x3+25x4≤215000335x1+40x2+15x3+25x4≤26250041500≤x1≤2500, 2000≤x2≤6000, 2000≤x3≤2500, 1000≤x1≤1500,且x1,x2,x3,x4 ∈N .注:为避免总和为数值而非文本,在初始设定四个变量的值分别为 1、2、3、4。
2)将线性规划的目标函数和约束条件输入到Excel。
(如表2)对于目标函数在单元格中F4输入公式 =SUMPRODUCT(B3:E3,B4:E4)对于约束条件的第一个式子的左边,在单元格输入公式=SUMPRODUCT(B3:E3,B5:E5)其他的两个约束条件依照上述方法输入对应的公式。
EXCEL规划求解案例分析

什么是规划问题?
在计划管理中常会遇到:人力资源的调度、
产品生产的安排、运1输、线约路束的条规划件、的生表产达材 料的搭配、采购批次2的、确目定标等的问题数。学描述
这类问题有一个共3同、点应,用即需Ex要ce解l的决:规如划 何合理利用各种存在求约解束的工资具源对,问而题获求得解最
佳的经济效益,也就是达到利润最大、成本 最低等目标。这就是本节要解决的“在约束 条件下寻求目标函数最优解的规划问题”。
规划问题的特点(共性)
一般来讲,规划问题都具有如下特点:
1. 所求问题都有单一的目标(如求生产的最低 成本,求运输的最佳路线,求产品的最大盈 利,求产品周期的最短时间),要求求目标 函数的最优解。
2. 对于问题涉及的对象(如路程、原材料等) 存在有明确的可以用不等式表达约束条件。
3. 问题的表达可以描述为:一组约束条件(不 等式),和一个目标方程。
4. 利用Excel技术可以简单的求得问题满足约束 条件求的目标最优解。
2.如何加载“规划求解”
1) 在“工具”菜单上,单击“加载宏”
2) 在弹出的对话框中的“可用加载宏”列表框 中,选定待添加的加载宏“规划求解”选项旁 的复选框,然后单击“确定”.单击“确定” 后,“工具”菜单下就会出现一项“规划求解”
设产品I和II的产量分别为x1和x2,其数学 模型为:
max Z= 6x1 +8x2 5x1 + 10x2 ≤60
st. 4x1 + 4x2 ≤40 x1 , x2 ≥0
其最优解,即最优生产计划为x1=8件, x2=2件,max Z=64元。
例2 假设在前面例子中,计划人员被要求 考虑如下意见:
应如何安排这四种家具的日产量,使得该厂的日利 润最大?
EXCEL规划求解功能操作说明

Excel规划求解功能操作说明以Microsoft Excel2003为例,说明使用Excel的求解线性规划问题功能的使用方法。
一、加载规划求解功能1.点击【工具】按钮,在下拉菜单中选择【加载宏】功能。
2.在弹出的【可加载宏】选项卡中勾选【规划求解】,点击确定按钮。
此时,【工具】下拉菜单中增加规划求解功能,表示加载成功。
二、构造表格Excel表格并填入各项数据以教材18页【例题2-8】为例,构造表格如下:1.录入约束条件系数约束条件(1)为5x1+x2-x3+x4=3,则在约束系数的第一行的x1,x2,x3,x4,x5,限制条件,常数b列下分别录入5,1,-1,1,0,=,3如下图所示。
约束系数区的第二行录入约束条件(2)的系数、限制符号及常数b,即-10,6,2,0,1,=,2;约束系数区的第三行录入约束条件(3)(x1≥0)的系数、限制符号及常数b,即1,0,0,0,0,≥,0;约束系数区的第四行录入约束条件(4)(x2≥0)的系数、限制符号及常数b,即0,1,0,0,0,≥,0;约束系数区的第五行录入约束条件(5)(x3≥0)的系数、限制符号及常数b,即0,0,1,0,0,≥,0;约束系数区的第六行录入约束条件(6)(x4≥0)的系数、限制符号及常数b,即0,0,0,1,0,≥,0;约束系数区的第七行录入约束条件(7)(x5≥0)的系数、限制符号及常数b,即0,0,0,0,1,≥,0。
如下图所示。
2.录入目标函数系数目标函数为maxZ=4x1-2x2-x3,则在目标函数的x1,x2,x3,x4,x5列下分别录入4,-2,-1,0,0,如下图所示。
3. 录入约束条件的计算公式双击约束条件(1)行的“总和”单元格,录入以下内容:“=B3*B12+C3*C12+D3*D12+E3*E12+F3*F12”说明:录入的内容即是约束条件(1)的计算公式,其中“B3*B12”代表5x 1; “C3*C12”代表1x 2;“D3*D12”代表-1x 3;“E3*E12”代表1x 4;“F3*F12”代表0x 5。
Excel 财务应用 经济价值最优的生产决策问题

Excel 财务应用 经济价值最优的生产决策问题人们在各种生产活动和经济活动中,总是希望最大限度的利用资源和设备,完成最佳的任务;或者在统筹安排下,在最短的时间内,使用最少的人力、物力和投资,即利用最小的资源消耗,完成规定的任务。
因此,就需要管理者做出相应的生产决策。
生产决策是根据企业的经营战略方案和企业内外经营环境的状况,来确定企业的生产方向、生产目标、生产方针以及生产方案的过程或职能。
下面就利用线性规划,解决企业中最优经济价值的生产决策问题。
在使用线性规划做出分析决策之前,需要先加载规划求解宏,以便日后使用。
依次单击Office 按钮和【Excel 选项】按钮,在弹出的对话框中,选择【加载项】选项卡,并单击【转到】按钮,即可弹出【加载宏】对话框。
然后,在该对话框中,启用【规划求解】复选框,如图9-1所示。
图9-1 加载规划求解宏例如,某钢厂生产螺纹钢和带钢两种类型的钢材,已知生产一吨螺纹钢需要A 种原材料2吨,B 种原材料6吨;生产一吨带钢需要A 种原材料5吨,B 种原材料3吨,而工厂要求所用的A 、B 两种原料分别不能超过10吨和18吨。
每吨螺纹钢可以获得4万元的利润,售出每吨带钢可以获得3万元的利润,要求计算生产螺纹钢和带钢两种产品各多少吨时,产值最大?在利用线性规划模型求解时,任何一个线性规划模型都包含有表示要做决策的决策变量、表述这些决策变量的可行值、现值的约束条件和表示问题完全绩效测度的目标函数。
因此,可以将问题中的已知条件、约束值以及所求变量都输入到Excel 工作表中,如图9-2所示。
图9-2 输入已知条件、约束值和变量上图所表述内容是对该问题在Excel 工作表中的数学描述。
其中,生产每吨螺纹钢和带 提 示 在【加载宏】对话框中单击【确定】按钮之后,系统将自动弹出安装过程对话框,安装完成之后重新启动计算机,即可在【数据】选项卡的分析组中,添加【规划求解】按钮。
启用输入条件钢所需要的两种原材料和销售产品产生的利润,均属于已知条件;工厂要求使用的两种原材料吨数为约束条件;而绿色单元格区域则表示问题中需要计算的两个变量值,默认情况下,其值为0。
EXCEL规化求解功能详解

EXCEL规化求解功能详解【摘要】随着OFFICE办公软件的日益更新,OFFICE办公软件依然能站在市场的前言,这不能不归功于它的功能强大。
尤其是其中的EXCEL,原来只是用到他的许多统计的功能,没想到他还可以解决很多复杂的数学问题,如果我们用常规的函数去做的话非常麻烦,但用它的规化求解功能问题便独迎刃而解,非常方便快捷。
对于今天的社会来说很是实用,因为今天我们面临的选择很多,商家企业会考虑如何能用最小的成本(人员费用、材料费用、厂房费用、机器费用等)达到最大的收益,各行各业都面临这种多个变量如何实现最优的问题,这个用数学方法来计算都需要很长时间,但用EXCEL两分钟就可以出结果,让人兴奋。
本文就它的这个功能做一详细的介绍。
【关键词】EXCEL;规化求解大学教程中线性代数中有讲到,就是满足给定条件下,求变量如何分配可以取得函数的极值。
在实际生活中应用非常广泛,如求如何在各种成本(人力、原材料、水电费等)最低的情况下去实现利润最大化,如果公司只生产一种产品,不用算只需投产;但如果是多种产品,那就需要一系列复杂的运算,考虑每一种产品的消耗;综合考虑每一种因素;最终才可以得出如何投入可以获得最大的利润。
但在EXCEL中却可以很容易的得到答案。
不管是EXCEL2003,还是2007,还是2010,虽然版本不同,但都能运用规化求解功能来解决实际的问题。
本文就EXCEL的规化求解的一实例具体来探讨它的好处与应用。
例如某公司生产和销售两种产品,两种产品一个单位各需要工时4.2小时和7.3小时,用电量4.1千瓦和5.3千瓦,需要原材料8公斤和4.6公斤。
公司可提供的工时为300小时,可提供的电量为250千瓦,可提供的原材料为420公斤。
两种产品的单位利润分别为190元和220元。
该公式如何安排两种产品的生产才能获得最大的利润。
诸如此类问题,可以再加入产品,再增加条件,但形式一样。
我们首先根据题目内容,读董题意,题目是想在不超出给定工时、电量、原材料的情况下,如何安排两种产品的生产可能得到最大利润。
利用excel软件求解线性规划问题讲解

下面我们通过一个例子来解释怎样用“规划求解”来求解数学规划问题。
例1 公司通常需要确定每月(或每周)生产计划,列出每种产品必须生产的数量。
具体来说就是,产品组合问题就是要确定公司每月应该生产的每种产品的数量以使利润最大化。
产品组合通常必须满足以下约束:● 产品组合使用的资源不能超标。
● 对每种产品的需求都是有限的。
我们每月生产的产品不能超过需求的数量,因为生产过剩就是浪费(例如,易变质的药品)。
下面,我们来考虑让某医药公司的最优产品组合问题。
该公司有六种可以生产的药品,相关数据如下表所示。
设该公司生产药品1~6的产量分别为126,,,x x x (磅),则最优产品组合的线性规划模型为123456123456123456123456max 6 5.3 5.4 4.2 3.8 1.86543 2.5 1.545003.2 2.6 1.50.80.70.316009609281041..977108410550,16j z x x x x x x x x x x x x x x x x x x x x x s t x x x x j =++++++++++≤⎧⎪+++++≤⎪⎪≤⎪≤⎪⎪≤⎨⎪≤⎪≤⎪⎪≤⎪⎪≥≤≤⎩下面用规划求解加载宏来求解这个问题: 首先,如下如所示,在Excel 工作表内输入目标函数的系数、约束方程的系数、右端常数项;其次,选定目标函数单元、可变单元、约束函数单元,定义目标函数、约束函数其中,劳动力约束函数的定义公式是“=MMULT(B3:G3, J5:J10)”,原料约束函数的定义公式是“=MMULT(B4:G4,J5:J10)”,目标函数的定义公式是“MMULT(B5:G5, J5:J10)”。
注:函数MMULT(B3:G3, J5:J10)的意义是:单元区B3:G3表示的行向量与单元区J5:J10表示的列向量的内积。
这一要特别注意的是,第一格单元区必须是行,第二格单元区必须是列,并且两个单元区所含的单元格个数必须相等。
