材料力学99
材料力学考研重点总结

材力基本考试就那几块,从第一册开始第二章第三章轴向拉压,扭转,一般只出选择,通常与第二册第一章弯曲中心结合着考,每年两个选择差不多,注意一下基础知识,仔细看一下书,总结一下基础知识就可以,把拉压和扭转的能量公式记住,在第二册能量法计算位移和力的时候会用到,第四章弯曲要出两道大题,主要是画剪力弯矩图和杆件的强度校核,强度校核一般与第七章强度理论和主应力还有第二册主应变结合在一起考,这章是重点要把课后的五十八道习题仔细做一遍,做会了。
第五章挠度和转角只看叠加法,记住书后附表中的每一个基本图示,把书上的例题和课后几道题看透了就行,第六章一般与第二册能量法结合起来考一个用能量法解超静定的题,要是时间不够的话就不要看了,直接等看第二册能量法的时候再一起看,第七章很重要,要出选择和大题,强度理论不用说每年都是重点,应力应变计算那主要看一类题就行,就是:用应变片测得在三十度的应变是多少多少,告诉你弹模,泊松比,让你求应力一类题,我忘记是课后哪个题了,我记得课后给的一般是30或者45度角的,总之看这一类题就行了,第八章主攻弯剪扭组合变形,只要这一个弄懂,其他什么弯扭组合,斜弯曲就迎刃而解了,对于铆钉连接计算看一下书上的例题就行,剪切和挤压也是以例题为主。
第九章通常与第二册动应力结合起来,考一个压杆稳定的大题,这部分以真题为主,看一下真题就知道他的具体类型和具体形式了。
接下来是第二册,第一章主看开口薄壁界面的弯曲中心和切应力流,第二章不看,第三章能量法必看,从头看到尾,遇题就做,遇知识点就背,可以说这章是真正花时间的,一定要看好,理解透。
第四章看一下应变片的贴法和主应变和应变圆的画法,这里会与第七章结合出大题,但是有一点,凡是用应变圆可以解决的都可以用应力圆解决,接下来就是看一下动荷载和疲劳验算,疲劳不出大题,动荷载只需要记住匀加速上升,水平冲击,自由落体,向下匀速冲击几种情况下的动荷载系数Kd就行。
基本就是这些,其他就没什么了,等我再回去看看有什么落下的,我再给你补充,哦对了我QQ是344963551,你可以直接加我QQ,我们再聊也材力下册重点概括材力第二册,第一章主看开口薄壁界面的弯曲中心和切应力流,第二章不看,第三章能量法必看,从头看到尾,遇题就做,遇知识点就背,课后题自己选三分之二来做,可以说这章是真正花时间的,一定要看好,理解透。
材料力学复习资料全

材料力学复习资料全材料力学复习资料一、填空题K为了保证机器或结构物正常地工作,要求每个构件都有足够的抵抗破坏的能力,即要求它们有足够的强度:冋时要求他们有足够的抵抗变形的能力?即要求它们有足够的刚度:另外,对于受压的细长直杆,还要求它们工作时能保持原有的平衡状态,即要求其有足够的稳定性「2、材料力学是研究构件强度、刚度、稳定性的学科。
3、强度是指构件抵抗破坏的能力:冈帔是指构件抵抗变形的能力:稳左性是指构件维持其原有的平衡状态的能力。
4、在材料力学中,对变形固体的基本假设是连续性假设、均匀性假设、各向同性假设5、随外力解除而消失的变形叫弹性变形;外力解除后不能消失的变形叫舉性变形。
6、截面法是计算力的基本方法。
7、应立是分析构件强度问题的重要依据。
8、线应变和切应变是分析构件变形程度的基本量。
9、轴向尺寸远大于横向尺寸,称此构件为枉。
10、构件每单位长度的伸长或缩短,称为线应变°11、单元体上相互垂直的两根棱边夹角的改变量.称为切应变-12、轴向拉伸与压缩时直杆横截而上的力,称为轴力,13、应力与应变保持线性关系时的最大应力,称为比例极限14、材料只产生弹性变形的最大应力,称为弹性极根:材料能承受的最大应力,称为强度极限。
15、弹性模量E是衡量材料抵抗弹性变形能力的指标。
16、延伸率6是衡量材料的塑性指标。
6 M5%的材料称为塑性材料:§ V5%的材料称为脆性材料。
17、应力变化不大,而应变显著增加的现象,称为屈服或流动18、材料在卸载过程中,应力与应变成线性关系。
19、在常温下把材料冷拉到强化阶段,然后卸载,当再次加载时,材料的比例极限提高,而塑性降低,这种现象称为冷作硬化20、使材料丧失正常工作能力的应力,称为极限应力,21、在工程计算中允许材料承受的最大应力,称为许用应力。
22、当应力不超过比例极限时,横向应变与纵向应变之比的绝对值,称为泊松比一23、胡克定律的应力适用恫是应力不超过材料的比例极限。
第五版材料力学答案

第五版材料力学答案1. 什么是材料的弹性模量?材料的弹性模量是描述材料在受力作用下的变形能力的物理量,它是应力和应变之间的比值。
弹性模量越大,材料的刚度越大,变形能力越小;弹性模量越小,材料的刚度越小,变形能力越大。
常见的弹性模量有弹性模量、剪切模量和体积模量等。
2. 什么是材料的屈服强度?材料的屈服强度是指材料在受到外力作用下开始发生塑性变形的应力值。
超过屈服强度后,材料将发生不可逆的塑性变形。
屈服强度是材料的重要力学性能参数,对于材料的强度和使用性能有重要影响。
3. 什么是材料的断裂韧性?材料的断裂韧性是描述材料在受到外力作用下抵抗断裂的能力。
断裂韧性越大,材料在受到外力作用下越不容易发生断裂。
断裂韧性是衡量材料抗断裂能力的重要指标,对于材料的使用安全性具有重要意义。
4. 什么是材料的疲劳强度?材料的疲劳强度是指材料在交变应力作用下能够承受的最大应力值。
材料在长期交变应力作用下容易发生疲劳破坏,疲劳强度是描述材料抗疲劳破坏能力的重要参数,对于材料的使用寿命具有重要影响。
5. 什么是材料的弹性极限?材料的弹性极限是指材料在受到外力作用下发生弹性变形的极限应力值。
超过弹性极限后,材料将发生塑性变形。
弹性极限是描述材料在受力作用下的弹性变形能力的重要参数,对于材料的设计和使用具有重要意义。
6. 什么是材料的刚度?材料的刚度是描述材料在受力作用下的变形能力的物理量,它是应力和应变之间的比值。
刚度越大,材料在受力作用下的变形能力越小;刚度越小,材料在受力作用下的变形能力越大。
刚度是描述材料力学性能的重要参数,对于材料的设计和使用具有重要影响。
7. 什么是材料的蠕变强度?材料的蠕变强度是指材料在高温和持续应力作用下发生蠕变变形的能力。
蠕变强度是描述材料在高温条件下的稳定性能的重要参数,对于材料在高温环境下的使用具有重要影响。
总结,材料力学是工程学、材料学和力学的交叉学科,对于材料的性能分析和设计具有重要意义。
材料力学

4.应力集中敏感性:脆性材料对应力集中敏感,以导致破坏
2.5.4 许用应力
������������ 或 ������0.2
������������
������������
脆性材料
[ σ ]=
2
2.2.5 圆柱薄壁容器的应力
1.横截面上的应力������������
=
������������ 4������
2.纵截面上的环向应力������������
=
������������ 2������
=
2������������
D 为圆柱薄壁容器的平均直径 (平均直径为内外径的平均值), δ 为壁厚,q 为内压
全应力
p
=
lim∆A→0
∆������ ∆������
正应力
σ=lim∆A→0
∆������������ ∆������
切应力
τ=lim∆A→0
∆������������ ∆������
FN= ������������������
3.静力学关系式
Fsy= ������������������������ Fsz= ������������������������ T= ������������ sin(������, ������) ������������
轴力、弯矩只与正应力有关 剪力,扭矩只与切应力有关
My= ������������������������
1
Mz= ������������������������
材料力学
4.截面法:①截开 ②画脱离物体受力图 ③列平衡方程,解方程
(完整版)材料力学必备知识点

材料力学必备知识点1、 材料力学的任务:满足强度、刚度和稳定性要求的前提下,为设计既经济又安全的构件,提供必要的理论基础和计算方法。
2、 变形固体的基本假设:连续性假设、均匀性假设、各向同性假设。
3、 杆件变形的基本形式:拉伸或压缩、剪切、扭转、弯曲。
4、 低碳钢:含碳量在0.3%以下的碳素钢。
5、 低碳钢拉伸时的力学性能:弹性阶段、屈服阶段、强化阶段、局部变形阶段 极限:比例极限、弹性极限、屈服极限、强化极限6、 名义(条件)屈服极限:将产生0.2%塑性应变时的应力作为屈服指标7、 延伸率δ是衡量材料的塑性指标塑性材料 随外力解除而消失的变形叫弹性变形;外力解除后不能消失的变形叫塑性变形。
>5%的材料称为塑性材料: <5%的材料称为脆性材料8、 失效:断裂和出现塑性变形统称为失效9、 应变能:弹性固体在外力作用下,因变形而储存的能量10、应力集中:因杆件外形突然变化而引起的局部应力急剧增大的现象11、扭转变形:在杆件的两端各作用一个力偶,其力偶矩大小相等、转向相反且作用平面垂直于杆件轴线,致使杆件的任意两个横截面都发生绕轴线的相对转动。
12、翘曲:变形后杆的横截面已不再保持为平面;自由扭转:等直杆两端受扭转力偶作用且翘曲不受任何限制;约束扭转:横截面上除切应力外还有正应力13、三种形式的梁:简支梁、外伸梁、悬臂梁14、组合变形:由两种或两种以上基本变形组合的变形15、截面核心:对每一个截面,环绕形心都有一个封闭区域,当压力作用于这一封闭区域内时,截面上只有压应力。
16、根据强度条件 可以进行(强度校核、设计截面、确定许可载荷)三方面的强度计算。
17、低碳钢材料由于冷作硬化,会使(比例极限)提高,而使(塑性)降低。
18、积分法求梁的挠曲线方程时,通常用到边界条件和连续性条件;因杆件外形突然变化引起的局部应力急剧增大的现象称为应力集中;轴向受压直杆丧失其直线平衡形态的现象称为失稳19、圆杆扭转时,根据(切应力互等定理),其纵向截面上也存在切应力。
材料力学基础知识PPT课件

3
材料力学的建立
强度。(屈服强度,抗拉强度,抗弯强度, 抗剪强度),如钢材Q235,屈服强度为 235MPa
塑性。一般用伸长率或断面收缩率表示。 如Q235伸长率为δ5=21-26
表示轴力沿杆轴变化情况的图线,称为轴力图。 例如上图中的坐标图即为杆的轴力图。
31
4.2轴力与轴力图
例1 图中所示为右端固定梯形杆,承受轴向载荷F1与F2作 用,已知F1=20KN(千牛顿),F2=50KN,试画杆的轴力 图,并求出最大轴力值。
解:(1)计算支反
力
A F1
B F2
设杆右端的支反力为
12
3.3外力与内力
内力与截面法
内力:物体内部的相互作用力。由于载荷作用引起的内力称为附加内 力。简称内力。内力特点:引起变形,传递外力,与外力平衡。 截面法:将杆件假想地切成两部分,以显示内力,称为截面法。
13
3.3外力与内力
应用力系简化理论,将上述分布内力向横截面的形心简化,得
轴力 :Fx沿杆件轴线方向内力分量,产生轴向(伸长,缩短)
C FR
FR,则由整个杆的平 F1
FN1 FN2
FR
衡方程
FN
20kN
ΣFx=0,F2-FR=0 得
+ 0
30kN
FR=F2-F1=50KN-20KN
=30KN
32
4.2轴力与轴力图
(2)分段计算轴力
设AB与BC段的轴力
A
均为拉力,并分别用FN1 F1
与FN2表示,则可知
(完整版)材料力学基本概念和公式

(完整版)材料力学基本概念和公式第一章绪论第一节材料力学的任务1、组成机械与结构的各组成部分,统称为构件。
2、保证构件正常或安全工作的基本要求:a)强度,即抵抗破坏的能力;b)刚度,即抵抗变形的能力;c)稳定性,即保持原有平衡状态的能力。
3、材料力学的任务:研究构件在外力作用下的变形与破坏的规律,为合理设计构件提供强度、刚度和稳定性分析的基本理论与计算方法。
第二节材料力学的基本假设1、连续性假设:材料无空隙地充满整个构件。
2、均匀性假设:构件内每一处的力学性能都相同3、各向同性假设:构件某一处材料沿各个方向的力学性能相同。
木材是各向异性材料。
第三节内力1、内力:构件内部各部分之间因受力后变形而引起的相互作用力。
2、截面法:用假想的截面把构件分成两部分,以显示并确定内力的方法。
3、截面法求内力的步骤:①用假想截面将杆件切开,一分为二;②取一部分,得到分离体;③对分离体建立平衡方程,求得内力。
4、内力的分类:轴力N F ;剪力S F ;扭矩T ;弯矩M第四节应力1、一点的应力:一点处内力的集(中程)度。
全应力0limA Fp A→?=?;正应力σ;切应力τ;p =2、应力单位:Pa (1Pa=1N/m 2,1MPa=1×106 Pa ,1GPa=1×109 Pa )第五节变形与应变1、变形:构件尺寸与形状的变化称为变形。
除特别声明的以外,材料力学所研究的对象均为变形体。
2、弹性变形:外力解除后能消失的变形成为弹性变形。
3、塑性变形:外力解除后不能消失的变形,称为塑性变形或残余变形。
4、小变形条件:材料力学研究的问题限于小变形的情况,其变形和位移远小于构件的最小尺寸。
对构件进行受力分析时可忽略其变形。
5、线应变:ll ?=ε。
线应变是无量纲量,在同一点不同方向线应变一般不同。
6、切应变:tan γγ≈。
切应变为无量纲量,切应变单位为rad 。
第六节杆件变形的基本形式1、材料力学的研究对象:等截面直杆。
工程材料力学性能基准讨论

工程材料力学性能基准讨论宋锋涛董本正等《基于Matlab的碳纤维复合材料的B基准值算法》中说到,为了保证材料的结构的可靠性和安全性,需要用到一些高级的统计学方法来确定其合理的设计许用值,一般采用B基准值。
B基准值是建立在统计学上的衡量材料性能的参数,在95%的置信度下,90%性能数值群的值高于此值。
而马鑫《复合材料B 基准值计算程序》一文中给出了B基准的定义。
B 基准值的定义为:一个力学性能的限定值,在95%的置信度下,90%的性能数值群的值不低于其值。
王亮等在《复合材料破坏数据B基准值计算的程序设计》中表示B 基准值是指力学性能的一个限定值, 在95% 的置信度下, 数值母体中90% 的性能值不小于其值。
王翔等在《基于统计的复合材料B基准值计算方法研究》中对材料性能的A、B做了介绍。
A 基准值指力学性能的一个限定值, 在95% 的置信度下, 99% 的性能数值群的最小值。
B 基准值指力学性能的一个限定值, 在95% 的置信度下, 90%的性能数值群的最小值。
另外给出了M IL- HDBK- 17对B类和A 类基准值单一环境下最低采样要求。
DOT /FAA /AR- 03 /19要求在每个试验条件下至少3 批次, 每批次至少6个数据。
如表1所示。
冯振宇等在《复合材料飞机结构材料和设计许用值的确定方法》中做A、B 基准的使用范围做了详细说明。
材料许用值是通过对试验数据进行统计分析得到的材料性能值( 例如模量、应变或应力等) 。
材料许用值通常用平均值( 用于模量) 、B 基准值( 用于超静定结构)和 A 基准值( 用于静定结构) 表征。
静强度设计许用值包括拉伸强度、压缩强度( 包括构件稳定性设计) 和剪切强度许用值。
总所周知工程材料力学性能有三个基准,即A/B/S。
那么S基准到底是什么含义呢?它的使用范围有包含那些东西呢??在美国的金属材料性能研发与标准化手册(MMPDS)中S基准很常见,但是它没有对S基准进行解释。
材料力学习题大全及答案
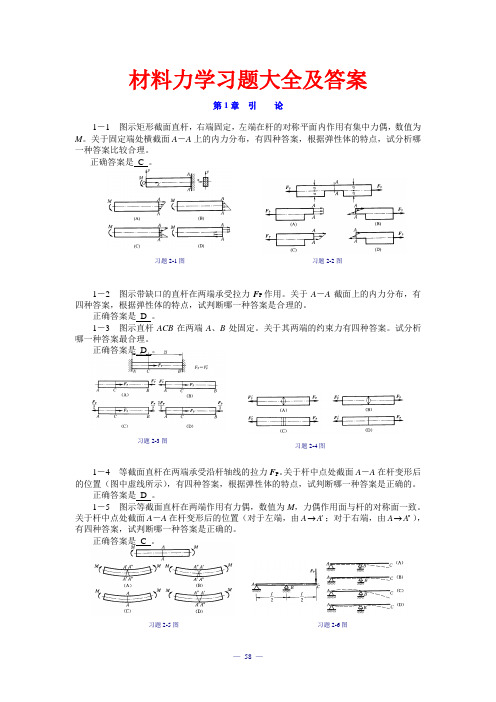
习题2-1图 习题2-2图习题2-3图 习题2-4图习题2-5图 习题2-6图材料力学习题大全及答案第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C 。
1-2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
1-3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
正确答案是 C 。
习题2-1图习题2-2图习题2-3图习题2-4图1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是 C 。
第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A )d d Q x F d M(B )d d Q x F (C )d d Q x F (D )d d Q xF 2-2 对于图示承受均布载荷q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中哪几种是正确的。
材料力学(填空、简答、判断、选择)

(填空、简答、判断、选择)一、填空题1、为了保证机器或结构物正常地工作,要求每个构件都有足够的抵抗破坏的能力,即要求它们有足够的强度;同时要求他们有足够的抵抗变形的能力,即要求它们有足够的刚度;另外,对于受压的细长直杆,还要求它们工作时能保持原有的平衡状态,即要求其有足够的稳定性。
2、材料力学是研究构件强度、刚度、稳定性的学科。
3、强度是指构件抵抗破坏的能力;刚度是指构件抵抗变形的能力;稳定性是指构件维持其原有的平衡状态的能力。
4、在材料力学中,对变形固体的基本假设是连续性假设、均匀性假设、各向同性假设。
5、随外力解除而消失的变形叫弹性变形;外力解除后不能消失的变形叫塑性变形。
6、截面法是计算内力的基本方法。
7、应力是分析构件强度问题的重要依据。
8、线应变和切应变是分析构件变形程度的基本量。
9、轴向尺寸远大于横向尺寸,称此构件为杆。
10、构件每单位长度的伸长或缩短,称为线应变。
11、单元体上相互垂直的两根棱边夹角的改变量,称为切应变。
12、轴向拉伸与压缩时直杆横截面上的内力,称为轴力。
13、应力与应变保持线性关系时的最大应力,称为比例极限。
14、材料只产生弹性变形的最大应力,称为弹性极根;材料能承受的最大应力,称为强度极限。
15、弹性模量E是衡量材料抵抗弹性变形能力的指标。
16、延伸率δ是衡量材料的塑性指标。
δ≥5%的材料称为塑性材料;δ<5%的材料称为脆性材料。
17、应力变化不大,而应变显著增加的现象,称为屈服或流动。
18、材料在卸载过程中,应力与应变成线性关系。
19、在常温下把材料冷拉到强化阶段,然后卸载,当再次加载时,材料的比例极限提高,而塑性降低,这种现象称为冷作硬化。
20、使材料丧失正常工作能力的应力,称为极限应力。
21、在工程计算中允许材料承受的最大应力,称为许用应力。
22、当应力不超过比例极限时,横向应变与纵向应变之比的绝对值,称为泊松比。
23、胡克定律的应力适用范围是应力不超过材料的比例极限。
完整版)材料力学知识点总结

完整版)材料力学知识点总结Summary of Material MechanicsI。
Basic nsAxial n and n: External forces act along the axis of the rod。
and internal XXX nal plane.n: XXX to the axis of the rod.Bending: Axial force N is defined as positive for XXX to the axis of the rod or in a plane containing the axis of the rod.Shear: Q is defined as positive for a XXX.Twisting: XXX.XXX: dQ/dx=q。
dM/dx=QII。
XXXXXX:XXX: ε=dΔl/dx=constantXXX:XXX: γ=ρdφ/dx=ρφXXX:XXX: ε=My/IzXXX: σ=Mz/WyShear stress: τ=QS*/IbNormal stress: σ=N/APlastic material: σu=σsXXX: σu=σbCircular shaft: XXX limitτ=GγXXX bending: XXX limit Normal bending stress:1.[σt]≤[σc]σmax≤[σ]2.[σt]≠[σc]σtmax≤[σt]。
σcmac≤[σc]Shear bending stress: τmax=Q/Iz b Elastic modulus:XXX: εmax≤[ε]n: φmax≤[φ]Bending: ymax≤[y]。
θmax≤[θ]Note: Units are XXX.N: XXXL: LengthE: Elastic modulusA: nal aread: DiameterI: Moment of inertiaP: Perimeterh: Heightb: WidthW: n modulusZ: Polar moment of inertia剪切公式:tau=\dfrac{Q}{A}\leq [\tau]$ A$—剪切面积挤压公式:sigma_{bs}=\dfrac{P}{A_j}\leq [\sigma_{bs}]$ A_j$—挤压面积圆形:tau_{max}=\dfrac{3Q}{2A}$矩形:tau_{max}=\dfrac{Q}{2A}$以上两式均发生在中性轴上截面几何性质:平行移轴公式:I_Z=I_{ZC}+a^2A$I_{YZ}=I_{ZC}+abA$组合截面:形心:bar{y}=\dfrac{\sum\limits_{i=1}^nA_iy_{ci}}{\sum\limits_ {i=1}^nA_i}$bar{z}=\dfrac{\sum\limits_{i=1}^nA_iz_{ci}}{\sum\limits_{ i=1}^nA_i}$静矩:S_Z=\sum\limits_{i=1}^nA_iy_{ci}$S_Y=\sum\limits_{i=1}^nA_iz_{ci}$惯性矩:I_Z=\sum\limits_{i=1}^n(I_Z)_i$I_Y=\sum\limits_{i=1}^n(I_Y)_i$应力分析:二向应力状态(解析法、图解法)解析法:sigma_y=\dfrac{\sigma_x+\sigma_y}{2}+\dfrac{\sigma_x-\sigma_y}{2}\cos 2\alpha-\tau_x\sin 2\alpha$tau_{xy}=\dfrac{\sigma_x-\sigma_y}{2}\sin2\alpha+\tau_x\cos 2\alpha$tau_{max}=\sqrt{\left(\dfrac{\sigma_x-\sigma_y}{2}\right)^2+\tau_x^2}$三向应力圆:sigma_{max}=\sigma_1$sigma_{min}=\sigma_1-\sigma_3$tau_{max}=\dfrac{\sigma_2}{3}$应力圆:sigma$: 拉为“+”,压为“-”tau$: 使单元体顺时针转动为“+”alpha$: 从$x$轴逆时针转到截面的法线为“+”广义虎克定律:dfrac{\epsilon_1}{E_1}=\dfrac{\epsilon_2}{E_2}=。
材料力学题库及答案

《材料力学》试题库及答案一、判断题(共266小题)材料力学主要研究杆件受力后变形与破坏的规律。
( A )2、内力只能是力。
( B )3、若物体各点均无位移,则该物体必定无变形。
( A )4、截面法是分析应力的基本方法。
( B )5、构件抵抗破坏的能力,称为刚度。
( B )6、构件抵抗变形的能力,称为强度。
( B )7、构件在原有几何形状下保持平衡的能力,称为构件的稳定性。
( A )8、连续性假设,是对变形固体所作的基本假设之一。
( A )9、材料沿不同方向呈现不同的力学性能,这一性质称为各向同性。
( B )10、材料力学只研究处于完全弹性变形的构件。
( A )11、长度远大于横向尺寸的构件,称为杆件。
( A )12、研究构件的内力,通常采用实验法。
( B )13、求内力的方法,可以归纳为“截-取-代-平”四个字。
( A )14、1MPa=109Pa=1KN/mm2。
( B )15、轴向拉压时 45º斜截面上切应力为最大,其值为横截面上正应力的一半( A )16、杆件在拉伸时,纵向缩短,ε<0。
( B )17、杆件在压缩时,纵向缩短,ε<0;横向增大,ε'>0。
( A )18、σb是衡量材料强度的重要指标。
( A)19、δ=7%的材料是塑性材料。
( A )20、塑性材料的极限应力为其屈服点应力。
( A )21、“许用应力”为允许达到的最大工作应力。
( A )22、“静不定系统”中一定存在“多余约束力”。
( A )23、用脆性材料制成的杆件,应考虑“应力集中”的影响。
( A )24、进行挤压计算时,圆柱面挤压面面积取为实际接触面的正投影面面积。
( A )25、冲床冲剪工件,属于利用“剪切破坏”问题。
( A )26、同一件上有两个剪切面的剪切称为单剪切。
( B )27、等直圆轴扭转时,横截面上只存在切应力。
( A )28、圆轴扭转时,最大切应力发生在截面中心处。
( B )29、在截面面积相等的条件下,空心圆轴的抗扭能力比实心圆轴大。
材料力学

斜弯曲 一、斜弯曲:外力通过弯心,且不与形心主轴平行或重合,则为 斜弯曲[杆件产生弯曲变形,但弯曲后,挠曲线与外力(横 向力)不共面。] 二、斜弯曲的研究方法 : 1.分解:将外载沿横截面的两个形心主轴分解,于是得到两个正交 的平面弯曲。
z P
j
Pz Py y z Pz
x
Py
y
P
2.叠加:对两个平面弯曲进行研究;然后将计算结果叠加起来。
xM
y
Myz Iy
P Mz y Myz x A Iz Iy
例4 图示不等截面与等截面杆,受力P=350kN,试分别求出两柱
内的绝对值最大正应力。 解:两柱均为压应力
P P
P M P 1max A1 Wz1
350000 350 506 0.20.3 0.20.32
z0 y cos 0 sinj )0 j Iy Iz
中性轴
y0 I z tg ctg j z0 I y
P z j z
Py
D2
可见:只有当Iy = Iz时,中性轴与外力才垂直。 D1 P ④最大正应力
y 在中性轴两侧,距中性轴最远的点为拉压最大正应力点。
Lmax D1
⑤变形计算
My引起的应力: M z引起的应力: 合应力: m
Myz Iy
Mz cos j Iy
Mz y M y sinj Iz Iz
z Iy y Iz
M ( cosj sinj )
x z
j
P L
Pz
z
y
x
m
L
Pz P
Py
Py
y
③中性轴方程
