生成m序列与gold序列
扩频编码M序列和gold序列
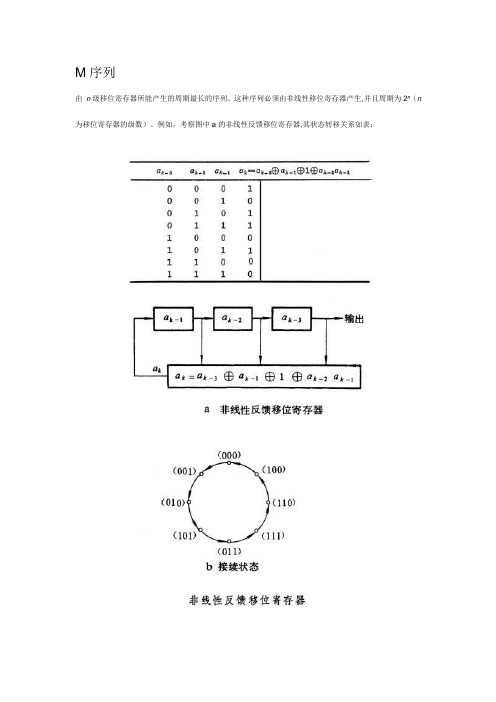
M序列由n级移位寄存器所能产生的周期最长的序列。
这种序列必须由非线性移位寄存器产生,并且周期为2n(n 为移位寄存器的级数)。
例如,考察图中a的非线性反馈移位寄存器,其状态转移关系如表:状态(a k-3,a k-2,a k-1)的接续状态是(a k-2,a k-1,a k),其中a k=a k-3嘰a k-1嘰1嘰a k-2a k-1是一种非线性逻辑。
从任一状态出发,例如从(000)出发,其接续状态恰好构成一个完全循环(图b),由此产生一个周期为23=8的3级序列。
M序列最早是用抽象的数学方法构造的。
它出现于组合数学的一些数学游戏中,例如L.欧拉关于哥尼斯堡的七桥问题等。
后来发现这种序列具有某些良好的伪随机特性。
例如,M序列在一个周期中,0与1的个数各占一半。
同时,同样长度的0游程与1游程也各占一半。
所有这些性质在数据通信、自动控制、光学技术和密码学诸领域中均有重要应用。
隐蔽通信内容的通信方式。
为了使非法的截收者不能理解通信内容的含义,信息在传输前必须先进行各种形式的变化,成为加密信息,在收信端进行相应的逆变化以恢复原信息。
电报通信、电话通信、图像通信和数据通信,都有相应的保密技术问题。
另一方面,为了从保密通信中获得军事、政治、经济、技术等机密信息,破译技术也在发展。
保密技术和破译技术是在相互对立中发展起来的。
1881年世界上出现了第一个电话保密专利。
电话保密开始是采用模拟保密或置乱的方法,即把话音的频谱或时间分段打乱。
置乱后的信号仍保持连续变化的性质。
在第二次世界大战期间,频域和时域的置乱器在技术上已基本成熟。
70年代以来,由于采用集成电路,电话保密通信得到进一步完善。
但置乱器仍是有线载波和短波单边带电话保密通信的主要手段。
模拟保密还可以采用加噪声掩盖、人工混响或逆向混响等方法,但因恢复后话音的质量大幅度下降或保密效果差,这些方法没有得到推广应用。
数字保密是由文字密码发展起来的。
数字信号(包括由模拟信号转换成的数字信号),由相同速率的密码序列加密,成为数字保密信号;保密信号传输到收信端后由同一密码序列去密,恢复原数字信号。
GOLD 序列码产生及特性分析实验

实验二 GOLD 序列码产生及特性分析实验一、实验目的1. 了解Gold 码的性质和特点;2. 熟悉Gold 码的产生方法;二、实验内容1. 熟悉Gold 码的的产生方法;2. 测试Gold 码的的波形;三、实验原理m 序列虽然性能优良,但同样长度的m 序列个数不多,且m 序列之间的互相关函数值并不理想(为多值函数)。
1967年,R .Gold 提出和讨论了一种新的序列,即Gold 码序列。
这种序列有较为优良的自相关和互相关特性,构造简单,产生的序列数多,因而得到广泛的应用。
a) m 序列优选对m 序列优选对是指在m 序列集中,其互相关函数最大值的绝对值满足下式的两条n 阶m 序列:表2-1给出了部分m 序列优选对。
表2-1 部分优选对码表 级数 基准本原多项式 配对本原多项式 7 211 217,235,277,325,203,357,301,323 9 1021 1131,133310 2415 2011,3515,317711 4445 4005,5205,5337,52632.Gold 码的产生方法Gold 码是m 序列的组合码,由同步时钟控制的两个码字不同的m 序列优选对逐位模2加得到,其原理如图2-1所示。
这两个码发生器的周期相同,速率也相同,因而两者保持一整除为偶数,但不能被位奇数41212)(2/)2(2/)1(n n R n n xy ⎩⎨⎧++≤++τ定的相位关系,这样产生的组合码与这两个子码序列的周期也相同。
当改变两个m 序列的相对位移时,会得到一个新的Gold 码。
Gold 码虽然是m 序列模2加得到的,但它已不再是m 序列,不过仍具有与m 序列近似的优良特性,各个码组之间的互相关特性与原来两个m 序列之间的互相关特性一样,最大的互相关值不会超过原来两个m 序列间最大互相关值。
Gold 码最大的优点是具有比m 序列多得多的独立码组。
图2-1 Gold 码序列发生器Gold 码序列具有以下性质:(1)两个m 序列优选对经不同移位相加产生的新序列都是Gold 序列,两个n 级移位寄存器可以产生2n +1个Gold 序列,周期均为2n -1。
gold码生成过程

Gold码是由m序列的优选对移位模二加构成的。
具体生成过程如下:
1.选择两个长度相同、码时钟速率相同的m序列。
2.这两个m序列构成一对优选对,优选对的定义是它们的互相关函数最大值的绝对值小于某个值。
3.如果一个序列保持不动,另一个序列随时钟进行移位,再将两者进行模2加,即可得到相应的
Gold码。
4.每改变优选对中两个m序列的相对位移就可得到一个新的Gold码。
5.两个n级移位寄存器可以产生2n+1个Gold码。
希望上述信息对你有所帮助。
如果你还有其他问题,请随时提问。
GOLD码产生与特性分析实验

实验八GOLD码特性实验一、实验目的1、掌握GOLD码的编解码原理。
2、掌握GOLD码的软件仿真方法。
3、掌握GOLD码的硬件仿真方法。
4、掌握GOLD码的硬件设计方法。
二、预习要求1、掌握GOLD码的编解码原理和方法。
2、熟悉matlab的应用和仿真方法。
3、熟悉Quatus的应用和FPGA的开发方法。
三、实验原理1、GOLD序列简介GOLD序列是由m序列的“优选对”构成的。
所谓优选对是指m序列中互相关值为[-1,-t(n),t(n)-2]的一对序列。
其中下表为部分m序列的部分优选对表1 部分m序列的部分优选对n基序序列配对序列3131554575,67,766103147,1337211217,235,277,203,301910211131,1461,1423,1167,1333,1365,1533 1020112415,2157,3515,34711140054445,4215,6015,4143,4053,7335,5747,5575,4161上表中的m序列采用8进制(可参见PN码实验)。
2、GOLD序列由m序列中的优选对{xi}和{yi}本身加上它们的相对移位模二相加构成的2n-1个序列组成,序列总数为2n+1。
任一队序列之间的互相关函数都是三值的,即即,GOLD序列的最大互相关值为下表为GOLD序列的t(n)值及其与自相关峰值Rs(0)的比值,同时给出GOLD序列族中的序列数。
表为部分GOLD序列的t(n)值、Rs(0)、序列数表级数n356791011序列长7316312751110232047序列数9336512951310252049t(n)591717336565t(n)/Rs(0)0.710.290.270.130.060.060.03四、GOLD的产生及特性分析1、建立GOLD的仿真文件(GOLD.MDL)GOLD1…GOLD7的Sample Time均设置为SampleTime;Preferred polynomial(1)设置为[1 0 1 1];Initial states(1)设置为[0 0 1]; Preferred polynomial(2)设置为[1 1 0 1];Initial states(2)设置为[0 01]。
m序列与Gold序列比较
第一章介绍了无线扩
频通信技术的发展状态以及国内外开发扩频通信芯片的现状,并给出了本论文的研究内容和安排。
第二章主要介绍了扩频通信的基本原理,主要
包括扩频通信的理论基础和分类。并结合QPSK调制方式对本论文重点研究的直接序列扩频通信方式的数学模型进行了分析。
第三章主要介绍了扩
频通信关键技术之一——伪随机序列的产生与性质。从最基础的移位寄存器序列分析引入m序列,并可以通过选择两个m序列优选对相加产生Gold序列。
首先,研究了直接扩
频通信系统中比较常用的各种伪随机序列的特性以及它们的产生方法,着重介绍了m序列,Gold序列,Walsh码和复合序列并对它们的性能做了比较,最
难得到 $",1$,"#,,#00,0"","%#$…位的 - 序列。
另外,- 序列的自相关函数由下式计算:
{ !(!)’
" "
+ 2
# , ":“%”的位数 # # :“"”的位数
令 $ ’ " 2 # ’ #% + "
则:
{ !(!)’
",! ’ %
+
" $
,!
"
%
设 % ’ $,$ ’ #$ + " ’ ,,则:
长周期的序列。对于何种抽头能产生何种长度和结
构的码序列,已 经 进 行 了 大 量 的 研 究 工 作。 现 在 已
经得到 $ . "%% 级 - 序 列 发 生 器 的 连 接 图 和 所 产 生
的 - 序列的结 构。 例 如 / 级 移 位 寄 存 器 产 生 的 "0
位的 - 序列之一为 """"%"%""%%"%%%。 同 理,我 们 不
m 序列与gold 序列性能分析比较 包含程序

m序列与gold序列性能分析比较赵新宁北京邮电大学信息工程学院,北京(100876)E-mail:zhaoxinning106@摘要:在扩频系统中,伪随机序列具有十分重要的作用。
m序列和gold序列作为最常用和实用的伪随机序列,各有其特点。
本文分析其基本原理和产生方式,并特别对其性能方面做了仿真比较。
关键词:扩频;m序列;gold序列中图分类号:TN91在扩频通信系统中,伪随机序列是关键技术之一。
伪随机序列码的码型影响码序列的相关特性,序列长度决定了扩展频谱的宽度。
因此,在扩频系统中,对于伪随机序列有如下的要求:首先,伪随机序列的长度(即伪码比特率)应该足够长,能够满足扩展带宽的需要;第二,伪随机序列要具有尖锐的自相关特性(用作地址码),和良好的互相关特性;第三,伪随机序列要有足够多的数量,以满足码分多址的需求;第四,应具有近似噪声的频谱特性,即近似连续谱,且均匀分布;工程上易于实现。
通常,作为扩频通信系统工程实现上的伪随机序列一般是m序列和gold序列。
目前,在cdma2000系统中采用伪随机序列中的m序列(长码)来区分用户,wcdma系统中则用gold码来区分用户。
1.m序列的原理和产生在所有的伪随机序列中,m序列是最重要、最基本的一种伪随机序列。
而另外的多种伪随机序列都是由它引出并且产生的。
m序列是一种周期性的伪随机序列,又被称作最长线性移位寄存器序列;是由带线性反馈的移位寄存器产生的周期最长的序列[1]。
其周期为2n-1(n 为移位寄存器级数)。
m序列具有与随机噪声类似的尖锐的自相关特性,但它不是真正随机的,而是按照一定的规律周期性的变化。
这种特性使得m序列适合于工程应用。
m序列最大长度决定于移位寄存器的级数,而序列构成则决定于反馈系数的不同设置。
并非所有的反馈系数的设置都可以产生对应长度的m序列。
m序列具有平衡性和其游程特性,即一个序列周期中,“1”的数目与“0”的数目最多相差一个;同时,长度为n的元素游程出现的次数比长度为n+1的游程出现的次数多一倍。
Gold序列与m序列仿真应用

1. 绪论m序列具有优良的双值自相关特性,但互相关特性不是很好。
作为CDMA通信地址码时,由于互相关特性不理想,使得系统内多址干扰影响增大,且可用地址码数量较少。
在某些应用场合,利用狭义伪随机序列复合而成复合序列更为有利。
这是因为通过适当方法构造的复合序列具有某些特殊性质。
Gold序列就是一种复合序列,而且具有良好的自相关与互相关特性,地址码数量远大于m序列,且易于实现、结构简单,在工程上得到广泛应用。
表1是m序列和Gold序列的主要性能比较,表中为m序列的自相关峰值,为自相关主峰;为Gold序列的互相关峰值,为其自相关主峰。
从表1中可以看出:当级数n一定时,Gold序列中可用序列个数明显多于m序列数,且Gold序列的互相关峰值和主瓣与旁瓣之比都比m序列小得多,这一特性在实现码分多址时非常有用。
表1. m序列和Gold序列性能比较在引入Gold序列概念之前先介绍一下m序列优选对。
m序列优选对,是指在m序列集中,其互相关函数绝对值的最大值(称为峰值互相关函数)最接近或达到互相关值下限(最小值)的一对m序列。
设{ai}是对应于r次本原多项式F1(x)所产生的m序列, {bi} 是另一r次本原多项式F2(x)产生的m序列,峰值互相关函数满足(1)则m序列{ai}与{bi}构成m序列优选对。
例如:的本原多项式与所产生的m序列与,其峰值互相关函数。
满足式(1),故与构成m序列优选对。
而本原多项式所产生的m序列,与m序列的峰值互相关函数,不满足上式,故与不是m序列优选对。
2. Gold序列1967年,R·Gold指出:“给定移位寄存器级数r时,总可找到一对互相关函数值是最小的码序列,采用移位相加方法构成新码组,其互相关旁瓣都很小,且自相关函数和互相关函数均有界”。
这样生成的序列称为Gold码(Gold序列)。
Gold序列是m序列的复合序列,由两个码长相等、码时钟速率相同的m序列优选对的模2和序列构成。
m序列和Gold序列特性研究要点上课讲义

m序列和G o l d序列特性研究要点Harbin Institute of Technology扩频通信实验报告课程名称:扩频通信实验题目:Gold码特性研究院系:电信学院班级:通信一班姓名:学号:指导教师:迟永钢时间: 2012年5月8日哈尔滨工业大学第1章实验要求1.以r=5 1 45E为基础,抽取出其他的m序列,请详细说明抽取过程;2.画出r=5的全部m序列移位寄存器结构,并明确哪些序列彼此是互反多项式;3.在生成的m序列集中,寻找出m序列优选对,请确定优选对的数量,并画出它们的自相关和互相关函数图形;4.依据所选取的m序列优选对生成所有Gold序列族,确定产生Gold序列族的数量,标出每个Gold序列族中的所有序列,并实例验证族内序列彼此的自相关和互相关特性;5.在生成的每个Gold序列族内,明确标出平衡序列和非平衡序列,并验证其分布关系。
6.完整的作业提交包括:纸质打印版和电子版两部分,要求两部分内容统一,且在作业后面附上源程序,并加必要注释。
7.要求统一采用Matlab软件中的M文件实现。
第2章 实验原理2.1 m 序列二元m 序列是一种伪随机序列,有优良的自相关函数,是狭义伪随机序列。
m 序列易于产生于复制,在扩频技术中得到了广泛应用。
2.1.1 m 序列的定义r 级非退化的移位寄存器的组成如图1所示,移位时钟源的频率为c R 。
r 级线性移位寄存器的反馈逻辑可用二元域GF(2)上的r 次多项式表示2012() {0,1}r r i f x c c x c x c x c =++++∈L (1)图 2-1 r 级线性移位寄存器式(1)称为线性移位寄存器的特征多项式,其给出的表示反馈网络的而逻辑关系式是现行的。
因此成为线性移位寄存器。
否则称为,非线性移位寄存器。
对于动态线性移位寄存器,其反馈逻辑也可以用线性移位寄存器的递归关系式来表示112233 {0,1}i i i i r i r i a c a c a c a c a c ----=++++∈L (2) 特征多项式(1)与递归多项式(2)是r 级线性移位寄存器反馈逻辑的两种不同种表示法,因其应用的场合不同而采用不同的表示方法。
Gold码

通信08-1 艾盼盼0850283101设计Gold序列发生器姓名:艾盼盼学号:0850283101 班级:通信08-1摘要:m序列,尤其是m序列优选对,是特性很好的伪随机序列。
但是,它们能彼此构成优选对的数目很少,不便于在码分多址系统中应用。
R.Gold于1967年提出了一种基于m 序列优选对的码序列,称为Gold序列。
它是m序列的组合码,由优选对的两个m序列逐位模2加得到,当改变其中一个m序列的相位(向后移位)时,可得到一新的Gold序列。
Gold 序列虽然是由m序列模2加得到的,但它已不是m序列,不过它具有与m序列优选对类似的自相关和互相关特性,而且构造简单,产生的序列数多,因而获得广泛的应用。
【关键词】:m序列优选对,Gold序列,模2加,自相关1. Gold码的概述1.1 gold码定义R.Gold于1967年提出了一种基于m序列优选对的码序列,称为Gold序列。
它是m序列的组合码,由优选对的两个m序列逐位模2加得到,当改变其中一个m序列的相位(向后移位)时,可得到一新的Gold序列。
Gold序列虽然是由m序列模2加得到的,但它已不是m 序列,不过它具有与m序列优选对类似的自相关和互相关特性,而且构造简单,产生的序列数多,因而获得广泛的应用。
1.2 gold码基本功能单元Gold码发生器的基本功能单元为线性反馈移位寄存器LFSR(Linear Fdddback Bhift Register)。
2.Gold序列的设计2.1 m序列优选对寻找方法产生gold序列的必要条件是m序列优选对,设A是对应于n级本原多项式f(x)所产生的m序列,B是对应于n级本原多项式g(x)所产生的m序列,当它们的互相关函数|Ra.b(k)|满足:则f(x)和g(x)所产生的m序列A和B构成一对优选对。
寻找m序列优选对的方法还有硬件计算法,分圆陪集法,逐步移位模2加法,三值判别法。
2.2gold序列设计的理论证明证明,若F1(x),F2(x)为两个不同的本原多项式,令F1(x)产生的序列为G(F1),F2(x)产生的序列为G(F2),F1(x). F2(x)所产生的序列为G(F1,F2),则有上式表明两本原多项式乘积所产生的序列等于两个本原多项式分别产生的模2和序列。
MATLAB仿真m序列和Gold序列自相关与互相关

MATLAB仿真m序列和Gold序列自相关与互相关MATLAB 是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。
MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
本章正是运用MATLAB来仿真m序列和Gold序列的相关特性,以及OCDMA 系统的误码率同用户数N的关系曲线。
su1 仿真过程在理论分析的基础上,下面使用附录上两段程序,通过MATLAB仿真得出m序列和Gold序列的自己相关性。
这段m序列产生程序采用了8个移位寄存器,将最后两个移位寄存器的值进行异或处理反馈给第一个移位寄存器,然后向前移位,输出最后一个移位寄存器的值,Gold序列的产生只是将两个m序列中的一个进行延时移位,再进行异或,产生的主要原理和m序列并无较大差异。
在这两段程序个前半部分m序列和Gold序列生成的基础上,只要将y1=xcorr(x1)改为y1=xcorr(x1,x2)即可求出它们的互相关仿真。
2 仿真结果在系统中采用上述序列仿真得到自相关和互相关特性曲线如图1 , 2及图3 所示。
图1 m 序列的自相关曲线图4-2 m 序列与Gold序列的自相关曲线图4-3 m 序列与Gold 序列的互相关曲线附录程序1X1=1;X2=0;X3=1;X4=0; %移位寄存器输入Xi初T态(0101), Yi为移位寄存器各级输出m=120; %置M序列总长度for i=1:m %1#Y8=X8; Y7=X7; Y6=X6; Y5=X5; Y4=X4; Y3=X3; Y2=X2; Y1=X1;X8=Y7; X7=Y6; X6=Y5; X5=Y4; X4=Y3; X3=Y2; X2=Y1;X1=xor(Y7,Y8); %异或运算if Y8==0U(i)=-1;elseU(i)=Y8;endendM=U%绘图i1=it=1:1:i1;x1=[(2*M)-1]’;%将运行结果m序列M从单极性序列变为双极性序列y1=xcorr(x1);%求自相关性t=1:1:i1;plot(t,y1(1:i1));axis([1,120,-12,288])%绘出信号的相关图gridxlabel('t')ylabel('相关性')title('移位寄存器产生的M序列的相关性')程序2function c=gold()n=7;a=[1 1 1 1 1 1 1 1];co=[];for v=1:2^n-1co=[co,a(1)];a(8)=mod(a(5)+a(1),2);a(1)=a(2);a(2)=a(3);a(3)=a(4);a(4)=a(5);a(5)=a(6);a(6)=a(7);a(7)=a(8);endm1=co;b=[1 0 1 0 0 0 0 1];co=[];for v=1:2^n-1co=[co,b(1)];m=mod(b(5)+b(1),2);p=mod(b(6)+m,2);b(8)=mod(b(5)+b(1),2);b(1)=b(2);b(2)=b(3);b(3)=b(4);b(4)=b(5);b(5)=b(6);b(6)=b(7);b(7)=b(8);endm2=co;c=xor(m1,m2);x2=[(2*c)-1]’;%将运行结果Gold序列c从单极性序列变为双极性序列y1=xcorr(x2);%求自相关性t=1:1:120;plot(t,y1(1:120));axis([1,120,-12,288])%绘出信号的相关图gridxlabel('t')ylabel('相关性')title('移位寄存器产生的Gold序列的相关性')。
m序列对及平衡Gold序列的产生与搜索

平衡Gold序列的产生与搜索方法
平衡Gold序列是一类具有优良伪随机性和自相关性的二元序列。产生平衡 Gold序列的方法主要有两种:一是通过平衡Gold多项式产生平衡Gold序列; 二是通过选择适当的m序列和反馈函数产生平衡Gold序列。搜索方法主要有基 于差分编码的搜索算法和基于自相关函数的搜索算法。
3、信息隐藏:平衡Gold序列可以用于信息隐藏中的隐写术,以隐藏敏感信息 在公开信息中。由于平衡Gold序列具有优良的自相关性,它可以用于构造高效 的隐写算法,提高信息隐藏的安全性和鲁棒性。
未来展望
随着技术的发展,平衡Gold序列的研究将面临新的挑战和机遇。以下是一些未 来可能的研究方向:
1、高效产生方法:目前平衡Gold序列的产生方法还比较耗时,因此研究更高 效的产生方法以提高搜索速度和降低计算成本是未来的一个研究方向。
1、反馈函数设计:反馈函数是m序列发生器的核心部分,其设计的好坏直接影 响到m序列的性能。一个好的反馈函数应该具有较低的误码率、较高的线性复 杂度、易于实现等优点。常用的反馈函数包括异或、同或、与等运算。
2、LFSR级数和反馈位数选择:m序列发生器的性能与LFSR的级数和反馈位数 密切相关。一般来说,增加LFSR的级数和反馈位数可以提高m序列的性能,但 同时也会增加硬件实现的复杂度和功耗。因此,在设计中需要根据实际需求选 择合适的LFSR级数和反馈位数。
在软件实现中,可以使用各种编程语言如C、C++、Python等编写m序列发生器。 软件实现具有灵活度高、易于调试和修改等优点,但也存在运行速度较慢和需 要运行额外的处理器等缺点。
m序列发生器的应用
m序列发生器在信号处理、通信技术等领域具有广泛的应用。以下是m序列发生 器的一些典型应用:
gold序列产生原理

gold序列产生原理Gold序列是一种特殊的数列,其产生原理可以通过递归函数来描述。
Gold序列的特点是,每个数都是前面两个数的和,即第n个数等于第n-1个数加上第n-2个数。
具体来说,第一个数和第二个数是预先给定的,接下来的每个数都是前面两个数的和。
为了更好地理解Gold序列的产生原理,我们可以通过一个简单的例子来说明。
假设我们规定第一个数为0,第二个数为1。
那么根据递归函数,第三个数就是0+1=1,第四个数是1+1=2,第五个数是1+2=3,以此类推。
通过上述例子,我们可以看出,Gold序列的产生过程是通过不断将前面两个数相加而得到的。
这个过程可以用递归函数来表示,即f(n) = f(n-1) + f(n-2),其中f(n)表示第n个数。
通过递归函数的定义,我们可以根据已知的前两个数,依次计算出后面的数。
值得注意的是,Gold序列的产生原理并不依赖于具体的初始值。
无论我们规定第一个数和第二个数是什么,只要按照递归函数的规则计算,最终得到的数列都是Gold序列。
这是因为递归函数的定义保证了每个数都是前面两个数的和。
Gold序列在数学和计算机科学中都有广泛的应用。
在数学中,Gold序列被用来研究一些数论和代数的问题,例如斐波那契数列和黄金分割数等。
在计算机科学中,Gold序列常常被用来生成随机数序列或用作密码学中的密钥序列。
在生成随机数序列的应用中,Gold序列通过将两个序列进行异或运算来产生新的序列。
这样做的好处是,由于递归函数的特性,Gold 序列的数值分布相对均匀,具有较好的随机性质。
这使得Gold序列在随机数生成算法中得到了广泛应用。
在密码学中,Gold序列常被用作加密算法中的密钥序列。
由于Gold序列具有较好的随机性质和良好的扩散性质,使得生成的密钥序列能够提供较高的安全性。
因此,Gold序列在密码学中被广泛应用于对称加密算法和流密码算法中。
总结起来,Gold序列是一种通过递归函数产生的数列,其产生原理是每个数都是前面两个数的和。
m序列、Gold序列和正交Gold序列的扩频通信系统仿真研究

机 码 C£进 行 模 二 加 , 生 扩 频 序 列 d t , 用 扩 频 序 列 d () 产 () 再
() 调制 载 波 f进 而得 到 已 扩频 调 制 的射 频 信 号 s £ 。 接 去 , () 在
直 接 序 列 扩 频 通 信 系统 ( S S Drc Sq ec ped D S ,i t e uneS ra e
S s m) 是 目前 应 用 很 广 泛 的 扩 频 系 统 , 早 出 现 于 第 二 次 yt , e 最
送 框 图 , 2为 直 扩 系 统 接 收 框 图 。 发射 端 , 源输 出 信 号 a 图 信
的 结论 。
关键 词 :扩 频 增 益 :扩 频 码 ;信 噪 比 ;直 接 序 列 扩 频 通 信
中图分类号 : N 1. Biblioteka 91 6文献标识码 : A
文 章 编 号 :1 7 — 2 6 2 1 ) 8 0 4 - 3 6 4 6 3 (0 2 1- 18 0
Re e r h a d sm u a i n O m -e ue c s.Go d s qu n e nd o t g n lGo d s a c n i l to n s q n e l e e c sa r ho o a l s q n e fs r a p c r e ue c s o p e d s e t um o m u i a i n y t m cm n c to s s e
Ab t a t De ci e et e r t a a i o ie t p e d s e t m o sr c : s r st o e i l ss f r c r a p cr b h h c b d s u c mmu i ai n a d mo e ,mal b p o r mmi gt r u h a nc t n d l o t rga a n o g h dr c p e d s e t m o i t r a p cr c mmu ia in s se d sg n e oma c i l t n o e s se , n u d r i e e t o d t n e s u n c t y tm e in a d p r r n esmu a i f h y t m r n e f r n n i o s o f o t u d c i
m序列和Gold序列特性研究要点

扩频通信实验报告Harbin Institute of Technology扩频通信实验报告课程名称:扩频通信实验题目:Gold码特性研究院系:电信学院班级:通信一班姓名:学号:指导教师:迟永钢时间: 2012年5月8日哈尔滨工业大学- I-第1章实验要求1.以r=5 1 45E为基础,抽取出其他的m序列,请详细说明抽取过程;2.画出r=5的全部m序列移位寄存器结构,并明确哪些序列彼此是互反多项式;3.在生成的m序列集中,寻找出m序列优选对,请确定优选对的数量,并画出它们的自相关和互相关函数图形;4.依据所选取的m序列优选对生成所有Gold序列族,确定产生Gold序列族的数量,标出每个Gold序列族中的所有序列,并实例验证族内序列彼此的自相关和互相关特性;5.在生成的每个Gold序列族内,明确标出平衡序列和非平衡序列,并验证其分布关系。
6.完整的作业提交包括:纸质打印版和电子版两部分,要求两部分内容统一,且在作业后面附上源程序,并加必要注释。
7.要求统一采用Matlab软件中的M文件实现。
第2章 实验原理2.1 m 序列二元m 序列是一种伪随机序列,有优良的自相关函数,是狭义伪随机序列。
m 序列易于产生于复制,在扩频技术中得到了广泛应用。
2.1.1 m 序列的定义r 级非退化的移位寄存器的组成如图1所示,移位时钟源的频率为c R 。
r 级线性移位寄存器的反馈逻辑可用二元域GF(2)上的r 次多项式表示2012() {0,1}r r i f x c c x c x c x c =++++∈ (1)图 2-1 r 级线性移位寄存器式(1)称为线性移位寄存器的特征多项式,其给出的表示反馈网络的而逻辑关系式是现行的。
因此成为线性移位寄存器。
否则称为,非线性移位寄存器。
对于动态线性移位寄存器,其反馈逻辑也可以用线性移位寄存器的递归关系式来表示112233 {0,1}i i i i r i r i a c a c a c a c a c ----=++++∈ (2) 特征多项式(1)与递归多项式(2)是r 级线性移位寄存器反馈逻辑的两种不同种表示法,因其应用的场合不同而采用不同的表示方法。
生成m序列与gold序列

一、生成m序列function [mseq] = m_sequence(fbconnection);n = length(fbconnection);N = 2^n-1; %m序列的长度register = [zeros(1,n - 1) 1]; %定义移位寄存器的初始状态mseq(1)= register(n); %m序列的第一个输出码元for i = 2:Nnewregister(1)= mod(sum(fbconnection.*register),2); %寄存器与反馈的模2和for j = 2:n,newregister(j)= register(j-1);end;register = newregister; %移位后的寄存器mseq(i) = register(n); %新的寄存器输出endclear all;close all;clc;fbconnection=[0 0 1 0 1]; %输入本原多项式系数,从C1开始m_sequence=m_sequence(fbconnection);stem(m_sequence); %对m序列绘图axis([0 35 -0.2 1.2]);grid on;二、生成gold序列function goldseq = g_sequence(connection1,connection2); msequence1 = m_sequence(connection1); %生成第一个m序列msequence2 = m_sequence(connection2); %生成第二个m序列N=2^length(connection1)-1; %gold序列长度for i = 1:N;s = mod(msequence1+msequence2,2); %两个m序列模二加产生gold序列goldseq = s;endclear all;close all;clc;connection1=[0 0 0 0 1 1];connection2=[1 0 0 1 1 1];goldseq = g_sequence(connection1,connection2);stem(goldseq);axis([0 65 -0.2 1.2]);grid on;THANKS !!!致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求欢迎您的下载,资料仅供参考。
M序列产生及其特性仿真实验报告

M序列产生及其特性仿真实验报告一、三种扩频码序列简介1.1 m序列它是由多级移位寄存器或其他延迟元件通过线性反馈产生的最长的码序列。
m序列的特性1、最长周期序列:N=2n-12、功率平衡性:‘1’的个数比‘0’的个数多13、‘0’、‘1’随机分布:近似高斯噪声4、相移不变性:任意循环移位仍是m序列,仅初相不同5、离散自相关函数:‘0’->+1,‘1’->-11.2 Gold序列Gold序列是两个等长m序列模二加的复合序列两个m序列应是“优选对”特点:1、包括两个优选对m序列,一个Gold序列族中共有2n+1个Gold序列2、Gold序列族中任一个序列的自相关旁瓣及任意两个序列的互相关峰值均不超过两个m序列优选对的互相关峰值1.3OVSF序列又叫正交可变扩频因子,系统根据扩频因子的大小给用户分配资源,数值越大,提供的带宽越小,是一个实现码分多址(CDMA)信号传输的代码,它由Walsh函数生成,OVSF码互相关为零,相互完全正交。
OVSF序列的特点1、序列之间完全正交2、极适合用于同步码分多址系统3、序列长度可变,不影响正交性,是可变速率码分系统的首选多址扩频码4、自相关性很差,需与伪随机扰码组合使用二、三种扩频码序列产生仿真一、M序列的产生代码:X1=1;X2=0;X3=1;X4=0; %移位寄存器输入Xi初T态(0101), Yi为移位寄存器各级输出m=60; %置M序列总长度for i=1:m %1#Y4=X4; Y3=X3; Y2=X2; Y1=X1;X4=Y3; X3=Y2; X2=Y1;X1=xor(Y3,Y4); %异或运算if Y4==0U(i)=-1;elseU(i)=Y4;endendM=U%绘图i1=ik=1:1:i1;plot(k,U,k,U,'rx')xlabel('k')ylabel('M序列')title('移位寄存器产生的M序列')用阶梯图产生表示:X1=1;X2=0;X3=1;X4=0; %移位寄存器输入Xi初T态(0101),Yi为移位寄存器各级输出m=60; %置M序列总长度for i=1:m %1#Y4=X4; Y3=X3; Y2=X2; Y1=X1;X4=Y3; X3=Y2; X2=Y1;X1=xor(Y3,Y4); %异或运算if Y4==0U(i)=-1;elseU(i)=Y4;endendM=U%绘图stairs(M);二、GOLD序列的产生:M序列A的生成:X1=1;X2=0;X3=1;X4=0; %移位寄存器输入Xi初T态(1010), Yi为移位寄存器各级输出m=60; %置M序列总长度for i=1:m %1#Y4=X4; Y3=X3; Y2=X2; Y1=X1;X4=Y3; X3=Y2; X2=Y1;X1=xor(Y3,Y4); %异或运算if Y4==0A(i)=0;elseA(i)=Y4;endendM=A%绘图i1=ik=1:1:i1;plot(k,A,k,A,'rx')xlabel('k')ylabel('M序列')title('移位寄存器产生的M序列')M序列B的生成:X1=0;X2=1;X3=0;X4=1; %移位寄存器输入Xi初T态(0101), Yi为移位寄存器各级输出m=60; %置M序列总长度for i=1:m %1#Y4=X4; Y3=X3; Y2=X2; Y1=X1;X4=Y3; X3=Y2; X2=Y1;X1=xor(Y3,Y4); %异或运算if Y4==0B(i)=0;elseB(i)=Y4;endendN=B%绘图i1=ik=1:1:i1;plot(k,B,k,B,'rx')xlabel('k')ylabel('M序列')title('移位寄存器产生的M序列') 生成gold序列:c=xor(A,B);stairs(c);三、OVSF序列的产生:%Function [OVSF_Codes]=OVSF_Generator(Spread_Fator,Code_Number)%Code_Number=-1 表示生成所有扩频因子=Spread_Factor的ovsf码Code_Number=-1;Spread_Fator=8;OVSF_Codes=1;if Spread_Fator==1return;endfor i=1:1:log2(Spread_Fator)Temp=OVSF_Codes;for j=1:1:size(OVSF_Codes,1)if j==1OVSF_Codes=[Temp(j,:),Temp(j,:) Temp(j,:),(-1)*Temp(j,:)];elseOVSF_Codes=[OVSF_Codes Temp(j,:),Temp(j,:) Temp(j,:),(-1)*Temp(j,:)];endendend%if Code_Number>-1% OVSF_Codes=OVSF_Codes((Code_Number+1),:);%endfigure(3)[b4,t4]=stairs([1:length(OVSF_Codes)],OVSF_Codes); plot(b4,t4);axis([0 130 -1.1 1.1]);title('OVSF序列')三、三种扩频码序列特性仿真(一)M序列自相关函数X1=1;X2=0;X3=1;X4=0; %移位寄存器输入Xi初T态(0101), Yi为移位寄存器各级输出m=2^8-1; %置M序列总长度for i=1:m %1#Y4=X4; Y3=X3; Y2=X2; Y1=X1;X4=Y3; X3=Y2; X2=Y1;X1=xor(Y3,Y4); %异或运算if Y4==0U(i)=-1;elseU(i)=Y4;y = xcorr(U);stairs(y);end互相关函数:输入两个m序列clcclear allclose allm1 = [0 1 0 0 1 1 0 0 1 0 1 0 1 0 0 1 1 0 1 1 0 0 0 1] m2 = [1 0 1 0 1 1 1 0 0 1 1 1 0 0 1 0 1 0 0 1 1 1 0 1]y = xcorr(m1,m2,'unbiased');stairs(y)(二)Gold码的自相关函数x2=[(2*c)-1];%将运行结果Gold序列c从单极性序列变为双极性序列y1=xcorr(x2,'unbiased');%求自相关性stairs(y1);gridxlabel('t')ylabel('相关性')title('移位寄存器产生的Gold序列的相关性')互相关性gold序列和m序列的互相关性y1=xcorr(c,m1,'unbiased'); stairs(y1);(三)ovsf码的互相关和自相关a=[1 -1 1 1 -1 1 -1 -1];b=[1 -1 -1 1 1 -1 -1 1];P=length(a);%求序列a的自相关函数Ra(1)=sum(a.*a);for k=1:P-1Ra(k+1)=sum(a.*circshift(a,[0,k])); end%求序列b的自相关函数Rb(1)=sum(b.*b);for k=1:P-1Rb(k+1)=sum(b.*circshift(b,[0,k])); end%求序列a和b的互相关函数Rab(1)=sum(a.*b);for k=1:P-1Rab(k+1)=sum(a.*circshift(b,[0,k])); endx=[0:P-1];figure(9)subplot(3,1,1);stem(x,Rab);ylabel('a和b的互相关函数');axis([0 P-1 -10 12]);grid;xlabel('偏移量');subplot(3,1,2);stem(x,Ra);ylabel('a自相关函数');xlabel('偏移量');%axis([0 P-1 -5 30]);subplot(3,1,3);stem(x,Rb);%plot(x,Rb)xlabel('偏移量');ylabel('b的自相关函数');四、总结一、M序列自相关函数近似于冲激函数的形状,不同序列间的互相关特性一致性不好。
m序列产生要点
out1(k)=reg1(1);
end
reg2=ones(1,7); %寄存器初始状态
coeff2=[1 10 0 1 1 1]; %设置系数
N=2^length(reg2)-1;
for k=1:N
a_n=mod(sum(reg2.*coeff2(1:length(coeff2)-1)),2); %移位,反馈
[3]吴先用,邹学玉.一种m序列伪码发生器的产生方法[J].西安:西安电子科技大学出版社.2003
附录
clear;
reg1=ones(1,7); %寄存器初始状态
coeff1=[1 0 0 0 0 1 1]; %设置系数
N=2^length(reg1)-1;
%产生m序列
for k=1:N
a_n=mod(sum(reg1.*coeff1(1:length(coeff1)-1)),2);
Simulink是MATLAB最重要的组件之一,它提供了一个动态系统建模,仿真和综合分析的集成环境。在此环境中无需大量书写程序,而只需通过简单直观的鼠标操作,就可构造出复杂的系统。Simulink具有适应性广,结构及流程清晰及仿真精细等优点,基于以上优点,Simulink已被广泛的运用到控制理论和数字信号处理的复杂仿真和设计。
m序列是最长线性反馈移位寄存器序列的简称,m序列是由带线性反馈的移位寄存器产生的。
由n级串联的移位寄存器和反馈逻辑线路可组成动态移位寄存器,如果反馈逻辑线路只由模2和构成,则称为线性反馈移位寄存器。
带线性反馈逻辑的移位寄存器设定初始状态后,在时钟触发下,每次移位后各级寄存器会发生变化,其中任何一级寄存器的输出,随着时钟节拍的推移都会产生一个序列,该序列称为移位寄存器序列。
