湖北省武汉市蔡甸区部分学校2015届九年级十月联考数学试题
湖北省武汉市2015年中考数学试卷(解析版)

2015年武汉市初中毕业生学业考试数学试卷一、选择题(共10小题,每小题3分,共30分) 1.在实数-3、0、5、3中,最小的实数是( ) A .-3B .0C .5D .32.若代数式2-x 在实数范围内有意义,则x 的取值范为是( ) A .x ≥-2 B .x >-2 C .x ≥2 D .x ≤2 3.把a 2-2a 分解因式,正确的是( )A .a (a -2)B .a (a +2)C .a (a 2-2)D .a (2-a ) 4.一组数据3、8、12、17、40的中位数为( ) A .3B .8C .12D .175.下列计算正确的是( ) A .2x 2-4x 2=-2B .3x +x =3x 2C .3x ·x =3x 2D .4x 6÷2x 2=2x 36.如图,在直角坐标系中,有两点A (6,3)、B (6,0).以原点O 为位似中心,相似比为31,在第一象限内把线段AB 缩小后得到线段CD ,则点C 的坐标为( ) A .(2,1) B .(2,0) C .(3,3)D .(3,1)7.如图,是由一个圆柱体和一个长方体组成的几何体,其主视图是( )8.下面的折线图描述了某地某日的气温变化情况,根据图中信息,下列说法错误的是( )A .4:00气温最低B .6:00气温为24℃C .14:00气温最高D .气温是30℃的为16:009.在反比例函数xmy 31-=图象上有两点A (x 1,y 1)、B (x 2,y 2),x 1<0<y 1,y 1<y 2,则m 的取值范围是( ) A .m >31 B .m <31 C .m ≥31 D .m ≤3110.如图,△ABC、△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是()2-A.33+B.1C.23-D.1二、填空题(共6小题,每题3分,共18分)11.计算:-10+(+6)=_________12.中国的领水面积约为370 000 km2,将数370 000用科学记数法表示为_________13.一组数据2、3、6、8、11的平均数是_________14.如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省__元15.定义运算“*”,规定x*y=ax2+by,其中a、b为常数,且1*2=5,2*1=6,则2*3=_________ 16.如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是_________三、解答题(共8小题,共72分)17.(本题8分)已知一次函数y=kx+3的图象经过点(1,4)求这个一次函数的解析式求关于x的不等式kx+3≤6的解集18.(本题8分)如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF 于点F,AC=DF求证:(1) △ABC≌△DEF(2)AB∥DE19.(本题8分)一个不透明的口袋中有四个完全相同的小球,它们分别标号为1,2,3,4(1) 随机摸取一个小球,直接写出“摸出的小球标号是3”的概率(2) 随机摸取一个小球然后放回,再随机摸出一个小球,直接写出下列结果:①两次取出的小球一个标号是1,另一个标号是2的概率②第一次取出标号是1的小球且第二次取出标号是2的小球的概率20.(本题8分),如图,已知点A(-4,2)、B(-1,-2),□ABCD的对角线交于坐标原点O(1) 请直接写出点C、D的坐标(2) 写出从线段AB到线段CD的变换过程(3) 直接写出□ABCD的面积21.(本题8分)如图,AB是⊙O的直径,∠ABT=45°,AT=AB(1) 求证:AT是⊙O的切线(2) 连接OT交⊙O于点C,连接AC,求tan∠TAC的值22.(本题8分)已知锐角△ABC 中,边BC 长为12,高AD 长为8(1) 如图,矩形EFGH 的边GH 在BC 边上,其余两个顶点E 、F 分别在AB 、AC 边上,EF 交AD 于点K ① 求AKEF的值 ② 设EH =x ,矩形EFGH 的面积为S ,求S 与x 的函数关系式,并求S 的最大值(2) 若AB=AC ,正方形PQMN 的两个顶点在△ABC 一边上,另两个顶点分别在△ABC 的另两边上,直接写出正方形PQMN 的边长23.(本题10分)如图,△ABC 中,点E 、P 在边AB 上,且AE =BP ,过点E 、P 作BC 的平行线,分别交AC 于点F 、Q .记△AEF 的面积为S 1,四边形EFQP 的面积为S 2,四边形PQCB 的面积为S 3(1) 求证:EF +PQ =BC (2) 若S 1+S 3=S 2,求AEPE的值 (3) 若S 3-S 1=S 2,直接写出AEPE的值24.(本题12分)已知抛物线y=x2+c与x轴交于A(-1,0),B两点,交y轴于点C(1) 求抛物线的解析式(2) 点E(m,n)是第二象限内一点,过点E作EF⊥x轴交抛物线于点F,过点F作FG⊥y轴于点G,连接CE、CF,若∠CEF=∠CFG,求n的值并直接写出m的取值范围(利用图1完成你的探究)(3) 如图2,点P是线段OB上一动点(不包括点O、B),PM⊥x轴交抛物线于点M,∠OBQ =∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长2015年武汉市初中毕业生学业考试数学试卷解析一、选择题(共10小题,每小题3分,共30分)1.在实数-3、0、5、3中,最小的实数是()A.-3 B.0 C.5 D.31.A【解析】有理数中,负数小于0,零小于正数,所以最小的是-3.备考指导:有理数大小比较的一般方法:①正数都大于0,负数都小于0,正数大于一切负数,两个负数绝对值大的反而小;②在数轴上表示的数,右边的总比左边的大.2.若代数式2x在实数范围内有意义,则x的取值范为是()A.x≥-2 B.x>-2 C.x≥2D.x≤22.C【解析】二次根式有意义,被开方数是非负数,故x-2≥0,x大于等于2.备考指导:代数式有意义的条件,一般从三个方面考虑:(1)当表达式是整式时,可取全体实数;(2)当表达式是分式时,考虑分式的分母不能为0;(3)当表达式是二次根式时,被开方数非负.3.把a2-2a分解因式,正确的是()A.a(a-2) B.a(a+2) C.a(a2-2) D.a(2-a)3.A【解析】考查提取公因式法分解因式.原式=a(a-2).备考指导:因式分解的一般步骤:若有公因式,先提公因式;然后再考虑用公式法或其它方法分解;直到每个因式都不能再分解为止.4.一组数据3、8、12、17、40的中位数为()A.3 B.8 C.12 D.174.C【解析】本题共5个数据,已经从小到大排列好,第3个数据12就是这组数据的中位数.备考指导:找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数,当数据个数为奇数时,即为中间的一个,当数据个数为偶数时,中位数就是中间两个数的平均数.5.下列计算正确的是()A.2x2-4x2=-2 B.3x+x=3x2 C.3x·x=3x2 D.4x6÷2x2=2x35.C 【解析】 本题考查整式的基本运算,对选项进行逐项分析选项 逐项分析正误 A 2x 2-4x 2=-2x 2≠-2 × B 3x +x =4x ≠3 x 2 × C 3x ·x =3 x 2 √ D4x 6÷2x 2=2x 4≠2x 3×备考指导:整式加减,实质是合并同类项,只把系数相加减,字母及字母的指数不变;整式乘法,系数相乘作为积的系数,相同的字母按照同底数幂的乘法法则相乘,单独的字母(式)作为积的一个因式;整式相除,系数相除作为商的系数,相同的字母按照同底数幂的除法法则相除,被除式中单独的字母(式)作为积的一个因式.6.如图,在直角坐标系中,有两点A (6,3)、B (6,0).以原点O 为位似中心,相似比为31,在第一象限内把线段AB 缩小后得到线段CD ,则点C 的坐标为( )A .(2,1)B .(2,0)C .(3,3)D .(3,1)6.A 【解析】∵线段CD 和线段AB 关于原点位似,∴△ODC ∽△OBA ,∴31OB ==AB CD OD ,即3136==CD OD ,∴CD =1,OD =2,∴C (2,1). 一题多解—最优解:设C (x ,y ),∵线段CD 和线段AB 关于原点位似,∴3136==y x ,∴x =2,y =1,∴C (2,1).备考指导:每对对应点的连线所在的直线都相交于一点的相似图形叫做位似图形.位似图形对应点到位似中心的距离比等于位似比(相似比);在平面直角坐标系中,如果位似图形是以原点为位似中心,那么位似图形对应点的坐标比等于相似比.7.如图,是由一个圆柱体和一个长方体组成的几何体,其主视图是( )7.B 【解析】圆柱的主视图是长方形,长方体的主视图是长方形,因此这个几何体的主视图是两个长方形组成,下面长方形的长大于上面长方形的长,且上面长方形位于下面长方形的中间,所以选择B .备考指导:确定简单组合体的三视图,首先确定每一个组成部分的三视图,再按照几何体组合方式确定各个组成部分的排放位置.8.下面的折线图描述了某地某日的气温变化情况,根据图中信息,下列说法错误的是( )A .4:00气温最低B .6:00气温为24℃C .14:00气温最高D .气温是30℃的为16:008.D 【解析】从图像可以看出最低点对应点时间是4:00时,即4:00时温度最低,故A 正确;6:00对应的温度为24℃,故B 正确;图形最高点对应14:00时,即14:00时温度最高,故C 正确;气温是30℃时对应两个时间12:00时和16时,故D 错误.备考指导:解决此类问题的时,要注意结合函数图像和题意弄清横轴、纵轴的实际意义,以及图像上特殊点的实际意义.此类问题一般的解答方式是根据一个坐标找到对应图像上的点,再确定这个点的另一个坐标;图像的最高(低)点对应函数最大(小)值. 9.在反比例函数xmy 31-=图象上有两点A (x 1,y 1)、B (x 2,y 2),x 1<0<y 1,y 1<y 2,则m 的取值范围是( ) A .m >31B .m <31C .m ≥31D .m ≤319.D 【解析】x 1<0<x 2时,y 1<y 2,说明反比例函数图像位于一三象限,故1-3m >0,所以m ≤31. 易错警示:对于x 1<0<x 2时,y 1<y 2,部分同学容易误认为y 随x 增大而增大,故错误得出1-3m <0.考虑反比例函数增减性要在同一个分支上,x 1<0<x 2说明点A 、B 不在同一个分支上,故不能利用增减性来解答. 备考指导:①反比例函数k xky (=为常数,且)0≠k 的图像是双曲线,当0>k 时,双曲线的两支分别位于第一、第三象限,在每个象限内y 值随x 值的增大而减小;当0<k 时,双曲线的两支分别位于第二、第四象限,在每个象限内y 值随x 值的增大而增大.②两个点若在双曲线同一分支上,则两点纵坐标符号相同,横坐标符号相同,两个点若不在双曲线同一分支上,则两点纵坐标符号相反,横坐标符号相反.10.如图,△ABC 、△EFG 均是边长为2的等边三角形,点D 是边BC 、EF 的中点,直线AG 、FC 相交于点M .当△EFG 绕点D 旋转时,线段BM 长的最小值是( )A .32-B .13+C .2D .13-10.D 【解析】先考虑让△EFG 和△BCA 重合,然后把△EFG 绕点D 顺时针旋转,连结AG 、DG ,根据旋转角相等,旋转前后的对应线段相等,容易发现∠ADG =∠FDC ,DA =DG ,DF =DC ,故∠DFC =∠DCF =∠DAG =∠DGA .又根据等腰三角形的“三线合一”可知∠FDG =90°,所以∠DFG +∠DGF =90°,即∠DFC +∠CFG +∠DGF =90°. 所以∠AMC =∠MGF +∠CFG =∠AGD +∠DGF +∠CFG =∠DFC +∠DGF +∠CFG =90°.故点M 始终在以AC 为直径的圆上,作出该圆,设圆心为O ,连结BO 与⊙O 相交于点P ,线段BP的长即为线段BM 长的最小值.BP =AO -OP 1,故选D .【难点突破】本题发现点M 始终在以AC 为直径的圆上是解题的重要突破口.考虑让△EFG 和△BCA 重合,然后把△EFG 绕点D 顺时针旋转,借助旋转的性质找出解题思路是分析有关旋转问题的重要方法.二、填空题(共6小题,每题3分,共18分) 11.计算:-10+(+6)=_________ 11.-4 【解析】-10+(+6)=-(10-6)=-4.备考指导:有理数加法法则:同号两数相加,取相同的符号,并把绝对值相加;异号两数相加,绝对值相等时其和为零,绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.12.中国的领水面积约为370 000 km 2,将数370 000用科学记数法表示为_________ 12.3.7×105 【解析】∵370 000的整数数位有6位,∴a =3.7,n =6-1=5,即370 000=3.7×105. 备考指导:用科学记数法表示一个数,就是把一个数写成a ×10n的形式(其中1≤a <10,n 为整数),其方法是(1)确定a ,a 是只有一位整数的数;(2)确定n ,当原数的绝对值≥10时, n 等于原数的整数位数减1;当原数的绝对值<1时,n 为负整数,n 的绝对值等于原数中左起第一个非零数前零的个数(含整数位数上的零).13.一组数据2、3、6、8、11的平均数是_________ 13.6 【解析】65118632=++++.备考指导:平均数计算公式为算术平均数:x 1,x 2…x n 的平均数 -x =n1(x 1+x 2+ x 3…x n ).14.如图所示,购买一种苹果,所付款金额y (元)与购买量x (千克)之间的函数图象由线段OA 和射线AB 组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省__元14.2【解析】当每次买苹果少于2千克时,每千克20÷2=10元/千克,故3千克分三次且每次买1千克时需10×3=30元;设AB 表达式为y =kx +b ,把(2,20)、(36,4)代入上式⎩⎨⎧+=+=bk b436k 220,解得k =8,b =4,所以y =8x +4,当x =3时,y =28,故可节省30-28=2元.备考指导:分段函数要注意自变量适用范围,要确定好函数图象的“拐点”,确定函数值一定要分清需要根据哪一段函数图象来解答.根据图象提供已知点的坐标确定每段图像的表达式是解答此类题目的前提.15.定义运算“*”,规定x *y =ax 2+by ,其中a 、b 为常数,且1*2=5,2*1=6,则2*3=_________ 15. 10【解析】由题意知,⎩⎨⎧=+=+6452a b a b ,所以⎩⎨⎧==21a b ,所以x ※y =x 2+2y ,所以2※3=22+2×3=10.新定义翻译:新定义的实质是解二元一次方程组,从而确定常数值,最后转化为求代数式的值.本题以新定义的形式出现,使简单问题新颖化,能很好的考查同学们的阅读理解能力.16.如图,∠AOB =30°,点M 、N 分别在边OA 、OB 上,且OM =1,ON =3,点P 、Q 分别在边OB 、OA 上,则MP +PQ +QN 的最小值是_________16.10【解析】作M 关于ON 对称点M 1,点N 关于OA 的对称点N 1,连接M 1N 1分别交OA 、ON 于Q ,P ,此时MP +PQ +NQ 的值最小.由对称性质知,M 1P =MP ,N 1Q =NQ ,所以MP +PQ +NQ = M 1N 1.连接ON 1、OM 1,则∠M 1OP =∠POM =∠N 1OM =30°,所以∠N 1OM 1=90°.又ON 1=ON =3,OM 1 =OM =1,所以M 1N 1=11ON OM =10.【指点迷津】线段和的最小值问题,一般都是将几条线段转化为同一条线段长度,根据两点之间线段最短来说明.一般是通过做对称点转化到同一条线段上,根据勾股定理计算最小值.三、解答题(共8小题,共72分)17.(本题8分)已知一次函数y =kx +3的图象经过点(1,4) 求这个一次函数的解析式 求关于x 的不等式kx +3≤6的解集17.【思路分析】(1)把(1,4)代入y =kx +3可确定表达式;(2)移项、合并同类项、系数化1,可确定不等式解集.解:(1)把(1,4)代入y =kx +3得, 4=k +3 K =1∴一次函数解析式为y =x +3; (2) kx +3≤6 X +3≤6 ∴x ≤3.备考指导:(1)确定函数解析式,用待定系数法,将已知点坐标代入表达式解出常数即可;(2)解不等式的基本步骤是:①去分母;②去括号;③移项;④合并同类项;⑤系数化为1,注意在不等式两边同乘或同除一个不为的0的数,需考虑正负对不等号方向的影响.18.(本题8分)如图,点B 、C 、E 、F 在同一直线上,BC =EF ,AC ⊥BC 于点C ,DF ⊥EF 于点F ,AC =DF求证:(1) △ABC≌△DEF(2) AB∥DE18.【思路分析】由AC⊥BC,DF⊥EF,知∠ACB=∠DFE,结合AC=DF,BC=EF可说明△ABC≌△DEF;(2)△ABC≌△DEF,故∠ACB=∠DFE,所以AB∥DE.证明:(1)∵AC⊥BC,DF⊥EF,∴∠ACB=∠DFE,∵AC=DF,BC=EF,∴△ABC≌△DEF;(2)∵△ABC≌△DEF,∴∠ACB=∠DFE,∴AB∥DE.备考指导:(1)当题目中已知两边“SS”时,根据三角形全等的判定条件,可选择“SAS”,或“SSS”进一步探索推理的思路;若已知一边一角“SA”时,可根据题意再补上一角或另一边,应用“SAS”,或“ASA”,或“AAS”进行说理;若已知两角“AA”时,则应补上一边,利用“AAS”,或“ASA”进行推理.总之,应根据具体条件灵活选择适当的判定方法;(2)证明两直线平行,就要说明这两条直线形成的内错角相等或同为角相等或同旁内角互补.19.(本题8分)一个不透明的口袋中有四个完全相同的小球,它们分别标号为1,2,3,4(1) 随机摸取一个小球,直接写出“摸出的小球标号是3”的概率(2) 随机摸取一个小球然后放回,再随机摸出一个小球,直接写出下列结果:①两次取出的小球一个标号是1,另一个标号是2的概率②第一次取出标号是1的小球且第二次取出标号是2的小球的概率19. 【思路分析】(1)所有等可能结果有四种,“摸出的小球标号是3”的结果有一种,故“摸出的小球标号是3”的概率为41; (2)首先找到所有的等可能情况数和满足条件的情况数,然后根据概率的公式进行计算即可.解:(1)P 摸出的小球标号是3=41 (2)列表如下:1 2 3 4 1 (1,1) (1,2) (1,3) (1,4) 2 (2,1) (2,2) (2,3) (2,4) 3 (3,1) (3,2) (3,3) (3,4) 4(4,1)(4,2)(4,3)(4,4)①由列表可知:共有16种等可能的结果,其中一个标号是1,另一个标号是2结果共有2种,∴P (一个标号是1,另一个标号是2)=81162=; ②共有16种等可能的结果,其中第一次取出标号是1的小球且第二次取出标号是2的结果共有1种,∴P (第一次取出标号是1的小球且第二次取出标号是2)= 161. 备考指导:求概率的方法: (1)直接公式法:()A mP n=,其中n 为所有事件的总和,m 为事件A 发生的总次数; (2)列举(列表或画树状图)法:当一次试验涉及多个因素(对象)时,由于不能直观的得到事件A 发生的次数m 及总事件发生的结果数n ,所以需要借助于列表或画树状图的方法来清晰的列举出来,再根据公式进行计算.一般步骤为:①判断使用列表法还是画树状图法:列表法一般适用于两步计算概率;画树状图法适合于两步以上求概率;②不重不漏的列举出所有事件出现的可能结果,并判定每种事件发生的可能性是否相等;③确定所有可能出现的结果数n及所求事件A出现的结果m;④用公式()A mPn求事件A发生的概率.20.(本题8分),如图,已知点A(-4,2)、B(-1,-2),□ABCD的对角线交于坐标原点O(1) 请直接写出点C、D的坐标(2) 写出从线段AB到线段CD的变换过程(3) 直接写出□ABCD的面积20. 【思路分析】(1)平行四边形是中心对对称图形,对称中心是原点,所以可以根据点关于原点的对称规律写出C、D坐标:(2)可以从中心对称、平移或旋转的角度来说明;(3)点B、C的纵坐标相同,故BC∥x轴,同理AD∥x轴.BC长度可由点B、C的很坐标来计算,BC上的高是A、B两点纵坐标的差.解:(1)C(4,-2)、D(1,2);(2)AB绕点O旋转180°得到线段CD,或作AB关于原点O的中心对称图形得到线段CD;(3)BC=5,BC上的高为4,所以平行四边形ABCD的面积为5×4=20.备考指导:在平面直角坐标系内,关于x轴对称的两点,横坐标不变,纵坐标互为相反数;关于y轴对称的两点,横坐标互为相反数,纵坐标不变;关于原点对称的两点, 横纵坐标都互为相反数.21.(本题8分)如图,AB是⊙O的直径,∠ABT=45°,AT=AB(1) 求证:AT是⊙O的切线(2) 连接OT交⊙O于点C,连接AC,求tan∠TAC的值21. 【思路分析】(1)由AB =AT ,知∠ATB =∠B =45°,故∠BAT =90°,AT 是⊙O 的切线; (2)设⊙O 半径为r ,延长TO 交⊙O 于D ,连接AD ,则∠CAD =∠BAT =90°,∠TAC =∠OAD =∠D .通过△TAC ∽△TDA ,说明TA 2=TC ·TD ,即4r 2= TC (TC +2r ),可以用r 表示TC ,tan ∠TAC = tan ∠D =ATTCAD AC =. 证明:(1)∵AB =AT , ∴∠ATB =∠B =45°, ∴∠BAT =90°, ∴AT 是⊙O 的切线;(2)设⊙O 半径为r ,延长TO 交⊙O 于D ,连接AD . ∵CD 是直径, ∴∠CAD =∠BAT =90°, ∴∠TAC =∠OAD =∠D . 又∠ATC =∠DTA , ∴△TAC ∽△TDA , ∴ATTCTD TA =, ∴TA 2=TC ·TD ,即即4r 2= TC (TC +2r ), 解得TA =r 1-5)(,∴tan ∠TAC = tan ∠D =AT TC AD AC ==2r 1)r -5(=21-5.备考指导:(1) 圆的切线的判定方法有三种:①和圆只有一个公共点的直线是圆的切线;这种方法不常用.②若圆心到直线的距离等于圆的半径,则这条直线是圆的切线;这种证明方法通常是在直线和圆没有公共点时,通过“作垂直,证半径”的方法来证明直线是圆的切线. ③经过半径外端并且垂直于这条半径的直线是圆的切线.这种证明方法通常是在直线和圆有公共点,通过“连半径,证垂直”的方法来证明直线是圆的切线.(2)涉及角的三角函数时,应该把这个角放在直角三角形中来考虑,如果这个角不在直角三角形中,可以在其他直角三角形中用它的等角来替换,最终把三角函数关系转化为直角三角形边的比值来解答.22.(本题8分)已知锐角△ABC 中,边BC 长为12,高AD 长为8(1) 如图,矩形EFGH 的边GH 在BC 边上,其余两个顶点E 、F 分别在AB 、AC 边上,EF 交AD 于点K ① 求AKEF的值 ② 设EH =x ,矩形EFGH 的面积为S ,求S 与x 的函数关系式,并求S 的最大值 (2) 若AB=AC ,正方形PQMN 的两个顶点在△ABC 一边上,另两个顶点分别在△ABC 的另两边上,直接写出正方形PQMN 的边长22. 【思路分析】(1)根据△AEF ∽△ABC ,对应高的比等于相似比可得ADAKBC EF =,即ADDK -AD BC EF =,代入数值可确定AK EF的值;(2)结合AKEF的值,用x 表示EF,从而可以把矩形EFGH 的面积为S 写成x 的二次函数,根据二次函数可确定矩形的最大面积.(3)分两种可能:①两顶点M 、N 在底边BC 上,根据(1)知23AK PQ =和AK =8-PQ 求解;②两顶点M 、N 在腰AB 上时,作AB 上的高,转化为(1)形式求解. 解:(1)∵EF ∥BC ,∴△AEF ∽△ABC ,∴AD AK BC EF =,即8AK12EF = ∴23AK EF =; (2)由题意知EH =KD =x ,AK =8-x .∵23AK EF =, ∴23x -8EF =, ∴EF =)8(23x -,∴S =EF ×EH =)8(23x -x =244-x 23-2+)(,∴S 的最大值是24;(3)①两顶点在底边BC 上时,由(1)知23AK PQ =,∵PQMN 是正方形, ∴AK =AD -DK =AD -PQ =8-PQ , ∴23PQ -8PQ =,∴PQ =4.8;②正方形两顶点M 、N 在腰AB 上时如图时,作CH ⊥AB 于H ,交PQ 于G ,则CG =CH -HG =CH -PQ =9.6-PQ , 如图:∵AB =AC ,AD ⊥BC , ∴BD =6 又AD =8, ∴AB =10,∴AB ×CH =BC ×AD , ∴CH =9.6.由(1)知2425CH AB CG PQ ==,即2425PQ -9.6PQ =, ∴PQ =49240, 综上,正方形PQMN 的边长为4.8或49240.备考指导:(1)相似三角形对应高的比等于对应边的比;(2)最值问题,最终转化为二次函数最值问题来解答.根据相似列比例式、勾股定理、三角函数都表示线段长度的方法;(3)对于“神同形异”、层层递进式的几何证明计算题,后面的结论一般都需要前面结论来证明,注意前后结论之间的“继承性”.23.(本题10分)如图,△ABC 中,点E 、P 在边AB 上,且AE =BP ,过点E 、P 作BC 的平行线,分别交AC 于点F 、Q .记△AEF 的面积为S 1,四边形EFQP 的面积为S 2,四边形PQCB 的面积为S 3 (1) 求证:EF +PQ =BC (2) 若S 1+S 3=S 2,求AEPE的值 (3) 若S 3-S 1=S 2,直接写出AEPE的值【思路分析】(1)作QN ∥AB ,交BC 于N ,通过证明△AEF ≌△QNC 可以证明EF +PQ =BC ;(2)△AEF ∽△APQ ,根据面积比等于相似比的平方,用PE 、AE 、S 1表示S 2,再由△AEF ∽△ABC ,用PE 、AE 、S 1表示S 2,两种表示方法列等式可求解;(3)根据△AEF ∽△ABC ,用PE 、AE 、S 1表示S 3,根据S 3-S 1=S 2列等式可求解.证明:(1)作QN ∥AB ,交BC 于N ,则∠NQP =∠A ,∠QNC =∠B .∵EF ∥BC ,∴∠AEF =∠B ,∴∠AEF =∠QNC .∵PQ ∥BC ,∴四边形PQNB 是平行四边形,∴BN =PQ ,QN =PB =AE ,∴△AEF ≌△QNC ,∴EE =NC ,∴BC =BN +NC =EF +PQ ;(2)∵EF ∥PQ ∥BC ,∴△AEF ∽△APQ ∽△ABC ∴2222211PE AE AE AP AE S S S )(+==+ 整理得S 2=122S AE PE PE AE 2+⋅①; 同理22223211PB PE AE AE AB AE S S S S )(++==++=22PE AE 2AE )(+, ∵S 1+S 3=S 2, ∴=++3211S S S S =212S S 22PE AE 2AE )(+, 整理得S 2=122S 2AEPE AE 2)(+②, ①=②即122S AE PE PE AE 2+⋅=122S 2AE PE AE 2)(+整理得PE 2=4AE 2,PE =2AE , ∴AEPE =2;(3) ∵△AEF ∽△ABC , ∴22223211PB PE AE AE AB AE S S S S )(++==++=22PE AE 2AE )(+, ∵S 3- S 1=S 2, ∴=++3211S S S S =312S S 22PE AE 2AE )(+, 整理得S 3=122S 2AE PE AE 2)(+, ∴122S 2AE PE AE 2)(+-S 1=122S AEPE PE AE 2+⋅ 整理得PE 2=2AE 2,∴PE =2AE ,AE PE =2.备考指导:(1)证明两条线段的和等于一条线段一般是把长线段分为两段,证明这两段分别与已知的两段相等;(2)当题目中涉及多个量时,根据他们的数量关系用其中一个量表示出其他量,再列式求解,相似、三角函数等都是数量之间互相转化的工具.24.(本题12分)已知抛物线y =x 2+c 与x 轴交于A (-1,0),B 两点,交y 轴于点C(1) 求抛物线的解析式(2) 点E (m ,n )是第二象限内一点,过点E 作EF ⊥x 轴交抛物线于点F ,过点F 作FG ⊥y 轴于点G ,连接CE 、CF ,若∠CEF =∠CFG ,求n 的值并直接写出m 的取值范围(利用图1完成你的探究)(3) 如图2,点P 是线段OB 上一动点(不包括点O 、B ),PM ⊥x 轴交抛物线于点M ,∠OBQ =∠OMP ,BQ 交直线PM 于点Q ,设点P 的横坐标为t ,求△PBQ 的周长【思路分析】(1)因为A 点在抛物线上,把A 点坐标代入抛物线即可求出c 的值,从而求出抛物线的解析式.(2)先在第二象限内取一合适的点E ,作出符合题目条件的图形,如答题图,因为题目所求与点E 的坐标有关,故想到要构造直角三角形,使其长度能用含m ,n 的代数式表示.过点C 作CH ⊥EF 于点H ,FG ⊥y 轴于点G 后,很容易发现△EHC ∽△FGC ,从而利用相似三角形的对应边成比例求n 的值,把y =n 代入抛物线的解析式,确定出m 的取值范围.(3)首先用含t 的代数式表示出PB 的长度,然后需要表示PQ 和QB 的长度.根据图形易发现△OPM ∽△QPB ,利用相似三角形的对应边成比例可表示出PQ 的长度,再利用勾股定理求出QB 的长度,即可求出△PBQ 的周长.解:(1)把(1,0)代入y =c x +221,得c =-1,所以抛物线解析式为y =21212-x ; (2)作CH ⊥EF 于点H ,则,△EHC ∽△FGC .∵E (m ,n ),∴F (m ,21m 212-), 又C (0,-21), ∴EH =n +21,CH =-m ,FG =-m ,CG =21m 2, ∵△EHC ∽△FGC ,∴CG FG CH EH =,即22m -m -21n m =+, ∴n +21=2, ∴n =23(-2<m <0);(3)由题意知点P (t ,0)的横坐标为,M (t ,21t 212-),△OPM ∽△QPB , ∴PBPQ PM OP =, 其中,OP =t ,PM =221-21t ,PB =1-t ,PQ =t t +12,BQ =22PQ PB +=tt ++112, ∴PQ +BQ +PB =t t +12+tt ++112+1-t =2. 难点突破:本题中的第(2)小题探索题,作出符合题目条件的图形是突破口,题目涉及点的坐标时,过点作x 轴或y 轴的垂线,构造出直角三角形,利用相似三角形来解答是解答此类题目一般思路.备考指导:中考压轴题,基本都是二次函数和几何图形的综合考查,解答方法万变不离其宗:用坐标表示线段,列方程求解.在这两个过程中,相似、三角函数、勾股定理是最常用的运算工具,是连接数形之间的桥梁 .。
2015年湖北省武汉市中考数学试卷答案与解析

2015年湖北省武汉市中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,共30分)下列各题中均有四个备选答案,其中有且只有一个是正确的,请在答题卡上将正确答案的代号涂黑.2.(3分)(2015•武汉)若代数式在实数范围内有意义,则x的取值范围是()26.(3分)(2015•武汉)如图,在直角坐标系中,有两点A(6,3),B(6,0),以原点O 位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为(),相似比是,=7.(3分)(2015•武汉)如图,是由一个圆柱体和一个长方体组成的几何体.其主视图是()B8.(3分)(2015•武汉)下面的折线图描述了某地某日的气温变化情况.根据图中信息,下列说法错误的是()9.(3分)(2015•武汉)在反比例函数y=图象上有两点A(x1,y1),B (x2,y2),<10.(3分)(2015•武汉)如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是()﹣+1 ﹣1=,BO==OM=AC=1OM=二、填空题(共6小题,每小题3分,共18分)请将答案填在答题卡对应题号的位置上.11.(3分)(2015•武汉)计算:﹣10+(+6)=﹣4.12.(3分)(2015•武汉)中国的领水面积约为370 000km2,将数370 000用科学记数法表示为 3.7×105.13.(3分)(2015•武汉)一组数据2,3,6,8,11的平均数是6.,则=14.(3分)(2015•武汉)如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省2元.)代入得:,15.(3分)(2015•武汉)定义运算“*”,规定x*y=ax2+by,其中a、b为常数,且1*2=5,2*1=6,则2*3=10.16.(3分)(2015•武汉)如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是.==故答案为三、解答题(共8小题,共72分)下列各题解答应写出文字说明,证明过程或演算过程.17.(8分)(2015•武汉)已知一次函数y=kx+3的图象经过点(1,4).(1)求这个一次函数的解析式;(2)求关于x的不等式kx+3≤6的解集.18.(8分)(2015•武汉)如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.求证:(1)△ABC≌△DEF;(2)AB∥DE.,19.(8分)(2015•武汉)一个不透明的口袋中有四个完全相同的小球,它们分别标号为1,2,3,4.(1)随机摸取一个小球,直接写出“摸出的小球标号是3”的概率;(2)随机摸取一个小球然后放回,再随机摸出一个小球,直接写出下列结果:①两次取出的小球一个标号是1,另一个标号是2的概率;②第一次取出标号是1的小球且第二次取出标号是2的小球的概率.;的概率为:=;的小球的概率为:.20.(8分)(2015•武汉)如图,已知点A(﹣4,2),B(﹣1,﹣2),平行四边形ABCD 的对角线交于坐标原点O.(1)请直接写出点C、D的坐标;(2)写出从线段AB到线段CD的变换过程;(3)直接写出平行四边形ABCD的面积.21.(8分)(2015•武汉)如图,AB是⊙O的直径,∠ABT=45°,AT=AB.(1)求证:AT是⊙O的切线;(2)连接OT交⊙O于点C,连接AC,求tan∠TAC.OT=(=,即=,从而求得x﹣==,即=﹣x=TAC==22.(10分)(2015•武汉)已知锐角△ABC中,边BC长为12,高AD长为8.(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.①求的值;②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC 的另两边上,直接写出正方形PQMN的边长.,可得,所以,据此求出,再根据=的值是.=EF=EF=x+24.AB=AC=.的边长是或.23.(10分)(2015•武汉)如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P 作BC的平行线,分别交AC于点F、Q,记△AEF的面积为S1,四边形EFQP的面积为S2,四边形PQCB的面积为S3.(1)求证:EF+PQ=BC;(2)若S1+S3=S2,求的值;(3)若S3﹣S1=S2,直接写出的值.)由平行线得出比例式,得出,得出,得出AN=﹣ah(﹣(ah+(((ah=((),=1=,﹣ah﹣(ah+(h=﹣=3=2(ah=﹣±)1+=1+=24.(12分)(2015•武汉)已知抛物线y=x2+c与x轴交于A(﹣1,0),B两点,交y轴于点C.(1)求抛物线的解析式;(2)点E(m,n)是第二象限内一点,过点E作EF⊥x轴交抛物线于点F,过点F作FG⊥y 轴于点G,连接CE、CF,若∠CEF=∠CFG.求n的值并直接写出m的取值范围(利用图1完成你的探究).(3)如图2,点P是线段OB上一动点(不包括点O、B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长.,∴抛物线解析式为,),m=2(﹣,,PQ=.PQ+BQ+PB=.。
湖北省武汉市武昌区C组联盟2015届九年级10月月考数学试题及答案

2014-2015学年上学期九年级北片联考命题人:熊利 审题人:张蓉华一、选择题(共10小题,每小题3分,共30分) 1、下列图形中,不是中心对称图形........的是A. B. C. D. 2.下列方程中是关于x 的一元二次方程的是A .2215x x+= B .2230x xy y +-= C. 210x x ++= D .20ax bx c ++=3.如图可以看作是一个等腰直角三角形旋转若干次得到,则每次旋转的度数可以是A .900B .60C . 45D .304.下列方程中有相等的实数根的是A. 210x x ++=B.2810x x ++=C.220x x ++=D.2210x x -+=5.抛物线1)3(22+-=x y 的顶点坐标是A .(3,1)B .(3,-1)C .(-3,1)D .(-3,-1)6.若点(2,5),(4,5)在抛物线2y ax bx c =++上,则它的对称轴是 A .0x = B .1x = C .2x = D .3x =7.如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是A.点MB.格点NC.格点PD.格点Q8.用配方法解方程2870x x ++=,则配方正确的是A. ()249x -= B. ()249x += C. ()2816x -= D. ()2857x +=9.某品牌电脑2009年的销售单价为7200元,由于科技进步和新型电子原材料的开发运用,该品牌电脑成本不断下降,销售单价也逐年下降.至2011年该品牌电脑的销售单价为4900元,设2009年至2010年,2010年至2011年这两年该品牌电脑的销售单价年平均降低率均为x ,则可列出的正确的方程为A. 24900(1)7200x += B. 7200(12)4900x -= C. 4900(1)7200(1)x x +=- D. 27200(1)4900x -=10.若1212,()x x x x <是关于x 的方程()()()x a x b a b a b --=-<的两个根,则实数12,,,x x a b 的大小关系为A.12x x a b <<<B. 12x a b x <<<C. 12a x x b <<<D. 12a x b x <<<二、填空题(共6小题,每小题3分,共18分)11. 函数21y x x =-+的图象与y 轴的交点坐标是 ;12. 若12,x x 是一元二次方程2430x x ++=的两个根,则12x x 的值是 ;13. 关于x 的一元二次方程22(1)10p x x p --+-=的一个根为,则实数的值是 ;14. 参加某次商品交易会的每两家公司之间都签订了一份合同,所有公司共签 订了36份合同,则共有 家公司参加了本次商品交易会。
武汉市黄陂区2015届九年级上10月联考数学试题及答案

部分学校九年级十月联考数学试卷一、选择题(每题3分,共30分)1.一元二次方程x2=2x的根为()A.x1=0,x2=2B.x=±2C.x=0D.x=22.下列电视台的台标,是中心对称图形的是()3.设方程x2-3x-1=0的两根分别为x1,x2,则x1+x2=( )A.-3B.3C.-1D.14.如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是()A.-1<x<5 B.x>5C.x<-1且x>5D. C.x<-1或x>55.如图,PA、PB是⊙O的两条切线,A、B为切点,AC为⊙O的直径,∠P=70°,则∠PBC=()A.110°B.120ºC.135°D.145°6.在平面直角坐标系中,将抛物线y=2x2向上平移2个单位,所得图象的解析式为()A. y=2x2-2B.y= 2x2+2C.y= 2(x-2)2D.y= 2(x+2)27. 某品牌电脑2009年的销售单价为7200元,由于科技进步和新型电子原材料的开发运用,该品牌电脑成本不断下降,销售单价也逐年下降.至2011年该品牌电脑的销售单价为4900元,设2009年至2010年,2010年至2011年这两年该品牌电脑的销售单价年平均降低率均为x,则可列出的正确的方程为( )A.4900(1+x)2=7200 B.7200(1-2x)=4900C.7200(1-x)=4900(1+x)D.7200(1-x)2=49008.如图,点A1、A2、A3、…、A n在抛物线y=x2图象上,点B1、B2、B3、…、B n在y轴上,若△A1B0B1、△A2B1B2、…、△A n B n-1B n都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于()A.2013B.2014C.第8题9.如图,△ABC是⊙O的内接三角形,C=120°,则⊙O的半径为()10. 如图,△ABC,∠C=90°,,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接BC′,则线段BC′的长为()。
湖北省武汉市2015年中考数学试题
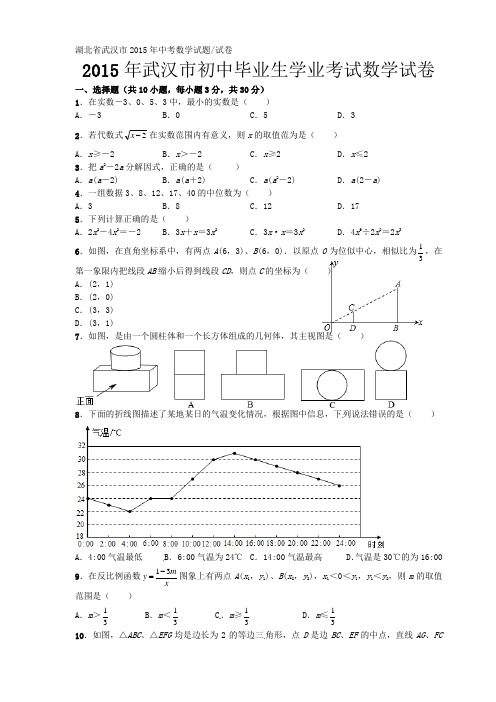
湖北省武汉市2015年中考数学试题/试卷2015年武汉市初中毕业生学业考试数学试卷一、选择题(共10小题,每小题3分,共30分) 1.在实数-3、0、5、3中,最小的实数是( ) A .-3 B .0 C .5D .32.若代数式2-x 在实数范围内有意义,则x 的取值范为是( ) A .x ≥-2 B .x >-2 C .x ≥2D .x ≤2 3.把a 2-2a 分解因式,正确的是( )A .a (a -2)B .a (a +2)C .a (a 2-2) D .a (2-a ) 4.一组数据3、8、12、17、40的中位数为( )A .3B .8C .12D .175.下列计算正确的是( )A .2x 2-4x 2=-2B .3x +x =3x 2C .3x ·x =3x2D .4x 6÷2x 2=2x 36.如图,在直角坐标系中,有两点A (6,3)、B (6,0).以原点O 为位似中心,相似比为31,在第一象限内把线段AB 缩小后得到线段CD ,则点C 的坐标为( ) A .(2,1) B .(2,0) C .(3,3) D .(3,1)7.如图,是由一个圆柱体和一个长方体组成的几何体,其主视图是( )8.下面的折线图描述了某地某日的气温变化情况,根据图中信息,下列说法错误的是( )A .4:00气温最低B .6:00气温为24℃C .14:00气温最高D .气温是30℃的为16:009.在反比例函数xmy 31-=图象上有两点A (x 1,y 1)、B (x 2,y 2),x 1<0<y 1,y 1<y 2,则m 的取值范围是( ) A .m >31B .m <31C .m ≥31D .m ≤3110.如图,△ABC 、△EFG 均是边长为2的等边三角形,点D 是边BC 、EF 的中点,直线AG 、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是()A.32-B.13+C.2D.13-二、填空题(共6小题,每题3分,共18分)11.计算:-10+(+6)=_________12.中国的领水面积约为370 000 km2,将数370 000用科学记数法表示为_________13.一组数据2、3、6、8、11的平均数是_________14.如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省__元15.定义运算“*”,规定x*y=ax2+by,其中a、b为常数,且1*2=5,2*1=6,则2*3=_________ 16.如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是_________三、解答题(共8小题,共72分)17.(本题8分)已知一次函数y=kx+3的图象经过点(1,4)求这个一次函数的解析式求关于x的不等式kx+3≤6的解集18.(本题8分)如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF求证:(1) △ABC≌△DEF(2) AB∥DE19.(本题8分)一个不透明的口袋中有四个完全相同的小球,它们分别标号为1,2,3,4(1) 随机摸取一个小球,直接写出“摸出的小球标号是3”的概率(2) 随机摸取一个小球然后放回,再随机摸出一个小球,直接写出下列结果:①两次取出的小球一个标号是1,另一个标号是2的概率②第一次取出标号是1的小球且第二次取出标号是2的小球的概率20.(本题8分),如图,已知点A (-4,2)、B (-1,-2),□ABCD 的对角线交于坐标原点O (1) 请直接写出点C 、D 的坐标(2) 写出从线段AB 到线段CD 的变换过程 (3) 直接写出□ABCD 的面积21.(本题8分)如图,AB 是⊙O 的直径,∠ABT =45°,AT =AB (1) 求证:AT 是⊙O 的切线(2) 连接OT 交⊙O 于点C ,连接AC ,求tan ∠TAC 的值22.(本题8分)已知锐角△ABC 中,边BC 长为12,高AD 长为8(1) 如图,矩形EFGH 的边GH 在BC 边上,其余两个顶点E 、F 分别在AB 、AC 边上,EF 交AD 于点K ① 求AKEF的值 ② 设EH =x ,矩形EFGH 的面积为S ,求S 与x 的函数关系式,并求S 的最大值(2) 若ABAC ,正方形PQMN 的两个顶点在△ABC 一边上,另两个顶点分别在△ABC 的另两边上,直接写出正方形PQMN 的边长23.(本题10分)如图,△ABC 中,点E 、P 在边AB 上,且AE =BP ,过点E 、P 作BC 的平行线,分别交AC 于点F 、Q .记△AEF 的面积为S 1,四边形EFQP 的面积为S 2,四边形PQCB 的面积为S 3 (1) 求证:EF +PQ =BC (2) 若S 1+S 3=S 2,求AEPE的值 (3) 若S 3-S 1=S 2,直接写出AEPE的值24.(本题12分)已知抛物线y=x2+c与x轴交于A(-1,0),B两点,交y轴于点C(1) 求抛物线的解析式(2) 点E(m,n)是第二象限内一点,过点E作EF⊥x轴交抛物线于点F,过点F作FG⊥y轴于点G,连接CE、CF,若∠CEF=∠CFG,求n的值并直接写出m的取值范围(利用图1完成你的探究)(3) 如图2,点P是线段OB上一动点(不包括点O、B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长。
2015年武汉市部分学校九年级10月数学联考试卷

2015年武汉市部分学校九年级10月数学联考试卷一、选择题(每小题3分,共30分)1、一元二次方程x x 22=的根为( )A 、2,021==x xB 、2±=xC 、0=xD 、2=x2、设方程0132=--x x 的两根分别为21,x x ,则=+21x x ( )A 、-3B 、3C 、-1D 、13、若方程()a x =-24有解,则a 的取值范围是( ) A 、0≤a B 、0≥a C 、0>a D 、无法确定4、关于x 的一元二次方程012=-+kx x 的根的情况是( )A 、有两根不相等实数根B 、没有实数根C 、有两根相等的实数根D 、不能确定5、如图是二次函数c bx ax y ++=2的部分图象,由图象可知不等式02<++c bx ax 的解集是( )A 、51<<-xB 、5>xC 、51>-<x x ,且D 、51>-<x x 或6、某机械厂七月份生产零件50万个,第三季度生产零件196万个。
设该厂八、九月份平均每月的增长率为x ,那么x 满足的方程是( )A 、()1961502=+xB 、()196150502=++x C 、()()196150150502=++++x x D 、()()196215015050=++++x x 7、吧抛物线22x y -=向左平移5个单位长度,然后向上平移3个单位长度,则平移后抛物线的解析式为( )A 、()3522---=x yB 、()3522-+-=x yC 、()3522+--=x y D 、()3522++-=x y 8、二次函数c bx ax y ++=2的图象恒在x 轴上方的条件是( )A 、04,02>->ac b aB 、04,02<->ac b aC 、04,02>-<ac b aD 、04,02<-<ac b a9、如图,点n A A A A 、、、321在抛物线2x y =图象上,点n B B B B 321、、在y 轴上,若n n n B B A B B A B B A 1212101-∆∆∆ 、、都为等腰直角三角形(点0B 是坐标原点),则201420132014B B A ∆的腰长等于( )A 、2013B 、2014C 、22013D 、2201410、已知二次函数()02≠++=a c bx ax y 的图象如图所示,给出下列结论:①ac b 42>;②0>abc ;③02=-b a ;④08<+c a ;⑤039<++c b a ,其中结论正确的有( )A 、2个B 、3个C 、4个D 、5个二、填空题(每小题3分,共18分)11、已知抛物线322-+=x x y ,则它的顶点坐标是 。
2015-2016学年湖北省武汉市部分学校联考九年级(上)期末数学试卷

2015-2016学年湖北省武汉市部分学校联考九年级(上)期末数学试卷一、选择题(共10小题,每小题3分,共30分)1.(3分)(2015秋•武汉校级期末)将方程x2﹣8x=10化为一元二次方程的一般形式,其中二次项系数为1,一次项系数、常数项分别是()A.﹣8、﹣10 B.﹣8、10 C.8、﹣10 D.8、102.(3分)(2015•潍坊)如图汽车标志中不是中心对称图形的是()A.B. C.D.3.(3分)(2016•抚顺模拟)袋子中装有10个黑球、1个白球,它们除颜色外无其他差别,随机从袋子中摸出一个球,则()A.这个球一定是黑球B.摸到黑球、白球的可能性的大小一样C.这个球可能是白球D.事先能确定摸到什么颜色的球4.(3分)(2003•泸州)抛物线y=﹣3(x﹣1)2+2的对称轴是()A.x=1 B.x=﹣1 C.x=2 D.x=﹣25.(3分)(2016•抚顺模拟)一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时是绿灯的概率是()A.B.C.D.6.(3分)(2015•常德)如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为()A.50°B.80°C.100°D.130°7.(3分)(2015秋•武汉校级期末)圆的直径为10cm,如果点P到圆心O的距离是d,则()A.当d=8cm时,点P在⊙O内B.当d=10cm时,点P在⊙O上C.当d=5cm时,点P在⊙O上D.当d=6cm时,点P在⊙O内8.(3分)(2015秋•武汉校级期末)某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是13,则每个支干长出()A.2根小分支B.3根小分支C.4根小分支D.5根小分支9.(3分)(2015•凉山州)关于x的一元二次方程(m﹣2)x2+2x+1=0有实数根,则m的取值范围是()A.m≤3 B.m<3 C.m<3且m≠2 D.m≤3且m≠210.(3分)(2015秋•武汉校级期末)如图,扇形OAB的圆心角的度数为120°,半径长为4,P为弧AB 上的动点,PM⊥OA,PN⊥OB,垂足分别为M、N,D是△PMN的外心.当点P运动的过程中,点M、N分别在半径上作相应运动,从点N离开点O时起,到点M到达点O时止,点D运动的路径长为()A.πB.πC.2 D.2二、填空题(本大题共6个小题,每小题3分,共18分)11.(3分)(2013•沈阳)在平面直角坐标系中,点(﹣3,2)关于原点对称的点的坐标是.12.(3分)(2015秋•常州期末)如图,转盘中8个扇形的面积都相等,任意转动转盘1次.当转盘停止转动时,指针指向大于5的数的概率为.13.(3分)(2015秋•武汉校级期末)某村种的水稻前年平均每公顷产7 200kg,今年平均每公顷产8 450kg.设这两年该村水稻每公顷产量的年平均增长率为x,根据题意,所列方程为.14.(3分)(2015秋•武汉校级期末)在直角坐标系中,将抛物线y=﹣x2﹣2x先向下平移一个单位,再向右平移一个单位,所得新抛物线的解析式为.15.(3分)(2016•抚顺模拟)如图,要拧开一个边长为a=12mm的六角形螺帽,扳手张开的开口b至少要mm.16.(3分)(2015秋•武汉校级期末)我们把a、b、c三个数的中位数记作Z|a,b,c|,直线y=kx+(k >0)与函数y=Z|x2﹣1,x+1,﹣x+1|的图象有且只有2个交点,则k的取值为.三、解答题(共8题,共72分)17.(8分)(2015秋•武汉校级期末)已知3是一元二次方程x2﹣2x+a=0的一个根,求a的值和方程的另一根.18.(8分)(2015秋•武汉校级期末)有6张看上去无差别的卡片,上面分别写着1、2、3、4、5、6 (1)一次性随机抽取2张卡片,用列表或画树状图的方法求出“两张卡片上的数都是偶数”的概率(2)随机摸取1张后,放回并混在一起,再随机抽取1张,直接写出“第二次取出的数字小于第一次取出的数字”的概率.19.(8分)(2016•襄城区模拟)如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AD交⊙O于点E(1)求证:AC平分∠DAB(2)连接CE,若CE=6,AC=8,直接写出⊙O直径的长.20.(8分)(2015秋•武汉校级期末)如图,正方形ABCD和直角△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF.(1)在图中画出点O和△CDF,并简要说明作图过程;(2)若AE=12,AB=13,求EF的长.21.(8分)(2015秋•武汉校级期末)图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:(1)求拱桥所在抛物线的解析式;(2)当水面下降1m时,则水面的宽度为多少?22.(10分)(2015秋•武汉校级期末)用一段长32m的篱笆和长8m的墙,围成一个矩形的菜园.(1)如图1,如果矩形菜园的一边靠墙AB,另三边由篱笆CDEF围成①设DE等于x m,直接写出菜园面积y与x之间的函数关系式,并写出自变量的取值范围;②菜园的面积能不能等于110m2?若能,求出此时x的值;若不能,请说明理由;(2)如图2,如果矩形菜园的一边由墙AB和一节篱笆BF构成,另三边由篱笆ADEF围成,求菜园面积的最大值.23.(10分)(2015秋•武汉校级期末)如图,∠BAC=60°,∠CDE=120°,AB=AC,DC=DE,连接BE,P为BE的中点.(1)如图1,若A、C、D三点共线,求∠PAC的度数;(2)如图2,若A、C、D三点不共线,求证:AP⊥DP;(3)如图3,若点C线段BE上,AB=1,CD=2,请直接写出PD的长度.24.(12分)(2015秋•武汉校级期末)问题探究:在直线y=x+3上取点A(2,4)、B,使∠AOB=90°,求点B的坐标.小明同学是这样思考的,请你和他一起完成如下解答:将线段OA绕点O逆时针旋转90°得到OC,则点C的坐标为:所以,直线OC的解析式为:点B为直线AB与直线OC的交点,所以,点B的坐标为:问题应用:已知抛物线y=﹣的顶点P在一条定直线l上运动.(1)求直线l的解析式;(2)抛物线与直线l的另一个交点为Q,当∠POQ=90°时,求m的值.2015-2016学年湖北省武汉市部分学校联考九年级(上)期末数学试卷参考答案一、选择题(共10小题,每小题3分,共30分)1.A;2.B;3.C;4.A;5.C;6.D;7.C;8.B;9.D;10.A;二、填空题(本大题共6个小题,每小题3分,共18分)11.(3,-2);12.; 13.7200(1+x)2=8450;14.y=-x2;15.12;16.;三、解答题(共8题,共72分)17.;18.;19.;20.;21.;22.;23.;24.(-4,2);y=-x;(-3,);。
湖北省武汉市部分学校2015届九年级10月联考数学试题(含答案)

EDCBAM GF EDCBA2014年秋武汉市部分学校九年级10月月考数学试题一、选择题(每小题3分,共30分)1.抛物线()5322-+=x y 的顶点坐标是( )A. (-3,-5)B. (-3,5)C. (3,-5)D. (3,5) 2.方程3242=+-x x 中二次项系数、一次项系数、常数项分别是( ) A. 4、-1、-1 B. 4、-1、2 C. 4、-1、3 D. 4、-1、5 3.下列图案中既是中心对称图形,又是轴对称图形的是( )4.若1x 、2x 是方程01322=++x x 的两个根,则21x x +的值是( ) A. -3 B.23 C. 21 D. 23- 5.将⊿ABC 绕点A 逆时针旋转一定的角度后,得到⊿ADE ,且点B 的对应点D 恰好落在BC 边上,若∠B =70°,则∠CAE 的度数是( ) A. 70° B. 50° C. 40° D. 30°6.将抛物线52312-+-=x x y 配成()k h x a y +-=2的形式为( )A. ()63312-+-=x yB. ()83312-+-=x yC. ()23312---=x yD. ()43312+--=x y7.如图,点C 为线段BD 上一点,分别以BC 、CD 为边在BD 的同侧作等边⊿ABC 和等边⊿CDE 。
AD 分别交BE 、CE 于点M 、F ,BE 交AC 于点G ,则图中可通过旋转而相互得到的三角形的对数有( )A. 1对B.2对C.3对D.4对8.一个QQ 群里共有x 个好友,每个好友都分别给群里的其他好友发一条信息,共发信息1980条,则可列方程( )AB DA.1980)1(21=-x x ;B. 1980)1(=-x x ;C. 1980)1(21=+x x ;D.1980)1(=+x x 9.已知抛物线22-+=x x y 与直线m x y -=5没有公共点,则m 的取值范围是( )A. 6<mB.6>mC.6≤m D. 2≥m10.如图,在⊿ABC 中,∠A ﹤90°,∠C =30°,AB =4,BC =6,E 为AB 的中点,P 为AC 边上一动点,将⊿ABC 绕点B 逆时针旋转α角(︒≤<︒3600α)得到11BC A ∆,点P 的对应点为1P ,连1EP ,在旋转过程中,线段1EP 的长度的最小值是( ) A.13- B. 1 C.23D. 2 二、填空题(每小题3分,共18分) 11.将抛物线5)1(22+-=x y 先向右平移2个单位,再向下平移3个单位后得到的抛物线的解析式为 。
湖北省武汉市2015年初中毕业生学业考试数学试题(附答案)

武汉市2015年初中毕业生学业考试数学(本试卷满分120分,考试时间120分钟)第Ⅰ卷(选择题共30分)一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.在实数-3,0,5,3中,最小的实数是()A.-3 B.0 C.5 D.3答案:A 【解析】本题考查有理数的大小比较,难度较小.有理数中,负数小于0,零小于正数,所以最小的是-3,故选A.2.若代数式在实数范围内有意义,则x的取值范围是()A.x≥-2 B.x>-2 C.x≥2 D.x≤2答案:C 【解析】本题考查二次根式,难度较小.二次根式有意义,被开方数是非负数,故x-2≥0,x≥2,故选C.3.把a2-2a分解因式,正确的是()A.a(a-2) B.a(a+2) C.a(a2-2) D.a(2-a)答案:A 【解析】本题考查提取公因式法分解因式,难度较小.原式=a(a-2),故选A.4.-组数据3,8,12,17,40的中位数为()A.3 B.8 C.12 D.17答案:C 【解析】本题考查中位数,难度较小.从小到大排列:3,8,12,17,40,第3个数据12就是这组数据的中位数.故选C.5.下列计算正确的是()A.2x2-4x2=-2 B.3x+x=3x2C.3x·x=3x2D.4x6÷2x2=2x3答案:C 【解析】本题考查整式的基本运算,难度较小.2x2-4x2=-2x2,A错误;3x+x=4x,B错误;3x·x=3x2,C正确;4x6÷2x2=2x4,D错误,故选C.6.如图,在直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为()A.(2,1) B.(2,0)C.(3,3) D.(3,1)答案:A 【解析】本题考查位似图形、三角形相似的判定与性质,难度中等.∵线段CD和线段AB关于原点位似,∴△ODC∽△OB A,∴,即,∴CD=1,OD=2,∴C(2,1),故选A.7.如图,是由一个圆柱体和一个长方体组成的几何体,其主视图是()A B C D答案:B 【解析】本题考查几何体的三视图,难度较小.圆柱的主视图是长方形,长方体的主视图是长方形,因此这个几何体的主视图是两个长方形组成,下面长方形的长大于上面长方形的长,且上面长方形位于下面长方形的中间,故选B.8.下面的折线图描述了某地某日的气温变化情况.根据图中信息,下列说法错误的是()A.4:00气温最低B.6:00气温为24℃C.14:00气温最高D.气温是30℃的时刻为16:00答案:D 【解析】本题考查函数图象的坐标意义,难度中等.从图象可以看出最低点对应点时间是4:00时,即4:00时温度最低,故A正确;6:00对应的温度为24℃,故B正确;图象最高点对应14:00时,即14:00时温度最高,故C正确;气温是30℃时对应两个时间:12:00时和16:00时,故D错误,故选D.9.在反比例函数图象上有两点A(x1,y1),B(x2,y2),x1<0<x2,y1<y2,则m 的取值范围是()A.B.C.D.答案:B 【解析】本题考查反比例函数图象的特征,难度中等.x1<0<x2时,y1<y2,说明反比例函数的图象位于一、三象限,故1-3m>0,所以,故选B.【易错分析】对于x1<0<x2时,y1<y2,考生容易误认为y随x增大而增大,故错误得出1-3m<0.考虑反比例函数增减性要在同一个分支上,x1<0<x2说明点A,B不在同一个分支上,故不能利用增减性来解答.10.如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC,EF的中点,直线AG,FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是()A.B.C.D.答案:D 【解析】本题考查三角形全等的应用、旋转的性质、等腰三角形的性质等知识,难度较大.因为△EFG≌△BCA,所以让△EFG和△BCA重合,把△EFG绕点D顺时针旋转,连接AD,DG,根据旋转角相等,旋转前后的对应线段相等,∴∠ADG=∠FDC,DA=DG,DF=DC,故∠DFC=∠DCF=∠DAG=∠DGA.又根据等腰三角形的“三线合一”可知∠FDG=90°,∴∠DFG+∠DGF=90°,即∠DFC+∠CFG+∠DGF=90°.所以∠AMC=∠MGF+∠CFG=∠AGD+∠DGF+∠CFG=∠DFC+∠DGF+∠CFG=90°.故点M始终在以AC为直径的圆上,作出该圆,设圆心为O,连接BO与⊙O相交于点P,线段BP的长即为线段BM长的最小值.,故选D.第Ⅱ卷(非选择题共90分)二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上)11.计算:-10+(+6)=_________.答案:-4 【解析】本题考查有理数的加减运算,难度较小.-10+(+6)=-4.12.中国的领水面积约为370000 km2,将数370000用科学记数法表示为_________.答案:3.7×105【解析】本题考查科学记数法,难度较小.用科学记数法表示一个数,就是把一个数写成a×10n的形式(其中1≤|a|<10,n为整数),其方法是(1)确定a,a 是只有一位整数的数;(2)确定n,当原数的绝对值≥10时,n等于原数的整数位数减1;当原数的绝对值<1时,n为负整数,n的绝对值等于原数中左起第一个非零数前零的个数(含整数位数上的零).370000=3.7×105.13.一组数据2,3,6,8,11的平均数是_________.答案:6 【解析】本题考查平均数,难度较小..14.如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省_________元.答案:2 【解析】本题考查待定系数法求函数解析式、函数图象的应用,难度中等.当每次买苹果少于2千克时,每千克20÷2=10元,故3千克分三次且每次买1千克时,需10×3=30元;设直线AB的表达式为y=kx+b,把(2,20),(4,36)代入上式,得解得k=8,b=4,所以y=8x+4,当x=3时,y=28,故可节省30-28=2元.15.定义运算“*”,规定x*y=ax2+by,其中a,b为常数,且1*2=5,2*1=6,则2*3=_________.答案:10 【解析】本题是新定义问题,考查解二元一次方程组,难度中等.由题意知所以所以x*y=x2+2y,所以2*3=22+2×3=10.16.如图,∠AOB=30°,点M,N分别在边OA,OB上,且OM=1,ON=3,点P,Q 分别在边OB,OA上,则MP+PQ+QN的最小值是_________.答案:【解析】本题考查对称、最值,难度较大.作点M关于ON的对称点M1,点N关于OA的对称点N1,连接M1N1,分别交OA,ON于点Q,P,此时MP+PQ+NQ 的值最小.由对称性质知,M1P=MP,N1Q=NQ,所以MP+PQ+NQ=M1N1.连接ON1,OM1,则∠M1OP=∠POM=∠N1OM=30°,∴∠N1OM1=90°.又ON1=ON=3,OM1=OM=1,∴.三、解答题(本大题共8小题,共72分.解答应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分8分)已知一次函数y=kx+3的图象经过点(1,4).(1)求这个一次函数的解析式;(2)求关于x的不等式kx+3≤6的解集.答案:本题考查解一元一次不等式,难度较小.解:(1)把(1,4)代入一次函数的解析式y=kx+3中得k+3=4,(2分)解得k=1,∴这个一次函数的解析式为y=x+3.(4分)(2)由(1)得x+3≤6,(6分)∴x≤3.(8分)18.(本小题满分8分)如图,点B,C,E,F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC =DF.求证:(1)△ABC≌△DEF;(2)AB∥DE.答案:本题考查三角形全等的判定和性质,难度较小.证明:(1)∵AC⊥BC,DE⊥EF,∴∠ACB=∠DFE=90°,(2分)在△ABC和△DEF中,∴△ABC≌△DEF.(4分)(2)∵△ABC≌△DEF,∴∠ABC=∠DEF,(6分)∴AB∥DE.(8分)19.(本小题满分8分)一个不透明的口袋中有四个完全相同的小球,它们分别标号为1,2,3,4.(1)随机摸取一个小球,直接写出“摸出的小球标号是3”的概率;(2)随机摸取一个小球然后放回,再随机摸出一个小球,直接写出下列结果:①两次取出的小球一个标号是1,另一个标号是2的概率;②第一次取出标号是1的小球且第二次取出标号是2的小球的概率.答案:本题考查列表法和树状图、概率,难度较小.解:(1).(2分)(2)①;(5分)②.(8分)20.(本小题满分8分)如图,已知点A(-4,2),B(-1,-2),□ABCD的对角线交于坐标原点O.(1)请直接写出点C,D的坐标;(2)写出从线段AB到线段CD的变换过程;(3)直接写出□ABCD的面积.答案:本题考查平行四边形的性质和面积的计算、点和线段平移,难度中等.解:(1)C(4,-2),D(1,2).(4分)(2)从线段AB到线段CD,可以看作是将线段AB绕O点旋转180°得到的.(6分)(3)20.(8分)21.(本小题满分8分)如图,AB是⊙O的直径,∠ABT=45°,AT=A B.(1)求证:AT是⊙O的切线;(2)连接OT交⊙O于点C,连接AC,求tan∠TAC的值.答案:本题考查圆的切线的判定、解直角三角形,难度中等.解:(1)证明:∵∠ABT=45°,AT=AB,∴∠ATB=45°,∠BAT=90°.(2分)∠AB是⊙O的直径,∴AT是⊙O的切线.(3分)(2)作CD⊥AB于点D.∵∠BAT=90°,∴CD∥AT.∴△OCD∽△OTA,∴,∴CD=2OD.(5分)设OD=a,则CD=2a,∴,∴.(7分)∵CD∥AT,∴∠TAC=∠ACD.∴.(8分)22.(本小题满分10分)已知锐角△ABC中,边BC长为12,高AD长为8.(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E,F分别在AB,AC边上,EF交AD于点K.①求的值;②设EH=x,矩形EFGH的面积为S.求S与x的函数关系式,并求S的最大值;(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.答案:本题考查三角形相似的判定和性质、相似形的相似比、矩形的面积、二次函数的最值、正方形的性质,难度中等.解:(1)①∵四边形EFGH是矩形,∴EF∥BC.∴△AEF∽△ABC,∴,(2分)∴;(3分)②由①得.(4分)∴(5分).(6分)∵0<x<8,∴当x=4时,S有最大值24.答:矩形EFGH的面积的最大值是24.(7分)(2)或.(10分)23.(本小题满分10分)如图,△ABC中,点E,P在边AB上,且AE=BP,过点E,P作BC的平行线,分别交AC于点F,Q.记△AEF的面积为S1,四边形EFQP的面积为S2,四边形PQCB的面积为S3.(1)求证:EF+PQ=BC;(2)若S1+S3=S2,求的值;(3)若S3-S1=S2,直接写出的值.答案:本题考查平行线的性质、三角形全等的判定和性质、相似的判定和性质、相似比与面积比的关系,难度中等.解:(1)证明:作CD∥AB,交PQ的延长线于点D,∵BC∥PQ,∴四边形BCDP是平行四边形,∠DCQ=∠A,∠CQD=∠AQP,BP=CD,PD=BC.∵EF∥BC∥PQ,∴∠AFE=∠AQP,∴∠CQD=∠AFE.∵AE=BP,∴AE=CD,∴△CQD≌△AFE,(2分)∴QD=EF.∴EF+PQ=QD+PQ=DP=BC.(3分)另解:∵EF∥BC∥PQ,∴△AEF∽△APQ∽△ABC,∴,,∴,.(2分)∵AE=BP,∴.(3分)(2)解法一:作CG∥AB,分别交PQ,EF的延长线于D,G,作QH∥AB,交EG于点H.∵△CQD≌△AFE,∴S△CQD=S△AFE=S1,∴S□BCDP=S1+S3.(4分)∵EF∥BC∥PQ,∴四边形BCDP,DGEP均为平行四边形,∠FCG=∠A,∠CFG=∠AQP.∵AE=BP,∴BE=AP,∴CG=AP,∴△CGF≌△APQ,∴S△CGF=S△APQ.S四边形DQFG=S四边形EFQP=S2,S□DPEG=2S2.(5分)∵S1+S3=S2,∴S□DPEG=2S□BCDP.(6分)∴PE=2BP=2AE,∴.(7分)解法二:设AE=BP=a,PE=b,∵EF∥PQ∥BC,∴△AEF∽△APQ∽△ABC.∴S△AEF:S△APQ:S△ABC=AE2:AP2:AB2.∴,,(5分)∵S1+S3=S2,∴,,∴.(6分)∴4a2-b2=0,∴b=2a或b=-2a(舍),∴.(7分)解法三:作□ABCT,设PQ,EF的延长线分别交CT于点D,G.∵EF∥BC∥PQ∥AT,∴四边形BCDP,AEGT,EPDG均为平行四边形,则S□BCDP+S□AEGT=S1+S3,(4分)S□EPDG=2S2,(5分)∵S1+S3=S2,∴S□EPDG=2S□BCDP.(6分)∴PE=2BP=2AE,∴.(7分)(3).(10分)24.(本小题满分12分)已知抛物线与x轴交于A(-1,0),B两点,交y轴于点C.(1)求抛物线的解析式;(2)点E(m,n)是第二象限内一点,过点E作EF⊥x轴交抛物线于点F,过点F作FG⊥y轴于点G,连接CE,CF,若∠CEF=∠CFG,求n的值并直接写出m的取值范围(利用图1完成你的探究);(3)如图2,点P是线段OB上一动点(不包括点O,B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长.答案:本题是二次函数和几何图形的综合题,考查二次函数的图象和性质、三角形相似的判定和性质、三角函数、勾股定理等,难度较大.解:(1)∵抛物线经过点A(-1,0),∴,(1分)∴.∴抛物线的解析式为.(2分)(2)作直线EH⊥y轴于H点,交抛物线于点D.∵E点坐标为(m,n),∴F点的坐标为,∴EH=FG=-m.(3分)由(1)得,∴,.(4分)∵EF∥y轴,∴∠CFG=∠CEF=∠ECH,∴tan∠CFG=tan∠ECH,即,(5分)∴.(6分)-2<m<0.(7分)(3)由抛物线得B(1,0),∵点P的横坐标为t,∴PB=1-t,点M的坐标为,∴.(8分)∵∠OBQ=∠OMP,∴△OMP∽△QBP,∴,(9分)即,∴,(10分)∴△PBQ的周长为(11分).(12分)综评:从试卷考查的内容来看,本套试卷几乎覆盖了数学《课程标准》所列的主要知识点,并且对初中数学的主要内容都作了重点考查.整体上呈现以下特点:1.突出考查考生的基础知识、基本技能.试卷紧密联系考生生活的实际问题,注重对数学核心内容的考查,加强了数学知识的有效整合,提高了试卷的概括性和综合性.2.注重考查考生的动态思维以及属性结合思想,如第24题,提高了考生的综合分析能力.本套试卷适合考生前期复习检测使用.。
2015年湖北省武汉市中考数学试题及解析

(2)若 AB=AC,正方形 PQMN 的两个顶点在△ABC 一边上,另两个顶点分别在△ABC 的另两边上,直接写出正方形 PQMN 的边长.
23.(10 分)(2015•武汉)如图,△ABC 中,点 E、P 在边 AB 上,且 AE=BP,过点 E、P 作 BC 的平行线,分别交 AC 于点 F、Q,记△AEF 的面积为 S1,四边形 EFQP 的面积为 S2, 四边形 PQCB 的面积为 S3. (1)求证:EF+PQ=BC; (2)若 S1+S3=S2,求 的值; (3)若 S3+S1=S2,直接写出 的值.
A (2,1) .
B (2,0) .
C (3,3) .
D (3,1) .
7.(3 分)(2015•武汉)如图,是由一个圆柱体和一个长方体组成的几何体.其主视图是( )
第 1页(共 24页)
A
B
C
D
.
.
.
.
8.(3 分)(2015•武汉)下面的折线图描述了某地某日的气温变化情况.根据图中信息,下 列说法错误的是( )
A x≥﹣2 .
B x>﹣2 .
在实数范围内有意义,则 x 的取值范围是( )
C x≥2 .
D x≤2 .
3.(3 分)(2015•武汉)把 a2﹣2a 分解因式,正确的是( )
A a(a﹣2)
B a(a+2)
C a(a2﹣2)
.
.
.
D a(2﹣a) .
4.(3 分)(2015•武汉)一组数据 3,8,12,17,40 的中位数为( )
18.(8 分)(2015•武汉)如图,点 B、C、E、F 在同一直线上,BC=EF,AC⊥BC 于点 C, DF⊥EF 于点 F,AC=DF.求证: (1)△ABC≌△DEF; (2)AB∥DE.
武汉市部分学校2015年10月九年级联考数学考试试题

1 / 5武汉市部分学校九年级10月月考数学试卷一、选择题:( 每小题3分,共30分 )1、下列方程是一元二次方程的是( ) A. 220x -= B. 3235x += C. 134x x+= D. 24x y += 2、若方程20x x m -+=的一个根是x=﹣1,则m 的值为( ) A. 2 B. ﹣2 C. 1 D. ﹣1 3、不解方程,判别方程:290x -+=的根的情况是( )A. 有两个相等的实数根B. 有两个不相等的实数根C. 只有一个实数根D. 没有实数根4、设一元二次方程2240x x --=的两个实数根为1x 和2x ,则下列结论正确的是( ) A. 122x x += B. 124x x +=- C. 122x x ⋅=- D. 124x x ⋅=5、下列各点,在抛物线24y x =-上的点是( )A. (4 ,4)B. (1 ,﹣4)C. (2 ,0)D. (0 ,4) 6、对于抛物线2(1)2y x =--的图象,下列说法正确的是( ) A. 开口向下 B. 对称轴是直线x=﹣1 C. 顶点坐标是(1 ,2) D. 与x 轴有两个交点 7、若1(0,)A y ,2B(1,)y ,3C(3,)y 在抛物线22(1)y x k =--+上,则( )A. 1y >2y >3yB. 2y > 1y >3yC. 3y > 2y >1yD. 1y >2y =3y 8、将抛物线2y=3x 向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )A. 2y=3x 3(+2)+ B. 2y=3x 3(-2)+ C. 2y=3x 3(+2)- D. 2y=3x 3(-2)- 9、已知三角形两边长分别为2和9,第三边的长为一元二次方程214480x x -+=的一根,则这个三角形的周长为( )A. 11B. 17C. 17或19D. 1910、已知:抛物线2(1)y a x =+的顶点为A ,图象与y 轴负半轴交点为B ,且OB=OA ,若点 C (﹣3 ,b )在抛物线上,则△ABC 的面积为( )A. 3B. 3.5C. 4D. 4.5二、填空题:(每小题3分,共18分)11、2014年一月份越南发生禽流感的养鸡场100家,后来二, 三月份新发生禽流感的养鸡场共250家,设二, 三月份平均每月禽流感的感染率为x ,依题意列出的方程是12、关于x 的一元二次方程22(1)x 10a x a -++-=的一个根是0 ,则a 的值为13、若关于x 的方程220x ax -+=与2(1)0x a x a -++=有一个相同的实数根,则a 的值是 14、已知抛物线2y x =沿直线y=x个单位后,所得的抛物线为15、如图,在平面直角坐标系中,二次函数2y ax c =+(a ≠0)的图象过正方形ABOC 的三个顶点A 、B 、C ,则ac 的值为16、关于x 的一元二次方程22(2k 1)x k 20x +++-=的两实数根的平方和等于11,则k 的值 为三、解答题:(共72分)17(8分)、解方程: (1) 2470x x --= (2) x x x 22)1(3-=-18(8分)、有一个人患了流感,经过两轮传染后,共有100人患了流感,求每轮传染中平均一个人传染多少个人?x2 / 519(8分)、已知二次函数的图象的顶点坐标为(1 ,2),且经过点(3 ,-10),求这个抛物线的解析式;20(8分)、已知关于x 的方程0)3(4122=+--m x m x 有两个不相等的实数根,求m 取最大整数值时方程的解;21(8分)、已知关于x 的一元二次方程210ax bx ++=中,1b m =+ ; (1)若a=4 ,求b 的值;(2)若方程210ax bx ++=有两个相等的实数根,求方程的根;22(8分)、如图,利用一面墙(墙EF 最长可利用28米),围成一个矩形的花园ABCD ,与围墙平行的一边BC 上要预留2米宽的入口(如图中虚线MN 所示,不用砌墙),用砌60米长的墙的材料;(1)当矩形的长BC 为多少米时,矩形花园的面积为(2)能否围成480平方米的矩形花园,为什么?23(10分)、如图,直线AB :3y kx =+过点(—2 ,4)与抛物线212y x =交于A 、B 两点; (1)直接写出点A 、点B 的坐标;(2)在直线AB 的下方的抛物线上求点P ,使△ABP 的面积等于5;24(12分)、如图,抛物线2(1)y x m =-+的图象与x 轴交于A 、B 两点,与y 轴交于点C ,且AB=4 ;(1)求抛物线的解析式;(2)将抛物线沿对称轴向上平移k 个单位长度后与线段BC 交于D 、E 两个不同的点,求k 的取值范围; (3)M 为线段OB 上一点(不含O 、B 两点)过点M 作y 轴的平行线交抛物线于点N ,交线段BC 于点P ,若△PCN 为等腰三角形,求M 点的坐标;蔡甸区部分学校九年级10月月考数学试卷一、选择题(共10小题,每小题3分,共30分)x x xx3 / 5二、填空题(共6小题,每小题3分,共18分)11、 _ 12、 13、14、 15、 16、4 / 518、 19x = 211x =-(舍) 19、 23(1)2y x =--+ 20、 4x =-±21、 b=5 ,121x x ==-22、 (1) 112x = 250x =(舍) (2)不能 23、 (1) A (2 ,2) B (—3,92) (2) P (1,12)或P (—2 ,2) 24、 (1) 223y x x =-- (2) 0≤k <94(3) M (2 ,0)或 M (1 ,0)或 M (3-,0)5 / 5。
湖北省武汉市蔡甸区部分学校2015届九年级十月联考物理(附答案)$477950

2014~2015学年度武汉市蔡甸区部分学校九年级调研测试物理试题(满分70分)2014年10月31日一、单项选择题(每小题3分,12小题,共36分)1.研究物理问题时经常用到科学的研究方法。
如探究“真空能否传声”就是在实验基础上进行理想推理而得出结论,研究以下问题的方法与此方法相同的是()A.分子热运动B.牛顿第一定律C.电阻上的电流与两端电压的关系D.研究压力产生的效果2.如图是某物质加热时温度随时间变化的图象。
下列对图象的分析正确的是()A.该物质一定是晶体B.T2一定是物质的沸点C.0~t1时间内物质的分子热运动加剧D.t1~t2时间内物质的温度不变,内能不变3.物理研究中常用图像来表示两个量(x,y)之间的关系,以使研究的问题变得直观明了。
下列两个量之间的关系不符合如图所示的是()A.物质的密度与质量的关系B.物体受到的重力与质量的关系C.匀速运动的物体通过的路程与时间的关系D.同一导体中通过的电流与该导体两端电压的关系4.如图所示,电源电压保持不变,当闭合开关S,滑动变阻器的滑片P向右移动的过程中,下列说法正确的是()A.电压表V1的示数增大,电压表V2的示数减小B.通过电阻R1和R2的电流不一定相等C.电压表V1减小的示数等于V2增大的示数D.电压表V1减小的示数小于V2增大的示数5.如图所示的电路中,闭合开关,发现每个电表都有一定的示数.向右移动变阻器的滑片,则()A.电流表A1示数减小,电流表A2和电压表V示数增加B.电流表A1和A2示数都减小,电压表V示数增加C.电流表A1、A2和电压表V示数都减小D.电流表A1、A2和电压表V示数都增加6.某同学在探究串联电路电流规律的实验中,按下图接好电路,闭合开关后,发现灯L1、L2都不发光,电流表示数为零.他用电压表分别接到电流表、灯L1、灯L2两端测量电压,发现电流表、灯L1两端电压均为零,灯L2两端电压不为零.电路的故障可能是()A.电流表断路B.灯L1断路C.灯L2断路D.灯L2短路第5题第6题第7题7.如图所示的电路中,当开关S闭合后()A.若A表是电流表,B表是电压表,则电阻R1、R2并联B.若A表是电流表,B表是电压表,则电阻R1、R2串联C.若A表是电压表,B表是电流表,则电阻R1、R2并联D.若A表是电压表,B表是电流表,则电阻R1、R2串联8.电现象中有四个同学们非常熟悉的实验:a、探究电流与电压的关系;b、探究电流与电阻的关系;c、伏安法测小灯泡的电阻;d、探究影响电阻大小的因素。
武汉市蔡甸区部分学校2015届九年级十月联考数学试题

A.k<1
B. k<-1 C.k≥1
D.k>1
3.抛物线 y (x 1)2 A.(1,4) B.(-1,44的) 顶点C坐.(1标,-是4) (
D.()-1,-4)
4. 下列图形中,中心对称图形有( ).
5.如图 CD 是⊙O 直径,圆心角∠BOD=102°,则圆周角∠BAC 的大小为(
A、156°
(1)直接写出 y 与 x、c 与 y 之间的函数关系式。
(2)若一天的销售利润 w=xy-c
①直接写出每一天的利润 w 与 x 之间的函数关系式。
②当销售价格 x 为多少时,w 最大?最大值是多少?
24.(本题 10 分)如图(1) , 已 知 △ ABC 是 等 腰 直 角 三 角 形 , ∠ BAC= 90°,点 D 是 BC 的中点.作正方形 DEFG,使点 A、C 分别在 DG 和 DE
21.(本题 8 分)如 图 :在 Rt△ ABC 中 , AC=4, BC=8,
(1)以 C 为原点,建立适当的平面直角坐标系,求线段 AB 所在直线的解析 式。 (2)点 D 为线段 AB 上一动点,求 AD 长度为多少时,矩形 DECF 面积最大,并求出最大值。
B
D
E
A
FC
22. (本题 8 分)如图,AC 为⊙O 的弦,CE⊥AC 交⊙O 于 E,B 为 AC 上的一
A、8
B、9
C、10
D、11
8. 已知 y=ax2﹣2x+1 与 x 轴没有交点,那么该抛物线的顶点在第( )象限。
A.一
B.二
C.三
D.四
三、解答题(共 9 小题,共 72 分) 17.(本题 6 分)解方程: x 2 18·(本题 6 分)若一元二次方-3x程-1(=0k+2) x 2 +4x-2=0 有实数根,求 k 的最小整数 值. 19.(本题 6 分)某商店 4 月份销售额为 50 万元,第二季度的总销售额为 182 万元, 若 5、6 两个月的月增长率相同,求月增长率. 20.(本题 6 分)如图,将一个钝角△ABC(其中∠ABC=120°)绕点 B 顺时针旋转,使 得点 A 对应点 A1,C 点落在 AB 的延长线上的点 C1 处,连结 AA1. (1)写出旋转角的度数;(2)求证:∠A1AC=∠C1.
湖北省武汉市2015年中考数学真题试题(含扫描答案)

中考衣食住用行衣:中考前这段时间,提醒同学们出门一定要看天气,否则淋雨感冒,就会影响考场发挥。
穿着自己习惯的衣服,可以让人在紧张时产生亲切感和安全感,并能有效防止不良情绪产生。
食:清淡的饮食最适合考试,切忌吃太油腻或者刺激性强的食物。
如果可能的话,每天吃一两个水果,补充维生素。
另外,进考场前一定要少喝水!住:考前休息很重要。
好好休息并不意味着很早就要上床睡觉,根据以往考生的经验,太早上床反而容易失眠。
考前按照你平时习惯的时间上床休息就可以了,但最迟不要超过十点半。
用:出门考试之前,一定要检查文具包。
看看答题的工具是否准备齐全,应该带的证件是否都在,不要到了考场才想起来有什么工具没带,或者什么工具用着不顺手。
行:看考场的时候同学们要多留心,要仔细了解自己住的地方到考场可以坐哪些路线的公交车?有几种方式可以到达?大概要花多长时间?去考场的路上有没有修路堵车的情况?考试当天,应该保证至少提前20分钟到达考场。
2015年武汉市初中毕业生学业考试数学试卷一、选择题(共10小题,每小题3分,共30分)1.在实数-3、0、5、3中,最小的实数是()A.-3 B.0 C.5 D.32.若代数式2x在实数范围内有意义,则x的取值范为是()A.x≥-2 B.x>-2 C.x≥2 D.x≤23.把a2-2a分解因式,正确的是()A.a(a-2) B.a(a+2) C.a(a2-2) D.a(2-a)4.一组数据3、8、12、17、40的中位数为( )A .3B .8C .12D .175.下列计算正确的是( )A .2x 2-4x 2=-2B .3x +x =3x 2C .3x ·x =3x2D .4x 6÷2x 2=2x 36.如图,在直角坐标系中,有两点A (6,3)、B (6,0).以原点O 为位似中心,相似比为31,在第一象限内把线段AB 缩小后得到线段CD ,则点C 的坐标为( ) A .(2,1) B .(2,0) C .(3,3) D .(3,1)7.如图,是由一个圆柱体和一个长方体组成的几何体,其主视图是( )8.下面的折线图描述了某地某日的气温变化情况,根据图中信息,下列说法错误的是( )A .4:00气温最低B .6:00气温为24℃C .14:00气温最高D .气温是30℃的为16:009.在反比例函数x my 31-=图象上有两点A (x 1,y 1)、B (x 2,y 2),x 1<0<y 1,y 1<y 2,则m 的取值范围是( )A .m >31B .m <31C .m ≥31D .m ≤3110.如图,△ABC 、△EFG 均是边长为2的等边三角形,点D 是边BC 、EF 的中点,直线AG 、FC 相交于点M .当△EFG 绕点D 旋转时,线段BM 长的最小值是( ) A .32- B .13+ C .2D .13-二、填空题(共6小题,每题3分,共18分)11.计算:-10+(+6)=_________12.中国的领水面积约为370 000 km2,将数370 000用科学记数法表示为_________13.一组数据2、3、6、8、11的平均数是_________14.如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA 和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省__元15.定义运算“*”,规定x*y=ax2+by,其中a、b为常数,且1*2=5,2*1=6,则2*3=_________ 16.如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA 上,则MP+PQ+QN的最小值是_________三、解答题(共8小题,共72分)17.(本题8分)已知一次函数y=kx+3的图象经过点(1,4)求这个一次函数的解析式求关于x的不等式kx+3≤6的解集18.(本题8分)如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC =DF求证:(1) △ABC≌△DEF(2) AB∥DE19.(本题8分)一个不透明的口袋中有四个完全相同的小球,它们分别标号为1,2,3,4(1) 随机摸取一个小球,直接写出“摸出的小球标号是3”的概率(2) 随机摸取一个小球然后放回,再随机摸出一个小球,直接写出下列结果:①两次取出的小球一个标号是1,另一个标号是2的概率②第一次取出标号是1的小球且第二次取出标号是2的小球的概率20.(本题8分),如图,已知点A(-4,2)、B(-1,-2),□ABCD的对角线交于坐标原点O(1) 请直接写出点C、D的坐标(2) 写出从线段AB到线段CD的变换过程(3) 直接写出□ABCD的面积21.(本题8分)如图,AB 是⊙O 的直径,∠ABT =45°,AT =AB (1) 求证:AT 是⊙O 的切线(2) 连接OT 交⊙O 于点C ,连接AC ,求tan ∠TAC 的值22.(本题8分)已知锐角△ABC 中,边BC 长为12,高AD 长为8(1) 如图,矩形EFGH 的边GH 在BC 边上,其余两个顶点E 、F 分别在AB 、AC 边上,EF 交AD 于点K ① 求AKEF的值 ② 设EH =x ,矩形EFGH 的面积为S ,求S 与x 的函数关系式,并求S 的最大值(2) 若ABAC ,正方形PQMN 的两个顶点在△ABC 一边上,另两个顶点分别在△ABC 的另两边上,直接写出正方形PQMN 的边长23.(本题10分)如图,△ABC 中,点E 、P 在边AB 上,且AE =BP ,过点E 、P 作BC 的平行线,分别交AC 于点F 、Q .记△AEF 的面积为S 1,四边形EFQP 的面积为S 2,四边形PQCB 的面积为S 3 (1) 求证:EF +PQ =BC (2) 若S 1+S 3=S 2,求AEPE的值 (3) 若S 3-S 1=S 2,直接写出AEPE的值24.(本题12分)已知抛物线y=x2+c与x轴交于A(-1,0),B两点,交y轴于点C(1) 求抛物线的解析式(2) 点E(m,n)是第二象限内一点,过点E作EF⊥x轴交抛物线于点F,过点F作FG⊥y轴于点G,连接CE、CF,若∠CEF=∠CFG,求n的值并直接写出m的取值范围(利用图1完成你的探究)(3) 如图2,点P是线段OB上一动点(不包括点O、B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长。
2015年湖北省武汉市中考数学试卷及详细解析

2015年湖北省武汉市中考数学试卷及详细解析一、选择题(共10小题,每小题3分,共30分)下列各题中均有四个备选答案,其中有且只有一个是正确的,请在答题卡上将正确答案的代号涂黑.1.(3分)(2015•武汉)在实数﹣3,0,5,3中,最小的实数是()A.﹣3 B. 0 C. 5 D. 32.(3分)(2015•武汉)若代数式在实数范围内有意义,则x的取值范围是()A.x≥﹣2 B.x>﹣2 C.x≥2 D.x≤23.(3分)(2015•武汉)把a2﹣2a分解因式,正确的是()A.a(a﹣2)B.a(a+2)C.a(a2﹣2)D.a(2﹣a)4.(3分)(2015•武汉)一组数据3,8,12,17,40的中位数为()A. 3 B. 8 C. 12 D. 175.(3分)(2015•武汉)下列计算正确的是()A.2a2﹣4a2=﹣2 B.3a+a=3a2C.3a•a=3a2D.4a6÷2a3=2a26.(3分)(2015•武汉)如图,在直角坐标系中,有两点A(6,3),B(6,0),以原点O位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为()A.(2,1)B.(2,0)C.(3,3)D.(3,1)7.(3分)(2015•武汉)如图,是由一个圆柱体和一个长方体组成的几何体.其主视图是()A.B.C.D.8.(3分)(2015•武汉)下面的折线图描述了某地某日的气温变化情况.根据图中信息,下列说法错误的是()A . 4:00气温最低B . 6:00气温为24℃C .14:00气温最高 D . 气温是30℃的时刻为16:009.(3分)(2015•武汉)在反比例函数y=图象上有两点A (x 1,y 1),B (x 2,y 2),x 1<0<x 2,y 1<y 2,则m 的取值范围是( )A . m >B . m <C .m ≥D .m ≤10.(3分)(2015•武汉)如图,△ABC ,△EFG 均是边长为2的等边三角形,点D 是边BC 、EF 的中点,直线AG 、FC 相交于点M .当△EFG 绕点D 旋转时,线段BM 长的最小值是( )A . 2﹣B .+1 C . D . ﹣1二、填空题(共6小题,每小题3分,共18分)请将答案填在答题卡对应题号的位置上. 11.(3分)(2015•武汉)计算:﹣10+(+6)=12.(3分)(2015•武汉)中国的领水面积约为370 000km 2,将数370 000用科学记数法表示为. 13.(3分)(2015•武汉)一组数据2,3,6,8,11的平均数是. 14.(3分)(2015•武汉)如图所示,购买一种苹果,所付款金额y (元)与购买量x (千克)之间的函数图象由线段OA 和射线AB 组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省 元.15.(3分)(2015•武汉)定义运算“*”,规定x*y=ax2+by,其中a、b为常数,且1*2=5,2*1=6,则2*3=.16.(3分)(2015•武汉)如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是.三、解答题(共8小题,共72分)下列各题解答应写出文字说明,证明过程或演算过程.17.(8分)(2015•武汉)已知一次函数y=kx+3的图象经过点(1,4).(1)求这个一次函数的解析式;(2)求关于x的不等式kx+3≤6的解集.18.(8分)(2015•武汉)如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.求证:(1)△ABC≌△DEF;(2)AB∥DE.19.(8分)(2015•武汉)一个不透明的口袋中有四个完全相同的小球,它们分别标号为1,2,3,4.(1)随机摸取一个小球,直接写出“摸出的小球标号是3”的概率;(2)随机摸取一个小球然后放回,再随机摸出一个小球,直接写出下列结果:①两次取出的小球一个标号是1,另一个标号是2的概率;②第一次取出标号是1的小球且第二次取出标号是2的小球的概率.20.(8分)(2015•武汉)如图,已知点A(﹣4,2),B(﹣1,﹣2),平行四边形ABCD的对角线交于坐标原点O.(1)请直接写出点C、D的坐标;(2)写出从线段AB到线段CD的变换过程;(3)直接写出平行四边形ABCD的面积.21.(8分)(2015•武汉)如图,AB是⊙O的直径,∠ABT=45°,AT=AB.(1)求证:AT是⊙O的切线;(2)连接OT交⊙O于点C,连接AC,求tan∠TAC.22.(10分)(2015•武汉)已知锐角△ABC中,边BC长为12,高AD长为8.(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.①求的值;②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.23.(10分)(2015•武汉)如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P 作BC的平行线,分别交AC于点F、Q,记△AEF的面积为S1,四边形EFQP的面积为S2,四边形PQCB的面积为S3.(1)求证:EF+PQ=BC;(2)若S1+S3=S2,求的值;(3)若S3+S1=S2,直接写出的值.24.(12分)(2015•武汉)已知抛物线y=x2+c与x轴交于A(﹣1,0),B两点,交y轴于点C.(1)求抛物线的解析式;(2)点E(m,n)是第二象限内一点,过点E作EF⊥x轴交抛物线于点F,过点F作FG⊥y 轴于点G,连接CE、CF,若∠CEF=∠CFG.求n的值并直接写出m的取值范围(利用图1完成你的探究).(3)如图2,点P是线段OB上一动点(不包括点O、B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长.1.考点:实数大小比较.分析:正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,据此判断即可.解答:解:根据实数比较大小的方法,可得﹣3<0<3<5,所以在实数﹣3,0,5,3中,最小的实数是﹣3.故选:A.点评:此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.2.考点:二次根式有意义的条件.分析:根据二次根式的性质,被开方数大于等于0,就可以求解.解答:解:根据题意得:x﹣2≥0,解得x≥2.故选:C.点评:本题考查了二次根式有意义的条件,知识点为:二次根式的被开方数是非负数.3.考点:因式分解-提公因式法.专题:计算题.分析:原式提取公因式得到结果,即可做出判断.解答:解:原式=a(a﹣2),故选A.点评:此题考查了因式分解﹣提公因式法,熟练掌握提取公因式的方法是解本题的关键.4..考点:中位数.分析:首先把这组数据3,8,12,17,40从小到大排列,然后判断出中间的数是多少,即可判断出这组数据的中位数为多少.解答:解:把3,8,12,17,40从小到大排列,可得3,8,12,17,40,所以这组数据3,8,12,17,40的中位数为12.故选:C.点评:此题主要考查了中位数的含义和求法的应用,要熟练掌握,解答此题的关键是要明确:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.5.解:A、原式=﹣2a2,错误;B、原式=4a,错误;C、原式=3a2,正确;D、原式=2a3,错误.故选C.6.解:由题意得,△ODC∽△OBA,相似比是,∴=,又OB=6,AB=3,∴OD=2,CD=1,∴点C的坐标为:(2,1),故选:A.7.解:从正面看下面是一个比较长的矩形,上面是一个比较宽的矩形.故选:B.8.解:A、由横坐标看出4:00气温最低是24℃,故A正确;B、由纵坐标看出6:00气温为24℃,故B正确;C、由横坐标看出14:00气温最高31℃;D、由横坐标看出气温是30℃的时刻是12:00,16:00,故D错误;故选:D.9.解:∵x1<0<x2时,y1<y2,∴反比例函数图象在第一,三象限,∴1﹣3m>0,解得:m<.故选B.10.解:连接AD、DG、BO、OM,如图.∵△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,∴AD⊥BC,GD⊥EF,DA=DG,DC=DF,∴∠ADG=90°﹣∠CDG=∠FDC,=,∴△DAG∽△DCF,∴∠DAG=∠DCF.∴A、D、C、M四点共圆.根据两点之间线段最短可得:BO≤BM+OM,即BM≥BO﹣OM,当M在线段BO与该圆的交点处时,线段BM最小,此时,BO===,OM=AC=1,则BM=BO﹣OM=﹣1.故选D.11.考点:有理数的加法.专题:计算题.分析:原式利用异号两数相加的法则计算即可得到结果.解答:解:原式=﹣(10﹣6)=﹣4.故答案为:﹣4.点评:此题考查了有理数的加法,熟练掌握运算法则是解本题的关键.12.解:370 000=3.7×105,故答案为:3.7×105.13.解:(2+3+6+8+11)÷5=30÷5=6所以一组数据2,3,6,8,11的平均数是6.故答案为:6.14.解:由线段OA的图象可知,当0<x<2时,y=10x,1千克苹果的价钱为:y=10,设射线AB的解析式为y=kx+b(x≥2),把(2,20),(4,36)代入得:,解得:,∴y=8x+4,当x=3时,y=8×3+4=28.当购买3千克这种苹果分三次分别购买1千克时,所花钱为:10×3=30(元),30﹣28=2(元).则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省2元.15.解:根据题中的新定义化简已知等式得:,解得:a=1,b=2,则2*3=4a+3b=4+6=10,故答案为:10.16.解:作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值.根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,∴△ONN′为等边三角形,△OMM′为等边三角形,∴∠N′OM′=90°,∴在Rt△M′ON′中,M′N′==.故答案为.17.解:(1)∵一次函数y=kx+3的图象经过点(1,4),∴4=k+3,∴k=1,∴这个一次函数的解析式是:y=x+3.(2)∵k=1,∴x+3≤6,∴x≤3,即关于x的不等式kx+3≤6的解集是:x≤3.18证.明:(1)∵AC⊥BC于点C,DF⊥EF于点F,∴∠ACB=∠DFE=90°,在△ABC和△DEF中,,∴△ABC≌△DEF(SAS);(2)∵△ABC≌△DEF,∴∠B=∠DEF,∴AB∥DE.19.解:(1)∵一个不透明的口袋中有四个完全相同的小球,它们分别标号为1,2,3,4,∴随机摸取一个小球,直接写出“摸出的小球标号是3”的概率为:;(2)画树状图得:则共有16种等可能的结果;①∵两次取出的小球一个标号是1,另一个标号是2的有2种情况,∴两次取出的小球一个标号是1,另一个标号是2的概率为:=;②∵第一次取出标号是1的小球且第二次取出标号是2的小球的只有1种情况,∴第一次取出标号是1的小球且第二次取出标号是2的小球的概率为:.20.解:(1)∵四边形ABCD是平行四边形,∴四边形ABCD关于O中心对称,∵A(﹣4,2),B(﹣1,﹣2),∴C(4,﹣2),D(1,2);(2)线段AB到线段CD的变换过程是:线段AB向右平移5个单位得到线段CD;(3)由(1)得:A到y轴距离为:4,D到y轴距离为:1,A到x轴距离为:2,B到x轴距离为:2,∴S ABCD的可以转化为边长为;5和4的矩形面积,∴S ABCD=5×4=20.21解:(1)∵∠ABT=45°,A T=AB.∴∠TAB=90°,∴TA⊥AB,∴AT是⊙O的切线;(2)作CD⊥AT于D,∵TA⊥AB,TA=AB=2OA,设OA=x,则AT=2x,∴OT=x,∴TC=(﹣1)x,∵CD⊥AT,TA⊥AB∴CD∥AB,∴==,即==,∴CD=(1﹣)x,TD=2(1﹣)x,∴AD=2x﹣2(1﹣)x=x,∴tan∠TAC===﹣1.22..解:(1)①∵EF∥BC,∴,∴=,即的值是.②∵EH=x,∴KD=EH=x,AK=8﹣x,∵=,∴EF=,∴S=EH•EF=x(8﹣x)=﹣+24,∴当x=4时,S的最大值是24.(2)设正方形的边长为a,①当正方形PQMN的两个顶点在BC边上时,,解得a=.②当正方形PQMN的两个顶点在AB或AC边上时,∵AB=AC,AD⊥BC,∴BD=CD=12÷2=6,∴AB=AC=,∴AB或AC边上的高等于:AD•BC÷AB=8×12÷10=∴,解得a=.综上,可得正方形PQMN的边长是或.23.(1)证明:∵EF∥BC,PQ∥BC,∴,,∵AE=BP,∴AP=BE,∴==1,∴=1,∴EF+PQ=BC;(2)解:过点A作AH⊥BC于H,分别交PQ于M、N,如图所示:设EF=a,PQ=b,AM=h,则BC=a+b,∵EF∥PQ,∴△AEF∽△APQ,∴=,∴AN=,MN=(﹣1)h,∴S1=ah,S2=(a+b)(﹣1)h,S3=(b+a+b)h,∵S1+S3=S2,∴ah+(a+b+b)h=(a+b)(﹣1)h,解得:b=3a,∴=3,∴=2;(3)解:∵S3﹣S1=S2,∴(a+b+b)h﹣ah=(a+b)(﹣1)h,解得:b=(1±)a(负值舍去),∴b=(1+)a,∴=1+,∴=.24.解:(1)把A(﹣1,0)代入得c=﹣,∴抛物线解析式为(2)如图1,过点C作CH⊥EF于点H,∵∠CEF=∠CFG,FG⊥y轴于点G∴△EHC∽△FGC∵E(m,n)∴F(m,)又∵C(0,)∴EH=n+,CH=﹣m,FG=﹣m,CG=m2又∵,则∴n+=2∴n=(﹣2<m<0)(3)由题意可知P(t,0),M(t,)∵PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,∴△OPM∽△QPB.∴.其中OP=t,PM=,PB=1﹣t,∴PQ=.BQ=∴PQ+BQ+PB=.∴△PBQ的周长为2.。
武汉市武昌区C组联盟2015届九年级10月月考数学试题及答案

2014-2015学年上学期九年级北片联考命题人:熊利 审题人:张蓉华一、选择题(共10小题,每小题3分,共30分) 1、下列图形中,不是中心对称图形........的是A. B. C. D. 2.下列方程中是关于x 的一元二次方程的是 A .2215x x+= B .2230x xy y +-= C. 210x x ++= D .20ax bx c ++=3.如图可以看作是一个等腰直角三角形旋转若干次得到,则每次旋转的度数可以是A .900B .60C . 45D .304.下列方程中有相等的实数根的是A. 210x x ++=B.2810x x ++=C.220x x ++=D.2210x x -+=5.抛物线1)3(22+-=x y 的顶点坐标是A .(3,1)B .(3,-1)C .(-3,1)D .(-3,-1)6.若点(2,5),(4,5)在抛物线2y ax bx c =++上,则它的对称轴是 A .0x = B .1x = C .2x = D .3x =7.如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是A.点MB.格点NC.格点PD.格点Q8.用配方法解方程2870x x ++=,则配方正确的是A. ()249x -= B. ()249x += C. ()2816x -= D. ()2857x +=9.某品牌电脑2009年的销售单价为7200元,由于科技进步和新型电子原材料的开发运用,该品牌电脑成本不断下降,销售单价也逐年下降.至2011年该品牌电脑的销售单价为4900元,设2009年至2010年,2010年至2011年这两年该品牌电脑的销售单价年平均降低率均为x ,则可列出的正确的方程为A. 24900(1)7200x += B. 7200(12)4900x -= C. 4900(1)7200(1)x x +=- D. 27200(1)4900x -=10.若1212,()x x x x <是关于x 的方程()()()x a x b a b a b --=-<的两个根,则实数12,,,x x a b 的大小关系为A.12x x a b <<<B. 12x a b x <<<C. 12a x x b <<<D. 12a x b x <<<二、填空题(共6小题,每小题3分,共18分)11. 函数21y x x =-+的图象与y 轴的交点坐标是 ;12. 若12,x x 是一元二次方程2430x x ++=的两个根,则12x x 的值是 ;13. 关于x 的一元二次方程22(1)10p x x p --+-=的一个根为,则实数的值是 ;14. 参加某次商品交易会的每两家公司之间都签订了一份合同,所有公司共签 订了36份合同,则共有 家公司参加了本次商品交易会。
2022-2023学年湖北省武汉市蔡甸区九年级(上)月考数学试卷(10月份)(附答案详解)

2022-2023学年湖北省武汉市蔡甸区九年级(上)月考数学试卷(10月份)一、选择题(本大题共10小题,共30.0分。
在每小题列出的选项中,选出符合题目的一项)1.方程2x2−2x−1=0的一次项系数、常数项分别是( )A. 1、2B. 2、−1C. −2、−1D. −2、12.方程x2−x−1=0的根的情况是( )A. 有两个不等实根B. 有两个相等实根C. 无实根D. 以上三种情况都有可能3.已知m是一元二次方程x2−4x+1=0的一个根,则2021−m2+4m的值为( )A. −2021B. 2021C. 2020D. 20224.已知方程x2+px+q=0的两个根分别是2和−3,则( )A. p=−1,q=−6B. p=1,q=6C. p=1,q=−6D. p=−1,q=65.顶点(−5,−1),且开口方向、形状与函数y=−13x2的图象相同的抛物线的是( )A. y=13(x−5)2+1 B. y=−13x2−5C. y=−13(x+5)2−1 D. y=13(x−5)2−16.将抛物线y=x2+1先向上平移2个单位,再向右平移1个单位后所得的抛物线是( )A. y=(x−1)2+3B. y=(x+1)2+3C. y=(x+2)2D. y=(x+1)2−17.已知二次函数y=3(x−1)2+ℎ的图象上有三点,A(−0.5,y1),B(2.5,y2),C(3,y3),则y1,y2,y3的大小关系为( )A. y1=y2<y3B. y1<y2<y3C. y1<y2=y3D. y3<y1=y28.某种细胞分裂,一个细胞经过两轮分裂后,共有a个细胞,设每轮分裂中平均一个细胞分裂成n个细胞,那么可列方程为( )A. n2=aB. (1+n)2=aC. 1+n+n2=aD. n+n2=a9.下列说法:①若一元二次方程x2+bx+a=0有一个根是−a(a≠0),则代数式a−b的值是−1②若a+b+c=0,则x=a+b+c是一元二次方程ax2+bx+c=0的一个根③若b=2a+3c,则一元二次方程ax2+bx+c=0有不相等的两个实数根④当m取整数−1或1时,关于x的一元二次方程mx2−4x+4=0与x2−4mx+4m2−4m−5=0的解都是整数.其中正确的有( )A. 1个B. 2个C. 3个D. 4个10.设关于x的方程ax2+(a+2)x+9a=0有两个不相等的实数根x1、x2,且x1<1<x2,那么实数a的取值范围是( )A. a<-211B. 27<a<25C. a>25D. -211<a<0二、填空题(本大题共6小题,共18.0分)11.方程x2=2x的根为______.12.已知x=1是方程x2+ax+2=0的一个根,则a的值为______ .13.抛物线y=x2−2x−2的顶点坐标是______ .14.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t−32t2.在飞机着陆滑行中,最后4s滑行的距离是______m.15.抛物线y=ax2+bx+c的对称轴为直线x=−1,部分图象如图所示,下列判断中:①abc>0;②2a−b=0;③b2−4ac>0;④4a+2b+c>0.其中判断正确的序号是______.16.如图,△ABC是等边三角形,AB=6,点D在边AB上,且BD=√3,E是边AC的中点,将线段BD绕点B顺时针旋转,点D的对应点为F,连接AF,EF,当△AEF为直角三角形时,AF=______.三、解答题(本大题共8小题,共72.0分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
蔡甸区部分学校2015九年级10月月考数学试卷
一、选择题(每小题3分,共30分)
1.已知a 是方程012=--x x 的一个根,则代数式a a -2的值等于( ) A .-1 B .0 C .1 D .2
2.若关于x 的方程 k x -=+1)1(2 没有实数根,则K 的取值范围是( ) A.k<1 B. k<-1 C.k≥1 D.k>1
3.抛物线4)1(y 2-+=x 的顶点坐标是 ( )
A.(1,4) B.(-1,4) C.(1,-4) D.(-1,-4) 4. 下列图形中,中心对称图形有( ).
5.如图CD 是⊙O 直径,圆心角∠BOD=102°,则圆周角∠BAC 的大小为( ) A 、156° B 、78° C 39° D 12°
6.若方程01x 32=--x 的两根1x ,2x ,则2
11
1x x +的值为( )
A .3
B .-3
C .31 D
.3
1
-
7.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、
支干和小分支的总数是91,则每个支干长出( )支小分支. A 、8 B 、9 C 、10 D 、11
8. 已知y=ax 2
﹣2x+1与x 轴没有交点,那么该抛物线的顶点在第( )象限。
A .一 B .二 C .三 D .四
9.如图,四边形ABCD 中,∠B+∠D=180°,AB=AD ,∠BAD=60°,
ABCD
S 4
=四边形,则线段AC 的长为( ) A .1 C 第10题图
10. 如图,Rt △ABC 中,∠C=90°,∠A=30°,在AC 边上取点O 为圆心画圆,使⊙O 经过A 、B 两点,下列结论:
①AO=2CO ②AO=BC ③以O 圆心,OC 为半径的圆与AB 相切 ④延长
BC 交⊙O 于D ,则A 、B 、D 是⊙O 的三等分点。
其中正确的序号
D
C
B
A
是()
A 、①②③④
B 、①②③
C 、②③④
D 、①③④ 二、填空题(每小题3分,共18分)
11.点(-2, 1)关于原点对称的点的坐标为 .
12.方程240x kx -+=有两个相等的实数根,则k 的值是 . 13.直线17+=x y 与抛物线532++=x x y 的图象有 个交点。
14. 将抛物线12+=x y 向左平移2个单位,再向下平移3个单位,所得到的抛物线的关系式为 。
15.汽车刹车后行驶的距离s与行驶时间t(秒)的函数关系是2615s t t -=,汽车从刹车到停下来所用时间是 秒。
16. 如图,BC 为⊙O 的直径,BC=42,弧AB=弧AC ,P 为BC 上一动点,M 为AB 的中点,设△PAM 的周长为m ,则m 的取值范围是 。
三、解答题(共9小题,共72分) 17.(本题6分)解方程:2
x -3x-1=0
18〃(本题6分)若一元二次方程(k+2)2x +4x-2=0有实数根,求k 的最小整数值. 19.(本题6分)某商店4月份销售额为50万元,第二季度的总销售额为182万元,若5、6两个月的月增长率相同,求月增长率.
20.(本题6分)如图,将一个钝角△ABC (其中∠ABC =120°)绕点B 顺时针旋转,使得点A 对应点A 1,C 点落在AB 的延长线上的点C 1处,连结AA 1. (1)写出旋转角的度数;(2)求证:∠A 1AC =∠C 1.
21.(本题8分)如图:在Rt △ABC 中,AC=4,BC=8,
(1)以C 为原
点,建
立适当的平面直角坐标系,求线段AB 所在直线的解析式。
(2)点D 为线段AB 上一动点,求AD 长度为多少时,矩形DECF 面积最大,并求出最大值。
22. (本题8分)如图,AC 为⊙O 的弦,CE ⊥AC 交⊙O 于E ,B 为AC 上的一 点,BC=CE,EF ⊥BE 交⊙O 于F ,⊙O 的直径为13,BE=52 .
(1)求证:BE ∥AF (2)求AB 的长 (3)求BF 的长
23. (本题10分)物价局规定A 产品的市场销售单价在15元到40元之间。
某商店在销售A 产品的过程中发现:销售A 产品的成本c (单位:元)与销售件数y (单位:件)成正比例,同时每天的销售件数y 与销售价格x (单位:元╱件)之间满足一次
(1 (2)若一天的销售利润w=xy -c
①直接写出每一天的利润w 与x
之间的函数关系式。
②当销售价格x 为多少时,w 最大?最大值是多少?
24.(本题10分)如图(1),
已知
△ABC 是等腰直角三角形,∠BAC=
90°,点D 是BC 的中点.作正方形DEFG ,使点A 、C 分别在DG 和DE 上,连接AE 、BG .
(1)试猜想线段BG
E
B
和AE的关系,请写出你的结论并加以证明;
(2)将正方形DEFG绕点D逆时针方向旋转一角度a后(0°<a<90°),如图(2),通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由:
(3)若BC=DE=2,正方形DEFG绕点D逆时针方向旋转角度a(0°<a<360°)过程中,当AE为最大值时,则AF的值为.
25. (本题12分)如图1,抛物线c
=2与x轴交于A,B两点(点A在点B
+
bx
ax
y+
的左侧),与y轴相交于点C,顶点为D,且A(-1,0),B(3,0),C(0,3)
(1)求抛物线的解析式和抛物线的对称轴。
