第5章 多电子原子泡利原理
多电子原子∶泡利原理

第五章多电子原子:泡利原理基本要求:1、掌握电子组态的描述,L-S耦合和j-j耦合法则。
2、掌握泡利不相容原理的叙述,懂得写出同科电子合成的原子状态。
3、初步掌握原子结构和元素性质周期变化之间的内在联系。
掌握周期表中原子内层电子分布的一般规律。
重点和难点:1、多电子原子的能级、洪特定则和朗德间隔定则;2、多电子原子跃迁的选择定则;3、泡利原理、能量最低原理;4、元素的基态原子态的确定。
教学方案如下在以前几章中我们讨论了单电子原子体系和具有一个价电子的碱金属原子的光谱,从而获得这些原子能级的情况,并通过电子自旋说明了怎样出现双层结构。
从那些讨论,我们对最简单原子的内部状况已有了一个扼要的了解。
这些知识也是进一步研究较复杂原子结构的基础,本章将讨论具有两个价电子的原子,其中最重要的内容是泡利原理,同时对三个和三个以上价电子的原子作概括性的论述。
§24 氦的光谱和能级最简单的多电子原子是氦原子。
所以我们研究多电子原子时首先讨论的就是氦原子。
一、氦原子的实验光谱结构实验的观察发现氦及周期系第二族元素如铍、镁、钙、锶、钡、镭、锌、镉、汞的光谱有相仿的结构,具有两套谱线系。
两套谱线系之间的区别很大,有一套是单线,另一套较复杂。
从这些元素的光谱,可以推得它们的能级都分成两套,一套是单层的,另一套具有三层结构。
下面我们具体地讨论氦原子的光谱和能级特点。
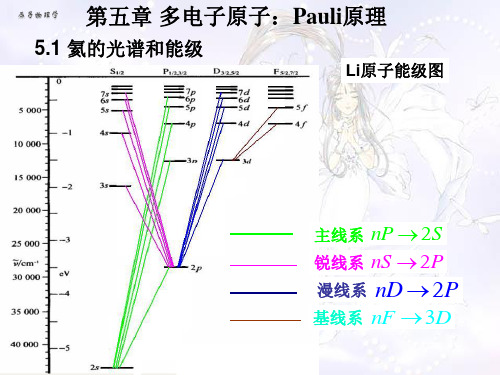
氦的光谱与碱金属光谱一样,存在一系列的谱线系,如图,因此可借鉴碱金属光谱的分析方法来分析氦原子光谱。
因为具有两套线系,即两个主线系,两个第一辅线系,两个第二辅线系等,之间没有多大联系,并且差别较大,科学家在早期便以为是两种氦原子的光谱。
简单的是仲氦,复杂的是正氦。
现在知道并不是两种氦原子,而是分为两套能级。
二、氦原子的能级结构1.两套结构。
如图,左边是单层,能级对应的总自旋量子数等于0,导致重数为1,所以叫单能级;右边是三层,能级的重数为3。
这两套能级之间不发生跃迁。
原子物理学 第五章 多电子原子:Pauli原理
,
1 2
0
大连理工大学物理系
原子物理学
pp组态
两个电子都处于l 1态
L—S耦合
s1
1 2
,s2
1 2
,l1
1,l2
1
S=0, 1, L 2,1,0
S=0 J= 2,1,0
1S0,1P1,1D2
大连理工大学物理系
原子物理学
S=1, L 2
J 3, 2, 1 3D3,2,1 S=1, L 1
构成6种相互作用:
G1 s1s2 、G2 l1l2 、G3 l1s1 G4 l2s2 、G5 l1s2 、G6 l2s1
G5 l1s2 、G6 l2s1 相互作用较弱
大连理工大学物理系
原子物理学
L—S耦合
G1 s1s2 、G2 l1l2
LS耦合一般出现大部分 原子中
大连理工大学物理系
大连理工大学物理系
原子物理学
4)选择规则
li
1
i
j—j 耦合
j 0, 1 J 0, 1
大连理工大学物理系
原子物理学
5)由电子的组态到原子态 ss组态
L—S耦合
s1
1 2
,s2
1 2
,l1
0,l2
0
S=0, 1, L 0
J 0,1
1S0,3S1
J—J耦合
s1
1 2
,s2
1 2
,l1
0,l2
原子物理学
J—J耦合
G3 l1s1 、G4 l2s2
由元素组态的能级实 际情况可判断原子态 属哪种耦合。
JJ 耦 合 一 般 出 现 在 某 些 高激发态和较重的原子 中
大连理工大学物理系
第五篇多电子原子:泡利原理.PP

(3)电子组态的能量——壳层的次序
1s, 2s, 2 p, 3s, 3p, 4s, 3d, 4 p, 5s, 4d, 5 p, 6s, 4 f , L
等电子体系光谱的比较:
T
RZ *2 Байду номын сангаас2
T 1 (Z )
Rn
E hcT
(4)原子基态
洪特定则(1925年):对于一个给定的电子组态形 成的一组原子态,当某原子态具有的S最大时,它处 的能级位置最低;对同一个S,又以L值大的为最低; 对同一L而不同J,正常次序(同科电子数小于或等 于满壳层的一半)和倒转次序(同科电子数大于满壳 层的一半)。
1916—1918年间,玻尔首先尝试对元素周期表给予 物理解释;
1925年,泡利提出不相容原理,结合能量最小原理, 对元素的周期性给出了成功的解释。
(2)壳层中电子的数目
决定原子中电子 状态的两条准则
泡利不相容原理 能量最小原理
决定了每一壳层 中电子的数目
决定了壳层的次序
n=1,2,3,4……称为主壳层 K,L,M,N……
l=0,1,2,…,(n-1)称为相应主壳层下的支壳层 s,p,d,f,g,h
电子状态由(n , l , ml , ms)表示,根据泡利不相 容原理: 每一次壳层(n,l相同)可容纳的最多电子数:
Nl 2(2l 1)
每一壳层(n相同)可容纳的最多电子数:
n1
Nn 2(2l 1) 2n2 l0
利用泡利不相容原理,可以解释原子内部的电子分布 状况和元素周期性。
(3)应用举例 1、氦原子的基态
基态电子组态1s1s
(n , l , ml , ms) (1,0,0,+1/2)
(1,0,0,-1/2)
原子物理讲义 第五章 多电子原子

第五章 多电子原子:泡利原理(YCS )§5-1 氦光谱和能级氦原子是1868年分析日全蚀光谱时发现的,30年后在地球矿物中找到.实验表明,氦及元素周期表第二族元素铍、镁、钙、锶、钡、镭、锌、镉、汞的光谱结构相仿.氦原子光谱的特点(详见P.213氦原子能级图)(氦能谱的以上4个特点分别包含着4个物理概念):1)明显地分成两套谱线系,左边一套为单层,右边一套多为三层;两套能级间无跃迁,各自内部的跃迁产生了两套独立的光谱.每一套都象碱金属原子光谱一样含有主线系,辅线系和伯格曼系等.但两套线系的构成截然不同.2)存在几个亚稳态,表明某种选择规则限制了这些态以自发辐射的形式发生衰变;3)基态01S 1与第一激发态13S 2间能量相差很大,为eV.7719;电离能也是所有元素中最大的,为eV .5824;4)在三层结构那套能级中没有来自2(1S)的能级.§5-2 电子组态和原子态1.电子组态:原子中各电子状态的组合描述一个电子的状态可用s l m m l n 、、、四个量子数.考虑电子的自旋-轨道相互作用,s l m m 、不再有确定值,则电子的状态用j j m l n 、、、描述.氢原子只有一个电子,在不考虑原子核运动时,电子状态就表示原子状态.对于碱金属原子,理论上可证明原子实的总角动量为0且不易被激发,被激发的只是价电子,可认为价电子的状态就表示碱金属原子状态.多电子原子则必须考虑电子间的相互作用,原子的状态是价电子运动状态的耦合.由于轨道运动的能量只取决于量子数l n 、,所以常用nl 来标记电子状态.例如:氢原子处于基态时,电子处于01=、=l n 的状态,记为s 1;氦原子处于基态时,两个电子都处于s 1态,则用两个电子状态的组合s 1s 1或21s 来表示;若一个原子有3个电子,其中两个处在0,2==l n 的状态,另一个处在1,2==l n 的状态,则电子组态为p s222.在给定的电子组态中,各电子的轨道角动量大小是确定的,但其轨道角动量和自旋角动量的方向不确定.因此每一个电子组态可耦合成若干原子态,由同一电子组态耦合成的不同原子态将且具有不同的能量,因为不同的角动量耦合产生的附加能量不同. 2.价电子间的相互作用价电子间的相互作用除电子自身的轨道与自旋耦合外,电子间的轨道与轨道、自旋与自旋、轨道与自旋等角动量都要发生耦合作用.如两个价电子间可有6种耦合方式(如图示):),(),(),(),(),(),(126215224113212211s l G s l G s l G s l G s s G l l G 、、、、、.这6种耦合的强弱不等,一般情况下,65G G 、较弱可不考虑.下面考虑两种极端情况. 1)S L -耦合:21G G 、较43G G 、强得多,将两个轨道角动量和两个自旋角动量分别合成总轨道角动量L 和总自旋角动量S ,再将L 和S合成总角动量J .(S L -耦合对于较轻元素的低激发态成立,适用性较广)2)j j -耦合:43G G 、较21G G 、强得多,将各个电子的轨道与自旋耦合成各个电子的总角动量1j 和2j,再将其耦合成原子的总角动量J .(j j -耦合则较少见,只在较重元素的激发态中出现)对于多电子耦合的情况可记为:⎩⎨⎧==-==-J j j j l s l s l s j j JL S l l l s s s S L )())()((:),(),,)(,,(:3233221132132113.S L-耦合的原子态21l l L +=.L的大小为: 212121,,1,,)1(l l l l l l L L L L --++=+= 21s s S +=.S 的大小为:⎩⎨⎧=±=+=01,)1(21s s S S S S原子的总角动量S L J+=,量子数S L S L S L J --++=,,1,对于具有两个价电子的原子,当L 给定时,对应于0,1==S S 的两种情况,J 的取值分别为:1)0=S时,L J =,表示原子只有一个可能的角动量状态,所以是单态. 2)1=S 时,1,,1-+=L L L J ,所以原子是三重态.由以上分析知,具有两个价电子的原子都有单态和三重态的能级结构. 例:原子有两个价电子,其角动量状态分别为 21,2;21,12211====s l s l ,用S L-耦合确定其原子态.总自旋量子数1,0=S ,3,2,1=L ,则当0=S 时,3,2,1==L J ;原子态为11P 、21D 、31F当1,1==L S 时,⎪⎩⎪⎨⎧=012J ,原子态为⎪⎩⎪⎨⎧031323P P P ;当2,1==L S 时, ⎪⎩⎪⎨⎧=123J ,原子态为⎪⎩⎪⎨⎧132333D D D ;当3,1==L S 时,⎪⎩⎪⎨⎧=234J ,原子态为⎪⎩⎪⎨⎧233343F F F共有12种可能的原子态.为了简洁,可排列成右上表.S L-耦合方法用于氦原子,即可证实其状态.(此略) 4.j j -耦合组成的原子态当每个电子自身的自旋-轨道耦合作用强,而电子间的耦合作用很弱时,采用j j -耦合.设第i 个电子的轨道角动量和自旋角动量分别为i l 和i s ,则第i 个电子的总角动量为i i i s l j +=,按量子力学规则,每个电子的总角动量的量子数为:ii i i i i i s l s l s l j --++=,,1,原子的总角动量为:21j j J +=其大小为)1(+=J J J ,212121,,1,j j j j j j J --++=j j -耦合组成的原子态常用符号J j j ),(21表示.如pd 电子组态形成的原子态为:1,22,30,1,2,31,2,3,4)23,21(;)25,21(;)23,23(;)25,23(,也是12种可能的原子态.结论:同一电子态,用S L -耦合形成的原子态与用j j -耦合形成的原子态的个数相等.5.两个角动量耦合的一般法则(以轨道角动量为例说明)⎪⎪⎩⎪⎪⎨⎧--++=+=+=+=⇒+=21212122211121,1,,)1()1()1(l l l l l l l l l L l l L l l L L L L其中若21l l >,则l 共有)12(2+l 个取值.(见下例)例:两个电子的角动量为⎩⎨⎧-=-=⎩⎨⎧==101101z ,112111,,m ,,m l l l l 方向的投影分别为在.因角动量相加只要将其投影值相加即可(详见教材中例子).6.电子组态变动的跃迁选择定则: 原子中各电子的量子数之和∑il为偶(奇)数时原子具有偶(奇)宇称.辐射跃迁只能发生在不同的宇称状态之间.即:偶宇称态⇔奇宇称态 7.耦合的选择定则:S L -耦合的选择定则:⎪⎩⎪⎨⎧→±=∆±=∆=∆)00(1,010除外J L Sj -j 耦合的选择定则:⎩⎨⎧→±=∆±=∆)00(1010j 除外,,J耦合的选择规则决定了氦原子的能谱.由于S L -耦合中0=∆S ,决定了氦的两套能级间不可能发生相互跃迁.对于氦,两个价电子的原子态有单态(0S =)和三重态(1S =)两类,选择定则0=∆S 要求两类能级之间不能发生跃迁(须注意0=∆S 这一规则并非对所有原子适用),好像这两类能级属于不同原子一样,因而产生两套谱线系.人们把产生单重线的叫仲氦,产生多重线的叫正氦.实际上,仲氦是两电子自旋取向相反(0S =)的氦原子,而正氦是两电子自旋取向相同(1S =)的氦原子.氦原子之间可通过相互碰撞来交换能量,这不必服从选择规则,故正常的氦气是“正氦”与“仲氦”的混合.关于氦的三重态谱线,有著名的黄色3D 线,1868年8月18日在太阳日珥的光谱中观察到这条线,从而发现了氦.用高分辨仪器可看出此线有三成分.从光谱看三重态和单态间没有跃迁,有一条很弱的06.591A =λ的线,最初认为是氦的三重态和单态间间的跃迁,后来证实这是氖的谱线.§5-3 泡利不相容原理1.历史回顾:玻尔对元素周期系的解释作了很多工作,曾特别讨论了氦原子内层轨道的“填满”问题,关于为什么每一轨道上只能放有限数目电子的问题,玻尔猜测:“只有当电子和睦时,才可能接受具有相同量子数的电子”,否则就“厌恶接受”.(牵强解释)泡利于1921年(时年21岁)涉足原子内电子的填充问题,他意识到,元素周期系的背后隐藏着一个重要的原理.至1925年,泡利通过对原子光谱和强磁场内的塞曼效应的分析,建立了他的不相容原理,使玻尔的解释有了牢固的基础.1940年泡利又证明了不相容原理对自旋为半整数的粒子不是附加的新原理,而是相对论性波动方程的必然结果. 2.不相容原理(1925年):在一个原子中不可能有两个或两个以上的电子具有完全相同的四个量子数(s l m m l n ...),即原子中的每一个状态只能容纳一个电子.另一种更普通的表述:在费米子(自旋为21的奇数倍的微观粒子)组成的系统中,不能有两个或更多的粒子处于完全相同的状态.(电子、质子、中子等均为费米子)泡利不相容原理是微观粒子运动的基本规律之一.利用它可解释原子内部的电子分布状况和元素周期律.泡利不相容原理反映的这种严格的排斥性的物理本质是什么?至今仍是个谜. 3.泡利不相容原理的应用1)氦原子的基态按L -S 耦合规则,氦的基态应有01S 和13S 两个态,但实际上只有1S ,这是因为两个电子的lm l n ,,相同(0,0,1===l m ln ),但s m 必定不能相同之故,不可能出现三重态13S .2)原子的大小玻尔曾认为原子的半径随Z 的增大而减小(核外电子都要占据能量最低的轨道,故受到的引力相等;Z 增大,核外电子受到的引力增大导致离核的距离减小).这是错误的.按泡利原理,虽第一层的轨道半径小了,但电子是分层排列的,但轨道层数增加了,原子的大小随Z 而变的变更甚微.所以原子的大小几乎都一样.(这是经典物理和旧量子论解释不了的)3)金属中的电子对金属加热过程中,核与核外电子得到的能量不均匀,几乎全由原子核得到.为什么?金属中,要使底层电子得到能量而激发十分困难,因为它附近的能态已被占满.而加热1万度才能给电子约1eV 的能量,但实际上,当加热到几百度时,金属的晶格点阵就被破坏而熔解了.所以金属中除最外层电子能从加热中得到少许能量外,其余能量均被核吸收了.4)原子核内独立核子运动按泡利原理,密度甚高的原子核内,基态附近的状态均被占满,核子之间没有相互碰撞,表现为独立的运动. 5) 核子内的有色夸克基本粒子中约95%的粒子为强子,强子的性质比较有规律,这说明强子的内部结构有相似之处.在海森堡的核子同位旋概念、坂田昌一(1956年)的强子内部对称性模型基础上,1961年美国的盖尔曼和奈曼提出对强子进行分类的“八重法”,据其理论预言的重子-Ω于1964年被实验所证实.盖尔曼进一步的研究使他提出了“夸克模型”,使这种对称性理论得到真正的进展.盖尔曼用具有一定对称性的上夸克(u )、下夸克(d )和奇异夸克(s )替换了坂田模型中的三种粒子.夸克是自然界中更为基本的物质微粒,所有的强子都由这三种夸克u 、d 、s 及其反粒子粲夸克(c )、底夸克(b )和顶夸克(t )组成.人们推测具有相同性质的粒子必定成批出现的,并且根据已知的一些粒子的性质可以预见尚未发现的其它粒子.夸克模型能成功地解释许多事实,把曾经很复杂的问题简单化了.夸克是自旋为21的费米子,设这三个夸克均处于基态,当两个夸克的自旋方向确定后,第三个夸克的取向必与前两个中的一个相同,这显然违反了泡利原理.但这种危机并未发生,这是因为基于夸克有适当的全同粒子的对称性,人们以红、绿、蓝三种颜色作为描写夸克量子状态的量子数(即三维自由度),解决了这一问题,并由此生发了描述强相互作用的量子色动力学. 4.同科电子*n 和l 相同的电子称同科电子.由于受泡利原理的限制,同科电子形成的原子态要少得多,这是因为对于同科电子,本来可能有的角动量状态由于泡利原理被去除了,从而使同科电子产生的状态数目大大减少.例如:0111S s s →,而1301,21S S s s →斯莱特图解法:例如:具有相同n 的两个电子,其组态为2np ,依泡利原理,两组量子数),,,(s l m m l n 不能全同,因1,0±=l m 有3个取值,21±=s m 有两个取值,则得到可能的l m 和s m 的取值见表26.1(教材P.223)(注意:经典物理中两个粒子可区分,但量子物理中两个全同电子是不可区分,不可加以“标记”的,这是经典物理与量子物理的原则区别之一)将表26.1数据用LS M M -图表示,图中每一小方块相应于不同的L S M M -值,方块中数字代表状态数,(a )一共有15种可能的状态,与表相符.(b)、(c)、(d)分别代表三种态项.3np 组态的电子合成的态项详见P.225.同科电子的态项与非同科电子的态项(详见P.225表)§5-4 元素周期表1.元素性质的周期性19世纪中叶人们已认识到元素的许多性质随着原子核的电荷数Z 的增加呈周期性的变化,这是原子结构随Z 的增加而呈周期性变化的结果.如摩尔体积、熔点、线胀系数、原子光谱、电离能等.元素的电离能随Z 的变化关系(详见P.226图示):表明元素的化学性质的周期变化特性. 2.元素周期表人们将化学性质相近的金属元素和卤族元素分别列为两个元素族.1869年,门捷列夫提出元素周期表,将当时所知道的62个元素按原子量(现在认识到应按原子序数)增加的次序排列,则原子的属性表现出有规律的重复,从而完成对所有元素的分族.当时有不少空缺的元素尚待发现,但可预言这些未知元素的性质.1874-1875年,化学家据预言发现了三个元素:钪、镓、锗,随后又陆续发现一些,元素周期表不断得到充实.到目前这止,公认的共109种元素.元素周期表中,每行称为一个周期,共有七个周期.同一列的元素称为一族,同族元素具有具有相似的化学性质和物理性质.左起第一族为碱金属,化合价为正1价,原子光谱都具有双重结构,电离能最小.第二族为碱土金属,化合价为正2价,原子光谱有单重和三重结构两套线系.最右一族为惰性气体,化学性质不活泼,电离能最大.元素周期表提出后的50余年内.人们不能对元素的周期性做出满意解释.玻尔在提出氢原子的量子理论后,就致力于周期表的解释.他凭直觉提出原子内的电子是按壳层排列的,同一壳层的电子具有相同的主量子数n.他的设想被证实,但他未说明为什么每一壳层只能容纳一定数量的电子.直至1925年泡利提出不相容原理后,才认识到元素的周期性是电子组态的周期性反映,而电子组态的周期性则联系于特定轨道的可容性.这样,化学性质的周期性用原子结构的物理图象得到了说明,使化学概念“物理化”,化学不再是一门和物理学互不相通的学科了.3.原子中电子的壳层中结构(结合元素电离能随Z 而变的规律分析)决定原子壳层结构(即电子所处状态)的两条准则: 1)泡利不相容原理.它决定壳层中电子的数目.2)能量最小原理.体系能量最低时,体系最稳定,它决定壳层的次序. 元素周期表就是按以上两条准则排列的.主量子数n 决定能量的主要部分,n 相同的电子分布在一个壳层上, ,3,2,1=n 的壳层分别称为K,L,M,N,O, …壳层.n 一定时,角量子数可取n 个值,对应于1,,3,2,1,0-=n l的支壳层分别用s,p,d,f,g,h …表示.l一定时,s m 有两种取向,l m 有)12(+l )种取值.因此每一角量子数为l 的支壳层中最多可容纳的电子数为:)12(2+=l N ln 一定时,)1(,,2,1,0-=n l ,共有n 个取值,因此每一壳层最多可容纳的电子数为:2122)12(22)12(2n n n l N n l n =-+=+=∑-=各支壳层和壳层中最多可容纳的电子数(见表)电子壳层的填充:按泡利原理从能量最低的状态开始填充,填满最低能态后才依次填充更高的能态.一般说来,n 越小或n 一定时l 越小,则能量越低. 某一特定壳层的电子能量,不仅取决于n ,还与l 有关,实际判断原子能级高低的经验规则:1))(l n +的值相同,则n 小的能级低;2) )(l n +的值不同,若n 相同,则l 小的能级低;若n 不同,则n 小的能级低.具体次序为: p d f s p d f s p d s p d s p s p s s 7,6,5,7,6,5,4,6.5,4,5,4.3,4,3.3,2,2,14.原子基态对于某一特定的原子,可按照其Z 确定其电子组态.一个电子组态可合成若干原子态,需按照泡利原理选出物理上允许的原子态,然后按洪特定则确定这些原子态的能量次序.其中能量最低的即为原子基态.1) 洪特定则(1925提出的经验规则):同一电子组态形成的原子态,(1)具有相同L 值的能级中, S 值最大(即重数最高)的能级位置最低;(2)具有相同S 值的能级中,具有最大L 值的能级位置最低.针对同科电子的洪特附加定则:对于同一l 值而J 值不同的能级,有以下两种情况 1)正常次序:当同科电子数小于或等于闭壳层占有数的一半时,具有最小J 值的能级(即SL -)处在最低;2)倒转次序:当同科电子数大于闭壳层占有数的一半时,具有最大J 值的能级(即SL -)处在最低2)朗德间隔定则:在三重态中,一对相邻能级间的间隔与两个J 值中较大的那个值成正比. 3)矢量合成法对由同科电子构成的组态,考虑到必须遵从泡利原理,通常不直接用S L-耦合的方法,而用合成投影合成法.要点如下:(1)按洪特定则,同科电子填入同一支壳层时,表现为尽可能以相同方向的自旋分别填入lm 不同的态,写出各电子的自旋量子数的值,求出总的自旋量子数:∑===Ni siS m M S1(2)在不违背泡利原理的前提下(即同科电子的si m 和li m 不全同),将各同科电子可能取的轨道磁量子数lim 的最大值相加,即得原子基态的总轨道量子数:∑===Ni li L m M L1(3)按洪特定则,决定原子基态光谱项的总角动量量子数,最后写出原子基态的光谱项.5.电离能变化的解释He 2:同一壳层的两个电子都受到e 2+的库仑力作用,结合能都很大;Li 3:由于静电屏蔽作用,最外层电子只受到e 1+的库仑力作用,且外层电子距核较远,结合能较小;而内层的两个电子受到e 3+的库仑力作用,其结合能较He 2中的电子要大;Be 4:最外层的两个电子受到e 2+的库仑力作用,…可见,随着壳层的增加,外层电子的结合能依次增高.如右图所示,Na 11的外层电子只受到一个有效正电荷的作用,而Ar 18外层的8个电子中的每一个都受到8个有效电荷的作用,因此,Ar 18要远比Na 11稳定.。
原子物理学 多电子原子:泡利原理 (5.4.2)--确定同科电子构成的原子态

原子中各电子在 n l 壳层的排布称电子组态。如:双电子 的氦的基态电子组态是 1s1s 。当一个电子被激发到 2s , 2p 后的电子组态是 1s2s , 1s2p 。
泡利不相容原理限制了 L-S 耦合、 j-j 耦合的形成的原子态
01234 S P DF G
例题 1 :( 1 )求 ns n´p 电子组态的原子态 ( 2 )求 3p4p 电子组态的原子态
解: ( 1 )考虑 ns n´p 电子组态的 L-S 耦合可能导致的
原子态 2s + 1Lj ,按照 L-S 耦合规则: PS = ps1 + ps2 ,总
自旋量子数取 S = ½ + ½ = 1 , ½ - ½ = 0 两个值; l1
法又称偶数定则。 电子组态形成封闭壳层结构
时, ML=0 , MS=0 。因此闭合壳层角动 量为零,即 L=0,S=0,J=0 。(原子实正是 这样)。由此 l=1 的 p 子壳层中的 np1 和 np5 ; np2 和 np4 具有相同的角动量大小 (方向相反),因而有相同的原子态。 .
L=0 1 2
(1S0) 1P1 (1D2)
3S1 (3P2,1,0) D 3
3,2,1
二、同科电子 ( 等效电子 ) 组态的原 子态 ( L-S 耦合)
nl 相同的电子组态称同科电子组态,同科电子由于全
同粒子的不可区分和不相容原理限制,由同科电子(如
nPnP ) L-S 耦合的原子态少于非同科电子组态 (nP n´P)
1
ML
Ms 坐标系中
ML
Ms
Ms
Ms
L=2 , S=0 , 1D2
L=1
第五章:多电子原子 泡利原理 《原子物理学》课堂课件

能级
五
章
多
实验表明,氦原子的光谱也是由这些线系
电 构成的,与碱金属原子光谱不同的是:
子
原
子
氦原子光谱的上述四个线系都出现双份,
:
泡 即两个主线系,两个锐线系等。
利
原
理
首页
上一页
下一页
氦及周期系第二族元素的光谱和能级
➢ 第二族元素:铍、镁、钙、锶、钡、镭、锌、镉、汞。 (都具有两个价电子 光谱和化学性质) ➢ 氦及第二族元素的能级都分成两套,一套是单层的,另 一套是三层的;各自形成两套光谱。
Atomic Physics 原子物理学
第五章:多电子原子 :泡利原理
第一节 氦的光谱和能级 第二节 两个电子的耦合 第三节 泡利原理 第四节 元素周期表
H原子:
Tn
R n2
En
Rhc n2
类H离子:
Tn
Z2
R n2
En
Z 2
Rhc n2
碱金属原子:
Tnl
(n
R l)2
Enl
(n
Rhc l)2
能级
五
章
即
原子实+2个价电子。
多
电
子
原
子 由此可见,能级和光谱的形成都是二个价电子
: 泡
各种相互作用引起的.
利
原
理
首页
上一页
下一页
第二节:两个电子的耦合
电子的组态
1.定义: 两个价电子处在各种状态的组合,
称电子组态。
电子的组 态
比如,氦的两个电子都在1s态,那么氦的电
第 五
子组态是1s1s;
一个电子在1s,
若核(实)外有两个电子,由两个价电子跃迁而形 成的光谱如何?能级如何?原子态如何?
第五章泡利原理

第五章多电子原子:泡利原理一、学习要点1. 氦原子和碱土金属原子:氦原子光谱和能级(正氦(三重态)、仲氦(单态))2. 重点掌握L-S耦合,了解j-j耦合3.洪特定则、朗德间隔定则、泡利不相容原理;4.两个价电子原子的电偶极辐射跃迁选择定则;5.元素周期律:元素周期表,玻尔解释.6.原子的电子壳层:主壳层:K LMNO P Q次壳层(课本表72页)、次支壳层电子填充壳层的原则:泡利不相容原理、能量最小原理7.原子基态的电子组态(P228表27.2)、莫塞莱定律二、基本练习(一)教材习题:杨书P255--256:5—2、5—4、5—5、5—8、5—9、5—11(二)第五章自测云南师范大学2009—2010学年____原子物理学(5)自测卷学院________专业_________年级______学号___________ 姓名_________考试方式:闭卷考考试时量:120分钟试卷编号:(A、B、C卷):A卷1.选择题(从A、B、C和D中选一,在题号上打“√”,每题2分,共64分)(1)关于氦原子光谱下列说法错误的是:A.第一激发态不能自发的跃迁到基态;B.1s2p 3P2,1,0能级是正常顺序;C.基态与第一激发态能量相差很大;D.三重态与单态之间没有跃迁(2)氦原子由状态1s2p 3P2,1,0向1s2s 3S1跃迁,可产生的谱线条数为:A.0;B.2;C.3;D.1(3)氦原子由状态1s3d 3D3,2,1向1s2p3P2,1,0跃迁时可产生的谱线条数为:A.3;B.4;C.6;D.5(4)氦原子有单态和三重态两套能级,从而它们产生的光谱特点是:A.单能级各线系皆为单线,三重能级各线皆为三线;B.单重能级各线系皆为双线,三重能级各线系皆为三线;C.单重能级各线系皆为单线,三重能级各线系皆为双线;D.单重能级各线系皆为单线,三重能级各线系较为复杂,不一定是三线.(5)下列原子状态中哪一个是氦原子的基态?A.1P1;B.3P1 ;C.3S1; D.1S0;(6)氦原子的电子组态为n1pn2s,则可能的原子态:A.由于n不确定不能给出确定的J值,不能决定原子态;B.为n1pn2s 3D2,1,0和n1pn2s 1D1;C.由于违背泡利原理只存单态不存在三重态;D.为n1pn2s 3P2,1,0和n1pn2s 1P1.(7)氦原子有单态和三重态,但1s1s3S1并不存在,其原因是:A.因为自旋为1/2,l 1=l2=0 故J=1/2 ;B.泡利不相容原理限制了1s1s3S1的存在;C..因为三重态能量最低的是1s2s3S1;D.因为1s1s3S1和 1s2s3S1是简并态(8)若某原子的两个价电子处于2s2p组态,利用L-S耦合可得到其原子态的个数是:A.1;B.3;C.4;D.6.(9)4D3/2 态的轨道角动量的平方值是:A.-3 2 ; B.6 2; C.-2 2; D.2 2(10)一个p电子与一个 s电子在L-S耦合下可能有原子态为:A.3P0,1,2, 3S1 ;B.3P0,1,2 , 1S0;C.1P1, 3P0,1,2 ;D.3S1 ,1P1(11)设原子的两个价电子是p电子和d电子,在L-S耦合下可能的原子态有:A.4个;B.9个;C.12个;D.15个;(12)电子组态2p4d所形成的可能原子态有:A.1P 3P 1F 3F; B. 1P 1D 1F 3P 3D 3F;C.3F 1F; D.1S 1P 1D 3S 3P 3D.(13)铍(Be)原子若处于第一激发态,则其电子组态:A.2s2s;B.2s3p;C.1s2p;D.2s2p(14)若镁原子处于基态,它的电子组态应为:A.2s2s B.2s2p C.3s3s D.3s3p(15)电子组态1s2p所构成的原子态应为:A1s2p1P1 , 1s2p3P2,1,0 B.1s2p1S0 ,1s2p3S1C1s2p1S0, 1s2p1P1 , 1s2p3S1 , 1s2p3P2,1,0; D.1s2p1S0,1s2p1P1(16)判断下列各谱项中那个谱项不可能存在:A.3F2;B.4P5/2;C.2F7/2;D.3D1/2(17)试判断原子态:1s1s3S1,1s2p3P2,1s2p1D1, 2s2p3P2中下列哪组是完全存在的?A. 1s1s3S1 1s2p3P2 2s2p3P2 B .1s2p3P2 1s2p1D1C. 1s2p3P2 2s2p3P2D.1s1s3S1 2s2p3P2 1s2p1D1(18)在铍原子中,如果3D1,2,3对应的三能级可以分辨,当有2s3d3D1,2,3到2s2p3P2,1,0的跃迁中可产生几条光谱线?A.6 B.3 C.2 D.9(19)钙原子的能级应该有几重结构?A.双重; B.一、三重; C.二、四重; D.单重(20)元素周期表中:A.同周期各元素的性质和同族元素的性质基本相同;B.同周期各元素的性质不同,同族各元素的性质基本相同C.同周期各元素的性质基本相同,同族各元素的性质不同D.同周期的各元素和同族的各元素性质都不同(21)当主量子数n=1,2,3,4,5,6时,用字母表示壳层依次为:A.K LMONP;B.KLMNOP;C.KLMOPN;D.KMLNOP;(22)下列哪一个元素其最外层电子具有最小电离能?A.氟(Z=9);B.氖(Z=10);C.钠(Z=11);D.镁(Z=12)(23)在原子壳层结构中,当l=0,1,2,3,…时,如果用符号表示各次壳层,依次用下列字母表示:A.s,p,d,g,f,h....B.s,p,d,f,h,g...C.s,p,d,f,g,h...D.s,p,d,h,f,g...(24)电子填充壳层时,下列说法不正确的是:A.一个被填充得支壳层,所有的角动量为零;B.一个支壳层被填满半数时,总轨道角动量为零;C.必须是填满一个支壳层以后再开始填充另一个新支壳层;D.一个壳层中按泡利原理容纳的电子数为2n2(25)实际周期表对K.L.M.N.O.P主壳层所能填充的最大电子数依次为:A.2,8,18,32,50,72;B.2,8,18,18,32,50;C.2,8,8,18,32,50;D.2,8,8,18,18,32.(26)按泡利原理,主量子数n确定后可有多少个状态?A.n2; B.2(2l+1); C.2j+1; D.2n2(27)某个中性原子的电子组态是1s22s22p63s3p,此原子是:A.处于激发态的碱金属原子;B.处于基态的碱金属原子;C.处于基态的碱土金属原子;D.处于激发态的碱土金属原子;(28)氩(Z=18)原子基态的电子组态及原子态是:A.1s22s22p63p81S0; B.1s22s22p62p63d83P0C.1s22s22p63p61S0; D. 1s22s22p63p43d22D1/2(29)某个中性原子的电子组态是1s22s22p63s23p65g1,此原子是:A.处于激发态的碱土金属原子;B.处于基态的碱土金属原子;C.处于基态的碱金属原子;D.处于激发态的碱金属原子.(30)有一原子,n=1,2,3的壳层填满,4s支壳层也填满,4p支壳层填了一半,则该元素是:A.Br(Z=35); B.Rr(Z=36); C.V(Z=23); D.As(Z=33)(31)由电子壳层理论可知,不论有多少电子,只要它们都处在满壳层和满支壳层上,则其原子态就都是:A.3S0;B.1P1;C.2P1/2;D.1S0.(32)氖原子的电子组态为1s22s22p6,根据壳层结构可以判断氖原子基态为:A.1P1;B.3S1;C.1S0;D.3P0.2.简答题(共12分,每题各4分)(1)简要解释下列概念:泡利不相容原理、洪特定则、朗德间隔定则、能量最小原理、莫塞莱定律.(2)L-S耦合的某原子的激发态电子组态是2p3p,可能形成哪些原子态?若相应的能级顺序符合一般规律,应如何排列?并画出此原子由电子组态2p3p向2p3s可能产生的跃迁.(首都师大1998)(3)写出铍原子基态、第一激发态电子组态及相应光谱项.(1991中山大学)3.计算题(共24分,每题各12分。
第五章 多电子原子:泡利原理

二、多重性的交替律:
按周期表顺序的元素,交替的具有偶数或 奇数的多重态。
交替的多重态
19
K 20Ca 21Sc 22Ti 23V 24 Cr 25Mn 26Fe27Co 28Ni 29Cu
单一
单一
单一
单一
单一
双重
双重
三重 三重
双重
三重
双重
三重
双重
三重
双重
四重
五重
四重
五重
四重
五重
四重
五重
四重
六重
七重
j1 ( j1 1),
j
1
1 l 1 s1 l 1 2
(2)
Pj 2 Ps 2 Pl 2
1 s2 2 l 2 0,1,2 (n 2 1) 1 j 2 l 2 s2 l 2 2
P s 2 s 2 (s 2 1), P l 2 l 2 (l 2 1), P j 2 j 2 (j 2 1),
泡利生平简介
4.同科电子
在一原子中,主量子数 n 和角量子数 相同的 电子,称为同科电子。
5.同科电子形成的原子态
对非同科电子2p3p可形成哪些原子态?
多电子原子光谱的一般规律
一、光谱和能级的位移律: 实验观察到:具有原子序数Z的中性原子的 光谱和能级,同具有原子序数Z+1的原子一次 电离后的离子的光谱和能级结构相似。 例如:H同He+, He同Li+
3P 0,1,2 3S 1
3P 0,1,2
1s2s1S0
3S 1
1s1s1S0
3S 1
氦原子能级图
1s3d1D2
1s3p1P1 1s3s1S0 1s2p1P1
第五章 多电子原子

,| l1 l2 |
,| s1 s2 | ,| l s |
例题:两各价电子一个处于 p 态,一个处于
d 态,求 L-S 耦合后的量子数 l、s 和 j。
解:由题目知道 l1=1,l2=2, 可得:l=3、2、1 又因为 s1=1/2、s2=1/2 所以有 s=0、1 当 s=1,l=1 时,j=2、1、0
示了微观粒子遵从的一个重要规律。
一、确定电子状态的量子数
主量子数n:决定了原子能量的主要部分。
n=1、2、3、 4、 5、 6…
K、L、M、N、O、 P… 轨道角量子数l:决定了轨道的角动量,并由于 轨道形状的不同而影响能级,同一n分成不同l 的 能级。
l =0、1、2、3、4、5、6……
s、p、d、f、g、h……
一般来说, 同一电子组态形成的原子态
中,三重态能级低于单态能级,因为三重态
s=1,两个电子的自旋是同向的
1、氦原子光谱:两套(单线、多线)
氦原子光谱的线系可分成两组,其中一组 的几个系都是单线;
一组中的几个线系都是复杂结构,其中主 线系和第二辅线系的每一条谱线都分裂成靠 得很近的三条谱线,第一辅线系的每一条谱 线都分裂成靠得很近的六条谱线。
历史 上曾分 别把它 们叫做 正氦 (s=0)和 仲氦 (s=1), 后来得 知这是 同一种 氦原子 的两种 不同自 旋状态 。
2、氦原子能级:单重、三重
经光谱分析可得氦原子的能级有两 套,一套是单能级,另一套是三重能 级。两套能级之间没有跃迁,在两套 能级中各自内部的跃迁,就产生了两 组相互独立的谱线。
5.2 角动量耦合和对氦光谱的解释
第五章 多电子原子

2、j-j耦合
G4 (l2 , s2 ) 时, G2 (l1, l2 ) << G3 (l1, s1 ) 、 当 G1(s1, s2 ) 、 J1 L1 S1 J 2 L2 S2 J J1 J 2
h h J 2 j2 ( j2 1) J1 j1 ( j1 1) 2 2 h j j j j j 1 j1 j2 1 2 J j ( j 1) 1 2 2 例4:利用j-j耦合,求2p3d态的原子态。 1 1 3 j l 1 s 解: 1 1 , 1 2 2 2 1 3 5 l2 2 s2 j , 2 2 2 2 1 3 3 3 3 5 1 5 ( , ) 2,1 ( , ) 3, 2 ( , )3, 2,1,0 ( , ) 4,3, 2,1 2 2 2 2 2 2 2 2 仍有12个态,且 j 值相同。一般的原子态表示为:
J MJ
F3
j - j 耦合的跃迁选择定则:
l 1 j 0, 1 J 0, 1 ( J 0 J /除外)
由元素组态 的能级实际 情况可判断 原子态属哪 种耦合。 j-j 耦 合 一 般 出现在某些 高激发态和 较重的原子 中
§26 泡利不相容原理
一、泡利原理:在一个原子中,不可能有两个或两个以上 的电子具有完全相同的状态(完全相同的四个量子数)。 ml , ms ) 二、确定电子状态的量子数 (n,l, 1.主量子数n-确定原子中电子在核外空间运动轨道的大小和能 量的高低。一般说来,n大,能量高,轨道半径大。 2.轨道角量子数l l决定电子轨道的形状和角动量的大小,同时也与能量有关. n相同时,l大,能量高。 3.轨道磁量子数 ml h L m l 表示轨道角动量在外场方向的投影: z 2
多电子原子-泡利原理

四个 (n,l,ml,ms) 即可。
back
next 目录 结束
②泡利原理的量子表述表述
在一个原子中,不可能有两个或两个以上的电子具 有完全相同的四个量子数 (n,l,ml,ms) 。
3.泡利原理的普遍表述
泡利原理不仅适用于原子,也适用于其它微观体系, 是微观粒子运动的基本规律之一。即:
在由费米子组成的系统中,不可能有两个或两个以
6.由同一电子组态所形成的三重态和单重态中,三重态 的能级总低于和单重态的能级。
back
next 目录 结束
§25 两个电子的耦合
①单线结构 氦光谱
②多线结构
①单层结构: 氦能级
②三层结构:两个电子的耦合 Nhomakorabeaback
next 目录 结束
一、电子组态 1.电子组态
处于一定状态的若干个(价)电子的组合 。 2.电子组态的表示
实验表明,氦原子的光谱也是由这些线系构成的,但 不同的是:氦原子光谱的上述四个线系都出现双份,即 两个主线系,两个锐线系等。而且这两套谱线的结构有 明显的差异,一套谱线由单线构成,另一套谱线却十分 复杂。
back
next 目录 结束
氦光谱除具有原子光谱的一般规律外,还具有以下特点:
氦的光谱分两套
单线结构 多线结构
主线系 第一辅线系 第二辅线系 伯格曼线系 主线系 第一辅线系 第二辅线系 伯格曼线系
每一条谱 线只有一 个成分
三线结构 六线结构
back
next 目录 结束
二、氦能级的特点 从氦光谱出发分析推断出的氦能级图如下:
back
next 目录 结束
1.能级分为两套
①单层结构:各S、P、D、F能级都是单层,用原子态符
第五章.多电子原子

j1 1/ 2 j 1,2 j2 3 / 2
(1/ 2,1/ 2)1, (1/ 2,1/ 2)0 , (1/ 2,3 / 2)1, (1/ 2,3 / 2)2 (2)L S 耦合
s 0 j 1 l 1
原子态为:
1
s 1 j 0,1,2 l 1
多电子原子中电子的填充次序
每主壳排n亚 壳,45度斜 连接优先无 空缺
原子的壳层结构
(1916 , W.Kossel )
主量子数 n 相同的电子属于同一主壳层 n = 1 , 2 , 3 , 4 , 5 , 6 , …. K , L , M , N , O , P , …. 同一壳层中( n 相同),l 相同的电子组成同一亚壳层或分壳层 l = 0,1 , 2 , 3 , … s, p, d, f, … 根据泡利不相容原理:一个多电子原子系统中,不可能有两个或两个
VI. 多电子原子:泡利原理
多电子原子中电子的分布 多电子原子状态——原子态 同科电子形成的原子态 泡利不相容原理的其他应用 原子态的验证——氦的光谱和能级 元素周期表 亚壳层能级顺序及交叉 等电子体系莫塞莱公式
返回
单电子近似法
认为被研究电子在原子实提供的中心势场中运动,
多电子原子状态—原子态
满壳层
电子已被填满的壳层叫满壳层,或封闭壳层 满壳层电子总的角动量及磁矩均等于零. 设总的磁量子数为ML及MS,
M L ml 0, M S ms 0 L 0, S 0
例如:Ne原子,其1s,2s,2p均填满,电子状态分别为:
(1,0,0,1/2) (2,1,1,-1/2) (1,0,0,-1/2) (2,1,0,1/2) (2,0,0,1/2) (2,0,0,-1/2) (2,1,1,1/2)
第五章:多电子原子 泡利原理

ml1
2l1 1种可能的取值
2l2 1种可能的取值
ml2
耦合之前的独立状态[(ml1) (ml1)]数目是(2l1+1)× (2l2+1)
(4)耦合之后的独立状态数目
[2(l2 l1 ) 1] [2(l2 l1 1) 1] .............. [2(l2 l1 ) 1]
例:氦原子基态: 1s1s
镁原子基态: 3s3s 第一激发态: 3s3p
第一激发态: 1s2s
同一电子组态可以有多种不同的能量,即一种电 子组态可以与多种原子态相对应。 我们知道,一种原 子态在能级图上与一个实实在在的能级相对应。
举例:氢原子 例如 2p, 3d
未考虑角动量的耦合 (包含但不限于自旋)
在两个价电子的情形中,每一个价电子都有它自己的 轨道与自旋运动,因此情况比较复杂。设两个价电子的轨 道运动和自旋运动分别是 l1,l2,s1,s2 , 则在两个电子间可能 的相互作用有六种: 一个电子的轨道运动和另 G (l s ) 一个电子自旋的相互作用
6 2 1
两个电子自 G (s s ) 1 1 2 旋相互作用
耦合实质:
PJ
PL
PL 2
PL1
PS 2 PS PS 1
LS耦合的矢量图
原子态的标记法
(s=0 )1
(s=1 )3
2 S 1
LJ
2
L+1, L, L-1(S=1)
L(S=0)
比较 单电子原子态
0 1 2 3 4
S P DF G
1 Lj , j l 2
例题:求一个n1s电子和一个n2p电子可能形成的原子态。
第五章 多电子原子:泡利原理 26节 泡利不相容原理2

更普遍的表述:费米子系统中一个状态只能容纳一个费米子。
费米子:自旋为半整数的粒子。
如电子、质子、中子等;
玻色子:自旋为整数或0的粒子。
如光子、π介子等。
三、应用举例
1、氦原子的基态
氦原子基态电子组态:s s 11,按S L -耦合,可以构造两个原子态:011S 、131S 。
实际上,131S 不存在。
原因:121==n n ,021==l l ,021==l l m m 211=s m ,2
12-=s m (两个电子自旋反平行),构成原子态 011S ; 211=s m ,2
12=s m (两个电子自旋同向平行),构成原子态 131S ,此时,4个量子数完全相同, 违反了泡利原理,故不可能存在。
同理,Be 原子的基态电子组态s s 22不能构成原子态132S 。
注意:
① 微观粒子具有全同性,是不可区分,因而不可编号。
两个电子自旋全向上或 全向下是等同的。
② 当l m 与s m 的取向不同时,即空间取向不同时,空间距离大,势能低,体系更稳 定,故在轨道与自旋的空间取向上,电子排列按先优先反向排列,后同向排列的顺序 进行。
2、原子的大小
实验表明,所有原子的大小几乎是相同的。
解释:较重的原子,Z 大,核外电子所受到的电场吸引力增大,原子半径r 应减小; 另一方面,电子受泡利原理的限制,不能都处于同一轨道,排列的层次增加,故 r 应增加。
综合竞争的结果,原子的大小不随Z 改变。
3、金属中的电子。
第五章 多电子原子:泡利原理2

偶性态(=偶数)奇性态(=奇数)∑i l ∑i l 跃迁只能发生在不同宇称状态之间,即从偶性宇称到奇性宇称或反之。
6. 辐射跃迁的普用选择定则宇称(或电子组态)跃迁选择定则j-j 耦合跃迁选择定则L-S 耦合跃迁选择定则(在两个电子同时受激发时才出现)0=∆L 10100±=±==,∆J ,∆L ∆S (J =0→J’=0 除外))0'0( 1 0,)2 ,1( 1 0,除外=→=±=∆=±=∆J J J i j i第三节:泡利原理He原子的基态电子组态是1s1s;在L-S 耦合下,可能的原子态是(1s1s) 1S0 和(1s1s) 3S1,但在能级图上,却找不到原子态3S1,事实上这个态是不存在的,这又是为什么?1925年,奥地利物理学家Pauli提出了不相容原理,回答了上述问题。
揭示了微观粒子遵从的一个重要规律。
1. 描述电子运动状态的量子数主量子数n :n = 1, 2, 3,……角量子数l :l = 0, 1 ,2,…,(n -1)轨道磁量子数m l :m l = 0,±1,…,±l 自旋量子数s :s = 1/2自旋磁量子数m s :m s =±1/2因为s=1/2 对所有电子都是相同的,不能作为区分状态的量子数,因此描述电子运动状态的是四个量子数(n, l, m l , m s );一组量子数(n, l, m l , m s )可以完全确定电子的状态。
比如总能量,角动量,轨道的空间取向,自旋的空间取向等物理量都可以由这组量子数确定。
2.Pauli原理的描述1925年,年仅25岁的泡利提出不相容原理:原子中每个状态只能容纳一个电子,换言之原子中不可, m s)相能有两个以上的电子占据四个量子数(n, l, ml 同的态。
3.Pauli原理的应用He原子的基态在氦的基态中,两个1s 电子的n和l 都相同,ml就必须有差又都等于0,根据泡利不相容原理,ms别,m只能有两个数值+1/2 和-1/2,这就是说两s个电子的自旋必须相反。
原子物理第五章 多电子原子泡利原理

例:两电子分别处于f 态和d 态,则 l1 3 , l2 1 ,合成总
轨道角动量为 Pl , 由于l1>l2,所以L的取值总数为2l2+1=3。那么L=4、3、2。
Pl1 12 Pl2 2 L 4 , 3 , 2
PL L(L 1) 20 , 12 , 6
3P2
总轨道
L=2 1D2
l1 1 , l2 2 L3 , 2 ,1
L=3
1F3
3D3 3F4
单态
S=1
3P1
3P0
3D2
3D1
3F3
3F2
三重态
•电子组态和原子态
例如:对于1s2p组态,由L-S耦合可以构成原子态3P2.1.0和1P1。 而对于3s3p组态,由L-S耦合可以构成原子态3P2.1.0和1P1。
5、一种电子态对应于多种原子态。 不仅氦 的能级和光谱有上述特点,人们发现,元素 周期表中第二族元素:
Be(4)、Mg(12)、Ca(20)、Sr(38)、 Ba(56)、Ra(88)、Zn(30)、Cd(48)、Hg(80) 的光谱都与氦有相同的线系结构。
谱线 能级
即
原子实+2个价电子。
由此可见,能级和光谱的形成都是二个价电子 各种相互作用引起的.
次壳层电子的数目
2(2l+1)
角动量 l
0
1
2
3
4
符号
s
p
d
f
g
状态数 2(2l+1) 2
6
10 14 18
壳层电子的数目
n1
Nn 22l 1 2n2 l 0
原子物理学第5章 多电子原子

2 1 2
G3 (l1 , s1 )
4
2
2
5 1
2
6
2
1
两个电子的自旋相互作用: 两个电子的自旋相互作用: 两个电子的轨道相互作用: 两个电子的轨道相互作用 一个电子的自旋轨道相互作用: 一个电子的自旋轨道相互作用
G1 ( s1 , s2 )
G2 (l1, l2 )
G3 (l1 , s1 )
漫、基线系由六条谱线构成
氦原子的光谱由两套 谱线构成, 谱线构成,一套是单层 另一套是三层, 的,另一套是三层,这 两套能级之间没有相互 跃迁, 跃迁,它们各自内部的 跃迁便产生了两套独立 的光谱, 的光谱,早先人们以为 有两种氦, 有两种氦,把具有复杂 结构的氦称为正氦, 结构的氦称为正氦,而 产生单线光谱的称为仲 氦,现在认识到只有一 种氦, 种氦,只是能级结构分 为两套。 为两套。
第二辅线系: 第二辅线系:
六个成份Βιβλιοθήκη n≥3n≥3~ ν =23P0,1, 2 n3S1
三个成份
基线系: 基线系:
~ ν =33 D1 n 3F2 ~ 2 ν =3 D2 n 3F2,3 ~ 3 3 ν =3 D3 n F2,3, 4
六个成份
n≥4
三、能级和能级图的特点
1、能级分为两套,单层和三层能级间没有跃迁;氦的基态是 能级分为两套,单层和三层能级间没有跃迁; (1s1s)11S0; 2、状态(1s1s)13S1不存在,且基态(1s1s)11S0和第一激发态 状态(1s1s)1 不存在,且基态(1s1s)1 之间能差很大, 19.77eV; (1s2s)23S1 之间能差很大,为19.77eV;电离能也是所有元素中最 大的, 24.58eV; 大的,为24.58eV; 态都是单层的; 3、所有的3S1态都是单层的; 4、(1s2s)21S0和(1s2s)23S1是氦的两个亚稳态;(不能跃迁到更低能 是氦的两个亚稳态;( ;(不能跃迁到更低能 级的状态称为亚稳态,当原子处在亚稳态时, 级的状态称为亚稳态,当原子处在亚稳态时,必须将其激发到更高 能,方可脱离此态回到基态) 方可脱离此态回到基态) 5、一种电子态对应于多种原子态。不仅氦的能级和光谱有上述特 一种电子态对应于多种原子态。 点,人们发现,元素周期表中第二族元素的光谱都与氦有相同的 人们发现,元素周期表中第二族元素的光谱都与氦有相同的 线系结构。 线系结构。 由此可见,能级和光谱的形成都是二个价电子各种相互作用引起的。 由此可见,能级和光谱的形成都是二个价电子各种相互作用引起的。
原子物理第五章

实际值为 146.16 77.15 1.9 ,与2十分接近。
例3、已知某种原子的一个多重态有三个能级,相邻两 对能级的间隔的比例为3:5,其能级结构如图所示。试给 出各能级对应的量子数S,L,J。 解:设下面一对能级的间隔为 , 于是较高的一对能级的间隔为5 3 。
5 3
J0 2
J0 1
J0
已知相邻能级的J值差为1,所以若最低能级的J值为 J 0 , 则其他两个能级为 J 0 1和 J 0 2 。
根据朗德间隔定则,得
2 L, S J0 1
③ 三重态的能级总是低于相应的单态的能级。例如 21 S0 比 23 S1高0.8eV。 ④ n=1的原子态不存在三重态。 ⑤ 第一激发态 21 S0 和 23 S1都是亚稳态,如果氦原子被 激发到这两个状态,则通过辐射跃迁到基态的几率是 极小的,这两个能级的寿命很长,实验测得 21 S0 的寿 命为19.5毫秒。
氦原子能级图
在氦的能级图中, 除基态外,所有能级 都是一个电子留在最 低态,另一个电子被 激发所形成的。图中, 最高能级是第二个电 子被电离,剩下一个 价电子在最低态时的 能级。也有可能两个 都被激发,但那样需 要更大的能量,很难 观察到。
§5.2、两个电子的耦合
一、电子的组态
原子中的原子实是一个稳固完整的结构,它的总角 动量和总磁矩是零。因此讨论原子态的形成,不需要考 虑原子实,只要从价电子来考虑就可以了。对于我们所 讨论的对象,具有两个价电子,这两个价电子可以处在 各种状态,它们合称电子组态,也即是由原子中各电子 的主量子数和角量子数所表示的原子状态。
线实际上包含有三条波长非常接近的成分。
氦原子的能级有以下几个特点: ① 有两套能级。一套能级是单层的,而另一套有三层结构, 与这两套能级相对应的原子多重态称为单态和三重态。在实 验观测的光谱中没有发现存在三重态和单态之间的跃迁,这 说明在两套能级间没有跃迁,只是由每套能级各自的跃迁产 生了相应的两套光谱线系。 ② 基态和第一激发态之间的能量差很大,为19.77eV。而 氦的电离能是所有元素中最大的,其值为24.58eV。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 多电子原子:泡利原理§5-1 氦光谱和能级氦原子是1868年分析日全蚀光谱时发现的,30年后在地球矿物中找到.实验表明,氦及元素周期表第二族元素铍、镁、钙、锶、钡、镭、锌、镉、汞的光谱结构相仿.氦原子光谱的特点(详见P.213氦原子能级图)(氦能谱的以上4个特点分别包含着4个物理概念):1)明显地分成两套谱线系,左边一套为单层,右边一套多为三层;两套能级间无跃迁,各自内部的跃迁产生了两套独立的光谱.每一套都象碱金属原子光谱一样含有主线系,辅线系和伯格曼系等.但两套线系的构成截然不同.2)存在几个亚稳态,表明某种选择规则限制了这些态以自发辐射的形式发生衰变;3)基态01S 1与第一激发态13S 2间能量相差很大,为eV .7719;电离能也是所有元素中最大的,为eV .5824;4)在三层结构那套能级中没有来自2(1S)的能级.§5-2 电子组态和原子态1.电子组态:原子中各电子状态的组合描述一个电子的状态可用s l m m l n 、、、四个量子数.考虑电子的自旋-轨道相互作用,s l m m 、不再有确定值,则电子的状态用j j m l n 、、、描述.氢原子只有一个电子,在不考虑原子核运动时,电子状态就表示原子状态.对于碱金属原子,理论上可证明原子实的总角动量为0且不易被激发,被激发的只是价电子,可认为价电子的状态就表示碱金属原子状态.多电子原子则必须考虑电子间的相互作用,原子的状态是价电子运动状态的耦合.由于轨道运动的能量只取决于量子数l n 、,所以常用nl 来标记电子状态.例如:氢原子处于基态时,电子处于01=、=l n 的状态,记为s 1;氦原子处于基态时,两个电子都处于s 1态,则用两个电子状态的组合s 1s 1或21s 来表示;若一个原子有3个电子,其中两个处在0,2==l n 的状态,另一个处在1,2==l n 的状态,则电子组态为p s 222.在给定的电子组态中,各电子的轨道角动量大小是确定的,但其轨道角动量和自旋角动量的方向不确定.因此每一个电子组态可耦合成若干原子态,由同一电子组态耦合成的不同原子态将且具有不同的能量,因为不同的角动量耦合产生的附加能量不同.2.价电子间的相互作用价电子间的相互作用除电子自身的轨道与自旋耦合外,电子间的轨道与轨道、自旋与自旋、轨道与自旋等角动量都要发生耦合作用.如两个价电子间可有6种耦合方式(如图示):),(),(),(),(),(),(126215224113212211s l G s l G s l G s l G s s G l l G 、、、、、.这6种耦合的强弱不等,一般情况下,65G G 、较弱可不考虑.下面考虑两种极端情况.1)S L -耦合:21G G 、较43G G 、强得多,将两个轨道角动量和两个自旋角动量分别合成总轨道角动量L 和总自旋角动量S ,再将L 和S 合成总角动量J .(S L -耦合对于较轻元素的低激发态成立,适用性较广)2)j j -耦合:43G G 、较21G G 、强得多,将各个电子的轨道与自旋耦合成各个电子的总角动量1j 和2j ,再将其耦合成原子的总角动量J .(j j -耦合则较少见,只在较重元素的激发态中出现)对于多电子耦合的情况可记为:⎩⎨⎧==-==-J j j j l s l s l s j j J L S l l l s s s S L )())()((:),(),,)(,,(:323322113213211 3.S L -耦合的原子态21l l L +=.L 的大小为: 212121,,1,,)1(l l l l l l L L L L --++=+=21s s S +=.S 的大小为:⎩⎨⎧=±=+=01,)1(21s s S S S S 原子的总角动量S L J +=,量子数S L S L S L J --++=,,1,对于具有两个价电子的原子,当L 给定时,对应于0,1==S S 的两种情况,J 的取值分别为:1)0=S 时,L J =,表示原子只有一个可能的角动量状态,所以是单态.2)1=S 时,1,,1-+=L L L J ,所以原子是三重态.由以上分析知,具有两个价电子的原子都有单态和三重态的能级结构.例:原子有两个价电子,其角动量状态分别为21,2;21,12211====s l s l ,用S L -耦合确定其原子态. 总自旋量子数1,0=S ,3,2,1=L ,则当0=S 时,3,2,1==L J ;原子态为11P 、21D 、31F当1,1==L S 时,⎪⎩⎪⎨⎧=012J ,原子态为⎪⎩⎪⎨⎧031323P P P ;当2,1==L S 时, ⎪⎩⎪⎨⎧=123J ,原子态为⎪⎩⎪⎨⎧132333D D D ; 当3,1==L S 时,⎪⎩⎪⎨⎧=234J ,原子态为⎪⎩⎪⎨⎧233343F F F共有12种可能的原子态.为了简洁,可排列成右上表.S L -耦合方法用于氦原子,即可证实其状态.(此略)4.j j -耦合组成的原子态当每个电子自身的自旋-轨道耦合作用强,而电子间的耦合作用很弱时,采用j j -耦合.设第i个电子的轨道角动量和自旋角动量分别为i l 和i s ,则第i 个电子的总角动量为i i i s l j +=,按量子力学规则,每个电子的总角动量的量子数为:i i i i i i i s l s l s l j --++=,,1,原子的总角动量为:21j j J += 其大小为 )1(+=J J J ,212121,,1,j j j j j j J --++=j j -耦合组成的原子态常用符号J j j ),(21表示.如pd 电子组态形成的原子态为:1,22,30,1,2,31,2,3,4)23,21(;)25,21(;)23,23(;)25,23(,也是12种可能的原子态. 结论:同一电子态,用S L -耦合形成的原子态与用j j -耦合形成的原子态的个数相等.5.两个角动量耦合的一般法则(以轨道角动量为例说明)⎪⎪⎩⎪⎪⎨⎧--++=+=+=+=⇒+=21212122211121,1,,)1()1()1(l l l l l l l l l L l l L l l L L L L其中 若21l l >,则l 共有)12(2+l 个取值.(见下例)例:两个电子的角动量为⎩⎨⎧-=-=⎩⎨⎧==101101z ,112111,,m ,,m l l l l 方向的投影分别为在.因角动量相加只要将其投影值相加即可(详见教材中例子).6.电子组态变动的跃迁选择定则:原子中各电子的量子数之和∑i l 为偶(奇)数时原子具有偶(奇)宇称.辐射跃迁只能发生在不同的宇称状态之间.即:偶宇称态⇔奇宇称态7.耦合的选择定则:S L -耦合的选择定则:⎪⎩⎪⎨⎧→±=∆±=∆=∆)00(1,010除外J L S j -j 耦合的选择定则:⎩⎨⎧→±=∆±=∆)00(1010j 除外,,J 耦合的选择规则决定了氦原子的能谱.由于S L -耦合中0=∆S ,决定了氦的两套能级间不可能发生相互跃迁.对于氦,两个价电子的原子态有单态(0S =)和三重态(1S =)两类,选择定则0=∆S 要求两类能级之间不能发生跃迁(须注意0=∆S 这一规则并非对所有原子适用),好像这两类能级属于不同原子一样,因而产生两套谱线系.人们把产生单重线的叫仲氦,产生多重线的叫正氦.实际上,仲氦是两电子自旋取向相反(0S =)的氦原子,而正氦是两电子自旋取向相同(1S =)的氦原子.氦原子之间可通过相互碰撞来交换能量,这不必服从选择规则,故正常的氦气是“正氦”与“仲氦”的混合.关于氦的三重态谱线,有著名的黄色3D 线,1868年8月18日在太阳日珥的光谱中观察到这条线,从而发现了氦.用高分辨仪器可看出此线有三成分.从光谱看三重态和单态间没有跃迁,有一条很弱的06.591A =λ的线,最初认为是氦的三重态和单态间间的跃迁,后来证实这是氖的谱线.§5-3 泡利不相容原理1.历史回顾:玻尔对元素周期系的解释作了很多工作,曾特别讨论了氦原子内层轨道的“填满”问题,关于为什么每一轨道上只能放有限数目电子的问题,玻尔猜测:“只有当电子和睦时,才可能接受具有相同量子数的电子”,否则就“厌恶接受”.(牵强解释)泡利于1921年(时年21岁)涉足原子内电子的填充问题,他意识到,元素周期系的背后隐藏着一个重要的原理.至1925年,泡利通过对原子光谱和强磁场内的塞曼效应的分析,建立了他的不相容原理,使玻尔的解释有了牢固的基础.1940年泡利又证明了不相容原理对自旋为半整数的粒子不是附加的新原理,而是相对论性波动方程的必然结果.2.不相容原理(1925年):在一个原子中不可能有两个或两个以上的电子具有完全相同的四个量子数(s l m m l n ...),即原子中的每一个状态只能容纳一个电子.另一种更普通的表述:在费米子(自旋为 21的奇数倍的微观粒子)组成的系统中,不能有两个或更多的粒子处于完全相同的状态.(电子、质子、中子等均为费米子)泡利不相容原理是微观粒子运动的基本规律之一.利用它可解释原子内部的电子分布状况和元素周期律.泡利不相容原理反映的这种严格的排斥性的物理本质是什么?至今仍是个谜.3.泡利不相容原理的应用1)氦原子的基态按L -S 耦合规则,氦的基态应有01S 和13S 两个态,但实际上只有01S ,这是因为两个电子的l m l n ,,相同(0,0,1===l m l n ),但s m 必定不能相同之故,不可能出现三重态13S .2)原子的大小玻尔曾认为原子的半径随Z 的增大而减小(核外电子都要占据能量最低的轨道,故受到的引力相等;Z 增大,核外电子受到的引力增大导致离核的距离减小).这是错误的.按泡利原理,虽第一层的轨道半径小了,但电子是分层排列的,但轨道层数增加了,原子的大小随Z 而变的变更甚微.所以原子的大小几乎都一样.(这是经典物理和旧量子论解释不了的)3)金属中的电子对金属加热过程中,核与核外电子得到的能量不均匀,几乎全由原子核得到.为什么?金属中,要使底层电子得到能量而激发十分困难,因为它附近的能态已被占满.而加热1万度才能给电子约1eV 的能量,但实际上,当加热到几百度时,金属的晶格点阵就被破坏而熔解了.所以金属中除最外层电子能从加热中得到少许能量外,其余能量均被核吸收了.4)原子核内独立核子运动按泡利原理,密度甚高的原子核内,基态附近的状态均被占满,核子之间没有相互碰撞,表现为独立的运动.5) 核子内的有色夸克基本粒子中约95%的粒子为强子,强子的性质比较有规律,这说明强子的内部结构有相似之处.在海森堡的核子同位旋概念、坂田昌一(1956年)的强子内部对称性模型基础上,1961年美国的盖尔曼和奈曼提出对强子进行分类的“八重法”,据其理论预言的重子-Ω于1964年被实验所证实.盖尔曼进一步的研究使他提出了“夸克模型”,使这种对称性理论得到真正的进展.盖尔曼用具有一定对称性的上夸克(u )、下夸克(d )和奇异夸克(s )替换了坂田模型中的三种粒子.夸克是自然界中更为基本的物质微粒,所有的强子都由这三种夸克u 、d 、s 及其反粒子粲夸克(c )、底夸克(b )和顶夸克(t )组成.人们推测具有相同性质的粒子必定成批出现的,并且根据已知的一些粒子的性质可以预见尚未发现的其它粒子.夸克模型能成功地解释许多事实,把曾经很复杂的问题简单化了. 夸克是自旋为 21的费米子,设这三个夸克均处于基态,当两个夸克的自旋方向确定后,第三个夸克的取向必与前两个中的一个相同,这显然违反了泡利原理.但这种危机并未发生,这是因为基于夸克有适当的全同粒子的对称性,人们以红、绿、蓝三种颜色作为描写夸克量子状态的量子数(即三维自由度),解决了这一问题,并由此生发了描述强相互作用的量子色动力学.4.同科电子*n 和l 相同的电子称同科电子.由于受泡利原理的限制,同科电子形成的原子态要少得多,这是因为对于同科电子,本来可能有的角动量状态由于泡利原理被去除了,从而使同科电子产生的状态数目大大减少.例如:0111S s s →,而1301,21S S s s →斯莱特图解法:例如:具有相同n 的两个电子,其组态为2np ,依泡利原理,两组量子数),,,(s l m m l n 不能全同,因1,0±=l m 有3个取值,21±=s m 有两个取值,则得到可能的l m 和s m 的取值见表26.1(教材P.223)(注意:经典物理中两个粒子可区分,但量子物理中两个全同电子是不可区分,不可加以“标记”的,这是经典物理与量子物理的原则区别之一)将表26.1数据用L S M M -图表示,图中每一小方块相应于不同的L S M M -值,方块中数字代表状态数,(a )一共有15种可能的状态,与表相符.(b)、(c)、(d)分别代表三种态项.3np 组态的电子合成的态项详见P.225.同科电子的态项与非同科电子的态项(详见P.225表)§5-4 元素周期表1.元素性质的周期性19世纪中叶人们已认识到元素的许多性质随着原子核的电荷数Z 的增加呈周期性的变化,这是原子结构随Z 的增加而呈周期性变化的结果.如摩尔体积、熔点、线胀系数、原子光谱、电离能等.元素的电离能随Z 的变化关系(详见P.226图示):表明元素的化学性质的周期变化特性.2.元素周期表人们将化学性质相近的金属元素和卤族元素分别列为两个元素族.1869年,门捷列夫提出元素周期表,将当时所知道的62个元素按原子量(现在认识到应按原子序数)增加的次序排列,则原子的属性表现出有规律的重复,从而完成对所有元素的分族.当时有不少空缺的元素尚待发现,但可预言这些未知元素的性质.1874-1875年,化学家据预言发现了三个元素:钪、镓、锗,随后又陆续发现一些,元素周期表不断得到充实.到目前这止,公认的共109种元素.元素周期表中,每行称为一个周期,共有七个周期.同一列的元素称为一族,同族元素具有具有相似的化学性质和物理性质.左起第一族为碱金属,化合价为正1价,原子光谱都具有双重结构,电离能最小.第二族为碱土金属,化合价为正2价,原子光谱有单重和三重结构两套线系.最右一族为惰性气体,化学性质不活泼,电离能最大.元素周期表提出后的50余年内.人们不能对元素的周期性做出满意解释.玻尔在提出氢原子的量子理论后,就致力于周期表的解释.他凭直觉提出原子内的电子是按壳层排列的,同一壳层的电子具有相同的主量子数n.他的设想被证实,但他未说明为什么每一壳层只能容纳一定数量的电子.直至1925年泡利提出不相容原理后,才认识到元素的周期性是电子组态的周期性反映,而电子组态的周期性则联系于特定轨道的可容性.这样,化学性质的周期性用原子结构的物理图象得到了说明,使化学概念“物理化”,化学不再是一门和物理学互不相通的学科了.3.原子中电子的壳层中结构(结合元素电离能随Z 而变的规律分析)决定原子壳层结构(即电子所处状态)的两条准则:1)泡利不相容原理.它决定壳层中电子的数目.2)能量最小原理.体系能量最低时,体系最稳定,它决定壳层的次序.元素周期表就是按以上两条准则排列的.主量子数n 决定能量的主要部分,n 相同的电子分布在一个壳层上, ,3,2,1=n 的壳层分别称为K,L,M,N,O, …壳层.n 一定时,角量子数可取n 个值,对应于1,,3,2,1,0-=n l 的支壳层分别用s,p,d,f,g,h …表示.l 一定时,s m 有两种取向,l m 有)12(+l )种取值.因此每一角量子数为l 的支壳层中最多可容纳的电子数为:)12(2+=l N l n 一定时,)1(,,2,1,0-=n l ,共有n 个取值,因此每一壳层最多可容纳的电子数为:21022)12(22)12(2n n n l N n l n =-+=+=∑-= 各支壳层和壳层中最多可容纳的电子数(见表) 电子壳层的填充:按泡利原理从能量最低的状态开始填充,填满最低能态后才依次填充更高的能态.一般说来,n 越小或n 一定时l 越小,则能量越低.某一特定壳层的电子能量,不仅取决于n ,还与l 有关,实际判断原子能级高低的经验规则:1) )(l n +的值相同,则n 小的能级低;2) )(l n +的值不同,若n 相同,则l 小的能级低;若n 不同,则n 小的能级低.具体次序为: p d f s p d f s p d s p d s p s p s s 7,6,5,7,6,5,4,6.5,4,5,4.3,4,3.3,2,2,14.原子基态对于某一特定的原子,可按照其Z 确定其电子组态.一个电子组态可合成若干原子态,需按照泡利原理选出物理上允许的原子态,然后按洪特定则确定这些原子态的能量次序.其中能量最低的即为原子基态.1) 洪特定则(1925提出的经验规则):同一电子组态形成的原子态,(1)具有相同L 值的能级中, S 值最大(即重数最高)的能级位置最低;(2)具有相同S 值的能级中,具有最大L 值的能级位置最低.针对同科电子的洪特附加定则:对于同一l 值而J 值不同的能级,有以下两种情况1)正常次序:当同科电子数小于或等于闭壳层占有数的一半时,具有最小J 值的能级(即S L -)处在最低;2)倒转次序:当同科电子数大于闭壳层占有数的一半时,具有最大J 值的能级(即S L -)处在最低2)朗德间隔定则:在三重态中,一对相邻能级间的间隔与两个J 值中较大的那个值成正比.3)矢量合成法 对由同科电子构成的组态,考虑到必须遵从泡利原理,通常不直接用S L -耦合的方法,而用合成投影合成法.要点如下:(1)按洪特定则,同科电子填入同一支壳层时,表现为尽可能以相同方向的自旋分别填入l m 不同的态,写出各电子的自旋量子数的值,求出总的自旋量子数:∑===N i si S mM S 1(2)在不违背泡利原理的前提下(即同科电子的si m 和li m 不全同),将各同科电子可能取的轨道磁量子数li m 的最大值相加,即得原子基态的总轨道量子数:∑===N i li L mM L 1(3)按洪特定则,决定原子基态光谱项的总角动量量子数,最后写出原子基态的光谱项.5.电离能变化的解释He 2:同一壳层的两个电子都受到e 2+的库仑力作用,结合能都很大; Li 3:由于静电屏蔽作用,最外层电子只受到e 1+的库仑力作用,且外层电子距核较远,结合能较小;而内层的两个电子受到e 3+的库仑力作用,其结合能较He 2中的电子要大;Be 4:最外层的两个电子受到e 2+的库仑力作用,…可见,随着壳层的增加,外层电子的结合能依次增高.如右图所示,Na 11的外层电子只受到一个有效正电荷的作用,而Ar 18外层的8个电子中的每一个都受到8个有效电荷的作用,因此,Ar 18要远比Na 11稳定.。
