almost flat manifolds

合集下载

数学专业英语第2章课后答案

2.12.比:ratio 比例:proportion 利率:interest rate 速率:speed 除:divide 除法:division 商:quotient 同类量:like quantity 项:term 线段:line segment 角:angle 长度:length 宽:width高度:height 维数:dimension 单位:unit 分数:fraction 百分数:percentage3.(1)一条线段和一个角的比没有意义,他们不是相同类型的量.(2)比较式通过说明一个量是另一个量的多少倍做出的,并且这两个量必须依据相同的单位.(5)为了解一个方程,我们必须移项,直到未知项独自处在方程的一边,这样就可以使它等于另一边的某量.4.(1)Measuring the length of a desk, is actually comparing the length of the desk to that of a ruler.(3)Ratio is different from the measurement, it has no units. The ratio of the length and the width of the same book does not vary when the measurement unit changes.(5)60 percent of students in a school are female students, which mean that 60 students out of every 100 students are female students.2.22.初等几何:elementary geometry 三角学:trigonometry 余弦定理:Law of cosines 勾股定理/毕达哥拉斯定理:Gou-Gu theorem/Pythagoras theorem 角:angle 锐角:acute angle 直角:right angle 同终边的角:conterminal angles 仰角:angle of elevation 俯角:angle of depression 全等:congruence 夹角:included angle 三角形:triangle 三角函数:trigonometric function直角边:leg 斜边:hypotenuse 对边:opposite side 临边:adjacent side 始边:initial side 解三角形:solve a triangle 互相依赖:mutually dependent 表示成:be denoted as 定义为:be defined as3.(1)Trigonometric function of the acute angle shows the mutually dependent relations between each sides and acute angle of the right triangle.(3)If two sides and the included angle of an oblique triangle areknown, then the unknown sides and angles can be found by using the law of cosines.(5)Knowing the length of two sides and the measure of the included angle can determine the shape and size of the triangle. In other words, the two triangles made by these data are congruent.4.(1)如果一个角的顶点在一个笛卡尔坐标系的原点并且它的始边沿着x轴正方向，这个角被称为处于标准位置.(3)仰角和俯角是以一条以水平线为参考位置来测量的,如果正被观测的物体在观测者的上方,那么由水平线和视线所形成的角叫做仰角.如果正被观测的物体在观测者的下方,那么由水平线和视线所形成的的角叫做俯角.(5)如果我们知道一个三角形的两条边的长度和对着其中一条边的角度,我们如何解这个三角形呢?这个问题有一点困难来回答,因为所给的信息可能确定两个三角形,一个三角形或者一个也确定不了.2.32.素数:prime 合数:composite 质因数:prime factor/prime divisor 公倍数:common multiple 正素因子: positive prime divisor 除法算式:division equation 最大公因数:greatest common divisor(G.C.D) 最小公倍数: lowest common multiple(L.C.M) 整除:divide by 整除性:divisibility 过程:process 证明:proof 分类:classification 剩余:remainder辗转相除法:Euclidean algorithm 有限集:finite set 无限的:infinitely 可数的countable 终止:terminate 与矛盾:contrary to3.(1)We need to study by which integers an integer is divisible, that is , what factor it has. Specially, it is sometime required that an integer is expressed as the product of its prime factors.(3)The number 1 is neither a prime nor a composite number;A composite number in addition to being divisible by 1 and itself, can also be divisible by some prime number.(5)The number of the primes bounded above by any given finite integer N can be found by using the method of the sieve Eratosthenes.4.(1)数论中一个重要的问题是哥德巴赫猜想,它是关于偶数作为两个奇素数和的表示.(3)一个数,形如2p-1的素数被称为梅森素数.求出5个这样的数.(5)任意给定的整数m和素数p,p的仅有的正因子是p和1,因此仅有的可能的p和m的正公因子是p和1.因此,我们有结论:如果p是一个素数,m是任意整数,那么p整除m,要么(p,m)=1.2.42.集:set 子集:subset 真子集:proper subset 全集:universe 补集:complement 抽象集:abstract set 并集:union 交集:intersection 元素:element/member 组成:comprise/constitute包含:contain 术语:terminology 概念:concept 上有界:bounded above 上界:upper bound 最小的上界:least upper bound 完备性公理:completeness axiom3.(1)Set theory has become one of the common theoretical foundation and the important tools in many branches of mathematics.(3)Set S itself is the improper subset of S; if set T is a subset of S but not S, then T is called a proper subset of S.(5)The subset T of set S can often be denoted by {x}, that is, T consists of those elements x for which P(x) holds.(7)This example makes the following question become clear, that is, why may two straight lines in the space neither intersect nor parallel.4.(1)设N是所有自然数的集合,如果S是所有偶数的集合,那么它在N中的补集是所有奇数的集合.(3)一个非空集合S称为由上界的,如果存在一个数c具有属性:x<=c对于所有S中的x.这样一个数字c被称为S的上界.(5)从任意两个对象x和y，我们可以形成序列（x，y），它被称为一个有序对，除非x=y，否则它当然不同于（y，x）.如果S和T是任意集合，我们用S*T表示所有有序对（x,y),其中x术语S，y属于T.在R.笛卡尔展示了如何通过实轴和它自己的笛卡尔积来描述平面的点之后，集合S*T被称为S和T的笛卡尔积.2.52.竖直线:vertical line 水平线:horizontal line 数对:pairs of numbers 有序对:ordered pairs 纵坐标:ordinate 横坐标:abscissas 一一对应:one-to-one 对应点:corresponding points圆锥曲线:conic sections 非空图形:non vacuous graph 直立圆锥:right circular cone 定值角:constant angle 母线:generating line 双曲线:hyperbola 抛物线:parabola 椭圆:ellipse退化的:degenerate 非退化的:nondegenerate任意的:arbitrarily 相容的:consistent 在几何上:geometrically 二次方程:quadratic equation 判别式:discriminant 行列式:determinant3.(1)In the planar rectangular coordinate system, one can set up aone-to-one correspondence between points and ordered pairs of numbers and also a one-to-one correspondence between conic sections and quadratic equation.(3)The symbol can be used to denote the set of ordered pairs（x，y）such that the ordinate is equal to the cube of the abscissa.（5）According to the values of the discriminate，the non-degenerate graph of Equation （iii） maybe known to be a parabola， a hyperbolaor an ellipse.4.（1）在例1，我们既用了图形，也用了代数的代入法解一个方程组（其中一个方程式二次的，另一个是线性的）。

漫谈微分几何、多复变函数与代数几何(Differential geometry, functions

漫谈微分几何、多复变函数与代数几何（Differential geometry, functions of complex variable and algebraic geometry）Differential geometry and tensor analysis, developed with the development of differential geometry, are the basic tools for mastering general relativity. Because general relativity's success, to always obscure differential geometry has become one of the central discipline of mathematics.Since the invention of differential calculus, the birth of differential geometry was born. But the work of Euler, Clairaut and Monge really made differential geometry an independent discipline. In the work of geodesy, Euler has gradually obtained important research, and obtained the famous Euler formula for the calculation of normal curvature. The Clairaut curve of the curvature and torsion, Monge published "analysis is applied to the geometry of the loose leaf paper", the important properties of curves and surfaces are represented by differential equations, which makes the development of classical differential geometry to reach a peak. Gauss in the study of geodesic, through complicated calculation, in 1827 found two main curvature surfaces and its product in the periphery of the Euclidean shape of the space not only depends on its first fundamental form, the result is Gauss proudly called the wonderful theorem, created from the intrinsic geometry. The free surface of space from the periphery, the surface itself as a space to study. In 1854, Riemann made the hypothesis about geometric foundation, and extended the intrinsic geometry of Gauss in 2 dimensional curved surface, thus developing n-dimensional Riemann geometry, with the development of complex functions. A group of excellentmathematicians extended the research objects of differential geometry to complex manifolds and extended them to the complex analytic space theory including singularities. Each step of differential geometry faces not only the deepening of knowledge, but also the continuous expansion of the field of knowledge. Here, differential geometry and complex functions, Lie group theory, algebraic geometry, and PDE all interact profoundly with one another. Mathematics is constantly dividing and blending with each other.By shining the charming glory and the differential geometric function theory of several complex variables, unit circle and the upper half plane (the two conformal mapping establishment) defined on Poincare metric, complex function theory and the differential geometric relationships can be seen distinctly. Poincare metric is conformal invariant. The famous Schwarz theorem can be explained as follows: the Poincare metric on the unit circle does not increase under analytic mapping; if and only if the mapping is a fractional linear transformation, the Poincare metric does not change Poincare. Applying the hyperbolic geometry of Poincare metric, we can easily prove the famous Picard theorem. The proof of Picard theorem to modular function theory is hard to use, if using the differential geometric point of view, can also be in a very simple way to prove. Differential geometry permeates deep into the theory of complex functions. In the theory of multiple complex functions, the curvature of the real differential geometry and other series of calculations are followed by the analysis of the region definition metric of the complex affine space. In complex situations, all of the singular discrete distribution, and in more complex situations, because of the famous Hartogsdevelopment phenomenon, all isolated singularities are engulfed by a continuous region even in singularity formation is often destroyed, only the formation of real codimension 1 manifold can avoid the bad luck. But even this situation requires other restrictions to ensure safety". The singular properties of singularities in the theory of functions of complex functions make them destined to be manifolds. In 1922, Bergman introduced the famous Bergman kernel function, the more complex function or Weyl said its era, in addition to the famous Hartogs, Poincare, Levi of Cousin and several predecessors almost no substantive progress, injected a dynamic Bergman work will undoubtedly give this dead area. In many complex function domains in the Bergman metric metric in the one-dimensional case is the unit circle and Poincare on the upper half plane of the Poincare, which doomed the importance of the work of Bergman.The basic object of algebraic geometry is the properties of the common zeros (algebraic families) of any dimension, affine space, or algebraic equations of a projective space (defined equations),The definitions of algebraic clusters, the coefficients of equations, and the domains in which the points of an algebraic cluster are located are called base domains. An irreducible algebraic variety is a finite sub extension of its base domain. In our numerical domain, the linear space is the extension of the base field in the number field, and the dimension of the linear space is the number of the expansion. From this point of view, algebraic geometry can be viewed as a study of finite extension fields. The properties of algebraic clusters areclosely related to their base domains. The algebraic domain of complex affine space or complex projective space, the research process is not only a large number of concepts and differential geometry and complex function theory and applied to a large number of coincidence, the similar tools in the process of research. Every step of the complex manifold and the complex analytic space has the same influence on these subjects. Many masters in related fields, although they seem to study only one field, have consequences for other areas. For example: the Lerey study of algebraic topology that it has little effect on layer, in algebraic topology, but because of Serre, Weil and H? Cartan (E? Cartan, eldest son) introduction, has a profound impact on algebraic geometry and complex function theory. Chern studies the categories of Hermite spaces, but it also affects algebraic geometry, differential geometry and complex functions. Hironaka studies the singular point resolution in algebraic geometry, but the modification of complex manifold to complex analytic space and blow up affect the theory of complex analytic space. Yau proves that the Calabi conjecture not only affects algebraic geometry and differential geometry, but also affects classical general relativity. At the same time, we can see the important position of nonlinear ordinary differential equations and partial differential equations in differential geometry. Cartan study of symmetric Riemann space, the classification theorem is important, given 1, 2 and 3 dimensional space of a Homogeneous Bounded Domain complete classification, prove that they are all homogeneous symmetric domains at the same time, he guessed: This is also true in the n-dimensional equivalent relation. In 1959, Piatetski-Shapiro has two counterexample and find the domain theory of automorphic function study in symmetry, in the 4 and 5dimensional cases each find a homogeneous bounded domain, which is not a homogeneous symmetric domain, the domain he named Siegel domain, to commemorate the profound work on Siegel in 1943 of automorphic function. The results of Piatetski-Shapiro has profound impact on the theory of complex variable functions and automorphic function theory, and have a profound impact on the symmetry space theory and a series of topics. As we know, Cartan transforms the study of symmetric spaces into the study of Lie groups and Lie algebras, which is directly influenced by Klein and greatly develops the initial idea of Klein. Then it is Cartan developed the concept of Levi-Civita connection, the development of differential geometry in general contact theory, isomorphic mapping through tangent space at each point on the manifold, realize the dream of Klein and greatly promote the development of differential geometry. Cartan is the same, and concluded that the importance of the research in the holonomy manifold twists and turns, finally after his death in thirty years has proved to be correct. Here, we see the vast beauty of differential geometry.As we know, geodesic ties are associated with ODE (ordinary differential equations), minimal surfaces and high dimensional submanifolds are associated with PDE (partial differential equations). These equations are nonlinear equations, so they have high requirements for analysis. Complex PDE and complex analysis the relationship between Cauchy-Riemann equations coupling the famous function theory, in the complex case, the Cauchy- Riemann equations not only deepen the unprecedented contact and the qualitative super Cauchy-Riemann equations (the number of variables is greater than the number of equations) led to a strange phenomenon. This makes PDE and the theory ofmultiple complex functions closely integrated with differential geometry.Most of the scholars have been studying the differential geometry of the intrinsic geometry of the Gauss and Riemann extremely deep stun, by Cartan's method of moving frames is beautiful and concise dumping, by Chern's theory of characteristic classes of the broad and profound admiration, Yau deep exquisite geometric analysis skills to deter.When the young Chern faced the whole differentiation, he said he was like a mountain facing the shining golden light, but he couldn't reach the summit at one time. But then he was cast as a master in this field before Hopf and Weil.If the differential geometry Cartan development to gradually change the general relativistic geometric model, then the differential geometry of Chern et al not only affect the continuation of Cartan and to promote the development of fiber bundle in the form of gauge field theory. Differential geometry is still closely bound up with physics as in the age of Einstein and continues to acquire research topics from physicsWhy does the three-dimensional sphere not give flatness gauge, but can give conformal flatness gauge? Because 3D balls and other dimension as the ball to establish flat space isometric mapping, so it is impossible to establish a flatness gauge; and n-dimensional balls are usually single curvature space, thus can establish a conformal flat metric. In differential geometry, isometry means that the distance between the points on the manifold before and after the mapping remains the same. Whena manifold is equidistant from a flat space, the curvature of its Riemann cross section is always zero. Since the curvature of all spheres is positive constant, the n-dimensional sphere and other manifolds whose sectional curvature is nonzero can not be assigned to local flatness gauge.But there are locally conformally flat manifolds for this concept, two gauge G and G, if G=exp{is called G, P}? G between a and G transform is a conformal transformation. Weyl conformal curvature tensor remains unchanged under conformal transformation. It is a tensor field of (1,3) type on a manifold. When the Weyl conformal curvature tensor is zero, the curvature tensor of the manifold can be represented by the Ricci curvature tensor and the scalar curvature, so Penrose always emphasizes the curvature =Ricci+Weyl.The metric tensor g of an n-dimensional Riemann manifold is conformally equivalent to the flatness gauge locally, and is called conformally flat manifold. All Manifolds (constant curvature manifolds) whose curvature is constant are conformally flat, so they can be given conformal conformal metric. And all dimensions of the sphere (including thethree-dimensional sphere) are manifold of constant curvature, so they must be given conformal conformal metric. Conversely, conformally flat manifolds are not necessarily manifolds of constant curvature. But a wonderful result related to Einstein manifolds can make up for this regret: conformally conformally Einstein manifolds over 3 dimensions must be manifolds of constant curvature. That is to say, if we want conformally conformally flat manifolds to be manifolds of constant curvature, we must call Ric= lambda g, and this is thedefinition of Einstein manifolds. In the formula, Ric is the Ricci curvature tensor, G is the metric tensor, and lambda is constant. The scalar curvature S=m of Einstein manifolds is constant. Moreover, if S is nonzero, there is no nonzero parallel tangent vector field over it. Einstein introduction of the cosmological constant. So he missed the great achievements that the expansion of the universe, so Hubble is successful in the official career; but the vacuum gravitational field equation of cosmological term with had a Einstein manifold, which provides a new stage for mathematicians wit.For the 3 dimensional connected Einstein manifold, even if does not require the conformal flat, it is also the automatic constant curvature manifolds, other dimensions do not set up this wonderful nature, I only know that this is the tensor analysis summer learning, the feeling is a kind of enjoyment. The sectional curvature in the real manifold is different from the curvature of the Holomorphic cross section in the Kahler manifold, and thus produces different results. If the curvature of holomorphic section is constant, the Ricci curvature of the manifold must be constant, so it must be Einstein manifold, called Kahler- Einstein manifold, Kahler. Kahler manifolds are Kahler- Einstein manifolds, if and only if they are Riemann manifolds, Einstein manifolds. N dimensional complex vector space, complex projective space, complex torus and complex hyperbolic space are Kahler- and Einstein manifolds. The study of Kahler-Einstein manifolds becomes the intellectual enjoyment of geometer.Let's go back to an important result of isometric mapping.In this paper, we consider the isometric mapping between M and N and the mapping of the cut space between the two Riemann manifolds, take P at any point on M, and select two non tangent tangent vectors in its tangent space, and obtain its sectional curvature. In the mapping, the two tangent vectors on the P point and its tangent space are transformed into two other tangent vectors under the mapping, and the sectional curvature of the vector is also obtained. If the mapping is isometric mapping, then the curvature of the two cross sections is equal. Or, to be vague, isometric mapping does not change the curvature of the section.Conversely, if the arbitrary points are set, the curvature of the section does not change in nature, then the mapping is not isometric mapping The answer was No. Even in thethree-dimensional Euclidean space on the surface can not set up this property. In some cases, the limit of the geodesic line must be added, and the properties of the Jacobi field can be used to do so. This is the famous Cartan isometry theorem. This theorem is a wonderful application of the Jacobi field. Its wide range of promotion is made by Ambrose and Hicks, known as the Cartan-Ambrose-Hicks theorem.Differential geometry is full of infinite charm. We classify pseudo-Riemannian spaces by using Weyl conformal curvature tensor, which can be classified by Ricci curvature tensor, or classified into 9 types by Bianchi. And these things are all can be attributed to the study of differential geometry, this distant view Riemann and slightly closer to the Klein point of the perfect combination, it can be seen that the great wisdom Cartan, here you can see the profound influence of Einstein.From the Hermite symmetry space to the Kahler-Hodge manifold, differential geometry is not only closely linked with the Lie group, but also connected with algebra, geometry and topologyThink of the great 1895 Poicare wrote the great "position analysis" was founded combination topology unabashedly said differential geometry in high dimensional space is of little importance to this subject, he said: "the home has beautiful scenery, where Xuyuan for." (Chern) topology is the beauty of the home. Why do you have to work hard to compute the curvature of surfaces or even manifolds of high dimensions? But this versatile mathematician is wrong, but we can not say that the mathematical genius no major contribution to differential geometry? Can not. Let's see today's close relation between differential geometry and topology, we'll see. When is a closed form the proper form? The inverse of the Poicare lemma in the region of the homotopy point (the single connected region) tells us that it is automatically established. In the non simply connected region is de famous Rham theorem tells us how to set up, that is the integral differential form in all closed on zero.Even in the field of differential geometry ignored by Poicare, he is still in a casual way deeply affected by the subject, or rather is affecting the whole mathematics.The nature of any discipline that seeks to be generalized after its creation, as is differential geometry. From the curvature, Euclidean curvature of space straight to zero, geometry extended to normal curvature number (narrow Riemann space) andnegative constant space (Lobachevskii space), we know that the greatness of non Euclidean geometry is that it not only independent of the fifth postulate and other alternative to the new geometry. It can be the founder of triangle analysis on it. But the famous mathematician Milnor said that before differential geometry went into non Euclidean geometry, non Euclidean geometry was only the torso with no hands and no feet. The non Euclidean geometry is born only when the curvature is computed uniformly after the metric is defined. In his speech in 1854, Riemann wrote only one formula: that is, this formula unifies the positive curvature, negative curvature and zero curvature geometry. Most people think that the formula for "Riemann" is based on intuition. In fact, later people found the draft paper that he used to calculate the formula. Only then did he realize that talent should be diligent. Riemann has explored the curvature of manifolds of arbitrary curvature of any dimension, but the quantitative calculations go beyond the mathematical tools of that time, and he can only write the unified formula for manifolds of constant curvature. But we know,Even today, this result is still important, differential geometry "comparison theorem" a multitude of names are in constant curvature manifolds for comparison model.When Riemann had considered two differential forms the root of two, this is what we are familiar with the Riemann metric Riemannnian, derived from geometry, he specifically mentioned another case, is the root of four four differential forms (equivalent to four yuan product and four times square). This is the contact and the difference between the two. But he saidthat for this situation and the previous case, the study does not require substantially different methods. It also says that such studies are time consuming and that new insights cannot be added to space, and the results of calculations lack geometric meaning. So Riemann studied only what is now called Riemann metric. Why are future generations of Finsler interested in promoting the Riemann's not wanting to study? It may be that mathematicians are so good that they become a hobby. Cartan in Finsler geometry made efforts, but the effect was little, Chern on the geometric really high hopes also developed some achievements. But I still and general view on the international consensus, that is the Finsler geometry bleak. This is also the essential reason of Finsler geometry has been unable to enter the mainstream of differential geometry, it no beautiful properties really worth geometers to struggle, also do not have what big application value. Later K- exhibition space, Cartan space will not become mainstream, although they are the extension of Riemannnian geometry, but did not get what the big development.In fact, sometimes the promotion of things to get new content is not much, differential geometry is the same, not the object of study, the more ordinary the better, but should be appropriate to the special good. For example, in Riemann manifold, homogeneous Riemann manifold is more special, beautiful nature, homogeneous Riemann manifolds, symmetric Riemann manifold is more special, so nature more beautiful. This is from the analysis of manifold Lie group action angle.From the point of view of metric, the complex structure is given on the even dimensional Riemann manifold, and the complexmanifold is very elegant. Near complex manifolds are complex manifolds only when the near complex structure is integrable. The complex manifold must be orientable, because it is easy to find that its Jacobian must be nonnegative, whereas the real manifold does not have this property in general. To narrow the scope of the Kahler manifold has more good properties, all complex Submanifolds of Kahler manifolds are Kahler manifolds, and minimal submanifolds (Wirtinger theorem), the beautiful results captured the hearts of many differential geometry and algebraic geometry, because other more general manifolds do not set up this beautiful results. If the first Chern number of a three-dimensional Kahler manifold is zero, the Calabi-Yau manifold can be obtained, which is a very interesting manifold for theoretical physicists. The manifold of mirrors of Calabi-Yau manifolds is also a common subject of differential geometry in algebraic geometry. The popular Hodge structure is a subject of endless appeal.Differential geometry, an endless topic. Just as algebraic geometry requires double - rational equivalence as a luxury, differential geometry requires isometric transformations to be difficult. Taxonomy is an eternal subject of mathematics. In group theory, there are single group classification, multi complex function theory, regional classification, algebraic geometry in the classification of algebraic clusters, differential geometry is also classified.The hard question has led to a dash of young geometry and old scholars, and the prospect of differential geometry is very bright.。

微积分术语中英文对照

微积分术语中英文对照A、B:Absolute convergence ：绝对收敛Absolute extreme values ：绝对极值Absolute maximum and minimum ：绝对极大与极小Absolute value ：绝对值Absolute value function ：绝对值函数Acceleration ：加速度Antiderivative ：原函数,反导数Approximate integration ：近似积分<法> Approximation ：逼近法by differentials ：用微分逼近linear ：线性逼近法by Simpson’s Rule ：Simpson法则逼近法by the Trapezoidal Rule ：梯形法则逼近法Arbitrary constant ：任意常数Arc length ：弧长Area ：面积under a curve ：曲线下方之面积between curves ：曲线间之面积in polar coordinates ：极坐标表示之面积of a sector of a circle ：扇形之面积of a surface of a revolution ：旋转曲面之面积Asymptote ：渐近线horizontal ：水平渐近线slant ：斜渐近线vertical ：垂直渐近线Average speed ：平均速率Average velocity ：平均速度Axes, coordinate ：坐标轴Axes of ellipse ：椭圆之对称轴Binomial series ：二项式级数Binomial theorem：二项式定理C:Calculus ：微积分differential ：微分学integral ：积分学Cartesian coordinates ：笛卡儿坐标一般指直角坐标Cartesian coordinates system ：笛卡儿坐标系Cauch’s Mean Value Theorem ：柯西中值定理Chain Rule ：链式法则Circle ：圆Circular cylinder ：圆柱体,圆筒Closed interval ：闭区间Coefficient ：系数Composition of function ：复合函数Compound interest ：复利Concavity ：凹性Conchoid ：蚌线Conditionally convergent：条件收敛Cone ：圆锥Constant function ：常数函数Constant of integration ：积分常数Continuity ：连续性at a point ：在一点处之连续性of a function ：函数之连续性on an interval ：在区间之连续性from the left ：左连续from the right ：右连续Continuous function ：连续函数Convergence ：收敛interval of ：收敛区间radius of ：收敛半径Convergent sequence ：收敛数列series ：收敛级数Coordinates：坐标Cartesian ：笛卡儿坐标cylindrical ：柱面坐标polar ：极坐标rectangular ：直角坐标spherical ：球面坐标Coordinate axes ：坐标轴Coordinate planes ：坐标平面Cosine function ：余弦函数Critical point ：临界点Cubic function ：三次函数Curve ：曲线Cylinder：圆筒, 圆柱体, 柱面Cylindrical Coordinates ：圆柱坐标D:Decreasing function ：递减函数Decreasing sequence ：递减数列Definite integral ：定积分Degree of a polynomial ：多项式之次数Density ：密度Derivative ：导数of a composite function ：复合函数之导数 of a constant function ：常数函数之导数directional ：方向导数domain of ：导数之定义域of exponential function ：指数函数之导数higher ：高阶导数partial ：偏导数of a power function ：幂函数之导数of a power series ：羃级数之导数of a product ：积之导数of a quotient ：商之导数as a rate of change ：导数当作变化率right-hand ：右导数second ：二阶导数as the slope of a tangent ：导数看成切线之斜率Determinant ：行列式Differentiable function ：可导函数Differential ：微分Differential equation ：微分方程partial ：偏微分方程Differentiation ：求导法implicit ：隐求导法partial ：偏微分法term by term ：逐项求导法Directional derivatives ：方向导数Discontinuity ：不连续性Disk method ：圆盘法Distance ：距离Divergence ：发散Domain ：定义域Dot product ：点积Double integral ：二重积分change of variable in ：二重积分之变数变换in polar coordinates ：极坐标二重积分E、F、G:Ellipse ：椭圆Ellipsoid ：椭圆体Epicycloid ：外摆线Equation ：方程式Even function ：偶函数Expected Valued ：期望值Exponential Function ：指数函数Exponents , laws of ：指数率Extreme value ：极值Extreme Value Theorem ：极值定理Factorial ：阶乘First Derivative Test ：一阶导数试验法First octant ：第一卦限Focus ：焦点Fractions ：分式Function ：函数Fundamental Theorem of Calculus ：微积分基本定理Geometric series ：几何级数Gradient ：梯度Graph ：图形Green Formula ：格林公式H:Half-angle formulas ：半角公式Harmonic series ：调和级数Helix ：螺旋线Higher Derivative ：高阶导数Higher mathematics 高等数学Horizontal asymptote ：水平渐近线Horizontal line ：水平线Hyperbola ：双曲线Hyperboloid ：双曲面I:Implicit differentiation ：隐求导法Implicit function ：隐函数Improper integral ：反常积分, 广义积分Increasing,Decreasing Test ：递增或递减试验法Increment ：增量Increasing Function ：增函数Indefinite integral ：不定积分Independent variable ：自变量Indeterminate from ：不定型Inequality ：不等式Infinite point ：无穷极限点Infinite series ：无穷级数Inflection point ：反曲点Instantaneous velocity ：瞬时速度Integer ：整数Integral ：积分Integrand ：被积函数Integration ：积分Integration by part ：分部积分法Intercepts ：截距Intermediate value of Theorem ：中值定理Interval ：区间Inverse function ：反函数Inverse trigonometric function ：反三角函数Iterated integral ：逐次积分L:Laplace transform ：Laplace 变换Law of sines：正弦定理Law of Cosines ：余弦定理Least upper bound ：最小上界Left-hand derivative ：左导数Left-hand limit ：左极限Lemniscate ：双钮线Length ：长度Level curve ：等高线L'Hospital's rule ：洛必达法则Limacon ：蚶线Limit ：极限Linear approximation：线性近似Linear equation ：线性方程式Linear function ：线性函数Linearity ：线性Linearization ：线性化Line in the plane ：平面上之直线Line in space ：空间之直线Local extreme ：局部极值Local maximum and minimum ：局部极大值与极小值Logarithm ：对数Logarithmic function ：对数函数M、N、O:Maximum and minimum values ：极大与极小值Mean Value Theorem ：均值定理Multiple integrals ：重积分Multiplier ：乘子Natural exponential function ：自然指数函数Natural logarithm function ：自然对数函数Natural number ：自然数Normal line ：法线Normal vector ：法向量Number ：数Octant ：卦限Odd function ：奇函数One-sided limit ：单边极限Open interval ：开区间Optimization problems ：最佳化问题Order ：阶Ordinary differential equation ：常微分方程Origin ：原点Orthogonal ：正交的P、Q:Parabola ：拋物线Parabolic cylinder ：抛物柱面Paraboloid ：抛物面Parallelepiped ：平行六面体Parallel lines ：平行线Parameter ：参数Partial derivative ：偏导数Partial differential equation ：偏微分方程Partial fractions ：部分分式Partial integration ：部分积分Partition ：分割Period ：周期Periodic function ：周期函数Perpendicular lines ：垂直线Piecewise defined function ：分段定义函数Plane ：平面Point of inflection ：反曲点Polar axis ：极轴Polar coordinate ：极坐标Polar equation ：极方程式Pole ：极点Polynomial ：多项式Positive angle ：正角Point-slope form ：点斜式Power function ：幂函数Product ：积Quadrant ：象限Quotient Law of limit ：极限的商定律Quotient Rule ：商定律R:Radius of convergence ：收敛半径Range of a function ：函数的值域Rate of change ：变化率Rational function ：有理函数Rationalizing substitution ：有理代换法Rational number ：有理数Real number ：实数Rectangular coordinates ：直角坐标Rectangular coordinate system ：直角坐标系Relative maximum and minimum ：相对极大值与极小值Revenue function ：收入函数Revolution , solid of ：旋转体Revolution , surface of ：旋转曲面Riemann Sum ：黎曼和Right-hand derivative ：右导数Right-hand limit ：右极限Root ：根S:Saddle point ：鞍点Scalar ：纯量Secant line ：割线Second derivative ：二阶导数Second Derivative Test ：二阶导数试验法Second partial derivative ：二阶偏导数Sector ：扇形Sequence ：数列Series ：级数Set ：集合Shell method ：剥壳法Sine function ：正弦函数Singularity ：奇点Slant, Oblique asymptote ：斜渐近线Slope ：斜率Slope-intercept equation of a line ：直线的斜截式Smooth curve ：平滑曲线Smooth surface ：平滑曲面Solid of revolution ：旋转体Space ：空间Speed ：速率Spherical coordinates ：球面坐标Squeeze Theorem ：夹挤定理Step function ：阶梯函数Strictly decreasing ：严格递减Strictly increasing ：严格递增Substitution rule ：替代法则Sum ：和Surface ：曲面Surface integral ：面积分Surface of revolution ：旋转曲面Symmetry ：对称T:Tangent function ：正切函数Tangent line ：切线Tangent plane ：切平面Tangent vector ：切向量Taylor’s formula ：泰勒公式Total differential ：全微分Trigonometric function ：三角函数Trigonometric integrals ：三角积分Trigonometric substitutions ：三角代换法Tripe integrals ：三重积分V、X、Z:Value of function ：函数值Variable ：变量Vector ：向量Velocity ：速度Vertical asymptote ：垂直渐近线Volume ：体积X-axis ：x轴X -coordinate ：x坐标X -intercept ：x截距Zero vector ：函数的零点Zeros of a polynomial ：多项式的零点。

常用的相似准则数

常用的相似准则数相似性准则是一种用于测量或衡量两个或多个对象之间的相似性或相关性的方法或模型。

在不同领域和应用中，存在许多常用的相似性准则，以下是其中一些常见的准则。

1. 欧几里德距离（Euclidean Distance）：欧几里德距离是空间中两个点之间的直线距离，根据勾股定理计算。

2. 曼哈顿距离（Manhattan Distance）：曼哈顿距离是两个点在坐标系上的绝对差值之和，通常用于城市街区距离的度量。

3. 余弦相似度（Cosine Similarity）：余弦相似度是向量空间中两个向量的夹角余弦值，可用于衡量文本、图像等数据的相似性。

4. 杰卡德相似系数（Jaccard Similarity Coefficient）：杰卡德相似系数用于衡量两个集合的相似度，计算两个集合交集的大小与并集的大小之比。

5. 皮尔逊相关系数（Pearson Correlation Coefficient）：皮尔逊相关系数是一种用于衡量两个连续变量之间线性相关程度的方法，取值范围为-1到16. 汉明距离（Hamming Distance）：汉明距离是用于衡量两个等长字符串之间的差异度量，计算相同位置不同字符的个数。

7. K-L散度（Kullback-Leibler Divergence）：K-L散度是一种度量两个概率分布之间差异的方法，用于衡量一个概率分布相对于另一个分布的不确定性。

10. 汉明重量（Hamming Weight）：汉明重量是二进制数中非零位的个数，用于衡量两个二进制数的相似性。

11. 简化模式（Simplification Metric）：简化模式是一种度量模型简化程度的方法，通常用于优化问题解的复杂度。

这些相似性准则在数据挖掘、机器学习、自然语言处理、图像处理等领域中得到广泛应用。

它们可以帮助我们理解和比较不同对象之间的相似性、相关性或差异性，从而为我们提供洞察和决策支持。

Submanifolds of generalized complex manifolds

SUBMANIFOLDS OF GENERALIZED (ALMOST) COMPLEX MANIFOLDS
arXiv:math/0309013v1 [math.DG] 1 Sep 2003
OREN BEN-BASSAT AND MITYA BOYARCHENKO Abstract. The main goal of our paper is the study of several classes of submanifolds of generalized complex manifolds. Along with the generalized complex submanifolds deﬁned by Gualtieri and Hitchin in [4], [8] (we call these “generalized Lagrangian submanifolds” in our paper), we introduce and study three other classes of submanifolds. For generalized complex manifolds that arise from complex (resp., symplectic) manifolds, all three classes specialize to complex (resp., symplectic) submanifolds. In general, however, all three classes are distinct. We discuss some interesting features of our theory of submanifolds, and illustrate them with a few nontrivial examples. We then support our “symplectic/Lagrangian viewpoint” on the submanifolds introduced in [4], [8] by deﬁning the “generalized complex category”, modelled on the constructions of Guillemin-Sternberg [5] and Weinstein [14]. We argue that our approach may be useful for the quantization of generalized complex manifolds.

美国大学生数学建模MCM 数学专用名词

美国大学生数学建模MCM 数学专用名词augmented matrix增广矩阵asymptotic渐进的asymptote渐进线asymmetrical非对称的associative law结合律ascending上升的arrangement排列arithmetic算术argument幅角，幅度，自变量，论证area面积arc length弧长apothem边心距apex顶点aperiodic非周期的antisymmetric反对称的antiderivative原函数anticlockwise逆时针的annihilator零化子angular velocity角速度angle of rotation旋转角angle of incidence入射角angle of elevation仰角angle of depression俯角angle of circumference圆周角analytic space复空间analytic geometry解析几何analytic function解析函数analytic extension解析开拓amplitude幅角，振幅alternative互斥的alternate series交错级数almost everywhere几乎处处algebraic topology代数拓扑algebraic expression代数式algebraic代数的affine仿射(几何学)的admissible error容许误差admissible容许的adjugate伴随转置的adjoint operator伴随算子adjoint伴随的adjacency邻接additive加法，加性acute angle锐角accumulation point聚点accidential error偶然误差accessible point可达点abstract space抽象空间abstract algebra抽象代数absolute value绝对值absolute integrable绝对可积absolute convergent绝对收敛Abelian阿贝尔的，交换的balance equation平衡方程bandwidth带宽barycenter重心base基base vectors基向量biased error有偏误差biased statistic有偏统计量bilinear双线性的bijective双射的bilateral shift双侧位移的binomial二项式bisector二等分线，平分线boundary边界的，边界bounded有界的broken line折线bundle丛，把，卷calculus微积分calculus of variations变分法cancellation消去canonical典型的，标准的canonical form标准型cap交，求交运算capacity容量cardinal number基数Cartesian coordinates笛卡尔坐标category范畴，类型cell单元，方格，胞腔cell complex胞腔复形character特征标characterization特征circuit环路，线路，回路circular ring圆环circulating decimal循环小数clockwise顺时针方向的closed ball闭球closure闭包cluster point聚点coefficient系数cofinal共尾的cohomology上同调coincidence重合，叠和collinear共线的collective集体的columnar rank列秩combinatorial theory组合理论common tangent公切线commutative交换的compact紧的compact operator紧算子compatibility相容性compatible events相容事件complementary余的，补的complete完全的，完备的complex analysis复变函数论complex potential复位势composite复合的concave function凹函数concentric circles同心圆concurrent共点conditional number条件数confidence interval置信区间conformal共形的conic圆锥的conjugate共轭的connected连通的connected domain连通域consistence相容，一致constrained约束的continuable可延拓的continuity连续性contour周线，回路，轮廓线convergence收敛性convexity凸形convolution对和，卷积coordinate坐标coprime互质的，互素的correspondence对应coset陪集countable可数的counterexample反例covariance协方差covariant共变的covering覆盖critical临界的cubic root立方根cup并，求并运算curl旋度curvature曲率curve曲线cyclic循环的decade十进制的decagon十边形decimal小数的，十进制的decision theory决策论decomposable可分解的decreasing递减的decrement减量deduction推论，归纳法defect亏量，缺陷deficiency亏格definition定义definite integral定积分deflation压缩deflection挠度，挠率，变位degenerate退化的deleted neighborhood去心邻域denominator分母density稠密性，密度density function密度函数denumerable可数的departure偏差，偏离dependent相关的dependent variable因变量derangement重排derivation求导derivative导数descent下降determinant行列式diagram图，图表diameter直径diamond菱形dichotomy二分法diffeomorphism微分同胚differentiable可微的differential微分differential geometry微分几何difference差，差分digit数字dimension维数directed graph有向图directed set有向集direct prodect直积direct sum直和direction angle方向角directional derivative方向导数disc圆盘disconnected不连通的discontinuous不连续的discrete离散的discriminant判别式disjoint不相交的disorder混乱，无序dissection剖分dissipation损耗distribution分布，广义函数divergent发散的divisor因子，除数division除法domain区域，定义域dot product点积double integral二重积分dual对偶dynamic model动态模型dynamic programming动态规划dynamic system动力系统eccentricity离心率econometrics计量经济学edge棱，边eigenvalue特征值eigenvector特征向量eigenspace特征空间element元素ellipse椭圆embed嵌入empirical equation经验公式empirical assumption经验假设endomorphism自同态end point端点entropy熵entire function整函数envelope包络epimorphism满同态equiangular等角equilateral等边的equicontinuous等度连续的equilibrium平衡equivalence等价error estimate误差估计estimator估计量evaluation赋值，值的计算even number偶数exact sequence正合序列exact solution精确解excenter外心excision切割，分割exclusive events互斥事件exhaustive穷举的expansion展开，展开式expectation期望experimental error实验误差explicit function显函数exponent指数extension扩张，外延face面factor因子factorial阶乘fallacy谬误fiducial置信field域，场field theory域论figure图形，数字finite有限的finite group有限群finite iteration有限迭代finite rank有限秩finitely covered有限覆盖fitting拟合fixed point不动点flag标志flat space平旦空间formula公式fraction分数，分式frame架，标架free boundary自由边界frequency频数，频率front side正面function函数functional泛函functor函子，算符fundamental group基本群fuzzy模糊的gain增益，放大率game对策gap间断，间隙general topology一般拓扑学general term通项generalized普遍的，推广的generalized inverse广义逆generalization归纳，普遍化generating line母线genus亏格geodesic测地线geometrical几何的geometric series几何级数golden section黄金分割graph图形，网格half plane半平面harmonic调和的hexagon六边形hereditary可传的holomorphic全纯的homeomorphism同胚homogeneous齐次的homology同调homotopy同伦hyperbola双曲线hyperplane超平面hypothesis假设ideal理想idempotent幂等的identical恒等，恒同identity恒等式，单位元ill-condition病态image像点，像imaginary axis虚轴imbedding嵌入imitation模仿，模拟immersion浸入impulse function脉冲函数inclination斜角，倾角inclined plane斜面inclusion包含incomparable不可比的incompatible不相容的，互斥的inconsistent不成立的indefinite integral不定积分independence无关（性），独立（性）index指数，指标indivisible除不尽的inductive归纳的inductive definition归纳定义induced诱导的inequality不等式inertia law惯性律inference推理，推论infimum下确界infinite无穷大的infinite decimal无穷小数infinite series无穷级数infinitesimal无穷小的inflection point拐点information theory信息论inhomogeneous非齐次的injection内射inner point内点instability不稳定integer整数integrable可积的integrand被积函数integral积分intermediate value介值intersection交，相交interval区间intrinsic内在的，内蕴的invariant不变的inverse circular funct反三角函数inverse image逆像，原像inversion反演invertible可逆的involution对合irrational无理的，无理数irreducible不可约的isolated point孤立点isometric等距的isomorphic同构的iteration迭代joint distribution联合分布kernel核keyword关键词knot纽结known已知的large sample大样本last term末项lateral area侧面积lattice格子lattice point格点law of identity同一律leading coefficient首项系数leaf蔓叶线least squares solution最小二乘解lemma引理Lie algebra李代数lifting提升likelihood似然的limit极限linear combination线性组合linear filter线性滤波linear fraction transf线性分linear filter线性滤波式变换式变换linear functional线性泛函linear operator线性算子linearly dependent线性相关linearly independent线性无关local coordinates局部坐标locus(pl.loci)轨迹logarithm对数lower bound下界logic逻辑lozenge菱形lunar新月型main diagonal主对角线manifold流形mantissa尾数many-valued function多值函数map into映入map onto映到mapping映射marginal边缘master equation主方程mathermatical analysis数学分析mathematical expectati数学期望matrix(pl. matrices)矩阵maximal极大的，最大的maximum norm最大模mean平均，中数measurable可测的measure测度mesh网络metric space距离空间midpoint中点minus减minimal极小的，最小的model模型modulus模，模数moment矩monomorphism单一同态multi-analysis多元分析multiplication乘法multipole多极mutual相互的mutually disjoint互不相交natural boundary自然边界natural equivalence自然等价natural number自然数natural period固有周期negative负的，否定的neighborhood邻域nil-factor零因子nilpotent幂零的nodal节点的noncommutative非交换的nondense疏的，无处稠密的nonempty非空的noncountable不可数的nonlinear非线性的nonsingular非奇异的norm范数normal正规的，法线normal derivative法向导数normal direction法方向normal distribution正态分布normal family正规族normal operator正规算子normal set良序集normed赋范的n-tuple integral重积分number theory数论numerical analysis数值分析null空，零obtuse angle钝角octagon八边形octant卦限odd number奇数odevity奇偶性off-centre偏心的one-side单侧的open ball开球operations reserach运筹学optimality最优性optimization最优化optimum最佳条件orbit轨道order阶，级，次序order-preserving保序的order-type序型ordinal次序的ordinary寻常的，正常的ordinate纵坐标orient定方向orientable可定向的origin原点original state初始状态orthogonal正交的orthonormal规范化正交的outer product外积oval卵形线overdetermined超定的overlaping重叠，交迭pairity奇偶性pairwise两两的parabola抛物线parallel平行parallel lines平行线parallelogram平行四边形parameter参数parent population母体partial偏的，部分的partial ordering偏序partial sum部分和particle质点partition划分，分类path space道路空间perfect differential全微分period周期periodic decimal循环小数peripheral周界的，外表的periphery边界permissible容许的permutable可交换的perpendicular垂直perturbation扰动，摄动phase相，位相piecewise分段的planar平面的plane curve平面曲线plane domain平面区域plane pencil平面束plus加point of intersection交点pointwise逐点的polar coordinates极坐标pole极，极点polygon多边形polygonal line折线polynomial多项式positive正的，肯定的potency势，基数potential位势prime素的primitive本原的principal minor主子式prism棱柱proof theory证明论probability概率projective射影的，投影proportion比例pure纯的pyramid棱锥，棱锥体quadrant像限quadratic二次的quadric surface二次曲面quantity量，数量quasi-group拟群quasi-norm拟范数quasi-normal拟正规queuing theory排队论quotient商radial径向radical sign根号radication开方radian弧度radius半径ramified分歧的random随机randomize随机化range值域，区域，范围rank秩rational有理的raw data原始数据real function实函数reciprocal倒数的，互反的reciprocal basis对偶基reciprocity互反性rectangle长方形，矩形rectifiable可求长的recurring decimal循环小数reduce简化，化简reflection反射reflexive自反的region区域regular正则regular ring正则环related function相关函数remanent剩余的repeated root重根residue留数，残数resolution分解resolvent预解式right angle直角rotation旋转roundoff舍入row rank行秩ruled surface直纹曲面runs游程，取遍saddle point鞍点sample样本sampling取样scalar field标量场scalar product数量积，内积scale标尺，尺度scattering散射，扩散sectorial扇形self-adjoint自伴的semicircle半圆semi-definite半定的semigroup半群semisimple半单纯的separable可分的sequence序列sequential相继的，序列的serial序列的sheaf层side face侧面similar相似的simple curve简单曲线simplex单纯形singular values奇异值skeleton骨架skewness偏斜度slackness松弛性slant斜的slope斜率small sample小样本smooth manifold光滑流形solid figure立体形solid geometry立体几何solid of rotation旋转体solution解solvable可解的sparse稀疏的spectral theory谱论spectrum谱sphere球面，球形spiral螺线spline function样条函数splitting分裂的statistics统计，统计学statistic统计量stochastic随机的straight angle平角straight line直线stream-line流线subadditive次可加的subinterval子区间submanifold子流形subset子集subtraction减法sum和summable可加的summand被加数supremum上确界surjective满射的symmetric对称的tabular表格式的tabulation列表，造表tangent正切，切线tangent space切空间tangent vector切向量tensor张量term项terminal row末行termwise逐项的tetrahedroid四面体topological拓扑的torsion挠率totally ordered set全序集trace迹trajectory轨道transcendental超越的transfer改变，传transfinite超限的transformation变换式transitive可传递的translation平移transpose转置transverse横截、trapezoid梯形treble三倍，三重trend趋势triad三元组triaxial三轴的，三维的trigon三角形trigonometric三角学的tripod三面角tubular管状的twist挠曲，扭转type类型，型，序型unbiased无偏的unbiased estimate无偏估计unbounded无界的uncertainty不定性unconditional无条件的unequal不等的uniform一致的uniform boundness一致有界uniformly bounded一致有界的uniformly continuous一致连续uniformly convergent一致收敛unilateral单侧的union并，并集unit单位unit circle单位圆unitary matrix酉矩阵universal泛的，通用的upper bound上界unrounded不舍入的unstable不稳定的valuation赋值value值variation变分，变差variety簇vector向量vector bundle向量丛vertex顶点vertical angle对顶角volume体积，容积wave波wave form波形wave function波函数wave equation波动方程weak convergence弱收敛weak derivatives弱导数weight权重，重量well-ordered良序的well-posed适定的zero零zero divisor零因子zeros零点zone域，带</Words>。

卡尔曼滤波简介和实例讲解(精品WORD文档)

卡尔曼，美国数学家和电气工程师。

1930年5月 19日生于匈牙利首都布达佩斯。

1953年在美国麻省理工学院毕业获理学士学位,1954年获理学硕士学位,1957年在哥伦比亚大学获科学博士学位。

1957～1958年在国际商业机器公司(IBM)研究大系统计算机控制的数学问题。

1958～1964年在巴尔的摩高级研究院研究控制和数学问题。

1964～1971年到斯坦福大学任教授。

1971年任佛罗里达大学数学系统理论研究中心主任，并兼任苏黎世的瑞士联邦高等工业学校教授。

1960年卡尔曼因提出著名的卡尔曼滤波器而闻名于世。

卡尔曼滤波器在随机序列估计、空间技术、工程系统辨识和经济系统建模等方面有许多重要应用。

1960年卡尔曼还提出能控性的概念。

能控性是控制系统的研究和实现的基本概念，在最优控制理论、稳定性理论和网络理论中起着重要作用。

卡尔曼还利用对偶原理导出能观测性概念，并在数学上证明了卡尔曼滤波理论与最优控制理论对偶。

为此获电气与电子工程师学会(IEEE)的最高奖──荣誉奖章。

卡尔曼著有《数学系统概论》(1968)等书。

什么是卡尔曼滤波最佳线性滤波理论起源于40年代美国科学家Wiener和前苏联科学家Ｋолмогоров等人的研究工作，后人统称为维纳滤波理论。

从理论上说，维纳滤波的最大缺点是必须用到无限过去的数据，不适用于实时处理。

为了克服这一缺点，60年代Kalman把状态空间模型引入滤波理论，并导出了一套递推估计算法，后人称之为卡尔曼滤波理论。

卡尔曼滤波是以最小均方误差为估计的最佳准则，来寻求一套递推估计的算法，其基本思想是：采用信号与噪声的状态空间模型，利用前一时刻地估计值和现时刻的观测值来更新对状态变量的估计，求出现时刻的估计值。

它适合于实时处理和计算机运算。

卡尔曼滤波的实质是由量测值重构系统的状态向量。

它以“预测—实测—修正”的顺序递推，根据系统的量测值来消除随机干扰，再现系统的状态，或根据系统的量测值从被污染的系统中恢复系统的本来面目。

manifold用法

“manifold”这个词有多种用法。

作为形容词，它表示多种多样的，多方面的，有多种形式的，有多种用途的。

作为名词，它表示具有多种形式的东西，多支管，歧管（汽车引擎用于进气或排气）。

作为及物动词，它表示复写，复印，增多，使…多样化。

在微分几何中，manifold是一个n维空间，其局部外观像R^n。

一个n维manifold由M的每个点P的邻近的局部模型定义。

这些局部模型是R^n的开集同胚于M在P点的开集。

此外，流形中的点可能会被好几个图所表示，如果两个图重叠，它们的部分会表示流形的同一个区域。

这些部分之间的关联代表流形上同一点的坐标点的映射，称作坐标变换、变换函数或转换函数、转换映射。

以上信息仅供参考，如需了解更多信息，建议查阅英语同义词词典获取更多关于“manifold”的释义及用途。

数学专业英语词汇（F）

数学专业英语词汇(F)f distribution f分布f ratio 方差比f space f空间f test f检定face 面face centered 面心的face centered cubic 面心立方体的face of a polyhedron 多面体面face operator 面算子factor 因子factor analysis 因子分析factor combination 因子组合factor group 商群factor groupoid 商广群factor loading 因子载荷factor matrix 因子矩阵factor model 因子模型factor module 商模factor of a polynomial 多项式的因子factor of proportionality 比例系数factor out 提出撰因子factor ring 商环factor set 商集factor space 商空间factor system 因子组factor theorem 因子定理factorability 因子可分解性factorable 可因子分解的factorial 阶乘factorial cumulant 阶乘累积量factorial design 因子设计factorial experiment 析因实验factorial notation 阶乘记号factorial of an integer 整数的阶乘factorial polynomial 阶乘多项式factorial series 阶乘级数factoring 因式分解factorizable 可因子分解的factorization 因式分解factorization method 因子分解方法factorization theorem 因子分解定理factorize 因子分解fair game 适当对策faithful anti representation 一一反表示faithful functor 一一的函子faithful module 一一的模faithful representation 一一表示faithfully flat ring 一一平坦环false 假的false conclusion 假结论family 族family of curves 曲线族family of elements 元素族family of functions 函数族family of orthogonal curves 正交曲线族family of planes 平面族family of sets 集族family of solutions 解族family of surfaces 曲面族fan 扇形farey series 法雷级数fast fourier transformation 快速傅里叶变换fatou lemma 法都引理favorable case 有利情形favorable event 有利事件feasible base 可行基feasible constraint 可行约束feasible control 可行控制feasible direction 可行方向feasible point 可行点feasible region 可行区域feasible restriction 可行约束feasible solution 可行解feeble solution 弱解fermat last theorem 费马最后定理fermat number 费马数fermat spiral 费马螺线fermat theorem 费马定理feynman integral 费曼积分fiber 纤维fiber bundle 纤维丛fiber map 纤维映射fiber preserving mapping 保纤映射fiber space 纤维空间fibonacci number 斐波那契数fibring 纤维空间fiducial distribution 置信分布fiducial estimation 置信估计fiducial inference 置信推理fiducial limit 置信限fiducial probability 置信概率fiducial region 置信区域field 域;场field of algebraic functions 代数函数域field of constants 常数域field of definition 定义域field of events 事件场field of extremals 极值曲线场field of forces 力场field of numbers 数域field of rational functions 有理函数域field of rationals 有理数域field of real numbers 实数域field of scalars 系数域field of sets 集域field theory 域论;场论figure 图形filter 滤子filter base 滤子基filtered category 滤子化范畴filtered degree 滤子化次数filtered group 过滤群filtering 过滤filtration 过滤final decision 最后判决final functor 尾函子final state 终态final topology 终拓扑fine sheaf 强层fine topology 细拓扑fineness 细度finer topology 较细拓扑finish time 终止时间finite automaton 有限自动机finite base 有限基finite cardinal 有限基数finite constructibility 有限可构成性finite continued fraction 有限连分数finite cyclic group 有限循环群finite definability 有限可定义性finite difference approximation 有限差分逼近finite difference equation 有限差分方程finite dimensional 有限维的finite dimensional extension field 有限维扩张域finite dimensional operator 有限维算子finite discontinuity 有限不连续性finite element method 有限元法finite equation 有限方程finite extension 有限维扩张域finite field 有限域finite function 有限函数finite game 有限对策finite group 有限群finite induction 有限归纳法finite mathematics 有限数学finite measure 有限测度finite model 有限模型finite multiplier 有限乘数finite nilpotent group 有限幂零群finite number plane 有限数平面finite ordinal number 有限序数finite part 有限部分finite partition 有限划分finite point 有限点finite presentation 有限表示finite progression 有限级数finite quantity 有限量finite sequence 有限序列finite series 有限级数finite set 有限集finite sum 有限和finite valued function 有限值函数finitely additive 有限加性的finitely additive measure 有限加性测度finitely cocomplete category 有限共完全范畴finitely complete category 有限完全范畴finitely generatable vector space 有限可生成向量空间finitely generated abelian group 有限生成阿贝耳群finitely generated algebra 有限生成代数finitely generated extension field 有限生成扩张域finitely generated group 有限生成群finitely generated ideal 有限生成理想finitely generated module 有限生成模finitely presented 有限出现的finitely presented group 有限出现群finitely representable 有限可表示的finitely valued function 有限值函数finiteness 有限性finiteness principle 有限性原理finiteness theorem 有限性原理finsler manifold 芬斯莱廖first approximation 首次近似first axiom of countability 第一可数性公理first boundary condition 狄利克雷边界条件first boundary value problem 狄利克雷问题first class 第一类first comparison test 第一比较检验first derivative 一阶导数first fundamental form 第一基本形式first fundamental form of surface 曲面的第一基本形式first integral 初积分first isomorphism theorem 同态定理first mean value theorem 平均值定理first obstruction 第一障碍类first order theory 一阶理论first quadrant 第一象限first quartile 第一四分位数first term 首项first theorem of the mean 第一平均值定理fisher z distribution 费歇耳z分布fitted curve 拟合曲线fitting 拟合five color theorem 五色定理five figure 五位数的five point finite difference scheme 五点有限差分格式five sided 五面的fix 固定fixed element 不变元fixed error 偏倚fixed point 定点fixed point calculation 定点计算fixed point method 不动点法fixed point of mapping 映射的不动点fixed point representation 定点表示法fixed point theorem 不动点定理fixed sample 固定样本fixed vector 固定向量flabby resolution 松弛分解flabby sheaf 散射层flag 旗flag manifold 旗廖flat morphism 平坦射flat point 平坦点flat space 平坦空间flat surface 平面flatness 平坦性flecnode 拐结点flex 拐点floating point 浮点floating point calculation 浮点记数法floating point notation 浮点记数法floating point representation 浮点记数法flow 流flow line 吝flow of scalar field 纯量场的流flow problem 潦题fluctuation 起状fluent 变数fluid 铃fluid dynamics 铃动力学fluid mechanics 铃力学flux 量flux of the vector 量fluxion 导数focal axis 焦轴focal chord 焦弦focal circle 焦圆focal conic 焦点圆锥曲线focal distance 焦距focal length 焦距focal line 焦线focal plane 焦平面focal point 焦点focal radius 焦半径focal strip 焦带focal surface 焦曲面focus 焦点focus of a parabola 抛物线的焦点fold singularity 折奇性folding 卷积foliated manifold 叶状廖foliation 叶状结构folium 叶形线folium of descartes 笛卡儿叶形线follow 跟foot 垂足foot of a perpendicular 垂足force 力force function 力函数force of gravity 重力force of inertia 惯性力force polygon 力的多角形force triangle 力三角形force vector 力向量forced oscillation 受迫振动forced vibration 受迫振动forcing method 力迫法forecasting 预报form 形式formal 形式的formal derivative 形式导数formal language 形式语言formal logic 形式逻辑formal model 形式模型formal power series 形式幂级数formal system 形式系统formally real field 形式实域formation 形成formation rule 形成规则formless 无形状的formula 公式formula language 公式语言formula of computation 计算公式formula of propositional logic 命题逻辑公式formulate 公式化formulation 用公式表示forward difference 前向差分forward difference operator 前向差分算子forward difference quotient 前向差商forward solution 前向解法foundation 基础foundation of geometry 几何基础foundations of geometry 几何基础foundations of mathematics 数学基础four address 四地址的four address instruction 四地址指令four color conjecture 四色猜想four color problem 四色问题four color theorem 四色定理four digit 四位的four dimensional 四维的four dimensionality 四维性four fold table 四重表four vector 四元向量four vertex theorem 四顶点定理fourier analysis 傅里叶分析fourier analyzer 傅里叶分析仪fourier bessel series 傅里叶贝塞耳级数fourier bessel transformation 汉克尔变换fourier coefficient 傅里叶系数fourier cosine transform 傅里叶余弦变换fourier expansion 傅里叶展开fourier integral 傅里叶积分fourier integral equation 傅里叶积分方程fourier integral theorem 傅里叶积分定理fourier kernel 傅里叶核fourier series 傅里叶级数fourier sine transform 傅里叶正弦变换fourier synthesis 傅里叶综合法fourier transform 傅里叶变换fourierstieltjes transform 傅里叶斯蒂尔吉斯变换fractal 分形fractal dimension 分形维数fraction 分数fraction in lowest terms 最简分数fractional derivative 分数导数fractional equation 分数方程fractional exponent 分式指数fractional function 分数函数fractional ideal 分式理想fractional integral 分数次积分fractional number 分数fractional part 分数部分fractional rational function 分数有理函数fractional replication 分数配置fractionary ideal 分式理想frame 架frechet derivative 弗雷谢导数frechet differentiable function 弗莱谢可微函数frechet differential 弗雷谢微分frechet space f空间fredholm alternative 弗雷德霍姆择一fredholm alternative theorem 弗雷德霍姆择一定理fredholm determinant 弗雷德霍姆行列式fredholm integral equation 弗雷德霍姆积分方程fredholm operator 弗雷德霍姆算子fredholm point 弗雷德霍姆点fredholm radius 弗雷德霍姆半径fredholm type integral equation 弗雷德霍姆型积分方程free decision variable 自由决策变量free end 自由端free group 自由群free groupoid 自由广群free index 自由指标free liberty 自由可动性free mobility 自由可动性free monoid 自由独异点free optimization problem 自由最优化问题free product 自由积free semigroup 自由半群free subscript 自由添标free ultrafilter 自由超滤子free variable 自由变量free vector 自由向量frequency 频率frequency curve 频率曲线frequency diagram 频率图frequency distribution 频率分布frequency function 频率函数frequency polygon 频数多边形frequency theory of probability 概率的频率论fresnel integral 菲涅耳积分friction 摩擦frobenius algebra 弗罗宾尼斯代数frobenius automorphism 弗罗宾尼斯自同构frobenius group 弗罗宾尼斯群front 前面frontier 边界frontier point 边界点frustum of a paraboloid 平截头抛物面体frustum of cone 平截头圆锥体frustum of pyramid 截棱锥fubini theorem 富比尼定理fuchsian function 富克斯函数fuchsian group 富克斯群fulcrum 支点full inhomogeneous lorentz group 完全非齐次洛伦茨群full line 实线full linear group 全线性群full solid angle 完全立体角full subcategory 完全子范畴full unimodular group 完全幺模群fully faithful 完全一一的fully faithful functor 完全一一函子fully normal space 仿紧空间fully reducible star body 完全可约星形体fully transitive group 全可迁群function 函数function algebra 函数代数function chart 函数尺function code 操纂function constant 函数常数function continuous on the right 右连续函数function field 函数域function of bounded variation 有界变差函数function of class 类函数function of complex variable 复变函数function of confluent type 合镣函数function of function 合成函数function of n variables n元函数function of one variable 一元函数function of several real variables 多实元函数function of several variables 多元函数function of third order 三阶函数function of unbounded variation 无界变差函数function representation 函数表示function sequence 函数序列function series 函数级数function space 函数空间function symbol of n arguments n变数函数符号function theoretic 函数论的function theoretic null set 函数论的零集function theory 函数论function value 函数值function variable 函数变数functional 泛函functional analysis 泛函分析functional calculus 函项演算functional constant 函数常数functional dependence 函数相关functional determinant 函数行列式functional differential equation 泛函微分方程functional equation 函数方程functional expression 函数式functional matrix 函数矩阵functional relation 函数关系functional scale 函数尺functional space 函数空间functional symbol 函数符号functional transformation 泛函变换functionelement 函数元素functor 函子fundamental 基本的fundamental class 基本类fundamental cocycle 基本上循环fundamental conjunction 基本合取fundamental constants 基本常数fundamental curve 基本曲线fundamental cycle 基本闭链fundamental determinant 基本行列式fundamental discriminant 基本判别式fundamental domain 基本域fundamental element 基本元素fundamental equations 基本方程fundamental form 基本形式fundamental formulae 基本公式fundamental frequency 基频fundamental function 特寨数fundamental group 基本群fundamental groupoid 基本广群fundamental homology class 基本同掂fundamental identity 基本恒等式fundamental invariant 基本不变量fundamental law 基本律fundamental lemma 基本引理fundamental lemma of calculus of variation 变分法的基本引理fundamental matrix 基本矩阵fundamental net 基本有向点族fundamental parallelepipedon 基本平行六面体fundamental period 基本周期fundamental period parallellogram 基本周期平行四边形fundamental period parallelogram 原始周期平行四边形fundamental point 基本点fundamental polygon 基本多角形fundamental sequence 柯悟列fundamental set 基本集fundamental solution 基本解fundamental surface 基本曲面fundamental system of solutions 基本解组fundamental tensor 基本张量fundamental tetrahedron 基本四面体fundamental theorem 基本定理fundamental theorem of algebra 代数基本定理fundamental theorem of calculus 微积分基本定理fundamental transformation 基本变换fundamental unit 基本单位fundamentals 原理fuzzy set 模糊集。

国际经济学英文第七版克鲁格曼英文经济名词翻译

Key Terms of International EconomicsChapter3 Labor Productivity and Comparative Advantage Comparative advantage 比较优势Absolute advantage 绝对优势Opportunity cost 机会成本Production possibility frontier 生产可能性边界Unit labor requirement 单位产品劳动投入Relative price 相对价格Relative demand curve相对需求曲线Relative supply curve 相对供给曲线Relative wage 相对工资Relative quantity 相对产量Ricardian model 李嘉图模型Pauper labor argument 贫民劳动论Nontraded goods 非贸易商品Chapter 4 Resources and Trade: the Heckscher-Ohlin Model Abundant factor 丰裕要素Biased expansion of production 偏向性生产扩张Equalization of factor prices 要素价格均等化Factor abundance 要素丰裕度Factor intensity 要素密集度Scarce factor 稀缺要素Leontief paradox 里昂惕夫悖论land-intensive 土地密集型Labor-intensive劳动密集型the ratio of 2 factor prices 要素价格比Wage-rental ratio 工资-租金比Land-labor ratio ，the ratio of land to labor 土地劳动比Chapter 5 The standard Trade Model--------------------------精品文档，可以编辑修改，等待你的下载，管理，教育文档----------------------------------------------------------------------------------------------------------------------------------------------------------------Biased growth 偏向性增长Export-biased growth 出口偏向性增长Immiserizing growth 贫困化增长Import-biased growth 进口偏向性增长Isovalue line等价值线Marginal propensity to spend边际消费倾向T erms of trade贸易条件Transfers of income转移支付Chapter 6 Economies of Scale, Imperfect Competition, and in ternational TradeDumping 倾销External economies of scale外部规模经济Imperfect competition 不完全竞争Interindustry trade 产业间贸易Intraindustry trade 产业内贸易Internal economies of scale内在规模经济Monopolistic competion垄断竞争Reciprocal dumping 相互倾销Increasing return 报酬递增Chapter 7 The Instruments of Trade policyad valorem tariff从价税Specific tariff从量税Consumer surplus消费者剩余Producer surplus生产者剩余Production distortion loss生产扭曲损失Consumption distortion loss消费扭曲损失Effective rate of protection有效保护率Efficiency loss效率损失Export restraint出口限制Export subsidy出口补贴Import quota进口配额--------------------------精品文档，可以编辑修改，等待你的下载，管理，教育文档----------------------------------------------------------------------------------------------------------------------------------------------------------------Voluntary export restraint自愿出口限制Local content requirement国产化程度要求nontariff barriers非关税避垒Quota rent配额租金Chapter 8 National Income Accounting and the Balance of Payments The Balance of Payment AccountsCurrent accountFinancial accountCapital accountChapter 9 Exchange Rates and the Foreign Exchange Market:An Asset ApproachAppreciation升值Arbitrage套汇、套利Depreciation贬值Exchange rate汇率Forward exchange rate远期汇率Interest parity condition利率平价条件Rate of appreciation升值率Rate of depreciation贬值率Real rate of return实际收益率Spot exchange rate即期汇率Vehicle currency载体货币Foreign exchange外汇Chapter 10 Money, Interest Rates, and Exchange ratesMoney Supply 货币供给Money Demand 货币需求Short-Run Price Rigidity 短期价格粘性Long-run Price Flexibility 长期灵活价格permanent increase in the U.S. money supply 货币供给永久性增长overshooting 超调--------------------------精品文档，可以编辑修改，等待你的下载，管理，教育文档----------------------------------------------------------------------------------------------------------------------------------------------------------------Chapter 11 Price Levels and the Exchange Rate in the Long Run Law of one price 一价定律Nominal exchange rate 名义汇率Nominal interest rate 名义利率Purchasing power parity 购买力平价Real appreciation实际升值Real depreciation 实际贬值Real exchange rate 实际汇率Relative PPP相对购买力平价Market rigidity市场刚性Price rigidity价格刚性Price stickiness价格粘性Chapter 12 Output and the Exchange Rate in the Short Run Aggregate demand 总需求Fiscal policy 财政政策J-curve J曲线Real exchange rate 实际汇率Real appreciation 实际升值Real depreciation 实际贬值Chapter 13 Fixed, Floating Exchange Rate and Policies Effects Sterilization冲销Sterilized foreign exchange intervention冲销性外汇干预Devaluation法定贬值Revaluation法定升值Clean float 清洁浮动Dirty float 肮脏浮动Capital flight 资本抽逃Chapter 14 The Theory of Optimum Currency Areas--------------------------精品文档，可以编辑修改，等待你的下载，管理，教育文档----------------------------------------------------------------------------------------------------------------------------------------------------------------optimum currency areas 最优货币区Monetary efficiency gain 货币效率收益Economic integration 经济一体化Floating exchange rate 浮动汇率Fixed exchange rate 固定汇率--------------------------精品文档，可以编辑修改，等待你的下载，管理，教育文档----------------------------------------------------------------------------------------------------------------------------------------------------------------。

度分布从而得到歹和尸的更高阶近似...

硕士论文UKF算法及其改进算法的研究中南大学硕士学位论文UKF算法及其改进算法的研究姓名:刘铮申请学位级别:硕士专业:控制科学与工程指导教师:樊晓平20090501摘要由于卡尔曼滤波器具有结构简单、性能最优、易于被掌握和应用等一系列的优点,其已被广泛应用于状态跟踪和估计等科学领域。

值得一提的是,由于其线性的推导和计算过程,决定了卡尔曼滤波器不能应用于非线性系统。

然而,滤波方法却可以通过一组代表着均值和方差分布的采样点来对非线性系统进行非线性计算,在不对非线性方程线性近似的条件下,达到线性卡尔曼滤波器的滤波性能。

随着滤波器在非线性状态估计领域的不断发展,越来越多的学者开始关注和研究妤滤波方法。

本文主要研究的是滤波方法的滤波性能、现存问题和改进方法。

首先,介绍和分析了几种重要的采样策略。

同时,提出了一种自适应比例采样策略,并且进行仿真实验证明了其有效性。

然后, 对该自适应采样策略中的比例因子进行了有益的讨论,并详细研究了该采样策略的适用范围和优缺点。

然后,详细讨论了存在模型误差的算法。

为减小线性化误差对非线性系统状态估计的影响,本文采用采样滤波器中的渐消记忆方法进行高精度滤波。

同时深入研究的自适应渐消记忆策略,以增强对建模误差的鲁棒性和对突变状态的跟踪能力,提高状态估计.的精度和快速性。

最后,为了提高滤波器的滤波精度和收敛速度,采用了一种混合动态系统传递模型下的噪声自适应算法。

基于方差匹配法和对噪声的缩放,该自适应算法能自动的使整个系统达到最优。

关键词非线性系统,,自适应采样,模型误差,处理噪声估计.., . ?,. , ., ..,.. .,, .,.嘞..,., ,原创性声明本人声明,所呈交的学位论文是本人在导师指导下进行的研究工作及取得的研究成果。

尽我所知,除了论文中特别加以标注和致谢的地方外,论文中不包含其他人已经发表或撰写过的研究成果,也不包含为获得中南大学或其他单位的学位或证书而使用过的材料。

哈罗德多玛模型的方程式

哈罗德多玛模型的方程式
哈罗德多玛模型是一种生物数学模型，用于描述一个种群的增长过程。

它的方程式可以表示为：
dN/dt = rN(1-N/K)
其中，N 是种群数量，t 是时间，r 是种群增长率，K 是种群的容纳量。

这个方程式描述了种群数量随时间的变化率，它有两个关键的部分：第一个是增长率 rN，它表示种群数量的增长速度与当前种群数量成正比；第二个是(1-N/K)，它表示种群数量相对于最大容纳量的剩余空间，即种群数量接近最大容纳量时增长速度会变慢。

这个方程式可以用于预测种群的增长和稳定状态，以及人口、动物和植物生态系统的研究。

城乡迁移、失业与私有化：托达罗假说

Lett Spat Resour Sci(2012)5:85–94DOI10.1007/s12076-011-0069-5O R I G I NA L PA P E RUrban-rural migration,unemployment,and privatization:a synthesis of Harris-Todaro modeland a mixed duopolyTohru NaitoReceived:21June2011/Accepted:7October2011/Published online:27October2011©Springer-Verlag2011Abstract The purpose of this paper is to analyze the effect of privatization on unem-ployment under the dualistic economy where the manufactured goods sector in urban area is the mixed duopoly and the agricultural goods sector in rural area is competi-tive.The result shows that the privatization of publicﬁrm in urban area makes worse the urban unemployment.The partial privatization is optimal when the environmental damage is high,relatively.Keywords Mixed duopoly·Privatization·Urban unemployment·Environmental pollutionJEL Classiﬁcation L32·Q56·R111IntroductionThe purpose of this paper is to analyze the effect of privatization of publicﬁrm on urban unemployment in a dualistic economy.Some developing countries face on not only urban unemployment but also environmental problems.These countries need a prescription to solve an environmental problem and the unemployment problem at the same time.As for urban unemployment problem,Harris and Todaro(1970) elucidated the mechanism to bring about the unemployment caused by migration be-tween urban area and rural area in developing countries.Some researchers extend this model by introducing environmental factor into Harris and Todaro model.Fukuyama and Naito(2007)also consider the environmental policies in the framework of Harris T.Naito()The University of Tokushima,Institute of Socio-Arts and Sciences,1-1Minamijosanjima-cho, Tokushima,7708502,Japane-mail:naito@ias.tokushima-u.ac.jp86T.Naito and Todaro model,in which the manufactured goods sector in urban area faces on competitive market.On the other hand,some developing countries have promoted the privatization of some public sector due to any economic policy.Some researchers have concerned about the privatization of publicﬁrm and analyzed the mixed oligopoly market.De Fraja and Delbono(1989)is one of pioneer studies in mixed oligopoly market.Mat-sumura(1998)or,Beladi and Chao(2006)consider the partial privatization of public ﬁrm in mixed oligopoly.In this paper,we construct the model,which synthesize three factors;mixed oligopoly market,dualistic economy,and environmental factor.We analyze the ef-fect of privatization of publicﬁrm on urban unemployment or optimal privatization level under this synthesized model.The paper proceeds as follows.The next section outlines the basic model.Section3shows the effect of privatization of publicﬁrm on the equilibrium and optimal privatization in the model.Finally,Sect.4contains our concluding remarks.2The modelWe consider the economy where all households have a common preference and reside in either urban area or rural area.We consider two kinds of products:agricultural goods and manufactured goods.The labor is used as the factors of production for both the agricultural good and the manufactured good.We assume that the urban wage is ﬁxed above the market-clearing level,and that it has downward rigidity attributable to the minimum wage system and so on.Particularly,let¯w x(=w x)represent the minimum wage in the urban area,which is higher than the rural wage w y.1That rural wage is determined in the labor market of the agricultural goods sector and is equal to the marginal product of labor in the agricultural goods sector.Moreover,we assume that labor has free mobility between urban area and rural areas,and we deal with the agricultural goods as numeraire in our model.We normalize total population in the economy as one.The proﬁt of agricultural goods sector and aggregated land rent in rural area are redistributed to all households.2.1HouseholdsSince we assume that all households have common preference,they have the follow-ing same utility function.U i(x,y;D)=ax−12x2+y−D(¯X)(i=x,u,y)(1)where x,y,and D are the consumption of manufactured goods,that of agricultural goods,and environmental damage caused by the production of manufactured good sector,respectively.Though the environmental damage D depends on the production level of manufactured goods(¯X),the households deal with this environmental dam-age as given.Thus,households cannot control this level,though the environmental1This assumption is followed by Harris and Todaro(1970).Urban-rural migration,unemployment,and privatization87 damage affects the utility level of households.All households have a unit of laborand supply it to either manufactured goods sector or agricultural goods sector inelas-tically.Thus,households employed by manufactured goods sector in urban area earnthe wage income w x(=¯w x)and those employed by agricultural goods sector in ruralarea earn the wage income w y.Households residing in the urban area are unemployedif they are not hired by the manufacturing goods sector.They do not earn wage in-come(w u=0)and can get only redistribution from the proﬁt of agricultural goods sector and the aggregated land lent in rural area.Here the budget constraint of eachhousehold is as follows.w i+I=px+y(i=x,u,y)(2) where p and I denote the price of manufactured goods and resitribution for each household.Here,I is composed of land rent revenue and the proﬁt of agricultural goods sector.Maximizing(1)subject to each budget constraint(2),the demand func-tion of manufactured goods of households is as follows.x=a−p(3) Substituting(3)into each budget constraint,each household’s demand of agricultural goods are as follows.y i=w i+I−p(a−p)(i=x,u,y)(4) Moreover,substituting(3)and(4)into(1),we can derive the following indirect utility function of each household.Let v i(i=x,u,y)represent the indirect utility function of households employed by manufactured goods sector in urban area,unemployed households in urban area,households in rural area,respectively.v i=12(a−p)2+w i+I−D(¯X)(i=x,u,y)(5)After deriving(3)as the demand function of manufactured goods of each household, we consider the total demand of manufactured goods in the economy.Let L x,L y, and L u represent the numbers of households employed by manufactured goods sec-tor,households employed by agricultural goods sector,and unemployed households, respectively.Assuming that the population in the economy is normalized to one,the (inverse)demand function of manufactured goods in an economy is as follows.p=a−¯X(6) Similar to Harris and Todaro model,the migration equilibrium between urban area and rural area is established when the expected utility level in urban area is equal to the utility level in rural area.Now we deﬁneλas the urban unemployment rate.λ≡L uL x u(7)Thus,the migration equilibrium condition(Harris and Todaro condition)is given by (1−λ)v x+λv u=v y⇐⇒(1−λ)¯w x=w(8) Assuming that total population in the economy is one,the population constraint is as follows.L x+L u+L y=1(9)88T.Naito Plugging(7)and(9),the population constraint is rewritten as follows.L x+(1−λ)L y=(1−λ)(10) 2.2Production2.2.1Agricultural goods sectorWe assume that labor and land are required for the production of agricultural goods. We assume that¯S y is theﬁxed land input and that it is normalized land input to one. We set up the production function as follows.Y=(L y)σ(¯S y)1−σ,σ∈(0,1)(11) Since we deal with agricultural goods as numeraire and assume that agricultural goods market is competitive,the wage rate of household employed by agricultural goods sector is equal to marginal product of product in its sector.w=σ(L y)σ−1(12) 2.2.2Manufactured goods sectorNext we construct the model of manufactured goods sector.Here,labor is only input factor for manufactured goods production.Though the agricultural goods sector mar-ket is competitive,the manufactured good sector faces the mixed duopoly,in which publicﬁrm and privateﬁrm exist in the same market.Manufactured goods are pro-duced in domestic country and are consumed there.Thus,we do not consider both import and export of manufactured goods in this model.Moreover,the publicﬁrm is owned by domestic government and maximize the domestic social welfare.On the other hand,the purpose of privateﬁrm is maximization of his proﬁt and it is owned by the foreign country entrepreneur.We assume that the minimum wage rate in urban area is¯w x as well as Harris and Todaro(1970).We label the publicﬁrm and private ﬁrm asﬁrm0andﬁrm1,respectively.Now we assume that the production function of manufactured goods is a linear function with respect to labor.Thus,we describe the production function ofﬁrm i(i=0,1)as follows.2X i=L i xm,m>0(i=0,1)(13)Here taking account of labor as only input of manufactured goods production and the shape of(13),the marginal cost C i ofﬁrm i is given byC i=¯w x mX i(14) We assume that the environmental damage is caused by pollution,which the man-ufactured goods sector emits in the process of his production.Let¯X represent thetotal amount of manufactured goods produced by publicﬁrm and privateﬁrm,that is, 2See Daitoh(2010).Urban-rural migration,unemployment,and privatization 89¯X=X 0+X 1.We set up the environmental damage caused by manufactured goods production as follows.D(¯X)=d 2(X 0+X 1)2(0<d <1)(15)Moreover we deﬁne ˆWas the domestic social welfare function.Since the private ﬁrm is owned by foreign country entrepreneur in our model,the social welfare function does not include the proﬁt of private ﬁrm.Thus the social welfare function is com-posed of consumer surplus,the proﬁt of public ﬁrm,and environmental damage.3ˆW =12(¯X)2+π0+¯w x L x +wL y −D(¯X)+I Here we consider that the government owns the share of (1−θ)of public ﬁrm as well as Matsumura (1998).Thus,the purpose of public ﬁrm (ﬁrm 0)is to maximize the weighted average of social welfare and its proﬁt,which is deﬁned by V (θ).It is possible for us to take account of partial privatization as to optimal privatization level.V (θ)=θπ0+(1−θ)ˆW =π0+(1−θ) 1−d 2(X 0+X 1)2+m ¯w x (X 0+X 1)+σL σy +I (16)The proﬁt function of ﬁrm 1,π1,is given by π1= a −(X 0+X 1) X 1−¯w x mX 1(17)Thus,differentiating (17)with respect to X 1,the ﬁrst order condition for proﬁt max-imization of ﬁrm 1is as follows.∂π1∂X 1=a −X 0−2X 1−m ¯w x =0(18)On the other hand,as the public ﬁrm maximizes (16),the ﬁrst order condition to maximize the weighted average of social welfare and proﬁt is as follows.∂V ∂X 0=a −θm ¯w x + (1−θ)(1−d)−2 X 0+ (1−θ)(1−d)−1 X 1=0(19)Solving (18)and (19),the equilibrium production of each ﬁrm can be derived as X ∗0and X ∗1:X ∗0=[1+(1−θ)(1−d)]a +[1−2θ−(1−θ)(1−d)]m ¯w x 3−(1−θ)(1−d)(20)X ∗1=[1−(1−θ)(1−d)]a −[2−θ−(1−θ)(1−d)]m ¯w x3−(1−θ)(1−d)(21)3The deﬁnition of social welfare used here is followed by Fukuyama and Naito (2007).Some countries like China do not permit ﬁrms owned by 100%foreign capital to operate in those countries.However,the Malaysian government permits 100%foreign capital to operate their ﬁrms in Malaysia after 2009.We consider the later situation in this model.90T.Naito Comparing(20)with(21),we know that the publicﬁrm production is larger than the privateﬁrm production when the parameter d,which means the environmental damage caused by manufactured goods sector,satisﬁes0<d<1.This result is the same as the results derived in previous literatures about mixed oligopoly theory and the publicﬁrm’s behavior outsells that of privateﬁrms.¯X=2a−(1+θ)m¯w x3−(1−θ)(1−d)(22) Here let L x represent the labor demand of manufactured goods sector.Since we spec-ify(13)as the production function of manufactured goods,the labor demand of man-ufactured goods sector in equilibrium is as follows.L x=L0x+L1x=m[2a−(1+θ)m¯w x]3−(1−θ)(1−d)(23)where L i x(i=0,1)denotes the labor input ofﬁrm i(=1,2).Substituting(22)into (6),we derive the equilibrium price of manufactured goods as follows.p∗=a[1−(1−θ)(1−d)]+(1+θ)m¯w x3−(1−θ)(1−d)(24)Next we consider the effect of privatization of publicﬁrm on total production in manufactured goods sector.Differentiating(22)with respect toθ,we derive the following function.∂¯X∂θ=−(1−d)a+[3−2(1−θ)(1−d)]m¯w x<0(25)Thus,we know that the effect of privatization on total production depends on the de-gree for environmental damage,which is denoted by d.Here we assume that d is pos-itive and smaller than one.So the privatization of publicﬁrm leads to decrease total manufactured goods production.Moreover,since we assume the production function is linear with respect to labor,the effect of privatization on the required labor input in equilibrium is as follows.∂L x ∂θ=−m{(1−d)a+[3−2(1−θ)(1−d)]m¯w x}<0(26)The required labor input in manufactured goods sector depends on the degree for environmental damage,too.We derive the following lemma from(25)and(26). Lemma1The privatization of publicﬁrm decreases the total amount of manufac-tured goods production and the required labor input for its production.3The effect of privatization on urban unemploymentWe have speciﬁed the behaviors of households,agricultural goods sector,and manu-factured goods sector.We consider the migration between urban area and rural areaUrban-rural migration,unemployment,and privatization91 under the above speciﬁcation.The wage rate in rural area is given by(12).So substi-tuting(12)into Harris-Todaro condition(8),L y is derived as follows.L∗y=(1−λ)¯w xσ1σ−1(27)Moreover,substituting(23)and(27)into(10),we derive the following equation.m[2a−(1+θ)m¯w x] 3−(1−θ)(1−d)+(1−λ)σσ−1¯w xσ1σ−1=(1−λ)(28)Solving(28)with respect toλ,we can describeλas the function of¯w x,θ,m,d, andσ.Using the implicit function theorem to(28),dλdθis given bydλdθ=m[2(1−d)a+(1−θ)dm¯w x][(σ1−σ)(1−λ)1σ−1(¯w xσ)1σ−1+1][3−(1−θ)(1−d)]2>0(29)We know that the effect of privatization of publicﬁrm on urban unemployment de-pends on the degree for environmental damage caused by manufactured good sector.Since1−d is positive,the sign of dλdθis positive.Thus,we derive the followingproposition.Proposition1When the degree of environmental damage caused by manufactured goods production is smaller than one,the privatization of publicﬁrm makes worse the unemployment rate in urban area.We show that it is possible to make worse the unemployment rate by the pri-vatization of publicﬁrm under any degree of environmental damage due to Propo-sition1.Next we consider how the privatization affects the environmental damage in an economy.As we know from(15),the increase of manufactured goods pro-duction leads to increase the environmental damage in an economy.We consider the effect of privatization on total manufactured goods production in equilibrium. Differentiating D(¯X(θ))with respect toθ,we know the following relationship from(25).dD(¯X) dθ=dD(¯X)d¯X·d¯Xdθ<0(30)Therefore,the effect of publicﬁrm’s privatization on environmental damage dependson the sign of(25).Supposed that d is smaller than one,d¯Xdθis negative,that is,the privatization improves the environmental damage.The publicﬁrm determines his production level to maximize the social welfare and produces more excessive than the privateﬁrm under the mixed oligopoly model.Since the privatization of publicﬁrm affects the unemployment rate and environmental damage,each effect of privatization is opposite.Thus,it is necessary to analyze the effect of privatization on social welfare in equilibrium in order to derive the optimal privatization level of92T.Naito Fig.1Optimal privatizationand environmental damagepublicﬁrm.Since equilibrium output of publicﬁrm is determined by(20),the social welfare in equilibrium is as follows.¯W∗=1−d2(¯X)2+p∗X∗0+m¯w x L∗x+wL∗y+I(31) Differentiating¯W∗with respect toθ,we derive the following equation.∂¯W∗∂θ=−1(2+θ+(1−θ)d)32(1−d)a+(1+2d)m¯w x×3(1+d)θ−da+2−m+θ−2m(θ+d)+(1−θ)d(32)Urban-rural migration,unemployment,and privatization93Determiningθ∗to satisfy∂¯W∗∂θ=0,the optimal privatization level is given as thefunction of d.4θ∗=(a+2m−1)d+m−2(3a−1)d+(3a−2m+1)(33)The sign of(32)depends on the environmental damage parameter d and the produc-tivity of manufactured goods m.Now we consider about relationship between optimalprivatization level and the environmental damage parameter d.Figure1describes the relationship between optimal privatization levelθ∗and theenvironmental damage parameter d under each parameter of manufactured goodsproductivity.As we know from Fig.1,the optimal privatization level is the increas-ing function of environmental damage parameter.Since we assume that the range ofparameter d is d∈[0,1],θ∗=1(full privatization)is not optimal despite the produc-tivity of manufactured goods.On the other hand,it is possible thatθ∗=0(full nation-alization)is optimal when the environmental damage parameter d is low relatively.Moreover,the range of environmental damage parameter,where full nationalizationis optimal,is the decreasing function of the productivity of manufactured goods.Inother words,the partial privatization is optimal when the environmental damage ishigh relatively.4Concluding remarksWe construct the model introducing the environmental damage having an effect onhousehold’s utility into Harris and Todaro model,which describes a dualistic econ-omy in developing countries.Though Fukuyama and Naito(2007)introduced theenvironmental damage into Harris and Todaro model and assumed that both manu-factured goods market and agricultural goods market are competitive,we considerthe manufactured good market is mixed duopoly market.The results show that theprivatization of publicﬁrm always makes worse urban unemployment rate and thatthe partial privatization is optimal when the productivity of manufactured goods andenvironmental damage is high relatively.Acknowledgements The previous version of this paper presented at2011Japanese Economic Associ-ation spring meeting,86th annual conference in Western Economic Association International,Institution and Economics International Conference2011,Regional Science Workshop in Tohoku University,and Applied Economics Workshop in Kyushu University.The author thanks to Yasunori Fujita,Jy S.Wu,Hi-rofumi Fukuyama,Dao-Zhi Zeng,Tatsuhito Kono,Asao Ando,Nobuaki Hori,Konari Uchida.Moreover, the author also thanks to two anonymous referees for their valuable comments in the previous version of this paper.This study is supported by Grant-in-Aid for Scientiﬁc Research B(22330095)from Japan Society of the Promotion of Science.ReferencesBeladi,H.,Chao,C.:Mixed ownership,unemployment,and welfare for a developing economy.Rev.Dev.Econ.10(4),604–611(2006)4Here we assume that the second order condition is satisﬁed.Though we use“optimal privatization level”, this level is notﬁrst best solution because of existence of urban unemployment.94T.Naito Daitoh,I.:International oligopoly market and the strategic trade policy in developing countries:the un-employment problem in developing countries and the optimal export policy in developed countries.Mimeo(2010)De Fraja,G.,Delbono,F.:Alternative strategies of a public enterprise in oligopoly.Oxf.Econ.Pap.41, 302–311(1989)Fukuyama,H.,Naito,T.:Unemployment,trans-boundary pollution,and environmental policy in a dualistic economy.RURDS,Rev.Urb.Reg.Dev.Stud.19(2),154–172(2007)Harris,J.R.,Todaro,M.P.:Migration unemployment and development:a two-sector analysis.Am.Econ.Rev.60,126–142(1970)Matsumura,T.:Partial privatization in mixed duopoly.J.Public Econ.70(3),473–483(1998)。

计算机控制系统习题及部分解答 (1)

∞
∞
∞
∞
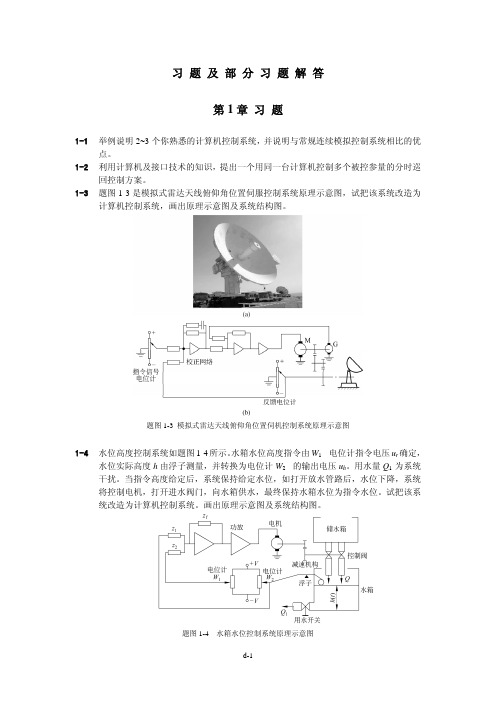
∑ ∑ ∑ ∑ F * (s) = f (kT )e−kTs = (1 − e−kT )e−kTs = e−kTs − e−kT (s+1)
k =0
k =0
k =0
k =0
∑ 因为
∞
ekTs
k =0
= 1 + e−Ts
+
e−2Ts
+
⋅
⋅
⋅
⋅
⋅
=
1
−
1 e−Ts
,
e−Ts < 1 ，(依等比级数公式)
g0=(1/T)*5*abs(1/(10+(GW+ws)*i)); G11=[g0];
g0=(1/T)*5*abs(1/(10+(GW-ws)*i)); G12=[g0];
g0=(1/T)*5*abs(1/(10+(GW+2*ws)*i)); G21=[g0];
g0=(1/T)*5*abs(1/(10+(GW-2*ws)*i)); G22=[g0];
题图 1-6 飞机连续模拟式姿态角控制系统结构示意图
第2章习题
2-1 下述信号被理想采样开关采样，采样周期为 T，试写出采样信号的表达式。
(1) f (t) = 1(t)
(2) f (t) = te−at
(3) f (t) = e−at sin(ωt)
解：
∞
∑ (1) f *(t) = 1(kT )δ (t − kT ) ； k =0 ∞
连续幅频曲线可以用如下 MATLAB 程序绘图：
step=0.1; Wmax=100; w2=-Wmax; y2=5*abs(1/(10+w2*i)); W=[w2]; Y=[y2]; for w=-Wmax:step:Wmax

manifold数学意思

manifold数学意思
【1】manifold的概念
在数学中，manifold（流形）一词通常用于描述一个具有多个维度的几何对象。

它可以被视为一个高维空间中的子集，其中每个点都与一组切向量相关联。

这些切向量构成了流形在该点处的局部坐标系。

简单来说，流形可以被看作是一个可以变形的高维曲面，其局部性质与二维曲面类似。

【2】manifold在数学中的重要作用
流形在数学领域中具有广泛的应用，尤其是在微分几何、拓扑学和数学物理等领域。

流形的引入使得我们可以研究更高维的空间问题，并且为复杂数学结构的分析提供了一种便捷的方式。

流形理论为数学家提供了一个统一框架，使得他们可以研究不同领域中的共同问题。

【3】manifold的多种类型
根据不同的定义和性质，流形可以分为多种类型，如光滑流形、可微流形、定向流形、复流形等。

每种类型的流形都有其独特的性质和结构，例如光滑流形具有连续的微分结构，可微流形在微分意义下具有连续的切向量场，定向流形具有固定的外积结构，复流形则是具有复结构的流形。

【4】manifold在实际应用中的价值
流形在实际应用中具有很高的价值。

例如，在计算机图形学中，流形被用于建模和渲染复杂的三维场景；在机器学习中，流形学习算法可以帮助我们发现高维数据中的低维结构；在物理学中，流形理论为弦论和量子引力提供了理论基础；在生物学中，流形被用于研究细胞和组织的形态和功能。

总之，manifold作为数学中的一个重要概念，不仅在理论研究中具有重要意义，同时在实际应用中也发挥着关键作用。

最大三次聚类准则

最大三次聚类准则
最大三次聚类准则是一种评估聚类质量的方法，其思想是通过比较不同聚类结果的准则值，选择最好的聚类划分。

最大三次聚类准则包括以下三个准则：
1. 最小总平方和（WCSS）：衡量样本与其所属聚类中心的距
离之和，即各样本与其所在聚类的内部差异。

较小的总平方和表示较好的聚类效果。

2. 最大平均轮廓系数（Silhouette Coefficient）：对于每个样本，计算其与同一聚类中其他样本的平均距离（a）和与最近邻的
其他聚类中样本的平均距离（b），然后计算轮廓系数为(b-
a)/max(a,b)。

轮廓系数的取值范围为[-1,1]，越接近1表示样本
与其所在的聚类越相似，越接近-1表示样本与其所在的聚类
越不相似。

较大的平均轮廓系数表示较好的聚类效果。

3. 最大Calinski-Harabasz指数：通过计算类间平均离差与类内
平均离差的比值，来评估聚类的紧密性与分离度。

指数值越大表示聚类效果越好。

以上三个准则都是通过计算距离或差异来衡量聚类的质量，具体的评估方法和计算公式可以根据具体的聚类算法和问题进行调整和变化。

慢特征分析名词解释

慢特征分析名词解释
慢特征分析（ManifoldFeatureAnalysis，简称MFA）是一种数据挖掘算法，可以从大量包含复杂关系的高维数据中，寻找出低维潜在特征。

该算法专注于对潜在结构进行建模，从而有助于数据分析人员更有效地发现他们感兴趣的关系。

MFA的模型主要包括数据映射，维度压缩和结构学习三个主模型。

首先，MFA从输入数据中提取局部特征，将高维数据映射到一个较低维的特征空间中。

这时，数据的潜在特征更容易显现出来。

根据这些局部特征，MFA将输入特征压缩到较小的空间中，从而节省数据分析时间。

最后，MFA采用结构学习方法，将局部特征组合成潜在的全局表达形式，从而发现数据中的潜在结构。

MFA可以用于多种应用，例如可视化复杂关系，聚类，特征选择，机器学习，推荐系统，网络分析等。

它也可以被用于多种类型的数据，包括文本，图像，音频，视频等。

MFA的优点主要有三：首先，它可以将非线性关系投射到较低维空间中，从而有助于数据分析；其次，MFA涉及到数学计算比较快，大大缩短了模型构建时间；最后，它有助于发现数据中的隐藏相关性，这有助于改善机器学习的效果。

总而言之，MFA是一种有效的数据挖掘算法，可以有效地发现数据中的潜在特征，帮助数据分析人员进行更有效的数据分析。

它的主要模型包括数据映射，维度压缩和结构学习，可以用于多种应用，有助于改善机器学习的效果。