第八章习题解答
初二物理第八章练习题含答案

初二物理第八章练习题含答案1. 选择题(1) 以下属于力的性质是:A. 大小B. 方向C. 作用点D. 面积答案:A、B、C(2) 能够使物体发生位移的只有:A. 摩擦力B. 重力C. 弹力和悬挂力D. 正确答案全部都对答案:C(3) 法拉第一定律指出的是:A. 外力作用于物体上时,物体一定保持静止或匀速直线运动B. 外力作用于物体上时,物体的速度将发生变化C. 物体受到的合力为零时,物体一定保持静止或匀速直线运动D. 物体受到的合力为零时,物体的速度将发生变化答案:C2. 填空题(1) 一个力从右往左作用于一个物体,这个物体产生的反作用力的方向是______。
答案:从左往右(2) 一个力从上往下作用于一个物体,这个物体产生的反作用力的方向是______。
答案:从下往上(3) 一个物体受到A力的作用产生加速度a,如果力A的大小不变,改变作用方向,则产生的加速度为______。
答案:-a3. 解答题(1) 什么是力?力的三要素是什么?解答:力是物体之间相互作用的结果,是导致物体发生变化的原因。
力的三要素包括大小、方向和作用点。
大小表示力的强弱程度,方向表示力作用的直线方向,作用点表示力作用的具体位置。
(2) 什么是合力?如何求合力?解答:合力是同时作用在物体上的多个力的共同效果。
求合力的方法是将所有作用在物体上的力按照大小和方向合成,可以通过向量法或图示法来求解。
(3) 描述牛顿第一定律,并用实例说明其应用。
解答:牛顿第一定律也称为惯性定律,指出在没有外力作用时,物体将保持静止或匀速直线运动的状态。
例如,当我们用力推动一张光滑的桌子上的书时,如果力的大小和方向适当,书就会保持匀速直线运动,直到受到其他力的作用。
这说明物体在没有外力干扰时具有惯性,保持原来的状态不发生变化。
总结:初二物理第八章练习题主要涉及力的性质和作用、法拉第一定律等内容。
通过选择题和填空题加深对知识点的理解,同时通过解答题展开思考和拓展。
第8章习题答案

第八章多态1.单选题(1).下列关于运算符重载的描述中,( D )是正确的。
(A) 可以改变参与运算的操作数个数 (B) 可以改变运算符原来的优先级(C) 可以改变运算符原来的结合性(D) 不能改变原运算符的语义(2).下列函数中,不能重载运算符的函数是( b )。
(A) 成员函数(B) 构造函数(C) 普通函数 (D) 友员函数(3).要求用成员函数重载的运算符是( A )。
(A) =(B) == (C) <= (D) ++(4).要求用友员函数重载的运算符是( C )。
(A) = (B) [] (C) <<(D) ()(5).在C++中,要实现动态联编,必须使用( D )调用虚函数。
(A) 类名(B) 派生类指针(C) 对象名(D) 基类指针(6).下列函数中,不能说明为虚函数的是( C )。
(A) 私有成员函数(B) 公有成员函数(C) 构造函数(D) 析构函数(7).在派生类中,重载一个虚函数时,要求函数名、参数的个数、参数的类型、参数的顺序和函数的返回值( A )。
(A) 相同(B)不同(C) 相容(D) 部分相同(8).C++中,根据(D )识别类层次中不同类定义的虚函数版本。
(A) 参数个数(B) 参数类型(C) 函数名(D) this指针类型(9).虚析构函数的作用是(C )。
(A) 虚基类必须定义虚析构函数(B) 类对象作用域结束时释放资源(C)delete动态对象时释放资源(D) 无意义(10).下面函数原型中,( B )声明了fun为纯虚函数。
(A) void fun()=0; (B) virtual void fun()=0;(C) virtual void fun(); (D) virtual void fun(){ };(11).若一个类中含有纯虚函数,则该类称为( C )。
(A) 基类(B)纯基类(C) 抽象类(D) 派生类(12).假设Aclass为抽象类,下列正确的说明语句是( B )。
大学物理习题解答 第八章

8-1.已知波源在原点(x=0)的平面简谐波的方程为)cos(Cx Bt A y -=式中A,B,C 为正值恒量.试求:(1)波的振幅,波速,频率,周期与波长;(2)写出传播放向上距离波源l 处一点的振动方程;(3)试求任何时刻,在波传播放向上相距为D 的两点的位相差;解:(1) ∵A 、B 、C 为正值恒量,所以该波沿X 轴正方向传播,与平面简谐波的波动方程)(cos cxt A y -=ω比较系数,可得波的振幅为A ,B =ω, π2B f =, B T π2=, C c=ω,C B C c ==ω ,因为f c λ=,所以C B C B CT ππλ22=⋅==. 所以该波的振幅为A,波速为CB,频率为π2B ,周期为B π2,波长为C π2.(2)传播方向上距波源l 处一点的振动方程为:)cos(Cl Bt A y -=.(3)设t 时刻,传播方向上相距为D 的两点分别为x 1,x 2. 那么这两点所对应的波动方程分别为: )cos(11Cx Bt A y -= )cos(22Cx Bt A y -= 所以这两点的相位差Δφ为CD x x C =-=-=∆1221φφφ.8-2. 一列横波沿绳子传播时的波动方程为)410cos(05.0x t y ππ-=,式中x,y 以m 计,t 以s 计.(1)求此波的振幅、波速、频率、和波长;(2)求绳子上各质点振动时的最大速度和最大加速度;(3)求x=0.2m 处的质点在t=1s 时的相位,它是原点处质点在哪一时刻的位相. 这一位相所代表的运动状态在t=1.25s 时刻到达哪一点?在t=1.5s 时刻到达哪一点?(4)分别图示t=1s,1.1s,1.25s,1.5s 各时刻的波形.解:(1)通过与平面简谐波的波动方程比较系数,可得 此波的振幅为:A=0.05m, 波速为:ππ410=c =2.5(m/s). 频率为:ππ210=f =5(HZ). 波长为:f c =λ=0.5(m).答:该波的振幅为0.05m, 波速为2.5m/s, 频率为5HZ,波长为0.5m.(2) ∵平面简谐波的波动方程为:)(cos cxt A y -=ω.∴绳子上各质点的振动速度为: )(sin cxt A t y v --=∂∂=ωω.绳子上各质点的振动加速度为: )(cos 222c xt A ty a --=∂∂=ωω.∴绳子上各质点振动时的最大速度为 ωA v =max =0.5π=1.57(m/s). 绳子上各质点振动时的最大加速度为 2m ax ωA a = =52π=49.35(m/s 2). 答:绳子上各质点振动时的最大速度为1.57m/s ,最大加速度为49.35m/s 2. (3)X=0.2m 处的质点在t=1s 时的位相: φ=9.2π 设该位相是原点处质点在t 时刻的位相,可得 φ=9.2π=10πt t=0.92(s) 这一位相代表的运动状态在t=1.25s 时距离原点的位置为: )(825.0)125.1(2.02.0m c t c x =-+=∆+=同理,在t=1.5s 时,该位相所代表的运动状态,距离原点的位置为: t c x '∆+=2.0=1.45 (m). (4)t=1s 时,x y π4cos 05.0=. t=1.1s 时,x y π4cos 05.0-=. t=1.25s 时,x y π4sin 05.0=. t=1.5s 时,x y π4cos 05.0-=.8-3. 已知平面余弦波波源的振动周期T=21s,所激起的波的波长λ=10m,振幅为0.1m,当t=0时,波源处振动的位移恰为正方向的最大值,取波源处为原点并设波沿+X 方向传播,求: (1)此波的方程;(2)沿波传播方向距离波源为2λ处的振动方程; (3)当4T t =时,波源和距离波源为 4λ,2λ,43λ及λ的各点各自离开平衡位置的位移;(4)当4T t =时,波源和距离波源为 4λ,2λ,43λ及λ的各点自离开平衡位置的位移;并根据(3)(4)计算结果画出波形(y-x)曲线; (5)当4T t =和2T 时,距离波源4λ处质点的振动速度. 解:(1)根据题意可知,该平面余弦波的振幅 A=0.1m, 频率f =2(HZ),波速f c λ==20(m/s),初相位φ0=0. 当取波源为原点并沿该波沿+X 方向传播时,波动方程为 )54cos(1.0x t y ππ-=.(2)沿波传播方向距离波源为λ/2处的振动方程为: )254cos(1.0λππ⋅-=t y =-0.1cos4πt.(3)距离波源分别为4λ,2λ,43λ和λ的各点的振动方程为 t y π4sin 1.0=, t y π4cos 1.0-= t y π4sin 1.0-=, t y π4cos 1.0=当4Tt =时,它们各自离开平衡位置的位移为 44sin 1.01Ty ⋅=π=0.1(m), 2y =0(m),3y =-0.1(m), 4y =0(m)(4)与(3)的方法类似,易求得 4λ=x 时, y=0(m). 2λ=x 时, y=0.1(m).43λ=x 时,y=0(m). λ=x 时,y=-0.1(m).(5)各质点的振动速度,)54sin(4.0x t t y v πππ--=∂∂= 当4Tt =时,距离波源4λ处质点的振动速度为: )4544sin(4.0λπππ⨯-⨯-=T v =0(m/s)同理,当2T t =时,距离波源4λ处质点的振动速度为:v =-0.4π(m/s)答:当4Tt =和2T 时,距离波源4λ处质点的振动速度分别为0m/s 和-0.4πm/s. 8-4. 一波源做简谐振动,周期为1001s,经平衡位置向正方向运动时,作为计时起点.设此振动以c=400m/s 的速度沿直线传播,求: (1)这波沿某一波线的方程;(2)距波源为16m 处和20m 处质点振动方程和初位相; (3)距波源为15m 和16 m 的两质点的位相差是多少?解:(1)根据题意可知,该简谐波的频率为ƒ=100(HZ), 波速c=400m/s, 初相位20πφ-=, 设该平面简谐波的波动方程为 )22cos(0φλπλπ+-=x ct A y 将上面的结果代入可得,)222cos(πλππ--=x t T A y =)22200cos(πππ--x t A(2)距波源为16m 和20m 处质点振动方程为:将x=16m 代入上式,得 )2200()2216200cos(1πππππ-=-⨯-=t Aos t A y同理,)2200cos()2220200cos(2πππππ-=-⨯-=t A t A y 初相位分别为:t=0时,210πφ-=,220πφ-=.(3)距波源为15m 和16m 的两质点的位相差: λπφ2⨯∆=∆x =2π. 8-5. 已知某平面简谐波的波源振动方程为)2sin(06.0πt y =,式中y 以m 计,t 以s计.设波速为2m/s,试求离波源5m 处质点的振动方程.这点的位相所表示的运动状态相当波源在哪一时刻的运动状态?解:离波源5m 处质点的振动方程为:将X=5m 代入波动方程得 )5(2sin06.0c t y -=π=)452sin(06.0ππ-t 设该点的位相所代表的运动状态相当波源在t ′时刻的运动状态,所以 t t '=-2452πππ可得 t ′=(t-2.5)(s).8-6.如图所示,A 和B 是两个同位相的波源,相距d=0.10m,同时以30Hz 的频率发出波动,波速为0.50m/s.P 点位于AB 上方,AP 与AB 夹角为30o ,且PA=4m ,求两波通过P 点位相差.解:依题意可知,PA=4m,AB=0.1m, 利用余弦定理,可得 PB=3.91(m),两波通过P 点相位差: λπφ2)(⨯-=∆PB PA又∵fc=λ ∴Δφ=10.8π. 8-7. S 1和S 2是两个相干波源,相距41波长,S 1比S 2的位相超前2π.设两列波在 S 1,S 2连线方向的强度相同且不随距离变化,问S 1,S 2连线上在S 1外侧各点处的合成波的强度如何?又在S 2外侧各点的强度如何?解:两列相干波在空间任意点P 所形成的振动的振幅为 α∆=cos A 2A +A +A 212221A其中Δα为两列相干波在空间任一点所引起的两个振动的位相差 λπααα2)(1212⨯---=∆r r当P 点在S 1外侧时,根据题中所给的条件,可得 πλλππλπααα-=⨯--=⨯---=∆4222)(1212r r∴0)cos(-2A 2A 2020=+=πA 又∵波的强度与振幅的平方成正比 ∴I=0. 同理,当P 点在S 2外侧时, 02)4(22)(1212=⨯---=⨯---=∆λπλπλπαααr r ⇒A=2A 0 ∴04I I =答:S 1,S 2连线上在S 1外侧各点处的合成波的强度为0,而在S 2外侧合成波的强度为4I 0.8-8.图所示,设平面横波1沿BP 方向传播,它在B 点的振动方程为t y πcos 102.021-⨯=,平面横波2沿AP 方向传播,A 点的振动方程为)2cos(102.022ππ+⨯=-t y ,两式中y 以m计,t以s计,P处与B相距0.40m ,与A 相距0.05m,波速为0.20m/s.求: (1)两波传到P 处的为相差; (2)在P 处合振动的振幅;(3)如果在P 处相遇的两横波,振动方向是互相垂直的,则合振动的振幅又如何?解:(1)两波传到P 处的位相差Δα: λπααα2)(1212⨯---=∆r r由题中给出A,B 两点的振动方程可知,A 比B 的位相超前π ∴ππωππλππα5.22)(22)(-=⨯-⨯-=--=∆CPB PA PB PA (2)在P 处合振动的振幅为:α∆++=cos A 2A A A 2010220210A 21083.2-⨯= (m). (3)由于两列横波振幅相同,频率相同,相位差Δα=25π, 所以,当振动方向相互垂直时,合成的结果是圆周运动. ∴A=A 10=0.2×10-2(m).8-9. 一列正弦式空气波,沿直径为0.14m 的圆柱形管行进,波的平均强度为18*10-3J/s ·m 2,频率为300Hz,波速为300m/s,问: (1)波中的平均能量密度和最大能量密度是多少?(2)每两个相邻的,相位差为2π的同相面(亦即相距1波长的两同相面)之间的波段中有多少能量?解:(1)根据题中所给的条件,由C I ω= 则cI=ω=300/10183-⨯=5106-⨯(J ·m -3). 由)(sin 222c rt A -=ωωρω 可得ωωρω222max ==A =4102.1-⨯(J ·m -3)(2)V W ∆⋅=ωd r 2πω==9.23×710-(J)8-10. 为了保持波源的振动不变,需要消耗4W 的功率,如果波源发出的是球面波,且认为媒质不吸收波的 能量,求距离波源1m 和2m 处的能流密度. 解:因为IS P =,所以距离波源1m 处的能流密度为ππ1442111===r S P I =0.318(w ·m -2)距离波源2m 处的能流密度为222244r S P I π===0.08(w ·m -2). 8-11. 两个波在一根很长的细绳上传播,它们的方程设为 )4(cos 06.01t x y -=π,)4(cos 06.02t x y +=π,式中x,y 以m 计,t 以s 计;(1) 求各波的频率,波长,波速和传播方向;(2) 试求这细绳上是做驻波式振动,求节点的位置和腹点的位置; (3)波腹处的振幅多大?在x=1.2m 处振幅多大?解:(1)与波动方程形式)cos(crt A y -=ω作比较,可得)4(4cos 06.01x t y -=π, )4(4cos 06.02xt y +=ππω41= ⇒πω211=f =2(Hz), s m c /41= 111T c =λ=2(m) 传播方向沿x 轴正方向 πω42=, ƒ2=2(Hz), C 2=-4m/s.222T c =λ =2(m). 传播方向沿x 轴负方向(2)由于两列波同频率,同振幅,同振动方向,并且传播速率相同方向相反,故满足驻波条件,所以做的是驻波式振动t x y y y ππ4cos cos 12.021⋅=+= 节点的位置: 2)12(ππ+=k x (k=0,±1, ±2,………) ⇒2)12(+=k x . 腹点的位置: ππk x = (k=0,±1, ±2, ……) ⇒k x =. (3)波腹处的振幅为0.12m.x=1.2m 处的振幅: )2.1cos(12.0π=0.097(m). 8-12. 设入射波的波动方程为)(2cos 1λπxT t A y +=,在x=0处发生反射,反射点为一自由端.求: (1)反射波的波动方程;(2)合成波(驻波)的方程,并由合成波方程说明哪些点是波腹,哪些点是波节.解:(1)反射波的波动方程为: )(2cos 2λπxT t A y -=(2) )2cos()2cos(221T tx A y y πλπ⋅=+波腹点:πλπk x =2 (k=0,±1, ±2,………) ⇒2λk x =.波节点位置:2)12(2πλπ+=k x (k=0,±1, ±2,………) ⇒4)12(λ+=k x8-13. 在实验室中做驻波试验时,将一根长3米的弦线的一端系于电动音叉的一个臂上,这音叉在 垂直于眩线长度的方向撒谎那个以60Hz 的频率做振动,眩线的质量为60*0.001kg.如果使这根弦线产生有四个波腹的振动,必须给这根弦线施多大的力.解:由8.14题的结论可知 μυTl n n 2=(n=1, 2,3,………) 根据题中所给的已知条件,可得 l =3m,n=44υ=60HZ, μ=60·10-3/3=kg 2102-⨯. 代入上式,解得24)2(nlT υμ==162(N).8-14. 把两端固定的一根弦线波动一下,就有横向振动弦线的两固定端传去,并被反射回来形成驻波图样, 一根长度为l 的弦线,它的驻波图样是一定的,所以它可按呈现一个波腹,二个波腹,三个波腹,……的形式做振动或这种基本振动叠加.试证明:一根长度为l 的弦线只能发出下列一些固有频率.μυTl n n 2=n=1,2,3,….. 式中μ是弦线单位的质量,T 是绳中的张力.证明:假设长度为l 的弦线,它的驻波图样可以产生n 个波腹,则n 2λ=l ① 又因波在弦线中传播的速率为 μTc =其中T 是绳中的张力,μ是弦线单位长度的质量μυυλTc nn == ②联立①②,解得 μυTl n n 2=. 故结论得证. 8-15. (1)有一支频率未知的音叉和一支频率已知为384Hz 的标准音叉一起振动时每秒产生三个拍,当这音叉上涂上少量石蜡时,拍频减少,沃尔玛这支音叉频率是多少?(2)某一波形可以用下式表示:11sin sin 3sin 535Y A x A x A x =+++试分别作出该级数前三项的图形,并作出叠加之后的图形. 解:(1)由拍频的定义,可知 123υυυ-==∴ 312±=υυ 即2υ=387或381(Hz). (2)图如下:11。
大学物理第八章课后习题答案

大学物理第八章课后习题答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第八章电磁感应电磁场8 -1一根无限长平行直导线载有电流I,一矩形线圈位于导线平面内沿垂直于载流导线方向以恒定速率运动(如图所示),则()(A)线圈中无感应电流(B)线圈中感应电流为顺时针方向(C)线圈中感应电流为逆时针方向(D)线圈中感应电流方向无法确定分析与解由右手定则可以判断,在矩形线圈附近磁场垂直纸面朝里,磁场是非均匀场,距离长直载流导线越远,磁场越弱.因而当矩形线圈朝下运动时,在线圈中产生感应电流,感应电流方向由法拉第电磁感应定律可以判定.因而正确答案为(B).8 -2将形状完全相同的铜环和木环静止放置在交变磁场中,并假设通过两环面的磁通量随时间的变化率相等,不计自感时则()(A)铜环中有感应电流,木环中无感应电流(B)铜环中有感应电流,木环中有感应电流(C)铜环中感应电动势大,木环中感应电动势小(D)铜环中感应电动势小,木环中感应电动势大23分析与解 根据法拉第电磁感应定律,铜环、木环中的感应电场大小相等,但在木环中不会形成电流.因而正确答案为(A ).8 -3 有两个线圈,线圈1 对线圈2 的互感系数为M 21 ,而线圈2 对线圈1的互感系数为M 12 .若它们分别流过i 1 和i 2 的变化电流且ti t i d d d d 21<,并设由i 2变化在线圈1 中产生的互感电动势为ε12 ,由i 1 变化在线圈2 中产生的互感电动势为ε21 ,下述论断正确的是( ).(A )2112M M = ,1221εε=(B )2112M M ≠ ,1221εε≠(C )2112M M =, 1221εε<(D )2112M M = ,1221εε<分析与解 教材中已经证明M21 =M12 ,电磁感应定律t i M εd d 12121=;ti M εd d 21212=.因而正确答案为(D ). 8 -4 对位移电流,下述四种说法中哪一种说法是正确的是( )(A ) 位移电流的实质是变化的电场(B ) 位移电流和传导电流一样是定向运动的电荷(C ) 位移电流服从传导电流遵循的所有定律(D ) 位移电流的磁效应不服从安培环路定理分析与解 位移电流的实质是变化的电场.变化的电场激发磁场,在这一点位移电流等效于传导电流,但是位移电流不是走向运动的电荷,也就不服从焦耳热效应、安培力等定律.因而正确答案为(A ).48 -5 下列概念正确的是( )(A ) 感应电场是保守场(B ) 感应电场的电场线是一组闭合曲线(C ) LI Φm =,因而线圈的自感系数与回路的电流成反比(D ) LI Φm =,回路的磁通量越大,回路的自感系数也一定大 分析与解 对照感应电场的性质,感应电场的电场线是一组闭合曲线.因而正确答案为(B ).8 -6 一铁心上绕有线圈100匝,已知铁心中磁通量与时间的关系为()Wb π100sin 100.85t Φ⨯=,求在s 100.12-⨯=t 时,线圈中的感应电动势.分析 由于线圈有N 匝相同回路,线圈中的感应电动势等于各匝回路的感应电动势的代数和,在此情况下,法拉第电磁感应定律通常写成tψt ΦN ξd d d d -=-=,其中ΦN ψ=称为磁链. 解 线圈中总的感应电动势()()t tΦNξπ100cos 51.2d d =-= 当s 100.12-⨯=t 时,V 51.2=ξ. 8 -7 有两根相距为d 的无限长平行直导线,它们通以大小相等流向相反的电流,且电流均以tI d d 的变化率增长.若有一边长为d 的正方形线圈与两导线处于同一平面内,如图所示.求线圈中的感应电动势.5分析 本题仍可用法拉第电磁感应定律tΦξd d -=来求解.由于回路处在非均匀磁场中,磁通量就需用⎰⋅=SΦS B d 来计算(其中B 为两无限长直电流单独存在时产生的磁感强度B 1 与B 2 之和). 为了积分的需要,建立如图所示的坐标系.由于B 仅与x 有关,即()B B x =,故取一个平行于长直导线的宽为dx 、长为d 的面元dS ,如图中阴影部分所示,则x d S d d =,所以,总磁通量可通过线积分求得(若取面元y x S d d d =,则上述积分实际上为二重积分).本题在工程技术中又称为互感现象,也可用公式tl M E M d d -=求解. 解1 穿过面元dS 的磁通量为()x d xI μx d d x I μΦd π2d π2d d d d 0021-+=⋅+⋅=⋅=S B S B S B 因此穿过线圈的磁通量为()43ln π2d π2d π2d 02020Id μx x Id μx d x Id μΦΦd d dd =-+==⎰⎰⎰ 再由法拉第电磁感应定律,有6tI d μt ΦE d d 43ln π2d d 0⎪⎭⎫ ⎝⎛=-= 解2 当两长直导线有电流I 通过时,穿过线圈的磁通量为 43ln π20dI μΦ=线圈与两长直导线间的互感为 43ln π20d μI ΦM == 当电流以tl d d 变化时,线圈中的互感电动势为 tI d μt I M E d d 43ln π2d d 0⎪⎭⎫ ⎝⎛=-= 试想:如线圈又以速率v 沿水平向右运动,如何用法拉第电磁感应定律求图示位置的电动势呢此时线圈中既有动生电动势,又有感生电动势.设时刻t ,线圈左端距右侧直导线的距离为ξ,则穿过回路的磁通量()ξf ΦS,1d =⋅=⎰S B ,它表现为变量I 和ξ的二元函数,将Φ代入t ΦE d d -= 即可求解,求解时应按复合函数求导,注意,其中v =tξd d ,再令ξ=d 即可求得图示位置处回路中的总电动势.最终结果为两项,其中一项为动生电动势,另一项为感生电动势.8 -8 有一测量磁感强度的线圈,其截面积S =4.0 cm 2 、匝数N =160 匝、电阻R =50Ω.线圈与一内阻R i =30Ω的冲击电流计相连.若开始时,线圈的平面与均匀磁场的磁感强度B 相垂直,然后线圈的平面很快地转到与B 的方向平行.此时从冲击电流计中测得电荷值54.010C q -=⨯.问此均匀磁场的磁感强度B 的值为多少7分析 在电磁感应现象中,闭合回路中的感应电动势和感应电流与磁通量变化的快慢有关,而在一段时间内,通过导体截面的感应电量只与磁通量变化的大小有关,与磁通量变化的快慢无关.工程中常通过感应电量的测定来确定磁场的强弱. 解 在线圈转过90°角时,通过线圈平面磁通量的变化量为NBS NBS ΦΦΦ=-=-=0Δ12 因此,流过导体截面的电量为ii R RNBS R R Φq +=+=Δ 则 ()T 050.0=+=NSR R q B i 8 -9 如图所示,一长直导线中通有I =5.0 A 的电流,在距导线9.0 cm 处,放一面积为0.10 cm 2 ,10 匝的小圆线圈,线圈中的磁场可看作是均匀的.今在1.0 ×10-2 s 内把此线圈移至距长直导线10.0 cm 处.求:(1) 线圈中平均感应电动势;(2) 设线圈的电阻为1.0×10-2Ω,求通过线圈横截面的感应电荷.8分析 虽然线圈处于非均匀磁场中,但由于线圈的面积很小,可近似认为穿过线圈平面的磁场是均匀的,因而可近似用NBS ψ=来计算线圈在始、末两个位置的磁链.解 (1) 在始、末状态,通过线圈的磁链分别为1011π2r ISμN S NB ψ==,2022π2r IS μN S NB ψ== 则线圈中的平均感应电动势为 V 1011.111πΔ2ΔΔ8210-⨯=⎪⎪⎭⎫ ⎝⎛-==r r t IS μN t ΦE 电动势的指向为顺时针方向.(2) 通过线圈导线横截面的感应电荷为tΦE d d -= 8 -10 如图(a)所示,把一半径为R 的半圆形导线OP 置于磁感强度为B 的均匀磁场中,当导线以速率v 水平向右平动时,求导线中感应电动势E 的大小,哪一端电势较高9分析 本题及后面几题中的电动势均为动生电动势,除仍可由tΦE d d -=求解外(必须设法构造一个闭合回路),还可直接用公式()l B d ⋅⨯=⎰l E v 求解.在用后一种方法求解时,应注意导体上任一导线元dl 上的动生电动势()l B d d ⋅⨯=v E .在一般情况下,上述各量可能是dl 所在位置的函数.矢量(v ×B )的方向就是导线中电势升高的方向. 解1 如图(b)所示,假想半圆形导线O P 在宽为2R 的静止形导轨上滑动,两者之间形成一个闭合回路.设顺时针方向为回路正向,任一时刻端点O 或端点P 距 形导轨左侧距离为x ,则B R Rx Φ⎪⎭⎫ ⎝⎛+=2π212 即B R tx RB t ΦE v 2d d 2d d -=-=-= 由于静止的 形导轨上的电动势为零,则E =-2R v B .式中负号表示电动势的方向为逆时针,对OP 段来说端点P 的电势较高. 解2 建立如图(c )所示的坐标系,在导体上任意处取导体元dl ,则()θR θB l θB E o d cos d cos 90sin d d v v ==⋅⨯=l B vB R θθBR E v v 2d cos d E π/2π/2===⎰⎰- 由矢量(v ×B )的指向可知,端点P 的电势较高.10 解3 连接OP 使导线构成一个闭合回路.由于磁场是均匀的,在任意时刻,穿过回路的磁通量==BS Φ常数.由法拉第电磁感应定律tΦE d d -=可知,E =0 又因 E =E OP +E PO即 E OP =-E PO =2R v B由上述结果可知,在均匀磁场中,任意闭合导体回路平动所产生的动生电动势为零;而任意曲线形导体上的动生电动势就等于其两端所连直线形导体上的动生电动势.上述求解方法是叠加思想的逆运用,即补偿的方法.8 -11 长为L 的铜棒,以距端点r 处为支点,以角速率ω绕通过支点且垂直于铜棒的轴转动.设磁感强度为B 的均匀磁场与轴平行,求棒两端的电势差.分析 应该注意棒两端的电势差与棒上的动生电动势是两个不同的概念,如同电源的端电压与电源电动势的不同.在开路时,两者大小相等,方向相反(电动势的方向是电势升高的方向,而电势差的正方向是电势降落的方向).本题可直接用积分法求解棒上的电动势,亦可以将整个棒的电动势看作是O A 棒与O B 棒上电动势的代数和,如图(b)所示.而E O A 和E O B 则可以直接利用第8 -2 节例1 给出的结果.解1 如图(a)所示,在棒上距点O 为l 处取导体元dl ,则()()r L lB ωl lB ωE L-r r AB AB 221d d --=-=⋅⨯=⎰⎰-l B v 因此棒两端的电势差为()r L lB ωE U AB AB 221--== 当L >2r 时,端点A 处的电势较高解2 将AB 棒上的电动势看作是O A 棒和O B 棒上电动势的代数和,如图(b)所示.其中221r ωB E OA =,()221r L B ωE OB -= 则()r L BL ωE E E OB OA AB 221--=-= 8 -12 如图所示,长为L 的导体棒OP ,处于均匀磁场中,并绕OO ′轴以角速度ω旋转,棒与转轴间夹角恒为θ,磁感强度B 与转轴平行.求OP 棒在图示位置处的电动势.分析 如前所述,本题既可以用法拉第电磁感应定律t ΦE d d -= 计算(此时必须构造一个包含OP 导体在内的闭合回路, 如直角三角形导体回路OPQO ),也可用()l B d ⋅⨯=⎰lE v 来计算.由于对称性,导体OP 旋转至任何位置时产生的电动势与图示位置是相同的.解1 由上分析,得()l B d ⋅⨯=⎰OP OP E v l αB l o d cos 90sin ⎰=v()()l θB θωl o d 90cos sin ⎰-=l()⎰==L θL B ωl l θB ω022sin 21d sin 由矢量B ⨯v 的方向可知端点P 的电势较高.解2 设想导体OP 为直角三角形导体回路OPQO 中的一部分,任一时刻穿过回路的磁通量Φ为零,则回路的总电动势QO PQ OP E E E t ΦE ++==-=0d d 显然,E QO =0,所以()221PQ B ωE E E QO PQ OP ==-= 由上可知,导体棒OP 旋转时,在单位时间内切割的磁感线数与导体棒QP 等效.后者是垂直切割的情况.8 -13 如图(a)所示,金属杆AB 以匀速12.0m s -=⋅v 平行于一长直导线移动,此导线通有电流I =40A .求杆中的感应电动势,杆的哪一端电势较高分析 本题可用两种方法求解.(1) 用公式()l B d ⋅⨯=⎰lE v 求解,建立图(a )所示的坐标系,所取导体元x l d d =,该处的磁感强度xI μB π20=.(2) 用法拉第电磁感应定律求解,需构造一个包含杆AB 在内的闭合回路.为此可设想杆AB 在一个静止的形导轨上滑动,如图(b)所示.设时刻t ,杆AB 距导轨下端CD 的距离为y ,先用公式⎰⋅=SΦS B d 求得穿过该回路的磁通量,再代入公式tΦE d d -=,即可求得回路的电动势,亦即本题杆中的电动势. 解1 根据分析,杆中的感应电动势为()V 1084.311ln 2πd 2πd d 50m 1.1m 1.00-⨯-=-=-==⋅⨯=⎰⎰v v v I μx x μxl E AB AB l B 式中负号表示电动势方向由B 指向A ,故点A 电势较高. 解2 设顺时针方向为回路AB CD 的正向,根据分析,在距直导线x 处,取宽为dx 、长为y 的面元dS ,则穿过面元的磁通量为x y xI μΦd 2πd d 0=⋅=S B 穿过回路的磁通量为11ln 2πd 2πd 0m1.1m 1.00⎰⎰-===S Iy μx y x I μΦΦ 回路的电动势为V 1084.32πd d 11ln 2πd d 500-⨯-=-=-=-=Iy μt y x I μt ΦE 由于静止的形导轨上电动势为零,所以 V 1084.35-⨯-==E E AB式中负号说明回路电动势方向为逆时针,对AB 导体来说,电动势方向应由B 指向A ,故点A 电势较高.8 -14 如图(a)所示,在“无限长”直载流导线的近旁,放置一个矩形导体线框,该线框在垂直于导线方向上以匀速率v 向右移动,求在图示位置处,线框中感应电动势的大小和方向.分析 本题亦可用两种方法求解.其中应注意下列两点:1.当闭合导体线框在磁场中运动时,线框中的总电动势就等于框上各段导体中的动生电动势的代数和.如图(a)所示,导体eh 段和fg 段上的电动势为零[此两段导体上处处满足()0l B =⋅⨯d v ],因而线框中的总电动势为()()()()hg ef hgef gh ef E E E -=⋅⨯-⋅⨯=⋅⨯+⋅⨯=⎰⎰⎰⎰l B l B l B l B d d d d v v v v 其等效电路如图(b)所示.2.用公式tΦE d d -=求解,式中Φ是线框运动至任意位置处时,穿过线框的磁通量.为此设时刻t 时,线框左边距导线的距离为ξ,如图(c )所示,显然ξ是时间t 的函数,且有v =tξd d .在求得线框在任意位置处的电动势E (ξ)后,再令ξ=d ,即可得线框在题目所给位置处的电动势.解1 根据分析,线框中的电动势为hg ef E E E -=()()⎰⎰⋅⨯-⋅⨯=hgef l B l B d d v v ()⎰⎰+-=2201000d 2πd 2πl l l l d I μl d I μv v ()1202πl d I I μ+=1vI 由E ef >E hg 可知,线框中的电动势方向为efgh .解2 设顺时针方向为线框回路的正向.根据分析,在任意位置处,穿过线框的磁通量为()()ξl ξξx Il μdx ξx Il μΦl 120020ln π2π21++=+=⎰ 相应电动势为()()1120π2d d l ξξl l I μt ΦξE +=-=v 令ξ=d ,得线框在图示位置处的电动势为 ()1120π2l d d l l I μE +=v 由E >0 可知,线框中电动势方向为顺时针方向.*8 -15 有一长为l ,宽为b 的矩形导线框架,其质量为m ,电阻为R .在t =0时,框架从距水平面y =0 的上方h 处由静止自由下落,如图所示.磁场的分布为:在y =0 的水平面上方没有磁场;在y =0 的水平面下方有磁感强度为B 的均匀磁场,B 的方向垂直纸面向里.已知框架在时刻t 1 和t 2 的位置如图中所示.求在下述时间内,框架的速度与时间的关系:(1) t 1 ≥t >0,即框架进入磁场前;(2) t 2 ≥t ≥t 1 ,即框架进入磁场, 但尚未全部进入磁场;(3)t >t 2 ,即框架全部进入磁场后.分析 设线框刚进入磁场(t 1 时刻)和全部进入磁场(t 2 时刻)的瞬间,其速度分别为v 10 和v 20 .在情况(1)和(3)中,线框中无感应电流,线框仅在重力作用下作落体运动,其速度与时间的关系分别为v =gt (t <t 1)和v =v 20 +g (t -t 2 )(t >t 2 ).而在t 1<t <t 2这段时间内,线框运动较为复杂,由于穿过线框回路的磁通量变化,使得回路中有感应电流存在,从而使线框除受重力外,还受到一个向上的安培力F A ,其大小与速度有关,即()A A F F =v .根据牛顿运动定律,此时线框的运动微分方程为()tv v d d m F mg A =-,解此微分方程可得t 1<t <t 2 时间内线框的速度与时间的关系式.解 (1) 根据分析,在1t t ≤时间内,线框为自由落体运动,于是()11t t gt ≤=v 其中1t t =时,gh 2101==v v(2) 线框进入磁场后,受到向上的安培力为v Rl B IlB F A 22== 根据牛顿运动定律,可得线框运动的微分方程tv m v d d 22=-R l B mg 令mRl B K 22=,整理上式并分离变量积分,有 ⎰⎰=-t t t g 110d d vv Kv v 积分后将gh 210=v 代入,可得()()[]1212t t K e gh K g g K----=v (3) 线框全部进入磁场后(t >t 2),作初速为v 20 的落体运动,故有()()()[]()222031221t t g e gh K g g Kt t g t t K -+--=-+=--v v 8 -16 有一磁感强度为B 的均匀磁场,以恒定的变化率t d d B 在变化.把一块质量为m 的铜,拉成截面半径为r 的导线,并用它做成一个半径为R 的圆形回路.圆形回路的平面与磁感强度B 垂直.试证:这回路中的感应电流为td d π4B d ρm I =式中ρ 为铜的电阻率,d 为铜的密度. 解 圆形回路导线长为πR 2,导线截面积为2πr ,其电阻R ′为22rR ρS l ρR ==' 在均匀磁场中,穿过该回路的磁通量为BS Φ=,由法拉第电磁感应定律可得回路中的感应电流为t t t d d 2πd d π1d d 122B ρRr B R R ΦR R E I ='='='= 而2ππ2r R d m =,即dm Rr π2π2=,代入上式可得 td d π4B d ρm I = 8 -17 半径为R =2.0 cm 的无限长直载流密绕螺线管,管内磁场可视为均匀磁场,管外磁场可近似看作零.若通电电流均匀变化,使得磁感强度B 随时间的变化率td d B 为常量,且为正值,试求:(1) 管内外由磁场变化激发的感生电场分布;(2) 如1s T 010.0d d -⋅=tB ,求距螺线管中心轴r =5.0 cm 处感生电场的大小和方向.分析 变化磁场可以在空间激发感生电场,感生电场的空间分布与场源———变化的磁场(包括磁场的空间分布以及磁场的变化率td d B 等)密切相关,即S B l E d d ⋅∂∂-=⎰⎰S S k t .在一般情况下,求解感生电场的分布是困难的.但对于本题这种特殊情况,则可以利用场的对称性进行求解.可以设想,无限长直螺线管内磁场具有柱对称性,其横截面的磁场分布如图所示.由其激发的感生电场也一定有相应的对称性,考虑到感生电场的电场线为闭合曲线,因而本题中感生电场的电场线一定是一系列以螺线管中心轴为圆心的同心圆.同一圆周上各点的电场强度E k 的大小相等,方向沿圆周的切线方向.图中虚线表示r <R 和r >R 两个区域的电场线.电场线绕向取决于磁场的变化情况,由楞次定律可知,当0d d <t B 时,电场线绕向与B 方向满足右螺旋关系;当0d d >t B 时,电场线绕向与前者相反.解 如图所示,分别在r <R 和r >R 的两个区域内任取一电场线为闭合回路l (半径为r 的圆),依照右手定则,不妨设顺时针方向为回路正向.(1) r <R , tB r t r E E k l k d d πd d d π2d 2-=⋅-=⋅=⋅=⎰⎰S B l E tB r E k d d 2-= r >R , t B R t r E E k lk d d πd d d π2d 2-=⋅-=⋅=⋅=⎰⎰S B l E tB r R E k d d 22-= 由于0d d >tB ,故电场线的绕向为逆时针. (2) 由于r >R ,所求点在螺线管外,因此tB r R E k d d 22-= 将r 、R 、tB d d 的数值代入,可得15m V 100.4--⋅⨯-=k E ,式中负号表示E k 的方向是逆时针的.8 -18 在半径为R 的圆柱形空间中存在着均匀磁场,B 的方向与柱的轴线平行.如图(a)所示,有一长为l 的金属棒放在磁场中,设B 随时间的变化率tB d d 为常量.试证:棒上感应电动势的大小为分析 变化磁场在其周围激发感生电场,把导体置于感生电场中,导体中的自由电子就会在电场力的作用下移动,在棒内两端形成正负电荷的积累,从而产生感生电动势.由于本题的感生电场分布与上题所述情况完全相同,故可利用上题结果,由⎰⋅=lk E l E d 计算棒上感生电动势.此外,还可连接OP 、OQ ,设想PQOP 构成一个闭合导体回路,用法拉第电磁感应定律求解,由于OP 、OQ 沿半径方向,与通过该处的感生电场强度E k 处处垂直,故0d =⋅l E k ,OP 、OQ 两段均无电动势,这样,由法拉第电磁感应定律求出的闭合回路的总电动势,就是导体棒PQ 上的电动势.证1 由法拉第电磁感应定律,有 22Δ22d d d d d d ⎪⎭⎫ ⎝⎛-==-==l R l t B t B S t ΦE E PQ 证2 由题8 -17可知,在r <R 区域,感生电场强度的大小tB r E k d d 2= 设PQ 上线元dx 处,E k 的方向如图(b )所示,则金属杆PQ 上的电动势为()()222202/2d d d 2/d d 2d cos d l R l t B x r l R t B r x θE E l k k PQ -=-==⋅=⎰⎰x E 讨论 假如金属棒PQ 有一段在圆外,则圆外一段导体上有无电动势 该如何求解8 -19 截面积为长方形的环形均匀密绕螺绕环,其尺寸如图(a)所示,共有N 匝(图中仅画出少量几匝),求该螺绕环的自感L .分析 如同电容一样,自感和互感都是与回路系统自身性质(如形状、匝数、介质等)有关的量.求自感L 的方法有两种:1.设有电流I 通过线圈,计算磁场穿过自身回路的总磁通量,再用公式IΦL =计算L .2.让回路中通以变化率已知的电流,测出回路中的感应电动势E L ,由公式t I E L L d /d =计算L .式中E L 和tI d d 都较容易通过实验测定,所以此方法一般适合于工程中.此外,还可通过计算能量的方法求解.解 用方法1 求解,设有电流I 通过线圈,线圈回路呈长方形,如图(b)所示,由安培环路定理可求得在R 1 <r <R 2 范围内的磁场分布为xNI μB π20=由于线圈由N 匝相同的回路构成,所以穿过自身回路的磁链为 12200ln π2d π2d 21R R hI N μx h x NI μN N ψS R R ==⋅=⎰⎰S B 则1220ln π2R R h N μI ψL = 若管中充满均匀同种磁介质,其相对磁导率为μr ,则自感将增大μr 倍.8 -20 如图所示,螺线管的管心是两个套在一起的同轴圆柱体,其截面积分别为S 1 和S 2 ,磁导率分别为μ1 和μ2 ,管长为l ,匝数为N ,求螺线管的自感.(设管的截面很小)分析 本题求解时应注意磁介质的存在对磁场的影响.在无介质时,通电螺线管内的磁场是均匀的,磁感强度为B 0 ,由于磁介质的存在,在不同磁介质中磁感强度分别为μ1 B 0 和μ2 B 0 .通过线圈横截面的总磁通量是截面积分别为S 1 和S 2 的两部分磁通量之和.由自感的定义可解得结果.解 设有电流I 通过螺线管,则管中两介质中磁感强度分别为I L N μnl μB 111==,I LN μnl μB 222== 通过N 匝回路的磁链为221121S NB S NB ΨΨΨ+=+=则自感2211221S μS μlN I ψL L L +==+= 8 -21 有两根半径均为a 的平行长直导线,它们中心距离为d .试求长为l的一对导线的自感(导线内部的磁通量可略去不计).分析 两平行长直导线可以看成无限长但宽为d 的矩形回路的一部分.设在矩形回路中通有逆时针方向电流I ,然后计算图中阴影部分(宽为d 、长为l )的磁通量.该区域内磁场可以看成两无限长直载流导线分别在该区域产生的磁场的叠加.解 在如图所示的坐标中,当两导线中通有图示的电流I 时,两平行导线间的磁感强度为()r d I μr I μB -+=π2π200 穿过图中阴影部分的磁通量为 aa d l μr Bl ΦS a d a -==⋅=⎰⎰-ln πd d 0S B 则长为l 的一对导线的自感为aa d l μI ΦL -==ln π0 如导线内部磁通量不能忽略,则一对导线的自感为212L L L +=.L 1 称为外自感,即本题已求出的L ,L 2 称为一根导线的内自感.长为l 的导线的内自感8π02l μL =,有兴趣的读者可自行求解. 8 -22 如图所示,在一柱形纸筒上绕有两组相同线圈AB 和A ′B ′,每个线圈的自感均为L ,求:(1) A 和A ′相接时,B 和B ′间的自感L 1 ;(2) A ′和B 相接时,A 和B ′间的自感L 2 .分析 无论线圈AB 和A ′B ′作哪种方式连接,均可看成一个大线圈回路的两个部分,故仍可从自感系数的定义出发求解.求解过程中可利用磁通量叠加的方法,如每一组载流线圈单独存在时穿过自身回路的磁通量为Φ,则穿过两线圈回路的磁通量为2Φ;而当两组线圈按(1)或(2)方式连接后,则穿过大线圈回路的总磁通量为2Φ±2Φ,“ ±”取决于电流在两组线圈中的流向是相同或是相反.解 (1) 当A 和A ′连接时,AB 和A ′B ′线圈中电流流向相反,通过回路的磁通量亦相反,故总通量为0221=-=ΦΦΦ,故L 1 =0.(2) 当A ′和B 连接时,AB 和A ′B ′线圈中电流流向相同,通过回路的磁通量亦相同,故总通量为ΦΦΦΦ4222=+=, 故L I ΦI ΦL 4422===. 本题结果在工程实际中有实用意义,如按题(1)方式连接,则可构造出一个无自感的线圈.8 -23 如图所示,一面积为4.0 cm 2 共50 匝的小圆形线圈A ,放在半径为20 cm 共100 匝的大圆形线圈B 的正中央,此两线圈同心且同平面.设线圈A 内各点的磁感强度可看作是相同的.求:(1) 两线圈的互感;(2) 当线圈B 中电流的变化率为-50 A·s-1 时,线圈A 中感应电动势的大小和方向.分析 设回路Ⅰ中通有电流I 1 ,穿过回路Ⅱ的磁通量为Φ21 ,则互感M =M 21 =Φ21I 1 ;也可设回路Ⅱ通有电流I 2 ,穿过回路Ⅰ的磁通量为Φ12 ,则21212I ΦM M == . 虽然两种途径所得结果相同,但在很多情况下,不同途径所涉及的计算难易程度会有很大的不同.以本题为例,如设线圈B 中有电流I 通过,则在线圈A 中心处的磁感强度很易求得,由于线圈A 很小,其所在处的磁场可视为均匀的,因而穿过线圈A 的磁通量Φ≈BS .反之,如设线圈A 通有电流I ,其周围的磁场分布是变化的,且难以计算,因而穿过线圈B 的磁通量也就很难求得,由此可见,计算互感一定要善于选择方便的途径.解 (1) 设线圈B 有电流I 通过,它在圆心处产生的磁感强度R I μN B B 200=穿过小线圈A 的磁链近似为 A B A A A A S RI μN N S B N ψ200== 则两线圈的互感为H 1028.6260-⨯===RS μN N I ψM A B A A (2)V 1014.3d d 4-⨯=-=tI M E A 互感电动势的方向和线圈B 中的电流方向相同.8 -24 如图所示,两同轴单匝线圈A 、C 的半径分别为R 和r ,两线圈相距为d .若r 很小,可认为线圈A 在线圈C 处所产生的磁场是均匀的.求两线圈的互感.若线圈C 的匝数为N 匝,则互感又为多少解 设线圈A 中有电流I 通过,它在线圈C 所包围的平面内各点产生的磁感强度近似为()2/322202d R IR μB +=穿过线圈C 的磁通为 ()22/32220π2r d R IR μBS ψC +==则两线圈的互感为 ()2/3222202πdR R r μI ψM +== 若线圈C 的匝数为N 匝,则互感为上述值的N 倍. 8 -25 如图所示,螺绕环A 中充满了铁磁质,管的截面积S 为2.0 cm 2 ,沿环每厘米绕有100 匝线圈,通有电流I 1 =4.0 ×10 -2 A ,在环上再绕一线圈C ,共10 匝,其电阻为0.10 Ω,今将开关S 突然开启,测得线圈C 中的感应电荷为2.0 ×10 -3C .求:当螺绕环中通有电流I 1 时,铁磁质中的B 和铁磁质的相对磁导率μr .分析 本题与题8 -8 相似,均是利用冲击电流计测量电磁感应现象中通过回路的电荷的方法来计算磁场的磁感强度.线圈C 的磁通变化是与环形螺线管中的电流变化相联系的. 解 当螺绕环中通以电流I 1 时,在环内产生的磁感强度110I n μμB r =则通过线圈C 的磁链为S I n μμN BS N ψr c 11022==设断开电源过程中,通过C 的感应电荷为q C ,则有()RS I n μμN ψR ψR qc r c c 110201Δ1=--=-= 由此得 T 10.02110===S N Rqc I n μμB r 相对磁导率1991102==I n μS N Rqc μr8 -26 一个直径为0.01 m ,长为0.10 m 的长直密绕螺线管,共1 000 匝线圈,总电阻为7.76 Ω.求:(1) 如把线圈接到电动势E =2.0 V 的电池上,电流稳定后,线圈中所储存的磁能有多少 磁能密度是多少*(2) 从接通电路时算起,要使线圈储存磁能为最大储存磁能的一半,需经过多少时间分析 单一载流回路所具有的磁能,通常可用两种方法计算:(1) 如回路自感为L (已知或很容易求得),则该回路通有电流I 时所储存的磁能221LI W m =,通常称为自感磁能.(2) 由于载流回路可在空间激发磁场,磁能实际是储存于磁场之中,因而载流回路所具有的能量又可看作磁场能量,即V w W V m m d ⎰=,式中m w 为磁场能量密度,积分遍及磁场存在的空间.由于μB w m 22=,因而采用这种方法时应首先求载流回路在空间产生的磁感强度B 的分布.上述两种方法还为我们提供了计算自感的另一种途径,即运用V w LI V m d 212⎰=求解L . 解 (1) 密绕长直螺线管在忽略端部效应时,其自感l S N L 2=,电流稳定后,线圈中电流RE I =,则线圈中所储存的磁能为J 1028.3221522202-⨯===lRSE N μLI W m 在忽略端部效应时,该电流回路所产生的磁场可近似认为仅存在于螺线管。
理论力学习题解答第八章
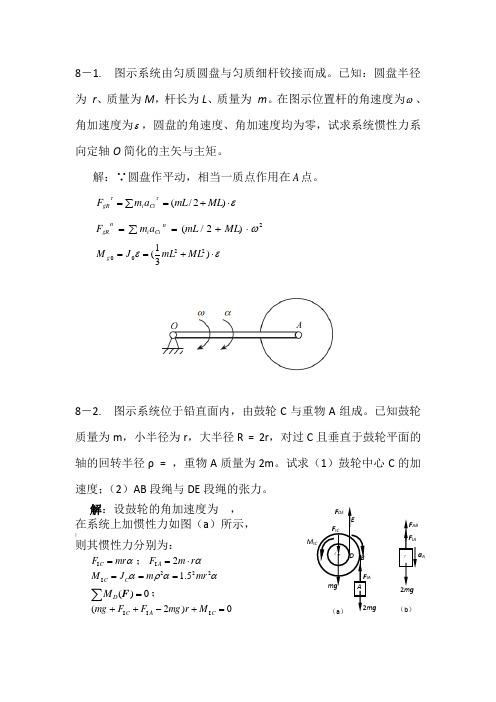
8-1. 图示系统由匀质圆盘与匀质细杆铰接而成。
已知:圆盘半径为 r 、质量为M ,杆长为L 、质量为 m 。
在图示位置杆的角速度为ω、角加速度为ε,圆盘的角速度、角加速度均为零,试求系统惯性力系向定轴O 简化的主矢与主矩。
解:∵圆盘作平动,相当一质点作用在A 点。
εττ⋅+==∑)2/(ML mL a m F Ci i gR 2)2/(ω⋅+==∑ML mL a m F n Ci i ngR εε⋅+==)31(2200ML mL J M g8-2. 图示系统位于铅直面内,由鼓轮C 与重物A 组成。
已知鼓轮质量为m ,小半径为r ,大半径R = 2r ,对过C 且垂直于鼓轮平面的轴的回转半径ρ = ,重物A 质量为2m 。
试求(1)鼓轮中心C 的加速度;(2)AB 段绳与DE 段绳的张力。
解:设鼓轮的角加速度为, 在系统上加惯性力如图(a )所示, |则其惯性力分别为:αmr F C =I ;αr m F A ⋅=2I ααρα222I 5.1mr m J M C C === ∑=0)(F D M ;0)2(I I I =+-++C A C M r mg F F mg?AM I CF I Cm g F DE (a )A B 《D E2gF A F I A F AB (b )g g r a C 2145.132=+==α ∑=0y F ;02I I =--+-mg mg F F F A C DE ;mg mr mg F DE 21593=-=α 取重物A 为研究对象,受力如图(b )所示,∑=0y F ;02I =-+mg F F A AB ;mg mg mr mg F AB 2134)2141(222=-=-=α:8-3. 11-15重力的大小为100N 的平板置于水平面上,其间的摩擦因数f = ,板上有一重力的大小为300N ,半径为20cm 的均质圆柱。
圆柱与板之间无相对滑动,滚动摩阻可略去不计。
第八章习题解答
第八章 机械波一、选择、填空题:1、若一平面简谐波的波动方程为y=A cos (Bt-Cx )(SI ),式中A 、B 、C 为正值恒量,则( )。
A.波速为C ;B.周期为1/B ;C.波长为2π/C ;D.角频率为B /2π。
答案 C解:)(2cos λ-π=xT t A y 与y =A cos (Bt -Cx )比较即得答案。
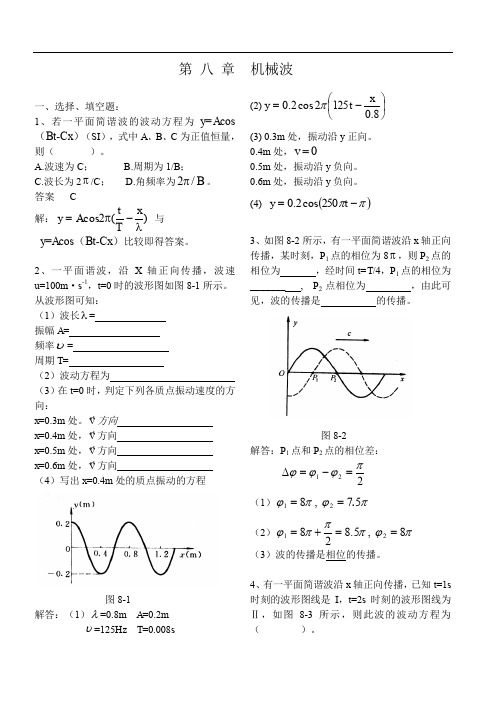
2、一平面谐波,沿X 轴正向传播,波速u =100m ·s -1,t =0时的波形图如图8-1所示。
从波形图可知:(1)波长λ= 振幅A = 频率υ= 周期T =(2)波动方程为 (3)在t=0时,判定下列各质点振动速度的方向:x =0.3m 处。
v方向x =0.4m 处,v方向x =0.5m 处,v方向x =0.6m 处,v方向(4)写出x =0.4m 处的质点振动的方程图8-1解答:(1)λ=0.8m A =0.2mυ=125Hz T =0.008s(2)⎪⎭⎫ ⎝⎛-=8.01252cos 2.0x t y π (3) 0.3m 处,振动沿y 正向。
0.4m 处,0=v0.5m 处,振动沿y 负向。
0.6m 处,振动沿y 负向。
(4) ()ππ-=t y 250cos 2.03、如图8-2所示,有一平面简谐波沿x 轴正向传播,某时刻,P 1点的相位为8π,则P 2点的相位为 ,经时间t=T /4,P 1点的相位为_______ , P 2点相位为 ,由此可见,波的传播是 的传播。
图8-2 解答:P 1点和P 2点的相位差: 221πϕϕϕ=-=∆(1)πϕπϕ57 , 821.== (2)πϕπππϕ8 , 8.52821==+=(3)波的传播是相位的传播。
4、有一平面简谐波沿x 轴正向传播,已知t =1s 时刻的波形图线是I ,t =2s 时刻的波形图线为Ⅱ,如图8-3所示,则此波的波动方程为( )。
图8-3A . m )232(cos 20+-=x t y π.B .m )4(cos 20xt y -=π.C .m )214(cos 20+-=x t y π.D .m )234(cos 20+-=x t y π.答案 D解:由图知:1-s m 4124m,20⋅=-==u A . 1-s 2 , s 2ππω===T T 可得; []ϕπ+-=)4(c o s 20xt y .对于波线I 上的O 点:. 0 , 0 , s 1 , 0<===v y t x其振动的相位为:)10( , 22,=+=+k k ππϕπ)2( , 23ππϕ-=∴5、在弦线上有一简谐波,其表达式是()SI x t y ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=32002.02cos 02.01ππ为了在此弦线上形成驻波,并且在x =0处为一波节,此弦线上还应有一简谐波,其表达式为:( )。
运筹学答案第八章

page 24 8 August 2024
School of Management
运筹学教程
第八章习题解答
8.15 如图8-59,发点S1,S2分别可供应10和15个 单边位上,数收为c点ij。t1,t2可以接收10和25个单位,求最大流,
page 25 8 August 2024
School of Management
运筹学教程
第八章习题解答
8.11 求图8-56中v1到各点的最短路。
page 17 8 August 2024
School of Management
运筹学教程
第八章习题解答
page 18 8 August 2024
School of Management
运筹学教程
第八章习题解答
8.12 求图8-57网络中各顶点间的最短路。
page 31 8 August 2024
School of Management
运筹学教程
第八章习题解答
page 32 8 August 2024
School of Management
运筹学教程
第八章习题解答
心B货1B,中18,B心.22B,的02,运B某3B输每种3。能天货A力需物1,由、求A2单分个2的位别仓库运为库存费9At量,如1,分5表At别,28运—为64t送。每,到天各求31仓运个3t库费配,到最货9t配;省中
20 0 36 14 32
D(4)
0
20
18
0
32
12
48
9
0
V1 V2 V3 V4 V5
V1 0 5 16 19 12
V2 20 0 36 14 32
第八章(焊缝、螺栓连接)--钢结构习题参考解答

8.4 有一工字形钢梁,采用I50a (Q235钢),承受荷载如图8-83所示。
F=125kN ,因长度不够而用对接坡口焊缝连接。
焊条采用E43型,手工焊,焊缝质量属Ⅱ级,对接焊缝抗拉强度设计值2205/w t f N mm =,抗剪强度设计值2120/w v f N mm =。
验算此焊缝受力时是否安全。
图8-83 习题8.4解:依题意知焊缝截面特性:A=119.25cm 2,Wx =1858.9cm 3,Ix=46472cm 4,Sx=1084.1cm 3,截面高度h=50cm ,截面宽度b=158mm ,翼缘厚t=20mm ,腹板厚tw=12.0mm 。
假定忽略腹板与翼缘的圆角,计算得到翼缘与腹板交点处的面积矩S 1=20×158×(250-10)=7.584×105mm 3。
对接焊缝受力:125V F kN ==;2250M F kN m =⨯=⋅ 焊缝应力验算:最大正应力:622325010134.5/205/1858.910w t x M N mm f N mm W σ⨯===<=⨯ 最大剪应力:33224125101084.11024.3/120/464721012w x v x w VS N mm f N mm I t τ⨯⨯⨯===<=⨯⨯ 折算应力:22127.2/205/w zs t N mm f N mm σ=<= 故焊缝满足要求。
8.5 图8-84所示的牛腿用角焊缝与柱连接。
钢材为Q235钢,焊条用E43型,手工焊,角焊缝强度设计值2f 160/w f N mm =。
T=350kN ,验算焊缝的受力。
图8-84 习题8.5 图8-84-1 焊缝截面计算简图解:(注:焊缝上下翼缘长度114mm 有些问题,应取2130210110l tmm -=-⨯=,黄钜枝06年6月19日)如图8-84-1,截面特性计算如下:2(11425242882)0.75667.2f A h mm =⨯+⨯+⨯⨯= 228820.73225.6w f A h mm =⨯⨯=32741288288[2882114(16)252()4]0.77.913101222f f I h mm =⨯⨯+⨯+⨯+⨯⨯⨯=⨯焊缝受力:247.52N kN ==;247.52V kN ==; 49.5M V e kN m =⋅=⋅ 应力验算:危险点为a 、b 两点,下面分别验算: 对a 点: 32247.51043.67/5667.2N aN N mm A σ⨯===62749.510160100.09/7.91310M a af My N mm I σ⨯⨯===⨯ 2243.67100.09143.76/195.2/N Mw a a f f N mm f N mm σσβ+=+=<=对b 点:32247.51076.73/3225.6V bw V N mm A τ⨯=== 243.67/N Nb a N mm σσ==62749.51014490.16/7.91310M b bf My N mm I σ⨯⨯===⨯22133.87/160/w f N mm f N mm =<=故焊缝强度满足要求。
第八章 电解质溶液习题解答

第八章 习题解答1、在300K 和100kPa 压力下,用惰性电极电解水以制备氢气。
设所用直流电的强度为5A ,电流效率为100%。
来电解稀H 2SO 4溶液,如欲获得1m 3氢气,须通电多少时间?如欲获得1m 3氧气,须通电多少时间?已知在该温度下水的饱合蒸气压为3565Pa 。
解 电解时放出气体的压力为 p=(100000-3565)Pa=96435Pa 1m 3气体的物质的量为311(96435)(1)/()38.6637(8.314)(300)Pa m n pV RT mol J K mol K --⨯===⋅⋅⨯氢气在阴极放出,电极反应为 2H ++2e -→H 2(g)根据法拉第定律,It=ξzF=(Δn B /νB )〃zF , t=(Δn B /νB I)〃zF放氢时,12=H ν,z=2,11(38.6637)2(96500)1492418.821(5)mol t C mol s C s --=⨯⨯⋅=⨯⋅。
氧气在阳极放出,电极反应为 2H 2O-4e -→O 2(g)+4H + 放氧时,12=O ν,z=4,11(38.6637)4(96500)2984837.641(5)mol t C mol s C s --=⨯⨯⋅=⨯⋅。
2、用电解NaCl 水溶液的方法制备NaOH ,在通电一段时间后,得到了浓度为1.0mol·dm -3的NaOH 溶液0.6dm 3,在与之串联的铜库仑计中析出了30.4g 的Cu(s)。
试计算该电解池的电流效率。
解 析出Cu(s)的反应为Cu 2++2e -→Cu电解NaCl 水溶液制备NaOH 的反应为阴极上的反应 2H 2O+2e -→2OH -+H 2(g) 阳极上的反应 2Cl --2e -→Cl 2(g)电解总反应为 2H 2O+2NaCl →Cl 2(g)+H 2(g)+ 2NaOH即铜库仑计中若析出1molCu(s),则理论上在电解池中可得到2 mol 的NaOH 。
基础化学习题解答(8)

习题解答(第八章)一、选择题1. 下列反应中,属于氧化还原反应的是( C )A.硫酸与氢氧化钡溶液的反应B.石灰石与稀盐酸的反应C.二氧化锰与浓盐酸在加热条件下反应D.醋酸钠的水解反应2. 单质A和单质B化合成AB(其中A显正价),下列说法正确的是( C )A. B被氧化B. A是氧化剂C. A发生氧化反应D. B具有还原性3. 对于原电池的电极名称,叙述中有错误的是( B )A.电子流入的一极为正极B.发生氧化反应的一极是正极C.电子流出的一极为负极D.比较不活泼的金属构成的一极为正极4. 根据下列反应:2FeCl3+Cu→2FeCl2+CuCl22Fe3++Fe→3Fe2+2KMnO4+10FeSO4+8H2SO4→2MnSO4+5Fe2(SO4)3+K2SO4+8H2O 判断电极电势最大的电对为( C )A.Fe3+/Fe2+B.Cu2+/CuC.MnO4-/Mn2+D.Fe2+/Feϕ5. 在含有Cl-,Br-,I-离子的混合溶液中,欲使I-氧化成I2,而Br-,Cl-不被氧化,根据φ值大小,应选择下列氧化剂中的( B )A.KMnO4B.K2Cr2O7C.(NH4)2S2O8D.FeCl36. 在酸性溶液中和标准状态下,下列各组离子可以共存的是( D )A.MnO4- 和Cl-B.Fe3+ 和Sn2+C.NO3- 和Fe2+D.I- 和Sn4+7. 利用标准电极电势表判断氧化反应进行的方向,正确的说法是( B )A.氧化态物质与还原态物质起反应;ϕ较大电对的氧化态物质与φϕ较小电对的还原态物质起反应;B. φC.氧化性强的物质与氧化性弱的物质起反应;D.还原性强的物质屯还原性弱的物质起反应。
二、是非题(下列叙述中对的打“√”,错的打“×”)1. MnO4-离子中,Mn和O的化合价分别为+8和-2。
( ×)2. 根据标准电极电势判定SnCl2 + HgCl2 =SnCl4 + Hg反应能自发向右进行。
第8章习题参考答案

第8章习题参考答案1.如果认为CPU等待设备的状态信号是处于非工作状态(即踏步等待),那么在下面几种主机与设备之间的数据传送中: A 主机与设备是串行工作的;B 主机与设备是并行工作的,C 主程序与设备是并行运行的。
A.程序查询方式B.程序中断方式C.DMA方式2.中断向量地址是 B 。
A.子程序入口地址B.中断服务程序入口地址C.中断服务程序入口地址指示器D.例行程序入口地址3.利用微型机制作了对输入数据进行采样处理的系统。
在该系统中,每抽取一个输入数据就要中断CPU一次,中断处理程序接收采样的数据,将其放到主存的缓冲区内。
该中断处理需时x秒,另一方面缓冲区内每存储n个数据,主程序就将其取出进行处理,这种处理需时y秒。
因此该系统可以跟踪到每秒 A 次的中断请求。
A.n/(n×x+y) B.n/(x+y)·n C.min(1/x,n/y)4.采用DMA方式传送数据时,每传送一个数据就要占用一个 C 的时间。
A.指令周期B.机器周期C.存储周期D.总线周期5.通道的功能是:(1) 控制外围设备,(2) 组织外围设备和内存之间进行数据传输。
按通道的工作方式分,通道有选择通道、数组多路通道和字节多路通道三种类型。
6.在图8.9中,当CPU对设备B的中断请求进行服务时,如设备A提出请求,CPU能够响应吗?为什么?如果设备B一提出请求总能立即得到服务,问怎样调整才能满足此要求? 答:不能,因为A、B是同级别的中断。
要使设备B一提出请求总能立即得到服务,除非将B提高到上一级,并令IM3=0,即构成一个3级IR。
7.在图8.9中,假定CPU取指并执行一条指令的时间为t1,保护现场需t2,恢复现场需t3,中断周期需t4,每个设备的设备服务时间为t A,t B,…,t G。
试计算只有设备A,D,G 时的系统中断饱和时间。
答:依次处理设备A,设备D,设备G的时间为:T1 =t1+t2+t3+t4+t AT2 = t1+t2+t3+t4+t DT3 = t1+t2+t3+t4+t G总时间为T = T1+T2+T3 = 3*( t1+t2+t3+t4)+ t A + t D + t G8.设某机有5级中断;L0,L1,L2,L3,L4,其中断响应优先次序为:L0最高,L1次之,L4最低。
第八章刚体的平面运动习题解答

故
向
即
8-21图8-48所示机构中,圆轮A的半径R=0.2m,圆轮B的半径r=0.1m,两轮均在水平轨道上作纯滚动。在图示瞬时,A轮上C点在最高位置,轮心速度vA=2m/s,加速度aA=2m/s2,试求轮B滚动的角速度和角加速度。
图8-48
加速度分析
圆轮A
杆BC
故
向
8-22轮O在水平面上作纯滚动,如图8-49所示。轮缘上固定销钉B,此销钉可在摇杆O1A的槽内滑动,并带动摇杆绕轴O1转动。已知轮心O的速度是一常量,vO=0.2m/s,轮的半径R=0.5m,图示位置时,O1A是轮的切线,摇杆与水平面的夹角为 。试求该瞬时摇杆的角速度和角加速度。
图8-59
以O为动点,杆AB为动系
(1)速度分析
(2)加速度分析
圆轮O
以O为基点,分析C点
向y
8-33图8-60所示机构中,已知曲柄OA以匀角速度 绕定轴O转动,OA=100mm,l=500mm。在图示位置, ,试确定杆BD的角速度和角加速度。
图8-60
以A为动点,杆AB为动系
(1)速度分析
(2)加速度分析
图8-33
瞬心法
基点法
8-7在如图8-34所示的筛动机构中,筛子BC的摆动是由曲柄连杆机构所带动。已知曲柄长OA=0.3m,转速为n=40r/min。当筛子运动到与点O在同一水平线上时, ,试求此时筛子BC的速度。
图8-34
速度投影定理
8-8长为l=1.2m的直杆AB作平面运动,某瞬时其中点C的速度大小为vC=3m/s,方向与AB的夹角为 ,如图8-35所示。试求此时点A可能有的最小速度以及该瞬时杆AB的角速度。
8-20半径为r的圆盘可在半径为R的固定圆柱面上纯滚动,滑块B可在水平滑槽内滑动,如图8-47所示。已知r=125mm,R=375mm;杆AB长l=250mm。图示瞬时,vB=500mm/s,aB=750mm/s2;O、A、O1三点位于同一铅垂线上,试求此时圆盘的角加速度。
习题参考答案
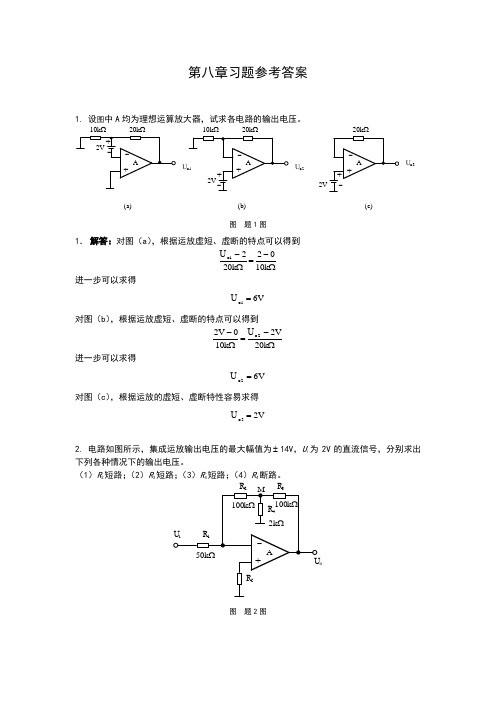
第八章习题参考答案1. 设图中A 均为理想运算放大器,试求各电路的输出电压。
Ωk 10Ωk 20(a)U o2Ωk 10Ωk 20(b)2V(c)U o3图 题1图1. 解答:对图(a ),根据运放虚短、虚断的特点可以得到Ω-=Ω-k 1002k 2021o U 进一步可以求得V 61o =U对图(b ),根据运放虚短、虚断的特点可以得到Ω-=Ω-k 20V2k 100V 22o U 进一步可以求得V 62o =U对图(c ),根据运放的虚短、虚断特性容易求得V 2o3=U2. 电路如图所示,集成运放输出电压的最大幅值为±14V ,U i 为2V 的直流信号,分别求出下列各种情况下的输出电压。
(1)R 2短路;(2)R 3短路;(3)R 4短路;(4)R 4断路。
o图 题2图2. 解答:(1)02=R 时可以得到⎪⎩⎪⎨⎧-==1i 3o M 0R U R U U ,求得V 4o -=U(2)03=R 时可以得到⎪⎩⎪⎨⎧=-=-=M oi 12M V4UU U R R U(3)04=R 时2R 支路无电流,放大电路相当于开环应用, V 14o -=U (4)∞=4R 时可以得到V 8i 132o -=+-=U R R R U3. 如图所示电路,设A 为理想集成运算放大器。
(1) 写出U o 的表达式;(2) 若R f =3k Ω,R 1=Ω,R 2=1k Ω,稳压管VZ 的稳定电压值U Z =,求U o 的值。
图 题3图3.解答:(1)图中的集成运算放大器组成了同相比例运算电路,其输出电压表达式为P 1f N 1f o 11U R R U R R U ⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛+= 当稳压管VZ 的稳定电压值V 10Z <U 时,Z P U U =,输出电压表达式为Z 1f o 1U R R U ⎪⎪⎭⎫⎝⎛+= 当稳压管VZ 的稳定电压值V 10Z >U 时,k P U U =,输出电压表达式为k 1f o 1U R R U ⎪⎪⎭⎫ ⎝⎛+= (2)V 10V 5.1Z <=U ,故输出电压表达式为Z 1f o 1U R U ⎪⎪⎭ ⎝+= 将Ω=k 3f R ,Ω=k 5.11R ,V 5.1Z =U 代入上式得V 5.4V 5.1k 5.1k 31o =⨯⎪⎭⎫ ⎝⎛ΩΩ+=U4. 如图所示电路中,A 为理想运算放大器,已知R 1=R w =10k Ω,R 2=20k Ω,U i =1V ,输出电压的最大值为±12V ,试分别求出当电位器R w 的滑动端移到最上端、中间位置和最小端时的输出电压U o 的值。
第8章习题解答

第8章思考题及习题8参考答案一、填空1. 单片机存储器的主要功能是存储和。
答:程序、数据。
2.假设外部数据存储器2000H单元的内容为80H,执行下列指令后累加器A中的内容为。
MOV P2,#20HMOV R0,#00HMOVX A,@R0答:80H。
3.在存储器扩展中,无论是线选法还是译码法最终都是为扩展芯片的端提供控制信号。
答:片选。
4.起止范围为0000H~3FFFH的数据存储器的容量是 KB。
答:16KB。
5.在AT89S52单片机中,PC和DPTR都用于提供地址,但PC是为访问存储器提供地址,而DPTR是为访问存储器提供地址。
答:程序、数据。
6.11条地址线可选个存储单元,16KB存储单元需要条地址线。
答:2K,14。
7.4KB RAM存储器的首地址若为0000H,则末地址为 H。
答:0FFF。
8.若单片机外扩32KB 数据存储器的首地址若为4000H,则末地址为 H。
答:BFFF9. 设计一个以AT89S52单片机为核心的系统,如果不外扩程序存储器,使其内部8KB闪烁程序存储器有效,则其引脚应该接。
答:EA*,+5V10.74LS138是具有3个输入的译码器芯片,其输出常作片选信号,可选中片芯片中的任一芯片,并且只有1路输出为电平,其它输出均为电平。
答:8,低,高;二、单选1.区分AT89S51单片机片外程序存储器和片外数据存储器的最可靠方法是。
A.看其位于地址范围的低端还是高端B.看其离AT89S51单片机芯片的远近C.看其芯片的型号是ROM还是RAMD.看其是与RD信号连接还是与PSEN信号连接答:D2.访问片外数据存储器的寻址方式是。
A.立即寻址B.寄存器寻址C.寄存器间接寻址D.直接寻址答:C3.若要同时扩展4片2KB的RAM和4片4KB的ROM,则最少需要根地址线。
A、12B、13C、14D、154.当EA=1时,AT89S52单片机可以扩展的外部程序存储器的最大容量为。
A. 64KB B.60KB C.58KB D.56KB答:D5. 若某数据存储器芯片地址线为12根,那么它的存储容量为。
第8章习题解答

第8章习题解答一. 选择题1. 关于类和对象,不正确的说法是()A. 类是一种数据类型,它封装了数据和函数B. 类是对某一类对象的抽象C. 可以基于类这种数据类型定义类的引用D. 一个类的对象只有一个【答案】D【解析】类是一种数据类型,可以基于“类”这种数据类型定义多个称为“对象”的变量。
2. 类定义的外部,可以被访问的类的成员有()A. public 的类成员B. public或private的类成员C. private或protected的类成员D. public或private 的类成员【答案】A【解析】类的成员数据或成员函数的访问属性分为三种情况:private、public和protected,即私有访问属性、公有访问属性和保护访问属性,类定义的外部只能访问公有访问属性的成员。
3 关于this 指针,说法错误的是()A. this指针必须显式说明B. 当创建一个对象后,this 指针就指向该对象C. 成员函数拥有this指针D. 静态成员函数拥有this指针【答案】D【解析】this指针是一种特殊的指针,它指向成员函数当前操作的数据所属的对象。
不同的对象调用相同的成员函数时,this指针将指向不同的对象,也就可以访问不同对象的成员数据。
而静态成员函数是一个类的所有对象共享的成员,而不仅仅是某一对象的成员。
因此,可以在没有任何对象存在的情况下,可以使用静态成员函数,而使用this指针必须有明确的对象所指。
4. 调用形式参数为普通对象的函数时,系统会自动调用相应类的()A. 名字不同于类名的一般成员函数B. 构造函数C. 析构函数D. 拷贝构造函数【答案】D【解析】若函数的形参为类的对象,调用函数时,实参赋值给形参,系统自动调用拷贝构造函数实现拷贝赋值。
5. 定义某类的对象后,再删除该对象,系统会自动调用()A. 名字不同于类名的一般成员函数B. 拷贝构造函数C. 构造函数D. 析构函数【答案】D【解析】当对象生存期结束时,需要调用析构函数,释放对象所占的内存空间。
高等数学课后答案第八章习题详细解答

习 题 8-11.设有一个面薄板(不计其厚度),占有xOy 面上的闭区域D ,薄板上分布有面密度为(,)x y μμ=的电荷,且(,)x y μ在D 上连续,试用二重积分表达该板上的全部电荷Q .解 用一组曲线将D 分成n 个小闭区域i σ∆,其面积也记为(1,2,,)i i n σ∆=.任取一点(,)i i i ξησ∈∆,则i σ∆上分布的电量(,)i i i Q μξησ∆≈∆.通过求和、取极限,便得到该板上的全部电荷为1lim (,)(,)d ,ni i i i DQ x y λμξησμσ→==∆=∑⎰⎰其中1max{i i nλσ≤≤=∆的直径}.2. 设12231()d D I x y σ=+⎰⎰其中1{(,)11,22}D x y x y =-≤≤-≤≤;又22232()d D I x y σ=+⎰⎰其中2{(,)01,02}D x y x y =≤≤≤≤.试利用二重积分的几何意义说明1I 与2I 之间的关系.解 由二重积分的几何意义知,1I 表示底为1D 、顶为曲面223()z x y =+的曲顶柱体1Ω的体积;2I 表示底为2D 、顶为曲面223()z x y =+的曲顶柱体2Ω的体积.由于位于1D 上方的曲面223()z x y =+关于yOz 面和zOx 面均对称,故yOz 面和zOx 面将1Ω分成四个等积的部分,其中位于第一卦限的部分即为2Ω.由此可知124I I =.3. 利用二重积分定义证明: (1) d ()DD σσσ=⎰⎰其中为的面积;(2) (,)d (,)d ()DDkf x y k f x y k σσ=⎰⎰⎰⎰其中为常数;(3)12(,)d (,)d (,)d ,DD D f x y f x y f x y σσσ=+⎰⎰⎰⎰⎰⎰其中12D DD =,1D 、2D 为两个无公共内点的闭区域.证 (1) 由于被积函数(,)1f x y ≡,故由二重积分定义得11d lim (,)lim lim .nniiii i i Df λλλσξησσσσ→→→===∆=∆==∑∑⎰⎰(2) 011(,)d lim (,)lim (,)(,)d .nni i i i i i i i DDkf x y kf k f k f x y λλσξησξησσ→→===∆=∆=∑∑⎰⎰⎰⎰(3) 因为函数(,)f x y 在闭区域D 上可积,故不论把D 怎样分割,积分和的极限总是不变的,因此在分割D 时,可以使1D 和2D 的公共边界永远是一条分割线。
大学物理第八、九章习题解答

第八章习题解答8-1选择题(1) 正方形的两对角线处各放置电荷Q ,另两对角线各放置电荷q ,若Q 所受到合力为零,则Q 与q 的关系为:()(A )3/22Q q =- (B)3/22Q q = (C)2Q q =- (D)2Q q =(1)、解:[答案:A]利用库仑定律分别求出受力电荷Q 与三个施力电荷q 、Q 、q 之间作用力的大小及方向,再将三力合成,令合力为零即可建立方程导出答案。
(2) 下面说法正确的是:()(A )若高斯面上的电场强度处处为零,则该面内必定没有电荷; (B )若高斯面内没有电荷,则该面上的电场强度必定处处为零; (C )若高斯面上的电场强度处处不为零,则该面内必定有电荷; (D )若高斯面内有电荷,则该面上的电场强度必定处处不为零。
(2)、解:[答案:D]高斯定理的原意。
(3) 一半径为R 的导体球表面的面点荷密度为σ,则在距球面R 处的电场强度() (A )0?/σε (B )0/2σε (C )/4σε(D )0/8σε(3)、解:[答案:C]利用均匀带电球面的场强公式计算02004qq rπε==F E r ,其中σπ24R q =, R 2r =(4)下列说法正确的是( )(A) 电场强度为零的点,电势也一定为零 (B) 电场强度不为零的点,电势也一定不为零 (C) 电势为零的点,电场强度也一定为零(D) 电势在某一区域内为常量,则电场强度在该区域内必定为零(4)、解:[答案:D].根据场强与电势的微分关系或积分关系均可以证明。
8-2填空题(1) 在静电场中,电势不变的区域,场强必定为 。
(1)、解:[答案:0] 根据场强与电势的微分关系或积分关系均可以证明。
(2) 一个点电荷q 放在立方体中心,则穿过某一表面的电通量为 ,若将点电荷由中心向外移动至无限远,则总通量将 。
(2)、解:[答案:0/6q ε, 将为零],第一空:根据高斯定理知:正六面体的六个对称面组成的闭合面总通量为εq,故每个面是总量的61。
(完整版)大学物理学(课后答案)第8章

第八章课后习题解答一、选择题8-1如图8-1所示,一定量的理想气体,由平衡态A 变到平衡态B ,且它们的压强相等,即=A B p p 。
则在状态A 和状态B 之间,气体无论经过的是什么过程,气体必然[ ](A) 对外作正功 (B) 内能增加 (C) 从外界吸热 (D) 向外界放热分析:由p V -图可知,A A B B p V p V =,即知A B T T <,则对一定量理想气体必有B A E E >,即气体由状态A 变化到状态B ,内能必增加。
而作功、热传递均是过程量,与具体的热力学过程相关,所以(A )、(C )、(D )不是必然结果,只有(B )正确。
8-2 两个相同的刚性容器,一个盛有氢气,一个盛有氦气(均视为刚性分子理想气体)。
开始时它们的压强和温度都相同。
现将3 J 热量传给氦气,使之升高到一定的温度。
若使氢气也升高同样的温度,则应向氢气传递热量为[ ](A) 6 J (B) 3 J (C) 5 J (D) 10 J分析:由热力学第一定律Q E W =∆+知在等体过程中Q E =∆。
故可知欲使氢气和氦气升高相同的温度,由理想气体的内能公式2m i E R T M '∆=∆,知需传递的热量之比22222:():():5:3HHe H He H He H He H Hem m Q Q i i i i M M ''===。
故正确的是(C )。
8-3 一定量理想气体分别经过等压、等温和绝热过程从体积1V 膨胀到体积2V ,如图8-3所示,则下述正确的是[ ]习题8-1图(A) A C →吸热最多,内能增加(B) A D →内能增加,作功最少(C) A B →吸热最多,内能不变(D) A C →对外作功,内能不变分析:根据p V -图可知图中A B →为等压过程,A C →为等温过程,A D →为绝热过程。
又由理想气体的物态方程pV vRT =可知,p V -图上的pV 积越大,则该点温度越高,因此图中D A B C T T T T <==,又因对于一定量的气体而言其内能公式2i E vRT =,由此知0AB E ∆>,0AC E ∆=,0AD E ∆<。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.7
见下图题(a),点源置于透镜前焦点,全息图可以记录透镜的像差试证明:用共扼参考光 照明(图(b))可以补偿透镜像差,在原点源处产生一个理想的衍射斑。
解:将点源置于透镜前焦点,由于透镜有像差,通过透镜出射的波面 ΣO 不为平面。参考光波 用平面波,在全息平面上物光和参考光波的复振幅分布为
U O ( x, y ) = AeiφO ( x , y ) , U R ( x, y ) = Reikx sin θ
(b) 物体位于透镜前 f − dO 处,应用公式(5.3.17)得到后焦面上的光场分布为 U O ( x, y ) = C ′e
ik x2 + y 2 2 dO
∫∫ g ( x
∞
O
, yO )e
− ik
xxO + yyO dO
dxO dyO = C ′e
ik
x2 + y 2 2 dO
G (ξ ,η )
(b)所示。而其它两项不在轴线方向而发散了。
采用全息图校正板后,在限视场的情况下可以改善成像质量。但也有如下缺点:全息图
4
的衍射效率低;由于全息图存在色散效应,必须采用单色光;全息图校正又引入了自身的像 差。
8.8
彩虹全息照相中使用狭缝的作用是什么?为什么彩虹全息图的色模糊主要发生在与狭缝 垂直的方向上?
8.9
说明博里叶变换全息图的记录和再现过程中,可以采用平行光入射和点光源照明两种方 式,并且这两种方式是独立的。
答:傅里叶变换全息图的核心是(a)通过一个傅里叶变换装置将物频谱记录下;(b) 再通过一 个傅里叶装置将物谱还原成物。因此,不管记录和再现装置有何具体差异,只要有傅里叶变 换功能即可。 当把物体置于变换透镜的前焦面,若用平行光照明,则透镜的后焦面则为物的标准频谱 面;若用点光源的物像共轭面即为物的标准频谱面。因此,记录时无论用平行光或点光源照 明,均可在相应的共轭面处记录下标准的物谱。同样,再现时无论用平行光照明或点光源照 明均可在共轭面处得到物。平行光照明和点光源照明可任意配置,这两种方式是独立的。
yO max = 0.2 mm, yO min = 0.1 mm, yR = 0 , z = 20 mm。这样有:
ηmax = ηmin
0.2 = 105 周/mm 10 × 20 0.1 = −7 = 0.5 × 105 周/mm 10 × 20
−7
因此,这样一张全息图所记录的空间频率范围为
0.5 × 105 ≤ η ≤ 105 (2) 当用 600nm 的单色平面波垂直照射这张全息图时,设 U ( x, y, 0) 为透过全息图的光场
I ( x, y ) = R 2 + C ′2 | G (ξ ,η ) |2 + RC ′e − i 2πξ b G (ξ ,η ) + RC ′ei 2πξ b G * (ξ ,η )
由此可见,二次相位因子已相互抵消,只有倾斜因子和物频谱,故记录了物的傅里叶频谱, 但记录面又不是物的准确傅里叶变换平面,所以称为准傅里叶变换全息图。
解:由式(8.5.20)可得:
(1) zi = ∓7.7 cm (2) zi = ∓15.4 cm, M = 2
8.3
证明: 若 λ2 = λ1 , 及 z p = zR , 则得到一个放大率为 1 的虚像; 而若 λ2 = λ1 , 及 z p = − z R 时,
1
则得到一个放大率为 1 的实像。 证明:由式 (8.5.20) 的第二组可得 zi = zO , M = 1 ,左方,虚像。由式 (8.5.20) 的第一组可得
8.5
证明下图(a)和(b)的光路都可以记录物体的准傅里叶变换全息图。
证明:(a) 物体位于透镜前 d O 处,应用公式(5.3.10),这里 q = f ,则物体 g ( xO , yO ) 在记录平 面上后焦面上的光场分布为
U O ( x, y ) = C ′e
ik f − dO
2f2
( x2 + y 2 )
∫∫ g ( xO , yO )e
∞
− i 2π (ξ xO +η yO )
dxO dyO = C ′e
ik
f − dO
2f2
( x2 + y 2 )
G (ξ ,η )
式中, G (ξ ,η ) 是 g ( xO , yO ) 的频谱, ξ = x / λ f ,η = y / λ f 。参考光在后焦面上形成分布为:
答:在彩虹全息照相中使用狭缝的目的是为了能在白光照明下再现准单色像。在普通全息照 相中,若用白光照明全息图再现时,不同波长的光同时进入人眼,我们将同时观察到相互错 位的不同颜色的再现像,造成再现像的模糊,即色模糊。在彩虹全息照相中,由于狭缝起了 分色作用,再现过程中不同波长的光对应不同的水平狭缝位置,通过某一狭缝位置只能看到 某一准单色的像,从而避免了色模糊。 在彩虹全息照相中,为了便于双眼观察,参考平面波的选择总是使全息图的光栅结构主 要沿水平方向,因而色散沿竖直方向。狭缝沿水平方向放置,这样色散方向与狭缝垂直,即 色模糊订发生在与狭缝垂直方向上。这样做的结果便于人眼上下移动选择不同颜色的准单色 像。
zi = − zO , M = 1 ,右方,实像。
8.4
下表列举了几种底片的 MTF 的近似截止频率 型号
Kodak Kodak Kodak Agfa Tri-x
线/mm
50 60 300 600
高反差片
SO-243 Agepam FF
设用 632nm 波长照明,采用无透镜傅里叶变换记录光路,参考点和物体离底片 10cm。 若物点位于某一大小的圆(在参考点附近)之外,则不能产生对应的像点,试对每种底片 估计这个圆的半径大小。 解:由式(8.7.24)可求得圆半径 rmax 的大小依次为:3.16,3.8,19,37 mm
2
U R ( x, y ) = R ⋅ e
ik
f − dO
2f2
( x2 + y 2 )
∫∫ δ ( xO + b, yO )e
∞
− i 2π ( ξ xO +η yO )
dxO dyO = R ⋅ e
ik
f − dO
2f2
( 的记录平面并不是物和参考光的准确傅里叶变换平面,多了一个二次相位因子,因此说 全息图是物光场分布的准傅里叶变换平面。全息图平面上的光强分布为
再现光用参考光波的共轭波,即 C = R* ,再现光波场为
U ( x, y ) = R*t = Rtb e − ikx sin θ + β ′eiφO ( x , y )− 2 ikx sin θ + β ′ ARe-iφO ( x , y )
如果使 e− iφO ( x , y ) 代表的光波 Σ* O 通过透镜,则与透镜所产生的有像差的波面 Σ O 形状相同,方向 相反,再经过透镜后可变成平面波。因此,在焦点平面上形成一个理想系统的衍射斑,所图
ik
x2 + y 2 2 dO
ei 2πξ b
全息图平面上的光强分布为
I ( x, y ) = R 2 + C ′2 | G (ξ ,η ) |2 + RC ′e − i 2πξ b G (ξ ,η ) + RC ′ei 2πξ b G * (ξ ,η )
由于物光波和参考光波有相同的相位因子,可相互抵消,从而得到物体的准傅里叶变换全息 图。
对于共轭实像(第一组符号)有
zi = − zO , xi = xO , yi = yO − zO (tan θ p + tan θ R )
不管是原始虚像或共轭实像, zi 均与 xO , yO 无关,即不管物点在物平面上位于何处,其像 点均在同同一平面内,但位置有变化,随参考光波和再现光波的不同而在像平面内发生平移。
8.10
曾有人提出用波长为 0.1nm 的辐射来记录一张 X 射线全息图,然后用波长为 600.0nm 的可见光来再现像。选择如下图题(上部)所示的无透镜傅里叶变换记录光路,物体的宽 度为 0.1mm,物体和参考点源之间的最小距离选为 0.1mm,以确保孪生像和“同轴”干 涉分离开,轴”干涉分离开.X 射线底片放在离物体 2cm 处。
复振幅分布,则它的角谱为
cos α cos β A , λ λ
由于 ξ =
cos α
− i 2π = ∫∫ U ( x, y, 0)e ∞
cosα
λ
x+
cos β y λ
dxdy
λ
,η =
cos β
λ
,所以
5 5 cos α cos β 不为零 0.5 × 10 ≤ cos β / λ ≤ 10 A , = λ 其他 λ 0
习 题 8
8.1 证明:若一平面物体的全息图记录在一个与物体相平行的平面内,则最后所得到的像将 在一个与全息图平行的平面内。(为简单起见,可设参考光为一平面波。) 证明:利用点源全息图公式 (8.5.20)~(8.5.22) ,取物平面上任一点来研究。为简单起见,设
λ1 = λ2 ,参考光波和再现光波是波矢平行于 y − z 平面的平面波,即 z p = z R = ∞ , x p = xR = 0 。
全息图上的光强分布为
I ( x, y ) = A2 + R 2 + AReiφO ( x , y )−ikx sin θ + ARe-iφO ( x , y ) +ikx sin θ
全息图的振幅透为:
t = tb + β ′eiφO ( x , y ) −ikx sin θ + β ′ ARe-iφO ( x , y )+ ikx sin θ
8.2
制作一全息图, 记录时用的是氩离子激光器波长为 488.0nm 的光, 而成像时则是用 He-Ne 激光器波长为 632.8nm 的光:
