直线段方位角计算
方位角计算公式
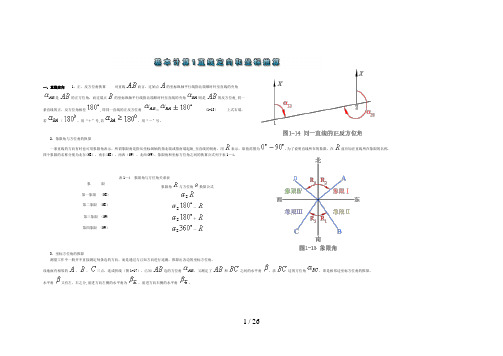
一、直线定向1、正、反方位角换算对直线而言,过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角,而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角,同一条直线的正、反方位角相差,即同一直线的正反方位角= (1-13〉上式右端,若〈,用“+”号,若,用“-”号。
2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。
所谓象限角是指从坐标纵轴的指北端或指南端起始,至直线的锐角,用表示,取值范围为.为了说明直线所在的象限,在前应加注直线所在象限的名称.四个象限的名称分别为北东<NE)、南东<SE)、南西(SW〉、北西(NW>。
象限角和坐标方位角之间的换算公式列于表1—4。
表1—4 象限角与方位角关系表象限象限角与方位角换算公式第一象限〈NE)=第二象限<SE)=-第三象限<SW)=+第四象限<NW)=-3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向,而是通过与已知方向进行连测,推算出各边的坐标方位角。
设地面有相邻的、、三点,连成折线〈图1-17),已知边的方位角,又测定了和之间的水平角,求边的方位角,即是相邻边坐标方位角的推算。
水平角又有左、右之分,前进方向左侧的水平角为,前进方向右侧的水平角。
1 / 26设三点相关位置如图1-17(〉所示,应有=++ (1—14〉设三点相关位置如图1-17(〉所示,应有=++-=+- (1-15〉若按折线前进方向将视为后边,视为前边,综合上二式即得相邻边坐标方位角推算的通式:=+(1-16〉显然,如果测定的是和之间的前进方向右侧水平角,因为有=-,代入上式即得通式=-(1—17〉上二式右端,若前两项计算结果<,前面用“+”号,否则前面用“-”号。
2 / 26二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。
坐标正算,就是根据直线的边长、坐标方位角和一个端点的坐标,计算直线另一个端点的坐标的工作。
测量学导线测量常用计算公式

一、方位角的计算公式二、平曲线转角点偏角计算公式三、平曲线直缓、缓直点的坐标计算公式四、平曲线上任意点的坐标计算公式五、竖曲线上点的高程计算公式六、超高计算公式七、地基承载力计算公式八、标准差计算公式九、坐标中线测量与计算十、全站仪的使用方法和坐标测量步骤一、方位角的计算公式1. 字母所代表的意义:x1:QD的X坐标y1:QD的Y坐标x 2:ZD 的X 坐标 y 2:ZD 的Y 坐标 S :QD ~ZD 的距离 α:QD ~ZD 的方位角2. 计算公式:()()212212y y x x S -+-=1)当y 2- y 1>0,x 2- x 1>0时:1212x x y y arctg--=α 2)当y 2- y 1<0,x 2- x 1>0时:1212360x x y y arctg --+︒=α 3)当x 2- x 1<0时:1212180x x y y arctg--+︒=α 二、 平曲线转角点偏角计算公式1. 字母所代表的意义:α1:QD ~JD 的方位角 α2:JD ~ZD 的方位角 β:JD 处的偏角2. 计算公式:β=α2-α1(负值为左偏、正值为右偏)三、 平曲线直缓、缓直点的坐标计算公式1. 字母所代表的意义:U :JD 的X 坐标 V :JD 的Y 坐标 A :方位角(ZH ~JD )T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=D :JD 偏角,左偏为-、右偏为+2. 计算公式:直缓(直圆)点的国家坐标:X ′=U+T cos(A+180°)Y ′=V+T sin(A+180°)缓直(圆直)点的国家坐标:X ″=U+Tcos(A+D)Y ″=V+Tsin(A+D)四、 平曲线上任意点的坐标计算公式1. 字母所代表的意义:P :所求点的桩号B :所求边桩~中桩距离,左-、右+ M :左偏-1,右偏+1C :JD 桩号 D :JD 偏角L s :缓和曲线长 A :方位角(ZH ~JD ) U :JD 的X 坐标 V :JD 的Y 坐标T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=I=C-T :直缓桩号 J=I+L :缓圆桩号s L DRJ H -+=180π:圆缓桩号K=H+L :缓直桩号2. 计算公式: 1)当P<I 时中桩坐标:X m =U+(C-P)cos(A+180°) Y m =V+(C-P)sin(A+180°) 边桩坐标:X b =X m +Bcos(A+90°) Y b =Y m +Bsin(A+90°)2)当I<P<J 时()s230RL I P MA O π-︒+= ()()2390R I P I P G ---=中桩坐标:X m =U+Tcos(A+180°)+GcosOY m =V+Tsin (A+180°)+G sinO()s290RL I P W π-︒=边桩坐标:X b =X m +Bcos(A+MW +90°) Y b =Y m +Bsin(A+MW +90°)3)当J<P<H 时()()R J P L M A R J P R L M A O s s πππ-+︒+=⎪⎭⎫⎝⎛-︒+︒+=909090 ()RJ P R G π-︒=90sin2 中桩坐标:()O G R L M A R L L A T U X s ss m cos 30cos 90180cos 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()O G R L M A R L L A T V Y s ss m sin 30sin 90180sin 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()RJ P W π-︒=90边桩坐标:X b =X m +Bcos(O+MW +90°) Y b =Y m +Bsin(O+MW +90°)4)当H<P<K 时()sRL K P MMD A O π230180-︒-︒++= ()2390R P K P K G ---=中桩坐标:X m =U+Tcos(A+MD)+GcosO Y m =V+Tsin(A+MD)+GsinO()s290RL K P W π-︒=边桩坐标:X b =X m +Bcos(A+MD-MW +90°) Y b =Y m +Bsin(A+MD-MW +90°)5)当P>K 时中桩坐标:X m =U+(T+P-K)cos(A+MD) Y m =V+(T+P-K)sin(A+MD) 边桩坐标:X b =X m +Bcos(A+MD +90°) Y b =Y m +Bsin(A+MD +90°)注:计算公式中距离、长度、桩号单位:“米”;角度测量单位:“度”;若要以“弧度”为角度测量单位,请将公式中带°的数字换算为弧度。
方位角

方位角(azimuthangle):从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角,叫方位角。
(一)方位角的种类由于每点都有真北、磁北和坐标纵线北三种不同的指北方向线,因此,从某点到某一目标,就有三种不同方位角。
(1)真方位角。
某点指向北极的方向线叫真北方向线,而经线,也叫真子午线。
由真子午线方向的北端起,顺时针量到直线间的夹角,称为该直线的真方位角,一般用A表示。
通常在精密测量中使用。
(2)磁方位角。
地球是一个大磁体,地球的磁极位置是不断变化的,某点指向磁北极的方向线叫磁北方向线,也叫磁子午线。
在地形图南、北图廓上的磁南、磁北两点间的直线,为该图的磁子午线。
由磁子午线方向的北端起,顺时针量至直线间的夹角,称为该直线的磁方位角,用Am表示。
(3)坐标方位角。
由坐标纵轴方向的北端起,顺时针量到直线间的夹角,称为该直线的坐标方位角,常简称方位角,用a表示。
方位角在测绘、地质与地球物理勘探、航空、航海、炮兵射击及部队行进时等,都广泛使用。
不同的方位角可以相互换算。
军事应用:为了计算方便精确,方位角的单位不用度,用密位作单位。
换算作:360度=6000密位。
(二)三种方位角之间的关系因标准方向选择的不同,使得一条直线有不同的方位角。
同一直线的三种方位角之间的关系为:A=Am+δA=a+γa=Am+δ-γ(三)坐标方位角的推算1.正、反坐标方位角每条直线段都有两个端点,若直线段从起点1到终点2为直线的前进方向,则在起点1处的坐标方位角a12称为直线12的正方位角,在终点2处的坐标方位角a21称为直线12的反方位角。
a反=a正±180°式中,当a正<180°时,上式用加180°;当a正>180°时,上式用减180°。
2.坐标方位角的推算实际工作中并不需要测定每条直线的坐标方位角,而是通过与已知坐标方位角的直线连测后,推算出各直线的坐标方位角。
方位角计算公式
辅助 计算
点名 2 BM1 1
2
3
BM2
测站数 3 8 3 4 5
20
表 2-2 附合水准路线计算
观测高差 /m
改正数 /m
改正后高差 /m
4
5
6
+8.364
- 0.014
+8.350
- 1.433
- 0.005
- 1.438
- 2.745
- 0.007
- 2.752
+4.661
- 0.008
+4.653
+ 8.847
- 0.034
一、直线定向
1、正、反方位角换算
对直线
而言,过始点
的坐标纵轴平行线指北端顺时针至直线的夹角
是
的正方位角,而过端点
的坐标纵轴平行线指北端顺时针至直线的夹角
则是
的反方位角,同
一条直线的正、反方位角相差
,即同一直线的正反方位角
=
(1-13>
上式右
端,若
<
,用“+”号,若
,用“-”号。
2、象限角与方位角的换算
算
各
待
定
点
的
高
程
。
如上 所述,闭 合水准 路线的 计算方法除高差 闭合差 的计算有 所区别 而外,其余与附 合路线 的计算 完全相 同。
二
、
举
例
1.
附
合
水
准
路
线
算
例
5 / 26
下图 2-18 所示附合水准路线为例,已知水准点 A 、 B 和待定点 1、2、3 将整个路线分为四个测段。
测段号 1 1 2 3
坐标及方位角计算

坐标及方位角计算坐标和方位角是地理学和导航中常用的概念,用于确定一个地点在地球上的位置和方向。
坐标通常用经度和纬度表示,而方位角则是用于确定一个地点相对于另一个地点的方向。
在本文中,我们将介绍坐标和方位角的计算方法。
1.坐标的计算方法:坐标是用经度和纬度来表示一个地点在地球上的位置。
经度是指一个地点距离地球上子午线的距离,而纬度是指一个地点距离地球赤道的距离。
计算经度和纬度的方法如下:-经度的计算方法:经度的取值范围是从-180度到180度。
以本初子午线(通过伦敦的经线)为基准,向东为正,向西为负。
可以通过使用全球定位系统(GPS)或使用地图上的比例尺来确定一个地点的经度。
-纬度的计算方法:纬度的取值范围是从-90度到90度。
以地球赤道为基准,向北为正,向南为负。
可以通过使用全球定位系统(GPS)或使用地图上的比例尺来确定一个地点的纬度。
2.方位角的计算方法:方位角是用于确定一个地点相对于另一个地点的方向的角度。
方位角通常使用正北方向为基准,顺时针方向计算。
计算方位角的方法如下:-使用经纬度计算方位角:首先,计算两个地点的经度差和纬度差。
然后,使用三角函数(正弦、余弦或正切)计算两个地点之间的夹角。
最后,将夹角转换为以度为单位的方位角。
-使用几何图形计算方位角:将两个地点的经纬度绘制在一张地图上,并为两个地点之间的连线添加标记。
然后,使用直线夹角定理计算连线的夹角。
最后,使用罗盘或直尺等工具,将夹角转换为以度为单位的方位角。
总结:坐标和方位角是地理学和导航中常用的概念,用于确定一个地点在地球上的位置和方向。
坐标使用经度和纬度来表示一个地点的位置,而方位角用于确定一个地点相对于另一个地点的方向。
计算坐标和方位角的方法可以通过使用全球定位系统(GPS)、地图上的比例尺或几何图形等方法来进行。
EXCEL曲线坐标计算公式

公式解析一.坐标转换X =A +N COSα-E SINαY =B +N SINα+E COSαN=(X-A) COSα±(Y-B)SINαE=(Y-B)COSα±(X-A)SINαA,B为施工坐标系坐标原点α为施工坐标系与北京坐标系X轴的夹角(旋转角)即大地坐标系方位角X,Y为北京坐标值N,E为施工坐标值二.方位角计算1.直线段方位角: α=tanˉ¹ [(Y b-Y a)/(X b-X a)]2.交点转角角度: α=2 tanˉ¹ (T/R)计算结果①为﹢且<360,则用原数;②为﹢且>360,则减去360;③为﹣,则加上180.3.缓和曲线上切线角: α=ƟZH±90°*Lo²/(π*R* Ls)α= Lo/(2ρ)=Lo²/(2 A²)=Lo²/(2R*Ls)ρ—该点的曲率半径4.圆曲线上切线角: α=ƟHY±180°*Lo/(π*R)ƟZH—直缓点方位角, ƟHY—缓圆点方位角,注:以计算方向为准,左偏,取"﹣";右偏,取"﹢"。
左偏,则第一段缓和曲线和圆曲线上取"﹣",第二段缓和曲线上取"﹢" ;右偏,则第一段缓和曲线和圆曲线上取"﹢",第二段缓和曲线上取"﹣" .。
符号说明:A—回旋线参数(A²=R* Ls)Ls—缓和曲线长度R—曲线半径Lo—曲线长度:计算点位到特殊点(ZH、HY、YH、HZ)的长度三.坐标值计算1.直线段坐标计算公式:直线两端点A.B间距离为S;A点坐标为A(X a, Y a);方位角为αX b= X a+S*cosαY b= Y a+S*sinα2.缓和曲线及圆曲线坐标计算公式:①缓和曲线坐标计算公式:X=X ZH+(Lo-Lo^5/(40*R^2*Ls^2)+Lo^9/(3456*R^4*Ls^4)-Lo^13/( 599040*R^6*Ls^6)+Lo^17/(175472640*R^8*Ls^8))*cosα-(Lo^3/(6 *R*Ls)-Lo^7/(336*R^3*Ls^3)+Lo^11/(42240*R^5*Ls^5)-Lo^15/(9 676800*R^7*Ls^7)+Lo^19/(3530096640*R^9*Ls^9))*sinαY=Y ZH+(Lo-^5/(40*R^2*Ls^2)+Lo^9/(3456*R^4*Ls^4)-Lo^13/(59 9040*R^6*Ls^6)+Lo^17/(175472640*R^8*Ls^8))*sinα+(Lo^3/(6* R*Ls)-Lo^7/(336*R^3*Ls^3)+Lo^11/(42240*R^5*Ls^5)-Lo^15/(96 76800*R^7*Ls^7)+Lo^19/(3530096640*R^9*Ls^9))* cosα符号说明:X ZH—直缓点X坐标值Y ZH—直缓点Y坐标值A—回旋线参数(A²=R* Ls)Lo—计算点位到特殊点的长度Ls—缓和曲线长度R—曲线半径α—方位角注:式中,紫色部分为缓和曲线任意点的坐标增量(支距坐标)。
公路工程各点方位角及坐标计算公式

公路工程各点方位角及坐标计算公式建筑 2009-10-16 09:41 阅读1962 评论3字号:大中小(一)各点方位角计算:1、第一直线段(K0~ZH):F=arctgΔY/ΔX注:直线方位角要考虑象限角才能定出正确线路走向2、第一缓和曲线段(KZH~KHY):δ1=(K0-KZH)2/(2RLh)×180/π3、圆曲线段(KHY~KYH):δ2=[2(K0-KZH)-Lh]/2R×180/πδ2=(KHY-KZH)/2R×180/π+(K0-KHY)/R×180/π无缓和曲线时:δ2=(K0-KHY)/R×180/π(即圆曲线圆心角)4、第二缓和曲线段(KYH~KHZ):δ3=(KHZ-K0)2/(2RLh)×180/π5、第二直线段(KHZ~KZH):F±α (左偏时F-α,右偏时F+α)注:K0——计算点的里程α——曲线交点偏角Lh——缓和曲线长(注意有时第一和第二缓和曲线长不一样)(二)各点坐标计算XZH=XJD-T?CosF XHZ=XJD+T?Cos(F±α)YZH=YJD-T?SinF YHZ=YJD+T?Sin(F±α)1、第一直线段:X=XZH+(K0-KZH)?CosF中桩Y=YZH+(K0-KZH)?SinFX边=X中±B?Cos(F-Δ)边桩Y边=Y中±B?Sin(F-Δ)注:B——中桩至所求点的距离(左幅时为+B,右幅时为-B,当设计轴线与线路不垂直时B取斜长,即B/SinΔ)设计轴线线路方向BΔ图S-12、第一缓和曲线段:XX=XZH-Y′?Sinθ+X′?CosθX X′X′中桩′Y=YZH+Y′?Cosθ+X′?SinθYZH Yθ HZX边=X中±B?Cos(F+μδ1-Δ)HY YH边桩Y边=Y中±B?Sin(F+μδ1-Δ)JDY′注:(本公式只适用与图S-2线形)图S-2μ——曲线左转为-1,右转为+1θ——线路方位角与Y轴所夹的锐角,见图S-2Y′=L-L5/(40R2Lh2);X′=L3/(6RLh)-L7/(336R3Lh3);(R—圆曲线半径,L—缓和曲线上任一点至曲线起点长度)3、圆曲线段:X=XHY+2R?Sinφ?Cos(F+μ(ξ+φ))中桩Y=YHY+2R?Sinφ?Sin(F+μ(ξ+φ))X边=X中±B?Cos(F+μδ2-Δ)边桩Y边=Y中±B?Sin(F+μδ2-Δ)注:φ=(K0-KHY)/2R×180/π;ξ=(KHY-KZH)/2R×180/π4、第二缓和曲线段:X=XHZ-Y′?Sinθ+X′?Cosθ中桩Y=YHZ-Y′?Cosθ-X′?SinθX边=X中±B?Cos(F+μδ1-Δ)边桩Y边=Y中±B?Sin(F+μδ1-Δ)注:1、本公式只适用与图S-2线形,其他线形可根据本线形公式变换2、式中符号与第一缓和曲线意义相同3、注意有时第一缓和曲线长和第二缓和曲线长不一样4、第二直线段:X=XHZ+(K0-KHZ)?Cos(F±α)中桩Y=YHZ+(K0-KHZ)?Sin(F±α)X边=X中±B?Cos(F±α-Δ)边桩Y边=Y中±B?Sin(F±α-Δ)注:F——第一直线段的方位角(三)用CASIO fx-4500P计算已知坐标点在线路上的里程和距中线距离1、直线段(已知坐标X、Y)Pol(X-XHZ,Y-YHZ):K=V?Cos(F-W)+KHZ B=V?Sin(F-W)注:1、在fx-4500P中计算结果存入变量储存区V和W,要显示储存区内容时按RCL V 、 W 键。
方位角距离计算坐标

方位角距离计算坐标方位角距离是一种常用的坐标计算方法,用于确定一个点相对于另一个点的位置。
它由方位角和距离两个参数组成,方位角表示与参考点的连线与北方向之间的夹角,距离表示两点之间的直线距离。
方位角是以北为基准的角度,以顺时针方向计算。
通常使用度数表示,范围从0度到360度。
如果方位角为0度,则表示目标点在参考点的正北方向;如果方位角为90度,则表示目标点在参考点的正东方向。
距离是两点之间的直线距离,通常以米或千米为单位。
它可以通过测量实际距离或使用地理信息系统(GIS)等工具来计算。
方位角距离的计算可以基于不同的坐标系。
在平面坐标系中,可以使用直角坐标系或极坐标系来计算。
在球面坐标系中,可以使用经纬度坐标系来计算。
在直角坐标系中,可以使用三角函数来计算方位角距离。
假设参考点的坐标为(x1, y1),目标点的坐标为(x2, y2),则可以通过以下公式计算方位角距离:距离 = sqrt((x2 - x1)^2 + (y2 - y1)^2)方位角 = atan2(y2 - y1, x2 - x1)其中,sqrt表示平方根,atan2表示反正切函数。
在极坐标系中,可以使用极坐标系下的公式来计算方位角距离。
假设参考点的极坐标为(r1, θ1),目标点的极坐标为(r2, θ2),则可以通过以下公式计算方位角距离:距离 = sqrt(r1^2 + r2^2 - 2 * r1 * r2 * cos(θ2 - θ1))方位角= atan2(r2 * sin(θ2 - θ1), r1 - r2 * cos(θ2 - θ1)) + θ1其中,cos表示余弦函数,sin表示正弦函数。
在经纬度坐标系中,可以使用球面三角学来计算方位角距离。
假设参考点的经纬度为(λ1, φ1),目标点的经纬度为(λ2, φ2),则可以通过以下公式计算方位角距离:距离= R * arccos(sin(φ1) * sin(φ2) + cos(φ1) * cos(φ2) * cos(λ2 - λ1))方位角= atan2(sin(λ2 - λ1) * cos(φ2), cos(φ1) * sin(φ2) - sin(φ1) * cos(φ2) * cos(λ2 - λ1))其中,R表示地球的半径。
方位角的计算方法

方位角的计算方法方位角是指在平面直角坐标系中,特定点与正方向x轴之间逆时针方向的夹角。
它在数学、地理、航空航天等领域中都有广泛的应用。
计算方位角的方法主要有以下几种:1.基于直角坐标系的计算:假设有两个点A(x1, y1)和B(x2, y2),首先需要计算出两点之间的直线斜率k = (y2 - y1) / (x2 - x1)。
然后利用反正切函数,通过求解arctan(k)得到弧度值θ。
最后利用单位换算,将弧度值θ转化为角度值α=θ * 180 / π,即为所求的方位角。
2.基于极坐标系的计算:在极坐标系中,一个点可以通过距离r和极角θ来表示。
假设有两个点A(r1,θ1)和B(r2,θ2),要计算两点之间的方位角,首先需要将两点的极角θ转化为弧度制,然后通过计算Δθ=θ2-θ1得到两点之间的相对角度。
最后利用单位换算,将相对角度Δθ转化为角度值α=Δθ*180/π,即得到方位角。
3.基于方向向量的计算:假设有两个点A(x1, y1)和B(x2, y2),可以将两点之间的连线看作一个方向向量。
首先需要计算出两点之间的方向向量V(x2 - x1, y2 - y1)。
然后利用反正切函数,通过求解arctan(Vy / Vx)得到弧度值θ。
最后利用单位换算,将弧度值θ转化为角度值α=θ * 180 / π,即为所求的方位角。
需要注意的是,在计算方位角时,可能会遇到特殊情况,例如:-当两点在同一直线上时,方位角为0或180度;-当两点重合时,方位角没有定义。
总结起来,方位角的计算方法有基于直角坐标系、极坐标系和方向向量三种方法,根据具体情况选择适合的方法进行计算。
角度、坐标测量计算公式细则

计算细则1、坐标计算:X¹=X+Dcosα,Y¹=Y+Dsinα。
式中Y、X为已知坐标,D为两点之间的距离,Α为方位角。
2、方位角计算:1)、方位角=tan=两坐标增量的比值,然后用计算器按出他们的反三角函数(±号判断象限)。
2)、方位角:arctan(y²-y¹)/(x²-x¹)。
加减180(大于180就减去180(还大于360就在减去360)、小于180就加180如果x轴坐标增量为负数,则结果加180°。
如果为正数,则看y轴的坐标增量,如果Y轴上的结果为正,则算出来的结果就是两点间的方位角,如果为负值,加360°。
S=√(y²-y¹)+(x²-x¹),1)、当y²-y¹>0,x²-x¹>0时;α=arctan(y²-y¹)/(x²-x¹)。
2)、当y²-y¹<0,x²-x¹>0时;α=360°+arctan (y²-y¹)/(x²-x¹)。
3)、当x²-x¹<0时;α=180°+arctan(y²-y¹)/(x²-x¹)。
再用两点之间的距离公式可算距离(根号下两个坐标距离差的平方相加)。
拨角:arctan(y²-y¹)/(x²-x¹)1、例如:两条巷道要互相平行掘进的话,求它们的拨角:方法(前视边方位角减后视边方位)在此后视边方位要加减180°,若拨角结果为负值为左偏“逆时针”(+360°就可化为右偏,正值为右偏“顺时针”。
2、在图上标识方位的方法:就是导线边与Y轴的夹角。
(整理)方位角计算公式

一、直线定向1、正、反方位角换算对直线而言,过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角,而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角,同一条直线的正、反方位角相差,即同一直线的正反方位角= (1-13)上式右端,若<,用“+”号,若,用“-”号。
2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。
所谓象限角是指从坐标纵轴的指北端或指南端起始,至直线的锐角,用表示,取值范围为。
为了说明直线所在的象限,在前应加注直线所在象限的名称。
四个象限的名称分别为北东(NE)、南东(SE)、南西(SW)、北西(NW)。
象限角和坐标方位角之间的换算公式列于表1-4。
表1-4 象限角与方位角关系表象限象限角与方位角换算公式=第一象限(NE)第二象限(SE)=-=+第三象限(SW )第四象限(NW)=-3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向,而是通过与已知方向进行连测,推算出各边的坐标方位角。
设地面有相邻的、、三点,连成折线(图1-17),已知边的方位角,又测定了和之间的水平角,求边的方位角,即是相邻边坐标方位角的推算。
水平角又有左、右之分,前进方向左侧的水平角为,前进方向右侧的水平角。
设三点相关位置如图1-17()所示,应有=++ (1-14)设三点相关位置如图1-17()所示,应有=++-=+- (1-15)若按折线前进方向将视为后边,视为前边,综合上二式即得相邻边坐标方位角推算的通式:=+(1-16)显然,如果测定的是和之间的前进方向右侧水平角,因为有=-,代入上式即得通式=- (1-17)上二式右端,若前两项计算结果<,前面用“+”号,否则前面用“-”号。
二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。
坐标正算,就是根据直线的边长、坐标方位角和一个端点的坐标,计算直线另一个端点的坐标的工作。
如图1所示,设直线AB的边长DAB和一个端点A的坐标XA、YA为已知,则直线另一个端点B的坐标为:XB=XA+ΔXABYB=YA+ΔYAB式中,ΔXAB、ΔYAB称为坐标增量,也就是直线两端点A、B的坐标值之差。
角度坐标测量计算公式细则

角度坐标测量计算公式细则文件编码(008-TTIG-UTITD-GKBTT-PUUTI-WYTUI-8256)计算细则1、坐标计算:X1=X+Dcosα,Y1=Y+Dsinα。
式中 Y、X为已知坐标,D为两点之间的距离,Α为方位角。
2、方位角计算:1)、方位角=tan=两坐标增量的比值,然后用计算器按出他们的反三角函数(±号判断象限)。
2)、方位角:arctan(y2-y1)/(x2-x1)。
加减180(大于180就减去180(还大于360就在减去360)、小于180就加180如果x轴坐标增量为负数,则结果加180°。
如果为正数,则看y轴的坐标增量,如果Y轴上的结果为正,则算出来的结果就是两点间的方位角,如果为负值,加360°。
S=√(y2-y1)+(x2-x1),1)、当y2-y1>0,x2-x1>0时;α=arctan(y2-y1)/(x2-x1)。
2)、当y2-y1<0,x2-x1>0时;α=360°+arctan(y2-y1)/(x2-x1)。
3)、当x2-x1<0时;α=180°+arctan(y2-y1)/(x2-x1)。
再用两点之间的距离公式可算距离(根号下两个坐标距离差的平方相加)。
拨角:arctan(y2-y1)/(x2-x1)1、例如:两条巷道要互相平行掘进的话,求它们的拨角:方法(前视边方位角减后视边方位)在此后视边方位要加减180°,若拨角结果为负值为左偏“逆时针”(+360°就可化为右偏,正值为右偏“顺时针”。
2、在图上标识方位的方法:就是导线边与Y轴的夹角。
3、高程计算:目标高程=测点高程+h+仪器高—占标高。
4、直角坐标与极坐标的换算:(直角坐标用坐标增量表示;极坐标用方位角和边长表示)1)、坐标正算(极坐标化为直角坐标)已知一个点的坐标及该点至未知点的距离和方位角,计算未知点坐标方位角,知A(Xa,Ya)、Sab、αab,求B(Xa,Ya)解:Xab=Sab×COSαab 则有Xb=Xa+XabYab=Sab×SINαab Yb=Ya+Yab2)、坐标反算,已知两点的坐标,求两点的距离(称反算边长)和方位角(称反算方位角)的方法已知A(Xa,Ya)、B(Xb,Yb),求αab、Sab。
方位角计算公式

方位角计算公式部门: xxx时间: xxx整理范文,仅供参考,可下载自行编辑一、直线定向1、正、反方位角换算对直线而言,过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角,而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角,同一条直线的正、反方位角相差,即同一直线的正反方位角= (1-13> 上式右端,若<,用“+”号,若,用“-”号。
2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。
所谓象限角是指从坐标纵轴的指北端或指南端起始,至直线的锐角,用表示,取值范围为。
为了说明直线所在的象限,在前应加注直线所在象限的名称。
四个象限的名称分别为北东<NE)、南东<SE)、南西(SW>、北西(NW>。
象限角和坐标方位角之间的换算公式列于表1-4。
象限角与方位角换算公式==-=+=-3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向,而是通过与已知方向进行连测,推算出各边的坐标方位角。
设地面有相邻的、、三点,连成折线<图1-17),已知边的方位角,又测定了和之间的水平角,求边的方位角,即是相邻边坐标方位角的推算。
水平角又有左、右之分,前进方向左侧的水平角为,前进方向右侧的水平角。
设三点相关位置如图1-17(>所示,应有=++ (1-14>设三点相关位置如图1-17(>所示,应有=++-=+- (1-15>若按折线前进方向将视为后边,视为前边,综合上二式即得相邻边坐标方位角推算的通式:=+(1-16>显然,如果测定的是和之间的前进方向右侧水平角,因为有=-,代入上式即得通式=- (1-17>上二式右端,若前两项计算结果<,前面用“+”号,否则前面用“-”号。
二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。
坐标正算,就是根据直线的边长、坐标方位角和一个端点的坐标,计算直线另一个端点的坐标的工作。
方位角计算公式

一、直线定向1、正、反方位角换算对直线而言,过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角,而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角,同一条直线的正、反方位角相差,即同一直线的正反方位角= (1-13)上式右端,若<,用“+”号,若,用“-”号。
2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。
所谓象限角是指从坐标纵轴的指北端或指南端起始,至直线的锐角,用表示,取值范围为。
为了说明直线所在的象限,在前应加注直线所在象限的名称。
四个象限的名称分别为北东(NE)、南东(SE)、南西(SW)、北西(NW)。
象限角和坐标方位角之间的换算公式列于表1-4。
表1-4 象限角与方位角关系表3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向,而是通过与已知方向进行连测,推算出各边的坐标方位角。
设地面有相邻的、、三点,连成折线(图1-17),已知边的方位角,又测定了和之间的水平角,求边的方位角,即是相邻边坐标方位角的推算。
水平角又有左、右之分,前进方向左侧的水平角为,前进方向右侧的水平角。
设三点相关位置如图1-17()所示,应有=++ (1-14)设三点相关位置如图1-17()所示,应有=++-=+- (1-15)若按折线前进方向将视为后边,视为前边,综合上二式即得相邻边坐标方位角推算的通式:=+(1-16)显然,如果测定的是和之间的前进方向右侧水平角,因为有=-,代入上式即得通式=- (1-17)上二式右端,若前两项计算结果<,前面用“+”号,否则前面用“-”号。
二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。
坐标正算,就是根据直线的边长、坐标方位角和一个端点的坐标,计算直线另一个端点的坐标的工作。
如图1所示,设直线AB的边长DAB和一个端点A的坐标XA、YA为已知,则直线另一个端点B的坐标为:XB=XA+ΔXABYB=YA+ΔYAB式中,ΔXAB、ΔYAB称为坐标增量,也就是直线两端点A、B的坐标值之差。
直线坐标计算公式

圆曲线坐标计算公式直线坐标计算公式β=180°/π×L/R X=X1+cosα×L△X=sinβ×R Y=Y1+sinα×L△Y=(1-cosβ)×R X1、Y1代表起算点坐标值。
C= 2X2Yα代表直线段方位角。
X=X1+cos(α±β/2)×C L代表起算点到准备算的距离。
Y=Y1+sin(α±β/2)×Cβ代表偏角,△X、△Y代表增量值。
X、Y代表准备求的坐标。
X1、Y1代表起算点坐标值。
α代表起算点的方位角。
缓和曲线坐标计算公式左右边桩计算方法β=L2/2RL S×180°/π X边=X中+cos(α±90°)×LC=L-L5/90R2L S2 Y边=Y中+sin(α±90°)×LX=X1+cos(α±β/3)×C 在计算左右边桩时,先求出中桩坐Y=Y1+sin(α±β/3)×C 标,在用此公式求左右边桩。
如果L代表起算点到准备算的距离。
在线路方向左侧用中桩方位角减去L S代表缓和曲线总长。
90°,线路右侧加90°,乘以准备算X1、Y1代表起算点坐标值。
的左右宽度。
例题:直线坐标计算方法α(方位角)=18°21′47″X1=84817.831 Y1=352.177 起始里程DK184+714.029 求DK186+421.02里程坐标解:根据公式 X=X1+cosα×LX=84817.831+COS18°21′47″×(86421.02—84714.029)=86437.901Y=Y1+sinα×LY=352.177+sin18°21′47″×(86421.02—84714.029)=889.943求DK186+421.02里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos(α±90°)×LX边=86437.901+cos(18°21′47″- 90°)×3.75=86439.082Y边=Y中+sin(α±90°)×LY边=889.943+sin(18°21′47″- 90°)×3.75=886.384 线路右侧计算:X边=X中+cos(α±90°)×LX边=86437.901+cos(18°21′47″+ 90°)×7.05=86435.680Y边=Y中+sin(α±90°)×LY边=889.943+sin(18°21′47″+90°)×7.05=896.634例题:缓和曲线坐标计算方法α(ZH点起始方位角)=18°21′47″X1=86437.901 Y1=889.941 起始里程DK186+421.02 曲线半径2500 缓和曲线长120m求HY点坐标,也可以求ZH点到HY点任意坐标解:根据公式β=L2/2RL S×180°/πβ={1202/(2×2500×120)}×(180°/π)= 1°22′30.36″C=L-L5/90R2L S2C=120-1205/(90×25002×1202)=119.997X=X1+cos(α±β/3)×CX=86437.901+cos(18°21′47″-1°22′30.36″/3)×119.997=86552.086Y=Y1+sin(α±β/3)×CY=889.941+sin(18°21′47″-1°22′30.36″/3)×119.997=926.832求DK186+541.02里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos(α±90°)×LX边=86552.086+cos{(18°21′47″-1°22′30.36″)- 90°}×3.75=86553.182Y边=Y中+sin(α±90°)×LY边=926.832+sin{(18°21′47″-1°22′30.36″)- 90°}×3.75=923.246线路右侧计算:X边=X中+cos(α±90°)×LX边=86552.086+cos{(18°21′47″-1°22′30.36″)+ 90°}×7.05=86550.026Y边=Y中+sin(α±90°)×LY边=926.832+sin{(18°21′47″-1°22′30.36″)+ 90°}×7.05=933.574 缓和曲线方位角计算方法α=(起始方位角±β偏角)= 18°21′47″-1°22′30.36″=16°59′16.64″注:缓和曲线在计算坐标时,此公式只能从两头往中间推,只能从ZH点往HY点推,HZ点往YH点推算,如果YH往HZ点推算坐标,公式里的β为β2/3.例题:圆曲线坐标计算方法α(HY点起始方位角)= 16°59′16.64″ X1=86552.086 Y1=926.832曲线半径2500曲线长748.75起始里程DK186+541.02求YH点坐标,也可以求QZ点坐标或任意圆曲线一点坐标.解:根据公式β=180°/π×L/Rβ=180°/π×748.75/2500=17°09′36.31″△X=sinβ×R△X=sin17°09′36.31″×2500=737.606△Y=(1-cosβ)×R△Y=(1-cos17°09′36.31″)×2500=111.290C= 2X2YC=745.954X=X1+cos(α±β/2)×CX= 86552.086 +cos(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=87290.023 Y=Y1+sin(α±β/2)×CY=926.832+ sin(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=1035.905圆曲线方位角计算方法α=(起始方位角±β偏角)= 16°59′16.64″+360°-17°09′36.31″=359°49′40.33″求DK187+289.77里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos(α±90°)×LX边=87290.023+cos(359°49′40.33″-90°)×3.75=87290.012Y边=Y中+sin(α±90°)×LY边=1035.905+sin(359°49′40.33″-90°)×3.75=1032.155线路右侧计算:X边=X中+cos(α±90°)×LX边=87290.023+cos(359°49′40.33″+90°)×7.05=87290.044Y边=Y中+sin(α±90°)×LY边=1035.905+sin(359°49′40.33″+90°)×7.05=1042.955。
起算方位角计算公式

起算方位角计算公式方位角是指一个点相对于另一个点的方向角度,通常以北方向为基准,顺时针方向为正角度,逆时针方向为负角度。
在地理测量、导航和工程测量等领域,方位角的计算是非常重要的。
在本文中,我们将介绍起算方位角的计算公式及其应用。
起算方位角的计算公式如下:tan(θ) = (sin(Δλ) cos(φ2)) / (cos(φ1) sin(φ2) sin(φ1) cos(φ2) cos(Δλ))。
其中,θ表示起算方位角,Δλ表示目标点经度与起始点经度的差值,φ1和φ2分别表示起始点和目标点的纬度。
在实际应用中,我们通常使用这个公式来计算两个点之间的方位角,以便进行导航、测量或定位。
首先,我们需要确定起始点和目标点的经纬度坐标。
然后,根据上述公式,计算出起算方位角。
这个角度可以帮助我们确定目标点相对于起始点的方向,从而进行导航或测量。
在地理测量中,起算方位角的计算也经常用于确定地表上两个点之间的距离和方向。
通过测量起算方位角,我们可以计算出两点之间的直线距离,从而进行地图绘制、土地测量等工作。
另外,起算方位角的计算还可以应用于航空导航和航海导航中。
飞行员和航海员可以利用起算方位角来确定飞行或航行的方向,从而确保航线的准确性和安全性。
在工程测量中,起算方位角的计算也是必不可少的。
工程师们可以利用这个公式来确定工程项目中各个点之间的方向和距离,从而进行工程测量和设计。
总之,起算方位角的计算公式是地理测量、导航和工程测量等领域中非常重要的工具。
通过这个公式,我们可以准确地计算出两个点之间的方向角度,从而进行导航、测量和定位工作。
希望本文对您有所帮助,谢谢阅读!。
