3平面问题的三角形单元8
第二章.三角形单元有限元

m(7)
j (1) i (2)
x
特别指出:为使求得面积的值为正值,本单元节点号 的次序必须是逆时针转向,如图所示。至于将哪个节 点作为起始节点i,则没有关系。 将式(2-14)代入式(2-12)的第一式,整理后得
1 u [( ai bi x ci y)ui (a j b j x c j y)u j (am bm x cm y)u m ] 2A 同理 1 [( ai bi x ci y) i (a j b j x c j y) j (am bm x cm y) m ] 2A
1 u [( ai bi x ci y)ui (a j b j x c j y)u j (am bm x cm y)u m ] 2A (2-16) 1 [( ai bi x ci y) i (a j b j x c j y) j (am bm x cm y) m ] 2A
1 a1 uj 2A um ui xi xj xm yi yj ym
1 a2 1 uj 2A 1 um
1 ui
yi yj ym
(2-14)
1 a3 1 xj 2A 1 xm
1
xi
ui uj um
式中,
y A为三角形单元的面积,有
1 A 1 xj 2 1 xm
1
xi
yi yj ym
(2-15)
[N]为形函数矩阵,写成分块形式:
[ N ] [[Ni ] [ N j ] [ N [ Ni ] Ni [ I ] 0 Ni [I]是2×2的单位矩阵。
(i, j, m) (2-22)
2.3 单元应变和应力 1、单元应变 根据几何方程(2-6)和位移函数(2-16)可以求 得单元应变。
求总体刚度矩阵-平面三角形单元最新实用版
求和得到的(实际只是对相关单元求和),其中各子块
矩阵均为2行×2列,整体刚度矩阵用子块矩阵可以表示 为
2021/8/23
平面问题有限元分析-总刚
3
5.1 整体刚度矩阵
y
K11 K12 K13 K14 K15 K16
1
K K K K K K 例平:面问如题图有所限示元有分限析元-模总2型刚1 ,弹性2模2量为 ,23厚度为 2,4为简化计25算取 26,求整体刚度矩阵。
5.1 整体刚度矩阵
例: 如图所示有限元模型,弹性模量为 E,厚度为 t,为
简化计算取 0,求整体刚度矩阵。E=1,t=1
y
1
a
a
2①
3
③
②
④
x
4 a
5
6
a
2021/8/23
平面问题有限元分析-总刚
1
5.1 整体刚度矩阵
解:该模型中共有6个节点,4个单元, 各单元的信息如表所示。
单元编号
各单元信息
46
解:该模型中共有6个节点,4个单元,各单元的信息如表所示。
K K K K K K 平面问题有限元分析-总5刚1
52பைடு நூலகம்
53
54
55
56
4 a
5
6
a
,由图形可知,25边为单元②和③的共用边,则
K K K K K K 平面问题有限元分析-总6刚1
62
63
64
65
66
以整体编码表示的单元刚度矩阵子块
K(2) 24
K(2) 44
K(2) 54
K(2) 25
K(2) 45
K(2) 55
Et 4
平面直角坐标系中的等腰三角形问题

平面直角坐标系中的等腰三角形问题一、解答题(本大题共5小题,共40.0分)1.如图,在平面直角坐标系中,AB∥OC,A(0,12),B(a,c),C(b,0),并且a,b满足b=√a−21+√21−a+16.动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点B运动;动点Q从点O出发,在线段OC上以每秒1个单位长度的速度向点C运动,点P,Q分别从点A,O同时出发,当点P运动到点B时,点Q随之停止运动.设运动时间为t(秒).(1)求B,C两点的坐标;(2)当t为何值时,△PQC是以PQ为腰的等腰三角形?并求出P,Q两点的坐标.2.如图(1),像∠G=∠HMN=∠Q=∠α这样,由△GHM和△MNQ组合成的封闭图形,我们称之为K型GHMNQ.在平面直角坐标系中,A(0,6),B(6,0),点C,D,E分别在线段AB,AO,BO上运动,且ADCEB为K型.(1)如图(2),若点D运动到点O时,过点O作OF⊥CO,交CE的延长线为F,连接BF,①求证:△ACO≌△BFO;②若AC=2√2,求OC的长;(2)如图(3),若C是AB中点,当△DCE为等腰三角形时,请直接写出AD的长.3.如图,平面直角坐标系中,点A的坐标为(4,0),以OA为一边,在第四象限作等边△OAB,点C是y轴上一动点,连接AC,以AC为一边,在直线AC的下方作等边△ACD.(1)随着点C的运动,∠ABD的大小是否会发生变化?请说明理由.(2)是否存在点C,使得△ABD是等腰三角形?如果有可能,若存在,求此时C点坐标;若不存在,请说明理由.4.长方形OABC在平面直角坐标系内位置如图所示,点A,C分别在y轴,x轴上,点D(4,3)在AB上,点E在OC上,沿DE折叠,使点B与点O重合,点C与点C1重合.(1)求点C1坐标;(2)若点P在坐标轴上,且ΔAPC1面积是9,请直接写出点P坐标.5.如图,在平面直角坐标系中,已知A(7,0),B(0,−7),点C为x轴负半轴上一点,AD⊥AB,∠1=∠2.(1)求∠BCD+∠BAD的度数;(2)如图①,若点C的坐标为(−3,0),求点D的坐标;(3)如图②,在(2)的条件下,过点D作DE⊥y轴于点E,DF⊥x轴于点F,点M为线段DF上一点,若第一象限内存在点N(n,2n−3),使△EMN为等腰直角三角形,请求出所有符合条件的N点坐标.6.直角坐标系中,A(6,0),B(0,8),连结AB,点C为AB的中点,点P为y轴正半轴上的一个动点,连结PC,如图,如图,作CQ⊥CP,且CQ=CP.(1)OC=________;点C的坐标为________;(2)当点Q恰好落在线段OC上时,求OP的长;(3)当△OAQ为等腰三角形时,求所有满足条件的点Q的坐标.7.如图①,我们在“格点”直角坐标系上可以清楚看到:要找AB或DE的长度,显然是转化为求Rt△ABC或Rt△DEF的斜边长.下面:以求DE为例来说明如何解决:从坐标系中发现:D(−7,5),E(4,−3).所以DF=|5−(−3)|=8,EF=|4−(−7)|= 11,所以由勾股定理可得:DE=√82+112=√185.下面请你参与:(1)在图①中:AC=______,BC=______,AB=______.(2)在图②中:设A(x1,y1),B(x2,y2),试用x1,x2,y1,y2表示AC=______,BC=______,AB=______.(3)(2)中得出的结论被称为“平面直角坐标系中两点间距离公式”,请用此公式解决如下题目:已知:A(2,1),B(4,3),C为坐标轴上的点,且使得△ABC是以AB为底边的等腰三角形.请求出C点的坐标.8.如图①,平面直角坐标系中,ABCD为长方形,其中点A、C坐标分别为(−4,2)、(1,−4),且AD∥x轴,交y轴于M点,AB交x轴于N.(1)求B、D两点坐标和长方形ABCD的面积;(2)如图②,一动点P从A出发(不与A点重合),以1个单位/秒的速度沿AB向B点运2动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;(3)是否存在某一时刻t,使三角形AMP的面积等于长方形面积的1若存在,求t的值3并求此时点P的坐标;若不存在请说明理由.9.等腰Rt△ACB,,AC=BC,点A、C分别在x轴、y轴的正半轴上.(1)如图1,求证:∠BCO=∠CAO;(2)如图2,若OA=5,OC=2,求B点的坐标;(3)如图3,点C(0,3),Q、A两点均在x轴上,且S△CQA=24.分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,连接MN交y轴于P点,则OP=______.。
现代设计方法第三章试题

现代设计方法 第三章试题第一部分 选择题一、单项选择题 (每小题1分) 在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在题后的括号内。
1、若把平面应力问题的单元刚度矩阵改为平面应变问题的单元刚度矩阵只需将( ) A.E 换成E/(1-μ2),μ换成μ/(1-μ2) B.E 换成E/(1-μ2),μ换成μ/(1-μ) C.E 换成E/(1-μ),μ换成μ/(1-μ2) D.E 换成E/(1-μ),μ换成μ/(1-μ) 2、对一根只受轴向载荷的杆单元,k ij 为负号的物理意义可理解为( ) A.当节点j 沿轴向产生位移时,在节点i 引起的载荷与其方向相同 B.当节点j 沿轴向产生位移时,在节点i 引起的载荷与其方向相反 C.当节点j 沿轴向产生位移时,在节点i 引起的位移与其方向相同 D.当节点j 沿轴向产生位移时,在节点i 引起的位移与其方向相反3、某平面三角形单元,其局部码依次对应的总码分别为8、2和6。
该单元刚度矩阵中的元素k 25,应放入总体刚度矩阵[K]的( )A.第20行5列B.第16行11列C.第20行10列D.第16行8列 4、平面刚架结构与桁架结构的单元刚度矩阵各为( )A. 6×6,6×6B. 6×6,4×4C. 4×4,6×6D. 4×4,4×4 5、平面刚架单元刚度矩阵的坐标转化为( )A.[K ](e)=T(e)[T][k ](e)[T ](e) B.[K ](e)=[T ](e)[k ](e)T(e)[T]C.[K ](e)=T(e)[T][k ](e)-1(e)[T]D.[K ](e)=-1(e)[T][k ](e)T(e)[T]6、半斜带宽矩阵r 行s 列的元素对应于竖带矩阵元素( )。
A.r 行s 列B.r 行s-r 列C.r 行s-r+1列D.r 行s-r-1列 7、图示三角形单元非节点载荷的节点等效载荷(厚度t=1cm )( )A. F yi =-100KN F yj =-50KN F yk =0B. F yi =-80KN F yj =-70KN F yk =0C. F yi =-70KN F yj =-80KN F yk =0D. F yi =-50KN F yj =-100KN F yk =08、对于平面桁架中的杆单元,每个节点在整体坐标系中的位移分量个数为( ) A 、1 B 、2 C 、3 D 、4 9、在任何一个单元内( )A 、只有节点符合位移模式B 、只有边界点符合位移模式C 、只有边界点和节点符合位移模式D 、单元内任意点均符合位移模式10、对于每节点具有三个位移分量的杆单元,两节点局部码为1,2,总码为4和3.则其单元刚度矩阵中的元素k 12应放入总体刚度矩阵[K ]的( ) A 、第1行第2列上 B 、第4行第3列上 C 、第4行第6列上 D 、第10行第11列上 11、平面应力问题中(Z 轴与该平面垂直),所有非零应力分量均位于( )A 、XY 平面内B 、XZ 平面内C 、YZ 平面内D 、XYZ 空间内 12、平面三角形单元内任意点的位移可表示为三个节点位移的( )A 、算术平均值B 、代数和C 、矢量和D 、线性组合 13、坐标转换矩阵可归类为( )A 、正交矩阵B 、奇异矩阵C 、正定矩阵D 、对称矩阵14、在一平面桁架中,节点3处铅直方向位移为已知,若用置大数法引入支承条件,则应将总体刚度矩阵中的()A、第3行和第3列上的所有元素换为大数AB、第6行和第6列上的对角线元素乘以大数AC、第3行和第3列上的所有元素换为零D、第6行和第6列上的所有元素换为零15、图示平面结构的总体刚度矩阵[K]和竖带矩阵[K*]的元素总数分别是()A、400和200B、400和160C、484和200D、484和16016、图示弹簧系统的总体刚度矩阵为()A、1B、C、D、17、轴对称问题中,值等于零的应变是()A.γrθB.γrzC.εθD.εr18、在有限元分析中,划分单元时,在应力变化大的区域应该()A、单元数量应多一些,单元尺寸小一些B、单元数量应少一些,单元尺寸大一些C、单元数量应多一些,单元尺寸大一些D、单元尺寸和数量随便确定22、在弹性力学平面刚架问题中,已知相邻节点总码的最大差值为5,则半宽值为( )A. 10B. 18C. 15D. 1223、图示的四根杆组成的平面刚架结构,用杆单元进行有限元分析,单元和节点的划分如图示,则总体刚度矩阵的大小为()A、8×8阶矩阵B、10×10阶矩C、12×12阶矩阵D、16×16阶矩阵24、已知单元的节点局部与总码的对应关系如下,单元e:1(e)、2(e)、3(e)——5 、3 、2试写出单元e 在整体坐标中的单元刚度矩阵为( )A.[K ](e)= 222325323335525355K K K K K K KK K B.[K ](e)=555352353332252322K K K K K K KK K C.[K ](e)=223252233353253555K KK K K K K K K D.[K ](e)=223525533323523222K KK K K K K K K25、对薄平板来说其沿板厚方向的应力问题( )A.应力为零,应变为零B.应力不为零,应变为零C.应力为零,应变不为零D.应力不为零,应变不为零 26、 从作图的结构体中取出单元体进行应力状态分析,正确的是( ) A 、σx =σy =0,τxy ≠0 B 、τxy =τyz =0,σx =σy ≠0 C 、τyz =τxz =0,σz =0 D 、σx =σy ≠0,τxy =027、如图所示由5根弹簧组成的系统中,每根弹簧的刚度系数如图,系统4个节点,系统的总体刚度矩阵中K 13为( )。
八年级上册数学第十一章 三角形 单元测试题 (3)200809(含答案解析)
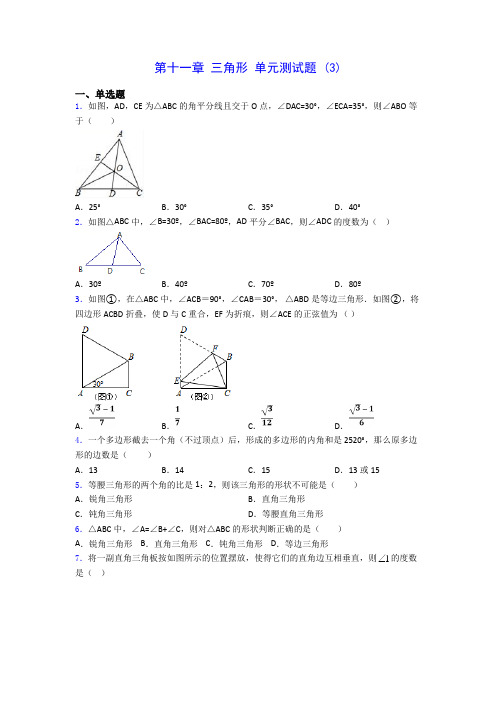
第十一章三角形单元测试题 (3)一、单选题1.如图,AD,CE为△ABC的角平分线且交于O点,∠DAC=30°,∠ECA=35°,则∠ABO等于()A.25°B.30°C.35°D.40°2.如图△ABC中,∠B=30º,∠BAC=80º,AD平分∠BAC,则∠ADC的度数为()A.30º B.40º C.70º D.80º3.如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的正弦值为()A.B.C.D.4.一个多边形截去一个角(不过顶点)后,形成的多边形的内角和是2520°,那么原多边形的边数是()A.13 B.14 C.15 D.13或155.等腰三角形的两个角的比是1:2,则该三角形的形状不可能是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰直角三角形6.△ABC中,∠A=∠B+∠C,则对△ABC的形状判断正确的是()A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形的度数7.将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则1是()A .95︒B .100︒C .105︒D .110︒ 8.△ABC 中,∠C=80°,∠B-∠A=20°,则∠B 的度数是( ) A .60°B .40°C .30°D .20° 9.如图,//AB CD ,AD 和BC 相交于点O ,35A ∠=︒,75AOB ∠=︒,则C ∠等于( )A .35︒B .75︒C .70︒D .80︒ 10.一个多边形的外角和等于其内角和的29,则它的边数为( ) A .12B .11C .10D .9 11.三个内角之比是1:5:6的三角形是( ) A .锐角三角形B .直角三角形C .钝角三角形D .等腰直角三角形 12.若一个多边形的每个内角都相等,且内角是其外角的4倍,则从此多边形的一个顶点出发的对角线的条数是( )A .5B .6C .7D .8二、填空题13.不能构成三角形的三条整数长度的线段的长度和的最小值为1+1+2=4;若四条整数长度的线段中,任意三条不能构成三角形,则该四条线段的长度和的最小值为1+1+2+3=7;……,依此规律,若八条整数长度的线段中,任意三条不能构成三角形,则该八条线段的长度和的最小值为________.14.已知30AON ︒∠=,点P 是射线ON 上一动点,点B 是射线OA 上一动点,点B ,P 均不与点O 重合,当B ∠=_____时,BOP △为直角三角形;如果使得BOP △为钝角三角形,则B 的取值范围是_____.15.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠J=_____°.16.如图,以正方形ABCD 的AB 边向外作正六边形ABEFGH ,连接DH ,则∠ADH=____________°17.如图,在△ABC 中,∠A=36°,∠B=60°,EF ∥BC ,FG 平分∠AFE ,则∠AFG 的度数为_______.18.如图,直线//MN PQ ,点A 、B 分别在MN PQ 、上,033MAB ∠=.过线段AB 上的点C 作CD AB ⊥交PQ 于点D ,则CDB ∠的大小为_____度.三、解答题19.(概念学习)在平面中,我们把大于180°且小于360°的角称为优角.如果两个角相加等于360°,那么称这两个角互为组角,简称互组.(1)若1∠、2∠互为组角,且1135∠=,则2∠= °.(理解应用)习惯上,我们把有一个内角大于180°的四边形俗称为镖形.(2)如图甲,在镖形ABCD 中,优角BCD ∠与钝角BCD ∠互为组角,试探索A ∠、B 、D ∠与钝角BCD ∠之间的数量关系,并说明理由.(拓展延伸)(3)如图乙,已知四边形ABCD 中,延长AD BC 、交于点Q ,延长AB DC 、交于点P ,APD AQB ∠∠、的平分线交于点M ,180A QCP ∠+∠=.①写出图中一对互组的角 (两个平角除外);②直接运用(2)中的结论,试说明:PM QM ⊥.20.求出图形中x 的值.21.一个正多边形的每一个内角为140°,求它的边数。
数学北师大版八年级上册第三章:回顾与思考之平面直角坐标系中的三角形面积问题

第三章:回顾与思考(第三课时)——专题复习:平面直角坐标系中三角形面积问题西安市文景中学安文鹏一、教学目标(1)知识与技能:进一步掌握在平面直角坐标系中已知点的坐标求三角形的面积和已知三角形的面积求点的坐标的方法。
(2)过程与方法通过渗透割补、转化(化复杂为简单、化未知为已知)、数形结合、分类讨论等数学思想,让学生学会学习数学的方法。
(3)情感态度与价值观积累学习经验,培养学生分析归纳能力和思维发散能力,同时培养学生的思维严谨性,提高学生学习数学的兴趣。
二、教学重点解决已知点的坐标求三角形面积和已知三角形的面积求点的坐标问题。
三、教学难点已知三角形的面积求点的坐标问题。
四、教学方法引导探究法五、教学过程(一)诗歌引入著名数学家华罗庚说过:“数缺形时少直观,形缺数时难入微。
数形结合万般好,一旦分离万事休。
”数形结合不仅为我们解题提供思路,也是揭示数学本质的有力工具。
本节课让我们一起利用数形结合的数学思想来专题复习平面直角坐标系中的三角形面积问题(教师板书课题)(二)探究已知点的坐标求面积思考:(1)你能否直接求出问题1、问题2、问题3、问题4中AOB S 的面积? 要求:问题1、问题2学生直接口答;问题3、问题4学生在讲义上独立完成,教师巡视指导并用红笔批改,之后随机选学生讲解,其他学生记录、质疑,教师补讲、点讲)(2)在平面直角坐标系中具备什么样特点的三角形就可以直接求出它的面积? 师生共同归纳:(1) 当三角形两边分别在横轴和纵轴时,可直接计算三角形的面积; (2) 当三角形有一边在横轴上时,则以横轴上的边为底边,其长等于坐标轴上的两个顶点的横坐标差的绝对值,这边上的高等于另一顶点纵坐标的绝对值;(3) 当三角形的一边在纵轴上时,则以坐标轴上的边为底边,其长等于坐标轴上的两个顶点纵坐标差的绝对值,这边上的高,等于另一顶点的横坐标的绝对值;(4) 当三角形的一边和坐标轴平行时,则以和坐标轴平行的线段为底边,这边上的高等于另一顶点的到这个坐标轴的距离。
平面问题

上一页 下一页 返回
5.5 平面矩形单元
• 式中 • 则形函数为:
其中,
i =1, 2, 3, 4。
上一页 下一页 返回
5.5 平面矩形单元
• 2. 单元刚度矩阵 • 应变矩阵[B]的分块矩阵为:
上一页 下一页 返回
5.2 平面杆单元
• 为了求整体结构的力与位移的关系,需要引入整体结构节点位移分量
•
和单元位移分
为单元编号)之间的协调关系,即:
(上标“i”
上一页 下一页 返回
5.2 平面杆单元
• 另外,根据力的平衡条件,作用在节点上的外力应该等于与该节点相 连的各单元所受到的节点力之和。因此,可得到结构的力与位移的关 系为:
5.4 平面三角形单元
• 2)确定结构整体载荷列阵
• 设某单元的三个节点(1、2、3 节点)对应的整体编号分别为i、j、
m,(i、j、m 的次序按从小到大排列),每个单元三个节点的等效
节点力分别记为
,
• 其中,
。
• 将弹性体的所有单元的节点力列阵 2n×1 阶列阵,即:
加以扩充,使之成为
上一页 下一页 返回
上一页 下一页 返回
5.3 平面悬臂梁单元
• 进一步整理,得: • 式中 [k]——平面梁单元的刚度矩阵,
上一页 下一页 返回
5.3 平面悬臂梁单元
• [B]是x 的函数,对上式积分得到平面梁的刚度矩阵为:
上一页
返回
5.4 平面三角形单元
• 5.4.1 单元分析
• 对三角形的单元分析依次分为位移函数、单元力学特性分析、载荷移 置和整体分析四步。
有限元复习题及答案

1.两种平面问题的根本概念和根本方程;答:弹性体在满足一定条件时,其变形和应力的分布规律可以用在某一平面内的变形和应力的分布规律来代替,这类问题称为平面问题。
平面问题分为平面应力问题和平面应变问题。
平面应力问题设有张很薄的等厚薄板,只在板边上受到平行于板面并且不沿厚度变化的面力,体力也平行于板面且不沿厚度变化。
由于平板很薄,外力不沿厚度变化,因此在整块板上有:,,剩下平行于XY面的三个应力分量未知。
平面应变问题设有很长的柱体,支承情况不沿长度变化,在柱面上受到平行于横截面而且不沿长度变化的面力,体力也如此分布。
平面问题的根本方程为:平衡方程几何方程物理方程〔弹性力学平面问题的物理方程由广义虎克定律得到〕•平面应力问题的物理方程平面应力问题有•平面应变问题的物理方程平面应变问题有在平面应力问题的物理方程中,将E替换为、替换为,可以得到平面应变问题的物理方程;在平面应变问题的物理方程中,将E替换为、替换为,可以得到平面应力问题的物理方程。
2弹性力学中的根本物理量和根本方程;答:根本物理量有:空间弹性力学问题共有15个方程,3个平衡方程,6个几何方程,6个物理方程。
其中包括6个应力分量,6个应变分量,3个位移分量。
平面问题共8个方程,2个平衡方程,3个几何方程,3个物理方程,相应3个应力分量,3个应变分量,2个位移分量。
根本方程有:1.平衡方程及应力边界条件:平衡方程:边界条件:2.几何方程及位移边界条件:几何方程:边界条件:3.物理方程:3.有限元中使用的虚功方程。
对于刚体,作用在其上的平衡力系在任意虚位移上的总虚功为0,这就是刚体的平衡条件,或者称为刚体的虚功方程。
对于弹性变形体,其虚位移原理为:在外力作用下处于平衡的弹性体,当给予物体微小的虚位移时,外力的总虚功等于物体的总虚应变能。
设想一处于平衡状态的弹性体发生了任意的虚位移,相应的虚应变为,作用在微元体上的平衡力系有〔X,Y,Z〕和面力。
外力的总虚功为实际的体力和面力在虚位移上所做的功,即:在物体产生微小虚变形过程中,整个弹性体内应力在虚应变上所做的功为总虚应变能,即:其中为弹性体单位体积内的应力在相应的虚应变上做的虚功,由此得到虚功方程:4.节点位移,单元位移及它们的关系。
第8章 空间实体单元分析

(8-10)
将式(8-5)、(8-9)(8-10)统一用矩阵式表示,可得与
平面问题式(2-20)类似的公式
u { f } v [ N ]{ }e w
(8-11)
式中 [N] 为单元形函数矩阵,其维数为 3×12 。进一步可写 为与平面问题式(2-21)、(2-22)类似的子块形式
[ N ] [ Ni N j Nm Nn ]
其中,子矩阵
Ni Ni 0 0 0 Ni 0
(8-12)
0 0 N i I (i, j, m, n ) (8-13) Ni
式中,I为3阶单位矩阵。 2、应变矩阵
在空间问题中,每点有6个应变分量。几何方程为:
第8章
8.1 概述
空间实体单元
许多工程实际问题属于空间问题。用有限元法分析空间
问题和分析平面问题在原理、思路和解题方法完全相同,
基本未知量仍然是节点位移。不同的是单元具有三维特点
节点位移在x、y、z三个坐标轴方向都有分量: u、v、w。
它的基本方程比平面问题要多,有3个平衡方程,6个几何
方程,6个物理方程。分析方法仍然是先进行单元分析,再 进行系统分析,最后求解系统的节点平衡方程,解算内力 或应力。
yj ym yn 1 1 1 zj zm zn
zj zm zn
1 bi 1 1 xj d i xm xn
yj ym yn yj ym yn
zj zm zn 1 1 1
(i, j, m, n)
(8-7)
1
xi
yi yj ym yn
zi zj zm zn
(8-8)
1 xj V 1 xm 1 xn
u j a1 a 2 x j a3 y j a 4 z j u m a1 a 2 x m a3 y m a 4 z m u n a1 a 2 x n a3 y n a 4 z n
有限元分析第4章 平面问题有限单元法1

6
P
3
4 5
4
2
位移协调条件:各单元共享节点的位移相等 节点平衡条件:各节点单元内力与节点外力构成平衡力系
最终数学模型: K Q
基本概念
单元(element) 节点 (node)
回顾
单元节点位移 (node displacement)
单元节点内力 (node force)
单元刚度矩阵 (element stiffness matrix)
e
bx u by v
d
S
e p
px u py v dS
代入
u v
N
e
{} [B]{ }e
{ } [S]{ }e
得
内力虚功=
e x x y y xy xy d
T d
cj
y)v j
(am
bmx
cm y)vm ]
二、平面问题三角形单元分析
三角形单元形函数
形函数
u x,
y
1 2A
[(ai
bi x
ci
y)ui
(a j
bj x
cj
y)u j
(am
bm x
cm
y)um ]
v x,
y
1 2A
[(ai
bi x
ci
y)vi
(a j
插值系数的确定:待定系数法
ui a1 a2 xi a3 yi u j a1 a2 x j a3 y j um a1 a2 xm a3 ym
有限元方法第五章平面三角形单元

图3-1 弹性体和有限元计算模型
y
vj (Vj )
j
uj (Uj )
um (Um )
vi (Vi )
i ui (Ui )
m
um (Um )
o
x
图3--2 平面三角形单元
二、位 移
首先,我们来分析一下三角形单元的力学特性,即
建立以单元节点位移表示单元内各点位移的关系式。设
单元e的节点编号为i、j、m,如图3-2所示。由弹性力学
(i , j , m轮换)
现在我们来讨论一下形函数所具有的一些性质。根据行列 式的性质:行列式的任一行(或列)的元素与其相应的代 数余子式的乘积之和等于行列式的值,而任一行(或列) 的元素与其他行(或列)对应元素的代数余子式乘积之和 为零,并注意到(5-9)式中的常数ai 、bi 、ci ,aj 、bj 、
四、应 力
求得应变之后,再将(3-13)式代入物理方程 D,
便可推导出以节点位移表示的应力。即
DBe
(5-16)
令
S DB
(h)
则
Se
(5-17)
其中 [S]叫做应力矩阵,若写成分块形式,有
S D Bi Bj Bm Si S j Sm
(5-18)
对于平面应力问题,弹性矩阵[D]为
7. 由单元的结点位移列阵计算单元应力
解出整体结构的结点位移列阵 后,再根据单元结点的 编号找出对应于单元的位移列阵 e,将 e代入(5-3)式就
可求出各单元的应力分量值。
8. 计算结果输出
求解出整体结构的位移和应力后,可有选择地整理 输出某些关键点的位移值和应力值,特别要输出结构的 变形图、应力图、应变图、结构仿真变形过程动画图及 整体结构的弯矩、剪力图等等。
人教版数学八年级上册《三角形》单元综合测试卷(含答案)

《三角形》单元测试
(时间:120分钟 满分:150分)
一、选择题:
1.已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为
A 2B.3C.5D.13
2.如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是()
A.锐角三角形B.直角三角形C.钝角三角形D.不能确定
A.2条B.3条C.4条D.5条
12.如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F= (∠BAC﹣∠C);④∠BGH=∠ABE+∠C.
其中正确的是( )
A. ①②③B. ①③④C. ①②③④D. ①②④
11.如图,已知△ABC中,AB=7,AC=5,BC=3,在△ABC所在平面内一条直线,将△ABC分割成两个三角形,使其中有一个边长为3的等腰三角形,则这样的直线最多可画( )
A.2条B.3条C.4条D.5条
【答案】C
【解析】
【分析】
根据等腰三角形的性质分别利用CB为底以及CB为腰得出符合题意的图形即可.
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:;
(2)图2中,当∠D=50度,∠B=40度时,求∠P的度数.
(3)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样 数量关系.
一、选择题:
1.已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为
∵∠1=∠DAA′+∠DA′A,∠2=∠EAA′+∠EA′A.
∵∠DAA′=∠DA′A,∠EAA′=∠EA′A,∴∠1+∠2=2(∠DAA′+∠EAA′)=2∠BAC=80°.
现代设计方法4-3 三角形三节点平面单元概要

单元分析的步骤:
节点 (1) 位移
单元内部 各点位移
(2)
单元 (3) 应变
单元 应力
(4)
节点 力
单元分析
2.1 由节点位移求单元内部任一点位移
(1) 单元位移模式
有限元法中,通常采用位移法进行计算,即取节点的位移分量
{a }=[L]{d }e
为三角形单元面积。
1 1 A 1 xj yj 2 2 1 xm ym 1 xi yi
1 ( x j ym xm yi xi y j xm y j xi ym x j yi ) 2
将a写成矩阵形式,有{a }=[L]{d }e
ai b i 1 ci L 0 2 0 0 0 a j 0 am 0 0 b j 0 bm 0 0 c j 0 cm 0 ai 0 a j 0 am bi 0 b j 0 bm ci 0 c j 0 cm
ui xi xj xm yi yj ym
ui 1 xi u j 1 x j u 1 x m m
1 ui yi yj ym
yi a1 yj a 2 a ym 3
1 xi ui
(a)
1 a1 uj A um
v ( x, y ) 0
a1 a 2 x y 0 0 0 a 3 (4.23) m ( x , y ) a a 0 0 1 x y 4 a 5 a 6
(2) 由单元节点位移{d }e求位移参数{a }
4.3 平面问题的有限单元法
有限元2-弹性力学平面问题(24矩形单元,25六节点三角形单元)

u 1 1 2 3 4 u 2 1 2 3 4
u 3 1 2 3 4
u 4 1 2 3 4
有限单元法
土木工程学院
P-9/44
解方程组便可求得待定常数。将这些参数代回式 (2-4-4),经整理得:
(1,1)
有限单元法
土木工程学院
P-6/44
二、结点位移列阵和结点力列阵
每个结点2个位移分量,共8个位移分量, 设结点位移和结点力列阵分别为:
d u v u v u v u v
e
2 4 2 e T F X Y X Y X Y X Y 1 1 2 2 3 3 4 4 2 4 3
有限单元法
土木工程学院
P-18/44
第2章 弹性力学平面问题有限单元法
2.1 三角形单元 2.2 三角形单元中几个问题的讨论 2.3 平面问题有限元程序设计 2.4 矩形单元 2.5 六结点三角形单元 2.6 四结点四边形单元 2.7 八结点曲线四边形等参元 2.8 几个问题的补充
有限单元法
土木工程学院
3
1
2
(1 ,1 )
(1,1)
有限单元法
土木工程学院
P-11/44
如果引进参数: ξ0=ξiξ, η0=ηiη(i=1, 2, 3, 4), (ξi, ηi)是矩形单元4个结点的局部坐标。结点i(ξi, ηi)的 坐标值分别是 (-1,-1), (1,-1),(1,1), (-1,-1)。代入 上式,则可将上式简记成:
Ai Li A
Lj Aj A
Am Lm A
i
m
Aj
三节点三角形单元算例

三节点三角形单元算例1.引言1.1 概述概述部分(1.1)概述部分旨在介绍本篇文章的主题和背景信息。
本文将重点讨论三节点三角形单元算例,并对其进行详细的分析和结果总结。
三节点三角形单元是有限元分析中常用的一个基本单元,用于建模和模拟复杂的结构系统。
它由三个节点和三条连接这些节点的边组成。
通过这些节点和边的组合,我们可以将结构系统离散成数学模型,进而进行计算和分析。
本文将首先介绍节点的定义和作用。
节点是结构系统中的一个关键概念,它代表了结构的局部特点和重要信息。
在有限元分析中,节点不仅仅是一个几何点,更是一个存储了与该节点相关信息的数据点。
节点的定义和位置决定了单元的布局以及整个结构系统的建模精度。
接着,本文将详细讨论三角形单元的定义和特征。
三角形单元是由三个节点和三条连接这些节点的边组成的简单形状。
这种单元具有较好的适应性和计算效率,广泛应用于各类结构系统的模拟和分析。
通过对三角形单元的了解,我们可以更好地理解和应用有限元方法进行结构分析。
在本文的结论部分,将以一个具体的算例为例,展示三节点三角形单元的应用和分析过程。
通过该算例的分析,我们将得出一些结论和总结,并对三节点三角形单元的适用性和精度进行评估。
在本文的后续章节中,将对节点定义、三角形单元定义、算例分析以及结果总结等内容进行详细阐述,并对相关问题进行讨论和分析。
通过全面的介绍和讨论,我们旨在提供一个全面、准确和有用的指南,帮助读者更好地理解和应用三节点三角形单元算例。
文章结构部分的内容可以按如下方式编写:1.2 文章结构本文共分为引言、正文和结论三个部分。
引言部分首先概述了本文的背景和意义。
随后,介绍了文章的结构,包括本文主要从节点定义和三角形单元定义两个方面展开,以及结语部分。
正文部分主要包括节点定义和三角形单元定义两个子部分。
节点定义部分介绍了在三节点三角形单元中节点的定义和作用。
三角形单元定义部分则详细介绍了三角形单元的结构和数学表示,以及其在有限元分析中的应用。
相似三角形(8大题型)(48道压轴题专练)(原卷版)—2024-2025学年九年级数学上册单元速记巧
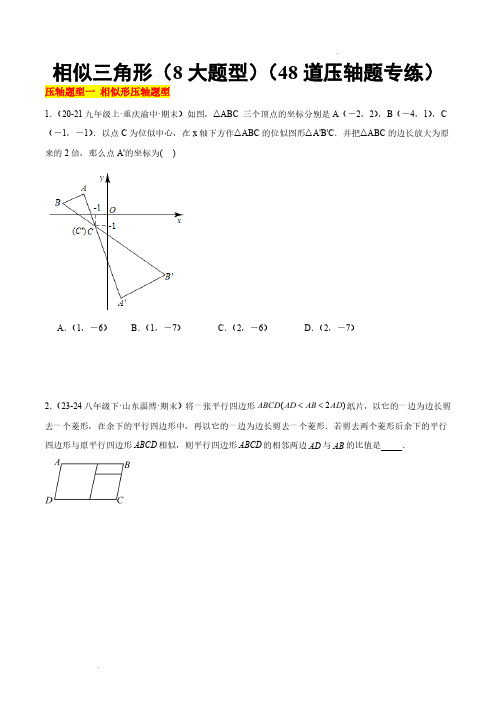
相似三角形(8大题型)(48道压轴题专练) 压轴题型一 相似形压轴题型1.(20-21九年级上·重庆渝中·期末)如图,△ABC 三个顶点的坐标分别是A (-2,2),B (-4,1),C (-1,-1).以点C 为位似中心,在x 轴下方作△ABC 的位似图形△A'B'C .并把△ABC 的边长放大为原来的2倍,那么点A'的坐标为( )A .(1,-6)B .(1,-7)C .(2,-6)D .(2,-7)2.(23-24八年级下·山东淄博·(2)ABCD AD AB AD <<纸片,以它的一边为边长剪去一个菱形,在余下的平行四边形中,再以它的一边为边长剪去一个菱形.若剪去两个菱形后余下的平行四边形与原平行四边形ABCD 相似,则平行四边形ABCD 的相邻两边AD 与AB 的比值是 .3.(2024·湖北武汉·一模)如图是由小正方形组成的网格,四边形ABCD的顶点都在格点上,仅用无刻度的直尺在所给定的网格中按要求完成下列画图,画图过程用虚线表示,画图结果用实线表示.(1)在图1中,先以点A为位似中心,将四边形ABCD缩小为原来的12,画出缩小后的四边形111AB C D,再在AB上画点E,使得DE平分四边形ABCD的周长;(2)在图2中,先在AB上画点F,使得CF BC=,再分别在AD,AB上画点M,N,使得四边形BCMN 是平行四边形.4.(23-24九年级上·江苏南京·阶段练习)形状相同(即长与宽之比相等)的矩形是相似矩形,已知一个矩形长为()1a a³,宽为1.一分为二(1)如图1,将矩形分割为一个正方形(阴影部分)和小矩形,小矩形恰与原矩形相似,则a的值为______.(2)如图2,将矩形分割为两个矩形,使每个小矩形均与原矩形相似,则a的值为______.一分为多(3)有同学说“无论a为何值,该矩形总可以分割为几个小矩形,这几个小矩形都与原矩形相似”,你同意这个说法吗?若同意,在图3中画出一种可行的分割方案;若不同意,举出反例.一分为三(4)将矩形分割为三个矩形,使每个小矩形均与原矩形相似.画出所有可能的分割方案的示意图,并在每个示意图下方直接写出对应的a 的值.5.(20-21八年级下·山东淄博·期末)如图,四边形ABCD ∽四边形A B C D ¢¢¢¢,且62A Ð=°,75B Ð=°,140D Т=°,9AD =,11A B ¢¢=,6A D ¢¢=,8B C ¢¢=.(1)请直接写出:C Ð= 度;(2)求边AB 和BC 的长.6.(23-24九年级上·广西南宁·阶段练习)如图,在平面直角坐标系中,ABC V 的三个顶点坐标分别为()1,1A ,()3,2B ,()2,3C (每个方格的边长均为1个单位长度),请按下列要求画图:(1)111A B C △与ABC V 关于原点O 成中心对称,画出111A B C △并写出点1A 的坐标;(2)以原点O 为位似中心,相似比为2,在第一象限内将ABC V 放大,画出放大后的222A B C △并写出点2B 的坐标;(3)根据信息回答问题:已知ABC V 的面积为32,AB ,请直接写出222A B C △的面积和22A B 边上的高的值.压轴题型二 比例线段压轴题型1.(2020古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底0.618≈,称为黄金分割比例),如图,著名的“断臂维纳斯”便是如此.此外,.若某人满足上述两个黄金分割比例,且腿长为105cm ,头顶至脖子下端的长度为26cm ,则其身高可能是( )A .165cmB .175cmC .185cmD .190cm2.(2024·四川乐山·一模)古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G 将线段MN 分为两线段MG ,GN ,使得其中较长的一段MG 是全长MN 与较短的一段GN 的比例中项,即满足MG GN MN MG ==这个数称为“黄金分割”数,把点G 称为线段MN 的“黄金分割”点.如图,在ABC V 中,已知3AB AC ==,4BC =,若D ,E 是边BC 的两个“黄金分割”点,则ADE V 的面积为 .3.(23-24八年级下·贵州六盘水·期末)已知a ,b ,c ,d ,e ,f 六个数,如果()0a c e k b d f b d f ===++¹,那么a c e k b d f++=++.理由如下:∵()0a c e k b d f b d f===++¹∴a bk =,c dk =,e fk =(第一步)∴()k b d f a c e bk dk fk k b d f b d f b d f++++++===++++++(第二步)(1)解题过程中第一步应用了______的基本性质;在第二步解题过程中,()k b d f k b d f ++=++应用了______的基本性质;(2)应用此解题过程中的思路和方法解决问题:①如果22567a b c ===,则218a b c ++=______;②已知0345x y z ==¹,求23x y z x y z -++-的值.4.(23-24九年级上··的矩形叫黄金矩形.如图①,已知黄金矩形ABCD 的宽1AB =.(1)黄金矩形ABCD 的长BC = ;(2)如图②,将图①中的黄金矩形裁剪掉一个以AB 为边的正方形ABEF ,得到新的矩形DCEF ,猜想矩形DCEF 是否为黄金矩形,并证明你的结论;(3)在图②中,连接AE ,求点D 到线段AE 的距离.5.(22-23九年级上·浙江·周测)若实数a b c ,,满足a b c b c a a c b c a b +-+-+-==,求()()()a b b c a c abc+×+×+的值.6.(23-24九年级下·山东淄博·期末)已知a ,b ,c ,d 为四个不为0的数.(1)如果3a b =,求a b b +与a b a b -+的值;(2)如果(),a c a b c d b d =¹¹,求证a c b a d c =--;(3)如果a c a b d b +=+,求证a c b d=.压轴题型三 相似三角形的判定压轴题型1.(21-22九年级上·陕西咸阳·期中)如图,在矩形ABCD 中,E 是AD 边的中点,BE ^F ,连接DF ,分析下列四个结论,①AEF CAB △∽△,②CF 2AF =;③DF DC =;④CD AC =.其中正确的结论有( )A .4个B .3个C .2个D .1个2.(2024·广东深圳·二模)如图,在等腰直角ABC V 中,4AB BC ==,D 为BC 上一点,E 为BC 延长线上一点,且45DAE =°∠,2AE AD =,则BD = .3.(2024·广东梅州·模拟预测)(1)如图1,在矩形ABCD 中,点C ,D 分别在边DC ,BC 上,AB AB ^,垂足为点G .求证:ADE DCF ∽V V .【问题解决】(2)如图2,在正方形ABCD 中,点E ,F 分别在边DC ,BC 上,AE DF =,延长BC 到点H ,使CH DE =,连接DH .求证:ADF H Ð=Ð.【类比迁移】(3)如图3,在菱形ABCD 中,E F 分别在边DC ,BC 上,10AE DF ==,7DE =,60AED Ð=°,求CF 的长.4.(2024·山西晋中·二模)综合与实践问题情境:数学活动课上,老师要求同学们以正方形为背景探索几何图形运动变化中的数学结论.如图1,正方形ABCD 中,4AB =,点E ,F 分别是边AB ,AD 的中点,连接EF ,点G 是线段EF 上的一个动点,连接AG ,将线段AG 绕点A 逆时针方向旋转90°,得到AH ,连接HD ,GB .猜想证明:(1)针对老师给出的问题背景,“智慧小组”发现GB HD =,请你证明这一结论;操作探究:(2)“善思小组”提出问题:如图2,当点G 为线段EF 的中点时,连接FH ,试判断四边形AGFH 的形状,并说明理由;深入探究:(3)“创新小组”BG 与直线DH 交于点M ,当AHD V 为直角三角形时,请直接写出四边形AGMH 的面积.5.(2024·安徽蚌埠·一模)如图1,在四边形ABCD 中,120ABC Ð=°,60ADC Ð=°,对角线AC ,BD 相交于点O ,且AC AD =,BD 平分ABC Ð.(1)求证:DB AB CB =+;(2)如图2,过点D 作DE AB ∥,使DE BC =,连接AE ,取AE 中点 F ,连接DF ,求证:22AC DF OD =×.6.(23-24九年级上·湖南常德·期中)(1)如图1,在四边形ABCD 中,90BAD BCD Ð=Ð=°,连接AC BD ,,过点A 作AE AC ^交CB 的延长线于点E ,求证:E ACD Ð=Ð.(2)如图2,在四边形ABCD 中,AB AD =,(1)中的其它条件不变,点M ,N 分别是BD EC ,的中点,连接AN AM ,,MN .①求证:AE AC =﹔②求证:N ABE AM ∽△△.压轴题型四 相似三角形的性质压轴题型1.(22-23九年级上·上海长宁·期中)已知点D 在ABC V 的边BC 上,联结AD ,如果ABD △与ACD V 相似,那么下列四个说法:①BAD C Ð=Ð;②AD BC ^;③2AD BD CD =×;④22AB BD AC CD =.一定成立的是( ).A .②④B .①③C .①②③D .②③④2.(2024·上海浦东新·三模)如图,在ABC V 中,3AC BC ==,90C Ð=°,点D 在边BC 上(不与点B ,点C 重合),连接AD ,点E 在边AB 上,EDB ADC Ð=Ð.已知点H 在射线AC 上,连接EH 交线段AD 于点G ,当1CH =,且AEH BED Ð=Ð时,则BE AB = .3.(23-24八年级下·山东威海·期末)如图1,矩形ABCD ,点E ,点F 分别为AD ,BC 上的点,将矩形沿EF 折叠,使点B 的对应点B ¢落在CD 上,连接BB ¢.(1)如图2,当点B ¢与点D 重合时,连接BE ,试判断四边形BEB F ¢的形状,并说明理由;(2)若6AB =,8BC =,求折痕EF 的最大值.4.(23-24八年级下·山东东营·期末)综合与探究(1)如图1,在正方形ABCD 中,点E ,F 分别在边BC CD ,上,且AE BF ^,则线段AE 与BF 的之间的数量关系为_____________;(2)【类比探究】如图2,在矩形ABCD 中,35AB AD ==,,点E ,F 分别在边BC ,CD 上,且AE BF ^,请写出线段AE 与BF 的数量关系,并证明你的结论.(3)【拓展延伸】如图3,在Rt ABC V 中,9046ABC AB BC Ð=°==,,,D 为BC 上一点,且2BD =,连接AD ,过点B 作BE AD ^于点F ,交AC 于点E ,求BE 的长.5.(23-24九年级下·广西南宁·阶段练习)已知等边ABC V ,以AC 为斜边向外作Rt ACD △,定义Rt ACD △为等边ABC V 的“关联直角三角形”,连接BD 交AC 于点E ,下面我们来研究与DE BE的值有关的问题.(1)如图①,当“关联直角三角形”是等腰直角三角形时,DE BE的值为______;(2)如图②,当“关联直角三角形”是含30°的直角三角形时,求DE BE的值;(3)如图③,当“关联直角三角形”是一般的直角三角形时,若16,3DE AB BE ==,求BD 的值.6.(2024·安徽·中考真题)如图1,ABCD Y 的对角线AC 与BD 交于点O ,点M ,N 分别在边AD ,BC 上,且AM CN =.点E ,F 分别是BD 与AN ,CM 的交点.(1)求证:OE OF =;(2)连接BM 交AC 于点H ,连接HE ,HF .(ⅰ)如图2,若HE AB ∥,求证:HF AD ∥;(ⅱ)如图3,若ABCD Y 为菱形,且2MD AM =,60EHF Ð=°,求AC BD 的值.压轴题型五 相似三角形的应用压轴题型1.(2024·浙江温州·三模)图1是《九章算术》中记载的“测井深”示意图,译文指出:“如图2,今有井直径CD 为5尺,不知其深AD .立5尺长的木CE 于井上,从木的末梢E 点观察井水水岸A 处,测得“入径CF ”为4寸,问井深AD 是多少?(其中1尺10=寸)”根据译文信息,则井深AD 为( )A .500寸B .525寸C .550寸D .575寸2.(2022·浙江金华·一模)将一本高为17cm (即17cm EF =)的词典放入高(AB )为16cm 的收纳盒中(如图1).恰好能盖上盒盖时,测得底部F 离收纳盒最左端B 处8cm ,若此时将词典无滑动向右倒,书角H 的对应点H ¢恰为CD 中点.(1)收纳盒的长BC = ;(2)现将若干本同样的词典放入此有盖的收纳盒中,如图2放置,则最多有本书可与边BC 有公共点.3.(2024·江苏南京·一模)在光学中,由实际光线会聚成的像,称为实像,而光线能会聚的是因为折射.图中,凸透镜EF 的焦距为f ,主光轴l EF ^,A ,B ,C ,D 都在l 上,其中O 是光心,2OB OD f ==,蜡烛PQ l ^(蜡烛可移动,且OQ f >),光线PG l ∥,其折射光线GC 与另一条经过光心的光线PP ¢相交于点P ¢(P Q l ¢¢^)即为蜡烛在光屏上所成的实像.图中所有点都在同一平面内.记物高()PQ 为h ,像高()P Q ¢¢为h ¢,物距()OQ ,像距()OQ ¢为v .(1)若10cm f =,10cm h =,15cm u =,=v cm .(2)求证111u v f+=.(3)当f 一定时,画出v 与u 之间的函数图象()u f >,并结合图象描述v 是怎么随着u 的变化而变化的?4.(23-24九年级上·河北邢台·1,小红家的阳台上放置了一个晒衣架,图2是晒衣架的侧面示意图,立杆AB 、CD 相交于点O ,B 、D 两点在地面上,经测量得到136cm AB CD ==,51cm OA OC ==,34cm OE OF ==,现将晒衣架完全稳固张开,扣链EF 成一条线段.发现:连接AC .则AC 与EF 有何位置关系?并说明理由;探究:若32cm EF =,求利用夹子垂挂在晒衣架上的连衣裙总长度小于多少时,连衣裙才不会拖在地面上?5.(22-23九年级上·浙江·单元测试)如图,Rt ABC V 为一块铁板余料,90B Ð=°,6cm BC =,8cm AB =,要把它加工成正方形小铁板,有如图所示的两种加工方案,请你分别计算这两种加工方案的正方形的边长.6.(2022九年级·全国·专题练习)阅读理解:如图1,AD 是△ABC 的高,点E 、F 分别在AB 和AC 边上,且EF //BC ,可以得到以下结论:AH EF AD BC=.拓展应用:(1)如图2,在△ABC 中,BC =3,BC 边上的高为4,在△ABC 内放一个正方形EFGM ,使其一边GM 在BC 上,点E 、F 分别在AB 、AC 上,则正方形EFGM 的边长是多少?(2)某葡萄酒庄欲在展厅的一面墙上,布置一个腰长为100cm ,底边长为160cm 的等腰三角形展台.现需将展台用隔板沿平行于底边,每间隔10cm 分隔出一排,再将每一排尽可能多的分隔成若干个无盖正方体格子,要求每个正方体格子内放置一瓶葡萄酒.平面设计图如图3所示,将底边BC 的长度看作是0排隔板的长度.①在分隔的过程中发现,当正方体间的隔板厚度忽略不计时,每排的隔板长度(单位:厘米)随着排数(单位:排)的变化而变化.请完成下表:排数/排0123…隔板长度/厘米160__________________…若用n 表示排数,y 表示每排的隔板长度,试求出y 与n 的关系式;②在①的条件下,请直接写出该展台最多可以摆放多少瓶葡萄酒?压轴题型六 重心的性质压轴题型1.(23-24九年级上·浙江宁波·期末)如图,点G 是ABC V 的重心,过点G 作MN BC ∥分别交AB AC ,于点M ,N ,过点N 作ND AB ∥交BC 于点D ,则四边形BDNM 与ABC V 的面积之比是( )A .1:2B .2:3C .4:9D .7:92.(2023·上海·一模)在Rt ABC △中,9030B BAC BC Ð=°Ð=°=,,1,以AC 为边在ABC V 外作等边ACD V ,设点E 、F 分别是ABC V 和ACD V 的重心,则两重心E 与F 之间的距离是 .3.(2024·江苏盐城·中考真题)如图1,E 、F 、G 、H 分别是平行四边形ABCD 各边的中点,连接AF CE 、交于点M ,连接AG 、CH 交于点N ,将四边形AMCN 称为平行四边形ABCD 的“中顶点四边形”.(1)求证:中顶点四边形AMCN 为平行四边形;(2)①如图2,连接AC BD 、交于点O ,可得M 、N 两点都在BD 上,当平行四边形ABCD 满足________时,中顶点四边形AMCN 是菱形;②如图3,已知矩形AMCN 为某平行四边形的中顶点四边形,请用无刻度的直尺和圆规作出该平行四边形.(保留作图痕迹,不写作法)4.(23-24七年级下·江苏扬州·阶段练习)作图.(1)直尺作图:如图1,已知D 、E 分别为AB 、AC 中点,过点A 作AF 平分ABC V 面积;(2)直尺作图:如图2,已知AD BC ∥,在四边形ABCD 中作一点O ,使AOB COD S S =△△;(3)尺规作图:如图3,已知D 为AC 中点,点M 在BC ,在AC 上作点N 使MN 平分ABC V 面积.5.(2024·辽宁丹东·二模)阅读与思考:三角形的重心定义:三角形三条中线相交于一点,这个交点叫做三角形的重心.三角形重心的一个重要性质:重心与一边中点的连线的长是对应中线长的13.下面是小明证明性质的过程.如图,在ABC V 中,D 、E 分别是边BC 、AC 的中点,AD 、BE 相交于点G ,求证:13GE GD BE AD ==证明:连接ED ,∵D ,E 是边BC ,AC 的中点,∴DE AB ∥,12DE AB =(依据1)∴ABG DEGV V ∽∴12GE GD DE GB GA AB ===(依据2)∴13GE GD BE AD ==(1)任务一,在小明的证明过程中,依据1和依据2的内容分别是:依据1:______________________依据2:______________________(2)应用①如图,在ABC V 中,点G 是ABC V 中的重心,连接AG 并延长交BC 与点E ,若 3.5GE =,求AG 长.②在ABC V 中,中线AD 、BE 相交于点O ,若ABC V 的面积等于30,求BOD V 的面积.6.(2024·河南周口·三模)(1)古往今来,人们在生产和生活中对三角形的应用层出不穷,三角形也是我们平时研究的重点,如图1,已知ABC V 是等边三角形. P 是ABC V 的重心,连接BP CP ,并延长分别交边AC AB ,于点E ,D .试判断:①BPD Ð的度数为 ;②线段PB PD PE ,,之间的数量关系:PB PD PE +;(填写“>”“<”或“=”)(2)如图2,若在等边ABC V 中,点E 是射线AC 上一动点(其中点E 不与点A 重合,且12CE AC <),连接BE ,作边BA 关于直线 BE 的对称线段 BD ,直线CD ,BE 相交于点 P ,试探究线段PB PC PD ,,的数量关系,并说明理由.压轴题型七 平面向量的线性运算压轴题型1.(23-24九年级上·上海·期中)下列判断不正确的是( )A .()222a b a b +=+r r r r ;B .如果向量a r 与b r 均为单位向量,那么a b =r r 或a b =-r r ;C .如果a b =r r ,那么a b =r r ;D .对于非零向量b r ,如果()0a k b k =×¹r r ,那么a b r r P .2.(2024·上海普陀·二模)如图,梯形ABCD 中,AD BC ∥,过点A 作AE DC ∥分别交BD 、BC 于点F 、E ,23BE BC =,设AD a =uuu r r ,AB b =uuu r r ,那么向量FE uuu r 用向量a r 、b r 表示为 .3.(23-24八年级下·上海崇明·期末)如图,点E 在平行四边形ABCD 的对角线BD 的延长线上.(1)填空:BA AB +uuu r uuu r = ,BA AE ED DC +++uuu r uuu r uuu r uuu r = ;(2)图中与AB uuu r 相等的向量是 ,与AD uuu r 相反的向量是 ;(3)求作:DC DE +uuu r uuu r (不写作法,保留作图痕迹,写出结论).4.(23-24八年级下·上海·期末)如图,在四边形ABCD 中,AD BC ∥,点O 是对角线AC 的中点,DO 的延长线与BC 相交于点E ,设AB a uuu r r =,AD b =uuu r r ,BE c =uuu r r .(1)试用向量a r 、b r 、c r 表示向量:ED =uuu r ______;(2)写出图中所有与AD uuu r 互为相反向量的向量:______;(3)求作:AD OC +uuu r uuu r.(画出所求向量,并直接写出结论)5.(23-24八年级下·上海闵行·期末)如图,已知梯形ABCD 中,AB DC P ,点E 在AB 上,ED BC ∥.(1)填空:BE ED DC CB +++=uuu r uuu r uuu r uuu r ,(2)填空:BA AD DC EA ++-=uuu r uuu r uuu r uuu r ;(3)在图中直接作出AE ED AB +-uuu r uuu r uuu r .(不写作法,写结论)6.(2022八年级下·上海·专题练习)如图,已知点M 是△ABC 边BC 上一点,设AB uuu r =a r ,AC uuu r =b r .(1)当BM MC=2时,AM uuuu r =______;(用a r 与b r 表示)(2)当AM uuuu r =4377a b +r r 时,BM MC =______;(3)在原图上作出AM uuuu r 在AB uuu r 、AC uuu r 上的分向量.压轴题型八 相似三角形的动点问题1.(2020·山西·一模)如图,在ABC V 中,8AB AC ==,6BC =,点P 从点B 出发以1个单位长度/秒的速度向点A 运动,同时点Q 从点C 出发以2个单位长度/秒的速度向点B 运动,其中一点到达另一点即停.当以B ,P ,Q 为顶点的三角形与ABC V 相似时,运动时间为( )A .2411秒B .95秒C .2411秒或95秒D .以上均不对2.(2023八年级上·江苏·专题练习)如图,在ABC V 中,90C Ð=°,3AC =,4BC =,动点P 从点B 出发以每秒1个单位长度的速度沿B A ®匀速运动;同时点Q 从点A 出发同样的速度沿A C B ®®匀速运动.当点P 到达点A 时,P 、Q 同时停止运动,设运动时间为t 秒,当t 为 时,以B 、P 、Q 为顶点的三角形是等腰三角形.3.(2024·吉林长春·三模)如图,在Rt ABC △中,90ABC Ð=°,8AB =,6BC =,点D 为AC 中点,动点P 从点A 出发,沿边AB 以每秒5个单位长度的速度向终点B 运动,连结DP ,将线段DP 绕点D 逆时针旋转90°得线段DE ,连结PE .设点P 运动的时间为t 秒.(1)用含t 的代数式表示点P 到AC 的距离为________;(2)当点E 落在ABC V 内部(不包括边界)时,求t 的取值范围;(3)当PE 与ABC V 的一边平行时,求线段PE 的长度;(4)当经过点E 与ABC V 的一个顶点的直线平分ABC V 面积时,直接写出t 的值.4.(2024·江苏苏州·二模)如图,矩形ABCD 中,4AB =厘米,3BC =厘米,点E 从A 出发沿AB BC -匀速运动,速度为1厘米/秒;同时,点F 从C 出发沿对角线CA 向A 匀速运动,速度为1厘米/秒,连接DE DF EF 、、,设运动时间为t 秒.请解答以下问题:(1)当0 2.5t <<时①t 为何值时,EF AD ∥;②设DEF V 的面积为y ,求y 关于t 的函数;5.(2023·吉林松原·模拟预测)已知ABC V 中,90C Ð=°,3cm AC =,4cm CD =,BD AD =.点F 从点A 出发,沿AC CD -运动,速度为1cm/s ,同时点E 从点B 出发,沿BD DA -运动,运动速度为1cm/s ,一个点到达终点,另一点也停止运动.设AEF △ 的面积为S 2cm ,点E ,F 运动时间为t s .(1)求BD 的长;(2)用含t 的代数式表示DE ;(3)求S 与t 的函数关系式,并写出t 的取值范围.6.(23-24九年级下·河北邯郸·阶段练习)如图1和2,在矩形ABCD 中,6,8AB BC ==,点K 在CD 边上.且73CK =.点M N ,分别在,AB BC 边上,且2AM CN ==.点P 从点M 出发沿折线MB BN -匀速运动,点E 在CD 边上随P 移动,且始终保持^PE AP ;点Q 从点D 出发沿DC 匀速运动,点P Q ,同时出发,点Q 的速度是点P 的一半,点P 到达点N 时停止,点Q 随之停止.设点P 移动的路程为x .(1)当点Q 与点K 重合时,通过计算确定点P 的位置;(2)若点P 在BN 上,当BP CE =时,如图2,求x 的值;(3)在点P 沿折线MB BN -运动过程中,求点Q ,E 的距离(用含x 的式子表示);(4)已知点P 从点M 到点B 再到点N 共用时20秒,请直接写出点K 在线段QE 上(包含端点)的总时长.。
弹性力学平面问题2

i
ui
j
uj
o
x
(1)
单元及其位移表示
为待定常数
ui = a1 + a2xi + a3 yi vi = a4 + a5xi + a6 yi
(2)
位移(1)在结点上有: 位移 在结点上有: 在结点上有
uj = a1 + a2xj + a3 yj vj = a4 + a5xj + a6 yj uk = a1 + a2xm + a3 ym vm = a4 + a5xm + a6 ym
Ω SσΒιβλιοθήκη 对于平面问题:{ε * }T {σ }dxdy = ∫∫ {u * }T { f }dxdy + ∫ {u * }{ f }dS ∫∫
Ω Ω Sσ
相容位移:即为满足位移边界条件的位移。 相容位移:即为满足位移边界条件的位移。
最小势能原理 在一切可能位移和形变中,真正的位移和形变使总势能取最小值; 在一切可能位移和形变中,真正的位移和形变使总势能取最小值;反 使总势能取最小值者也必是真正的位移和形变。 之,使总势能取最小值者也必是真正的位移和形变。
弹性力学平面问题的有限元法
一 弹性力学的基本方程 二 弹性力学的变分原理 三 平面问题的三角形单元 四 平面问题的四边形等参单元
一 弹性力学基本方程
1、基本物理量
位移
{u} = {u( x, y, z), v( x, y, z), w( x, y, z )}
ui (i = 1, 2,3)
张量表示: 张量表示:
, ci =
1 xm ym
1 xj 1 xm
有限元 第8-9讲 矩形单元和6节点三角形单元

因此,单元内任一点的面积坐标满足关系: Li+ Lj+ Lm=1 即3个面积坐标只有2个面积坐标是独立的。
•
面积坐标与直角坐标之间有确定的变换关系,因此,对三角形单
元的描述完全可以用面积坐标进行。
直角坐标表示面积坐标
不难导出下列变换关系:
1 Li (ai bi x ci y ) 2A
第四章 平面问题高精度单元
§4.1
提高有限元求解精度的途径
三、建立高精度单元的原理和途径 • 原理:提高单元位移模式多项式的阶次,从而增强单元拟合局部区 域位移、应力变化的能力。 • • 途径:主要是增加单元的节点数。 对平面问题,先考虑采用4节点矩形单元和6节点三角形单元。
第四章 平面问题高精度单元
§4.2
Nk N 0 0 Nk
矩形单元
Nl 0 0 Nl Nm 0 0 Nm Nn 0 0 Nn
形函数矩阵
•
各形函数为:
1 x y (1 )(1 ) 4 a b 1 x y N l (1 )(1 ) 4 a b 1 x y N m (1 )(1 ) 4 a b 1 x y N n (1 )(1 ) 4 a b Nk
•
•
采用面积坐标后,单元刚度矩阵和等效节点力的计算都比较方便。
6节点三角形单元列式推导原理与其它单元相同。
第四章 平面问题高精度单元
第四章 平面问题高精度单元
T
第四章 平面问题高精度单元
§4.2
•
矩形单元
单元内位移多项式设4项,为双线性多项式:
u a1 a2 x a3 y a4 xy v a5 a6 x a7 y a8 xy
