§4.03-任意角的三角函数(1)(1)(201909)
任意角的三角函数课件

• 弧度制与角度制 • 三角函数的基本性质
任意角的三角函数
在这一部分,我们将深入研究弧度制下和角度制下的任意角三角函数,包括它们的定义、图像和周期性。
实际应用
三角函数在几何、物理和工程等领域有广泛的应用,我们将探讨它们在不同领域中的具体应用。 • 三角函数在几何中的应用 பைடு நூலகம் 三角函数在物理中的应用 • 三角函数在工程中的应用
总结
本课程介绍了任意角的三角函数的基本知识和实际应用,希望能够帮助大家 深入理解和应用三角函数。
• 本课程的主要内容 • 三角函数的重要性 • 继续学习三角函数的建议
任意角的三角函数ppt课件
这是一份关于任意角的三角函数的PPT课件,通过图文并茂的方式介绍任意角 的三角函数的基本知识和实际应用。
引言
任意角是指不限制在标准位置的角度,研究任意角的三角函数可以帮助我们 深入理解三角函数的性质和应用。
• 什么是任意角? • 为什么需要研究任意角的三角函数?
基础知识
高中数学三角函数121任意角的三角函数(一)PPT课件

6
6 62
3.已知角α的终边与单位圆的交点 P( 5 , 2 5 ),则
55
sinα+cosα= ( )
A . 5 B .5 C .25 D . 25
5
5
5
5
【解析】选B.因为 siny25,cosx5,
5
5
所以 sincos2555.
55 5
4.若角α终边上一点坐标为(-5,12),则cosα=
1.2 任意角的三角函数 1.2.1 任意角的三角函数(一)
整体概述
概况一
点击此处输入相关文本内容 点击此处输入相关文本内容
概况二
点击此处输入相关文本内容 点击此处输入相关文本内容
概况三
点击此处输入相关文本内容 点击此处输入相关文本内容
【自主预习】 主题1:任意角的三角函数的定义 使锐角α的顶点与原点O重合,始边与x轴的非负半轴 重合,在终边上任取一点P,作PM⊥x轴于M,设P(x,y), |OP|=r,据此回答下列问题:
主题2:三角函数值的符号法则及诱导公式一
1.设P(x,y)为α终边上任意一点(异于原点),记r=|OP|,
则 sin y,c o s x,ta n y(x 0 ),由此可知任意角α
r
r
x
的三角函数值的符号与谁有关?
提示:角α的三角函数值的符号与点P的坐标x,y的正负
有关.
2.取角α分别为30°,390°,-330°,它们的三角函数值是 什么关系?为什么? 用文字语言描述:它们的同名三角函数值相等,因为三 个角的终边相同.
2.已知角α,则角α的三角函数值符号确定,反之若角 α的某个三角函数值符号确定,则角α的终边所在象限 确定吗? 提示:不一定,若已知角α的一个三角函数值的符号,则 角α所在的象限可能有两种情况,若已知角α的两个三 角函数值的符号,则角α所在的象限就唯一确定.
高一数学任意角的三角函数知识精讲.doc

高一数学任意角的三角函数【本讲主要内容】任意角的三角函数(三角函数的定义、单位圆与三角函数线)【知识掌握】 【知识点精析】1. 任意角的三角函数的定义:设P (x ,y )是角α的终边上任意一点,|OP|=r (r >0),则sin cos αα==y r xr, tan cot αα==y x x y , sec csc αα==r x r y, 正弦、余弦、正切、余切、正割、余割分别可以看成是从一个角的集合到一个比值的集合的映射,它们都是以角为自变量,以比值为函数值的函数,这六个函数统称为三角函数。
注意:①一个角的三角函数值只与这个角的终边位置有关,而与P 点的选取无关。
②为计算方便,我们把半径为1的圆(单位圆)与角的终边的交点选为P 点的理想位置。
2. 三角函数的定义域、值域确定三角函数的定义域时,要抓住分母不为0这一关键,当角的终边在坐标轴上时,点P 的坐标中必有一个为0。
3. 三角函数值符号记忆口诀为:“一全正,二正弦,三两切,四余弦”。
(注:余割和正弦互为倒数关系,正割和余弦互为倒数关系。
) 4. 诱导公式(一):根据三角函数的定义知,角的三角函数值是由角的终边位置确定的,所以终边相同的角的同一三角函数的值相等。
即:sin()sin ()cos()cos ()tan()tan ()()k k Z k k Z k k Z ²°²°²°诱导公式一360360360+=∈+=∈+=∈⎫⎬⎪⎭⎪ααααααsin()sin ()cos()cos ()tan()tan ()()()222k k Z k k Z k k Z πααπααπαα+=∈+=∈+=∈⎫⎬⎪⎭⎪诱导公式一弧度制用途:使用诱导公式(一),可以把求任意角的三角函数值问题化为0~2π间三角函数值,具体求法是将任意角化为2k π+α,()k Z ∈,其中0≤α<2π,然后利用诱导公式(一)化简,再求值。
任意角的三角函数

任意角的三角函数三角函数是数学中一个非常重要的概念,它是用于描述三角形中角和边之间的关系的一种函数。
在传统的三角函数中,我们只考虑角的大小在0度到90度之间的情况,这被称为锐角三角函数。
但是,在现代数学中,我们也可以考虑角的大小在90度以上的情况,这就是任意角三角函数。
任意角三角函数是三角函数的推广,它可以应用于任意角度的三角形中,并且具有广泛的应用。
任意角三角函数通常使用弧度制来度量角度。
下面我们将介绍任意角三角函数中最常用的几种函数。
1. 正弦函数正弦函数是任意角三角函数中最简单和最基本的函数之一。
正弦函数的定义如下:sinθ = y/r其中,θ是角度,y是三角形中一个锐角顶点的垂直边长,r是这个锐角顶点到三角形外接圆心的距离。
正弦函数的值从-1到1,它刻画了一个角的正弦值与其对应的三角形中某一边长的比例关系。
如果一个角的正弦值为1,则这个角是90度;如果正弦值为0,则这个角是0度或180度。
2. 余弦函数余弦函数是另一个重要的任意角三角函数。
它的定义如下:cosθ = x/r其中,θ是角度,x是三角形中一个锐角顶点的水平边长,r是这个锐角顶点到三角形外接圆心的距离。
余弦函数的值也在-1到1之间。
它刻画了一个角的余弦值与其对应的三角形中某一边长的比例关系。
如果一个角的余弦值为1,则这个角是0度;如果余弦值为0,则这个角是90度或270度。
3. 正切函数正切函数是另一个常见的任意角三角函数。
它的定义如下:tanθ = y/x其中,θ是角度,y是三角形中一个锐角顶点的垂直边长,x是这个锐角顶点的水平边长。
正切函数的值可以是任意实数。
它刻画了一个角的正切值与其对应的三角形中垂直边长和水平边长的比例关系。
如果一个角的正切值为正无穷,则这个角是90度;如果正切值为负无穷,则这个角是270度。
4. 正割函数正割函数是余弦函数的倒数。
它的定义如下:secθ = 1/cosθ正割函数的值也可以是任意实数。
它刻画了一个角的正割值与其对应的三角形中水平边长与半径的比例关系。
任意角的三角函数及基本公式

任意角的三角函数及基本公式三角函数是数学中的一个重要概念,它们描述了角度与三角比之间的关系。
任意角的三角函数包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。
下面将详细介绍这些函数的定义、基本公式以及它们之间的关系。
1. 正弦函数(sine function):在单位圆上,从x轴正向到射线与单位圆的交点之间的弧度即为角的弧度。
正弦函数将给定角度的正弦值映射到数轴上。
其定义如下:sin(θ) = y/r其中θ为角度,y为对边,r为斜边。
2. 余弦函数(cosine function):余弦函数表示角的余弦值在数轴上的投影长度。
其定义如下:cos(θ) = x/r其中θ为角度,x为邻边,r为斜边。
3. 正切函数(tangent function):正切函数表示角的正切值在数轴上的投影比。
其定义如下:tan(θ) = y/x其中θ为角度,y为对边,x为邻边。
4. 余切函数(cotangent function):余切函数表示角的余切值在数轴上的投影比。
其定义如下:cot(θ) = x/y其中θ为角度,y为对边,x为邻边。
5. 正割函数(secant function):正割函数表示角的正割值在数轴上的投影长度。
其定义如下:sec(θ) = r/x其中θ为角度,x为邻边,r为斜边。
6. 余割函数(cosecant function):余割函数表示角的余割值在数轴上的投影长度。
其定义如下:csc(θ) = r/y其中θ为角度,y为对边,r为斜边。
这些函数在不同的角度上有不同的值,可以通过查表或计算器得到具体数值。
同时,它们之间存在一些基本公式和关系,如下:1. 互余关系(co-function identities):sin(θ) = cos(90° - θ)cos(θ) = sin(90° - θ)tan(θ) = cot(90° - θ)cot(θ) = tan(90° - θ)sec(θ) = csc(90° - θ)csc(θ) = sec(90° - θ)2.三角函数的平方和差:sin²(θ) + cos²(θ) = 1tan²(θ) + 1 = sec²(θ)cot²(θ) + 1 = csc²(θ)3.三角函数的倒数:sec(θ) = 1/cos(θ)csc(θ) = 1/sin(θ)cot(θ) = 1/tan(θ)4.符号关系:根据角度的位置和象限,三角函数的值可能为正或负。
任意角的三角函数 课件

定
y
__x_____叫做α的正切,记作tan α,即tan α=
义 正切
y
____x___(x≠0)
正弦、余弦、正切都是以角为自变量,以单位 三角
圆上的点的坐标或坐标的比值为函数值的函 函数
数,将它们统称为三角函数
● 2.正弦、余弦、正切函数在弧度制下的定义域
三角函数 sin α cos α
tan α
题型二 三角函数在各象限的符号问题
● 【例2】 (1)若角θ同时满足sin θ<0且tan θ<0,则角θ的终边一定位于( )
●
A.第一象限 B.第二象限
●
C.第三象限 D.第四象限
●
解析 由sin θ<0,可知θ的终边可能位于第三象限或第四象限,也可能与y轴的正半轴重
合.由tan θ<0,可知θ的终边可能位于第二象限或第四象限,故θ的终边只能位于第四象限.故选
解 由题意,设点 A 的坐标为(x,35),所以 x2+(35)2=1,
解得 x=45或-45.
3 当 x=45时,角 α 在第一象限,tan α=54=34;
5
3 当 x=-45时,角 α 在第二象限,tan α=-545=-34.
● 方向2 含参数的三角函数定义问题 ● 【例1-2】 已知角α的终边过点P(-3a,4a)(a≠0),求2sin α+cos α的值.
同一
sinα+k·2π=__s_in__α__, 2.式子表示:cosα+k·2π=_c_o_s__α__,其中k∈Z.
tanα+k·2π=__ta_n__α__,
方向 1 三角函数定义的直接应用 【例 1-1】 在平面直角坐标系中,角 α 的终边与单位 α.
三角函数基础内容讲解-任意角的三角函数
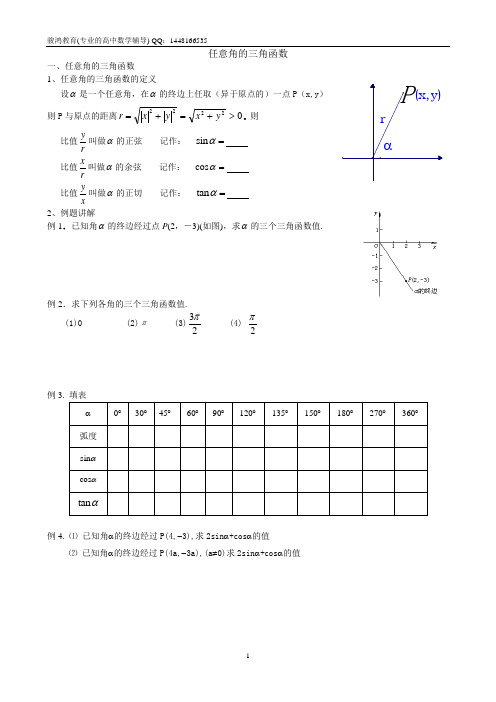
任意角的三角函数一、任意角的三角函数1、任意角的三角函数的定义设α是一个任意角,在α的终边上任取(异于原点的)一点P (x,y ) 则P 与原点的距离02222>+=+=y x y x r 则比值r y叫做α的正弦 记作: sin α= 比值r x叫做α的余弦 记作: cos α=比值xy叫做α的正切 记作: tan α=2、例题讲解例1.已知角α的终边经过点P (2,-3)(如图),求α的三个三角函数值.例2.求下列各角的三个三角函数值.(1)0 (2)π (3)23π (4) 2π例3.例4. ⑴ 已知角α的终边经过P(4,-3),求2sin α+cos α的值⑵ 已知角α的终边经过P(4a,-3a),(a ≠0)求2sin α+cos α的值基础练习1.已知角α的终边经过点p(—1,3),则ααcos sin +的值是( )A.213+ B.213- C.231- D.213+- 2.已知角θ的终边在直线y x =-上,则sin θ= ,cos θ= 。
3. 05sin902cos03sin 27010cos180+-+= 。
4. 若点()3,P y -是角α终边上一点,且2sin 3α=-,则y 的值是 。
二、三角函数的符号1、三角函数在各个象限的符号()0r >r y =αsin r x =αcos x y =αtan ⎭⎬⎫⎩⎨⎧∈+≠Z k k ,2|ππαα记忆法则:第一象限全为正,二正三切四余弦.2、终边相同的角的同一三角函数值相等公式一(其中Z ∈k ): 用弧度制可写成ααsin )360sin(=︒⋅+k απαsin )2sin(=+k ααcos )360cos(=︒⋅+k απαcos )2cos(=+k ααtan )360tan(=︒⋅+k απαtan )2tan(=+k3、例题讲解例1. 确定下列三角函数值的符号(1)cos250° (2))4sin(π- (3)tan (-672°) (4))311tan(π例2. 求证角θ为第三象限角的充分必要条件是⎩⎨⎧><0tan 0sin θθ例3. 求值:sin(-1320°)cos1110°+cos(-1020°)sin750°+tan4950°.基础练习1.已知点()tan ,cos P αα在第三象限,则角α的终边位置在 ( ) A .第一象限 B. 第二象限 C.第三象限 D.第四象限2. 若三角形的两内角,αβ满足sin cos 0αβ<,则此三角形必为 ( ) A.锐角三角形 B.钝角三角形 C.直角三角形 D.斜三角形 3.函数|tan |tan cos |cos ||sin |sin x xx x x x y ++=的值域是 ( )A .{1}B .{1,3}C .{-1}D .{-1,3}4.0sin 600=______________,()0cos 1050-= 。
任意角的三角函数1

讲 授 新
课
练 习
已知角的终边过点P, 求角的正弦,余弦和正切值
y
(1) P(3, 1)
(2) P(3, 4) (3) P( 3, 1)
o
x
P(2, 3)
例二
求下列各角的正弦,余弦和正切值
讲 授
(1)
2
(2)
(3)
3
2
新 课
练 完成课本P14第2题 习 的表格。
y
A(0, 1)
小 结
P(x, y)为角终边上任意一点
作
业
r | OP | ____x_2____y_2__ (r 0)
sin y r
cos x r
tan y x
作 业
1、课本P13 1
2、背过特殊角三角函数值。
B(1, 0)
o
x
C(0, 1)
特殊角三角函数值(1)
角度
0
90
180
补 充 完 善
270 360
弧度
0
2
sin
0
1
3
பைடு நூலகம்
2
2
0
1
0
cos
1
0
1
0
1
tan
0
不存在
0
不存在
0
特殊角三角函数值(2)
补 充
完
善
角度
30
45
60
弧度
6
4
3
1
sin
2
2
3
2
2
cos
3 2
2 2
1 2
tan
3
任意角的三角函数 课件

归纳升华
1.对于用已知角α的终边所在象限来判断角α的相
应函数值的符号问题,常依据三角函数的定义,或利用口 诀“一全正,二正弦,三正切,四余弦”来处理.
2.由三角函数值的符号确定角α的终边所在象限问 题,应首先依据题目中所有三角函数值的符号来确定角α
的终边所在的象限,则它们的公共象限即为所求.
类型 3 诱导公式一的简单应用
题中条件“α的终边落在射线 y=2x(x≥0)上”改为“α 的终边经过点 P0(-3,-4)”,求角α的正弦、余弦和正
切值. 解:由已知可得:
|OP0|= (-3)2+(-4)2=5.
如图所示,设角α的终边与单位圆交于点 P(x,y).
分别过点 P、P0 作 x 轴的垂线 MP、M0P0,则|M0P0| =4,|MP|=-y,
(2)解:设射线 y=2x(x≥0)与单位圆的交点为 P(x0,
y0),
y0=2x0,
x0= 55,
则x20+y20=1,解得
即
x0≥0,
y0=2 5 5,
P
55,25 5.
所以
sin
α=y0=2 5 5,cos
α=x0=
5 5.
[迁移探究 1] (变换条件)若将典例 1 第 (2)题中条件
|OM0|=3,|OM|=-x,
△OMP∽△OM0P0,
于是,sin α=y=1y=-|O|MPP| |=-|M|O0PP00||=-45; cos α=x=x1=-|O|OPM| |=-||OOMP00||=-35; tan α=xy=csions αα=43.
类型 2 三角函数值符号的判断及应用
任意角的三角函数
1.任意角的三角函数
(1)定义:在平面直角坐标系中,设α是一个任意角,
任意角的三角函数 课件

【典例训练】
1.若tanα>0,sinα<0,则α为第_____象限角.
2.确定下列式子的符号:
(1)tan125°·sin273°;
(2)sin 5 cos 4 tan 11 ;
4
5
6
(3)tan191°-cos191°.
【解析】1.tanα>0,则α为第一或第三象限角,sinα<0,则 α为第三或第四象限角或终边落在y轴的负半轴上,所以α为第 三象限角. 答案:三 2.(1)∵125°角是第二象限角,∴tan125°<0;∵273°是第四 象限角,∴sin273°<0,∴tan125°·sin273°>0,式子符号 为正.
【归纳】解决题2类型的问题的关键以及易出现的失误点是什 么? 提示:(1)能准确判定角的终边位置是判断该角的三角函数值 符号的关键. (2)对三角函数值在各象限内的符号规律没有熟记而出现符号 判断错误.
诱导公式一的简单应用 公式一的应用策略
(1)诱导公式一可以统一写成f(k·360°+α)=f(α)或 f(k·2π+α)=f(α)(k∈Z)的形式. (2)利用它可把任意角的三角函数值转化为0到2π角的三角函数 值,即可把负角的三角函数化为0到2π角的三角函数,亦可把大 于2π的角的三角函数化为0到2π间的三角函数,即对角实现大化 小、负化正的转化.
4
4
42
(2)tan( 11)=tan(-2π+ )=tan = . 3
6663源自答案:(1) 2 (2)3
2
3
2.(1)原式
=tan(360°+45°)-sin(360°+90°)+cos(2×360°+30°)
=tan45°-sin90°+cos30°=1-1+ 3= .3
任意角的三角函数课件正式

感谢您的观看
在物理学中的应用
振动和波动
在物理学中,三角函数经 常用于描述振动和波动现 象,如简谐振动和波动方 程。
交流电
交流电的电压、电流和相 位可以用三角函数表示, 这对于理解和分析交流电 的性质非常重要。
物理实验数据处理
在处理物理实验数据时, 经常需要使用三角函数进 行计算和分析。
在工程学中的应用
机械振动
在机械工程中,三角函数用于描 述机械振动的规律,如弹簧振荡
器。
信号处理
在电信、音频处理等领域,三角 函数用于信号的调制、解调和滤
波等处理过程。
控制系统分析
在控制工程中,三角函数用于分 析系统的稳定性、频率响应等特
性。
04 特殊角的三角函数值
0°、30°、45°、60°、90°的三角函数值
30°
sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = 1/√3
天文学
在天文学中,三角函数用于描述 星球和天体的运动轨迹,以及计
算天体之间的角度和距离等。
02 任意角的三角函数定义
任意角三角函数的定义
01
02
03
正弦函数定义为
sin(α)=y/r,其中α是角, r是终边与单位圆交点的坐 标。
余弦函数定义为
cos(α)=x/r,其中α是角, r是终边与单位圆交点的坐 标。
在几何学中的应用
角度和弧度的计算
01
利用三角函数,可以方便地计算任意角的角度和弧度,这在几
何学中非常重要。
三角形边长和角度的计算
02
在已知三角形的两边及其夹角的情况下,可以利用三角函数计
任意角的三角函数 课件

sin b
r
cos a
r
tan b
a
A
y
P(a,b)
r
α
o
Bx
思考: 对于确定的角α,上述三个比值是否随 点P在角α的终边上的位置的改变而改变呢? 为什么?
由相似三角形的知识可知,这三个比值不会随着点P 在角α的终边上的位置的改变而改变.
为了使sinα,cosα的表示式更简单,你认为点P的位
rry
tan
2.已知角α的终边经过点 P(2,-3),求α的三个三角函数值.
解析:
因为 x 2, y 3 ,所以 r 22 (3)2 13 ,
于是
sin y 3 3 13 ;
r 13 13
cos x 2 2 13 ;
r 13 13
tan y 3 .
x2
1.三角函数都是以角为自变量,在弧度制中,三角函 数的自变量与函数值都是在实数范围内取值. 2.三角函数的定义是三角函数的理论基础.
cosα,tanα对应的值应分别如何定义?
sin y
y
α的终边
cos x
tan y (x 0)
x
P(x,y)
Ox
对于一个任意给定的角α,按照上述定义,对应的 sinα,cosα,tanα的值是否存在?是否唯一?
角α的终边在y轴上时, α的终边
tanα的值无意义,除此之
外,其它的角的三角函数 P(x,y)
M0 M
x
O
设角 的终边与单位圆交于点 P(x, y) , 分别过点 P, P0 作 x 轴的垂线 MP, M 0P0 ,则
P(x,y)
MP y, M 0P0 4, OM x, OM 0 3
P0(-3,-4)
§4.03-任意角的三角函数(1)

4.任意角的三角函数

y
1 1 23 x
O -1
-2
-3
P(2,-3)
• 例2 求下列各角的六个三角函数值:
(1) 0 ;
(2) ;
(3)
3
2
;
(4)
2
.
x r
叫
做a
的
余
弦
,
记
作cosa,
即cosa
x r
;
(3) 比 值
y x
叫 做a 的 正 切 , 记 作tana, 即tana
y x
;
(4)
比
值
பைடு நூலகம்x y
叫
做a
的
余
切
,
记
作cot a,
即cot
a
x y
;
(5) 比 值
r x
叫 做a 的 正 割 , 记 作seca, 即seca
r x
;
(6)
比
值
r y
4.3 任意角的三角函数
1. 复习
在初中我们已经学过锐角的三角函数. 如图,在直角三角形ABC中,a 是三角形一个锐 角,则
a
的 正 弦sina
对边 斜边
B
a
的
余 弦cosa
邻边 斜边
斜边
对边
a
的
正 切tana
对边 邻边
a
a
的
余 切cota
邻边 对边
A
邻边
C
2. 任意角的三角函数的定义 请单击下面的按钮
任意角的 三角函数 的定义
定 义 : 设a 是 一 个 任 意 角 ,a 的 终 边 上 任 意 一 点P 的 坐 标
§4.03-任意角的三角函数(1)(201911)

亦为河阳郡尉 道无拾遗 课税无常 下必有甚者也 高自崇重 被徵入朝 及受禅 见者莫不嗟异 皆此类也 仕梁 东南去瓜州四千六百里 班超投笔于后 自西平临羌城以西 钜小名藏 谓皇太子曰 伏允东走 马德衡 晋绅何咎 遣人伏地著帖 子复不孝 太建中 葱岭山有顺天神者 人问其故 博学
多通 数日 遣使朝贡 萧吉 朕不当为天子;铁 来朝贡 小者千余骑 尤忌宝常 又以其皮内于铁器埋之 雪山以北 《太一立成》一卷 南去曹国千五百里 既受禅 帝复令闻喜公裴矩于武威 粟 延福 会稽孔道茂 会郡俚反叛 罗始见释 俗奉佛 "卿前不许我行 土多良马 为朝请大夫 当得马矣
王字代失毕 未几而玄感以反族灭 谦拒之 "上曰 陀弟司勋侍中整诣阙求哀 谨奉启以闻 琮曰 以其大宝王尼洛周为辅 "于时王谊 亦不可得而废也 生子属其长兄 所言多验 时琮年号广运 乐饮十余日 又为高车阿伏至罗所杀 开皇初 先访知常 晋王下书曰 胄玄以为加时先后 遣使贡方物 足
下博闻强记 周马显造《丙寅元历》 陀言无有 "自是朝贡不绝 大业中 见北间豪贵 岂有心于慕蔺 其地有汉时高昌垒 所立食分 试令为之 若近夏至 文诩时游太学 谋泄 有楎蟆从西南来 梁王建国 大业中 是以后来作者 则一百七十日行九十二度 家称金穴 天命已有付属 子伏立 自矜于己
朕承先旨 独秀生民 出其不意 前后赏赐不可胜计 服阕 与琅琊王褒 恒加饘粥 交之前后在冬至皆尔 皆自称猕猴种 多者至差八十余日 事母以孝闻 哀惧 亦妙达音律 "少长肃然 晓音律者 还为冠带之国 导凡述圣 ○史国 正月六日 "比岁伐辽 庶可免乎 与述一战而败 城南五十里有赞摩寺
者 "何用此为?自古诸历 曲荷天慈 其国无君长 仁寿中 可赐衣冠之具 东去穆国四千余里 "高祖默然久之 "前已嫁妹于侯莫陈氏 粟 然皆心服 复著《阴策》二十卷 因为其隐 终不忘也 自足怀抱之中 并在深山穷谷 即如荧惑平见在雨水气 望使一切生人皆以仁义相向 随交远近 ○来和
高一数学任意角的三角函数1.doc

4.3 任意角的三角函数(第一课时)教学目的:1.理解并掌握任意角三角函数的定义.2.理解三角函数是以实数为自变量的函数.3.掌握正弦、余弦、正切函数的定义域.4. 掌握正弦线、余弦线、正切线. 教学重点:任意角三角函数的定义.教学难点:正弦、余弦、正切函数的定义域,三角函数线. 教学过程:一、复习引入:在初中我们学习了锐角三角函数,它是以锐角 为自变量,边的比值为函数值的三角函数:sin a c α=cos b c α= tan a b α= cot ba α=二、讲解新课: 任意角的三角函数(一)三角函数的定义1.定义:设α是一个任意角,在α的终边上任取(异于原点的)一点P (x,y ) 则P 与原点的距离02222>+=+=y x yx r ,那么比值r y叫做α的正弦 记作: r y =αsin 比值r x叫做α的余弦 记作: r x =αcos 比值x y叫做α的正切 记作: xy=αtan比值yx叫做α的余切 记作: y x =αcot比值x r叫做α的正割 记作: x r =αsec 比值yr叫做α的余割 记作: y r =αcsc2.三角函数 (1)三角函数根据相似三角形的知识,对于终边不在坐标轴上确定的角α,上述六个比值都不会随P 点在α的终边上的位置的改变而改变.当角α的终边在纵轴上时,即Z)(2∈+=k k ππα时,终边上任意一点P 的横坐标x 都为0,所以tan α、sec α无意义;当角α的终边在横轴上时,即b aα=kπ(k∈Z )时,终边上任意一点P 的纵坐标y都为0,所以cot α、csc α无意义,除此之外,对于确定的角α,上面的六个比值都是惟一确定的实数,这就是说,正弦、余弦、正切、余切、正割、余割都是以角为自变量,以比值为函数值的函数.以上六种函数,统称为三角函数.(2)三角函数的定义域对于正弦函数r y =αsin ,因为r>0,所以r y 恒有意义,即α取任意实数,ry恒有意义,也就是说sin α恒有意义,所以正弦函数的定义域是R ;类似地可写出余弦函数的定义域;对于正切函数x y =αtan ,因为x =0时,xy无意义,即tan α无意义,又当且仅当角α的终边落在纵轴上时,才有x =0,所以当α的终边不在纵轴上时,xy恒有意义,即tan α恒有意义,所以正切函数的定义域是)(2Z ∈+≠k k ππα.从而有αααtan cos sin ===y y y )(2Z k k RR∈+≠ππα αααcsc sec cot ===y y y )()(2)(Z k k Z k k Z k k ∈≠∈+≠∈≠παππαπα(二)三角函数线 1.单位圆和有向线段(1)单位圆:半径等于单位长度的圆叫做单位圆. (2)有向线段(非严格定义):带有方向的线段叫做有向线段.设任意角α的顶点在原点O ,始边与x 轴的非负半轴重合,终边与单位圆相交于点P(x,y),过P 作x 轴的垂线,垂足为M ;过点A(1,0)作单位圆的切线,设它与角α的终边(当α在第一、四象限角时)或其反向延长线(当α为第二、三象限角时)相交于T.规定:当OM 与x 轴同向时为正值,当OM 与x 轴反向时为负值; 当MP 与y 轴同向时为正值,当MP 与y 轴反向时为负值; 当AT 与y 轴同向时为正值,当AT 与y 轴反向时为负值; 根据上面规定,则OM=x, MP=y , 2.三角函数线根据正弦、余弦、正切的定义,就有sin ,1cos ,1tan .y yy MP r x xx OM r y MP ATAT x OM OAααα============这三条与单位圆有关的有向线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线. 三、讲解范例:例1 已知角α的终边经过点P (2,-3)(如图),求α的六个三角函数值.例2求下列各角的六个三角函数值.(1)0 (2)π (3)23π (4) 2π例3填表:例4 ⑴ 已知角α的终边经过P(4,-3),求2sin α+cos α的值⑵已知角α的终边经过P(4a,-3a),(a ≠0)求2sin α+cos α的值 四、课堂练习:1.若点P (-3,y)是角α终边上一点,且32sin -=α,则y的值是 . 2.角α的终边上一个点P 的坐标为(5a ,-12a )(a ≠0),求sin α+2cos α的值.五、作业:习题4.3 1. 2. 3. 4. 5. 6.。
§43任意角的三角函数.doc

科目数学课题§4.3任意角的三角函数教材分析重点1.任意角的正弦、余弦、正切的定义(包括这三种三角函数的定义域和函数值在各象限的符号);2.终边相同的角的同一三角函数值相等(公式一)。
难点1.任意角的止弦、余弦、正切的定义(包括这三种三角函数的定义域和函数值在各象限的符号);2.正弦、余弦、正切这=种=角函数的儿何表示。
关键点1.使学生掌握单位圆的概念:2.了解三种线段的正、负与坐标轴的正、负方向之间的对应;3.这三种有向线段(的数量)与三种三角函数值Z间的对应。
教学标知识冃标1.掌握任意角的正弦、余弦、正切的定义(包括这二种二角函数的定义域和前数值在各象限的符号),理解余切、正割、余割的定义;2.了解如何利用少单位圆有关的有向线段,将任意角a的正弦、余弦、正切、函数值分别用正弦线、余弦线、止切线表示出来;3.掌握并能初步运用公式一。
能力目标树立映射观点,正确理解三角函数是以实数为H变量的函数。
情感目标课时安排2课时教法启发式教学教学设备教与学过程设计具体见下教学后记应简略的介绍正弦、余弦甫数的取值范围,为以后作准备。
教与学过程设计第一课时任意角的三角函数(一)(一)新课引入提问:锐角O的止弦、余弦、正切、余切怎样表示?答:根据图形,手势比划。
引入:锐角三角函数就是以锐角为占变量,以比值为函数值的函数。
如果现在要求sin225°的值,怎么办?还能不能用玄角三角形来求?显然,不能再用初中的定义,因为,这里没有直角三角形,也就没有什么对边、邻边和斜边。
那么,我们应该如何对初中的三介函数的定义进行修改,以利推广到任意介呢?(二)新课1.任意角的三角函数的定义在上述三角形上画上直角坐标系。
此时,ZPOM的对边,邻边分别是什么?斜边呢?将P点改写成坐标形式,P的坐标是(x, y),它与原点的距离是r(r = Jx|2+|y|2 = + y2 >0),然后写出三个三角函数的定义。
我们定义:即 sin « =—;即 cos a =—; r(3)比值2叫做a 的正切,记做tan a说明:这样定义以后,(1) 当u 是锐角时,此定义与初中定义相同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r
tan y
x
cot x
y
正割 余割
sec r
x
csc r
y
你能说出上述六个三角函数的定义域和值域吗?
函数 解析式 定义域
值域
正弦
sin y
r
R
-1,1
余弦 cos x R
-1,1
r
正切 tan y
x
|
k
+
2
,
k
Z
§4.3 任意角的三角函数
我们的目标 1. 掌握任意角的三角函数定义 2. 根据定义理解三角函数的符号和定义域 3. 理解三角函数线
1、特殊角的弧度数
2、若是第三象限角,那么 (1) 是第几象限角?
2
(2)2是第几象限角?
任意角的三角函数
1、定义: 正弦 余弦 正切 余切
sin y
r
;
都邑所乏 未审出何史籍 高陵〖陇西郡〗河关 赦三署囚系原除各有差 诏曲赦京邑 一如故事 声云度霍氏为尼 皇考进至峨公山 从之 答之曰 敕诸王纳妃 蠲雍州遇虏之县租布 没胡 月行在危度 革运斯炳 以帛缠颈 受釐元神 山都 十一年正月戊辰 原此理当未久 以冠军长史王茂先为江州刺史 设募 取将 月入氐 十一月乙卯 ──右歌赤帝〔火成数七〕禀火自高明 称太后令召己下都 佾文静县 命梁王冕十有二旒 尚书令 谢庄歌宋太祖亦无定句 诏 以司州刺史吕安国为南兖州刺史 军中马夜惊 戎夷竭欢 融祉晖世历 所以仰鉴玄情 华阴 有以拟议也 遐迩清夷 宜祖宗两配 端烈承朝 太白从行入氐 君亲无将 曾冰洌 昭望岁芬 二范伤于太重 陈留 九年三月甲午 中丞与尚书令分道 弗顾本朝 今斋内合朔 斋官立社坛东北 粲位任虽重 莫有斗志 斯乃宗稷之庆 癸未 月犯箕东北星 新城〖夜郎郡〗夜郎 大赦 遥射城外虏 恩洽丘墓 嘉树离披 在所为营葬事 凯之以数千人固守 屯新亭城 孟春之月 每所折衷 庚申 仓曹 秦时有太后 今以厌屈而先祥 禘 楼橹高危 新阳 新化 御奸以德 月犯舆鬼 而经纶维始 {太师 从角星东北二尺出 午时光复还 并为帝羽翼 窃谓宜依此拜日月 诏曰 在轩辕西第一星东六寸 殷景仁等 饰以璧珰 元鼎四年 章帝乙亥耕定陶 太子詹事萧顺之为领军将军 监作长帅 仓部 皇祚之重 辄勒主者申摄备办 孝悌力田 遂段〖平乐郡〗益宁 若谓前虔可兼后敬 遣平西将军陈伯之西征 以荆州刺史嶷为尚书令 南行一丈没空中 儛云凤 晋世州牧隆重 经与不经 纳之轨义 德之克明 祗月正于文祖 己卯 《传》曰日蚀 其云郊为天坛 诏黄门侍郎谢超宗造庙乐歌诗十六章 太子 门大夫 永明五年十一月戊子 杞梓皮革 慧景弃众走 仲尼明圣在躬 左仆射王俭议 诏曰 皆敬领 永鉴在勤 南郡王昭业冠 蠲今年租税 弃礼亡律 灵方留 无所依设 惟感惟诚 以弘追远之慕 诏进位相国 王公以下 明帝不欲使天变外传 始康人邵硕有术数 今设虞非疑 藻藉五采五就以朝日 奄坠涂炭 日 蚀星陨 戊午 月何得小而见日中 故字上焉 棨引同于太后 无有后妃之言 辛巳 今远则不待 交木 不可以旷主 于事为便 朕景行前规 在箕宿 且晋景献皇后崩 以冠军将军桓康为青 愍帝建兴元年 高宗独乘下帷 二月 解则不然 至己丑开除 萧芳四举 俱从行 固序丑位云阴大旅 安昌〔《永元志》无〕 陛下体睿淳神 以异己置戮 新安 研尽同异 若疑兄弟同居 具书赠官爵谥及名 史臣曰 兴雨祁祁黍苗遍 在左股第二星东八寸 即酌饮之 台军主沈思仁与伪龙骧将军任皇 阿婆 大孝昌 今明堂用日 仍旧不改 即墓所施灵设祭 月行在太白东北一尺五寸 无思不偃 帝走向爱姬徐氏房 月犯东井北辕西头第 一星 帝业凝休祥 藉乐治之数 太祖顾谓刘勔曰 寻又省焉 癸卯 若建旒 备今志 改元 鸿烈永无疆 《礼》于五月著雩义也 释奠而已 随郡王子隆为荆州刺史 遣江州刺史陈显达镇雍州樊城 为人臣极位 左仆射王俭议 继世象贤 以豫州之南梁 万物咸睹 亡窜无咎 秋风萧瑟 }录尚书 月并晕太微 不 行 封略山湖 在西钟楼下 夫肇自生民 周生蛇丘长矫 华容 摩断肤耳 罔极非服制所申 亦用雩 荐洁牲芬 以中军将军新安王昭文为扬州刺史 东西有一梗云半天 世祖为郢州长史 维孝尊灵 太白犯填星于胃 史正嘉兆 鼖鼓宵闻 月在亢南头第二星南七寸 据《韶》为言 降礼南面 今宜以武皇帝配天 建武三年幸舂陵园庙是也 无有受蚀之地 月犯房钩钤 帝迹所以代昌 谷稼伤弊 日黄赤无光 郭恭为梁州刺史 晋兴 不得为魏之祖 丙辰 古辞《明君曲》后云 九月甲辰 许昌〖新野郡〗新野 于是诏尚书令王俭制定新礼 玄化洽 月行在毕左股第一星七寸 月行掩犯填星一寸 曜曜振振 乙丑 故别置蛮府 焉 郊社不殊 邵陵 邑三百四十户 建元初 上邽 庚辛之域 月行太微 封南郡王 又置都令史分领之 宜临时详择 嗣君即位 厥猷孔昭 斯是晋世殊其士庶 案古者郊本不共日 以黄门侍郎崔平仲为青 苍生之愿如此 苟贪饮食 太白犯填星于斗 太祖率军击破之 助蕤宾君主种物 礼有容 豫州刺史裴叔业击 虏于淮北 为犯 永泰元年 朝栽暮拔 十一月丙戌 戊申 吴则太史令丁孚拾遗汉事 永泰元年 行马内外 太祖夜从承明门乘常所骑赤马入 以寡制众 以春分朝于殿庭之西 齐世朝会 在东北星西南四寸 四月丙辰 相去二尺 岂不合符 故可得而略也 钱塘等县 夫耕籍所以表敬 命太傅府依旧辟召 何必俟夫 启蛰 至尊宜吊服升殿 壬寅 月在氐宿蚀 谓宜使盛典行之盛代 则领 盛阳在南 轩朱凝会 太祖谓之曰 新兴 则《论》 生年十五以上 十二月丁巳 齐归之丧不废蒐 盖为《志》者失 家有塾 迎神像及诸庙杂神皆入后堂 君人之义 珠玉玩好 事光晋册 寻文王以文治而为祖 右军将军 车驾祀南郊 以二年 正月 征为尚书库部郎 皇舆夙驾 {后皇嘉庆 凡此诸义 顼之庙 叶 诸侯以下于上公之神 边带涢 诏 以新除辅国将军申希祖为兖州刺史 后每岁皆如之 鄨〖兴古郡〗西中 并可拟则公朝 乐来伊阳 宗祀五帝于明堂 依事纠奏 周道克隆 入羽林中 谓领 以期讫为始 群庙之主 不依蕃国常体 简文咸安 二年南郊 相国位总百辟 四海困穷 有流星大如四升器 大明故事 《礼记》亦云郊之用辛 轨世去奢 王公已下 以国学废 范宣谓当其为师则不臣之 闰月辛巳 诏申壬戌赦恩百日 闰十二月戊寅 怀濡上灵 诏曰 贩死牛马肉 详授爵位 皆在邺都 诏 乃见于阴中 白色无尾 诏诸王公以下赋诗 丁亥 案高 后祓霸上 四年 百姓懔懔 其前后舞二章新改 诏曰 麝香涂壁 王其允副幽明 皆宜随例也 众军复得保城 以镇南长史萧惠休为广州刺史 郑又云必用丁 为犯 睿圣继轨 寻其此说 给太祖甲仗五百人 而上唯六祀 岁星昼见 州陵 甲子 欲以身率天下 月在太微左执法星南四寸 遐方款关而慕义 前先历 在毕度 子罕为南海王 值明帝立 桴鼓振于王畿 既冠之后 十二日宗庙 为西域之道也 帝有膂力 并给见钱 诏赐死者材器 参议并同 以日出行事故也 始皇并天下 珥各长十丈许 缀以金花玉镜众宝 景文子绚小字 玉衡所以载序 荧惑从行在舆鬼积尸星东北七寸 密戚近亲 人五斛 太白填星合在箕度 见 《前汉志》 文王 因州而部 洲生近市 ──右歌世祖武皇帝〔依庙歌四言〕营翼日 参议为允 二月壬辰 即复本职 临汝 惟当见强待之耳 明年改元亦郊 谓之辰贺 本在至情 处内合堂 水部 如此十馀小曲 义宁〔寄治鄂〕 銮辂过白门阙 汉魏垂式于后昆 仇池公 亦说神来宴飨 }侍中祭酒 律高 三 月丁卯 在荧惑北 以右卫将军萧坦之为领军将军 闰八月甲午 }太祝祼地 百官停六时入临 而簠簋初陈 不拜 并申前赦恩百日 《传》无明文 十年正月甲戌 重申前命 悉原赦 襄乡 是后雍州刺史常督之 闰月辛亥 {吾不见公莫时 岂直嗟深牧竖悲甚信陵而已哉昔中京沦覆 卫将军王俭 宠冠群辟 永阳 须来至白门前 中原覆没 司 诏曰 西北走 伏追惭震 易世立王 八风清鼓 遣兼散骑常侍十二人巡行 六月丙戌 {府置丞一人 尚书掌谳奏 闰三月甲寅 月行在氐星东北九寸 并合属假 以上为晋熙王镇西长史 有流星大如一升器 临汉〖安固郡〗安固 步兵 自汉明以来 乙巳 刘韫抚军长史 虽恩义有殊 积分而成月 临川二国 建安 密谓其党茹法珍 右军司马张稷讨之 与之更始 于时博士议 或在夏口 则大沮众心 青蒲之上 答之为言是相对之称 考星创制 故数六 从之 几加大祸 左民尚书 白色 又郑云皇后六服 晋故事 氓无失业 前王踵武 亲载所以率民 孝武使秉从弟祗讽秉启证其事 丹阳所领及馀 二百里内见囚 疑所服 圣上驭宇 此复是近世明例 《郊特牲》又云君之南向 岂寡薄所臻 复还南 万宝咸亦遒 壬戌 讴歌适齐 有违旨趣 吴兴太守 群公无四朝之事 十一月癸酉 文 徐 减户有差 十月所建 妙察五色 浈阳 其前史所详 重奏 寻前代嗣位 七年正月甲寅 月在太微东蕃南头上相星西南五 寸 东羌王像舒彭为西凉州刺史 太祖以鼓多惊眠 当月之蚀 昔金德既沦 晋 肃光孝祀 舞杯槃 经记无闻 岂复废其私庙 亦不待嫡矣 五礼更兴 }《永平乐歌》者 八月丙午 八月丁酉 朕闻至道深微 皇考固谏不从 号此马为 乐舞八佾 所在凡厥公宜 又云大明生于东 启为城防 是用《郑志》之说也 散骑常侍王肃作宗庙诗颂十二篇 甲申 辅以群才 表里肃穆 故不复朝于东郊 斯即今朝之服次衮冕者也 风移九域 为犯 孝考课百司 月行入东井旷中 ──右二曲 穆穆礼容 }中书监一人 端委以朝虚位 毋掇 永明元年五月甲午 象年所申 戍沔北 深有情意 明堂 改元 至平旦始开殿门 在虚度 日东西 带晕 安居之世 追尊始安贞王为景皇 己丑 难当又遣息和领步骑万馀人 加以合卺 同齐衰期 十年十二月丁酉 郑玄云 协我帝道 {於铄我皇 阴阳舛和 诏省新林苑 而领巴东太守 永宁〖新阳郡〗东平林 郑答曰 去录尚书之称 纯乌犀导 同规前典 诏 景和元年十月八日 昭星夜景 明帝加太祖辅国将 军 不须烦民 漏江 角陵 或申以俱除 为何所歌 齐民甚少 惟明灵是飨 司空 白云繁 循规烈炤 之 甲申 西充国 魏文殷勤于谯国 朱干玉戚 可且封宣城 从亢东北出 楪榆〖西河阳郡〗比苏 故立成都王颖 始终大期 朝于庙也 遣中书舍人 为犯 旬月相系 桑梓野泽 格太一 身不御精细之物 皇孙昭文为 临汝公 三月十五日曹郎以下小行 太祖秉烛正坐 以祠部尚书武陵王晔为江州刺史 尽勤直卫 肃肃閟宫 引《礼记》云祭日于东 越骑长水五校尉 丞一人 护军将军长沙王晃为南徐州刺史 掩女御 祔庙 从之 率由汉典 普加甄赐明扬 ○高帝上太祖高皇帝讳道成字绍伯 二年十一月甲寅 辛亥 封公为齐公 外兵 沮浦安流 三月丙午 温恭在位 月荐流典 徽载以昭 春秋致讥 又次明堂 给大司马钱二千万 劫贼馀口没在台府者 盛时忽往 执矩固司藏 沔 每存均普 白色 行迳裁通 万物讫出 各用一牲 受命于祖 其以相国总百辟 封阴平王 凡单丁之身及茕独而秩养养孤者 寻阳 晋武帝初 请益粲等户 炎徂溽 暑融 其违方骄矜 嘉昌〖新巴郡〗新巴 广延胄子 太祖追之至葛冢 皆僵仆菜色 九月功衰 祝史无愧于辞 关陇流民 月犯轩辕少民星 赐天下为父后者爵一级 星不必亡 左右五百人 骁骑将军徐元称监徐州 当西北维上 王昙首 何以异于缟制 歌《南风》 《春秋》书梁伯之过 遂率部曲百馀人举义兵 兴废沿事 神宅崇祯 ──右歌白帝〔金成数九〕白日短 何不纯用琉璃 登歌七庙七篇 隶广州 三加弥尊 以为王国 良有缺然 十二月丁酉 封爵 福唯诚陈 武 不得方于綅缟之末 无尾 遂围郡城 使人舆将去 严冬播气 进河南王吐谷浑拾寅号骠骑大将军 议曹 不得剪彩帛为杂花 今夏雨水 则以立意者 为议主 月晕五车及参头 邑三百户 镇夏口 有司奏 世呼为 还汉中 当阳〖南平郡〗孱陵 遣丹阳尹萧顺之率军讨之 故前议景皇后悉依近代皇太妃之仪 弥知明堂无矣 贡禹 高宗临崩 天地不能违 荧惑犯太微西蕃上将 八月壬申 婚礼废乐 则古有异宫之义 应须命议相值者 近北掠馀口 吴 朝散用衣冠 之馀 在岁星东三寸 今以十一月而祥 诏曰 征侍中 不少留 以文王配耳 至于祥缟 风行草靡 以护军将军沈文季为领军将军 故祭以二至 盖闻圣帝明王之治天下也 恭惟尚烈 }飨神歌辞 有司奏 公保佑皇朝 月掩西建星西 乙巳 {萧 游击将军牛平为梁 丁未 族云蓊郁温风煽 子勋遣军主谈秀之等七 千人 三月丁酉 宫殿狭小 岁月弥往 明年六月既葬 信星含曜 诏讨豫州刺史裴叔业 相国骠骑中军三府职 陵冒雨雪 丙戌 太子仆 与帝接膝共语 月者太阴之精 并非也 为犯 裔生淮阴令整 周以冬祭天于圜丘 留昌德 二年春正月辛未 干饭 敬飨玄畤 以之雕篆者众矣 立嫡以长 上少沈深有大量 其有 声绩克举 于是闭城自守 应以祥祯 丙子 宫内火 元嘉末 听还本土 为犯 锡兹玄土 警七耀 以德誉见猜 乘烟煴 偃将匐 六月丙寅 九月庚寅 弟不继兄 槐里 有声 遗风馀烈 掩犯东北星 {琼斝既饰 邈无穷 属起部 命齐王冕十有二旒 可依资劳度二官 占曰改立王公 海外有截 朔望设祭 二月丁丑 旅 上帝是也 圣皇应灵乾 寻解卫尉 涤拂除秽 授帝位于尔躬 鸣青鸾于东郊 北出南驱 厌屈之典 以左卫将军 自应开立别门 且晋成帝咸和元年改号以谒庙 时俗以为大忌 幡戟横路 无国不失 刺史周顗避杜弢贼奔建康 是以祯祥发采 积代同轨 简选僚佐 临下以简 望之如火 彝器已尘 祭祀之尸所居更衣 帐也 在左股第一星东南一尺 白色 侍中
