湖南省邵阳市一中2009-2010学年第一学期高一数学期中考试试题

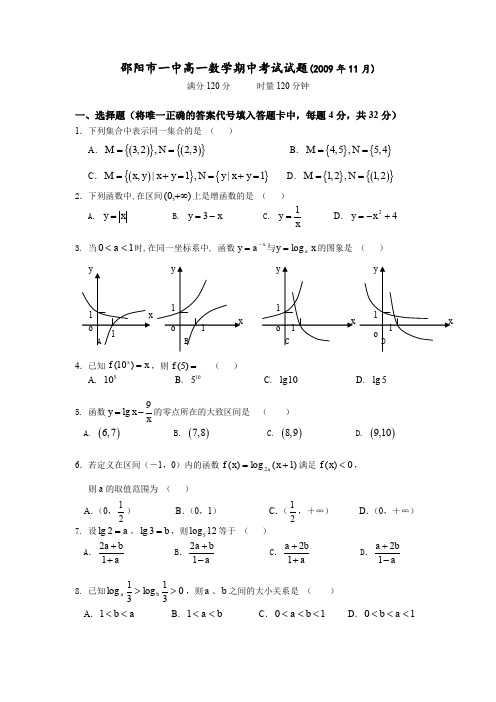
邵阳市一中高一数学期中考试试题(2009年11月)满分120分 时量120分钟一、选择题（将唯一正确的答案代号填入答题卡中，每题4分，共32分）1．下列集合中表示同一集合的是 （ ）A ．(){}(){}3,2,2,3M N == B ．{}{}4,5,5,4M N == C ．(){}{},|1,|1M x y x y N y x y =+==+= D ．{}(){}1,2,1,2M N ==2．下列函数中,在区间),0(+∞上是增函数的是 （ ） A. x y = B. x y -=3 C. x y 1=D ．42+-=x y3. 当10<<a 时,在同一坐标系中, 函数x y a y a x log ==-与的图象是 （ ）4．已知(10)x f x =，则(5)f = （ ）A . 510B . 105C . lg10D . lg 55. 函数9lg y x x=-的零点所在的大致区间是 （ ） A. ()6,7 B. ()7,8 C. ()8,9 D. ()9,106．若定义在区间（－1，0）内的函数)1(log )(2+=x x f a 满足0)(<x f ，则a 的取值范围为 （ ）A ．（0，21）B ．（0，1）C ．（21，＋∞） D ．（0，＋∞） 7. 设a =2lg ，b =3lg ，则5log 12等于 （ ）A ．21a b a ++B ．21a b a +-C ．21a b a ++D ．21a b a +-8. 已知031log 31log >>b a ，则a 、b 之间的大小关系是 （ ） A ．a b <<1 B ．b a <<1 C ．10<<<b a D ．10<<<a b二、填空题（每题4分，共28分）9．若幂函数)(x f y =的图象经过点（9,13）, 则)25(f 的值是_______ 10．函数()()251x f x a a +=+>的图像必过一定点，该点的坐标是11．已知函数⎩⎨⎧=x x x f 3log )(2)0()0(≤>x x ，则)]41([f f 的值是 12. 函数()23log 21y ax x =-+的定义域为R ，则a 的取值范围是13．用二分法求函数x 的一个零点，其参考数据如下:据此数据, 可得方程043=--x x 的一个近似解(精确到0.01)为14．方程2)21(2=+x x 的解的个数是 个. 15．三个函数①1;y x=②2;x y -=③3y x =-中，在其定义域内既是奇函数又是减函数 的是 （写出所有正确命题的序号）三、解答题（每题10分,共60分）16．已知函数f (x )=2xx a a -+（a >0，a ≠1，a 为常数，x ∈R ） （Ⅰ）若f (m )=6，求f (－m )的值；（Ⅱ）若f (1)=3，求f (2)的值.17. 计算：5log 21122++50lg 2lg 5lg 2+18．设集合{})1(log |2-==x y x A ，{}R x x x y y B ∈-+-==,22|2（Ⅰ）求集合B A ,（Ⅱ）若集合C =}02|{<+a x x ，且满足C C B = ，求实数a 的取值范围。

19. 已知函数()f x 是定义在[1,1]-上的奇函数，且()f x 在定义域上是减函数， （Ⅰ）求函数(1)y f x =-定义域；（Ⅱ）若(2)(1)0f x f x -+-<，求x 的取值范围．20．某旅游景点有50辆自行车供游客租赁使用，管理这些自行车的费用是每日115元．根据经验，若每辆自行车的日租金不超过6元，则自行车可以全部租出；若超过6元，则每提高1元，租不出去的自行车就增加3辆．规定：每辆自行车的日租金不超过20元，每辆自行车的日租金x 元只取整数，并要求出租所有自行车一日的总收入必须超过一日的管理费用，用y 表示出租所有自行车的日净收入（即一日中出租所有自行车的总收入减去管理费后的所得）．（Ⅰ）求函数)(x f y =的解析式及定义域；（Ⅱ）试问日净收入最多时每辆自行车的日租金应定为多少元？日净收入最多为多少元？21．已知函数()f x 定义在()1,1-上，对于任意的,(1,1)x y ∈-， 有()()()1x y f x f y f xy++=+，且当0x <时，()0f x >。

（Ⅰ）验证函数1()ln 1x f x x-=+是否满足这些条件； （Ⅱ）判断这样的函数是否具有奇偶性和其单调性，并加以证明； （Ⅲ）若1()12f -=，求函数21)(+=x f y 的零点。

高一数学期中考试参考答案一、BACD DCBD二、9．15 10．)6,2(- 11．91 12. 1>a 13．1.56 14．2 15．③三、16．解：（Ⅰ）∵ f (－x )=2xx a a +-=f (x ) ∴ f (x )为偶函数∴ f (－m )=f (m )=6. …5分 （Ⅱ）∵f (1)=3 ∴a +a1=6 ∴ 22212)1(a a a a ++=+=36 ∴221a a +=34∴ f (2)=34/2=17 ……10分 17. 解：原式=)5lg 1(2lg 5lg 2225log 212+++⨯ …………………………………4分 =2lg )5lg 2(lg 5lg 52+++ ……………………………………8分 =152+ …………………………………………………………10分18．解：（Ⅰ）()1,A =+∞ ………2分 (],1B =-∞- ………5分 （Ⅱ）,2a C ⎛⎫=-∞- ⎪⎝⎭………………………………………………………6分 B C C ⋃= B C ∴⊆ ……………………………………8分122a a ∴->-∴< …………………………………………… 10分19. 解：（Ⅰ）依题意得：111x -≤-≤，解得02x ≤≤函数(1)y f x =-定义域为{|02}x x ≤≤………………………………4分（Ⅱ） ()f x 是奇函数，且(2)(1)0f x f x -+-<∴ 得(2)(1)(1)f x f x f x -<--=- …………………………………6分()f x 在[1,1]-上是单调递减函数，则12111121x x x x -≤-≤⎧⎪-≤-≤⎨⎪->-⎩ 解得130232x x x ⎧⎪≤≤⎪≤≤⎨⎪⎪>⎩……………………………………9分即322x <≤ ∴x 的取值范围3{|2}2x x <≤……………………………10分20．解：（Ⅰ）当x ≤6时，11550-=x y ，令011550>-x ，解得3.2>x ．∵∈x N ，∴x ≥3，∴3≤x ≤6，且∈x N ．…………………………………………2分 当x <6≤20时，115)]6(350[---=x x y 1156832-+-=x x ．…………………4分综上可知⎩⎨⎧∈≤<-+-∈≤≤-=).,206(,115683),,63(,115502N N x x x x x x x y ……………………………5分 （Ⅱ）当3≤x ≤6，且∈x N 时，∵11550-=x y 是增函数，∴当6=x 时，185max =y 元．……………………………………………………7分 当x <6≤20，∈x N 时，1156832-+-=x x y 3811)334(32+--=x ， ∴当11=时，270max =y 元．…………………………………………………………9分 综上所述，当每辆自行车日租金定在11元时才能使日净收入最多，为270元．……10分21．解：（Ⅰ）由101x x->+可得11x -<<，即其定义域为()1,1- 又1111()()ln ln ln()1111x y x y f x f y x y x y----+=+=⋅++++ 111ln ln 111x yx y xy xy x y x y xy xy+---++==++++++()1x y f xy +=+ 又当0x <时，110,x x ->+>111x x -∴>+1ln 01x x -∴>+ 故1()ln 1x f x x-=+满足这些条件。

………………………………………………3分 （Ⅱ）(0)(0)(0)(0)0f f f f +=⇒=()()(0)0()()f x f x f f x f x ∴-+==⇒-=-∴()f x 在()1,1-上是奇函数。

…………………………………………………5分()()()()()1x y f x f y f x f y f xy--=+-=- 当11x y -<<<时，01x y xy-<-，由条件知()01x y f xy ->-，即()()0f x f y -> ∴()f x 在()1,1-上是减函数。

……………………………………………………7分 （Ⅲ）11()1()122f f -=∴=- 方程021)(=+x f 即为2212()1()()()()12x f x f x f x f f x =-⇔+==+ ()f x 在()1,1-上是减函数2221410212x x x x x ∴=⇔-+=⇔=±+又(1,1)2x x ∈-∴= ………………………………………………………10分。