高考数学理一轮总复习必修部分开卷速查47立体几何中的向量方法(二)求空间角与距离(含解析)新人教A版
2020届高考数学一轮复习立体几何中的向量法(第2课时)求空间角与距离课时作业理(含解析)

第2课时 求空间角与距离课时作业1.在棱长为4的正方体ABCD -A 1B 1C 1D 1中,点P 在棱CC 1上,且CC 1=4CP ,求点P 到平面ABD 1的距离.解:建立如图所示的空间直角坐标系,则由题设条件易知A (4,0,0),B (4,4,0),P (0,4,1),D 1(0,0,4).AB →=(0,4,0),AD 1→=(-4,0,4),过P 点作PH ⊥平面ABD 1,垂足为H ,则PH 即为点P 到平面ABD 1的距离. 设点H 的坐标为(x ,y ,z ),则PH →=(x ,y -4,z -1),AH →=(x -4,y ,z ), ∵PH ⊥平面ABD 1,∴PH →⊥AB →,PH →⊥AD 1→,PH →⊥AH →, ∴⎩⎪⎨⎪⎧PH →·AB →=y -=0,PH →·AD 1→=-4x +z -=0,PH →·AH →=x x -+y y -+z z -=0,解得x =32,y =4,z =52或x =0,y =4,z =1(舍去),∴H ⎝ ⎛⎭⎪⎫32,4,52,PH →=⎝ ⎛⎭⎪⎫32,0,32,∴|PH →|=322.故点P 到平面ABD 1的距离为322.2.(2019漳州5月)如图,在三棱台ABC -DEF 中,二面角B -AD -C 是直二面角,AB ⊥AC ,AB =3,AD =DF =FC =12AC =1.(1)求证:AB ⊥平面ACFD ;(2)求二面角F -BE -D 的平面角的余弦值.解析:(1)连接CD ,在等腰梯形ACFD 中,过D 作DG ⊥AC 交于G ,因为AD =DF =FC =12AC=1,所以AG =12,DG =32,CG =32,所以CD =3,所以AD 2+CD 2=AC 2,即CD ⊥AD ,又二面角B -AD -C 是直二面角,CD平面ACFD ,所以CD ⊥平面ABED ,又AB平面ABED ,所以AB ⊥CD ,又因为AB ⊥AC ,AC ∩CD =C ,AC 、CD平面ACFD ,所以AB ⊥平面ACFD .(2)如图,在平面ACFD 内,过点A 作AH ⊥AC ,由(1)可知AB ⊥AH ,以A 为原点,AB →,AC →,AH →的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系A -xyz .则B (3,0,0),D ⎝ ⎛⎭⎪⎫0,12,32,F ⎝ ⎛⎭⎪⎫0,32,32,C (0,2,0),所以BC →=(-3,2,0),CF →=⎝ ⎛⎭⎪⎫0,-12,32,设n =(x ,y ,z )是平面FBE 的一个法向量,则⎩⎪⎨⎪⎧n ⊥BC→n ⊥CF→,所以⎩⎨⎧-3x +2y =0-y +3z =0,取x =2,则y =3,z =3, 即n =(2,3,3), 由(1)可知CD ⊥平面BED ,所以CD →=⎝ ⎛⎭⎪⎫0,-32,32是平面BED 的一个法向量,所以cos 〈n ,CD →〉=n ·CD →|n |·|CD →|=-343=-34,又二面角F -BE -D 的平面角为锐角, 所以二面角F -BE -D 的平面角的余弦值为34.3.如图,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC =4,AB =6,BC =3.点E 是CD 边的中点,点F ,G 分别在线段AB ,BC 上,且AF =2FB ,CG =2GB .(1)证明:PE ⊥FG ;(2)求二面角P -AD -C 的正切值; (3)求直线PA 与直线FG 所成角的余弦值. 解:(1)证明:∵PD =PC 且E 为CD 的中点,∴PE ⊥DC .又平面PDC ⊥平面ABCD ,且平面PDC ∩平面ABCD =CD ,PE 平面PDC ,∴PE ⊥平面ABCD .又FG 平面ABCD , ∴PE ⊥FG .(2)∵四边形ABCD 是矩形,∴AD ⊥DC ,又平面PDC ⊥平面ABCD ,且平面PDC ∩平面ABCD =CD ,AD 平面ABCD ,∴AD ⊥平面PCD ,又CD ,PD平面PDC ,∴AD ⊥DC ,AD ⊥PD ,∴∠PDC 即为二面角P -AD -C 的平面角,在Rt △PDE 中,PD =4,DE =12AB =3,PE =PD 2-DE 2=7,∴tan ∠PDC =PE DE =73,即二面角P -AD -C 的正切值为73. (3)如图所示,连接AC .∵AF =2FB ,CG =2GB , 即AF FB =CGGB=2,∴AC ∥FG ,∴∠PAC 为直线PA 与直线FG 所成角或其补角, 在△PAC 中,PA =PD 2+AD 2=5,AC =AD 2+CD 2=35,由余弦定理可得cos ∠PAC =PA 2+AC 2-PC 22PA ·AC =52+52-422×5×35=9525,∴直线PA 与直线FG 所成角的余弦值为9525.4.如图,在三棱柱ABC -A 1B 1C 1中,侧面ACC 1A 1与侧面CBB 1C 1都是菱形,∠ACC 1=∠CC 1B=60°,AC=2.(1)证明:AB1⊥CC1;(2)若三棱柱ABC-A1B1C1的体积为3,求二面角B1-AC-C1的余弦值.解析:(1)取CC1的中点O,连接AO、AC1、B1C、B1O,由菱形的性质及∠ACC1=∠CC1B1=60°.得△ACC1,△B1CC1为正三角形.∴AO⊥CC1,B1O⊥CC1,且AO∩B1O=O.∴CC1⊥平面AOB1,∴CC1⊥AB1.(2)三棱锥A-A1B1C1的体积是三棱柱ABC-A1B1C1体积的三分之一,得四棱锥A-BCC1B1的体积是柱体体积的三分之二,即等于2.平行四边形BCC1B1的面积为SBCC1B=2×2×sin 60°=2 3.设四棱锥A-BCC1B1的高为h,则:13×23×h =2,∴h =3, 又AO =3=h ,AO ⊥平面BCC 1B 1, 建立如图直角坐标系:O -xyz ,则A (0,0,3),B 1(3,0,0),C (0,-1,0),CB 1→=(3,1,0),CA →=(0,1,3),设平面CAB 1的一个法向量为n 1=(x ,y ,z ), 则⎩⎪⎨⎪⎧n 1·CA →=y +3z =0n 1·CB 1→=3x +y =0,取一个法向量为n 1=(3,-3,3), 显然n 2=(1,0,0)是平面C 1CA 的一个法向量. 则cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=315=55.二面角B 1-AC -C 1的余弦值为55. 5.如图,在四棱柱ABCD -A 1B 1C 1D 1中,侧棱A 1A ⊥底面ABCD ,AB ⊥AC ,AB =1,AC =AA 1=2,AD =CD =5,且点M 和N 分别为B 1C 和D 1D 的中点.(1)求证:MN ∥平面ABCD ; (2)求二面角D 1-AC -B 1的正弦值;(3)设E 为棱A 1B 1上的点,若直线NE 和平面ABCD 所成角的正弦值为13,求线段A 1E 的长.解:如图,以A 为原点建立空间直角坐标系,依题意可得A (0,0,0),B (0,1,0),C (2,0,0),D (1,-2,0),A 1(0,0,2),B 1(0,1,2),C 1(2,0,2),D 1(1,-2,2),又因为M ,N 分别为B 1C 和D 1D 的中点,得M (1,12,1),N (1,-2,1).(1)证明:依题意,可得n =(0,0,1)为平面ABCD 的一个法向量,MN →=(0,-52,0),由此可得,MN →·n =0,又因为直线MN 平面ABCD ,所以MN ∥平面ABCD .(2)AD 1→=(1,-2,2),AC →=(2,0,0),设n 1=(x ,y ,z )为平面ACD 1的一个法向量,则 ⎩⎪⎨⎪⎧n 1·AD 1→=0,n 1·AC →=0,即⎩⎪⎨⎪⎧x -2y +2z =0,2x =0.不妨设z =1,可得n 1=(0,1,1),设n 2=(x ,y ,z )为平面ACB 1的一个法向量,则⎩⎪⎨⎪⎧n 2·AB 1→=0,n 2·AC →=0,又AB 1→=(0,1,2),得⎩⎪⎨⎪⎧y +2z =0,2x =0.不妨设z =1,可得n 2=(0,-2,1). 因此有cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=-1010,于是sin 〈n 1,n 2〉=31010,所以二面角D 1-AC -B 1的正弦值为31010.(3)依题意,可设A 1E →=λA 1B 1→,其中λ∈[0,1],则E (0,λ,2),从而NE →=(-1,λ+2,1),又n =(0,0,1)为平面ABCD的一个法向量,由已知得cos 〈NE →,n 〉=NE →·n |NE →|·|n |=1-2+λ+2+12=13,整理得λ2+4λ-3=0,又因为λ∈[0,1],解得λ=7-2,所以线段A 1E 的长为7-2.6.(2018承豫南九校)如图,在四棱锥P -ABCD 中,底面ABCD 是平面四边形,AB =AC =2,AD =22,PB =32,PB ⊥AC .(1)求证:平面PAB ⊥平面PAC ;(2)若∠PBA =45°,试判断棱PA 上是否存在与点P ,A 不重合的点E ,使得直线CE 与平面PBC 所成角的正弦值为33,若存在,求出AEAP的值;若不存在,请说明理由. 解析:(1)因为四边形ABCD 是平行四边形,AD =22,所以BC =AD =22, 又AB =AC =2,所以AB 2+AC 2=BC 2,所以AC ⊥AB , 又PB ⊥AC ,且AB ∩PB =B ,所以AC ⊥平面PAB , 因为AC平面PAC ,所以平面PAB ⊥平面PAC .(2)由(1)知AC ⊥AB ,AC ⊥平面PAB ,如图,分别以AB ,AC 所在直线为x 轴、y 轴,平面PAB 内过点A 且与直线AB 垂直的直线为z 轴,建立空间直角坐标系A -xyz ,则A (0,0,0),B (2,0,0),C (0,2,0),AC →=(0,2,0),BC →=(-2,2,0) 由∠PBA =45°,PB =32,可得P (-1,0,3), 所以AP →=(-1,0,3),BP →=(-3,0,3),假设棱PA 上存在点E ,使得直线CE 与平面PBC 所成角的正弦值为33, 设AE AP=λ(0<λ<1),则AE →=λAP →=(-λ,0,3λ),CE →=AE →-AC →=(-λ,-2,3λ), 设平面PBC 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·BC →=0n ·BP →=0,即⎩⎪⎨⎪⎧-2x +2y =0-3x +3z =0,令z =1,可得x =y =1,所以平面PBC 的一个法向量为n =(1,1,1), 设直线CE 与平面PBC 所成的角为θ,则 sin θ=|cos 〈n ,CE →〉|=|-λ-2+3λ|3·-λ2+-2+λ2=|2λ-2|3·10λ2+4=33, 整理得3λ2+4λ=0,因为0<λ<1,所以3λ2+4λ>0,故3λ2+4λ=0无解, 所以棱PA 上不存在与点P ,A 不重合的点E ,使得直线CD 与平面PBC 所成角的正弦值为33.。
高考数学一轮复习:44 立体几何中的向量方法(二)--求空间角(理科专用)

高考数学一轮复习:44 立体几何中的向量方法(二)--求空间角(理科专用)姓名:________班级:________成绩:________一、 单选题 (共 13 题;共 26 分)1. (2 分) 如图,三棱柱 ABC﹣A′B′C′的所有棱长都相等,侧棱与底面垂直,M 是侧棱 BB′的中点,则二 面角 M﹣AC﹣B 的大小为( )A . 30° B . 45° C . 60° D . 75° 2. (2 分) (2018 高二上·临汾月考) 如图,在正方体 则下列结论不正确的是( )中,若 是线段上的动点,A . 三棱锥的正视图面积是定值B . 异面直线, 所成的角可为C . 异面直线, 所成的角为第 1 页 共 12 页D . 直线与平面所成的角可为3. (2 分) 正方形 ABCD 中,E、F 为 AB、CD 的中点,M、N 为 AD、BC 的中点,将正方形沿 MN 折成一个直二面 角,则异面直线 MF 与 NE 所成角的大小为( )A.B.C . arcsinD . arccos4. (2 分) (2018 高二上·阜城月考) 在三棱柱.若分别是棱角的余弦值为( )上的点,且中,底面为正三角形,侧棱垂直底面,,则异面直线与 所成A. B. C. D. 5. (2 分) 下列命题:第 2 页 共 12 页①两个相交平面组成的图形叫做二面角; ②异面直线 a,b 分别和一个二面角的两个面垂直,则 a,b 所成的角与这个二面角相等或互补; ③二面角的平面角是从棱上一点出发,分别在两个面内作射线所成角的最小角; ④二面角的大小与其平面角的顶点在棱上的位置没有关系,其中正确的是( ) A . ①③ B . ②④ C . ③④ D . ①②6. (2 分) 二面角内一点到两个面的距离分别为, 到棱的距离为 , 则二面角的度数是( )A.B.C.D.7. (2 分) 如图,正方体 ABCD﹣A1B1C1D1 中,E 为 DD1 的中点,则 BD1 与平面 ACE 所成的角为( )A . 0° B . 30° C . 45° D . 90°第 3 页 共 12 页8. (2 分) 如图,在四面体 ABCD 中,AB⊥BD,CD⊥DB,若 AB 与 CD 所成的角的大小为 60°,则二面角 C﹣BD ﹣A 的大小为( )A . 60°或 90°B . 60°C . 60°或 120°D . 30°或 150°9. (2 分) 在教材中,我们学过“经过点 P(x0 , y0 , z0),法向量为 =(A,B,C)的平面的方程是:A(x﹣x0)+B(y﹣y0)+C(z﹣z0)=0”.现在我们给出平面 α 的方程是 x﹣y+z=1,平面 β 的方程是 由这两平面所成的锐二面角的余弦值是( ),则A.B.C.D. 10. (2 分) (2016·铜仁) 正方体 ABCD—A1B1C1D1 中直线 与平面夹角的余弦值是( )A. B. C.第 4 页 共 12 页D.11. (2 分) (2015 高二上·承德期末) 如图所示的长方体中,AB=2 ,AD= ,=,E、F 分别为的中点,则异面直线 DE、BF 所成角的大小为( )A.B.C.D.12. (2 分) (2018 高二上·临汾月考) 在正三角形中,过其中心 作边与 , ,将沿折起到的位置,使点 在平面的中点 ,则二面角的平面角的大小是( )的平行线,分别交 , 上的射影恰是线段A.B.C.D.13. (2 分) 设四面体的六条棱的长分别为 1,1,1,1, 和 a,且长为 a 的棱与长为 的棱异面,则 a 的 取值范围是( )A.B.第 5 页 共 12 页C.D.二、 填空题 (共 3 题;共 3 分)14. (1 分) (2018 高二上·承德期末) 已知四棱锥面,且,点 是棱 的中点, 在棱所成角的正弦值为________.的底面是菱形,上,若,则直线,平与平面15. (1 分) (2015 高一上·西安期末) 三棱锥 P﹣ABC 的两侧面 PAB,PBC 都是边长为 2 的正三角形,AC= , 则二面角 A﹣PB﹣C 的大小为________.16. (1 分) 设动点 P 在棱长为 1 的正方体 ABCD﹣A1B1C1D1 的对角线 BD1 上,记 时,则 λ 的取值范围是________. 当∠APC 为钝角三、 解答题 (共 5 题;共 50 分)17. (10 分) (2018 高一下·北京期中) 正四棱锥的侧面积是底面积的 2 倍,高是 3,求它的全面积.18. (10 分) (2018 高二上·抚顺期末) 在三棱柱,。
高考数学 《立体几何中的向量方法(二)——求空间角与距离易错点》

立体几何中的向量方法(二)——求空间角与距离备考策略易错点主标题:立体几何中的向量方法(二)——求空间角与距离备考策略易错点副标题:从考点分析立体几何中的向量方法(二)——求空间角与距离备考策略易错点,为学生备考提供简洁有效的备考策略。
关键词:空间角,距离,易错点难度:2重要程度:4【易错点】1.直线的方向向量与平面的法向量(1)若n 1,n 2分别是平面α,β的法向量,则n 1∥n 2⇔α∥β.(×)(2)两直线的方向向量的夹角就是两条直线所成的角.(×)(3)已知a =(-2,-3,1),b =(2,0,4),c =(-4,-6,2),则a ∥c ,a ⊥b .(√)2.空间角(4)两异面直线夹角的范围是⎝ ⎛⎦⎥⎤0,π2,直线与平面所成角的范围是⎣⎢⎡⎦⎥⎤0,π2,二面角的范围是[0,π].(√)(5)已知向量m ,n 分别是直线l 和平面α的方向向量、法向量,若cos<m ,n >=-12,则l 与α所成的角为150°.(×)(6)已知两平面的法向量分别为m =(0,1,0),n =(0,1,1),则两平面所成的二面角的大小为45°.(×)(7)在如图所示的正方体ABCD -A 1B 1C 1D 1中,异面直线A 1B 与B 1C 所成角的大小为60°.(√)剖析:1.利用空间向量求空间角,避免了寻找平面角和垂线段等诸多麻烦,使空间点线面的位置关系的判定和计算程序化、简单化.主要是建系、设点、计算向量的坐标、利用数量积的夹角公式计算.2.两种关系一是异面直线所成的角与其方向向量的夹角:当异面直线的方向向量的夹角为锐角或直角时,就是该异面直线的夹角;否则向量夹角的补角是异面直线所成的角,如(2).二是二面角与法向量的夹角:利用平面的法向量求二面角的大小时,当求出两半平面α,β的法向量n1,n2时,要根据向量坐标在图形中观察法向量的方向,从而确定二面角与向量n1,n2的夹角是相等,还是互补,如(6).。
高三数学第一轮复习课时作业(43)立体几何中的向量方法(二)——空间角与距离求解
课时作业(四十三) 第43讲 立体几何中的向量方法(二)——空间角与距离求解时间:45分钟 分值:100分基础热身1.如图K43-1所示,PD 垂直于正方形ABCD 所在平面,AB =2,E 为PB 的中点,cos 〈,〉=33.若以DA 、DC 、DP 所在直线分别为x 、y 、z 轴建立坐标系,则点E 的坐标为( )A .(1,1,1)B .(2,1,1)C.⎝⎛⎭⎫2,12,12D.⎝⎛⎭⎫1,1,122.若a =(1,2,1),b =(-2,0,1)分别是直线l 1,l 2的方向向量,则l 1,l 2的位置关系是( ) A .平行 B .异面C .相交D .相交或异面3.两平行平面α,β分别经过坐标原点O 和点A (2,1,1),且两平面的一个法向量n =(-1,0,1),则两平面间的距离是( )A.32B.22C. 3 D .3 2 4.方向向量为s =(1,1,1)的直线l 经过点A (1,0,0),则坐标原点O (0,0,0)到该直线的距离是( ) A. 3 B. 2 C.62 D.63能力提升5.如图K43-2,长方体ABCD -A 1B 1C 1D 1中,底面是边长为2的正方形,高为1,则异面直线AD 1和C 1D 所成角的余弦值是( )A.55 B .-55 C.15 D.256.在平行四边形ABCD 中,AB =AC =1,∠ACD =90°,将它沿对角线AC 折起,使AB 和CD 成60°角(如图K43-3),则B 、D 间的距离为( )图K43A .1 B .2 C. 2 D .2或 2 7.2011·河南六市联考 在正方体ABCD -A 1B 1C 1D 1中,E 是A 1B 1的中点,则异面直线AD 1与CE 所成角为( )A.π6B.π4C.π3D.π28.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为棱AA 1、BB 1的中点,G 为棱A 1B 1上的一点,且A 1G =λ(0≤λ≤1),则点G 到平面D 1EF 的距离为( )A. 3B.22 C.2λ3 D.559.如图K43-4,四棱锥P -ABCD 中,底面ABCD 是矩形,PD ⊥平面ABCD ,且PD =AD =1,AB =2,点E 是AB 上一点,当二面角P -EC -D 的平面角为π4时,AE =( )A .1 B.12C .2- 2D .2- 310.已知三棱锥O -ABC 的侧棱OA ,OB ,OC 两两垂直,E 为OC 的中点,且OA =1,OB =OC =2,则平面EAB 与平面ABC 夹角的余弦值是________.11.如图K43-5,已知四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 是边长为a 的正方形,侧棱AA 1长为b ,且AA 1与A 1B 1,A 1D 1的夹角都是60°,则AC 1的长等于________.-5K43-612.如图K43-6,AO ⊥平面α,BC ⊥OB ,BC 与平面α的夹角为30°,AO =BO =BC =a ,则AC =________________________________________________________________________.13.如图K43-7,在空间直角坐标系中有棱长为a 的正方体ABCD -A 1B 1C 1D 1,点M 是线段DC 1上的动点,则点M 到直线AD 1距离的最小值为________.14.(10分)如图K43-8,放置在水平面上的组合体由直三棱柱ABC -A 1B 1C 1与正三棱锥B -ACD 组成,其中,AB ⊥BC .它的主视图、俯视图、左视图的面积分别为22+1,22+1,1.(1)求直线CA 1与平面ACD 所成角的正弦值;(2)在线段AC 1上是否存在点P ,使B 1P ⊥平面ACD ?若存在,确定点P 的位置;若不存在,说明理由.15.(13分)2011·安徽师大附中三模如图K43-9,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.(1)求证:AF∥平面BCE;(2)求证:平面BCE⊥平面CDE;(3)求直线BF和平面BCE所成角的正弦值.难点突破16.(12分)2011·湖北卷如图K43-10,已知正三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.(1)当CF=1时,求证:EF⊥A1C;(2)设二面角C-AF-E的大小为θ,求tanθ的最小值.图K43-10课时作业(四十三)【基础热身】1.A 解析 可知A (2,0,0)、B (2,2,0)、C (0,2,0), 令P (0,0,2m )(m >0),则E (1,1,m ),=(-1,1,m ),=(0,0,2m ),∴cos 〈,〉=2m 21+1+m 2·2m=33,m =1.∴E 的坐标为(1,1,1).2.D 解析 根据共线向量定理,显然a ,b 不平行,所以l 1,l 2的位置关系是相交或异面.3.B 解析 两平面的一个单位法向量n 0=⎝ ⎛⎭⎪⎫-22,0,22,故两平面间的距离d =|·n 0|=22.4.D 解析 直线l 的一个单位法向量s 0=⎝ ⎛⎭⎪⎫33,33,33,向量=(1,0,0),故点O 到直线l 的距离为d =|OA →|2-|OA →·s 0|2=1-⎝⎛⎭⎪⎫332=63.【能力提升】5.C [解析] 建立如图所示的空间直角坐标系.则A (2,0,0),D (0,0,0),D 1(0,0,1),C 1(0,2,1),1=(-2,0,1),=(0,2,1),故异面直线AD 1和C 1D 所成角的余弦值为|cos 〈1,1〉|==15.6.D [解析] ∵∠ACD =90°,∴·=同理·=0,∵AB 和CD 成60°角,∴〈,〉=60°或120°. ∵=++, ∴2=2+2+2+2·+2·+2· =2+2+2+2·=3+2×1×1×cos 〈,〉 =∴||=2或2,即B 、D 间的距离为2或2,故选D.7.D [解析] 建立如图所示的空间直角坐标系,设正方体棱长为1,则有A (0,0,0),D 1(1,0,1),C (1,1,0),E ⎝⎛⎭⎫0,12,1,所以=(1,0,1),=⎝⎛⎭⎫-1,-12,1,∴·=0,即异面直线AD 1与CE 所成角为π2.8.D [解析] 如图,如果过点G 1H ,如果我们能求出向量,那么||就是点G 到平面D 1EF 的距离.在正方体中,建立空间直角坐标系非常方便,因此用坐标的方法,解决这个问题.如图,以射线DA ,DC ,DD 1分别为x ,y ,z 轴的正方向建立空间直角坐标系,则G (1,λ,1),E ⎝⎛⎭⎫1,0,12,=⎝⎛⎭⎫0,-λ,-12,F ⎝⎛⎭⎫1,1,12,=(0,1,0),D 1(0,0,1),1=⎝⎛⎭⎫-1,0,12.过点G 向平面D 1EF 作垂线,垂足为H ,由于点H 在平面D 1EF 内,故存在实数x ,y 使=+x +y 1=⎝⎛⎭⎫-y ,-λ+x ,-12+12y ,由于GH ⊥EF ,GH ⊥ED 1,所以⎩⎨⎧⎝⎛⎭⎫-y ,-λ+x ,-12+12y ·(0,1,0)=0,⎝⎛⎭⎫-y ,-λ+x ,-12+12y ·⎝⎛⎭⎫-1,0,12=0,解得⎩⎪⎨⎪⎧x =λ,y =15,故=⎝⎛⎭⎫-15,0,-25,所以||=55,即点G 到平面D 1EF 的距离是55.9.D [解析] 以D 为原点,射线DA ,DC ,DP 为x ,y ,z 轴正方向建立空间直角坐标系,如图,设E (1,y 0,0)(0≤y 0≤2),则=(-1,2-y 0,0), 设平面PEC 的法向量为n 1=(x ,y ,z ),∴⇒⎩⎨⎧-x +y (2-y 0)=0,2y -z =0⇒x ∶y ∶z =(2-y 0)∶1∶2,记n 1=(2-y 0,1,2),而平面ECD 的法向量n 2=(0,0,1),则二面角P -EC -D 的平面角θ满足cos θ=|cos 〈n 1,n 2〉|=22, ∴cos θ=|n 1·n 2||n 1|·|n 2|=2(2-y 0)2+12+22·122⇒y 0=2- 3.∴当AE =2-3时,二面角P -EC -D 的平面角为π4.10.7618[解析] 以O 为原点,OB ,OC ,OA 分别为x ,y ,z 轴建立空间直角坐标系,则有A (0,0,1),B (2,0,0),C (0,2,0),E (0,1,0).设平面ABC 的法向量为n 1=(x ,y ,z ),则由11n 1⊥知n 1·=2y -z =0,取n 1=(1,1,2).设平面EAB 的法向量为n =(x ,y ,z ),则由n ⊥知n ·=2x -z =0,由n ⊥知n ·=2x -y =0,取n =(1,2,2).则cos 〈n ,n 1〉=n ·n 1|n ||n 1|=1+2+49×6=7618,所以平面EAB 与平面ABC 夹角的余弦值为7618. 11.2a 2+b 2-2ab [解析] 由已知〈1,〉=〈1,〉=120°,〈,〉=90°. |1|2=|1++|2=|1|2+||2+||2+21·+2·+21·=b 2+a 2+a 2-ab -ab =2a 2+b 2-2ab ,故|1|=2a 2+b 2-2ab . 12.2a [解析] =++, 其中〈,〉=〈,〉=90°,〈,〉=120°,故||2=|++|2=||2+||2+||2+2·+2·+2·=3a 2+2a 2cos120°=2a 2,故||=2a ,即AC =2a .13.33a [解析] 设M (0,m ,m )(0≤m ≤a ),=(-a,0,a ),直线AD 1的一个单位方向向量s 0=⎝ ⎛⎭⎪⎫-22,0,22,由=(0,-m ,a -m ),故点M 到直线AD 1的距离d =|MD 1→|2-|MD 1→·s 0|2=m 2+(a -m )2-12(a -m )2=32m 2-am +12a 2,根式内的二次函数当m =--a 2×32=a 3时取最小值32⎝⎛⎫a 32-a ×a 3+12a 2=13a 2,故d 的最小值为33a . 14.[解答] 由已知可得AB ⊥平面BB 1C 1C ,由于三棱锥B -ACD 是正三棱锥,所以CD ⊂平面BB 1C 1C ,D ,B ,B 1三点共线,AB =BC =BD .设AB =a ,BB 1=b .则其主视图和俯视图的面积都是ab +12a 2,左视图的面积是12a 2,根据已知解得a =2,b=2.以点B 为坐标原点,射线BC ,BB 1,BA 分别为x ,y ,z 轴的正方向建立空间直角坐标系,如图,则A (0,0,2),C (2,0,0),D (0,-22,0),A 1(0,2,2). (1)由于三棱锥B -ACD ⎭⎪⎫,23,则BG ⊥平面ACD ,故可取向量n =(1,-1,1)为平面ACD 的一个法向量,=(-2,2,2),故可取v =(1,-2,-1)为直线CA 1的一个方向向量.设直线CA 1与平面ACD 所成角为θ,则sin θ=|cos 〈n ,v 〉|=|n ·v ||n ||v |=223=66.(2)设=m =(2m,2m ,-2m ),则=+=(2m,2m -2,2-2m ),如果B 1P ⊥平面ACD ,则∥n ,即(2m,2m -2,2-2m )=(λ,-λ,λ),由此得方程组⎩⎨⎧2m =λ,①2m -2=-λ,②2-2m =λ,③由①③得m =12,λ=22,代入②则-1=-22,矛盾,这说明不存在满足题目要求的点P .15.[解答] 方法一:(1)证法一:取CE 的中点G ,连接FG 、BG .∵F 为CD 的中点,∴GF ∥DE 且GF =12DE ,∵AB ⊥平面ACD ,DE ⊥平面ACD , ∴AB ∥DE ,∴GF ∥AB .又AB =12DE ,∴GF =AB .又DE =2AB ,∴四边形GFAB 为平行四边形,则AF ∥BG . ∵AF ⊄平面BCE ,BG ⊂平面BCE , ∴AF ∥平面BCE .证法二:取DE 的中点M ,连接AM 、FM , ∵F 为CD 的中点,∴FM ∥CE .∵AB ⊥平面ACD ,DE ⊥平面ACD ,∴DE ∥AB .又AB =12DE =ME ,∴四边形ABEM 为平行四边形,则AM ∥BE . ∵FM 、AM ⊄平面BCE ,CE 、BE ⊂平面BCE , ∴FM ∥平面BCE ,AM ∥平面BCE .又FM ∩AM =M ,∴平面AFM ∥平面BCE . ∵AF ⊂平面AFM , ∴AF ∥平面BCE .(2)证明:∵△ACD 为等边三角形,F 为∴AF ⊥CD .∵DE ⊥平面ACD ,AF ⊂平面ACD ,∴DE ⊥AF . 又CD ∩DE =D ,故AF ⊥平面CDE . ∵BG ∥AF ,∴BG ⊥平面CDE . ∵BG ⊂平面BCE ,∴平面BCE ⊥平面CDE .(3)在平面CDE 内,过F 作FH ⊥CE 于H ,连接BH , ∵平面BCE ⊥平面CDE ,∴FH ⊥平面BCE . ∴∠FBH 为BF 和平面BCE 所成的角. 设AD =DE =2AB =2a ,则FH =CF sin45°=22a , BF =AB 2+AF 2=a 2+(3a )2=2a ,在Rt △FHB 中,sin ∠FBH =FH BF =24. ∴直线BF 和平面BCE 所成角的正弦值为24. 方法二:设AD =DE =2AB =2a ,建立如图所示的坐标系A -xyz ,则A (0,0,0),C (2a,0,0),B (0,0,a ),D (a ,3a,0),E (a ,3a,2a ).∵F 为CD 的中点,∴F ⎝ ⎛⎭⎪⎫32a ,32a ,0.(1)证明:=⎝ ⎛⎭⎪⎫32a ,32a ,0,=(a ,3a ,a ),=(2a,0,-a ),∵=12(+),AF ⊄平面BCE ,∴AF ∥平面BCE .(2)证明:∵=⎝ ⎛⎭⎪⎫32a ,32a ,0,=(-a ,3a,0),=(0,0,-2a ),∴·=0,·=0,∴⊥,⊥.∴⊥平面CDE ,又AF ∥平面BCE , ∴平面BCE ⊥平面CDE .(3)设平面BCE 的法向量为n =(x ,y ,z ),由n ·=0,n ·=0可得x +3y +z =0,2x -z =0,取n =(1,-3,2).又=⎝ ⎛⎭⎪⎫32a ,32a ,-a ,设BF 和平面BCE 所成的角为θ,则sin θ==2a 2a ·22=24.∴直线BF 和平面BCE 所成角的正弦值为24. 【难点突破】16.[解答] 解法1:过E 作EN ⊥AC 于N ,连接EF .(1)如图①,连接NF 、AC 1,由直棱柱的性质知,底面ABC ⊥侧面A 1C ,又底面ABC ∩侧面A 1C =AC ,且EN ⊂底面ABC ,所以EN ⊥侧面A 1C ,NF 为EF 在侧面A 1C 内的射影, 在Rt △CNE 中,CN =CE cos60°=1,则由CF CC 1=CN CA =14,得NF ∥AC 1.又AC 1⊥A 1C ,故NF ⊥A 1C , 由三垂线定理知EF ⊥A 1C .(2)如图②,连接AF ,过N 作NM ⊥AF 于M ,连接ME , 由(1)知EN ⊥侧面A 1C ,根据三垂线定理得EM ⊥AF ,所以∠EMN 是二面角C -AF -E 的平面角,即∠EMN =θ, 设∠FAC =α,则0°<α≤45°.在Rt △CNE 中,NE =EC ·sin60°=3, 在Rt △AMN 中,MN =AN ·sin α=3sin α, 故tan θ=NE MN =33sin α. 又0°<α≤45°,∴0<sin α≤22, 故当sin α=22,即当α=45°时,tan θ达到最小值, tan θ=33×2=63,此时F 与C 1重合.解法2:(1)建立如图③所示的空间直角坐标系,则由已知可得A (0,0,0),B (23,2,0),C (0,4,0),A 1(0,0,4),E (3,3,0),F (0,4,1),于是=(0,-4,4),=(-3,1,1),则·=(0,-4,4)·(-3,1,1)=0-4+4=0,故EF ⊥A 1C .(2)设CF =λ(0<λ≤4),平面AEF 的一个法向量为m =(x ,y ,z ),则由(1)得F (0,4,λ), =(3,3,0),=(0,4,λ),于是由m ⊥,m ⊥可得即⎩⎪⎨⎪⎧3x +3y =0,4y +λz =0,取m =(3λ,-λ,4),又由直三棱柱的性质可取侧面A 1C 的一个法向量为n =(1,0,0),于是由θ为锐角可得cos θ=|m·n||m|·|n|=3λ2λ2+4,sin θ=λ2+162λ2+4,所以tan θ=λ2+163λ=13+163λ2, 由0<λ≤4,得1λ≥14,即tan θ≥13+13=63, 故当λ=4,即点F 与点C 1重合时,tan θ取得最小值63.。
高三数学一轮总复习 第七章 立体几何 7.8 立体几何中的向量方法(二)——求空间角与距离
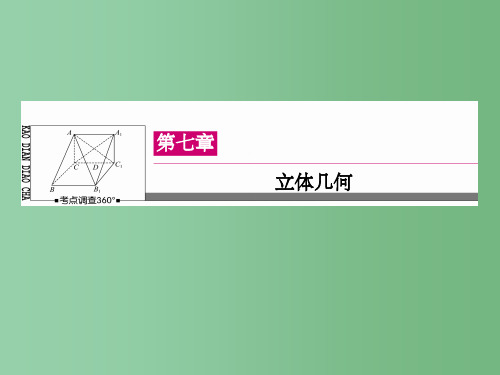
→ DD1
、
→ DC
、
→ DA
分别为z轴、y轴、x轴的正向,
1 2
→ |DD1|为1个单位长度建立空间直角坐标系。
由题设知点E、F、G1、E1的坐标分别为(1,2,1),(0,1,2),(0,0,1),(0,2,1),
→
→
→
∴FE1=(0,1,-1),FG1=(0,-1,-1),EE1=(-1,0,0),
第七章
立体几何
第八节 立体几何中的向量方法(二)——求空间角与距离
课前学案 基础诊断
课堂学案 考点通关
高考模拟 备考套餐
考纲 导学
1.能用空间向量方法解决直线与直线、直线与平面、平面与平面的 夹角的计算问题。 2.了解向量方法在研究立体几何问题中的应用。
课前学案 基础诊断
夯基固本 基础自测
1.空间向量与空间角的关系
4.在正方体A1B1C1D1-ABCD中,E是C1D1的中点,则异面 直线DE与AC夹角的余弦值为( )
A.-
10 10
B.-210
1
10
C.20 D. 10
解析:如图建立直角坐标系D-xyz,设DA=1,A(1,0,0),
C(0,1,0),E
0,21,1
,则
→ AC
=(-1,1,0),
→ DE
=
→→
→→
→→→→
∴FG1·EE1=0,FG1·FE1=0⇒FG1⊥EE1,FG1⊥FE1,∴FG1⊥EE1,FG1⊥FE1。
又∵EE1∩FE1=E1.∴FG1⊥平面FEE1。
(2)求异面直线E1G1与EA所成角的正弦值。
解析:(2)由题意知点A的坐标为(2,0,0),
→
高考数学一轮复习学案 第44讲 立体几何中的向量方法(二)--求空间角(理科专版)(解析版)

第44讲 立体几何中的向量方法(二) ------求空间角(理科专版)(解析版)考 点内容解读要求 常考题型1.立体几何中用向量方法求空间角 理解空间向量求解空间距离与角度的原理,会用向量法求空间角。
Ⅱ 解答题知识要点梳理 1.空间的角(1)异面直线所成的角:如图,已知两条异面直线a 、b ,经过空间任一点O 作直线a ′∥a ,b ′∥b .则把a ′与b ′所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角).(2)平面的一条斜线和它在平面内的射影所成的锐角,叫做这条直线和这个平面所成的角.①直线垂直于平面,则它们所成的角是直角;②直线和平面平行,或在平面内,则它们所成的角是0°的角. (3)二面角的平面角如图在二面角α-l -β的棱上任取一点O ,以点O 为垂足,在半平面α和β内分别作垂直于棱l 的射线OA 和OB ,则∠AOB 叫做二面角的平面角. 2.空间向量与空间角的关系(1)设异面直线l 1,l 2的方向向量分别为m 1,m 2,则l 1与l 2的夹角θ满足cos θ=|cos 〈m 1,m 2〉.(2)设直线l 的方向向量和平面α的法向量分别为m ,n ,则直线l 与平面α的夹角θ满足sin θ=|cos 〈m ,n 〉|. (3)求二面角的大小(ⅰ)如图①,AB 、CD 是二面角α-l -β的两个面内与棱l 垂直的直线,则二面角的大小θ=〈AB →,CD →〉. (ⅱ)如图② ③,n 1,n 2分别是二面角α-l -β的两个半平面α,β的法向量,则二面角的大小θ满足cos θ=cos〈n 1,n 2〉或-cos 〈n 1,n 2〉.考点一 求异面直线所成的角例1:已知ABCD -A 1B 1C 1D 1是底面边长为1的正四棱柱,高AA 1=2,求:(1)异面直线BD 与AB 1所成角的余弦值; (2)四面体AB 1D 1C 的体积.【解析】(1)如图建立空间直角坐标系A 1-xyz ,由已知条件: B (1,0,2),D (0,1,2), A (0,0,2),B 1(1,0,0). 则BD →=(-1,1,0),AB 1→=(1,0,-2) 设异面直线BD 与AB 1所成角为θ, cos θ=|cos 〈BD →,AB 1→〉|=1010.(2)VAB 1D 1C =VABCDA 1B 1C 1D 1-4VCB 1C 1D 1=23.类题通解异面直线所成角范围是(0°,90°],若异面直线a ,b 的方向向量为m ,n ,异面直线a ,b 所成角为θ,则cos θ=|cos 〈m ,n 〉|.解题过程是:(1)建系;(2)求点坐标;(3)表示向量;(4)计算. 变式训练1.已知正方体ABCD -A 1B 1C 1D 1中,E 为C 1D 1的中点,则异面直线AE 与BC 所成角的余弦值为________.【解析】如图建立直角坐标系D -xyz ,设DA =1,由已知条件 A (1,0,0),E ⎝⎛⎭⎫0,12,1, B (1,1,0),C (0,1,0), AE →=⎝⎛⎭⎫-1,12,1,BC →=(-1,0,0) 设异面直线AE 与BC 所成角为θ. cos θ=|cos 〈AE →,BC →〉|=|AE ,→·BC →||AE →||BC →|=23.【答案】 23考点二 利用向量求直线与平面所成的角例2:如图所示,已知点P 在正方体ABCD -A ′B ′C ′D ′的对角线BD ′上,∠PDA =60°.(1)求DP 与CC ′所成角的大小; (2)求DP 与平面AA ′D ′D 所成角的大小.【解析】如图所示,以D 为原点,DA 为单位长度建立空间直角坐标系D -xyz . 则DA →=(1,0,0),CC ′→=(0,0,1).连接BD ,B ′D ′. 在平面BB ′D ′D 中,延长DP 交B ′D ′于H .设DH →=(m ,m ,1)(m >0),由已知〈DH →,DA →〉=60°,即DA →·DH →=|DA →||DH →|cos 〈DH →,DA →〉, 可得2m =2m 2+1. 解得m =22,所以DH →=⎝⎛⎭⎫22,22,1. (1)因为cos 〈DH →,CC ′→〉=22×0+22×0+1×11×2=22,所以〈DH →,CC ′→〉=45°,即DP 与CC ′所成的角为45°. (2)平面AA ′D ′D 的一个法向量是DC →=(0,1,0). 因为cos 〈DH →,DC →〉=22×0+22×1+1×01×2=12,所以〈DH →,DC →〉=60°,可得DP 与平面AA ′D ′D 所成的角为30°. 类题通解(1)异面直线的夹角与向量的夹角有所不同,应注意思考它们的区别与联系.(2)直线与平面的夹角可以转化成直线的方向向量与平面的法向量的夹角,由于向量方向的变化,所以要注意它们的区别与联系. 变式训练1.已知三棱锥P -ABC 中,P A ⊥平面ABC ,AB ⊥AC ,P A =AC =12AB ,N 为AB 上一点,AB =4AN ,M ,S 分别为PB ,BC 的中点. (1)证明:CM ⊥SN ;(2)求SN 与平面CMN 所成角的大小.【解析】设P A =1,以A 为原点,射线AB ,AC ,AP 分别为x ,y ,z 轴正向建立空间直角坐标系如图.则P (0,0,1),C (0,1,0),B (2,0,0),M ⎝⎛⎭⎫1,0,12,N ⎝⎛⎭⎫12,0,0,S ⎝⎛⎭⎫1,12,0.(1)证明:CM →=(1,-1,12),SN →=⎝⎛⎭⎫-12,-12,0, 因为CM →·SN →=-12+12+0=0,所以CM ⊥SN .(2)NC →=⎝⎛⎭⎫-12,1,0, 设a =(x ,y ,z )为平面CMN 的一个法向量,则⎩⎪⎨⎪⎧CM ,→·a =0NC ,→·a =0∴⎩⎨⎧x -y +12z =0,-12x +y =0,取x =2,得a =(2,1,-2).因为|cos 〈a ,SN →〉|=⎪⎪⎪⎪⎪⎪-1-123×22=22,所以SN 与平面CMN 所成角为45°.考点三 利用空间向量求二面角例3:如图,四棱锥P -ABCD 中,底面ABCD 为平行四边形,∠DAB =60°,AB =2AD ,PD ⊥底面ABCD . (1)证明:P A ⊥BD ;(2)若PD =AD ,求二面角A -PB -C 的余弦值.【解析】(1)证明 因为∠DAB =60°,AB =2AD ,由余弦定理得BD =3AD . 从而BD 2+AD 2=AB 2,故BD ⊥AD .又PD ⊥底面ABCD ,可得BD ⊥PD .又AD ∩PD =D . 所以BD ⊥平面P AD .故P A ⊥BD .(2)如图,以D 为坐标原点,AD 的长为单位长,射线DA 为x 轴的正半轴建立空间直角坐标系D -xyz ,则A (1,0,0),B (0,3,0),C (-1,3,0),P (0,0,1). AB →=(-1,3,0),PB →=(0,3,-1),BC →=(-1,0,0).设平面P AB 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·AB ,→=0,n ·PB ,→=0.即⎩⎨⎧-x +3y =0,3y -z =0.因此可取n =(3,1,3).设平面PBC 的法向量为m ,则⎩⎪⎨⎪⎧m ·PB ,→=0,m ·BC ,→=0.可取m =(0,-1,-3),则cos 〈m ,n 〉=-427=-277.故二面角A -PB -C 的余弦值为-277.类题通解求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角是锐角还是钝角. 变式训练1.如图,在四棱锥P -ABCD 中,底面ABCD 是矩形,P A ⊥平面ABCD ,AP =AB =2,BC =22,E ,F 分别是AD ,PC 的中点. (1)证明:PC ⊥平面BEF ;(2)求平面BEF 与平面BAP 夹角的大小.【解析】(1)如图,以A 为坐标原点,AB ,AD ,AP 所在直线分别为x ,y ,z 轴建立空间直角坐标系. ∵AP =AB =2,BC =AD =22,四边形ABCD 是矩形,∴A ,B ,C ,D ,P 的坐标为A (0,0,0),B (2,0,0),C (2,22,0),D (0,22,0),P (0,0,2).又E ,F 分别是AD ,PC 的中点,∴E (0,2,0),F (1,2,1). ∴PC →=(2,22,-2),BF →=(-1,2,1),EF →=(1,0,1). ∴PC →·BF →=-2+4-2=0,PC →·EF →=2+0-2=0. ∴PC →⊥BF →,PC →⊥EF →∴PC ⊥BF ,PC ⊥EF .又BF ∩EF =F , ∴PC ⊥平面BEF .(2)由(1)知平面BEF 的一个法向量n 1=PC →=(2,22,-2),平面BAP 的一个法向量n 2=AD →=(0,22,0),∴n 1·n 2=8. 设平面BEF 与平面BAP 的夹角为θ,则cos θ=|cos 〈n 1,n 2〉|=|n 1·n 2||n 1||n 2|=84×22=22,∴θ=45°.∴平面BEF 与平面BAP 的夹角为45°.1.如果平面的一条斜线与它在这个平面上的射影的方向向量分别是a =(1,0,1),b =(0,1,1),那么,这条斜线与平面所成的角是( ).A .90°B .30°C .45°D .60°【解析】∵cos 〈a ,b 〉=12·2=12,又∵〈a ,b 〉∈[0,π],∴〈a ,b 〉=60°. 【答案】D2.已知两平面的法向量分别为m =(0,1,0),n =(0,1,1),则两平面所成的二面角的大小为( ). A .45° B .135° C .45°或135°D .90°【解析】 cos 〈m ,n 〉=m·n|m ||n |=11×2=22,即〈m ,n 〉=45°,其补角为135°, ∴ 两平面所成的二面角为45°或135°. 【答案】 C3.已知向量m ,n 分别是直线l 和平面α的方向向量、法向量,若cos 〈m ,n 〉=-12,则l 与α所成的角为( ).A .30°B .60°C .120°D .150°【解析】设l 与α所成的角为θ,则sin θ=|cos 〈m ,n 〉|=12,∴θ=30°.【答案】A4.在如图所示的正方体A 1B 1C 1D 1-ABCD 中,E 是C 1D 1的中点,则异面直线DE 与AC 夹角的余弦值为( ). A .-1010 B .-120 C .120 D .1010【解析】如图建立直角坐标系D -xyz ,设DA =1,A (1,0,0),C (0,1,0),E ⎝⎛⎭⎫0,12,1. 则AC →=(-1,1,0),DE →=⎝⎛⎭⎫0,12,1,若异面直线DE 与AC 所成的角为θ, cos θ=|cos 〈AC →,DE →〉|=1010.【答案】D5.如图所示,在三棱柱ABC -A 1B 1C 1中,AA 1⊥底面ABC ,AB =BC =AA 1,∠ABC =90°,点E 、F 分别是棱AB 、BB 1的中点,则直线EF 和BC 1所成的角是________. 【解析】建立如图所示的空间直角坐标系.设AB =BC =AA 1=2,则C 1(2,0,2),E (0,1,0),F (0,0,1) 则EF →=(0,-1,1),BC 1→=(2,0,2),∴EF →·BC 1→=2, ∴ cos 〈EF →,BC 1→〉=22×22=12, ∴ EF 和BC 1所成角为60°. 【答案】 60°6.点M 在z 轴上,它与经过坐标原点且方向向量为s =(1,-1,1)的直线l 的距离为6,则点M 的坐标是( )A .(0,0,±2)B .(0,0,±3)C .(0,0,±3)D .(0,0,±1) 【解析】设M (0,0,z ),直线的一个单位方向向量s 0=⎝⎛⎭⎫33,-33,33,故点M 到直线的距离d =|OM →|2-|OM →·s 0|2=z 2-13z 2=6,解得z =±3.【答案】B7.若a =(1,2,1),b =(-2,0,1)分别是直线l 1,l 2的方向向量,则l 1,l 2的位置关系是( ) A .平行 B .异面 C .相交 D .相交或异面 【解析】根据共线向量定理,显然a ,b 不平行,所以l 1,l 2的位置关系是相交或异面. 【答案】D8.两平行平面α,β分别经过坐标原点O 和点A (2,1,1),且两平面的一个法向量n =(-1,0,1),则两平面间的距离是( )A .32B .22 C .3 D .3 2【解析】 两平面的一个单位法向量n 0=⎝⎛⎭⎫-22,0,22,故两平面间的距离d =|OA →·n 0|=22. 【答案】B9.方向向量为s =(1,1,1)的直线l 经过点A (1,0,0),则坐标原点O (0,0,0)到该直线的距离是( )A. 3 B . 2 C .62 D .63【解析】 直线l 的一个单位法向量s 0=⎝⎛⎭⎫33,33,33,向量OA →=(1,0,0),故点O 到直线l 的距离为d =|OA →|2-|OA →·s 0|2=1-⎝⎛⎭⎫332=63. 【答案】 D10.如图,长方体ABCD -A 1B 1C 1D 1中,底面是边长为2的正方形,高为1,则异面直线AD 1和C 1D 所成角的余弦值是( )A.55 B .-55 C.15 D.25【解析】建立如图所示的空间直角坐标系.则A (2,0,0),D (0,0,0),D 1(0,0,1),C 1(0,2,1),AD →1=(-2,0,1),DC 1→=(0,2,1),故异面直线AD 1和C 1D 所成角的余弦值为|cos 〈AD →1,DC →1〉|=|AD →1·DC →1||AD →1||DC →1|=15.【答案】C11.在平行四边形ABCD 中,AB =AC =1,∠ACD =90°,将它沿对角线AC 折起,使AB 和CD 成60°角(如图),则B 、D 间的距离为( )A .1B .2 C. 2 D .2或 2 【解析】∵∠ACD =90°,∴AC →·CD →=0. 同理BA →·AC →=0,∵AB 和CD 成60°角,∴〈BA →,CD →〉=60°或120°. ∵BD →=BA →+AC →+CD →,∴BD →2=BA →2+AC →2+CD →2+2BA →·CD →+2BA →·AC →+2AC →·CD →=BA →2+AC →2+CD →2+2BA →·CD → =3+2×1×1×cos 〈BA →,CD →〉=⎩⎪⎨⎪⎧4〈BA →,CD →〉=60°,2〈BA →,CD →〉=120°,∴|BD →|=2或2,即B 、D 间的距离为2或2,故选D. 【答案】D12.三棱锥的三条侧棱两两互相垂直,长度分别为6,4,4,则其顶点到底面的距离为( ) A.143 B .217 C.62211 D.2173【解析】设三棱锥为P -ABC ,且P A =6,PB =PC =4,以P 为原点建立空间直角坐标系如图,则P (0,0,0),A (6,0,0),B (0,4,0),C (0,0,4),P A →=(6,0,0),AB →=(-6,4,0),AC →=(-6,0,4),设面ABC 的一个法向量为n =(x ,y ,z ),则n ⊥AB →,n ⊥AC →,所以⎩⎪⎨⎪⎧-6x +4y =0,-6x +4z =0⇒y =z =32x ,所以可选面ABC 的一个法向量为n=(2,3,3),所以P 到面ABC 的距离d =|P A →||cos 〈P A →,n 〉|=|P A →·n ||n |=124+9+9=62211【答案】C13.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为棱AA 1、BB 1的中点,G 为棱A 1B 1上的一点,且A 1G =λ(0≤λ≤1),则点G 到平面D 1EF 的距离为( ) A. 3 B.22 C.2λ3 D.55【解析】如图,如果过点G 直接向平面D 1EF 作垂线,垂足为H ,如果我们能求出向量GH →,那么|GH →|就是点G 到平面D 1EF 的距离.在正方体中,建立空间直角坐标系非常方便,因此用坐标的方法,解决这个问题。
高考数学 考点突破——空间向量与立体几何:立体几何中的向量方法(二)求空间角学案-人教版高三全册数学

立体几何中的向量方法(二)求空间角【考点梳理】1.异面直线所成的角设a ,b 分别是两异面直线l 1,l 2的方向向量,则a 与b 的夹角βl 1与l 2所成的角θ范围(0,π)求法cos β=a ·b|a ||b |cos θ=|cos β|=|a ·b ||a ||b |2.求直线与平面所成的角设直线l 的方向向量为a ,平面α的法向量为n ,直线l 与平面α所成的角为θ,则sinθ=|cos 〈a ,n 〉|=|a ·n ||a ||n |. 3.求二面角的大小(1)如图①,AB ,CD 是二面角α-l -β的两个面内与棱l 垂直的直线,则二面角的大小θ=__〈AB →,CD →〉.(2)如图②③,n 1,n 2 分别是二面角α-l -β的两个半平面α,β的法向量,则二面角的大小θ满足|cos θ|=|cos 〈n 1,n 2〉|,二面角的平面角大小是向量n 1与n 2的夹角(或其补角). 【考点突破】考点一、利用空间向量求异面直线所成的角【例1】在直三棱柱 ABC -A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为( )A .110B .25C .3010D .22[答案] C[解析] 建立如图所示的空间直角坐标系C -xyz ,设BC =2,则B (0,2,0),A (2,0,0),M (1,1,2),N (1,0,2),所以BM →=(1,-1,2),AN →=(-1,0,2),故BM 与AN 所成角θ的余弦值cos θ=|BM →·AN →||BM →|·|AN →|=36×5=3010.【类题通法】1.利用向量法求异面直线所成角的一般步骤是:①选好基底或建立空间直角坐标系;②求出两直线的方向向量v 1,v 2;③代入公式|cos 〈v 1,v 2〉|=|v 1·v 2||v 1||v 2|求解.2.两异面直线所成角的范围是θ∈⎝⎛⎦⎥⎤0,π2,两向量的夹角α的范围是[0,π],当异面直线的方向向量的夹角为锐角或直角时,就是该异面直线的夹角;当异面直线的方向向量的夹角为钝角时,其补角才是异面直线的夹角. 【对点训练】在正方体A 1B 1C 1D 1-ABCD 中,AC 与B 1D 所成的角的大小为( ) A .π6 B .π4 C .π3 D .π2[答案] C[解析] 建立如图所示的空间直角坐标系,设正方体边长为1,则A (0,0,0),C (1,1,0),B 1(1,0,1),D (0,1,0).∴AC →=(1,1,0),B 1D →=(-1,1,-1), ∵AC →·B 1D →=1×(-1)+1×1+0×(-1)=0, ∴AC →⊥B 1D →,∴AC 与B 1D 所成的角为π2.考点二、利用空间向量求直线与平面所成的角【例2】如图,在三棱柱ABC -A 1B 1C 1中,B 1B =B 1A =AB =BC ,∠B 1BC =90°,D 为AC 的中点,AB ⊥B 1D .(1)求证:平面ABB 1A 1⊥平面ABC ;(2)求直线B 1D 与平面ACC 1A 1所成角的正弦值.[解析] (1)取AB 中点为O ,连接OD ,OB 1, ∵B 1B =B 1A ,∴OB 1⊥AB . 又AB ⊥B 1D ,OB 1∩B 1D =B 1, ∴AB ⊥平面B 1OD ,∵OD ⊂平面B 1OD ,∴AB ⊥OD . ∵∠B 1BC =90°,即BC ⊥BB 1,又OD ∥BC ,∴OD ⊥BB 1,又AB ∩BB 1=B , ∴OD ⊥平面ABB 1A 1, 又OD ⊂平面ABC , ∴平面ABC ⊥平面ABB 1A 1.(2)由(1)知,OB ,OD ,OB 1两两垂直.以O 为坐标原点,OB →的方向为x 轴的方向,|OB →|为单位长度1,建立如图所示的空间直角坐标系O -xyz .由题设知B 1(0,0,3),D (0,1,0),A (-1,0,0),C (1,2,0),C 1(0,2,3). 则B 1D →=(0,1,-3),AC →=(2,2,0),CC 1→=(-1,0,3).设平面ACC 1A 1的一个法向量为m =(x ,y ,z ),则由⎩⎪⎨⎪⎧m ·AC →=0,m ·CC 1→=0,得⎩⎨⎧x +y =0,-x +3z =0,取m =(3,-3,1).∴cos 〈B 1D →,m 〉=B 1D →·m|B 1D →||m |=0×3+1×(-3)+(-3)×102+12+(-3)2×(3)2+(-3)2+12=-217, ∴直线B 1D 与平面ACC 1A 1所成角的正弦值为217. 【类题通法】利用向量法求线面角的方法:(1)分别求出斜线和它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角);(2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角或钝角的补角,取其余角就是斜线和平面所成的角. 【对点训练】如图,三棱柱ABC -A 1B 1C 1中,底面ABC 为等腰直角三角形,AB =AC =1,BB 1=2,∠ABB 1=60°.(1)证明:AB ⊥B 1C ;(2)若B 1C =2,求AC 1与平面BCB 1所成角的正弦值.[解析] (1)连接AB 1,在△ABB 1中,AB =1,BB 1=2,∠ABB 1=60°, 由余弦定理得,AB 21=AB 2+BB 21-2AB ·BB 1·cos ∠ABB 1=3, ∴AB 1=3,∴BB 21=AB 2+AB 21, ∴AB 1⊥AB .又△ABC 为等腰直角三角形,且AB =AC , ∴AC ⊥AB ,∵AC ∩AB 1=A , ∴AB ⊥平面AB 1C .又B 1C ⊂平面AB 1C ,∴AB ⊥B 1C .(2)∵AB 1=3,AB =AC =1,B 1C =2, ∴B 1C 2=AB 21+AC 2,∴AB 1⊥AC .如图,以A 为原点,以AB →,AC →,AB 1→的方向分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,则A (0,0,0),B 1(0,0,3),B (1,0,0),C (0,1,0),∴BB 1→=(-1,0,3),BC →=(-1,1,0). 设平面BCB 1的一个法向量为n =(x ,y ,z ),由⎩⎪⎨⎪⎧BB 1→·n =0,BC →·n =0,得⎩⎨⎧-x +3z =0,-x +y =0,令z =1,得x =y =3,∴平面BCB 1的一个法向量为n =(3,3,1).∵AC 1→=AC →+CC 1→=AC →+BB 1→=(0,1,0)+(-1,0,3)=(-1,1,3), ∴cos 〈AC 1→,n 〉=AC 1→·n|AC 1→||n |=35×7=10535,∴AC 1与平面BCB 1所成角的正弦值为10535.考点三、利用空间向量求二面角【例3】如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,平面ABEF 为正方形,AF =2FD ,∠AFD =90°,且二面角D -AF -E 与二面角C -BE -F 都是60°.(1)证明:平面ABEF ⊥平面EFDC ; (2)求二面角E -BC -A 的余弦值.[解析] (1)由已知可得AF ⊥DF ,AF ⊥EF , 所以AF ⊥平面EFDC . 又AF ⊂平面ABEF , 故平面ABEF ⊥平面EFDC .(2)过D 作DG ⊥EF ,垂足为G . 由(1)知DG ⊥平面ABEF .以G 为坐标原点,GF →的方向为x 轴正方向,|GF →|为单位长,建立如图所示的空间直角坐标系G -xyz .由(1)知∠DFE 为二面角D -AF -E 的平面角,故∠DFE =60°,则|DF |=2,|DG |= 3. 可得A (1,4,0),B (-3,4,0),E (-3,0,0),D (0,0,3). 由已知得AB ∥EF ,所以AB ∥平面EFDC . 又平面ABCD ∩平面EFDC =CD , 故AB ∥CD ,CD ∥EF .由BE ∥AF ,可得BE ⊥平面EFDC ,所以∠CEF 为二面角C -BE -F 的平面角,∠CEF =60°. 从而可得C (-2,0,3).所以EC →=(1,0,3),EB →=(0,4,0),AC →=(-3,-4,3),AB →=(-4,0,0). 设n =(x ,y ,z )是平面BCE 的法向量, 则⎩⎪⎨⎪⎧n ·EC →=0,n ·EB →=0,即⎩⎨⎧x +3z =0,4y =0,所以可取n =(3,0,-3).设m 是平面ABCD 的法向量,则⎩⎪⎨⎪⎧m ·AC →=0,m ·AB →=0,同理可取m =(0,3,4).则cos 〈n ,m 〉=n ·m |n ||m |=-21919.故二面角E -BC -A 的余弦值为-21919.【类题通法】利用向量计算二面角大小的常用方法:(1)找法向量法:分别求出二面角的两个半平面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角的大小.(2)找与棱垂直的方向向量法:分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量,则这两个向量的夹角的大小就是二面角的大小. 【对点训练】如图,在四棱锥P ABCD 中,AB ∥CD ,且∠BAP =∠CDP =90°. (1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,∠APD =90°,求二面角A PB C 的余弦值.[解析] (1)由已知∠BAP =∠CDP =90°,得AB ⊥AP ,CD ⊥PD . 因为AB ∥CD ,所以AB ⊥PD . 又AP ∩PD =P ,所以AB ⊥平面PAD . 又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD . (2)在平面PAD 内作PF ⊥AD ,垂足为F . 由(1)可知,AB ⊥平面PAD , 故AB ⊥PF ,又AD ∩AB =A , 可得PF ⊥平面ABCD .以F 为坐标原点,FA ―→的方向为x 轴正方向,|AB ―→|为单位长度,建立如图所示的空间直角坐标系F xyz .由(1)及已知可得A ⎝⎛⎭⎪⎫22,0,0,P ⎝ ⎛⎭⎪⎫0,0,22,B ⎝ ⎛⎭⎪⎫22,1,0,C ⎝ ⎛⎭⎪⎫-22,1,0.所以PC ―→=⎝ ⎛⎭⎪⎫-22,1,-22,CB ―→=(2,0,0),PA ―→=⎝ ⎛⎭⎪⎫22,0,-22,AB ―→=(0,1,0).设n =(x 1,y 1,z 1)是平面PCB 的法向量, 则⎩⎪⎨⎪⎧ n ·PC ―→=0,n ·CB ―→=0,即⎩⎪⎨⎪⎧-22x 1+y 1-22z 1=0,2x 1=0.所以可取n =(0,-1,-2). 设m =(x 2,y 2,z 2)是平面PAB 的法向量, 则⎩⎪⎨⎪⎧m ·PA ―→=0,m ·AB ―→=0,即⎩⎪⎨⎪⎧22x 2-22z 2=0,y 2=0.所以可取m =(1,0,1).则cos 〈n ,m 〉=n ·m |n ||m |=-23×2=-33.由图知二面角A PB C 为钝角, 所以二面角A PB C 的余弦值为-33.。
2019高考数学考点突破——空间向量与立体几何(理科专用):立体几何中的向量方法(二)求空间角

立体几何中的向量方法(二)求空间角【考点梳理】1.异面直线所成的角设a ,b 分别是两异面直线l 1,l 2的方向向量,则设直线l 的方向向量为a ,平面α的法向量为n ,直线l 与平面α所成的角为θ,则sinθ=|cos 〈a ,n 〉|=|a ·n ||a ||n |. 3.求二面角的大小(1)如图①,AB ,CD 是二面角α-l -β的两个面内与棱l 垂直的直线,则二面角的大小θ=__〈AB →,CD →〉.(2)如图②③,n 1,n 2 分别是二面角α-l -β的两个半平面α,β的法向量,则二面角的大小θ满足|cos θ|=|cos 〈n 1,n 2〉|,二面角的平面角大小是向量n 1与n 2的夹角(或其补角).【考点突破】考点一、利用空间向量求异面直线所成的角【例1】在直三棱柱 ABC -A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为( )A .110B .25C .3010D .22[答案] C[解析] 建立如图所示的空间直角坐标系C -xyz ,设BC =2,则B (0,2,0),A (2,0,0),M (1,1,2),N (1,0,2),所以BM →=(1,-1,2),AN →=(-1,0,2),故BM 与AN 所成角θ的余弦值cos θ=|BM →·AN →||BM →|·|AN →|=36×5=3010.【类题通法】1.利用向量法求异面直线所成角的一般步骤是:①选好基底或建立空间直角坐标系;②求出两直线的方向向量v 1,v 2;③代入公式|cos 〈v 1,v 2〉|=|v 1·v 2||v 1||v 2|求解. 2.两异面直线所成角的范围是θ∈⎝ ⎛⎦⎥⎤0,π2,两向量的夹角α的范围是[0,π],当异面直线的方向向量的夹角为锐角或直角时,就是该异面直线的夹角;当异面直线的方向向量的夹角为钝角时,其补角才是异面直线的夹角.【对点训练】在正方体A 1B 1C 1D 1-ABCD 中,AC 与B 1D 所成的角的大小为( )A .π6B .π4C .π3D .π2[答案] C[解析] 建立如图所示的空间直角坐标系,设正方体边长为1,则A (0,0,0),C (1,1,0),B 1(1,0,1),D (0,1,0).∴AC →=(1,1,0),B 1D →=(-1,1,-1),∵AC →·B 1D →=1×(-1)+1×1+0×(-1)=0,∴AC →⊥B 1D →, ∴AC 与B 1D 所成的角为π2.考点二、利用空间向量求直线与平面所成的角【例2】如图,在三棱柱ABC -A 1B 1C 1中,B 1B =B 1A =AB =BC ,∠B 1BC =90°,D 为AC 的中点,AB ⊥B 1D .(1)求证:平面ABB 1A 1⊥平面ABC ;(2)求直线B 1D 与平面ACC 1A 1所成角的正弦值.[解析] (1)取AB 中点为O ,连接OD ,OB 1,∵B 1B =B 1A ,∴OB 1⊥AB .又AB ⊥B 1D ,OB 1∩B 1D =B 1,∴AB ⊥平面B 1OD ,∵OD ⊂平面B 1OD ,∴AB ⊥OD .∵∠B 1BC =90°,即BC ⊥BB 1,又OD ∥BC ,∴OD ⊥BB 1,又AB ∩BB 1=B ,∴OD ⊥平面ABB 1A 1,又OD ⊂平面ABC ,∴平面ABC ⊥平面ABB 1A 1.(2)由(1)知,OB ,OD ,OB 1两两垂直.以O 为坐标原点,OB →的方向为x 轴的方向,|OB →|为单位长度1,建立如图所示的空间直角坐标系O -xyz .由题设知B 1(0,0,3),D (0,1,0),A (-1,0,0),C (1,2,0),C 1(0,2,3). 则B 1D →=(0,1,-3),AC →=(2,2,0),CC 1→=(-1,0,3).设平面ACC 1A 1的一个法向量为m =(x ,y ,z ),则由⎩⎪⎨⎪⎧m ·AC →=0,m ·CC 1→=0,得⎩⎨⎧x +y =0,-x +3z =0,取m =。
高考数学一轮总复习第七章立体几何第八节立体几何中的向量方法二求空间角练习理

高考数学一轮总复习第七章立体几何第八节立体几何中的向量方法二求空间角练习理【最新考纲】 1.能用向量方法解决直线与直线,直线与平面,平面与平面的夹角的计算问题;2.了解向量方法在研究立体几何问题中的应用.1.异面直线所成的角设a ,b 分别是两异面直线l 1,l 2的方向向量,则2.求直线与平面所成的角设直线l 的方向向量为a ,平面α的法向量为n ,直线l 与平面α所成的角为θ,则sin θ=|cos 〈a ,n 〉|=|a·n||a||n|.3.求二面角的大小①若AB 、CD 分别是二面角αlβ的两个面内与棱l 垂直的异面直线,则二面角的大小就是向量AB →与CD →的夹角.②设n 1,n 2分别是二面角αlβ的两个面α,β的法向量,则向量n 1与n 2的夹角(或其补角)的大小就是二面角的平面角的大小(如图②③).1.(质疑夯基)判断下列结论的正误.(正确的打“√”,错误的打“×”) (1)两直线的方向向量所成的角就是两条直线所成的角.( )(2)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角.( ) (3)两个平面的法向量所成的角是这两个平面所成的角.( )(4)两异面直线夹角的范围是⎣⎢⎡⎦⎥⎤0,π2,直线与平面所成角的范围是⎝⎛⎦⎥⎤0,π2,二面角的范围是[0,π].( )答案:(1)× (2)× (3)× (4)×2.已知两平面的法向量分别为m =(0,1,0),n =(0,1,1),则两平面所成的二面角为( )A .45°B .135°C .45°或135°D .90° 解析:cos 〈m ,n 〉=m·n |m||n|=11×2=22,即〈m ,n 〉=45°.∴两平面所成二面角为45°或180°-45°=135°. 答案:C3.(2016·泰安质检)已知向量m ,n 分别是直线l 和平面α的方向向量和法向量,若cos 〈m ,n 〉=-12,则l 与α所成的角为( )A .30°B .60°C .120°D .150°解析:设l 与α所成角为θ,∵cos 〈m ,n 〉=-12,∴sin θ=|cos 〈m ,n 〉|=12,∵0°≤θ≤90°,∴θ=30°.答案:A4.(2014·课标全国Ⅱ卷)在直三棱柱ABCA 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为( )A.110 B.25 C.3010 D.22解析:建立如图所示的空间直角坐标系Cxyz ,设BC =2,则B(0,2,0),A(2,0,0),M(1,1,2),N(1,0,2),所以BM →=(1,-1,2),AN →=(-1,0,2),故BM 与AN 所成角θ的余弦值cos θ=|BM →·AN →||BM →|·|AN →|=36×5=3010.答案:C5.(2016·石家庄模拟)过正方形ABCD 的顶点A 作线段PA⊥平面ABCD ,若AB =PA ,则平面ABP 与平面CDP 所成的二面角为________.解析:如图建立空间直角坐标系,设AB =PA =1,则A(0,0,0),D(0,1,0),P(0,0,1),由题意,AD ⊥平面PAB ,设E 为PD 的中点,连接AE ,则AE⊥PD,又CD⊥平面PAD ,∴CD ⊥AE ,从而AE⊥平面PCD.所以AD →=(0,1,0),AE →=(0,12,12)分别是平面PAB ,平面PCD 的法向量,且〈AD →,AE →〉=45°,故平面PAB 与平面PCD 所成的二面角为45°.答案:45°三个范围1.异面直线所成角的范围是⎝ ⎛⎦⎥⎤0,π2;2.直线与平面所成角的范围是⎣⎢⎡⎦⎥⎤0,π2; 3.二面角的范围是[0,π]. 三种关系1.求两异面直线a ,b 夹角θ,须求出它们的方向向量a ,b 的夹角,则cos θ=|cos 〈a ,b 〉|.2.求直线l 与平面α所成的角θ,可先求出平面α的法向量n 与直线l 的方向向量a 的夹角,则sin θ=|cos 〈n ,a 〉|.3.求二面角αlβ的大小θ,可先求出两个平面的法向量n 1,n 2所成的角,则θ=〈n 1,n 2〉或π-〈n 1,n 2〉.一个易错点利用平面的法向量求二面角的大小时,当求出两个半平面α,β的法向量n 1,n 2时,要根据向量坐标在图形中观察法向量的方向,从而确定二面角与向量n 1,n 2的夹角是相等(一个平面的法向量指向二面角的内部,另一个平面的法向量指向二面角的外部),还是互补(两个法向量同时指向二面角的内部或外部),这是利用向量求二面角的难点、易错点.A 级 基础巩固一、选择题1.(2016·秦皇岛模拟)已知正四棱柱ABCD A 1B 1C 1D 1中,AA 1=2AB ,E 为AA 1的中点,则异面直线BE 与CD 1所成角的余弦值为( )A.1010 B.15 C.31010 D.35解析:以D 为坐标原点,建立空间直角坐标系,如图,设AA 1=2AB =2,则D(0,0,0),C(0,1,0),B(1,1,0),E(1,0,1),D 1(0,0,2).所以BE →=(0,-1,1),CD 1→=(0,-1,2).所以cos 〈BE →,CD 1→〉=BE →·CD 1→|BE →|·|CD 1→|=32×5=31010.答案:C 2.正方体ABCD A 1B 1C 1D 1的棱长为a ,点M 在AC 1上且AM →=12MC 1→,N 为B 1B 的中点,则|MN →|为( )A.216 a B.66a C.156 a D.153a 解析:以D 为原点建立如图所示的空间直角坐标系D xyz ,则A(a ,0,0),C 1(0,a ,a),N(a ,a ,a2).设M(x ,y ,z),∵点M 在AC 1上 且AM →=12MC 1→,(x -a ,y ,z) =12(-x ,a -y ,a -z) ∴x =23a ,y =a 3,z =a 3.得M ⎝ ⎛⎭⎪⎫2a 3,a 3,a 3, ∴|MN →|= ⎝ ⎛⎭⎪⎫a -23a 2+⎝ ⎛⎭⎪⎫a -a 32+⎝ ⎛⎭⎪⎫a 2-a 32=216a. 答案:A 3.在正方体ABCDA 1B 1C 1D 1中,点E 为BB 1的中点,则平面A 1ED 与平面ABCD 所成的锐二面角的余弦值为( )A.12B.23C.33D.22解析:以A 为原点建立如图所示的空间直角坐标系A xyz ,设棱长为1,则A 1(0,0,1),E(1,0,12),D(0,1,0),∴A 1D →=(0,1,-1),A 1E →=(1,0,-12),设平面A 1ED 的一个法向量为n 1=(1,y ,z), 所以有⎩⎪⎨⎪⎧A 1D →·n 1=0,A 1E →·n 1=0,即⎩⎪⎨⎪⎧y -z =0,1-12z =0,解得⎩⎪⎨⎪⎧y =2,z =2.∴n 1=(1,2,2).∵平面ABCD 的一个法向量为n 2=(0,0,1),∴cos 〈n 1,n 2〉=23×1=23.即所成的锐二面角的余弦值为23.答案:B 4.已知三棱柱ABCA 1B 1C 1的侧棱与底面垂直,体积为94,底面是边长为3的正三角形.若P 为底面A 1B 1C 1的中心,则PA 与平面ABC 所成角的大小为( )A.5π12 B.π3 C.π4 D.π6解析:如图所示:S △ABC =12×3×3×sin 60°=334.∴VABC A 1B 1C 1=S △ABC ·OP=334·OP =94,∴OP = 3. 又OA =32×3×23=1,∴tan ∠OAP =OPOA=3, 又0<∠OAP<π2,∴∠OAP =π3.答案:B5.在四面体P-ABC 中,PA ,PB ,PC 两两垂直,设PA =PB =PC =a ,则点P 到平面ABC 的距离为( )A.63 B.33a C.a3D.6a 解析:根据题意,可建立如图所示的空间直角坐标系Pxyz ,则P(0,0,0),A(a ,0,0),B(0,a ,0),C(0,0,a).过点P 作PH⊥平面ABC ,交平面ABC 于点H ,则PH 的长即为点P 到平面ABC 的距离.∵PA =PB =PC ,∴H 为△ABC 的外心.又△ABC 为等边三角形,∴H 为△ABC 的重心,则H ⎝ ⎛⎭⎪⎫a 3,a 3,a 3. ∴PH =⎝ ⎛⎭⎪⎫a 3-02+⎝ ⎛⎭⎪⎫a 3-02+⎝ ⎛⎭⎪⎫a 3-02=33a. ∴点P 到平面ABC 的距离为33a. 答案:B 二、填空题6.(2016·郑州模拟)在长方体ABCD A 1B 1C 1D 1中,AB =2,BC =AA 1=1,则D 1C 1与平面A 1BC 1所成角的正弦值为________.解析:以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,设n =(x ,y ,z)为平面A 1BC 1的法向量.则n·A 1B →=0,n·A 1C 1→=0,即⎩⎪⎨⎪⎧2y -z =0,-x +2y =0,令z =2,则y =1,x =2, 于是n =(2,1,2),D 1C 1→=(0,2,0)设所求线面角为α,则sin α=|cos 〈n ,D 1C 1→〉|=13.答案:137.如图所示,在三棱柱ABCA 1B 1C 1中,AA 1⊥底面ABC ,AB =BC =AA 1,∠ABC =90°,点E 、F 分别是棱AB 、BB 1的中点,则直线EF 和BC 1所成的角是________.解析:以BC 为x 轴,BA 为y 轴,BB 1为z 轴,建立空间直角坐标系.设AB =BC =AA 1=2,则C 1(2,0,2),E(0,1,0),F(0,0,1), 则EF →=(0,-1,1),BC 1→=(2,0,2), ∴EF →·BC 1→=2, ∴cos 〈EF →,BC 1→〉=22×22=12,∴EF 和BC 1所成的角为60°. 答案:60°8.正△ABC 与正△BCD 所在平面垂直,则二面角ABDC 的正弦值为________.解析:取BC 中点O ,连接AO ,DO.建立如图所示坐标系,设BC =1,则A ⎝ ⎛⎭⎪⎫0,0,32,B(0,-12,0), D ⎝⎛⎭⎪⎫32,0,0. ∴OA →=⎝ ⎛⎭⎪⎫0,0,32,BA →=⎝ ⎛⎭⎪⎫0,12,32,BD →=⎝ ⎛⎭⎪⎫32,12,0.设平面ABD 的法向量为n =(x 0,y 0,z 0), 则BA →·n =0,且BD →·n =0, ∴y 02+32z 0=0且32x 0+y 02=0, 解之得y 0-3z 0,且y 0=-3x 0,取x 0=1,得平面ABD 的一个法向量n =(1,-3,1), 由于OA →=⎝ ⎛⎭⎪⎫0,0,32为平面BCD 的一个法向量.∴cos 〈n ,OA →〉=55,∴sin 〈n ,OA →〉=255.答案:255三、解答题9.(2014·广东卷)如图,四边形ABCD 为正方形,PD ⊥平面ABCD ,∠DPC =30°,AF ⊥PC 于点F ,EF ∥CD ,交PD 于点E.(1)证明:CF⊥平面ADF;(2)求二面角D AF E的余弦值.(1)证明:∵ED⊥平面ABCD,AD⊂平面ABCD,∴ED⊥AD.又∵四边形ABCD为正方形,因此AD⊥CD.∵ED∩CD=D,∴AD⊥平面CDEF.由于CF⊂平面CDEF,∴AD⊥CF.又AF⊥CF,AF∩AD=A.故CF⊥平面ADF.(2)解:如图所示,建立空间直角坐标系,点D为坐标原点,设DC=1.由于∠DPC=30°,PD⊥CD,所以PC=2,PD= 3.由于CF⊥FD,FE∥CD,所以DF=32,DE=34,EF =34.从而D ,A ,C ,F ,E 五点的坐标分别为D(0,0,0),A(0,0,1),C(0,1,0),F ⎝ ⎛⎭⎪⎫34,34,0,E(34,0,0). 计算得CF →=⎝ ⎛⎭⎪⎫34,-14,0,FA →=⎝ ⎛⎭⎪⎫-34,-34,1,EF →=⎝ ⎛⎭⎪⎫0,34,0.设平面AEF 的法向量为n 1=(x 1,y 1,z 1), 则n 1⊥EF →,n 1⊥FA →,因此⎩⎨⎧y 1=0,-3x 1-3y 1+4z 1=0,取x 1=4,则n 1=(4,0,3)为平面AEF 的一个法向量. 由于CF⊥平面ADF ,故平面ADF 的一个法向量n 2=(3,-1,0). 由图可见所求二面角θ的余弦值为cos θ=|n 1·n 2||n 1||n 2|=4316+3×(3)2+(-1)2=25719. 10.如图,在直棱柱ABCD-A 1B 1C 1D 1中AD∥BC,∠BAD =90°,AC ⊥BD ,BC =1,AD =AA 1=3.(1)证明:AC⊥B 1D ;(2)求直线B 1C 1与平面ACD 1所成角的正弦值.(1)证明:易知,AB ,AD ,AA 1两两垂直.如图,以A 为坐标原点,AB ,AD ,AA 1所成直线分别为x 轴,y 轴,z 轴建立空间直角坐标系.设AB =t ,则相关各点的坐标为A(0,0,0),B(t ,0,0),B 1(t ,0,3),C(t ,1,0),C 1(t ,1,3),D(0,3,0),D 1(0,3,3).从而B 1D →=(-t ,3,-3),AC →=(t ,1,0),BD →=(-t ,3,0). 因为AC⊥BD,所以AC →·BD →=-t 2+3+0=0, 解得t =3或t =-3(舍去).于是B 1D →=(-3,3,-3),AC →=(3,1,0). 因为AC →·B 1D →=-3+3+0=0, ∴AC →⊥B 1D →,则AC⊥B 1D.(2)解:由(1)知,AD 1→=(0,3,3),AC →=(3,1,0),B 1C 1→=(0,1,0). 设n =(x ,y ,z)是平面ACD 1的一个法向量, 则⎩⎪⎨⎪⎧n ·AC →=0,n ·AD 1→=0,即⎩⎨⎧3x +y =0,3y +3z =0,令x =1,则n =(1,-3,3).设直线B 1C 1与平面ACD 1所成角为θ, 则sin θ=|cos 〈n ,B 1C 1→〉|=⎪⎪⎪⎪⎪⎪⎪⎪n ·B 1C 1→|n|·|B 1C 1→| =37=217.即直线B 1C 1与平面ACD 1所成角的正弦值为217.B 级 能力提升1.(2016·西安调研)如图所示,在空间直角坐标系中有直三棱柱ABC A 1B 1C 1,CA =CC 1=2CB ,则直线BC 1与直线AB 1夹角的余弦值为( )A.55 B.53 C.255 D.35解析:不妨令CB =1,则CA =CC 1=2.可得O(0,0,0),B(0,0,1),C 1(0,2,0),A(2,0,0), B 1(0,2,1),∴BC 1→=(0,2,-1),AB 1→=(-2,2,1),∴cos 〈BC 1→,AB 1→〉=BC 1→·AB 1→|BC 1→||AB 1→|=4-15×9=15=55>0.∴BC 1→与AB 1→的夹角即为直线BC 1与直线AB 1的夹角, ∴直线BC 1与直线AB 1夹角的余弦值为55. 答案:A2.二面角的棱上有A ,B 两点,直线AC ,BD 分别在这个二面角的两个半平面内,且都垂直于AB.已知AB =4,AC =6,BD =8,CD =217,则该二面角的大小为________.解析:∵CD →=CA →+AB →+BD →, ∴|CD →|=(CA →+AB →+BD→)2 =36+16+64+2CA →·BD →=116+2CA →·BD →=217.∴CA →·BD →=|CA →|·|BD →|·cos 〈CA →,BD →〉=-24. ∴cos 〈CA →,BD →〉=-12.又所求二面角与〈CA →,BD →〉互补, ∴所求二面角为60°. 答案:60°3.(2015·广东卷)如图,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC =4,AB =6,BC =3.点E 是CD 边的中点,点F ,G 分别在线段AB ,BC 上,且AF =2FB ,CG =2GB.(1)证明:PE⊥FG; (2)求二面角PADC 的正切值;(3)求直线PA 与直线FG 所成角的余弦值. 解:在△PCD 中,∵E 为CD 的中点,且PC =PD , ∴PE ⊥CD.又∵平面PCD⊥平面ABCD ,且平面PCD∩平面ABCD =CD ,PE ⊂平面PCD , ∴PE ⊥平面ABCD. 取AB 的中点H ,连接EH ,∵四边形ABCD 是长方形,则EH⊥CD.如图所示,以E 为原点,EH ,EC ,EP 所在直线分别为x ,y ,z 轴建立空间直角坐标系.∵PD =PC =4,AB =6,BC =3,AF =2FB ,CG =2GB.∴E(0,0,0),P(0,0,7),F(3,1,0),G(2,3,0),A(3,-3,0),D(0,-3,0),C(0,3,0).(1)证明:∵EP →=(0,0,7),FG →=(-1,2,0), ∴EP →·FG →=(0,0,7)·(-1,2,0)=0, 因此EP →⊥FG →,EP ⊥FG. (2)解:∵PE⊥平面ABCD ,∴平面ABCD 的法向量为EP →=(0,0,7).设平面ADP 的一个法向量为n =(x 1,y 1,z 1),AP →=(-3,3,7),DP →=(0,3,7). 由于⎩⎪⎨⎪⎧AP →·n =0,DP →·n =0,即⎩⎨⎧-3x 1+3y 1+7z 1=0,3y 1+7z 1=0,令z 1=3,则x 1=0,y 1=-7, ∴n =(0,-7,3). 由图可知二面角PADC 是锐角,设为α,则cos α=⎪⎪⎪⎪⎪⎪⎪⎪n ·EP →|n||EP →|=3747=34, ∴sin α=74,tan α=73. (3)解:∵AP →=(-3,3,7),FG →=(-1,2,0),设直线PA 与直线FG 所成角为θ, 则cos θ=⎪⎪⎪⎪⎪⎪⎪⎪AP →·FG →|AP →||FG →|=3+69+9+7×5=9525. ∴直线PA 与FG 所成角的余弦值为9525.立体几何中的高考热点题型1.立体几何是高考的重要内容,每年基本上都是一个解答题,两个选择题或填空题.小题主要考查学生的空间观念,空间想象能力及简单计算能力.解答题主要采用“论证与计算”相结合的模式,即首先是利用定义、定理、公理等证明空间的线线、线面、面面平行或垂直,再利用空间向量进行空间角的计算.重在考查学生的逻辑推理能力及计算能力.热点题型主要有平面图形的翻折、探索性的存在问题等;2.思想方法:(1)转化与化归(空间问题转化为平面问题);(2)数形结合(根据空间位置关系利用向量转化为代数运算).热点1 空间点、线、面位置关系以空间几何体(主要是柱、锥或简单组合体)为载体,通过空间平行、垂直关系的论证命制,主要考查公理4及线、面平行与垂直的判定定理与性质定理,常与平面图形的有关性质及体积的计算等知识交汇考查,考查学生的空间想象能力和推理论证能力以及转化与化归思想,一般以解答题的形式出现,难度中等.(2014·北京卷)如图,在三棱柱ABC A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.(1)求证:平面ABE⊥平面B1BCC1;(2)求证:C1F∥平面ABE;(3)求三棱锥E-ABC的体积.(1)证明:在三棱柱ABC-A1B1C1中,BB1⊥底面ABC.所以BB 1⊥AB.又因为AB⊥BC,所以AB⊥平面B 1BCC 1. 所以平面ABE⊥平面B 1BCC 1.(2)证明:法一 如图1,取AB 中点G ,连接EG ,FG. 因为E ,F 分别是A 1C 1,BC 的中点, 所以FG∥AC,且FG =12AC.因为AC∥A 1C 1,且AC =A 1C 1, 所以FG∥EC 1,且FG =EC 1. 所以四边形FGEC 1为平行四边形. 所以C 1F ∥EG.又因为EG ⊂平面ABE ,C 1F ⊄平面ABE , 所以C 1F ∥平面ABE.法二 如图2,取AC 的中点H ,连接C 1H ,FH. 因为H ,F 分别是AC ,BC 的中点,所以HF∥AB, 又因为E ,H 分别是A 1C 1,AC 的中点, 所以EC 1AH ,所以四边形EAHC 1为平行四边形,所以C 1H ∥AE ,又C 1H ∩HF =H ,AE ∩AB =A , 所以平面ABE∥平面C 1HF , 又C 1F ⊂平面C 1HF , 所以C 1F ∥平面ABE.(3)解:因为AA 1=AC =2,BC =1,AB ⊥BC , 所以AB =AC 2-BC 2= 3. 所以三棱锥E-ABC 的体积V =13S △ABC ·AA 1=13×12×3×1×2=33.1.(1)证明面面垂直,将“面面垂直”问题转化为“线面垂直”问题,再将“线面垂直”问题转化为“线线垂直”问题.(2)证明C 1F ∥平面ABE :①利用判定定理,关键是在平面ABE 中找(作)出直线EG ,且满足C 1F ∥EG.②利用面面平行的性质定理证明线面平行,则先要确定一个平面C 1HF 满足面面平行,实施线面平行、面面平行的转化.2.计算几何体的体积时,能直接用公式时,关键是确定几何体的高,而不能直接用公式时,注意进行体积的转化.【变式训练】 (2015·四川卷)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.(1)请将字母F ,G ,H 标记在正方体相应的顶点处(不需说明理由); (2)判断平面BEG 与平面ACH 的位置关系,并证明你的结论; (3)证明:直线DF⊥平面BEG.(1)解:标出点F 、G 、H 的位置如图所示.(2)解:平面BEG∥平面ACH. 证明如下: 因为ABCDEFGH 为正方体,所以BC∥FG,BC =FG. 又FG∥EH,FG =EH , 所以BC∥EH,BC =EH ,于是四边形BCHE 为平行四边形. 所以BE∥CH.又CH ⊂平面ACH ,BE ⊄平面ACH , 所以BE∥平面ACH. 同理BG∥平面ACH.又BE∩BG=B ,所以平面BEG∥平面ACH. (3)证明:连接FH ,与EG 交于点O ,连接BD. 因为ABCDEFGH 为正方体,所以DH⊥平面EFGH.因为EG ⊂平面EFGH ,所以DH⊥EG.又EG⊥FH,DH ∩FH =H ,所以EG⊥平面BFHD. 又DF ⊂平面BFHD ,所以DF⊥EG. 同理DF⊥BG.又EG∩BG=G ,所以DF⊥平面BEG.热点2 平面图形折叠成空间几何体(真题探源)将平面图形折叠成空间几何体,并以此为载体考查点、线、面间的位置关系及有关几何量的计算是近年高考的热点,考查学生的空间想象能力、知识迁移能力和转化思想.试题以解答题为主要呈现形式,中档难度.(2015·陕西卷)如图①,在直角梯形ABCD 中,AD ∥BC ,∠BAD =π2,AB =BC =1,AD =2,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到△A 1BE 的位置,如图②.(1)证明:CD⊥平面A 1OC ;(2)若平面A 1BE ⊥平面BCDE ,求平面A 1BC 与平面A 1CD 夹角的余弦值.命题立意:本题以翻折问题为背景,主要考查空间点、线、面的位置关系和空间角(二面角)的计算.考查学生的识图、用图的空间想象能力,以及考查学生的运算求解能力和数学推理论证能力,突出考查方程思想和转化化归思想.(1)证明:在题图①中,因为AB =BC =1,AD =2,E 是AD 的中点,∠BAD =π2,所以BE⊥AC.即在题图②中,BE ⊥OA 1,BE ⊥OC , 从而BE⊥平面A 1OC.又CD∥BE,所以CD⊥平面A 1OC. (2)解:由已知,平面A 1BE ⊥平面BCDE , 又由(1)知,BE ⊥OA 1,BE ⊥OC , 所以∠A 1OC 为二面角A 1BEC 的平面角,所以∠A 1OC =π2.如图,以O 为原点,建立空间直角坐标系,因为A 1B =A 1E =BC =ED =1, BC ∥ED , 所以B ⎝⎛⎭⎪⎫22,0,0,E ⎝ ⎛⎭⎪⎫-22,0,0,A 1⎝ ⎛⎭⎪⎫0,0,22,C ⎝ ⎛⎭⎪⎫0,22,0,得BC →=⎝ ⎛⎭⎪⎫-22,22,0,A 1C →=⎝ ⎛⎭⎪⎫0,22,-22,CD →=BE →=(-2,0,0).设平面A 1BC 的法向量n 1=(x 1,y 1,z 1),平面A 1CD 的法向量n 2=(x 2,y 2,z 2),平面A 1BC 与平面A 1CD 的夹角为θ,则⎩⎪⎨⎪⎧n 1·BC →=0,n 1·A 1C →=0,得⎩⎪⎨⎪⎧-x 1+y 1=0,y 1-z 1=0,取n 1=(1,1,1);⎩⎪⎨⎪⎧n 2·CD →=0,n 2·A 1C →=0,得⎩⎪⎨⎪⎧x 2=0,y 2-z 2=0,取n 2=(0,1,1), 从而cos θ=|cos 〈n 1,n 2〉|=23×2=63, 即平面A 1BC 与平面A 1CD 夹角的余弦值为63. 【真题探源】 本题源于人教A 版选修2-1P 119B 组第3题,两题都考查空间角的计算、数学逻辑推理论证和空间想象能力以及教材习题比较,高考真题“增添”平面图形的折叠背景,并将原题的第(1)问“体积计算”变为“线面垂直”的证明,突显数学证明和图形翻折热点内容的考查.求解的关键在于搞清翻折前后图形中线面位置关系和度量关系的变化情况.试题的导向有利于指导中学数学教学,而且有利于高校选拔合格新生.《人教A 版选修2-1》P 119习题B 组第3题: 如图所示,在四棱锥SABCD 中,底面是直角梯形,AB 垂直于AD 和BC ,侧棱SA⊥底面ABCD ,且SA =AB =BC =1,AD =0.5.(1)求四棱锥S ABCD的体积;(2)求平面SCD与平面SAB所成二面角的余弦值.【变式训练】如图,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4,点E,F 分别是AB,CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF.(1)当AG+GC最小时,求证:BD⊥CG;(2)当2V B ADGE=V D GBCF时,求二面角D BG C的平面角的余弦值.(1)证明:∵点E、F分别是AB、CD的中点.∴EF∥BC,又∠ABC=90°,∴AE⊥EF,∵平面AEFD⊥平面EBCF.∴AE⊥平面EBCF,AE⊥EF,AE⊥BE,又BE⊥EF,如图建立空间直角坐标系E-xyz.翻折前,连接AC 交EF 于点G ,此时点G 使得AG +GC 最小,EG =12BC =2,又知EA =EB=2,则A(0,0,2),B(2,0,0),C(2,4,0),D(0,2,2),E(0,0,0),G(0,2,0),∴BD →=(-2,2,2),CG →=(-2,-2,0),∴BD →·CG →=(-2,2,2)·(-2,-2,0)=0,∴BD ⊥CG. (2)解:设EG =k.∵AD ∥平面EFCB ,∴点D 到平面EFCB 的距离即为点A 到平面EFCB 的距离. ∵S 四边形GBCF =12[(3-k)+4]×2=7-k ,∴V D GBCF=13·S 四边形GBCF ·AE =23(7-k). 又V B ADGE=13S 四边形ADGE ·BE =23(2+k), 2V BADGE=V DGBCF,∴43(2+k)=23(7-k),∴k =1,即EG =1.设平面DBG 的法向量为n 1=(x ,y ,z),∵G(0,1,0),∴BG →=(-2,1,0),BD →=(-2,2,2), 则⎩⎪⎨⎪⎧n 1·BD →=0,n 1·BG →=0,即⎩⎪⎨⎪⎧-2x +2y +2z =0-2x +y =0,取x =1,则y =2,z =-1,∴n 1=(1,2,-1). 平面BCG 的一个法向量为n 2=(0,0,1), 则cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=-66.∵所求二面角DBGC 的平面角为锐角,∴此二面角的平面角的余弦值为66. 热点3 立体几何中的探索开放问题此类试题一般以解答题形式呈现,常涉及线、面平行、垂直位置关系的探索或空间角的计算问题,是高考命题的热点,一般有两种考查形式:(1)根据条件作出判断,再进一步论证.(2)利用空间向量,先假设存在点的坐标,再根据条件判断该点的坐标是否存在.(2015·天津高考改编)如图,在四棱柱ABCD A 1B 1C 1D 1中,侧棱A 1A⊥底面ABCD ,AB ⊥AC ,AB =1,AC =AA 1=2,AD =CD =5,且点M 和N 分别为B 1C 和D 1D 的中点.(1)求证:M N∥平面ABCD ; (2)求二面角D 1ACB 1的正弦值;(3)在棱A 1B 1上是否存在点E ,使得直线NE 与平面ABCD 所成角的正弦值为13?若存在,求出线段A 1E 的长;若不存在,请说明理由.解:如图,以A 为原点建立空间直角坐标系,依题意可得A(0,0,0),B(0,1,0),C(2,0,0),D(1,-2,0),A 1(0,0,2),B 1(0,1,2),C 1(2,0,2),D 1(1,-2,2).又因为M ,N 分别为B 1C 和D 1D 的中点,所以M ⎝ ⎛⎭⎪⎫1,12,1,N(1,-2,1).(1)证明:依题意,可得n =(0,0,1)为平面ABCD 的一个法向量,MN →=⎝ ⎛⎭⎪⎫0,-52,0,由此可得MN →·n =0.又因为直线MN ⊄平面ABCD ,所以MN∥平面ABCD.(2)解:AD 1→=(1,-2,2),AC →=(2,0,0),设n 1=(x 1,y 1,z 1)为平面ACD 1的一个法向量,则⎩⎪⎨⎪⎧n 1·AD 1→=0,n 1·AC →=0,即⎩⎪⎨⎪⎧x 1-2y 1+2z 1=0,2x 1=0. 不妨设z 1=1,可得n 1=(0,1,1).设n 2=(x 2,y 2,z 2)为平面ACB 1的一个法向量, 则⎩⎪⎨⎪⎧n 2·AB 1→=0,n 2·AC →=0.又AB 1→=(0,1,2),所以⎩⎪⎨⎪⎧y 2+2z 2=0,2x 2=0,不妨设z 2=1,可得n 2=(0,-2,1). 因此有cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=-1010,于是sin 〈n 1,n 2〉=31010,所以,二面角D 1ACB 1的正弦值为31010.(3)解:假设存在点E ,使得NE 与平面ABCD 所成角的正弦值为13.依题意,可设A 1E →=λA 1B 1→,其中λ∈[0,1],则E(0,λ,2), 从而NE →=(-1,λ+2,1).又n =(0,0,1)为平面ABCD 的一个法向量,由已知,得 |cos 〈NE →,n 〉|=|NE →·n||NE →||n|=1(-1)2+(λ+2)2+12=13, 整理得λ2+4λ-3=0,解得λ=-2±7. 又因为λ∈[0,1],所以λ=7-2.因此,存在点E 满足题设条件,且线段A 1E =7-2.1.对于存在判断型问题的求解,应先假设存在,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等.2.对于位置探究型问题,通常借助向量,引进参数,综合已知和结论列出等式,解出参数.【变式训练】(2016·河北保定调研)如图,在三棱柱ABC A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.(1)求证:AA1⊥平面ABC;(2)求二面角A1-BC1-B1的余弦值;(3)在线段BC1上是否存在点D,使得AD⊥A1B?若存在,试求出BDBC1的值.(1)证明:在正方形AA1C1C中,A1A⊥AC.又平面ABC⊥平面AA1C1C,且平面ABC∩平面AA1C1C=AC,∴AA1⊥平面ABC.(2)解:由(1)知AA1⊥AC,AA1⊥AB,由题意知,在△ABC中,AC=4,AB=3,BC=5,∴BC2=AC2+AB2,∴AB⊥AC.∴以A为坐标原点,建立如图所示空间直角坐标系A-xyz.A 1(0,0,4),B(0,3,0),C 1(4,0,4),B 1(0,3,4),于是A 1C 1→=(4,0,0),A 1B →=(0,3,-4),B 1C 1→=(4,-3,0),BB 1→=(0,0,4). 设平面A 1BC 1的法向量n 1=(x 1,y 1,z 1),平面B 1BC 1的法向量n 2=(x 2,y 2,z 2). ∴⎩⎪⎨⎪⎧A 1C 1→·n 1=0,A 1B →·n 1=0⇒⎩⎪⎨⎪⎧4x 1=0,3y 1-4z 1=0,∴取向量n 1=(0,4,3). 由⎩⎪⎨⎪⎧B 1C 1→·n 2=0,BB 1→·n 2=0⇒⎩⎪⎨⎪⎧4x 2-3y 2=0,4z 2=0.取向量n 2=(3,4,0) ∴cos θ=n 1·n 2|n 1||n 2|=165×5=1625.由题图可判断二面角A 1BC 1B 1为锐角,故二面角A 1BC 1B 1的余弦值为1625.(3)解:假设存在点D(x ,y ,z)是线段BC 1上一点, 使AD⊥A 1B ,且BD →=λBC 1→.∴(x ,y -3,z)=λ(4,-3,4), 解得x =4λ,y =3-3λ,z =4λ, ∴AD →=(4λ,3-3λ,4λ),又AD⊥A 1B ,∴0+3(3-3λ)-16λ=0,解得λ=925,因为925∈[0,1],所以在线段BC 1上存在点D ,使得AD⊥A 1B ,此时BD BC 1=925. 热点4 空间向量在几何体中的应用(多维探究)在高考中主要考查通过建立恰当的空间直角坐标系,利用空间向量的坐标运算证明空间中的线、面的平行与垂直关系,计算空间角(特别是二面角),常与空间几何体的结构特征,空间线、面位置关系的判定定理与性质定理等知识综合,以解答题形式出现,难度中等.角度一 线线角、线面角的计算1.(2016·上饶模拟)(1)如图所示,已知三棱柱ABCA 1B 1C 1的所有棱长都相等,且AA 1⊥面ABC ,M 是侧棱CC 1的中点,则异面直线AB 1和BM 所成的角的大小是________.(2)已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.①证明:BN ⊥平面C 1B 1N.②设直线C 1N 与平面CNB 1所成的角为θ,求cos θ的值.解:(1)不妨设三棱柱ABC-A 1B 1C 1的棱长为2,以BA →,BC →,BB 1→作为基向量. 由于AA 1⊥平面ABC , 所以BB 1→·BA →=0,BB 1→·BC →=0. ∵AB 1→=BB 1→-BA →,BM →=BC →+12BB 1→,∴AB 1→·BM →=(BB 1→-BA →)·(BC →+12BB 1→)=0+12BB 1→2-BA →·BC →=2-|BA →|·|BC →|·cos 60°=2-2=0. 因此,AB 1→⊥BM →,则直线AB 1与BM 成90°的角. 答案:90°(2)①证明:该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则BA ,BC ,BB 1两两垂直.以BA ,BB 1,BC 分别为x ,y ,z 轴建立空间直角坐标系,则N(4,4,0),B 1(0,8,0),C 1(0,8,4),C(0,0,4), 因为BN →·NB 1→=0,BN →·B 1C 1→=0,所以BN⊥NB 1,且BN⊥B 1C 1,又因为B 1N ∩B 1C 1=B 1, 所以BN ⊥平面B 1NC 1.②解:设n =(x 0,y 0,z 0)为平面CNB 1的一个法向量, 则⎩⎪⎨⎪⎧n ·CN →=0,n ·NB 1→=0即⎩⎪⎨⎪⎧x 0+y 0-z 0=0,x 0-y 0=0,令x 0=1,则n =(1,1,2). 又C 1N →=(4,-4,-4),则sin θ=|cos 〈n ,C 1N →〉|=23,从而cos θ=73.1.第(1)题利用空间向量的线性运算,关键是选择好基底,第(2)题利用垂直关系,建立空间直角坐标系,运用向量的坐标运算,其关键是写对点的坐标.2.解决与折叠有关的问题的关键是搞清折叠前后的变化量和不变量.一般情况下,长度是不变量,而位置关系往往会发生变化.角度二 二面角的计算2.(2015·重庆卷)如图,三棱锥P-ABC 中,PC ⊥平面ABC ,PC =3,∠ACB =π2.D ,E分别为线段AB ,BC 上的点,且CD =DE =2,CE =2EB =2.(1)证明:DE⊥平面PCD ; (2)求二面角A-PD-C 的余弦值.(1)证明:由PC⊥平面ABC ,DE ⊂平面ABC , 得PC⊥DE.由CE =2,CD =DE =2得△CDE 为等腰直角三角形, 故CD⊥DE.由PC∩CD=C ,DE 垂直于平面PCD 内两条相交直线,故DE⊥平面PCD.(2)解:由(1)知,△CDE 为等腰直角三角形,∠DCE =π4. 如图,过D 作DF 垂直CE 于F ,易知DF =FC =FE =1.又已知EB =1,故FB =2. 由∠ACB=π2,得DF∥AC,∴DF AC =FB BC =23, 故AC =32DF =32.以C 为坐标原点,分别以CA →,CB →,CP →的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,则C(0,0,0),P(0,0,3),A(32,0,0),E(0,2,0),D(1,1,0),ED →=(1,-1,0),DP →=(-1,-1,3),DA →=(12,-1,0).设平面PAD 的法向量为n 1=(x 1,y 1,z 1), 由n 1·DP →=0,n 1·DA →=0, 得⎩⎪⎨⎪⎧-x 1-y 1+3z 1=0,12x 1-y 1=0,取n 1=(2,1,1).由(1)可知DE⊥平面PCD ,故平面PCD 的法向量n 2可取为ED →,即n 2=(1,-1,0), 从而法向量n 1,n 2的夹角的余弦值为 cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=36,故所求二面角A-PD-C 的余弦值为36.1.本题主要考查数学推理论证能力,利用空间向量进行数学运算能力,同时考查化归转化的数学思想.2.求二面角APDC 的余弦值,转化为求两个半平面所在平面的法向量.通过两个平面的法向量的夹角求得二面角的大小,但要注意结合实际图形判断所求角的大小.角度三 根据空间角的大小求相关量3.(2014·课标全国Ⅱ卷)如图,四棱锥P-ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(1)证明:PB∥平面AEC.(2)设二面角D-AE-C 为60°,AP =1,AD =3,求三棱锥E ACD 的体积.(1)证明:连接BD 交AC 于点O ,连接EO. 因为ABCD 为矩形,所以O 为BD 的中点. 又E 为PD 的中点, 所以EO∥PB,又EO ⊂平面AEC ,PB ⊄平面AEC.所以PB∥平面AEC.(2)解:因为PA⊥平面ABCD ,ABCD 为矩形,所以AB ,AD ,AP 两两垂直. 如图,以A 为坐标原点,AB →的方向为x 轴的正方向,建立空间直角坐标系A-xyz ,则D(0,3,0),E ⎝ ⎛⎭⎪⎫0,32,12,AE →=⎝⎛⎭⎪⎫0,32,12. 设B(m ,0,0)(m>0),则C(m ,3,0),AC →=(m ,3,0). 设n 1=(x ,y ,z)为平面ACE 的法向量,则⎩⎪⎨⎪⎧n 1·AC →=0,n 1·AE →=0,即⎩⎪⎨⎪⎧mx +3y =0,32y +12z =0,可取n 1=⎝⎛⎭⎪⎫3m ,-1,3. 又n 2=(1,0,0)为平面DAE 的法向量, 由题设|cos 〈n 1,n 2〉|=12,即33+4m 2=12,解得m =32. 因为E 为PD 的中点,所以三棱锥E-ACD 的高为12.三棱锥E-ACD 的体积V =13×12×3×32×12=38.建立恰当的空间直角坐标系,将两平面的法向量用与待求相关的参数(字母)表示,利用两向量的夹角公式构建方程或不等式或函数,进而求解.【变式训练】 (2015·江苏卷)如图,在四棱锥PABCD 中,已知PA⊥平面ABCD ,且四边形ABCD 为直角梯形,∠ABC =∠BAD=π2,PA =AD =2,AB =BC =1.(1)求平面PAB 与平面PCD 所成二面角的余弦值;(2)点Q 是线段BP 上的动点,当直线CQ 与DP 所成的角最小时,求线段BQ 的长. 解:以{AB →,AD →,AP →}为正交基底建立如图所示的空间直角坐标系A-xyz ,则各点的坐标为B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2).(1)由题意知,AD ⊥平面PAB ,所以AD →=(0,2,0)是平面PAB 的一个法向量. 因为PC →=(1,1,-2),PD →=(0,2,-2). 设平面PCD 的法向量为m =(x ,y ,z), 则m·PC →=0,m·PD →=0,即⎩⎪⎨⎪⎧x +y -2z =0,2y -2z =0.令y =1,解得z =1,x =1. 所以m =(1,1,1)是平面PCD 的一个法向量. 从而cos 〈AD →,m 〉=AD →·m |AD →||m|=33,所以平面PAB 与平面PCD 所成二面角的余弦值为33. (2)因为BP →=(-1,0,2),设BQ →=λBP →=(-λ,0,2λ)(0≤λ≤1),又CB →=(0,-1,0),则CQ →=CB →+BQ →=(-λ,-1,2λ). 又DP →=(0,-2,2),从而cos 〈CQ →,DP →〉=CQ →·DP →|CQ →|·|DP →|=1+2λ10λ2+2. 设1+2λ=t ,t ∈[1,3].则cos 2〈CQ →,DP →〉=2t 25t 2-10t +9=29⎝ ⎛⎭⎪⎫1t -592+209≤910.当且仅当t =95,即λ=25时,|cos 〈CQ →,DP →〉|的最大值为31010.因为y =cos x 在⎝⎛⎭⎪⎫0,π2上是减函数,所以此时直线CQ 与DP 所成角取得最小值. 又因为BP =12+22=5, 所以BQ =25BP =255.1.如图所示,已知直三棱柱ABC-A 1B 1C 1中,△ABC 为等腰直角三角形,∠BAC =90°,且AB =AA 1,D ,E ,F 分别为B 1A ,C 1C ,BC 的中点.求证:(1)DE∥平面ABC ; (2)B 1F ⊥平面AEF.证明:(1)如图建立空间直角坐标系A-xyz ,令AB =AA 1=4,则A(0,0,0),E(0,4,2),F(2,2,0),B(4,0,0),B 1(4,0,4).取AB 中点为N ,连接CN , 则N(2,0,0),C(0,4,0), D(2,0,2),∴DE →=(-2,4,0),NC →=(-2,4,0), ∴DE →=NC →,∴DE ∥NC ,又∵NC ⊂平面ABC ,DE ⊄平面ABC. 故DE∥平面ABC.(2)B 1F →=(-2,2,-4),EF →=(2,-2,-2), AF →=(2,2,0).B 1F →·EF →=(-2)×2+2×(-2)+(-4)×(-2)=0, B 1F →·AF →=(-2)×2+2×2+(-4)×0=0. ∴B 1F →⊥EF →,B 1F →⊥AF →,即B 1F ⊥EF ,B 1F ⊥AF , 又∵AF∩FE=F ,∴B 1F ⊥平面AEF.2.(2016·西安质检)如图所示,在长方体ABCD-A 1B 1C 1D 1中,AB =λAD=λAA′(λ>0),E ,F 分别是A′C′和AD 的中点,且EF⊥平面A′BCD′.(1)求λ的值;(2)求二面角C-A ′B-E 的余弦值.解:以D 为原点,DA ,DC ,DD ′分别为x ,y ,z 轴建立空间直角坐标系.设AA′=AD =2,则AB =2λ,D(0,0,0),A ′(2,0,2),D ′(0,0,2),B(2,2λ,0),C(0,2λ,0),E(1,λ,2),F(1,0,0).(1)EF →=(0,-λ,-2),D ′A ′→=(2,0,0),A ′B →=(0,2λ,-2), ∵EF ⊥D ′A ′,EF ⊥A ′B , ∴EF →·D ′A ′→=0,EF →·A ′B →=0, 即-2λ2+4=0,∴λ= 2.(2)设平面EA′B 的一个法向量为m =(1,y ,z), 则⎩⎪⎨⎪⎧m ·A′B →=0m ·A′E →=0∵A ′B →=(0,22,-2),A ′E →=(-1,2,0),∴⎩⎨⎧22y -2z =0,-1+2y =0.∴y =22,z =1,∴m =⎝ ⎛⎭⎪⎫1,22,1.由已知,EF →=(0,-2,-2)是平面A′BCD′的一个法向量. ∴cos 〈m ,EF →〉=m ·EF →|m|·|EF →|=0-1-252×6=-155.又二面角C-A ′B-E 为锐二面角, 故二面角C-A ′B-E 的余弦值为155. 3.(2015·课标全国Ⅰ卷)如图,四边形ABCD 为菱形,∠ABC =120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE =2DF ,AE ⊥EC.(1)证明:平面AEC⊥平面AFC ;(2)求直线AE 与直线CF 所成角的余弦值. (1)证明:如图所示,连接BD ,设BD∩AC=G ,连接EG ,FG ,EF.在菱形ABCD 中,不妨设GB =1. 由∠ABC=120°,可得AG =GC = 3. 由BE⊥平面ABCD ,AB =BC ,可知AE =EC. 又AE⊥EC,所以EG =3,且EG⊥AC. 在Rt △EBG 中,可得BE =2,故DF =22. 在Rt △FDG 中,可得FG =62. 在直角梯形BDFE 中,由BD =2,BE =2,DF =22, 得EF =322.从而EG 2+FG 2=EF 2,所以EG⊥FG. 又AC∩FG=G ,所以EG⊥平面AFC.因为EG ⊂平面AEC ,所以平面AEC⊥平面AFC.(2)解:如图,以G 为坐标原点,分别以GB →,GC →的方向为x 轴,y 轴正方向,|GB →|为单位长度,建立空间直角坐标系Gxyz.由(1)可得A(0,-3,0),E(1,0,2),F ⎝ ⎛⎭⎪⎫-1,0,22,C(0,3,0), 所以AE →=(1,3,2),CF →=⎝ ⎛⎭⎪⎫-1,-3,22.故cos 〈AE →,CF →〉=AE →·CF →|AE →||CF →|=-33.所以直线AE 与直线CF 所成角的余弦值为33. 4.(2015·济南质检)如图,在四棱锥PABCD 中,PA ⊥平面ABCD ,AC ⊥AD ,AB ⊥BC ,∠BAC =45°,PA =AD =2,AC =1.(1)证明:PC⊥AD;(2)求二面角APCD 的正弦值;(3)设E 为棱PA 上的点,满足异面直线BE 与CD 所成的角为30°,求AE 的长. (1)证明:如图,以点A 为原点建立空间直角坐标系,依题意,得A(0,0,0),D(2,0,0),C(0,1,0),B ⎝ ⎛⎭⎪⎫-12,12,0,P(0,0,2). 易得PC →=(0,1,-2),AD →=(2,0,0),于是PC →·AD →=0,所以PC⊥AD. (2)解:PC →=(0,1,-2),CD →=(2,-1,0). 设平面PCD 的法向量n =(x ,y ,z),则⎩⎪⎨⎪⎧n ·PC →=0,n ·CD →=0,即⎩⎪⎨⎪⎧y -2z =0,2x -y =0.不妨令z =1,可得n =(1,2,1). 可取平面PAC 的法向量m =(1,0,0). 于是cos 〈m ,n 〉=m·n |m||n|=16=66,从而sin 〈m ,n 〉=306, 所以二面角APCD 的正弦值为306. (3)解:设点E 的坐标为(0,0,h),其中h∈[0,2]. 由此得BE →=⎝ ⎛⎭⎪⎫12,-12,h .由CD →=(2,-1,0), 故cos 〈BE →,CD →〉=BE →·CD →|BE →||CD →|=310+20h 2所以310+20h2=cos 30°=32, 解得h =1010,即AE =1010. 5.已知四棱锥P-ABCD 的底面ABCD 是矩形,PA ⊥平面ABCD ,AD =2,AB =1,E 、F 分别是线段AB 、BC 的中点.(1)求证:PF⊥FD;(2)在PA 上找一点G ,使得EG∥平面PFD ;(3)若PB 与平面ABCD 所成的角为45°,求二面角A-PD-F 的余弦值. (1)证明:建立如图所示的空间直角坐标系A-xyz ,则A(0,0,0),B(1,0,0),F(1,1,0),D(0,2,0), 不妨令P(0,0,t),t>0.∵PF →=(1,1,-t),DF →=(1,-1,0), ∴PF →·DF →=1×1+1×(-1)+(-t)×0=0. ∴PF ⊥FD.(2)解:设平面PFD 的法向量为n =(x ,y ,z), 由⎩⎪⎨⎪⎧n ·PF →=0,n ·DF →=0.得⎩⎪⎨⎪⎧x +y -tz =0x -y =0,则⎩⎪⎨⎪⎧tz =2x ,y =x.取z =1,则n =⎝ ⎛⎭⎪⎫t 2,t 2,1. 设G(0,0,m),∵E(12,0,0),∴EG →=(-12,0,m),由题意EG →·n =0,∴-t 4+m =0,∴m =14t ,∴当G 是线段PA 的靠近于A 的一个四等分点时,使得EG∥平面PFD. (3)解:∵PA⊥平面ABCD ,∴∠PBA 就是PB 与平面ABCD 所成的角, 即∠PBA=45°,∴PA =AB =1,P(0,0,1), 由(2)知平面PFD 的一个法向量为n =(12,12,1).易知平面PAD 的一个法向量为AB →=(1,0,0), ∴cos 〈AB →,n 〉=AB →·n |AB →||n|=1214+14+1=66. 由图知,二面角A-PD-F 的平面角为锐角,所以,二面角A-PD-F 的余弦值为66. 6.(2015·湖南卷)如图,已知四棱台ABCDA 1B 1C 1D 1的上、下底面分别是边长为3和6的正方形,A 1A =6,且A 1A ⊥底面ABCD ,点P ,Q 分别在棱DD 1,BC 上.(1)若P 是DD 1的中点,证明:AB 1⊥PQ ;(2)若PQ∥平面ABB 1A 1,二面角P-QD-A 的余弦值为37,求四面体ADPQ 的体积.解:由题设知,AA 1,AB ,AD 两两垂直,以A 为坐标原点,AB ,AD ,AA 1所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则相关各点的坐标为A(0,0,0),B 1(3,0,6),D(0,6,0),D 1(0,3,6),Q(6,m ,0),其中m =BQ ,0≤m ≤6.(1)证明:若P 是DD 1的中点,则P(0,92,3),PQ →=(6,m -92,-3).又AB 1→=(3,0,6),于是AB 1→·PQ →=18-18=0, 所以AB 1→⊥PQ →,即AB 1⊥PQ.(2)解:由题设知,DQ →=(6,m -6,0),DD 1→=(0,-3,6)是平面PQD 内的两个不共线向量.设n 1=(x ,y ,z)是平面PQD 的一个法向量, 则⎩⎪⎨⎪⎧n 1·DQ →=0,n 1·DD 1→=0,即⎩⎪⎨⎪⎧6x +(m -6)y =0,-3y +6z =0.取y =6,得n 1=(6-m ,6,3).又平面AQD 的一个法向量是n 2=(0,0,1), 所以cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=3(6-m )2+62+32·1=3(6-m )2+45. 而二面角P-QD-A 的余弦值为37.因此3(6-m )2+45=37, 解得m =4或m =8(舍去),此时Q(6,4,0).设DP →=λDD 1→(0<λ≤1),而DD 1→=(0,-3,6),由此得点P(0,6-3λ,6λ),所以PQ →=(6,3λ-2,-6λ). 因为PQ∥平面ABB 1A 1,且平面ABB 1A 1的一个法向量是n 3=(0,1,0), 所以PQ →·n 3=0,即3λ-2=0,亦即λ=23,从而P(0,4,4).于是,将四面体ADPQ 视为以△ADQ 为底面的三棱锥P-ADQ ,则其高h =4, 故四面体ADPQ 的体积V =13S △ADQ ·h =13×12×6×6×4=24.。
高考数学考点突破——空间向量与立体几何(理科专用):立体几何中的向量方法(二)求空间角

立体几何中的向量方法(二)求空间角【考点梳理】1.异面直线所成的角设a ,b 分别是两异面直线l 1,l 2的方向向量,则设直线l 的方向向量为a ,平面α的法向量为n ,直线l 与平面α所成的角为θ,则sin θ=|cos 〈a ,n 〉|=|a ·n ||a ||n |.3.求二面角的大小(1)如图①,AB ,CD 是二面角α-l -β的两个面内与棱l 垂直的直线,则二面角的大小θ=__〈AB →,CD →〉.(2)如图②③,n 1,n 2 分别是二面角α-l -β的两个半平面α,β的法向量,则二面角的大小θ满足|cos θ|=|cos 〈n 1,n 2〉|,二面角的平面角大小是向量n 1与n 2的夹角(或其补角). 【考点突破】考点一、利用空间向量求异面直线所成的角【例1】在直三棱柱 ABC -A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为( )A .110B .25C .3010D .22[答案] C[解析] 建立如图所示的空间直角坐标系C -xyz ,设BC =2,则B (0,2,0),A (2,0,0),M (1,1,2),N (1,0,2),所以BM →=(1,-1,2),AN →=(-1,0,2),故BM 与AN 所成角θ的余弦值cos θ=|BM →·AN →||BM →|·|AN →|=36×5=3010.【类题通法】1.利用向量法求异面直线所成角的一般步骤是:①选好基底或建立空间直角坐标系;②求出两直线的方向向量v 1,v 2;③代入公式|cos 〈v 1,v 2〉|=|v 1·v 2||v 1||v 2|求解.2.两异面直线所成角的范围是θ∈⎝⎛⎦⎥⎤0,π2,两向量的夹角α的范围是[0,π],当异面直线的方向向量的夹角为锐角或直角时,就是该异面直线的夹角;当异面直线的方向向量的夹角为钝角时,其补角才是异面直线的夹角. 【对点训练】在正方体A 1B 1C 1D 1-ABCD 中,AC 与B 1D 所成的角的大小为( ) A .π6 B .π4 C .π3 D .π2[答案] C[解析] 建立如图所示的空间直角坐标系,设正方体边长为1,则A (0,0,0),C (1,1,0),B 1(1,0,1),D (0,1,0).∴AC →=(1,1,0),B 1D →=(-1,1,-1), ∵AC →·B 1D →=1×(-1)+1×1+0×(-1)=0, ∴AC →⊥B 1D →,∴AC 与B 1D 所成的角为π2.考点二、利用空间向量求直线与平面所成的角【例2】如图,在三棱柱ABC -A 1B 1C 1中,B 1B =B 1A =AB =BC ,∠B 1BC =90°,D 为AC 的中点,AB ⊥B 1D .(1)求证:平面ABB 1A 1⊥平面ABC ;(2)求直线B 1D 与平面ACC 1A 1所成角的正弦值.[解析] (1)取AB 中点为O ,连接OD ,OB 1, ∵B 1B =B 1A ,∴OB 1⊥AB . 又AB ⊥B 1D ,OB 1∩B 1D =B 1, ∴AB ⊥平面B 1OD ,∵OD ⊂平面B 1OD ,∴AB ⊥OD . ∵∠B 1BC =90°,即BC ⊥BB 1,又OD ∥BC ,∴OD ⊥BB 1,又AB ∩BB 1=B , ∴OD ⊥平面ABB 1A 1, 又OD ⊂平面ABC , ∴平面ABC ⊥平面ABB 1A 1.(2)由(1)知,OB ,OD ,OB 1两两垂直.以O 为坐标原点,OB →的方向为x 轴的方向,|OB →|为单位长度1,建立如图所示的空间直角坐标系O -xyz .由题设知B 1(0,0,3),D (0,1,0),A (-1,0,0),C (1,2,0),C 1(0,2,3). 则B 1D →=(0,1,-3),AC →=(2,2,0),CC 1→=(-1,0,3).设平面ACC 1A 1的一个法向量为m =(x ,y ,z ),则由⎩⎪⎨⎪⎧m ·AC →=0,m ·CC 1→=0,得⎩⎨⎧x +y =0,-x +3z =0,取m =(3,-3,1).∴cos 〈B 1D →,m 〉=B 1D →·m|B 1D →||m |=0×3+1×(-3)+(-3)×102+12+(-3)2×(3)2+(-3)2+12=-217, ∴直线B 1D 与平面ACC 1A 1所成角的正弦值为217. 【类题通法】利用向量法求线面角的方法:(1)分别求出斜线和它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角);(2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角或钝角的补角,取其余角就是斜线和平面所成的角. 【对点训练】如图,三棱柱ABC -A 1B 1C 1中,底面ABC 为等腰直角三角形,AB =AC =1,BB 1=2,∠ABB 1=60°.(1)证明:AB ⊥B 1C ;(2)若B 1C =2,求AC 1与平面BCB 1所成角的正弦值.[解析] (1)连接AB 1,在△ABB 1中,AB =1,BB 1=2,∠ABB 1=60°, 由余弦定理得,AB 21=AB 2+BB 21-2AB ·BB 1·cos ∠ABB 1=3, ∴AB 1=3,∴BB 21=AB 2+AB 21, ∴AB 1⊥AB .又△ABC 为等腰直角三角形,且AB =AC , ∴AC ⊥AB ,∵AC ∩AB 1=A , ∴AB ⊥平面AB 1C .又B 1C ⊂平面AB 1C ,∴AB ⊥B 1C .(2)∵AB 1=3,AB =AC =1,B 1C =2, ∴B 1C 2=AB 21+AC 2,∴AB 1⊥AC .如图,以A 为原点,以AB →,AC →,AB 1→的方向分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,则A (0,0,0),B 1(0,0,3),B (1,0,0),C (0,1,0),∴BB 1→=(-1,0,3),BC →=(-1,1,0). 设平面BCB 1的一个法向量为n =(x ,y ,z ),由⎩⎪⎨⎪⎧BB 1→·n =0,BC →·n =0,得⎩⎨⎧-x +3z =0,-x +y =0,令z =1,得x =y =3,∴平面BCB 1的一个法向量为n =(3,3,1).∵AC 1→=AC →+CC 1→=AC →+BB 1→=(0,1,0)+(-1,0,3)=(-1,1,3), ∴cos 〈AC 1→,n 〉=AC 1→·n|AC 1→||n |=35×7=10535,∴AC 1与平面BCB 1所成角的正弦值为10535.考点三、利用空间向量求二面角【例3】如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,平面ABEF 为正方形,AF =2FD ,∠AFD =90°,且二面角D -AF -E 与二面角C -BE -F 都是60°.(1)证明:平面ABEF ⊥平面EFDC ; (2)求二面角E -BC -A 的余弦值.[解析] (1)由已知可得AF ⊥DF ,AF ⊥EF , 所以AF ⊥平面EFDC . 又AF ⊂平面ABEF , 故平面ABEF ⊥平面EFDC .(2)过D 作DG ⊥EF ,垂足为G . 由(1)知DG ⊥平面ABEF .以G 为坐标原点,GF →的方向为x 轴正方向,|GF →|为单位长,建立如图所示的空间直角坐标系G -xyz .由(1)知∠DFE 为二面角D -AF -E 的平面角,故∠DFE =60°,则|DF |=2,|DG |= 3. 可得A (1,4,0),B (-3,4,0),E (-3,0,0),D (0,0,3). 由已知得AB ∥EF ,所以AB ∥平面EFDC . 又平面ABCD ∩平面EFDC =CD , 故AB ∥CD ,CD ∥EF .由BE ∥AF ,可得BE ⊥平面EFDC ,所以∠CEF 为二面角C -BE -F 的平面角,∠CEF =60°. 从而可得C (-2,0,3).所以EC →=(1,0,3),EB →=(0,4,0),AC →=(-3,-4,3),AB →=(-4,0,0). 设n =(x ,y ,z )是平面BCE 的法向量, 则⎩⎪⎨⎪⎧n ·EC →=0,n ·EB →=0,即⎩⎨⎧x +3z =0,4y =0,所以可取n =(3,0,-3).设m 是平面ABCD 的法向量,则⎩⎪⎨⎪⎧m ·AC →=0,m ·AB →=0,同理可取m =(0,3,4).则cos 〈n ,m 〉=n ·m |n ||m |=-21919.故二面角E -BC -A 的余弦值为-21919.【类题通法】利用向量计算二面角大小的常用方法:(1)找法向量法:分别求出二面角的两个半平面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角的大小.(2)找与棱垂直的方向向量法:分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量,则这两个向量的夹角的大小就是二面角的大小. 【对点训练】如图,在四棱锥P ABCD 中,AB ∥CD ,且∠BAP =∠CDP =90°. (1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,∠APD =90°,求二面角A PB C 的余弦值.[解析] (1)由已知∠BAP =∠CDP =90°, 得AB ⊥AP ,CD ⊥PD . 因为AB ∥CD ,所以AB ⊥PD . 又AP ∩PD =P ,所以AB ⊥平面PAD . 又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD . (2)在平面PAD 内作PF ⊥AD ,垂足为F . 由(1)可知,AB ⊥平面PAD , 故AB ⊥PF ,又AD ∩AB =A , 可得PF ⊥平面ABCD .以F 为坐标原点,FA ―→的方向为x 轴正方向,|AB ―→|为单位长度,建立如图所示的空间直角坐标系F xyz .由(1)及已知可得A ⎝ ⎛⎭⎪⎫22,0,0,P ⎝ ⎛⎭⎪⎫0,0,22,B ⎝ ⎛⎭⎪⎫22,1,0,C ⎝ ⎛⎭⎪⎫-22,1,0.所以PC ―→=⎝ ⎛⎭⎪⎫-22,1,-22,CB ―→=(2,0,0),PA ―→=⎝ ⎛⎭⎪⎫22,0,-22,AB ―→=(0,1,0).设n =(x 1,y 1,z 1)是平面PCB 的法向量, 则⎩⎪⎨⎪⎧ n ·PC ―→=0,n ·CB ―→=0,即⎩⎪⎨⎪⎧-22x 1+y 1-22z 1=0,2x 1=0.所以可取n =(0,-1,-2). 设m =(x 2,y 2,z 2)是平面PAB 的法向量, 则⎩⎪⎨⎪⎧m ·PA ―→=0,m ·AB ―→=0,即⎩⎪⎨⎪⎧22x 2-22z 2=0,y 2=0.所以可取m =(1,0,1).则cos 〈n ,m 〉=n ·m |n ||m |=-23×2=-33.由图知二面角A PB C 为钝角, 所以二面角A PB C 的余弦值为-33.。
高考数学大一轮复习 第八章 立体几何与空间向量 第8讲 立体几何中的向量方法(二)——求空间角试题

中的向量方法(二)——求空间角试题理新人教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018版高考数学大一轮复习第八章立体几何与空间向量第8讲立体几何中的向量方法(二)——求空间角试题理新人教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018版高考数学大一轮复习第八章立体几何与空间向量第8讲立体几何中的向量方法(二)——求空间角试题理新人教版的全部内容。
几何中的向量方法(二)——求空间角试题理新人教版基础巩固题组(建议用时:40分钟)一、选择题1.(2016·长沙模拟)在正方体A1B1C1D1-ABCD中,AC与B1D所成的角的大小为( )A。
错误!B。
错误! C.错误! D.错误!解析建立如图所示的空间直角坐标系,设正方体边长为1,则A(0,0,0),C(1,1,0),B(1,0,1),D(0,1,0)。
1∴错误!=(1,1,0),错误!=(-1,1,-1),∵错误!·错误!=1×(-1)+1×1+0×(-1)=0,∴错误!⊥错误!,∴AC与B1D所成的角为错误!。
答案D2。
(2017·郑州调研)在正方体ABCD-A1B1C1D1中,BB1与平面ACD1所成角的正弦值为( )A。
错误! B.错误! C.错误! D.错误!解析设正方体的棱长为1,以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,如图所示。
则B(1,1,0),B1(1,1,1),A(1,0,0),C(0,1,0),D(0,0,1),1所以错误!=(0,0,1),错误!=(-1,1,0),错误!=(-1,0,1)。
高考数学总复习 第七篇 立体几何与空间向量(必修2、选修2-1)第7节 立体几何中的向量方法(第二课

第二课时求空间角与距离【选题明细表】知识点、方法题号向量法求异面直线所成的角4,9向量法求直线和平面所成的角2,5,11,12,13向量法求二面角1,6,7,10,14向量法求空间距离3,8基础巩固(建议用时:25分钟)1.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角为( C )(A)45°(B)135°(C)45°或135°(D)90°解析:cos<m,n>===,即<m,n>=45°.所以两平面所成二面角为45°或135°.2.设直线l与平面α相交,且l的方向向量为a,平面α的法向量为n,若<a,n>=,则l与α所成的角为(C)(A)(B)(C)(D)解析:线面角的X围是[0,].因为<a,n>=π,所以l与平面α的法向量所在直线所成角为,所以l与α所成的角为.故选C.3.已知平面α的一个法向量为n=(-2,-2,1),点A(-1,3,0)在平面α内,则点P(-2,1,4)到平面α的距离为( D )(A)10 (B)3 (C) (D)解析:点P到平面α的距离d===.4.在棱长为1的正方体ABCD A1B1C1D1中,M,N分别为A1B1,BB1的中点,那么直线AM与所成角的余弦值等于( D )(A)(B)(C)(D)解析:建立如图所示的空间直角坐标系,则A(1,0,0),M(1,,1),C(0,1,0),N(1,1,),所以=(1,0,),=(0,,1).故cos<,>===.故直线AM与所成角的余弦值等于.故选D.5.如图,正三棱柱ABC-A1B1C1的所有棱长都相等,E,F,G分别为AB,AA1,A1C1的中点,则B1F与平面GEF所成角的正弦值为( A )(A)(B)(C)(D)解析:设正三棱柱的棱长为2,取AC的中点D,连接DG,DB,分别以DA,DB,DG所在的直线为x轴、y轴、z轴建立空间直角坐标系,如图所示,则B1(0,,2),F(1,0,1),E(,,0),G(0,0,2),=(1,-,-1),=(,-,1),=(1,0,-1).设平面GEF的法向量为n=(x,y,z),则即取x=1,则z=1,y=,故n=(1,,1)为平面GEF的一个法向量,所以cos<n,>==-,所以B1F与平面GEF所成角的正弦值为.故选A.6.在正方体ABCD A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为( B )(A)(B)(C)(D)解析:以A为原点建立如图所示的空间直角坐标系Axyz,设棱长为1,则A1(0,0,1),E(1,0,),D(0,1,0),所以=(0,1,-1),=(1,0,-),设平面A1ED的一个法向量为n1=(x,y,z),则即令x=1,则所以n1=(1,2,2).又平面ABCD的一个法向量为n2=(0,0,1),所以cos<n1,n2>==.即平面A1ED与平面ABCD所成的锐二面角的余弦值为.故选B.7.如图所示,已知点P为菱形A B C D外一点,且P A⊥平面A B C D,PA=AD=AC,点F为PC的中点,则二面角C-BF-D的正切值为.解析:如图所示,连接BD,AC∩BD=O,连接OF.以O为原点,OB,OC,OF所在直线分别为x轴、y轴、z轴建立空间直角坐标系Oxyz.设PA=AD=AC=1,则BD=.所以B(,0,0),F(0,0,),C(0,,0),D(-,0,0).结合图形可知,=(0,,0)且为平面BOF的一个法向量,由=(-,,0),=(,0,-),可求得面BCF的一个法向量为n=(1,,).所以cos<n,>=,sin<n,>=,所以tan<n,>=.答案:8.已知正方体ABCD-A1B1C1D1的棱长为2,E,F,G分别是CC1,D1A1,AB的中点,则点A到平面EFG的距离等于.解析:如图,建立空间直角坐标系Dxyz,则A(2,0,0),E(0,2,1),F(1,0,2),G(2,1,0).所以=(1,-2,1),=(2,-1,-1),=(0,-1,0).设n=(x,y,z)是平面EFG的一个法向量,则由n⊥,n⊥,得即解得x=y=z.令x=1,得n=(1,1,1).因为在n方向上的投影为==,所以点A到平面EFG的距离为.答案:能力提升(建议用时:25分钟)9.如图所示,在空间直角坐标系中有直三棱柱ABC A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( A )(A)(B)(C)(D)解析:不妨令CB=1,则CA=CC1=2.可得O(0,0,0),B(0,0,1),C1(0,2,0),A(2,0,0),B1(0,2,1),所以=(0,2,-1),=(-2,2,1),所以cos<,>===>0.所以与的夹角即为直线BC1与直线AB1的夹角,所以直线BC1与直线AB1夹角的余弦值为.故选A.10.在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2.若二面角B1-DC-C1的大小为60°,则AD的长为( A )(A)(B)(C)2 (D)解析:如图,以C为坐标原点,CA,CB,CC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则C(0,0,0),A(1,0,0),B1(0,2,2),C1(0,0,2).设AD=a,则D点坐标为(1,0,a),=(1,0,a),=(0,2,2).设平面B1CD的法向量为m=(x,y,z).由得令z=-1,则m=(a,1,-1).又平面C1DC的一个法向量为n=(0,1,0),则由 cos 60°=,得=,解得a=,所以AD=.故选A.11.如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=2,CF=3.若直线FO与平面BED所成的角为45°,则AE=.解析:如图,以O为原点,以OA,OB所在直线分别为x轴、y轴,以过点O且平行于CF的直线为z轴建立空间直角坐标系.设AE=a,则B(0,,0),D(0,-,0),F(-1,0,3),E(1,0,a),所以=(-1,0,3),=(0,2,0),=(-1,,-a).设平面BED的法向量为n=(x,y,z),则即则y=0,令z=1,得x=-a,所以n=(-a,0,1),所以cos<n,>==.因为直线FO与平面BED所成角的大小为45°,所以=,解得a=2或a=-(舍去),所以AE=2.答案:212.如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ABC=∠BAD=90°,且PA=AB=BC=AD=1,PA⊥平面ABCD.(1)求PB与平面PCD所成角的正弦值;(2)棱PD上是否存在一点E满足∠AEC=90°?若存在,求AE的长;若不存在,说明理由.解:(1)依题意,以A为坐标原点,分别以AB,AD,AP为x,y,z轴建立空间直角坐标系Axyz,则P(0,0,1),B(1,0,0),C(1,1,0),D(0,2,0),从而=(1,0,-1),=(1,1,-1),=(0,2,-1),设平面PCD的法向量为n=(a,b,c),则n·=0,且n·=0,即a+b-c=0,且2b-c=0,不妨取c=2,则b=1,a=1,所以平面PCD的一个法向量为n=(1,1,2),此时cos<,n>==-,所以PB与平面PCD所成角的正弦值为.(2)设=λ(0≤λ≤1),则E(0,2λ,1-λ),则=(-1,2λ-1,1-λ),=(0,2λ,1-λ),由∠AEC=90°,得·=2λ(2λ-1)+(1-λ)2=0,化简得,5λ2-4λ+1=0,该方程无解,所以,棱PD上不存在一点E满足∠AEC=90°.13.(2018·某某瓦房店一模)如图,已知AB⊥BC,BE∥CD,∠DCB=90°,平面BCDE⊥平面ABC,AB=BC=BE=2,CD=4,F为AD的中点.(1)证明:EF⊥平面ACD;(2)求直线CE与平面ABD所成角的余弦值.(1)证明:设AC的中点为G,连接FG,BG,因为F为AD的中点,所以FG∥DC,FG=DC,又由题意BE∥CD,BE=CD,所以EB∥FG,且EB=FG,所以四边形BEFG为平行四边形,所以EF∥BG.因为∠DCB=90°,所以DC⊥BC,又因为平面BCDE⊥平面ABC,平面BCDE∩平面ABC=BC,DC⊂平面BCDE,所以DC⊥平面ABC.又BG⊂平面ABC,所以DC⊥BG,所以DC⊥EF.又AB=BC,AG=CG,所以AC⊥BG,所以AC⊥EF.因为AC∩DC=C,AC⊂平面ACD,DC⊂平面ACD,所以EF⊥平面ACD.(2)解:以点B为原点,以BA方向为x轴,以BC方向为y轴,以BE方向为z轴,建立如图所示坐标系,B(0,0,0),E(0,0,2),A(2,0,0),C(0,2,0),D(0,2,4),设平面ABD的法向量为n=(x,y,z),则所以取z=1,得n=(0,-2,1),=(0,-2,2),所以cos<,n>===,设直线CE与平面ABD所成角为θ,则sin θ=,所以cos θ=,即直线CE与平面ABD所成角的余弦值为.14.(2018·某某九校联考)如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.(1)求二面角B-PD-A的大小;(2)在线段PD上是否存在一点M,使得CM⊥PA?若存在,求出PM的长;若不存在,说明理由. 解:(1)因为梯形ABCD中,AD∥BC,AD⊥AB,所以BC⊥AB,因为PB⊥平面ABCD,所以PB⊥AB,PB⊥BC,如图,以B为原点,B C,B A,B P所在直线为x,y,z轴建立空间直角坐标系,所以C(1,0,0),D(3,3,0),A(0,3,0),P(0,0,3).设平面BPD的一个法向量为n=(x,y,z),平面APD的一个法向量为m=(a,b,c),因为=(3,3,-3),=(0,0,3),所以即取x=1,得n=(1,-1,0),同理可得m=(0,1,1),所以cos<n,m>==-,因为二面角B PD A为锐角,所以二面角B PD A为.(2)假设存在点M,设=λ=(3λ,3λ,-3λ), 所以=+=(-1+3λ,3λ,3-3λ),因为=(0,3,-3),所以·=9λ-3(3-3λ)=0,解得λ=,所以存在点M,且PM=PD=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
开卷速查(四十七) 立体几何中的向量方法(二)——求空间角与距离A级基础巩固练1.[2014·陕西]四面体ABCD及其三视图如图所示,过棱AB的中点E作平行于AD,BC 的平面分别交四面体的棱BD,DC,CA于点F,G,H.(1)证明:四边形EFGH是矩形;(2)求直线AB与平面EFGH夹角θ的正弦值.解析:(1)由该四面体的三视图可知,BD⊥DC,BD⊥AD,AD⊥DC,BD=DC=2,AD=1.由题设,BC∥平面EFGH,平面EFGH∩平面BDC=FG,平面EFGH∩平面ABC=EH,∴BC∥FG,BC∥EH,∴FG∥EH.同理EF∥AD,HG∥AD,∴EF∥HG,∴四边形EFGH是平行四边形.又∵AD⊥DC,AD⊥BD,∴AD⊥平面BDC,∴AD⊥BC,∴EF⊥FG,∴四边形EFGH是矩形.(2)如图,以D为坐标原点建立空间直角坐标系,则D(0,0,0),A(0,0,1),B(2,0,0),C(0,2,0),DA→=(0,0,1),BC→=(-2,2,0),BA→=(-2,0,1).设平面EFGH的法向量n=(x,y,z),∵EF∥AD,FG∥BC,∴n·DA →=0,n ·BC →=0,得⎩⎪⎨⎪⎧z =0,-2x +2y =0,取n =(1,1,0),∴sin θ=||cos 〈BA →,n 〉=⎪⎪⎪⎪⎪⎪⎪⎪BA →·n |BA →||n |=25×2=105. 2.[2014·天津]如图,在四棱锥P -ABCD 中,PA ⊥底面ABCD ,AD ⊥AB ,AB ∥DC ,AD =DC =AP =2,AB =1,点E 为棱PC 的中点.(1)证明:BE ⊥DC ;(2)求直线BE 与平面PBD 所成角的正弦值;(3)若F 为棱PC 上一点,满足BF ⊥AC ,求二面角F -AB -P 的余弦值.解析:方法一:依题意,以点A 为原点建立空间直角坐标系(如下图),可得B (1,0,0),C (2,2,0),D (0,2,0),P (0,0,2).由E 为棱PC 的中点,得E (1,1,1).(1)向量BE →=(0,1,1),DC →=(2,0,0),故BE →·DC →=0. 所以,BE ⊥DC .(2)向量BD →=(-1,2,0),PB →=(1,0,-2). 设n =(x ,y ,z )为平面PBD 的法向量. 则⎩⎪⎨⎪⎧n ·BD →=0,n ·PB →=0,即⎩⎪⎨⎪⎧-x +2y =0,x -2z =0.不妨令y =1,可得n =(2,1,1)为平面PBD 的一个法向量,于是有cos 〈n ,BE →〉=n ·BE →|n |·|BE →|=26×2=33.所以,直线BE 与平面PBD 所成角的正弦值为33. (3)向量BC →=(1,2,0),CP →=(-2,-2,2),AC →=(2,2,0),AB →=(1,0,0).由点F 在棱PC 上,设CF →=λCP →,0≤λ≤1.故BF →=BC →+CF →=BC →+λCP →=(1-2λ,2-2λ,2λ).由BF ⊥AC ,得BF →·AC →=0,因此,2(1-2λ)+2(2-2λ)=0,解得λ=34.即BF →=(-12,12,32).设n 1=(x ,y ,z )为平面FAB 的法向量,则⎩⎪⎨⎪⎧n 1·AB →=0,n 1·BF →=0,即⎩⎪⎨⎪⎧x =0,-12x +12y +32z =0.不妨令z =1,可得n 1=(0,-3,1)为平面FAB 的一个法向量.取平面ABP 的法向量n 2=(0,1,0),则cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=-310×1=-31010.易知,二面角F -AB -P 是锐角,所以其余弦值为31010.方法二:(1)如图,取PD 中点M ,连接EM ,AM .由于E ,M 分别为PC ,PD 的中点,故EM ∥DC ,且EM =12DC ,又由已知,可得EM ∥AB 且EM =AB ,故四边形ABEM 为平行四边形,所以BE ∥AM .因为PA ⊥底面ABCD ,故PA ⊥CD ,而CD ⊥DA ,从而CD ⊥平面PAD ,因为AM ⊂平面PAD ,于是CD ⊥AM ,又BE ∥AM ,所以BE ⊥CD .(2)连接BM ,由(1)有CD ⊥平面PAD ,得CD ⊥PD ,而EM ∥CD ,故PD ⊥EM ,又因为AD =AP ,M 为PD 的中点,故PD ⊥AM ,可得PD ⊥BE ,所以PD ⊥平面BEM ,故平面BEM ⊥平面PBD .所以,直线BE 在平面PBD 内的射影为直线BM ,而BE ⊥EM ,可得∠EBM 为锐角,故∠EBM 为直线BE 与平面PBD 所成的角.依题意,有PD =22,而M 为PD 中点,可得AM =2,进而BE = 2.故在直角三角形BEM 中,tan ∠EBM =EM BE =AB BE =12,因此sin ∠EBM =33.所以,直线BE 与平面PBD 所成角的正弦值为33. (3)如图,在△PAC 中,过点F 作FH ∥PA 交AC 于点H .因为PA ⊥底面ABCD ,故FH ⊥底面ABCD ,从而FH ⊥AC .又BF ⊥AC ,得AC ⊥平面FHB ,因此AC ⊥BH .在底面ABCD 内,可得CH =3HA ,从而CF =3FP .在平面PDC 内,作FG ∥DC 交PD 于点G ,于是DG =3GP .由于DC ∥AB ,故GF ∥AB ,所以A ,B ,F ,G 四点共面.由AB ⊥PA ,AB ⊥AD ,得AB ⊥平面PAD ,故AB ⊥AG .所以∠PAG 为二面角F-AB -P 的平面角.在△PAG 中,PA =2,PG =14PD =22,∠APG =45°,由余弦定理可得AG =102,cos ∠PAG=31010. 所以,二面角F -AB -P 的余弦值为31010.B 级 能力提升练3.如图是多面体ABC -A 1B 1C 1和它的三视图.(1)线段CC 1上是否存在一点E ,使BE ⊥平面A 1CC 1?若不存在,请说明理由,若存在,请找出并证明;(2)求平面C 1A 1C 与平面A 1CA 夹角的余弦值.解析:(1)由题意知AA 1,AB ,AC 两两垂直,建立如图所示的空间直角坐标系,则A (0,0,0),A 1(0,0,2),B (-2,0,0),C (0,-2,0),C 1(-1,-1,2),则CC 1→=(-1,1,2),A 1C 1→=(-1,-1,0),A 1C →=(0,-2,-2).设E (x ,y ,z ),则CE →=(x ,y +2,z ),EC 1→=(-1-x ,-1-y,2-z ).设CE →=λEC 1→,则⎩⎪⎨⎪⎧x =-λ-λx ,y +2=-λ-λy ,z =2λ-λz ,则E ⎝⎛⎭⎪⎫-λ1+λ,-2-λ1+λ,2λ1+λ,BE →=⎝ ⎛⎭⎪⎫2+λ1+λ,-2-λ1+λ,2λ1+λ.由⎩⎪⎨⎪⎧BE →·A 1C 1→=0,BE →·A 1C →=0,得⎩⎪⎨⎪⎧-2+λ1+λ+2+λ1+λ=0,-2-λ1+λ+2λ1+λ=0,解得λ=2,所以线段CC 1上存在一点E ,CE →=2EC 1→,使BE ⊥平面A 1CC 1. (2)设平面C 1A 1C 的法向量为m =(x ,y ,z ), 则由⎩⎪⎨⎪⎧m ·A 1C 1→=0,m ·A 1C →=0,得⎩⎪⎨⎪⎧-x -y =0,-2y -2z =0.取x =1,则y =-1,z =1.故m =(1,-1,1),而平面A 1CA 的一个法向量为n =(1,0,0),则cos 〈m ,n 〉=m·n |m ||n |=13=33,故平面C 1A 1C 与平面A 1CA 夹角的余弦值为33.4.如图,三棱柱ABC -A 1B 1C 1的侧棱AA 1⊥底面ABC ,∠ACB =90°,E 是棱CC 1上的动点,F 是AB 的中点,AC =1,BC =2,AA 1=4.(1)当E 是棱CC 1的中点时,求证:CF ∥平面AEB 1;(2)在棱CC 1上是否存在点E ,使得二面角A -EB 1-B 的余弦值是21717?若存在,求CE的长,若不存在,请说明理由.解析:(1)证明:取AB 1的中点G ,连接EG ,FG . ∵F ,G 分别是棱AB ,AB 1的中点, ∴FG ∥BB 1,FG =12BB 1,又B 1B 綊C 1C ,EC =12C 1C ,∴B 1B ∥EC ,EC =12B 1B .∴FG 綊EC .∴四边形FGEC 是平行四边形,∴CF ∥EG . ∵CF ⊄平面AEB 1,EG ⊂平面AEB 1, ∴CF ∥平面AEB 1.(2)以C 为坐标原点,射线CA ,CB ,CC 1为x ,y ,z 轴正半轴,建立如图所示的空间直角坐标系C -xyz ,则C (0,0,0),A (1,0,0),B 1(0,2,4).设E (0,0,m )(0≤m ≤4),平面AEB 1的法向量n 1=(x ,y ,z ). 则AB 1→=(-1,2,4), AE →=(-1,0,m ).由AB 1→⊥n 1,AE →⊥n 1,得⎩⎪⎨⎪⎧-x +2y +4z =0,-x +mz =0.令z =2,则n 1=(2m ,m -4,2). 连接BE ,∵CA ⊥平面C 1CBB 1,∴CA →是平面EBB 1的一个法向量,令n 2=CA →, ∵二面角A -EB 1-B 的余弦值为21717,∴21717=cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=2m 4m 2+m -42+4, 解得m =1(0≤m ≤4).∴在棱CC 1上存在点E ,符合题意,此时CE =1.。
