2012高考文科试题立体几何(打印版)

合集下载

2012年高考数学试题解析分项版之专题08 立体几何学生版文.pdf

单元测试(二)　方程与不等式(时100分钟　满分：150分)题号一二三四五六七八总分合分人复分人得分一、选择题(本大题共10小题每小题4分满分40分)(滚动考查相反数与绝对值的概念)－的相反数是( )－4 2．(滚动考查科学记数法)南海资源丰富其面积约为350万平方千米相当于我国的渤海、黄海和东海总面积的3倍．其中350万用科学记数法表示为( )B．3.5×107 C．3.5×106 D．35×105 3．(滚动考查分式性质)下列等式成立的是( )＋＝＝＝D.＝－把不等式组的解集表示在数轴上正确的为图中的( ) 5．(兼顾考查因式分解、一元二次方程的解、实数与整式运算)在一节数学复习课上王老师在小黑板上写＝－3；②分解因式：16x－1＝(4x＋1)(4x－1)；③方程x(x＋2)＝3(x＋2)的解是x＝3；④化简：x＋2x＝3x其中正确的个数是( )个．个．个．个已知二元一次方程组则x＋y等于( )(滚动考查列代数式的实际应用)岳西某村贫困家庭的孩子读书享受“两免一补”(即免学杂费、免课本费补助寄宿生活费)加上免收农业税该家庭现在平均每月可减少40的费用支出．若该家庭原来平均每月支出m元则现在每月的支出为( ) B. C．60%m D．40%m 8．不等式组的解集在数轴上表示正确的是( ) 9．为了丰富同学们的业余生活体育委员小强到体育用品商店购买羽毛球拍和乒乓球拍若购买1副羽毛球拍和1副乒乓球拍共需50元小强一共用了320元购买了6副同样的羽毛球拍和10副同样的乒乓球拍若设每副羽毛球拍x元每副乒乓球拍y元可列二元一次方程组为( ) B. C. D. 10．(2015·哈尔滨)今年我市计划扩大城区绿地面积现有一块长方形绿地它的短边长为60 若将短边增大到与长边相等(长边不变)使扩大后的绿地的形状是正方形则扩大后的绿地面积比原来增加1 600时．设扩大后的正方形绿地边长为x 下面所列方程正确的是( )(x－60)＝1 600 ．(x＋60)＝1 600(x＋60)＝1 600 ．(x－60)＝1 600二、填空题(本大题共4小题每小题5分满分20分)(2014·怀远模拟)分式方程＝的解为x＝________. 12．(2014·宣城模拟)方程组的解是________．如图数轴上所表示的不等式组的解集是____________________． 14．(2015·咸宁)如果实数x满足方程组则x－y的值为________．三、(本大题共2小题每小题8分满分16分)解方程：5(x－5)＋2x＝－4.解方程：x＋3x＝2.四、(本大题共2小8分满分16分)7．(兼顾考查整式的运算和一元二次方程的解法)已知x－4x＝0求代数式(2x－1)－(2x＋y)(2x－y)－y的值．解不等式组：五、(本大题共2小题每小题10分满分20分)(兼顾考查分式的运算和分式方程的解法)已知y＝－当x为何值时的值为？(兼定义新运算：对于任意实数a都有ab＝a(a－b)＋1等式右边是通常的加法、减法及乘法运算比如：25＝2×(2－5)＋1＝2×(－3)＋1＝－6＋1＝－5.(1)求(－2)3的值；(2)若3x的值小于13求x的取值范围并在数轴上表示出来．六、(本题满分12分)小明在超市帮妈请你根据图中的信息若小明把50个纸杯整齐叠放在一起你能帮小明求出它的高度吗？七、(本题满分12分)年底某市汽车拥有量为100万辆而截止2015年底该市的汽车拥有量已达到144万辆．求2013年底至2015年底该市汽车拥有量的年平均增长率．八、(本题满分14分)(兼顾考查二元一次方程组、一元一次不等式及一次函数的应用)(2015·常德)某物流公司承接A、B两种货物的运输业务已知5月份A货物运费单价为50元/吨货物运费单价为30元/吨共收运费9 500元；6月份由于油价上涨运费单价上涨为：A货物70元/吨货物40元/吨．该物流公司6月份承接的A种货物和B种货物数量与5月份相同13 000元．问：(1)该物流公司5月份运输两种货物各多少吨？(2)该物流公司预计7月份运输这两种货物共330吨且A货物的数量不大于B货物的2倍在运费单价与6月份相同的情况下该物流公司7月份最多将收取多少运输费？　2.　3.　4.B　5.　6.　7.　8.　9.　10.　11.1　12.　13.－1＜x≤2(其他表示也可) 14.－ 15.去括号得：5x－25＋2x＝－4移项得：7x＝21系数化为1得：x＝3. 16.∵a＝1＝3＝－2＝＝＝＝ 17.原式＝4x－4x＋1－4x＋y－y＝－4x＋1.∵x2－4x＝0解得x＝4＝0. 当x＝4时原式＝－4x＋1＝－4×4＋1＝－15；当x＝0时原式＝－4x＋1＝－4×0＋1＝1. 18.由①去分母得：3－(x－1)≥0化简得：－x≥－4解得x≤4；由②去括号得：3－(2x－2)＜3x即3－2x＋2＜3x解得x＞1把两解集表示在数轴上如图所示： ∴不等式组的解集为1＜x≤4. 19.原式＝－＝－当y的值为时－＝解得x＝－3经检验x＝－3是这个方程的解且原式有意义当x＝－3时的值为 20.(1)(－2)3＝－2×(－2－3)＋1＝－2×(－5)＋1＝10＋1＝11. (2)∵3x＜13(3－x)＋1＜13－3x＋1＜13－3x＜3x＞－1.在数轴上表示如图所示： 21．设每两个纸杯叠放在一起比单独的一个纸杯增高单独一个纸杯的高度为y 则解得则49x＋y＝49×1＋7＝56. 答：把50个纸杯整齐地叠放在一起时的高度约是56 22.设2013年底至2015年底该市汽车拥有量的年平均增长率为x根据题意得 100(1＋x)＝144.解得x＝0.2＝20＝－2.2(不合题意舍去)．答：2013年底至2015年底该市汽车拥有量的年平均增长率为20 23.1)设该物流公司5月份运输A、B两种货物各x吨、y吨依题意得解得答：该物流公司5月份运输A种货物100吨运输B种货物150吨． (2)设物流公司7月份运输A种货物a吨收取w元运输费则依题意有： a≤2(330－a)则a≤220. ∴a最大为220.w＝70a＋40(330－a)＝30a＋13 200. ∵k＝30>0随a的增大而增大． ∴当a＝220时最大＝30×220＋13 200＝19 800(元)．答：该物流公司7月份最多将收取运输费19 800元．初中学习网，资料共分享！我们负责传递知识！。

2012年高考试题文科数学分类汇编：立体几何

2012年高考试题分类汇编：立体几何一、选择题1.【2012高考新课标文7】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（）【答案】B2.【2012高考新课标文8】平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π 【答案】B3.【2012高考全国文8】已知正四棱柱1111ABCD A B C D -中，2AB =，1CC =E 为1CC 的中点，则直线1AC 与平面BED 的距离为（A ）2 （B （C （D ）1 【答案】D4.【2012高考陕西文8】将正方形（如图1所示）截去两个三棱锥，得到图2所示的几何体，则该几何体的左视图为（）8.【答案】B.5.【2012高考江西文7】若一个几何体的三视图如图所示，则此几何体的体积为 A ．112 B.5 C.4 D. 92【答案】D6.【2012高考湖南文4】某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能．．．是【答案】D7.【2012高考广东文7】某几何体的三视图如图1所示，它的体积为A. 72πB. 48πC. 30πD. 24π【答案】C8.【2102高考福建文4】一个几何体的三视图形状都相同，大小均等，那么这个几何体不可以是 A 球 B 三棱锥 C 正方体 D 圆柱【答案】D.9.【2012高考重庆文9】设四面体的六条棱的长分别为1，1，1，1和a 且长为a的棱异面，则a 的取值范围是（A）（B）（C）（D）【答案】A10.【2012高考浙江文3】已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积是 A.1cm 3 B.2cm 3 C.3cm 3 D.6cm 3 【答案】C11.【2012高考浙江文5】设l 是直线，a ，β是两个不同的平面A. 若l ∥a ，l ∥β，则a ∥βB. 若l ∥a ，l ⊥β，则a ⊥βC. 若a ⊥β，l ⊥a ，则l ⊥βD. 若a ⊥β, l ∥a ，则l ⊥β 【答案】B12.【2012高考四川文6】下列命题正确的是（）A 、若两条直线和同一个平面所成的角相等，则这两条直线平行B 、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C 、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D 、若两个平面都垂直于第三个平面，则这两个平面平行【答案】C13.【2012高考四川文10】如图，半径为R 的半球O 的底面圆O 在平面α内，过点O 作平面α的垂线交半球面于点A ，过圆O 的直径CD 作平面α成45角的平面与半球面相交，所得交线上到平面α的距离最大的点为B ，该交线上的一点P 满足60BOP ∠=，则A 、P 两点间的球面距离为（）图1正视图俯视图侧视图A、arccos4R B 、4R π C、R D 、3R π 【答案】A14.【2102高考北京文7】某三棱锥的三视图如图所示，该三棱锥的表面积是（A ）28+B ）30+C ）56+D ）60+【答案】B二、填空题15.【2012高考四川文14】如图，在正方体1111ABCD A B C D -中，M 、N 分别是CD 、1CC 的中点，则异面直线1A M 与DN 所成的角的大小是____________。

2012-2020年全国卷高考立体几何大题汇编(文科)

立体几何大题汇编（文科）1.（2020年全国一卷文19）如图、为圆锥曲线的顶点，底面的内接正三角形，为上一点，（1平面（2）设，圆锥的侧面积为，求三棱锥2.（2020年全国二卷文20的底面是正三角形，侧面是矩形，分别为，的中点，为上一点，过和的平面交于，交于（1）证明：面（2）设为的中心，若，面，且求四棱锥3.（2020年全国三卷文19）如图、在长方体中，点分别在棱，（1）证明：当时，（2）证明：点在平面内4.（2019年全国一卷文19）如图，直四棱柱的底面是棱形，，，，，分别是，的中点（1（2）求点到平面的距离5.（2019年全国二卷文科17）如图，长方体的底面是正方形，点在棱（1平面（2，，求四棱锥6.（2019年全国三卷文科19）图是矩形组成的一个平面图形，其中，将其沿，折起使得与重合，连接，如图（1）证明：图平面（2）求图中的四边形的面积7.（2018年全国三卷文科19）如图，边长为的正方形所在的平面与半圆弧所在平面垂直，是上异于的点（1（2）在线段上是否存在点？请说明理由8.（2018年全国二卷文科19）如图，在三棱锥中，，，为的中点（1（2）若点在棱，求点到平面的距离9.（2018年全国一卷文科18）如图，在平行四边形中，，以到达点（1平面（2）为线段上一点，为线段上一点，且，求三棱锥的体积10.（2017年全国三卷文科19）如图，在四面体是正三角形，（1（2）是直角三角形，，若为棱上与不重合的点，求四面体与四面体的体积比11.（2017年全国二卷文科18）如图，四棱锥中，侧面为等边三角形且垂直于底面，（1（2，求四棱锥的体积12.（2017年全国一卷文科18）如图，在四棱锥，，且（1平面（2）若，求该四棱锥的侧面积13.（2016年全国三卷文科19）如图，底面，，，，为线段，为的中点（1（2的体积14.（2016年全国二卷文科19）如图，菱形的对角线与交于点，点分别在，上，交于点（1（2）若，，15.（2016年全国一卷文科18）如图，的侧面是直角三角形，，顶点在平面内正投影为点，在平面内的正投影为点，连接并延长交于点（1）证明：是的中点（2）大答题卡第题中作出点在平面内的正投影（说明作法及理由），并求四面体的体积16.（2015年全国二卷文科19）如图，长方体中，，，点，分别在，上，，过点，的平面与此长方体的面相交，交线围成一个正方形。

2012年高考立体几何

三、解答题28.【2012高考新课标理19】（本小题满分12分）如图，直三棱柱111ABC A B C -中，112A CBC A A ==，D 是棱1AA 的中点，BD DC ⊥1（1）证明：BC DC ⊥1（2）求二面角11C BD A --的大小. 【答案】（1）在R t D A C ∆中，AD AC = 得：45ADC ︒∠=同理：1114590A D C C D C ︒︒∠=⇒∠=得：111,DC DC DC BD DC ⊥⊥⇒⊥面1BCD DC BC ⇒⊥ （2）11,DC BC CC BC BC ⊥⊥⇒⊥面11ACC A BC AC ⇒⊥取11A B 的中点O ，过点O 作O H BD ⊥于点H ，连接11,C O C H 111111A CBC C O A B =⇒⊥，面111A B C ⊥面1A BD 1C O ⇒⊥面1A B D 1O H B D C H B D ⊥⇒⊥得：点H 与点D 重合且1C D O ∠是二面角11C BD A --的平面角设A C a =，则12C O =，111230CD C O C DO ︒==⇒∠=既二面角11C BD A --的大小为30︒29.【2012高考江苏16】（14分）如图，在直三棱柱111ABC A B C -中，1111A B A C =，D E ，分别是棱1BC CC ，上的点（点D 不同于点C ），且AD DE F ⊥，为11B C 的中点．求证：（1）平面AD E ⊥平面11BCC B ；（2）直线1//A F 平面ADE ．【答案】证明：（1）∵111ABC A B C -是直三棱柱，∴1CC ⊥平面A B C 。

又∵AD ⊂平面A B C ，∴1CC AD ⊥。

又∵1AD DE CC DE ⊥⊂，，平面111BCC B CC DE E = ，，∴AD ⊥平面11BCC B 。

又∵AD ⊂平面ADE ，∴平面AD E ⊥平面11BCC B 。

2012年全国高考文科数学试题和答案-新课标word版

绝密*启用前2012年普通高等学校招生全国统一考试（新课标卷）文科数学注息事项:1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分。

答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2.问答第Ⅰ卷时。

选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动.用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效.3.回答第Ⅱ卷时。

将答案写在答题卡上.写在本试卷上无效·4.考试结束后.将本试卷和答且卡一并交回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的。

1、已知集合A={x |x 2－x －2<0}，B={x |－1<x <1}，则（A ）A ⊂≠B （B ）B ⊂≠A （C ）A=B （D ）A ∩B=∅（2）复数z ＝－3+i 2+i 的共轭复数是（A ）2+i （B ）2－i （C ）－1+i （D ）－1－i3、在一组样本数据（x 1，y 1），（x 2，y 2），…，（x n ，y n ）（n ≥2，x 1,x 2,…,x n 不全相等）的散点图中，若所有样本点（x i ，y i ）(i =1,2,…,n )都在直线y =12x +1上，则这组样本数据的样本相关系数为（A ）－1 （B ）0 （C ）12 （D ）1（4）设F 1、F 2是椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，P 为直线x =3a 2上一点，△F 1PF 2是底角为30°的等腰三角形，则E 的离心率为（）（A ）12 （B ）23 （C ）34 （D ）455、已知正三角形ABC 的顶点A(1,1)，B(1,3)，顶点C 在第一象限，若点（x ，y ）在△ABC 内部，则z =－x+y 的取值范围是（A ）(1－3，2) （B ）(0，2) （C ）(3－1，2) （D ）(0，1+3)（6）如果执行右边的程序框图，输入正整数N(N ≥2)和实数a 1,a 2,…,a N ，输出A,B ，则（A ）A+B 为a 1,a 2,…,a N 的和（B ）A ＋B 2为a 1,a 2,…,a N 的算术平均数（C ）A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数（D ）A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数（7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（A）6（B）9（C）12（D）18(8)平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π（9）已知ω>0，0<φ<π，直线x =π4和x =5π4是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴，则φ=（A ）π4 （B ）π3 （C ）π2 （D ）3π4（10）等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线y 2=16x 的准线交于A ，B 两点，|AB|=43，则C 的实轴长为（A ） 2 （B ）2 2 （C ）4 （D ）8(11)当0<x ≤12时，4x <log a x ，则a 的取值范围是（A ）(0，22) （B ）(22，1) （C ）(1，2) （D ）(2，2)（12）数列{a n }满足a n +1＋(－1)n a n ＝2n －1，则{a n }的前60项和为（A ）3690 （B ）3660 （C ）1845 （D ）1830第Ⅱ卷本卷包括必考题和选考题两部分。

立体几何测试题(文科)

立体几何文科试题一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的． 1、设有直线m 、n 和平面α、β.下列四个命题中，正确的是( )A.若m ∥α,n ∥α,则m ∥nB.若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥βC.若α⊥β，m ⊂α,则m ⊥βD.若α⊥β，m ⊥β，m ⊄α,则m ∥α 2、已知直线,l m与平面αβγ，，满足//l l m βγαα=⊂ ，，和mγ⊥，则有A ．αγ⊥且l m⊥ B ．αγ⊥且//m β C ．//m β且lm⊥ D ．//αβ且αγ⊥3.若()0,1,1a =- ，()1,1,0b = ，且()a b a λ+⊥，则实数λ的值是（）A .－1 B.0 C.1 D.－24、已知平面α⊥平面β，α∩β= l ，点A ∈α，A ∉l ，直线AB ∥l ，直线AC ⊥l ，直线m ∥α，m ∥β，则下列四种位置关系中，不一定．．．成立的是（） A. AB ∥m B. AC ⊥m C. AB ∥β D. AC ⊥β5一个几何体的三视图及长度数据如图，则几何体的表面积与体积分别为()3,27+A ()328，+B()2327，+C ()23,28+D6、已知长方体的表面积是224cm ，过同一顶点的三条棱长之和是6cm ，则它的对角线长是（）A. B. 4cm C. D.7、已知圆锥的母线长5l cm =，高4h cm =，则该圆锥的体积是____________3cmA. 12π B 8π C. 13π D. 16π8、某几何体的三视图如图所示，当ba +取最大值时，这个几何体的体积为（）A ．61 B ．31 C ．32 D ．219、已知,,,A B C D 在同一个球面上,,AB BCD ⊥平面,BC CD ⊥若6,AB =AC =8A D =,则,B C 两点间的球面距离是（）A. 3πB. 43π C. 23π D. 53π10、四面体A B C D 的外接球球心在C D 上，且2C D =，3=AB ，在外接球面上A B ，两点间的球面距离是（） A ．π6B ．π3C ．2π3D ．5π611、半径为2cm 的半圆纸片做成圆锥放在桌面上，一阵风吹倒它，它的最高处距桌面（） A ．4cmB ．2cmC ．cm 32D ．cm 312、有一正方体，六个面上分别写有数字1、2、3、4、5、6，有三个人从不同的角度观察的结果如图所示.如果记3的对面的数字为m ，4的对面的数字为n ，那么m+n 的值为（） A ．3B ．7C ．8D ．11二．填空题：本大题共4个小题。

2012高考真题分类汇编：立体几何

实用文档2012高考真题分类汇编：立体几何一、选择题1、【2012高考真题北京理7】某三棱锥的三视图如图所示，该三梭锥的表面积是（）A. 28+65B. 30+65C. 56+ 125D. 60+1252、【2012高考真题浙江理10】已知矩形ABCD ，AB=1，BC=2。

将△沿矩形的对角线BD 所在的直线进行翻折，在翻折过程中。

A.存在某个位置，使得直线AC 与直线BD 垂直.B.存在某个位置，使得直线AB 与直线CD 垂直.C.存在某个位置，使得直线AD 与直线BC 垂直.D.对任意位置，三对直线“AC 与BD ”，“AB 与CD ”，“AD 与BC ”均不垂直3、【2012高考真题新课标理7】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（）()A 6 ()B 9 ()C 12 ()D 18实用文档4、【2012高考真题新课标理11】已知三棱锥S ABC -的所有顶点都在球O 的求面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =；则此棱锥的体积为（）()A 26 ()B 36 ()C 23 ()D 225、【2012高考真题全国卷理4】已知正四棱柱ABCD- A 1B 1C 1D 1中，AB=2，CC 1=22 E 为CC 1的中点，则直线AC 1与平面BED 的距离为A 2 B3 C 2 D 16、【2012高考真题重庆理9】设四面体的六条棱的长分别为1，1，1，12和a ，且长为a 的棱2的棱异面，则a 的取值范围是（A ）2) （B ）3) （C ）2) （D ）3)7、【2012高考真题福建理4】一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是A.球B.三棱柱C.正方形D.圆柱8、【2012高考真题广东理6】某几何体的三视图如图所示，它的体积为A．12π B.45π C.57π D.81π9、【2012高考真题湖北理4】已知某几何体的三视图如图所示，则该几何体的体积为实用文档A．8π3B．3πC．10π3D．6π10、【2012高考真题湖南理3】某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能是实用文档实用文档11、【2012高考真题陕西理5】如图，在空间直角坐标系中有直三棱柱111ABC A B C -，12CA CC CB ==，则直线1BC 与直线1AB 夹角的余弦值为（） A. 55B.53C. 25D. 3512、【2012高考真题四川理10】如图，半径为R 的半球O 的底面圆O 在平面α内，过点O 作平面α的垂线交半球面于点A ，过圆O 的直径CD 作平面α成45角的平面与半球面相交，所得交线上到平面α的距离最大的点为B ，该交线上的一点P 满足60BOP ∠=，则A 、P 两点间的球面距离为（）αC AO DBPA 、2arccos4R B 、4R π C 、3arccos 3R D 、3R π13、【2012高考真题四川理6】下列命题正确的是（）A 、若两条直线和同一个平面所成的角相等，则这两条直线平行B 、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行实用文档C 、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D 、若两个平面都垂直于第三个平面，则这两个平面平行二、填空题14、【2012高考真题安徽理12】某几何体的三视图如图所示，该几何体的表面积是_____．15、【2012高考真题四川理14】如图，在正方体1111ABCD A B C D 中，M 、N 分别是CD 、1CC 的中点，则异面直线1A M 与DN 所成角的大小是____________。

2012年高考文科立体几何(无错版)

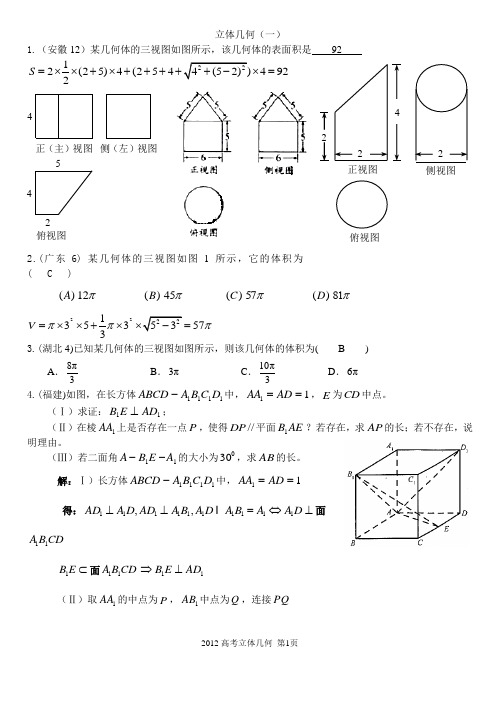
立体几何（一）1.（安徽12）某几何体的三视图如图所示，该几何体的表面积是 9212(25)4(2544922S =⨯⨯+⨯++++⨯=2.(广东6) 某几何体的三视图如图1所示，它的体积为( C )()A 12π ()B 45π ()C π57 ()D π81221353573V πππ=⨯⨯+⨯=3.(湖北4)已知某几何体的三视图如图所示，则该几何体的体积为( B )A ．8π3 B ．3π C ．10π3D ．6π 4.(福建)如图，在长方体1111D C B A ABCD -中，11==AD AA ，E 为CD 中点。

（Ⅰ）求证：11AD E B ⊥；（Ⅱ）在棱1AA 上是否存在一点P ，使得//DP 平面AE B 1？若存在，求AP 的长；若不存在，说明理由。

（Ⅲ）若二面角11A E B A --的大小为030，求AB 的长。

解：Ⅰ）长方体1111D C B A ABCD -中，11==AD AA 得：1111111111,,AD A D AD A B A D A B A A D ⊥⊥=⇔⊥ 面11A B CD1B E ⊂面11A B CD 11B E AD ⇒⊥（Ⅱ）取1AA 的中点为P ，1AB 中点为Q ，连接PQ侧（左）视图正（主）视图 45 俯视图42 俯视图侧视图正视图4在11AA B ∆中，111111//,////////22PQ A B DE A B PQ DE PD QE PD ⇒⇒⇒面AE B 1 此时11122AP AA == （Ⅲ）设11A D AD O = ，连接AO ，过点O 作1OH B E ⊥于点H ，连接AH1AO ⊥面11A B CD ，1O H B E ⊥1A H B E⇒⊥ 得：AHO ∠是二面角11A E B A --的平面角30AHO ο⇒∠=在Rt AOH ∆中，30,90,2AHO AOH AH OH οο∠=∠==⇒=在矩形11A B CD 中，1,CD x A D ==11112222222228B OE x xS x ∆=--⨯-⨯=122x =⇔= 得：2AB =5.（湖南3）某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能是( D )6.（辽宁13）一个几何体的三视图如图所示，则该几何体的表面积为 387.（辽宁16）已知正三棱锥-P ABC ，点,,,P A B C 的球面上，若,,PA PB PC 两两相互垂直，则球心到截面ABC 的距离为38.（江苏7）如图，在长方体1111ABCD A B C D -中，3cm AB AD ==，12cm AA =，则四棱锥11A BB D D -的体积为 6 cm 3。

2012年高考真题文科数学汇编10：立体几何.pdf

一、 ? 说明文 1、如何给概念下定义？（常见问题：根据文章内容给“xx”下定义。

）答：下定义必须由四部分组成：被定义概念及其上一级概念、定义词（如“叫”、“是”等）、对象的本质特点。

缺一不可，且不能使用生动语言。

2、如何阐述说明方法的作用？（常见问题：划线句运用了哪些说明方法？有何作用？）答：（1）首先讲清说明方法本身的作用：如打比方“生动形象地说明了……”，举例子“具体说明了……”，作比较“突出说明了……”，列数字“准确说明了……”，分类别“有条理地说明了……”等；（2）说明方法的运用是为了说明某个结论（对象及其特点），此结论可以有现成的，也可以从具体句子中去提炼。

3、如何阐述词语的表达作用？（常见问题：某词语有何表达作用？某词语能否删除？某词语能否换作xx词？）（1）首先阐述词语本身的含义或作用；（2）其次结合语境阐述词语在句子中的作用；（主要结合说明对象和该词所修饰的中心词）；（3）加个套语：这体现了说明文用词的准确性或生动性。

4、说明顺序有哪几种？其中常见的逻辑顺序有哪些？答：说明顺序主要有时间顺序、空间顺序和逻辑顺序。

其中常见的逻辑顺序有：由概括到具体、由一般到个别、由整体到局部、由表及里（由现象到本质）、由主到次、由此及彼、由因到果等。

5、如何从文中提炼信息答题？答：（1）顺着文章总段和各段中心句确定答题所依据的原文范围；（2）根据该题分值推测要点数（一般1分对应一个要点）。

6、如何分析说明文的语言特点？答：（1）语言的准确性，主要抓住词语（如“大约、之一、至少、到目前为止”等）展开；（2）语言的生动性，主要抓住修辞方法、描写、抒情和叙述展开。

? 二、 ? 议论文 1、如何把握中心论点？答：（1）它必须围绕论题展开；（2）必须是陈述句；（3）位于标题或总段中，除了开头引析材料或先驳敌论再立论会位于文章中间以外，一般则位于文章标题和首尾；（4）没有现成的中心论点可结合论题、分论点或围绕的问题进行归纳，也可由论据进行反推。

2012年立体几何高考真题(文科)

2012年高考（文科）数学立体几何汇编1.(2012安徽)平面图形111A B B A C C 如图4所示，其中11BB C C 是矩形，12,4B C B B ==，2AB AC ==，11115A B AC ==。

现将该平面图形分别沿BC 和11B C 折叠，使ABC ∆与111A B C ∆所在平面都与平面11BB C C 垂直，再分别连接111,,AA BA CA ,得到如图2所示的空间图形，对此空间图形解答下列问题。

（Ⅰ）证明：1AA BC ⊥；（Ⅱ）求1AA 的长；（Ⅲ）求二面角1A BC A --的余弦值。

2.（2012江苏）如图，在直三棱柱111ABC A B C -中，1111AB AC =，D E ，分别是棱1BC CC ，上的点（点D 不同于点C ），且AD DE F ⊥，为11B C 的中点．求证：（1）平面ADE ⊥平面11BCC B ；（2）直线1//A F 平面ADE ．1A1CFDCAE1B3.（2012安徽）如图，长方体1111D C B A ABCD -中，底面1111D C B A 是正方形，O 是BD 的中点，E 是棱1AA 上任意一点。

（Ⅰ）证明：BD 1EC ⊥ ；（Ⅱ）如果AB =2，AE =2，1EC OE ⊥,，求1AA 的长。

4.（2012北京）如图1，在Rt ABC ∆中，90C ∠=，,D E 分别为,AC AB 的中点，点F 为线段CD 上的一点，将ADE ∆沿DE 折起到1A DE ∆的位置，使1A F CD ⊥，如图2。

（Ⅰ）求证：//DE 平面1ACB ；（Ⅱ）求证：1A F BE ⊥；（Ⅲ）线段1A B 上是否存在点Q ，使1AC ⊥平面DEQ ？5.（2012福建）如图，在长方体1111D C B A ABCD -中，2,11===AA AD AB ，M 为棱1DD 上的一点。

（I ）求三棱锥1MCC A -的体积；（II ）当MC M A +1取得最小值时，求证：⊥M B 1平面MAC 。

2012年全国新课标高考文科数学真题及答案(Word版)

绝密*启用前2012年普通高等学校招生全国统一考试文科数学注息事项：1. 本试卷分第I 卷(选择题)和第n 卷号填写在本试卷和答题卡相应位置上。

2. 问答第I 卷时。

选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动擦干净后，再选涂其它答案标号。

写在本试卷上无效3.回答第n 卷时。

将答案写在答题卡上 .写在本试卷上无效•4. 考试结束后.将本试卷和答且卡一并交回。

1y i ) (i=1,2,…,n)都在直线y=2x+1上，则这组样本数据的样本相关系数为x 2 y 2 3aF 2是椭圆E ：耸+ y^= 1(a>b>0)的左、右焦点，P 为直线x=3a 上一点，△ F 1PF 2是底角为30°a b 2 的等腰三角形，则 E 的离心率为()(A) 1 ( B ) 2 (C ) 4( D ) 4 5、已知正三角形 ABC 的顶点A(1,1)，B(1,3)，顶点C 在第一象限，若点(x ，丫)在厶ABC 内部，贝U z= —x+y 的取值范围是 (A ) (1 — 3, 2) ( B ) (0, 2)( C ) ( 3— 1, 2)( D ) (0，1+ 3)(6)如果执行右边的程序框图，输入正整数 N(N >2)和实数a 1,a 2,…,a N ,输出A,B ，则(A)A+B 为 a 1,a 2,…,a N 的和 A + B(B)—2 —为a1,a 2,…,a N 的算术平均数(A )— 1(B) 0 (D) 1(非选择题)两部分。

答卷前，考生务必将自己的姓名、准考证.用橡皮、选择题: 本大题共 12小题, 每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的。

1、已知集合 A={ x|x 2— x — 2<0}, B={ x|— 1<x<1},(A) A B(B ) B A (C ) A=B(D ) A n B=(2)复数 z =—的共轭复数是2+i(A) 2+i( B ) 2 — i(C )— 1+i (D )— 1— i3、在一组样本数据(X 1, y 1), (x 2, y 2),…，(x n .y n ) ( n > 2, X 1,x 2,…,X n 不全相等)的散点图中，若所有样本点(X i ,(4)设 F 1、(C) A和B分别是a i,a2,…,a N中最大的数和最小的数(D) A和B分别是a i,a2,…,a N中最小的数和最大的数(7) 如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为(A) 6(B) 9(C) 12(D)18(8) 平面a截球0的球面所得圆的半径为1球心O到平面a的距离为，2，则此球的体积为(A) 6n ( B) 4 3n (C) 4 6n (D) 6 3n(9) 已知3>0, 0< o <n直线x=4和x=5^函数f(x)=sin( ®x+妨图像的两条相邻的对称轴，贝Un n n 3 n(A ) 4 (B) 3 ( C) 2 ( D) G(10) 等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=l6x的准线交于A , B两点, 则C的实轴长为(A ) 2 (B) 2 2 (C) 4 ( D) 8(11) 当0<x< 2时，4x<|og a x，贝y a的取值范围是(A ) (0,子) (B)(今，1) (C) (1 , 2) ( D) (.2, 2)(12) 数列｛a n｝满足a n+1 + (- 1)n a n = 2n- 1，则｛a n｝的前60项和为(A) 3690 ( B) 3660 (C) 1845 ( D) 1830本卷包括必考题和选考题两部分。

2012高考文科数学立体几何_(答案详解)

选择题1.（12年四川卷）如图，半径为R 的半球O 的底面圆O 在平面α内，过点O 作平面α的垂线交半球面于点A ，过圆O 的直径CD 作平面α成45 角的平面与半球面相交，所得交线上到平面α的距离最大的点为B ，该交线上的一点P 满足60BOP ∠= ，则A 、P 两点间的球面距离为（）A. arccos4R B. 4R πC. arccos 3RD. 3R π 2.（12年广东卷）某几何体的三视图如图1所示，它的体积为( )A. 72πB. 48πC. 30πD. 24π3.（12年重庆卷）设四面体的六条棱的长分别为1，1，1，1和a 且长为a的棱与长为的棱异面，则a 的取值范围是（）A.B.C.D.4.（12年浙江卷）已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积是（） A.1cm 3 B.2cm 3 C.3cm 3 D.6cm3图1C5.（12年浙江卷）设l 是直线，αβ，是两个不同的平面（）A.若l ∥α，l ∥β，则α∥βB. 若l ∥α，l ⊥β，则α⊥βC. 若α⊥β，l ⊥α，则l ⊥βD. 若α⊥β， l ∥α，则l ⊥β6.（12年新课标卷）如图，网格上小正方形的边长为1，粗线画出的是某几何体的三视图，则几何体的体积为（）A .6B .9C .12D .187. 某三棱锥的三视图如图所示，该三棱锥的表面积是（）A．28+ B．30+ C．56+ D ．60+ 8.（12年福建卷）一个几何体的三视图形状都相同，大小均等，那么这个几何体不可以是（）A ．球B ．三棱锥C ．正方体D ．圆柱 9.（12年湖南卷）某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能．．．是（）10.（12年江西卷）若一个几何体的三视图如图所示，则此几何体的体积为 ( )A B C DA ．112B.5C.4D. 9211.（12年大纲卷）已知正四棱柱1111ABCD A B C D -中，2AB =，1CC =E 为1CC 的中点，则直线1AC 与平面BED 的距离为（）A ．2BCD ．1 12.（12年陕西卷）将正方体（如图1所示）截去两个三棱锥，得到图2所示的几何体，则该几何体的左视图为（）填空题1．（12年湖北卷）已知某几何体的三视图如图所示，则该几何体的体积为 .左视图主视图俯视图侧视图正视图俯视图2.（12年四川卷）如图，在正方体1111ABCD A B C D -中，M 、N 分别是CD ，1CC 的中点，则异面直线1A M 与DN 所成的角的大小是____________.3.（12年山东卷）如图，正方体1111D C B A ABCD -的棱长为1，E 为线段C B 1上的一点，则三棱锥1DED A -的体积为___________ .4.（12年安徽卷）某几何体的三视图如图所示，该几何体的体积是_____.5.（12年江苏卷）如图，在长方体1111ABCD A B C D -中，3cm AB AD ==，12cm AA =，则四棱锥11A BB D D -的体积为 cm 3．NA 1A B CC 1 A 1 侧（左）视图正（主）视图 4俯视图 5 4 26.（12年辽宁卷）一个几何体的三视图如图所示，则该几何体的体积为_______________.7.（12年辽宁卷）已知点P A B C D ，，，，是球O 表面上的点，PA ABCD ⊥平面，四边形ABCD是边长为.若PA =，则OAB ∆的面积为______________. 8.（12年大纲卷）已知正方形1111ABCD A B C D -中，,E F 分别为1BB ，1CC 的中点，那么异面直线AE 与1D F 所成角的余弦值为．9.（12年上海卷）一个高为2的圆柱，底面周长为2π，该圆柱的表面积为 . 10.（12年天津卷）一个几何体的三视图如图所示（单位：m ），则该几何体的体积 3m.2.（12年山东卷）(本小题满分12分)如图，几何体E ABCD -是四棱锥，△ABD 为正三角形，,CB CD EC BD =⊥. (Ⅰ)求证：BE DE =；(Ⅱ)若∠120BCD =︒，M 为线段AE 的中点，求证：DM ∥平面BEC .3.（12年广东卷）(本小题满分13分)如图所示，在四棱锥P ABCD -中，AB ⊥平面PAD ，//,AB CD PD AD =，E 是PB 中点，F 是DC 上的点，且12DF AB =，PH 为PAD ∆中AD 边上的高. （1）证明：PH ⊥平面ABCD ；（2）若1,1PH AD FC ===，求三棱锥E BCF -的体积；（3）证明：EF ⊥平面PAB ． 6.（12年新课标卷）（本小题满分12分）如图，三棱柱111ABC A B C -中，侧棱垂直底面，o 90ACB ∠=，112AC BC AA ==，D 是棱1AA 的中点.(Ｉ) 证明：平面BDC ⊥平面1BDC（Ⅱ）平面1BDC 分此棱柱为两部分，求这两部分体积的比.选择题1.【答案】A【分析】由已知可知，AOP CBD ⊥面面，∴cos cos cos AOP AOB BOP = ∠∠∠，带入数据得1cos ==224AOP ∠，arccos4AP R ∴=. 2. 【答案】C【分析】几何体是半球与圆锥叠加而成它的体积为32141π3π330π233V =⨯⨯+⨯⨯= 3.【答案】：A【分析】：如图所示，取,E F 分别为,PC AB 的中点，依题意可得PB BC ⊥，所以GEAB FCPD HBE ==.在BEF ∆中，BF BE <，所以2AB BF =<4. 【答案】C【分析】由题意判断出，底面是一个直角三角形，两个直角边分别为1和2，整个棱锥的高由侧视图可得为3，所以三棱锥的体积为11123132⨯⨯⨯⨯=. 5.【答案】B【分析】利用排除法可得选项B 是正确的，∵l ∥α，l ⊥β，则α⊥β．如选项A ：l ∥α，l ∥β时，α⊥β或α∥β；选项C ：若α⊥β，l ⊥α时，l ∥β或l β⊂；选项D ：若α⊥β，l ∥α时，l ∥β或l ⊥β．6. 【答案】B【分析】由三视图知，其对应几何体为三棱锥，其底面为一边长为6，底边上高为3的等腰三角形，棱锥的高为3，故其体积为1163332⨯⨯⨯⨯=9，故选B. 7. 【答案】B 【分析】从所给的三视图可以得到该几何体为三棱锥，本题所求表面积为三棱锥四个面的面积之和.利用垂直关系和三角形面积公式，可得：=10=10=10S S S S 后右左底，，，因此该几何体表面积30S =+，故选B .8. 【答案】D【分析】圆的正视图（主视图）、侧视图（左视图）和俯视图均为圆；三棱锥的正视图（主视图）、侧视图（左视图）和俯视图可以为全等的三角形；正方体的正视图（主视图）、侧视图（左视图）和俯视图均为正方形；圆柱的正视图（主视图）、侧视图（左视图）为矩形，俯视图为圆.9. 【答案】D【分析】本题是组合体的三视图问题，由几何体的正视图和侧视图均相同，原图下面部分应为圆柱或直四棱柱，上面是圆柱或直四棱柱或下底是直角的三棱柱，A ，B ，C 都可能是该几何体的俯视图，D 不可能是该几何体的俯视图，因为它的正视图上面部分应为中间有条虚线的矩形..10. 【答案】C【分析】通过观察几何体的三视图可知，该几何体是一个底面为六边形（2条对边长为1，其余4，高为1的直棱柱.所以该几何体的体积为112122142V sh ⎛⎫==⨯+⨯⨯⨯⨯= ⎪⎝⎭，故选D.11. 【答案】D【分析】因为底面的边长为2，高为,AC BD ，得到交点为O ，连接EO ，1//EO AC ，则点1C 到平面BDE 的距离等于C 到平面BDE 的距离，过点C 作CH OE ⊥，则CH 即为所求，在三角形OCE 中，利用等面积法，可得1CH =，故选答案D. 12.【答案】B【分析】显然从左边看到的是一个正方形，因为割线1AD 可见，所以用实线表示；而割线1B C 不可见，所以用虚线表示．故选B ．填空题1. 【答案】12π【分析】该几何体的左中右均为圆柱体，其中左右圆柱体全等，是底面半径为2，高为1的圆柱体；中间部分是底面半径为1，高为4的圆柱体，所以所求的体积为：22π212π14=12πV =⨯⨯⨯+⨯⨯.2. 【答案】o 90【分析】方法一：连接D 1M ，易得DN ⊥A 1D 1 ，DN ⊥D 1M ，所以，DN ⊥平面A 1MD 1，又A 1M ⊂平面A 1MD 1，所以，DN ⊥A 1M ，故夹角为o 90 方法二：以D 为原点，分别以DA ， DC ， DD 1为x ， y ， z 轴，建立空间直角坐标系D —xyz .设正方体边长为2，则D （0，0，0），N （0，2，1），M （0，1，0），A 1（2，0，2）故1(0,2,1)(2,1,2)DN MA ==- ，所以， 111cos ,0DN MA DN MA DN MA <>==，故DN ⊥A 1M ，所以夹角为o 90.3. 【答案】61 【分析】求1DED A -的体积，显然为定值，也就是说三棱锥的底面面积与三棱锥的高都为定值，因此，我们需要找一个底面为定值的三角形，三角形1ADD 的面积为21（为定值），而E 点到底面1ADD 的高恰为正方体的高为1（为定值），因此体积为61. 4. 【答案】56 【分析】该几何体是底面是直角梯形，高为4的直四棱柱，几何体的的体积是：()12544562V =⨯+⨯⨯=5. 【答案】6【分析】∵长方体底面A B C D 是正方形，∴△ABD 中BD cm ，BD 边上的高（它也是四棱锥11A BB D D -的高）∴四棱锥11A BB D D -的体积为123⨯6. 【答案】12π+【分析】由三视图可知该几何体为一个长方体和一个等高的圆柱的组合体，其中长方体的长、宽、高分别为4、3、1，圆柱的底面直径为2，高位1，所以该几何体的体积为3411112ππ⨯⨯+⨯⨯=+7.【答案】【分析】点P A B C D O 、、、、为球内接长方体的顶点，14O OAB ∴∆球心为该长方体对角线的中点，的面积是该长方体对角面面积的，164OAB AB PA S ∆===⨯=8. 【答案】35【分析】首先根据已知条件，连接DF ，则由//DF AE 可知1DFD ∠或其补角为异面直线AE 与1D F 所成的角，设正方体的棱长为2，则可以求解得到112DF D F DD ===，再由余弦定理可得22211115543cos 2255D F DF D D DFD D F DF +-+-∠===⋅⨯. 9. 【答案】π6【分析】根据该圆柱的底面周长得底面圆的半径为1=r ，所以该圆柱的表面积为：22π2π4π2π6πS rh r =+=+=.10. 【答案】30【分析】由三视图可知这是一个下面是个长方体，上面是个平躺着的底面为直角梯形的直四棱柱构成的组合体.长方体的体积为24243=⨯⨯，直四棱柱的体积是6412)21(=⨯⨯+，所以几何体的总体积为30.2. 【证明】(Ⅰ)设BD 的中点为O ，连接,OC OE , 则由BC CD CO BD =知垂直又CE BD ⊥，所以BD OCE ⊥平面所以BD OE ⊥，即OD 是BE 的垂直平分线BE DE =所以(Ⅱ)取AB 的中点为N ，连接MN ,DN 因为M 是AE 的中点，，所以//MN BEO NM因为ABD ∆是等边三角形，所以DN ⊥AB由o o 12030BCD CBD ∠=∠=知，所以o 90ABC ∠=，即BC ⊥AB 所以ND //BC所以平面MND //平面BEC ，故DM //平面BEC3. 【解】（1）AB ⊥平面PAD ，PH ⊂面PAD PH AB ⇒⊥ 又,PH AD AD AB A PH ⊥=⇒⊥ 面ABCD （2）E 是PB 中点⇒点E 到面BCF 的距离1122h PH ==三棱锥E BCF -的体积11111133262BCF V S h FC AD h ∆=⨯=⨯⨯⨯⨯=⨯=（3）过D 作DG PA G ⊥于，连接EG ，易得EG PAD ⊥面由AB ⊥平面PAD ⇒面PAD ⊥面PAB DG ⇒⊥面PAB E P B E GP A A B P是的中点，⊥，⊥ 11//,//////22EG AB DF AB EG DF DG EF ⇒⇒⇒ 得：EF ⊥平面PAB6. 【解】（Ⅰ）由题设知1BC CC ⊥，BC AC ⊥，1CC AC C =∩，∴BC ⊥面11ACC A又∵1DC ⊂面11ACC A ，∴1DC BC ⊥，由题设知01145A DC ADC ∠=∠=，∴1CDC ∠=090，即1DC DC ⊥，又∵DC BC C =∩，∴1DC ⊥面BDC ， ∵1DC ⊂面1BDC ， ∴面BDC ⊥面1BDC ；（Ⅱ）设棱锥1B DACC -的体积为1V ，AC =1，由题意得，1V =1121132+⨯⨯⨯=12，由三棱柱111ABC A B C -的体积V =1，∴11():V V V -=1:1，∴平面1BDC 分此棱柱为两部分体积之比为1:1.。

2012年立体几何(文科)教师版

2012年 G 立体几何G1 空间几何体的结构1．G1[2012·重庆卷] 设四面体的六条棱的长分别为1,1,1,1，2和a ，且长为a 的棱与长为2的棱异面，则a 的取值范围为( )A ．(0，2)B ．(0，3)C ．(1，2)D ．(1，3)图1－21．A [解析] 如图1－2所示，设AB ＝a ，CD ＝2，BC ＝BD ＝AC ＝AD ＝1，则∠ACD ＝∠BCD ＝45°，要构造一个四面体，则△ACD 与△BCD 不能共面，即：①当△BCD 与△ACD 重合时，a ＝0；②当A 、B 、C 、D 四点共面，且A 、B 两点在DC 的两侧时，在△ABC 中，∠ACB ＝∠ACD ＋∠BCD ＝45°＋45°＝90°，AB ＝AC 2＋BC 2＝2，所以a 的取值范围是(0，2)．2．G1、G2[2012·陕西卷] 将正方体(如图1－3①所示)截去两个三棱锥，得到图②所示的几何体，则该几何体的左视图为( )2．B [解析] 分析题目中截几何体所得的新的几何体的形状，结合三视图实线和虚线的不同表示可知对应的左视图应该为B.3．G1、G12[2012·安徽卷] 若四面体ABCD 的三组对棱分别相等，即AB ＝CD ，AC ＝BD ，AD ＝BC ，则________(写出所有正确结论的编号)．①四面体ABCD 每组对棱相互垂直；②四面体ABCD 每个面的面积相等；③从四面体ABCD 每个顶点出发的三条棱两两夹角之和大于90°而小于180°；④连接四面体ABCD 每组对棱中点的线段相互垂直平分；⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长．3．②④⑤ [解析] 如图，把四面体ABCD 放入长方体中，由长方体中相对面中相互异面的两条面对角线不一定相互垂直可知①错误；由长方体中△ABC ≌△ABD ≌△DCB ≌△DCA ，可知四面体ABCD 每个面的面积相等，同时四面体ABCD 中过同一顶点的三个角之和为一个三角形的三个内角之和，即为180°，故②正确，③错误；长方体中相对面中相互异面的两条面对角线中点的连线相互垂直，故④正确；从四面体ABCD 每个顶点出发的三条棱可以移到一个三角形中，作为一个三角形的三条边，故⑤正确．答案为②④⑤.4．G1[2012·上海卷] 一个高为2的圆柱，底面周长为2π，该圆柱的表面积为________．4．6π [解析] 考查圆柱的表面积，利用圆的周长求得圆柱的底面半径．由圆柱的底面周长可得底面圆的半径，2πr ＝2π，∴r ＝1，得圆柱的表面积S ＝2πr 2＋2πh ＝2π＋4π＝6π.5．G1、G11[2012·上海卷] 如图1－1，在三棱锥P －ABC 中，PA ⊥底面ABC ，D 是PC 的中点，已知∠BAC ＝π2，AB ＝2，AC ＝23，PA ＝2，求： (1)三棱锥P －ABC 的体积；(2)异面直线BC 与AD 所成的角的大小(结果用反三角函数值表示)．5．解：(1)S △ABC ＝12×2×23＝23，三棱锥P －ABC 的体积为V ＝13S △ABC ×PA ＝13×23×2＝433. (2)取PB 的中点E ，连接DE 、AE ，则ED ∥BC ，所以∠ADE(或其补角)是异面直线BC 与AD 所成的角．在△ADE中，DE ＝2，AE ＝2，AD ＝2，cos ∠ADE ＝22＋22－22×2×2＝34，所以∠ADE ＝arccos 34.因此，异面直线BC 与AD 所成的角的大小是arccos 34.G2 空间几何体的三视图和直观图6．G2[2012·天津卷] 一个几何体的三视图如图1－2所示(单位：m)，则该几何体的体积为________m 3.6．30[解析] 由三视图可得该几何体为两个直四棱柱的组合体，其体积V ＝3×4×2＋12(1＋2)×1×4＝30.7．G2[2012·辽宁卷] 一个几何体的三视图如图1－3所示，则该几何体的体积为________．7.本小题主要考查三视图和体积公式．解题的突破口为通过观察分析三视图，得出几何体的形状，是解决问题的根本．由三视图可知，几何体是一个长方体与一个圆柱构成的组合体，所以该几何体的体积为V ＝V 长方体＋V 圆柱＝4×3×1＋π×12×1＝12＋π.8．G2[2012·课标全国卷] 如图1－2，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为( )A ．6B ．9C ．12D ．188．B[解析]根据三视图可知该几何体是三棱锥，其底面是斜边长为6的等腰直角三角形(斜边上的高为3)，有一条长为3的侧棱垂直于底面，所以该几何体的体积是V ＝13×12×6×3×3＝9，故选B. 9. G2、G7[2012·浙江卷] 已知某三棱锥的三视图(单位：cm)如图1－1所示，则该三棱锥的体积是( )A ．1 cm 3B ．2 cm 3C ．3 cm 3D ．6 cm 39．A[解析]本题考查三棱锥的三视图与体积计算公式，考查学生对数据的运算能力和空间想象能力．由三视图可知，该几何体为一个正三棱锥，则V ＝13Sh ＝13×12×1×2×3＝1.10.G2[2012·湖北卷] 已知某几何体的三视图如图1－4所示，则该几何体的体积为________．10.[解析] 由三视图可知，该几何体是由左右两个相同的圆柱(底面圆半径为2，高为1)与中间一个圆柱(底面圆半径为1，高为4)组合而成，故该几何体的体积是V ＝π×22×1×2＋π×12×4＝12π.11．G2[2012·广东卷] 某几何体的三视图如图1－1所示，它的体积为( )A ．72πB ．48πC ．30πD ．24π11．C [解析] 根据三观图知该几何体是由半球与圆锥构成，球的半径R ＝3，圆锥半径R ＝3，高为4，所以V 组合体＝V 半球＋V 圆锥＝12×43π×33＋13π×32×4＝30π，所以选择C.12．G2[2012·福建卷] 一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是( )A ．球B ．三棱锥C ．正方体D ．圆柱12．D [解析] 球的三视图大小、形状相同，三棱锥的三视图也可能相同，正方体三种视图也相同，只有D 不同． 13．G2、G7[2012·安徽卷] 某几何体的三视图如图1－2所示，则该几何体的体积等于________．13．56 [解析] 如图，根据三视图还原的实物图为底面是直角梯形的直四棱柱，其体积为V ＝Sh ＝12()2＋5×4×4＝56.14．G2、G7[2012·北京卷] ( )A ．28＋6 5B ．30＋6 5C ．56＋12 5D ．60＋12 514．B [解析] 本题考查三棱锥的三视图与表面积公式．由三视图可知，几何体为一个侧面和底面垂直的三棱锥，如图所示，可知S 底面＝12×5×4＝10，S 后＝12×5×4＝10，S 左＝12×6×25＝65，S 右＝12×4×5＝10，所以S 表＝10×3＋65＝30＋6 5. 15．G2[2012·湖南卷] 某几何体的正视图和侧视图均如图1－1所示，则该几何体的俯视图不可能．．．是( )15．C [解析] 握．选项A, B, D ，都有可能，选项C 的正视图应该有看不见的虚线，故C 是不可能的．[易错点] 本题由于对三视图的不了解，易错选D ，三视图中看不见的棱应该用虚线标出．16．G2[2012·江西卷] 若一个几何体的三视图如图1－2A.112 B ．5 C.92D ．4 16．D [解析] 该几何体是直六棱柱，由左视图知其高为1面面积S ＝(1＋3)×1＝4，因此其体积为4，故选D.G3 平面的基本性质、空间两条直线 G4 空间中的平行关系17．G4、G5[2012·山东卷] 如图1－6，几何体E －ABCD 是四棱锥，△ABD CD ，EC ⊥BD. (1)求证：BE ＝DE ；(2)若∠BCD ＝120°，M 为线段AE BEC.17．证明：(1)取BD 的中点O ，连接CO ，EO.由于CB ＝CD ，所以CO ⊥BD ，又EC ⊥BD ，EC∩CO ＝C ，CO ，EC ⊂平面EOC ，所以BD ⊥平面EOC ，因此BD ⊥EO ，又O 为BD 的中点，所以BE ＝DE.(2)证法一：取AB 的中点N ，连接DM ，DN ，MN ，因为M 是AE 的中点，所以MN ∥BE.又MN ⊄平面BEC ，BE ⊂平面BEC ，所以MN ∥平面BEC ，又因为△ABD 为正三角形，所以∠BDN＝30°，又CB ＝CD ，∠BCD ＝120°，因此∠CBD ＝30°，所以DN ∥BC ，又DN ⊄平面BEC ，所以DN ∥平面BEC ，又MN∩DN ＝N ，故平面DMN ∥平面BEC ，又所以DM ∥平面BEC.证法二：延长AD ，BC 交于点F ，连接EF.因为CB ＝CD ，∠BCD ＝120°.所以∠CBD ＝30°.因为△ABD 为正三角形．所以∠BAD ＝60°，∠ABC ＝90°，因此∠AFB ＝30°，所以AB ＝12AF.又AB ＝AD ，所以D 为线段AF 的中点．连接DM ，由点M 是线段AE 的中点，因此DM ∥EF.又DM ⊄平面BEC ，EF ⊂平面BEC ，所以DM ∥平面BEC.18．G4、G7[2012·辽宁卷] 如图1－5，直三棱柱ABC －A′B′C′，∠BAC ＝90°，AB ＝AC ＝2，AA′＝1，点M ，N 分别为A′B 和B′C′的中点．(1)证明：MN ∥平面A′ACC′；(2)求三棱锥A′－MNC 的体积．(锥体体积公式V ＝13Sh ，其中S 为底面面积，h 为高) 18．解：(1)(证法一)连结AB′，AC′，由已知∠BAC ＝90°，AB ＝AC ，三棱柱ABC －A′B′C′为直三棱柱，所以M 为AB′中点，又因为N 为B′C′的中点，所以MN ∥AC′.又MN ⊄平面A′ACC′，AC′⊂平面A′ACC′，因此MN ∥平面A′ACC′.(证法二)取A′B′中点P ，连结MP ，NP ，M 、N 分别为AB′与B′C′的中点，所以MP ∥AA′，PN ∥A′C′，所以MP ∥平面A′ACC′，PN ∥平面A′ACC′，又MP∩NP ＝P ，因此平面MPN ∥平面A′ACC′，而MN ⊂平面MPN.因此MN ∥平面A′ACC′.(2)(解法一)连结BN ，由题意A′N ⊥B′C′，平面A′B′C′∩平面B′BCC′＝B′C′，所以A′N ⊥平面NBC.又A′N ＝12B′C′＝1，故V A′－MNC ＝V N －A′MC ＝12V N －A′BC ＝12V A′－NBC ＝16.(解法二)V A′－MNC ＝V A′－NBC －V M －NBC ＝12V A′－NBC ＝16. 19．G4、G5[2012·江苏卷] 如图1－4，在直三棱柱ABC －A 1B 1C 1中，A 1B 1＝A 1C 1，D ，E 分别是棱BC ，CC 1上的点(点D 不同于点C)，且AD ⊥DE ，F 为B 1C 1的中点．求证：(1)平面ADE ⊥平面BCC 1B 1；(2)直线A 1F ∥平面ADE.19．证明：(1)因为ABC －A1B 1C 1是直三棱柱，所以CC 1⊥平面ABC ，又AD ⊂平面ABC ，所以CC 1⊥AD.又因为AD ⊥DE ，CC 1，DE ⊂平面BCC 1B 1，CC 1∩DE ＝E ，所以AD ⊥平面BCC 1B 1.又AD ⊂平面ADE ，所以平面ADE ⊥平面BCC 1B 1.(2)因为A 1B 1＝A 1C 1，F 为B 1C 1的中点，所以A 1F ⊥B 1C 1.因为CC 1⊥平面A 1B 1C 1，且A 1F ⊂平面A 1B 1C 1，所以CC 1⊥A 1F.又因为CC 1，B 1C 1⊂平面BCC 1B 1，CC 1∩B 1C 1＝C 1，所以A 1F ⊥平面BCC 1B 1.由(1)知AD ⊥平面BCC 1B 1，所以A 1F ∥AD.又AD ⊂平面ADE ，A 1F ⊄平面ADE ，所以A 1F ∥平面ADE.20．G4、G5[2012·浙江卷] 设l 是直线，α，β是两个不同的平面( )A ．若l ∥α，l ∥β，则α∥βB ．若l ∥α，l ⊥β，则α⊥βC ．若α⊥β，l ⊥α，则l ⊥βD ．若α⊥β，l ∥α，则l ⊥β20．B [解析] 本题考查了线面、面面平行，线面、面面垂直等简单的立体几何知识，考查学生对书本知识的掌握情况以及空间想象、推理能力．对于选项A ，若l ∥α，l ∥β，则α∥β或平面α与β相交；对于选项B ，若l ∥α，l ⊥β，则α⊥β；对于选项C ，若α⊥β，l ⊥α，则l ∥β或l 在平面β内；对于选项D ，若α⊥β，l ∥α，则l 与β平行、相交或l 在平面β内．G5 空间中的垂直关系21．G5[2012·江西卷] 如图1－7，在梯形ABCD 中，AB ∥CD ，E ，F 是线段AB 上的两点，且DE ⊥AB ，CF ⊥AB ，AB ＝12，AD ＝5，BC ＝42，DE ＝4，现将△ADE ，△CFB 分别沿DE ，CF 折起，使A ，B 两点重合于点G ，得到多面体CDEFG.(1)求证：平面DEG ⊥平面CFG ； (2)图1－721．解：(1)证明：因为DE ⊥EF ，CF ⊥EF ，所以四边形CDEF 为矩形，由GD ＝5，DE ＝4，得GE ＝GD 2－DE 2＝3.由GC ＝42，CF ＝4，得FG ＝GC 2－CF 2＝4，所以EF ＝5.在△EFG 中，有EF 2＝GE 2＋FG 2，所以EG ⊥GF ，又因为CF ⊥EF ，CF ⊥FG ，得，CF ⊥平面EFG ，所以CF ⊥EG ，所以EG ⊥平面CFG ，即平面DEG ⊥平面CFG .(2)如图，在平面EGF 中，过点G 作GH ⊥EF 于点H ，则GH ＝EG·GF EF ＝125.CDEF ⊥平面EFG ，得GH ⊥平面CDEF ，V CDEFG ＝13S CDEF ·GH ＝16. 22．G5、G7[2012·陕西卷] 直三棱柱ABC －A 1B 1C 1中，AB ＝AA 1，∠CAB ＝π2. (1)证明：CB 1⊥BA 1；(2)已知AB ＝2，BC ＝5，求三棱锥C －ABA 的体积．22AB 1，ABC －A 1B 1C 1是直三棱柱，∠CAB ＝π2，∴AC ⊥平面ABB 1A 1，故AC ⊥BA 1. 又∵AB ＝AA 1，∴四边形ABB 1A 1是正方形，∴BA 1⊥AB 1，又CA∩AB 1＝A.∴BA 1⊥平面CAB 1，故CB 1⊥BA 1.(2)∵AB ＝AA 1＝2，BC ＝5，∴AC ＝A 1C 1＝1，由(1)知，A 1C 1⊥平面ABA 1，∴VC 1－ABA 1＝13S △ABA 1·A 1C 1＝13×2×1＝23. 23．G5、G12[2012·广东卷] 如图1－5所示，在四棱锥P －ABCD 中，AB ⊥平面PAD ，AB ∥CD ，PD ＝AD ，E 是PB 的中点，F 是DC 上的点且DF ＝12AB ，PH 为△PAD 中AD 边上的高． (1)证明：PH ⊥平面ABCD ；(2)若PH ＝1，AD ＝2，FC ＝1，求三棱锥E －BCF 的体积；(3)证明：EF ⊥平面PAB.23．解：(1)由于AB ⊥平面PAD ，PH ⊂平面PAD ，故AB ⊥PH.又因为PH 为△PAD 中AD 边上的高，故AD ⊥PH. ∵AB∩AD ＝A ，AB ⊂平面ABCD ，AD ⊂平面ABCD ，∴PH ⊥平面ABCD.由于PH ⊥平面ABCD ，E 为PB 的中点，PH ＝1，故E 到平面ABCD 的距离h ＝12PH ＝12.又因为AB∥CD，AB⊥AD，所以AD⊥CD，故S△BCF＝12·FC·AD＝12·1·2＝22.因此V E－BCF＝13S△BCF·h＝13·22·12＝212.(3)证明：过E作EG∥AB交PA于G，连接DG.由于E为PB的中点，所以G为PA的中点．因为DA＝DP，故△DPA为等腰三角形，所以DG⊥PA.∵AB⊥平面PAD，DG⊂平面PAD，∴AB⊥DG. 又∵AB∩PA＝A，AB⊂平面PAB，PA⊂平面PAB，∴DG⊥平面PAB.又∵GE綊12AB，DF綊12AB，∴GE綊DF.所以四边形DFEG为平行四边形，故DG∥EF.于是EF⊥平面PAB.24．G5、G11[2012·安徽卷] 如图1－3，长方体ABCD－A1B1C1D1中，底面A1B1C1D1是正方形，O是BD的中点，E是棱AA1上任意一点．(1)证明：BD⊥EC1；(2)如果AB＝2，AE＝2，OE⊥EC1，求AA1的长．24．解：(1)证明：连接AC，A1C1.AA1⊥平面ABCD，BD⊆平面ABCD，所以AA1⊥BD.又由AA1∩AC＝A，所以BD⊥平面111⊆平面AA1C1C知，BD⊥EC1.(2)设AA1的长为h，连接OC1.在Rt△OAE中，AE＝2，AO＝2，故OE2＝(2)2＋(2)2＝4.在Rt△EA1C1中，A1E＝h－2，A1C1＝2 2.故EC21＝(h－2)2＋(22)2.在Rt△OCC1中，OC＝2，CC1＝h，OC21＝h2＋(2)2.因为OE⊥EC1，所以OE2＋EC21＝OC21，即4＋(h－2)2＋(22)2＝h2＋(2)2，解得h＝3 2.所以AA1的长为3 2.G6 三垂线定理G7 棱柱与棱锥25．G7[2012·山东卷] 如图1－3所示，正方体ABCD－A1B1C1D1的棱长为1，E为线段B1C上的一点，则三棱锥A －DED1的体积为________．25. [解本题考查棱锥的体积公式，考查空间想象力与转化能力，容易题．V A－DED1＝VE－DD1A＝13×12×1×1×1＝16.26．G7[2012·江苏卷] 如图1－2，在长方体ABCD－A1B1C1D1中，AB＝AD＝3 cm，AA1＝2 cm，则四棱锥A－BB1D1D 的体积为________cm3.26．6[解析] 本题考查四棱锥体积的求解以及对长方体性质的运用．解题突破口为寻找四棱锥的高．连AC交BD于点O，因四边形ABCD为正方形，故AO为四棱锥A－BB1D1D的高，从而V＝13×2×32×322＝6.G8 多面体与球27．G8[2012·辽宁卷] 已知点P，A，B，C，D是球O表面上的点，PA⊥平面ABCD，四边形ABCD是边长为23的正方形，若PA＝26，则△OAB的面积为________．27．33 [解析] 本小题主要考查球的概念与性质．解题的突破口为弄清PC 为球的直径，问题转换为求长方体的对角线．因为四边形ABCD 是边长为23的正方形，故而AB ＝AD ＝23，如图1－4所示，PA ，AB ，AD 两两垂直，可以补充成以PA ，AB ，AD 为棱的球内接长方体，故而2R ＝PA 2＋AB 2＋AD 2＝43，所以R ＝23，故而△OAB 为等边三角形，S △OAB ＝34×(23)2＝3 3. 28．G8[2012·课标全国卷] 平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为( )A.6π B ．43π C ．46π D ．63π28．B [解析] 由题意，球的半径为R ＝12＋22＝3，所以球的体积为V ＝43πR 3＝43π.故选B. G12 单元综合29．G12[2012·四川卷] 下列命题正确的是( )A ．若两条直线和同一个平面所成的角相等，则这两条直线平行B ．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C ．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D ．若两个平面都垂直于第三个平面，则这两个平面平行39．C [解析] 对于A ，可以考虑一个圆锥的两条母线与底面所成角都相等，但它们不平行，A 错．对于B ，当三个点在同一条直线上，且该直线平行于一个平面时，不能保证两个平面平行；或者当其中两个点在平面一侧，第三点在平面异侧，且它们到平面距离相等，也不能保证两个平面平行，故B 错．对于C ，记平面外的直线为a ，两平面记为α、β，它们的交线为l.过a 作平面γ与平面α相交于b ，并使得b 不在β内，由a ∥α，可知a ∥b ，又a ∥β，故b ∥β.过b 的平面α与β相交于l ，由线面平行的性质定理可得：b ∥l ，再由公理可得：a ∥l.C 正确．对于D ，观察一个正方体共顶点的三个面，即可知D 错误．2012模拟题40．[2012·韶关调研] 三棱柱的直观图和三视图(正视图和俯视图是正方形，侧视图是等腰直角三角形)如图K27－3所示，则这个三棱柱的全面积等于( )图A ．12＋4 2 B ．6＋2 2 C ．8＋4 2 D ．440．A [解析] 由三视图的数据可知，三棱柱的全面积为S ＝2×12×2×2＋(2＋2＋22)×2＝12＋42，选A. 41．[2012·辽宁两校联考] 已知球的直径SC ＝4，A ，B 是球面上的两点，AB ＝2，∠BSC ＝∠ASC ＝45°，则棱锥S －ABC 的体积是( )A.33B.233C.433D.53341.令球心为O ，因为SC 是直径，所以SA ⊥AC ，SB ⊥BC ，则AO ＝BO ＝SC 2＝2＝AB ，AO ⊥SC ，BO ⊥SC ，所以△AOB 为正三角形，则点A 到BO 的距离为3，因为AO ⊥SC ，BO ⊥SC ，所以SC ⊥面AOB ，所以点A 到平面SBC 的距离h 等于点A 到BO 的距离，即h ＝3，所以棱锥S －ABC 的体积为S △SBC h 3＝SC·BO·h 6＝433. 42．[2012·辽宁部分重点中学联考] 棱长为1的正方体和它的外接球被一个平面所截，截面是一个圆及其内接正三角形，那么球心到截面的距离等于________．42. 36[解析] 在正方体ABCD －A 1B 1C 1中，球心到截面的距离即为O 到三角形ACB 1的中心H 的距离，根据点B 到平面ACB 1的距离是正方体的体对角线的13，而正方体的体对角线为3，∴O 到三角形ACB 1的中心H 的距离为：OB －BH ＝32－33＝36.。

2012年高考题立体几何

2012年高考题1.[2012·陕西卷] (1)如图所示，证明命题“a 是平面π内的一条直线，b 是π外的一条直线(b 不垂直于π)，c 是直线b 在π上的投影，若a ⊥b ，则a ⊥c ”为真；(2)写出上述命题的逆命题，并判断其真假(不需证明)．解：(1)证法一：如下图，过直线b 上任一点作平面π的垂线n ，设直线a ，b ，c ，n 的方向向量分别是a ，b ，c ，n ，则b ，c ，n 共面．根据平面向量基本定理，存在实数λ，μ使得c ＝λb ＋μn ，则a·c ＝a ·(λb ＋μn )＝λ(a·b )＋μ(a·n )，因为a ⊥b ，所以a·b ＝0，又因为a π，n ⊥π，所以a·n ＝0，故a·c ＝0，从而a ⊥c .证法二：如图，记c ∩b ＝A ，P 为直线b 上异于点A 的任意一点，过P 作PO ⊥π，垂足为O ，则O ∈c .∵PO ⊥π，a π，∴直线PO ⊥a ，又a ⊥b ，b 平面P AO ，PO ∩b ＝P ， ∴a ⊥平面P AO ，又c 平面P AO ，∴a ⊥c .(2)逆命题为：a 是平面π内的一条直线，b 是π外的一条直线(b 不垂直于π)，c 是直线b 在π上的投影，若a ⊥c ，则a ⊥b .逆命题为真命题．2.[2012·全国卷] 如图，四棱锥P －ABCD 中，底面ABCD 为菱形，P A ⊥底面ABCD ，AC ＝22，P A ＝2，E 是PC 上的一点，PE ＝2EC .(1)证明：PC ⊥平面BED ；(2)设二面角A －PB －C 为90°，求PD 与平面PBC 所成角的大小．解：方法一：(1)因为底面ABCD 为菱形，所以BD ⊥AC ，又P A ⊥底面ABCD ，所以PC ⊥BD .设AC ∩BD ＝F ，连结EF .因为AC ＝22，P A ＝2，PE ＝2EC ，故PC ＝23，EC ＝233，FC ＝2，从而PC FC ＝6，AC EC ＝ 6.因为PC FC ＝AC EC，∠FCE ＝∠PCA ，所以△FCE ∽△PCA ，∠FEC ＝∠P AC ＝90°，由此知PC ⊥EF .PC 与平面BED 内两条相交直线BD ，EF 都垂直，所以PC ⊥平面BED .(2)在平面P AB 内过点A 作AG ⊥PB ，G 为垂足．因为二面角A －PB －C 为90°，所以平面P AB ⊥平面PBC .又平面P AB ∩平面PBC ＝PB ，故AG ⊥平面PBC ，AG ⊥BC .BC 与平面P AB 内两条相交直线P A ，AG 都垂直，故BC ⊥平面P AB ，于是BC ⊥AB ，所以底面ABCD 为正方形，AD ＝2，PD ＝P A 2＋AD 2＝2 2.设D 到平面PBC 的距离为d .因为AD ∥BC ，且AD ⊄平面PBC ，BC ⊂平面PBC ，故AD ∥平面PBC ，A 、D 两点到平面PBC 的距离相等，即d ＝AG ＝ 2.设PD 与平面PBC 所成的角为α，则sin α＝d PD ＝12.所以PD 与平面PBC 所成的角为30°.方法二：(1)以A 为坐标原点，射线AC 为x 轴的正半轴，建立如图所示的空间直角坐标系A －xyz .设C (22，0,0)，D (2，b,0)，其中b >0，则P (0,0,2)，E ⎝⎛⎭⎫423，0，23，B (2，－b,0)．于是PC →＝(22，0，－2)，BE →＝⎝⎛⎭⎫23，b ，23，DE →＝⎝⎛⎭⎫23，－b ，23，从而PC →·BE →＝0，PC →·DE →＝0，故PC ⊥BE ，PC ⊥DE .又BE ∩DE ＝E ，所以PC ⊥平面BDE . (2)AP →＝(0,0,2)，AB →＝(2，－b,0)．设m ＝(x ，y ，z )为平面P AB 的法向量，则m ·AP →＝0，m ·AB →＝0，即2z ＝0，且2x －by ＝0，令x ＝b ，则m ＝(b ，2，0)．设n ＝(p ，q ，r )为平面PBC 的法向量，则n ·PC →＝0，n ·BE →＝0，即22p －2r ＝0且2p 3＋bq ＋23r ＝0，令p ＝1，则r ＝2，q ＝－2b ，n ＝⎝⎛⎭⎫1，－2b ，2. 因为面P AB ⊥面PBC ，故m·n ＝0，即b －2b＝0，故b ＝2，于是n ＝(1，－1，2)，DP →＝(－2，－2，2)，cos 〈n ，DP →〉＝n ·DP →|n ||DP →|＝12，〈n ，DP →〉＝60°. 因为PD 与平面PBC 所成角和〈n ，DP →〉互余，故PD 与平面PBC 所成的角为30°.3.[2012·福建卷] 如图，在长方体ABCD －A 1B 1C 1D 1中，AA 1＝AD ＝1，E 为CD 中点．(1)求证：B 1E ⊥AD 1；(2)在棱AA 1上是否存在一点P ，使得DP ∥平面B 1AE ？若存在，求AP 的长；若不存在，说明理由；(3)若二面角A －B 1E －A 1的大小为30°，求AB 的长．解：(1)以A 为原点，AB →，AD →，AA 1→的方向分别为x 轴，y 轴，z 轴的正方向建立空间直角坐标系(如图)．设AB ＝a ，则A (0,0,0)，D (0,1,0)，D 1(0,1,1)，E ⎝⎛⎭⎫a 2，1，0，B 1(a,0,1)，故AD 1＝(0,1,1)，B 1E →＝⎝⎛⎭⎫－a 2，1，－1，AB 1→＝(a,0,1)，AE →＝⎝⎛⎭⎫a 2，1，0. ∵AD 1→·B 1E →＝－a 2×0＋1×1＋(－1)×1＝0，∴B 1E ⊥AD 1.(2)假设在棱AA 1上存在一点P (0,0，z 0)，使得DP ∥平面B 1AE .此时DP →＝(0，－1，z 0)．又设平面B 1AE 的法向量n ＝(x ，y ，z )．∵n ⊥平面B 1AE ，∴n ⊥AB 1→，n ⊥AE →，得⎩⎪⎨⎪⎧ ax ＋z ＝0，ax 2＋y ＝0. 取x ＝1，得平面B 1AE 的一个法向量n ＝⎝⎛⎭⎫1，－a 2，－a . 要使DP ∥平面B 1AE ，只要n ⊥DP →，有a 2－az 0＝0，解得z 0＝12. 又DP ⊄平面B 1AE ，∴存在点P ，满足DP ∥平面B 1AE ，此时AP ＝12. (3)连接A 1D ，B 1C ，由长方体ABCD －A 1B 1C 1D 1及AA 1＝AD ＝1，得AD 1⊥A 1D .∵B 1C ∥A 1D ，∴AD 1⊥B 1C .又由(1)知B 1E ⊥AD 1，且B 1C ∩B 1E ＝B 1，∴AD 1⊥平面DCB 1A 1.∴AD 1→是平面A 1B 1E 的一个法向量，此时AD 1→＝(0,1,1)．设AD 1→与n 所成的角为θ，则cos θ＝n ·AD 1→|n ||AD 1→|＝－a 2－a 21＋a 24＋a 2. ∵二面角A －B 1E －A 1的大小为30°，∴|cos θ|＝cos30°，即3a221＋5a 24＝32，解得a ＝2，即AB 的长为2.4. [2012·江苏卷] 如图，在直三棱柱ABC －A 1B 1C 1中，A 1B 1＝A 1C 1，D ，E 分别是棱BC ，CC 1上的点(点D 不同于点C )，且AD ⊥DE ，F 为B 1C 1的中点．求证：(1)平面ADE ⊥平面BCC 1B 1；(2)直线A 1F ∥平面ADE .证明：(1)因为ABC －A 1B 1C 1是直三棱柱，所以CC 1⊥平面ABC ，又AD ⊂平面ABC ，所以CC 1⊥AD .又因为AD ⊥DE ，CC 1，DE ⊂平面BCC 1B 1，CC 1∩DE ＝E ，所以AD ⊥平面BCC 1B 1.又AD ⊂平面ADE ，所以平面ADE ⊥平面BCC 1B 1.(2)因为A 1B 1＝A 1C 1，F 为B 1C 1的中点，所以A 1F ⊥B 1C 1.因为CC 1⊥平面A 1B 1C 1，且A 1F ⊂平面A 1B 1C 1，所以CC 1⊥A 1F .又因为CC 1，B 1C 1⊂平面BCC 1B 1，CC 1∩B 1C 1＝C 1，所以A 1F ⊥平面BCC 1B 1.由(1)知AD ⊥平面BCC 1B 1，所以A 1F ∥AD .又AD ⊂平面ADE ，A 1F ⊄平面ADE ，所以A 1F ∥平面ADE .5.[2012·辽宁卷] 如图，直三棱柱ABC －A ′B ′C ′，∠BAC ＝90°，AB ＝AC ＝λAA ′，点M ，N 分别为A ′B 和B ′C ′的中点．(1)证明：MN ∥平面A ′ACC ′；(2)若二面角A ′－MN －C 为直二面角，求λ的值．解：(1)(证法一)连结AB ′，AC ′，由已知∠BAC ＝90°，AB ＝AC ，三棱柱ABC －A ′B ′C ′为直三棱柱．所以M 为AB ′中点．又因为N 为B ′C ′的中点．所以MN ∥AC ′.又MN ⊄平面A ′ACC ′， AC ′⊂平面A ′ACC ′，因此MN ∥平面A ′ACC ′.(证法二)取A ′B ′中点P ，连结MP ，NP ，M ，N 分别为AB ′与B ′C ′的中点，所以MP ∥AA ′，PN ∥A ′C ′，所以MP ∥平面A ′ACC ′，PN ∥平面A ′ACC ′，又MP ∩NP ＝P ，因此平面MPN ∥平面A ′ACC ′，而MN ⊂平面MPN ，因此MN ∥平面A ′ACC ′.(2)以A 为坐标原点，分别以直线AB ，AC ，AA ′为x 轴，y 轴，z 轴建立直角坐标系O －xyz ，如图所示．设AA ′＝1，则AB ＝AC ＝λ，于是A (0,0,0)，B (λ，0,0)，C (0，λ，0)，A ′(0,0,1)，B ′(λ，0,1)，C ′(0，λ，1)．所以M ⎝⎛⎭⎫λ2，0，12，N ⎝⎛⎭⎫λ2，λ2，1.设m ＝(x 1，y 1，z 1)是平面A ′MN 的法向量，由⎩⎪⎨⎪⎧ m ·A ′M →＝0，m ·MN →＝0得⎩⎨⎧ λ2x 1－12z 1＝0，λ2y 1＋12z 1＝0，可取m ＝(1，－1，λ)．设n ＝(x 2，y 2，z 2)是平面MNC 的法向量，由⎩⎪⎨⎪⎧ n ·NC →＝0，n ·MN →＝0得⎩⎨⎧ －λ2x 2＋λ2y 2－z 2＝0，λ2y 2＋12z 2＝0.可取n ＝(－3，－1，λ)．因为A ′－MN －C 为直二面角，所以m ·n ＝0.即－3＋(－1)×(－1)＋λ2＝0，解得λ＝ 2.6.[2012·重庆卷] 如图，在直三棱柱ABC －A 1B 1C 1中，AB ＝4，AC ＝BC ＝3，D 为AB 的中点．(1)求点C 到平面A 1ABB 1的距离；(2)若AB 1⊥A 1C ，求二面角A 1－CD －C 1的平面角的余弦值．解：(1)由AC ＝BC ，D 为AB 的中点，得CD ⊥AB .又CD ⊥AA 1，故CD ⊥面A 1ABB 1，所以点C 到平面A 1ABB 1的距离为CD ＝BC 2－BD 2＝ 5.(2)解法一：如图，取D 1为A 1B 1的中点，连结DD 1，则DD 1∥AA 1∥CC 1.又由(1)知CD ⊥面A 1ABB 1，故CD ⊥A 1D ，CD ⊥DD 1，所以∠A 1DD 1为所求的二面角A 1－CD －C 1的平面角．因A 1D 为A 1C 在面A 1ABB 1上的射影，又已知AB 1⊥A 1C ，由三垂线定理的逆定理得AB 1⊥A 1D ，从而∠A 1AB 1、∠A 1DA 都与∠B 1AB 互余，因此∠A 1AB 1＝∠A 1DA ，所以Rt △A 1AD ∽Rt △B 1A 1A .因此AA 1AD ＝A 1B 1AA 1，即AA 21＝AD ·A 1B 1＝8，得AA 1＝2 2. 从而A 1D ＝AA 21＋AD 2＝2 3.所以，在Rt △A 1DD 1中，cos ∠A 1DD 1＝DD 1A 1D ＝AA 1A 1D ＝63.解法二：如图，过D 作DD 1∥AA 1交A 1B 1于点D 1，在直三棱柱中，易知DB ，DC ，DD 1两两垂直．以D 为原点，射线DB ，DC ，DD 1分别为x 轴、y 轴、z 轴的正半轴建立空间直角坐标系D －xyz .设直三棱柱的高为h ，则A (－2,0,0)，A 1(－2,0，h )，B 1(2,0，h )，C (0，5，0)，C 1(0，5，h )，从而AB 1→＝(4,0，h )，A 1C →＝(2，5，－h )．由AB 1→⊥A 1C →，有8－h 2＝0，h ＝2 2.故DA 1→＝(－2,0,22)，CC 1→＝(0,0,22)，DC →＝(0，5，0)．设平面A 1CD 的法向量为m ＝(x 1，y 1，z 1)，则m ⊥DC →，m ⊥DA 1→，即⎩⎨⎧5y 1＝0，－2x 1＋22z 1＝0，取z 1＝1，得m ＝(2，0,1)，设平面C 1CD 的法向量为n ＝(x 2，y 2，z 2)，则n ⊥DC →，n ⊥CC 1→，即⎩⎨⎧5y 2＝0，22z 2＝0，取x 2＝1，得n ＝(1,0,0)，所以cos 〈m ，n 〉＝m·n |m ||n |＝22＋1·1＝63. 所以二面角A 1－CD －C 1的平面角的余弦值为63. 7. [2012·浙江卷] 如图1－5所示，在四棱锥P －ABCD 中，底面是边长为23的菱形，∠BAD ＝120°，且P A ⊥平面ABCD ，P A ＝26，M ，N 分别为PB ，PD 的中点．(1)证明：MN ∥平面ABCD ；(2)过点A 作AQ ⊥PC ，垂足为点Q ，求二面角A －MN －Q 的平面角的余弦值．解：(1)因为M ，N 分别是PB ，PD 的中点，所以MN 是△PBD 的中位线，所以MN ∥BD . 又因为MN ⊄平面ABCD ，所以MN ∥平面ABCD .(2)方法一：连结AC 交BD 于O .以O 为原点，OC ，OD 所在直线为x ，y 轴，建立空间直角坐标系Oxyz ，如图所示．在菱形ABCD 中，∠BAD ＝120°，得AC ＝AB ＝23，BD ＝3AB ＝6.又因为P A ⊥平面ABCD ，所以P A ⊥AC .在Rt △P AC 中，AC ＝23，P A ＝26，AQ ⊥PC ，得QC ＝2，PQ ＝4.由此知各点坐标如下，A (－3，0,0)，B (0，－3,0)，C (3，0,0)，D (0,3,0)，P (－3，0,26)，M ⎝⎛⎭⎫－32，－32， 6，N ⎝⎛⎭⎫－32，32， 6，Q ⎝⎛⎭⎫33，0，263. 设m ＝(x ，y ，z )为平面AMN 的法向量．由AM →＝⎝⎛⎭⎫32，－32，6，AN →＝⎝⎛⎭⎫32，32，6知⎩⎨⎧ 32x －32y ＋6z ＝0，32x ＋32y ＋6z ＝0.取z ＝－1，得m ＝(22，0，－1)．设n ＝(x ，y ，z )为平面QMN 的法向量．由QM →＝⎝⎛⎭⎫－536，－32，63，QN →＝⎝⎛⎭⎫－536，32，63知⎩⎨⎧ －536x －32y ＋63z ＝0，－536x ＋32y ＋63z ＝0，取z ＝5，得n ＝(22，0,5)．于是cos 〈m ，n 〉＝m·n |m |·|n |＝3333.所以二面角A －MN －Q 的平面角的余弦值为3333. 方法二：在菱形ABCD 中，∠BAD ＝120°，得AC ＝AB ＝BC ＝CD ＝DA ，BD ＝3AB . 又因为P A ⊥平面ABCD ，所以P A ⊥AB ，P A ⊥AC ，P A ⊥AD .所以PB ＝PC ＝PD .所以△PBC ≌△PDC .而M ，N 分别是PB ，PD 的中点，所以MQ ＝NQ ，且AM ＝12PB ＝12PD ＝AN . 取线段MN 的中点E ，连结AE ，EQ ，则AE ⊥MN ，QE ⊥MN ，所以∠AEQ 为二面角A －MN －Q 的平面角．由AB ＝23，P A ＝26，故在△AMN 中，AM ＝AN ＝3，MN ＝12BD ＝3，得AE ＝332. 在直角△P AC 中，AQ ⊥PC ，得AQ ＝22，QC ＝2，PQ ＝4.在△PBC 中，cos ∠BPC ＝PB 2＋PC 2－BC 22PB ·PC ＝56，得MQ ＝PM 2＋PQ 2－2PM ·PQ cos ∠BPC ＝5.在等腰△MQN 中，MQ ＝NQ ＝5，MN ＝3，得QE ＝MQ 2－ME 2＝112. 在△AEQ 中，AE ＝332，QE ＝112，AQ ＝22，得cos ∠AEQ ＝AE 2＋QE 2－AQ 22AE ·QE ＝3333. 所以二面角A －MN －Q 的平面角的余弦值为3333. 8. [2012·天津卷] 如图所示，在四棱锥P -ABCD 中，P A ⊥平面ABCD ，AC ⊥AD ，AB ⊥BC ，∠BAC ＝45°，P A ＝AD ＝2，AC ＝1.(1)证明PC ⊥AD ；(2)求二面角A －PC －D 的正弦值；(3)设E 与棱P A 上的点，满足异面直线BE 与CD 所成的角为30°，求AE 的长．解：方法一：如图所示，以点A 为原点建立空间直角坐标系，依题意得A (0,0,0)，D (2,0,0)，C (0,1,0)，B ⎝⎛⎭⎫－12，12，0，P (0,0,2)．(1)易得PC →＝(0,1，－2)，AD →＝(2,0,0)，于是PC →·AD →＝0，所以PC ⊥AD .(2)PC →＝(0,1，－2)，CD →＝(2，－1，0)．设平面PCD 的法向量n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ n ·PC →＝0，n ·CD →＝0，即⎩⎪⎨⎪⎧y －2z ＝0，2x －y ＝0.不妨令z ＝1，可得n ＝(1,2,1)．可取平面P AC 的法向量m ＝(1,0,0)．于是cos 〈m ，n 〉＝m·n |m|·|n |＝16＝66，从而sin 〈m ，n 〉＝306.所以二面角A －PC －D 的正弦值为306. (3)设点E 的坐标为(0,0，h )，其中h ∈[0,2]．由此得BE →＝⎝⎛⎭⎫12，－12，h ，由CD →＝(2，－1,0)，故cos 〈BE →，CD →〉＝BE →·CD →|BE →||CD →|＝3212＋h 2×5＝310＋20 h 2，所以，310＋20 h 2＝cos30°＝32，解得h ＝1010，即AE ＝1010. 方法二：(1)由P A ⊥平面ABCD ，可得P A ⊥AD .又由AD ⊥AC ，P A ∩AC ＝A ，故AD ⊥平面P AC ，又PC ⊂平面P AC ，所以PC ⊥AD .(2)如图所示，作AH ⊥PC 于点H ，连接DH .由PC ⊥AD ，PC ⊥AH ，可得PC ⊥平面ADH ，因此DH ⊥PC ，从而∠AHD 为二面角A －PC －D 的平面角.在Rt △P AC 中，P A ＝2，AC ＝1，由此得AH ＝25.由(1)知AD ⊥AH .故在Rt △DAH 中，DH ＝AD 2＋AH 2＝2305.因此sin ∠AHD ＝AD DH ＝306.所以二面角A －PC －D 的正弦值为306. (3)如图所示，因为∠ADC ＜45°，故过点B 作CD 的平行线必与线段AD 相交，设交点为F ，连接BE ，EF .故∠EBF 或其补角为异面直线BE 与CD 所成的角．由BF ∥CD ，故∠AFB ＝∠ADC .在Rt △DAC 中，CD ＝5，sin ∠ADC ＝15，故sin ∠AFB ＝15 .在△AFB 中，由BF sin ∠F AB ＝AB sin ∠AFB ，AB ＝12，sin ∠F AB ＝sin135°＝22，可得BF ＝52. 由余弦定理，BF 2＝AB 2＋AF 2－2AB ·AF ·cos ∠F AB ，可得AF ＝12.设AE ＝h . 在Rt △EAF 中，EF ＝AE 2＋AF 2＝h 2＋14.在Rt △BAE 中，BE ＝AE 2＋AB 2＝h 2＋12. 在△EBF 中，因为EF ＜BE ，从而∠EBF ＝30°，由余弦定理得cos30°＝BE 2＋BF 2－EF 22BE ·BF ，可解得h ＝1010.所以AE ＝1010. 9.[2012·四川卷] 如图所示，在正方体ABCD －A 1B 1C 1D 1中，M 、N 分别是棱CD 、CC 1的中点，则异面直线A 1M 与DN 所成的角的大小是________．答案：90° [解析] 因为ABCD －A 1B 1C 1D 1为正方体，故A 1在平面CDD 1C 1上的射影为D 1，即A 1M 在平面CDD 1C 1上的射影为D 1M ，而在正方形CDD 1C 1中，由tan ∠DD 1M ＝tan ∠CDN ＝12，可知D 1M ⊥DN ，由三垂线定理可知，A 1M ⊥DN .10. [2012·江苏卷] 如图1－4，在直三棱柱ABC －A 1B 1C 1中，A 1B 1＝A 1C 1，D ，E 分别是棱BC ，CC 1上的点(点D 不同于点C )，且AD ⊥DE ，F 为B 1C 1的中点．求证：(1)平面ADE ⊥平面BCC 1B 1；(2)直线A 1F ∥平面ADE .证明：(1)因为ABC －A 1B 1C 1是直三棱柱，所以CC 1⊥平面ABC ，又AD ⊂平面ABC ，所以CC 1⊥AD .又因为AD ⊥DE ，CC 1，DE ⊂平面BCC 1B 1，CC 1∩DE ＝E ，所以AD ⊥平面BCC 1B 1.又AD ⊂平面ADE ，所以平面ADE ⊥平面BCC 1B 1.(2)因为A 1B 1＝A 1C 1，F 为B 1C 1的中点，所以A 1F ⊥B 1C 1.因为CC 1⊥平面A 1B 1C 1，且A 1F ⊂平面A 1B 1C 1，所以CC 1⊥A 1F .又因为CC 1，B 1C 1⊂平面BCC 1B 1，CC 1∩B 1C 1＝C 1，所以A 1F ⊥平面BCC 1B 1.由(1)知AD ⊥平面BCC 1B 1，所以A 1F ∥AD .又AD ⊂平面ADE ，A 1F ⊄平面ADE ，所以A 1F ∥平面ADE .11. [2012·湖南卷] 如图，在四棱锥P －ABCD 中，P A ⊥平面ABCD ，AB ＝4，BC ＝3，AD ＝5，∠DAB ＝∠ABC ＝90°，E 是CD 的中点．(1)证明：CD ⊥平面P AE ；(2)若直线PB 与平面P AE 所成的角和PB 与平面ABCD 所成的角相等，求四棱锥P －ABCD 的体积．解：解法1：(1)如下图(1)，连结AC .由AB ＝4，BC ＝3，∠ABC ＝90°得AC ＝5.又AD ＝5，E 是CD 的中点，所以CD ⊥AE .因为P A ⊥平面ABCD ，CD ⊂平面ABCD ，所以P A ⊥CD .而P A ，AE 是平面P AE 内的两条相交直线，所以CD ⊥平面P AE .(2)过点B 作BG ∥CD ，分别与AE 、AD 相交于点F ，G ，连结PF .由(1)CD ⊥平面P AE 知，BG ⊥平面P AE .于是∠BPF 为直线PB 与平面P AE 所成的角，且BG ⊥AE .由P A ⊥平面ABCD 知，∠PBA 为直线PB 与平面ABCD 所成的角．由题意∠PBA ＝∠BPF ，因为sin ∠PBA ＝P A PB ，sin ∠BPF ＝BF PB，所以P A ＝BF . 由∠DAB ＝∠ABC ＝90°知，AD ∥BC ，又BG ∥CD ，所以四边形BCDG 是平行四边形．故GD ＝BC ＝3.于是AG ＝2.在Rt △BAG 中，AB ＝4，AG ＝2，BG ⊥AF ，所以BG ＝AB 2＋AG 2＝25，BF ＝AB 2BG ＝1625＝855.于是P A ＝BF ＝855. 又梯形ABCD 的面积为S ＝12×(5＋3)×4＝16，所以四棱锥P －ABCD 的体积为V ＝13×S ×P A ＝ 13×16×855＝128515.解法2：如上图(2)，以A 为坐标原点，AB ，AD ，AP 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系．设P A ＝h ，则相关各点的坐标为：A (0,0,0)，B (4,0,0)，C (4,3,0)，D (0,5,0)，E (2,4,0)，P (0,0，h )．(1)易知CD →＝(－4,2,0)，AE →＝(2,4,0)，AP →＝(0,0，h )．因为CD →·AE →＝－8＋8＋0＝0，CD →·AP →＝0，所以CD ⊥AE ，CD ⊥AP .而AP ，AE 是平面P AE 内的两条相交直线，所以CD ⊥平面P AE .(2)由题设和(1)知，CD →，P A →分别是平面P AE ，平面ABCD 的法向量．而PB 与平面P AE 所成的角和PB 与平面ABCD 所成的角相等，所以|cos 〈CD →，PB →〉|＝|cos 〈P A →，PB →〉|，即⎪⎪⎪⎪⎪⎪CD →·PB →|CD →|·|PB →|＝⎪⎪⎪⎪⎪⎪P A →·PB →|P A →|·|PB →|.由(1)知，CD →＝(－4,2,0)，P A →＝(0,0，－h )，又PB →＝(4,0，－h )，故⎪⎪⎪⎪⎪⎪－16＋0＋025·16＋h 2＝⎪⎪⎪⎪⎪⎪0＋0＋h 2h ·16＋h 2.解得h ＝855. 又梯形ABCD 的面积为S ＝12×(5＋3)×4＝16，所以四棱锥P －ABCD 的体积为V ＝13×S ×P A ＝13×16×855＝128515.。

2012高考数学试题汇编立体几何

内的两条相交直线，所以 CD 平面PAE .
(Ⅱ)由题设和（Ⅰ）知， CD, AP 分别是平面PAE ，平面ABCD 的法向量，而 PB 与
平面PAE 所成的角和 PB 与平面ABCD 所成的角相等，所以
CD PB PA PB cos CD, PB cos PA, PB ,即 . CD PB PA PB
又梯形 ABCD 的面积为 S 6 3 3 5 15
【点评】本题考查空间线面垂直关系的证明，考查空间角的应用，及几何体体积计算.第一问只要证明 PA CD 即可，第二问算出梯形的面积和棱锥的高，由 V 积，或者建立空间直角坐标系，求得高几体积.
BG
AB 2 16 8 5 AB AG 2 5, BF . BG 5 2 5
2 2
于是 PA BF
8 5 . 5
1 (5 3) 4 16, 所以四棱锥 P ABCD 的体积为 2
又梯形 ABCD 的面积为 S
V
1 1 8 5 128 5 S PA 16 . 3 3 5 15
2012年普通高等学校招生全国统一考试(辽宁卷) 数学(供理科考生使用)
(18)(本小题满分 12 分) 如图，直三棱柱 ABC A B C ， BAC 90 ，
/ / /
AB AC AA/ , 点 M，N 分别为 A/ B 和 B / C / 的中点。
(Ⅰ)证明： MN ∥平面 A ACC ; (Ⅱ)若二面角 A/ MN C 为直二面角，求的值。
（Ⅰ）易知 CD ( 4, 2, 0), AE (2, 4, 0), AP (0, 0, h ). 因为

2012立体几何高考题

2012年高考立体几何选作1、[2012·课标全国卷] 已知三棱锥S －ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 为球O 的直径，且SC ＝2，则此棱锥的体积为( ) A.26 B.36 C.23 D.222、[2012·辽宁卷] 已知正三棱锥P －ABC ，点P ，A ，B ，C 都在半径为3的球面上．若P A ，PB ，PC 两两相互垂直，则球心到截面ABC 的距离为________．3、[2012·北京卷] 如图1，在Rt △ABC 中，∠C ＝90°，BC ＝3，AC ＝6，D ，E 分别是AC ，AB 上的点，且DE ∥BC ，DE ＝2，将△ADE 沿DE 折起到△A 1DE 的位置，使A 1C ⊥CD ，如图2(1)求证：A 1C ⊥平面BCDE ；(2)若M 是A 1D 的中点，求CM 与平面A 1BE 所成角的大小；(3)线段BC 上是否存在点P ，使平面A 1DP 与平面A 1BE 垂直？说明理由．A CB DE A C E D M 图1 图24、[2012·湖北卷] 如图1所示，∠ACB ＝45°，BC ＝3，过动点A 作AD ⊥BC ，垂足D 在线段BC 上且异于点B ，连结AB ，沿AD 将△ABD 折起，使∠BDC ＝90°(如图2)．(1)当BD 的长为多少时，三棱锥A －BCD 的体积最大？(2)当三棱锥A －BCD 的体积最大时，设点E ，M 分别为棱BC ，AC 的中点，试在棱CD 上确定一点N ，使得EN ⊥BM ，并求EN 与平面BMN 所成角的大小．5、[2012·全国卷] 如图，四棱锥P －ABCD 中，底面ABCD 为菱形，P A ⊥底面ABCD ，AC ＝22，P A ＝2，E 是PC 上的一点，PE ＝2EC .(1)证明：PC ⊥平面BED ；(2)设二面角A －PB －C 为90°，求PD 与平面PBC 所成角的大小．A B C D AD BC M E 图1 图2PABC E6、[2012·辽宁卷] 如图，直三棱柱ABC －A ′B ′C ′，∠BAC ＝90°，AB ＝AC ＝λAA ′，点M ，N 分别为A ′B 和B ′C ′的中点．(1)证明：MN ∥平面A ′ACC ′；(2)若二面角A ′－MN －C 为直二面角，求λ的值．7、[2012·天津卷] 如图所示，在四棱锥P -ABCD 中，P A ⊥平面ABCD ，AC ⊥AD ，AB ⊥BC ，∠BAC ＝45°，P A ＝AD ＝2，AC ＝1.(1)证明PC ⊥AD ；(2)求二面角A －PC －D 的正弦值；(3)设E 与棱P A 上的点，满足异面直线BE 与CD 所成的角为30°，求AE 的长．A BCC /A /B /M N PA B C8、[2012·福建卷] 如图，在长方体ABCD －A 1B 1C 1D 1中，AA 1＝AD ＝1，E 为CD 中点．(1)求证：B 1E ⊥AD 1；(2)在棱AA 1上是否存在一点P ，使得DP ∥平面B 1AE ？若存在，求AP 的长；若不存在，说明理由；(3)若二面角A －B 1E －A 1的大小为30°，求AB 的长．9、[2012·湖南卷] 如图，在四棱锥P －ABCD 中，P A ⊥平面ABCD ，AB ＝4，BC ＝3，AD ＝5，∠DAB ＝∠ABC ＝90°，E 是CD 的中点．(1)证明：CD ⊥平面P AE ；(2)若直线PB 与平面P AE 所成的角和PB 与平面ABCD 所成的角相等，求四棱锥P －ABCD 的体积．A A 1B 1C 1D 1 D CE B B C EDP A。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2012高考文科试题解析分类汇编：立体几何一、选择题
.3.【2012高考全国文8】已知正四棱柱1111ABCD A BC D -中，
2AB =，122CC =，E 为1CC 的中点，则直线1AC 与平面BED 的距离为
（A ）2 （B ）3 （C ）2 （D ）．1
4.【2012高考陕西文8】将正方形（如图1所示）截去两个三棱锥，得到图2所示的几何体，则该几何体的左视图为（）
7.【2012高考广东文7】某几何体的三视图如图1所示，它的体积为
A ．72π
B ． 48π
C 30π
D ．24π
9.【2012高考重庆文9】设四面体的六条棱的长分别为1，1，1，1，2和a 且长为a 的棱与长为2的棱异面，则a 的取值范围是
（A ）．(0,2) （B ）(0,3) （C ）(1,2)（D ）(1,3)
图
1
正视图俯视图
侧视图
5
5
6
3
5
5 6
3
11.【2012高考浙江文5】设l 是直线，a ，β是两个不同的平面
A ．若l ∥a ，l ∥β，则a ∥β
B 若l ∥a ，l ⊥β，则a ⊥β
C ．若a ⊥β，l ⊥a ，则l ⊥β
D ．若a ⊥β, l ∥a ，则l ⊥β 12.【2012高考四川文6】下列命题正确的是（）
A 、若两条直线和同一个平面所成的角相等，则这两条直线平行
B 、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行
C ．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行
D 、若两个平面都垂直于第三个平面，则这两个平面平行
14.【2102高考北京文7】某三棱锥的三视图如图所示，该三棱锥的表面积是
（A ）28+65（B ）．30+65（C ）56+125（D ）60+125
二、填空题
15.【2012高考四川文14】如图，在正方体1111ABCD A BC D -中，
M 、N 分别是CD 、1CC 的中点，则异面直线1A M 与DN 所成的角的大小是____________。

N M
B 1
A 1
C 1
D 1B
D
C A
16.【2012高考上海文5】一个高为2的圆柱，底面周长为2π，该圆柱的表面积为
19.【2012高考江苏7】（5分）如图，在长方体1111ABCD A B C D -中，
3cm AB AD ==，12cm AA =，
则四棱锥11A BB D D -的体积为 ▲ cm 3
．
25.【2012高考全国文16】已知正方体1111ABCD A B C D -中，E 、F 分别为11BB CC 、的中点，那么异面直线AE 与1D F 所成角的余弦值为____________.
三、解答题
29.【2012高考重庆文20】（本小题满分12分，（Ⅰ）小问4分，（Ⅱ）小问8分）已知
直三棱柱111ABC A B C -中，
4AB =，3AC BC ==，D 为AB 的中点。

（Ⅰ）求异面直线1CC 和AB 的距离；（Ⅱ）若11AB AC ⊥，求二面角11A CD B --的平面角的余弦值。

【答案】（Ⅰ）（Ⅱ）
13
31.【2012高考新课标文19】（本小题满分12分）
如图，三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB=90°，AC=BC=1
2AA 1，D 是棱AA 1
的中点
(Ｉ)证明：平面BDC 1⊥平面BDC
（Ⅱ）平面BDC 1分此棱柱为两部分，求这两部分体积的比.1:1
32.【2012高考湖南文19】（本小题满分12分）
如图6，在四棱锥P-ABCD 中，PA ⊥平面ABCD ，底面ABCD 是等腰梯形，AD ∥BC ，AC ⊥BD.
（Ⅰ）证明：BD ⊥PC ；（Ⅱ）若AD=4，BC=2，直线PD 与平面PAC 所成的角为30°，求四棱锥P-ABCD 的体积
.12
B 1
C B
A D
C 1
A 1。