高等数学第八章二重积分试题及答案
高等数学课后习题答案--第八章

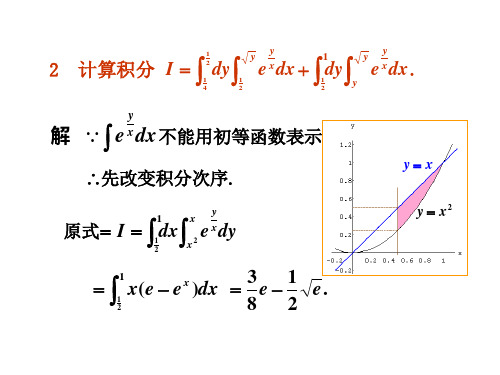
第八章 多元函数积分学 §3 三重积分的计算及其应用 习 题
1. 计算下列三重积分 (1) ∫∫∫ xy 2 z 3 dσ ,其中 Ω 是曲面 z = xy 和平面 y = x, x = 1, z = 0 所围成的区域;
Ω
(2) ∫∫∫ xzdσ ,其中 Ω 是由平面 z = 0 , x = y, y = z 以及抛物柱面 y = x 2 所围成的
D D
的大小。 【解】 利用 sin 2 x ≤ x 2 .则 sin 2 ( x + 2 y + 3z ) ≤ ( x + 2 y + 3z ) 2 积分得
∫∫∫ sin
D
2
( x + 2 y + 3 z )dσ ≤ ∫∫∫ ( x + 2 y + 3 z ) 2 dσ
D
4. 利用重积分的性质,估计积分值
(1) ∫∫ sin( x 2 + y 2 )dσ ,其中 D = {( x, y ) |
D
π
4
≤ x2 + y2 ≤
3π }; 4
dxdy , 其中 D = {( x, y ) | 0 ≤ x ≤ 4,0 ≤ y ≤ 8}; ln(4 + x + y ) D 2 2 1 (3) ∫∫ e x + y dσ ,其中 D = {( x, y ) | x 2 + y 2 ≤ }. 4 D
习题参考资料
第八章 多元函数积分学 §2 二重积分的计算 习 题
1. 计算二重积分
(1) ∫∫ xye xy dσ ,其中 D = {( x, y ) | 0 ≤ x ≤ 1,0 ≤ y ≤ 1};
2
D
(2) ∫∫
二重积分(答案)

第五次课一.(上册)回顾一元定积分的定义,牛顿-莱布尼兹公式(很重要,要掌握)二.二重积分的定义 几何意义(了解), 课本65页三.二重积分的性质(课本68页)四.二重积分的计算(重点) 课本70页(注:最主要的是确定积分的上限限)1. 直角坐标系下计算二重积分(X 型, Y 型,如何选择)2. 极坐标系下计算二重积分一.选择题1.设D 是以(0,0),(1,0),(1,2),(0,1)O A B C 为顶点的梯形所围成的有界闭区域,(,)f x y 是域D 上的连续函数,则二重积分(,)Df x y dxdy =⎰⎰ ( B )(A )1101(,)xdx f x y dy +⎰⎰(B )110(,)xdx f x y dy +⎰⎰(C )11211(,)(,)y dx f x y dy dx f x y dy -+⎰⎰⎰⎰(D )112111(,)(,)y dx f x y dy dx f x y dy -+⎰⎰⎰⎰2.二次积分⎰⎰22),(x dy y x f dx 的另一种积分次序是 ( A )(A )⎰⎰402),(ydx y x f dy (B )⎰⎰40),(ydx y x f dy (C )⎰⎰4022),(x dx y x f dy (D )⎰⎰402),(ydx y x f dy3.设f 是连续函数,而D :122≤+y x 且0>y ,则dxdy y x f D)(22⎰⎰+= ( A )(A )⎰1)(dr r rf π (B )⎰1)(dr r f π (C )2⎰1)(dr r rf π (D )2⎰1)(dr r f π二.填空题1.若积分区域D 是2214x y ≤+≤,则=3D dxdy π⎰⎰2.改换积分的次序⎰⎰⎰⎰-+102120),(),(xxdy y x f dx dy y x f dx =三.计算题1.设区域D 由22,y x y x ==所围成,求2()Dx y d +σ⎰⎰解:原式=241122200)[)]22x x x dx x y dy x x dx +=+-⎰⎰=54142033()22140x x x x dx -+-=⎰2.设D 是由直线2x =,y x =及1xy =所围成的平面区域,求22Dx dxdy y⎰⎰解:原式=222312119()4xxx dx dy x x dx y=-+=⎰⎰⎰ 解:原式=111200111(1)()266xdx x y dy x x dx ---=-+=⎰⎰⎰3.计算(课本81页 例题13)4. (课本81页 例题12).:222a y x D ≤+120(,)yydy f x y dx -⎰⎰,d d 22⎰⎰--Dy x y x e。
高等数学课后答案 第八章 习题详细解答

习 题 8-11.设有一个面薄板(不计其厚度),占有xOy 面上的闭区域D ,薄板上分布有面密度为(,)x y μμ=的电荷,且(,)x y μ在D 上连续,试用二重积分表达该板上的全部电荷Q .解 用一组曲线将D 分成n 个小闭区域i σ∆,其面积也记为(1,2,,)i i n σ∆= .任取一点(,)i i i ξησ∈∆,则i σ∆上分布的电量(,)i i i Q μξησ∆≈∆.通过求和、取极限,便得到该板上的全部电荷为1lim (,)(,)d ,ni i i i DQ x y λμξησμσ→==∆=∑⎰⎰其中1max{i i nλσ≤≤=∆的直径}.2. 设12231()d D I x y σ=+⎰⎰其中1{(,)11,22}D x y x y =-≤≤-≤≤;又22232()d D I x y σ=+⎰⎰其中2{(,)01,02}D x y x y =≤≤≤≤.试利用二重积分的几何意义说明1I 与2I 之间的关系.解 由二重积分的几何意义知,1I 表示底为1D 、顶为曲面223()z x y =+的曲顶柱体1Ω的体积;2I 表示底为2D 、顶为曲面223()z x y =+的曲顶柱体2Ω的体积.由于位于1D 上方的曲面223()z x y =+关于yOz 面和zOx 面均对称,故yOz 面和zOx 面将1Ω分成四个等积的部分,其中位于第一卦限的部分即为2Ω.由此可知124I I =.3. 利用二重积分定义证明: (1) d ()DD σσσ=⎰⎰其中为的面积;(2) (,)d (,)d ()DDkf x y k f x y k σσ=⎰⎰⎰⎰其中为常数;(3)12(,)d (,)d (,)d ,DD D f x y f x y f x y σσσ=+⎰⎰⎰⎰⎰⎰其中12D D D= ,1D 、2D 为两个无公共内点的闭区域.证 (1) 由于被积函数(,)1f x y ≡,故由二重积分定义得11d lim (,)lim lim .nniiii i i Df λλλσξησσσσ→→→===∆=∆==∑∑⎰⎰(2) 011(,)d lim (,)lim (,)(,)d .nni i i i i i i i DDkf x y kf k f k f x y λλσξησξησσ→→===∆=∆=∑∑⎰⎰⎰⎰(3) 因为函数(,)f x y 在闭区域D 上可积,故不论把D 怎样分割,积分和的极限总是不变的,因此在分割D 时,可以使1D 和2D 的公共边界永远是一条分割线。
二重积分习题答案

二重积分习题答案 Revised by BLUE on the afternoon of December 12,2020.第八章二重积分习题答案练习题1.设D:0y ≤0x a ≤≤,由二重积分的几何意义计算d Dx y解:d Dx y=200d πθ⎰⎰=222001()2r d a r πθ=--⎰⎰2. 设二重积分的积分区域为2214x y ≤+≤,则2dxdy =⎰⎰ 解:2dxdy =⎰⎰22126d rdr πθπ=⎰⎰练习题1.2d Dx σ⎰⎰其中D 是两个圆,y x 122=+与,y x 422=+围成的环型区域.解:2d Dx σ⎰⎰=22222301001515cos [cos2]84d r dr d d πππθθθθθπ=+=⎰⎰⎰⎰ 2计算二重积分σd yx D)341(--⎰⎰,其中D 是由直线2,,2=-=x x ;1,1=-=y y 围成的矩形。
解:σd y x D)341(--⎰⎰= 221211212(1)[(1)]4346x y x y dx dy y dx ------=--⎰⎰⎰=222(1)84xdx --=⎰3. 应用二重积分,求在xy 平面上由曲线224x x y x y -==与所围成的区域D 的面积.解:22242202320(42)28(2)|33x x xDA dxdy dx dy x x x x -===-=-=⎰⎰⎰⎰⎰4. 求旋转抛物面224z x y =--与xy 平面所围成的立体体积 解: 2222220(4)(4)48DV x y d d r rdr d ππσθθπ=--=-==⎰⎰⎰⎰⎰习 题 八一.判断题1.d Dσ⎰⎰等于平面区域D 的面积.(√)2.二重积分 100f(x,y)d ydy x ⎰⎰交换积分次序后为11f(x,y)d xdx x ⎰⎰ (×)二.填空题1.二重积分的积分区域为2214x y ≤+≤,则4dxdy =⎰⎰12π12π.2.二重积分d d Dxy x y ⎰⎰的值为112,其中2:0D y x ≤≤,01x ≤≤.1123.二重积分10(,)ydy f x y dx ⎰⎰交换积分次序后为11(,)xdx f x y dy⎰⎰. 11(,)xdx f x y dy ⎰⎰4.设区域D 为1x ≤,1y ≤,则⎰⎰(sin x x -)d d x y =0.05.交换积分次序1d (,)y f x y dx ⎰=211(,)(,)x dx f x y dy f x y dy+⎰⎰.211(,)(,)x dx f x y dy f x y dy +⎰⎰6.设D 是由221x y +≤所确定的区域。
高等数学第八章习题详细答案

习 题 8-11.设有一个面薄板(不计其厚度),占有xOy 面上的闭区域D ,薄板上分布有面密度为(,)x y μμ=的电荷,且(,)x y μ在D 上连续,试用二重积分表达该板上的全部电荷Q .解 用一组曲线将D 分成n 个小闭区域i σ∆,其面积也记为(1,2,,)i i n σ∆= .任取一点(,)i i i ξησ∈∆,则i σ∆上分布的电量(,)i i i Q μξησ∆≈∆.通过求和、取极限,便得到该板上的全部电荷为1lim (,)(,)d ,ni i i i DQ x y λμξησμσ→==∆=∑⎰⎰其中1max{i i nλσ≤≤=∆的直径}.2. 设11D I σ=其中1{(,)|1,0,0}D x y x y x y =+≤≥≥;又22D I σ=其中222{(,)1,0,0}D x y x y x y =+≤≥≥.试利用二重积分的几何意义说明1I 与2I 之间的关系.解 由二重积分的几何意义知,1I 表示底为1D 、顶为曲面z =1Ω的体积;2I 表示底为2D 、顶为曲面z =2Ω的体积.由于当0,1x y ≤≤时,12()()S D S D <且12D D ⊂,位于1D 上方的曲面z 始终不低于曲面z =12I I <.3. 利用二重积分定义证明: (1) d ()DD σσσ=⎰⎰其中为的面积;(2) (,)d (,)d ()DDkf x y k f x y k σσ=⎰⎰⎰⎰其中为常数;(3)12(,)d (,)d (,)d ,DD D f x y f x y f x y σσσ=+⎰⎰⎰⎰⎰⎰其中12D D D= ,1D 、2D 为两个无公共内点的闭区域.证 (1) 由于被积函数(,)1f x y ≡,故由二重积分定义得11d lim (,)lim lim .nniiii i i Df λλλσξησσσσ→→→===∆=∆==∑∑⎰⎰(2) 011(,)d lim (,)lim (,)(,)d .nni i i i i i i i DDkf x y kf k f k f x y λλσξησξησσ→→===∆=∆=∑∑⎰⎰⎰⎰(3) 因为函数(,)f x y 在闭区域D 上可积,故不论把D 怎样分割,积分和的极限总是不变的,因此在分割D 时,可以使1D 和2D 的公共边界永远是一条分割线。
高等数学第八章二重积分试题及答案

第八章 多元函数积分学一、二重积分的概念与性质1.定义设()y x f ,是定义在有界闭区域D 上的有界函数,如果对任意分割D 为n 个小区域,,,,21n σσσ∆∆∆ 对小区域()n k k ,,2,1 =∆σ上任意取一点()k k ηξ,都有()k nk k kd f σηξ∆∑=→1,lim存在,(其中k σ∆又表示为小区域k σ∆的面积,k d 为小区域k σ∆的直径,而k nk d d ≤≤=1max ) 则称这个极限值为()y x f ,在区域D 上的二重积分 记以()⎰⎰Dd y x f σ,,这时就称()y x f ,在D 上可积。
如果()y x f ,在D 上是有限片上的连续函数,则()y x f ,在D 上是可积的。
2.几何意义当()y x f ,为闭区域D 上的连续函数,且()0,≥y x f ,则二重积分()⎰⎰Dd y x f σ,表示以曲面()y x f z ,=为顶,侧面以D 的边界曲线为准线,母线平行于z 轴的曲顶柱体的体积。
当封闭曲面S 它在xy 平面上的投影区域为D ,上半曲面方程为()y x f z ,2=,下半曲面方程为()y x f z ,1=,则封闭曲面S 围成空间区域的体积为()()[]σd y x f y x f D⎰⎰-,,123.基本性质 (1)()()⎰⎰⎰⎰=DDd y x f k d y x kf σσ,,(k 为常数)(2)()()[]()()σσσd y x g d y x f d y x g y x f DDD⎰⎰⎰⎰⎰⎰±=±,,,,(3)()()()⎰⎰⎰⎰⎰⎰+=12,,,D D Dd y x f d y x f d y x f σσσ 其中21UDD D =,除公共边界外,1D 与2D 不重叠。
(4)若()()y x g y x f ,,≤,()D y x ∈,,则()()⎰⎰⎰⎰≤DDd y x g d y x f σσ,,(5)若()M y x f m ≤≤,,()D y x ∈,,则()⎰⎰≤≤DMS d y x f mS σ, 其中S 为区域D 的面积。
高等数学教材二重积分答案

高等数学教材二重积分答案在进行高等数学学习的过程中,二重积分是一个非常重要的概念。
掌握了二重积分的求解方法以及相应的答案,对于我们理解和应用高等数学知识有着至关重要的作用。
本文将回答一些关于二重积分的题目,以帮助读者更好地理解和应用这一概念。
1. 求解二重积分∬(x^2+y^2)dxdy,其中积分区域为x^2+y^2≤1。
首先要确定积分区域,由于条件限制为x^2+y^2≤1,因此积分区域为单位圆。
接下来我们可以将此二重积分转换成极坐标下的积分形式。
当x和y用极坐标表示时,x=rcosθ,y=rsinθ,其中r为极径,θ为极角,那么根据雅可比行列式的性质,dx dy=r dr dθ。
现在我们将原来的二重积分改写成极坐标下的形式:∬(r^2) r dr dθ。
由于积分区域为单位圆,所以对于极径r,积分范围为0到1;对于极角θ,积分范围为0到2π。
将上述积分范围代入原式,得到二重积分的答案为:∫[0,2π]∫[0,1](r^3) dr dθ。
2. 求解二重积分∬(2xy-3x^2)dydx,其中积分区域为0≤x≤1,0≤y≤2。
根据题目给定的积分区域,可以直接进行二重积分的计算。
首先计算内层的y方向的积分,即对2xy-3x^2关于y进行积分,得到xy^2-3x^2y。
然后再对x进行积分,积分范围是0到1。
将上一步得到的结果乘以x的积分范围并进行积分,即∫[0,1] (xy^2-3x^2y)dx。
计算这一步的结果,得到(1/4)y^2-(3/4)y。
最后,将y的积分范围0到2代入上一步得到的结果进行积分,即∫[0,2] [(1/4)y^2-(3/4)y]dy。
将这一步的计算结果代入,得到最终的答案为(-11/2)。
通过以上两个例子的解答,我们可以看到在求解二重积分时,首先需要确定积分区域,然后根据积分区域的不同,选择合适的计算方法。
在一些情况下,我们可以将二重积分转换成极坐标下的形式,从而简化计算过程。
高等数学课后答案 第八章 习题详细解答

习 题 8-11.设有一个面薄板(不计其厚度),占有xOy 面上的闭区域D ,薄板上分布有面密度为(,)x y μμ=的电荷,且(,)x y μ在D 上连续,试用二重积分表达该板上的全部电荷Q .解 用一组曲线将D 分成n 个小闭区域i σ∆,其面积也记为(1,2,,)i i n σ∆= .任取一点(,)i i i ξησ∈∆,则i σ∆上分布的电量(,)i i i Q μξησ∆≈∆.通过求和、取极限,便得到该板上的全部电荷为1lim (,)(,)d ,ni i i i DQ x y λμξησμσ→==∆=∑⎰⎰其中1max{i i nλσ≤≤=∆的直径}.2. 设12231()d D I x y σ=+⎰⎰其中1{(,)11,22}D x y x y =-≤≤-≤≤;又22232()d D I x y σ=+⎰⎰其中2{(,)01,02}D x y x y =≤≤≤≤.试利用二重积分的几何意义说明1I 与2I 之间的关系.解 由二重积分的几何意义知,1I 表示底为1D 、顶为曲面223()z x y =+的曲顶柱体1Ω的体积;2I 表示底为2D 、顶为曲面223()z x y =+的曲顶柱体2Ω的体积.由于位于1D 上方的曲面223()z x y =+关于yOz 面和zOx 面均对称,故yOz 面和zOx 面将1Ω分成四个等积的部分,其中位于第一卦限的部分即为2Ω.由此可知124I I =.3. 利用二重积分定义证明: (1) d ()DD σσσ=⎰⎰其中为的面积;(2) (,)d (,)d ()DDkf x y k f x y k σσ=⎰⎰⎰⎰其中为常数;(3)12(,)d (,)d (,)d ,DD D f x y f x y f x y σσσ=+⎰⎰⎰⎰⎰⎰其中12D D D= ,1D 、2D 为两个无公共内点的闭区域.证 (1) 由于被积函数(,)1f x y ≡,故由二重积分定义得11d lim (,)lim lim .nniiii i i Df λλλσξησσσσ→→→===∆=∆==∑∑⎰⎰(2) 011(,)d lim (,)lim (,)(,)d .nni i i i i i i i DDkf x y kf k f k f x y λλσξησξησσ→→===∆=∆=∑∑⎰⎰⎰⎰(3) 因为函数(,)f x y 在闭区域D 上可积,故不论把D 怎样分割,积分和的极限总是不变的,因此在分割D 时,可以使1D 和2D 的公共边界永远是一条分割线。
二重积分习题答案精编WORD版

二重积分习题答案精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】第八章二重积分习题答案练习题8.11.设D :0y ≤,0x a ≤≤,由二重积分的几何意义计算d Dx y解:d Dx y =20d πθ⎰⎰=22201()2r d a r πθ=--⎰⎰2. 设二重积分的积分区域为2214x y ≤+≤,则2dxdy =⎰⎰ 解:2dxdy =⎰⎰22126d rdr πθπ=⎰⎰练习题8.21.2d Dx σ⎰⎰其中D 是两个圆,y x 122=+与,y x 422=+围成的环型区域.解:2d Dx σ⎰⎰=22222301001515cos [cos2]84d r dr d d πππθθθθθπ=+=⎰⎰⎰⎰ 2计算二重积分σd yx D)341(--⎰⎰,其中D 是由直线2,,2=-=x x ;1,1=-=y y 围成的矩形。
解:σd yx D)341(--⎰⎰= 221211212(1)[(1)]4346x y x y dx dy y dx ------=--⎰⎰⎰=222(1)84xdx --=⎰3. 应用二重积分,求在xy 平面上由曲线224x x y x y -==与所围成的区域D 的面积.解:22242202320(42)28(2)|33x x xDA dxdy dx dy x x x x -===-=-=⎰⎰⎰⎰⎰4. 求旋转抛物面224z x y =--与xy 平面所围成的立体体积解: 222222(4)(4)48DV x y d d r rdr d ππσθθπ=--=-==⎰⎰⎰⎰⎰习 题 八一.判断题1.d Dσ⎰⎰等于平面区域D 的面积.(√)2.二重积分 100f(x,y)d ydy x ⎰⎰交换积分次序后为11f(x,y)d xdx x ⎰⎰ (×)二.填空题1.二重积分的积分区域为2214x y ≤+≤,则4dxdy =⎰⎰12π12π.2.二重积分d d Dxy x y ⎰⎰的值为112,其中2:0D y x ≤≤,01x ≤≤.1123.二重积分10(,)ydy f x y dx ⎰⎰交换积分次序后为11(,)xdx f x y dy⎰⎰. 11(,)xdx f x y dy ⎰⎰4.设区域D 为1x ≤,1y ≤,则⎰⎰(sin x x -)d d x y =0.05.交换积分次序1d (,)y f x y dx ⎰=211(,)(,)x dx f x y dy f x y dy+⎰⎰⎰⎰.211(,)(,)x dx f x y dy f x y dy +⎰⎰6.设D 是由221x y +≤所确定的区域。
二重积分习题解答

二重积分习题解答(一) 选择题(在每小题给出的四个选项中,只有一项符合题目要求,选出正确的选项) 1.12200I dy x y dx =⎰,则交换积分次序后得 C 。
(A)1220I dy x y dy =⎰; (B)12203I x y dy =⎰;(C )2112203x I dx x y dx -=⎰⎰; (D )2112203x I dx x y dy +=⎰⎰。
2.设积分域为{(,)|11,11}D x y x y =-≤≤-≤≤,则x yDedxdy +=⎰⎰ D. .(A)2)1(-e , (B)21)(2--e e , (C) 42)1(-e , (D) 21)(--e e ;3. 设积分域D 由直线,2,2y x x y x =+==围成,则(,)D f x y dxdy =⎰⎰ C(A)120(,)xx dx f x y dy -⎰⎰, (B) 21(,)yydyf x y dx -⎰⎰, (C) 212(,)xxdx f x y dy -⎰⎰, (D) 1(,)xdx f x y dy ⎰⎰.;4.22x y DI e dxdy --=⎰⎰,D :221x y +≤,化为极坐标形式是 D 。
(A )221[]r I e dr d πθ-=⎰⎰;(B )2124[]r I e dr d πθ-=⎰⎰;(C )21202[]r I e rdr d πθ-=⎰⎰;(D )221[]r I e rdr d πθ-=⎰⎰。
5. 2DI xy d σ=⎰⎰, 其中22:1D x y +≤的第一象限部分,则 C 。
(A)120I dy dy =⎰; (B )1120I dx xy dy =⎰⎰;(C)12I dx dy =⎰;(D )1232cos sin I d r dr πθθθ=⎰⎰。
填空题1.交换二次积分次序,1(,)xI f x y dy =⎰= 。
故211(,)(,)yxy I dx f x y dy dy f x y dx ==⎰⎰⎰2.设积分域D 由11,22,x y -≤≤-≤≤围成,则3(2)Dx y dxdy +=⎰⎰ 0 3.设积分域为22{(,)|14,}D x y x y y x =≤+≤≥,则积分22()Df xy dxdy +=⎰⎰在极坐标下的二次积分为 。
高等数学习题详解-第8章 二重积分[优质文档]
![高等数学习题详解-第8章 二重积分[优质文档]](https://img.taocdn.com/s3/m/e984d1d4aeaad1f346933f94.png)
习题8-11. 设有一平面薄片,在xOy 平面上形成闭区域D ,它在点(x ,y )处的面密度为μ(x ,y ),且μ(x ,y )在D 连续,试用二重积分表示该薄片的质量. 解:(,)Dm x y d μσ=⎰⎰.2. 试比较下列二重积分的大小:(1) 2()Dx y d σ+⎰⎰与3()Dx y d σ+⎰⎰,其中D 由x 轴、y 轴及直线x +y =1围成;(2)ln()Dx y d σ+⎰⎰与2ln()Dx y d σ+⎡⎤⎣⎦⎰⎰,其中D 是以A (1,0),B (1,1),C (2,0)为顶点的三角形闭区域.解:(1)在D 内,()()2301x y x y x y ≤+≤+≥+,故,23()()DDx y d x y d σσ+≥+⎰⎰⎰⎰.(2) 在D 内,212ln()1,ln()ln ()x y x y x y x y ≤+≤≤+≤+≥+,故0从而, 2ln()[ln()]DDx y d x y d σσ+≥+⎰⎰⎰⎰习题8-21. 画出积分区域,并计算下列二重积分:(1) ()Dx y d σ+⎰⎰,其中D 为矩形闭区域:1,1x y ≤≤;(2) (32)Dx y d σ+⎰⎰,其中D 是由两坐标轴及直线x +y =2所围成的闭区域;(3) 22()D xy x d σ+-⎰⎰,其中D 是由直线y =2,y =x ,y =2x 所围成的闭区域;(4) 2Dx y d σ⎰⎰,其中D 是半圆形闭区域:x 2+y 2≤4,x ≥0; (5) ln Dx y d σ⎰⎰,其中D 为:0≤x ≤4,1≤y ≤e ;(6)22Dx d σy ⎰⎰其中D 是由曲线11,,2xy x y x ===所围成的闭区域. 解:(1) 111111()()20.Dx y d dx x y dy xdx σ---+=+==⎰⎰⎰⎰⎰ (2) 222200(32)(32)[3(2)(2)]x Dx y d dx x y dy x x x dx σ-+=+=-+-⎰⎰⎰⎰⎰223202220[224]4.330x x dx x x x =-++=-++=⎰(3) 32222222002193()()()248yy Dy x y x d dy x y x dx y dy σ+-=+-=-⎰⎰⎰⎰⎰43219113.96860y y -= (4) 因为被积函数是关于y 的奇函数,且D 关于x 轴对称,所以20.Dx yd σ=⎰⎰(5) 44201041ln ln (ln ln )2(1)2110e De e e x yd dx x ydy x y y y dx x e σ-==-==-⎰⎰⎰⎰⎰.(6) 122224111311122222119()()124642x x Dx x x x x x d dx dy dx x x dx y y y x σ==-=-=-=⎰⎰⎰⎰⎰⎰.2. 将二重积分(,)Df x y d σ⎰⎰化为二次积分(两种次序)其中积分区域D 分别如下:(1) 以点(0,0),(2,0),(1,1)为顶点的三角形;(2) 由直线y =x 及抛物线y 2=4x 所围成的闭区域;(3) 由直线y =x ,x =2及双曲线1y x=所围成的闭区域;(4) 由曲线y =x 2及y =1所围成的闭区域. 解:(1) 1221201(,)(,)(,).xx y ydx f x y dy dx f x y dy dy f x y dx --+=⎰⎰⎰⎰⎰⎰(2) 2441004(,)(,).y x y dx f x y dy dy f x y dx =⎰⎰⎰⎰(3) 12222111112(,)(,)(,).xyyxdy f x y dx dy f x y dx dx f x y dy +=⎰⎰⎰⎰⎰⎰(4) 21111(,)(,).xdx f x y dy dy f x y dx -=⎰⎰⎰3. 交换下列二次积分的积分次序:(1) 10(,)ydy f x y dx ⎰⎰; (2)2220(,)yydy f x y dx ⎰⎰;(3) ln 10(,)e xdx f x y dy ⎰⎰; (4) 123301(,)(,)y ydy f x y dx dy f x y dx -+⎰⎰⎰⎰.解:(1) 111(,)(,)yxdy f x y dx dx f x y dy =⎰⎰⎰⎰.(2) 222402(,)(,).y x ydy f x y dx dx f x y dy =⎰⎰⎰⎰(3) ln 11(,)(,)y e xeedx f x y dy dy f x y dx =⎰⎰⎰⎰(4) 123323012(,)(,)(,)yyxxdy f x y dx dy f x y dx dx f x y dy --+=⎰⎰⎰⎰⎰⎰.4. 求由平面x =0,y =0,x =1,y =1所围成的柱体被平面z =0及2x +3y +z =6截得的立体体积.解:11100037(623)(62).22V dx x y dy x dx =--=--=⎰⎰⎰5. 求由平面x =0,y =0,x +y =1所围成的柱体被平面z =0及曲面x 2+y 2=6-z 截得的立体体积.解:3111222000(1)34(6)[6(1)(1)).312x x V dx x y dy x x x dx --=--=----=⎰⎰⎰习题8-31. 画出积分区域,把二重积分(,)Df x y d σ⎰⎰化为极坐标系下的二次积分,其中积分区域D是:(1) x 2+y 2≤a 2 (a >0); (2) x 2+y 2≤2x ;(3) 1≤x 2+y 2≤4; (4) 0≤y ≤1-x ,0≤x ≤1. 解:(1) 20(,)(cos ,sin ).aDf x y d d f r r rdr πσθθθ=⎰⎰⎰⎰(2) 2cos 202(,)(cos ,sin ).Df x y d d f r r rdr πθπσθθθ-=⎰⎰⎰⎰(3) 221(,)(cos ,sin ).D f x y d d f r r rdr πσθθθ=⎰⎰⎰⎰(4)12cos sin 0(,)(cos ,sin ).Df x y d d f r r rdr πθθσθθθ+=⎰⎰⎰⎰2. 把下列积分化为极坐标形式,并计算积分值:(1)220)ady x y dx +⎰;(2)21;xxdx ⎰⎰解:(1)4422320)248aaa a dy x y dx d r dr πππθ+==⋅=⎰⎰⎰.(2) 2sin 31244cos 600001sin 3cos x x dx d r dr d πθπθθθθθ==⎰⎰⎰⎰⎰244466400011c o s 111(c o s )[(c o s )(c o s )]33cos cos cos d d d πππθθθθθθθ-=-=--⎰⎰⎰531cos cos 4()3530πθθ--=--+= 3. 在极坐标系下计算下列二重积分:(1)22x y De d σ+⎰⎰,其中D 是圆形闭区域: x 2+y 2≤1;(2) 22ln(1)Dxy d σ++⎰⎰,其中D 是由圆周x 2+y 2=1及坐标轴所围成的在第一象限内的闭区域;(3)arctanDyd σx⎰⎰,其中D 是由圆周x 2+y 2=1,x 2+y 2=4及直线y =0,y =x 所围成的在第一象限内的闭区域;(4)Dσ其中D 由圆周x 2+y 2=Rx (R >0)所围成.解:(1) 22222100112(1).20xy r r De d d e rdr e e πσθππ+==⋅=-⎰⎰⎰⎰(2)23112222221ln(1)ln(1)[ln(1)]221Dr r xy d d r rdr r dr rππσθ++=+=+-+⎰⎰⎰⎰⎰ 212(1)[ln 22](2ln 21)441r r r dr rππ+-=-=-+⎰. (3) 222244010133arctan arctan(tan ).32264Dy d d rdr d rdr x ππππσθθθθ=⋅==⋅=⎰⎰⎰⎰⎰⎰(4)Dσ3cos 22222022cos 12()230R R d R r d ππθππθθθ--==--⎰⎰⎰ 3333221(s i n )33R R R d πππθθ-=--=⎰. 4. 求由曲面z =x 2+y 2与z =所围成的立体体积.解:两条曲线的交线为x 2+y 2=1,因此,所围成的立体体积为:212220()]().6DV x y d d r r rdr ππσθ=+=-=⎰⎰⎰⎰习题8-41. 计算反常二重积分()x y De dx dy -+⎰⎰,其中D :x ≥0,y ≥x .2. 计算反常二重积分222()Ddx dyx y +⎰⎰,其中D :x 2+y 2≥1. 解:1.22201()2a aaax yx x aaa xe dx edy eedx e e ---------=-=-+-⎰⎰⎰所以2()211lim ().22a x y a a a De edxdy e e --+--→+∞-=-+-=⎰⎰2. 由232011112()22R d dr r R πθπ=-⎰⎰,得222211lim 2().2()2R Ddxdy x y R ππ→+∞=-=+⎰⎰复习题8(A )1. 将二重积分d d (,)Df x y x y ⎰⎰化为二次积分(两种次序都要),其中积分区域D 是:(1) ︱x ︱≤1,︱y ︱≤2;(2) 由直线y =x 及抛物线y 2=4x 所围成. 解:(1) 12211221(,)(,).dx f x y dy dy f x y dx ----=⎰⎰⎰⎰(2) 244004(,)(,).yy xdx f x y dy dy f x y dx =⎰⎰⎰⎰2. 交换下列两次积分的次序:(1)d d 10(,)yy f x y x ⎰;(2)d d 20(,)a x x y y ⎰;(3)d d +d d 12201(,)(,)xxx f x y y x f x y y -⎰⎰⎰⎰.解:(1)211d (,)d d (,)d x yxy f x y x x f x y y =⎰⎰⎰.(2) 200d (,)d d (,)d aaa a x f x y y y f x y x =⎰⎰⎰.(3)1221201d (,)d +d (,)d d (,)d xxy yx f x y y x f x y y y f x y x --=⎰⎰⎰⎰⎰⎰.3. 计算下列二重积分:(1) e d x y Dσ+⎰⎰, D : ︱x ︱≤1,︱y ︱≤1;(2) d d 2D xy x y ⎰⎰,D 由直线y =1,x =2及y =x 围成;(3) d d (1)Dx x y -⎰⎰,D 由y =x 和y =x3围成;(4) d d 22()Dx y x y +⎰⎰,D :︱x ︱+︱y ︱≤1; (5) d 1sin Dy σy ⎰⎰,D 由22y x π=与y =x 围成; (6)d (4)Dx y σ--⎰⎰,D 是圆域x 2+y 2≤R 2;解: (1) 1111111211111e d ()()()1x y x y x x x x Ddx e dy e e dx e e e e σ+++-+----==-=-=--⎰⎰⎰⎰⎰.(2)5322224211121129d d ()()2253151xDx x xy x y dx x ydy x x dx ==-=-=⎰⎰⎰⎰⎰.(3) 3112430011117(1)d d (1)()325460x x Dx x y dx x dy x x x x dx -=-=--+=--+=-⎰⎰⎰⎰⎰.(4)1122220()d d 4()xDx y x y dx x y dy -+=+⎰⎰⎰⎰33241201412124(2)4()33323330x x x x x x dx x =--+=--+=⎰. (5) 222200sin 12sin d (sin sin )y y Dy y dy dx y y y dy y y πππσπ==-⎰⎰⎰⎰⎰222222sin (cos )1(cos sin )10ydy yd y y y y ππππππ=+=+-=-⎰⎰. (6)322200(4)d (4cos sin )[2(cos sin )]3RDR x y d r r rdr R d ππσθθθθθθ--=--=-+⎰⎰⎰⎰⎰3222[2(sin cos )]430R R R πθθθπ=--=.4. 已知反常二重积分e d 2y Dx σ-⎰⎰收敛,求其值.其中D 是由曲线y =4x 2与y =9x 2在第一象限所围成的区域.解:设2249(0)a D y x y x y a a ===>是由曲线、和在第一象限所围成.则22222200015555ed ()236144144144aaa a y y y y a D x dy dx ye dy e d y e σ-----==⋅=--=-⎰⎰⎰⎰⎰. 所以225e d lime d 144ay ya DD x x σσ--→+∞==⎰⎰⎰⎰. 5. 计算e d 2x x +∞--∞⎰.解:由第四节例2以及2y =e x -是偶函数,可知2e d x x +∞--∞=⎰.6. 求由曲面z =0及z =4-x 2-y 2所围空间立体的体积.解:曲面z =0和z =4-x 2-y 2的交线为x 2+y 2 =4.因此,所围空间立体的体积为:222220016(4)d d (4)2(8)84D x y x y d r rdr πθππ--=-=-=⎰⎰⎰⎰.7. 已知曲线y =ln x 及过此曲线上点(e ,1)的切线ey x 1=.(1) 求由曲线y =ln x ,直线ey x 1=和y =0所围成的平面图形D 的面积;(2) 求以平面图形D 为底,以曲面z =e y 为顶的曲顶柱体的体积.解:(1) 1ln (ln )12221e e e ee S xdx x x x =-=--=-⎰.(2) 221120013()()2220y y e yyyy y ye e V dy e dx e ye dy ye e ==-=-+=-⎰⎰⎰.(B )1. 交换积分次序:(1) 311(,)xxdx f x y dy -⎰⎰; (2)0112(,)y dy f x y dx --⎰⎰;(3) 224(,)x x f x y dy -⎰;(4) 110(,)dx f x y dy ⎰.解:(1) 3111(,)(,)x xydx f x y dy dy f x y dx -=⎰⎰⎰.(2) 01101221(,)(,)yxdy f x y dx dx f x y dy ---=⎰⎰⎰⎰.。
二重积分习题及答案1
去掉绝对值符号.
解 采用直角坐标
1
( x y )dxdy 4 dx
1x2 ( x y)dy 8
D
0
0
3
【注】在利用对称性计算二重积分时,要同时考虑被积
函数的奇偶性和积分区域的对称性,不能只注意积分区域
关于坐标轴的对称性,而忽视了被积函数应具有相应的奇
偶性.
6
证明
b
dx
x
(xΒιβλιοθήκη y)n23 d4sin r 2 rdr
15(
3).
D
6
2sin
2
sin cos
8
计算 ( x2 y2 )dxdy,其 D 为由圆
D
x2 y2 2 y, x2 y2 4 y及直线 x 3 y 0,
y 3x 0 所围成的平面闭区域.
解
y
3x
0
2
3
x2 y2 4 y r 4sin
x
3y
0
1
6
x2 y2 2 y r 2sin
( x2 y2 )dxdy
1
yx
D1
D2
o
1x
2D2 (x y)dxdy 2D dxdy
2 ( 2 1)
3
2
说明: 若不用对称性, 需分块积分以去掉绝对值符号.
5 计算 ( x y )dxdy, D : x2 y2 1
D
分析 积分区域D关于x、y轴均对称, 被积函数
f ( x, y) x y 关于x,y均是偶函数,利用对称性
D
式,其中积分区域
D {( x, y) | 1 x y 1 x2 , 0 x 1}.
解
在极坐标系下
(整理)高等数学课后答案第八章习题详细解答

习 题 8-11.设有一个面薄板(不计其厚度),占有xOy 面上的闭区域D ,薄板上分布有面密度为(,)x y μμ=的电荷,且(,)x y μ在D 上连续,试用二重积分表达该板上的全部电荷Q .解 用一组曲线将D 分成n 个小闭区域i σ∆,其面积也记为(1,2,,)i i n σ∆=.任取一点(,)i i i ξησ∈∆,则i σ∆上分布的电量(,)i i i Q μξησ∆≈∆.通过求和、取极限,便得到该板上的全部电荷为1lim (,)(,)d ,ni i i i DQ x y λμξησμσ→==∆=∑⎰⎰其中1max{i i nλσ≤≤=∆的直径}.2. 设12231()d D I x y σ=+⎰⎰其中1{(,)11,22}D x y x y =-≤≤-≤≤;又22232()d D I x y σ=+⎰⎰其中2{(,)01,02}D x y x y =≤≤≤≤.试利用二重积分的几何意义说明1I 与2I 之间的关系.解 由二重积分的几何意义知,1I 表示底为1D 、顶为曲面223()z x y =+的曲顶柱体1Ω的体积;2I 表示底为2D 、顶为曲面223()z x y =+的曲顶柱体2Ω的体积.由于位于1D 上方的曲面223()z x y =+关于yOz 面和zOx 面均对称,故yOz 面和zOx 面将1Ω分成四个等积的部分,其中位于第一卦限的部分即为2Ω.由此可知124I I =.3. 利用二重积分定义证明: (1) d ()DD σσσ=⎰⎰其中为的面积;(2) (,)d (,)d ()DDkf x y k f x y k σσ=⎰⎰⎰⎰其中为常数;(3)12(,)d (,)d (,)d ,DD D f x y f x y f x y σσσ=+⎰⎰⎰⎰⎰⎰其中12D DD =,1D 、2D 为两个无公共内点的闭区域.证 (1) 由于被积函数(,)1f x y ≡,故由二重积分定义得11d lim (,)lim lim .nniiii i i Df λλλσξησσσσ→→→===∆=∆==∑∑⎰⎰(2) 011(,)d lim (,)lim (,)(,)d .nni i i i i i i i DDkf x y kf k f k f x y λλσξησξησσ→→===∆=∆=∑∑⎰⎰⎰⎰(3) 因为函数(,)f x y 在闭区域D 上可积,故不论把D 怎样分割,积分和的极限总是不变的,因此在分割D 时,可以使1D 和2D 的公共边界永远是一条分割线。
二重积分练习题

二重积分练习题一、定义和性质在微积分中,二重积分是对二元函数在给定区域上的积分运算。
它可以看作是对一个平面区域上的函数进行求和。
1. 定义设函数 f(x,y) 在闭区域 D 上有界,将 D 分成若干个小区域ΔDi(i=1,2,...,n),其中ΔDi 的面积为ΔSi,选定任意一点(xi*, yi*) 属于ΔDi,作数值ΔZi= f(xi*, yi*)ΔSi,当ΔSi 的最大值趋于 0 时,如果和 I 的极限存在,则称 I 为 f(x,y) 在区域 D 上的二重积分,记作:∬ D f(x,y)dS = limΣΔZi2. 性质二重积分具有以下性质:(1)线性性质:对于常数 a 和 b,有∬ D (af(x,y) + bf(x,y))dS = a∬D f(x,y)dS + b∬ D f(x,y)dS(2)可加性:若 D = D1 ∪ D2,则有∬ D f(x,y)dS = ∬ D1 f(x,y)dS + ∬ D2 f(x,y)dS(3)保号性:若f(x,y)≥0,那么∬ D f(x,y)dS ≥ 0二、计算方法1. 求解一般二重积分对于一般的二重积分∬D f(x,y)dS,可以根据具体情况使用极坐标、直角坐标或变量代换等方法进行计算。
下面以几个实例为例进行说明。
例1:计算二重积分∬ D (x^2 + y)dS,其中 D 的边界由直线 y = x和 y = 2 - x 所确定。
解:根据题意,D 的边界可以表示为D = {(x,y) | 0 ≤ x ≤ 1, x ≤ y ≤ 2- x}。
使用直角坐标系计算时,可以将 f(x,y) 中的 x 和 y 分别看作是自变量,然后将 D 投影到 xy 平面得到关于 x 和 y 的积分限。
在本例中,可以先固定 y,让 x 遍历从 0 到 1 的范围,再让 y 遍历从 x 到 2 - x 的范围。
因此,二重积分可以表示为:∫(0,1)∫(x,2-x)(x^2 + y)dydx接下来按照一定的顺序进行积分运算,最终得到结果。
二重积分练习题答案

8、 ∫∫ x − y dxdy , D : x = 0, y = 0, x = 1, y = 1 y
D
1
解: 原式 = ∫∫ ( y − x)dxdy + ∫∫ ( x − y )dxdy
D1 D2
D1
D2
0
1
x
= ∫ dx
0
1
∫x ( y − x)dy + ∫ dx
1 0
1
∫0 ( x − y) 2 y
f ( x, y )dx
D
.
( -1,-1)
⎞ ⎛ 1 ⎜ - ,-1⎟ ⎝ 2 ⎠
1
高等数学——Copyright©2012 by Samw. All rights reserved.
3、 D : x 2 + y 2 ≥ ax , 2 + y 2 ≤ 2 ax ( a > 0) 将 ∫∫ f ( x, y ) dxdy 设 x
二重积分练习题
一、填空
x2 1、设 D : x = 2, y = x, xy = 1, ∫∫ 3 dxdy = y D
2 x x 2 x2 ∫∫ y3 dxdy = ∫1 dx ∫1x y 3 dy D
13 5
.
(2, 2)
(1,1)
1 (2, ) 2
2、设 D : y = x, y = 2 x, y = −1,将 ∫∫ f ( x, y )dxdy 化为累 次积分 =
D1 D2
0
1
x
= ∫ dθ
4 0
π
∫
sec θ
0
f (r cosθ , r sin θ )rdr f (r cosθ , r sin θ )rdr
重积分习题答案

第八章二重积分习题答案练习题8.11.设D:0y ≤,0x a ≤≤,由二重积分的几何意义计算d Dx y解:d Dx y=200d πθ⎰⎰=222001()2d a r πθ=--⎰⎰ 2. 设二重积分的积分区域为2214x y ≤+≤,则2dxdy =⎰⎰ 解:2dxdy =⎰⎰22126d rdr πθπ=⎰⎰练习题8.21.2d Dx σ⎰⎰其中D 是两个圆,y x 122=+与,y x 422=+围成的环型区域.解:2d Dx σ⎰⎰=22222301001515cos [cos2]84d r dr d d πππθθθθθπ=+=⎰⎰⎰⎰ 2计算二重积分σd yx D)341(--⎰⎰,其中D 是由直线2,,2=-=x x ;1,1=-=y y 围成的矩形。
解:σd yx D)341(--⎰⎰= 221211212(1)[(1)]4346x y x y dx dy y dx ------=--⎰⎰⎰ =222(1)84xdx --=⎰3. 应用二重积分,求在xy 平面上由曲线224x x y x y -==与所围成的区域D 的面积.解:22242202320(42)28(2)|33x x xDA dxdy dx dy x x x x -===-=-=⎰⎰⎰⎰⎰4. 求旋转抛物面224z x y =--与xy 平面所围成的立体体积 解: 222222(4)(4)48DV x y d d r rdr d ππσθθπ=--=-==⎰⎰⎰⎰⎰习 题 八一.判断题1.d Dσ⎰⎰等于平面区域D 的面积.(√)2.二重积分 100f(x,y)d ydy x ⎰⎰交换积分次序后为11f(x,y)d xdx x ⎰⎰ (×)二.填空题1.二重积分的积分区域为2214x y ≤+≤,则4dxdy =⎰⎰12π12π.2.二重积分d d Dxy x y ⎰⎰的值为112,其中2:0D y x ≤≤,01x ≤≤.1123.二重积分10(,)ydy f x y dx ⎰⎰交换积分次序后为11(,)xdx f x y dy⎰⎰. 11(,)xdx f x y dy ⎰⎰4.设区域D 为1x ≤,1y ≤,则⎰⎰(sin x x -)d d x y =0.05.交换积分次序1d (,)y f x y dx ⎰=211(,)(,)x dx f x y dy f x y dy+⎰⎰.211(,)(,)x dx f x y dy f x y dy +⎰⎰6.设D 是由221x y +≤所确定的区域。
酱菜学校二重积分习题参考答案

第八章二重积分习题参考答案(2012)练习8.11.二重积分定义中,极限过程为什么不取0σ∆→{}12(max ,,...,)n σσσσ∆=∆∆∆,即最大区域面积趋于零来描述“对D 的无限细分”?答:n 无限增大,精细的分割是指分割后每个小区域的任意两点的距离很小,这样(,)k k k f ξησ∆才接近实际值;直线上小区间长度很短就能保证其内任意两点距离很小,而平面上,小区域面积很小和其内任意两点距离很小却不是一回事,比如非常扁的长条面积虽小,但两头的点的距离却很大;定义的里0d →必有0σ∆→,但0σ∆→,不一定0d →,故不取0σ∆→来描述“对D 的无限细分”.2.有人说:“二重积分(,)Df x y d σ⎰⎰的几何意义是以(,)z f x y =为曲顶,以D 为底的曲顶柱体的体积.”是否正确?为什么?答:不正确,二重积分(,)Df x y d σ⎰⎰的几何意义包含三种情形而不是这一种情况.3.比较下列二重积分的大小: (1)2322()():(2)(1) 2.DDx y d x y d D x y σσ++-+-≤⎰⎰⎰⎰与(2)2ln()[ln()]DDx y d x y d σσ++⎰⎰⎰⎰与:(1,),(1,1),(2,0)D A B C 顶点为0的三角形闭区域.解:(1)在D 内显然有1x y +≥,所以在D 内有23()()x y x y +≤+故23()()DDx y d x y d σσ+≤+⎰⎰⎰⎰.xx y +(2)由已知可得BC 的直线方程为2,x y +=从而D 内有12, 0ln()1x y x y ≤+≤≤+< 所以2ln()[ln()]DDx y d x y d σσ+≥+⎰⎰⎰⎰.4.利用二重积分性质估计下列积分值: (1)(1),:01,02;DI x y d D x y σ=++≤≤≤≤⎰⎰ (2)2222(9),: 4.DI x y d D x y σ=+++≤⎰⎰解:(1)由于114(,)x y x y D ≤++≤∈ 所以(1)4DDDd x y d d σσσ≤++≤⎰⎰⎰⎰⎰⎰(1)4(2D D D DS x y d S S D σ≤++≤=⎰⎰为面积)21)8Dx y d σ≤++≤⎰⎰(.(2) 因为229913(,)x y x y D ≤++≤∈所以229(9)134D D D DS x y d S S σπ≤++≤=⎰⎰2236(9)52Dx y d πσπ≤++≤⎰⎰.5.判断二重积分22ln()DI x y d σ=+⎰⎰值的符号,: 1.D x y +≤解: 因为(,)x y D ∈有1x y +≤,所以2()1x y +≤22121x y xy +≤-≤即 所以22()0In x y +≤于是22()0DIn x y d σ+≤⎰⎰ 故I 取负号.练习8.21.若(,)f x y 在:,D a x b c y d ≤≤≤≤上两个二次积分都存在,则它们必定相等,即(,)(,)b dd baccadx f x y dy dy f x y dx =⎰⎰⎰⎰对否?为什么?xxyx解:对. 因为根据定理1有(,)(,)bdacDf x y d dx f x y dy σ=⎰⎰⎰⎰(,)(,)d bcaDf x y d dy f x y dx σ=⎰⎰⎰⎰,所以等式成立.2. 交换下列二次积分次序: (1)2211(,)x dx f x y dy ⎰⎰; 解:由已知的二次积分得积分区域2:12,1D x y x ≤≤≤≤推出D 由2,1,2y x y x ===围成;写成y 型区域:142D y x ≤≤≤≤故2211(,)x dx f x y dy =⎰⎰⎰⎰Dd y x f σ),(=⎰⎰241),(ydx y x f dy .(2)10(,)y dy f x y dx ⎰ 解:由已知得积分区域D 为: y x y y ≤≤≤≤,10 推出D 由2,y x y x ==围成; 写成x 型区域 2:01,D x x y x ≤≤≤≤故1(,)ydy f x y dx =⎰⎰⎰Dd y x f σ),(=21(,)xxdx f x y dy ⎰⎰.(3)211(,)yydy f x y dx ⎰⎰解:由已知得积分区域D 为: y x yy ≤≤≤≤121,推出D 由1,,2y y x y x===围成; 将D 写成x 型区域y xyx=12y =x1D :111,22x y x≤≤≤≤ 2D :12,2x x y ≤≤≤≤故211(,)y ydy f x y dx ⎰⎰=12112(,)xdx f x y dy ⎰⎰+221(,)xdx f x y dy ⎰⎰.(4)1220010(,)(,).x xdx f x y dy dx f x y dy -+⎰⎰⎰⎰ 解:由已知得积分区域D 由1D 和2D 构成1D : 01,0x y x ≤≤≤≤2D : 12,02x y x ≤≤≤≤-推出D 由,0,2y x y x y ==+=围成; 写成y 型区域 :012D y y x y ≤≤≤≤-, 故12201(,)(,)xxdx f x y dy dx f x y dy -+=⎰⎰⎰⎰⎰⎰-yydx y x f dy 210),(.3.计算下列二重积分:(1)323(3)Dx x y y d σ++⎰⎰,其中D 是矩形闭区域x y ≤≤≤≤01,01;解:1132332300(3)(3)Dx x y y d dx x x y y dy σ++=++⎰⎰⎰⎰24132100(3)24y y x y xdx =++⎰ 132031()24x x dx =++⎰43111()1424x x x =++=.(2)223/2(1)Dyd x y σ++⎰⎰,其中D 是矩形闭区域x y ≤≤≤≤01,01; 解:3322112222(1)(1)Dyy d dx dy xy x y σ=++++⎰⎰⎰⎰=32112220011[]2(1)dy dx x y ++⎰⎰x31122220011[(1)]2(1)d x y dx x y =++++⎰⎰121221001[(2)(1)]2x y dx -=⋅-⋅++⎰ 11221220[(2)(1)]x x dx --=-+-+⎰=11-⎰⎰(利用第六章公式)1100ln(ln(x x =+-ln(1ln(1=-+2)ln(1=-.(3)cos()Dx x y d σ+⎰⎰,其中D 是三顶点分别为,πππ(0,0),(,0)和()的三角形闭区域;解:由已知推出D 由,0,y x y x π===围成;:0,0D x y x π≤≤≤≤cos()cos()xDx x y d dx x x y dy πσ+=+⎰⎰⎰⎰=00[sin()]xx x y dx π+⎰(sin 2sin )x x x dx π=-⎰sin 2sin x xdx x xdx ππ=-⎰⎰01(cos 2)cos 2xd x xd x ππ=-+⎰⎰ 00001(cos 2cos 2)cos cos 2x x xdx x x xdx ππππ=-++-⎰⎰0011(cos 2cos 22)sin 22xd x x πππππ=-+--⎰ 322πππ=--=-.(4)2Dxy dxdy ⎰⎰,其中D 是由22(0)2py px x p ==>,围成的闭区域.解:D 为:2,,22y pp y p x p -≤≤≤≤ x22222p y pp pDxy dxdy dy xy dx -=⎰⎰⎰⎰=22222p y p px y dy -⎰=2422()88pp p y y dy p --⎰ 22621()88pp p y y dy p-=-⎰ 237502122838721p p p y y p p =⋅⋅-⋅⋅=. 4.将下列二重积分(,)Df x y dxdy ⎰⎰化为极坐标形式的二次积分:(1)222:D x y a +≤; 解: 因为222:D x y a +≤将cos ,sin x r y r θθ== 代入222x y a +=得222(r a x y a =+=的极坐标方程)极坐标系下:020D r a θπ≤≤≤≤, 所以200(,)(cos ,sin )aDf x y dxdy d f r r rdr πθθθ=⎰⎰⎰⎰(2)22:2.D x y x +≤解: 因为22:2D x y x +≤,即22(1)1x y -+≤ 将cos ,sin x r y r θθ== 代入222x y x +=得222cos (2r x y x θ=+=的极坐标方程)极坐标系下:02cos 22D r ππθθ-≤≤≤≤,所以2cos 202(,)(cos ,sin )Df x y dxdy d f r r rdr πθπθθθ-=⎰⎰⎰⎰.xx2px2a =5.将下列二次积分转化为极坐标系下的二次积分: (1)2200()Rdx f x y dy +⎰;解:已知:0,0D x R y ≤≤≤≤为推出D 由222,0,0x y R y x +===围成; 极坐标系下:002D r R πθ≤≤≤≤,22()Rdx f x y dy +⎰2200()Rd f r rdr πθ=⎰⎰.(2)200(,).Rdy f x y dx ⎰解:已知D为:02,0y R x ≤≤≤≤ 推出D 由222x y Ry +=即222(),0x y R R x +-==将cos ,sin x r y r θθ== 代入222x y Ry +=得222sin (2r R x y Ry θ=+=的极坐标方程)极坐标系下:002sin 2D r R πθθ≤≤≤≤,20(,)Rdy f x y dx ⎰2sin 200(cos ,sin )R d f r r rdr πθθθθ=⎰⎰.6.利用极坐标计算下列二重积分: (1){}22(4)(,)|4Dx y d D x y x y σ--+≤⎰⎰,=解: 22:4D x y +≤极坐标系下:0202D r θπ≤≤≤≤,22(4)(4cos sin )(4cos sin )DDx y d r r rdrd d r r rdrπσθθθθθθ--=--=--⎰⎰⎰⎰⎰⎰332222200(2cos sin )33r r rd πθθθ=--⎰ 2088(8cos sin )33d πθθθ=--⎰xxx2R 422()y R R -=2208816sin cos 1633πππθθπ=-+=.(2)22:1,0,0DD x y x y σ+≤≥≥, 解:22:1,0,0D x y x y +≤≥≥ 极坐标系下:0012D r πθ≤≤≤≤,200Dd πσθ=⎰⎰2d πθ=⎰⎰02π=⎰2200()44r t ππ===⎰⎰111()44ππ==-⎰⎰⎰21101(arcsin 42t π=-⎰121[(1)]422t ππ=+-⎰()(1)(2)42428ππππππ==-=-. (3)22ln(1)Dx y d σ++⎰⎰,其中D 是由圆周224x y +=以及坐标轴所围成的在第一象限的区域; 解: 222:2,0,0D x y x y +≤≥≥极坐标系下:0022D r πθ≤≤≤≤,22222ln(1)ln(1)Dx y d d r rdr πσθ++=+⎰⎰⎰⎰220ln(1)2r rdr π=+⎰2220ln(1)4r dr π=+⎰2220ln(1)(1)4r d r π=++⎰521ln (1)4tdt r t π=+=⎰x1=x45511(ln )4t t dt π=-⎰(5ln 54)4π=-.(4)222222sin(),:4,0,0.Dx y dxdy D x y x y ππ+≤+≤≥≥⎰⎰解: 2222:4,0,0D x y x y ππ≤+≤≥≥极坐标系下:022D r πθππ≤≤≤≤,22222sin()sin Dx y dxdy d r rdr πππθ+=⎰⎰⎰⎰ 222()(s i n )d r r d r πππθ=⋅⎰⎰ 22222sin sin 24r rdr r dr ππππππ==⎰⎰2222(cos )(cos cos 4)44r ππππππ=-=-.练习8.3(不作要求)1. 用二重积分变换计算: (1)22(),:;Dx y dxdy D x y x y ++≤+⎰⎰解: 22x y x y +≤+由,得22211()()22x y -+-≤令11,,22u x v y =-=-作变换11,,22x u y v =+=+101001J ==≠ 在变换下D 变成221:2D u v '+≤11()()(1)22DD D x y dxdy u v J dudv u v dudv ''+=+++=++⎰⎰⎰⎰⎰⎰:0202D r θπ'≤≤≤≤=,20()cos sin 1)Dx y dxdy d r r rdr πθθθ+=++⎰⎰⎰20[(cos sin )d πθθθ=+⎰x22001sin )124d d ππθθθθ=++⎰⎰220cos )1242ππθπθθ=-+=.(2)222222(),:1,0,0.Dx y x y dxdy D a b a b ++≤>>⎰⎰解:令,,x y u v a b== 作变换,,x au y bv ==000a J ab b==≠ 在变换下D 变成22:1D u v '+≤ 222222()()DD xy dxdy a u b v abdudv '+=+⎰⎰⎰⎰:0201D r θπ'≤≤≤≤,21222222220()(cos sin )Dx y dxdy d a r b r abrdr πθθθ+=+⎰⎰⎰⎰ 21222230(cos sin )d a b abr dr πθθθ=+⎰⎰42222210(cos sin )4rab a b d πθθθ=+⎰22222200(cos sin )4ab a d b d ππθθθθ=+⎰⎰2222001cos 21cos 2()422ab a d b d ππθθθθ+-=+⎰⎰222222011[(sin 2)(sin 2)42222ab a b ππππθθθθ=++-22()4ab a b π=+. 2. 用二重积分求由直线,(0),x y m x y n m n +=+=<<,(0)y ax y bx a b ==<< 所围成的区域D 的面积S . 解: 令 ,,yu x y v x=+= 作变换,.11u uv x y v v==++x122211(1)0(1)1(1)u v v uJ v u v vv -++==≠+++在变换下D 变成:D m u n a v b '≤≤≤≤221()[](1)(1)n b m a DD D u S dxdy J dudv dudv udu dv v v ''====⋅++⎰⎰⎰⎰⎰⎰⎰⎰ 2221()()()()212(1)(1)n b ma ub a n m v a b --=⋅-=+++.习题八 1. 填空题(1)设D 是第II 象限内的一个有界闭区域,且01y <<记32312,DDI yx d I y x d σσ==⎰⎰⎰⎰1323,DI y x d σ=⎰⎰则123I I I 、、的大小顺序为 . 答案:312I I I <<分析:因为01y <<,所以122y y y <<;而30x <,于是133232y x yx y x <<,故312I I I <<.(2)若D 是由直线1x y +=与两坐标轴围成的三角形区域,且1()()Df x dxdy x dx ϕ=⎰⎰⎰,则()x ϕ= .xax n答案: ()(1)()x x f x ϕ=-分析:因为1100()()xDf x dxdy dx f x dy -=⎰⎰⎰⎰1100()(1)()f x x dx x dx ϕ=-=⎰⎰所以()(1)()x x f x ϕ=-(3)设D 由(0)01y kx k y x =>==、、围成的有界闭区域,且21,15Dxy dxdy =⎰⎰则k = . 答案: 1k =分析:311220003kxkxDy xy dxdy dx xy dy xdx ==⎰⎰⎰⎰⎰3353141001,3351515k k x k x dx ====⎰ 31(0)k k =>,所以 1k =.(4)设()00(,)(,)(0)aa x ady f x y dx dx f x y dy a ϕ-=>⎰⎰⎰,则()x ϕ= .答案:()x ϕ=分析:因为0,y a x ≤≤-≤推出D 为222x y a +=的上半圆;换积分次序有:,0D a x a y -≤≤≤≤()(,)(,)(,)aaa x aady f x y dx dx f x y dy dx f x y dy ϕ--==⎰⎰⎰⎰所以()x ϕ=(5)设{}(,)10D x y x y x =+≤≥且,按先y 后x 的积分次序写二次积分()Dx y dxdy +⎰⎰= (结果中被积函数不含绝对值符号).答案:10110100()()xx dx x y dy dx x y dy ---++⎰⎰⎰⎰ 分析:由12D D D =1:01,10,D x x y ≤≤-≤≤ 2:01,01,D x y x ≤≤≤≤-有10110100()()()xx Dx y dxdy dx x y dy dx x y dy --+=-++⎰⎰⎰⎰⎰⎰.(6) 若322111()00()(,)(,)x y x y dx f x y dy dy f x y dx ϕϕ=⎰⎰⎰⎰,则12((),())y y ϕϕ= .答案:12((),())y y ϕϕ=分析:因为3223113200(,)(,)([0,1])x x x x dx f x y dy dx f x y dy x x x =-∈≤⎰⎰⎰⎰(,)Df x y dxdy =-⎰⎰由已知推出D 由32,y x y x ==围成;换积分次序有:01,D y x ≤≤≤原二次积分1100(,)(,)dy f x y dx dy f x y dx =-=⎰⎰211()()(,)y y dy f x y dx ϕϕ=⎰⎰故 12((),())y y ϕϕ=.(7) 若{}222(,)D x y x y a =+≤(0)a >,Dπ=,则a = .答案:a = 分析:因为:020D r a θπ≤≤≤≤,2Dd πθ=⎰⎰322222320001122()[()]2[()()]2233ad a r a r a πθπππ=⋅--=-⋅-==⎰⎰33231,32a a ==, 所以a =. (8)已知22222()():(0)DF t f x y dxdy D x y t t =++≤>⎰⎰,则()F t '= .答案:2()2()F t tf t π'=分析: 由积分区域222x y t +≤和被积函数22()f x y +的形式知用极坐标计算 :02,0D r t θπ≤≤≤≤222()()()DDF t f x y dxdy f r rdrd θ=+=⎰⎰⎰⎰222220()()[()]2()t t td f r rdr d f r rdr f r rdr ππθθπ==⋅=⎰⎰⎰⎰⎰得 2()2()F t tf t π'=.2. 选择题 (1)估计积分22||||101100cos cos x y I dxdy x y +≤=++⎰⎰的值,则正确的是( ). A. 11.042I << B. 1.04 1.96I << C. 1.962I << D. 2 2.14I << 答案:C分析:由已知有1410102002D S =⋅⋅⋅=,根据二重积分中值定理有22200(,)100cos cos D I f S ξηξη=⋅=++ (,)D ξη∈ 又220cos cos 2ξη<+<, 得 200200102100I << 即1.962I <<, 故选C .(2) 设区域12:11,22;:01,02,D x y D x y -≤≤-≤≤≤≤≤≤又1222322312(),(),D D I x y d I x y d σσ=+=+⎰⎰⎰⎰则正确的是( ).A. 124I I >B. 124I I <C .124I I = D. 122I I = 答案: C分析:因为2D 与1D 在第一象限重合,1D 关于x 轴、y 轴都对称,被积函数关于y 、x 都是偶函数,x所以124I I =,故选C .(3)设22:1,0,0,D x y x y +≤≥≥则Dxydxdy ⎰⎰=( ).A. 100dx ⎰ B. 00C. 100dx ⎰ D. 110dx xydy ⎰⎰答案: C分析:因为:01,0D x y ≤≤≤≤所以100Dxydxdy dx =⎰⎰⎰,故选C . (4)cos 200(cos ,sin )d f r r rdr πθθθθ⎰⎰=( ).A. 1100(,)dx f x y dy ⎰⎰ B. 100(,)dy f x y dx ⎰C. 100(,)dx f x y dy ⎰ D. 1(,)dy f x y dx ⎰答案: C分析:已知:00cos 2D r πθθ≤≤≤≤由cos r θ=有2cos r r θ=得22x y x +=即22211()()22x y -+=,推出D 为22211()()22x y -+=的上半圆;所以:010D x y ≤≤≤≤于是cos 20(cos ,sin )d f r r rdr πθθθθ=⎰⎰10(,)dx f x y dy ⎰, 故选C.(5)设(,)f x y 是所给积分区域上的连续函数,则下列等式成立的是( ).A. (,)(,)bddba c c a dx f x y dy dx f x y dy =⎰⎰⎰⎰ B. (,)(,)bddba c c a dx f x y dy dy f x y dx =⎰⎰⎰⎰ C. ()()()()(,)(,)bg x g x ba x x a dx f x y dy dy f x y dx ϕϕ=⎰⎰⎰⎰D. ()()()()(,)(,)b g x b g x a x a x dx f x y dy dy f x y dx ϕϕ=⎰⎰⎰⎰ 答案:B分析:正确的是(,)(,)bdd ba ccadx f x y dy dy f x y dx =⎰⎰⎰⎰, 故选B .(6)1100(,)xdx f x y dy -=⎰⎰( ).A. 1100(,)x dy f x y dx -⎰⎰B. 1100(,)xdy f x y dx -⎰⎰ C. 1100(,)dy f x y dx ⎰⎰ D. 1100(,)ydy f x y dx -⎰⎰ 答案:D分析:已知:0101D x y x ≤≤≤≤-,推出D 由1,0,0x y y x +===围成;换积分次序有:0101D y x y ≤≤≤≤- 所以1100(,)xdx f x y dy -=⎰⎰110(,)ydy f x y dx -⎰⎰, 故选D .(7)圆1r =之外和圆r θ=之内的公共部分的面积S =( ). A./60d rdr πθθ⎰B. /6d rdr πθθ⎰C. /602d rdr πθθ⎰D. /62d rdr πθθ⎰答案:C分析: 由1r =有21r =得221x y +=2cos r r θθ=由有22222(x y x x y +=+=得即 12DD S d d σσ==⎰⎰⎰⎰, 1D 是D 在x 轴上方部分22221x y x y x ⎧+=⎪⎨+=⎪⎩交点:11(),()2222- 故有1sin ,26πθθ==1:016D r πθθ≤≤≤≤于是S=1/60122D d d rdr πθσθ=⎰⎰⎰, 故选C .(8)当D 是由( )围成的区域时,112Ddxdy =⎰⎰.A. 0x =,0y =及220x y +-=B. 1x =,2x =及3y =,4y =C. 11,22x y == D. 1,1x y x y +=-= 答案:D分析:1111122222A I S ∆==⋅⋅⋅=, 111(21)(43)222B I S ==-⋅-=矩,211111[()]22222C I S ==--=矩, 11144111222D I S ∆=⋅=⋅⋅⋅⋅=即112D DI dxdy ==⎰⎰ 故选D . (9)下列结论中不成立的有( ).A. (,)0Dd f x y dxdy =⎰⎰B. (,)0D f x y dxdy x ∂=∂⎰⎰ C.(,)0Df x y dxdy y ∂=∂⎰⎰ D. 111000(,)(,)dv f u v du f u x du x∂=∂⎰⎰⎰答案:D分析:因为(,)Df x y d x d y=⎰⎰常数,所以(,)0Dd f x y dxdy =⎰⎰,(,)0D f x y dxdy x ∂=∂⎰⎰,(,)0Df x y dxdy y ∂=∂⎰⎰均成立, 故选D .(10)设12(,)()()f x y f x f y =且11()()F x f x '=,22()()F y f y '=,则11(,)dx f x y dy ⎰⎰=( ).A. (1,1)(0,0)f f -B. 1212(1)(1)(0)(0)F F F F ⋅-⋅C. 111200()()F x dx F y dy ⋅⎰⎰D. 12121212(1)(1)(0)(1)(1)(0)(0)(0)F F F F F F F F ⋅-⋅-⋅+⋅ 答案:D 分析:1111120(,)()()dx f x y dy dx f x f y dy =⋅⎰⎰⎰⎰11120(())(())f x dx f y dy =⋅⎰⎰111020[()][()]F x F y =⋅1122[(1)(0)][(1)(0)]F F F F =-⋅-12121212(1)(1)(0)(1)(1)(0)(0)(0)F F F F F F F F =⋅-⋅-⋅+⋅, 故选D .(11) 100(,)xdx f x y dy =⎰⎰( );A. 100(,)xdy f x y dx ⎰⎰ B. 10(,)x dy f x y dx ⎰⎰ C. 110(,)y dy f x y dx ⎰⎰ D. 100(,)xdx f x y dy ⎰⎰ 答案:C分析:已知:010D x y x ≤≤≤≤, 推出D 由,0,1y x y x ===围成;交换积分次序:011D y y x ≤≤≤≤1(,)x dx f x y dy ⎰⎰=110(,)ydy f x y dx ⎰⎰, 故选C .(12) 设22:14D x y ≤+≤,则Ddxdy =⎰⎰( );A. πB. 3πC. 4πD. 15π 答案:B分析:因为22213D Ddxdy S πππ==⋅-⋅=⎰⎰, 故选B .(13)设12D D D = ,而1D 是以(0,0),(2,1),(2,0)为顶点的三角形区域,2D 是以(0,0),(2,0),(21-,)为顶点的三角形区域,则(,)Df x y dxdy =⎰⎰( );A. 0B. 1(,)D f x y dxdy ⎰⎰+ 2(,)D f x y dxdy ⎰⎰C. 2(,)D f x y dxdy ⎰⎰ D. 1(,)D f x y dxdy ⎰⎰答案:B分析: 由已知显然有12D D S S =,但被积函数只是记号(,)f x y 不是具体解析式,而12D D D = ,所以(,)Df x y dxdy ⎰⎰12(,)(,)D D f x y dxdy f x y dxdy =+⎰⎰⎰⎰,故选B .(14)若D 是以(1,1),(1,1),(11---,)为顶点的三角形区域,1D 是D 在第一象限部分,则(cos sin )Dxy x y dxdy +=⎰⎰( );A. 21cos sin D x ydxdy ⎰⎰ B. 21D xydxdy ⎰⎰C. 41(cos sin )D xy x y dxdy +⎰⎰ D. 41cos sin D x ydxdy ⎰⎰答案:A分析:设1234D D D D D = (如图)12:D D 图形关于y 轴对称,被积函数中cos sin x y关于x 是偶函数,xy 关于x 是奇函数;34:D D 图形关于x 轴对称,被积函数关于y 是奇函数;1234(cos sin )(cos sin )(cos sin )DD D D D xy x y dxdy xy x y dxdy xy x y dxdy+=+++⎰⎰⎰⎰⎰⎰112cos sin 002cos sin D D x ydxdy x ydxdy =++=⎰⎰⎰⎰, 故选A .(15)若已知00()dx xf y dy ππ⎰⎰=1,则0()f x dx π=⎰( );A. 1πB.21π C. 22π D. 不能确定 答案: C分析:因为2000000()()[()]()[()]2x dx xf y dy xdx f y dy f y dy ππππππ=⋅=⋅⎰⎰⎰⎰⎰ 2()12f y dy ππ==⎰, 所以22()()f y dy f x dx πππ==⎰⎰, 故选C(16)设平面区域22:1D x y +≤,0y ≥,且DI f dxdy =⎰⎰的被积函数在D 上连续,则在极坐标下,I =( );A. 10()rf r dr π⎰ B. 102()rf r dr π⎰ C. 102()f r dr π⎰ D. 10()f r dr π⎰ 答案: A 分析::001D r θπ≤≤≤≤1()DI f dxdy d f r rdr πθ==⎰⎰⎰⎰1100()()()f r rdr rf r dr πθπ=⋅=⎰⎰, 故选A .(17)若{(,)2D xy x y x =≤≤,则在极坐标下(,)Df x y dxdy =⎰⎰( ); A. /4100(cos ,sin )d f r r rdr πθθθ⎰⎰ B. /21/40(cos ,sin )d f r r rdr ππθθθ⎰⎰ C. /42cos 00(cos ,sin )d f r r rdr πθθθθ⎰⎰ D. /22cos /4(cos ,sin )d f r r rdr πθπθθθ⎰⎰答案:D分析:由已知22222(1)1y x y x x y =+=-+=有得推出D 由222x y x +=即22(1)1,x y y x -+==围成; 将cos ,sin x r y r θθ== 代入222x y x +=得222cos (2r x y x θ=+=的极坐标方程)所以极坐标系下:02cos 42D r ππθθ≤≤≤≤(,)Df x y dxdy =⎰⎰/22cos /4(cos ,sin )d f r r rdr πθπθθθ⎰⎰, 故选D .(18)二重积分I 在极坐标系下为100(cos ,sin )I d f r r rdr πθθθ=⎰⎰,则在直角坐标系下I =( );A. 100(,)dx f x y dy ⎰B. 102(,)dx f x y dy ⎰C. 110(,)dx f x y dy -⎰D. 1(,)dy f x y dx ⎰答案: C分析:由已知的:001D r θπ≤≤≤≤推出D 为单位圆221x y +=的上半圆部分,所以直角坐标系下:110D x y -≤≤≤≤110(,)I dx f x y dy -=⎰, 故选C .(19) 设31()DI ln x y d σ=+⎰⎰,32()DI x y d σ=+⎰⎰,33sin ()DI x y d σ=+⎰⎰,D 是由0x =,0y =,12x y +=与1x y +=围成的区域,则( );123321132312....A I I I B I I I C I I I D I I I <<<<<<<<答案: C分析:由已知的D 可知112x y ≤+≤,1ln 2lnln()ln102x y -=≤+≤= 3()0ln x y +≤非正,3()0x y +>,3sin ()0x y +>而sin()x y x y +<+,于是333()sin ()()ln x y x y x y +<+<+ 所以132I I I <<, 故选C . (20) 设sin (,)xf x y x=,则(,)f x y 在由0y =,y x =及1x =围成的平面区域D 上的平均值为( ).A. 22cos1-B. 1sin1-C. cos11-D. 1 答案:A分析:由已知有:010D x y x ≤≤≤≤10011sin (,)(,)1112xDDxf f x y dxdy dx dy S xξη==⋅⋅⎰⎰⎰⎰11002sin 2cos 22cos1xdx x ==-=-⎰, 故选A . 3.利用二重积分性质估计下列积分值: (1)2222(49),:4DI x y d D x y σ=+++≤⎰⎰;解:由22(,)49f x y x y =++,22:4D x y +≤ 显然有(0,0)9m f ==最大值在边界2222x y +=上取得,即求22(,)49f x y x y =++ 满足2222x y +=的最值,方法①:将224y x =-代入有222()4(4)9325f x x x x =+-+=-+()60f x x '=-=令得唯一驻点 0x =,()6f x ''=-,(0)60f ''=-< 0x =是极大值点也就是最大值点,(0)25M f ==方法②:令2222(,,)49(4)F x y x y x y λλ=++++-2222084200x y F x x F y y F x y λλλ+-'=+==⎧⎪'=+=⎨⎪'=⎩解得0x =,2y =±;0y =,2x =± 可能的极值点(0,2),(0,2),(2,0),(2,0)--检验可得(0,2)(0,2)25f f -==为最大值,即25M = 于是2294925(,)x y x y D ≤++≤∈所以 229(49)25D D DS x y d S σ≤++≤⎰⎰, 4D S π=即 2236(49)100Dx y d πσπ≤++≤⎰⎰ 故 36100I ππ≤≤.(2)22221(),:1DI ln x y d D x y eσ=+≤+≤⎰⎰;解:因为2211(,)x y x y D e≤+≤∈所以2211ln ln()ln10x y e-=≤+≤=22()0D DS In x y d σ-≤+≤⎰⎰ 2211(1)D S eπππ=⋅-=- 221(1)()0DIn x y d e πσ--≤+≤⎰⎰ 所以1(1)0I e π-≤≤.(3)22sin sin ,:0,0.DI x yd D x y σππ=≤≤≤≤⎰⎰解:由:0,0D x y ππ≤≤≤≤ 有22220sin sin sin sin 122x y ππ≤≤=于是2220sin sin D Dx yd S σπ≤≤=⎰⎰ 所以20I π≤≤.4.化二重积分(,)Df x y d σ⎰⎰为二次积分(两种积分次序都要):(1){}(,)|||1,|1D x y x y =≤≤; 解::11,11D x y -≤≤-≤≤1111(,)(,)Df x y d dx f x y dy σ--=⎰⎰⎰⎰ (先对y 积分,后对x 积分)1111(,)dy f x y dx --=⎰⎰. (先对x 积分,后对y 积分)(2)D 是由0x =,1y =及y x =围成的区域; 解:将D 表示成x 型:1,10≤≤≤≤y x x(,)Df x y d σ⎰⎰11(,)xdx f x y dy =⎰⎰ (先对y 积分,后对x 积分)将D 表示成y 型:y x y ≤≤≤≤0,10(,)Df x y d σ⎰⎰1(,)ydy f x y dx =⎰⎰. (先对x 积分,后对y 积分)(3)D 是由0y =,ln y x =及x e =围成的区域. 解:将D 表示成x 型:1,0ln x e y x ≤≤≤≤(,)Df x y d σ⎰⎰1(,)eInxdx f x y dy =⎰⎰(先对y 积分,后对x 积分)将D 表示成y 型:01,y y e x e ≤≤≤≤(,)Df x y d σ⎰⎰10(,)y eedy f x y dx =⎰⎰ (先对x 积分,后对y 积分)5.交换下列二次积分次序: (1)1120(,)xxdx f x y dy -⎰⎰;解:积分区域为:10,12x x y x ≤≤≤≤-换成y 型: 11:0,02D y x y ≤≤≤≤ 21:1,012D y x y ≤≤≤≤-1120(,)xxdx f x y dy -⎰⎰120(,)ydy f x y dx =⎰⎰+11102(,)ydy f x y dx -⎰⎰.(2)122001(,)(,)xdx f x y dy dx f x y dy -+⎰⎰⎰;解:第一项积分的积分区域1:01,0D x y ≤≤≤≤ 第二项积分的积分区域2:12,02D x y x ≤≤≤≤-22222(1)1y x y x x y =+=-+=由有即,22y x x =-=-+将两区域合并成区域D 并表示成y 型::01,12D y x y ≤≤≤≤-1221(,)(,)xdx f x y dy dx f x y dy -+⎰⎰⎰1201(,)ydy f x y dx -=⎰⎰.(3)2122002(,)(,)x dx f x y dy f x y dy +⎰⎰⎰;解:第一项积分的积分区域为 211:0202D x y x ≤≤≤≤,,第二项积分的积分区域为 2:20D x y ≤≤≤≤228y x y =+=由得,212y x =将两区域合并成区域D 并表示成y 型:: 02,D y x ≤≤≤21222(,)(,)x dx f x y dy f x y dy +⎰⎰⎰2(,)dy f x y dx =⎰.(4)10(,).dx f x y dy ⎰解:积分区域:01,D x y ≤≤≤≤222211()24y x y x x y =+=-+=由得即,y =将D 表示成y 型域要分成三个区域123D D D 、、:211:1,12D y y x ≤≤≤≤2211:0,22D y y x ≤≤≤≤=31:0,12D y x ≤≤≤≤10(,)dx f x y dy⎰22111122102(,)(,)(,)yy dy f x y dx dy f x y dx dy f x y dx =++⎰⎰⎰⎰.6.计算下列二重积分:(1)(6)Dx y dxdy +⎰⎰,其中D 是由y x =,5y x =及1x =围成的区域;解::015D x x y x ≤≤≤≤ (x 型)(6)Dx y dxdy +⎰⎰150(6)xxdx x y dy =+⎰⎰⎰⋅+=1052)26(dx y xy xx 3763767613102=⋅==⎰x dx x . (2)x y De d σ+⎰⎰,其中D 是由1x y +≤所确定的闭区域;解:将D 表示成x 型分为:1:1011D x x y x -≤≤--≤≤+,2:01,11D x x y x ≤≤-≤≤-x yDe d σ+⎰⎰12x y x y D D e dxdy e dxdy ++=+⎰⎰⎰⎰ 01111101xxx y x y xx dx e dy dx e dy +-++----=+⎰⎰⎰⎰1111110x y xx yxx x e edx e e dx +-----=+⎰⎰0111111()()x x x x x x e e e dx e e e dx +-----=-+-⎰⎰ 0112112111x x e dx e dx e dx edx +----=--+⎰⎰⎰⎰111111()()22e e e e e e e e=----+=-. (3)22()Dx y x d σ+-⎰⎰,其中D 是由直线2y =,y x =及2y x =所围成的闭区域;解::022yD y x y ≤≤≤≤(y 型)22()Dxy x d σ+-⎰⎰22220()y ydy x y x dx =+-⎰⎰232220()32y y x x y x dy =+-⎰ 232193()248y y dy =-⎰ 432019113()24486y y =-=. (4)22y Dx e dxdy -⎰⎰,其中D 由直线y x =,1y =及y 轴所围成;解::01,0D y x y ≤≤≤≤ (y 型)22y Dx edxdy -⎰⎰2120yy dy x edx -=⎰⎰231003y yx edy -=⋅⎰ 213013y e y dy -=⋅⎰2122016y e y dy -=⋅⎰ 21016t y tte dt=-=⎰111()6t t te e dt --=--⎰110111()663t e e e--=-+=-. (5)cos Dxdxdy x⎰⎰,其中D 由曲线2y x =与y x =所围成. 解;2:01,D x x y x ≤≤≤≤ (x 型)cos Dxdxdy x ⎰⎰221100cos cos ()x x x x x x dx dy y dx x x ==⎰⎰⎰ 120cos ()xx x dx x =-⎰10(cos cos )x x x dx =-⎰ 1111000sin sin sin1(sin sin )x xd x x x xdx =-=--⎰⎰10sin1(sin1cos )1cos1x =-+=-.7.将下列二重积分(,)Df x y dxdy ⎰⎰化为极坐标系下的二次积分:(1)22:14D x y ≤+≤; 解::02,12D r θπ≤≤≤≤(,)Df x y dxdy ⎰⎰221(cos ,sin )d f r r rdr πθθθ=⎰⎰(2)22:(1)(1) 1.D x y -+-≤解:由22221112210x y x y x y -+-=+--+=()()得将cos ,sin x r y r θθ==代入有22(cos sin )10r r θθ-++=r =cos sin θθ=+或由22221112210x y x y x y -+-≤+--+≤()()得将cos ,sin x r y r θθ==代入有22(cos sin )10r r θθ-++≤222(cos sin )(cos sin )2sin cos 0r r θθθθθθ-+++-≤ 2[(cos sin )]sin 2r θθθ-+≤,(cos sin )r θθ-+≤cos sin cos sin r θθθθ+≤≤+故极坐标系下:0,2D πθ≤≤cos sin cos sin r θθθθ+≤≤+(,)Df x y dxdy⎰⎰cos sin 20cos sin (cos ,sin )d f r r rdr πθθθθθθθ++=⎰⎰8.将下列二次积分转化为极坐标系下的二次积分: (1)20x dx f dy ⎰;解:由已知的:02D x x y ≤≤≤推出D由,,2y x y x ==围成,tan 14y x x x πθθ====,tan 3y x πθθ==== 2cos 22sec (2x r r x θθ====由,有,得的极坐标方程)所以极坐标系下:02sec 43D r ππθθ≤≤≤≤故22sec 3004()x dx f dy d f r rdr πθπθ=⎰⎰⎰.(2)2100(,).x dx f x y dy ⎰⎰解:由已知的2:010D x y x ≤≤≤≤推出D 由2,0,1y x y x ===围成, 将cos ,sin x r y r θθ== 代入2,1y x x ==得2sec tan (r y x θθ==的极坐标方程)sec (1r x θ==的极坐标方程)所以极坐标系下1:00sec 4D r πθθ≤≤≤≤2:00sec tan 4D r πθθθ≤≤≤≤故21sec sec tan 440(,)(cos ,sin )(cos ,sin )x dx f x y dy d f r r rdr d f r r rdrππθθθθθθθθθ=-⎰⎰⎰⎰⎰⎰sec sec tan 40[(cos ,sin )(cos ,sin )]f r r rdr f r r rdr d πθθθθθθθθ=-⎰⎰⎰2sec 040ec tan [(cos ,sin )(cos ,sin )]s f r r rdr f r r rdr d πθθθθθθθθ=+⎰⎰⎰sec 40sec tan [(cos ,sin )]f r r rdr d πθθθθθθ=⎰⎰sec 40sec tan (cos ,sin )d f r r rdr πθθθθθθ=⎰⎰9.利用极坐标计算下列二重积分: (1)22,:DD x y x +≤;解:由2222211()()22x y x x y +≤-+≤有 将cos ,sin x r y r θθ== 代入22x y x +=得22cos (r x y x θ=+=的极坐标方程)所以极坐标系下:,0cos 22D r ππθθ-≤≤≤≤cos 0Dd rdr πθπθ=⎰⎰2-25cos 222)r d πθπθ-=⎰3222cos 5d ππθθ-=⎰2204(1sin )sin 5d πθθ=-⎰ 2304sin 8(sin )5315πθθ=-=. (2)1222()Dx y dxdy -+⎰⎰,D :y x =与2y x =所围成的闭区域.解:将cos ,sin x r y r θθ== 代入2y x =得2sec tan (r y x θθ==的极坐标方程)所以极坐标系下:00sec tan 4D r πθθθ≤≤≤≤1sec tan 22421()Dx y dxdy d rdr rπθθθ-+=⎰⎰⎰⎰4sec tan d πθθθ=⎰4sec 1πθ==.10.利用适当的坐标系计算下列二重积分: (1)22Dx d yσ⎰⎰,其中D 是由直线2x =,y x =及曲线1xy =所围成的闭区域; 解:1:12,D x y x x≤≤≤≤ (x 型)2221221x x Dx x d dx dy y y σ=⎰⎰⎰⎰22111()xxx dx y =-⎰2211()x x dx x =-+⎰=42232119()()424x x x x dx -=-=⎰. (2)22()Dx y d σ+⎰⎰,其中D 是由直线y x =,y x a =+,y a =,3(0)y a a =>所围成的区域;解::3,D a y a y a x y ≤≤-≤≤(y 型)22()Dx y d σ+⎰⎰=322()a y ay ady x y dx -+⎰⎰332()3a y y y ay aax y xdy --=+⎰33321{[()]}3aa y y a ay dy =--+⎰443333411()1434343a aa aaay y a y aa -=-+=.(3)Dσ⎰⎰,其中D 是由圆周22x y Rx +=所围成的区域.解: 由22222()()22R R x y Rx x y +≤-+≤有 将cos ,sin x r y r θθ== 代入22x y Rx +=得22cos (r R x y Rx θ=+=的极坐标方程)所以极坐标系下:,0cos 22D r R ππθθ-≤≤≤≤Dσ⎰⎰22cos 0R d ππθθ-=⎰⎰22cos 20R d ππθθ-=⎰⎰22cos 2201()2R d R r ππθθ-=--⎰⎰ 223222cos 012()23R R r d ππθθ-=--⎰ 223331(sin )3R R d ππθθ-=--⎰ 23302133R d R πθπ==⎰. 11.用二重积分求由24x y y =-及4x y +=所围成的平面图形的面积. 解:由224(2)4x y y x y =-=--+有241,44x y y y y x y ⎧=-==⎨+=⎩得 2:14,44D y y x y y ≤≤-≤≤-(y 型)24414y y yDS d dy dx σ--==⎰⎰⎰⎰421(44)y y y dy =--+⎰23424119(54)(54)232y y y y dy y =--=--=⎰.12.计算2110.x y I dy e dx ⎰⎰=解:由已知的:01,1D y y x ≤≤≤≤推出D 由,0,1y x y x ===围成, 将D 表示成x 型:01,0x y x ≤≤≤≤221110xx x yI dy e dx dx e dy ==⎰⎰⎰⎰2211000()x xx e y dx e xdx =⋅=⋅⎰⎰ 221210111(1)222x x e dx e e ===-⎰. 13.求由曲面22z x y =+、三坐标平面和平面1x y +=所围成的立体体积. 解:因为 22()DV x y dxdy =+⎰⎰而:01,01D x y x ≤≤≤≤-所以 112200()xV dx x y dy -=+⎰⎰312100()3x y x y dx -=+⎰12301[(1)(1)]3x x x dx =-+-⎰ 123011(6431)36x x x dx =--+=⎰. *14.计算1(0,0).ln b ax x I dx a b x->>⎰= 解:这题是求定积分,但积分难以进行. 注意到ln ln yb a byb aax x x x dy xx-==⎰,因此I 可化为二次积分. 111000()ln b ab b y y a a x x I dx x dy dx dx x dy x-===⎰⎰⎰⎰⎰ 交换二次积分次序:111001()1bbyy aaI dy x dx x dy y +==⋅+⎰⎰⎰ 11ln 1ln(1)ln(1)ln11bb aab dy y b a y a +==+=+-+=++⎰. *15.设(,)f x y 连续,且(,)(,)Df x y xy f u v dudv =+⎰⎰,其中D 是由20,,y y x ==1x =所围成的区域,求(,)f x y .解:将(,)(,)Df x y xy f u v dudv =+⎰⎰两边同时二重积分(,)[(,)]DDDDf x y dxdy xydxdy f u v dudv dxdy =+⎰⎰⎰⎰⎰⎰⎰⎰(,)DDDxydxdy f u v dudv dxdy =+⋅⎰⎰⎰⎰⎰⎰(,)D DDxydxdy S f u v dudv =+⋅⎰⎰⎰⎰(1)(,)D DDS f x y dxdy xydxdy -=⎰⎰⎰⎰。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章 多元函数积分学一、二重积分的概念与性质1.定义设()y x f ,是定义在有界闭区域D 上的有界函数,如果对任意分割D 为n 个小区域,,,,21n σσσ∆∆∆ 对小区域()n k k ,,2,1 =∆σ上任意取一点()k k ηξ,都有()k nk k kd f σηξ∆∑=→1,lim存在,(其中k σ∆又表示为小区域k σ∆的面积,k d 为小区域k σ∆的直径,而k nk d d ≤≤=1max ) 则称这个极限值为()y x f ,在区域D 上的二重积分 记以()⎰⎰Dd y x f σ,,这时就称()y x f ,在D 上可积。
如果()y x f ,在D 上是有限片上的连续函数,则()y x f ,在D 上是可积的。
2.几何意义当()y x f ,为闭区域D 上的连续函数,且()0,≥y x f ,则二重积分()⎰⎰Dd y x f σ,表示以曲面()y x f z ,=为顶,侧面以D 的边界曲线为准线,母线平行于z 轴的曲顶柱体的体积。
当封闭曲面S 它在xy 平面上的投影区域为D ,上半曲面方程为()y x f z ,2=,下半曲面方程为()y x f z ,1=,则封闭曲面S 围成空间区域的体积为()()[]σd y x f y x f D⎰⎰-,,123.基本性质 (1)()()⎰⎰⎰⎰=DDd y x f k d y x kf σσ,,(k 为常数)(2)()()[]()()σσσd y x g d y x f d y x g y x f DDD⎰⎰⎰⎰⎰⎰±=±,,,,(3)()()()⎰⎰⎰⎰⎰⎰+=12,,,D D Dd y x f d y x f d y x f σσσ 其中21UDD D =,除公共边界外,1D 与2D 不重叠。
(4)若()()y x g y x f ,,≤,()D y x ∈,,则()()⎰⎰⎰⎰≤DDd y x g d y x f σσ,,(5)若()M y x f m ≤≤,,()D y x ∈,,则()⎰⎰≤≤DMS d y x f mS σ, 其中S 为区域D 的面积。
(6)()()σσd y x f d y x f DD⎰⎰⎰⎰≤,,(7)积分中值定理 设()y x f ,在有界闭区域D 上连续,S 为D 的面积,则存在()D ∈ηξ,,使得()()S f d y x f D⋅=⎰⎰ηξσ,,我们也把()⎰⎰Dd y x f Sσ,1称为()y x f ,在D 上的积分平均值。
4.对称区域上奇偶函数的积分性质定理1.设()y x f ,在有界闭区域D 上连续,若D 关于x 轴对称,则()()()()⎰⎰⎰⎰⎪⎩⎪⎨⎧=DDy y x f d y x f y y x f d y x f 为偶函数对为奇函数对, ,,2,,0,1σσ其中1D 为D 在x 轴的上半平面部分。
定理2.设()y x f ,在有界闭区域D 上连续,若D 关于y 轴对称,则()()()()⎰⎰⎰⎰⎪⎩⎪⎨⎧=DDx y x f d y x f x y x f d y x f 为偶函数对为奇函数对, ,,2,,0,2σσ其中2D 为D 在y 轴的右半平面部分。
定理3.设()y x f ,在有界闭区域D 上连续,若D 关于原点对称,则()()()()()()()()⎰⎰⎰⎰⎪⎩⎪⎨⎧∈=--∈-=--=DD D y x y x f y x f d y x f D y x y x f y x f d y x f ,,,,, ,,2,,,,,,0,3σσ其中3D 为D 的上半平面或右半平面。
定理4.设()y x f ,在有界闭区域D 上连续,若D 关于直线x y =对称,则()()⎰⎰⎰⎰=DDd x y f d y x f σσ,,若54D D D =,4D ,5D 分别为D 在x y =的上方与下方部分,则()()σσd x y f d y x f D D ⎰⎰⎰⎰=54,,二、在直角坐标系中化二重积分为累次积分以及交换积分顺序问题 模型I :设有界闭区域()()(){}x y x b x a y x D 21,,ϕϕ≤≤≤≤=其中()x 1ϕ,()x 2ϕ在[]b a ,上连续,()y x f ,在D 上连续。
则()()⎰⎰⎰⎰=DDdxdy y x f d y x f ,,σ ()()()⎰⎰=bax x dy y x f dx 21,ϕϕ模型II :设有界闭区域()()(){}y x y d y c y x D 21,,ψψ≤≤≤≤= 其中()y 1ψ,()y 2ψ在[]d c ,上连续,()y x f ,在D 上连续。
则()()⎰⎰⎰⎰=DDdxdy y x f d y x f ,,σ()()()⎰⎰=dc y y dx y x f dy 21,ψψ关于二重积分的计算主要根据模型I 或模型II 把二重积分化为累次积分从而进行计算,对于比较复杂的区域D ,如果既不符合模型I 中关于D 的要求,又不符合模型II 中关于D 的要求,那么就需要把D 分解成一些小区域,使得每一个小区域能够符合模型I 或模型II 中关于区域的要求,利用二重积分性质,把大区域上二重积分等于这些小区域上二重积分之和,而每个小区域上的二重积分则可以化为累次积分进行计算。
在直角坐标系中,两种不同顺序的累次积分的互相转化是一种很重要的手段,具体做法是先把给定的累次积分反过来化为二重积分,求出它的积分区域D ,然后根据D 再把二重积分化为另外一种顺序的累次积分。
三、在极坐标系中化二重积分为累次积分在极坐标系中一般只考虑一种顺序的累次积分,也即先固定θ对γ进行积分,然后再对θ进行积分,由于区域D 的不同类型,也有几种常用的模型。
模型I :设有界闭区域()()(){}θϕγθϕβθαθγ21,,≤≤≤≤=D其中()θϕ1,()θϕ2在[]βα,上连续,()()θγθγsin ,cos ,f y x f =在D 上连续,()()⎰⎰⎰⎰=DDd d f d y x f θγγθγθγσ sin ,cos ,()()()⎰⎰=βαθϕθϕγγθγθγθ21 sin ,cos d f d模型II :设有界闭区域()()(){}θϕγθϕπθθγ21,20,≤≤≤≤=D其中()()θϕθϕ21,在[]π2,0上连续,()()θγθγsin ,cos ,f y x f =在D 上连续,则()()⎰⎰⎰⎰=DDd d f d y x f θγγθγθγσ sin ,cos ,()()()⎰⎰=πθϕθϕγγθγθγθ20s i n ,c o s 21d f d模型III :设有界闭区域()(){}θϕγβθαθγ≤≤≤≤=0,,D其中()θϕ在[]βα,上连续,()()θγθγsin ,cos ,f y x f =在D 上连续,则()()⎰⎰⎰⎰=DDd d f d y x f θγγθγθγσ sin ,cos ,()()⎰⎰=βαθϕγγθγθγθ0s i n ,c o s d f d 模型IV :设有界闭区域()(){}θϕγπθθγ≤≤≤≤=0,20,D其中()θϕ在[]π2,0上连续,()()θγθγsin ,cos ,f y x f =在D 上连续,则()()θγγθγθγσd d f d y x f DDsin ,cos ,⎰⎰⎰⎰= ()()⎰⎰=πθϕγγθγθγθ200sin ,cos d f d例题:一、选择题1.设f(x,y) 为连续函数,则使=⎰≤+122),(y x dxdy y x f 4⎰2/0πθd rdrr r f )sin ,cos (1⎰θθ成立的充分条件是A f(-x,-y)=f(x,y)B f(-x,-y)=-f(x,y)C f(-x,y)= f(x,-y)=-f(x,y)D f(-x,y)= f(x,-y)=f(x,y)2. 设D :122≤+y x ,y ≥0;D 1:122≤+y x ,x ≥0,y ≥0则A ⎰⎰⎰⎰=DD xydxdy xydxdy 12 B ⎰⎰⎰⎰=DD xdxdy ydxdy 12C⎰⎰⎰⎰=DD ydxdy xdxdy 12 D⎰⎰⎰⎰+=+DDdxdy y x dxdy y x )(2)(3. 设D 是xoy 平面以(1,1),(-1,1),和(-1,-1)为顶点的三角形区域,D 1是D 的第一象限的部分,且f(x,y)=xy+⎰⎰Dy)dxdy f(x,则A ⎰⎰⎰⎰=DD dxdy y x dxdy y x 1),f(),f( B⎰⎰⎰⎰=DD dxdy y x dxdy y x 1),f(2),f(C ⎰⎰⎰⎰=DD dxdy dxdy y x 1x)f(y,2),f( D ⎰⎰⎰⎰=DDdxdy dxdy y x x)f(y,),f(4. 设D 是xoy 平面以(1,1),(-1,1),和(-1,-1)为顶点的三角形区域,D 1是D 的第一象限的部分,则⎰⎰+Ddxdy y x xy )sin cos (等于A ⎰⎰1sin cos 2D ydxdy x B ⎰⎰12D xydxdyC 4⎰⎰+1)sin cos (D dxdy y x xy D 05. ⎰⎰=θπθθθcos 02)sin ,cos (rdr r r f d I 化为在直角坐标系下的二次积分的正确结果为( )A⎰1dy ⎰-20),(y y dx y x f B⎰10dy ⎰-210),(y dx y x f C⎰1dx ⎰1),(dy y x f D⎰10dx ⎰-2),(x x dy y x f二、改变下列积分次序: 1.⎰⎰--ax a ax a dy y x f dx 022222),( 2.⎰⎰⎰⎰-+312301),(),(2x x dy y x f dx dy y x f dx3.⎰⎰⎰⎰----+2221201),(),(x xx xdy y x f dx dy y x f dx 4.⎰⎰πsin 0),(xdy y x f dx三、求解下列二重积分: 1.⎰⎰⎰⎰+422212sin2sinxxxdy yxdx dy yxdx ππ 2. ⎰⎰-x y dy edx 021023.⎰⎰Ddxdy xy6, D: 由y = x 4-x 3的上凸弧段部分与x 轴所形成的曲边梯形 4.dx e dy edx edy eyy R x RR y x Ry ⎰⎰⎰⎰-----+0222222225.:由与所围的区域6.⎰⎰+Ddxdy yx xy22, D: y ≥ x 及1 ≤ x 2 + y 2 ≤ 2 7. 求)DI y d σ=⎰⎰, 1)1(4:2222≥++≤+y x y x D 8.⎰⎰⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-Ddxdy b y a x 221, D: 12222≤+b y a x9.计算dxdy y x x x y y D⎰⎰++++++2221)1ln(1,其中D={(x,y)|0,122≥≤+y y x } 10.设f(x)连续且恒不为零,求dxdy y f x f y bf x af I R y x ⎰⎰≤+++=222)()()()( 11.计算二重积分I=⎰⎰+++++D yx y x y x 22221)1ln()1ln(dxdy,其D={(x,y)|10,10≤≤≤≤y x } 。
