2014年高考广西文科数学试题及答案(word解析版)

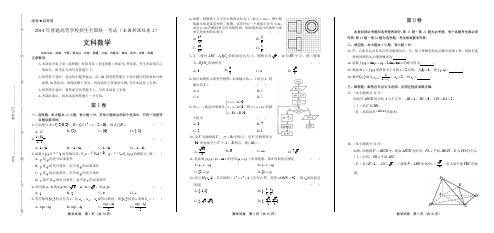
2014年普通高等学校招生全国统一考试（广西卷）数学（文科）第Ⅰ卷（共60分）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． （1）【2014年广西，文1，5分】设集合{12468}{123567}M N ==,,,,，,,,,,，则M N I 中元素的个数为（ ）（A ）2 （B ）3 （C ）5 （D ）7 【答案】B【解析】{}1,2,6M N =I ，所以M N I 中元素的个数为3，故选B ．【点评】此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键． （2）【2014年广西，文2，5分】已知角α的终边经过点(43)-，，则cos α=（ ）（A ）45 （B ）35 （C ）35- （D ）45-【答案】D【解析】由三角函数定义知4cos 5==-，故选D ．【点评】本题主要考查任意角的三角函数的定义，两点间的距离公式的应用，属于基础题．（3）【2014年广西，文3，5分】不等式组(2)0||1x x x +>⎧⎨<⎩的解集为（ ）（A ）{|21}x x -<<- （B ）{|10}x x -<< （C ）{|01}x x << （D ）{|1}x x > 【答案】C【解析】由()20x x +>得0x >或2x <-；由1x <得11x -<<，所以不等式组的解集为{}01x x <<，故选C ． 【点评】本题主要考查一元二次不等式、绝对值不等式的解法，属于基础题． （4）【2014年广西，文4，5分】已知正四面体ABCD 中，E 是AB 的中点，则异面直线CE 与BD 所成角的余弦值为（ ）（A ）16 （B （C ）13（D【答案】B【解析】如图，取AD 的中点F ，连接EF 、CF ．因为E 、F 分别是AB 、AD 的中点，所以=1//2EF BD ，故CEF ∠或其补角是异面直线CE 、BD 所成的角．设正四面体ABCD 的棱长为a ，易知CE CF =，12EF a =．在CEF △中，由余弦定理可得22212cos a CEF ⎫⎫⎛⎫+-⎪⎪ ⎪⎪⎪∠=B ． 【点评】本题考查异面直线及其所成的角，关键是找角，考查了余弦定理的应用，是中档题．（5）【2014年广西，文5，5分】函数)()ln11y x =>-的反函数是（ ）（A ）()()311x y e x =->-（B ）()()311x y e x =->-（C ）()()31x y e x =-∈R （D ）()()31x y e x =-∈R【答案】D 【解析】由)ln1y=1e y =，即()3e 1y x =-，又由1x >-可知y ∈R ，所以原函数的反函数为()()3e 1y y y =-∈R ，故选D ．【点评】本题考查反函数解析式的求解，属基础题． （6）【2014年广西，文6，5分】已知，a b 为单位向量，其夹角为60o ，则(2)-⋅=a b b （ ）FE DBA【解析】()2222211cos 6010-⋅=⋅-=⨯⨯⨯-=o a b b a b b ，故选B ．【点评】本题主要考查两个向量的数量积的定义，属于基础题． （7）【2014年广西，文7，5分】有6名男医生、5名女医生，从中选出2名男医生、1名女医生组成一个医疗小组，则不同的选法共有（ ）（A ）60种 （B ）70种 （C ）75种 （D ）150种 【答案】C【解析】根据题意，先从6名男医生中选2人，有2615C =种选法，再从5名女医生中选出1人，有155C =种选法，则不同的选法共有15×5=75种，故选C ．【点评】本题考查分步计数原理的应用，注意区分排列、组合的不同． （8）【2014年广西，文8，5分】设等比数列{}n a 的前n 项和为n S ，若24315S S ==，，则6S =（ ）（A ）31 （B ）32 （C ）63 （D ）64 【答案】C【解析】由等比数列的性质得()()242264S S S S S -=⋅-，即()2612315S =⨯-，解得663S =，故选C ． 【点评】本题考查等比数列的性质，得出2S ，42S S -，64S S -成等比数列是解决问题的关键，属基础题．（9）【2014年广西，文9，5分】已知椭圆C ：22221x y a b+=(0)a b >>的左、右焦点为1F 、2F ，离心率为3，过2F 的直线l 交C 于A 、B 两点，若1AF B ∆的周长为43，则C 的方程为（ ） （A ）22132x y += （B ）2213x y += （C ）221128x y += （D ）221124x y +=【答案】A【解析】∵1AF B ∆的周长为43，∴443a =，∴3a =，∵离心率为3，∴1c =，∴222b a c =-=，∴椭圆C 的方程为22132x y+=，故选A ．【点评】本题考查椭圆的定义与方程，考查椭圆的几何性质，考查学生的计算能力，属于基础题． （10）【2014年广西，文10，5分】正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（ ）（A ）814π （B ）16π （C ）9π （D ）274π【答案】A【解析】设球的半径为R ，则∵棱锥的高为4，底面边长为2，∴()()22242R R =-+，∴94R =，∴球的表面积为2981444ππ⎛⎫⋅= ⎪⎝⎭，故选A ．【点评】本题考查球的表面积，球的内接几何体问题，考查计算能力，是基础题．（11）【2014年广西，文11，5分】双曲线C ：22221(00)x y a b a b-=>>，的离心率为2，焦点到渐近线的距离为3，则C 的焦距等于（ ）（A ）2 （B ）22 （C ）4 （D ）42 【答案】C【解析】由已知得2c e a ==，所以12a c =，故223b c a c =-=，从而双曲线的渐进线方程为3by x x a=±=±，由焦点到渐进线的距离为3，得33c=，解得2c =，故24c =，故选C ．【点评】本题主要考查是双曲线的基本运算，利用双曲线的离心率以及焦点到直线的距离公式，建立方程组是解决本题的关键，比较基础．（12）【2014年广西，文12，5分】奇函数()f x 的定义域为R ，若(2)f x +为偶函数，且(1)1f =，则(8)(9)f f +=（ ）【解析】由()2f x +是偶函数可得()()22f x f x -+=+，又由()f x 是奇函数得()()22f x f x -+=-，所以()()22f x f x +=-，()()4f x f x +=，故()f x 是以4为周期的周期函数， 所以()()()924111f f f =⨯+==，又()f x 是定义在R 上的奇函数，所以()00f =， 所以()()800f f ==，故()()891f f +=，故选D ．【点评】本题主要考查函数值的计算，利用函数奇偶性的性质，得到函数的对称轴是解决本题的关键．第II 卷（共100分）二、填空题：本大题共4小题，每小题5分． （13）【2014年广西，文13，5分】6(2)x -的展开式中3x 的系数为 （用数字作答）． 【答案】160【解析】通项()()66166C 22C r r r r rr r T x x --+=⋅⋅-=-⋅，令63r -=，得3r =，所以3x 的系数为()3362C 160-=-． 【点评】本题考查二项式定理的应用，关键要得到()62x -的展开式的通项．（14）【2014年广西，文14，5分】函数cos22sin y x x =+的最大值为 ．【答案】32【解析】221312sin 2sin 2sin 22y x x x ⎛⎫=-+=--+ ⎪⎝⎭，因为1sin 1x -剟，所以当1sin 2x =时，max 32y =．【点评】本题主要考查二倍角的余弦公式，二次函数的性质应用，正弦函数的值域，属于基础题．（15）【2014年广西，文15，5分】设x 、y 满足约束条件02321x y x y x y -≥⎧⎪+≤⎨⎪-≤⎩，则4z x y =+的最大值为 ．【答案】5【解析】由约束条件02321x y x y x y -≥⎧⎪+≤⎨⎪-≤⎩作出可行域如图，联立023x y x y -=⎧⎨+=⎩，解得()1,1C ．化目标函数4z x y =+为直线方程的斜截式，得144zy x =-+．由图可知，当直线144zy x =-+过C 点时，直线在y 轴上的截距最大，z 最大．此时max 1415z =+⨯=．【点评】本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题． （16）【2014年广西，文16，5分】直线1l 和2l 是圆222x y +=的两条切线，若1l 与2l 的交点为()1,3，则1l 与2l的夹角的正切值等于____________． 【答案】43【解析】设1l 与2l 的夹角为2θ，由于1l 与2l 的交点()1,3A 在圆的外部，且点A 与圆心O 之间的距离为：1910OA =+=，圆的半径为2r =，∴2sin 10r OA θ==，22cos 10θ=，sin 1tan cos 2θθθ==， 22tan 14tan 211tan 314θθθ===--． 【点评】本题主要考查直线和圆相切的性质，直角三角形中的变角关系，同角三角函数的基本关系、二倍角的正切公式的应用，属于中档题．三、解答题：本大题共6题，共75分． （17）【2014年广西，文17，10分】数列{}n a 满足12211222n n n a a a a a ++===-+，，．（1）设1n n n b a a +=-，证明{}n b 是等差数列；（2）求{}n a 的通项公式．解：（1）由2122n n n a a a ++=-+得，2112n n n n a a a a +++-=-+，即12n n b b +=+．又1211b a a =-=．所以{}n b 是首项为1，公差为2的等差数列．（2）由（1）得()121n b n =+-，即121n n a a n +-=-．于是()()11121nnk k k k a a k +==-=-∑∑，所以211n a a n +-=，211n a n a +=+．又11a =，所以{}n a 的通项公式为2122n a n n +=-+．【点评】本题考查了等差数列的定义、通项公式、前n 项和公式，及累加法求数列的通项公式和转化思想，属于中档题．（18）【2014年广西，文18，12分】ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ，已知3cos 2cos a C c A =，1tan 3A =，求B ．解：根据正弦定理，由3cos 2cos 3sin cos 2sin cos a C c A A C C A =⇒=sin sin 323tan 2tan cos cos A CA C A C⇒⨯=⨯⇒=因为1tan 3A =，所以1132tan tan 32C C ⨯=⇒=，所以11tan tan 32tan()1111tan tan 132A C A C A C +++===--⨯ 因为0A C π<+<，所以4A C π+=，由三角形的内角和可得344B πππ=-=．【点评】本题考查了正弦定理、同角的三角函数基本关系式、两角和差的正切公式、诱导公式等基础知识与基本技能方法，考查了推理能力和计算能力，属于中档题．（19）【2014年广西，文19，12分】如图，三棱柱111ABC A B C -中，点1A 在平面ABC 内的射影D在AC 上，090ACB ∠=，11,2BC AC CC ===．（1）证明：11AC A B ⊥；（2）设直线1AA 与平面11BCC B 的距离为3，求二面角1A AB C --的大小． 解：解法一： （1）因为1A D ⊥平面ABC ，1A D ⊆平面11AAC C ，故平面11AA C C ⊥平面ABC ． 又BC AC ⊥，所以BC ⊥平面11AA C C ．连结1A C ．因为侧面11AA C C 为菱形，故11AC A C ⊥． 由三垂线定理得11AC A B ⊥．（2）BC ⊥平面11AA C C ，BC ⊆平面11BCC B ，故平面11AA C C ⊥平面11BCC B ．作11A E CC ⊥，E 为垂足，则1A E ⊥平面11BCC B ．又直线1//A A 平面11BCC B ，因而1A E 为直线1A A与平面11BCC B 的距离，13A E =．因为1A C 为11A CC ∠的平分线，故113A D A E ==．作DF AB ⊥， F 为垂足，连结1A F ．由三垂线定理得1A F AB ⊥，故1A FD ∠为二面角1A AB C --的平面角．由22111AD AA A D =-=得D 为C A 中点，15=25AC BC DF AB ⨯⨯=，11tan 15A D A FD DF ∠==． 所以二面角1A AB C --的大小为arc tan 15． 解法二：以C 为坐标原点，射线CA 为x 轴的正半轴，以CB 的长为单位长，建立如图所示的空间直角 坐标系C xyz -，由题设知1A D 与x 轴平行，z 轴在平面11AA C C 内（1）设1(,0,)A a c ，由题设有2,(2,0,0),(0,1,0)a A B ≤，则(2,1,0),(2,0,0)AB AC =-=-u u u r u u u r ， 1(2,0,)AA a c =-u u u r，111(4,0,),(,1,)AC AC AA a c BA a c =+=-=-u u u u r u u u r u u u r u u u r ………………2分由221||2(2)2AA a c =⇒-+=u u u r，即2240a a c -+=①于是221140AC BA a a c ⋅=-+=u u u u r u u u r，所以11AC A B ⊥． ……………………5分（2）设平面11BCC B 的法向量(,,)m x y z =u r，则1,m CB m BB ⊥⊥u r u u u r u r u u u r ，所以10,0m CB m BB ⋅=⋅=u r u u u r u r u u u r ， 因11(0,1,0),(2,0,)CB BB AA a c ===-u u u r u u u r u u u r ，所以0(2)0y a x cz =⎧⎨-+=⎩，令x c =，则2z a =-，(,0,2)m c a ∴=-u u u r ，点A 到平面11BCC B的距离为2|||cos ,|2||CA m cCA m CA c m ⋅⋅<>=====u u u r u ru u u r u r u u u r ur ， 又依题设，A 到平面11BCC Bc =代入①解得3a =（舍去）或1a = ……8分于是1(AA =-u u u r ，设平面1ABA 的法向量(,,)n p q r =r ，则1,n AA n AB ⊥⊥r u u u r r u u u r 所以10,0n AA n AB ⋅=⋅=r u u u r r u u u r，所以0202p r p p q q p⎧⎧-==⎪⎪⇒⎨⎨-+=⎪⎩⎪=⎩，令p =，则1,q r n ===r ，又(0,0,1)p =u r 为平面ABC的法向量，故1cos ,4||||n p n p n p ⋅<>===⋅r u rr u r r u r ， 所以二面角1A AB C --的大小为1arccos 4． ………………………………………………………12分【点评】本题考查二面角的求解，作出并证明二面角的平面角是解决问题的关键，属中档题． （20）【2014年广西，文20，12分】设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.60.50.50.4、、、，各人是否需使用设备相互独立．（1）求同一工作日至少3人需使用设备的概率；（2）实验室计划购买k 台设备供甲、乙、丙、丁使用．若要求“同一工作日需使用设备的人数大于k ”的概率小于0.1，求k 的最小值．解：记i A 表示事件：同一工作日乙、丙中恰有i 人需使用设备，0,1,2i =，B 表示事件：甲需使用设备，C 表示事件：丁需使用设备，D 表示事件：同一工作日至少3人需使用设备（1）122D A B C A B A B C =⋅⋅+⋅+⋅⋅，22()0.6,()0.4,()0.5,0,1,2ii P B P C P A C i ====， 所以122()()P D P A B C A B A B C =⋅⋅+⋅+⋅⋅122()()()P A B C P A B P A B C =⋅⋅+⋅+⋅⋅122()()()()()()()()P A P B P C P A P B P A P B P C =++0.31=．（2）由（1）知，若2k =，则()0.310.1P F =>．又2E B C A =⋅⋅，()()()()()220.06P E P B C A P B P C P A =⋅⋅==．若3k =，则()0.60.1F =<．所以k 的最小值时为3．【点评】本题主要考查相互独立事件的概率乘法公式，体现了分类讨论的数学思想，属于中档题． （21）【2014年广西，文21，12分】函数32()+33(0)f x ax x x a =+≠．（1）讨论()f x 的单调性； （2）若()f x 在区间(12)，是增函数，求a 的取值范围．解：（1）()363f x ax x '=++，()0f x '=的判别式()361a ∆=-．（i ）若1a …，则()0f x '…，且当且仅当1a =，1x =-．故此时()f x 在R 上是增函数． （ii ）由于0a ≠，故当1a <时，()0f x '=有两个根：1x =2x =．若01a <<，则当()2,x x ∈-∞或()1,x x ∈+∞时，()0f x '>，故()f x 在()2,x -∞，()1,x +∞上是增函数；当()21,x x x ∈时，()0f x '<，故()f x 在()21,x x 上是减函数；若0a <，则当()1,x x ∈-∞或()2,x +∞时，()0f x '<，故()f x 在()1,x -∞，()2,x +∞上是减函数； 当()21,x x x ∈时，()0f x '>，故()f x 在()12,x x 上是增函数．（2）当0a >，0x >时，()23630f x ax x '=++>，故当0a >时，()f x 在区间()1,2上是增函数．当0a <时，()f x 在区间()1,2上是增函数当且仅当()10f '…且()20f '…，解得504a -<…．综上，a 的取值范围是()5,00,4⎡⎤-+∞⎢⎥⎣⎦U ．【点评】本题考查函数的导数的应用，判断函数的单调性以及已知单调性求解函数中的变量的范围，考查分类讨论思想的应用．（22）【2014年广西，文22，12分】已知抛物线C ：22(0)y px p =>的焦点为F ，直线4y =与y 轴的交点为P ，与C 的交点为Q ，且54QF PQ =．（1）求C 的方程；（2）过F 的直线l 与C 相交于A ，B 两点，若AB 的垂直平分线l '与C 相交于M ，N 两点，且A ，M ，B ，N 四点在同一圆上，求l 的方程．解：（1）设()0,4Q x ，代入22y px =得08x p =．所以8PQ P=，0822p p QF x p =+=+．由题设得85824p p p +=+，解得2p =-（舍去）或2p =．所以C 的方程为24y x =．（2）依题意知l 与坐标轴不垂直，故可设l 的方程为()10x my m =+≠．代入24y x =得2440y my --=．设()11,A x y ，()22,B x y ，则124y y m +=，124y y =-．故AB 的中点为()221,2D m m +，()21241AB y m =-=+．又l '的斜率为m -，所以l '的方程为2123x y m m=-++． 将上式代入24y x =，并整理得()2244230y y m m +-+=．设()33,M x y ，()44,N x y ，则344y y +=-，()234423y y m ⋅=-+．故MN 中点为222223,E m mm ⎛⎫++- ⎪⎝⎭，(234241m MN y m +-=． 由于MN 垂直平分AB ，故A ，M ，B ，N 四点在同一圆上等价于12AE BE MN ==，从而2221144AB DE MN +=，即()()()2222222244121224122m m m m m m m ++⎛⎫⎛⎫+++++= ⎪ ⎪⎝⎭⎝⎭． 化简得210m -=，解得1m =或1m =-．所求直线l 的方程为10x y --=或10x y +-=．【点评】本题主要考查求抛物线的标准方程，直线和圆锥曲线的位置关系的应用，韦达定理、弦长公式的应用，体现了分类讨论的数学思想，属于中档题．。