2014年高考全国1卷文科数学试题及答案(详细解析版,精校版)

合集下载

2014年高考文科数学全国卷1(含详细答案)

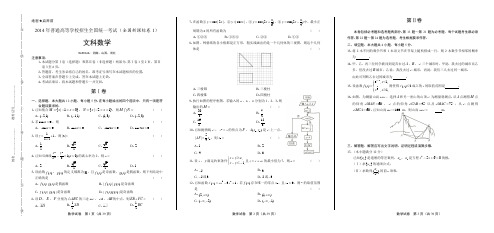
数学试卷第1页（共39页）数学试卷第2页（共39页）数学试卷第3页（共39页）绝密★启用前2014年普通高等学校招生全国统一考试（全国新课标卷1）文科数学使用地区：河南、山西、河北注意事项：1.本试题分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.第Ⅰ卷1至2页，第Ⅱ卷3至6页.2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置.3.全部答案在答题卡上完成，答在本试题上无效.4.考试结束后，将本试题和答题卡一并交回.第Ⅰ卷一、选择题：本大题共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{|13}M x x =-<<，{|21}N x x =-<<，则M N = ( ) A .(2,1)- B .(1,1)- C .(1,3) D .(2,3)-2.若tan 0α>，则( )A . sin 0α>B .cos 0α>C . sin20α>D .cos20α> 3.设1i 1iz =++，则|z |=( )A .12B .22 C .32D .24.已知双曲线2221(0)3x y a a -=>的离心率为2，则a = ( )A .2B .62C .52D .1 5.设函数()f x ，()g x 的定义域都为R ，且()f x 是奇函数，()g x 是偶函数，则下列结论中正确的是( )A .()f x ()g x 是偶函数B .|()|f x ()g x 是奇函数C .()f x |()|g x 是奇函数D .|()()|f x g x 是奇函数6.设D ，E ，F 分别为ABC △的三边BC ，CA ，AB 的中点，则EB FC += ( )A .ADB .12AD C .BCD .12BC 7.在函数①cos |2|y x =，②|cos |y x =，③πcos(2)6y x =+，④πtan(2)4y x =-中，最小正周期为π的所有函数为( )A .①②③B .①③④C .②④D .①③8.如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是( )A .三棱锥B .三棱柱C .四棱锥D .四棱柱 9.执行如图的程序框图，若输入的a ，b ，k 分别为1，2，3.则输出的M =( )A .203B .72C .165D .15810.已知抛物线C ：2y x =的焦点为F ，00(,)A x y 是C 上一点，05||4AF x =，则0x = ( )A .1B .2C .4D .811.设x ，y 满足约束条件,1,x y a x y +⎧⎨--⎩≥≤且z x ay =+的最小值为7，则a =( )A .5-B .3C .5-或3D .5或3-12.已知函数32()31f x ax x =-+，若()f x 存在唯一的零点0x ，且00x >，则a 的取值范围是( )A .(2,)+∞B .(1,)+∞C .(,2)-∞-D .(,1)-∞-第Ⅱ卷本卷包括必考题和选考题两部分.第13题～第21题为必考题，每个试题考生都必须作答.第22题～第24题为选考题，考生根据要求作答. 二、填空题：本大题共4小题，每小题5分.13.将2本不同的数学书和1本语文书在书架上随机排成一行，则2本数学书相邻的概率为 .14.甲、乙、丙三位同学被问到是否去过A ，B ，C 三个城市时，甲说：我去过的城市比乙多，但没去过B 城市；乙说：我没去过C 城市；丙说：我们三人去过同一城市. 由此可判断乙去过的城市为 .15.设函数113e ,1,(),1,x x f x x x -⎧⎪=⎨⎪⎩＜≥则使得()2f x ≤成立的x 的取值范围是 .16.如图，为测量山高MN ，选择A 和另一座山的山顶C 为测量观测点.从A 点测得M 点的仰角60MAN ∠=，C 点的仰角45CAB ∠=以及75MAC ∠=；从C 点测得60MCA ∠=.已知山高100BC = m ，则山高MN = m .三、解答题：解答应写出文字说明、证明过程或演算步骤. 17.（本小题满分12分）已知{}n a 是递增的等差数列，2a ，4a 是方程2560x x -+=的根. （Ⅰ）求{}n a 的通项公式；（Ⅱ）求数列{}2nn a 的前n 项和.姓名________________ 准考证号_____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷第4页（共39页）数学试卷第5页（共39页）数学试卷第6页（共39页）18.（本小题满分12分）从某企业生产的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量结（Ⅰ）在答题卡上作出这些数据的频率分布直方图：（Ⅱ）估计这种产品质量指标值的平均数及方差（同一组中的数据用该组区间的中点值作代表）；（Ⅲ）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定？19.（本小题满分12分）如图，三棱柱111ABC A B C -中，侧面11BB C C 为菱形，1B C 的中点为O ，且AO ⊥平面11BB C C .（Ⅰ）证明：1B C AB ⊥；（Ⅱ）若1AC AB ⊥，160CBB ∠=，1BC =，求三棱柱111ABC A B C -的高.20.（本小题满分12分）已知点(2,2)P ，圆C ：2280x y y +-=，过点P 的动直线l 与圆C 交于A ，B 两点，线段AB 的中点为M ，O 为坐标原点. （Ⅰ）求M 的轨迹方程；（Ⅱ）当||||OP OM =时，求l 的方程及POM △的面积.21.（本小题满分12分）设函数21()ln (1)2a f x a x x bx a -=+-≠，曲线()y f x =在点(1,(1))f 处的切线斜率为0.（Ⅰ）求b ；（Ⅱ）若存在01x ≥，使得0()1af x a <-，求a 的取值范围.请考生在第22、23、24三题中任选一题作答.注意：只能做所选定的题目.如果多做，则按所做的第一个题目计分，作答时请用2B 铅笔在答题卡上将所选题号后的方框涂黑. 22.（本小题满分10分）选修4—1：几何证明选讲如图，四边形ABCD 是O 的内接四边形，AB 的延长线与DC 的延长线交于点E ，且CB CE =.（Ⅰ）证明：D E ∠=∠；（Ⅱ）设AD 不是O 的直径，AD 的中点为M ，且MB MC =，证明：ADE △为等边三角形.23.（本小题满分10分）选修4—4：坐标系与参数方程已知曲线C ：22149x y +=，直线l ：2,22,x t y t =+⎧⎨=-⎩(t 为参数). （Ⅰ）写出曲线C 的参数方程，直线l 的普通方程；（Ⅱ）过曲线C上任意一点P 作与l 夹角为30的直线，交l 于点A ，求||PA 的最大值与最小值.24.（本小题满分10分）选修4—5：不等式选讲若0a >，0b >，且11a b+=（Ⅰ）求33a b +的最小值；（Ⅱ）是否存在a ，b ，使得236a b +=？并说明理由.3 / 132014年普通高等学校招生全国统一考试（全国新课标卷1）文科数学答案解析第Ⅰ卷一、选择题 1.【答案】B【解析】根据集合的运算法则可得：{|11}MN x x =-<<，即选B ．【提示】集合的运算用数轴或者Venn 图可直接计算。

2014年全国统一高考数学试卷(文科)

2014年全国统一高考数学试卷（文科）（新课标Ⅰ）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的3．（5分）（2014•河南）设z=+i，则|z|=（）．C D4．（5分）（2014•河南）已知双曲线﹣=1（a＞0）的离心率为2，则a=（）C D5．（5分）（2014•河南）设函数f（x），g（x）的定义域都为R，且f（x）是奇函数，g（x）是偶函数，则下列结论6．（5分）（2014•河南）设D，E，F分别为△ABC的三边BC，CA，AB的中点，则+=（）．C D．7．（5分）（2014•河南）在函数①y=cos丨2x丨，②y=丨cosx丨，③y=cos（2x+）④y=tan（2x﹣）中，8．（5分）（2014•河南）如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是（）9．（5分）（2014•河南）执行如图的程序框图，若输入的a，b，k分别为1，2，3，则输出的M=（）．C D．10．（5分）（2014•河南）已知抛物线C：y2=x的焦点为F，A（x0，y0）是C上一点，|AF|=x0，x0=（）11．（5分）（2014•河南）设x，y满足约束条件，且z=x+ay的最小值为7，则a=（）12．（5分）（2014•河南）已知函数f（x）=ax3﹣3x2+1，若f（x）存在唯一的零点x0，且x0＞0，则a的取值范围二、填空题：本大题共4小题，每小题5分13．（5分）（2014•河南）将2本不同的数学书和1本语文书在书架上随机排成一行，则2本数学书相邻的概率为_________．14．（5分）（2014•河南）甲、乙、丙三位同学被问到是否去过A，B，C三个城市时，甲说：我去过的城市比乙多，但没去过B城市；乙说：我没去过C城市；丙说：我们三人去过同一城市；由此可判断乙去过的城市为_________．15．（5分）（2014•河南）设函数f（x）=，则使得f（x）≤2成立的x的取值范围是_________．16．（5分）（2014•河南）如图，为测量山高MN，选择A和另一座山的山顶C为测量观测点，从A点测得M点的仰角∠MAN=60°，C点的仰角∠CAB=45°，以及∠MAC=75°；从C点测得∠MCA=60°．已知山高BC=100m，则山高MN=_________m．三、解答题：解答应写出文字说明．证明过程或演算步骤17．（12分）（2014•河南）已知{a n}是递增的等差数列，a2，a4是方程x2﹣5x+6=0的根．（1）求{a n}的通项公式；（2）求数列{}的前n项和．18．（12分）（2014•河南）从某企业生产的产品中抽取100件，测量这些产品的一项质量指标值，由测量结果得如（2）估计这种产品质量指标的平均数及方差（同一组中的数据用该组区间的中点值作代表）；（3）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定？19．（12分）（2014•河南）如图，三棱柱ABC﹣A1B1C1中，侧面BB1C1C为菱形，B1C的中点为O，且AO⊥平面BB1C1C．（1）证明：B1C⊥AB；（2）若AC⊥AB1，∠CBB1=60°，BC=1，求三棱柱ABC﹣A1B1C1的高．20．（12分）（2014•河南）已知点P（2，2），圆C：x2+y2﹣8y=0，过点P的动直线l与圆C交于A，B两点，线段AB的中点为M，O为坐标原点．（1）求M的轨迹方程；（2）当|OP|=|OM|时，求l的方程及△POM的面积．21．（12分）（2014•河南）设函数f（x）=alnx+x2﹣bx（a≠1），曲线y=f（x）在点（1，f（1））处的切线斜率为0，（1）求b；（2）若存在x0≥1，使得f（x0）＜，求a的取值范围．请考生在第22，23，24题中任选一题作答，如果多做，则按所做的第一题记分，作答时清写清题号。

2014年高考(大纲全国卷)数学(文科) 详细答案解析

2014年普通高等学校招生全国统一考试(大纲全国卷)数学(文科)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合M={1,2,4,6,8},N={1,2,3,5,6,7},则M∩N中元素的个数为().A.2B.3C.5D.7【答案】B【解析】∵M={1,2,4,6,8},N={1,2,3,5,6,7},∴M∩N={1,2,6},∴M∩N中元素的个数为3,故选B.2.已知角α的终边经过点(-4,3),则cosα=().A.45B.35C.- 35D.- 45【答案】D【解析】设角α的终边上点(-4,3)到原点O的距离为r,则r=√(-4)2+32=5,∴由余弦函数的定义,得cosα=xr =-45,故选D.3.不等式组{x(x+2)>0,|x|<1的解集为().A.{x|-2<x<-1}B.{x|-1<x<0}C.{x|0<x<1}D.{x|x>1} 【答案】C【解析】{x(x+2)>0,①|x|<1,②由①得,x<-2或x>0,由②得,-1<x<1,因此原不等式组的解集为{x|0<x<1},故选C.4.已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为().A.16B.√36C.13D.√33【答案】B【解析】如图所示,取AD的中点F,连EF,CF,则EF∥BD, ∴异面直线CE与BD所成的角即为CE与EF所成的角∠CEF.由题知,△ABC ,△ADC 为正三角形,设AB=2,则CE=CF=√3,EF=12BD=1.∴在△CEF 中,由余弦定理, 得cos ∠CEF=CE 2+EF 2-CF 22CE·EF=√3)22√3)22×√3×1=√36,故选B .5.函数y=ln(√x 3+1)(x>-1)的反函数是( ). A .y=(1-e x )3(x>-1) B .y=(e x -1)3(x>-1) C .y=(1-e x )3(x ∈R ) D .y=(e x -1)3(x ∈R ) 【答案】D【解析】由y=ln(√x 3+1),得e y =√x 3+1,∴√x 3=e y -1,x=(e y -1)3,∴f -1(x )=(e x -1)3. ∵x>-1,∴y ∈R ,即反函数的定义域为R . ∴反函数为y=(e x -1)3(x ∈R ),故选D .6.已知a ,b 为单位向量,其夹角为60°,则(2a -b )·b =( ). A .-1 B .0 C .1 D .2 【答案】B【解析】由已知得|a |=|b |=1,<a ,b >=60°,∴(2a -b )·b =2a ·b -b 2=2|a ||b |cos <a ,b >-|b |2 =2×1×1×cos 60°-12=0,故选B .7.有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( ).A .60种B .70种C .75种D .150种【答案】C【解析】从6名男医生中选出2名有C 62种选法,从5名女医生中选出1名有C 51种选法,故共有C 62·C 51=6×52×1×5=75种选法,选C .8.设等比数列{a n }的前n 项和为S n .若S 2=3,S 4=15,则S 6=( ). A .31 B .32 C .63 D .64 【答案】C【解析】∵S 2=3,S 4=15,∴由等比数列前n 项和的性质,得S 2,S 4-S 2,S 6-S 4成等比数列, ∴(S 4-S 2)2=S 2(S 6-S 4),即(15-3)2=3(S 6-15),解得S 6=63,故选C .9.已知椭圆C :x 2a 2+y 2b 2=1(a>b>0)的左、右焦点为F 1,F 2,离心率为√33,过F 2的直线l 交C 于A ,B 两点.若△AF 1B 的周长为4√3,则C 的方程为( ). A .x 23+y 22=1 B .x 23+y 2=1 C .x 212+y 28=1 D .x 212+y 24=1【答案】A 【解析】∵x 2a2+y 2b2=1(a>b>0)的离心率为√33, ∴ca =√33,∴a ∶b ∶c=3∶√6∶√3.又∵过F 2的直线l 交椭圆于A ,B 两点, △AF 1B 的周长为4√3, ∴4a=4√3,∴a=√3. ∴b=√2,∴椭圆方程为x 23+y 22=1,选A .10.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( ). A .81π4B .16πC .9πD .27π4【答案】A【解析】由图知,R 2=(4-R )2+2,∴R 2=16-8R+R 2+2,∴R=94,∴S 表=4πR 2=4π×8116=814π,选A .11.双曲线C :x 2a 2−y 2b 2=1(a>0,b>0)的离心率为2,焦点到渐近线的距离为√3,则C 的焦距等于( ).A .2B .2√2C .4D .4√2 【答案】C【解析】∵e=2,∴ca =2.设焦点F 2(c ,0)到渐近线y=ba x 的距离为√3, 渐近线方程为bx-ay=0,∴√b 2+a 2=√3.∵c 2=a 2+b 2,∴b=√3. 由ca =2,得√c 2-b 2=2,∴c 2c 2-3=4,解得c=2.∴焦距2c=4,故选C .12.奇函数f (x )的定义域为R .若f (x+2)为偶函数,且f (1)=1,则f (8)+f (9)=( ). A .-2 B .-1 C .0 D .1 【答案】D【解析】∵奇函数f (x )的定义域为R ,∴f (-x )=-f (x ),且f (0)=0.∵f (x+2)为偶函数,∴f (-x+2)=f (x+2).∴f [(x+2)+2]=f (-x-2+2)=f (-x )=-f (x ),即f (x+4)=-f (x ). ∴f (x+8)=f [(x+4)+4]=-f (x+4)=-(-f (x ))=f (x ). ∴f (x )是以8为周期的周期函数,∴f (8)=f (0)=0,f (9)=f (8+1)=f (1)=1. ∴f (8)+f (9)=0+1=1.故选D .第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.(x-2)6的展开式中x 3的系数为 .(用数字作答) 【答案】-160【解析】由通项公式得T 4=C 63x 6-3(-2)3=-8C 63x 3,故展开式中x 3的系数为-8C 63=-8×6×5×43×2×1=-160.14.函数y=cos 2x+2sin x 的最大值为 . 【答案】32【解析】∵y=cos 2x+2sin x=1-2sin 2x+2sin x=-2(sinx -12)2+32,∴当sin x=12时,y max =32.15.设x ,y 满足约束条件{x -y ≥0,x +2y ≤3,x -2y ≤1,则z=x+4y 的最大值为 .【答案】5【解析】画出x , y 的可行域如图阴影区域.由z=x+4y ,得y= - 14x+z4.先画出直线y=-14x ,再平移直线y=-14x , 当经过点B (1,1)时,z=x+4y 取得最大值为5.16.直线l 1和l 2是圆x 2+y 2=2的两条切线.若l 1与l 2的交点为(1,3),则l 1与l 2的夹角的正切值等于 . 【答案】43【解析】如图所示,设l 1与圆O :x 2+y 2=2相切于点B ,l 2与圆O :x 2+y 2=2相切于点C , 则OB=√2,OA=√10,AB=2√2. ∴tan α=OB AB=√22√2=12.∴tan ∠BAC=tan 2α=2tanα1−tan 2α=2×121−14=43.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)数列{a n }满足a 1=1,a 2=2,a n+2=2a n+1-a n +2. (1)设b n =a n+1-a n ,证明{b n }是等差数列; (2)求{a n }的通项公式.分析:本题主要考查等差数列的概念、通项公式以及累加法求数列通项公式.(1)可用定义证明b n+1-b n =2(常数)即可.(2)利用(1)的结果,求出{b n }的通项公式及a n+1-a n 的表达式,再用累加法可求数列{a n }的通项公式.(1)证明:由a n+2=2a n+1-a n +2得a n+2-a n+1=a n+1-a n +2, 即b n+1=b n +2. 又b 1=a 2-a 1=1,所以{b n }是首项为1,公差为2的等差数列. (2)解:由(1)得b n =1+2(n-1),即a n+1-a n =2n-1.于是∑k=1n(a k+1-a k )=∑k=1n(2k-1),所以a n+1-a 1=n 2,即a n+1=n 2+a 1.又a 1=1,所以{a n }的通项公式为a n =n 2-2n+2.18.(本小题满分12分)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知3a cos C=2c cos A , tan A=13,求B.分析:先由已知及正弦定理,将边的关系转化为角的关系,再由同角三角函数基本关系化弦为切,求出tan C.根据三角形内角和定理及两角和的正切公式求出tan B ,即可求角B. 解:由题设和正弦定理得3sin A cos C=2sin C cos A.故3tan A cos C=2sin C ,因为tan A=13,所以cos C=2sin C ,tan C=12. 所以tan B=tan[180°- (A+C )]= - tan(A+C ) =tanA+tanC tanAtanC -1=-1,即B=135°.19.(本小题满分12分)如图,三棱柱ABC-A 1B 1C 1中,点A 1在平面ABC 内的射影D 在AC 上,∠ACB=90°,BC=1,AC=CC 1=2. (1)证明:AC 1⊥A 1B ;(2)设直线AA 1与平面BCC 1B 1的距离为√3,求二面角A 1-AB-C 的大小.分析:解法一:(1)由已知可证平面AA 1C 1C ⊥平面ABC ,再由面面垂直证线面垂直,利用三垂线定理即得线线垂直.(2)为利用已知,先寻找并证明AA 1与平面BCC 1B 1的距离为A 1E.再由三垂线定理,确定二面角A 1-AB-C 的平面角为∠A 1FD.最后通过解直角三角形求出∠A 1FD 的正切值,即可得出二面角的大小.解法二:建立空间直角坐标系,利用向量知识求解.(1)设出A 1点坐标,确定点及向量坐标,利用数量积为0,证明线线垂直. (2)设法向量,由已知垂直关系,确定坐标.利用向量夹角公式求二面角大小.解法一:(1)证明:因为A 1D ⊥平面ABC ,A 1D ⊂平面AA 1C 1C ,故平面AA 1C 1C ⊥平面ABC. 又BC ⊥AC ,所以BC ⊥平面AA 1C 1C.连结A 1C.因为侧面AA 1C 1C 为菱形,故AC 1⊥A 1C. 由三垂线定理得AC 1⊥A 1B.(2)BC ⊥平面AA 1C 1C ,BC ⊂平面BCC 1B 1, 故平面AA 1C 1C ⊥平面BCC 1B 1.作A 1E ⊥CC 1,E 为垂足,则A 1E ⊥平面BCC 1B 1. 又直线AA 1∥平面BCC 1B 1,因而A 1E 为直线AA 1与平面BCC 1B 1的距离,A 1E=√3. 因为A 1C 为∠ACC 1的平分线,故A 1D=A 1E=√3.作DF ⊥AB ,F 为垂足,连结A 1F.由三垂线定理得A 1F ⊥AB , 故∠A 1FD 为二面角A 1-AB-C 的平面角.由AD=√AA 12-A 1D 2=1得D 为AC 中点,DF=12×AC×BC AB=√55,tan ∠A 1FD=A 1DDF =√15.所以二面角A 1-AB-C 的大小为arctan √15.解法二:以C 为坐标原点,射线CA 为x 轴的正半轴,以CB 的长为单位长,建立如图所示的空间直角坐标系C-xyz. 由题设知A 1D 与z 轴平行,z 轴在平面AA 1C 1C 内. (1)证明:设A 1(a ,0,c ),由题设有a ≤2,A (2,0,0),B (0,1,0), 则AB ⃗⃗⃗⃗⃗ =(-2,1,0),AC ⃗⃗⃗⃗⃗ =(-2,0,0),AA 1⃗⃗⃗⃗⃗⃗⃗ =(a-2,0,c ), AC 1⃗⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ +AA 1⃗⃗⃗⃗⃗⃗⃗ =(a-4,0,c ),BA 1⃗⃗⃗⃗⃗⃗⃗⃗ =(a ,-1,c ). 由|AA 1⃗⃗⃗⃗⃗⃗⃗ |=2得√(a -2)2+c 2=2, 即a 2-4a+c 2=0.①于是AC 1⃗⃗⃗⃗⃗⃗⃗ ·BA 1⃗⃗⃗⃗⃗⃗⃗⃗ =a 2-4a+c 2=0,所以AC 1⊥A 1B.(2)设平面BCC 1B 1的法向量m =(x ,y ,z ),则m ⊥CB ⃗⃗⃗⃗⃗ ,m ⊥BB 1⃗⃗⃗⃗⃗⃗⃗ , 即m ·CB ⃗⃗⃗⃗⃗ =0,m ·BB 1⃗⃗⃗⃗⃗⃗⃗ =0.因CB ⃗⃗⃗⃗⃗ =(0,1,0),BB 1⃗⃗⃗⃗⃗⃗⃗ =AA 1⃗⃗⃗⃗⃗⃗⃗ =(a-2,0,c ), 故y=0,且(a-2)x+cz=0.令x=c ,则z=2-a ,m =(c ,0,2-a ),点A 到平面BCC 1B 1的距离为 |CA ⃗⃗⃗⃗⃗ |·|cos <m ,CA⃗⃗⃗⃗⃗ >|=|CA ⃗⃗⃗⃗⃗·m||m|=√c 2+(2−a)2= c.又依题设,A 到平面BCC 1B 1的距离为√3,所以c=√3. 代入①解得a=3(舍去)或a=1.于是AA 1⃗⃗⃗⃗⃗⃗⃗ =(-1,0,√3). 设平面ABA 1的法向量n =(p ,q ,r ), 则n ⊥AA 1⃗⃗⃗⃗⃗⃗⃗ ,n ⊥AB ⃗⃗⃗⃗⃗ ,即n ·AA 1⃗⃗⃗⃗⃗⃗⃗ =0,n ·AB ⃗⃗⃗⃗⃗ =0, -p+√3r=0,且-2p+q=0.令p=√3,则q=2√3,r=1,n =(√3,2√3,1). 又p =(0,0,1)为平面ABC 的法向量, 故cos <n ,p >=n·p |n||p|=14.所以二面角A 1-AB-C 的大小为arccos 14.20.(本小题满分12分)设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6,0.5,0.5,0.4,各人是否需使用设备相互独立. (1)求同一工作日至少3人需使用设备的概率;(2)实验室计划购买k 台设备供甲、乙、丙、丁使用.若要求“同一工作日需使用设备的人数大于k”的概率小于0.1,求k 的最小值.分析:(1)先用字母表示各事件,再由互斥与独立事件的概率可求.(2)由(1)分析k 的可能取值情况,比较即得结果.解:记A i 表示事件:同一工作日乙、丙中恰有i 人需使用设备,i=0,1,2,B 表示事件:甲需使用设备,C 表示事件:丁需使用设备,D 表示事件:同一工作日至少3人需使用设备,E 表示事件:同一工作日4人需使用设备,F 表示事件:同一工作日需使用设备的人数大于k. (1)D=A 1·B ·C+A 2·B+A 2·B ·C ,P (B )=0.6,P (C )=0.4,P (A i )=C 2i×0.52,i=0,1,2,所以P (D )=P (A 1·B ·C+A 2·B+A 2·B ·C )=P (A 1·B ·C )+P (A 2·B )+P (A 2·B ·C )=P (A 1)P (B )P (C )+P (A 2)P (B )+P (A 2)P (B )P (C ) =0.31.(2)由(1)知,若k=2,则P (F )=0.31>0.1. 又E=B ·C ·A 2,P (E )=P (B ·C ·A 2)=P (B )P (C )P (A 2)=0.06. 若k=3,则P (F )=0.06<0.1. 所以k 的最小值为3.21.(本小题满分12分)函数f (x )=ax 3+3x 2+3x (a ≠0). (1)讨论f (x )的单调性;(2)若f (x )在区间(1,2)是增函数,求a 的取值范围.分析:(1)由于导函数的判别式含参数a ,因此要根据导数值的正负判断单调性,需对a 进行分类讨论.当判别式为正时,导函数有两根,为比较两根的大小,需对a 进行二重讨论.(2)根据f (x )在(1,2)上是增函数可列出关于a 的不等式,注意对a>0或a<0进行讨论. 解:(1)f'(x )=3ax 2+6x+3,f'(x )=0的判别式Δ=36(1-a ).①若a ≥1,则f'(x )≥0,且f'(x )=0当且仅当a=1,x=-1. 故此时f (x )在R 上是增函数.②由于a ≠0,故当a<1时,f'(x )=0有两个根: x 1=-1+√1−aa,x 2=-1-√1−aa.若0<a<1,则当x ∈(-∞,x 2)或x ∈(x 1,+∞)时f'(x )>0, 故f (x )分别在(-∞,x 2),(x 1,+∞)是增函数; 当x ∈(x 2,x 1)时f'(x )<0,故f (x )在(x 2,x 1)是减函数; 若a<0,则当x ∈(-∞,x 1)或(x 2,+∞)时f'(x )<0, 故f (x )分别在(-∞,x 1),(x 2,+∞)是减函数; 当x ∈(x 1,x 2)时f'(x )>0,故f (x )在(x 1,x 2)是增函数.(2)当a>0,x>0时,f'(x )=3ax 2+6x+3>0,故当a>0时,f (x )在区间(1,2)是增函数. 当a<0时,f (x )在区间(1,2)是增函数当且仅当f'(1)≥0且f'(2)≥0,解得 - 54≤ a<0.综上,a 的取值范围是[-54,0)∪(0,+∞).22.(本小题满分12分)已知抛物线C :y 2=2px (p>0)的焦点为F ,直线y=4与y 轴的交点为P ,与C 的交点为Q ,且|QF|=54|PQ|. (1)求C 的方程;(2)过F 的直线l 与C 相交于A ,B 两点,若AB 的垂直平分线l'与C 相交于M ,N 两点,且A ,M ,B ,N 四点在同一圆上,求l 的方程.分析:(1)设出Q 点坐标,利用|QF|=54|PQ|列出关于p 的方程,借助于p 的几何意义及抛物线的性质确定p.(2)通过题设分析判断直线l 与x 轴不垂直.因直线l 过F (1,0),可设l 的方程为x=my+1(m ≠0).直线l 方程与抛物线方程联立,利用韦达定理得到y 1+y 2,y 1y 2关于m 的表达式,借助弦长公式得|AB|=√m 2+1|y 1-y 2|(其中A (x 1,y 1),B (x 2,y 2)),同理可得|MN|=√1+1m |y 3-y 4|(其中M (x 3,y 3),N (x 4,y 4)).由题目中的A ,M ,B ,N 四点在同一圆上得到关于m 的方程,进而求出m ,得到直线l 的方程.解:(1)设Q (x 0,4),代入y 2=2px 得x 0=8p .所以|PQ|=8p ,|QF|=p2+x 0=p2+8p . 由题设得 p2+8p=54×8p,解得p=-2(舍去)或p=2. 所以C 的方程为y 2=4x. (2)依题意知l 与坐标轴不垂直, 故可设l 的方程为x=my+1(m ≠0). 代入y 2=4x 得y 2-4my-4=0.设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=4m ,y 1y 2=-4. 故AB 的中点为D (2m 2+1,2m ), |AB|=2+1|y 1-y 2|=4(m 2+1).又l'的斜率为-m ,所以l'的方程为x=-1m y+2m 2+3. 将上式代入y 2=4x ,并整理得y 2+4m y-4(2m 2+3)=0. 设M (x 3,y 3),N (x 4,y 4),则y 3+y 4=-4m ,y 3y 4=-4(2m 2+3). 故MN 的中点为E (2m 2+2m 2+3,−2m ), |MN|=√1+1m 2|y 3-y 4|=4(m 2+1)√2m 2+1m .由于MN 垂直平分AB ,故A ,M ,B ,N 四点在同一圆上等价于|AE|=|BE|=12|MN|, 从而14|AB|2+|DE|2=14|MN|2,即4(m 2+1)2+(2m +2m )2+(2m 2+2)2=4(m 2+1)2(2m 2+1)m 4,化简得m 2-1=0,解得m=1或m=-1.所求直线l的方程为x-y-1=0或x+y-1=0.。

2014年高考数学(文科)试题及参考答案(新课标I卷)

2014年普通高等学校招生全国统一考试（课标I 文科卷）数学（文科）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合{}{}12|,31|≤≤-=≤≤-=x x B x x M ，则MB =（）A. )1,2(-B. )1,1(-C. )3,1(D. )3,2(- （2）若0tan >α，则A. 0sin >αB. 0cos >αC. 02sin >αD. 02cos >α（3）设i iz ++=11，则=||z A. 21 B. 22 C. 23 D. 2（4）已知双曲线)0(13222>=-a y a x 的离心率为2，则=a A. 2 B. 26 C. 25D. 1（5）设函数)(),(x g x f 的定义域为R ，且)(x f 是奇函数，)(x g 是偶函数，则下列结论中正确的是A. )()(x g x f 是偶函数B. )(|)(|x g x f 是奇函数C. |)(|)(x g x f 是奇函数D. |)()(|x g x f 是奇函数（6）设F E D ,,分别为ABC ∆的三边AB CA BC ,,的中点，则=+FC EB A. AD B.21 C. 21D. BC （7）在函数①|2|cos x y =，②|cos |x y = ，③)62cos(π+=x y ,④)42tan(π-=x y 中，最小正周期为π的所有函数为A.①②③B. ①③④C. ②④D. ①③8.如图，网格纸的各小格都是正方形，粗实线画出的事一个几何体的三视图，则这个几何体是（） A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱9.执行右面的程序框图，若输入的,,a b k 分别为1,2,3，则输出的M =( ) A.203 B.72 C.165 D.15810.已知抛物线C ：x y =2的焦点为F ,()y x A 0,是C 上一点，zxxk x F A 045=，则=x 0（）A. 1B. 2C. 4D. 8 （11）设x ，y 满足约束条件,1,x y a x y +≥⎧⎨-≤-⎩且z x ay =+的最小值为7，则a =（A ）-5 （B ）3 （C ）-5或3 （D ）5或-3（12）已知函数32()31f x ax x =-+，若()f x 存在唯一的零点0x ，且00x >，则a 的取值范围是（A ）()2,+∞ （B ）()1,+∞ （C ）(),2-∞- （D ）(),1-∞-第II 卷二、填空题：本大题共4小题，每小题5分（13）将2本不同的数学书和1本语文书在书架上随机排成一行，则2本数学书相邻的概率为________. （14）甲、乙、丙三位同学被问到是否去过A 、B 、zxxk C 三个城市时，甲说：我去过的城市比乙多，但没去过B 城市；乙说：我没去过C 城市；丙说：我们三人去过同一城市；由此可判断乙去过的城市为________.（15）设函数()113,1,,1,x e x f x x x -⎧<⎪=⎨⎪≥⎩则使得()2f x ≤成立的x 的取值范围是________.（16）如图，为测量山高MN ，选择A 和另一座山的山顶C 为测量观测点.从A 点测得 M 点的仰角60MAN ∠=︒，C 点的仰角45CAB ∠=︒以及75MAC ∠=︒；从C 点测得60MCA ∠=︒.已知山高100BC m =，则山高MN =________m.三、解答题：解答应写出文字说明，证明过程或演算步骤. （17）（本小题满分12分）已知{}n a 是递增的等差数列，2a ，4a 是方程2560x x -+=的根。

2014年全国高考文科数学试题及答案-全国卷

2014年普通高等学校统一考试（大纲）文科第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设集合{1,2,4,6,8},{1,2,3,5,6,7}M N ==，则M N 中元素的个数为（）A ．2B ．3C ．5D ．72. 已知角α的终边经过点(4,3)-，则cos α=（）A ．45B ．35C ．35-D ．45- 3. 不等式组(2)0||1x x x +>⎧⎨<⎩的解集为（）A ．{|21}x x -<<-B ．{|10}x x -<<C ．{|01}x x <<D ．{|1}x x > 4. 已知正四面体ABCD 中，E 是AB 的中点，则异面直线CE 与BD 所成角的余弦值为（）A ．16B C ．13D5. 函数1)(1)y x =>-的反函数是（）A ．3(1)(1)x y e x =->- B ．3(1)(1)xy e x =->- C ．3(1)()x y e x R =-∈ D ．3(1)()xy e x R =-∈6. 已知a b 、为单位向量，其夹角为060，则(2)a b b -∙=（） A ．-1 B ．0 C ．1 D ．27. 有6名男医生、5名女医生，从中选出2名男医生、1名女医生组成一个医疗小组，则不同的选法共有（）A ．60种B ．70种C ．75种D ．150种8. 设等比数列{}n a 的前n 项和为n S ，若243,15,S S ==则6S =（）A ．31B ．32C ．63D ．649. 已知椭圆C ：22221x y a b+=(0)a b >>的左、右焦点为1F 、2F，过2F 的直线l 交C 于A 、B 两点，若1AF B ∆的周长为C 的方程为（）A ．22132x y +=B ．2213x y += C ．221128x y += D ．221124x y += 10. 正四棱锥的顶点都在同一球面上，若该棱锥的高位4，底面边长为2，则该球的表面积为（）A ．814π B ．16π C ．9π D ．274π11. 双曲线C ：22221(0,0)x y a b a b-=>>的离心率为2，，则C 的焦距等于（）A ．2 B． C ．4 D．12. 奇函数()f x 的定义域为R ，若(2)f x +为偶函数，且(1)1f =，则(8)(9)f f +=（）A ．-2B ．-1C ．0D ．1第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上） 13. 6(2)x -的展开式中3x 的系数为 .（用数字作答） 14. 函数cos22sin y x x =+的最大值为 .15. 设x 、y 满足约束条件02321x y x y x y -≥⎧⎪+≤⎨⎪-≤⎩，则4z x y =+的最大值为 .16. 直线1l 和2l 是圆222x y +=的两条切线，若1l 与2l 的交点为（1,3），则1l 与2l 的夹角的正切值等于 .三、解答题（本大题共6小题. 解答应写出文字说明、证明过程或演算步骤.） 17. （本小题满分10分）数列{}n a 满足12212,2,22n n n a a a a a ++===-+. （1）设1n n n b a a +=-，证明{}n b 是等差数列；（2）求{}n a 的通项公式. 18. （本小题满分12分）ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ，已知13cos 2cos ,tan 3a C c A A ==，求B.19. （本小题满分12分）如图，三棱柱111ABC A B C -中，点1A 在平面ABC 内的射影D 在AC 上，090ACB ∠=，11,2BC AC CC ===.（1）证明：11AC A B ⊥；（2）设直线1AA 与平面11BCC B 1A AB C --的大小. 20.（本小题满分12分）设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6，0.5,0.5,0.4，各人是否使用设备相互独立，（1）求同一工作日至少3人需使用设备的概率；（2）实验室计划购买k 台设备供甲、乙、丙、丁使用，若要求“同一工作日需使用设备的人数大于k ”的概率小于0.1，求k 的最小值.21. （本小题满分12分）函数32()33(0)f x ax x x a =++≠.（1）讨论函数()f x 的单调性；（2）若函数()f x 在区间（1，2）是增函数，求a 的取值范围. 22. （本小题满分12分）已知抛物线C:22(0)y px p =>的焦点为F ，直线4y =与y 轴的交点为P ，与C 的交点为Q ，且54QF PQ =. （1）求抛物线C 的方程；（2）过F 的直线l 与C 相交于A,B 两点，若AB 的垂直平分线l '与C 相交于M,N 两点，且A,M,B,N四点在同一个圆上，求直线l的方程.参考答案一、选择题1.B2.D3.C4.B5.D6.B7.C8.C9.A10.A11.C12.D二、填空题13. -16014.3215. 5 16.43三、解答题：解答应写出文字说明，证明过程或演算步骤。

2014年全国统一高考数学试卷(文科)(新课标ⅰ)(附参考答案+详细解析Word打印版)

2014年全国普通高等学校招生统一考试数学试卷（文科）（新课标Ⅰ）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的1．（5分）已知集合M={x|﹣1＜x＜3}，N={x|﹣2＜x＜1}，则M∩N=（）A．（﹣2，1）B．（﹣1，1）C．（1，3） D．（﹣2，3）2．（5分）若tanα＞0，则（）A．sinα＞0 B．cosα＞0 C．sin2α＞0 D．cos2α＞03．（5分）设z=+i，则|z|=（）A．B．C．D．24．（5分）已知双曲线﹣=1（a＞0）的离心率为2，则实数a=（）A．2 B．C．D．15．（5分）设函数f（x），g（x）的定义域都为R，且f（x）是奇函数，g（x）是偶函数，则下列结论正确的是（）A．f（x）•g（x）是偶函数B．|f（x）|•g（x）是奇函数C．f（x）•|g（x）|是奇函数D．|f（x）•g（x）|是奇函数6．（5分）设D，E，F分别为△ABC的三边BC，CA，AB的中点，则+=（）A．B．C．D．7．（5分）在函数①y=cos|2x|，②y=|cosx|，③y=cos（2x+），④y=tan（2x﹣）中，最小正周期为π的所有函数为（）A．①②③B．①③④C．②④D．①③8．（5分）如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是（）A．三棱锥B．三棱柱C．四棱锥D．四棱柱9．（5分）执行如图的程序框图，若输入的a，b，k分别为1，2，3，则输出的M=（）A．B．C．D．10．（5分）已知抛物线C：y2=x的焦点为F，A（x0，y0）是C上一点，AF=|x0|，则x0=（）A．1 B．2 C．4 D．811．（5分）设x，y满足约束条件且z=x+ay的最小值为7，则a=（）A．﹣5 B．3 C．﹣5或3 D．5或﹣312．（5分）已知函数f（x）=ax3﹣3x2+1，若f（x）存在唯一的零点x0，且x0＞0，则实数a的取值范围是（）A．（1，+∞）B．（2，+∞）C．（﹣∞，﹣1）D．（﹣∞，﹣2）二、填空题：本大题共4小题，每小题5分13．（5分）将2本不同的数学书和1本语文书在书架上随机排成一行，则2本数学书相邻的概率为．14．（5分）甲、乙、丙三位同学被问到是否去过A，B，C三个城市时，甲说：我去过的城市比乙多，但没去过B城市；乙说：我没去过C城市；丙说：我们三人去过同一城市；由此可判断乙去过的城市为．15．（5分）设函数f（x）=，则使得f（x）≤2成立的x的取值范围是．16．（5分）如图，为测量山高MN，选择A和另一座的山顶C为测量观测点，从A点测得M点的仰角∠MAN=60°，C点的仰角∠CAB=45°以及∠MAC=75°；从C点测得∠MCA=60°，已知山高BC=100m，则山高MN=m．三、解答题：解答应写出文字说明．证明过程或演算步骤17．（12分）已知{a n}是递增的等差数列，a2，a4是方程x2﹣5x+6=0的根．（1）求{a n}的通项公式；（2）求数列{}的前n项和．18．（12分）从某企业生产的产品中抽取100件，测量这些产品的一项质量指标值，由测量结果得如下频数分布表：（1）在表格中作出这些数据的频率分布直方图；（2）估计这种产品质量指标的平均数及方差（同一组中的数据用该组区间的中点值作代表）；（3）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定？19．（12分）如图，三棱柱ABC﹣A1B1C1中，侧面BB1C1C为菱形，B1C的中点为O，且AO⊥平面BB1C1C．（1）证明：B1C⊥AB；（2）若AC⊥AB1，∠CBB1=60°，BC=1，求三棱柱ABC﹣A1B1C1的高．20．（12分）已知点P（2，2），圆C：x2+y2﹣8y=0，过点P的动直线l与圆C交于A，B两点，线段AB的中点为M，O为坐标原点．（1）求M的轨迹方程；（2）当|OP|=|OM|时，求l的方程及△POM的面积．21．（12分）设函数f（x）=alnx+x2﹣bx（a≠1），曲线y=f（x）在点（1，f （1））处的切线斜率为0，（1）求b；（2）若存在x0≥1，使得f（x0）＜，求a的取值范围．请考生在第22，23，24题中任选一题作答，如果多做，则按所做的第一题记分。

2014年全国高考文科数学试题及答案-全国卷

2014年普通高等学校统一考试（大纲）文科第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设集合，则中元素的个数为（）{1,2,4,6,8},{1,2,3,5,6,7}M N ==M N A ．2B ．3C ．5D ．72. 已知角的终边经过点，则（）α(4,3)-cos α=A ．B ．C ．D ． 453535-45-3. 不等式组的解集为（）(2)0||1x x x +>⎧⎨<⎩A ．B ．C ．D ． {|21}x x -<<-{|10}x x -<<{|01}x x <<{|1}x x >4. 已知正四面体ABCD 中，E 是AB 的中点，则异面直线CE 与BD 所成角的余弦值为（）A ．B C ． D 16135. 函数的反函数是（）1)(1)y x =>-A ． B ． 3(1)(1)x y e x =->-3(1)(1)xy e x =->-C ． D ．3(1)()x y e x R =-∈3(1)()xy e x R =-∈6. 已知为单位向量，其夹角为，则（） a b 、60(2)a b b -∙= A ．-1 B ．0 C ．1 D ．27. 有6名男医生、5名女医生，从中选出2名男医生、1名女医生组成一个医疗小组，则不同的选法共有（）A ．60种B ．70种C ．75种D ．150种8. 设等比数列的前n 项和为，若则（）{}n a n S 243,15,S S ==6S =A ．31B ．32C ．63D ．649. 已知椭圆C ：的左、右焦点为、，过的直线交22221x y a b+=(0)a b >>1F 2F 2F l C 于A 、B 两点，若的周长为C 的方程为（）1AF B ∆A ． B ． C ． D ．22132x y +=2213x y +=221128x y +=221124x y +=10. 正四棱锥的顶点都在同一球面上，若该棱锥的高位4，底面边长为2，则该球的表面积为（） A ．B ．C ．D ． 814π16π9π274π11. 双曲线C ：的离心率为2，，则C 的焦距等22221(0,0)x y a b a b-=>>于（）A ．2B ．．4 D ．12. 奇函数的定义域为R ，若为偶函数，且，则（）()f x (2)f x +(1)1f =(8)(9)f f +=A ．-2 B ．-1 C ．0 D ．1第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上） 13. 的展开式中的系数为 .（用数字作答） 6(2)x -3x 14. 函数的最大值为 .cos 22sin y x x =+15. 设x 、y 满足约束条件，则的最大值为 .2321x y x y x y -≥⎧⎪+≤⎨⎪-≤⎩4z x y =+16. 直线和是圆的两条切线，若与的交点为（1,3），则与的夹角的正切值1l 2l 222x y +=1l 2l 1l 2l 等于 .三、解答题（本大题共6小题. 解答应写出文字说明、证明过程或演算步骤.） 17. （本小题满分10分）数列满足. {}n a 12212,2,22n n n a a a a a ++===-+（1）设，证明是等差数列； 1n n n b a a +=-{}n b （2）求的通项公式. {}n a 18. （本小题满分12分）的内角A 、B 、C 的对边分别为a 、b 、c ，已知，求B.ABC ∆13cos 2cos ,tan 3a C c A A ==19. （本小题满分12分）如图，三棱柱中，点在平面ABC 内的射影D 在AC 上，，111ABC A B C -1A 090ACB ∠=.11,2BC AC CC ===（1）证明：；11AC A B ⊥（2）设直线与平面，求二面角的大小. 1AA 11BCC B 1A AB C --20.（本小题满分12分）设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6，0.5,0.5,0.4，各人是否使用设备相互独立，（1）求同一工作日至少3人需使用设备的概率；（2）实验室计划购买k 台设备供甲、乙、丙、丁使用，若要求“同一工作日需使用设备的人数大于k”的概率小于0.1，求k 的最小值.21. （本小题满分12分）函数.32()33(0)f x ax x x a =++≠（1）讨论函数的单调性；()f x （2）若函数在区间（1，2）是增函数，求的取值范围. ()f x a 22. （本小题满分12分）已知抛物线C:的焦点为F ，直线与y 轴的交点为P ，与C 的交点为Q ，22(0)y px p =>4y =且. 54QF PQ =（1）求抛物线C 的方程；（2）过F 的直线与C 相交于A,B 两点，若AB 的垂直平分线与C 相交于M,N 两点，且A,M,B,Nl l 'l四点在同一个圆上，求直线的方程.参考答案一、选择题1.B2.D3.C4.B5.D6.B7.C8.C9.A10.A11.C12.D二、填空题13. -16014.15. 5 16.3243三、解答题：解答应写出文字说明，证明过程或演算步骤。

2014年全国I卷文科数学高考试卷(原卷答案)

绝密★启用前2014年普通高等学校招生全国统一考试(全国I 卷)(适用地区：河南、河北、山西)文科数学本试卷共24题，共150分。

考试结束后，将本试卷和答题卡一并交回。

注意事项：1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一．选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合M=｛x|-1＜x ＜3｝，N=｛x|-2＜x ＜1｝则M ∩N=（）A. )1,2(−B. )1,1(−C. )3,1(D. )3,2(−（2）若0tan >α，则A. 0sin >αB. 0cos >αC. 02sin >αD. 02cos >α （3）设i iz ++=11，则=||z A.21 B. 22 C. 23 D. 2 （4）已知双曲线)0(13222>=−a y a x 的离心率为2，则=aA. 2B.26 C. 25D. 1 (5)设函数)(),(x g x f 的定义域都为R ，且)(x f 是奇函数，)(x g 是偶函数，则下列结论中正确的是A. )()(x g x f 是偶函数B. )(|)(|x g x f 是奇函数C. |)(|)(x g x f 是奇函数D. |)()(|x g x f 是奇函数（6）设F E D ,,分别为ABC ∆的三边AB CA BC ,,的中点，则=+FC EBA. ADB.AD 21 C. BC D. BC 21(7)在函数①|2|cos x y =，②|cos |x y = ，③)62cos(π+=x y ,④)42tan(π−=x y 中，最小正周期为π的所有函数为A.①②③B. ①③④C. ②④D. ①③（8）如图，网格纸的各小格都是正方形，粗实线画出的事一个几何体的三视图，则这个几何体是（）A.三棱锥B.三棱柱C.四棱锥D.四棱柱（9）执行右面的程序框图，若输入的,,a b k 分别为1,2,3，则输出的M =( )A.203B.72C.165D.158（10）已知抛物线C ：x y =2的焦点为F,A(x 0,y 0)是C 上一点，x F A 045=，则x 0=（）A. 1B. 2C. 4D. 8 （11）设x ，y 满足约束条件,1,x y a x y +≥⎧⎨−≤−⎩且z x ay =+的最小值为7，则a =A ．-5 B. 3C ．-5或3 D. 5或-3（12）已知函数32()31f x ax x =−+，若()f x 存在唯一的零点0x ，且00x >，则a 的取值范围是A.()2,+∞B.()1,+∞C.(),2−∞−D.(),1−∞−第II 卷二、填空题：本大题共4小题，每小题5分（13）将2本不同的数学书和1本语文书在书架上随机排成一行，则2本数学书相邻的概率为_ _. （14）甲、乙、丙三位同学被问到是否去过A 、B 、C 三个城市时，甲说：我去过的城市比乙多，但没去过B 城市；乙说：我没去过C 城市；丙说：我们三人去过同一城市；由此可判断乙去过的城市为____ ____.（15）设函数()113,1,,1,x e x f x x x −⎧<⎪=⎨⎪≥⎩则使得()2f x ≤成立的x 的取值范围是__ _____.（16）如图，为测量山高MN ，选择A 和另一座山的山顶C 为测量观测点.从A 点测得 M 点的仰角60MAN ∠=︒，C 点的仰角45CAB ∠=︒以及75MAC ∠=︒；从C 点测得60MCA ∠=︒.已知山高100BC m =，则山高MN =_ ___m .三、解答题：解答应写出文字说明，证明过程或演算步骤. （17）（本小题满分12分）已知{}n a 是递增的等差数列，2a ，4a 是方程2560x x −+=的根。

2014年全国统一高考数学试卷(文科)(大纲版)解析版

2014年全国统一高考数学试卷（文科）（大纲版）解析版参考答案与试题解析一、选择题（本大题共12小题，每小题5分）1．（5分）设集合{1M =，2，4，6，8}，{1N =，2，3，5，6，7}，则M N 中元素的个数为( ) A ．2B ．3C ．5D ．7【考点】1A ：集合中元素个数的最值；1E ：交集及其运算【专题】5J ：集合【分析】根据M 与N ，找出两集合的交集，找出交集中的元素即可．【解答】解：{1M =，2，4，6，8}，{1N =，2，3，5，6，7}， {1MN ∴=，2，6}，即MN 中元素的个数为3．故选：B ．【点评】此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键． 2．（5分）已知角α的终边经过点(4,3)-，则cos (α= ) A ．45B ．35C ．35-D ．45-【考点】9G ：任意角的三角函数的定义【专题】56：三角函数的求值【分析】由条件直接利用任意角的三角函数的定义求得cos α的值．【解答】解：角α的终边经过点(4,3)-，4x ∴=-，3y =，5r ==． 44cos 55x r α-∴===-，故选：D ．【点评】本题主要考查任意角的三角函数的定义，两点间的距离公式的应用，属于基础题． 3．（5分）不等式组(2)0||1x x x +>⎧⎨<⎩的解集为( )A ．{|21}x x -<<-B ．{|10}x x -<<C ．{|01}x x <<D ．{|1}x x >【考点】7E ：其他不等式的解法【专题】59：不等式的解法及应用【分析】解一元二次不等式、绝对值不等式，分别求出不等式组中每个不等式的解集，再取交集，即得所求．【解答】解：由不等式组(2)0||1x x x +>⎧⎨<⎩可得2,011x x x ⎧-⎨-<<⎩或，解得01x <<，故选：C ．【点评】本题主要考查一元二次不等式、绝对值不等式的解法，属于基础题．4．（5分）已知正四面体ABCD 中，E 是AB 的中点，则异面直线CE 与BD 所成角的余弦值为( )A ．16B C ．13D 【考点】LM ：异面直线及其所成的角【专题】5G ：空间角【分析】由E 为AB 的中点，可取AD 中点F ，连接EF ，则CEF ∠为异面直线CE 与BD 所成角，设出正四面体的棱长，求出CEF ∆的三边长，然后利用余弦定理求解异面直线CE 与BD 所成角的余弦值．【解答】解：如图，取AD 中点F ，连接EF ，CF ，E 为AB 的中点，//EF DB ∴，则CEF ∠为异面直线BD 与CE 所成的角，ABCD 为正四面体，E ，F 分别为AB ，AD 的中点， CE CF ∴=．设正四面体的棱长为2a ，则EF a =，CE CF =．在CEF ∆中，由余弦定理得：2222cos 2CE EF CF CEF CE EF +-∠==故选：B ．【点评】本题考查异面直线及其所成的角，关键是找角，考查了余弦定理的应用，是中档题．5．（5分）函数1)(1)y ln x =>-的反函数是( ) A ．3(1)(1)x y e x =->- B ．3(1)(1)x y e x =->- C ．3(1)()x y e x R =-∈ D ．3(1)()x y e x R =-∈【考点】4R ：反函数【专题】51：函数的性质及应用【分析】由已知式子解出x ，然后互换x 、y 的位置即可得到反函数．【解答】解：3(1)y ln =，∴1y e +=1y e =-，3(1)y x e ∴=-，∴所求反函数为3(1)x y e =-，故选：D ．【点评】本题考查反函数解析式的求解，属基础题．6．（5分）已知a ，b 为单位向量，其夹角为60︒，则(2)(a b b -= ) A ．1-B ．0C ．1D ．2【考点】9O ：平面向量数量积的性质及其运算【专题】5A ：平面向量及应用【分析】由条件利用两个向量的数量积的定义，求得a b 、2b 的值，可得(2)a b b -的值．【解答】解：由题意可得，111cos602a b =⨯⨯︒=，21b =， 2(2)20a b b a b b ∴-=-=，故选：B ．【点评】本题主要考查两个向量的数量积的定义，属于基础题．7．（5分）有6名男医生、5名女医生，从中选出2名男医生、1名女医生组成一个医疗小组，则不同的选法共有( ) A ．60种B ．70种C ．75种D ．150种【考点】9D ：排列、组合及简单计数问题【专题】5O ：排列组合【分析】根据题意，分2步分析，先从6名男医生中选2人，再从5名女医生中选出1人，由组合数公式依次求出每一步的情况数目，由分步计数原理计算可得答案．【解答】解：根据题意，先从6名男医生中选2人，有2615C =种选法，再从5名女医生中选出1人，有155C =种选法，则不同的选法共有15575⨯=种；故选：C ．【点评】本题考查分步计数原理的应用，注意区分排列、组合的不同．8．（5分）设等比数列{}n a 的前n 项和为n S ．若23S =，415S =，则6(S = ) A ．31B ．32C ．63D ．64【考点】89：等比数列的前n 项和【专题】54：等差数列与等比数列【分析】由等比数列的性质可得2S ，42S S -，64S S -成等比数列，代入数据计算可得．【解答】解：212S a a =+，2423412()S S a a a a q -=+=+，4645612()S S a a a a q -=+=+，所以2S ，42S S -，64S S -成等比数列，即3，12，615S -成等比数列，可得26123(15)S =-，解得663S = 故选：C ．【点评】本题考查等比数列的性质，得出2S ，42S S -，64S S -成等比数列是解决问题的关键，属基础题．9．（5分）已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点为1F 、2F ，，过2F 的直线l 交C 于A 、B 两点，若△1AF B 的周长为，则C 的方程为( )A ．22132x y +=B ．2213x y +=C ．221128x y +=D ．221124x y +=【考点】4K ：椭圆的性质【专题】5D ：圆锥曲线的定义、性质与方程【分析】利用△1AF B 的周长为a =，可得1c =，求出b ，即可得出椭圆的方程．【解答】解：△1AF B 的周长为△1AF B 的周长1212||||||||224AF AF BF BF a a a =+++=+=，4a ∴=a ∴=离心率为，∴c a =，1c =，b ∴=∴椭圆C 的方程为22132x y +=．故选：A ．【点评】本题考查椭圆的定义与方程，考查椭圆的几何性质，考查学生的计算能力，属于基础题．10．（5分）正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为( ) A ．814πB ．16πC ．9πD ．274π【考点】LG ：球的体积和表面积；LR ：球内接多面体【专题】11：计算题；5F ：空间位置关系与距离【分析】正四棱锥P ABCD -的外接球的球心在它的高1PO 上，记为O ，求出1PO ，1OO ，解出球的半径，求出球的表面积．【解答】解：设球的半径为R ，则棱锥的高为4，底面边长为2，222(4)R R ∴=-+，94R ∴=， ∴球的表面积为29814()44ππ=．故选：A ．【点评】本题考查球的表面积，球的内接几何体问题，考查计算能力，是基础题．11．（5分）双曲线2222:1(0,0)x y C a b a b-=>>的离心率为2C 的焦距等于( )A ．2B ．C ．4D ．【考点】KC ：双曲线的性质【专题】5D ：圆锥曲线的定义、性质与方程【分析】根据双曲线的离心率以及焦点到直线的距离公式，建立方程组即可得到结论．【解答】解：2222:1(0,0)x y a b a b-=>>的离心率为2，2c e a ∴==，双曲线的渐近线方程为b y x a =±，不妨取by x a=，即0bx ay -=，则2c a =，b =，焦点(,0)F c 到渐近线0bx ay -=d ∴==3ac === 解得2c =，则焦距为24c =，故选：C ．【点评】本题主要考查是双曲线的基本运算，利用双曲线的离心率以及焦点到直线的距离公式，建立方程组是解决本题的关键，比较基础．12．（5分）奇函数()f x 的定义域为R ，若(2)f x +为偶函数，且f （1）1=，则f （8）f +（9）(= ) A ．2-B ．1-C ．0D ．1【考点】3K ：函数奇偶性的性质与判断【专题】51：函数的性质及应用【分析】根据函数的奇偶性的性质，得到(8)()f x f x +=，即可得到结论．【解答】解：(2)f x +为偶函数，()f x 是奇函数，∴设()(2)g x f x =+，则()()g x g x -=，即(2)(2)f x f x -+=+， ()f x 是奇函数，(2)(2)(2)f x f x f x ∴-+=+=--，即(4)()f x f x +=-，(8)(44)(4)()f x f x f x f x +=++=-+=，则f （8）(0)0f ==，f （9）f =（1）1=， f ∴（8）f +（9）011=+=，故选：D ．【点评】本题主要考查函数值的计算，利用函数奇偶性的性质，得到函数的对称轴是解决本题的关键．二、填空题(本大题共4小题，每小题5分)13．（5分）6(2)x -的展开式中3x 的系数是 160- ．（用数字作答）【考点】DA ：二项式定理【专题】11：计算题【分析】根据题意，由二项式定理可得6(2)x -的展开式的通项，令x 的系数为3，可得3r =，将3r =代入通项，计算可得34160T x =-，即可得答案．【解答】解：根据题意，6(2)x -的展开式的通项为66166(2)(1)2r r r r r r r r T C x C x --+=-=-，令63r -=可得3r =，此时3333346(1)2160T C x x =-=-，即3x 的系数是160-；故答案为160-．【点评】本题考查二项式定理的应用，关键要得到6(2)x -的展开式的通项． 14．（5分）函数cos22sin y x x =+的最大值是 32．【考点】HW ：三角函数的最值【专题】11：计算题【分析】利用二倍角公式对函数化简可得2213cos22sin 12sin 2sin 2(sin )22y x x x x x =+=-+=--+，结合1sin 1x -剟及二次函数的性质可求函数有最大值【解答】解：2213cos22sin 12sin 2sin 2(sin )22y x x x x x =+=-+=--+又1sin 1x -剟当1sin 2x =时，函数有最大值32 故答案为：32【点评】本题主要考查了利用二倍角度公式对三角函数进行化简，二次函数在闭区间上的最值的求解，解题中要注意1sin 1x -剟的条件．15．（5分）设x ，y 满足约束条件02321x y x y x y -⎧⎪+⎨⎪-⎩………，则4z x y =+的最大值为 5 ．【考点】7C ：简单线性规划【专题】31：数形结合【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，由图得到最优解，联立方程组求出最优解的坐标，代入目标函数得答案．【解答】解：由约束条件02321x y x y x y -⎧⎪+⎨⎪-⎩………作出可行域如图，联立023x y x y -=⎧⎨+=⎩，解得(1,1)C ．化目标函数4z x y =+为直线方程的斜截式，得144z y x =-+．由图可知，当直线144zy x =-+过C 点时，直线在y 轴上的截距最大，z 最大．此时1415max z =+⨯=．故答案为：5．【点评】本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题． 16．（5分）直线1l 和2l 是圆222x y +=的两条切线，若1l 与2l 的交点为(1,3)，则1l 与2l 的夹角的正切值等于43．【考点】IV ：两直线的夹角与到角问题【专题】5B ：直线与圆【分析】设1l 与2l 的夹角为2θ，由于1l 与2l 的交点(1,3)A 在圆的外部，由直角三角形中的边角关系求得sin r OA θ= 的值，可得cos θ、tan θ 的值，再根据22tan tan 21tan θθθ=-，计算求得结果．【解答】解：设1l 与2l 的夹角为2θ，由于1l 与2l 的交点(1,3)A 在圆的外部，且点A 与圆心O 之间的距离为OA =圆的半径为r =sin r OA θ∴==，cos θ∴=，sin 1tan cos 2θθθ==，22tan 14tan 211tan 314θθθ∴===--，故答案为：43．【点评】本题主要考查直线和圆相切的性质，直角三角形中的变角关系，同角三角函数的基本关系、二倍角的正切公式的应用，属于中档题．三、解答题17．（10分）数列{}n a 满足11a =，22a =，2122n n n a a a ++=-+．（Ⅰ）设1n n n b a a +=-，证明{}n b 是等差数列；（Ⅱ）求{}n a 的通项公式．【考点】83：等差数列的性质；84：等差数列的通项公式；8H ：数列递推式【专题】54：等差数列与等比数列【分析】（Ⅰ）将2122n n n a a a ++=-+变形为：2112n n n n a a a a +++-=-+，再由条件得12n n b b +=+，根据条件求出1b ，由等差数列的定义证明{}n b 是等差数列；（Ⅱ）由（Ⅰ）和等差数列的通项公式求出n b ，代入1n n n b a a +=-并令n 从1开始取值，依次得(1)n -个式子，然后相加，利用等差数列的前n 项和公式求出{}n a 的通项公式n a ．【解答】解：（Ⅰ）由2122n n n a a a ++=-+得， 2112n n n n a a a a +++-=-+，由1n n n b a a +=-得，12n n b b +=+，即12n n b b +-=，又1211b a a =-=，所以{}n b 是首项为1，公差为2的等差数列．（Ⅱ）由（Ⅰ）得，12(1)21n b n n =+-=-，由1n n n b a a +=-得，121n n a a n +-=-，则211a a -=，323a a -=，435a a -=，⋯，12(1)1n n a a n --=--，所以，11352(1)1n a a n -=+++⋯+-- 2(1)(123)(1)2n n n -+-==-，又11a =，所以{}n a 的通项公式22(1)122n a n n n =-+=-+．【点评】本题考查了等差数列的定义、通项公式、前n 项和公式，及累加法求数列的通项公式和转化思想，属于中档题．18．（12分）ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ，已知3cos 2cos a C c A =，1tan 3A =，求B ．【考点】GL ：三角函数中的恒等变换应用；HP ：正弦定理【专题】58：解三角形【分析】由3cos 2cos a C c A =，利用正弦定理可得3sin cos 2sin cos A C C A =，再利用同角的三角函数基本关系式可得tan C ，利用tan tan[()]tan()B A C A C π=-+=-+即可得出．【解答】解：3cos 2cos a C c A =，由正弦定理可得3sin cos 2sin cos A C C A =， 3tan 2tan A C ∴=， 1tan 3A =，12tan 313C ∴=⨯=，解得1tan 2C =．11tan tan 32tan tan[()]tan()1111tan tan 132A C B A C A C A C π++∴=-+=-+=-=-=---⨯， (0,)B π∈， 34B π∴=【点评】本题考查了正弦定理、同角的三角函数基本关系式、两角和差的正切公式、诱导公式等基础知识与基本技能方法，考查了推理能力和计算能力，属于中档题．19．（12分）如图，三棱柱111ABC A B C -中，点1A 在平面ABC 内的射影D 在AC 上，90ACB ∠=︒，1BC =，12AC CC ==．（Ⅰ）证明：11AC A B ⊥；（Ⅱ）设直线1AA 与平面11BCC B 1A AB C --的大小．【考点】LW ：直线与平面垂直；MJ ：二面角的平面角及求法【专题】5F ：空间位置关系与距离【分析】（Ⅰ）由已知数据结合线面垂直的判定和性质可得；（Ⅱ）作辅助线可证1A FD ∠为二面角1A AB C --的平面角，解三角形由反三角函数可得．【解答】解：（Ⅰ）1A D ⊥平面ABC ，1A D ⊂平面11AA C C ，∴平面11AAC C ⊥平面ABC ，又BC AC ⊥BC ∴⊥平面11AA C C ，连结1A C ，由侧面11AA C C 为菱形可得11AC AC ⊥，又1AC BC ⊥，1A CBC C =，1AC ∴⊥平面1A BC ，1AB ⊂平面1A BC ， 11AC A B ∴⊥；（Ⅱ）BC ⊥平面11AA C C ，BC ⊂平面11BCC B ，∴平面11AAC C ⊥平面11BCC B ，作11A E CC ⊥，E 为垂足，可得1A E ⊥平面11BCC B ，又直线1//AA 平面11BCC B ，1A E ∴为直线1AA 与平面11BCC B 的距离，即1A E =1A C 为1ACC ∠的平分线，11A D A E ∴==作DF AB ⊥，F 为垂足，连结1A F ，又可得1AB A D ⊥，111A FA D A =，AB ∴⊥平面1A DF ，1A F ⊂平面1A DF1A F AB ∴⊥，1A FD ∴∠为二面角1A AB C --的平面角，由1AD 可知D 为AC 中点，12AC BC DF AB ⨯∴=⨯，11tan A DA FD DF∴∠=∴二面角1A AB C --的大小为【点评】本题考查二面角的求解，作出并证明二面角的平面角是解决问题的关键，属中档题． 20．（12分）设每个工作日甲，乙，丙，丁4人需使用某种设备的概率分别为0.6，0.5，0.5，0.4，各人是否需使用设备相互独立．（Ⅰ）求同一工作日至少3人需使用设备的概率；（Ⅱ）实验室计划购买k 台设备供甲，乙，丙，丁使用，若要求“同一工作日需使用设备的人数大于k ”的概率小于0.1，求k 的最小值．【考点】8C ：相互独立事件和相互独立事件的概率乘法公式【专题】5I ：概率与统计【分析】（Ⅰ）把4个人都需使用设备的概率、4个人中有3个人使用设备的概率相加，即得所求．（Ⅱ）由（Ⅰ）可得若2k =，不满足条件．若3k =，求得“同一工作日需使用设备的人数大于3”的概率为0.060.1<，满足条件，从而得出结论．【解答】解：（Ⅰ）由题意可得“同一工作日至少3人需使用设备”的概率为0.60.50.50.4(10.6)0.50.50.40.6(10.5)0.50.40.60.5(10.5)0.40.60.50.5(10.4)0.31⨯⨯⨯+-⨯⨯⨯+⨯-⨯⨯+⨯⨯-⨯+⨯⨯⨯-=．（Ⅱ）由（Ⅰ）可得若2k =，则“同一工作日需使用设备的人数大于2”的概率为0.310.1>，不满足条件．若3k =，则“同一工作日需使用设备的人数大于3”的概率为0.60.50.50.40.060.1⨯⨯⨯=<，满足条件．故k 的最小值为3．【点评】本题主要考查相互独立事件的概率乘法公式，体现了分类讨论的数学思想，属于中档题．21．（12分）函数32()33(0)f x ax x x a =++≠．（Ⅰ）讨论()f x 的单调性；（Ⅱ）若()f x 在区间(1,2)是增函数，求a 的取值范围．【考点】6B ：利用导数研究函数的单调性；6D ：利用导数研究函数的极值【专题】53：导数的综合应用【分析】（Ⅰ）求出函数的导数，通过导数为0，利用二次函数的根，通过a 的范围讨论()f x 的单调性；（Ⅱ）当0a >，0x >时，()f x 在区间(1,2)是增函数，当0a <时，()f x 在区间(1,2)是增函数，推出f '（1）0…且f '（2）0…，即可求a 的取值范围．【解答】解：（Ⅰ）函数32()33f x ax x x =++，2()363f x ax x ∴'=++，令()0f x '=，即23630ax x ++=，则△36(1)a =-，①若1a …时，则△0…，()0f x '…，()f x ∴在R 上是增函数；②因为0a ≠，1a ∴…且0a ≠时，△0>，()0f x '=方程有两个根，1x =，2x =，当01a <<时，则当2(,)x x ∈-∞或1(x ，)+∞时，()0f x '>，故函数在2(,)x -∞或1(x ，)+∞是增函数；在2(x ，1)x 是减函数；当0a <时，则当1(,)x x ∈-∞或2(x ，)+∞，()0f x '<，故函数在1(,)x -∞或2(x ，)+∞是减函数；在1(x ，2)x 是增函数；（Ⅱ）当0a >，0x >时，2()3630f x ax x '=++> 故0a >时，()f x 在区间(1,2)是增函数，当0a <时，()f x 在区间(1,2)是增函数，当且仅当：f '（1）0…且f '（2）0…，解得504a -<…，a 的取值范围5[,0)(04-⋃，)+∞．【点评】本题考查函数的导数的应用，判断函数的单调性以及已知单调性求解函数中的变量的范围，考查分类讨论思想的应用．22．（12分）已知抛物线2:2(0)C y px p =>的焦点为F ，直线4y =与y 轴的交点为P ，与C 的交点为Q ，且5||||4QF PQ =．（Ⅰ）求C 的方程；（Ⅱ）过F 的直线l 与C 相交于A 、B 两点，若AB 的垂直平分线l '与C 相交于M 、N 两点，且A 、M 、B 、N 四点在同一圆上，求l 的方程．【考点】KH ：直线与圆锥曲线的综合【专题】5E ：圆锥曲线中的最值与范围问题【分析】（Ⅰ）设点Q 的坐标为0(x ，4)，把点Q 的坐标代入抛物线C 的方程，求得08x p=，根据5||||4QF PQ =求得p 的值，可得C 的方程．（Ⅱ）设l 的方程为1x my =+(0)m ≠，代入抛物线方程化简，利用韦达定理、中点公式、弦长公式求得弦长||AB ．把直线l '的方程代入抛物线方程化简，利用韦达定理、弦长公式求得||MN ．由于MN 垂直平分线段AB ，故A M B N 四点共圆等价于1||||||2AE BE MN ==，由此求得m 的值，可得直线l 的方程．【解答】解：（Ⅰ）设点Q 的坐标为0(x ，4)，把点Q 的坐标代入抛物线2:2(0)C y px p =>，可得08x p=，点(0,4)P ，8||PQ p ∴=．又08||22p p QF x p =+=+，5||||4QF PQ =， ∴85824p p p+=⨯，求得2p =，或2p =-（舍去）．故C 的方程为24y x =．（Ⅱ）由题意可得，直线l 和坐标轴不垂直，24y x =的焦点(1,0)F ，设l 的方程为1(0)x my m =+≠，代入抛物线方程可得2440y my --=，显然判别式△216160m =+>，124y y m +=，124y y =-．AB ∴的中点坐标为2(21D m +，2)m ，弦长212|||4(1)AB y y m -+．又直线l '的斜率为m -，∴直线l '的方程为2123x y m m=-++．过F 的直线l 与C 相交于A 、B 两点，若AB 的垂直平分线l '与C 相交于M 、N 两点，把线l '的方程代入抛物线方程可得2244(23)0y y m m +-+=，344y y m-∴+=，2344(23)y y m =-+．故线段MN的中点E 的坐标为222(23m m++，2)m-，23421)21|||m MN y y m +∴=-=，MN 垂直平分线段AB ，故AMBN 四点共圆等价于1||||||2AE BE MN ==， ∴2221144AB DE MN +=， 22222222422116(1)(21)4(1)(2)(2)4m m m m m m m++∴+++++=⨯，化简可得210m -=， 1m ∴=±，∴直线l 的方程为10x y --=，或10x y +-=．【点评】本题主要考查求抛物线的标准方程，直线和圆锥曲线的位置关系的应用，韦达定理、弦长公式的应用，体现了转化的数学思想，属于难题．。

2014年全国高考数学卷文科卷1试题及答案解析课件.doc

2014 年全国高考数学卷文科卷 17 ．在函数①y cos | 2x |，②y | cos x| ，③y cos( 2x ) , ④6一、选择题（题型注释）1．已知集合M x| 1 x 3 ,N x| 2 x 1 ，则M N （）y tan(2 x)中，最小正周期为的所有函数为4A. ①②③B. ①③④C. ②④D. ①③A. ( 2 ,1)B. ( 1,1 )C. (1,3)D. ( 2,3 ) 2．若tan 0，则8．如图，网格纸的各小格都是正方形，粗实线画出的事一个几何体的三视图，则这个几何体是（）A. sin 0B. cos 0C. sin 2 0D. cos2 013．设z i1 i，则| z|A. 12B.22C.32D. 22 2x y4．已知双曲线1( 0)a2a 3 的离心率为2，则aA. 三棱锥B. 三棱柱C. 四棱锥D. 四棱柱9．执行右面的程序框图，若输入的a, b,k 分别为1,2,3 ，则输出的M ( )A. 2B.6 C.25 D. 125．设函数 f (x), g(x)的定义域为R ，且 f (x) 是奇函数，g (x) 是偶函数，则下列结论中正确的是A. f ( x)g( x) 是偶函数B. | f ( x) | g( x) 是奇函数C. f ( x) | g( x) | 是奇函数D. | f (x)g(x) |是奇函数6．设D, E,F 分别为ABC 的三边BC, CA, AB 的中点，则EB FC1 A. AD B. AD21C. BC2D. BC试卷第 1 页，总 4 页A. 203B.72C.165D.15816．如图，为测量山高MN ，选择A 和另一座山的山顶 C 为测量观测点. 从A 点测得M 点的仰角MAN 60 ，C 点的仰角CAB 45 以及52 的焦点为 F ,A x y10．已知抛物线C：y x 0, 是C上一点，AF x0 4 ，MAC 75 ；从C 点测得MCA 60 . 已知山高BC 100m ，则山高MN ________ m.则x0 （）A. 1B. 2C. 4D. 811．已知函数 3 2f (x) ax 3x 1，若f (x) 存在唯一的零点x0 ，且x0 0，则a的取值范围是（A）2, （B）1, （C）, 2 （D）, 1二、填空题（题型注释）三、解答题（题型注释）12．设x，y 满足约束条件x y a,且z x ay 的最小值为7，则ax y 1,17．已知 a 是递增的等差数列，a2 ，a4 是方程n2 5 6 0x x 的根。

2014年高考全国1卷文科数学试题及答案(详细解析版,精校版)

2014年普通高等学校招生全国统一考试（全国I 卷）文科数学一、选择题，本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合M ={x |-1<x <3}，N ={x |-2<x <1}，则M ∩N =( )A ．(-2,1)B ．(-1,1)C ．(1,3)D ．(-2,3) 2．若tan α>0，则( )A ．sin α>0B ．cos α>0C ．sin2α>0D ．cos2α>03．设i iz ++=11，则|z |=( )A ．21B ．22C ．23D ．24．已知双曲线)0(13222>=-a y a x 的离心率为2，则a=( ) A ．2 B ．26 C ．25D ．15．设函数f (x )，g (x )的定义域为R ，且f (x )是奇函数，g (x )是偶函数，则下列结论中正确的是( )A ．f (x )g (x )是偶函数B ．|f (x )|g (x )是奇函数C ．f (x )|g (x )|是奇函数D ．|f (x )g (x )|是奇函数6．设D ,E ,F 分别为ΔABC 的三边BC ,CA ,AB 的中点，则=+FC EB ( )A ．ADB ．AD 21C ．BC 21D ．BC7．在函数① y=cos|2x|，②y=|cos x |，③)62cos(π+=x y ，④)42tan(π-=x y 中，最小正周期为π的所有函数为( )A ．①②③B ．①③④C ．②④D ．①③ 8．如图，网格纸的各小格都是正方形，粗实线画出的一个几何体的三视图，则这个几何体是( )A ．三棱锥B ．三棱柱C ．四棱锥D ．四棱柱9．执行下面的程序框图，若输入的a ,b ,k 分别为1,2,3，则输出的M =( )A ．203B ．72C ．165D ．15810．已知抛物线C：y2=x的焦点为F，A(x0,y0)是C上一点，|AF|=54x0，则x0=( )A．1 B．2 C．4 D．811．设x，y满足约束条件,1,x y ax y+≥⎧⎨-≤-⎩且z=x+ay的最小值为7，则a= ( )A．-5 B．3 C．-5或3 D．5或-312．已知函数f(x)=ax3-3x2+1，若f(x)存在唯一的零点x0，且x0>0，则a的取值范围是( )A．(2,+∞)B．(1,+∞)C．(-∞, -2) D．(-∞, -1)二、填空题：本大题共4小题，每小题5分，共20分．把答案填在横线上．13．将2本不同的数学书和1本语文书在书架上随机排成一行，则2本数学书相邻的概率为________.14．甲、乙、丙三位同学被问到是否去过A、B、C三个城市时，甲说：我去过的城市比乙多，但没去过B城市；乙说：我没去过C城市；丙说：我们三人去过同一城市；由此可判断乙去过的城市为________.15．设函数113,1(),1xe xf xx x-⎧<⎪=⎨⎪≥⎩，则使得f(x)≤2成立的x的取值范围是______.16．如图，为测量山高MN，选择A和另一座山的山顶C为测量观测点. 从A点测得M点的仰角：∠MAN=60°，C点的仰角∠CAB=45°以及∠MAC=75°；从C点测得∠MCA=60°. 已知山高BC=100m，则山高MN=______m.三、解答题：解答应写出文字说明，证明过程或演算步骤.只做6题，共70分. 17．（本小题满分12分）已知{a n}是递增的等差数列，a2，a4是方程x2-5x+6=0的根.(Ⅰ)求{a n}的通项公式；(Ⅱ)求数列2n na⎧⎫⎨⎬⎩⎭的前n项和.从某企业生产的某种产品中抽取100件，测量这些产品的一项质量指标值，质量指标值分组[75,85) [85,95) [95,105) [105,115) [115,125) 频数 6 26 38 22 8(Ⅱ)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表)；(Ⅲ)根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定？19．(本题满分12分)如图，三棱柱ABC-A1B1C1中，侧面BB1C1C为菱形，B1C的中点为O，且AO⊥平面BB1C1C.(Ⅰ)证明：B1C⊥AB;(Ⅱ)若AC⊥AB1，∠CBB1=60°，BC=1，求三棱柱ABC-A1B1C1的高.20．（本小题满分12分）已知点P(2,2)，圆C: x2+y2-8y=0，过点P的动直线l与圆C交于A,B两点，线段AB的中点为M，O为坐标原点.(Ⅰ)求M的轨迹方程；(Ⅱ)当|OP|=|OM|时，求l的方程及ΔPOM的面积.设函数f (x )= a ln x+212a x --bx (a ≠1)，曲线y =f (x )在点(1, f (1))处的切线斜率为0 (Ⅰ)求b ; (Ⅱ)若存在x 0≥1，使得f (x 0)<1aa -，求a 的取值范围.请考生从第22、23、24三题中任选一题作答.多答按所答的首题进行评分. 22.（本小题满分10分）选修4—1：几何证明选讲如图，四边形ABCD 是⊙O 的内接四边形，AB 的延长线与DC 的延长线交于点E ，且CB=CE （Ⅰ）证明：∠D=∠E ；（Ⅱ）设AD 不是⊙O 的直径，AD 的中点为M ，且MB=MC ，证明：△ADE 为等边三角形.23.（本小题满分10分）选修4—4：坐标系与参数方程已知曲线C ：22149x y +=，直线l ：222x t y t =+⎧⎨=-⎩（t 为参数）.（Ⅰ）写出曲线C 的参数方程，直线l 的普通方程；（Ⅱ）过曲线C 上任意一点P 作与l 夹角为o 30的直线，交l 于点A ，求||PA 的最大值与最小值.24. （本小题满分10分）选修4—5：不等式选讲若0,0a b >>，且11ab a b+=.（Ⅰ）求33a b +的最小值；（Ⅱ）是否存在,a b ，使得236a b +=？并说明理由.2014年高考全国1卷文科数学参考答案1．解：取M ， N 中共同的元素的集合是(-1,1)，故选B2．解：tan α>0，α在一或三象限，所以sin α与cos α同号，故选C3．解：111,12222i i z i i z i -=+=+=+∴==+，故选B4．解：2c e a ====，解得a=1，故选D 5．解：设F (x )=f (x )|g (x )|，依题可得F (-x )=-F (x )，∴ F (x )为奇函数，故选C6．解：+EB FC EC CB FB BC +=++=111()222AC AB AB AC AD +=+=,故选A7．解：由cos y x =是偶函数可知①y=cos|2x|=cos2x ，最小正周期为π；②y=|cos x |的最小正周期也是π；③中函数最小正周期也是π；正确答案为①②③，故选A8．解：几何体是一个横放着的三棱柱. 故选B9．解：运行程序M,a,b,n 依次为33(,2,,2)22;838(,,,3)323;15815(,,,4)838；输出158M =.故选D.10．解：根据抛物线的定义可知|AF |=001544x x +=，解之得x 0=1. 故选A11．解：联立x+y=a 与x-y =-1解得交点M 11(,)22a a -+，z 取得最值11722a a a -++⨯=，解之得a =-5或a =3. 但a =-5时，z 取得最大值，舍去，所以a =3，故选B.12．解：依题a≠0，f '(x )=3ax 2-6x ，令f '(x )=0，解得x =0或x =2a，当a >0时，在(-∞, 0)与(2a ,+∞)上，f '(x )>0，f (x )是增函数.在(0,2a) 上，f '(x )<0，f (x )是减函数.且f (0)=1>0，f (x )有小于零的零点，不符合题意.当a <0时，在(-∞,2a )与(0,+∞)上，f '(x )<0，f (x )是减函数.在(2a,0)上，f '(x )>0，f (x )是增函数.要使f (x )有唯一的零点x 0，且x 0>0，只要2()0f a>，即a 2>4，所以a <-2．故选C另解：依题a≠0，f (x )存在唯一的正零点，等价于3113a x x=-有唯一的正零根，令1t x=，则问题又等价于a =-t 3+3t 有唯一的正零根，即y =a 与y =-t 3+3t 有唯一的交点且交点在在y 轴右侧，记g (t )=-t 3+3t ，g '(t )=-3t 2+3，由g '(t )=0，解得t =±1，在(-∞,-1)与(1,+∞)上，g '(t )<0，g (t )是减函数.在(-1,1)上，g '(t )>0，g (t )是增函数.要使a =-t 3+3t 有唯一的正零根，只要a <g (-1)=-2，故选C 二、填空题13．23 14．A 15．(-∞,8] 16．15013．解：设数学书为1，2，语文书为A ，则所有的排法有(1,2,A)，(1,A,2)，(2,1, A)，(2, A,1)，(A,1,2)，(A,2,1)共6 种，其中2 本数学书相邻的情况有4 种情况，故所求概率为4263P ==.14．解：∵丙说：三人同去过同一个城市，甲说没去过B 城市，乙说：我没去过C 城市，∴三人同去过同一个城市应为Ａ，∴乙至少去过Ａ，若乙再去城市B ，甲去过的城市至多两个，不可能比乙多，∴可判断乙去过的城市为A.本题考查逻辑推理，反证法的思想.15．解：当x<1时，由e x -1≤2可得x ≤1+ln 2，故x<1；当x≥1时，由13x ≤2可得x ≤8，故1≤x ≤8，综上可得x ≤8.16．解：在RtΔABC 中，由条件可得AC =，在ΔMAC 中，∠MAC=45°；由正弦定理可得sin60sin 45AM AC =︒︒，故AM =在直角RtΔMAN 中，MN=AM sin60°=150.三、解答题17．解：(Ⅰ) 解x 2-5x +6=0得的两个根为2，3，依题a 2=2，a 4=3，…2分所以2d =1，故12d =，从而132a =， …4分所以通项公式为a n =a 2+(n -2)d 112n =+ …6分(Ⅱ) 由(Ⅰ)知1222n n n a n ++=，设{}2n na 的前n 项和为S n ，则 2313412...2222n n n n n S +++=++++，① 341213412 (22222)n n n n n S ++++=++++，② …8分①-②得3412131112...242222n n n n n S ++++=++++-123112(1)4422n n n -++=+--所以，1422n n n S ++=- …12分18．解：(Ⅰ)…4分(Ⅱ)质量指标值的样本平均数为 x =80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100. 所以平均数估计值为100，…6分质量指标值的样本方差为 s 2=(-20)2×0.06+(-10)2×0.26+0×0.38+(10)2×0.22+(20)2×0.08=104. 方差的估计值为104. …8分(Ⅲ)依题0.38+0.22+0.08=0.68 < 80％，所以该企业生产的这种产品不符合“质量指标值不低于95的产品至少要占全部产品的 80％”的规定. …12分19．(Ⅰ)证明：连接 BC 1，则O 为B 1C 与BC 1的交点，∵AO ⊥平面BB 1C 1C . ∴AO ⊥B 1C ， …2分因为侧面BB 1C 1C 为菱形，∴BC 1⊥B 1C ，…4分 ∴BC 1⊥平面ABC 1，∵AB ⊂平面ABC 1，故B 1C ⊥AB . …6分(Ⅱ)作OD ⊥BC ，垂足为D ，连结AD ，∵AO ⊥BC ，∴BC ⊥平面AOD ，又BC ⊂平面ABC ，∴平面ABC ⊥平面AOD ，交线为AD ，作OH ⊥AD ，垂足为H ，∴OH ⊥平面ABC . …9分∵∠CBB 1=60°，所以ΔCBB 1为等边三角形，又BC =1，可得OD 3由于AC ⊥AB 1，∴11122OA B C ==，∴2274AD OD OA =+=，由 OH·AD=OD·OA ，可得OH=2114，又O 为B 1C 的中点，所以点B 1到平面ABC 的距离为217，所以三棱柱ABC-A 1B 1C 1的高高为217. …12分另解(等体积法)：∵∠CBB 1=60°，所以ΔCBB 1为等边三角形，又BC =1，可得BO 3AC ⊥AB 1，∴111OA B C ==，∴AB =1，2，…9分则等腰三角形ABC 的面积为2212271()24-，设点B 1到平面ABC 的距离为d ，由V B 1-ABC =V A-BB 1C 73121,27d ==解得，所以三棱柱ABC-A 1B 1C 1的高高为217. …12分20．解：(Ⅰ)圆C 可化为x 2+(y -4)2=16，所以圆心为C (0,4)，半径为4. …2分设M (x ,y )，则(,4)CM x y =-，(2,2)MP x y =--，由题知0CM MP =，…4分故x (2-x )+(y -4)(2-y )=0，整理得(x -1)2+(y -3)2=2，由于点P 在圆C 的内部，所以M 的轨迹方程是(x -1)2+(y -3)2=2 …6分(Ⅱ)由(Ⅰ)可知M 的轨迹是以点N (1,3)2 为半径的圆.由于|OP |=|OM |22=O 在线段PM 的垂直平分线上，又P 在圆N 上，从而ON ⊥PM . …8分因为ON 的斜率为3，所以l 的斜率为13-，直线l 的方程为：12(2)3y x -=--，即1833y x =-+， …10分又|OP |=|OM |22=O 到l 410，410||PM =，所以ΔPOM 的面积为165. …12分另解：因为|OP |=|OM |22=P ,M 也在圆x 2+y 2=8上，点P ,M 也在圆(x -1)2+(y -3)2=2，…8分两式相减可得公共弦方程2x +6y -16=0，即1833y x =-+，就是线l 的方程. …10分21．解：(Ⅰ) ()(1)af x a x b x'=+--(x >0)，依题f '(1)=0，解得b =1， …3分(Ⅱ)由(Ⅰ)知f (x )= a ln x+212a x --x ，2(1)(1)[(1)]()a x x a x a x a f x x x--+---'==，因为a ≠1，所以f '(x )=0有两根：x =1或1ax a=-. …4分(1)若12a ≤，则11aa≤-，在(1,+∞)上，f '(x )>0，f (x )单调递增.所以存在x 0≥1，使得f (x 0)<1a a -，的充要条件为(1)1a f a ≤-，即1121a aa--<-，解得2121a -<<. …6分(2)若112a <<，则11a a >-，在 (1,1a a -)上，f '(x ) <0 , f (x )单调递减，在(,1aa+∞-)时，f '(x )>0，f (x )单调递增. 所以存在x 0≥1，使得f (x 0)<1a a -，的充要条件为()11a af a a≤--，而()2()ln 112111a a a a a f a a a a a a=++>-----，所以不合题意. …9分(3) 若a >1，则11(1)1221a a af a ---=-=<-.存在x 0≥1，符合条件.…11分综上，a 的取值范围为：(21,21)(1,)---⋃+∞. …12分22.证明：（Ⅰ）由题设得，A ，B ，C ，D 四点共圆，所以，D CBE ∠=∠又CB CE =，CBE E ∴∠=∠，所以D E ∠=∠ （Ⅱ）设BC 的中点为N ，连结MN ，如图所示，则由MC MB =知BC MN ⊥，所以，O 在MN 上，又AD不是⊙O 的直径，M 为AD 的中点，故AD OM ⊥，即AD MN ⊥，所以BC AD //，故D A ∠=∠，由（Ⅰ）D E ∠=∠，所以△ADE 为等边三角形. 23.解：（Ⅰ）C:⎩⎨⎧==θθsin 3cos 2y x l ：062=-+y x（Ⅱ）P 到直线l 的距离为|6sin 3cos 4|55-+=θθd |6sin 3cos 4|55230sin ||0-+==θθd PA ，从而||PA 的最大值为5522，最小值为552 24.解：（I ）由112ab a b ab=+≥，得2ab ≥，且当2a b ==时取等号．故33a b +33242a b ≥≥，且当2a b ==时取等号．所以33a b +的最小值为42． ……5分（II ）由（I ）知，232643a b ab +≥≥．由于436>，从而不存在,a b ，使得236a b +=．……10分N。

2014年高考(课标全国Ⅰ)数学(文科)

【解析】由于 y=cos|2x|=cos 2x,所以该函数的周期为2π=π;由函数 y=|cos x|的图象易知
2
其周期为π;函数 y=cos 2 + π 的周期为2π=π;函数 y=tan 2 - π 的周期为π,故最小正周
6
2
4
2
期为π的函数是①②③,故选 A.
8.(2014 课标全国Ⅰ,文 8)如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体
当 a>0 时,f'(x)=3ax2-6x=3ax - 2 ,
令 f'(x)=0,得 x1=0,x2=2,
所以 f(x)在 x=0 处取得极大值 f(0)=1,在 x=2处取得极小值 f 2 =1- 42, 要使 f(x)有唯一的零点,需 f 2 >0,但这时零点 x0 一定小于 0,不合题意;
当 a<0 时,f'(x)=3ax2-6x=3ax - 2 ,
B.(-1,1)
C.(1,3)
D.(-2,3)
【解析】由已知得 M∩N={x|-1<x<1}=(-1,1),故选 B.
2.(2014 课标全国Ⅰ,文 2)若 tan α>0,则( ).
A.sin α>0 【答案】C
B.cos α>0
C.sin 2α>0
D.cos 2α>0
【解析】由 tan α>0 知角α是第一或第三象限角,当α是第一象限角时,sin 2α=2sin αcos
两式相减,得12Sn=34 +
1 23
+
…
+
2
1
+1
+2 2 +2

2014全国新课标1卷数学文科详解

2014年高招全国课标1 -文科数学解题样卷一．选择题：本大题共10小题，每小题5分，共50分.（1）已知集合{}13M x x =-<<， {}21N x x =-<<，则M N =（）A. )1,2(-B. )1,1(-C. )3,1(D. )3,2(-【参考答案】：在数轴上表示出对应的集合，可得M N = (-1,1),选B【解题方法】①直接计算②取特值如令x=2代入排除C,D 再取x=-1可选B 【规律提炼】：集合的运算用数轴或者Venn 图可直接计算（2）若0tan >α，则A. 0sin >αB. 0cos >αC. 02sin >αD. 02cos >α 【参考答案】：由tan α > 0可得:k π <α < k π +2π(k ∈Z )，故2k π <2α <2 k π +π (k ∈Z )，正确的结论只有sin 2α > 0. 选C【解题方法】：①观察计算②特值法如取α=0225进行排除【规律提炼】：判断三角函数的符号可先确定角所在的象限（3）设i iz ++=11，则=||z A.21 B. 22 C. 23 D. 2 【参考答案】：11111222i z i i i i -=+=+=++，z ==，选B 【解题方法】：求模一般直接法【规律提炼】：复数的除法用分母实数化，求复数的模用公式z =（4）已知双曲线)0(13222>=-a y a x 的离心率为2，则=a A. 2 B.26 C. 25 D. 1 【参考答案】：由双曲线的离心率可得2a=，解得1a =，选D.【解题方法】：①把选项中的a 值逐一代入检验可得D. ②利用公式e =【规律提炼】：求离心率关键在于寻找a,b 或者a,c之间的关系，用公式e =c e a =（5）设函数)(),(x g x f 的定义域为R ，且)(x f 是奇函数，)(x g 是偶函数，则下列结论中正确的是 A. )()(x g x f 是偶函数 B. )(|)(|x g x f 是奇函数 C. |)(|)(x g x f 是奇函数 D. |)()(|x g x f 是奇函数【参考答案】：设()()()F x f x g x =，则()()()F x f x g x -=--，∵()f x 是奇函数，()g x 是偶函数，∴()()()()F x f x g x F x -=-=-，()F x 为奇函数，选C.【解题方法】：①把四个选项逐一分析，②利用性质)(x f 奇，|()|f x 为偶，奇奇=偶，奇偶=奇。

2014年全国高考新课标1卷文科数学试题(word文档完整版小题也有详解)

2014年全国高考新课标1卷文科数学试题一、选择题，本大题共12小题,每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合M =｛x |—1<x <3}，N ={x |—2<x <1},则M ∩N =( ）A ．(-2，1)B ．(-1,1）C ．(1，3)D ．(—2，3） 2．若tan α>0，则( ）A ．sin α〉0B ．cos α>0C ．sin2α〉0D ．cos2α〉03．设i iz ++=11,则｜z |=( )A ．21B ．22C ．23D ．24．已知双曲线)0(13222>=-a y a x 的离心率为2,则a=( ) A ．2 B ．26 C ．25D ．15．设函数f (x ），g (x ）的定义域为R ，且f (x )是奇函数，g （x )是偶函数，则下列结论中正确的是（）A ．f （x ）g （x ）是偶函数B ．|f （x ）｜g (x ）是奇函数C ．f （x )｜g （x ）|是奇函数D ．|f (x )g （x )|是奇函数6．设D ,E ，F 分别为ΔABC 的三边BC ,CA ，AB 的中点，则=+FC EB ( ）A ．ADB ．AD 21C ．BC 21D ．BC7．在函数① y=cos ｜2x|，②y=｜cos x ｜，③)62cos(π+=x y ，④)42tan(π-=x y 中,最小正周期为π的所有函数为( ）A ．①②③B ．①③④C ．②④D ．①③ 8．如图,网格纸的各小格都是正方形,粗实线画出的一个几何体的三视图，则这个几何体是（）A ．三棱锥B ．三棱柱C ．四棱锥D ．四棱柱9．执行下面的程序框图,若输入的a ,b ,k 分别为1，2,3,则输出的M =（ )A ．203B ．72C ．165D ．15810．已知抛物线C ：y 2=x 的焦点为F ，A （x 0，y 0）是C 上一点，|AF ｜=54x 0,则x 0=( ）A ．1B ．2C ．4D ．811．设x，y满足约束条件,1,x y ax y+≥⎧⎨-≤-⎩且z=x+ay的最小值为7，则a=（）A．—5 B．3 C．-5或3 D．5或—312．已知函数f（x）=ax3-3x2+1，若f(x）存在唯一的零点x0，且x0>0，则a的取值范围是（）A．（2,+∞）B．（1，+∞）C．（-∞，-2）D．（-∞, —1）二、填空题:本大题共4小题，每小题5分，共20分．把答案填在横线上．13．将2本不同的数学书和1本语文书在书架上随机排成一行,则2本数学书相邻的概率为________.14．甲、乙、丙三位同学被问到是否去过A、B、C三个城市时,甲说：我去过的城市比乙多，但没去过B城市；乙说：我没去过C城市;丙说：我们三人去过同一城市；由此可判断乙去过的城市为________。

2014年高考全国1卷文科数学试题及答案(详细解析版,精校版)

2014年高考文科数学全国卷1(含详细答案)

2014年全国统一高考数学试卷(文科)

2014年高考(大纲全国卷)数学(文科) 详细答案解析

2014年高考数学(文科)试题及参考答案(新课标I卷)

2014年全国高考文科数学试题及答案-全国卷

2014年全国统一高考数学试卷(文科)(新课标ⅰ)(附参考答案+详细解析Word打印版)

2014年全国高考文科数学试题及答案-全国卷

2014年全国I卷文科数学高考试卷(原卷 答案)

2014年全国统一高考数学试卷(文科)(大纲版)解析版

2014年全国高考数学卷文科卷1试题及答案解析课件.doc

2014年高考全国1卷文科数学试题及答案(详细解析版,精校版)

2014年高考(课标全国Ⅰ)数学(文科)

2014全国新课标1卷数学文科详解

2014年全国高考新课标1卷文科数学试题(word文档完整版小题也有详解)

2014年全国I卷文科数学高考试卷(原卷答案)