利用微分估算误差举例

常微分方程数值解法的误差分析汇总

淮北师范大学2013届学士学位论文常微分方程数值解法的误差分析学院、专业数学科学学院数学与应用数学研究方向计算数学学生姓名李娜学号 20091101070指导教师姓名陈昊指导教师职称讲师年月日常微分方程数值解法的误差分析李娜（淮北师范大学数学科学学院，淮北，235000）摘要自然界与工程技术中的很多现象，往往归结为常微分方程定解问题。

许多偏微分方程问题也可以化为常微分方程问题来近似求解。

因此，研究常微分方程的数值解法是有实际应用意义的。

数值解法是一种离散化的数学方法，可以求出函数的精确解在自变量一系列离散点处的近似值。

随着计算机计算能力的增强以及数值计算方法的发展，常微分方程的数值求解方法越来越多，比较成熟的有Euler 法、后退Euler法、梯形方法、Runge—Kutta方法、投影法和多步法，等等．本文将对这些解的误差进行分析,以求能够得到求解常微分数值解的精度更好的方法。

关键词：常微分方程, 数值解法, 单步法, 线性多步法, 局部截断误差Error Analysis of Numerical Method for Solving theOrdinary Differential EquationLi Na(School of Mathematical Science, Huaibei Normal University, Huaibei, 235000)AbstractIn nature and engineering have many phenomena , definite solution of the problem often boils down to ordinary differential equations. So study the numerical solution of ordinary differential equations is practical significance. The numerical method is a discrete mathematical methods, and exact solution of the function can be obtained in the approximation of a series of discrete points of the argument.With the enhanced computing power and the development of numerical methods,ordinary differential equations have more and more numerical solution,there are some mature methods. Such as Euler method, backward Euler method, trapezoidal method, Runge-Kutta method, projection method and multi-step method and so on.Therefore, numerical solution of differential equation is of great practical significance. Through this paper, error of these solutions will be analyzed in order to get a the accuracy better way to solve the numerical solution of ordinary differential.Keywords:Ordinary differential equations, numerical solution methods, s ingle ste p methods, l inear multi-step methods, local truncation error目录引言 (1)一、常微分方程 (1)1、定义 (1)2、常微分方程初值问题描述 (2)3、数值解法的基本思想与途径 (2)4、数值解的分类 (3)5、问题(1)解的存在惟一性定理 (4)二、几种常用的数值解法及其误差分析 (4)1、单步法 (4)(一)、欧拉法 (5)(二)、向后EuIer方法 (6)(三)、- 法 (7)(四)、改进欧拉法 (7)(五)Runge—Kutta方法 (9)2、线性多步法 (14)总结 (16)参考文献: (17)引言自然界中很多事物的运动规律可用微分方程来刻画。

数值微分公式的误差分析

(n 1)!
n1(x) xxi
i 0,1, , n
(6 2)
故一般限于对节点上的导数值采用插值多项式的相应导数值进行近似计算，
以便估计误差。
一般地 Lnk (xi ) f k (xi ) i 0,1, , n; k 1,2,
这类公式称为插值型数值微分公式。
6.1.1 常用的数值微分公式
nn 0
ji
t j hdt i j
j0
j0
b a (1)ni
nn
(t j)dt
n i!(n i)! 0 ji
j0
记
Cin
(1)ni i!(n i)!n
n 0
n
(t j)dt
ji
j0
则 Ai (b a)，CNin-C求积公式表示为
n
In (b a) Cin f (xi ) i0
y2
f (x1 h)
f
( x1 )
hf
( x1 )
h2 2
f
( x1 )
h3 3!
f
( x1
)
h4 4!
f 4 1
y0
f (x1 h)
f
(
x1 )
hf
( x1 )
h2 2
f
(
x1
)
h3 3!
f
( x1
)
h4 4!
f 4(2 )
这里 x1 1 x2 , x0 2 x1
相加得
y2
x2 x2
y0
x x0 x x2 x1 x0 x1 x2
y1
x x0 x x2 x0 x2
x1 x1
y2
f
(x0 )

微分方程中的数值解误差分析方法

微分方程中的数值解误差分析方法在数学领域中，微分方程是描述自然现象和物理现象的一个非常重要的工具。

然而，大多数微分方程很难用解析的方法求解，因此我们通常使用数值方法来近似求解。

然而，这些数值解不可避免地会引入误差。

本文将介绍微分方程中的数值解误差分析方法。

一、局部截断误差在使用数值方法求解微分方程时，我们通常会引入一个步长h。

在每个步长上，我们通过一系列迭代计算来逼近真实的解。

然而，由于近似计算和舍入误差等原因，我们得到的数值解与真实解之间存在误差。

这个误差被称为局部截断误差。

局部截断误差可以通过泰勒展开来近似计算。

假设我们使用的数值方法是Euler方法，那么可以得到如下的局部截断误差公式：$$LTE = \frac{y(t_{n+1}) - [y(t_n) + hf(t_n, y(t_n))]}{h}$$其中，$y(t_n)$是真实解在时间点$t_n$的值，$f(t_n, y(t_n))$是微分方程的右侧函数在$t_n$和$y(t_n)$处的取值。

二、全局截断误差除了局部截断误差之外，我们还需要考虑全局截断误差。

全局截断误差是指在整个求解过程中，数值解与真实解之间的误差累积情况。

通过对局部截断误差进行逐步累积，我们可以得到全局截断误差的估计。

例如，使用Euler方法求解微分方程，假设总共迭代了N步，步长为h，则全局截断误差的估计为：$$GTE = \frac{LTE}{h} \times N = \frac{y(T) - y(t_0)}{h} = O(h)$$其中，$y(T)$是真实解在求解区间的终点处的值，$y(t_0)$是真实解在求解区间的起点处的值。

三、稳定性分析除了局部截断误差和全局截断误差，稳定性也是数值解的一个重要性质。

在数值方法中，一个稳定的方法可以保证数值解不会因为舍入误差或者数值不稳定性而发散。

稳定性分析通常通过稳定性函数来进行判断。

对于一个给定的数值方法，我们可以将其误差传播到未来的时间点，然后观察误差是否会趋于无穷大。

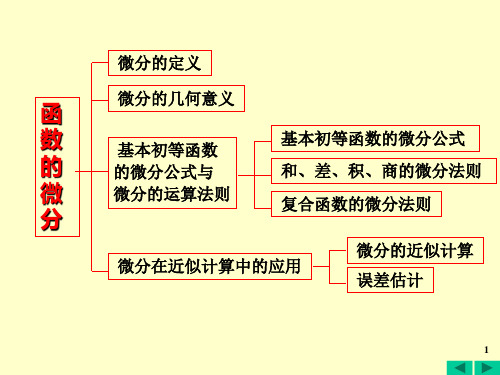
函数的微分及其在近似计算中的应用

3
3、问题：函数可微的条件是什么？ A = ? 问题：函数可微的条件是什么？可微, 则有(1)成立成立，设函数 y = f (x) 在点 x0 可微则有成立，即
∆y = A∆x + o(∆x)
等式两端除以 ∆x , 得
o( ∆ x ) ∆y = A+ . ∆x ∆x
于是, 于是当 ∆x → 0时, 由上式就得到 o(∆x ) ∆y = lim A + lim = A. f ′( x 0 ) = ∆ x → 0 ∆x →0 ∆x ∆x 可微，因此, 因此如果函数 f (x) 在点 x 0 可微，则 f (x)在点 x 0也一定可导且也一定可导,
函数在任意点的微分,称为函数的微分,记作函数在任意点的微分称为函数的微分记作 dy 或 df ( x ), 即称为函数的微分 dy = f ′( x ) ∆ x . 如函数 y = cos x 的微分为
dy = (cos x )' ∆ x = − sin x ∆ x 显然，显然，函数的微分 dy = f ′( x )∆x 与 x 和 ∆x 有关。有关。
′
1 d (log a x ) = dx, x ln a 1 d (ln x ) = dx , x 1 d (arcsinx) = dx, 2 1− x 1 d (arccosx) = − dx, 1 − x2 1 d (arctanx) = dx, 2 1+ x
1 (arccot x) = − 2 . 1+ x
dy = ( x 3 )′∆x = 3 x 2 ∆x.
再求函数当 x = 2 , ∆ x = 0 . 02 时的微分
dy
x =2 ∆x =0.02

定位误差的微分算法

定位误差的微分算法华侨大学机电及自动化学院定位误差的微分算法定位误差微分算法基本原理定位误差微分算法步骤定位误差微分算法举例定位误差微分算法的基本原理调整法加工中工序尺寸的定位误差即为设计基准工序基准在加工尺寸方向上的位置变动量工序基准位置的变动量是某一包含工序基准的尺寸的变化量该变化量对于尺寸来说是一个微量可以看做微分定位误差微分法计算步骤找到工序尺寸的设计基准或工序基准把工序基准沿尺寸方向与夹具上的某一固定点相连计算两点间尺寸的变化量即微分的定位误差定位误差的微分算法例1sinadodoaocoa计算内孔表面键槽加工尺寸h工序基准b夹具固定点a外圆中心o计算外圆表面键槽加工尺寸h以圆柱心轴在内孔表面定位工序基准a外圆中心o
定位误差的微分算法
定位误差的微分算法
定位误差微分算法基本原理定位误差微分算法步骤定位误差微分算法举例
定位误差微分算法的基本原理
➢ 调整法加工中，工序尺寸的定位误差即为设计基准（工序基准）在加工尺寸方向上的位置变动量
➢ 工序基准位置的变动量是某一包含工序基准的尺寸的变化量
➢ 该变化量对于尺寸来说，是一个微量，可以看做微分
H3
O3 A O1A O1O2 O2O3
d1 2
O1O2
D2 2
d3 2
A
dw
O3 A
Td1 2
TD2 2
Td3 2
t
O1O2
B
α
A
dw
AB
Td 2 sin
2
TD 2
t
定位误差的微分算法例3
计算外圆表面键槽加
工尺寸H3的定位误差
内孔与外圆间同轴度
O3
H3
O1 O2
公差Φt
以圆柱心轴在内孔表

组合表面定位误差的微分法计算

△ ＝ｙ蔷，其，传系。中茜为递数
应不大于零件精度的１ —１。／／３５定位误差主要由基准位移误差Ａｙ和基准不重２工件以一面两孔定位时转角误差计算合误差ＡＢ组成。前者主要是由于定位元件的制造误差、工作定位面的制造公差等造成；后者主要是由于实例１为加工如图１所示的托架，以Ａ面及两
工件定位时定位基准、工序基准、设计基准之间不重个８。８定位＋０＋５０粗镗尺３孔，证加工尺寸４保脚合而造成，两者之综合形成定位误差。５０）ｍ，２圆柱销４，，８削边销对单一表面定位的定位误差，已在文献［、］２［等（ ± ．ｍ使用两销为：］３８．４５００多有描述，本处不再重复。但组合表面的定位误差，咖删０销间距为（１ ± ．）ｍ计算定位误差。１００１ｍ，０
ａ８
— 一 —
Ｏ２４％（－—Ｄ－２ ’ ＤＬＤｌｄ＋２ｄ２ｔ）
一
ａ一北２ｌｄ＋２ｄ）＋ — ｌ－￣Ｄ ’ 丝
ＯＬ＝２Ｄｄ＋２￣（ｄＤ－，ｄ）
△ ＝２ｎＩ×１＝２．０６６×９．２＝０１。２ｔ △ ｘａＩ２ ×００９Ｂ０３６．３砌Ｉ
当各组成要求尺寸出现一个微小的增量 △ ，以则ｙ的变动可近似地用全微分表达
△Ｙ＝ｌ△ ２ △ ，，＋ｌ＋２ …
收稿日期：０２ｏ — ６２１－１２
△ ＿ｌ２＝，７ … ，
图２一面两孔定位的转角误差

ad微分积分误差

ad微分积分误差AD微分积分误差微积分是数学的重要分支，其应用广泛，对于科学研究和工程实践都有着重要的作用。

在微积分中，微分和积分是两个基本的运算符号，它们可以帮助我们研究函数的变化和计算曲线下的面积。

然而，在实际应用中，由于计算机计算的有限精度和数值算法的局限性，微分和积分的计算结果往往会存在误差。

这篇文章将讨论AD微分积分误差的问题。

AD（Automatic Differentiation）自动微分是一种基于微分规则的计算方法，它可以通过计算导数来近似计算函数的微分。

AD方法具有高精度、高效率的特点，被广泛应用于科学计算、优化问题求解等领域。

然而，即使使用AD方法进行微分计算，也无法完全消除误差的产生。

这是因为计算机在进行浮点数运算时存在舍入误差，而AD方法本质上也是基于浮点数运算的。

微分误差是指在进行微分计算时，由于浮点数运算的舍入误差而引入的误差。

在函数的微分计算中，我们通常使用数值的近似方法，例如有限差分法或符号微分法。

有限差分法是一种常用的数值方法，它通过计算函数在某一点附近的两个近似值之差来近似计算导数。

然而，由于有限差分法在计算过程中需要进行除法运算，而除法运算是容易引入舍入误差的运算，所以有限差分法计算的微分结果往往存在误差。

AD方法通过利用链式法则来计算导数，避免了除法运算，从而减小了微分误差。

但是，AD方法也无法完全消除微分误差的产生。

这是因为在计算机进行浮点数运算过程中，存在舍入误差，而AD方法的基本运算仍然是浮点数运算。

另外，AD方法在计算导数时，需要构建计算图和反向传播，这些过程也会引入一定的误差。

积分误差是指在进行积分计算时，由于数值算法的近似性而引入的误差。

在实际应用中，我们通常使用数值积分方法来计算曲线下的面积。

数值积分方法包括梯形法则、辛普森法则等，它们都是通过将曲线分割成多个小区间，然后计算每个小区间的面积，最后将这些小区间的面积相加来近似计算整个曲线下的面积。

微积分在近似运算中的应用

例3 正方形边长为2.41 0.005米, 求出它的面积 ,
并估计绝对误差与相对误差.
解设正方形边长为 x , 面积为y, 则 y x .
2
当x 2.41时,
y (2.41) 2 5.8081(m 2 ).
x 2.41
y
x 2.41
2x
4.82.
边长的绝对误差为 x 0.005,
一、计算函数增量的近似值
若y f ( x )在点x0处的导数f ( x0 ) 0, 且 x 很小时,
y
x x0
dy
x x0
f ( x0 ) x .
, 半径伸长了例1 半径10厘米的金属圆片加热后 0.05厘米,问面积增大了多少 ?
2 设 A r , r 10厘米, r 0.05厘米. 解
二、利用微分计算当 x 由45 变到 4510 时，函数 y cos x 的增量的近似值(1 0.017453弧度).
,ห้องสมุดไป่ตู้
练习题
三、已知单摆的振动周期T 2
l ，其中g 980 厘 g
米/秒 2， l 为摆长（单位为厘米），设原摆长为 20 T 增大 0.05 秒，摆长约需加长多厘米，为使周期少？
1 (1) 1 x 1 x; ( 2) sin x x ( x为弧度); n ( 3) tan x x ( x为弧度); (4) e x 1 x; (5) ln(1 x ) x . 1 1 1 n 证明 (1) 设 f ( x ) n 1 x , f ( x ) (1 x ) , n 1 f (0) 1, f (0) . n x f ( x ) f ( 0) f ( 0) x 1 . n

微分方程的数值解法与误差估计

微分方程的数值解法与误差估计微分方程是数学中的重要分支，广泛应用于物理、工程、经济等领域。

解微分方程的数值方法是研究微分方程的一个重要方面，它通过数值计算来近似求解微分方程，为实际问题提供了有效的数值解。

本文将介绍微分方程的数值解法以及误差估计的相关内容。

一、欧拉方法欧拉方法是一种常见的数值解微分方程的方法。

它基于微分方程的定义，将微分方程转化为差分方程。

具体而言，对于一阶常微分方程dy/dx=f(x,y)，我们可以将其转化为差分方程(y_(i+1)-y_i)/(x_(i+1)-x_i)=f(x_i,y_i)，其中x_i和y_i分别表示第i个点的x坐标和y坐标。

然后，通过给定的初始条件y_0，可以使用迭代公式y_(i+1)=y_i+(x_(i+1)-x_i)f(x_i,y_i)来逐步计算出近似解。

然而，欧拉方法存在一定的误差。

首先，它是基于线性逼近的，因此在非线性问题上可能会产生较大的误差。

其次，由于每次迭代的误差会累积，欧拉方法的误差随着步长的增加而增加。

因此，在使用欧拉方法时需要注意选择合适的步长，以保证结果的准确性。

二、改进的欧拉方法为了克服欧拉方法的缺点，人们提出了改进的欧拉方法，如改进的欧拉法和改进的欧拉-克罗默法。

这些方法通过引入更高阶的近似公式来减小误差，并提高数值解的精度。

改进的欧拉法是通过使用中点来近似解的方法，即在每个小区间上使用中点的斜率来计算近似解。

这样做可以减小误差，并提高数值解的精度。

改进的欧拉-克罗默法是通过使用梯形法则来近似解的方法，即在每个小区间上使用梯形的斜率来计算近似解。

这种方法比改进的欧拉法更精确，但计算量也更大。

三、龙格-库塔方法龙格-库塔方法是一种常用的数值解微分方程的方法，它通过使用不同阶数的近似公式来计算近似解，并通过比较不同阶数的结果来估计误差。

其中最常用的是四阶龙格-库塔方法，也称为RK4方法。

RK4方法通过计算不同阶数的斜率来逐步逼近真实解。

偏微分方程数值解法在流体力学中的应用及误差分析

偏微分方程数值解法在流体力学中的应用及误差分析摘要流体力学是一门研究流体运动及其与周围环境相互作用的学科，其基本方程组为一组偏微分方程。

由于解析解往往难以获得，数值解法成为了解决流体力学问题的关键工具。

本文将首先介绍流体力学中常见的偏微分方程及其特点，然后重点阐述几种常用的数值解法，包括有限差分法、有限元法和有限体积法，并分析其优缺点和适用范围。

最后，本文将深入探讨数值解法的误差分析，包括截断误差、舍入误差以及数值稳定性等方面，并给出降低误差的策略。

关键词：偏微分方程，数值解法，流体力学，误差分析1. 绪论流体力学广泛应用于航空航天、能源、环境等各个领域，其研究对象涵盖从气体到液体等多种流体。

流体力学的基本方程组由质量守恒方程、动量守恒方程和能量守恒方程组成，这些方程都是非线性偏微分方程，其解析解往往难以获得。

因此，数值解法成为了解决流体力学问题的关键工具。

数值解法通过将连续的物理问题离散化，转化为一系列代数方程，并利用计算机进行求解，从而得到问题的近似解。

目前，常用的数值解法包括有限差分法、有限元法和有限体积法等。

这些方法各有优缺点，在不同的应用场景下有着不同的适用范围。

2. 流体力学中的偏微分方程流体力学中常见的偏微分方程包括：*质量守恒方程 (Continuity equation)：描述流体质量守恒定律，其数学表达式为：$\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{u}) = 0$其中 $\rho$ 为流体密度，$\mathbf{u}$ 为流体速度。

*动量守恒方程(Navier-Stokes equation)：描述流体动量守恒定律，其数学表达式为：$\rho \frac{\partial \mathbf{u}}{\partial t} + \rho (\mathbf{u} \cdot \nabla) \mathbf{u} =- \nabla p + \mu \nabla^2 \mathbf{u} + \rho \mathbf{f}$其中 $p$ 为流体压力，$\mu$ 为流体粘度，$\mathbf{f}$ 为作用于流体的体积力。

微分在近似计算与误差估计中的应用

微分在近似计算与误差估计中的应用一、预备知识1．利用一元函数的微分进行近似计算和误差估计若一元函数y＝f(x)在点x0可微，则当|Δx|很小时，有f(x0＋Δx)－f(x0)≈f′(x0)Δx要计算f(x)的值，可找一个邻近于x的x0，使f(x0)与f′(x0)易于计算，然后用x代换(1)式中的x0＋Δx，求得f(x)的近似值为f(x0)＋f′(x0)Δx，其中Δx＝x－x0．2．利用全微分进行近似计算与误差估计若二元函数z＝f(x，y)在点(x0，y0)可微，则Δz＝dz＋o(ρ)＝f′x(x0，y0)Δx＋f′y(x0，y0)Δy＋0(ρ)Δz≈dz＝f′x(x0，y0)Δx＋f′y(x0，y0)Δy或f(x0＋Δx，y0＋Δy)≈f(x0，y0)＋f′x(x0，y0)Δx＋f′x(x0，y0)Δy(3)若三元函数u＝f(x，y，z)在点(x0，y0，z0)可微，则Δu≈du＝f′x(x0，y0，z0)Δx＋f′y(x0，y0，z0)Δy＋f′x(x0，y0，z0)Δz或f(x0＋Δx，y0＋Δy，z0＋Δz)≈f(x0，y0，z0)＋3．绝对误差、相对误差在实际工作中，某个量的精确值往往是无法知道的，于是绝对误差和相对误差也就无法求得．但是根据测量仪器的精度等因素，有时能够确定误差在某一个范围内，如果某个量的精确值是A，测得它的近似值是a，又知道它的误差不超过δA，即|A－a|≤δA二、应用例题例1求sin29°的近似值．例2证明：近似公式利用上面公式，则例3为了计算出球的体积准确到1％，问度量球半径R时，所产生的相对误差应不超过多少？所以度量球半径R时，所产生的相对误差不得超过0.33％．例4证明：根据正切对数表所求得的角度，比用具有同样多位小数正弦对数表求得的角度更为精确．证明设y1(x)＝lntanx，y2(x)＝lnsinx，则若对数表具有n位，则一般来说，根据正切对数表所求得的角度，比用具有同样多位小数的正弦对数表求得的角度更为精确．例5求1.083.96的近似值．解设f(x，y)＝x y，令x0＝1，y0＝4，Δx＝0.08，Δy＝－0.04，由公式(3)，有1.083.96＝f(x0＋Δx，y0＋Δy)≈f(1，4)＋f′x(1，4)×0.08＋f′y(1，4)×(－0.04)＝1＋4×0.08＋1×ln1×(－0.04)＝1＋0.32＝1.32例6现测得某三角形两边及其夹角分别为a＝12.50，b＝8.30，C＝30°．测量a，b的误差为±0.01，C的误差为±0.1°，求用公式计算三角形面积时，所产生的绝对误差与相对误差．解依题意测量a，b，C绝对误差限分别为|Δa|＝0.01，|Δb|由公式(4)，有将各数据代入上式得S的绝对误差为|ΔS|≈0.13．及从而，S的相对误差为求方程的近似解，可分两步进行：第一步是确定根的大致范围，即确定一个区间[a，b]，使所求的根是位于这个区间内的唯一实根，称为根的隔离，并称此区间[a，b]为隔离区间．第二步是以根的隔离区间的端点作为根的初始近似值，逐步提高根的近似值的精确度，直至得到满足精确度要求的近似解为止．1．二分法设函数f(x)在区间[a，b]上连续，f(a)·f(b)＜0，且方程f(x)＝0在(a，b)内仅有一个实根ξ，于是[a，b]即为这个根的一个隔离区间．例7用二分法求方程x3＋1.1x2＋0.9x－1.4＝0的实根的近似值，精确到10-3(即误差不超过10-3)．解设f(x)＝x3＋1.1x2＋0.9x－1.4，x∈R显然，f(x)在R上连续，可导，且f′(x)＝3x2＋2.2x＋0.9上严格递增，方程f(x)＝0仅有一个实根．由f(0)＝－1.4＜0与f(1)＝1.6＞0知，方程f(x)＝0的根在[0，1]内，取a＝0，b＝1，则[0，1]即是一个隔离区间．经计算，有ξ1＝0.5，f(ξ1)＝－0.55＜0，取a1＝0.5，b1＝1；ξ2＝0.75，f(ξ2)＝0.32＞0，取a2＝0.5，b2＝0.75；ξ3＝0.625，f(ξ3)＝－0.16＜0，取a3＝0.625，b3＝0.75；ξ4＝0.687，f(ξ4)＝0.062＞0，取a4＝0.625，b4＝0.687；ξ5＝0.656，f(ξ5)＝－0.054＜0，取a5＝0.656，b5＝0.687；ξ6＝0.672，f(ξ6)＝0.005＞0，取a6＝0.656，b6＝0.672；ξ7＝0.664，f(ξ7)＝－0.025＜0，取a7＝0.664，b7＝0.672；ξ8＝0.668，f(ξ8)＝－0.010＜0，取a8＝0.668，b8＝0.672；ξ9＝0.672，f(ξ9)＝－0.002＜0，取a9＝0.670，b9＝0.672；ξ10＝0.671，f(ξ10)＝0.001＞0，取a10＝0.670，b10＝0.671．于是，0.670＜ξ＜0.671．要用0.670作为根的不足近似值，或用0.671作为根过剩近似值，其误差都小于10-3．设f(x)在[a，b]上存在二阶导数，f(a)·f(b)＜0，且f′(x)与f″(x)在[a，b]上保持定号，则方程f(x)＝0在(a，b)内有且仅有一个实根ξ．[a，b]即为根的一个隔离区间，由f′(x)与f″(x)的正、负号之间有不同的组合，曲线y=f(x)在[a，b]上图形只有如图所示的四种不同的情形．2．弦位法标作为方程根的近似值，这种方法称为弦位法．如果f′(x)与f″(x)同号，令x0＝a，以点A(x0，f(x0))为已知点的弦AB方程为令y＝0，求得这弦与x轴的交点横坐标x1是如果f′(x)与f″(x)异号，令x0＝b，用同样方法，求得弦与x轴的交点横坐标x1是由图可见，弦AB与x轴的交点的横坐标x1比a(情形(a)，(d))或比b(情形(b)，(c))更接近方程根ξ．用同样方法，从新区间[x1，b]或[a，x1)出发，可得比x1更接近ξ的x2，如此继续下去，一般地，从区间[xn-1，b]或[a，xn-1]出发，得根的近似值为当n→∞时，xn→ξ，其中满足(3)近似根数列，有a＜x1＜x2＜…＜xn＜…＜ξ，满足(4)式的近似根数列，有ξ＜…＜xn＜xn-1＜…＜x2＜x1＜b．在区间[xn，ξ]或[ξ，xn]上应用拉格朗日定理，有f(xn)＝f(xn)－f(ξ)＝(xn－ξ)f′(c)(在xn与ξ构成区间内)这样，由(5)式就可判定近似根xn与ξ近似程度．例8用弦切法求方程x3－2x2－4x－7＝0的实根的近似值，精确到10-2．f′(x)＝3x3－4x－4＞0，令x1＝3.52，由(1)式，有同法可得显然f(x i)＜0，i＝1，2，3，所以x0＜x1＜x2＜x3＜ξ．由误差估计公式，有于是，以3.63作为根的近似值，其误差小于10-2．例9用弦切法求方程x－0.1sinx－2＝0的实根近似值，精确到10-3．解f(x)＝x－0.1sinx－2，x∈Rf′(x)＝1－0.1cosx＞0由f(2)＝－0.1sin2＝－0.1×0.9093＝－0.0904＜0，f(2.1)＝0.1×(1－sin2.1)＝0.1×0.1368＝0.00137＞0，f″(x)＝－0.1sinx＞0与f′(x)同号，令x1＝2，由(1)式，有从而f(x1)＝0.0868－0.1 sin 2.0868≈－0.0002＜0于是，方程的根ξ∈(2.0868，2.0870)．其误差不超过10-3．3．切线法如图，用曲线弧一端的切线来代替曲线弧，从而求出方程实根的近似值，这种方法称为切线法．在曲线弧的端点纵坐标与f″(x)同号的曲线端点处作曲线的切线，如图，情形(a)，(d)作点B处(情形(b)，(c)作点A处)的曲线切线．令x0＝b(x0＝a)，则点B(x0，f(x0)(A(x0，f(x0))处曲线切线方程为y－f(x0)＝f′(x0)(x－x0)令y＝0，求得这切线与x轴交点横坐标x1是由图可见，端点B处(A处)的曲线切线与x轴交点的横坐标x1比b(情形(a)，(d))或a(情形(b)，(c))更接近方程根ξ．再在点(x1，f(x1)作切线，可得根的近似值x2，如此继续下去，一般地，在点(xn-1f(xn-1)作切线，得根的近似值为例10用切线法求方程x3＋1.1x2＋0.9x－1.4＝0的实根的近似值，精确到10-3．f′(x)＝3x2＋2.2x＋0.9＞0f″(x)＝6x＋2.2＞0．由f(0)＜0，f(1)＞0，则f″(x)与f(1)同号，令x0＝1，由(6)式，有同法可得出现此种情形，不能再继续算下去．显然，f(x i)(i＝1，2，…)与f″(x)同号，即f(0.671)＞0，经计算知f(0.670)＜0，于是，有0.670＜ξ＜0.671以0.670或0.671作为根的近似值，其误差都小于10-3．。

微分方程中的数值解误差分析方法

微分方程中的数值解误差分析方法微分方程是描述自然界中各种变化规律的数学工具，在科学研究和工程实践中有着广泛的应用。

然而，在实际问题中，常常无法通过解析方法求得微分方程的精确解，因此需要借助数值方法来求解微分方程的数值解。

但是，数值解并非完全准确，会存在一定的误差。

因此，对数值解的误差进行分析是非常重要的，可以帮助我们评估数值解的可靠性，指导数值方法的选择以及参数的调整。

一、截断误差在数值解微分方程时，我们常常会使用近似方法来替代微分方程中的导数，例如使用差分法或插值法。

这样就会引入截断误差，即在每次近似计算中产生的误差。

截断误差通常与步长有关，步长越小，截断误差越小。

二、舍入误差在计算机上进行数值计算时，由于计算机的存储精度有限，会导致舍入误差的产生。

舍入误差是由于对于无限小数进行有限位数的近似表示而引起的误差。

舍入误差在数值计算中是不可避免的，但可以通过控制计算精度和合理选择数值方法来减小舍入误差的影响。

三、稳定性分析除了截断误差和舍入误差外，还有一个重要的误差来源是数值方法的稳定性。

稳定性分析主要是研究数值方法对微小扰动的抵抗能力，即微小误差是否会被放大。

一个稳定的数值方法可以保证数值解的误差不会随着计算的进行而迅速增大，而是保持在一个可控范围内。

四、数值解误差的评估对于数值解的误差评估是数值计算中非常重要的一环。

常用的评估方法包括绝对误差、相对误差、误差限制和收敛性分析等。

在实际应用中，我们需要根据具体情况选择合适的误差评估方法，并根据误差分析的结果来调整数值方法的参数。

通过以上的误差分析，我们可以更加全面地了解数值解的可靠性和精度，指导我们选择合适的数值方法和参数，提高数值计算的准确性和效率。

在研究微分方程和进行工程计算时，对数值解误差的分析是必不可少的一步，有助于我们更加有效地利用数值方法解决实际问题。

微分方程数值解的误差估计

微分方程数值解的误差估计在微分方程数值解的误差估计方面，我们可以采用以下格式来撰写文章：--------微分方程数值解的误差估计在数值计算的领域，微分方程数值解的误差估计是一个重要的研究方向。

准确地估计数值解的误差可以帮助我们评估数值算法的可行性，并为进一步优化算法提供指导。

本文将介绍微分方程数值解的误差估计方法，并探讨其中的关键技术。

1. 误差源的分析微分方程数值解的误差来源于多个方面，包括离散化误差、截断误差、舍入误差等。

在准确估计误差之前，我们需要仔细分析这些误差的来源，并确定相应的解决策略。

离散化误差是因为将连续的微分方程转化为离散的差分方程而引入的，截断误差则是因为在差分方程的推导过程中对无穷级数进行了截断。

舍入误差则是由计算机中的浮点数表示和计算过程中的舍入引入的。

2. 误差估计的方法为了准确估计微分方程数值解的误差，我们需要借助数学理论和计算机技术。

一种常用的方法是利用残差的计算来估计误差。

我们可以比较数值解与解析解之间的差异，通过计算残差来估计误差的上界。

此外，还可以利用局部截断误差的估计方法，将整个区域划分为若干个子区间，在每个子区间内进行误差估计，然后求得整个区域上误差的上界。

3. 关键技术与工具在误差估计过程中，我们需要运用一些关键的技术和工具。

一种常用的技术是有限元法，它将微分方程的求解区域进行剖分，构建一组局部基函数，并利用这些基函数对数值解进行逼近。

通过对逼近解与真解之间的差异进行分析，可以得到误差的估计。

此外，还有其他技术如有限差分法、有限体积法等，在不同问题中，选择合适的技术是很重要的。

4. 数值实验与结果分析为了验证误差估计的有效性，我们可以设计相应的数值实验，并对实验结果进行分析。

实验中我们可以选择一些已知精确解的微分方程，通过不同的数值算法求解，并与解析解进行比较。

通过对比真实误差和估计误差之间的差距，可以评估误差估计方法的准确性和可靠性。

结论微分方程数值解的误差估计是一个复杂而关键的问题。

微分法分析误差的局限

微分法分析误差的局限
仪器误差的微分法的分析与局限性
仪器的输出和各元件特性参数、结构参数之间的关系如果能用数学关系表达，那么这种关系式就称为作用方程式或仪器方程式。

若此时误差源为上述元件特性参数或结构参数则可以对作用方程式做全
微分，进行误差分析与计算。

例32自准直仪制造误差分析。

例31给出了自准直仪原理误差的分析，这是基于各元件参数理想情况。

如果存在制造误差，哪些零件的误差会影响测角精度呢？由式（39）这就是自准直仪的作用方程式。

对式（312）进行微分，有式（313）两边同除以α，得到相对误差关系式（314）右边*项是分划板刻线的相对误差，第二项是物镜焦距的相对误差。

可见测角误差与这两个元件的制造误差有关；同时这两项误差的贡献符号相反，可考虑在制定零件公差时，一个给正偏差一个给负偏差，使它们对仪器测角误差的影响起到某种程度的抵消作用。

微分法的优点是利用微分运算解决误差计算问题，简单快速。

其局限性是无法分析不能列入仪器作用方程式的误差源，如度盘安装偏心等。

此类误差通常产生于装配调整环节，与仪器作用方程式无关。

微分在近似计算中的应用

4
误差的类型
1、间接测量误差：由于测量仪器的精度、测量条件和测量方法等各种因素的影响，测得的数据往往有误差，而根据带有误差的数据计算所得的结果也会有误差，我们把它叫做间接测量误差。
2、绝对误差：如果某一个量的精确度为A，它的近似
值为, 那么 A 叫做的绝对误差。 3、相对误差：如果的绝对误差为 A , 那么，
A
, 就叫做的相对误差。

5
4、绝对误差限：若 A A, 则称 A 为
测量A的绝对误差限。（为测量A时的近似值。）
5、相对误差限：若 A 为测量A 的绝对误差限，则
称
A
为测量A的相对误差限。
注：1、在实际工作中，精确值往往无法知道，但可以确定其测量的精度等因素引起的误差的范围，即误差限。
2
DD
即 A 的绝对误差限约为
A

2
DD

2
60.03 0.05

4.715
mm2
A 的相对误差限约为
A
A

2
D

D
D2
0.17%
7
4
2-8 微分在近似计算中的应用
近似计算的原理近似计算的举例误差的类型
误差的例
1
近似计算原理
设 y f x 可微，且在 x0 有 f x0 0, 在 x 很小时, 这时
dy 近似于y 的相对误差也很小，即 y dy 由 y dy 得：
f x f x0 f x0 x x0 f x f x0 f x0 x x0 即可微函数 f x 可近似表示为 x 的线性形式。（线性化的

定位误差的微分计算法

定位误差的微分计算法设计夹具时，必须对定位误差进行分析计算。

当工序尺寸为与定位基准成线性关系的量时，定位误差等于基准不重合误差与基准位移误差之和，计算较为简单。

但对于平面尺寸系统和空间尺寸系统，由于尺寸方向不一致以及存在角度误差，使定位误差的计算变得较为复杂。

应用定位误差微分计算法则可使上述问题较易得到解决。

定位误差微分计算法是高等数学微分近似计算原理的应用。

设函数y=F(x1，x2，…，xn)，当自变量x1，x2，…，xn分别在x01，x02，…，x0n处的变动量|?x1|，|?x2|，…，|?xn|均较小时，y的变动量可近似用全微分表示为?y=n∑i=1?y?xi?x0i(1)由微分概念的极限原理可知，|?xi|越小，则?y的近似程度越高。

由于可将工序尺寸L 视为工件和定位元件上若干尺寸l1，l2，…，ln的函数，即L=F(l1，l2，…，ln)。

根据工件定位的标准位置概念，令l1=l01±??l1，l2=l02±??l2，…，ln=l0n±??ln。

由于尺寸偏差?li比基本尺寸(平均尺寸)l0i小得多，故可运用微分近似公式(1)计算定位误差，即?L=2n∑i=1?L?li=n∑i=1?L?li?l0i2?l0i(2)下面通过计算实例具体说明定位误差微分计算法的应用。

例1：如图1所示，盘形工件以外圆表面靠在新型V型铁的两个圆柱销上定位，工序尺寸H为所加工孔与工件的中心距，显然工件中心O为工序基准，现用微分法计算其定位误差。

工序尺寸H的函数表达式为H=h-OA=h-?[(D+d)2-b2]?(3)式中：d——两圆柱销直径b——两圆柱销中心距h——机床轴线到两圆柱销中心连线的距离视d、b、h 为常量，D=D0±??D为变量，因此工序尺寸H为工件直径D的函数，按式(2)对式(3)取微分得?H=-1D0+d?D=?D=?D2[(D0+d)2-b2] ?2{1-[b/(D0+d)]2]}?2cosa 0(4)式中d0=arcsin[b/(D0+d)] 式(4)中第一步求导后出现的负号表示工序尺寸H 随D 的增大而减小。

微分方程数值解的误差估计

微分方程数值解的误差估计在实际应用中，微分方程是很常见的数学模型。

由于有些微分方程形式复杂，解析解往往难以获得，因此数值解法成为解决这类问题的一种重要手段。

然而，数值解在计算过程中往往会带来误差，因此对数值解的误差估计是非常重要的。

一、误差来源与分类在了解误差估计之前，首先需要明确误差的来源。

在数值解中，误差主要来自以下几个方面：1. 离散化误差：将连续的微分方程转化为离散的差分方程时，会产生离散化误差。

这种误差通常来自于差分步长的选择，步长越大误差越大。

2. 截断误差：截断误差是指数值方法近似求解时对于某个被忽略的项的误差。

3. 舍入误差：由于计算机内部数值的有限精度，进行计算时会产生舍入误差。

根据误差产生的方式和性质，可以将误差分为绝对误差和相对误差。

绝对误差是指数值解与精确解之间的差值，而相对误差是绝对误差与精确解之间的比值。

二、误差估计方法为了评估数值解的准确性，需要进行误差估计。

下面介绍几种常用的误差估计方法。

1. 解析解法：当微分方程存在解析解时，可以将解析解与数值解进行比较，计算其差值即可得到误差。

但是，解析解往往难以获得，所以这种方法应用较为有限。

2. 步长收缩方法：通过多次计算采用不同步长的数值解，利用步长收缩时误差与步长的关系进行估计。

当步长趋近于零时，数值解也会接近准确解。

3. 泰勒级数展开法：根据一阶导数、二阶导数等与准确解的关系，利用泰勒级数展开计算估计误差。

通过比较泰勒级数展开结果与数值解之间的差异，可以获得误差的估计值。

4. 向后差分法：向后差分法是使用后项的差分来逼近微分方程的方法，利用向后差分法可以计算出数值解与实际解之间的差异，并进行误差估计。

这种方法在实际应用中非常常见。

三、误差控制与提高数值解的精度误差估计不仅可以评估数值解的准确性，还可以用于误差控制和提高数值解的精度。

在控制误差方面，通常采用自适应步长策略，即根据误差估计结果自动调整步长，使误差在允许范围内。

微分求近似值

微分求近似值
微分求近似值是数学中的一个常见问题,旨在找到一个函数的近似值,使其与原函数的误差达到最小。

在数学、物理、工程等领域中,近似值非常重要,可以帮助我们进行各种分析和计算。

本文将探讨微分求近似值的方法和应用。

微分求近似值的方法可以分为两类:基于函数的导数和基于函数的极值。

其中,基于函数的导数的求近似值方法是最常用的方法。

在这种方法中,我们首先求出函数的导数,然后利用导数的正负性来近似原函数。

具体来说,设我们要计算的函数为$f(x)$,则我们可以对其求导数,得到$f'(x)$。

然后,我们利用导数的正负性来决定如何近似$f(x)$。

如果$f'(x)>0$,则我们通常可以沿$x$轴正方向求近似值;如果$f'(x)<0$,则我们通常可以沿$x$轴负方向求近似值。

这种方法可以有效地将原函数近似为$f(x)+k$,其中$k$是一个常数。

基于函数的极值的求近似值方法相对较为复杂。

在这种方法中,我们首先需要找到函数的极值点,然后利用这些极值点来近似$f(x)$。

这种方法比较适用于一些比较复杂的函数,比如$e^x$函数。

微分求近似值的应用非常广泛。

在数学领域中,微分求近似值可以用来计算各种数值,比如微积分、微分方程等。

在物理领域中,微分求近似值可以用来计算物理量的大小,比如速度、加速度等。

在工程领域中,微分求近似值可以用来计算各种实际问题,比如机械效率、电路中的电流等。

微分求近似值的方法可以有效地求解很多实际问题,实现重要的近似计算。

不仅如此,还可以为其他数值求解提供一个重要的数学工具。