高三攀枝花市高三第四次统一考试
四川省攀枝花市2023届高三第二次统一考试理科数学试题

四川省攀枝花市2023届高三第二次统一考试理科数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知全集{1,2,3,4,5,6}U =,集合{1,2,3}M =,{3,4}N =,则()()U U M N ⋃=( ) A .{3} B .{5,6} C .{1,2,3,4}D .{1,2,4,5,6}2.已知复数z 满足i(1)12i z +=-+(其中i 为虚数单位),则z =( ) A .1i - B .1i + C .3i --D .3i -+3.已知等比数列{an }满足a 1a 6=a 3,且a 4+a 5=32,则a 1=( )A .18B .14C .4D .84.某国有企业响应国家关于进一步深化改革,加强内循环的号召,不断自主创新提升产业技术水平,同时积极调整企业旗下的甲、乙、丙、丁、戊等5种系列产品的结构比例,近年来取得了显著效果.据悉该企业2021年5种系列产品年总收入是2020年的2倍,其中5种系列产品的年收入构成比例如下图所示.则以下说法错误的是( )A .2021年甲系列产品收入和2020年的一样多B .2021年乙和丙系列产品收入之和比2020年的企业年总收入还多C .2021年丁系列产品收入是2020年丁系列产品收入的13D .2021年戊系列产品收入是2020年戊系列产品收入的2倍还多5.将一直角三角形绕其一直角边旋转一周后所形成的几何体的三视图如图所示,则该几何体的侧面积是A .2π3B .2πCD .3π6.我国著名数学家华罗庚先生曾说:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休”,在数学的学习和研究中,有时可凭借函数的图象分析函数解析式的特征.已知函数()f x 的部分图象如图所示,则函数()f x 的解析式可能为( )A .()2e1ln ||()2exxx f x -⋅=B .()()2e1ln 2exxx f x +⋅=C .()22e ()e 1ln ||xxf x x =-⋅D .22e 1()ex x f x x -=7.已知四边形ABCD 中,2AB DC =,0AD AB ⋅=,|||2|2AB AD ==,E 为BC 的中点,则AC DE ⋅=( )A .14B .34C .1D .28.一排11个座位,现安排甲、乙2人就座,规定中间的3个座位不能坐,且2人不能相邻,则不同排法的种数是( ) A .28B .32C .38D .449.如图,正方体1111ABCD A B C D -中,P 是1A D 的中点,给出下列结论: ①1//PB D C ;①//PB 平面11B D C ①1PB B C ⊥;①PB ⊥平面11AC D 其中正确的结论个数为( )A .1B .2C .3D .410.已知正项数列{}n a 的前n 项和为n S ,且221n n n a S a =+,设12log n n nS b S +=,数列{}n b 的前n 项和为n T ,则满足2n T ≥的n 的最小正整数解为( ) A .15B .16C .3D .411.已知函数π()sin cos 22x f x x ⎛⎫=+⋅ ⎪⎝⎭,则下列说法正确的是( )A .()y f x =是奇函数B .()y f x =的图象关于直线πx =对称C .()f x 在3π,2π2⎛⎫⎪⎝⎭上单调递减 D .()f x 是最小正周期为2π的周期函数12.已知2a =,32e 2b =,88ln2c =-,则( )A .b a c <<B .a b c <<C .a c b <<D .c<a<b二、填空题13.已知平面向量(2,1)a =,(,2)b x =-,若a b ⊥,则||b =_________.14.()241(1)ax x -+的展开式中3x 的系数为12,则=a _________.15.已知边长为3的正ABC 的三个顶点都在球O (O 为球心)的表面上,且OA 与平面ABC 所成的角为30,则球O 的体积为___________.16.已知函数()()()ln 1,111,1x x f x k x x ⎧->⎪=⎨-+<⎪⎩,若存在非零实数0x ,使得()()0011f x f x -=+成立,则实数k 的取值范围是_________.三、解答题17.攀枝花市地处川滇交界处,攀西大裂谷中段,这里气候条件独特,日照充足,盛产芒果、石榴、枇杷、甘蔗等热带亚热带水果.根据种植规模与以往的种植经验,产自某种植基地的单个“红玉软籽”石榴质量()g 在正常环境下服从正态分布()602,625N . (1)10000个产自该基地的“红玉软籽”石榴,估计有多少个质量()g 在(]577,652内; (2)2023年该基地考虑增加人工投入,现有以往的人工投入增量x (人)与年收益增量y (万元)的数据如下:该基地为了预测人工投入增量与年收益增量的关系,建立了y 与x 的回归模型,试根据表中统计数据,求出y 关于x 的线性回归方程y bx a =+并预测人工投入增量为10人时的年收益增量. 参考数据:若随机变量()2,XN μσ,则()0.6827P X μσμσ-<≤+≈,(22)0.9545P X μσμσ-<≤+≈,(33)0.9973P X μσμσ-<≤+≈,回归直线ˆˆˆybxa =+的斜率和截距的最小二乘估计分别为()()()1122211ˆn ni iii i nniiii i x y nx y x x y y bxnxx x ====-⋅--==--∑∑∑∑,ˆˆay bx =-. 18.在①ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且cos sin b b A B -=. (1)求A ;(2)线段BC 上一点D 满足1AD BD ==,3CD =,求①ADC 的面积.19.如图,直四棱柱1111ABCD A B C D -的底面是菱形,14AA =,2AB =,60BAD ∠=︒,E 为AD 的中点,112D F FC =.(1)证明:B ,E ,F ,1C 四点共面; (2)求1D C 与平面1BEFC 所成角的正弦值. 20.已知抛物线2:2(0)E y px p =>与双曲线22134x y -=的渐近线在第一象限的交点为P ,且点P 的横坐标为3. (1)求抛物线E 的标准方程;(2)点A 、B 是第一象限内抛物线E 上的两个动点,点(,0)C t 为x 轴上的动点,若ABC 为等边三角形,求实数t 的取值范围. 21.已知函数2()ln ()f x x a x x a =-+∈R . (1)当3a =时,求函数()f x 的极值;(2)设函数()()g x f x x =-,若()g x 有两个零点1x ,()212x x x <,且0x 为()g x 的唯一极值点,求证:1202x x x +>.22.在平面直角坐标系xOy 中,曲线1C的参数方程为12x y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数).以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2(cos sin )ρθθ=-.(1)求曲线1C 的极坐标方程和曲线2C 的直角坐标方程; (2)设曲线1C 与曲线2C 交于P 、Q 两点,求||||OP OQ ⋅的值. 23.已知()|2||2|()f x x ax a =++-∈R . (1)当2a =时,解不等式()12f x <;(2)若1x ∀≥,不等式2()3f x x x ≤++恒成立,求a 的取值范围.。
湖北省新高考联考协作体2024-2025学年高三上学期开学测试化学参考答案及解析

高三化学试题答案和给分标准1-15.(每题3分,共45分)1.D2.A3.D4.B5.C6.A7.C8.D9.B 10.C11.C 12.B 13.D 14.A 15.C16.(共14分)(1)3d 74s 2(1分)第四周期VIII 族(2分,周期和族各1分,不互相牵连)+3(1分)(2)abc (2分,选对两个得1分,有错或只选对1个0分)(3)[]4+22242222LiCoO +H C O +8Cl 6H 22CO +4H O Co +2Li Cl -+-+=+↑(2分,要么0分要么2分)(4)9.44×10-3(2分,没有用科学计数法或者没有保留3位有效数字者不得分)(5)1:4(2分)降低反应温度或带走过多热量,反应速率减慢(2分,合理即得分)17.(共14分)(1)CH 4(g)+CO 2(g)2CO(g)+2H 2(g)ΔH =+247.4kJ·mol -1(2分,ΔH 的值没有标明正号者不扣分,无单位或者没配平、没写状态者无分)(2)①0.025(2分)②AC (2分,只写对一个得1分,有错者无分)(3)①<(2分)②(2分)(4)①<(2分)②1324k k k k ⨯⨯(2分)湖北省新高考联考协作体2024-2025学年上学期开学测试18.(共13分)(1)222Cu H O Cu(OH)=+↓(2分,没有沉淀符号者得1分);2Cu 2e Cu -+-=(1分)(2)222442Cu H O H SO CuSO 2H O ++=+(2分,若写成离子方程式,写对了,得1分);产生的铜离子催化了过氧化氢分解(1分)(3)对于2Cu 2e Cu -+-=,加入氨水,氨水与2Cu +形成()234Cu NH +⎡⎤⎣⎦,使()2c Cu +减小,提高了Cu 的还原性(2分,合理即得2分);向U 型管右侧溶液中滴加硫酸(1分,没说清楚是右侧者不得分)(4)在还原反应或氧化反应(半反应)中,增大反应物浓度或降低生成物浓度,氧化剂(还原剂)的氧化性(还原性)增强。
2024届四川省攀枝花市高三上学期第一次统一考试理综全真演练物理试题

2024届四川省攀枝花市高三上学期第一次统一考试理综全真演练物理试题一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题2024年春天,中国航天科技集团研制的50kW级双环嵌套式霍尔推力器,成功实现点火并稳定运行,标志着我国已跻身全球嵌套式霍尔电推进技术领先行列。
嵌套式霍尔推力器不用传统的化学推进剂,而是使用等离子体推进剂,它的一个显著优点是“比冲”高。
比冲是航天学家为了衡量火箭引擎燃料利用效率引入的一个物理量,英文缩写为,是单位质量的推进剂产生的冲量,比冲这个物理量的单位应该是( )A.m/s B.C.D.第(2)题用控制变量法,可以研究影响电荷间相互作用力的因素.如图所示,O是一个带电的物体,若把系在丝线上的带电小球先后挂在横杆上的P1、P2、P3等位置,可以比较小球在不同位置所受带电物体的作用力的大小。
这个力的大小可以通过丝线偏离竖直方向的角度θ显示出来。
若物体O的电荷量用Q表示,小球的电荷量用q表示,物体与小球间距离用d表示,物体和小球之间的作用力大小用F表示。
则以下对该实验现象的判断正确的是( )A.保持Q、q不变,增大d,则θ变大,说明F与d有关B.保持Q、q不变,减小d,则θ变大,说明F与d成反比C.保持Q、d不变,减小q,则θ变小,说明F与q有关D.保持q、d不变,减小Q,则θ变小,说明F与Q成正比第(3)题如图所示,一颗人造卫星原来在椭圆轨道1绕地球E运行,在P点变轨后进入轨道2做匀速圆周运动.下列说法正确的是:()A.不论在轨道1还是轨道2运行,卫星在P点的速度都相同B.不论在轨道1还是轨道2运行,卫星在P点的加速度都相同C.卫星在轨道1的任何位置都具有相同加速度D.卫星在轨道2的任何位置都具有相同动量(动量P=mv,v为瞬时速度)第(4)题2024年4月20日,我国首次利用核电商用堆批量生产碳14同位素,这标志着将彻底破解国内碳14同位素依赖进口的难题,实现碳14供应全面国产化。
四川省攀枝花市2025届高三化学上学期第一次统一考试试题

四川省攀枝花市2025届高三化学上学期第一次统一考试试题可能用到的相对原子质量:H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27 Si-28S-32 Cl-35.5 Ca-40 Ti-48 Fe-56 Cu-64 Pd(钯)-1067. 化学与生活、生产亲密相关。
下列叙述不正确...的是A. 高纯硅可用于制作光导纤维B.二氧化氯可用于自来水的杀菌消毒C.氯化铁溶液可用于刻制铜质印刷线路板D.海水里的钢闸门可连接电源的负极进行防护8.依据下列事实书写的离子方程式中,错误的是A.向Na2SiO3溶液中加入稀盐酸得到硅酸胶体: SiO32- + 2H+ H2SiO3(胶体)B.向FeSO4溶液中加入NH4HCO3溶液得到FeCO3沉淀:Fe2++ 2HCO3-FeCO3↓+ CO2↑+ H2O C.向AlCl3溶液中加入足量稀氨水:Al3++ 4NH3·H2O Al3++ NH4+ + 2H2OD.在稀硫酸存在下,MnO2将CuS中的硫元素氧化为硫单质:MnO2 +CuS + 4H+Mn2++ Cu2++ S + 2H2O9.依据反应2NaIO3 + 5SO2 + 4H2O I2 + 3H2SO4 + 2NaHSO4,利用下列装置从含NaIO3的废液中得到碘的CCl4溶液并回收NaHSO4。
其中装置正确且能达到相应试验目的是A.②④ B.①②③ C.②③④ D.①②③④10.海冰是海水冻结而成的咸水冰。
海水冻结时,部分来不及流走的盐分以卤汁的形式被包围在冰晶之间,形成“盐泡” (假设盐分以一个NaCl计),其大致结构如下图所示,若海冰的冰龄达到1年以上,溶化后的水为淡水。
下列叙述正确的是A.海冰内层“盐泡”越多,密度越小B. 海冰冰龄越长,内层的“盐泡”越多C. 海冰内层“盐泡”内的盐分主要以NaCl分子的形式存在D. 海冰内层NaCl的浓度约为10-4mol/L(设冰的密度为0.9g/cm3)11.如图是工业利用菱镁矿(主要含MgCO3,还含有Al2O3、FeCO3杂质)制取氯化镁的工艺流程。
四川省攀枝花市2014届高三第四次统一考试地理试题 Word版含答案
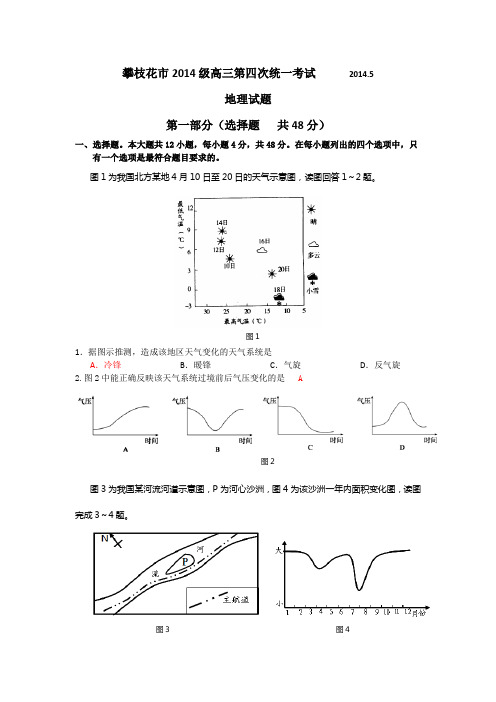
攀枝花市2014级高三第四次统一考试 2014.5地理试题第一部分(选择题 共48分)一、选择题。
本大题共12小题,每小题4分,共48分。
在每小题列出的四个选项中,只有一个选项是最符合题目要求的。
图1为我国北方某地4月10日至20日的天气示意图,读图回答1~2题。
1.据图示推测,造成该地区天气变化的天气系统是 A .冷锋 B .暖锋 C .气旋 D .反气旋 2.图2中能正确反映该天气系统过境前后气压变化的是 A图3为我国某河流河道示意图,P 为河心沙洲,图4为该沙洲一年内面积变化图,读图完成3~4题。
3.该河位于我国的 A .青藏地区 B .东北地区 C .华北地区 D .长江中下游地区图2 图1图4 图34.下列的叙述,正确的有①该河段河水由西南流向东北 ②该河段为水流较慢的河流下游地区 ③该河流以季节性积雪融水补给为主 ④若河流上游修筑水坝,则河心洲面积增长速度减慢 A .①② B .③④ C .①③ D .②④图5为世界某岛屿图,读图回答5~6题。
5.图中洋流对相邻陆地环境的影响是 A .降低了温、湿程度 B .增加了温、湿程度C .减轻了寒冷、加剧了干燥状况D .加剧了寒冷、减轻了干燥状况 6.该岛A. 温泉众多地热资源丰富B. 亚寒带针叶林遍布全岛C .西岸筑港水域条件较好 D. 最冷月平均气温约为-4℃图6是三种农业地域类型基本情况比较图,读图回答7~8题。
7.有关三种农业地域类型的说法,不正确...的是 A .①类型,农民可根据市场的需求调整农业生产结构 B .②类型,以小农经营为主,机械化和科技水平比较低 C .②类型,单位面积产量高,但要投入大量劳动力精耕细作 D .③类型,生产规模大、机械化水平高、农业科学技术先进 8.图7四个地区发展的农业地域类型,与图6中对应合理的是A .甲~①B .乙~②C .丙~③D .丁~③图6图7图5图8表示多年平均情况的、图9表示某年情况的陆地(用110°E 代表)与海洋(用160°E 代表)气压梯度(大陆气压与海洋气压之差,单位:百帕)的时空分布状况图。
四川省攀枝花市高2014届高三第四次统考试题及答案

四川省攀枝花市2014级高三第四次统考化学试题2014.03可能用到的相对原子质量:H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27 S-32Cl-35.5 Ca-40 Fe-56 Cu-64 Zn-65 Ag-108 Ba-137选择题(42分)本题包括7个小题,每小题6分,共42分,每小题只有一个..选项符合题意1.化学与生活、环境密切相关。
下列有关叙述中,正确的是A.凡是含有食品添加剂的食物都对人体健康有害,不能食用B.塑化剂是一种应用很广的化工塑料软化剂,可大量添加到婴幼儿食品、玩具中C.回收废弃塑料制成燃油替代汽油、柴油,可节约化石能源和减轻环境污染D.绿色化学的核心是应用化学原理对环境污染进行治理2.下列有关物质性质的应用正确的是A.液氨汽化时要吸收大量的热,可用作制冷剂B.二氧化硅不与强酸反应,可用石英器皿盛放氢氟酸C.生石灰具有很强的吸水性,可用来干燥氯气D.氯化铝是一种电解质,常用于电解法制铝3.我国地质学家发现一种化学式为Ca3Li2(BeSiO4)3F2的矿石。
下列说法正确的是A.该矿石所含非金属元素的简单氢化物中,SiH4的沸点最高B.该矿石所含金属元素中,Be的原子半径最小C.该矿石所含金属元素都是+2价D.该矿石中所含元素都是短周期元素4.设N A为阿伏加德罗常数的值。
下列说法正确的是A.25℃时,1 L pH=1的硫酸溶液中H+的数目为0.2N AB.78 g 苯含有C=C 键的数目为3N AC.常温常压下,22.4L 由SO2与CO2组成的混合气体含有的氧原子数目为2N A D.T℃时,MgCO3的Ksp=4×10-8,则该温度下1L饱和MgCO3溶液中含有的Mg2+数目为2×10-4 N A5.气体的自动化检测中常常应用原电池原理的传感器。下图为电池的工作示意图:气体扩散进入传感器,在敏感电极上发生反应,传感器就会接收到电信号。下表列出了待测气体及敏感电极上部分反应产物。则下列说法中正确的是待测气体部分电极反应产物A .检测NO 2、CO 气体时,敏感电极均作电池正极B .检测H 2S 气体时,电解质溶液中的阴离子向对电极作定向移动C .检测Cl 2气体时,敏感电极的电极反应为:Cl 2 + 2e -= 2Cl -D .检测同体积的含H 2S 和CO 体积分数相同的两份空气样本时,传感器上产生的电流大小相同6.25℃时,pH 均为3的盐酸和醋酸溶液分别加水稀释(忽略温度变化),其pH 随溶液体积变化的曲线如图所示。
攀枝花市2023届高三第三次统一考试语文参考答案及评分细则

攀枝花市2023届高三第三次统考试题2023.04语文参考答案及评分细则一、现代文阅读(36分)(一)现代文文本阅读I(本题共3小题,9分)1.(3分)答案:B。
(根据原文,“类脑芯片”是“数据生命”产生的关键,而“数字生命”则需要高精度仪器拍摄大脑结构快照,完美的脑机接口、成熟的全脑仿真技术、极强算力的设备支撑等复杂因素。
)2.(3分)答案:C。
(“从科学技术和现实运用层面进行了可行性分析,结论依据充分”错,从分析来看,目前还有许多“不可行”因素,作者也并未给出明确的结论。
)3.(3分)答案:D。
(数字生命是否将从科幻走进现实,作者并未给出明确的答案。
)(二)现代文文本阅读II(本题共3小题,12分)4.(3分)答案:C。
(材料主要强调孙晶岩的创作品质,如《西望胡杨》就不能说明国力的发展壮大是其作品产生广泛影响的根本原因。
)5.(3分)答案:D。
(D选项还是属于体育范畴,与提问中“您说写《中国冬奥》绝不是就体育写体育”矛盾。
)6.(6分)答案:①材料二立足《中国冬奥》这本书(1分),围绕创作动力、创作方法、创作困难等方面展开提问(1分),侧重于展现创作者的创作过程(创作品质)(1分)。
②材料三关注作者创作的多部报告文学(1分),侧重展现孙晶岩创作视野宏大的理念(关注现实)(1分),以及她的个人品质和对国家和人民的爱。
(1分)(答案分为三个层面,一是采访围绕某一部作品和围绕多部作品的区别;二是提问的核心内容概括不同;三是从采访的展现的目的不同。
意思对即可。
)(三)现代文文本阅读III(本题共3小题,15分)7.(3分)答案:D。
(错在“失望”,更多的是“痛惜失落”。
)8.(6分)参考答案:①采用白描手法,凸显住处环境的清寒,清寒的环境衬托出王梅邨的落寞。
(3分)②用语极其精简,连用数词“一”,突出了梅邨居住环境的简约与清寒,揭示了梅邨先生的落魄的处境,暗示了梅邨斩断书缘的原因。
(3分)(或:连用短句,句子整齐,适合表现简约明净具有古典气息的环境氛围,符合读书人的气质。
2023届四川省攀枝花市高三第三次统一考试数学(文)试题【含答案】

2023届四川省攀枝花市高三第三次统一考试数学(文)试题一、单选题1.设集合,,则( ){}13,Z M x x x =-<≤∈{}1,0,1,2N =-M N ⋂=A .B .C .D .{}12x x -<≤{}1,0,1,2-{}0,1,2{}1,0,1,2,3-【答案】C【分析】化简集合,根据交集的定义求解即可.M 【详解】因为,{}13,Z M x x x =-<≤∈所以,又,{}0,1,2,3M ={}1,0,1,2N =-所以.{}0,1,2M N = 故选:C.2.如果一个复数的实部和虚部相等,则称这个复数为“等部复数”,若复数(i 为虚数单位)i1i z a =-为“等部复数”,则实数a 的值为( )A .B .C .0D .13-1-【答案】B【分析】先化简复数,利用“等部复数”的定义:实部和虚部相等,列出方程求出的值.z a 【详解】,222(1i)i i 1i ((1i i 1i 1i))111a a a z a a a a a a +-+-==+-==++++-复数为“等部复数”,i1i z a =-,22111a a a -∴=++1a ∴=-故选:B .3.攀枝花昼夜温差大,是内陆地区发展特色农业的天然宝地,干热河谷所孕育的早春蔬菜为大家送去新鲜优质的维生素和膳食纤维.下图为攀枝花年月日至日的最高气温与最低气温的天20233612气预报数据,下列说法错误的是( )A .这天的单日最大温差为度的有天7172B .这天的最高气温的中位数为度729C .这天的最高气温的众数为度729D .这天的最高气温的平均数为度729【答案】D【分析】确定这天的单日最大温差为度的日期,可判断A 选项;利用中位数的定义可判断B 717选项;利用众数的概念可判断C 选项;利用平均数公式可判断D 选项.【详解】对于A 选项,这天的单日最大温差为度为月日、月日,共天,A 对;7173103112对于B 选项,这天的最高气温由小到大依次为:、、、、、、(单位:),728282929293031C故这天的最高气温的中位数为度,B 对;729对于C 选项,这天的最高气温的众数为度,C 对;729对于D 选项,这天的最高气温的平均数为,D 错.728229330312042977⨯+⨯++=>故选:D.4.如图所示的程序框图中,若输出的函数值在区间内,则输入的实数x 的取值范围是()f x []3,2-( )A .B .[]4,1-[]2,4-C .D .[]1,4-[]1,2-【答案】B【分析】根据程序框图,明确该程序的功能是求分段函数的值,由此根据该函2log ,1()1,1x x f x x x >⎧=⎨-≤⎩数值域,可求得答案.【详解】由程序框图可知:运行该程序是计算分段函数的值,该函数解析式为 ,2log ,1()1,1x x f x x x >⎧=⎨-≤⎩输出的函数值在区间 内 ,[]3,2-必有当时,,,1x >20log 2x <≤14x ∴<≤当 时 ,,,1x ≤310x -≤-≤21x ∴-≤≤即得 .[2,4]x ∈-故选∶B .5.若角的终边上有一点,则( )β()2,1P tan 2β=A .B .C .D .4343-4545-【答案】A【分析】根据正切函数的定义及二倍角的正切公式求解.【详解】因为角的终边上有一点,β()2,1P 所以,1tan 2β=所以,22tan 14tan 211tan 314βββ===--故选:A6.对于直线m 和平面,,下列命题中正确的是( )αβA .若,,则B .若,,则//m α//αβ//m βm β⊥αβ⊥//m αC .若,,则D .若,,则m α⊥//αβm β⊥m α⊂αβ⊥m β⊥【答案】C【分析】根据线面关系和面面关系逐项判断可得出答案.【详解】对于A ,若,,则或,故A 错误;//m α//αβ//m βm β⊂对于B ,若,,则或,故B 错误;m β⊥αβ⊥//m αm α⊂对于C ,若,,则,故C 正确;m α⊥//αβm β⊥对于D ,若,,则与相交或或,故D 错误.m α⊂αβ⊥m β//m βm β⊂故选:C.7.已知,,,,若“p 且q ”是真命题,则实数a:[1,2]p x ∀∈20x a -≥0:q x ∃∈R 200220x ax a ++-=的取值范围是( )A .B .C .或D .且2a ≤-1a ≤2a ≤-1a =2a >-1a ≠【答案】C【分析】分类讨论为真和为真时,的取值,进而利用集合的交集关系,即可求解p qa 【详解】若p 真,则;若q 真,则或.又因为“p 且q ”是真命题,所以或1a ≤2a ≤-1a ≥2a ≤-.1a =故选:C .8.已知,c =sin1,则a ,b ,c 的大小关系是( )0.0232log 8,π==a b A .c <b <a B .c <a <bC .a <b <cD .a <c <b【答案】D【分析】由对数的运算法则求出a ,然后根据指数函数与正弦函数的单调性分别对b ,c 进行放缩,最后求得答案.【详解】由题意,,,533223log 8log 20.65a ====0.020ππ1b =>=,则.ππsinsin1sin 43c <<⇒<<a c b <<故选:D.9.八角星纹是大汶口文化中期彩陶纹样中具有鲜明特色的花纹.八角星纹以白彩绘成,黑线勾边,中为方形或圆形,具有向四面八方扩张的感觉.图2是图1抽象出来的图形,在图2中,圆中各个三角形为等腰直角三角形.若向图2随机投一点,则该点落在白色部分的概率是( )A .B .C .D .32π2π1285π【答案】D【分析】计算出白色部分对应的面积后根据几何概型的概率公式可求概率.【详解】设圆的半径为2,如图设与交于,设的中点为,连接.HC AF P AF M ,OM AO 则,设,则,故,OM AF ⊥AP a =222354222a a a ⎛⎫⎛⎫+== ⎪ ⎪⎝⎭⎝⎭285a =而题设中空白部分的面积为,22214342a a ⎫⨯⨯⨯+=⎪⎪⎭故点落在白色部分的概率是,22484ππ5πa a ==故选:D.10.已知双曲线,A 为双曲线C 的左顶点,B 为虚轴的上顶点,直线l 垂()2222:10,0x y C a b a b -=>>直平分线段,若直线l 与C 存在公共点,则双曲线C 的离心率的取值范围是( )AB A .B .C .D.)+∞)+∞(【答案】B【分析】先根据题意求得直线l 的斜率,再根据直线l 与C 存在公共点,只需直线l 的斜率大于渐近线的斜率即可求解.ba -【详解】依题意,可得,则,()(),0,0,A a B b -00AB b bk a a -==+又因为直线l 垂直平分线段,所以,AB l a k b =-因为直线l 与C 存在公共点,所以,即,a b ba ->-22a b <则,即,解得222a c a <-2222,2c e a <>e >所以双曲线C 的离心率的取值范围是.)+∞故选:B11.已知函数对任意都有,则当取到最大值时,()()πsin 03f x x ωω⎛⎫=+> ⎪⎝⎭3π0,8x ⎛⎫∈ ⎪⎝⎭()12f x >ω图象的一条对称轴为( )()f x A .B .π8x =3π16x =C .D .π2x =3π4x =【答案】A【分析】先根据,得到,结合,得到的范围,求3π0,8x ⎛⎫∈ ⎪⎝⎭ππ3ππ3383x ωω<+<+1()2f x >3ππ83ω+出的范围,进而得到的最大值为,再利用整体法求出函数的对称轴,得到答案.ωω43【详解】,,3π0,8x ⎛⎫∈ ⎪⎝⎭ 0ω>,ππ3ππ3383x ωω∴<+<+,1()2f x >,π3ππ5π3836ω∴<+≤,所以的最大值为,403ω∴<≤ω43当时,令,43ω=4π()sin 33f x x ⎛⎫=+ ⎪⎝⎭4πππ,Z 332x k k +=+∈解得,π3π,Z 84x k k =+∈当时,对称轴为,经检验,其他三个均不合要求.0k =π8x =故选:A12.定义在R 上的连续函数满足,且为奇函数.当时,()f x ()()11f x f x -=+()42y f x =+(]2,3x ∈,则( )()()()3232f x x x =---(2022)(2023)f f +=A .B .C .2D .01-2-【答案】B【分析】首先根据题意,得到,,从而得到函数的周期()()2=f x f x -()()22f x f x -+=-+()f x 为,再根据求解即可.4()()20233f f =【详解】因为函数满足,所以关于对称,()f x ()()11f x f x -=+()f x 1x =即①.()()2=f x f x -又因为为奇函数,所以,()42y f x =+()()4242f x f x -+=-+即②.()()22f x f x -+=-+由①②知,()()2=-+f x f x 所以,()()()24f x f x f x +=-+=-即,所以函数的周期为,()()4f x f x =+()f x 4所以,()()()2023505433f f f =⨯+=,()()()2022505422=⨯+=f f f 因为时,,(]2,3x ∈()()()3232f x x x =---所以,3(3)(32)3(32)2f =---=-又为奇函数,所以当时,,(42)y f x =+0x =(2)0f =所以,(2022)(2023)022f f +=-=-故选:B.二、填空题13.已知实数x ,y 满足约束条件,则的最大值为___________.010x y x y x -≤⎧⎪+≤⎨⎪≥⎩2z x y =+【答案】2【分析】画出约束条件所表示的平面区域,结合图象确定目标函数的最优解,代入即可求解.【详解】作出约束条件对应的平面区域,如图所示,010x y x y x -≤⎧⎪+≤⎨⎪≥⎩由,可得直线,2z x y =+122z y x =-+当直线过点A 时,此时直线在轴上的截距最大,此时取得最大值,122zy x =-+y z 又由,解得,010x x y =⎧⎨+-=⎩(0,1)A 所以的最大值为.z 0212z =+⨯=故答案为:2.14.已知抛物线的焦点为F ,过F 的直线l 与C 交于A ,B 两点,O 为坐标原点,则2:4C y x =________.OA OB ⋅=【答案】3-【分析】求出抛物线的焦点坐标,用点斜式求出直线的方程,将直线方程与抛物线联立得到一AB 元二次方程,利用韦达定理得到,,由即可求出.126x x +=121=x x 1212OA OB x x y y ⋅=+【详解】抛物线的焦点为,24y x =()1,0设A ,B 两点的坐标为和,由题意得直线的方程为,11(,)x y 22(,)x y AB 1y x =-将直线和抛物线联立,可得,241y x y x ⎧=⎨=-⎩2610x x -+=其中,364320∆=-=>则,,126x x +=121=x x .1212OA OB x x y y ⋅=+()()121211x x x x +--=()121221x x x x =-++21613=⨯-+=-故答案为:3-15.如图,圆台中,O 在线段上,上下底面的半径分别为12O O 12O O =12OO ,________.11r =2r =【答案】69π5【分析】列出外接球半径所满足的方程,解出半径,得外接球表面积.【详解】设外接球半径为R,,=26920R =所以外接球表面积为,269π4π5R =故答案为:.69π516.如图,四边形中,与相交于点O ,平分,ABCD AC BD AC DAB ∠,,则的值_______.π3ABC ∠=33AB BC ==sin DAB ∠【分析】由余弦定理求出AC =sin BAC ∠=【详解】在中,,ABC π,3,13ABC AB BC ∠===由余弦定理得2222cos AC AB BC AB BC ABC ∠=+-⨯⨯,2213123172=+-⨯⨯⨯=所以.AC =由正弦定理得,sin sin BC ACBAC ABC =∠∠即sin sin BC ABC BAC AC ∠∠⋅===cos BAC ∠=又因为平分,所以.AC DAB∠sin 2sin cos DAB BACBAC ∠∠∠==三、解答题17.某企业从生产的一批产品中抽取个作为样本,测量这些产品的一项质量指标值,由测量结100果制成如图所示的频率分布直方图.(1)求这件产品质量指标值的样本平均数(同一组数据用该区间的中点值作代表)和中位数;100x(2)用频率代替概率,按分层抽样的方法从质量指标值位于、内的产品中随机抽取[)15,25[)35,45个,再从这个产品中随机抽个,求这个产品质量指标值至少有一个位于内的概率.6622[)35,45【答案】(1)平均数为,中位数为25x =23.75(2)35【分析】(1)将每个矩形底边的中点值乘以对应矩形的面积,将所得结果全部相加可得出,利用x 中位数的定义可求得样本的中位数;(2)分析可知质量落在有个,分别记为、、、,质量落在有个,分别[)15,254A B C D [)35,452记为、,列举出所有的事件,并确定所求事件所包含的基本事件,利用古典概型的概率公式可a b 求得所求事件的概率.【详解】(1)解:由已知得.100.01510200.04010300.02510400.0201025x =⨯⨯+⨯⨯+⨯⨯+⨯⨯=因为.设中位数为,则,0.150.40.5+>x ()15,25x ∈则,解得.()0.015100.04150.5x ⨯+⨯-=23.75x =(2)解:质量指标值位于、内的产品的频率分别为,[)15,25[)35,450.04100.4⨯=,其中,0.02100.2⨯=0.4:0.22:1=所以用分层抽样的方法抽取的个产品中,质量落在有个,6[)15,254分别记为、、、,质量落在有个,分别记为、,A B C D [)35,452a b 则从这个产品中随机抽个,共种情况,如下:、、、、、、6215AB AC AD Aa Ab BC 、、、、、、、、,这种情况发生的可能性是相等的.BD Ba Bb CD Ca Cb Da Db ab 15设事件为从这个产品中随机抽个,M 62这个产品质量指标值至少有一个位于内,2[)35,45有、、、、、、、、,共种情况.Aa Ab Ba Bb Ca Cb Da Db ab 9则.()93155P M ==18.已知等差数列的公差为,前n 项和为,现给出下列三个条件:①成等{}n a ()0d d ≠n S 124,,S S S 比数列;②;③.请你从这三个条件中任选两个解答下列问题.432S =()6632S a =+(1)求数列的通项公式;{}n a (2)若,且,设数列的前n 项和为,求证:.()122n n n b b a n --=≥13b =1n b ⎧⎫⎨⎬⎩⎭n T 1132n T ≤<【答案】(1)42n a n =-(2)证明见解析【分析】(1)先分析条件①②③分别化简,若选①②,①③,②③,联立化简后条件求首项与公差得出通项公式即可;(2)由,利用累加法求出求出,再由裂项相消法求出的前n 项和,结()122n n n b b a n --=≥n b 1n b ⎧⎫⎨⎬⎩⎭合的单调性可得证.n T 【详解】(1)由条件①得,因为,,成等比数列,则,1S 2S 4S 2214S S S =即,又,则,()()2111246a d a a d +=+0d ≠12d a =由条件②得,即,414632S a d =+=13162a d +=由条件③得,可得,即.()6632S a =+()11615352a d a d +=++12a =若选①②,则有,可得,则;1122316d a a d =⎧⎨+=⎩124a d =⎧⎨=⎩()1142n a a n d n =+-=-若选①③,则,则;124d a ==()1142n a a n d n =+-=-若选②③,则,可得,所以.1343162a d d +=+=4d =()1142n a a n d n =+-=-(2)由,且,()12284n n n b a n b n -=--=≥13b =当时,2n ≥则有()()()()1213213122084n n n b b b b b b b b n -=+-+-++-=++++- ()()2841213412n n n -+-=+=-又也满足,故对任意的,有,13b =241n b n =-*n ∈N 241n b n =-则,()()11111212122121n b n n n n ⎛⎫==- ⎪-+-+⎝⎭所以,21111112111121233521121n T n n n ⎡⎤⎛⎫⎛⎫⎛⎫=-+-++- ⎪ ⎪ ⎪⎢⎥-+⎝⎛⎫=-< ⎪+⎝⎭⎝⎭⎭⎝⎭⎣⎦ 由于单调递增,所以,21n n T n =+113n T T ≥=综上:.1132n T ≤<19.如图1,圆O 的内接四边形中,,,直径.将圆沿折ABCD 45DAC ∠=︒60CAB ∠=︒2AC =AC 起,并连接、、,使得为正三角形,如图2.OB OD BD BOD(1)证明:图2中的平面;AB ⊥BCD (2)在图2中,求三棱锥的体积.D OBC -【答案】(1)证明见解析【分析】(1)利用勾股定理证明,然后结合可证;AB BD ⊥AB BC ⊥(2)利用可求答案.12D OBC O BCD A BCDV V V ---==【详解】(1)由题意得到,.1AB BD ==AD =222AD AB BD =+所以.AB BD ⊥因为为直径所对的圆周角,所以.ABC ∠AB BC ⊥又,平面,平面,BD BC B ⋂=BD ⊂BCD BC ⊂BCD 平面.∴AB ⊥BCD (2)因为平面,平面,AB ⊥BCD CD ⊂BCD所以,因为,,AB CD ⊥AD CD ⊥AB AD A ⋂=所以平面,因为平面,所以,DC ⊥ABD BD ⊂ABD DC BD ⊥所以1122D OBC O BCD A BCD V V V AB BD DC ---===⋅⋅20.已知椭圆的焦点坐标为和,且椭圆经过点.C ()12,0F -()22,0F G ⎛ ⎝(1)求椭圆的标准方程;C (2)椭圆的上、下顶点分别为点和,动点在圆上,动点在椭圆上,直线、C M N A 221x y +=B C MA 的斜率分别为、,且.证明:、、三点共线.MB 1k 2k 125k k =N A B 【答案】(1)2215x y +=(2)证明见解析【分析】(1)求出的值,利用椭圆的定义可求得,进而可求得的值,由此可得出椭圆的标c a b C 准方程;(2)计算得出,结合已知条件可得出,即可证得结论成立.15BM BN k k ⋅=-AN BN k k =【详解】(1)易知椭圆的.2c =点在椭圆上,且G 12GF GF +==∴2a a =⇒=由得,椭圆的标准方程为:.222a b c =+1b =∴C 2215x y +=(2)设,()22,B x y因为.22222222222211111555BM BNy y y y k k x x x y -+--⋅=⋅===--由得.125k k =21115BN k k k =-=-为圆的直径,所以,,.MN 221x y +=NA MA ⊥∴11AN BN k k k =-=故、、三点共线.N A B 【点睛】关键点点睛:本题考查三点共线的证明,解题的关键在于根据椭圆的方程计算得出,以及由圆的几何性质得出,结合斜率关系来进行证明.15BM BN k k ⋅=-NA MA ⊥21.已知函数在处的切线方程为.()e ln x f x x a x=-1x =()2e 1y x b =+-(),a b R ∈(1)求实数a ,b 的值;(2)当时,恒成立,求正整数m 的最大值.1,12x ⎡⎤∈⎢⎥⎣⎦()2e 0x f x x m --+<【答案】(1),1a =-e 1b =+(2)3【分析】(1)求出导数,根据题意列出方程组求解即可得解;(2)分离参数转化为的最小值,利用导数判断单调性及极值确定最小值()()2e ln x g x x x x=-+-+为,根据单调性求出的范围即可得解.()00212g x x x =-++()0g x 【详解】(1)定义域为,.()0,∞+()()1e x af x x x '=+-由题意知,()()12e 2e 112e 1e f a f b ⎧=-=+⎪⎨=+-='⎪⎩解得,.1a =-e 1b =+(2)由题意有恒成立,即恒成立()2e ln 0x x x x m -+-+<()2e ln x m x x x <-+-+设,,.()()2e ln xg x x x x =-+-+1,12x ⎡⎤∈⎢⎥⎣⎦()()11e x g x x x ⎛⎫'=-- ⎪⎝⎭当时,,∴112x ≤≤10x -≥令,其中,则()1e x h x x =-1,12x ⎡⎤∈⎢⎥⎣⎦()21e 0x h x x '=+>所以函数在上单调递增()1e x h x x =-1,12x ⎡⎤∈⎢⎥⎣⎦因为,,所以存在唯一,1202h ⎛⎫=< ⎪⎝⎭()1e 10h =->01,12x ⎛⎫∈ ⎪⎝⎭使得,即,可得.()0001e 0x h x x =-=001e x x =00ln x x =-当时,,此时函数单调递减,012x x <<()0g x '>()g x 当时,,此时函数单调递增.01x x <<()0g x '<()g x ,∴()()()()00000000min 00122ln 2212x g x g x x e x x x x x x x ==-+-+=-+⋅+=-++,由对勾函数性质知函数在递减,21122(1y x x x x =-++=+-()0,1x ∈,.01,12x ⎛⎫∈ ⎪⎝⎭∴()()0002123,4g x x x =-++∈当时,不等式对任意恒成立,∴3m ≤()2e ln xm x x x <-+-+1,12x ⎡⎤∈⎢⎥⎣⎦正整数m 的最大值是3.∴【点睛】关键点点睛:第一个关键点首先要分离参数,将问题转化为恒成立,()2e ln x m x x x<-+-+第二个关键在于求取函数的最小值,需结合零点存在性定理得出隐零点()()2e ln x g x x x x=-+-+,分析的范围.01,12x ⎛⎫∈ ⎪⎝⎭()000212g x x x =-++22.在平面直角坐标系中,曲线的参数方程为(t 为参数),曲线xOy 1C 11x t t y t t ⎧=+⎪⎪⎨⎪=-⎪⎩,以坐标原点O 为极点,x 轴的非负半轴为极轴建立极坐标系.()222:24C x y -+=(1)求,的极坐标方程;1C 2C (2)若射线分别与曲线,相交于A ,B 两点,求的面积.()π06θρ=≥1C 2C 2C AB △【答案】(1),2cos 24ρθ=4cos ρθ=【分析】(1)两式平方相减消去参数即可得出曲线普通方程;利用将直角坐标方程1C cos sin x y ρθρθ=⎧⎨=⎩转化为极坐标方程;(2)利用极坐标的几何意义,求得的长,利用直线与夹角为及的长,求得AB 2OC π6θ=π62OC 边上的高,从而求得面积.AB 【详解】(1)依题意得,化简整理得:2222221212x t t y t t ⎧=++⎪⎪⎨⎪=-+⎪⎩224x y -=令,,化简得.cos x ρθ=sin y ρθ=2cos 24ρθ=对于,化简得:.()22222440x y x y x -+=⇒+-=4cos ρθ=(2)设,(),A A ρθ(),B B ρθ依题意得,解得2cos 24π6ρθθ⎧=⎪⎨=⎪⎩A ρ=,解得,4cos π6ρθθ=⎧⎪⎨=⎪⎩Bρ=∴B A AB ρρ=-=-设到射线的距离为d ,2C π6θ=,解得,2πsin6d OC =1d =∴(21122C AB S AB d =⋅==△23.已知函数.()13f x x x =-+-(1)解不等式;()1f x x ≤+(2)设函数的最小值为c ,正实数a ,b 满足,求的最小值.()f x a b c +=111a b ++【答案】(1)[]1,5(2)43【分析】(1)分类讨论去绝对值符号解不等式;(2)利用绝对值三角不等式得c 的值,再利用基本不等式求的最小值.111a b ++【详解】(1)当时,不等式可化为,,1x <4211x x x -≤+⇒≥x ∈∅当时,不等式可化为,得,即.13x ≤≤21x ≤+1x ≥13x ≤≤当时,不等式可化为,得,即.3x >241x x -≤+5x ≤35x <≤综上所述,原不等式的解集为.[]1,5(2)由绝对值不等式性质得,()()13132x x x x -+-≥-+-=所以,即.2c =2a b +=所以.()1111111412131313b a a b a b a b a b +⎛⎫⎛⎫⎡⎤+=+++=++≥ ⎪ ⎪⎣⎦+++⎝⎭⎝⎭当且仅当,即时取到等号,21a b a b +=⎧⎨=+⎩3212a b ⎧=⎪⎪⎨⎪=⎪⎩所以的最小值为.111a b ++43。
四川省绵阳市2024高三冲刺(高考数学)人教版考试(综合卷)完整试卷
四川省绵阳市2024高三冲刺(高考数学)人教版考试(综合卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题函数的大致图像是()A.B.C.D.第(2)题设,是两个不同的平面,,,是三条不同的直线.下列说法不正确的是()A.若,,则B.若,,则C.若,,则D.若,,,,则第(3)题若向量满足,则在上的投影向量为()A.B.C.D.第(4)题若集合,,那么()A.B.C.D.第(5)题如图所示,多面体ABCDEF中,已知平面ABCD是边长为3的正方形,,,EF到平面ABCD的距离为2,则该多面体的体积V为()A.B.5C.6D.第(6)题已知函数在上恰有1个零点,则的取值范围是()A.B.C.D.第(7)题已知,,,则a,b,c的大小关系是().A.B.C.D.第(8)题在内,使成立的的取值范围是A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题已知函数及其导函数的定义域均为,,,且当时,,则()A.B.C.D.第(2)题已知可导函数及其导函数的定义域均为,若是奇函数,,且对任意,恒有,则一定有()A.B.C.D.第(3)题已知函数,则下列说法正确的是()A.函数的最小正周期是B.,使C.在内有4个零点D.函数的图像是中心对称图形三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题如图,正方体ABCD-A1B1C1D1中,与AD1异面且与AD1所成角为90°的面对角线共有_______条.第(2)题在数列中,,则__________.第(3)题我国南北朝时期的数学家祖暅提出了计算体积的祖暅原理:“幂势既同,则积不容异.”意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.如图,阴影部分是由双曲线与它的渐近线以及直线所围成的图形,将此图形绕y轴旋转一周,得到一个旋转体,如用与x轴相距为,且垂直于y轴的平面,截这个旋转体,则截面图形的面积为______;这个旋转体的体积为______.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题从①前n项和②且这两个条件中任选一个,填至横线上,并完成解答.在数列中,,________,其中.(1)求数列的通项公式;(2)若,,成等比数列,其中m,,且,求m的最小值.(注:如果选择多个条件分别解答,那么按第一个解答计分)第(2)题已知是数列的前n项和,,______.①,;②数列为等差数列,且的前3项和为6.从以上两个条件中任选一个补充在横线处,并求解:(1)求;(2)设,求数列的前6项和.注:如果选择多个条件分别解答,按第一个解答计分.第(3)题在中,内角所对的边分别为且.(1)求角的大小;(2)若,且的面积为,求的周长.第(4)题在中,角,,的对边分别为,,,且.(1)求大小;(2)若为锐角三角形,且,求面积的取值范围.第(5)题已知.(1)若在处的切线的斜率是,求当在恒成立时的的取值范围;(2)设,当时有唯一零点,求a的取值范围.。
四川省攀枝花市2024高三冲刺(高考数学)人教版模拟(综合卷)完整试卷

四川省攀枝花市2024高三冲刺(高考数学)人教版模拟(综合卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:①y与x负相关且=2.347x﹣6.423;②y与x负相关且=﹣3.476x+5.648;③y与x正相关且=5.437x+8.493;④y与x正相关且=﹣4.326x﹣4.578.其中一定不正确的结论的序号是( )A.①②B.②③C.③④D.①④第(2)题不等式的解集为()A.B.C.D.或,第(3)题以下三组数据的标准差分别为,,.5,5,5,5,5,5,5,5,53,3,4,4,5,6,6,7,72,2,2,2,5,8,8,8,8则有()A.B.C.D.第(4)题已知为等边三角形,AB=2,设点P,Q满足,,,若,则=A.B.C.D.第(5)题已知集合,则()A.B.C.D.第(6)题在棱长为1的正方体中,、为线段上的两个三等分点,动点在内,且,则点的轨迹长度为()A.B.C.D.第(7)题,,则()A.B.C.D.第(8)题二项式展开式中,的系数为()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题已知圆,则()A.圆的圆心坐标为B.圆的周长为C.圆与圆外切D.圆截轴所得的弦长为3第(2)题在长方形ABCD中,,,点E,F分别为边BC和CD上两个动点(含端点),且,设,,则()A.,B.为定值C.的最小值50D.的最大值为第(3)题下列说法中,正确的是()A.设有一个经验回归方程为,变量增加1个单位时,平均增加2个单位B.已知随机变量,若,则C.两组样本数据和的方差分别为.若已知且,则D.已知一系列样本点的经验回归方程为,若样本点与的残差相等,则三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题已知函数(,),若为奇函数,且在上单调递减,则ω的最大值为______.第(2)题如图,该“四角反棱柱”是由两个相互平行且全等的正方形经过旋转、连接而成,其侧面均为等边三角形,则该“四角反棱柱”外接球的表面积与侧面面积的比为__________.第(3)题在四边形中,为中点.记,用表示_____________________;若,则的最大值为_____________________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知数列的前项和为,满足,且为,的等比中项.(1)求数列的通项公式;(2)设为数列的前项和,证明:.第(2)题为更好地发挥高考的育才作用,部分新高考试题采用了多选题这一新题型.多选题的评分规则如下:对于多选题,每个小题给出的四个选项中有两项或三项是正确的,满分6分.全部选对得6分,有错选或全不选的得0分.正确答案为两项时,选对1个得3分;正确答案为三项时,选对1个得2分,选对2个得4分.某数学小组研究发现,多选题正确答案是两个选项的概率为,正确答案是三个选项的概率为.现有一道多选题,学生李华完全不会,此时他有三种答题方案:Ⅰ.随机选一个选项;Ⅱ.随机选两个选项;Ⅲ.随机选三个选项.(1)若,且学生李华选择方案I,求本题得分的数学期望;(2)以本题得分的数学期望为决策依据,的取值在什么范围内唯独选择方案Ⅰ最好?第(3)题已知椭圆的上顶点为B,右焦点为F,点B、F都在直线上.(1)求椭圆的标准方程及离心率;(2)设直线与椭圆相切于第一象限内的点,不过原点且平行于的直线与椭圆交于不同的两点,,点关于原点的对称点为.记直线的斜率为,直线的斜率为,求的值.第(4)题已知双曲线E:的右焦点为,一条渐近线方程为.(1)求双曲线E的方程;(2)是否存在过点的直线l与双曲线E的左右两支分别交于A,B两点,且使得,若存在,求出直线l的方程;若不存在,说明理由.第(5)题商场对某种商品进行促销,顾客只要在商场中购买该商品,就可以在商场中参加抽奖活动.规则如下:先赋予参加抽奖的顾客5分的原始分,然后从装有4个红球,2个白球,2个黑球的盒中有放回地随机取球若干次,每次取出一个球,若为红球,则加1分,否则扣1分,过程中若顾客持有分数变为0分,抽奖结束;若顾客持有分数达到15分,则获得一等奖,抽奖结束.(1)求顾客3次取球后持有分数的数学期望;(2)设顾客在抽奖过程中持有分数为分最终获得一等奖的概率为;①证明:是等差数列;②求顾客获得一等奖的概率.。
高2013级第四次统考试题

攀枝花市2013级高三第四次统考英语本试卷分第一卷(选择题)和第二卷(非选择题)两部分。
共150分。
考试时间120分钟。
第一卷1至10页,第二卷11至12页。
第I卷(选择题,共90分)注意事项:1. 答第一卷时,考生务必将自己的姓名、准考证号、考试科目、试卷类型用铅笔涂写在答题卡上。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试卷上。
第一部分:英语知识运用(共两节,满分40分)第一节单项填空(共10小题;每小题1分,满分10分)从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
1. —I am sorry I broke your coffee cup.—______. I’m thinking to throw it away.A. That’s rightB. Forget itC. Not at allD. Don’t mention it2. Now that his cellphone is broken, John _____ buying a new one, but he hasn’t decided yet.A. had consideredB. has been consideringC. consideredD. is going to consider3. Ladies and gentlemen, would you please ______ your cellphones? Our plane is taking off in a minute.A. switch offB. keep offC. show offD. pay off4. —Why don’t you buy a car?—I . It takes me about twenty minutes to walk to my office.A. can’tB. may notC. shouldn’tD. needn’t5. She has been working for the last seven years as a night cleaner, ______ offices in a big building.A. cleansB. to cleanC. cleaningD. cleaned6. —Do you know something about Margret Thatcher, the former prime minister of Great Britain?—To tell you the truth, I have no knowledge whatever ______ her.A. onB. toC. ofD. in7. My experience tells me it is not ______ you are given but how you make use of it that determines who you are.A. whatB. thatC. whyD. whether8. The book is of great value. But I don’t think anything can be enjoyed ______ you absorb it.A. althoughB. becauseC. whenD. unless9. He graduated from a university ______ tradition is to encourage students to question what seems to be truth.A. whichB. whoseC. whenD. where10. It’s polite for you to say ―Thank you just the same.‖ if you really don’t need it when ______ help.A. offeringB. to offerC. offeredD. to be offered第二节完形填空(共20小题;每小题1.5分,满分30分)阅读下面短文,从短文后各题所给的四个选项(A、B、C和D)中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
四川省攀枝花市2023届高三第三次统一考试理科数学试题

中该金属含量低于最原始的 5%时,至少需要循环使用该技术的次数为( )(参考数
据: lg2 » 0.301)
A.12
B.13
C.14
D.15
10.已知函数
f
(
x)
=
sin
æ çè
w
x
+
π 3
ö ÷ø
(w
>
0)
对任意
x
Î
æ çè
0,
3π 8
ö ÷ø
都有
f
(
x)
>
1 2
w ,则当
取
到最大值时, f ( x) 图象的一条对称轴为( )
7
天的最高气温的平均数为
28 ´
2
+
29 ´3 7
+
30
+
31
=
204 7
>
29
,D
错.
故选:D. 4.B
【分析】根据程序框图,明确该程序的功能是求分段函数
f
(x)
=
ìíîlxo-g12 ,xx,
x > 1的值,由此根 £1
据该函数值域,可求得答案. 【详解】由程序框图可知:运行该程序是计算分段函数的值,
(2)若射线q
=
π 6
(r
³
0) 分别与曲线 C1 , C2 相交于 A,B
两点,求△C2 AB
的面积.
23.已知函数 f ( x) = x -1 + x - 3 .
(1)解不等式 f ( x) £ x +1;
(2)设函数
f
(x)
的最小值为
c,正实数
湖北省新高考联考协作体2024-2025学年高三上学期11月期中考试数学试题

湖北省新高考联考协作体2024-2025学年高三上学期11月期中考试数学试题一、单选题1.已知集合{}2340A x x x =--<,{}1,B x x x =>∈Z ,则A B = ()A .{}1,2,3-B .{}2,3C .{}3,2--D .{}3,2,0--2.若1i z =+,则i 3z z +=()A .B .C .D .3.已知x ,y 是任意实数,则:4p x y +≥是:1q x ≥且3y ≥的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.设,a b 均为非零向量,且()a ab ⊥- ,2b a = ,则a与b 的夹角为()A .6πB .4πC .3πD .23π5.若35log 2a =,0.115b -⎛⎫= ⎪⎝⎭,0.125c -⎛⎫= ⎪⎝⎭,则a ,b ,c 的大小关系为().A .a c b<<B .a b c<<C .c a b<<D .c b a<<6.已知等比数列{}n a 的前3项和为28,0n a >且5256a a -=,则6a =()A .28B .56C .64D .1287.已知π02βα<<<,()4sin 5αβ-=,tan tan 2αβ⋅=,则sin sin αβ=()A .15B .25C .12D .28.英国数学家牛顿在17世纪给出了一种求方程近似根的方法—牛顿迭代法,做法如下:如图,设r 是()0f x =的根,选取0x 作为r 的初始近似值,过点0,0作曲线=的切线()()()000:l y f x f x x x '-=-,则l 与x 轴的交点的横坐标10x x =-()()()()0000f x f x f x ''≠,称1x 是r 的第一次近似值;过点1,1作曲线=的切线,则该切线与x 轴的交点的横坐标为2x ,称2x 是r 的第二次近似值;重复以上过程,得r 的近似值序列,其中()()()()10n n n n n f x x x f x f x +''=-≠,称1n x +是r 的1n +次近似值,这种求方程()0f x =近似解的方法称为牛顿迭代法.若使用该方法求方程23x =的近似解,则下列正确的是()A .若取初始近似值为1,则过点1,1作曲线=的切线23y x =-B .若取初始近似值为1,则该方程解的第二次近似值为75C .()()()()()()01230012f x f x f x x x f x f x f x =--'''+D .()()()()()()()()01210012n n n f x f x f x f x x x f x f x f x f x +=---'--''' 二、多选题9.设等差数列{}n a 的前n 项和为n S ,公差为d ,10a >,670a a +>,670a a ⋅<,下列结论正确的是().A .60a <,70a >B .0d <C .130S <D .当7n =时,n S 最大10.已知实数,a b 满足()lg lg lg 4a b a b +=+,则下列结论正确的是()A .a b +的最小值为9B .1ab的最大值为14CD .lg lg a b +的最小值为4lg 211.函数()12xf x a b ⎛⎫=+ ⎪⎝⎭的图象过原点,且无限接近直线2y =但又不与该直线相交,则下列结论正确的是()A .2a =B .()()21f f ->C .若120x x <<,则()()1212122x x f f x f x +⎛⎫⎡⎤>+ ⎪⎣⎦⎝⎭D .方程()()2102f x f x -=有3个实数根三、填空题12.已知函数=,∈,且()03f =,()()0.520f f =,()()120.5f f =, ,()()()0.520.51f n f n =-,*n ∈N ,则()3f =.13.如图,函数()()()0,0πf x x ωϕωϕ=+><<的部分图象如图所示,已知点A ,D 为()f x 的零点,点B ,C 为()f x 的极值点,212AB DC AB ⋅=-,则ϕ=.14.若1n a n =-,*n ∈N ,记数列{}n a 的前n 项和为n S ,则2250n nS S +的最小值为.四、解答题15.已知函数()21cos sin 2f x x x x =+-.(1)求()f x 的单调减区间;(2)将函数=的图象向左平移π6个单位长度,再将所得图象上各点的横坐标变为原来的2倍(纵坐标不变),得到函数=的图象.若对任意1x ,2π,π6x ⎡⎤∈⎢⎥⎣⎦,()()12g x g x a-≤求实数a 的最小值.16.已知函数()323f x ax bx x =+-在点()()1,1f --处的切线方程为2y =(1)求函数()f x 的解析式;(2)若2m ≠-,且过点()1,m 可作曲线()y f x =的三条切线,求实数m 的取值范围.17.在ABC V 中,角A ,B ,C 所对的边分别为a ,b ,c ,且sin sin 2A C b C c +=(1)求角B 的大小;(2)设D 是边AC 上一点,BD 为角平分线且3AD DC =,求cos A 的值.18.已知函数()()212ln 2f x x ax x a =-+-∈R .(1)若3a =,求()f x 极值;(2)求函数()f x 的单调区间;(3)若函数()f x 有两个极值点1x ,()212x x x <,求证:()()12293ln 2f x f x +>-.19.把满足任意x ,y ∈R 总有()()()()2f x y f x y f x f y ++-=的函数称为“类余弦型”函数.(1)已知()f x 为“类余弦型”函数()0f x >,()1728f =,求1的值;(2)在(1)的条件下,定义数列:()()()*21n a f n f n n =+-∈N ,求10012222log log log 333a a a++⋅⋅⋅+的值;(3)若()g x 为“类余弦型”函数,且()g 00>,对任意非零实数t ,总有()g 1t >.设有理数1x ,2x 满足21x x >,判断()2g x 与()1g x 的大小关系,并给出证明.。
四川省成都市2024高三冲刺(高考数学)统编版测试(评估卷)完整试卷

四川省成都市2024高三冲刺(高考数学)统编版测试(评估卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知函数.若存在,使得成立,则实数a的最大值是()A.B.C.D.第(2)题牟合方盖是由我国古代数学家刘徽发现并采用的,一种用于计算球体体积的方法,类似于现在的微元法.由于其采用的模型像一个牟合的方形盒子,故称为牟合方盖.本质上来说,牟合方盖是两个半径相等并且轴心互相垂直的圆柱体相交而成的三维图形,如图1所示.刘徽发现牟合方盖后200多年,祖冲之及他的儿子祖暅,推导出牟合方盖八分之一部分的体积计算公式为(为构成牟合方盖的圆柱底面半径).图2为某牟合方盖的部分,且图2正方体的棱长为1,则该牟合方盖的体积为()A.B.C.D.第(3)题设,,,则a,b,c的大小关系是()A.B.C.D.第(4)题已知焦点为的抛物线上有一点,准线交轴于点.若,则直线的斜率()A.B.C.D.第(5)题的展开式中的系数是()A.B.0C.35D.70第(6)题若直线的一个方向向量,平面的一个法向量,则与所成角为()A.B.C.或D.或第(7)题动点到定点的距离与到定直线:的距离的比等于,则动点的轨迹方程是()A.B.C.D.第(8)题已知a,b是单位向量,a·b=0.若向量c满足|c-a-b|=1,则|c|的最大值为()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题如图,已知,点M,N满足,,BN与CM交于点P,AP交BC于点D,.则()A.B.C.D.第(2)题下列说法中正确的有()A.在回归分析中,决定系数越大,说明回归模型拟合的效果越好B.已知相关变量满足回归方程,则该方程对应于点的残差为1.1C.已知随机变量,若,则D.以拟合一组数据时,经代换后的经验回归方程为,则第(3)题已知函数的部分图象如图所示,若将函数的图象纵坐标不变,横坐标缩短到原来的,再向右平移个单位长度,得到函数的图象,则下列命题正确的有()A.函数的解析式为B.函数的最小正周期为C .函数在区间上单调递减D .是函数图象的一个对称中心三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题若直线是曲线与曲线的公切线,则___________,___________.第(2)题已知的展开式中只有第4项的二项式系数最大,且项的系数为,则______.第(3)题设是首项为的等比数列,是其前项和,若,则______.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题如图,已知三棱柱的侧棱垂直于底面,,,点,分别为和的中点.(1)证明:平面;(2)设,当为何值时,平面?试证明你的结论.第(2)题京剧被誉为中国文化的瑰宝.每个脸谱都有其独特的象征意义,是京剧中不可或缺的一个组成部分.某商店售卖的京剧脸谱娃娃共有三种款式,有直接购买和盲盒购买两种方式.若直接购买京剧脸谱娃娃,则每个京剧脸谱娃娃售价54元,可选定款式;若盲盒购买京剧脸谱娃娃,则每个盲盒售价27元,盲盒中的一款京剧脸谱娃娃是随机的.(1)甲采用盲盒购买的方式,每次购买一个盲盒并打开,若买到的京剧脸谱娃娃中出现相同款式,则停止购买.用表示甲购买盲盒的个数,求的分布列.(2)乙计划收集一套京剧脸谱娃娃(三种款式各一个),先购买盲盒,每次购买一个盲盒并打开(乙最多购买3个盲盒),若未集齐一套京剧脸谱娃娃,再直接购买没买到的款式,以购买费用的期望值为决策依据,问乙应购买多少个盲盒?第(3)题设函数.(1)当时,求的单调区间;(2)若f(x)有两个极值点,,求a的取值范围.第(4)题已知正项数列满足,.(1)若,请判断并证明数列的单调性;(2)若,求数列的前项和.第(5)题如图,已知椭圆,点是抛物线的焦点,过点F作直线交抛物线于M,N两点,延长,分别交椭圆于A,B两点,记,的面积分别是,.(1)求的值及抛物线的准线方程;(2)求的最小值及此时直线的方程.。
高三年级1月工作简讯

高三年级工作动态一、主要活动:1. 在年级主任杨树贵、顾迎宏、曹勇洪老师的组织下,全年级师生的共同配合下,本月顺利完成四次考试,分别为1月6日、7日的玉溪市市统测、1月12日、13日的攀枝花统测、1月24日的第十次周清、1月31日的期末考试,学科组长及时完成成绩统计分析并上报年级。
2.1月22日,全体师生在文化堂顺利召开玉溪市市统测学生表彰会。
会上,年级主任杨树贵、顾迎宏老师分别对本次成绩进行分析,对全体学生鼓励。
林云志老师的演讲振奋人心,让师生充满斗志。
王莉淇同学以激昂的情感带领全体学生宣誓。
3.高三学生综合素质档案于1月4日全部上交。
4. 1月9日——12日,高三部分学生参加学业水平考试补考,无缺考。
5. 本月共组织三次宿舍卫生安全纪律督查,时间分别为:1月4日、1月15日、1月20日。
第一次盘查较多违禁物品,以充电宝、不健康书籍为主,卫生情况、安全情况良好。
第二次第三次督查较第一次有很大好转,违禁物品明显减少。
6.美术考生于1月2日外出培训并考试。
出发前三位年级主任及班主任做了安全教育并签下安全责任书,由美术专业教师张志强带领,赴昆明做最后的考前准备,计划于2月4日艺考结束后返校。
7.1月15日,全体高三教师的教学常规、教研送至学术中心检查。
8.1月16日,高职机电专业学生返校。
9. 1月17——18日,体育教师张正富、蒋洪海及班主任杨发翠组织体育专业学生专业模拟检测。
二、教育研究:1.我校全体教师于1月12日、13日参加了攀枝花市的教学业务大练兵。
高三年级每位教师都能以平和的心态应对,认真参加相应学科的考试。
2. 1月4日,高三年级召开学科组长会,会上年级主任杨树贵老师做了统筹安排,各学科组长畅所欲言,对一轮复习进行总结,并初步规划二轮复习所用资料及方案。
三、其他工作:1.艺考学生返校相关安排2.体育考生外出考试准备3.寒假安排(放假时间、收假时间、寒假作业、假期安全)。
四川省乐山市2024高三冲刺(高考物理)统编版(五四制)质量检测(备考卷)完整试卷

四川省乐山市2024高三冲刺(高考物理)统编版(五四制)质量检测(备考卷)完整试卷一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题一石块做自由落体运动,当下落速度为v时,其下落时间t和下降高度h分别为( )A.,B.,C.,D.,第(2)题如图所示,质量为m2的物体Q通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与另一质量为m1的物体P相连,P与水平地面之间的动摩擦因数μ=0.3,轻绳OA与竖直方向的夹角θ=37°,轻绳OA能承受的最大拉力为300 N.欲使Q、P均保持静止,且轻绳OA不断裂,则P、Q的质量可能为(已知sin 37°=0.6,cos 37°=0.8,g取10 m/s2,设最大静摩擦力等于滑动摩擦力) ( )A.m1=80 kg,m2=30 kg B.m1=70 kg,m2=30 kgC.m1=65 kg,m2=20 kg D.m1=45 kg,m2=20 kg第(3)题如图所示,两个可视为质点的带同种电荷的小球a和b,放置在一个光滑绝缘半球面内,已知小球a和b的质量分别为m1、m2,电荷量分别为q1、q2,两球处于平衡状态时α<β.则以下判断正确的是A.m1>m2B.m1<m2C.q1>q2D.q1<q2第(4)题对于光的认识,下列说法正确的是( )A.光不容易观察到衍射现象是因为光的速度太大B.偏振光可以是横波,也可以是纵波C.照相机镜头的偏振滤光片可使水下影像清晰D.雨后路面上的油膜呈现彩色,是光的折射现象第(5)题如图所示为杂技“顶竿”表演,一人站在地上,肩上扛一质量为M的竖直竹竿,竿上有一质量为m的人可以看成质点,当此人沿着竖直竿以加速度a加速下滑时,竿对地面上的人的压力大小为( )A.(M+m)g+ma B.(M+m)g-maC.(M+m)g D.(M-m)g第(6)题图(a)所示的我国首次火星探测任务“天问一号”探测器成功实施第三次近火制动,进入火星停泊轨道,若探测器的停泊轨道可简化为图(b)所示的椭圆轨道,其中的P点为近火点,Q点为远火点,则可知( )A.探测器在P点的速度小于在Q点的速度B.探测器在P点的加速度小于在Q点的加速度C.探测器从P点运动到Q点的过程中,机械能逐渐减小D.探测器从P点运动到Q点的过程中,机械能保持不变第(7)题2021年国庆期间播放的电视剧《功勋》中,介绍了我国核潜艇之父黄旭华隐姓埋名30年,埋下头甘心做沉默的砥柱,如深海中的潜艇,无声但有无穷的力量。
四川省成都市2024高三冲刺(高考数学)人教版质量检测(综合卷)完整试卷

四川省成都市2024高三冲刺(高考数学)人教版质量检测(综合卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题过点作抛物线的两条切线,切点分别为,则的最小值为()A.B.C.D.第(2)题在三棱锥中,侧面是等边三角形,平面平面,且,则三棱锥外接球的表面积为()A.B.C.D.第(3)题已知双曲线的右焦点为,一条渐近线方程为,则C的方程为()A.B.C.D.第(4)题对于每一对实数,,函数满足函数方程,如果,那么满足的的个数是()A.1个B.2个C.3个D.无数多个第(5)题甲、乙两同学进行棒球比赛,约定连胜两局者胜出,比赛结束,最多比赛五局,若前四局不分胜负,则第五局胜者获胜,比赛结束.已知甲每局获胜的概率为,每局比赛没有平局,结果相互独立,则甲第一局获胜并最终获得胜利的概率为()A.B.C.D.第(6)题已知某圆台的上底面和下底面的面积分别为、,高为,则该圆台的体积为()A.B.C.D.第(7)题已知复数满足,则()A.B.C.D.第(8)题已知双曲线为坐标原点,若直线与双曲线的两条渐近线分别交于点,则内切圆的半径等于()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题若,,则()A.B.C.D.第(2)题为庆祝江西籍航天员邓清明顺利从太空返航,邓清明家乡的某所中学举办了一场“我爱星辰大海”航天知识竞赛,满分100分,该校高一(1)班代表队6位参赛学生的成绩(单位:分)分别为:84,100,91,95,95,98,则关于这6位参赛学生的成绩.下列说法正确的是()A.众数为95B.中位数为93C.平均成绩超过93分D.第分位数是91第(3)题函数,(,,)在一个周期内的图象如图所示,则()A.B.C.D.三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题已知,则的最小值为____________.第(2)题在正三棱柱中,D为棱AB的中点,与交于点E,若,则CD与所成角的余弦值为___.第(3)题已知函数的定义域为,为单调函数且对任意的都有,若方程有两解,则实数的取值范围是___________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知数列是公差为的等差数列,且满足.(1)求的通项公式;(2)设,求数列的前10项和.第(2)题某学校为了解本校文、理科学生的学业水平模拟测试数学成绩情况,分别从理科班学生中随机抽取人的成绩得到样本甲,从文科班学生中随机抽取人的成绩得到样本乙,根据两个样本数据分别得到如下直方图:甲样本数据直方图乙样本数据直方图已知乙样本中数据在的有个.(1)求和乙样本直方图中的值;(2)试估计该校理科班学生本次模拟测试数学成绩的平均值和文科班学生本次模拟测试数学成绩的中位数(同一组中的数据用该组区间中点值为代表).第(3)题设正项等比数列满足,.(1)求的通项公式;(2)记,为数列的前项和,求使得的的取值范围.第(4)题已知是坐标原点,抛物线的焦点为,点在上,线段是圆的一条直径,且的最小值为.(1)求的方程;(2)过点作圆的两条切线,与分别交于异于点的点,求直线斜率的最大值.第(5)题已知椭圆的长轴长为,其离心率与双曲线的离心率互为倒数.(1)求椭圆的方程;(2)将椭圆上每一点的横坐标扩大为原来的倍,纵坐标不变,得到曲线,若直线与曲线交于、两个不同的点,为坐标原点,是曲线上的一点,且四边形是平行四边形,求四边形的面积.。
四川省眉山市2024高三冲刺(高考物理)统编版(五四制)真题(评估卷)完整试卷

四川省眉山市2024高三冲刺(高考物理)统编版(五四制)真题(评估卷)完整试卷一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题如图所示,质量为m、带电荷量为的小球(可视为质点)与长为L的绝缘轻绳相连,轻绳另一端固定在O点,整个系统处在与竖直方向夹角为的匀强电场中。
已知A、B、C、D、E、F为圆周上的点,为水平直径,为竖直直径,过O点且与的夹角为,当小球绕O点在竖直平面内做半径为L的圆周运动时,小球运动到A点时的速度最小,最小速度为,g为重力加速度的大小,则下列说法正确的是( )A.匀强电场的电场强度大小为B.小球从A点运动到B点时,合力做的功为C.小球运动到B点时轻绳拉力的大小为D.小球运动到F点时的机械能最大第(2)题两个点电荷固定在x轴上的M、N点,x轴上各点的电场强度E与各点位置坐标x之间的关系如图所示。
取x轴正方向为电场强度的正方向,无穷远电势为零,下列说法正确的是( )A.固定在M点的点电荷电量比固定在N点的点电荷电量小B.Q点的电势等于零C.从C点由静止释放一正点电荷,仅在电场力作用下,到D点前它将一直做加速运动D.从P点由静止释放一负点电荷,仅在电场力作用下,在它向左运动过程中电势能将一直减小第(3)题中国北斗导航系统是中国自主研制的全球卫星导航系统,北斗导航系统由24颗中圆地球轨道卫星、3颗地球静止轨道同步卫星和3颗倾斜地球轨道卫星,共30颗卫星组成。
关于这3颗地球静止轨道卫星,下列说法正确的是( )A.向心加速度相同B.可能经过广州上空C.受到的向心力大小相同D.线速度小于第一宇宙速度第(4)题如图,商场内某顾客站在自动扶梯上随扶梯一起上行,扶梯与水平面夹角为,速度为,将速度沿水平和竖直方向分解,则顾客在竖直方向的分速度为( )A.B.C.D.第(5)题核潜艇是以核反应堆为动力来源,若反应堆的一个核反应方程式为,则( )A.,Y为元素B.,Y为C.有56个质子,144个中子D.核比核的比结合能小第(6)题我国于2024年1月研发出全球首款民用核电池.该核电池利用半衰期约为100年的镍63来工作,其衰变方程为:Ni→Y+X,则( )A.X是电子B.X是粒子C.Y与Ni是同位素D.Y的中子数为29第(7)题如图所示,一个质量为m的物块,左端与轻弹簧栓接,轻弹簧的另一端固定在墙上的O点,物块和地面间的动摩擦因数为。
四川省甘孜藏族自治州2024高三冲刺(高考物理)统编版(五四制)模拟(评估卷)完整试卷

四川省甘孜藏族自治州2024高三冲刺(高考物理)统编版(五四制)模拟(评估卷)完整试卷一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题在地质、地震、勘探、气象和地球物理等领域的研究中,需要精确的重力加速度g值,g值可由实验精确测得,近年来测g值的一种方法叫“对称自由下落法”,它是将测g转变为测长度和时间,具体做法是:将真空长直管沿竖直方向放置,自其中O点上抛的小球又落回原处的时间为T2,在小球运动过程中经过比O点高H的P点,小球离开P点到又回到P点所用的时间为T1,测得T1、T2和H,可求得g等于( )A.B.C.D.第(2)题波源按照的规律振动,时刻在介质中形成的波形图如图,由此可知该波在5s时间内传播的距离为( )A.10m B.8mC.5m D.2m第(3)题质量为1kg的物块放在一个纵截面为矩形的静止木箱内,物块和木箱水平底面之间的动摩擦因数为0.3,开始时物块被一根轻弹簧用1.6N的水平拉力向左拉着而保持静止;如图所示。
设最大静摩擦力等于滑动摩擦力,g取10m/s2。
则()A.木箱以2m/s2的加速度竖直向下加速时,物块与木箱之间发生相对滑动B.木箱以2m/s2的加速度竖直向上加速时,物块与木箱之间发生相对滑动C.木箱以4m/s2的加速度水平向左加速时,物块与木箱之间发生相对滑动D.木箱以1m/s2的加速度水平向右加速时,物块所受的摩擦力为2.6N第(4)题下列四幅图涉及不同的物理知识,其中说法不正确的是( )A.图甲是在显微镜下观察到的一个布朗微粒一段时间内的运动径迹B.普朗克为了解释图乙黑体辐射规律最先提出了能量子的概念C.卢瑟福通过分析图丙α粒子散射实验结果建立了原子核式结构模型D.电子束通过铝箔后在胶片上得到图丁的图样说明了电子具有波动性第(5)题在如图所示的光电效应实验中,将滑动触头P移到a端。
用单色光M照射阴极K时,电流计G的指针不会发生偏转;将滑动触头P移到b端,用单色光N照射阴极K时,电流计G的指针会发生偏转,则下列说法正确的是( )A.M光的强度一定小于N光的强度B.M光的频率一定大于N光的频率C.用N光照射阴极K时将P移到a端,电流计G的指针一定会发生偏转D.用M光照射阴极K时将P移到c处,电流计G的指针可能会发生偏转第(6)题在我国北方部分地区经常出现低温雨雪冰冻天气,高压输电线因结冰而造成严重损毁,如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
攀枝花市高三第四次统一考试理科综合·物理理科综合考试时间共150分钟,满分300分,其中物理110分,化学100分,生物90分。
物理试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)。
共4页。
考生作答时,须将答案答在答题卡物理答题区上,在本试题卷、草稿纸上答题无效。
第Ⅰ卷(选择题 共42分)注意事项:1.答题前,务必将自己的姓名、考号填写在答题卡规定的位置上。
并用2B 铅笔将答题卡考号对应数字标号涂黑。
2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
第Ⅰ卷共7题,每题6分。
每题给出的四个选项中,有的只有一个选项、有的有多个选项符合题目要求,全部选对的得6分,选对但不全的得3分,有选错的得0分。
1.关于电磁波的下列叙述中,正确的是 A .波长越大的电磁波,越容易发射 B .把传递信号“加”到载波的过程叫调谐C .根据光速不变原理,电磁波在不同介质中的传播速度相同D .赫兹第一次用实验证实了电磁波的存在2.如图甲所示是用干涉法检查厚玻璃板a 的上表面是否平整的装置, b 是标准样板。
图乙所示干涉条纹,是两个表面反射光的叠加而形成的,这两个表面是 A .a 的上表面、b 的下表面 B .a 的上表面、b 的上表面 C .a 的下表面、b 的上表面 D .a 的下表面、b 的下表面 3.矩形金属线圈共110匝,在匀强磁场中绕与磁感线垂直的轴匀速转动,如图甲所示.产生的感应电动势如图乙所示,则 A .此交流电的频率为0.5Hz B .t =0.5s 时,线圈平面平行于磁场C .此交变电动势有效值为220VD .穿过线圈的最大磁通量为501Wb 4.如图所示,三个重均为100N 的物块,叠放在水平桌面上,各接触面水平,水平拉力F =20N 作用在物块2上,三条轻质绳结于O 点,水平绳与物块3连接,竖直绳悬挂重物B ,倾斜绳通过定滑轮与物体A 连接,已知倾斜绳与水平绳间的夹角为120o ,A 物体重40N ,不计滑轮质量及摩擦,整个装置处于静止状态。
则物块3受力个数为-2s图乙a 乙甲A .3个B .4个C .5个D .6个5.一列沿x 轴正向传播的简谐横波,波速为2m/s ,在t =1.5s 时刻的波形如右图,图中x =2m 处的质点振动图象应是下图中的哪个6. MA VEN 火星探测器于2014年9月进入火星轨道,至今年4月的第二周完成了绕火星运行的第1000圈。
若MA VEN 火星探测器在地球、火星表面受到的重力分别为G 1、G 2,已知地球半径为R 1,火星半径为R 2,地球表面处的重力加速度为g ,则A .火星表面处的重力加速度为g G G 12B .火星与地球的质量之比为212221R G R G C .火星与地球的第一宇宙速度之比为1122R G R G D .MA VEN 火星探测器沿火星表面轨道上做匀速圆周运动的周期为1222gG G R π7. 如图所示,在xOy 坐标平面内,质量为m 、电荷量为e 的质子以某一初速度从坐标原点O 沿x 轴正方向进入场区(第一象限内),若场区仅存在平行于y 轴向上的匀强电场时,质子通过P (2d ,d )点时的动能为k E ;若场区仅存在垂直于xOy 平面的匀强磁场时,质子也能通过P 点。
不计质子的重力。
设上述匀强电场的电场强度大小为E 、匀强磁场的磁感应强度大小为B ,则下列说法中正确的是A.edEE k= B.edE E k2=C.edmE B k 52=D.edmE B k 52=第Ⅱ卷 (非选择题 共68分)注意事项:ABCD必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答。
作图题可先用铅笔绘出,确认后再用0.5毫米黑色签字笔描清楚。
答在试题卷上、草稿纸上无效。
8.(17分) (1)(5分)图为验证机械能守恒定律的实验装置示意图。
现有的器材为:带铁夹的铁架台、电磁打点计时器、纸带、带铁夹的重锤、天平、秒表。
回答下列问题:①为完成此实验,除了所给的器材,还需要的器材为 。
②上述器材中,实验不需要的器材有 。
(2)(12分)如图甲是利用伏安法测量电源的电动势和内阻的电路图,图中的器材为:A.待测电源;B.电压表(量程1.5V ,内阻1.5kΩ);C.电流表(量程0.6A ,内阻约为0.1Ω);D.滑动变阻器(阻值0―50Ω);定值电阻(R 0=500Ω)。
①按电路图在图乙虚线框内各实物图之间画出连线。
②在你连接的实物图中,开关S 闭合前,滑动变阻器的滑片P 置于 端(填a 或b )。
③闭合开关S ,移动滑动变阻器的滑动端P 至某一位置,读出电流表、电压表读数。
多次改变滑动端P 的位置,得到的数据如下:在图丙所示的坐标纸上以U 为纵坐标,I 为横坐标,画出对应的U -I 图象。
④实验测得的电源电动势E = V ,内阻r = Ω。
9.(15分)图甲A_ +ES图乙图丙abP上海大众生产的一款豪华型小汽车,搭载有EA888发动机和7挡双离合变速箱,整车质量为1.5×103kg ,EA888发动机的最大输出功率为120kw ,该车在某段路面上行驶的最大速度为180km/h 。
设汽车行驶过程中受到的阻力恒定,重力加速度g 取10m/s 2。
求: (1) 汽车在该路段上行驶过程中受到的阻力是车重的多少倍;(2) 汽车由静止开始以2m/s 2的加速度,在该路段上匀加速直线行驶的最长时间。
10.(17分)如图所示,相距均为L =1m 的光滑倾斜导轨MN 、PQ 与粗糙水平导轨NS 、QT 连接,水平导轨处在磁感应强度大小B =0.5T ,方向水平向左的匀强磁场中。
倾斜导轨的ef 、gh 之间的区域存在磁感应强度大小也为0.5T ,方向垂直于倾斜导轨所在平面向下的匀强磁场。
金属导体棒ab 、cd 垂直于导轨分别放在倾斜导轨和水平导轨上,并与导轨接触良好,不计导轨电阻。
连接导体棒cd 的绝缘细线通过定滑轮悬挂物体C (静止)。
细线沿导轨中心线且在导轨平面内,细线及滑轮质量、滑轮摩擦均不计。
已知棒ab 质量m 1=0.2kg ,棒cd 质量m 2=0.1kg,两棒电阻均为R =0.25Ω,C 的质量m c =0.025kg ,倾斜导轨与水平面的夹角θ=300,重力加速度g 取10m/s 2,ef 、gh 之间的距离S =1m ,棒cd 与水平导轨间的动摩擦因数μ=0.5,导轨足够长,C 距地面足够远,现将导体棒ab 从距ef 一定距离的位置由静止释放,刚好能匀速通过ef 、gh 间的区域,试求:(1) 导体棒ab 通过ef 、gh 间的区域的速度大小。
(2) 导体棒cd 在水平轨道上运动的最大距离。
11.(19分)如图甲所示,在xOy 平面内,正六边形ONPQRS 的边长为L ,某一顶点O 与坐标原点重合,边OS 与x 轴重合,正六边形内有垂于xOy 平面的恒定匀强磁场,正六边形的ON 边左下方有沿平面的匀强电场,场强大小为03E ,方向与x 轴的夹角为300。
一质量为m ,带电量为+q 的带电粒子从A 点由静止释放,刚好从正六边形的PQ 边中点垂直于PQ 边射出,已知A 点到原点O 的距离为L ,不计粒子所受重力,求:(1) 粒子进入磁场时的速度大小;(2) 粒子在磁场中的运动时间及磁场的磁感应强度的大小;(3) 若正六边形内的匀强磁场按图乙所示的规律随时间变化,0时刻粒子进入磁场,4T 0时刻粒子从正六边形的QR 边中点垂直于QR 边射出,已知乙图中的qLmE B 002,磁场方向垂直纸面向里为正,求T 0多大?攀枝花市2015届高三第四次统一考试 2015.5理科综合·物理参考答案及评分标准第Ⅰ卷选择题(每小题6分,共42分,全对6分,对而不全得3分)8.(1)①低压交流电源、刻度尺(3分);②天平、秒表(2分)。
(2)①如图(3分);②a (与图对应)(2分);③如图(3分);④1.99(1.97-2.00)(2分),0.8(0.75-0.85)(2分)9.解:(1)设汽车受到的阻力为车重的k 倍,则由功率公式得:m V F P 0=额(2分)汽车以最大速度运动时kmg f F ==0(2分) 联立以上各式并代入数据得:16.0=k (2分)(2)汽车以加速度a 匀加速运动时,由牛顿第二定律得:ma f F =-(3分)设保持这一加速度匀加速运动的最大速度为v m ,则由功率公式得:m Fv P =额(2分)由匀变速运动公式得:m m at v =(2分) 联立以上各式并代入数据得:1.119100≈=m t s (2分) 10.解:(1)设导体棒ab 通过ef 、gh 间区域的速度大小为v ,则由法拉弟电磁感应定律、欧姆定律、安培力公式及力的平衡得:BLv E =(1分)REI 2=(1分)BIL F =(1分)θsin 1g m F =(1分) 联立以上各式并代入数据得:2=v m/s (1分)(2)棒ab 进入磁场前,棒cd 处于静止状态。
设棒ab 在磁场中运动过程中,水平导轨对棒cd 的支持力为N 1,由平衡条件得:030sin 102.0101.0sin 01221=⨯⨯-⨯=-=-=θg m g m F g m N (1分)A_ +ES图乙图丙abP棒cd 、物体C 受力如图,由牛顿第二定律得:121a m T =(1分) 11a m T g m c c =-(1分)棒ab 通过磁场的时间:vSt =1(1分)此时间内棒cd 运动的距离:211121t a s =(1分)棒ab 离开磁场,棒cd 速度:111t a v =(1分)棒ab 离开磁场后,棒cd 、物体C 受力如图,由牛顿第二定律得:222a m T f =- (1分) 22a m g m T c c =-(1分) g m N f 2μμ==(1分)设棒ab 离开磁场后,棒cd 运动的最大距离为s 2,则222120s a v -=-(1分)联立以上各式并代入数据得棒cd 运动的最大距离:5.025.025.021=+=+=s s s m (2分) 11.解:(1)设粒子进入磁场时的速度大小为v ,由动能定理得:2002130cos 3mv L qE =(3分) mL qE v 03=(2分) (2)粒子在磁场中的运动轨迹如图,由几何知识可得,轨道半径为:L r 23=(2分) 由洛仑兹力公式及匀速圆周运动公式得:qBv f =rv m F n 2= f F n =(2分)联立以上各式得:qLmE B 320=(2分)(3)设如图乙所示的磁场中运动的轨道半径为r 0,由洛仑兹力公式及匀速圆周运动公式得:vqB f 00=020r v m F n = 00f F n =(2分)粒子在磁场中运动的轨迹如图中的曲线DEFG 。
