第四章 传热习题参考答案
《传热学》课后习题答案-第四章
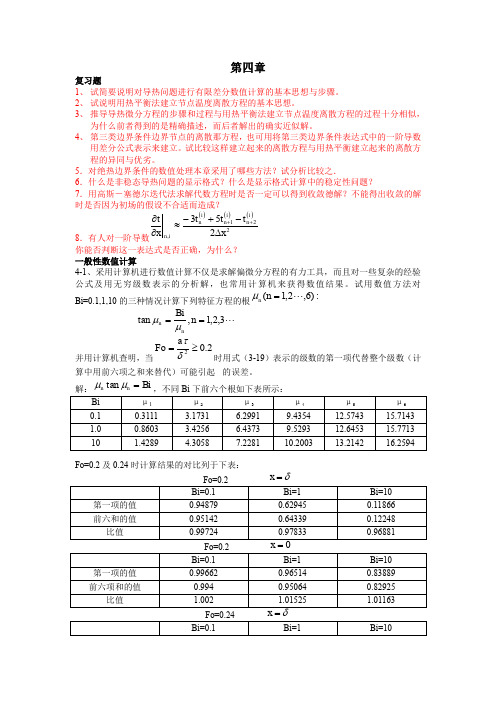
t k i,j 1 t k i,j t k i,j 1 t k i , j r r rj rj r 2 r 2 rj r
并简化,可以得出与上式完全一样相同的结果。
4-7、 一金属短圆柱在炉内受热厚被竖直地移植到空气中冷却, 底面可以认为是绝热的。为用数值法确定冷却过程中柱体温 度的变化, 取中心角为 1rad 的区域来研究 (如本题附图所示) 。 已知柱体表面发射率,自然对流表面传热系数,环境温度, 金属的热扩散率,试列出图中节点(1,1) , (M,1)(M,n)及 (M,N) 的离散方程式。 在 r 及 z 方向上网格是各自均分的。 解:应用热平衡法来建立四个节点点离散方程。 节点(1,1) :
, 离散方程的建立 4-5、试将直角坐标中的常物性无内热源的二维稳态导热微分方程化为显式差分格式,并指 出其稳定性条件( x y) 。 解:常物性无内热源二维非稳态方程微分方程为
4.3636t 2 2.53t1 1.8336t f
t2
2.53t f 1.8336t f
2t 2t t a x 2 y 2
Bi=0.1,1,10 的三种情况计算下列特征方程的根
n (n 1,2,6) :
n a Fo 2 0.2 并用计算机查明,当 时用式(3-19)表示的级数的第一项代替整个级数(计
算中用前六项之和来替代)可能引起 的误差。 解: n Bi 0.1 1.0 10
tan n
第四章
复习题 1、 试简要说明对导热问题进行有限差分数值计算的基本思想与步骤。 2、 试说明用热平衡法建立节点温度离散方程的基本思想。 3、 推导导热微分方程的步骤和过程与用热平衡法建立节点温度离散方程的过程十分相似, 为什么前者得到的是精确描述,而后者解出的确实近似解。 4、 第三类边界条件边界节点的离散那方程,也可用将第三类边界条件表达式中的一阶导数 用差分公式表示来建立。试比较这样建立起来的离散方程与用热平衡建立起来的离散方 程的异同与优劣。 5.对绝热边界条件的数值处理本章采用了哪些方法?试分析比较之. 6.什么是非稳态导热问题的显示格式?什么是显示格式计算中的稳定性问题? 7.用高斯-塞德尔迭代法求解代数方程时是否一定可以得到收敛德解?不能得出收敛的解 时是否因为初场的假设不合适而造成?
化工原理:传热习题(含答案)

第四章 传热一、填空题:1、在包有二层相同厚度保温材料的园形管道上,应该将 材料包在内层,其原因是 , 导热系数小的 减少热损失 降低壁面温度2、厚度不同的三种平壁,各层接触良好,已知321b b b >>;导热系数321λλλ<<。
在稳定传热过程中,各层的热阻R 1 R 2 R 3 各层的导热速率Q 1 Q 2 Q 3 在压强恒定的条件下,空气的粘度随温度降低而—————————— 。
解①R 1>R 2>R 3 , Q 1=Q 2=Q 3 ②降低 3、①物体辐射能力的大小与 成正比,还与 成正比。
②流体沸腾根据温度差大小可分为 、 、 、三个阶段,操作应控制在 。
因为40100⎪⎭⎫⎝⎛==T c E E b εε ∴E ∝T 4 ,E ∝ε ②自然对流 泡状沸腾 膜状沸腾 泡状沸腾段 4、①列管式换热器的壳程内设置折流的作用在于 ,折流挡板的形状有 等。
②多层壁稳定导热中,若某层的热阻最大,则该层两侧的温差 ;若某层的平均导热面积最大,则通过该层的热流密度 。
解①提高壳程流体的流速,使壳程对流传热系数提高 , 园缺形(弓形),园盘和环形②最大 , 最小 5、①在确定列管换热器冷热流体的流径时,一般来说,蒸汽走管 ;易结垢的流体走管 ;高压流体走管 ;有腐蚀性液体走管 ;粘度大或流量小的流体走管 。
①外, 内 ,内 , 内 , 外 6、①在一卧式加热器中,利用水蒸汽冷凝来加热某种液体,应让加热蒸汽在 程流动,加热器顶部设置排气阀是为了 。
②列管换热器的管程设计成多程是为了 ;在壳程设置折流挡板是为了 ; 解 ①壳程 , 排放不凝气,防止壳程α值大辐度下降 ②提高管程值 α , 提高壳程值α 7、①间壁换热器管壁wt 接近α 侧的流体温度;总传热系数K 的数值接近 一侧的α值。
②对于间壁式换热器:mt KA t t Cp m T T Cp m ∆=-=-)()(122'2211'1等式成立的条件是 、 、 。
化工原理课后习题答案第4章传热习题解答

化工原理课后习题答案第4章传热习题解答习 题1. 如附图所示。
某工业炉的炉壁由耐火砖λ1=1.3W/(m·K )、绝热层λ2=0.18W/(m·K )及普通砖λ3=0.93W/(m·K )三层组成。
炉膛壁内壁温度1100o C ,普通砖层厚12cm ,其外表面温度为50 o C 。
通过炉壁的热损失为1200W/m 2,绝热材料的耐热温度为900 o C 。
求耐火砖层的最小厚度及此时绝热层厚度。
设各层间接触良好,接触热阻可以忽略。
已知:λ1=1.3W/m·K ,λ2=0.18W/m·K ,λ3=0.93W/m·K ,T 1=1100 o C ,T 2=900 o C ,T 4=50o C ,3δ=12cm ,q =1200W/m 2,Rc =0求: 1δ=?2δ=? 解: ∵δλT q ∆=∴1δ=m q T T 22.0120090011003.1211=-⨯=-λ又∵33224234332322λδλδδλδλ+-=-=-=T T T T T T q ∴W K m q T T /579.093.012.01200509002334222⋅=--=--=λδλδ得:∴m 10.018.0579.0579.022=⨯==λδ习题1附图 习题2附图2. 如附图所示。
为测量炉壁内壁的温度,在炉外壁及距外壁1/3厚度处设置热电偶,测得t 2=300 o C ,t 3=50 o C 。
求内壁温度t 1。
设炉壁由单层均质材料组成。
已知:T 2=300o C ,T 3=50o C求: T 1=?解: ∵δλδλ31323T T T Tq -=-=∴T 1-T 3=3(T 2-T 3)T 1=2(T 2-T 3)+T 3=3×(300-50)+50=800 o C3. 直径为Ø60×3mm 的钢管用30mm 厚的软木包扎,其外又用100mm 厚的保温灰包扎,以作为绝热层。
化工原理答案 第四章 传热

第四章 传 热热传导【4-1】有一加热器,为了减少热损失,在加热器的平壁外表面,包一层热导率为(m·℃)、厚度为300mm 的绝热材料。
已测得绝热层外表面温度为30℃,另测得距加热器平壁外表面250mm 处的温度为75℃,如习题4-1附图所示。
试求加热器平壁外表面温度。
解 2375℃, 30℃t t ==计算加热器平壁外表面温度1t ,./()W m λ=⋅016℃ (1757530025005016016)t --= ..145025********t =⨯+=℃【4-2】有一冷藏室,其保冷壁是由30mm 厚的软木做成的。
软木的热导率λ= W/(m·℃)。
若外表面温度为28℃,内表面温度为3℃,试计算单位表面积的冷量损失。
解 已知.(),.123℃, 28℃, =0043/℃ 003t t W m b m λ==⋅=, 则单位表面积的冷量损失为【4-3】用平板法测定材料的热导率,平板状材料的一侧用电热器加热,另一侧用冷水冷却,同时在板的两侧均用热电偶测量其表面温度。
若所测固体的表面积为0.02m 2,材料的厚度为0.02m 。
现测得电流表的读数为2.8A ,伏特计的读数为140V ,两侧温度分别为280℃和100℃,试计算该材料的热导率。
解 根据已知做图热传导的热量 .28140392Q I V W =⋅=⨯=.().()12392002002280100Qb A t t λ⨯==-- 【4-4】燃烧炉的平壁由下列三层材料构成:耐火砖层,热导率λ=(m·℃),厚度230b mm =;绝热砖层,热导率λ=(m·℃);普通砖层,热导率λ=(m·℃)。
耐火砖层内侧壁面温度为1000℃,绝热砖的耐热温度为940℃,普通砖的耐热温度为130℃。
(1) 根据砖的耐热温度确定砖与砖接触面的温度,然后计算绝热砖层厚度。
若每块绝热砖厚度为230mm ,试确定绝热砖层的厚度。
化工原理习题及答案

第四章传热一、名词解释1、导热若物体各部分之间不发生相对位移,仅借分子、原子和自由电子等微观粒子的热运动而引起的热量传递称为热传导(导热)。
2、对流传热热对流是指流体各部分之间发生相对位移、冷热流体质点相互掺混所引起的热量传递。
热对流仅发生在流体之中, 而且必然伴随有导热现象。
3、辐射传热任何物体, 只要其绝对温度不为零度 (0K), 都会不停地以电磁波的形式向外界辐射能量, 同时又不断地吸收来自外界物体的辐射能, 当物体向外界辐射的能量与其从外界吸收的辐射能不相等时, 该物体就与外界产生热量的传递。
这种传热方式称为热辐射。
4、传热速率单位时间通过单位传热面积所传递的热量(W/m2)5、等温面温度场中将温度相同的点连起来,形成等温面。
等温面不相交。
二、单选择题1、判断下面的说法哪一种是错误的()。
BA 在一定的温度下,辐射能力越大的物体,其黑度越大;B 在同一温度下,物体吸收率A与黑度ε在数值上相等,因此A与ε的物理意义相同;C 黑度越大的物体吸收热辐射的能力越强;D 黑度反映了实际物体接近黑体的程度。
2、在房间中利用火炉进行取暖时,其传热方式为_______ 。
CA 传导和对流B 传导和辐射C 对流和辐射3、沸腾传热的壁面与沸腾流体温度增大,其给热系数_________。
CA 增大B 减小C 只在某范围变大D 沸腾传热系数与过热度无关4、在温度T时,已知耐火砖辐射能力大于磨光铜的辐射能力,耐火砖的黑度是下列三数值之一,其黑度为_______。
AA 0.85B 0.03C 15、已知当温度为T时,耐火砖的辐射能力大于铝板的辐射能力,则铝的黑度______耐火砖的黑度。
DA 大于B 等于C 不能确定是否大于D 小于6、多层间壁传热时,各层的温度降与各相应层的热阻_____。
AA 成正比B 成反比C 没关系7、在列管换热器中,用饱和蒸汽加热空气,下面两项判断是否正确: A甲、传热管的壁温将接近加热蒸汽温度;乙、换热器总传热系数K将接近空气侧的对流给热系数。
第四章传热习题测验答案

第四章 传热习题答案4-1一炉壁由三层不同材料组成,第一层为耐火砖,导热系数为1.7 W/(m·℃),允许最高温度为1450℃,第二层为绝热砖,导热系数为0.35 W/(m·℃),允许最高温度为1100℃,第三层为铁板,导热系数为40.7W/(m·℃),其厚度为6mm ,炉壁内表面温度为1350℃,外表面温度为220℃。
在稳定状态下通过炉壁的热通量为4652 W/m 2,试问各层应该多厚时才能使壁的总厚度最小?解:当绝热材料达到最高允许温度时,总壁厚为最小btq ∆=λ,q t b ∆=λ()mm m b 1920.09136/4652110013501.7==-⨯= 0.006/40.70.35/22011004652+-=2bmm m b 2660.066==因第二层绝热砖已达到最高温度,故第一层耐火砖的厚度不可再小,所以现在所得总厚为其最小厚度:mm b b b 32116466692min =++=++=δ4-2一根直径为φ60mm×3mm 的铝铜合金钢管,导热系数为45 W/(m·℃)。
用30mm 厚的软木包扎,其外又用30mm 厚的保温灰包扎作为绝热层。
现测得钢管内壁面温度为-110℃,绝热层外表面温度10℃。
求每米管每小时散失的冷量。
如将两层绝热材料位置互换,假设互换后管内壁温度及最外保温层表面温度不变,则传热量为多少?已知软木和保温灰的导热系数分别为0.043和0.07W/(m·℃)。
解:()()mW 34.4m W 3060/2303060/2ln 0.07160/23060/2ln 0.0431/2326060/2ln 451101103.142ln ln ln -=++++++⨯---⨯⨯=++-=34323212141r r 21r r 21r r 21t t L Q πλπλπλ两层互换位置后,热损失为()()mW 39m W 3060/2303060/2ln 0.043160/23060/2ln 0.071/2326060/2ln 451101103.142ln 2ln 2ln 2-=++++++⨯---⨯⨯=++-=34323212141r r 1r r 1r r 1t t L Q πλπλπλ4-3一炉壁面由225mm 厚的耐火砖,120mm 厚的绝热转及225mm 厚的建筑转所组成。
第四章传热(习题及解答2007版)(20200919085422)

单层平 壁导热4.1红砖平壁墙,厚度为500 mm , 一侧温度为200 C,另一侧温度为30 C,设红砖的平均导热 系数可取0.57 W/(m :C ),试求:(1)单位时间,单位面积导过的热量 q 为多少W/m 2,并换算成工程单位制kCal/(m 2h)。
(2) 距离高温侧350 mm 处的温度为多少?(3)如红砖导热系数与温度关系可表示为: 入=0.51+5 x -1t0则q 又为多少? 多层平壁导热4.2某燃烧炉的炉墙由三种砖依次砌成:第一层为耐火砖,厚b 1=0.23 m , "1.05 W/(m •C ); 第二层为绝热砖, “ =0.151 W/(m C-);第三层为普通砖,b 3 =0.24 m , & =0 .93 W/(m C )。
若已 知耐火砖内侧温度为 1000 C,耐火砖与绝热砖接触处温度为940 C,绝热砖与普通砖接触面温 度不得超过138 C ;试求:(1) 绝热砖层的厚度;(2) 普通砖外侧温度。
序号材料 厚度b (mm ) 导热系数入(W/m- C) 1 (内层)耐火砖 200 1.07 2绝热砖 100 0.14 3 钢板 6 45若耐火砖层内表面温度 t 1=1150 C,钢板外表面温度t 4 =30 C,试计算导热的热通量。
又实测通过炉壁的热损失为 300 W/m 2,如计算值与实测不符,试分析原因并计算附加热阻。
多层圆筒导热4.4 一外径为100 mm 的蒸汽管,外包一层 50 mm 绝热材料 A , M =0.07 W/(m C ),其外再包一 层25 mm 的绝热材料 B ,居=0.087 W/(m C )。
设A 的内侧温度为170 C, B 外侧温度为38 C 。
试求每米管上的热损失及 A 、B 界面的温度。
4.5①60 >3 mm 铝合金管(其导热系数可取为 45 W/(m C )),外包一 层厚30mm 石棉,之外再包一层厚 30 mm 的软木,石棉和软木的 导热系数分别为0.16 W/(m C )和0.04 W/(m C )。
第四章传热(习题及解答2007版)(20200919085422)

单层平 壁导热4.1红砖平壁墙,厚度为500 mm , 一侧温度为200 C,另一侧温度为30 C,设红砖的平均导热 系数可取0.57 W/(m :C ),试求:(1)单位时间,单位面积导过的热量 q 为多少W/m 2,并换算成工程单位制kCal/(m 2h)。
(2) 距离高温侧350 mm 处的温度为多少?(3)如红砖导热系数与温度关系可表示为: 入=0.51+5 x -1t0则q 又为多少? 多层平壁导热4.2某燃烧炉的炉墙由三种砖依次砌成:第一层为耐火砖,厚b 1=0.23 m , "1.05 W/(m •C ); 第二层为绝热砖, “ =0.151 W/(m C-);第三层为普通砖,b 3 =0.24 m , & =0 .93 W/(m C )。
若已 知耐火砖内侧温度为 1000 C,耐火砖与绝热砖接触处温度为940 C,绝热砖与普通砖接触面温 度不得超过138 C ;试求:(1) 绝热砖层的厚度;(2) 普通砖外侧温度。
序号材料 厚度b (mm ) 导热系数入(W/m- C) 1 (内层)耐火砖 200 1.07 2绝热砖 100 0.14 3 钢板 6 45若耐火砖层内表面温度 t 1=1150 C,钢板外表面温度t 4 =30 C,试计算导热的热通量。
又实测通过炉壁的热损失为 300 W/m 2,如计算值与实测不符,试分析原因并计算附加热阻。
多层圆筒导热4.4 一外径为100 mm 的蒸汽管,外包一层 50 mm 绝热材料 A , M =0.07 W/(m C ),其外再包一 层25 mm 的绝热材料 B ,居=0.087 W/(m C )。
设A 的内侧温度为170 C, B 外侧温度为38 C 。
试求每米管上的热损失及 A 、B 界面的温度。
4.5①60 >3 mm 铝合金管(其导热系数可取为 45 W/(m C )),外包一 层厚30mm 石棉,之外再包一层厚 30 mm 的软木,石棉和软木的 导热系数分别为0.16 W/(m C )和0.04 W/(m C )。
化工原理传热题库完整

第四章《传热》练习题一、选择题1、关于传热系数K,下述说法中错误的是()A、传热过程中总传热系数K实际是个平均值;B、总传热系数K随着所取的传热面不同而异;C、总传热系数K可用来表示传热过程的强弱,与冷、热流体的物性无关;D、要提高K值,应从降低最大热阻着手;答案:C2、揭示了物体辐射能力与吸收率之间关系的定律是()。
A、斯蒂芬-波尔兹曼定律;C、折射定律;B、克希霍夫定律;D、普郎克定律;答案:B3、在确定换热介质的流程时,通常走管程的有(),走壳程的有()。
A、高压流体;B、蒸汽;C、易结垢的流体;D、腐蚀性流体;E、粘度大的流体;F、被冷却的流体;答案:A、C、D;B、E、F4、影响对流传热系数的因素有( )。
A、产生对流的原因;B、流体的流动状况;C、流体的物性;D、流体有无相变;E、壁面的几何因素;答案:A、B、C、D、E5、某套管换热器,管间用饱和水蒸气将湍流流动的空气加热至指定温度,若需进一步提高空气出口温度,拟将加热管管径增加一倍(管长、流动状态及其他条件均不变),你认为此措施是( )。
A 、不可行的;B 、可行的;C 、可能行,也可能不行;D 、视具体情况而定;答案:A解:原因是:流量不变 2d u =常数当管径增大时,a. 2/u l d ∝,0.80.2 1.8/1/u dd α∝= b. d 增大时,α增大,dα∝ 综合以上结果, 1.81/A d α∝,管径增加,A α下降根据()21p mc t t KA -=m Δt 对于该系统K α≈∴2112ln m t t KA t A T t T t α-∆≈-- 即 121ln p mc AT t T t α=--∵A α↓ 则12lnT t T t -↓-∴2t ↓ ⇒ 本题在于灵活应用管内强制湍流表面传热系数经验关联式:0.80.023Re Pr n u N =,即物性一定时,0.80.2/u d α∝。
根据连续性方程,流量不变时,24V d u π==常数,所以管径变化,管内流速也发生变化。
第四章传热习题答案电子教案

第四章 传热习题答案4-1一炉壁由三层不同材料组成,第一层为耐火砖,导热系数为1.7 W/(m·℃),允许最高温度为1450℃,第二层为绝热砖,导热系数为0.35 W/(m·℃),允许最高温度为1100℃,第三层为铁板,导热系数为40.7W/(m·℃),其厚度为6mm ,炉壁内表面温度为1350℃,外表面温度为220℃。
在稳定状态下通过炉壁的热通量为4652 W/m 2,试问各层应该多厚时才能使壁的总厚度最小?解:当绝热材料达到最高允许温度时,总壁厚为最小btq ∆=λ,q t b ∆=λ()mm m b 1920.09136/4652110013501.7==-⨯= 0.006/40.70.35/22011004652+-=2bmm m b 2660.066==因第二层绝热砖已达到最高温度,故第一层耐火砖的厚度不可再小,所以现在所得总厚为其最小厚度:mm b b b 32116466692min =++=++=δ4-2一根直径为φ60mm×3mm 的铝铜合金钢管,导热系数为45 W/(m·℃)。
用30mm 厚的软木包扎,其外又用30mm 厚的保温灰包扎作为绝热层。
现测得钢管内壁面温度为-110℃,绝热层外表面温度10℃。
求每米管每小时散失的冷量。
如将两层绝热材料位置互换,假设互换后管内壁温度及最外保温层表面温度不变,则传热量为多少?已知软木和保温灰的导热系数分别为0.043和0.07W/(m·℃)。
解:()()mW 34.4m W 3060/2303060/2ln 0.07160/23060/2ln 0.0431/2326060/2ln 451101103.142ln ln ln -=++++++⨯---⨯⨯=++-=34323212141r r 21r r 21r r 21t t L Q πλπλπλ两层互换位置后,热损失为()()mW 39m W 3060/2303060/2ln 0.043160/23060/2ln 0.071/2326060/2ln 451101103.142ln 2ln 2ln 2-=++++++⨯---⨯⨯=++-=34323212141r r 1r r 1r r 1t t L Q πλπλπλ4-3一炉壁面由225mm 厚的耐火砖,120mm 厚的绝热转及225mm 厚的建筑转所组成。
第四章传热习题答案

第四章 传热习题答案4-1一炉壁由三层不同材料组成,第一层为耐火砖,导热系数为1.7 W/(m·℃),允许最高温度为1450℃,第二层为绝热砖,导热系数为0.35 W/(m·℃),允许最高温度为1100℃,第三层为铁板,导热系数为40.7W/(m·℃),其厚度为6mm ,炉壁内表面温度为1350℃,外表面温度为220℃。
在稳定状态下通过炉壁的热通量为4652 W/m 2,试问各层应该多厚时才能使壁的总厚度最小?解:当绝热材料达到最高允许温度时,总壁厚为最小btq ∆=λ,q t b ∆=λ()mm m b 1920.09136/4652110013501.7==-⨯= 0.006/40.70.35/22011004652+-=2bmm m b 2660.066==因第二层绝热砖已达到最高温度,故第一层耐火砖的厚度不可再小,所以现在所得总厚为其最小厚度:mm b b b 32116466692min =++=++=δ4-2一根直径为φ60mm×3mm 的铝铜合金钢管,导热系数为45 W/(m·℃)。
用30mm 厚的软木包扎,其外又用30mm 厚的保温灰包扎作为绝热层。
现测得钢管内壁面温度为-110℃,绝热层外表面温度10℃。
求每米管每小时散失的冷量。
如将两层绝热材料位置互换,假设互换后管内壁温度及最外保温层表面温度不变,则传热量为多少?已知软木和保温灰的导热系数分别为0.043和0.07W/(m·℃)。
解:()()mW 34.4m W 3060/2303060/2ln 0.07160/23060/2ln 0.0431/2326060/2ln 451101103.142ln ln ln -=++++++⨯---⨯⨯=++-=34323212141r r 21r r 21r r 21t t L Q πλπλπλ两层互换位置后,热损失为()()mW 39m W 3060/2303060/2ln 0.043160/23060/2ln 0.071/2326060/2ln 451101103.142ln 2ln 2ln 2-=++++++⨯---⨯⨯=++-=34323212141r r 1r r 1r r 1t t L Q πλπλπλ4-3一炉壁面由225mm 厚的耐火砖,120mm 厚的绝热转及225mm 厚的建筑转所组成。
化工原理答案第四章传热

第四章 传 热热传导【4-1】有一加热器,为了减少热损失,在加热器的平壁外表面,包一层热导率为(m·℃)、厚度为300mm 的绝热材料。
已测得绝热层外表面温度为30℃,另测得距加热器平壁外表面250mm 处的温度为75℃,如习题4-1附图所示。
试求加热器平壁外表面温度。
解 2375℃, 30℃t t ==计算加热器平壁外表面温度1t ,./()W m λ=⋅016℃ (1757530025005016016)t --= ..145025********t =⨯+=℃【4-2】有一冷藏室,其保冷壁是由30mm 厚的软木做成的。
软木的热导率λ= W/(m·℃)。
若外表面温度为28℃,内表面温度为3℃,试计算单位表面积的冷量损失。
解 已知.(),.123℃, 28℃, =0043/℃ 003t t W m b m λ==⋅=,则单位表面积的冷量损失为【4-3】用平板法测定材料的热导率,平板状材料的一侧用电热器加热,另一侧用冷水冷却,同时在板的两侧均用热电偶测量其表面温度。
若所测固体的表面积为0.02m 2,材料的厚度为0.02m 。
现测得电流表的读数为2.8A ,伏特计的读数为140V ,两侧温度分别为280℃和100℃,试计算该材料的热导率。
解 根据已知做图热传导的热量 .28140392Q I V W =⋅=⨯=.().()12392002002280100Qb A t t λ⨯==-- 【4-4】燃烧炉的平壁由下列三层材料构成:耐火砖层,热导率λ=(m·℃),厚度230b mm =;绝热砖层,热导率λ=(m·℃);普通砖层,热导率λ=(m·℃)。
耐火砖层内侧壁面温度为1000℃,绝热砖的耐热温度为940℃,普通砖的耐热温度为130℃。
(1) 根据砖的耐热温度确定砖与砖接触面的温度,然后计算绝热砖层厚度。
若每块绝热砖厚度为230mm ,试确定绝热砖层的厚度。
第四章传热习题答案

第四章 传热习题答案4-1一炉壁由三层不同材料组成,第一层为耐火砖,导热系数为1.7 W/(m·℃),允许最高温度为1450℃,第二层为绝热砖,导热系数为0.35 W/(m·℃),允许最高温度为1100℃,第三层为铁板,导热系数为40.7W/(m·℃),其厚度为6mm ,炉壁内表面温度为1350℃,外表面温度为220℃。
在稳定状态下通过炉壁的热通量为4652 W/m 2,试问各层应该多厚时才能使壁的总厚度最小?解:当绝热材料达到最高允许温度时,总壁厚为最小btq ∆=λ,q t b ∆=λ()mm m b 1920.09136/4652110013501.7==-⨯= 0.006/40.70.35/22011004652+-=2bmm m b 2660.066==因第二层绝热砖已达到最高温度,故第一层耐火砖的厚度不可再小,所以现在所得总厚为其最小厚度:mm b b b 32116466692min =++=++=δ4-2一根直径为φ60mm×3mm 的铝铜合金钢管,导热系数为45 W/(m·℃)。
用30mm 厚的软木包扎,其外又用30mm 厚的保温灰包扎作为绝热层。
现测得钢管内壁面温度为-110℃,绝热层外表面温度10℃。
求每米管每小时散失的冷量。
如将两层绝热材料位置互换,假设互换后管内壁温度及最外保温层表面温度不变,则传热量为多少?已知软木和保温灰的导热系数分别为0.043和0.07W/(m·℃)。
解:()()mW 34.4m W 3060/2303060/2ln 0.07160/23060/2ln 0.0431/2326060/2ln 451101103.142ln ln ln -=++++++⨯---⨯⨯=++-=34323212141r r 21r r 21r r 21t t L Q πλπλπλ两层互换位置后,热损失为()()mW 39m W 3060/2303060/2ln 0.043160/23060/2ln 0.071/2326060/2ln 451101103.142ln 2ln 2ln 2-=++++++⨯---⨯⨯=++-=34323212141r r 1r r 1r r 1t t L Q πλπλπλ4-3一炉壁面由225mm 厚的耐火砖,120mm 厚的绝热转及225mm 厚的建筑转所组成。
化原第四章传热习题答案

b1 t1
t2
b2 b3
t3 t4
11. 水以5kg/s的流量通过一内径为5cm的光滑管,其管壁的 温度为80 ℃,水从10 ℃被加热到30 ℃,试求所需管道的长 度? 解:Δt=80-(30+10)/2=60 ℃
Φ=hAΔt=qmcp(30-10) =5×4.187×103×20 =418.7×103w h=0.023(λ/d)Re0.8Pr0.4 Re=(0.05×5/(0.785×0.052))/1×10-3=127389 Pr=(cpη/λ)=4.187×103×10-3/0.599=7 h=0.023×0.599/0.05×127390.8×70.4=7301w/(m2.K) A=418.7×103/(7301×60)=0.956m2 l=0.956/(3.14×0.05)=6.09m
解: q= Δt/(b1/λ1+ b2/λ2+ b3/λ3) =(1200-330)/(0.225/1.4+0.120/0.2+0.225/0.7) = 870/(0.16+0.6+0.32)=804W/m2
t2=t1-qb1/λ1=1200-804×0.225/1.4=1071K t3=qb3/λ3+t4=804×0.225/0.7+330=588K
34.测定某氨合成炉部列管式换热器的传热系数。反应后气体走管内,流 量为6100kg/h,进口温度分别为485℃,154℃,Cp=3.04kJ/(kg.K)。原 料气走管外,流量为5800kg/h,进口温度为50 ℃, Cp=3.14kJ/(kg.K) 。 换热面积A=30m2,逆流传热,试计算传热系数K。(忽略热损失)
b1 t1
t2
b2 b3t3 t4 Nhomakorabeabmin=92+66+6=164mm
化工原理答案传热定稿版

化工原理答案传热HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】第四章 传热热传导【4-1】有一加热器,为了减少热损失,在加热器的平壁外表面,包一层热导率为0.16W/(m·℃)、厚度为300mm 的绝热材料。
已测得绝热层外表面温度为30℃,另测得距加热器平壁外表面250mm 处的温度为75℃,如习题4-1附图所示。
试求加热器平壁外表面温度。
解 2375℃, 30℃t t ==计算加热器平壁外表面温度1t ,./()W m λ=⋅016℃ (1757530025005016016)t --= ..145025********t =⨯+=℃ 【4-2】有一冷藏室,其保冷壁是由30mm 厚的软木做成的。
软木的热导率λ=0.043 W/(m·℃)。
若外表面温度为28℃,内表面温度为3℃,试计算单位表面积的冷量损失。
解 已知.(),.123℃, 28℃, =0043/℃ 003t t W m b m λ==⋅=,则单位表面积的冷量损失为【4-3】用平板法测定材料的热导率,平板状材料的一侧用电热器加热,另一侧用冷水冷却,同时在板的两侧均用热电偶测量其表面温度。
若所测固体的表面积为0.02m 2,材料的厚度为0.02m 。
现测得电流表的读数为2.8A ,伏特计的读数为140V ,两侧温度分别为280℃和100℃,试计算该材料的热导率。
解 根据已知做图热传导的热量 .28140392Q I V W =⋅=⨯=.().()12392002002280100Qb A t t λ⨯==-- 【4-4】燃烧炉的平壁由下列三层材料构成:耐火砖层,热导率λ=1.05W/(m·℃),厚度230b mm =;绝热砖层,热导率λ=0.151W/(m·℃);普通砖层,热导率λ=0.93W/(m·℃)。
耐火砖层内侧壁面温度为1000℃,绝热砖的耐热温度为940℃,普通砖的耐热温度为130℃。
最新第四章-传热习题参考答案

第四章 传热3 直径为φ60×3mm 的钢管用30mm 厚的软木包扎,其外又用100mm 厚的保温灰包扎,以作为绝热层。
现测得钢管外壁面温度为-110℃,绝热层外表面温度为10℃。
软木和保温灰的导热系数分别为0.043和0.07W/(m. ℃),试求每米管长的冷损失量。
解:m W r r r r t L Q /25207.0)60/160ln(2043.0)30/60ln(101102)/ln(2)/ln(223112-=⨯⨯+⨯⨯--=+∆=πππλπλ4 蒸汽管道外包扎有两层导热系数不同而厚度相同的绝热层,设外层的平均直径为内层的两倍。
其导热系数也为内层的两倍。
若将两层材料互换位置,而假定其它条件不变,试问每米管长的热损失将改变多少?说明在本题情况下,哪一种材料包扎在内层较为合适?解:内层管内径r 1,外径r 2,外层管外径r 32(221r r +)=(223r r +) , 2312r r r r -=- 23125,3r r r r ==⇒ 122λλ=πλπλπλπλ4)3/5ln(2)3ln(2)/ln(2)/ln(11223112+∆=+∆=t r r r r t L Qπλπλπλπλ2)3/5ln(4)3ln(2)/ln(2)/ln('11123212+∆=+∆=tr r r r t L Q 25.1)3/5ln(3ln 2)3/5ln(23ln '=++=⇒Q Q 所以导热系数小的应该包扎在内层。
7 在并流换热器中,水的进出口温度分别为15℃和40℃,油的进、出口温度分别为150℃和100℃。
现因生产任务要求油的出口温度降至80℃,假设油和水的流量、进口温度和物性均不变,若原换热器的管长为1m 。
试求此换热器的管长增至若干米才能满足要求。
设换热器的热损失可忽略。
解:''''''''m m m m m m t tQ Q S S t S t S t KS t KS Q Q ∆∆⋅=⇒∆∆=∆∆= (1) 其中:4.110015080150)()(''21'2'1=--=--=T T C W T T C W Q Q ph h ph h (2) 又由:C t t t t t T T T T t t C W T T C W t t C W T T C W pc c ph h pc c ph h ︒=⇒--=--⇒⎭⎬⎫-=--=-50''')'()'()()(21212212112211221 C t m ︒=-=∆∴5.9260/135ln 60135C t m ︒=-=∆8.6930/135ln 30135' (3)将(2)(3)代入(1)即得。
化工原理传热习题解答

第四章习题1)用平板法测定材料的导热系数,其主要部件为被测材料构成的平板,其一侧用电热器加热,另一侧用冷水将热量移走,同时板的两侧用热电偶测量其表面温度。
设平板的导热面积为0.03m 2,厚度为0.01m 。
测量数据如下:试求:①该材料的平均导热系数。
②如该材料导热系数与温度的关系为线性:,则λ0和a 值为多少?001825.0)/(4786.0]2/)50200(1[5878.0]2/)100300(1[6533.0)/(6206.02/)()/(5878.01153.201.0/03.0)50200()/(6533.01408.201.0/03.0)200300(/)(1][000002102201121=⋅=++=++=∴⋅=+=⋅=⨯=⨯-⋅=⨯=⨯-∴=-=a C m w a a C m w C m w C m w VIL S t t Q m λλλλλλλλλλλ得)解2)通过三层平壁热传导中,若测得各面的温度t 1、t 2、t 3和t 4分别为500℃、400℃、200℃和100℃,试求合平壁层热阻之比,假定各层壁面间接触良好。
12112)100200()200400(21200400400500(/)(/)(/)(][3213221343232121::::::::)):(:解==--==--=-=-=-=R R R R R R R R T T R T T R T T Q3)某燃烧炉的平壁由耐火砖、绝热砖和普通砖三种砌成,它们的导热系数分别为1.2W/(m ·℃),0.16 W/(m ·℃)和0。
92 W/(m ·℃),耐火砖和绝热转厚度都是0.5m ,普通砖厚度为0.25m 。
已知炉内壁温为1000℃,外壁温度为55℃,设各层砖间接触良好,求每平方米炉壁散热速率。
221/81.247)]92.0/25.0()16.0/5.0()112/5.0/[)551000()//(/][m w b t t S Q i i =++-=-=∑(()解λ4)在外径100mm 的蒸汽管道外包绝热层。
第四章传热(习题及解答2007版)

四传热单层平壁导热4.1 红砖平壁墙,厚度为500 mm,一侧温度为200 ℃,另一侧温度为30 ℃,设红砖的平均导热系数可取0.57 W/(m·℃),试求:(1)单位时间,单位面积导过的热量q为多少W/m2,并换算成工程单位制kCal/ (m2·h) 。
(2)距离高温侧350 mm处的温度为多少?(3)如红砖导热系数与温度关系可表示为:λ=0.51+5×10 -4t,则q又为多少?多层平壁导热4.2 某燃烧炉的炉墙由三种砖依次砌成:第一层为耐火砖,厚b1=0.23 m,λ1=1.05 W/(m·℃);第二层为绝热砖,λ2 =0.151 W/(m·℃);第三层为普通砖,b3 =0.24 m,λ3 =0 .93 W/(m·℃)。
若已知耐火砖内侧温度为1000 ℃,耐火砖与绝热砖接触处温度为940 ℃,绝热砖与普通砖接触面温度不得超过138℃;试求:(1)绝热砖层的厚度;(2)普通砖外侧温度。
4.3 平壁炉壁由三种材料组成,其厚度和导热系数如下:序号材料厚度b(mm)导热系数λ(W/m·℃)1(内层)耐火砖200 1.072 绝热砖100 0.143 钢板 6 45若耐火砖层内表面温度t1=1150 ℃,钢板外表面温度t4 =30 ℃,试计算导热的热通量。
又实测通过炉壁的热损失为300 W/m2,如计算值与实测不符,试分析原因并计算附加热阻。
多层圆筒导热4.4 一外径为100 mm的蒸汽管,外包一层50 mm绝热材料A,λA =0.07 W/(m·℃),其外再包一层25 mm的绝热材料B,λB =0.087 W/(m·℃)。
设A的内侧温度为170 ℃,B外侧温度为38 ℃。
试求每米管上的热损失及A、B界面的温度。
4.5 Φ60×3 mm铝合金管(其导热系数可取为45 W/(m·℃)),外包一层厚30 mm石棉,之外再包一层厚30 mm的软木,石棉和软木的导热系数分别为0.16 W/(m·℃)和0.04 W/(m·℃) 。
第四章传热(习题及解答2007版)

四传热单层平壁导热4.1 红砖平壁墙,厚度为500 mm,一侧温度为200 ℃,另一侧温度为30 ℃,设红砖的平均导热系数可取0.57 W/(m·℃),试求:(1)单位时间,单位面积导过的热量q为多少W/m2,并换算成工程单位制kCal/ (m2·h) 。
(2)距离高温侧350 mm处的温度为多少?(3)如红砖导热系数与温度关系可表示为:λ=0.51+5×10 -4t,则q又为多少?多层平壁导热4.2 某燃烧炉的炉墙由三种砖依次砌成:第一层为耐火砖,厚b1=0.23 m,λ1=1.05 W/(m·℃);第二层为绝热砖,λ2 =0.151 W/(m·℃);第三层为普通砖,b3 =0.24 m,λ3 =0 .93 W/(m·℃)。
若已知耐火砖内侧温度为1000 ℃,耐火砖与绝热砖接触处温度为940 ℃,绝热砖与普通砖接触面温度不得超过138℃;试求:(1)绝热砖层的厚度;(2)普通砖外侧温度。
4.3 平壁炉壁由三种材料组成,其厚度和导热系数如下:序号材料厚度b(mm)导热系数λ(W/m·℃)1(内层)耐火砖200 1.072 绝热砖100 0.143 钢板 6 45若耐火砖层内表面温度t1=1150 ℃,钢板外表面温度t4 =30 ℃,试计算导热的热通量。
又实测通过炉壁的热损失为300 W/m2,如计算值与实测不符,试分析原因并计算附加热阻。
多层圆筒导热4.4 一外径为100 mm的蒸汽管,外包一层50 mm绝热材料A,λA =0.07 W/(m·℃),其外再包一层25 mm的绝热材料B,λB =0.087 W/(m·℃)。
设A的内侧温度为170 ℃,B外侧温度为38 ℃。
试求每米管上的热损失及A、B界面的温度。
4.5 Φ60×3 mm铝合金管(其导热系数可取为45 W/(m·℃)),外包一层厚30 mm石棉,之外再包一层厚30 mm的软木,石棉和软木的导热系数分别为0.16 W/(m·℃)和0.04 W/(m·℃) 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 传热
3 直径为φ60×3mm 的钢管用30mm 厚的软木包扎,其外又用100mm 厚的保温灰包扎,以作为绝热层。
现测得钢管外壁面温度为-110℃,绝热层外表面温度为10℃。
软木和保温灰的导热系数分别为0.043和0.07W/(m. ℃),试求每米管长的冷损失量。
解:
m W r r r r t L Q /25207.0)60/160ln(2043.0)30/60ln(101102)/ln(2)/ln(22311
2-=⨯⨯+⨯⨯--=+
∆=πππ
λπλ
4 蒸汽管道外包扎有两层导热系数不同而厚度相同的绝热层,设外层的平均直径为内层的两倍。
其导热系数也为内层的两倍。
若将两层材料互换位置,而假定其它条件不变,试问每米管长的热损失将改变多少?说明在本题情况下,哪一种材料包扎在内层较为合适?
解:内层管内径r 1,外径r 2,外层管外径r 3
2(
22
1r r +)=(2
23r r +) , 2312r r r r -=- 23125,3r r r r ==⇒ 122λλ=
πλπλπλπλ4)3/5ln(2)3ln(2)/ln(2)/ln(1122311
2+∆=+
∆=t r r r r t L Q
πλπλπ
λπλ2)
3/5ln(4)3ln(2)/ln(2)/ln('11123212+∆=+∆=t
r r r r t L Q 25.1)
3/5ln(3ln 2)
3/5ln(23ln '=++=⇒
Q Q 所以导热系数小的应该包扎在内层。
7 在并流换热器中,水的进出口温度分别为15℃和40℃,油的进、出口温度分别为150℃和100℃。
现因生产任务要求油的出口温度降至80℃,假设油和水的流量、进口温度和物性均不变,若原换热器的管长为1m 。
试求此换热器的管长增至若干米才能满足要求。
设换热器的热损失可忽略。
解:
'
'''''''m m m m m m t t
Q Q S S t S t S t KS t KS Q Q ∆∆⋅=⇒∆∆=∆∆= (1) 其中:4.1100
15080150)()(''
21'
2'1=--=--=T T C W T T C W Q Q ph h ph h (2) 又由:
C t t t t t T T T T t t C W T T C W t t C W T T C W pc c ph h pc c ph h ︒=⇒--=--⇒⎭⎬
⎫-=--=-50''')'()'()()(21
21
2212112211221 C t m ︒=-=
∆∴5.9260/135ln 60135C t m ︒=-=∆8.6930
/135ln 30
135' (3)
将(2)(3)代入(1)即得。
8.重油和原油在单程套管换热器中呈并流流动,两种油的初温分别为243℃和128℃;终温分别为167℃和157℃。
若维持两种油的流量和初温不变,而将两流体改为逆流,试求此时流体的平均温度差及它们的终温。
假设在两种流动情况下,流体的物性和总传热系数均不变化,换热器的热损失可以忽略。
解:采用传热单元数法求解。
并流时,根据76
29
16724312815721121
=
--=--=
=
T T t t C W C W R pc
c ph h (1) 可知热流体为最小值流体,以后以热流体为基准计-算。
并流
C t m ︒=∆43
77.143
16724321min 1=-=∆-=∆==m ph h m t T T C W t Q C KS
NTU (2)
改为逆流时,流体的物性和总传热系数均不变化,所以R ,NTU 不变。
由(1)(2)查逆流下图4-23得:C T t T T T ︒=⇒--==6.15576.0'21
1'
21ε
又
C t C t T T t t C W C W m pc
c ph h ︒=∆⇒︒=⇒--=
8.492.161''
''
22112
13. 在一单程管壳式换热器中,用饱和蒸汽加热原料油。
温度为160℃的饱和蒸汽在壳程冷凝(排出时为饱和液体),原料油在管程流动,并由20℃加热到160℃。
管壳式换热器尺寸为:列管直径φ19×2mm 、管长4m ,共有25根管子。
若换热器的传热量为125kW ,蒸汽冷凝传热系数为7000 W/(m2·℃),油侧污垢热阻可取为0.0005 m2·℃/W ,管壁热阻和蒸汽侧垢层热阻可忽略,试求管内油侧对流传热系数。
又若油的流速增加一倍,此时若换热器的总传热系数为原来总传热系数的1.75倍,试求油的出口温度。
假设油的物性不变。
解:297.5m L d n S o O
==π, C t o m 27.90=∆
根据m O O t S K Q ∆=得到)/(2322C m W t S Q
K m
O O
︒⋅=∆=
)/(3601112C m W d d R d d
K i i
O si i O i O O ︒⋅=⇒⋅+⋅+=ααα 若油的流速增加一倍,
C t t K t K Q Q t t W t t W t t C W t t C W Q Q m m c c pc c pc c ︒=⇒⎪⎪⎭
⎪⎪⎬⎫∆∆=
--=--=100''')()(')()('''
2121'
2121'2
15 在一逆流套管换热器中,冷、热流体进行热交换。
两流体进、出口温度分别为t1=20℃、t2=85℃;T1=100℃、T2=70℃。
当冷流体流量增加一倍时,试求两流体的出口温度和传热量的变化情况。
假设两种情况下总传热系数不变,换热器热损失可忽略。
解:用传热单元数法求解。
原工况:根据65
30
12212
=
--=
=
t t T T C W C W R ph
h pc c (1) 知冷流体为最小值流体,以下按冷流体为基准计算。
8125.020
10020
851112=--=--=
t T t t ε (2)
由(1)(2)查表可得23.22
=NTU
新工况:
C t t T t t R R NTU NTU ︒=⇒--==⇒⎪⎭
⎪⎬⎫====
6353.0'6560211.121''21
11'22'222ε 由此结合热量衡算式可确定Q ’/Q ,以及'
2T
也可利用总传热速率方程,热量衡算及对数平均温差的公式对两流体的出口温度解二元二次方程求解。
