多元函数微分学__考试重点
多元函数微分学知识点梳理

多元函数微分学知识点梳理
第九章多元函数微分学
内容复
一、基本概念
1.多元函数的基本概念包括n维空间、n元函数、二重极限、连续等。
其中,偏导数和全微分也是重要的概念。
2.重要定理:
1)二元函数中,可导、连续、可微三者的关系为偏导数
连续→可微。
同时,偏导数存在和函数连续是可微的必要条件。
2)二元函数的极值必须满足必要条件和充分条件。
二、基本计算
一)偏导数的计算
1.偏导数值的计算有三种方法:先代后求法、先求后代法
和定义法。
2.偏导函数的计算包括简单的多元初等函数和复杂的多元
初等函数。
对于复杂的函数,可以使用链式法则,或者隐函数求导法。
3.高阶导数的计算需要注意记号表示和求导顺序。
二)全微分的计算
1.叠加原理可以用于计算全微分,即dz=∂z/∂x dx+∂z/∂y dy。
2.一阶全微分形式不变性对于自变量和中间变量均成立。
三、偏导数的应用
在优化方面,多元函数的极值和最值是常见的应用。
1.无条件极值可以用必要条件和充分条件来求解。
2.条件极值可以使用Lagrange乘数法来求解。
3.最值可以通过比较区域内部驻点处函数值和区域边界上最值的大小来确定。
高等数学-第八章 多元函数微分学

(ex ) e x
(loaxg)x
1 ln
a
(arcxs)in
1
1
x
2
(lnx) 1
x
(arccx)os 1
1 x2
(arcxt)an
1
1
x
2
(acrc ox)t
1
1 x
2
2. 求一点处偏导数的方法
• 利用定义: fx (x 0 ,y 0 ) lx 0 if( m x 0 x ,y 0 x ) f(x 0 ,y 0 )
第八章 多元函数微分学 知识总结
一. 多元函数的基本概念 二. 多元函数的偏导数、微分与方向导数 三. 多元函数微分法 四. 多元函数微分学的几何应用 五. 多元函数的极值和最值
一. 多元函数的基本概念
1. 区域 2. 多元函数概念
3. 多元函数的极限 4. 多元函数的连续性
1) 函数 f(P)在P0连续 P l iP 0 m f(P)f(P 0)
例.
设
f(x,y,z)xco y syco zs zco x,求 sdf 1co x s co y s co z s
(0,0,0) .
解: f(x,0,0) x 3cosx
fx(0,0,0)
x
3cosx
x0
1 4
利用轮换对称性 , 可得 fy(0,0,0)fz(0,0,0)1 4
d f( 0 ,0 ,0 ) f x ( 0 ,0 ,0 ) d x fy ( 0 ,0 ,0 ) d y f z ( 0 ,0 ,0 ) d z
(1) 检验函数是否连续,若不连续一定不可微
(2 )求 fx (x 0 ,y 0)、 fy (x 0 ,y 0) 注 : 若 有 一 个 不 存 在 则 一 定 不 可 微
高等数学第九章多元函数微分学试题及答案

第九章 多元函数微分学§9.1 多元函数的概念、极限与连续性一、多元函数的概念1.二元函数的定义及其几何意义设D 是平面上的一个点集,如果对每个点()D y x P ∈,,按照某一对应规则f ,变量z 都有一个值与之对应,则称z 是变量x ,y 的二元函数,记以()y x f z ,=,D 称为定义域。
二元函数()y x f z ,=的图形为空间一卦曲面,它在xy 平面上的投影区域就是定义域D 。
例如 221y x z --=,1:22≤+y x D , 此二元函数的图形为以原点为球心,半径为1的上半球面,其定义域D 就是 xy 平面上以原点为圆心,半径为1的闭圆。
2.三元函数与n 元函数()z y x f u ,,= ()Ω∈z y x ,,空间一个点集称为三元函数()n x x x f u ,,21 = 称为n 元函数它们的几何意义不再讨论,在偏导数和全微分中会用到三元函数。
条件极值中,可能会遇到超过三个自变量的多元函数。
二、二元函数的极限设函数),(y x f 在区域D 内有定义,),(000y x P 是D 的聚点,如果存在常数A ,对于任意给定的0>ε,总存在0>δ,当),(y x P 满足δ<-+-=<20200)()(0y y x x PP 时,恒有ε<-A y x f ),(成立。
则记以()A y x f y y x x =→→,lim 0或()()()A y x f y x y x =→,lim00,,。
称当()y x ,趋于()00,y x 时,()y x f ,的极限存在,极限值A ,否则称为极限不存在。
值得注意:这里()y x ,趋于()00,y x 是在平面范围内,可以按任何方式沿任意曲线趋于()00,y x ,所以二元函数的极限比一元函数的极限复杂;但考试大纲只要求知道基本概念和简单的讨论极限存在性和计算极限值,不像一元函数求极限要求掌握各种方法和技巧。
多元函数微分学知识点

多元函数微分学知识点多元函数微分学是微积分的重要内容,它研究的是在多变量条件下函数的导数和微分的性质。
在实际应用中,多元函数微分学为我们解决各种问题时提供了有效的数学工具。
本文将介绍一些多元函数微分学的基本知识点,包括偏导数、全微分和梯度。
多元函数微分学的第一个知识点是偏导数。
在一元函数中,导数表示函数在某一点上的变化率。
而在多元函数中,我们需要引入偏导数的概念。
偏导数表示函数在某一点上沿着一个坐标轴的变化率。
对于一个两个自变量的函数f(x, y),偏导数可以用∂f/∂x和∂f/∂y表示。
它们分别表示函数沿x轴和y轴的变化率。
偏导数可以帮助我们理解函数的局部变化情况,并在解决最优化问题时提供重要的线索。
第二个知识点是全微分。
全微分是多元函数微分学中的一个重要概念,它表示函数在某一点上的微小变化量。
全微分可以用df表示,其中df = ∂f/∂x*dx + ∂f/∂y*dy。
全微分可以帮助我们推导函数的逼近值和误差,从而得出函数在某一点的性质和特点。
例如,在工程学中,通过对一个物理过程的全微分分析,我们可以推导出近似解,并估计误差。
最后一个知识点是梯度。
梯度是多元函数微分学中的一个重要工具,它表示函数在某一点的最大变化方向。
对于一个函数f(x, y),梯度可以用∇f = (∂f/∂x, ∂f/∂y)表示。
梯度的方向是函数变化最快的方向,它的模长表示函数的变化速率。
通过研究梯度,我们可以找到函数的极大值、极小值和鞍点,并解决最优化问题。
多元函数微分学是高级数学中的一个重要分支,它在各个学科领域都有广泛的应用。
在物理学中,我们可以通过多元函数微分学的方法推导出物理方程,并解决各种动力学问题。
在经济学中,多元函数微分学可以帮助我们分析供求关系,推导出边际效应,并解决最优决策问题。
在金融学中,多元函数微分学可以帮助我们研究金融风险和资产定价。
综上所述,多元函数微分学是微积分的重要内容之一,它研究的是多变量条件下函数的导数和微分的性质。
考研数学:多元函数微分学考点和常考题型分析

考研数学:多元函数微分学考点和常考题型分析在研究生入学考试中,高等数学是数一、数二、数三考试的公共内容。
数一、数三均占56%(总分150分),考察4个选择题(每题4分,共16分)、4个填空题(每题4分,共16分)、5个解答题(总分50分)。
数二不考概率论,高数占78%,考察6个选择题(每题4分,共24分)、4个填空题(每题5分,共20分)、7个解答题(总分72分)。
由高数所占比例易知,高数是考研数学的重头戏,因此一直流传着“得高数者得数学。
”高等数学包含函数、极限与连续、一元函数微分学、一元函数积分学、多元函数微分学、多元函数积分学、常微分方程和无穷级数等七个模块,老师在梳理分析函数、极限与连续、一元函数微分学、一元函数积分学的基础上,继续梳理多元函数微分学,希望对学员有所帮助。
1、考试内容(1)多元函数的概念二元函数的几何意义;(2)二元函数的极限与连续的概念,有界闭区域上二元连续函数的性质 ;(3)多元函数偏导数的概念与计算;(4)多元复合函数的求导法与隐函数求导法;(5)二阶偏导数;(6)全微分;(7)多元函数的极值和条件极值,最大值和最小值。
2、考试要求(1)了解多元函数的概念,了解二元函数的几何意义;(2)了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质;(3)了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,会求多元隐函数的偏导数;(4)了解多元函数极值和条件极值的概念;(5)掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件;(6)会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决简单的应用问题.3、常考题型(1)多元函数的极限;(2)多元函数微分学的概念;(3)连续、可导、可微的关系;(4)求函数的偏导数;(5)变换下关于偏导数方程的变形;(6)求函数的无条件极值;(7)求函数的条件极值。
多元函数微分学单元测试题及答案解析

多元函数微分学单元测试题A一、选择题1. 极限24200limy x y x yy x x +→→= ( )A.等于0;B.不存在;C.等于 12;D.存在且不等于0或12. 2.设),(b a f y '存在,则yy b a f y b a f y ),(),(lim 0--+→= ( )A.),(b a f y ';B. 0; C . 2),(b a f y '; D.21),(b a f y '. 3. 若函数) ,(y x f 在点) ,(00y x 处不连续,则 ( ) A.) ,(lim 00y x f y y x x →→必不存在; B.) ,(00y x f 必不存在;C. ) ,(y x f 在点) ,(00y x 必不可微;D.) ,(), ,(0000y x f y x f y x 必不存在.4.函数()y x f ,在点()00,y x 处连续是函数在该点可微分的 ( ) A. 充分而不必要条件; B. 必要而不充分条件; C. 必要而且充分条件; D. 既不必要也不充分条件.5.函数xy xyz +=arcsin的定义域是 ( ) A.{}0,|),(≠≤x y x y x ; B.{}0,|),(≠≥x y x y x ;C.{}0,0|),(≠≥≥x y x y x {}0,0|),(≠≤≤⋃x y x y x ;D.{}{}0,0|),(0,0|),(<<⋃>>y x y x y x y x .6、函数22(,)ln()f x y x y =-的定义域是( )(A) 220x y +>; (B )220x y ->; (C )220x y +<; (D )220x y -<.7、二元函数333()z x y x y =+--的极值点是 ( D ) A 、(1,2) B 、(1,-2) C 、(-1,2) D 、(-1,-1) 二、判断题1. 点集E 的内点必属于E. ( )2. 设y x z ln 2+=,则yx x z 12+=∂∂. ( ) 3. 若函数),(y x f z =在),(00y x P 处的两个偏导数),(00y x f x 与),(00y x f y 均存在,则该函数在P 点处未必连续 ( )4.二阶混合偏导数与求偏导的次序无关 ( )5.具有偏导数的函数的驻点必定是极值点. ( ) 6、若(,)(,)xy yx f x y f x y 和都在点00(,)x y 连续,则0000(,)(,)xy yx f x y f x y =。
(完整版)多元函数微分学复习题及答案

第八章 多元函数微分法及其应用 复习题及解答一、选择题1. 极限lim x y x yx y→→+00242= (提示:令22y k x =) ( B ) (A) 等于0 (B) 不存在 (C) 等于12 (D) 存在且不等于0或12 2、设函数f x y x y y xxy xy (,)sin sin=+≠=⎧⎨⎪⎩⎪1100,则极限lim (,)x y f x y →→0= ( C )(提示:有界函数与无穷小的乘积仍为无穷小)(A) 不存在 (B) 等于1 (C) 等于0 (D) 等于23、设函数f x y xy x y x y x y (,)=++≠+=⎧⎨⎪⎩⎪222222000,则(,)f x y ( A )(提示:①在220x y +≠,(,)f x y 处处连续;②在0,0x y →→ ,令y kx =,200(0,0)x x y f →→→=== ,故在220x y +=,函数亦连续.所以,(,)f x y 在整个定义域内处处连续.)(A) 处处连续 (B) 处处有极限,但不连续 (C) 仅在(0,0)点连续 (D) 除(0,0)点外处处连续4、函数z f x y =(,)在点(,)x y 00处具有偏导数是它在该点存在全微分的 ( A ) (A)必要而非充分条件(B)充分而非必要条件(C)充分必要条件 (D)既非充分又非必要条件5、设u y x =arctan ,则∂∂u x = ( B )(A)xx y 22+(B) -+y x y 22 (C) yx y 22+(D)-+xx y 226、设f x y yx(,)arcsin=,则f x '(,)21= ( A ) (A )-14(B )14 (C )-12 (D )127、设yxz arctan=,v u x +=,v u y -=,则=+v u z z ( C )(A )22v u v u -- (B )22v u u v -- (C )22v u v u +- (D )22v u uv +-8、若f x x x x f x x x x (,),(,)'232612=+=+,则f x x y '(,)2= ( D ) (A) x +32(B) x -32(C) 21x + (D) -+21x 9、设z y x =,则()(,)∂∂∂∂z x zy+=21 ( A ) (A) 2 (B) 1+ln2 (C) 0 (D) 110、设z xye xy =-,则z x x x'(,)-= ( D ) (A)-+2122x x e x () (B)2122x x e x ()- (C)--x x e x ()122 (D)-+x x e x ()12211、曲线x t y t z t ===24sin ,cos ,在点(,,)202π处的法平面方程是 (C )(A) 242x z -=-π (B) 224x z -=-π (C) 42y z -=-π (D) 42y z -=π12、曲线45x y y z ==,,在点(,,)824处的切线方程是 (A )(A)842204x z y --=-= (B)x y z +==+122044 (C) x y z -=-=-85244 (D)x y z -=-=351413、曲面x z y x z cos cos +-=ππ22在点ππ2120,,-⎛⎝ ⎫⎭⎪处的切平面方程为 (D )(A )x z -=-π1 (B )x y -=-π1 (C )x y -=π2 (D )x z -=π214、曲面x yz xy z 2236-=在点(,,)321处的法线方程为 (A ) (A )x y z +=--=--58531918 (B )x y z -=-=--3823118(C )83180x y z --= (D )831812x y z +-=15、设函数z x y =-+122,则点 (,)00是函数 z 的 ( B ) (A )极大值点但非最大值点 (B )极大值点且是最大值点 (C )极小值点但非最小值点 (D )极小值点且是最小值点 16、设函数z f x y =(,)具有二阶连续偏导数,在P x y 000(,)处,有2)()(,0)()(,0)(,0)(000000======P f P f P f P f P f P f yx xy yy xx y x ,则( C )(A )点P 0是函数z 的极大值点 (B )点P 0是函数z 的极小值点 (C )点P 0非函数z 的极值点 (D )条件不够,无法判定 17、函数f x y z z (,,)=-2在222421x y z ++=条件下的极大值是 ( C )(A) 1 (B) 0 (C)-1 (D) -2 二、填空题 1、极限limsin()x y xy x→→0π= ⎽⎽⎽⎽⎽⎽⎽ .答:π 2、极限limln()x y x y e x y→→++01222=⎽⎽⎽⎽⎽⎽⎽ .答:ln23、函数z x y =+ln()的定义域为 ⎽⎽⎽⎽⎽⎽⎽ .答:x y +≥14、函数z xy=arcsin 的定义域为 ⎽⎽⎽⎽⎽⎽⎽ .答:-≤≤11x ,y ≠0 5、设函数f x y x y xy y x (,)ln =++⎛⎝ ⎫⎭⎪22,则f kx ky (,)= ⎽⎽⎽⎽⎽⎽⎽ .答:k f x y 2⋅(,)6、设函数f x y xy x y (,)=+,则f x y x y (,)+-= ⎽⎽⎽⎽⎽⎽⎽ .答:222x y x-(22()()(,)()()2x y x y x y f x y x y x y x y x+--+-==++-Q )7、设f x y x y x y A x y (,)ln()//=-⋅+<+≥⎧⎨⎩11212222222,要使f x y (,)处处连续,则A= ⎽⎽⎽⎽⎽⎽⎽ .答:-ln28、设f x y x y x y x y Ax y (,)tan()(,)(,)(,)(,)=++≠=⎧⎨⎪⎩⎪22220000,要使f x y (,)在(0,0)处连续,则A= ⎽⎽⎽⎽⎽⎽⎽ .答:1 9、函数221x y z x +=-的间断点是 .答:直线10x -=上的所有点10、函数f x y x y yx (,)cos =-122的间断点为 ⎽⎽⎽⎽⎽⎽⎽ .答:直线y x =±及x =011、设z x y y =-+sin()3,则∂∂z xx y ===21_________ .答:3cos512、设f x y x y (,)=+22,则f y (,)01= _________ .答:113、设u x y z x y z(,,)=⎛⎝ ⎫⎭⎪,则)3,2,1(d u =_________ .答:38316182d d ln d x y z --14、设u x x y =+22,则在极坐标系下,∂∂ur= _________ .答:0 15、设u xy y x =+,则∂∂22u x = _________.答:23yx16、设u x xy =ln ,则∂∂∂2u x y = ___________ .答:1y17、函数y y x =()由12+=x y e y 所确定,则d d y x = ___________ .答:22xye xy - 18、设函数z z x y =(,)由方程xy z x y z 2=++所确定,则∂∂zy= _______ .答:2112xyz xy --19、由方程xyz x y z +++=2222所确定的函数z z x y =(,)在点(1,0,-1)处的全微分d z = _________ .答:d d x y -220、曲线x t y t z t ===23213,,在点(,,)1213处的切线方程是_________.答:x y z -=-=-12221321、曲线x te y e z t e t t t ===232222,,在对应于 t =-1点处的法平面方程是___________. 答:01132=+--e y x 22、曲面xe y e z e ey z x ++=+223321在点(,,)210-处的法线方程为_________ . 答:e ze y x 22212=-+=- 23、曲面arctan y xz 14+=π在点(,,)-210处的切平面方程是_________.答:y z +=2124、设函数z z x y =(,)由方程123552422x xy y x y e z z +--+++=确定,则函数z的驻点是_________ .答:(-1,2) 27、函数z x y x y =----2346122的驻点是_________.答:(1,1)25、若函数f x y x xy y ax by (,)=+++++22236在点 (,)11-处取得极值,则常数a =_________, b =_________.答:a =0,b =426、函数f x y z x (,,)=-22在x y z 22222--=条件下的极大值是_______答:-4 三、计算题1、求下列二元函数的定义域,并绘出定义域的图形.(1) z = (2)ln()z x y =+ (3)1ln()z x y =+ (4)ln(1)z xy =-解:(1)要使函数z =有意义,必须有2210x y --≥,即有221x y +≤.故所求函数的定义域为22{(,)|1}D x y x y =+≤,图形为图3.1(2)要使函数ln()z x y =+有意义,必须有0x y +>.故所有函数的定义域为{}(,)|0D x y x y =+>,图形为图3.2(3)要使函数1ln()z x y =+有意义,必须有ln()0x y +≠,即0x y +>且1x y +≠.故该函数的定义域为{}(,)|01D x y x y x y =+>+≠,,图形为图3.3(4)要使函数ln(1)z xy =-有意义,必须有10xy ->.故该函数的定义域为{(,)|1}D x y xy =>,图形为图3.4图3.1 图3.2图3.3 图3.42、求极限limsin x y y xxy →→+-0211.解:lim sin x y y xxy →→+-0211=⋅++→→lim sin ()x y y x xy xy 00211= 43、求极限lim sin()x y x y x yxy →→-+0023211. 解:原式=lim ()sin()x y x y x y x y xy →→-++0232211=-++⋅→→limsin()x y x y xy xy 002111=-124、求极限lim x y xxye xy→→-+0416 . 解:lim x y xxye xy→→-+00416=++-→→lim ()x y x xye xy xy 00416= -85、设u x y y x =+sin cos ,求 u u x y ,. 解:u y y x x =-sin sinu x y x y =+cos cos6、设z xe ye y x =+-,求z z x y ,. 解:z e ye x y x =--z xe e y y x =+-7、设函数z z x y =(,)由yz zx xy ++=3所确定,试求∂∂∂∂z x zy,(其中x y +≠0). 解一:原式两边对x 求导得yz x x zxz y ∂∂∂∂+++=0,则∂∂z x z y y x =-++同理可得:∂∂z y z x y x =-++ 解二:xy xz F F y z xy y z F F x z x y y x ++-=-=++-=-=∂∂∂∂, 8、求函数z x xy y x y =-++-+23243122的极值.解:由z x y z x y x y=-+==-+-=⎧⎨⎩43403430,得驻点(,)-10074334>=--==yy yxxy xx z z z z D z xx =>40,函数z 在点(,)-10处取极小值z (,)-=-101.9、设z e x y =+32,而x t y t ==cos ,2,求d d z t. 解:d d (sin )()zte t e t x y x y =-+++3223232=-++(sin )3432t t e x y10、设z y xy x =ln(),求∂∂∂∂z x z y,. 解:z y y xy xy x x x =⋅+ln ln 1 z xy xy yy y x x =+-11ln() 11、设u a x a x yz a =->+ln ()0,求d u . 解:∂∂u x a a ax x yz =-+-ln 1,∂∂u y a z a x yz =⋅+ln ,∂∂u zya a x yz =+ln d (ln )d ln (d d )u a a ax x a a z y y z x yz x yz =-+++-+112、求函数z x y e xy =++ln()22的全微分.解:∂∂∂∂z x x ye x y e z y y xe x y e xyxyxyxy=+++=+++222222,[]d ()d ()d z x y ex ye x y xe y xyxy xy =+++++12222 四、应用题1、要造一容积为128立方米的长方体敞口水池,已知水池侧壁的单位造价是底部的2倍,问水池的尺寸应如何选择,方能使其造价最低? 解:设水池的长、宽、高分别为x y z ,,米.水池底部的单位造价为a .则水池造价()S xy xz yz a =++44 且 xyz =128令 ()L xy xz yz xyz =+++-44128λ由 ⎪⎪⎩⎪⎪⎨⎧=-==++==++==++=01280440404xyz L xy y x L xz z x L yz z y L z y x λλλλ得 x y z ===82由于实际问题必定存在最小值,因此当水池的长、宽、高分别为8米、8米、2米时,其造价最低.2、某工厂生产两种商品的日产量分别为x 和y (件),总成本函数22128),(y xy x y x C +-=(元).商品的限额为42=+y x ,求最小成本. 解:约束条件为042),(=-+=y x y x ϕ,构造拉格朗日函数22(,,)812(42)F x y x xy y x y λλ=-+++-,解方程组160240420x y F x y F x y F x y λλλ'⎧=-+=⎪'=-++=⎨⎪'=+-=⎩,得唯一驻点)17,25(),(=y x ,由实际情况知,)17,25(),(=y x 就是使总成本最小的点,最小成本为8043)17,25(=C (元).3、某工厂生产两种产品甲和乙,出售单价分别为10元与9元,生产x 单位的产品甲与生产y 单位的产品乙的总费用是)33(01.03240022y xy x y x +++++元, 求取得最大利润时,两种产品的产量各为多少?解:),(y x L 表示获得的总利润,则总利润等于总收益与总费用之差,即有利润目标函数)]33(01.032400[)910(),(22y xy x y x y x y x L +++++-+=)0,0(,400)33(01.06822>>-++-+=y x y xy x y x ,令⎩⎨⎧=+-='=+-='0)6(01.060)6(01.08y x L y x L yx,解得唯一驻点(120,80).又因06.0,01.0,006.0-=''=-=''=<-=''=yy xy xx L C L B L A ,得0105.332>⨯=--B AC .得极大值320)80,120(=L . 根据实际情况,此极大值就是最大值.故生产120单位产品甲与80单位产品乙时所得利润最大320元. 五、证明题 1、设)11(yx e z +-=, 求证z yz y x z x 222=∂∂+∂∂.证明: 因为2)11(1x e xzy x ⋅=∂∂+-, 2)11(1ye y z y x ⋅=∂∂+-, 所以 z e e yz y x z x y x y x 2)11()11(22=+=∂∂+∂∂+-+-2、证明函数nx ey tkn sin 2-=满足关系式22x y k t y ∂∂=∂∂ 证明:因为nx e kn kn nx e ty tkn t kn sin )(sin 2222⋅-=-⋅⋅=∂∂--, nx nex y tkn cos 2-=∂∂, nx e n xy t kn sin 2222--=∂∂, nx e kn xyk t kn sin 2222--=∂∂,所以22x y k t y ∂∂=∂∂.3、设z =xy +xF (u ), 而xyu =, F (u )为可导函数, 证明xy z y z y x z x +=∂∂+∂∂⋅.证明:y z y x z x ∂∂⋅+∂∂⋅])([])()([yu u F x x y x u u F x u F y x ∂∂'+⋅+∂∂'++=)]([)]()([u F x y u F xyu F y x '+⋅+'-+==xy +xF (u )+xy =z +xy .。
多元函数微分学习题.-共28页

第五部分 多元函数微分学(1)[选择题]容易题1—36,中等题37—87,难题88—99。
1.设有直线⎩⎨⎧=+--=+++031020123:z y x z y x L 及平面0224:=-+-z y x π,则直线L ( )(A) 平行于π。
(B) 在上π。
(C) 垂直于π。
(D) 与π斜交。
答:C2.二元函数⎪⎩⎪⎨⎧=≠+=)0,0(),(,0)0,0(),(,),(22y x y x y x xyy x f 在点)0,0(处 ( )(A) 连续,偏导数存在 (B) 连续,偏导数不存在 (C) 不连续,偏导数存在 (D) 不连续,偏导数不存在 答:C3.设函数),(),,(y x v v y x u u ==由方程组⎩⎨⎧+=+=22v u y v u x 确定,则当v u ≠时,=∂∂x u( ) (A)v u x - (B) v u v -- (C) v u u -- (D) vu y- 答:B4.设),(y x f 是一二元函数,),(00y x 是其定义域内的一点,则下列命题中一定正确的是( )(A) 若),(y x f 在点),(00y x 连续,则),(y x f 在点),(00y x 可导。
(B) 若),(y x f 在点),(00y x 的两个偏导数都存在,则),(y x f 在点),(00y x 连续。
(C) 若),(y x f 在点),(00y x 的两个偏导数都存在,则),(y x f 在点),(00y x 可微。
(D) 若),(y x f 在点),(00y x 可微,则),(y x f 在点),(00y x 连续。
答:D 5.函数2223),,(z y x z y x f +++=在点)2,1,1(-处的梯度是( )(A) )32,31,31(- (B) )32,31,31(2- (C) )92,91,91(- (D) )92,91,91(2- 答:A6.函数z f x y =(.)在点(,)x y 00处具有两个偏导数f x y f x y x y (,),(,)0000 是函数存在全 微分的( )。
第7章多元函数的微分学总复习剖析

x2 y2
x2 y2
总复习(第7章) 四、抽象复合函数的一阶偏导数
——填空、选择
2、设z f( x2 y2,e xy ),其中f 为可微函数,求zx ,zy .
解 设u x2 y2 ,v e xy , 则z f(u,v),
zx zu ux zv vx fu(u,v) 2x fv(u,v) ye xy
1. u xe y z2
解 du u dx u dy u dz
x
y
z
e y z2dx xe y z2dy 2 xze ydz.
2. z ln( x2 y2)
解 dz z dx z dy
x
y
( x2
y
2
) x
dx
( x2
y
2
) y
dy
x2 y2
x2 y2
2x
2 y
dx
dy
1. x 2 y z 2xyz 0.
解 令F( x, y,z) x 2 y z 2xyz
Fx 1 2 yz, Fy 2 2xz, Fz 1 2xy
z Fx
x
Fz
1 2yz 1 2xy
z Fy
y
Fz
2 2xz 1 2xy
总复习(第7章)
2. x2 z2 ln z ln y
2 xf ( x2 y2 ,e xy ) ye xy f ( x2 y2 ,e xy )
zy zu uy zv v y fu(u,v) (2 y) fv(u,v) xexy 2 yf ( x2 y2 ,e xy ) xe xy f ( x2 y2 ,e xy )
总复习(第7章)
144 p1 4 p2
总复习(第7章)
高等数学 多元函数微分学复习

第六章 多元函数微分学及其应用6.1 多元函数的基本概念一、二元函数的极限定义 f (P )= f (x ,y )的定义域为D , 0P ),(00y x 是D 的聚点. 对常数A ,对于任意给定的正数ε,总存在正数δ,使得当点P (x ,y )∈D ),(0δP U o⋂,即δ<-+-<<20200)()(||0y y x x P P时,都有|f (P )–A |=|f (x ,y )–A |<ε成立,那么就称常数A 为函数f (x ,y )当(x ,y )→),(00y x 时的极限,记作A y x f y x y x =→),(lim),(),(00或f (x ,y )→A ((x ,y )→),(00y x ),也记作A P f P P =→)(lim 0或 f (P ) →A (P →0P )为了区别于一元函数的极限,上述二元函数的极限也称做二重极限. 二、二元函数的连续性=→),(lim),(),(00y x f y x y x f ),(00y x ,0lim )0,0(),(=∆→∆∆z y x如果函数f (x , y )在D 的每一点都连续,那么就称函数f (x , y )在D 上连续,或者称f (x , y )是D 上的连续函数.如果函数f (x , y )在点0P ),(00y x 不连续,则称0P ),(00y x 为函数f (x , y )的间断点. 多元连续函数的和、差、积仍为连续函数;连续函数的商在分母不为零处仍连续;多元连续函数的复合函数也是连续函数。
一切多元初等函数在其定义区域内是连续的.多元初等函数的极限值就是函数在该点的函数值,即)()(lim00P f P f p p =→.有界性与最大值最小值定理 在有界闭区域D 上的多元连续函数,必定在D 上有界,且能取得它的最大值和最小值. 介值定理 在有界闭区域D 上的多元连续函数必取复介于最大值和最小值之间的任何值。
高等数学二专升本教材讲解

高等数学二专升本教材讲解高等数学二是专升本考试中的一门重要科目,为了帮助准备参加专升本考试的考生更好地掌握该科目的知识,本文将对高等数学二的教材进行详细讲解。
第一章:多元函数微分学1.1 隐函数与多元函数的导数在高等数学二的多元函数微分学中,我们首先学习了隐函数与多元函数的导数。
隐函数的求导是一项重要的技巧,我们需要通过求偏导数的方法来确定隐函数的导数。
在具体的计算过程中,我们需要运用链式法则和隐函数定理等概念。
1.2 多元函数的微分和全微分多元函数的微分和全微分是高等数学二中的核心内容。
通过多元函数的微分和全微分,我们可以更好地理解多元函数的变化规律和性质。
在计算全微分时,我们需要运用到偏导数,以及导数在计算微分中的应用。
1.3 复合函数的导数复合函数的导数在高等数学二的多元函数微分学中也是一项重要的内容。
我们需要通过链式法则和复合函数的求导法则来计算复合函数的导数。
此外,还需掌握常见的复合函数导数计算方法,如指数函数、对数函数和三角函数等。
第二章:多元函数积分学2.1 重积分重积分是高等数学二中的重要概念,其主要应用于多元函数的积分。
我们需要学习二重积分和三重积分的计算方法,并了解其几何意义。
此外,还需掌握重积分在求取平均值、质心和质量等方面的应用。
2.2 曲线、曲面积分曲线积分和曲面积分是高等数学二中的重要知识点,对于多元函数的积分具有重要的意义。
我们需要学习曲线积分和曲面积分的计算方法,并了解其几何意义和物理应用。
2.3 用重积分计算物理量在高等数学二的多元函数积分学中,我们还需要运用重积分来计算物理量。
通过建立积分与物理问题之间的联系,我们可以更好地理解和运用重积分的概念和方法。
第三章:无穷级数3.1 数项级数数项级数是高等数学二中关键的内容,我们需要学习数项级数的收敛性和敛散性判别方法。
掌握级数的概念和应用,对于解决实际问题具有重要的意义。
3.2 幂级数幂级数是高等数学二中的一个重要概念,其在数学和工程领域中具有广泛的应用。
第八章(理工)多元函数的微分学

4、过曲面 z − e + 2 xy = 3 上点 (1, 2, 0) 处的切平面方程为 解析:切点的方向向量为 n = (2 y , 2 x,1 − e ) ⇒ n
z
G
G
(1,2,0)
= (4, 2, 0) = (2,1, 0) ,则有点向式 2( x −1) + ( y − 2) = 0
⇒ 2x + y − 4 = 0
∂2 z ∂ 2 w ∂u ∂ 2 w ∂v ∂ 2 w ∂u ∂ 2 w ∂v ∂2w ∂2w ∂2w 2 = − − − − = − − − ∂x 2 ∂u 2 ∂x ∂u∂v ∂x ∂u∂v ∂x ∂v 2 ∂x ∂u 2 ∂u∂v ∂v 2 ∂2 z ∂ 2 w ∂u ∂ 2 w ∂v ∂ 2 w ∂u ∂ 2 w ∂v ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w 2 = − − + + = − + + − = − + − ∂y 2 ∂u 2 ∂y ∂u∂v ∂y ∂u∂v ∂y ∂v 2 ∂y ∂u 2 ∂u∂v ∂u∂v ∂v 2 ∂u 2 ∂u∂v ∂v 2 ∂2 z ∂ 2 w ∂u ∂ 2 w ∂v ∂ 2 w ∂u ∂ 2 w ∂v ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w = 1− 2 − + + = 1− 2 − + + = 1− 2 + 2 ∂x∂y ∂u ∂x ∂u∂v ∂x ∂u∂v ∂x ∂v 2 ∂x ∂u ∂u∂v ∂u∂v ∂v 2 ∂u ∂v ∂2 z ∂2 z ∂2 z ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w +2 + = − 2 −2 − + 2(1 − 2 + 2 ) − 2 +2 − =− 4 2 + 2 ∂x 2 ∂x∂y ∂y 2 ∂u ∂u∂v ∂v 2 ∂u ∂v ∂u ∂u∂v ∂v 2 ∂u
《数学分析》第四章多元函数微分学

《数学分析》第四章多元函数微分学第四章多元函数微分学一、本章知识脉络框图极限连续重极限与累次极限基本概念有界性极限存在的判别方法极值和最值基本性质极限与连续介值性偏导数可微性概念可微和连续可微的必要条件可微的充分条件复合函数微分隐函数微分计算参数方程微分多元函数微分学全微分(三元为例)df=f x dx+f y dy+f z dz 条件极值应用高阶导数与微分多元极值切线、法线、法平面、切平面泰勒公式二、本章重点及难点本章需要重点掌握以下几个方面内容:● 偏导数、全微分及其几何意义,可微与偏导存在、连续之间的关系,复合函数的偏导数与全微分,一阶微分形式不变性,方向导数与梯度,高阶偏导数,混合偏导数与顺序无关性,二元函数中值定理与Taylor 公式.● 隐函数存在定理、隐函数组存在定理、隐函数(组)求导方法、反函数组与坐标变换. ● 几何应用(平面曲线的切线与法线、空间曲线的切线与法平面、曲面的切平面与法线. ● 极值问题(必要条件与充分条件),条件极值与Lagrange 乘数法.三、本章的基本知识要点(一)平面点集与多元函数1.任意一点A 与任意点集E 的关系.1) 内点. 若存在点A 的某邻域()U A ,使得()U A E ?,则称点A 是点集E 的内点。
2) 外点. 若存在点A 的某邻域()U A ,使得()U A E ?=?,则称点A 是点集E 的外点。
3) 界点(边界点). 若在点A 的任何邻域内既含有属于E 得的点,又含有不属于E 的点,则称点A 是点集E 的界点。
4) 聚点. 若在点A 的任何空心邻域()oUA 内部都含有E 中的点,则称点A 是点集E的聚点。
5) 孤立点. 若点A E ∈,但不是E 的聚点,则称点A 是点集E 的孤立点。
2. 几种特殊的平面点集.1) 开集. 若平面点集E 所属的每一点都是E 的内点,则称E 为开集。
2)闭集. 若平面点集E 的所有聚点都属于E ,则称E 为闭集。
《数学分析》第四章多元函数微分学
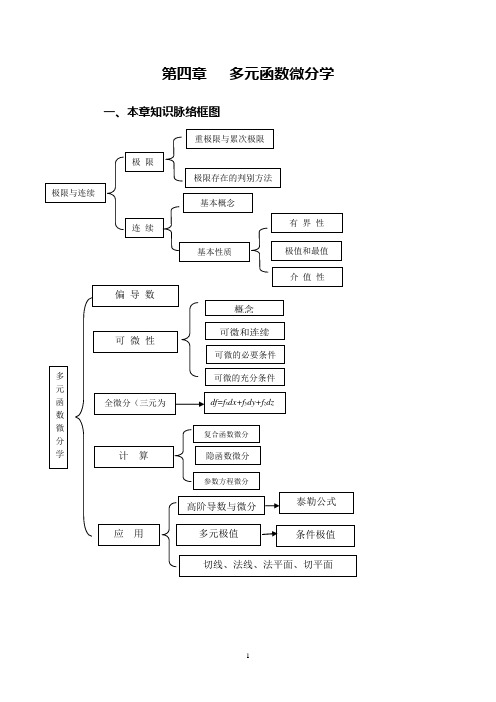
第四章 多元函数微分学一、本章知识脉络框图极 限 连 续重极限与累次极限 基本概念有 界 性极限存在的判别方法极值和最值 基本性质极限与连续介 值 性偏 导 数可 微 性概念可微和连续可微的必要条件可微的充分条件 复合函数微分隐函数微分计 算参数方程微分多元函数微分学全微分(三元为例)df=f x dx+f y dy+f z dz 条件极值应 用高阶导数与微分多元极值切线、法线、法平面、切平面泰勒公式二、本章重点及难点本章需要重点掌握以下几个方面内容:● 偏导数、全微分及其几何意义,可微与偏导存在、连续之间的关系,复合函数的偏导数与全微分,一阶微分形式不变性,方向导数与梯度,高阶偏导数,混合偏导数与顺序无关性,二元函数中值定理与Taylor 公式.● 隐函数存在定理、隐函数组存在定理、隐函数(组)求导方法、反函数组与坐标变换. ● 几何应用(平面曲线的切线与法线、空间曲线的切线与法平面、曲面的切平面与法线. ● 极值问题(必要条件与充分条件),条件极值与Lagrange 乘数法.三、本章的基本知识要点(一)平面点集与多元函数1.任意一点A 与任意点集E 的关系.1) 内点. 若存在点A 的某邻域()U A ,使得()U A E ⊂,则称点A 是点集E 的内点。
2) 外点. 若存在点A 的某邻域()U A ,使得()U A E ⋂=∅,则称点A 是点集E 的外点。
3) 界点(边界点). 若在点A 的任何邻域内既含有属于E 得的点,又含有不属于E 的点,则称点A 是点集E 的界点。
4) 聚点. 若在点A 的任何空心邻域()oUA 内部都含有E 中的点,则称点A 是点集E的聚点。
5) 孤立点. 若点A E ∈,但不是E 的聚点,则称点A 是点集E 的孤立点。
2. 几种特殊的平面点集.1) 开集. 若平面点集E 所属的每一点都是E 的内点,则称E 为开集。
2)闭集. 若平面点集E 的所有聚点都属于E ,则称E 为闭集。
第9章多元函数微分学知识点总结

第9章多元函数微分学知识点总结1.多元函数的偏导数:-定义:对于多元函数来说,当变量除了要考虑沿着自变量方向变化外,还要考虑其他自变量是否保持不变,用偏导数来表示。
-计算方法:求各个偏微分时,将其他自变量视为常数,只对需要求的变量求导即可。
2.全微分:-定义:全微分是多元函数在其中一点上沿各个偏导数方向的和所对应的微分形式。
-计算方法:使用偏导数对各个自变量求导数,并乘以相应的变化量,再相加得到全微分。
3.方向导数:-定义:方向导数是函数在其中一点上沿着指定方向的变化率,表征了函数沿着该方向上变化的快慢程度。
-计算方法:先对多元函数求偏导数,然后将其与方向向量进行点积运算,再乘以方向向量的模长。
4.梯度:-定义:梯度是一个向量,其方向是函数在其中一点增大最快的方向,大小表示函数在该点变化率的大小。
-计算方法:求多元函数在其中一点的各个偏导数,并写成一个向量,即为该点的梯度。
5.方向导数与梯度的关系:-定理:函数在其中一点上的方向导数等于该点的梯度向量与方向向量的点积。
6.极值点:-定义:多元函数的极值点是指函数取得极大值或极小值的点。
-判定方法:通过求偏导数等于零的点,再利用二阶导数进行判定。
7.拉格朗日乘数法:-定义:拉格朗日乘数法是求解给定条件下多元函数的极值问题的一种方法。
-使用方法:通过构造拉格朗日函数,利用偏导数为零和给定条件进行求解。
8.海森矩阵:-定义:海森矩阵是多元函数的二次导数在其中一点上的矩阵形式。
-计算方法:对多元函数的各个偏导数再次求偏导数,并按照顺序组成矩阵。
9.二次型:-定义:二次型是多元函数二阶偏导数在其中一点上的二次齐次多项式。
-判定方法:通过海森矩阵的特征值进行判别,判断其正负来决定函数在该点上的行为。
以上是第9章多元函数微分学的主要知识点总结。
掌握了这些知识点,我们可以更好地理解多元函数的变化规律,求解问题时也能够更有效地运用微分学的方法进行分析和计算。
4考研数学大纲知识点解析(第四章多元函数的微分学-数一

满足 .
.则
【解析】由题设
可知,当
时,有
且
,从而有
由二元函数全微分的定义, 有
在点
处可微,且
. ,
. ,故
【全微分存在的必要条件和充分条件】 【极限,连续,偏导数,可微分之间的关系】 一元函数:
二元函数:
【例题】(02 年,数学一)考虑二元函数
的下面 条性质:
①
在点
处连续. ②
在点
处的两个偏导数连续,
确.
选项(C),(D)取 不存在,故排除(C),(D).
,显然
在点
处可微,但
【综合题】设
在
点处( ).
(A)不连续. (B)偏导函数不存在. (C)不可微. (D)可微.
【解析】(1)
,
在
点连续.
(2)
同理
(3)
从而
不存在.
在
点不可微. 故选(C).
【综合题】设
则在
(A)偏导不存在. (B)偏导函数连续. (C)可微. (D)不可微.
第四章 多元函数的微分学 【多元函数的概念】 【二元函数的定义】
类似的可以定义三元函数 【二元函数的几何意义】 二元函数
. 一般表示空间直角坐标系下的一个空间曲面.
【二元函数极限的概念】
【注】二元函数极限存在,是指 以所有路径趋于
时,对应的函数值趋于相同
的一个常数.如果 沿着两条不同路径趋于
时,对应的函数值趋于不同的值,
设
有连续的一阶偏导数,又函数
及
分别由下列两式确定
:
求.
和
,
【解析】
由
两边对 求导,得
即
.
高等数学题库第08章(多元函数微分学).

- 1 -第八章多元函数微积分习题一一、填空题1. 设f(x,y)=x-3y. ,则f(2,-1)=_______,f(-1,2)=________x2+y2_______. 2. 已知f(x,y)=2x2+y2+1,则f(x,2x)=__________二、求下列函数的定义域并作出定义域的图形 1.z=3. z=y-x 2. z=-x+-y 4-x2-y24. z=log2xy习题二一、是非题1. 设z=x+lny,则2∂z1=2x+ ()∂xy2. 若函数z=f(x,y)在P(x0,y0)处的两个偏导数fx(x0,y0)与fy(x0,y0)均存在,则该函数在P点处一定连续()3. 函数z=f(x,y)在P(x0,y0)处一定有fxy(x0,y0)=fyx(x0,y0) ()xy⎧,x2+y2≠0⎪4. 函数f(x,y)=⎨x2+y2在点(0,0)处有fx(0,0)=0及⎪0,x2+y2=0⎩fy(0,0)=0 ()5. 函数z=x2+y2在点(0,0)处连续,但该函数在点(0,0)处的两个偏导数zx(0,0),zy(0,0)均不存在。
()二、填空题- 2 -1. 设z=lnx∂z∂z,则=___________;∂x∂yy2x=2y=1=___________;2. 设f(x,y)在点(a,b)处的偏导数fx(a,b)和fy(a,b)均存在,则limh→0f(a+h,b)-f(a,b-2h)=_________.h2xy+sin(xy);x2+ey三、求下列函数的偏导数:1. z=x3y-y3x+1;2. z=3. z=(1+xy)y;4. z=lntanx; y5. u=xy2+yz2+zx2∂2z∂2z∂2z四、求下列函数的2,和:∂x∂y2∂x∂y3241. z=x+3xy+y+2;2. z=xy五、计算下列各题1. 设f(x,y)=e-sinx(x+2y),求fx(0,1),fy(0,1);∂2z2. 设f(x,y)=xln(x+y),求2∂x六、设z=ln(x+y),证明:x1313∂2z,2x=1∂yy=2∂2z,x=1∂x∂yy=2.x=1y=2∂z∂z1+y=. ∂x∂y3习题三一、填空题2xy_____. 1.z=xy+e在点(x,y)处的dz=__________ 2.z=xx+y_____. 在点(0,1)处的dz=__________- 3 -3.设z=f(x,y)在点(x0,y0)处的全增量为∆z,全微分为dz,则f(x,y)在点(x0,y0) 处的全增量与全微分的关系式是__________________.二、选择题1.在点P处函数f(x,y)的全微分df存在的充分条件为()A、f的全部二阶偏导数均存在B、f连续C、f的全部一阶偏导数均连续D、f连续且fx,fy均存在2.使得df=∆f的函数f为()A、ax+by+c(a,b,c为常数)B、sin(xy)C、e+eD、x2+y22三、设z=xy,当∆x=0.1,∆y=0.2时,在(1,2)点处,求∆z和dz。
多元函数微分学题目简析

暑期培训(多元函数微分学)一、多元函数的偏导数1. f(x,y)可微,f(0,0)=0,m f x =)0,0(/,n f y =)0,0(/,)),(,()(t t f t f t =ϕ,求)0(/ϕ。
知识点:抽象的复合函数求偏导 关键:理清函数结构 答案:2m mn n ++ 难度:易2. z=z(x,y)由f(y-x, yz)=0所确定,f 对各变量的二阶偏导函数连续,求x z ∂∂,22xz ∂∂。
知识点:抽象的复合函数、隐函数求偏导关键:理清函数结构答案://///11122/2,(,),(,);f zf f y x yz f f y x yz x yf ∂==-=-∂()()()22//////////2122211121232/22.f f f f f f f zxy f--+∂=∂难度:易 3.(,)z f x y z xyz =++,求,,.z x yx y z∂∂∂∂∂∂知识点:抽象的复合函数求偏导关键:3个变量,1个方程在一定条件下可确定一个2元函数,该2元函数的因变量可以是z ,也可以是x 或者.y答案://////121212//////1212121;;.1f yzf f xzf f xyf zx y x f xyf y f yzf z f xzf ++--∂∂∂==-=∂--∂+∂+ 难度:易4. z=f(x,y)在(0,1)的某邻域内可微,且22),(321)1,(y x O y x y x f +=+++=+ρρ,一元函数y(x)由f(x,y)=1所确定,求)0(/y知识点:多元函数全微分的定义关键:找到两个已知条件:“z=f(x,y)在(0,1)的某邻域内可微”与“(,1)123(),f x y x y O ρρ+=+++=之间的联系,从而从已知条件中发现求)0(/y 所需要的东西。
答案:23- 难度:中 5.3(),(),,uu f xyz F t t xyz x y z∂===∂∂∂求().F t知识点:3元的抽象的复合函数求偏导 关键:理清函数结构+耐心 答案:///2(3)()3()().f t tf t t f t ++难度:易6. 2(1,1)(,),.u uu e xy u u x y x y ∂+==∂∂确定了求知识点:隐函数求偏导关键:求出2u x y∂∂∂的表达式,明确(,)(1,1)x y =时?u =答案:///2(3)()3()().f t tf t t f t ++难度:易7. ,ln )1()(x y x x y xf z -+=f 二阶可微,求-∂∂222x z x 222yz y ∂∂. 知识点:抽象的复合函数求偏导关键:处理好()y f x答案:(1).x y + 难度:易 8.2222(),x y z xyf z f++=可微,求.z z xy x y∂∂+∂∂ 知识点:抽象的复合函数求偏导 关键:理清函数结构、处理好2()f z答案:/2.1()zxyf z - 难度:易 9.(,,)u v w ϕ有二阶连续偏导数,(,)z z x y =由(,,)0bz cy cx az ay bx ϕ---=所确定,求.z za b x y∂∂+∂∂知识点:抽象的复合函数求偏导 关键:等号左边的ϕ有3个中间变量;(,)z z x y =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dz f x ( x, y) dx f y ( x, y)z y e x y , x
在点 (2,1) 处的全微分.
z xex y y
z 2 e2 y (2,1)
z e2 , x (2,1)
例6. 计算函数
的全微分.
1 y 解: du 1 dx ( cos z e y z )d y y e y z d z 2 2
x 时,相应地函数有增量 f ( x0 x, y0 ) f ( x0 , y0 ), f ( x0 x , y0 ) f ( x0 , y0 ) 如果 lim 存在,则称 x 0 x 此极限为函数 z f ( x , y )在点( x0 , y0 )处对 x 的
偏导数,记为
例2 求函数 z x ( x 0, x 1) 的偏导数. 解
z yx y 1 , x
z x y ln x. y
2、高阶偏导数
函数 z f ( x , y ) 的二阶偏导数为
z 2 z z 2 z 2 f yy ( x , y ), 2 f xx ( x , y ), x x x y y y
z f , ,z x x x x 0 x x x 0 y y y y
0 0
x x0 或 y y0
f x ( x 0 , y0 ) .
同理可定义函数 z f ( x , y )在点( x0 , y0 )处对 y 的偏导数, 为
f ( x 0 , y0 y ) f ( x 0 , y 0 ) lim y 0 y z f 记为 , , z y x x0 或 f y ( x 0 , y0 ) . y y0 y x x 0 y x x 0 y y y y
t
z
e t cos t e t sin t
u
t
v
t
e t (cos t sin t ).
定理 2
如果 u ( x , y ) 及 v ( x , y )都在点
( x , y )具有对 x和 y 的偏导数,且函数 z f ( u, v )
在对应点( u, v ) 具有连续偏导数,则复合函数
2z 2z 2z 2z 求 2, , , x yx xy y 2
z z 3 2 2 2 3 解 2 x y 9 xy x; 3 x y 3 y y, y x
z z 2 6 xy , 2 x 3 18 xy; x 2 y 2 2 z 2z 6 x 2 y 9 y 2 1, 6 x 2 y 9 y 2 1. xy yx
(3) z
(
ln( x y ) x y
(4) z
x y
x2 y2 , 则 f (2,3) _______. 2. 设 f ( x , y ) 2 xy
二、多元函数的极限
定义 设函数 z f ( x , y ) 的定义域为 D , P0 ( x0 , y0 ) D , z 当点 P 无限趋近于点 P0 时, f ( x , y ) 无限地趋近于一
dz z du z dv . dt u dt v dt
dz 以上公式中的导数 称为全导数. dt
z
u
t
v
t
dz 例 7 设 z uv ,而 u e , v cos t ,求全导数 . dt
t
解
dz z du z dv dt u dt v dt
ve u sin t
z z 求 和 . x y
解
z z u z v x u x v x
e u sin v y e u cos v 1 e u ( y sinv cos v ),
z z u z v y u y v y u u e sin v x e cos v 1 e u ( x sinv cos v ).
其中 ( x ) ( y ) ,则称函数 z f ( x , y ) 在点( x , y )可微分。称 f x ( x, y) x f y ( x, y) y
2 2
为函数 z f ( x , y )在点( x , y )的全微分,记为 dz,即 dz f x ( x, y) x f y ( x, y) y , 或
0 0
例1 求 z x 3 xy y 在点 (1, 2) 处的偏导数.
2 2
解
z 2x 3 y ; x
x 1 y 2
z 3x 2 y . y
x 1 y 2
z x
z 2 1 3 2 8 , y
y
3 1 2 2 7 .
练
习
三
z z 2 z 2 z z e xy ( x y ), 求 , 2, , 1、设 x y y yx z z , dz (1,1) . , 2、已知 z x 3 y , 求 x y
3、 设 z
y ex,
z z , . 求 x x y
1 . 2
三、多元函数的连续性
定义3 . 设二元函数 f ( P )定义在 D 上, P0 ( x0 , y0 ) D, 如果存在
P P0
lim f ( P ) f ( P0 )
则称 二元函数 f ( P ) 在点 P0 连续, 否则称为不连续, 此时 称为间断点 . 如果函数在 D 上各点处都连续, 则称此函数在 D 上
z f [ ( x , y ), ( x , y )]在对应点( x , y )的两个偏
导数存在,且可用下列公式计算
z z u z v , x u x v x z z u z v . y u y v y
z
u v
x
y x
y
例8
设 z e u sin v ,而 u xy , v x y ,
y 0
1 lim y sin 0 x0 x y0
无穷小乘有界量仍是无穷小
原式 0.
例2
xy 1 1 求 lim . x 0 xy y0
xy 1 1 1 解 原式 lim lim x 0 xy( xy 1 1) x 0 xy 1 1 y0 y0
2
2.
3.
du 设 u e ( y z ), 而 y a sin x, z cos x, 求 . dx
ax
七、隐函数的求导法则
(1) F ( x , y ) 0
隐函数存在定理 1 设函数 F ( x , y )在点 P ( x0 , y0 )的 某一邻域内具有连续的偏导数,且 F ( x0 , y0 ) 0, F y ( x0 , y0 ) 0 ,则方程 F ( x , y ) 0 在点 P ( x0 , y0 )的 某一邻域内恒能唯一确定一个单值连续且具有连续 导数的函数 y f ( x ) ,它满足条件 y0 f ( x0 ),并 有
纯偏导
z 2 z z 2 z f xy ( x , y ), f yx ( x , y ). y x xy x y yx
混合偏导
定义 二阶及二阶以上的偏导数统称为高阶偏 导数.
例3
设 z x 3 y 2 3 xy 3 xy 1
2
六、复合函数求导法则(链式法则)
定理 1 如果函数及 u ( t ), v ( t ) 都在点 t 可 导,函数 z f ( u, v )在对应点( u, v ) 具有连续偏导 数, 则复合函数 z f [ (t ), (t )] 在对应点 t 可导, 且其导数可用下列公式计算:
dz 例9. 设 z u v sin t , u e , v cos t , 求全导数 . dt
t
解:
d z z du d t u d t
z t
v et
t
cos t
z
u v t
e (cos t sin t ) cos t
t
t
练 习 四
1.
z z 设 z u sin v , 而 u xy , v x y , 求 和 . x y z z x 已知 z u ln v , 而 u , v 2 x 3 y , 求 和 . x y y
2
2
例4. 求函数 z e 解:
x2 y
的二阶偏导数.
z x2 y e x
z x2 y e 2 x
2
z x2 y 2e y
z x2 y 2e x y
2
z x2 y 2 e y x
2
z x2 y 4e 2 y
2
五、全微分概念 如果函数 z f ( x , y )在点( x , y )的全增量 z f ( x x , y y ) f ( x , y )可以表示为 z f x ( x, y) x f y ( x, y) y o( ) ,
个确定的常数 A ,则称 A 为函数 z f ( x , y ) 当 x x 0 , y y0 时的极限,记为 (或 f ( x, y) A ( P P0 ) ).
x x0 y y0
lim f ( x , y ) A
说明:
(1)定义中 P P0 的方式是任意的;
确定的值和它对应,则称 z 是变量 x, y 的二元函 数,记为 z f ( x , y ) (或记为 z f (P ) ).
类似地可定义三元及三元以上函数.
n 当 n 2 时, 元函数统称为多元函数.
