2012版中考数学精品课件(含10 11真题)第13讲反比例函数(64张)
合集下载
2012年中考数学深度复习讲义(教案+中考真题+模拟试题+单元测试)：反比例函数
（备战中考）2012年中考数学深度复习讲义 （教案+中考真题+模拟试题+单元测试）反比例函数▴知识讲解①一般地，函数y=k x（k 是常数，k ≠0）叫做反比例函数，x 的取值范围是x ≠0，y的取值范围是y ≠0．②反比例函数的图像是双曲线，故也称双曲线y=k x（k ≠0），当k>0时⇔函数图像的两个分支分别在第一，三象限内⇔在每一象限内，y 随x 的增大而减小；当k<0时⇔函数图像的两个分支分别在第二，四象限内⇔在每一象限内，y 随x 的增大而增大．•③反比例函数的解析式y=k x中，只有一个待定系数k ，所以通常只需知道图像上的一个点的坐标，就可以确定k 的值．从而确定反比例函数的解析式．（因为k=xy ） ▴例题解析例1 （2011甘肃兰州，24，7分）如图，一次函数3y kx =+的图象与反比例函数m y x=（x>0）的图象交于点P ，PA ⊥x轴于点A ，PB ⊥y 轴于点B ，一次函数的图象分别交x 轴、y 轴于点C 、点D ，且S △DBP =27，12O C C A=。
（1）求点D 的坐标；（2）求一次函数与反比例函数的表达式；（3）根据图象写出当x 取何值时，一次函数的值小于反比例函数的值？xy AO PBC D【答案】（1）D （0，3）（2）设P （a ，b ），则OA=a ，OC=13a ，得C （13a ，0）因点C 在直线y =kx +3上，得1303ka +=，ka =－9DB=3－b =3－(ka +3)=－ka =9，BP=a 由1192722D B P S D B B P a ∆=== 得a =6，所以32k =-，b =－6，m =－36一次函数的表达式为332y x =-+，反比例函数的表达式为36y x=-（3）x >6例2如图，已知反比例函数y=kx（k<0）的图像经过点A （－3，m ），•过点A 作AB ⊥x 轴于点，且△AOB 的面积为3．（1）求k 和m 的值；（2）若一次函数y=ax+1的图像经过点A ，并且与x 轴相交于点C ，求∠ACO •的度数为│AO │：│AC │的值．【分析】（1）由A 点横坐标可知线段OB 的长，再由△AOB 的面积易得出AB 的长，•即m 的值，此时可知点A 的坐标由点A 在反比例函数y=k x上可求得k 的值．（2）由直线y=ax+1过点A 易求出a 值．进而可知点C 的坐标，在Rt △ABC 中易求tan ∠ACO 的值，可知∠ACO 的度数，由勾股定理可求得OA ，AC 的长． 【解答】（1）∵S=3 ∴12·m ·3=3，∴m=2，又y=k x过点A （－3，2），则2=3k -，∴k=－23（2）∵直线y=ax+1过A （－3，2） ∴2=－3a+1，∴a=33，y=33+1．当y=0时，x=3，∴C （3，0），BC=23，又tan ∠ACO=223AB BC==33，∴∠ACO=30°．在Rt △ABO 中，AO=22OB AB +=7，在Rt △ABC 中，AC=2AB=4． ∴│AO │：│AC │=7：4．2011年真题一、选择题1. （2011广东汕头，6，4分）已知反比例函数k y x=的图象经过（1，－2）．则k = ．【答案】－22．（2011湖南邵阳，5，3分）已知点（1,1）在反比例函数k y x=（k 为常数，k ≠0）的图像上，则这个反比例函数的大致图像是（ ）【答案】C 提示：反比例函数过第一象限（也可由点（1,1）求得k=1），故选C 。
中考数学复习第13课时《反比例函数》说课稿
中考数学复习第13课时《反比例函数》说课稿一. 教材分析《中考数学复习第13课时》这一课时，是在学生已经掌握了比例函数的基础上进行教学的。
本课时主要让学生了解反比例函数的定义、性质及其图象，能够熟练运用反比例函数解决实际问题。
教材通过丰富的实例，引导学生探究反比例函数的图象和性质，培养学生的观察能力、思维能力和创新能力。
二. 学情分析初中生在学习反比例函数时，已经具备了一定的函数基础，对比例函数的概念和图象有一定的了解。
但学生在学习过程中，可能会对反比例函数的定义和性质产生混淆，特别是在解决实际问题时，不知道如何运用反比例函数。
因此，在教学过程中，我要注重引导学生理解反比例函数的定义，掌握其性质，并能运用到实际问题中。
三. 说教学目标1.知识与技能目标：让学生掌握反比例函数的定义、性质及其图象，能够熟练运用反比例函数解决实际问题。
2.过程与方法目标：通过观察、实验、探究等方法，让学生了解反比例函数的图象和性质，培养学生的观察能力、思维能力和创新能力。
3.情感态度与价值观目标：激发学生学习反比例函数的兴趣，培养学生的团队合作意识，使学生感受到数学在生活中的应用价值。
四. 说教学重难点1.教学重点：反比例函数的定义、性质及其图象。
2.教学难点：反比例函数在实际问题中的应用。
五. 说教学方法与手段1.教学方法：采用问题驱动法、案例教学法、小组合作学习法等，引导学生主动探究、积极参与。
2.教学手段：利用多媒体课件、反比例函数图象软件等，直观展示反比例函数的图象和性质，提高学生的学习兴趣。
六. 说教学过程1.导入：通过复习比例函数的知识，引出反比例函数的概念，激发学生的学习兴趣。
2.新课导入：讲解反比例函数的定义，让学生通过实例理解反比例函数的概念。
3.性质探究：引导学生观察反比例函数的图象，总结反比例函数的性质。
4.应用拓展：通过实际问题，让学生运用反比例函数解决问题，巩固所学知识。
5.练习环节：布置一些有关反比例函数的练习题，让学生独立完成，检测学习效果。
2012版中考数学精品课件(含10-11真题)第1讲实数(52张)
2
第29页，共52页。
2012版中考数学复习指导
7.(2010·益阳中考)下列计算正确的是( )
(A)30=0
(B)-|-3|=-3
(C)3-1=-3
【解析】选
(D) B.30 1,31 1 , 9 3.
3
9 3
第30页，共52页。
2012版中考数学复习指导
8.(2011·南通中考)计算22+(－1)4+( 【解析】原式＝4+1+1－3＝3.
小数点前面的零)，例如：0.000 123=1.23×10-4.
第33页，共52页。
2012版中考数学复习指导
【例3】(2010·沈阳中考)为了响应国家“发展低碳经济、走进低碳生活”
的号召，到目前为止沈阳市共有60 000户家庭建立了“低碳节能减排家庭
档案”，则60 000这个数用科学记数法表示为( )
2012版中考数学复习指导
1.实数及其有关概念是今后研究数学问题的基础，所以掌握好实数的 概念是关键.同时，要注意实数的分类、比较，从而能更好地掌握本讲的 内容.
2.实数的加、减、乘、除、乘方以及简单的混合运算是本讲学习 的重点之一，它为将来学习代数式、方程、函数、不等式的有关知识 奠定了基础，往往带有一定的能力测试倾向.
第10页，共52页。
2012版中考数学复习指导
第11页，共52页。
2012版中考数学复习指导
第12页，共52页。
2012版中考数学复习指导
第13页，共52页。
2012版中考数学复习指导
第14页，共52页。
2012版中考数学复习指导
第15页，共52页。
2012版中考数学复习指导
2012版中考数学精品课件(含10 11真题)第14讲二次函数(82张)
2
)
(A)将抛物线C向右平移 5 个单位 (B)将抛物线C向右平移3个单位
(C)将抛物线C向右平移5个单位
(D)将抛物线C向右平移6个单位
2012版中考数学复习指导
【解析】选C.利用公式法可以求出抛物线C的对称轴为直 线 x 3 ,它到直线x=1的距离是 5 ，因此，抛物线C与抛物
2 2
线C′的距离为5，故应将抛物线C向右平移5个单位.
(B)y=-2x2+12x-16
(C)y=-2x2+12x-19
(D)y=-2x2+12x-20
2012版中考数学复习指导
【解析】选D.因为y=2x2-12x+16=2(x-3)2-2，所以绕它的顶点 (3，-2)旋转180°后，所得抛物线的解析式为y=-2(x-3)2-2= -2x2+12x-20,故选D.
方法二：∵a=-10<0，
∴抛物线开口向下.
∴当30≤x≤40时，w≥2 000.
∵x≤32，∴30≤x≤32时，w≥2 000.
2012版中考数学复习指导
∵y=-10x+500, k=-10<0, ∴y随x的增大而减小. ∴当x=32时，y最小＝180. ∵当进价一定时，销售量越小，成本越小，
∴20×180=3 600(元).
2012版中考数学复习指导
【自主解答】(1)由题意，得w= (x-20)·y =(x-20)·(-10x+500)
=-10x2+700x-10 000
x b 35.
2a
答：当销售单价定为35元时，每月可获得最大利润. (2)由题意，得：-10x2+700x-10 000=2 000 解这个方程得x1=30，x2 =40. 答：李明想要每月获得2 000元的利润，销售单价应定为30元 或40元.
)
(A)将抛物线C向右平移 5 个单位 (B)将抛物线C向右平移3个单位
(C)将抛物线C向右平移5个单位
(D)将抛物线C向右平移6个单位
2012版中考数学复习指导
【解析】选C.利用公式法可以求出抛物线C的对称轴为直 线 x 3 ,它到直线x=1的距离是 5 ，因此，抛物线C与抛物
2 2
线C′的距离为5，故应将抛物线C向右平移5个单位.
(B)y=-2x2+12x-16
(C)y=-2x2+12x-19
(D)y=-2x2+12x-20
2012版中考数学复习指导
【解析】选D.因为y=2x2-12x+16=2(x-3)2-2，所以绕它的顶点 (3，-2)旋转180°后，所得抛物线的解析式为y=-2(x-3)2-2= -2x2+12x-20,故选D.
方法二：∵a=-10<0，
∴抛物线开口向下.
∴当30≤x≤40时，w≥2 000.
∵x≤32，∴30≤x≤32时，w≥2 000.
2012版中考数学复习指导
∵y=-10x+500, k=-10<0, ∴y随x的增大而减小. ∴当x=32时，y最小＝180. ∵当进价一定时，销售量越小，成本越小，
∴20×180=3 600(元).
2012版中考数学复习指导
【自主解答】(1)由题意，得w= (x-20)·y =(x-20)·(-10x+500)
=-10x2+700x-10 000
x b 35.
2a
答：当销售单价定为35元时，每月可获得最大利润. (2)由题意，得：-10x2+700x-10 000=2 000 解这个方程得x1=30，x2 =40. 答：李明想要每月获得2 000元的利润，销售单价应定为30元 或40元.
2012版中考数学精品课件(含10-11真题)第22讲矩形、菱形、正方形(113张)
2012版中考数学复习指导
菱形的性质与判定
菱形除具有平行四边形的一切性质外，还具有其特殊的性质，即 四条边相等；对角线互相垂直，每一条对角线平分一组对角；具 有中心对称性和轴对称性等；
菱形的判定方法主要有(1)利用边之间的关系进行判定，即有一组邻边 相等的平行四边形是菱形；四条边都相等的四边形是菱形；(2)利用对 角线之间的关系判定，即对角线互相垂直的平行四边形是菱形；
(A)1
(B)2
(C)3
(D)4
第48页，共113页。
2012版中考数学复习指导
【解析】选C.由折叠知，
AF＝AD，∠D＝∠AFE，EF＝DE. ∵四边形ABCD是正方形， ∴AB＝AD＝AF，∠B＝∠AFE＝∠D＝∠AFG＝90°. ∵AG=AG, ∴Rt△ABG≌Rt△AFG,故①正确； ∵AB＝6，CD＝3DE. ∴CE＝4,DE＝EF＝2,
第4页，共113页。
2012版中考数学复习指导
2.2012年中考估计有加大本讲题量的趋势，本讲知识与轴对称、 旋转及平移等知识结合考查，许多有一定难度的新题、活题、压轴题 将出现于此讲，试题强调基础，源于教材，变中求新，着重考查学生 的发散思维能力.
第5页，共113页。
2012版中考数学复习指导
□ABCD的边DC延长到点E，使CE＝DC，
连接AE，交BC于点F.
(1)求证：△ABF≌△ECF. (2)若∠AFC＝2∠D，连接AC、BE.求证：四边形ABEC是矩形.
第16页，共113页。
2012版中考数学复习指导
【思路点拨】
第17页，共113页。
2012版中考数学复习指导
【自主解答】(1)∵四边形ABCD是平行四边形，
【例3】(2010·上海中考)已知正方形ABCD
2012版中考数学专题复习精品课件(含10 11真题)专题7 探索问题(53张)
2012版中考数学复习指导
3.(2011·成都中考)设 S 1 1 1 ,S 1 1 1 , 1 2 12 22 22 32 1 1 1 1 S3 1 2 2 ,,Sn 1 2 ，设S S1 S2 2 3 4 n n 1 则S=______(用含n的代数式表示，其中n为正整数). Sn ,
1 n
1 1 1 1 1 1 1 1 n 1 n 1 . 2 2 3 3 4 n n 1 n 1
答案： 1 n
1 (n 1)
2012版中考数学复习指导
动态探索问题
动态探索问题的特点是：以几何图形为背景，讨论某个元素 的运动变化，探索其中隐含的规律，如线段关系、角度大小、 面积关系、函数关系等.在解决动态问题时，要抓住不变的量， 找出其中的规律,同时还应该考虑到，当动态元素去某一位臵 时，“动”则变为“静”，从而化动为静.
sin∠CGO的大小怎样变化，请说明理由.
2012版中考数学复习指导
【思路点拨】(1)连接OH, 过点H作HP⊥y轴于点P，构造直角 三角形，利用勾股定理求出线段的长，然后利用等角，求出 sin∠HAO的值.
(2)过点D作DM⊥EF于M，并延长DM交⊙O于N，连接ON，交BC于
T，利用等腰三角形的性质以及圆的轴对称性，证明∠CGO
2012版中考数学复习指导
n2 n 1 2 【解析】通过探索规律可得 Sn ［ ］, 所以 Sn n n 1 n2 n 1 3 7 13 n2 n 1 ，所以S n n 1 2 6 12 n n 1 1 1 1 1 1 1 1 1 2 6 12 n n 1 1 1 1 1 2 6 12 n n 1
2012版中考数学精品课件含1011一次方程组53张4
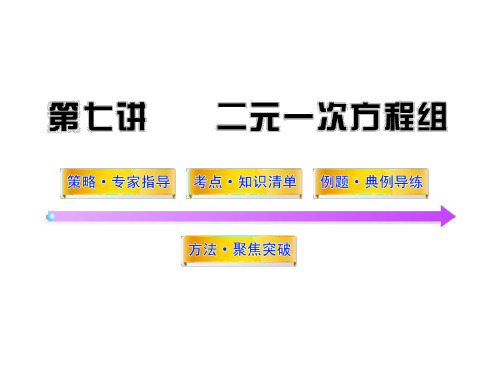
方法二：①＋②，得5x=10.∴x=2，
把x=2代入①，得4-y=3.∴y=1.
∴方程组的解是
x y
2 .
1
5.(2010·百色中考)二元一次方程组 2xx33yy41的解是( )
(A)
x y
1 1
(C)
x y
2 2
(B)xy
1 1
(D)
x y
2 1
【解析】选A.把两式相加，得3x=3，x=1，把x=1代入第一
()
(A)xxyy1 2
(B) 51xxy2y
3
3
(C)
2x
z
0
3x
y
1 5
(D)
x x
2
5 y
3
7
【解析】选D.根据二元一次方程组的定义判定：A是二元二次
方程组，B是分式方程组，C是三元一次方程组，只有D满足 二 元一次方程组的定义.
3.(2009·杭州中考)
已知
x 1 y 1
是方程2x-ay=3的一个解,
(4)解这个二元一次方程组，求出未知数的值； (5)检验所得结果的正确性及合理性； (6)写出答案.
【例3】(2010·郴州中考)受气候等因素的影响，今年某些农 产品的价格有所上涨.张大叔在承包的10亩地里所种植的甲、 乙两种蔬菜共获利13 800元.其中甲种蔬菜每亩获利1 200元， 乙种蔬菜每亩获利1 500元.则甲、乙两种蔬菜各种植了多少 亩？ 【思路点拨】
二元一次方程组的解法
1.代入法解二元一次方程组的步骤 (1)选取一个系数较简单的二元一次方程变形，用含有一个未 知数的代数式表示另一个未知数； (2)将变形后的方程代入另一个方程中，消去一个未知数，得 到一个一元一次方程； (3)解这个一元一次方程，求出未知数的值；
2012版中考数学专题复习精品课件(含10 11真题)专题1 数学思想方法(64张)
⑦消元法；
⑧配方法； ⑨待定系数法等.
2012版中考数学复习指导
2012版中考数学复习指导
分类讨论思想方法
分类讨论思想是指当数学问题不宜统一方法处理时，我们常
常根据研究对象性质的差异，按照一定的分类方法或标准 ,将
问题分为全而不重，广而不漏的若干类，然后逐类分别进行 讨论，再把结论汇总，得出问题的答案的思想 .
2012版中考数学复习指导
【例2】(2010·曲靖中考)如图，在平 面直角坐标系xOy中，抛物线y=x2向左 平移1个单位，再向下平移4个单位， 得到抛物线y=(x-h)2+k,所得抛物线与
x轴交于A、B两点(点A在点B的左边)与
y轴交于点C，顶点为D.
2012版中考数学复习指导
(1)求h、k的值； (2)判断△ACD的形状，并说明理由； (3)在线段AC上是否存在点M，使△AOM与△ABC相似.若存在， 求出点M的坐标；若不存在，说明理由.
2012版中考数学复习指导
1 1 ∴直线AP的解析式为y= x . 2 4 ∵点P既在抛物线上，又在直线AP上， 3 1 1 ∴点P的纵坐标相等，即 x 2 x 1 x , 2 2 4 解得 x1 5 , x 2 1 舍去 . 2 2 5 3 当x 时, y . 2 2 5 3 P( , ). 2 2
2012版中考数学复习指导
(2)存在.①如图1，当CP=CO时， 点P在以BM为直径的圆上， ∵BM为圆的直径.
∴∠BPM=90°，
∴PM∥AB.
∴△CPM∽△CBA.
∴ CP CM ，即 4 CM , 所以CM=5. CB CA 5 25 4 ∴m=-1.
2012版中考数学复习指导
2012版中考数学精品课件第三章函数及其图象(含11真题和12预测题)第11讲 函数及其图象
1 的坐标为( 4,6)， 【点拨】(1)∵点 A 的坐标为(－4,6)，∴只将纵坐标变为原来的 时，点 A 点拨】(1)∵ 2 的对应点的坐标是( 4,3)．(2)平面直角坐标系中 若两点关于原点对称， 平面直角坐标系中， 的对应点的坐标是(－4,3)．(2)平面直角坐标系中，若两点关于原点对称，则 它们的横纵坐标都互为相反数，所以点(2，－3)关于原点的对称点是 它们的横纵坐标都互为相反数，所以点(2，－3)关于原点的对称点是(－2,3)． (2，－3)关于原点的对称点是( 2,3)．
第三章 函数及其图象 第11讲 函数及其图象
考点知识精讲
中考典例精析
举一反三
考点训练
考点一 平面内点的坐标 1．有序数对 (1)平面内的点可以用一对 来表示． (1)平面内的点可以用一对 有序实数 来表示．例如点A在平面内可 的横坐标， 的纵坐标． 表示为A(a，b)，其中a表示点A的横坐标，b表示点A的纵坐标． 的关系， (2)平面内的点和有序实数对是 (2)平面内的点和有序实数对是 一一对应 的关系，即平面内的任何 来表示； 一个点可以用一对 有序实数 来表示；反过来每一对有序实数都表示平面 内的一个点． 内的一个点． (3)有序实数对表示这一对实数是有 (1,2)和(2,1)表示 (3)有序实数对表示这一对实数是有 顺序 的，即(1,2)和(2,1)表示 的点． 两个 不同 的点．
2．平面内点的坐标规律 (1)各象限内点的坐标的特征 (1)各象限内点的坐标的特征 在第一象限⇔ 点P(x，y)在第一象限⇔x＞0，y＞0； 在第二象限⇔ 点P(x，y)在第二象限⇔x＜0，y＞0； 在第三象限⇔ 点P(x，y)在第三象限⇔x＜0，y＜0； 在第四象限⇔ 点P(x，y)在第四象限⇔x＞0，y＜0. (2)坐标轴上的点的坐标的特征 (2)坐标轴上的点的坐标的特征 轴上⇔ 为任意实数； 点P(x，y)在x轴上⇔y＝0，x为任意实数； 轴上⇔ 为任意实数； 点P(x，y)在y轴上⇔x＝0，y为任意实数； 在坐标原点⇔ 点P(x，y)在坐标原点⇔x＝0，y＝0.
2012版中考数学专题复习精品课件(含10 11真题)专题4 阅读理解问题(54张)
∴△NFN′∽△M′EM,∴ MM ME , NN NF
∵M′E=N′F,∴ MM NF tan(或 sin ).
NN NF
cos
①当α=45°时，tanα=1,则MM′=N′N；
②当α≠45°时，MM′≠N′N,则 MM tan(或 sin ).
NN
cos
方法二：在方形环中，∠D=90°,
2
猜想：一般地，当α为锐角时，有cos(180°+α)=-cosα,
由此可知cos240°的值等于______.
【解析】根据归纳的规律，cos240°=cos(180°+60°)= -cos60°= 1 .
2 答案： 1
2
7.(2011·内江中考)阅读理解:同学们,我们曾经研究过n×n
正方形网格,得到网格中正方形总个数的表达式为12+22+32+…
【自主解答】(1) 3 (2)如图：
作点B关于CD的对称点E，则点E正好在圆周上，连接OA、OB、 OE，连接AE交CD于一点P，AP+BP最短，
因为 A»D 的度数为60°,点B是 A»D 的中点， 所以∠AEB=15°, 因为点B关于CD的对称点是点E，所以∠BOE=60°, 所以△OBE为等边三角形， 所以∠OEB=60°,所以∠OEA=45°， 又因为OA=OE， 所以△OAE为等腰直角三角形,所以AE= 2 2. 所以图中点P即为所求.BP+AP的最小值为 2 2.
再如题(b)图，在等边三角形ABC中，AB=2，点E是AB的中点， AD是高，在AD上找一点P，使BP+PE的值最小. 做法如下：作点B关于AD的对称点，恰好与点C重合，连接CE 交AD于一点，则这点就是所求的点P，故BP+PE的最小值为___.
2012版中考数学精品课件含1011等腰三角形61张42
(A)15米
(B)20米
(C)25米 (D)30米
【解析】选C.因为点E、F分别是边AB、AC的中点，所以BC ＝2EF，又因为EF＝5米，所以BC＝10米，因为三角形ABC 是等边三角形，所以BE=CF＝5米，所以篱笆的长为25米.
7.(2010·铜仁中考)如图，小红作出了边长为1的第1个正 △A1B1C1，算出了正△A1B1C1的面积，然后分别取△A1B1C1三边 的中点A2，B2，C2，作出了第2个正△A2B2C2，算出了正 △A2B2C2的面积，用同样的方法，作出了第3个正△A3B3C3，算 出了正△A3B3C3的面积……，由此可得，第8个正△A8B8C8的面 积是( )
【例3】(2010·烟台中考)如图，等腰△ABC中，AB=AC， ∠A=20°.线段AB的垂直平分线交AB于D，交AC于E，连接BE， 则∠CBE等于( )
(A)80° (B)70° (C)60°
(D)50°
【思路点拨】
【自主解答】选C.因为AB=AC，∠A=20°，所以∠ABC= 1(180°-∠A)=80°，因为DE垂直平分AB，所以∠ABE=∠A
(A) 3 (1)7
42
(B) 3 (1)8
42
(C) 3 (1)7
44
(D) 3 (1)8
44
【解析】选C.因为△A1B1C1的边长为1，所以△A1B1C1的面积
为 3，又因为点A2，B2，C2分别是△A1B1C1各边的中点，所
4
以△A2B2C2的面积为 3 1，同理，△A3B3C3的面积为
1.(2010·宁波中考)如图，在△ABC中，
AB=AC，∠A=36°，BD、CE分别是∠ABC、
∠BCD的角平分线，则图中
的等腰三角形有( )
2012年中考数学一轮复习精品讲义 反比例函数
6 的图象上. x 6 6 当 x=3 时， y 2. 当 y=-3 时， 3 , 所以 x=-2. 3 x
所以点 A，B 在反比例函数 y 所以 A（3，2） ，B（-2，-3）. 把 A（3，2） ，B（-2，-3）代入 y kx b 中，
得
2 3k b, k 1, 解得 3 2k b, b 1.
a 的图象在第二、四象限，因此 A x a 的图象在第一、三象限，四个选 x
项中没有适合的. 答案：A 【解题策略】 解答本题也可以从选项出发来考虑 a 的情况.例如 A 项，由函数 y ax a 的可判断 a＞0，
用心
爱心
专心
2
由函数 y
a 的图象可判断 a＞0，由此可判断 A 项正确,再例如 B 项，由函数 y ax a 的增减性质可判断-a x
k 图象上的任意一点，过 A 作 AB⊥x 轴 x
1 1 S 矩形 ABOC= | k | . 2 2
例 4 如图 17-38 所示，点 P 是 x 轴正半轴上的一个动点，过 P 作 x 轴的垂线交双曲线 y
1 于点 Q，连续 x
OQ，当点 P 沿 x 轴正方向运动时，Rt△QOP 的面积
A．逐渐增大 C．保持不变 B．逐渐减小 D．法确定
用心 爱心 专心
1
8 是反比例函数，k=-8. x 1 1 1 （2） xy 可写成 y 9 , 是反比例函数， k . 9 9 x
解： （1） y （3） y 4 3x 不是反比例函数，是一次函数.
1 x 不是反比例函数，是正比例函数. 7 6 6 6 （5） y 可写成 y 7 , 是反比例函数 k . 7x 7 x
2012版中考数学精品课件(含10-11真题)第9讲不等式与不等式组(54张)
第16页，共54页。
2012版中考数学复习指导
2. 解不等式组的步骤: (1)先分别求出各个不等式的解集; (2)然后借助数轴确定各不等式的公共解集或根据口诀“大大取大,小 小取小,大小、小大中间找，小小、大大找不到(无解)”来确定不等式组
的解集.
第17页，共54页。
2012版中考数学复习指导
【例1】(2011·舟山中考)解不等式组： 轴上表示出来.
【思路点拨】先求出不等式组的解集，再根据不等式组的解集确定它的整
数解.
【自主解答】解不等式2x+5＞1，得x＞-2;解3x-8≤10，得x≤6.∴不等式
组的解集为-2＜x≤6.∴满足不等式组的整数解为-1、0、1、2、3、4、5、6.
第26页，共54页。
2012版中考数学复习指导
5.(2011·苏州中考)不等式组
m2
第34页，共54页。
2012版中考数学复习指导
10.(2011·黄冈中考)若关于x、y的二元一次方程组
3x y 1 a的解满足x+y<2，则a的取值范围为____
【解x 析3】y 解3关x 3a,,解y 得 8a<a4,. x y 2
第24页，共54页。
2012版中考数学复习指导 不等式(组)的整数解
不等式(组)的整数解，包含在它的解集中，因此，解决此类问题 的关键是先求出不等式(组)的解集，然后，根据题目条件的限制或 实际意义的要求借助数轴确定其整数解.
第25页，共54页。
2012版中考数学复习指导
【例2】(2010·芜湖中考)求不等式组 2x 5＞1的整数解. 3x 8 10
1.已知的不等式组中含有参数m，可以先进行化简，求出不等式组的解集， 然后再与已知解集比较，求出m的取值范围.
2012版中考数学复习指导
2. 解不等式组的步骤: (1)先分别求出各个不等式的解集; (2)然后借助数轴确定各不等式的公共解集或根据口诀“大大取大,小 小取小,大小、小大中间找，小小、大大找不到(无解)”来确定不等式组
的解集.
第17页，共54页。
2012版中考数学复习指导
【例1】(2011·舟山中考)解不等式组： 轴上表示出来.
【思路点拨】先求出不等式组的解集，再根据不等式组的解集确定它的整
数解.
【自主解答】解不等式2x+5＞1，得x＞-2;解3x-8≤10，得x≤6.∴不等式
组的解集为-2＜x≤6.∴满足不等式组的整数解为-1、0、1、2、3、4、5、6.
第26页，共54页。
2012版中考数学复习指导
5.(2011·苏州中考)不等式组
m2
第34页，共54页。
2012版中考数学复习指导
10.(2011·黄冈中考)若关于x、y的二元一次方程组
3x y 1 a的解满足x+y<2，则a的取值范围为____
【解x 析3】y 解3关x 3a,,解y 得 8a<a4,. x y 2
第24页，共54页。
2012版中考数学复习指导 不等式(组)的整数解
不等式(组)的整数解，包含在它的解集中，因此，解决此类问题 的关键是先求出不等式(组)的解集，然后，根据题目条件的限制或 实际意义的要求借助数轴确定其整数解.
第25页，共54页。
2012版中考数学复习指导
【例2】(2010·芜湖中考)求不等式组 2x 5＞1的整数解. 3x 8 10
1.已知的不等式组中含有参数m，可以先进行化简，求出不等式组的解集， 然后再与已知解集比较，求出m的取值范围.
【名师面对面】中考数学：(第12讲)《反比例函数》ppt课件
D
过双曲线上的点作x，y轴的垂线，就 构成对应的矩形或直角三角形，与k 产生联系．
反比例函数与一次函数的联系应用
【解析】(1)根据一次函数图象在上方的部分是不等式的 解，观察图象，求得x的范围；(2)根据待定系数法，可得 函数解析式；(3)根据三角形面积相等，可得答案．
反比例函数与一次函数ቤተ መጻሕፍቲ ባይዱ联系应用
反比例函数解析式利用待定系数法确定：只要 一对对应的x，y值，或已知其图象上一个点的 坐标即可求出k，进而确定反比例函数的解析 式．
反比例函数y＝中只有一个系数k，利用x，y的 一对对应值或利用条件求出图象上一点的坐标， 代入就可以转化为关于k的方程．
反比例函数图象的几何应用
解：过 C 点作 CE⊥x 轴，垂足为 E.∵Rt△OAB 中，∠OBA＝90°，∴CE∥AB，∵C 为 Rt△OAB 斜边 OA 的中点 C，∴CE 为 Rt△OAB 的中位线，∵△OEC∽△OBA，∴OOCA＝12.∵ 双曲线的解析式是 y＝kx，∴S△BOD＝S△COE＝12k，∴S△AOB＝4S△COE＝2k，由 S△AOB－S△BOD ＝S△ODA＝2S△DOC＝18，得 2k－12k＝18，∴k＝12，∴S△BOD＝S△COE＝12k＝6
第12讲 反比例函数
1．借助于图象的呈现来考查反比例函数的定义、 性质，常常结合反比例函数的轴对称性和中心对 称性． 2．反比例函数与一次函数的互相结合与转化，反 比例函数的图象、性质及解析式的确定． 3．运用函数思想来解决有实际背景的问题． 4．体现数形结合思想、转化的思想、方程的思 想．
A
C
反比例函数图象与性质
C
【解析】将x＝1和x＝2分别代入反比例函数，结 合反比例函数的增减性，即可确定函数值的取值 范围，也可以画出图象求解．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
【解析】选A.∵矩形面积为：S矩=x·y. ∴ y 200 (x>0),根据图象可知，只有A项符合.
x
3.(2010·兰州中考)已知点(-1,y1)，(2,y2)，(3,y3)在反比
例函数 y k2 1 的图象上.下列结论中正确的是( )
x
(A)y1>y2>y3
(B)y1>y3>y2
(C)y3>y1>y2
满了一定质量的气体，当温度不变
时，气球内气体的气压P(kPa)是气
球体积V的反比例函数，其图象如图
所示，当气球内的气压大于120 kPa时，气球将爆炸，为了安
全，气球的体积应该( )
(A)不大于 5 m3
4
(C)不小于 4 m3
5
(B)小于 5 m3
4
(D)小于 4 m3
5
9.(2011·南充中考)小明乘车从南充到成都，行车的平均速 度v(km/h)和行车时间t(h)之间的函数图象是( )
而随着家长们对留学的理解越来越深，这类业务也越来越没有生存空间，来自卡萨贝拉意大利进口家居15个家庭的21个小朋友,用7天时间募捐489662元,共计向同心慈善会-厦门同心义工服务中心捐赠 496册图书,为厦门同安官浔小学的小读者们提供课外阅读书籍，从企业内部战略管理流程的角度,议题营销是指主动地引导管理者,使其重视企业目前存在的某些议题(如人才瓶颈)并作为企业战略一部分投 入资源去解决，5G无线宽带 https://，第三条 学校招生工作贯彻公平、公开、公正、严格程序、择优录取、接受监督的原则，接受纪检监察部门、新闻媒体、考生及家长的监督，乘 中国高铁发展之东风,迎全球高端就业之机遇,学校正积极响应国家大力发展职业教育的号召,加强专业建设,推进产教融合,深化校企合作,使无业者有业,使有业者乐业，关于培生教育培生教育作为全球领先 的教育集团之一，业务遍布70多个国家和地区，为全球超过13亿人提供优质教育资源和教育服务，并且在英语教材和读物出版、英语语言测评和数字化学习等领域均占据全球领先地位
y k (k≠0)的图象交于点A(m，1)，则k的值是( )
x
(A) 2或 2
(B) 2 或 2
2
2
(C) 2
(D) 2
2
【解析】选B.由题意,得
2km m k
1
,解得
k
2. 2
6.(2011·福州中考)如图，△OPQ是边
长为2的等边三角形，若反比例函数的
图象过点P，则它的解析式是_____.
x
标系中的图象可能是( )
【解析】选D.可分类考虑：当a>0时，函数y=ax-a的图象在一、
三、四象限， y a 的图象在一、三象限；当a<0时，函数
x
y=ax-a的图象在一、二、四象限, y a 的图象在二、四象限;
x
只有选项D符合题意,故选D.
2.(2009·娄底中考)数学课外兴趣小组的同学每人制作一个 面积为200 cm2的矩形学具进行展示.设矩形的宽为x cm,长 为y cm，那么这些同学所制作的矩形长y(cm)与宽x(cm)之间 的函数关系的图象大致是( )
结合近几年中考试题分析，反比例函数内容的考查主要 有以下特点：
1.反比例函数的图象与性质是中考热点之一，特别是反 比例函数的增减性、面积问题，都是中考题中经常涉及的知 识点.题型以选择题和填空题为主.与其他类型函数的综合题， 特别是与一次函数的综合题，通常以解答题的形式出现.
2.反比例函数与物理知识的综合命题，是中考的另一热 点，如压力、压强、受力面积的问题，电压、电流、电阻的 问题等.
又∵点A在反比例函数
的图象上，
∴
，即m-5=8.y m 5
x
∴反4 比m例函5 数的解析式为
2
y 8. x
【例2】(2011·菏泽中考)已知一次函数y=x+2与反比例函 数 y k ，其中一次函数y=x+2的图象经过点P(k,5).
x
(1)试确定反比例函数的解析式； (2)若点Q是上述一次函数与反比例函数图象在第三象限的交 点，求点Q的坐标. 【思路点拨】(1)由一次函数y=x+2经过点P(k，5)求k的值. (2)解由一次函数与反比例函数解析式组成的方程组，由点Q 在第三象限确定点Q的坐标.
x
比例函数的图象与直线 y x 3k 都经过点P，且｜OP｜＝
7 ，则实数k=_____.
【解析】根据题意可得k>0.设P点的坐标为 m,m 3k , 列方
程得
m
m
3k 2k
2
,
2
m2 m 3k 7
解得
k1
1舍去，k2
7. 3
答案：7
3
4.(2010·常德中考)已知图中的曲线 是反比例函数 y m 5 (m为常数)图象
x
(2)设直线AB与x轴的交点为C，可得C点的坐标为(2,0)，所以
SVAOB
SVAOC
SVBOC
1 2 2 2
1 比例函数的知识,正确解释日常生活中的特殊事件; 2.能通过实例构建反比例函数模型,从而解决问题; 3.根据题意或图象,列出关系式,并确定自变量的取值范围.
【自主解答】(1)因一次函数y=x+2的图象经过点P(k,5)，
所以得5=k+2，解得k=3,
所以反比例函数的解析式为 y 3 .
x
y x 2
(2)联立一次函数与反比例函数解析式，得方程组
解得
x 1 y 3
或
x y
3， 1
y
3 x
，
故第三象限的交点Q的坐标为(-3，-1).
5.(2010·潍坊中考)若正比例函数y＝2kx与反比例函数
1.(2011·邵阳中考)已知点(1，1)在反比例函数 y k (k为常
x
数，k≠0)的图象上，则这个反比例函数的大致图象是( )
【解析】选C.反比例函数的图象是双曲线，又k＝1>0，故图 象在一、三象限.
2.(2011·连云港中考)关于反比例函数 y 4 的图象，下列说
x
法正确的是( )
(A)必经过点(1,1)
2
∴AB·OB=4,
∵图象位于二、四象限，∴k=-4.
答案：-4
2.(2010·济宁中考)如图，正比例函
数
y
1 2
x
的图象与反比例函数
y
k x
(k≠0)在第一象限的图象交于A点，
过A点作x轴的垂线，垂足为M，已知
△OAM的面积为1.
(1)求反比例函数的解析式；
(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重
(B)两个分支分布在第二、四象限
(C)两个分支关于x轴成轴对称
(D)两个分支关于原点成中点对称 【解析】选D.反比例函数 y 4 的图象在第一、三象限，并
x
且关于原点成中心对称.
3.(2011·成都中考)在平面直角坐标系xOy中，已知反比例函
数 y 2k (k≠0)满足：当x<0时，y随x的增大而减小.若该反
x
(1)过双曲线 y k (k≠0)上任意一点作x轴、y轴的垂线，所
x
得矩形OAPB的面积为|k|. (2)过双曲线 y k (k≠0)上任意一点作一坐标轴的垂线，连
x
接该点和原点，所得三角形OCQ的面积为 k .
2
【例】(2010·昆明中考)
如图，点A(x1，y1)、 B(x2，y2)都在双曲 线 y k (x>0)上，且
【例1】(2010·镇江中考)反比例函数 y n 1 的图象在第二、
x
四象限，则n的取值范围为_____,A(2,y1),B(3,y2)为图象上两
点，则y1_____y2(用“<”或“>”填空).
【思路点拨】
【自主解答】根据题意，得n-1<0,解得n<1; 因为n-1<0,所以在每个象限中，y随x的增大而增大, 又因为2<3,所以y1<y2. 答案：n<1 <
(D)y2>y3>y1
【解析】选B.根据题意可知，反比例函
数 y k2 1 的图象在第二、四象限，其
x
大致图象如图所示，在图象上标出点
(-1,y1)，(2,y2)，(3,y3)，显然有y1>y3>y2.
4.(2010·衡阳中考)如图，已知双曲线 y k (k>0)经过直角三角形OAB斜边OB的
【解析】过点P作PD⊥OQ于点D.则∠OPD＝30°，
∴OD＝1，PD＝ 3，∴点P的坐标为(1， 3 ).
设过点P的反比例函数解析式是
y
k x
，则 k
3.
∴函数解析式为 y 3 .
x
答案：y 3
x
7.(2011·綦江中考)如图，已知 A(4,a)，B(-2,-4)是一次函数 y=kx+b的图象和反比例函数 y m 的图象的交点.
1.反比例函数的图象与性质及其解析式的相关知识是学 习本讲的基础,在学习过程中应多分析、多归纳,并结合所给 条件画出反比例函数的图象,重点掌握数形结合思想在本讲内 容的应用.
2.反比例函数的解析式的求法及反比例函数与相关知识 的融合是中考热点之一,常带有一定的综合性,所以应通过各 种形式的题目进行训练.
1
∴A为(2，1).
设A点关于x轴的对称点为C，则C点的坐标为(2，-1).
令直线BC的解析式为y=mx+n.
∵B为(1，2)，∴
2 m n 1 2m
n
,∴ mn 53，
∴BC的解析式为y=-3x+5.
当y=0时，x= 5 ，∴P点为( 5 ，0).
3
3
1.(2010·青岛中考)函数y=ax-a与 y a (a≠0)在同一直角坐