哈工大版理论力学答案详解第13章
哈尔滨工业大学理论力学课后习题问题详解

实用标准文档----------------------------------------理论力学(第七版)课后题答案 哈工大.高等教育出版社-------------------------------- 第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体 A ,ABC 或构件 AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
F N1A PF N 2(a) (a1)F TA PF N(b)(b1)AF N1P BF N 3F N 2(c) (c1)F TBF AyP 1P 2AF Ax(d) (d1)F AF BFAB(e)(e1)qFF Ay F BF AxA B(f) (f1)FBC F CAF A(g) (g1)F Ay FCCA F Ax BP1 P2(h) (h1)BFCF CF AxDAF Ay(i) (i1)(j) (j1)BF B FCPF AyF AxA(k) (k1)F CAF AB ′ F AC CA′ F ABBF ACF BAA P (l) (l1)(l2)(l3)图 1-11-2 画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所 有接触处均为光滑接触。
F N 2C′ F P 2(a1) F N1N(a)BF N1BC F N 2F NP 2P1P1F AyF Ay F AxF AxAA(a2) (a3)F N1AP1F N3B P 2F N 2(b) (b1)′ F NF N3F N1ABP 2P1F N F N 2(b2)(b3)F AyF AxACD F N2B P2P1F N1(c) (c1)F AyF TA F AxD′FF N2 TBP1F N1 P2(c2) (c3)F AyF BqBA FAxC DF C(d) (d1)F DyF Ay F BqqD′FDxBA F Ax C F Dx D′FDyF C(d2) (d3)F Ay′FBxq BF AyF AxqA B ′FByF AxF Cx CF Cy PF BxA BPF Cx(e1)C F By F Cy(e) (e2) (e3)F1 CF2F Ay FByA BF Ax F Bx(f) (f1)F Cx′ FCxCCF 1F CyF ′ F 2 F AyCyF ByAF BxF Ax B(f2)(f3)F BF AyCBAF AxP(g)(g1)′ F CyF T′FCxCF AyF BF TDCF AxBAF Cx P (g2)(g3)DF 1F CyF B ′ F 2F BBCF CxBF Ay AF Ax(h)(h1)(h2)A F AxF AyF CyF CxC′ A F EF CyF F OyCDF OxF Cx ′EO B(i)(i1)(i2)AA ′FAx′FE′FAyFEC DF ByF ByF OyF BxF Ox F BxOB B(i3) (i4)F AyD EF CxF TA F AxF ByCCH FBy F CyB PF Bx F BxB(j) (j1) (j2)F Ay F Dy′′FEy′F CF Cx′E F AxT 2D F T 2 ′FExF Ex A D F Dx′ EF DxF T3F T1 ′FCyF Dy F Ey(j3) (j4) (j5)EF F BC ED ′ BFCxθ′′FDEFCy(k) (k1)F BFFCB FCxθ E CF Cy90°−θFDED DF AyF AyA AF Ax F Ax(k2) (k3)F B′ FBF 1F DBBDCAF AF C(l)(l1)(l2)F 2′ D F DF 1F 2D BAC EE F EF AF C F E(l3)(l4)或′ ′ F DyF 2F 1F F Dy F 2F 1B ′ DF DxF DxBBD D F ExA C E C E F ExF CF EyF AF CF Ey(l2)’(l3)’ (l4)’′ F ADAF CyF CxCF 1B(m)(m1)F ADDF ADHEF 2A DF EF HF AD ′(m2)(m3)F N AAF kF N BF OyF OxBO(n) (n1)F N1B Dq′ F BF N 2F N3(n2)FB D FF C F E F AF G GCEA(o)(o1)FBBDFDF BF E F F F CF D′ FEA F AF B ′ CD(o2)(o3) (o4) 图 1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A ,B 和 C 处受 3个力作用,如图 2-1a 所示。
理论力学复习题及答案(哈工大版)汇总

一、是非题1、力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
(√)2、在理论力学中只研究力的外效应。
(√)3、两端用光滑铰链连接的构件是二力构件。
(×)4、作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
(√)5、作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
(×)6、三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
(×)7、平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
(√)8、约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
(×)9、在有摩擦的情况下,全约束力与法向约束力之间的(应是最大)夹角称为摩擦角。
(×)10、用解析法求平面汇交力系的平衡问题时,所建立的坐标系x,y轴一定要相互垂直。
(×)11、一空间任意力系,若各力的作用线均平行于某一固定平面,则其独立的平衡方程最多只有3个。
(×)12、静摩擦因数等于摩擦角的正切值。
(√)13、一个质点只要运动,就一定受有力的作用,而且运动的方向就是它受力方向。
(×)14、已知质点的质量和作用于质点的力,质点的运动规律就完全确定。
(×)15、质点系中各质点都处于静止时,质点系的动量为零。
于是可知如果质点系的动量为零,则质点系中各质点必都静止。
(×)16、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
(×)17、力对于一点的矩不因力沿其作用线移动而改变。
(√)18、在自然坐标系中,如果速度υ= 常数,则加速度α= 0应是切线方向加速度为零。
(×)19、设一质点的质量为m,其速度 与x轴的夹角为α,则其动量在x轴上的投影为mvx =mvcos a。
(√)20、用力的平行四边形法则,将一已知力分解为F1和F2两个分力,要得到唯一解答,必须具备:已知F1和F2两力的大小;或已知F1和F2两力的方向;或已知F1或F2中任一个力的大小和方向。
哈工大理论力学教案 第13章.

r0
r F
drr
k
r
2
2
2 0
0 0为零势能点, 则
V k2
2
(3)万有引力场中的势能
V A0
由于erAr
r F
drr
A0
drr
A
dr有
fm1m2 r2
r er
drr
V
r1 fm1m2
r
r2
dr
1
fm1m2
r1
1 r
取零势能点在无穷远
V fm1m2 r
r1
(4)质点系受到多个有势力作用 质点系的零势能位置:各质点都处于其零势能点的一组位置.
2 dt
1 2
m
J R2
ds dt
2
P重力
mg
ds dt
, P弹性力
ks
ds dt
dT dt P重力 P弹性力
m
J R2
ds dt
d2s dt 2
mg
ds dt
ks ds dt
m
J R2
d2s dt 2
mg
ks
令
为弹簧静伸长,即mg=k
0
,0以
平衡位置为原点
s 0 x
s R
Fs 2Fds
Fs 2mg fs
不作功的力可不考虑,因此亦可如下计算:
W
(F
Fd )s
Fd R
s R
Fs
2Fd s
§13-2 质点和质点系的动能
1、质点的动能
T 1 mv2 2
2、质点系的动能
(1)平移刚体的动能
T
1 2
mi
vi
2
哈尔滨工业大学 第七版 理论力学.13
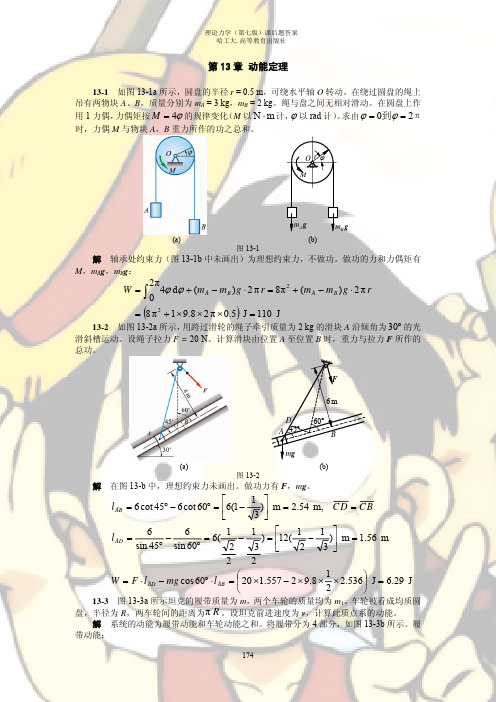
1 2 T履 = ∑ mi vi = TI + TII + TIII + TIV 2
D II A
(a) 图 13-3
IV
2v
C
ω
v
III
Iv=0
(b)
B
由于 v1 = 0, vIV = 2v ,且由于每部分履带长度均为π R ,因此
mI = mII = mIII = mIV = TI =
m 4
1 2 mI vI = 0 2 1 1 m m 2 TIV = mIV v IV = × (2v) 2 = v 2 2 2 4 2 m m 2 II、III 段可合并看作 1 滚环,其质量为 ,转动惯量为 J = R ,质心速度为 v,角速度 2 2 v 为 ω = ,则 R 1 m 1 mv 2 1 m 2 v 2 m 2 TII + TIII = ⋅ v 2 + Jω 2 = + ⋅ R ⋅ 2 = v 2 2 2 4 2 2 2 R m m T履 = 0 + v 2 + v 2 = mv 2 2 2
理论力学(第七版)课后题答案 哈工大.高等教育出版社
第 13 章 动能定理
13-1 如图 13-1a 所示,圆盘的半径 r = 0.5 m,可绕水平轴 O 转动。在绕过圆盘的绳上 吊有两物块 A、B,质量分别为 mA = 3 kg,mB = 2 kg。绳与盘之间无相对滑动。在圆盘上作 用 1 力偶, 力偶矩按 M = 4ϕ 的规律变化 (M 以 N ⋅ m 计, ϕ 以 rad 计) 。 求由 ϕ = 0到ϕ = 2π 时,力偶 M 与物块 A,B 重力所作的功之总和。
第 2 阶段 :系统通过搁板继续运动 x2 距离后静止。由动能定理
哈工大理论力学第七版课后习题答案(高清无水印版)

第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体A ,ABC 或构件AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
2F(a)(a1)(b) (b1)2N F 3N(c) (c1)Ax(d) (d1)B(e) (e1)Bq(f) (f1)(g)1F 2(h)(h1)Ax(i)(i1)(j)(j1)F(k) (k1)BA F FF ′ (l) (l2) (l3)图1-11-2画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所有接触处均为光滑接触。
22N(a1)2AxFAx(a2)3N(b)(b1)N3′(b2) (b3)1N2AxF(c)(c1)1N2N2Ax(c2)(c3)(d) (d1)CDy(d2)(d3)CxBxByF By′(e) (e1)(e2) (e3)ByBxAx(f) (f1)AxBx F′(f2)(f3)FB(g) (g1)BCx′F(g3)(h)(h1)FFAxC(i) (i1) (i2)F(i3)(i4)AyFFFCy (j) (j1)(j2) 2TFDx3TEyFCyEx′(j3) (j4) (j5)BBDECyF(k)(k1)BBCx (k2) (k3) DEA(l) (l1) (l2)A C E(l3) (l4)或CDxFEyFEy(l2)’(l3)’ (l4)’F′(m)(m1)EADFH2FAD′(m2) (m3)BN(n)q3N(n2)G(o)(o1)BADB(o2) (o3) (o4)图1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心A ,B 和C 处受3个力作用,如图2-1a 所示。
N 1001=F ,沿铅直方向;N 503=F ,沿水平方向,并通过点A ;N 502=F ,力的作用线也通过点A ,尺寸如图。
求此力系的合力。
(a)(b)图2-1解 (1) 几何法作力多边形abcd ,其封闭边ad 即确定了合力F R 的大小和方向。
哈工大理论力学笔记

第一章静力学公理和物体的受力分析§1—1静力学公理一.公理1:力的平行四边形法则①作用在物体上同一点的两个力,可以合成一个合力②合力的作用点在该点,合力的大小和方向,由这两个力为边构成的平行四边形的对角线确定或:合力矢等于这两个边矢的几何和,即21R F F F +=※:也可另作一三角形,求两汇交力合力的大小和方向二.公理2:二力平衡条件作用在刚体上的两个力(如1F 与2F ),使刚体保持平衡的必要和充分条件是:这两个力的大小相等,方向相反,且作用在同一直线上三.公理3:加减平衡力系原理在已知力上加上或减去任意的平衡力系,并不改变原力系对刚体的作用四.两个推理:1.推理1:力的可传性(1)内容:作用于刚体上的某点的力,可以沿着它的作用线移到刚体内任意一点,并不改变该力对刚体的作用(2)证明:用加减平衡力系原理先加一平衡力系,再减一平衡力系(3)说明的问题:①作用于刚体上的力的三要素:力的大小、方向、作用线②作用于刚体上的力可以沿着作用线移动→滑动矢量2.推理2:三力平衡汇交定理(1)内容:作用于刚体上三个力相互平衡的力,若其中两个力的作用线汇交于一点,则此三力必在同一平面内,且第三个力的作用线通过汇交点(2)证明:用力的可传性、平行四边形法则、二力平衡的条件证明五.公理4:作用和反作用定律作用力和反作用力总是同时存在,两力的大小相等、方向相反,沿着同一直线,分别作用在两个相互作用的物体上F F '-=※:作用力与反作用力不能看成平衡力系六.公理5:刚化原理(1)内容:变形体在某一力系作用下处于平衡,如将此变形体刚化为刚体,其平衡状态保持不变(2)说明的问题:①变形体看作刚体模型的条件:在某一力系作用下处于平衡②刚体平衡条件与变形体平衡条件的关系:刚体平衡是变形体平衡的必要条件,而不是充分条件§1—2约束和约束力一.约束1.自由体和非自由体:(1)自由体:位移不受限制的物体(2)非自由体:位移受到限制的物体2.约束:对非自由体的某些位移起限制作用的周围物体二.约束力1.约束力的含义:约束对物体所施加的,阻碍物体位移的力2.约束力的方向:与该约束所能阻碍的位移方向相反※:利用这个准则可以确定约束力的方向或作用线的位置3.约束力的大小:(1)特点:约束力的大小是未知的(2)静力学中的求法:约束力与主动力组成平衡力系→用平衡条件求约束力三.几种常见的约束及相应约束力的方向1.具有光滑接触面的约束(1)约束的特点:不能限制物体沿约束表面切线的位移,只能阻碍物体沿接触表面法线并向约束内部的位移(2)约束力:作用在接触点处,方向沿接触表面的公法线,并指向被约束的物体→法向约束力F表示※:用N2.由柔软的绳索、链条或胶带等构成的约束F表示(1)绳索对物体的约束力,作用在接触点,方向沿着绳索背离物体,用F或T(2)绕在轮子上的链条或胶带对轮子的约束力沿轮缘的切线方向3.光滑铰链约束1)向心轴承(径向轴承)(1)结构与简图(2)约束的特点:①轴可在孔内任意转动,也可沿孔的中心线移动②轴承阻碍着轴沿径向向外的位移(3)约束力:①作用位置与方向:作用在接触点,且沿公法线指向轴心,并且与轴线垂直②特点:主动力不同,轴和孔的接触点的位置不同→主动力不确定时,约束力的方向预先不能确定③通常的处理:用通过轴收的两个大小未知的正交分力Ax F ,Ay F 表示,且Ax F ,Ay F 的方向暂可任意假定2)圆柱铰链和固定铰链支座(1)一个示例:(2)圆柱铰链(铰链):①结构:由销钉将两个钻有同样大小孔的构件连接在一起而成②简图:(3)固定铰链支座(固定铰支):①结构:铰链连接中有一个固定在地面或机架上作为支座②简图:(3)分析约束力时销钉的处理:①铰链处约束力的分析:常将销钉固连在其中一个构件上→相互连接的两构件互为约束②固定铰链支座处的销钉:将销钉固连在支座上③说明:当需要分析销钉受力时,才将销钉分离出来单独研究(4)约束力的实质:①约束的实质:轴与光滑孔的配合②约束力情况:与轴承具有同样的约束,即约束力的作用线不能预先定出,但约束力垂直并通过铰链中心(5)约束力分析图3)光滑铰链约束的特点:只限制两物体径向的相对移动,而不限制两物体绕铰链中心的相对转动及沿轴向的位移4.其他约束:1)滚动支座:(1)结构:在固定铰链支座与光滑支承面之间装有几个辊轴而构成(辊轴支座)(2)约束特点:可以沿支承面移动※:约束性质与光滑面约束相同(3)约束力:垂直支承面,且通过铰链中心2)球铰链(1)结构:通过圆球和球壳将两个构件连接在一起的约束(2)约束的特点:使构件的球心不能有任何位移,但构件可绕球心任意转动(3)约束力:①通过接触点与球心,但方向不能预先确定的一个空间约束力②处理方法:用三个正交分力表示3)止推轴承(1)约束特点:除了能限制轴的径向位移外,还能限制轴沿轴向的位移(2)约束力特点:有三个正交分量(3)简图与约束力:§1—3物体的受力分析和受力图一.物体受力的类型:(1)主动力(一般是已知的)(2)被动力:约束对于物体的约束力二.受力分析的要求:(1)要将受力物分离出来,画出它的简图→取研究对象或分离体(2)画出物体所受的所有力,注意每个力的作用位置与作用方向三.有用模型→二力构件(二力杆):只在两个力作用平衡的构件,两个力必沿两作用点的连线,且等值反向第二章平面汇交力系与平面力偶系§2—1平面汇交力系合成与平衡的几何法一.平面汇交力系合成的几何法、多边形法则1.平面汇交力系的含义:各力的作用线都在同一平面内且汇交于一点的力系2.平面汇交力系可合成:①力的可传性→将各力沿作用线移至汇交点②平行四边形法则→所有的力可合成一个合力3.平面汇交力系合成的几何法:①平行四边形法则;②多边形法则4.结论:平面汇交力系可简化为一合力,其合力的大小与方向等于各分力的矢量和(几何和),合力的作用线通过汇交点∑==+++=n1i in 21R F F F F F 二.平面汇交力系平衡的几何条件:1.平面汇交力系平衡的充要条件:该力系的合力等于零F =∑=n1i i 2.平面汇交力系平衡的几何条件:该力系的力多边形自行封闭3.求解平面汇交力系平衡问题的几何法:①按比例先画出封闭的力多边形,量得所要求的未知量②根据图形的几何关系,用三角公式计算出所要求的未知量§2—2平面汇交力系合成与平衡的解析法一.平面汇交力系合成的解析法ji F F F y x Ry Rx R F F +=+=⎪⎪⎩⎪⎪⎨⎧=+++==+++=∑∑==n 1i yi yn y2y1y n 1i xi xn x2x1x F F F F F F F F F F ,()()()()⎪⎪⎩⎪⎪⎨⎧====+=+=∑∑∑∑R yi R y R R xi R x R 2yi 2xi 2y 2x R F F F F ,cos ,F F F F ,cos F F F F F j F i F 二.平面汇交力系的平衡方程:1.平面汇交力系的平衡条件:各力在两个坐标轴上的投影的代数和分别等于02.平面汇交力系的平衡方程:0F xi =∑,0F yi =∑§2—3平面力对点之矩的概念及计算一.力对点之矩(力矩)1.问题的提出:(1)力对刚体的作用效果:使刚体的运动状态发生改变(2)刚体的运动状态:移动与转动(3)力对刚体的移动效应由力矢量度2.力臂:某点O 到力的作用线的垂直距离h 称为力对O 点的力臂※:点O 称为矩心3.力对点之矩(力矩):(1)含义:①是一个代数量②力对点之矩的绝对值等于力的大小与力臂的乘积③力对点之矩的正负为:力使物体绕矩心逆时针转向时为正,反之为负(2)力矩的表达式:Fh)(M O ±=F (3)力矩的单位:m N ⋅,m kN ⋅,mm N ⋅,mmkN ⋅(4)力矩的物理意义:力矩表示力对刚体的转动效应二.合力矩定理与力矩的解析表达式1.合力矩定理:平面汇交力系的合力对于平面内任一点之矩等于所有各分力对于该点之矩的代数和∑==n1i i O R O )(M )(M F F 2.力矩的解析表达式:x y O yF xF )(M -=F ,()∑=-=n 1i xii yi i R O F y F x )(M F §2—4平面力偶一.力偶与力偶矩1.力偶的定义:①力偶:由两个大小相等,方向相反且不共线的平行力组成的力系※:两力分别记作F ,F '②力偶臂:力偶的两力之间的垂直距离d③力偶的作用面:力偶所在的平面2.力偶的作用效果:①力偶的矢量和为零→力偶对刚体没有移动效应②力偶对各点的力矩不等于零→力偶改变刚体的转动状态※:力与力偶是静力学中的两个基本要素3.力偶矩:(1)力偶对作用面内任意点的力矩的代数和:①大小等于力与力偶臂的乘积,正负一定②大小、正负都与矩心位置无关(2)力偶矩的定义:力偶矩是一个代数量,其绝对值等于力的大小与力偶臂的乘积,正负号表示力偶的转向:以逆时针转向为正,反之为负FdM ±=※:力偶矩等于力偶中两个力对任意点的力矩的代数和二.同平面内力偶的等效定理1.定理:在同平面内的两个力偶,如果力偶矩相等,则两力偶彼此等效※:理由:①力偶只改变物体的转动状态②力偶对物体的转动效应由力偶矩度量2.推论:①任一力偶可以在它的作用面内任意移转,而不改变它对刚体的作用→力偶对刚体的作用与力偶在其作用面内的位置无关②只要保持力偶矩的大小和力偶的转向不变,可以同时改变力偶中力的大小和力偶臂的长短,而不改变力偶对刚体的作用3.结论:力偶矩是平面力偶作用的唯一量度,而力偶的臂和力的大小都不是力偶的特征量三.平面力偶系的合成和平衡条件:1.平面力偶系的合成:在同一平面内的任意个力偶可合成一个合力偶,合力偶矩等于各个力偶矩的代数和∑==n1i iM M ※:推导过程:①将各力偶在保持力偶矩不变的前提下同时改变力偶臂与力的大小,使各力偶的力偶臂大小相等②在平面内将各偶移转,使它们的作用线重合③分别求两作用线上的合力2.平面力偶系的平衡条件:平面力偶系平衡的必要和充分条件是:所有各力偶矩的代数和等于零M n1i i =∑=第三章平面任意力系§3—1平面任意力系向作用面内一点简化一.力的平移定理:可以把作用在刚体上点A 的力F 平行移到任一点B ,但必须同时附加一个力偶,这个力偶的矩等于原来的力对新作用点B 的矩※:证明过程:在B 点加一对大小与F 相等,方向与F 平行的平衡力,其中与F相反的力与F 组成一个力偶二.平面任意力系向作用面内一点简化·主矢和主矩1.平面任意力系向作用面内一点简化1)平移:力的平移定理→将作用在刚体上的平面任意力系1F ,2F ,…,n F 中的各力向简化中心O 平移,同时附加一个相应的力偶→平面任意力系等效为两个简单力系:平面汇交力系1F ',2F ',…,n F '和平面力偶系1M ,2M ,…,n M※:i i F F =',)(M M i O i F =2)合成:(1)主矢:将平面汇交力系1F ',2F ',…,n F '合成为一个通过简化中心的合力R F '→主矢∑∑==='='n1i i n 1i i RF F F (2)主矩:将平面力偶系1M ,2M ,…,n M 可合成为一个力偶O M →主矩∑∑====n1i i O n 1i i i )(M M M F (3)说明:主矢与简化中心无关,主矩与简化中心有关3)结论:平面任意力系向作用面内任选一点简化,可得一个力和一个力偶。
《理论力学》课后习题解答(赫桐生版)
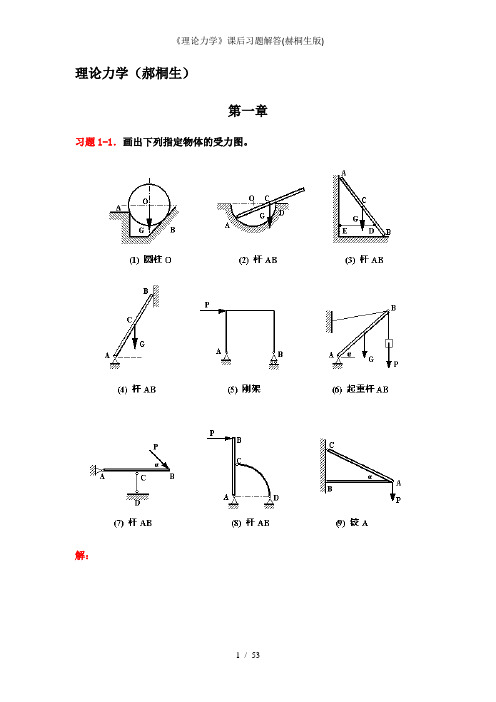
理论力学(郝桐生)第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1)研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB与水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
理论力学(哈工大第八版)-教学课件-第13章

ma F FN
F FN ma 0
令 FI ma
惯性力
有 F FN FI 0
质点的达朗贝尔原理:作用在质点的主动力、
约束力和虚加的惯性力在形式上组成平衡力系.
例13-1
已知: m 0.1kg, l 0.3m, 60
求:惯性力系向点O简化的结果(方向在图上画出).
解:
FItO
m
l
2
FIOn
m
l 2
2
M IO
1 3
ml 2
例13-5
已知:如图所示,电动机定子及其外壳总质量为m1,质心位于O
处.转子的质量为m2 ,质心位于C 处,偏心矩OC=e ,
图示平面为转子的质量对称面.电动机用地角螺钉固定
于水平基础上,轴O与水平基础间的距离为h.运动开始时,
解得
fs
Fs FN
3m1
2m1 m2
A
mg
D m2 g
FN
FS
M IA
FIA
FIC
B
§ 13-4 绕定轴转动刚体的轴承动约束力
Fx 0 FAx FBx FRx FI x 0 Fy 0 FAy FB y FR y FI y 0
Fz 0 FBz FRz 0
M IO ri FIi ri (miaC ) ( miri ) aC
mrC aC
惯性力系向质心简化. 只简化为一个力
M IC 0 FIR maC
平移刚体的惯性力系可以简化为通过质心的合力, 其大小等于刚体的质量与加速度的乘积,合力的方向与 加速度方向反向。
哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题-达朗贝尔原理(圣才出品)

图 13-4 解:以整体为研究对象,受力分析如图 13-5 所示。
5 / 33
圣才电子书
十万种考研考证电子书、题库视频学习平台
图 13-5
作出所有主动力、约束力和惯性力。
由平衡方程
可得
解得 当两轮压力相等时,
,解得
13-3 图 13-6 所示均质矩形块质量 m1=100 kg,置于平台车上,车质量 m2=50 kg, 此车沿光滑的水平面运动,不计定滑轮质量。车和矩形块在一起由质量为 m3 的物体牵引, 使之作加速运动。设物块与车之间的摩擦力足够阻止相互滑动,求能够使车加速运动的质量 m3 的最大值,以及此时车的加速度大小。
2 / 33
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 13-3 答:(a)满足动平衡,(b)满足静平衡,(c)、(d)不满足。 二、习题 13-1 图 13-1 所示由相互铰接的水平臂连成的传送带,将圆柱形零件从一高度传送到 另一个高度。设零件与臂之间的摩擦因数 fs=0.2。求:(1)降落加速度 a 为多大时,零件 不致在水平臂上滑动;(2)在此加速度 a 下,比值 h/d 等于多少时,零件在滑动之前先倾 倒。
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 13-3
当零件处于倾倒的临界状态时,由 M A = 0 可得
因为
,所以
,即
时零件先倾倒。
13-2 图 13-4 所示汽车总质量为 m,以加速度 a 作水平直线运动。汽车质心 G 离地 面的高度为 h,汽车的前后轴到通过质心垂线的距离分别等于 c 和 b。求其前后轮的正压力; 又,汽车应如何行驶能使前后轮的压力相等?
图 13-9 解:以圆盘 B 为研究对象,受力分析如图 13-10 所示。
CUGB理论力学习题解答PPT课件

40
FRy F1 sin1 F2 sin2 F3
50 F3 F4
x FRy 20N
MO 30F1 sin1 40F1 cos1 20F2 sin2 60F2 cos2 50F4 2000
MO 1000Nmm
3-1 已知:F1
50 N
,1
arctan
3 4
,
F2
30
2N ,2 45o
2
55.80kN
2-16 在一钻床上水平放置工件,在工件上同时钻四个等直径
的孔,每个钻头的力偶矩为 m1 m2 m3 m4 15N m 求工件的总切削力偶矩和A 、B端水平反力?
解: 各力偶的合力偶距为
n
FA
M Mi
i 1
M m1 m2 m3 m4
FB
4 (15) 60N m
求:力系的主矢和对O点的主矩。 z
MOy M y
b
c F1
e
b b2
c2
F1d
d
O
x
e
F2
y
e2 d 2 F2d
d e2
d2
F2 b
e
M Oy
0.3 0.5
100
0.3
1 10 5
5 0.2
2 10 5
5 0.2
6Nm
1-4 已知:F1= 100N,F2=10√5N, b= 0.3m , c= 0.4m , d = 0.2m , e= 0.1m 。
Mo
M
2 x
M
2 y
M
2 z
2
674 52Nm
arccos 40 39.7o 105.2o 54.8o
52
【推荐】理论力学(哈工大版)课后习题答案

第三章 平面任意力系
第四章空间力系
第五章摩擦
第六章 点的运动学
第七章 刚体的简单运动
第八章 点的合成运动
第九章 刚体的平面运动
第十章 质点动力学的基本方程
第十一章动量定理
第十二章 动量矩定理
第十三章 动能定理
理论力学作业答案第一章静力学公理和物体的受力分析1112第二章平面汇交力系与平面力偶系第三章平面任意力系第四章空间力系第五章摩擦第六章点的运动学第七章刚体的简单运动第八章点的合成运动第九章刚体的平面运动第十章质点动力学的基本方程第十一章动量定理第十二章动量矩定理第十三章动能定理
理论力学作业答案
第一章静力学公理和物体的受力分析
理论力学课后习题答案1-13章

则有
即
联立求解得
2-24一悬臂圈梁,其轴线为 =4m的 圆弧。梁上作用着垂直匀布荷载, =2kN/m。求该匀布荷载的合力及其作用线位置。
解:合力大小 ,铅直向下。
作用线位置在圆弧的形心处即平分轴上距离圆心
处
3-1作下列指定物体的示力图。物体重量除图上已注明者外,均略去不计。假设接触处都是光滑的。
解:整体:
先判断零杆如图。
取Ⅰ-Ⅰ截面右半部分
5-5 (b)试用最简捷的方法求图示桁架指定杆件的内力。
解:取Ⅰ-Ⅰ截面上半部分
取Ⅱ-Ⅱ截面右半部分
,
5-8杆系铰接如图所示,沿杆3与杆5分别作用着力FP1与FP2,试求各杆内力。
解:先判断零杆如图。 ,则
5-21板 长 , 、 两端分别搁在倾角 =50°, =30°的两斜面上。已知板端与斜面之间的摩擦角 =25°。欲使物块M放在板上而板保持水平不动,试求物块放置的范围。板重不计。
2.绕A点滚动,B点达到极限状态
,
3.绕B点滚动,A点达到极限状态
,
故,FT的最小值为 。
5-29一个半径为300mm、重为3kN的滚子放在水平面上。在过滚子重心 而垂直于滚子轴线的平面内加一力 ,恰足以使滚子滚动。若滚动摩擦因数δ=5mm,求 的大小。
解:滚子受力如图
6-5半圆形凸轮以匀速v=10mm/s沿水平方向向左运动,活塞杆AB长l,沿铅直方向运动。当运动开始时,活塞杆A端在凸轮的最高点上。如凸轮的半径R=80mm,求活塞B的运动方程和速度方程。
解:OA杆力偶系平衡(由于A滑块,FA垂直O1A)
整体力偶系平衡
4—14求下列面积的形心。图中长度单位是m。
理论力学(机械工业出版社)第十三章达朗伯原理习题解答

理论力学(机械工业出版社)第十三章达朗伯原理习题解答习题13-1 如图13-16所示,一飞机以匀加速度a 沿与水平线成仰角b 的方向作直线运动。
已知装在飞机上的单摆的悬线与铅垂线所成的偏角为f ,摆锤的质量为m 。
试求此时飞机的加速度a 和悬线中的张力F T 。
图13-16ma F =I0cos sin 0I T =-=∑β?F F F x ?βsin cos IT F F =0sin cos 0I T =--=∑mg F F F y β?0sin cos sin cos I I =--mg F F β??β0sin )cos(I=-+mg F ?β? mg ma=+?β?sin )cos( )cos(sin β??+=g amg maF F )cos(cos sin cos sin cos I T β?ββ?β+===13-2 球磨机的简图如图13-17所示,滚筒作匀速转动,内装钢球及被粉碎的原料,当钢球随滚筒转到某一角度f 时,将脱离筒壁作抛射运动,由于钢球的撞击,从而破碎与研磨原料。
已知钢球脱离筒壁的最佳位置'4054?=?,滚筒半径R =0.6m 。
试求使钢球在'4054?=?处脱离滚筒的滚筒转速。
图13-172n I ωmR ma F == 0cos 0I N n =-+=∑F mg F F ?)cos (cos cos 22I N ?ω?ω?g R m mg mR mg F F -=-=-=令0N =F0cos 2=-?ωg RRg ?ωcos =min r/35.296.00454cos 8.9π30cos π30π30='??===R g n ?ω13-3 一质量为m 的物块A 放在匀速转动的水平转台上,如图13-18所示。
已知物块的重心距转轴的距离为r ,物块与台面之间的静摩擦因数为s μ。
试求物块不致因转台旋转而滑出时水平转台的最大转速。
图13-182n I ωmr ma F ==00N =-=∑mg F F ymg F =N 00I =-=∑F F F x0N s 2=-F mr μω 0s 2=-mg mr μωrgs μω=rgn s max π30π30μω==13-4 离心调速器的主轴以匀角速度w 转动,如图13-19所示。
