数模发展历程
数学建模竞赛简介

数学建模竞赛简介数学建模就是建立、求解数学模型的过程和方法,首先要通过分析主要矛盾,对各种实际问题进行抽象简化,并按照有关规律建立起变量,参数间的明确关系,即明确的数学模型,然后求出该数学问题的解,并通过一定的手段来验证解的正确性。
数学建模竞赛于1985年起源于美国,起初竞赛题目通常由工业部门、军事部门提出,然后由数学工作者简化或修正。
1989年我国大学生开始参加美国大学生数学建模竞赛,1990年我国开始创办我国自己的大学生数学建模竞赛。
1993年国家教委(现教育部)高教司正式发文,要求在全国普通高等学校中开展数学建模竞赛。
从1994年开始,大学生数学建模竞赛成为教育部高教司和中国工业的应用数学学会共同主办,每年一届的,面向全国高等院校全体大学生的一项课外科技竞赛活动。
2010年全国共有30省(市、自治区)九百多所院校一万多个队三万多名大学生参赛,成为目前全国高等学校中规模最大的课外科技活动。
数学建模竞赛是教育主管部门主办的大学生三大竞赛之一。
现在的竞赛题目来源于更广泛的领域,都是各行各业的实际问题经过适当简化,提炼出来的极富挑战性的问题,每次两道题,学生任选一题,可以使用计算机、软件包,可以参阅任何资料(含上网参阅任何资料)。
竞赛以三人组成的队为单位,三人之间通力合作,在三天三夜内完成一篇论文。
不给论文评分,而是按论文的水平为四档:全国一等奖、全国二等奖、赛区一等奖,赛区二等奖,成功参赛奖。
我校于2001年开始参加这项竞赛活动。
多次获全国一等奖、二等奖、湖北赛区一等奖、二等奖。
数学建模竞赛活动培养了学生的创造力、应变能力、团队精神和拼搏精神,适应了21世纪经济发展和人才培养的挑战。
不少参加过全国大学生数学建模竞赛的同学都深有感触,他们说:“参加这次活动是我们大学四年中最值得庆幸的一件事,我们真正体会这几年内学到了什么,自己能干什么。
”“那不寻常的三天在我们记忆中留下了永恒的一瞬,真是一次参赛,终身受益。
数学建模竞赛介绍

数学建模竞赛参赛方式
• 数学建模竞赛是按参赛队为单位来参赛的
•每队 人 ( 须属于同一所学校 ) , 专业不限 。 每队3人 须属于同一所学校) 专业不限。 每队 竞赛分本科、 专科两组进行, 竞赛分本科 、 专科两组进行 , 本科生参加本科 组竞赛, 专科生参加专科组竞赛( 组竞赛 , 专科生参加专科组竞赛 ( 也可参加本 科组竞赛) 科组竞赛),
班级以对为单位:
三人一队, 建议不要同专业的,本科专科分开。不同院 系不同专业搭配。 最好计算机专业的童鞋或计算机爱好者分布 到每个队伍当中 建议男女搭配,三人中至少一个男生和一个 女生
数学建模竞赛介绍
数学建模竞赛的起源
• 美国大学生数学建模竞赛开始于1985年 美国大学生数学建模竞赛开始于1985 1985年
• 我国高校的数学建模竞赛开始于1992年 我国高校的数学建模竞赛开始于1992年 1992 近年来数学建模教育发展非常迅速,现在许多院校 近年来数学建模教育发展非常迅速, 正在将数学建模与教学改革相结合, 正在将数学建模与教学改革相结合,努力探索有效的 数学建模教学法和培养面向21世纪人才的新思路。 21世纪人才的新思路 数学建模教学法和培养面向21世纪人才的新思路。
•竞赛题目 竞赛题目 来源于工程技术和管理科学等方面经过适 当简化加工的实际问题,不要求参赛者预先 掌握深入的专门知识,只需要学过普通高校 的数学课程。 题目有较大的灵活性供参赛者发挥其创造 能力。参赛者应根据题目要求,完成一篇包 括模型的假设、建立和求解、计算方法的设 计和计算机实现、结果的分析和检验、模型 的改进等方面的论文(即答卷)。竞赛评奖 以假设的合理性、建模的创造性、结果的正 确性竞赛有
•美国大学生数学建模竞赛(每年2月左右) 美国大学生数学建模竞赛(每年2月左右) 美国大学生数学建模竞赛 •网址 网址 •全国大学生数学建模竞赛(每年9月左右) 全国大学生数学建模竞赛(每年 月左右 月左右) 全国大学生数学建模竞赛 网址: •全国大学生电工数学建模竞赛(每2年11月左右) 全国大学生电工数学建模竞赛( 月左右) 全国大学生电工数学建模竞赛 年 月左右 网址: •全国研究生数学建模竞赛(每年 月下旬) 全国研究生数学建模竞赛( 月下旬) 全国研究生数学建模竞赛 每年9月下旬 网址:
数学建模概念的发展研究

数学建模概念的发展研究数学建模是将数学方法应用于真实世界问题,通过数学模型来描述和预测现象和过程的一种方法。
它已经成为了现代科学和工程领域中必不可少的工具之一。
从古代就开始有数学建模的思想和方法,但它的概念与应用在20世纪才得到广泛的认识和发展。
以下是数学建模概念的发展研究:1. 古代数学建模在古代,人们对自然现象和过程的研究主要通过观察和实验来进行。
例如,在古希腊时期,阿基米德就利用切割球体的方法来确定球体的体积,并使用“阿基米德原理”来解释浮力现象。
此外,古代埃及人也在建筑和土木工程中应用了一些数学知识。
这些都可以看作是数学建模的早期实践。
在14世纪的意大利文艺复兴时期,欧洲开始注重人文主义和研究自然科学。
一些科学家开始将数学应用于自然现象和社会问题的研究中。
例如,深奥的数学方法被用于计算天体运动和建立地图。
此外,经济学也开始应用数学来研究货币流通和市场供求关系,这也被认为是早期的数学建模。
随着科学和工程技术的发展,数学建模得到了更广泛的应用。
20世纪初期,电力、石油、化学和航空工业的发展需要对各种物理现象和过程进行建模和控制。
例如,在火箭推进器研究中,研究人员利用不同的数学模型优化行星编队任务,以避免碰撞和损伤。
此外,建筑师也开始利用数学模型来设计结构和计算负荷。
4. 数学建模在科学和医学中的应用在医学和生命科学中,数学模型被广泛应用于疾病预测、药物研发和疾病治疗等方面。
例如,伦敦大学学院的研究人员开发了一种数学模型,可以预测新流感病毒的传播方式。
此外,数学建模还被用于癌症治疗的优化和药物研发。
综上所述,数学建模概念的发展经历了古代、早期现代应用、工程建模和科学医学应用等阶段,如今已成为现代科学和工程领域的基础工具之一。
对数学建模方法的研究与应用

对数学建模方法的研究与应用1. 概述数学建模方法是一种应用数学的方法,它利用数学工具和技术来解决实际问题。
随着科技的迅速发展,数学建模方法的应用越来越广泛,它已经成为现代工程、科学和技术的重要组成部分。
本文将介绍数学建模方法的发展历程,主要的数学建模方法以及其在实际问题中的应用。
2. 数学建模方法的发展历程数学建模方法在过去几十年中发展迅速。
数学建模起源于20世纪50年代,当时一些科学家开始将数学建模方法应用于预测天气、经济和人口增长等方面。
随着计算机技术的发展,数学建模方法的应用范围越来越广泛。
数学建模方法的发展可以分为三个阶段。
第一阶段是数学模型的发展阶段。
此阶段的研究侧重于数学模型的构建和修改。
第二阶段是计算机技术的发展阶段。
此阶段的研究侧重于模型的数值计算和仿真。
第三阶段是对数学建模方法的深入研究和应用阶段。
此阶段的研究侧重于数学建模方法的理论和实践应用。
3. 主要的数学建模方法3.1 常微分方程模型常微分方程模型是数学建模中应用最广泛的一种模型。
它可以用来描述自然界中的许多物理和生物现象。
例如,温度变化、人口增长、生态平衡等等。
常微分方程模型不仅具有广泛的应用,而且具有较强的理论基础。
例如,常微分方程的解存在唯一性和稳定性定理等。
3.2 偏微分方程模型偏微分方程模型是一种适用于描述分布现象的数学模型。
例如,流体力学中的Navier-Stokes方程、热传导方程、扩散方程等等。
偏微分方程模型的求解需要较高的数学技巧。
近年来,高维偏微分方程的数值计算和控制成为热门研究方向。
3.3 随机过程模型随机过程模型是用来描述随机现象的数学模型。
例如,股市波动、气候变化、交通流量等等。
随机过程模型的求解需要使用概率和统计学的知识。
在现代金融等领域中,随机过程模型的应用越来越广泛。
4. 数学建模方法的应用4.1 环境保护与气候预测数学建模方法可以应用于环境保护中的水质监测、土地利用规划等问题。
例如,利用水文运动方程模拟湖泊环境变化,运用气象学知识建立气候预测模型等等,这些都是利用数学建模方法来解决实际问题。
数模发展史

1. 数值模拟技术开始于1954年.由Aronofsky和Jenkins应用于分析一维一相气体非稳态径向流.第一个商业数值模拟软件诞生于1966年, 由D.R.McCord联合公司研发.2. 岩芯实验公司稍后推出了自己的数值模拟软件.3. 1968年成立的INTERCOMP及科学软件公司主导了70年代数值模拟软件市场, Kaneb 服务公司于1977年收购了INTERCOMP公司并于1983年售于科学软件公司,两家公司合并为后来的SSI公司,现被贝克休斯收购.其开发的数值模拟软件为Simbest2.4. Ian cheshire博士于70年代在英国原子能源部率领小组开发PORES数值模拟软件,于1981年10月同John Appleyard和Jon Holmes成立ECL公司,开始研发后来主导数值模拟软件市场的ECLIPSE软件.ECLIPSE是"ECL's Implicit Program for Simulation Engineering"的缩写.1983年11月发布第一个版本.该版本创下几个世界第一.是第一个全隐式模拟全油田的数值模拟软件.是第一个采用嵌套因式分解法的数值模拟软件.首创角点网格.首次采用优化内存管理,模拟双孔双渗而且首次可以运行在不同的硬件平台.1986年INTERA收购ECL公司.1995年斯仑贝谢GeoQuest收购INTERA公司软件部.5. CMG公司1977年成立于加拿大卡尔加里,其开发的数值模拟软件为STAR,IMEX及GEM.STAR应用于热采研究,IMEX应用于黑油模型,GEM应用于组分模型.CMG公司目前在中国,美国,英国,委内瑞拉建立了办事处.6. J.S.Nolen联合公司成立于1979年,其公司创设人为J.S.Nolen.该公司于1985年被西方阿特拉斯收购.1996年兰德马克公司收购了西方阿特拉斯数模业务.兰德马克于1996年7月被哈里伯顿公司宣布收购,成为其下子公司. 其开发的数值模拟软件为VIP.VIP为Vectorized Implicit Program的缩写.1991年开始研发并行算法.7. SimTech成立于1982年,1996年5月16日被Intera收购.Intera为Duke工程服务公司的子公司,主要做环境及水资源评价.8. 数值模拟研究公司(RSRC)成立于1982年,1996年被Smedvig收购.1999年Smedvig 技术公司与多流体ASA合并组成新的Roxar公司.其模拟软件为MORE. MORE为Modular Oil Reservoir Evaluation的缩写.9. Hot (Heinemann Oil Technology and Engineering)公司1986年成立于奥地利Leoben.其模拟软件为SURE,包括SUREGrid, SURESim,SUREPlot,SUREPVT,SUREFrac. SURE的主要特色是采用PEBI网格.1999年12月RC2收购HOT公司SURE软件,2001年2月Viritas DGC公司收购RC2和SURE.2003年9月地震微技术公司(SMT)收购RC2和SURE.10.其他数值模拟软件有:IFP的Athos. ConocoPhilipse的SENSOR,壳牌的MORES.油藏数值模拟未来10年发展预测进入二十一世纪,伴随着计算机的飞速发展以及互连网的普及应用,科技以令人难以想象的速度在突飞猛进。
数学建模竞赛简介

数学建模竞赛简介全国大学生数学建模竞赛是教育部高等教育司和中国工业与应用数学学会共同主办的面向全国大学生的群众性科技活动,竞赛创办于1992年,每年一届,目前已成为全国高校规模最大的基础性学科竞赛,也是世界上规模最大的数学建模竞赛。
目的在于激励学生学习数学的积极性,提高学生建立数学模型和运用计算机技术解决实际问题的综合能力,鼓励广大学生踊跃参加课外科技活动,开拓知识面,培养创造精神及合作意识,推动大学数学教学体系、教学内容和方法的改革。
随着社会的发展,数学的应用在各个领域发挥越来越重要的作用,社会对数学的需求除了一些数学家和研究人员以外,越来越倾向于在日常生活中可以用数学思维和方法来解决实际问题,从而创造经济效益和社会效益的人才。
数学建模就是从复杂的实际问题进行分析,发现其中可以用数学语言来描述的关系或规律,把这个实际问题化成一个数学问题,建立数学模型的过程。
数学模型也可以称之为数学问题和实际问题之间的一座桥梁,通过模型就可以利用数学方法对实际问题进行分析和求解,并结合实际问题的信息来验证所求的解答数学建模竞赛的起源•一些西方国家的大学在二十世纪六、七十年代开始开设《数学模型》或《数学建模》课程,我国在八十年代初将《数学建模》引入课堂。
美国大学生数学建模竞赛(MCM)•1985年开始举办,此后每年一次(2月),“国际竞赛”•1999年起又同时推出交叉学科竞赛(Interdisciplinary Contest in Modeling – ICM) •1989年清华、北大、北理工首次参加,英文答卷。
此后每年都有其它院校参加。
•每年赛题和优秀答卷刊登于同年UMAP杂志。
中国大学生数学建模竞赛(CUMCM)•1990年上海举办首次省、市级大学生数模竞赛。
•1992年中国工业与应用数学学会(CSIAM)组织首届全国大学生数模竞赛。
•1994年起教育部高教司和CSIAM共同举办(每年9月)•赛题和优秀答卷于次年“数学的实践与认识”(2001年起刊登于当年“工程数学学报”数学建模竞赛的内容与形式内容:赛题:工程、管理中经过简化的实际问题答卷:一篇包含问题分析、模型假设、建立、求解(通常用计算机)、结果分析和检验等的论文形式: A. 全国统一竞赛题目,采取通讯竞赛方式,以相对集中的形式进行;B. 竞赛每年举办一次,一般在某个周末前后的三天内举行;C. 大学生以队为单位参赛,每队3人,专业不限。
数模发展史

1. 数值模拟技术开始于1954年.由Aronofsky和Jenkins应用于分析一维一相气体非稳态径向流.第一个商业数值模拟软件诞生于1966年, 由D.R.McCord联合公司研发.2. 岩芯实验公司稍后推出了自己的数值模拟软件.3. 1968年成立的INTERCOMP及科学软件公司主导了70年代数值模拟软件市场, Kaneb 服务公司于1977年收购了INTERCOMP公司并于1983年售于科学软件公司,两家公司合并为后来的SSI公司,现被贝克休斯收购.其开发的数值模拟软件为Simbest2.4. Ian cheshire博士于70年代在英国原子能源部率领小组开发PORES数值模拟软件,于1981年10月同John Appleyard和Jon Holmes成立ECL公司,开始研发后来主导数值模拟软件市场的ECLIPSE软件.ECLIPSE是"ECL's Implicit Program for Simulation Engineering"的缩写.1983年11月发布第一个版本.该版本创下几个世界第一.是第一个全隐式模拟全油田的数值模拟软件.是第一个采用嵌套因式分解法的数值模拟软件.首创角点网格.首次采用优化内存管理,模拟双孔双渗而且首次可以运行在不同的硬件平台.1986年INTERA收购ECL公司.1995年斯仑贝谢GeoQuest收购INTERA公司软件部.5. CMG公司1977年成立于加拿大卡尔加里,其开发的数值模拟软件为STAR,IMEX及GEM.STAR应用于热采研究,IMEX应用于黑油模型,GEM应用于组分模型.CMG公司目前在中国,美国,英国,委内瑞拉建立了办事处.6. J.S.Nolen联合公司成立于1979年,其公司创设人为J.S.Nolen.该公司于1985年被西方阿特拉斯收购.1996年兰德马克公司收购了西方阿特拉斯数模业务.兰德马克于1996年7月被哈里伯顿公司宣布收购,成为其下子公司. 其开发的数值模拟软件为VIP.VIP为Vectorized Implicit Program的缩写.1991年开始研发并行算法.7. SimTech成立于1982年,1996年5月16日被Intera收购.Intera为Duke工程服务公司的子公司,主要做环境及水资源评价.8. 数值模拟研究公司(RSRC)成立于1982年,1996年被Smedvig收购.1999年Smedvig 技术公司与多流体ASA合并组成新的Roxar公司.其模拟软件为MORE. MORE为Modular Oil Reservoir Evaluation的缩写.9. Hot (Heinemann Oil Technology and Engineering)公司1986年成立于奥地利Leoben.其模拟软件为SURE,包括SUREGrid, SURESim,SUREPlot,SUREPVT,SUREFrac. SURE的主要特色是采用PEBI网格.1999年12月RC2收购HOT公司SURE软件,2001年2月Viritas DGC公司收购RC2和SURE.2003年9月地震微技术公司(SMT)收购RC2和SURE.10.其他数值模拟软件有:IFP的Athos. ConocoPhilipse的SENSOR,壳牌的MORES.油藏数值模拟未来10年发展预测进入二十一世纪,伴随着计算机的飞速发展以及互连网的普及应用,科技以令人难以想象的速度在突飞猛进。
数模介绍

面向对象:
广大理工商科同学。 主要方法: 数学方法和计算机技术。 题目内容: 社会,生活,实事,经济,环境,工程技术等 方面的实际问题 比赛形式: 三人、三天,针对题目进行分析、建模、处理, 最终以论文形式提交结果。
第一届数学建模竞赛:美国,1985年 我校首次开设该课程:1983年 全国第一届数模竞赛:1992年 我校第一届数模竞赛:1994年
现存竞赛中历史最悠久、影响范围最广的竞赛
之一。每年的竞赛约有300名同学参赛,范围 涵盖所有理、工、商科院系,涵盖四个年级。
不同规格的建模比赛:校内、全国、美国
校内赛成为国际比赛赛前练手的极好机会!
校内赛获奖团队将得到后续赛事的经费支持以
及数学系老师的专业指导,增大国际比赛获奖 机会!
毛学长(美赛后获中医院兼职邀请):“数模
竞赛在团队精神,搜索学术资源、快速阅读的 能力(美赛的话主要是英文),写作学术文章 的方法,数学模型的基本知识方面锻炼了我”
黄学长(现就读于加州大学伯克利分校):数
学建模竞赛获奖对深造申请,很有好处。
汪学长:“我去年7月从清华毕业,现在斯坦福
大学读EE PhD,做计算机系统方面的研究。去 年申请时,除斯坦福外,还得到了Berkeley, CMU, UCLA等六七所学校的offer。参加比赛对 于能力和信心的提高挺有帮助的……很多锻炼和 收获都是潜移默化的,希望有更多同学能从数 学建模中有所收获。”
参赛时间短,形式灵活。 资料查找、知识应用以及沟通合作料临时学 习应用非本专业知识(各专业都如此),同时 将专业知识发挥到最大限度。一次有价值的奋 斗体验。 比赛需要成员充分发挥其自身的优势,贯彻团 队合作从而最终解答,队员通过竞赛建立起深 厚的友谊。是一次有价值的团队体验。 对题目十分感兴趣的同学们则可在竞赛结束后 对问题进行进一步的思考,完善论文并最终发 表。这是一次有价值的科研体验。
中国大学生数学建模竞赛发展史
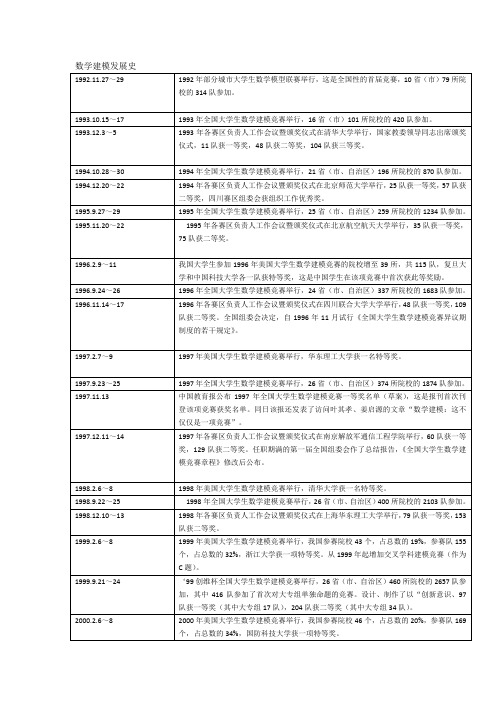
2000网易杯全国大学生数学建模竞赛举行,27省(市、自治区)517所院校的3210队参加,其中608队参加大专组竞赛,香港城市大学有1个队首次参赛
2000.12.6~8
2000年各赛区负责人工作会议暨颁奖仪式在中山大学珠海校区举行,119队获一等奖(其中大专组23队),245队获二等奖(其中大专组55队)。
1998年全国大学生数学建模竞赛举行,26省(市、自治区)400所院校的2103队参加。
1998.12.10~13
1998年各赛区负责人工作会议暨颁奖仪式在上海华东理工大学举行,79队获一等奖,153队获二等奖。
1999.2.6~8
1999年美国大学生数学建模竞赛举行,我国参赛院校43个,占总数的19%,参赛队155个,占总数的32%,浙江大学获一项特等奖。从1999年起增加交叉学科建模竞赛(作为C题)。
2003.2
2003年美国大学生数学建模竞赛(MCM)和交叉学科竞赛(ICM)举行,我国共参加300队,占总数的47%,浙江大学、北京大学、东南大学、东华大学各一队获特等奖。
2003.9.22~25
2003高教社杯全国大学生数学建模竞赛举行,30省(市、自治区)637所院校的5406队参加。
2003.12.6~7
2003年各赛区工作会议暨颁奖仪式在厦门举行,厦门大学承办,608队获全国奖,其中本科组一等奖151队,二等奖306队,大专组一等奖48队,二等奖103队。
2004.2
2004年美国大学生数学建模竞赛(MCM)和交叉学科竞赛(ICM)举行,我国共参加398队,占总数的54%,成都电子科技大学一队获特等奖。
数学建模发展史
1992.11.27~29
1992年部分城市大学生数学模型联赛举行,这是全国性的首届竞赛,10省(市)79所院校的314队参加。
数学建模概念的发展研究

数学建模概念的发展研究一、数学建模的历史数学建模的历史可以追溯到古希腊时期,当时的数学家开始用几何图形来描述天体运动和地球形状。
随着数学的发展,人们开始将数学方法应用于实际问题的解决,比如天文学、物理学、经济学等领域的问题。
直到20世纪初,数学建模才成为一个独立的学科。
随着计算机技术的发展,数学建模得到了迅速的发展,成为一种独立的学科,并逐渐应用于更广泛的领域。
二、数学建模的应用领域数学建模的应用领域非常广泛,涉及自然科学、工程技术、社会经济等各个领域。
在自然科学方面,数学建模被广泛应用于力学、流体力学、材料科学等领域,用于描述和预测物质的力学性质、流体的流动规律等;在工程技术领域,数学建模被用于设计和优化各种系统和设备,包括航天器、汽车、电子设备等;在社会经济领域,数学建模被用于分析和预测经济走势、人口增长、资源分配等问题。
数学建模已经成为现代科学技术和社会经济发展的重要工具。
三、数学建模的发展趋势随着实际问题的复杂性和多样性不断增加,数学建模也面临着新的挑战和发展机遇。
一方面,数学建模需要不断更新和完善自身的理论和方法,以应对日益复杂的问题;数学建模还需要与其他学科进行交叉融合,结合现代信息技术、大数据分析等手段,才能更好地应用于实际问题的解决。
数学建模的发展趋势可以概括为:理论创新、方法完善、跨学科融合。
在未来,数学建模有望成为更加重要和有效的工具,为人类的科学探索和社会经济发展提供更有力的支持。
随着人工智能、大数据分析等技术的发展,数学建模将更加注重数据的挖掘和分析,以及模型的精确描述和预测能力。
数字化技术也将使数学建模更加普及和便捷,让更多的科研人员和工程技术人员能够轻松进行数学建模工作。
数学建模有望在未来发挥更加重要的作用,为人类的发展进步做出更大的贡献。
数学建模竞赛发展历程

数学建模竞赛发展历程数学建模竞赛是一项旨在培养学生数学建模能力的比赛,其发展历程可以追溯到20世纪60年代。
在这个过程中,数学建模竞赛经历了多个阶段的发展和变革。
起初,数学建模竞赛的范围相对较窄,主要侧重于数学理论和方法的应用。
参赛者需要解决一些抽象的数学问题,通过运用已有的数学知识和技巧来推导和证明结论。
这个阶段的竞赛题目较为抽象,解决问题的方式相对固定,对学生的综合能力要求较高。
随着时间的推移,数学建模竞赛逐渐开始注重实际问题的建模和解决。
竞赛题目涉及的领域也逐渐扩展,除了数学本身,还包括了物理、化学、生物、经济等其他学科。
这使得竞赛更加贴近实际,增加了学生的兴趣和参与度。
在发展过程中,数学建模竞赛也开始引入了计算机技术的应用。
计算机可以帮助学生更快地处理和分析大量的数据,提高解题效率。
同时,计算机模拟和仿真技术也使得学生可以更加直观地观察和探索问题。
这一变革使得数学建模竞赛更加灵活和高效。
随着社会和科技的进步,数学建模竞赛也逐渐定位为培养创新人才的重要途径。
竞赛题目开始注重培养学生的创新思维和实践能力,鼓励学生提出新颖的解决方案和方法。
竞赛评价标准也从简单的答案是否正确转变为解决问题的方法是否合理、是否具有实际应用价值等方面。
当前的数学建模竞赛已经成为一项具有广泛影响力和参与度的学科竞赛。
不仅学生和教师参与其中,还有许多企业和科研机构提供支持和赞助。
竞赛的题目也愈加贴近实际和前沿,涉及的领域更加广泛。
此外,一些国际性的数学建模竞赛也开始兴起,为学生提供了一个与世界各地的优秀选手交流的机会。
总的来说,数学建模竞赛经历了从理论到实践、从抽象到具体、从计算机辅助到创新思维的发展历程。
通过这项竞赛,学生不仅可以提高数学建模能力,还可以培养创新思维和实践能力,为未来的学习和工作打下良好的基础。
中国大学生数学建模竞赛发展史

中国大学生数学建模竞赛发展史自20世纪80年代初,中国大学生数学建模竞赛便在我国高校间兴起并得到广泛关注。
这一竞赛活动不仅提供了一种展示学生数学建模能力的机会,更培养了学生的创新精神和团队合作能力。
以下将介绍中国大学生数学建模竞赛的发展史及其影响。
1. 初期阶段(1984-1993)中国大学生数学建模竞赛起始于1984年,当时仅有百余所高校参与其中,但其知名度和影响力逐渐扩大。
竞赛组织者积极探索比赛规则,优化题目设计,并引入专家评审,以提高竞赛的专业性和公正性。
2. 发展壮大(1994-2003)在1994年至2003年这一时期,中国大学生数学建模竞赛规模持续扩大,参赛高校增加到500余所。
组织者进一步改进比赛形式,创新题目的类型和难度,逐渐提高竞赛的技术含量与实践能力要求。
3. 制度完善(2004-2013)2004年至2013年期间,中国大学生数学建模竞赛进一步规范化和制度化,参赛高校数量激增至近千所。
组织者增加了作品评价标准,设置了多轮复赛来提高竞赛的选拔效果。
同时,各省级及全国范围内的选拔赛也逐渐建立起来。
4. 国际交流(2014至今)自2014年以来,中国大学生数学建模竞赛开始与国际接轨,允许外国大学生参赛。
通过国际合作与交流,中国大学生数学建模竞赛与国际间的接轨逐渐加深,为学生提供了更广阔的发展平台。
此外,竞赛还积极组织学生赴国外参加国际数学建模竞赛,为他们拓宽国际视野和培养全球竞争力奠定了基础。
中国大学生数学建模竞赛的发展深深地影响着我国的教育体制和学生的学习态度。
通过参与竞赛,学生在解决实际问题的过程中锻炼了自己的数学建模和创新思维能力。
而竞赛的组织和评审过程也刺激了高校教师的教学研究和专业提升。
总的来说,中国大学生数学建模竞赛在我国高校教育中的地位越来越重要。
它不仅是一项促进数学教育发展的有效方式,也是培养学生创新能力和团队协作精神的重要途径。
随着竞赛不断发展,我们有理由相信,中国大学生数学建模竞赛将为培养更多有实践能力和创新精神的优秀人才做出更大的贡献。
数学建模课程和竞赛的发展与数学教学改革.

二. 数学实验课的开设及实践
内容 集数值计算、优化方法、数理统计、数学建模及数学软 件技术于一体,以“了解数学基本原理、掌握主要数值算法、 会用计算机软件实现、培养数学建模能力”为基本要求; 在大学数学教学体系中起着承上(数学基础课)、启下(后续 课及数学的应用)的作用。 实施 针对课程需要知识面广、实例多、方法与软件计算交叉 等特点,采用多媒体课件,实例生动、信息量大、便于接受; 精心安排学生的实验,保证上机时间,对实验报告提出严格、 合理的要求。学生一学期需完成10个实验报告; 期末考试完全开卷,在计算机实验室进行,期末根据实验报告 成绩,辅以面试,给予部分学生免试。
六. 数学建模与数学实验课的关系
• 课程目的基本一致:着重培养“用数学”的能力 • 课程内容差别较大: 1)数学实验课介绍若干数学方法(数值计算、优化、 统计)及相应的软件,能方便地完成模型的求解; 数学建模课很少涉及模型明确 地看出用哪种数学方法);数学建模课传授丰富的 建模案例。
五. 国外教材和数学实验课程给数学建模教学的启示
借助数学软件研究模型(利用软件的数值解和图形功 能),适当增加数值计算、数值模拟及敏感性分析; 扩大优化模型的范围,如线性规划和整数规划模型 内容(建立模型、软件求解、敏感性分析); 增加统计回归模型内容(变量挑选、模型选择、软件 求解、奇异值处理、结果分析); 加强项目练习(Projects),提供更多的题目。
三. 两本国外数学建模教材
Douglas D. Mooney and Randall J. Swift, A Course in Mathematical Modeling,1999
内容 离散模型(动态系统、随机模拟、马氏链),经验模型 (回归分析),连续模型(动态系统、特征根和相轨线、排队 模型及模拟、生灭过程); 案例以经济和生态领域为主,多数包含用软件做的数值计算。
数模发展历程

什么是数学模型与数学建模简单地说:数学模型就是对实际问题的一种数学表述。
具体一点说:数学模型是关于局部现实世界为某种目的的一个抽象的简化的数学构造。
更确切地说:数学模型就是对于一个特定的对象为了一个特定目标,根据特有的内在规律,做出一些必要的简化假设,运用适当的数学工具,得到的一个数学构造。
数学构造可以是数学公式,算法、表格、图示等。
数学建模就是建立数学模型,建立数学模型的过程就是数学建模的过程〔见数学建模过程流程图〕。
数学建模是一种数学的思考方法,是运用数学的语言和方法,通过抽象、简化建立能近似刻划并"解决"实际问题的一种强有力的数学手段。
美国大学生数学建模竞赛的由来:1985年在美国出现了一种叫做MCM的一年一度大大学生数学模型〔1987年全称为Mathematical Competition in Modeling,1988年改全称为Mathematical Contest in Modeling,其所写均为MCM〕。
这并不是偶然的。
在1985年以前美国只有一种大学生数学竞赛〔The william Lowell Putnam mathematial Competition,简称Putman(普特南〕数学竞赛〕,这是由美国数学协会〔MAA--即Mathematical Association of America的缩写〕主持,于每年12月的第一个星期六分两试进展,每年一次。
在国际上产生很大影响,现已成为国际性的大学生的一项著名赛事。
该竞赛每年2月或3月进展。
我国自1989年首次参加这一竞赛,历届均取得优异成绩。
经过数年参加美国赛说明,中国大学生在数学建模方面是有竞争力和创新联想能力的。
为使这一赛事更广泛地展开,1990年先由中国工业与应用数学学会后与国家教委联合主办全国大学生数学建模竞赛〔简称CMCM〕,该项赛事每年9月进展。
数学模型竞赛与通常的数学竞赛不同,它来自实际问题或有明确的实际背景。
数学建模概念的发展研究

数学建模概念的发展研究数学建模是数学与实际问题相结合,通过数学方法来描述、分析与解决实际问题的过程。
它是数学与现实世界之间的桥梁,为各行各业的发展提供了理论支持和解决方案。
数学建模的概念及其发展历程,对于了解数学建模的本质和意义,以及对实际问题进行定量分析和解决具有重要的指导意义。
本文将对数学建模概念的发展进行研究,探讨其历史渊源、主要发展阶段及未来发展方向。
一、数学建模概念的形成和发展历程数学建模的概念最早可以追溯到古希腊时期,当时数学家们开始探讨几何学和代数学以及它们在解决实际问题中的应用。
真正系统地将数学与实际问题相结合,进行定量分析和解决实际问题的过程还是在20世纪初才逐渐形成。
20世纪50年代后,随着计算机技术的发展,数学建模逐渐成为了一个独立的学科领域,并在科学研究、工程技术和社会经济等领域得到了广泛的应用。
在数学建模概念的形成和发展过程中,可以归纳为以下几个阶段:初级阶段、发展阶段和成熟阶段。
在初级阶段,数学建模主要集中在物理、化学、生物等自然科学领域,主要目的是用数学方法来解决自然现象中的问题。
在发展阶段,数学建模逐渐扩展到了工程技术、经济管理等应用领域,形成了一系列的数学模型和方法。
而到了成熟阶段,数学建模已经成为了一门独立的学科,涵盖了广泛的研究领域和应用领域,不仅在学术研究中发挥重要作用,也成为了解决实际问题的有效工具。
二、数学建模概念的内涵和意义数学建模的概念涉及到了数学方法、实际问题和解决过程三个方面。
数学方法是指数学在解决实际问题中的应用,包括代数学、几何学、概率统计、微分方程等数学内容。
实际问题是指现实世界中的各种具体问题,包括自然现象、工程技术、社会经济等领域的问题。
解决过程是指通过数学建模来描述实际问题、分析问题的本质、提出解决方案的过程。
数学建模是将数学方法应用于实际问题的过程,通过建立数学模型来描述实际问题、分析问题、进行定量分析和解决问题的过程。
数学建模的意义主要体现在以下几个方面:一是为科学研究和工程技术提供了重要的理论支持和分析工具,从而推动了科学技术的发展和进步;二是为社会经济和管理决策提供了重要的预测和决策支持,帮助人们更好地认识和把握现实世界;三是为学生和研究人员提供了宝贵的学习和研究机会,有助于培养学生的数学思维和解决问题的能力。
数学建模竞赛的类型、发展PPT

如: A15010021_张三_李四_王五
表示:选作A题,山东赛区,参赛学校为山东大 学,队员:张三、李四、王五
每个学校都有唯一编号,可登陆山东赛区组委 会网址查询
参赛队校内编号由参赛学校统一指定,应保证
• 运筹学或数学规划---线性、整数、0-1、非线性、多目 标规划
• 图论与网络优化
• 多因素综合评价
• 数值计算方法---数值微分,数值积分,插值与拟合等 • 差分与微分方程等机理分析建模方法
• 排队论、对策论、决策论
• 其他:模糊数学、 随机规划与决策、随机模拟、灰色
系 统理论、优化算法(神经网络、遗传算法、蚁群算
• 论文写作:尽早开始组织编写,以免因时间限制, 造成遗憾;
• 预防措施:所有程序、计算结果、所编写的论 文应注意随时做好备份,以免丢失;
2020/3/25
数学建模竞赛的类型、发展
9
• 竞赛结束后 提交论文:提交论文前应仔细阅读全国组 委会和山东赛区组委会有关论文格式要求, 以及提交流程,按规定仔细检查后再上传 论文。
3人一个参赛队, 利用3天时间完成一 篇竞赛论文
全国征集,网络下载
数学建模竞赛的类型、发展
1
发展规模
历年CUMCM 参赛队数统计
2020/3/25
数学建模竞赛的类型、发展
2
三、竞赛组织和赛题分析
• 组队:时间越早越好,最好从大一开始
• 组队要求:
1、建模知识与能力尽可能全面;
2、尽可能地让能力、素质方面不同的学生
钢管的订购和运输问题
数学建模的起源与发展历史是什么?

数学建模的起源与发展历史是什么?、数学建模的起源数学建模是在20世纪60和70年代进入一些西方国家大学的,我国的几所大学也在80年代初将数学建模引入课堂。
经过20多年的发展现在绝大多数本科院校和许多专科学校都开设了各种形式的数学建模课程和讲座,为培养学生利用数学方法分析、解决实际问题的能力开辟了一条有效的途径。
大学生数学建模竞赛最早是1985年在美国出现的,1989年在几位从事数学建模教育的教师的组织和推动下,我国几所大学的学生开始参加美国的竞赛,而且积极性越来越高,近几年参赛校数、队数占到相当大的比例。
可以说,数学建模竞赛是在美国诞生、在中国开花、结果的。
1992年由中国工业与应用数学学会组织举办了我国10城市的大学生数学模型联赛,74所院校的314队参加。
教育部领导及时发现、并扶植、培育了这一新生事物,决定从1994年起由教育部高教司和中国工业与应用数学学会共同主办全国大学生数学建模竞赛,每年一届。
十几年来这项竞赛的规模以平均年增长25%以上的速度发展。
全国大学生数学建模竞赛是全国高校规模最大的课外科技活动之一。
本竞赛每年9月(一般在中旬某个周末的星期五至下周星期一共3天,72小时)举行,竞赛面向全国大专院校的学生,不分专业(但竞赛分本科、专科两组,本科组竞赛所有大学生均可参加,专科组竞赛只有专科生(包括高职、高专生)可以参加)。
2008 年全国有31个省/市/自治区(包括香港)1023所院校、12846个队(其中甲组10384队、乙组2462队)、3万8千多名来自各个专业的大学生参加竞赛,是历年来参赛人数最多二、数学建模的定义简单地说:数学模型就是对实际问题的一种数学表述。
具体一点说:数学模型是关于部分现实世界为某种目的的一个抽象的简化的数学结构。
更确切地说:数学模型就是对于一个特定的对象为了一个特定目标,根据特有的内在规律,做出一些必要的简化假设,运用适当的数学工具,得到的一个数学结构。
数模竞赛历史

·数模竞赛历史1、美国(MCM / ICM)竞赛1983年起,美国一些专家开始探讨组织一项应用数学方面的竞赛的可能性。
经过论证和争取资助,终于在1985年开始有了美国的第一届大学生数学建模竞赛,简称MCM(1987年前称Mathematical Competition in Modeling, 之后更名为Mathematical Contest in Modeling)。
竞赛由美国工业与应用数学学会和美国运筹学会联合主办。
从1985年起,每年举行一届,在每年二月的某个星期五到星期日举行。
到2004年已举行了20届。
MCM官方网站:Mathematical Contest in Modeling (MCM), challenges teams of students to clarify, analyze, and propose solutions to open-ended problems. The contest attracts diverse students and faculty advisors from over 500 institutions around the world.The Interdisciplinary Contest in Modeling (ICM), an international contest for high school students and college undergraduates. ICM is an extension of the Mathematical Contest in Modeling (MCM). It is designed to develop and advance interdisciplinary problem-solving skills as well as competence in written communication.2、全国大学生数学建模竞赛受到美国先进教育的影响,早在1983年,我校数学系就首先开设了数学建模课程,当时仅面向数学系同学,用的是美国的教材。
数学建模概念的发展研究

数学建模概念的发展研究
数学建模是一种将实际问题转化为数学公式并用数学方法求解的过程。
它不仅在科学领域有着广泛的应用,而且在社会、经济、工程等领域也有着非常重要的作用。
随着科技的不断发展,数学建模理论和应用规模也不断拓展。
本文将探讨数学建模概念的发展研究。
数学建模理论最早出现于18世纪,当时主要应用于静力和弹性的问题研究。
19世纪后期,数学建模理论出现了飞速发展,形成了以应用为导向的数学建模。
Faraday在研究电场的变化规律时,首次提出数学模型的概念。
之后,众多学者,如Laplace、Poisson、Fourier、Gauss等人纷纷应用数学模型来解决实际问题,从而让数学建模更加深入人心。
20世纪,数学建模理论得到了更深入的发展。
20世纪50年代,美国国防部开始对数学建模理论进行研究,旨在解决国防领域中的实际问题。
此外,20世纪60年代末,计算机技术的发展使得数学建模能够更加高效地进行。
通过借助计算机,数学建模能够对复杂问题进行模拟和分析,从而加快了解决实际问题的速度。
随着社会和经济的发展,数学建模的应用范围也进一步拓展。
在工程领域,数学建模常常被应用于对电力输送和供应系统的稳定性进行分析。
在医学领域,数学建模可以帮助研究人员探索疾病的传播机制,为治疗疾病提供有力支持。
在金融领域,数学建模可以帮助投资者控制投资风险,从而提高投资收益。
总之,数学建模的发展研究经历了从模型简单到模型复杂、从理论发展到实际应用的不断深入和拓展的历程。
随着技术的不断进步,数学建模将拥有更加广泛和深入的实际应用,为社会的发展和进步做出更大的贡献。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
什么是数学模型与数学建模
简单地说:数学模型就是对实际问题的一种数学表述。
具体一点说:数学模型是关于部分现实世界为某种目的的一个抽象的简化的数学结构。
更确切地说:数学模型就是对于一个特定的对象为了一个特定目标,根据特有的内在规律,做出一些必要的简化假设,运用适当的数学工具,得到的一个数学结构。
数学结构可以是数学公式,算法、表格、图示等。
数学建模就是建立数学模型,建立数学模型的过程就是数学建模的过程(见数学建模过程流程图)。
数学建模是一种数学的思考方法,是运用数学的语言和方法,通过抽象、简化建立能近似刻划并"解决"实际问题的一种强有力的数学手段。
美国大学生数学建模竞赛的由来:
1985年在美国出现了一种叫做MCM的一年一度大大学生数学模型(1987年全称为Mathematical Competition in Modeling,1988年改全称为Mathematical Contest in Modeling,其所写均为MCM)。
这并不是偶然的。
在1985年以前美国只有一种大学生数学竞赛(The william Lowell Putnam mathematial Competition,简称Putman(普特南)数学竞赛),这是由美国数学协会(MAA--即Mathematical Association of America的缩写)主持,于每年12月的第一个星期六分两试进行,每年一次。
在国际上产生很大影响,现已成为国际性的大学生的一项著名赛事。
该竞赛每年2月或3月进行。
我国自1989年首次参加这一竞赛,历届均取得优异成绩。
经过数年参加美国赛表明,中国大学生在数学建模方面是有竞争力和创新联想能力的。
为使这一赛事更广泛地展开,1990年先由中国工业与应用数学学会后与国家教委联合主办全国大学生数学建模竞赛(简称CMCM),该项赛事每年9月进行。
数学模型竞赛与通常的数学竞赛不同,它来自实际问
题或有明确的实际背景。
它的宗旨是培养大学生用数学方法解决实际问题的意识和能力,整个赛事是完成一篇包括问题的阐述分析,模型的假设和建立,计算结果及讨论的论文。
通过训练和比赛,同学们不仅用数学方法解决实际问题的意识和能力有很大提高,而且在团结合作发挥集体力量攻关,以及撰写科技论文等方面将都会得到十分有益的锻炼。
数学建模方法
一、机理分析法从基本物理定律以及系统的结构数据来推导出模型。
1. 比例分析法--建立变量之间函数关系的最基本最常用的方法。
2. 代数方法--求解离散问题(离散的数据、符号、图形)的主要方法。
3. 逻辑方法--是数学理论研究的重要方法,对社会学和经济学等领域的实际问题,在决策,对策等学科中得到广泛应用。
4. 常微分方程--解决两个变量之间的变化规律,关键是建立"瞬时变化率"的表达式。
5. 偏微分方程--解决因变量与两个以上自变量之间的变化规律。
二、数据分析法从大量的观测数据利用统计方法建立数学模型。
1. 回归分析法--用于对函数f(x)的一组观测值(xi,fi)i=1,2,…,n,确定函数的表达式,由于处理的是静态的独立数据,故称为数理统计方法。
2. 时序分析法--处理的是动态的相关数据,又称为过程统计方法。
3. 回归分析法--用于对函数f(x)的一组观测值(xi,fi)i=1,2,…,n,确定函数的表达式,由于处理的是静态的独立数据,故称为数理统计方法。
4. 时序分析法--处理的是动态的相关数据,又称为过程统计方法。
三、仿真和其他方法
1. 计算机仿真(模拟)--实质上是统计估计方法,等效于抽样试验。
①离散系统仿真--有一组状态变量。
②连续系统仿真--有解析表达式或系统结构图。
2. 因子试验法--在系统上作局部试验,再根据试验结果进行不断分析修改,求得所需的模型结构。
3. 人工现实法--基于对系统过去行为的了解和对未来希望达到的目标,并考虑到系统有关因素的可能变化,人为地组成一个系统。
(参见:齐欢《数学模型方法》,华中理工大学出版社,1996)
题型:
赛题题型结构形式有三个基本组成部分:
一、实际问题背景 1. 涉及面宽--有社会,经济,管理,生活,环境,自然现象,工程技术,现代科学中出现的新问题等。
2. 一般都有一个比较确切的现
实问题。
二、若干假设条件有如下几种情况: 1. 只有过程、规则等定性假设,无具体定量数据; 2. 给出若干实测或统计数据; 3. 给出若干参数或图形; 4. 蕴涵着某些机动、可发挥的补充假设条件,或参赛者可以根据自己收集或模拟产生数据。
三、要求回答的问题往往有几个问题(一般不是唯一答案): 1. 比较确定性的答案(基本答案);
2. 更细致或更高层次的讨论结果(往往是讨论最优方案的提法和结果)。
竞赛答卷:
提交一篇论文,基本内容和格式大致分三大部分:
一、标题、摘要部分:
1.题目--写出较确切的题目(不能只写A题、B 题)。
2.摘要--200-300字,包括模型的主要特点、建
模方法和主要结果。
3.内容较多时最好有个目录。
二、中心部分:
1.问题提出,问题分析。
2.模型建立:
①补充假设条件,明确概念,引进参数;
②模型形式(可有多个形式的模型);
③模型求解;
④模型性质;
3.计算方法设计和计算机实现。
4.结果分析与检验。
5.讨论--模型的优缺点,改进方向,推广新思想。
6.参考文献--注意格式。
三、附录部分:
1.计算程序,框图。
2.各种求解演算过程,计算中间结果。
3.各种图形、表格。
竞赛题汇集:
推荐资料:
----国际数学和计算机建模协会,International Association for Mathematical and Computer Modelling Home Page。
----应用数学建模,Applied Mathematical Modelling (Elsevier)。
----应用数学和计算,Applied Mathematics and Computation。
----欧洲应用数学杂志,European Journal of Applied Mathematics (Cambridge)。
----IMA 应用数学杂志,The IMA Journal of Applied Mathematics (Oxford)。
----SIMA的应用数学杂志,SIAM
Journal on Applied Mathematics。
----数学建模和数值分析杂志,Journal Mathematical Modelling and Numerical Analysis-Rairo。
----数学建模和分析杂志,Journal of mathematical modelling and analysis。
----美国工业和应用数学会评论,SIAM Review 。
