新人教版苏科版七年级数学上册5.4主视图、左视图、俯视图(1)课件(共19张PPT)
七年级数学上册 5.4 主视图、左视图、俯视图 什么是左视图素材 苏科版(2021学年)

七年级数学上册5.4主视图、左视图、俯视图什么是左视图素材(新版)苏科版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(七年级数学上册5.4 主视图、左视图、俯视图什么是左视图素材(新版)苏科版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为七年级数学上册5.4 主视图、左视图、俯视图什么是左视图素材(新版)苏科版的全部内容。
什么是左视图难易度:★★★★关键词:三视图答案:从左面观察一个物体时看到的形状图,叫物体的左视图。
【举一反三】典题:如图的几何体,左视图是( )。
思路导引:从左面观察一个物体时看到的形状图,叫物体的左视图。
标准答案:选B.以上就是本文的全部内容,可以编辑修改。
高尔基说过:“书是人类进步的阶梯。
”我希望各位朋友能借助这个阶梯不断进步。
物质生活极大丰富,科学技术飞速发展,这一切逐渐改变了人们的学习和休闲的方式。
很多人已经不再如饥似渴地追逐一篇文档了,但只要你依然有着这样一份小小的坚持,你就会不断成长进步,当纷繁复杂的世界牵引着我们疲于向外追逐的时候,阅读一文或者做一道题却让我们静下心来,回归自我。
用学习来激活我们的想象力和思维,建立我们的信仰,从而保有我们纯粹的精神世界,抵御外部世界的袭扰。
The above is the whole content of this article, Gorky said: "the book is the ladder of human progress." Ihope you can make p rogress withthe help ofthis ladder. Material lifeis ex tremely rich, scienceand technologyare developing rapidly, allof which gradually changethe way of people'sstudy and leisure. Manypeople are no longer eager to pursuea document, but as long as you still havesucha small persistence, you willcontinue to grow and progress. When the complex world leads us to chase out, reading an article or doinga problem makes us calmdown and return to ourselves. With learning, wecan activate ourimagination and thinking, establish our belief, keep our purespiritual world and resist the attack of theexternal world.。
苏科版七年级数学上册《5.4主视图、左视图、俯视图(1)》课件

(2) 正视图
(3) 俯视图
从
上
(2)桌上放着
面 看
一个长方体、一个
棱锥和一个圆柱, 请说出下面的三幅 从左面看
图分别是从哪个方
向看到的?
(1)
正视图
(2)
左视图
(3)
俯视图
观察下表中所示物体,并将看到的图 形填入表中.
从三个方向看
长 高
主视图
宽
宽
左视图
主俯长相等 主左高平齐 俯左宽相等
从上面看
从左面看
试 左视图为 (2) .
一
试
(1)
(2)
(3)
如右图所示的物体,你 知道下面的三幅图分别是从 哪个方向看到的吗?你能说 出这三幅视图的名称吗?
(1) 左视图
(2) 主视图
(3) 俯视图
从
上
面
(1)桌面上放着
看
一个圆柱和一个长方
体,请说出下面三幅 从左面看 图分别是从哪一个方
向看到的?
(1) 左视图
看一看
?
这是两幅意大利比萨斜塔的照片, 你知道为什么第二幅照片中的斜塔 不斜呢?
5.4 主视图、左视图、 俯视图(1)
(1)从上面、左面、正面看一个 圆柱,看到的图形分别是什么?
从
上
从上面看
面
看
从左面看
从左面看
从正面看
立体图形
平面图形
(2)从正面、左面、上面看一个四 棱锥,看到的图形分别是什么?
图)
说
)
…
• 不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面 上的话,另一眼睛看到纸的背面。2022年4月13日星期三上午2时9分55秒02:09:5522.4.13
5.4 左视图、主视图、俯视图-2020秋苏科版七年级数学上册课件(共16张PPT)

随堂练习
2.下列几何体中,主视图与俯视图不相同的是( B )
课堂小结
主视图:从正面看到的图形
主视图、左视 图、俯视图
左视图:从左面看到的图形 俯视图:从上面看到的图形
课程讲授
1 主视图、左视图、俯视图
问题3:如右图所示的物体,你知道下面的三幅图分别 是从哪个方向看到的吗?你能说出这三幅视图的名 称吗?
(1) 左视图
(2) 主视图
(3) 俯视图
课程讲授
1 主视图、左视图、俯视图
练一练:如图所示的几何体的主视图是( C )
随堂练习
1.如图是由三个相同的小正方体组成的几何体,则该几 何体的左视图是( C )
三视图
正面
侧面 水平面
主视图
左视图
高高
长
宽
长
俯视图
宽
课程讲授
1 主视图、左视图、俯视图
主视图
左视图
高高
长
宽
长
俯视图
宽
定义:一般地,我们把从正面看到的图形,称为主视
图;把从左面看到的图形,称为左视图;把从上面看 到的图形,称为俯视图.
课程讲授
1 主视图、左视图、俯视图
问题2:桌面上放着一个圆柱和一个长方体,请说出下 面三幅图分别是从哪一个方向看到的? 从 上 面 看
问题1:根据下图中对玩偶各个面的观察,你能想同学 描述这个玩偶的基本特征吗?
正面
侧面
背面Biblioteka 定义:当我们从某一方向观察一个物体时,所看到的
图形叫做物体的一个视图.
课程讲授
1 主视图、左视图、俯视图
为了全面反映物体的形状,生产实践中往往采用多个 视图来反映同一物体不同方面的形状.
苏科版七年级数学上 5.4 主视图,左视图,俯视图(共37张PPT)

半圆柱
根据三视图,猜猜是哪个几何体?
主视图 左视图 俯视图
我们发现:
从三个方向看
立体图形
平面图形
空间想象
#
活动二:
下面为由小立方体搭成的几何体的三个视图, 你能想象出这个几何体的形状吗?
能用手中的立方体纸盒搭出来吗?
主视图 左视图
俯视图
#
先想一想,再搭一搭
下面是由若干个小立方体搭成的几何体的三个视图, 你能想象出这个几何体的形状吗?请用小立方体搭出相应 的几何体。
主视图 左视图
俯视图 长方体
(1)
主视图 左视图
俯视图 圆柱
(2)
根据图中的三视图,说出相应 几何体的名称.
主视图 左视图 俯视图
三棱锥
(3)
根据图中的三视图,说出相应 几何体的名称.
主视图 左视图
主视图 左视图
俯视图 三棱柱俯视图
根据图中所示的三个视图, 想象相应物体的形状.
主视图 左视图 俯视图
平面图形 立体图形
几何体可能是:
圆锥
四棱锥
通过一个或两个视图, 不 能确定一个物体的形状和 大小!
平面图形 立体图形
已知三个视图,能确定吗?
主视图,左视图,俯视图都是正方形
平面图形 立体图形
主视图,左视图,俯视图都是圆
通过三个视图, 能确定一 个物体的形状和大小!
根据图中的三视图,说出相应 几何体的名称.
生活中处处有数学!
在一个仓库里堆积着正
方体的货箱若干,要搬运这 些箱子很困难,可是仓库管 主视图 理员要核实一下箱子的数量, 于是就想出一个办法:将这 堆货物的三视图画了出来, 你能根据图中的三视图,帮 他清点一下箱子的数量吗? 俯视图
最新苏科版七年级上册数学《5.4 主视图、左视图、俯视图》精品教学课件 (9)

中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
三棱柱
人教版初中数学精品教学课件设计
四棱锥
3、根据三个视图,分别说出相应几何体 的名称。
六棱锥
人教版初中数学精品教学课件设计
圆锥
根据下图的三个视图,分别 想象相应的物体的形状
人教版初中数学精品教学课件设计
你能根据三视图用小方块搭出相应的几何体吗?
用小立方块搭出符合下列三视图的几何体:
人教版初中数学精品教学课件设计
俯视图
如图是由几个小立方块所搭几何体的 俯视图,小正方形中的数字表示在该 位置小立方块的个数,请画出这个几 何体的主视图和左视图。
21
12
主视图
左视图
人教版初中数学精品教学课件设计
如图所示是由几个小立方块所搭几 何体的俯视图,小正方形中的数字 表示在该位置小立方块的个数,画 出相应几何体的主视图、左视图。
13
21
主视图
人教版初中数学精品教学课件设计
左视图
如图所示的是由几个小立方块所搭几何体的俯 视图,小正方形中的数字表示在该位置小立方 块的个数,请画出相应几何体的主视图和左视 图。
23
1
主视图
人教版初中数学精品教学课件设计
左视图
如下图是由几个小立方块所搭几何体的俯视图 ,小正方形中的数字表示在 该位置的小立方块的个数,这个几何体的主视图是( )
用小立方块搭出符合下列三视图的几何体,
需要______块小立6 方块.
人教版初中数学精品教学课件设计
21 1 1
人教版初中数学精品教学课件设计
苏科版七年级上册第五章第四节主视图、左视图、俯视图(1)学案

5.4主视图、左视图、俯视图(1)【学习目标】1.经历从不同方向观察物体的活动过程,发展学生的空间观念;2.会画简单物体的三视图,能判断简单物体的视图;3.进一步感知立体图形与平面图形的关系.【学习重点】掌握立体图形的三视图以及会画出简单图形的三视图.【学习难点】从不同方向画简单组合体的三视图.【学习过程】一、情境创设1.引用苏轼《题西林壁》中的诗句:横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.2.显示飞机的三视图.感悟:从不同方向看同一个物体,看到的图形往往是不同的。
二、探索新知1.桌上放着一个长方体和1个圆柱,从不同方向观察这两个物体,指出右边的3幅图分别是从哪一个方向看到的?2.桌上放着一个长方体、一个棱锥和一个圆柱,请说出右面的三幅图分别是从哪个方向看到的?生活中,你有类似的体验吗?请举例说明。
3.观察下表中所示物体,并将看到的图形填入表中.人们从不同的方向观察某个物体,可以看到不同的图形。
一般地,我们把从正面看到的图形,称为主视图;从左面看到的图形,称为左视图;从上面看到的图形,称为俯视图。
由于三个视图反映的是同一个物体,所以每两个视图之间必有一个相同的度量.因此得到:主、俯视图等长;主、左视图等高;俯、左视图等宽.三、例题精讲如下图所示的物体,你知道下面的三幅图分别是从哪个方向看到的吗?你能说出这三幅视图的名称吗?四、课堂练习1.画出图中两个物体的主视图、左视图、俯视图.2.甲、乙、丙、丁四人分别面对面坐在一个四边形桌子旁边,桌上一张纸写着数字“9”,甲说他看到的是“6”,乙说他看到的是“”,丙说他看到的是“”,丁说他看到的是“9”,则下列说法正确的是().A.甲在丁的对面,乙在甲的左边,丙在丁的右边;B.丙在乙的对面,丙的左边是甲,右边是乙;C.甲在乙的对面,甲的右边是丙,左边是丁;D.甲在丁的对面,乙在甲的右边,丙在丁的右边.3.如图是一个由4个相同的正方体组成的立体图形,它的左视图是()A.B.C.D.4.如图所示的几何体是由一个圆柱体挖去一个长方体后得到的,它的主视图是()A.B.C.D.5.如图是一个由7个相同正方体组合而成的几何体,它的主视图为()A.B.C.D.6.如图是由4个小立方块搭成的几何体,则下列说法正确的是()A.主视图的面积最大B.俯视图的面积最大C.左视图的面积最大D.三个视图的面积一样大7.在下面的四个几何体中,主视图、俯视图、左视图都相同的几何体的个数有()A.1个B.2个C.3个D.4个8.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是()A.主视图B.俯视图C.左视图D.一样大9.图①是五棱柱形状的几何体,则它的三视图为()A.B.C.D.10.如图是由长方体和圆柱组成的几何体,它的俯视图是()A.B.C.D.11.将一个长方体内部挖去一个圆柱(如图所示),它的主视图是()A.B.C.D.12.如图是将一个底面为正方形的长方体切掉一个角后得到的几何体,则从上面看到的几何体的形状图是()A.B.C.D.五、拓展提高一个几何体由一些大小相同的小正方体搭成,如图是从上面看到的这个几何体的形状图,小正方形中的数字表示在该位置的小正方体的个数,请画出从正面和从左面看到的几何体的形状图.六、小结与思考通过本节课的学习你有哪些收获?七、课后作业《同步练习》第95,96页。
苏科版七年级数学上册 主视图、左视图、俯视图(课件)

所以这个几何体最多有10个正方体组成.故答案为8,10.
)
由三视图还原几何体
2.某几何体的三视图如图所示,因此几何体是( )
A.长方形
B.圆柱
C.球
D.正三棱柱
3.由若干个相同的小正方体搭成的一个几何体的主视图和俯
视图如图所示,则组成这个几何体的小正方体的个数最多有
(3)3×4×3=36cm2,
∴这个几何体的侧面积为36 cm2
课后回顾
课后回顾
01
02
03
A.4
B.5
C.6
D.7
【解析】
由主视知这个几何体共有2层,由俯视图易得最底层有4个小正方体,由主视图可得二
层最多有2个小正方体,第那么搭成这个几何体的小正方体最多为4+2=6个。故选C。
三视图的相关计算
4.如图,是由一些棱长为1cm的小正方体构成的立体图形的三种视图,那
么这个立体图形的表面积是(
情景引入
题西林壁
横看成岭侧成峰,
远近高低各不同。
不识庐山真面目,
只缘身在此山中。
你知道这是为什么吗?
探索与思考
下图为某产品的设计图,你能指出这些设计图是从哪几个方向来描绘物体的吗?
视图
当我们从某一方向观察一个物体时,所看到的图形叫做物体的一个
视图。视图也可以看作物体在某一个方向的光线下的正投影,对于同
∴设高为h,则5×3×h=30,解得:h=2,
∴它的表面积是:5×3×2+5×2×2+3×2×2=30+20+12=62.
6 如图是一个几何体从三个方向看所得到的形状图.
《主视图、左视图、俯视图》课件+【2022版新课标】苏科版七年级数学上册

高平齐
长对正
宽相等
俯视图
主视图与俯视图的长对正,主视图与左视 图的高平齐,左视图与俯视图的宽相等.
画三视图
画三视图的方法: 第一步,确定主视图的位置,画出主视图; 第二步,在主视图正下方画出俯视图,注意 与主视图长对正; 第三步,在主视图正右方画出左视图,注意 与主视图高平齐,与俯视图宽相等. 画三视图时,看得见部分的轮廓线画成实线, 看不见部分的轮廓线画成虚线;规定在视图中加画 点划线表示圆柱、圆锥的对称轴.
正对着物体看: 物体左右之间的水平距 离是物体的长; 前后之间的水平距离是 物体的宽; 上下之间的竖直距离是 物体的高.
正面
宽 长
水平面
高 侧面
请观察三个视图,在三 视图中长宽高有什么特 点?
主、左视图等高“高平齐”; 主、俯视图等长“长对正”; 俯、左视图等宽“宽相等”
Байду номын сангаас
主
左
视
视
图
高高
图
长
宽
长 宽
左
面
面
看
看
从 上 面 看
练习:如图,右面三幅图分别是从哪个方向看 这个棱柱得到的?
上面 正面 左面
探究:右图是一个 由 9 个正方体组成的 立 体图形,分别从正面、
左面、上面观察这个 图
形,各能得到什么平 面 图形?
正面
左面
上面
练一练:
从正面、左面、上面 看这个由正方体组合成的 立体图形各能得到什么平 面图形?
立体图形 从正面看 从左面看 从上面看
.
三视图
人们从不同的方向观察某个物 体,可以看到不同的图形,一 般地,我们把从正面看到的图 形,称为主视图;从左面看到 的图形,称为左视图;从上面 看到的图形称为俯视图.
主视图、左视图、俯视图(同步课件)七年级数学上册(苏科版)

三视图
人们从不同的方向观察某个物体,可以看到不同的图形: 从正面看到的图形,称为主视图; 从左面看到的图形,称为左视图; 从上面看到的图形,称为俯视图;
从这三个方向上看到的图形,叫做这个几何体的三视图。
02 知识精讲
圆柱
圆锥
棱柱
从正面看 从左面看 从上面看
主视图 左视图 俯视图
02 知识精讲 练一练1:把物体的主视图、左视图、俯视图的名称填在下图相应 的括号内
的左视图是( B )
A.
B.
C.
D.
03 典例精析
例4、如图所示是由若干个相同的小立方体搭成的几何体的俯视图
和左视图,则小立方体的个数不可能是( D )
A.6个 B.7个 C.8个 D.9个
11
这一行至少有一个位 置上是2个,最多三 个位置上都是2个
最少需要6个小立方块, 最多需要8个小立方块。
03 典例精析
例5、某几何体由若干个大小相同的小正方体搭成,其主视图与左
视图如图所示,则搭成这个几何体的小正方体最少有( B )
A.3个 B.5个 C.7个 D.9个
3 1 1
俯视图占格子 最少的情况:
最少需要5个小正方块
人们从不同的方向观察某个物体,可以看到不同的图形: 从正面看到的图形,称为主视图; 从左面看到的图形,称为左视图; 从上面看到的图形,称为俯视图; 从这三个方向上看到的图形,叫做这个几何体的三视图。
教学目标
01 从不同方向观察同一物体,发展空间观念 02 能画简单几何体的三视图 03 能根据三视图还原几何体,进一步感受立体图形与平面图形
的关系
三视图的概念 与画法
01 情境引入
横看成岭侧成峰,远近高低各不同; 不识庐山真面目,只缘身在此山中。
5.4 从三个方向看教学课件(2) (苏科版七年级上)

2. 已知两个视图能确定几何体吗?
(1)主视图是长方形,俯视图是三角形
(2)主视图和左视图都是长方形
给出某些视图,你能想象出相应的几何体吗?
3、根据三个视图,分别说出相应几何 体的名称。
练一练
• P138 练一练1、2
你能根据以下立方块组合体的三 个视图, 搭出组合体的形状吗?
我们经常在由几个小正方体所搭几 何体的俯视图中标上数字, 用来表示在该位置小正方体的个数, 如:
§5.4从三个方向看(2)
回顾与思考
1、什么是几何体的三个视图?
2、画三个视图时应注意些什么?
给出某些视图,你能想象出相应的几何体吗? 1、已知一个几何体的一个视图 (1)主视图是圆的几何体可能是什么? (2)俯视图是长方形的几何体可能是什么? (3)左视图是三角形的几何体可能是什么?
给出某些视图,你能想象出相应的几何体吗?
1 2 1 2 主视图 左视图
如图是由几个小立方块所搭几何体的俯 视图,小正方形中的数字表示在该位置 小立方块的个数,请画出它的主视图和 左视图.
1 2 3 1
主视图
左视图
做一做
• PБайду номын сангаас37(在俯视图中标出小正方形个数)
1
2 1
1
想一想:能用主视图或是左视图作相应的改造来表 示这个几何体吗?
我们经常在由几个小正方体所搭 几何体的俯视图中标上数字, 用来表示在该位置小正方体的个 数,如:
1
2
3
1
如图是由几个小立方块所搭几何体的 俯视图,小正方形中的数字表示在该 位置小立方块的个数,请先搭出这个 物体,再画出它的主视图和左视图.
苏科版数学七年级上册教学设计《5-4主视图、左视图、俯视图(第1课时)》

苏科版数学七年级上册教学设计《5-4主视图、左视图、俯视图(第1课时)》一. 教材分析《5-4主视图、左视图、俯视图(第1课时)》这部分内容是苏科版数学七年级上册的重点内容。
它主要介绍了三视图的概念及其之间的关系。
通过学习,学生能够理解并掌握主视图、左视图、俯视图的定义,能够根据物体的形状描述出它的三视图,并能够通过三视图来还原物体的形状。
这一部分内容为后续学习立体几何打下基础。
二. 学情分析七年级的学生已经具备了一定的空间想象能力,但是对于三视图的概念和应用可能还比较陌生。
因此,在教学过程中,需要引导学生从实际生活中的例子出发,培养他们的空间想象能力,帮助他们理解和掌握三视图的概念。
三. 教学目标1.知识与技能:学生能够理解主视图、左视图、俯视图的概念,能够根据物体的形状描述出它的三视图,并能够通过三视图来还原物体的形状。
2.过程与方法:通过观察实际生活中的例子,培养学生的空间想象能力,帮助他们理解和掌握三视图的概念。
3.情感态度价值观:培养学生对数学的兴趣,提高他们解决实际问题的能力。
四. 教学重难点1.重点:学生能够理解并掌握主视图、左视图、俯视图的定义,能够根据物体的形状描述出它的三视图,并能够通过三视图来还原物体的形状。
2.难点:学生能够灵活运用三视图的概念来解决实际问题。
五. 教学方法采用情境教学法、案例教学法和小组合作学习法。
通过观察实际生活中的例子,引导学生培养空间想象能力;通过分析典型案例,让学生深入理解和掌握三视图的概念;通过小组合作学习,促进学生之间的交流和合作,提高他们解决实际问题的能力。
六. 教学准备1.准备相关的教学案例和图片,用于引导学生观察和思考。
2.准备教学课件,用于辅助讲解和展示。
3.准备练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)通过展示一些实际生活中的例子,如房屋、车辆等,引导学生观察并思考:如果你要从不同的角度去观察这些物体,你能够看到什么?从而引出主视图、左视图、俯视图的概念。
七年级数学上册知识讲义-5.4物体的主视图、左视图、俯视图-苏科版
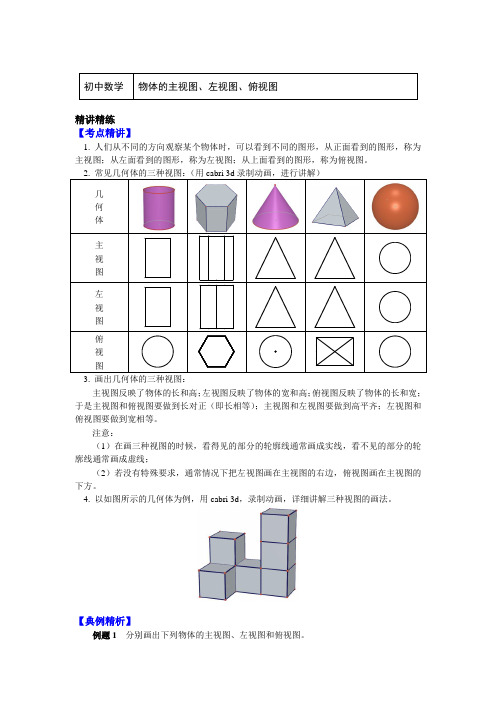
初中数学物体的主视图、左视图、俯视图精讲精练【考点精讲】1. 人们从不同的方向观察某个物体时,可以看到不同的图形,从正面看到的图形,称为主视图;从左面看到的图形,称为左视图;从上面看到的图形,称为俯视图。
2. 常见几何体的三种视图:(用cabri 3d录制动画,进行讲解)几何体主视图左视图俯视图3. 画出几何体的三种视图:主视图反映了物体的长和高;左视图反映了物体的宽和高;俯视图反映了物体的长和宽;于是主视图和俯视图要做到长对正(即长相等);主视图和左视图要做到高平齐;左视图和俯视图要做到宽相等。
注意:(1)在画三种视图的时候,看得见的部分的轮廓线通常画成实线,看不见的部分的轮廓线通常画成虚线;(2)若没有特殊要求,通常情况下把左视图画在主视图的右边,俯视图画在主视图的下方。
4. 以如图所示的几何体为例,用cabri 3d,录制动画,详细讲解三种视图的画法。
【典例精析】例题1 分别画出下列物体的主视图、左视图和俯视图。
图1 图2 图3 思路导航:按照定义,分别从正面、左面和上面去观察几何体,然后画出看到的平面图形即可。
为了更加直观、形象,也为了培养学生的空间想象能力,录制动画,进行讲解。
答案:图1 所示几何体的主视图、左视图和俯视图如下图所示:俯视图左视图主视图图2 所示几何体的主视图、左视图和俯视图如下图所示: 主视图俯视图左视图图3 所示几何体的主视图、左视图和俯视图如下图所示: 左视图俯视图主视图点评:几何体的主视图、左视图和俯视图的画法及步骤:①确定主视图的位置,并且想象从几何体的正面进行观察,画出主视图;②在主视图的下方画俯视图,并且想象从几何体的正上方进行观察,注意与主视图“长对正”;③在主视图的正右方画左视图,并且想象从几何体的左边进行观察,注意与主视图“高平齐”,与俯视图要做到“宽相等”。
例题2 用若干个棱长为1m 的正方体堆成如图所示的物体(并且将其固定在地面上),现在要用油漆喷涂所有的暴露面,则需要喷涂油漆的总面积是多少?思路导航:分别画出主视图、左视图和俯视图,求出其面积,借助于主视图、左视图和俯视图的面积来求暴露面的面积。
苏科版数学七年级上册5.4《主视图、左视图、俯视图》教学设计1

苏科版数学七年级上册5.4《主视图、左视图、俯视图》教学设计1一. 教材分析《苏科版数学七年级上册5.4《主视图、左视图、俯视图》》这一节内容,主要让学生掌握三视图的概念,了解主视图、左视图、俯视图之间的关系,并能够熟练地进行图形的转换。
教材通过实例的展示,引导学生观察、思考,从而发现并掌握三视图的绘制方法。
二. 学情分析七年级的学生已经具备了一定的空间想象能力和图形认知能力,他们对平面图形有一定的了解。
但是,对于三维图形和三视图的概念,可能还比较陌生。
因此,在教学过程中,教师需要通过生动的实例和直观的演示,帮助学生建立起三视图的空间形象,使他们能够更好地理解和掌握这一部分内容。
三. 教学目标1.了解主视图、左视图、俯视图的概念,知道它们之间的关系。
2.能够根据物体的三视图,还原出物体的形状。
3.能够运用三视图的知识,解决一些实际问题。
四. 教学重难点1.重点:主视图、左视图、俯视图的概念及它们之间的关系。
2.难点:如何根据三视图还原出物体的形状,以及如何运用三视图解决实际问题。
五. 教学方法1.情境教学法:通过实例的展示,让学生在实际情境中感受三视图的概念,提高他们的空间想象力。
2.合作学习法:引导学生分组讨论,共同探讨三视图的绘制方法,提高他们的合作能力。
3.实践操作法:让学生动手操作,实际绘制一些简单物体的三视图,增强他们的实践能力。
六. 教学准备1.准备一些常见物体的三视图图片,如圆柱、正方体等。
2.准备一些绘图工具,如直尺、圆规等。
3.准备一些练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)教师通过展示一些常见物体的三视图图片,引导学生观察、思考,让学生初步了解三视图的概念。
2.呈现(10分钟)教师通过讲解和演示,详细介绍主视图、左视图、俯视图的概念,以及它们之间的关系。
同时,让学生动手绘制一些简单物体的三视图,加深他们对三视图的理解。
3.操练(10分钟)教师提出一些练习题,让学生分组讨论,共同完成。
苏科版数学七年级上册5.4《主视图、左视图、俯视图》教学设计2

苏科版数学七年级上册5.4《主视图、左视图、俯视图》教学设计2一. 教材分析《苏科版数学七年级上册5.4《主视图、左视图、俯视图》》这一节主要让学生了解主视图、左视图、俯视图的概念,以及它们之间的关系。
通过观察长方体和正方体的三视图,让学生能够识别和理解三视图所反映的物体的形状。
教材通过丰富的图片和实例,让学生在实际操作中掌握三视图的知识,培养学生的空间想象能力和抽象思维能力。
二. 学情分析七年级的学生已经具备了一定的几何知识,对立体图形有一定的了解。
但是,对于主视图、左视图、俯视图的概念以及它们之间的关系,可能还比较模糊。
因此,在教学过程中,需要通过大量的实例和操作,让学生深入理解三视图的知识。
三. 教学目标1.知识与技能:让学生掌握主视图、左视图、俯视图的概念,能够识别和理解三视图所反映的物体的形状。
2.过程与方法:通过观察、操作、思考,培养学生的空间想象能力和抽象思维能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作意识和探究精神。
四. 教学重难点1.重点:主视图、左视图、俯视图的概念及其关系。
2.难点:如何通过三视图识别和理解物体的形状。
五. 教学方法1.情境教学法:通过丰富的图片和实例,让学生在实际操作中掌握三视图的知识。
2.小组合作学习:引导学生进行观察、讨论,培养学生的团队合作意识和探究精神。
3.启发式教学:教师提问,引导学生思考,激发学生的学习兴趣。
六. 教学准备1.准备长方体和正方体的模型,以及它们的三视图图片。
2.准备投影仪或大屏幕,用于展示图片和实例。
3.准备练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)利用图片和实例,引导学生观察长方体和正方体的三视图,让学生初步了解主视图、左视图、俯视图的概念。
2.呈现(10分钟)展示长方体和正方体的三视图,让学生直观地感受三视图之间的关系。
教师引导学生观察、思考,总结出主视图、左视图、俯视图的特点和规律。
最新苏科版七年级上册数学《5.4 主视图、左视图、俯视图》精品教学课件 (7)

由4个小立方体搭成的一个物体, 它的主视图与左视图如图所示:
你能画出俯视图吗? 主视图 左视图
人教版初中数学精品教学课件设计
用小立方块搭一个几何体,使得它的主 视图和俯视图如图所示,它最少需要多 少个小立方块?最多需要多少个立方块?
主视图
人教版初中数学精品教学课件设计
俯视图
中小学精品教学资源 中小学精品教学资源
4.长方体的主视图与左视图如图所示(单位:cm),则其
俯视图的面积是
.
主视图
2 4
左视图
2 3
人教版初中数学精品教学课件设计
想一想 1.已知一个几何体的一个视图 (1)主视图是圆的几何体可能是?
人教版初中数学精品教学课件设计
想一想 1.已知一个几何体的一个视图 (2)俯视图是长方形的几何体是什么?
人教版初中数学精品教学课件设计
人教版初中数学精品教学课件设计
活动一
1.从正面、左面、上面看一个四棱锥,看 到的图形分别是什么?
从 上 面 看
从左面看
立体图形 人教版初中数学精品教学课件设计
平面图形
2. 观察下表中所示的物体,并将看到的图形填入表 中
物体
观察 角度
圆柱
从正面看
从左面看
从上面看
人教版初中数学精品教学课件设计
人教版初中数学精品教学课件设计
例2 画出如图所示物体的主视图、俯视图、 左视图.
人教版初中数学精品教学课件设计
1.如图所示几何体的左视图是( )
2.由两块大小不同的正方体搭成如图所示的几何体, 它的主视图是( )
人教版初中数学精品教学课件设计
3.如图所示的几何体的俯视图是( )
人教版初中数学精品教学课件设计
5.4主视图、左视图、俯视图(1)课件(共19张PPT

解 这个正三棱柱的三视图如下图所示.
你能看出这个正三棱 柱的主视图与左视图的区 别吗?
练习
1.画出如图摆放的正三棱柱的三视图. 答:这个正三棱柱的三视图如下图所示:
2.画出如图所示物体的三视图. 答:这个物体的三视图如下图所示:
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月4日星期五2022/3/42022/3/42022/3/4 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/42022/3/42022/3/43/4/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/42022/3/4March 4, 2022 •4、享受阅读快乐,提高生活质量。2022/3/42022/3/42022/3/42022/3/4
第三步:从上往下看,画出圆柱在置于它的 下方的水平面上的正投影,这称为
“俯视图”.通俗地说,就是从圆柱 的上面看这个圆柱.
从前后、左右、上下三个方向观察物体, 能够比较全面地了解物体的大小和形状,我们 把主视图、左视图、俯视图统称为“三视图” . 下图即为圆柱的三视图.
在画三视图时,俯视 图在主视图的下边,左视 图在主视图的右边.
谢谢观赏
You made my day!
我们,还在路上……
动脑筋
制造一个圆柱形家具,为了让工人师傅知道 工件的准确形状和大小,设计人员应该如何画出 这个工件的图?
可以采用下述方法来画圆柱的视图.
第一步,从前往后看,画出圆柱在立于它的 后面的竖直平面上的正投影,如图, 这为“主视图”.通俗地说,就是 从圆柱的正面看这个圆柱.
七年级数学上册 5.4 主视图、左视图、俯视图课件 苏科苏科级上册数学课件

5-4-74
2.如图5-4-74,将图中扇形BOC部分剪掉,用剩余部分围成一个几何
体的侧面,使AB、DC重合,则所围成的几何体的俯视图是____ (画图).
12/6/2021
答案:
知识拓展
1.如果一个立体图形的三个视图都是正方形,那么关于这个立体图 形的三种说法正确的有( B ) ①这个立体图形是四棱柱; ②这个立体图形是正方体; ③这个立体图形是四棱锥;
A.1个
12/6/2021
B.2个
C.3个
D.以上全不对
12/6/2021
12/6/2021
课堂练习
2.如图5-4-67是一个立体图形的三视图,请写出这个立体图形的 名称,并计算这个立体图形的体积.(结果保留 π)
答案:该立体图形是圆柱,它的体积为:π(
10 2
)²x10
12/6/2021
=250π .
课后作业
1.图5-4-72的几何体的三视图是( C )
5-4-72
12/6/2021
知识梳理
知识点2:与图形计算有关的视图问题
【例】如图5-4-54是一个几何体的三视图,则这个几何体的侧面积是( A )
A.18cm2
B.20cm2
C.22cm2
D.24cm2
主视图
俯视图
左视图
【讲解】根据三视图判断出该几何体是底面边长为2cm,侧棱长为
3cm的正三棱柱,然后根据矩形的面积公式列式计算即可
5-4-49
知识梳理
知识点1:由三视图确定基本几何体
【例】如图5-4-51所示,是一个物体的三视图,则它是( A ) A.六棱柱 B.六棱锥 C.六面体 D.不能确定
主视图
俯视图
5-4主视图左视图俯视图22-23苏科版七年级数学上册

(1)
(2)
(3)
成果汇报
2.从棱长为2a的正方体零件的一角,挖去一个棱长为 a的小正方体,得到一个如图所示的零件,则这个
零件的俯视图是( B )
3.沿圆柱体上底面直径截去一部分的物体如图所示,
它的俯视图是( D )
A
B
C
D
成果汇报
4.如图是一块带有圆形空洞和方形空洞的小 木板,则下列物体中既可以堵住圆形空洞,又
可以堵住方形空洞的是 ( B )
A
B
C
D
成果汇报
5.画出该几何体的主视图、左视图、俯视图.
灵活应用
主视图
左视图
俯视图
正面
生活应用
生活应用
课堂小结
通过本节课的学习, 你学习了哪些知识, 有什么收获呢?
感谢大家
你看到什么?
横看成岭侧成峰, 远近高低各不同。
定性判断
定性判断
如图所示的物体,你知道下面的三幅图分别是从 哪个方向看到的吗?
定性判断
几何体
正方体
长方体
球体
圆柱
圆锥
从正面看
从左面看 从上面看
概念巩固
主视图 俯视图
左视图
从左面看
从上面看 从正面看
概念巩固
1.如图是由5个大小相同的正方体组成的几何体,
则该几何体的主视图是( A )
A.
B.
C.
D.
2.下面四个几何体中,左视图是四边形的几何体共有( B)
圆柱
圆锥
球
A.1个 B.2个 C.3个
正方体
D.4个
概念辨析
小黄狗的回答对吗?如果不对,错在哪里?
主视图
这还不简单, 看好了!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1 画球的三视图(如下图所示). 分析 一个球无论在哪个平面上的正投影都是 圆,并且圆的半径与球的半径相等,所 以球的主视图、左视图、俯视图都是半 径与球的半径相等的圆及其内部.
解
这个球的三视图如下图所示.
例2
画圆锥的三视图(如下图所示).
分析 从正面看这个圆锥,它的投影是一个等腰 三角形及其内部;从左面看这个圆锥,它 的投影是和主视图一样的等腰三角形及其 内部;从上面看这个圆锥,它的投影是一 个圆及其内部,其中圆锥顶点的投影是这 个圆的圆心.
动脑筋
制造一个圆柱形家具,为了让工人师傅知道 工件的准确形状和大小,设计人员应该如何画出 这个工件的图?
可以采用下述方法来画圆柱的视图.
第一步,从前往后看,画出圆柱在立于它的 后面的竖直平面上的正投影,如图, 这称为“主视图”.通俗地说,就是 从圆柱的正面看这个圆柱.
第二步:从左往右看,画出圆柱在立于它的右边 的竖直平面上的正投影,这称为“左视 图”.通俗地说,就是从圆柱的左面看这 个圆柱.
解
这个正三棱柱的三视图如下图所示.
你能看出这个正三棱 柱的主视图与左视图的区 别吗?
练习
1.画出如图摆放的正三棱柱的三视图. 答:这个正三棱柱的三视图如下图所示:
2.画出如图所示物体的三视图. 答:这个物体的三视图如下图所示:
5.4
主视图、左视图、俯视图(1)
物体形状→三视图
议一议
如图,在正午的阳光下,一个物体在地面上的 影子是一个圆,你能确定这个物体的形状吗?
影子是圆的物体可以是圆盘,可以 是球,在正午的阳光下, 还可以是立着 的圆柱,……
单凭在地面上的影子, 不可以确定 物体的形状.
因此,只从一个方向看物体,不能确定物体 Biblioteka 形状,应该从多个方向对物体进行观察.
解
这个圆锥的三视图如下图所示.
例3 如图,这是一个底面为等边三角形的 正三棱柱,画出它的三视图.
分析 从正面看,这个正三棱柱的投影是一个矩形 及其内部,其中侧棱CC1的投影是这个矩形 的上、下两边中点的连线段,由于看不见, 因此用虚线表示;从左面看,这个正三棱柱 的投影是一个矩形及其内部;从上面看,这 个正三棱柱的投影是正三角形及其内部.
第三步:从上往下看,画出圆柱在置于它的 下方的水平面上的正投影,这称为 “俯视图”.通俗地说,就是从圆柱 的上面看这个圆柱.
从前后、左右、上下三个方向观察物体, 能够比较全面地了解物体的大小和形状,我们 把主视图、左视图、俯视图统称为“三视图” .
下图即为圆柱的三视图.
在画三视图时,俯视 图在主视图的下边,左视 图在主视图的右边.
