2018年高考湖南卷(理)
2018年湖南理综高考试题及答案
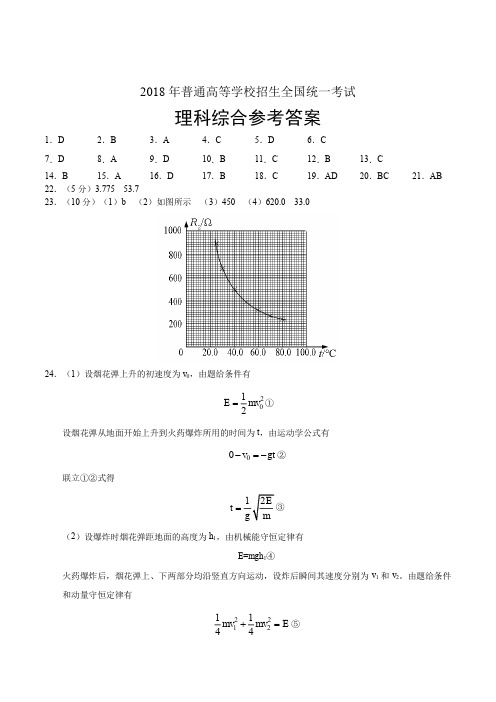
2018年普通高等学校招生全国统一考试理科综合参考答案1.D 2.B 3.A 4.C 5.D 6.C 7.D8.A9.D10.B11.C12.B13.C 14.B 15.A 16.D 17.B 18.C 19.AD 20.BC21.AB22.(5分)3.775 53.723.(10分)(1)b (2)如图所示 (3)450 (4)620.0 33.024.(1)设烟花弹上升的初速度为v 0,由题给条件有2012E mv =①设烟花弹从地面开始上升到火药爆炸所用的时间为t ,由运动学公式有00v gt -=-②联立①②式得t =(2)设爆炸时烟花弹距地面的高度为h 1,由机械能守恒定律有E =mgh 1④火药爆炸后,烟花弹上、下两部分均沿竖直方向运动,设炸后瞬间其速度分别为v 1和v 2。
由题给条件和动量守恒定律有22121144mv mv E +=⑤1211022mv mv +=⑥ 由⑥式知,烟花弹两部分的速度方向相反,向上运动部分做竖直上抛运动。
设爆炸后烟花弹上部分继续上升的高度为h 2,由机械能守恒定律有2121142mv mgh =⑦ 联立④⑤⑥⑦式得,烟花弹上部分距地面的最大高度为122Eh h h mg=+=⑧ 25.(1)11H 在电场中做类平抛运动,在磁场中做圆周运动,运动轨迹如图所示。
设11H 在电场中的加速度大小为a 1,初速度大小为v 1,它在电场中的运动时间为t 1,第一次进入磁场的位置到原点O 的距离为s 1。
由运动学公式有111s v t =①21112h a t =② 由题给条件,11H 进入磁场时速度的方向与x 轴正方向夹角160θ=︒。
11H 进入磁场时速度y 分量的大小为1111tan a t v θ=③联立以上各式得1s =④ (2)11H 在电场中运动时,由牛顿第二定律有1qE ma =⑤设11H 进入磁场时速度的大小为1v ',由速度合成法则有1v '= 设磁感应强度大小为B ,11H 在磁场中运动的圆轨道半径为R 1,由洛伦兹力公式和牛顿第二定律有2111mv qv B R ''=⑦由几何关系得1112sin s R θ=⑧联立以上各式得B =(3)设21H 在电场中沿x 轴正方向射出的速度大小为v 2,在电场中的加速度大小为a 2,由题给条件得222111222m v mv =()⑩ 由牛顿第二定律有22qE ma =⑪设21H 第一次射入磁场时的速度大小为2v ',速度的方向与x 轴正方向夹角为2θ,入射点到原点的距离为s 2,在电场中运动的时间为t 2。
2018年高考全国1卷理科数学试题及答案

理科数学试题 第1页(共9页)2018年普通高等学校招生全国统一考试理科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设1i2i 1iz -=++,则||z = A .0B .12C .1D .22.已知集合2{|20}A x x x =-->,则A =RA .{|12}x x -<<B .{|12}x x -≤≤C .{|1}{|2}x x x x <->D .{|1}{|2}x x x x -≤≥3.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番. 为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 4.记n S 为等差数列{}n a 的前n 项和. 若3243S S S =+,12a ,则5aA .12-B .10-C .10D .125.设函数32()(1)f x x a x ax =+-+. 若()f x 为奇函数,则曲线()y f x =在点(0,0)处的切线方程为 A .2y x =-B .y x =-C .2y x =D .y x =6.在ABC △中,AD 为BC 边上的中线,E 为AD 的中点,则EB = A .3144AB AC -B .1344AB AC -。
2018年高考理综真题及答案(全国卷)

2018年高考理综真题及答案(全国卷)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
学·科网可能用到的相对原子质量:H 1 Li 7 C 12 N 14 O 16 Na23 S 32 Cl 35.5 Ar 40 Fe 56 I 127一、选择题:本题共13个小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.生物膜的结构与功能存在密切的联系。
下列有关叙述错误的是A.叶绿体的类囊体膜上存在催化ATP合成的酶B.溶酶体膜破裂后释放出的酶会造成细胞结构的破坏C.细胞的核膜是双层膜结构,核孔是物质进出细胞核的通道D.线粒体DNA位于线粒体外膜上,编码参与呼吸作用的酶2.生物体内的DNA常与蛋白质结合,以DNA—蛋白质复合物的形式存在。
下列相关叙述错误的是A.真核细胞染色体和染色质中都存在DNA—蛋白质复合物B.真核细胞的核中有DNA—蛋白质复合物,而原核细胞的拟核中没有C.若复合物中的某蛋白参与DNA复制,则该蛋白可能是DNA 聚合酶D.若复合物中正在进行RNA的合成,则该复合物中含有RNA 聚合酶3.下列有关植物根系吸收利用营养元素的叙述,错误的是A.在酸性土壤中,小麦可吸收利用土壤中的N2和NO-3B.农田适时松土有利于农作物根细胞对矿质元素的吸收C.土壤微生物降解植物秸秆产生的无机离子可被根系吸收D.给玉米施肥过多时,会因根系水分外流引起“烧苗”现象4.已知药物X对细胞增值有促进作用,药物D可抑制药物X的作用。
某同学将同一瓶小鼠皮肤细胞平均分为甲、乙、丙三组,分别置于培养液中培养,培养过程中进行不同的处理(其中甲组未加药物),每隔一段时间测定各组细胞数,结果如图所示。
2018年湖南理综高考试题文档版(含答案)

2018年普通高等学校招生全国统一考试(湖南卷)理科综合能力测试注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
学·科网可能用到的相对原子质量:H 1 Li 7 C 12 N 14 O 16 Na 23 S 32 Cl 35.5 Ar40 Fe 56 I 127一、选择题:本题共13个小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.生物膜的结构与功能存在密切的联系。
下列有关叙述错误的是A.叶绿体的类囊体膜上存在催化ATP合成的酶B.溶酶体膜破裂后释放出的酶会造成细胞结构的破坏C.细胞的核膜是双层膜结构,核孔是物质进出细胞核的通道D.线粒体DNA位于线粒体外膜上,编码参与呼吸作用的酶2.生物体内的DNA常与蛋白质结合,以DNA—蛋白质复合物的形式存在。
下列相关叙述错误的是A.真核细胞染色体和染色质中都存在DNA—蛋白质复合物B.真核细胞的核中有DNA—蛋白质复合物,而原核细胞的拟核中没有C.若复合物中的某蛋白参与DNA复制,则该蛋白可能是DNA聚合酶D.若复合物中正在进行RNA的合成,则该复合物中含有RNA聚合酶3.下列有关植物根系吸收利用营养元素的叙述,错误的是A.在酸性土壤中,小麦可吸收利用土壤中的N2和NO-3B.农田适时松土有利于农作物根细胞对矿质元素的吸收C.土壤微生物降解植物秸秆产生的无机离子可被根系吸收D.给玉米施肥过多时,会因根系水分外流引起“烧苗”现象4.已知药物X对细胞增值有促进作用,药物D可抑制药物X的作用。
某同学将同一瓶小鼠皮肤细胞平均分为甲、乙、丙三组,分别置于培养液中培养,培养过程中进行不同的处理(其中甲组未加药物),每隔一段时间测定各组细胞数,结果如图所示。
2018湖南高考数学(理科)高考试题(word版)(附答案)

绝密★启用前2018年普通高等学校招生全国统一考试理科数学注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设1i2i 1iz -=++,则||z =A .0B .12C .1D2.已知集合{}220A x x x =-->,则A =R ð A .{}12x x -<< B .{}12x x -≤≤C .}{}{|1|2x x x x <->UD .}{}{|1|2x x x x ≤-≥U3.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:建设前经济收入构成比例 建设后经济收入构成比例则下面结论中不正确的是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 4.设n S 为等差数列{}n a 的前n 项和,若3243S S S =+,12a =,则=5a A .12-B .10-C .10D .125.设函数32()(1)f x x a x ax =+-+,若()f x 为奇函数,则曲线()y f x =在点(0,0)处的切线方程为 A .2y x =-B .y x =-C .2y x =D .y x =6.在ABC △中,AD 为BC 边上的中线,E 为AD 的中点,则EB =u u u rA .3144AB AC -u u ur u u u rB .1344AB AC -u u ur u u u rC .3144AB AC +u u ur u u u rD .1344AB AC +u u ur u u u r7.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A .172B .52C .3D .28.设抛物线C :y 2=4x 的焦点为F ,过点(–2,0)且斜率为23的直线与C 交于M ,N 两点,则FM FN ⋅u u u u r u u u r =A .5B .6C .7D .89.已知函数e 0()ln 0x x f x x x ⎧≤=⎨>⎩,,,,()()g x f x x a =++.若g (x )存在2个零点,则a 的取值范围是 A .[–1,0)B .[0,+∞)C .[–1,+∞)D .[1,+∞)10.下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC 的斜边BC ,直角边AB ,AC .△ABC 的三边所围成的区域记为I ,黑色部分记为II ,其余部分记为III .在整个图形中随机取一点,此点取自I ,II ,III 的概率分别记为p 1,p 2,p 3,则A .p 1=p 2B .p 1=p 3C .p 2=p 3D .p 1=p 2+p 311.已知双曲线C :2213x y -=,O 为坐标原点,F 为C 的右焦点,过F 的直线与C 的两条渐近线的交点分别为M 、N .若△OMN 为直角三角形,则|MN |= A .32B .3 C. D .412.已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为 ABCD二、填空题:本题共4小题,每小题5分,共20分。
2018高考全国1卷理科数学试卷及答案

2018高考全国1卷理科数学试卷及答案2018年普通高等学校招生全国统一考试(全国一卷)理科数学一、选择题,本题共12小题,每小题5分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设 $z=\frac{1-i+2i}{1+i}$,则 $z=$A.0B.1C.1/2D.22.已知集合 $A=\{x|x-x-2>0\}$,则 $C_R A=$A。
$\{x|-1<x<2\}$B。
$\{x|-1\leq x\leq 2\}$C。
$\{x|x2\}$D。
$\{x|x\leq -1\}\cup\{x|x\geq 2\}$3.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番。
为更好地了解该地区农村的经济收入变化情况,统计和该地图新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是A.新农村建设后,种植收入减少B.新农村建设后,其他收入增加了一倍以上C.新农村建设后,养殖收入增加了一倍D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4.记 $S_n$ 为等差数列 $\{a_n\}$ 的前 $n$ 项和,若$3S_3=S_2+S_4$,$a_1=2$,则 $a_5=$A。
$-12$B。
$-10$C。
10D。
125.设函数 $f(x)=x+(a-1)x+ax$,若 $f(-x)$ 为奇函数,则曲线 $y=f(x)$ 在点 $(3,32)$ 处的切线方程为A。
$y=-2x$B。
$y=-x$XXXD。
$y=x$6.在 $\triangle ABC$ 中,$AD$ 为 $BC$ 边上的中线,$E$ 为 $AD$ 的中点,则 $EB=\frac{1}{3}AB-\frac{1}{4}AC$A。
$\frac{3}{11}AB-\frac{8}{11}AC$B。
$\frac{4}{11}AB-\frac{7}{11}AC$C。
$\frac{7}{11}AB-\frac{4}{11}AC$D。
2018湖南高考数学[理科]高考试题[版][附答案解析]
![2018湖南高考数学[理科]高考试题[版][附答案解析]](https://img.taocdn.com/s3/m/77fb15551eb91a37f1115cf7.png)
绝密★启用前2018年普通高等学校招生全国统一考试理科数学注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设1i2i 1iz -=++,则||z =A .0B .12C .1D2.已知集合{}220A x x x =-->,则A =R ð A .{}12x x -<< B .{}12x x -≤≤ C .}{}{|1|2x x x x <->D .}{}{|1|2x x x x ≤-≥3.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:建设前经济收入构成比例 建设后经济收入构成比例则下面结论中不正确的是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 4.设n S 为等差数列{}n a 的前n 项和,若3243S S S =+,12a =,则=5a A .12-B .10-C .10D .125.设函数32()(1)f x x a x ax =+-+,若()f x 为奇函数,则曲线()y f x =在点(0,0)处的切线方程为A .2y x =-B .y x =-C .2y x =D .y x =6.在ABC △中,AD 为BC 边上的中线,E 为AD 的中点,则EB = A .3144AB AC - B .1344AB AC - C .3144AB AC + D .1344AB AC + 7.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A .172B .52C .3D .28.设抛物线C :y 2=4x 的焦点为F ,过点(–2,0)且斜率为23的直线与C 交于M ,N 两点,则FM FN ⋅= A .5B .6C .7D .89.已知函数e 0()ln 0x x f x x x ⎧≤=⎨>⎩,,,,()()g x f x x a =++.若g (x )存在2个零点,则a 的取值范围是 A .[–1,0)B .[0,+∞)C .[–1,+∞)D .[1,+∞)10.下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC 的斜边BC ,直角边AB ,AC .△ABC 的三边所围成的区域记为I ,黑色部分记为II ,其余部分记为III .在整个图形中随机取一点,此点取自I ,II ,III 的概率分别记为p 1,p 2,p 3,则A .p 1=p 2B .p 1=p 3C .p 2=p 3D .p 1=p 2+p 311.已知双曲线C :2213x y -=,O 为坐标原点,F 为C 的右焦点,过F 的直线与C 的两条渐近线的交点分别为M 、N .若△OMN 为直角三角形,则|MN |= A .32B .3 C. D .412.已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为 ABCD二、填空题:本题共4小题,每小题5分,共20分。
2018年全国高考理综试题物理部分解析(全国卷Ⅲ)

2018年全国统一考试理科综合能力测试物理部分(全国卷Ⅲ)二、选择题:第14~17题只有一项符合题目要求,第18~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.1934年,约里奥-居里夫妇用α粒子轰击铝核2713Al ,产生了第一个人工放射性核素X :2713α+Al n+X 。
X 的原子序数和质量数分别为( ) A .15和28 B .15和30 C .16和30 D .17和3114【答案】B 【解析】本题考查核反应方程遵循的质量数守恒和电荷数守恒规律及其相关的知识点。
根据核反应遵循的质量数守恒和电荷数守恒可知,X 的电荷数为2+13=15,质量数为4+27-1=30,根据原子核的电荷数等于原子序数,可知X 的原子序数为15,质量数为30,B 正确。
15.为了探测引力波,“天琴计划”预计发射地球卫星P ,其轨道半径约为地球半径的16倍;另一地球卫星Q 的轨道半径约为地球半径的4倍。
P 与Q 的周期之比约为( )A .2:1B .4:1C .8:1D .16:115【答案】C 【解析】 设地球半径为R ,根据题述,地球卫星P 的轨道半径为R P =16R ,地球卫星Q 的轨道半径为R Q =4R ,根据开普勒定律,所以P 与Q 的周期之比为T P ∶T Q =8∶1,C 正确。
16.一电阻接到方波交流电源上,在一个周期内产生的热量为Q 方;若该电阻接到正弦交变电源上,在一个周期内产生的热量为Q 正。
该电阻上电压的峰值为u 0,周期为T ,如图所示。
则Q 方: Q 正等于( )A .1:2 B .2:1 C .1:2 D .2:116【答案】D 02,而方波交流电的有效值为u 0,根据焦耳定律和欧姆定律,Q =I 2RT =2U RT ,可知在一个周期T 内产生的热量与电压有效值的二次方成正比,Q 方∶Q 正= u 02∶(02u )2=2∶1,选项D 正确。
2018年 全国统一高考 物理试卷(含答案解析)

2018年全国统一高考物理试卷(含答案解析)一、选择题:本题共8小题,每小题6分,共48分.在每小题给出的四个选项中,第1~5题只有一顶符合题目要求,第6~8题有多项符合题目要求.全部选对的得6分,选对但不全的得3分,有选错的得0分.1.(6分)高铁列车在启动阶段的运动可看作初速度为零的匀加速直线运动,在启动阶段,列车的动能()A.与它所经历的时间成正比B.与它的位移成正比C.与它的速度成正比D.与它的动量成正比2.(6分)如图,轻弹簧的下端固定在水平桌面上,上端放有物块P,系统处于静止状态,现用一竖直向上的力F作用在P上,使其向上做匀加速直线运动,以x表示P离开静止位置的位移,在弹簧恢复原长前,下列表示F和x之间关系的图象可能正确的是()A.B.C.D.3.(6分)如图,三个固定的带电小球a,b和c,相互间的距离分别为ab=5cm,bc=3cm,ca=4cm,小球c所受库仑力的合力的方向平行于a,b的连线,设小球a,b所带电荷量的比值的绝对值为k,则()A.a,b的电荷同号,k= B.a,b的电荷异号,k=C.a,b的电荷同号,k= D.a,b的电荷异号,k=4.(6分)如图,导体轨道OPQS固定,其中PQS是半圆弧,Q为半圆弧的中点,O为圆心。
轨道的电阻忽略不计。
OM是有一定电阻。
可绕O转动的金属杆,M端位于PQS上,OM与轨道接触良好。
空间存在与半圆所在平面垂直的匀强磁场,磁感应强度的大小为B,现使OM从OQ位置以恒定的角速度逆时针转到OS位置并固定(过程Ⅰ);再使磁感应强度的大小以一定的变化率从B增加到B′(过程Ⅱ)。
在过程Ⅰ、Ⅱ中,流过OM的电荷量相等,则等于()A.B.C.D.25.(6分)如图,abc是竖直面内的光滑固定轨道,ab水平,长度为2R;bc是半径为R的四分之一圆弧,与ab相切于b点。
一质量为m的小球,始终受到与重力大小相等的水平外力的作用,自a点处从静开始向右运动。
重力加速度大小为g。
【新课标II卷】2018年全国统一高考理科综合试卷(含答案)

2018年普通高等学校招生全国统一考试理科综合能力测试本试卷共38题,共100分,共16页,考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,条形码准确粘贴在条形码区域内。
2.选择题必须使用2B铅笔填涂:非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带刮纸刀。
可能用到的相对原子质量:H1 C12 N14 O16 Na23 P31 S32 Fe56一、选择题:本题共13小题,每小题6分,共78分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列关于人体中蛋白质功能的叙述,错误的是A.浆细胞产生的抗体可结合相应的病毒抗原B.肌细胞中的某些蛋白质参与肌肉收缩的过程C.蛋白质结合Mg2+形成的血红蛋白参与O2运输,D.细胞核中某些蛋白质是染色体的重要组成成分2.下列有关物质跨膜运输的叙述,正确的是A.巨噬细胞摄入病原体的过程属于协助扩散B.固醇类激素进入靶细胞的过程属于主动运输C.神经细胞受到刺激时产生的Na+内流属于被动运输D.护肤品中的甘油进入皮肤细胞的过程属于主动运输3.下列有关人体内激素的叙述,正确的是A.运动时,肾上腺素水平升高,可使心率加快,说明激素是高能化合物B.饥饿时,胰高血糖素水平升高,促进糖原分解,说明激素具有酶的催化活性C.进食后,胰岛素水平升高,其既可加速糖原合成,也可作为细胞的结构组分D.青春期,性激素水平升高,随体液到达靶细胞,与受体结合可促进机体发育4.有些作物的种子入库前需要经过风干处理,与风干前相比,下列说法错误的是A.风干种子中有机物的消耗减慢B.风干种子上微生物不易生长繁殖C.风干种子中细胞呼吸作用的强度高D.风干种子中结合水与自由水的比值大5.下列关于病毒的叙述,错误的是A.从烟草花叶病毒中可以提取到RNAB.T2噬菌体可感染肺炎双球菌导致其裂解C.HIV可引起人的获得性免疫缺陷综合征D.阻断病毒的传播可降低其所致疾病的发病率6.在致癌因子的作用下,正常动物细胞可转变为癌细胞。
2018年全国卷高考真题(理科)

伪满时期的哈尔滨市立医院,如今仍是医院。后来得知赵一曼女士曾在这里 住过院,我便翻阅了她的一些资料。 赵一曼女士, 是一个略显瘦秀且成熟的女性。在她身上弥漫着拔俗的文人气 质和职业军人的冷峻。在任何地方,你都能看出她有别于他人的风度。 赵一曼女士率领的抗联活动在小兴安岭的崇山峻岭中, 那儿能够听到来自坡 镇的钟 声,冬夜里,钟声会传得很远很远。钟声里,抗联的兵士在森林里烤火,烤野味 儿,或者唱着“火烤胸前暖,风吹背后寒......战士们哟”......这些都给躺在 病床上的赵一曼女士留下清晰回忆。 赵一曼女士单独一间病房,由警察昼夜看守。 白色的小柜上有一个玻璃花瓶,里面插着丁香花。赵一曼女士喜欢丁香花。 这束丁香花,是女护士韩勇义折来摆放在那里的。听说,丁香花现在已经成为这 座城市的“市花”了。 她是在山区中了日军的子弹后被捕的。滨江省警务厅的大野泰治对赵一曼女 士进行了严刑拷问,始终没有得到有价值的回答,他觉得很没面子。 大野泰治在向上司呈送的审讯报告上写道: 赵一曼是中国共产党珠河县委委员,在该党工作上有与赵尚志同等的权 力。她是北满共产党的重要干部,通过对此人的严厉审讯,有可能澄清中共与苏 联的关系。 1936 年初,起一曼女士以假名“王氏”被送到医院监禁治疗。 《滨江省警务厅关于赵一曼的情况》扼要地介绍了赵一曼女士从市立医院逃 走和被害的情况。 赵一曼女士是在 6 月 28 日逃走的。夜里,看守董宪勋在他叔叔的协助下, 将赵一曼抬出医院的后门。一辆雇好的出租车已等在那里。几个人上了车, 车立刻就开走了。出租车开到文庙屠宰场的后面,韩勇义早就等候在那里, 扶着赵一曼女士上了雇好的轿子,大家立刻向宾县方向逃去。 赵一曼女士住院期间, 发现警士董宪勋似乎可以争取。经过一段时间的观 察、分析,她觉得有把握去试一试。 她躺在病床上,和蔼地问董警士:“董先生,您一个月的薪俸是多少?” 董警士显得有些忸怩,“十多块钱吧……” 赵一曼女士遺憾地笑了,说:“真没有想到,薪俸会这样少。” 董警士更加忸怩了。 赵一曼女士神情端庄地说:“七尺男儿,为着区区十几块钱,甘为日本人役 使,不是太愚蠢了吗?” 董警士无法再正视这位成熟女性的眼睛了,只是哆哆嗦嗦给自己点了一颗
2018年高考湖南卷数学(理)试卷及答案

2018年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)本试卷包括选择题、填空题和解答题三部分,共5页,时量120分钟,满分150分。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数()()1z i i i =+为虚数单位在复平面上对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限 2.某学校有男、女学生各500名.为了解男女学生在学习兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取100名学生进行调查,则宜采用的抽样方法是A .抽签法B .随机数法C .系统抽样法D .分层抽样法 3.在锐角中ABC ∆,角,A B 所对的边长分别为,a b .若2sin ,a B A =则角等于 A .12π B .6π C .4π D .3π 4.若变量,x y 满足约束条件211y xx y y ≤⎧⎪+≤⎨⎪≥-⎩,2x y +则的最大值是A .5-2 B .0 C .53 D .525.函数()2ln f x x =的图像与函数()245g x x x =-+的图像的交点个数为 A .3 B .2 C .1 D .06. 已知,a b 是单位向量,0a b =.若向量c 满足1,c a b c --=则的取值范围是A.⎤⎦B.⎤⎦C.1⎡⎤⎣⎦D.1⎡⎤⎣⎦7.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 A .1 B.2 D.28.在等腰三角形ABC 中,=4AB AC =,点P 是边AB 上异于,A B 的一点,光线从点P 出发,经,BC CA 发射后又回到原点P (如图1).若光线QR 经过ABC ∆的中心,则AP 等A .2B .1C .83 D .43二、填空题:本大题共8小题,考生作答7小题,每小题5分,共35分.(一)选做题(请考生在第9、10、11三题中任选两题作答,如果全做,则按前两题计分)9.在平面直角坐标系xoy 中,若,3cos ,:(t )C :2sin x t x l y t a y ϕϕ==⎧⎧⎨⎨=-=⎩⎩为参数过椭圆 ()ϕ为参数的右顶点,则常数a 的值为 .10.已知222,,,236,49a b c a b c a b c ∈++=++则的最小值为 12 .11.如图2O 中,弦,AB CD 相交于点,2P PA PB ==,1PD =,则圆心O 到弦CD 的距离为 .必做题(12-16题) 12.若209,Tx dx T =⎰则常数的值为 .13.执行如图3所示的程序框图,如果输入1,2,a b a ==则输出的的值为 9 .14.设12,F F 是双曲线2222:1(0,0)x y C a b a b-=>>的两个焦点,P 是C 上一点,若216,PF PF a +=且12PF F ∆的最小内角为30,则C 的离心率为___。
(完整版)2018年高考真题——物理试题全国卷1(含答案)
绝密★启用前2018年普通高等学校招生全国统一考试理科综合能力测试 全国1卷一、单项选择题:每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
14.高铁列车在启动阶段的运动可看作初速度为零的均加速直线运动,在启动阶段列车的动能A .与它所经历的时间成正比B .与它的位移成正比C .与它的速度成正比D .与它的动量成正比15.如图,轻弹簧的下端固定在水平桌面上,上端放有物块P ,系统处于静止状态,现用一竖直向上的力F 作用在P 上,使其向上做匀加速直线运动,以x 表示P 离开静止位置的位移,在弹簧恢复原长前,下列表示F 和x 之间关系的图像可能正确的是16.如图,三个固定的带电小球a 、b 和c ,相互间的距离分别为ab =5 cm ,bc =3 cm ,ca =4 cm 。
小球c 所受库仑力的合力的方向平行于a 、b 的连线。
设小球a 、b 所带电荷量的比值的绝对值为k ,则A .a 、b 的电荷同号,169k=B.a 、b 的电荷异号,169k =A B C DC.a、b的电荷同号,6427 k=D.a、b的电荷异号,6427 k=17.如图,导体轨道OPQS固定,其中PQS是半圆弧,Q为半圆弧的中心,O为圆心。
轨道的电阻忽略不计。
OM是有一定电阻。
可绕O转动的金属杆。
M端位于PQS上,OM与轨道接触良好。
空间存在半圆所在平面垂直的匀强磁场,磁感应强度的大小为B,现使OQ位置以恒定的角速度逆时针转到OS位置并固定(过程Ⅰ);再使磁感应强度的大小以一定的变化率从B增加到B'(过程Ⅱ)。
在过程Ⅰ、Ⅱ中,流过OM的电荷量相等,则BB'等于A.54B.32C.74D.218.如图,abc是竖直面内的光滑固定轨道,ab水平,长度为2R:bc是半径为R的四分之一的圆弧,与ab相切于b点。
一质量为m的小球。
始终受到与重力大小相等的水平外力的作用,自a点处从静止开始向右运动,重力加速度大小为g。
最新-2018年普通高等学校招生全国统一考试数学理试题

2018年普通高等学校招生全国统一考试数学理试题(湖南卷,含答案)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}1,2,3M =,{}2,3,4N =,则 A .M N ⊆ B .N M ⊆ C .{}2,3MN = D .{}1,4M N =2.下列命题中的假命题...是 A .R x ∀∈,120x -> B .N x *∀∈,()10x -2>C .R x ∃∈,lg x <1D . R x ∃∈,tan 2x =3.极坐标方程cos ρθ=和参数方程1,23x t y t =--⎧⎨=+⎩(t 为参数)所表示的图形分别是A .圆、直线B .直线、圆C .圆、圆D .直线、直线4.在Rt ABC ∆中,90C ∠=,4AC =,则AB AC 等于 A .16- B .8- C .8 D .16 5.421d x x⎰等于 A .2ln 2- B .2ln 2 C .ln 2- D .ln 26.在ABC ∆中,角A ,B ,C 所对的边长分别为a ,b ,c .若120C ∠=,c =,则A .a >bB .a <bC .a =bD .a 与b 的大小关系不能确定7.在某种信息传输过程中,用4个数字的一个排列(数字允许重复)表示一个信息,不同排列表示不同信息,若所用数字只有0和1,则与信息0110至多有两个对应位置上的数字相同的信息个数为A.10B.11C.12D.158.用{}min ,a b 表示,a b 两数中的最小值.若函数{}()min ,f x x x t =+的图像关于直线12x =-对称,则t 的值为A .2-B .2C .1-D .1二、填空题:本大题共7小题,每小题5分,共35分.把答案填在答题卡...中对应题号后的横线上.9.已知一种材料的最佳加入量在110g 到210g 之间.若用0.618法安排实验,则第一次试点的加入量可以是 g .10.如图1所示,过O 外一点P 作一条直线与O 交于A,B 两点.已知PA=2,点P 到O 的切线长PT=4,则弦AB 的长为 .11.在区间[]1,2-上随机取一个数x ,则1x ≤的概率为 .12.图2是求222123+++2…+100的值的程序框图,则正整数n = .13.图3中的三个直角三角形是一个体积为203cm 的几何体的三视图,则h = cm .图214.过抛物线22(0)x py p =>的焦点作斜率为1的直线与该抛物线交于,A B 两点,,A B 在x 轴上的正射影分别为,D C .若梯形ABCD 的面积为,则p = .15.若数列{}n a 满足:对任意的n N *∈,只有有限个正整数m 使得m a n <成立,记这样的m 的个数为()n a *,则得到一个新数列{}()n a *.例如,若数列{}n a 是1,2,3,n …,…,则数列{}()n a *是0,1,2,1,n -…,….已知对任意的N n *∈,2n a n =,则5()a *= ,(())n a **= .三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分12分)已知函数2()22sin f x x x =-. (Ⅰ)求函数()f x 的最大值; (Ⅱ)求函数()f x 的零点的集合. 17.(本小题满分12分)图4是某城市通过抽样得到的居民某年的月均用水量(单位:吨)的频率分布直方图. (Ⅰ)求直方图中x 的值.(Ⅱ)若将频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用水量在3至4吨的居民数X 的分布列和数学期望. 18.(本小题满分12分)如图5所示,在正方体1111ABCD A B C D -中,E 是棱1DD 的中点. (Ⅰ)求直线BE 的平面11ABB A 所成的角的正弦值;(Ⅱ)在棱11C D 上是否存在一点F ,使1B F ∥平面1A BE ?证明你的结论.19.(本小题满分13分)为了考察冰川的融化状况,一支科考队在某冰川上相距8km 的A ,B 两点各建一个考察基地.视冰川面为平面形,以过A ,B 两点的直线为x 轴,线段AB 的垂直平分线为y 轴建立平面直角坐标系(图6).在直线2x =的右侧,考察范围为到点B 的距离不超过km 的区域;在直线2x =的左侧,考察范围为到A ,B 两点的距离之和不超过的区域. (Ⅰ)求考察区域边界曲线的方程;(Ⅱ)如图6所示,设线段12PP ,23P P 是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km ,以后每年移动的距离为前一年的2倍,求冰川边界线移动到考察区域所需的最短时间. 20.(本小题满分13分)已知函数2()(,),f x x bx c b c R =++∈对任意的x R ∈,恒有'()f x ≤()f x . (Ⅰ)证明:当0x ≥时,2()()f x x c ≤+;(Ⅱ)若对满足题设条件的任意b ,c ,不等式22()()()f c f b M c b -≤-恒成立,求M 的最小值. 21.(本小题满分13分)数列{}*()n a n N ∈中,11,n a a a +=是函数322211()(3)332n n n f x x a n x n a x =-++的极小值点.(Ⅰ)当0a =时,求通项n a ;(Ⅱ)是否存在a ,使数列{}n a 是等比数列?若存在,求a 的取值范围;若不存在,请说明理由.参考答案一、选择题1.C2.B3.A4.D5.D6.A7.B8.D 二、填空题9.171.8或148.2 10.6 11.2312.100 13.4 14.2 15.2 2n 三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.解法2:由()0f x =得2cos 2sin x x x =,于是sin 0x =sin x x =即tan x =由sin 0x =可知x k π=;由tan x =3x k ππ=+.故函数()f x 的零点的集合为,,3x x k x k k Z πππ⎧⎫==+∈⎨⎬⎩⎭或17.(本小题满分12分)解:(Ⅰ)依题意及频率分布直方图知,0.020.10.370.391x ++++=,解得0.12x =. (Ⅱ)由题意知,XB(3,0.1).因此031233P(0)0.90.729,(1)0.10.90.243X C P X C ==⨯===⨯⨯=,223333P(2)0.10.90.027,(3)0.10.001X C P X C ==⨯⨯===⨯=.XX 的数学期望为EX=30.1=0.3⨯.18.(本小题满分12分)解法1:设正方体的棱长为1.如图所示,以1ABAD AA ,,为单位正交基底建立空间直角坐标系.(Ⅰ)依题意,得1(1,0,0),(0,1,),(0,0,0),(0,1,0)2B E A D , 所以1=(1,1,),(0,1,0)2BE AD -=.在正方体1111ABCD A BC D -中,因为11AD ABB A ⊥平面,所以AD 是平面11ABB A 的一个法向量,设直线BE 和平面11ABB A 所成的角为θ,则12sin 3312BE AD BE ADθ===⨯. 即直线BE 和平面11ABB A 所成的角的正弦值为23.设F 是棱11C D 上的点,则(,1,1)(01)F t t ≤≤.又1(1,0,1)B ,所以1(1,1,0)B F t =-.而11B F A BE ⊄平面,于是11110(1,1,0)(2,1,2)02(1)102B F A BE B F n t t t F ⇔=⇔-=⇔-+=⇔=⇔∥平面为11C D 的中点,这说明在棱11C D 上存在点F(11C D 的中点),使11B F A BE ∥平面 解法2:(Ⅰ)如图(a )所示,取1AA 的中点M ,连结EM,BM.因为E 是1DD 的中点,四边形11DD A A 为正方形,所以EM ∥AD.即直线BE 和平面11ABB A 所成的角的正弦值为23.(Ⅱ)在棱11C D 上存在点F ,使11B F A BE ∥平面.事实上,如图(b )所示,分别取11C D 和CD 的中点F ,G ,连结1EG,BG,,FG CD .因1111A D B C BC ∥∥,且11A D BC =,所以四边形11A BCD 是平行四边形,因此11D C A B ∥.又E,G 分别为1D D ,CD 的中点,所以1DC EG ∥,从而1B EG ∥A .这说明1A ,B ,G ,E 共面,所以1BG BE ⊂平面A .因四边形11C CDD 与11B BCC 皆为正方形,F ,G 分别为11C D 和CD 的中点,所以11FG C B B ∥C ∥,且11FG C B B =C=,因此四边形1B BGF 是平行四边形,所以1BG B F ∥.而11⊄B F 平面A BE ,1BG BE ⊂平面A ,故11B F A BE ∥平面.19.(本小题满分13分)解:(Ⅰ)设边界曲线上点P 的坐标为(,)x y , 当2x ≥时,由题意知2236(4)5x y -+=.当2x <时,由PA PB +=点P 在以A ,B 为焦点,长轴长为2a =.此时短半轴长2b ==.因而其方程为221204x y +=. 故考察区域边界曲线(如图)的方程为22221236:(4)(2):1(2)5204x y C x y x C x -+=≥+=<和.(Ⅱ)设过点12,P P 的直线为1l ,过点23,P P 的直线为2l ,则直线1l ,2l 的方程分别为14,6y y =+=.程为8y +,l 与1l 之间的距离为3d ==.又直线2l 到1C 和2C 的最短距离6d '=,而3d '>,所以考察区域边界到冰川边界线的最短距离为3.设冰川边界线移动到考察区域所需的时间为n 年,则由题设及等比数列求和公式,得0.2(21)321n -≥-,所以4n ≥.故冰川边界线移动到考察区域所需的最短时间为4年. 20.(本小题满分13分)解:(Ⅰ)易知()2f x x b '=+.由题设,对任意的2,2x R x b x bx c ∈+≤++,即2(2)0x b x c b +-+-≥恒成立,所以2(2)4()0b c b ---≤,从而214b c ≥+.于是1c ≥,且c b ≥=,因此2()0c b c c b -=+->.故当0x ≥时,有2()()(2)(1)0x c f x c b x c c +-=-+-≥. 即当0x ≥时,2()()f x x c ≤+.当c b =时,由(Ⅰ)知,2,2b c =±=.此时()()8f c f b -=-或0,220c b -=,从而223()()()2f c f b c b -≤-恒成立. 综上所述,M 的最小值为3221.(本小题满分13分)解:易知2222()(3)3(3)()n n n n f x x a n x n a x a x n '=-++=--. 令212()03,n n f x x a x n '===,得. (1)若23n a n <,则当3n x a <时,()0,()n n f x f x '>单调递增; 当23n a x n <<时,()0,()n n f x f x '<单调递减; 当2x n >时,()0,()n n f x f x '>单调递增.故()n f x 在2x n =取得极小值.由此猜测:当3n ≥时,343n n a -=⨯.下面先用数学归纳法证明:当3n ≥时,23n a n >. 事实上,当3n =时,由前面的讨论知结论成立.假设当(3)n k k =≥时,23k a k >成立,则由(2)知,213k k a a k +=>,从而22213(1)3(1)2(2)210k a k k k k k k +-+>-+=-+->,所以213(1)k a k +>+. 故当3n ≥时,23n a n >成立.于是由(2)知,当3n ≥时,13n n a a +=,而34a =,因此343n n a -=⨯. 综上所述,当0a =时,10a =,21a =,343(3)n n a n -=⨯≥. (Ⅱ)存在a ,使数列{}n a 是等比数列.事实上,由(2)知,若对任意的n ,都有23n a n >,则13n n a a +=.即数列{}n a 是首项为a ,公比为3的等比数列,且33n n a a -=.而要使23n a n >,即23na n >对一切n N *∈都成立,只需23n n a >对一切n N *∈都成立.记23n n b =,则123141,,,.393b b b ===令23xxy=,则()()22112ln3233x xy x x x x'=-<-.因此,当2x≥时,0y'<,从而函数当13a<时,可得1234,1,4,12,,a a a a a====数列{}n a不是等比数列.综上所述,存在a,使数列{}n a是等比数列,且a的取值范围为4,9⎛⎫+∞⎪⎝⎭.。
(完整版)2018高考全国二卷全国卷理综试题和答案解析

完美WORD 格式.整理整理. 专业资料分享专业资料分享. 2018年高考全国卷Ⅱ理综试题二、选择题:本题共8小题,每小题6分,共48分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.(考点一:动能定理)如图,某同学用绳子拉动木箱,使它从静止开始沿粗糙水平路面运动至具有某一速度,木箱获得的动能一定A .小于拉力所做的功B .等于拉力所做的功C .等于克服摩擦力所做的功D .大于克服摩擦力所做的功15.(考点二:动量定理)高空坠物极易对行人造成伤害。
若一个50 g 的鸡蛋从一居民楼的25层坠下,与地面的撞击时间约为2 ms ,则该鸡蛋对地面产生的冲击力约为A .10 NB .102 NC .103 ND .104 N 16.(考点三:万有引力,圆周运动)2018年2月,我国500 m 口径射电望远镜(天眼)发现毫秒脉冲星“J0318+0253”,其自转周期T =5.19 ms ,假设星体为质量均匀分布的球体,已知万有引力常量为11226.6710N m /kg -⨯⋅。
以周期T 稳定自转的星体的密度最小值约为A .93510kg /m ⨯B .123510kg /m ⨯ C .153510kg /m ⨯D .183510kg /m ⨯ 17.(考点四:光电效应)用波长为300 nm 的光照射锌板,的光照射锌板,电子逸出锌板表面的最大初动能为电子逸出锌板表面的最大初动能为1.28⨯10-19 J 。
已知普朗克常量为6.63⨯10-34 J·J·s s ,真空中的光速为3.00⨯108 m·m·s s -1,能使锌产生光电效应的单色光的最低频率约为A .1⨯1014 HzB .8⨯1014 HzC .2⨯1015 HzD .8⨯1015 Hz 18.(考点五:法拉第电磁感应定律,楞次定律)如图,在同一平面内有两根平行长导轨,导轨间存在依次相邻的矩形匀强磁场区域,区域宽度均为l ,磁感应强度大小相等、方向交替向上向下。
高考试题——(湖南卷)数学理(全解析)

2018年高考湖南卷理科数学全解全析一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的]1.已知集合,,则A.B.C. D.【答案】C【解读】故选C.【命题意图】本题考查集合的交集与子集的运算,属容易题.2.下列命题中的假命题...是A., B.,[C., D.,【答案】B【解读】对于B选项x=1时,,故选B.【命题意图】本题考查余弦定理,特殊角的三角函数值,不等式的性质,比较法,属中档题。
7.在某种信息传输过程中,用4个数字的一个排列<数字也许重复)表示一个信息,不同排列表示不同信息,若所用数字只有0和1,则与信息0110至多有两个对应位置上的数字相同的信息个数为A .10 B.11 C.12 D.15 【答案】B【解读】与信息0110至多有两个对应位置上的数字相同的信息包括三类:第一类:与信息0110有两个对应位置上的数字相同有【命题意图】本题通过新定义考察学生的创新能力,考察函数的图象,考察考生数形结合的能力,属中档题。
二、填空题:本大题共7小题,每小题5分,共35分.把答案填在答题卡...对应题号后的横线上。
9.已知一种材料的最佳加入量在110g到210 g之间,若用0.618法安排实验,则第一次试点的加入量可以是_____________g.【答案】171.8或148.2【解读】根据0.618法,第一次试点加入量为110+<210-110)0.618=171.8或210-<210-110)0.618=148.2【命题意图】本题考察优选法的0.618法,属容易题。
10.如图1所示,过外一点P作一条直线与交于A,B两点,已知PA=2,点P到的切线长PT =4,则弦AB的长为________.【答案】6【解读】根据切线长定理所以【命题意图】本题考察平面几何的切线长定理,属容易题。
11.在区间上随机取一个数x,则≤1的概率为________.【答案】【解读】P<≤1)=【命题意图】本题考察几何概率,属容易题。
2018年湖南省高考物理试题与答案

2018年湖南省高考物理试题与答案(考试时间:60分钟试卷满分:110分)一、选择题:本题共8小题,每小题6分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
1.高铁列车在启动阶段的运动可看作初速度为零的均加速直线运动,在启动阶段列车的动能A.与它所经历的时间成正比 B.与它的位移成正比C.与它的速度成正比 D.与它的动量成正比2.如图,轻弹簧的下端固定在水平桌面上,上端放有物块P,系统处于静止状态,现用一竖直向上的力F作用在P上,使其向上做匀加速直线运动,以x表示P离开静止位置的位移,在弹簧恢复原长前,下列表示F和x之间关系的图像可能正确的是A. B.C. D.3.如图,三个固定的带电小球a、b和c,相互间的距离分别为ab=5 cm,bc=3 cm,ca=4 cm。
小球c所受库仑力的合力的方向平衡于a、b的连线。
设小球a、b所带电荷量的比值的绝对值为k,则A.a、b的电荷同号,169k= B.a、b的电荷异号,169k=C.a、b的电荷同号,6427k= D.a、b的电荷异号,6427k=4.如图,导体轨道OPQS固定,其中PQS是半圆弧,Q为半圆弧的中心,O为圆心。
轨道的电阻忽略不计。
OM是有一定电阻。
可绕O转动的金属杆。
M端位于PQS上,OM与轨道接触良好。
空间存在半圆所在平面垂直的匀强磁场,磁感应强度的大小为B,现使OQ位置以恒定的角速度逆时针转到OS位置并固定(过程Ⅰ);再使磁感应强度的大小以一定的变化率从B增加到B'(过程Ⅱ)。
在过程Ⅰ、Ⅱ中,流过OM的电荷量相等,则BB'等于A.54B.32C.74D.25.如图,abc是竖直面内的光滑固定轨道,ab水平,长度为2R:bc是半径为R的四分之一的圆弧,与ab相切于b点。
一质量为m的小球。
始终受到与重力大小相等的水平外力的作用,自a点处从静止开始向右运动,重力加速度大小为g。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)本试卷包括选择题、填空题和解答题三部分,共5页,时量120分钟,满分150分。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数()()1z i i i =+为虚数单位在复平面上对应的点位于[来源:]A .第一象限B .第二象限C .第三象限D .第四象限2.某学校有男、女学生各500名.为了解男女学生在学习兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取100名学生进行调查,则宜采用的抽样方法是A .抽签法B .随机数法C .系统抽样法D .分层抽样法 3.在锐角中ABC ∆,角,A B 所对的边长分别为,a b .若2sin ,a B A =则角等于 A .12π B .6π C .4π D .3π 4.若变量,x y 满足约束条件211y xx y y ≤⎧⎪+≤⎨⎪≥-⎩,2x y +则的最大值是A .5-2B .0C .53D .525.函数()2ln f x x =的图像与函数()245g x x x =-+的图像的交点个数为 A .3 B .2 C .1 D .06. 已知,a b 是单位向量,0a b =.若向量c 满足1,c a b c --=则的取值范围是A.⎤⎦B.⎤⎦C.1⎡⎤⎣⎦D.1⎡⎤⎣⎦7.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 A .1 BC.2 D.28.在等腰三角形ABC 中,=4AB AC =,点P 是边AB 上异于,A B 的一点,光线从点P 出发,经,BC CA 发射后又回到原点P (如图1).若光线QR 经过ABC ∆的中心,则AP 等A .2B .1C .83 D .43[来源:学科网ZXXK] 二、填空题:本大题共8小题,考生作答7小题,每小题5分,共35分.(一)选做题(请考生在第9、10、11三题中任选两题作答,如果全做,则按前两题计分)9.在平面直角坐标系xoy 中,若,3cos ,:(t )C :2sin x t x l y t a y ϕϕ==⎧⎧⎨⎨=-=⎩⎩为参数过椭圆[来源:学|科|网Z|X|X|K]()ϕ为参数的右顶点,则常数a 的值为 .10.已知222,,,236,49a b c a b c a b c ∈++=++则的最小值为 12 .[来源:Z_xx_]11.如图2的O 中,弦,AB CD 相交于点,2P PA PB ==,1PD =,则圆心O 到弦CD 的距离为 .必做题(12-16题) 12.若209,Tx dx T =⎰则常数的值为 .13.执行如图3所示的程序框图,如果输入1,2,a b a ==则输出的的值为 9 .14.设12,F F 是双曲线2222:1(0,0)x y C a b a b-=>>的两个焦点,P 是C 上一点,若216,PF PF a +=且12PF F ∆的最小内角为30,则C 的离心率为___。
15.设n S 为数列{}n a 的前n 项和,1(1),,2nn n n S a n N *=--∈则 (1)3a =_____; (2)12100S S S ++⋅⋅⋅+=___________。
16.设函数(),0,0.xxxf x a b c c a c b =+->>>>其中(1)记集合{}(,,),,M a b c a b c a =不能构成一个三角形的三条边长,且=b ,则(,,)a b c M ∈所对应的()f x 的零点的取值集合为____。
(2)若,,a b c ABC ∆是的三条边长,则下列结论正确的是 .(写出所有正确结论的序号)①()(),1,0;x f x ∀∈-∞>②,,,xxxx R xa b c ∃∈使不能构成一个三角形的三条边长; ③若()()1,2,0.ABC x f x ∆∃∈=为钝角三角形,则使三、解答题:本大题共6小题,共75分。
解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知函数2()sin()cos().()2sin 632xf x x xg x ππ=-+-=。
(I )若α是第一象限角,且()f α=()g α的值; (II )求使()()f x g x ≥成立的x 的取值集合。
18.(本小题满分12分)某人在如图4所示的直角边长为4米的三角形地块的每个格点(指纵、横的交叉点记忆三角形的顶点)处都种了一株相同品种的作物。
根据历年的种植经验,一株该种作物的年收获这里,两株作物“相近”是指它们之间的直线距离不超过1米。
(I )从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率; (II )从所种作物中随机选取一株,求它的年收获量的分布列与数学期望。
19.(本小题满分12分)如图5,在直棱柱1111//ABCD A B C D AD BC -中,,90,,1BAD AC BD BC ∠=⊥=,13AD AA ==。
(I )证明:1AC B D ⊥; (II )求直线111B C ACD 与平面所成角的正弦值。
20.(本小题满分13分)在平面直角坐标系xOy 中,将从点M 出发沿纵、横方向到达点N 的任一路径成为M 到N 的一条“L 路径”。
如图6所示的路径1231MM M M N MN N 与路径都是M 到N 的“L 路径”。
某地有三个新建的居民区,分别位于平面xOy 内三点(3,20),(10,0),(14,0)A B C -处。
现计划在x 轴上方区域(包含x 轴)内的某一点P 处修建一个文化中心。
(I )写出点P 到居民区A 的“L 路径”长度最小值的表达式(不要求证明);(II )若以原点O 为圆心,半径为1的圆的内部是保护区,“L 路径”不能进入保护区,请确定点P 的位置,使其到三个居民区的“L 路径”长度值和最小。
21.(本小题满分13分)过抛物线2:2(0)E x py p =>的焦点F 作斜率分别为12,k k 的两条不同的直线12,l l ,且122k k +=,1l E与相交于点A ,B ,2l E 与相交于点C ,D 。
以AB ,CD 为直径的圆M ,圆N (M ,N 为圆心)的公共弦所在的直线记为l 。
(I )若120,0k k >>,证明;22FM FN P <;(II )若点M 到直线l ,求抛物线E 的方程。
[来源:学,科,网Z,X,X,K]22.(本小题满分13分)已知0a >,函数()2x af x x a-=+。
(I )记[]()0,4f x a 在区间上的最大值为g(),求a g()的表达式;(II )是否存在a ,使函数()y f x =在区间()0,4内的图像上存在两点,在该两点处的切线相互垂直?若存在,求a 的取值范围;若不存在,请说明理由。
参考答案一、选择题 1.B 2.D 3.D 4.C 5.B 6.A 7.C 8.D 9.3 10.12 11.23[来源:学&科&网] 12.3 13.9 14.315.116-;10011(1)32- 16.(1)]10(, (2)①②③17.解: (I )533sin 3)(sin 3sin 23cos 21cos 21sin 23)(==⇒=++-=ααf x x x x x x f . 51cos 12sin 2)(,54cos )2,0(,53sin 2=-===⇒∈=⇒ααααπααg 且(II )21)6sin(cos 21sin 23cos 1sin 3)()(≥+=+⇒-≥⇒≥πx x x x x x g x f [来源:] Z k k k x k k x ∈+∈⇒++∈+⇒],322,2[]652,62[6ππππππππ18.解: (Ⅰ) 由图知,三角形边界共有12个格点,内部共有3个格点.从三角形上顶点按逆时针方向开始,分别有0,0,1,1,0,1,1,0,0,1,2,1对格点,共8对格点恰好“相近”。
所以,从三角形地块的内部和边界上分别随机选取一株作物,它们恰好“相近”的概率923128=⋅=P (Ⅱ)三角形共有15个格点。
与周围格点的距离不超过1米的格点数都是1个的格点有2个,坐标分别为(4,0),(0,4)。
154)51(==Y P 所以 与周围格点的距离不超过1米的格点数都是2个的格点有4个,坐标分别为(0,0), (1,3), (2,2),(3,1)。
154)48(==Y P 所以 与周围格点的距离不超过1米的格点数都是3个的格点有6个,坐标分别为(1,0), (2,0), (3,0),(0,1,) ,(0,2),(0,3,)。
156)45(==Y P 所以 与周围格点的距离不超过1米的格点数都是4个的格点有3个,坐标分别为(1,1), (1,2), (2,1)。
153)42(==Y P 所以 如下表所示:1544815251)(⋅+⋅=Y E46)(=∴Y E .19.解: (Ⅰ) AC BB ABCD BD ABCD BB D C B A ABCD ⊥⇒⊂⊥∴-111111,面且面是直棱柱D B AC BDB D B BDB AC B BB BD BD AC 11111,,⊥∴⊂⊥∴=⋂⊥,面。
面且又 . (证毕)(Ⅱ)。
的夹角与平面的夹角即直线与平面直线θ111111,////ACD AD ACD C B AD BC C B ∴轴正半轴。
为轴正半轴,为点,量解题。
设原点在建立直角坐标系,用向X AD Y AB A ()BD AC y BD y AC y C y B D D A ⊥-== ),0,,3(),0,,1()0,,1(),0,,0(),3,0,3(),0,0,3(,00,01,则,设).3,0,3(),0,3,1(.30,003012==∴=⇒>=+-⇒=⋅AD AC y y y BD AC ),,(),,(的一个法向量平面则的法向量为设平面303,313-.0,111==⇒⎪⎩⎪⎨⎧=⋅=⋅AD n ACD AD n AC n n ACD 7213733|,cos |sin 003,313-1=⋅=><=⇒==∴AD n AD n ACD θ),,(),,(的一个法向量平面 72111夹角的正弦值为与平面所以ACD BD 。
20.解: .0),,(≥y y x P 且设点(Ⅰ) d L A P 路径”的最短距离的“到点点)20,3(,[来源:学科网]|20 -y | + |3 -x |=+d 垂直距离,即等于水平距离,其中.,0R x y ∈≥(Ⅱ)本问考查分析解决应用问题的能力,以及绝对值的基本知识。
