中考数学压轴题(讲义及答案)含答案
【精品】人教版九年级数学中考压轴试题(含答案解析)

【精品】人教版九年级数学中考压轴试题(含答案)1.(8分)如图,已知Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上的一点(不与A、B重合).过点B作BE⊥CD,垂足为E.将线段CE绕点C顺时针旋转90°,得到线段CF,连结EF.设∠BCE度数为α.(1)①补全图形.②试用含α的代数式表示∠CDA.(2)若=,求α的大小.(3)直接写出线段AB、BE、CF之间的数量关系.【分析】(1)①根据要求画出图形即可;②利用三角形的外角的性质计算即可;(2)只要证明△FCE∽△ACB,可得==,Rt△CFA中,∠CFA=90°,cos∠FCA=,推出∠FCA=30°,即α=30°.(3)在Rt△ABC,和Rt△CBE中,利用勾股定理即可解决问题;【解答】解:(1)①补全的图形如图所示:②∵CA=CB,∠ACB=90°,∴∠A=∠ABC=45°,∴∠CDA=∠DBC+∠BCD=45°+α.(2)在△FCE和△ACB中,∠CFE=∠CAB=45°,∠FCE=∠ACB=90°,∴△FCE∽△ACB,∴=∵=∴=连结FA,∵∠FCA=90°﹣∠ACE,∠ECB=90°﹣∠ACE,∴∠FCA=∠BCE=α,在Rt△CFA中,∠CFA=90°,cos∠FCA=∴∠FCA=30°,即α=30°.(3)结论:AB2=2CF2+2BE2.理由:∵AB2=AC2+BC2=2BC2,BC2=CE2+BE2=CF2+BE2,∴AB2=2CF2+2BE2.【点评】本题考查相似三角形综合题、相似三角形的判定和性质、等腰直角三角形的性质、勾股定理、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.2.(8分)已知在平面直角坐标系xOy中的点P和图形G,给出如下的定义:若在图形G上存在一点Q,使得P、Q之间的距离等于1,则称P为图形G的关联点.(1)当⊙O的半径为1时,①点P1(,0),P2(1,),P3(0,3)中,⊙O的关联点有P1,P2.②直线经过(0,1)点,且与y轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标x的取值范围.(2)已知正方形ABCD的边长为4,中心为原点,正方形各边都与坐标轴垂直.若正方形各边上的点都是某个圆的关联点,求圆的半径r的取值范围.【分析】(1)①利用两圆的位置关系即可判断;②根据定义分析,可得当最小y=﹣x上的点P到原点的距离在1到3之间时符合题意,设P(x,﹣x),根据两点间的距离公式即可得到结论;(2)根据关联点的定义求出圆的半径r的最大值与最小值即可解决问题;【解答】解:(1)①∵点P1(,0),P2(1,),P3(0,3)∴OP1=,OP2=2,OP3=3,∴半径为1的⊙P1与⊙O相交,半径为1的⊙P2与⊙O相交,半径为1的⊙P3与⊙O相离1,∴⊙O的关联点是P1,P2;故答案为:P1,P2;②如图,以O为圆心,2为半径的圆与直线y=1交于 P1,P2两点.线段P1,P2上的动点P(含端点)都是以O为圆心,1为半径的圆的关联点.故此﹣≤x≤.(2)由已知,若P为图形G的关联点,图形G必与以P为圆心1为半径的圆有交点.∵正方形ABCD边界上的点都是某圆的关联点,∴该圆与以正方形边界上的各点为圆心1为半径的圆都有交点故此,符合题意的半径最大的圆是以O为圆心,3为半径的圆;符合题意的半径最小的圆是以O为圆心,2﹣1 为半径的圆.综上所述,2﹣1≤r≤3.【点评】本题考查一次函数综合题、圆、正方形的有关性质等知识,解题的关键是理解题意,学会用转化的思想思考问题,学会用分类讨论的思想思考问题,属于中考压轴题.3.(5分)如图,Rt△ABC中,∠C=90°,AC=BC,AB=4cm.动点D沿着A→C→B的方向从A点运动到B点.DE⊥AB,垂足为E.设AE长为xcm,BD长为ycm(当D与A重合时,y=4;当D与B重合时y=0).小云根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小云的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:x/cm 0 0.5 1 1.5 2 2.5 3 3.5 4y/cm 4 3.5 3.2 2.8 2.1 1.4 0.7 0补全上面表格,要求结果保留一位小数.则t≈ 2.9 .(2)在下面的网格中建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.(3)结合画出的函数图象,解决问题:当DB=AE时,AE的长度约为2.3 cm.【分析】(1)按题意,认真测量即可;(2)利用数据描点、连线;(3)当DB=AE时,y=x,画图形测量交点横坐标即可.【解答】解:(1)根据题意量取数据为2.9故答案为:2.9(2)根据已知数据描点连线得:(3)当DB=AE时,y与x满足y=x,在(2)图中,画y=x图象,测量交点横坐标为2.3.故答案为:2.3【点评】本题以考查画函数图象为背景,应用了数形结合思想和转化的数学思想.4.(7分)已知抛物线:y=mx2﹣2mx+m+1(m≠0).(1)求抛物线的顶点坐标.(2)若直线l1经过(2,0)点且与x轴垂直,直线l2经过抛物线的顶点与坐标原点,且l1与l2的交点P在抛物线上.求抛物线的表达式.(3)已知点A(0,2),点A关于x轴的对称点为点B.抛物线与线段AB恰有一个公共点,结合函数图象写出m的取值范围.【分析】(1)利用配方法把解析式配成顶点式即可得到抛物线的顶点坐标;(2)先确定P点坐标,然后把P点坐标代入y=mx2﹣2mx+m+1求出m 即可;(3)分别把A、B点的坐标代入y=mx2﹣2mx+m+1求出对应的m的值,然后根据二次函数的性质确定满足条件的m的范围.【解答】(1)解:∵y=mx2﹣2mx+m+1=m(x﹣1)2+1,∴抛物线的顶点坐标为(1,1);(2)易得直线l2的表达式为y=x,当x=2时,y=x=2,则P(2,2),把P(2,2)代入y=mx2﹣2mx+m+1得4m﹣4m+m+1=2,解得m=1,∴抛物线解析式为y=x2﹣2x+2;(3)点A(0,2)关于x轴的对称点B的坐标为(0,﹣2),当抛物线过A(0,2)时,把A(0,2)代入y=mx2﹣2mx+m+1得m+1=2,解得m=1,结合图象可知,当抛物线开口向上且和线段AB恰有一个公共点时,0<m≤1;当抛物线过B(0,﹣2)时,把B(0,﹣2)代入y=mx2﹣2mx+m+1得m+1=﹣2,解得m=﹣3,结合图象可知,当抛物线开口向上且和线段AB恰有一个公共点时,﹣3≤m<0;综上所述,m的取值范围是 0<m≤1或﹣3≤m<0.【点评】本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.也考查了二次函数的性质.5.(5分)如图,AB是⊙O的直径,C、D是⊙O上两点, =.过点B作⊙O的切线,连接AC并延长交于点E,连接AD并延长交于点F.(1)求证:AC=CE.(2)若AE=8,sin∠BAF=求DF长.【分析】(1)连接BC,想办法证明AC=BC,EC=BC即可解决问题;(2)首先证明∠DBF=∠BAF,可得sin∠BAF=sin∠DBF==,由此即可解决问题;【解答】(1)证明:连结BC.∵AB是的直径,C在⊙O上∴∠ACB=90°,∵=,∴AC=BC∴∠CAB=45°.∵AB是⊙O的直径,EF切⊙O于点B,∴∠ABE=90°,∴∠AEB=45°,∴AB=BE,∴AC=CE.(2)在Rt△ABE中,∠ABE=90°,AE=8,AE=BE ∴AB=8,在Rt△ABF中,AB=8,sin∠BAF=,解得:BF=6,连结BD,则∠ADB=∠FDB=90°,∵∠BAF+∠ABD=90°,∠ABD+∠DBF=90°,∴∠DBF=∠BAF,∵sin∠BAF=,∴sin∠DBF=,∴=,∴DF=.【点评】本题考查切线的性质、圆周角定理、解直角三角形、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.6.(5分)在平面直角坐标系xOy中,一次函数y=x+b的图象与x轴交于点A(2,0),与反比例函数y=的图象交于点B(3,n).(1)求一次函数与反比例函数的表达式;(2)若点P为x轴上的点,且△PAB的面积是2,则点P的坐标是(﹣2,0)或(6,0).【分析】(1)利用待定系数法即可解决问题;(2)利用三角形的面积公式求出PA的长即可解决问题;【解答】解:(1)∵一次函数y=x+b的图象与x轴交于点A(2,0),∴2+b=0,∴b=﹣2,∴y=x﹣2,当x=3时,y=1,∴B(3,1),代入y=中,得到k=3,∴反比例函数的解析式为y=.(2)∵△PAB的面积是2,∴PA=4,∴P(﹣2,0)或(6,0).【点评】本题考查一次函数的性质、反比例函数的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.7.(5分)如图,小明想测量山的高度.他在点B处仰望山顶A,测得仰角∠ABN=30°,再向山的方向(水平方向)行进100m至索道口点C处,在点C处仰望山顶A,测得仰角∠ACN=45°.求这座山的高度.(结果精确到0.1m,小明的身高忽略不计)(参考数据:≈1.41,≈1.73)【分析】作AH⊥BN于H,设AH=xm,根据正切的概念表示出CH、BH,根据题意列出方程,解方程即可.【解答】解:如图,作AH⊥BN于H,设AH=xm,∵∠ACN=45°,∵tanB=,∴BH=x,则BH﹣CH=BC,即x﹣x=100,解得x=50(+1).答:这座山的高度为50(+1)m;【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,正确作出辅助线、熟记锐角三角函数的概念是解题的关键.8.(5分)如图,四边形ABCD是平行四边形,CE⊥AD于点E,DF⊥BA交BA的延长线于点F.(1)求证:△ADF∽△DCE;(2)当AF=2,AD=6,且点E恰为AD中点时,求AB的长.【分析】(1)由平行四边形的性质知CD∥AB,即∠DAF=∠CDE,再由CE⊥AD、DF⊥BA知∠AFD=∠DEC=90°,据此可得;(2)根据△ADF∽△DCE知=,据此求得DC=9,再根据平行四边形的性质可得答案.【解答】解:(1)∵四边形ABCD是平行四边形,∴CD∥AB,∴∠DAF=∠CDE,又∵CE⊥AD、DF⊥BA,∴∠AFD=∠DEC=90°,∴△ADF∽△DCE;(2)∵AD=6、且E为AD的中点,∴DE=3,∵△ADF∽△DCE,∴=,即=,解得:DC=9,∵四边形ABCD是平行四边形,∴AB=CD=9.【点评】本题主要考查相似三角形的判定和性质,解题的关键是熟练掌握相似三角形的判定和性质及平行四边形的性质.9.(5分)二次函数y=x2﹣2mx+5m的图象经过点(1,﹣2).(1)求二次函数图象的对称轴;(2)当﹣4≤x≤1时,求y的取值范围.【分析】(1)根据抛物线的对称性和待定系数法求解即可;(2)根据二次函数的性质可得.【解答】解:(1)把点(1,﹣2)代入y=x2﹣2mx+5m中,可得:1﹣2m+5m=﹣2,解得:m=﹣1,所以二次函数y=x2﹣2mx+5m的对称轴是x=﹣,(2)∵y=x2+2x﹣5=(x+1)2﹣6,∴当x=﹣1时,y取得最小值﹣6,由表可知当x=﹣4时y=3,当x=﹣1时y=﹣6,∴当﹣4≤x≤1时,﹣6≤y≤3.【点评】本题考查了二次函数图象与性质及待定系数法求函数解析式,熟练掌握二次函数的图象与性质是解题的关键.10.(6分)如图,AC是⊙O的直径,点D是⊙O 上一点,⊙O的切线CB与AD的延长线交于点B,点F是直径AC上一点,连接DF并延长交⊙O于点E,连接AE.(1)求证:∠ABC=∠AED;(2)连接BF,若AD=,AF=6,tan∠AED=,求BF的长.【分析】(1)直接利用圆周角定理以及切线的性质定理得出∠ACD=∠ABC,进而得出答案;(2)首先得出DC的长,即可得出FC的长,再利用已知得出BC的长,结合勾股定理求出答案.【解答】(1)证明:连接DC,∵AC是⊙O的直径,∴∠BDC=90°,∴∠ABC+∠BCD=90°,∵⊙O的切线CB与AD的延长线交于点B,∴∠BCA=90°,∴∠ACD+∠BCD=90°,∴∠ACD=∠ABC,∴∠ABC=∠AED;(2)解:连接BF,∵在Rt△ADC中,AD=,tan∠AED=,∴tan∠ACD==,∴DC=AD=,∴AC==8,∵AF=6,∴CF=AC﹣AF=8﹣6=2,∵∠ABC=∠AED,∴tan∠ABC==,∴=,解得:BD=,故BC=6,则BF==2.【点评】此题主要考查了切线的性质与判定以及勾股定理等知识,正确得出∠ACD=∠ABC是解题关键.11.(7分)在平面直角坐标系xOy中,抛物线y=﹣x2+mx+n经过点A (﹣1,0)和B(0,3).(1)求抛物线的表达式;(2)抛物线与x轴的正半轴交于点C,连接BC.设抛物线的顶点P 关于直线y=t的对称点为点Q,若点Q落在△OBC的内部,求t的取值范围.【分析】(1)利用待定系数法即可解决问题;(2)分别求出点Q落在直线BC和x轴上时的t的值即可判断;【解答】解:(1)∵抛物线y=﹣x2+mx+n经过点A(﹣1,0)和B(0,3),∴,解得,∴抛物线的解析式为y=﹣x2+2x+3.(2)如图,易知抛物线的顶点坐标为(1,4).观察图象可知当点P关于直线y=t的对称点为点Q中直线BC上时,t=3,当点P关于直线y=t的对称点为点Q在x轴上时,t=2,∴满足条件的t的值为2<t<3.【点评】本题考查二次函数的性质、待定系数法、轴对称等知识,解题的关键是熟练掌握基本知识,学会寻找特殊点解决问题,属于中考常考题型.。
中考数学——一元二次方程的综合压轴题专题复习含答案解析

一、一元二次方程 真题与模拟题分类汇编(难题易错题)1.已知关于x 的方程230x x a ++=①的两个实数根的倒数和等于3,且关于x 的方程2(1)320k x x a -+-=②有实数根,又k 为正整数,求代数式2216k k k -+-的值. 【答案】0.【解析】【分析】 由于关于x 的方程x 2+3x +a =0的两个实数根的倒数和等于3,利用根与系数的关系可以得到关于a 的方程求出a ,又由于关于x 的方程(k -1)x 2+3x -2a =0有实数根,分两种情况讨论,该方程可能是一次方程、有可能是一元二次方程,又k 为正整数,利用判别式可以求出k ,最后代入所求代数式计算即可求解.【详解】解:设方程①的两个实数根分别为x 1、x 2则12123940x x x x a a +-⎧⎪⎨⎪-≥⎩=== , 由条件,知12121211x x x x x x ++==3, 即33a -=,且94a ≤, 故a =-1,则方程②为(k -1)x 2+3x +2=0,Ⅰ.当k -1=0时,k =1,x =23-,则22106k k k -=+-. Ⅱ.当k -1≠0时,∆=9-8(k -1)=17-6-8k ≥0,则178k ≤, 又k 是正整数,且k≠1,则k =2,但使2216k k k -+-无意义. 综上,代数式2216k k k -+-的值为0 【点睛】本题综合考查了根的判别式和根与系数的关系,在解方程时一定要注意所求k 的值与方程判别式的关系.要注意该方程可能是一次方程、有可能是一元二次方程,2.已知关于x 的方程221(1)104x k x k -+++=有两个实数根. (1)求k 的取值范围;(2)若方程的两实数根分别为1x ,2x ,且221212615x x x x +=-,求k 的值.【答案】(1)32k ≥(2)4 【解析】试题分析: 根据方程的系数结合根的判别式即可得出230k ∆=-≥ ,解之即可得出结论. 根据韦达定理可得:212121114x x k x x k ,+=+⋅=+ ,结合221212615x x x x +=- 即可得出关于k 的一元二次方程,解之即可得出k 值,再由⑴的结论即可确定k 值.试题解析:因为方程有两个实数根,所以()22114112304k k k ⎛⎫⎡⎤∆=-+-⨯⨯+=-≥ ⎪⎣⎦⎝⎭, 解得32k ≥. 根据韦达定理,()221212111141 1.114k k x x k x x k +-++=-=+⋅==+, 因为221212615x x x x +=-,所以()212128150x x x x +-+=,将上式代入可得 ()2211811504k k ⎛⎫+-++= ⎪⎝⎭,整理得2280k k --= ,解得 1242k k ,==- ,又因为32k ≥,所以4k =.3.沙坪坝区各街道居民积极响应“创文明城区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A ,B 两个社区,B 社区居民人口数量不超过A 社区居民人口数量的2倍. (1)求A 社区居民人口至少有多少万人?(2)街道工作人员调查A ,B 两个社区居民对“社会主义核心价值观”知晓情况发现:A 社区有1.2万人知晓,B 社区有1.5万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A 社区的知晓人数平均月增长率为m %,B 社区的知晓人数第一个月增长了45m %,第二月在第一个月的基础上又增长了2m %,两个月后,街道居民的知晓率达到92%,求m 的值.【答案】(1)A 社区居民人口至少有2.5万人;(2)m 的值为50.【解析】【分析】(1)设A 社区居民人口有x 万人,根据“B 社区居民人口数量不超过A 社区居民人口数量的2倍”列出不等式求解即可;(2)A社区的知晓人数+B社区的知晓人数=7.5×92%,据此列出关于m的方程并解答.【详解】解:(1)设A社区居民人口有x万人,则B社区有(7.5-x)万人,依题意得:7.5-x≤2x,解得x≥2.5.即A社区居民人口至少有2.5万人;(2)依题意得:1.2(1+m%)2+1.5×(1+45m%)+1.5×(1+45m%)(1+2m%)=7.5×92%,解得m=50答:m的值为50.【点睛】本题考查了一元二次方程和一元一次不等式的应用,解题的关键是读懂题意,找到题中相关数据的数量关系,列出不等式或方程.4.小王经营的网店专门销售某种品牌的一种保温杯,成本为30元/只,每天销售量y (只)与销售单价x(元)之间的关系式为y=﹣10x+700(40≤x≤55),求当销售单价为多少元时,每天获得的利润最大?最大利润是多少元?【答案】当销售单价为50元时,每天获得的利润最大,利润的最大值为4000元【解析】【分析】表示出一件的利润为(x﹣30),根据总利润=单件利润乘以销售数量,整理成顶点式即可解题.【详解】设每天获得的利润为w元,根据题意得:w=(x﹣30)y=(x﹣30)(﹣10x+700)=﹣10x2+1000x﹣21000=﹣10(x ﹣50)2+4000.∵a=﹣10<0,∴当x=50时,w取最大值,最大值为4000.答:当销售单价为50元时,每天获得的利润最大,利润的最大值为4000元.【点睛】本题考查了一元二次函数的实际应用,中等难度,熟悉函数的性质是解题关键.5.某社区决定把一块长50m,宽30m的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小形状都相同的矩形) ,空白区域为活动区,且四周的4个出口宽度相同,当绿化区较长边x为何值时,活动区的面积达到21344m?【答案】当13x m =时,活动区的面积达到21344m【解析】【分析】根据“活动区的面积=矩形空地面积﹣阴影区域面积”列出方程,可解答.【详解】解:设绿化区宽为y ,则由题意得502302x y -=-.即10y x =-列方程: 50304(10)1344x x ⨯--=解得13x =- (舍),213x =.∴当13x m =时,活动区的面积达到21344m【点睛】本题是一元二次方程的应用题,确定等量关系是关键,本题计算量大,要细心.6.如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB ,BC 各为多少米?【答案】羊圈的边长AB ,BC 分别是20米、20米.【解析】试题分析:设AB 的长度为x 米,则BC 的长度为(100﹣4x )米;然后根据矩形的面积公式列出方程.试题解析:设AB 的长度为x 米,则BC 的长度为(100﹣4x )米. 根据题意得 (100﹣4x )x=400,解得 x 1=20,x 2=5. 则100﹣4x=20或100﹣4x=80. ∵80>25, ∴x 2=5舍去. 即AB=20,BC=20考点:一元二次方程的应用.7.为了让学生亲身感受合肥城市的变化,蜀山中学九(1)班组织学生进行“环巢湖一日研学游”活动,某旅行社推出了如下收费标准:(1)如果人数不超过30人,人均旅游费用为100元;(2)如果超过30人,则每超过1人,人均旅游费用降低2元,但人均旅游费用不能低于80元.该班实际共支付给旅行社3150元,问:共有多少名同学参加了研学游活动?【答案】共有35名同学参加了研学游活动.【解析】试题分析:由该班实际共支付给旅行社3150元,可以判断出参加的人数在30人以上,等量关系为:(100﹣在30人基础上降低的人数×2)×参加人数=3150,得到相关解后根据人均活动费用不得低于80元作答即可.试题解析:∵100×30=3000<3150,∴该班参加研学游活动的学生数超过30人. 设九(1)班共有x 人去旅游,则人均费用为[100﹣2(x ﹣30)]元,由题意得: x[100﹣2(x ﹣30)]=3150,整理得x 2﹣80x+1575=0,解得x 1=35,x 2=45,当x=35时,人均旅游费用为100﹣2(35﹣30)=90>80,符合题意.当x=45时,人均旅游费用为100﹣2(45﹣30)=70<80,不符合题意,应舍去. 答:该班共有35名同学参加了研学旅游活动.考点:一元二次方程的应用.8.解方程:(x 2+x )2+(x 2+x )=6.【答案】x 1=﹣2,x 2=1【解析】【分析】设x 2+x =y ,将原方程变形整理为y 2+y ﹣6=0,求得y 的值,然后再解一元二次方程即可.【详解】解:设x 2+x =y ,则原方程变形为y 2+y ﹣6=0,解得y 1=﹣3,y 2=2.①当y =2时,x 2+x =2,即x 2+x ﹣2=0,解得x 1=﹣2,x 2=1;②当y =﹣3时,x 2+x =﹣3,即x 2+x+3=0,∵△=12﹣4×1×3=1﹣12=﹣11<0,∴此方程无解;∴原方程的解为x 1=﹣2,x 2=1.【点睛】本题考查了换元法和一元二次方程的解法,设出元化简原方程是解答本题的关键.9.阅读材料:若22228160m mn n n -+-+=,求m 、n 的值.解: 22228160m mn n n -+-+=,222(2)(816)0m mn n n n ∴-++-+=22()(4)0m n n ∴-+-=,0,40m n n ∴-=-=,4,4n m ∴==.根据你的观察,探究下面的问题:(1)己知2222210x xy y y ++++=,求x y -的值.(2)已知△ABC 的三边长a 、b 、c 都是正整数,且满足2268250a b a b +--+=,求边c 的最大值.(3) 若己知24,6130a b ab c c -=+-+=,求a b c -+的值.【答案】(1)2(2)6(3)7【解析】【分析】(1)将多项式第三项分项后,结合并利用完全平方公式化简,根据两个非负数之和为0,两非负数分别为0求出x 与y 的值,即可求出x ﹣y 的值;(2)将已知等式25分为9+16,重新结合后,利用完全平方公式化简,根据两个非负数之和为0,两非负数分别为0求出a 与b 的值,根据边长为正整数且三角形三边关系即可求出c 的长;(3)由a ﹣b =4,得到a =b +4,代入已知的等式中重新结合后,利用完全平方公式化简,根据两个非负数之和为0,两非负数分别为0求出b 与c 的值,进而求出a 的值,即可求出a ﹣b +c 的值.【详解】(1)∵x 2+2xy +2y 2+2y +1=0∴(x 2+2xy +y 2)+(y 2+2y +1)=0∴(x +y )2+(y +1)2=0∴x +y =0 y +1=0解得:x =1,y =﹣1∴x ﹣y =2;(2)∵a 2+b 2﹣6a ﹣8b +25=0∴(a 2﹣6a +9)+(b 2﹣8b +16)=0∴(a ﹣3)2+(b ﹣4)2=0∴a ﹣3=0,b ﹣4=0解得:a =3,b =4∵三角形两边之和>第三边∴c <a +b ,c <3+4,∴c <7.又∵c 是正整数,∴△ABC 的最大边c 的值为4,5,6,∴c 的最大值为6;(3)∵a ﹣b =4,即a =b +4,代入得:(b +4)b +c 2﹣6c +13=0,整理得:(b 2+4b +4)+(c 2﹣6c +9)=(b +2)2+(c ﹣3)2=0,∴b +2=0,且c ﹣3=0,即b =﹣2,c =3,a =2,则a ﹣b +c =2﹣(﹣2)+3=7.故答案为7.【点睛】本题考查了因式分解的应用,以及非负数的性质,熟练掌握完全平方公式是解答本题的关键.10.解方程:x 2-2x =2x +1.【答案】x 1=2,x 2=2【解析】试题分析:根据方程,求出系数a 、b 、c ,然后求一元二次方程的根的判别式,最后根据求根公式2b x a -=求解即可.试题解析:方程化为x 2-4x -1=0.∵b 2-4ac =(-4)2-4×1×(-1)=20,∴x=,∴x1=2,x 2=2。
全国各地中考数学压轴题精选(含详细答案)

12.(黄冈)已知:如图,在直角梯形COAB中,OC∥AB,以O为原点建立平面直角坐标系 ,A,B,C三点的坐标分别为A(8,0),B(8,10),C(0,4),点D为线段BC的中点, 动点P从点O出发,以每秒1个单位的速度,沿折线OABD的路线移动,移动的时间为t秒. (1)求直线BC的解析式; (2)若动点P在线段OA上移动,当t为何值时,四边形OPDC的面积是梯形COAB面积的 ; (3)动点P从点O出发,沿折线OABD的路线移动过程中,设△OPD的面积为S,请直接写出S 与t的函数关系式,并指出自变量t的取值范围;
8
点F重合时,梯形ABCD停止移动.观察得知:在梯形ABCD移动过程中,其腰BC始终经过坐 标原点O.(如图2) ①设点A的坐标为(a,b),梯形ABCD与梯形OEFG重合部分的面积为S,试求a与何值时, S的值恰好等于梯形OEFG面积的 ;
②当点A在EF上滑动时,设AD与x轴的交点为M,试问:在y轴上是否存在点P,使得△PAM 是底角为30°的等腰三角形?如果存在,请求出所有符合条件的点P的坐标;如果不存在, 请说明理由.(利用图3进行探索)
【最新】人教版九年级数学中考压轴试题(及答案解析)

【精品】人教版九年级数学中考压轴试题(含答案)1.(8分)一般地,我们把半径为1的圆叫做单位圆,在平面直角坐标系xOy中,设单位圆的圆心与坐标原点O重合,则单位圆与x轴的交点分别为(1,0),(﹣1,0),与y轴的交点分别为(0,1),(0,﹣1).在平面直角坐标系xOy中,设锐角a的顶点与坐标原点O重合,a的一边与x轴的正半轴重合,另一边与单位圆交于点P(x1,y1),且点P在第一象限.(1)x1= cosα(用含a的式子表示);y1= sinα(用含a的式子表示);(2)将射线OP绕坐标原点O按逆时针方向旋转90°后与单位圆交于点Q(x2,y2).①判断y1与x2的数量关系,并证明;②y1+y2的取值范围是:1<y1+y2≤..【分析】(1)如图作PF⊥x轴于F,QE⊥x轴于E.则OF=OP•cosα,PF=OP•sinα,由此即可解决问题;(2)①过点P作PF⊥x轴于点F,过点Q作QE⊥x轴于点E.只要证明△QOE≌△OPF即可解决问题;②当P在x轴上时,得到y1+y2的最小值为1,由y1+y2=PF+QE=OE+OF=EF,四边形QEFP是直角梯形,PQ=,EF≤PQ,即可推出当EF=PQ=时,得到y1+y2的最大值为;【解答】解:(1)如图作PF⊥x轴于F,QE⊥x轴于E.则OF=OP•cosα,PF=OP•sinα,∴x1=cosα,y1=sinα,故答案为cosα,sinα;(2)①结论:y1=﹣x2.理由:过点P作PF⊥x轴于点F,过点Q作QE⊥x轴于点E.∴∠PFO=∠QEO=∠POQ=90°,∴∠POF+∠OPF=90°,∠POF+∠QOE=90°,∴∠QOE=∠OPF,∵OQ=OP,∴△QOE≌△OPF,∴PF=OE,∵P(x1,y1),Q(x2,y2),∴PF=y1,OE=﹣x2,∴y1=﹣x2②当P在x轴上时,得到y1+y2的最小值为1,∵y1+y2=PF+QE=OE+OF=EF,∵四边形QEFP是直角梯形,PQ=,EF≤PQ,∴当EF=PQ=时,得到y1+y2的最大值为,∴1<y1+y2≤.故答案为1<y1+y2≤.【点评】本题考查圆综合题、解直角三角形、全等三角形的判定和性质、锐角三角函数、直角梯形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.2.(5分)点P(1,4),Q(2,m)是双曲线y=图象上一点.(1)求k值和m值.(2)O为坐标原点.过x轴上的动点R作x轴的垂线,交双曲线于点S,交直线OQ于点T,且点S在点T的上方.结合函数图象,直接写出R的横坐标n的取值范围.【分析】(1)利用待定系数法即可解决问题;(2)利用图象法即可解决问题;【解答】(1)解:∵点P(1,4),Q(2,m )是双曲线y=图象上一点.∴4=,m=,∴k=4,m=2.(2)观察函数图象可知,R的横坐标n的取值范围:0<n<2或n<﹣2.【点评】本题考查反比例函数图象上点的特征、待定系数法等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.3.(5分)小明同学要测量学校的国旗杆BD的高度.如图,学校的国旗杆与教学楼之间的距AB=20m.小明在教学楼三层的窗口C测得国旗杆顶点D的仰角为14°,旗杆底部B的俯角为22°.(1)求∠BCD的大小.(2)求国旗杆BD的高度(结果精确到1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin14°≈0.24,cos14°≈0.97,tan14°≈0.25)【分析】(1)过C作CE∥AB交BD于E.根据题意可得答案;(2)在Rt△CEB中,利用三角函数可得tan∠ECB=,代入数据可得BE的长,然后在Rt△CED中可得tan∠DCE==≈0.25,进而可得ED长,再求和即可.【解答】解:(1)过C作CE∥AB交BD于E.由已知,∠DCE=14°,∠ECB=22°,∴∠DCB=36°;(2)在Rt△CEB中,∠CEB=90°,AB=20,∠ECB=22°,∴tan∠ECB==≈0.4,∴BE≈8,在Rt△CED中,∠CED=90°,CE=AB=20,∠DCE=14°,∴tan∠DCE==≈0.25,∴DE≈5,∴BD≈13,∴国旗杆BD的高度约为13米.【点评】此题主要考查了解直角三角形的应用,关键是读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.4.(5分)如图,AB是⊙O的直径,C、D是⊙O上两点, =.过点B作⊙O的切线,连接AC并延长交于点E,连接AD并延长交于点F.(1)求证:AC=CE.(2)若AE=8,sin∠BAF=求DF长.【分析】(1)连接BC,想办法证明AC=BC,EC=BC即可解决问题;(2)首先证明∠DBF=∠BAF,可得sin∠BAF=sin∠DBF==,由此即可解决问题;【解答】(1)证明:连结BC.∵AB是的直径,C在⊙O上∴∠ACB=90°,∵=,∴AC=BC∴∠CAB=45°.∵AB是⊙O的直径,EF切⊙O于点B,∴∠ABE=90°,∴∠AEB=45°,∴AB=BE,∴AC=CE.(2)在Rt△ABE中,∠ABE=90°,AE=8,AE=BE∴AB=8,在Rt△ABF中,AB=8,sin∠BAF=,解得:BF=6,连结BD,则∠ADB=∠FDB=90°,∵∠BAF+∠ABD=90°,∠ABD+∠DBF=90°,∴∠DBF=∠BAF,∵sin∠BAF=,∴sin∠DBF=,∴=,∴DF=.【点评】本题考查切线的性质、圆周角定理、解直角三角形、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.5.如图,P是所对弦AB上一动点,过点P作PC⊥AB交于点C,取AP中点D,连接CD.已知AB=6cm,设A,P两点间的距离为xcm,C.D两点间的距离为ycm.(当点P与点A重合时,y的值为0;当点P与点B重合时,y的值为3)小凡根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小凡的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:x/cm0 1 2 3 4 5 6y/cm0 2.2 2.9 3.2 3.4 3.3 3 (2)建立平面直角坐标系,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合所画出的函数图象,解决问题:当∠C=30°时,AP的长度约为 3.3 cm.【分析】(1)根据对称性可知:当x=2和x=4时,PA=BP′=2,因为PC⊥AB,P′C′⊥AB,即可推出PC=P′C′=,再利用勾股定理即可解决问题;(2)利用描点法即可解决问题;(3)函数图象与直线y=x的交点的横坐标即为PA的长,利用图象法即可解决问题;【解答】解:(1)如图,根据对称性可知:根据对称性可知:当x=2和x=4时,PA=BP′=2,∵PC⊥AB,P′C′⊥AB,∴PC=P′C′=,∴CD=≈2.9.故答案为2.9.(2)利用描点法画出图象如图所示:(3)当∠DCP=30°时,CD=2PD,即y=x,观察图象可知:与函数图象与直线y=x的交点为(3.3,3.3),∴AP的长度为3.3.【点评】本题属于圆综合题,考查了勾股定理,函数图象,直角三角形30度角的性质等知识,解题的关键是理解题意,学会利用对称性解决问题,学会利用图象法解决问题,属于中考压轴题.6.如图,△ABC是等边三角形,D,E分别是AC,BC边上的点,且AD=CE,连接BD,AE相交于点F.(1)∠BFE的度数是60°;(2)如果=,那么= 1 ;(3)如果=时,请用含n的式子表示AF,BF的数量关系,并证明.【分析】(1)易证△ABD≌△ACE,可得∠DAF=∠ABF,根据外角等于不相邻两个内角的和即可解题.(2)如图1中,当=时,由题意可知:AD=CD,BE=CE.利用等腰三角形的性质即可解决问题;(3)设AF=x,BF=y,AB=BC=AC=n.AD=CE=1,由△ABD≌△CAE,推出BD=AE,设BD=AE=m,利用相似三角形的性质,列出关系式即可解决问题;【解答】解:(1)∵△ABC是等边三角形,∴AB=AC,∠BAD=∠C=60°,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS)∴∠DAF=∠ABD,∴∠BFE=∠ABD+∠BAF=∠DAF+∠BAF=∠BAD=60°,故答案为:60°.(2)如图1中,当=时,由题意可知:AD=CD,BE=CE.∵△ABC是等边三角形,BE=EC,AD=CD,∴∠BAE=∠BAC=×60°=30°,∠ABD=∠ABC=30°,∴∠FAB=∠FBA,∴FA=FB,∴=1.故答案为1.(3)设AF=x,BF=y,AB=BC=AC=n.AD=CE=1,∵△ABD≌△CAE,∴BD=AE,∠DAF=∠ABD,设BD=AE=m,∵∠ADF=∠BDA,∴△ADF∽△BDA,∴=,∴=①,∵∠FBE=∠CBD,∠BFE=∠C=60°,∴△BFE∽△BCD,∴=,∴=②,①÷②得到:=,∴=.【点评】本题属于三角形综合题,考查了等边三角形的性质,相似三角形的判定和性质的等知识,解题的关键是正确寻找相似三角形解决问题,学会利用参数解决问题,属于中考压轴题.7.对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C 上存在一个点M,使得MP=MC,则称点P为⊙C的“等径点”,已知点D(,),E(0,2),F(﹣2,0).(1)当⊙O的半径为1时,①在点D,E,F中,⊙O的“等径点”是D,E;②作直线EF,若直线EF上的点T(m,n)是⊙O的“等径点”,求m的取值范围.(2)过点E作EG⊥EF交x轴于点G,若△EFG各边上所有的点都是某个圆的“等径点”,求这个圆的半径r的取值范围.【分析】(1)①根据“等径点”的定义可知,“等径点”到圆心的距离小于等于圆的半径的2倍,由此即可判定;②如图2中,设直线EF交半径为2的⊙O于点K,连接OK,作KM⊥OF于M.当点T在线段FK上时,点T是“等径点”,求出点K的坐标即可解决问题;(2)因为△EFG各边上所有的点都是某个圆的“等径点”,所以这个圆的圆心Q是线段FG的中点,易知Q(2,0),设这个圆的半径为r.根据QG≤2r,构建不等式即可解决问题;【解答】解:(1)根据“等径点”的定义可知,“等径点”到圆心的距离小于等于圆的半径的2倍.即半径为1的⊙O的“等径点”在以O为圆心2为半径的圆内或圆上.如图1中,观察图象可知:在点D,E,F中,⊙O的“等径点”是D,E.故答案为D,E;②如图2中,设直线EF交半径为2的⊙O于点K,连接OK,作KM⊥OF于M.∵OF=2,OE=2,∴tan∠EFO==,∴∠OFK=60°,∵OF=OK,∴△OFK是等边三角形,∴OF=OK=FK=2,∵KM⊥OF,∴FM=OM=1,KM==,∴K(﹣1,),∵当点T在线段FK上时,点T是“等径点”,∴﹣2≤m≤﹣1.(2)如图3中,∵△EFG是直角三角形,∠FEG=90°,∠EFG=60°,∴EF=2OF=4,FG=2EF=8,∴OG=6,由题意△EFG各边上所有的点都是某个圆的“等径点”,这个圆的圆心Q是线段FG的中点,Q(2,0),设这个圆的半径为r.由题意:QG≤2r∴4≤2r,∴r≥2,即这个圆的半径r的取值范围为r≥2.【点评】本题属于圆综合题,考查了“等径点”的定义,解直角三角形,勾股定理,锐角三角函数等知识,解题的关键是理解题意,学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.。
初中数学中考数学压轴题(讲义及答案)附解析

一、中考数学压轴题1.已知AM//CN,点B为平面内一点,AB⊥BC于B.(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠EBC的度数.2.综合与实践A纸是我们学习工作最常用的纸张之一,其长宽之比是2:1,我们定义:长宽之比是42:1的矩形纸片称为“标准纸”.操作判断:()1如图1所示,矩形纸片2=是一张“标准纸”,将纸片折叠一次,使点()ABCD AD ABAB=求CF的B与D重合,再展开,折痕EF交AD边于点,E交BC边于点F,若1,长,()2如图2,在()1的基础上,连接,BD折痕EF交BD于点O,连接,BE判断四边形BFDE的形状,并说明理由.探究发现:()3如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点A 与点C 重合,再展开,痕MN 交AD 边于点M ,BC 交边于点,N 交BD 也是点O .然后将四边形ENFM 剪下,探究纸片ENFM 是否为“标准纸”,说明理由.3.如果关于x 的一元二次方程20ax bx c ++=有两个不相等的实数根,且其中一个根为另一个根的一半,则称这样的方程为“半等分根方程”.(1)①方程2280x x --= 半等分根方程(填“是”或“不是”);②若(1)()0x mx n -+=是半等分根方程,则代数式2252m mn n ++= ; (2)若点(,)p q 在反比例函数8x y =的图象上,则关于x 的方程260px x q -+=是半等分根方程吗?并说明理由; (3)如果方程20ax bx c ++=是半等分根方程,且相异两点(1,)M t s +,(4,)N t s -都在抛物线2y ax bx c =++上,试说明方程20ax bx c ++=的一个根为53. 4.如图,在平面直角坐标中,点O 为坐标原点,ABC ∆的三个顶点坐标分别为()A O m ,,(),B m O -,(),C n O ,5AC =且OBA OAB ∠=∠,其中m ,n 满足725m n m n +=⎧⎨-=⎩.(1)求点A ,C 的坐标;(2)点P 从点A 出发,以每秒1个单位长度的速度沿y 轴负方向运动,设点P 的运动时间为t 秒.连接BP 、CP ,用含有t 的式子表示BPC ∆的面积为S (直接写出t 的取值范围);(3)在(2)的条件下,是否存在t 的值,使得ΔΔ32PAB POC S S =,若存在,请求出t 的值,并直接写出BP 中点Q 的坐标;若不存,请说明理由.5.如图一,矩形ABCD 中,AB=m ,BC=n ,将此矩形绕点B 顺时针方向旋转θ(0°<θ<90°)得到矩形A 1BC 1D 1,点A 1在边CD 上.(1)若m=2,n=1,求在旋转过程中,点D 到点D 1所经过路径的长度;(2)将矩形A 1BC 1D 1继续绕点B 顺时针方向旋转得到矩形A 2BC 2D 2,点D 2在BC 的延长线上,设边A 2B 与CD 交于点E ,若161A E EC=-,求n m 的值. (3)如图二,在(2)的条件下,直线AB 上有一点P ,BP=2,点E 是直线DC 上一动点,在BE 左侧作矩形BEFG 且始终保持BE n BG m =,设AB=33,试探究点E 移动过程中,PF 是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.6.如图,抛物线2y x bx c =-++与x 轴相交于A 、B 两点,与y 轴相交于点C ,且点B 与点C 的坐标分别为()3,0B ,()0,3C ,点M 是抛物线的顶点.(1)求二次函数的关系式.(2)点P 为线段MB 上一个动点,过点P 作PD x ⊥轴于点D .若OD m =,PCD 的面积为S .①求S 与m 的函数关系式,写出自变量m 的取值范围.②当S 取得最值时,求点P 的坐标.(3)在MB 上是否存在点P ,使PCD 为直角三角形?如果存在,请直接写出点P 的坐标;如果不存在,请说明理由.7.平面直角坐标系中,点A 、B 分别在x 轴正半轴、y 轴正半轴上,AO =BO ,△ABO 的面积为8.(1)求点A 的坐标;(2)点C 、D 分别在x 轴负半轴、y 轴正半轴上(D 在B 点上方),AB ⊥CD 于E ,设点D 纵坐标为t ,△BCE 的面积为S ,求S 与t 的函数关系;(3)在(2)的条件下,点F 为BE 中点,连接OF 交BC 于G ,当∠FOB +∠DAE =45°时,求点E 坐标.8.对于平面内的点M 和点N ,给出如下定义:点P 为平面内的一点,若点P 使得PMN 是以M ∠为顶角且M ∠小于90°的等腰三角形,则称点P 是点M 关于点N 的锐角等腰点P .如图,点P 是点M 关于点N 的锐角等腰点.在平面直角坐标系xOy 中,点O 是坐标原点.(1)已知点(2,0)A ,在点123(0,2),(1,3),(1,3)P P P -,4(2,2)P -中,是点O 关于点A 的锐角等腰点的是___________.(2)已知点(3,0)A ,点C 在直线2y x b =+上,若点C 是点O 关于点A 的锐角等腰点,求实数b 的取值范围.(3)点D 是x 轴上的动点,(,0),(2,0)D t E t -,点(,)F m n 是以D 为圆心,2为半径的圆上一个动点,且满足0n ≥.直线24y x =-+与x 轴和y 轴分别交于点H K ,,若线段HK 上存在点E 关于点F 的锐角等腰点,请直接写出t 的取值范围.9.小明研究了这样一道几何题:如图1,在ABC 中,把AB 绕点A 顺时针旋转()0180a a ︒<<︒得到AB ',把AC 绕点A 逆时针旋转β得到AC ',连接B C ''.当180a β+=︒时,请问AB C ''△边B C ''上的中线AD 与BC 的数量关系是什么?以下是他的研究过程:特例验证:(1)①如图2,当ABC 为等边三角形时,猜想AD 与BC 的数量关系为AD =_______BC ;②如图3,当90BAC ∠=︒,8BC =时,则AD 长为________. 猜想论证:(2)在图1中,当ABC 为任意三角形时,猜想AD 与BC 的数量关系,并给予证明.拓展应用:(3)如图4,在四边形ABCD ,90C ∠=︒,120A B ∠+∠=︒,3BC =6CD =,3DA =P ,使PDC △与PAB △之间满足小明探究的问题中的边角关系?若存在,请画出点P 的位置(保留作图痕迹,不需要说明)并直接写出PDC △的边DC 上的中线PQ 的长度;若不存在,说明理由.10.已知:菱形 ABCD ,点 E 在线段 BC 上,连接 DE ,点 F 在线段 AB 上,连接 CF 、DF , CF 与 DE 交于点 G ,将菱形 ABCD 沿 DF 翻折,点 A 恰好落在点 G 上.(1)求证:CD=CF ;(2)设∠CED = x ,∠DCF = y ,求 y 与 x 的函数关系式;(不要求写出自变量的取值范围) (3)在(2)的条件下,当 x =45°时,以 CD 为底边作等腰△CDK ,顶角顶点 K 在菱形 ABCD 的内部,连接 GK ,若 GK ∥CD ,CD =4 时,求线段 KG 的长.11.如图,抛物线214y x bx c =++与x 轴交于点A (-2,0),交y 轴于点B (0,52-).直线32y kx =+过点A 与y 轴交于点C ,与抛物线的另一个交点是D .(1) 求抛物线214y x bx c =++与直线32y kx =+的解析式; (2)点P 是抛物线上A 、D 间的一个动点,过P 点作PM ∥CE 交线段AD 于M 点.①过D 点作DE ⊥y 轴于点E ,问是否存在P 点使得四边形PMEC 为平行四边形?若存在,请求出点P 的坐标;若不存在,请说明理由;②作PN ⊥AD 于点N ,设△PMN 的周长为m ,点P 的横坐标为x ,求m 关于x 的函数关系式,并求出m 的最大值.12.如图,已知抛物线y =2ax bx c ++与x 轴交于A 3,0-(),B 33,0()两点,与y 轴交于点C 0,3().(1)求抛物线的解析式及顶点M 坐标;(2)在抛物线的对称轴上找到点P ,使得PAC 的周长最小,并求出点P 的坐标; (3)在(2)的条件下,若点D 是线段OC 上的一个动点(不与点O 、C 重合).过点D 作DE //PC 交x 轴于点E .设CD 的长为m ,问当m 取何值时,PDE ABMC 1S S 9=四边形. 13.在平面直角坐标系中,直线4(0)3y x b b =-+>交x 轴于点A ,交y 轴于点B ,10AB =.(1)如图1,求b 的值;(2)如图2,经过点B 的直线(4)(40)y n x b n =++-<<与直线y nx =交于点C ,与x 轴交于点R ,//CD OA ,交AB 于点D ,设线段CD 长为d ,求d 与n 的函数关系式; (3)如图3,在(2)的条件下,点F 在第四象限,CF 交OA 于点E ,45AEF ∠=︒,点P 在第一象限,PH OA ⊥,点N 在x 轴上,点M 在PH 上,MN 交PE 于点G ,PH EN =,过点E 作EQ CF ⊥,交PH 于点Q , 32==EQ EF PM ,∠=∠OBR HNM ,BC CR =,点G 的坐标为1927,55⎛⎫ ⎪⎝⎭,连接FN ,求EFN 的面积.14.在ABC ∆中,若存在一个内角角度,是另外一个内角角度的n 倍(n 为大于1的正整数),则称ABC ∆为n 倍角三角形.例如,在ABC ∆中,80A ∠=︒,75B ∠=︒,25C ∠=︒,可知3∠=∠B C ,所以ABC ∆为3倍角三角形.(1)在ABC ∆中,55A ∠=︒,25B ∠=︒,则ABC ∆为________倍角三角形;(2)若DEF ∆是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的13,求DEF ∆的最小内角. (3)若MNP ∆是2倍角三角形,且90M N P ∠<∠<∠<︒,请直接写出MNP ∆的最小内角的取值范围.15.在菱形ABCD 中,P 为直线DA 上的点,Q 为直线CD 上的点,分别连接PC ,PQ ,且PC PQ =.(1)若60B ∠=︒,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图①,易证:DQ PD AB +=(不需证明);(2)如图②,若∠B =120°,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图③,猜想线段DQ ,PD 和AB 之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.16.如图,在平面直角坐标系中,Rt ABC △的斜边在AB 在x 轴上,点C 在y 轴上90ACB ∠=︒,OC 、OB 的长分别是一元二次方程2680x x -+=的两个根,且OC OB <.(1)求点A 的坐标;(2)D 是线段AB 上的一个动点(点D 不与点A ,B 重合),过点D 的直线l 与y 轴平行,直线l 交边AC 或边BC 于点P ,设点D 的横坐标为t ,线段DP 的长为d ,求d 关于t 的函数解析式;(3)在(2)的条件下,当12d =时,请你直接写出点P 的坐标.17.已知抛物线y=﹣x 2﹣2x+3交x 轴于点A 、C (点A 在点C 左侧),交y 轴于点B .(1)求A ,B ,C 三点坐标;(2)如图1,点D 为AC 中点,点E 在线段BD 上,且BE=2DE ,连接CE 并延长交抛物线于点M ,求点M 坐标;(3)如图2,将直线AB 绕点A 按逆时针方向旋转15°后交y 轴于点G ,连接CG ,点P 为△ACG 内一点,连接PA 、PC 、PG ,分别以AP 、AG 为边,在它们的左侧作等边△APR 和等边△AGQ ,求PA+PC+PG 的最小值,并求当PA+PC+PG 取得最小值时点P 的坐标(直接写出结果即可).18.如图,在平面直角坐标系中,矩形ABCD 的顶点,A D 在坐标轴上,两点的坐标分别是点()0,,A m 点(),0,D m 且m 322m m -62=AB 与x 轴交于点,E 点F 是边AD 上一动点,连接FB ,分别与x 轴,y 轴交于点,P 点,H 且FD BE =.(1)求m 的值;(2)若45,APF ∠=︒求证:AHF HFA ∠=∠;(3)若点F 的纵坐标为,n 则线段HF 的长为 .(用含n 的代数式表示)19.在Rt ABC ∆中,6AB =,90B ∠=︒,8BC =,点P 从A 出发沿AC 方向在运动速度为3个单位/秒,点Q 从C 出发向点B 运动,速度为1个单位/秒,P 、Q 同时出发,点Q 到点B 时两点同时停止运动.(1)点P 在线段AC 上运动,过P 作DP PQ ⊥交边AB 于D ,2t =时,求PD PQ的值; (2)运动t 秒后,90BPQ ∠=︒,求此时t 的值;(3)t =________时,AQ QP =. 20. 在平面直角坐标系中,点O 为坐标原点,直线y =﹣x+4与x 轴交于点A ,过点A 的抛物线y =ax 2+bx 与直线y =﹣x+4交于另一点B ,且点B 的横坐标为1.(1)该抛物线的解析式为;(2)如图1,Q为抛物线上位于直线AB上方的一动点(不与B、A重合),过Q作QP⊥x 轴,交x轴于P,连接AQ,M为AQ中点,连接PM,过M作MN⊥PM交直线AB于N,若点P的横坐标为t,点N的横坐标为n,求n与t的函数关系式;在此条件下,如图2,连接QN并延长,交y轴于E,连接AE,求t为何值时,MN∥AE.(3)如图3,将直线AB绕点A顺时针旋转15度交抛物线对称轴于点C,点T为线段OA 上的一动点(不与O、A重合),以点O为圆心、以OT为半径的圆弧与线段OC交于点D,以点A为圆心、以AT为半径的圆弧与线段AC交于点F,连接DF.在点T运动的过程中,四边形ODFA的面积有最大值还是有最小值?请求出该值.21.如图,四边形AOBC是正方形,点C的坐标是(82,0).(1)正方形AOBC的边长为,点A的坐标是;(2)将正方形AOBC绕点O顺时针旋转45︒,点A,B,C旋转后的对应点为A',B',C',求点A'的坐标及旋转后的正方形与原正方形的重叠部分的面积;(3)动点P从点O出发,沿折线OACB方向以1个单位/秒的速度匀速运动,同时,另一动点Q从点O出发,沿折线OBCA方向以2个单位/秒的速度匀速运动,运动时间为t△为等腰三角形时,求出t的值(直接写出结果秒,当它们相遇时同时停止运动,当OPQ即可).22.如图,在▱ABCD中,对角线AC⊥BC,∠BAC=30°,BC=23,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,则AF=_____.23.已知四边形ABCD为矩形,对角线AC、BD相交于点O,AD=AO.点E、F为矩形边上的两个动点,且∠EOF=60°.(1)如图1,当点E、F分别位于AB、AD边上时,若∠OEB=75°,求证:DF=AE;(2)如图2,当点E、F同时位于AB边上时,若∠OFB=75°,试说明AF与BE的数量关系;(3)如图3,当点E 、F 同时在AB 边上运动时,将△OEF 沿OE 所在直线翻折至△OEP ,取线段CB 的中点Q .连接PQ ,若AD =2a (a >0),则当PQ 最短时,求PF 之长.24.如图,在ABC 中,35,7,tan 4AB BC B ===,动点P 从点A 出发,沿AB 以每秒53个单位长度的速度向终点B 运动,过P 作PQ BC ,交AC 于点Q ,以PQ PB 、为邻边作平行四边形PQDB ,同时以PQ 为边向下作正方形PQEF ,设点P 的运动时间为t 秒()0t >.(1)点A 到直线EF 的距离______________;(用含t 的代数式表示)(2)当点D 落在落在PF 上时,求t 的值;(3)设平行四边形PQDB 与正方形PQEF 重叠部分的面积为()0S S >,求S 与t 之间的函数关系式,并求出S 的最大值.(4)设:PDE APE S S m =△△,当112m 时,直接写出t 的取值范围.25.如图,在等边△ABC 中,AB =BC =AC =6cm ,点P 从点B 出发,沿B →C 方向以1.5cm/s 的速度运动到点C 停止,同时点Q 从点A 出发,沿A →B 方向以1cm/s 的速度运动,当点P 停止运动时,点Q 也随之停止运动,连接PQ ,过点P 作BC 的垂线,过点Q 作BC 的平行线,两直线相交于点M .设点P 的运动时间为x (s ),△MPQ 与△ABC 重叠部分的面积为y (cm 2)(规定:线段是面积为0的图形).(1)当x = (s )时,PQ ⊥BC ;(2)当点M 落在AC 边上时,x = (s );(3)求y 关于x 的函数解析式,并写出自变量x 的取值范围.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题1.A解析:(1)∠A+∠C=90°;(2)证明见解析;(3)99°.【解析】【分析】(1)根据平行线的性质以及直角三角形的性质进行证明即可;(2)先过点B作BG∥DM,根据同角的余角相等,得出∠ABD=∠CBG,再根据平行线的性质,得出∠C=∠CBG,即可得到∠ABD=∠C;(3)先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,再设∠DBE=a,∠ABF=b,根据∠CBF+∠BFC+∠BCF=180°,可得(2a+b)+5a+(5a+b)=180°,根据AB⊥BC,可得b+b+2a=90°,最后解方程组即可得到∠ABE=9°,即可得出∠EBC的度数.【详解】解:(1)如图1,设AM与BC的交点为O,AM//CN,∴∠C=∠AOB,∵AB⊥BC,∴∠ABO=90°,∴∠A+∠AOB=90°,即∠A+∠C=90°,故答案为:∠A+∠C=90°;(2)证明:如图2,过点B作BG//DM,∵BD AM,∴∠BDM=90°,∵BG//DM,BDM DBG,∴∠+∠=︒180∴90∠=︒DBG ,即∠ABD +∠ABG =90°,∵AB BC ⊥,∴∠ABC =90°,∴∠CBG +∠ABG =90°,∴∠ABD =∠CBG ,∵AM //CN ,BG //DM ,∴BG //CN ,∴∠C =∠CBG ,∴∠ABD =∠C ;(3)如图3,过点B 作BG //DM ,∵BF 平分∠DBC ,BE 平分∠ABD ,∴∠DBF =∠CBF ,∠DBE =∠ABE ,由(2)可得∠ABD =∠CBG ,∴∠-∠=∠-∠DBF ABD CBF CBG ,即∠ABF =∠GBF ,设∠DBE =a ,∠ABF =b ,则∠ABE =a ,∠ABD =∠CBG =2a ,∠GBF =∠ABF =b ,∠BFC =5∠DBE =5a ,∴∠CBF =∠CBG +∠GBF =2a +b ,∵BG //DM ,∴∠AFB =∠GBF =b ,∴∠AFC =∠BFC +∠AFB =5a +b ,∵AM //CN ,∴∠AFC +∠NCF =180°,∵∠FCB +∠NCF =180°,∴∠FCB =∠AFC =5a +b ,在△BCF 中,由∠CBF +∠BFC +∠BCF =180°可得:(2a +b )+5a +(5a +b )=180°,化简得:6=90+︒a b ,由AB BC ,可得:b +b +2a =90°,化简得:=45+︒a b ,联立6=9045a b a b +︒⎧⎨+=︒⎩,解得:=936a b ︒⎧⎨=︒⎩, ∴∠ABE =9°,∴∠EBC =∠ABE +∠ABC =9°+90°=99°.【点睛】本题主要考查了平行线的性质的运用,解决问题的关键是作平行线构造内错角,运用等角的余角(补角)相等进行推导.余角和补角计算的应用,常常与等式的性质、等量代换相关联.解题时注意方程思想的运用.2.(1) CF ;(2) 四边形BFDE 是菱形,理由见解析;(3) 纸片ENFM 是“标准纸",理由见解析【解析】【分析】(1)1AB =,则AD =ABCD 是矩形,得到1,CD AB BC AD ==-=FB FD =,设CF x =,则FB FD x ==,在Rt DCF △中,222+=CD CF DF ,可得)2221x x +=即可求解.(2)当顶点B 与点D 重合时,折痕EF 垂直平分BD ,可得OB OD =,90BOF DOE ∠=∠=,在矩形ABCD 中,//AD BC ,得到OBF ODE ∠=∠,在BOF 和DOE △中,,OBF ODE OB OD BOF DOE ∠=∠=∠=∠,,可得BOF DOE ≅,OE OF =,再根据OB OD =,可得四边形BFDE 是平行四边形,最后根据EF BD ⊥,即可求证平行四边形BFDE 是菱形.(3)由()2可知,OE OF =,同理可知,OM ON =,可得四边形ENFM 是平行四边形,根据90DOE DAB ∠=∠=︒,得到DOE DAB ,再根据AD =,可得2OE AB OD AD ===,进而得到2OE OD =,2EF BD =,同理可得,2MN AC =,根据四边形ABCD 是矩形,可得AC BD =,EF MN =,四边形ENFM是矩形,90EMF ∠=,MF OD tan FEM ME OE ∠===MF =,即可求证纸片ENFM 是“标准纸".【详解】解:()11,AB =则AD AB ==四边形ABCD 是矩形1,CD AB BC AD ∴==-=由折叠得FB FD =设CF x =,则FB FD x ==在Rt DCF △中,222+=CD CF DF)2221x x +=24x = 答:CF 长为24()2四边形BFDE 是菱形.理由:当顶点B 与点D 重合时,折痕EF 垂直平分,BDOB OD ∴=,90BOF DOE ∠=∠=在矩形ABCD 中,//,AD BCOBF ODE ∴∠=∠在BOF 和DOE △中,,OBF ODE OB OD BOF DOE ∠=∠=∠=∠,BOF DOE ∴≅OE OF ∴=OB OD =∴四边形BFDE 是平行四边形EF BD ⊥平行四边形BFDE 是菱形.()3纸片ENFM 是“标准纸”理由如下:由()2可知,,OE OF =同理可知,,OM ON =∴四边形ENFM 是平行四边形90DOE DAB ∠=∠=︒DOE DAB ∴2AD =2OE AB OD AD ∴===OE ∴=2EF BD ∴=同理可得,2MN AC = 四边形ABCD 是矩形,AC BD ∴=,EF MN ∴=∴四边形ENFM 是矩形.90EMF ∴∠=.MF OD tan FEM ME OE∴∠===MF ∴=.∴纸片ENFM 是“标准纸".【点睛】此题主要考查矩形的判定和性质、勾股定理、全等三角形的判定和性质、菱形的判定及三角函数,灵活运用判定和性质是解题关键.3.(1)①不是;②0;(2)若点(,)p q 在反比例函数8y x=的图象上,则关于x 的方程260px x q -+=是半等分根方程,理由详见解析;(3)详见解析【解析】【分析】(1)①解方程2280x x --=,根据“半等分根方程”定义作出判断即可;②解方程(1)()0x mx n -+=得11x =,2n x m =-,所以12n m -=或2n m -=,即:n =-2m 或m =-2n ,分别代入代数式2252m mn n ++=结果均为0 (2)根据点(,)p q 在反比例函数8y x =的图象上,得到8q p =,代入260px x q -+=,得到关于x 的方程2860px x p-+=,解方程,用含p 的式子表示x ,根据“半等分根方程”定义判断即可; (3)根据两点(1,)M t s +,(4,)N t s -都在抛物线上,且纵坐标相等,可以求出对称轴为52x =,根据方程20ax bx c ++=是半等分根方程,得到两根关系,根据抛物线对称轴为 12522x x +=,即可求出两个根,问题得证. 【详解】解:(1)①解方程2280x x --=得124,2x x ==-,不符合“半等分根方程”定义, 故答案为:不是;②解方程(1)()0x mx n -+=得11x =,2n x m =-,所以12n m -=或2n m-=,即:n =-2m 或m =-2n , 当n =-2m 时,()()22225522022m mn n m m n m ++=+-+-=; 当m =-2n 时,()()22225522022m mn n n n n n ++=-+-+=; 故答案为:0;(2)若点(,)p q 在反比例函数8y x=的图象上,则关于x 的方程260px x q -+=是半等分根方程理由:∵点(,)p q 在反比例函数8y x=的图象上 ∴8q p =代入方程260px x q -+=得: 2860px x p -+= 解得:12x p =,24x p = ∵1212x x = ∴方程260px x q -+=是半等分根方程(3)∵相异两点(1,)M t s +,(4,)N t s -都在抛物线2y ax bx c =++上, ∴抛物线的对称轴为:(1)(4)522t t x ++-== 又∵方程20ax bx c ++=是半等分根方程∴设20ax bx c ++=的两个根分别为1x 和2x 令1212x x =则有:12522x x += 所以153x =,2103x =所以方程20ax bx c ++=的一个根为53得证. 【点睛】本题为“新定义问题”,考查了学生自主学习的能力,解决此题关键是理解新定义概念,并结合所学数学知识进行解答.4.A 解析:(1)A (0,4),C (3,0);(2)S=()()51004251042t t t t ⎧-+<<⎪⎪⎨⎪->⎪⎩;(3)存在,满足条件的t 的值为3617或36,点Q 的坐标为162,17⎛⎫- ⎪⎝⎭或()2,16--. 【解析】【分析】(1)解方程组求出m ,n 即可解决问题.(2)分两种情形:如图1中,当0<t <4时,如图2中,当t >4时,根据S=12•BC•OP 求解即可.(3)分两种情形分别构建方程求解即可.【详解】 解:(1)由725m n m n +=⎧⎨-=⎩, 解得:43m n =⎧⎨=⎩, ∴A (0,4),C (3,0);(2)如图1中,当0<t <4时,S=12•BC•OP=12×5×(4-t )=-52t+10. 如图2中,当t >4时,S=12•BC•OP=12×5×(t-4)=52t-10. 综上所述,S=()()51004251042t t t t ⎧-+<<⎪⎪⎨⎪->⎪⎩, (3)当04t <<时,由题意,1314(4)3222t t ⨯⨯=⨯⨯-⨯, 解得3617t =, 此时,363241717OP =-=, 32(0,)17P ∴, (4,0)B -,BQ ∴的中点Q 的坐标为162,17⎛⎫- ⎪⎝⎭, 当4t >时,由题意,1314(4)3222t t ⨯⨯=⨯⨯-⨯, 解得36t =,此时36432OP =-=,(0,32)P ∴-,(4,0)B -,BP ∴的中点Q 的坐标为(2,16)--.综上所述,满足条件的t 的值为3617或36.点Q 的坐标为16(2,)17-或(2,16)--. 【点睛】本题属于三角形综合题,考查了解方程组,三角形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型. 5.A解析:(15;(233)存在,63【解析】【分析】(1)作A 1H ⊥AB 于H ,连接BD ,BD 1,则四边形ADA 1H 是矩形.解直角三角形,求出∠ABA 1,得到旋转角即可解决问题;(2)由△BCE ∽△BA 2D 2,推出222A D CE n CB A B m ==,可得CE=2n m,由161A E EC =-推出16A C EC =,推出A 1C=26n m •,推出BH=A 1C=26n m•,然后由勾股定理建立方程,解方程即可解决问题;(3)当A 、P 、F ,D ,四点共圆,作PF ⊥DF ,PF 与CD 相交于点M ,作MN ⊥AB ,此时PF 的长度为最小值;先证明△FDG ∽△FME ,得到3FG F FM FE D ==,再结合已知条件和解直角三角形求出PM 和FM 的长度,即可得到PF 的最小值.【详解】解:(1)作A 1H ⊥AB 于H ,连接BD ,BD 1,则四边形ADA 1H 是矩形.∴AD=HA 1=n=1,在Rt △A 1HB 中,∵BA 1=BA=m=2,∴BA 1=2HA 1,∴∠ABA 1=30°,∴旋转角为30°,∵22125+=∴D 到点D 1所经过路径的长度3055π⋅⋅=; (2)∵△BCE ∽△BA 2D 2, ∴222A D CE n CB A B m==, ∴2n CE m=, ∵161EA EC=,∴16A C EC =, ∴A 1C=26n m⋅, ∴BH=A 1C=2226n m n m -=⋅, ∴42226n m n m-=⋅, ∴m 4﹣m 2n 2=6n 4, ∴242416n n m m-=•, ∴3n m =(负根已舍去). (3)当A 、P 、F ,D ,四点共圆,作PF ⊥DF ,PF 与CD 相交于点M ,作MN ⊥AB ,此时PF 的长度为最小值;由(2)可知,3BE n BG m ==, ∵四边形BEFG 是矩形,∴3FG FE = ∵∠DFG+∠GFM=∠GFM+∠MFE=90°,∴∠DFG=∠MFE ,∵DF ⊥PF ,即∠DFM=90°,∴∠FDM+∠GDM=∠FDM+∠DFM=∠FDM+90°,∴∠FDG=∠FME ,∴△FDG ∽△FME ,∴3FG F FM FE D ==, ∵∠DFM=90°,tan 3FD FMD FM ∠==,∴∠FDM=60°,∠FMD=30°,∴FM DM =;在矩形ABCD 中,有AD AB =3=,则3AD =, ∵MN ⊥AB ,∴四边形ANMD 是矩形,∴MN=AD=3,∵∠NPM=∠DMF=30°,∴PM=2MN=6,∴NP=AB =,∴DM=AN=BP=2,∴2FM DM ===∴6PF PM MF =+=【点睛】本题考查点的运动轨迹,旋转变换、解直角三角形、弧长公式、矩形的性质、相似三角形的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于压轴题,中考常考题型.正确作出辅助线,正确确定动点的位置,注意利用数形结合的思想进行解题.6.B解析:(1)2y x 2x 3=-++;(2)①23S m m =-+,13m ≤≤;②P (32,3);(3)3,32⎛⎫ ⎪⎝⎭或(3-+-【解析】【分析】(1)将点B 、C 的坐标代入2y x bx c =-++即可; (2)①求出顶点坐标,直线MB 的解析式等,由PD ⊥x 轴且OD=m 知P (m ,-2m+6),即可用含m 的代数式表示出S ;②在和①的情况下,将S 和m 的关系式化为顶点式,由二次函数的图象和性质即可写出点P 的坐标;(3)分情况讨论,当∠CPD=90°时,推出PD=CO=3,则点P 的纵坐标为3,即可求出点P 的坐标;当∠PCD=90°时,证∠PDC=∠OCD ,由锐角三角函数可求出m 的值,即可写出点P 的坐标;当∠PDC=90°时,不存在点P .【详解】解:(1)将()3,0B ,()0,3C 代入2y x bx c =-++,得0=-9+3b 33c +⎧⎨=⎩, 解得23b c =⎧⎨=⎩, ∴二次函数的解析式为2y x 2x 3=-++; (2)①∵()222314y x x x =-++=--+∴顶点M (1,4),将直线BM 的解析式设为y kx b =+,将点()3,0B ,M (1,4)代入,可得304k b k b +=⎧⎨+=⎩, 解得26k b =-⎧⎨=⎩, ∴直线BM 的解析式为26y x =-+,如图∵PD ⊥x 轴且OD=m ,∴P (m ,-2m+6), ∴211(26)322PCD S S PD OD m m m m ==⋅=-+=-+, 即23S m m =-+,∵点P 为线段MB 上一个动点且()3,0B ,M (1,4),∴13m ≤≤; ②22393()24S m m m =-+=--+, ∴当32m =时,S 取最大值94,∴P (32,3); (3)存在,理由如下:如图,当∠CPD=90°时,90COD ODP CPD ,∴四边形CODP 为矩形, ∵PD=CO=3,将3y =代入直线26y x =-+,得32x =, ∴P 3,32⎛⎫ ⎪⎝⎭;如图,当∠PCD=90°时,∵OC=3,OD=m ,22229CD OC OD m , //PD OC PDCOCD , cos cos PDC OCD ,DC OC PD DC∴=, 2DC PD OC ∴=⋅,293(26)m m ,解得1332m(舍去),13m =-+∴(3P -+-;当∠PDC=90°时,∵PD ⊥x 轴,∴不存在点P ; 综上所述,点P 的坐标为3,32⎛⎫ ⎪⎝⎭或(3-+-.【点睛】本题考查了待定系数法求函数解析式,函数的思乡曲求极值以及直角三角形的存在性与动点结合等,解题的关键是注意分类讨论思想在解题过程中的运用. 7.A解析:(1)A (4,0);(2)2144S t =-;(3)(4,8)E - 【解析】【分析】(1)利用三角形的面积公式构建方程即可解决问题.(2)证明△CEA 和△COD 是等腰直角三角形,由EN ⊥AC ,推出42t CN NE NA +===,AC=4+t ,根据S=S △AEC -S △ABC 计算即可.(3)过点F 作FM ⊥AC 于点M ,由(2)求出点F 的坐标为(1,3)44t t -+,从而得到 1144t t OM =-=-,34t FM =+,由∠ABO=∠BDA+∠BAD=45°,∠FOB +∠DAE =45°,得出∠FOB=∠BDA ,进而得出∠MFO=∠ODA ,tan ∠MFO =tan ∠ODA ,故而OA OM OD MF =, 即14434t t t -=+,解出t 的值,再求点E 的坐标即可. 【详解】 (1)由题意可得:211•••822AOB S OA OB OA ===, ∴OA 2=16,∵OA >0,∴OA=OB=4,∴A (4,0),B (0,4).(2)如图,过点E 作EN ⊥AC 于点N .∵∠AOB=90°,OA=OB ,∴∠OAB=45°,∵AB ⊥CD ,∴∠CEA=90°,∴∠ECA=45°,∴△CEA 是等腰直角三角形,∵∠ECA=45°,∠COD=90°,∴∠CDO=45°,∴△CDO 是等腰直角三角形.∵点D 纵坐标为t ,∴CO=DO=t.∵OA=OB=4,∴AC=t+4. ∴42t CN NE NA +===, ∴()()2141144442224AEC ABC t S S S t t t +⎛⎫=-=⨯+⨯-⨯+⨯=- ⎪⎝⎭; ∴S 与t 的函数关系是:2144S t =-. (3)如图,过点F 作FM ⊥AC 于点M ,由(2)可知,42t CN NE +==,∴22t ON OC CN =-=-, ∴点E 的坐标为(2,2)22t t -+, ∵点B (0,4),点F 为BE 中点,∴点F 的坐标为(1,3)44t t -+, ∴1144t t OM =-=-,34t FM =+, ∵∠ABO=∠BDA+∠BAD=45°,∠FOB +∠DAE =45°,∴∠FOB=∠BDA ,∴OF ∥AD ,∵FM ⊥AC ,∴FM ∥DO ,∴∠MFO=∠ODA ,∴tan ∠MFO =tan ∠ODA , ∴OA OM OD MF=, 即14434t t t -=+, 解得t=12或4=-4(不合题意,舍去)∴点E 的坐标为(4,8)-.【点睛】本题考查三角形综合题,解题的关键是正确作出辅助线,灵活运用所学知识,利用参数构建方程解决问题.8.E解析:(1)24P P ,;(2)3b -≤<;(3)64t >≥-【解析】【分析】(1)根据等腰锐角点的定义即得;(2)先确定极限位置:直线与圆相切于第四象限及直线过(0,3)时b 的值,进而确定范围;(3)分类讨论:E 点和F 点位于线段HK 左侧;E 点和F 点位于线段HK 右侧;利用一线三垂直模型及相似三角形的性质确定极限位置t 的值,进而确定范围.【详解】(1)∵点P 是点O 关于点A 的锐角等腰点,(2,0)A∴OA=OP=2如下图:当1(0,2)P 时,OP 1=2,OP 1⊥OA ,不成立; 当(23P 时,过P 2作P 2M ⊥x 轴 ∴OM=1,P 23∴在2Rt P MO 中,22222OP OM P M =+= ∵290P OA ∠<︒ ∴点(23P 是点O 关于点A 的锐角等腰点; 当(33P -时,390POA >︒∠ ∴点(33P -不是点O 关于点A 的锐角等腰点; 当42,2P 时,过P 4作P 4N ⊥x 轴 ∴2,P 42∴在4Rt P NO 中,22442OP ON P N =+=,445P ON =︒∠ ∴点42,2P 是点O 关于点A 的锐角等腰点. ∴点O 关于点A 的锐角等腰点有(23P ,42,2P 故答案为:24P P , (2)以O 为圆心,OA=3为半径作圆,当直线2y x b =+与圆O 相切与第四象限时,切点即为点O 关于点A 的锐角等腰点,如下图点C .由题意,得:OB=-b ,OD=2b ∴在Rt DOB 中,225DB OD OB =+= ∵11122OD OB DB OC = ∴21532b =⨯ 解得:35b =-如上图:当直线2y x b =+过点E ()03,时,3b =,OE ⊥OA ∴要使在直线2y x b =+上存在点C 是点O 关于点A 的锐角等腰点,3b <综上所述:353b -≤<时,直线2y x b =+上存在点C 是点O 关于点A 的锐角等腰点 .(3)如下图:当E F ,在直线左侧,4EF =时,过E 作EG HK ⊥∵90KOH EGH KHO GHE ==︒∠=∠∠∠,∴H EGH KO ∽∴KO KH EG EH= ∵()()()()0420020K H D t E t -,,,,,,, ∴KO=4,KH=5EH=4-t∴EG=8525425t -= ∵要使线段HK 上存在点E 关于点F 的锐角等腰点,则4EG ≤ ∴85545t ≤∴425t ≥-当E 点和F 点位于线段HK 右侧时,即:4t ≥时,如下图,过E 作EB ⊥EF ,过B 作BM ⊥x 轴,过点F 作FL ⊥x 轴当BE EF =时,F BME EL ≌∴BM EL =,ME FL =∵()F m n ,,()(),020D t E t -,,∴ME FL n ==,2BM EL m t ==-+∴2OM t n =--∴()22B t n m t ---+,将点()22B t n m t ---+,代入直线24y x =-+得:()2224m t t n -+=---+解得:62t n m =+-∴当62t n m <+-时,线段HK 上存在点E 关于点F 的锐角等腰点.∵2m t ≥-,20n ≥≥∴62622212t n m t t <+-≤+⨯-+=-,即6t <综上所述:64t >≥-HK 上存在点E 关于点F 的锐角等腰点【点睛】本题考查了等腰三角形的定义,全等三角形的判定及性质,切线的性质,相似三角形的判定及性质,圆的定义及一次函数,解题关键是将动点问题转化问各个状态,进而应用等量关系列出方程求解,得出极限状态的未知量的值,进而得出取值范围.9.(1)①12;②4,(2)12AD BC =;理由见解析,(3)存在; 【解析】【分析】 (1)①首先证明ADB '∆是含有30的直角三角形,可得1122AD AB BC '==,即可解决问题;②首先证明BAC B AC ''∆∆≌,根据直角三角形斜边中线定理即可解决问题. (2)AD 与BC 的数量关系为12AD BC =,如图5,延长AD 到M ,使AD DM =,连接B M '、C M ',先证四边形AC MB ''是平行四边形,再证明BAC AB M '∆∆≌,即可解决问题.(3)存在,如图6,延长AD 交BC 的延长线于M ,作BE AD ⊥于E ,做直线BC 的垂直平分线交BE 于P ,交BC 于F ,连接PA 、PD 、PC ,作PDC ∆的中线PQ ,连接DF 交PC 于O ,先证明PA PD =,PB PC =,再证明+180APD BPC ∠∠=︒,即可得出结论,再在Rt PDQ ∆中,根据勾股定理,即可求出PQ 的长.【详解】(1)①如图2,∵ABC ∆是等边三角形,把AB 绕点A 顺时针旋转α得到AB ',把AC 绕点A 逆时针旋转β得到AC ',∴===AB AC BC AB AC ''=,又∵AD 是AB C ''△边B C ''上的中线,∴=DB DC '',∴AD B C ''⊥,即90ADB '∠=︒,∵60BAC ∠=︒,180BAC B AC ''∠+∠=︒,∴120B AC ''∠=︒,∴=30B C ''∠∠=︒,∴在ADB '∆中,90ADB '∠=︒,30B '∠=︒, ∴1122AD AB BC '==. 故答案为:12. ②如图3,∵90BAC ∠=︒,+=180BAC B AC ''∠∠︒,∴==90BAC B AC ''∠∠︒,即ABC ∆和AB C ''∆为直角三角形,∵把AB 绕点A 顺时针旋转α得到AB ',把AC 绕点A 逆时针旋转β得到AC ',∴=AB AB ',=AC AC ',∴在ABC ∆和AB C ''∆中,===AB AB BAC B AC AC AC '''∠'⎧⎪∠⎨⎪⎩∴BAC B AC ''∆∆≌,∴=BC B C '',∵AD 是AB C ''△边B C ''上的中线,AB C ''∆为直角三角形, ∴1122AD B B C C ''==, 又∵8BC =, ∴11=8=422AD BC =⨯. 故答案为:4. (2)12AD BC =, 如图5,延长AD 到M ,使AD DM =,连接B M '、C M ',图5∵=B D DC '',AD DM =,∴四边形AC MB ''是平行四边形,∴AC B M AC ''==,∵+=180BAC B AC ''∠∠︒,+=180B AC AB M '''∠∠︒,∴=BAC AB M '∠∠,∵=AB AB ',∴在BAC ∆和AB M '∆中,==AC B M BAC AB M AB AB ''=⎧'⎪∠∠⎨⎪⎩∴BAC AB M '∆∆≌,∴BC AM =,∴12AD BC =.(3)存在,如图6,延长AD 交BC 的延长线于M ,作BE AD ⊥于E ,作直线BC 的垂直平分线交BE 于P ,交BC 于F ,连接PA 、PD 、PC ,作PDC ∆的中线PQ ,连接DF 交PC 于O ,图6∵+=120A B ∠∠︒,∴=180=60M A B ∠︒-∠-∠︒,∵=90C ∠︒,∴=180=30MDC M MCD ∠︒-∠-∠︒,在Rt DCM ∆中,∵=6CD ,=90DCM ∠︒,=30MDC ∠︒, ∴=23CM =43DM =60M ∠︒,在Rt BEM ∆中,∵=90BEM ∠︒,143BM BC CM =+==30MDC ∠︒, ∴1732EM BM ==, ∴33DE EM DM =-=, ∵=63AD =AE DE ,∵BE AD ⊥,∴PA PD =,PB PC =,在Rt CDF ∆中,∵=6CD ,=63CF ∴tan 3CDF ∠=∴60CDF CPF =︒=∠∠,∴FCP CFD ∆∆≌,∴CD PF =,∵//CD PF ,∴四边形CDPF 是矩形,∴=90CDP ∠︒,∴=60ADP ADC CDP ∠∠-∠=︒,∴ADP ∆是等边三角形, ∴==63PA PD AD =∵=60BPF CPF ∠∠=︒,∴120BPC ∠=︒,∴+180APD BPC ∠∠=︒,∴PDC ∆与PAB ∆之间满足小明探究的问题中的边角关系,在Rt PDQ ∆中,∵=90PDQ ∠︒,PD PA AD ===132DQ CD ==,∴PQ ==【点睛】本题考查了三角形的综合问题.掌握全等三角形的性质以及判定定理、直角三角形斜边中线定理、解直角三角形、勾股定理、中线的性质是解题的关键.在处理三角形的边旋转问题时,旋转前后边长不变,根据已知角度变化,求得线段之间关系.在证明某点是否存在问题时,先假设这点存在,能求出相关线段或坐标,即证实存在性. 10.D解析:(1)见解析;(2)y=1603x +;(2)2 【解析】【分析】(1)根据翻折的性质得△DFG ≌△DFA ,从而推导得出∠FDC=∠DFG ,进而得到CF=DC ; (2)在等腰△DGC 和等腰△CFD 中,可用y 表示出∠GDC 、∠FDC 的值,从而求出∠ADF ,根据∠ADE=∠DEC ,得出y 与x 的关系式;(3)先证△KCD 是等腰直角三角形,根据CD 的长得到KC 的值,然后再△KGC 中求得KG 的值.【详解】(1)∵将菱形ABCD 沿DF 翻折,点A 恰好落在点G 上∴△DFG ≌△DFA ,∠AFD=∠FDC∴∠AFD=∠DFG∴∠FDC=∠DFG∴CF=DC ;(2)∵AD=DG=DC=FC ,∠DCF=y∴在△DGC 中,∠DGC=y ,∠GDC=180-2y在△CFD 中,∠CFD=∠CDF=902y -∴∠FDG=∠FDC -∠GDC=3902y - ∴∠ADF=∠FDG=3902y -,∴∠ADE=3y -180 ∵AD ∥BC∴∠ADE=∠DEC ,即3y -180=x。
初三数学压轴题及答案

⼀、图形运动产⽣的⾯积问题知识点睛研究_基本_图形分析运动状态:①由起点、终点确定t的范围;②对t分段,根据运动趋势画图,找边与定点,通常是状态转折点相交时的特殊位置.分段画图,选择适当⽅法表达⾯积.⼆、精讲精练已知,等边三⾓形ABC的边长为4厘⽶,长为1厘⽶的线段MN在△ABC的边AB上,沿AB⽅向以1厘⽶/秒的速度向B点运动(运动开始时,点与点重合,点N到达点时运动终⽌),过点M、N分别作边的垂线,与△ABC的其他边交于P、Q两点,线段MN 运动的时间为秒.(1)线段MN在运动的过程中,为何值时,四边形MNQP恰为矩形?并求出该矩形的⾯积.(2)线段MN在运动的过程中,四边形MNQP的⾯积为S,运动的时间为t.求四边形MNQP的⾯积S随运动时间变化的函数关系式,并写出⾃变量t的取值范围.1题图 2题图如图,等腰梯形ABCD中,AB∥CD,AB=, CD=,⾼CE=,对⾓线AC、BD交于点H.平⾏于线段BD的两条直线MN、RQ 同时从点A出发,沿AC⽅向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对⾓线AC于F、G,当直线RQ到达点C时,两直线同时停⽌移动.记等腰梯形ABCD被直线MN扫过的⾯积为,被直线RQ扫过的⾯积为,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒. (1)填空:∠AHB=____________;AC=_____________; (2)若,求x.如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,点P、Q同时从点C出发,以1cm/s的速度分别沿CA、CB匀速运动,当点Q到达点B时,点P、Q同时停⽌运动.过点P作AC的垂线l交AB于点R,连接PQ、RQ,并作△PQR关于直线l对称的图形,得到△PQ'R.设点Q的运动时间为t(s),△PQ'R与△PAR重叠部分的⾯积为S(cm2). (1)t为何值时,点Q' 恰好落在AB上? (2)求S与t的函数关系式,并写出t的取值范围.(3)S能否为?若能,求出此时t的值;若不能,请说明理由.如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm,动点P从点A出发,沿AB⽅向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA⽅向以1cm/s的速度向点A运动.当点P到达点B时,P,Q两点同时停⽌运动.以AP为边向上作正⽅形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正⽅形APDE和梯形BCFQ重叠部分的⾯积为Scm2.(1)当t=_____s时,点P与点Q重合;(2)当t=_____s时,点D在QF上;(3)当点P在Q,B两点之间(不包括Q,B两点)时,求S与t之间的函数关系式.如图,在平⾯直⾓坐标系中,已知点A(0,1)、D(-2,0),作直线AD并以线段AD为⼀边向上作正⽅形ABCD.(1)填空:点B的坐标为________,点C的坐标为_________.(2)若正⽅形以每秒个单位长度的速度沿射线DA向上平移,直⾄正⽅形的顶点C落在y轴上时停⽌运动.在运动过程中,设正⽅形落在y轴右侧部分的⾯积为S,求S关于平移时间t(秒)的函数关系式,并写出相应的⾃变量t的取值范围.如图,在平⾯直⾓坐标系xOy中,已知直线l1:y=x与直线l2:y=-x+6相交于点M,直线l2与x轴相交于点N. (1)求M,N的坐标.(2)已知矩形ABCD中,AB=1,BC=2,边AB在x轴上,矩形ABCD沿x轴⾃左向右以每秒1个单位长度的速度移动.设矩形ABCD与△OMN重叠部分的⾯积为S,移动的时间为t(从点B与点O重合时开始计时,到点A与点N重合时计时结束).求S与⾃变量t之间的函数关系式,并写出相应的⾃变量t的取值范围.⼆、⼆次函数中的存在性问题⼀、知识点睛解决“⼆次函数中存在性问题”的基本步骤:①画图分析.研究确定图形,先画图解决其中⼀种情形.②分类讨论.先验证①的结果是否合理,再找其他分类,类⽐第⼀种情形求解.③验证取舍.结合点的运动范围,画图或推理,对结果取舍.⼆、精讲精练如图,已知点P是⼆次函数y=-x2+3x图象在y轴右侧部分上的⼀个动点,将直线y=-2x沿y轴向上平移,分别交x轴、y轴于A、B 两点. 若以AB为直⾓边的△PAB与△OAB相似,请求出所有符合条件的点P的坐标.抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.点P在抛物线上,直线PQ//BC交x轴于点Q,连接BQ.(1)若含45°⾓的直⾓三⾓板如图所⽰放置,其中⼀个顶点与点C重合,直⾓顶点D在BQ上,另⼀个顶点E在PQ上,求直线BQ的函数解析式;(2)若含30°⾓的直⾓三⾓板的⼀个顶点与点C重合,直⾓顶点D在直线BQ上(点D不与点Q重合),另⼀个顶点E在PQ上,求点P的坐标.如图,矩形OBCD的边OD、OB分别在x轴正半轴和y轴负半轴上,且OD=10,OB=8.将矩形的边BC绕点B逆时针旋转,使点C恰好与x轴上的点A重合.(1)若抛物线经过A、B两点,求该抛物线的解析式:______________;(2)若点M是直线AB上⽅抛物线上的⼀个动点,作MN⊥x轴于点N.是否存在点M,使△AMN与△ACD相似?若存在,求出点M的坐标;若不存在,说明理由.已知抛物线经过A、B、C三点,点P(1,k)在直线BC:y=x3上,若点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的四边形为平⾏四边形?若存在,请求出点M的坐标;若不存在,请说明理由.抛物线与y轴交于点C,与直线y=x交于A(-2,-2)、B(2,2)两点.如图,线段MN在直线AB上移动,且,若点M的横坐标为m,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以P、M、Q、N为顶点的四边形否为平⾏四边形?若能,请求出m的值;若不能,请说明理由.三、⼆次函数与⼏何综合⼀、知识点睛 “⼆次函数与⼏何综合”思考流程: 整合信息时,下⾯两点可为我们提供便利:①研究函数表达式.⼆次函数关注四点⼀线,⼀次函数关注k、b; ②)关键点坐标转线段长.找特殊图形、特殊位置关系,寻求边和⾓度信息.⼆、精讲精练如图,抛物线y=ax2-5ax+4(a<0)经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC. (1)求抛物线的解析式.(2)在抛物线的对称轴上是否存在点M,使|MA-MB|?若存在,求出点M的坐标;若不存在,请说明理由.如图,已知抛物线y=ax2-2ax-b(a>0)与x轴交于A、B两点,点A在点B的右侧,且点B的坐标为(-1,0),与y轴的负半轴交于点C,顶点为D.连接AC、CD,∠ACD=90°. (1)求抛物线的解析式;(2)点E在抛物线的对称轴上,点F在抛物线上,且以B、A、F、E四点为顶点的四边形为平⾏四边形,求点的坐标.如图,在平⾯直⾓坐标系中,直线与抛物线交于A、B两点,点A在x轴上,点B的横坐标为-8. (1)求该抛物线的解析式;(2)点P是直线AB上⽅的抛物线上⼀动点(不与点A、B重合),过点P作x轴的垂线,垂⾜为C,交直线AB于点D,作PE⊥AB于点E.设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的值.已知,抛物线经过A(-1,0),C(2,)两点,与x轴交于另⼀点B. (1)求此抛物线的解析式;(2)若抛物线的顶点为M,点P为线段OB上⼀动点(不与点B重合),点Q在线段MB上移动,且∠MPQ=45°,设线段OP=x,MQ=,求y2与x的函数关系式,并直接写出⾃变量x的取值范围.已知抛物线的对称轴为直线,且与x轴交于A、B两点,与y轴交于点C,其中A(1,0),C(0,-3). (1)求抛物线的解析式; (2)若点P在抛物线上运动(点P异于点A),①如图1,当△PBC的⾯积与△ABC的⾯积相等时,求点P的坐标; ②如图2,当∠PCB =∠BCA时,求直线CP的解析式.四、中考数学压轴题专项训练1.如图,在直⾓梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1),B(3,1).动点P从点O出发,沿x轴正⽅向以每秒1个单位长度的速度移动.过点P作PQ⊥OA,垂⾜为Q.设点P移动的时间为t秒(0△OPQ与直⾓梯形OABC重叠部分的⾯积为S. (1)求经过O,A,B三点的抛物线解析式. (2)求S与t的函数关系式.(3)将△OPQ绕着点P顺时针旋转90°,是否存在t,使得△OPQ的顶点O或Q在抛物线上?若存在,直接写出t的值;若不存在,请说明理由.2.如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于点C,与过点C且平⾏于x轴的直线交于另⼀点D,点P是抛物线上⼀动点. (1)求抛物线的解析式及点D的坐标.(2)点E在x轴上,若以A,E,D,P为顶点的四边形是平⾏四边形,求此时点P的坐标.(3)过点P作直线CD的垂线,垂⾜为Q.若将△CPQ沿CP翻折,点Q的对应点为Q′,是否存在点P,使点Q′恰好在x轴上?若存在,求出此时点P的坐标;若不存在,请说明理由. 3.(11分)如图,已知直线与坐标轴交于A,B两点,以线段AB为边向上作正⽅形ABCD,过点A,D,C的抛物线与直线的另⼀个交点为E. (1)请直接写出C,D两点的坐标,并求出抛物线的解析式;(2)若正⽅形以每秒个单位长度的速度沿射线AB下滑,直⾄顶点D落在x轴上时停⽌,设正⽅形落在x轴下⽅部分的⾯积为S,求S关于滑⾏时间t的函数关系式,并写出相应⾃变量t的取值范围;(3)在(2)的条件下,抛物线与正⽅形⼀起平移,同时停⽌,求抛物线上C,E两点间的抛物线弧所扫过的⾯积.4.(11分)如图,抛物线y=ax2+bx+c交x轴于点A(-3,0),点B(1,0),交y轴于点E(0,-3).点C是点A关于点B的对称点,点F 是线段BC的中点,直线l过点F且与y轴平⾏.直线y=-x+m过点C,交y轴于点D. (1)求抛物线的解析式; (2)点K为线段AB上⼀动点,过点K作x轴的垂线,交直 线CD于点H,交抛物线于点G,求线段HG长度的值;(3)在直线l上取点M,在抛物线上取点N,使以A,C,M,N为顶点的四边形是平⾏四边形,求点N的坐标.5.(11分)如图,在平⾯直⾓坐标系中,直线与抛物线交于A,B两点,点A在x轴上,点B的横坐标为-8.(1)求抛物线的解析式.(2)点P是直线AB上⽅的抛物线上⼀动点(不与点A,B重合),过点P作x轴的垂线,垂⾜为C,交直线AB于点D,作PE⊥AB于点E.①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的值.②连接PA,以PA为边作图⽰⼀侧的正⽅形APFG.随着点P的运动,正⽅形的⼤⼩、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.6.(11分)如图1,点A为抛物线C1:的顶点,点B的坐标为 (1,0),直线AB交抛物线C1于另⼀点C.(1)求点C的坐标;(2)如图1,平⾏于y轴的直线x=3交直线AB于点D,交抛物线C1于点E,平⾏于y轴的直线x=a交直线AB于点F,交抛物线C1于点G,若FG:DE=4:3,求a的值;(3)如图2,将抛物线C1向下平移m(m>0)个单位得到抛物线C2,且抛物线C2的顶点为P,交x轴负半轴于点M,交射线AB于点N,NQ⊥x轴于点Q,当NP平分∠MNQ时,求m的值. 附:参考答案 ⼀、图形运动产⽣的⾯积问题1. (1)当t=时,四边形MNQP恰为矩形.此时,该矩形的⾯积为平⽅厘⽶.(2)当0<t≤1时,;当1<t≤2时,;当2<t<3时,2.(1)90°;4 (2)x=2.3.(1)当t=时,点Q' 恰好落在AB上. (2)当0<t≤时,;当<t≤6时, (3)由(2)问可得,当0<t≤时,; 当<t≤6时,; 解得,或,此时.4.(1)1 (2)(3)当1<t≤时,;当<t<2时,.5.(1)(﹣1,3),(﹣3,2)(2)当0<t≤时,;当<t≤1时,;当1<t≤时,.6.(1)M(4,2) N(6,0)(2)当0≤t≤1时,;当1<t≤4时,;当4<t≤5时,;当5<t≤6时,;当6<t≤7时,⼆、⼆次函数中的存在性问题1.解:由题意,设OA=m,则OB=2m;当∠BAP=90°时,△BAP∽△AOB或△BAP∽△BOA;若△BAP∽△AOB,如图1,可知△PMA∽△AOB,相似⽐为2:1;则P1(5m,2m),代⼊,可知,若△BAP∽△BOA,如图2,可知△PMA∽△AOB,相似⽐为1:2;则P2(2m,),代⼊,可知,当∠ABP=90°时,△ABP∽△AOB或△ABP∽△BOA;若△ABP∽△AOB,如图3,可知△PMB∽△BOA,相似⽐为2:1;则P3(4m,4m),代⼊,可知,若△ABP∽△BOA,如图4,可知△PMB∽△BOA,相似⽐为1:2;则P4(m,),代⼊,可知,2.解:(1)由抛物线解析式可得B点坐标(1,3).要求直线BQ的函数解析式,只需求得点Q坐标即可,即求CQ长度.过点D作DG⊥x轴于点G,过点D作DF⊥QP于点F.则可证△DCG≌△DEF.则DG=DF,∴矩形DGQF为正⽅形.则∠DQG=45°,则△BCQ为等腰直⾓三⾓形.∴CQ=BC=3,此时,Q点坐标为(4,0)可得BQ解析式为y=-x+4.(2)要求P点坐标,只需求得点Q坐标,然后根据横坐标相同来求点P坐标即可.⽽题⽬当中没有说明∠DCE=30°还是∠DCE=60°,所以分两种情况来讨论.当∠DCE=30°时,a)过点D作DH⊥x轴于点H,过点D作DK⊥QP于点K.则可证△DCH∽△DEK.则,在矩形DHQK中,DK=HQ,则.在Rt△DHQ中,∠DQC=60°.则在Rt△BCQ中,∴CQ=,此时,Q点坐标为(1+,0)则P点横坐标为1+.代⼊可得纵坐标.∴P(1+,).b)⼜P、Q为动点,∴可能PQ在对称轴左侧,与上⼀种情形关于对称轴对称.由对称性可得此时点P坐标为(1-,)当∠DCE=60°时,过点D作DM⊥x轴于点M,过点D作DN⊥QP于点N.则可证△DCM∽△DEN.则,在矩形DMQN中,DN=MQ,则.在Rt△DMQ中,∠DQM=30°.则在Rt△BCQ中,∴CQ=BC=,此时,Q点坐标为(1+,0)则P点横坐标为1+.代⼊可得纵坐标.∴P(1+,).b)⼜P、Q为动点,∴可能PQ在对称轴左侧,与上⼀种情形关于对称轴对称.由对称性可得此时点P坐标为(1-,)综上所述,P点坐标为(1+,),(1-,),(1+,)或(1-,).3.解:(1)∵AB=BC=10,OB=8 ∴在Rt△OAB中,OA=6 ∴ A(6,0)将A(6,0),B(0,-8)代⼊抛物线表达式,得,(2)存在:如果△AMN与△ACD相似,则或设M(0假设点M在x轴下⽅的抛物线上,如图1所⽰:当时,,即∴∴如图2验证⼀下当时,,即∴(舍)2)如果点M在x轴上⽅的抛物线上:当时,,即∴∴M此时, ∴∴△AMN∽△ACD ∴M满⾜要求当时,,即∴m=10(舍)综上M1,M24.解:满⾜条件坐标为:思路分析:A、M、N、P四点中点A、点P为顶点,则AP可为平⾏四边形边、对⾓线;(1)如图,当AP为平⾏四边形边时,平移AP;∵点A、P纵坐标差为2 ∴点M、N纵坐标差为2;∵点M的纵坐标为0 ∴点N的纵坐标为2或-2①当点N的纵坐标为2时解:得⼜∵点A、P横坐标差为2 ∴点M的坐标为:、 ②当点N的纵坐标为-2时 解:得⼜∵点A、P横坐标差为2 ∴点M的坐标为:、(2)当AP为平⾏四边形边对⾓线时;设M5(m,0)MN⼀定过AP的中点(0,-1)则N5(-m,-2),N5在抛物线上∴(负值不符合题意,舍去)∴∴综上所述:符合条件点P的坐标为:5.解:分析题意,可得:MP∥NQ,若以P、M、N、Q为顶点的四边形为平⾏四边形,只需MP=NQ即可。
中考数学《压轴题》专题训练含答案解析

压轴题1、已知,在平行四边形OABC 中,OA=5,AB=4,∠OCA=90°,动点P 从O 点出发沿射线OA 方向以每秒2个单位的速度移动,同时动点Q 从A 点出发沿射线AB 方向以每秒1个单位的速度移动.设移动的时间为t 秒. (1)求直线AC 的解析式;(2)试求出当t 为何值时,△OAC 与△PAQ 相似; (3)若⊙P 的半径为58,⊙Q 的半径为23;当⊙P 与对角线AC 相切时,判断⊙Q 与直线AC 、BC 的位置关系,并求出Q 点坐标。
解:(1)42033y x =-+ (2)①当0≤t≤2.5时,P 在OA 上,若∠OAQ=90°时, 故此时△OAC 与△PAQ 不可能相似.当t>2.5时,①若∠APQ=90°,则△APQ ∽△OCA ,∵t>2.5,∴符合条件.②若∠AQP=90°,则△APQ ∽△∠OAC ,∵t>2.5,∴符合条件.综上可知,当时,△OAC 与△APQ 相似.(3)⊙Q 与直线AC 、BC 均相切,Q 点坐标为(109,531)。
2、如图,以矩形OABC 的顶点O 为原点,OA 所在的直线为x 轴,OC 所在的直线为y 轴,建立平面直角坐标系.已知OA =3,OC =2,点E 是AB 的中点,在OA 上取一点D ,将△BDA 沿BD 翻折,使点A 落在BC 边上的点F 处. (1)直接写出点E 、F 的坐标;(2)设顶点为F 的抛物线交y 轴正半轴...于点P ,且以点E 、F 、P 为顶点的三角形是等腰三角形,求该抛物线的解析式;(3)在x 轴、y 轴上是否分别存在点M 、N ,使得四边形MNFE 的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.解:(1)(31)E ,;(12)F ,.(2)在Rt EBF △中,90B ∠=, 2222125EF EB BF ∴=+=+=.设点P 的坐标为(0)n ,,其中0n >,顶点(12)F ,, ∴设抛物线解析式为2(1)2(0)y a x a =-+≠.①如图①,当EF PF =时,22EF PF =,221(2)5n ∴+-=.解得10n =(舍去);24n =.(04)P ∴,.24(01)2a ∴=-+.解得2a =. ∴抛物线的解析式为22(1)2y x =-+(第2题)②如图②,当EP FP =时,22EP FP =,22(2)1(1)9n n ∴-+=-+. 解得52n =-(舍去).③当EF EP =时,53EP =<,这种情况不存在. 综上所述,符合条件的抛物线解析式是22(1)2y x =-+. (3)存在点M N ,,使得四边形MNFE 的周长最小. 如图③,作点E 关于x 轴的对称点E ',作点F 关于y 轴的对称点F ',连接E F '',分别与x 轴、y 轴交于点M N ,,则点M N ,就是所求点.(31)E '∴-,,(12)F NF NF ME ME '''-==,,,.43BF BE ''∴==,.FN NM ME F N NM ME F E ''''∴++=++=22345+=.又5EF =,∴55FN NM ME EF +++=+,此时四边形MNFE 的周长最小值是553、如图,在边长为2的等边△ABC 中,A D ⊥BC,点P 为边AB 上一个动点,过P 点作PF//AC 交线段BD 于点F,作PG ⊥AB 交AD 于点E,交线段CD 于点G,设BP=x . (1)①试判断BG 与2BP 的大小关系,并说明理由;②用x 的代数式表示线段DG 的长,并写出自变量x 的取值范围;(2)记△DEF 的面积为S,求S 与x 之间的函数关系式,并求出S 的最大值;(3)以P 、E 、F 为顶点的三角形与△EDG 是否可能相似?如果能相似,请求出BP 的长,如果不能,请说明理由。
中考数学——一元二次方程组的综合压轴题专题复习含答案

中考数学——一元二次方程组的综合压轴题专题复习含答案一、一元二次方程 1.解下列方程:(1)x 2﹣3x=1.(2)12(y+2)2﹣6=0.【答案】(1)12x x ==1222y y =-+=-- 【解析】试题分析:(1)利用公式法求解即可; (2)利用直接开方法解即可;试题解析:解:(1)将原方程化为一般式,得x 2﹣3x ﹣1=0,∵b 2﹣4ac=13>0∴.∴1233,22x x +-==.(2)(y+2)2=12,∴或,∴1222y y =-+=--2.解方程:(2x+1)2=2x+1. 【答案】x=0或x=12-. 【解析】试题分析:根据因式分解法解一元二次方程的解法,直接先移项,再利用ab=0的关系求解方程即可.试题解析:∵(2x+1)2﹣(2x+1)=0,∴(2x+1)(2x+1﹣1)=0,即2x (2x+1)=0, 则x=0或2x+1=0, 解得:x=0或x=﹣12.3.发现思考:已知等腰三角形ABC 的两边分别是方程x 2﹣7x+10=0的两个根,求等腰三角形ABC 三条边的长各是多少?下边是涵涵同学的作业,老师说他的做法有错误,请你找出错误之处并说明错误原因. 涵涵的作业解:x 2﹣7x+10=0a=1 b=﹣7 c=10∵b2﹣4ac=9>0∴73 2±∴x1=5,x2=2所以,当腰为5,底为2时,等腰三角形的三条边为5,5,2.当腰为2,底为5时,等腰三角形的三条边为2,2,5.探究应用:请解答以下问题:已知等腰三角形ABC的两边是关于x的方程x2﹣mx+m2﹣14=0的两个实数根.(1)当m=2时,求△ABC的周长;(2)当△ABC为等边三角形时,求m的值.【答案】错误之处及错误原因见解析;(1)当m=2时,△ABC的周长为72;(2)当△ABC为等边三角形时,m的值为1.【解析】【分析】根据三角形三边关系可以得到等腰三角形的三条边不能为2、2、5.(1)先解方程,再确定边,从而求周长;(2)是等边三角形,则两根相等,即△=(﹣m)2﹣4(m2﹣14)=m2﹣2m+1,可求得m.【详解】解:错误之处:当2为腰,5为底时,等腰三角形的三条边为2、2、5.错误原因:此时不能构成三角形.(1)当m=2时,方程为x2﹣2x+34=0,∴x1=12,x2=32.当12为腰时,12+12<32,∴12、12、32不能构成三角形;当32为腰时,等腰三角形的三边为32、32、12,此时周长为32+32+12=72.答:当m=2时,△ABC的周长为72.(2)若△ABC为等边三角形,则方程有两个相等的实数根,∴△=(﹣m)2﹣4(m2﹣14)=m2﹣2m+1=0,∴m 1=m 2=1.答:当△ABC 为等边三角形时,m 的值为1.【点睛】本题考核知识点:二元一次方程的运用.解题关键点:熟练掌握二元一次方程的解法和等腰三角形性质.4. y 与x 的函数关系式为:y=1.7x (x≤m );或( x≥m) ;5.已知为正整数,二次方程的两根为,求下式的值:【答案】【解析】 由韦达定理,有,.于是,对正整数,有原式=6.解下列方程: (1)2x 2-4x -1=0(配方法); (2)(x +1)2=6x +6.【答案】(1)x 1=1+2x 2=1-21=-1,x 2=5. 【解析】试题分析:(1)根据配方法解一元二次方程的方法,先移项,再加减一次项系数一半的平方,完成配方,再根据直接开平方法解方程即可;(2)根据因式分解法,先移项,再提公因式即可把方程化为ab=0的形式,然后求解即可.试题解析:(1)由题可得,x 2-2x =12,∴x 2-2x +1=32.∴(x -1)2=32.∴x -1=±2.∴x 1=1x 2=1 (2)由题可得,(x +1)2-6(x +1)=0,∴(x +1)(x +1-6)=0. ∴x +1=0或x +1-6=0. ∴x 1=-1,x 2=5.7.已知关于x 的一元二次方程()220x m x m -++=(m 为常数)(1)求证:不论m 为何值,方程总有两个不相等的实数根; (2)若方程有一个根是2,求m 的值及方程的另一个根. 【答案】(1)见解析;(2) 即m 的值为0,方程的另一个根为0. 【解析】 【分析】(1)可用根的判别式,计算判别式得到△=(m+2)2−4×1⋅m=m 2+4>0,则方程有两个不相等实数解,于是可判断不论m 为何值,方程总有两个不相等的实数根; (2)设方程的另一个根为t ,利用根与系数的关系得到2+t=21m + ,2t=m,最终解出关于t 和m 的方程组即可. 【详解】 (1)证明:△=(m+2)2−4×1⋅m=m 2+4, ∵无论m 为何值时m 2≥0, ∴m 2+4≥4>0, 即△>0,所以无论m 为何值,方程总有两个不相等的实数根. (2)设方程的另一个根为t ,()220x m x m -++=根据题意得2+t=21m + ,2t=m , 解得t=0, 所以m=0,即m 的值为0,方程的另一个根为0. 【点睛】本题考查根的判别式和根于系数关系,对于问题(1)可用根的判别式进行判断,在判断过程中注意对△的分析,在分析时可借助平方的非负性;问题(2)可先设另一个根为t ,用根于系数关系列出方程组,在求解.8.用适当的方法解下列一元二次方程:(1)2x 2+4x -1=0;(2)(y +2)2-(3y -1)2=0.【答案】(1)x 1=-1x 2=-12)y 1=-14,y 2=32.【解析】试题分析:(1)根据方程的特点,利用公式法解一元二次方程即可;(2)根据因式分解法,利用平方差公式因式分解,然后再根据乘积为0的方程的解法求解即可.试题解析:(1)∵a=2,b=4,c=-1 ∴△=b 2-4ac=16+8=24>0∴=41222-=-±⨯∴x 1=-1,x 2=-1 (2)(y +2)2-(3y -1)2=0[(y+2)+(3y-1)][ (y+2)-(3y-1)]=0 即4y+1=0或-2y+3=0 解得y 1=-14,y 2=32.9.关于x 的一元二次方程()22210x k x k +-+=有两个不等实根1x ,2x . (1)求实数k 的取值范围;(2)若方程两实根1x ,2x 满足121210x x x x ++-=,求k 的值. 【答案】(1) k <14;(2) k=0. 【解析】 【分析】(1)根据一元二次方程的根的判别式得出△>0,求出不等式的解集即可;(2)根据根与系数的关系得出x 1+x 2=-(2k-1)=1-2k ,x 1•x 2=k 2,代入x 1+x 2+x 1x 2-1=0,即可求出k 值. 【详解】解:(1)∵关于x 的一元二次方程x 2+(2k-1)x+k 2=0有两个不等实根x 1,x 2,∴△=(2k-1)2-4×1×k 2=-4k+1>0, 解得:k <14, 即实数k 的取值范围是k <14;(2)由根与系数的关系得:x1+x2=-(2k-1)=1-2k,x1•x2=k2,∵x1+x2+x1x2-1=0,∴1-2k+k2-1=0,∴k2-2k=0∴k=0或2,∵由(1)知当k=2方程没有实数根,∴k=2不合题意,舍去,∴k=0.【点睛】本题考查了解一元二次方程根的判别式和根与系数的关系等知识点,能熟记根的判别式和根与系数的关系的内容是解此题的关键,注意用根与系数的关系解题时要考虑根的判别式,以防错解.10.阅读下面的材料,回答问题:解方程x4﹣5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:设x2=y,那么x4=y2,于是原方程可变为y2﹣5y+4=0 ①,解得y1=1,y2=4.当y=1时,x2=1,∴x=±1;当y=4时,x2=4,∴x=±2;∴原方程有四个根:x1=1,x2=﹣1,x3=2,x4=﹣2.(1)在由原方程得到方程①的过程中,利用法达到的目的,体现了数学的转化思想.(2)解方程(x2+x)2﹣4(x2+x)﹣12=0.【答案】(1)换元,降次;(2)x1=﹣3,x2=2.【解析】【详解】解:(1)在由原方程得到方程①的过程中,利用换元法达到降次的目的,体现了数学的转化思想;(2)设x2+x=y,原方程可化为y2﹣4y﹣12=0,解得y1=6,y2=﹣2.由x2+x=6,得x1=﹣3,x2=2.由x2+x=﹣2,得方程x2+x+2=0,b2﹣4ac=1﹣4×2=﹣7<0,此时方程无实根.所以原方程的解为x1=﹣3,x2=2.11.关于x的一元二次方程x2﹣(m﹣3)x﹣m2=0.(1)证明:方程总有两个不相等的实数根;(2)设这个方程的两个实数根为x1,x2,且|x1|=|x2|﹣2,求m的值及方程的根.【答案】(1)证明见解析;(2)x1=﹣,x2=﹣1或【解析】试题分析:(1)根据一元二次方程的判别式△=b2﹣4ac的结果判断即可,当△>0时,有两个不相等的实数根,当△=0时,有两个相等的实数根,当△<0时,方程没有实数根;(2)根据一元二次方程根与系数的关系x1+x2=-ba,x1•x2=ca,表示出两根的关系,得到x1,x2异号,然后根据绝对值的性质和两根的关系分类讨论即可求解.试题解析:(1)一元二次方程x2﹣(m﹣3)x﹣m2=0,∵a=1,b=﹣(m﹣3)=3﹣m,c=﹣m2,∴△=b2﹣4ac=(3﹣m)2﹣4×1×(﹣m2)=5m2﹣6m+9=5(m﹣35)2+365,∴△>0,则方程有两个不相等的实数根;(2)∵x1•x2=ca=﹣m2≤0,x1+x2=m﹣3,∴x1,x2异号,又|x1|=|x2|﹣2,即|x1|﹣|x2|=﹣2,若x1>0,x2<0,上式化简得:x1+x2=﹣2,∴m﹣3=﹣2,即m=1,方程化为x2+2x﹣1=0,解得:x1=﹣x2=﹣1,若x1<0,x2>0,上式化简得:﹣(x1+x2)=﹣2,∴x1+x2=m﹣3=2,即m=5,方程化为x2﹣2x﹣25=0,解得:x1=1,x212.解方程:(x2+x)2+(x2+x)=6.【答案】x1=﹣2,x2=1【解析】【分析】设x2+x=y,将原方程变形整理为y2+y﹣6=0,求得y的值,然后再解一元二次方程即可.【详解】解:设x2+x=y,则原方程变形为y2+y﹣6=0,解得y1=﹣3,y2=2.①当y=2时,x2+x=2,即x2+x﹣2=0,解得x1=﹣2,x2=1;②当y=﹣3时,x2+x=﹣3,即x2+x+3=0,∵△=12﹣4×1×3=1﹣12=﹣11<0,∴此方程无解;∴原方程的解为x1=﹣2,x2=1.【点睛】本题考查了换元法和一元二次方程的解法,设出元化简原方程是解答本题的关键.13.今年以来猪肉价格不断走高,引起了民众与区政府的高度关注,当市场猪肉的平均价格每 千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.据统计:从今年年初至 11月 10 日,猪排骨价格不断走高,11 月 10 日比年初价格上涨了 75%.今年 11 月 10 日某市 民于 A 超市购买 5 千克猪排骨花费 350 元. (1)A 超市 11 月排骨的进货价为年初排骨售价的32倍,按 11 月 10 日价格出售,平均一天能销售出 100 千克,超市统计发现:若排骨的售价每千克下降 1 元,其日销售量就增加 20千克,超市为了实现销售排骨每天有 1000 元的利润,为了尽可能让顾客优惠应该将排骨的 售价定位为每千克多少元?(2)11 月 11 日,区政府决定投入储备猪肉并规定排骨在 11 月 10 日售价的基础上下调 a %出售,A 超市按规定价出售一批储备排骨,该超市在非储备排骨的价格不变情况下,该天的两种猪排骨总销量比 11 月 10 日增加了 a %,且储备排骨的销量占总销量的57,两种排骨销售的总金额比 11 月 10 日提高了128a %,求 a 的值. 【答案】(1)售价为每千克65元;(2)a =35. 【解析】 【分析】(1)先根据题意计算出11月10的售价和11月的进货价,设每千克降价x 元,则每千克的利润为10-x 元,日销量为100+20x 千克,根据销量×单利润=总利润列出方程求解,并根据为了尽可能让顾客优惠,对所得的解筛选;(2)根据销售总金额=储备排骨销售单价×储备排骨销售数量+非储备排骨销售单价×非储备排骨销售数量,即可得出关于a 的一元二次方程,解之取其正值即可得出结论. 【详解】解:(1)11月10日的售价为350÷5=70元/千克 年初的售价为:350÷5÷175%=40元/千克, 11月的进货价为: 340602?元/千克设每千克降价x 元,则每千克的利润为70-60-x=10-x 元,日销量为100+20x 千克 则(10020)(10)1000x x +-=, 解得10x =,25x =因为为了尽可能让顾客优惠,所以降价5元,则售价为每千克65元. (2)根据题意可得52170(1%)100(1%)70100(1%)701001%7728a a a a ⎛⎫-++⨯+=⨯+⎪⎝⎭解得135a =,20a =(舍去) 所以a =35. 【点睛】本题考查一元二次方程的应用,(1)中理清销售量随着单价的变化而变化的数量关系是解题关键;(2)中在求解时有些难度,可先设令%a t =,解方程求出t 后再求a 的值.14.阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现: 当a >0,b >0时:)2=a ﹣b ≥0∴a +b a =b 时取等号. 请利用上述结论解决以下问题: (1)请直接写出答案:当x >0时,x +1x 的最小值为 .当x <0时,x +1x的最大值为 ;(2)若y =27101x x x +++,(x >﹣1),求y 的最小值;(3)如图,四边形ABCD 的对角线AC 、BD 相交于点O ,△AOB 、△COD 的面积分别为4和9,求四边形ABCD 面积的最小值.【答案】(1)2;﹣2.(2)y 的最小值为9;(3)四边形ABCD 面积的最小值为25. 【解析】 【分析】(1)当x >0时,按照公式a +b a =b 时取等号)来计算即可;当x <0时,﹣x >0,1x->0,则也可以按公式a +b a =b 时取等号)来计算;(2)将y 27101x x x ++=+的分子变形,分别除以分母,展开,将含x 的项用题中所给公式求得最小值,再加上常数即可;(3)设S △BOC =x ,已知S △AOB =4,S △COD =9,由三角形面积公式可知:S △BOC :S △COD =S △AOB :S △AOD ,用含x 的式子表示出S △AOD ,再表示出四边形的面积,根据题中所给公式求得最小值,加上常数即可. 【详解】(1)当x >0时,x 1x +≥=2; 当x <0时,﹣x >0,1x->0.∵﹣x 1x -≥=2,∴则x 1x +=-(﹣x 1x -)≤﹣2,∴当x >0时,x 1x +的最小值为 2.当x <0时,x 1x+的最大值为﹣2. 故答案为:2,﹣2.(2)∵x >﹣1,∴x +1>0,∴y 27101x x x ++=+()2(1)5141x x x ++++=+=(x +1)41x +++5=4+5=9,∴y 的最小值为9. (3)设S △BOC =x ,已知S △AOB =4,S △COD =9则由等高三角形可知:S △BOC :S △COD =S △AOB :S △AOD ,∴x :9=4:S △AOD ,∴S △AOD 36x=,∴四边形ABCD 面积=4+9+x 36x +≥=25. 当且仅当x =6时,取等号,∴四边形ABCD 面积的最小值为25. 【点睛】本题考查了配方法在最值问题中的应用.对不能直接应用公式的,需要正确变形才可以应用.15.阅读材料:各类方程的解法求解一元一次方程,根据等式的基本性质,把方程转化为x=a 的形式。
中考数学几何压轴题(有关三角形、四边形)的综合专题(含答案解析)
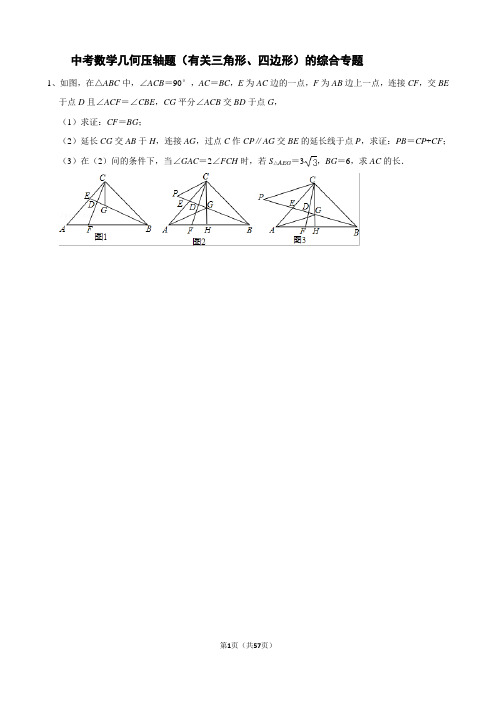
中考数学几何压轴题(有关三角形、四边形)的综合专题1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△,可推证△CEF是三角形,从而求得∠DCE=.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.3、(2019秋•锦江区校级期末)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.4、(2019•镇平县三模)如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为;∠EFC的度数为;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.5、(2017春•西城区校级期末)如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.7、(1)如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.9、(2018•大东区一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于时,线段BC的长取得最大值,且最大值为(用含b,c的式子表示)(直接填空).模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.13、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.14、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)16、在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.17、在△ABC中,∠BAC=60°,点D、E分别在边AC、AB上,AD=AE,连接CE、BD相交于点F,且∠BEC=∠ADF,连接AF.(1)如图1,连接ED,求证:∠ABD=∠CED;(2)如图2,求证:EF+FD=AF;(3)如图3,取BC的中点G,连接AG交BD于点H,若∠GAC=3∠ABD,BH=7,求△ABH的面积.18、点D,E分别在△ABC的边AC,BD上,BD,CE交于点F,连接AF,∠F AE=∠F AD,FE=FD.(1)如图1,若∠AEF=∠ADF,求证:AE=AD;(2)如图2,若∠AEF≠∠ADF,FB平分∠ABC,求∠BAC的度数;(3)在(2)的条件下,如图3,点G在BE上,∠CFG=∠AFB若AG=6,△ABC的周长为20,求BC长.中考数学几何压轴题(有关三角形、四边形)的综合专题参考答案1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.证明:(1)如图1,∵∠ACB=90°,AC=BC,∴∠A=45°,∵CG平分∠ACB,∴∠ACG=∠BCG=45°,∴∠A=∠BCG,在△BCG和△CAF中,∵,∴△BCG≌△CAF(ASA),∴CF=BG;(2)如图2,∵PC∥AG,∴∠PCA=∠CAG,∵AC=BC,∠ACG=∠BCG,CG=CG,∴△ACG≌△BCG,∴∠CAG=∠CBE,∵∠PCG=∠PCA+∠ACG=∠CAG+45°=∠CBE+45°,∠PGC=∠GCB+∠CBE=∠CBE+45°,∴∠PCG=∠PGC,∴PC=PG,∵PB=BG+PG,BG=CF,∴PB=CF+CP;(3)解法一:如图3,过E作EM⊥AG,交AG于M,∵S△AEG=AG•EM=3,由(2)得:△ACG≌△BCG,∴BG=AG=6,∴×6×EM=3,EM=,设∠FCH=x°,则∠GAC=2x°,∴∠ACF=∠EBC=∠GAC=2x°,∵∠ACH=45°,∴2x+x=45,x=15,∴∠ACF=∠GAC=30°,在Rt△AEM中,AE=2EM=2,AM==3,∴M是AG的中点,∴AE=EG=2,∴BE=BG+EG=6+2,在Rt△ECB中,∠EBC=30°,∴CE=BE=3+,∴AC=AE+EC=2+3+=3+3.解法二:同理得:∠CAG=30°,AG=BG=6,如图4,过G作GM⊥AC于M,在Rt△AGM中,GM=3,AM===3,∵∠ACG=45°,∠MGC=90°,∴GM=CM=3,∴AC=AM+CM=3+3.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△ADB,可推证△CEF是等腰直角三角形,从而求得∠DCE=135°.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.解:[问题初探]如图2,过点E作EF⊥BC交直线BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=135°,故答案为:ADB,等腰直角,135;[继续探究]如图3,过点E作EF⊥BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=45°;[拓展延伸]如图4,在△ABC中,∠ABC=90°,AB=BC=,∴∠ACB=45°当点D在射线BC上时,由[问题初探]知,∠BCM=135°,∴∠ACM=∠BCM﹣∠ACB=90°,当点D在线段CB的延长线上时,由[继续探究]知,∠BCE=45°,∴∠ACN=∠ACB+∠BCM=90°,∴点E是过点C垂直于AC的直线上的点,∴当BE⊥MN时,BE最小,∵∠BCE=45°,∴∠CBE=45°=∠BCE,∴BE=CE,∴BE最小=BC=,即:BE的最小值为.3、在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.证明:(1)如图1,过点D作DE⊥AB,∵BD是△ABC的角平分线,DE⊥AB,∠ACB=90°,∴DC=DE,∵∠A=30°,DE⊥AB,∴AD=2DE,∴AD=2DC;(2)如图2,过点M作ME∥BD,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵BD是△ABC的角平分线,∴∠ABD=∠DBC=30°,∵BM平分∠CBD,∴∠CBM=15°=∠DBM,∵ME∥BD,∴∠MEC=∠CBD=30°,∠EMB=∠DBM=∠MBE,∴ME=BE,∵∠MEC=30°,∠C=90°∴CE=MC=,ME=2MC=2=BE,∴BC=+2,∵∠CBD=30°,∠C=90°,∴BC=CD,∴CD=1+,∴DM=,∴△DBM的面积=××(+2)=1+;(3)若点N在CD上时,AD=DG+DN,理由如下:如图3所示:延长ED使得DW=DN,连接NW,∵∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E,∴∠ADE=∠BDE=60°,AD=BD,∵DN=DW,且∠WDN=60°∴△WDN是等边三角形,∴NW=DN,∠W=∠WND=∠BNG=∠BDN=60°,∴∠WNG=∠BND,在△WGN和△DBN中,∴△WGN≌△DBN(SAS),∴BD=WG=DG+DN,∴AD=DG+DN.(3)若点N在AD上时,AD=DG﹣DN,理由如下:如图4,延长BD至H,使得DH=DN,连接HN,由(1)得DA=DB,∠A=30°.∵DE⊥AB于点E.∴∠2=∠3=60°.∴∠4=∠5=60°.∴△NDH是等边三角形.∴NH=ND,∠H=∠6=60°.∴∠H=∠2.∵∠BNG=60°,∴∠BNG+∠7=∠6+∠7.即∠DNG=∠HNB.在△DNG和△HNB中,∴△DNG≌△HNB(ASA).∴DG=HB.∵HB=HD+DB=ND+AD,∴DG=ND+AD.∴AD=DG﹣ND.4、如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为EF=CF;∠EFC的度数为120°;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.解:(1)如图1中,∵DE⊥AB,∴∠BED=90°,∵∠BCD=90°,BF=DF,∴FE=FB=FD=CF,∴∠FBE=∠FEB,∠FBC=∠FCB,∴∠EFC=∠EFD+∠CFD=∠FBE+∠FEB+∠FBC+∠FCB=2(∠FBE+∠FBC)=2∠ABC=120°,故答案为:EF=CF,120°.(2)结论成立.理由:如图2中,取AB的中点M,AD的中点N,连接MC,MF,ED,EN,FN.∵BM=MA,BF=FD,∴MF∥AD,MF=AD,∵AN=ND,∴MF=AN,MF∥AN,∴四边形MFNA是平行四边形,∴NF=AM,∠FMA=∠ANF,在Rt△ADE中,∵AN=ND,∠AED=90°,∴EN=AD=AN=ND,同理CM=AB=AM=MB,在△AEN和△ACM中,∠AEN=∠EAN,∠MCA=∠MAC,∵∠MAC=∠EAN,∴∠AMC=∠ANE,又∵∠FMA=∠ANF,∴∠ENF=∠FMC,在△MFC和△NEF中,,∴△MFC≌△NEF(SAS),∴FE=FC,∠NFE=∠MCF,∵NF∥AB,∴∠NFD=∠ABD,∵∠ACB=90°,∠BAC=30°,∴∠ABC=60°,△BMC是等边三角形,∠MCB=60°∴∠EFC=∠EFN+∠NFD+∠DFC=∠MCF+∠ABD+∠FBC+∠FCB=∠ABC+∠MCB=60°+60°=120°.(3)如图3中,作EH⊥AB于H.在Rt△ABC中,∵∠BAC=30°,BC=3,∴AB=2BC=6,在Rt△AED中,∠DAE=30°,AD=2,∴DE=AD=1,在Rt△DEH中,∵∠EDH=60°,DE=1,∴EH=ED•sin60°=,DH=ED•cos60°=,在Rt△EHG中,EG==.5、如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.解:(1)BC=2BD,理由:如图2,连接CD,由旋转可得,CP=DP,∠CPD=60°,∴△CDP是等边三角形,∴∠CDP=60°=∠PCD,又∵P是AB的中点,AB=AC,∠A=60°,∴等边三角形ABC中,∠PCB=30°,CP⊥AB,∴∠BCD=30°,即BC平分∠PCD,∴BC垂直平分PD,∴∠BDC=∠BPC=90°,∴Rt△BCD中,BC=2BD.(2)如图3,取BC中点F,连接PF,∵∠A=90°,AB=AC,∴△ABC是等腰直角三角形,∵P是AB的中点,F是BC的中点,∴PF是△ABC的中位线,∴PF∥AC,∴∠PFB=∠ACB=45°,∠BPF=∠A=90°,∴△BPF是等腰直角三角形,∴BF=BP,BP=PF,∵∠DPC=∠BPF=90°,∴∠BPD=∠FPC,又∵PD=PC,∴△BDP≌△FCP,∴BD=CF,∵BC=BF+FC,∴BC=BD+BP.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.【发现问题】解:延长CA到M,作∠MAC的平分线AN,在AN上截取AD=AC,连接CD,即可得到等腰直角△ACD;连接BD、CE,如图1所示:∵△ABE与△ACD都是等腰直角三角形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE,【拓展探究】解:BD=CE;理由如下:∵四边形AEFB与四边形ACGD都是正方形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;【解决问题】解:以AB为边向外作等边三角形ABE,连接CE,如图3所示:则∠BAE=60°,BE=AB=AE=8,∵AD=CD,∠ADC=60°,∴△ACD是等边三角形,∴∠CAD=60°,AC=AD,∴∠CAD+∠BAC=∠BAE+∠BAC,即∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;当C、B、E三点共线时,CE最大=BC+BE=15+8=23,∴BD的最大值为23.7、如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为a+b(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.(1)解:∵点C为线段AB外一动点,且AC=b,AB=a,∴当点C位于BA的延长线上时,线段BC的长取得最大值,且最大值为AC+AB=a+b,(2)①证明:如图2中,∵△ACD与△BCE是等边三角形,∴CD=AC,CB=CE,∠ACD=∠BCE=60°,∴∠DCB=∠ACE,在△CAD与△EAB中,,∴△CAD≌△EAB(SAS),∴AE=BD.②∵线段AE长的最大值=线段BD的最大值,由(1)知,当线段BD的长取得最大值时,点D在BA的延长线上,∴最大值为AD+AB=3+10=13;(3)如图3中,连接BN,∵将△AMN绕着点M顺时针旋转90°得到△PBM,连接AP,则△APM是等腰直角三角形,∴MA=MP=2,BP=AN,∴P A=2,∵AB=6,∴线段AN长的最大值=线段BP长的最大值,∴当P在线段BA的延长线时,线段BP取得最大值最大值=AB+AP=6+2.8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是∠BAE+∠F AD=∠EAF;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.解:(1)∠BAE+∠F AD=∠EAF.理由:如图1,延长FD到点G,使DG=BE,连接AG,根据SAS可判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再根据SSS可判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF.故答案为:∠BAE+∠F AD=∠EAF;(2)仍成立,理由:如图2,延长FD到点G,使DG=BE,连接AG,∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,∴∠B=∠ADG,又∵AB=AD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AE=AG,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF;(3)∠EAF=180°﹣∠DAB.证明:如图3,在DC延长线上取一点G,使得DG=BE,连接AG,∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,∴∠ADC=∠ABE,又∵AB=AD,∴△ADG≌△ABE(SAS),∴AG=AE,∠DAG=∠BAE,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠F AE=∠F AG,∵∠F AE+∠F AG+∠GAE=360°,∴2∠F AE+(∠GAB+∠BAE)=360°,∴2∠F AE+(∠GAB+∠DAG)=360°,即2∠F AE+∠DAB=360°,∴∠EAF=180°﹣∠DAB.9、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.解:(1)CP=BQ,理由:如图1,连接OQ,由旋转知,PQ=OP,∠OPQ=60°⊅∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(2)CP=BQ,理由:如图2,连接OQ,由旋转知,PQ=OP,∠OPQ=60°∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(3)如图3,在Rt△ABC中,∠A=30°,AC=,∴BC=AC•tan∠A=,过点O作OH⊥BC,∴∠OHB=90°=∠BCA,∴OH∥AB,∵O是AB中点,∴CH=BC=,OH=AC=,∵∠BPQ=45°,∠OHP=90°,∴∠BPQ=∠PQH,∴PH=OH=,∴CP=PH﹣CH=﹣=,连接BQ,同(1)的方法得,BQ=CP=.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于线段BA的延长线上时,线段BC的长取得最大值,且最大值为b+c(用含b,c的式子表示)(直接填空)模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为5.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.解:当点C位于线段BA的延长线上时,线段BC的长取得最大值,最大值为b+c,故答案为:线段BA的延长线上;b+c;模型应用:(1)证明:∵△ACD、△BCE都是等边三角形,∴CD=CA=AD,CB=CE,∠ACD=60°,∠BCE=60°,∴∠DCB=∠ACE,在△DCB和△ACE中,,∴△DCB≌△ACE(SAS)∴BD=AE;(2)当点D位于线段BA的延长线上时,线段BD的长取得最大值,最大值为AB+AD=AB+AC=3+2=5,∵AE=BD,∴线段AE长的最大值为5,模型拓展:取AB的中点G,连接OG、CG,在Rt△AOB中,G为AB的中点,∴OG=AB=4,在Rt△CAG中,CG===5,当点O、G、C在同一条直线上时,OC最大,最大值为4+5=9.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.(1)证明:如图1中,∵BE⊥AD于E,∴∠AEF=∠BCF=90°,∵∠AFE=∠CFB,∴∠DAC=∠CBF,∵BC=CA,∴△BCF≌△ACD,∴BF=AD.(2)结论:BD=2CF.理由:如图2中,作EH⊥AC于H.∵∠AHE=∠ACD=∠DAE=90°,∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,∴∠DAC=∠AEH,∵AD=AE,∴△ACD≌△EHA,∴CD=AH,EH=AC=BC,∵CB=CA,∴BD=CH,∵∠EHF=∠BCF=90°,∠EFH=∠BFC,EH=BC,∴△EHF≌△BCF,∴FH=CF,∴BD=CH=2CF.(3)如图3中,同法可证BD=2CM.∵AC=3CM,设CM=a,则AC=CB=3a,BD=2a,∴==.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.(1)①证明:如图1中,∵AB=AC,∠ABC=60°∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BN,∴∠ADB=90°,∵∠MBN=30°,∠BFD=60°=∠1+∠BAF=∠2+∠BAF,∴∠1=∠2②证明:如图2中,在Rt△BFD中,∵∠FBD=30°,∴BF=2DF,∵BF=2AF,∴BF=AD,∵∠BAE=∠FBC,AB=BC,∴△BFC≌△ADB,∴∠BFC=∠ADB=90°,∴BF⊥CF(2)在BF上截取BK=AF,连接AK.∵∠BFE=∠2+∠BAF,∠CFE=∠4+∠1,∴∠CFB=∠2+∠4+∠BAC,∵∠BFE=∠BAC=2∠EFC,∴∠1+∠4=∠2+∠4∴∠1=∠2,∵AB=AC,∴△ABK≌CAF,∴∠3=∠4,S△ABK=S△AFC,∵∠1+∠3=∠2+∠3=∠CFE=∠AKB,∠BAC=2∠CEF,∴∠KAF=∠1+∠3=∠AKF,∴AF=FK=BK,∴S△ABK=S△AFK,∴=2.13、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.(1)解:如图1中,在AB上取一点M,使得BM=ME,连接ME.在Rt△ABE中,∵OB=OE,∴BE=2OA=2,∵MB=ME,∴∠MBE=∠MEB=15°,∴∠AME=∠MBE+∠MEB=30°,设AE=x,则ME=BM=2x,AM=x,∵AB2+AE2=BE2,∴(2x+x)2+x2=22,∴x=(负根已经舍弃),∴AB=AC=(2+)•,∴BC=AB=+1.方法二:作EH⊥BC于H,求出BH,CH即可解决问题.(2)证明:如图2中,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.∵BE⊥AP,∴∠AHB=90°,∴∠ABH+∠BAH=90°,∵∠BAH+∠P AC=90°,∴∠ABE=∠P AC,在△ABE和△CAP中,,∴△ABE≌△CAP,∴AE=CP=CF,∠AEB=∠P,在△DCF和△DCP中,,∴△DCF≌△DCP,∴∠DFC=∠P,∴∠GFE=∠GEF,∴GE=GF,∵GM⊥EF,∴FM=ME,∵AE=CF,∴AF=CE,∴AM=CM,在△GAH和△GAM中,,∴△AGH≌△AGM,∴AH=AM=CM=AC(3)解:结论:AG=EF.理由:如图3中,作CM⊥AC交AD的延长线于M,连接PG交AC于点O.由(2)可知△ACM≌△BAE,△CDF≌△CDM,∴∠AEB=∠M=∠GEF,∠M=∠CFD=∠GFE,AE=CM=CF,∴∠GEF=∠GFE,∴GE=GF,∵△EFP是由△EFG翻折得到,∴EG=EP=GF=PF,∴四边形EGFP是菱形,∴PG⊥AC,OE=OF,∵AE=CF,∴AO=OC,∵AB∥OP,∴BP=PC,∵PF∥BE,∴EF=CF=AE,∵PB=PC,AO=OC,∴PO=OG=AB,∴AB=PG,AB∥PG,∴四边形ABPG是平行四边形,∴AG∥BC,∴∠GAO=∠ACB=45°,设EO=OF=a,则OA=OG=3a,AG=3a,∴==,∴AG=EF14、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.解:(1)∵E为AC中点,作ED⊥AC交AB于D,∴AD=CD,∵∠ACB=90°,∴BC∥DE,∴AD=BD,∴CD=BD,∴AB=2CD;(2)如图2,连接CH,∵点E是AC的中点,∴AE=CE,∵DE⊥AC,∴CH=AH,∴∠ACH=∠CAH,∵∠ACB=90°,∴∠B+∠BAC=90°,∵CF⊥AB,∴∠BAC+∠ACF=90°,∴∠ACF=∠B,∴∠HCG=∠ACH+∠ACF=∠CAH+∠B,∠AHG=2∠B∴在四边形AHGF中,∠AFG+∠FGH+∠AHG+∠F AH=360°,∴∠FGH=360°﹣(∠AFG+∠AHG+∠F AH)=360°﹣(90°+2∠B+∠CAH+∠BAC)=360°﹣(90°+2∠B+∠CAH+90°﹣∠B)=360°﹣(180°+∠B+∠CAH)=180°﹣(∠B+∠CAH),∵∠CGH=180°﹣∠FGH=∠B+∠CAH=∠HCG,∴CH=GH,∵CH=AH,∴AH=GH;(3)如图3,由(1)知,DE∥BC,∴∠B=∠ADE,在△BFC和△DEA中,,∴△BFC≌△DEA,∴BC=AD,∵AD=BD=CD,∴BC=BD=CD,∴△BCD是等边三角形,∴∠B=60°,在Rt△ABC中,AC=6,∴BC=2,AB=4,∵CF⊥BD,∴DF=,CF=3,∵∠BAC=30°,∴∠ADE=60°,∵∠EDG=90°,∠FDG=30°,在Rt△DFG中,DF=,∴FG=1,DG=2,∴CG=CF﹣FG=2过点H作HN⊥CF,由(2)知,CH=GH,∴NG=CG=1,∴FN=NG+FG=2,过点H作HM⊥AB,∴∠FMH=∠NFM=∠HNF=90°,∴四边形NFMH是矩形,∴HM=FN=2,在Rt△DMH中,∠ADE=60°,HM=2,∴DH=,在Rt△HDG中,根据勾股定理得,HG==.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)(1)证明:∵AC=BC,∠ACB=90°,∴∠A=∠B=45°,∵CD⊥AB,∴∠CDB=90°,∴∠DCB=45°,∵∠ECF=∠DCB+∠1=45°+∠1,∠EFC=∠B+∠2=45°+∠2,∠1=∠2,∴∠ECF=∠EFC,∴CE=EF,∵CD⊥AB,FG⊥AB,∴∠CDE=∠EGF=90°,在△CDE和△EGF中,,∴△CDE≌△EGF(AAS);(2)证明:由(1)得:CE=EF,∠A=∠B,∵CE平分∠ACD,∴∠ACE=∠1,∵∠1=∠2,∴∠ACE=∠2,在△ACE和△BEF中,,∴△ACE≌△BEF(AAS),∴AE=BF;(3)AE=BF,作EH⊥BC与H,如图3所示:设DE=x,根据题意得:BE=DE=x,AD=BD=2x,CD=AD=2x,AE=3x,根据勾股定理得:BC=AC=2x,∵∠ABC=45°,EH⊥BC,∴BH=x,∴CH=BC﹣BH=x,∵EC=EF,∴FH=CH=x,∴BF=x﹣x=x,∴=,∴AE=.16、在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线。
(完整)中考数学压轴题精选含答案

一、解答题1.如图,在直角梯形ABCD 中,AB ∥CD ,∠B =90°,AB =4,BC =8,CD =2m (m >2),P 为CD 中点,以P 为圆心,CP 为半径作半圆P ,交线段AC 于点E ,交线段AD 于点F .(1)当E 为CA 中点时,①求证:E 是弧CF 的中点.②求此时m 的值.(2)连结PF ,若PF 平行△ABC 的某一边时求出满足条件的m 值.(3)连结PE ,将PE 绕着点E 顺时针旋转90°得到EP ',连结AP ',当AP '⊥AC 时,求此时CE 的长.2.如图1,在菱形ABCD 中,∠D =120°,AB =8,点M 从A 开始,以每秒1个单位的速度向点B 运动;点N 从C 出发,沿C →D →A 方向,以每秒2个单位的速度向点A 运动,若M 、N 同时出发,其中一点到达终点时,另一个点也随之停止运动.设运动的时间为t 秒,过点N 作NQ ⊥DC ,交AC 于点Q .(1)当t =2时,求线段NQ 的长;(2)设△AMQ 的面积为S ,直接写出S 与t 的函数关系式及t 的取值范围;(3)在点M 、N 运动过程中,是否存在t 值,使得△AMQ 为等腰三角形?若存在,请求出t 的值;若不存在,请说明理由.3.如图,在平面直角坐标系中,抛物线2y x bx c =-++,与y 轴交于点A 与x 轴交于点E 、B .且点()0,5A ,()5,0B ,点P 为抛物线上的一动点.(1)求二次函数的解析式;(2)如图1,过点A 作AC 平行于x 轴,交抛物线于点C ,若点P 在AC 的上方,作PD 平行于y 轴交AB 于点D ,连接PA ,PC ,当245AOE APCD S S ∆=四边形时,求点P 坐标; (3)设抛物线的对称轴与AB 交于点M ,点Q 在直线AB 上,当以点M 、E 、P 、Q 为顶点的四边形为平行四边形时,请直接写出点Q 的坐标.4.如图,抛物线2y ax bx c =++与x 轴交于A ,B 两点,与y 轴交于C 点,OA =1,OB =OC =3.(1)求抛物线的表达式;(2)如图1,点D 为第一象限抛物线上一动点,连接DC ,DB ,BC ,设点D 的横坐标为m ,△BCD 的面积为S ,求S 的最大值;(3)如图2,点P (0,n )是线段OC 上一点(不与点O 、C 重合),连接PB ,将线段PB 以点P 为中心,旋转90°得到线段PQ ,是否存在n 的值,使点Q 落在抛物线上?若存在,请求出满足条件的n 的值,若不存在,请说明理由.5.如图,抛物线223y x x =--+与x 轴交于A 、B 两点,与y 轴交于C 点.(1)在第二象限内的抛物线上确定一点P ,使四边形PBOC 的面积最大.求出点P 的坐标.(2)点M 为抛物线上一动点,x 轴上是否存在一点Q ,使点B 、C 、M 、Q 的顶点的四边形是平行四边形,若存在,请直接写出Q 点的坐标;若不存在,请说明理由.6.已知抛物线经过()30A -,,()1,0B ,52,2C ⎛⎫ ⎪⎝⎭三点,其对称轴交x 轴于点H ,一次函数()0y kx b k =+≠的图象经过点C ,与抛物线交于另一点D (点D 在点C 的左边),与抛物线的对称轴交于点E . (1)求抛物线的解析式;(2)在抛物线上是否存在点F ,使得点A 、B 、E 、F 构成的四边形是平行四边形,如果存在,求出点F 的坐标,若不存在请说明理由(3)设∠CEH=α,∠EAH =β,当αβ>时,直接写出k 的取值范围7.如图1,直线l 1:y =kx 与直线l 2:y =﹣12x +b 相交于点A (4,3),直线l 2:y =﹣12x +b 与x 轴交于点B ,点E 为线段AB 上一动点,过点E 作EF ∥y 轴交直线l 1于点F ,连接BF .(1)求k、b的值;(2)如图2,若点F坐标为(8,6),∠OFE的角平分线交x轴于点M.①求线段OM的长;②点N在直线l1的上方,当△OFN和△OFM全等时,直接写出点N的坐标.8.如图,抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,与y轴交于点C.直线l与抛物线交于A、D两点,与y轴交于点E,点D的坐标为(4,3).(1)求抛物线的解析式与直线l的解析式;(2)若点P是抛物线上的点且在直线l上方,连接PA、PD,求当△PAD面积最大时点P 的坐标及该面积的最大值;(3)若点Q是y轴上的点,且∠ADQ=45°,求点Q的坐标.9.如图,在△ABC中,AB=AC,⊙是△ABC的外接圆,连接BO并延长交边AC于点D.(1)如图1,求证:∠BAC=2∠ABD;(2)如图2,过点B作BH⊥AC于点H,延长BH交⊙O于点G,连接OC,CG,OC交BG于点F,求证:BF=2HG;(3)如图3,在(2)的条件下,若AD=2,CD=3,求线段BF的长.10.如图1,在平面直角坐标系中,抛物线y=ax2+154x+c与x轴负半轴相交于点A(﹣20,0),与y轴相交于点B(0,﹣15).(1)求抛物线的函数表达式及直线AB的函数表达式;(2)如图2,点C是第三象限内抛物线上的一个动点,连接AC、BC,直线OC与直线AB 相交于点D,当△ABC的面积最大时,求此时△ABC面积的最大值及点C的坐标;(3)在(2)的条件下,点E为线段OD上的一个动点,点E从点O开始沿OD以每秒10个单位长度的速度向点D运动(运动到点D时停止),以OE为边,在OD的左侧做正方形OEFG,设正方形OEFG与△OAD重叠的面积为S,运动时间为t秒.当t>3时,请直接写出S与t之间的函数关系式为(不必写出t的取值范围).11.在平面直角坐标系xOy中,点A(a,b)和点B(c,d).给出如下定义:以AB为边,作等边三角形ABC,按照逆时针方向排列A,B,C三个顶点,则称等边三角形ABC为点A,B的逆序等边三角形.例如,当1,0,3,0a b c d=-===时,点A,B的逆序等边三角形ABC如图①所示.(1)已知点A(-1,0),B(3,0),则点C的坐标为___;请在图①中画出点C,B的逆序等边三角形CBD,点D的坐标为___.(2)图②中,点B(3,0),点A在以点M(-2,0)为圆心1为半径的圆上,求点A,B的逆序等边三角形ABC的顶点C的横坐标取值范围.(3)图③中,点A在以点M(-2,0)为圆心1为半径的圆上,点B在以N(3,0)为圆心2为半径的圆上,且点B的纵坐标0d>,点A,B的逆序等边三角形ABC如图③所示.若点C 恰好落在直线y x t=+上,直接写出t的取值范围.12.已知:如图1,一次函数y=mx+5m的图像与x轴、y轴分别交于点A、B,与函数y=-23x的图像交于点C,点C的横坐标为-3.(1)求点B的坐标;(2)若点Q为直线OC上一点,且S△QAC=2S△AOC,求点Q的坐标;(3)如图2,点D为线段OA上一点,∠ACD=∠AOC.点P为x轴负半轴上一点,且点P到直线CD和直线CO的距离相等.①在图2中,只利用圆规.....作图找到点P的位置; (保留作图痕迹,不得在图2中作无关元素.)②求点P的坐标.13.在平面直角坐标系xOy中,⊙O的半径为1.对于线段AB,给出如下定义:若线段AB沿着某条直线l对称可以得到⊙O的弦A′B′,则称线段AB是⊙O的以直线l为对称轴的“反射线段”,直线l称为“反射轴”.(1)如图,线段CD,EF,GH中是⊙O的以直线l为对称轴的“反射线段”有;(2)已知A点坐标为(0,2),B点坐标为(1,1),①若线段AB是⊙O的以直线l为对称轴的“反射线段”,求反射轴l与y轴的交点M的坐标.②若将“反射线段”AB沿直线y=x的方向向上平移一段距离S,其反射轴l与y轴的交点的纵坐标yM的取值范围为12≤yM136≤,求S.(3)已知点M,N是在以原点为圆心,半径为2的圆上的两个动点,且满足MN=1,若MN是⊙O的以直线l为对称轴的“反射线段”,当M点在圆上运动一周时,求反射轴l未经过的区域的面积.(4)已知点M,N是在以(2,013MN2=MN是⊙O的以直线l为对称轴的“反射线段”,当M点在圆上运动一周时,请直接写出反射轴l与y轴交点的纵坐标的取值范围.14.△ABC为等边三角形,AB=4,AD⊥BC于点D,点E为AD的中点.(1)如图1,将AE绕点A顺时针旋转60°至AF,连接EF交AB于点G,求证:G为EF中点.(2)如图2,在(1)的条件下,将△AEF绕点A顺时针旋转,旋转角为α,连接BE,H为BE的中点,连接DH,GH.当30°<α<120°时,猜想∠DHG的大小是否为定值,并证明你的结论.(3)在△AEF绕点A顺时针旋转过程中,H为BE的中点,连接CH,问线段CH何时取得最大值,请说明理由,并直接写出此时△ADH的面积.15.在ABC中,AB AC=,D是边AC上一点,F是边AB上一点,连接BD、CF交于点E,连接AE,且.(1)如图1,若90BAC∠=︒,,,求点B到AE的距离;(2)如图2,若E为BD中点,连接FD,FD平分,G为CF上一点,且,求证:;(3)如图3,若,12BC=,将ABD△沿着AB翻折得,点H为的中点,连接HA、HC,当周长最小时,请直接写出的值.16.在平面直角坐标系xOy中,已知抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y轴交于C点,D为抛物线顶点.(1)连接AD,交y轴于点E,P是抛物线上的一个动点.①如图一,点P是第一象限的抛物线上的一点,连接PD交x轴于F,连接,若,求点P的坐标.②如图二,点P在第四象限的抛物线上,连接AP、BE交于点G,若,则w有最大值还是最小值?w的最值是多少?(2)如图三,点P是第四象限抛物线上的一点,过A、B、P三点作圆N,过点P作PM x⊥轴,垂足为I,交圆N于点M,点P在运动过程中,线段是否变化?若有变化,求出MI的取值范围;若不变,求出其定值.(3)点Q是抛物线对称轴上一动点,连接OQ、AQ,设AOQ外接圆圆心为H,当的值最大时,请直接写出点H的坐标.17.如图,在平面直角坐标系中,矩形OABC,点A在y轴上,点C在x轴上,其中B(﹣2,3),已知抛物线y=﹣34x2+bx+c经过点A和点B.(1)求抛物线解析式;(2)如图1,点D (﹣2,﹣1)在直线BC 上,点E 为y 轴右侧抛物线上一点,连接BE 、AE ,DE ,若S △BDE =4S △ABE ,求E 点坐标;(3)如图2,在(2)的条件下,P 为射线DB 上一点,作PQ ⊥直线DE 于点Q ,连接AP ,AQ ,PQ ,若△APQ 为直角三角形,请直接写出P 点坐标.18.如图1,点A ,点B 的坐标分别(a ,0),(0,b ),且b =+4,将线段BA 绕点B 逆时针旋转90°得到线段BC .(1)直接写出a = ,b = ,点C 的坐标为 ;(2)如图2,作CD ⊥x 轴于点D ,点M 是BD 的中点,点N 在△OBD 内部,ON ⊥DN ,求2+ON =DN .(3)如图3,点P 是第二象限内的一个动点,若∠OPB =90°,求线段CP 的最大值.19.如图1,已知抛物线)(3343y x x =+-与x 轴交于A 、B 两点,与y 轴交于点C ,(1)写出A 、B 、C 三点的坐标.(2)若点P 为OBC 内一点,求OP BP CP ++的最小值.(3)如图2,点Q 为对称轴左侧抛物线上一动点,点()4,0D ,直线DQ 分别与y 轴、直线AC 交于E 、F 两点,当CEF △为等腰三角形时,请直接写出CE 的长.20.已知等边△ABC ,M 在边BC 上,MN ⊥AC 于N ,交AB 于点P .(1)求证:BP =BM ;(2)若MC =2BM ,求证:MP =MN .(3)若E ,F 分别在AB 、AC 上,且△MEF 为等边三角形,当MEF ABC S S ∆∆的值最小时,BM BC= .【参考答案】**科目模拟测试 一、解答题 1.(1)①见解析;②5m =;(2)m 的值为25或6;(3)25CE =【解析】【分析】(1)①连接DE ,证明ADC ∆是等腰三角形,根据“三线合一”的性质可得ADE CDE ∠=∠,证得EC EF =,从而可得结论;②根据勾股定理得到AC 45=,由E 为AC 中点得EC 25=,再证明DEC CBA ,由相似三角形的性质列出比例式,求出m 的值即可;(2)分PF //AC 和PF //BC 两种情况求解即可; (3)设CE =x ,作PG ⊥AC ,则2x GE =,45AE x =- 证明PGE EAP '≅得AP GE '=,再证明AP EBAC ',列比例式求出x 的值即可.【详解】解:(1)如图,连接DE∵CD 是圆P 的直径,∴∠DEC =90°,即DE ⊥AC∵E 为CA 中点∴AE =CE∴AD =CD∴ADE CDE ∠=∠∴EC EF =∴E 是CF 的中点;②在Rt △ABC 中,∠B =90°,AB =4,BC =8,∴22224845AC AB BC +=+∵E 是AC 的中点∴11452522EC AC ==⨯= ∵AB //CD ,90B ∠=︒∴90B DCB ∠+∠=︒∴90DCB∠=︒,即90DCE BCA∠+∠=︒∵90CDE DCE∠+∠=︒∴CDE BCA∠=∠又90B DEC∠=∠=︒∴DEC CBA∆∆∽∴CE DCAB AC=,即252=445m解得,5m=;(2)分两种情况:①当PF//AC时,如图,则有PDF CDA∆∆∴PF PDAC CD=,即245PF mm=∴25=PF∴25m=②当PF//BC时,如图,过点A作AH⊥DC,垂足为H,则四边形AHCB是矩形,∴AH//BC,HC=AB=4,AH=BC=8∴PF//AH∵90DCB∠=︒∴90FPD∠=︒∴45PDF PFD∠=∠=︒∴45HAD HDA∠=∠=︒∴DH=AH,即248m-=解得,6m=综上,m的值为256;(3)过点P 作PG AC ⊥于点G ,如图,∵PE =PC ∴1,2GE CE EPG CPG =∠=∠ ∵90PEP '∠=︒∴90P EA PEG '∠+∠=︒又90PEG GPE ∠+∠=︒∴P EA EPG '∠=∠又90P AE PGE '∠=∠=︒,PE P E '=∴P AE EPG '∆≅∆∴AP GE '=设CE x =,则45,2x AE x GE AP '=== ∵90,90BCA DCA GPC PCH ∠+∠=︒∠+∠=︒∴GPC BCA ∠=∠∴EPG BCP ∠=∠∴P EA BCA '∠=∠又90P AE B '∠=∠=︒∴AP E BAC '∆∆ ∴AP AB AE BC '=42825x = ∴5x =25CE =【点睛】本题主要考查了全等三角形的判定与性质,圆的基本概念,相似三角形的判定与性质,正确作出辅助线以及进行分类讨论是解答本题的关键.2.(143;(2)S =()()22330434348t t t ⎧+≤≤⎪⎪⎨⎪≤⎪⎩<;(3)存在,当t =247s 或(32-163)s或163s时,△AMQ为等腰三角形.【解析】【分析】(1)首先求得CN的长,在直角△CNQ中利用三角函数即可求得NQ的长;(2)当0≤t≤4时,N在CD上,首先求得CQ,则AQ长即可求得,再根据△CAB=30°,AM=t,据此即可求得△AMQ的长;当4<t≤8时,利用相似求得AQ的长,进而求得△AMQ的面积,得到函数解析式;(3)分三种情形讨论求解即可.【详解】解:(1)当t=2时,CN=2×2=4,∵在△ACD中,AD=DC,∴∠DCA=1801202︒-︒=30°,在直角△CNQ中,NQ=CN•tan30°=4×33=433;(2)由题意得,AM=t,当0≤t≤4时,CN=2t,∵∠D=120°,AB=CD=8,∴∠DCA=30°,连接BD,与AC相交于点定O,过点Q作QG⊥AB于点G,∴OC=CD•cos30︒3AC3∴在Rt△CNQ中,NQ23t,CQ43t,∴AQ=AC-CQ343,QG=12AQ,∴S=12AM• QG =233t+,当4<t≤8时,延长QN,交AB于G,交CD延长线于H,如图:ND =2t -8,∠HDN =60°,∴HD =12ND =t -4, ∴CH =t -4+8=t +4,∴CQ =23cos303CH =︒(t +4), ∴AQ =AC -CQ =83-233(t +4),QG =12AQ , S =12•AM • QG 234363t t =-+. 综上,S =()()223230433434863t t t t t t ⎧-+≤≤⎪⎪⎨⎪-+≤⎪⎩<; (3)①当0<t ≤4时,只有MA =MQ 符合条件,过点M 作ME ⊥AC 于点E ,则AE =EQ =AM •cos30︒=32t , ∴AQ =3t ,由(2)知AQ 343, 3433, 解得t =247; ②当4<t ≤8时,由(2)知AQ 323t +4),AQ =AM 时,)4t +=t ,解得tAQ =MQ 时,AM ,t )4t ⎤+⎥⎦, 解得t =163.综上所述,当t =247s 或(s 或163s 时,△AMQ 为等腰三角形. 【点睛】本题考查了菱形的性质以及三角函数,正确进行分请情况进行讨论是关键.3.(1)245y x x =-++;(2)1(2,9)P ,2(3,8)P ;(3)1(9,4)Q -,2(0,5)Q ,3(1,6)Q -,4(5,10)Q -【解析】【分析】(1)直接将(0,5)A ,(5,0)B 代入2y x bx c =-++,求解即可;(2)先求出AB 的解析式,设点P 的横坐标为t ,则()2,45P t t t -++,(,5)D t t -+,用t 表示出PD ,最后利用245AOE APCD S S ∆=四边形求出结果; (3)分三种情况讨论解答:①当EM 为平行四边形的对角线时;②当EP 为对角线时;③当EQ 为对角线时.【详解】(1)将点(0,5)A ,(5,0)B 分别代入2y x bx c =-++得25505b c c -++=⎧⎨=⎩, 45b c =⎧∴⎨=⎩, ∴二次函数的解析式为245y x x =-++;(2)//AC x 轴,点()0,5A ,∴当5y =时,2455x x -++=,10x ∴=,24x =,()4,5C ∴,4AC ∴=,设直线AB 的解析式为y mx n =+,将(0,5)A ,(5,0)B 分别代入得505n m n =⎧⎨=+⎩, 解得:1m =-,5n =∴直线AB 的解析式为5y x =-+;设点P 的横坐标为t ,则()2,45P t t t -++,(,5)D t t -+()2245(5)5PD t t t t t ∴=-++--+=-+,4AC =,()22114521022APCD S AC PD t t t t ∴=⨯=⨯⨯-+=-+四边形 函数245y x x =-++,当0y =时,有2450x x -++=,11x ∴=-,25x =,(1,0)E ∴-,1OE ∴=,又5OA =,11515222AOE S OE OA ∆∴=⨯⨯=⨯⨯=, 245AOE APCD S S ∆=四边形, 22452101252t t ∴-+=⨯=, 解得:12t =,23t =,∴点1(2,9)P ,2(3,8)P ;(3)∵2(2)9y x =--+,∴当x =2时,y =-2+5=3,∴M (2,3),设P (m ,2(2)9m --+,(,5)Q n n -+,而E (-1,0),①当EM 为平行四边形的对角线时,(平行四边形的对角线互相平分)得:21222(2)950322m n m n +-+⎧=⎪⎪⎨--+-++⎪=⎪⎩, 解得121261,52m m n n ==-⎧⎧⎨⎨=-=⎩⎩ (舍), ∴点Q 的坐标为(-5,10);②当EP 为对角线时,212220(2)93522m m m n -++⎧=⎪⎪⎨--+-+⎪=⎪⎩,解得121223,10m m n n ==⎧⎧⎨⎨=-=⎩⎩, ∴点Q 的坐标为(-1,6)或(0,5);③当EQ 为对角线时,21222053(2)922n m n m -++⎧=⎪⎪⎨-+--+⎪=⎪⎩, 解得121261,92m m n n ==-⎧⎧⎨⎨==⎩⎩(舍), 点Q 的坐标为(9,-4),综上所得:1(9,4)Q -,2(0,5)Q ,3(1,6)Q -,4(5,10)Q -.【点睛】本题考查了待定系数法求函数关系式,平行四边形的性质和判定,解本题的关键是分类思想的运用.4.(1)2y x 2x 3=-++;(2)278;(3)存在,n =1或n 3+33- 【解析】【分析】(1)通过待定系数法求解函数解析式即可;(2)作DF ⊥x 轴于点F ,交BC 于点E ,根据12S DE OB =⋅求得S 关于m 的解析式,根据二次函数的性质求解即可;(3)过点P 作PB 的垂线,交抛物线于点1Q 和2Q ,作1Q M y ⊥轴于点M ,2Q N y ⊥轴于点N ,利用全等三角形的性质求解即可.【详解】解:(1)设函数关系式为2y ax bx c =++由题意,得A (-1,0),B (3,0),C (0,3)∴(1)(3)y a x x =+-把C (0,3)代入得,1a =-∴2y x 2x 3=-++(2)作DF ⊥x 轴于点F ,交BC 于点E设直线BC 关系式为y =kx +b ,代入(3,0),(0,3)得k =-1,b =3,∴y =-x +3∵点D 的横坐标为m ,则DF =223m m -++,EF =-m +3∴DE =23m m -+22133327(3)()22228S DE OB m m m =⋅=-+=--+ ∵302-<,∴S 的最大值是278(3)过点P 作PB 的垂线,交抛物线于点1Q 和2Q ,作1Q M y ⊥轴于点M ,2Q N y ⊥轴于点N∴1290Q MP Q NP BOP ∠=∠=∠=︒∵1190Q PM PQ M ∠+∠=︒,190Q PM BPO ∠+∠=︒,∴1PQ M BPO ∠=∠又∵1BP PQ =,∴1Q PM PBO △≌△∴1MQ OP n ==,3MP OB ==,∴1()3Q n n +,代入抛物线,得2323n n n +=-++解得11n =,20n =(舍去)同理,2PN Q PBO ≌,∴2Q (-n ,n -3)代入抛物线,得2323n n n =-+-- 解得13+33n -=2333n --=舍去) 综上,存在n 的值,n =1或n 3+33-【点睛】 此题考查了二次函数与几何的综合应用,涉及了待定系数法求解析式,二次函数的性质,全等三角形的判定与性质,解题的关键是熟练掌握二次函数以及全等三角形的判定与性质.5.(1)315,24⎛⎫- ⎪⎝⎭;(2)Q 1(-5,0),Q 2(-1,0),Q 3 ()720,,Q 4)720,. 【解析】【分析】(1)分别求出点B 、C 的坐标,连接PB ,PC ,PO ,设点P 坐标为()2,23m m m --+,四边形PBOC 的面积为S ,根据=BOP COP S S S +△△得到S 关于m 的二次函数解析式,根据二次函数的性质即可求解;(2)分点M 在x 轴上方或点M 在x 轴下方两种情况讨论,分别求出点M 的坐标,根据平行四边形的性质即可求出点Q 的坐标. 【详解】解:(1)把0x =代入223y x x =--+得y =3, ∴点C 坐标为(0,3);把y =0代入223y x x =--+得2x 2x 30--+=, 解得123,1x x =-=, ∵点B 在x 轴负半轴上, ∴点B 坐标为(-3,0); 如图1,连接PB ,PC ,PO ,∵点P 在第二象限抛物线223y x x =--+上,∴设点P 坐标为()2,23m m m --+(-3<m <0),设四边形PBOC 的面积为S , ∴=BOP COP S S S +△△2211232m m OB O m C =--++ ()()2332223m m m +=+--- 2399222m m =--+, ∵302-<,∴当322b m a =-=-时,S 有最大值, 此时,215234m m --+=, ∴当点P 坐标为315,24⎛⎫- ⎪⎝⎭时,四边形PBOC 的面积最大;(2)存在,如图2,分点M 在x 轴上方或点M 在x 轴下方两种情况讨论. ①当点M 在x 轴上方时,点M 与点C 纵坐标相等,∴2233x x --+=, 解得122,0x x =-=, ∴CM 1=2,∵四边形BQCM 1是平行四边形, ∴CM =BQ =2,∴满足条件的点Q 有两个,分别是Q 1(-5,0),Q 2(-1,0); ②当点M 在x 轴下方时,点M 与点C 纵坐标互为相反数, ∴2233x x --+=-, 解得1271,71x x =--=-,∴点M 2坐标为()713---,,点M 3坐标为()713--,,由平行四边形的性质得点B 向右平移3个单位,向上平移3个单位得到点C ,∴点M 2向右平移3个单位,向上平移3个单位得到点Q 3,点M 3向右平移3个单位,向上平移3个单位得到点Q 4,∴Q 3的坐标为()720-+,,Q 4的坐标为()720+,;综上所述,满足条件的点Q 的坐标有四个,分别是Q 1(-5,0),Q 2(-1,0),Q 3()720-+,,Q 4()720+,.【点睛】本题为二次函数综合题,难度较大,解决第(1)步,关键是理解函数图象上点的坐标特点,将四边形分割为两个三角形,分别表示出三角形面积,得到函数解析式,并利用二次函数性质求解;解决第(2)步关键是理解平行四边形的性质,利用分类讨论思想求解,注意要充分考虑各种情况,不要漏解.6.(1)y =12x 2+x −32;(2)(3,6)或(-5,6)或(−1,-2);(3)−12<k <56且k≠0或56<k<43【解析】【分析】(1)把A(−3,0),B(1,0),52,2C⎛⎫⎪⎝⎭代入y=ax2+bx+c,解方程组即可;(2)把C点坐标代入直线CD,得2k+b=52,分两种情况:①若AB为平行四边形的边时,②若AB为平行四边形的对角线时,得关于k、b的方程组,解方程组即可求解;(3)分两种情况:①当E点在x轴上方时,②E点在x轴下方时,根据当α=β时,列方程,可求出k的值,进而求出k的取值范围.【详解】解:(1)设抛物线的解析式为y=ax2+bx+c,∵抛物线经过A(−3,0),B(1,0),C(2,52)三点,∴9305 422a b ca b ca b c⎧⎪-+=⎪++=⎨⎪⎪++=⎩,∴12132abc⎧⎪⎪⎨⎪⎪-⎩===,∴抛物线的解析式为y=12x2+x−32;(2)如图1所示,将C点坐标代入直线CD,得2k+b=52,当x=−1时,y=−k+b,即E(−1,−k+b).①若AB为平行四边形的边时,则F(-1+4,−k+b)或F(-1-4,−k+b),即:F(3,−k +b )或F (-5,−k +b ), 把F (3,−k +b )代入y =12x 2+x −32,得−k +b =6, 把F (-5,−k +b ),代入y =12x 2+x −32,得−k +b =6, 又∵2k +b =52, ∴k =76-,b =296∴F (3,6)或(-5,6);②若AB 为平行四边形的对角线时,则F 和E 关于x 轴对称, ∴F (−1,k -b ), ∴k -b =-2, 又∵2k +b =52, ∴k =16,b =136,∴F (−1,-2),综上所述:F 的坐标为(3,6)或(-5,6)或(−1,-2); (3)如图2所示,①当E 点在x 轴上方时,如图2所示,当α=β时,∵∠EHA =90°, ∴∠AEC =90°, ∴∠AEH =∠EGH , ∵∠AHF =∠FHG =90°, ∴AHF FHG ∽, ∴AE AHEG EH=, ∵A (−3,0),E (−1,−k +b ),G (bk-,0),∴()()2222221k bk bbk bk+-+=-+⎛⎫-++-+⎪⎝⎭,∴k2−bk−2=0,联立方程220522k bkk b⎧--=⎪⎨+=⎪⎩,解得k=−12(k=43舍去),随着E点向下移动,∠CEH的度数越来越大,∠EAH的度数越来越小,当E点和H点重合时(如图3所示),α和β均等于0,此时联立方程522k bk b⎧+⎪⎨⎪-+⎩==,解得5656kb⎧=⎪⎪⎨⎪=⎪⎩,因此当−12<k<56且k≠0时,α>β;②E点在x轴下方时,如图4所示,当α=β时,∵∠EHA=90°,∴∠AEC=90°,根据①可得此时k=43(k=−12舍去),随着E点向下移动,∠CEH的度数越来越小,∠EAH的度数越来越大,因此当56<k <43时,α>β.综上所述可得,当α>β时,k 取值范围为−12<k <56且k ≠0或56<k <43.【点睛】本题考查的是一次函数、二次函数和相似三角形的判定和性质的综合应用,掌握待定系数法求函数解析式和数形结合思想方法是解题的关键.7.(1)34k =,5b =;(2)①OM =5;②()3,6N 或724,55N ⎛⎫ ⎪⎝⎭【解析】 【分析】(1)分别将将(4,3)A 代入y kx =和12y x b =-+中,求解即可;(2)①设直线AB 与y 轴交与点C ,与FM 交于点D ,证明△AFD ≌△EFD ,得到AD =ED ,利用中点坐标公式求得点D 坐标,用待定系数法求得直线FD 的函数表达式,令0y =,即可求得点M 的坐标,从而求得OM ;②点N 在直线l 1的上方,当△OFN 和△OFM 全等时,满足题意的点N 有两个,分别画出相关的图形,分类讨论求解即可. 【详解】解:(1)∵直线l 1:y kx =和直线l 2:12y x b =-+相交于点A∴将(4,3)A 代入y kx =中,得:43k = 解得:34k =∴将(4,3)A 代入12y x b =-+中,得:1432b -⨯+=解得:5b =∴3,54k b == (2)① 设直线AB 与y 轴交与点C ,与FM 交于点D ,如下图:∵34k =,5b = ∴直线l 1的函数表达式为34y x =,直线l 2的函数表达式为152y x =-+∵(4,3)A ∴22345OA +设直线AB 与y 轴交与点C ,与FM 交于点D 则()0,5C ∴5OC = ∴5OA OC == ∴∠OCA =∠OAC ∵//FE y 轴 ∴∠OCA =∠FEA 又∵∠OAC =∠FAE ∴∠FAE =∠FEA ∴FA =FE又∵FM 是∠OFE 的角平分线 ∴∠AFM =∠EFM 又∵FD =FD ∴△AFD ≌△EFD ∴AD =ED ∴点D 为AE 的中点 ∵//FE y 轴∴点F 和点E 的横坐标相同 将8x =代入152y x =-+中,得1y =∴()8,1E ∵(4,3)A ,()8,1E ∴()6,2D设线段FM 所在的直线函数表达式为()0y ax b a =+≠将()()8,6,6,2F D 代入y ax b =+中,得:8662k b k b +=⎧⎨+=⎩解得:210k b =⎧⎨=-⎩∴线段FM 所在的直线函数表达式为210y x =- 令0y =,得2100x -= 解得:5x = ∴()5,0M ∴OM =5② 当,OFN FOM 全等时,有两种情况,情况一,如下图所示:∵OFN FOM ≅△△∴∠OFN =∠FOM ,FN =OM ,ON =FM ∴//FN OM ∵OM =5 ∴FN =5,8F x =∴853N x =-=,6N F y y == ∴()3,6N情况二,当△OMF 和△ONF 关于直线l 1对称时,如下图所示:∵OFN FOM ≅△△∴ON =OM =5,∠NOF =∠MOF ∵OP =OP ∴△NOP ≌△MOP ∴PN =PM ∵()8,6F∴10OF 又∵1122OMFF SOM y OF PM =⋅=⋅ ∴F OM y OF PM ⋅=⋅ ∴56==310PM ⨯∴MN =2PM =6,OP 4 ∵1122OMN N S MN OP OM y =⋅=⋅△ ∴642455N y ⨯==∴75N x ==∴724,55N ⎛⎫⎪⎝⎭综上所述,满足题意点有两个,分别是:()3,6N 或724,55N ⎛⎫⎪⎝⎭【点睛】本题考查用待定系数法求一次函数表达式,三角形全等的性质和证明,两条直角交点的求法以及三角形的等面积法等知识点,牢记相关内容并能灵活应用数形结合思想解题是本题的关键.8.(1)y 14=-x 2+x +3;y 12=x +1;(2)△PAD 的面积的最大值为274,P (1,154);(3)点Q 的坐标为(0,133)或(0,﹣9) 【解析】 【分析】(1)由A (﹣2,0)、B (6,0)设抛物线的解析式为y =a (x +2)(x ﹣6),把D (4,3)的代入解析式解方程即可,再利用待定系数法求解一次函数的解析式; (2)如图1中,过点P 作PT y ∥轴交AD 于点T .设P (m ,14- m 2+m +3),则T(m,12m+1),再利用面积列函数关系式,再利用二次函数的性质求解最值即可;(3)如图2中,将线段AD绕点A逆时针旋转90°得到AT,则T(﹣5,6),设DT交y轴于点Q,则∠ADQ=45°,再求解直线DT的解析式为y13=-x133+,作点T关于AD的对称点T′(1,﹣6),求解直线DT′的解析式为y=3x﹣9,设DQ′交y轴于点Q′,则∠ADQ′=45°,从而可得答案.【详解】解:(1)∵抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,∴设抛物线的解析式为y=a(x+2)(x﹣6),∵D(4,3)在抛物线上,∴3=a(4+2)×(4﹣6),解得a14 =-,∴抛物线的解析式为y14=-(x+2)(x﹣6)14=-x2+x+3,∵直线l经过A(﹣2,0)、D(4,3),设直线l的解析式为y=kx+m(k≠0),则2043k mk m-+=⎧⎨+=⎩,解得,121km⎧=⎪⎨⎪=⎩,∴直线l的解析式为y12=x+1;(2)如图1中,过点P作PT y∥轴交AD于点T.设P(m,14-m2+m+3),则T(m,12m+1).∵S△PAD12=•(xD﹣xA)•PT=3PT,∴PT的值最大值时,△PAD的面积最大,∵PT14=-m2+m+312-m﹣114=-m212+m+214=-(m﹣1)294+,∵14-<0,抛物线开口向下,∴m=1时,PT的值最大,最大值为94,此时△PAD的面积的最大值为274,P(1,154).(3)如图2中,将线段AD绕点A逆时针旋转90°得到AT,过D作DM x⊥轴于,M过T作TN x轴于,N90,,TNA AMD TAD AD AT90,TAN ATN TAN DAM,ATN DAM,ATN DAM≌6,3,235,TN AM AN DM ON∴T(﹣5,6),设DT交y轴于点Q,则∠ADQ=45°,∵D(4,3),∴直线DT的解析式为y13=-x133+,∴Q(0,133),作点T关于AD的对称点T',同理可得T'(1,﹣6),则直线DT′的解析式为y=3x﹣9,设DQ′交y轴于点Q′,则∠ADQ′=45°,∴Q′(0,﹣9),综上所述,满足条件的点Q的坐标为(0,133)或(0,﹣9).【点睛】本题属于二次函数综合题,考查了二次函数的性质,一次函数的性质,待定系数法,等腰直角三角形的性质等知识,解题的关键是学会利用参数构建二次函数解决最值问题,学会构造特殊三角形解决问题,属于中考压轴题.二次函数综合题中面积问题的解题通法:(1)直角坐标系中图形面积的求法,以“S三角形=12×水平底×铅直高”为基础求解.(2)图形面积的数量关系:①找出所求图形的顶点,其中动点的坐标根据函数关系式用含未知数的代数式表示出来;②结合图形作辅助线,并将关键线段的长度用含未知数的代数式表示出来;③利用面积公式用含未知数的代数式表示出图形的面积;④列方程求解.(3)图形面积的最值,解题思路跟(1)中的前三步相同,然后利用函数的增减性求解.9.(1)证明见解析;(2)证明见解析,(3)15714BF=.【解析】【分析】(1)连接OA并延长AO交BC于E,证明∠BAC=2∠BAE和∠ABD=∠BAE即可得结论,(2)利用直角三角形两锐角互余、圆周角定理进行导角,得出MCG△和△FCG是等腰三角形,得出BM=MC=FG=CG,MH=HG,进而由BF=BM+MH-FH=FG-FH+HG,得出结论;(3)过O点作OP⊥AC,由垂径定理得出12PD=,再由52ABOADOS AB BOS AD OD===和平行线分线段成比例定理求出7724DH DP==,由勾股定理进而可求BH,再利用相似三角形对应边成比例求出HG,即可得BF长.【详解】解:(1)连接OA并延长AO交BC于E,∵AB=AC,∴AB AC=,∵AE过圆心O,∴AE BC⊥,BE EC=,∴∠BAC=2∠BAE,∵OA=OB,∴∠ABD=∠BAE,∴∠BAC=2∠ABD;(2)如解图(2),连接OA并延长AO交BC于E,AE交BF于M,连接MC,设2BACα∠=,则ABD BAE EACα∠=∠=∠=∵AE =EC ,AE ⊥BC ,∴BM =MC ,∴∠MBC =∠MCB ,∵BG ⊥AC ,AE ⊥BC ,∴∠EAC +∠ACE =90°,∠HBC +∠ACE =90°,∴EAC HBC MCB α∠=∠=∠=,∴2CMG MBC MCB α∠=∠+∠=,∵BC BC =,∴2G BAC α∠=∠=,∴∠G =∠CMG ,∴CG =CM =BM ,∵AC ⊥BG ,∴MH =HG ,∵OA =OC ,∴ACO EAC α∠=∠=∴9090CFG ACO α∠=︒-∠=︒-,∵180FCG CFG G ∠=︒-∠-∠,即180(90)290FCG ααα∠=︒-︒--=︒-,∴FCG CFG ∠=∠,∴FG =CG ,∴BM =MC =FG =CG ,又∵MH =HG ,∴BF =BM +MH -FH =FG -FH +HG ,∴BF =2HG .(3)过O 点作OP ⊥AC ,如解图(3)∵AO 是∠BAC 的角平分线,∴点O 到AB 、AC 的距离相等, ∴ABO ADO SAB BO S AD OD==, ∵AD =2,CD =3,∴AB =AC =5, ∴5=2BO OD ,即:2=7OD BD , ∵OP ⊥AC ,∴52AP PC ==,12PD =, ∵BH AC ⊥, ∴OP //BH ,∴27DP OP OD DH BH BD ===, ∴7724DH DP ==, ∴154AH AD DH =+=,5-4HC DC DH ==,∵在Rt ABH中,BH == ∵BAH G ∠=∠,AHB GHC ∠=∠, ∴AHB GHC △△,∴AH BH HG CH = 即:AH HC BHHG =, 51544=⨯, ∴HG =, 由(2)得BF =2HG ,∴BF = 【点睛】 本题是圆的综合题,主要考查了圆周角定理,涉及了相似三角形的判定和性质、勾股定理、等腰三角形的判定和性质等知识点,解题关键是利用同弧或等弧所对圆周角相等、直角三角形的两锐角相等找出图中角之间的关系,从而利用相似或勾股定理解题.10.(1)291515404y x x =+-,y =﹣34x ﹣15;(2)面积最大值225,C (﹣10,﹣30);(3)S =﹣2553t +160t ﹣240. 【解析】【分析】(1)利用待定系数法将点A (﹣20,0),B (0,﹣15)代入抛物线y =ax 2+154x +c 即可求出抛物线的函数表达式;设AB 的函数表达式是y =kx +b ,然后利用待定系数法将点A (﹣20,0),B (0,﹣15)代入y =kx +b 即可求出直线AB 的函数表达式;(2)作CE ⊥OA 于E ,交AB 于F ,设C (a ,940a 2+154a ﹣15),F (a ,﹣34a ﹣15),根据题意表示出CF 的长度,进而表示出ABC S ∆,然后利用二次函数的性质求解即可;(3)作AN ⊥OD 于N ,AD 与FG 交于点I ,首先根据题意求出OC 的解析式,然后联立33154y x y x =⎧⎪⎨=--⎪⎩求出点D 的坐标,然后求出AD OD =,利用等腰三角形三线合一性质求出ON 的长度,进而利用勾股定理求出AN 的长度,表示出S △AON ,然后证明出△GFI ∽△OGH ∽△ANO ,利用相似三角形的性质表示出S △IJF =803(t ﹣3)2,S △GOH =253t ,最后利用面积之间的关系即可求出S 与t 之间的函数关系式.【详解】解:(1)由题意得,将点A (﹣20,0),B (0,﹣15)代入抛物线y =ax 2+154x +c 得, 21515(20)(20)04c a c =-⎧⎪⎨-+⨯-+=⎪⎩, ∴15940c a =-⎧⎪⎨=⎪⎩, ∴291515404y x x =+-, 设AB 的函数表达式是y =kx +b ,将点A (﹣20,0),B (0,﹣15)代入y =kx +b 得,∴15200b k b =-⎧⎨-+=⎩, ∴1534b k =-⎧⎪⎨=-⎪⎩, ∴y =﹣34x ﹣15; (2)如图1,作CE ⊥OA 于E ,交AB 于F ,设C (a ,940a 2+154a ﹣15),F (a ,﹣34a ﹣15), ∴FC =(﹣315)4a -﹣(2940a +154a ﹣15)=﹣2940a ﹣92a , ∴ABC S ∆=12CF •AO =12(﹣2940a ﹣92a )×20=﹣94(a +10)2+225, ∴当a =﹣10时,ABC S ∆=225, 当a =﹣10时,y =29(10)40⨯-+()15104⨯-﹣15=﹣30, ∴C (﹣10,﹣30);(3)如图2,作AN ⊥OD 于N ,∵C (﹣10,﹣30),∴OC 的解析式是:y =3x ,由33154y x y x =⎧⎪⎨=--⎪⎩得, 412x y =-⎧⎨=-⎩, ∴D (﹣4,﹣12),∵A (﹣20,0),OD 22412+10∴AD ()2220412-++=20,∴AD OD=,又∵AN⊥OD,∴ON=12OD=AN=S△AON=1160 22AN ON=⨯=,∵OE,OD=,∴DE=,∴JE=3(),∴FJ=EF﹣JEt﹣3(t)=(t﹣3),∵OG AN FJ∥∥,∴GOH OAN DAN AJF∠=∠=∠=∠,又∵90G ANO F∠=∠=∠=︒,∴△GFI∽△OGH∽△ANO,∴IJFAONSS∆∆=(FJAN)2=2,GOHAONSS∆∆=(OGAN)2)2,∴S△IJF=803(t﹣3)2,S△GOH=253t,∴S=S正方形OEFG﹣S△IJF﹣S△GOH=10t2﹣53t2﹣803(t﹣3)2=﹣2553t+160t﹣240,故答案是:S=﹣2553t+160t﹣240.【点睛】此题考查了待定系数法求二次函数和一次函数表达式,二次函数与一次函数综合问题,相似三角形的性质和判定,二次函数中最大面积问题等知识,解题的关键是正确分析题目中的条件,设出点的坐标,根据相似三角形的性质以及勾股定理表示出相应的线段和面积.11.(1)(1,,图见解析(2)1322Cx-≤≤1122t<≤【解析】【分析】(1)根据等边三角形的性质,勾股定理求解即可;(2)根据题意以MB为边作等边三角形MM B',以M'为圆心1为半径作M',根据线段中点坐标公式求解即可;(3)在(2)的基础上,先求得最小值,再确定2个圆心,第1个是A 点运动点C 对应的圆心P ',第2个是点B 的运动时点C 轨迹的对应的圆心P ,进而根据线段和最大,当,,P P Q '共线时候,t 最大,根据(2)的方法求解即可.(1)过点C 作CE x ⊥轴于点E ,作出点C ,B 的逆序等边三角形CBD ,如图1,()()1,03,0A B -,,ABC 是等边三角形()1131222AE BE AB ∴===--=,33CE AE ==()1,0E ∴,(1,3C ,ABC BCD 是等边三角形∴60DCB ABC ∠=∠=︒,AB AC BC CD BD ====,CD AB CD AB ∴=∥(5,23D ∴ 故答案为:(1,23,(5,23(2)如图2,以MB 为边作等边三角形MM B ',以M '为圆心1为半径作M ', 点B (3,0),点A 在以点M (-2,0)为圆心1为半径的圆上, ∴点A ,B 的逆序等边三角形ABC 的顶点C 在M '23122M x '-+∴== M '的半径为1∴111122C x -≤≤+ 即1322C x -≤≤(3)如图3,设N 与x 轴交于点G ,以GM 为边向上作等边三角形MGH ,以点H 为圆心1为半径,作H ,设直线y x =为1l ,y x t =+为2l ,过点H 作1HJ l ⊥,交x 轴于点J ,交1l 于点S ,交2l 于点L ,过点H ,作HI x ⊥轴于点I ,设2l 与x 轴的交点为T ,则OT t =根据题意,当C 点在第二象限时,能找到t 的最小值,根据定义可知,B 点与G 点重合时,A 点在M 上运动,则C 点在H 上运动,当2l 与H 相切时,t 最小, ()2,0M -,()3,0N ,M 的半径为1,N 的半径为2, 2,321OM OG ∴==-=3MG ∴=33HI ∴=1322MI MG == 1,02I ⎛⎫∴- ⎪⎝⎭ 1332H ⎛∴- ⎝⎭1l 与x 轴的夹角为45°,1HJ l ⊥,HI x ⊥轴, HIJ ∴是等腰直角三角形 HI IJ ∴=HJ ∴===12OI =12OJ ∴1,02J ⎫∴⎪⎪⎝⎭1LJ HJ HL ∴=-=12l l ∥ LTJ ∴是等腰直角三角形1TJ ∴===⎝3122OJ =1122TO TJ JO ⎫=-==⎪⎪⎝⎭即t 12, B 的纵坐标0d >,则12t > 如图4,作,M N 的逆序等边三角形MNP ',以P '为圆心,1为半径作P ',则1PP AM '==,连接,AM PP ',ANP MNP '是等边三角形,,,60AN NP MN NP ANP MNP ''∴==∠=∠=︒PNP ANM '∴∠=∠PP N AMN '≌∴当,,P P Q '共线时候,t 最大以P 为圆心,2为半径作半圆P ,当直线y x t =+与半圆P 相切时,设切点为Q ,当C 点与Q 点重合时,即可取得t 的最大值,最大值即为T O '的长,()()2,0,3,0M N - ∴1532P ⎛' ⎝⎭过点P '作P P x '''⊥轴于点P '',如图,。
中考初三数学整合压轴题100题附答案

中考初三数学整合压轴题100题附答案一、中考压轴题1.用两种方法解答:已知m、n是关于x的方程x2+(p﹣2)x+1=0两个实数根,求代数式(m2+mp+1)(n2+np+1)的值.【分析】本题主要是利用韦达定理来计算.已知m、n是关于x的方程x2+(p﹣2)x+1=0两个实数根,有四个等式可供使用:m+n=2﹣p①,mn=1②,m2+(p﹣2)m+1=0③,n2+(p﹣2)n+1=0④.通过变形方法,合理地选择解题方法.【解答】解:∵m、n是x2+(p﹣2)x+1=0的根,∴m+n=2﹣p,mn=1.方法一:m2+(p﹣2)m+1=0,n2+(p﹣2)n+1=0.即m2+pm+1=2m,n2+pn+1=2n.原式=2m×2n=4mn=4.方法二:(m2+mp+1)(n2+np+1)=(m2+mp)(n2+np)+m2+mp+n2+np+1=m2n2+m2np+mpn2+mnp2+m2+mp+n2+np+1=1+mp+np+p2+m2+n2+mp+np+1=2+p2+m2+n2+2(m+n)p=2+p2+m2+n2+2(2﹣p)p=2+p2+m2+n2+4p﹣2p2=2+(m+n)2﹣2mn+4p﹣2p2+p2=2+(2﹣p)2﹣2+4p﹣2p2+p2=4﹣4p+p2+4p﹣p2=4.【点评】本题主要是通过根与系数的关系来求值.注意把所求的代数式转化成m+n=2﹣p,mn=1的形式,正确对所求式子进行变形是解题的关键.2.已知:y关于x的函数y=(k﹣1)x2﹣2kx+k+2的图象与x轴有交点.(1)求k的取值范围;(2)若x1,x2是函数图象与x轴两个交点的横坐标,且满足(k﹣1)x12+2kx2+k+2=4x1x2.①求k的值;②当k≤x≤k+2时,请结合函数图象确定y的最大值和最小值.【分析】(1)分两种情况讨论,当k=1时,可求出函数为一次函数,必与x轴有一交点;当k≠1时,函数为二次函数,若与x轴有交点,则△≥0.(2)①根据(k﹣1)x12+2kx2+k+2=4x1x2及根与系数的关系,建立关于k的方程,求出k 的值;②充分利用图象,直接得出y的最大值和最小值.【解答】解:(1)当k=1时,函数为一次函数y=﹣2x+3,其图象与x轴有一个交点.当k≠1时,函数为二次函数,其图象与x轴有一个或两个交点,令y=0得(k﹣1)x2﹣2kx+k+2=0.△=(﹣2k)2﹣4(k﹣1)(k+2)≥0,解得k≤2.即k≤2且k≠1.综上所述,k的取值范围是k≤2.(2)①∵x1≠x2,由(1)知k<2且k≠1,函数图象与x轴两个交点,∴k<2,且k≠1.由题意得(k﹣1)x12+(k+2)=2kx1①,将①代入(k﹣1)x12+2kx2+k+2=4x1x2中得:2k(x1+x2)=4x1x2.又∵x1+x2=,x1x2=,∴2k•=4•.解得:k1=﹣1,k2=2(不合题意,舍去).∴所求k值为﹣1.②如图,∵k1=﹣1,y=﹣2x2+2x+1=﹣2(x﹣)2+.且﹣1≤x≤1.由图象知:当x=﹣1时,y最小=﹣3;当x=时,y最大=.∴y的最大值为,最小值为﹣3.【点评】本题考查了抛物线与x轴的交点、一次函数的定义、二次函数的最值,充分利用图象是解题的关键.3.如图①,有四张编号为1、2、3、4的卡片,卡片的背面完全相同.现将它们搅匀并正面朝下放置在桌面上.(1)从中随机抽取一张,抽到的卡片是眼睛的概率是多少?(2)从四张卡片中随机抽取一张贴在如图②所示的大头娃娃的左眼处,然后再随机抽取一张贴在大头娃娃的右眼处,用树状图或列表法求贴法正确的概率.【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.【解答】解:(1)所求概率为;(2)方法①(树状图法)共有12种可能的结果:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)∵其中有两种结果(1,2),(2,1)是符合条件的,∴贴法正确的概率为,方法②(列表法)1 2 3 4第一次抽取第二次抽取1(2,1)(3,1)(4,1)2(1,2)(3,2)(4,2)3(1,3)(2,3)(4,3)4(1,4)(2,4)(3,4)共有12种可能的结果:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),∵其中有两种结果(1,2),(2,1)是符合条件的,∴贴法正确的概率为.【点评】此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.4.如图,反比例函数的图象经过点A(4,b),过点A作AB⊥x轴于点B,△AOB 的面积为2.(1)求k和b的值;(2)若一次函数y=ax﹣3的图象经过点A,求这个一次函数的解析式.【分析】(1)由△AOB的面积为2,根据反比例函数的比例系数k的几何意义,可知k的值,得出反比例函数的解析式,然后把x=4代入,即可求出b的值;(2)把点A的坐标代入y=ax﹣3,即可求出这个一次函数的解析式.【解答】解:(1)∵反比例函数的图象经过点A,AB⊥x轴于点B,△AOB的面积为2,A(4,b),∴OB×AB=2,×4×b=2,∴AB=b=1,∴A(4,1),∴k=xy=4,∴反比例函数的解析式为y=,即k=4,b=1.(2)∵A(4,1)在一次函数y=ax﹣3的图象上,∴1=4a﹣3,∴a=1.∴这个一次函数的解析式为y=x﹣3.【点评】本题主要考查了待定系数法求一次函数的解析式和反比例函数中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.5.我国年人均用纸量约为28公斤,每个初中毕业生离校时大约有10公斤废纸;用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树.(1)若我市2005年4万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使多少亩森林免遭砍伐?(2)我市从2000年初开始实施天然林保护工程,大力倡导废纸回收再生,如今成效显著,森林面积大约由2003年初的50万亩增加到2005年初的60.5万亩.假设我市年用纸量的20%可以作为废纸回收、森林面积年均增长率保持不变,请你按全市总人口约为1000万计算:在从2005年初到2006年初这一年度内,我市因回收废纸所能保护的最大森林面积相当于新增加的森林面积的百分之几?(精确到1%)【分析】(1)因为每个初中毕业生离校时大约有10公斤废纸,用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树,所以有40000×10÷1000×18÷80,计算出即可求出答案;(2)森林面积大约由2003年初的50万亩增加到2005年初的60.5万亩,可先求出森林面积年均增长率,进而求出2005到2006年新增加的森林面积,而因回收废纸所能保护的最大森林面积=1000×10000×28×20%÷1000×18÷50,然后进行简单的计算即可求出答案.【解答】解:(1)4×104×10÷1000×18÷80=90(亩).答:若我市2005年4万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使90亩森林免遭砍伐.(2)设我市森林面积年平均增长率为x,依题意列方程得50(1+x)2=60.5,解得x1=10%,x2=﹣2.1(不合题意,舍去),1000×104×28×20%÷1000×18÷50=20160,20160÷(605000×10%)≈33%.答:在从2005年初到2006年初这一年度内,我市因回收废纸所能保护的最大森林面积相当于新增加的森林面积的33%.【点评】本题以保护环境为主题,考查了增长率问题,阅读理解题意,并从题目中提炼出平均增长率的数学模型并解答的能力;解答时需仔细分析题意,利用方程即可解决问题.6.广安市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.(1)求平均每次下调的百分率.(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?【分析】(1)根据题意设平均每次下调的百分率为x,列出一元二次方程,解方程即可得出答案;(2)分别计算两种方案的优惠价格,比较后发现方案①更优惠.【解答】解:(1)设平均每次下调的百分率为x,则6000(1﹣x)2=4860,解得:x1=0.1=10%,x2=1.9(舍去),故平均每次下调的百分率为10%;(2)方案①购房优惠:4860×100×(1﹣0.98)=9720(元);方案②可优惠:80×100=8000(元).故选择方案①更优惠.【点评】本题主要考查一元二次方程的实际应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解,属于中档题.7.如图,一次函数y=﹣x﹣2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=(x<0)的图象于点Q,且tan∠AOQ=.(1)求k的值;(2)连接OP、AQ,求证:四边形APOQ是菱形.【分析】(1)由一次函数解析式确定A点坐标,进而确定C,Q的坐标,将Q的坐标代入反比例函数关系式可求出k的值.(2)由(1)可分别确定QC=CP,AC=OC,且QP垂直平分AO,故可证明四边形APOQ是菱形.【解答】(1)解:∵y=﹣x﹣2令y=0,得x=﹣4,即A(﹣4,0)由P为AB的中点,PC⊥x轴可知C点坐标为(﹣2,0)又∵tan∠AOQ=可知QC=1∴Q点坐标为(﹣2,1)将Q点坐标代入反比例函数得:1=,∴可得k=﹣2;(2)证明:由(1)可知QC=PC=1,AC=CO=2,且A0⊥PQ∴四边形APOQ是菱形.【点评】本题考查了待定系数法求函数解析式,又结合了几何图形进行考查,属于综合性比较强的题目,有一定难度.8.某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A类杨梅包装后直接销售;B类杨梅深加工后再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2)之间的函数关系如图;B类杨梅深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.(1)直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式;(2)第一次,该公司收购了20吨杨梅,其中A类杨梅有x吨,经营这批杨梅所获得的毛利润为w万元(毛利润=销售总收入﹣经营总成本).①求w关于x的函数关系式;②若该公司获得了30万元毛利润,问:用于直销的A类杨梅有多少吨?(3)第二次,该公司准备投入132万元资金,请设计一种经营方案,使公司获得最大毛利润,并求出最大毛利润.【分析】(1)这是一个分段函数,分别求出其函数关系式;(2)①当2≤x<8时及当x≥8时,分别求出w关于x的表达式.注意w=销售总收入﹣经营总成本=w A+w B﹣3×20;②若该公司获得了30万元毛利润,将30万元代入①中求得的表达式,求出A类杨梅的数量;(3)本问是方案设计问题,总投入为132万元,这笔132万元包括购买杨梅的费用+A类杨梅加工成本+B类杨梅加工成本.共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,分别求出当2≤x<8时及当x≥8时w关于x的表达式,并分别求出其最大值.【解答】解:(1)①当2≤x<8时,如图,设直线AB解析式为:y=kx+b,将A(2,12)、B(8,6)代入得:,解得,∴y=﹣x+14;②当x≥8时,y=6.所以A类杨梅平均销售价格y与销售量x之间的函数关系式为:y=;(2)设销售A类杨梅x吨,则销售B类杨梅(20﹣x)吨.①当2≤x<8时,w A=x(﹣x+14)﹣x=﹣x2+13x;w B=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x∴w=w A+w B﹣3×20=(﹣x2+13x)+(108﹣6x)﹣60=﹣x2+7x+48;当x≥8时,w A=6x﹣x=5x;w B=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x∴w=w A+w B﹣3×20=(5x)+(108﹣6x)﹣60=﹣x+48.∴w关于x的函数关系式为:w=.②当2≤x<8时,﹣x2+7x+48=30,解得x1=9,x2=﹣2,均不合题意;当x≥8时,﹣x+48=30,解得x=18.∴当毛利润达到30万元时,直接销售的A类杨梅有18吨.(3)设该公司用132万元共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,则购买费用为3m万元,A类杨梅加工成本为x万元,B类杨梅加工成本为[12+3(m﹣x)]万元,∴3m+x+[12+3(m﹣x)]=132,化简得:x=3m﹣60.①当2≤x<8时,w A=x(﹣x+14)﹣x=﹣x2+13x;w B=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12∴w=w A+w B﹣3×m=(﹣x2+13x)+(6m﹣6x﹣12)﹣3m=﹣x2+7x+3m﹣12.将3m=x+60代入得:w=﹣x2+8x+48=﹣(x﹣4)2+64∴当x=4时,有最大毛利润64万元,此时m=,m﹣x=;②当x≥8时,w A=6x﹣x=5x;w B=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12∴w=w A+w B﹣3×m=(5x)+(6m﹣6x﹣12)﹣3m=﹣x+3m﹣12.将3m=x+60代入得:w=48∴当x>8时,有最大毛利润48万元.综上所述,购买杨梅共吨,其中A类杨梅4吨,B类吨,公司能够获得最大毛利润,最大毛利润为64万元.【点评】本题是二次函数、一次函数的综合应用题,难度较大.解题关键是理清售价、成本、利润三者之间的关系.涉及到分段函数时,注意要分类讨论.9.经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时,研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.(1)求大桥上车流密度为100辆/千米时的车流速度;(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/小时,应控制大桥上的车流密度在什么范围内?(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.【分析】(1)当20≤x≤220时,设车流速度v与车流密度x的函数关系式为v=kx+b,根据题意的数量关系建立方程组求出其解即可;(2)由(1)的解析式建立不等式组求出其解即可;(3)设车流量y与x之间的关系式为y=vx,当x<20和20≤x≤220时分别表示出函数关系由函数的性质就可以求出结论.【解答】解:(1)设车流速度v与车流密度x的函数关系式为v=kx+b,由题意,得,解得:,∴当20≤x≤220时,v=﹣x+88,当x=100时,v=﹣×100+88=48(千米/小时);(2)由题意,得,解得:70<x<120.∴应控制大桥上的车流密度在70<x<120范围内;(3)设车流量y与x之间的关系式为y=vx,当0≤x≤20时y=80x,∴k=80>0,∴y随x的增大而增大,∴x=20时,y最大=1600;当20≤x≤220时y=(﹣x+88)x=﹣(x﹣110)2+4840,∴当x=110时,y最大=4840.∵4840>1600,∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆.【点评】本题考查了车流量=车流速度×车流密度的运用,一次函数的解析式的运用,一元一次不等式组的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.10.⊙O1与⊙O2相交于A、B两点,如图(1),连接O2O1并延长交⊙O1于P点,连接P A、PB并分别延长交⊙O2于C、D两点,连接CO2并延长交⊙O2于E点.已知⊙O2的半径为R,设∠CAD=α.(1)求CD的长(用含R、α的式子表示);(2)试判断CD与PO1的位置关系,并说明理由;(3)设点P’为⊙O1上(⊙O2外)的动点,连接P’A、P’B并分别延长交⊙O2于C’、D’,请你探究∠C’AD’是否等于α?C’D’与P’O1的位置关系如何?并说明理由.(注:图(2)与图(3)中⊙O1和⊙O2的大小及位置关系与图(1)完全相同,若你感到继续在图(1)中探究问题(3),图形太复杂,不便于观察,可以选择图(2)或图(3)中的一图说明理由).【分析】(1)作⊙O2的直径CE,连接DE.根据圆周角定理的推论,得∠E=∠CAD=α,再利用解直角三角形的知识求解;(2)连接AB,延长PO1与⊙O1相交于点E,连接AE.根据圆内接四边形的性质,得∠ABP′=∠C′,根据圆周角定理的推论,得∠ABP′=∠E,∠EAP′=90°,从而证明∠AP′E+∠C′=90°,则CD与PO1的位置关系是互相垂直;(3)根据同弧所对的圆周角相等,则说明∠C’AD’等于α;根据(2)中的证明过程,则可以证明C’D’与P’O1的位置关系是互相垂直.【解答】解:(1)连接DE.根据圆周角定理的推论,得∠E=∠CAD=α.∵CE是直径,∴∠CDE=90°.∴CD=CE•sin E=2R sinα;(2)CD与PO1的位置关系是互相垂直.理由如下:连接AB,延长PO1与⊙O1相交于点E,连接AE.∵四边形BAC′D′是圆内接四边形,∴∠ABP′=∠C′.∵P′E是直径,∴∠EAP′=90°,∴∠AP′E+∠E=90°.又∠ABP′=∠E,∴∠AP′E+∠C′=90°,即CD与PO1的位置关系是互相垂直;(3)根据同弧所对的圆周角相等,则说明∠C’AD’等于α;根据(2)中的证明过程,则可以证明C’D’与P’O1的位置关系是互相垂直.【点评】此题综合运用了圆周角定理及其推论、直角三角形的性质、圆内接四边形的性质.注意:连接两圆的公共弦、构造直径所对的圆周角都是圆中常见的辅助线.11.如图,已知直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,连接PC 并延长PC交y轴于点D(0,3).(1)求证:△POD≌△ABO;(2)若直线l:y=kx+b经过圆心P和D,求直线l的解析式.【分析】(1)首先连接PB,由直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,可求得∠APB=∠DPO=60°,∠ABO=∠POD=90°,即可得△P AB是等边三角形,可得AB=OP,然后由ASA,即可判定:△POD≌△ABO;(2)易求得∠PDO=30°,由OP=OD•tan30°,即可求得点P的坐标,然后利用待定系数法,即可求得直线l的解析式.【解答】(1)证明:连接PB,∵直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,∴∠APB=∠DPO=×180°=60°,∠ABO=∠POD=90°,∵P A=PB,∴△P AB是等边三角形,∴AB=P A,∠BAO=60°,∴AB=OP,∠BAO=∠OPD,在△POD和△ABO中,∴△POD≌△ABO(ASA);(2)解:由(1)得△POD≌△ABO,∴∠PDO=∠AOB,∵∠AOB=∠APB=×60°=30°,∴∠PDO=30°,∴OP=OD•tan30°=3×=,∴点P的坐标为:(﹣,0)∴,解得:,∴直线l的解析式为:y=x+3.【点评】此题考查了圆周角定理、全等三角形的判定与性质、直角三角形的性质、等边三角形的判定与性质以及待定系数法求一次函数的解析式.此题综合性较强,难度适中,注意准确作出辅助线,注意数形结合思想的应用.12.如图,△ABC内接于⊙O,AB=6,AC=4,D是AB边上一点,P是优弧BAC的中点,连接P A、PB、PC、PD.(1)当BD的长度为多少时,△P AD是以AD为底边的等腰三角形?并证明;(2)在(1)的条件下,若cos∠PCB=,求P A的长.【分析】(1)根据等弧对等弦以及全等三角形的判定和性质进行求解;(2)过点P作PE⊥AD于E.根据锐角三角函数的知识和垂径定理进行求解.【解答】解:(1)当BD=AC=4时,△P AD是以AD为底边的等腰三角形.∵P是优弧BAC的中点,∴=.∴PB=PC.又∵∠PBD=∠PCA(圆周角定理),∴当BD=AC=4,△PBD≌△PCA.∴P A=PD,即△P AD是以AD为底边的等腰三角形.(2)过点P作PE⊥AD于E,由(1)可知,当BD=4时,PD=P A,AD=AB﹣BD=6﹣4=2,则AE=AD=1.∵∠PCB=∠P AD(在同圆或等圆中,同弧所对的圆周角相等),∴cos∠P AD=cos∠PCB=,∴P A=.【点评】综合运用了等弧对等弦的性质、全等三角形的判定和性质、锐角三角函数的知识以及垂径定理.13.已知⊙O1与⊙O2相交于A、B两点,点O1在⊙O2上,C为⊙O2上一点(不与A,B,O1重合),直线CB与⊙O1交于另一点D.(1)如图(1),若AD是⊙O1的直径,AC是⊙O2的直径,求证:AC=CD;(2)如图(2),若C是⊙O1外一点,求证:O1C丄AD;(3)如图(3),若C是⊙O1内的一点,判断(2)中的结论是否成立?【分析】(1)连接C01,利用直径所对圆周角等于90度,以及垂直平分线的性质得出即可;(2)根据已知得出四边形AEDB内接于⊙O1,得出∠ABC=∠E,再利用=,得出∠E=∠AO1C,进而得出CO1∥ED即可求出;(3)根据已知得出∠B=∠EO1C,又∠E=∠B,即可得出∠EO1C=∠E,得出CO1∥ED,即可求出.【解答】(1)证明:连接C01∵AC为⊙O2直径∴∠AO1C=90°即CO1⊥AD,∵AO1=DO1∴DC=AC(垂直平分线的性质);(2)证明:连接AO1,连接AB,延长AO1交⊙O1于点E,连接ED,∵四边形AEDB内接于⊙O1,∴∠E+∠ABD=180°,∵∠ABC+∠ABD=180°,∴∠ABC=∠E,又∵=,∴∠ABC=∠AO1C,∴∠E=∠AO1C,∴CO1∥ED,又AE为⊙O1的直径,∴ED⊥AD,∴O1C⊥AD,(3)(2)中的结论仍然成立.证明:连接AO1,连接AB,延长AO1交⊙O1于点E,连接ED,∵∠B+∠AO1C=180°,∠EO1C+∠AO1C═180°,∴∠B=∠EO1C,又∵∠E=∠B,∴∠EO1C=∠E,∴CO1∥ED,又ED⊥AD,∴CO1⊥AD.【点评】此题主要考查了圆周角定理以及相交两圆的性质和圆内接四边形的性质,根据圆内接四边形的性质得出对应角之间的关系是解决问题的关键.14.如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且=,弦AD的延长线交切线PC于点E,连接BC.(1)判断OB和BP的数量关系,并说明理由;(2)若⊙O的半径为2,求AE的长.【分析】(1)首先连接OC,由PC切⊙O于点C,可得∠OCP=90°,又由∠BAC=30°,即可求得∠COP=60°,∠P=30°,然后根据直角三角形中30°角所对的直角边等于斜边的一半,证得OB=BP;(2)由(1)可得OB=OP,即可求得AP的长,又由=,即可得∠CAD=∠BAC=30°,继而求得∠E=90°,继而在Rt△AEP中求得答案.【解答】解:(1)OB=BP.理由:连接OC,∵PC切⊙O于点C,∴∠OCP=90°,∵OA=OC,∠OAC=30°,∴∠OAC=∠OCA=30°,∴∠COP=60°,∴∠P=30°,在Rt△OCP中,OC=OP=OB=BP;(2)由(1)得OB=OP,∵⊙O的半径是2,∴AP=3OB=3×2=6,∵=,∴∠CAD=∠BAC=30°,∴∠BAD=60°,∵∠P=30°,∴∠E=90°,在Rt△AEP中,AE=AP=×6=3.【点评】此题考查了切线的性质、直角三角形的性质以及圆周角定理.此题难度适中,注意掌握数形结合思想的应用,注意掌握辅助线的作法.15.如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.(1)设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形越接近于正方形.①若菱形的一个内角为70°,则该菱形的“接近度”等于40;②当菱形的“接近度”等于0时,菱形是正方形.(2)设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a﹣b|,于是|a﹣b|越小,矩形越接近于正方形.你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.【分析】(1)根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,相似图形的“接近度”相等.所以若菱形的一个内角为70°,则该菱形的“接近度”等于|m﹣n|;当菱形的“接近度”等于0时,菱形是正方形;(2)不合理,举例进行说明.【解答】解:(1)①∵内角为70°,∴与它相邻内角的度数为110°.∴菱形的“接近度”=|m﹣n|=|110﹣70|=40.②当菱形的“接近度”等于0时,菱形是正方形.(2)不合理.例如,对两个相似而不全等的矩形来说,它们接近正方形的程度是相同的,但|a﹣b|却不相等.合理定义方法不唯一.如定义为,越接近1,矩形越接近于正方形;越大,矩形与正方形的形状差异越大;当时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.【点评】正确理解“接近度”的意思,矩形的“接近度”|a﹣b|越小,矩形越接近于正方形.这是解决问题的关键.16.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)①画出△ABC关于x轴对称的△A1B1C1;②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;③△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;④△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.【分析】(1)将三角形的各顶点,向x轴作垂线并延长相同长度得到三点的对应点,顺次连接;(2)将三角形的各顶点,绕原点O按逆时针旋转90°得到三点的对应点.顺次连接各对应点得△A2B2C2;(3)从图中可发现成轴对称图形,根据轴对称图形的性质画出对称轴即连接两对应点的线段,做它的垂直平分线;(4)成中心对称图形,画出两条对应点的连线,交点就是对称中心.【解答】解:如下图所示:(3)成轴对称图形,根据轴对称图形的性质画出对称轴即连接两对应点的线段,作它的垂直平分线,或连接A1C1,A2C2的中点的连线为对称轴.(4)成中心对称,对称中心为线段BB2的中点P,坐标是(,).【点评】本题综合考查了图形的变换,在图形的变换中,关键是找到图形的对应点.17.图(1)是一个10×10格点正方形组成的网格.△ABC是格点三角形(顶点在网格交点处),请你完成下面的两个问题:(1)在图(1)中画出与△ABC相似的格点△A1B1C1和△A2B2C2,且△A1B1C1与△ABC的相似比是2,△A2B2C2与△ABC的相似比是;(2)在图(2)中用与△ABC,△A1B1C1,△A2B2C2全等的格点三角形(每个三角形至少使用一次),拼出一个你熟悉的图案,并为你设计的图案配一句贴切的解说词.【分析】(1)△A1B1C1与△ABC的相似比是2,则让△ABC的各边都扩大2倍就可.△A2B2C2与△ABC的相似比是;△ABC的直角边是2,所以△A2B2C2与的直角边是即一个对角线的长度.斜边为2.依此画图即可;(2)拼图有审美意义即可,答案不唯一.【解答】解:【点评】本题主要考查了相似图形的画法,做这类题时根据的是相似图形的性质,即相似比相等.对应角相等.18.如图,矩形ABCD的边AD、AB分别与⊙O相切于点E、F,(1)求的长;(2)若,直线MN分别交射线DA、DC于点M、N,∠DMN=60°,将直线MN沿射线DA方向平移,设点D到直线的距离为d,当时1≤d≤4,请判断直线MN与⊙O的位置关系,并说明理由.【分析】(1)连接OE、OF,利用相切证明四边形AFOE是正方形,再根据弧长公式求弧长;(2)先求出直线M1N1与圆相切时d的值,结合1≤d≤4,划分d的范围,分类讨论.【解答】解:(1)连接OE、OF,∵矩形ABCD的边AD、AB分别与⊙O相切于点E、F,∴∠A=90°,∠OEA=∠OF A=90°∴四边形AFOE是正方形∴∠EOF=90°,OE=AE=∴的长==π.(2)如图,将直线MN沿射线DA方向平移,当其与⊙O相切时,记为M1N1,切点为R,交AD于M1,交BC于N1,连接OM1、OR,∵M1N1∥MN∴∠DM1N1=∠DMN=60°∴∠EM1N1=120°∵MA、M1N1切⊙O于点E、R∴∠EM1O=∠EM1N1=60°在Rt△EM1O中,EM1===1∴DM1=AD﹣AE﹣EM1=+5﹣﹣1=4.过点D作DK⊥M1N1于K在Rt△DM1K中DK=DM1×sin∠DM1K=4×sin∠60°=2即d=2,∴当d=2时,直线MN与⊙O相切,当1≤d<2时,直线MN与⊙O相离,当直线MN平移到过圆心O时,记为M2N2,点D到M2N2的距离d=DK+OR=2+=3>4,∴当2<d≤4时,MN直线与⊙O相交.【点评】本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d 与圆半径大小关系完成判定.19.如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.(1)试判断DE与BD是否相等,并说明理由;(2)如果BC=6,AB=5,求BE的长.【分析】(1)可通过连接AD,AD就是等腰三角形ABC底边上的高,根据等腰三角形三线合一的特点,可得出∠CAD=∠BAD,根据圆周角定理即可得出∠DEB=∠DBE,便可证得DE=DB.(2)本题中由于BE⊥AC,那么BE就是三角形ABC中AC边上的高,可用面积的不同表示方法得出AC•BE=CB•AD.进而求出BE的长.【解答】解:(1)DE=BD证明:连接AD,则AD⊥BC,在等腰三角形ABC中,AD⊥BC,∴∠CAD=∠BAD(等腰三角形三线合一),∴=,∴DE=BD;(2)∵AB=5,BD=BC=3,∴AD=4,∵AB=AC=5,∴S△ABC=•AC•BE=•CB•AD,∴BE=4.8.【点评】本题主要考查了等腰三角形的性质,圆周角定理等知识点的运用,用等腰三角形三线合一的特点得出圆周角相等是解题的关键.20.下框中是小明对一道题目的解答以及老师的批改.题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧内墙保留3m的空地,其他三侧内墙各保留1m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288m2?解:设矩形蔬菜种植区域的宽为xm,则长为2xm,根据题意,得x•2x=288.解这个方程,得x1=﹣12(不合题意,舍去),x2=12所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)答:当温室的长为28m,宽为14m时,矩形蔬菜种植区域的面积是288m2.我的结果也正确!小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.结果为何正确呢?(1)请指出小明解答中存在的问题,并补充缺少的过程:变化一下会怎样…(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.【分析】(1)根据题意可得小明没有说明矩形蔬菜种植区域的长与宽之比为2:1的理由,所以应设矩形蔬菜种植区域的宽为xm,则长为2xm,然后由题意得,矩形蔬菜种植区域的长与宽之比为2:1,再利用小明的解法求解即可;(2)由使矩形A′B′C′D′∽矩形ABCD,利用相似多边形的性质,可得,即,然后利用比例的性质,即可求得答案.【解答】解:(1)小明没有说明矩形蔬菜种植区域的长与宽之比为2:1的理由.在“设矩形蔬菜种植区域的宽为xm,则长为2xm.”前补充以下过程:设温室的宽为xm,则长为2xm.则矩形蔬菜种植区域的宽为(x﹣1﹣1)m,长为(2x﹣3﹣1)m.∵,∴矩形蔬菜种植区域的长与宽之比为2:1;(2)要使矩形A′B′C′D′∽矩形ABCD,就要,即,即,即2AB﹣2(b+d)=2AB﹣(a+c),∴a+c=2(b+d),即.【点评】此题考查了相似多边形的性质.此题属于阅读性题目,注意理解题意,读懂题目是解此题的关键.21.二次函数y=ax2+bx+c图象的一部分如图所示,则a的取值范围是﹣1<a<0.。
(完整)中考数学压轴题精选及答案
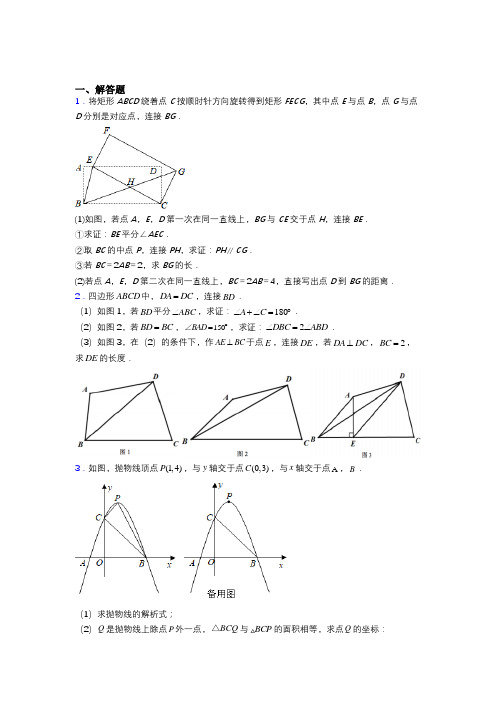
一、解答题1.将矩形ABCD 绕着点C 按顺时针方向旋转得到矩形FECG ,其中点E 与点B ,点G 与点D 分别是对应点,连接BG .(1)如图,若点A ,E ,D 第一次在同一直线上,BG 与CE 交于点H ,连接BE . ①求证:BE 平分∠AEC .②取BC 的中点P ,连接PH ,求证:PH ∥CG . ③若BC =2AB =2,求BG 的长.(2)若点A ,E ,D 第二次在同一直线上,BC =2AB =4,直接写出点D 到BG 的距离. 2.四边形ABCD 中,DA DC =,连接BD .(1)如图1,若BD 平分ABC ∠,求证:180A C ∠+∠=︒. (2)如图2,若BD BC =,150=︒∠BAD ,求证:2DBC ABD ∠=∠.(3)如图3,在(2)的条件下,作AE BC ⊥于点E ,连接DE ,若DA DC ⊥,2BC =,求DE 的长度.3.如图,抛物线顶点(1,4)P ,与y 轴交于点(0,3)C ,与x 轴交于点A ,B .(1)求抛物线的解析式;(2)Q 是抛物线上除点P 外一点,BCQ △与BCP 的面积相等,求点Q 的坐标:(3)M 是线段BC 上方抛物线上一个动点,过点M 作x 轴的垂线,交线段BC 于点D ,再过点M 做MN //x 轴交抛物线于点N ,连结DN ,请问是否存在点M 使MDN △为等腰直角三角形?若存在,求出点M 的坐标;若不存在,说明理由.4.某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:观察与猜想(1)①如图1,在正方形ABCD 中,点E ,F 分别是AB ,AD 上的两点,连接DE ,CF ,DE CF ⊥,则DECF的值为 ; ②如图2,在矩形ABCD 中,7AD =,4CD =,点E 是AD 上的一点,连接CE ,BD ,且CE BD ⊥,则CEBD的值为 ; 类比探究(2)如图3,在四边形ABCD 中,90A B ∠=∠=︒,点E 为AB 上一点,连接DE ,过点C 作DE 的垂线交ED 的延长线于点G ,交AD 的延长线于点F ,求证:DE AB CF AD ⋅=⋅;拓展延伸(3)如图4,在Rt ABD △中,90BAD ∠=︒,3AB =,9AD =,将Rt ABD △沿BD 翻折,点A 落在点C 处得CBD ,点E ,F 分别在边AB ,AD 上,连接DE ,CF ,DE CF ⊥.请问DECF是定值吗?若是求出其值,若不是说明理由; 5.如图,在平面直角坐标系中,ABC 的边AB 在x 轴上,且OB OA >,以AB 为直径的圆过点C .若点C 的坐标为()0,4,10AB =,(1)求抛物线的解析式;(2)点P为该函数在第一象限内的图象上一点(不与BC重合),过点P作PQ BC⊥,垂足为点Q,连接PC.若以点P、C、Q为顶点的三角形与COA相似,求点P的坐标;(3)若ACB∠平分线所在的直线l交x轴与点E,过点E任作一直线l'分别交射线CA,CB(点C除外)于点M,N.则11CM CN+的是否为定值?若是,求出该定值;若不是,请说明理由.6.在平面直角坐标系xOy中,规定:抛物线y=a(x﹣h)2+k的“伴随直线”为y=a(x﹣h)+k.例如:抛物线y=2(x+1)2﹣3的“伴随直线”为y=2(x+1)﹣3,即y=2x﹣1.(1)在上面规定下,抛物线y=(x+1)2﹣5的顶点坐标为_____,“伴随直线”为_____.(2)如图,顶点在第一象限的抛物线y=a(x﹣1)2﹣4a(a≠0)与其“伴随直线”相交于点A,B(点A在点B的左侧),与x轴交于点C,D.①若△ABC为等腰三角形时,求a的值;②如果点P(x,y)是直线BC上方抛物线上的一个动点,△PBC的面积记为S,当S取得最大值274时,求a的值.7.如图1,抛物线y=ax2﹣94x+c与x轴交于A(﹣1,0)和B两点,与y轴交于C(0,﹣3),E为抛物线顶点,抛物线的对称轴交x轴于点H.(1)求抛物线的解析式;(2)已知点3(0,2)2F,点P在对称轴右侧的抛物线上运动,连接PO,PO与对称轴交于点D,连接DF.当DF平分∠ODE时,求点P的坐标;(3)如图2,平移对称轴EH交抛物线于M,交直线BC于N.以N为圆心,NM为半径作⊙N.当⊙N与坐标轴相切时,请直接写出⊙N的半径长.8.等腰Rt△ABC,CA=CB,D在AB上,CD=CE,CD⊥CE.(1)如图1,连接BE,求证:AD=BE.(2)如图2,连接AE,CF⊥AE交AB于F,T为垂足,①求证:FD=FB;②如图3,若AE交BC于N,O为AB中点,连接OC,交AN于M,连FM、FN,当S OF2+BF2的最小值.52FMN9.如图,在△ABC中,AB=AC,⊙是△ABC的外接圆,连接BO并延长交边AC于点D.(1)如图1,求证:∠BAC=2∠ABD;(2)如图2,过点B作BH⊥AC于点H,延长BH交⊙O于点G,连接OC,CG,OC交BG于点F,求证:BF=2HG;(3)如图3,在(2)的条件下,若AD=2,CD=3,求线段BF的长.10.问题背景如图(1),△ABC 为等腰直角三角形,∠BAC =90°,直线l 绕着点A 顺时针旋转,过B ,C 两点分别向直线l 作垂线BD ,CE ,垂足为D ,E ,此时△ABD 可以由△CAE 通过旋转变换得到,请写出旋转中心、旋转方向及旋转角的大小(取最小旋转角度). 尝试应用如图(2),△ABC 为等边三角形,直线l 绕着点A 顺时针旋转,D 、E 为直线l 上两点,∠BDA =∠AEC =60°.△ABD 可以由△CAE 通过旋转变换得到吗?若可以,请指出旋转中心O 的位置并说明理由;拓展创新如图(3)在问题背景的条件下,若AB =2,连接DC ,直接写出CD 的长的取值范围.11.如图1,菱形ABCD 绕点A 顺时针旋转()0180αα︒<<︒,得到菱形AEFG ,连接AC ,AF 、分别与BD ,EG 相交于点O ,O '.射线BD ,GE 交于点P ,BPG β∠=.(1)当90α=︒时,四边形AOPO '的形状为 . (2)求α与β的数量关系.(3)如图2.连接PA ,若42BAD ∠=°,PA PB =,求α的值.(4)如图3,连接PC ,PF ,若5AB =,4BD =,四边形AFPC 能否为菱形?若能,直接写出α的值和AP 的长;若不能,请说明理由.12.如图,在平面直角坐标系xOy中,直线AP交x轴于点P(p,0),与y轴交于点A (0,a),且a、p满足+(p﹣1)2=0.(1)求直线AP的解析式;(2)如图1,直线x=﹣2与x轴交于点N,点M在x轴上方且在直线x=﹣2上,若△MAP 的面积等于6,请求出点M的坐标;(3)如图2,已知点C(﹣2,4),若点B为射线AP上一动点,连接BC,在坐标轴上是否存在点Q,使△BCQ是以BC为底边的等腰直角三角形,直角顶点为Q,若存在,请求出点Q坐标;若不存在,请说明理由.13.我们把方程(x﹣m)2+(y﹣n)2=r2称为圆心为(m,n)、半径长为r的圆的标准方程.例如,圆心为(1,﹣2)、半径长为3的圆的标准方程是(x﹣1)2+(y+2)2=9.如图,在平面直角坐标系中,⊙C与x轴交于A,B两点,且点B的坐标为(8,0),与y轴相切于点D(0,4),过点A,B,D的抛物线的顶点为E.(1)求⊙C的标准方程;(2)试判断直线AE 与⊙C 的位置关系,并说明理由; (3)连接CE ,求sin∠AEC 的值.14.如图,ABC 为O 的内接三角形,AB 为O 的直径,过点A 作O 的切线交BC 的延长线干点D .(1)求证:ABC ∽;(2)若E 为AD 上一点,使得,连接OE ,求证:OE 平分;(3)若点F 为直径AB 下方半圆的中点,连接CF 交AB 于点G ,且,2AB =,求CG的长.15.如图,在平面直角坐标系中,抛物线y =ax 2+bx +2与直线y =x ﹣2交于点A (m ,0)和点B (﹣2,n ),与y 轴交于点C .(1)求抛物线的解析式及顶点D 的坐标;(2)若向下平移抛物线,使顶点D 落在x 轴上,原来的抛物线上的点P 平移后的对应点为P ',若,求点P 的坐标;(3)在抛物线上是否存在点Q ,使△QAB 的面积是△ABC 面积的一半?若存在,直接写出点Q 的坐标;若不存在,请说明理由.16.已知抛物线24y ax bx =++(a ≠0)与x 轴交于点A (3-,0)、B (2,0),与y 轴交于点C ,直线y mx n =+经过两点A 、C .(1)求a,b的值;(2)如图1,点Р在已知抛物线上,且位于第二象限,当四边形PABC的面积最大时,求点P的坐标.(3)如图2,将已知抛物线向左平移12个单位,再向下平移2个单位.记平移后的抛物线为'y,若抛物线'y与原抛物线的对称轴交于点Q.点E是新抛物线'y的对称轴上一动点,在(2)的条件下,当△PQE是等腰三角形时,请直接写出点E的坐标.17.如图,已知四边形ABCD内接于⊙O,直径DF交BC于点G.(1)如图1,求证:∠BAD-∠BCF=90°;(2)如图2,连接AC,当∠BAC=∠CFD+∠ACD时,求证:CA=CB;(3)如图3,在(2)的条件下,AC交DF于点H,∠BAC=∠DGB,45CGBG,AC=9,求△CDH的面积.18.设抛物线y=ax2+bx-2与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90度.(1)求m 的值;(2)求抛物线的解析式,并验证点D (1,﹣3)是否在抛物线上;(3)已知过点A 的直线y =x +1交抛物线于另一点E .问:在x 轴上是否存在点P ,使以点P 、B 、D 为顶点的三角形与△AEB 相似?若存在,请求出所有符合要求的点P 的坐标;若不存在,请说明理由.19.图形的旋转变换是研究数学相关问题的重要手段之一,在研究三角形的旋转过程中,发现下列问题:如图1,在ABC 中,AB AC =,BAC α∠=,MN 分别为AB 、BC 边上一点,连接MN ,且MN AC ∥,将ABC 绕点B 在平面内旋转.(1)观察猜想ABC 绕点B 旋转到如图2所示的位置,若60α=︒,则AMCN的值为______. (2)类比探究若90α=︒,将ABC 绕点B 旋转到如图3所示的位置,求AMCN的值. (3)拓展应用若90α=︒,M 为AB 的中点,4AB =,当AM BN ⊥时,请直接写出CN 的值. 20.如图1,在菱形ABCD 中,对角线AC 与BD 相交于点O ,且AC =16,BD =12. (1)求菱形ABCD 的面积及周长;(2)点M 是射线DA 上一个动点,作射线BM ,交射线CA 于点E .将射线BM 绕点B 逆时针旋转后交射线CA 于点N ,旋转角为∠MBN ,且∠MBN =12BAD ∠,连接MN .①如图2,当点N 与点O 重合时,求△AMN 的周长;②当AE =BE 时,请直接写出AM 的长为 ; ③BN =35时,请直接写出AM 的长为 .【参考答案】**科目模拟测试一、解答题1.(1)7 57221【解析】 【分析】(1)①根据旋转的性质得到CB CE =,求得EBC BEC ∠=∠,根据平行线的性质得到EBC BEA ∠=∠,于是得到结论;②如图1,过点B 作CE 的垂线BQ ,根据角平分线的性质得到AB BQ =,求得=CG BQ ,根据全等三角形的性质得到BH GH =,根据三角形的中位线定理即可得到结论; ③如图2,过点G 作BC 的垂线GM ,解直角三角形即可得到结论.(2)如图3,连接DB ,DG ,过G 作GP BC ⊥交BC 的延长线于P ,GN DC ⊥交DC 的延长线于N ,根据旋转的性质得到4==CE BC ,2CD AB ==,解直角三角形得到1NG =,3PG =(1)解:①证明:矩形ABCD 绕着点C 按顺时针方向旋转得到矩形FECG ,CB CE ∴=,EBC BEC ∴∠=∠,又//AD BC ,EBC BEA ∴∠=∠,BEA BEC ∴∠=∠,BE ∴平分AEC ∠;②证明:如图1,过点B 作CE 的垂线BQ ,BE 平分AEC ∠,BA AE ⊥,BQ CE ⊥,AB BQ ∴=,CG BQ ∴=,90BQH GCH ∠=∠=︒,BQ AB CG ==,BHQ GHC ∠=∠,()BHQ GHC AAS ∴∆≅∆,BH GH ∴=,即点H 是BG 中点, 又点P 是BC 中点,//PH CG ∴;③解:如图2,过点G 作BC 的垂线GM ,22BC AB ==,1BQ ∴=,30BCQ ∴∠=︒,90ECG ∠=︒,60GCM ∴∠=︒,1CG AB CD ===,3GM ∴12CM =,222253()()722BG BM MG ∴=+=+=; (2)解:如图3,连接DB ,DG ,过G 作GP BC ⊥交BC 的延长线于P ,GN DC ⊥交DC 的延长线于N ,24BC AB ==,2AB ∴=,将矩形ABCD 绕着点C 按顺时针方向旋转得到矩形FECG ,4CE BC ∴==,2CD AB ==,点A ,E ,D 第二次在同一直线上,90CDE ,12CD CE ∴=, 30DEC ∴∠=︒,60DCE ∴∠=︒,30NCG ∴∠=︒,2CG =,1NG ∴=,3PG =523DBG DBC DCG BCG S S S S ∆∆∆∆∴=++=+2227BG BP PG +257221DBG S DM BG ∆∴= 【点睛】本题考查了旋转的性质,全等三角形的判定和性质,矩形的性质,三角形的中位线定理,勾股定理,解直角三角形,解题的关键是正确地作出辅助线.2.(1)见解析;(2)见解析;(32【解析】【分析】(1)过点D 分别作DF BC ⊥于点F ,DE BA ⊥交BA 的延长线于点E ,根据角平分线的性质可得ED FD =,结合已知条件HL 证明Rt DAE ≌Rt DCF △,继而可得C EAD ∠=∠,根据平角的定义以及等量代换即可证明180BAD BCD ∠+∠=︒;(2)过点D 分别作DF BC ⊥于点F ,DE BA ⊥交BA 的延长线于点E ,过点B 作BG DC ⊥,根据含30度角的直角三角形的性质可得12ED AD =,根据三线合一,可得12DG DC =,进而可得DE DG =,根据角平分线的判定定理可推出12ABD DBG DBC ∠=∠=∠,进而即可证明2DBC ABD ∠=∠; (3)先证明四边形DMEF 是矩形,证明△MAD ≌FCD ,进而证明四边形DMEF 是正方形,设ABD α∠=,根据(2)的结论以及三角形内角和定理,求得15α=︒,进而求得30DBC ∠=︒,根据含30度角的直角三角形的性质,即可求得EF ,进而在Rt DEF △中,勾股定理即可求得DE 的长.【详解】(1)如图,过点D 分别作DF BC ⊥于点F ,DE BA ⊥交BA 的延长线于点E ,BD 平分ABC ∠,ED FD ∴=DA DC =,在Rt DAE 与Rt DCF △中AD DC ED FD =⎧⎨=⎩∴Rt DAE ≌Rt DCF △(HL )C EAD ∴∠=∠180DAB EAD DAB C ∴∠+∠=∠+∠=︒即180BAD BCD ∠+∠=︒(2)如图,过点D 作DE BA ⊥交BA 的延长线于点E ,过点B 作BG DC ⊥,BD BC = 11,22DG GC DC DBG CBG DBC ∴==∠=∠=∠ 150=︒∠BAD ,18015030EAD ∴∠=︒-︒=︒12ED AD ∴= DA DC =ED DG ∴=,ED BE DG BG ⊥⊥EBD GBD ∴∠=∠12ABD DBC ∴∠=∠ 即2DBC ABD ∠=∠(3)如图,过点D 分别作DF BC ⊥于点F ,DM EA ⊥交EA 的延长线于点M ,AE BC ⊥,,DM ME DF FE ⊥⊥∴四边形DMEF 是矩形90MDF ∴∠=︒90MDA ADF ∴∠+∠=︒DA DC⊥90ADC∴∠=︒90ADF FDC∴∠+∠=︒FDC MDA∴∠=∠在△MAD与FCD中MDA FDCDMA DFCDA DC∠=∠⎧⎪∠=∠⎨⎪=⎩∴△MAD≌FCDDM DF∴=,MDA FDC∠=∠∴四边形DMEF是正方形DF EF∴=设ABDα∠=∴22DBC ABDα∠=∠=BD BC=()11802902BDC BCDαα∴∠=∠=︒-=-90MDA FDC BCDα∴∠=∠=︒-∠=90DAE M MDAα∴∠=∠+∠=︒+150BAD∠=︒60BAEα∴∠=-在BAE中9030ABE BAEα∠=︒-∠=︒+23ABE ABD DBCααα∠=∠+∠=+=15α∴=︒230DBCα∴∠==︒2BD =112122DF BD∴==⨯=在Rt DEF△中,1EF DF==DE∴==【点睛】本题考查了三角形全等的性质与判定,角平分线的性质与判定,三角形内角和定理,三角形的外角性质,勾股定理,正方形的性质与判定,正确的添加辅助线是解题的关键.3.(1)2y x 2x 3=-++;(2)1(2,3)Q ,2317117(,)22Q +--,3317117(,)22Q --+;(3)存在,(2,3)M 或5175317(,)22--+ 【解析】【分析】 (1)设2(1)4(0)y a x a =-+≠,把C(0,3)代入求出a ,即可得出答案;(2)①过P 作PQ //BC ,交抛物线于点Q ,如图1所示;②求出点G 坐标,可得2PG GH ==,过H 作直线23Q Q //BC ,交x 轴于点H ,分别求出Q 的坐标即可;(3)MDN △为等腰直角三角形,则MN MD =,求出MN 、MD 的长度即可列出等量关系式,从而得出答案.【详解】(1)设2(1)4(0)y a x a =-+≠,把C(0,3)代入抛物线解析式得:43a +=,即1a =-,则抛物线解析式为22(1)423 y x x x =--+=-++;(2)由(3,0)B ,C(0,3),得到直线BC 解析式为3y x =-+,①过P 作1PQ //BC ,交抛物线于点1Q ,如图1所示,(1,4)P ,∴直线PQ 解析式为5y x =-+,联立得:2235y x x y x ⎧=-++⎨=-+⎩, 解得:14x y =⎧⎨=⎩或23x y =⎧⎨=⎩, 即1(2,3)Q ;②过P 作PH x ⊥轴,交BC 于点G ,交x 轴于点H ,令1x =,代入3y x =-+,得2y =,(1,2)G ∴,2PG GH ∴==,过H 作直线23Q Q //BC ,则直线23Q Q 解析式为1y x =-+,联立得:2231y x x y x ⎧=-++⎨=-+⎩,解得:x y ⎧=⎪⎪⎨⎪=⎪⎩或x y ⎧⎪⎪⎨⎪=⎪⎩2Q ∴,3Q , 综上所述:点Q 的坐标为1(2,3)Q,2Q,3Q ; (3)MDN △为等腰直角三角形,则MN MD =,点()2,23M m m m -++,令x m =,代入3y x =-+得:3y m =-+,(,3)D m m ∴-+,函数的对称轴为:1x =,则点N 的横坐标为:2m -,则|22|MN m =-,2223(3)3MD m m m m m =-++--+=-+,2223m m m ∴-=-+,2223m m m -=-+或2223m m m -+=-+,解得:12m =或21m =-(舍)或3m =4m = 当2m =时,2233m m -++=,当m =223m m -++= 故点M 的坐标为:(2,3)或. 【点睛】 本题考查了二次函数综合题,设计知识有:用待定系数法求函数解析式、同底等高的面积计算、等腰直角三角形的性质,一次函数与二次函数交点问题,熟练掌握相关知识点是解决本题的关键.4.(1)①1;②47;②见解析;(3)是定值,53 【解析】【分析】(1)①如图1,设DE 与CF 交于点G ,由正方形的性质得出∠A =∠FDC =90°,AD =CD ,可证明△AED ≌△DFC (AAS ),由全等三角形的性质得出DE =CF ,则可得出结论;②如图2,设DB 与CE 交于点G ,根据矩形性质得出∠A =∠EDC =90°,由直角三角形的性质证出∠ECD =∠ADB ,由相似三角形的判定定理证出△DEC ∽△ABD 即可;(2)如图3,过点C 作CH ⊥AF 交AF 的延长线于点H ,证明△DEA ∽△CFH ,由相似三角形的性质得出DE AD CF CH =,则可得出结论; (3)过点C 作CG ⊥AD 于点G ,连接AC 交BD 于点H ,CG 与DE 相交于点O ,根据等积关系可得AH 、DH 和CG 的长,,再证明△DEA ∽△CFG ,得出比例线段DE AD CF CG=则可求出答案.【详解】解:(1)①如图1,设DE 与CF 交于点G ,∵四边形ABCD 是正方形,∴∠A =∠FDC =90°,AD =CD ,∵DE ⊥CF ,∴∠DGF =90°,∴∠ADE +∠CFD =90°,∠ADE +∠AED =90°,∴∠CFD =∠AED ,在△AED 和△DFC 中,A FDC CFD AED AD CD ∠∠⎧⎪∠∠⎨⎪⎩===, ∴△AED ≌△DFC (AAS ),∴DE =CF ,∴DE CF=1 故答案为:1;②如图2,设DB 与CE 交于点G ,∵四边形ABCD 是矩形,∴∠A=∠EDC=90°,∵CE⊥BD,∴∠DGC=90°,∴∠CDG+∠ECD=90°,∠ADB+∠CDG=90°,∴∠ECD=∠ADB,∵∠CDE=∠A,∴△DEC∽△ABD,∴4,7 CE DCBD AD==,故答案为:47.(2)证明:如图3,过点C作CH⊥AF交AF的延长线于点H,∵CG⊥EG,∴∠G=∠H=∠A=∠B=90°,∴四边形ABCH为矩形,∴AB=CH,∠FCH+∠CFH=∠DFG+∠FDG=90°,∴∠FCH=∠FDG=∠ADE,∠A=∠H=90°,∴△DEA∽△CFH,∴DE AD CF CH=,∴DE AD CF AB=,∴DE•AB=CF•AD;(3)是定值,如图4,过点C作CG⊥AD于点G,连接AC交BD于点H,CG与DE相交于点O,则AC BD ⊥于H∵CF ⊥DE ,GC ⊥AD ,∴∠FCG +∠CFG =∠CFG +∠ADE =90°,∴∠FCG =∠ADE ,∠BAD =∠CGF =90°,∴△DEA ∽△CFG , ∴DE AD CF CG=, 在Rt △ABD 中,AD =9,AB =3, ∴222293310BD AB AD ++ 又1122AD AB BD AH = ∴93910310AD AB AH BD ⨯=== ∴AC =2AH 91052222910279()101010DH AD AH =-=- ∵1122ADC S AC DH AD CG ∆=⋅=⋅, ∴192711010925102CG =⨯, ∴CG =275,由(1)可得,ADE GCF ∆∆∴952735DE AD CF CG ===【点睛】此题是相似形综合题,主要考查了正方形的性质,矩形的性质,勾股定理,相似三角形的判定与性质,全等三角形的判断和性质,三角形的面积,解本题的关键是熟练掌握相似三角形的判定与性质.5.(1)213442y x x =-++;(2)点P 的坐标为:(6,4171,2172);(3)11NC MC += 【解析】【分析】(1)根据题意,先证明AOC ∆∽COB ∆,得到AO OC CO OB=,求出点A 、B 的坐标,然后利用待定系数法,即可求出抛物线解析式;(2)根据题意,可分为两种情况:AOC ∆∽PQC ∆或AOC ∆∽CQP ∆,结合解一元二次方程,相似三角形的判定和性质,分别求出点P 的坐标,即可得到答案;(3)过点E 作EI ⊥AC 于I ,EJ ⊥CN 于J ,然后由角平分线的性质定理,得到EI =EJ ,再证明△MEI ∽△MNC ,△NEJ ∽△NMC ,得到111NC MC EI +=,然后求出EI 一个定值,即可进行判断.【详解】解:(1)∵以AB 为直径的圆过点C ,∴∠ACB =90°,∵点C 的坐标为()0,4,∴CO ⊥AB ,∴∠AOC =∠COB =90°,∴∠ACO +∠OCB =∠ACO +∠OAC =90°,∴∠OCB =∠OAC ,∴AOC ∆∽COB ∆, ∴AO OC CO OB =, ∵4CO =,10AO BO AB +==,∴10AO OB =-, ∴1044OB OB-=, 解得:2OB =或8OB =,经检验,满足题意,∵OB OA >,∴8OB =,∴点A 为(2-,0),点B 为(8,0).设抛物线的解析式为2y ax bx c =++,把点A 、B 、C 三点的坐标代入,有44206480c a b c a b c =⎧⎪-+=⎨⎪++=⎩,解得:14324a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩,∴抛物线的解析式为213442y x x =-++; (2)根据题意,如图:当AOC ∆∽PQC ∆时,∴ACO PCQ ∠=∠,∵90ACO OCB ∠+∠=︒,∴90PCQ OCB ∠+∠=︒, ∴PC ⊥OC ,∴点P 的纵坐标为4,当4y =时,有2134442x x -++=, 解得:16x =或20x =(舍去);∴点P 的坐标为(6,4);当AOC ∆∽CQP ∆时,则此时BC 垂直平分OP ,作PG ⊥y 轴,垂足为G ,如上图, ∴90CQP AOC ∠=∠=︒,∴AC ∥OP ,∴∠ACO =∠POG ,∵90PGO AOC ∠=∠=︒,∴AOC ∆∽PGO ∆,∴AO OC PG GO=, 设点P 为(x ,213442x x -++), ∴PG x =,213442GO x x =-++, ∴22413442x x x =-++, 解得:171x =, ∵点P 在第一象限, ∴171x =,∴2134217242x x -++=,∴点P 的坐标为(171-,2172-);综合上述,点P 的坐标为:(6,4)或(171-,2172-);(3)过点E 作EI ⊥AC 于I ,EJ ⊥CN 于J ,如图:∵CE 是∠ACB 的角平分线,∴EI =EJ , ∵EI ∥CN ,EJ ∥CM ,∴△MEI ∽△MNC ,△NEJ ∽△NMC ,∴EI ME NC MN =,EJ NE MC MN =, ∴1EI EJ ME NE NC MC MN MN +=+=, ∴1EI EI NC MC +=, ∴111NC MC EI+=, ∵△ACO ∽△AEI , ∴12AI AO EI CO ==, ∵222425AC =+∵AC AI IC AI EI =+=+,2512EI -=, 解得:45EI =∴11135NC MC EI +== ∴11NC MC+是一个定值. 【点睛】本题考查了二次函数的综合应用,求二次函数的解析式,二次函数的性质,相似三角形的判定和性质,解一元二次方程,角平分线的性质定理等知识,解题的关键是熟练掌握题意,正确的作出辅助线,运用数形结合的思想进行解题.6.(1)(﹣1,﹣5),y =x ﹣4;(2)①a 的值为a =﹣2. 【解析】【分析】(1)由“伴随直线”的定义即可求解; (2)①先求y =a (x −1)2−4a 的伴随直线为y =ax −5a ,再联立方程组2(1)45y a x a y ax a ⎧=--⎨=-⎩,求出A (1,−4a ),B (2,−3a ),C (−1,0),D (3,0),由于当△ABC 为等腰三角形时,只存在一种可能为AC =BC ,即可求a 的值;②先求直线BC 解析式为y =−ax −a ,过P 作x 轴的垂线交BC 于点Q ,设点P 的横坐标为x ,则P [x ,a (x −1)2−4a ],Q (x ,−ax −a ),23127()228PBC S a x a ∆=--,即可求面积的最大值,进而求a 的值.【详解】(1)∵抛物线y =(x +1)2﹣5,∴顶点坐标为(﹣1,﹣5),“伴随直线”为y =x ﹣4,故答案为:(﹣1,﹣5),y =x ﹣4;(2)①由“伴随直线”定义可得:y =a (x ﹣1)2﹣4a 的伴随直线为y =ax ﹣5a , 联立2(1)45y a x a y ax a ⎧=--⎨=-⎩, 解得14x y a =⎧⎨=-⎩或23x y a =⎧⎨=-⎩, ∴A (1,﹣4a ),B (2,﹣3a ),在y =a (x ﹣1)2﹣4a 中,令y =0可解得x =﹣1或x =3,∴C (﹣1,0),D (3,0),∴AC 2=4+16a 2,BC 2=9+9a 2,∵当△ABC 为等腰三角形时,只存在一种可能为AC =BC ,∴AC 2=BC 2,即4+16a 2=9+9a 2,解得=a ∵抛物线开口向下,∴a =∴若△ABC 为等腰三角形时,a 的值为 ②设直线BC 的解析式为y =kx +b ,∵B (2,﹣3a ),C (﹣1,0),∴200k b k b +=⎧⎨-+=⎩,解得k a b a =-⎧⎨=-⎩,∴直线BC 解析式为y =﹣ax ﹣a ,如图,过P 作x 轴的垂线交BC 于点Q ,设点P 的横坐标为x ,∴P [x ,a (x ﹣1)2﹣4a ],Q (x ,﹣ax ﹣a ),∵P 是直线BC 上方抛物线上的一个动点, ∴22219(1)4(2)()24PQ a x a ax a a x x a x ⎡⎤=--++=--=--⎢⎥⎣⎦, ∴23127()228PBC S a x a ∆=--, ∴当12x =时,△PBC 的面积有最大值278-a , ∴S 取得最大值274时,即272784-=a ,解得a =﹣2.【点睛】本题考查二次函数的综合应用,熟练掌握二次函数的图象及性质,理解新定义,将所求问题转化为直线与抛物线的知识是解题的关键.7.(1)y =239344x x --;(2)点P 的坐标为:13313-13313-或(3,3);(3)⊙N 的半径为163或83或1. 【解析】【分析】(1)代入点A 、C 的坐标求出解析式;(2)先求出直线OD 的解析式,再和二次函数为的解析式y =239344x x -+联立即可求解;(3)先求出直线BC 的解析式,设N (m ,3m 34-),则M (m ,239344m m --),求出MN 的距离,最后利用“当⊙N 与y 轴相切时,MN =m ”,得出结果.【详解】解:(1)将点A (-1,0),C (0,3)代入抛物线的解析式得,9043a c c ⎧++=⎪⎨⎪=-⎩, 解得343a c ⎧=⎪⎨⎪=-⎩, 故二次函数的解析式为y =239344x x --; (2)∵抛物线y =239344x x --=23325()423x --, ∴抛物线的顶点E 的坐标为(325,23-), ∵DF 平分∠ODE ,∴∠ODF =∠FDE ,∵EH ∥y 轴,∴∠FDE =∠OFD ,∴OD =OF ,∵(0,F , ∴OD =OF设D (32,m ),则OD ²=223()2m +,即2(=223()2m +,解得:m =-32或32, ∴D (32,32-)或(32,32), 设直线OD 的解析式为y =kx , ∴32-=32k 或32=32k ,解得:k =-1或k =1, ∴直线OD 的解析式为:y =x 或y =-x , 联立239344y x y x x =⎧⎪⎨=--⎪⎩或239344y x y x x =-⎧⎪⎨=--⎪⎩, 解得:x舍去);或x =3或43-(舍去); ∴y3, ∴点P 的坐标为:或(3,3);(3)由(1)得二次函数为:y =239344x x --, 当y =0时,239344x x --=0,解得:121,4x x =-=, ∴B (4,0),设直线BC 为:y =kx +b ,经过点C (0,-3),则有043k b b =+⎧⎨=-⎩, 解得:343k b ⎧=⎪⎨⎪=-⎩ , ∴直线BC 为:y=334x -, 设N (m ,3m 34-),则M (m ,239344m m --), ∴MN =M N y y -=239333444m m m ---+=2334m m - 当⊙N 与y 轴相切时,MN =m , ∴2334m m -=m , 解2334m m -=m ,得m =163或0(舍去), 解2334m m -=-m ,得m =83或0(舍去), ∴⊙N 的半径为163或83; 当⊙N 与x 轴相切时,MN =334m -+, ∴2334m m -=334m -+,解2334m m -=334m -+,得m =4(舍去)或-1(舍去), 解2334m m -=3m 34-,得m =4(舍去)或1, ∴⊙N 的半径为1;综上,⊙N 的半径为163或83或1.【点睛】本题考查了待定系数法求二次函数及一次函数的解析式,两点之间的距离公式,圆的切线的性质,解本题的关键用方程的思想解决问题.8.(1)见解析;(2)①见解析;②202【解析】【分析】(1)利用SAS 证明△ACD ≌△BCE ,从而利用全等三角形的性质即可得出结论;(2)①过点D 作DH ⊥CF 于H ,过点B 作BG ⊥CF ,交CF 的延长线于G ,首先证明△ACT ≌△BCG 及△DCH ≌△ECT ,得到CT =BG ,CT =DH ,通过等量代换得出DH =BG ,再证明△DHF ≌△BGF ,则可证明结论;②首先利用等腰三角形的性质和ASA 证明△AOM ≌△COF ,则有OM =OF ,然后利用等腰直角三角形的性质得出FK 2,然后利用三角形的面积得出OF×BF =2,最后利用平方的非负性和完全平方公式求解即可.【详解】证明:(1)∵△ABC 是等腰直角三角形,AC =BC ,∴∠ACB =90°,∵CD ⊥CE ,∴∠ACB =∠DCE =90°,∴∠ACD +∠BCD =∠BCE +∠BCD ,即∠ACD =∠BCE ,在△ACD 和△BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩, ∴△ACD ≌△BCE (SAS ),∴AD =BE ;(2)①如图2,过点D 作DH ⊥CF 于H ,过点B 作BG ⊥CF ,交CF 的延长线于G ,∵CF ⊥AE ,∴∠ATC =∠ATF =90°,∴∠ACT +∠CAT =90°,又∵∠ACT +∠BCG =90°,∴∠CAT =∠BCG ,在△ACT 和△CBG 中,90CAT BCG ATC CGB AC CB ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩, ∴△ACT ≌△CBG (AAS ),∴CT =BG ,同理可证△DCH ≌△ECT ,∴CT =DH ,∴DH =BG ,在△DHF 和△BGF 中,90DFH BFG DHF BGF DH BG ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩, ∴△DHF ≌△BGF (AAS ),∴DF =BF ;②如图3,过点F 作FK ⊥BC 于K , ∵等腰Rt △ABC ,CA =CB ,点O 是AB 的中点, ∴AO =CO =BO ,CO ⊥AB ,∠ABC =45°, ∴∠OCF +∠OFC =90°,∵AT ⊥CF ,∴∠ATF =90°,∴∠OFC +∠FAT =90°,∴∠FAT =∠OCF ,在△AOM 和△COF 中,90MAO FCO OA OCAOM COF ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ∴△AOM ≌△COF (ASA ),∴OM =OF ,又∵CO ⊥AO ,∴∠OFM =∠OMF =45°,222MF OF OM =+, ∴∠OFM =∠ABC ,MF, ∴MF //BC ,∴∠MFK =∠BKF =90°,∵∠ABC =45°,FK ⊥BC ,∴∠ABC =∠BFK =45°,∴FK =BK ,∵222BF FK BK =+,∴FK=22BF,∵S△FMN=52,∴12×MF×FK=52,∴2OF×22BF=102,∴OF×BF=102,∵(BF﹣OF)2≥0,∴BF2+OF2﹣2BF×OF≥0,∴BF2+OF22=2∴BF2+OF2的最小值为2.【点睛】本题主要考查全等三角形的判定及性质,等腰直角三角形的性质与判定,平行线的性质与判定,三角形面积,完全平方公式等等,掌握等腰直角三角形的性质与判定和全等三角形的判定方法及性质是解题的关键.9.(1)证明见解析;(2)证明见解析,(3)157 BF=【解析】【分析】(1)连接OA并延长AO交BC于E,证明∠BAC=2∠BAE和∠ABD=∠BAE即可得结论,(2)利用直角三角形两锐角互余、圆周角定理进行导角,得出MCG△和△FCG是等腰三角形,得出BM=MC=FG=CG,MH=HG,进而由BF=BM+MH-FH=FG-FH+HG,得出结论;(3)过O点作OP⊥AC,由垂径定理得出12PD=,再由52ABOADOS AB BOS AD OD===和平行线分线段成比例定理求出7724DH DP==,由勾股定理进而可求BH,再利用相似三角形对应边成比例求出HG,即可得BF长.【详解】解:(1)连接OA并延长AO交BC于E,∵AB=AC,∴AB AC=,∵AE过圆心O,∴AE BC⊥,BE EC=,∴∠BAC=2∠BAE,∵OA=OB,∴∠ABD=∠BAE,∴∠BAC=2∠ABD;(2)如解图(2),连接OA并延长AO交BC于E,AE交BF于M,连接MC,设2BACα∠=,则ABD BAE EACα∠=∠=∠=∵AE=EC,AE⊥BC,∴BM=MC,∴∠MBC=∠MCB,∵BG⊥AC,AE⊥BC,∴∠EAC+∠ACE=90°,∠HBC+∠ACE=90°,∴EAC HBC MCBα∠=∠=∠=,∴2CMG MBC MCBα∠=∠+∠=,∵BC BC=,∴2G BACα∠=∠=,∴∠G=∠CMG,∴CG =CM =BM ,∵AC ⊥BG ,∴MH =HG ,∵OA =OC ,∴ACO EAC α∠=∠=∴9090CFG ACO α∠=︒-∠=︒-,∵180FCG CFG G ∠=︒-∠-∠,即180(90)290FCG ααα∠=︒-︒--=︒-,∴FCG CFG ∠=∠,∴FG =CG ,∴BM =MC =FG =CG ,又∵MH =HG ,∴BF =BM +MH -FH =FG -FH +HG ,∴BF =2HG .(3)过O 点作OP ⊥AC ,如解图(3)∵AO 是∠BAC 的角平分线,∴点O 到AB 、AC 的距离相等, ∴ABO ADO SAB BO S AD OD==, ∵AD =2,CD =3,∴AB =AC =5, ∴5=2BO OD ,即:2=7OD BD , ∵OP ⊥AC , ∴52AP PC ==,12PD =, ∵BH AC ⊥, ∴OP //BH ,∴27DP OP OD DH BH BD ===, ∴7724DH DP ==, ∴154AH AD DH =+=,5-4HC DC DH ==,∵在Rt ABH中,BH==∵BAH G∠=∠,AHB GHC∠=∠,∴AHB GHC△△,∴AH BHHG CH=即:AH HC BH HG=,51544=⨯,∴HG=,由(2)得BF=2HG,∴BF=【点睛】本题是圆的综合题,主要考查了圆周角定理,涉及了相似三角形的判定和性质、勾股定理、等腰三角形的判定和性质等知识点,解题关键是利用同弧或等弧所对圆周角相等、直角三角形的两锐角相等找出图中角之间的关系,从而利用相似或勾股定理解题.10.(1)旋转中心为BC边的中点O,旋转方向为逆时针,旋转角度为90°;(2)可以,旋转中心为为等边△ABC三边垂直平分线的交点O,理由见解析;(3)11CD≤≤【解析】【分析】问题背景(1)根据等腰直角三角形的性质,以及旋转的性质确定即可;尝试应用(2)首先通过证明△ABD和△CAE全等说明点A和点B对应,点C和点A对应,从而作AB和AC的垂直平分线,其交点即为旋转中点;拓展创新(3)首先确定出D点的运动轨迹,然后结合点与圆的位置关系,分别讨论出CD 最长和最短时的情况,并结合勾股定理进行求解即可.【详解】解:问题背景(1)如图所示,作AO⊥BC,交BC于点O,由等腰直角三角形的性质可知:∠AOC=90°,OA=OC,∴点A是由点C绕点O逆时针旋转90°得到,同理可得,点B是由点A绕点O逆时针旋转90°得到,点D是由点E绕点O逆时针旋转90°得到,∴△ABD可以由△CAE通过旋转变换得到,旋转中心为BC边的中点O,旋转方向为逆时针,旋转角度为90°;尝试应用(2)∵△ABC 为等边三角形,∴AB =AC ,∠BAC =60°,∵∠DAC =∠DAB +∠BAC =∠AEC +∠EAC ,∠BAC =∠AEC =60°,∴∠DAB =∠ECA ,在△ABD 和△CAE 中,BDA AEC DAB ECA AB CA ∠⎪∠⎧=∠∠=⎪⎨⎩= ∴△ABD ≌△CAE (AAS ),∴△ABD 的A 、B 、D 三点的对应点分别为△CAE 的C 、A 、E 三点,则AC 、AB 分别视作两组对应点的连线,此时,如图所示,作AC 和AB 的垂直平分线交于点O ,∵△ABC 为等边三角形,∴由等边三角形的性质可知,OC =OA =OB ,∠AOC =120°,∴△ABD 可以由△CAE 通过旋转变换得到,旋转中心为为等边△ABC 三边垂直平分线的交点O ;拓展创新(3)由(1)知,在直线l 旋转的过程中,总有∠ADB =90°,∴点D 的运动轨迹为以AB 为直径的圆,如图,取AB 的中点P ,连接CP ,交⊙P 于点Q ,则当点D 在CP 的延长线时,CD 的长度最大,当点D 与Q 点重合时,CD 的长度最小,即CQ 的长度,∵AB =AC ,AB =2,∴AP =1,AC =2,在Rt △APC 中,225CP AP AC =+=,由圆的性质,PD =AP =1,∴PD =PQ =1,∴51CD CP PD =+=+,51CQ CP PQ =-=-,∴CD 的长的取值范围为:5151CD -≤≤+.【点睛】本题主要考查旋转三要素的确定,以及旋转的性质,主要涉及等腰直角三角形和等边三角形的性质,全等三角形的判定与性质,以及动点最值问题,掌握旋转的性质,确定出动点的轨迹,熟练运用圆的相关知识点是解题关键.11.(1)正方形;(2)α+β=180°;(3)α=96°;(4)能,α的值为120°,AP 的长为221.【解析】【分析】(1)由旋转的性质得到AO =AO ′,∠OAO ′=90°,由菱形的性质得到∠POA =∠AO ′P =90°,可以推出四边形AOPO ′为正方形;(2)利用旋转的性质推出∠AEP +∠AEG =∠AEP +∠ABD =180°,再结合四边形的内角和即可推出结论;(3)结合已知条件可分别先求出各部分角度,然后结合旋转的性质推出∠BPG 的度数,再结合(2)的结论求解即可;(4)利用勾股定理即可求得AO 的长,根据菱形的性质推出BD 是AC 的垂直平分线,证明△PAC 是等边三角形,即可求解.【详解】:(1)当α=90°时,四边形AOPO ′的形状为正方形.∵菱形AEFG 是菱形ABCD 旋转得到的,且点O ,O ′是对角线的交点,∴AO=AO′,∠OAO′=90°,∠POA=∠AO′P=90°,∴四边形AOPO′为正方形,故答案为:正方形;(2)由题意△BAD≌△EAG,∴∠ABD=∠AEG,∵射线BD,GE交于点P,∴∠AEP+∠AEG=∠AEP+∠ABD=180°,在四边形ABPE中,∠BAE+∠BPG=360°-(∠AEP+∠ABD)=180°,∴∠BAE=a,∠BPG=β,∴α+β=180°;(3)由菱形的性质知,AB=AD,△ABD为等腰三角形,∴当∠BAD=42°时,∠ABD=∠ADB=69°,∵PA=PB,∴∠ABP=∠BAP=69°,∴∠BPA=42°,∵AO=AO′,∴PA平分∠BPG,即:∠BPA=∠GPA=42°,∴∠BPG=84°,即:β=84°,由①知:α +β=180°,∴α=180°-84°=96°;(4)能,理由如下:连接PA,∵四边形ABCD 是菱形,且对角线交点为O ,AB =5,BD =4,∴BO =DO =2,AO =CO ,∠BOA =90°,∴AO =CO 2221AB BO -=∴AC 21 同理:21,AF 由旋转对称性可得,PC PF =∴ 当30CPB ∠=︒时,2221,PC CO PF ===∴ 四边形AFPC 是菱形,∵四边形ABCD 是菱形,∴BD 是AC 的垂直平分线,∴PC =PA ,∴△PAC 是等边三角形,∴PA =PC 21PAC =60°,∴∠CAF =120°,即α的值为120°,AP 的长为21【点睛】本题是四边形综合题,考查了菱形的性质,旋转的性质,勾股定理,等腰三角形的性质,等边三角形的判定和性质等,解答时灵活运用菱形的性质和旋转变化的性质是解题关键.12.(1)y =3x -3;(2)(-2,3);(3)Q 的坐标为(-72,0)或(0,74)或(0,132) 【解析】【分析】(1)根据算术平方根的非负性及偶次方的非负性得到a +3=0,p -1=0,求出a ,p ,得到点P ,A 的坐标,设直线AP 的解析式为y=kx+b ,利用待定系数法求出函数解析式;(2)过M 作MD交x 轴于D ,连接AD ,由MD ,△MAP 的面积等于6,顶点△DAP 的面积等于6,求出DP ,得到点D 坐标,求出直线DM 的解析式,即可求出M 的坐标;(3)设B (t ,3t -3),分三种情况,①当点Q 在轴负半轴时,过B 作BE ⊥x 轴于E ,证明△BEQ ≌△QNC (AAS ),得到O Q=QE-OE=ON+QN ,即4-t =2+3-3t ,求出t 值即可;②当Q在y轴正半轴上时,过C作CF⊥y轴于F,过B作BG⊥y轴于G,证明△CQF≌△QBG(AAS),得到O Q=OG-QG=OF-QF,即3t-3-2=4-t,求出t即可;③当Q在y轴正半轴上时,过点C作CF⊥y轴于F,过B作BT⊥y轴于T,同②可证△CFQ≌△QTB(AAS),得到OQ=OT+QT=OF+QF,即3t-3+2=4+t,求出t值即可.(1)解:∵+(p﹣1)2=0.∴a+3=0,p-1=0,解得a=-3,p=1,∴P(1,0),A(0,-3),设直线AP的解析式为y=kx+b,∴,解得,∴直线AP的解析式为y=3x-3;(2)解:过M作MD交x轴于D,连接AD,∵MD,△MAP的面积等于6,∴△DAP的面积等于6,∴,即,∴DP=4,∴D(-3,0)设直线DM的解析式为y=3x+c,则,∴c=9,∴直线DM的解析式为y=3x+9,令x=-2,得y=3,∴M(-2,3);(3)解:存在设B(t,3t-3),。
初三数学综合题压轴题100题(含答案解析)

初三数学综合题压轴题100题(含答案解析)一、中考压轴题1.某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A类杨梅包装后直接销售;B类杨梅深加工后再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2)之间的函数关系如图;B类杨梅深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.(1)直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式;(2)第一次,该公司收购了20吨杨梅,其中A类杨梅有x吨,经营这批杨梅所获得的毛利润为w万元(毛利润=销售总收入﹣经营总成本).①求w关于x的函数关系式;②若该公司获得了30万元毛利润,问:用于直销的A类杨梅有多少吨?(3)第二次,该公司准备投入132万元资金,请设计一种经营方案,使公司获得最大毛利润,并求出最大毛利润.【分析】(1)这是一个分段函数,分别求出其函数关系式;(2)①当2≤x<8时及当x≥8时,分别求出w关于x的表达式.注意w=销售总收入﹣经营总成本=w A+w B﹣3×20;②若该公司获得了30万元毛利润,将30万元代入①中求得的表达式,求出A类杨梅的数量;(3)本问是方案设计问题,总投入为132万元,这笔132万元包括购买杨梅的费用+A类杨梅加工成本+B类杨梅加工成本.共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,分别求出当2≤x<8时及当x≥8时w关于x的表达式,并分别求出其最大值.【解答】解:(1)①当2≤x<8时,如图,设直线AB解析式为:y=kx+b,将A(2,12)、B(8,6)代入得:,解得,∴y=﹣x+14;②当x≥8时,y=6.所以A类杨梅平均销售价格y与销售量x之间的函数关系式为:y=;(2)设销售A类杨梅x吨,则销售B类杨梅(20﹣x)吨.①当2≤x<8时,w A=x(﹣x+14)﹣x=﹣x2+13x;w B=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x∴w=w A+w B﹣3×20=(﹣x2+13x)+(108﹣6x)﹣60=﹣x2+7x+48;当x≥8时,w A=6x﹣x=5x;w B=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x∴w=w A+w B﹣3×20=(5x)+(108﹣6x)﹣60=﹣x+48.∴w关于x的函数关系式为:w=.②当2≤x<8时,﹣x2+7x+48=30,解得x1=9,x2=﹣2,均不合题意;当x≥8时,﹣x+48=30,解得x=18.∴当毛利润达到30万元时,直接销售的A类杨梅有18吨.(3)设该公司用132万元共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,则购买费用为3m万元,A类杨梅加工成本为x万元,B类杨梅加工成本为[12+3(m﹣x)]万元,∴3m+x+[12+3(m﹣x)]=132,化简得:x=3m﹣60.①当2≤x<8时,w A=x(﹣x+14)﹣x=﹣x2+13x;w B=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12∴w=w A+w B﹣3×m=(﹣x2+13x)+(6m﹣6x﹣12)﹣3m=﹣x2+7x+3m﹣12.将3m=x+60代入得:w=﹣x2+8x+48=﹣(x﹣4)2+64∴当x=4时,有最大毛利润64万元,此时m=,m﹣x=;②当x≥8时,w A=6x﹣x=5x;w B=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12∴w=w A+w B﹣3×m=(5x)+(6m﹣6x﹣12)﹣3m=﹣x+3m﹣12.将3m=x+60代入得:w=48∴当x>8时,有最大毛利润48万元.综上所述,购买杨梅共吨,其中A类杨梅4吨,B类吨,公司能够获得最大毛利润,最大毛利润为64万元.【点评】本题是二次函数、一次函数的综合应用题,难度较大.解题关键是理清售价、成本、利润三者之间的关系.涉及到分段函数时,注意要分类讨论.2.如图,在矩形ABCD中,AB=8,AD=6,点P、Q分别是AB边和CD边上的动点,点P从点A向点B运动,点Q从点C向点D运动,且保持AP=CQ.设AP=x.(1)当PQ∥AD时,求x的值;(2)当线段PQ的垂直平分线与BC边相交时,求x的取值范围;(3)当线段PQ的垂直平分线与BC相交时,设交点为E,连接EP、EQ,设△EPQ的面积为S,求S关于x的函数关系式,并写出S的取值范围.【分析】(1)根据已知条件,证明四边形APQD是矩形,再根据矩形的性质和AP=CQ 求x即可;(2)连接EP、EQ,则EP=EQ,设BE=y,列出等式(8﹣x)2+y2=(6﹣y)2+x2然后根据函数的性质来求x的取值范围;(3)由图形的等量关系列出方程,再根据函数的性质来求最值.【解答】解:(1)当PQ∥AD时,则∠A=∠APQ=90°,∠D=∠DQP=90°,又∵AB∥CD,∴四边形APQD是矩形,∴AP=QD,∵AP=CQ,AP=CD=,∴x=4.(2)如图,连接EP、EQ,则EP=EQ,设BE=y.∴(8﹣x)2+y2=(6﹣y)2+x2,∴y=.∵0≤y≤6,∴0≤≤6,∴≤x≤.(3)S△BPE=•BE•BP=••(8﹣x)=,S△ECQ==•(6﹣)•x=,∵AP=CQ,∴S BPQC=,∴S=S BPQC﹣S△BPE﹣S△ECQ=24﹣﹣,整理得:S==(x﹣4)2+12(),∴当x=4时,S有最小值12,当x=或x=时,S有最大值.∴12≤S≤.【点评】解答本题时,涉及到了矩形的判定、矩形的性质、勾股定理以及二次函数的最值等知识点,这是一道综合性比较强的题目,所以在解答题目时,一定要把各个知识点融会贯通,这样解题时才会少走弯路.3.(1)已知一元二次方程x2+px+q=0(p2﹣4q≥0)的两根为x1、x2;求证:x1+x2=﹣p,x1•x2=q.(2)已知抛物线y=x2+px+q与x轴交于A、B两点,且过点(﹣1,﹣1),设线段AB的长为d,当p为何值时,d2取得最小值,并求出最小值.【分析】(1)先根据求根公式得出x1、x2的值,再求出两根的和与积即可;(2)把点(﹣1,﹣1)代入抛物线的解析式,再由d=|x1﹣x2|可知d2=(x1﹣x2)2=(x1+x2)2﹣4 x1•x2=p2,再由(1)中x1+x2=﹣p,x1•x2=q即可得出结论.【解答】证明:(1)∵a=1,b=p,c=q∴△=p2﹣4q∴x=即x1=,x2=∴x1+x2=+=﹣p,x1•x2=•=q;(2)把(﹣1,﹣1)代入y=x2+px+q得1﹣p+q=﹣1,所以,q=p﹣2,设抛物线y=x2+px+q与x轴交于A、B的坐标分别为(x1,0)、(x2,0)∵d=|x1﹣x2|,∴d2=(x1﹣x2)2=(x1+x2)2﹣4x1•x2=p2﹣4q=p2﹣4p+8=(p﹣2)2+4当p=2时,d2的最小值是4.【点评】本题考查的是抛物线与x轴的交点及根与系数的关系,熟知x1,x2是方程x2+px+q =0的两根时,x1+x2=﹣p,x1x2=q是解答此题的关键.4.已知:y关于x的函数y=(k﹣1)x2﹣2kx+k+2的图象与x轴有交点.(1)求k的取值范围;(2)若x1,x2是函数图象与x轴两个交点的横坐标,且满足(k﹣1)x12+2kx2+k+2=4x1x2.①求k的值;②当k≤x≤k+2时,请结合函数图象确定y的最大值和最小值.【分析】(1)分两种情况讨论,当k=1时,可求出函数为一次函数,必与x轴有一交点;当k≠1时,函数为二次函数,若与x轴有交点,则△≥0.(2)①根据(k﹣1)x12+2kx2+k+2=4x1x2及根与系数的关系,建立关于k的方程,求出k 的值;②充分利用图象,直接得出y的最大值和最小值.【解答】解:(1)当k=1时,函数为一次函数y=﹣2x+3,其图象与x轴有一个交点.当k≠1时,函数为二次函数,其图象与x轴有一个或两个交点,令y=0得(k﹣1)x2﹣2kx+k+2=0.△=(﹣2k)2﹣4(k﹣1)(k+2)≥0,解得k≤2.即k≤2且k≠1.综上所述,k的取值范围是k≤2.(2)①∵x1≠x2,由(1)知k<2且k≠1,函数图象与x轴两个交点,∴k<2,且k≠1.由题意得(k﹣1)x12+(k+2)=2kx1①,将①代入(k﹣1)x12+2kx2+k+2=4x1x2中得:2k(x1+x2)=4x1x2.又∵x1+x2=,x1x2=,∴2k•=4•.解得:k1=﹣1,k2=2(不合题意,舍去).∴所求k值为﹣1.②如图,∵k1=﹣1,y=﹣2x2+2x+1=﹣2(x﹣)2+.且﹣1≤x≤1.由图象知:当x=﹣1时,y最小=﹣3;当x=时,y最大=.∴y的最大值为,最小值为﹣3.【点评】本题考查了抛物线与x轴的交点、一次函数的定义、二次函数的最值,充分利用图象是解题的关键.5.如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于点M对称,定点M叫做对称中心.此时,M是线段PQ的中点.如图,在直角坐标系中,△ABO的顶点A,B,O的坐标分别为(1,0),(0,1),(0,0).点列P1,P2,P3,…中的相邻两点都关于△ABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称…对称中心分别是A,B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),试求出点P2,P7,P100的坐标.【分析】通过作图可知6个点一个循环,那么P7的坐标和P1的坐标相同,P100的坐标与P4的坐标一样,通过图中的点可很快求出.【解答】解:P2的坐标是(1,﹣1),P7的坐标是(1,1),P100的坐标是(1,﹣3).理由:作P1关于A点的对称点,即可得到P2(1,﹣1),分析题意,知6个点一个循环,故P7的坐标与P1的坐标一样,P100的坐标与P4的坐标一样,所以P7的坐标等同于P1的坐标为(1,1),P100的坐标等同于P4的坐标为(1,﹣3).【点评】解决本题的关键是读懂题意,画出图形,仔细观察,分析,得到相应的规律.6.用两种方法解答:已知m、n是关于x的方程x2+(p﹣2)x+1=0两个实数根,求代数式(m2+mp+1)(n2+np+1)的值.【分析】本题主要是利用韦达定理来计算.已知m、n是关于x的方程x2+(p﹣2)x+1=0两个实数根,有四个等式可供使用:m+n=2﹣p①,mn=1②,m2+(p﹣2)m+1=0③,n2+(p﹣2)n+1=0④.通过变形方法,合理地选择解题方法.【解答】解:∵m、n是x2+(p﹣2)x+1=0的根,∴m+n=2﹣p,mn=1.方法一:m2+(p﹣2)m+1=0,n2+(p﹣2)n+1=0.即m2+pm+1=2m,n2+pn+1=2n.原式=2m×2n=4mn=4.方法二:(m2+mp+1)(n2+np+1)=(m2+mp)(n2+np)+m2+mp+n2+np+1=m2n2+m2np+mpn2+mnp2+m2+mp+n2+np+1=1+mp+np+p2+m2+n2+mp+np+1=2+p2+m2+n2+2(m+n)p=2+p2+m2+n2+2(2﹣p)p=2+p2+m2+n2+4p﹣2p2=2+(m+n)2﹣2mn+4p﹣2p2+p2=2+(2﹣p)2﹣2+4p﹣2p2+p2=4﹣4p+p2+4p﹣p2=4.【点评】本题主要是通过根与系数的关系来求值.注意把所求的代数式转化成m+n=2﹣p,mn=1的形式,正确对所求式子进行变形是解题的关键.7.我国年人均用纸量约为28公斤,每个初中毕业生离校时大约有10公斤废纸;用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树.(1)若我市2005年4万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使多少亩森林免遭砍伐?(2)我市从2000年初开始实施天然林保护工程,大力倡导废纸回收再生,如今成效显著,森林面积大约由2003年初的50万亩增加到2005年初的60.5万亩.假设我市年用纸量的20%可以作为废纸回收、森林面积年均增长率保持不变,请你按全市总人口约为1000万计算:在从2005年初到2006年初这一年度内,我市因回收废纸所能保护的最大森林面积相当于新增加的森林面积的百分之几?(精确到1%)【分析】(1)因为每个初中毕业生离校时大约有10公斤废纸,用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树,所以有40000×10÷1000×18÷80,计算出即可求出答案;(2)森林面积大约由2003年初的50万亩增加到2005年初的60.5万亩,可先求出森林面积年均增长率,进而求出2005到2006年新增加的森林面积,而因回收废纸所能保护的最大森林面积=1000×10000×28×20%÷1000×18÷50,然后进行简单的计算即可求出答案.【解答】解:(1)4×104×10÷1000×18÷80=90(亩).答:若我市2005年4万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使90亩森林免遭砍伐.(2)设我市森林面积年平均增长率为x,依题意列方程得50(1+x)2=60.5,解得x1=10%,x2=﹣2.1(不合题意,舍去),1000×104×28×20%÷1000×18÷50=20160,20160÷(605000×10%)≈33%.答:在从2005年初到2006年初这一年度内,我市因回收废纸所能保护的最大森林面积相当于新增加的森林面积的33%.【点评】本题以保护环境为主题,考查了增长率问题,阅读理解题意,并从题目中提炼出平均增长率的数学模型并解答的能力;解答时需仔细分析题意,利用方程即可解决问题.8.如图,反比例函数的图象经过点A(4,b),过点A作AB⊥x轴于点B,△AOB的面积为2.(1)求k和b的值;(2)若一次函数y=ax﹣3的图象经过点A,求这个一次函数的解析式.【分析】(1)由△AOB的面积为2,根据反比例函数的比例系数k的几何意义,可知k的值,得出反比例函数的解析式,然后把x=4代入,即可求出b的值;(2)把点A的坐标代入y=ax﹣3,即可求出这个一次函数的解析式.【解答】解:(1)∵反比例函数的图象经过点A,AB⊥x轴于点B,△AOB的面积为2,A(4,b),∴OB×AB=2,×4×b=2,∴AB=b=1,∴A(4,1),∴k=xy=4,∴反比例函数的解析式为y=,即k=4,b=1.(2)∵A(4,1)在一次函数y=ax﹣3的图象上,∴1=4a﹣3,∴a=1.∴这个一次函数的解析式为y=x﹣3.【点评】本题主要考查了待定系数法求一次函数的解析式和反比例函数中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.9.我们学习了利用函数图象求方程的近似解,例如:把方程2x﹣1=3﹣x的解看成函数y=2x﹣1的图象与函数y=3﹣x的图象交点的横坐标.如图,已画出反比例函数y=在第一象限内的图象,请你按照上述方法,利用此图象求方程x2﹣x﹣1=0的正数解.(要求画出相应函数的图象;求出的解精确到0.1)【分析】根据题意可知,方程x2﹣x﹣1=0的解可看做是函数y=和y=x﹣1的交点坐标,所以根据图象可知方程x2﹣x﹣1=0的正数解约为1.1.【解答】解:∵x≠0,∴将x2﹣x﹣1=0两边同时除以x,得x﹣1﹣=0,即=x﹣1,把x2﹣x﹣1=0的正根视为由函数y=与函数y=x﹣1的图象在第一象限交点的横坐标.如图:∴正数解约为1.1.【点评】主要考查了反比例函数和一元二次方程之间的关系.一元二次方程的解都可化为一个反比例函数和一次函数的交点问题求解.10.九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.【分析】利用三角形相似中的比例关系,首先由题目和图形可看出,求AB的长度分成了2个部分,AH和HB部分,其中HB=EF=1.6m,剩下的问题就是求AH的长度,利用△CGE∽△AHE,得出,把相关条件代入即可求得AH=11.9,所以AB=AH+HB=AH+EF=13.5m.【解答】解:∵CD⊥FB,AB⊥FB,∴CD∥AB∴△CGE∽△AHE∴即:∴∴AH=11.9∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).【点评】主要用到的解题思想是把梯形问题转化成三角形问题,利用三角形相似比列方程来求未知线段的长度.11.如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.(1)求证:△AEC≌△DEB;(2)若∠ABC=∠DCB=90°,AB=2 cm,求图中阴影部分的面积.【分析】(1)在△AEC和△DEB中,已知AE=DE,BE=CE,且夹角相等,根据边角边可证全等.(2)由图可知,在连接EO并延长EO交BC于点F,连接AD之后,整个图形是一个以EF所在直线对称的图形.即△AEO和△DEO面积相等,只要求出其中一个即可,而三角形AEO面积=•OE•FB,所以解题中心即为求出OE和FB,有(1)中结论和已知条件即可求解.【解答】(1)证明:∵∠AEB=∠DEC=90°,∴∠AEB+∠BEC=∠DEC+∠BEC,即∠AEC=∠DEB,∵△BEC是等边三角形,∴CE=BE,又AE=DE,∴△AEC≌△DEB.(2)解:连接EO并延长EO交BC于点F,连接AD.由(1)知AC=BD.∵∠ABC=∠DCB=90°,∴∠ABC+∠DCB=180°,∴AB∥DC,AB==CD,∴四边形ABCD为平行四边形且是矩形,∴OA=OB=OC=OD,又∵BE=CE,∴OE所在直线垂直平分线段BC,∴BF=FC,∠EFB=90°.∴OF=AB=×2=1,∵△BEC是等边三角形,∴∠EBC=60°.在Rt△AEB中,∠AEB=90°,∠ABE=∠ABC﹣∠EBC=90°﹣60°=30°,∴BE=AB•cos30°=,在Rt△BFE中,∠BFE=90°,∠EBF=60°,∴BF=BE•cos60°=,EF=BE•sin60°=,∴OE=EF﹣OF==,∵AE=ED,OE=OE,AO=DO,∴△AOE≌△DOE.∴S△AOE=S△DOE∴S阴影=2S△AOE=2וEO•BF=2×××=(cm2).【点评】考查综合应用等边三角形、等腰三角形、解直角三角形、直角三角形性质,进行逻辑推理能力和运算能力.12.如图,已知直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,连接PC 并延长PC交y轴于点D(0,3).(1)求证:△POD≌△ABO;(2)若直线l:y=kx+b经过圆心P和D,求直线l的解析式.【分析】(1)首先连接PB,由直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,可求得∠APB=∠DPO=60°,∠ABO=∠POD=90°,即可得△P AB是等边三角形,可得AB=OP,然后由ASA,即可判定:△POD≌△ABO;(2)易求得∠PDO=30°,由OP=OD•tan30°,即可求得点P的坐标,然后利用待定系数法,即可求得直线l的解析式.【解答】(1)证明:连接PB,∵直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,∴∠APB=∠DPO=×180°=60°,∠ABO=∠POD=90°,∵P A=PB,∴△P AB是等边三角形,∴AB=P A,∠BAO=60°,∴AB=OP,∠BAO=∠OPD,在△POD和△ABO中,∴△POD≌△ABO(ASA);(2)解:由(1)得△POD≌△ABO,∴∠PDO=∠AOB,∵∠AOB=∠APB=×60°=30°,∴∠PDO=30°,∴OP=OD•tan30°=3×=,∴点P的坐标为:(﹣,0)∴,解得:,∴直线l的解析式为:y=x+3.【点评】此题考查了圆周角定理、全等三角形的判定与性质、直角三角形的性质、等边三角形的判定与性质以及待定系数法求一次函数的解析式.此题综合性较强,难度适中,注意准确作出辅助线,注意数形结合思想的应用.13.如图,有一直径MN=4的半圆形纸片,其圆心为点P,从初始位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚至位置Ⅴ,其中,位置Ⅰ中的MN平行于数轴,且半⊙P与数轴相切于原点O;位置Ⅱ和位置Ⅳ中的MN垂直于数轴;位置Ⅲ中的MN在数轴上;位置Ⅴ中的点N到数轴的距离为3,且半⊙P与数轴相切于点A.解答下列问题:(1)位置Ⅰ中的MN与数轴之间的距离为2;位置Ⅱ中的半⊙P与数轴的位置关系是相切;(2)求位置Ⅲ中的圆心P在数轴上表示的数;(3)纸片半⊙P从位置Ⅲ翻滚到位置Ⅳ时,求点N所经过路径长及该纸片所扫过图形的面积;(4)求OA的长.[(2),(3),(4)中的结果保留π].【分析】(1)先求出圆的半径,再根据切线的性质进行解答;(2)根据位置Ⅰ中的长与数轴上线段ON相等求出的长,再根据弧长公式求出的长,进而可得出结论;(3)作NC垂直数轴于点C,作PH⊥NC于点H,连接P A,则四边形PHCA为矩形,在Rt△NPH中,根据sin∠NPH==即可∠NPH、∠MP A的度数,进而可得出的长,【解答】解:(1)∵⊙P的直径=4,∴⊙P的半径=2,∵⊙P与直线有一个交点,∴位置Ⅰ中的MN与数轴之间的距离为2;位置Ⅱ中的半⊙P与数轴的位置关系是相切;故答案为:2,相切;(2)位置Ⅰ中的长与数轴上线段ON相等,∵的长为=π,NP=2,∴位置Ⅲ中的圆心P在数轴上表示的数为π+2.(3)点N所经过路径长为=2π,S半圆==2π,S扇形==4π,半⊙P所扫过图形的面积为2π+4π=6π.(4)如图,作NC垂直数轴于点C,作PH⊥NC于点H,连接P A,则四边形PHCA为矩形.在Rt△NPH中,PN=2,NH=NC﹣HC=NC﹣P A=1,于是sin∠NPH==,∴∠NPH=30°.∴∠MP A=60°.从而的长为=,于是OA的长为π+4+π=π+4.【点评】本题考查的是直线与圆的关系、弧长的计算、扇形的面积公式,在解答此题时要注意Ⅰ中的长与数轴上线段ON相等的数量关系.14.已知⊙O1与⊙O2相交于A、B两点,点O1在⊙O2上,C为⊙O2上一点(不与A,B,O1重合),直线CB与⊙O1交于另一点D.(1)如图(1),若AD是⊙O1的直径,AC是⊙O2的直径,求证:AC=CD;(2)如图(2),若C是⊙O1外一点,求证:O1C丄AD;(3)如图(3),若C是⊙O1内的一点,判断(2)中的结论是否成立?【分析】(1)连接C01,利用直径所对圆周角等于90度,以及垂直平分线的性质得出即可;(2)根据已知得出四边形AEDB内接于⊙O1,得出∠ABC=∠E,再利用=,得出∠E=∠AO1C,进而得出CO1∥ED即可求出;(3)根据已知得出∠B=∠EO1C,又∠E=∠B,即可得出∠EO1C=∠E,得出CO1∥ED,即可求出.【解答】(1)证明:连接C01∵AC为⊙O2直径∴∠AO1C=90°即CO1⊥AD,∵AO1=DO1∴DC=AC(垂直平分线的性质);(2)证明:连接AO1,连接AB,延长AO1交⊙O1于点E,连接ED,∵四边形AEDB内接于⊙O1,∴∠E+∠ABD=180°,∵∠ABC+∠ABD=180°,∴∠ABC=∠E,又∵=,∴∠ABC=∠AO1C,∴∠E=∠AO1C,∴CO1∥ED,又AE为⊙O1的直径,∴ED⊥AD,∴O1C⊥AD,(3)(2)中的结论仍然成立.证明:连接AO1,连接AB,延长AO1交⊙O1于点E,连接ED,∵∠B+∠AO1C=180°,∠EO1C+∠AO1C═180°,∴∠B=∠EO1C,又∵∠E=∠B,∴∠EO1C=∠E,∴CO1∥ED,又ED⊥AD,∴CO1⊥AD.【点评】此题主要考查了圆周角定理以及相交两圆的性质和圆内接四边形的性质,根据圆内接四边形的性质得出对应角之间的关系是解决问题的关键.15.⊙O1与⊙O2相交于A、B两点,如图(1),连接O2O1并延长交⊙O1于P点,连接P A、PB并分别延长交⊙O2于C、D两点,连接CO2并延长交⊙O2于E点.已知⊙O2的半径为R,设∠CAD=α.(1)求CD的长(用含R、α的式子表示);(2)试判断CD与PO1的位置关系,并说明理由;(3)设点P’为⊙O1上(⊙O2外)的动点,连接P’A、P’B并分别延长交⊙O2于C’、D’,请你探究∠C’AD’是否等于α?C’D’与P’O1的位置关系如何?并说明理由.(注:图(2)与图(3)中⊙O1和⊙O2的大小及位置关系与图(1)完全相同,若你感到继续在图(1)中探究问题(3),图形太复杂,不便于观察,可以选择图(2)或图(3)中的一图说明理由).【分析】(1)作⊙O2的直径CE,连接DE.根据圆周角定理的推论,得∠E=∠CAD=α,再利用解直角三角形的知识求解;(2)连接AB,延长PO1与⊙O1相交于点E,连接AE.根据圆内接四边形的性质,得∠ABP′=∠C′,根据圆周角定理的推论,得∠ABP′=∠E,∠EAP′=90°,从而证明∠AP′E+∠C′=90°,则CD与PO1的位置关系是互相垂直;(3)根据同弧所对的圆周角相等,则说明∠C’AD’等于α;根据(2)中的证明过程,则可以证明C’D’与P’O1的位置关系是互相垂直.【解答】解:(1)连接DE.根据圆周角定理的推论,得∠E=∠CAD=α.∵CE是直径,∴∠CDE=90°.∴CD=CE•sin E=2R sinα;(2)CD与PO1的位置关系是互相垂直.理由如下:连接AB,延长PO1与⊙O1相交于点E,连接AE.∵四边形BAC′D′是圆内接四边形,∴∠ABP′=∠C′.∵P′E是直径,∴∠EAP′=90°,∴∠AP′E+∠E=90°.又∠ABP′=∠E,∴∠AP′E+∠C′=90°,即CD与PO1的位置关系是互相垂直;(3)根据同弧所对的圆周角相等,则说明∠C’AD’等于α;根据(2)中的证明过程,则可以证明C’D’与P’O1的位置关系是互相垂直.【点评】此题综合运用了圆周角定理及其推论、直角三角形的性质、圆内接四边形的性质.注意:连接两圆的公共弦、构造直径所对的圆周角都是圆中常见的辅助线.16.一个不透明的口袋里有红、黄、绿三种颜色的球(除颜色外其余都相同),其中红球有2个,黄球有1个,任意摸出一个黄球的概率为.(1)试求口袋里绿球的个数;(2)若第一次从口袋中任意摸出一球(不放回),第二次任意摸出一球,请你用树状图或列表法,求出两次都摸到红球的概率.【分析】(1)根据概率的求解方法,利用方程求得绿球个数;(2)此题需要两步完成,所以采用树状图法或者列表法都比较简单,解题时要注意是放回实验还是不放回实验,此题为不放回实验.【解答】解:(1)设口袋里绿球有x个,则,解得x=1.故口袋里绿球有1个.(2)红一红二黄绿红一红二,红一黄,红一绿,红一红二红一,红二黄,红一绿,红二黄红一,黄红二,黄绿,黄绿红一,绿红二,绿黄,绿故,P(两次都摸到红球)=.【点评】(1)解题时要注意应用方程思想;(2)列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.17.经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时,研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.(1)求大桥上车流密度为100辆/千米时的车流速度;(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/小时,应控制大桥上的车流密度在什么范围内?(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.【分析】(1)当20≤x≤220时,设车流速度v与车流密度x的函数关系式为v=kx+b,根据题意的数量关系建立方程组求出其解即可;(2)由(1)的解析式建立不等式组求出其解即可;(3)设车流量y与x之间的关系式为y=vx,当x<20和20≤x≤220时分别表示出函数关系由函数的性质就可以求出结论.【解答】解:(1)设车流速度v与车流密度x的函数关系式为v=kx+b,由题意,得,解得:,∴当20≤x≤220时,v=﹣x+88,当x=100时,v=﹣×100+88=48(千米/小时);(2)由题意,得,解得:70<x<120.∴应控制大桥上的车流密度在70<x<120范围内;(3)设车流量y与x之间的关系式为y=vx,当0≤x≤20时y=80x,∴k=80>0,∴y随x的增大而增大,∴x=20时,y最大=1600;当20≤x≤220时y=(﹣x+88)x=﹣(x﹣110)2+4840,∴当x=110时,y最大=4840.∵4840>1600,∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆.【点评】本题考查了车流量=车流速度×车流密度的运用,一次函数的解析式的运用,一元一次不等式组的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.18.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)①画出△ABC关于x轴对称的△A1B1C1;②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;③△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;④△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.【分析】(1)将三角形的各顶点,向x轴作垂线并延长相同长度得到三点的对应点,顺次连接;(2)将三角形的各顶点,绕原点O按逆时针旋转90°得到三点的对应点.顺次连接各对应点得△A2B2C2;(3)从图中可发现成轴对称图形,根据轴对称图形的性质画出对称轴即连接两对应点的线段,做它的垂直平分线;(4)成中心对称图形,画出两条对应点的连线,交点就是对称中心.【解答】解:如下图所示:(3)成轴对称图形,根据轴对称图形的性质画出对称轴即连接两对应点的线段,作它的垂直平分线,或连接A1C1,A2C2的中点的连线为对称轴.(4)成中心对称,对称中心为线段BB2的中点P,坐标是(,).【点评】本题综合考查了图形的变换,在图形的变换中,关键是找到图形的对应点.19.下框中是小明对一道题目的解答以及老师的批改.题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧内墙保留3m的空地,其他三侧内墙各保留1m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288m2?解:设矩形蔬菜种植区域的宽为xm,则长为2xm,根据题意,得x•2x=288.解这个方程,得x1=﹣12(不合题意,舍去),x2=12所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)答:当温室的长为28m,宽为14m时,矩形蔬菜种植区域的面积是288m2.我的结果也正确!小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.结果为何正确呢?(1)请指出小明解答中存在的问题,并补充缺少的过程:变化一下会怎样…(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.【分析】(1)根据题意可得小明没有说明矩形蔬菜种植区域的长与宽之比为2:1的理由,所以应设矩形蔬菜种植区域的宽为xm,则长为2xm,然后由题意得,矩形蔬菜种植区域的长与宽之比为2:1,再利用小明的解法求解即可;(2)由使矩形A′B′C′D′∽矩形ABCD,利用相似多边形的性质,可得,即,然后利用比例的性质,即可求得答案.【解答】解:(1)小明没有说明矩形蔬菜种植区域的长与宽之比为2:1的理由.在“设矩形蔬菜种植区域的宽为xm,则长为2xm.”前补充以下过程:设温室的宽为xm,则长为2xm.则矩形蔬菜种植区域的宽为(x﹣1﹣1)m,长为(2x﹣3﹣1)m.∵,∴矩形蔬菜种植区域的长与宽之比为2:1;(2)要使矩形A′B′C′D′∽矩形ABCD,就要,即,即,即2AB﹣2(b+d)=2AB﹣(a+c),∴a+c=2(b+d),即.【点评】此题考查了相似多边形的性质.此题属于阅读性题目,注意理解题意,读懂题目是解此题的关键.20.如图,AD是⊙O的直径.(1)如图①,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是22.5°,∠B2的度数是67.5°;(2)如图②,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,分别求∠B1,∠B2,∠B3的度数;(3)如图③,垂直于AD的n条弦B1C1,B2C2,B3C3,…,B n∁n把圆周2n等分,请你用含n的代数式表示∠B n的度数(只需直接写出答案).【分析】根据条件可以先求出圆的各段弧的度数,根据圆周角等于所对弧的度数的一半,就可以求出圆周角的度数.【解答】解:(1)垂直于AD的两条弦B1C1,B2C2把圆周4等分,则是圆的,因而度数是45°,因而∠B1的度数是22.5°,同理的度数是135度,因而,∠B2的度数是67.5°;(2)∵圆周被6等分∴===360°÷6=60°∵直径AD⊥B1C1∴==30°,∴∠B1==15°∠B2==×(30°+60°)=45°。
初三中考数学压轴题精选100题(含答案)

初三中考数学压轴题精选100题(含答案)一、中考压轴题1.在△ABC中,AB=BC,将△ABC绕点A沿顺时针方向旋转得△A1B1C1,使点C1落在直线BC上(点C1与点C不重合),(1)如图,当∠C>60°时,写出边AB1与边CB的位置关系,并加以证明;(2)当∠C=60°时,写出边AB1与边CB的位置关系(不要求证明);(3)当∠C<60°时,请你在如图中用尺规作图法作出△AB1C1(保留作图痕迹,不写作法),再猜想你在(1)、(2)中得出的结论是否还成立并说明理由.【分析】(1)AB1∥BC.因为等腰三角形,两底角相等,再根据平行线的判定,内错角相等两直线平行,可证明两直线平行.(2)当∠C=60°时,写出边AB1与边CB的位置关系也是平行,证明方法同(1)题.(3)成立,根据旋转变换的性质画出图形.利用三角形全等即可证明.【解答】解:(1)AB1∥BC.证明:由已知得△ABC≌△AB1C1,∴∠BAC=∠B1AC1,∠B1AB=∠C1AC,∵AC1=AC,∴∠AC1C=∠ACC1,∵∠C1AC+∠AC1C+∠ACC1=180°,∴∠C1AC=180°﹣2∠ACC1,同理,在△ABC中,∵BA=BC,∴∠ABC=180°﹣2∠ACC1,∴∠ABC=∠C1AC=∠B1AB,∴AB1∥BC.(5分)(2)如图1,∠C=60°时,AB1∥BC.(7分)(3)如图,当∠C<60°时,(1)、(2)中的结论还成立.证明:显然△ABC≌△AB1C1,∴∠BAC=∠B1AC1,∴∠B1AB=∠C1AC,∵AC1=AC,∴∠AC1C=∠ACC1,∵∠C1AC+∠AC1C+∠ACC1=180°,∴∠C1AC=180°﹣2∠ACC1,同理,在△ABC中,∵BA=BC,∴∠ABC=180°﹣2∠ACC1,∴∠ABC=∠C1AC=∠B1AB,∴AB1∥BC.(13分)【点评】考查图形的旋转,等腰三角形的性质,平行线的判定.本题实质是考查对图形旋转特征的理解,旋转前后的图形是全等的.2.我们学习了利用函数图象求方程的近似解,例如:把方程2x﹣1=3﹣x的解看成函数y =2x﹣1的图象与函数y=3﹣x的图象交点的横坐标.如图,已画出反比例函数y=在第一象限内的图象,请你按照上述方法,利用此图象求方程x2﹣x﹣1=0的正数解.(要求画出相应函数的图象;求出的解精确到0.1)【分析】根据题意可知,方程x2﹣x﹣1=0的解可看做是函数y=和y=x﹣1的交点坐标,所以根据图象可知方程x2﹣x﹣1=0的正数解约为1.1.【解答】解:∵x≠0,∴将x2﹣x﹣1=0两边同时除以x,得x﹣1﹣=0,即=x﹣1,把x2﹣x﹣1=0的正根视为由函数y=与函数y=x﹣1的图象在第一象限交点的横坐标.如图:∴正数解约为1.1.【点评】主要考查了反比例函数和一元二次方程之间的关系.一元二次方程的解都可化为一个反比例函数和一次函数的交点问题求解.3.汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2005年盈利1500万元,到2007年盈利2160万元,且从2005年到2007年,每年盈利的年增长率相同.(1)该公司2006年盈利多少万元?(2)若该公司盈利的年增长率继续保持不变,预计2008年盈利多少万元?【分析】(1)需先算出从2005年到2007年,每年盈利的年增长率,然后根据2005年的盈利,算出2006年的利润;(2)相等关系是:2008年盈利=2007年盈利×每年盈利的年增长率.【解答】解:(1)设每年盈利的年增长率为x,根据题意得1500(1+x)2=2160解得x1=0.2,x2=﹣2.2(不合题意,舍去)∴1500(1+x)=1500(1+0.2)=1800答:2006年该公司盈利1800万元.(2)2160(1+0.2)=2592答:预计2008年该公司盈利2592万元.【点评】本题的关键是需求出从2005年到2007年,每年盈利的年增长率.等量关系为:2005年盈利×(1+年增长率)2=2160.4.如图,△ABC内接于⊙O,AB=6,AC=4,D是AB边上一点,P是优弧BAC的中点,连接P A、PB、PC、PD.(1)当BD的长度为多少时,△P AD是以AD为底边的等腰三角形?并证明;(2)在(1)的条件下,若cos∠PCB=,求P A的长.【分析】(1)根据等弧对等弦以及全等三角形的判定和性质进行求解;(2)过点P作PE⊥AD于E.根据锐角三角函数的知识和垂径定理进行求解.【解答】解:(1)当BD=AC=4时,△P AD是以AD为底边的等腰三角形.∵P是优弧BAC的中点,∴=.∴PB=PC.又∵∠PBD=∠PCA(圆周角定理),∴当BD=AC=4,△PBD≌△PCA.∴P A=PD,即△P AD是以AD为底边的等腰三角形.(2)过点P作PE⊥AD于E,由(1)可知,当BD=4时,PD=P A,AD=AB﹣BD=6﹣4=2,则AE=AD=1.∵∠PCB=∠P AD(在同圆或等圆中,同弧所对的圆周角相等),∴cos∠P AD=cos∠PCB=,∴P A=.【点评】综合运用了等弧对等弦的性质、全等三角形的判定和性质、锐角三角函数的知识以及垂径定理.5.广安市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.(1)求平均每次下调的百分率.(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?【分析】(1)根据题意设平均每次下调的百分率为x,列出一元二次方程,解方程即可得出答案;(2)分别计算两种方案的优惠价格,比较后发现方案①更优惠.【解答】解:(1)设平均每次下调的百分率为x,则6000(1﹣x)2=4860,解得:x1=0.1=10%,x2=1.9(舍去),故平均每次下调的百分率为10%;(2)方案①购房优惠:4860×100×(1﹣0.98)=9720(元);方案②可优惠:80×100=8000(元).故选择方案①更优惠.【点评】本题主要考查一元二次方程的实际应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解,属于中档题.6.如图,已知直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,连接PC并延长PC交y轴于点D(0,3).(1)求证:△POD≌△ABO;(2)若直线l:y=kx+b经过圆心P和D,求直线l的解析式.【分析】(1)首先连接PB,由直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,可求得∠APB=∠DPO=60°,∠ABO=∠POD=90°,即可得△P AB是等边三角形,可得AB=OP,然后由ASA,即可判定:△POD≌△ABO;(2)易求得∠PDO=30°,由OP=OD•tan30°,即可求得点P的坐标,然后利用待定系数法,即可求得直线l的解析式.【解答】(1)证明:连接PB,∵直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,∴∠APB=∠DPO=×180°=60°,∠ABO=∠POD=90°,∵P A=PB,∴△P AB是等边三角形,∴AB=P A,∠BAO=60°,∴AB=OP,∠BAO=∠OPD,在△POD和△ABO中,∴△POD≌△ABO(ASA);(2)解:由(1)得△POD≌△ABO,∴∠PDO=∠AOB,∵∠AOB=∠APB=×60°=30°,∴∠PDO=30°,∴OP=OD•tan30°=3×=,∴点P的坐标为:(﹣,0)∴,解得:,∴直线l的解析式为:y=x+3.【点评】此题考查了圆周角定理、全等三角形的判定与性质、直角三角形的性质、等边三角形的判定与性质以及待定系数法求一次函数的解析式.此题综合性较强,难度适中,注意准确作出辅助线,注意数形结合思想的应用.7.如图1,在直角坐标系中,点A的坐标为(1,0),以OA为边在第四象限内作等边△AOB,点C为x轴的正半轴上一动点(OC>1),连接BC,以BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.(1)试问△OBC与△ABD全等吗?并证明你的结论;(2)随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由;(3)如图2,以OC为直径作圆,与直线DE分别交于点F、G,设AC=m,AF=n,用含n的代数式表示m.【分析】(1)由等边三角形的性质知,OBA=∠CBD=60°,易得∠OBC=∠ABD,又有OB=AB,BC=BD故有△OBC≌△ABD;(2)由1知,△OBC≌△ABD⇒∠BAD=∠BOC=60°,可得∠OAE=60°,在Rt△EOA 中,有EO=OA•tan60°=,即可求得点E的坐标;(3)由相交弦定理知1•m=n•AG,即AG=,由切割线定理知,OE2=EG•EF,在Rt△EOA中,由勾股定理知,AE==2,故建立方程:()2=(2﹣)(2+n),就可求得m与n关系.【解答】解:(1)两个三角形全等.∵△AOB、△CBD都是等边三角形,∴OBA=∠CBD=60°,∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD;∵OB=AB,BC=BD,△OBC≌△ABD;(2)点E位置不变.∵△OBC≌△ABD,∴∠BAD=∠BOC=60°,∠OAE=180°﹣60°﹣60°=60°;在Rt△EOA中,EO=OA•tan60°=,或∠AEO=30°,得AE=2,∴OE=∴点E的坐标为(0,);(3)∵AC=m,AF=n,由相交弦定理知1•m=n•AG,即AG=;又∵OC是直径,∴OE是圆的切线,OE2=EG•EF,在Rt△EOA中,AE==2,()2=(2﹣)(2+n)即2n2+n﹣2m﹣mn=0解得m=.【点评】命题立意:考查圆的相交弦定理、切线定理、三角形全等等知识,并且将这些知识与坐标系联系在一起,考查综合分析、解决问题的能力.8.我国年人均用纸量约为28公斤,每个初中毕业生离校时大约有10公斤废纸;用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树.(1)若我市2005年4万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使多少亩森林免遭砍伐?(2)我市从2000年初开始实施天然林保护工程,大力倡导废纸回收再生,如今成效显著,森林面积大约由2003年初的50万亩增加到2005年初的60.5万亩.假设我市年用纸量的20%可以作为废纸回收、森林面积年均增长率保持不变,请你按全市总人口约为1000万计算:在从2005年初到2006年初这一年度内,我市因回收废纸所能保护的最大森林面积相当于新增加的森林面积的百分之几?(精确到1%)【分析】(1)因为每个初中毕业生离校时大约有10公斤废纸,用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树,所以有40000×10÷1000×18÷80,计算出即可求出答案;(2)森林面积大约由2003年初的50万亩增加到2005年初的60.5万亩,可先求出森林面积年均增长率,进而求出2005到2006年新增加的森林面积,而因回收废纸所能保护的最大森林面积=1000×10000×28×20%÷1000×18÷50,然后进行简单的计算即可求出答案.【解答】解:(1)4×104×10÷1000×18÷80=90(亩).答:若我市2005年4万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使90亩森林免遭砍伐.(2)设我市森林面积年平均增长率为x,依题意列方程得50(1+x)2=60.5,解得x1=10%,x2=﹣2.1(不合题意,舍去),1000×104×28×20%÷1000×18÷50=20160,20160÷(605000×10%)≈33%.答:在从2005年初到2006年初这一年度内,我市因回收废纸所能保护的最大森林面积相当于新增加的森林面积的33%.【点评】本题以保护环境为主题,考查了增长率问题,阅读理解题意,并从题目中提炼出平均增长率的数学模型并解答的能力;解答时需仔细分析题意,利用方程即可解决问题.9.一个不透明的口袋里有红、黄、绿三种颜色的球(除颜色外其余都相同),其中红球有2个,黄球有1个,任意摸出一个黄球的概率为.(1)试求口袋里绿球的个数;(2)若第一次从口袋中任意摸出一球(不放回),第二次任意摸出一球,请你用树状图或列表法,求出两次都摸到红球的概率.【分析】(1)根据概率的求解方法,利用方程求得绿球个数;(2)此题需要两步完成,所以采用树状图法或者列表法都比较简单,解题时要注意是放回实验还是不放回实验,此题为不放回实验.【解答】解:(1)设口袋里绿球有x个,则,解得x=1.故口袋里绿球有1个.(2)红一红二黄绿红一红二,红一黄,红一绿,红一红二红一,红二黄,红一绿,红二黄红一,黄红二,黄绿,黄绿红一,绿红二,绿黄,绿故,P(两次都摸到红球)=.【点评】(1)解题时要注意应用方程思想;(2)列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.10.如图,在矩形ABCD中,AB=8,AD=6,点P、Q分别是AB边和CD边上的动点,点P从点A向点B运动,点Q从点C向点D运动,且保持AP=CQ.设AP=x.(1)当PQ∥AD时,求x的值;(2)当线段PQ的垂直平分线与BC边相交时,求x的取值范围;(3)当线段PQ的垂直平分线与BC相交时,设交点为E,连接EP、EQ,设△EPQ的面积为S,求S关于x的函数关系式,并写出S的取值范围.【分析】(1)根据已知条件,证明四边形APQD是矩形,再根据矩形的性质和AP=CQ 求x即可;(2)连接EP、EQ,则EP=EQ,设BE=y,列出等式(8﹣x)2+y2=(6﹣y)2+x2然后根据函数的性质来求x的取值范围;(3)由图形的等量关系列出方程,再根据函数的性质来求最值.【解答】解:(1)当PQ∥AD时,则∠A=∠APQ=90°,∠D=∠DQP=90°,又∵AB∥CD,∴四边形APQD是矩形,∴AP=QD,∵AP=CQ,AP=CD=,∴x=4.(2)如图,连接EP、EQ,则EP=EQ,设BE=y.∴(8﹣x)2+y2=(6﹣y)2+x2,∴y=.∵0≤y≤6,∴0≤≤6,∴≤x≤.(3)S△BPE=•BE•BP=••(8﹣x)=,S△ECQ==•(6﹣)•x=,∵AP=CQ,∴S BPQC=,∴S=S BPQC﹣S△BPE﹣S△ECQ=24﹣﹣,整理得:S==(x﹣4)2+12(),∴当x=4时,S有最小值12,当x=或x=时,S有最大值.∴12≤S≤.【点评】解答本题时,涉及到了矩形的判定、矩形的性质、勾股定理以及二次函数的最值等知识点,这是一道综合性比较强的题目,所以在解答题目时,一定要把各个知识点融会贯通,这样解题时才会少走弯路.11.某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A 类杨梅包装后直接销售;B类杨梅深加工后再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2)之间的函数关系如图;B类杨梅深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.(1)直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式;(2)第一次,该公司收购了20吨杨梅,其中A类杨梅有x吨,经营这批杨梅所获得的毛利润为w万元(毛利润=销售总收入﹣经营总成本).①求w关于x的函数关系式;②若该公司获得了30万元毛利润,问:用于直销的A类杨梅有多少吨?(3)第二次,该公司准备投入132万元资金,请设计一种经营方案,使公司获得最大毛利润,并求出最大毛利润.【分析】(1)这是一个分段函数,分别求出其函数关系式;(2)①当2≤x<8时及当x≥8时,分别求出w关于x的表达式.注意w=销售总收入﹣经营总成本=w A+w B﹣3×20;②若该公司获得了30万元毛利润,将30万元代入①中求得的表达式,求出A类杨梅的数(3)本问是方案设计问题,总投入为132万元,这笔132万元包括购买杨梅的费用+A类杨梅加工成本+B类杨梅加工成本.共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,分别求出当2≤x<8时及当x≥8时w关于x的表达式,并分别求出其最大值.【解答】解:(1)①当2≤x<8时,如图,设直线AB解析式为:y=kx+b,将A(2,12)、B(8,6)代入得:,解得,∴y=﹣x+14;②当x≥8时,y=6.所以A类杨梅平均销售价格y与销售量x之间的函数关系式为:y=;(2)设销售A类杨梅x吨,则销售B类杨梅(20﹣x)吨.①当2≤x<8时,w A=x(﹣x+14)﹣x=﹣x2+13x;w B=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x∴w=w A+w B﹣3×20=(﹣x2+13x)+(108﹣6x)﹣60=﹣x2+7x+48;当x≥8时,w A=6x﹣x=5x;w B=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x∴w=w A+w B﹣3×20=(5x)+(108﹣6x)﹣60=﹣x+48.∴w关于x的函数关系式为:w=.②当2≤x<8时,﹣x2+7x+48=30,解得x1=9,x2=﹣2,均不合题意;当x≥8时,﹣x+48=30,解得x=18.∴当毛利润达到30万元时,直接销售的A类杨梅有18吨.(3)设该公司用132万元共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,则购买费用为3m万元,A类杨梅加工成本为x万元,B类杨梅加工成本为[12+3(m﹣x)]∴3m+x+[12+3(m﹣x)]=132,化简得:x=3m﹣60.①当2≤x<8时,w A=x(﹣x+14)﹣x=﹣x2+13x;w B=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12∴w=w A+w B﹣3×m=(﹣x2+13x)+(6m﹣6x﹣12)﹣3m=﹣x2+7x+3m﹣12.将3m=x+60代入得:w=﹣x2+8x+48=﹣(x﹣4)2+64∴当x=4时,有最大毛利润64万元,此时m=,m﹣x=;②当x≥8时,w A=6x﹣x=5x;w B=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12∴w=w A+w B﹣3×m=(5x)+(6m﹣6x﹣12)﹣3m=﹣x+3m﹣12.将3m=x+60代入得:w=48∴当x>8时,有最大毛利润48万元.综上所述,购买杨梅共吨,其中A类杨梅4吨,B类吨,公司能够获得最大毛利润,最大毛利润为64万元.【点评】本题是二次函数、一次函数的综合应用题,难度较大.解题关键是理清售价、成本、利润三者之间的关系.涉及到分段函数时,注意要分类讨论.12.⊙O1与⊙O2相交于A、B两点,如图(1),连接O2O1并延长交⊙O1于P点,连接P A、PB并分别延长交⊙O2于C、D两点,连接CO2并延长交⊙O2于E点.已知⊙O2的半径为R,设∠CAD=α.(1)求CD的长(用含R、α的式子表示);(2)试判断CD与PO1的位置关系,并说明理由;(3)设点P’为⊙O1上(⊙O2外)的动点,连接P’A、P’B并分别延长交⊙O2于C’、D’,请你探究∠C’AD’是否等于α?C’D’与P’O1的位置关系如何?并说明(注:图(2)与图(3)中⊙O1和⊙O2的大小及位置关系与图(1)完全相同,若你感到继续在图(1)中探究问题(3),图形太复杂,不便于观察,可以选择图(2)或图(3)中的一图说明理由).【分析】(1)作⊙O2的直径CE,连接DE.根据圆周角定理的推论,得∠E=∠CAD=α,再利用解直角三角形的知识求解;(2)连接AB,延长PO1与⊙O1相交于点E,连接AE.根据圆内接四边形的性质,得∠ABP′=∠C′,根据圆周角定理的推论,得∠ABP′=∠E,∠EAP′=90°,从而证明∠AP′E+∠C′=90°,则CD与PO1的位置关系是互相垂直;(3)根据同弧所对的圆周角相等,则说明∠C’AD’等于α;根据(2)中的证明过程,则可以证明C’D’与P’O1的位置关系是互相垂直.【解答】解:(1)连接DE.根据圆周角定理的推论,得∠E=∠CAD=α.∵CE是直径,∴∠CDE=90°.∴CD=CE•sin E=2R sinα;(2)CD与PO1的位置关系是互相垂直.理由如下:连接AB,延长PO1与⊙O1相交于点E,连接AE.∵四边形BAC′D′是圆内接四边形,∴∠ABP′=∠C′.∵P′E是直径,∴∠EAP′=90°,∴∠AP′E+∠E=90°.又∠ABP′=∠E,∴∠AP′E+∠C′=90°,即CD与PO1的位置关系是互相垂直;(3)根据同弧所对的圆周角相等,则说明∠C’AD’等于α;根据(2)中的证明过程,则可以证明C’D’与P’O1的位置关系是互相垂直.【点评】此题综合运用了圆周角定理及其推论、直角三角形的性质、圆内接四边形的性质.注意:连接两圆的公共弦、构造直径所对的圆周角都是圆中常见的辅助线.13.已知⊙O1与⊙O2相交于A、B两点,点O1在⊙O2上,C为⊙O2上一点(不与A,B,O1重合),直线CB与⊙O1交于另一点D.(1)如图(1),若AD是⊙O1的直径,AC是⊙O2的直径,求证:AC=CD;(2)如图(2),若C是⊙O1外一点,求证:O1C丄AD;(3)如图(3),若C是⊙O1内的一点,判断(2)中的结论是否成立?【分析】(1)连接C01,利用直径所对圆周角等于90度,以及垂直平分线的性质得出即可;(2)根据已知得出四边形AEDB内接于⊙O1,得出∠ABC=∠E,再利用=,得出∠E=∠AO1C,进而得出CO1∥ED即可求出;(3)根据已知得出∠B=∠EO1C,又∠E=∠B,即可得出∠EO1C=∠E,得出CO1∥ED,即可求出.【解答】(1)证明:连接C01∵AC为⊙O2直径∴∠AO1C=90°即CO1⊥AD,∵AO1=DO1∴DC=AC(垂直平分线的性质);(2)证明:连接AO1,连接AB,延长AO1交⊙O1于点E,连接ED,∵四边形AEDB内接于⊙O1,∴∠E+∠ABD=180°,∵∠ABC+∠ABD=180°,∴∠ABC=∠E,又∵=,∴∠ABC=∠AO1C,∴∠E=∠AO1C,∴CO1∥ED,又AE为⊙O1的直径,∴ED⊥AD,∴O1C⊥AD,(3)(2)中的结论仍然成立.证明:连接AO1,连接AB,延长AO1交⊙O1于点E,连接ED,∵∠B+∠AO1C=180°,∠EO1C+∠AO1C═180°,∴∠B=∠EO1C,又∵∠E=∠B,∴∠EO1C=∠E,∴CO1∥ED,又ED⊥AD,∴CO1⊥AD.【点评】此题主要考查了圆周角定理以及相交两圆的性质和圆内接四边形的性质,根据圆内接四边形的性质得出对应角之间的关系是解决问题的关键.14.如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.(1)求证:△AEC≌△DEB;(2)若∠ABC=∠DCB=90°,AB=2 cm,求图中阴影部分的面积.【分析】(1)在△AEC和△DEB中,已知AE=DE,BE=CE,且夹角相等,根据边角边可证全等.(2)由图可知,在连接EO并延长EO交BC于点F,连接AD之后,整个图形是一个以EF所在直线对称的图形.即△AEO和△DEO面积相等,只要求出其中一个即可,而三角形AEO面积=•OE•FB,所以解题中心即为求出OE和FB,有(1)中结论和已知条件即可求解.【解答】(1)证明:∵∠AEB=∠DEC=90°,∴∠AEB+∠BEC=∠DEC+∠BEC,即∠AEC=∠DEB,∵△BEC是等边三角形,∴CE=BE,又AE=DE,∴△AEC≌△DEB.(2)解:连接EO并延长EO交BC于点F,连接AD.由(1)知AC=BD.∵∠ABC=∠DCB=90°,∴∠ABC+∠DCB=180°,∴AB∥DC,AB==CD,∴四边形ABCD为平行四边形且是矩形,∴OA=OB=OC=OD,又∵BE=CE,∴OE所在直线垂直平分线段BC,∴BF=FC,∠EFB=90°.∴OF=AB=×2=1,∵△BEC是等边三角形,∴∠EBC=60°.在Rt△AEB中,∠AEB=90°,∠ABE=∠ABC﹣∠EBC=90°﹣60°=30°,∴BE=AB•cos30°=,在Rt△BFE中,∠BFE=90°,∠EBF=60°,∴BF=BE•cos60°=,EF=BE•sin60°=,∴OE=EF﹣OF==,∵AE=ED,OE=OE,AO=DO,∴△AOE≌△DOE.∴S△AOE=S△DOE∴S阴影=2S△AOE=2וEO•BF=2×××=(cm2).【点评】考查综合应用等边三角形、等腰三角形、解直角三角形、直角三角形性质,进行逻辑推理能力和运算能力.15.经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时,研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.(1)求大桥上车流密度为100辆/千米时的车流速度;(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/小时,应控制大桥上的车流密度在什么范围内?(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.【分析】(1)当20≤x≤220时,设车流速度v与车流密度x的函数关系式为v=kx+b,根据题意的数量关系建立方程组求出其解即可;(2)由(1)的解析式建立不等式组求出其解即可;(3)设车流量y与x之间的关系式为y=vx,当x<20和20≤x≤220时分别表示出函数关系由函数的性质就可以求出结论.【解答】解:(1)设车流速度v与车流密度x的函数关系式为v=kx+b,由题意,得,解得:,∴当20≤x≤220时,v=﹣x+88,当x=100时,v=﹣×100+88=48(千米/小时);(2)由题意,得,解得:70<x<120.∴应控制大桥上的车流密度在70<x<120范围内;(3)设车流量y与x之间的关系式为y=vx,当0≤x≤20时y=80x,∴k=80>0,∴y随x的增大而增大,∴x=20时,y最大=1600;当20≤x≤220时y=(﹣x+88)x=﹣(x﹣110)2+4840,∴当x=110时,y最大=4840.∵4840>1600,∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆.【点评】本题考查了车流量=车流速度×车流密度的运用,一次函数的解析式的运用,一元一次不等式组的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.16.如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.(1)设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形越接近于正方形.①若菱形的一个内角为70°,则该菱形的“接近度”等于40;②当菱形的“接近度”等于0时,菱形是正方形.(2)设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a﹣b|,于是|a﹣b|越小,矩形越接近于正方形.你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.【分析】(1)根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,相似图形的“接近度”相等.所以若菱形的一个内角为70°,则该菱形的“接近度”等于|m﹣n|;当菱形的“接近度”等于0时,菱形是正方形;(2)不合理,举例进行说明.【解答】解:(1)①∵内角为70°,∴与它相邻内角的度数为110°.∴菱形的“接近度”=|m﹣n|=|110﹣70|=40.②当菱形的“接近度”等于0时,菱形是正方形.(2)不合理.例如,对两个相似而不全等的矩形来说,它们接近正方形的程度是相同的,但|a﹣b|却不相等.合理定义方法不唯一.如定义为,越接近1,矩形越接近于正方形;越大,矩形与正方形的形状差异越大;当时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.【点评】正确理解“接近度”的意思,矩形的“接近度”|a﹣b|越小,矩形越接近于正方形.这是解决问题的关键.17.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)①画出△ABC关于x轴对称的△A1B1C1;②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;③△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;④△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.【分析】(1)将三角形的各顶点,向x轴作垂线并延长相同长度得到三点的对应点,顺次连接;(2)将三角形的各顶点,绕原点O按逆时针旋转90°得到三点的对应点.顺次连接各对应点得△A2B2C2;(3)从图中可发现成轴对称图形,根据轴对称图形的性质画出对称轴即连接两对应点的线段,做它的垂直平分线;(4)成中心对称图形,画出两条对应点的连线,交点就是对称中心.【解答】解:如下图所示:(3)成轴对称图形,根据轴对称图形的性质画出对称轴即连接两对应点的线段,作它的垂直平分线,或连接A1C1,A2C2的中点的连线为对称轴.(4)成中心对称,对称中心为线段BB2的中点P,坐标是(,).【点评】本题综合考查了图形的变换,在图形的变换中,关键是找到图形的对应点.18.如图,矩形ABCD的边AD、AB分别与⊙O相切于点E、F,(1)求的长;(2)若,直线MN分别交射线DA、DC于点M、N,∠DMN=60°,将直线MN沿射线DA方向平移,设点D到直线的距离为d,当时1≤d≤4,请判断直线MN与⊙O的位置关系,并说明理由.【分析】(1)连接OE、OF,利用相切证明四边形AFOE是正方形,再根据弧长公式求弧长;(2)先求出直线M1N1与圆相切时d的值,结合1≤d≤4,划分d的范围,分类讨论.【解答】解:(1)连接OE、OF,∵矩形ABCD的边AD、AB分别与⊙O相切于点E、F,∴∠A=90°,∠OEA=∠OF A=90°∴四边形AFOE是正方形∴∠EOF=90°,OE=AE=∴的长==π.(2)如图,将直线MN沿射线DA方向平移,当其与⊙O相切时,记为M1N1,切点为R,交AD于M1,交BC于N1,连接OM1、OR,∵M1N1∥MN∴∠DM1N1=∠DMN=60°∴∠EM1N1=120°∵MA、M1N1切⊙O于点E、R∴∠EM1O=∠EM1N1=60°在Rt△EM1O中,EM1===1∴DM1=AD﹣AE﹣EM1=+5﹣﹣1=4.过点D作DK⊥M1N1于K在Rt△DM1K中DK=DM1×sin∠DM1K=4×sin∠60°=2即d=2,∴当d=2时,直线MN与⊙O相切,当1≤d<2时,直线MN与⊙O相离,当直线MN平移到过圆心O时,记为M2N2,点D到M2N2的距离d=DK+OR=2+=3>4,∴当2<d≤4时,MN直线与⊙O相交.【点评】本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d 与圆半径大小关系完成判定.19.如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.(1)求证:AP=AO;(2)求证:PE⊥AO;(3)当AE=AC,AB=10时,求线段BO的长度.【分析】(1)根据等角的余角相等证明即可;(2)过点O作OD⊥AB于D,根据角平分线上的点到角的两边的距离相等可得CO=DO,利用“SAS”证明△APE和△OAD全等,根据全等三角形对应角相等可得∠AEP=∠ADO=90°,从而得证;(3)设C0=3k,AC=8k,表示出AE=CO=3k,AO=AP=5k,然后利用勾股定理列式求出PE=4k,BC=BD=10﹣4k,再根据相似三角形对应边成比例列式求出k=1然后在Rt △BDO中,利用勾股定理列式求解即可.【解答】(1)证明:∵∠C=90°,∠BAP=90°∴∠CBO+∠BOC=90°,∠ABP+∠APB=90°,又∵∠CBO=∠ABP,∴∠BOC=∠APB,∵∠BOC=∠AOP,∴∠AOP=∠APB,∴AP=AO;(2)证明:如图,过点O作OD⊥AB于D,∵∠CBO=∠ABP,∴CO=DO,∵AE=OC,∴AE=OD,∵∠AOD+∠OAD=90°,∠P AE+∠OAD=90°,∴∠AOD=∠P AE,在△AOD和△P AE中,,∴△AOD≌△P AE(SAS),∴∠AEP=∠ADO=90°∴PE⊥AO;(3)解:设AE=OC=3k,∵AE=AC,∴AC=8k,∴OE=AC﹣AE﹣OC=2k,∴OA=OE+AE=5k.由(1)可知,AP=AO=5k.如图,过点O作OD⊥AB于点D,∵∠CBO=∠ABP,∴OD=OC=3k.在Rt△AOD中,AD===4k.∴BD=AB﹣AD=10﹣4k.∵OD∥AP,∴,即解得k=1,∵AB=10,PE=AD,∴PE=AD=4K,BD=AB﹣AD=10﹣4k=6,OD=3在Rt△BDO中,由勾股定理得:BO===3.【点评】本题考查了全等三角形的判定与性质,角平分线上的点到角的两边的距离相等的性质,勾股定理,相似三角形的判定与性质,(2)作辅助线构造出过渡线段DO并得到全等三角形是解题的关键,(3)利用相似三角形对应边成比例求出k=1是解题的关键.20.下框中是小明对一道题目的解答以及老师的批改.题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧内墙保留3m的空地,其他三侧内墙各保留1m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288m2?解:设矩形蔬菜种植区域的宽为xm,则长为2xm,根据题意,得x•2x=288.解这个方程,得x1=﹣12(不合题意,舍去),x2=12所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)答:当温室的长为28m,宽为14m时,矩形蔬菜种植区域的面积是288m2.我的结果也正确!小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.结果为何正确呢?(1)请指出小明解答中存在的问题,并补充缺少的过程:变化一下会怎样…(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.。
中考数学一元二次方程-经典压轴题及答案

中考数学一元二次方程-经典压轴题及答案一、一元二次方程真题与模拟题分类汇编(难题易错题)21.解方程:(1-2x)(x2-6x+9)。
答案】x1=1/4,x2=-2/3.解析】题目分析:先对方程的右边因式分解,然后直接开平方或移项之后再因式分解法求解即可。
解题分析】因式分解,得到22(1-2x)=(x-3)。
开平方,得到1-2x=x-3,或1-2x=-(x-3)。
解得x1=1/4,x2=-2/3.2.已知关于x的一元二次方程mx-(m+2)x+2m-3=0.1)当m取什么值时,方程有两个不相等的实数根?2)当m=4时,求方程的解。
答案】(1)当m>-1且m≠0时,方程有两个不相等的实数根;(2)x1= (3+5)/4,x2= (3-5)/4.解析】分析】(1)方程有两个不相等的实数根,Δ>0,代入求m取值范围即可,注意二次项系数≠0;(2)将m=4代入原方程,求解即可。
详解】1) 当mx-(m+2)x+2m-3=0,即(m-2)x+2m-3=0.根据求根公式,得到Δ=(m+2)2-4m(m-2)=4m+4>0.因为m≠0,所以m>-1,解得m>-1.因为二次项系数≠0,所以m≠2,解得m≠2.所以当m>-1且m≠0时,方程有两个不相等的实数根。
2) 当m=4时,将m=4代入原方程,得到4x2-6x+1=0.根据求根公式,得到x1=(3+5)/4,x2=(3-5)/4.所以当m=4时,方程的解为x1=(3+5)/4,x2=(3-5)/4.点睛】本题考查一元二次方程根的情况以及求解,熟练掌握根的判别式以及一元二次方程求解是解决本题的关键。
3.某社区决定把一块长50m,宽30m的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,当绿化区较长边x为何值时,活动区的面积达到1344m2?答案】当x=13m时,活动区的面积达到1344m2.解析】分析】根据“活动区的面积=矩形空地面积-阴影区域面积”列出方程,可解答。
中考数学压轴题100题含答案解析

中考数学压轴题100题精选【含答案】【001】如图,已知抛物线y a(x 3 3( a z 0)经过点A2 °),抛物线的顶点为D , 过O作射线OM // AD •过顶点D平行于x轴的直线交射线OM于点C , B在x轴正半轴上,连结BC •(1)求该抛物线的解析式;(2)若动点P从点0出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为t(s) •问当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?(3)若0C °B,动点P和动点Q分别从点0和点B同时出发,分别以每秒1个长度单位和2 个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动•设它们的运动的时间为t (s),连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.【002】如图16,在Rt A ABC中,/ C=90 , AC = 3 , AB = 5 .点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t >0).(1) 当t = 2时,AP = ,点Q到AC的距离是:(2) 在点P从C向A运动的过程中,求△ APQ的面积S与t的函数关系式;(不必写出t的取值范围)(3) 在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值.若不能,请说明理由;(4) 当DE经过点C时,请直接写出t的值.【003】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B (4, 0)、C ( 8, 0)、D ( 8,8) •抛物线y=ax2+bx过A、C两点.(1) 直接写出点A的坐标,并求出抛物线的解析式;(2) 动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD 向终点D运动.速度均为每秒1个单位长度,运动时间为t秒•过点P作PE丄AB交AC于点E,①过点E作EF丄AD于点F,交抛物线于点G.当t为何值时,线段EG最长?②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△ CEQ是等腰三角形?请直接写出相应的t值。
初中数学中考压轴题(含答案)

中考数学专题复习——压轴题1.已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A (-1,0)、B (0,3)两点,其顶点为D. (1) 求该抛物线的解析式;(2) 若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积; (3) △AOB 与△BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由.(注:抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22解:(1c=3,b=2∴抛物线的线的解析式为223y x x =-++ (2)由顶点坐标公式得顶点坐标为(1,4)所以对称轴为x=1,A,E 关于x=1对称,所以E(3,0) 设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形=111()222AO BO BO DF OF EF DF ⋅++⋅+⋅ =11113(34)124222⨯⨯++⨯+⨯⨯ =9(3)相似如图,=====所以2220BD BE +=, 220DE =即: 222BD BE DE +=,所以BDE ∆是直角三角形 所以90AOB DBE ∠=∠=︒,且2AO BO BD BE ==, 所以AOBDBE ∆∆.2.如图,在平面直角坐标系中,直线y =x 轴交于点A ,与y 轴交于点C ,抛物线2(0)y ax x c a =+≠经过A B C ,,三点.(1)求过A B C ,,三点抛物线的解析式并求出顶点F 的坐标; (2)在抛物线上是否存在点P ,使ABP △为直角三角形,若存在,直接写出P 点坐标;若不存在,请说明理由;(3)试探究在直线AC 上是否存在一点M ,使得MBF △的周长最小,若存在,求出M 点的坐标;若不存在,请说明理由.解:过点F 作AC 的垂线交y 轴于点H ,则点H 为点F 关于直线AC 的对称点.连接BH 交AC 于点M ,则点M 即为所求. ······过点F 作FG y ⊥轴于点G ,则OB FG ∥,BC FH ∥.90BOC FGH ∴∠=∠=,BCO FHG ∠=∠ HFG CBO ∴∠=∠同方法一可求得(30)B ,. 在Rt BOC △中,t a n 3O B C ∠=,30OBC ∴∠=,可求得3G H G C ==, GF ∴为线段CH 的垂直平分线,可证得CFH △为等边三角形, AC ∴垂直平分FH .即点H 为点F 关于AC 的对称点.0H ⎛∴ ⎝⎭,··········设直线BH 的解析式为y kx b =+,由题意得03k b b =+⎧⎪⎨=⎪⎩解得k b ⎧=⎪⎪⎨⎪=⎪⎩ y ∴=·························y y ⎧=⎪∴⎨⎪=-⎩解得37x y ⎧=⎪⎪⎨⎪=⎪⎩37M ⎛∴- ⎝⎭, ∴在直线AC 上存在点M ,使得M B F △的周长最小,此时377M ⎛- ⎝⎭,. 13. 已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E .x(1)写出直线BC 的解析式. (2)求ABC △的面积.(3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积最大,最大面积是多少?解:(1)在2334y x =-+中,令23304x ∴-+=12x ∴=,22x =-(20)A ∴-,,(20)B , 又点B 在34y x b =-+上 302b ∴=-+32b =BC ∴的解析式为3342y x =-+ ······················· 2分 (2)由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩,得11194x y =-⎧⎪⎨=⎪⎩ 2220x y =⎧⎨=⎩ ················ 4分 914C ⎛⎫∴- ⎪⎝⎭,,(20)B ,4AB ∴=,94CD =···························· 5分 1994242ABC S ∴=⨯⨯=△ ··························· 6分(3)过点N 作NP MB ⊥于点P EO MB ⊥NP EO ∴∥BNP BEO ∴△∽△ BN NP BE EO ∴=································ 8分 由直线3342y x =-+可得:302E ⎛⎫⎪⎝⎭, ∴在BEO △中,2BO =,32EO =,则52BE = 25322t NP∴=,65NP t ∴= ······················16(4)25S t t ∴=-2312(04)55S t t t =-+<< ·····················2312(2)55S t =--+ ························此抛物线开口向下,∴当2t =时,125S =最大∴当点M 运动2秒时,MNB △的面积达到最大,最大为125.4. 已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A (-1,0)、B (0,3)两点,其顶点为D. (1)求该抛物线的解析式;(2)若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积; (3)△AOB 与△BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由.(注:抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫⎝⎛--a b ac a b 44,22)解:( 1)由已知得:310c b c =⎧⎨--+=⎩解得c=3,b=2∴抛物线的线的解析式为223y x x =-++(2)由顶点坐标公式得顶点坐标为(1,4)所以对称轴为x=1,A,E 关于x=1对称,所以E(3,0) 设对称轴与x 轴的交点为F 所以四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形 =111()222AO BO BO DF OF EF DF ⋅++⋅+⋅ =11113(34)124222⨯⨯++⨯+⨯⨯ =9(3)相似如图,====所以2220BD BE +=, 220DE =即: 222BD BE DE +=,所以BDE ∆是直角三角形所以90AOB DBE ∠=∠=︒,且AO BO BD BE ==,所以AOB DBE ∆∆.5. (2014.临夏州)如图14(1),抛物线22y x x k =-+与x 轴交于A 、B 两点,与y 轴交于点C (0,3-).[图14(2)、图14(3)为解答备用图](1)k = ,点A 的坐标为 ,点B 的坐标为 ;(2)设抛物线22y x x k =-+的顶点为M ,求四边形ABMC 的面积; (3)在x 轴下方的抛物线上是否存在一点D ,使四边形ABDC 的面积最大?若存在,请求出点D 的坐标;若不存在,请说明理由。
中考数学专题复习――压轴题(含答案)

中考数学专题复习――压轴题(含答案)中考数学专题复习――压轴题1.已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.(1)求该抛物线的解析式;(2)若该抛物线与x轴的另一个交点为E. 求四边形ABDE 的面积;(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.b4ac b2(注:抛物线y=ax+bx+c(a≠0)的顶点坐标为2a,4a )2.2. 已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8,23),C(0,2),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;(1)求∠OAB的度数,并求当点A′在线段AB上时,S关于t 的函数关系式;(2)当纸片重叠部分的图形是四边形时,求t的取值范围;(3)S存在最大值吗?若存在,求出这个最大值,并求此时t 的值;若不存在,请说明理由.3. 如图,在Rt△ABC中,A 90,AB 6,AC 8,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向运动,过点P作PQ BC于Q,过点Q作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ x,QR y.(1)求点D到BC的距离DH的长;(2)求y关于x的函数关系式(不要求写出自变量的取值范围);(3)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由.H QC4.在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN 为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.(1)用含x的代数式表示△MNP的面积S;(2)当x为何值时,⊙O与直线BC相切?(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?P 图35、如图1,已知双曲线y=BD 图2B图1k(k0)与直线y=k′x交于A,B两点,点A在第一象限.试x解答下列问题:(1)若点A的坐标为(4,2).则点B的坐标为;若点A的横坐标为m,则点B的坐标可表示为;(2)如图2,过原点O作另一条直线l,交双曲线y=k(k0)于P,Q两点,点P在第一x象限.①说明四边形APBQ一定是平行四边形;②设点A.P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出mn应满足的条件;若不可能,请说明理由.6. 如图1,在平面直角坐标系中,己知ΔAOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连结AP,并把ΔAOP绕着点A按逆时针方向旋转.使边AO与AB重合.得到ΔABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D 的坐标;(3)是否存在点P,使ΔOPD的面积等于3,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由. 47.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE 的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.(2)将原题中正方形改为矩形(如图4―6),且AB=a,BC=b,CE=ka,CG=kb (a b,k 0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.(3)在第(2)题图5中,连结DG、BE,且a=3,b=2,k= 1,求BE2 DG2的值.28.如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C作直线l.将直线l平移,平移后的直线l与x轴交于点D,与y轴交于点E.(1)将直线l向右平移,设平移距离CD为t(t 0),直角梯形OABC被直线l扫过的面积(图中阴影部份)为s,s关于t的函数图象如图2所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.①求梯形上底AB的长及直角梯形OABC的面积;②当2 t 4时,求S关于t的函数解析式;(2)在第(1)题的条件下,当直线l向左或向右平移时(包括l与直线BC重合),在直线上是否存在点P,使PDE为等腰直角三角形?若存在,请直接写出所有满..AB..足条件的点P的坐标;若不存在,请说明理由.9.如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.(1)求证:△BDE≌△BCF;(2)判断△BEF的形状,并说明理由;(3)设△B EF的面积为S,求S的取值范围.10.如图,抛物线L1:y x2 2x 3交x轴于A、B两点,交y轴于M点.抛物线L1向右平移2个单位后得到抛物线L2,L2交x 轴于C、D两点. (1)求抛物线L2对应的函数表达式;(2)抛物线L1或L2在x轴上方的部分是否存在点N,使以A,C,M,N为顶点的四边形是平行四边形.若存在,求出点N的坐标;若不存在,请说明理由;(3)若点P是抛物线L1上的一个动点(P不与点A、B重合),那么点P关于原点的对称点Q是否在抛物线L2上,请说明理由.11 20XX年5月1日,目前世界上最长的跨海大桥――杭州湾跨海大桥通车了.通车后,苏南A地到宁波港的路程比原来缩短了120千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时.(1)求A地经杭州湾跨海大桥到宁波港的路程.(2)若货物运输费用包括运输成本和时间成本,已知某车货物从A地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元?(3)A地准备开辟宁波方向的外运路线,即货物从A地经杭州湾跨海大桥到宁波港,再从宁波港运到B地.若有一批货物(不超过10车)从A地按外运路线运到B地的运费需8320元,其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?12.如图1,把一张标准纸一次又一次对开,得到“2开”纸、“4开”纸、“8开”纸、“16开”纸.已知标准纸的短边长为a....(1)如图2,把这张标准纸对开得到的“16开”张纸按如下步骤折叠:第一步将矩形的短边AB与长边AD对齐折叠,点B落在AD上的点B 处,铺平后得折痕AE;第二步将长边AD与折痕AE对齐折叠,点D正好与点E重合,铺平后得折痕AF.则AD:AB的值是,AD,AB的长分别是,.(2)“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等?若相等,直接写出这个比值;若不相等,请分别计算它们的比值.(3)如图3,由8个大小相等的小正方形构成“L”型图案,它的四个顶点E,F,G,H分别在“16开”纸的边AB,BC,CD,DA上,求DG的长.(4)已知梯形MNPQ中,MN∥PQ,∠M 90,MN MQ 2PQ,且四个顶点M,N,P,Q都在“4开”纸的边上,请直接写出2个符合条件且大小不同的直角梯形的面积.4开a2开8开开图1D FA ED GBE 图2CBF 图3C13.如图,在梯形ABCD中,AB∥CD,AB=7,CD=1,AD =BC=5.点M,N分别在边AD,BC上运动,并保持MN∥AB,ME⊥AB,NF⊥AB,垂足分别为E,F.(1)求梯形ABCD的面积;(2)求四边形MEFN面积的最大值.(3)试判断四边形MEFN能否为正方形,若能,求出正方形MEFN的面积;若不能,请说明理由.C A E F B14.如图,点A(m,m+1),B(m+3,m-1)都在反比例函数y (1)求m,k的值;(2)如果M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.友情提示:本大题第(1)小题4分,第(2)小题7分.对完成第(2)小题有困难的同学可以做下面的(3)选做题.选做题2分,所得分数计入总分.但第(2)、(3)小题都做的,第(3)小题的得分不重复计入总分.(3)选做题:在平面直角坐标系中,点P的坐标为(5,0),点Q的坐标为(0,3),把线段PQ向右平移4个单位,然后再向上平移2个单位,得到线段P1Q1,则点P1的坐标为,点Q1的坐标为.k的图象上.x15.我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图12,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.(1) 请你求出“蛋圆”抛物线部分的解析式,并写出自变量的取值范围;(2)你能求出经过点C的“蛋圆”切线的解析式吗?试试看;(3)开动脑筋想一想,相信你能求出经过点D的“蛋圆”切线的解析式.0),A(6,0),C(0,3).动点Q从点16.将一矩形纸片OABC 放在平面直角坐标系中,O(0,2秒时,动点P从点A出发以3相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的O出发以每秒1个单位长的速度沿OC向终点C运动,运动运动时间为t(秒).(1)用含t的代数式表示OP,OQ;PQ沿PQ翻折,点O恰好落在CB边上的点D处,求点D (2)当t 1时,如图1,将△O的坐标;(4)连结AC,将△OPQ沿PQ翻折,得到△EPQ,如图2.问:PQ与AC能否平行?PE与AC能否垂直?若能,求出相应的t值;若不能,说明理由.图117.如图16,在平面直角坐标系中,直线y x轴交于点A,与y轴交于点C,抛物线y ax2x c(a 0)经过A,B,C三点.3(1)求过A,B,C三点抛物线的解析式并求出顶点F的坐标;(2)在抛物线上是否存在点P,使△ABP为直角三角形,若存在,直接写出P点坐标;若不存在,请说明理由;(3)试探究在直线AC上是否存在一点M,使得△MBF的周长最小,若存在,求出M点的坐标;若不存在,请说明理由.18.(20XX年沈阳市)如图所示,在平面直角坐标系中,矩形ABOC的边BO在x轴的负半轴上,边OC在y轴的正半轴上,且AB1,OB ABOC绕点O按顺时针方向旋转60后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C 的对应点为点D,抛物线y ax2 bx c过点A,E,D.(1)判断点E 是否在y轴上,并说明理由;(2)求抛物线的函数表达式;(3)在x轴的上方是否存在点P,点Q,使以点O,B,P,Q为顶点的平行四边形的面积是矩形ABOC面积的2倍,且点P 在抛物线上,若存在,请求出点P,点Q的坐标;若不存在,请说明理由.19.(20XX年四川省巴中市) 已知:如图14,抛物线y 与直线y32x 3与x轴交于点A,点B,433x b相交于点B,点C,直线y x b与y轴交于点E.44(1)写出直线BC的解析式.(2)求△ABC的面积.(3)若点M在线段AB上以每秒1个单位长度的速度从A 向B运动(不与A,B重合),同时,点N在射线BC上以每秒2个单位长度的速度从B向C运动.设运动时间为t秒,请写出△MNB的面积S与t的函数关系式,并求出点M运动多少时间时,△MNB的面积最大,最大面积是多少?20.(20XX年成都市)如图,在平面直角坐标系xOy中,△OAB 的顶点A的坐标为(10,0),顶点B在第一象限内,且AB sin∠OAB=. 5(1)若点C是点B关于x轴的对称点,求经过O、C、A三点的抛物线的函数表达式;(2)在(1)中,抛物线上是否存在一点P,使以P、O、C、A为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由;(3)若将点O、点A分别变换为点Q(-2k ,0)、点R(5k,0)(k1的常数),设过Q、R两点,且以QR的垂直平分线为对称轴的抛物线与y轴的交点为N,其顶点为M,记△QNM的面积为S QMN,△QNR的面积S QNR,求S QMN∶S QNR的值.21.(20XX年乐山市)在平面直角坐标系中△ABC的边AB在x 轴上,且OAOB,以AB为直径的圆过点C若C的坐标为(0,2),AB=5,A,B两点的横坐标XA,XB是关于X的方程x2 (m 2)x n 1 0的两根:(1) 求m,n的值(2) 若∠ACB的平分线所在的直线l交x轴于点D,试求直线l对应的一次函数的解析式(3) 过点D任作一直线l分别交射线CA,CB(点C除外)于点M,N,则是否为定值,若是,求出定值,若不是,请说明理由`11 的值CMCNL`22.(20XX年四川省宜宾市)已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D. (1)求该抛物线的解析式;(2)若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积;(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.b4ac b2(注:抛物线y=ax+bx+c(a≠0)的顶点坐标为2a,4a )223.(天津市20XX年)已知抛物线y 3ax2 2bx c,(Ⅰ)若a b 1,c 1,求该抛物线与x轴公共点的坐标;(Ⅱ)若a b 1,且当1 x 1时,抛物线与x轴有且只有一个公共点,求c的取值范围;x2 1时,(Ⅲ)若a b c 0,且x1 0时,对应的y1 0;对应的y2 0,试判断当0 x 1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.24.(20XX年大庆市)如图①,四边形AEFG和ABCD都是正方形,它们的边长分别为a,b(b≥2a),且点F在AD上(以下问题的结果均可用a,b的代数式表示).(1)求S△DBF;(2)把正方形AEFG绕点A按逆时针方向旋转45°得图②,求图②中的S△DBF;(3)把正方形AEFG绕点A旋转一周,在旋转的过程中,S△DBF是否存在最大值、最小值?如果存在,直接写出最大值、最小值;如果不存在,请说明理由. .GAF①GAB② ECDC25. (20XX年上海市)已知AB 2,AD 4,DAB 90,AD∥BC (如图13).E是射线BC上的动点(点E与点B不重合),M是线段DE的中点.(1)设BE x,△ABM的面积为y,求y关于x的函数解析式,并写出函数的定义域;(2)如果以线段AB为直径的圆与以线段DE为直径的圆外切,求线段BE的长;(3)联结BD,交线段AM于点N,如果以A,N,D为顶点的三角形与△BME相似,求线段BE的长.AC B B E C备用图图1326. (20XX年陕西省)某县社会主义新农村建设办公室,为了解决该县甲、乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站.由供水站直接铺设A管道到另外两处.如图,甲,乙两村坐落在夹角为30的两条公路的AB段和CD段(村子和公路的宽均不计),点M表示这所中学.点B在点M的北偏西30的3km处,点A在点M的正西方向,点D在点M的南偏西60的处.为使供水站铺设到另两处的管道长度之和最短,现有如下三种方案:方案一:供水站建在点M处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;方案二:供水站建在乙村(线段CD某处),甲村要求管道建设到A处,请你在图①中,画出铺设到点A和点M处的管道长度之和最小的线路图,并求其最小值;方案三:供水站建在甲村(线段AB某处),请你在图②中,画出铺设到乙村某处和点M处的管道长度之和最小的线路图,并求其最小值.综上,你认为把供水站建在何处,所需铺设的管道最短?27. (20XX年山东省青岛市)已知:如图①,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题:(1)当t为何值时,PQ∥BC?(2)设△AQP的面积为y(cm),求y与t之间的函数关系式;(3)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;(4)如图②,连接PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时刻t,使四边形PQP′C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.2图①P28. (20XX年江苏省南通市)已知双曲线yk1与直线y x相交于A、B两点.第一象限x4k上的点M(m,n)(在A点左侧)是双曲线y 上的动点.过点B作BD∥y轴于点D.过Nxk(0,-n)作NC∥x轴交双曲线y 于点E,交BD于点C.x(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA =pMP,MB=qMQ,求p-q的值.29. (20XX年江苏省无锡市)一种电讯信号转发装置的发射直径为31km.现要求:在一边长为30km的正方形城区选择若干个安装点,每个点安装一个这种转发装置,使这些装置转发的信号能完全覆盖这个城市.问:(1)能否找到这样的4个安装点,使得这些点安装了这种转发装置后能达到预设的要求?(2)至少需要选择多少个安装点,才能使这些点安装了这种转发装置后达到预设的要求?答题要求:请你在解答时,画出必要的示意图,并用必要的计算、推理和文字来说明你的理由.(下面给出了几个边长为30km的正方形城区示意图,供解题时选用)图1 图2 图3 图4压轴题答案c 31. 解:(1)由已知得:解得1 b c 0c=3,b=2∴抛物线的线的解析式为y x 2x 3 (2)由顶点坐标公式得顶点坐标为(1,4)所以对称轴为x=1,A,E关于x=1对称,所以设对称轴与x轴的交点为F所以四边形ABDE的面积=S ABO S梯形BOFD S2111AO BO (BO DF) OF EF DF*****= 1 3 (3 4) 1 2 4 222==9(3)相似如图,222所以BD BE 20, DE 20即:BD BE DE,所以BDE是直角三角形222所以AOB DBE 90 ,且所以AOBAOBO,BDBE2DBE.2. (1) ∵A,B两点的坐标分别是A(10,0)和B(8,23),∴tan OAB233,10 8∴ OAB 60当点A在线段AB上时,∵ OAB 60 ,TA=TA,∴△ATA是等边三角形,且TP TA ,∴TP (10 t)sin60113(10 t),A P AP AT (10 t),222∴S S A TP1 A P TP (10 t)2,282 当A与B重合时,AT=AB= 4,sin60所以此时6 t 10.(2)当点A在线段AB的延长线,且点P在线段AB(不与B重合)上时,纸片重叠部分的图形是四边形(如图(1),其中E是TA 与CB的交点),当点P与B重合时,AT=2AB=8,点T的坐标是(2,又由(1)中求得当A与B重合时,T的坐标是(6,0) 所以当纸片重叠部分的图形是四边形时,2 t 6.(3)S存在最大值1当6 t 10时,S ○(10 t)2,8在对称轴t=10的左边,S的值随着t的增大而减小,∴当t=6时,S的值最大是23.2当2 t 6时,由图○1,重叠部分的面积S S○ A TP S A EB ∵△AEB的高是A Bsin60 ,∴S31(10 t)2 (10 t 4)2 822( t2 4t 28) (t 2)2 43 88当t=2时,S的值最大是4;3当0 t 2,即当点A和点P都在线段AB的延长线是(如图○2,其中E是TA与○CB的交点,F是TP与CB的交点),∵ EFT FTP ETF,四边形ETAB是等腰形,∴EF=ET=AB=4,∴S11EF OC 4 23 43 22综上所述,S的最大值是4,此时t的值是0 t 2. 3. 解:(1)A Rt ,AB 6,AC 8,BC 10.1点D为AB中点,BD AB 3.DHB A 90,B B.△BHD∽△BAC,*****12 AC 8 .,DH *****05(2)QR∥AB,QRC A 90.C C,△RQC∽△ABC,RQQCy10 x,,*****3x 6.5即y关于x的函数关系式为:y (3)存在,分三种情况:①当PQ PR时,过点P作PM QR于M,则QM RM.1 2 90,C 2 90,1 C.H QC84QM4cos 1 cosC ,,105QP51 3x 6 425 ,x 18.*****②当PQ RQ时,HQCQ312x 6 ,55x 6.③当PR QR时,则R为PQ中垂线上的点,于是点R为EC 的中点,11CR CE AC 2.24QRBAtanC ,CRCA3x 6156 ,x .2281815综上所述,当x为或6或时,△PQR为等腰三角形.524. 解:(1)∵MN∥BC,∴∠AMN=∠B,∠ANM=∠C.∴ △AMN ∽ △ABC.图1xAN∴ AM AN,即.43ABAC3∴ AN=x.……………2分4∴ S=S MNP S AMN133x x x2.(0<x<4)……………3分2481MN.2(2)如图2,设直线BC与⊙O相切于点D,连结AO,OD,则AO =OD =在Rt△ABC中,BC.由(1)知△AMN ∽ △ABC.BQD 图2xMN∴ AM MN,即.45ABBCx,45∴ OD x.…………………5分8∴ MN过M点作MQ⊥BC 于Q,则MQ OD5x.8在Rt△BMQ与Rt△BCA中,∠B是公共角,∴ △BMQ∽△BCA.∴ BM QM.BCAC55 x25x,AB BM MA 25x x 4.∴ BM*****96.4996∴ 当x=时,⊙O与直线BC相切. (7)分49(3)随点M的运动,当P点落在直线BC上时,连结AP,则O点为AP的中点.∵ MN∥BC,∴ ∠AMN=∠B,∠AOM=∠APC∴ △AMO ∽ △ABP.∴ x=∴ AM AO 1.AM=MB=2.ABAP2故以下分两种情况讨论:3① 当0<x≤2时,y SΔPMN x2.8∴ 当x=2时,y最大3232 . ……………………………………8分82P② 当2<x<4时,设PM,PN分别交BC于E,F.∵ 四边形AMPN是矩形,∴ PN∥AM,PN=AM=x.又∵ MN∥BC,∴ 四边形MBFN是平行四边形.∴ FN=BM=4-x.∴ PF x 4 x 2x 4.又△PEF ∽ △ACB.图4PF S PEF∴ .AB S ABC∴ S PEF232x 2 .……………………………………………… 9分23392y S MNP S PEF=x2 x 2 x2 6x 6.……………………10分8282929 8当2<x<4时,y x 6x 6 x 2.88 38时,满足2<x<4,y最大2.……………………11分38综上所述,当x 时,y值最大,最大值是2.…………………………12分3k5. 解:(1)(-4,-2);(-m,-)m∴ 当x(2) ①由于双曲线是关于原点成中心对称的,所以OP=OQ,OA=OB,所以四边形APBQ。
2020年中考数学压轴题专题讲解:四边形综合题(含答案)

备战2020年中考数学压轴题专题讲解:四边形综合题1.如图,四边形ABCD是菱形,120BAD∠=︒,点E在射线AC上(不包括点A和点)C,过点E的直线GH交直线AD于点G,交直线BC于点H,且//GH DC,点F在BC的延长线上,CF AG=,连接ED,EF,DF.(1)如图1,当点E在线段AC上时,①判断AEG∆的形状,并说明理由.②求证:DEF∆是等边三角形.(2)如图2,当点E在AC的延长线上时,DEF∆是等边三角形吗?如果是,请证明你的结论;如果不是,请说明理由.2.(1)如图1,在四边形ABCD中,AB AD=,180B D∠+∠=︒,E,F分别是边BC,CD上的点,且12EAF BAD∠=∠,则BE,EF,DF之间的数量关系是EF BE DF=+.(2)如图2,若E,F分别是边BC,CD延长线上的点,其他条件不变,则BE,EF,DF 之间的数量关系是什么?请说明理由.(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30︒的A处,舰艇乙在指挥中心南偏东70︒的B处,并且两舰艇到指挥中心的距离相等,接到行动命令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50︒的方向以80海里/小时的速度前进,1.5小时后,指挥中心观察到舰艇甲、乙分别到达E,F处,且两舰艇与指挥中心O 连线的夹角70EOF∠=︒,试求此时两舰艇之间的距离.3.将一个等边三角形纸片AOB 放置在平面直角坐标系中,点(0,0)O ,点(6,0)B .点C 、D 分别在OB 、AB 边上,//DC OA ,23CB =.()I 如图①,将DCB ∆沿射线CB 方向平移,得到△D C B '''.当点C 平移到OB 的中点时,求点D '的坐标;()II 如图②,若边D C ''与AB 的交点为M ,边D B ''与ABB ∠'的角平分线交于点N ,当BB '多大时,四边形MBND '为菱形?并说明理由.()III 若将DCB ∆绕点B 顺时针旋转,得到△D C B '',连接AD ',边D C ''的中点为P ,连接AP ,当AP 最大时,求点P 的坐标及AD '的值.(直接写出结果即可).4.如图(1),在ABC ∆中,AB AC =,90BAC ∠=︒,AD BC ⊥于点D ,20BC cm =,10AD cm =.点P 从点B 出发,在线段BC 上以每秒2cm 的速度向点C 匀速运动,与此同时,垂直于AD 的直线t 从点A 沿AD 出发,以每秒1cm 的速度沿AD 方向匀速平移,分别交AB 、AC 、AD 于M 、N 、E .当点P 到达点C 时,点P 与直线l 同时停止运动,设运动时间为t 秒(0)t >.(1)在运动过程中(点P 不与B 、C 重合),连接PN ,求证:四边形MBPN 为平行四边形;(2)如图(2),以MN 为边向下作正方形MFGN ,FG 交AD 于点H ,连结PF 、PG ,当1003t <<时,求PFG ∆的面积最大值; (3)在整个运动过程中,观察图(2)、(3),是否存在某一时刻t ,使PFG ∆为等腰三角形?若存在,直接写出t 的值;若不存在,请说明理由.5.如图①,在矩形ABCD 中,动点P 从点A 出发,以1/cm s 的速度沿AD 向终点D 移动,设移动时间为()t s ,连接PC ,以PC 为一边作正方形PCEF ,连接DE 、DF ,设PCD ∆的面积为2()y cm ,y 与t 之间的函数关系如图②所示. (1)AB = cm ,AD = cm ;(2)当t 为何值时,DEF ∆的面积最小?请求出这个最小值; (3)当t 为何值时,DEF ∆为等腰三角形?请简要说明理由.6.如图,在平行四边形ABCD 中,AC BC ⊥,10AB =.6AC =.动点P 在线段BC 上从点B 出发沿BC 方向以每秒1个单位长的速度匀速运动;动点Q 在线段DC 上从点D 出发沿DC 的力向以每秒1个单位长的速度匀速运动,过点P 作PE BC ⊥.交线段AB 于点E .若P 、Q 两点同时出发,当其中一点到达终点时整个运动随之停止,设运动时间为t 秒.(1)当t 为何值时,//QE BC ?(2)设PQE ∆的面积为S ,求出S 与t 的函数关系式:(3)是否存在某一时刻t ,使得PQE ∆的面积S 最大?若存在,求出此时t 的值; 若不存在,请说明理由.(4)是否存在某一时刻t ,使得点Q 在线段EP 的垂直平分线上?若存在,求出此时t 的值;若不存在,请说明理由.7.如图一,在射线DE的一侧以AD为一条边作矩形ABCD,53AD=,5CD=,点M是线段AC上一动点(不与点A重合),连结BM,过点M作BM的垂线交射线DE于点N,连接BN.(1)求CAD∠的大小;(2)问题探究:动点M在运动的过程中,①是否能使AMN∆为等腰三角形,如果能,求出线段MC的长度;如果不能,请说明理由.②MBN∠的大小是否改变?若不改变,请求出MBN∠的大小;若改变,请说明理由.(3)问题解决:如图二,当动点M运动到AC的中点时,AM与BN的交点为F,MN的中点为H,求线段FH的长度.8.如图,点E,F分别在正方形ABCD的边CD,BC上,且DE CF=,点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转90︒得到线段EG,过点E作GD的垂线QH,垂足为点H,交射线BC于点Q.(1)如图1,若点E是CD的中点,点P在线段BF上,线段BP,QC,EC的数量关系为+=.BP QC EC(2)如图2,若点E不是CD的中点,点P在线段BF上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.(3)正方形ABCD的边长为6,3QC=,请直接写出线段BP的长.=,1AB DE9.小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.(1)温故:如图1,在ABC ∆中,AD BC ⊥于点D ,正方形PQMN 的边QM 在BC 上,顶点P ,N 分别在AB ,AC 上,若BC a =,AD h =,求正方形PQMN 的边长(用a ,h 表示).(2)操作:如何画出这个正方形PQMN 呢?如图2,小波画出了图1的ABC ∆,然后按数学家波利亚在《怎样解题》中的方法进行操作:先在AB 上任取一点P ',画正方形P Q M N '''',使点Q ',M '在BC 边上,点N '在ABC ∆内,然后连结BN ',并延长交AC 于点N ,画NM BC ⊥于点M ,NP NM ⊥交AB 于点P ,PQ BC ⊥于点Q ,得到四边形PQMN .(3)推理:证明图2中的四边形PQMN 是正方形.(4)拓展:小波把图2中的线段BN 称为“波利亚线”,在该线上截取NE NM =,连结EQ ,EM (如图3),当90QEM ∠=︒时,求“波利亚线” BN 的长(用a ,h 表示).请帮助小波解决“温故”、“推理”、“拓展”中的问题.10.性质探究如图①,在等腰三角形ABC 中,120ACB ∠=︒,则底边AB 与腰AC 的长度之比为 3 .理解运用(1)若顶角为120︒的等腰三角形的周长为843+,则它的面积为;(2)如图②,在四边形EFGH中,EF EG EH==.①求证:EFG EHG FGH∠+∠=∠;②在边FG,GH上分别取中点M,N,连接MN.若120EF=,直接写出FGH∠=︒,10线段MN的长.类比拓展顶角为2α的等腰三角形的底边与一腰的长度之比为(用含α的式子表示).11.如图1,在矩形ABCD中,3BC=,动点P从B出发,以每秒1个单位的速度,沿射线t s.BC方向移动,作PAB∆关于直线PA的对称PAB∆',设点P的运动时间为()(1)若23AB=.①如图2,当点B'落在AC上时,显然PAB∆'是直角三角形,求此时t的值;②是否存在异于图2的时刻,使得PCB∆'是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由.(2)当P点不与C点重合时,若直线PB'与直线CD相交于点M,且当3t<时存在某一时刻有结论45PAMt>的任意时刻,结论“45∠=︒”是否总是PAM∠=︒成立,试探究:对于3成立?请说明理由.12.如图,在以点O为中心的正方形ABCD中,4AD=,连接AC,动点E从点O出发沿∆的外→以每秒1个单位长度的速度匀速运动,到达点C停止.在运动过程中,ADEO C接圆交AB于点F,连接DF交AC于点G,连接EF,将EFG∆.∆沿EF翻折,得到EFH (1)求证:DEF∆是等腰直角三角形;(2)当点H 恰好落在线段BC 上时,求EH 的长;(3)设点E 运动的时间为t 秒,EFG ∆的面积为S ,求S 关于时间t 的关系式.13.操作体验:如图,在矩形ABCD 中,点E 、F 分别在边AD 、BC 上,将矩形ABCD 沿直线EF 折叠,使点D 恰好与点B 重合,点C 落在点C '处.点P 为直线EF 上一动点(不与E 、F 重合),过点P 分别作直线BE 、BF 的垂线,垂足分别为点M 和N ,以PM 、PN为邻边构造平行四边形PMQN . (1)如图1,求证:BE BF =;(2)特例感知:如图2,若5DE =,2CF =,当点P 在线段EF 上运动时,求平行四边形PMQN 的周长;(3)类比探究:若DE a =,CF b =.①如图3,当点P 在线段EF 的延长线上运动时,试用含a 、b 的式子表示QM 与QN 之间的数量关系,并证明;②如图4,当点P 在线段FE 的延长线上运动时,请直接用含a 、b 的式子表示QM 与QN 之间的数量关系.(不要求写证明过程)14.在矩形ABCD 中,连结AC ,点E 从点B 出发,以每秒1个单位的速度沿着B A C →→的路径运动,运动时间为t (秒).过点E 作EF BC ⊥于点F ,在矩形ABCD 的内部作正方形EFGH .(1)如图,当8AB BC ==时,①若点H 在ABC ∆的内部,连结AH 、CH ,求证:AH CH =;②当08t <时,设正方形EFGH 与ABC ∆的重叠部分面积为S ,求S 与t 的函数关系式;(2)当6AB=,8BC=时,若直线AH将矩形ABCD的面积分成1:3两部分,求t的值.15.如图,在平面直角坐标系xOy中,矩形ABCD的边4AB=,6BC=.若不改变矩形ABCD 的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y 轴的正半轴上随之上下移动.(1)当30OAD∠=︒时,求点C的坐标;(2)设AD的中点为M,连接OM、MC,当四边形OMCD的面积为212时,求OA的长;(3)当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值,并求此时cos OAD∠的值.参考答案1、【解答】(1)①解:AEG ∆是等边三角形;理由如下: 四边形ABCD 是菱形,120BAD ∠=︒,//AD BC ∴,AB BC CD AD ===,//AB CD ,1602CAD BAD ∠=∠=︒, 180BAD ADC ∴∠+∠=︒, 60ADC ∴∠=︒, //GH DC ,60AGE ADC ∴∠=∠=︒, 60AGE EAG AEG ∴∠=∠=∠=︒, AEG ∴∆是等边三角形;②证明:AEG ∆是等边三角形, AG AE ∴=, CF AG =, AE CF ∴=,四边形ABCD 是菱形, 120BCD BAD ∴∠=∠=︒, 60DCF CAD ∴∠=︒=∠,在AED ∆和CFD ∆中,AD CD EAD FCD AE CF =⎧⎪∠=∠⎨⎪=⎩,()AED CFD SAS ∴∆≅∆DE DF ∴=,ADE CDF ∠=∠,60ADC ADE CDE ∠=∠+∠=︒, 60CDF CDE ∴∠+∠=︒,即60EDF ∠=︒, DEF ∴∆是等边三角形;(2)解:DEF ∆是等边三角形;理由如下: 同(1)①得:AEG ∆是等边三角形, AG AE ∴=,CF AG =, AE CF ∴=,四边形ABCD 是菱形, 120BCD BAD ∴∠=∠=︒,1602CAD BAD ∠=∠=︒, 60FCD CAD ∴∠=︒=∠,在AED ∆和CFD ∆中,AD CD EAD FCD AE CF =⎧⎪∠=∠⎨⎪=⎩,()AED CFD SAS ∴∆≅∆, DE DF ∴=,ADE CDF ∠=∠,60ADC ADE CDE ∠=∠-∠=︒, 60CDF CDE ∴∠-∠=︒,即60EDF ∠=︒, DEF ∴∆是等边三角形.2、【解答】解:(1)延长FD 到点G ,使DG BE =,连结AG ,如图1所示: 在ABE ∆和ADG ∆中,90BE DG B ADG AB AD =⎧⎪∠=∠=︒⎨⎪=⎩,()ABE ADG SAS ∴∆≅∆, AE AG ∴=,BAE DAG ∠=∠,12EAF BAD ∠=∠, GAF DAG DAF BAE DAF BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=∠,在AEF ∆和GAF ∆中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,()AEF AGF SAS ∴∆≅∆, EF FG ∴=,FG DG DF BE DF =+=+, EF BE DF ∴=+,故答案为:EF BE DF =+;(2)BE ,EF ,DF 之间的数量关系是:EF BE DF =-;理由如下: 在CB 上截取BM DF =,连接AM ,如图2所示:180B D ∠+∠=︒,180ADC ADF ∠+∠=︒,B ADF ∴∠=∠,在ABM ∆和ADF ∆中,AB ADB ADF BM DF=⎧⎪∠=∠⎨⎪=⎩,()ABM ADF SAS ∴∆≅∆,AF AM ∴=,DAF BAM ∠=∠,BAD MAF ∴∠=∠,2BAD EAF ∠=∠,2MAF EAF ∴∠=∠,MAE EAF ∴∠=∠,在FAE ∆和MAE ∆中,AE AEFAE MAE AF AM=⎧⎪∠=∠⎨⎪=⎩,()FAE MAE SAS ∴∆≅∆,EF EM BE BM BE DF ∴==-=-,即EF BE DF =-;(3)连接EF ,延长AE 、BF 相交于点C ,如图3所示:3090(9070)140AOB ∠=︒+︒+︒-︒=︒,70EOF ∠=︒,12EOF AOB ∴∠=∠,OA OB =,(9030)(7050)180OAC OBC ∠+∠=︒-︒+︒+︒=︒,∴符合(1)中的条件,即结论EF AE BF =+成立,1.5(6080)210EF ∴=⨯+=(海里).答:此时两舰艇之间的距离是210海里.3、【解答】解:(Ⅰ)如图①中,作DH BC ⊥于H .AOB ∆是等边三角形,//DC OA ,60DCB AOB ∴∠=∠=︒,60CDB A ∠=∠=︒,CDB ∴∆是等边三角形, 23CB =DH CB ⊥,3CH HB ∴==3DH =,(63D ∴,3),3C B '=,233CC ∴'=-,233DD CC ∴'='=-,(33D ∴'+3).(Ⅱ)当3BB '=时,四边形MBND '是菱形.理由:如图②中,ABC ∆是等边三角形,60ABO ∴∠=︒,180120ABB ABO '∴∠=︒-∠=︒, BN 是ACC '∠的角平分线, 1602NBB ABB D C B ''∴∠'=∠=︒=∠'',//D C BN ''∴,//AB B D ''∴四边形MBND '是平行四边形,60ME C MCE '''∠=∠=︒,60NCC NC C ''∠=∠=︒,∴△MC B ''和NBB '∆是等边三角形,MC CE '∴=,NC CC '=,23B C ''=,四边形MBND '是菱形,BN BM ∴=,132BB B C '''∴==;(Ⅲ)如图连接BP ,在ABP ∆中,由三角形三边关系得,AP AB BP <+,∴当点A ,B ,P 三点共线时,AP 最大,如图③中,在△D BC ''中,由P 为D C ''的中点,得AP D C ''⊥,3PD '=,3CP ∴=,639AP ∴=+=,在Rt APD '∆中,由勾股定理得,AD '==此时15(2P ,.4、【解答】(1)证明:l AD ⊥,BC AD ⊥,//l BC ∴, ∴AM ANAB AC =,AB AC =,AM AN ∴=,90BAC ∠=︒,ME NE ∴=,22MN AE t ∴==,2BP t =,MN BP ∴=,∴四边形MBPN 为平行四边形;(2)解:四边形MFGN 是正方形,22FG MN MF AE t ∴====,2EH MF t ==,103DH AD AH t ∴=-=-,2115252(103)3()2233PFG S FG DH t t t ∆∴==⨯⨯-=--+,30a =-<,1003t <<,∴当53t =时,PFG S ∆最大253=;(3)解:存在,当t =5t =或10t =时,PFG ∆为等腰三角形;理由如下:利用勾股定理得:222(103)PF t =-,222(103)(10)PG t t =-+-,又22(2)FG t =, 当PF FG =时,则222(103)(2)t t -=,解得:t =,当PF PG =时,2222(103)(103)(10)t t t -=-+-,解得:5t =,或0t =(舍去);当FG PG =时,222(2)(103)(10)t t t =-+-,解得:10t =,或103t =(舍去);综上所述,t =5t =或10t =时,PFG ∆为等腰三角形.5、【解答】解:(1)由图②知:5AD =,当0t =时,P 与A 重合,152y AD CD =⨯⨯=,1552CD ⨯⨯=,2CD cm =,四边形ABCD 是矩形,2AB CD cm ∴==,故答案为:2,5;(2)由题意得:AP t =,5PD t =-,112(5)522y CD PD t t ∴==-=-,四边形EFPC 是正方形,12DEF PDC EFPC S S S ∆∆∴+=正方形,222PC PD CD =+,22222(5)1029PC t t t ∴=+-=-+,222111913(1029)(5)4(4)22222DEF S t t t t t t ∆∴=-+--=-+=-+,当t 为4时,DEF ∆的面积最小,且最小值为32;(3)当DEF ∆为等腰三角形时,分四种情况:①当FD FE =时,如下图所示,过F 作FG AD ⊥于G ,四边形EFPC 是正方形,PF EF PC ∴==,90FPC ∠=︒,PF FD ∴=,FG PD ⊥, 12PG DG PD ∴==, 90FPG CPD CPD DCP ∠+∠=∠+∠=︒,FPG DCP ∴∠=∠,90FGP PDC ∠=∠=︒,()FPG PDC AAS ∴∆≅∆,2PG DC ∴==,4PD ∴=,541AP ∴=-=,即1t =;②当DE DF =时,如下图所示,E 在AD 的延长线上,此时正方形EFPC 是正方形,2PD CD ==,523AP t ∴==-=;③当DE EF =时,如下图所示,过E 作EG CD ⊥于G ,FE DE EC ==,112CG DG CD ∴===, 同理得:()PDC CGE AAS ∆≅∆,1PD CG ∴==,514AP t ∴==-=,④当DF EF =时,如下所示,2PC EF PF ===,且PC BC ⊥,此时P 与D 重合,5t =, 综上,当1t s =或3s 或4s 或5s 时,DEF ∆为等腰三角形.6、【解答】解:(1)如图1,记EQ 与AC 的交点为G ,AC BC ⊥,90ACB ∴∠=︒,在Rt ABC ∆中,10AB =,6AC =,根据勾股定理得,8BC =,3tan 4AC B BC ==, 四边形ABCD 是平行四边形,10CD AB ∴==,8AD BC ==,由运动知,BP t =,DQ t =,8PC t ∴=-,10CQ t =-,PE BC ⊥,90BPE ∴∠=︒,在Rt BPE ∆中,3sin 5B =,4cos 5B =,3tan 4PE PE B BP t ===, 34PE t ∴=, //EQ BC ,90PEQ BPE ∴∠=∠=︒,∴四边形CPEG 是矩形,34CG PE t ∴==, //EQ BC ,CGQ CAD ∴∆∆∽, ∴CG CQ AC CD=, ∴3104610t t -=. 409t ∴=;(2)如图2,过点Q 作QH BC ⊥交BC 的延长线于H ,四边形ABCD 是平行四边形,//AB CD ∴,DCH B ∴∠=∠,在Rt CHQ ∆中,3sin 105QH QH QCH CQ t ∠===-, 3(10)5QH t ∴=-,4cos 105CH CH HCQ CQ t ∠===-, 4(10)5CH t ∴=-, 498(10)1655PH PC CH t t t ∴=+=-+-=-, ()()2133919327404010161610()25452554093QPH QHPE S S S t t t t t t ∆⎡⎤⎛⎫⎛⎫∴=-=-+⨯--⨯-⨯-=--+ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭梯形,点E 在线段AB 上,∴点P 在线段BC 上,08t ∴<,点Q 在CD 上,010t ∴<<,08t ∴<, 即:2274040()(08)4093S t t =--+<;(3)由(2)知,2274040()(08)4093S t t =--+<;409t ∴=时,403S =最大;(4)如图3,过点Q 作QM PE ⊥于M ,交AC 于N , 点Q 在线段EP 的垂直平分线上,1328PM PE t ∴==,同(2)的方法得,3(10)5CN t =-,易知,四边形PCNM 是矩形,PM CN ∴=,∴33(10)85t t =-,8013t ∴=.7、【解答】解:(1)如图一(1)中,四边形ABCD 是矩形,90ADC ∴∠=︒,53tan 353DC DAC AD ∠===,30DAC ∴∠=︒.(2)①如图一(1)中,当AN NM =时,90BAN BMN ∠=∠=︒,BN BN =,AN NM =, Rt BNA Rt BNM(HL)∴∆≅∆,BA BM ∴=,在Rt ABC ∆中,30ACB DAC ∠=∠=︒,5AB CD ==, 210AC AB ∴==,60BAM ∠=︒,BA BM =,ABM ∴∆是等边三角形,5AM AB ∴==,5CM AC AM ∴=-=.如图一(2)中,当AN AM =时,易证15AMN ANM ∠=∠=︒,90BMN ∠=︒,75CMB ∴∠=︒,30MCB ∠=︒,180753075CBM ∴∠=︒-︒-︒=︒,CMB CBM ∴∠=∠,3CM CB ∴==,综上所述,满足条件的CM 的值为5或53②结论:30MBN ∠=︒大小不变.理由:如图一(1)中,180BAN BMN ∠+∠=︒,A ∴,B ,M ,N 四点共圆,30MBN MAN ∴∠=∠=︒.如图一(2)中,90BMN BAN ∠=∠=︒,A ∴,N ,B ,M 四点共圆,180MBN MAN ∴∠+∠=︒,180DAC MAN ∠+∠=︒,30MBN DAC ∴∠=∠=︒,综上所述,30MBN ∠=︒.(3)如图二中,AM MC =,BM AM CM ∴==,2AC AB ∴=,AB BM AM ∴==,ABM ∴∆是等边三角形,60BAM BMA ∴∠=∠=︒,90BAN BMN ∠=∠=︒,30NAM NMA ∴∠=∠=︒,NA NM ∴=,BA BM =,BN ∴垂直平分线段AM ,52FM ∴=,53cos303FM NM ∴==︒,90NFM ∠=︒,NH HM =,12FH MN ∴==8、【解答】解:(1)BP QC EC +=;理由如下: 四边形ABCD 是正方形,BC CD ∴=,90BCD ∠=︒,由旋转的性质得:90PEG ∠=︒,EG EP =,90PEQ GEH ∴∠+∠=︒,QH GD ⊥,90H ∴∠=︒,90G GEH ∠+∠=︒,PEQ G ∴∠=∠,又90EPQ PEC ∠+∠=︒,90PEC GED ∠+∠=︒, EPQ GED ∴∠=∠,在PEQ ∆和EGD ∆中,EPQ GEDEP EG PEQ G∠=∠⎧⎪=⎨⎪∠=∠⎩,()PEQ EGD ASA ∴∆≅∆,PQ ED ∴=,BP QC BC PQ CD ED EC ∴+=-=-=,即BP QC EC +=;故答案为:BP QC EC +=;(2)(1)中的结论仍然成立,理由如下:由题意得:90PEG ∠=︒,EG EP =,90PEQ GEH ∴∠+∠=︒,QH GD ⊥,90H ∴∠=︒,90G GEH ∠+∠=︒,PEQ G ∴∠=∠,四边形ABCD 是正方形,90DCB ∴∠=︒,BC DC =,90EPQ PEC ∴∠+∠=︒,90PEC GED ∠+∠=︒,GED EPQ ∴∠=∠,在PEQ ∆和EGD ∆中,EPQ GEDEP EG PEQ G∠=∠⎧⎪=⎨⎪∠=∠⎩,()PEQ EGD ASA ∴∆≅∆,PQ ED ∴=,BP QC BC PQ CD ED EC ∴+=-=-=,即BP QC EC +=;(3)分两种情况:①当点P 在线段BC 上时,点Q 在线段BC 上,由(2)可知:BP EC QC =-,36AB DE ==,2DE ∴=,4EC =,413BP ∴=-=;②当点P 在线段BC 上时,点Q 在线段BC 的延长线上,如图3所示:同(2)可得:()PEQ EGD AAS ∆≅∆,2PQ DE ∴==,1QC =,1PC PQ QC ∴=-=,615BP BC PC ∴=-=-=;综上所述,线段BP 的长为3或5.9、【解答】(1)解:如图1中,//PN BC,APN ABC∴∆∆∽,∴PN AEBC AD=,即PN h PNa h-=,解得ah PNa h=+(2)能画出这样的正方形,如图2中,正方形PNMQ即为所求.(3)证明:如图2中,由画图可知:90QMN PQM NPQ BM N∠=∠=∠=∠''=︒,∴四边形PNMQ是矩形,//MN M N'',∴△BN M BNM''∆∽,∴M N BN MN BN'''=,同理可得:P N BN PN BN '''=∴M N P N MN PN''''=,M N P N''='',MN PN∴=,∴四边形PQMN是正方形(4)如图,过点N作ND ME⊥于点D图3MN EN =,ND ME ⊥,NEM MNE ∴∠=∠,ED DM =90BMN QEM ∠=∠=︒90EQM EMQ ∴∠+∠=︒,90EMQ EMN ∠+∠=︒EMN EQM ∴∠=∠,且MN QN =,90QEM NDM ∠=∠=︒()QEM MDN AAS ∴∆≅∆12EQ DM EM ∴==,90BMN QEM ∠=∠=︒90BEQ NEM ∴∠+∠=︒,90BME NME ∠+∠=︒BEQ BME ∴∠=∠,且MBE MBE ∠=∠BEQ BME ∴∆∆∽ ∴12BQ BE EQ BE BM EM ===,2BM BE ∴=,2BE BQ =4BM BQ ∴=3QM BQ MN ∴==,5BN BQ = ∴3355MN BQ BN BQ ==55()33ahBN MN a h ∴==+10、【解答】性质探究解:作CD AB ⊥于D ,如图①所示:则90ADC BDC ∠=∠=︒,AC BC =,120ACB ∠=︒,AD BD ∴=,30A B ∠=∠=︒,2AC CD ∴=,AD =,2AB AD ∴==,∴AB AC =;理解运用(1)解:如图①所示:同上得:2AC CD =,AD =,8AC BC AB ++=+,48CD ∴+=+解得:2CD =,AB ∴=,ABC ∴∆的面积11222AB CD =⨯=⨯=故答案为:(2)①证明:EF EG EH ==,EFG EGF ∴∠=∠,EGH EHG ∠=∠,EFG EHG EGF EGH FGH ∴∠+∠=∠+∠=∠; ②解:连接FH ,作EP FH ⊥于P ,如图②所示: 则PF PH =,由①得:120EFG EHG FGH ∠+∠=∠=︒,360120120120FEH ∴∠=︒-︒-︒=︒,EF EH =,30EFH ∴∠=︒,152PE EF ∴==,PF ∴==,2FH PF ∴==,点M 、N 分别是FG 、GH 的中点,MN ∴是FGH ∆的中位线, 1532MN FH ∴==;类比拓展解:如图③所示:作AD BC ⊥于D ,AB AC =,BD CD ∴=,12BAD BAC α∠=∠=,sin BDAB α=,sin BD AB α∴=⨯,22sin BC BD AB α∴==⨯,∴2sin 2sin BC AB AB AB αα==;故答案为:2sin α.11、【解答】解:(1)①如图1中,四边形ABCD 是矩形,90ABC ∴∠=︒,2221AC AB BC ∴=+=PCB ACB ∠'=∠,90PB C ABC ∠'=∠=︒, PCB ACB ∴∆'∆∽,∴CB PB CB AB ''=,∴2123323PB -'=,274PB ∴'=-.274t PB ∴==-. ②如图21-中,当PCB ∠’ 90=︒时,四边形ABCD 是矩形,90D ∴∠=︒,23AB CD ==,3AD BC ==,22(23)33DB ∴'=-=,3CB CD DB ∴'=-'=,在Rt PCB ∆'中,222B P PC B C '=+',222(3)(3)t t ∴=+-,2t ∴=.如图22-中,当PCB ∠’ 90=︒时,在Rt ADB ∆'中,223DB AB AD '='-=, 33CB ∴'=在Rt PCB ∆’中则有:222(33)(3)t t +-=,解得6t =. 如图23-中,当CPB ∠’ 90=︒时,易证四边形ABP ’为正方形,易知23t =.综上所述,满足条件的t 的值为2s 或6s 或23s .(2)如图31-中,45PAM ∠=︒2345∴∠+∠=︒,1445∠+∠=︒又翻折,12∴∠=∠,34∠=∠,又ADM AB ∠=∠’ M ,AM AM =, ()AMD AMB AAS ∴∆≅∆',AD AB ∴=’ AB =,即四边形ABCD 是正方形,如图,设APB x ∠=.90PAB x ∴∠=︒-,DAP x ∴∠=,易证MDA ∆≅△B ’ ()AM HL , BAM DAM ∴∠=∠,翻折,PAB PAB ∴∠=∠’ 90x =︒-, DAB ∴∠’ PAB =∠’ 902DAP x -∠=︒-, 12DAM DAB ∴∠=∠’ 45x =︒-,45MAP DAM PAD ∴∠=∠+∠=︒.12、【解答】(1)证明:四边形ABCD 是正方形, 45DAC CAB ∴∠=∠=︒,FDE CAB ∴∠=∠,DFE DAC ∠=∠, 45FDE DFE ∴∠=∠=︒, 90DEF ∴∠=︒,DEF ∴∆是等腰直角三角形;(2)设OE t =,连接OD , 90DOE DAF ∴∠=∠=︒, OED DFA ∠=∠,DOE DAF ∴∆∆∽,∴22OEODAF AD ==,∴2AF t =,又AEF ADG ∠=∠,EAF DAG ∠=∠,AEF ADG ∴∆∆∽, ∴AE AFAD AG =, ∴42AG AE AD AF t ==,又AE OA OE t =+=+,∴AG =,EG AE AG ∴=-=当点H 恰好落在线段BC 上454590DFH DFE HFE ∠=∠+∠=︒+︒=︒, ADF BFH ∴∆∆∽,∴FH FB FD AD ==, //AF CD ,∴FG AF DG CD ==∴FG DF =∴=,解得:1t =-,2t =(舍去),EG EH ∴====-;(3)过点F 作FK AC ⊥于点K ,由(2)得EG =,DE EF =,90DEF ∠=︒,DEO EFK ∴∠=∠,()DOE EKF AAS ∴∆≅∆,FK OE t ∴==, 31242EFG t S EG FK ∆+∴==13、【解答】(1)证明:如图1中,四边形ABCD 是矩形,//AD BC ∴,DEF EFB ∴∠=∠,由翻折可知:DEF BEF ∠=∠,BEF EFB ∴∠=∠,BE BF ∴=.(2)解:如图2中,连接BP ,作EH BC ⊥于H ,则四边形ABHE 是矩形,EH AB =.5DE EB BF ===,2CF =,7AD BC ∴==,2AE =,在Rt ABE ∆中,90A ∠=︒,5BE =,2AE =,225221AB ∴=-=,BEF PBE PBF S S S ∆∆∆=+,PM BE ⊥,PN BF ⊥, ∴111222BF EH BE PM BF PN =+, BE BF =,21PM PN EH ∴+==,四边形PMQN 是平行四边形,∴四边形PMQN 的周长2()221PM PN =+=(3)①证明:如图3中,连接BP ,作EH BC ⊥于H .ED EB BF a ===,CF b =,AD BC a b ∴==+,AE AD DE b ∴=-=, 22EH AB a b ∴==-,EBP BFP EBF S S S ∆∆∆-=,∴111222BE PM BF PN BF EH -=, BE BF =,22PM PN EH a b ∴-==-,四边形PMQN 是平行四边形,22()QN QM PM PN a b ∴-=-=-.②如图4,当点P 在线段FE 的延长线上运动时,同法可证:22QM QN PN PM a b -=-=-.14、【解答】解:(1)①如图1中,四边形EFGH 是正方形,AB BC =,BE BG ∴=,AE CG =,90BEH BGH ∠=∠=︒,90AEH CGH ∴∠=∠=︒,EH HG =,()AEH CGH SAS ∴∆≅∆,AH CH ∴=.②如图1中,当04t <时,重叠部分是正方形EFGH ,2S t =.如图2中,当48t <时,重叠部分是五边形EFGMN ,2211882(8)163222ABC AEN CGM S S S S t t t ∆∆∆=--=⨯⨯-⨯-=-+-.综上所述,22(04)1632(48)t t S t t t ⎧<=⎨-+-<⎩. (2)如图31-中,设直线AH 交BC 于M ,当4BM CM ==时,直线AH 将矩形ABCD 的面积分成1:3两部分.//EH BM ,∴AE EH AB BM =, ∴664t t -=, 125t ∴=. 如图32-中,设直线长AH 交CD 于M 交BC 的延长线于K ,当3CM DM ==时,直线AH 将矩形ABCD 的面积分成1:3两部分,易证8AD CK ==,//EH BK ,∴AE EH AB BK=,∴6616t t -=, 4811t ∴=. 如图33-中,当点E 在线段AC 上时,设直线AH 交CD 于M ,交BC 的延长线于N .当CM DM =时,直线AH 将矩形ABCD 的面积分成1:3两部分,易证8AD CN ==.在Rt ABC ∆中,226810AC =+=,//EF AB ,∴CE EFCA AB =,∴16106tEF-=,3(16)5EF t ∴=-,//EH CN ,∴EH AECN AC =,∴3(16)65810t t --=,解得727t =.当正方形EFGH 在AC 的左边时,由EH AE CN AC =,可得3(16)65410t t --=,解得12t =.综上所述,满足条件的t 的值为125或4811或727或12.15、【解答】解:(1)如图1,过点C 作CE y ⊥轴于点E ,矩形ABCD 中,CD AD ⊥,90CDE ADO ∴∠+∠=︒,又90OAD ADO ∠+∠=︒,30CDE OAD ∴∠=∠=︒,∴在Rt CED ∆中,122CE CD ==,2223DE CD CE =-=在Rt OAD ∆中,30OAD ∠=︒,132OD AD ∴==,∴点C 的坐标为(2,33)+(2)M 为AD 的中点,3DM ∴=,6DCM S ∆=, 又212OMCD S =四边形,92ODM S ∆∴=,9OAD S ∆∴=,设OA x =、OD y =,则2236x y +=,192xy =,222x y xy ∴+=,即x y =,将x y =代入2236x y +=得218x =, 解得32x =(负值舍去),32OA ∴=(3)OC 的最大值为8,如图2,M 为AD 的中点,3OM ∴=,225CM CD DM =+=,8OC OM CM ∴+=,当O 、M 、C 三点在同一直线时,OC 有最大值8,连接OC ,则此时OC 与AD 的交点为M ,过点O 作ON AD ⊥,垂足为N , 90CDM ONM ∠=∠=︒,CMD OMN ∠=∠,CMD OMN ∴∆∆∽, ∴CDDMCMON MN OM ==,即4353ON MN ==, 解得95MN =,125ON =,65AN AM MN ∴=-=,在Rt OAN ∆中,22655OA ON AN =+=,5cos 5ANOAD OA ∴∠==.。
2022届中考数学压轴题押题及答案解析

2022年中考数学压轴题1.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、C(3,0),点B为抛物线顶点,直线BD为抛物线的对称轴,点D在x轴上,连接AB、BC.(1)如图1,若∠ABC=60°,则点B的坐标为B(1,2√3);(2)如图2,若∠ABC=90°,AB与y轴交于点E,连接CE.①求这条抛物线的解析式;②点P为第一象限抛物线上一个动点,设△PEC的面积为S,点P的横坐标为m,求S关于m的函数关系式,并求出S的最大值;③如图3,连接OB,抛物线上是否存在点Q,使直线QC与直线BC所夹锐角等于∠OBD,若存在请直接写出点Q的坐标;若不存在,说明理由.解:(1)∵A(﹣1,O)、C(3,0),∴AC=4∵直线BD为抛物线的对称轴,∴AB=CB,BD⊥AC,AD=CD=2∴D(1,0),∵∠ABC=60°,∴△ABC是等边三角形∴∠ABC=60°,=60°∴tan∠ABC=BDAD,即BD=AD•tan∠ABC=2tan60°=2√3,∴B(1,2√3);故答案为:B(1,2√3);(2)①∵A(﹣1,0),C(3,0)∴AC=4∵直线BD为对称轴∴AD=CD=12AC=2,AB=BC∴D(1,0)∵∠ABC=90°∴△ABC为等腰直角三角形∴B(1,2)设抛物线解析式为y=a(x﹣1)2+2,图象过A(﹣1,0),则0=a(﹣1﹣1)2+2,解得a=−1 2,∴y=−12(x﹣1)2+2,即y=−12x2+x+32;②如图2,过点P作PF⊥y轴于点F,则P(m,−12m2+m+32)∵AB=BC,∠ABC=90°∴∠BAC=45°在Rt△AOE中,∠AOE=90°,∴∠AEO=∠EAO=45°∴AO=EO=1∴E(0,1)∴S=S四边形FPCO﹣S△PEF﹣S△CEO=12(m+3)(−12m2+m+32)−12m(−12m2+m+32−1)−12×1×3 =−34m2+2m+34=−34(m−43)2+2512∵−34<0,∴当m=43时,S最大值=2512,∴S关于m的函数关系式为S=−34m2+2m+34,S的最大值为2512;③抛物线上存在点Q,使直线QC与直线BC所夹锐角等于∠OBD,如图3,在Rt△ABC中,∠ABC=90°,AB=BC,AC=4∴△ABC是等腰直角三角形,AB=BC=2√2∵E(0,1)∴BE =AE =12BC ,即tan ∠BCE =BE BC =12∵tan ∠OBD =OD BD =12∴tan ∠BCE =tan ∠OBD ,即∠BCE =∠OBD 易求得直线CE 解析式为y =−13x +1, 联立方程组{y =−13x +1y =−12x 2+x +32, 解得{x 1=3y 1=0,{x 2=−13y 2=109;∴Q 1(−13,109)在直线AB 上截取BG =12BC ,∴tan ∠BCG =BG BC =12=tan ∠OBD ∴∠BCG =∠OBD ,过点G 作GL ⊥y 轴于L ,则△OAE ∽△LGE ∴GL OA=EL OE=EG AE=21∴GL =2OA =2,EL =2OE =2,OL =OE +EL =1+2=3 ∴G (2,3)∴直线CG 解析式为y =﹣3x +9,解方程组{y =−3x +9y =−12x 2+x +32得{x 1=3y 1=0,{x 2=5y 2=−6 ∴Q 2(5,﹣6),综上所述,点Q 的坐标为:Q 1(−13,109),Q 2(5,﹣6).2.如图,在平面直角坐标系中,抛物线y=12x2+bx+c交x轴正半轴于点A、点B,交y轴于点C,直线y=﹣x+6经过点B、点C;(1)求抛物线的解析式;(2)点D在x轴下方的抛物线上,连接DB、DC,点D的横坐标为t,△BCD的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围;(3)在(2)的条件下,点E在x轴上方的抛物线上,过点E作EF⊥x轴,垂足为点F,连接DE,将射线ED沿直线EF折叠,得到对应射线EG,直线DF交射线EG于点H,当S=12,EF=√5FH时,求点E的坐标.解:(1)在y=﹣x+6中,令x=0,得y=6,∴C(0,6),令y=0,得x=6,∴B(6,0)将B(6,0),C(0,6)代入y=12x2+bx+c中,得{12×62+6b+c=0c=6,解得{b=−4c=6∴抛物线的解析式为:y=12x2−4x+6;(2)如图1,过点D作DL⊥BC于L,作DK∥y轴交BC于K,则∠DLK=∠BOC=90°,∵DK∥y轴∴∠DKL=∠BCO∴∠DKL∽∠BCO∴DLDK =OBBC∴DL •BC =DK •OB∵D (t ,12t 2−4t +6),K (t ,﹣t +6)∴DK =﹣t +6﹣(12t 2−4t +6)=−12t 2+3t∴S =12DL •BC =12DK •OB =12×(−12t 2+3t )×6=−32t 2+9t ,在y =12x 2−4x +6中,令y =0,得12x 2−4x +6=0,解得:x 1=2,x 2=6,∵点D 在x 轴下方的抛物线上,∴2<t <6, ∴S =−32t 2+9t (2<t <6);(3)当S =12时,−32t 2+9t =12,解得:t 1=2,t 2=4,∵2<t <6,∴t =4,∴D (4,﹣2)如图2,点E 在x 轴上方对称轴左侧时,过D 作DG ∥x 轴交射线EG 于G ,交EF 于R ,设E (m ,12m 2−4m +6),m <2,则F (m ,0),G (2m ﹣4,﹣2)∴直线DE 解析式为y =12(m ﹣4)x +6﹣2m ,直线GE 解析式为y =12(4﹣m )x +m 2﹣6m +6 直线DH 解析式为y =2m−4x −2mm−4 ∵12(4﹣m )×2m−4=−1∴GE ⊥DH∴∠EHG =∠ERD =90° ∵∠REG =∠RED ∴△EFH ∽△EDR ∴DR ER=FH EH,∵EF =√5FH ,∴EH =2FH∴ER =2DR ,即12m 2−4m +6+2=2(4﹣m ),解得:m 1=0,m 2=4(舍去) ∴E 1(0,6);如图3,点E 在x 轴上方对称轴右侧时,过D 作DG ∥x 轴交射线EG 于G ,交EF 于R ,设E (m ,12m 2−4m +6),m >6,与上述方法相同可得:ER =2DR ,即12m 2−4m +6+2=2(m ﹣4),解得:m 1=4(舍去),m2=8,∴E2(8,6);综上所述,点E的坐标为:E1(0,6),E2(8,6).3.已知,在平面直角坐标系中,抛物线y=−12x2+2x﹣1与直线y=﹣x﹣1相交于A,B两点,点C为顶点,连接AC.(1)如图1,连接BC,点P为线段AB上一动点,过点P作PE⊥x轴于点E,PF⊥BC 于点F,过点P作PQ∥x轴交抛物线于点Q(点Q在点P左侧),当PE•PF取得最大值时,在y轴上取一点R,连接QR,求PQ+2QR+√2RO的最小值;(2)如图2,将抛物线沿射线AC方向平移,记平移后的抛物线为y′,顶点为K,当AC=CK时,点N为平移后的抛物线y′上一点,其横坐标为8.点M为线段AB上一点,连接CM,且CM=BM,将△ACM绕点B顺时针旋转α度(0<α<180),旋转后的三角形为△A′C′M′,记直线A′C′与直线AB相交于点S,直线C′M′与直线AB相交于点T,连接NS,NT.是否存在点S和点T,使△C′ST为等腰三角形,若存在,请直接写出△NST的面积;若不存在,请说明理由.解:(1)由抛物线y =−12x 2+2x ﹣1=−12(x ﹣2)2+1得:C (2,1),解方程组{y =−12x 2+2x −1y =−x −1,得:{x 1=0y 1=−1,{x 2=6y 2=−7;∴A (0,﹣1),B (6,﹣7),过C 作CS ⊥y 轴于S ,过B 作BK ⊥y 轴于K ,则∠ASC =∠AKB =90° ∵CS =2,AS =1﹣(﹣1)=2,BK =6,AK =﹣1﹣(﹣7)=6 ∴AS =CS ,AK =BK∴△ACS 和△ABK 均为等腰直角三角形, ∴∠CAS =∠BAK =45°,AC =2√2,AB =6√2 ∴∠BAC =90°,BC =√AC 2+AB 2=4√5设P (m ,﹣m ﹣1),0≤m ≤6,则PE =﹣(﹣m ﹣1)=m +1,PB =√2(6﹣m ), ∵PF ⊥BC∴∠BFP =∠BAC =90° △BPF ∽△BCA ∴PF BP=AC BC=√24√5,∴PF =√55(6﹣m ) ∴PE •PF =(m +1)×√55(6﹣m )=−√55(m −52)2+49√520,∵−√55<0,∴当m =52时,PE •PF 取得最大值,此时,P (52,−72),∵PQ ∥x 轴∴Q (﹣1,−72),在x 正半轴上截取OG =OR ,连接RG ,过O 作OT ⊥RG 于T ,则RT =√22RO ,∵PQ +2QR +√2RO =PQ +2(QR +√22RO )求PQ +2QR +√2RO 的最小值,即求QR +√22RO 的最小值,当Q ,R ,T 三点共线时,QR +√22RO 的值最小;∵∠ORG =45° ∴∠PQR =∠QRK =45° ∴QR =√2,RO =52, ∴PQ +2QR +√2RO 的最小值=52−(﹣1)+2(√2+√22×52)=7+9√22; (2)∵AC =CK ,∴K (4,3)∴平移后的抛物线为y ′=−12(x ﹣4)2+3, ∴N (8,﹣5)过点N 作NZ ⊥AB 于Z ,作NN ′∥x 轴交AB 于N ′,则∠NN ′Z =45°,N ′(4,﹣5) ∴NN ′=8﹣4=4,NZ =√22×4=2√2∵点M 为线段AB 上一点,且CM =BM ,设M (t ,﹣t ﹣1) ∴(t ﹣2)2+(﹣t ﹣1﹣1)2=(t ﹣6)2+(﹣t ﹣1+7)2,解得:t =83∴M (83,−113)∴CM =BM =10√23,AM =AB ﹣BM =8√23∴AC :AM :CN =3:4:5,△C ′ST 为等腰三角形,可以分三种情形:①C ′T =ST ,如图2,作TL ⊥SC ′于L ,则∠TSC ′=∠C ′=∠ACM ,SL =LC ′=12SC ′, ∴sin ∠TSC ′=sin ∠ACM =45,∵BA ′=BA =6√2, ∴BS =BA′sin∠TSC′=6√245=15√22,∴S (−32,12),∵A′BA′S=tan ∠TSC ′=tan ∠ACM =43,∴A ′S =34A ′B =9√22,SC ′=A ′S +A ′C ′=13√22,SL =13√24, ∴ST =53SL =65√212∴S △NST =12ST •NZ =12×65√212×2√2=656, ②C ′S =C ′T ,如图3,作C ′H ⊥AB 于H ,作TL ⊥SC ′于L ,作NZ ⊥AB 于Z , 由①知AC :AM :CN =3:4:5,即:A ′C ′:A ′M ′:C ′M ′=3:4:5, ∵TL ∥A ′M ′,∴C ′L :LT :C ′T =3:4:5,设C ′L =3k ,LT =4k ,C ′T =5k ∴C ′S =C ′T =5k ,LS =2k ,ST =√LS 2+LT 2=2√5k ,A ′S =5k ﹣2√2, ∵LT ∥A ′B∴A ′S :A ′B =SL :LT =1:2,即:2A ′S =A ′B ,2(5k ﹣2√2)=6√2,解得:k =√2 ∴ST =2√5×√2=2√10 ∴S △NST =12ST •NZ =12×2√10×2√2=4√5; ③C ′S =ST ,如图4,作SB ⊥C ′T 于B ′,作TL ⊥SC ′于L ,作NZ ⊥AB 于Z , 则C ′B ′=B ′T ,∠STC ′=∠C ′=∠ACM ∴SB′SC′=LT C′T =sin ∠ACM =45,设SB ′=4t ,SC ′=5t ,则C ′B =B ′T =3t ,ST =5t∴C ′L =35C ′T =185t ,SL =SC ′﹣C ′L =75t ,LT =245t , ∵LT ∥BA ′ ∴SA′A′B=SL LT=724,24SA ′=7A ′B∴24(5t ﹣2√2)=7×6√2,解得:t =3√24 ∴ST =15√24 ∴S △NST =12ST •NZ =12×15√24×2√2=152, 综上所述,△C ′ST 为等腰三角形时,△NST 的面积为:656或4√5或152.4.如图,在Rt △ABC 中,∠ACB =90°,D 为AB 边上的一点,以AD 为直径的⊙O 交BC 于点E ,交AC 于点F ,过点C 作CG ⊥AB 交AB 于点G ,交AE 于点H ,过点E 的弦EP 交AB 于点Q (EP 不是直径),点Q 为弦EP 的中点,连结BP ,BP 恰好为⊙O 的切线.(1)求证:BC 是⊙O 的切线.(2)求证:EF̂=ED ̂. (3)若sin ∠ABC ═35,AC =15,求四边形CHQE 的面积.(1)证明:连接OE ,OP ,∵AD 为直径,点Q 为弦EP 的中点,∴PE ⊥AB ,点Q 为弦EP 的中点,∴AB 垂直平分EP ,∴PB =BE ,∵OE =OP ,OB =OB ,∴△BEO ≌△BPO (SSS ),∴∠BEO=∠BPO,∵BP为⊙O的切线,∴∠BPO=90°,∴∠BEO=90°,∴OE⊥BC,∴BC是⊙O的切线.(2)证明:∵∠BEO=∠ACB=90°,∴AC∥OE,∴∠CAE=∠OEA,∵OA=OE,∴∠EAO=∠AEO,∴∠CAE=∠EAO,̂=ED̂.∴EF(3)解:∵AD为的⊙O直径,点Q为弦EP的中点,∴EP⊥AB,∵CG⊥AB,∴CG∥EP,∵∠ACB=∠BEO=90°,∴AC∥OE,∴∠CAE=∠AEO,∵OA=OE,∴∠EAQ=∠AEO,∴∠CAE=∠EAO,∵∠ACE=∠AQE=90°,AE=AE,∴△ACE≌△AQE(AAS),∴CE=QE,∵∠AEC+∠CAE=∠EAQ+∠AHG=90°,∴∠CEH=∠AHG,∵∠AHG=∠CHE,∴∠CHE=∠CEH,∴CH =CE ,∴CH =EQ ,∴四边形CHQE 是平行四边形,∵CH =CE ,∴四边形CHQE 是菱形,∵sin ∠ABC ═sin ∠ACG ═AG AC =35, ∵AC =15,∴AG =9,∴CG =√AC 2−AG 2=12,∵△ACE ≌△AQE ,∴AQ =AC =15,∴QG =6,∵HQ 2=HG 2+QG 2,∴HQ 2=(12﹣HQ )2+62,解得:HQ =152,∴CH =HQ =152,∴四边形CHQE 的面积=CH •GQ =152×6=45.5.如图,△ABC 中,AB =AC ,⊙O 是△ABC 的外接圆,BO 的延长线交边AC 于点D .(1)求证:∠BAC =2∠ABD ;(2)当△BCD 是等腰三角形时,求∠BCD 的大小;(3)当AD =2,CD =3时,求边BC 的长.(1)证明:连接OA.∵AB=AC,̂=AĈ,∴AB∴OA⊥BC,∴∠BAO=∠CAO,∵OA=OB,∴∠ABD=∠BAO,∴∠BAC=2∠ABD.(2)解:如图2中,延长AO交BC于H.①若BD=CB,则∠C=∠BDC=∠ABD+∠BAC=3∠ABD,∵AB=AC,∴∠ABC=∠C,∴∠DBC=2∠ABD,∵∠DBC +∠C +∠BDC =180°,∴8∠ABD =180°,∴∠C =3∠ABD =67.5°.②若CD =CB ,则∠CBD =∠CDB =3∠ABD , ∴∠C =4∠ABD ,∵∠DBC +∠C +∠CDB =180°,∴10∠ABD =180°,∴∠BCD =4∠ABD =72°.③若DB =DC ,则D 与A 重合,这种情形不存在. 综上所述,∠C 的值为67.5°或72°.(3)如图3中,作AE ∥BC 交BD 的延长线于E .则AE BC =AD DC =23, ∴AO OH =AE BH =43,设OB =OA =4a ,OH =3a , ∵BH 2=AB 2﹣AH 2=OB 2﹣OH 2,∴25﹣49a 2=16a 2﹣9a 2,∴a 2=2556,∴BH =5√24, ∴BC =2BH =5√22.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、中考数学压轴题1.已知AM //CN ,点B 为平面内一点,AB ⊥BC 于B .(1)如图1,直接写出∠A 和∠C 之间的数量关系;(2)如图2,过点B 作BD ⊥AM 于点D ,求证:∠ABD =∠C ;(3)如图3,在(2)问的条件下,点E 、F 在DM 上,连接BE 、BF 、CF ,BF 平分∠DBC ,BE 平分∠ABD ,若∠FCB +∠NCF =180°,∠BFC =5∠DBE ,求∠EBC 的度数.2.如图所示,在平面直角坐标系中,点(),C m m 在一三象限角平分线上,点(),0B n 在x 轴上,且m=2n -+2n -+4,点A 在y 轴的正半轴上;四边形AOBC 的面积为6 (1)求点A 的坐标;(2)P 为AB 延长线上一点,//PQ OC ,交CB 延长线于Q ,探究OAP ∠、ABQ ∠、Q ∠的数量关系并说明理由;(3)作AD 平行CB 交CO 延长线于D ,BE 平分CBx ∠,BE 反向延长线交CO 延长线于,若设ADO α∠=,F β∠=,试求2αβ+的值.3.已知:如图,在平面直角坐标系中,点O 为坐标原点,()2,0C .直线26y x =+与x 轴交于点A ,交y 轴于点B .过C 点作直线AB 的垂线,垂足为E ,交y 轴于点D . (1)求直线CD 的解析式;(2)点G 为y 轴负半轴上一点,连接EG ,过点E 作EH EG ⊥交x 轴于点H .设点G 的坐标为()0,t ,线段AH 的长为d .求d 与t 之间的函数关系式(不要求写出自变量的取值范围)(3)过点C 作x 轴的垂线,过点G 作y 轴的垂线,两线交于点M ,过点H 作HN GM⊥于点N ,交直线CD 于点K ,连接MK ,若MK 平分NMB ∠,求t 的值.4.如图1,已知,⊙O 是△ABC 的外接圆,AB=AC=10,BC=12,连接AO 并延长交BC 于点H .(1)求外接圆⊙O 的半径;(2)如图2,点D 是AH 上(不与点A ,H 重合)的动点,以CD ,CB 为边,作平行四边形CDEB ,DE 分别交⊙O 于点N ,交AB 边于点M .①连接BN ,当BN ⊥DE 时,求AM 的值;②如图3,延长ED 交AC 于点F ,求证:NM ·NF=AM ·MB ;③设AM=x ,要使2ND -22DM <0成立,求x 的取值范围.5.综合与实践4A 纸是我们学习工作最常用的纸张之一, 其长宽之比是2:1,我们定义:长宽之比是2:1的矩形纸片称为“标准纸”.操作判断:()1如图1所示,矩形纸片2()ABCD AD AB =是一张“标准纸”,将纸片折叠一次,使点B 与D 重合,再展开,折痕EF 交AD 边于点,E 交BC 边于点F ,若1,AB =求CF 的长,()2如图2,在()1的基础上,连接,BD 折痕EF 交BD 于点O ,连接,BE 判断四边形BFDE 的形状,并说明理由.探究发现:()3如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点A 与点C 重合,再展开,痕MN 交AD 边于点M ,BC 交边于点,N 交BD 也是点O .然后将四边形ENFM 剪下,探究纸片ENFM 是否为“标准纸”,说明理由.6.对于平面直角坐标系xOy 中的任意点()P x y ,,如果满足x y a += (x ≥0,a 为常数),那么我们称这样的点叫做“特征点”.(1)当2≤a ≤3时,①在点(1,2),(1,3),(2.5,0)A B C 中,满足此条件的特征点为__________________;②⊙W 的圆心为(,0)W m ,半径为1,如果⊙W 上始终存在满足条件的特征点,请画出示意图,并直接写出m 的取值范围;(2)已知函数()10Z x x x=+>,请利用特征点求出该函数的最小值.7.问题背景:如图,四边形ABCD 中,AD BC ∥,8BC =,17AD =+,32AB =,45ABC ∠=︒,P 为边AD 上一动点,连接BP 、CP .问题探究(1)如图1,若30PBC ∠=︒,则AP 的长为__________.(2)如图2,请求出BPC △周长的最小值;(3)如图3,过点P 作PE BC ⊥于点E ,过点E 分别作EM PB ⊥于M ,EN PC ⊥于点N ,连接MN①是否存在点P ,使得PMN 的面积最大?若存在,求出PMN 面积的最大值,若不存在,请说明理由;②请直接写出PMN 面积的最小值.8.平面直角坐标系中,点A 、B 分别在x 轴正半轴、y 轴正半轴上,AO =BO ,△ABO 的面积为8.(1)求点A 的坐标;(2)点C 、D 分别在x 轴负半轴、y 轴正半轴上(D 在B 点上方),AB ⊥CD 于E ,设点D 纵坐标为t ,△BCE 的面积为S ,求S 与t 的函数关系;(3)在(2)的条件下,点F 为BE 中点,连接OF 交BC 于G ,当∠FOB +∠DAE =45°时,求点E 坐标.9.如图,在ABC 中,90ABC ∠=︒,AB BC <,O 为AC 中点,点D 在BO 延长线上,CD BC =,AE BC ∥,CE CA =,AE 交BD 于点G .(1)若28DCE ∠=︒,求AOB ∠的度数;(2)求证:AG GE =;(3)设DC 交GE 于点M .①若3AB =,4BC =,求::AG GM ME 的值;②连结DE ,分别记ABG ,DGM ,DME 的面积为1S ,2S ,3S ,当AC DE 时,123::S S S = .(直接写出答案)10.附加题:在平面直角坐标系中,抛物线21y ax a =-与y 轴交于点A ,点A 关于x 轴的对称点为点B ,(1)求抛物线的对称轴;(2)求点B 坐标(用含a 的式子表示);(3)已知点11,P a ⎛⎫ ⎪⎝⎭,(3,0)Q ,若抛物线与线段PQ 恰有一个公共点,结合函数图像,求a 的取值范围.11.如图,一张半径为3cm 的圆形纸片,点O 为圆心,将该圆形纸片沿直线l 折叠,直线l 交O 于AB 、两点.(1)若折叠后的圆弧恰好经过点O ,利用直尺和圆规在图中作出满足条件的一条直线l (不写作法,保留作图痕迹),并求此时线段AB 的长度.(2)已知M 是O 一点,1cm OM =.①若折叠后的圆弧经过点M ,则线段AB 长度的取值范围是________.②若折叠后的圆弧与直线OM 相切于点M ,则线段AB 的长度为_________cm .12.如图1,在O 中,弦AB ⊥弦CD ,垂足为点E ,连接AD 、BC 、AO ,AD AB =.(1)求证:2CAO CDB ∠=∠(2)如图2,过点O 作OH AD ⊥,垂足为点H ,求证:2OH CE DE +=(3)如图3,在(2)的条件下,延长DB 、AC 交于点F ,过点D 作DM AC ⊥,垂足为M ,交AB 于N ,若12BC =,3AF BF =,求MN 的长.13.如图,抛物线2(40) y ax bx a =++≠与x 轴交于()() 3,0, 4,0A C -两点,与y 轴交于点B .()1求这条抛物线的顶点坐标;()2已知AD AB =(点D 在线段AC 上),有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动:同时另一个点Q 以某一速度从点B 沿线段BC 移动,经过()t s 的移动,线段PQ 被BD 垂直平分,求t 的值;()3在()2的情况下,抛物线的对称轴上是否存在一点M ,使MQ MC +的值最小?若存在,请求出点M 的坐标:若不存在,请说明理由.14.如图①,在△ABC 中,∠ACB =90°,∠B =30°,AC =1,D 为AB 的中点,EF 为△ACD 的中位线,四边形EFGH 为△ACD 的内接矩形(矩形的四个顶点均在△ACD 的边上). (1)计算矩形EFGH 的面积;(2)将矩形EFGH 沿AB 向右平移,F 落在BC 上时停止移动.在平移过程中,当矩形与△CBD 重叠部分的面积为316时,求矩形平移的距离; (3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形1111E F G H ,将矩形1111E F G H 绕1G 点按顺时针方向旋转,当1H 落在CD 上时停止转动,旋转后的矩形记为矩形2212E F G H ,设旋转角为α,求cos α的值.15.已知:AB 为⊙O 的直径,点C 为弧AB 的中点,点D 为⊙O 上一点,连接CD ,交AB 于点M ,AE 为∠DAM 的平分线,交CD 于点E .(1)如图1,连接BE ,若∠ACD=22°,求∠MBE 的度数;(2) 如图2,连接DO 并延长,交⊙O 于点F ,连接AF ,交CD 于点N .①求证:DM 2+CN 2=CM 2;②如图3,当AD=1,AB=10时,请直接写出....线段ME 的长. 16.我们知道,在等腰直角三角形中,底边与一边腰长比为2:1.如图1,90A ∠=︒,AB AC =,则2BC AB=.知识应用:(1)如图2,ADE ∆和ABC ∆均为等腰直角三角形,90DAE BAC ∠=∠=︒,D ,E ,C 三点共线,若2AD =,2BD =,求CD 的长. 知识外延:(2)如图3,正方形ABCD 中,BE 和BC 关于BG 对称,C 点的对应点为E 点,AE 交BG 的延长线于F 点,连接CF .①求证:GF EC =;②若2AE =,2CE =,求BF 的长.17.如图,平面直角坐标系中,抛物线228y ax ax a =--与x 轴交于B 、C 两点(点B 在点C 右侧),与y 轴交于点A ,连接AB ,25AB =.(1)求抛物线的解析式;(2)点P 在第二象限的抛物线上,连接PB 交y 轴于D ,取PB 的中点E ,过点E 作EH x ⊥轴于点H ,连接DH ,设点P 的横坐标为t .ODH 的面积为S ,求S 与t 的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,作PF y ⊥轴于F ,连接CP 、CD ,CP CD =,点S 为PF 上一点,连接BS 交y 轴于点T ,连接BF 并延长交抛物线于点R .SBC FBO 45∠+∠=︒,在射线CS 上取点Q.连接QF ,QF RF =,求直线TQ 的解析式.18.如图,已知ABF 为等腰直角三角形,90BAF ∠=︒,D 、C 为直线AF 上两点,且满足DF AC =,连接BD 、BC ,过点A 作AE BD ⊥于点E ,交BF 于点H ,连接CH .(1)若30BAE ∠=︒,1BE =,求DE 的长;(2)若点M 是线段BF 上的动点,连AM 并延长交BD 于N ,当M 在线段BF 的什么位置上时,AH BN =?请说明理由;(3)在(2)的结论下,判断线段CH 、AH 、BD 的数量关系.请说明理由.19.阅读材料:等腰三角形具有性质“等边对等角”.事实上,不等边三角形也具有类似性质“大边对大角”:如图1.在△ABC 中,如果AB >AC ,那么∠ACB >∠ABC .证明如下:将AB 沿△ABC 的角平分线AD 翻折(如图2),因为AB >AC ,所以点B 落在AC 的延长线上的点B '处.于是,由∠ACB >∠B ',∠ABC =∠B ',可得∠ACB >∠ABC .(1)灵活运用:从上面的证法可以看出,折纸常常能为证明一个命题提供思路和方法.由此小明想到可用类似方法证明“大角对大边”:如图3.在△ABC 中,如果∠ACB >∠ABC ,那么AB >AC .小明的思路是:沿BC 的垂直平分线翻折……请你帮助小明完成后面的证明过程.(2)拓展延伸:请运用上述方法或结论解决如下问题:如图4,已知M 为正方形ABCD 的边CD 上一点(不含端点),连接AM 并延长,交BC 的延长线于点N .求证:AM +AN >2BD .20.如图1,Rt △ABC 中,点D ,E 分别为直角边AC ,BC 上的点,若满足AD 2+BE 2=DE 2,则称DE 为R △ABC 的“完美分割线”.显然,当DE 为△ABC 的中位线时,DE 是△ABC 的一条完美分割线.(1)如图1,AB =10,cos A =45,AD =3,若DE 为完美分割线,则BE 的长是 . (2)如图2,对AC 边上的点D ,在Rt △ABC 中的斜边AB 上取点P ,使得DP =DA ,过点P 画PE ⊥PD 交BC 于点E ,连结DE ,求证:DE 是直角△ABC 的完美分割线.(3)如图3,在Rt △ABC 中,AC =10,BC =5,DE 是其完美分割线,点P 是斜边AB 的中点,连结PD 、PE ,求cos ∠PDE 的值.21.在平面直角坐标系xOy 中,点A 、B 为反比例函数()4x 0x y =>的图像上两点,A 点的横坐标与B 点的纵坐标均为1,将()4x 0x y =>的图像绕原点O 顺时针旋转90°,A 点的对应点为A’,B 点的对应点为B’.(1)点A’的坐标是 ,点B’的坐标是 ;(2)在x 轴上取一点P ,使得PA+PB 的值最小,直接写出点P 的坐标. 此时在反比例函数()4x 0xy =>的图像上是否存在一点Q ,使△A’B’Q 的面积与△PAB 的面积相等,若存在,求出点Q 的横坐标;若不存在,请说明理由;(3)连接AB’,动点M 从A 点出发沿线段AB’以每秒1个单位长度的速度向终点B’运动;动点N 同时从B’点出发沿线段B’A’以每秒1个单位长度的速度向终点A’运动.当其中一个点停止运动时,另一个点也随之停止运动.设运动的时间为t 秒,试探究:是否存在使△MNB’为等腰直角三角形的t 值.若存在,求出t 的值;若不存在,说明理由.22.如图,二次函数23y x x m =-++的图象与x 轴的一个交点为(4,0)B ,另一个交点为A ,且与y 轴相交于C 点(1)则m =_________;C 点坐标为___________;(2)在直线BC 上方的抛物线上是否存在一点M ,使得它与B ,C 两点构成的三角形面积最大,若存在,求出此时M 点坐标;若不存在,请简要说明理由.(3)P 为抛物线上一点,它关于直线BC 的对称点为Q①当四边形PBQC 为菱形时,求点P 的坐标;②点P 的横坐标为(04)t t <<,当t =________时,四边形PBQC 的面积最大.23.如图①,在ABC ∆中,90C ∠=︒,10,8AB BC ==.点,D E 分别是边,AC BC 上的动点,连接DE .设CD x =(0x >),BE y =,y 与x 之间的函数关系如图②所示.(1)求出图②中线段PQ所在直线的函数表达式;(2)将DCE沿DE翻折,得DME.∆的某条角平分线上?如果可以,求出相应x的值;如果不可①点M是否可以落在ABC以,说明理由;∆重叠部分面积的最大值及相应x的值.②直接写出....DME与ABC24.已知,在四边形ABCD中,AD∥BC,AB∥DC,点E在BC延长线上,连接DE,∠A+∠E=180°.(1)如图1,求证:CD=DE;(2)如图2,过点C作BE的垂线,交AD于点F,请直接写出BE、AF、DF 之间的数量关系_______________________;(3)如图3,在(2)的条件下,∠ABC的平分线,交CD于G,交CF于H,连接FG,若∠FGH=45°,DF=8,CH=9,求BE的长.25.已知:如图,在平面直角坐标系中,点 A 的坐标为(6,0),2,点 P 从点 O 出发沿线段 OA 向终点 A 运动,点 P 的运动速度是每秒 2 个单位长度,点 D 是线段 OA 的中点.(1)求点B 的坐标;(2)设点P 的运动时间为点t 秒,△BDP 的面积为S,求S 与t 的函数关系式;(3)当点P 与点D 重合时,连接BP,点E 在线段AB 上,连接PE,当∠BPE=2∠OBP 时,求点E 的坐标.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题1.A解析:(1)∠A+∠C=90°;(2)证明见解析;(3)99°.【解析】【分析】(1)根据平行线的性质以及直角三角形的性质进行证明即可;(2)先过点B作BG∥DM,根据同角的余角相等,得出∠ABD=∠CBG,再根据平行线的性质,得出∠C=∠CBG,即可得到∠ABD=∠C;(3)先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,再设∠DBE=a,∠ABF=b,根据∠CBF+∠BFC+∠BCF=180°,可得(2a+b)+5a+(5a+b)=180°,根据AB⊥BC,可得b+b+2a=90°,最后解方程组即可得到∠ABE=9°,即可得出∠EBC的度数.【详解】解:(1)如图1,设AM 与BC 的交点为O ,AM //CN ,∴∠C =∠AOB ,∵AB ⊥BC ,∴∠ABO =90°,∴∠A +∠AOB =90°,即∠A +∠C =90°,故答案为:∠A +∠C =90°;(2)证明:如图2,过点B 作BG //DM ,∵BD AM ,∴∠BDM =90°,∵BG //DM ,180∴∠+∠=︒BDM DBG ,∴90∠=︒DBG ,即∠ABD +∠ABG =90°,∵AB BC ⊥,∴∠ABC =90°,∴∠CBG +∠ABG =90°,∴∠ABD =∠CBG ,∵AM //CN ,BG //DM ,∴BG //CN ,∴∠C =∠CBG ,∴∠ABD =∠C ;(3)如图3,过点B 作BG //DM ,∵BF 平分∠DBC ,BE 平分∠ABD ,∴∠DBF =∠CBF ,∠DBE =∠ABE ,由(2)可得∠ABD =∠CBG ,∴∠-∠=∠-∠DBF ABD CBF CBG ,即∠ABF =∠GBF ,设∠DBE =a ,∠ABF =b ,则∠ABE =a ,∠ABD =∠CBG =2a ,∠GBF =∠ABF =b ,∠BFC =5∠DBE =5a ,∴∠CBF =∠CBG +∠GBF =2a +b ,∵BG //DM ,∴∠AFB =∠GBF =b ,∴∠AFC =∠BFC +∠AFB =5a +b ,∵AM //CN ,∴∠AFC +∠NCF =180°,∵∠FCB +∠NCF =180°,∴∠FCB =∠AFC =5a +b ,在△BCF 中,由∠CBF +∠BFC +∠BCF =180°可得:(2a +b )+5a +(5a +b )=180°,化简得:6=90+︒a b ,由AB BC ,可得:b +b +2a =90°,化简得:=45+︒a b ,联立6=9045a b a b +︒⎧⎨+=︒⎩,解得:=936a b ︒⎧⎨=︒⎩, ∴∠ABE =9°,∴∠EBC =∠ABE +∠ABC =9°+90°=99°.【点睛】本题主要考查了平行线的性质的运用,解决问题的关键是作平行线构造内错角,运用等角的余角(补角)相等进行推导.余角和补角计算的应用,常常与等式的性质、等量代换相关联.解题时注意方程思想的运用.2.A解析:(1)A (0,1)(2)结论:∠ABQ +∠OAB ﹣∠Q =135°.(3)α+2β=45°.【解析】【分析】(1)利用二次根式的性质求出m、n的值,求出B、C两点坐标,由S四边形AOBC=S△OBC+S△AOC,推出1 2×2×4+12×OA×4=6,求出OA即可;(2)如图2中,结论:∠ABQ+∠OAB﹣∠Q=135°.根据三角形内角和定理,三角形的外角的性质即可解决问题;(3)由AD∥BC,推出∠ADC=∠DCB=α,由BE平分∠CBx,推出∠CBE=∠EBx,由∠CBE=∠F+∠OCB=α+β,推出∠OBF=∠EBx=α+β,由OC平分∠AOB,可得∠COB=45°=∠F+∠OBF=α+(α+β),由此即可解决问题;【详解】解:(1)由题意2020nn-≥⎧⎨-≥⎩,,得,解得n=2,∴m=4,B(2,0),C(4,4).如图:∵S四边形AOBC=S△OBC+S△AOC,∴12×2×4+12×OA×4=6,∴OA=1,∴A(0,1).(2)结论:∠ABQ+∠OAB﹣∠Q=135°.如图:理由如下:∵OC∥PQ,∴∠Q=∠OCB,∵∠ABQ =∠1+∠OCB =∠1+∠Q ,∠1=180°﹣∠OAB ﹣∠AOC =180°﹣∠OAB ﹣45°=135°﹣∠OAB ,∴∠ABQ =∠Q +135°﹣∠OAB ,∴∠ABQ +∠OAB ﹣∠Q =135°.(3)如图:∵AD ∥BC ,∴∠ADC =∠DCB =α,∵BE 平分∠CBx ,∴∠CBE =∠EBx ,∵∠CBE =∠F +∠OCB =α+β,∴∠OBF =∠EBx =α+β,∵C (4,4),∴OC 平分∠AOB ,∴∠COB =45°=∠F +∠OBF =α+(α+β),∴α+2β=45°.【点睛】本题考查平行线的判定和性质、角平分线的定义、三角形的内角和定理、三角形的外角性质等知识,解题的关键是灵活运用所学知识解决问题,属于压轴题.3.C解析:(1)112y x =-+;(2)1d t =-+;(3)6215t -= 【解析】【分析】(1)根据互相垂直两直线斜率积为-1,设出直线CE 的解析式,再将点C 坐标代入即可求解;(2)过点E 作EM ⊥y 轴于点M ,过点E 作EN x ⊥轴于点N ,通过解直角三角形可证EDM ≌EAN ,ENH ≌EMG ,得到AN =DM ,HN =GM ,进而得到AH DG =,再根据CE 解析式求出D 点坐标,即可找出d 与t 之间的函数关系式;(3)过点B 作BT CM ⊥于点T ,在直线BT 上截取TL NK =,证四边形BGMT 与四边形HNMC 均为矩形,得MN MT =,再进一步证明ENH ≌EMG ,利用全等三角形的性质通过角度计算,得出△BML为等腰三角形且BM BL=,再用含有t的代数式表示BM,最后在Rt△BMG中利用勾股定理建立等式,求出t的值.【详解】解:(1)∵CE⊥AB,∴设直线CE的解析式为:1 2y x c=-+,把点C(2,0)代入上述解析式,得1c=,∴直线CD的解析式为:112y x=-+;(2)过点E作EM⊥y轴于点M,过点E作EN x⊥轴于点N,令26112y xy x=+⎧⎪⎨=-+⎪⎩,解得22xy=-⎧⎨=⎩,∴()2,2E-,易证EDM≌EAN,ENH≌EMG,∴AN=DM,HN=GM,∴AH DG=,由直线CE的解析式112y x=-+,可求点D(0,1)∴DG=1—t,∴1d t=-+;(3)过点B作BT CM⊥于点T,在直线BT上截取TL NK=,易证四边形BGMT 与四边形HNMC 均为矩形,由(2)问可知1t AH GD ==-,则6t HC =-∴6t BG MT ==-,∴MN MT =,∵90KNM LTM ∠=∠=︒,∴ENH ≌EMG ,∴L NKM ∠=∠,设KMN α∠=,则KMB KMN α∠=∠=,∴90NKM α∠=︒-,∴90NKM L α∠=∠=︒-,∵//BL MN ,∴2MBL BMN α∠=∠=,∴18090BML MBL L α∠=︒-∠-∠=︒-,∴BM BL =, ∵1tan 2KCH ∠=, ∴11322KH CH t ==-, ∴133322KN KH HN t t t TL =+=--=-=, ∴352BL BT TL t BM =+=-=, 在Rt BMG △中, 222BM BG GM =+, 解得64215t +=(不合题意舍去)或64215t -= 故,6215t -=. 【点睛】本题一次函数综合题,考查了待定系数法求解析式,一次函数的性质,全等三角形的判定与性质,角平分线的性质,勾股定理等,利用已知条件求相等交,相等线段是解决本题的关键.4.A解析:(1)O 半径为254;(2)①458AM =;②详见解析;③当1251017x <<时,有2220ND DM -<成立.【解析】【分析】(1)如下图,在Rt △ABH 中,先求得AH 的值,设OA=r ,在Rt △OBH 中,利用勾股定理可求得r 的长;(2)①如下图,在Rt BCN ,可求得BN 的长,然后在矩形NBHD 中,求得AD 的值,最后利用cos ∠MAD 求得AM ;②如下图,同过证AMN NFC △∽△可得结论;③如下图,通过转换,先得出222ND DM -=22AM MB DM ⋅这个等式,然后利用3sin 5DM MAD AM ∠==,设AM=x ,可得到关于x 的方程,进而求出x 的取值范围. 【详解】 解:(1)如图1,连接OB ,∵AH 过圆心O ,∴AH BC ⊥,∵AB AC =,∴162BH CH BC ===, 在Rt ABH △中,221068AH =-=,设半径OA OB r ==,则8OH r =-,在Rt OBH 中,222(8)6r r -+=, 解得254r =,即O 半径为254. (2)①如图2,连接CN在平行四边形CDEB 中,DE BC ∥,∴ENB NBC ∠=∠. ∵BN DE ⊥,即90ENB ∠=︒,∴90NBC ∠=︒. ∴CN 是O 的直径.2522CN r ==. ∴在Rt BCN 中,2272BN CN BC =-=. ∵四边形CDEB 是平行四边形,NB ⊥BH ,DH ⊥BH ∴四边形NBHD 是矩形,∴72DH BN ==,6ND BH ==,∴79822AD AH DH =-=-=. ∴在Rt ADM △中,4cos 5AD AH MAD AM AB ∠===,∴458AM =, ②如图3,连接AN ,CN ,∵DE BC ∥,∴DNC NCB ∠=∠.∵NAB NCB ∠=∠,∴NAB DNC ∠=∠. 由DE BC ∥,AB AC =可得AMD ABC ACB AFD ∠=∠=∠=∠, ∴AMN NFC ∠=∠,AM AF =.∴AMN NFC △∽△,MB CF =.∴NM NM AM CF MB NF==,即NM NF AM MB ⋅=⋅. ③∵AH BC ⊥,DE BC ∥,∴AD MF ⊥,∵AM AF =,∴MD DF =, ∴222222ND DM ND DM DM -=-- 2()()ND DM ND DM DM =-+-2NM NF DM =⋅-22AM MB DM =⋅.∵AM x =,∴10BM x =-,由3sin 5DM MAD AM ∠==,得35DM x =, ∴22223342(10)10525ND DM x x x x x ⎛⎫-=--=-+ ⎪⎝⎭.(010)x <<该函数图象的示意图如图4易求得点P 坐标为125,017⎛⎫⎪⎝⎭∴当1251017x <<时,有2220ND DM -<成立. 【点睛】本题考查几何图形的综合,解题过程中用到了勾股定理、相似、三角函数和平行四边形、圆的性质,解题关键是将这些知识点综合起来分析题干. 5.(1) CF 长为24;(2) 四边形BFDE 是菱形,理由见解析;(3) 纸片ENFM 是“标准纸",理由见解析 【解析】 【分析】(1)1AB =,则2AD =ABCD 是矩形,得到1,2CD AB BC AD ==-=FB FD =,设CF x =,则2FB FD x ==,在Rt DCF △中,222+=CD CF DF ,可得)22212x x +=即可求解.(2)当顶点B 与点D 重合时,折痕EF 垂直平分BD ,可得OB OD =,90BOF DOE ∠=∠=,在矩形ABCD 中,//AD BC ,得到OBF ODE ∠=∠,在BOF 和DOE △中,,OBF ODE OB OD BOF DOE ∠=∠=∠=∠,,可得BOF DOE ≅,OE OF =,再根据OB OD =,可得四边形BFDE 是平行四边形,最后根据EF BD ⊥,即可求证平行四边形BFDE 是菱形.(3)由()2可知,OE OF =,同理可知,OM ON =,可得四边形ENFM 是平行四边形,根据90DOE DAB ∠=∠=︒,得到DOEDAB ,再根据2AD AB =,可得222OE AB OD AD ===,进而得到22OE OD =,22EF BD =,同理可得,22MN AC =,根据四边形ABCD 是矩形,可得AC BD =,EF MN =,四边形ENFM 是矩形,90EMF ∠=,2MF ODtan FEM ME OE∠===,2MF ME =,即可求证纸片ENFM 是“标准纸". 【详解】 解:()11,AB =则2,2AD AB ==四边形ABCD 是矩形1,2CD AB BC AD ∴==-=由折叠得FB FD = 设CFx =,则2FB FD x ==- 在Rt DCF △中,222+=CD CF DF()22212x x +=-24x =答:CF 长为24()2四边形BFDE 是菱形.理由:当顶点B 与点D 重合时,折痕EF 垂直平分,BDOB OD ∴=,90BOF DOE ∠=∠=在矩形ABCD 中,//,AD BCOBF ODE ∴∠=∠在BOF 和DOE △中,,OBF ODE OB OD BOF DOE ∠=∠=∠=∠,BOF DOE ∴≅OE OF ∴= OB OD =∴四边形BFDE 是平行四边形EF BD ⊥平行四边形BFDE 是菱形.()3纸片ENFM 是“标准纸”理由如下:由()2可知,,OE OF =同理可知,,OM ON =∴四边形ENFM 是平行四边形90DOE DAB ∠=∠=︒ DOEDAB ∴2AD =222OE AB OD AD ∴===2OE ∴= 22EF BD ∴=同理可得,22MN AC =四边形ABCD 是矩形,AC BD ∴=, EF MN ∴=∴四边形ENFM 是矩形.90EMF ∴∠=.2,MF ODtan FEM ME OE∴∠=== 2MF ME ∴=.∴纸片ENFM 是“标准纸".【点睛】此题主要考查矩形的判定和性质、勾股定理、全等三角形的判定和性质、菱形的判定及三角函数,灵活运用判定和性质是解题关键.6.A解析:(1)①(1,2),(2.5,0)A C ;②2232m ≤;(2)最小值为2.【解析】 【分析】(1)①根据“特征点”的定义判断即可;②如图2中,当⊙W 1与直线y =−x +2相切时,1(22,0)W -,当⊙W 2与直线y =−x +3相切时,2(32,0)W +,结合图象,⊙W 与图中阴影部分有交点时,⊙W 上存在满足条件的特征点.(2)特征点的图象是由原点向外扩大,当与反比例函数的图象第一次有交点时,1x x+的值最小(如图3中). 【详解】解:(1)①∵1+2=3,1+3=4,2.5+0=2.5, 又∵2≤a ≤3, ∴A ,C 是特征点,故答案为:(1,2),(2.5,0)A C ; ②如图1,∵2≤a ≤3,∴直线y =−x +2和直线y =−x +3之间的区域(包括两直线)上的点都为“特征点”, 直线y =−x +2和直线y =−x +3分别与x 轴的交点为(2,0)P ,(3,0)Q ,当⊙W 1与直线y =−x +2相切时,设切点为M ,此时2OP =,1MW MP ⊥,145MPW ∠=︒,则1MPW 为等腰直角三角形, ∵⊙W 1半径为1,即11MW =,∴12PW =1122OW OP PW =-=- ∴1(22,0)W ,当⊙W 2与直线y =−x +3相切时,设切点为N ,此时3OQ =,2NW NQ ⊥,245NQW ∠=︒,则2NQW 为等腰直角三角形, 同理得:22QW =,则2232OW OQ QW =+=+, ∴2(32,0)W +,观察图象可知满足条件的m 取值范围为:2232m -≤≤+; (2)根据0x >,在第一象限画出1y x=的图象, ∴在此坐标系中图象上的点就是1x x ⎛⎫⎪⎝⎭,,∵特征点满足x y a +=(x ≥0,a 为常数), ∴在此图象上对应的就是1x a x+=, ∴将特征点的图象由原点向外扩大,当与反比例函数1y x =的图象第一次有交点时,1x x+出现最小值, 如图2,由x >0可将1x a x+=整理得:210x ax -+=, ∴2()40a ∆=--=,解得:12a =,22a =-(舍去),∴2a =, ∴12Z x x =+=,即()10Z x x x=+>的最小值为2.【点睛】本题属于反比例函数综合题,考查了直线与圆的位置关系,反比例函数的性质等知识,解题的关键是理解题意,学会利用图象法解决问题,属于中考压轴题.7.B解析:(1)333-;(2)18;(3)①2716;②972625【解析】 【分析】(1)过点B 作BF ⊥AD ,交DA 的延长线于点F ,利用等腰直角三角形ABF 求得AF 和BF 的长,再利用Rt △PBF 求得PF 的长,进而得解;(2)作点B 关于直线AD 的对称点B',连接B'C ,交AD 于点P',连接BP',根据两点之间线段最短可知当B',P ,C 三点共线时,BPC △周长取得最小值,再利用勾股定理计算即可;(3)①②根据EM PB ⊥,EN PC ⊥可得点E 、M 、P 、N 在以PE 为直径的圆上,利用圆周角定理和直角三角形两锐角互余可证得△MPN ∽△CPB ,进而可知当MN 最大时,PMN 面积的最大,当MN 最小时,PMN 面积的最小,由圆的性质可知当MN 为直径时MN 最大,当MN ⊥PE 时,MN 最小,最后利用勾股定理、等积法和相似三角形的性质求解即可. 【详解】解:(1)如图,过点B 作BF ⊥AD ,交DA 的延长线于点F ,∵AD ∥BC ,∠ABC =45°, ∴∠FAB =∠ABC =45°, ∵BF ⊥AD ,∴在Rt △ABF 中,AF 2+BF 2=AB 2, ∵32AB = ∴AF =BF =22AB =23232⨯=, ∵AD ∥BC ,∠PBC =30°, ∴∠FPB =∠PBC =30°, ∵在Rt △PBF 中,tan ∠FPB =BFPF∴tan30°=33PF =, ∴33PF=∴333AP PF AF =-=-;(2)如图,作点B 关于直线AD 的对称点B',连接B'C ,交AD 于点P',连接BP',∵点B 与点B'关于直线AD 对称, ∴AD 垂直平分BB',BF =B'F =3, ∴P'B =P'B',BB'=6,∴当点P 在点P'时,PB+PC 取得最小值,最小值为B'C 的长,此时△BPC 的周长最小, 在Rt △BB'C 中,B'C 22226810'BB BC ++=, ∴△BPC 的周长最小值为B'C +BC =10+8=18; (3)①∵EM PB ⊥,EN PC ⊥,∴∠EMP =∠ENP =90°,∴点E 、M 、P 、N 在以PE 为直径的圆上,如图所示,则∠PMN =∠PEN , ∵PE BC ⊥,EN PC ⊥, ∴∠PEC =∠ENC =90°,∴∠PEN+∠NEC =∠NEC+∠PCB =90°, ∴∠PEN =∠PCB , ∴∠PMN =∠PCB , 又∵∠MPN =∠CPB , ∴△MPN ∽△CPB ,∴2PMN PCB S MN S BC ⎛⎫=⎪⎝⎭∵PE BC ⊥, ∴PE =3, ∴11831222PCBSBC PE ==⨯⨯= ∴2128PMN SMN ⎛⎫= ⎪⎝⎭∴当MN 取得最大值时,PMN 的面积取得最大值,当MN =PE =3时,23128PMN S⎛⎫= ⎪⎝⎭解得2716PMNS=即当MN =PE =3时,PMN 的面积最大,最大值为2716; ②由①可知,2128PMNSMN ⎛⎫= ⎪⎝⎭,∴当MN 取得最小值时,PMN 的面积取得最小值, 由垂径定理可知,当MN ⊥PE 时,MN 取得最小值,如图,当MN ⊥PE 时,则弧ME =弧NE∴∠MPE =∠NPE , ∵PE BC ⊥, ∴∠PEB =∠PEC =90°, ∴△PEB ≌△PEC , ∴EB =EC =12BC =4, 在Rt △BEP 中,BP5==, ∵1122BEPS BE PE BP ME == ∴1143522ME ⨯⨯=⨯ ∴125ME =, 在Rt △PME 中,PM 95== ∵1122PMES PM ME PE MH == ∴1912132552MH ⨯⨯=⨯ ∴3625MH =, ∴72225MN MH ==, ∴227292512825PMN S ⎛⎫ ⎪⎛⎫== ⎪ ⎪⎝⎭⎪⎝⎭,解得972625PMNS=, ∴PMN 面积的最小值为972625. 【点睛】本题考查了等腰直角三角形、特殊角的三角函数、相似三角形的判定及性质、勾股定理、垂径定理和圆周角定理等相关知识,有点难度,属中考压轴题,能够将第(3)问转化为利用圆的相关知识和相似三角形的性质解决是解决本题的关键.8.A解析:(1)A (4,0);(2)2144S t =-;(3)(4,8)E -【解析】 【分析】(1)利用三角形的面积公式构建方程即可解决问题.(2)证明△CEA 和△COD 是等腰直角三角形,由EN ⊥AC ,推出42t CN NE NA +===,AC=4+t ,根据S=S△AEC -S △ABC 计算即可.(3)过点F 作FM ⊥AC 于点M ,由(2)求出点F 的坐标为(1,3)44t t-+,从而得到 1144t t OM =-=-,34tFM =+,由∠ABO=∠BDA+∠BAD=45°,∠FOB +∠DAE =45°,得出∠FOB=∠BDA ,进而得出∠MFO=∠ODA ,tan ∠MFO =tan ∠ODA ,故而OA OMOD MF=, 即14434t t t -=+,解出t 的值,再求点E 的坐标即可. 【详解】(1)由题意可得:211•••822AOB S OA OB OA ===,∴OA 2=16, ∵OA >0, ∴OA=OB=4,∴A (4,0),B (0,4).(2)如图,过点E 作EN ⊥AC 于点N .∵∠AOB=90°,OA=OB , ∴∠OAB=45°, ∵AB ⊥CD , ∴∠CEA=90°, ∴∠ECA=45°,∴△CEA 是等腰直角三角形, ∵∠ECA=45°,∠COD=90°,∴∠CDO=45°,∴△CDO 是等腰直角三角形. ∵点D 纵坐标为t , ∴CO=DO=t. ∵OA=OB=4, ∴AC=t+4.∴42t CN NE NA +===, ∴()()2141144442224AECABCt S SSt t t +⎛⎫=-=⨯+⨯-⨯+⨯=- ⎪⎝⎭; ∴S 与t 的函数关系是:2144S t =-. (3)如图,过点F 作FM ⊥AC 于点M ,由(2)可知,42t CN NE +==, ∴22tON OC CN =-=-, ∴点E 的坐标为(2,2)22t t-+, ∵点B (0,4),点F 为BE 中点, ∴点F 的坐标为(1,3)44t t-+, ∴1144t t OM =-=-,34tFM =+, ∵∠ABO=∠BDA+∠BAD=45°,∠FOB +∠DAE =45°, ∴∠FOB=∠BDA , ∴OF ∥AD , ∵FM ⊥AC , ∴FM ∥DO , ∴∠MFO=∠ODA , ∴tan ∠MFO =tan ∠ODA ,∴OA OM OD MF=,即14434ttt-=+,解得t=12或4=-4(不合题意,舍去)∴点E的坐标为(4,8)-.【点睛】本题考查三角形综合题,解题的关键是正确作出辅助线,灵活运用所学知识,利用参数构建方程解决问题.9.A解析:(1)详见解析;(2)详见解析;(3)①::32:7:25AG GM ME=;②6:1:2.【解析】【分析】(1)根据∠AOB=∠OBC+∠OCB,只要求出∠OBC,∠OCB即可.(2)想办法证明CG⊥AE即可解决问题.(3)①如图2中,作MH⊥CE于H,解直角三角形求出AG,GM,ME即可解决问题.②如图3所示:连接DE.首先证明四边形OCED是平行四边形,再证明EC=2DG,利用平行线分线段成比例定理即可解决问题.【详解】解:(1)∵CE CA=,CD BC=,∴CAE CEA∠=∠,CBD CDB∠=∠.∵AE BC∥,∴CAE OCB∠=∠.∵90ABC∠=︒,O为AC中点,∴OB OC=.∴CBD OCB CAE∠=∠=∠.∴ACE BCD∠=∠.即28ACB DCE∠=∠=︒.∴56AOB OBC OCB∠=∠+∠=︒.(2)连结CG(如图1).∵AE BC∥,AO CO=,∴BO OG =.∵90ABC ∠=︒,∴四边形ABCG 为矩形.∴CG AE ⊥.∵CE CA =,∴AG GE =.(3)①作MH CE ⊥于H (如图2).由AG BC ,AG GE BC ==,则四边形GBCE 是平行四边形,∴E OBC OCB DCE ∠=∠=∠=∠.∴MC ME =,2222345CE BG AC AB BC ===+=+=. ∵MH CE ⊥,∴522CE HE ==. ∵4cos cos 5E OCB =∠=, ∴25cos 8HE ME E ==. ∵4GE AG BC ===, ∴257488GM GE ME =-=-=. ∴725::4::32:7:2588AG GM ME ==. ②如图3所示:连接DE .∵OA=OC ,∠ABC=90°,∴BO=OA=OC ,∴∠OBC=∠OCB ,∵AE ∥BC ,∴∠CAE=∠ACB ,∠AGO=∠OBC ,∵CA=CE ,∴∠CAE=∠CAE ,∴∠AGB=∠AEC ,∴AD ∥CE ,∵DE ∥AC ,∴四边形OCED 是平行四边形,∴OD=CE=CA ,∵∠OAG=∠OGA ,∴OA=OG ,∴OA=OC=OG=DG ,∵DG ∥EC , ∴12GM DG ME CF ==, ∴1212S S =, 设S 2=m ,则S 3=2m ,∴S △DGE =3m ,∵OG=GD ,∠AGO=∠DGE ,∠OAG=∠DEG ,∴△AGO ≌△EGD (AAS ),∴S △AOG =S △DEG =3m ,∵OB=OG ,∴S △ABG =2S △AOG =6m ,∴S 1:S 2:S 3=6m :m :2m=6:1:2.故答案为:6:1:2.【点睛】本题考查相似三角形的判定和性质,解直角三角形,平行四边形的判定和性质,三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题.10.B解析:(1)直线x=0;(2)B (0,1a );(3)≤a ≤13-或13≤a【解析】【分析】(1)根据抛物线的表达式直接得出对称轴即可;(2)根据题意得出点A 的坐标,再利用关于x 轴对称的点的坐标规律得出点B 坐标; (3)分a >0和a <0两种情况分别讨论,画图图像,求出a 的范围.【详解】解:(1)在抛物线21y axa=-中,2a-=,∴对称轴为直线x=0,即y轴;(2)∵抛物线与y轴交于点A,∴A(0,1a -),∵点A关于x轴的对称点为点B,∴B(0,1a);(3)当a>0时,点A(0,1a-)在y轴负半轴上,当点P恰好在抛物线上时,代入得:11aa a -=,解得:2a=或2-(舍),当点Q恰好在抛物线上时,代入得:190 aa-=,解得:13a=或13-(舍),∴当13≤a≤2时,抛物线与线段PQ恰有一个公共点;当a<0时,点A(0,1a-)在y轴正半轴上,同理可知:当点P恰好在抛物线上时,代入得:11aa a -=,解得:2a=2-,当点Q恰好在抛物线上时,代入得:190 aa-=,解得:13a=(舍)或13-,∴当2-≤a ≤13-时,抛物线与线段PQ 只有一个公共点;综上:若抛物线与线段PQ 恰有一个公共点,a 的取值范围是2-≤a ≤13-或13≤a ≤2. 【点睛】本题是一道二次函数的综合题目,主要考查二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,画出相应的函数图象,利用分类讨论的方法和数形结合的思想解答.11.A解析:(1)图见解析,33cm ;(2)①25cm 42cm AB ≤≤;②26【解析】【分析】(1)连接AO ,直线l 垂直平分PO .13cm 22OH PO ==,在Rt △AHO 中即可求解; (2)①分两种情况求解;②过O 作弦AB 的垂直与圆交于点D ,与弧AB 交于点C ,与AB 交于点E ,过M 作OM 的垂线,两条垂线的交点为O',连接AO ,得到OO'垂直平分AB ,O'为弧ABM 所在圆的圆心,10cm OO '=,在Rt △ADO 中即可求解;【详解】(1)如图,直线l 为所求,连接AO .∵点P 与点O 关于直线l 对称,∴直线l 垂直平分PO .∴13cm 22OH PO ==. 在Rt AHO ∆中,∵222AH HO AO +=, ∴2233cm 2AH AO HO =-=. 在O 中,∵PO AB ⊥,PO 为半径, ∴233cm AB AH ==.(2)如图1:∵弧AB 翻折与M 重合,OM=1,∴DM=1,在Rt△ADO 中,AO=3,DO=2,∴5AD =;如图2:∵弧AB 翻折与M 重合,OM=1,∴MD=2,DO=1,在Rt△ADO 中,AO=3,∴22AD =∴2542AB ≤≤故答案为2542AB ≤≤(3)如图3:过O 作弦AB 的垂线与圆O 交于点C ,与AB 交于点D ,连接OM ,过点M 作OM 的垂线,两条垂线的交点为O',连接AO ,。
