九年级数学下册-26.2-二次函数的图象与性质(第3课时)课件-(新版)华东师大版
合集下载
26.2.3 求二次函数的表达式 公开课获奖课件

解:(1)∵抛物线 y=13x2+bx+c 经过 A(- 3,0),B(0,
- 3) 两 点 , ∴ 13×(- 3)2- 3b+c=0, 解 得 c=-3,
b=-23 c=-3.
3, ∴此抛物线所对应的函数关系式为
y
=
1 3
x2
-
2 3 3x-3 (2)由(1)可得此抛物线的对称轴为直线 x= 3,顶
二、填空题(每小题 4 分,共 16 分) 12.已知抛物线 y=x2+mx-5 经过点(2,-3), 则该抛物线的解析式为__y=x2-x-5__. 13.已知抛物线与 x 轴交于点 A(-1,0),B(1, 0),与 y 轴交点的纵坐标为 1,则该抛物线的解析式为 __y=-x2+1__. 14.抛物线 y=ax2+bx+c 的顶点在 x 轴上,对称 轴是直线 x=1,并且抛物线经过点(2,2),则这条抛 物线的解析式为__y=2(x-1)2__. 15.一个二次函数,当自变量 x=-1 时,函数值 y=2;当 x=0 时,y=-1;当 x=1 时,y=-2,那 么,这个二次函数的解析式为__y=x2-2x-1__.
最后还想推一下萧绎的《幽逼诗》四 首:
【南史曰:元帝避建邺则都江陵,外 迫强敌 ,内失 人和。 魏师至 ,方征 兵四方 ,未至 而城见 克。在 幽逼求 酒,饮 之,制 诗四绝 。后为 梁王詧 所害。 】 南风且绝唱,西陵最可悲。今日还蒿 里,终 非封禅 时。 人世逢百六,天道异贞恒。何言异蝼 蚁,一 旦损鲲 鹏。 松风侵晓哀,霜雰当夜来。寂寥千载 后,谁 畏轩辕 台。 夜长无岁月,安知秋与春。原陵五树 杏,空 得动耕 人。
B.2,-4
C.-2,4 D.-2,-4
9.已知抛物线 y=ax2+bx+c 过(-1,2),(0,1),
2 二次函数的图象与性质2.二次函数y=ax2+bx+c的图象与性质第3课时PPT课件(华师大版)

首先要将二次函数的关系式化为顶点式,然后按照“左加右减,上加下
减”的平移规律,确定平移后的抛物线对应的函数关系式.
第3课时
二次函数y=a(x-h)2+k的图象与性质
目标三 理解二次函数y=a(x-h)2+k的性质
例 3 [高频考题]
已知函数 y=3 - +9.
(1)确定此函数图象的开口方向、对称轴和顶点坐标;
第3课时
二次函数y=a(x-h)2+k的图象与性质
知识点二 二次函数y=a(x-h)2+k的图象与性质
二次
a的
图象的开 图象的 图象的顶
函数值的
图象
函数
符号
最值
口方向
对称轴 点坐标
变化情况
当x>h时,y随x的
y=
a(x-
a>0
向上
直线
( h , 增大而 增大 ;
图象有最 低点,
当x=h时,y有最
x=h
2
称轴分别为 y 轴,直线 x=1,直线 x=1;顶点坐标分别为
(0,0),(1,0),(1,-2).
第3课时
二次函数y=a(x-h)2+k的图象与性质
【归纳总结】画二次函数 y=a(x-h)2+k 的图象的技巧:
(1)找到对称轴直线 x=h(即顶点的横坐标 h);
(2)列表时选取的 x 值中把 h 放在中间,比 h 小和比 h 大的数各取若干个
k
)
当x<h时,y随x的
h)2+k
增大而
增大
大值
k
第3课时
二次函数y=a(x-h)2+k的图象与性质
反思
减”的平移规律,确定平移后的抛物线对应的函数关系式.
第3课时
二次函数y=a(x-h)2+k的图象与性质
目标三 理解二次函数y=a(x-h)2+k的性质
例 3 [高频考题]
已知函数 y=3 - +9.
(1)确定此函数图象的开口方向、对称轴和顶点坐标;
第3课时
二次函数y=a(x-h)2+k的图象与性质
知识点二 二次函数y=a(x-h)2+k的图象与性质
二次
a的
图象的开 图象的 图象的顶
函数值的
图象
函数
符号
最值
口方向
对称轴 点坐标
变化情况
当x>h时,y随x的
y=
a(x-
a>0
向上
直线
( h , 增大而 增大 ;
图象有最 低点,
当x=h时,y有最
x=h
2
称轴分别为 y 轴,直线 x=1,直线 x=1;顶点坐标分别为
(0,0),(1,0),(1,-2).
第3课时
二次函数y=a(x-h)2+k的图象与性质
【归纳总结】画二次函数 y=a(x-h)2+k 的图象的技巧:
(1)找到对称轴直线 x=h(即顶点的横坐标 h);
(2)列表时选取的 x 值中把 h 放在中间,比 h 小和比 h 大的数各取若干个
k
)
当x<h时,y随x的
h)2+k
增大而
增大
大值
k
第3课时
二次函数y=a(x-h)2+k的图象与性质
反思
2019_2020学年九年级数学第26章二次函数26.2二次函数的图象与性质教学课件(新版)华东师大版

(3)图象 与x轴有交点吗?如果有,交点坐标是什么?
(4)在对称轴左侧,随着x值的增大,y 的值如何变化?在对 称轴右侧呢?
(5)当x取什么值时,y的值最小?最小值是什么?你是如 何知道的?
y x2
这条抛物线关于 y轴对称,y轴就
是它的对称轴.
对称轴与抛物 线的交点叫做 抛物线的顶点.
(1)二次函数y=-x2的图象是什么形状?
2
2
图象
想一想, 这个函数的图象和性质会是什么样?
描点,连线 y 20
16
y 1 x2 2
12
y 1 x 22
2
-12 -10 -8 -6
8
4 2
-4 -2 0 2
直线x-=2-2
x
4 6 8 10 12
函数 y 1 与 x 22 2
的y 1 x2 2
图象有什么关系?说出它
的顶点坐标和对称轴
1
(5)y=- 2 (x+ 3)2
2、根据下列函数的解析式回答 当x为何值时,y随x的增大而 增大?
(1)y=(x+1)2 (2)y=-(x-5)2
(3)y=2(x-3)2(4)y=- 2(x-1)2
1
(5)y=- 2 (x+
3)2
第4课时
函数y=ax²+bx+c的图象
二次函数y=3x2-6x+5的图象是什么形状?它与我 们已经作过的二次函数的图象有什么关系?
在同一个直角坐标系里画出函数
y
1 2
x2与y
1 x 22
2
的
图象.
y 描点,连线
20 16
y 1 x2 2
12
8
华东师大版九年级下册数学课件:26.二次函数y=ax2的图象和性质(共23张)
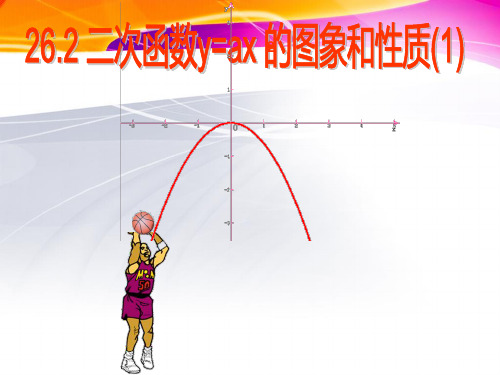
像都是轴对称图形,y轴是它们的对称轴.
抛物线与对称轴的交点叫做抛物线的顶点.
抛物线y=x2的顶点(0,0)是它的最低点.
抛物线y=-x2的顶点(0,0)是它的最高点.
y x2
y 1 x2 2
y x2
y 2x2
y 2 x2 3
二次函数y=ax2的图象形如物体抛射时 所经过的路线,我们把它叫做抛物线。
(2) 描点
y=-
1 2
x2
…
-8 -4.5 -2 -0.5 0 -0.5 -2 -4.5 -8
…
x
……
-2 -8
-1.5 -4.5
-1 -2
-0.5 -0.5
0 0.5 1 0 -0.5 -2
1.5 2 -4.5 -8
……
(3) y连=线-2x2
y 1
函数y=- x2,y21=-2x2的图 -5 -4 -3 -2 -1-1 o 1 2 3 4 5 x
y轴
位置
在y轴左右两侧同时向上无限延伸
在x轴的上方(除顶点外)
y= ax2 (a<0)
(0,0) 最高点
y轴
在y轴左右两侧同时向下无限延伸
在x轴的下方( 除顶点外)
开口方向
向上
向下
最值
当x=0时,最小值为0.
当x=0时,最大值为0.
增减性 开口大小
在对称轴的左侧,y随着x的增大而减小. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
2
1、二次函数的一般情势是怎样的?
y=ax²+bx+c(a,b,c是常数,a≠ 0)
最新华师大版九年级数学下册电子课本课件【全册】

最新华师大版九年级数学下册电子 课本课件【全册】
1. 圆的基本元素
最新华师大版九年级数学下册电子 课本课件【全册】
2. 圆的对称性
最新华师大版九年级数学下册电子 课本课件【全册】
最新华师大版九年级数学下册电子 课本课件【全册】
26.3 实践与探索
最新华师大版九年级数学下册电子 课本课件【全册】
第27章 圆
最新华师大版九年级数学下册电子 课本课件【全册】
27.1 圆的认识
最新华师大版九年级数学下册电 子课本课件【全册】目录
0002页 0062页 0100页 0158页 0229页 0261页 0285页 0322页 0336页 0387页 0443页 0466页 0497页 0 2. 二次函数y=ax2+bx+c的图象与性质 26.3 实践与探索 27.1 圆的认识 2. 圆的对称性 27.2 与圆有关的位置关系 2. 直线与圆的位置关系 27.3 圆中的计算问题 第28章 样本与总体 1. 普查和抽样调查 28.2 用样本估计总体 2. 简单随机抽样调查可靠吗 1. 借助调查作决策
第26章 二次函数
最新华师大版九年级数学下册电子 课本课件【全册】
26.1 二次函数
最新华师大版九年级数学下册电子 课本课件【全册】
26.2 二次函数的图象与性质
最新华师大版九年级数学下册电子 课本课件【全册】
1. 二次函数y=ax2的图象与性质
最新华师大版九年级数学下册电子 课本课件【全册】
2. 二次函数y=ax2+bx+c的图象 与性质
最新华师大版九年级数学下册电子 课本课件【全册】
3. 求二次函数的表达式
1. 圆的基本元素
最新华师大版九年级数学下册电子 课本课件【全册】
2. 圆的对称性
最新华师大版九年级数学下册电子 课本课件【全册】
最新华师大版九年级数学下册电子 课本课件【全册】
26.3 实践与探索
最新华师大版九年级数学下册电子 课本课件【全册】
第27章 圆
最新华师大版九年级数学下册电子 课本课件【全册】
27.1 圆的认识
最新华师大版九年级数学下册电 子课本课件【全册】目录
0002页 0062页 0100页 0158页 0229页 0261页 0285页 0322页 0336页 0387页 0443页 0466页 0497页 0 2. 二次函数y=ax2+bx+c的图象与性质 26.3 实践与探索 27.1 圆的认识 2. 圆的对称性 27.2 与圆有关的位置关系 2. 直线与圆的位置关系 27.3 圆中的计算问题 第28章 样本与总体 1. 普查和抽样调查 28.2 用样本估计总体 2. 简单随机抽样调查可靠吗 1. 借助调查作决策
第26章 二次函数
最新华师大版九年级数学下册电子 课本课件【全册】
26.1 二次函数
最新华师大版九年级数学下册电子 课本课件【全册】
26.2 二次函数的图象与性质
最新华师大版九年级数学下册电子 课本课件【全册】
1. 二次函数y=ax2的图象与性质
最新华师大版九年级数学下册电子 课本课件【全册】
2. 二次函数y=ax2+bx+c的图象 与性质
最新华师大版九年级数学下册电子 课本课件【全册】
3. 求二次函数的表达式
九年级数学下册27.2二次函数的图象与性质2.3二次函数y=ax2bxc的图象与性质第3课时课件华东师大版

【规律总结】
函数y=a(x-h)2+k与y=ax2的性质比较
函数 开口方向 对称轴 顶点坐标
增减性
最值
y轴(直 y=ax2
线x=0) 当a>0时,
开口向上;
当a<0时,
y=a(x- 开口向下 直线
h)2+k
x=h
(0,0) (h,k)
a>0,当x=0时, 当a>0时,在 对称轴的左侧, y最小=0;a<0, y随x的增大而 当x=0时,y最大
抛物线y=a(x-h)2+k与y=ax2的平移 【例1】把抛物线y=x2+bx+c向上平移2个单位,再向左平移4个 单位,得到抛物线y=x2,求b,c的值. 【解题探究】(1)抛物线y=x2+bx+c向上平移2个单位,再向左平 移4个单位,得到抛物线y=x2,也可以是抛物线y=x2先向右平移 4个单位,再向下平移2个单位得到抛物线y=x2+bx+c.
④函数y=(x-1)2+1的图象也可以看作是函数y=x2的图象沿x轴向 _右__平移_1_个单位,再沿直线x=1向_上__平移_1_个单位得到的; ⑤函数y=(x-1)2的对称轴是x=_1_,y=(x-1)2+1的对称轴是x=_1_; 函数y=(x-1)2的顶点坐标为_(_1_,__0_)_, y=(x-1)2+1的顶点坐标为_(_1_,__1_)_.
2.(2012·扬州中考)将抛物线y=x2+1先向左平移2个单位,再向
下平移3个单位,那么所得抛物线的函数关系式是( )
Байду номын сангаас
(A)y=(x+2)2+2
(B)y=(x+2)2-2
华师版九年级下册数学第26章 二次函数 二次函数y=a(x-h)2+k的图象与性质

图②的位置,m 逐渐减小,点 B 沿 y 轴向上移动,
当点 B 与 O 重合时,-12m2+4=0, 解得 m=2 2或 m=-2 2, 当点 B 与点 D 重合时,如图②, 顶点 A 也与 B、D 重合,点 B 到达最高点, ∴点 B(0,4),∴-12m2+4=4,解得 m=0.
当抛物线从图②的位置继续向左平移 时,如图③,点 B 不在线段 OD 上, ∴B 点在线段 OD 上时,m 的取值范 围是 0≤m<1 或 1<m<2 2.
(1)当m=5时,求n的值;
解:当 m=5 时,y=-12(x-5)2+4, 当 x=1 时,n=-12×42+4=-4.
(2)当n=2时,若点A在第一象限内,结合图象,求当y≥2 时,自变量x的取值范围;
解:当 n=2 时,将 C(1,2)的坐标代入函数表达式 y=-12(x-m)2+4,得 2=-12(1-m)2+4, 解得 m=3 或 m=-1(舍去), ∴此时抛物线的对称轴为 x=3, 根据抛物线的对称性可知,当 y=2 时,x=1 或 x=5, ∴x 的取值范围为 1≤x≤5.
7 ∴tan ∠ABC=OOCB=37=13.
12.把二次函数 y=a(x-h)2+k 的图象先向左平移 2 个单位 长度,再向上平移 4 个单位长度,得到二次函数 y=12(x +1)2-1 的图象.
(1)试确定 a、h、k 的值; 解:a=12,h=1,k=-5.
(2)指出二次函数y=a(x-h)2+k图象的开口方向、对称轴 和顶点坐标.
【答案】①②④
10.【中考·舟山】二次函数 y=-(x-1)2+5,当 m≤x≤n 且
mn<0 时,y 的最小值为 2m,最大值为 2n,则 m+n 的
值为( )
A.52
当点 B 与 O 重合时,-12m2+4=0, 解得 m=2 2或 m=-2 2, 当点 B 与点 D 重合时,如图②, 顶点 A 也与 B、D 重合,点 B 到达最高点, ∴点 B(0,4),∴-12m2+4=4,解得 m=0.
当抛物线从图②的位置继续向左平移 时,如图③,点 B 不在线段 OD 上, ∴B 点在线段 OD 上时,m 的取值范 围是 0≤m<1 或 1<m<2 2.
(1)当m=5时,求n的值;
解:当 m=5 时,y=-12(x-5)2+4, 当 x=1 时,n=-12×42+4=-4.
(2)当n=2时,若点A在第一象限内,结合图象,求当y≥2 时,自变量x的取值范围;
解:当 n=2 时,将 C(1,2)的坐标代入函数表达式 y=-12(x-m)2+4,得 2=-12(1-m)2+4, 解得 m=3 或 m=-1(舍去), ∴此时抛物线的对称轴为 x=3, 根据抛物线的对称性可知,当 y=2 时,x=1 或 x=5, ∴x 的取值范围为 1≤x≤5.
7 ∴tan ∠ABC=OOCB=37=13.
12.把二次函数 y=a(x-h)2+k 的图象先向左平移 2 个单位 长度,再向上平移 4 个单位长度,得到二次函数 y=12(x +1)2-1 的图象.
(1)试确定 a、h、k 的值; 解:a=12,h=1,k=-5.
(2)指出二次函数y=a(x-h)2+k图象的开口方向、对称轴 和顶点坐标.
【答案】①②④
10.【中考·舟山】二次函数 y=-(x-1)2+5,当 m≤x≤n 且
mn<0 时,y 的最小值为 2m,最大值为 2n,则 m+n 的
值为( )
A.52
九年级数学下册第26章二次函数26.2二次函数的图象与性质1课件新版华东师大版ppt课件

在对称轴的右 侧,y随着x的增大而增大;
在对称轴的左 侧,y随着x的增大而减小,
当x= 0
时,函数y的值最小,是 0 。
(2)抛物线 y 的 开2口x 2方向
,对向称下轴是 ,顶点是
(当0x,>00时),y随着x3的增大而
;
当x<0时,y随着x的 增大而
;
减小
当x=0时,函数y的值最大,是
.
增大
y轴;
0
高效讨论,实现目标
重点讨论:1.如何画二次函数的图象 ? 2.二次函数y=ax2有哪些性质?
1.全体同学站起来讨论。 2.先对桌一对一讨论,相互解疑答难,并不断完善导学案。 3.一对一讨论过后,再进行组内讨论,互相解决疑难问题。同时确定好展 示和点评的同学,并做好准备。展示的同学去黑板板书展示的内容。 4.通过讨论小组内的每一位组员都能把导学案的问题弄明白,搞清楚。 5.讨论的同时,注意用红色笔修改完善导学案。 注意:站起讨论时要轻轻地将凳子放到桌子下面,讨论达标后自主坐下。
目标引领方向,奋斗点燃激情!
自主纠错
要求: 1.面对疑难不要慌张,认真分析问题涉及的知 识与方法,用红笔进行方法与总结; 2.写出题目规范的解答过程,小题也要写出解 答过程;自己解决不了的题目用红笔标出,以 备讨论时解决。
合抱之木,生于毫末;九层之台,起于垒土;千里之行,始于足下。 ——老子
预习导学
当x=0时,y最小值为0
向下
y轴 (直线x=0)
(0,0)
在对称轴的左侧,y随x的增大而增大;在对称 轴的右侧,y随x的增大而减小.
当x=0时,y最大值为0
y 2x2
y 2 x2 3
1、根据左边已画好的函数图象填空:
华师版九年级数学下册教学课件(HS) 第26章 二次函数 二次函数y=ax2的图象与性质

y
O
x
5.若抛物线y=ax2 (a ≠ 0),过点(-1,2).
(1)则a的值是
;2
(2)对称轴是
,y轴开口
. 向上
(3)顶点坐标是
(,0顶,0)点是抛物线上的最 值 .
小
抛物线在x轴的 方(上除顶点外).
(4) 若A(x1,y1),B(x2,y2)在这条抛物线上,且x1<x2<0, 则y1 y>2.
. 减小
y
O
x
y x
O
3、如右图,观察函数y=( k-1)x2的图象,则k的取值范围
是
.
k>1
4、说出下列抛物线的开口方向、对称轴和顶点:
y 3x2
y 3x 2 y 1 x2 3
y 1 x2 3
开口方向 向上 向下 向上 向下
对称轴 y轴 y轴 y轴 y轴
顶点 (0,0) (0,0) (0,0) (0,0)
4.5
2 0.5
0 0.5 2 4.5 8 ···
思考1:从二次函数 关系?
y x2
y 1 x2 , y x开2 ,口y大小2与x2a的大小有什么
2
y 2x2
8
6
4
y 1 x2
2
2
-4
-2
2
4
当a>0时,a越大,开口越小.
练一练:在同一直角坐标系中,画出函数
的y 图象1.x2 , y 2x2
讲授新课
一 二次函数y=ax2的图象
典例精析
例1 画出二次函数y=x2的图象. 1. 列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应 值:
x
…
-3
华师版九年级数学下册_26.2.2 二次函数y=ax2+bx+c的图象与性质

(h,k)
(h,0) (0,k) (0,0)
直线x=h
y轴
感悟新知
特别解读
知4-讲
1. 抛物线y=ax2,y=ax2+k,y=a(x-h)2,y=a(x-h)2+k中a
的值相等,所以这四条抛物线的形状、开口方向完全
一样,故它们之间可通过互相平移得到.
2. 抛物线的平移规律是“左加右减,上加下减”,不同的
而减小. 其中正确结论有__①__③__④__.
解题秘方:紧扣二次函数y=a(x-h)2+k 的图象和 性质逐一判断.
感悟新知
知3-练
解:∵ a=-1<0,∴抛物线的开口向下,故①正确; 对称轴为直线x=-1,故②错误;顶点坐标为 (-1,3),故③正确;当x>1 时,y 随x 的增大 而减小,故④正确.
y轴
当x<0 时,y随x的 当x<0 时,y 随x 的
增大而减小;当x> 增大而增大;当x>
0 时,y随x的增大而 0 时,y 随x的增大
增大
而减小
当x=0 时,y最小值=k 当x=0 时,y最大值=k
感悟新知
知1-讲
3. 二次函数y=ax2+k 的图象的画法 (1)描点法:即按列表→描点→连线的顺序作图. (2)平移法:将二次函数y=ax2 的图象,向上(k > 0)或向 下(k < 0)平移|k| 个单位,即可得到二次函数y=ax2+k 的图象.
解:由图象知,对于一切x的值,总有y ≤ 2.
感悟新知
知4-练
4-1. [中考·湖州] 将抛物线y=x2 向上平移3 个单位,所得抛 物线的表达式是( A ) A. y=x2+3 B. y=x2-3 C. y=(x+3)2 D. y=(x-3)2
华师大版九年级数学下册电子课本课件【全册】

华师大版九年级数学下册电子课本 课件【全册】
第27章 圆
华师大版九年级数学下册电子课本 课件【全册】
27.1 圆的认识
华师大版九年级数学下册电子课本 课件【全册】
1. 圆的基本元素
华师大版九年级数学下册电子课本 课件【全册】
2. 二次函数y=ax2+bx+c的图象 与性质
华师大版九年级数学下册电子课本 课件【全册】
3. 求二次函数的表达式
华师大版九年级数学下册电子课本 课件【全册】
26.3 实践与探索
华师大版九年级数学下册电子课 本课件【全册】目录
0002页 0044页 0070页 0100页 0145页 0173页 0175页 0213页 0230页 0281页 0283页 0310页 0345页 0次函数的图象与性质 2. 二次函数y=ax2+bx+c的图象与性质 26.3 实践与探索 27.1 圆的认识 2. 圆的对称性 27.2 与圆有关的位置关系 2. 直线与圆的位置关系 27.3 圆中的计算问题 第28章 样本与总体 1. 普查和抽样调查 28.2 用样本估计总体 2. 简单随机抽样调查可靠吗 1. 借助调查作决策
华师大版九年级数学下册电子课本 课件【全册】
2. 圆的对称性
华师大版九年级数学下册电子课本 课件【全册】
第26章 二次函数
华师大版九年级数学下册电子课本 课件【全册】
26.1 二次函数
华师大版九年级数学下册电子课本 课件【全册】
26.2 二次函数的图象与性质
华师大版九年级数学下册电子课本 课件【全册】
1. 二次函数y=ax2的图象与性质
第27章 圆
华师大版九年级数学下册电子课本 课件【全册】
27.1 圆的认识
华师大版九年级数学下册电子课本 课件【全册】
1. 圆的基本元素
华师大版九年级数学下册电子课本 课件【全册】
2. 二次函数y=ax2+bx+c的图象 与性质
华师大版九年级数学下册电子课本 课件【全册】
3. 求二次函数的表达式
华师大版九年级数学下册电子课本 课件【全册】
26.3 实践与探索
华师大版九年级数学下册电子课 本课件【全册】目录
0002页 0044页 0070页 0100页 0145页 0173页 0175页 0213页 0230页 0281页 0283页 0310页 0345页 0次函数的图象与性质 2. 二次函数y=ax2+bx+c的图象与性质 26.3 实践与探索 27.1 圆的认识 2. 圆的对称性 27.2 与圆有关的位置关系 2. 直线与圆的位置关系 27.3 圆中的计算问题 第28章 样本与总体 1. 普查和抽样调查 28.2 用样本估计总体 2. 简单随机抽样调查可靠吗 1. 借助调查作决策
华师大版九年级数学下册电子课本 课件【全册】
2. 圆的对称性
华师大版九年级数学下册电子课本 课件【全册】
第26章 二次函数
华师大版九年级数学下册电子课本 课件【全册】
26.1 二次函数
华师大版九年级数学下册电子课本 课件【全册】
26.2 二次函数的图象与性质
华师大版九年级数学下册电子课本 课件【全册】
1. 二次函数y=ax2的图象与性质
初中数学华东师大九年级下26.2 二次函数的图象与性质(第3课时)

6.若一次函数 y= ax + b 的图象经过第二、三、四象限,
则二次函数y = ax2 + bx - 3的大致图象是
( C)
y
y
y
y
ox -3
A
ox -3
B
ox -3
C
ox -3
D
7.在同一直角坐标系中,二次函数y=ax2+bx+c 与一次函数y=ax+c的大致图象可能是 (C )
y
y
y
y
ox
ox
1.y 2x2 12 x 13; 2.y 5x2 80 x 319;
3.y 2 x 1 x 2; 4.y 32x 12 x.
2
例:指出抛物线: y x2 5x 4 的开口方向,求出它的对称轴、顶点坐 标、与y轴的交点坐标、与x轴的交点坐 标。并画出草图。
在x轴上,求c的值。
变化:抛物线y=x2-4x+c的顶点在 y=x+1上,求c的值。
解题时可以考虑多种方法
已知抛物线y=-3x2-2x+m的顶点在
1 直线 y=3x+3 上,求m的值
例5:抛物线y=2x2+bx的对称轴在 y轴的右侧。求b的取值范围。
例6:已知二
次函数 y m x2 2(m 2)x m 3
A.直线y = x上 B.直线y = - x上
C.x轴上
D.y轴上
)
3.若二次函数y=ax2 + 4x+a- 1的最小值是2,则a的值是 A
A. 4
B. -1
C. 3
D.4或-1
4.若二次函数 y=ax2 + b x + c 的图象如下,与x
华东师大版九年级数学下册 26.2.1 二次函数y=ax2的图象与性质【名校课件+集体备课】

在对称轴左侧递增 在对称轴右侧递减
新课进行时
典例精析
例1 已知二次函数y=x2. (1)判断点A(2,4)在二次函数图象上吗? (2)请分别写出点A关于x轴的对称点B的坐标,关 于y轴的对称点C的坐标,关于原点O的对称点D的 坐标; (3)点B、C、D在二次函数y=x2的图象上吗?在二 次函数y=-x2的图象上吗?
6
课后作业
课后作业
1、完成教材本课时对应习题; 2、完成同步练习册本课时的习题。
文本
文本
文本
文本
谢谢欣赏
THANK YOU FOR LISTENING
3.图象关于y轴对称;
4.顶点( 0 ,0 ); 5.图象有最低点.
o
x
新课进行时
说说二次函数y=-x2的图象有哪些性质,与同伴交流。
1.y=-x2是一条抛物线; 2.图象开口向下; 3.图象关于y轴对称; 4.顶点( 0 ,0 ); 5.图象有最高点.
y
o
x
y=-x2
新课进行时
知识要点
二次函数y=ax2 的图象性质: 1. 顶点都在原点; 2. 图像关于y轴对称; 3.当a>0时,开口向上; 当a<0时,开口向下.
们的对称轴, ∴OA=OB, ∴在长方形ABCD内,左边阴影部分面积等于右
边空白部分面积,∴S阴影部分面积之和=2×8=16.
新课进行时
方法总结
二次函数y=ax2的图象关于y轴对称,因此左右 两部分折叠可以重合,在二次函数比较大小中,我 们根据图象中点具有的对称性转变到同一变化区域 中(全部为升或全部为降),根据图象中函数值高低去 比较;对于求不规则的图形面积,采用等面积割补 法,将不规则图形转化为规则图形以方便求解。
华师大版九年级数学下册第二十六章《二次函数的图象与性质(第3课时)》优质公开课课件

线
.
4、把抛物线 y=2x 2 向 平移 个单位,
可得到抛物线 y=2(x+-13)) 22
5、把抛物线
向 平移 个单位,
可得到抛物线 yyy==--22323x(x2(x+-258))x228
6、把抛物线 yy=22((xx+-13) 22
向 平移 个单位, 可得到抛物线 y=2x 2
二次函数y=a(x-h)2的性质
1.顶点坐标与对称轴 2.位置与开口方向
3.增减性与最值
抛物线
y=a(x-h)2 (a>0)
y=a(x-h)2 (a<0)
顶点坐标
(h,0)
(h,0)
对称轴
直线x=h
直线x=h
位置 在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
开口方向
向上
向下
增减性 最值
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在同一个直角坐标系里画出
函数y 1 x2与y 1 x 22
2
2
的图象.
描点,连线
y 20
16
y 1 x2 2
观察这两个12函数的图y 1象x ,22
它们有什么84关系? 2
2
x
-12 -10 -8 -6 -4 -2 0 2 4 6 8 10 12 -2
描点,连线
y
20
y 1 x2 2
当x=h时,最小值为0.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
当x=h时,最大值为0.
开口大小 a 越大,开口越小.
a 越小,开口越大.
九年级数学下册 26.2 二次函数的图象与性质(第3课时)课件 (新版)华东师大版

第十五页,共22页。
二次函数(hánshù)y=a(x-h)2的性 质1.顶点(dǐngdiǎn)坐标与
对2称.位轴置(wèi zhi)与开口 方3.向增减性与最值
抛物线
y=a(x-h)2 (a>0)
顶点坐标
(h,0)
对称轴
直线x=h
位置 在x轴的上方(除顶点外)
开口方向
向上
增减性 最值
在对称轴的左侧,y随着x的增大而减小. 在对称轴 的右侧, y随着x的增大而增大.
与y= x22的图象有什么关系?它2是
轴对称图形吗?它的对称轴和顶
点坐标分别是什么?
第六页,共22页。
直线x=2
y
O2
x
顶图点象是(d轴ǐn对gd称iǎ图n形)坐(t 对称轴是是点平(行2,于0).
y轴的直线:x=2.
函数y= 1(x-2)2的图象与y= 1x2 的图象有2 什么关系?它是轴对2称 图形吗?它的对称轴和顶点 (dǐngdiǎn)坐标分别是什么?
1
(5)y=- 2 (x+ 3)2
第十八页,共22页。
3、把抛物线
向左右平
移43 个单位 可得到(dédào
(dānwèi), 抛物
线
.
第十九页,共22页。
4、把抛物线 y=2x2 向 平移 个单位, 可得到抛物线
第二十页,共22页。
5、把抛物线 向 平移 个单位,
可得到抛物线 yy=- 223x(x2 +28)2x 8
当x=h时,最小值为0.
a 越大,开口越小.
第十六页,共22页。
y=a(x-h)2 (a<0)
(h,0) 直线x=h
在x轴的下方( 除顶点外)
二次函数(hánshù)y=a(x-h)2的性 质1.顶点(dǐngdiǎn)坐标与
对2称.位轴置(wèi zhi)与开口 方3.向增减性与最值
抛物线
y=a(x-h)2 (a>0)
顶点坐标
(h,0)
对称轴
直线x=h
位置 在x轴的上方(除顶点外)
开口方向
向上
增减性 最值
在对称轴的左侧,y随着x的增大而减小. 在对称轴 的右侧, y随着x的增大而增大.
与y= x22的图象有什么关系?它2是
轴对称图形吗?它的对称轴和顶
点坐标分别是什么?
第六页,共22页。
直线x=2
y
O2
x
顶图点象是(d轴ǐn对gd称iǎ图n形)坐(t 对称轴是是点平(行2,于0).
y轴的直线:x=2.
函数y= 1(x-2)2的图象与y= 1x2 的图象有2 什么关系?它是轴对2称 图形吗?它的对称轴和顶点 (dǐngdiǎn)坐标分别是什么?
1
(5)y=- 2 (x+ 3)2
第十八页,共22页。
3、把抛物线
向左右平
移43 个单位 可得到(dédào
(dānwèi), 抛物
线
.
第十九页,共22页。
4、把抛物线 y=2x2 向 平移 个单位, 可得到抛物线
第二十页,共22页。
5、把抛物线 向 平移 个单位,
可得到抛物线 yy=- 223x(x2 +28)2x 8
当x=h时,最小值为0.
a 越大,开口越小.
第十六页,共22页。
y=a(x-h)2 (a<0)
(h,0) 直线x=h
在x轴的下方( 除顶点外)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-6
-4
-2
2
4
6
8
10
直线x=-2
1 2 函数 y 2 x 2 1 2
的图象可以看成由 y x 的图象向 _____ 右 平移___ 2 个单 2 位得到,它们的形状和开口大小相同
1 2 函数y x 2 的图象可以看成由 1 2 2 y x 的图象向 ____ 左 平移 ___ 2 个单位 2
得到,它们的形状和开口大小相同
这里的平移方向有什么规律?
2 函数y=a(x-h) (a≠0)的图象和
性质
1.函数y=a(x-h)2(a≠0)的图象可 由函数y=ax2的图象平移得到. 当h>0 时,向___ h 个单位 右 平移___ 当h<0 时,向___ ____个单位 左 平移|h| 对称轴为:_________. ____ 直线x=h 顶点为(h,0)
二次函数y=a(x-h)2的性质
1.顶点坐标与对称轴 2.位置与开口方向 3.增减性与最值 抛物线 顶点坐标 对称轴 位置 y=a(x-h)2 (a>0) (h,0) 直线x=h 在x轴的上方(除顶点外) 向上
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
y=a(x-h)2 (a<0) (h,0) 直线x=h 在x轴的下方( 除顶点外) 向下
y
在同一个直角坐标系里画出 1 2 1 2 函数 y x 和 y x 2 的图 2 2 象
想一想, 这个函数的图象和 性质会是什么样?
列表描点,连线
y
20
1 2 y x 2
1 2 y x 2 2
16
观察函数 与 的 图象,它们有什么关系?
4 2 0 -2 -12 -10 -8 -6 -4 -2 2 4 6 8 10
3、把抛物线
2 右 y=2x 向左平
可得到抛物 移4 3 个单位,
线 .
4、把抛物线 向
2 y=2x
平移
个单位,
2 2 y=2(x-1) y=2(x+3)
可得到抛物线
5、把抛物线 向 平移 个单位,
22 2 2 2 (x-5) (x+2) yy=2 x 8 x 8 可得到抛物线 y=33
10
y
8
y=x2+1
y=x2 y=x2-2
5
4
y
2
y=-x2+3
5
6
4
-10
-5
O
-2
x
10
2
y=-x2 y=-x2-2
-4
-10 -5
O
-2
x
10
-6
-8
当a>0时,抛物线y=ax2+k的开口 向上 ,对称轴 是 y轴 ,顶点坐标是(0,k),在对称轴的左侧,y随x的 增大而 减小,在对称轴的右侧,y随x的增大而 增大, 当x= 0 时,取得最 小 值,这个值等于 k ; 当a<0时,抛物线y=ax2+k的开口 向下,对称轴 是y轴 ,顶点坐标是(0,k),在对称轴的左侧,y随x的 增大而 增大,在对称轴的右侧,y随x的增大而 减小, 当x= 0 时,取得最 大 值,这个值等于 k 。
y
的图象有什么关系 ? 它是轴对
称图形吗 ? 它的对称轴和顶点 坐标分别是什么?
y
直线x=2
顶点坐标 图象是轴对称图形 对称轴是平行于 是点(2,0). y轴的直线:x=2.
x
O
2
1 1 函数 y= (x-2)2 的图象与 y= x2 2 2
的图象有什么关系 ? 它是轴对 称图形吗 ? 它的对称轴和顶点 坐标分别是什么?
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
开口方向
增减性 最值
当x=h时,最小值为0.
a 越大,开口越小.
当x=h时,最大值为0.
a 越小,开口越大.
1、说出下列抛物线的开口方向、 顶点坐标和对称轴:
( 1) (3)
2 y=(x+1)
(2)
2 y=-(x-5)
在对称轴(直线:x=2) 顶点是最低点 , 函数 左侧(即x<2时), y的值 有最小值 . 当 x=2 时 , 在对称轴 ( 直线 :x=2) 随x的增大而减小,. 最小值是 0..时), y的值 右侧 ( 即 x>2 O 2 x 随x的增大而增大,. 1 x取哪些值时,函数y= (x-1)2的值 2 随x值的增大而减小?x取哪些值 1 时,函数y= (x-1)2的值随x的增大 2 而增大?
1 2 y 8 x 2 2
12
1 2 y x 2
x
12
列表描点,连线
y
20
1 2 y x 2
函数 与 的 图象有什么关系?说出它 1 y x 2 的顶点坐标和对称轴 2
8 4 2 0 -2
2
1 16 2 y x 2 2 12
1 2 y x 2
x 12
-12 -10 -8
函数y=a(x-h)2(a≠0) 的图象和性质
2.当a>0时,抛物线在x轴的上方 (除顶点外),它的开口向上,并 且向上无限伸展; 当a<0时,抛物线在x轴的下方 (除顶点外),它的开口向下,并 且向下无限伸展.
直线 x=h
3.当a>0时,在对称轴(x=h)的左侧,y 随着x的增大而减小;在对称轴(x=h) 右侧,y随着x的增大而增大;当x=h时 函数y的值最小(是0). 当a<0时,在对称轴(x=h)的左侧,y随 着x的增大而增大;在对称轴(x=h)的 右侧,y随着x增大而减小;当x=h时,函 数y的值最大(是0).
2 2 6、把抛物线 y=2(x+3) y=2(x-1)向 Nhomakorabea平移
个单位,
2 y=2x
可得到抛物线
在同一个直角坐标系里画出
1 1 2 2 函数 y x 与 y x 2 2 2
的图象.
列表,描点,连线 1
y
y
20 16 12 8 4 2 -12 -10 -8 -6 -4 -2 0 -2 2 4
2
x
2
1 2 y x 2 2
x 6 8 10 12
两个二次函数的图象 二次项系数 形状相同 ,可以看作是 1 2 相同 抛物线 y=a>0, x 整体 2 沿 x 轴向右平移了 2 开口都向上 , x O 2 个单位 1 2 1 2 函数 y= (x-2) 的图象与 y= x 2 2
(第3课时)
y x2
二次函数y=ax2的性质
y x2
1.抛物线y=ax2的顶点是原点, 对称轴是y轴.
2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外), 它的开口向上,并且向上无限伸展; 当a<0时,抛物线y=ax2在x轴的下方(除顶点外), 它的开口向下,并且向下无限伸展.
3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对 称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小. 当a<0时,在对称轴的左侧,y随着x的增大而增大;在对 称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.
2 2(x-1)
2 y=y=2(x-3) (4)
1 2 y=- (x+ 3) ( 5) 2
2、根据下列函数的解析式回答 当x为何值时,y随x的增大而 增大? (1)
2 y=(x+1)
(2)
2 y=-(x-5)
2 2(x-1)
(3)
2 y=y=2(x-3) (4)
1 2 (5)y=- 2 (x+ 3)
