广东省14市2016届高三上学期期末考试数学文试题分类汇编:立体几何
【全国百强校】广东省广州市执信中学2016届高三上学期期末考试数学(文)试题

2015-2016学年度第一学期高三级(文科)数学期末考试试卷本试卷分选择题和非选择题两部分,共4页,满分为150分.考试用时120分钟.第一部分选择题(共 60 分)一、选择题:共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.解已知全集R U =,集合},1|{},01|{≥=<-=x x B xx x A 则集合}0|{≤x x 等于( * ) A .B A B .B A C .)(B A C U D .)(B A C U 2.已知复数()πθθθ<≤+=0sin cos i z ,则使12-=z 的θ的值为( * ) A. 0 B.4π C. 2πD. 43π3.设γβα,,为平面,l n m ,,为直线,则β⊥m 的一个充分条件是( * ) A .l m l ⊥=⊥,,βαβαB .βαα⊥⊥⊥n m n ,,C .αγβγα⊥⊥⊥m ,,D . γβγαγα⊥=⊥,,m 4.设函数)2)(21cos(3)21sin()(πθθθ<+-+=x x x f ,且其图像关于y 轴对称,则函数()y f x =在下列区间中单调递减的是( * )A .)2,0(πB .),2(ππC .)4,2(ππ--D .)2,23(ππ5.某林区的的森林蓄积量每年比上一年平均增长%4.10,要增长到原来的x 倍,需经过y 年,则函数)(x f y =的图象大致为( * )6.据《法制晚报》报道,2009年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共28800人,图1是对这28800人血液中酒精含量进行检测所得结果的频率分布直方图,从左到右各直方块表示的人数依次记为1A 、2A 、……、8A (例如2A 表示血液酒精浓度在30~40 mg/100 ml 的人数),图2是对图1中血液酒精浓度在某一范围内的人数进行统计的程序框图。
这个程序框图输出的=s ( * )A.24480B.24380C. 23040D. 231407.某几何体的三视图如右图,其正视图中的曲线部分为半个圆弧,则该几何体的表面积为( * )A .219cm π+ B .2224cm π+C. 210624cm π++ D .213624cm π++8.若||2||||a b a b a =-=+,则向量b a +与a 的夹角为( * ) A .6π B .3π C .32πD .65π9.已知抛物线的顶点在原点,焦点在x 轴的正半轴上,若抛物线的准线与双曲线20522=-y x 的两条渐近线围成的三角形的面积等于54,则抛物线的方程为( * ) A .x y 42= B .x y 82= C .y x 42= D .y x 82=10.已知圆222:r y x O =+,点)0(),,(≠ab b a P 是圆O 内的一点,过点P 的圆O 的最短弦在直线1l 上,直线2l 的方程为2r ay bx =-,那么( * )A .21//l l 且2l 与圆O 相交 B.21l l ⊥且2l 与圆O 相切 C .21//l l 且2l 与圆O 相离 D.21l l ⊥且2l 与圆O 相离图12cm3cm 侧视图3cm2cm俯视图2cm正视图图211.已知椭圆C 的方程为13422=+y x ,过C 的右焦点F 的直线与C 相交于A 、B 两点,向量)4,1(--=m ,若向量OF m OB OA --与共线,则直线AB 的方程是( * )A .022=--y xB .022=-+y xC .022=+-y xD .022=++y x12.已知函数2|log |,02()sin(),2104x x f x x x π<<⎧⎪=⎨≤≤⎪⎩,若存在实数1x ,2x ,3x ,4x ,满足1234x x x x <<<,且1234()()()()f x f x f x f x ===,则3412(2)(2)x x x x -⋅-⋅的取值范围是( * )A .(4,16)B .(0,12)C . (9,21)D .(15,25)第二部分非选择题 (共 90 分)二.填空题:本大题共4小题, 每小题5分, 共20分. 把答案填在答卷的相应位置 13.已知等差数列{}n a 的公差为2,若431,,a a a 成等比数列,则2a =____14.已知函数x x x f 4ln )(+=,求曲线)(x f 在点(1,(1))f 处的切线方程__________________ 15.在正三棱锥S ABC -中,M 是SC 的中点,且AM SB ⊥,底面边长22AB =,则正三棱锥S ABC -的体积为 ,其外接球的表面积为 .16.已知)(x f 是定义在R 上的增函数,函数)1(-=x f y 的图象关于点(1,0)对称.若对任意的R y x ∈,,不等式0)8()216(22<-++-y y f x x f 恒成立,则当3>x 时,22y x +的取值范围是_______三.解答题:必做大题共5小题,共60分;选做大题三选一,共10分;解答应写出文字说明、证明过程或演算步骤17.(本小题满分共12分)已知函数()()sin 03f x x πωω⎛⎫=-> ⎪⎝⎭图象的相邻的两条对称轴之间的距离为2π. (1)求函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的值域;(2)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,已知sin sin sin sin cos21A B B C B ⋅+⋅+=且()0,,2f C C ππ⎛⎫=∈ ⎪⎝⎭,求三边长之比::a b c .18 .(本小题满分共12分)为了美化城市环境,某市针对市民乱扔垃圾现象进行罚款处理。
广东省14市2016届高三数学上学期期末考试精彩试题分类总汇编三角函数理

A. 1 2
B. 2 2
C. 3 2
D. 3 3
12、(市 2016 年普通高考测试(一))已知 sin 2 ,则 cos( 2 ) = 3
A、- 5 3
B、- 1 9
C、 1 9
D、 5 3
13、(市
2016
届高三第二次统测(期末))已知函数
f
(x)
2sin x
6
的最小正周期为
,则函数
y
f
2、(市 2016 届高三上期末)在平面,已知四边形 ABCD,CD⊥AD,∠CBD= ,AD=5,AB 12
=7,且 cos2∠ADB+3cos∠ADB=1,则 BC 的长为
3、(市 2016 届高三教学质量检测(一))在 ABC中,角 A 、 B 、C 的对边分别为 a 、b 、
c , M 是 BC 的中点, BM 2 , AM c b ,则 ABC面积的最大值为
省 14 市 2016 届高三上学期期末考试数学理试题分类汇编
三角函数
一、选择题
1、(市 2016 届高三上期末)函数 f (x) sin(x )( 0|, | ) 的部分图象如图所示, 2
如果
x1,
x2
(
6
,
3
)
,且
f (x1)
f (x2 ) ,则
f
( x1 x2 ) 等于 2
A、 1 2
2a sin A (2b c)sin B (2c b)sin C.则 A 的大小是 .
(A) 1 , (B) 1 , (C) 1 , (D) 1 ,
4
42
2
22
7、(市 2016 届高三第一次高考模拟考试)已知 cos 1 , 0 ,则 tan
广东省广州市执信中学2016届高三数学上学期期末考试试题文

...x 3 2x 4 20 时,x32 x 4 24 2 8 212,当 t 1 时,往下平移,x 1 x 2 的值越大, 因为当 tx 1x 21 1x 3 2 x 4222 10 20,所以x 3 2 x 42的取值X 围是0,12 ,应选 B .x 1 x 21x 1x 222法二、log 2 x 1 log 2 x 2 log 2 x 1 log 2 x 2 0 log 2 x 1x 2 log 2 1x 1 x 21x 3x 4 6 x 412 x 32( x 32)( x 4 2) ( x 3 2)( x 4 2) (x 32)(12 x 32) x 3212x 3 20( x 36)2 16 (2 x 3 4)x 1x 213 解:∵a 4=a 1+6,a 3=a 1+4,a 1,a 3,a 4 成等比数列,22=a ×〔 a +6〕,解得 a =﹣ 8,∴a =a +2=﹣ 6.∴a=a ?a ,即〔 a +4〕3 141111 2 114解 f (1)(ln x 4) x(ln x 4) x3 ln x3 ln14又∵ f ( x)x 2x 2,∴ f (1)23 .1∴ f ( x) 在点 (1, f (1))处的切线方程为: y4 3(x 1) ,即 3x y7 0.15. 4,12解:取AC 中点D ,那么SDAC ,BDAC ,又∵ SDBD D ,∴AC平面 SBD ,3∵ SB平面 SBD ,∴ AC SB ,又∵ AMSB , AM ACA ,∴ SB平面 SAC ,∴SASB ,SASCSB ,根据对称性可知 SASC ,从而可知, SB , SC 两两垂直,如下列图所示,将其补2,∴V S1 12 24为立方体,其棱长为ABCVC ASB2 ,其外接球即为立方体的外接球,32 3半径 r3 23,外表积 S4 312 .216 解:∵函数 y=f 〔x ﹣ 1〕的图象关于点〔 1, 0〕对称∴函数 y=f 〔 x 〕的图象关于点〔 0, 0〕对 称,即函数 y=f 〔 x 〕为奇函数,那么 f 〔﹣ x 〕 =﹣ f 〔x 〕 又∵ f 〔 x 〕是定义在 R 上的增函数且f 〔 x 2﹣ 6x+21〕 +f 〔y 2﹣ 8y 〕< 0 恒成立∴〔 x 2﹣ 6x+21〕<﹣ f 〔 y 2﹣ 8y 〕=f 〔 8y ﹣y 2 〕成立∴ x 2﹣ 6x+21< 8y ﹣ y 2 ∴〔 x ﹣ 3〕2+〔 y ﹣ 4〕2< 4 恒成立设 M 〔 x ,y 〕,那么当 x > 3 时, M 表示以〔 3, 4〕为圆心 2 为半径的右半圆内的任意一点,那么 x 2+y 2表示在半圆内任取一点与原点的距离的平方, 由图可知, 最短距离为OA=,最大距离OB=OC+BC=5+2=7∴13< x 2+y 2< 490 时,32 x 4 24 2 8 212,当 t 1 时,往下平移,x 1 x 2 的值越大, 因为当 tx 1x 21 1x 3 2 x 4222 10 20,所以x 3 2 x 42的取值X 围是0,12 ,应选 B .x 1 x 21x 1x 222法二、log 2 x 1 log 2 x 2 log 2 x 1 log 2 x 2 0 log 2 x 1x 2 log 2 1x 1 x 21x 3x 4 6 x 412 x 32( x 32)( x 4 2) ( x 3 2)( x 4 2) (x 32)(12 x 32) x 3212x 3 20( x 36)2 16 (2 x 3 4)x 1x 213 解:∵a 4=a 1+6,a 3=a 1+4,a 1,a 3,a 4 成等比数列,22=a ×〔 a +6〕,解得 a =﹣ 8,∴a =a +2=﹣ 6.∴a=a ?a ,即〔 a +4〕3 141111 2 114解 f (1)(ln x 4) x(ln x 4) x3 ln x3 ln14又∵ f ( x)x 2x 2,∴ f (1)23 .1∴ f ( x) 在点 (1, f (1))处的切线方程为: y4 3(x 1) ,即 3x y7 0.15. 4,12解:取AC 中点D ,那么SDAC ,BDAC ,又∵ SDBD D ,∴AC平面 SBD ,3∵ SB平面 SBD ,∴ AC SB ,又∵ AMSB , AM ACA ,∴ SB平面 SAC ,∴SASB ,SASCSB ,根据对称性可知 SASC ,从而可知, SB , SC 两两垂直,如下列图所示,将其补2,∴V S1 12 24为立方体,其棱长为ABCVC ASB2 ,其外接球即为立方体的外接球,32 3半径 r3 23,外表积 S4 312 .216 解:∵函数 y=f 〔x ﹣ 1〕的图象关于点〔 1, 0〕对称∴函数 y=f 〔 x 〕的图象关于点〔 0, 0〕对 称,即函数 y=f 〔 x 〕为奇函数,那么 f 〔﹣ x 〕 =﹣ f 〔x 〕 又∵ f 〔 x 〕是定义在 R 上的增函数且f 〔 x 2﹣ 6x+21〕 +f 〔y 2﹣ 8y 〕< 0 恒成立∴〔 x 2﹣ 6x+21〕<﹣ f 〔 y 2﹣ 8y 〕=f 〔 8y ﹣y 2 〕成立∴ x 2﹣ 6x+21< 8y ﹣ y 2 ∴〔 x ﹣ 3〕2+〔 y ﹣ 4〕2< 4 恒成立设 M 〔 x ,y 〕,那么当 x > 3 时, M 表示以〔 3, 4〕为圆心 2 为半径的右半圆内的任意一点,那么 x 2+y 2表示在半圆内任取一点与原点的距离的平方, 由图可知, 最短距离为OA=,最大距离OB=OC+BC=5+2=7∴13< x 2+y 2< 490 时,32 x 4 24 2 8 212,当 t 1 时,往下平移,x 1 x 2 的值越大, 因为当 tx 1x 21 1x 3 2 x 4222 10 20,所以x 3 2 x 42的取值X 围是0,12 ,应选 B .x 1 x 21x 1x 222法二、log 2 x 1 log 2 x 2 log 2 x 1 log 2 x 2 0 log 2 x 1x 2 log 2 1x 1 x 21x 3x 4 6 x 412 x 32( x 32)( x 4 2) ( x 3 2)( x 4 2) (x 32)(12 x 32) x 3212x 3 20( x 36)2 16 (2 x 3 4)x 1x 213 解:∵a 4=a 1+6,a 3=a 1+4,a 1,a 3,a 4 成等比数列,22=a ×〔 a +6〕,解得 a =﹣ 8,∴a =a +2=﹣ 6.∴a=a ?a ,即〔 a +4〕3 141111 2 114解 f (1)(ln x 4) x(ln x 4) x3 ln x3 ln14又∵ f ( x)x 2x 2,∴ f (1)23 .1∴ f ( x) 在点 (1, f (1))处的切线方程为: y4 3(x 1) ,即 3x y7 0.15. 4,12解:取AC 中点D ,那么SDAC ,BDAC ,又∵ SDBD D ,∴AC平面 SBD ,3∵ SB平面 SBD ,∴ AC SB ,又∵ AMSB , AM ACA ,∴ SB平面 SAC ,∴SASB ,SASCSB ,根据对称性可知 SASC ,从而可知, SB , SC 两两垂直,如下列图所示,将其补2,∴V S1 12 24为立方体,其棱长为ABCVC ASB2 ,其外接球即为立方体的外接球,32 3半径 r3 23,外表积 S4 312 .216 解:∵函数 y=f 〔x ﹣ 1〕的图象关于点〔 1, 0〕对称∴函数 y=f 〔 x 〕的图象关于点〔 0, 0〕对 称,即函数 y=f 〔 x 〕为奇函数,那么 f 〔﹣ x 〕 =﹣ f 〔x 〕 又∵ f 〔 x 〕是定义在 R 上的增函数且f 〔 x 2﹣ 6x+21〕 +f 〔y 2﹣ 8y 〕< 0 恒成立∴〔 x 2﹣ 6x+21〕<﹣ f 〔 y 2﹣ 8y 〕=f 〔 8y ﹣y 2 〕成立∴ x 2﹣ 6x+21< 8y ﹣ y 2 ∴〔 x ﹣ 3〕2+〔 y ﹣ 4〕2< 4 恒成立设 M 〔 x ,y 〕,那么当 x > 3 时, M 表示以〔 3, 4〕为圆心 2 为半径的右半圆内的任意一点,那么 x 2+y 2表示在半圆内任取一点与原点的距离的平方, 由图可知, 最短距离为OA=,最大距离OB=OC+BC=5+2=7∴13< x 2+y 2< 490 时,32 x 4 24 2 8 212,当 t 1 时,往下平移,x 1 x 2 的值越大, 因为当 tx 1x 21 1x 3 2 x 4222 10 20,所以x 3 2 x 42的取值X 围是0,12 ,应选 B .x 1 x 21x 1x 222法二、log 2 x 1 log 2 x 2 log 2 x 1 log 2 x 2 0 log 2 x 1x 2 log 2 1x 1 x 21x 3x 4 6 x 412 x 32( x 32)( x 4 2) ( x 3 2)( x 4 2) (x 32)(12 x 32) x 3212x 3 20( x 36)2 16 (2 x 3 4)x 1x 213 解:∵a 4=a 1+6,a 3=a 1+4,a 1,a 3,a 4 成等比数列,22=a ×〔 a +6〕,解得 a =﹣ 8,∴a =a +2=﹣ 6.∴a=a ?a ,即〔 a +4〕3 141111 2 114解 f (1)(ln x 4) x(ln x 4) x3 ln x3 ln14又∵ f ( x)x 2x 2,∴ f (1)23 .1∴ f ( x) 在点 (1, f (1))处的切线方程为: y4 3(x 1) ,即 3x y7 0.15. 4,12解:取AC 中点D ,那么SDAC ,BDAC ,又∵ SDBD D ,∴AC平面 SBD ,3∵ SB平面 SBD ,∴ AC SB ,又∵ AMSB , AM ACA ,∴ SB平面 SAC ,∴SASB ,SASCSB ,根据对称性可知 SASC ,从而可知, SB , SC 两两垂直,如下列图所示,将其补2,∴V S1 12 24为立方体,其棱长为ABCVC ASB2 ,其外接球即为立方体的外接球,32 3半径 r3 23,外表积 S4 312 .216 解:∵函数 y=f 〔x ﹣ 1〕的图象关于点〔 1, 0〕对称∴函数 y=f 〔 x 〕的图象关于点〔 0, 0〕对 称,即函数 y=f 〔 x 〕为奇函数,那么 f 〔﹣ x 〕 =﹣ f 〔x 〕 又∵ f 〔 x 〕是定义在 R 上的增函数且f 〔 x 2﹣ 6x+21〕 +f 〔y 2﹣ 8y 〕< 0 恒成立∴〔 x 2﹣ 6x+21〕<﹣ f 〔 y 2﹣ 8y 〕=f 〔 8y ﹣y 2 〕成立∴ x 2﹣ 6x+21< 8y ﹣ y 2 ∴〔 x ﹣ 3〕2+〔 y ﹣ 4〕2< 4 恒成立设 M 〔 x ,y 〕,那么当 x > 3 时, M 表示以〔 3, 4〕为圆心 2 为半径的右半圆内的任意一点,那么 x 2+y 2表示在半圆内任取一点与原点的距离的平方, 由图可知, 最短距离为OA=,最大距离OB=OC+BC=5+2=7∴13< x 2+y 2< 490 时,3 2 x 4 2 4 2 8 2 12,当 t 1 时,往下平移, x 1 x 2的值越大, 因为当 t x 1x 2 1 1x 3 2 x 4 2 2 2 10 2 0,所以 x 3 2 x 4 2的取值X 围是 0,12 ,应选 B .x 1 x 21x 1x 222 法二、log 2 x 1 log 2 x 2 log 2 x 1 log 2 x 2 0 log 2 x 1x 2 log 2 1 x 1 x 2 1 x 3 x 4 6 x 4 12 x 32 ( x3 2)( x4 2) ( x 3 2)( x 4 2) (x 3 2)(12 x 3 2) x 32 12x 3 20 ( x 3 6)2 16 (2 x 3 4) x 1x 2 13 解:∵a 4=a 1+6,a 3=a 1+4,a 1,a 3,a 4 成等比数列,2 2 =a ×〔 a +6〕,解得 a =﹣ 8,∴a =a +2=﹣ 6.∴a =a ?a ,即〔 a +4〕3 14 1 1 1 1 2 1 14解 f (1) (ln x 4) x (ln x 4) x 3 ln x 3 ln14又∵ f ( x) x 2 x 2 ,∴ f (1) 2 3 . 1 ∴ f ( x) 在点 (1, f (1))处的切线方程为: y 4 3(x 1) ,即 3x y 7 0.15. 4,12 解:取AC 中点D ,那么SD AC ,BD AC ,又∵ SD BD D ,∴AC 平面 SBD , 3 ∵ SB 平面 SBD ,∴ AC SB ,又∵ AM SB , AM AC A ,∴ SB 平面 SAC ,∴ SA SB , SASC SB ,根据对称性可知 SA SC ,从而可知, SB , SC两两垂直,如下列图所示,将其补2,∴V S 1 1 2 2 4为立方体,其棱长为 ABC V C ASB 2 ,其外接球即为立方体的外接球,3 2 3 半径 r 3 2 3,外表积 S4 3 12 . 2 16 解:∵函数 y=f 〔x ﹣ 1〕的图象关于点〔 1, 0〕对称∴函数 y=f 〔 x 〕的图象关于点〔 0, 0〕对 称,即函数 y=f 〔 x 〕为奇函数,那么 f 〔﹣ x 〕 =﹣ f 〔x 〕 又∵ f 〔 x 〕是定义在 R 上的增函数且 f 〔 x 2﹣ 6x+21〕 +f 〔y 2﹣ 8y 〕< 0 恒成立∴〔 x 2﹣ 6x+21〕<﹣ f 〔 y 2﹣ 8y 〕=f 〔 8y ﹣y 2 〕成立∴ x 2﹣ 6x+21< 8y ﹣ y 2 ∴〔 x ﹣ 3〕2+〔 y ﹣ 4〕2< 4 恒成立 设 M 〔 x ,y 〕,那么当 x > 3 时, M 表示以〔 3, 4〕为圆心 2 为半径的右半圆内的任意 一点,那么 x 2+y 2表示在半圆内任取一点与原点的距离的平方, 由图可知, 最短距离为 OA=,最大距离 OB=OC+BC=5+2=7∴13< x 2+y 2< 490 时,3 2 x 4 2 4 2 8 2 12,当 t 1 时,往下平移, x 1 x 2的值越大, 因为当 t x 1x 2 1 1x 3 2 x 4 2 2 2 10 2 0,所以 x 3 2 x 4 2的取值X 围是 0,12 ,应选 B .x 1 x 21x 1x 222 法二、log 2 x 1 log 2 x 2 log 2 x 1 log 2 x 2 0 log 2 x 1x 2 log 2 1 x 1 x 2 1 x 3 x 4 6 x 4 12 x 32 ( x3 2)( x4 2) ( x 3 2)( x 4 2) (x 3 2)(12 x 3 2) x 32 12x 3 20 ( x 3 6)2 16 (2 x 3 4) x 1x 2 13 解:∵a 4=a 1+6,a 3=a 1+4,a 1,a 3,a 4 成等比数列,2 2 =a ×〔 a +6〕,解得 a =﹣ 8,∴a =a +2=﹣ 6.∴a =a ?a ,即〔 a +4〕3 14 1 1 1 1 2 1 14解 f (1) (ln x 4) x (ln x 4) x 3 ln x 3 ln14又∵ f ( x) x 2 x 2 ,∴ f (1) 2 3 . 1 ∴ f ( x) 在点 (1, f (1))处的切线方程为: y 4 3(x 1) ,即 3x y 7 0.15. 4,12 解:取AC 中点D ,那么SD AC ,BD AC ,又∵ SD BD D ,∴AC 平面 SBD , 3 ∵ SB 平面 SBD ,∴ AC SB ,又∵ AM SB , AM AC A ,∴ SB 平面 SAC ,∴ SA SB , SASC SB ,根据对称性可知 SA SC ,从而可知, SB , SC两两垂直,如下列图所示,将其补2,∴V S 1 1 2 2 4为立方体,其棱长为 ABC V C ASB 2 ,其外接球即为立方体的外接球,3 2 3 半径 r 3 2 3,外表积 S4 3 12 . 2 16 解:∵函数 y=f 〔x ﹣ 1〕的图象关于点〔 1, 0〕对称∴函数 y=f 〔 x 〕的图象关于点〔 0, 0〕对 称,即函数 y=f 〔 x 〕为奇函数,那么 f 〔﹣ x 〕 =﹣ f 〔x 〕 又∵ f 〔 x 〕是定义在 R 上的增函数且 f 〔 x 2﹣ 6x+21〕 +f 〔y 2﹣ 8y 〕< 0 恒成立∴〔 x 2﹣ 6x+21〕<﹣ f 〔 y 2﹣ 8y 〕=f 〔 8y ﹣y 2 〕成立∴ x 2﹣ 6x+21< 8y ﹣ y 2 ∴〔 x ﹣ 3〕2+〔 y ﹣ 4〕2< 4 恒成立 设 M 〔 x ,y 〕,那么当 x > 3 时, M 表示以〔 3, 4〕为圆心 2 为半径的右半圆内的任意 一点,那么 x 2+y 2表示在半圆内任取一点与原点的距离的平方, 由图可知, 最短距离为 OA=,最大距离 OB=OC+BC=5+2=7∴13< x 2+y 2< 49。
广东省14市2016届高三数学上学期期末考试试题分类汇编数列理

广东省14市2016届高三上学期期末考试数学理试题分类汇编数列一、选择题1、(清远市2016届高三上期末)已知数列{}n a 满足:111,(*)2nn n a a a n N a +==∈+,12(1)()1n n C a n λ=+-+,若{}n C 是单调递减数列,则实数λ的取值范围是( ) A 、λ13≥B 、λ13>C 、λ43≥D 、λ43> 2、(东莞市2016届高三上期末)已知各项为正的数列{}n a 的前n 项的乘积为n T ,点(2,15)n T n n -在函数12log y x =的图象上,则数列{}2log n a 的前10项和为(A )-140 (B )100 (C )124 (D )1563、(广州市2016届高三1月模拟考试)各项均为正数的等差数列{}n a 中,3694=a a ,则前12项和12S 的最小值为(A )78 (B )48 (C )60(D )724、(揭阳市2016届高三上期末)在等差数列{}n a 中,已知35710132,9a a a a a +=++=,则此数列的公差为 (A )13 (B )3 (C )12 (D )165、(清远市2016届高三上期末)已知数列{}n a 的前n 项和为22n S n n =-,则317a a +=( )A 、36B 、35C 、34D 、336、(汕尾市2016届高三上期末)已知是等差数列{}n a ,且28a a +=16,则数列{}n a 的前9 项和等于( )A.36B.72C.144D.2887、(湛江市2016年普通高考测试(一))设n S 为等差数列{}n a 的前n 项和,若11a =,公差d =2,2n n S S +-=36,则n =A 、5B 、6C 、7D 、88、(肇庆市2016届高三第二次统测(期末))设等差数列{}n a 的前n 项和为n S ,若11a =,315S =,则6S =(A )62 (B )66 (C )70 (D )74选择题答案:1、B2、C3、D4、A5、C6、B7、D8、 B 二、填空题1、(惠州市2016届高三第三次调研考试)设数列{}n a 的前n 项和为n S ,且121a a ==,{}(2)n n nS n a ++为等差数列,则数列{}n a 的通项公式n a = .2、(揭阳市2016届高三上期末)设n S 是数列{}n a 的前n 项和,且1111,n n n a a S S ++=-=,则数列{}n a 的通项公式n a = 3、(汕尾市2016届高三上期末)已知数列 为等比数列,,若数列满足则的前n 项和n S = .填空题答案1、12n n- 2、1,(1)1.(2)(1)n n n n -=⎧⎪⎨≥⎪-⎩3、1n n +三、解答题1、(潮州市2016届高三上期末)已知正项等差数列{}n a 的前n 项和为n S ,且满足215313a a a +=,756S =。
广东省14市2016届高三数学上学期期末考试试题分类汇编三角函数理

广东省14市2016届高三数学上学期期末考试试题分类汇编三角函数理广东省14市2016届高三上学期期末考试数学理试题分类汇编三角函数一、选择题1、(潮州市2016届高三上期末)函数()sin()(0,)2f x x πω?ω?=+><||的部分图象如图所示,如果12,(,)63x x ππ∈-,且12()()f x f x =,则12()2x x f +等于A 、12 BC D 、12、(潮州市2016届高三上期末)已知cos()63πθ+=-,则sin(2)6πθ-=A 、13 B 、23 C 、-13 D 、-233、(佛山市2016届高三教学质量检测(一))已知30π=x 是函数)2sin()(?+=x x f 的一个极大值点,则)(x f 的一个单调递减区间是() A .)32,6(ππ B .)65,3(ππ C .),2(ππD .),32(ππ4、(广州市2016届高三1月模拟考试)已知3s i n 5?=,且2?π??∈π,,函数()sin()(0)f x x ω?ω=+>的图像的相邻两条对称轴之间的距离等于2π,则4f π?? ???的值为(A )35-5- (C )35 (D )45 5、(惠州市2016届高三第三次调研考试)已知34cos sin =+θθ)40(πθ<<,则θθcos si n -的值为()A .32B .32-C .31D .31-6、(揭阳市2016届高三上期末)函数24()cos cos f x x x =-的最大值和最小正周期分别为(A )1,4π (B )1,42π (C )1,2π (D )1,22π7、(茂名市2016届高三第一次高考模拟考试)已知()=-παcos 12,0πα-<<,则tan α= ()C. D. 8、(茂名市2016届高三第一次高考模拟考试)将函数??? ??-=32sin )(πx x f 的图像向右平移3π个单位得到函数)(x g 的图像,则)(x g 的一条对称轴方程可以为()A. 43π=x π= C. 127π=x D. 12π=x 9、(汕头市2016届高三上期末)将函数sin()()6y x x R π=+∈的图象上所有点的纵坐标不变横坐标缩小到原来的倍,再把图象上各点向左平移4π个单位长度,则所得的图象的解析式为( ) A .)652sin(π+=x y B .)621sin(π+=x y C .)322sin(π+=x y D .)12521sin(π+=x y 10、(汕尾市2016届高三上期末)下列选项中是函数的零点的是()11、(韶关市2016届高三1月调研)22cos 165sin 15-= ( )A .12 B .2 C 12、(湛江市2016年普通高考测试(一))已知2sin 3α=,则cos(2)πα-=A B 、-19 C 、19 D13、(肇庆市2016届高三第二次统测(期末))已知函数()2sin 6f x x πω?=-的最小正周期为π,则函数()y f x =在区间0,2π??上的最大值和最小值分别是(A )2和2- (B )2和0 (C )2和1- (D)2和2-14、(珠海市2016=( ) A .1- BC .1 D.15、(佛山市2016届高三教学质量检测(一))已知21tan = x ,则)4(sin 2π+x =() A .101 B .51 C .53 D .10916、16、(汕头市2016) A 17、(韶关市2016届高三1月调研)已知函数()sin()(0,0)f x x ω?ωπ?=+>-<<的最小正周期是π,将函数()f x 图象向左平移3 π个单位长度后所得的函数图象过点(0,1)P ,则函数()sin()f x x ω?=+ () A.在区间[,]63ππ-上单调递减 B.在区间[,]63ππ-上单调递增 C.在区间[,]36ππ-上单调递减 D.在区间[,]36ππ-上单调递增18、(珠海市2016届高三上期末)如图是函数()cos()f x A x ω?=+的一段图像,则函数()f x 图像上的最高点坐标为( )A .(2)2k k Z π∈,, B .(2)k k Z π∈,, C .(22)6k k Z ππ-∈,, D .(2)12k k Z ππ-∈,,选择题答案:1、D2、C3、B4、B5、B6、B7、A8、A9、C 10、D 11、 C 12、B 13、C 14、C 15、D 16、D 17、B 18、D 二、填空题 1、(潮州市2016届高三上期末)在△ABC 中,内角A ,B ,C 所对应的边分别为a ,b ,c ,若(第5题图) 2-23π6πsin cos 0b A B =,且2b ac =,则a cb+的值为____2、(东莞市2016届高三上期末)在平面内,已知四边形ABCD ,CD ⊥AD ,∠CBD =12π,AD =5,AB =7,且cos2∠ADB +3cos ∠ADB =1,则BC 的长为 3、(佛山市2016届高三教学质量检测(一))在ABC ?中,角A 、B 、C 的对边分别为a 、b 、c ,M 是BC 的中点,2=BM ,b c AM -=,则A B C ?面积的最大值为.4、(广州市2016届高三1月模拟考试)已知()1cos 3θ+π=-,则s i n 22θπ?+= ??. 5、(茂名市2016届高三第一次高考模拟考试)CD CB AD AC AD AB ,AB D ABC 3,,3,===?且的一个三等分点为中在,则B cos =6、(汕头市2016届高三上期末)在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且.sin )2(sin )2(sin 2C b c B c b A a +++=则A 的大小是.7、(肇庆市2016届高三第二次统测(期末))在ABC ?中,角,,A B C 所对的边分别为,,a b c ,且cos cos 2sin a B b A C+=,2c =,角C 是锐角,则a b c ++的取值范围为 .8、(珠海市2016届高三上期末)如右下图,四边形ABCD 中,0135BAD ∠=,0120ADC ∠=,045BCD ∠=,060ABC ∠=,2BC =,则线段AC 长度的取值范围是.填空题答案 1、2 2、BCDA(第16题图)3、 4、-79 5、1867 6、,32π或 120 7、(]4,6 8、2)三、解答题1、(惠州市2016届高三第三次调研考试)如图所示,在四边形ABCD 中,D ∠=2B ∠,且1AD =,3CD =,cos 3B =.(Ⅰ)求△ACD 的面积;AB 的长.2、(揭阳市2016届高三上期末)已知a,b,c 分别是△ABC 内角A ,B ,C的对边,且sin cos A a C =(Ⅰ)求C 的值(Ⅱ)若2,c a b ==ABC 的面积3、(清远市2016届高三上期末)已知函数)(21cos 2sin 23)(2R x x x x f ∈--=,设ABC ?的内角C B A ,,的对应边分别为c b a ,,,且0)(,3==C f c .(1)求C 的值.(2)若向量)sin ,1(A m =与向量)sin ,2(B n =共线,求ABC ?的面积.4、(汕尾市2016届高三上期末)在锐角△ABC 中,角 A,B,C 的对边分别是a ,b ,c,若(1) 求角A 的大小; (2) 若a =3,△ABC 的面积 S=,求b + c 的值.5、(肇庆市2016届高三第二次统测(期末))在ABC ?中,角,,A B C 的对边分别为,,a b c ,ABCD。
广东省14市2016届高三上学期期末考试数学文试题分类汇编:选修(4-1与4-4)

广东省14市2016届高三上学期期末考试数学文试题分类汇编 选修4-1与选修4-41、(潮州市2016届高三上学期期末) (22)、(本小题满分10分)选修4-1:如图所示,已知AB 是圆O 的直径,AC 是弦,AD ⊥CE ,垂足为D ,AC 平分∠BAD 。
(I )求证:直线CE 是圆O 的切线; (II )求证:AC 2=AB•AD 。
(23)、(本小题满分10分)选修4-4:在直角坐标系xoy 中,圆C 的参数方程1cos (sin x y ϕϕϕ=+⎧⎨=⎩为参数)。
以O 为极点,x 轴的非负半轴为极轴建立极坐标系。
(I )求圆C 的极坐标方程; (II )射线OM :4πθ=学科网与圆C 的交点O 、P 两点,求P 点的极坐标。
2、(东莞市2016届高三上学期期末)(22).(本小题满分10分)选修4—1:几何证明选讲如图,已知圆O 的内接四边形BCED ,BC 为圆O 的直径,BC =2,延长CB 、ED 交于A 点,使得∠DOB =∠ECA ,过A 作圆O 的切线,切点为P 。
(I )求证:BD =DE ;(II )若∠ECA =45°,求AP 2的值。
(23).(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系xoy 中,以原点O 为极点,x 轴正半轴为极轴,建立极坐标系,已知曲线DCBAP图5C的参数方程是sin )sin )x cos y cos θθθθ⎧=+⎪⎨=-⎪⎩(θ为参数),曲线C 与l 的交点的极坐标为(2,3π)和(2,6π)。
(I )求直线l 的普通方程;(II)设P 点为曲线C 上的任意一点,求P 点到直线l 的距离的最大值。
3、(佛山市2016届高三教学质量检测(一)(期末) (22).(本小题满分10分)选修41-:几何证明选讲如图5,四边形ABCD 是圆内接四边形,BA 、CD 的延长线交于点P ,且AB AD =,2BP BC =. (Ⅰ) 求证:2PD AB =;(Ⅱ) 当2BC =,5PC =时,求AB 的长.(23).(本小题满分10分)选修44-:坐标系与参数方程选讲已知直线l 的方程为4y x =+,圆C 的参数方程为2cos 22sin x y θθ=⎧⎨=+⎩(θ为参数),以原点为极点,x 轴正半轴为极轴,建立极坐标系. (Ⅰ) 求直线l 与圆C 的交点的极坐标;(Ⅱ) 若P 为圆C 上的动点,求P 到直线l 的距离d 的最大值. 4、(广州市2016届高三1月模拟考试)(22)(本小题满分10分)选修4—1:几何证明选讲如图90ACB ∠=︒,CD AB ⊥于点D ,以BD 为直径的O e 与BC 交于点E . (Ⅰ)求证:BC CE AD DB ⋅=⋅;(Ⅱ)若4BE =,点N 在线段BE 上移动,90ONF ∠=o,NF 与O e 相交于点F ,求NF 的最大值.(23)(本小题满分10分)选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,已知曲线1C :1,12x t y t=+⎧⎨=-⎩(t 为参数)与曲线2C :图4OE BDC P A cos 3sin x a y θθ=⎧⎨=⎩,(θ为参数,0a >). (Ⅰ)若曲线1C 与曲线2C 有一个公共点在x 轴上,求a 的值;(Ⅱ)当3a =时, 曲线1C 与曲线2C 交于A ,B 两点,求A ,B 两点的距离. 5、(惠州市2016届高三第三次调研)(22)(本小题满分10分)选修4—1:几何证明选讲如图,正方形ABCD 的边长为2,以D 为圆心、DA 为半径的圆弧 与以BC 为直径的半圆O 交于点F ,连结CF 并延长交AB 于点E . (Ⅰ)求证:AE EB =;(Ⅱ)求EF FC ⋅的值.(23)(本小题满分10分)选修4—4:坐标系与参数方程已知曲线C 的参数方程是⎩⎨⎧+=+=θθsin 2cos 1y x (θ为参数),直线l 的极坐标方程为24sin =⎪⎭⎫⎝⎛+πθρ.(其中坐标系满足极坐标原点与直角坐标系原点重合,极轴与直角坐标系x 轴正半轴重合,单位长度相同。
广东省13市2017届高三上学期期末考试数学理试题分类汇编:立体几何含答案

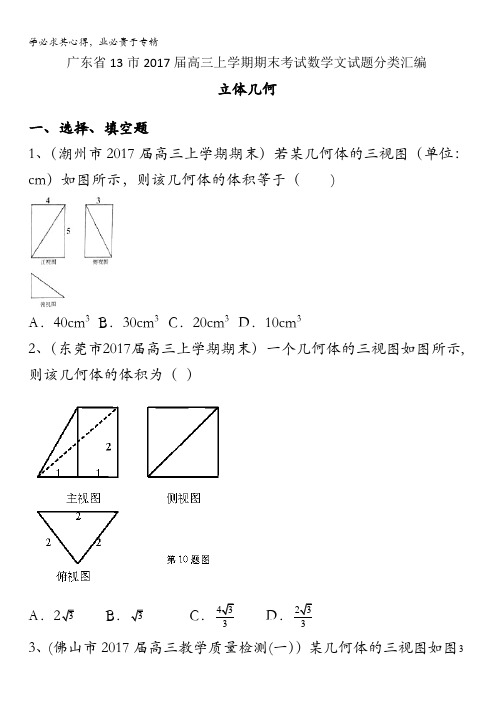
广东省13市2017届高三上学期期末考试数学理试题分类汇编立体几何一、选择、填空题1、(潮州市2017届高三上学期期末)若某几何体的三视图(单位:cm )如图所示,则该几何体的体积等于( )A .40cm 3B .30cm 3C .20cm 3D .10cm 32、(东莞市2017届高三上学期期末)一个几何体的三视图如右图所示,则该几何体的体积为A .12 B. 1 C.32D 。
2 3、(佛山市2017届高三教学质量检测(一))某几何体的三视图如图2所示,则该几何体的体积为( ) A .6 B .320 C .7 D .3224、(广州市2017届高三12月模拟)如图, 网格纸上小正方形的边长为1, 粗线画出的是某三棱锥的三视图,则该三棱锥的外接球的表面积是(A ) π25 (B ) π425(C) π29 (D) π4295、(惠州市2017届高三第三次调研)某四棱锥的三视图如图3所示,该四棱锥最长棱的棱长为( ) (A)1 (B )错误! (C )错误!(D )26、(江门市2017届高三12月调研)如图,正方体ABCD-A 1B 1C 1D 1中,E 为棱BB 1的中点,用过点A 、E 、C 1的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是7、(揭阳市2017届高三上学期期末)若空间四条直线a 、b 、c 、d ,两个平面α、β,满足b a ⊥,d c ⊥,α⊥a ,α⊥c ,则(A )α//b(B )b c ⊥(C )d b //(D )b 与d 是异面直线8、(茂名市2017届高三第一次综合测试)一个几何体的三视图如图3所示, 其表面积为62+ππ,则该几何体的体积为( ) A .4π B .2π C .113π D . 3π 图39、(清远市清城区2017届高三上学期期末)已知某几何体的三视图如图所示,则该几何体的表面积为( )A. 40 B。
30 C。
36 D.4210、(汕头市2017届高三上学期期末)已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是.-的三视图如图所示,其五个顶点都在同一球面上,若四棱锥11、(韶关市2017届高三1月调研)四棱锥P ABCD-的侧面积等于4(12)P ABCD+,则该外接球的表面积是(A) 4π(B)12π(C)24π(D)36π12、(肇庆市2017届高三第二次模拟)如图是某几何体的三视图,则该几何体的体积为2 222 2正视图俯视图侧视图(A)8 3(B)4 3(C)82 3(D)42 313、(珠海市2017届高三上学期期末)某几何体的三视图如图所示(图中每个小网格的边长为1 个单位),其中俯视图为扇形,则该几何体的体积为()A.23πB.43πC.143πD.169π14、(潮州市2017届高三上学期期末)已知正四棱锥的底面边长为1,高为1,则这个正四棱锥的外接球的表面积为.15、(东莞市2017届高三上学期期末)轴截面为等边三角形的圆锥的表面积与其外接球表面积之比为___________。
广东省13市2017届高三上学期期末考试数学文试题分类汇编:立体几何含答案
广东省13市2017届高三上学期期末考试数学文试题分类汇编立体几何一、选择、填空题1、(潮州市2017届高三上学期期末)若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于()A.40cm3B.30cm3C.20cm3D.10cm32、(东莞市2017届高三上学期期末)一个几何体的三视图如图所示,则该几何体的体积为()A.23B3C43D233、(佛山市2017届高三教学质量检测(一))某几何体的三视图如图3所示,则该几何体外接球的表面积为()A.π4B.π12C.π48D.π364、(广州市2017届高三12月模拟)如图, 网格纸上小正方形的边长为1, 粗线画出的是某三棱锥的三视图,则该三棱锥的外接球的表面积是25(A) π25(B) π429(C)π29(D)π45、(惠州市2017届高三第三次调研)如图所示,将图(1)中的正方体截去两个三棱锥,得到图(2)中的几何体,则该几何体的侧视图为()6、(江门市2017届高三12月调研)一个长方体的棱长分别为1、2、2,它的顶点都在同一个球面上,这个球的体积为A.9πB.92πC.18πD.36π47、(揭阳市2017届高三上学期期末)若空间四条直线a、b、c、d,两个平面α、β,满足bc⊥,α⊥a,α⊥c,则a⊥,d(A )α//b (B )b c ⊥ (C)d b // (D )b 与d 是异面直线8、(茂名市2017届高三第一次综合测试)一个几何体的三视图如图2所示,其表面积为62+ππ,则该几何体的体积为( )A .4B .2C .113π D .39、(清远市清城区2017届高三上学期期末)一个几何体的三视图如图所示,其中俯视图与左视图均为半径是1的圆,则这个几何体的体积是_________A .43πB .3π C .23πD .π10、(汕头市2017届高三上学期期末)已知三棱柱111C B A ABC -的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为32,2=AB ,1=AC , 60=∠BAC ,则此球的表面积等于()A .π5B .π20 C.π8 D .π1611、(韶关市2017届高三1月调研)正方体1111ABCD A BC D -中,,E F 分别是1,AD DD 的中点,4AB =,则过,,B E F 的平面截该正方体所得的截面周长为 (A)6245+(B )6225+(C )3245+ (D )3225+12、(肇庆市2017届高三第二次模拟)如图是某几何体的三视图,则该几何体的体积为(A )83(B )43(C )823(D )42313、(珠海市2017届高三上学期期末)一个几何体的三视图如图所示,则该几何体的表面积为A. 2 + 43 B 。
广东省14市2016届高三上学期期末考试数学理试题分类汇编:圆锥曲线综述

广东省14市2016届高三上学期期末考试数学理试题分类汇编圆锥曲线一、选择题1、(潮州市2016届高三上期末)已知双曲线22221(0,0)x y a b a b-=>>的一个焦点恰为抛物线28y x =的焦点,且离心率为2,则该双曲线的标准方程为A 、2213y x -= B 、221412x y -= C 、2213x y -= D 、221124x y -= 2、(东莞市2016届高三上期末)已知圆22()4x m y -+=上存在两点关于直线20x y --=对称,若离心率为2的双曲线22221(0,0)x y a b a b-=>>的两条渐近线与圆相交,则它们的交点构成的图形的面积为(A )1 (B )3 (C )23 (D )43、(佛山市2016届高三教学质量检测(一))已知1F 、2F 分别是双曲线12222=-b y a x (0>a ,0>b )的左、右两个焦点,若在双曲线上存在点P ,使得︒=∠9021PF F ,且满足12212F PF F PF ∠=∠,那么双曲线的离心率为( )A .13+B .2C .3D .254、(广州市2016届高三1月模拟考试)过双曲线22221(0,0)x y a b a b-=>>的一个焦点F 作一条渐近线的垂线,垂足为点A ,与另一条渐近线交于点B ,若2FB FA =uu r uu r,则此双曲线的离心率为(A )2 (B )3 (C )2 (D )55、(惠州市2016届高三第三次调研考试)若双曲线22221(0,0)x y a b a b-=>>与直线2y x =无交点,则离心率e 的取值范围是( ) A .(1,2)B .(1,2]C .(1,5)D . (1,5]6、(揭阳市2016届高三上期末)如果双曲线经过点(2,2)p ,且它的一条渐近线方程为y x =,那么该双曲线的方程式(A )22312y x -= (B ) 22122x y -= (C )22136x y -= (D )22122y x -= 7、(茂名市2016届高三第一次高考模拟考试)设双曲线2214y x -=上的点P 到点(0,5)的距离为6,则P 点到(0,5)-的距离是( )A .2或10 B.10 C.2 D.4或88、(清远市2016届高三上期末)已知双曲线C :2221x my +=的两条渐近线互相垂直,则抛物线E :2y mx =的焦点坐标是( )A 、(0,1)B 、(0,-1)C 、(0,12) D 、(0,-12) 9、(东莞市2016届高三上期末)已知直线l 过抛物线E :22(0)y px p =>的焦点F 且与x 轴垂直,l 与E 所围成的封闭图形的面积为24,若点P 为抛物线E 上任意一点,A (4,1),则|PA |+|PF |的最小值为(A )6 (B )4+22 (C )7 (D )4+2310、(汕尾市2016届高三上期末)已知双曲线22221(0,0)x y a b a b-=>>的左右焦点为,点 A 在其右半支上, 若12AF AF =0, 若,则该双曲线的离心率e 的取值范围为A. (1,2) B.(1, 3) C. (2, 3) D. (2, 6)11、(韶关市2016届高三1月调研)曲线221(6)106x y m m m +=<--与曲线221(59)59x y n n n+=<<--的( ) A .焦距相等 B . 离心率相等 C .焦点相同 D .顶点相同12、(珠海市2016届高三上期末)点00()P x y ,为双曲线22:149x y C -=上一点,12B B 、为C 的虚轴顶点,128PB PB ⋅<u u u r u u u r,则0x 的范围是( )A .626626(2][2)1313--,,U B .626626(2)(2)1313--,,U C .(222][222)--U ,, D .(222)(222]--,,U13、(湛江市2016年普通高考测试(一))等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,|AB |=43,则C 的实轴长为:C A 、2 B 、22 C 、4 D 、814、(潮州市2016届高三上期末)若双曲线2221(0)y x b b-=>的一条渐近线与圆22(2)x y +-=1至多有一个交点,则双曲线的离心率的取值范围是A 、(1,2)B 、[2,+∞)C 、(1,3]D 、B 、[3,+∞)选择题答案:1、A2、D3、A4、C5、D6、B7、A8、D9、C 10、A 11、A 12、C 13、 14、A 二、解答题1、(潮州市2016届高三上期末)已知椭圆22221(0)x y a b a b+=>>右顶点与右焦点的距离为3-1,短轴长为22。
广东省14市2016届高三上学期期末考试数学文试题分类汇编:数列

广东省14市2016届高三上学期期末考试数学文试题分类汇编 数列一、选择题1、(潮州市2016届高三上学期期末)在等差数列{}n a 中,首项1a =0,公差d ≠0,若1237k a a a a a =+++⋅⋅⋅+,则k =A 、22B 、23C 、24D 、252、(东莞市2016届高三上学期期末)已知各项为正的数列{}n a 的前n 项的乘积为n T ,点(2,15)n T n n -在函数12log y x =的图象上,则数列{}2log n a 的前10项和为(A )-140 (B )100 (C )124 (D )1563、(佛山市2016届高三教学质量检测(一)(期末))在等差数列{}n a 中,13a =,1033a a =,则{}n a 的前12项和12S =( )A . 120B . 132C . 144D .1684、(广州市2016届高三1月模拟考试)在数列{}n a 中,已知1221n n a a a ++⋅⋅⋅+=-,则22212n a a a ++⋅⋅⋅+等于(A )2(21)n- (B )2(21)3n - (C )41n- (D )413n -5、(惠州市2016届高三第三次调研)设n S 为等差数列{}n a 的前n 项和,且65101=-+a a a ,则11S =( )(A )55 (B )66 (C )110 (D )1326、(揭阳市2016届高三上学期期末学业水平考试)在等差数列{}n a 中,已知35710132,9,a a a a a +=++=则此数列的公差为(A)31 (B)3 (C) 12 (D) 167、(茂名市2016届高三第一次高考模拟)已知数列{}n a 、{}n b 满足2log ,*n n b a n N =∈,其中{}n b 是等差数列,且9200814a a =g ,则1232016b b b b +++⋅⋅⋅+=( ) A 、-2016 B 、2016 C 、2log 2016 D 、10088、(惠州市2016届高三第三次调研)设记数列{}n a 的前n 项和为n S ,若2(1)4n n S a n++=,则n a =( ) (A )2n n (B )12n n -g (C )2nn g (D )12n n - 9、(汕头市2016届高三上学期期末)已知数列{}n a 的前n 项和为n S ,11a =,12n n S a +=,则当1n >时,n S =( )A .132n -⎛⎫ ⎪⎝⎭B .12n - C .123n -⎛⎫⎪⎝⎭D .111132n -⎛⎫-⎪⎝⎭10、(韶关市2016届高三上学期调研)已知{}n a 为等比数列,设n S 为{}n a 的前n 项和,若21n n S a =-,则6a =( )A . 32B .31C .64D .6211、(湛江市2016年普通高考测试(一))已知数列{}n a 是公比为2的等比数列,数列{}n b 是公差为3且各项均为正整数的等差数列,则数列{}n b a 是 A 、公差为5的等差数列 B 、公差为6的等差数列C 、公比为6的等比数列D 、公比为8的等比数列12、(肇庆市2016届高三第二次统测(期末))在等比数列{}n a 中,已知613a a =678910111213a a a a a a a a =(A )4 (B ) (C )2 (D13、(肇庆市2016届高三第二次统测(期末))设各项均为正数的数列{}n a 的前n 项和为n S ,且n S 满足222(34)n n S n n S ---22(3n -)0n -=,n ∈N *. 则数列{}n a 的通项公式是(A )32n a n =- (B )43n a n =- (C )21n a n =- (D )21n a n =+ 14、(珠海市2016届高三上学期期末)等比数列{}n a 的前n 项和为n S ,已知12310a a S +=,95=a ,则 1a = ( )A .31B .31-C .91- D .91参考答案: 1、A 2、3、D4、D5、B6、A7、A8、D9、A 10、A 11、D 12、A 13、A 14、D二、填空题1、(东莞市2016届高三上学期期末)已知各项为正的等比数列{}n a 的前n 项和为n S ,430S =,过点P (2,log n n a )和Q (212,log n n a ++)(*n N ∈)的直线的斜率为1,设2122212log log log n n n na b a a ++=g ,则数列{}n b 的前n 项和为n T = 2、(广州市2016届高三1月模拟考试)设数列{}n a 的各项都是正数,且对任意*n ∈N ,都有242n n n S a a =+,其中n S 为数列{}n a 的前n 项和,则数列{}n a 的通项公式为n a = .3、(揭阳市2016届高三上学期期末学业水平考试)数列{}n a 的通项公式(1)2cos()n n n a n n π=-⋅+⋅,其前n 项和为n S ,则10S 等于 .4、(茂名市2016届高三第一次高考模拟)在数列{}n a 中,111,1,n n n a a a S +==+为{}n a 的前n 项和,若n S =21,则n =5、(汕头市2016届高三上学期期末)已知正项等比数列{}n a 的公比2q =,若存在两项m a ,n a 14m n a a a =,则14m n+的最小值为 . 6、(韶关市2016届高三上学期调研)等差数列{}n a 中,21a =,69a =,则{}n a 的前7项和7S = .参考答案: 1、2、2n3、6874、65、326、35三、解答题1、(潮州市2016届高三上学期期末)若n S 是公差为不为等差数列{}n a 的前n 项和为,且124,,S S S 成等比数列。
广东省14市高三数学上学期期末考试试题分类汇编 圆锥曲线 理

广东省14市2016届高三上学期期末考试数学理试题分类汇编圆锥曲线一、选择题1、(潮州市2016届高三上期末)已知双曲线22221(0,0)x y a b a b-=>>的一个焦点恰为抛物线28y x =的焦点,且离心率为2,则该双曲线的标准方程为A 、2213y x -= B 、221412x y -= C 、2213x y -= D 、221124x y -= 2、(东莞市2016届高三上期末)已知圆22()4x m y -+=上存在两点关于直线20x y --=对22221(0,0)x y a b a b-=>>的两条渐近线与圆相交,则它们的交点构成的图形的面积为(A )1 (B (C ) (D )43、(佛山市2016届高三教学质量检测(一))已知1F 、2F 分别是双曲线12222=-b y a x (0>a ,0>b )的左、右两个焦点,若在双曲线上存在点P ,使得︒=∠9021PF F ,且满足12212F PF F PF ∠=∠,那么双曲线的离心率为( )A .13+B .2C .3D .254、(广州市2016届高三1月模拟考试)过双曲线22221(0,0)x y a b a b-=>>的一个焦点F 作一条渐近线的垂线,垂足为点A ,与另一条渐近线交于点B ,若2FB FA =uu r uu r,则此双曲线的离心率为(A (B (C )2 (D 5、(惠州市2016届高三第三次调研考试)若双曲线22221(0,0)x y a b a b-=>>与直线2y x =无交点,则离心率e 的取值范围是( )A .(1,2)B .(1,2]C .D .6、(揭阳市2016届高三上期末)如果双曲线经过点p ,且它的一条渐近线方程为y x =,那么该双曲线的方程式(A )22312y x -= (B ) 22122x y -= (C )22136x y -= (D )22122y x -=7、(茂名市2016届高三第一次高考模拟考试)设双曲线2214y x -=上的点P 到点的距离为6,则P 点到(0,的距离是( )A .2或10 B.10 C.2 D.4或88、(清远市2016届高三上期末)已知双曲线C :2221x my +=的两条渐近线互相垂直,则抛物线E :2y mx =的焦点坐标是( ) A 、(0,1) B 、(0,-1) C 、(0,12) D 、(0,-12) 9、(东莞市2016届高三上期末)已知直线l 过抛物线E :22(0)y px p =>的焦点F 且与x 轴垂直,l 与E 所围成的封闭图形的面积为24,若点P 为抛物线E 上任意一点,A (4,1),则|PA |+|PF |的最小值为(A )6 (B )4+ (C )7 (D )4+10、(汕尾市2016届高三上期末)已知双曲线22221(0,0)x y a b a b-=>>的左右焦点为,点 A 在其右半支上, 若12AF AF =0, 若,则该双曲线的离心率e 的取值范围为B.(C.D.11、(韶关市2016届高三1月调研)曲线221(6)106x y m m m +=<--与曲线221(59)59x y n n n+=<<--的( ) A .焦距相等 B . 离心率相等 C .焦点相同 D .顶点相同12、(珠海市2016届高三上期末)点00()P x y ,为双曲线22:149x y C -=上一点,12B B 、为C 的虚轴顶点,128PB PB ⋅<u u u r u u u r,则0x 的范围是( )A .(2][2-UB .(2)(2-UC .(2][2--UD .(2)(2--U13、(湛江市2016年普通高考测试(一))等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,|AB |=C 的实轴长为:CA B 、 C 、4 D 、814、(潮州市2016届高三上期末)若双曲线2221(0)y x b b-=>的一条渐近线与圆22(2)x y +-=1至多有一个交点,则双曲线的离心率的取值范围是A 、(1,2)B 、[2,+∞)C 、D 、B 、∞)选择题答案:1、A2、D3、A4、C5、D6、B7、A8、D9、C 10、A 11、A 12、C 13、 14、A 二、解答题1、(潮州市2016届高三上期末)已知椭圆22221(0)x y a b a b+=>>-1,短轴长为(I )求椭圆的方程;(II )过左焦点F 的直线与椭圆分别交于A 、B 两点,若△OAB (O 为直角坐标原点)的面积为4,求直线AB 的方程。
广东省14市2016届高三上学期期末考试数学文试题分类汇编:立体几何

广东省14市2016届高三上学期期末考试数学文试题分类汇编立体几何一、选择题1、(潮州市2016届高三上学期期末)右图是一个几何体的正视图和侧视图,其俯视图是面积为82的矩形,则该几何体的体积是A、8B、42C、16D、16 32、(东莞市2016届高三上学期期末)已知一个几何体的三视图如图所示,图中小正方形的边长为1,则该几何体的体积为(A)103(B)4(C)6(D)103、(佛山市2016届高三教学质量检测(一)(期末))某一简单几何体的三视图如图2所示,该几何体的外接球的表面积是( )A. 13πB. 16πC. 25πD. 27π4、(广州市2016届高三1月模拟考试)一个几何体的三视图如图所示,其中正视图与侧视图都是斜边长为2的直角三角形,俯视图是半径为1的四分之一圆周和两条半径,则这个几何体的表面积为(A)312π(B)36π(C)34π(D)33π22322正视图侧视图俯视图图25、(惠州市2016届高三第三次调研)某几何体的三视图如图,其正视图中的曲线部分为半个圆弧,则该几何体的表面积为( ) (A )π42616++ (B )π32616++ (C )π42610++ (D )π32610++6、(揭阳市2016届高三上学期期末学业水平考试)已知棱长为2的正方体ABCD-A 1B 1C 1D 1的一个面A 1B 1C 1 D 1在一半球底面上,且A 、B 、C 、D 四个顶点都在此半球面上,则此半球的体积为(A) 46π (B) 26π (C) 163π (D) 86π7、(茂名市2016届高三第一次高考模拟)一个几何体的三视图如图所示,则该几何体的体积为( )A 、43 B 、23 C 、13D 、2 8、(清远市2016届高三上学期期末)一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( ) A .3 B .23 C . 33 D .439、(汕头市2016届高三上学期期末)某几何体的三视图如图2所示,则该几何体的外接球表面积为( )正视图俯视图侧视图2232311A.43πB.12πC.24πD.48π10、(汕尾市2016届高三上学期调研)一个几何体的三视图如图所示,该几何体的体积为( )11、(韶关市2016届高三上学期调研)如图,圆柱内有一个直三棱柱,三棱柱的底面在圆柱底面内,12,圆柱的底面直径与母线长相且底面是正三角形. 如果三棱柱的体积为3等,则圆柱的侧面积为12A.π14B.π16C.π18D.π12、(湛江市2016年普通高考测试(一))一个几何体的三视图如右图所示,则该几何体的表面积为A 、64+8πB 、48+12πC 、48+8πD 、48+12π13、(肇庆市2016届高三第二次统测(期末))若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图2所示,则此几何体的表面积是 (A )24π (B )2482ππ+ (C )2442ππ+ (D )32π14、(珠海市2016届高三上学期期末)已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是 ( )A .2B .4C .6D .12侧视图正视图 俯视图2222第11题图1、A2、C3、C4、A5、C6、A7、B8、A9、B 10、A 11、C 12、A 13、C 14、B二、填空题1、(潮州市2016届高三上学期期末)已知一个长方体的长、宽、高分别是5,4,3,则该长方体的外接球的表面积等于__2、(东莞市2016届高三上学期期末)如图,等腰直角三角形ABC ,|AB |=2,AC L ,三角形ABC 绕直线L 旋转一周,得到的几何体的体积为3、(惠州市2016届高三第三次调研)已知三棱锥S ABC -所在顶点都在球O 的球面上,且SC ⊥平面ABC ,若1SC AB AC ===,120BAC ∠=︒,则球O 的表面积为 .4、(揭阳市2016届高三上学期期末学业水平考试)如图2,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则被截去部分的几何体的表面积为 .5、(汕尾市2016届高三上学期调研)若正方体的棱长为2,则该正方体外接球的表面积为6、(肇庆市2016届高三第二次统测(期末))已知各顶点都在一个球面上的正四棱柱的高为4,体积为16,则这个球的体积为 .1、π502、3、【答案】5π【解析】记底面三角形ABC 的外接圆为⊙O ′,半径为r,则22sin120BCr ==︒,所以记球的半径为R ,因为SC ⊥平面ABC ,则()2222145R r SC =+=+=,所以球O 的表面积为2254452S R πππ⎛⎫==⨯⨯= ⎪ ⎪⎝⎭4、54183+5、12π6、86π三、解答题1、(潮州市2016届高三上学期期末)如图,四棱锥P -ABCD 的底面ABCD 是矩形,侧面PAB 是正三角形,AB =2,BC =2,PC =6,E ,H 分别为PA 、AB 中点。
广东省13大市高中数学上学期期末试题分类汇编 立体几何 文

广东省13大市2013届高三上期末考数学文试题分类汇编立体几何一、选择题1、(潮州市2013届高三上学期期末)对于平面α和共面的两直线m 、n ,下列命题中是真命题的为A .若m α⊥,m n ⊥,则//n αB .若//m α,//n α,则//m nC .若m α⊥,n α⊥,则//m nD .若m β⊂,n β⊂,//m α,//n α,则//αβ 答案:C2、(东莞市2013届高三上学期期末)点M 、N 分别是正方体1111ABCD A B C D -的棱11A B 、11A D 中点,用过A 、M 、N 和D 、N 、1C 的两个截面截去正方体的两个角后得到的几何体如右图,则该几何体的正视图、侧视图(左视图)、俯视图依次为A .①、②、③B .②、③、④C .①、③、④D .②、④、③ 答案:B 3、(佛山市2013届高三上学期期末)一个长方体被一个平面截去一部分后所剩几何体的正视图和俯视图如图所示,则该几何体的侧视图可以为A .B .C .D .答案:B4、(广州市2013届高三上学期期末)设n m ,是两条不同的直线,γβα,,是三个不同的平面,下列命题正确的是A .αα//,//,//n m n m 则若B .βαγβγα//,,则若⊥⊥C .n m n m //,//,//则若ααD .n m n m ⊥⊥则若,//,αα答案:D5、(惠州市2013届高三上学期期末)已知,m n 是两条不同直线,αβγ,,是三个不同平正视图俯视图第9题图面,下列命题中正确的有( )A. m n m n αα若,,则‖‖‖; B. αγβγαβ⊥⊥若,,则‖; C. m m αβαβ若,,则‖‖‖; D. m n m n αα⊥⊥若,,则‖. 答案:D6、(江门市2013届高三上学期期末)图1,将一个正三棱柱截去一个三棱锥,得到几何体DEF BC -,则该几何体的正视图(或称主视图)是A .B .C .D . 答案:C 7、(茂名市2013届高三上学期期末)若某一几何体的正视图与侧视图均为边长是1的正方 形,且其体积为12,则该几何体的俯视图可以是( )答案:C8、(汕头市2013届高三上学期期末)如图正四棱锥(底面是正方形,顶点在底面的射影是底面的中心)P-ABCD 的底面边长为6cm ,侧棱长为5cm ,则它的侧视图的周长等于( ).A.17cmB.1195cm +学科网学科网C.16cmD.14cm答案:D9、(增城市2013届高三上学期期末)给出三个命题:(1)若两直线和第三条直线所成的角相等,则这两直线互相平行. (2)若两直线和第三条直线垂直,则这两直线互相平行. (3)若两直线和第三条直线平行,则这两直线互相平行.其中正确命题的个数是A .0B . 1C . 2D . 3 答案:B10、(湛江市2013届高三上学期期末)一个几何体的三视图如图所示,其中主视图和左视图都是边长为2的正三角形,俯视图为圆,那么该几何体的表面积为A 、6πB 、4πC 、3πD 、2 π 答案:C11、(肇庆市2013届高三上学期期末)某三棱锥的三视图如图2所示,该三棱锥的体积是为( )A. 80B. 40C.803D. 403答案:D解析:从图中可知,三棱锥的底为两直角边分别为4和5的直角三角形,高为4 体积为11404(23)4323V =⨯⨯⨯+⨯= 12、(中山市2013届高三上学期期末)如图,在透明塑料制成的长方体1111D C B A ABCD -容器内灌进一些水,将容器底面一边BC 固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:①水的部分始终呈棱柱状;②水面四边形EFGH 的面积不改变; ③棱11D A 始终与水面EFGH 平行; ④当1AA E ∈时,BF AE +是定值.其中所有正确的命题的序号是( ) A .①②③ B .①③ C .②④ D .①③④答案:D13、(珠海市2013届高三上学期期末)已知直线l ,m 和平面α, 则下列命题正确的是 A .若l ∥m ,m ⊂α,则l ∥α B .若l ∥α,m ⊂α,则l ∥m C .若l ⊥m ,l ⊥α,则m ∥αHG FE D1C1B1A1DCBAD .若l ⊥α,m ⊂α,则l ⊥m 答案:D 二、填空题1、(潮州市2013届高三上学期期末)若一个正三棱柱的三视图如下图所示,则这个正三棱柱的体积为_______. 答案:83由左视图知正三棱柱的高2h =,设正三棱柱的底面边长a ,则3232a=, 故4a =,底面积1423432S =⨯⨯=,故43283V Sh ==⨯=. 三、解答题1、(潮州市2013届高三上学期期末)已知梯形ABCD 中//AD BC ,2π=∠=∠BAD ABC ,42===AD BC AB ,E 、F 分别是AB 、CD 上的点,//EF BC ,x AE =.沿EF 将梯形ABCD 翻折,使平面AEFD ⊥平面EBCF (如图).G 是BC 的中点. (1)当2=x 时,求证:BD ⊥EG ;(2)当x 变化时,求三棱锥D BCF -的体积()f x 的函数式.(1)证明:作EF DH ⊥,垂足H ,连结BH ,GH , …… 2分 ∵平面AEFD ⊥平面EBCF ,交线EF ,DH ⊂平面EBCF ,∴⊥DH 平面EBCF ,又⊂EG 平面EBCF ,故DH EG ⊥. …… 4分 ∵12EH AD BC BG ===,//EF BC ,90ABC ∠=o . ∴四边形BGHE 为正方形,故BH EG ⊥. ………… 6分 又BH 、DH ⊂平面DBH ,且BH DH H =I ,故⊥EG 平面DBH . 又⊂BD 平面DBH ,故BD EG ⊥. ………… 8分(2)解:∵AE EF ⊥,平面AEFD ⊥平面EBCF ,交线EF ,AE ⊂平面AEFD .∴AE ⊥面EBCF .又由(1)⊥DH 平面EBCF ,故//AE GH ,……10分 ∴四边形AEHD 是矩形,DH AE =,故以F 、B 、C 、D 为顶点的三棱锥D BCF -的高DH AE x ==. …………11分又114(4)8222BCF S BC BE x x ∆==⨯⨯-=-⋅. ………… 12分 ∴三棱锥D BCF -的体积()f x =13BFC S DH ∆⋅13BFC S AE ∆=⋅2128(82)333x x x x =-=-+………… 14分19.解:(1)由1112S a ==,得112a b =+;由21243S a a =+=,得4423a b =+. ∴223a b a b +=⎧⎨+=⎩,解得11a b =⎧⎨=⎩,故21n n S n =+; ………… 4分(2)当2n ≥时,2232212(1)(1)(1)11(1)n n n n n n n n n n a S S n n n n n n----++-=-=-==+++. 由于112a =也适合221n n n a n n +-=+. ……… 8分 ∴221n n n a n n +-=+; ……… 9分(3)21111(1)1n n a b n n n n n n ===-+-++. ……… 10分 ∴数列{}n b 的前n 项和1211111111122311n n n T b b b b n n n n -=++++=-+-++-+--+L L 1111nn n =-=++. ……… 14分2、(东莞市2013届高三上学期期末)在等腰梯形PDCB(见图a )中,DC//PB ,,DA PB ⊥,垂足为A ,将PAD ∆沿AD 折起,使得PA AB ⊥,得到四棱锥P-ABCD (见图b ). 在图b 中完成下面问题:(I)证明:平面PAD ⊥平面PCD;(2)点M 在棱PB 上,平面AMC 把四棱锥P-ABCD 分成两个几何体(如图b ),当这两个几何体的体积之比5:4PM ACD M ABC V V --=时,求PMMB的值; (3)在(2)的条件下,证明:PD ‖平面AMC.证明:(1)因为在图a 的等腰梯形PDCB 中,PB DA ⊥,所以在四棱锥ABCD P -中,AB DA ⊥, PA DA ⊥. …………1分 又PA AB ⊥,且AB DC //,所以PA DC ⊥,DA DC ⊥, …………2分 而⊂DA 平面PAD ,⊂PA 平面PAD ,A DA PA =I ,所以⊥DC 平面PAD . …………3分 因为⊂DC 平面PCD ,所以平面⊥PAD 平面PCD . …………4分 解:(2)因为PA DA ⊥,且AB PA ⊥ 所以⊥PA 平面ABCD , 又⊂PA 平面PAB ,所以平面⊥PAB 平面ABCD . 如图,过M 作AB MN ⊥,垂足为N , 则⊥MN 平面ABCD . ……5分 在等腰梯形PDCB 中,PB DC //, 2,33===PD DC PB ,PB DA ⊥,所以1=PA ,2=AB ,122=-=PA PD AD . …………6分设h MN =,则 h h h DA AB h S V ABC ABC M 31122131213131=⨯⨯⨯⨯=⨯⨯⨯⨯=⋅=∆-. …………7分 2111221312)(3131=⨯⨯+⨯=⨯⨯+⨯=⋅=-PA AD AB DC PA S V ABCD ABCDP 梯形. ABDCOPMNh V V V ABC M ABCD P ACD PM 3121-=-=---. …………8分 因为4:5:=--ABC M ACD PM V V ,所以4:531:)3121(=-h h ,解得32=h .………9分在PAB ∆中,32==PA MN BP BM , 所以BP BM 32=,BP MP 31=.所以2:1:=MB PM . …………10分 (3)在梯形ABCD 中,连结AC 、BD 交于点O ,连结OM .易知AOB ∆∽DOC ∆,所以21==AB DC OB DO . …………11分 又21=MB PM , 所以MB PMOB DO =, …………12分 所以在平面PBD 中,有MO PD //. …………13分 又因为⊄PD 平面AMC ,⊂MO 平面AMC ,所以PD //平面AMC . …………14分3、(佛山市2013届高三上学期期末)如图所示,已知圆O 的直径AB 长度为4,点D 为 线段AB 上一点,且13AD DB =,点C 为圆O 上一点,且BC =.点P 在圆O 所在平面上的正投影为点D ,PD BD =.(1)求证:CD ⊥平面PAB ; (2)求点D 到平面PBC 的距离.解析:(Ⅰ)法1:连接CO ,由3AD DB =知,点D 又∵AB 为圆O 的直径,∴AC CB ⊥,BC =知,60CAB ∠=o,∴ACO ∆为等边三角形,从而CD AO ⊥.-----------------3分 ∵点P 在圆O 所在平面上的正投影为点D , ∴PD ⊥平面ABC ,又CD ⊂平面ABC , ∴PD CD ⊥,-----------------5分由PD AO D =I 得,CD ⊥平面PAB .-----------------6分(注:证明CD ⊥平面PAB 时,也可以由平面PAB ⊥平面ACB 得到,酌情给分.) 法2:∵AB 为圆O 的直径,∴AC CB ⊥, ∵在Rt ABC ∆中,4AB =,∴由3AD DB =BC =得,3DB =,4AB =,BC =,∴BD BC BC AB ==,则BDC BCA ∆∆∽, ∴BCA BDC ∠=∠,即CD AO ⊥.-----------------3分 ∵点P 在圆O 所在平面上的正投影为点D , ∴PD ⊥平面ABC ,又CD ⊂平面ABC , ∴PD CD ⊥,-----------------5分由PD AO D =I 得,CD ⊥平面PAB .-----------------6分 法3:∵AB 为圆O 的直径,∴AC CB ⊥,在Rt ABC ∆BC =得,30ABC ∠=o,∵4AB =,由3AD DB =得,3DB =,BC = 由余弦定理得,2222cos303CD DB BC DB BC =+-⋅=o, ∴222CD DB BC +=,即CD AO ⊥.-----------------3分 ∵点P 在圆O 所在平面上的正投影为点D , ∴PD ⊥平面ABC ,又CD ⊂平面ABC , ∴PD CD ⊥,-----------------5分由PD AO D =I 得,CD ⊥平面PAB .-----------------6分(Ⅱ)法1:由(Ⅰ)可知CD =,3PD DB ==,--------7分(注:在第(Ⅰ)问中使用方法1时,此处需要求出线段的长度,酌情给分.)∴1111133332322P BDC BDC V S PD DB DC PD -∆=⋅=⋅⋅⋅=⨯⨯=.--------10分又PB ==,PC ==BC ==∴PBC ∆为等腰三角形,则12PBC S ∆=⨯=.--------12分 设点D 到平面PBC 的距离为d ,由P BDC D PBC V V --=得,132PBC S d ∆⋅=,解得5d =.--------14分法2:由(Ⅰ)可知CD =3PD DB ==,DP侧视D CB AP 图5图4过点D 作DE CB ⊥,垂足为E ,连接PE ,再过点D 作DF PE ⊥,垂足为F .-----------------8分∵PD ⊥平面ABC ,又CB ⊂平面ABC , ∴PD CB ⊥,又PD DE D =I , ∴CB ⊥平面PDE ,又DF ⊂平面PDE , ∴CB DF ⊥,又CB PE E =I ,∴DF ⊥平面PBC ,故DF 为点D 到平面PBC 的距离.--------10分 在Rt DEB ∆中,3sin 302DE DB =⋅=o,PE ==,在Rt PDE ∆中,3352PD DE DF PE ⨯⋅===,即点D 到平面PBC 的距离为.-------14分 4、(广州市2013届高三上学期期末)已知四棱锥P ABCD -的正视图是一个底边长为4、腰长为3的等腰三角形,图4、图5 分别是四棱锥P ABCD -的侧视图和俯视图. (1)求证:AD PC ⊥;(2)求四棱锥P ABCD -的侧面PAB 的面积.(1)证明:依题意,可知点P 在平面ABCD 上的正射影是线段CD 的中点E ,连接PE , 则PE ⊥平面ABCD . …………… 2分 ∵AD ⊂平面ABCD ,∴AD PE ⊥. …………… 3分 ∵AD CD ⊥,CD PE E CD ,=⊂I 平面PCD ,PE ⊂平面PCD , ∴AD ⊥平面PCD . …………… 5分 ∵PC ⊂平面PCD ,∴AD PC ⊥. …………… 6分(2)解:依题意,在等腰三角形PCD 中,3PC PD ==,2DE EC ==, 在Rt △PED中,PE ==,…………… 7分过E 作EF AB ⊥,垂足为F ,连接PF ,∵PE ⊥平面ABCD ,AB ⊂平面ABCD ,∴AB PE ⊥. …………… 8分∵EF ⊂平面PEF ,PE ⊂平面PEF ,EF PE E =I , ∴AB ⊥平面PEF . …………… 9分 ∵PF ⊂平面PEF ,∴AB PF ⊥. …………… 10分 依题意得2EF AD ==. …………… 11分 在Rt △PEF 中, 223PF PE EF =+=, …………… 12分∴△PAB 的面积为162S AB PF ==g g . ∴四棱锥P ABCD -的侧面PAB 的面积为6. …………… 14分5、(惠州市2013届高三上学期期末)如图所示,在棱长为2的正方体1111ABCD A B C D -中,E 、F 分别为1DD 、DB 的中点.(1)求证:EF //平面11ABC D ; (2)求证:1CF B E ⊥; (3)求三棱锥1C B FE V -的体积.解:(1)连结1BD ,在B DD 1∆中,E 、F 分别为1D D ,DB 的中点,则∵EF 为中位线…………2分1//EF D B ∴而1D B ⊂面11ABC D ,EF ⊄面11ABC D//EF ∴面11ABC D …………4分(2)等腰直角三角形BCD 中,F 为BD 中点BD CF ⊥∴①…………5分Θ正方体1111ABCD A B C D -ABCD 1面⊥∴DD ,ABCD 面⊂CF CF DD ⊥∴1②…………7分综合①②,且1111,,B BDD BD DD D BD DD 面⊂=⋂11B BDD CF 面⊥∴,而111B E BDD B ⊂面,PD CBANE B CF 1⊥∴…………………………………………………9分(3)由(2)可知11CF BDD B ⊥Q 平面1CF EFB ∴⊥平面 即CF 为高,CF BF ==10分112EF BD ==Q,1B F ===13B E ===∴22211EF B F B E += 即190EFB ∠=o∴223211=⋅=∆F B EF S EF B …………12分11113B EFC C B EF B EF V V S CF --∆∴==⋅⋅=1222331=⋅⋅…………14分 6、(江门市2013届高三上学期期末)如图6,四棱锥ABCD P -的底面是边长是1的正方形,侧棱PD ⊥平面ABCD ,M 、N 分别是AB 、PC 的中点.⑴求证://MN 平面PAD ;⑵记x MN =,)(x V 表示四棱锥ABCD P -的体积, 求)(x V 的表达式(不必讨论x 的取值范围).证明与求解:⑴取CD 的中点E ,连接ME 、NE ,则AD ME //,PD NE //……2分, 因为E NE ME =I ,所以平面//MNE 平面PAD ……4分, ⊂MN 平面MNE ,所以//MN 平面PAD ……6分.⑵PD NE //,PD ⊥平面ABCD ,所以NE ⊥平面ABCD ……8分, ⊂ME 平面ABCD ,ME NE ⊥……9分,222NE ME MN +=,所以1222-=-=x ME MN NE ……10分,由⑴知1222-==x NE PD ……11分, 所以PD S Sh x V ABCD ⨯⨯==3131)(……13分,1322-=x ……14分.7、(茂名市2013届高三上学期期末)在如图所示的多面体ABCDE 中,AB ⊥平面ACD ,DE ⊥平面ACD,1AB CD ==,3AC =,AD=DE=2,G 为AD 的中点。
广东省14市2019届高三上学期期末考试数学理试题分类汇编:立体几何

广东省14市2019届高三上学期期末考试数学理试题分类汇编立体几何一、选择、填空题 1、(东莞市2019届高三上学期期末)已知某几何体的三视图如图1所示(侧视图中曲线为四分之一圆弧),则该几何体的体积为A 、1-4π B 、3+2π C 、2+4πD 、4 2、(广州市2019届高三12月调研考试)如图为一个多面体的三视图,则该多面体的体积为A .6B .7C .223 D .2333、(惠州市2019届高三第三次调研考试)一个几何体的三视图如图所示,则这个几何的体积为( )立方单位。
A .32316π33+ B .16π833+ C .3236π3+D .836π+4、(江门市 2019届普通高中高三调研)已知两条直线m n 、,两个平面αβ、,给出下面四个命题:①//,////m n m n αα⇒ ②//,//,m n m n αβαβ⊥⇒⊥ ③,//m n m n αα⊥⊥⇒或n α⊂ ④,//m m αβαβ⊥⇒⊥ 其中,正确命题的个数是( ) A .1 B .2 C .3 D .4 5、(揭阳市2019届高三上学期期末)某几何体示意图的三视图如图示,已知其主视图的周长为8,则该几何体侧面积的最大值为A .πB .2πC .4πD .16π6、(雷州市2019届高三上学期期末)正四面体ABCD 中,CD 在平面α内,点E 是线段AC 的中点,在该四面体绕CD 旋转的过程中,直线BE 与平面α所成角不可能是 A .0 B .6π C .3π D .2π7、(茂名市2019届高三上期末)如图2,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则此几何体的体积为( ). A 、6 B 、18 C 、12 D 、368、(清远市2019届高三上期末)如图为某几何体的三视图,图中的三个正方形的边长均为2,则该几何体的体积为A.316B. 8-π32C.332D.8+π329、(汕头市2019届高三上学期期末)已知一个简单几何体的三视图如图所示, 若该几何体的体积为 24π+48, 则 r =A 、2B 、4C 、1D 、310、(汕尾市2019届高三上学期期末)某几何体的三视图如图所示,则该几何体的体积为 A .23 B .13 C .43 D .5611、(韶关市2019届高三上学期期末)已知三棱柱ABC-A 1B 1C 1的底面边长和侧棱长都相等,侧棱AA 1⊥底面ABC ,则直线BC 1与AC 所成角的余弦值是 A 、24 B 、-24 C 、22 D 、一2212、(肇庆市2019届高三上学期期末)在长方体1111ABCD A B C D -中,124AA AB BC ===,E 是AB 的中点,则三棱锥11E D C C -外接球的表面积为A .36πB .32πC .9πD .8π 13、(珠海市2019届高三上学期期末)如图是某几何体的三视图,其中正视图和侧视图为正方形,俯视图是腰长为2的等腰直角三角形,则该几何体的体积是( )A 、43 B 、223 C 、83D 、42314、(佛山市2019届高三上学期期末)参考答案 一、填空题1、A2、B3、D4、B5、C6、D7、A8、B9、A 10、A 11、A 12、B 13、B 14、D二、解答题1、(东莞市2019届高三上学期期末)如图所示,在四棱锥P 一ABCD 中,底面ABCD 为菱形,PA ⊥底面ABCD ,点M 是PC 上的 一个动点,PA =AB ,∠DAB =3π. (1)当PC ⊥DM 时,求证:PC ⊥BM ;(2)当PA ∥平面MBD 时,求二面角P 一BD -M 的余弦值.2、(广州市2019届高三12月调研考试)如图,多面体ABCDEF 中,四边形ABCD 为矩形,二面角A CD F --为60︒,DE CF ∥,,2CD DE AD ⊥=,3DE DC ==,6CF =.(1)求证:BF ∥平面ADE ;(2)在线段CF 上求一点G ,使锐二面角B EG D --的余弦值为14.3、(惠州市2019届高三第三次调研考试)在四棱锥P ABCD -中,侧面PAD ⊥底面ABCD ,底面ABCD 为直角梯形,BC ∥AD ,090ADC ∠=,1BC CD ==,2AD =,3PA PD ==,E 为AD 的中点,F 为PC 的中点。
高三数学上期末考试分类汇编《立体几何》文科
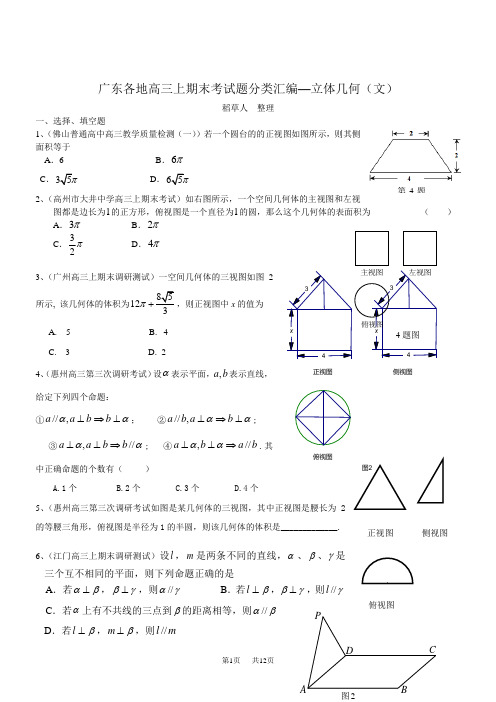
图2侧视图俯视图正视图4x33x4CDP广东各地高三上期末考试题分类汇编—立体几何(文)稻草人 整理一、选择、填空题 1、(佛山普通高中高三教学质量检测(一))若一个圆台的的正视图如图所示,则其侧面积等于A .6B .C .D .2、(高州市大井中学高三上期末考试)如右图所示,一个空间几何体的主视图和左视图都是边长为的正方形,俯视图是一个直径为的圆,那么这个几何体的表面积为( )A .B .C .D .3、(广州高三上期末调研测试)一空间几何体的三视图如图2所示, 该几何体的体积为8512π+,则正视图中x 的值为 A. 5 B . 4 C. 3 D . 24、(惠州高三第三次调研考试)设表示平面,表示直线,给定下列四个命题:①; ②; ③; ④.其中正确命题的个数有( )A.1个B.2个C.3个D.4个5、(惠州高三第三次调研考试如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是_____________.6、(江门高三上期末调研测试)设,是两条不同的直线,、、是三个互不相同的平面,则下列命题正确的是 A .若,,则B .若,,则C .若上有不共线的三点到的距离相等,则D .若,,则6π35π65π11π3π2π23π4αb a ,αα⊥⇒⊥b b a a ,//αα⊥⇒⊥b a b a ,//αα//,b b a a ⇒⊥⊥b a b a //,⇒⊥⊥ααl m αβγβα⊥γβ⊥γα//β⊥l γβ⊥γ//l αββα//β⊥l β⊥m m l //第4题4题图主视图俯视图左视图正视图 俯视图侧视图C D D俯视图左视图主视图侧视图7、(江门高三上期末调研测试)如图2所示,为正三角形,四边形为正方形,平面平面.点为平面内的一个动点,且满足,则点在正方形的轨迹为8、(揭阳市高三上学期学业水平考试).设,是两条不同的直线,是一个平面,则下列命题正确的是()A.若,,则B.若,,则C.若,,则D.若,,则9、(揭阳市高三上学期学业水平考试).四棱锥的顶点P在底面ABCD中的投影恰好是A,其三视图如上图所示,根据图中的信息,在四棱锥的任两个顶点的连线中,互相垂直的异面直线对数为.10、(茂名高三上期末考试)设是两条直线,是两个平面,则的一个充分条件是A.B.C.D.11、(汕头10-11普通高中毕业班教学质量监测)若、为两条不重合的直线,、为两个不重合的平面,则下列命题中的真命题个数是( )①若、都平行于平面,则、一定不是相交直线;②若、都垂直于平面,则、一定是平行直线;③已知、互相垂直,、互相垂直,若,则;④、在平面内的射影互相垂直,则、互相垂直.A.1 B.2 C.3 D.412、(汕头10-11普通高中毕业班教学质量监测)一个几何体的三视图如图所示,则这个几何体的表面积为( )A.72 B.66 C.60 D.3013、(肇庆中小学教学质量评估10-11高三上期末)图1是一个几何体的ADP∆ABCD⊥ADP ABCDM ABCDMCMP=M ABCDl mαl m⊥mα⊂lα⊥lα⊥l m//mα⊥lα//mα⊂l m//lα//mα//l m//P ABCD-P ABCD-a,b,αβa b⊥,//,a bαβαβ⊥⊥,,//a bαβαβ⊥⊥,,//a bαβαβ⊂⊥,//,a bαβαβ⊂⊥m nαβm nαm nm nαm nαβm nα⊥mβ⊥nm nαm n三视图,根据图中数据, 可得该几何体的表面积是 A . 9 B . 10C . 11D . 1214、(中山高三上期末统考)已知某几何体的俯视图是如图所示的边长为的正方形,主视图与左视图是边长为的正三角形,则其全面积是 A .8 B .12C .D .15、(珠海高三上期末考试题)已知、是三个互不重合的平面,是一条直线,下列命题中正确命题是( )A .若,则B .若上有两个点到的距离相等,则C .若,则D .若,则答案:1、C2、C3、C 4.【解析】考虑的情形,则排除①③,故正确命题有②、④,故选B 。
广东省14市2019届高三上学期期末考试数学理试题分类汇编:立体几何
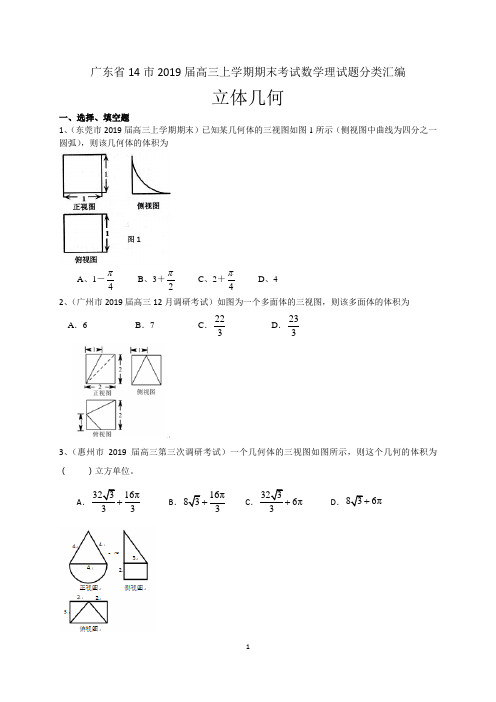
广东省14市2019届高三上学期期末考试数学理试题分类汇编立体几何一、选择、填空题 1、(东莞市2019届高三上学期期末)已知某几何体的三视图如图1所示(侧视图中曲线为四分之一圆弧),则该几何体的体积为A 、1-4π B 、3+2π C 、2+4πD 、4 2、(广州市2019届高三12月调研考试)如图为一个多面体的三视图,则该多面体的体积为 A .6 B .7 C .223 D .2333、(惠州市2019届高三第三次调研考试)一个几何体的三视图如图所示,则这个几何的体积为( )立方单位。
A .32316π33+ B .16π833+ C .3236π3+D .836π+4、(江门市 2019届普通高中高三调研)已知两条直线m n 、,两个平面αβ、,给出下面四个命题: ①//,////m n m n αα⇒ ②//,//,m n m n αβαβ⊥⇒⊥ ③,//m n m n αα⊥⊥⇒或n α⊂ ④,//m m αβαβ⊥⇒⊥其中,正确命题的个数是( ) A .1 B .2 C .3 D .4 5、(揭阳市2019届高三上学期期末)某几何体示意图的三视图如图示,已知其主视图的周长为8,则该几何体侧面积的最大值为A .πB .2πC .4πD .16π6、(雷州市2019届高三上学期期末)正四面体ABCD 中,CD 在平面α内,点E 是线段AC 的中点,在该四面体绕CD 旋转的过程中,直线BE 与平面α所成角不可能是 A .0 B .6π C .3π D .2π7、(茂名市2019届高三上期末)如图2,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则此几何体的体积为( ). A 、6 B 、18 C 、12 D 、368、(清远市2019届高三上期末)如图为某几何体的三视图,图中的三个正方形的边长均为2,则该几何体的体积为 A.316 B. 8-π32C.332D.8+π329、(汕头市2019届高三上学期期末)已知一个简单几何体的三视图如图所示, 若该几何体的体积为 24π+48, 则 r =A 、2B 、4C 、1D 、310、(汕尾市2019届高三上学期期末)某几何体的三视图如图所示,则该几何体的体积为 A .23 B .13 C .43 D .5611、(韶关市2019届高三上学期期末)已知三棱柱ABC-A 1B 1C 1的底面边长和侧棱长都相等,侧棱AA 1⊥底面ABC ,则直线BC 1与AC 所成角的余弦值是 A 、24 B 、-24 C 、22 D 、一2212、(肇庆市2019届高三上学期期末)在长方体1111ABCD A B C D -中,124AA AB BC ===,E 是AB 的中点,则三棱锥11E D C C -外接球的表面积为A .36πB .32πC .9πD .8π13、(珠海市2019届高三上学期期末)如图是某几何体的三视图,其中正视图和侧视图为正方形,俯视图是腰长为2的等腰直角三角形,则该几何体的体积是( )A、43B、223C、83D、42314、(佛山市2019届高三上学期期末)参考答案一、填空题1、A2、B3、D4、B5、C6、D7、A8、B9、A10、A 11、A12、B13、B14、D二、解答题 1、(东莞市2019届高三上学期期末)如图所示,在四棱锥P 一ABCD 中,底面ABCD 为菱形,PA ⊥底面ABCD ,点M 是PC 上的 一个动点,PA =AB ,∠DAB =3π. (1)当PC ⊥DM 时,求证:PC ⊥BM ;(2)当PA ∥平面MBD 时,求二面角P 一BD -M 的余弦值.2、(广州市2019届高三12月调研考试)如图,多面体ABCDEF 中,四边形ABCD 为矩形,二面角A CD F --为60︒,DE CF ∥,,2CD DE AD ⊥=,3DE DC ==,6CF =.(1)求证:BF ∥平面ADE ;(2)在线段CF 上求一点G ,使锐二面角B EG D --的余弦值为14.3、(惠州市2019届高三第三次调研考试)在四棱锥P ABCD -中,侧面PAD ⊥底面ABCD ,底面ABCD 为直角梯形,BC ∥AD ,090ADC ∠=,1BC CD ==,2AD =,3PA PD ==,E 为AD 的中点,F 为PC 的中点。
广东省各地高三上学期期末考试数学理试题分类汇编:立体几何 Word版含答案[ 高考]
![广东省各地高三上学期期末考试数学理试题分类汇编:立体几何 Word版含答案[ 高考]](https://img.taocdn.com/s3/m/13021c1ee2bd960591c67724.png)
图1图1广东省各地2014届高三上学期期末考试数学理试题分类汇编立体几何一、选择题1、(佛山市2014届高三教学质量检测(一))某由圆柱切割获得的几何体的三视图如图1所示,其中俯视图是中心角为60︒的扇形,则该几何体的体积为A .3πB .23πC .π ks5uD .2π答案:D2、(惠州市2014届高三第三次调研考)右图是一个几何体的三视图,根据图中数据可得该几何体的表面积是( )A .9πB .10πC .11πD .12π答案:D3、(江门市2014届高三调研考试)如图1,E 、F 分别是正方体1111D C B A ABCD -中1AD 、C B 1上的动点(不含端点),则四边形FDE B 1的俯视图可能是A .B .C .D . 答案:B4、(揭阳市2014届高三学业水平考试)图(1)中的网格纸是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为A.4B.8C.16D.20 答案:C俯视图正(主)视图 侧(左)视图2 3225、(汕头市2014届高三上学期期末教学质量监测)三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正视 图(如图所示)的面积为8,则侧视图的面积为( ) A. 8 B. 4 C.43 D.3答案:C6、(肇庆市2014届高三上学期期末质量评估)某几何体的三视图如图2所示(单位:cm), 则其体积和表面积分别是( )A. 6π3cm 和12(1)π+2cm B. 6π3cm 和12π2cm C. 12π3cm 和12(1)π+2cm D. 12π3cm 和12π2cm答案:A7、(中山市2014届高三上学期期末考试)把边长为1的正方形ABCD 沿对角线BD 折起,使得平面⊥ABD 平面CBD ,形成三棱锥ABD C -的正视图与俯视图如下图所示,则侧视图的面积为 ( )A .21B .41C .42D . 22 答案:B8、(珠海市2014届高三上学期期末)一个四棱锥的三视图如图所示,其中主视图是腰长为1的等腰直角三角形,则这个几何体的体积是( ) A 、12 B 、1 C 、23D 、2答案:A9、(珠海一中等六校2014届高三第三次联考)已知正方形ABCD 的对角线AC 与BD 相交于E 点,将ACD ∆沿对角线AC 折起,使得平面ABC ⊥平面ADC (如图),则下列命题中正确的为( C ) A. 直线AB ⊥直线CD, 且直线AC ⊥直线BDB. 直线AB ⊥平面BCD ,且直线AC ⊥平面BDEC. 平面ABC ⊥平面BDE ,且平面ACD ⊥平面BDED. 平面ABD ⊥平面BCD ,且平面ACD ⊥平面BDE 答案:C10、(东莞市2014届高三上学期期末调研测试)一个空间几何体的正视图与侧视图都是边长为2的正三角形,俯视图是半径为1的圆,则该几何体的体积是答案:A 二、填空题1、(省华附、省实、广雅、深中四校2014届高三上学期期末)某几何体的三视图如图所示,其中正(主)视图与侧(左)视图的边界均为直角三角形,俯视图的边界为直角梯形,则该几何体的体积为 .答案:82、(江门市2014届高三调研考试)若α、β是不重合的平面,a 、b 、c 是互不相同的空间直线,则下列命题中为真命题的是 .(写出所有真命题的序号) ① 若α//a ,α//b ,则b a // ② 若α//c ,α⊥b ,则b c ⊥ ③ 若α⊥c ,β//c ,则βα⊥④ 若α⊂b ,α⊂c 且b a ⊥,c a ⊥,则α⊥a 答案:②③(对1个3分,错1个2-分)解法二图ABCD PEFHxy z解法一图A BC DPEF. .ACDBEF图5图6ABCD PEF三、解答题1、(佛山市2014届高三教学质量检测(一))如图5,矩形A B C D 中,12AB =,6AD =,E 、F 分别为CD 、AB 边上的点,且3DE =,4BF =,将BCE ∆沿BE 折起至PBE ∆位置(如图6所示),连结AP 、EF 、PF ,其中25PF =.(Ⅰ)求证:PF ⊥平面ABED ; (Ⅱ)求直线AP 与平面PEF 所成角的正弦值.【解析】(Ⅰ)由翻折不变性可知,6PB BC ==,9PE CE ==, 在PBF ∆中,222201636PF BF PB +=+==,所以PF BF ⊥ ……………2分 在图1中,易得()226123461EF =+--=, ………3分在PEF ∆中,222612081EF PF PE +=+==,所以PF EF ⊥ …………………4分 又BF EF F =,BF ⊂平面ABED ,EF ⊂平面ABED ,所以PF ⊥平面ABED . ………………6分(注:学生不写BFEF F =扣1分)(Ⅱ)方法一:以D 为原点,建立空间直角坐标系D xyz -如图所示,则()6,0,0A ,()6,8,25P ,()0,3,0E ,()6,8,0F ,所以()0,8,25AP =,()0,0,25FP =,()6,5,0EF =, …………8分 设平面PEF 的法向量为(),,x y z =n ,则00FP EF ⎧⋅=⎪⎨⋅=⎪⎩n n ,即250650z x y ⎧⋅=⎪⎨+=⎪⎩,解得560x y z ⎧=-⎪⎨⎪=⎩令6y =-,得()5,6,0=-n ,……………………………………………12分 设直线AP 与平面PEF 所成角为θ,则48sin 8461AP AP θ⋅===⨯n n81281427.所以直线AP 与平面PEF 所成角的正弦值为81281427. ……………………14分 方法二:过点A 作AH EF ⊥于H ,由(Ⅰ)知PF ⊥平面ABED ,而AH ⊂平面ABED 所以PF AH ⊥,又EF PF F =,EF ⊂平面PEF ,PF ⊂平面PEF ,所以AH ⊥平面PEF ,所以APH ∠为直线AP 与平面PEF 所成的角. ………………………9分在Rt APF ∆中,226420221AP AF PF =+=+= …………………………11分在AEF ∆中,由等面积公式得AF ADAH EF ⋅==4861………………………………13分 在Rt APH ∆中,16381281sin 42761221AH APH AP ∠==⨯=所以直线AP 与平面PEF 所成角的正弦值为81281427. ………………………14分 2、(广州市2014届高三1月调研测试)在如图6的几何体中,平面CDEF 为正方形,平面ABCD 为等腰梯形,AB ∥CD ,BC AB 2=,60ABC ︒∠=,AC FB ⊥.(1)求证:⊥AC 平面FBC ;(2)求直线BF 与平面ADE 所成角的正弦值.(1)证明1:因为BC AB 2=,60ABC ︒∠=,在△ABC 中,由余弦定理可得BC AC 3=.……………………………2分所以222AC BC AB +=.所以BC AC ⊥.………………………………………………………………3分 因为AC FB ⊥,BF BC B =,BF 、BC ⊂平面FBC ,所以⊥AC 平面FBC .……………………………………………………………4分 证明2:因为60ABC ︒∠=,设BAC α∠=()0120α<<,则120ACB α∠=-.在△ABC 中,由正弦定理,得()sin sin 120BC ABαα=-.……………………1分 因为BC AB 2=,所以()sin 1202sin αα-=.整理得3tan 3α=,所以30α=.……………………………………………2分 图6ABCDE F所以BC AC ⊥.………………………………………………………………3分 因为AC FB ⊥,BF BC B =,BF 、BC ⊂平面FBC ,所以⊥AC 平面FBC .…………………………………………………4分(2)解法1:由(1)知,⊥AC 平面FBC ,FC ⊂平面FBC ,所以FC AC ⊥.因为平面CDEF 为正方形,所以FC CD ⊥.因为AC CD C =,所以⊥FC 平面ABCD .……………………………6分取AB 的中点M ,连结MD ,ME ,因为ABCD 是等腰梯形,且BC AB 2=,60DAM ∠=, 所以MD MA AD ==.所以△MAD 是等边三角形,且MEBF .………………7分取AD 的中点N ,连结MN ,NE ,则MN AD ⊥.………8分 因为MN ⊂平面ABCD ,ED FC ,所以ED MN ⊥.因为ADED D =,所以MN ⊥平面ADE . ……………9分所以MEN ∠为直线BF 与平面ADE 所成角. ……………10分 因为NE ⊂平面ADE ,所以MN ⊥NE .…………………11分因为32MN AD =,222ME MD DE AD =+=,……………………………12分 在Rt △MNE 中,6sin 4MN MEN ME ∠==.………………………………13分 所以直线BF 与平面ADE 所成角的正弦值为64.……………………………14分 解法2:由(1)知,⊥AC 平面FBC ,FC ⊂平面FBC ,所以FC AC ⊥.因为平面CDEF 为正方形,所以FC CD ⊥.因为AC CD C =,所以⊥FC 平面ABCD .……………………………………6分所以CA ,CB ,CF 两两互相垂直,建立如图的空间直角坐标系xyz C -.………………………7分 因为ABCD 是等腰梯形,且BC AB 2=,60ABC ︒∠= 所以CB CD CF ==.不妨设1BC =,则()0,1,0B ,()0,0,1F ,()3,0,0A,31,,022D ⎛⎫- ⎪ ⎪⎝⎭,31,,122E ⎛⎫- ⎪ ⎪⎝⎭, MN ABCD EFx AB CDEFyz所以()0,1,1BF =-,31,,022DA ⎛⎫=⎪ ⎪⎝⎭,()0,0,1DE =.………………………9分 设平面ADE 的法向量为=()x,y,z n ,则有0,0.DA DE ⎧⋅=⎪⎨⋅=⎪⎩n n 即30,220.y x z ⎧+=⎪⎨⎪=⎩取1x =,得=n ()1,3,0-是平面ADE 的一个法向量.…………………………11分 设直线BF 与平面ADE 所成的角为θ, 则()()0,1,11,3,06sin cos ,422BF BF BF --⋅θ=〈〉===n n n.………………13分 所以直线BF 与平面ADE 所成角的正弦值为64.………………………………14分 3、(增城市2014届高三上学期调研)如图3,边长为2的正方形ABCD ,E,F 分别是AB,BC 的中点,将△AED , △DCF 分别沿DE,DF 折起,使A,C 两点重合于A '。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省14市2016届高三上学期期末考试数学文试题分类汇编立体几何一、选择题1、(潮州市2016届高三上学期期末)右图是一个几何体的正视图和侧视图,其俯视图是面积为82的矩形,则该几何体的体积是A、8B、42C、16D、16 32、(东莞市2016届高三上学期期末)已知一个几何体的三视图如图所示,图中小正方形的边长为1,则该几何体的体积为(A)103(B)4(C)6(D)103、(佛山市2016届高三教学质量检测(一)(期末))某一简单几何体的三视图如图2所示,该几何体的外接球的表面积是( )A. 13πB. 16πC. 25πD. 27π4、(广州市2016届高三1月模拟考试)一个几何体的三视图如图所示,其中正视图与侧视图都是斜边长为2的直角三角形,俯视图是半径为1的四分之一圆周和两条半径,则这个几何体的表面积为(A)312π(B)36π(C)34π(D)33π22322正视图侧视图俯视图图25、(惠州市2016届高三第三次调研)某几何体的三视图如图,其正视图中的曲线部分为半个圆弧,则该几何体的表面积为( ) (A )π42616++ (B )π32616++ (C )π42610++ (D )π32610++6、(揭阳市2016届高三上学期期末学业水平考试)已知棱长为2的正方体ABCD-A 1B 1C 1D 1的一个面A 1B 1C 1 D 1在一半球底面上,且A 、B 、C 、D 四个顶点都在此半球面上,则此半球的体积为(A) 46π (B) 26π (C) 163π (D) 86π7、(茂名市2016届高三第一次高考模拟)一个几何体的三视图如图所示,则该几何体的体积为( )A 、43 B 、23 C 、13D 、2 8、(清远市2016届高三上学期期末)一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( ) A .3 B .23 C . 33 D .439、(汕头市2016届高三上学期期末)某几何体的三视图如图2所示,则该几何体的外接球表面积为( )正视图俯视图侧视图2232311A.43πB.12πC.24πD.48π10、(汕尾市2016届高三上学期调研)一个几何体的三视图如图所示,该几何体的体积为( )11、(韶关市2016届高三上学期调研)如图,圆柱内有一个直三棱柱,三棱柱的底面在圆柱底面内,12,圆柱的底面直径与母线长相且底面是正三角形. 如果三棱柱的体积为3等,则圆柱的侧面积为12A.π14B.π16C.π18D.π12、(湛江市2016年普通高考测试(一))一个几何体的三视图如右图所示,则该几何体的表面积为A 、64+8πB 、48+12πC 、48+8πD 、48+12π13、(肇庆市2016届高三第二次统测(期末))若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图2所示,则此几何体的表面积是 (A )24π (B )2482ππ+ (C )2442ππ+ (D )32π14、(珠海市2016届高三上学期期末)已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是 ( )A .2B .4C .6D .12侧视图正视图 俯视图2222第11题图1、A2、C3、C4、A5、C6、A7、B8、A9、B 10、A 11、C 12、A 13、C 14、B二、填空题1、(潮州市2016届高三上学期期末)已知一个长方体的长、宽、高分别是5,4,3,则该长方体的外接球的表面积等于__2、(东莞市2016届高三上学期期末)如图,等腰直角三角形ABC ,|AB |=2,AC L ,三角形ABC 绕直线L 旋转一周,得到的几何体的体积为3、(惠州市2016届高三第三次调研)已知三棱锥S ABC -所在顶点都在球O 的球面上,且SC ⊥平面ABC ,若1SC AB AC ===,120BAC ∠=︒,则球O 的表面积为 .4、(揭阳市2016届高三上学期期末学业水平考试)如图2,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则被截去部分的几何体的表面积为 .5、(汕尾市2016届高三上学期调研)若正方体的棱长为2,则该正方体外接球的表面积为6、(肇庆市2016届高三第二次统测(期末))已知各顶点都在一个球面上的正四棱柱的高为4,体积为16,则这个球的体积为 .1、π502、3、【答案】5π【解析】记底面三角形ABC 的外接圆为⊙O ′,半径为r,则22sin120BCr ==︒,所以记球的半径为R ,因为SC ⊥平面ABC ,则()2222145R r SC =+=+=,所以球O 的表面积为2254452S R πππ⎛⎫==⨯⨯= ⎪ ⎪⎝⎭4、54183+5、12π6、86π三、解答题1、(潮州市2016届高三上学期期末)如图,四棱锥P -ABCD 的底面ABCD 是矩形,侧面PAB 是正三角形,AB =2,BC =2,PC =6,E ,H 分别为PA 、AB 中点。
(I )求证:PH ⊥平面ABCD ; (II )求三棱锥P -EHD 的体积。
2、(东莞市2016届高三上学期期末)如图,四棱锥P -ABCD 中,底面四边形ABCD 是正方形,PA =AB =1,PA ⊥平面ABCD ,E 为棱PB 上一点,PD ∥平面ACE ,过E 作PC 的垂线,垂足为F 。
(I )求证:PC ⊥平面AEF ; (II )求三棱锥P -AEF 的体积。
图3B 1C 1A 1DC BA3、(佛山市2016届高三教学质量检测(一)(期末))如图4,三棱柱111ABC A B C -中,侧面11AAC C⊥侧面11ABB A ,12AC AA AB ==,1160AAC∠=︒, 1AB AA ⊥,H 为棱1CC 的中点,D 为1BB 的中点.(Ⅰ) 求证:1A D ⊥平面1AB H ;(Ⅱ) 若2AB =,求三棱柱111ABC A B C -的体积.4、(广州市2016届高三1月模拟考试)在直三棱柱111ABC A B C -中,13AB AC AA ===,2BC =,D 是BC 的中点,F 是1C C 上一点.(Ⅰ)当2CF =时,证明:1B F ⊥平面ADF ; (Ⅱ)若D B FD 1⊥,求三棱锥1B ADF -的体积.5、(惠州市2016届高三第三次调研)如图,已知等腰梯形ABCD 中,1//,2,2A D B C A BA DBC E ===是BC 的中点,A EB D M = ,将BAE ∆沿着AE 翻折成1B AE ∆.(Ⅰ)求证:CD ⊥平面1B DM ;(Ⅱ)若101=C B ,求棱锥1B CDE -的体积6、(揭阳市2016届高三上学期期末学业水平考试)如图4,在三棱柱ABC -A 1B 1C 1中,底面△ABC 是边长为2的等边三角形,D 为AB 中点.(Ⅰ)求证:BC 1∥平面A 1CD ;(Ⅱ)若四边形CB B 1C 1是正方形,且15,A D =求多面体11CAC BD 的体积.ABCA 1B 1C 1DH图4A BCDFA 1B 1C 1ABDC EMAM1B DE C图47、(茂名市2016届高三第一次高考模拟) 如图,在直角梯形ABCD 中,AB ∥CD ,且AB =AD =2,CD =4,四边菜ADE 1F 1是正方形,且平面ADE 1F 1⊥平面ABCD ,M 是E 1C 的中点。
(1)证明:BM ∥平面ADE 1F 1; (2)求三棱锥D -BME 1的体积。
8、(清远市2016届高三上学期期末)如图,直三棱柱111ABC A BC -中,AC =CB ,D ,E 分别是AB ,1BB 的中点。
(1)证明://1BC 平面CD A 1; (2)求证:CD ⊥平面ABB 1A 1;(3)设12,22AA AC CB AB ====,求E 到截面DC A 1的距离d.9、(汕头市2016届高三上学期期末)如图4,在直三棱柱111C C AB -A B 中,底面C ∆AB 为等腰直角三角形,C 90∠AB = ,4AB =,16AA =,点M 是1BB 中点.(I )求证:平面1C A M ⊥平面11C C AA ; (II )求点A 到平面1C A M 的距离.GFEDCBA10、(汕尾市2016届高三上学期调研)如图,在四棱锥P —ABCD 中,侧面PAB 为正三角形,侧面PAB ⊥底面ABCD ,E 为PD 的中点,AB ⊥AD , BC ∥AD ,且AB=BC=12AD=2. (1)求证CE ∥平面PAB ;(2)求四棱锥P —ABCD 的体积.11、(韶关市2016届高三上学期调研)如图,四边形ABCD 是矩形,1,2AB AD ==,E 是AD 的中点,BE 与AC 交于点F , GF ⊥平面ABCD . (Ⅰ)求证:AF ⊥面BEG ;(Ⅱ) 若AF FG =,求点E 到平面ABG 距离.12、(湛江市2016年普通高考测试(一))如图,三棱柱ABC -A 1B 1C 1中,侧棱AA 1⊥平面ABC ,AB 1⊥平面A 1CD ,AC ⊥BC ,D 为AB 中点。
(I )证明:CD ⊥平面AA 1B 1B ;(II )若AA 1=1,AC =2,求三棱锥C 1-A 1DC 的体积。
EH PADCBF13、(肇庆市2016届高三第二次统测(期末))如图3,正方形ABCD 的边长为22,E 、F 分别是DC 和BC 的中点,H 是正方形的对角线AC 与EF 的交点,N 是正方形两对角线的交点,现沿EF 将CEF ∆折起到PEF ∆的位置,使得PH AH ⊥,连结PA ,PB ,PD (如图4).(Ⅰ)求证:BD ⊥AP ; (Ⅱ)求三棱锥A BDP -的高.14、(珠海市2016届高三上学期期末)如图,四棱锥P ABCD -底面ABCD 为平行四边形,且AC BD O = ,PA PC =,PB BD ⊥,平面PBD ⊥平面PAC (I)求证PB ⊥面ABCD(II)若PAC ∆为正三角形,60BAD ∠=︒,且四棱锥P ABCD -的体积为66,求侧面PCD ∆的面积.参考答案:1、(Ⅰ)证明:∵PAB ∆是正三角形且H 是AB 的中点,∴PH AB ⊥.……………………..………………1分∵在PBC ∆中,2PB AB ==,2BC =,6PC =,∴222PC PB BC =+.∴BC PB ⊥.…………………………….…..……3分 又BC BA ⊥,且PB BA B = , PB 、BA ⊂平面PAB ,∴BC ⊥平面PAB ,…………………………………4分又PH ⊂平面PAB ,∴BC PH ⊥.………………………………………5分又AB BC B = ,AB 、BC ⊂平面ABCD , ∴PH ⊥平面ABCD .…………………………..………6分 (Ⅱ)解法一:O DAPBC第19题图E H PADCB由(Ⅰ)可知PH 是三棱锥P AHD -的高. 在Rt PAH ∆中,2PA AB ==,112AH AB ==. ∴22413PH PA AH =-=-=.………………7分又11212222AHD S AH AD ∆=⋅⋅=⨯⨯=, ∴112633326P AHD AHD V S PH -∆=⋅⋅=⨯⨯=.………………9分 过点E 作//EF PA ,交AB 于点F ,又点E 是PA 的中点, 所以EF ⊥平面AHD ,且1322EF PH ==. ∴11236332212E AHD AHD V S EF -∆=⋅=⨯⨯=.………………11分 ∴三棱锥P EHD -的体积为66661212P EHD P AHD E AHD V V V ---=-=-=.……12分 解法二:在Rt PAH ∆中,2PA AB ==,112AH AB ==. 所以22413PH PA AH =-=-=.…………………………7分又E 是PA 的中点, 所以11111313222224PEH PAH S S AH PH ∆∆==⨯⋅⋅=⨯⨯⨯=…9分 由(Ⅰ)可知BC ⊥平面PAB 且2BC =. 又//AD BC 且AD BC =,所以AD ⊥平面PAB 且2AD =.………………10分 所以1136233412P EHD D PEH PEH V V S AD --∆==⋅⋅=⨯⨯=………………12分 2、GMHDC 1B 1A 1CBA3、【解析】(Ⅰ)连结1AC ,因为1ACC ∆为正三角形,H 为棱1CC 的中点,所以1AH CC ⊥,从而1AH AA ⊥,又面11AAC C ⊥面11ABB A , 面11AAC C 面11ABB A 1AA=,AH ⊂面11AAC C , 所以AH ⊥面11ABB A ,又1A D ⊂面11ABB A ,所以AH ⊥1A D …①,……2分 设2AB a =,由12AC AA AB ==,所以12AC AA a ==,1DB a =,11111112DB A B B A AA ==,又111190DB A B A A ∠=∠=︒,所以1111A DB AB A ∆∆ , 所以1111B AA B A D ∠=∠,又11190B A D AA D ∠+∠=︒, 所以11190B AA AA D ∠+∠=︒,设11AB A D O = ,则11A D AB ⊥…②,…………………5分由①②及1AB AH A = ,可得1A D ⊥平面1AB H .…………………6分(Ⅱ)方法一:取1AA 中点M ,连结1C M ,则1//C M AH ,所以1C M ⊥面11ABB A .…………7分 所以11111111623333C AB A AB A V S C M -∆=⋅=⨯⨯=,…………………10分 所以三棱柱111ABC A B C -的体积为11136C AB A V -=.…………………12分 方法二:取11AC 中点G ,连结AG ,因为11AAC ∆为正三角形,所以11AG AC ⊥, 因为面11AAC C ⊥面11ABB A ,面11AAC C 面11ABB A 1AA =,11A B ⊂面11ABB A ,111A B AA ⊥,所以11A B ⊥面11AAC C ,又AG ⊂面11AAC C ,所以11A B AG ⊥,又11111AC A B A = ,所以AG ⊥平面111A B C ,所以AG 为三棱柱111ABC A B C -的高,……9分 经计算3AG =,11111111122222A B C S A B AC ∆=⋅=⨯⨯=,………………11分所以三棱柱111ABC A B C -的体积111236A B C V S AG ∆=⋅=⨯=.………………12分4、5、【解析】(I ) 连接DE ,由题意可知四边形ABED 和AECD 是平行四边形, 又AB=AD ,所以ABED 是菱形 (2分)故BM AE ⊥,.DM AE ⊥ 即AE M B ⊥1,.DM AE ⊥ (4分)D 1B 1C 1A 1DCBAEHB 1C 1A 1DCBA又因为M M B DM =⋂1,MD 、⊂M B 1平面MD B 1,所以⊥AE 平面MD B 1.(5分) 由题可得AE ∥CD ,所以1CD B DM ⊥平面 (6分) (Ⅱ) 连接CM ,由(Ⅰ)得AB=AE=BE=2 ,所以1B AE ∆为等边三角形 ,31=∴M B (7分)又722=+=CD DM CM ,101=C B 21221C B CM M B =+∴,即1B M MC ⊥ (9分)又AE M B ⊥1,MC AE M ⋂=,⊥∴M B 1平面CDE (10分)3322121=⨯⨯=⋅=∆DM AE S CDE (11分) 111133133B CDE CDE V S B M -∆∴=⋅=⨯⨯= (12分)6、(I)证法1:连结AC 1,设AC 1与A 1C 相交于点E ,连接DE ,则E 为AC 1中点,--------2分 ∵D 为AB 的中点,∴DE ∥BC 1,-----4分 ∵BC 1Ë平面A 1CD ,DE Ì平面A 1CD ,------------5分 ∴BC 1∥平面A 1CD . -----------------------------6分 【证法2:取11A B 中点1D ,连结1BD 和11C D ,-----1分 ∵BD 平行且等于11A D ∴四边形BD 11A D 为平行四边形 ∴11//A D BD -----------------------------------2分 ∵1A D ⊂平面1ACD ,1BD ⊄平面1ACD ∴1//BD 平面1ACD ,------------------------------3分 同理可得11//C D 平面1ACD ------------------------4分 ∵1111BD C D D = ∴平面1ACD //平面11BD C 又∵1BC ⊂平面11BD C∴BC 1∥平面A 1CD. -------------------------------6分】 (Ⅱ) 222115AD +A A =A D = 1,A A A D \^-------------------------------------7分又111,//B B BC B B A A ^ 1A A BC \^,又AD BC B = 1A A \^面ABC -------------------------------------------9分 (法一)∴所求多面体的体积V =1111111ABC A B C A ACD B A B C V V V ----------------------------10分111111133ABC ACD A B C AA S AA S BB S ∆∆∆=⨯-⋅⨯-⋅⨯ 112ABC AA S ∆=⋅⨯2113223222=⋅⋅⋅⋅= 即所求多面体11CAC BD 的体积为3.----------------12分【(法二)过点1A 作111A H B C ⊥于H ,∵平面11BB C C ⊥平面111A B C 且平面11BB C C 平面111A B C 11B C =∴1A H ⊥平面11BB C C ,------10分∴所求多面体的体积V =1111A ACD A ACC V V --+1111133BCD BCC S AA S A H ∆∆=⋅+⋅ 113114243332432=⨯⨯⨯⨯+⨯⨯⨯=.------------------------------------------12分】 7、8、【证明】:(1)连接AC 1交A 1C 于点F ,则F 为AC 1的中点, ………………1分 又D 是AB 的中点,连接DF ,则BC 1∥DF . ………………2分DF ⊂平面A 1CD ,1BC ⊄平面A 1CD ………………3分 ∴BC 1∥平面A 1CD ………………4分(2) ABC -A 1B 1C 1是直三棱柱,∴AA 1⊥平面ABC,……5分 CD ⊂平面ABC ,∴AA 1⊥CD , ………………6分 由已知AC =CB ,D 为AB 的中点,∴CD ⊥AB ,…………7分又AA 1∩AB =A ,于是CD ⊥平面ABB 1A 1, ………………8分 (3)由AA 1=AC =CB =2,AB=22得∠ACB =90°,CD =2,A 1D =6,DE =3,A 1E =3, 故A 1D 2+DE 2=A 1E 2,DE ⊥A 1D ,………………9分∴123621311=⨯⨯⨯⨯=-DEA C V ………………10分又C D ⊥A 1D,∴△A 1DC 为直角三角形,……………………11分 ∴11D EA C D CA E V V --= ∴1331=⋅⨯d , ∴ 3=d ……………12分法2:∵ CD ⊥平面ABB 1A 1 ,且CD ⊂平面A 1DC.∴ 平面A 1CD ⊥平面ABB 1A 1 . ……………………………………………………10 ∵ 平面A 1CD ∩平面ABB 1A 1=DA 1且ED ⊥DA 1∴ED ⊥平面A 1CD ,∴ED 为E 到平面A 1CD 的距离………………………………11 在Rt △DBE 中,ED=322=+BE DB ………………………………………12 9、解:(Ⅰ)记1AC 与C A 1的交点为E .连结ME .直三棱柱111C B A ABC -,点M 是1BB 中点,2211435MA MA MC MC ∴====+=……2分因为点E 是1AC 、C A 1的中点,所以1AC ME ⊥ , C A ME 1⊥, ……4分 又11AC AC E = 从而ME ⊥平面11AAC C .因为ME ⊂平面1A MC ,所以平面1A MC ⊥平面11AAC C . ……6分(Ⅱ)过点A作1AH AC ⊥于点H , 由(Ⅰ)平面1A MC ⊥平面11AAC C ,平面1A MC 平面111AAC C AC =, 而AH ⊥平面11AAC C ……2分∴AH 即为点A 到平面1A MC 的距离. ……3分在1A AC ∆中,190A AC ∠=︒,11642,68AA AC AC ===,1164224343468AA AC AH AC ⋅⨯∴===即点A 到平面1A MC 的距离为243434……6分 10、11、证法1:∵四边形ABCD 为矩形,∴AEF ∆∽CBF ∆, ∴21===BC AE BF EF CF AF ……………1分 又∵矩形ABCD 中,2,1==AD AB ,∴3,22==AC AE 在BEA Rt ∆中,2622=+=AE AB BE ∴3331==AC AF ,3632==BE BD ……………2分 在ABF ∆中,222221)36()33(AB BF AF ==+=+ ∴90=∠AFB ,即BE AC ⊥ ……………4分∵⊥GF 平面ABCD ,⊂AC 平面ABCD ∴GF AC ⊥ ……………5分 又∵F GF BE = ,⊂GF BE ,平面BCE ∴⊥AF 平面BEG ……………6分 证法2:(坐标法)证明1-=⋅BE AC K K ,得BE AC ⊥,往下同证法1.(2)在AGF Rt ∆中,22GF AF AG +=36)33()33(22=+= 在BGF Rt ∆中,22GF BF BG +=1)33()36(22=+= ………… ……………8分 在ABG ∆中,36=AG ,1==AB BG ∴2)66(13621-⨯⨯=∆ABG S 656303621=⨯⨯=………………………………10分 设点E 到平面ABG 的距离为d ,则GF S d S ABF ABG ⋅=⋅∆∆3131, ………………………………11分 ∴ABG ABFS GF S d ∆⋅=1030653312221=⨯⨯⨯= ………………………………12分12、13、(Ⅰ)证明: ∵E 、F 分别是CD 和BC 的中点,∴EF //BD . (1分) 又∵AC BD ⊥,∴AC EF ⊥,故折起后有PH EF ⊥. (2分) 又PH AH⊥,所以PH ⊥平面ABFED . (3分)又∵BD ⊂平面ABFED ,∴PH BD ⊥, (4分) ∵AH PH H = ,,AH PH ⊂平面APH ,∴BD ⊥平面APH , (5分) 又AP ⊂平面APH ,∴BD ⊥AP (6分) (Ⅱ)解:∵正方形ABCD 的边长为22,∴4AC BD ==,2,1AN NH PH ===,PE PF = (7分) ∴PBD ∆是等腰三角形,连结PN ,则PN BD ⊥,222PN NH PH =+=∴PBD ∆的面积11422222PBD S BD PN ∆=⋅=⨯⨯= (8分) 设三棱锥A BDP -的高为h ,则三棱锥A BDP -的体积为12233A BDP PBD hV S h -∆=⋅= (9分)由(Ⅰ)可知PH 是三棱锥P ABD -的高,∴三棱锥P ABD -的体积:11111422221332323P ABD ABD V S PH AB AD PH -∆=⋅=⨯⋅⋅=⨯⨯⨯⨯= (11分)∵A BDP P ABD V V --=,即22433h =,解得2h =,即三棱锥A BDP -的高为2. (12分) 14、(I)证明:由于四边形ABCD 为平行四边形,所以O 为AC 的中点;连接PO PA PC =∴AC PO ⊥ ———1分 平面PBD ⊥平面PAC ,又 平面PBD 平面=PAC PO ,AC ∈平面PAC ∴AC ⊥面PBD ∴AC ⊥PB —————4分又 PB BD ⊥,且AC BD O = ,AC BD ABCD ∈、面∴PB ⊥面ABCD —————6分(II)解:由(I)知AC ⊥面PBD ,所以AC ⊥BD ,可知底面ABCD 为菱形; 设AB BC a ==,又因为60BAD ∠=︒,所以BD a =,3AC a =因为PAC ∆为正三角形,所以3PC a = —————7分由(I)知PB BC ⊥,从而PBC ∆为直角三角形,2PB a ∴= —————8分21116323326P ABCD ABCD V S PB a a -=== 解得:1a = ———9分 所以3PC =、1CD =、2PB = 223PD PB BD ∴=+= —————10分取CD 的中点E ,连接PE ,可知PE CD ⊥22112PE PC CE =-=11124PCD S CD PE == —12分 OD APB C E。
