第1章 时域离散随机信号的分析
第1章离散信号与系统时域分析2

因此
当0 n 3时,y (n) 1 n 1
m 0 3 n
当4 n 6时,y(n)
数字信号处理
数字信号处理
DIGITAL SIGNALS PROCESSING
1.3.1 线性系统
• 满足叠加原理的系统称为线性系统。设x1(n)和 x2(n)分别作为系统的输入序列,其输出分别用 y1(n)和y2(n)表示,即
y1 (n) T [ x1 (n)], y2 (n) T [ x2 (n)]
DIGITAL SIGNALS PROCESSING
1.3.3 线性时不变系统输入与输 出之间的关系——卷积
设系统的输入x(n)=δ(n),系统输出y(n)的初 始状态为零,定义这种条件下系统输出称为 系统的单位脉冲响应,用h(n)表示。用公式 表示为
h(n) T [ (n)] (1.3.6)
数字信号处理
DIGITAL SIGNALS PROCESSING
(1.3.8) (1.3.9) (1.3.10)
线性卷积的运算规则
x(n) (n)
m
x(m) (n m) x(n)
(1.3.11)
x(n) (n n0 ) x(n n0 )
数字信号处理
DIGITAL SIGNALS PROCESSING
1.3.4系统的因果性和稳定性
判断线性时不变系统因果性的 充分必要条件:
h(n) 0, n 0
数字信号处理
DIGITAL SIGNALS PROCESSING
信号分析与处理-程耕国 第1章 信号及信号的时域分析

2 f (n )
N
信号与系统
SIGNALS AND SYSTEMS
15
1.1.4能量信号与功率信号
1.能量信号 能量信号的归一化能量为有限值,归一化功率为零。即满 足 0 W ,P 0 。
2.功率信号 功率信号的归一化功率为有限值,归一化能量为无限大。 即满足 W , 0 P 。一般,周期信号为功率信号。
t
cos Ω t
Im f t Ae
t
sin Ω t
Re 的波形相似,只是相位相差 f t 信号 Re f t 的波形与 。 两者均为实信号,而且是频率相同,幅值随时间变化的正( 2 余)弦振荡信号。
Re f t 0 Im f t 0
f (t )
A
f (n)
A N
-T
-T/2
0 -A (a)
T/2
T t
-N
0
N
2N
n
(b)
图1-5周期信号
信号与系统
SIGNALS AND SYSTEMS
13
1.1.3周期信号与非周期信号
2.非周期信号: 不满足周期信号定义的信号称为非周期信号。 周期分别为T1 、T 2 的2个信号相加产生的信号 f t ,其周期 最小公倍数 T 0 为:
N
W 0
所以该信号为能量信号。
信号与系统
SIGNALS AND SYSTEMS
19
1.1.5 实信号与复信号
1.实信号 在各时刻 t (或 n )上的信号幅值为实数的信号为实信号。 例如,单边指数信号,正、余弦信号等。实信号是可以物 理实现的。 2.复信号 函数(或序列)值为复数的信号称为复信号,最常用的是复 指数信号。连续时间的复指数信号通常表示为:
第一章 离散随机信号统计分析基础

❖ 如果我们把对温漂电压的观察看作为一个随机试验,那么,每一次的记录,就是
随机试验的一次实现,相应的结果就是一个样本函数:
xi (t)
❖
所能有经样历本的函整数个的过x集程i (合,t)该集合就i=是1一,个2随,…机过,N程,,N也→即随∞机,信就号构,成记了之温为漂:电压可
X(t)
物随机变理量 意义:x1 (t1 ), x2 (t1 ), , xN (t1 )
lim
M
1 2M
1
M
x(n)x(n
nM
m)
x
(m)
例1.2.3 讨论例1.2.1随机相位正弦序列的各
态遍历性。
解 对 X (n) Asin(2fnTs ),其单一的时间样本
x(n) Asin(2fnTs ) , 为一常数,对 X (n)
作时间平均,显然
mx (n)
lim
M
2
1 M
自相关函数和自协方差函数的关系
❖ 1 X (m) X (m) mX2 XY (m) XY (m) mX mY
❖ 2当 mX 0 时
X (m) X (m) XY (m) XY (m)
工程实际中,当m趋于无穷大时,可以认 为不相关,存在:
lim
m
X
(m)
E[
X
*
(n)
X
自相关函数 X (n1, n2 ) 和 n1,n2 的选取无关,而仅和 n1, n之2 差有关,那么,我 们称X(n)为宽平稳的随机信号,或广义平稳随机信号 。其具有以下的统 计特征. ❖ 1)均值为常值。
2)自相关函数和自协方差函数均只是m的函数。
目的:使问题简化,实际工程中大部分属于这种
严平稳随机信号:指概率特性不随时间的平移而变化(或说与 时间基准点无关)的随机信号。只有当X(n)是高斯随机过程 时,宽平稳才是严平稳。
数字信号处理-时域离散随机信号处理课件:时域离散随机信号的分析

数字信号处理——时域离散随机信号处理
x1(tn
t
图 1.1.1 n部接收机的输出噪声
数字信号处理——时域离散随机信号处理
x1(n) x2(n) xn(n)
数字信号处理——时域离散随机信号处理
一般均方值和方差都是n的函数, 但对于平稳随机序列, 它 们与n无关, 是常数。如果随机变量Xn代表电压或电流,其均方 值表示在n时刻消耗在1 Ω电阻上的集合平均功率,方差则表示 消耗在1Ω电阻上的交变功率的集合平均。有时将σx称为标准方 差。
数字信号处理——时域离散随机信号处理
3. 随机序列的相关函数和协方差函数
我们知道, 在随机序列不同时刻的状态之间,存在着关联 性, 或者说不同时刻的状态之间互相有影响,包括随机序列 本身或者不同随机序列之间。 这一特性常用自相关函数和互 相关函数进行描述。
自相关函数定义为
rxx
(n,
m)
E[
X
* n
X
m
]
xn*
xm
pX
n
,
X
m
数字信号处理——时域离散随机信号处理
时域离散随机信号的分析
1.1 引言 1.2 时域离散随机信号的统计描述 1.3 随机序列数字特征的估计 1.4 平稳随机序列通过线性系统 1.5 时间序列信号模型
数字信号处理——时域离散随机信号处理
1.1 引 言
信号有确定性信号和随机信号之分。 所谓确定性信号,就 是信号的幅度随时间的变化有一定的规律性, 可以用一个明确 的数学关系进行描述,是可以再现的。 而随机信号随时间的变 化没有明确的变化规律,在任何时间的信号大小不能预测, 因 此不可能用一明确的数学关系进行描述,但是这类信号存在着 一定的统计分布规律,它可以用概率密度函数、概率分布函数、 数字特征等进行描述。
数字信号处理知识点归纳整理

数字信号处理知识点归纳整理第一章时域离散随机信号的分析1.1. 引言实际信号的四种形式:连续随机信号、时域离散随机信号、幅度离散随机信号和离散随机序列。
本书讨论的是离散随机序列()X n ,即幅度和时域都是离散的情况。
随机信号相比随机变量多了时间因素,时间固定即为随机变量。
随机序列就是随时间n 变化的随机变量序列。
1.2. 时域离散随机信号的统计描述 1.2.1概率描述1. 概率分布函数(离散情况)随机变量n X ,概率分布函数: ()()n X n n n F x ,n P X x =≤(1)2. 概率密度函数(连续情况)若n X 连续,概率密度函数: ()()n n X X n nF x,n p x ,n x ∂=∂ (2)注意,以上两个表达式都是在固定时刻n 讨论,因此对于随机序列而言,其概率分布函数和概率密度函数都是关于n 的函数。
当讨论随机序列时,应当用二维及多维统计特性。
()()()()121212,,,121122,,,12,,,1212,1,,2,,,,,,,1,,2,,,,1,,2,,,NNNx XX N N N N x XX N x XX N NF x x x N P X x X x X x F x x x N p x x x N x x x =≤≤≤∂=∂∂∂1.2.2 数字特征1. 数学期望 ()()()()n xx n n m n E x n x n p x ,n dx ∞-∞==⎡⎤⎣⎦⎰ (3)2. 均方值与方差均方值: ()()22n n x n n E X x n p x ,n dx ∞-∞⎡⎤=⎣⎦⎰ (4)方差: ()()()2222xn x n x n E X m n E X m n σ⎡⎤⎡⎤=-=-⎣⎦⎣⎦(5)3. 相关函数和协方差函数自相关函数:()()nm**n m n m X ,X n m n m r n,m E X X x x p x ,n,x ,m dx dx ∞∞-∞-∞⎡⎤==⎣⎦⎰⎰ (6)自协方差函数:()()()()**cov ,,n m nmn m n X mX xx XXX X E X m Xm r n m m m ⎡⎤=--⎢⎥⎣⎦=- (7)由此可进一步推出互相关函数和互协方差函数。
数字信号处理ppt课件

三.自相关函数与 自协方差函数的性质
24
性质1 :相关函数与协方差函数的关系
Cxx m rxx m mx 2
Cxy m rxy m m*xmy
当 mx 0
Cxx m rxx m Cxy m rxy m
25
性质2:均方值、方差与相关函数和协方差函数
rxx
0
E
xn
2
Cxx 0 rxx 0 mx 2
五、功率谱密度
44
维纳——辛钦定理
1. 复频域
rxx
(m)
1
2
j
c Sxx (z)zm1dz,
Sxx
(z)
m
rxx
(m)z
m
C (Rx , Rx )
45
2. 频域
{ rxx(m)
1
2
Pxx (e j )e jm d
2
Pxx (e j ) rxx (m)e jm
m
46
3.性质
实平稳随机信号 rxx m rxx m
rxx m E x x n1 n1m
x1x2 p x1 , x2 ; m dx1dx2
18
自协方差函数
Cxx (m) E (xn1 mx )*(xn2 mx ) E (xn1 mx )*(xn1m mx )
rxx m mx 2
19
对于均值为零的随机过程 rxx m Cxx m
①偶函数
Pxx e j Pxx e j
②实函数
Pxx e j Pxx e j
③极点互为倒数出现
Sxx
z
Sxx
1 z
47
④功率谱在单位圆上的积分等于平均功率
E
x2
数字信号处理课件ppt

相关卷积定理:
卷积的相关函数等于相关函数的卷积
e(n)=a(n)*b(n)
f(n)=c(n)*d(n) ref(m)=rac(m) * rbd(m)
ryy(m)= rxx(m)*v(m)=rxy(m)*h(-m)
r h (m) h(m), rh (m) h(m)
时间序列信号模型:
| rws (k ) |2
2 w
1 dz 1 C Sss ( z) H opt ( z)S xs ( z ) z 2πj
通过前面的分析, 因果维纳滤波器设计的一般方法可以按 下面的步骤进行:
(1) 根据观测信号x(n)的功率谱求出它所对应的信号模型的
传输函数,即采用谱分解的方法得到B(z)。 S xs ( z) (2) 求 B( z 1 ) 的Z反变换,取其因果部分再做Z变换,即 S xs ( z ) 舍掉单位圆外的极点,得 B( z 1 ) (3) 积分曲线取单位圆,应用(2.3.38)式和(2.3.39)式,计 算Hopt(z), E[|e(n)|2]min。
m0
k=0, 1, 2, …
利用白化x(n)的方法求解维纳-霍夫方程:
x(n)=s(n)+υ (n)
H(z) (a)
ˆ y ( n) s ( n)
x(
x(n)
1 B( z )
w(n)
G(z) (b)
ˆ y ( n) s ( n)
x(
图2.3.5 利用白化x(n)的方法求解维纳-霍夫方程
2 S xx ( z ) S xs ( z ) S ss ( z ) B( z ) B( z 1 )
1 z N S xs ( z ) 1 H opt ( z ) 2 [ z N B( z )] B( z ) B( z 1 ) B( z ) 1
时域离散信号实验报告(3篇)

第1篇一、实验目的1. 理解时域离散信号的基本概念和特性。
2. 掌握时域离散信号的表示方法。
3. 熟悉常用时域离散信号的产生方法。
4. 掌握时域离散信号的基本运算方法。
5. 通过MATLAB软件进行时域离散信号的仿真分析。
二、实验原理时域离散信号是指在时间轴上取离散值的一类信号。
这类信号在时间上不连续,但在数值上可以取到任意值。
时域离散信号在数字信号处理领域有着广泛的应用,如通信、图像处理、语音处理等。
时域离散信号的基本表示方法有:1. 序列表示法:用数学符号表示离散信号,如 \( x[n] \) 表示离散时间信号。
2. 图形表示法:用图形表示离散信号,如用折线图表示序列。
3. 时域波形图表示法:用波形图表示离散信号,如用MATLAB软件生成的波形图。
常用时域离散信号的产生方法包括:1. 单位阶跃信号:表示信号在某个时刻发生突变。
2. 单位冲激信号:表示信号在某个时刻发生瞬时脉冲。
3. 正弦信号:表示信号在时间上呈现正弦波形。
4. 矩形脉冲信号:表示信号在时间上呈现矩形波形。
时域离散信号的基本运算方法包括:1. 加法:将两个离散信号相加。
2. 乘法:将两个离散信号相乘。
3. 卷积:将一个离散信号与另一个离散信号的移位序列进行乘法运算。
4. 反褶:将离散信号沿时间轴翻转。
三、实验内容1. 实验一:时域离散信号的表示方法(1)使用序列表示法表示以下信号:- 单位阶跃信号:\( u[n] \)- 单位冲激信号:\( \delta[n] \)- 正弦信号:\( \sin(2\pi f_0 n) \)- 矩形脉冲信号:\( \text{rect}(n) \)(2)使用图形表示法绘制以上信号。
2. 实验二:时域离散信号的产生方法(1)使用MATLAB软件生成以下信号:- 单位阶跃信号- 单位冲激信号- 正弦信号(频率为1Hz)- 矩形脉冲信号(宽度为2)(2)观察并分析信号的波形。
3. 实验三:时域离散信号的基本运算(1)使用MATLAB软件对以下信号进行加法运算:- \( u[n] \)- \( \sin(2\pi f_0 n) \)(2)使用MATLAB软件对以下信号进行乘法运算:- \( u[n] \)- \( \sin(2\pi f_0 n) \)(3)使用MATLAB软件对以下信号进行卷积运算:- \( u[n] \)- \( \sin(2\pi f_0 n) \)(4)使用MATLAB软件对以下信号进行反褶运算:- \( u[n] \)4. 实验四:时域离散信号的仿真分析(1)使用MATLAB软件对以下系统进行时域分析:- 系统函数:\( H(z) = \frac{1}{1 - 0.5z^{-1}} \)(2)观察并分析系统的单位冲激响应。
随机信号分析第一章

02
随机信号的统计描
述
概率密度函数
定义
概率密度函数(PDF) 是描述随机信号在各个 时刻取值概率分布的函 数。
性质
概率密度函数具有非负 性、归一化性质,即概 率密度函数在全域上的 积分等于1。
计算方法
可以通过直方图法、核 密度估计法等方法计算 概率密度函数。
概率分布函数
定义
概率分布函数(CDF)是描述随机信号取值小于或等 于某个值的概率的函数。
随机信号的特性
统计特性
随机信号的统计特性包括均值、 方差、概率分布等,这些特性描 述了信号的平均行为和不确定性 。
时间特性
随机信号的时间特性包括自相关 函数、互相关函数、功率谱密度 等,这些特性描述了信号在不同 时间点的相关性以及频率成分。
随机信号的应用
通信
在通信领域,随机信号可用 于扩频通信、无线通信等领 域,以提高通信的抗干扰能 力和保密性。
05
随机信号的采样定
理
采样定理的内容
采样定理定义
对于一个时间连续的模拟信号,如果以不高于其最高频率分量的频 率进行采样,则可以无失真地恢复原始信号。
采样定理的数学表达式
如果信号的最高频率为Fmax,则采样频率应不小于2Fmax。
采样定理的意义
采样定理是数字信号处理的基础,它确保了从离散样本中能够准确 重建原始信号。
雷达与声呐
在雷达与声呐领域,随机信 号可用于目标检测、测距、 定位等方面,以提高探测的 精度和可靠性。
地球物理学
在地球物理学领域,随机信 号可用于地震勘探、矿产资 源探测等方面,以揭示地球 内部结构和物质分布。
金融与经济
在金融与经济领域,随机信 号可用于股票价格分析、市 场预测等方面,以揭示市场 动态和经济发展趋势。
第1章 2时域离散信号

N1=2/ω1=10, N2=2/ω2=6
序 列 x(n) 的 周 期 N 为 N1 和 N2 的 最 小 公 倍 数 , 可 得
N=[10,6]=30
第1章 时域离散信号和系时域离散系统
除常用的典型序列外,对任意序列,可用单位采样序 列的移位加权和表示,即
x ( n)
m
x(m) (n m)
axis([-5, 6, -1.2, 1.2]); xlabel('n'); ylabel('x(n)')
运行程序输出波形如图1.2.1所示。
第1章 时域离散信号和系时域离散系统
1.2.1
常用的典型序列
1. 单位采样序列δ(n) n0 1 ( n) 0 n 0
(1.2.2)
也称单位脉冲序列:仅在n=0时值为1,其它均为零。
第1章 时域离散信号和系时域离散系统
图1.2.7
用单位采样序列移位加权和表示序列
第1章 时域离散信号和系时域离散系统
1.2.2
序列的运算
序列的简单运算有加法、乘法、移位、翻转及尺度
变换。
1. 加法和乘法
序列之间的加法和乘法,是指它的同序号的序列值 逐项对应相加和相乘,如图1.2.8所示。
第1章 时域离散信号和系时域离散系统
(1.2.12)
这种任意序列的表示方法,在信号分析中很有用。
如, 如图1.2.7所示的x(n) 波形,可用(1.2.12)式表示成:
x(n) 2 (n 2) 0.5 (n 1) 2 (n) (n 1) 1.5 (n 2) (n 4) 2 (n 5) (n 6)
第1章 时域离散信号和系时域离散系统
时域离散信号和系统ppt课件

问题: u(n)的作用 ? 递推方向?
2021精选ppt
8
第1章 时域离散信号和时域离散系统
结论: 1. 对同一个差分方程和同一个输入信号,因为初始条件不同
得到的输出信号是不相同的。
2. 一个差分方程不一定代表因果系统,初始条件不同,则可 能得到非因果系统 。
y1(n)=ay1(n-1)+δ(n)
和例1.4.1(2)相同,输出如下:
y1(n)=(1+a)an u(n)
2021精选ppt11源自第1章 时域离散信号和时域离散系统
(2) x2(n)=δ(n-1),y2(-1)=1 y2(n)=ay2(n-1)+δ(n-1)
n=0时,n=1时,n=2时, …n=n时,
y2(0)=ay2(-1)+δ(-1)=a y2(1)=a y2(0)+δ(0)=1+a2 y2(2)=a y2(1)+δ(1)=(1+ a2)a y2(n)=(1+ a2)a n-1 y2(n)=(1+ a2)a n-1 u(n-1)+aδ(n)
2021精选ppt
12
第1章 时域离散信号和时域离散系统
n=1: y(0)=a-1(y(1)-δ(1))=0
n=0: y(-1)=a-1(y(0)-δ(0))=-a-1
n=-1: y(-2)=a-1(y(-1)-δ(-1))=-a-2
n=-|n| y(n-1)=-a n-1
通式
将n-1用n代替,得到
y(n)=-an u(-n-1) ? 非因果序列 2021精选ppt
P20
10
第1章 时域离散信号和时域离散系统
第1章 离散时间信号与系统的时域分析
-3 -2 -1 0 1 2 3
y(n) 4 3 2 1 0 1 2 3 4 5 6 7
y(n) x(n) * h(n)
n
例1-7 设x(n)=3δ(n)+2δ(n-1)+δ(n-2), h(n)=2δ(n)+δ(n-1)+δ(n-2), 求y(n)=x(n)*h(n)。 解:采用列表法。
1 1 1 3 2 1 1 2 2 1 1 1 6 2 1 1 7 7 3 2 1 n=?
2
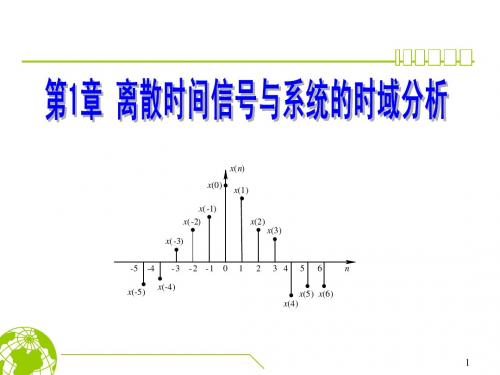
1. 2 离散时间信号
离散时间信号是指一个实数或复数的数字序列,它是整 数自变量n的函数,表示为x(n)。离散时间信号也常用图形 描述。
x(n) x(0) x(1) x(-1) x(2) x(-2) x(3) x(-3) -5 -4 -3 -2 -1 0 1 2 3 4 5 6 n x(-5) x(-4) x(5)x(6) x(4)
y(n)
x(n)
y(n)
x(n) * [h1 (n) + h2 (n)] x(n) * h1 (n) + x(n) * h2 (n)
4
2.单位阶跃序列u(n)
u (n )
1 u(n) 0
n0 n0
1 … n 0 1 2 3
3.矩形序列
R4 (n )
1 R N ( n) 0
0 n N 1 n为 其 它
1
n 0 1 2 3
矩形序列(N=4)
5
4.实指数序列
x(n) a n u(n)
a为实数
21
x(n) T[] -2 -1 01 2 3 4 n
y(n)
-2 -1 01 2 3 4
n
x(n-2) T[] 0 123456 n
数字信号处理知识点整理

第一章 时域离散随机信号的分析1.1. 引言实际信号的四种形式:连续随机信号、时域离散随机信号、幅度离散随机信号和离散随机序列。
本书讨论的是离散随机序列()X n ,即幅度和时域都是离散的情况。
随机信号相比随机变量多了时间因素,时间固定即为随机变量。
随机序列就是随时间n 变化的随机变量序列。
1.2. 时域离散随机信号的统计描述 1.2.1概率描述1. 概率分布函数(离散情况)随机变量n X ,概率分布函数: ()()n X n n n F x ,n P X x =≤ (1)2. 概率密度函数(连续情况)若n X 连续,概率密度函数: ()()n n X X n nF x,n p x ,n x ∂=∂ (2)注意,以上两个表达式都是在固定时刻n 讨论,因此对于随机序列而言,其概率分布函数和概率密度函数都是关于n 的函数。
当讨论随机序列时,应当用二维及多维统计特性。
()()()()121212,,,121122,,,12,,,1212,1,,2,,,,,,,1,,2,,,,1,,2,,,NNNx XX N N N N x XX N x XX N NF x x x N P X x X x X x F x x x N p x x x N x x x =≤≤≤∂=∂∂∂1.2.2 数字特征1. 数学期望 ()()()()n xx n n m n E x n x n p x ,n dx ∞-∞==⎡⎤⎣⎦⎰ (3)2. 均方值与方差均方值: ()()22n n x n n E X x n p x ,n dx ∞-∞⎡⎤=⎣⎦⎰ (4)方差: ()()()2222xn x n x n E X m n E X m n σ⎡⎤⎡⎤=-=-⎣⎦⎣⎦(5)3. 相关函数和协方差函数自相关函数:()()n m**xxn m n m X,X n m n m r n,m E X X x x p x ,n,x ,m dx dx ∞∞-∞-∞⎡⎤==⎣⎦⎰⎰ (6)自协方差函数:()()()()**cov ,,n m nmn m n XmX xx XXX X E X m Xm r n m m m ⎡⎤=--⎢⎥⎣⎦=- (7)由此可进一步推出互相关函数和互协方差函数。
01随机序列及数字特征

17
3.实平稳随机序列的相关函数, 协方差函数的性质
(1)是 m 的偶函数:
Rxx (m) Rxx (m) Rxy (m) Ryx (m)
Cxx (m) Cxx (m) Cxy (m) Cyx (m)
参见:
(1.2.20)
[1]王永德.随机信号分析基础(第二
(1.2.6)
●意义: 如果 X n 代表电流或电压, 均方值则表示在 n时刻 消耗在1电阻上的集合平均功率。
(2)方差 (二阶中心矩)
●定义:
x 2(n )E [|X nm x(n )|2]
(1.2.7)
有时将x称为标准方差
10
●意义: 方差表示 X n 取值的分散程度(或偏离中心值的大 小)。如果 X n 代表电流或电压,方差则表示消耗在1电 阻上的交变功率的集合平均.
(1.2.28)
22
p (x )p (x1,x2, ,xN ) dNxdx1dx2 dxN
● x的自相关矩阵 R x x 是一个 N阶正半定对称矩阵: Rxx E[xxT]
(1.2.29)
● x的自协方差矩阵 C x x 也是一个N阶正半定对称矩阵: C x xE [(xm )(xm )T ]
上式含义: n与 m点的随机变量 X n 与 X m ,其取值同时满
足 Xn xn 及 Xm xm的概率, 亦称“二维联合概率分布函 数”。
6
2.概率密度函数
●一维: 设 X n 取连续值, 则一维概率密度函数定义为:
pXn(xn,n)xn FXn(xn,n)
(1.2.3)
因此,FXn (xn,n) 可等价表示为:
●互相关函数:
(1.2.17)
R x y(m ) E [x (n )y (n m )]
第一章 时域离散随机信号

•自协方差序列
* c o v (, X X ) E [ ( X m ) ( X m ) ] n m n X m X
n m
可以证明
* c o v ( X , X ) r ( n , m ) m m n m x x XX
n m
m 0 ,有 对于零均值随机序列, m X X
n m
c o v ( X , X ) r (, n m ) n m x x
' ' * r ( mE ) [ xn ()( y nm ) ] ( 3 ) r ( m ) E [( x n ) x ( n m ) ] , x y x x
*
三种定义之间的关系为
' ' ' ' ' ' rmr () ( mr ) ( m ) rm () r ( m ) r ( m ) , x y x y y x x x x x x x
F ( x ,n ) P ( X x ) X n n n n
•概率密度函数 如果 X n 是连续随机变量,X n 的概率密度函数定义为
pXn (xn,n) F ) Xn (x n, n xn
3
•概率质量函数
如果 X n 是离散随机变量,则它的概率密度函数不存在,定义 一个概率质量函数来描述它。
( n ) E [ Xm ] E [ X m ]
2 x 2 2 n x n m x
* r ( m ) r ( n , n m ) E [ X X ] x x x x nn m
* r ( m ) r ( m ) x x x x
o v () m c o v ( n , n m ) 自协方差序列: c x x x x
第一章 时域离散信号与系统

8
1.2.3 常用的时域离散信号
单位脉冲序列
(n)
1 0
n0 n0
单位脉冲序列也称为单位采样序列。特点是仅在n=0处 取值为1,其他均为零。
9
单位阶跃序列
1 u(n)
n≥ 0
0 n 0
单位阶跃序列的特点是只有在n≥0时,它才取非零值1,
当n<0时,均取零值。
u(n)可以用单位脉冲序列表示为
数字信号处理:用数值计算的方法对数字信号进行处理
信号处理系统:模拟系统、时域离散系统、数字系统 (处理对象分别对应上面的三种信号)以及数字和模 拟的混合系统。
2
1.2 模拟信号、时域离散信号和数字信号
1.2.1 时域离散信号和数字信号 1.2.2 时域离散信号的表示方法 1.2.3 常用的时域离散信号
上式的运算关系被称作卷积运算,式中的*代表两个序 列的卷积运算。
25
卷积运算的图解法
y(n ) x(m )h (nm )x(n )*h (n ) m
(1)画出x(m)和h(m)的波形;
(2)反转平移:h(m)反转→ h(-m),右移n → h(n – m)
(3)乘积: x(m) h(n – m)
x 2 (n ) u (n ) u (n 3 ),试求信号x(n),它满足 x(n )x 1(n )x2(n ),并画出x(n)的波形。
解:这是一个典型的解线性卷积的题目。
x(n)x1(n)x2(n)= [(n)3(n1)2(n2) ][u(n)u(n3)] = [(n)3(n1)2(n2) ]R3(n)
h 1 (n )
h 2 (n )
h1(n) * h2(n)
h 1 (n )+h 2 (n )
时域离散信号

fs
第1章 时域离散信号和时域离散系统
6. 复指数序列
x(n)=e(σ+jω0)n
式中ω0为数字域频率,设σ=0,用极坐标和实部 虚部表示如下
x(n)=ejω0n x(n)=cos(ω0n)+jsin(ω0n)
由于n取整数,下面等式成立:
e j(ω0+2πM)n= e jω0n, M=0,±1,±2…
图像等。目的:提高图像质量、提取特征、 压缩以便于传输、模式识别等 4、生物医学信号处理:脑电、心电、视觉信号处理等,医用图像
处理 5、控制过程的信号处理:对随机信号的波形特征、信号状态进行
估计,如维纳滤波、卡尔曼滤波、系统 辩识等。
第1章 时域离散信号和时域离散系统
四、数字信号处理研究的内容
离散时间信号与系统理论 离散傅里叶变换理论
第1章 时域离散信号和时域离散系统
1.2.2 离散系统的分类
• 线性与非线性 • 时变与时不变 • 因果性
第1章 时域离散信号和时域离散系统
2. 移位、
设序列x(n)用图1.1.8(a)表示,其移位序 列x(n-n0)(当n0 =2时)用图1.1.8(b)表示;当 n0 >0时称为x(n)的延时序列;当n0 <0时,称 为x(n)的超前序列。x(-n)则是x(n)的翻转序 列 , 用 图 1.1.8(c) 表 示 。 x(mn) 是 x(n) 序 列 每 隔m点取一点形成的,相当于时间轴n压缩了m 倍。当m=2时,其波形如图1.1.8(d)所示。
y(n)=T[x(n)] 其框图如图1.2.1所示。
第1章 时域离散信号和时域离散系统
x(n)
y(n)
T[•]
图1.2.1 时域离散系统
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 x
rxx ( m ) cov xx (m )
2 mx
m 0 自相关函数和自协方差函数曲线图
2014年11月26日星期三 15:44:45 24
99
1.2 时域离散随机信号的统计描述
1.2.4 平稳随机序列的功率密度谱(PSD:Power Spetral Density)
平稳随机序列:非周期函数,能量无限,傅里叶变换不存在。
99
1.2 时域离散随机信号的统计描述
平稳序列的各态历经性:如果平稳随机序列满足下面两式,称
其具有各态历经性:
<x(n)>=mx=E[ X(n)] (1.2.48)
<x*(n)x(n+m)>=rxx(m)=E[X*(n)X(n+m)]
(1.2.49)
各态历经性实际意义:用时间平均代替集合平均, 这给研究平
2014年11月26日星期三 15:44:45 1
99
学时分配:总学时:48
第一章 时域离散随机信号的分析:6学时 第二章 维纳滤波和卡尔曼滤波: 第三章 自适应数字滤波器: 8学时 8学时
第四章 功率谱估计:
小波分析: 其它内容:
8学时
6学时 6学时
基础:
信号与系统,数字信号处理, 数理统计与随机过程。
稳随机序列带来很大的方便。而且实际中遇到的平稳随机序列,
一般都是各态历经性的。
2014年11月26日星期三 15:44:45 31
99
1.2 时域离散随机信号的统计描述
1.2.6 1. 正态(高斯)随机序列 正态随机序列x(n)的N维联合概率密度函数:
其中
特点:正态随机序列仅决定于均值矢量M和协方差矩阵varX。
2014年11月26日星期三 15:44:45 33
99
1.2 时域离散随机信号的统计描述
2.
平稳白噪声序列的定义: (1) 两两不相关 (2) 功率谱为常数 cov(xn, xm)=σ2δmn Pxx(ejω)=σ2=常数 (1.2.54)
正态(高斯)白噪声序列:白噪声序列服从正态分布。 注意:正态和白色是两个不同的概念,前者是指信号取值服从
1.
随机变量Xn的概率分布函数:
(1.2.1)
2. 概率一维密度函数
(1.2.2)
2014年11月26日星期三
15:44:45
8
99
1.2 时域离散随机信号的统计描述
对于随机序列,不同 n 的随机变量之间并不是独立的, 为了更加完整地描述随机序列, 需要用二维及多维统计特性。 (1.2.3) (1.2.4)
说明 :为简单起见,常用小写字母 x(n)或xn表示随机序列, 只
要概念清楚,容易分清楚。
2014年11月26日星期三
15:44:45
6
99
1.1 引 言
随机序列举例:n部接收机输出噪声的时域离散化
2014年11月26日星期三
15:44:45
7
99
1.2 时域离散随机信号的统计描述
§1.2 时域离散随机信号的统计描述 1.2.1
2014年11月26日星期三
15:44:45
15
99
1.2 时域离散随机信号的统计描述
3. 随机序列的相关函数和协方差函数 相同或不同随机序列在不同时刻的状态之间,存在着关联
性, 这种关联性可以用自相关函数和互相关函数进行描述。
自相关函数定义
*表示复数共轭
(1.2.11)
2014年11月26日星期三 15:44:45 16
现代数字信号处理
教材:
•丁玉美,数字信号处理—时域离散随机
信号处理 ,西电出版社,2002 •自编讲义
参考书:
•张贤达,现代信号处理,清华出版社,2002 •姚天任,现代数字信号处理,华中科大出版社,1999 •胡广书,现代信号处理教程,清华出版社,2004
•皇甫堪,现代数字信号处理,电子工业出版社,2003
15:44:45
11
99
1.2 时域离散随机信号的统计描述
f x
=1 =5
2 2
2
方差描述随 机变量相对 于均值的偏 离程度
= 10
x
m1 = 50
均值相同方差不同的高斯分布
2014年11月26日星期三 15:44:45 12
99
数学期望是随 机过程所有样 本函数的统计 平均函数。
说明:由于实际中无法得到概率分布函数, 数字特征比较容
易进行测量和计算, 因此也可以用数字特征描述随机序列。
常用的数字特征有数学期望、 方差和相关函数。
2014年11月26日星期三 15:44:45 9
99
1.2 时域离散随机信号的统计描述
1.2.2
1. 数学期望(统计平均值) (1.2.7) 说明:E表示求统计平均值。 一般情况:数学期望是n的函数。 平稳随机序列:数学期望是常数,与n无关。
由于 (1.2.34)
如果z1是其极点,1/z*1也是极点。如果z1在单位圆内, z 1 必须 在单位圆外,收敛域一定包含单位圆,即:
1
*
0≤Ra≤1
互相关函数及其Z变换:
(1.2.35)
2014年11月26日星期三 15:44:45 26
99
1.2 时域离散随机信号的统计描述
由于Pxx(z)的收敛域包含单位圆意味着rxx(m)的傅里叶变换存 在。令z=exp(jω) 有 (1.2.37) (1.2.38)
2014年11月26日星期三 15:44:45 32
99
1.2 时域离散随机信号的统计描述
高斯—马尔可夫过程:具有指数型自相关函数的平稳高斯过程。
例如:
高斯 —马尔可夫的特点 :是一种常见的随机信号,适合于大多
数物理过程,具有较好的精确性,数学描述简单。因为当
m→∞时, 自相关函数趋近于0,所以均值为0,过程的自相关 函数特性完全描述了过程的特性。
99
1.2 时域离散随机信号的统计描述
自协方差函数定义 (1.2.12) 容易证明 特殊情况:mXn= mXm=0 (1.2.13)
自协方差函数=自相关函数
2014年11月26日星期三 15:44:45 17
99
1.2 时域离散随机信号的统计描述
互相关函数的定义 联合概率密度
互协方差函数定义
特殊情况:mXn=mYm =0 cov(Xn, Ym)=rxy(n, m)
自相关函数及其 Z变换:由性质(4)知当mx=0, rxx(m)是收敛序列, Z变换存在,而且维纳-欣钦定理保证自相关函数的Z变换就是 平稳序列的功率谱。 (1.2.32) 反变换
2014年11月26日星期三 15:44:45
(1.2.33)
25
99
1.2 时域离散随机信号的统计描述
Pxx(z)的收敛域:Biblioteka 15:44:455
99
1.1 引 言
随机信号的计算机处理 :计算机只能处理随机数字信号。如
果忽略计算机有限字长效应,随机数字信号近似为随机序列。
因此,我们针对时域离散随机信号(随机序列)展开讨论。 符号说明: X(t)->连续随机信号 xi(t)-> X(t)的第i个样本函数 X(n)->随机序列或随机变量 xi(n)-> X(n)的第i个样本函数
2014年11月26日星期三 15:44:45 20
99
1.2 时域离散随机信号的统计描述
两个平稳且联合平稳复序列的数字特征: (1.2.22) 复平稳序列的两个重要性质: (1.2.23) (1.2.24) 两随机序列相互正交:对于所有m ,rxy(m)=0 两随机序列互不相关:对于所有m, rxy(m)=mxmy, covxy (m)=0
正态分布, 后者指信号不同时刻取值的独立性。
2014年11月26日星期三 15:44:45 34
99
1.2 时域离散随机信号的统计描述
3. 谐波过程
(1.2.55)
其中Ai和ωi是常数,θi是服从均匀分布的独立随机变量: (1.2.56)
可以证明:谐波过程是平稳的。
99
1.2 时域离散随机信号的统计描述
1.2.5 随机序列的各态历经性
集合平均或统计平均:求大量样本在同一时刻的平均, 实际中无
法实现。
时间平均:仅对一条样本在时间上求平均,实际中容易实现。
时间平均值的计算:
(1.2.46)
时间自相关函数的计算:
(1.2.47)
2014年11月26日星期三 15:44:45 式中,〈 · 〉表示时间平均算子。 30
2014年11月26日星期三 15:44:45 2
99
第一章 时域离散随机信号的分析
1.1 引言 1.2 时域离散随机信号的统计描述 1.3 随机序列数字特征的估计 1.4 平稳随机序列通过线性系统 1.5 时间序列信号模型
2014年11月26日星期三
15:44:45
3
99
1.1 引 言
§1.1 引 言 信号有确定性信号和随机信号之分。
确定性信号:信号幅度随时间变化有一定规律性, 可以用一个
明确的数学关系描述,是可以再现的。
随机信号:随时间变化没有明确的规律,任何时间信号的大小
不能预测, 不能用明确的数学关系进行描述。但存在着一定的 统计规律,可以用概率密度函数、概率分布函数、数字特征描 述。
2014年11月26日星期三 15:44:45 4
2014年11月26日星期三 15:44:45 18
99
1.2 时域离散随机信号的统计描述
1.2.3
平稳随机序列:N维概率分布函数或N维概率密度函数与时间n
的起始位置无关。又称为狭义(严)平稳随机序列。
