数字信号处理-时域离散随机信号处理(丁玉美) 第四章习题答案
数字信号处理(丁玉美版)教案第4章

7
4.2.1 直接计算DFT的问题及改进的途径
DFT及IDFT的定义
X (k ) x (n )W
n 0
N 1
kn N
k=0, 1, …, N-1
kn N
1 x(n) N
X (k )W
k 0
N 1
n=0, 1, …, N-1
8
可见,DFT 与 IDFT 的计算成本基本相同。 直接计算N点DFT 时: 对应一个k需要N次复数乘和(N-1)次 复数加;对所有N个k值,则需要 N² 复数乘和N (N-1)次复数加 。 其中: 一次复数乘需要4次实数乘和2次实数加方能 完成。当N较大时,运算量很大。
分成四个1点的序列
24
the butterfly(蝶形运算)
2点DFT 4点DFT
x(0)
X1(0)
X(0)
x(2)
W20
-1
X1(1)
X(1)
x(1)
X2(0)
W40 W41
-1
X(2)
x(3)
W20
X2(1)
-1
-1
X(3)
1点序列的DFT就是序列本身,即不用计算
25
如N>4,则 将 x1(r) 再按r的奇偶进一步分解成两个 N/4点长的子序列:
x2(3)
0 2
W
W
0 8 1 8 2 8 3 8
34
求IFFT,也可用DIT-FFT的流程来实现。
x 3(l ) x1(2l )
N l 0,1,..., 1 4 x 4(l ) x1(2l 1)
26
X 1(k )
N / 4 1 l 0
x (2l )W
数字信号处理第四章答案
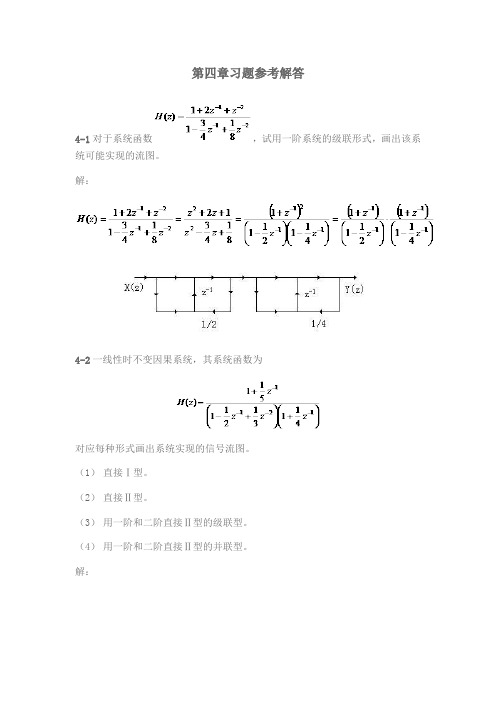
第四章习题参考解答4-1对于系统函数,试用一阶系统的级联形式,画出该系统可能实现的流图。
解:4-2一线性时不变因果系统,其系统函数为对应每种形式画出系统实现的信号流图。
(1)直接Ⅰ型。
(2)直接Ⅱ型。
(3)用一阶和二阶直接Ⅱ型的级联型。
(4)用一阶和二阶直接Ⅱ型的并联型。
解:直接Ⅰ型直接Ⅱ型用一阶和二阶直接Ⅱ型的级联型用一阶和二阶直接Ⅱ型的并联型4-3已知模拟滤波器的传输函数,试用脉冲响应不变法将转换成数字传输函数。
(设采样周期T=0.5)解:4-4若模拟滤波器的传输函数为,试用脉冲响应不变法将转换成数字传输函数。
(设采样周期T=1)解:4-5用双线性变换法设计一个三阶的巴特沃滋数字低通滤波器,采样频率,截至频率。
解:,4-6用双线性变换法设计一个三阶的巴特沃滋数字高通滤波器,采样频率,截至频率。
解:,,归一化,4-7用双线性变换法设计一个三阶的巴特沃滋数字带通滤波器,采样频率,上下边带截至频率分别为,。
解:,,,4-8设计一个一阶数字低通滤波器,3dB截至频率为,将双线性变换应用于模拟巴特沃滋滤波器。
解:一阶巴特沃滋,4-9试用双线性变换法设计一低通数字滤波器,并满足:通带和阻带都是频率的单调下降函数,而且无起伏;频率在处的衰减为-3.01dB;在处的幅度衰减至少为15dB。
解:设,则:,通带:,即阻带:,即阶数:,查表得二阶巴特沃滋滤波器得系统函数为双线性变换实现数字低通滤波器4-10一个数字系统的采样频率,已知该系统收到频率为100Hz的噪声干扰,试设计一个陷波滤波器去除该噪声,要求3dB的边带频率为95Hz和105Hz,阻带衰减不小于14dB。
解:,令,,,,设N=2,则。
数字信号处理课后答案+第4章(高西全丁美玉第三版)

令 y(n)=x1(n)+jx2(n) Y(k)=DFT[y(n)] 则
这样, 通过一次N点IFFT计算就完成了计算2N点DFT。 当然还要进行由Y(k)求X1(k)、 X2(k)和X(k)的运算(运算量相对
k=0, 1, …, N-1
⎧ ⎛n⎞ ⎪ x1 ⎜ 2 ⎟ ⎪ ⎝ ⎠ x (n) = ⎨ ⎪x ⎛ n −1 ⎞ ⎪ 2⎜ 2 ⎟ ⎠ ⎩ ⎝
n = 偶数 n = 奇数
在编程序实现时, 只要将存放x1(n)和x2(n)的两个数组的元 素分别依次放入存放x(n)的数组的偶数和奇数数组元素中 即可。
运算流图。 但画图占篇幅较大, 这里省略本题解答, 请 读者自己完成。
很少)。 (2) 与(1)相同, 设 x1(n)=x(2n) n=0, 1, …, N-1 x2(n)=x(2n+1) n=0, 1, …, N-1 X1(k)=DFT[x1(n)] X2(k)=DFT[x2(n)] 则应满足关系式
1 X 1 ( k ) = DFT[ x1 ( n)] = Yep ( k ) = [Y ( k ) + Y * ( N − k )] 2 1 jX 2 (k ) = DFT[ jx2 (n)] = Yep (k ) = [Y ( k ) − Y * ( N − k )] 2
4. 设x(n)是长度为2N的有限长实序列, X(k)为x(n)的 2N点DFT。 (1) 试设计用一次N点FFT完成计算X(k)的高效算法。 (2) 若已知X(k) ,试设计用一次N点IFFT实现求X(k)的 2N点IDFT运算。
x1(n)和x2(n)均为实序列, 所以根据DFT的共轭对称性, 可用
② 由X1(k)和X2(k)构成N点频域序列Y(k): Y(k)=X1(k)+jX2(k)=Yep(k)+Yop(k)
数字信号处理(第三版)-课后习题答案全-(原题+答案+图)
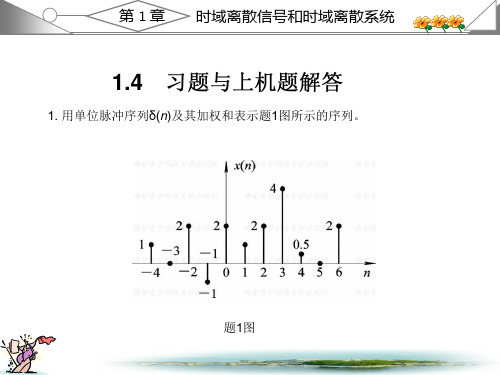
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(2n)+2δ(n-1)+δ(n-2)
+4.5δ(n-3)+2δ(n-4)+δ(n-5)
第 1 章 时域离散信号和时域离散系统
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况,
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
(5)y(n)=x2(n)
(6)y(n)=x(n2)
(7)y(n)=
n
(8)y(n)=x(n)sin(ωxn(m) )
m0
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
数字信号处理 答案 第四章

z −1
r sin θ
− r sin θ r cos θ
y ( n)
z −1
网络Ⅱ 解 网络Ⅰ:根据信号流程图写出差分方程
y (n) = 2r cos θ y (n − 1) − r 2 y (n − 2) + x(n)
由差分方程得系统函数
H1 ( z ) =
Y ( z) 1 = X ( z ) 1 − 2r cos θ z −1 + r 2 z −1 1 )(rz −1 − e jθ )
(4)并联型
x ( n)
z −1
1/4 10/3
-7/3
y ( n)
z −1
1/2 将系统函数写成部分分式形式
H ( z) =
−7 / 3 10 / 3 + 1 −1 1 1− z 1 − z −1 4 2
4.4 用直接Ⅰ型和直接Ⅱ型结构实现以下系统函数; (1)
H(z)=
−5 + 2 z −1 − 0.5 z −2 1 + 3z −1 + 3z −2 + z −3
3z 3 + 2 z 2 + 2 z + 5 (2) H(x)=0.8 3 z + 4 z 2 + 3z + 2
解 (1)根据系统函数写出差分方程
y (n) + 3 y (n − 1) + 3 y (n − 2) + y (n − 3) = −5 x(n) + 2 x(n − 1) − 0.5 x(n − 2)
可见网络Ⅰ和网络Ⅱ具有相同极点。 4.3 一个因果线性离散系统由下列差分方程描述:
3 1 1 y(n)- y(n-1)+ y(n-2)=x(n)+ x(n-1) 4 8 3
数字信号处理第四章附加习题及答案-new

第四章附加题1. 请推导出三阶巴特沃思低通滤波器的系统函数,设1/c rad s Ω=。
解:幅度平方函数是:2261()()1A H j Ω=Ω=+Ω令: 22s Ω=- ,则有:61()()1a a H s H s s -=- 各极点满足121[]261,26k j k s ek π-+==所得出的6个 k s 为:15==j es 2321321jes j +-==π12-==πj e s 2321343jes j --==π2321354j es j -==π2321316j es j +==π15==j e s 2321321je s j +-==π12-==πj e s 2321343je s j --==π2321354j es j -==π2321316j es j +==π122))()(()(233210+++=---=s s s k s s s s s s k s H a 1221)(23+++==s s s s H a 代入s=0时, ,可得,故:1=)s (H a 10=k2. 设计一个满足下列指标的模拟Butterworth 低通滤波器,要求通带的截止频率6,p f kHz =,通带最大衰减3,p A dB =,阻带截止频率12,s f kHz =,阻带的最小衰减25s A dB =,求出滤波器的系统函数。
解: 2,2s s p p f f ππΩ=Ω= 0.10.1101lg 101N 2lg()s pA A sp⎛⎫- ⎪-⎝⎭≥ΩΩ=4.15取N=5,查表得H(p)为:221()(0.6181)( 1.6181)(1)H p p p p p p =+++++因为3,p A dB =所以c p Ω=Ω[]52222()()0.618 1.618cs p c c c c c c H s H p s s s s s =Ω=Ω=⎡⎤⎡⎤+Ω-Ω+Ω-Ω+Ω⎣⎦⎣⎦3. 设计一个模拟切比雪夫低通滤波器,要求通带的截止频率 f p =3kHz ,通带衰减要不大于0.2dB ,阻带截止频率 f s = 12kHz ,阻带衰减不小于 50dB 。
数字信号处理(第三版)教程及答案第4章

第 4 章 时域离散系统的网络结构及数字信号处理的实现
4.4 例
[例4.4.1] 例
题
设FIR滤波器的系统函数为
1 H ( z ) = (1 + 0.9 z −1 + 2.1z − 2 + 0.9 z −3 + z − 4 ) 10
求出其单位脉冲响应, 判断是否具有线性相位, 画出直 接型结构和线性相位结构(如果存在)。
第 4 章 时域离散系统的网络结构及数字信号处理的实现
4.1 教材第 章学习要点 教材第5章学习要点
数字信号处理系统设计完毕后, 得到的是该系统的系 统函数或者差分方程, 要实现还需要按照系统函数设计一 种具体的算法。 不同的算法会影响系统的成本、 运算的复 杂程度、 运算时间以及运算误差等。 教材第5章的学习要点 如下: (1) 由系统流图写出系统的系统函数或者差分方程。
: 解: 上式的分子分母是因式分解形式, 再写成下式:
− 8 + 20 z −1 − 6 z −2 H ( z ) = 16 + (1 − 0.5 z −1 )(1 − z −1 + 0.5 z −2 )
上式的第二项已是真分式, 可以进行因式分解。
第 4 章 时域离散系统的网络结构及数字信号处理的实现
时域离散系统的网络结构及数字信号处理的实现41教材第5章学习要点42按照系统流图求系统函数或者差分方程43按照系统函数或者差分方程画系统流图44例题45教材第章学习要点46教材第章习题与上机题解答时域离散系统的网络结构及数字信号处理的实现41教材第5章学习要点数字信号处理系统设计完毕后得到的是该系统的系统函数或者差分方程要实现还需要按照系统函数设计一种具体的算法
− 8 + 20 z −1 − 6 z −2 H1 ( z) = (1 − 0.5 z −1 )(1 − z −1 + 0.5 z − 2 )
数字信号处理-西安电子科技大学出版(_高西全丁美玉)第三版_课后习题答案(全)
18
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
28
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
第 1 章 时域离散信号和时域离散系统
解法(二) 采用解析法。 按照题7图写出x(n)和h(n)的表达式分别为
5. 设系统分别用下面的差分方程描述, x(n)与y(n)分别表示系统输入和输 出, 判断系统是否是线性非时变的。
(1)y(n)=x(n)+2x(n-1)+3x(n-2) (2)y(n)=2x(n)+3 (3)y(n)=x(n-n0) n0 (4)y(n)=x(-n)
15
第 1 章 时域离散信号和时域离散系统
非零区间如下:
0≤m≤3 -4≤m≤n
第 1 章 时域离散信号和时域离散系统
根据非零区间, 将n分成四种情况求解: ① n<0时, y(n)=0
② 0≤n≤3时, y(n)= ③ 4≤n≤7时, y(n)= ④ n>7时, y(n)=0
1=n+1
n
1=8-m n0
