专题6由运动产生的线段和差问题
专题6 全等三角形与三条线段的和差问题(原卷版)

专题6 全等三角形与三条线段的和差问题(原卷版)类型一a=b+c或a=b-c类型解决策略一等量代换名师点金:通过图中线段来代换另一条线段,将线段的和差问题转化为证两线段相等的问题,通过全等得到线段等,直接代换,将分散的线段转化到同一直线上解决问题.模型一旋转型全等1.(2021秋•临沂期末)△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD交CD所在的直线于点E,交直线AC于F.(1)点D在边AB上时,如图,试探索AB、F A和BD之间的等量关系,并说明理由;(2)点D在AB的延长线或反向延长线上时,请选择一种情况,画出图形,写出AB、F A和BD之间的等量关系,并说明理由.模型二一线三垂直模型2.已知:如图,在△ABC中,∠BAC=90°,AB=AC,l是过点A的一条直线,BD⊥l,CE⊥l,垂足分别为D、E.(1)如图①,求证:DE=BD+CE;(2)若直线l绕A点旋转到图②位置时,其余条件不变,请把图形补充完整,写出BD、CE与DE之间的数量关系,并证明你的结论.模型三一线三等角(不为直角)模型3.(2023春•惠民县期末)如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E,F分别是直线CD上两点,且∠BEC=∠CF A=α.(1)若直线CD经过∠BCA的内部,且E,F在射线CD上.①如图1,若∠BCA=90°,α=90°,证明BE=CF.②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件,使①中的结论仍然成立,并说明理由.(2)如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.解决策略二截长补短法名师点金:截长:在长线段中截取一段等于另两条中的一条,然后证明剩下部分等于另一条;补短:将一条短线段延长,延长部分等于另一条短线段,然后证明新线段等于长线段;或者将短线段直接延长至等于长线段。
2019年中考数学复习1.7因动点产生的线段和差问题
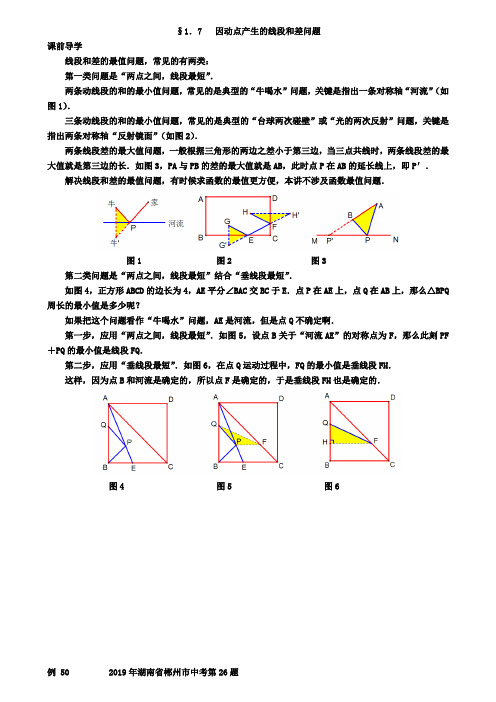
§1.7 因动点产生的线段和差问题课前导学线段和差的最值问题,常见的有两类:第一类问题是“两点之间,线段最短”.两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1).三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2).两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长.如图3,PA与PB的差的最大值就是AB,此时点P在AB的延长线上,即P′.解决线段和差的最值问题,有时候求函数的最值更方便,本讲不涉及函数最值问题.图1 图2 图3第二类问题是“两点之间,线段最短”结合“垂线段最短”.如图4,正方形ABCD的边长为4,AE平分∠BAC交BC于E.点P在AE上,点Q在AB上,那么△BPQ 周长的最小值是多少呢?如果把这个问题看作“牛喝水”问题,AE是河流,但是点Q不确定啊.第一步,应用“两点之间,线段最短”.如图5,设点B关于“河流AE”的对称点为F,那么此刻PF +PQ的最小值是线段FQ.第二步,应用“垂线段最短”.如图6,在点Q运动过程中,FQ的最小值是垂线段FH.这样,因为点B和河流是确定的,所以点F是确定的,于是垂线段FH也是确定的.图4 图5 图6例 50 2019年湖南省郴州市中考第26题已知抛物线y =ax 2+bx +c 经过A(-1, 0)、B(2, 0)、C(0, 2)三点. (1)求这条抛物线的解析式;(2)如图1,点P 是第一象限内此抛物线上的一个动点,当点P 运动到什么位置时,四边形ABPC 的面积最大?求出此时点P 的坐标;(3)如图2,设线段AC 的垂直平分线交x 轴于点E ,垂足为D ,M 为抛物线的顶点,那么在直线DE 上是否存在一点G ,使△CMG 的周长最小?若存在,请求出点G 的坐标;若不存在,请说明理由.图1 图2动感体验请打开几何画板文件名“14郴州26”,拖动点P 运动,可以体验到,当点P 运动到CB 的中点的正上方时,四边形ABPC 的面积最大.拖动点G 运动,可以体验到,当A 、G 、M 三点共线时,GC +GM 最小,△CMG 的周长最小. 思路点拨1.设交点式求抛物线的解析式比较简便.2.连结OP ,把四边形ABPC 的面积分割为三个三角形的面积和.3.第(3)题先用几何说理确定点G 的位置,再用代数计算求解点G 的坐标. 图文解析(1)因为抛物线与x 轴交于A(-1, 0)、B(2, 0)两点,设y =a(x +1)(x -2). 代入点C(0, 2),可得a =-1.所以这条抛物线的解析式为y =-(x +1)(x -2)=-x 2+x +2. (2)如图3,连结OP .设点P 的坐标为(x,-x 2+x +2). 由于S △AOC =1,S △POC =x ,S △POB =-x 2+x +2,所以S 四边形ABPC =S △AOC +S △POC +S △POB =-x 2+2x +3=-(x -1)2+4. 因此当x =1时,四边形ABPC 的面积最大,最大值为4.此时P(1, 2). (3)第一步,几何说理,确定点G 的位置:如图4,在△CMG 中,CM 为定值,因此当GC +GM 最小时,△CMG 的周长最小. 由于GA =GC ,因此当GA +GM 最小时,GC +GM 最小. 当点G 落在AM 上时,GA +GM 最小(如图5).图3 图4 图5 第二步,代数计算,求解点G 的坐标:如图6,AC =cos ∠CAO =AD AO AE AC ==52AE ==,E 3(,0)2.如图7,由y =-x 2+x +2=219()24x --+,得M 19()24,. 由A(-1, 0)、M 19()24,,得直线AM 的解析式为3322y x =+.作GH ⊥x 轴于H .设点G 的坐标为33(,)22x x +.由于tan ∠GEH =tan ∠ACO =12,所以12GH EH =,即EH =2GH .所以3332()222x x -=+.解得38x =-.所以G 315(,)816-.图6 图7 图8考点伸展第(2)题求四边形ABPC 的面积,也可以连结BC (如图8).因为△ABC 的面积是定值,因此当△PCB 的面积最大时,四边形ABPC 的面积也最大. 过点P 作x 轴的垂线,交CB 于F .因为△PCF 与△PBF 有公共底边PF ,高的和等于C 、B 两点间的水平距离,所以当PF 最大时,△PCB 的面积最大.设点P(x,-x 2+x +2),F(x,-x +2),那么PF =-x 2+2x . 当x =1时,PF 最大.此时P(1, 2).例 51 2019年湖南省湘西州中考第25题如图1,抛物线y =ax 2+bx +c 关于y 轴对称,它的顶点在坐标原点O ,点B 4(2)3-,和点C(-3,-3)均在抛物线上,点F 3(0)4-,在y 轴上,过点3(0)4,作直线l 与x 轴平行.(1)求抛物线的解析式和直线BC 的解析式;(2)设点D(x, y)是线段BC 上的一个动点(点D 不与B 、C 重合),过点D 作x 轴的垂线,与抛物线交于点G ,设线段GD 的长为h ,求h 与x 之间的函数关系式,并求出当x 为何值时,线段GD 的长度h 最大,最大长度h 的值是多少?(3)若点P(m, n)是抛物线上位于第三象限的一个动点,连结PF 并延长,交抛物线于另一点Q ,过点Q 作QS ⊥l ,垂足为S ,过点P 作PN ⊥l ,垂足为N ,试判断△FNS 的形状,并说明理由;(4)若点A(-2, t)在线段BC 上,点M 为抛物线上的一个动点,连结AF ,当点M 在何位置时,MF +MA 的值最小.请直接写出此时点M 的坐标与MF +MA 的最小值.图1动感体验请打开几何画板文件名“14湘西25”,点击屏幕左下方的按钮(2),拖动点D 在BC 上运动,可以体验到,当点D 是BC 的中点时,GD 最大.点击按钮(3),拖动点P 运动,可以体验到,△FNS 保持直角三角形的形状.点击按钮(4),拖动点M 运动,可以体验到,ME 与MF 保持相等,当AE 是垂线段时,ME +MA 最小. 思路点拨1.第(2)题用x 表示G 、D 两点的纵坐标,GD 的长就转化为关于x 的二次函数. 2.第(3)题是典型结论:抛物线上任意一点到直线l 的距离等于它与点F 间的距离. 3.第(4)题要经过两步说理,得到MF +MA 的最小值是点A 到l 的垂线段长. 图文解析(1)因为抛物线的顶点在坐标原点,所以y =ax 2.代入点C(-3,-3),得13a =-.所以抛物线的解析式为213y x =-.设直线BC 的解析式为y =kx +b ,代入B 4(2)3-,、C(-3,-3),得42,33 3.k b k b ⎧+=-⎪⎨⎪-+=-⎩ 解得13k =,b =-2.所以直线BC 的解析式为123y x =-.(2)由于点D 、G 分别在直线BC 和抛物线上,所以D 1(,2)3x x -,G 21(,)3x x -. 所以h =GD =211(2)33x x ---=21125(+)+3212x -.因此当12x=-时,h取得最大值,最大值为2512.(3)如图2,设点3(0)4,为H.设直线PQ的解析式为34y kx=-.联立直线PQ:34y kx=-与抛物线213y x=-,消去y,得21334x kx+-=.所以x1·x2=94-.它的几何意义是HS·HN=94.又因为HF=32.所以HF2=HS·HN.所以HF HSHN HF=.所以tan∠1=tan∠2.所以∠1=∠2.又因为∠1与∠3互余,所以∠2与∠3互余.所以△FNS是直角三角形.(4)MF+MA的最小值是83,此时点M的坐标是4(2,)3--.图2 图3 图4考点伸展第(3)题也可以通过计算得到PF=PN.同理得到QF=QS.这样我们就可以根据“等边对等角”及“两直线平行,内错角相等”,得到∠NFC=90°.应用这个结论,就容易解答第(4)题:如图3,作ME⊥l于E,那么MF=ME.当ME+MA的值最小时,MF+MA的值也最小.当A、M、E三点共线时,ME+MA的值最小,最小值为AE.而AE的最小值为点A到l的垂线段,即AE⊥l时,AE最小(如图4).2019-2020学年数学中考模拟试卷一、选择题1.如图,在Rt △ABC 中,∠C =30°,AB =4,D ,F 分别是AC ,BC 的中点,等腰直角三角形DEH 的边DE 经过点F ,EH 交BC 于点G ,且DF =2EF ,则CG 的长为( )A .B . 1C .52D 2.四个命题:①有两边和其中一边的对角对应相等的两个三角形全等;②三角形的一条中线能将三角形分成面积相等的两部分;③点P (1,2)关于原点的对称点坐标为(﹣1,﹣2);④两圆的半径分别是3和4,圆心距为d ,若两圆有公共点,则1<d <7.其中正确的是( ) A .①②B .①③C .②③D .③④3.某市连续10天的最低气温统计如下(单位:℃):4,5,4,7,7,8,7,6,5,7,该市这10天的最低气温的中位数是( ) A .6℃B .6.5℃C .7℃D .7.5℃4.如图,AB 是☉O 的直径,弦CD ⊥AB 于点E,点P 在☉O 上,PB 与CD 交于点F,∠PBC=∠C.若∠PBC=22.5°,☉O 的半径R=2,则劣弧AC 的长度为 ( )A.πB.C.2πD.π5.如图,正方形ABCD 内接于圆O ,4AB =,则图中阴影部分的面积是( ).A .416π-B .3216π-C .1632π-D .816π-6.如图是由5个相同的小正方体组成的几何体,其左视图是( )A .B .C .D .7.如图是直尺和一个等腰直角三角尺画平行线的示意图,图中∠α的度数为( )A .30°B .45°C .60°D .90°8.下列各数中,最小的实数是( )A.﹣5B.3C.09.如图,在△ABC 中,∠C=90°,AC=BC=3cm ,动点P 从点A cm/s 的速度沿AB 方向运动到点B ,动点Q 同时从点A 出发,以1cm/s 的速度沿折线AC→CB 方向运动到点B ,先到达点B 的点保持与点B 重合,待另一个点到达点B 后同时停止运动。
八年级数学专题:证明线段的和差问题常用两种方法

八年级数学专题:证明线段的和差问题常用两种方法
总结归纳初中数学典型例题、常考易错题,中考试题等,提炼通法,构建模型,助力中小学数学教育。
初中数学视频课程(配电子讲义)
初中数学全套视频课程,如需资料,请关
注后私信回复“初中数学”
线段的和差问题
要证明两条线段的和与一条线段相等时常用的两种方法:
一、可在长线段上截取与两条线段中一条
相等的一段,然后证明剩余的线段与另一条线
段相等(割)
二、把一个三角形移到另一位置,使两线
段补成一条线段,再证明它与长线段相等(补)
三、注意辅助线的作法及语言的表达,辅
助线只能实现一种功能。
无锡新领航教育2012年全国中考数学(100套)压轴题分类解析汇编专题6:由运动产生的线段和差问题

无锡新领航教育
2012年全国中考数学(100套)压轴题分类解析汇编
专题6:由运动产生的线段和差问题
1.(2012北京市8分)在平面直角坐标系xoy 中,对于任意两点P 1(x 1,y 1)与P 2(x 2,y 2)的“非常距离”, 给出如下定义:
若∣x 1-x 2∣≥∣y 1-y 2∣,则点P 1与点P 2的“非常距离”为∣x 1-x 2∣;
若∣x 1-x 2∣<∣y 1-y 2∣,则点P 1与点P 2的“非常距离”为∣y 1-y 2∣.
例如:点P 1(1,2),点P 2(3,5),因为∣1-3∣<∣2-5∣,所以点P 1与点P 2的“非常距离”为 ∣2-5∣=3,也就是图1中线段P 1Q 与线段P 2Q 长度的较大值(点Q 为垂直于y 轴的直线P 1Q 与垂直于x 轴的直线P 2Q 的交点)。
(1)已知点A 1
(0)2-,,B 为y 轴上的一个动点, ①若点A 与点B 的“非常距离”为2,写出一个满足条件的点B 的坐标;
②直接写出点A 与点B 的“非常距离”的最小值;
(2)已知C 是直线3
y x 34=+上的一个动点,
①如图2,点D 的坐标是(0,1),求点C 与点D 的“非常距离”的最小值及相应的点C 的坐标; ②如图3,E 是以原点O 为圆心,1为半径的圆上的一个动点,求点C 与点E 的“非常距离”的最 小值及相应的点E 和点C 的坐标。
【答案】解:(1)①(0,-2)或(0,2)。
②21。
(2)①设C 坐标为003x x 34⎛
⎫+ ⎪⎝⎭,,如图,过点C 作
CP ⊥x 轴于点P ,作CQ ⊥y 轴于点Q 。
由“非常距离”的定义知,当OP=DQ 时,点C 与点
D 的“非常距离”最小,。
压轴题专题——因动点产生的线段和差问题
教师姓名张雯学生姓名eagle 填写时间2012.11.23 周五学科初中数学年级初二教材版本人民教育出版社课题名称压轴题专题——因动点产生的线段和差问题本人课时统计第( 1、2 )课时共()课时上课时间11.23 周五14:00-16:00教学目标同步教学知识内容因动点产生的线段和差问题的几种类型归纳个性化学习问题解决掌握因动点问题产生线段和差问题的解题思路教学重点因动点产生的线段和差问题的几种类型及解题方法教学难点能够利用归纳的解题思路解决因动点产生的线段和差问题教学过程、课堂设计【课程介绍】本教案针对的是(150分考120分以上)的学生,该类型的学生失分点主要是在压轴题上,也就是在倒数一二大题上,所以如果要取得高分,我们就要争取把压轴题做好。
而动点问题是福州中考数学必考的压轴题类型之一,考试的分值在14分左右。
例如:2008年考的是因动点产生的面积问题、因动点产生的相似三角形问题;2009年考的是因动点产生的面积问题;2010年考的是因动点产生的面积问题;2011年考的是因动点产生的平行四边形问题;2012年考的是因动点产生的菱形问题;那么2013年福州中考会考什么类型的动点问题呢?它除了考上述的几种类型之外,还有可能考因动点产生的特殊三角形问题、因动点产生的特殊四边形问题以及因动点产生的线段和差问题,而这也是本节课老师所要讲的重点,根据我对2008——2012福州质检、中考的统计研究,得到如下数据:【本节课知识网络】因动点产生的线段和差问题两定一动型一定两动型两定两动型两定两动定长型三动一定长型xyOx =1第25题AC B【题型一】两定一动型1.和的最小值例题.已知:在l 上求作一点M ,使得AM +BM 最小.解析:取两定点中的一个定点做动点所在直线的对称点,连接该点与另一定点交动点所在直线的点即为所求的点,满足和最小!练习.(聊城市中考)如图,已知抛物线()20y ax bx c a =++≠的对称轴为x =1,且抛物线经过()1,0A -()0,3C -两点,与x 轴交于另一点B .(1)求这条抛物线所对应的函数关系式;(2)在抛物线的对称轴x =1上求一点M ,使点M 到点A 的距离与到点C 的距离之和最小,并求出此时点M的坐标;2.差最大例题.在l 上求作一点M ,使得|AM -BM |最大;(1)两定点在同侧(2)两定点在异侧练习.(福州市2012年质检22)如图,已知抛物线243y x bx c =++经过()()3,0,0,4A B 两点, (1)求此抛物线的解析式(2)若点D是第二象限内一点,以点D为圆心的圆分别于x轴,y轴,直线AB相交于点E,F,H。
专题:线段的和差问题

F E DBGA C 线 段 的 和 差 问 题几何中有许多题目要证明一线段等于另两线段的和(或差),解决这类问题常用的方法大体有五种,即,利用等量线段代换、截短法、接长法、利用面积证明、旋转等五种。
一、利用等量线段代换:证一线段等于另两线段的和(或差),只需证这条全线段的两部分,分别等于较短的两条线段,问题就解决了。
例1 已知:已知:如图,在△ABC 中,∠B 和∠C 的角平分线BD 、CD 相交于一点D ,过D 点作EF ∥BC 交AB 与点E ,交AC 与点F 。
求证:EF=BE+CF例2 已知:如图,在△ABC 中,∠ABC 的平分线与∠ACB 相邻外角∠ACG 的平分线相交于D ,DE∥BC 交AB 于E ,交AC 于F .求证:EF=BE-CF .二、截长法(在第三条线段上截取一段等于第一条线段,然后证明余下的线段等于第二条线段)三、补短法(延长一条线段,作出两条线段的和,然后证明这条线段等于第三条线段)例3 如图所示,已知三角形ABC中,AD平分∠BAC,∠B=2∠C,求证:AB+BD=AC.四、旋转法:通过旋转变换,而得全等三角形是解决正方形中有关题目类型的一种技巧。
例4 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,求证:EF=BE+FD五、等积变换法:利用三角形的面积进行证明。
例5 已知:如图,已知在△ABC 中,AB=AC ,BD 为AC 边上的高,如果在BC 上取一点F ,过F 作FG ⊥AB 于G ,作FH ⊥AC 于H.求证:FG+FH=BD.练习:1、 已知:如图,△ABC 中,∠BAC=90o ,AB=AC ,AE 是过点A 的一条直线且B ,C 在AE 的异侧,BD⊥AE 于D ,CE⊥AE 于E 。
求证:BD=DE+CE . E DCAB2、 如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于 D .求证:AD+BC=AB .3、如图,已知在△ABC中,∠BAC为直角,AB=AC,BD平分∠ABC,CE⊥BD于E.求证CE=1/2 BD4、已知:如图,在△ABC中,∠A=90º,D是AC上一点,BD=CD,P是BC上任一点,PE⊥BD于E,PF⊥AC于F.求证:PE+PF=AB.。
线段和差问题与截长补短法(含答案)

线段和差问题的截长补短方案(一题多解)系列文章之一线段和差问题与截长补短法(含答案)四川崇州 平生曜曜数学好玩,因为定题型、树模型,招式路数皆可寻。
几何中的线段和差问题,截长补短法在实施过程中都有四种截长方案,八种补短方案,可谓十二重关。
本文即将推出一道线段和差问题,希望同学们努力破之。
作者曾闲着没事碰巧把这十二种方案都尝试成功了,所以对于同学而言这十二关障的破解就不再是渺茫的探求,而是一个已经有了答案的考题。
同学们尽管去尝试,要深信这十二种方案皆能破题,但也仅限于本文所推题目而已,至于其它的线段和差问题十二关障能否一一告破就不好说了。
比如本人正在攻克一道线段和差问题,被弄得昏天地转,仍未冲破牛角,现在只得将之当作休闲佐料耳。
作者打心底告诉各位同学,把一道“典型题”做透了,会领悟n 多,积淀一抹多。
但说得再多也是空谈,当你正真去把它做实,你才能感受到其中的丰富与藕联,而后你再通过提炼啊,总结啊,什么,什么的,定能铸就非凡的解题技艺。
数学可玩,因为按需补、应需造,综合分析可当道。
好了,大家来凑凑热闹,去感受那应需而生的几何构造是如何美妙? 如图,等边⊿ABC 中M 、N 分别为线段AB 、BC 上的两点,且BM=CN ,AN 、CM 相交于点E ,将⊿ABC 绕点C 旋转,使CB 与CA 重合得到⊿ACD ,连结DE.(1)、求证:⊿BCM ≌⊿CAN ; (2)、求∠AED 的度数; (3)、求证:AE + CE = DE ;第一篇章:探讨第(1)、(2)问的解答第(1)问的解答(1)、∵⊿ABC 是等边三角形 , ∴ BC = AC ,∠B =∠ACN又∵BM = CN ,∴⊿BCM ≌⊿CAN .第(2)问的解答〈分析一〉:通过量角器测量,可大胆猜想ο∠AED,怎样求证?60= Array由(1)题,容易证获CAN=∠,BCM∠再由外角性质易证ο∠AEM,从而∠=60得ο∠AEC,那么关键环节来了!120=在四边形AECD中,欲证边AD所对“帆尖角”ο60∠ACD,所以=60=∠AED,考虑到边AD所对另一“帆尖角”ο只需去求证“A、E、C、D”四点共圆即可。
线段的和差(53张PPT)数学

答案
解析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
CD
CB
解析 由题图可知:BD=BC+CD,AD=AC+BD-CB.
(2)如果CD=4 cm,BD=7 cm,B是AC的中点,那么AB的长为_____cm.
答案
解析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
3
解析 如果CD=4 cm,BD=7 cm,B是AC的中点,则BC=BD-CD=7-4=3 cm,∴AB=BC=3 cm.
∴点O是线段AB的中点;∵AB=2OB,∴点O是线段AB的中点.故选C.
答案
解析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
4.如图,C是线段AB上的一点,点D是线段BC的中点,若AB=10,AC=6,则AD等于( )A.4 B.6 C.7.5 D.8
D
解析 ∵BC=AB-AC=4,点D是线段BC的中点,∴CD=DB= BC=2,∴AD=AC+CD=6+2=8.故选D.
中点
知识点2 与中点有关的计算
答案
自我检测2.点C是线段AB的中点,则下列结论不成立的是( )A.AC=BC B.AC= ABC.AB=2AC D.BC= AB
B
答案
返回
备考2019中考数学高频考点剖析几何动态之线段和差问题(适用浙教版).doc

备考2019中考数学高频考点剖析几何动态之线段和差问题(适用浙教版)考点扫描☆聚焦中考几何动态中的线段和差问题,是每年中考的压轴题中的必考内容之一,考查的知识点包括和差为定值问题、和差最大问题和和差最小问题。
,总体来看,难度系数偏高,以计算解答题为主。
也有少量的探究题。
探究题主要以证明为主。
结合2017、2018年全国各地屮考的实例和2019年名校小考模拟试题,我们从三方面进行实数的概念和计算问题的探讨:(1)几何动态和差为定值问题;(2)儿何动态和差为最大值问题;(3)几何动态和差为最小值问题.考点剖析☆典型例题匹(2017-杭州一模)(1)如图①,四边形ABCD是正方形,点G是BC上的任意一点,BF丄AG于点F, DE丄AG于点E,探究BF, DE, EF之间的数量关系,第一学习小组合作探究后,得到DE - BF二EF, 请证明这个结论;(2)若(1)中的点G在CB的延2线上,其余条件不变,请在图②中画出图形,并直接写出此时BF, DE, EFZ间的数量关系;(3)如图③,四边形ABCD内接于00, AB=AD, E, F是AC上的两点,且满足ZAED=ZBFA=ZBCD, 试判断AC, DE, BF之间的数量关系,并说明理由.【考点】MR:圆的综合题.【分析】(1)如图1中,结论:DE-BF二EF.只要证明厶ABF^ADAE,即可解决问题.(2)结论EF二DE+BF.证明方法类似(1).(3)如图3屮,结论:AC二BF+DE.只要证明厶ADE^ABAF以及DE=EC即可解决问题.【解答】解:(1)如图1中,结论:DE・BF二EF.理由如下:图①图②图③图①•・•四边形ABCD是正方形,AAB-AD, ZBAD-900 ,TBF丄AG于点F, DE丄AG于点E,.\ZAFB-ZDEA=90° ,VZBAF+ZDAE=90° , ZDAE+ZADE二90° , :.ZBAF=ZADE,在Z\ABF 和Z\DAE 中,fZAFB=ZAEDZAFB 二ZAED,[AB二ADAAABF^ADAE,・・・BF=AE, AF=DE,TAF・ AE=EF,ADE - BF二EF.(2)结论EF二DE+BF・理由如下:如图2屮,EF], ________G B C图②・・•四边形ABCD是正方形,・・・AB二AD, ZBAD二90° ,TBF丄AG于点F, DE丄AG于点E, .•.ZAEB=ZDEA=90° ,VZBAF+ZDAE=90° , ZDAE+ZADE=90° ,・・・ZBAF 二ZADE,在AABF和ADAE屮,(ZAFB 二ZAED{ZAFB二Z AED,[AB二ADAAABF^ADAE,・・・BF二AE, AF二DE,・・・EF=AF+AF 二DE+BF.(3)如图3中,结论:AOBF+DE.理由如下:连接BD.图③V ZDBC+ZBDC+ZDCB=180° , ZDAE+ZADE+ZAED二180° ,又V ZDBC=ZDAE, ZDCB=ZAED,.\ZADE=ZBDC,•••ZBDOZBAF,AZADE=ZBAF, VAD=AB, ZAED=ZAFB,AAADE^ABAF,AAE=BF,TAD二AB,.\ZADB=ZABD=ZACD,VZADE=ZCDB,A ZCDE=ZADB,A ZEDC=ZECD,ADE=CE,・・・AC二BF+DE.【点评】本题考查圆综合题、正方形的性质、全等三角形的点评和性质、等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.丽综合题(1) 阅读理解:如图①,在AABC 中,若AB=10, AC 二6,求BC 边上的中线AD 的取值范围. 解决此问题可以用如下方法:延长AD 到点E 使DE 二AD,再连接BE (或将AACD 绕着点D 逆吋针旋转 180°得到AEBD),把AB 、AC, 2AD 集中在△ ABE 中,利用三角形三边的关系即可判断.屮线AD 的取值范围是 ________ ;(2) 问题解决: 如图②,在Z\ABC 中,D 是BC 边上的中点,DE 丄DF 于点D, DE 交AB 于点E, DF 交AC 于点F,连接 EF,求证:BE+CF>EF ;(3) 问题拓展:如图③,在四边形A BCD ZB+ZD=180° , CB 二CD, ZBCD=140° ,以C 为顶点作一个70°角,角 的两边分别交AB, AD 于E 、F 两点,连接EF,探索线段BE, DF, EF 之间的数量关系,并加以证明.【分析】(1)解:延长AD 至E,使DE 二AD,连接BE,由SAS 证出△ BDE^ACDA,由全等三角形的性 质得出BE 二AC 二6,在Z\ABE 屮,由三角形的三边关系得:- BEVAEVAB+BE,即可求出AD 的取值范 围;(2) 延长FD 至点M,使DM 二DF,连接BM 、EM,同(1)得厶BMD^ACFD,得出BM 二CF,由线段垂直 平分线的性质得LLiEM 二EF,在中,由三角形的三边关系得:BE+BM>EM 即可得出结论;(3) 延长八B 至点N,使BN=DF,连接CN,证出ZNBC 二ZD,由SAS 证出△ NBC^AFDC,得出CN=CF, ZNCB 二ZFCD,证出ZECN=70° =ZECF,再由 SAS 证出△ NCE^AFCE,得出 EN 二EF,即可得出结论。
2013中考压轴题选讲专题6:由运动产生的线段和差问题(排版+答案)

2012年中考数学压轴题分类解析专题6:由运动产生的线段和差问题授课老师:黄立宗典型例题选讲:例题1:如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.例题2:如图,抛物线l交x轴于点A(﹣3,0)、B(1,0),交y轴于点C(0,﹣3).将抛物线l沿y轴翻折得抛物线l1.(1)求l1的解析式;(2)在l1的对称轴上找出点P,使点P到点A的对称点A1及C两点的距离差最大,并说出理由;(3)平行于x轴的一条直线交抛物线l1于E、F两点,若以EF为直径的圆恰与x轴相切,求此圆的半径.备用图巩固练习1、(2012湖北黄冈14分)如图,已知抛物线的方程C1:()()1y x2(x m)m0m=-+->与x 轴相交于点B、C,与y 轴相交于点E,且点B 在点C 的左侧.(1)若抛物线C1过点M(2,2),求实数m 的值.(2)在(1)的条件下,求△BCE的面积.(3)在(1)的条件下,在抛物线的对称轴上找一点H,使BH+EH最小,并求出点H的坐标.(4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.2、(2012湖南郴州10分)如图,已知抛物线2=++经过A(4,0),B(2,3),C(0,3)三点.y ax bx c(1)求抛物线的解析式及对称轴.(2)在抛物线的对称轴上找一点M,使得MA+MB的值最小,并求出点M的坐标.(3)在抛物线上是否存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.3、如图,抛物线y =x 2-6x +8与x 轴交于A 、B 两点(点A 在点B 的左侧),直线y =21x +2交y 轴于点C ,且过点D (8,m ).左右平移抛物线y =x 2-6x +8,记平移后点A 的对应点为A ′,点B 的对应点为B ′.(1)求线段AB 、CD 的长;(2)当抛物线向右平移到某个位置时,A ′D +B ′D 最小,试确定此时抛物线的表达式; (3)是否存在某个位置,使四边形A ′B ′DC 的周长最小?若存在,求出此时抛物线的表达式和四边形A ′B ′DC 的周长最小值;若不存在,请说明理由.参考答案例题1【答案】解:(1)由抛物线y=﹣x 2+bx+c 过点A (﹣1,0)及C (2,3)得,1b+c=04+2b+c=3--⎧⎨-⎩,解得b=2c=3⎧⎨⎩。
动态几何之和差问题探讨 OK

动态几何之和差问题探讨动态题是近年来中考的的一个热点问题,动态包括点动、线动和面动三大类,解这类题目要“以静制动”,即把动态问题,变为静态问题来解,而静态问题又是动态问题的特殊情况。
常见的题型包括最值问题、面积问题、和差问题、定值问题和存在性问题等。
我们从四方面进行动态几何之和差问题的探讨:(1)静态和差问题;(2)和差为定值问题;(3)和差最大问题;(4)和差最小问题。
一、静态和差问题:典型例题:例1:如图,在△ABC中,∠B与∠C的平分线交于点O. 过O点作DE∥BC,分别交AB、AC于D、E.若AB=5,AC=4,则△ADE的周长是.例2:如图,已知正方形ABCD的对角线长为2,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为【】A.8B.4C.8 D.6例3:如图,在矩形ABCD中,AB=10,BC=5点E、F分别在AB、CD上,将矩形ABCD沿EF折叠,使点A、D分别落在矩形ABCD外部的点A1、D1处,则阴影部分图形的周长为【】A.15B.20C.25D.30例4:如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为【】A、14B、16C、20D、28例5:在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD 于点F,若AB=5,BC=6,则CE+CF的值为【】A.11+1132B.11-1132C.11+1132或11-1132D.11-1132或1+32例6:已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.(1)求证:AB=BC;(2)当BE⊥AD于E时,试证明:BE=AE+CD.例7:如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于E,BF∥DE,交AG于F.(1)求证:AF﹣BF=EF;(2)将△ABF绕点A逆时针旋转,使得AB与AD重合,记此时点F的对应点为点F′,若正方形边长为3,求点F′与旋转前的图中点E之间的距离.例8:已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD 于点E,∠1=∠2.(1)若CE=1,求BC的长;(2)求证:AM=DF+ME.例9:如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME 的面积记为S2;当AB=3时,△AME的面积记为S3;…;当AB=n时,△AME的面积记为S n.当n≥2时,S n﹣S n﹣1=.例10:如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为【】A.6B.7C.8D.9例11:如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=【】A.150°B.210°C.105°D.75°例12:已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β-∠γ的值是【】A.45ºB.60ºC.90ºD.180º例13:(2012湖南长沙3分)如图,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=度.趁热打铁:1.如图在直角△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连接AE,则△ACE的周长为【】A、16B、15C、14D、132. 如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,则△AED的周长是_ ____.3. 如图,Rt△ABC中,∠C=90°,AC = BC = 6,E是斜边AB上任意一点,作EF⊥AC于F,EG⊥BC于G,则矩形CFEG的周长是.4. 如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥HG,EH∥FG,则四边形EFGH的周长是【】A.10 B.13 C.210 D.2135.如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E , AD⊥EC于点D且交⊙O于点F,连接BC , CF , AC。
中考专题训练:定值和最值问题

(一)定值问题1、如图,在平面直角坐标系x O y中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)2. 以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t秒,当t=2秒时PQ=5(1)求点D的坐标,并直接写出t的取值范围;(2)连接AQ并延长交x轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△A EF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.(3)在(2)的条件下,t为何值时,四边形APQF是梯形?2、如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC.CD上滑动,且E、F不与B.C.D重合.(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF和△CEF的面积是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.(二)由运动产生的线段和差问题(最值问题)1、如图所示,已知A 11(,y )2,B 2(2,y )为反比例函数1y x图像上的两点,动点P (x,0)在x 正半轴上运动,当线段AP 与线段BP 之差达到最大时,点P 的坐标是【 】A. 1(,0)2B. (1,0)C. 3(,0)2D. 5(,0)22、如图,抛物线l 交x 轴于点A (﹣3,0)、B (1,0),交y 轴于点C (0,﹣3).将抛物线l 沿y 轴翻折得抛物线l 1.(1)求l 1的解析式;(2)在l 1的对称轴上找出点P ,使点P 到点A 的对称点A 1及C 两点的距离差最大,并说出理由;3、如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.4、如图,已知抛物线2y ax bx c =++经过A (4,0),B (2,3),C (0,3)三点.(1)求抛物线的解析式及对称轴.(2)在抛物线的对称轴上找一点M ,使得MA+MB 的值最小,并求出点M 的坐标.(3)在抛物线上是否存在一点P ,使得以点A 、B 、C 、P 四点为顶点所构成的四边形为梯形?若存在,请求出点P 的坐标;若不存在,请说明理由.。
资料介绍

《2012年全国中考数学(100套)压轴题分类解析汇编》在对100套中考数学试卷解析的基础上将押轴题单独汇编构成10个专题。
每条题目给出了;1.原始题目(对照扫描试卷逐条检验,力求无差错),2.完整解答(解答全面,完整绘图,对网上流传的错误答题进行了更正),3.归纳考点,4.详细分析,5.考题出处,6.考题分值。
10专题为:专题1:动点问题,专题2:函数问题,专题3:面积问题,专题4:三角形四边形存在性问题,专题5:定值问题,专题6:由运动产生的线段和差问题,专题7:几何三大变换相关问题,专题8:实践操作、探究类问题,专题9:几何综合问题,专题10:代数综合问题。
中考数学复习压轴题冲刺 代几综合题 第五讲 动点产生的线段和差问题

2021年
8
(3)知识应用:
2021年
9
证明:(2)①由托勒密定理可知 PB • AC + PC • AB = PA • BC ∵ △ ABC 是 等 边 三 角 形 ,∴ AB = AC = BC, ∴PB + PC = PA,
② P'A P'B P'C P'A (P'B P'C) P'A P′D,
∴ MB MK 的最小值是 BP . 即 BP 的长是 DN NM MK 的最小值. ∵BK∥AD, ∴ BKP 90 . 在 Rt△BKP 中,由勾股定理得 BP = 8. ∴ DN NM MK 的最小值为 8.
2021年
15
动点产生的 线段和差
问题
利用平移、对 称、旋转把线 段放Fra bibliotek一条直2
2021年
14
(3)∵点 D、B 关于直线 AK 对称, ∴ DN MN 的最小值是 MB . 过 K 作 KF⊥x 轴于 F 点. 过点 K 作直线 AD 的对称点 P, 连接 KP,交直线 AD 于点 Q, ∴KP⊥AD. ∵AK 是∠DAB 的角平分线,
∴ KF KQ PQ 2 3 .
AD 为△ABC 的费马距离.
2021年
10
例 2.如图,在平面直角坐标系 xOy 中,点 B 的坐标为 (0, 2) ,点 D 在 x 轴的正半轴上,ODB 30 ,OE 为△ BOD 的中线,
2021年
11
【解析】1)过 E 作 EG ⊥ OD 于 G .∴ OG 3 .∴ 点 E 的坐标为 ( 3,1)
利用三角形两边
之和大于第三边,
或者垂线段最短 来求;
线段的和差 PPT课件 1 浙教版

2、如图,下列说法 ,不能判断点C是线段AB
的中点的是( C)
A、AC=CB
B、AB=2AC
C、AC+CB=AB
D、CB=
1 2
AB
随堂练习
1、如图 AB=8cm,点C是AB的中点,点D 是CB的中点,则AD=____cm
2、如图,下列说法 ,不能判断点C是线段AB 的中点的是( )
•
80、乐观者在灾祸中看到机会;悲观者在机会中看到灾祸。
•
11、明天是世上增值最快的一块土地,因它充满了希望。
•
12、得意时应善待他人,因为你失意时会需要他们。
•
13、人生最大的错误是不断担心会犯错。
•
14、忍别人所不能忍的痛,吃别人所不能吃的苦,是为了收获别人得不到的收获。
•
15、不管怎样,仍要坚持,没有梦想,永远到不了远方。
•
16、心态决定命运,自信走向成功。
解: A
OB
C
AC=AB+BC=5+2=7cm
AO=OC= 1 AC=3.5cm 2
OB=AB-AO=5-3.5=1.5cm(或OB=OC-BC=3.5-2=1.5cm)
答:线段OB的长等于1.5cm.
小狗、小猫为什么都选择直的路?
A B
D
C
想一想
如图,从小明家到学校共有三条路,小明为 了尽快到学校,应选择第 ⑵ 条路。为什么?
•
74、先知三日,富贵十年。付诸行动,你就会得到力量。
•
75、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。
•
76、好习惯成就一生,坏习惯毁人前程。
数学《动点定值问题》专题(含答案)

数学动点定值问题专题一、选择题1.如图,直线l 是一条河,A ,B 两地相距5 km ,A ,B 两地到l 的距离分别为3 km ,6 km ,欲在l 上的某点M 处修建一个水泵站,向A ,B 两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是( )2.如图,A ,B 两个电话机离电话线l 的距离分别是3米,5米,CD =6米,若由l 上一点分别向A ,B 连线,最短为( )A .11米B .10米C .9米D .8米(第2题图) (第3题图) 3.如图,AC ⊥BC 于C ,连接AB ,点D 是AB 上的动点,AC =6,BC =8,AB =10,则点C 到点D 的最短距离是( ) A .6 B .8 C .403 D .245 (第4题图) ,第5题图) ,第6题图)4.如图Rt △ABC 中,AB =BC =4,D 为BC 的中点,在AC 边上存在一点E ,连接ED ,EB ,则△BDE 周长的最小值为( )A .2 5B .2 3C .25+2D .23+2二、填空题5.如图,从直线外一点A 到这条直线的所有线段中,线段__ __最短.6.如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是PB ,理由是__ _ _.7.如图,在等腰三角形△ABC 中,∠ABC =120°,P 是底边AC 上的一个动点,M ,N 分别是AB ,BC 的中点,若PM +PN 的最小值是2,则△ABC 的周长是__ __.,第7题图) ,第8题图)8.如图,在菱形ABCD 中,∠BAD =60°,点M 是AB 的中点,P 是对角线AC 上的一个动点,若PM +PB 的最小值是9,则AB 的长是__ __.9.如果P是边长为2的正方形ABCD的边CD上任意一点且PE⊥DB,PF⊥CA,垂足分别为E,F,则PE+PF =__ __.,第9题图),第10题图)10.如图,∠ABC=45°,BC=42,BD平分∠ABC交AC于点D,M,N分别是BD和BC上的动点(M与B,D两点不重合,N与B,C两点不重合),则CM+MN的最小值是__ __.典型例题:例1.小虎家新建一间房子,要在屋外的A处安装水表,从大路边到A处怎样接水管最近?把最短的线段画出来,并简要说明道理.例2.等边△ABC的边长是8,AD⊥BC,E是BD的中点,M,N分别是AB,AD上的动点,求MN+EN的最小值.例3.如图,∠AOB=45°,P是∠AOB内一定点,PO=10,Q,R分别是OA,OB上的动点,求△PQR周长的最小值.(要求画出示意图,写出解题过程)例4.如图,在菱形ABCD中,AB=4,∠A=135°,点P,M,N分别为对角线BD及边BC,CD上的动点,求PM+PN的最小值.例5.如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P,Q分别是AD和AE上的动点,求DQ+PQ的最小值.巩固练习:一、填空题1、如图,在反比例函数y=6x上有两点A(3,2),B(6,1),在直线y=-x上有一动点P,当P点的坐标为__ _时,PA+PB有最小值.二、解答题2.已知点M(3,2),N(1,-1),点P在y轴上,求使得△PMN的周长最小的点P的坐标.3.小明在学习轴对称的时候,老师留了一道思考题:如图1,若点A,B在直线m的同侧,在直线m上找一点P,使得AP+BP的值最小,小明通过独立思考,很快得出了解决这个问题的正确方法,他的做法是这样的:(a)作点B关于直线m的对称点B′,(b)连接AB′与直线m交于点P,则点P为所求.请你参考小明的做法解决下列问题:(1)如图2,在等边△ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P(尺规作图,保留作图痕迹,不写作法),使得BP+PE的值最小,并求出最小值;(2)如图3,在矩形ABCD中,AB=4,BC=6,G为边AD上的中点,若E,F为AB 边上的两个动点,点E在点F的左侧,且EF=1,当四边形CGEF的周长最小时,请你在图3中确定点E,F的位置(尺规作图,保留作图痕迹,不写作法),并求出四边形CGEF的周长的最小值.2.如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以1cm/s的速度沿FG方向移动,移动开始前点A与点F重合,在移动过程中,边AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为1cm,矩形EFGH的边FG,GH的长分别为4cm,3cm,设正方形移动时间为x(s),线段GP的长为y(cm),其中0≤x≤2.5.(1)试求出y关于x的函数关系式,并求当y=3时相应x的值;(2)记△DGP的面积为S1,△CDG的面积为S2.试说明S1﹣S2是常数;(3)当线段PD所在直线与正方形ABCD的对角线AC垂直时,求线段PD的长.中午作业:(分类练习)一、定值问题解1、如图,在平面直角坐标系x O y 中,矩形AOCD 的顶点A 的坐标是(0,4),现有两动点P 、Q ,点P 从点O 出发沿线段OC (不包括端点O ,C )以每秒2个单位长度的速度,匀速向点C 运动,点Q 从点C 出发沿线段CD (不包括端点C ,D )以每秒1个单位长度的速度匀速向点D 运动.点P ,Q 同时出发,同时停止,设运动时间为t 秒,当t=2秒时PQ=52.(1)求点D 的坐标,并直接写出t 的取值范围;(2)连接AQ 并延长交x 轴于点E,把AE 沿AD 翻折交CD 延长线于点F,连接EF ,则△A EF 的面积S 是否随t 的变化而变化?若变化,求出S 与t 的函数关系式;若不变化,求出S 的值.(3)在(2)的条件下,t 为何值时,四边形APQF 是梯形?(第1题图)2、如图所示,在菱形ABCD 中,AB=4,∠BAD=120°,△AEF 为正三角形,点E 、F 分别在菱形的边BC .CD 上滑动,且E 、F 不与B .C .D 重合. (1)证明不论E 、F 在BC .CD 上如何滑动,总有BE=CF ; (2)当点E 、F 在BC .CD 上滑动时,分别探讨四边形AECF 和△CEF 的面积是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.(2题图)(3题图) 二、由运动产生的线段和差问题(最值问题)3、如图所示,已知A 11(,y )2,B 2(2,y )为反比例函数1y x 图像上的两点,动 点P (x,0)在x 正半轴上运动,当线段AP 与线段BP 之差达到最大时,点P 的坐标是【 】A. 1(,0)2B. (1,0)C. 3(,0)2D. 5(,0)24、如图,抛物线l 交x 轴于点A (﹣3,0)、B (1,0),交y 轴于点C (0,﹣3).将抛物线l 沿y 轴翻折得抛物线l 1.(1)求l 1的解析式;(2)在l 1的对称轴上找出点P ,使点P 到点A 的对称点A 1及C 两点的距离差最大,并说出理由;5、如图,已知抛物线y=﹣x 2+bx+c 与一直线相交于A (﹣1,0),C (2,3)两点,与y 轴交于点N .其顶点为D .(1)抛物线及直线AC 的函数关系式;(2)设点M (3,m ),求使MN+MD 的值最小时m 的值;(3)若抛物线的对称轴与直线AC 相交于点B ,E 为直线AC 上的任意一点,过点E 作EF∥BD 交抛物线于点F ,以B ,D ,E ,F 为顶点的四边形能否为平行四边形?若能,求点E 的坐标;若不能,请说明理由;(4)若P 是抛物线上位于直线AC 上方的一个动点,求△APC 的面积的最大值.回家作业:(压轴题训练)1、如图,已知抛物线2y ax bx c =++经过A (4,0),B (2,3),C (0,3)三点.(1)求抛物线的解析式及对称轴.(2)在抛物线的对称轴上找一点M ,使得MA+MB 的值最小,并求出点M 的坐标.(3)在抛物线上是否存在一点P ,使得以点A 、B 、C 、P 四点为顶点所构成的四边形为梯形?若存在,请求出点P 的坐标;若不存在,请说明理由.2. 如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC.CD上滑动,且E、F不与B.C.D重合.(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF和△CEF的面积是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.3. 如图,一次函数y=﹣x+4的图象与x轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB与△OAP外接圆的交点,点P、Q与点A都不重合.(1)写出点A的坐标;(2)当点P在直线l上运动时,是否存在点P使得△OQB与△APQ全等?如果存在,求出点P的坐标;如果不存在,请说明理由.(3)若点M在直线l上,且∠POM=90°,记△OAP外接圆和△OAM外接圆的面积分别是S1、S2,求的值.参考答案:课前演练:1. B ;2. B ;3.D ;4. C ;5. AD ;6. 垂线段最短;7. 4+23;8. 63;9. 2;10. 4;2. 典型例题:例1.解:如图所示:沿AB 线段接水管最近,因为直线外一点与直线的所有连接线段中,垂直线段最短(例1答图)(例2答图)(例3答图)例2. 解:作点E 关于AD 的对称点H ,过点H 作HG ⊥AB 于G ,则MN +EN 的最小值是HG ,Rt △HBG 中,sin 60°=GH 6,解得,GH =3 3 。
6.4 线段的和差 课件(共27张PPT)

点拨 答案 变式训练
抓住M为AC中点这个条件,先求AC,再求AM, 而MB可看成AB-AM或MC-BC,也可看成AC- AM-BC.
§6.4 线段的和差
聚焦学练考·学案导学讲义
典例 · 精析区
以题说法 互动探究
【例1】 如图,已知线段BC=2,反向延长BC至A,使AB =2BC,若M为AC的中点,求AM和MB的长度.
111 1 MN=MC-NC=2AC-2BC=2×8-2×3=2.5.
§6.4 线段的和差
聚焦学练考·学案导学讲义
随堂 · 检测区
即时演练 查漏补缺
C. 头脑风暴(选做题,20分)
11. 位于某大道AB上有四个居民小区A、B、C、D,其中AC=CD =DB,现想要在AB段上建一家超市,要求各居民小区到超 市的路程之和最小,请你确定超市的位置,并说明理由.
归纳总结
1. 线段的和差实质是线段长度的和差,因此线段间 的数量关系就是长度上的数量关系.
2. 彻底理解中点的意义和寻找线段间的和差倍分关 系是解决线段计算类问题的关键.
3. 巧用代数设元是解决几何问题的一种重要思想. 4. 当点之间的相对位置不明确时,应进行分类讨论.
§6.4 线段的和差
聚焦学练考·学案导学讲义
连接起来.
作图:略
§6.4 线段的和差
聚焦学练考·学案导学讲义
随堂 · 检测区
即时演练 查漏补缺
8. 已知AB=4cm,P为直线AB上一点,且PA=3cm, 求PB的长.
解:PB=1或7
§6.4 线段的和差
聚焦学练考·学案导学讲义
随堂 · 检测区
即时演练 查漏补缺
B. 提高部分(共2题,每题10分)
9. 如图,已知线段AB的长为a,延长线段AB至点C, 使BC= 1AB. (1)求线段2 AC的长; 1
第8讲-因动点产生的线段和差问题.doc

第8讲因动点产生的线段和差问题例 1 福州市中考第26题如图1,抛物线y=x2-4x与x轴交于O、A两点,P为抛物线上一点,过点P的直线y=x+m与抛物线的对称轴交于点Q.(1)这条抛物线的对称轴是_________,直线PQ与x轴所夹锐角的度数是______;(2)若两个三角形的面积满足S△OQP=13S△P AQ,求m的值;(3)当点P在x轴下方的抛物线上时,过点C(2, 2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD·DQ的最大值.图思路点拨1.第(2)题△OQP与△P AQ是同底三角形,把面积比转化为对应高的比,进而确定线段OA的分点的位置,从而得到直线PQ与y轴的交点坐标.2.第(3)题中,△CQD保持等腰直角三角形的形状.满分解答(1)抛物线的对称轴为直线x=2,直线PQ与x轴的夹角为45°.(2)因为△OQP与△P AQ有公共边PQ,所以它们的面积比等于对应高的比.如图2,作OM⊥PQ于M,AN⊥PQ于N.当S△OQP=13S△P AQ时,13OMAN=.设直线PQ与x轴交于点H,那么13 OH OMAH AN==.由y=x2-4x=x(x-4),得A(4, 0).所以OA=4.①如图2,当点H在线段OA上时,OH=1,H(1, 0).此时m=-1.②如图3,当点H在AO的延长线上时,OH=2,H(-2, 0).此时m=2.(3)①如图4,由A(4, 0)、C(2, 2),得直线AC与x轴的夹角为45°,点C在抛物线的对称轴上.又因为直线PQ与x轴的夹角为45°,所以△CDQ是等腰直角三角形.作点Q关于直线AC的对称点Q′,那么△CQQ′是等腰直角三角形,CQ′//x轴.所以DQ=DQ′.因此PD+DQ=PD+DQ′=PQ′.作PP′⊥CQ′,垂足为P′,那么△PP′Q′是等腰直角三角形.当点P 运动到抛物线的顶点(2,-4)时,PP ′最大,最大值PP ′=6. 此时PQ ′的最大值为62,即PD +DQ 的最大值为62.图2 图3 图4 ②由于PD +DQ ≤62PD =a ,那么DQ ≤62a .因此PD ·QD ≤2(62)(32)18a a a =--+. 所以当a =32PD ·QD 的最大值为18.此时PD =DQ =32P 、Q 两点重合于抛物线的顶点.考点伸展第(3)①题可以用代数法来解:因为点P 在抛物线y =x 2-4x 上,设P (n , n 2-4n ). 将P (n , n 2-4n )代入直线y =x +m ,可得m =n 2-5n .所以直线PQ 可以表示为y =x +n 2-5n ,那么Q (2, 2+n 2-5n ).联立直线AC :y =-x +4和直线PQ :y =x +n 2-5n ,可得2x D =4-n 2+5n . 于是PD +DQ 2()2()D P D Q x x x x --2(2)D P Q x x x --222(452)2(2)62n n n n -+--=--+所以当n =2时,PD +DQ 的最大值为62n =2时点P 在抛物线的顶点.例2 广州市中考第24题已知平面直角坐标系中两定点A (-1, 0)、B (4, 0),抛物线y =ax 2+bx -2(a ≠0)过点A 、B ,顶点为C ,点P (m , n )(n <0)为抛物线上一点.(1)求抛物线的解析式和顶点C 的坐标; (2)当∠APB 为钝角时,求m 的取值范围;(3)若m >32,当∠APB 为直角时,将该抛物线向左或向右平移t (0<t <52)个单位,点C 、P 平移后对应的点分别记为C ′、P ′,是否存在t ,使得顺次首尾连接A 、B 、P ′、C ′所构成的多边形的周长最短?若存在,求t 的值并说明抛物线平移的方向;若不存在,请说明理由.思路点拨1.要探求∠APB 为钝角时点P 的范围,需要先找到∠APB 为直角时点P 的位置. 2.直径的两个端点与圆内一点围成的三角形是钝角三角形.3.求两条线段的和最小,是典型的“牛喝水”问题.本题的四条线段中,有两条的长是定值,把不定的两条线段通过“平行且相等”连接起来,就转化为“牛喝水”问题.满分解答(1)因为抛物线y =ax 2+bx -2与x 轴交于A (-1, 0)、B (4, 0)两点, 所以y =a (x +1)(x -4)=ax 2-3ax -4a .所以-4a =-2,b =-3a .所以12a =,32b =-.所以221313252()22228y x x x =--=--。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题6由运动产生的线段和差问题
1.(2012北京市8分)在平面直角坐标系xoy中,对于任意两点P1(x1,y1)与P2(x2,y2)
的“非常距离”,
给出如下定义:
若∣x1-x2∣≥∣y1-y2∣,则点P1与点P2的“非常距离”为∣x1-x2∣;
若∣x1-x2∣<∣y1-y2∣,则点P1与点P2的“非常距离”为∣y1-y2∣.
例如:点P1(1,2),点P2(3,5),因为∣1-3∣<∣2-5∣,所以点P1与点P2的“非常距离”为
∣2-5∣=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q 与垂直于x
轴的直线P2Q的交点)。
(1)已知点A
1
(0)
2
-,,B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
(2)已知C是直线
3
y x3
4
=+上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的
点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非
常距离”的最
小值及相应的点E和点C的坐标。
【答案】解:(1)①(0,-2)或(0,2)。
②2
1。
(2)①设C 坐标为003x x 34⎛⎫
+ ⎪⎝⎭
,,如图,过点C 作CP⊥x
轴于点P ,作CQ⊥y 轴于点Q 。
由“非常距离”的定义知,当OP=DQ 时,点C 与点
D 的“非常距离”最小,
∴003
x 0x 314
-=
+-。
两边平方并整理,得2007x 48x 64=0--,解得,08
x 7
=-
或0x 8=(大于
8
7
,舍去)。
∴点C 与点D 的“非常距离”的最小值距离为87,此时815C 77⎛⎫
- ⎪⎝⎭
,。
②设直线3
y x 3
4
=+与x 轴和y 轴交于点A ,B ,过点O
作直线3y x 34=
+的垂线交直线3
y x 34
=+于点C ,交圆于点E ,过点C 作CP⊥x 轴于点P ,作CQ⊥y 轴于点Q ,过点E 作EM⊥x 轴于点M ,作EN⊥y 轴于点N 。
易得,OA=4,OB=3,AB=5。
由△OAB∽△MEM,OE=1,得OM=35,ON=45。
∴34E 55⎛⎫
- ⎪⎝⎭
,。
设C 坐标为003x x 34⎛⎫
+ ⎪⎝⎭
,
由“非常距离”的定义知,当MP=NQ 时,点C 与点E 的“非常距离”最
小,
∴00334
x +
x 3545
=+-。
两边平方并整理,得200175x 840x 1792=0--, 解得,08x 5=-或0224x 35=(大于8
5
,舍去)。
∴点C 与点E 的“非常距离”的最小值距离为1,此时89C 55⎛⎫
- ⎪⎝⎭
,,
34E 55⎛⎫- ⎪⎝⎭
,。
【考点】新定义,直线上点的坐标与方程的关系,直线和圆的性质,解一元二次方程,勾股定理,相似三角形的和性质。
【分析】(1)根据“非常距离”的定义可直接求出。
(2)①解题关键是,过C 点向x 、y 轴作垂线,当CP 和CQ 长度相等的时候“非常距离”最短,理由是,如果向下(如左图)或向上(如右图)移动C 点到达C’点,其与点D 的“非常距离”都会增大。
故而C 、D 为正方形相对的两个顶点时有最小的非常距离。
②同①,同时理解当OC 垂直于直线3
y x 34
=+时,点C 与点E 的“非常距离”最小。
2. (2012广西南宁10分)已知点A (3,4),点B 为直线x=-1上的动点,设B (-1,y ). (1)如图1,若点C (x ,0)且-1<x <3,BC⊥AC,求y 与x 之间的函数关系式; (2)在(1)的条件下,y 是否有最大值?若有,请求出最大值;若没有,请说明理由; (3)如图2,当点B 的坐标为(-1,1)时,在x 轴上另取两点E ,F ,且EF=1.线段EF 在x 轴上平移,线段EF 平移至何处时,四边形ABEF 的周长最小?求出此时点E 的坐标.
【答案】解:(1)如图1,过点A 作AE⊥x 轴于点E .
在△BCD 与△CAE 中,
∵∠BCD=∠CAE=90°-∠ACE,∠BDC=∠CEA=90°, ∴△BCD∽△CAE,∴
BD CD
CE AE
=。
∵A(3,4),B (-1,y ),C (x ,0)且-1<x <3, ∴
y x 1
3x 4
+=-。
∴y 与x 之间的函数关系式为2113
y x x 424
=++(-1<x <3)。
(2)y 没有最大值。
理由如下:
∵222113131
y x x (x 2x)(x 1)1424444
=
++=-+=-+, 又∵-1<x <3,∴y 没有最大值。
(3)如图2,过点A 作x 轴的平行线,并且在这条平行线上截取线段AA′,使
AA′=1,作点B 关于x 轴的对称点B′,连接A′B′,交x 轴于点E ,在x 轴上截取线段EF=1,则此时四边形ABEF 的周长最小。
∵A(3,4),∴A′(2,4)。
∵B(-1,1),∴B′(-1,-1)。
设直线A′B′的解析式为y=kx+b ,
则2k b 4k b 1+=⎧⎨-+=-⎩,解得5k 3
2b 3⎧
=⎪⎪⎨⎪=⎪⎩。
∴直线A′B′的解析式为52
y x 33
=
+。
当y=0时,52x 033+=,解得2
x 5
=-。
∴线段EF 平移至如图2所示位置时,四边形ABEF 的周长最小, 此时点E 的坐标为(2
5
-
,0)。
【考点】一次函数综合题,待定系数法,曲线上点的坐标与方程的关系,相似三角形的判定和性质,二次函数的最值,轴对称的性质,三角形三边关系。
【分析】(1)过点A 作AE⊥x 轴于点E ,先证明△BCD∽△CAE,再根据相似三角形对应边成比例即可
求出y 与x 之间的函数关系式。
(2)先运用配方法将2113
y x x 424
=++写成顶点式,再根据自变量x 的取值范围即可求解。
(3)欲使四边形ABEF 的周长最小,由于线段AB 与EF 是定长,所以只需BE+AF 最小.为此,
先确定点E 、F 的位置:过点A 作x 轴的平行线,并且在这条平行线上截取线段AA′,使AA′=1,作点B 关于x 轴的对称点B′,连接A′B′,交x 轴于点E ,在x 轴上截取线段EF=1,则点E 、F 的位置确定.再根据待定系数法求出直线A′B′的解析式,然后令y=0,即可求出点E 的横坐标,从而得出点E 的坐标。
3. (2012山东滨州10分)如图,在平面直角坐标系中,抛物线y=ax 2
+bx+c 经过A (﹣2,﹣4),O (0,0),B (2,0)三点. (1)求抛物线y=ax 2
+bx+c 的解析式;
(2)若点M 是该抛物线对称轴上的一点,求AM+OM 的最小值.
【答案】解:(1)把A (﹣2,﹣4),O (0,0),B (2,0)三点的坐标代入y=ax 2
+bx+c 中,得
4a+2b+c=04a 2b+c=4c=0
⎧⎪
--⎨⎪⎩,解这个方程组,得1a=2b=1c=0⎧
-⎪⎪⎨⎪⎪
⎩。
∴抛物线的解析式为y=﹣12
x 2
+x 。
(2)由y=﹣12x 2+x=﹣12(x ﹣1)2+12
,可得 抛物线的对称轴为x=1,并且对称轴垂直平分线段OB 。
∴OM=BM。
∴OM+AM=BM+AM。
连接AB 交直线x=1于M 点,则此时OM+AM 最小。
过点A 作AN⊥x 轴于点N ,
在Rt△A BN 中,2222AB=AN +BN 4+442==, 因此OM+AM 最小值为42。
【考点】二次函数综合题,曲线上点的坐标与方程的关系,解方程组,二次函数的性质,线段中垂线的性质,三角形三边关系,勾股定理。
【分析】(1)已知抛物线上不同的三点坐标,利用待定系数法可求出该抛物线的解析。
(2)根据O 、B 点的坐标发现:抛物线上,O 、B 两点正好关于抛物线的对称轴对称,
那么只需连接A 、B ,直线AB 和抛物线对称轴的交点即为符合要求的M 点,而AM+OM 的最小值正好是AB 的长。
对x=1上其它任一点M′,根据三角形两边之和大于第三边的性质,总有: O M′+A M′= B M′+A M′>AB=OM+AM , 即OM+AM 为最小值。
