1.1.2 程序框图 课件1
合集下载
1.1.2 程序框图 课件1

条件结构
否
flag=1?
是
n是质数
n不是质数
结束
循环结构
否
d整除n?
是
flag=0
d=d+1
是
d<=n-1且flag=1?
否
小结: 1、程序框图的概念
2、程序框图图例的名称和意义(作用)
3、如何用程序框图表示顺序结构、选择结构 与循环结构的算法
图形描述
否
d=2 否 d整除n? 是 flag=0 是 d<=n-1且 flag=1? 否 flag=1? 是 n是质数 结束 d=d+1
否
n不是质数
开始
判断一个正整数是否是质数的算法 图形描述 思考:
否 输入n n=2? d=2 否 d整除n? 是 flag=0 是 d<=n-1且 flag=1? 否 flag=1? 是 n是质数 结束 d=d+1 是
开始
输入a,b,c
a+b>c,a+c > b, b+c > a是否同 时成立? 是
否
存在这样的 三角形
不存在这样 的三角形
结束
例5 设计一个计算1+2 +...+100的值的 算法,并画出程序框图.
开始
i=1
sum=0
i=i+1 sum=sum+1
i≤100?
否 输出sum 结束
是
练习巩固
1 看下面的程序框图,分析算法的作用
判断框
判断一个条件是否成立,用 “是”、“否”或“Y”、 “N”标明
例1 设计一算法:输入圆的半径,输出圆的面积,并画出流程图 算法分析:
开始
第一步:输入圆的半径
第二步:利用公式“圆的面 积=圆周率×(半径的平方)” 计算圆的面积; 第三步:输出圆的面积。
用1.1.2_程序框图与算法的基本逻辑结构课件(1)程序框图与顺序结构

解:分析框图可得该程序的作用是计算并输出b=1+3的值. ∴b=1+3=4, 故选C. 8.任何一个算法都必须有的基本结构是( A ) A.顺序结构 B.条件结构 C.循环结构 D.三个都有
归纳小结 1.程序框图的定义:又称流程图,是一种用规定的图形、指向线及文字说明来准 确、直观地表示算法的图形. 2.基本程序框图及其功能;
2.基本的程序框和它们各自表示的功能如下: 图形符号 名称 终端框(起止框) 输入、输出框 功能 表示一个算法的起始和结束 表示一个算法输入和输出的信息 赋值、计算
处理框(执行框)
判断框 流程线 连接点
判断某一条件是否成立,成立时在 出口处标明“是”或“Y”;不” 成立时标明“否”或“N”.
典 型 例 题
已知一个三角形的三边边长分别为a,b,c, 利用海伦-秦九韶公式设计一个算法,求出 它的面积,画出算法的程序框图. 算法步骤:
第三步,计算S p( p a)( p b)( p c).
第四步,输出 S.
海伦-秦九韶公式:已知三角形三边边长 分别为a,b,c,则三角形的面积为:
(2)
开始 输入a,b sum=a+b 输出sum 结束
输出c
结束 (1)求直角三角形斜边长;
(2)求两个数的和.
上 节 课 例 题 回 顾
例:写出交换两个大小相同的杯子中的液体(A 水、 B 酒)的一个算法. 第一步,找一个大小与A相同的空杯子C; ∵A 杯子里有水,∴B杯子中的 第二步,将A中的水倒入C中; 酒不可能直接倒在A杯子里,找 第三步,将B中的酒精倒入A中; 一个空杯子C中间过渡一下! 第四步,将C中的水倒入B中,结束. 中间过渡量法 例1 将两个数a=2,b=-6交换,使a=-6,b=2,下列语句正确的是( ) A.开始 B. 开始 C. 开始 D. 开始
人教A版 高中数学 必修3 第一章 1.1.2 循环结构的程序框图课件(共16张PPT)
巩固提高
1、设计一算法,求 积:1×2×3×…×100, 画出流程图
思考:该流程图与前面 的例1中求和的流程图有 何不同?
开始 i=0,S=1
i=i+1 S=S*i 否 i>=100?
是 输出S 结束
巩固提高
2、设计一算法输出1~1000以内能被3整除的整数
开始
算法:
i=0
S1:确定i的初始值为0;
开始 i=0,S=0
否 i<100? 是 i=i+1 S=S+ i
输出S 结束
思考:将步骤A和步骤B交换位 置,结果会怎样?能达到预期结果 吗?为什么?要达到预期结果,还 需要做怎样的修改?
步骤A
步骤B 答:达不到预期结果;
当i = 100时,退出循环,i 的值未能加入到S中;修 改的方法是将判断条件改 为i<101
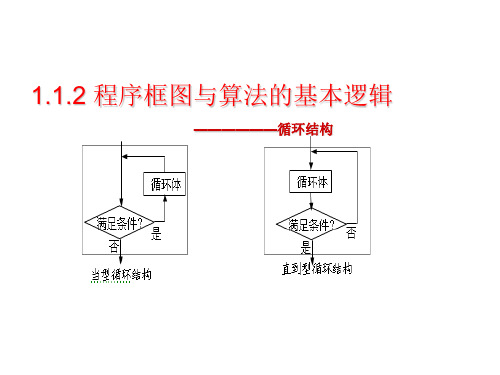
1.1.2 程序框图与算法的基本逻辑
——————循环结构
复习回顾
1、程序框图(流程图)的概念: 2、算法的三种逻辑结构: 3、顺序结构的概念及其程序框图: 4、条件结构的概念及其程序框图:
复习回顾
i) 顺序结构
ii) 条件结构
Yp N A
A
B
B
循环结构
循环结构:在一些算法中,也经常会出现从某处开始,
小结:
4.画循环结构流程图前: ①确定循环变量和初始条件; ②确定算法中反复执行的部分,即循环体; ③确定循环的转向位置; ④确定循环的终止条件.
循环结构的三要素:
循环变量,循环体、循环的终止条件。
其中顺序结构是最简单的结构,也是最基 本的结构,循环结构必然包含条件结构,所以 这三种基本逻辑结构是相互支撑的,无论怎样 复杂的逻辑结构,都可以通过这三种结构来表 达。
高中数学必修3 1.1.2程序框图与逻辑结构优秀课件

环 结
输出S
构
结束
算法分析:
第一步:令
i=1,S=0;
第二步:假设 i≤100成立,那 么执行第三步;
直 到
否那么,输出
型
S, 结束算法;
循
第三步:
环
S=S+i;
结
第四步:i=i+1,
构
返回第二步。
练习1:
(1).流程图的功能是 ( D ).
A.表示算法的起始和结束. B.表示算法的输入和输出信息. C.赋值、运算. D.按照算法顺序连接程序图框.
图形符号
名称
功能
终端框(起止框) 表示一个算法 的起始和结束
输入,输出框 表示算法的输入
和输出的信息
处理框(执行框) 赋值、计算
判断框 流程线
判断一条件是否成立, 用 “Y〞或“N〞标
明
连接程序框
连接点
连接程序框图的两局部
图形
指向线
流程图 文字说明
框
流程线
文字说明
程序
练习:
1.流程图的功能是:…………………..( ). A.表示算法的起始和结束. B.表示算法的输入和输出信息. C.赋值、运算. D.按照算法顺序连接程序图框.
练习3. 某工厂2005年的年生产总值为200万元,技术革新后 预计以后每年的年生产总值都比上一年增长5%.设计一程 序框图,输出预计年生产总值超过300万元的最早年份。
练习3. 某工厂2005年的年生产总值为200万元,技术革新后 预计以后每年的年生产总值都比上一年增长5%.设计一程 序框图,输出预计年生产总值超过300万元的最早年份。
是 △<0 否
b b x1 2a , x2 2a
课件5:1.1.2 程序框图

(3)图框④中,y2=ax+b的含义:该图框在执行③的前提下,即当x= -3时计算ax+b的值,并把这个值赋给y2.
(4)该程序框图解决的是求函数f(x)=ax+b的函数值的问题,其中输入 的是自变量x的值,输出的是x对应的函数值.
(5)y1=3,即2a+b=3① y2=-2,即-3a+b=-2②
1.1.2 程序框图
1.程序框图的概念 通常用一些通用图形符号构成一张图来表示算法,这种图称作程序框图(简称 框图)或流程图.
注意:(1)算法可以用自然语言来描述,但为了使算法的程序或步骤表达得更 为直观,我们经常用图形方式来表示它;
(2)流程图又称程序框图,是一种用规定的图形、指向线及文字说明来准确、 直观地表示算法的图形.
解:设某户有x人,根据题意,收取的卫生费y应是x的分段函数. 当x≤3时,y=5;当x>3时,y=5+(x-3)×1.2=1.2x+1.4.
S1 输入x; S2 如果x≤3,则y=5;如果x>3,则y=1.2x+1.4; S3 输出y.
相应的程序框图如图所示.
当堂检测 1.下列关于程序框图的说法中正确的个数是( ) ①用程序框图表示算法直观、形象、容易理解 ②程序框图能够清楚地展现算法的逻辑结构,也就是通常所说的一图 胜万言 ③在程序框图中,起止框是任何流程不可少的 ④输入和输出框可用在算法中任何需要输入、输出的位置 A.1个 B.2个 C.3个 D.4个
命题方向 程序框图的概念 [例1] 关于程序框图,有以下说法 ①程序框图只有一个入口,也只有一个出口 ②输入框只能在开始框之后,输出框只能在结束框前 ③判断框内的条件是惟一的 ④在程序框图中,大多数框图符号只有一个进入点和一个退出点,判断框 是惟一具有超过一个退出点的一个符号
⑤一种判断框是“是”与“不是”两分支的判断,而且有且仅有两个结 果,另一种是多分支判断,有几种不同的结果
(4)该程序框图解决的是求函数f(x)=ax+b的函数值的问题,其中输入 的是自变量x的值,输出的是x对应的函数值.
(5)y1=3,即2a+b=3① y2=-2,即-3a+b=-2②
1.1.2 程序框图
1.程序框图的概念 通常用一些通用图形符号构成一张图来表示算法,这种图称作程序框图(简称 框图)或流程图.
注意:(1)算法可以用自然语言来描述,但为了使算法的程序或步骤表达得更 为直观,我们经常用图形方式来表示它;
(2)流程图又称程序框图,是一种用规定的图形、指向线及文字说明来准确、 直观地表示算法的图形.
解:设某户有x人,根据题意,收取的卫生费y应是x的分段函数. 当x≤3时,y=5;当x>3时,y=5+(x-3)×1.2=1.2x+1.4.
S1 输入x; S2 如果x≤3,则y=5;如果x>3,则y=1.2x+1.4; S3 输出y.
相应的程序框图如图所示.
当堂检测 1.下列关于程序框图的说法中正确的个数是( ) ①用程序框图表示算法直观、形象、容易理解 ②程序框图能够清楚地展现算法的逻辑结构,也就是通常所说的一图 胜万言 ③在程序框图中,起止框是任何流程不可少的 ④输入和输出框可用在算法中任何需要输入、输出的位置 A.1个 B.2个 C.3个 D.4个
命题方向 程序框图的概念 [例1] 关于程序框图,有以下说法 ①程序框图只有一个入口,也只有一个出口 ②输入框只能在开始框之后,输出框只能在结束框前 ③判断框内的条件是惟一的 ④在程序框图中,大多数框图符号只有一个进入点和一个退出点,判断框 是惟一具有超过一个退出点的一个符号
⑤一种判断框是“是”与“不是”两分支的判断,而且有且仅有两个结 果,另一种是多分支判断,有几种不同的结果
1.1.2程序框图

不存在这样的三角
形。
结束
练习:
1.就逻辑结构,说 出其算法功能.
开始 max=a 输入b
max>b? 否
是
max=b
输出max
结束 答案:1.求两个数中的最大值.
小结
3.程序框图的三种基本的逻辑结构:
顺序结构 条件结构 循环结构
注:条件后面要加“?”
【回顾】求函数
x2 2x, x 2 y
程序框图:
算法步骤:第一步,输入a,b,c.
第二步:计算p的值.
开始
第三步:由海伦-秦九韶公式
输入a,b,c 求出三角形的面积S. 第四步:输出S.
p abc 2
计算机完成
S p( p a)(p b)(p c)
输出S 结束
将确定的数值赋给变量的语句叫 做赋值语句。给变量a赋值一个数 为12,则格式为:a = 12
练习:观察下面两个逻辑结构,说出各自的算法功能
(1)
开始
(2)
开始
输入正数a,b
输入ห้องสมุดไป่ตู้,b
d a2 b2
c d
s=(a+b)÷2 输出s
输出c
结束
结束
(1)求直角三角形斜边长;(2)求两个数的平均值.
2.已知梯形上底为2,下底为4,高为5,求其面积, 设计出该问题的流程图.
开始
a 2,b 4, h 5
1、程序框图:
又称流程图,是一种用程序框、流 程线及文字说明来准确、直观的表示 算法的图形.
2.基本的程序框和它们各自表示的功能如下:
图形符号
名称 终端框 (起止框) 输入、输 出框 处理框 (执行框)
1.1.2程序框图

第三步:输出结果。
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
相应的程序框图为:
开始
a=2,b=3
计算 x y 1
ab
输出结果
结束
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
练习3: 1、写出过两点P1(3,5),P2(-1,2)的 直线的斜率的一个算法,并画出程序框图。 2、写出求A(x1,y1),B(x2,y2)的两点 距离的一个算法,并画出程序框图。
广东省东莞沙田中学 罗朝举 Nhomakorabea天进步一点点,哪怕是1%的进步.
三、本课小结 1、程序框图 (1)程序框图由程序框、流程线和程 序框外必要的文字说明组成。 (2)程序框有:终端框、输入输出框、 处理框和判断框。
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
2、算法的基本逻辑结构:顺序结构、条件结 构和循环结构。 3、画程序框图的规则 (1)使用标准的框图符号; (2)框图一般从上到下、从左到右的方向画; (3)除判断框外,大多数框图符号只有一个 进入点(入口)和一个退出点(出口); (4)在框图符号内描述的语言要简练清楚。
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
基本的程序框和它们各自表示的功能如下:
图形符号
名称
功能
终端框 (起止框)
输入、输出 框
表示一个算法的起始 和结束
表示一个算法输入和 输出的信息
处理框 (执行框)
判断框
流程线
赋值、计算
判断某一条件是否成立,成立 时在出口处标明“是”或 “Y”;不成立时标明“否”
2、 ①有限性
②明确性
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
相应的程序框图为:
开始
a=2,b=3
计算 x y 1
ab
输出结果
结束
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
练习3: 1、写出过两点P1(3,5),P2(-1,2)的 直线的斜率的一个算法,并画出程序框图。 2、写出求A(x1,y1),B(x2,y2)的两点 距离的一个算法,并画出程序框图。
广东省东莞沙田中学 罗朝举 Nhomakorabea天进步一点点,哪怕是1%的进步.
三、本课小结 1、程序框图 (1)程序框图由程序框、流程线和程 序框外必要的文字说明组成。 (2)程序框有:终端框、输入输出框、 处理框和判断框。
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
2、算法的基本逻辑结构:顺序结构、条件结 构和循环结构。 3、画程序框图的规则 (1)使用标准的框图符号; (2)框图一般从上到下、从左到右的方向画; (3)除判断框外,大多数框图符号只有一个 进入点(入口)和一个退出点(出口); (4)在框图符号内描述的语言要简练清楚。
广东省东莞沙田中学 罗朝举
每天进步一点点,哪怕是1%的进步.
基本的程序框和它们各自表示的功能如下:
图形符号
名称
功能
终端框 (起止框)
输入、输出 框
表示一个算法的起始 和结束
表示一个算法输入和 输出的信息
处理框 (执行框)
判断框
流程线
赋值、计算
判断某一条件是否成立,成立 时在出口处标明“是”或 “Y”;不成立时标明“否”
2、 ①有限性
②明确性
数学:1.1.2《程序框图》课件

第一步:计算p的值.
第二步:由海伦-秦九韶公式求出三角形的面积S.
第三步:输出S的值.
第九页,编辑于星期日:十一点 三十八分。
(1)顺序结构-----是由若干个依次执行的处理 步骤组成的.这是任何一个算法都离不开的 基本结构.
例1:已知一个三角形的三边边长分别为2,3,4,利 用海伦-秦九韶公式设计一个算法,求出它的面积, 画出算法的程序框图.
流程线
连接程序框
连接点
连接程序框图的两部分
第六页,编辑于星期日:十一点 三十八分。
开始 输入n i=2
用程序框图来表示算法,有三 种不同的基本逻辑结构:
顺序结构
求n除以i的余数r
i=i+1
i≥n或r=0?
是
r=0?
是
n不是质数
否 否
n是质数
循环结构
条件结构
结束
第七页,编辑于星期日:十一点 三十八分。
第二步:判断a+b>c,a+c>b,b+c>a是否同时成立, 若是,则能组成三角形;若否,则组不成三角形.
第十四页,编辑于星期日:十一点 三十八分。
程序框图:
开始
输入a,b,c
a+b>c,a+c>b,b+c>a是否 同时成立?
是
存在这样的
三角形
结束
否
不存在这样的 三角形
第十五页,编辑于星期日:十一点 三十八分。
程序框图的三种基本的逻辑结构
顺序结构
条件结构
循环结构
第八页,编辑于星期日:十一点 三十八分。
(1)顺序结构-----是由若干个依次执行的处理 步骤组成的.这是任何一个算法都离不开的基 本结构.
第二步:由海伦-秦九韶公式求出三角形的面积S.
第三步:输出S的值.
第九页,编辑于星期日:十一点 三十八分。
(1)顺序结构-----是由若干个依次执行的处理 步骤组成的.这是任何一个算法都离不开的 基本结构.
例1:已知一个三角形的三边边长分别为2,3,4,利 用海伦-秦九韶公式设计一个算法,求出它的面积, 画出算法的程序框图.
流程线
连接程序框
连接点
连接程序框图的两部分
第六页,编辑于星期日:十一点 三十八分。
开始 输入n i=2
用程序框图来表示算法,有三 种不同的基本逻辑结构:
顺序结构
求n除以i的余数r
i=i+1
i≥n或r=0?
是
r=0?
是
n不是质数
否 否
n是质数
循环结构
条件结构
结束
第七页,编辑于星期日:十一点 三十八分。
第二步:判断a+b>c,a+c>b,b+c>a是否同时成立, 若是,则能组成三角形;若否,则组不成三角形.
第十四页,编辑于星期日:十一点 三十八分。
程序框图:
开始
输入a,b,c
a+b>c,a+c>b,b+c>a是否 同时成立?
是
存在这样的
三角形
结束
否
不存在这样的 三角形
第十五页,编辑于星期日:十一点 三十八分。
程序框图的三种基本的逻辑结构
顺序结构
条件结构
循环结构
第八页,编辑于星期日:十一点 三十八分。
(1)顺序结构-----是由若干个依次执行的处理 步骤组成的.这是任何一个算法都离不开的基 本结构.
课件4:1.1.2 程序框图

C.输入框只能紧接在起始框之后 D.用程序框图表达算法,其优点是使算法表示得非常直观、清晰
【解析】A 项中框图中的符号要严格标准,不能由个人确定;B 项中 只能执行判断问题,不能执行计算语句;C 项中输入框不一定紧
接在起始框之后;D 正确.
【答案】 D
变式训练
关于程序框图,有以下说法
①判断框内的条件是唯一的;
1.1.2 程序框图
1.了解程序框图的概念. 课标解 2.理解图形符号的意义和作用.(重点)
读 3.会利用图形符号描述一些简单问题的算法.(难点、 易混点)
知识一 程序框图的概念
【问题导思】 已知半径为 r 的圆的面积公式为 S=πr2. 问题 1:能否写出计算圆的面积的一个算法? 【提示】 能.
循环必须是有限循环;连接点连接同一个程序框图的不同部分. 【答案】 D
2.对起止框叙述正确的是( ) A.表示一个算法的开始或结束,图形符号是 B.表示一个算法输入和输出的信息,图形符号是
C.表示一个算法的开始或结束,图形符号是 D.表示一个算法中输入和输出的信息,图形符号是 【解析】 起、止框表示一个算法的开始或结束,用椭圆形的矩形 表示.故选 C. 【答案】 C
【答案】 C
类型二 程序框图的画法
例 2 三角形的面积公式为 S=12ah,写出当 a=10,h=20 时求三角形面 积数值的一个算法,并画出程序框图.
解: 算法: S1 取 a=10,h=20. S2 计算 S=12ah. S3 输出 S.
程序框图如图所示:
变式训练 已知梯形两底 a、b 和高 h,设计一个求梯形面积的算法,并画出程
3.如图所示的程序框图,若 R=8,则 a 等于( )
A.8
B.4
1.1.2程序框图ppt 人教课标版

12.02.2019
开始 输入 a , b , c
2 D b 4 a c
D0
N
Y
x (b D )/2 a 1
无实根
结束
江西省赣州一中刘利剑 整理 heishu800101@
三、概念形成
概念2.画程序框图的规则
为了使大家彼此之间能够 读懂各自画的框图,必须 遵守一些共同的规则: (4)一种判断框是二择 一形式的判断,有且仅有 两个可能结果;另一种是 多分支判断,可能有几种 不同的结果。
序,这些步骤或程序必须是明确的和有效的,而且
能够在有限步之内完成的。 一般来说,“用算法解决问题”可以利用计算机 帮助完成。
12.02.2019
江西省赣州一中刘利剑 整理 heishu800101@
一、复习引入
算法的要求
(1)写出的算法,必须能解决一类问题(例如解任意 一个二元一次方程组),并且能重复使用; (2)算法过程要能一步一步执行,每一步执行的操 作,必须确切,不能含混不清,而且在有限步之内 完成后能得出结果。
是 否
第四步,判断“r=0”是否成立. 若是,则n不是质数,结束算法,否则,i=i+1.
第五步,判断“i>(n-1)”是否成立。 若是,则n是质数;否则返回第三步。
r=0?
是
否
输出“n不是质数”
输出“n是质数”
12.02.2019
江西省赣州一中刘利剑 整理 heishu800101@
结束
2
x (b D )/2 a 1
无实根
1
12.02.2019
结束
江西省赣州一中刘利剑 整理 heishu800101@
三、概念形成
概念2.画程序框图的规则
开始 输入 a , b , c
2 D b 4 a c
D0
N
Y
x (b D )/2 a 1
无实根
结束
江西省赣州一中刘利剑 整理 heishu800101@
三、概念形成
概念2.画程序框图的规则
为了使大家彼此之间能够 读懂各自画的框图,必须 遵守一些共同的规则: (4)一种判断框是二择 一形式的判断,有且仅有 两个可能结果;另一种是 多分支判断,可能有几种 不同的结果。
序,这些步骤或程序必须是明确的和有效的,而且
能够在有限步之内完成的。 一般来说,“用算法解决问题”可以利用计算机 帮助完成。
12.02.2019
江西省赣州一中刘利剑 整理 heishu800101@
一、复习引入
算法的要求
(1)写出的算法,必须能解决一类问题(例如解任意 一个二元一次方程组),并且能重复使用; (2)算法过程要能一步一步执行,每一步执行的操 作,必须确切,不能含混不清,而且在有限步之内 完成后能得出结果。
是 否
第四步,判断“r=0”是否成立. 若是,则n不是质数,结束算法,否则,i=i+1.
第五步,判断“i>(n-1)”是否成立。 若是,则n是质数;否则返回第三步。
r=0?
是
否
输出“n不是质数”
输出“n是质数”
12.02.2019
江西省赣州一中刘利剑 整理 heishu800101@
结束
2
x (b D )/2 a 1
无实根
1
12.02.2019
结束
江西省赣州一中刘利剑 整理 heishu800101@
三、概念形成
概念2.画程序框图的规则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
开始
输入a,b
S=(a+b)*0.5
S>=60? 是
credit=2
否
credit=0
输出credit
精品课件
结束
课堂作业P11 开始
练习1
输入a
N
a ≥0
Y
输出 |a|=a
输出 |a|=-a
结束
精品课件
练习2
开始 X1=1 X2=2
m=(x1+x2)/2 N
m*m -3<>0 y
(x1*x1 -3)*(m*m -3) >0
算法初步
§1.1.2 程序框图
精品课件
复习 1、算法的概念 2、算法的特点 3、常见的几个例子 4、判断一个正整数是否是质数的算法
精品课件
算法的概念 算法是指解决给定问题的有穷操作步骤的 描述,简单的说,算法就是解决问题的步 骤和方法。
精品课件
算法的基本特点
1、有穷性
一个算法应包括有限的操作步骤,能在执行有穷的操作 步骤之后结束。
第二步:依次从2~ (n-1)检验是不是 n的因数,即能整除 n的数,若有这样的 数,则n不是质数; 若没有,则n是质数。
n=2? 否
d=2
d整除n? 是
flag=0
是
d<=n-1且
flag=1?
否
flag=1?3;1 否 n不是质数
开始
判断一个正整数是否是质数的算法
1 看下面的程序框图,分析算法的作用
(1)
开始 输入x y=3*x*x+4*x+5 输出y
(2)
开始 输入a,b
a<b? 是
输出a,b
结束
精品课件
结束
否 输出b,a
练习2
城区一中学生数学模块学分 认定由模块成绩决定,模块 成绩由模块考试成绩和平时 成绩构成,各占50%,若模块 成绩大于或等于60分,获得2 学分,否则不能获得学分 (为0分),设计一算法,通 过考试成绩和平时成绩计算 学分,并画出程序框图
M=240+(S-80)×5
输入面积S
否 S<=80 是
第三步:输出房租M的值。
M=3*S
M=240+5*(S-8)
思考:整个程序框图有什么特点?
精品课件
输出租金M 结束
例4 任意给定3个 正实数,设计一个 算法,判断分别以 这3个数为三边边 长的三角形是否 存在.画出这个算 法的程序框图..
开始
图形描述
输入n
思考:
1、flag的作用是 什么?
2、d=d+1是什么意 思?
n=2? 否
d=2
d整除n? 是
flag=0
3、整个图形中有哪 些基本的图形,各 自的意义和作用是 什么?
是
d<=n-1且
flag=1?
否
flag=1? 是
n是质数
精品课件
结束
是 否
d=d+1 否 n不是质数
程序框图又称流程图,是一种用规定的图形,指向线及 文字说明来准确、直观地表示算法的图形。
程序框
名称
功能
终端框(起 表示一个算法的起始和结束 止框)
输入、输出 表示算法的输入和输出的信
框
息
处理框(执 赋值、计算 行框)
判断框
判断一个条件是否成立,用 精品课“件 是”、“否”或“Y”、
“N”标明
例1 设计一算法:输入圆的半径,输出圆的面积,并画出流程图
算法分析:
第一步:输入圆的半径
第二步:利用公式“圆的面 积=圆周率×(半径的平方)” 计算圆的面积; 第三步:输出圆的面积。
精品课件
输出s 结束
例3 设计房租收费的算法,其要求是:住房面积80平方米
以内,每平方米收费3元,住房面积超过80平方米时,超过
部分,每平方米收费5元.输入住房面积数,输出应付的房
租.
算法分析:
开始
第一步:输入住房面积S
第二步:根据面积选择计费 方式:如果S小于或等于80,
则租金为M=s×3,否则为
精品课件
条件结构
否
flag=1?
是
n是质数
n不是质数
结束
精品课件
循环结构
否
d整除n?
是
flag=0
d=d+1
是
d<=n-1且flag=1?
精品否课件
小结: 1、程序框图的概念 2、程序框图图例的名称和意义(作用) 3、如何用程序框图表示顺序结构、选择结构 与循环结构的算法
精品课件
作业巩固:
P11 1.1 A组 B组
习题
3 2
精品课件
x1=m
x2=m
N |x1 -x2|<0.005 y
m=(x1+x2)/2
输出所求的近似值m
精品课件
结束
精品课件
开始
输入n
flag=1 否
n>2 是
d=2
d整除n? 是
flag=0
否 d=d+1
是 d<=n-1且flag=1?
否 否
flag=1? 是
n是质数
n不是质数
精品课件
结束
顺序结构
输入n flag=1
输入a,b,c
a+b>c,a+c > b, b+c > a是否同 时成立?
是 存在这样的
三角形
否
不存在这样 的三角形
结束
精品课件
开始
例5 设计一个计算1+2
+...+100的值的
i=1
算法,并画出程序框图.
sum=0
i≤100? 否
输出sum
精品课件 结束
i=i+1 sum=sum+1 是
练习巩固
开始 定义Pi=3.14 输入半径R 计算S=Pi*R*R
思考:整个程序框图有什么特点?
输出面积S
精品课件
结束
例2 已知一个三角形的三边长 确分别为2,3,4,利用海伧-秦九 韶公式设计一个算法,求出它的
面积,画出算法的程序框图.
开始 p=(2+3+4)/2
s=SQR(p*(p-2)*(p -3)*(p-4))
2、确定性
算法的计算规则及相应的计算步骤必须是唯一确定的, 既不能含糊其词,也不能有二义性。
3、可行性
算法中的每一个步骤都是可以在有限的时间内完成的基 本操作,并能得到确定的精结品课果件 。
判断一个正整数是否是质数的算法 开始
自然语言描述
图形描述
输入n
第一步:判断n是否等 于2?若n=2,则n是质 数,否则,执行第二 步;
