正比例和反比例判断精选习题
正比例反比例练习题

正比例反比例练习题一、正比例关系练习题1. 甲地的人口与时间之间存在着正比例关系,已知2010年时甲地的人口为500万人,而2020年时甲地的人口为600万人。
求2015年时甲地的人口数量。
2. 小明用固定的速度每小时跑5公里,已知小明连续跑了3个小时,求小明跑的总路程。
3. 某机构对某公司年度销售额与广告费用之间的关系进行研究,数据表明销售额与广告费用呈正比例关系,当广告费用为200万元时,销售额为1600万元。
问当广告费用为350万元时,销售额是多少?4. 某工厂生产零件的速度与机器运行时间存在正比例关系,已知机器连续运行10小时可以生产240个零件。
求机器连续运行16小时可以生产多少个零件?5. 一位股民投资了某只股票,大约过了一年,他发现自己的投资金额翻了6倍。
如果他最初投资了8万元,求现在他的投资金额有多少。
二、反比例关系练习题1. 甲地的公交车以固定的速度行驶,已知当车速为30千米/小时时,需要5小时才能到达目的地,求当车速为60千米/小时时,需要多长时间才能到达目的地。
2. 某机器完成一项任务需要的时间与工人数量之间存在反比例关系,已知当有6名工人时,任务可以在8个小时内完成,求如果只有3名工人,需要多长时间才能完成任务。
3. 某水泥厂生产水泥的速度与工人数量之间存在反比例关系,已知当有8名工人时,水泥厂可以生产200吨水泥,求如果只有4名工人,水泥厂可以生产多少吨水泥。
4. 某车间生产零件的速度与工人数量之间存在反比例关系,已知当有10名工人时,车间可以生产600个零件,求如果只有5名工人,车间可以生产多少个零件。
5. 甲地离某市的距离与到达市区所需时间之间存在反比例关系,已知距离为60千米时需要1个小时到达市区,求距离为30千米时需要多长时间才能到达市区。
以上所列的练习题涉及到了正比例关系和反比例关系,通过解题可以巩固对正比例关系和反比例关系的理解,并提高解决实际问题的能力。
在实际生活和工作中,我们常常会遇到各种与比例关系相关的问题,因此掌握好这些知识对我们的学习和工作都具有重要意义。
年级正比例和反比例比例练习题

年级正比例和反比例比例练习题
正比例和反比例是数学中重要的概念,在年级研究中经常会遇到这两种类型的题目。
以下是一些年级正比例和反比例比例练题,希望能帮助你更好地理解这两种关系。
正比例题目
1. 一辆汽车以每小时60公里的速度行驶,求2小时内汽车行驶的路程。
解答:
设汽车行驶的路程为x公里,则根据正比例关系可得:
60公里/1小时 = x公里/2小时
解方程得:x = 60 * 2 = 120公里
2. 小明去超市买苹果,苹果的单价是每个2元。
如果小明买了5个苹果,他要支付的金额是多少?
解答:
设小明支付的金额为y元,则根据正比例关系可得:
2元/1个 = y元/5个
解方程得:y = 2 * 5 = 10元
反比例题目
1. 一辆车以每小时60公里的速度行驶,行驶1小时后发现油
箱中的油量减少了1/6。
求这辆车油箱的容量。
解答:
设油箱的容量为z升,则根据反比例关系可得:
60公里/1小时 = z升/1/6升
解方程得:z = 60 * (1/6) = 10升
2. 5个工人需要3天时间完成一项任务,如果再增加3个工人,那么完成该任务需要多少天?
解答:
设完成任务需要的天数为t天,则根据反比例关系可得:
5个工人/3天 = 8个工人/t天
解方程得:t = 3 * 5 / 8 = 1.875天,约等于1.88天
以上是一些年级正比例和反比例比例练题的解答,在解题过程中需要注意明确所给的条件,并正确运用正比例和反比例的概念。
希望这些题目对你的研究有所帮助!。
判断正比例与反比例专项练习题

判断正比例与反比例专项练习题一、判断题:1、圆的面积和圆的半径成正比例。
()2、圆的面积和圆的半径的平方成正比例。
()3、圆的面积和圆的周长的平方成正比例。
()4、正方形的面积和边长成正比例。
()5、正方形的周长和边长成正比例。
()6、长方形的面积一定时,长和宽成反比例。
()7、长方形的周长一定时,长和宽成反比例。
()8、三角形的面积一定时,底和高成反比例。
()9、梯形的面积一定时,上底和下底的和与高成反比例。
()10、圆的周长和圆的半径成正比例。
()二.选择题时间与路程()。
A.成正比例 B.成反比例 C.不成比例(2A.三、看图表填空(2)根据规律判断比例关系,并填空。
与Y()。
A. 成正比例 B. 成反比例3.选择填空。
a÷b=c,当c一定时a和b();当a一定时b和c();当b一定时a和c()。
A. 成正比例B. 成反比例四、判断对错(1)路程一定,速度和时间成正比例。
()(2)一堆煤的总量不变,烧去的煤与剩下的煤成反比例。
()(3)花生的出油率一定,花生的重量与榨出花生油的重量成正比例。
()(4)平行四边形的面积不变,它的底与高成反比例。
()五、选择题(1)长方形的_________________,它的长和面积成正比例。
A.周长一定B.宽一定C.面积一定(2)圆柱体体积一定,________________和高成反比例。
A.底面半径B.底面积C.表面积六、练习1.判断下面每题中的三个量成什么比例?(1)速度、路程和时间(2)工作总量、工作效率和工作时间(3)单价、总价和数量(4)平行四边形的面积、底和高2.下列各题中的两种量是不是成比例,成什么比例,并说明理由。
(1)买相同的电脑,购买的电脑台数与总价单价(一定),(2)每捆练习本的本数相同,练习本的总本数与捆数每捆练习本的本数(一定)(3)总路程一定,已行的路程与未行的路程(4)分数值一定,分数的分子与分母比值(一定),(5)长方形的长一定,它的面积和宽不成比例(6)长方体的体积一定,底面积和高底面积×高=体积(一定)(7)一本书的总页数一定,看的天数与平均每天看的页数看的天数平均每天看的页数一本书的总页数(一定)(8)圆的周长和直径∏(一定)(9)订阅《扬子晚报》,订的份数与总价单价(一定)(10)图上距离一定,实际距离与比例尺图上距离(一定)(11)小麦的出粉率一定,小麦的质量与面粉的质量(12)六(1)班同学做操,每排站的人数与排数总人数(一定)。
正反比例练习题-正比例和反比例练习题

正反比例练习题-正比例和反比例练习题正比例或反比例练习题一、判断下面两个量是否成正比例或反比例,说明理由。
1、每箱木瓜的个数一定,运来木瓜的箱数和木瓜的总个数。
2、看一本书,每天看的页数和所看的天数。
3、房间的面积一定,铺地砖的块数与每块地砖的面积。
4、每块地砖的面积一定,铺地面积与所需地砖的块数。
二、用比例尺知识解决问题。
1、一条跑道全长200米,在图纸上的长度是10厘米。
这幅图的比例尺是多少?2、一个零件的实际长度是8毫米,在设计图上用4厘米表示,这幅图的比例尺是多少?3、在一幅比例尺是1:4500000的地图上,量得甲乙两地之间的距离是20厘米,甲乙两地的实际距离是多少千米?4、在一张图纸上,量得学校操场的长是12厘米,宽是8厘米。
这张图纸的比例尺是1:200,这个操场的实际面积是多少平方米?5、甲乙两地的实际距离是300千米,在一幅地图上量得两地之间的距离是6厘米。
在这一幅地图上,又量得甲丙之间的距离是4厘米,甲丙的实际距离是多少千米?三、用正反比例解决问题。
1、光辉服装厂4天加工服装160套,照这样计算,生产360套服装,需要多少天?2、化肥厂有一批煤,每天用12吨,可用40天。
如果这批煤要用60天,每天只能用多少吨?3、修路队3天修路150米,照这样的速度,再修10天,又修多少米?4、一辆汽车从甲城开往乙城,每小时行45千米,5小时到达。
返回时,每小时行驶50千米,几小时回到甲城?5、一间房子,用面积是16平方分米的方砖铺地,需要54块。
如果改用面积是9平方分米的方砖,需要多少块?7、用同样的砖铺地,铺18平方米要用砖618块。
如果铺24平方米,要用砖多少块?1、一幅图的比例尺是,那么图上的1厘米表示实际距离();实际距离50千米在图上要画()厘米。
把这个线段比例尺改写成数值比例尺是()。
3.一种微型零件的长5毫米,画在图纸上长20厘米,这幅图的比例尺是()。
4.判断下列各题中两种量是否成比例?成什么比例?(1)路程一定,车轮的周长和车轮滚动的圈数。
六年级下学期数学 正比例与反比例的判断50题训练 带答案

正比例与反比例的判断50题训练1、速度一定,路程和时间(正)比例路程一定,速度和时间(反)比例时间一定,路程和速度(正)比例2、工作效率一定,工作总量和工作时间(正)比例工作时间一定,工作效率和工作总量(正)比例工作总量一定,工作效率和工作时间(反)比例3、总价一定,单价和数量(反)比例数量一定,单价和总价(正)比例单价一定,数量和总价(正)比例4、每公顷产量一定,总产量和公顷数(正)比例公顷数一定,每公顷产量和总产量(正)比例总产量一定,每公顷产量和公顷数(反)比例5、份数一定,每份数和总数(正)比例每份数一定,份数和总数(正)比例总数一定,每份数和份数(反)比例6、商一定,除数和被除数(正)比例除数一定,商和被除数(正)比例被除数一定,除数和商(反)比例7、积一定,两个因数(反)比例一个因数一定,另一个因数和积(正)比例8、和一定,两个加数(不成)比例一个加数一定,另一个加数与和(不成)比例9、差一定,减数和被减数(不成)比例减数一定,被减数和差(不成)比例被减数一定,减数和差(不成)比例10、前项一定,比的后项和比值(反)比例比值一定,比的前项和后项(正)比例后项一定,比的前项和比值(正)比例11、分数值一定,分子和分母(正)比例分母一定,分数值和分子(正)比例分子一定,分数值和分母(反)比例12、在长方形中,长一定,面积和宽(正)比例宽一定,面积和长(正)比例面积一定,长和宽(反)比例周长一定,长和宽(不成)比例长一定,周长和宽(不成)比例宽一定,周长和长(不成)比例13、在平行四边形里,底一定,面积和高(正)比例高一定,面积和底(正)比例面积一定,底和高(反)比例14、在三角形里,底一定,面积和高(正)比例高一定,面积和底(正)比例面积一定,底和高(反)比例15、在正方形中,边长和周长(正)比例面积和边长(不成)比例16、在圆中,面积和半径(不成)比例周长和半径(正)比例直径和半径(正)比例直径和面积(不成)比例17、在长方体中,底面积一定,体积和高(正)比例体积一定,底面积和高(反)比例高一定,底面积和体积(正)比例18、在比例尺中,比例尺一定,图上距离和实际距离(正)比例图上距离一定,比例尺和实际距离(反)比例实际距离一定,比例尺和图上距离(正)比例19、用大豆榨油时,出油率一定时,油的重量和大豆的重量(正)比例大豆的重量一定,油的重量和出油率(正)比例油的重量一定时,大豆的重量和出油率(反)比例20、甲×乙=丙,当丙一定时,甲和乙(反)比例当甲一定时,丙和乙(正)比例当乙一定时,甲和丙(正)比例21、车轮的周长(或半径、直径)一定,车轮前进路程和转数(正)比例22、一堆煤的总重量一定,烧去的和剩下的(不成)比例23、要行的总路程一定,已经走过的路程和剩下的路程(不成)比例24、在规定的时间里,制造每个零件的时间和制造零件的个数(反)比例25、一批纸总页数一定,装订练习本本数和每本练习本的页数(反)比例26、每件上衣用布量一定,做上衣的件数和用布总米数(正)比例27、每块砖的面积一定,铺地总面积和用砖的总块数(正)比例28、铺地总面积一定,每块砖的面积和用砖的总块数(反)比例29、每立方厘米的铁的重量一定,铁的总重量和体积(正)比例30、购买各种货物的总价和数量(正)比例31、互相咬合的齿轮的齿数和转数(反)比例32、一个人的身高和体重(不成)比例33、总人数一定,每排人数和排数(反)比例34、一堆货物的总重量一定,每辆车的载重量和汽车辆数(反)比例35、正方体的棱长一定,它的体积和表面积(不成)比例36、一条公路的全长一定,已经修好的和没修好的(不成)比例37、同样的铁丝,每米长的重量一定,铁丝总重量和长度(正)比例38、正方体的棱长和体积(不成)比例。
六年级正反比例题100道

六年级正反比例题100道正比例题:1. 如果一个苹果的价格是2元,那么5个苹果的价格是多少元。
2. 5本书的价格是20元,那么每本书的价格是多少元。
3. 一个足球的价格是50元,购买3个足球需要多少钱。
4. 如果一辆车每小时行驶60公里,行驶2小时后能行驶多少公里。
5. 4个橙子的总价是16元,1个橙子多少钱。
6. 一条绳子长6米,3条绳子总长多少米。
7. 如果每辆车能载5人,10辆车能载多少人。
8. 一盒巧克力有10块,3盒巧克力有多少块。
9. 每个学生要交100元的学费,10个学生总共交多少钱。
10. 一台电脑的价格是4000元,4台电脑的总价是多少元。
11. 如果1升油的价格是8元,5升油的价格是多少元。
12. 一辆自行车的价格是300元,7辆自行车总共需要多少钱。
13. 1本书的页数是200页,5本书的总页数是多少页。
14. 如果每个学生需要2支铅笔,20个学生需要多少支铅笔。
15. 一棵树的高度是3米,5棵树的总高度是多少米。
16. 1块蛋糕的价格是15元,3块蛋糕总共多少钱。
17. 如果每本杂志售价10元,9本杂志总共多少钱。
18. 一辆车每小时行驶80公里,4小时能行驶多少公里。
19. 如果1公斤米的价格是5元,2公斤米总共多少钱。
20. 每个孩子要喝250毫升的牛奶,8个孩子需要多少牛奶。
21. 一支笔的价格是3元,12支笔总共多少钱。
22. 如果一个篮球的价格是120元,3个篮球的价格是多少元。
23. 一根铅笔的长度是20厘米,4根铅笔的总长度是多少厘米。
24. 如果一个人的工资是3000元,5个人的总工资是多少元。
25. 每条鱼的重量是200克,10条鱼的总重量是多少克。
26. 如果1个西瓜的价格是30元,4个西瓜的价格是多少元。
27. 一辆车的油耗是每公里8升,行驶100公里需要多少升油。
28. 每个学生要用5张纸,25个学生需要多少张纸。
29. 如果一个房间的面积是50平方米,5个这样的房间总面积是多少平方米。
正比例和反比例习题(含答案)

《正比例和反比例》习题一、对号入座。
1、35:()=20÷16==()%=()(填小数)2、因为X=2Y,所以X:Y=():(),X和Y成()比例。
3、一个长方形的长比宽多20%,这个长方形的长和宽的最简整数比是()。
4、向阳小学三年级与四年级人数比是3:4,三年级人数比四年级少()% 四年级比三年级多()%5、甲乙两个正方形的边长比是2:3,甲乙两个正方形的周长比是(),甲乙两个正方形的面积比是()。
6、一个比例由两个比值是2的比组成,又知比例的外项分别是1.2和5,这个比例是()。
7、已知被减数与差的比是5:3,减数是100,被减数是()。
8、在一幅地图上量得甲乙两地距离6厘米,乙丙两地距离8厘米;已知甲乙两地间的实际距离是120千米,乙丙两地间的实际距离是()千米;这幅地图的比例尺是()。
9、从2:8、1.6:和:这三个比中,选两个比组成的比例是()。
10、一块铜锌合金重180克,铜与锌的比是2:3,锌重()克。
如果再熔入30 克锌,这时铜与锌的比是()。
二、明辨是非。
1、一项工程,甲队40天可以完成,乙队50天可以完成。
甲乙两队的工作效率比是4:5。
()2、圆柱体与圆锥体的体积比是3:1,则圆柱体与圆锥体一定等底等高。
()3、甲数与乙数的比是3:4,甲数就是乙数的。
()4、比的前项和后项同时乘以同一个数,比值不变。
()5、总价一定,单价和数量成反比例。
()6、实际距离一定,图上距离与比例尺成正比例。
()7、正方体体积一定,底面积和高成反比例。
()8、订阅《今日泰兴》的总钱数和份数成正比例。
()三、选择题。
1、把一个直径4毫米的手表零件,画在图纸上直径是8厘米,这幅图纸的比例尺是()。
A、1:2B、2:1C、1:20D、20:12、已知=1.2、=1.2,所以X和Y比较()。
A、X大B、YC、一样大3、如果A×2=B÷3,那么A:B=()。
A、2:3B、3:2C、1:6 D 6:14、一个三角形的三个内角的度数比是2:3:4,这个三角形是()。
正比例和反比例习题(含答案)

《正比例和反比例》习题一、对号入座。
1、35:()=20÷16==()%=()(填小数)2、因为X=2Y,所以X:Y=():(),X和Y成()比例。
3、一个长方形的长比宽多20%,这个长方形的长和宽的最简整数比是()。
4、向阳小学三年级与四年级人数比是3:4,三年级人数比四年级少()% 四年级比三年级多()%5、甲乙两个正方形的边长比是2:3,甲乙两个正方形的周长比是(),甲乙两个正方形的面积比是()。
6、一个比例由两个比值是2的比组成,又知比例的外项分别是1.2和5,这个比例是()。
7、已知被减数与差的比是5:3,减数是100,被减数是()。
8、在一幅地图上量得甲乙两地距离6厘米,乙丙两地距离8厘米;已知甲乙两地间的实际距离是120千米,乙丙两地间的实际距离是()千米;这幅地图的比例尺是()。
9、从2:8、1.6:和:这三个比中,选两个比组成的比例是()。
10、一块铜锌合金重180克,铜与锌的比是2:3,锌重()克。
如果再熔入30 克锌,这时铜与锌的比是()。
二、明辨是非。
1、一项工程,甲队40天可以完成,乙队50天可以完成。
甲乙两队的工作效率比是4:5。
()2、圆柱体与圆锥体的体积比是3:1,则圆柱体与圆锥体一定等底等高。
()3、甲数与乙数的比是3:4,甲数就是乙数的。
()4、比的前项和后项同时乘以同一个数,比值不变。
()5、总价一定,单价和数量成反比例。
()6、实际距离一定,图上距离与比例尺成正比例。
()7、正方体体积一定,底面积和高成反比例。
()8、订阅《今日泰兴》的总钱数和份数成正比例。
()三、选择题。
1、把一个直径4毫米的手表零件,画在图纸上直径是8厘米,这幅图纸的比例尺是()。
A、1:2B、2:1C、1:20D、20:12、已知=1.2、=1.2,所以X和Y比较()。
A、X大B、YC、一样大3、如果A×2=B÷3,那么A:B=()。
A、2:3B、3:2C、1:6 D 6:14、一个三角形的三个内角的度数比是2:3:4,这个三角形是()。
小学数学正比反比练习题

小学数学正比反比练习题正文:一、正比例关系练习题1. 小明每天骑自行车上学,他的速度和用时的关系是什么?如果他以每小时15公里的速度骑行,那么骑行5小时能够走多远?2. 一辆汽车以每小时80公里的速度行驶,行驶4小时后,它能够走多远?3. 将正比例关系列为函数的形式:设x是小明骑自行车所花费的时间(小时),y是他骑行的距离(公里),写出函数y和x之间的关系式。
4. 小明骑自行车到山上游玩,用时与距离的关系是正比例关系。
他用时2小时到达离家20公里的山脚,那么他用时3小时能够到达离家多远的山脚?5. 一辆汽车以每小时60公里的速度行驶,行驶2小时15分钟后,它能够走多远?二、反比例关系练习题1. 公司A生产一批产品需要5个工人工作3天完成,那么如果只有3个工人参与生产,需要多少天才能完成?2. 某项工程由6个工人完成,需要12天,如果增加工人的数量,能否缩短工期?为什么?3. 设x是某项工程所需要的工人数,y是完成这项工程所需的天数。
当工人数增加时,工期缩短了吗?写出x和y之间的关系式。
4. 利用反比例关系解决实际问题:某项工程由10个工人完成,需要20天。
如果只有5个工人参与工作,那么需要多少天才能完成?5. 公司A和公司B生产某种产品,两个公司的产能成反比例关系。
如果公司B的产能是公司A的2倍,那么公司B需要多久才能完成和公司A一样多的产品?结语:通过以上练习题,我们可以更好地理解小学数学中的正比例关系和反比例关系。
掌握了这两种关系的概念和求解方法,我们可以更好地应用于实际生活中的问题求解。
希望同学们能够通过不断地练习,加深对正反比例关系的理解和运用能力。
六年级正比例和反比例习题精选

六年级正比例和反比例习题精选正比例与反比例基础题精选年月日姓名一、判断.1.一个因数不变,积与另一个因数成正比例.()2.长方形的长一定,宽和面积成正比例.()3.大米的总量一定,吃掉的和剩下的成反比例.()4.圆的半径和周长成正比例.()5.分数的分子一定,分数值和分母成反比例.()6.铺地面积一定,方砖的边长和所需块数成反比例.()7.铺地面积一定,方砖面积和所需块数成反比例.()8.除数一定,被除数和商成正比例.()二、选择.1.把一堆化肥装入麻袋,麻袋的数量和每袋化肥的重量.()A.成正比例B.成反比例C.不成比例2.和一定,加数和另一个加数.()A.成正比例B.成反比例C.不成比例3.在汽车每次运货吨数,运货次数和运货的总吨数这三种量中,成正比例关系是(),成反比例关系是().A.汽车每次运货吨数一定,运货次数和运货总吨数.B.汽车运货次数一定,每次运货的吨数和运货总吨数.C.汽车运货总吨数一定,每次运货的吨数和运货的次数.三、思考.1、如果,和成()比例,则∶=()∶()四、填空.1.两种()的量,一种量变化,另一种量(),如果这两种量中()的两个数的()一定,这两种量就叫做成正比例的量,它们的关系叫做(),关系式是().2.两种()的量,一种量变化,另一种量(),如果这两种量中()的两个数的()一定,这两种量就叫做成反比例的量,它们的关系叫做(),关系式是().3.一房间铺地面积和用砖数如下表,根据要求填空.(1)表中()和()是相关联的量,()随着()的变化而变化.(2)表中第三组这两种量相对应的两个数的比是(),比值是();第五组这两种量相对应的两个数的比是(),比值是().(3)上面所求出的比值所表示的的意义是(),铺地面积和砖的块数的()是一定的,所以铺地面积和砖的块数().4.练习本总价和练习本本数的比值是().当()一定时,()和()成()比例.五、判断下面每题中的两种量是不是成比例,成什么比例,并说明理由.1.平行四边形的高一定,它的底和面积.2.被除数一定,商和除数.3.小明的年龄和他的体重.4.天数一定,生产零件的总个数和每天生产零件的个数.六、思考.、、三种量的关系是:×=1.如果一定,那么和成()比例;2.如果一定,那么和成()比例;3.如果一定,那么和成()比例.参考答案一、判断.1.一个因数不变,积与另一个因数成正比例.(√)2.长方形的长一定,宽和面积成正比例.(√)3.大米的总量一定,吃掉的和剩下的成反比例.(×)4.圆的半径和周长成正比例.(√)5.分数的分子一定,分数值和分母成反比例.(√)6.铺地面积一定,方砖的边长和所需块数成反比例.(×)7.铺地面积一定,方砖面积和所需块数成反比例.(√)8.除数一定,被除数和商成正比例.(√)二、选择.1.把一堆化肥装入麻袋,麻袋的数量和每袋化肥的重量.(B)A.成正比例B.成反比例C.不成比例2.和一定,加数和另一个加数.(C)A.成正比例B.成反比例C.不成比例3.在汽车每次运货吨数,运货次数和运货的总吨数这三种量中,成正比例关系是(A、B),成反比例关系是(C).A.汽车每次运货吨数一定,运货次数和运货总吨数.B.汽车运货次数一定,每次运货的吨数和运货总吨数.C.汽车运货总吨数一定,每次运货的吨数和运货的次数.三、思考.如果,和成(正)比例,则∶=( 1 )∶( 8 )四、填空.1.两种(相关联)的量,一种量变化,另一种量(随着变化),如果这两种量中(相对应)的两个数的(比值)一定,这两种量就叫做成正比例的量,它们的关系叫做(正比例关系),关系式是( (一定)).2.两种(相关联)的量,一种量变化,另一种量(随着变化),如果这两种量中(相对应)的两个数的(积)一定,这两种量就叫做成反比例的量,它们的关系叫做(反比例关系),关系式是((一定)).3.一房间铺地面积和用砖数如下表,根据要求填空.1 2 3 4 5铺地面积(平方米)用砖块数25 50 75 100 125(1)表中(铺地面积)和(用砖块数)是相关联的量,(用砖块数)随着(铺地面积)的变化而变化.(2)表中第三组这两种量相对应的两个数的比是(75∶3),比值是(25);第五组这两种量相对应的两个数的比是(125∶5),比值是(25).(3)上面所求出的比值所表示的的意义是(每平方米用砖块数),铺地面积和砖的块数的(比值)是一定的,所以铺地面积和砖的块数(正比例).4.练习本总价和练习本本数的比值是(练习本单价).当(练习本单价)一定时,(练习本总价)和(练习本本数)成(正)比例.五、判断下面每题中的两种量是不是成比例,成什么比例,并说明理由.1.平行四边形的高一定,它的底和面积.理由:因为,高一定,就是平行四边形面积与底的比值一定.所以,平行四边形的面积与底成正比例.2.被除数一定,商和除数.理由:因为被除数一定,就是商和除数的乘积一定,所以,商和除数成反比例.3.小明的年龄和他的体重.理由:小明的年龄和他的体重虽然也是一对相关联的量,但是这两个量的变化并没有什么规律,找不出哪个是不变量,所以,小明的年龄和他的体重不成比例.4.天数一定,生产零件的总个数和每天生产零件的个数.理由:因为,天数一定,就是生产零件的总个数和每天生产零件的个数的比值一定,所以,生产零件的总个数和每天生产零件的个数成正比例.六、思考.、、三种量的关系是:×=1.如果一定,那么和成(正)比例;2.如果一定,那么和成(正)比例;3.如果一定,那么和成(反)比例.。
正比例与反比例练习题

正比例与反比例练习题1. 小明每天骑自行车上学,他发现骑行的时间和他的速度成正比。
如果他以每小时10公里的速度骑行,那么上学的时间是多少?解答: 假设骑行的时间是 x 小时,则速度和时间成正比,可以表示为 10/x = k,其中 k 是比例系数。
根据比例关系可得,x = 10/k。
由题意可知,当速度为10公里/小时时,上学时间为x小时,代入公式得到:x = 10/k。
因此,上学的时间为 10/k 小时。
2. 某工厂生产零件的速度和工人数量成正比。
如果有8个工人能够在5小时内生产完500个零件,那么10个工人需要多长时间才能生产1000个零件?解答: 假设生产零件的时间是 x 小时,则工人数量和时间成正比,可以表示为 8/5 = 10/x。
通过交叉乘积得到方程 8x = 50,解得 x = 6.25。
因此,10个工人需要6.25小时才能生产完1000个零件。
3. 小红做作业的速度和作业量成反比。
如果她能够在12小时内完成180页的作业,那么她在4小时内能完成多少页的作业?解答: 假设完成作业的页数是 y 页,则速度和作业量成反比,可以表示为 180/12 = y/4。
通过交叉乘积得到方程 180*4 = 12y,解得 y = 60。
因此,小红在4小时内能完成60页的作业。
4. 某项任务由8个工人在10天内完成,如果增加到12个工人,需要多少天才能完成同样的工作?解答: 假设完成任务的时间是 x 天,则工人数量和时间成反比,可以表示为 8*10 = 12*x。
通过交叉乘积得到方程 80 = 12x,解得 x = 6.67。
因此,增加到12个工人需要6.67天才能完成同样的工作。
由于天数不能为小数,可以向上取整,并得出需要7天才能完成。
5. 某车辆的速度和行驶时间成反比。
如果车辆以每小时80公里的速度行驶,那么行驶1000公里需要多长时间?解答: 假设行驶的时间是 y 小时,则速度和时间成反比,可以表示为 80/y = k,其中 k 是比例系数。
判断正比例与反比例专项练习题
判断正比例与反比例专项练习题
问题一:
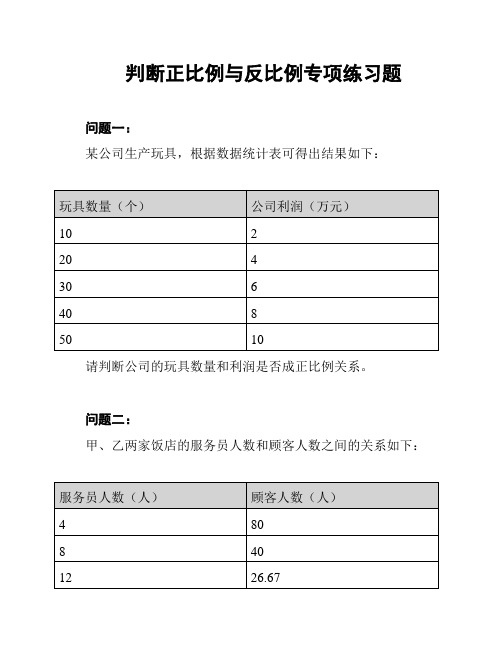
某公司生产玩具,根据数据统计表可得出结果如下:
请判断公司的玩具数量和利润是否成正比例关系。
问题二:
甲、乙两家饭店的服务员人数和顾客人数之间的关系如下:
请判断饭店的服务员人数和顾客人数是否成反比例关系。
问题三:
某池塘中的鱼的数量和水的深度之间的关系如下:
请判断池塘的水深和鱼的数量是否成反比例关系。
问题四:
某学校的学生数和书籍数的关系如下:
请判断学校的学生数和书籍数是否成反比例关系。
问题五:
某工厂织布时,织机每小时的织布米数与织物重量的关系如下:
请判断织机的织布米数和织物重量是否成正比例关系。
判断正比例与反比例专项练习题

判断正比例与反比例专项练习题
题目一
判断下列各组数据是否呈现正比例关系:
原始数据 | 比例数据 |
1.2.| 2.4.|
3.4.| 6.8.|
5.6.| 10.12.|
是正比例关系,因为每个原始数据乘以2都可以得到对应的比例数据。
题目二
判断下列各组数据是否呈现反比例关系:
原始数据 | 比例数据 |
2.3.| 6.4.|
4.5.| 10.8.|
6.7.| 14.12.|
不是反比例关系,因为每个原始数据乘以2并不等于对应的比例数据。
题目三
判断下列各组数据是否呈现正比例关系:
原始数据 | 比例数据 |
1.4.|
2.8.|
3.7.| 6.1
4.|
5.10.| 10.20.|
是正比例关系,因为每个原始数据乘以相同的倍数都可以得到对应的比例数据。
总结
通过观察原始数据和比例数据之间的关系,我们可以判断出是否存在正比例关系或反比例关系。
在正比例关系中,每个原始数据乘以同一个倍数都可以得到对应的比例数据;而在反比例关系中,每个原始数据乘以同一个倍数得到的结果是相反的。
正确地判断出正比例和反比例关系,有助于我们在数学问题中更好地理解和运用比例概念。
正比例反比例练习题

正比例反比例练习题一、选择题1. 已知A和B成正比例,若A=3时,B=9,则当A=6时,B的值为多少?A. 18B. 12C. 24D. 362. 某工厂的产量与工作时间成正比例,若工作8小时产量为160件,则工作10小时的产量是多少?A. 200B. 180C. 160D. 2203. 反比例函数y=1/x的图象上,当x=2时,y的值为多少?A. 0.5B. 1C. 2D. 44. 甲乙两地之间的距离是固定的,若汽车速度与所需时间成反比例,汽车以60公里/小时的速度行驶需要2小时,则以40公里/小时的速度行驶需要多少时间?A. 3B. 4C. 6D. 85. 已知反比例函数y=k/x,当x=3时,y=2,则k的值为多少?A. 6B. 5C. 3D. 2二、填空题6. 若A和B成正比例,比例系数为5,当A=10时,B的值为_________。
7. 某商品的单价与购买数量成反比例,若单价为10元时,购买数量为20件,则单价为20元时,购买数量为_________。
8. 已知正比例函数y=kx,当x=4时,y=8,则k的值为_________。
9. 反比例函数y=6/x的图象上,当x=3时,y的值为_________。
10. 若速度与时间成反比例,且当速度为5米/秒时,时间为10秒,则当速度为10米/秒时,时间为_________。
三、解答题11. 某工厂生产某种零件,其生产效率与所需时间成反比例。
若生产100个零件需要2小时,请回答:(1) 写出该工厂生产零件的反比例函数关系式。
(2) 若该工厂需要生产200个零件,需要多少时间?12. 某城市出租车的计价规则是:起步价为10元,之后每公里收费2元。
若乘客行驶了15公里,请计算乘客需要支付的费用。
13. 已知正比例函数y=kx,其中k=4,求当x=5时,y的值。
14. 某学校规定,学生的体育成绩与学习时间成正比例。
若学生学习2小时,体育成绩为80分,则学习3小时时,体育成绩为多少?15. 某工厂的产量与工作时间成正比例,若工作8小时产量为160件,求该工厂的产量与工作时间的正比例系数。
(完整版)正比例和反比例习题精选及答案

正比例和反比例习题精选一、判断.1.一个因数不变,积与另一个因数成正比例.()2.长方形的长一定,宽和面积成正比例.()3.大米的总量一定,吃掉的和剩下的成反比例.()4.圆的半径和周长成正比例.()5.分数的分子一定,分数值和分母成反比例.()6.铺地面积一定,方砖的边长和所需块数成反比例.()7.铺地面积一定,方砖面积和所需块数成反比例.()8.除数一定,被除数和商成正比例.()二、选择.1.把一堆化肥装入麻袋,麻袋的数量和每袋化肥的重量.()A.成正比例B.成反比例C.不成比例2.和一定,加数和另一个加数.()A.成正比例B.成反比例C.不成比例3.在汽车每次运货吨数,运货次数和运货的总吨数这三种量中,成正比例关系是(),成反比例关系是().A.汽车每次运货吨数一定,运货次数和运货总吨数.B.汽车运货次数一定,每次运货的吨数和运货总吨数.C.汽车运货总吨数一定,每次运货的吨数和运货的次数.三、填空.1.两种()的量,一种量变化,另一种量(),如果这两种量中()的两个数的()一定,这两种量就叫做成正比例的量,它们的关系叫做(),关系式是().2.两种()的量,一种量变化,另一种量(),如果这两种量中()的两个数的()一定,这两种量就叫做成反比例的量,它们的关系叫做(),关系式是().3.一房间铺地面积和用砖数如下表,根据要求填空.铺地面积(平方米)1 2 3 4 5用砖块数25 50 75 100 125(1)表中()和()是相关联的量,()随着()的变化而变化.(2)表中第三组这两种量相对应的两个数的比是(),比值是();第五组这两种量相对应的两个数的比是(),比值是().(3)上面所求出的比值所表示的的意义是(),铺地面积和砖的块数的()是一定的,所以铺地面积和砖的块数().4.练习本总价和练习本本数的比值是().当()一定时,()和()成()比例.二、判断下面每题中的两种量是不是成比例,成什么比例,并说明理由.1.平行四边形的高一定,它的底和面积.2.被除数一定,商和除数.3.小明的年龄和他的体重.4.天数一定,生产零件的总个数和每天生产零件的个数.三、思考.、、三种量的关系是:×=1.如果一定,那么和成()比例;2.如果一定,那么和成()比例;3.如果一定,那么和成()比例.参考答案一、判断.(√)(√)(×)(√)(√)(×)(√)(√)二、选择.1.(B )2.(C )3.(C ).1.两种(相关联)的量,一种量变化,另一种量(随着变化),如果这两种量中(相对应)的两个数的(比值)一定,这两种量就叫做成正比例的量,它们的关系叫做(正比例关系),关系式是((一定)).2.两种(相关联)的量,一种量变化,另一种量(随着变化),如果这两种量中(相对应)的两个数的(积)一定,这两种量就叫做成反比例的量,它们的关系叫做(反比例关系),关系式是((一定)).(1)表中(铺地面积)和(用砖块数)是相关联的量,(用砖块数)随着(铺地面积)的变化而变化.(2)表中第三组这两种量相对应的两个数的比是(75∶3),比值是(25);第五组这两种量相对应的两个数的比是(125∶5),比值是(25).(3)上面所求出的比值所表示的的意义是(每平方米用砖块数),铺地面积和砖的块数的(比值)是一定的,所以铺地面积和砖的块数(正比例).4.练习本总价和练习本本数的比值是(练习本单价).当(练习本单价)一定时,(练习本总价)和(练习本本数)成(正)比例.二、判断下面每题中的两种量是不是成比例,成什么比例,并说明理由.1.平行四边形的高一定,它的底和面积.理由:因为,高一定,就是平行四边形面积与底的比值一定.所以,平行四边形的面积与底成正比例.2.被除数一定,商和除数.理由:因为被除数一定,就是商和除数的乘积一定,所以,商和除数成反比例.3.小明的年龄和他的体重.理由:小明的年龄和他的体重虽然也是一对相关联的量,但是这两个量的变化并没有什么规律,找不出哪个是不变量,所以,小明的年龄和他的体重不成比例.4.天数一定,生产零件的总个数和每天生产零件的个数.理由:因为,天数一定,就是生产零件的总个数和每天生产零件的个数的比值一定,所以,生产零件的总个数和每天生产零件的个数成正比例.三、思考.、、三种量的关系是:×=1.如果一定,那么和成(正)比例;2.如果一定,那么和成(正)比例;3.如果一定,那么和成(反)比例.。
正比例和反比例习题(含答案)

《正比例和反比例》习题一、对号入座。
1、35:()=20÷16==()%=()(填小数)2、因为X=2Y,所以X:Y=():(),X和Y成()比例。
3、一个长方形的长比宽多20%,这个长方形的长和宽的最简整数比是()。
4、向阳小学三年级与四年级人数比是3:4,三年级人数比四年级少()% 四年级比三年级多()%5、甲乙两个正方形的边长比是2:3,甲乙两个正方形的周长比是(),甲乙两个正方形的面积比是()。
6、一个比例由两个比值是2的比组成,又知比例的外项分别是1.2和5,这个比例是()。
7、已知被减数与差的比是5:3,减数是100,被减数是()。
8、在一幅地图上量得甲乙两地距离6厘米,乙丙两地距离8厘米;已知甲乙两地间的实际距离是120千米,乙丙两地间的实际距离是()千米;这幅地图的比例尺是()。
9、从2:8、1.6:和:这三个比中,选两个比组成的比例是()。
10、一块铜锌合金重180克,铜与锌的比是2:3,锌重()克。
如果再熔入30 克锌,这时铜与锌的比是()。
二、明辨是非。
1、一项工程,甲队40天可以完成,乙队50天可以完成。
甲乙两队的工作效率比是4:5。
()2、圆柱体与圆锥体的体积比是3:1,则圆柱体与圆锥体一定等底等高。
()3、甲数与乙数的比是3:4,甲数就是乙数的。
()4、比的前项和后项同时乘以同一个数,比值不变。
()5、总价一定,单价和数量成反比例。
()6、实际距离一定,图上距离与比例尺成正比例。
()7、正方体体积一定,底面积和高成反比例。
()8、订阅《今日泰兴》的总钱数和份数成正比例。
()三、选择题。
1、把一个直径4毫米的手表零件,画在图纸上直径是8厘米,这幅图纸的比例尺是()。
A、1:2B、2:1C、1:20D、20:12、已知=1.2、=1.2,所以X和Y比较()。
A、X大B、YC、一样大3、如果A×2=B÷3,那么A:B=()。
A、2:3B、3:2C、1:6 D 6:14、一个三角形的三个内角的度数比是2:3:4,这个三角形是()。
正比反比练习题

正比例与反比例基础题精选年月日姓名一、判断.1.一个因数不变,积与另一个因数成正比例.()2.长方形的长一定,宽和面积成正比例.()3.大米的总量一定,吃掉的和剩下的成反比例.()4.圆的半径和周长成正比例.()5.分数的分子一定,分数值和分母成反比例.()6.铺地面积一定,方砖的边长和所需块数成反比例.()7.铺地面积一定,方砖面积和所需块数成反比例.()8.除数一定,被除数和商成正比例.()二、选择.1.把一堆化肥装入麻袋,麻袋的数量和每袋化肥的重量.()A.成正比例B.成反比例C.不成比例2.和一定,加数和另一个加数.()A.成正比例B.成反比例C.不成比例3.在汽车每次运货吨数,运货次数和运货的总吨数这三种量中,成正比例关系是(),成反比例关系是().A.汽车每次运货吨数一定,运货次数和运货总吨数.B.汽车运货次数一定,每次运货的吨数和运货总吨数.C.汽车运货总吨数一定,每次运货的吨数和运货的次数.三、思考.1、如果,和成()比例,则∶=()∶()四、填空.1.两种()的量,一种量变化,另一种量(),如果这两种量中()的两个数的()一定,这两种量就叫做成正比例的量,它们的关系叫做(),关系式是().2.两种()的量,一种量变化,另一种量(),如果这两种量中()的两个数的()一定,这两种量就叫做成反比例的量,它们的关系叫做(),关系式是().3.一房间铺地面积和用砖数如下表,根据要求填空.(1)表中()和()是相关联的量,()随着()的变化而变化.(2)表中第三组这两种量相对应的两个数的比是(),比值是();第五组这两种量相对应的两个数的比是(),比值是().(3)上面所求出的比值所表示的的意义是(),铺地面积和砖的块数的()是一定的,所以铺地面积和砖的块数().4.练习本总价和练习本本数的比值是().当()一定时,()和()成()比例.五、判断下面每题中的两种量是不是成比例,成什么比例,并说明理由.1.平行四边形的高一定,它的底和面积.2.被除数一定,商和除数.3.小明的年龄和他的体重.4.天数一定,生产零件的总个数和每天生产零件的个数.六、思考.1.如果一定,那么和成()比例;2.如果一定,那么和成()比例;3.如果一定,那么和成()比例.参考答案一、判断.1.一个因数不变,积与另一个因数成正比例.(√)2.长方形的长一定,宽和面积成正比例.(√)3.大米的总量一定,吃掉的和剩下的成反比例.(×)4.圆的半径和周长成正比例.(√)5.分数的分子一定,分数值和分母成反比例.(√)6.铺地面积一定,方砖的边长和所需块数成反比例.(×)7.铺地面积一定,方砖面积和所需块数成反比例.(√)8.除数一定,被除数和商成正比例.(√)二、选择.1.把一堆化肥装入麻袋,麻袋的数量和每袋化肥的重量.(B)A.成正比例B.成反比例C.不成比例2.和一定,加数和另一个加数.(C)A.成正比例B.成反比例C.不成比例3.在汽车每次运货吨数,运货次数和运货的总吨数这三种量中,成正比例关系是(A、B),成反比例关系是(C).A.汽车每次运货吨数一定,运货次数和运货总吨数.B.汽车运货次数一定,每次运货的吨数和运货总吨数.C.汽车运货总吨数一定,每次运货的吨数和运货的次数.三、思考.如果,和成(正)比例,则∶=( 1 )∶( 8 )四、填空.1.两种(相关联)的量,一种量变化,另一种量(随着变化),如果这两种量中(相对应)的两个数的(比值)一定,这两种量就叫做成正比例的量,它们的关系叫做(正比例关系),关系式是( (一定)).2.两种(相关联)的量,一种量变化,另一种量(随着变化),如果这两种量中(相对应)的两个数的(积)一定,这两种量就叫做成反比例的量,它们的关系叫做(反比例关系),关系式是((一定)).3.一房间铺地面积和用砖数如下表,根据要求填空.(1)表中(铺地面积)和(用砖块数)是相关联的量,(用砖块数)随着(铺地面积)的变化而变化.(2)表中第三组这两种量相对应的两个数的比是(75∶3),比值是(25);第五组这两种量相对应的两个数的比是(125∶5),比值是(25).(3)上面所求出的比值所表示的的意义是(每平方米用砖块数),铺地面积和砖的块数的(比值)是一定的,所以铺地面积和砖的块数(正比例).4.练习本总价和练习本本数的比值是(练习本单价).当(练习本单价)一定时,(练习本总价)和(练习本本数)成(正)比例.五、判断下面每题中的两种量是不是成比例,成什么比例,并说明理由.1.平行四边形的高一定,它的底和面积.理由:因为,高一定,就是平行四边形面积与底的比值一定.所以,平行四边形的面积与底成正比例.2.被除数一定,商和除数.理由:因为被除数一定,就是商和除数的乘积一定,所以,商和除数成反比例.3.小明的年龄和他的体重.理由:小明的年龄和他的体重虽然也是一对相关联的量,但是这两个量的变化并没有什么规律,找不出哪个是不变量,所以,小明的年龄和他的体重不成比例.4.天数一定,生产零件的总个数和每天生产零件的个数.理由:因为,天数一定,就是生产零件的总个数和每天生产零件的个数的比值一定,所以,生产零件的总个数和每天生产零件的个数成正比例.六、思考.、、三种量的关系是:×=1.如果一定,那么和成(正)比例;2.如果一定,那么和成(正)比例;3.如果一定,那么和成(反)比例.正比例和反比例练习题姓名_____________一、判断题:对的打√,错的打x。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.判断
1、圆的面积和圆的半径成正比例。
()
2、圆的面积和圆的半径的平方成正比例。
()
3、圆的面积和圆的周长的平方成正比例。
()
4、正方形的面积和边长成正比例。
()
5、正方形的周长和边长成正比例。
()
6、长方形的面积一定时,长和宽成反比例。
()
7、长方形的周长一定时,长和宽成反比例。
()
8、三角形的面积一定时,底和高成反比例。
()
9、梯形的面积一定时,上底和下底的和与高成反比例。
()
10、圆的周长和圆的半径成正比例。
()11.一个因数不变,积与另一个因数成正比例.()
12.长方形的长一定,宽和面积成正比例.()13.大米的总量一定,吃掉的和剩下的成反比例.()
14.圆的半径和周长成正比例.()15.分数的分子一定,分数值和分母
成反比例.()
16.铺地面积一定,方砖的边长和所需块数成反比例.()17.铺地面积一定,方砖面积和所需块数成反比例.()18.除数一定,被除数和商成正比例.()
19. 分母一定,分子和分数值成正比例()
20. 圆的面积一定,圆周率与半径成反比例()
21. 出勤率一定,实际出勤人数和应出勤人数成反比例()
22. 小明跳高的高度与他的身高成反比例()
23. 铺地面积一定,每块砖的面积与需要的块数成反比例()
24. 比的前项一定,比的后项和比值成反比例()
25. 文具盒的单价一定,买文具盒的个数和总价成正比例()
26. 水稻产量一定,水稻的种植面积和总产量成反比例()。
27. 一堆货物一定,运出的和剩下的成正比例()。
28. 汽车行驶的速度一定,行驶的时间和路程成正比例()。
29. 比值一定,比的前项和后项成正比例()。
30. 煤的总量一定,每天的烧煤量和烧的天数成正比例()。
31. 李叔叔从家到工厂,骑车的速度和所需要的时间成反比例
32. 玉华做12 道练习题,做完的与没做的题成正比例()。
33. 长方形面积一定,它的长和宽成正比例()。
34. 长方形的周长一定时,长和宽成反比例。
()
35. 三角形的面积一定时,底和高成反比例。
()
36. 车轮直径一定,所行路程和车轮的转数成反比例()
37. 直角三角形的两个锐角成反比例()
38. 一个因数(不为零)一定,积和另一个因数成正比例()
39. 同样的书,买的本数和钱数成正比例()
二、判断下面各题中的两个量成什么比例,并说明理由。
1、订《少先队员》的份数和总钱数。
2、三角形的面积一定,底和高。
3、总人数一定,行数和每行人数。
4、总价一定,单价和数量。
5、购买同一种钢笔的数量和总价。
6、正方形的周长与它的边长。
7、圆的面积与它的半径。
8、圆的周长与它的半径。
9、圆柱的侧面积一定,它的底面积周长与高。
10、长方形的长一定,它的面积与宽。
11、被减数一定,减数和差。
12、总人数一定,每行人数和行数。
13、长方体的底面积一定,体积和高。
14、路程一定,已走的路程和剩下的路程。
15、百米赛跑中,跑步速度和所用时间。
16、车轮的转数一定时,车轮的直径和行驶的路程。
17、x=2y ,(x、y 不为0)那么x 和y.
18、大豆的出油率一定,大豆的数量和出油的数量。
19、分数值一定,分子和分母。
20、一个加数一定,另一个加数与和。
21、路程一定,速度和时间。
22、圆柱的底面积一定,它的体积与高。
23、看一本故事书,每天看的页数和所剩下的页数。
24、圆锥的体积一定,它的底面积与高。
25、购买苹果的总价一定,购买苹果的千克数和单价。
26、正方体的棱长与表面积。
27. 时间一定,每小时织布的米数和织布总米数.
28. 平行四边形面积一定,它的底和高.
29. 分子一定,分母和分数值.
30. 报纸的单价一定,总价与订阅的份数.
31. 正方形的周长和边长.
32. 正方形的边长和面积.
33. 路程一定,车轮的直径与车轮的转数.
34. 被成数一定,成数与差.
35. 三角形的高一定,底和面积.
36. 甲、乙两数互为倒数,甲数和乙数
37. 铺地的总面积一定,每块砖的面积与需要的块数成正比例.
38. 班级学生的总人数一定,出勤率与缺勤率成正比例.
、填空:
1、 每块砖的面积一定,铺地面积与块数成(
)比例。
2、年级总人数一定,每班人数与班数成(
)比例。
3、被除数一定,商和除数成(
)比例。
4、糖水的含糖率一定,糖和水成(
)比例。
5、三角形的面积一定,它的底和高(
)比例。
6、如果=y , (x 不为0),那么x 和y 成( )比例。
7、如果x= y 十,那么x 和y 成( )比例。
四、根据圆柱的体积、底面积、高在个量之间的关系,完成关系式:
例。
五、选择.
1.
把一堆化肥装入麻袋,麻袋的数量和每袋化肥的重量. () A . 成正比例 B .成反比例 C .不成比例 2.
和一定,加数和另一个加数. () A . 成正比例 B .成反比例 C .不成比例
3•在汽车每次运货吨数,运货次数和运货的总吨数这三种量中,成正比例关系是( 玄阜 ( 系疋(
A. 汽车每次运货吨数一定,运货次数和运货总吨数.
B. 汽车运货次数一定,每次运货的吨数和运货总吨数.
C. 汽车运货总吨数一定,每次运货的吨数和运货的次数.
互为倒数的两个数成反比例关系
我认为它们是存在反比例关系的。
两个相关联的量,一个量变化,另一个量也随之变化,并且这两 个量的乘积一定,我们就说这两个量是反比例的量,他们的关系就是反比例关系。
从定义上可以看出, 反比例关系需要满足 3个条件,一:两个量是要有关联的,互为倒数的两个量很明显有关系;二:一个 量变化另一个量也随之变化,从命题上可以看出,对这两个数我们没有用固定的数字来表达,因此我们 看出这两个互为倒数的数是可以变化的并且也满足一个变化另一个也变化这个条件;三:这两个量的乘 积一定或者说是不变,什么叫互为倒数。
乘积是
1的两个互为倒数,所以我们可以很明显的看出这
2个
数的乘积是不变的并且都是 1。
在判断这个的过程中我们需要明白量和数字是不同的,比如说 2与1/2这两个数,我们就不能说他 们成反比例( )(一定),( )和(
)成
比例; ( )(一定),( )和( )成(
(
)(一定),( )和( )成( ) )比例; )比 ),成反比例关
关系,因为这两个只是数字。
量是可以产生变化的,而数字是固定不变的所以我认为互为倒数的两个数是成反比例关系。
