用栈进行表达式求值并输出逆波兰式(源代码)
中缀表达式转逆波兰式并求值

中缀表达式转逆波兰式并求值// 标题: 栈的应用——中缀表达式转逆波兰式 // 时间: 2015年4月14日// 所有者: Vae#include<stdio.h>#include<malloc.h>#include<stdlib.h>#include<windows.h>#include<Winuser.h>#define STACK_INIT_SIZE 100 #define STACKCREATE 10 #define OK 1 #define ERROR 0typedef struct double_stack {int *num;int *index;}DOUBLESTACK;typedef struct SqStack{DOUBLESTACK top; DOUBLESTACK base;int stacksize;}SqStack;// 函数名: InitStack // 形参类型: SqStack * // 函数功能构造一个栈void InitStack(SqStack *S) {S->base.index = (int *)malloc(sizeof(int)*STACK_INIT_SIZE);S->base.num = (int *)malloc(sizeof(int)*STACK_INIT_SIZE);if (!(S->base.num && S->base.index)){printf("构造栈失败!\n");exit(-1);}S->top.num = S->base.num;S->top.index = S->base.index;S->stacksize = STACK_INIT_SIZE;return ;}// 函数名: Push// 形参类型: SqStack *, int, int // 函数功能插入e为新的栈顶元素int Push(SqStack *S, int m, int n){if ((S->top.num - S->base.num) >= S->stacksize){S->base.index = (int *)realloc(S->base.index,sizeof(int)*(STACK_INIT_SIZE+STACKCREATE));S->base.num = (int *)realloc(S->base.num,sizeof(int)*(STACK_INIT_SIZE+STACKCREATE));if (!(S->base.num || S->base.index))return ERROR; }*S->top.index++ = n;*S->top.num++ = m;S->stacksize = S->stacksize + STACKCREATE;return OK;}// 函数名: Pop// 形参类型: SqStack *, int *, int * // 函数功能出栈并用e返回int Pop(SqStack *S, int *a, int *b) {if (S->base.num == S->top.num) return ERROR;*a = * --S->top.num;*b = * --S->top.index;return OK;}// 函数名: GetTop// 形参类型: SqStack *, int * // 函数功能用e返回栈顶元素int GetTop(SqStack S, int *e) {if (S.top.num == S.base.num)return ERROR;*e = *(S.top.num - 1);return OK;}// 函数名: EmptyStack // 形参类型: SqStack// 函数功能判断是否为空栈int EmptyStack(SqStack S) {if (S.base.num == S.top.num)return OK;elsereturn ERROR;}// 函数名: Precede// 形参类型: char, char// 函数功能判断运算符的优先关系char Precede(char t1, char t2) { char f;switch(t2){case '+':case '-':if(t1=='(' || t1=='\n')f = '<'; //t1<t2elsef = '>'; // t1>t2break;case '*':case '/':if (t1=='*' || t1=='/' || t1==')') f = '>';elsef = '<';break;case '(':if (t1 == ')'){printf("括号不匹配\n");exit(-1);}elsef = '<';break;case ')':switch(t1){case '(': f = '=';break;case '\n': printf("缺乏左括号\n"); exit(-1); default:f = '>';}break;case '\n':switch(t1){case '\n':f = '='; break; case '(':printf("缺乏右括号\n");exit(-1);default:f = '>'; }}return f;}// 函数名: In// 形参类型: char // 函数功能判断是否为7种运算符之一int In(char c){switch(c){case '+' :case '-' :case '*' :case '/' :case '(' :case ')' :case '\n': return OK;default : return ERROR;}}// 函数名: ShowStack // 形参类型: SqStack // 函数功能输出表达式的逆波兰式void ShowStack(SqStack S) {int a, b;SqStack q;InitStack(&q);while (!EmptyStack(S)){Pop(&S,&a,&b);Push(&q,a,b);}printf("原表达式转换成逆波兰式为\n"); while (!EmptyStack(q)){Pop(&q,&a,&b);if (b == 0)printf("%c ", a);elseprintf("%d ", a);}printf("\n");}// 函数名: Opertae // 形参类型: int, char, int // 函数功能做四则运算 a theta bint Operator_(int a, char theta, int b){switch(theta){case '+':return a+b; case '-':return a-b;case '*':return a*b;}return a/b;}// 函数名: GetValue // 形参类型: SqStack// 函数功能求的表达式的值void GetValue(SqStack S) {int a, b;SqStack q,p;int value;int m, n;int c, d;char z;InitStack(&q);InitStack(&p);while (!EmptyStack(S)) {Pop(&S,&a,&b);Push(&q,a,b); }while (!EmptyStack(q)) {Pop(&q,&a,&b);if (b == 0){Pop(&p,&m,&c);Pop(&p,&n,&d);z = toascii(a);value = Operator_(n,z,m); Push(&p,value,1);}elsePush(&p,a,1);}Pop(&p,&a,&b);printf("表达式的值为:%d\n", a);return ;}// 函数名: EvaLuateExpression // 形参类型: void// 函数功能得到逆置的后缀表达式void EvaluateExpression(){SqStack OPRT, OPND; // 设OPTR 和 OPND 分别为运算符栈和运算数栈d, x; charint y;char c;char z[11];int i;InitStack(&OPRT);InitStack(&OPND);Push(&OPRT,'\n',0); //将换行符压入运算符栈的栈底c = getchar();GetTop(OPRT,&x);//将运算符栈OPTR的栈顶元素赋值给xwhile (c!='\n' || x!='\n'){if (In(c)) //c是7种运算符之一{switch(Precede(x,c)) //判断x和c的优先级 {case '<':Push(&OPRT,c,0);c = getchar();break; case '=':Pop(&OPRT,&x,&y);c=getchar();break;case '>':Pop(&OPRT,&x,&y);Push(&OPND,x,y);}}else if (c>='0' && c<='9'){i = 0;while (c>='0' && c<= '9') {z[i++] = c;c = getchar(); }z[i] = '\0';d = atoi(z); //将z中保存的数值型字符窜转化为整型存于d中 Push(&OPND,d,1);}else{printf("出现非法字符!\n");exit(-1);}GetTop(OPRT,&x);}ShowStack(OPND);GetValue(OPND);}int main(void){printf("请输入表达式,负数用(0-正数)表示:"); EvaluateExpression();return 0;}。
利用栈来实现算术表达式求值的算法

利用栈来实现算术表达式求值的算法利用栈来实现算术表达式求值的算法算术表达式是指按照一定规则组成的运算式,包含数字、运算符和括号。
在计算机中,求解算术表达式是一项基本的数学运算任务。
根据算术表达式的性质,我们可以考虑利用栈这一数据结构来实现求值算法。
一、算法思路首先,我们需要明确一个重要概念——逆波兰表达式(ReversePolish notation)。
逆波兰表达式是一种没有括号的算术表达式,其运算规则是先计算后面的数字和运算符,再计算前面的数字和运算符。
例如,对于算术表达式“3+4*5-6”,其对应的逆波兰表达式为“3 45 * +6 -”。
那么,我们可以利用栈来实现将中缀表达式转化为逆波兰表达式的过程,具体步骤如下:1. 创建两个栈——操作数栈和操作符栈。
2. 从左到右扫描中缀表达式的每一个数字和运算符,遇到数字则压入操作数栈中,遇到运算符则进行如下操作:(1)如果操作符栈为空或当前运算符的优先级大于栈顶运算符的优先级,则将当前运算符压入操作符栈中。
(2)如果当前运算符的优先级小于或等于栈顶运算符的优先级,则将栈顶运算符弹出并加入操作数栈中,重复此过程直到遇到优先级较低的运算符或操作符栈为空为止,然后将当前运算符压入操作符栈中。
3. 扫描完中缀表达式后,若操作符栈不为空,则将其中所有运算符弹出并加入操作数栈中。
4. 最终,操作数栈中存放的就是逆波兰表达式,我们可以按照逆波兰表达式的计算规则来计算其结果。
二、算法优点利用栈来实现算术表达式求值的算法具有以下优点:1. 代码简洁易懂,易于实现和维护。
2. 由于将中缀表达式转化为逆波兰表达式后,可以减少运算符的优先级关系而消除括号,从而减少求值的复杂度,提高程序的执行效率。
三、代码实现下面是利用栈来实现算术表达式求值的算法的Python代码实现:```pythonclass Stack:def __init__(self):self.items = []def push(self, item):self.items.append(item)def pop(self):return self.items.pop()def peek(self):return self.items[-1]def is_empty(self):return len(self.items) == 0def size(self):return len(self.items)def calculate(op_num1, op_num2, operator):if operator == "+":return op_num1 + op_num2elif operator == "-":return op_num1 - op_num2elif operator == "*":return op_num1 * op_num2elif operator == "/":return op_num1 / op_num2def infix_to_postfix(infix_expr):opstack = Stack()postfix_expr = []prec = {"+": 1, "-": 1, "*": 2, "/": 2, "(": 0} token_list = infix_expr.split()for token in token_list:if token.isdigit():postfix_expr.append(token)elif token == '(':opstack.push(token)elif token == ')':top_token = opstack.pop()while top_token != '(':postfix_expr.append(top_token)top_token = opstack.pop()else:while (not opstack.is_empty()) and(prec[opstack.peek()] >= prec[token]):postfix_expr.append(opstack.pop())opstack.push(token)while not opstack.is_empty():postfix_expr.append(opstack.pop())return " ".join(postfix_expr)def postfix_eval(postfix_expr):opstack = Stack()token_list = postfix_expr.split()for token in token_list:if token.isdigit():opstack.push(int(token))else:op_num2 = opstack.pop()op_num1 = opstack.pop()result = calculate(op_num1, op_num2, token) opstack.push(result)return opstack.pop()infix_expr = "3 + 4 * 5 - 6"postfix_expr = infix_to_postfix(infix_expr)print(postfix_expr)print(postfix_eval(postfix_expr))```四、总结算术表达式求值是一项常见的数学运算任务,利用栈这一数据结构来实现求值算法是一种简单有效的方法,它将中缀表达式转化为逆波兰表达式后,可以消除括号并减少运算符的优先级关系,从而提高程序的执行效率。
C语言之逆波兰表达式完整代码(附算法)

C语言课程设计之逆波兰表达式//逆波兰表达式(后缀表达式)reverse polish notation//程序实现的功能是将中缀表达式转变为后缀表达式,再求出其值//主要运用的知识点有:isdigit函数,pow函数,system("cls")函数,堆栈,格式的强制转换#include<stdio.h>#include<ctype.h>#include<stdlib.h>#include<math.h>void shift( char notation[]); //中缀表达式转换为后缀表达式的转换函数float calculate(float a[][2],int k); //计算后缀表达式int judge(char notation[]); //判断输入的中缀表达式是否符合要求int grade(char a); //返回运算符的等级void display(float a[][2],int k); //在屏幕上显示后缀表达式//主函数void main(){char notation [100];char choice;do{printf("请输入正确的中缀表达式:\n");printf("例如:2*3+4/3-(2+1)\n");scanf("%s",¬ation);if(judge(notation)){shift(notation);}elseprintf("你的表达式有错误,请仔细检查!\n");fflush(stdin);printf("\n你是否需要继续计算(是输入Y/y,否输入其他任意键)\n");scanf("%c",&choice);getchar();system("cls");}while(choice=='Y'||choice=='y');printf("\n程序结束,谢谢使用!\n");}//判定函数int judge(char notation[]){int i,m,num=1,p1=0,p2=0;for(i=0;notation[i]!='\0';i++) //排除表达式外的字符{if(notation[i]!='('&¬ation[i]!=')'&¬ation[i]!='+'&¬ation[i]!='-'&¬ation[i]!='*'&¬ation[i]!='/'&&!isdigit(notation[i])&¬ation[i]!='.') {num=0;return num;}}if(notation[0]=='*'||notation[0]=='/'||notation[0]==')'||notation[0]=='.') //排除第一个字符为*,/,),.{num=0;return num;}for(i=0;notation[i]!='\0';i++) //排除'+','-','*','/','.'之间的连续出现以及'+','-','*','/','.'后面直接加')'{if(notation[i]!='('&¬ation[i]!=')'&&!isdigit(notation[i])){if(notation[i+1]!='('&&!isdigit(notation[i+1])){num=0;return num;}}if(notation[i]=='('&&(notation[i+1]==')'||notation[i+1]=='.'||notation[i+1]=='*'||notation[i+ 1]=='/')){ //排除'('和')','.','*','/'一起连用num=0;return num;}if(notation[i]==')'&&(notation[i+1]=='('||notation[i+1]=='.'))//排除')'和'(','.'一起连用{num=0;return num;}}for(i=0;notation[i]!='\0';i++) //小数位不得超过4位{if(notation[i]=='.'&¬ation[i+1]!='\0'&¬ation[i+2]!='\0'&¬ation[i+3]!='\0'&¬ation[i+4]!='\0'&¬ation[i+5]!='\0'){if(isdigit(notation[i+1])&&isdigit(notation[i+2])&&isdigit(notation[i+3])&&isdigit(notation[i+ 4])&&isdigit(notation[i+5])){num=0;return num;}}}for(i=0;notation[i]!='\0';i++) //排除一个小数中有两个小数点的情况{if(notation[i]=='.'){i++;while(isdigit(notation[i])){i++;}if(notation[i]=='.'){num=0;return 0;}}}for(i=0;notation[i]!='\0';i++) //排除')'后面不可以直接跟数字以及'('前面不可以加数字{if(notation[i]==')'&&isdigit(notation[i+1])){num=0;return num;}if(isdigit(notation[i])&¬ation[i+1]=='(' ){num=0;return num;}}for(i=0;notation[i]!='\0';i++) //约束数字的位数一共最多为七位{if(isdigit(notation[i])){m=0; //用来计数,数字的位数为7while(isdigit(notation[i])||notation[i]=='.'){i++;m++;if(notation[i]=='.'){m--;}}if(m>7){num=0;return num;}}}for(i=0;notation[i]!='\0';i++) //'('与')'需要配对存在{if(notation[i]=='(')p1++;if(notation[i]==')')p2++;if(p1!=p2){num=0;return num;}}return num;}//转换函数void shift( char notation[]){char s1[100];s1[0]='#';float s2[100][2]; //第一维放后缀表达式的元素,第二维表示小数点的位数以及是否是运算符int i=0,j=1,k=0,t=0;float sum,num1=0,num2=0; //num1为存储整数位num2为存储小数位while(notation[i]!='\0'){if(i==0&¬ation[i]=='+') //第一位为正号的情况{if(isdigit(notation[++i])){num1=0; //整数部分while(isdigit(notation[i])){num1=num1*10+(notation[i]-'0'); //notation[i]-'0'可以将字符转换为整数0~9i++;}num2=0; //小数部分t=0;if(notation[i]=='.'){i++;while(isdigit(notation[i])){num2=float (num2+pow(0.1,++t)*(notation[i]-'0'));i++;}}s2[k++][0]=float(num1+num2);s2[k-1][1]=float(t);}}if(i==0&¬ation[i]=='-') //第一位为负号的情况,代码与正号类似{if(isdigit(notation[++i])){num1=0;while(isdigit(notation[i])){num1=(-1)*num1*10+(-1)*(notation[i]-'0');i++;}num2=0;t=0;if(notation[i]=='.'){i++;while(isdigit(notation[i])){num2=float(num2+(-1)*pow(0.1,++t)*(notation[i]-'0'));i++;}}s2[k++][0]=float(num1+num2);s2[k-1][1]=float(t);}}if(isdigit(notation[i])) //当前字符为数字的情况与为正号的情况一样{num1=0;while(isdigit(notation[i])){num1=num1*10+(notation[i]-'0');i++;}num2=0;t=0;if(notation[i]=='.'){i++;while(isdigit(notation[i])){num2=float(num2+pow(0.1,++t)*(notation[i]-'0'));i++;}}s2[k++][0]=float(num1+num2);s2[k-1][1]=float(t);}if(notation[i]=='+'||notation[i]=='-'||notation[i]=='*'||notation[i]=='/'){ //当前的字符为操作符时,如果s1的站定为'('则将字符直接送入s1if(s1[j-1]=='('){s1[j++]=notation[i++];}}if(notation[i]=='+'||notation[i]=='-'||notation[i]=='*'||notation[i]=='/'){ //当前字符为操作符时的普通的情况if(grade(notation[i])>grade(s1[j-1])){s1[j++]=notation[i++];}else{s2[k++][0]=s1[--j];s2[k-1][1]=-1;s1[j++]=notation[i++];}}if(notation[i]=='(') //当前字符为'('的情况{s1[j++]=notation[i++];if(notation[i]=='+') //'('后跟正号的情况{if(isdigit(notation[++i])){num1=0;while(isdigit(notation[i])){num1=num1*10+(notation[i]-'0');i++;}num2=0;t=0;if(notation[i]=='.'){i++;while(isdigit(notation[i])){num2=float(num2+pow(0.1,++t)*(notation[i]-'0'));i++;}}s2[k++][0]=float(num1+num2);s2[k-1][1]=float(t);}}if(notation[i]=='-') //'('后跟负号的情况{if(isdigit(notation[++i])){num1=0;while(isdigit(notation[i])){num1=float((-1)*num1*10+(-1)*(notation[i]-'0'));i++;}num2=0;t=0;if(notation[i]=='.'){i++;while(isdigit(notation[i])){num2=float(num2+(-1)*pow(0.1,++t)*(notation[i]-'0'));i++;}}s2[k++][0]=float(num1+num2);s2[k-1][1]=float(t);}}}if(notation[i]==')') //当前字符为')'的情况{while(s1[--j]!='('){s2[k++][0]=s1[j];s2[k-1][1]=-1;}i++;}}while(j>0&&s1[--j]!='#') //依次将s1中的除了'#'外的所有操作符出栈,相当于最后的扫尾工作{s2[k++][0]=s1[j];s2[k-1][1]=-1;}printf("\n后缀表达式(逆波兰表达式):\n");display(s2,k-1);printf("\n表达式的值为:\n");sum=calculate(s2,k-1);printf("%7.4f",sum);}//计算函数float calculate(float a[][2],int k){int i,t=0,j=k;float b[100][2],c[100];for(i=k;i>=0;i--){b[i][0]=a[k-i][0];b[i][1]=a[k-i][1];}i=k;while(j>=0){if(b[i][1]!=-1){c[t]=float (b[i][0]);j--;i--;t++;}if(b[i][1]==-1) //每当遇到一个运算符则将栈最上面的两个数出栈进行运算,然后再入栈{if(int(b[i][0])=='+'){c[t-2]=float (c[t-2]+c[t-1]);}if(int(b[i][0])=='-'){c[t-2]=float (c[t-2]-c[t-1]);}if(int(b[i][0])=='*'){c[t-2]=float (c[t-2]*c[t-1]);}if(int(b[i][0])=='/'){c[t-2]= float (c[t-2]/c[t-1]);}j--;i--;t--;}}return c[0]; //运算到最后,栈中的元素即为结果}//等级函数int grade(char a) //按照运算符的优先级{if(a=='#')return 0;if(a=='(')return 1;if(a=='-'||a=='+')return 2;if(a=='*'||a=='/')return 3;if(a==')')return 4;elsereturn 5;}//显示函数void display(float a[][2],int k){int i;for(i=0;i<=k;i++){if(a[i][1]==0)printf(" %d",int(a[i][0]));if(a[i][1]==1)printf(" %7.1f",a[i][0]);if(a[i][1]==2)printf(" %7.2f",a[i][0]);if(a[i][1]==3)printf(" %7.3f",a[i][0]);if(a[i][1]==4)printf(" %7.4f",a[i][0]);if(a[i][1]==-1)printf(" %c",int (a[i][0]));}}算法实现一个表达式E的后缀形式可以如下定义:(1)如果E是一个变量或常量,则E的后缀式是E本身。
栈实现以及逆波兰表达式

栈实现以及逆波兰表达式栈和队列也是数据结构中经常⽤到的⼀种容器.栈是先进后出FILO,队列是先进先出FIFO.在C语⾔中,栈可以⽤数组或者链表来实现,在python中,list也就是列表也可以当做栈使⽤.⽐如在尾部压⼊元素可以⽤append的⽅法,压出元素可以⽤pop的⽅法.访问栈定元素可以⽤list[-1]的⽅法.但是list也同时提供了⼀⼤批栈不应该⽀持的操作,⽐如栈中未弹出的元素是存在的,但是list可以删除任意元素.因此为了实现完全的栈功能,我们可以⽤⼀个类来实现栈并将list隐藏在这个对象的内部.代码如下在内部定义了⼀个私有变量_elem.使得⽆法从外部实例进⾏访问,也就⽆从修改class stack():def __init__(self):self._elem=[]def is_empty(self):return self._elem == []def top(self):if self._elem == []:raise BaseException('top:stack empty')#当列表为空的时候,抛出异常return self._elem[-1]def push(self,elem):self._elem.append(elem)def pop(self):if self._elem == []:raise BaseException('pop:stack empyt')return self._elem.pop()if __name__=="__main__":s=stack()s.push(5)s.push(4)s.push(10)print s.pop()前⾯这个例⼦是通过内置的list来实现了栈队列,我们还可以采⽤列表的形式来实现栈代码如下:这⾥⾸先引⽤了第三章中的Lnode对象class Lnode(object):def __init__(self,elem,next_=None):self.elem=elemself.next=next_class Stack_node():def __init__(self):self._top=Nonedef is_emepy(self):return self._top == Nonedef top(self):if self._top== None:raise BaseException("top:stack is empty")return self._top.elemdef push(self,elem):self._top=Lnode(elem,self._top) #通过传⼊上⼀个Lnode对象进⾏链表链接def pop(self):if self._top == None:raise BaseException('pop:stack is empty')p=self._topself._top=p.nextreturn p.elemif __name__=="__main__":s=Stack_node()s.push(4)s.push(10)print s.pop()前⾯2个列⼦介绍了栈的两种实现⽅式,下⾯来看下栈的具体应⽤.⾸先来看第⼀个例⼦.括号匹配.在数字运算中有(),[],{}三种符号来进⾏各种封闭的运算.对于⼀个正常的计算公式⽽⾔,当前⽐括号应该与前⾯最近的尚未匹配的开括号匹配,下⼀个闭括号应与前⾯次进的括号匹配.因此在这⾥我们就可以应⽤到栈来实现括号的匹配.来看下具体的实现def check_parents(text):#⾸先定义parents代表所有的括号形式,然后定义open_parents表⽰所有的开括号然后定义oppsites⼀个字典,代表开括号和闭括号的对应关系.parents='()[]{}'open_parents='([{'oppsites={")":"(","]":"[","}":"{"}def parent_generate(text):i,text_len=0,len(text)while True:while i< text_len and text[i] not in parents: #当不属于括号的,则继续往后i+=1if i >= text_len:returnyield text[i],i #属于括号形式的则通过yield返回i+=1s=stack()for pt,i in parent_generate(text): #调⽤parent_generate⽣成器if pt in open_parents: #如果是开括号则进栈s.push(pt)elif s.pop()!=oppsites[pt]: #否则是闭括号,则与最近的⼀次进栈的括号进⾏⽐较,看是否匹配,如果不匹配则提⽰umatchprint 'unmatch was found at %d' % ireturn Falseelse: #如果匹配则不做任何操作passprint 'all are matched'return Trueif __name__=="__main__":check_parents('{[(a+b)+c]/3+1}+2')运⾏结果:/usr/bin/python2.7 /home/zhf/py_prj/data_struct/chapter5.pyall are matched如果修改下传⼊的text为check_parents('{[(a+b)+c/3+1}+2'),少了⼀个].则会提⽰umatch,并指⽰不匹配的位置./usr/bin/python2.7 /home/zhf/py_prj/data_struct/chapter5.pyunmatch was found at 13后缀表达式算是表达式有三种表达⽅式 中缀表达式,前缀表达式,后缀表达式.来看下三种表达式的区别中缀表达式: (3-5)*2+4前缀表达式:+*-3524后缀表达式:35-2*4+可以看到中缀表达式就和我们平常书写的运算公式是⼀样的,中缀表达式就是将运算符号写在运算符的前⾯,⽽后缀表达式就是将运算符号写在运算符的后⾯其实表达式之间的转换很简单,可以参考如下的⽅法:给出⼀个中缀表达式:a+b*c-(d+e)第⼀步:按照运算符的优先级对所有的运算单位加括号:式⼦变成拉:((a+(b*c))-(d+e))第⼆步:转换前缀与后缀表达式前缀:把运算符号移动到对应的括号前⾯则变成拉:-( +(a *(bc)) +(de))把括号去掉:-+a*bc+de 前缀式⼦出现后缀:把运算符号移动到对应的括号后⾯则变成拉:((a(bc)* )+ (de)+ )-把括号去掉:abc*+de+- 后缀式⼦出现那么这⼏种表达式有什么意义呢,中缀表达式对于我们正常⼿写运算来说很形象,但是对于计算机来说就很抽象了,⽽前缀表达式和后缀表达式来说则很形象.⽐如3+(2-5)*6/3这个表达式,对应的后缀表达式为3 2 5 - 6 3 / * +那么在计算借助到栈的⽅法进⾏运算1 如果是数字则直接进栈此时在栈的数据为5232 遇到运算符则将栈顶的2个数字出栈进⾏计算,此时遇到-则5,2出栈,进⾏运算2-5=-3并将-3重新⼊栈.并继续遍历表达式,此时栈的数据为36-333 遇到/则继续出栈2个数字进⾏运算6/3=2并将2⼊栈,此时栈的数据为2-334 遇到*则继续出栈2个数字进⾏运算2*-3=-6并⼊栈,此时栈数据为-635 遇到+则出栈2个数字进⾏运算-6+3=-3并⼊栈,此时栈数据为-3这样就得到了最终的数据.从上⾯的表⽰可以看出后缀表达式对于计算机的运算来说很⽅便,下⾯就来看下后缀表达式的实现:以:3+2*5-6/3为例.有个数据结构⼀个是后缀表达式队列⼀个是运算符栈队列a 遇到数字则加⼊后缀表达式列表b遇到运算符或者是(则进运算符栈c当遇到准备进栈的运算符优先级⼩于或等于栈顶的运算符,则将栈顶运算符出栈加⼊到后缀表达式列表中d如果准备进栈的运算符优先级⼤于栈顶的运算符则继续进栈第⼀步:数字3进⼊后缀表达式,同时+进⼊运算符栈后缀表达式队列 运算符栈3 +第⼆步:数字2进⼊后缀表达式,同时*进⼊运算符栈后缀表达式队列 运算符栈32 *+第三步:数字5进⼊后缀表达式,同时-准备进⼊运算符栈,由于-的优先级⼩于当前栈顶的*,因此*出栈并加⼊到后缀表达式队列中,并且-和+的优先级相同,因此+继续出栈并加⼊到后缀表达式队列中.最后-进栈后缀表达式队列 运算符栈325*+ -第四步:数字6进⼊后缀表达式,/进⼊运算符栈后缀表达式队列 运算符栈325*+6 /-第五步:数字3进⼊后缀表达式.此时将运算符依次出栈链接到后缀表达式队列之后.后缀表达式队列 运算符栈325*+63 /-最终⽣成的后缀表达式为325*+63/-下⾯来看下具体的代码实现,⾸先是后缀表达式⽣成的代码:def trans_infix_suffix(line):s=stack() #运算符栈exp=[] #后缀表达式队列priority={"(":1,"+":3,"-":3,"*":5,"/":5} #⽣成运算符优先级⼤⼩的字典infix_operator="+-/*()"for x in line:if x not in infix_operator: #如果不是运算符号,则进后缀表达式队列exp.append(x)elif s.is_empty() or x == '(': #如果是(则直接进栈s.push(x)elif x == ')': #如果是),则运算符出栈并加⼊到后缀表达式中,直到遇见'('while not s.is_empty() and s.top() != '(':exp.append(s.top)if s.is_empty():raise BaseException('stack is empty')s.pop() # '(' 出栈else: #⽐较栈顶的元素和当前运算符的优先级,如果⼤于则出栈加⼊到后缀表达式队列中.知道栈顶元算符优先级⼩于当前运算符的优先级while not s.is_empty() and priority[s.top()] >= priority[x]:exp.append(s.pop())s.push(x) #当前运算符⼊栈while not s.is_empty(): #栈运算符的运算符全部出栈加⼊到后缀表达式队列中.if s.top() == '(':raise BaseException('extra ( found')exp.append(s.pop())return exp得到了后缀表达式,那么下⼀步就是要针对后缀表达式进⾏运算了,代码如下:def exp_calculate(exp):operators='+-/*'s=stack()for x in exp:if x not in operators: #如果是⾮运算符,则直接进栈s.push(int(x))continueif s.depth() < 2:raise BaseException('lack of stack element')a=s.pop() #否则遇到运算符,则出栈2个数字进⾏运算b=s.pop()if x == '+':c=b+aelif x == '-':c=b-aelif x == '*':c=b*aelif x == '/':c=b/aelse:breaks.push(c) #将元算得到的数字进栈if s.depth() == 1: # 运算完返回最终的结果return s.pop()对于3+2*5-6/3这个表达式,得到运算结果为11.运算正确/usr/bin/python2.7 /home/zhf/py_prj/data_struct/chapter5.py ['3', '2', '5', '*', '+', '6', '3', '/', '-']11。
(编译原理)逆波兰式算法的源代码

一.实验目的1.深入理解算符优先分析法2.掌握FirstVt和LastVt集合的求法有算符优先关系表的求法3.掌握利用算符优先分析法完成中缀表达式到逆波兰式的转化二.实验内容及要求将非后缀式用来表示的算术表达式转换为用逆波兰式来表示的算术表达式,并计算用逆波兰式来表示的算术表达式的值。
程序输入/输出示例:输出的格式如下:(1)逆波兰式的生成及计算程序,编制人(2)输入一以#结束的中缀表达式(包括+—*/()数字#)(3)(4)逆波兰式备注:(1)在生成的逆波兰式中如果两个数相连则用&分隔,如28和68,中间用&分隔;(注意:1。
表达式中允许使用运算符(+-*/)、分割符(括号)、数字,结束符#;2。
如果遇到错误的表达式,应输出错误提示信息(该信息越详细越好);3.对学有余力的同学,测试用的表达式事先放在文本文件中,一行存放一个表达式,同时以分号分割。
同时将预期的输出结果写在另一个文本文件中,以便和输出进行对照;三.实验过程1、逆波兰式定义将运算对象写在前面,而把运算符号写在后面。
用这种表示法表示的表达式也称做后缀式。
逆波兰式的特点在于运算对象顺序不变,运算符号位置反映运算顺序。
采用逆波兰式可以很好的表示简单算术表达式,其优点在于易于计算机处理表达式。
2、产生逆波兰式的前提中缀算术表达式3、逆波兰式生成的实验设计思想及算法(1)首先构造一个运算符栈,此运算符在栈内遵循越往栈顶优先级越高的原则。
(2)读入一个用中缀表示的简单算术表达式,为方便起见,设该简单算术表达式的右端多加上了优先级最低的特殊符号“#”.(3)从左至右扫描该算术表达式,从第一个字符开始判断,如果该字符是数字,则分析到该数字串的结束并将该数字串直接输出。
(4)如果不是数字,该字符则是运算符,此时需比较优先关系。
做法如下:将该字符与运算符栈顶的运算符的优先关系相比较.如果,该字符优先关系高于此运算符栈顶的运算符,则将该运算符入栈.倘若不是的话,则将此运算符栈顶的运算符从栈中弹出,将该字符入栈。
c语言实现逆波兰表达式!

}else if(a[i] == ' '){ i++;
}else if(a[i] == '+'){ x1 = operNum[--top]; x2 = operNum[--top]; operNum[top++] = x1 + x2; i++;
博客园 用户登录 代码改变世界 密码登录 短信登录 忘记登录用户名 忘记密码 记住我 登录 第三方登录/注册 没有账户, 立即注册
c语 言 实 现 逆 波 兰 表 达 式 !
C语言实现逆波兰表达式 (栈的应用 )
#include<iostream> #include<cstdio> using namespace std; const int MAXSIZE = 110; char a[MAXSIZE]; double operNum[MAXSIZE]; double getSum(int* i){//地址传递,可以在边求值时边改变i的原值。如若是值传递,会导致值的重复算
}else if(a[i] == '-'){ x1 = operNum[--top]; x2 = operNum[--top]; operNum[top++] = x2 - x1; i++;
}else if(a[i] == '*'){ x1 = operNum[--top]; x2 = operNum[--top]; operNum[top++] = x1 * x2; i++;
使用栈实现逆波兰表达式

flag=0; //结束循环,搜索完成
}
else if(c=='('||pri(c)>=pri.insert(c);
k++;
}
else if(c==')'&&ops.read()=='(')
int flag=1;
char c=s[*k];
while(c>='0'&&c<='9'||c=='.')
{
*k=*k+1;
if(c>='0'&&c<='9')
if(flag==0)//小数点后面
{
x=x*0.1;
y=y+(c-'0')*x;
#pragma once
#include"iostream"
using namespace std;
template<class T>
class stack
{
private:
int size;
int top;
T *next;
public:
stack()
{
size=0;
case'/':z=x/y;break;
case'+':z=x+y;break;
case'-':z=x-y;break;
}
opd.insert(z);
}
(编译原理)逆波兰式算法的源代码

(编译原理)逆波兰式算法的源代码一.实验目的1.深入理解算符优先分析法2.掌握FirstVt和LastVt集合的求法有算符优先关系表的求法3.掌握利用算符优先分析法完成中缀表达式到逆波兰式的转化二.实验内容及要求将非后缀式用来表示的算术表达式转换为用逆波兰式来表示的算术表达式,并计算用逆波兰式来表示的算术表达式的值。
程序输入/输出示例:输出的格式如下:(1)(2)输入一以#结束的中缀表达式(包括+—*/()数字#)(3)(4)逆波兰式备注:(1)在生成的逆波兰式中如果两个数相连则用&分隔,如28和68,中间用&分隔;串。
注意:1.表达式中允许使用运算符(+-*/)、分割符(括号)、数字,结束符#;2.如果遇到错误的表达式,应输出错误提示信息(该信息越详细越好);3.对学有余力的同学,测试用的表达式事先放在文本文件中,一行存放一个表达式,同时以分号分割。
同时将预期的输出结果写在另一个文本文件中,以便和输出进行对照;三.实验过程1、逆波兰式定义将运算对象写在前面,而把运算符号写在后面。
用这种表示法表示的表达式也称做后缀式。
逆波兰式的特点在于运算对象顺序不变,运算符号位置反映运算顺序。
采用逆波兰式可以很好的表示简单算术表达式,其优点在于易于计算机处理表达式。
2、产生逆波兰式的前提中缀算术表达式3、逆波兰式生成的实验设计思想及算法(1)首先构造一个运算符栈,此运算符在栈内遵循越往栈顶优先级越高的原则。
(2)读入一个用中缀表示的简单算术表达式,为方便起见,设该简单算术表达式的右端多加上了优先级最低的特殊符号“#”。
(3)从左至右扫描该算术表达式,从第一个字符开始判断,如果该字符是数字,则分析到该数字串的结束并将该数字串直接输出。
(4)如果不是数字,该字符则是运算符,此时需比较优先关系。
做法如下:将该字符与运算符栈顶的运算符的优先关系相比较。
如果,该字符优先关系高于此运算符栈顶的运算符,则将该运算符入栈。
中缀表达式转逆波兰式并求值

InitStack(&OPRT);
InitStack(&OPND);
Push(&OPRT,'\n',0); //将换行符压入运算符栈的栈底
c = getchar();
GetTop(OPRT,&x);//将运算符栈OPTR的栈顶元素赋值给x
while (c!='\n' || x!='\n')
// 函数功能 用e返回栈顶元素
int GetTop(SqStack S, int *e)
{
if (S.top.num == S.base.num)
return ERROR;
*e = *(S.top.num - 1);
return OK;
} Βιβλιοθήκη // 函数名: EmptyStack
// 标题: 栈的应用——中缀表达式转逆波兰式
// 时间: 2015年4月14日
// 所有者: Vae
#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#include<windows.h>
#include<Winuser.h>
Push(&OPND,d,1);
}
else
{
printf("出现非法字符!\n");
exit(-1);
}
GetTop(OPRT,&x);
}
ShowStack(OPND);
GetValue(OPND);
简单的四则运算(栈+逆波兰)

逆波兰利用栈实现简单的四则运算一.逆波兰表达式引自/blog/472070逆波兰表达式解决四则运算逆波兰表达式又叫做后缀表达式,它将复杂表达式转换为可以依靠简单的操作得到计算结果的表达式,解决了四则运算中括号改变运算符优先级的问题。
四则运算的表达式一般都是中缀表达式如1+2*(3-4)+5,即操作符在两个操作数之间。
四则运算需要两个步骤,一是把中缀表达式转为后缀表达式,二是由后缀表达生成结果中缀表达式转为后缀表达式算法描述:(1)首先有个包含中缀表达式元素列表sourceList,然后创建一个符号列表destList保存最终后缀表达式,创建一个操作符堆栈opStack(2)从sourceList取出一个元素A(3a)如是数字则加入到destList中(3b)如果元素A是运算符,将操作符A与操作符堆栈opStack栈顶的运算符的优先关系相比较。
如果,优先关系高于opStack栈顶的运算符,则将该运算符压入操作符堆栈opStack。
倘若不是(低于或等于)的话,则将运算符栈opStack栈顶的运算符从栈中弹出保存到destList,重复此步骤,直到作符A压入操作符堆栈opStack。
(3c)若元素A是左括号"(",则压入操作符堆栈opStack(3d)若元素B是右括号")",则操作符堆栈opStack弹出操作符并加入到destList中,直到弹出左括号"("。
(5)从步骤2重复上述操作,所有元素处理完毕后将操作符堆栈opStack弹出操作符并加入到destList中,这样中缀式表示的简单算术表达式转化为逆波兰表示的简单算术表达式。
示例:中缀表达式如1+2*(3-4)+5,构造元素列表1,+,2,*,(,3,-,4,),5,构造一个空最终后缀表达式destList,一个操作符堆栈opStack1、取出“1”,destList【1】,opStack【】2、取出“+”,destList【1】,opStack【+】3、取出“2”,destList【1,2】,opStack【+】4、取出“*”,destList【1,2】,opStack【+,*】5、取出“(”,destList【1,2】,opStack【+,*,(】6、取出“3”,destList【1,2,3】,opStack【+,*,(】7、取出“-”,destList【1,2,3】,opStack【+,*,(,-】8、取出“4”,destList【1,2,3,4】,opStack【+,*,(,-】9、取出“)”,destList【1,2,3,4,-】,opStack【+,*】//操作符堆栈opStack弹出操作符并加入到destList中,直到弹出左括号"("10、取出“+”,destList【1,2,3,4,-,*,+】,opStack【+】//加号优先级不大于【+,*】11、取出“5”,destList【1,2,3,4,-,*,+,5】,opStack【+】12、处理完毕,destList【1,2,3,4,-,*,+,5,+】,opStack【】后缀表达式到计算结果算法描述:遍历储存后缀表达式的列表,将元素依次进栈,当遇到操作符时,连续出栈两个元素,进行运算,再将结果进栈,最后栈内留下的元素就是计算结果示例:后缀表达式destList【1,2,3,4,-,*,+,5,+】,结果堆栈resultStatck【】格式输入-->:结果[1,2,3,4]-->:resultStatck【1,2,3,4】[-]-->:resultStatck【1,2,3-4】[ * ]-->:resultStatck【1,2*(3-4)】[+]-->:resultStatck【1+2*(3-4)】[5]-->:resultStatck【1+2*(3-4),5】[+]-->:resultStatck【1+2*(3-4)+5】举例:正常的表达式逆波兰表达式a+b ---> a,b,+a+(b-c) ---> a,b,c,-,+a+(b-c)*d ---> a,b,c,-,d,*,+a+d*(b-c) ---> a,d,b,c,-,*,+a=1+3 ---> a=1,3 +二.自己写的简单四则运算的程序。
设计并实现将一个中缀表达式转换成逆波兰式,然后对此逆波兰表达式求值的算法。

/* Note:Your choice is C IDE */#include "stdio.h"#include "stdlib.h"#include "string.h"#define STACK_INIT_SIZE 100 //初始大小#define STACK_INCR_SIZE 10 //增加大小#define OVERFLOW -2typedef char SELemType;typedef struct{SELemType base[STACK_INIT_SIZE];int top;}SqStack;void InitStack(SqStack *s) //初始化{s->top=-1;}void Push(SqStack *s,SELemType e) //进栈{if(s->top==STACK_INIT_SIZE-1)exit(OVERFLOW);elses->base[++s->top]=e;}void Pop(SqStack *S, SELemType *e) //删除栈顶元素{if (S->top==-1)exit(OVERFLOW);else*e=S->base[S->top--];}char GetTop(SqStack S) //取栈顶元素{SELemType e;if (S.top == -1)exit(OVERFLOW);elsee=S.base[S.top];return e;}SELemType Operate(SELemType a[],SELemType O,SELemType b[]){char str[10];int m=0,n=0,result,i=0,j=0,O,R;while(a[i]!='\0'){m=m*10+(a[i]-'0');i++; }while(b[j]!='\0'){n=n*10+(b[j]-'0');j++; }O='+';switch(O){case '+':result=m+n;break; case '-':result=m-n;break; case '*':result=m*n;break; case '/':result=m/n;break; }R=result;i=0;do{result=result/10;i++;}while(result>0);for(j=i-1;j>=0;j--){result=R%10;R=R/10;str[j]=(result+'0');}str[i]='\0';return str;}SELemType Precede(SELemType a,SELemType b) {int m,n;SELemType operat[7][7]={'>','>','<','<','<','>','>','>','>','<','<','<','>','>','>','>','>','>','<','>','>','>','>','>','>','<','>','>','<','<','<','<','<','=',' ','>','>','>','>',' ','>','>','<','<','<','<','<',' ','=',}; switch(a){case '+':m=0;break;case '-':m=1;break;case '*':m=2;break;case '/':m=3;break;case '(':m=4;break;case ')':m=5;break;case '#':m=6;break;}switch(b){case '+':n=0;break;case '-':n=1;break;case '*':n=2;break;case '/':n=3;break;case '(':n=4;break;case ')':n=5;break;case '#':n=6;break;}return operat[m][n];}char EvaluateExpression() {SqStack OPND,OPTR;char c,x,theta; char a,b;int i=0,j;InitStack(&OPTR); Push(&OPTR,'#');InitStack(&OPND); c=getchar();while(c!='#'||GetTop(OPTR)!='#') {if(c!='+'&&c!='-'&&c!='*'&&c!='/'&&c!='('&&c!=')'&&c!=' #'){ Push(&OPND,c);str[i]=c;i++;c=getchar();}elseswitch (Precede(GetTop(OPTR),c)){ case '<': Push(&OPTR,c);c=getchar();break;case '=': Pop(&OPTR,&x);c=getchar();break;case '>': Pop(&OPTR,&theta);str[i]=theta;i++;Pop(&OPND,&b);Pop(&OPND,&a);Push(&OPND,Operate(a,theta,b));break;}}c=GetTop(OPND);/* DestroyStack(OPTR);DestroyStack(OPND);*/return c;}void main(){printf("%c",EvaluateExpression()); }。
(编译原理)逆波兰式算法地源代码

一.实验目的1.深入理解算符优先分析法2.掌握FirstVt和LastVt集合的求法有算符优先关系表的求法3.掌握利用算符优先分析法完成中缀表达式到逆波兰式的转化二.实验内容及要求将非后缀式用来表示的算术表达式转换为用逆波兰式来表示的算术表达式,并计算用逆波兰式来表示的算术表达式的值。
程序输入/输出示例:输出的格式如下:(1)(2)输入一以#结束的中缀表达式(包括+—*/()数字#)(3)(4)逆波兰式备注:(1)在生成的逆波兰式中如果两个数相连则用&分隔,如28和68,中间用&分隔;注意:1.表达式中允许使用运算符(+-*/)、分割符(括号)、数字,结束符#;2.如果遇到错误的表达式,应输出错误提示信息(该信息越详细越好);3.对学有余力的同学,测试用的表达式事先放在文本文件中,一行存放一个表达式,同时以分号分割。
同时将预期的输出结果写在另一个文本文件中,以便和输出进行对照;三.实验过程1、逆波兰式定义将运算对象写在前面,而把运算符号写在后面。
用这种表示法表示的表达式也称做后缀式。
逆波兰式的特点在于运算对象顺序不变,运算符号位置反映运算顺序。
采用逆波兰式可以很好的表示简单算术表达式,其优点在于易于计算机处理表达式。
2、产生逆波兰式的前提中缀算术表达式3、逆波兰式生成的实验设计思想及算法(1)首先构造一个运算符栈,此运算符在栈内遵循越往栈顶优先级越高的原则。
(2)读入一个用中缀表示的简单算术表达式,为方便起见,设该简单算术表达式的右端多加上了优先级最低的特殊符号“#”。
(3)从左至右扫描该算术表达式,从第一个字符开始判断,如果该字符是数字,则分析到该数字串的结束并将该数字串直接输出。
(4)如果不是数字,该字符则是运算符,此时需比较优先关系。
做法如下:将该字符与运算符栈顶的运算符的优先关系相比较。
如果,该字符优先关系高于此运算符栈顶的运算符,则将该运算符入栈。
倘若不是的话,则将此运算符栈顶的运算符从栈中弹出,将该字符入栈。
栈的应用(逆波兰表达式)

栈的应⽤(逆波兰表达式)栈的应⽤(逆波兰表达式的计算)因为中缀表达式对于操作符的优先级很不好计算,就将中缀转成计算机更容易识别的后缀表达式中缀转后缀表达式写法:a+b => a b +a+(b-c) => a b c - +a+(b-c)*d => a b c - d * +a+d*(b-c) => a d b c - * +a=1+3 => a 1 3 + =后缀表达式(逆波兰表达式)计算规则:从左向右扫描,遇到操作符就将左边的两个数取出进⾏运算然后将结果插⼊到原来取出两个数的位置,再向右扫描代码实现:遇到数字就⼊数栈,遇到操作符就取出栈顶和次栈顶的数进⾏运算然后将结果压⼊数栈中,这⾥就不需要操作符栈了,因为每遇到⼀个操作符就进⾏了运算分割数和操作符并存⼊链表public static List<String> getListString(String suffixExpression) {//将表达式分割String[] strs = suffixExpression.split(" ");ArrayList<String> list = new ArrayList<>();//forEach的参数传递的是⼀个消费型接⼝Arrays.stream(strs).forEach((str) -> {list.add(str);});return list;}public static int caculate(List<String> list) {// 创建⼀个栈,只需要⼀个栈,只需要存数字Stack<String> stack = new Stack<>();// 遍历listlist.stream().forEach((str) -> {//这⾥使⽤正则表达式来判断是否是数字if (str.matches("\\d+")) {//匹配的是多位数//⼊栈stack.push(str);} else {//从栈中pop两个数并运算,结果再⼊栈//先pop出来的是被* 被/数//后pop出来的是 / -数int num2 = Integer.parseInt(stack.pop());int num1 = Integer.parseInt(stack.pop());int res = 0;switch (str) {case "+":res = num1 + num2;break;case "-":res = num1 - num2;break;case "*":res = num1 * num2;break;case "/":res = num1 / num2;break;default:throw new RuntimeException("运算符有误");}//结果⼊栈stack.push(res + "");}});//最后留在stack中的数是运算结果return Integer.parseInt(stack.pop());}。
C语言利用栈实现对后缀表达式的求解
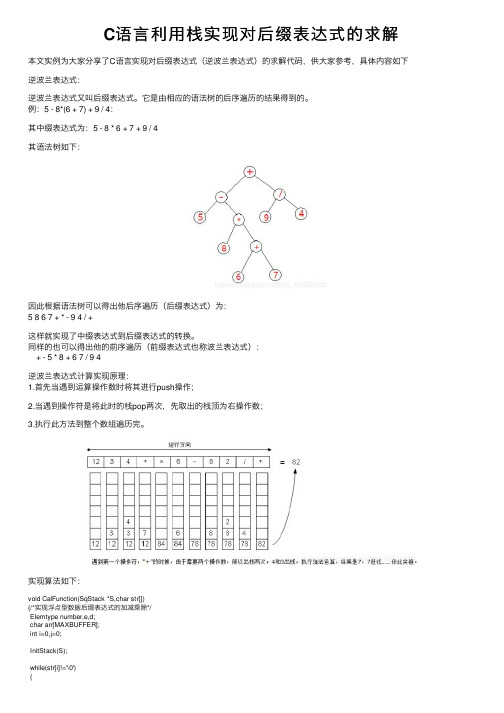
C语⾔利⽤栈实现对后缀表达式的求解本⽂实例为⼤家分享了C语⾔实现对后缀表达式(逆波兰表达式)的求解代码,供⼤家参考,具体内容如下逆波兰表达式:逆波兰表达式⼜叫后缀表达式。
它是由相应的语法树的后序遍历的结果得到的。
例:5 - 8*(6 + 7) + 9 / 4:其中缀表达式为:5 - 8 * 6 + 7 + 9 / 4其语法树如下:因此根据语法树可以得出他后序遍历(后缀表达式)为:5 867 + * - 9 4 / +这样就实现了中缀表达式到后缀表达式的转换。
同样的也可以得出他的前序遍历(前缀表达式也称波兰表达式): + - 5 * 8 + 6 7 / 9 4逆波兰表达式计算实现原理:1.⾸先当遇到运算操作数时将其进⾏push操作;2.当遇到操作符是将此时的栈pop两次,先取出的栈顶为右操作数;3.执⾏此⽅法到整个数组遍历完。
实现算法如下:void CalFunction(SqStack *S,char str[]){/*实现浮点型数据后缀表达式的加减乘除*/Elemtype number,e,d;char arr[MAXBUFFER];int i=0,j=0;InitStack(S);while(str[i]!='\0')while(isdigit(str[i])||str[i]=='.') //过滤数字{arr[j++]=str[i++];arr[j]='\0';if( j >= MAXBUFFER ){printf("输⼊单个数据过⼤!\n");return ;}if(str[i]==' '){number=atof(arr); //利⽤atof函数将数字字符串转化为double型数据PushStack(S,number); //将转换的数进⾏压栈j=0; //这⾥不要忘记将j重新初始化进⾏下个数据的转化break;}}/*如果遇到操作运算符则,弹出两个数据进⾏运算,然后将得出的结果重新⼊栈*/ switch(str[i]){case '+':PopStack(S,&e);PopStack(S,&d);PushStack(S,d+e);break;case '-':PopStack(S,&e);PopStack(S,&d);PushStack(S,d-e);break;case '*':PopStack(S,&e);PopStack(S,&d);PushStack(S,d*e);break;case '/':PopStack(S,&e);PopStack(S,&d);if(e == 0){printf("输⼊出错,分母为零!\n");return ;}PushStack(S,d/e);break;}i++; //继续遍历直到遍历字符串结束}PopStack(S,&e);printf("计算结果为:%lf",e);}完整代码如下:#include<stdio.h>#include<stdlib.h>#include<assert.h>#include<ctype.h>#define INITSIZE 20#define INCREMENT 10#define MAXBUFFER 10#define LEN sizeof(Elemtype)/*栈的动态分配顺序存储结构*/typedef double Elemtype;typedef struct{Elemtype *base;Elemtype *top;int StackSize;}SqStack;void InitStack(SqStack *S)S->base=(Elemtype*)malloc(LEN*INITSIZE);assert(S->base != NULL);S->top=S->base;S->StackSize=INITSIZE;}void PushStack(SqStack *S,Elemtype e){if(S->top - S->base >= S->StackSize){S->base=(Elemtype*)realloc(S->base,(S->StackSize+INCREMENT)*LEN); assert(S->base !=NULL);S->top=S->base+S->StackSize;S->StackSize+=INCREMENT;}*S->top =e;S->top++;}void PopStack(SqStack *S,Elemtype *e){*e=*--S->top;}void CalFunction(SqStack *S,char str[]){Elemtype number,e,d;char arr[MAXBUFFER];int i=0,j=0;InitStack(S);while(str[i]!='\0'){while(isdigit(str[i])||str[i]=='.') //过滤数字{arr[j++]=str[i++];arr[j]='\0';if( j >= MAXBUFFER ){printf("输⼊单个数据过⼤!\n");return ;}if(str[i]==' '){number=atof(arr); //利⽤atof函数将数字字符转化为double型数据PushStack(S,number); //将转换的数进⾏压栈j=0;break;}}switch(str[i]){case '+':PopStack(S,&e);PopStack(S,&d);PushStack(S,d+e);break;case '-':PopStack(S,&e);PopStack(S,&d);PushStack(S,d-e);break;case '*':PopStack(S,&e);PopStack(S,&d);PushStack(S,d*e);break;case '/':PopStack(S,&e);PopStack(S,&d);if(e == 0){return ;}PushStack(S,d/e);break;}i++;}PopStack(S,&e);printf("计算结果为:%lf",e);}int main(){char str[100];SqStack S;printf("请按逆波兰表达式输⼊数据,每个数据之间⽤空格隔开:");gets(str);CalFunction(&S,str);return 0;}// 检测⽤例 5 - (6 + 7) * 8 + 9 / 4// 输⼊:5 8 6 7 + * - 9 4 / + #// 输出: - 96.750000运⾏效果截图如下:以上就是本⽂的全部内容,希望对⼤家的学习有所帮助,也希望⼤家多多⽀持。
逆波兰表达式计算 java

逆波兰表达式计算 java逆波兰表达式是一种将运算符写在操作数之后的表示方法,计算逆波兰表达式可以使用栈来实现。
下面是一个使用Java实现逆波兰表达式计算的例子:```javaimport java.util.Stack;public class RPNCalculator {public static double evaluateRPN(String[] tokens) {Stack<Double> stack = new Stack<>();for (String token : tokens) {if (isOperator(token)) {double operand2 = stack.pop();double operand1 = stack.pop();double result = calculate(token, operand1, operand2);stack.push(result);} else {stack.push(Double.parseDouble(token));}}return stack.pop();}private static boolean isOperator(String token) {return token.equals("+") || token.equals("-") ||token.equals("*") || token.equals("/");}private static double calculate(String operator, double operand1, double operand2) {switch (operator) {case "+":return operand1 + operand2;case "-":return operand1 - operand2;case "*":return operand1 * operand2;case "/":return operand1 / operand2;default:throw new IllegalArgumentException("Unknown operator: " + operator);}}public static void main(String[] args) {String[] tokens = {"2", "1", "+", "3", "*"};double result = evaluateRPN(tokens);System.out.println("Result: " + result);String[] tokens2 = {"4", "13", "5", "/", "+"};double result2 = evaluateRPN(tokens2);System.out.println("Result: " + result2);}}```这个例子演示了如何使用栈来计算逆波兰表达式。
C++逆波兰式的实现代码

- 1 - #include"iostream.h"#include<stdlib.h>#include<stdio.h>#include<math.h>#define max 100char ex[max]; /*存储后缀表达式*/void trans(){ /*将算术表达式转化为后缀表达式*/char str[max]; /*存储原算术表达式*/char stack[max]; /*作为栈使用*/char ch;int sum,i,j,t,top=0;printf("*****************************************\n");printf("*输入一个求值的表达式,以#结束。
*\n");printf("******************************************\n");printf("算数表达式:");i=0; /*获取用户输入的表达式*/do{i++;cin>>str[i];/*此步我用的是C++ C 语言的话在后面 之所以用这个有一点区别 都*/ //scanf("%c",&str[i]);}while(str[i]!='#' && i!=max);sum=i;t=1;i=1;ch=str[i];i++;//while(ch!='#'){switch(ch){case '(': /*判定为左括号*/top++;stack[top]=ch;break;case ')': /*判定为右括号*/while(stack[top]!='('){ex[t]=stack[top];top--;t++;}top--;break;case '+': /*判定为加减号*/case '-':while(top!=0&&stack[top]!='('){ex[t]=stack[top];top--;t++;}top++;stack[top]=ch;break;- 2 - case '*': /*判定为乘除号*/case '/':while(stack[top]=='*'||stack[top]=='/'){ex[t]=stack[top];top--;t++;}top++;stack[top]=ch;break;case ' ':break;default:while(ch>='0'&&ch<='9'){ /*判定为数字*/ex[t]=ch;t++;ch=str[i];i++;}i--;ex[t]=' ';t++;}ch=str[i];i++;}while(top!=0){ex[t]=stack[top];t++;top--;}ex[t]=' ';printf("\n\t 原来表达式:");for(j=1;j<sum;j++)printf("%c",str[j]);printf("\n\t 逆波兰式:",ex);for(j=1;j<t;j++)printf("%c",ex[j]);}void compvalue(){ /*计算后缀表达式的值*/float stack[max],d; /*作为栈使用*/char ch;int t=1,top=0; /*t 为ex 下标,top 为stack 下标*/ch=ex[t];t++;while(ch!=' '){switch(ch){case '+':stack[top-1]=stack[top-1]+stack[top];top--;break;case '-':stack[top-1]=stack[top-1]-stack[top];top--;break;case '*':stack[top-1]=stack[top-1]*stack[top];top--;break;case '/':if(stack[top]!=0) stack[top-1]=stack[top-1]/stack[top];else{printf("\n\t除零错误!\n");exit(0); /*异常退出*/}top--;break;default:d=0;while(ch>='0'&&ch<='9'){d=10*d+ch-'0'; /*将数字字符转化为对应的数值*/ch=ex[t];t++;}top++;stack[top]=d;}ch=ex[t];t++;}printf("\n\t计算结果:%g\n",stack[top]);}void main(){trans();compvalue();}- 3 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用栈进行表达式求值并输出逆波兰式(源代码)#include "stdio.h"#include "malloc.h"#include "string.h"#define STACK_INIT_SIZE 100#define STACKINCREMENT 10typedef struct{char *top,*base;int csize;}*charstack,cstack;typedef struct{float *top,*base;int fsize;}*floatstack,fstack;charstack initcharstack(){charstack s;s=(charstack)malloc(sizeof(cstack));s->base=s->top=(char*)malloc(STACK_INIT_SIZE * sizeof(char));s->csize=STACK_INIT_SIZE;return s;}floatstack initfloatstack(){floatstack s;s=(floatstack)malloc(sizeof(fstack));s->base=s->top=(float*)malloc(STACK_INIT_SIZE * sizeof(float));*(s->top)=-1;s->fsize=STACK_INIT_SIZE;return s;}char chargettop(charstack s){return *(s->top-1);}float floatgettop(floatstack s){return *(s->top-1);}void charpush(charstack s,char c){if((s->top-s->base)>=s->csize){s->base =(char *)realloc(s->base ,(s->csize +STACKINCREMENT)*sizeof(char));s->top=s->base +s->csize ;s->csize +=STACKINCREMENT;}*s->top++=c;}void floatpush(floatstack s,float a){if((s->top-s->base)>=s->fsize){s->base =(float *)realloc(s->base ,(s->fsize +STACKINCREMENT)*sizeof(float));s->top=s->base+s->fsize ;s->fsize +=STACKINCREMENT;}*s->top++=a;}char charpop(charstack s){char c;c=*(s->top-1);s->top--;return c;}float floatpop(floatstack s){float a;a=*(s->top-1);s->top--;return a;}int in(char c){char s[7]={'+','-','*','/','(',')','#'};int i;for(i=0;i<7;i++)if(s[i]==c) return 1;return 0;}float operate(float a,char c,float b){switch(c){case '+':return (a+b);case '-':return (a-b);case '*':return (a*b);case '/':return (a/b);default :return 0.0;}}int charstackempty(charstack s){if(s->base==s->top)return 1;return 0;}char precede(char c1,char c2){char s[7]={'+','-','*','/','(',')','#'};char str[7][7]={'>','>','<','<','<','>','>','>','>','<','<','<','>','>','>','>','>','>','<','>','>','>','>','>','>','<','>','>','<','<','<','<','<','=',' ','>','>','>','>',' ','>','>','<','<','<','<','<',' ','='};int i=0,j=0;while(s[i]!=c1)i++;while(s[j]!=c2)j++;return str[i][j];}float evaluateexpression(char *str){charstack optr;floatstack opnd;char c1;float a,b;int i=0;optr=initcharstack();opnd=initfloatstack();charpush(optr,'#');while(str[i]!='#'||chargettop(optr)!='#'){if(!in(str[i])){floatpush(opnd,str[i]-48.0);i++;}else{if(chargettop(optr)=='#'){charpush(optr,str[i]);i++;}elseswitch(precede(chargettop(optr),str[i])){case '<':charpush(optr,str[i]);i++;break;case '=':c1=charpop(optr);i++;break;case '>':c1=charpop(optr);a=floatpop(opnd);b=floatpop(opnd);floatpush(opnd,operate(b,c1,a));break;}}}printf("\n");return floatgettop(opnd);}char* Ipn(char *s){charstack s1,s2;int length=0;char *p=s,ch,*result;s1=initcharstack();s2=initcharstack();charpush(s2,'#');for( ;*p!='#';p++){switch(*p){case '(':charpush(s2,*p);break;case ')':while(chargettop(s2)!='('){ch=charpop(s2);charpush(s1,ch);}ch=charpop(s2);break;case '+':case '-':for(ch=chargettop(s2);ch!='#';ch=chargettop(s2)){if(ch=='(')break;else{ch=charpop(s2);charpush(s1,ch);}}charpush(s2,*p);length++;break;case '*':case '/':for(ch=chargettop(s2);ch!='#'&&ch!='+'&&ch!='-';ch=chargettop(s2)){ if(ch=='(')break;else{ch=charpop(s2);charpush(s1,ch);}}charpush(s2,*p);length++;break;default:charpush(s1,*p);length++;}}while(!charstackempty(s2)&&chargettop(s2)!='#'){ch=charpop(s2);charpush(s1,ch);}result=(char*)malloc(sizeof(char)*(length+1));result+=length;*result='\0';result--;for( ;!charstackempty(s1);result--){ch=charpop(s1);*result=ch;}++result;return result;}void main(){float r;char str[100],*s;printf("Input one expression ending with #:\n\t");gets(str);s=Ipn(str);printf("The Reverse Polish Nation of the expression is:\n\t%s",s);printf("\n");r=evaluateexpression(str);printf("The result is %f.\n\n",r);}。
