永磁电机电磁计算
永磁电动机计算公式大全(电磁计算程序)精讲
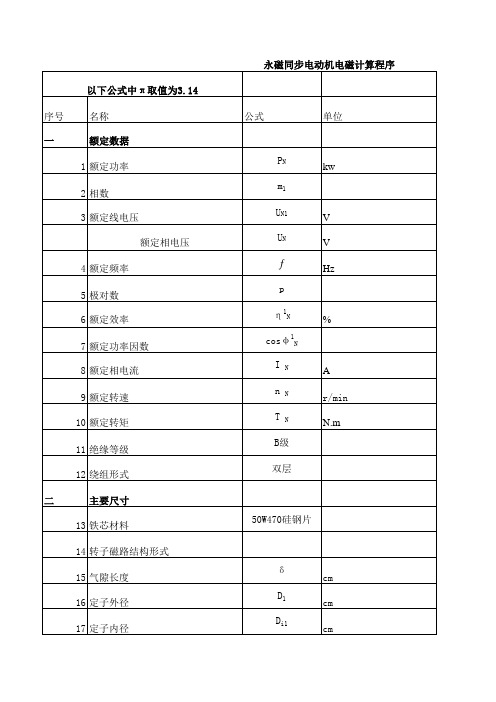
ƒ
p
1 N 1 N
%
cosφ I n T
N
A r/min N.m
N
N
B级 双层
18 转子外径 19 转子内径 20 定、转子铁心长度 21 铁心计算长度 铁心有效长度 铁心叠压系数 净铁心长 22 定子槽数 23 定子每级槽数 24 极距 25 定子槽形 梨形槽
D2 Di2 l1=l2 la=l1 leff Kfe lFe Q1 Qp1 τ p
26.65 6.3 12.19
根据I1q查表10-1得 1.38E+01 4.44E+00 0.448328451 0.801493714 0.893868894 3.25E+00 6.34E+00 0.999959394 2.72E+01 -5.17E-01 7.124891206 0.010084516 196.0756768 0.818432713 1.745334746 1.084150606 261.3172646
4.69E-01 6.28E-01 0.0205 1.65E-01 5.31E-01 1.63E+00 0.812981515 0.325192606 0.4 6.558622511 193.4528014 1.231451467 158.2920937 0.011846361 0.858709257 0.009949617 8.19E+00
12
cm A
Fδ Fδ q h1t1 bt1 Bt10 Ft1 Ht10 h1j1 l1j1 Bj10 Fj1 C1 Hj10 Kt ΣF ΣF
ad
T A A/cm cm cm T cm
A/cm
A A H H
aq
永磁同步电动机电磁计算程序

序号名称公式单位一额定数据1额定功率P Nkw2相数m13额定线电压U N1V 额定相电压U NV4额定频率ƒHz5极对数p6额定效率η1N%7额定功率因数cosφ1N8额定相电流I NA9额定转速n Nr/min10额定转矩T NN.m11绝缘等级B级12绕组形式双层二主要尺寸13铁芯材料50W470硅钢片14转子磁路结构形式15气隙长度δcm16定子外径D1cm17定子内径D i1cm永磁同步电动机电磁计算程序以下公式中π取值为3.1418转子外径D2cm19转子内径D i2cm20定、转子铁心长度l1=l2cm21铁心计算长度la=l1cm铁心有效长度l effcm铁心叠压系数K fe净铁心长l Fecm22定子槽数Q1 23定子每级槽数Q p1 24极距τp 25定子槽形梨形槽b s0cmh s0cmb s1cmh s1cmh s2cmrcm26每槽导体数N s1 27并联支路数a1 28每相绕组串联导体数NΦ129绕组线规N11S11mm230槽满率根据N11S11=1.54mm2,线径取d1/d1i=1.4mm/1.46mm,并绕根数N1(1)槽面积s scm2槽楔厚度hcm(2)槽绝缘占面积s icm2h1scm绝缘厚度C icm(3)槽有效面积s ecm2(4)槽满率sf% N1三永磁体计算31永磁材料类型铷铁棚32永磁体结构矩形33极弧系数a p34主要计算弧长b1pcm35主要极弧系数a1p 36永磁体Br温度系数a Br永磁体剩余磁通密度B r20T温度t℃t=80℃时剩余磁通密度B rT37永磁体矫顽力H c20KA/m永磁体H c温度系数a Hct=80℃时矫顽力Hc KA/m 38永磁体相对回复磁导率u ru0H/m39最高工作温度下退磁曲线的拐点b k40永磁体宽度b mcm41永磁体磁化方向厚度h Mcm42永磁体轴向长度l Mcm43提供每级磁通的截面积S M cm2四磁路计算44定子齿距t1cm45定子斜槽宽b skcm46斜槽系数K sk147节距y48绕组系数K dp1(1)分布系数K d1α°q1(2)短距系数K p1β49气隙磁密波形系数K f50气隙磁通波形系数KΦ51气隙系数Kδ52空载漏磁系数σ053永磁体空载工作点假设值b1m054空载主磁通Φδ0W b55气隙磁密Bδ056气隙磁压降δ12cm直轴磁路FδA交轴磁路Fδq 57定子齿磁路计算长度h1t1 58定子齿宽b t159定子齿磁密B t10T60定子齿磁压降F t1A查第2章附录图2E-3得H t10A/cm61定子轭计算高度h1j1cm62定子轭磁路计算长度l1j1cm63定子轭磁密B j10T64定子轭磁压降F j1cm查第2章附录图2C-4得C1查第2章附录图2E-3得H j10A/cm65磁路齿饱和系数K t66每对极总磁压降ΣF adAΣF aqA67气隙主磁导ΛδH68磁导基值ΛbH69主磁导标幺值λδ70外磁路总磁导λ1H71漏磁导标幺值λσ72永磁体空载工作点b m073气隙磁密基波幅值Bδ1T74空载反电动势E0V五参数计算75线圈平均半匝长l zl BcmdcmτycmsinαcosαC s76双层线圈端部轴向投影长f dcm77定子直流电阻R1ΩρΩ.mm2/mS1mm2d1mm78漏抗系数C x79定子槽比漏磁导λS1查第2章附录2A-3得K u1K L1λu1λL 1与假设值误差小于1%,不用重复计算80定子槽漏抗X s181定子谐波漏抗X d1Ω查第2章附录2A-4得ΣS82定子端部漏抗X e1Ω83定子斜槽漏抗X sk1Ω84定子漏抗X1Ω85直轴电枢磁动势折算系数K ad 86交轴电枢磁动势折算系数K aqK q87直轴电枢反应电流X adΩE dVI1dAF adA f1adb madΦδadW b88直轴同步电抗X dΩ89交轴磁化曲线(X aq-Iq)计算六工作性能计算90转矩角θ°91假定交轴电流I1q A92交轴电枢反应电抗X aqΩ见P428页表10-1 Xaq-Iq曲线93交轴同步电抗X qΩ94输入功率P1kwSINθSIN2θCOSθ95直轴电流I d A96交轴电流I q A97功率因数cosφ°ψ°φ°98定子电流I1A99负载气隙磁通ΦδW bEδV 100负载气隙磁密BδT 101负载定子齿磁密B t1T 102负载转子磁密B j2T 103铜耗P cu1W 104鉄耗(1)定子轭重量G j1kg(2)定子齿重量G t1kg(3)单位铁耗查第2章附录2E-4得p t1w/kgp j1w/kg(4)定子齿损耗P t1W(5)定子轭损耗P j1W(6)总损耗P Fe Wk1k2105杂耗P sP sN kw106机械损耗P fw w107总损耗ΣP kw108输出功率P2kw109效率η%110工作特性见P430表10-2111失步转矩倍数K MT max112永磁体额定负载工作点b mNf1adN113电负荷A1A/cmλ1n114电密J1A/mm2115热负荷A1J1(A/cm)(A/mm2)116永磁体最大去磁工作点b mhf1adhI adh Alaobusi算例4.00003.0000360.0000207.846096926.50003.00000.89601.00007.15960155253072.07547170.052314.814.74.8191919.10.9518.053667.7453333330.350.080.680.091.060.443213841.539699259 .4mm/1.46mm,并绕根数N1=11.0449520.20.1572481.150.030.887704 76.8400277610.82 6.4511733330.832911-0.121.22801.13216923-0.12856.544 1.0523700751.26E-063.61.219136.81.290888889 1.678155556 0.9808257135 0.932879761 0.965960169302 0.965753860.8333333331.2300402670.9406348791.2448267171.30.87 0.010365012 0.8411970220.02 1101.610936 833.7137955 1.2966666670.6405444441.793880386233.490 2.576666667 5.344105556 1.114305729 12.980832390.71.735 1.211871535 1347.991769 1080.094628 7.68922E-06 1.50683E-065.1029296776.63380858 1.5308789030.869003789 %,不用重复计算1.034706209201.529426831.682915872327.2568888890.5490852490.8357663494.3414579342.3838305111.7158936780.02171.53861.48.21E-010.9608659780.870.9050.403328710.6744.69E-016.28E-010.02051.65E-015.31E-011.63E+00 0.812981515 0.3251926060.4 6.558622511 193.4528014 1.231451467 158.2920937 0.011846361 0.858709257 0.0099496178.19E+0026.656.312.19根据I1q查表10-1得1.38E+014.44E+000.4483284510.8014937140.8938688943.25E+006.34E+000.9999593942.72E+01-5.17E-017.1248912060.010084516196.07567680.8184327131.7453347461.084150606261.317264623.264103534.2097075396.22.17 26.10018674 50.48310465 166.21667622.52 19.806546740.0227.9841 0.4753245883.97E+008.93E+010.18536125713.360.8611346311.04E-02 176.61978556.643 4.630762516 817.884282 0.4683161174.61E-014.79E+01。
永磁电机磁路计算基础

下面以隐极永磁同步电机为例,运用前 面介绍的磁路计算方法和概念,具体推导计 算永磁体体积的公式。 永磁同步发电机的额定容量(kVA)
40
41
42
可以看出:
43
44
45
46
21
22
23
2.3 解析法的应用 以上为了推导过程简洁,是从退磁曲线为直线、回复线与退磁曲线
重合的稀土木磁材料这一特例着手的。实际上,上述推导结果可以推广 应用于所有永磁材料。研究实践表明,在永磁电机运行时,永磁体工作 点是变化的,直接决定永磁体的磁密与场强关系的是回复线。或者说, 永磁体在电机内的基本工作曲线是回复线,并不是退磁曲线。而所有永 磁材料的回复线部近似认为是直线,区别在于它们并不都象稀土永磁那 样在第二象限内全部是直线,而是在退磁场强超过一定值后出现拐点; 而且,采用不同的稳磁处理引起起始点P的位置不同,导致回复线与纵轴 的交点随之改变;这些增加了分析计算的复杂性。经过分析研究可知, 只要针对不同情况进行处理,仍可应用上述方法。
29
30
应用比磁导
31
4 永磁体的最佳工作点 在设计永磁电机时,为了充分利用永磁
料,缩小永磁体和整个电机的尺寸,应该力 求用最小的永磁体体积在气隙中建立且有最 大磁能的磁场。
32
4.1 最大磁能的永磁体最佳工作点
33
34
4.2 最大有效磁能的永磁体最佳工作点
则具有最大有效磁能的永磁体最 佳工作点的标么值
27
28
3等效磁路的图解法 采用标么值的解析法的优点是计算简单,
适于应用计算机求解,但也存在不足,即不 够直观,尤其是当退磁曲线为曲线或具有拐 点和磁路饱和程度较高时。而应用图解法直 接画出永磁体工作图,则可以清晰地看出各 种因素的影响程度和工作点与拐点间的关系。 故工程上在应用解析法进行计算机求解的同 时,还常采用图解法进行补充分析。
永磁电机电磁计算
永磁电机电磁计算传统的电机学和电机设计中,习惯地把电机的分析和计算归结为电路和磁路的计算问题。
实际上,电路和磁路中的各个参数是由电机电磁场的场量得来,由于数值计算和仿真技术的不断发展,我们可以直接使用有限元对电机的电磁场进行分析和计算。
本文将应用ANSYS软件,对大型永磁电机的电磁场进行分析和计算。
这里只研究平行平面场问题,即二维电磁场,因而只有一个自由度即矢量磁势Az。
电机的对称周期取一对磁极范围。
考虑漏磁的影响,把转轴和机座作为模型的内外边界。
定义电机材料特性首先,定义硅钢片的材料属性与磁化曲线,如图1:永磁体的材料特性需要说明的是,永磁体的退磁曲线是指剩磁密度Br与矫顽力Hcb的曲线,以下简称BH曲线。
退磁曲线通常在第二象限,但ANSYS 程序中需按第一象限输入。
此外还需要知道永磁体的工作温度,即电机内部温度分布,Br的可逆温度系数,Hcb的可逆温度系数。
参数化建模参数化建模具有很多优点,各个变量物理意义明确,便于查找和修改。
而且可以通过对话框快速对电机尺寸参数进行调整,缩短调试程序和优化设计的时间。
这里采用ANSYS内部的对话框进行交互,可以方便其他设计人员对程序的调试,提高程序的通用性,如图2:有限元模型的建立和边界条件定、转子应分别建模,这样两部分模型不会相互干扰。
定、转子之间的气隙,可定义两层或更多层,再经过径向拼接得到整个求解区域。
分网时应注意疏密结合,气隙部分网格要足够稠密,而且沿径向应均匀分网。
其它部分网格可稀疏些。
模型尽量使用四边形网格,并保证节点连续。
这里只研究电机转速恒定情况,用有限元法进行电机的电磁场分析,要模拟电机定、转子之间的相对运动。
这里使用运动边界法,即假设定子模型静止不动,让转子部分旋转,和真实情况一样。
具体如下:气隙模型中有一条定、转子网格重合的公共运动边界,分别为定、转子的运动边界上的节点编号,并且保证相邻节点径向间距相等,这样能保证转子旋转后运动边界上的节点重合,压缩重合的关键点(KP)、节点(node),保持网格的连续性。
永磁直流电机电磁设计算例

永磁直流电机电磁设计算例假设我们要设计一个功率为500W的永磁直流电机,额定电压为24V。
首先,我们需要确定电机的转矩常数和电机的转速范围。
转矩常数表示电机在给定电压下的输出转矩大小。
常用的永磁直流电机转矩常数一般在0.02-0.06Nm/A之间。
假设我们选择一个转矩常数为0.04Nm/A的永磁直流电机。
根据功率和转矩常数的关系,我们可以计算出电机的额定电流为500/0.04=12.5A。
接下来,我们需要确定电机的磁路尺寸和磁路材料。
磁路尺寸决定了电机的体积和重量,而磁路材料的选择直接影响电机的性能和效率。
常见的磁路材料包括硅钢片、铁氧体和软磁合金等。
这里我们选择硅钢片作为磁路材料。
根据电机的功率和额定电流,我们可以计算出电机的额定转矩为500/12.5=40Nm。
接下来,我们需要根据额定转矩和转矩常数计算出永磁体的磁通。
磁通是永磁体产生的磁场大小,它与电机的转矩和电压密切相关。
磁通的计算公式为磁通=转矩/转矩常数=40/0.04=1000Wb。
接下来,我们需要计算出电机的磁场密度和磁力线密度。
磁场密度表示单位面积内的磁场大小,而磁力线密度表示单位长度内的磁场线条数。
根据磁场强度和磁路材料的磁导率,我们可以计算出磁场密度和磁力线密度。
最后,我们需要设计电机的线圈和定子参数。
根据额定电流和电压,我们可以计算出电机的线圈匝数和线圈直径。
定子参数的计算需要根据电机的磁通和磁场密度来决定。
综上所述,永磁直流电机的电磁设计是一个复杂的过程,需要根据电机的功率、转矩和工作条件来选择合适的磁路材料和定子参数。
设计过程需要综合考虑电机的性能、效率和成本等因素,从而确保电机的稳定运行和长寿命。
异步起动永磁同步电动机的电磁计算程序和算例

转子极距: τ2 πD2 , bp (τ2 b02) τ2 2p
67. 计算极弧系数: αi αp 0.889
, αp bp τ2
68. 气隙磁密波形系数: Kf
4 π
sin
αiπ 2
1.254
69, 气隙磁通波形系数: KΦ
计算剩磁密度: Br
[1 (t
20)αBr]1
IL 100
Br20
1.123
T
31.
计算矫顽力:
Hc [1 (t 20)αBr]1
IL 100
Hc20
854.896
kA/m
32. 真空磁导率: μ0 4π10 7 H/m
若 Lvv = 3或9,则 ht2 hr12 br1 2 br2 6 若 Lvv = 4或5,则齿部按三段磁路计算:槽上部段磁路计算长度: ht2t hr1 ;槽中部段磁路计算长度:
ht2m hr2 ;槽下部段磁路的计算长度: ht2b hr3
13. 额定相电流: IN
永磁同步伺服电机电磁计算流程_2

电机计算与磁场分析1.1 计算程序及算例注:计算采用手算和MathCAD 计算结合使用的方法所以计算结果保留到小数点后三位。
一、 额定数据1.额定功率 5KW N P =2.相数 3m =3.额定电压 直流输出电压 40V d U =额定相电压 217.949V 2.34d N U U +== 三相桥整流考虑二极管压降4.功率因数 cos 0.8ϕ= sin 0.6ϕ=5.额定相电流 310116.071A cos N N N P I m U ϕ⨯==⋅⋅ 6.效率 0.9N η=7.额定转速 100000rpm N n = 8.预取极对数 2p =9.频率 3333Hz 60N pnf ==10.冷却方式 空气冷却 11.转子结构 径向套环12.电压调整率 20%N U ∆≤二、永磁材料选择13.材料牌号 NSC27G 烧结钐钴材料,主要考虑到高温工作环境 该材料高温下退磁小。
14.预计温度 T= 250C 15.剩余磁通密度 20 1.0T r B =0.03%B r rB α=----的温度系数 0r I L B =---的不可逆损失率工作温度下 201(20)(1)0.931T100100Br r r IL B t B α⎡⎤=+--=⎢⎥⎣⎦ 16.计算矫顽力 20760kA/m c H =工作温度下 201(20)(1)707.56KA/m 100100Br C r IL H t H α⎡⎤=+--=⎢⎥⎣⎦17.相对回复磁导率 3010 1.047rr C B H μμ-=⨯=式中 70410H /m μπ-=⨯ 三、永磁体尺寸18.永磁体磁化方向长度 0.35cm M h =19.永磁体宽度 1.56cm M b =20.永磁体轴向长度 5.35cm M L = 21.永磁体段数 1W =22.永磁体每极截面积 28.346cm M M M A L b == 23.永磁体每对极磁化方向长度 20.7cm MP M h h == 24.永磁体体积 311.684cm m M MP V PA h == 25.永磁体质量 31095.812g m m m V ρ-=⨯= 稀土钴材料密度 38.2g/cm ρ=四、转子结构尺寸26.气隙长度 10.19cm δδ=∆+= 均匀气隙空气隙长度10.03cm δ= 非磁性套环长度 0.16cm ∆=27.转子外径 2 3.0cm D = 28.轴孔直径 2 1.0cm i D =29.转子铁心长度 2 5.35cm M L L ==30.衬套厚度 222()0.49cm 2i M h D D h h --∆+==31.极距 2(2)2.105cm 2D pπτ-∆== 径向瓦片形32.极弧系数 0.74p α=33.极间宽度 2(1)0.547cm p b ατ=-= 五、定子绕组和定子冲片34.定子外径 1 4.8cm D =35.定子内径 1212 3.06cm i D D δ=+= 36. 定子铁心长度 1 5.35cm M L L ==长径比λ=1.7537.每极每相槽数 1q =38. 定子槽数 212Q mpq ==39.绕组节距 3y = 整距绕组,影响下面一些系数40. 短距系数 180sin 12p K β==41. 分布因数 1d K = 42.斜槽因数 1sk K =43.绕组因数 1dp d p sk K K K K ==波形系数 sin()20.91.024i iK φαπα⋅==44.预估永磁体空载工作点 '00.67m b = 工作点范围在0.55-0.75Br 内但高速电机应取小一些。
永磁直流电机电磁设计算例.

手工输入公式计算,不可改.关键判定,提示说明.数据引用序号名称符号或算式单位一额定数据1额定功率P N W 2额定电压U N V额定转速n N rpm 额定电流I N A额定转矩T N=9.549*P N/n N N.m 起动转矩倍数T stN 二主要尺寸及永磁体尺寸选择额定效率ηN =P N/(U N*I N*COSØ*100%计算功率P'=((1+2η/100/(3ηN/100*P N W感应电势E'a=((1+(2ηN/100/3*U N V极对数p永磁材料类型预计永磁体工作温度t℃永磁体剩磁密度Bt20T工作时永磁体剩磁密度Br=(1-(t-20*αBr/100*(1-IL/100*Bt20T剩磁温度系数αBr%K-1剩磁温度不可逆损失率IL%永磁体计算矫顽力Hc20KA/M工作时永磁体计算矫顽力Hc=(1-(t-20*αBr/100*(1-IL/100*Hc20KA/M永磁体相对回复磁导率μr=Br/(μ0*Hc/1000真空磁导率μ=4*PI*10-7工作温度下退磁曲线的拐点b k电枢铁心材料铁芯叠加系数K Fe电负荷预估值A'A/cm 气隙磁密预估值B'δ=(0.60-0.85Br =0.8Br T 永磁直流电机电磁计算程序和算例:支路电流Ia=I N/(2*a预计电枢电流密度j'2=5-13A/mm²预计导线截面积A'Cua=Ia/j'2 并绕根数N t计算导线裸线线径d'=(4A'Cua/PI1/2导线裸线线径d0mm导线绝缘后线径d mm实际导线截面积ACUa=PI*Nt*d02/4mm²实际电枢电流密度j2=Ia/A CUa实际热负荷△=AJ2槽形选择槽口宽度b02cm槽口高度h02cm槽下度半径r22cm槽上部倒角半径r23cm槽上部高度h2, h2=r23cm槽上部宽度d1cm槽中部高度h22cm槽下部宽度d2cm槽下部倒角圆心距d3cm槽高ht2cm齿宽bt2, 近似取平行齿cm槽净面积As=PI*(r222+r232/2+h22(d1+2r22+r2 3*d3-Ci(PI*r22+2*h22+d1cm²槽绝缘厚度Ci cm槽满率Sf=Nt*Ns*d2/As%线圆平均半匝长度Lav=La+Ke*Da, Ke=(1.35,p=1cm 电枢绕组电阻Ra=ρ*N*Lav/(4*Acua*a2Ra20(ρa20=0.1785*10-3Ω.mm2/cmΩRa75(ρa75=0.217*10-3Ω.mm3/cmΩ转子冲片内径D i2, D i2=(0.15-0.25Da mm转子冲片内径圆整mm 电枢轭高h J2=(Da-2*ht2-Di2/2mm 电枢轭有效高hj21=h j2+Di2/8mm 四磁路计算气隙系数Kδ, Kδ=(1.01-1.1气隙磁通密度Bδ=Ф'δ*104/(α*τ*LefT每对极气隙磁位差Fδ=1.6*Kδ*δ*Bδ*104A0.2970.04142857110.2296704060.23OK0.25 漆膜厚度0.01mm 0.0415475636.979952136531.1938393半梨形槽0.270.1150.20.10.10.6950.6944412910.7230.7230.40.4951.1380.249441291 0.46018799 0.02336.6697966110.3741148.13518732 58.51728654 0.7860.8OK1.0821.1821.0890.269372444 375.48363780.000632167。
永磁直流电动机电磁计算程序
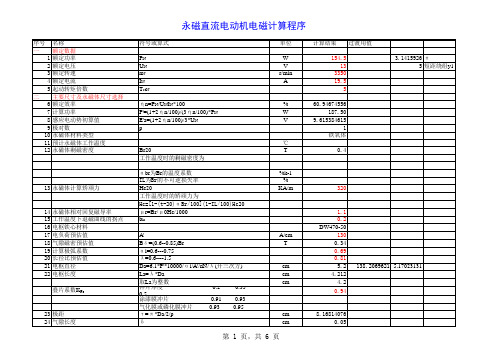
23 极距 24 气隙长度
永磁直流电动机电磁计算程序
符号或算式
单位
PN
W
UN
V
nN
r/min
IN
A
TstN
η n=PN/UNIN*100 P'=(1+2η n/100)/(3η n/100)*PN E'a=(1+2η n/100)/3*UN p
Br20 工作温度时的剩磁密度为
α br为Br的温度系数 IL为Br的不可逆损失率 Hc20 工作温度时的矫顽力为 Hc=[1-(t-20)α Br/100](1-IL/100)Hc20 μ r=Br/μ 0Hc/1000 bk
0.6 0.6
1 0.36
1 54.16666667
1.4 0.8
2.5 4.385139671 0.654498458 0.135005868 4.036484279 1.747272727 1.065527066 1.223684486 0.088166387 0.000171066 3.823841793
t'k=tk*De2/Dk(厘米)
要求bk<0.8τ (1-α δ )厘米
七 最大去磁校核
113 不同工作时的最大瞬时电流
A
突然起动时
A
瞬时堵转时
A
114 直轴电枢磁动势
A
A
115 交轴电枢磁动势 116 换向元件电枢磁动势 117 电枢总去磁磁动势 118 最大去磁时永磁体工作点
Amax
A/cm A A A
12 114.591561
9.75 22
0.443181818 1
0.75 0.78 0.441786459 22.06948582 2528.97683 半梨形槽
永磁电机频率计算公式

永磁电机频率计算公式永磁电机在现代工业和生活中的应用那可是相当广泛啦,从电动汽车到家用电器,到处都能看到它的身影。
要搞清楚永磁电机频率的计算,咱们得先明白几个关键的概念。
咱先来说说啥是频率。
频率呢,简单说就是电机在单位时间内完成的周期性变化的次数。
就好比咱们跑步,一分钟跑多少圈,这圈数就类似于电机的频率。
那永磁电机的频率是咋算出来的呢?其实有个挺重要的公式:f = p × n / 120 。
这里的“f”就是频率啦,“p”指的是电机的极对数,“n”呢则是电机的转速。
比如说,有个永磁电机,它的极对数是 2,转速是 1500 转每分钟,那按照公式算一下,频率 f 就等于 2×1500÷120 = 25 赫兹。
我记得有一次,我去一家工厂参观,正好看到工程师们在调试一台永磁电机。
他们拿着各种仪器,一边测量数据,一边嘴里念叨着这些公式。
我凑过去看,发现他们就是根据电机的实际转速和极对数,用这个公式来计算频率,然后再对照标准值,看看电机是否运行正常。
那时候我就在想,这小小的公式,居然能决定这么大一台机器的运行效果,真的是太神奇了!在实际应用中,要准确计算永磁电机的频率可不容易。
因为电机的转速可能会受到负载、电压等各种因素的影响而发生变化。
所以,要得到准确的频率值,就得综合考虑这些因素。
而且啊,不同类型的永磁电机,其频率计算可能还会有一些细微的差别。
比如说,在一些高性能的永磁电机中,可能还需要考虑磁场的变化、损耗等因素对频率的影响。
再比如说,在一些特殊的应用场景中,比如航空航天领域,对永磁电机频率的精度要求那是相当高的。
这时候,就不能仅仅依靠简单的公式计算了,还需要借助更先进的测量设备和复杂的算法来确保频率的准确性。
总之,永磁电机频率的计算虽然有公式可循,但要真正掌握并运用好,还需要我们对电机的工作原理有深入的理解,对各种影响因素有清晰的认识。
希望通过我上面的这些讲解,能让您对永磁电机频率的计算公式有更清楚的了解。
永磁直流电动机电磁计算程序

永磁直流电动机电磁计算程序以下是一个简单的永磁直流电动机电磁计算程序的示例:```pythonimport math#输入电机参数voltage = float(input("请输入电机电压(伏):"))current = float(input("请输入电机电流(安):"))speed = float(input("请输入电机转速(转/分钟):"))#计算电机电磁力flux_density = 0.95 # 磁通密度(特斯拉)pole_pairs = 2 # 极对数armature_length = 0.1 # 电枢长度(米)force_constant = 2 * math.pi * pole_pairs * flux_density * armature_length # 电机电磁力常数(牛)force = force_constant * current#计算电机功率和效率power = voltage * currentefficiency = power / (force * speed)#输出计算结果print("电磁力:", force, "牛")print("功率:", power, "瓦")print("效率:", efficiency * 100, "%")```在上述示例程序中,首先通过`input`函数获取用户输入的电机参数,包括电压、电流和转速。
然后,根据给定的参数计算电机的电磁力、功率和效率。
电机电磁力的计算使用了一些基本的电磁学公式,如电机电磁力常数的计算公式为`2 * math.pi * pole_pairs * flux_density *armature_length`,其中`math.pi`为圆周率,`pole_pairs`为极对数,`flux_density`为磁通密度,`armature_length`为电枢长度。
盘式永磁电机功率计算

盘式永磁电机功率计算
1.机械功率计算:首先需要确定电机的输出转速和输出扭矩。
输出转速可以通过电机的额定转速和负载转矩来确定。
输出扭
矩可以通过电机的额定输出功率和额定转速来确定。
机械功率
的计算公式为:机械功率=输出扭矩×输出转速。
2.电磁功率计算:电磁功率是指电机输入电功率和电机效率
的乘积。
输入电功率可以通过电机的额定电压和额定电流来确定。
电机效率可以通过电机的额定输出功率和输入电功率来计算,电磁功率的计算公式为:电磁功率=输入电功率×电机效率。
3.总功率计算:总功率等于机械功率加上电磁功率,即:总
功率=机械功率+电磁功率。
需要注意的是,在实际应用中,电机的效率可能会受到一些
因素的影响,例如负载情况、温度等。
因此,在计算功率时,
应该尽可能地考虑这些因素,并进行实际测量或者根据经验进
行修正。
永磁同步电机扭矩dq计算公式

永磁同步电机扭矩dq计算公式
永磁同步电机是一种高效率、高可靠性的电机类型,广泛应用于工业和交通领域。
扭矩dq计算公式是用于计算永磁同步电机在dq坐标系下的电磁转矩的数学公式。
在dq坐标系下,电机的d轴与磁极轴重合,而q轴与d轴垂直。
dq坐标系的
选择可以使得扭矩计算更加简化和准确。
永磁同步电机的扭矩dq计算公式如下:
Td = 3/2 * P * (Psi_d * I_q - Psi_q * I_d)
其中,Td表示电机的电磁转矩(单位为N·m),P表示电机的极对数,Psi_d
和Psi_q分别表示电机的磁链(单位为Wb),I_d和I_q分别表示电机在dq轴方
向的电流(单位为A)。
通过这个公式,可以根据电机的磁链和电流值,准确计算电机所产生的电磁转矩。
需要注意的是,这个公式仅适用于理想情况下的永磁同步电机。
在实际应用中,由于电机的非线性特性和其他因素的影响,可能需要考虑更复杂的模型和算法来计算电磁转矩。
总结而言,永磁同步电机的扭矩dq计算公式是一种重要的数学工具,用于准
确计算电机的电磁转矩。
在工程设计和研发过程中,合理利用这个公式可以帮助优化电机性能,提高系统效率。
直驱永磁风力发电机的瞬态电磁场计算

等
E o = U+I R + j l d Xd + j l q Xq U= I( R+ j x)
( 5 )
( 6 )
( 7 )
一
8一
电气牵引2 0 1 4 年第 2 期( 总第 1 2 8 期)
表 1 电机带不同负载时负载功率值
枢 电流滞后于空载感应电势 , 直轴电枢反应对气隙磁 场起去磁作用 ; 而容性负载使得电势电流超前于空载 感应电势, 直轴电枢反应起增磁作用。外电路阻抗达 到0 . 4 5 欧姆 以上时, 端电压增加较小 , 电机磁路趋 向 饱和状态。当电机带0 . 1 2 欧姆的阻性负载时 , 电机可 达到额定输出功率 。由于 电枢反应和外接负载的影
了空 载 和不 同阻 性 负 载 时永 磁 风 力发 电机 的 性 能 ,
数, 为槽满率 , , 为电流。 为 了考虑外电路 和电机端部效应 , 可用场路耦 合的方法计算 电磁瞬态过程 , 通过电枢绕组 的电动 势将上述电磁场有限元方程与绕组 电路方程联立 , 求解磁矢位和电流。感应电势和外电路方程如下 :
上式分别表示空气 区域 、 涡流区域 、 永磁区域和
绕 组 部分 的 电磁场 方 程 。式 中 A为 矢量 磁 位 , 为 磁导率 , 为 电导 率 , ,为 电流密 度 , Ⅳ 为槽 串联 匝
Байду номын сангаас
下 的某时刻的磁场分布 , 无法计算 出电机的实际运
行参数 ; 瞬态场计算可把外电路方程和有限元方程 联立 , 直接求解矢量磁位和绕组 电流。文献[ 1 ] 计算
最 大 的风 电市 场 , 风 电并 网装机 量位 居世 界前 列 , 目
前, 国内风力发 电机组主要采用异步风力发电机 、 双
KW调速永磁同步电动机电磁设计方案程序

11KW 变频起动永磁同步电动机电磁设计程序及电磁仿真1永磁同步电动机电磁设计程序1.1额定数据和技术要求除特殊注明外,电磁计算程序中的单位均按目前电机行业电磁计算时习惯 使用的单位,尺寸以cm (厘M )、面积以cm 2(平方厘M )、电压以V (伏)、电 流以A (安)、功率和损耗以(瓦)、电阻和电抗以门(欧姆)、磁通以Wb (韦伯)、磁密以T (特斯拉)、磁场强度以 A/cm (安培/厘 M )、转矩以N (牛 顿)为单位。
1额定功率P n = 11kW2相数g =3 3额定线电压U N 1 =38CV额定相电压丫接法U N二U N1/ .3 = 219.39V 4额定频率f =50HZ5电动机的极对数P=26额定效率N =0.87 7额定功率因数cos N =0.78 8失步转矩倍数 T poN = 2.2 9起动转矩倍数T ;N =2.2 10起动电流倍数I ;N =2.211额定相电流I NP N 105 R U N NCOS N11 105 3 219.39 0.87 0.78A - 24.6212额定转速n N =1000r/min13额定转矩T N二9.55P N103二9.55 11二105.039N.m n N100014绝缘等级:B级15绕组形式:双层叠绕Y接法1.2主要尺寸16铁心材料DW540-50硅钢片17转子磁路结构形式:表贴式18气隙长度:=0.07 cm19定子外径D1=26cm20定子内径D i1 =18cm21 转子外径D2=。
辺一2、=(18-2 0.07)cm =17.86 22转子内径D i2=6cm23定,转子铁心长度h J =15cm24铁心计算长度l a =12= 15cm铁心有效长度l ef =l a 2、=(15 2 0.07)cm = 15.14cm 25定子槽数Q厂36 26定子每极每相槽数q =Q1 /2m1p =36/2 3 3=227极距巨p=蔥/2P =3.14 18/2 3 = 9.728cm28定子槽形:梨形槽定子槽尺寸h01= 0.08cmb01= 0.38cmbi = 0.78cmr1 = 0.53cmh02= 1.72cm32定子轭计算高度33定子齿计算长度r ii h ti=h i21=i.720.53 =i.8967cm3334定子轭磁路计算长度JI JIL M (D i-h ii)(26-i.8467) = 6.3233cm4pi235每槽导体数N si =38 36并联支路数〉i =237每相绕组串联匝数N 二@血二型卫^二“厶口% 3 汉 2 38并绕根数-线径 也—d ii =i-i.2ON t2_d i2=i-i.2O39槽满率29定子齿距t iD ii 18■: Q i36 二 1.5708cm30定子斜槽距离 t sk t iQiQ i p停08 3Ji.50cm36 331定子齿宽二[D ii2(h0ihi2)]iiQ i-2ri沖8 2(°.08WOG "824954cm36i2 -Bi di 「si)]巾 J[i8 2(0.08 0.ii55)]_0.78 = 0.8249WmQ i36式中h si0.78—0.38tan 0.ii55cm6b ti -bti2.b tii —'bti2= 0.8249ii0.824954 -0.8259ii3二0.824940cmhjiD i -D ii-(h 0ih i2刍)=26_i8一(0.08 i.72 2 0.53) =i.8467cm3 2 322 0.53 0.78 0.53 2(1.72 -0.2) 1.8394cm 22式中槽楔厚h = 0.2cm ,槽绝缘占面积 A =G (21^2+2r , +R) =0.035x(3.44+ 0.53兀 +1.06+0.78) = 0.2678cm 2式中,绝缘厚度G 二0.03cm 槽有效面积代f二 A s-A =1.8396-0.2678 =1.5718槽满率N s [N t1(dn hdJ 2 N t2©2 h d2)2]Aef=38q (1.2 +0.08)2 +(1.2 + 0.08)2] _79 22% - 1.5718 - . %40节距y=541 绕组短距因数 K p1 =sin() =sin(5 ) =0.83332 12式中:二 y/mq = 5/6.q : 1 sin42绕组分布因数Kd120.9659.«1 q sin44绕组因数 K dp 二K d1K p1K sk1 =0.9659 0.8333 0.9909 = 0.9245 45绕组线圈平均半匝长 Lav2(d L e) =15 2 (1.5 5.106) = 28.212cm式中,绕组直线部分伸出长一般取1-3cm ,取d=1.5cm ;双层线圈端部斜边长 L E 二 y/(2cos : °) =9.728/(2 0.8497) = 5.106cm 。
ANSYS分析实例C

•
这里只研究电机转速恒定情况,用有限元法进行电机
的电磁场分析,要模拟电机定、转子之间的相对运动。这
里使用运动边界法,即假设定子模型静止不动,让转子部
分旋转,和真实情况一样。具体如下:气隙模型中有一条
定、转子网格重合的公共运动边界,分别为定、转子的运
动边界上的节点编号,并且保证相邻节点径向间距相等,
磁场转化成等效的多段磁路,并近似认为在每段磁路中磁
通沿截面和长度均匀分布,将磁场的计算转化为磁路的计
算,然后用各种系数修正,使各段磁路的磁位差等于磁场
中对应点之间的磁位差;
•
二、电磁场数值计算中的有限元法。有限元法是当今
数值计算领域应用最为广泛、最为成熟的一种计算方法,
其最大的优点是通用性强、精度高,可以进行专门问题的
某某某项目研讨会
演讲人:*************
一 、永 磁 电 机 电 磁 计 算
1.基本的思想和分析原则
大型电机和特种电机的设计技术都有了巨大的进步,电 机各项参数计算的精度要求越来越高,设计研发的周期越来 越短,传统的分析计算不能很好的满足上述要求。
有限元法作为一种电机电磁场数值解法臻于完善,其应 用也越来越广泛。作为一种近似的数值计算方法,有限元法 的计算精度很大程度上取决于网格剖分的疏密程度。对于一 台电机若采用三维模型计算,其计算量很大,不利于调试。
磁电机在冲击电流产生的电枢反应作用下,或者过高(钕
铁硼永磁)过低(铁氧体永磁)温度时,可能造成永磁体 的不可逆退磁,使电机性能降低甚至无法使用。
•
永磁同步发电机在正常工作时,电枢磁场的轴线和永
磁体的轴线一般不重合(我方采用的发电机为外转子旋转
磁极式),通常磁钢磁场的轴线位置超前电枢磁场的轴线
永磁同步电动机电磁转矩的计算

r2Br B d
1
•
式中:p为电机极对数; 角(机械弧度)。
1
、2
为求解区域的起、止
磁通法
永磁同步电动机的相量关系 如图1所示, 可以得到负载 气隙合成电动势的直轴分量 和交轴分量为:
式中, E0 、E 为空载反电 动势和负载气隙合成电动势。
麦克斯韦应力张量法
• 麦克斯韦应力张量法是由力学理论推导出的转矩 计算方法。在二维电磁场中,作用于电机定子或转 子上的切向电磁力密度
ft
1 u0
Bn Bt
• 电磁转矩由切向力产生,如果沿半径r的圆周积分,
则电磁转矩的表达式为
Tem
Lef u0
r2Br B d
麦克斯韦应力张量法
• 式中:r是位于气隙中的圆周半径; Br 、B 分别为半 径r处气隙磁密的径向和切向分量。Lef 是电机等
永磁同步电动机电磁转矩的计算
背景及意义
• 目前高性能永磁体广泛应用, 永磁电机也随之普遍 化, 但电机磁路结构的变化多样给电机的电磁计算 带来了不便, 随着有限元法的提出以及计算机性能 的提高, 永磁电机电磁转矩的计算也得到了改善。 电磁转矩是电机的一个重要指标,电磁转矩的准确 计算也会影响一台电机的性能。
样机电磁转矩计算
• 样机在额定负载运行状态下, 电磁转矩的测量值为 TemN 1220N • m , • 通过麦克斯韦应力张量法计算所得电磁转矩 TemMAX 1190.89N,• m ,误
差为
• 磁通法计算结果 TemCT 1182.76N • m , 误差为
两种计算结果与实际值的误差在合理范围内。
永磁直流电机电磁计算

永磁直流电机电磁计算一、磁路计算磁路计算是永磁直流电机电磁计算的基础。
磁路计算的主要目的是确定电机内部的磁场分布,从而为电磁场计算、转矩计算、损耗计算等提供基础数据。
在进行磁路计算时,需要先确定电机的主要参数,如气隙长度、绕组匝数、永磁体尺寸等。
然后,根据这些参数计算出磁路中的磁通密度分布,从而得出每个结构部分的磁通量和磁动势。
二、电磁场计算电磁场计算是永磁直流电机电磁计算的核心。
电磁场计算的主要目的是确定电机内部的电磁场分布,包括电势、电流、磁场等。
在进行电磁场计算时,需要使用数值计算方法,如有限元法、有限差分法等。
这些方法可以模拟电机的三维电磁场分布,从而得出每个结构部分的电磁特性和性能指标。
三、转矩计算转矩计算是永磁直流电机电磁计算的重要环节。
转矩计算的主要目的是确定电机输出的转矩大小和转矩方向。
在进行转矩计算时,需要考虑到电机的机械结构和工作原理。
通常采用的方法包括电动机转矩计算公式和能量转换公式等。
通过这些方法可以得出电机的输出转矩和效率等性能指标。
四、损耗计算损耗计算是永磁直流电机电磁计算的关键步骤之一。
损耗计算的主要目的是确定电机内部的能量损失,包括铜损、铁损、机械损失等。
在进行损耗计算时,需要考虑到电机的运行特性和结构特点。
通常采用的方法包括根据电阻和电流计算铜损、根据磁场和导体材料计算铁损、根据机械性能参数计算机械损失等。
通过这些方法可以得出电机的总损耗和各部分的能量损失。
五、温度场计算温度场计算是永磁直流电机电磁计算的重要环节之一。
温度场计算的主要目的是确定电机内部的温度分布,从而为电机的热设计和安全运行提供依据。
在进行温度场计算时,需要考虑到电机的热源和散热条件。
通常采用的方法包括有限元法和有限差分法等数值计算方法。
通过这些方法可以得出电机各个部分的温度分布和热应力分布等。
六、结构优化设计结构优化设计是永磁直流电机电磁计算的又一重要环节。
结构优化设计的主要目的是提高电机的性能和可靠性,包括优化电机结构、改进散热设计、提高机械强度等。
永磁同步电动机电磁计算程序

Λδ Λb λδ λ1 λσ
cm A
T A A/cm cm cm T cm
23.26410353 4.209707539
6.2
2.17 26.10018674 50.48310465 166.2166762
2.5 2
19.80654674 0.02
27.9841 0.475324588
3.97E+00 8.93E+01
0.185361257 13.36
0.861134631 1.04E-02
cm
Ksk1
y
Kdp1 Kd1
α
°
q1
Kp1
β
Kf
KΦ
Kδ
σ0
b1m0
Φδ0
Wb
Bδ0
56 气隙磁压降
直轴磁路 交轴磁路 57 定子齿磁路计算长度 58 定子齿宽 59 定子齿磁密 60 定子齿磁压降 查第2章附录图2E-3得 61 定子轭计算高度 62 定子轭磁路计算长度 63 定子轭磁密 64 定子轭磁压降 查第2章附录图2C-4得 查第2章附录图2E-3得 65 磁路齿饱和系数 66 每对极总磁压降
38 永磁体相对回复磁导率
ss
cm2
h
cm
si
cm2
h1s
cm
Ci
cm
se
cm2
sf
%
N1
铷铁棚 矩形
ap b1p a1p aBr Br20 t Br Hc20 aHc
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
永磁电机电磁计算吴海鹰(中船重工集团公司712研究所武汉 430064)摘要:本文采用有限元法,运用场——路结合方法进行电磁设计计算,验证电机结构参数的合理性。
利用电机的周期性和齿槽结构的重复性,采用简化计算的方法即只计算一个槽距范围,对得到的结果数据进行数据扩展,得到电机转子转过一对磁极范围的数据,可使计算速度提高几十倍。
用上述计算方法设计计算了兆瓦级船舶交流永磁推进电机,各种参数计算值与实验结果相比基本相符,能够满足设计的精度要求。
关键词:反电势电感叠压系数磁导率各项异性1引言科技飞速发展的今天,大型电机和特种电机的设计技术都有了巨大的进步,电机各项参数计算的精度要求越来越高,设计研发的周期越来越短,传统的分析计算不能很好的满足上述要求。
有限元法作为一种电机电磁场数值解法臻于完善,其应用也越来越广泛。
作为一种近似的数值计算方法,有限元法的计算精度很大程度上取决于网格剖分的疏密程度。
对于一台电机若采用三维模型计算,其计算量很大,不利于调试。
实践证明如果忽略电机端部的影响,采用二维的磁场分析也能满足设计的精度要求。
利用电机结构的周期性,选用充分、合理的电机计算区域作为有限元模型,可以对电机模型进一步的简化。
2分析过程本文应用ANSYS7.0有限元软件,对大型永磁电机的电磁场进行分析和计算。
这里只研究平行平面场即二维电磁场问题,因而只有一个自由度即矢量磁势Az。
电机的对称周期取一对磁极范围。
考虑漏磁的影响,把转轴和机座作为模型的内外边界。
电磁场的经典理论是麦克斯韦方程组,此处不再累述。
这里引入矢量磁势Az的重要意义在于对平行平面场,两点间矢量磁势的差值就是两点间沿z轴单位长度上的磁通。
要注意二维电磁场分析计算得到的基本结果数据都是Az值,通过对Az值进行处理可以方便的求出电机各处的磁密和磁场强度,磁通、反电势和电磁转矩等。
有限元分析的基本思路如图1所示。
收稿日期:2004-06-21 2.1 定义电机材料特性2.1.1 定义硅钢片的材料属性与磁化曲线定义硅钢片材料特性时要注意,有些大型电机使用各向异性的冷轧硅钢片,这里需考虑材料的正交各向异性。
对定子齿部,认为磁密的方向偏离轧制方向为0度;对定子轭部,磁密的方向偏离轧制方向为90度;对转子铁芯来说,偏离轧制方向为0度,导磁率按静磁场选择(f=0)。
输入BH曲线要注意:a) B值与H值要一一对应,并且单调连续,BH曲线缺省通过原点,(0,0)点不输入。
b) ANSYS程序根据BH曲线自动计算v-B曲线(v为磁阻率),它应该也是单调连续的。
因此如果v-B曲线不单调要重新修正B-H曲线上的数据点,如图2所示。
c) BH曲线应覆盖材料的全部工作范围,提供足够多的数据点以完整描述该材料特性。
有时要剔除那些数值较大的点,再观察曲线的单调性。
图1 有限元分析过程定义单元类型,材料属性电机的基本尺寸的参数化转子建模(含气隙)定子建模(含气隙)径向拼接模型处理模型的边界条件施加载荷求解后处理2.1.2 永磁体的材料特性需要说明的是永磁体的退磁曲线是指剩磁密度Br 与矫顽力Hcb 的曲线,以下简称BH 曲线。
退磁曲线通常在第二象限,但ANSYS 程序中需按第一象限输入。
此外还需要知道永磁体的工作温度,即电机内部温度分布,Br 的可逆温度系数,Hcb 的可逆温度系数。
2.2 参数化建模参数化建模具有很多优点,各个变量物理意义明确,便于查找和修改。
而且可以通过对话框快速对电机尺寸参数进行调整,缩短调试程序和优化设计的时间。
这里采用ANSYS 内部的对话框进行交互,可以方便其他设计人员对程序的调试,提高程序的通用性,如图3:图3 与用户交互的ANSYS 对话框可以在图3中输入不同功率对应的相电流和转速;也可以调整电机的气隙长度,定子内径和定子铁芯长等电机重要尺寸参数;可以输入用于保存磁通量和电磁转矩结果文件的文件名。
2.3 有限元模型的建立和边界条件定、转子应分别建模,这样两部分模型不会相互干扰。
定、转子之间的气隙,可定义两层或更多层,再经过径向拼接得到整个求解区域。
分网时应注意疏密结合,气隙部分网格要足够稠密,而且沿径向应均匀分网。
其它部分网格可稀疏些。
模型尽量使用四边形网格,并保证节点连续。
这里只研究电机转速恒定情况,用有限元法进行电机的电磁场分析,要模拟电机定、转子之间的相对运动。
这里使用运动边界法,即假设定子模型静止不动,让转子部分旋转,和真实情况一样。
具体如下:气隙模型中有一条定、转子网格重合的公共运动边界,分别为定、转子的运动边界上的节点编号,并且保证相邻节点径向间距相等,这样能保证转子旋转后运动边界上的节点重合,压缩重合的关键点(KP )、节点(node ),保持网格的连续性。
如图4。
2.4 后处理 2.4.1 反电势的计算图4 运动边界示意图单根导体的反电势的计算公式推导(不计斜槽)。
根据反电势计算的基本公式:dtd E ω=(1) 在转子为匀速旋转时:ωθd d dt =(2) 式中:θ——转子机械角(弧度) ω——转子机械角速度ψ——所求导体的磁链 对于单根导体:θωd d = (3)而根据矢量磁位的定义: z A d L d ×=1φ (4)式中:——定子铁心长度z A ——所求导体的Z 方向上的矢量磁位。
在进行有限元分析时,计算不同转子位置的磁场分布,而且每次旋转的角度Δθ是一个定值。
θω∆∆××=zA L E 1 (5)z A K E ∆×= (6)式中:θω∆×=1L K ,为常量。
2.4.2 ANSYS 程序中反电势的计算首先使用ANSYS 的APDL 语言在工作路径中创建数据文件写入每个线圈的Az 值,然后关闭文件。
循环计算中每次打开数据文件,数据以追加方式顺序写入。
最后使用上述公式(6)可计算出单根导体反电势,再根据一相下所有导体的串并联关系得到一相绕组的反电势。
2.4.3 反电势的简化计算利用电机的周期性和齿槽结构的重复性,对于空载情况可采用反电势的简化计算方法,快速得出计算结果(比上述方法快几十倍),并且结果与上述方法相同,这样可大量减少设计时间,快速对不同设计方案进行比较,从而得到最优方案。
这里反电势的简化计算是仅对定、转子在一个槽距范围的几个相对位置进行分析,而不是一对极距范围,然后对结果数据进行扩展得到一对极范围内的数据。
注意此方法不能用于负载情况,因负载时由于电枢反应电机电磁场发生畸变。
2.4.4 考虑斜槽对反电势的影响此处斜槽指把定子槽扭斜一个定子齿距,这样定子槽内一根导体沿轴向各部分感应的齿协波反电势相位就不同了,叠加起来就消弱了导体的齿协波反电势。
因上述计算都是二维平面场计算,只有一个自由度Az ,不能在模型中直接体现斜槽的影响。
对空载情况,只要把一个槽距范围内的计算结果相加求平均值即可。
对于负载情况因线圈中通电流,磁场发生畸变,在循环计算中取出沿轴向的多个计算平面分别进行计算(线圈中通的电流幅值和相位相同,但定转子的相对位置不同),对得到计算结果相加再求平均值的方法来考虑斜槽的影响。
图6、图7分别是不计斜槽和考虑斜槽时一相绕组空载反电势波形。
从图中可见,考虑斜槽时导体中反电势波形的幅值减小了,并且齿槽效应对波形的影响也明显减小了。
2.4.5 考虑硅钢片叠压系数的影响大型电机的定转子铁心多采用硅钢片叠压而成,因而应考虑叠压系数K ef 的影响,所以硅钢片的BH 曲线一般不能直接被程序调用,应该对硅钢片的磁化曲线进行修正。
如图8所示,已知硅钢片垂直于磁力线方向的截面积为S ,磁力线平行穿过硅钢片,因硅钢片之间有多层空气隙,实际的铁芯面积为S ×K ef 。
硅钢片的磁导率远远大于空气,铁芯中的磁力线都从硅钢片经过,因而铁芯中实际磁密值高于不考虑铁芯迭压系数时的磁密值。
2.4.6电机的计算转矩在后处理中还可以通过ANSYS 内部的torq2d 或torqc2d 磁宏命令计算电机的计算转矩,先用path 命令在气隙中定义一条圆弧路径(要注意圆弧路径轴向经过周期对称后应该是闭合的),再调用torq2d 宏命令。
注意此时的结果是电机一个周期下沿轴向单位长度的计算转矩,此结果乘以转子铁芯长,再乘以计算区域的周期数才是电机的计算电磁转矩,如图9所示。
2.4.7 损耗的计算这里电机的损耗主要研究定子铁耗的计算方法。
硅钢片的损耗系数(单位为W kg )通常按以下数值方程计算:he p =50/10P 2B 3.1)50(f 式中50/10P ——当B =1T ,f=50Hz 时,硅钢片单位质量的损耗。
硅钢片的基本铁耗的一般公式为:fe p =a K he p fe G式中fe G ——受交变磁化或旋转磁化作用的硅钢片的重量;a K ——经验系数。
较准确的计算方法是把电机定子沿径向分成“K”层,以保证磁密在每层范围内有足够的精度,总的损耗通过对各层损耗求和得到。
考虑到硅钢片的各向异性,沿轧制方向和垂直于轧制方向的单位损耗曲线是不同的,因而分别计算径向磁密和切向磁密的损耗值。
在后处理中取出电机有限元模型中定子硅钢片部分的每个单元的面积和该单元对应的切向磁密和径向磁密值。
由该单元的各磁密值分别从对应的硅钢片的单位损耗曲线上插值得到单位铁损。
每个单元的面积乘以对应的单位铁损再对所有定子硅钢片部分单元求和,所得值与定子铁芯长、叠压系数、硅钢片密度和极对数的乘积即为定子铁损。
2.4.8 气隙磁密波形和磁力线电机在进行能量转换时,无论是从机械能变成电能,或是从电能变成机械能,能量都是以电磁能的形式通过定、转子之间的气隙进行传递的,气隙空气硅钢片磁密是电机电磁场计算中重要的物理量。
气隙磁密波形和计算区域内磁力线分布如图10和图11所示。
2.4.9 后处理中还可以进行协波分析,漏磁系数和电感的计算等。
3 结论ANSYS 有限元软件为电机的仿真和电机参数的计算提供了非常好的数值计算方法,相信随着对有限元认识的加深,我们可以更加深入、细致、精确的对电机进行分析和计算,大大加快电机设计、生产的研发周期。
图11 磁力线分布参考文献:[1] 金建铭(美)著,王建国译,葛德彪校.电磁场有限元方法.西安电子科技大学出版社,1998年1月.[2] 唐任远等著.现代永磁电机理论与设计.北京:机械工业出版社,1997年12月.[3] 冯慈璋主编.电磁场(上下册).北京.高等教育出版社, 1983年10月,第二版.[4] 陈世坤主编.电机设计. 北京:机械电子出版社,1990年10月,第二版.[5] 李发海等著.电机学. 北京:科技出版社,1991年8月,第二版 .[6] ANSYS 7.0培训手册.Electromagnetic Field Calculation of AC PM Propulsive Motor for ShipsWu Haiying(Wuhan Marine Electric Propulsion Research Institute, CSIC , Wuhan 430064 , China)Abstract :On the basis of the electromagnet field analysis and calculation of the PM motor, we use the finite element method and field —current conjugation for EM field design to confirm structural parameters of the motor. With the periodicity of motor and the repeatability of the tooth space structure, by using a simplified calculation, that is calculating only one slot pitch, and extending resulting data, and then getting the data that the rotor rotates over a pair of magnetic poles, the speed of calculation is increased by several ten times. We have designed the megawatt AC PM propulsion motor of the ships, and the calculated result of the parameters is up to the experimental result basically.Key words :EMF ;inductance ;silicon sheet lamination-stacking ;magnetic inductivity anisotropy(×10) 8.6456.9165.1873.4581.7290-1.729-3.458-5.187-6.916-8.645(×10)。
