高一数学立体几何练习题及部分标准答案汇编
高一数学立体几何大题(含答案)

4.in/w).6=4r3.
例 3:如图,PD ⏊ 平面 ABCD,AD ⏊ CD,AB ⎳ CD,PQ ⎳ CD,AD
= CD = DP = 2PQ = 2AB = 2, 点 M 为 BQ 的中点 .
为 的 P Q C -
M-
大小
0 .
Sepm E 却 二
忙=
以 <m (
,
蕊 令 1
二
5 = -
3
※ 琴 㱺 sina.me
㱺 Somc 二 士 心 的 ✗
=r
.
二号 器 Q到 平面 阰 的 距离 为 : d = 2 5
.io
shnoifst.no
,
㱺 VQ-pmc-f-Somc.dk/nEfsio=fs'm0.
PCHEF 进而 1211 平面 ,
在 阳 仲 , PA-E.AE/,PC=0=)PA4AcEpc2=sAc-1A.
所以 又由 题 干 知 : A 4 P B ,
A
C
1
-
平面阳
13
.
13) 易知 SEFG 二 ftp.c , 所以 /7AB=fSopAB-AC.=f-li2nE.iS'm45J-l
1 求二面角 Q - PM - C 的正弦值;
2 若 N 为线段 CQ 上的点,且直线 DN 与平面 PMQ 所成的角为
π 6
,
求线段
QN
的长
.
子 (2) 由 山 知 二面⻆ QPMC 的 大小 为 ,
劝 的平面 PMQ所 成的 ⻆ 为 至
所以 叽 与平面PMC 所 成的 ⻆
高一立体几何试题及答案详解
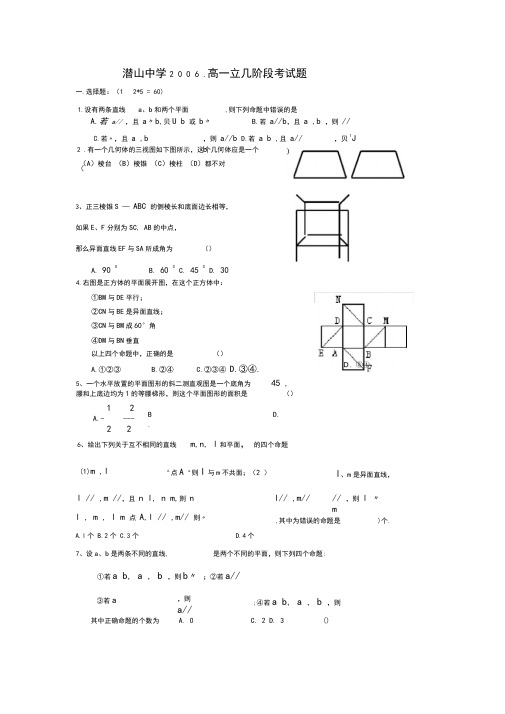
潜山中学2 0 0 6 .高一立几阶段考试题A.若 a// ,且 a 〃b,贝U b 或 b 〃B.若 a//b ,且 a ,b ,则 //l , m , l m 点 A,l // ,m// 则〃A.l 个B.2个C.3个D.4个7、设a 、b 是两条不同的直线,是两个不同的平面,则下列四个命题:①若a b, a , b ,则b 〃 ;②若a//一.选择题:(1 2*5 = 60) 1.设有两条直线a 、b 和两个平面,则下列命题中错误的是C .若〃,且 a ,b ,则 a//bD .若 a b ,且 a// ,贝1Jb 2 .有一个几何体的三视图如下图所示,这个几何体应是一个( (A )棱台 (B )棱锥 (C )棱柱 (D )都不对 3、正三棱锥S — ABC 的侧棱长和底面边长相等, 如果E 、F 分别为SC, AB 的中点, 那么异面直线EF 与SA 所成角为 () A. 90 0 B. 60 0 C. 45 0D. 30 4.右图是正方体的平面展开图,在这个正方体中: ①BM 与DE 平行; ②CN 与BE 是异面直线; ③CN 与BM 成60°角 ④DM 与BN 垂直 以上四个命题中,正确的是 () A.①②③ B.②④ C.②③④ D.③④. 5、一个水平放置的平面图形的斜二测直观图是一个底角为 45 ,腰和上底边均为1的等腰梯形,则这个平面图形的面积是()1 2 A.- --- 2 2 B.D. 6、给出下列关于互不相同的直线 m,n, l 和平面, 的四个命题 (1)m ,l A,点A m,则l 与m 不共面;(2 )l 、m 是异面直线,l // ,m //,且 n l, n m,则 n l// ,m//// ,则 l 〃m③若a,则a//;④若a b, a , b ,则其中正确命题的个数为A. 0C. 2D. 3 (),其中为错误的命题是)个.8 .定点P 不在4ABC 所在平面内,过P 作平面a ,使^ ABC 的三个顶点到a 的距离相等,二.填空题:(4*6 = 2 4)14.106山东•理】如图,在等腰梯形 ABCD 中,AB=2DC=2 , / DAB=60 中点,将 AADE 与4BEC 分别沿ED 、EC 向上折起,使 A 、B 重 合于点P,则三棱锥P —DCE 的外接球的体积为 II 5如图,一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞D, E, F ,且知有()(A ) 1 个 (B ) 2 个 9、下列各图是正方体或正四面体, (C) 3 个(D) 4 个P, Q, R, S 分别是所在棱的中点,这四个点中不共面的一个图是SSSSQQQ Q0、如图,在一根长 (B) (C) (D)11cm,外圆周长6cm 的圆柱形柱体外表面,用一根细铁丝缠绕,组成 如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为 (A) 61cm (B) J157 cm (C) J1021 cm1 .(天津卷10)如图,在长方体 ABCD A 1B 1c l D 1中,AB A D 1的两个平行截面将长方体分成三部分, 其体积分别记为 V I V AEA 1 DFD I ,V 3 VB I E I BC 1F 1C 。
高一数学立体几何练习题及部分答案大全

立体几何试题一.选择题(每题4分,共40分)1.已知AB 0300300150空间,下列命题正确的个数为( )(1)有两组对边相等的四边形是平行四边形,(2)四边相等的四边形是菱形(3)平行于同一条直线的两条直线平行 ;(4)有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 4 3.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是( )A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m αα过平面α外一点,作与α平行的平面,则这样的平面可作( ) A 1个 或2个 B 0个或1个 C 1个 D 0个6.如图,如果MC ⊥菱形ABCD 所在平面,那么MA 与BD 的位置关系是( )A 平行B 垂直相交C 异面D 相交但不垂直 7.经过平面α外一点和平面α内一点与平面α垂直的平面有( )A 0个B 1个C 无数个D 1个或无数个 8.下列条件中,能判断两个平面平行的是( ) A 一个平面内的一条直线平行于另一个平面; B 一个平面内的两条直线平行于另一个平面 C 一个平面内有无数条直线平行于另一个平面 D 一个平面内任何一条直线都平行于另一个平面 9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是( ) A //,,m n n m βα⊥⊂ B //,,m n n m βα⊥⊥ C ,,m n m n αβα⊥=⊂ D ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有( ) A 1个 B 2个 C 3个 D 4个二.填空题(每题4分,共16分)11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N ,设直线AB 与平面α交于点O ,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、 解答题15(10分)如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =。
高一数学立体几何练习题及部分答案大全.docx

立体几何试题一.选择题(每题 4 分,共 40 分)1. 已知 AB3003001500空间,下列命题正确的个数为()(1)有两组对边相等的四边形是平行四边形, (2)四边相等的四边形是菱形(4)有两边及其夹角对应相等的两个三角(3)平行于同一条直线的两条直线平行 ;形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是()A平行B相交C在平面内D平行或在平面内4. 已知直线 m过平面外一点,作与平行的平面,则这样的平面可作()A 1 个或 2 个B 0个或1个C1个 D 0个6.如图 , 如果 MC 菱形 ABCD 所在平面 , 那么 MA与 BD的位置关系是 ( )A平行B垂直相交C异面D相交但不垂直7. 经过平面外一点和平面内一点与平面垂直的平面有()A 0 个B 1个C无数个 D 1个或无数个8.下列条件中 , 能判断两个平面平行的是 ( )B一个平面内的两条直线平行于另一个平面C一个平面内有无数条直线平行于另一个平面D一个平面内任何一条直线都平行于另一个平面9. 对于直线m ,n 和平面,, 使成立的一个条件是 ( )A m // n, n, mB m // n, n,mC m n,I m, nD m n, m //, n //)10 . 已知四棱锥 , 则中 , 直角三角形最多可以有 (A 1个B2个 C 3个D4个二.填空题(每题 4 分,共16 分)11. 已知ABC的两边 AC,BC分别交平面于点M,N,设直线AB与平面交于点O,则点 O与直线 MN的位置关系为 _________12.过直线外一点与该直线平行的平面有 ___________个,过平面外一点与该平面平行的直线有_____________条13. 一块西瓜切 3 刀最多能切 _________块14.将边长是 a 的正方形 ABCD沿对角线 AC 折起 , 使得折起后 BD得长为 a, 则三棱锥D-ABC的体积为 ___________三、解答题15(10 分)如图,已知 E,F 分别是正方形ABCD A1B1C1 D1的棱 AA1和棱 CC1上的点,且 AE C1 F 。
高一必修二立体几何练习试题(含答案)

《立体几何初步》练习题一、 选择题1、一条直线和三角形的两边同时垂直,则这条直线和三角形的第三边的位置关系是( )A 、垂直B 、平行C 、相交不垂直D 、不确定 2. 在正方体1111ABCD A B C D -中, 与1A C 垂直的是( )A. BDB. CDC. BCD. 1CC3、线n m ,和平面βα、,能得出βα⊥的一个条件是( )A.βα//n ,//m ,n m ⊥B.m ⊥n ,α∩β=m ,n ⊂αC.αβ⊆⊥m n n m ,,//D.βα⊥⊥n m n m ,,//4、平面α与平面β平行的条件可以是( )A.α内有无穷多条直线与β平行;B.直线a//α,a//βC.直线a α⊂,直线b β⊂,且a//β,b//αD.α内的任何直线都与β平行 5、设m 、n 是两条不同的直线,,,αβγ是三个不同的平面,给出下列四个命题: ①若m ⊥α,n //α,则m n ⊥ ②若αβ//,βγ//,m ⊥α,则m ⊥γ ③若m //α,n //α,则m n // ④若αγ⊥,βγ⊥,则//αβ其中正确命题的序号是( ) A.①和② B.②和③ C.③和④ D.①和④6.点P 为ΔABC 所在平面外一点,PO ⊥平面ABC ,垂足为O,若PA=PB=PC ,则点O 是ΔABC 的( ) A.内心 B.外心 C.重心 D.垂心7. 若l 、m 、n 是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是( )A .若//,,l n αβαβ⊂⊂,则//l nB .若,l αβα⊥⊂,则l β⊥ C. 若,//l l αβ⊥,则αβ⊥ D .若,l n m n ⊥⊥,则//l m 8. 已知两个平面垂直,下列命题中正确的个数是( ) ①一个平面内的已知直线必垂直于另一个平面的任意一条直线; ②一个平面内的已知直线必垂直于另一个平面的无数条直线; ③一个平面内的任一条直线必垂直于另一个平面;④过一个平面内任意一点作交线的垂线,则垂线必垂直于另一个平面. A.3 B.2 C.1 D.09.(2013浙江卷)设m.n 是两条不同的直线,α.β是两个不同的平面,( )A .若m ∥α,n ∥α,则m ∥nB .若m ∥α,m ∥β,则α∥βC .若m ∥n,m ⊥α,则n ⊥αD .若m ∥α,α⊥β,则m ⊥β10.(2013广东卷)设l 为直线,,αβ是两个不同的平面,下列命题中正确的是( ) A .若//l α,//l β,则//αβ B .若l α⊥,l β⊥,则//αβ C .若l α⊥,//l β,则//αβ D .若αβ⊥,//l α,则l β⊥二、填空题11、在棱长为2的正方体ABCD —A 1B 1C 1D 1中,E ,F 分别是棱AB ,BC 中点,则三棱锥B —B 1EF 的体积为 .12.对于空间四边形ABCD ,给出下列四个命题:①若AB=AC ,BD=CD 则BC ⊥AD ;②若AB=CD ,AC=BD 则BC ⊥AD ;③若AB ⊥AC ,BD ⊥CD 则BC ⊥AD ;④若AB ⊥CD , BD ⊥AC 则BC ⊥AD ;其中真命题序号是 .13. 已知直线b//平面α,平面α//平面β,则直线b 与β的位置关系为 .14. 如图,△ABC 是直角三角形,∠ACB=︒90,PA ⊥平面ABC ,此ABCP图形中有 个直角三角形三、解答题15.如图,PA ⊥平面ABC ,平面PAB ⊥平面PBC 求证:AB ⊥BC16.如图,ABCD 和ABEF 都是正方形,M AC N FB ∈∈,,且AM FN =。
【必刷题】2024高一数学下册立体几何初步专项专题训练(含答案)

【必刷题】2024高一数学下册立体几何初步专项专题训练(含答案)试题部分一、选择题:1. 在空间直角坐标系中,点A(1,2,3)关于x轴的对称点的坐标是()A. (1,2,3)B. (1,2,3)C. (1,2,3)D. (1,2,3)2. 下列关于直线l:x=1,y=2+t,z=32t的描述,正确的是()A. 直线l平行于x轴B. 直线l平行于y轴C. 直线l平行于z轴D. 直线l垂直于x轴3. 一个正方体的对角线长度为6根号3,则其表面积为()A. 216B. 54C. 108D. 1444. 若长方体的长、宽、高分别为2cm、3cm、4cm,则其对角线长度为()A. 5cmB. 6cmC. 7cmD. 9cm5. 下列关于平面α:2x3y+z=6的描述,正确的是()A. 平面α平行于x轴B. 平面α平行于y轴C. 平面α平行于z轴D. 平面α垂直于x轴6. 下列关于点P(2,3,4)到平面α:x+y+z=6的距离,正确的是()A. 1B. 2C. 3D. 47. 若三棱锥的底面是边长为1的正三角形,侧棱长为根号3,则其体积为()A. 1/3B. 1/6C. 1/9D. 1/128. 下列关于球体的描述,正确的是()A. 球体的表面积与半径成正比B. 球体的体积与半径成正比C. 球体的表面积与半径的平方成正比D. 球体的体积与半径的平方成正比9. 若四面体的四个面均为等边三角形,边长为a,则其体积为()A. a^3/6B. a^3/12C. a^3/18D. a^3/2710. 下列关于空间向量夹角的描述,正确的是()A. 向量a与向量b的夹角为90°,则a·b=0B. 向量a与向量b的夹角为0°,则a·b=0C. 向量a与向量b的夹角为180°,则a·b=0D. 向量a与向量b的夹角为60°,则a·b=0二、判断题:1. 在空间直角坐标系中,点A(0,0,0)到点B(1,1,1)的距离等于根号3。
高一立体几何试卷及答案

高一立体几何试卷及答案The document was prepared on January 2, 2021立体几何试题一.选择题每题4分,共40分1.已知AB 0300300150空间,下列命题正确的个数为1有两组对边相等的四边形是平行四边形,2四边相等的四边形是菱形3平行于同一条直线的两条直线平行 ;4有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m αα过平面α外一点,作与α平行的平面,则这样的平面可作A 1个 或2个B 0个或1个C 1个D 0个6.如图,如果MC ⊥菱形ABCD 所在平面,那么MA 与BD 的位置关系是A 平行B 垂直相交C 异面D 相交但不垂直7.经过平面α外一点和平面α内一点与平面α垂直的平面有A 0个B 1个C 无数个D 1个或无数个8.下列条件中,能判断两个平面平行的是A 一个平面内的一条直线平行于另一个平面;B 一个平面内的两条直线平行于另一个平面C 一个平面内有无数条直线平行于另一个平面D 一个平面内任何一条直线都平行于另一个平面9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是A //,,m n n m βα⊥⊂B //,,m n n m βα⊥⊥C ,,m n m n αβα⊥=⊂D ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有A 1个B 2个C 3个D 4个二.填空题每题4分,共16分11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N,设直线AB 与平面α交于点O,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、 解答题1510分如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =.求证:四边形1EBFD 是平行四边形1610分如图,P 为ABC ∆所在平面外一点,AP=AC,BP=BC,D 为PC 的中点, 证明:直线PC 与平面ABD 垂直CB1712分如图,正三棱锥A-BCD,底面边长为a,则侧棱长为2a,E,F分别为AC,AD 上的动点,求截面BEF∆周长的最小值和这时E,F的位置.DC1812分如图,长方形的三个面的对角线长分别是a,b,c,求长方体对角线AC'的长C1bC BA答案1三点共线2无数 无数3a 1证明: 1AE C F = 11AB C D =11EAB FC D ∠=∠∴ 11EAB FC D ∆≅∆1EB FD ∴=过1A 作11//A G D F又由1A E ∥BG 且1A E =BG可知1//EB AG 1//EB D F ∴∴四边形1EBFD 是平行四边形2 ∵AP AC =D 为PC 的中点∴AD PC ⊥∵BP BC =D 为PC 的中点∴BD PC ⊥∴PC ⊥平面ABD∴AB PC ⊥3 提示:沿AB 线剪开 ,则BB '为周长最小值.易求得EF 的值为34a ,则周长最小值为114a . 4解:()()()222AC AC CC ''=+ ()()222()AB BC CC '=++222a b c =++。
高一数学立体几何练习题及部分答案汇编之欧阳法创编

立体几何试题一.选择题(每题4分,共40分)1.已知AB//PQ,BC//QR,则∠PQP等于()A 030B 030C 0150 D 以上结论都不对2.在空间,下列命题正确的个数为()(1)有两组对边相等的四边形是平行四边形,(2)四边相等的四边形是菱形(3)平行于同一条直线的两条直线平行;(4)有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是()A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m//平面α,直线n在α内,则m 与n的关系为()A 平行B 相交C 平行或异面D 相交或异面5.经过平面α外一点,作与α平行的平面,则这样的平面可作()A 1个或2个B 0个或1个C 1个D 0个6.如图,如果MC⊥菱形ABCD所在平面,那么MA 与BD的位置关系是( )A 平行B 垂直相交C 异面D 相交但不垂直7.经过平面α外一点和平面α内一点与平面α垂直的平面有()A 0个B 1个C 无数个D 1个或无数个8.下列条件中,能判断两个平面平行的是( )A 一个平面内的一条直线平行于另一个平面;B 一个平面内的两条直线平行于另一个平面C 一个平面内有无数条直线平行于另一个平面D 一个平面内任何一条直线都平行于另一个平面9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是( )A //,,m n n m βα⊥⊂B //,,m n n m βα⊥⊥C ,,m n m n αβα⊥=⊂D ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有( )A 1个B 2个C 3个D 4个二.填空题(每题4分,共16分)11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N ,设直线AB 与平面α交于点O ,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、解答题15(10分)如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =。
立体几何经典习题集(含答案)

立体几何基础A 组题一、选择题:1.下列命题中正确命题的个数是 ( ) ⑴ 三点确定一个平面⑵ 若点P 不在平面α内,A 、B 、C 三点都在平面α内,则P 、A 、B 、C 四点不在同一平面内 ⑶ 两两相交的三条直线在同一平面内⑷ 两组对边分别相等的四边形是平行四边形A.0B.1C.2D.3答案:A2.已知异面直线a 和b 所成的角为︒50,P 为空间一定点,则过点P 且与a 、b 所成的角都是︒30的直线条数有且仅有 ( ) A.1条 B.2条 C.3条 D.4条答案:B 3.已知直线⊥l 平面α,直线⊂m 平面β,下列四个命题中正确的是 ( ) (1) 若βα//,则m l ⊥ (2) 若βα⊥,则m l // (3) 若m l //,则βα⊥ (4) 若 m l ⊥,则βα//A.(3)与(4)B.(1)与(3)C.(2)与(4)D.(1)与(2)答案:B4.已知m 、n 为异面直线,⊂m 平面α,⊂n 平面β,l =βα ,则l ( ) A.与m 、n 都相交 B.与m 、n 中至少一条相交 C.与m 、n 都不相交 D.至多与m 、n 中的一条相交答案:B5.设集合A={直线},B={平面},B A C =,若A a ∈,B b ∈,C c ∈,则下列命题中的真命题是 ( )A. c a b a b c ⊥⇒⎭⎬⎫⊥// B.c a c b b a //⇒⎭⎬⎫⊥⊥ C.c a b c b a //////⇒⎭⎬⎫ D. c a b c b a ⊥⇒⎭⎬⎫⊥//答案:A6.已知a 、b 为异面直线,点A 、B 在直线a 上,点C 、D 在直线b 上,且AC=AD ,BC=BD ,则直线a 、b 所成的角为 ( ) A. ︒90 B. ︒60 C. ︒45 D. ︒30答案:A7.下列四个命题中正确命题的个数是 ( ) 有四个相邻侧面互相垂直的棱柱是直棱柱 各侧面都是正方形的四棱柱是正方体底面是正三角形,各侧面都是等腰三角形的三棱锥是正三棱锥A.1个B.2个C.3个D.0个答案:D8.设M={正四棱柱},N={长方体},P={直四棱柱},Q={正方体},则这些集合之间关系是 ( ) A.Q M N P B.Q M N P C.Q N M P D.Q N M P答案:B9.正四棱锥P —ABCD 中,高PO 的长是底面长的21,且它的体积等于334cm ,则棱AB 与侧面PCD 之间的距离是 ( ) A.cm 2 B. cm 2 C. cm 1 D.cm 22答案:A10.纬度为α的纬圈上有A 、B 两点,弧在纬圈上,弧AB 的长为απcos R (R 为球半径),则A 、B 两点间的球面距离为 ( )A. R πB. R )(απ-C. R )2(απ-D. R )2(απ-答案:D11.长方体三边的和为14,对角线长为8,那么 ( ) A.它的全面积是66 B.它的全面积是132C.它的全面积不能确定D.这样的长方体不存在答案:D12.正四棱锥P —ABCD 的所有棱长都相等,E 为PC 的中点,那么异面直线BE 与PA 所成角的余弦值等于( )A.21B. 22C. 32D. 33答案:D13.用一个过正四棱柱底面一边的平面去截正四棱柱,截面是 ( )A.正方形B.矩形C.菱形D.一般平行四边形答案:B二、填空题:14.正方体1111D C B A ABCD -中,E 、F 、G 分别为AB 、BC 、CC 1的重点,则EF 与BG 所成角的余弦值为________________________答案:510 15.二面角βα--a 内一点P 到两个半平面所在平面的距离分别为22和4,到棱a 的距离为24,则这个二面角的大小为__________________答案:︒︒16575或16.四边形ABCD 是边长为a 的菱形,︒=∠60BAD ,沿对角线BD 折成︒120的二面角A —BD —C 后,AC 与BD 的距离为_________________________答案:a 43 17.P 为︒120的二面角βα--a 内一点,P 到α、β的距离为10,则P 到棱a 的距离是_________________答案:3320 18.如图:正方形ABCD 所在平面与正方形ABEF 所在平面成︒60的二面角,则异面直线AD 与BF 所成角的余弦值是______________________答案:4219.已知三棱锥P —ABC 中,三侧棱PA 、PB 、PC 两两互相垂直,三侧面与底面所成二面角的大小分别为γβα,,,则=++γβα222cos cos cos _______________答案:1 20.若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积的值是_____________(只需写出一个可能的值)。
高一立体几何试卷及答案

立体几何试题一.选择题(每题4分,共40分)1.已知AB 0300300150空间,下列命题正确的个数为( )(1)有两组对边相等的四边形是平行四边形,(2)四边相等的四边形是菱形(3)平行于同一条直线的两条直线平行 ;(4)有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是( )A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m αα过平面α外一点,作与α平行的平面,则这样的平面可作( )A 1个 或2个B 0个或1个C 1个D 0个6.如图,如果MC ⊥菱形ABCD 所在平面,那么MA 与BD 的位置关系是( )A 平行B 垂直相交C 异面D 相交但不垂直7.经过平面α外一点和平面α内一点与平面α垂直的平面有( )A 0个B 1个C 无数个D 1个或无数个8.下列条件中,能判断两个平面平行的是( )A 一个平面内的一条直线平行于另一个平面;B 一个平面内的两条直线平行于另一个平面C 一个平面内有无数条直线平行于另一个平面D 一个平面内任何一条直线都平行于另一个平面9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是( )A //,,m n n m βα⊥⊂B //,,m n n m βα⊥⊥C ,,m n m n αβα⊥=⊂ID ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有( )A 1个B 2个C 3个D 4个二.填空题(每题4分,共16分)11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N ,设直线AB 与平面α交于点O ,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、 解答题15(10分)如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =。
高一数学立体几何练习题与部分答案汇编

⾼⼀数学⽴体⼏何练习题与部分答案汇编⽴体⼏何试题⼀.选择题(每题4分,共40分)1.已知AB//PQ,BC//QR,则∠PQP等于()A 0150 D 以上结论都不对30 B 030 C 02.在空间,下列命题正确的个数为()(1)有两组对边相等的四边形是平⾏四边形,(2)四边相等的四边形是菱形(3)平⾏于同⼀条直线的两条直线平⾏;(4)有两边及其夹⾓对应相等的两个三⾓形全等A 1B 2C 3D 43.如果⼀条直线与两个平⾏平⾯中的⼀个平⾏,那么这条直线与另⼀个平⾯的位置关系是()A 平⾏B 相交C 在平⾯内D 平⾏或在平⾯内4.已知直线m//平⾯α,直线n在α内,则m与n的关系为()A 平⾏B 相交C 平⾏或异⾯D 相交或异⾯5.经过平⾯α外⼀点,作与α平⾏的平⾯,则这样的平⾯可作()A 1个或2个B 0个或1个C 1个D 0个6.如图,如果MC⊥菱形ABCD所在平⾯,那么MA与BD的位置关系是( )A 平⾏B 垂直相交C 异⾯D 相交但不垂直7.经过平⾯α外⼀点和平⾯α内⼀点与平⾯α垂直的平⾯有()A 0个B 1个C ⽆数个D 1个或⽆数个 8.下列条件中,能判断两个平⾯平⾏的是( ) A ⼀个平⾯内的⼀条直线平⾏于另⼀个平⾯; B ⼀个平⾯内的两条直线平⾏于另⼀个平⾯ C ⼀个平⾯内有⽆数条直线平⾏于另⼀个平⾯ D ⼀个平⾯内任何⼀条直线都平⾏于另⼀个平⾯ 9.对于直线m ,n 和平⾯,αβ,使αβ⊥成⽴的⼀个条件是( ) A //,,m n n m βα⊥? B //,,m n n m βα⊥⊥ C ,,m n m n αβα⊥=?I D ,//,//m n m n αβ⊥ 10 .已知四棱锥,则中,直⾓三⾓形最多可以有( ) A 1个 B 2个 C 3个 D 4个⼆.填空题(每题4分,共16分)11.已知?ABC 的两边AC,BC 分别交平⾯α于点M,N ,设直线AB 与平⾯α交于点O ,则点O 与直线MN 的位置关系为_________12.过直线外⼀点与该直线平⾏的平⾯有___________个,过平⾯外⼀点与该平⾯平⾏的直线有_____________条13.⼀块西⽠切3⼑最多能切_________块14.将边长是a 的正⽅形ABCD 沿对⾓线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、解答题15(10分)如图,已知E,F 分别是正⽅形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =。
高中立体几何试题及答案

高中立体几何试题及答案一、选择题(每题3分,共15分)1. 空间中,如果直线a与平面α平行,那么直线a与平面α内的任意直线b的位置关系是:A. 平行B. 异面C. 相交D. 垂直2. 一个正方体的棱长为a,那么它的对角线长度为:A. a√2B. a√3C. 2aD. 3a3. 已知一个圆锥的底面半径为r,高为h,圆锥的体积是:A. πr²hB. 1/3πr²hC. 2πr²hD. 3πr²h4. 一个球的半径为R,那么它的表面积是:A. 4πR²B. 2πR²C. πR²D. R²5. 空间中,如果两个平面α和β相交于直线l,那么直线l与平面α和平面β的位置关系是:A. 平行B. 垂直C. 相交D. 包含二、填空题(每题2分,共10分)6. 空间直角坐标系中,点A(2,3,4)到原点O的距离是________。
7. 一个正四面体的每个顶点都与其它三个顶点相连,那么它的边长与高之比为________。
8. 已知一个长方体的长、宽、高分别为l、w、h,那么它的体积是________。
9. 空间中,如果一个点到平面的距离是d,那么这个点到平面上任意一点的距离的最大值是________。
10. 一个圆柱的底面半径为r,高为h,它的侧面积是________。
三、解答题(共75分)11. (15分)已知空间直角坐标系中,点A(1,2,3),B(4,5,6),点C 在平面ABC内,且AC=BC=2,求点C的坐标。
12. (20分)一个圆锥的底面半径为3,高为4,求圆锥的全面积和表面积。
13. (20分)一个长方体的长、宽、高分别为5、3、2,求其外接球的半径。
14. (20分)已知一个球的表面积为4π,求该球的体积。
答案:一、选择题1. A2. B3. B4. A5. C二、填空题6. √(1²+2²+3²)=√147. √3:18. lwh9. d+R10. 2πrh三、解答题11. 点C的坐标可以通过向量运算求得,设C(x,y,z),则向量AC=向量BC,即(1-x,2-y,3-z)=(x-4,5-y,6-z),解得x=3,y=4,z=5,所以点C的坐标为(3,4,5)。
(完整word版)高中立体几何大量习题及答案

立体几何一、选择题1. 给出下列四个命题①垂直于同一直线的两条直线互相平行;②垂直于同一平面的两个 平面互相平行;③若直线4与同一平面所成的角相等,则4互相平行;④若直线 /|仏是异面直线,则与都相交的两条直线是异面直线。
其中假命题的个数是()A. 1B. 2 C ・ 3 D. 42. 将正方形ABCD 沿对角线〃£)折成一个120。
的二面角,点C 到达点G ,这时异面直 线AD 与BCi 所成角的余弦值是()A. —B. -C.逅D.- 2 2 4 43. —个长方体一顶点的三个面的面积分别是血、巧、后,这个长方体对角线的长为()6. 正方体A ,B ,C ,D ,—ABCD 的棱长为a, EF 在AB 上滑动,且|EF|=b (b<a=9 Q 点在DC 上滑动,则四面体N —EFQ 的体积()A ・与E 、尸位置有关 B.与Q 位置有关C.与E 、F 、0位置都有关D.与E 、F 、0位買均无关,是定值 7. 三个两两垂直的平面,它们的三条交线交于一点O,点P 到三个平面的距离比为1 :2 : 3, PO=2V14 ,则P 到这三个平面的距离分别是()4. A. 2^3 B. 3^2 C. 6 如图,在正三角形ABC 中,D 、E 、尸分别为各边的中点,G 、H 、I 、丿分别为AF 、AD. BE 、DE 的中点.将△ ABC 沿QE 、EF 、Q 尸折成三棱锥以后,与〃所成角的度数为(A. 90° B ・ 60° C. 45。
5.两相同的正四棱锥组成如图所示的几何体,可放棱 长为1的正方体内,使正四棱锥的底面ABCD 与正 方体的某一个平面平行,且各顶点均在正方体的面 上,则这样的几何体体积的可能值有()A ・I 个B. 2个C. 3个 D0°D.A. 1, 2, 3 B・ 2, 4, 6 C・ 1, 4, 6 D・ 3, 6, 98. 如图,在四而体ABCD 中,截rfij AEF 经过四面 体的内切球(与四个面都相切的球)球心O,且 与BC, DC 分别截于E 、F,如果截面将四面体 分成体积相等的两部分,设四棱锥A —BEFD 与 三棱锥A-EFC 的表面积分别是Si ,52,则必有 ()A. S\<S2B. Si>S2C. S I =52D. 5I ,S2的大小关系不能确定 9. 条件甲:四棱锥的所有侧面都是全等三角形,条件乙:这个四棱锥是正四棱锥,则条 件甲是条件乙的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件10. 已知棱锥的顶点为P, P 在底面上的射影为O, PO=a,现用平行于底面的平面去截 这个棱锥,截面交PO 于点M,并使截得的两部分侧面积相等,设OM=b ,则a 与b 的关系是() B ・ h= ( V2 +1) aD.后土色 2 —♦ f11. 已知向量d=(2, 4, x ), 〃=(2, y, 2),若f |=6, “ 丄〃,则 x+y 的值是()12. 一个长方体共一顶点的三个面的面积分别是迈,JI 亦,这个长方体它的八个顶点都在同一个球面上,这个球的表面积是()A.1271B. 1871C.3671D. 6兀 13. 己知某个几何体的三视图如下,图中标出的尺寸(单位:cm ),则这个几何体的体积是()已知圆锥的全面积是底面积的3倍,那么该圆锥的侧tfri 展开图扇形的圆心角为( A.12O 0 B.15O 0 C.180° D.24O 0A ・ b= ( 5/2 —l)a A. 4000 14. A8000 正视图 俯视图20. 15.在一个倒置的正三棱锥容器内,放入一个钢球,钢球恰好与棱锥的四个而都接触,经 过棱锥的一条侧棱和高作截面,正确的截面图形是()“(-1,0,2),且几+》与必―》互相垂直,贝IJR 值是() 厂3 “7 C. — D.— 5516. 正四棱柱 ABCD-AiBiCiDi 中,AB=3, BBi=4.长为 1 的线段PQ 在棱AAi 上移动,长为3的线段MN 在棱 CCi±移动,点R 在棱BBi 上移动,则四棱锥R- PQMN 的体积是()A. 6B. 10 C ・12 D ・不确定17. 已知三棱锥0—ABC 中,OA 、OB 、OC 两两互相垂直,若x+y=4,则已知三棱锥O —ABC 体积的最大值是()1 2 >/3 B. — C. — D. 3 3 3 A.l18. 如图,在正四面体A-BCD 中,E 、F 、G 分别是三角形ADC 、ABD 、BCD 的中心, 则AEFG 在该正四面体各个面上的射影所有可能的序号是()A.①③B.②®® c.③④D.②④ A/ \ /◎、L ________ \ ① MB — — —②19. 如來底而直径和高相等的圆柱的侧面积是s •那么圆柱的体积等于A.-VSB.-J-C.-VSD.- 2 2V K 44 vn 已知直线AB. CD 是异面直线,AC 丄AB, AC 丄CD, BD 丄CD, 则异面直线AB 与CD 所成角的大小为()A. 30°B. 45° 且 AB=2, CD=1,C. 60°D. 75°已知向量”m°),B.- 5 A. 1 OC=1, OA=x, OB=y,22. 在四棱锥的四个侧面中,直角三角形最参可有()A.4个B.2个C.3个D.1个23. 三棱锥A-BCD 中,AC 丄BD, E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,则四边形EFGH 是()A.菱形B.矩形C.梯形D.正方形24. 在正四面体P —ABC 中,D 、E 、F 分别是AB 、BC 、CA 的中点,下面四个结论中不 成立的是()25. 一棱锥被平行于底面的平面所截,若截面1何积与底面面积的比为1: 3,则此截面把一条侧棱分成的两线段之比为()A.1: 3B.1: 2C.1:羽D.1:羽一 1 26. 正四面体P —ABC 中,M 为棱AB 的中点,则PA 与CM 所成角的余弦值为()A 並B 並C 返D 迴 A. 2 B. § C. 4 D. 327. —个三棱锥S —ABC 的三条侧棱SA 、SB 、SC 两两互相垂直,且长度分别为1, & ,3 已知该三棱锥的四个顶点都在一个球而上,则这个球的表面积为()A.16nB.32 兀C.36 兀D.64 兀28. 在棱长为。
高中数学立体几何习题(含答案与解析)

立体几何试卷五一、选择题1、线段AB 在平面α内,则直线AB 与平面α的位置关系是A 、AB α⊂ B 、AB α⊄C 、由线段AB 的长短而定D 、以上都不对 2、下列说法正确的是A 、三点确定一个平面B 、四边形一定是平面图形C 、梯形一定是平面图形D 、平面α和平面β有不同在一条直线上的三个交点 3、垂直于同一条直线的两条直线一定A 、平行B 、相交C 、异面D 、以上都有可能 4、在正方体1111ABCD A B C D -中,下列几种说法正确的是A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45角D 、11AC 与1B C 成60角 5、若直线l 平面α,直线a α⊂,则l 与a 的位置关系是A 、l aB 、l 与a 异面C 、l 与a 相交D 、l 与a 没有公共点6、下列命题中:(1)、平行于同一直线的两个平面平行;(2)、平行于同一平面的两个平面平行;(3)、垂直于同一直线的两直线平行;(4)、垂直于同一平面的两直线平行.其中正确的个数有 A 、1 B 、2 C 、3 D 、4 二、填空题1、等体积的球和正方体,它们的表面积的大小关系是S 球_____S 正方体(填”大于、小于或等于”).2、正方体1111ABCD A B C D -中,平面11AB D 和平面1BC D 的位置关系为3、已知PA 垂直平行四边形ABCD 所在平面,若PC BD ⊥,平行则四边形ABCD 一定是 .4、如图,在直四棱柱A 1B 1C 1 D 1-ABCD 中,当底面四边形ABCD 满足条件_________时,有A 1 B ⊥B 1 D 1. 5.正三棱锥P -ABC 中,三条侧棱两两垂直,且侧棱长为a ,则P 点到面ABC 的距离是6.三个平面两两垂直,它们的三条交线交于一点O ,P 到三个面的距离分别是6,8,10,则OP 的长为 。
(理科)已长方体的全面积是8,则其对角线长的最小值是 认为正确的一种条件即可,不必考虑所有可能的情形.) 三、解答题1、已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.(10分) 2、已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点,且EH∥FG.求证:EH ∥BD . (12分)3、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证:AD ⊥面SBC .(12分)4、一块边长为10cm 的正方形铁片按如图所示的阴影部分裁下,H G FE DB A CSD CB A四棱锥形容器,试建立容器的容积V 与x 的函数关系式,并求出函数的定义域. (12分)5、已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点. 求证:(1)1C O 面11AB D ;(2 )1AC ⊥面11AB D . (14分)6、已知△BCD 中,∠BCD =90°,BC =CD =1,AB ⊥平面BCD ,∠ADB =60°,E 、F 分别是AC 、AD 上的动点,且(01).AE AFAC AD λλ==<< (Ⅰ)求证:不论λ为何值,总有平面BEF ⊥平面ABC ;(Ⅱ)当λ为何值时,平面BEF ⊥平面ACD ? (14分)7、如图3所示,一个圆锥形的空杯子上面放着一个半球形冰淇淋,如果冰淇淋融化了,会溢出杯子吗?8、矩形ABCD 中,1,(0)AB BC a a ==>,PA ⊥平面AC ,BC 边上存在点Q ,使得PQ QD ⊥,求a 的取值范围.参考答案选择ACDDDB填空1、小于2、平行3、菱形4、1111AC B D 对角线与互相垂直5、设P 点到面ABC 的距离为h ,由体积公式可得:()3261231a h a =⋅,故a h 332=。
高中几何体试题及答案大全

高中几何体试题及答案大全试题一:直线与平面的关系题目:在空间直角坐标系中,直线l过点A(1, 2, 3)且与向量(2, -1, 0)平行。
求证:直线l与平面x - 2y + z = 6平行。
答案:首先,直线l的参数方程可以表示为:\[ x = 1 + 2t, \quad y = 2 - t, \quad z = 3 \]其中\( t \)为参数。
接下来,将直线l的参数方程代入平面方程x - 2y + z = 6,得到:\[ (1 + 2t) - 2(2 - t) + 3 = 6 \]\[ 1 + 2t - 4 + 2t + 3 = 6 \]\[ 4t = 6 \]\[ t = \frac{3}{2} \]由于直线l的参数方程中,参数\( t \)可以取任意实数,而代入平面方程后,\( t \)有唯一解,这表明直线l与平面x - 2y + z = 6平行。
试题二:立体几何体积计算题目:一个正方体的边长为a,求其外接球的体积。
答案:正方体的外接球的直径等于正方体的对角线长度,即:\[ 2R = a\sqrt{3} \]其中\( R \)为外接球的半径。
由此可得外接球的半径为:\[ R = \frac{a\sqrt{3}}{2} \]球的体积公式为:\[ V = \frac{4}{3}\pi R^3 \]代入\( R \)的值,得到正方体外接球的体积为:\[ V = \frac{4}{3}\pi \left(\frac{a\sqrt{3}}{2}\right)^3 =\frac{\pi a^3\sqrt{3}}{2} \]试题三:圆锥曲线问题题目:已知椭圆的方程为\( \frac{x^2}{a^2} + \frac{y^2}{b^2} =1 \),其中a > b > 0。
求椭圆的焦点坐标。
答案:椭圆的焦点位于主轴上,根据椭圆的性质,焦点到椭圆中心的距离为c,满足以下关系:\[ c^2 = a^2 - b^2 \]假设焦点位于x轴上,焦点的坐标为\( (c, 0) \)和\( (-c, 0) \)。
高中数学立体几何小题100题(含答案与解析)

立体几何小题100例一、选择题1.如图,已知正方体1111ABCD A B C D -的棱长为4,点E ,F 分别是线段AB ,11C D 上的动点,点P 是上底面1111A B C D 内一动点,且满足点P 到点F 的距离等于点P 到平面11ABB A 的距离,则当点P 运动时,PE 的最小值是( )A .5B .4C .42.5【答案】D 【解析】试题分析:因为点P 是上底面1111A B C D 内一动点,且点P 到点F 的距离等于点P 到平面11ABB A 的距离,所以,点P 在连接1111,A D B C 中点的连线上.为使当点P 运动时,PE 最小,须PE 所在平面平行于平面11AA D D ,2244()52PE =+=选D考点:1.平行关系;2.垂直关系;3.几何体的特征.2.如图在一个二面角的棱上有两个点A ,B ,线段,AC BD 分别在这个二面角的两个面内,并且都垂直于棱AB ,=46,AB cm AC cm =, 8,217BD cm CD cm ==,则这个二面角的度数为( )A .30︒B .60︒C .90︒D .120︒ 【答案】B 【解析】试题分析:设所求二面角的大小为θ,则,BD AC θ<>=,因为CD DB BA AC =++,所以22222()222CD DB BA AC DB BA AC DB BA DB AC BA AC =++=+++⋅+⋅+⋅CA DB而依题意可知,BD AB AC AB ⊥⊥,所以20,20DB BA BA AC ⋅=⋅=所以2222||||||||2CD DB BA AC BD AC =++-⋅即222417468286cos θ⨯=++-⨯⨯所以1cos 2θ=,而[0,]θπ∈,所以60θ=︒,故选B. 考点:1.二面角的平面角;2.空间向量在解决空间角中的应用.3.已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm )可得这 个几何体的体积是( )112222侧视图俯视图主视图A .343cmB .383cmC .33cmD .34cm【答案】B . 【解析】试题分析:分析题意可知,该几何体为一四棱锥,∴体积382231312=⨯⨯==Sh V . 考点:空间几何体的体积计算.4.如图,P 是正方体1111ABCD A B C D -对角线1AC 上一动点,设AP 的长度为x ,若PBD ∆的面积为(x)f ,则(x)f 的图象大致是( )【答案】A 【解析】试题分析:设AC 与BD 交于点O ,连接OP .易证得BD ⊥面11ACC A ,从而可得BD OP ⊥.设正方体边长为1,在1Rt ACC ∆中126cos 33C AC ∠==.在AOP ∆中 22OA =,设(),03AP x x =≤≤,由余弦定理可得2222226231222362OP x x x x ⎛⎫=+-⋅⨯=-+ ⎪ ⎪⎝⎭,所以223162OP x x =-+.所以()22231262f x x x =-+.故选A. 考点:1线面垂直,线线垂直;2函数图象.5.如图所示,正方体ABCD A B C D ''''-的棱长为1, ,E F 分别是棱AA ',CC '的中点,过直线,E F 的平面分别与棱BB '、DD '交于,M N ,设 BM x =,[0,1]x ∈,给出以下四个命题:(1)平面MENF ⊥平面BDD B '';(2)当且仅当x=12时,四边形MENF 的面积最小;(3)四边形MENF 周长()L f x =,[0,1]x ∈是单调函数; (4)四棱锥C MENF '-的体积()V h x =为常函数; 以上命题中假命题...的序号为( ) A .(1)(4) B .(2) C .(3) D .(3)(4) 【答案】C 【解析】试题分析:(1)由于AC EF //,B B AC BD AC '⊥⊥,,则D D B B ''⊥平面AC ,则D D B B EF ''⊥平面,又因为EMFN EF 平面⊂,则平面MENF ⊥平面BDD B '';(2)由于四边形MENF 为菱形,MN EF S MENF ⋅=21,2=EF ,要使四边形MENF 的面积最小,只需MN 最小,则当且仅当21=x 时,四边形MENF 的面积最小;(3)因为1)21(2+-=x MF ,1)21(4)(2+-=x x f ,)(x f 在]1,0[上不是单调函数;(4)NE C F EC M F MENF C V V V '-'--'+=,ME C S '∆=41121=⋅'E C ,F 到平面ME C '的距离为1,1214131=⋅='-ME C F V ,又41121=⋅'⋅='∆E C S NE C ,1214131=⋅='-NE C F V ,61)(=x h 为常函数.故选(3)考点:1.面面垂直的判定定理;2.建立函数模型.6.已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 上的射影为BC 的中点,则异面直线AB 与1CC 所成的角的余弦值为( )(A)4 (B )4 (C )4 (D )34【答案】D. 【解析】试题分析:连接B A 1;11//CC AA ,AB A 1∠∴是异面直线AB 与1CC 所成的角或其补角;在1ADA Rt ∆中,设11=AA ,则21,231==D A AD ;在1BDA Rt ∆中,2121=B A ;在1ABA ∆中,431122111cos 1=⨯⨯-+=∠AB A ;即面直线AB 与1CC 所成的角的余弦值为34. 考点:异面直线所成的角.7.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为A .π312B .π12C .π34D .π3 【答案】D 【解析】试题分析:由三视图可知,该几何体为四棱锥,侧棱垂直底面,底面是正方形,将此四棱锥还原为正方体,则正方体的体对角线即外接球的直径,32=r ,23=∴r ,因此ππ342==r S 表面积,故答案为D. 考点:由三视图求外接球的表面积.8.如图,棱长为1的正方体ABCD-A 1B 1C 1D 1中,P 为线段A 1B 上的动点,则下列结论错误的是( )A .11DC D P ⊥B .平面11D A P ⊥平面1A APC .1APD ∠的最大值为90 D .1AP PD +22+ 【答案】C 【解析】试题分析:111DC D A ⊥ ,11DC B A ⊥,1111A B A D A = ,⊥∴1DC 平面11BCD A ,⊂P D 1平面11BCD A 因此P D DC 11⊥,A 正确;由于⊥11A D 平面11ABB A ,⊂11A D 平面P A D 11,故平面⊥P A D 11平面AP A 1 故B 正确,当2201<<P A 时,1APD ∠为钝角,C 错;将面B AA 1与面11BCD A 沿B A 1展成平面图形,正视图 侧视图俯视图线段1AD 即为1PD AP +的最小值,利用余弦定理解221+=AD ,故D 正确,故答案为C .考点:棱柱的结构特征. 9.下列命题中,错误的是( )A .一条直线与两个平行平面中的一个相交,则必与另一个平面相交B .平行于同一平面的两条直线不一定平行C .如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βD .若直线l 不平行于平面α,则在平面α内不存在与l 平行的直线 【答案】B 【解析】试题分析: 由直线与平面的位置关系右知A 正确;平行于同一个平面的两条直线可以相交、平行或异面,故B 错,所以选B.考点:直线、平面平行与垂直的判定与性质.10.已知如图所示的正方体ABCD ﹣A 1B 1C 1D 1,点P 、Q 分别在棱BB 1、DD 1上,且=,过点A 、P 、Q作截面截去该正方体的含点A 1的部分,则下列图形中不可能是截去后剩下几何体的主视图的是( )【答案】A【解析】试题分析:当P 、B 1重合时,主视图为选项B ;当P 到B 点的距离比B 1近时,主视图为选项C ;当P 到B 点的距离比B 1远时,主视图为选项D ,因此答案为A. 考点:组合体的三视图11.一个几何体的三视图及尺寸如图所示,则该几何体的外接球半径为 ( )A. B. C. D.【答案】C 【解析】试题分析:由三视图可知:该几何体是一个如图所示的三棱锥P-ABC ,它是一个正四棱锥P-ABCD 的一半,其中底面是一个两直角边都为6的直角三角形,高PE=4. 设其外接球的球心为O ,O 点必在高线PE 上,外接球半径为R , 则在直角三角形BOE 中,BO 2=OE 2+BE 2=(PE-EO )2+BE 2, 即R 2=(4-R )2+(32)2,解得:R=174,故选C.考点:三视图,球与多面体的切接问题,空间想象能力12.如右图,在长方体1111ABCD A B C D -中,AB =11,AD =7,1AA =12,一质点从顶点A 射向点()4312E ,,,遇长方体的面反射(反射服从光的反射原理),将1i -次到第i 次反射点之间的线段记为()2,3,4i L i =,1L AE =,将线段1234,,,L L L L 竖直放置在同一水平线上,则大致的图形是( )【答案】C 【解析】 试题分析:因为37411>,所以1A E 延长交11D C 于F ,过F 作FM 垂直DC 于.M 在矩形1AA FM 中分析反射情况:由于35105AM =>,第二次反射点为1E 在线段AM 上,此时153E M =,第三次反射点为2E 在线段FM 上,此时24E M =,第四次反射点为3E 在线段1AF 上,由图可知,选C.考点:空间想象能力13.一块石材表示的几何体的三视图如图所示,将该石材切削、打磨、加工成球,则能得到的最大球的半径等于( )A.1B.2C.3D.4【答案】B【解析】试题分析:由图可得该几何体为三棱柱,因为正视图,侧视图,俯视图的内切圆半径最小的是正视图(直角三角形)所对应的内切圆,所以最大球的半径为正视图直角三角形内切圆的半径r , 则2286862r r r -+-+⇒=,故选B. 考点:三视图 内切圆 球 三棱柱14.已知二面角l αβ--为60︒,AB α⊂,AB l ⊥,A 为垂足,CD β⊂,C l ∈,135ACD ∠=︒,则异面直线AB 与CD 所成角的余弦值为 A .14 B .24 C .34 D .12【答案】B. 【解析】试题分析:如图作BE β⊥于E ,连结AE ,过A 作AG ∥CD ,作EG AG ⊥于G ,连结BG ,则.BG AG ⊥设2AB a =.在ABE ∆中,60,90,2,.BAE AEB AB a AE a ∠=︒∠=︒=∴=在Rt AEG ∆中,29045,90,cos 45.2GAE CAG AGE AG a a ∠=︒-∠=︒∠=︒∴=︒=在Rt ABG∆中,222cos 24AG BAG AB a ∠===∴异面直线AB 与CD 所成角的余弦值为24,故选B .βαElBDACG考点:1.三垂线定理及其逆定理;2. 空间角(异面直线所成角)的计算.15.在空间直角坐标系Oxyz 中,已知(2,0,0)(2,2,0),(0,2,0),(1,1,2)A B C D .若123,,S S S 分别是三棱锥D ABC -在,,xOy yOz zOx 坐标平面上的正投影图形的面积,则( )A .123S S S ==B .21S S =且23S S ≠C .31S S =且32S S ≠D .32S S =且31S S ≠ 【答案】D 【解析】试题分析:三棱锥ABC D -在平面xoy 上的投影为ABC ∆,所以21=S ,设D 在平面yoz 、zox 平面上的投影分别为2D 、1D ,则ABC D -在平面yoz 、zox 上的投影分别为2OCD ∆、1OAD ∆,因为)2,1,0(1D ,)2,0,1(2D ,所以212=-S S ,故选D.考点:三棱锥的性质,空间中的投影,难度中等.16.正方形ABCD 的边长为2,点E 、F 分别在边AB 、BC 上,且1AE =,12BF =,将此正 方形沿DE 、DF 折起,使点A 、C 重合于点P ,则三棱锥P DEF -的体积是( ) A .13B 523 D .23【答案】B【解析】试题分析:解:因为90,DPE DPF ∠=∠=所以,DP PE DP PF ⊥⊥又因为PE ⊂平面PEF ,PF ⊂平面PEF ,且PE PF P =,所以DP ⊥平面PEF在PEF ∆中,22223151,,1222PE PF EF EB BF ⎛⎫===+=+= ⎪⎝⎭所以222351222cos 33212EPF ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭∠==⨯⨯,225sin 133EPF ⎛⎫∠=-= ⎪⎝⎭ 所以11355sin 122234PEF S PE PF EPF ∆=⋅⋅∠=⨯⨯⨯= 115523346PEF P DEF D PEF V V DP S ∆--==⋅⋅=⨯⨯=三棱锥三棱锥 所以应选B.考点:1、直线与平面垂直的判定;2、正弦定理与余弦定理;3、棱锥的体积.17.高为的四棱锥S ﹣ABCD 的底面是边长为1的正方形,点S ,A ,B ,C ,D 均在半径为1的同一球面上,则底面ABCD 的中心与顶点S 之间的距离为( )A. B. C. D.【答案】A【解析】试题分析:由题意可知ABCD 是小圆,对角线长为,四棱锥的高为,推出高就是四棱锥的一条侧棱,最长的侧棱就是球的直径,然后利用勾股定理求出底面ABCD 的中心与顶点S 之间的距离.解:由题意可知ABCD 是小圆,对角线长为,四棱锥的高为,点S ,A ,B ,C ,D 均在半径为1的同一球面上,球的直径为2,所以四棱锥的一条侧棱垂直底面的一个顶点,最长的侧棱就是直径,所以底面ABCD 的中心与顶点S 之间的距离为:=故选A点评:本题是基础题,考查球的内接多面体的知识,能够正确推出四棱锥的一条侧棱垂直底面的一个顶点,最长的侧棱就是直径是本题的关键,考查逻辑推理能力,计算能力.18.二面角l αβ--为60°,A 、B 是棱l 上的两点,AC 、BD 分别在半平面,αβ内,AC l ⊥,BD l ⊥,且AB =AC =a ,BD =2a ,则CD 的长为( )A .2aB .5aC .aD .3a【答案】A【解析】试题分析:根据异面直线上两点间的距离公式2222cos EF d m n mn θ=++± ,对于本题中,d a =,m a =,2n =,60θ=,故()222222cos 602CD a a a a a a =++-⋅⋅⋅=.考点:异面直线上两点间距离,空间想象能力.19.长方体的表面积是24,所有棱长的和是24,则对角线的长是( ).A.14 B .4 C .32 D .23【答案】B【解析】试题分析:设出长方体的长、宽、高,表示出长方体的全面积,十二条棱长度之和,然后可得对角线的长度.考点:长方体的结构特征,面积和棱长的关系.20.已知棱长为l 的正方体1111ABCD A B C D -中,E ,F ,M 分别是AB 、AD 、1AA 的中点,又P 、Q 分别在线段11A B 11、A D 上,且11A P=A Q=x,0<x<1,设面MEF 面MPQ=l ,则下列结论中不成立的是( )A .//l 面ABCDB .l ⊥ACC .面MEF 与面MPQ 不垂直D .当x 变化时,l 不是定直线【答案】D【解析】试题分析:解:连结1111,,,AC BD AC B D ,,AC BD 交于点O 1111,AC B D 交于点1O由正方体的性质知,11111111////,,BD B D AC AC AC BD AC B D ⊥⊥,因为,E F 是,AD AB 的中点,所以//EF BD因为11A P A Q =,所以11//PQ B D所以//PQ EF ,所以//PQ 平面MEF ,//EF 平面MPQ , 由MEF 面MPQ=l ,EF ⊂ 平面MEF ,所以//EF l ,而EF ⊂平面ABCD ,l ⊂/平面ABCD , 所以,//l 面ABCD ,所以选项A 正确;由AC BD ⊥,//EF BD 得EF AC ⊥而//EF l ,所以l ⊥AC ,所以选项B 正确;连111,,MB MD O M ,则11//,O M AC 而1111,//,//AC A B AC BD BD EF A B MF ⊥⊥,所以,11,O M EF O M MF ⊥⊥,所以1O M ⊥平面MEF ,过直线l 与平面MEF 垂直的平面只能有一个,所以面MEF 与面MPQ 不垂直,所以选项C 是正确的;因为//EF l ,M 是定点,过直线外一点有且只有一条直线与已知直线平行,所以直线l 是唯一的,故选项D 不正确.考点:1、直线平面的位置关系;2、直线与直线,直线与平面,平面与平面的平行与垂直的判定及性质.21.如图,等边三角形ABC 的中线AF 与中位线DE 相交于G ,已知ED A '∆是△ADE 绕DE 旋转过程中的一个图形,下列命题中,错误的是( )A .动点A '在平面ABC 上的射影在线段AF 上B .恒有平面GF A '⊥平面BCDEC .三棱锥EFD A -'的体积有最大值D .异面直线E A '与BD 不可能垂直【答案】D【解析】试题分析:由于',A G DE FG DE ⊥⊥.所以DE ⊥平面'A FG .经过点'A 作平面ABC 的垂线垂足在AF上.所以A 选项正确.由A 可知B 选项正确.当平面'A DE 垂直于平面BCDE 时,三棱锥EFD A -'的体积最大,所以C 正确.因为BD EF ,设2AC a =.所以'EF A E a ==,当'2A F a =时,32'(')2a A G GF A G GF a <+==.所以异面直线E A '与BD 可能垂直.所以D 选项不正确.考点:1.线面位置关系.2.面面的位置关系.3.体积公式.4.异面直线所成的角.5.空间想象力.22.已知棱长为l 的正方体1111ABCD A B C D -中,E ,F ,M 分别是AB 、AD 、1AA 的中点,又P 、Q 分别在线段11A B 11、A D 上,且11A P=A Q=x,0<x<1,设面MEF 面MPQ=l ,则下列结论中不成立的是( )A .//l 面ABCDB .l ⊥ACC .面MEF 与面MPQ 不垂直D .当x 变化时,l 不是定直线【答案】D【解析】试题分析:解:连结1111,,,AC BD AC B D ,,AC BD 交于点O 1111,AC B D 交于点1O由正方体的性质知,11111111////,,BD B D AC AC AC BD AC B D ⊥⊥,因为,E F 是,AD AB 的中点,所以//EF BD因为11A P A Q =,所以11//PQ B D所以//PQ EF ,所以//PQ 平面MEF ,//EF 平面MPQ ,由MEF 面MPQ=l ,EF ⊂ 平面MEF ,所以//EF l ,而EF ⊂平面ABCD ,l ⊂/平面ABCD , 所以,//l 面ABCD ,所以选项A 正确;由AC BD ⊥,//EF BD 得EF AC ⊥而//EF l ,所以l ⊥AC ,所以选项B 正确;连111,,MB MD O M ,则11//,O M AC 而1111,//,//AC A B AC BD BD EF A B MF ⊥⊥,所以,11,O M EF O M MF ⊥⊥,所以1O M ⊥平面MEF ,过直线l 与平面MEF 垂直的平面只能有一个,所以面MEF与面MPQ不垂直,所以选项C是正确的;EF l,M是定点,过直线外一点有且只有一条直线与已知直线平行,所以直线l是唯一的,故选因为//项D不正确.考点:1、直线平面的位置关系;2、直线与直线,直线与平面,平面与平面的平行与垂直的判定及性质.23.把四个半径都是1的球中的三个放在桌面上,使它两两外切,然后在它们上面放上第四个球,使它与前三个都相切,求第四个球的最高点与桌面的距离()A.B.C.D.3【答案】A【解析】由题意,四球心组成棱长为2的正四面体的四个顶点,则正四面体的高.而第四个球的最高点到第四个球的球心距离为求的半径1,且三个球心到桌面的距离都为1,故第四个球的最高点与桌面的距离为,选A.24.如图所示,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=PD.则棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值是()A. 2:1B. 1:1C. 1:2D. 1:3【答案】C【解析】设AB =a.由题设知AQ 为棱锥Q -ABCD 的高,所以棱锥Q -ABCD 的体积V 1=.易证PQ ⊥面DCQ ,而PQ =,△DCQ 的面积为,所以棱锥P -DCQ 的体积V 2=.故棱锥Q -ABCD 的体积与棱锥P -DCQ 的体积的比值为1:1,选C.25.正四面体ABCD ,线段AB //平面α,E ,F 分别是线段AD 和BC 的中点,当正四面体绕以AB 为轴旋转时,则线段AB 与EF 在平面α上的射影所成角余弦值的范围是( )A . [0,22]B .[22,1]C .[21,1] D .[21,22] 【答案】B【解析】试题分析:如图,取AC 中点为G ,结合已知得GF //AB ,则线段AB 、EF 在平面α上的射影所成角等于GF 与EF 在平面α上的射影所成角,在正四面体中,AB ⊥CD ,又GE //CD ,所以GE ⊥GF,所以222GF GE EF +=,当四面体绕AB 转动时,因为GF //平面α,GE 与GF 的垂直性保持不变,显然,当CD 与平面α垂直时,GE 在平面上的射影长最短为0,此时EF 在平面α上的射影11F E 的长取得最小值21,当CD 与平面α平行时,GE 在平面上的射影长最长为21,11F E 取得最大值22,所以射影11F E 长的取值范围是 [21,22],而GF 在平面α上的射影长为定值21,所以AB 与EF 在平面α上的射影所成角余弦值的范围是[22,1].故选B 考点:1线面平行;2线面垂直。
高一数学(必修二)立体几何练习题(含答案)
一.选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的) 1、下列命题为真命题的是( )A. 平行于同一平面的两条直线平行;B.与某一平面成等角的两条直线平行;C. 垂直于同一平面的两条直线平行;D.垂直于同一直线的两条直线平行。
2、下列命题中错误的是:( )A. 如果α⊥β,那么α内一定存在直线平行于平面β;B. 如果α⊥β,那么α内所有直线都垂直于平面β;C. `D. 如果平面α不垂直平面β,那么α内一定不存在直线垂直于平面β;E. 如果α⊥γ,β⊥γ,α∩β=l,那么l ⊥γ.3、右图的正方体ABCD-A ’B ’C ’D ’ 中,异面直线AA ’与BC 所成的角是( ) A. 300 B.450 C. 600 D. 900 4、右图的正方体ABCD- A ’B ’C ’D ’中,【二面角D ’-AB-D 的大小是( ) A. 300 B.450 C. 600 D. 900 5.在空间中,下列命题正确的是A.若三条直线两两相交,则这三条直线确定一个平面B.若直线m 与平面α内的一条直线平行,则α//mC.若平面βα⊥,且l =βα ,则过α内一点P 与l 垂直的直线垂直于平面βD.若直线a 与直线b 平行,且直线a l ⊥,则b l ⊥6.设平面α∥平面β,A ,C ∈α,B ,D ∈β,直线AB 与CD 交于点S ,且点S 位于平面α,β之间,AS =8,BS =6,CS =12,则SD =( ) |A .3B .9C .18D .107.下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .9πB .10πC .11πD .12πA BDA ’B ’\C C ’ABD CE F8. 正方体的内切球和外接球的半径之比为( ) )A. 3:1B. 3:2C. 3:3D. 2:39.已知△ABC 是边长为a 2的正三角形,那么它的斜二侧所画直观图A B C 的面积为( )a 2 a 2 a 2 a 210.若正方体的棱长为2,则以该正方体各个面的中心为顶点的多面体的体积为( )11. 在空间四边形ABCD 中,AD=BC=2,E 、F 分别是AB 、CD 的中点,EF=2,求AD 与BC 所成角的大小.( )A. 30B. 45C. 60οD. 90 >12.如图,在多面体ABCDEF 中,已知平面ABCD 是边长为3的正方形,//EF AB ,32EF =,且EF 与平面ABCD 的距离为2,则该多面体的体积为( )A92 B 5 C 6 D 152二、填空题(共4小题,每小题5分,共20分,把答案填在题中的横线上)13. Rt ABC ∆中,3,4,5AB BC AC ===,将三角形绕直角边AB 旋转一周所成的几何体的体积为 .14.一个圆台的母线长为5 cm ,两底面面积分别为4πcm 2 和25π cm 2.则圆台的体积 ________. 15. 三棱锥S-ABC 中SA平面 ABC ,AB 丄 BC,SA = 2,AB =B C =1,则三棱锥S-ABC 的外接球的表面积等于______.16.如图,在直角梯形ABCD 中,,,BC DC AE DC ⊥⊥M 、N 分别是AD 、BE 的中点,将三角形ADE 沿AE 折起。
高一数学立体几何期末复习练习题

F H GEA BC Dp 高一数学立体几何期末复习练习题班级: 学号 姓名一、填空题;(每题7分,共70分)1、一条直线与一个平面平行,过该直线且与这个平面平行的平面有 ▲ 个。
2、夹在两个平行平面间的平行线段 ▲ 。
3、R t A B C ∆中,D 是斜边AB 的中点,AC=6,BC=8,EC ABC ⊥面,且EC=12,则ED= ▲ 。
4、已知l α⊥,则过l 与α垂直的平面有 ▲ 个5、已知空间四边形ABCD 中,AB=AD ,BC=CD ,则对角线BD 与AC 所成的角为 ▲ 。
6、共点的三条线段OA 、OB 、OC 两两垂直,则OA 与BC 所成角是 ▲ 。
7、P 在平面ABC 外,若到A B C ∆三个顶点的距离相等,则P 在平面ABC 上的射影是A B C ∆的 ▲ 心。
8、若斜线,a b 在面α上的射影是两条平行线,则,a b 的位置关系是 ▲ 。
9、若PA ABCD ⊥矩形,在面PAB 、PBC 、PCD 、PDA 中相互垂直的平面称为一对,则共有 ▲ 对。
10,则这个长方体对角线长为 ▲ 。
二、解答题:(每题15分,共30分)11、已知四棱锥P-ABCD 的底面为直角梯形,//,90A B D C D A B ∠= ,PA ABCD ⊥面,且1P A =A D =D C =12A B =, (1)求证:PAD PCD ⊥面面; (2)求AC 与PB 所成角的余弦值。
12、在正方体1111ABC D -A B C D 中棱长a ,M 、N 分别为1A B AC 和上的点,且1A M AN =, (1)求证:11//M N BB C C 面; (2)求线段MN 的最小值。
FH GEABCDp 高一数学立体几何期末复习练习题参考答案一、填空题;(每题7分,共70分)1、 12、 相等3、 134、 无数5、 906、 907、 外8、 平行、异面9、 3 10、二、解答题:(每题15分,共30分)11、,; (1):PA C D PA ABC D AD C D C D ⊥⎫⊥⇒⎬⊥⎭⇒⊥⇒⊥证明面面PAD 面PAD 面PCD(2)作AC 、PA 、AB 、PC 的中点G 、H 、E 、F 连结HF 、HE 、EF 、FG 、EG////////11112222H F AC H E PB FG PA EG BC H F AC H E PB FG PA EG BC ∴====EH F ∴∠(或其补角)即为AC 与PB 所成的角11,2P A A D D C A B ==== 且ABCD 是直角梯形B C A C P ∴12222FG EG H F EH ∴====2PA FG E EF ⊥∴⊥∴∆∴=面ABCD FG 面ABCD 是直角三角形222905FH EF FHEH EFH C O S EH F EH∴+=∴∠=∴∠==12、(1)证明: 分别过1M N //,//BB E BC F 1111、作ME A B 交于NF A B 交于 111111111111////ABC D A B C D A M AN BM C N AB A B AB A B M E BM C N N F A B A BACABM E N F M E N F-=∴==∴===∴= 正方体////A B C D M N E FM N E F M N A B C D∴∴=∴四边形为平行四边形面(2)解:设正方体棱长为,a BF b = 由(1)知:1B E b M N EF == 在90EBF EBF BE a b BF b ∆∠==-=中,EF ∴==222a b EF EF a M N a ==∴时,最小,即最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何试题一.选择题(每题4分,共40分)1.已知AB//PQ,BC//QR,则∠PQP等于()A 030B 030C 0150 D 以上结论都不对2.在空间,下列命题正确的个数为()(1)有两组对边相等的四边形是平行四边形,(2)四边相等的四边形是菱形(3)平行于同一条直线的两条直线平行;(4)有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是()A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m//平面α,直线n在α内,则m与n的关系为()A 平行B 相交C 平行或异面D 相交或异面5.经过平面α外一点,作与α平行的平面,则这样的平面可作()A 1个或2个B 0个或1个C 1个D 0个6.如图,如果MC⊥菱形ABCD所在平面,那么MA与BD的位置关系是( )A 平行B 垂直相交C 异面D 相交但不垂直7.经过平面α外一点和平面α内一点与平面α垂直的平面有()8.下列条件中,能判断两个平面平行的是( )A 一个平面内的一条直线平行于另一个平面;B 一个平面内的两条直线平行于另一个平面C 一个平面内有无数条直线平行于另一个平面D 一个平面内任何一条直线都平行于另一个平面9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是( )A //,,m n n m βα⊥⊂B //,,m n n m βα⊥⊥C ,,m n m n αβα⊥=⊂ID ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有( )A 1个B 2个C 3个D 4个二.填空题(每题4分,共16分)11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N ,设直线AB 与平面α交于点O ,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、解答题15(10分)如图,已知E,F 分别是正方形ABCD A B C D -的棱AA 和棱CC 上的点,且1AE C F =。
求证:四边形1EBFD 是平行四边形16(10分)如图,P 为ABC ∆所在平面外一点,AP=AC,BP=BC,D 为PC 的中点, 证明:直线PC 与平面ABD 垂直 PDBA17(12分)如图,正三棱锥A-BCD ,底面边长为a ,则侧棱长为2a ,E,F 分别为AC,AD 上的动点,求截面BEF ∆周长的最小值和这时E,F 的位置.DC18(12分)如图,长方形的三个面的对角线长分别是a,b,c ,求长方体对角线AC '的长C1b CBA答案1.D2.B3.D4.C5.C6.C7.D 8.D 9.A 10.D1三点共线2无数无数 3. 74 123a1证明: 1AE C F =Q11AB C D =11EAB FC D ∠=∠∴11EAB FC D ∆≅∆1EB FD ∴=过1A 作11//A G D F又由1A E ∥BG 且1A E =BG可知1//EB AG1//EB D F ∴∴四边形1EBFD 是平行四边形2 ∵AP AC =D 为PC 的中点∵BP BC =D 为PC 的中点∴BD PC ⊥∴PC ⊥平面ABD∴AB PC ⊥3 提示:沿AB 线剪开 ,则BB '为周长最小值.易求得EF 的值为34a ,则周长最小值为114a . 4解:()()()222AC AC CC ''=+ ()()222()AB BC CC '=++222a b c =++15(10分)如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =。
求证:四边形1EBFD 是平行四边形∆所在平面外一点,AP=AC,BP=BC,D为PC的中点,6(10分)如图,P为ABC证明:直线PC与平面ABD垂直B17(12分)如图,正三棱锥A-BCD,底面边长为a,则侧棱长为2a,E,F分别为AC,AD 上的动点,求截面BEF∆周长的最小值和这时E,F的位置.DC18(12分)如图,长方形的三个面的对角线长分别是a,b,c ,求长方体对角线AC '的长C1b CBA答案1证明: 1AE C F =Q11AB C D =11EAB FC D ∠=∠∴11EAB FC D ∆≅∆1EB FD ∴=过1A 作11//A G D F又由1A E ∥BG 且1A E =BG可知1//EB AG∴四边形1EBFD 是平行四边形4 ∵AP AC =D 为PC 的中点∴AD PC ⊥∵BP BC =D 为PC 的中点∴BD PC ⊥∴PC ⊥平面ABD∴AB PC ⊥5 提示:沿AB 线剪开 ,则BB '为周长最小值.易求得EF 的值为34a ,则周长最小值为114a . 4解:()()()222AC AC CC ''=+ ()()222()AB BC CC '=++222a b c =++高一数学必修2立体几何测试题试卷满分:100分考试时间:120分钟班级___________姓名__________ 学号_________ 分数___________第Ⅰ卷一、选择题(每小题3分,共30分)A 、AB α⊂ B 、AB α⊄C 、由线段AB 的长短而定D 、以上都不对2、下列说法正确的是A 、三点确定一个平面B 、四边形一定是平面图形C 、梯形一定是平面图形D 、平面α和平面β有不同在一条直线上的三个交点3、垂直于同一条直线的两条直线一定A 、平行B 、相交C 、异面D 、以上都有可能4、在正方体1111ABCD A B C D -中,下列几种说法正确的是A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45o 角D 、11AC 与1B C 成60o 角5、若直线l ∥平面α,直线a α⊂,则l 与a 的位置关系是A 、l ∥aB 、l 与a 异面C 、l 与a 相交D 、l 与a 没有公共点6、下列命题中:(1)平行于同一直线的两个平面平行;(2)平行于同一平面的两个平面平行;(3)垂直于同一直线的两直线平行;(4)垂直于同一平面的两直线平行.其中正确的个数有A 、1B 、2C 、3D 、47、在空间四边形ABCD 各边AB BC CD DA 、、、上分别取E F G H 、、、四点,如果与EF GH 、能相交于点P ,那么A 、点P 不在直线AC 上B 、点P 必在直线BD 上C 、点P 必在平面ABC 内D 、点P 必在平面ABC 外8、a ,b ,c 表示直线,M 表示平面,给出下列四个命题:①若a ∥M ,b ∥M ,则a ∥b ;②若b ⊂M ,a ∥b ,则a ∥M ;③若a ⊥c ,b ⊥c ,则a ∥b ;④若a ⊥M ,b ⊥M ,则a ∥b .其中正确命题的个数有A 、0个B 、1个C 、2个D 、3个9、已知二面角AB αβ--的平面角是锐角θ,α内一点C 到β的距离为3,点C 到棱AB 的距离为4,B1C 1A 1D 1BAC D那么tan θ的值等于A 、34 B、35CD 10、如图:直三棱柱ABC —A 1B 1C 1的体积为V ,点P 、Q 分别在侧棱AA 1和CC 1上,AP=C 1Q ,则四棱锥B —APQC 的体积为A 、2V B 、3V C 、4V D 、5V二、填空题(每小题4分,共16分)11、等体积的球和正方体,它们的表面积的大小关系是S 球_____S 正方体(填”大于、小于或等于”).12、正方体1111ABCD A B C D -中,平面11AB D 和平面1BC D 的位置关系为13、已知PA 垂直平行四边形ABCD 所在平面,若PC BD ⊥,平行则四边形ABCD 一定是 .14、如图,在直四棱柱A 1B 1C 1 D 1-ABCD 中,当底面四边形ABCD满足条件_________时,有A 1 B ⊥B 1 D 1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)第Ⅱ卷一、选择题(每小题3分,共30分)二、填空题(每小题4分,共16分)11、 12、 13、 14、三、解答题(共54分,要求写出主要的证明、解答过程)15、已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长. (7分)QP C'B'A'CBA16、已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点,且EH∥FG. 求证:EH ∥BD . (8分)17、已知ABC ∆中90ACB ∠=o ,SA ⊥面ABC ,ADSC ⊥,求证:AD ⊥面SBC .(8分)18、一块边长为10cm 的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积V 与x 的函数关系式,并求出函数的定义域. (9分)H G F ED BA CSDCBA点.19、已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交求证:(1) C 1O ∥面11AB D ;(2)1AC ⊥面11AB D . (10分)20、已知△BCD 中,∠BCD =90°,BC =CD =1,AB ⊥平面BCD , ∠ADB =60°,E 、F 分别是AC 、AD 上的动点,且(01).AE AFAC ADλλ==<< (Ⅰ)求证:不论λ为何值,总有平面BEF ⊥平面ABC ; (Ⅱ)当λ为何值时,平面BEF ⊥平面ACD ? (12分)1A FEDBAC高一立体几何试题一、选择题:(每题5分)1.下列说法中正确的个数为()①以直角梯形的一腰为轴旋转所得的几何体是圆台②用一个平面去截圆锥,得到一个圆锥和一个圆台③各个面都是三角形的几何体是三棱锥④以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥⑤棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是六棱锥⑥圆锥的顶点与底面圆周上的任意一点的连线都是母线。
A. 0 B. 1 C. 2 D. 3 2.如图,一几何体的三视图如下:则这个几何体是()A. 圆柱B. 空心圆柱C. 圆D. 圆锥3.一梯形的直观图是一个如上图所示的等腰梯形,且梯形OA /B /C /的面积为2,则原梯形的面积为 ( )A. 2B.2 C.D. 4俯视图正 视 图 侧视图4.圆锥的轴截面是等腰直角三角形,侧面积是,则圆锥的体积是() A .643πB 1283π C 64π D5. 一个圆台的上、下底面面积分别是12cm 和492cm ,一个平行底面的截面面积为252cm ,则这个截面与上、下底面的距离之比是 ( ) A 2: 1 B. 3: 1C.2: 1 D. 3: 16. 长方体的一个顶点上三条棱的边长分别为3、4、5,且它的八个顶点都在同一个球面上,这个球的表面积是()A. 220πB. 225πC. π50D. π200 7.下列命题中正确的个数是()①若直线l 上有无数个点不在平面α内,则l α∥②若直线l 与平面α平行,则l 与平面α内的任意一条直线都平行③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行 ④若直线l 与平面α平行,则l 与平面α内的任意一条直线都没有公共点 A. 0 B. 1 C. 2 D. 38.已知直线l α⊥平面,有以下几个判断:①若m l ⊥,则m α//;②若m α⊥,则m l //;③若m α//,则m l ⊥;④若m l //,则m α⊥.上述判断中正确的是()A. ①②③B. ②③④C. ①②④D. ①③④ 9.如图是正方体的展开图,则在这个正方体中,以下四个命题中正确的序号是() ①BM 与ED 平行.②CN 与BE 是异面直线. ③CN 与BM 成60˚角.④DM 与BN 垂直. A. ①②③ B. ③④ C. ②④ D. ②③④E10.在四面体ABCD 中,,E F 分别是,AC BD 的中点,若2,4,AB CD EF AB ==⊥,则AB 与CD 所成的角的度数为() A .030 B .45o C .60o D .90o11.在长方体ABCD-A 1B 1C 1D 1中,B 1B=BC=1,则面BD 1C 与面AD 1D 所成二面角的大小为()A .030B .45oC .60oD .90o12.蚂蚁搬家都选择最短路线行走,有一只蚂蚁沿棱长分别为 1cm,2cm,3cm 的长方体木块的顶点A 处沿表面达到顶点B 处(如图所示),这只蚂蚁走的路程是()A .cm 14B .cm 23C .cm 26D .1+cm 13 二、填空题(每题5分)13.半径为R 的半圆卷成一个圆锥,则它的体积为________________.14.已知a b ,是一对异面直线,且a b ,成70o 角,P 为空间一定点,则在过P 点的直线中与a b ,所成的角为70o 的直线有条。
