2016年吉林省长春市南关区中考模拟试题及答案
吉林省长春市南关区2016届九年第一次模拟考试英语试题.doc

九年级质量调研题(英语)参考答案2016.4I. 1. hold / give /join /attend /have 2. deep 3. myself 4. luckily 5. healthII. 6. argument 7. third 8. seeing 9. cleaner 10. excitingIII. 11-15 C B D A C 16-20 B A C D C 21-25 B C A D CIV. 26-30 B E C F AV. 31-35 D C D B A 36-40 A D C B A 41-45 D C B A CVI. 46-50 A C A B D 51-55 F F T T F 56-60 B D C C B 61-65 A E C D B66. His dream (It) was to journey with the sun. / Journeying with the sun. / It was journeying with the sun.67. He met an old man, a bum. (an old man 和a bum 答出一个即可赋分)68. The old man was one of the wealthiest men in the world. / The old man was very rich.69. Because he wanted to tell the young man not to judge a book by its cover.70. It’s wisdom. / Wisdom.VII. (A) 71. with 72. waste / pity / way 73. box 74. wear / keep 75. poor(B)此题共15分,内容和语言14分,字数1分。
按5个档次给分。
评分时根据其内容、语言表达的准确程度及其书写情况分档,最后确定分数。
吉林省长春市南关区2016届九年级语文第一次模拟试题

九年级质量调研题(语文)一、阅读(60分)(一)名句积累与运用(15分)1.采菊东篱下,。
(陶渊明《饮酒》)2.,。
无为在歧路,儿女共沾巾。
(王勃《送杜少府之任蜀州》)3.满眼风光北固楼。
?悠悠。
(辛弃疾《南乡子·登京口北固亭有怀》)4.子夏曰:“,,仁在其中矣。
”(《论语·子张》)5.白居易在《钱塘湖春行》中,借莺莺燕燕的动态,把大自然从秋冬沉睡中苏醒的情景和早春的活力生动地描绘了出来,给人一种清新明快、骀荡欢悦的感受的诗句是:,。
6.《春望》一诗中以“,”两句,真实地表达了诗人杜甫因战乱不息亲人消息隔绝,久盼音讯不至时的迫切心情。
7.成长的道路上总会有失意与挫折,当我们感到迷茫与困惑时,可以用李白《行路难》中“,”两句来激励自己,增添拼搏的信心和勇气,执着地追求人生的理想。
8.《小石潭记》中流水淙淙,树蔓青翠,鱼儿在清澈的潭水中畅游。
柳宗元面对如此美景却感到:“ ,”,这种感受正是他被贬之后的心情写照。
(二)文言文阅读(15分)(甲)阅读下文,回答问题。
(10分)醉翁亭记环滁皆山也。
其西南诸峰,林壑尤美,望之蔚然而深秀者,琅玡也。
山行六七里,渐闻水声潺潺,而泻出于两峰之间者,酿泉也。
峰回路转,有亭翼然临于泉上者,醉翁亭也。
作亭者谁?山之僧曰智仙也。
名之者谁?太守自谓也。
太守与客来饮于此,饮少辄醉,而年又最高,故自号曰醉翁也。
醉翁之意不在酒,在乎山水之间也。
山水之乐,得之心而寓之酒也。
若夫日出而林霏开,云归而岩穴暝,晦明变化者,山间之朝暮也。
野芳发而幽香,佳木秀而繁阴,风霜高洁,水落而石出者,山间之四时也。
朝而往,暮而归,四时之景不同,而乐亦无穷也。
至于负者歌于涂,行者休于树,前者呼,后者应,伛偻提携,往来而不绝者,滁人游也。
临溪而渔,溪深而鱼肥,酿泉为酒,泉香而酒洌,山肴野蔌,杂然而前陈者,太守宴也。
宴酣之乐,非丝非竹,射者中,弈者胜,觥筹交错,起坐而喧哗者,众宾欢也。
苍颜白发,颓然乎其间者,太守醉也。
2016年吉林省长春市中考考前物理模拟试卷和答案

2016年吉林省长春市中考考前物理模拟试卷一、选择题(共10小题,每小题2分,满分20分)1.(2分)一个验电器的两个金属箔片因带电而张开,则这两个金属箔片一定()A.带正电B.带负电C.带异种电荷D.带同种电荷2.(2分)将白酒进行加热,就可分离出水和酒精,这是利用了它们的()A.密度不同B.熔点不同C.沸点不同D.凝固点不同3.(2分)下列现象中,由光的反射形成的是()A.海市蜃楼B.池水看起来比实际浅C.山在水中形成“倒影” D.水中的筷子变“弯折”了4.(2分)下列物态变化中,放热的是()A.冰熔化成水B.地上的水变干C.衣柜中的樟脑丸变小了D.玻璃上形成“窗花”5.(2分)下列事例中,属于增大压强的是()A.书包背带加宽B.刀刃磨得锋利C.坦克装有履带D.铁轨铺在枕木上6.(2分)考试时,许多同学有一个不良习惯,将笔放在手指上不停地转圈,笔会经常掉到地面或桌面上发出噪声。
下列说法正确的是()A.笔在下落过程中不受力的作用B.笔停在静止的手指上时受到平衡力作用C.笔在手指拨动时才会连续转圈,说明力是维持物体运动的原因D.手指不拨动笔,笔也会在手指上继续转动一段时间,说明笔与手指间不存在摩擦力7.(2分)投影仪的镜头相当于一个焦距为10cm的凸透镜.下列有关投影仪的分析中正确()A.投影仪成的像是虚像B.投影仪成缩小的实像C.投影片离镜头的距离应该大于20cmD.如果想要银幕上的像变大,应将镜头向下移动8.(2分)关于家庭电路,下列说法正确的是()A.冰箱、彩电间是串联的B.控制灯泡的开关应该接在零线上C.电冰箱的金属外壳要接地D.家里的空气开关“跳闸”,一定是发生了短路9.(2分)如图所示,闭合开关S后发现,L1正常发光,L2只能微弱发光,以下分析合理的是()A.L2短路B.L2断路C.L2的电阻较小,实际功率较小D.L2的电阻较大,实际功率较小10.(2分)如图所示,两个斜面的粗糙程度相同,现将同一个物体分别从两个斜面的底端匀速拉到斜面的顶端,所用的时间相等.以下说法中正确的是()A.两物体运动的速度相同B.拉力F1、F2的大小相等C.拉力F1的功率小于拉力F2的功率D.上升过程中物体的动能转化为重力势能二、填空题(共6小题,每小题2分,满分12分)11.(2分)手机间是利用波传递信号的。
2016届吉林长春市中考模拟考试(十一)数学试卷(带解析)

试卷第1页,共21页绝密★启用前2016届吉林长春市中考模拟考试(十一)数学试卷(带解析)试卷副标题考试范围:xxx ;考试时间:151分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、如图,在平面直角坐标系中,点A 、B 的坐标分别为(4,0)、(0,2),点C 为线段AB 上任意一点(不与点A 、B 重合),CD ⊥OA 于点D ,点E 在DC 的延长线上,EF ⊥y 轴于点F ,若点C 为DE 的中点,则四边形ODEF 的周长为( )A .4B .6C .8D .10【答案】C. 【解析】试题解析:设直线AB 的解析式为y=kx+b , 将点A (4,0)、点B (0,2)代入y=kx+b 中,得:,解得:.试卷第2页,共21页∴直线AB 的解析式为y=-x+2.设点C 的坐标为(m ,- m+2)(0<m <4),则点E 的坐标为(m ,-m+4),∴OD=EF=m ,CD=2-m ,DE=4-m ,∵ED ⊥OA ,EF ⊥y 轴,BO ⊥OA , ∴∠O=∠F=∠ODE=90°, ∴四边形ODEF 为矩形.∴C 矩形ODEF =2×(OD+DE )=2×(m+4-m )=8. 故选C .考点:1.一次函数图象上点的坐标特征;2.坐标与图形性质;3.矩形的判定与性质. 2、如图,AB 是⊙O 的直径,点A 是弧CD 的中点,若∠B=25°,则∠AOC=( )A .25°B .30°C .40°D .50°【答案】D . 【解析】试题解析:∵点A 是弧CD 的中点, ∴,∴∠AOD=∠AOC=2∠B , ∵∠B=25°, ∴∠AOC=50°. 故选D .考点:圆周角定理;圆心角、弧、弦的关系.试卷第3页,共21页3、如图,在△ABC 中,点D 、E 、F 分别在边AC 、AB 、BC 上,EF ∥AC ,DF ∥AB ,若∠B=45°,∠C=65°,则∠EFD 的大小为( )A .45°B .70°C .80°D .100°【答案】B. 【解析】试题解析:∵EF ∥AC , ∴∠EFB=∠C=65°, ∵DF ∥AB , ∴∠DFC=∠B=45°,∴∠EFD=180°-∠EFB-∠DFC=180°-65°-45°=70°. 故选B .考点:平行线的性质.4、下列方程没有实数根的是( ) A .x 2-3x+4=0B .x 2=2xC .2x 2+3x-1=0D .x 2+2x+1=0【答案】A . 【解析】试题解析:A 、方程x 2-3x+4=0中,△=(-3)2-4×1×4=-7<0,故此方程无实数根; B 、由x 2=2x 得x 2-2x=0,△=(-2)2-4×1×0=4>0,故此方程有两个不相等实数根; C 、方程2x 2+3x-1=0中,△=32-4×2×(-1)=17>0,故此方程有两个不相等实数根; D 、方程x 2+2x+1=0中,△=22-4×1×1=0,故此方程有两个相等实数根; 故选A .考点:根的判别式.5、不等式x+5≥1的解集在数轴上表示正确的是( )试卷第4页,共21页【答案】B . 【解析】试题解析:移项得,x≥1-5, 合并同类项得,x≥-4, 在数轴上表示为:.故选B .考点:1.在数轴上表示不等式的解集;2.解一元一次不等式.6、如图是由5个高和底面直径相等的圆柱体搭成的立体图形,这个立体图形的左视图是( )【答案】C . 【解析】试题解析:从左边看第一层是两个小正方形,第二层是一个小正方形, 故选C .考点:简单组合体的三视图.7、据统计,长春市主城区2015年上半年机动车数量突破1000000辆大关,1000000这个数用科学记数法表示为( ) A .1×107B .0.1×107C .1×106D .10×101【答案】C . 【解析】试题解析:1000000用科学记数法表示为1×106. 故选C .考点:科学记数法—表示较大的数. 8、计算-5+1的结果为( ) A .-6B .-4C .4D .6【答案】B.试卷第5页,共21页【解析】试题解析:-5+1=-(5-1)=-4.故选B .考点:有理数的加法.试卷第6页,共21页第II 卷(非选择题)二、填空题(题型注释)9、如图,在平面直角坐标系中,点P 在第一象限,以P 为顶点的抛物线经过原点,与x 轴正半轴相交于点A ,⊙P 与y 轴相切于点B ,交抛物线交于点C 、点D .若点A 的坐标为(m ,0),CD=n ,则△PCD 的周长为 (用含m 、n 的代数式表示).【答案】m+n. 【解析】试题解析:过P 作PE ⊥OA 于E ,∵P 为抛物线的顶点,∴OE=OA=m ,连接PB ,∵⊙P 与y 轴相切于点B , ∴PB ⊥OB ,∴四边形PBOE 是矩形,∴PB=OE=m ,∴PC=PD=PB=m ,∴△PCD 的周长为=PC+PD+CD=m+n ,考点:1.切线的性质;2.二次函数图象上点的坐标特征.试卷第7页,共21页10、如图,在△ABC 和△ADE 中,∠C=∠AED=90°,点E 在线段AB 上,AD ∥CB ,若AC=AE=2,BC=3,则DE 的长为 .【答案】.【解析】试题解析:∵AD ∥CB , ∴∠B=∠DAE , 而∠C=∠AED=90°, ∴△ACB ∽△DEA ,∴AC :DE=BC :AE ,即2:DE=3:2, ∴DE=.考点:相似三角形的判定与性质.11、如图,在平面直角坐标系中,▱ABCD 的顶点A 在函数y=(k >0,x >0))的图象上,顶点B 、C 在y 轴正半轴上(点B 在点C 的上方),若点D 的坐标为(3,1),▱ABCD 的面积为4,5,则k 的值为 .【答案】7.5. 【解析】试题解析:设A (3,t ), ∵▱ABCD 的面积为4.5, ∴3(t-1)=4.5,解得t=2.5,试卷第8页,共21页∴A 点坐标为(3,2.5),把A (3,2.5)代入y=得k=3×2.5=7.5.考点:1.反比例函数图象上点的坐标特征;2.平行四边形的性质.12、购买1个单价为a 元的面包和3瓶单价为b 元的饮料,所需钱数为 元.【答案】(a+3b ). 【解析】试题解析:∵一个面包的价格为a 元,3瓶饮料的总价为3a 元∴购买1个单价为a 元的面包和3瓶单价为b 元的饮料,所需钱数为(a+3b )元. 考点:列代数式.13、分解因式:a 2-4= .【答案】(a+2)(a-2). 【解析】试题解析:a 2-4=(a+2)(a-2). 考点:因式分解-运用公式法. 14、计算:= .【答案】.【解析】试题解析:==.考点:二次根式的乘除法.三、解答题(题型注释)15、如图,在平面直角坐标系中,抛物线y=a (x-2)2-2与y 轴交于点A (0,1),直线AB ∥x 轴交抛物线于点B ,点P 是直线AB 上一点(不与A 、B 重合),PQ ∥y 轴交抛物线于点Q ,以PQ 为斜边向左作等腰直角三角形PQM ,设点P 的横坐标为m .试卷第9页,共21页(1)求这条抛物线所对应的函数表达式. (2)当线段PQ 被x 轴平分时,求m 的值.(3)当等腰直角三角形PQM 夹在x 轴与直线AB 之间的图形为轴对称三角形时,求m 的取值范围.(4)直接写出当等腰直角三角形PQM 的两条直角边与坐标轴有两个公共点时m 的取值范围.【答案】(1)y=(x-2)2-2,(2)m 1=2+,m 2=2-.(3)0<m≤2-或2-≤m≤2+或2+≤m <4,(4)0<m <或m >.【解析】试题分析:(1)将A 点坐标代入解析式直接求出a ;(2)由P 、Q 关于x 轴对称,且横坐标相同可设出Q 点坐标,代入抛物线解析式中,即可直接求出m 的值;(3)找到两个临界点:当Q 点刚好在x 轴上时;当M 点刚好在x 轴上时.算出这个两个临界状态时的m 值,即可确定符合要求的m 的取值范围;(4)等腰直角三角形PQM 的两条直角边与坐标轴有两个公共点,也就是y 轴同时与两直角边相交,所以只需算出M 点恰好在y 轴上的临界状态时的m 值即可. 试题解析:(1)把A (0,1)代入y=a (x-2)2-2中,得1=a (0-2)2-2,∴a=,∴y=(x-2)2-2,(2)设Q (m ,-1),试卷第10页,共21页则-1=(m-2)2-2,∴m 1=2+,m 2=2-.(3)当点Q 落在x 轴上时,PQ=1,∴1-[(m-2)2-2]=1,∴m 1=2-,m 2=2+,∴当0<m≤2-或2-≤m≤2+或2+≤m <4,为轴对称三角形,(4)当M 点刚好在y 轴上时:|1-[(m-2)2-2]|=m ,解得:m=或m=,∴0<m <或m >.考点:二次函数综合题.16、如图,在△ABC 中,∠ACB=90°,AC=2,BC=4,D 、E 分别是边AB 、BC的中点,点P 从点C 出发,沿线段CD 方向以每秒1个单位长度的速度运动,当点P 与点D 不重合时,以EP 、ED 为邻边作▱EDFP ,设点P 的运动时间为t (秒).(1)求AB 长.(2)当∠DPF=∠PFD 时,求t 的值.(3)当点P 在线段CD 上时,设▱EDFP 与△ABC 重叠部分图形的面积为y (平方单位),求y 与t 之间的函数关系式.(4)连结AF ,当△AFD 的面积与△PDE 的面积相等时,直接写出t 的值.试卷第11页,共21页【答案】(1)10;(2).(3) y=.(4) 0或.【解析】试题分析:(1)在RT △ABC 中利用勾股定理即可解决问题.(2)如图1中,当∠DPF=∠PFD 时,可以证明PE ∥AB ,PC=PD ,由此即可解决问题.(3)分两种情形①当0≤t≤时,如图2中,作PM ⊥DE 存在为M ,此时重叠部分面积就是平行四边形PEDF 的面积,②当<t <5时,如图3中,此时y=S △PHD +S △PDE .(4)两种情形①t=O 时,△ADF 与△PDE 面积相等.②如图4中,当A 、P 、E 共线时△ADF 与△PDE 面积相等,由DE ∥AC 得,求出PC 即可. 试题解析:(1)在△ABC 中,∵∠ACB=90°,AC=2,BC=4,∴AB=.(2)如图1中,∵四边形PEDF 是平行四边形, ∴PF ∥DE ,PE ∥DF , ∴∠DPF=∠PDE , ∵∠ACB=90°,AD=DB , ∴CD=DB=DA=5,∵CE=EB , ∴DE ⊥BC ,∠CDE=∠EDB ∵∠DPF=∠PFD , ∴∠PED=∠BDE ,试卷第12页,共21页∴PE ∥DB ,∵CE=EB ,∴PC=PD=,∴t=.(3)①当0≤t≤时,如图2中,作PM ⊥DE 存在为M , ∵PM ∥CE ,∴,∴,∴PM=(5-t ),∴y=DE•PM=•(5-t )=-2t+10.②当<t <5时,如图3中,试卷第13页,共21页∵PH ∥AC ,∴,∴,∴PH=(5-t ),∴y=S △PHD +S △PDE =•PH•PM+(-2t+10)=t 2-5t+15,综上所述:y=.(4)①t=O 时,△ADF 与△PDE 面积相等. ②如图4中,当A 、P 、E 共线时,∵AE ∥DF , ∴S △ADF =S △PDF =S △PED , ∵DE ∥AC ,∴,∴PC=,∴t=,试卷第14页,共21页∴t=0或时,△ADF 与△PDE 面积相等.考点:四边形综合题.17、探究:如图①,点E 、F 分别在正方形ABCD 的边BC 、CD 上,∠EAF=45°,连结EF ,求证:EF=BE+DF .应用:如图②,在四边形ABCD 中,点E 、F 分别在BC 、CD 上,AB=AD ,∠B+∠D=90°,∠EAF=∠BAD ,若EF=3,BE=2,则DF= .【答案】(1)证明见解析;(2).【解析】试题分析:(1)如图①中,把△ABE 绕点A 逆时针旋转90°得到△ADE′,只要证明△AFE ≌△AFE′即可解决问题.(2)如图②中,将△ABE 绕点A 旋转到△ADE′位置连接E′F .,只要证明△FAE ≌△FAE′得EF=FE′,在RT △E′DF 中利用勾股定理即可解决问题. 试题解析:(1)如图①中,在正方形ABCD 中,∵AB=AD ,∠BAD=∠ADC=∠B=90°, 把△ABE 绕点A 逆时针旋转90°得到△ADE′, ∵∠ADF=∠ADE′=90°, ∴点F 、D 、E′共线,试卷第15页,共21页∴∠E′AF=90°-45°=45°=∠EAF , 在△AFE 和△AFE′中,,∴△AFE ≌△AFE′, ∵EF=FE′=DE′+DF=DE+DF . (2)如图②中,因为AB=AD ,所以可以将△ABE 绕点A 旋转到△ADE′位置,连接E′F . ∵∠B+∠ADF=90°,∠B=∠E′DA , ∴∠E′DF=∠E′DA+′ADF=90°,∵∠BAE+∠DAF=∠EAF ,∠E′AD=∠BAE , ∴∠E′AF=∠EAF , 在△FAE 和△FAE′中,,∴△FAE ≌△FAE′, ∴EF=FE′=3,在RT △E′DF 中,∵∠E′DF=90°,E′F=3,DE′=BE=2, ∴DF=.考点:1.全等三角形的判定与性质;2.正方形的性质;3.旋转的性质.18、十一期间,小明和小亮相约从长春出发到某市某游乐园游玩,小明乘私家车从长春出发1小时后,小亮乘“和谐号”动车从长春出发,先到某市火车站A ,然后乘出租车去游乐园B (换车时间忽略不计),两人恰好同时到达游乐园,他们离开长春的距离y (千米)与小明乘车时间t (时)的函数图象如图所示.试卷第16页,共21页(1)求“和谐号”动车的速度.(2)当小亮到达某市火车站时,求小明距离游乐园的距离.(3)若小明乘私家车从长春到达游乐园的时间比原来要提前18分钟,则私家车速度应比原来增加多少?【答案】(1)240千米/时.(2)56千米.(3)10千米/时. 【解析】试题分析:(1)根据速度=路程÷时间,可得出“和谐号”动车的速度;(2)根据距离=速度×时间可得出小亮乘“和谐号”动车的函数表达式,由图象交点横坐标为1.5可得出此时距离游乐园的距离,由该点的坐标可得出小明乘私家车的函数表达式,求出t=2时y 的值,用216减去此时的y 值即可得出结论;(3)先通过(2)中得出的小明乘私家车的函数表达式计算出小明到达游乐园的时间,在此时间上减去0.3小时(18分钟),再根据速度=路程÷时间得出提速后的速度,用此速度减去提速前的速度即可得出结论.试题解析:(1)240÷(2-1)=240(千米/时). 答:“和谐号”动车的速度为240千米/时.(2)由(1)知,小亮乘“和谐号”动车的函数表达式为y=240(t-1)=240t-240(1≤t≤2), 当t=1.5时,y=240×1.5-240=120.设小明乘私家车的函数表达式为y=kt ,则有120=1.5k , 解得:k=80, ∴y=80t .当t=2时,y=80×2=160, 216-160=56(千米).∴当小亮到达某市火车站时,小明距离游乐园的距离为56千米. (3)当y=216时,则有80t=216, 解得:t=2.7.试卷第17页,共21页∵18分钟=0.3小时, ∴2.7-0.3=2.4(小时), ∴216÷2.4=90(千米/时), 90-80=10(千米/时).答:私家车速度应比原来增加10千米/时. 考点:一次函数的应用.19、近年来,“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n 名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题: n 名学生对使用计算器影响计算能力的发展看法人数统计表(1)求n 的值;(2)统计表中的m= ;(3)估计该校1800名学生中认为“影响很大”的学生人数.【答案】(1)200;(2)100;(3)900. 【解析】试题分析:(1)将“没有影响”的人数÷其占总人数百分比=总人数n 即可; (2)用总人数减去“没有影响”和“影响不大”的人数可得“影响很低”的人数m ; (3)将样本中“影响很大”的人数所占比例乘以该校总人数即可得. 试题解析:(1)n=40÷20%=200(人). 答:n 的值为200; (2)m=200-40-60=100;(3)1800×=900(人).答:该校1800名学生中认为“影响很大”的学生人数约为900人.试卷第18页,共21页故答案为:(2)100.考点:1.扇形统计图;2.用样本估计总体.20、如图,一艘货轮位于灯塔P 北偏东53°方向,距离灯塔100海里的A 处,另一艘客轮位于货轮正南方向,且在灯塔P 南偏东45°方向的B 处,求此时两艘轮船之间的距离AB .(结果精确到1海里)【参考数据:sin53°=0.799,cos53°=0.602,tan53°=1.327】【答案】两艘轮船之间的距离AB 约为140海里. 【解析】试题分析:通过解直角△ACP 得到AC 、PC 的长度;然后结合等腰直角三角形的性质来求BC 的长度,则易求AB=AC+BC . 试题解析:由题意,得∠A=53°,BC=PC . 在直角△APC 中,AC=100cos53°=100×0.602=60.2, BC=PC=100sin53°=100×0.799=79.9,所以AB=AC+BC=60.2+79.9=140.1≈140(海里). 答:两艘轮船之间的距离AB 约为140海里.考点:解直角三角形的应用-方向角问题.试卷第19页,共21页21、如图,在△ABC 中,D 、E 分别是边AB 、AC 的中点,点F 是BC 延长线上一点,且CF=BC ,连结CD 、EF .求证:CD=EF .【答案】证明见解析. 【解析】试题分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得DE ∥BC ,DE=BC ,然后求出四边形DEFC 是平行四边形,再根据平行四边形的对边相等证明即可.试题解析:∵D 、E 分别是边AB 、AC 的中点,∴DE ∥BC ,DE=BC ,∵CF=BC ,∴DE=CF ,∴四边形DEFC 是平行四边形, ∴CD=EF .考点:1.三角形中位线定理;2.平行四边形的判定与性质.22、学校计划选购甲、乙两种图书作为“校园读书节”的奖品,已知甲种图书的单价是乙种图书单价的1.5倍,用600元单独购买甲种图书的册数比单独购买乙种图书要少10册,求甲、乙两种图书的单价.【答案】甲种图书的单价为30元/册,乙种图书的单价为20元/册. 【解析】试题分析:设乙种图书的单价为x 元/册,则甲种图书的单价为1.5x 元/册,根据册数=总价÷单价,结合用600元单独购买甲种图书的册数比单独购买乙种图书要少10册,可列出关于x 的分式方程,解方程即可求出x 的值,由此亦可得出甲种图书的单价.试卷第20页,共21页试题解析:设乙种图书的单价为x 元/册,则甲种图书的单价为1.5x 元/册,依题意,得,解得:x=20,或x=0(舍去).经检验,x=20是原方程的解且符合题意, 所以甲种图书的单价为1.5×20=30(元).答:甲种图书的单价为30元/册,乙种图书的单价为20元/册. 考点:分式方程的应用.23、有甲、乙两个不透明的盒子,甲盒里有3张卡片,分别写有字母A 、B 、C ;乙盒里有2张卡片,分别写有字母C 、D ,这些卡片除所标字母不同外其余均相同,先从甲盒中随机抽取1张卡片,再从乙盒中随机抽取1张卡片,请用画树状图(或列表)的方法.求抽取的两张卡片中都含有字母C 的概率.【答案】.【解析】试题分析:如图所示:,一共有6种可能,抽取的两张卡片中都含有字母C 的可能有1种,故抽取的两张卡片中都含有字母C 的概率为:.试题解析:根据题意画出树状图,进而利用概率公式求出答案. 考点:列表法与树状图法.24、先化简,再求值:(3a+2)2-9a (a+1),其中a=.【答案】5. 【解析】试题分析:先利用完全平方式和单项式乘以多项式将原式展开,再合并同类项,将a 的值代入计算可得.试题解析:原式=9a 2+12a+4-9a 2-9a =3a+4,试卷第21页,共21页 当a=时, 原式=3×+4=5. 考点:整式的混合运算—化简求值.。
2016长春中考物理模拟题(1)

15.江波同学看到江中停着一艘轮船.他想:如果地球对所有物体的引力都突然增大一倍,这艘船的质量和浮沉情况会怎样变化呢
甲乙三、计算题(每小题
(1)如图所示图甲是即将完成的该实验的电路图.请在图中三个“○”内正确填入“灯泡”、“电
流表 ”和“电压表”的电路符号,完成该电路图.
(2)按电路图连接完电路,闭合开关快速试触的瞬间,电流表和电压表出现了如图乙所示的情况,
经检查,所有仪器、元件完好。
请分析出现以上现象的可能原因(两表各写一条). 电流表: ;电压表: 。
(3)小军问题解决后,再次接通电路,为了使小灯泡能够正常发光,应调节滑动变阻器使电压表
示数为 V .小灯泡正常发光时,电流表的示数如图丙所示,则流过小灯泡的电流为 A ,该灯泡正常工作时的电阻是 Ω.。
2016年长春市中考数学模拟试卷(十一)
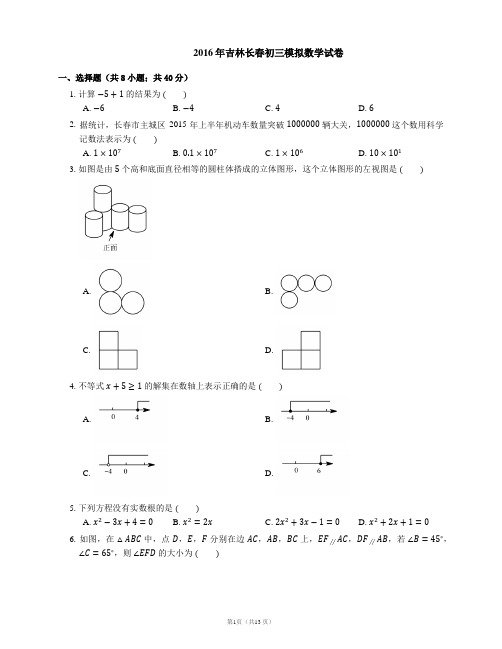
2016年吉林长春初三模拟数学试卷一、选择题(共8小题;共40分)1. 计算的结果为A. B. C. D.2. 据统计,长春市主城区2015年上半年机动车数量突破辆大关,这个数用科学记数法表示为A. B. C. D.3. 如图是由个高和底面直径相等的圆柱体搭成的立体图形,这个立体图形的左视图是A. B.C. D.4. 不等式的解集在数轴上表示正确的是A. B.C. D.5. 下列方程没有实数根的是A. B. C. D.6. 如图,在中,点,,分别在边,,上,,,若,,则的大小为A. B. C. D.7. 如图,是的直径,点是弧的中点,若,则A. B. C. D.8. 如图,在平面直角坐标系中,点,的坐标分别为,,点为线段上任意一点(不与点,重合),于点,点在的延长线上,轴于点,若点为的中点,则四边形的周长为A. B. C. D.二、填空题(共6小题;共30分)9. 计算:.10. 分解因式:.11. 购买个单价为元的面包和瓶单价为元的饮料,所需钱数为元.12. 如图,在平面直角坐标系中,平行四边形的顶点在函数(,)的图象上,顶点,在轴正半轴上(点在点的上方),若点的坐标为,平行四边形的面积为,则的值为.13. 如图,在和中,,点在线段上,,若,,则的长为.14. 如图,在平面直角坐标系中,点在第一象限,以为顶点的抛物线经过原点,与轴正半轴相交于点,与轴相切于点,交抛物线于点、点.若点的坐标为,,则的周长为(用含,的代数式表示).三、解答题(共10小题;共130分)15. 先化简,再求值:,其中.16. 有甲、乙两个不透明的盒子,甲盒里有张卡片,分别写有字母,,;乙盒里有张卡片,分别写有字母,,这些卡片除所标字母不同外其余均相同,先从甲盒中随机抽取张卡片,再从乙盒中随机抽取张卡片,请用画树状图(或列表)的方法.求抽取的两张卡片中都含有字母的概率.17. 学校计划选购甲、乙两种图书作为“校园读书节”的奖品,已知甲种图书的单价是乙种图书单价的倍,用元单独购买甲种图书的册数比单独购买乙种图书要少册,求甲、乙两种图书的单价.18. 如图,在中,,分别是边,的中点,点是延长线上一点,且,连接,.求证:.19. 如图,一艘货轮位于灯塔北偏东方向,距离灯塔海里的处,另一艘客轮位于货轮正南方向,且在灯塔南偏东方向的处,求此时两艘轮船之间的距离.(结果精确到海里)【参考数据:,,】20. 近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:名学生对使用计算器影响计算能力的发展看法人数统计表(1)求的值;(2)统计表中的;(3)估计该校名学生中认为“影响很大”的学生人数.21. 十一期间,小明和小亮相约从长春出发到某市某游乐园游玩,小明乘私家车从长春出发小时后,小亮乘“和谐号“动车从长春出发,先到某市火车站,然后乘出租车去游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开长春的距离(千米)与小明乘车时间(时)的函数图象如图所示.(1)求“和谐号”动车的速度.(2)当小亮到达某市火车站时,求小明距离游乐园的距离.(3)若小明乘私家车从长春到达游乐园的时间比原来要提前分钟,则私家车速度应比原来增加多少?22. (1)探究:如图①,点,分别在正方形的边,上,,连接,求证:.(2)应用:如图②,在四边形中,点,分别在,上,,,,若,,则.23. 如图,在中,,,,,分别是边,的中点,点从点出发,沿线段方向以每秒个单位长度的速度运动,当点与点不重合时,以,为邻边作平行四边形,设点的运动时间为(秒).(1)求长.(2)当时,求的值.(3)当点在线段上时,设平行四边形与重叠部分图形的面积为(平方单位),求与之间的函数关系式.(4)连接,当的面积与的面积相等时,直接写出的值.24. 如图,在平面直角坐标系中,抛物线与轴交于点,直线轴交抛物线于点,点是直线上一点(不与,重合),轴交抛物线于点,以为斜边向左作等腰直角三角形,设点的横坐标为.(1)求这条抛物线所对应的函数表达式;(2)当线段被轴平分时,求的值.(3)当等腰直角三角形夹在轴与直线之间的图形为轴对称三角形时,求的取值范围;(4)直接写出当等腰直角三角形的两条直角边与坐标轴有两个公共点时的取值范围.答案第一部分1. B2. C3. C4. B5. A6. B7. D8. C 【解析】设直线的解析式为,将点,点代入中,得:解得:直线的解析式为.设点的坐标为,则点的坐标为,,,,轴,,,四边形为矩形..矩形第二部分9.10.11.12.13.14.第三部分15. 原式当时,原式16. 如图所示:一共有种等可能的情况,抽取的两张卡片中都含有字母的情况有种,故抽取的两张卡片中都含有字母的概率为:.17. 设乙种图书的单价为元/册,则甲种图书的单价为元/册,依题意,得解得:经检验,是原方程的解且符合题意,甲种图书的单价为(元).答:甲种图书的单价为元/册,乙种图书的单价为元/册.18. ,分别是边,的中点,,,,,四边形是平行四边形,.19.由题意,得,.在直角中,(海里),(海里),所以(海里).答:两艘轮船之间的距离约为海里.20. (1)(人).答:的值为;(2)【解析】;(3)(人).答:该校名学生中认为“影响很大”的学生人数约为人.21. (1)(千米 / 时).答:“和谐号”动车的速度为千米 / 时.(2)由(1)知,小亮乘“和谐号”动车过程中与的函数表达式为,当时,.设小明乘私家车的函数表达式为,则有,解得:,.当时,,(千米).当小亮到达某市火车站时,小明距离游乐园的距离为千米.(3)当时,则有,解得:.分钟小时,(小时),(千米 / 时),(千米 / 时).答:私家车速度应比原来增加千米 / 时.22. (1)如图①中,在正方形中,,,把绕点逆时针旋转得到,,点,,共线,,在和中,,.(2)【解析】如图②中,因为,所以可以将绕点旋转到位置,连接.,,,,,,在和中,,,在中,,,,.23. (1)在中,,,,.(2)如图1中,四边形是平行四边形,,,.,,,,,,.,,,,,.(3)①当时,如图2中,作于点,,,,,,...②当时,如图3中,作于点.,,,,,综上所述:.(4)①时,与面积相等.②如图4中,当,,共线时,,与同底等高,,四边形是平行四边形,,,,,,,或时,与面积相等.24. (1)把代入中,得,,.(2)设,则,,.(3)当点落在轴上时,,,,,当点落在轴上时,,两点关于轴轴对称,由(2)可知,,,当或或,等腰直角三角形夹在轴于直线之间的图形为轴对称三角形.(4)当点刚好在轴上时:,解得:或,显然或时满足题意.当时三角形的两条直角边和轴有个交点.因此当两条直角边均与轴没有交点,即点在轴上方时,满足题意.此时.当直角边经过原点时,,,,符合题意.当直角边经过原点时,设点坐标为,代入抛物线方程解得舍或.综上所述,满足题意的的取值范围为或或或.。
2016届吉林省长春市九年级中考模拟物理试卷(带解析)

绝密★启用前2016届吉林省长春市九年级中考模拟物理试卷(带解析)试卷副标题考试范围:xxx ;考试时间:61分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、已知甲物体在光滑的水平面上运动,乙物体在粗糙的水平面上运动,现用相同的水平推力分别使甲、乙两个物体沿力的方向移动相同的距离,两次推力所做的功分别是W甲,W 乙,则W 甲 W 乙.【答案】= 【解析】试题分析:功等于力与距离的乘积,即W=Fs ,由于用相同的水平推力,所以F 相同,同时,甲、乙两个物体沿力的方向移动相同的距离,所以s 也相同,故所做的功相等,即W 甲=W 乙.2、在如图所示电路中,电源电压保持不变,R 1为定值电阻,R 2为滑动变阻器.开关S 闭合后,将滑动变阻器R 2的滑片P 向左移动过程中( )A .电流表的示数不变试卷第2页,共16页B .电压表V 1的示数不变C .电压表V 2的示数变小D .电压表V 1的示数和电流表的示数比值不变【答案】D 【解析】试题分析:由电路图可知,R 1与R 2串联,电压表V 1测R 1两端的电压,电压表V 2测R 2两端的电压,电流表测电路中的电流.将滑动变阻器R 2的滑片P 向左移动过程中,接入电路中的电阻变大,电路中的总电阻变大,由I=可知,电路中的电流变小,即电流表的示数变小,故A 错误; 由U=IR 可知,R 1两端的电压变小,即电压表V 1的示数变小,故B 错误; 因串联电路中总电压等于各分电压之和,所以,R 2两端的电压变大,即电压表V 2的示数变大,故C 错误; 由R=可知,电压表V 1的示数和电流表的示数比值等于R 1的阻值, 则电压表V 1的示数和电流表的示数比值不必,故D 正确. 故选D .3、起重机吊着一重力为G 的物体,静止时拉力为F 1,当以2m/s 的速度匀速竖直上升时拉力为F 2,当以3m/s 的速度匀速竖直下降时拉力为F 3,则有( ) A .F 3>F 2>F 1=G B .F 3=F 2=F 1=G C .F 2>F 1=G >F 3D .F 1=G >F 3>F 2【答案】B 【解析】试题分析:物体静止在空中时,受到重力和拉力F 1的作用,由于物体处于平衡状态,所以受到的重力和拉力是一对平衡力,根据二力平衡的条件可知,拉力等于重力,即:F 1=G .物体以2m/s 的速度匀速竖直上升时,受到重力G 和拉力F 2的作用,此时物体处于平衡状态,所以受到的重力和拉力是一对平衡力,根据二力平衡的条件可知,拉力等于重力,即:F 2=G .同理物体3m/s 的速度匀速竖直下降时,受到的拉力F 3与重力G 仍然是平衡力,仍相等:F 3=G .由此可知:F 3=F 2=F 1=G . 综上分析故选B .4、如图所示,从车箱顶的A 处有一小球自由落下,结果落在底板上的B 处,则此时该车箱所处的运动状态可能是( )A .匀速向左运动B .向左加速运动C .匀速向右运动D .向右减速运动【答案】BD 【解析】试题分析:(1)如果车匀速向左运动和匀速向右运动,小球从车顶落下时,由于惯性,小球向车行方向的运动速度和车前进的速度相同,小球会落到A 点的正下方. (2)如果车向左进行加速运动,当小球从车顶落下时,小球向左的运动速度小于车前进的速度,小球会落到A 点的右侧.(3)如果车向右进行减速运动,当小球从车顶落下时,小球向右的运动速度大于车前进的速度,小球会落到A 点的右侧. 故选BD .5、如图所示,一束光线射向O 处的光学元件后会聚于主光轴上的S 点,去掉光学元件后,光线会聚于S 1点,则该元件一定是( )A .平面镜B .凹面镜C .凸透镜D .凹透镜【答案】D 【解析】试题分析:由题意可知,光线通过该元件发生了折射,故应为透镜.而凹透镜对光起发散作用,使光线会聚于主光轴上的S 点. 故选D .6、把标有“220V 40W”和“220V 25W”的甲、乙两盏灯串联接在220V 的电源上(设灯丝电阻不变),则下列分析正确的是()试卷第4页,共16页A .两盏灯的总功率等于65WB .甲灯两端的电压大于乙灯两端的电压C .两盏灯的总功率小于25WD .乙灯消耗的功率小于甲灯消耗的功率【答案】C【解析】试题分析:两灯功率不是额定功率,所以总功率不是两灯额定功率之和,故A 错..因为串联电流相等,甲灯电阻小,所以电压也小,消耗的功率也小,故B 、D 错. 此时电路电流,两盏灯的总功率,故C 对.故选C .7、一物体放在装满甲液体的溢水杯中沉底,排出甲液体的质量为m 甲,放在装满乙液体的溢水杯中漂浮,排出乙液体的质量为m 乙,则( ) A .m 甲<m 乙 B .m 甲>m 乙 C .m 甲=m 乙D .无法确定【答案】A 【解析】试题分析:物体放在装满甲液体的溢水杯中沉底,则物体受到的浮力小于重力,根据阿基米德原理可知,排开甲液体的重力小于物体的重力,即m 甲<m 物;物体放在装满乙液体的溢水杯中漂浮,此时浮力等于重力,根据阿基米德原理可知,排开乙液体的重力等于物体的重力,即m 乙=m 物; 故m 甲<m 乙. 故选A .8、关于物体的内能,下列说法正确的是( ) A .温度为0℃的物体没有内能B .物体内能增加,一定是通过外界对物体做功C .正在沸腾的水吸收热量,温度增加,内能不变D .在相同物态下,同一物体温度降低,它的内能会减少【答案】D【解析】试题分析:A、温度为0℃的物体也具有内能,故A错误;B、物体的内能增加,可能是外界对物体做功,也可能是从外界吸收了热量,故B错误;C、正在沸腾的水吸收热量,温度不变,内能增加,故C错误;D、在相同物态下,同一物体温度降低,它的内能会减少,故D正确.故选D.9、下列说法中,正确的是()A.家里的空气开关的最大额定电流越大越好B.物体内能增加,温度一定升高C.运动员跑得越快到达终点越不容易停下来是因为速度越大惯性越大D.科学家奥斯特发现电流周围存在磁场【答案】D【解析】试题分析:A、家里的空气开关的最大额定电流应根据实际进行选择,并不是越大越好,如果太大,则不一定起到保护作用,故A错误;B、物体内能增加,温度不一定升高,如晶体熔化时,吸热内能增大,但温度不变,故B错误;C、惯性的大小只与物体的质量有关,与运动的速度等无关,故C错误;D、科学家奥斯特发现电流周围存在磁场,即电流的磁效应,故D正确.故选D.10、A.冬天,温暖车厢的车窗模糊是因为车外水蒸气液化B.夏天,洒在地上的水变干了是液化现象C.秋天的早晨花草上出现的小露珠,这是液化现象,要吸收热量D.冬天,河水结成冰是凝固现象【答案】D【解析】试题分析:A、冬天,温暖的室内窗玻璃变模糊,是车内的水蒸气遇到温度较低的玻璃液化成小水珠形成的,故A错误.B、夏天,洒在地上的水变干了是汽化现象,故B错误.C、秋天,草叶上结有小露珠,是空气中的水蒸气遇冷液化形成的,要放出热量,故C试卷第6页,共16页错误.D 、河水结冰,液态变为了固态,是凝固现象,故D 正确. 故选D .11、下列估测值中,最接近实际的是() A .体育课中常用的实心球质量为50g B .乒乓球的直径约为10cm C .一块橡皮的质量约为500g D .普通课桌的高度约为0.8m【答案】D 【解析】试题分析:A 、一个鸡蛋的质量在50g 左右,实心球的质量比一个鸡蛋的质量大得多.此选项不符合实际;B 、乒乓球的直径在4cm 左右.此选项不符合实际;C 、一块橡皮的质量在5g 左右,比500g 小得多.此选项不符合实际;D 、中学生的身高在165cm 左右,课桌的高度大约是中学生身高的一半,在80cm=0.8m 左右.此选项符合实际. 故选D .第II 卷(非选择题)二、填空题(题型注释)12、在弹簧测力计悬挂一圆柱体,从盛水的烧杯上方某一高度缓慢下降,圆柱体浸没后继续下降,直到圆柱体底面与烧杯底部将要接触为止(水未溢出),如图所示是圆柱体下降过程中弹簧测力计读数F 随圆柱体下降高度h 变化的图象:求:(1)分析图象可知,圆柱体重力是 N ; (2)圆柱体浸没在水中时,受到的浮力是 N ; (3)圆柱体的密度是 kg/m 3(g=10N/kg );(4)在圆柱体浸没后逐渐下降的过程中,水对烧杯底的压力 ,烧杯底对桌面的压强 (选填“变大”“变小”或“不变”)【答案】(1)12; (2)8; (3)1.5×103; (4)不变;不变 【解析】试题分析:(1)由图象可知,当h=0时,弹簧测力计示数为12N , 此时圆柱体处于空气中,根据二力平衡条件可知,G=F 拉=12N .(2)从h=7cm 开始,弹簧测力计示数不变,说明此时圆柱体已经浸没在水中,对圆柱体受力分析可知,F 浮=G ﹣F 拉=12N ﹣4N=8N .(3)由阿基米德原理F 浮=ρ液V 排g 得:V 排===8×10﹣4m 3,因为物体是全部浸没,所以V 物=V 排=8×10﹣4m 3, 由公式G=mg 可求出物体的质量,试卷第8页,共16页m===1.2kg ,ρ物===1.5×103kg/m 3;(5)在圆柱体浸没后逐渐下降的过程中,排开水的体积不变,液面不再上升,所以水对容器底的压强和压力都不变;烧杯底对桌面的压力不变,压强不变.13、如图,凸透镜放置在光具座的C 点处,光具座上所标的A 、B 、D 、E 四点中,恰有两点到C 点的距离同为该透镜的一倍焦距、或同为该透镜的两倍焦距.①该透镜的焦距为 厘米或 厘米;②接着,小王将发光物置于光具座上距B 点15厘米处,在DE 间移动光屏找像,可能在光屏上得到 的像(选填“缩小”或“等大”或“放大”).【答案】①10;20;②放大 【解析】试题分析:①因凸透镜放置在光具座的C 点处,距凸透镜距离相同的两点分别是B 、D ,距离为20cm ,由题意知:20cm 为该透镜的一倍焦距、或为该透镜的两倍焦距;则透镜的焦距为20cm 或10cm .②将发光物置于光具座上距B 点15厘米的左侧处,则凸透镜的焦距可能为:20cm ;即物体可能在在二倍焦距和一倍焦距之间;若能在DE 间移动光屏找到像的话,在光屏上得到的是倒立放大的像.14、如图甲所示的电路中,电源电压为8V 且保持不变,灯泡上标有“6V 6W”字样,此灯泡的电流随电压变化关系如图乙所示,灯泡正常发光时电流表的示数为 ;当电流表示数为0.6A 时,此时电压表的示数为 ,此时滑动变阻器R 接入电路的阻值为 .【答案】1.0A ;2V ;10Ω【解析】试题分析:(1)由P=UI ,可得,小灯泡正常发光时的电流:I===1A ; 因为电流表测量电路中的电流,因此灯泡正常发光时,电流表的示数为1A ; (2)由图可知,当电流表示数为0.6A 时,小灯泡两端的电压为2V ,即电压表示数为2V ;因为灯泡和滑动变阻器串联,因此滑动变阻器两端电压U′=8V ﹣2V=6V ; 则滑动变阻器接入电路的电阻R===10Ω.15、如图所示是一些小冰块的温度随加热时间变化的图象,由图象可知:冰的熔化过程共持续 min ;加热至第15min 时,物质的状态为 .【答案】10;液态 【解析】试题分析:从图象上看,冰从第5min 开始熔化,到第15min 完全熔化完,所以熔化过程经历了15min ﹣5min=10min ,加热至第15min 时冰完全熔化处于液态.16、将一墨水瓶放在平面镜前6cm 处,像与墨水瓶间距离为 cm .若使墨水瓶向镜面靠近,墨水瓶在镜中像的大小 .【答案】12;不变 【解析】 试题分析:(1)将一墨水瓶放在镜前6cm 处,墨水瓶在镜中的像到平面镜距离也为6cm ,像与墨水瓶间距离为6cm+6cm=12cm .(2)物体在平面镜中成像大小跟物体大小有关,跟物体到平面镜的距离无关.所以不管是将墨水瓶靠近平面镜还是远离平面镜,墨水瓶在镜中像的大小都不变. 17、用水作汽车发动机的冷却液是因为 ,当发动机的冷却液温度升高时,内能 .【答案】水的比热容大;增大 【解析】试题分析:用水作汽车发动机的冷却液是因为水的比热容大,相同质量的水和其他物质相比较,改变相同的温度,水可以吸收更多的热量; 当发动机的冷却液温度升高时,内能增大.18、如图所示,底面积和质量都相同的A 、B 两容器,装有质量相同的不同液体,放在水平桌面上,则液体对容器底部的压强P A P B ,容器对桌面的压强P A ′ P B ′.(选填“大试卷第10页,共16页于”“等于”“小于”)【答案】小于;等于 【解析】试题分析:(1)两个容器底面积相同,形状不同,在液面等高的情况下,两个容器内液体的体积关系为:V A >V B ;由于两种液体质量相同,由ρ=得:ρA <ρB ;已知液面高度相同:h A =h B ,由液体压强公式P=ρgh 得: 两容器底部所受液体的压强关系是P A <P B ;(2)两个容器的质量以及所装液体的质量相同,即两个容器的总质量相同:m A =m B ; 所以两个容器对桌面的压力F=G=mg 相同,又已知容器底面积相等,即S A =S B ; 由p=得:两个容器对桌面的压强关系是P A ′=P B ′.三、实验题(题型注释)19、利用如图所示的电路可测量未知电阻R x 的阻值,其中R 为已知电阻.(1)请将电压表连入电路,使电路完整.(2)当开关S 1、S 2闭合时,电压表示数U 1=6V ;当开关S 1闭合、S 2断开时,电压表示数U 2=4V .己知R=10Ω,则电源电压U= V ,R x = Ω.(3)实验中若由于某个元件出现故障(短路或断路),导致电压表的示数U 1=U 2=6V ,则该元件及故障可能是 .试卷第11页,共16页【答案】(1)实物电路图如图所示(2)6;20;(3)R 短路或R x 断路 【解析】试题分析:(1)由电路图可知,可以用电压表先测出电源电压,然后再测出电阻两端电压,然后再根据串联电路特点与欧姆定律求出待测电阻阻值,电压表与待测电阻并联,实物电路图如图所示:(2)由电路图可知,当开关S 1、S 2闭合时,电压表测电源电压,电压表示数U 1=6V ,则电源电压U=U 1=6V ;当开关S 1闭合、S 2断开时,电压表测待测电阻两端电压,电压表示数U 2=4V ,此时电路电流:I====0.2A ,由I=可知,待测电阻阻值:R x ===20Ω.(3)电压表的示数U 1=U 2=6V ,说明两种情况下,电压表都测电源电压,定值电阻两端电压为零,则电阻R 发生短路或R x 断路.20、测量小灯泡功率的实验,所用小灯泡的额定电压为2.5V .试卷第12页,共16页(1)实验中所用电压表在未接入电路时表盘如图甲所示,在使用它测量前应进行的操作是 .(2)链接的电路如图乙所示,其中有一根导线连接不规范,导致开关没有闭合时 表就有读数.请在这根导线上打“×”,并用笔画线代替导线,将其改正.(3)改正电路后闭合开关,移动滑片,小灯泡正常发光,电流表示数如图丙所示则小灯泡的额定功率为 W .【答案】(1)对电压表进行调零,使指针指在零刻度线上; (2)电压;如图(3)0.65 【解析】 试题分析:(1)由图甲所示可知,电压表指针没有指在零刻度线上,在使用前应对电压表进行调零,使指针指在零刻度线上;(2)由图乙所示电路图可知,电压表连线错误,电压表与电源两极相连接,在闭合开关前,电压表有示数,修改后的电路图如图所示:;(3)移动滑片使电压表示数等于灯泡额定电压2.5V ,由图丙所示电流表可知,其量程为0~0.6A ,分度值为0.02A ,示数为0.26A , 所以灯泡额定功率:P=UI=2.5V×0.26A=0.65W .21、利用如图所示装置探究“物体的动能大小与哪些因素有关”.将小球A 、B 分别拉到与竖直方向成一定角度θ的位置,然后都由静止释放,当小球摆动到竖直位置时,将与静止在水平面上的木块C 发生碰撞,木块都会在水平面上滑行一定距离后停止.图中的摆长L 都相同,θ1<θ2,球A 、B 的质量分别为m A 、m B (m A <m B ).试卷第13页,共16页(1)本实验中,通过观察 比较小球动能的大小. (2)观察如图甲、乙所示现象,由此可得出结论: .(3)图乙中小球B 到达竖直位置时的速度 (选填“大于”、“小于”或“等于”)图丙中小球B 到达竖直位置时的速度.如图乙、丙所示,可得出结论: .【答案】(1)木块C 被推动的距离;(2)速度相同时,物体的质量越大,动能越大; (3)小于;质量相同时,物体的速度越大,动能越大 【解析】 试题分析:(1)由图知,小球将木块C 推动的距离大小判断其动能大小,采用了转换法的思想; (2)由图甲、乙可知,m A <m B ,两球的速度相同,B 球能将木块c 撞得更远,说明B 球的动能更大,因此可得:速度相同时,物体的质量越大,动能越大;(3)乙丙两图,小球的质量相同,θ1<θ2,所以丙图小球的速度更大,图丙中木块C 滑行得更远些,因此可得:质量相同时,物体的速度越大,动能越大.四、作图题(题型注释)22、(1)一束光照射到水面发生反射和折射,这束光经水面折射后的光束如图甲所示.请在图中画出它的入射光线和反射光线的大致方向.(2)如图乙所示,课桌的重心为O 点,若在课桌的C 点用力F 把桌腿B 抬离地面,在抬起时另一桌腿A 没有滑动,请在图中画出最小力F 的示意图及其力臂L . (3)小磁针的指向如图丙所示,请画出螺母管的极性和电流方向.【答案】【解析】试题分析:(1)光由空气斜射进入液体中时,折射光线向靠近法线方向偏折,根据折试卷第14页,共16页射角小于入射角画出入射光线.由光的反射定律的内容,首先过入射点画出法线,法线与界面垂直(虚线),根据反射角等于入射角画出反射光线;如下图所示:(2)连接AC ,则AC 就是最长的动力臂,根据杠杆平衡的条件,要使杠杆平衡动力方向向上,据此可画出最小的动力;如下图所示:(3)小磁针的右端为S 极,靠近螺线管的左端,根据磁极间作用规律可知,螺线管的左端为N 极,右端为S 极.根据螺线管的极性和线圈的绕向,利用安培定则可以确定螺线管中电流是从右端流入,左端流出.如下图所示:五、计算题(题型注释)23、如图所示,电源电压恒定不变,电阻R 1的阻值为5Ω,小灯泡上标有“12V 6W”字样,闭合开关S .(1)当开关S 1、S 2都闭合,滑动变阻器的滑片P 移到最右端时,电流表的读数为1.7A ,小灯泡恰能正常发光,求滑动变阻器的最大阻值.(2)当开关S 1、S 2都断开,滑动变阻器的滑片P 在最右端,求电流表的读数和滑动变阻器消耗的电功率.【答案】(1)滑动变阻器的最大阻值为10Ω;(2)当开关S 1、S 2都断开,滑动变阻器的滑片P 在最右端,电流表的读数为0.8A ,滑动变阻器消耗的电功率为6.4W【解析】试题分析:(1)当开关S 1、S 2都闭合,滑动变阻器的滑片P 移到最右端时,灯泡与滑动变阻器的最大阻值并联,由于并联电路中各支路两端的电压相等,且灯泡正常发光,试卷第15页,共16页所以电源的电压U=U L =12V ,因为P=UI ,且灯泡正常发光时的功率为6W , 所以通过小灯泡的电流: I L ===0.5A ,由于并联电路中干路电流等于各支路电流之和, 所以通过滑动变阻器的电流: I 2=I ﹣I L =1.7A ﹣0.5A=1.2A , 由I=可知,滑动变阻器的最大阻值: R 2===10Ω;(2)由于串联电路中的总电阻等于各分电阻之和, 所以此时电路中的电流即电流表的示数: I===0.8A ,此时滑动变阻器消耗的电功率: P 2=I 2R 2=(0.8A )2×10Ω=6.4W .24、斜面也是一种简易机械.如图所不,已知斜面上木箱的质量m=40kg ,人对木箱的拉力为75N ,木箱沿着斜面从底端匀速运动到斜面长4m 长的斜面顶端,斜面高0.5m .(g 取10N/kg )(1)斜面的机械效率.(2)木箱运动过程中受到的阻力.【答案】(1)斜面的机械效率为66.7%. (2)木箱运动过程中受到的阻力为25N 【解析】 试题分析:(1)木箱受到的重力: G=mg=40kg×10N/kg=400N ; 有用功W 有用=Gh=400N×0.5m=200J ,总功W 总=Fs=75N×4m=300J 斜面的机械效率:η=×100%=×100%≈66.7%;试卷第16页,共16页(3)因为W 总=W 有用+W 额,所以克服阻力做的额外功:W 额=W 总﹣W 有用=300J ﹣200J=100J ,因为W 额=fs ,所以木箱所受的阻力:f===25N。
初中数学吉林省长春市南关区中考模拟数学一模考试卷含答案解析
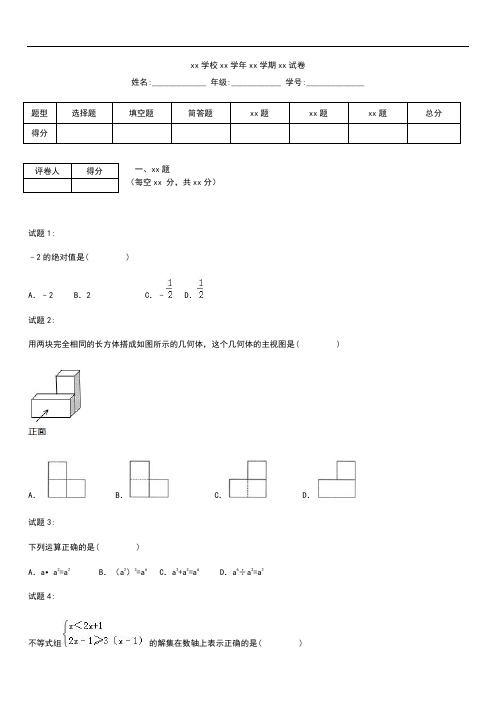
xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)试题1:﹣2的绝对值是( )A.﹣2 B.2 C.﹣ D.试题2:用两块完全相同的长方体搭成如图所示的几何体,这个几何体的主视图是( )A. B. C. D.试题3:下列运算正确的是( )A.a•a2=a2 B.(a2)3=a6 C.a2+a3=a6 D.a6÷a2=a3试题4:不等式组的解集在数轴上表示正确的是( )评卷人得分A. B. C. D.试题5:如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于EF 长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )A.20° B.25° C.30° D.40°试题6:如图,在Rt△ABC中,∠C=90°,AC<BC.斜边AB的垂直平分线交边BC于点D.若BD=5,CD=3,则△ACD的周长是( )A.7 B.8 C.12 D.13试题7:如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )A.130° B.120° C.110° D.100°试题8:如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=﹣(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )A. B. C. D.试题9:化简:﹣=__________.试题10:某种商品n千克的售价是m元,则这种商品8千克的售价是__________元.试题11:不解方程,判断方程2x2+3x﹣2=0的根的情况是__________.试题12:如图,在平面直角坐标系中,直线y=﹣x+2分别交x轴、y轴于A、B两点,点P(1,m)在△AOB的形内(不包含边界),则m的值可能是__________.(填一个即可)试题13:如图,在正方形ABCDE中,以BC为一边,在形内作等边△BCF,连结AF.则∠AFB的大小是__________度.试题14:如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小是__________度.试题15:先化简,再求值:(),其中x=.试题16:在一个不透明的口袋里装有2个红球、1个黄球和1个白球,它们除颜色不同外其余都相同.从口袋中随机摸出2个球,请你用画树状图或列表法的方法,求摸到的两个球都是红球的概率.试题17:某市政工程队承担着1200米长的道路维修任务.为了减少对交通的影响,在维修了240米后通过增加人数和设备提高了工程进度,工作效率是原来的4倍,结果共用了6小时就完成了任务.求原来每小时维修多少米?试题18:如图,在△ABC中,AD是BC边的中线,E是AD的中点,过A点作AF∥BC交BE的延长线于点F,连结CF.求证:四边形ADCF是平行四边形.试题19:2015年3月22日是第二十三届“世界水日”,宣传主题是“水与可持续发展”.小明同学为了解本校同学对“世界水日”的了解情况,从本校七、八、九年级学生中各随机抽取100人进行问卷调查,这些同学都交回了调查问卷,并都对“了解”和“不了解”这两个选项做了唯一的选择,小明根据所得数据绘制了统计图如下.根据相关信息,解答下列问题.(1)补全条形统计图.(2)求抽取的学生中了解“世界水日”的人数.(3)本校七、八、九年级各有学生500名,估计全校学生了解“世界水日”的人数.试题20:如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°,求路灯DE的顶端D点到桥面AB的垂直距离(即DF的长,精确到0.1m).【参考数据:sin14°=0.24,cos14°=0.97,tan14°=0.25】试题21:某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.(1)求甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式.(2)求甲、乙第一次相遇的时间.(3)直接写出乙回到侧门时,甲到侧门的路程.试题22:【发现问题】如图①,在△ABC中,分别以AB、AC为斜边,向△ABC的形外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点.求证:△DFM≌△MGE.【拓展探究】如图②,在△ABC中,分别以AB、AC为底边,向△ABC的形外作等腰三角形,顶角的顶点分别为D、E,且∠BAD+∠CAE=90°.点F、M、G分别为AB、BC、AC边的中点,若AD=5,AB=6,△DFM的面积为32,直接写出△MGE的面积.试题23:如图,在平面直角坐标系中,直线y=kx﹣3k(k>0)分别交x轴、y轴于点A、B.抛物线y=x2+(k﹣3)x﹣3k经过A、B 两点,点P在抛物线上,且在直线y=kx﹣3k(k>0)的下方,其横坐标为2k,连结PA、PB,设△PAB的面积为S.(1)求点P的坐标(用含k的代数式表示).(2)求S与k之间的函数关系式.(3)求S等于2时k的值.(4)求S取得最大值时此抛物线所对应的函数表达式.试题24:如图,在△ABC中,AC=BC=5cm,AB=6cm,CD⊥AB于点D.动点P、Q同时从点C出发,点P沿线CD做依次匀速往返运动,回到点C停止;点Q沿折线CA=AD向终点D做匀速运动;点P、Q运动的速度都是5cm/s.过点P作PE∥BC,交AB于点E,连结PQ.当点P、E不重合点P、Q不重合时,以线段PE∥BC,交AB于点E,连结PQ.当点P、E不重合且点P、Q不重合时,以线段PE、PQ为一组邻边作▱PEFQ.设点P运动的时间为t(s),▱PEFQ与△ABC重叠部分的面积为S(cm2).(1)用含t的代数式表示线段PE的长.(2)当点F在线段AB上时,求t的值.(3)当点Q在线段AB上运动时,求S与t之间的函数关系式.(4)在整个运动过程中,当▱PEFQ为矩形时,直接写出t的值.试题1答案:B【考点】绝对值.【分析】根据绝对值的定义,可直接得出﹣2的绝对值.【解答】解:|﹣2|=2.故选B.【点评】本题考查了绝对值的定义,关键是利用了绝对值的性质.试题2答案:C【考点】简单组合体的三视图.【分析】根据主视图的定义,找到从正面看所得到的图形即可.【解答】解:从物体正面看,左边1列、右边1列上下各一个正方形,且左右正方形中间是虚线,故选:C.【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图,解答时学生易将三种视图混淆而错误的选其它选项.试题3答案:B【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.【专题】计算题.【分析】A、原式利用同底数幂的乘法法则计算得到结果,即可做出判断;B、原式利用幂的乘方运算法则计算得到结果,即可做出判断;C、原式不能合并,错误;D、原式利用同底数幂的除法法则计算得到结果,即可做出判断.【解答】解:A、原式=a3,错误;B、原式=a6,正确;C、原式不能合并,错误;D、原式=a4,错误,故选B.【点评】此题考查了同底数幂的乘除法,合并同类项,以及幂的乘方与积的乘方,熟练掌握运算法则是解本题的关键.试题4答案:B【考点】在数轴上表示不等式的解集;解一元一次不等式组.【分析】分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.【解答】解:,由①得,x>﹣1;由②得,x≤2,故此不等式组的解集为:﹣1<x≤2.在数轴上表示为:【点评】本题考查的是在数轴上表示一元一次不等式组的解集,熟知实心圆点与空心圆点的区别是解答此题的关键.试题5答案:A【考点】作图—基本作图.【分析】根据题意可得AH平分∠CAB,再根据平行线的性质可得∠CAB的度数,再根据角平分线的性质可得答案.【解答】解:由题意可得:AH平分∠CAB,∵AB∥CD,∴∠C+∠CAB=180°,∵∠ACD=140°,∴∠CAB=40°,∵AH平分∠CAB,∴∠HAB=20°,∴∠AHC=20°.故选A.【点评】此题主要考查了平行线的性质,以及角平分线的作法,关键是掌握两直线平行,同旁内角互补,以及角平分线的做法.试题6答案:C【考点】线段垂直平分线的性质.【分析】根据线段的垂直平分线的性质得到AD=BD,根据勾股定理求出AC的长,根据三角形的周长公式计算即可.【解答】解:∵DE是AB的垂直平分线,∴AD=BD=5,又CD=3,由勾股定理得,AC==4,∴△ACD的周长=AC+CD+AD=12,故选:C.【点评】本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.试题7答案:D【考点】圆内接四边形的性质;圆周角定理.【分析】先根据圆内接四边形的性质得到∠D=180°﹣∠B=50°,然后根据圆周角定理求∠AOC.【解答】解:∵∠B+∠D=180°,∴∠D=180°﹣130°=50°,∴∠AOC=2∠D=100°.故选D.【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了圆内接四边形的性质.试题8答案:C【考点】反比例函数图象上点的坐标特征;坐标与图形变化-平移.【分析】先求出A点坐标,再根据图形平移的性质得出A1点的坐标,故可得出反比例函数的解析式,把O1点的横坐标代入即可得出结论.【解答】解:∵OB=1,AB⊥OB,点A在函数y=﹣(x<0)的图象上,∴当x=﹣1时,y=2,∴A(﹣1,2).∵此矩形向右平移3个单位长度到A1B1O1C1的位置,∴B1(2,0),∴A1(2,2).∵点A1在函数y=(x>0)的图象上,∴k=4,∴反比例函数的解析式为y=,O1(3,0),∵C1O1⊥x轴,∴当x=3时,y=,∴P(3,).故选C.【点评】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上点的坐标一定适合此函数的解析式是解答此题的关键.试题9答案:.【考点】二次根式的加减法.【分析】先把各根式化为最简二次根式,再根据二次根式的减法进行计算即可.【解答】解:原式=2﹣=.故答案为:.【点评】本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.试题10答案:元.【考点】列代数式.【分析】先求出1千克商品的价格,再乘以8,即可解答.【解答】解:根据题意,得:,故答案为:.【点评】本题考查了列代数式,解决本题的关键是先求出1千克商品的价格.试题11答案:有两个不相等的实数根.【考点】根的判别式.【分析】先求一元二次方程的判别式,由△与0的大小关系来判断方程根的情况.【解答】解:∵a=2,b=3,c=﹣2,∴△=b2﹣4ac=9+16=25>0,∴一元二次方程有两个不相等的实数根.故答案为:有两个不相等的实数根.【点评】此题考查一元二次方程根的情况与判别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没有实数根.试题12答案:1.(填一个即可)【考点】一次函数图象上点的坐标特征.【分析】先求出AB两点的坐标,进而可得出结论.【解答】解:∵直线y=﹣x+2分别交x轴、y轴于A、B两点,∴A(4,0),B(0,2),∴当点P在直线y=﹣x+2上时,﹣+2=m,解得m=,∵点P(1,m)在△AOB的形内,∴0<m<,∴m的值可以是1.故答案为:1.【点评】本题考查的是一次函数图象上点的坐标特征,熟知一次函数图象上图象上点的坐标一定适合此函数的解析式是解答此题的关键.试题13答案:66度.【考点】多边形内角与外角;等边三角形的性质.【分析】根据等边三角形的性质得到BF=BC,∠FBC=60°,由正五边形的性质得到AB=BC,∠ABC=108°,等量代换得到AB=BF,∠ABF=48°,根据三角形的内角和即可得到结论.【解答】解:∵△BCF是等边三角形,∴BF=BC,∠FBC=60°,∵在正方形ABCDE中,AB=BC,∠ABC=108°,∴AB=BF,∠ABF=48°,∴∠AFB=∠BAF==66°,故答案为:66.【点评】本题考查了正多边形的内角和,等边三角形的性质,等腰三角形的性质,熟记正多边形的内角的求法是解题的关键.试题14答案:80度.【考点】旋转的性质.【分析】由旋转的性质可知∠B=∠AB1C1,AB=AB1,由等腰三角形的性质和三角形的内角和定理可求得∠B=∠BB1A=∠AB1C1=40°,从而可求得∠BB1C1=80°.【解答】解:由旋转的性质可知:∠B=∠AB1C1,AB=AB1,∠BAB1=100°.∵AB=AB1,∠BAB1=100°,∴∠B=∠BB1A=40°.∴∠AB1C1=40°.∴∠BB1C1=∠BB1A+∠AB1C1=40°+40°=80°.故答案为:80.【点评】本题主要考查的是旋转的性质,由旋转的性质得到△ABB1为等腰三角形是解题的关键.试题15答案:【考点】分式的化简求值.【分析】先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.【解答】解:原式=÷(﹣)=÷=•=x2.当x=时,原式=()2=2.【点评】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.试题16答案:【考点】列表法与树状图法.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与摸到的两个球都是红球的情况,再利用概率公式即可求得答案.【解答】解:画树状图得:∵共有12种等可能的结果,摸到的两个球都是红球的有2种情况,∴摸到的两个球都是红球的概率为:=.【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.试题17答案:【考点】分式方程的应用.【分析】设原来每小时维修x米,则后来每小时维修4x米,等量关系是:原来维修240米所用时间+后来维修(1200﹣240)米所用时间=6小时,依此列出方程求解即可.【解答】解:设原来每小时维修x米.根据题意得+=6,解得x=80,经检验,x=80是原方程的解,且符合题意.答:原来每小时维修80米.【点评】本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.试题18答案:【考点】平行四边形的判定.【专题】证明题.【分析】首先利用全等三角形的判定方法得出△AEF≌△DEB(AAS),进而得出AF=BD,再利用一组对边平行且相等的四边形是平行四边形进而得出答案.【解答】证明:∵AF∥BC,∴∠AFE=∠EBD.在△AEF和△DEB中∵,∴△AEF≌△DEB(AAS).∴AF=BD.∴AF=DC.又∵AF∥BC,∴四边形ADCF为平行四边形.【点评】此题主要考查了平行四边形的判定以及全等三角形的判定与性质,得出△AEF≌△DEB是解题关键.试题19答案:【考点】条形统计图;用样本估计总体;扇形统计图.【分析】(1)求得八年级的人数,补全条形统计图即可;(2)求出总人数乘以40%即可得到结果;(3)由500乘以学生了解“世界水日”的百分比即可得到结果.【解答】解:(1)八年级一共300×40%﹣60﹣20=40人;画图如下:(2)100×3×40%=120人;(3)500×3×40%=600人.【点评】此题考查了条形统计图,扇形统计图,关键是正确从扇形统计图和条形统计图中,对比两个图中得到所用的信息.试题20答案:【考点】解直角三角形的应用-坡度坡角问题.【分析】首先得到∠EDF=∠ABC=14°,然后在Rt△DEF中利用余弦的定义得到DF=DEcos∠EDF即可.【解答】解:在Rt△BEG和Rt△DEF中,∵∠BEG=∠DEF,∴∠EDF=∠ABC=14°,在Rt△DEF中,∵cos∠EDF=,∴DF=DEcos∠EDF=5×cos14°=5×0.97=4.85≈4.9m.答:路灯DE的顶端D点到桥面AB的垂直距离为4.9米.【点评】本题考查了解直角三角形的知识,解题的关键是能够从实际问题中整理出直角三角形并选择合适的边角关系求解.试题21答案:【考点】一次函数的应用.【分析】(1)根据函数图象可知点(0,15)和点(1,10)在甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数图象上,从而可以解答本题;(2)根据函数图象可以分别求得甲乙刚开始两端对应的函数解析式,联立方程组即可求得第一次相遇的时间;(3)根据函数图象可以得到在最后一段甲对应的函数解析式,乙到侧门时时间为2.2h,从而可以得到乙回到侧门时,甲到侧门的路程.【解答】解:(1)设甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式为:y=kx+b,∵点(0,15)和点(1,10)在此函数的图象上,∴,解得k=﹣5,b=15.∴y=﹣5x+15.即甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式为:y=﹣5x+15.(2)设乙骑自行车从侧门匀速前往正门对应的函数关系式y=kx,将(1,15)代入可得k=15,∴乙骑自行车从侧门匀速前往正门对应的函数关系式y=15x,∴解得x=0.75.即第一次相遇时间为0.75h.(3)乙回到侧门时,甲到侧门的路程是7km.设甲休息了0.6小时后仍按原速继续行走对应的函数解析式为:y=kx+b.将x=1.2代入y=﹣5x+15得,y=9.∵点(1.8,9),(3.6,0)在y=kx+b上,∴,解得k=﹣5,b=18.∴y=﹣5x+18.将x=2.2代入y=﹣5x+18,得y=7.即乙回到侧门时,甲到侧门的路程是7km.【点评】本题考查一次函数的应用,解题的关键是能看懂题意,根据数形结合的数学思想,找出所求问题需要的条件.试题22答案:【考点】全等三角形的判定与性质;等腰直角三角形.【分析】【发现问题】根据等腰直角三角形的性质得到∠DFB=90°,DF=FA;∠EGC=90°,AG=GE,根据三角形的中位线的性质得到FM∥AC,MG∥AB,推出四边形AFMG是平行四边形,根据平行四边形的性质得到FM=AG,MG=FA,∠BFM=∠BAC,∠BAC=∠MGC,即可得到结论;【拓展探究】根据三角形的中位线的性质得到FM∥AC,MG∥AB,FM=AC=AG,MG=AB=AF,∠MGC=∠BAC=∠BFM,等量代换得到∠DFM=∠MGE,根据余角的性质得到∠1=∠3,根据三角函数的定义,推出,得到△DFM∽△MGE,根据相似三角形的性质即可得到结论.【解答】【发现问题】证明:∵△ADB是等腰直角三角形,F为斜边AB的中点,∴∠DFB=90°,DF=FA;∵△ACE是等腰直角三角形,G为斜边AC的中点,∴∠EGC=90°,AG=GE,∵点F、M、G分别为AB、BC、AC边的中点,∴FM∥AC,MG∥AB,∴四边形AFMG是平行四边形,∴FM=AG,MG=FA,∠BFM=∠BAC,∠BAC=∠MGC,∴DF=MG,∠DFM=∠MGE,FM=GE,在△DFM与△MGE中,,∴△DFM≌△MGE.【拓展探究】∵点F、M、G分别为AB、BC、AC边的中点,∴FM∥AC,MG∥AB,FM=AC=AG,MG=AB=AF,∠MGC=∠BAC=∠BFM,∴∠DFM=∠MGE,∵∠1+∠2=90°∠2+∠3=90°,∴∠1=∠3,∴tan∠1=tan∠3,即,∴,∵∠DFM=∠MGE,∴△DFM∽△MGE,∴,∴S△MGE=18.【点评】本题考查了全等三角形的判定和性质,相似三角形的判定和性质,直角三角形的性质.三角形的中位线的性质,等腰三角形的性质,证得△DFM∽△MGE是解题的关键.试题23答案:【考点】二次函数综合题.【分析】(1)把点P的横坐标2k代入抛物线y=x2+(k﹣3)x﹣3k,可求P的坐标(用含k的代数式表示).(2)过P点作PQ∥y轴交AB于点Q,过B点作BN⊥PQ于点N,过A点作AM⊥PQ于点M,可得P(2k,6k2﹣9k),Q(2k,2k2﹣3k),根据两点间的距离公式可得PQ,再根据S△PAB=S△PQB+S△PQA,可求S与k之间的函数关系式.(3)根据S等于2,可得关于k的方程,解方程可求k的值.(4)根据配方法可求S取得最大值时k的值,进一步得到抛物线所对应的函数表达式.【解答】解:(1)∵点P在抛物线y=x2+(k﹣3)x﹣3k上,且其横坐标为2k,∴y=4k2+(k﹣3)×2k﹣3k=6k2﹣9k,∴点P的坐标(2k,6k2﹣9k);(2)如图,过P点作PQ∥y轴交AB于点Q,过B点作BN⊥PQ于点N,过A点作AM⊥PQ于点M,则P(2k,6k2﹣9k),Q(2k,2k2﹣3k),则PQ=﹣4k2+6k),S△PAB=S△PQB+S△PQA=PQ•BN+PQ•AM=PQ(BN+AM)=PQ=﹣6k2+9k;(3)依题意有﹣6k2+9k=2,解得k1=,k2=;(4)S△PAB=﹣6k2+9k=﹣6(k﹣)2+,当k=时,△PAB面积最大值是,y=x2﹣x﹣.【点评】考查了二次函数综合题,解题的关键是熟练掌握两点间的距离公式,三角形面积,二次函数最值的知识点,同时涉及方程思想的应用,综合性较强,有一定的难度.试题24答案:【考点】相似形综合题.【专题】压轴题;数形结合.【分析】(1)根据题意,分两种情况:①当0<t<时;②当<t≤时;然后根据PE∥BC,可得,据此用含t 的代数式表示线段PE的长即可.(2)首先用含t的代数式表示出QF、QA,然后根据QA=QF,求出t的值是多少即可.(3)首先作PM⊥BC于点M,作QN⊥BC于点N,设▱PEFQ的高为h,分别用含t的代数式表示出PM、QN,进而用含t的代数式表示出h;然后根据三角形的面积的求法,求出S与t之间的函数关系式即可.(4)当▱PEFQ为矩形时,推得∠DQP=∠BCD,然后根据tan∠DQP=tan∠BCD==,可得,据此求出t的值是多少即可.【解答】解:(1)∵AC=BC=5cm,CD⊥AB于点D,∴点D是AB的中点,AD=6÷2=3(cm),∵AC=5cm,∴CD==(cm).①当0<t<时,如图1,∵PC=5t,∴PD=CD﹣PC=4﹣5t,∵PE∥BC,∴,∴PE==(4﹣5t)=5﹣t.②当<t≤时,如图2,,PD=5t﹣4,∵PE∥BC,∴,∴PE==(5t﹣4)=t﹣5.综上,可得PE=.(2)如图3,QF=PE=t﹣5∵CQ=5t,∴QA=AC﹣CQ=5﹣5t,∵PE∥BC,PE∥QF,∴QF∥BC,∴,∵AC=BC,∴QA=QF,∴5﹣5t=t﹣5,解得t=.(3)如图4,作PM⊥BC于点M,作QN⊥BC于点N,设▱PEFQ的高为h,∵sin∠PCM=,∴PM=PC•sin∠PCM=(8﹣5t)×=﹣3t,∵sin∠QBN==,∴QN=BQ•sin∠QBN=[6﹣(5t﹣5)]×=﹣4t,∴h=QN﹣PM=(﹣4t)﹣(﹣3t)=4﹣t,∴S==(t﹣5)×(4﹣t)=﹣t2+15t﹣10.(4)如图5,当▱PEFQ为矩形时,PD=5t﹣4,QD=8﹣5t,∵▱PEFQ为矩形,∴∠DQP+∠DEP=90°,∵∠B+BCD=90°,∠DEP=∠B,∴∠DQP=∠BCD,∴tan∠DQP=tan∠BCD==,∴,解得t=.【点评】(1)此题主要考查了相似形综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,要熟练掌握.(2)此题还考查了函数关系式的求法、矩形的性质和应用、三角函数的应用、三角形的面积的求法,要熟练掌握.。
吉林省长春市2016届九年级中考模拟试卷(三)数学试题解析(解析版)

一、选择题(共8小题,每小题3分,满分24分)1.若等式2□(﹣1)=3成立,则“□”内的运算符号是()A.+ B.﹣ C.× D.÷【答案】B.考点:有理数的运算.2.2015年10月1日,某市旅游景点接待游客约有61500人次,数据61500用科学记数法表示为()A.6.15×104 B.6.15×105C.61.5×103D.0.615×105【答案】A.【解析】试题解析:61500=6.15×104,故选A.考点:科学记数法—表示较大的数.3.如图是某个几何体的三视图,该几何体是()A.正方体 B.圆柱 C.圆锥 D.球【答案】B.【解析】试题解析:∵俯视图是圆,∴排除A,∵主视图与左视图均是长方形,∴排除C、D故选B.考点:简单几何体的三视图.4.如图,不等式组1232xx-≤⎧⎨+⎩<中的两个不等式的解集在同一个数轴上表示正确的是()【答案】C.考点:在数轴上表示不等式的解集.5.把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45°角)如图放置,使直角顶点C重合,若DE∥BC,则∠1的度数是()A.75° B.105° C.110° D.120°【答案】B.试题解析:∵DE∥BC,∴∠E=∠ECB=45°,∴∠1=∠ECB+∠B=45°+60°=105°,故选B.考点:平行线的性质.6.如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是()A.43B.3 C.5 D.274【答案】B.【解析】试题解析:∵AD∥BE∥CF,∴AB DE BC EF=,即:4.532DE=,∴DE=3,故选B.考点:平行线分线段成比例定理.7.如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A 的度数是()A.65° B.45° C.25° D.20°【答案】D.试题解析:∵OA⊥OB,∴∠AOB=90°,∴∠C=12∠AOB=45°,∠ADB=∠AOB﹣∠B=90°﹣25°=65°,∴∠A=∠ADB﹣∠C=20°.故选D.考点:圆周角定理.8.如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=﹣12x+1上,△ABO的面积是()A.12B.32C.2 D.3【答案】B. 【解析】试题解析:因为在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=﹣12x+1上,可得y=32,把y=32代入y=﹣12x+1,可得:x=﹣2,所以△ABO的面积=1332222⨯⨯=.故选B.考点:一次函数图象上点的坐标特点.二、填空题(共6小题,每小题3分,满分18分)9.计算:(2a)3a2= .【答案】8a5.试题解析:(2a)3a2=8a3×a2=8a5.考点:单项式乘以单项式.10.一元二次方程x2﹣3x﹣1=0根的判别式△=.【答案】13.【解析】试题解析:△=(﹣3)2﹣4×1×(﹣1)=13.考点:根的判别式.11.如图,AB是⊙O的直径,点C在⊙O上,连接AC、BC,CD平分∠ACB交⊙O于点D,若⊙O的半径是4,则AD的长度是.【答案】2π.【解析】试题解析:连接OD,∵AB是⊙O的直径,∴∠ACB=90°,∵CD平分∠ACB,∴∠ACD=45°,∴∠AOD=90°,则AD的长度是904180π⨯=2π.考点:1.圆周角定理;2.弧长的计算.12.如图,在△ABC中,AB=8,BC=6,AC=5,点D在AC上,连结BD,将△ABC沿BD翻折后,若点C恰好落在AB边上的点E处,则△ADE的周长为.【答案】7.【解析】试题解析:∵由翻折的性质可知:DC=DE,BC=EB=6.∴AD+DE=AD+DC=AC=5,AE=AB﹣BE=AB﹣CB=8﹣6=2.∴△ADE的周长=5+2=7.考点:翻折的性质.13.如图,反比例函数y1=1kx的图象与直线y2=k2x+b的一个交点的横坐标为2,当x=3时,y1y2(填“>”、“=”或“<”).【答案】<.【解析】试题解析:观察图象可知,x=3时,反比例函数图象在一次函数的图象的下面,所以y1<y2.考点:反比例函数与一次函数的计算问题.14.如图,在平面直角坐标系中,抛物线y=﹣x2+4x与x轴交于点O、A,点P在抛物线上,连结OP、AP,设点P的横坐标为m,△AOP的面积为S,若0<m<3,则S的取值范围是.【答案】0<S≤8.【解析】试题解析:由题意,P 点坐标为:(m ,﹣m 2+4m ),∵抛物线y=﹣x 2+4x 与x 轴交于点O 、A ,∴当y=0时,﹣x 2+4x=0,解得:x=0,或x=4,∴A(4,0),∴OA=4,由题意可得:P 到AB 的距离为﹣m 2+4m , ∴S=12×4×(﹣m 2+4m )=﹣2m 2+8m=﹣2(m ﹣2)2+8; ∵0<m <3,∴0<S≤8.考点:二次函数的综合题.三、解答题(共10小题,满分78分)15.先化简,再求值:22111a a a --+,其中a=﹣3. 【答案】14-. 【解析】试题分析: 先根据分式混合运算的法则把原式进行化简,再把a 的值代入进行计算即可.试题解析:原式=21(1)(1)(1)(1)a a a a a a --+-+- =2(1)(1)(1)a a a a --+- =11a -, 当a=﹣3时,原式=11314=---. 考点:分式的化简求值.16.从一副扑克牌中取出的两组牌如图所示,第一组牌是红桃1,2,3,第二组牌是方块1,2,3.将它们分别重新洗匀后,背面朝上放置,再从每组牌中各随机抽取1张.用画树状图(或列表)求抽出的两张牌的牌面数字之和是4的概率.【答案】13.【解析】试题分析:先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率即可.试题解析:列表如下:可得所有的结果有9种,两张牌的牌面数字之和是4的有3种,故P(摸出的两张牌的牌面数字之和是4)=31 93 =.考点:列表法或树状图法求概率.17.某条道路上安排了A、B两辆清扫车,A车比B车每小时多清扫路面2km,A车清扫路面35km与B车清扫路面25km所用的时间相同,求B车每小时清扫路面的长度.【答案】B车每小时清扫路面的长度为5km.【解析】试题分析:设设B车每小时清扫路面的长度为xkm,根据“A车清扫路面35km与B车清扫路面25km所用的时间相同”列出方程求解即可.试题解析:设B车每小时清扫路面的长度为xkm,由题意,得25352x x=+,解得x=5.经检验,x=5是所列方程的根,且符合题意.答:B车每小时清扫路面的长度为5km.考点:分式方程的应用.18.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,过点B作BE∥CD,过点C作CE∥AB,BE,CE相交于点E.求证:四边形BDCE是菱形.【答案】证明见解析.【解析】试题分析:根据平行四边形的判定得出四边形是平行四边形,根据直角三角形上的中线得出CD=BD,根据菱形的判定得出即可.试题解析:∵BE∥CD,CE∥AB,∴四边形BDCE是平行四边形.∵∠ACB=90°,CD是AB边上的中线,∴CD=BD,∴平行四边形BDCE是菱形.考点:1.直角三角形上的中线,2.平行四边形的判定,3.菱形的判定.19.“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,某市食品企业计划在今年推出:海参干贝棕、板栗鲜肉粽、水晶蜜浅粽、咖喱牛肉粽(以下分别用A、B、C、D表示)四种口味的粽子.该企业为了解市民对这四种不同口味粽子的喜爱情况,在端午节前派调查组到各社区调查,第一组抽取了某社区10%的居民调查,并将调查情况绘制成如下两幅不完整的统计图.(1)这个社区的居民共有多少人?(2)补全条形统计图.(3)若该市有20万居民,请估计爱吃C种粽子的人数.【答案】(1)8000;(2)补图见解析;(3)4万人.【解析】试题分析:(1)先求出调查的人数,再求出这个社区的居民总人数;(2)先求出喜欢吃C种粽子的人数,补全条形统计图即可;(3)利用全市爱吃C种粽子的人数=全市总人数×爱吃C种粽子的百分比.试题解析:(1)调查这个社区的居民人数为240÷30%=800(人),这个社区的居民总人数为:800÷10%=8000(人);(2)喜欢吃C种粽子的人数为800﹣240﹣80﹣320=160(人),补全条形统计图,;(3)爱吃C种粽子的人数为20×160800=4(万人).考点:1.条形统计图;2.扇形统计图.20.如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).【参考数据:sin17°=0.29,cos17°=0.96,tan17°=0.31】【答案】旗杆AB的高度约为11.8m.【解析】试题分析:试题解析:如图,由题意得EF=BC=9m,∠AEF=17°,∠BEF=45°,在Rt△BEF中,∵tan∠BEF=tan45°=BF EF,∴BF=EF=9m.在Rt△AEF中,∵tan17°=AF EF,∴AF=9×0.31=2.79m.∴AB=AF+BF=11.79≈11.8m.答:旗杆AB的高度约为11.8m.考点:解直角三角形的应用﹣仰角俯角问题.21.一个容器装有一个注水管和两个排水管,每个排水管每分钟排水7.5L,从某一时刻开始2min内只注水不排水,2min后开启一个排水管,容器内的水量y(L)与注水时间x(min)之间的函数关系如图所示.(1)求a的值.(2)当2≤x≤6时,求y与x的函数关系式.(3)若在6min之后,两个出水管均开启,注水管关闭,还需多长时间可排尽容器中的水?【答案】(1)30;(2)y=52x+15(2≤x≤6);(3)2小时.【解析】试题分析:(1)每分钟的进水量根据前2分钟的图象求出,根据后4分钟的水量变化即可求得a的值.(2)设当2≤x≤6时,y与x的函数关系式为y=kx+b.图象过(2,20)、(6,30),用待定系数法求对应的函数关系式;(3)根据每个出水管每分钟出水量,即可求得排完容器的水所有的时间.试题解析:(1)根据图象,每分钟进水20÷2=10L,在随后的4min内容器内的水量y=4(10﹣7.5)=10(L),∴a=20+10=30;(2)设当2≤x≤6时,y与x的函数关系式为y=kx+b.∵图象过(2,20)、(6,30),∴220 630k bk b+=⎧⎨+=⎩,解得:5215 kb⎧=⎪⎨⎪=⎩,∴当2≤x≤6时,y与x的函数关系式为y=52x+15(2≤x≤6);(3)30÷(2×7.5)=2.答:还需2小时可排尽容器中的水.考点:一次函数的应用.22.如图①,在△ABC中,∠ACB=90°,AC=BC,在AC、BC边上分别截取CD=CE,连结DE.将△DCE绕着点C顺时针旋转θ角,连结BE、AD.(1)当0°<θ<90°时,如图②,直线BE交直线AD于点F.①求证:△ACD≌△BCE.②求证:AF⊥BE.(2)当0°<θ<360°,AC=5,CD=3,四边形CDFE是正方形时,直接写出AF的长度.【答案】(1)证明见解析;(2)1.【解析】试题分析: (1)①根据旋转的性质和已知,运用SAS 证明即可;②由问题原型中的结论:△ACE≌△BCE 得出∠BFO=∠ACB,结合等量代换进行求解即可;(2)运用CD∥BE 结合初步探究中的结论,可证CD⊥AF,结合勾股定理即可求解.试题解析:(1)①如图②,∵△DCE 绕着点C 顺时针旋转θ角,由旋转的性质可知,∴∠ACD=∠BCE=θ,又∵AC=BC,CD=CE ,在△ACD 和△BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD≌△BCE;②如图②,设AF 与BC 交点于O ,∵△ACD≌△BCE,∴∠DAC=∠EBC,∵∠AOC=∠BOF,∴∠BFO=∠ACB=90°,∴AF⊥BE;(2)如图③,∵AC=5,CD=3,四边形CDFE是正方形时,∵AD⊥CD,=,4∴AF=4+3=7,如图4,∴AF=4﹣3=1.考点:旋转的性质.23.如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于O、A两点,与直线y=x交于点B,点A、B 的坐标分别为(3,0)、(2,2).点P在抛物线上,过点P作y轴的平行线交射线OB于点Q,以PQ为边向右作矩形PQMN,且PN=1,设点P的横坐标为m(m>0,且m≠2).(1)求这条抛物线所对应的函数表达式.(2)求矩形PQMN的周长C与m之间的函数关系式.(3)当矩形PQMN是正方形时,求m的值.【答案】(1)y=﹣x2+3x.(2)①当0<m<2时,C=﹣2m2+4m+2.②当m>2时,C=2m2﹣4m+2.(3)1或. 【解析】试题分析: (1)把A(3,0)、B(2,2)两点坐标代入y=ax2+bx,解方程组即可解决.(2)分两种情形:①0<m<2,②m>2,分别求出矩形PQMN的周长C与m之间的函数关系式即可.(3)分两种情形列出方程即可解决.试题解析:(1)把A(3,0)、B(2,2)两点坐标代入y=ax2+bx,得930422a ba b+=⎧⎨+=⎩,解得13ab=-⎧⎨=⎩.故抛物线所对应的函数表达式为y=﹣x2+3x.(2)∵点P在抛物线y=﹣x2+3x上,∴可以设P(m,﹣m2+3m),∵PQ∥y轴,∴Q(m,m).①当0<m<2时,如图1中,PQ=﹣m2+3m﹣m=﹣m2﹣2m,C=2(﹣m2+2m)+2=﹣2m2+4m+2.②当m>2时,如图2中,PQ=m﹣(﹣m2+3m)=m2﹣2m,C=2(m2﹣2m)+2=2m2﹣4m+2.(3)∵矩形PQMN是正方形,∴PQ=PN=1,当0<m<2时,如图3中,﹣m2+2m=1,解得m=1.当m>2时,如图4中,m2﹣2m=1,解得(或1不合题意舍弃).考点:二次函数综合题.24.如图,△ABC是等边三角形,AB=2,D是边BC的中点,点P从点A出发,沿AB﹣BD以每秒1个单位长度的速度向终点D运动.同时点Q从点C出发,沿CA﹣AC以每秒1个单位长度的速度运动.当点P停止运动时,点Q也随之停止运动,设点P的运动时间为t(秒),△PQD的面积为S.(1)求线段PB的长(用含t的代数式).(2)当△PQD是等边三角形时,求t的值.(3)当S>0时,求S与t的函数关系式.(4)若点D关于直线PQ的对称点为点D′,且S>0,直接写出点D′落在△ABC的边上时t的值.S=2<t<3时,【答案】(1)BP=t﹣2;(2)1;(3)当0≤t≤2时,22S=+4)1或2.5.【解析】试题分析: (1)根据当0≤t≤2和2≤t≤3时两种情况进行解答即可;(2)根据等边三角形的性质和AAS证明△BPD与△CDQ全等解答即可;(3)根据当0≤t≤2和2<t<3时两种情况,利用三角函数和三角形面积公式解答即可.(4)根据点D′落在△ABC 的边上两种情况解答即可.试题解析:(1)∵△ABC 是等边三角形,AB=2,∴当0≤t≤2时,BP=2﹣t ;当2≤t≤3时,BP=t ﹣2;(2)如图1,∵△PQD 是等边三角形,∴∠PDQ=60°,∴∠PDB+∠CDQ=120°,∵△ABC 是等边三角形,∴∠B=∠C=60°,∴∠PDB+∠BPD=120°,∴∠BPD=∠CDQ,∵BD=CD,在△BPD 与△CDQ 中,BPD CDQ B CBD DC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△BPD≌△CDQ(AAS ),∴BP=CQ,∴2﹣t=t ,∴t=1,(3)当0≤t≤2时,如图2,连接AD ,∵△ABC 是等边三角形,D 是边BC 的中点,∴∠ADB=90°,分别过点P ,Q 作PE⊥BC,QF⊥BC,垂足分别为点E ,F ,在R t△BPE t)-,在Rt△QCF , 过点Q 作QG⊥AB 于点G ,在Rt△AGQ t)-, ∴S △PQD =S △ABC ﹣S △BPD ﹣S △QCD ﹣S △APQ ,∴11112))2222PQD S t t t =⨯-----,∴2S =-+ 当2<t <3时,如图3过点Q 作QH⊥BC 于点H ,在Rt△CQH 中,∠CHQ=90°,t)-,∴211(3))22S PQD PD QH t t ==⨯--=+,∴2S =-+(4)点D′落在△ABC的边上,如图4,此时t=1;点D′落在△ABC的边上,如图5,此时t=2.5.考点:三角形综合题.。
2016年吉林省长春市南关区中考历史一模试卷(解析版)

2016年吉林省长春市南关区中考历史一模试卷一、选择题(每小题1分,共20分,每小题只有一个正确选项)1.这个刚刚点燃销烟烈火的第一英雄,就被发往新疆接受处罚.“第一英雄”是()A.林则徐B.邓世昌C.谭嗣同D.张之洞2.清末,学生经常看到政见的书报,其中“三大主义:曰民族、民权、民生”.应出自()A.《天演论》B.《万国公报》C.《民报》D.《海国图志》3.1919年的五四运动是一群青年揭开了一个时代的序幕.“一个时代”是()A.民主科学时代 B.资产阶级革命时代C.变法图强时代 D.新民主主义革命时代4.奠定了解放长江以南各省基础的战役是()A.辽沈战役 B.淮海战役 C.平津战役 D.渡江战役5.“列车呀,请慢一点儿开,让我们再看一眼朝鲜的亲人,让我们在这曾经洒过鲜血的土地上再停留片刻.”这里与朝鲜人民依依惜别的军队是()A.红军 B.八路军C.新四军D.中国人民志愿军6.探索社会主义道路的良好开端是()A.中共一大 B.遵义会议 C.中共七大 D.中共八大7.1980年我国建立的四个经济特区中,在福建省的是()A.深圳 B.珠海 C.汕头 D.厦门8.“21世纪的钟声即将敲响,神州大地上消除了最后一块殖民地的残痕,民族独立的历史使命完整而彻底地完成了.”材料描述的是()A.香港的回归B.“一国两制”的提出C.澳门的回归D.对台方针的提出9.1992年海峡两岸关系协会和海峡交流基金会达成的重要共识是()A.调整“三不”政策B.两岸坚持一个中国原则C.加强两岸经济交流 D.不以政治分歧干扰合作10.中美两国正式建立外交关系的时间是()A.1972年B.1979年C.1997年D.2001年11.某一文明古国境内,不同种姓之间不能通婚.这个文明古国是()A.古代印度 B.古代巴比伦C.古代希腊 D.古代埃及12.“由信仰、幻想和偏见织成的神学面纱最先在意大利烟消云散了.”这是由于()A.文艺复兴的兴起B.新航路的开辟C.启蒙火种的点燃D.信息时代的到来13.“当宣布登基的时候,他宣誓效忠于1789年的革命原则,也就是说尊重人权、自由、平等,他的一个重要思想就是要通过这个民法,确立革命的原则.”这里的“他”是()A.克伦威尔 B.华盛顿C.拿破仑D.亚历山大二世14.马克思主义诞生的标志是()A.《权利法案》的发表B.《人权宣言》的发表C.法典的发表D.《共产党宣言》的发表15.在1921~1922年召开的华盛顿会议上起主要作用的国家是()A.英、法、美B.英、法、日C.美、英、日D.法、美、日16.1939年8月31日,希特勒签署了关于实施“白色方案”的命令.其中写道:“进攻日期:1939年9月1日.”签署该命令是为了()A.突袭波兰 B.进攻苏联C.偷袭珍珠港D.包围斯大林格勒17.得知“珍珠港事件”爆发,英国首相丘吉尔流下眼泪,高兴地说:“敌人的敌人,才是我们的朋友”.这里的两个“敌人”分别指的是()A.日本、德国B.德国、美国C.日本、美国D.德国、苏联18.从漫画中可以提取到的信息是()A.欧盟是世界最大的经济体B.英国是欧盟的成员国之一C.欧盟各国使用统一的货币D.英国退出使欧盟面临解体19.二战后,逐步成为世界第二号资本主义经济大国的国家是()A.德国 B.美国 C.日本 D.法国20.当今世界经济发展趋势是()A.全球化B.信息化C.多极化D.规范化二、非选择题(4小题,共40分)21.观察下列“政治事件对国家经济影响示意图”,结合所学知识判断下列说法是否正确,正确涂“√”,否则涂“×”.(1)两幅示意图揭示的“影响”出现在第一次工业革命期间.(2)A处填入的国家是法国.(3)图一中的国家在1871年经济出现滑落,是由于资产阶级革命的爆发.(4)图二中的英国在1880年经济出现上涨,是由于对我国发动了鸦片战争.(5)图一曲线波动很大,图二曲线比较平滑,说明两国经济受政治变化影响的程度不同..22.阅读“东北衰退之谜”的部分报道:报道一:东北沈阳市铁西区,因位于南满铁路西部而得名.早在清朝,该地区集聚了大批手工作坊,成为铁西现代工业的萌芽.1945年,东北工业规模亚洲第一.铁西区被誉为“东方鲁尔”.1949年后,铁西区更成为中国制造业的一个重要标本.报道二:1990年代初期,单一的所有制结构和失衡的产业结构使东北地区许多传统产品因为竞争力低而逐渐被淘汰,而铁西区成为“东北现象”的典型代表.2003年,中央出台“振兴东北”战略.随后10年中,中央花费了大量的财力物力投资东北建设.报道三:2015年上半年,东三省的经济表现都不令人满意…东北经济再次告急的原因有多种,如资源枯竭、人才流失、经济结构未有实质性变化、市场缺乏活力等等.﹣﹣摘编自“界面新闻”请回答:(1)报道一中的南满铁路在1931年遭到日军怎样的摧毁?借此,日本发动了哪一侵华事变?1945年铁西区的“荣耀”,与哪场战争的胜利有关?新中国成立后,哪次经济计划的实施使它成为“标本”?任意写出此时东北取得的一项成就.(2)报道二中的铁西区的发展出现了怎样的状况?为了改变报道中“单一的所有制结构”,我国在城市中进行了哪一改革?后来又建立了哪一经济体制?依据报道指出,中央又做了哪些努力来加强东北建设?(3)依据报道三指出,东北经济再次告急的原因有哪些?针对原因提出一项改进建议.23.被称作“种族大熔炉”的美国是个典型的移民国家,请完成以下探究活动.【追根溯源】其移民历史最早可追溯到1620年…就连矗立在纽约的“自由女神像”也是在1886年从法国“移民”到美国的.(1)自由女神像“移民”到美国时,正逢美国诞辰多少周年?为了实现“诞生”美国土著居民与英国“移民”进行了哪些抗争?【移民运动】美国历史持续百年的三次移民潮…第二次移民高潮是从1861年到1880年.为了吸引欧洲移民来美国,在1864年,①总统游说国会通过了《鼓励外来移民法》.1865年,②战争结束后,美国迎来了工业化的高峰期.(2)依据材料指出美国历史上出现几次移民高潮?在材料的①②处,填入相应的内容.【移民人数】(3)图示①②两个时期,移民人数分别出现了怎样的趋势?1930年移民人数出现最低点,写出与之相关的事件.1950年后,移民人数趋于平稳阶段,这与美国陷入和苏联之间的哪场战争有关?【移民贡献】移民潮不但对美利坚民族性格的形成产生了深刻影响,而且使得美国在短短一百多年里能够迅速崛起…可以说移民潮铸就了美国的强大.﹣﹣以上材料均摘编自新华网(4)依据材料指出移民潮给美国带来了哪两点影响?对此,你有何感受?24.以下是从多种史观的视角审视近代西方列强对华的侵略.【革命史观】西方列强的侵略,损害了中国的主权,使我国的社会性质发生了深刻的变化,至此革命进入到旧民主主义革命时期.【文明史观】开启了近代中国向西方学习的进程…中国开始了从器物层面到制度层面,再到观念层面的近代化进程.【全球史观】加强了中国和世界的联系(尽管是被动的,但这是客观事实),中国被纳入了资本主义世界体系,成为资本主义世界体系的重要组成部分.(1)依据材料中划线部分所反映的史实,以《多视角诠释“侵略”》为题,撰写一篇历史小短文.要求:①文中需要包含八个历史事件,且事件需要涉及三个视角的维度(每个“史观”中至少写出与之相关的一个历史事件).②结合材料从两种不同的角度谈谈你对“侵略”的认识.③史实准确,表述清晰流畅,字数150字左右.(2)多视角审视问题的方法,对于你评析历史事件有着怎样的作用?2016年吉林省长春市南关区中考历史一模试卷参考答案与试题解析一、选择题(每小题1分,共20分,每小题只有一个正确选项)1.这个刚刚点燃销烟烈火的第一英雄,就被发往新疆接受处罚.“第一英雄”是()A.林则徐B.邓世昌C.谭嗣同D.张之洞【考点】林则徐虎门销烟.【分析】本题考查林则徐的事迹.【解答】题干中的关键信息“点燃销烟烈火的第一英雄”,根据已学知识可知,1839年6月3日,林则徐下令将缴获的鸦片,在虎门海滩当众销毁.虎门销烟是中国人民禁烟斗争的伟大胜利,显示了中国人民反抗外来侵略的坚强意志.领导这次斗争的林则徐是当之无愧的民族英雄.故选A.2.清末,学生经常看到政见的书报,其中“三大主义:曰民族、民权、民生”.应出自()A.《天演论》B.《万国公报》C.《民报》D.《海国图志》【考点】孙中山的历史功绩.【分析】本题主要考查孙中山的相关内容.【解答】根据已学知识可知:孙中山在《民报》的发刊词中,把同盟会的纲领阐发为“民族主义”“民权主义”“民生主义”三大主义,即“三民主义”.三民主义是孙中山领导辛亥革命的指导思想.故选C.3.1919年的五四运动是一群青年揭开了一个时代的序幕.“一个时代”是()A.民主科学时代 B.资产阶级革命时代C.变法图强时代 D.新民主主义革命时代【考点】五四运动.【分析】本题考查五四爱国运动.【解答】1919年5月,巴黎和会外交失败的消息,激起了中国人民无比的愤慨.一场以学生斗争为先导的爱国运动,首先在北京爆发,这就是五四运动.五四运动是中国近代史上一次彻底的反帝反封建的爱国运动,标志着中国新民主主义的开端.揭开的这个时代是新民主主义革命时代.故选D.4.奠定了解放长江以南各省基础的战役是()A.辽沈战役 B.淮海战役 C.平津战役 D.渡江战役【考点】辽沈、淮海、平津三大战役.【分析】本题考查了淮海战役的意义.【解答】题目直接设问考查奠定了解放长江以南各省基础的战役.在刘伯承、陈毅、邓小平、粟裕、谭震林等统一指挥下,中原解放军和华东解放军又发起了以徐州为中心的淮海战役,人民解放军先解放徐州,又在河南东部全歼敌军.淮海战役的胜利,奠定了解放长江以南各省的基础.故选B.5.“列车呀,请慢一点儿开,让我们再看一眼朝鲜的亲人,让我们在这曾经洒过鲜血的土地上再停留片刻.”这里与朝鲜人民依依惜别的军队是()A.红军 B.八路军C.新四军D.中国人民志愿军【考点】抗美援朝.【分析】本题考查抗美援朝的相关知识.【解答】题干中的关键信息“让我们再看一眼朝鲜的亲人,让我们在这曾经洒过鲜血的土地上再停留片刻”“与朝鲜人民依依惜别的军队”可知是中国人民志愿军,1950年10月彭德怀率领中国人民志愿军跨过鸭绿江,奔赴朝鲜前线,中国开始抗美援朝战争.故选D.6.探索社会主义道路的良好开端是()A.中共一大 B.遵义会议 C.中共七大 D.中共八大【考点】中共八大和社会主义建设总路线.【分析】本题考查学生对中共八大的认识.【解答】根据所学可知,1956年,中国共产党第八次全国代表大会在北京召开.大会指出,当前我国的主要矛盾是,人民对于建立先进的工业国的要求,同落后的农业国的现实之间的矛盾;人民对于经济文化迅速发展的需要,同当前经济文化不能满足人民需要的状况之间的矛盾.党和人民当前的主要任务,是集中力量把我国尽快地从落后的农业国变成先进的工业国.这次大会对当时中国社会主要矛盾和主要任务的分析是正确的,是对我国建设社会主义道路的一次成功探索.故选D.7.1980年我国建立的四个经济特区中,在福建省的是()A.深圳 B.珠海 C.汕头 D.厦门【考点】对外开放和深圳等经济特区的建立.【分析】本题主要考查了我国设立的经济特区.【解答】根据所学知识可知,1980年,我国在广东深圳、珠海、汕头和福建的厦门建立四个经济特区,后来又增设海南经济特区.故选D.8.“21世纪的钟声即将敲响,神州大地上消除了最后一块殖民地的残痕,民族独立的历史使命完整而彻底地完成了.”材料描述的是()A.香港的回归B.“一国两制”的提出C.澳门的回归D.对台方针的提出【考点】祖国统一大业.【分析】本题主要考查了祖国统一大业.【解答】从“21世纪的钟声即将敲响之前”、“最后一块帝国主义侵略造成的殖民地的残痕”等信息判断,材料表明的是1999年12月澳门回归祖国,澳门回归祖国洗雪了中华民族耻辱的一页,而且意味着西方在中国的殖民主义统治结束.故选C.9.1992年海峡两岸关系协会和海峡交流基金会达成的重要共识是()A.调整“三不”政策B.两岸坚持一个中国原则C.加强两岸经济交流 D.不以政治分歧干扰合作【考点】祖国统一大业.【分析】本题主要考查了两岸关系.【解答】1992年11月大陆的两岸关系协会与台湾的海峡交流基金会就解决两会事务性问题进行商谈,两会表明坚持一个中国原则,表达了“海峡两岸均坚持一个中国原则”的共识.故选B.10.中美两国正式建立外交关系的时间是()A.1972年B.1979年C.1997年D.2001年【考点】中美建交.【分析】本题考查了中美建交的时间.【解答】1979年,中国与美国正式建立外交关系.美国承认中有一个中国,台湾是中国的一部分.故选B.11.某一文明古国境内,不同种姓之间不能通婚.这个文明古国是()A.古代印度 B.古代巴比伦C.古代希腊 D.古代埃及【考点】古印度的种姓制度.【分析】本题考查了古印度文明代表﹣﹣种姓制度.【解答】根据题干给出的不同种姓之间不能通婚可知是国家是印度.雅利安人在进入古代印度后,逐渐产生不同等级,形成严格的等级制度,史称“种姓制度”.各等级之间高低贵贱有别,下一等级的人没资格从事高一等级的职业,不同等级的人不得通婚.它激化了当时的社会矛盾,并对后来印度社会的发展带来了不良影响.故选A.12.“由信仰、幻想和偏见织成的神学面纱最先在意大利烟消云散了.”这是由于()A.文艺复兴的兴起B.新航路的开辟C.启蒙火种的点燃D.信息时代的到来【考点】文艺复兴运动.【分析】本题考查文艺复兴,结合所学基础知识即可解答.【解答】中世纪的欧洲被宗教神学所笼罩,气氛沉闷、压抑.14﹣17世纪的文艺复兴运动,焕发出人性的光辉.文艺复兴的核心思想是人文主义,提倡人性,反对神性,主张人的价值是追求幸福,倡导个性解放,反对封建神学.意大利人但丁被称为文艺复兴的先驱,文艺复兴的实质就是新兴的资产阶级文化运动.意大利佛罗伦萨作为文艺复兴的发祥地,在诗歌、绘画、建筑、雕刻、音乐各方面成就突出.著名的文艺复兴三杰拉斐尔、米开朗基罗、达芬奇全部诞生在意大利.所以说文艺复兴运动使“由信仰、幻想和偏见织成的神学面纱最先在意大利烟消云散了”.故选A.13.“当宣布登基的时候,他宣誓效忠于1789年的革命原则,也就是说尊重人权、自由、平等,他的一个重要思想就是要通过这个民法,确立革命的原则.”这里的“他”是()A.克伦威尔 B.华盛顿C.拿破仑D.亚历山大二世【考点】法国大革命.【分析】本题考查的是法国资产阶级革命.应重点掌握拿破仑.【解答】A.克伦威尔是英国资产阶级革命的领导人.B.华盛顿是领导了美国独立战争,又开创了民主政治的先河.C.1804年,拿破仑制订了《拿破仑法典》,第一次确认了民事权利平等、废除贵族特权、财产所有权无限制和契约自由等资产阶级民法的基本原则.这是人类历史上资产阶级国家的第一部民法典.依据题干“尊重人权、自由、平等,他的一个重要思想就是要通过这个民法,确立革命的原则”判断是拿破仑.D.亚历山大二世领导了1861年俄国废除农奴制改革.故选C.14.马克思主义诞生的标志是()A.《权利法案》的发表B.《人权宣言》的发表C.法典的发表D.《共产党宣言》的发表【考点】《共产党宣言》.【分析】本题考查的是马克思主义诞生的知识点.【解答】1848年,马克思和恩格斯共同起草的纲领性文献《共产党宣言》的发表,标志着马克思主义的诞生.故选D.15.在1921~1922年召开的华盛顿会议上起主要作用的国家是()A.英、法、美B.英、法、日C.美、英、日D.法、美、日【考点】巴黎和会和凡尔赛体系.【分析】本题考查的是华盛顿会议.【解答】为协调美日在远东和太平洋地区的矛盾,在美国的倡议下,1921年﹣1922年,美、英、法、日、意、荷、比、葡、中九国在华盛顿举行会议,在会议上起主要作用的是美、英、日三国.故选C.16.1939年8月31日,希特勒签署了关于实施“白色方案”的命令.其中写道:“进攻日期:1939年9月1日.”签署该命令是为了()A.突袭波兰 B.进攻苏联C.偷袭珍珠港D.包围斯大林格勒【考点】第二次世界大战的爆发.【分析】本题考查德国突袭波兰.【解答】从题目中的时间可以得知讲的是德国突袭波兰.“白色方案”是二战初德军为了保障自己东部战略地的安全,而对波兰进行的攻击计划.1939年9月1日,德军突袭波兰,英法被迫对德宣战,第二次世界大战全面爆发.故选A.17.得知“珍珠港事件”爆发,英国首相丘吉尔流下眼泪,高兴地说:“敌人的敌人,才是我们的朋友”.这里的两个“敌人”分别指的是()A.日本、德国B.德国、美国C.日本、美国D.德国、苏联【考点】太平洋战争.【分析】本题考查的是二战期间珍珠港事件的相关史实.【解答】1941年12月7日,日本偷袭珍珠港,标志着二战规模进一步扩大,太平洋战争爆发,其中第一个敌人指的是珍珠港事件的发动者日本,第二个敌人指的是珍珠港事件的受害者美国.故选C.18.从漫画中可以提取到的信息是()A.欧盟是世界最大的经济体B.英国是欧盟的成员国之一C.欧盟各国使用统一的货币D.英国退出使欧盟面临解体【考点】欧盟的成立.【分析】本题考查欧盟的相关知识.【解答】英国保守党领袖、现任首相卡梅伦内阁会议后宣布,英国将与2016年6月23日就“英国是否留在欧盟”举行全民公投,他强调这将是“我们一生中英国面临的最重要的决定之一”.漫画中“英国”和“我们很可能退出欧盟”透露的信息是“英国退出使欧盟面临解体”.故选D.19.二战后,逐步成为世界第二号资本主义经济大国的国家是()A.德国 B.美国 C.日本 D.法国【考点】战后日本经济的高度发展.【分析】本题考查了二战后日本经济发展的成就.【解答】据所学知,二战后,日本利用良好的国内、国际环境,大力发展经济,使国民经济获得了高速发展,到1968年,日本国民生产总值已超过西德,成为资本主义世界第二经济大国.故选C.20.当今世界经济发展趋势是()A.全球化B.信息化C.多极化D.规范化【考点】世界经济全球化的影响.【分析】本题考查了当今世界经济发展趋势.【解答】据所学知,二战后,随着科学技术的发展,世界经济的全球化趋势日益加强,各国之间的联系越来越密切.经济全球化已成为不可逆转的大潮流,各国都在采取措施来顺应这一发展潮流.故选A.二、非选择题(4小题,共40分)21.观察下列“政治事件对国家经济影响示意图”,结合所学知识判断下列说法是否正确,正确涂“√”,否则涂“×”.(1)两幅示意图揭示的“影响”出现在第一次工业革命期间.×(2)A处填入的国家是法国.√(3)图一中的国家在1871年经济出现滑落,是由于资产阶级革命的爆发.×(4)图二中的英国在1880年经济出现上涨,是由于对我国发动了鸦片战争.×(5)图一曲线波动很大,图二曲线比较平滑,说明两国经济受政治变化影响的程度不同.√.【考点】史实辨析题;英国资产阶级革命;法国大革命;第一次工业革命.【分析】(1)本题考查的是工业革命的知识点.(2)本题考查的是法国的政治事件对国家经济影响的知识点.(3)本题考查的是巴黎公社的知识点.(4)本题考查的是鸦片战争发知识点.(5)本题考查的是法英两国政治事件对国家经济影响的知识点.【解答】(1)工业革命发生于18世纪60年代至19世纪的上半期,英国完成工业革命的时间是1840年前后.而材料反映的是1840年以后英国、法国的政治事件对国家经济的影响.因此两幅示意图揭示的“影响”不是出现在第一次工业革命期间.(2)由图一中“1848年革命”“1871年巴黎公社”的信息,可知图一反映的是法国的政治事件对国家经济的影响.(3)法国资产阶级革命爆发于1789年.1871年,法国巴黎的工人发动起义,建立的是巴黎公社,这是无产阶级建立政权的第一次伟大尝试.(4)英国发动鸦片战争是在1840年﹣﹣1842年,不是造成图二中的英国在1880年经济出现上涨的原因.(5)阅读《政治事件对国家经济影响示意图》,可知:图一曲线波动很大,说明法国的国家经济受政治事件的影响大;图二曲线比较平滑,说明英国的政治事件对国际经济的影响比法国要小.故答案为:(1)×;(2)√;(3)×;(4)×;(5)√.22.阅读“东北衰退之谜”的部分报道:报道一:东北沈阳市铁西区,因位于南满铁路西部而得名.早在清朝,该地区集聚了大批手工作坊,成为铁西现代工业的萌芽.1945年,东北工业规模亚洲第一.铁西区被誉为“东方鲁尔”.1949年后,铁西区更成为中国制造业的一个重要标本.报道二:1990年代初期,单一的所有制结构和失衡的产业结构使东北地区许多传统产品因为竞争力低而逐渐被淘汰,而铁西区成为“东北现象”的典型代表.2003年,中央出台“振兴东北”战略.随后10年中,中央花费了大量的财力物力投资东北建设.报道三:2015年上半年,东三省的经济表现都不令人满意…东北经济再次告急的原因有多种,如资源枯竭、人才流失、经济结构未有实质性变化、市场缺乏活力等等.﹣﹣摘编自“界面新闻”请回答:(1)报道一中的南满铁路在1931年遭到日军怎样的摧毁?借此,日本发动了哪一侵华事变?1945年铁西区的“荣耀”,与哪场战争的胜利有关?新中国成立后,哪次经济计划的实施使它成为“标本”?任意写出此时东北取得的一项成就.(2)报道二中的铁西区的发展出现了怎样的状况?为了改变报道中“单一的所有制结构”,我国在城市中进行了哪一改革?后来又建立了哪一经济体制?依据报道指出,中央又做了哪些努力来加强东北建设?(3)依据报道三指出,东北经济再次告急的原因有哪些?针对原因提出一项改进建议.【考点】材料解析题;九一八事变和中国局部抗战;抗日战争的胜利及历史意义;一五计划;城市国有企业改革;确立社会主义市场经济体制;历史开放性问题;阐述见解题.【分析】(1)本题考查九一八事变、抗日战争和一五计划.(2)本题考查“东北现象”、国有企业改革、社会主义市场经济体制和“振兴东北”战略.(3)本题考查东北经济再次告急.【解答】(1)1931年日军炸毁南满铁路柳条湖一小段铁轨,反诬中国军队破坏铁路,并以此为借口,发动九一八事变,中国人民开始局部抗战;1945年铁西区的“荣耀”与抗日战争有关,1945年抗日战争胜利,铁西区也回归祖国,被誉为“东方鲁尔”;新中国成立后,一五计划的实施使它成为“标本”,1953年至1957年我国编制并实施一五计划,集中力量发展重工业,铁西区的重工业成就显著,沈阳第一机床厂建成投产.(2)1990年代初期,单一的所有制结构和失衡的产业结构使东北地区许多传统产品因为竞争力低而逐渐被淘汰,而铁西区成为“东北现象”的典型代表;为了改变报道中“单一的所有制结构”,我国在城市中进行了国有企业改革,扩大企业的生产经营自主权,实行经营责任制;1992年党的十四大提出建立社会主义市场经济体制;2003年,中央出台“振兴东北”战略.随后10年中,中央花费了大量的财力物力投资东北建设.(3)依据报道三可知,东北经济再次告急的原因有资源枯竭、人才流失、经济结构未有实质性变化、市场缺乏活力.故答案为:(1)柳条湖事件;九一八事变;抗日战争;一五计划;沈阳第一机床厂建成投产.(2)单一的所有制结构和失衡的产业结构使东北地区许多传统产品因为竞争力低而逐渐被淘汰,而铁西区成为“东北现象”的典型代表;国有企业改革;社会主义市场经济体制;2003年,中央出台“振兴东北”战略.随后10年中,中央花费了大量的财力物力投资东北建设.。
2016年吉林省长春市中考物理模拟试卷和答案(一)

2016年吉林省长春市中考物理模拟试卷(一)一、选择题(每小题2分,共20分)1.(2分)生活中的一些数据,下列符合实际的是()A.长春市夏季最高气温可达70℃B.课桌高度大约50cmC.中学生的体重大约50ND.中学生的步行速度大约4km/h2.(2分)如图所示的现象中,属于光的反射现象的是()A.水中倒影B.日食形成C.小孔成像D.铅笔“折断”3.(2分)下列各种常见的现象中,属于液化的是()A.春天,清晨河面淡淡的白雾B.夏天,玻璃上的水很快变干C.秋天,日出后薄雾渐渐消散D.冬天,室外冰冻的衣服变干4.(2分)下列家用电器中,利用电流热效应工作的是()A.电风扇B.电饭锅C.电冰箱D.电视机5.(2分)关于家庭电路和安全用电,下列说法正确的是()A.客厅里一个开关可以控制四只灯泡,这四只灯泡一定是串联B.金属外壳的用电器用两脚插头和两孔插座C.严禁在高压线下放风筝,避免发生触电事故D.家庭电路中,开关一定要接在灯泡和零线之间6.(2分)关于温度、比热容、热量、内能,以下说法正确的是()A.一块0℃的冰没有内能B.一个物体吸收了热量,它的温度一定会升高C.一个物体温度升高了,它的内能一定增加D.钻木取火是用热传递的方式改变内能的7.(2分)如图所示,OB=BA,在A点施加一个力,使轻质杠杆OA在水平位置静止,以下说法正确的是()A.杠杆OA一定是一个省力杠杆B.杠杆OA一定是一个费力杠杆C.在A点施加的最小力的大小为D.在A点施加的力不能大于G8.(2分)如图甲所示,木块放在水平面上,用弹簧测力计沿水平方向拉木块使其做匀速直线运动,两次拉动木块得到的s﹣t图象分别是图乙中的图线①、②.两次对应的弹簧测力计示数分别为F1、F2,两次拉力的功率分别是P1、P2,则()A.F1=F2,P1>P2B.F1>F2 P1>P2C.F1=F2P1=P2D.F1>F2 P1<P2 9.(2分)如图甲所示,重力5N的铁块吸附在竖直放置足够长的磁性平板上,在竖直向上拉力F的作用系铁块沿直线竖直向上运动.铁块运动过程中速度v的大小随时间t变化的图象如图乙所示,下列说法正确的是()A.磁性平板对铁块的吸引力等于5NB.在0~2s内摩擦力逐渐变小C.在0~6s内摩擦力大小不变D.在2~6s内拉力逐渐增大10.(2分)甲和乙两灯的额定电压均为6V,图中是甲、乙两灯的电流随其两端电压变化的图象,以下说法正确的是()A.将两灯并联在4V的电源两端,电路总功率为4WB.将两灯串联,使其中一个灯泡正常发光,电源电压最大为9VC.将两灯串联起来,并保证都发光且不被烧坏时,甲灯比乙灯亮D.将两灯并联在6V的电源两端,干路电流为1.5A二、填空题(每空1分,共12分)11.(2分)小明所戴的眼镜对光有发散作用,则小明的眼镜是透镜,他的眼睛是(选填“近视眼”或“远视眼”).12.(2分)闭合开关S后,小磁针静止时北极的指向如图所示,则螺线管左端是极(选填“N”或“S”),电源左端是极(选填“正”或“负”).13.(1分)一辆在水平路面上匀速行驶的洒水车正在洒水作业.该洒水车在洒水的过程中,机械能.(选填“增大”“减小”或“不变”)14.(2分)如图所示,小明将烧热的八宝粥罐扣在气球上,过了一会儿,八宝粥罐“粘”在气球上了,这说明.在此过程中八宝粥罐中的空气温度降低,内能将.15.(2分)摩擦现象广泛存在于人们的生活与生产中.小梦对此很感兴趣,围绕生活中的摩擦现象进行了探究.小梦分别对物体在静止状态和水平运动状态下受摩擦力情况进行了研究,并绘制了图象,如图所示.请比较图象中A、B两点处拉力和摩擦力的大小F A f a,F B f b(选填“大于”、“小于”、“等于”或“不能确定”).16.(3分)如图,A灯标有“4V 4W”字样,B灯标有“4V 2W”字样,闭合开关,从右向左缓慢滑动变阻器滑片,直到其中一盏灯恰好正常发光,此时电路中的电流是A、电压表的示数是V,A灯的功率是W(不考虑温度对灯丝电阻的影响)。
2016年吉林省长春市中考数学模拟试卷(九)

2016年吉林省长春市中考数学模拟试卷(九)一、选择题(共8小题,每小题3分,满分24分)1.(3分)﹣的相反数是()A.B.﹣C.2 D.﹣22.(3分)下列图形中,是正方体表面展开图的是()A.B.C.D.3.(3分)2015年1﹣3月,全国网上商品零售额6310亿元,将6310用科学记数法表示应为()A.6.310×103B.63.10×102C.0.6310×104D.6.310×1044.(3分)不等式组的解集为()A.x≤2 B.x>﹣1 C.﹣1<x≤2 D.﹣1≤x≤25.(3分)如图,在平面直角坐标系中,直线y=﹣x+1上一点A关于x轴的对称点为B(2,m),则m的值为()A.﹣1 B.1 C.2 D.36.(3分)如图,在⊙O中,直径AB=5,弦BC=3,若点P为弧BC上任意一点,则AP的长不可能为()A.3 B.4 C.4.5 D.57.(3分)如图,在菱形ABCD中,E为边CD上一点,连结AE并延长,交BC的延长线于点F,若CE=1,DE=2,则CF长为()A.1 B.1.5 C.2 D.2.58.(3分)如图,在平面直角坐标系中,等腰直角三角形ABC的直角顶点A的坐标为(2,0),顶点B的坐标为(0,1),顶点C在第一象限,若函数y=(x>0)的图象经过点C,则k的值为()A.2 B.3 C.4 D.6二、填空题(共6小题,每小题3分,满分18分)9.(3分)计算:=10.(3分)若关于x的一元二次方程x2﹣4x+k﹣2=0有两个相等的实数根,则k的值为.11.(3分)如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°,若使直线b与直线a平行,则可将直线b绕着点A顺时针至少旋转度.12.(3分)如图,在△ABC中,∠C=90°,AC=6,BC=8.以点A为圆心,AC长为半径作圆弧交边AB于点D,则BD的长为.13.(3分)如图,四边形ABCD是⊙O的内接四边形,若∠B=130°,则∠AOC的大小为.14.(3分)如图,在平面直角坐标系中,过抛物线y=a(x+1)2﹣2(x≤0,a为常数)的顶点A作AB⊥x轴于点B,过抛物线y=﹣a(x﹣1)2+2(x≥0,a为常数)的顶点C作CD ⊥x轴于点D,连结AD、BC.则四边形ABCD的面积为.三、解答题(共10小题,满分78分)15.(6分)先将代数式因式分解,再求值:2x(a﹣2)﹣y(2﹣a),其中a=0.5,x=1.5,y=﹣2.16.(6分)在一个不透明的袋子里装有四只标号分别为1,2,3,4的乒乓球,这些乒乓球除所标数字不同其余均相同.先从袋子里随机摸出一个乒乓球(不放回),再从袋子里随机摸出一个乒乓球,请用画树状图(或列表)的方法,求两次摸出乒乓球的标号是连续整数的概率.17.(6分)甲、乙两地之间的公路长120千米,一辆汽车从甲地匀速驶往乙地,比原计划晚出发24分钟,该车实际行驶的速度是原计划行驶的速度的1.25倍,结果按原计划时间到达乙地,求该车实际行驶速度.18.(7分)如图,在▱ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F.四边形AFCE是菱形吗?请说明理由.19.(7分)如图,把两幅完全相同的长方形图片粘贴在一矩形宣传板EFGH上,除D点外,其他顶点均在矩形EFGH的边上.AB=50cm,BC=40cm,∠BAE=55°,求EF的长.参考数据:sin55°=0.82,cos55°=0.57,tan55°=1.43.20.(7分)为了解大学生参加公益活动的情况,几位同学设计了调查问卷,对几所大学的学生进行了随机调查,问卷如下:根据调查结果绘制出如下两幅不完整的统计图.请回答以下问题:(1)此次被调查的学生人数为人,扇形统计图中m的值为.(2)请补全条形统计图.(3)据统计,该市某大学有学生15000人,请估计这所大学2014﹣2015学年度第一学期参加过至少两次公益活动的人数.21.(8分)小明与小英同时从人们广场出发,沿同一路线骑自行车匀速前往净月潭公园,小明骑行20分钟后因事耽误一会儿,事后继续按原速骑行到达目的地.在小明和小英骑行过程中,二人骑行的路程y(千米)与小英的骑行时间x(分)之间的函数图象如图所示.(1)求小明比小英早到目的地的时间.(2)求图象中线段BC所对应的函数表达式.(3)直接写出在小明和小英所骑行的路程相差不超过1千米时x的取值范围.22.(9分)问题背景:在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.(1)请你将△ABC的面积直接填写在横线上;思维拓展:(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为、、(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积;探索创新:(3)若△ABC三边的长分别为、、(m>0,n>0,且m≠n),试运用构图法求出这三角形的面积.23.(10分)如图,在△ABC中,AB=7,BC=4,∠B=45°,动点P、Q同时出发,点P 沿A﹣C﹣B运动,在边AC的速度为每秒1个单位长度,在边CB的速度为每秒个单位长度;点Q沿B﹣A﹣B以每秒2个单位长度的速度运动,其中一个动点到达终点时,另一个动点也停止运动,在运动过程中,过点P作AB的垂线与AB交于点D,以PD为边向由作正方形PDEF;过点Q作AB的垂线l.设正方形PDEF与△ABC重叠部分图形的面积为y(平方单位),运动时间为t(秒).(1)当点P运动点C时,PD的长度为.(2)求点D在直线l上时t的值.(3)求y与t之间的函数关系式.(4)在运动过程中,是否存在某一时刻t使得在直线上任取一点H,均有HD=HE?若存在,请直接写出t的值;若不存在,请说明理由.24.(12分)原型:如图①,在Rt△ABC中,∠ACB=90°,C是在直线l上的一点,AD⊥l,BE⊥l,垂足分别为D、E.易证△ACD∽△CBE.(不需证明)应用:点A、B在抛物线y=x2上,且OA⊥OB,连结AB与y轴交于点C,点C的坐标为(0,d).过点A、B分别作x轴的垂线,垂足为M、N,点M、N的坐标分别为(m,0)、(n,0).(1)当OA=OB时,如图②,m=,d=;当OA≠OB,如图③,m=时,d=.(2)若将抛物线“y=x2”换成“y=2x2”,其他条件不变,当OA=OB时,d=;当OA≠OB,m=1时,d=.探究:若将抛物线“y=x2”换成“y=ax2(a>0)”,其他条件不变,解答下列问题:(1)完成下列表格.(2)猜测d与a的关系,并证明其结论.拓展:如图④,点A、B在抛物线y=ax2(a>0)上,且OA⊥OB,连结AB与y轴关于点C,AB的延长线与x轴交于点D.AE⊥x轴,垂足为E,当AE=时,△AOE与△CDO 的面积之比为.2016年吉林省长春市中考数学模拟试卷(九)参考答案一、选择题(共8小题,每小题3分,满分24分)1.A;2.A;3.A;4.C;5.B;6.A;7.B;8.D;二、填空题(共6小题,每小题3分,满分18分)9.;10.6;11.20;12.4;13.100°;14.4;三、解答题(共10小题,满分78分)15.;16.;17.;18.;19.;20.200;13;21.;22.;23.4;24.1;1;1;;;;2;4:9;。
吉林省长春市2016届九年级中考模拟试卷(十二)数学试题解析(解析版)

一、选择题(共8小题,每小题3分,满分24分)1.比1小2的数是()A.-3 B.-2 C.-1 D.0【答案】C.【解析】试题解析:1-2=-1.故选C.考点:有理数的减法.2.PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,数0.0000025用科学记数法表示为()A.25×10-7 B.2.5×10-6 C.0.25×10-5 D.2.5×10-7【答案】B.考点:科学记数法--表示较小的数.3.不等式组31xx-≤⎧⎨⎩>的解集在数轴上表示正确的是()【答案】A. 【解析】试题解析:不等式组31xx-≤⎧⎨⎩>的解集是-3<x≤1,在数轴上表示为:故选A.考点:用数轴表示不等式的解集.4.下列四个物体的俯视图与右边给出视图一致的是()【答案】C.【解析】试题解析:几何体的俯视图为,故选C考点:由三视图判断几何体.5.下列方程中,有两个相等的实数根的是()A.x2-4x+4=0 B.x2-2x+5=0 C.x2-2x=0 D.x2-2x-1=0【答案】A.考点:根的判别式.6.如图,AB∥CD,点E在直线CD上,EA平分∠CEB,若∠BED=40°,则∠A大小为()A.80° B.70° C.50° D.40°【答案】B.【解析】试题解析:∵∠BED=40°,∴∠BEC=180°-40°=140°,∵EA是∠CEB的平分线,∴∠AEC=70°,∵AB∥CD,∴∠A=∠AEC=70°,故选B.考点:平行线的性质.7.如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D 为切点,若∠BCD=120°,则∠APD的大小为()A.45° B.40° C.35° D.30°【答案】D.【解析】试题解析:连接DO,∵∠BCD=120°,∴∠DAB=180°-120°=60°,∴△ADO为等边三角形,∴∠ODA=60°,∵PD与⊙O相切,∴∠PDO=90°,∴∠ADP=90°-60°=30°,∴∠APD=∠ODA-∠ADP=60°-30°=30°.故选D.考点:切线的性质.8.如图,在平面直角坐标系中,△OAB的顶点A、B的坐标分别为(0,1)、(2,1),点C在边AB上(不与点B重合),设点C的横坐标为m,△BOC的面积为S,则下面能够反映S与m之间的函数关系的图象是()【答案】C.【解析】试题解析:由题意可得,(2)222BOCBC OA mS⨯-⨯===2-m,所以,S随着m的增大而减小,当m=0时,取得最大值2,m的取值范围是0≤m<2,故选C.考点:动点问题的函数图象.二、填空题(共6小题,每小题3分,满分18分)9.计算:(3x)2= .【答案】9x2.【解析】试题解析:(3x)2=32x2=9x2.考点:积的乘方.10.某种水果的售价为每千克a元,用面值为50元的人民币购买了3千克这种水果,应找回元(用含a的代数式表示).【答案】(50-3a).【解析】试题解析:∵购买这种售价是每千克a元的水果3千克需3a元,∴根据题意,应找回(50-3a)元.考点:列代数式.11.如图,在平面直角坐标系中,矩形OABC 的顶点A 、C 分别在x 轴、y 轴上一点B 在第一象限,函数y=k x (x >0)的图象经过BC 边上的点M ,且MB=2MC ,若矩形OABC 的面积为6,则k 的值为 .【答案】2.【解析】试题解析:如图作MN⊥x 轴垂足为N ,∵S 矩形ABCD =6,BM=2MC ,∴S 矩形MNOC =13×6=2, ∴k=S 矩形MNOC =2.考点:反比例函数k 的几何意义.12.如图,已知C ,D 是以AB 为直径的半圆周上的两点,O 是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于 .【答案】23π. 【解析】试题解析:图中阴影部分的面积=12π×22-21202360π⨯=2π-4 3π=23π.答:图中阴影部分的面积等于23π.考点:扇形面积的计算.13.如图,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC=13BC,DE∥AC,与AB边的交点为E,若DE=4,则BE的长为.【答案】8.【解析】试题解析:∵AD平分∠BAC,∴∠BAD=∠CAD,∵DE∥AC,∴∠CAD=∠EDA,∴∠EAD=∠EDA,∴EA=ED=4,∵DE∥AC,∴BE BD AE CD,而DC=13 BC,∴BE=2AE=8.考点:平行线分线段成比例.14.如图,在平面直角坐标系中,抛物线y=ax2-2ax+32(a<0)的顶点为A,与y轴的交点为B,点B关于抛物线对称轴的对称点为D,四边形ABCD为菱形,若点C在x轴上,则a的值为.【答案】-32. 【解析】 试题解析:∵y=ax 2-2ax+32=a (x-1)2-a+32, ∴顶点A 的坐标为(1,-a+32), 令x=0,则y=32, 所以,点B 的坐标为(0,32), ∵点B 关于抛物线对称轴的对称点为D ,四边形ABCD 为菱形,∴-a+32=2×32, 解得a=-32. 考点:1.菱形的轴对称性,2.二次函数的性质.三、解答题(共10小题,满分78分)15.先化简,再求值:21(1)11x x x ÷+--,其中1x =-.【答案】11x +. 【解析】试题分析:分式的化简,要熟悉混合运算的顺序,分子、分母能因式分解的先因式分解;除法要统一为乘法运算,注意化简后,将1x =,代入化简后的式子求出即可. 试题解析:21(1)11x x x ÷+-- =11()(1)(1)11x x x x x x -÷++---=(1)(1)1x x x x x ÷+-- =1(1)(1)x x x x x-⨯+- =11x +;把1x =-,代入原式= 考点:分式混合运算.16.如图,有3张不透明的卡片,除正面写有不同的数字外,其他均相同,将这3张卡片背面向上洗匀,从中随机抽取一张,记下数字后放回;重新洗匀后再从中随机抽取一张,将抽取的第一张、第二张卡片上的数字分别作为十位数字和个位数字组成两位数,请用画树状图(或列表)的方法,求这个两位数能被3整除的概率.【答案】49. 【解析】试题分析:根据题意直接画出树状图,进而利用概率公式求出答案.试题解析:如图所示:,故这个两位数能被3整除的概率为:49. 考点:树状图法求概率. 17.某超市2015年1月份的营业额为10000元,3月份的营业额为12100元,若该超市2015年前4个月营业额的月增长率相同,求该超市2015年4月份的营业额.【答案】该超市2015年4月份的营业额为13310元.【解析】试题分析:设该超市2015年前4个月营业额的月增长率为x,根据3月份的销售额=1月份的销售额×(1+增长率)的平方,列出关于x的一元二次方程,解方程即可求出x的值,再根据4月份的销售额=3月份的销售额×(1+增长率)即可得出结论.试题解析:设该超市2015年前4个月营业额的月增长率为x,由题意,得10000(1+x)2=12100,解得x=0.1,或x=-2.1(舍去),则12100×(1+10%)=13310(元).答:该超市2015年4月份的营业额为13310元.考点:一元二次方程的应用.18.如图,在△ABC中,AB=AC,D为BC边的中点,以AB、BD为邻边作▱ABDE,连接AD,EC.求证:四边形ADCE是矩形.【答案】证明见解析.【解析】试题分析:由等腰三角形的三线合一性质得出AD⊥BC,BD=CD,∠ADC=90°,由平行四边形的性质得出AE∥BD,AE=BD,得出AE∥CD,AE=CD,证出四边形ADCE是平行四边形,即可得出结论.试题解析:∵AB=AC,D为BC边的中点,∴AD⊥BC,BD=CD,∴∠ADC=90°,∵四边形ABDE是平行四边形,∴AE∥BD,AE=BD,∴AE∥CD,AE=CD,∴四边形ADCE是平行四边形,又∵∠ADC=90°,∴四边形ADCE是矩形.考点:1.等腰三角形的性质;2.平行四边形的判定与性质;3.矩形的判定.19.如图,某广场有一灯柱AB高7.5米,灯的顶端C离灯柱顶端A的距离CA为1.7米,且∠CAB=110°,求灯的顶端C距离地面的高度CD.(结果精确到0.1米)【参考数据:sin20°=0.34,cos20°=0.94,tan20°=0.36】【答案】灯的顶端C距离地面的高度CD约为8.1米.【解析】试题分析:过点C作地面的垂线,垂足为D,过点A作AE⊥CD于E,在RT△ACE中,利用sin∠CAE=CE AE,即可解决问题.试题解析:如图,过点C作地面的垂线,垂足为D,过点A作AE⊥CD于E,∵∠EDB=∠ABD=∠AEB=90°,∴四边形ABDE是矩形,∴ED=AB=7.5,∵∠CAE=∠CAB-90°=110°-90°=20°,在RT△CAE中,∠AEC=90°,∠CAE=90°,∠CAE=20°,AC=1.7,∵sin∠CAE=CE AE,∴CE=AEsin∠CAE=1.7×0.34=0.578,∴CD=CE+ED=0.578+7.5=8.078≈8.1米.答:灯的顶端C距离地面的高度CD约为8.1米.考点:解直角三角形.20.国家教育部规定“中小学生每天在校体育活动时间不低于1小时”.某中学为了解学生体育活动情况,随机抽查了520名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”,并根据调查结果绘制成如下不完整的统计图.根据统计图提供的信息,解答下列问题:(1)这520名毕业生中每天在校锻炼时间超过1消失的人数是.(2)请补全条形统计图.(3)2016年该中学所在城市的初中毕业生约为5.2万人,估计2016年该城市初中毕业生中因为没时间导致每天锻炼时间未超过1小时的人数.【答案】(1)399;(2)补图见解析;(3)0.7万人.【解析】试题分析:(1)将每天在校锻炼时间超过1小时所对应圆心角占周角的比例乘以总人数可得;(2)先求出锻炼时间未超过1小时的人数,再将未超过1小时人数减去“不喜欢”和“其他”的人数即可补全图形;(3)将样本中“没时间”的人数占调查人数的比例乘以总体中的人数可得.试题解析:(1)这520名毕业生中每天在校锻炼时间超过1小时的人数是:270360×520=390(人);(2)每天在校锻炼时间未超过1小时的人数是:520-390=130(人),则“没时间”的人数是:130-50-10=70(人),补全图形如下:(3)5.2×70520=0.7(万人),答:估计2016年该城市初中毕业生中因为没时间导致每天锻炼时间未超过1小时的人数约为0.7万人.考点:1.条形统计图;2.扇形统计图.21.感知:如图①,在矩形ABCD中,点E是边BC的中点,将△ABE沿AE折叠,使点B落在矩形ABCD内部的点F处,延长AF交CD于点G,连结FC,易证∠GCF=∠GFC.探究:将图①中的矩形ABCD改为平行四边形,其他条件不变,如图②,判断∠GCF=∠GFC是否仍然相等,并说明理由.应用:如图②,若AB=5,BC=6,则△ADG的周长为.【答案】探究:∠GCF=∠GFC,理由见解析;应用:16.【解析】试题分析:探究:由▱ABCD及折叠可得∠B+∠ECG=∠AFE+∠ECG=∠AFE+∠EFG=180°,即∠ECG=∠EFG,再根据EB=EF=EC得∠EFC=ECF,从而可得∠GCF=∠GFC;应用:由(1)中∠GCF=∠GFC得GF=GC,AF=AB,根据△ADG的周长AD+AF+GF+GD=AD+AB+GC+GD可得.试题解析:探究:∠GCF=∠GFC,理由如下:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠B+∠ECG=180°,又∵△AFE是由△ABE翻折得到,∴∠AFE=∠B,EF=BE,又∵∠AFE+∠EFG=180°,∴∠ECG=∠EFG,又∵点E是边BC的中点,∴EC=BE,∵EF=BE,∴EC=EF,∴∠ECF=∠EFC,∴∠ECG-∠ECF=∠EFG-∠EFC,∴∠GCF=∠GFC;应用:∵△AFE是由△ABE翻折得到,∴A F=AB=5,由(1)知∠GCF=∠GFC,∴GF=GC,∴△ADG的周长AD+AF+GF+GD=AD+AB+GC+GD=AD+AB+CD=6+5+5=16考点:1.翻折变换;2.平行四边形的性质.22.小明家、学校与图书馆依次在一条直线上,小明、小亮两人同时分别从小明家和学校出发沿直线匀速步行到图书馆借阅图书,小明到达图书馆花了20分钟,小亮每分钟步行40米,小明离学校的距离y(米)与两人出发时间x(分)之间的函数图象如图所示.(1)小明每分钟步行米,a= ,小明家离图书馆的距离为米.(2)在图中画出小亮离学校的距离y(米)与x(分)之间的函数图象.(3)求小明和小亮在途中相遇时二人离图书馆的距离.【答案】(1)60;960;1200.(2)画图见解析;(3) 小明和小亮在途中相遇时二人离图书馆的距离为480米.【解析】试题分析:(1)根据速度=路程÷时间可得出小明的速度,由此得出小明每分钟步行的路程;结合路程=速度×时间,可找出a的值;由小明家离图书馆的距离=小明家离学校的距离+学校离图书馆的距离,由此得出结论;(2)根据时间=路程÷速度,算出小亮到达图书馆的时间,由两点可画出小亮离学校的距离y(米)与x(分)之间的函数图象;(3)根据待定系数法求出小明从学校到图书馆这段路程对应的函数表达式以及小亮从学校到图书馆这段路程对应的函数表达式,由两关系式可得出交点坐标,由此可得出小明和小亮在途中相遇时二人离图书馆的距离.试题解析:(1)240÷4=60(米),60×(20-4)=960(米),240+960=1200(米).(2)960÷40=24(分钟).画出图形如图所示.(3)设小明从学校到图书馆这段路程对应的函数表达式为y=kx+b(k≠0),∵图象经过点(4,0)、(20,960),∴4020960k bk b+=⎧⎨+=⎩,解得60240kb=⎧⎨=-⎩.∴函数表达式为y=60x-240(4≤x≤20).又∵小亮每分钟步行40米,∴小亮从学校到图书馆这段路程对应的函数表达式为y=40x(0≤x≤24).∴当二人相遇时,有60x-240=40x,解得x=12.∴960-40×12=480(米).∴小明和小亮在途中相遇时二人离图书馆的距离为480米.考点:1.一次函数的应用;2.待定系数法求函数解析式.23.如图①,在△ABC 中,AB=7,tanA=34,∠B=45°.点P 从点A 出发,沿AB 方向以每秒1个单位长度的速度向终点B 运动(不与点A 、B 重合),过点P 作PQ⊥AB.交折线AC-CB 于点Q ,以PQ 为边向右作正方形PQMN ,设点P 的运动时间为t (秒),正方形PQMN 与△ABC 重叠部分图形的面积为S (平方单位).(1)直接写出正方形PQMN 的边PQ 的长(用含t 的代数式表示).(2)当点M 落在边BC 上时,求t 的值.(3)求S 与t 之间的函数关系式.(4)如图②,点P 运动的同时,点H 从点B 出发,沿B-A-B 的方向做一次往返运动,在B-A 上的速度为每秒2个单位长度,在A-B 上的速度为每秒4个单位长度,当点H 停止运动时,点P 也随之停止,连结MH .设MH 将正方形PQMN 分成的两部分图形面积分别为S 1、S 2(平方单位)(0<S 1<S 2),直接写出当S 2≥3S 1时t 的取值范围.【答案】(1) PQ=7-t .(2) t=145.(3) 当0<t≤145时,S=2916t .当145<t≤4,24135491622S t t =-+-.当4<t <7时, 2149722S t t =-+.(4)68157252t ≤<或2856915t ≤≤或5214t ≤<. 【解析】试题分析:(1)分两种情况讨论:当点Q 在线段AC 上时,当点Q 在线段BC 上时.(2)根据AP+PN+NB=AB ,列出关于t 的方程即可解答;(3)当0<t≤145时,当145<t≤4,当4<t <7时; (4)68157252t ≤<或2856915t ≤≤或5214t ≤<. 试题解析:(1)当点Q 在线段AC 上时,PQ=tanAAP=34t . 当点Q 在线段BC 上时,PQ=7-t .(2)当点M 落在边BC 上时,如图③,由题意得:t+34t+34t=7, 解得:t=145. ∴当点M 落在边BC 上时,求t 的值为145. (3)当0<t≤145时,如图④,S=2239()416t t =. 当145<t≤4,如图⑤,222915413549(7)16221622S t t t t =--=-+-. 当4<t <7时,如图⑥,221149(7)7222S t t t =-=-+. (4)68157252t ≤<或2856915t ≤≤或5214t ≤<.. 考点:四边形综合题.24.如图,在平面直角坐标系中,经过原点的抛物线y=-x2+4mx(m>0)与x轴的另一个交点为点A,过点P(1,m)作直线PB⊥x轴,交抛物线于点B,作点B关于抛物线对称轴的对称点C(点B、C不重合),连结BC,当点P、B不重合时,以BP、BC为边作矩形PBCQ,设矩形PBCQ的周长为l.(1)当m=1时,求点A的坐标.(2)当BC=12时,求这条抛物线所对应的函数表达式.(3)当点P在点B下方时,求l与m之间的函数关系.(4)连结CP,以CP为直角边作等腰直角三角形PCM,直接写出点M落在坐标轴上时m的值.【答案】(1) (4,0);(2) y=-x2+52x或y=-x2+32x.(3)l=-2m+2.(4)m=23,m=25.【解析】试题分析:(1)根据自变量与函数值的对应关系,可得答案;(2)根据BC的长,可得关于m的方程,根据解方程,可得m的值;(3)根据周长公式,可得答案;(4)利用直线PC的斜率求出直线PE的斜率,并求出直线PE的参数方程,讨论点E在x轴与y轴的情况,并分别求出点E的参数坐标,根据PC=PE,利用两点间距离公式求解.此题也可用开锁法进行求解.试题解析:(1)当m=1时,抛物线的解析式为y=-x2+4x.当y=0时,-x2+4x=0,解得x1=0,x2=4,即A点坐标为(4,0);(2)当y=-x2+4mx中x=1时,y=4m-1,B(1,4m-1).且抛物线的对称轴为x=-42(1)m⨯-=2m.当点B在对称轴左侧时,即m>12时,BC=2(2m-1)=4m-2.当BC=12时,4m-2=12.m=58,这条抛物线的解析式为y=-x2+52x.当BC=12时,2-4m=12.m=38,这条抛物线的解析式为y=-x2+32x.(3)当点B在对称轴左侧,同时点P在点B的下方,即13<m<12时,l=2[2(1-2m)+(4m-1-m)],l=-2m+2.(4)分三种情况:P在对称轴左侧,P(1,m),B(1,4m-1),C(4m-1,4m-1),BC=4m-2,BP=3m-1,①若∠CPQ=90°,PC=PQ,如图1,此时,△CBP≌△PFQ,∴CB=PF,即4m-2=m,解得m=23,②若∠PCQ=90°,CP=CQ,如图2,此时,△QFP≌△CDQ,∴DF=CD,即4m-1=4m-1,方程无解;∴此种情况不成立.③如图3,B(1,4m-1),P(1,m),C(4m-1,4m-1),若∠CPQ=90°,PC=PQ,△CBP≌△QFC,BP=CF,即3m-1=4m-1,解得m=0(舍),④如图4,∠CQP=90°,CQ=CP,△CBP≌△PFQ,BP=QF,即4m-1-m=1,解得m=23;⑤如图5,∠CQP=90°,CQ=CP,△CBP≌△PFQ,BC=PF,即2-4m=m,解得m=25;综上所述:m=23,m=25.考点:二次函数综合题.。
吉林省长春市南关区2016届中考化学一模试题(含解析)

2016年吉林省长春市南关区中考化学一模试卷一、考生注意:每小题只有一个选项符合题意;请用2B铅笔将答题卡上的相应序号涂黑.1.空气中含量较多且常用作保护气的是()A.氮气 B.氧气 C.稀有气体 D.二氧化碳2.生活中的下列现象中,一定发生化学变化的是()A.冰雪融化 B.酒精挥发 C.煤气燃烧 D.蔗糖溶解3.下列物质由分子构成的是()A.铁B.氯化钠C.氨气 D.金刚石4.下列实验操作中,正确的是()A.稀释浓硫酸B.蒸发结晶C.收集气体D.测溶液pH5.下列说法中,错误的是()A.用水能灭火,是因为水能降低可燃物的着火点B.液态氧变成氧气是物理变化,是因为氧分子本身没有变化C.酸溶液有相似的化学性质,是因为在不同的酸溶液中都含有H+D.湿衣服在阳光下比在阴凉处干的快,是因为温度高分子运动的快6.下列关于甲烷(CH4)的说法中,错误的是()A.甲烷是最简单的有机化合物B.甲烷是由碳元素和氢元素组成的C.甲烷分子由碳原子和氢原子构成D.甲烷中碳、氢元素质量比为1:47.下列对有关事实的解释中,正确的是()A.石墨和金刚石物理性质不同﹣﹣碳原子结构不同B.一氧化碳和二氧化碳的化学性质不同﹣﹣分子构成不同C.用CO2鉴别NaOH和Ca(OH)2溶液﹣﹣CO2只与Ca(OH)2反应D.用酚酞溶液不能鉴别稀硫酸和稀盐酸﹣﹣酚酞溶液遇两种酸都变红色8.下列说法中,正确的是()A.浓盐酸和浓硫酸都需要密封保存,都具有挥发性B.氧化铁、碳酸、氧气都含氧元素,都属于氧化物C.氢氧化钠、氢氧化钙都能与酸反应,都能改良酸性土壤D.氯化铵、硝酸铵、硫酸铵都是含铵根离子的盐,都能与可溶性碱反应9.下列有关实验操作的分析中,正确的是()A.配制氯化钠溶液:量取水时,俯视读数,导致浓度偏小B.测定空气中氧气含量:点燃红磷后缓慢伸入集气瓶中,导致进水偏少C.用滴管吸取液体:伸入试剂瓶中捏扁胶头赶尽气体再吸液,不会污染药品D.去除粗盐中难溶性杂质:提纯后所得精盐未完全干燥就称量,导致产率偏高10.下列实验中,能达到相应目的是()A.检验NaOH溶液是否变质:取样,滴入石蕊溶液B.鉴别NaCl溶液和Na2CO3溶液:取样,测酸碱度C.分离木炭粉和氧化铜的混合物:向固体中加入足量的稀硫酸后过滤D.除去CO中的CO2气体和水蒸气:将混合气体依次通过浓硫酸和NaOH溶液二、非选择题(共40分)考生注意:请在答题卡上的指定区域作答.11.回答下列问题.(1)氢气的化学式;(2)铁离子可表示为.12.图A是铝元素在元素周期表中的部分信息,图B是铝原子的结构示意图,回答问题.(1)铝的相对原子质量是;(2)铝元素属于(填“金属”或“非金属”)元素;(3)从图B可知,铝原子在化学反应中容易电子.13.请回答下列与水有关的问题.(1)生活中降低水的硬度可采用的方法是;(2)净化水过程中,利用活性炭的性除去水中的异味和有色物质;(3)水蒸发变成水蒸气时所占的体积变大,从微观角度看是因为.14.现有四种物质:①浓硫酸②氢氧化钠溶液③澄清石灰水④生石灰,回答下列问题.(1)能用来干燥氧气的是;(2)用澄清石灰水检验二氧化碳时的现象是;(3)生石灰做干燥剂时发生的反应可用化学方程式表示为.15.回答下列与含碳物质有关的问题.(1)石墨能用于制作干电池的电极是利用其优良的性;(2)将CO和CO2分别通入到石蕊溶液中,能使溶液变红的是;(3)天然气是一种重要的燃料,其主要成分充分燃烧可用化学方程式表示为;(4)在高炉炼铁3CO+Fe2O3 2Fe+3CO2反应中,表现出氧化性的物质是.16.根据给出的KNO3和NaCl两种物质的溶解度表及溶解度曲线,回答问题.(1)在0℃时,NaCl的溶解度为g;(2)观察曲线可知,从海水中提取氯化钠,通常采用的方法是;(3)在20℃时将20gKNO3放入100g水中,若保持温度不变,再加入KNO3g即可将其变成恰好饱和的溶液;(4)若KNO3中混有少量的NaCl,可先将混合物溶于水配成高温下的饱和溶液,然后再采用的方法就可以提纯KNO3.17.结合盐酸、硫酸的相关知识,回答下列问题.(1)人体胃液中含有少量的,帮助消化;(2)两种酸可以用BaCl2溶液鉴别,是因为两种酸溶液中存在的不同;(3)能与盐酸、稀硫酸发生化学反应产生气体的物质有两类:一类是含有的盐,另一类是活泼金属.18.实验室中用如下实验方案(图示)来研究铁、铝、铜三种金属活动性顺序及其在活动性顺序表中相对氢的位置.(1)乙实验中只要观察到现象,就证明二者已经发生反应;(2)若将实验乙中的CuSO4溶液替换为,即可达成实验目的;(3)现在按原有方案(图示)实验,实验结束后,将乙、丙实验后的剩余物倾倒在一个烧杯中,充分反应.然后将甲实验的剩余物倒入此烧杯,无气泡产生.下列说法中,正确的是.A.最后烧杯中的溶液一定不是无色的B.乙实验中,CuSO4溶液一定是过量的C.乙、丙混合过程中,可能没有发生化学反应D.最后烧杯中的溶液,一定含有Al2(SO4)3,可能含有FeSO4.19.在实验室里用浓度为98%的浓硫酸和蒸馏水配制稀硫酸.(1)要配制19.6%的稀硫酸100g,需要98%的浓硫酸g;(2)量取和混匀操作中需要的玻璃仪器包括烧杯、量筒、胶头滴管和;(3)若量取水时仰视读数,其它的操作均正确,则配制出的稀硫酸的浓度比19.6% ;(4)如图所示是某同学配制后贴在试剂瓶上的标签,有一处错误,请改正:.20.以下是在实验室里制取气体时常用的部分仪器,回答问题.(1)用分解过氧化氢的方法制备并收集氧气,已经选择了仪器a、b、c、i,则还需要从上图中选择的仪器是(填序号),完全反应后从剩余物中分离出二氧化锰可以用蒸发的方法,还可以用的方法是;(2)在(1)中所选仪器还可以制取CO2,若用73g10%的稀盐酸与足量的大理石充分反应,能产生CO2g;(3)上述两实验中使用仪器c的目的是;(4)制取的氧气可以用于铁丝燃烧实验,集气瓶底放入少许水的目的是.21.某实验小组在探究“酸与碱能否发生反应”时,用稀NaOH溶液、稀盐酸和酸碱指示剂进行实验的过程如图,回答下列相关问题.(1)所加试剂①是;(2)为了安全处理废液,要先验证最后得到的无色溶液中溶质的成分,下列所选药品能达到实验目的是.A.Fe2O3B.ZnC.AgNO3溶液D.NaOH溶液.22.有一包白色固体,可能由Na2CO3、BaCl2、Na2SO4、NaOH、CuSO4中的一种或几种组成,为了探究固体的成分,现做如下实验:(1)原固体中一定没有;(2)生成气体的化学方程式是;(3)无色溶液a中一定含有的溶质是;(4)下列关于溶液和白色沉淀的设想中,合理的是.A.鉴别稀盐酸和碳酸钠溶液:用溶液b、c、dB.除去硝酸钡溶液中的硝酸:加入过量的白色沉淀AC.除去氯化钠溶液中少量的盐酸:加入适量的无色溶液a.2016年吉林省长春市南关区中考化学一模试卷参考答案与试题解析一、考生注意:每小题只有一个选项符合题意;请用2B铅笔将答题卡上的相应序号涂黑.1.空气中含量较多且常用作保护气的是()A.氮气 B.氧气 C.稀有气体 D.二氧化碳【考点】空气的成分及各成分的体积分数.【专题】空气与水.【分析】由空气的成分按体积分数计算及各自的性质去分析解答.【解答】解:空气的成分按体积分数计算大约是:大约是氮气占(78%),氧气占(21%),稀有气体占(0.94%),二氧化碳占(0.03%),其它气体和杂质占(0.03%).A、由上面空气的成分可知氮气的含量最多,且氮气的化学性质不活泼,常用做保护气;故A正确;B、由上面空气的成分可知氧气的含量较多,但氧气是一种化学性质比较活泼的气体,不能用做保护气;故B错误;C、由上面空气的成分可知稀有气体的含量较少,故C错误;D、由上面空气的成分可知二氧化碳的含量较少;故D错误;故选A.【点评】空气的成分:氮气占(78%),氧气占(21%),稀有气体占(0.94%),二氧化碳占(0.03%),其它气体和杂质占(0.03%)是体积比而不是质量比.2.生活中的下列现象中,一定发生化学变化的是()A.冰雪融化 B.酒精挥发 C.煤气燃烧 D.蔗糖溶解【考点】化学变化和物理变化的判别.【专题】化学反应的分类思想;物质的变化与性质.【分析】化学变化是指有新物质生成的变化.物理变化是指没有新物质生成的变化.化学变化和物理变化的本质区别是否有新物质生成.【解答】解:A、冰雪融化的过程中没有新物质生成,属于物理变化;B、酒精挥发的过程中没有新物质生成,属于物理变化;C、煤气燃烧的过程中有新物质水和二氧化碳生成,属于化学变化;D、蔗糖溶解的过程中没有新物质生成,属于物理变化.故选C.【点评】解答本题要分析变化过程中是否有新物质生成,如果没有新物质生成就属于物理变化.如果有新物质生成就属于化学变化.3.下列物质由分子构成的是()A.铁B.氯化钠C.氨气 D.金刚石【考点】物质的构成和含量分析.【专题】物质的微观构成与物质的宏观组成.【分析】根据金属、大多数固态非金属单质等由原子构成,有些物质是由分子构成的,如水、氢气等,有些物质是由离子构成的,如氯化钠,进行分析判断即可.【解答】解:A、铁属于金属单质,是由铁原子直接构成的,故选项错误.B、氯化钠是由钠离子和氯离子构成的,故选项错误.C、氨气是由氨分子构成的,故选项正确.D、金刚石属于固态非金属单质,是由碳原子直接构成的,故选项错误.故选:C.【点评】本题难度不大,主要考查了构成物质的微观粒子方面的知识,掌握常见物质的粒子构成是正确解答本题的关键.4.下列实验操作中,正确的是()A.稀释浓硫酸B.蒸发结晶C.收集气体D.测溶液pH【考点】溶液的酸碱度测定;浓硫酸的性质及浓硫酸的稀释;蒸发与蒸馏操作;常用气体的收集方法.【专题】实验操作型;化学学习中的实验思想;常见仪器及化学实验基本操作.【分析】A、根据浓硫酸的稀释方法(酸入水,沿器壁,慢慢倒,不断搅)进行分析判断.B、根据蒸发操作的注意事项进行分析判断.C、根据收集气体的注意事项,进行分析判断.D、根据用pH试纸测定未知溶液的pH的方法进行分析判断.【解答】解:A、稀释浓硫酸时,要把浓硫酸缓缓地沿器壁注入水中,同时用玻璃棒不断搅拌,以使热量及时地扩散;一定不能把水注入浓硫酸中;图中所示操作错误.B、蒸发时,应用玻璃棒不断搅拌,以防液体受热不均匀,造成液体飞溅,图中所示操作正确.C、收集气体时,为利于空气的排出,导管应伸入集气瓶的底部,图中所示操作错误.D、用pH试纸测定未知溶液的pH时,正确的操作方法为用玻璃棒蘸取少量待测液滴在干燥的pH试纸上,与标准比色卡对比来确定pH.不能将pH试纸伸入待测液中,以免污染待测液,图中所示操作错误.故选:B.【点评】本题难度不大,熟悉各种仪器的用途及使用注意事项、常见化学实验基本操作的注意事项是解答此类试题的关键.5.下列说法中,错误的是()A.用水能灭火,是因为水能降低可燃物的着火点B.液态氧变成氧气是物理变化,是因为氧分子本身没有变化C.酸溶液有相似的化学性质,是因为在不同的酸溶液中都含有H+D.湿衣服在阳光下比在阴凉处干的快,是因为温度高分子运动的快【考点】灭火的原理和方法;酸的化学性质;分子的定义与分子的特性.【专题】化学与能源;微观和宏观相互转化思想;物质的微观构成与物质的宏观组成;常见的酸酸的通性.【分析】A、根据灭火的原理,进行分析判断.B、根据发生物理变化时分子本身不变,进行分析判断.C、根据酸溶液有相似的化学性质的原因,进行分析判断.D、根据分子的基本性质,进行分析判断.【解答】解:A、用水能灭火,是因为水能使温度降到着火点以下,而不是能降低可燃物的着火点,故选项说法错误.B、液态氧变成氧气是物理变化,是因为氧分子本身没有变化,故选项说法正确.C、酸溶液有相似的化学性质,是因为在不同的酸溶液中都含有H+,故选项说法正确.D、湿衣服在阳光下比在阴凉处干的快,是因为温度升高,分子运动的速率加快,故选项说法正确.故选:A.【点评】本题难度不大,掌握灭火的原理、分子恶基本性质、酸溶液有相似的化学性质的原因是正确解答本题的关键.6.下列关于甲烷(CH4)的说法中,错误的是()A.甲烷是最简单的有机化合物B.甲烷是由碳元素和氢元素组成的C.甲烷分子由碳原子和氢原子构成D.甲烷中碳、氢元素质量比为1:4【考点】化学式的书写及意义;有机物与无机物的区别;元素质量比的计算.【专题】化学用语和质量守恒定律.【分析】A、根据最简单的有机物是甲烷进行分析判断;B、根据物质是由元素组成的进行分析;C、根据甲烷的微观构成进行分析判断;D、根据甲烷中碳、氢元素质量比等于相对原子质量和原子个数乘积的比值进行分析.【解答】解:A、甲烷是结构最简单的有机物,故A正确;B、由化学式可知,甲烷是由碳元素和氢元素组成的,故B正确;C、甲烷是由甲烷分子构成的,1个甲烷分子中含有1个碳原子和4个氢原子,故C正确;D、甲烷中碳、氢元素质量比为:12:(1×4)=3:1,故D错误.故选:D.【点评】本题难度不大,考查同学们结合新信息、灵活运用化学式的含义与有关计算进行分析问题、解决问题的能力.7.下列对有关事实的解释中,正确的是()A.石墨和金刚石物理性质不同﹣﹣碳原子结构不同B.一氧化碳和二氧化碳的化学性质不同﹣﹣分子构成不同C.用CO2鉴别NaOH和Ca(OH)2溶液﹣﹣CO2只与Ca(OH)2反应D.用酚酞溶液不能鉴别稀硫酸和稀盐酸﹣﹣酚酞溶液遇两种酸都变红色【考点】酸、碱、盐的鉴别;分子的定义与分子的特性;碳元素组成的单质.【专题】物质的鉴别题;微观和宏观相互转化思想;物质的微观构成与物质的宏观组成;碳单质与含碳化合物的性质与用途.【分析】A、根据石墨和金刚石物理性质不同的原因,进行分析判断.B、同种的分子性质相同,不同种的分子性质不同,进行分析判断.C、根据碱溶液能与二氧化碳反应进行分析判断.D、无色酚酞溶液遇酸性溶液不变色,遇碱性溶液变红.【解答】解:A、石墨和金刚石物理性质不同,是因为碳原子的排列方式不同,故选项说法错误.B、一氧化碳和二氧化碳的化学性质不同,是因为它们分子的构成不同,不同种的分子性质不同,故选项解释正确.C、用CO2鉴别NaOH和Ca(OH)2溶液,不是因为CO2只与Ca(OH)2反应,二氧化碳也能与氢氧化钠溶液反应,但无明显变化,故选项说法错误.D、用酚酞溶液不能鉴别稀硫酸和稀盐酸,是因为酚酞溶液遇两种酸都不变色,故选项说法错误.故选:B.【点评】本题难度不大,掌握物质鉴别的原理、分子的基本性质(可以简记为:“两小运间,同同不不”)、碱的化学性质等是正确解答本题的关键.8.下列说法中,正确的是()A.浓盐酸和浓硫酸都需要密封保存,都具有挥发性B.氧化铁、碳酸、氧气都含氧元素,都属于氧化物C.氢氧化钠、氢氧化钙都能与酸反应,都能改良酸性土壤D.氯化铵、硝酸铵、硫酸铵都是含铵根离子的盐,都能与可溶性碱反应【考点】空气中常见酸碱盐的质量或性质变化及贮存法;证明铵盐;常见碱的特性和用途;从组成上识别氧化物.【专题】元素与化合物;物质的分类;常见的酸酸的通性;常见的碱碱的通性;常见的盐化学肥料.【分析】A、根据浓盐酸和浓硫酸的物理性质,进行分析判断.B、氧化物是指由两种元素组成且一种是氧元素的化合物.C、根据氢氧化钠具有强烈的腐蚀性,进行分析判断.D、根据铵盐能与碱性物质反应,进行分析判断.【解答】解:A、浓盐酸和浓硫酸都需要密封保存,分别是因为浓盐酸具有挥发性、浓硫酸具有吸水性,故选项说法错误.B、氧化铁是由钠元素和氧元素组成的化合物,属于氧化物;碳酸、氧气分别是由三种元素、一种元素组成,均不属于氧化物;故选项说法错误.C、氢氧化钠具有强烈的腐蚀性,不能用于改良酸性土壤,故选项说法错误.D、氯化铵、硝酸铵、硫酸铵都是含铵根离子的盐,都能与可溶性碱反应,故选项说法正确.故选:D.【点评】本题难度不大,掌握药品密封保存的原因、氧化物的特征、铵盐的性质等是正确解答解答本题的关键.9.下列有关实验操作的分析中,正确的是()A.配制氯化钠溶液:量取水时,俯视读数,导致浓度偏小B.测定空气中氧气含量:点燃红磷后缓慢伸入集气瓶中,导致进水偏少C.用滴管吸取液体:伸入试剂瓶中捏扁胶头赶尽气体再吸液,不会污染药品D.去除粗盐中难溶性杂质:提纯后所得精盐未完全干燥就称量,导致产率偏高【考点】化学实验方案设计与评价;液体药品的取用;一定溶质质量分数的溶液的配制;空气组成的测定;氯化钠与粗盐提纯.【专题】实验设计题;简单实验方案的设计与评价.【分析】A、量取水时,俯视读数,读数比实际液体体积大,进行分析判断.B、根据插入燃烧匙太慢,在塞紧瓶塞之前,瓶内部分空气受热逸出,进行分析判断.C、根据胶头滴管的使用方法,进行分析判断.D、根据提纯后所得精盐未完全干燥就称量,会导致获得的精盐的质量偏大,进行分析判断.【解答】解:A、量取水时,俯视读数,读数比实际液体体积大,会造成实际量取的水的体积偏小,则使溶质质量分数偏大,故选项说法错误.B、点燃红磷后缓慢伸入集气瓶中,瓶内部分空气受热逸出,使瓶内的气体除氧气之外的气体也跑到了瓶外,导致进水偏多,故选项说法错误.C、使用胶头滴管时,伸入液体前,应捏紧胶头,排出里面的空气,再伸入试剂中吸取液体,故选项说法错误.D、提纯后所得精盐未完全干燥就称量,会导致获得的精盐的质量偏大,导致产率偏高,故选项说法正确.故选:D.【点评】本题难度不是很大,化学实验方案的设计是考查学生能力的主要类型,同时也是实验教与学难点,在具体设计时要对其原理透彻理解,可根据物质的物理性质和化学性质结合实验目的进行分析判断.10.下列实验中,能达到相应目的是()A.检验NaOH溶液是否变质:取样,滴入石蕊溶液B.鉴别NaCl溶液和Na2CO3溶液:取样,测酸碱度C.分离木炭粉和氧化铜的混合物:向固体中加入足量的稀硫酸后过滤D.除去CO中的CO2气体和水蒸气:将混合气体依次通过浓硫酸和NaOH溶液【考点】化学实验方案设计与评价;常见气体的检验与除杂方法;碱的化学性质;酸、碱、盐的鉴别.【专题】实验设计题;简单实验方案的设计与评价.【分析】A、根据氢氧化钠不变质后生成的碳酸钠也显碱性,进行分析判断.B、根据NaCl溶液和Na2CO3溶液分别显中性、碱性,进行分析判断.C、根据氧化铜能与稀硫酸反应生成硫酸铜和水,进行分析判断.D、根据除去CO中的CO2气体和水蒸气,要后除水蒸气,进行分析判断.【解答】解:A、氢氧化钠不变质后生成的碳酸钠也显碱性,不能用滴入石蕊溶液的方法检验是否变质,故选项说法错误.B、NaCl溶液和Na2CO3溶液分别显中性、碱性,可用取样,测酸碱度的方法进行鉴别,故选项说法正确.C、氧化铜能与稀硫酸反应生成硫酸铜和水,木炭粉不与稀硫酸反应,但不能分离出氧化铜,故选项说法错误.D、除去CO中的CO2气体和水蒸气,应依次通过氢氧化钠溶液、浓硫酸,否则会再次引入水蒸气,故选项说法错误.故选:B.【点评】本题难度不是很大,化学实验方案的设计是考查学生能力的主要类型,同时也是实验教与学难点,在具体设计时要对其原理透彻理解,可根据物质的物理性质和化学性质结合实验目的进行分析判断.二、非选择题(共40分)考生注意:请在答题卡上的指定区域作答.11.回答下列问题.(1)氢气的化学式H2;(2)铁离子可表示为Fe3+.【考点】化学式的书写及意义;化学符号及其周围数字的意义.【专题】化学用语和质量守恒定律.【分析】(1)氢气属于气态非金属单质,在元素符号的右下角写上表示分子中所含原子数的数字.(2)离子的表示方法,在表示该离子的元素符号右上角,标出该离子所带的正负电荷数,数字在前,正负符号在后,带1个电荷时,1要省略.【解答】解:(1)氢气属于气态非金属单质,在元素符号的右下角写上表示分子中所含原子数的数字,其化学式为:H2.(2)由离子的表示方法,在表示该离子的元素符号右上角,标出该离子所带的正负电荷数,数字在前,正负符号在后,带1个电荷时,1要省略.铁离子可表示为:Fe3+.故答案为:(1)H2;(2)Fe3+.【点评】本题难度不大,掌握常见化学用语(化学式、离子符号等)的书写方法是正确解答此类题的关键.12.图A是铝元素在元素周期表中的部分信息,图B是铝原子的结构示意图,回答问题.(1)铝的相对原子质量是26.98 ;(2)铝元素属于金属(填“金属”或“非金属”)元素;(3)从图B可知,铝原子在化学反应中容易失去电子.【考点】元素周期表的特点及其应用;原子结构示意图与离子结构示意图.【专题】元素位置、结构与性质;化学用语和质量守恒定律.【分析】(1)根据图中元素周期表可以获得的信息:汉字下面的数字表示相对原子质量,进行分析解答.(2)金属元素名称一般有“钅”字旁,进行分析解答.(3)原子结构示意图中,圆圈内数字表示核内质子数,弧线表示电子层,弧线上的数字表示该层上的电子数,离圆圈最远的弧线表示最外层.若最外层电子数≥4,在化学反应中易得电子,若最外层电子数<4,在化学反应中易失去电子.【解答】解:(1)根据元素周期表中的一格可知,汉字下面的数字表示相对原子质量,该元素的相对原子质量为26.98.(2)铝带“钅”字旁,属于金属元素.(3)由铝原子结构示意图为可以看出:最外层弧线上的数字是3,最外层电子数是3,在化学反应中易失去3个电子而形成阳离子.故答案为:(1)26.98;(2)金属;(3)失去.【点评】本题难度不大,灵活运用元素周期表中元素的信息(原子序数、元素符号、元素名称、相对原子质量)、原子结构示意图的含义是正确解答本题的关键.13.请回答下列与水有关的问题.(1)生活中降低水的硬度可采用的方法是煮沸;(2)净化水过程中,利用活性炭的吸附性除去水中的异味和有色物质;(3)水蒸发变成水蒸气时所占的体积变大,从微观角度看是因为分子间的间隔变大.【考点】硬水与软水;分子的定义与分子的特性;碳单质的物理性质及用途.【专题】化学知识生活化;空气与水.【分析】(1)根据生活中降低水的硬度方法分析;(2)根据活性炭具有吸附性进行分析;(3)根据分子的基本特征:分子之间有间隔进行分析.【解答】解:(1)较为常用的将硬水软化的方法有加热煮沸或蒸馏,生活中可通过简单的加热煮沸方法来降纸水的硬度;故填:煮沸;(2)净化水过程中,利用活性炭的吸附性除去水中的异味和有色物质;故填:吸附;(3)水蒸发为水蒸气,所占体积变大,是因为温度升高,水分子间的间隔变大;故填;分子间的间隔变大.【点评】本题考查与生活相关的知识,体现了化学在生活中的应用,对生活的指导作用,难度不大,基础性强,注意掌握.14.现有四种物质:①浓硫酸②氢氧化钠溶液③澄清石灰水④生石灰,回答下列问题.(1)能用来干燥氧气的是①④;(2)用澄清石灰水检验二氧化碳时的现象是澄清石灰水变浑浊;。
2016年吉林省长春市中考模拟数学试卷(含答案)
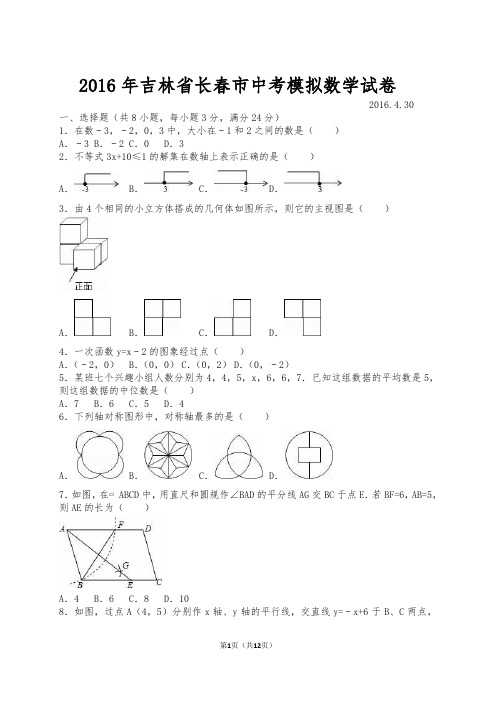
2016年吉林省长春市中考模拟数学试卷2016.4.30一、选择题(共8小题,每小题3分,满分24分)1.在数﹣3,﹣2,0,3中,大小在﹣1和2之间的数是()A.﹣3 B.﹣2 C.0 D.32.不等式3x+10≤1的解集在数轴上表示正确的是()A.B. C.D.3.由4个相同的小立方体搭成的几何体如图所示,则它的主视图是()A.B.C.D.4.一次函数y=x﹣2的图象经过点()A.(﹣2,0)B.(0,0)C.(0,2)D.(0,﹣2)5.某班七个兴趣小组人数分别为4,4,5,x,6,6,7.已知这组数据的平均数是5,则这组数据的中位数是()A.7 B.6 C.5 D.46.下列轴对称图形中,对称轴最多的是()A. B.C.D.7.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为()A.4 B.6 C.8 D.108.如图,过点A(4,5)分别作x轴、y轴的平行线,交直线y=﹣x+6于B、C两点,若函数y=(x>0)的图象△ABC的边有公共点,则k的取值范围是()A.5≤k≤20 B.8≤k≤20 C.5≤k≤8 D.9≤k≤20二、填空题(共6小题,每小题3分,满分18分)9.若2x+1=3,则6x+3的值为.11.如图,点A、C、F、B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA=58°,则∠GFB的大小为°.12.如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为3,则阴影部分的面积为(结果保留π).13.如图,平面直角坐标中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x 轴正方向平移,使⊙P与y轴相交,则平移的距离d的取值范围是.14.如图,抛物线y=ax2﹣4和y=﹣ax2+4都经过x轴上的A、B两点,两条抛物线的顶点分别为C、D.当四边形ACBD的面积为40时,a的值为.三、解答题(共10小题,满分78分)15.先化简,再求值:2a(a+2b)﹣(a+2b)2,其中a=﹣1,b=.16.一辆汽车从A地驶往B地,前路为普通公路,其余路段为高速公路,已知汽车在普通公路上行驶的速度为60km/h,在高速路上行驶的速度为100km/h,汽车从A地到B 地一共行驶了2.2h,普通公路和高速公路各是多少km?17.小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.(1)如果随机翻1张牌,那么抽中20元奖品的概率为(2)如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总值不低于30元的概率为多少?18.如图,在△ABC中,D、E分别是边AB、AC的中点,延长BC至点F,使得CF=BC,连结CD、DE、EF.(1)求证:四边形CDEF是平行四边形.(2)若四边形CDEF的面积为8,则△ABC的面积为.19.如图,某高楼CD与处地面垂直,要在高楼前的地面A处安装某种射灯,安装后,射灯发出的光线与地面的最大夹角∠DAC为70°,光线与地面的最小夹角∠DAB为35°,要使射灯发光时照射在高楼上的区域宽BC为50米,求A处到高楼的距离AD.(结果精确到0.1米)【参考数据:sin70°=0.94,cos70°=0.34,tan70°=2.75,sin35°=0.57,cos35°=0.82,tan35°=0.70】20.某校随机抽取部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类,学校根据调查进行了统计,并绘制了如下不完整的条形统计图和扇形统计图.结合图中信息,解答下列问题:(1)求本次共调查的学生人数.(2)求被调查的学生中,最喜爱丁类图书的学生人数.(3)求被调查的学生中,最喜爱甲类图书的人数占本次被调查人数的百分比.(4)该学校共有学生1600人,估计该校最喜爱丁类图书的人数.21.探索:如图①,以△ABC的边AB、AC为直角边,A为直角顶点,向外作等腰直角△ABD和等腰直角△ACE,连结BE、CD,试确定BE与CD有怎样数量关系,并说明理由.应用:如图②,要测量池塘两岸B、E两地之间的距离,已知测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.22.从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,设小明出发xh后,到达离乙地ykm的地方,图中的折线ABCDEF 表示y与x之间的函数关系.(1)小明骑车在平路上的速度为km/h,他在乙地休息了h.(2)分别求线段AB、EF所对应的函数关系式.(3)从甲地到乙地经过丙地,如果小明两次经过丙地的时间间隔为0.85h,求丙地与甲地之间的路程.23.如图,平面直角坐标系中,抛物线y=ax2+bx+2与x轴分别交于点A(﹣1,0)、B (3,0),与y轴交于点C,连结BC.点P是BC上方抛物线上一点,过点P作y轴的平行线,交BC于点N,分别过P、N两点作x轴的平行线,交抛物线的对称轴于点Q、M,设P点的横坐标为m.(1)求抛物线所对应的函数关系式.(2)当点P在抛物线对称轴左侧时,求四边形PQMN周长的最大值.(3)当四边形PQMN为正方形时,求m的值.24.如图①,平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,点B的坐标为(2,4),将矩形OABC绕着点A顺时针旋转90°得到矩形AFED,直线y=kx+b 经过点G(4,0),交y轴于点H.(1)点D、E的坐标分别为.(2)当直线GH经过EF中点K时,如图②,动点P从点C出发,沿着折线C﹣B﹣D以每秒1个单位速度向终点D运动,连结PH、PG,设点P运动的时间为t(秒),△PGH 的面积为S(平方单位).①求直线GH所对应的函数关系式.②求S与t之间的函数关系式.(3)当直线GH经过点E时,如图③,点Q是射线B﹣D﹣E﹣F上的点,过点Q作QM⊥GH于点M,作QN⊥x轴于点N,当△QMN为等腰三角形时,直接写出点Q的坐标.参考答案一、选择题1故选:C.2.故选:C.3.故选A.4.故选:D.5.故选C.6.故选:B.7.故选C.8.故选A.二、填空题9.故答案为:910.故答案为:m>n.11故答案为61°.12.故答案为:3π.13.故答案为:1<d<5.14.故答案是:0.16.三、解答题15.【解答】解:原式=2a2+4ab﹣a2﹣4ab﹣4b2=a2﹣4b2,当a=﹣1,b=时,原式=1﹣12=﹣11.16.【解答】解:设普通公路长为x(km),高速公路长为y(km).根据题意,得,解得,答:普通公路长为60km,高速公路长为120km.17.【解答】解:(1)∵1÷4=0.25=25%,∴抽中20元奖品的概率为25%.故答案为:25%.(2),∵所获奖品总值不低于30元有4种情况:30元、35元、30元、35元,∴所获奖品总值不低于30元的概率为:4÷12=.18.【解答】(1)证明:∵如图,在△ABC中,D、E分别是边AB、AC的中点,∴DE∥BC且DE=BC.又∵CF=BC,∴DE=CF,∴四边形CDEF是平行四边形.(2)解:∵DE∥BC,∴四边形CDEF与△ABC的高相等,设为h,又∵CF=BC,∴S△ABC=BC•h=CF•h=8,故答案是:8.19.【解答】解:∵CD⊥AD,∴∠CDA=90°,∴在Rt△ADB中,BD=ADtan∠BAD,在Rt△ADC中,CD=ADtan∠CAD,∴AD•tan70°﹣AD•tan35°=50,∴2.75AD﹣0.70AD=50,解得:AD=≈24.4,答:A处到高楼的距离AD为24.4米.20.【解答】解:(1)40÷20%=200(名)答:共调查的学生人为200名;(2)根据题意得:丁类学生数为200﹣(80+65+40)=15(名);(3)最喜爱甲类图书的人数占本次被调查人数的80÷200×100%=40%;(4)1600×=120(人)答:该校最喜爱丁类图书的人数为120人.21.【解答】解:探索:BE=CD,理由:∵∠BAD=∠CAE=90°,∴∠CAD=∠EAB,在△CAD和△EAB中∵,∴△CAD≌△EAB(SAS);应用:如图②,过点A作AD⊥AB,且AD=AB,连接BD,由探索,得△CAD≌△EAB,∴BE=DC,∵AD=AB=100m,∠DAB=90°,∴∠ABD=45°,BD=100m,∵∠ABC=45°,∴∠DBC=90°,在Rt△DBC中,BC=100m,BD=100m,∴CD==100(m),则BE=100m,答:BE的长为100m.22.【解答】解:(1)小明骑车上坡的速度为:(6.5﹣4.5)÷0.2=10(km/h),小明平路上的速度为:10+5=15(km/h),小明下坡的速度为:15+5=20(km/h),小明平路上所用的时间为:2(4.5÷15)=0.6h,小明下坡所用的时间为:(6.5﹣4.5)÷20=0.1h所以小明在乙地休息了:1﹣0.1﹣0.6﹣0.2=0.1(h).故答案为:15,0.1;(2)由题意可知:上坡的速度为10km/h,下坡的速度为20km/h,所以线段AB所对应的函数关系式为:y=6.5﹣10x,即y=﹣10x+6.5(0≤x≤0.2).线段EF所对应的函数关系式为y=4.5+20(x﹣0.9).即y=20x﹣13.5(0.9≤x≤1).(3)由题意可知:小明第一次经过丙地在AB段,第二次经过丙地在EF段,设小明出发a小时第一次经过丙地,则小明出发后(a+0.85)小时第二次经过丙地,6.5﹣10a=20(a+0.85)﹣13.5解得:a=.=1(千米).答:丙地与甲地之间的路程为1千米.23.【解答】解:(1)当x=0时,y=ax2+bx+2=2,则C(0,2),设抛物线解析式为y=a(x+1)(x﹣3),把C(0,2)代入得a•1•(﹣3)=2,解得a=﹣,所以抛物线的解析式为y=﹣(x+1)(x﹣3),即y=﹣x2+x+2;(2)∵抛物线与x轴分别交于点A(﹣1,0)、B(3,0),∴抛物线的对称轴为直线x=1,设直线BC的解析式为y=px+q,把C(0,2),B(3,0)代入得,解得,所以直线BC的解析式为y=﹣x2+2,设P(m,﹣ m2+m+2),则N(m,﹣ m+2),∴PN=﹣m2+m+2﹣(﹣m+2)=﹣m2+2m,而PQ=1﹣m,∴四边形PQMN周长=2(﹣m2+2m+1﹣m)=﹣m2+2m+2=﹣(m﹣)2+(0<m<1),∴当m=时,四边形PQMN周长有最大值,最大值为;(3)当0<m<1时,PQ=1﹣m,若PQ=PN时,四边形PQMN为正方形,即﹣m2+2m=1﹣m,整理得2m2﹣9m+3=0,解得m1=(舍去),m2=,当1<m<3时,PQ=m﹣1,若PQ=PN时,四边形PQMN为正方形,即﹣m2+2m=m﹣1,整理得2m2﹣3m﹣3=0,解得m1=(舍去),m2=,综上所述,当m=或m=时,四边形PQMN为正方形.24.【解答】(1)解:∵矩形OABC绕着点A顺时针旋转90°得到矩形AFED,且B(2,4),∴OA=AD=2,OC=AF=4,∴D(2,2),E(6,2);故答案为D(2,2),E(6,2);(2)①解:∵E(6,2),G(4,0),∴K(6,1),∵直线y=kx+b经过点G,K,∴,∴,∴直线GH的解析式为y=x﹣2,②当0≤t≤2时,延长CB交HG于W,如图1,S△PHG=S△SHW﹣S△HCP﹣S△PGW= [[6×12﹣6t﹣4(12﹣t)]=﹣t+12,②当2<t≤4时,延长BA交HG于T,如图2,S△PHG=S△PTH+S△PGT=×4(7﹣t)=﹣2t+14,第11页(共12页)(3)解;①当0≤t ≤2时,如图3,由题意,得N (2,0),Q (2,4﹣t ),M (,),∴QN2=(4﹣t )2,MN2=+,QM2=, (Ⅰ)、当QN=QM 时,即QN2=QM2,∴(4﹣t )2=+,∴t=(舍), (Ⅱ)、当QN=QM 时,方法同(Ⅰ)的一样,得t=(舍), (Ⅲ)、当MN=QM 时,方法同(Ⅰ)的一样,得到方程无解,②当2<t ≤6时,由题意,得N (t ,0),Q (t ,2),M (,), 方法和①(Ⅰ)一样,分三种情况,(Ⅰ)、当QN=QM 时,t=6+2(舍),或t=6﹣2∴Q (6﹣2,2); (Ⅱ)、当QN=MN 时,t=﹣8(舍)或t=2,∴Q (2,2);(Ⅲ)、当QM=MN 时,t=4,∴Q (4,2);②当6<t ≤8时,由题意,得N (6,0),Q (6,8﹣t ),M (,﹣), 方法和①(Ⅰ)一样,分三种情况,(Ⅰ)、当QN=QM 时,t=10+2(舍),或t=10﹣2∴Q (6,2﹣2); (Ⅱ)、当QN=MN 时,t=6(舍)或t=10(舍)(Ⅲ)、当QM=MN 时,t=8(舍);∴Q (6﹣2,2)或Q (2,2)或Q (4,2)或Q (6,2﹣2);第12页(共12页)。
吉林省长春市南关区2016届九年第一次模拟考试物理试题

九年级质量调研(物理)一.单项选择题(每小题分,共分)1. 人的正常体温约为(). ℃. ℃. ℃. ℃2.下列四种情境中,由于光的反射形成的是().鱼缸中金鱼.豹子在水中的倒影.钢笔错位.池水变浅了3. 以下常见的物态变化中,吸热的是(). 春天,积雪消融 . 夏天,雾气缭绕. 秋天,霜打枝头 . 冬天,大雪纷飞4. 在温度一定时比较两根铜导线的电阻,下列说法中正确的是(). 长导线的电阻一定比短导线的电阻大. 细导线的电阻一定比粗导线的电阻大. 长度相同,粗导线的电阻大. 粗细相同,长导线的电阻大5. 如图所示,忽略空气阻力,小球由空中处释放经过、两位置时,以下物理量不变的是() . 速度 . 动能 . 机械能 . 重力势能6. 电饭锅是常用的家庭电器,下列与之相关的说法错误的是(). 组成材料既有导体又有绝缘体 . 工作时,利用了电流的热效应. 工作时,通过热传递使温度升高 . 与其他家用电器是串联使用7. 假如水的比热容变得比砂石、干泥土还要小,则可能的是( ). 同体积的水质量会变小 . 沿海地区的夏季比内陆地区凉快. 沿海地区昼夜温差会变大 . 北方装水的暖气里取暖效果更好8. 下列关于平面镜成像说法中正确的是(). 比平面镜大的物体不能在平面镜中成完整的像. 遮光板在平面镜的后方会遮住平面镜内的像. 平面镜能使房间看起来更宽敞,是因为像比物体离平面镜更远. 物体不动,把竖直放置的平面镜沿竖直方向上下移动,像不动9.如图所示,杠杆可绕点转动,力作用在杠杆一端且始终与杠杆垂直,在将杠杆缓慢地由位置拉到位置的过程中,力(). 变大 .变小 .不变 .先变大后变小10.在如图所示电路,电源电压保持不变,电路出现了一处故障,故障可能发生在、处。
开关闭合前后,三个电表示数都没有变化,则电路中的故障是(). 短路 . 断路 . 短路 . 断路二.填空题(每空分,共分)11.是一种可以将个人电脑、手机等终端设备以无线方式互相连接的技术。
2016年吉林省长春市中考数学模拟试卷(四)含答案解析

2016年吉林省长春市中考数学模拟试卷(四)一、选择题(共8小题,每小题3分,满分24分)1.的绝对值是()A.B. C.D.2.如图所示,该几何体的俯视图是()A.B.C.D.3.2015年9月20日,吉图珺高铁正式开通运营,使长春至军春通勤时间缩短至3小时左右,项目总投资416亿元,416亿这个数用科学记数法表示为()A.416×108B.41.6×109C.4.16×1010 D.4.16×10114.不等式x﹣1≥1的解集在数轴上表示为()A.B.C.D.5.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是()A.5 B.6 C.12 D.166.下列计算正确的是()A.a6÷a3=a2B.3a2•2a=6a3C.(3a)2=3a2D.(a+b)2=a2+b27.如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为()A.B.C.D.8.在平面直角坐标系xOy中,函数y=(k1>0,x>0)、函数y=(k2<0,x<0)的图象分别经过▱OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为()A.4:9 B.2:3 C.3:2 D.9:4二、填空题(共6小题,每小题3分,满分18分)9.购买单价为a元的牛奶3盒,单价为b元的面包4个共需元(用含有a、b的代数式表示).10.因式分解:6x3y﹣12xy2+3xy=.11.如图,AB∥CD,∠A=41°,∠C=32°,则∠AEC的大小为度.12.如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;直线DF分别交l1、l2、l3于点D、E、F,若AB=3,BC=4,DE=2,则线段EF的长为.13.如图,在△ABC中,AB=AC,∠A=32°,以点C为圆心,BC长为半径作弧,交AB于点D,交AC于点E,连结BE,则∠ABE的大小为度.14.点A(1,a)是抛物线y=x2上的点,以点A为一个顶点作边长为2的等边△ABC,使点B、C中至少有一个点在这条抛物线上,这样的△ABC共有个.三、解答题(共10小题,满分78分)15.先化简,再求值:(),其中x=﹣.16.列方程或方程组解应用题:近年来,我国逐步完善养老金保险制度.甲、乙两人计划用相同的年数分别缴纳养老保险金15万元和10万元,甲计划比乙每年多缴纳养老保险金0.2万元.求甲、乙两人计划每年分别缴纳养老保险金多少万元?17.如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.(1)求证:四边形AEFD是菱形.(2)直接写出四边形AEFD的两条对角线的长.18.某中学为了了解初一年级学生数学学科的预习时间,在初一年级随机抽取了若干名学生进行调查,并把调查结果绘制成如下的不完整的统计表和统计图:根据上面提供的信息回答下列问题:(1)统计表中m的值为,并补全频数分布直方图;(2)预习时间的中位数落在第组;(3)估计该校初一年级400名学生中,数学学科预习时间少于10分钟的学生人数.19.双十一期间,某店铺推出的如图①所示的雪球夹销售火爆,其形状可近似的看成图②所示的图形,当雪球夹闭合时,测得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(精确到1厘米)【参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin14°≈0.24,cos14°≈0.97,tan14°≈0.25.20.甲乙两人玩一种游戏:三张大小、质地都相同的卡片上分别标有数字1,2,3,现将标有数字的一面朝下,洗匀后甲从中任意抽取一张,记下数字后放回;又将卡片洗匀,乙也从中任意抽取一张,计算甲乙两人抽得的两个数字之积,如果积为奇数则甲胜,若积为偶数则乙胜.(1)用列表或画树状图等方法,列出甲乙两人抽得的数字之积所有可能出现的情况;(2)请判断该游戏对甲乙双方是否公平?并说明理由.21.感知:如图①,点B、A、C在同一条直线上,DB⊥BC,EC⊥BC,且∠DAE=90°,AD=AE,易证△DBA≌△ACE.探究:如图②,在△DBA和△ACE中,AD=AE,若∠DAE=α(0°<α<90°),∠BAC=2α,∠B=∠C=180°﹣α,求证:△DBA≌△ACE.应用:如图②,在△DBA和△ACE中,AD=AE,若∠DAE=70°,∠BAC=140°,∠B=∠C=110°,则当∠D=°时,∠DAC的度数是∠E的3倍.22.甲、乙两车分别从相距480千米的A、B两地出发,匀速相向行驶,乙车比甲车先出发1小时,从B地直达A地.甲车出发t小时两车相遇后甲车停留1小时,因有事按原路返回A地,两车同时到达A地.从甲车出发时开始计时,时间为x(时),甲、乙两车距B地的路程y(千米)与x(时)之间的函数关系如图所示(1)乙车的速度是千米/时,t=.(2)求甲车距B地路程y与x之间的函数关系式,并写出自变量x的取值范围.(3)直接写出乙车出发多长时间两车相距30千米.23.如图,在矩形ABCD中,BC=1,将矩形ABCD绕点D逆时针旋转45°,得到矩形A′B′C′D′,点B′恰好落在BC的延长线上,边A′B′交边CD于点E.(1)求证:B′C=BC.(2)保持矩形A′B′C′D′不动,将矩形ABCD沿射线BB′方向以每秒1个单位的速度平移,设平移时间为t秒.①当矩形ABCD与矩形A′B′C′D′重叠部分为四边形时,求重叠部分的面积为S与t之间的函数关系式.②点A′关于AB的对称点记作点F,直接写出直线DF与矩形A′B′C′D′的边平行时t的值.24.边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.(1)求抛物线的解析式;(2)点P从点C出发,沿射线CB每秒1个单位长度的速度运动,运动时间为t秒.过点P作PF⊥CD 于点F,当t为何值时,以点P,F,D为顶点的三角形与△COD相似?(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.2016年吉林省长春市中考数学模拟试卷(四)参考答案与试题解析一、选择题(共8小题,每小题3分,满分24分)1.的绝对值是( )A .B .C .D .【考点】绝对值.【分析】绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.【解答】解:根据负数的绝对值等于它的相反数,得|﹣|=.故选A .【点评】考查了绝对值的性质.2.如图所示,该几何体的俯视图是( )A .B .C .D .【考点】简单组合体的三视图.【分析】根据从上面看得到的图形是俯视图,可得答案.【解答】解:从上面看是一个正方形,正方形的左下角是一个小正方形,故B 正确;故选:B .【点评】本题考查了简单组合体的三视图,从上面看得到的图形是俯视图.3.2015年9月20日,吉图珺高铁正式开通运营,使长春至军春通勤时间缩短至3小时左右,项目总投资416亿元,416亿这个数用科学记数法表示为( )A .416×108B .41.6×109C .4.16×1010D .4.16×1011【考点】科学记数法—表示较大的数.【分析】科学记数法就是将一个数字表示成(a×10的n次幂的形式),其中1≤|a|<10,n表示整数,即从左边第一位开始,在首位非零的后面加上小数点,再乘以10的n次幂.【解答】解:∵一亿=108,∴416亿用科学记数法表示为4.16×1010.故选:C.【点评】此题考查了对科学记数法的理解和运用和单位的换算.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.4.不等式x﹣1≥1的解集在数轴上表示为()A.B.C.D.【考点】在数轴上表示不等式的解集;解一元一次不等式.【分析】先求出不等式的解集,再在数轴上表示出来即可.【解答】解:移项得,x≥1+1,合并同类项得,x≥2.在数轴上表示为:.故选A.【点评】本题考查的是在数轴上表示不等式的解集,熟知“小于向左,大于向右”是解答此题的关键.5.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是()A.5 B.6 C.12 D.16【考点】三角形三边关系.【分析】设第三边的长为x,再由三角形的三边关系即可得出结论.【解答】解:设第三边的长为x,∵三角形两边的长分别是4和10,∴10﹣4<x<10+4,即6<x<14.故选C.【点评】本题考查的是三角形的三边关系,熟知三角形任意两边之和大于第三边,任意两边之差小于第三边是解答此题的关键.6.下列计算正确的是()A.a6÷a3=a2B.3a2•2a=6a3C.(3a)2=3a2D.(a+b)2=a2+b2【考点】同底数幂的除法;幂的乘方与积的乘方;单项式乘单项式;完全平方公式.【分析】根据同底数幂的除法底数不变指数相减;单项式的乘法:系数乘系数,同底数的幂相乘;积的乘方等于乘方的积;和的平方等于平方和加积的二倍,可得答案.【解答】解:A、同底数幂的除法底数不变指数相减,故A错误;B、系数乘系数,同底数的幂相乘,故B正确;C、积的乘方等于乘方的积,故C错误;D、和的平方等于平方和加积的二倍,故D错误;故选:B.【点评】本题考查了同底数幂的除法,熟记法则并根据法则计算是解题关键,注意完全平方公式是和的平方加积的二倍.7.如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为()A.B.C.D.【考点】扇形面积的计算.【分析】先根据三角形内角和定理得出∠ABC+∠ACB的度数,再由△OBD、△OCE是等腰三角形得出∠BDO+∠CEO的度数,由三角形内角和定理即可得出∠BOD+∠COD的度数,再根据扇形的面积公式即可得出结论.【解答】解:∵△ABC中,∠A=80°,∴∠ABC+∠ACB=180°﹣80°=100°,∵△OBD、△OCE是等腰三角形,∴∠BDO+∠CEO=∠ABC+∠ACB=100°,∴∠BOD+∠COE=360°﹣(∠BDO+∠CEO)﹣(∠ABC+∠ACB)=360°﹣100°﹣100°=160°,∵BC=4,∴OB=OC=2,==.∴S阴影故选:C.【点评】本题考查的是扇形面积的计算,解答此类问题时往往用到三角形的内角和是180°这一隐藏条件.8.在平面直角坐标系xOy中,函数y=(k1>0,x>0)、函数y=(k2<0,x<0)的图象分别经过▱OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为()A.4:9 B.2:3 C.3:2 D.9:4【考点】平行四边形的性质;反比例函数图象上点的坐标特征.【分析】作AF⊥OB于F,由AAS证明△ABF≌△OCE,得出AF=OE,因此OD=OE,由△AOD的面积=AD•OD=k1,△OCE的面积=CE•OE=|k2|,|k1|:|k2|=9:4,得出==即可.【解答】解:作AF⊥OB于F,如图所示:则∠AFB=∠OEC=∠ADO=90°,AF=OD,CE∥OB,∴∠OCE=∠BOC,∵四边形OABC是平行四边形,∴OC=AB,OC∥AB,∴∠ABF=∠BOC,∴∠ABF=∠OCE,在△ABF和△OCE中,,∴△ABF≌△OCE(AAS),∴AF=OE,∴OD=OE,∵△AOD的面积=AD•OD=k1,△OCE的面积=CE•OE=|k2|,|k1|:|k2|=9:4,∴==.故选:D.【点评】本题考查了平行四边形的性质、全等三角形的判定与性质、反比例函数图象上点的坐标特征、三角形面积的计算;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.二、填空题(共6小题,每小题3分,满分18分)9.购买单价为a元的牛奶3盒,单价为b元的面包4个共需(3a+4b)元(用含有a、b的代数式表示).【考点】列代数式.【分析】求买3盒牛奶和4个面包所用的钱数,用3盒牛奶的总价+4个面包的总价即可.【解答】解:购买单价为a元的牛奶3盒,单价为b元的面包4个共需(3a+4b)元.故答案为:(3a+4b).【点评】此题考查列代数式,解题关键是根据已知条件,把未知的数用字母正确的表示出来,然后根据题意列式计算即可得解.10.因式分解:6x3y﹣12xy2+3xy=3xy(2x2﹣4y+1).【考点】因式分解-提公因式法.【分析】直接找出公因式3xy,进而提取公因式得出答案.【解答】解:6x3y﹣12xy2+3xy=3xy(2x2﹣4y+1).故答案为:3xy(2x2﹣4y+1).【点评】此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.11.如图,AB∥CD,∠A=41°,∠C=32°,则∠AEC的大小为73度.【考点】平行线的性质;三角形的外角性质.【分析】根据两直线平行,内错角相等可得∠ABE=∠C,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【解答】解:∵AB∥CD,∴∠ABE=∠C=32°,在△ABE中,由三角形的外角性质得,∠AEC=∠A+∠ABE=41°+32°=73°.故答案为:73.【点评】本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.12.如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;直线DF分别交l1、l2、l3于点D、E、F,若AB=3,BC=4,DE=2,则线段EF的长为.【考点】平行线分线段成比例.【专题】计算题.【分析】利用平行线分线段成比例定理得到=,然后把AB=3,BC=4,DE=2代入计算即可.【解答】解:∵l1∥l2∥l3,∴=,即=,∴EF=.故答案为.【点评】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.13.如图,在△ABC中,AB=AC,∠A=32°,以点C为圆心,BC长为半径作弧,交AB于点D,交AC于点E,连结BE,则∠ABE的大小为21度.【考点】等腰三角形的性质.【分析】在△ABC中可求得∠ACB=∠ABC=74°,在△BCE中可求得∠EBC=53°,再根据角的和差关系可求出∠ABE的度数.【解答】解:∵AB=AC,∠A=32°,∴∠ABC=∠ACB=74°,又∵BC=EC,∴∠BEC=∠EBC=53°,∴∠ABD=∠ABC﹣∠EBC=74°﹣53°=21°.故答案为:21.【点评】本题主要考查等腰三角形的性质,掌握等边对等角是解题的关键,注意三角形内角和定理的应用.14.点A(1,a)是抛物线y=x2上的点,以点A为一个顶点作边长为2的等边△ABC,使点B、C中至少有一个点在这条抛物线上,这样的△ABC共有5个.【考点】二次函数图象上点的坐标特征;等边三角形的性质.【分析】根据题意画出图象,根据图象即可求得.【解答】解:如图,因为点A(1,a)是抛物线y=x2上的点,所以A(1,),所以,OA=2,以A为圆心,以OA为半径画圆交抛物线三个点,以这三个点和A点构成的线段为边作等边三角形作6个,其中重合一个,故可以作5个,故答案为5.【点评】本题考查了二次函数图象上点的坐标特征和等边三角形的性质,根据题意作出函数的图象是解题的关键,三、解答题(共10小题,满分78分)15.先化简,再求值:(),其中x=﹣.【考点】分式的化简求值.【分析】首先化简分式,进而利用分式乘除运算法则求出答案.【解答】解:()=(x+1+x﹣3)•=(2x﹣2)•=2x+2,当x=﹣时,原式=2×(﹣)+2=﹣1.【点评】此题主要考查了分式的混合运算,正确化简分式是解题关键.16.列方程或方程组解应用题:近年来,我国逐步完善养老金保险制度.甲、乙两人计划用相同的年数分别缴纳养老保险金15万元和10万元,甲计划比乙每年多缴纳养老保险金0.2万元.求甲、乙两人计划每年分别缴纳养老保险金多少万元?【考点】分式方程的应用.【专题】应用题.【分析】设乙每年缴纳养老保险金为x万元,则甲每年缴纳养老保险金为(x+0.2)万元,根据甲、乙两人计划用相同的年数分别缴纳养老保险金15万元和10万元列出方程,求出方程的解即可得到结果.【解答】解:设乙每年缴纳养老保险金为x万元,则甲每年缴纳养老保险金为(x+0.2)万元,根据题意得:=,去分母得:15x=10x+2,解得:x=0.4,经检验x=0.4是分式方程的解,且符合题意,∴x+0.2=0.4+0.2=0.6(万元),答:甲、乙两人计划每年分别缴纳养老保险金0.6万元、0.4万元.【点评】此题考查了分式方程的应用,找出题中等量关系“甲、乙两人计划用相同的年数分别缴纳养老保险金15万元和10万元”是解本题的关键.17.如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.(1)求证:四边形AEFD是菱形.(2)直接写出四边形AEFD的两条对角线的长.【考点】菱形的判定与性质;图形的剪拼;平移的性质.【分析】(1)根据平移的性质得到AE∥DF,AE=DF,则由此判定四边形AEFD是平行四边形;然后由“邻边相等的平行四边形是菱形”证得结论;(2)根据勾股定理,可得答案.【解答】(1)证明:由平移,得AE∥DF,AE=DF,∴四边形AEFD是平行四边形.又∵AE=AD=5,∴四边形AEFD是菱形.(2)依题意得:AB•AD=15,即5AB=15,故AB=3.在直角△ABE中,AB=3,AE=5,则由勾股定理得到:BE==4.如图,连接AF,ED.在直角△ABF中,由勾股定理得到:AF===3.在直角△DCE中,由勾股定理得到:DE==.【点评】本题考查了菱形的判定与性质、图形的剪拼以及平移的性质.通过解答该题,使学生学会能够灵活运用菱形、勾股定理知识解决有关问题.18.某中学为了了解初一年级学生数学学科的预习时间,在初一年级随机抽取了若干名学生进行调查,并把调查结果绘制成如下的不完整的统计表和统计图:根据上面提供的信息回答下列问题:(1)统计表中m的值为11,并补全频数分布直方图;(2)预习时间的中位数落在第3组;(3)估计该校初一年级400名学生中,数学学科预习时间少于10分钟的学生人数.【考点】频数(率)分布直方图;用样本估计总体;频数(率)分布表;中位数.【分析】(1)根据频数之和等于样本容量计算,补全频数分布直方图;(2)根据中位数的概念解答;(3)利用样本估计总体的方法计算即可.【解答】解:(1)50﹣8﹣18﹣13=11,故答案为:11.频数分布直方图如图所示:(2)50÷2=25,∴中位线是第25、26的平均数,∴预习时间的中位数落在第3组,故答案为:3.(3)数学学科预习时间少于10分钟的学生人数为:400×=152人.【点评】本题考查的是频数分布直方图、用样本估计总体、中位数的概念,正确读懂频数分布直方图、利用统计图获取信息是解题的关键.19.双十一期间,某店铺推出的如图①所示的雪球夹销售火爆,其形状可近似的看成图②所示的图形,当雪球夹闭合时,测得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(精确到1厘米)【参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin14°≈0.24,cos14°≈0.97,tan14°≈0.25.【考点】解直角三角形的应用.【分析】如图②中,作OM⊥AB于M,在RT△AOM中,利用sin∠AOM=求出AM,即可解决问题.【解答】解:如图②中,作OM⊥AB于M,则∠AMO=90°,∵OA=OB,∴AB=2AM,∠AOM=∠AOB=×28°=14°,在RT△AOM中,∠AMO=90°,∠AOM=14°,OA=14,∴sin∠AOM=,∴AM=O•sin∠AOM=14×sin14°≈14×0.24=3.36,∴AB=2AM=6.72≈7(厘米).答:这个雪球夹制作的雪球的直径AB的长度约为7厘米.【点评】本题考查解直角三角形的有关知识、等腰三角形的性质.解题的关键是转化为直角三角形去思考,体现了转化的思想,属于中考常考题型.20.甲乙两人玩一种游戏:三张大小、质地都相同的卡片上分别标有数字1,2,3,现将标有数字的一面朝下,洗匀后甲从中任意抽取一张,记下数字后放回;又将卡片洗匀,乙也从中任意抽取一张,计算甲乙两人抽得的两个数字之积,如果积为奇数则甲胜,若积为偶数则乙胜.(1)用列表或画树状图等方法,列出甲乙两人抽得的数字之积所有可能出现的情况;(2)请判断该游戏对甲乙双方是否公平?并说明理由.【考点】游戏公平性;列表法与树状图法.【专题】计算题.【分析】(1)列表得出所有等可能的情况数,找出甲乙两人抽得的数字之积所有可能出现的情况即可;(2)分别求出甲乙两人获胜的概率,比较即可得到结果.【解答】解:(1)列表如下:所有等可能的情况有9种,分别为(1,1);(1,2);(1,3);(2,1);(2,2);(2,3);(3,1);(3,2);(3,3),则甲乙两人抽得的数字之积所有可能出现的情况有1,2,3,2,4,6,3,6,9,共9种;(2)该游戏对甲乙双方不公平,理由为:其中积为奇数的情况有4种,偶数有5种,∴P(甲)<P(乙),则该游戏对甲乙双方不公平.【点评】此题考查了游戏的公平性,以及列表法与树状图法,判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.21.感知:如图①,点B、A、C在同一条直线上,DB⊥BC,EC⊥BC,且∠DAE=90°,AD=AE,易证△DBA≌△ACE.探究:如图②,在△DBA和△ACE中,AD=AE,若∠DAE=α(0°<α<90°),∠BAC=2α,∠B=∠C=180°﹣α,求证:△DBA≌△ACE.应用:如图②,在△DBA和△ACE中,AD=AE,若∠DAE=70°,∠BAC=140°,∠B=∠C=110°,则当∠D=35°时,∠DAC的度数是∠E的3倍.【考点】全等三角形的判定与性质.【分析】探究:利用AAS证明△DBA≌△ACE.应用:根据角之间的关系得到:∠DAC=70°+∠EAC,∠EAC=70°﹣∠E,得出3∠E=70°+70°﹣∠E,解得:∠E=35°,再根据△DBA≌△ACE,即可求出∠D的度数.【解答】解:探究:∵∠BAC=2α,∠DAE=α,∴∠DAB+∠EAC=α,∵∠B=180°﹣α,∴∠DAB+∠D=α,∴∠EAC=∠D,在△DBA和△ACE中,∴△DBA≌△ACE.应用:∵∠DAE=70°,∠BAC=140°,∠B=∠C=110°,∴∠DAC=∠DAE+∠EAC=70°+∠EAC,∠EAC=180°﹣∠C﹣∠E=180°﹣110°﹣∠E=70°﹣∠E,∴∠DAC=70°+70°﹣∠E,当∠DAC=3∠E,∴3∠E=70°+70°﹣∠E,解得:∠E=35°,∵△DBA≌△ACE.∴∠D=∠E=35°.故答案为:35.【点评】本题考查了全等三角形的性质定理与判定定理,解决本题的关键是证明△DBA≌△ACE.22.甲、乙两车分别从相距480千米的A、B两地出发,匀速相向行驶,乙车比甲车先出发1小时,从B地直达A地.甲车出发t小时两车相遇后甲车停留1小时,因有事按原路返回A地,两车同时到达A地.从甲车出发时开始计时,时间为x(时),甲、乙两车距B地的路程y(千米)与x(时)之间的函数关系如图所示(1)乙车的速度是60千米/时,t=3.(2)求甲车距B地路程y与x之间的函数关系式,并写出自变量x的取值范围.(3)直接写出乙车出发多长时间两车相距30千米.【考点】一次函数的应用.【分析】(1)由速度=路程÷时间可算出乙车的速度,根据在整个行驶的过程中甲为匀速运动(中间停留除外),可知甲返回A地时间与出发时间相同,由此得出关于时间t的一元一次方程,解方程即可得出t的值;(2)分别设出各线段的函数关系式,代入端点坐标,利用待定系数法即可得出结论;(3)根据乙车的速度得出乙车距B地路程y与x之间的函数关系式,结合(2)中的关系式分段讨论,由两车的距离差为30得出关于x的一元一次方程,解方程得出x的值,由于是求乙车出发的时间,故在x值上+1即可得出结论.【解答】解:(1)乙车的速度为60÷1=60(千米/时),∵甲车的速度不变,∴甲车返回的时间也为t小时,∴有t+1+t=(480﹣60)÷60,解得:t=3.故答案为:60;3.(2)根据题意,得:甲出发3小时时,与B地的距离为3×60+60=240;甲出发7小时后,与乙一同到B地.当0≤x≤3时,设所求函数关系式为y=kx+b,根据题意,得,解得.∴y=﹣80x+480;当3<x≤4时,y=240;当4<x≤7时,设所求函数关系式为y=mx+n,根据题意,得,解得.∴y=80x﹣80.综上可知:甲车距B 地路程y 与x 之间的函数关系式为y=.(3)乙车距B 地路程y 与x 之间的函数关系式为y=60(x+1)=60x+60,当0≤x ≤3时,﹣80x+480﹣60x ﹣60=30,解得:x=,x+1=;当3<x ≤4时,60x+60﹣240=30,解得:x=,x+1=;当4<x ≤7时,60x+60﹣80x+80=30,解得:x=,x+1=.综上可知:乙车出发、和小时时两车相距30千米. 【点评】本题考查了一次函数的应用、待定系数法求函数解析式以及解一元一次方程,解题的关键是:(1)找出关于时间t 的一元一次方程;(2)利用待定系数法分段求函数的解析式;(3)根据数量关系得出关于x 的一元一次方程.本题属于中档题,难度不大,解决该题型题目时,根据数量关系列出方程(方程组或函数关系式)是关键.23.如图,在矩形ABCD 中,BC=1,将矩形ABCD 绕点D 逆时针旋转45°,得到矩形A ′B ′C ′D ′,点B ′恰好落在BC 的延长线上,边A ′B ′交边CD 于点E .(1)求证:B ′C=BC .(2)保持矩形A ′B ′C ′D ′不动,将矩形ABCD 沿射线BB ′方向以每秒1个单位的速度平移,设平移时间为t 秒.①当矩形ABCD 与矩形A ′B ′C ′D ′重叠部分为四边形时,求重叠部分的面积为S 与t 之间的函数关系式.②点A ′关于AB 的对称点记作点F ,直接写出直线DF 与矩形A ′B ′C ′D ′的边平行时t 的值.【考点】几何变换综合题.【分析】(1)由矩形的性质和旋转的性质判断出△DBB′是等腰三角形;即可;(2)分三段计算,由矩形的性质旋转的性质先计算出S△A′D′G,S四边形D′GEF(3)先由矩形的性质和旋转的性质表示出相关的线段,再用比例式,计算即可.【解答】证明:(1)如图①,连接DB,DB′,∵四边形ABCD是矩形,∴∠BCD=90°,∴DC⊥BB′,由旋转有,DB=DB′,∴B′C=BC;(2)如图②,当0<t≤1﹣时,作D′G∥DC,交A′B′于G,∵四边形A′B′C′D′是矩形,∴A′B′∥D′C′∴四边形D′GEF是平行四边形,由旋转有∠A′D′G=45°,∵A′D′=1,∴S△A′D′G=×A′D′2=×1=,D′G=,由运动时间为t,∴DD′=t,=D′G×DD′=t,∴S四边形D′GEF=+t,∴S=S△A′D′G+S四边形D′GEF当t=1时,如图③,∵四边形ABCD,A′B′′D′是矩形,∴四边形AMCF是平行四边形,∴S=AM×AD=A′D′×AD=×1×1=;当1+≤t<2时,如图④,过B′作B′M∥AB,同理:四边形NMB′H是平行四边形,∴MN=B′H=B′C′=运动时间为t,∴BB′=2﹣t,∴S=S△B′C′M+S四边形NMB′H=×B′C′2+MN×BB′=×1+(2﹣t)=+2﹣t;(3)点A′关于AB的对称点记作点F,∴A′F⊥AB,∵四边形ABCD为矩形,∴AD⊥AB,∴A′F∥AD,∵直线DF与矩形A′B′C′D′的边平行①如图⑤,当DF∥A′D′时,四边形A′FDD′是平行四边形,∴A′F=DD′=t,∴AD′=1﹣t,∵点A′与F关于AB对称,∴A′M=FM=,∵∠AD′M=∠MA′F=45°,∴A′M=t,∴D′M=A′D′﹣A′M=1﹣t,∵AD∥A′F,∴,∴,∴t=2﹣;②如图⑥,当DF∥D′C′时,四边形D′GFD是平行四边形,∴GF=DD′=t,∵A′G=A′D′=,∴A′F=A′G+GF=+t,∵A′F=2(t﹣1+)=2t﹣2+,∴+t=2t﹣2+,∴t=2,即:直线DF与矩形A′B′C′D′的边平行时t的值为2﹣或2.【点评】此题是几何变换综合题,主要考查了矩形的性质,旋转的性质,三角形面积的计算,根据条件表示出线段是接本题的关键,难点是分段求函数解析式和分情况求t的值.24.边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.(1)求抛物线的解析式;(2)点P从点C出发,沿射线CB每秒1个单位长度的速度运动,运动时间为t秒.过点P作PF⊥CD 于点F,当t为何值时,以点P,F,D为顶点的三角形与△COD相似?(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.【考点】二次函数综合题.【专题】压轴题.【分析】(1)根据正方形的性质,可得OA=OC,∠AOC=∠DGE,根据余角的性质,可得∠OCD=∠GDE,根据全等三角形的判定与性质,可得EG=OD=1,DG=OC=2,根据待定系数法,可得函数解析式;(2)分类讨论:若△DFP∽△COD,根据相似三角形的性质,可得∠PDF=∠DCO,根据平行线的判定与性质,可得∠PDO=∠OCP=∠AOC=90,根据矩形的判定与性质,可得PC的长;若△PFD∽△COD,根据相似三角形的性质,可得∠DPF=∠DCO,=,根据等腰三角形的判定与性质,可得DF于CD的关系,根据相似三角形的相似比,可得PC的长;(3)分类讨论:▱MDNE,▱MNDE,▱NDME,根据一组对边平行且相等的四边形式平行四边,可得答案..【解答】解:(1)方法一:过点E作EG⊥x轴于G点.∵四边形OABC是边长为2的正方形,D是OA的中点,∴OA=OC=2,OD=1,∠AOC=∠DGE=90°.∵∠CDE=90°,∴∠ODC+∠GDE=90°.∵∠ODC+∠OCD=90°,∴∠OCD=∠GDE.在△OCD和△GED中,∴△ODC≌△GED (AAS),∴EG=OD=1,DG=OC=2.∴点E的坐标为(3,1).∵抛物线的对称轴为直线AB即直线x=2,∴可设抛物线的解析式为y=a(x﹣2)2+k,将C、E点的坐标代入解析式,得.解得,抛物线的解析式为y=(x﹣2)2+;方法二:过点E作EG⊥x轴于G点.DE⊥DC⇒∠CDO+∠EDH=90°,。
吉林省长春市2016届中考数学模拟试卷(二)含答案

吉林省长春市2016届中考数学模拟试卷(二)含答案2016年吉林省长春市中考数学模拟试卷(二)一、选择题(共8小题,每小题3分,满分24分)1.﹣3的相反数是()A.3 B.﹣3 C.D.﹣2.如图是由五个完全相同的小正方体组成的几何体,这个几何体的主视图是()A.B.C.D.3.吉林省交警总队公布的数据显示,截止到2015年9月1日,全省机动车保有量超过4530000辆,4530000这个数用科学记数法表示为()A.0.453×107B.4.53×106C.4.53×107D.45.3×1054.计算5x2﹣2x2的结果是()A.3 B.3x C.3x2D.3x45.不等式﹣3x≥6的解集在数轴上表示为()A.B.C.D.6.如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=55°,则∠2的大小为()A.55°B.65°C.75°D.85°7.如图,⊙O是△ABC的外接圆,连结OA、OB,且点C、O在弦AB的同侧,若∠ABO=50°,则∠ACB的度数为()A.50°B.45°C.30°D.40°8.若二次函数y=﹣x2+2x+m2+1的最大值为4,则实数m的值为()A.B.C.±2 D.±1二、填空题(共6小题,每小题3分,满分18分)9.分解因式:a2﹣a=.10.函数y=x+中,自变量x的取值范围是.11.如图,PA和PB是⊙O的切线,点A和点B是切点,若OA=9,∠P=40°,则的长为(结果保留π).12.如图,在平面直角坐标系中,菱形OABC的顶点B在y轴正半轴上,菱形的两条对角线的长分别是6和4,函数y=的图象经过点C,则k的值为.13.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是(用a、b的代数式表示).14.如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为.三、解答题(共10小题,满分78分)15.先化简,再求值:(x﹣1﹣),其中x=.16.某汽车专卖店销售A、B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,两种车型的销售总额为96万元;本周销售2辆A型车和1辆B型车,两种车型的销售总额为62万元,已知这两周两种型号汽车销售价格不变,求它们的销售单价.17.在一个不透明的箱子里,装有黄、白、黑各一个球,它们除了颜色之外没有其他区别,随机从箱子里取出1个球,放回搅匀再取一次,请你用画树状图或列表的方法表示所有可能出现的结果,求两次取出的都是白球的概率.18.如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC,求证:BE=AF.19.图①、②分别是一把水平放置的椅子的效果图与椅子侧面的示意图,椅子高为AC,椅面宽BE 为60cm,椅脚高ED为35cm,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得带你E的俯角为53°,求椅子高AC(精确到0.1cm).【参考数据:sin53°=0.739,cos53°=0.673,tan53°=1.099】20.某校团委为了了解学生孝敬父母的情况,在全校范围内随机抽取n名学生进行问卷调查.问卷中孝敬父母方式包括:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其他.每位学生在问卷调查时都按要求只选择了其中一种方式,该校团委收回全部问卷后,将收集到的数据整理并绘制成如下的统计图.(1)求n的值.(2)四种方式中被选择次数最多的方式为(用A、B、C、D作答);选择该种方式的学生人数占被调查的学生人数的百分比为.(3)根据统计结果,估计该校1600名学生中选择B方式的学生比选择A方式的学生多的人数.21.问题背景:在正方形ABCD的外侧,作△ADE和△DCF,连结AF、BE.特例探究:如图①,若△ADE与△DCF均为等边三角形,试判断线段AF与BE的数量关系和位置关系,并说明理由;拓展应用:如图②,在△ADE与△DCF中,AE=DF,ED=FC,且BE=4,则四边形ABFE的面积为.22.甲、乙两台机器各自加工相同数量的零件,工作时工作效率不变,甲机器先开始工作,中途停机检修了0.5小时.如图是甲、乙两台机器在整个工作过程中各自加工的零件个数y(个)与甲机器工作时间x(时)之间的函数图象.(1)求图中m和a的值.(2)机器检修后,求甲加工的零件个数y与x之间的函数关系式.(3)在乙机器工作期间,求两台机器加工的零件个数相差50个时x的值.23.(2016•长春模拟)如图,在平面直角坐标系中,抛物线y=ax2﹣4ax+1(a>0)与y轴交于点A,点D的坐标为(,1),过点D作DC∥y轴,交抛物线于点C,过点C作CB∥x轴,交y轴于点B,连结AD.(1)当点B的坐标为(0,2)时,求抛物线对应的函数表达式.(2)当矩形ABCD的边AD被抛物线分成1:3两部分时,求点C的坐标.(3)当矩形ABCD是正方形时,求a的值.(4)在抛物线的对称轴上有一点P,当△ABP为等腰直角三角形时,求点P的坐标.24.(2016•长春模拟)如图,在菱形ABCD中,AB=6,∠ABC=60°,AH⊥BC于点H.动点E从点B出发,沿线段BC向点C以每秒2个单位长度的速度运动.过点E作EF⊥AB,垂足为点F.点E出发后,以EF为边向上作等边三角形EFG,设点E的运动时间为t秒,△EFG和△AHC的重合部分面积为S.(1)CE=(含t的代数式表示).(2)求点G落在线段AC上时t的值.(3)当S>0时,求S与t之间的函数关系式.(4)点P在点E出发的同时从点A出发沿A﹣H﹣A以每秒2个单位长度的速度作往复运动,当点E停止运动时,点P随之停止运动,直接写出点P在△EFG内部时t的取值范围.2016年吉林省长春市中考数学模拟试卷(二)参考答案与试题解析一、选择题(共8小题,每小题3分,满分24分)1.﹣3的相反数是()A.3 B.﹣3 C.D.﹣【考点】相反数.【专题】常规题型.【分析】根据相反数的概念解答即可.【解答】解:﹣3的相反数是3,故选:A.【点评】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号;一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.2.如图是由五个完全相同的小正方体组成的几何体,这个几何体的主视图是()A.B.C.D.【考点】简单组合体的三视图.【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.【解答】解:从正面看易得第一层有3个正方形,第二层最右边有一个正方形.故选D.【点评】本题考查了三视图的知识,属于基础题,注意主视图是从物体的正面看得到的视图.3.吉林省交警总队公布的数据显示,截止到2015年9月1日,全省机动车保有量超过4530000辆,4530000这个数用科学记数法表示为()A.0.453×107B.4.53×106C.4.53×107D.45.3×105【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将4530000用科学记数法表示为:4.53×106.故选B.【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.4.计算5x2﹣2x2的结果是()A.3 B.3x C.3x2D.3x4【考点】合并同类项.【分析】根据合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变,进行运算即可.【解答】解:原式=5x2﹣2x2=3x2.故选:C.【点评】此题考查了合并同类项的知识,属于基础题,解答本题的关键是掌握合并同类项的法则.5.不等式﹣3x≥6的解集在数轴上表示为()A.B.C.D.【考点】在数轴上表示不等式的解集.【分析】根据不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),可得答案.【解答】解:﹣3x≥6,解得x≤﹣2.故选:C.【点评】本题考查了在数轴上表示不等式的解集,不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),注意在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.6.如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=55°,则∠2的大小为()A.55°B.65°C.75°D.85°【考点】平行线的性质;三角形内角和定理.【分析】先根据平行线性质求出∠3,再根据三角形内角和定理求出∠4,即可求出答案.【解答】解:∵直线l1∥l2,且∠1=55°,∴∠3=∠1=55°,∵在△AEF中,∠A=50°,∴∠4=180°﹣∠3﹣∠A=75°,∴∠2=∠4=75°,故选C.【点评】本题考查了平行线的性质和三角形内角和定理,对顶角相等的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.7.如图,⊙O是△ABC的外接圆,连结OA、OB,且点C、O在弦AB的同侧,若∠ABO=50°,则∠ACB的度数为()A.50°B.45°C.30°D.40°【考点】圆周角定理.【分析】利用等边对等角求得∠BAO的度数,然后根据三角形内角和定理求得∠AOB的度数,最后根据圆周角定理即可求解.【解答】解:∵OA=OB,∴∠BAO=∠ABO=50°,∴∠AOB=180°﹣50°﹣50°=80°.∴∠ACB=∠AOB=40°.故选D.【点评】本题考查了等腰三角形的性质定理以及圆周角定理,正确理解定理,求得∠AOB的度数是关键.8.若二次函数y=﹣x2+2x+m2+1的最大值为4,则实数m的值为()A.B.C.±2 D.±1【考点】二次函数的最值.【专题】探究型.【分析】先将二次函数y=﹣x2+2x+m2+1化为顶点式,又因为二次函数y=﹣x2+2x+m2+1的最大值为4,从而可以得到关于m的等式,从而可以得到m的值,本题得以解决.【解答】解:∵y=﹣x2+2x+m2+1=﹣(x﹣1)2+m2+2,二次函数y=﹣x2+2x+m2+1的最大值为4,∴m2+2=4,解得,m=,故选A.【点评】本题考查二次函数的最值,解题的关键时能将二次函数的一般式化为顶点式,找准对应关系.二、填空题(共6小题,每小题3分,满分18分)9.分解因式:a2﹣a=a(a﹣1).【考点】因式分解-提公因式法.【专题】因式分解.【分析】这个多项式含有公因式a,分解因式时应先提取公因式.【解答】解:a2﹣a=a(a﹣1).【点评】本题考查了提公因式法分解因式,比较简单,注意不要漏项.10.函数y=x+中,自变量x的取值范围是x≠2.【考点】函数自变量的取值范围.【分析】根据分母不等于0列式计算即可得解.【解答】解:由题意得,x﹣2≠0,解得x≠2.故答案为:x≠2.【点评】本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.11.如图,PA和PB是⊙O的切线,点A和点B是切点,若OA=9,∠P=40°,则的长为,7π(结果保留π).【考点】切线的性质;弧长的计算.【分析】根据切线的性质得出∠PAO=∠PBO=90°,求出∠AOB=140°,根据弧长公式求出即可.【解答】解:∵PA和PB是⊙O的切线,点A和点B是切点,∴∠PAO=∠PBO=90°,∵∠P=40°,∴∠AOB=360°﹣90°﹣90°﹣40°=140°,∴的长为=7π,故答案为:7π【点评】本题考查了切线的性质,弧长公式的应用,能根据切线的性质求出∠PAO=∠PBO=90°是解此题的关键,注意:圆的切线垂直于过切点的半径.12.如图,在平面直角坐标系中,菱形OABC的顶点B在y轴正半轴上,菱形的两条对角线的长分别是6和4,函数y=的图象经过点C,则k的值为﹣6.【考点】菱形的性质;反比例函数图象上点的坐标特征.【分析】先根据菱形的性质求出C点坐标,再把C点坐标代入反比例函数的解析式即可得出k的值.【解答】解:∵菱形的两条对角线的长分别是6和4,∴C(﹣3,2),∵点C在反比例函数y=的图象上,∴2=,解得k=﹣6.故答案为:﹣6.【点评】本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上各点的坐标一定满足此函数的解析式.13.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是ab(用a、b的代数式表示).【考点】平方差公式的几何背景.【专题】操作型.【分析】利用大正方形的面积减去4个小正方形的面积即可求解.【解答】解:设大正方形的边长为x1,小正方形的边长为x2,由图①和②列出方程组得,解得,②的大正方形中未被小正方形覆盖部分的面积=()2﹣4×()2=ab.故答案为:ab.【点评】本题考查了平方差公式的几何背景,正确求出大小正方形的边长列代数式,以及整式的化简,正确对整式进行化简是关键.14.如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为6.【考点】旋转的性质;相似三角形的判定与性质.【专题】几何图形问题.【分析】利用平行线的性质以及旋转的性质得出△CAD∽△B′A′C,再利用相似三角形的性质得出AD的长,进而得出BD的长.【解答】解:∵将△ABC绕点C按逆时针方向旋转得到△A′B′C,∴AC=CA′=4,AB=B′A′=2,∠A=∠CA′B′,∵CB′∥AB,∴∠B′CA′=∠D,∴△CAD∽△B′A′C,∴=,∴=,解得AD=8,∴BD=AD﹣AB=8﹣2=6.故答案为:6.【点评】此题主要考查了旋转的性质以及相似三角形的判定与性质等知识,得出△CAD∽△B′A′C 是解题关键.三、解答题(共10小题,满分78分)15.先化简,再求值:(x﹣1﹣),其中x=.【考点】分式的化简求值.【分析】先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.【解答】解:原式=•=•=,当x=时,原式==﹣.【点评】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.16.某汽车专卖店销售A、B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,两种车型的销售总额为96万元;本周销售2辆A型车和1辆B型车,两种车型的销售总额为62万元,已知这两周两种型号汽车销售价格不变,求它们的销售单价.【考点】二元一次方程组的应用.【分析】设每辆A型车售价为x万元,B型车的售价为y万元,根据1辆A型车和3辆B型车的销售总额为96万元,2辆A型车和1辆B型车的销售总额为62万元,列出二元一次方程组,求解即可.【解答】解:设每辆A型车售价为x万元,B型车的售价为y万元,根据题意,得,解得:,答:每辆A型车售价为18万元,B型车的售价为26万元.【点评】本题考查了二元一次方程组的应用,解答本题的关键在于读懂题意,设出未知数,找出合适的等量关系,列出正确的二元一次方程组并求解.17.在一个不透明的箱子里,装有黄、白、黑各一个球,它们除了颜色之外没有其他区别,随机从箱子里取出1个球,放回搅匀再取一次,请你用画树状图或列表的方法表示所有可能出现的结果,求两次取出的都是白球的概率.【考点】列表法与树状图法.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次取出白颜色球的情况,再利用概率公式即可求得答案.【解答】解:画树状图得:由树形图可知所有等可能的情况有9种,其中两次取出的都是白色球有1种,所以两次取出的都是白色球的概率=.【点评】此题考查的是用列表法或树状图法求概率,注意列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意此题属于放回实验.18.如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC,求证:BE=AF.【考点】平行四边形的判定与性质.【专题】证明题.【分析】由DE∥AB,EF∥AC,可证得四边形ADEF是平行四边形,∠ABD=∠BDE,又由BD是△ABC的角平分线,易得△BDE是等腰三角形,即可证得结论.【解答】证明:∵DE∥AB,EF∥AC,∴四边形ADEF是平行四边形,∠ABD=∠BDE,∴AF=DE,∵BD是△ABC的角平分线,∴∠ABD=∠DBE,∴∠DBE=∠BDE,∴BE=DE,∴BE=AF.【点评】本题考查了平行四边形的判定与性质、等腰三角形的判定与性质以及三角函数等知识.此题难度适中,注意掌握数形结合思想的应用.19.图①、②分别是一把水平放置的椅子的效果图与椅子侧面的示意图,椅子高为AC,椅面宽BE 为60cm,椅脚高ED为35cm,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得带你E的俯角为53°,求椅子高AC(精确到0.1cm).【参考数据:sin53°=0.739,cos53°=0.673,tan53°=1.099】【考点】解直角三角形的应用-仰角俯角问题.【专题】探究型.【分析】要求AC的长,只要求出AB和BC的长即可,根据题意可知BC与DE的长相等,根据∠AEB=53°和BE的长可以求得AB的长,从而可以求得AC的长,本题得以解决.【解答】解:∵AC⊥BE,AC⊥CD,AC∥ED,∴四边形BCDE是矩形,∠AEB=35°,∴BC=DE=35,在Rt△ABE中,∠ABE=90°,tan∠AEB=,BE=60,∴AB=BE•tan∠AEB=60×tan53°=60×1.009=65.94,∴AC=AB+BC=65.94+35=100.94≈100.9cm,即椅子的高约为100.9cm.【点评】本题考查解直角三角形的应用﹣仰角俯角问题,解题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数解答问题.20.某校团委为了了解学生孝敬父母的情况,在全校范围内随机抽取n名学生进行问卷调查.问卷中孝敬父母方式包括:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其他.每位学生在问卷调查时都按要求只选择了其中一种方式,该校团委收回全部问卷后,将收集到的数据整理并绘制成如下的统计图.(1)求n的值.(2)四种方式中被选择次数最多的方式为C(用A、B、C、D作答);选择该种方式的学生人数占被调查的学生人数的百分比为40%.(3)根据统计结果,估计该校1600名学生中选择B方式的学生比选择A方式的学生多的人数.【考点】条形统计图;用样本估计总体.【分析】(1)直接利用条形统计图可得出n的值;(2)利用条形统计图结合(1)中所求,得出C种方式的学生人数占被调查的学生人数的百分比;(3)利用条形统计图得出选择B方式的学生比选择A方式的学生多的人数.【解答】解:(1)n=36+60+96+48=240(人),故n的值为240;(2)由条形统计图可得:四种方式中被选择次数最多的方式为:C;选择该种方式的学生人数占被调查的学生人数的百分比为:×100%=40%;故答案为:C,40%;(3)由题意可得:600×﹣1600×=160(人),答:该校1600名学生中选择B方式的学生比选择A方式的学生多的人数为160人.【点评】此题主要考查了条形统计图的应用,正确利用条形统计图得出正确信息是解题关键.21.问题背景:在正方形ABCD的外侧,作△ADE和△DCF,连结AF、BE.特例探究:如图①,若△ADE与△DCF均为等边三角形,试判断线段AF与BE的数量关系和位置关系,并说明理由;拓展应用:如图②,在△ADE与△DCF中,AE=DF,ED=FC,且BE=4,则四边形ABFE的面积为8.【考点】正方形的性质;全等三角形的判定与性质.【分析】特例探究:易证△ADE≌△DCF,即可证明AF与BE的数量关系是:AF=BE,位置关系是:AF⊥BE;拓展应用:首先证得△ADE≌△CDF,由全等三角形的性质可得∠DAE=∠CDF,易得△BAE≌△ADF,可得AE=AF,同特例探究可得AF⊥BE,易得四边形ABFE的面积为:.【解答】解:特例探究:AF=BE,AF⊥BE.∵四边形ABCD为正方形,△ADE与△DCF均为等边三角形,∴AB=AD=CD,∠BAD=∠ADC,AE=AD=CD=DF,∠DAE=∠CDF,∴∠BAD+∠DAE=∠ADC+∠CDF,即∠BAE=∠ADF,在△ABE与△DAF中,,∴△ABE≌△DAF(SAS),∴AF=BE,∠ABE=∠DAF,∵∠DAF+∠BAF=90°,∴∠ABE+∠BAF=90°,∴AF⊥BE;拓展应用:在△ADE与△CDF中,∵,∴△ADE≌△CDF(SSS),∴∠DAE=∠CDF,∠ADF=∠ADC+∠CDF=90°+∠CDF,∠BAE=∠BAD+∠EAD=90°+∠EAD,∴∠ADF=∠BAE,在△ABE与△DAF中,,∴△ABE≌△DAF(SAS),∴AF=BE,∠ABE=∠DAF,∵∠DAF+∠BAF=90°,∴∠ABE+∠BAF=90°,∴AF⊥BE,∴S==8,四边形ABFE故答案为:8.【点评】本题主要考查了正方形的性质和等边三角形的性质,证得AF=BE,AF⊥BE是解答此题的关键.22.甲、乙两台机器各自加工相同数量的零件,工作时工作效率不变,甲机器先开始工作,中途停机检修了0.5小时.如图是甲、乙两台机器在整个工作过程中各自加工的零件个数y(个)与甲机器工作时间x(时)之间的函数图象.(1)求图中m和a的值.(2)机器检修后,求甲加工的零件个数y与x之间的函数关系式.(3)在乙机器工作期间,求两台机器加工的零件个数相差50个时x的值.【考点】一次函数的应用.【专题】函数及其图象.【分析】(1)根据已知和图象可以得到m的值,由甲、乙两台机器各自加工相同数量的零件,工作时工作效率不变,可以求得a的值;(2)由图象可以得到点B、C的点的坐标,从而可以得到机器检修后,甲加工的零件个数y与x之间的函数关系式;(3)根据题意可以列出相应的等式,从而可以求得x的值.【解答】解:(1)由题意可得,m=1.5﹣0.5=1,∵工作效率保持不变,∴,解得a=40,即m=1,a=40;(2)设机器检修后,甲加工的零件个数y与x之间的函数关系式是:y=k1x+b1,则,解得,即机器检修后,甲加工的零件个数y与x之间的函数关系式是:y=40x﹣20(3.5≤x≤7);(3)设CE所在直线的函数解析式为:y=k2x+b2,则解得,,即直线CE所在直线的解析式为:y=80x﹣160,则|(80x﹣160)﹣(40x﹣20)|=50,解得,或x=.即当甲机器工作小时或小时时,恰好相差50个.【点评】本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.23.(2016•长春模拟)如图,在平面直角坐标系中,抛物线y=ax2﹣4ax+1(a>0)与y轴交于点A,点D的坐标为(,1),过点D作DC∥y轴,交抛物线于点C,过点C作CB∥x轴,交y轴于点B,连结AD.(1)当点B的坐标为(0,2)时,求抛物线对应的函数表达式.(2)当矩形ABCD的边AD被抛物线分成1:3两部分时,求点C的坐标.(3)当矩形ABCD是正方形时,求a的值.(4)在抛物线的对称轴上有一点P,当△ABP为等腰直角三角形时,求点P的坐标.【考点】二次函数综合题.【分析】(1)由题意易得点C的坐标为:(,2),然后代入抛物线y=ax2﹣4ax+1,即可求得答案;(2)首先设抛物线交AD于点E,则点E的纵坐标为1,可求得点E的坐标,然后分别从AE=3DE 或3AE=DE去分析求解即可求得答案;(3)若矩形ABCD是正方形,则AD=CD,可求得点C的坐标,然后分别从点C在点D上方与点C在点D下方,去分析求解即可求得答案;(4)分别从∠BAP=90°,∠ABP=90°或∠APB=90°,去分析求解即可求得答案.【解答】解:(1)∵CB∥x轴,DC∥y轴,点B的坐标为(0,2),点D的坐标为(,1),∴点C的坐标为:(,2),∵抛物线y=ax2﹣4ax+1(a>0)过点C,∴﹣8+1=2,解得:a=,∴抛物线对应的函数表达式为:y=x2﹣x+1;(2)设抛物线交AD于点E,则点E的纵坐标为1,由ax2﹣4ax+1=1,解得:x1=0,x2=4,∴点E的坐标为(4,1),∵点D的坐标为(,1),则DE=﹣4,当AE=3DE时,4=3(﹣4),解得:a=,∴点C的坐标为:(,);当3AE=DE时,12=﹣4,解得:a=,∴点C的坐标为:(16,25);(3)若矩形ABCD是正方形,则AD=CD,∵点D的坐标为:(,1),且DC∥y轴,∴C(,﹣7),若点C在点D上方,则CD=﹣8,∴=﹣8,解得:a=;若点C在点D下方,则CD=8﹣,∴=8﹣,解得:a=;综上可得:a=或;(4)抛物线的对称轴方程为:x=﹣=﹣=2,∵△ABP为等腰直角三角形,∴若∠BAP=90°,则点P的坐标为:(2,1);若∠ABP=90°,则AB=BP=2,∴点P的坐标为:(2,3)或(2,﹣1);若∠APB=90°,AB=2×2=4,∴点P的坐标为:(2,3);综上所述:点P的坐标为:(2,1)或(2,3)或(2,﹣1).【点评】此题属于二次函数的综合题.考查了待定系数求二次函数解析式、矩形的性质、正方形的性质以及等腰直角三角形性质.注意掌握分类讨论思想的应用是解此题的关键.24.(2016•长春模拟)如图,在菱形ABCD中,AB=6,∠ABC=60°,AH⊥BC于点H.动点E从点B出发,沿线段BC向点C以每秒2个单位长度的速度运动.过点E作EF⊥AB,垂足为点F.点E出发后,以EF为边向上作等边三角形EFG,设点E的运动时间为t秒,△EFG和△AHC的重合部分面积为S.(1)CE=6﹣2t(含t的代数式表示).(2)求点G落在线段AC上时t的值.(3)当S>0时,求S与t之间的函数关系式.(4)点P在点E出发的同时从点A出发沿A﹣H﹣A以每秒2个单位长度的速度作往复运动,当点E停止运动时,点P随之停止运动,直接写出点P在△EFG内部时t的取值范围.【考点】四边形综合题.【分析】(1)由菱形的性质得出BC=AB=6得出CE=BC﹣BE=6﹣2t即可;(2)由菱形的性质和已知条件得出△ABC是等边三角形,得出∠ACB=60°,由等边三角形的性质和三角函数得出∠GEF=60°,GE=EF=BE•sin60°=t,证出∠GEC=90°,由三角函数求出CE==t,由BE+CE=BC得出方程,解方程即可;(3)分两种情况:①当<t≤2时,S=△EFG的面积﹣△NFN的面积,即可得出结果;②当2<t≤3时,由①的结果容易得出结论;(4)由题意得出t=时,点P与H重合,E与H重合,得出点P在△EFG内部时,t的不等式,解不等式即可.【解答】解:(1)根据题意得:BE=2t,∵四边形ABCD是菱形,∴BC=AB=6,∴CE=BC﹣BE=6﹣2t;故答案为:6﹣2t;(2)点G落在线段AC上时,如图1所示:∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC是等边三角形,∴∠ACB=60°,∵△EFG是等边三角形,∴∠GEF=60°,GE=EF=BE•sin60°=t,∵EF⊥AB,∴∠BEF=90°﹣60°=30°,∴∠GEB=90°,∴∠GEC=90°,∴CE===t,∵BE+CE=BC,∴2t+t=6,解得:t=2;(3)分两种情况:①当<t≤2时,如图2所示:S=△EFG的面积﹣△NFN的面积=××(t)2﹣××(﹣+2)2=t2+t﹣3,即S=t2+t﹣3;当2<t≤3时,如图3所示:S=t2+t﹣3﹣(3t﹣6)2,即S=﹣t2+t﹣;(4)∵AH=AB•sin60°=6×=3,3÷2=,3÷2=,∴t=时,点P与H重合,E与H重合,∴点P在△EFG内部时,﹣<(t﹣)×2<t﹣(2t﹣3)+(2t﹣3),解得:<t<;即点P在△EFG内部时t的取值范围为:<t<.【点评】本题是四边形综合题目,考查了菱形的性质、等边三角形的判定与性质、三角函数、三角形面积的计算等知识;本题综合性强,难度较大,特别是(3)中,需要进行分类讨论才能得出结果.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年吉林省长春市南关区中考模拟试题(数学)2016.4一、选择题(本大题共8小题,每小题3分,共24分) 1.6-的绝对值是(A )6-. (B )6. (C )16-. (D )16. 2.“十二五”期间,某市义务教育阶段在校学生人数达到654 000人.654 000这个数用科学记数法表示为 (A )60.65410⨯. (B )66.5410⨯. (C )56.5410⨯. (D )465.410⨯. 3.下列运算中,正确的是(A )235a a a ⋅=. (B )842a a a ÷=. (C )527()a a =. (D )235a b ab +=. 4.右图是由六个完全相同的小正方体组合而成的立体图形,它的主视图是(A ) (B ) (C ) (D ) (第4题)5.如图,直线a ∥b .若130∠=︒,2=45∠︒,则3∠的大小为(A )75︒. (B )80︒. (C )85︒. (D )105︒.(第5题) (第6题)6.如图,四边形ABCD 内接于⊙O .若⊙O 的半径为4,135D ∠=︒,则»AC 的长为 (A )π. (B )2π. (C )4π. (D )8π.ba 3217.如图,在△ABC 中,分别以点A 、C 为圆心,以大于2AC长为半径作圆弧,两弧分别相交于点E 、F ,连结EF 并延长交边BC 于点D ,连结AD .若6AB =,8BC =,则△ABD 的周长为 (A )8. (B )10. (C )12. (D )14.(第7题) (第8题)8.如图,在平面直角坐标系中,矩形ABCD 的边BC 在x 轴的正半轴上,点B 在点C 的左侧,直线y kx =经过点(3,3)A 和点P ,且OP =将直线y kx =沿y 轴向下平移得到直线y kx b =+,若点P 落在矩形ABCD 的内部,则b 的取值范围是(A )0<b <3. (B )3-<b <0. (C )6-<b <3-. (D )3-<b <3. 二、填空题(本大题共6小题,每小题3分,共18分)92.(填“>”、“=”或“<”) 10.不等式2(3)4x +-≤0的解集为 .11.一元二次方程2530x x -+=根的判别式的值为 .12.如图,AB 为⊙O 的直径,点C 、D 在⊙O 上.若40CAB ∠=︒,则D ∠的大小为 度.(第12题) (第13题) (第14题)13.如图,在平面直角坐标系中,点A 在函数ky x=(x >0) 的图象上,过点A 作AC ⊥y 轴于点C ,点B 在x 轴上,连结CB 、AB .若△ABC 的面积为4,则k 的值为 .14.如图,在平面直角坐标系中,抛物线2(2)1y a x =-+(a 为常数)的顶点为A ,过点A 作y 轴的平行线与抛物线21433y x x =--交于点B ,抛物线21433y x x =--的顶点为C ,连结CA 、CB .则△ABC 的面积为 .FEDB CA B、三、解答题(本大题共10小题,共78分)15.(6分)先化简,再求值:(4)(1)(1)a a a a -+-+,其中34a =.16.(6分)现有一副扑克牌中的3张牌,牌面数字分别为7、9、9,从中随机抽取一张然后放回,再随机抽取一张.用画树状图(或列表)的方法,求抽取的两张牌面数字相同的概率.17.(6分)某车间计划生产360个零件,由于改进了技术,该车间实际每天生产零件的个数是原计划的1.2倍,结果提前4天完成任务.求该车间原计划每天生产零件的个数.18.(7分)如图,在△ABC 中,AB =AC ,AD 平分BAC ∠交BC 于点D ,分别过点A 、D 作AE ∥BC 、DE∥AB ,AE 与DE 相交于点E ,连结CE .求证:四边形ADCE 是矩形.EDCBA19.(7分)如图,一艘海轮位于灯塔P 的北偏东30°方向,距离灯塔80海里的A 处.海轮沿正南方向航行一段时间后,到达位于灯塔P 的南偏东64°方向上的B 处.求海轮所在的B 处与灯塔P 的距离.(结果精确到0.1海里)【参考数据:sin 640.90cos640.44tan 64 2.05︒=︒=︒=,,】20.(7分)在“世界粮食日”前夕,某校团委随机抽取了n 名本校学生,对某日午餐剩饭菜情况进行问卷调查.问卷中的剩饭菜情况包括:A .饭和菜全部吃完;B .饭有剩余但菜吃完;C .饭吃完但菜有剩余;D .饭和菜都有剩余.每位学生在问卷调查时都按要求只选择了其中一种情况,该校团委收回全部问卷后,将收集到的数据整理并绘制成如下的条形统计图. (1)求n 的值.(2)饭和菜全部吃完的学生人数占被调查的学生人数的百分比为 . (3)根据统计结果,估计该校2400名学生中菜有剩余的学生人数.(第20题)剩饭菜情况n 名学生午餐剩饭菜情况的人数条形统计图64°30°北BAP21.(8分)甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队又用了2小时完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度y (米)与维修时间x (时)之间的函数图象如图所示. (1)甲队调离时,甲、乙两队已维修路面的总长度为 米. (2)求此次维修路面的总长度a .(3)求甲队调离后y 与x 之间的函数关系式.22.(9分)在菱形ABCD 中,60B ∠=︒,AC 为对角线.点E 、F 分别在边AB 、DA 或其延长线上,连结CE 、CF ,且60ECF ∠=︒.感知:如图①,当点E 、F 分别在边AB 、DA 上时,易证: AF BE =.(不要求证明) 探究:如图②,当点E 、F 分别在边AB 、DA 的延长线上时,CF 与边AB 交于点G .求证:AF BE =.应用:如图②,若12AB =,4AF =,求线段GE 的长. 图① 图②F EDCB A GF EDCBA时)y (米23.(10分)如图,在△ABC 中,90C ∠=︒,6AC BC ==. 点P 在边AC 上运动,过点P 作PD ⊥AB 于点D ,以AP 、AD 为邻边作□P ADE . 设□P ADE 与ABC △重叠部分图形的面积为y ,线段AP 的长为x (0<x ≤6).(1)求线段PE 的长(用含x 的代数式表示).(2)当点E 落在边BC 上时,求x 的值. (3)求y 与x 之间的函数关系式.(4)直接写出点E 到△ABC 任意两边所在直线距离相等时x 的值.24.(12分)如图,在平面直角坐标系中,抛物线2+5y ax bx =+与x 轴交于(1,0)A 、(5,0)B 两点,点D 是抛物线上横坐标为6的点.点P 在这条抛物线上,且不与A 、D 两点重合,过点P 作y 轴的平行线与射线AD 交于点Q ,过点Q 作QF 垂直于y 轴,点F 在点Q 的右侧,且2QF =,以QF 、QP 为邻边作矩形QPEF .设矩形QPEF 的周长为d ,点P 的横坐标为m . (1)求这条抛物线所对应的函数表达式.(2)求这条抛物线的对称轴将矩形QPEF 的面积分为1:2两部分时m 的值. (3)求d 与m 之间的函数关系式及d 随m 的增大而减小时d 的取值范围. (4)当矩形QPEF 的对角线互相垂直时,直接写出其对称中心的横坐标. ABC PED九年级数学质量调研题参考答案及评分标准 2016.4一、选择题(每小题3分,共24分)1B 2C 3A 4 D 5 A 6B 7D 8 C二、填空题(每小题3分,共18分)9.< 10.x ≤1- 11.13 12.50 13.8 14.10 三、解答题(本大题共10小题,共78分)15.原式224114.a a a a =-+-=- (4分) 当34a =时,原式=31414 2.4a -=-⨯=- (6分)16.所以5().9P 数字相同= (6分) 17.设该车间原计划每天生产零件x 个.根据题意,得36036041.2x x-=. (3分) 解得15x =. (5分 经检验,15x =是原方程的解,且符合题意.答:该车间原计划每天生产零件15个. (6分) 18.∵AE ∥BC 、DE ∥AB ,∴四边形ABDE 是平行四边形. (3分)∴.AE BD =又∵AB AC =,AD 平分BAC ∠,∴BD DC =,AD ⊥BC .∴AE DC =,90.ADC ∠=︒ (5分) 又∵AE ∥BC , ∴四边形ADCE 是平行四边形.∴四边形ADCE 是矩形. (7分)19.过点P 作PC ⊥AB 于点C .由题意可知,AB ∥PD , ∴30,64.A B ∠=︒∠=︒ 在Rt △APC 中,90,30,80.ACP A AP ∠=︒∠=︒=1sin3040.2PC AP AP =︒== (3分) 在Rt △PBC 中,90,64.BCP B ∠=︒∠=︒4044.44sin640.9PC PB ===︒≈44.4(海里). 答:海轮所在的B 处与灯塔P 的距离约为44.4海里. (7分) 20.(1)120402020200.n =+++= (2分) (2)60%. (4分) (3)20202400480200+⨯= (人). (7分) D C北B AP 64°30°(2)甲队调离前,甲、乙两队每小时维修路面的总长度为1503=50÷(米).∴乙队每小时维修路面的长度为503020-=. (4分)15020219a =+⨯=(米). (5分)(3)设所求函数关系式为y kx b =+.将点(3,150),(5,190)代入,得3150,5190.k b k b +=⎧⎨+=⎩ 解得20,90.k b =⎧⎨=⎩(7分) ∴2090y x =+(3<x ≤5). (8分) 22.探究:∵四边形ABCD 是菱形,60.ABC ∠=︒∴AC BC =. (1分)60.ACB DAC ABC ∠=∠=∠=︒ ∴180120.FAC DAC ∠=︒-∠=︒ 180120.EBC ABC ∠=︒-∠=︒∴.FAC EBC ∠=∠ (3分) 又∵60ECF ∠=︒∴60.ACF ACB GCB GCB ∠=∠-∠=︒-∠60.BCE ECF GCB GCB ∠=∠-∠=︒-∠∴.ACF BCE ∠=∠ (5分) ∴△ACF ≌△BCE .∴.AF BE = (6分)应用:∵四边形ABCD 是菱形,∴AD ∥CB .∴△AFG ∽△BCG .∴41.123GA AF GB BC === ∴3.GB GA = 又∵12.GA GB AB +== ∴312.GA GA +=∴ 3.GA = (8分) ∴9.GB =又∵AF BE =,∴9413.GE GB BE =+=+= (9分)23.(1)cos 45PE AD AP x ==︒=. (2分) (2)62xx +=. 4.x = (4分) (3)当0<x ≤4时,21.2y x == 当4<x ≤6 时, 16.2DG x =-13(6) 6.22GE x DG x x x =-=--=- G A B CP ED2221135(6)918.2228y x x x x =--=-+- (7分)(4)3,6,12(37 (10分)由116.22x x x =-- 得 3.x =由11(6).22x x x =-- 得 6.x =6.2xx =-- 得12(37x == 24.(1)把(1,0)A 、(5,0)B 代入2+5y ax bx =+50,25550.a b a b ++=⎧⎨++=⎩ 解得1,6.a b =⎧⎨=-⎩(2分) ∴26 5.y x x =-+ (2)对称轴为:63.22b x a -=-=-= 由3223m -=,得53m =.由3123m -=,得73m =. (4分)(3)当6x =时,22656665 5.y x x =-+=-⨯+=∴点D 的坐标为(6,5).射线AD 所对应的函数表达式为1y x =-(x >1). ∴2(,65)P m m m -+,(,1)Q m m -. 当1<m <6时,222(762)2148.d m m m m =-+-+=-+- (6分)当m >6时,222(762)21416.d m m m m =-++=-+ (8分)又2273321482).22d m m m =-+-=--+( ∴d 随m 的增大而减小时d 的取值范围是0<m ≤332. (9分)(4由2780.m m -+= 得12m m ==由2740.m m -+= 得 m m =(舍去) (12分)。
