课时1.实数的有关概念
实数的有关概念

第1讲┃实数的有关概念
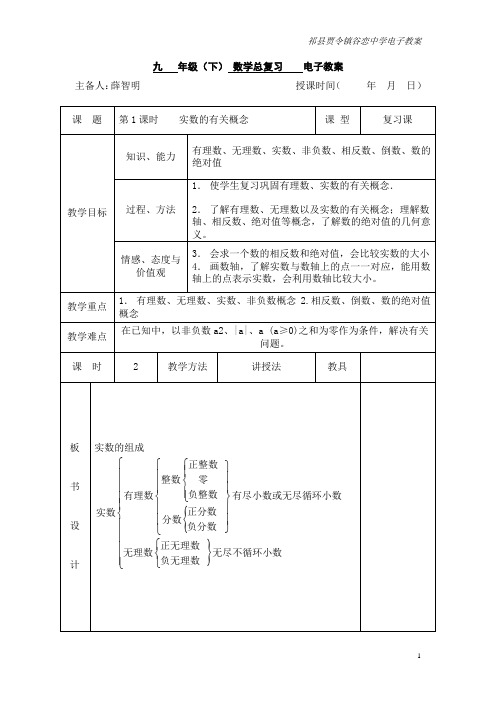
2.按正负分类: 正整数 正有理数 正分数 正实数 正无理数 零 实数 负整数 负有理数 负实数 负分数 负无理数
22 3 [注意](1)任何分数都是有理数,如 ,- 等; 7 11 (2)0 既不是正数,也不是负数,但 0 是自然数。
A. a的相反数是-a,0的相反数是0,如-2014的 相反数是2014; B.若a、b互为相反数,则a + b=0; C.在数轴上,表示互为相反数(0除外)的两个 点,位于原点两侧,并且到原点的距离相等.
5.倒数 (1)定义:如果两个数的乘积等于1,我们把 其中一个数叫做另一个数的倒数.
1 (2)性质:实数a(a≠0)的倒数为 ,特别地,0 a
第1课时 实数的有关概念
实数:有理数和无理数统称为实数.
有理数和无理数
(1)有理数:整数和分数统称为有理数.
有限小数与无限循环小数。 (2)无理数:无限不循环小数叫做无理数.
(3)初中阶段常见的几种无理数:
3 A.开方不尽的数,如 2 ,3 , 2 等; B.有规律但是不循环的无限小数,如
0.30300300030000…(两个3之间依次多一个0)
考点聚焦 归类探究 回归教材 中考预测
3.数轴:规定了原点、②_正方向 _______和单位长度的
直线叫做数轴.任何实数都可以用数轴上唯一的一 个点来表示,即实数与数轴上的点是一一对应的. 4.相反数 符号 不同,那 (1)定义:如果两个数只有③______ 么其中一个数叫做另一个数的相反数.
4(1):反数的性质
²² 9 2 3 -7.5, 15,4, , , -27,0.31,-π ,0.15。 17 3 ·· 2 3 -7.5,4, , -27,0.31,0.15 3 (1)有理数集合: { …}; 9 15, ,-π 17 (2)无理数集合: { …}; 9 2 ·· (3)正实数集合: { 15,4, …}; , ,0.31,0.15 17 3 3 (4)负实数集合: {-7.5, -27,-π …}。
1.实数的有关概念
从数轴上看,互为相反数的两个数所对应的点关于原点对称.
(4)绝对值
从数轴上看,一个数的绝对值就是表示这个数的点与原点的距离
(5)倒数
实数a(a≠0)的倒数是 (乘积为1的两个数,叫做互为倒数);零没有倒数.
例1①a的相反数是- ,则a的倒数是_______.
3.分析:考查绝对值、倒数、平方根的概念,明确各自的意义,不要混淆。
答案: ,-2/7,±2/3
4.分析:本题考查相反数和绝对值及根式的概念
5【学生练】对实数进行分类不能只看表面形式,应先化简,再根据结果去判断.
作
业
布置
山西省中考指导1-4页
教学反思
九年级(下)数学总复习电子教案
主备人:薛智明授课时间(年月日)
课 题
第1课时 实数的有关概念
课型
复习课
教学目标
知识、能力
有理数、无理数、实数、非负数、相反数、倒数、数的绝对值
过程、方法
1.使学生复习巩固有理数、实数的有关概念.
2.了解有理数、无理数以及实数的有关概念;理解数轴、相反数、绝对值等概念,了解数的绝对值的几何意义。
课时
2
教学方法
讲授法
教具
板
书
设
计
实数的组成
教
学
过
程
教师引导
学生活动
个性化修改
1、实数的有关概念
(1)实数的组成
(2)数轴:规定了原点、正方向和单位长度的直线叫做数轴(画数轴时,要注童上述规定的三要素缺一个不可),
实数与数轴上的点是一一对应的。
数轴上任一点对应的数总大于这个点左边的点对应的数,
第1课时 实数的有关概念优秀课件

考点 4 乘方、开方
1.正数的任何次幂是__正__数_;负数的偶次幂是__正_数_,负数的奇次幂是_负__数_;0的任何 正数次幂是_0___。 2. 实数a(a≥0)的平方根是_____ ,算数平方根是_____;实数a的立方根是_____。
第8页
第9页
第10页
第11页
第12页
第13页
(1)实数 0 (既不是正数,也不是负数)
返回思维导图
负数(<0)
(2)正负数的意义
正负数可以用于表示相反意义的量.如:规定“盈(+)”则“亏(-)”,“胜(+)”则“负 (-)”,“收入(+)”则“支出(-)”,“零上(+)”则“零下(-)”,“上升(+)”则“下降(- )”等.
考点 2
1. 数轴 (1)三要素:
3.绝对值 a(a>0)
(1)|a|= 0(a=0) -a (a<0)
返回思维导图
(2)几何意义:数轴上表示这个数的点到原点的距离, 离原点越远的数的绝对值越
____大____.
4((12. ))倒实非数数零实a、数b互a的为倒倒数数是⇔__a_b_=1_______._1_特_.别注意:0没有倒数,倒数是它本身的数是
数轴、相反数、绝对值、倒数
返回思维导图
(2)实数与数轴上的点是一 一对应的. 2. 相反数 (1)非零实数a的相反数为___-__a___,特别地,0的相反数为0; (2)实数a,b互为相反数⇔a+b=____0____; (3)几何意义:互为相反数的两个数分别位于数轴上原点的两侧,且到原点的距离 ___相__等___;
第1课时 实 数的有关概念
按定义分 实数的分类
按大小分
科学记数法
数轴 相反数 绝对值
九年级一轮复习第1、2、3部分 实数

A.2 2B.2 2 C.2 D.2。
二)填空题:
5.若 是同类项,则m + n=____________.
6.观察下面的单项式:x,-2x,4x3,-8x4,…….根据你发现的规律,写出第7个式子是.
7.大家一定熟知杨辉三角(Ⅰ),观察下列等式(Ⅱ)
第3课时:整式及其运算
【课前热身】
1.(09烟台)若 与 的和是单项式,则 .
2.(10泰安)计算 的结果是A. B. C. D.
3.(10临沂)下列计算正确的是()
A.x2‧x3=x6B.2x3x=5x2C.(x2)3=x6D.x6x2=x3。
4.计算(-x)2x3所得的结果是()A. B. C. D.
8.若a,b满足=0,则的值是
9.(09枣庄)
a是不为1的有理数,我们把 称为a的差倒数.如:2的差倒数是 , 的差倒数是 .已知 , 是 的差倒数, 是 的差倒数, 是 的差倒数,…,依此类推,则 .
10.(10枣庄)下列一串梅花图案是按一定规律排列的,请你仔细观察,在前2010个梅花图案中,共有__________个“”图案.
11.细心观察图形,认真分析各式,然后解答问题:
(1)请用含有n(n是正整数)的等式表示
上述变化规律;
(2)推算出OA10的长;
(3)求出 的值.
【强化训练】
1.判断题:
(1)如果a为实数,那么-a一定是负数;( )(2)对于任何实数a与b,|a-b|=|b-a|恒成立;( )
(3)两个无理数之和一定是无理数;( )(4)两个无理数之积不一定是无理数;( )
根据前面各式规律,则 .
课时1.实数的有关概念】

7.若 ,则 =_______.
8.某种电子元件大约只占0.00000063(毫米2),这个数用科学记数法表示为_______.
【自主演练】
1.-3的相反数是______, 的绝对值是_____, =______, ______.
2.某种零件,标明要求是φ20±0.02mm(φ表示直径,单位:毫米),经检查,一个零件的直径是19.9mm,该零件____________.(填“合格”或“不合格”)
20.在四个数0, ,一 ,0.3中最小的是_________.
《实数的概念》【限时训练A】
1.-的绝对值是____,-0.5的相反数是____,4的算术平方根是____, ___。
2.扬州2008年全年接待游客约113 Nhomakorabea0000人次,用科学记数法表示为________.
3.方程 的解的相反数是________.
11.下列各组数中,互为相反数的是()
A.6和 B.-6和- C.-6和|-6| D. 和
12. 的倒数是()
13.无理数是()A. B. C. D.
14.若x的相反数是3,│y│=5,则x+y的值为()
15.如图,数轴上A、B两点所表示的两数的()
A.和为正数B.和为负数C.积为正数D.积为负数
16.如图,数轴上点 表示的数可能是()
课时1.实数的有关概念
1.-2的倒数是_______.
2. 的相反数是_______.
3.-5的绝对值是_______.
4. 16的平方根是__________. 的算术平方根是_______.
5.在 ,3.14, , ,0.1010010001…,sin45°这些数中,无理数有()个。
第1课时 实数的有关概念

课件目录
首页
末页
类型之二 相反数、倒数和绝对值
(1)[2019·遂宁]-|- 2的值为( B )
A. 2
B.- 2
C.± 2
D.2
(2)[2019·滨州]下列各数中,负数是( B )
A.-(-2)
B.-|-2
C.(-2)2
D.(-2)0
【解析】 ∵-(-2)=2,-|-2=-2,(-2)2=4,(-2)0=1,∴负数是-|-2.
课件目录
首页
末页
2.数轴 定义:规定了 原点 、 正方向 和 单位长度 的直线叫做数轴. 大小比较:(1)在数轴上表示的两个数, 右边 的数总比 左边 的数大; (2)正数大于 0;负数 小于 0;正数 大于 一切负数;两个负数比较大小,绝对 值大的反而 小 .
注意:实数与数轴上的点一一对应.
课件目录
首页
末页
2.[2019·泰安]在实数|-3.14|,-3,- 3,π中,最小的数是( B )
类型之三 实数的大小比较 [2019·嘉兴]数轴上有两个实数a,b,且a>0,b<0,a+b<0,则四个数a,
b,-a,-b的大小关系为 b<-a<a<-b (用“<”号连接).
【解析】 ∵a>0,b<0,故有a>b,又∵a+b<0,说明a的绝对值小于b的绝对值, 故可得到b<-a<a<-b.
课件目录
A.-5
B.-1
C.0
D.1
【解析】 -5<-3<-1<0<1,∴比-3小的数是-5.故选A.
课件目录
首页
末页
4.[2019·邵阳]下列各数中,属于无理数的是( C )
课时1 实数的有关概念

1 1 【例5】(2013•泉州) 的立方根是______. 2 8
·数学
考点4
实数与数轴
【例6】(2013•包头)若|a|=-a,则实数a在数轴上的对应
点一定在 ( B)
A.
C.
B.原点或原点左侧
D.
思路点拨:根据|a|=-a,求出a的取值范围,再根据数轴的 特点即可得出答案. 解析:∵|a|=-a,∴a一定是非正数.∴实数a在数轴上的对应 点一定在原点或原点左侧,故选B.
·数学
三、相反数、倒数 符号 不同的两个数称互为相反数.a的相反数是______. -a 1.只有______ 若a,b互为相反数,则a+b=______ ,|a|______|b|. 0 = 1 乘积为1 的两个数互为倒数.a的倒数通常表示为______ 2. ________ a (a≠0).若a,b互为倒数,则ab=______. 1
2
A. B.-
2
2 2
2 2
C.
D. -
·数学
【例3】(2013•南京)-3的相反数是______ ;-3的倒数是 3 1 ______. 3 考点3 平方根与立方根
【例4】(2013•黔西南州) 81的平方根是______. 3 解析:∵ 81=9,9的平方根是±3,∴81 的平方根是 ±3.
·数学
考点5
近似数和科学记数法
【例7】(2013•湛江)国家提倡“低碳减排”,湛江某公司
计划在海边建风能发电站,电站年均发电量约为213 000 000 度,将数据213 000 000用科学记数法表示为 ( ) A.213×106 C.2.13×108 B.21.3×107 D.2.13×109
9.
3
课时1 实数的有关概念

课时1 实数的有关概念学习目标:了解有理数、无理数以及实数的有关概念;理解数轴、相反数、倒数、绝对值等概念,了解平方根、算术平方根、立方根的概念、了解近似数和有效数字的概念。
课前预习:【基础知识】1.有理数的意义⑴ 数轴的三要素为 、 和 . 数轴上的点与 构成一一对应. ⑵ 实数a 的相反数为________. 若a ,b 互为相反数,则b a += .⑶ 非零实数a 的倒数为______. 若a ,b 互为倒数,则ab = .(4)科学记数法:把一个数表示成 的形式,其中1≤a <10的数,n 是整数.(5) 绝对值⎪⎩⎪⎨⎧<=>=)0( )0( )0( a a a a . ⑹ 一般地,一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位.这时,从左边第一个不是 的数起,到 止,所有的数字都叫做这个数的有效数字.2.数的开方⑴ 任何正数a 都有______个平方根,它们互为________.其中正的平方根a 叫 _______________. 没有平方根,0的算术平方根为______.⑵ 任何一个实数a 都有立方根,记为 .⑶ =2a ⎩⎨⎧<≥=)0( )0( a a a . 3. 实数的分类 和 统称实数.【知识应用】1.2的倒数是;的相反数是 .2.若向南走2m 记作2m -,则向北走3m 记作 m .3.9的平方根是 ,14的算术平方根是 ,-64的立方根是 ; 4.在下列实数中,无理数是( )A .13B .πCD .2275.3-的绝对值是( ) A .3- B .3 C .13- D .13 6.随着电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.000 000 7(毫米2),这个数用科学记数法表示为( )A.7×10-6B. 0.7×10-6C. 7×10-7D. 70×10-8 7.如图,在数轴上点A 和点B 之间表示整数的点有___________个.8.若22(1)0m n ++-=,则2m n +的值为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⎪⎩⎪⎨⎧<=>=)0( )0( )0( a a a a 实数的有关概念 导学案(1)
学习目标:
1) 了解有理数、无理数、实数的概念,会比较实数的大小,知道实数与数轴上的点一一对应,会用科学计数法表示有理数。
2) 理解相反数和绝对值的概念及意义。
3)了解近似数,有效数字的概念。
一、自主学习
1、有理数的意义
⑴ 数轴的三要素为 、 和 . 数轴上的点与 构成一一对应. ⑵ 实数a 的相反数为________. 若a ,b 互为相反数,则b a += .
⑶ 非零实数a 的倒数为______. 若a ,b 互为倒数,则ab = .
⑷ 绝对值.
⑸ 科学记数法:把一个数表示成 的形式,其中1≤a <10的数,n 是整数. ⑹ 一般地,一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位.这时,从左边第一个不是 的数起,到 止,所有的数字都叫做这个数的有效数字.
2.数的开方
⑴ 任何正数a 都有______个平方根,它们互为________.其中正的平方根a 叫 _______________. 没有平方根,0的算术平方根为______.
⑵ 任何一个实数a 都有立方根,记为 .
⑶ ⎩
⎨⎧≤≥==002a a a a . 3. 实数的分类 和 统称实数.
4.易错知识辨析
(1)近似数、有效数字 如0.030是2个有效数字(3,0)精确到千分位;3.14×10
5是3个有效数字;精确到千位.3.14万是3个有效数字(3,1,4)精确到百位.
(2)绝对值2=x 的解为2±=x ;而22=-,但少部分同学写成22±=-.
(3)在已知中,以非负数a 2、|a|、(a ≥0)之和为零作为条件,解决有关问题.
二、合作探究
1. 在“()05,3.14 ,()33,()2
3-,cos 600 sin 450 ”这6个数中,无理数的个数是( )A .2个 B .3个 C .4个 D .5个
2. ⑴2--的倒数是( )A .2 B. 21 C. 2
1- D.-2 ⑵.若0)2(3-m 2=++n ,则2m n +的值为( )
A .4-
B .1-
C .0
D .4
⑶.如图,数轴上点P 表示的数可能是( )A.7 B. 7- C.—3.2 D.10-
3.下列说法正确的是( ) A .近似数3.9×103精确到十分位 B .按科学计数法表示的数8.04×105其原数是80400
C .把数50430保留2个有效数字得5.0×104.
D .用四舍五入得到的近似数8.1780精确到0.001
三、展示提升
1. -3的相反数是______,2
1-的绝对值是_____,2-1=______,2008(1)-= . 2. 某种零件,标明要求是φ20±0.02 mm (φ表示直径,单位:毫米),经检查,一个零件的直径是19.9 mm ,该零件 .(填“合格” 或“不合格”)
3. 下列各数中:-3,4
1,0,23
,0.31,722,2π,2.161 161 161…, (-2 005)0是无理数的是___________________________.
4.全世界人民踊跃为四川汶川灾区人民捐款,到6月3日止各地共捐款约423.64亿元,用科学记数法表示捐款数约为__________元.(保留两个有效数字)
5.若
0)1(32=++-n m ,则m n +的值为 . 6. 2.40万精确到__________位,有效数字有__________个.
四、有效训练 1. 51-的倒数是 ( )A .51- B .5
1 C .5- D .5 2.点A 在数轴上表示+2,从A 点沿数轴向左平移3个单位到点B ,则点B 所表示的实数是( ) A .3 B .-1 C .5 D .-1或3
3.如果□+2
1=0,那么“□”内应填的实数是( ) A .21 B .21- C .2
1± D .2 4.下列各组数中,互为相反数的是( )
A .2和21
B .-2和21--
C .-2和|-2|
D .2和2
1 5. 16的算术平方根是( )
A.4
B.-4
C.±4
D.16
6.实数a 、b 在数轴上的位置如图所示,则a 与b 的大小关系是( )
A .a > b
B . a = b
C . a < b
D .不能判断
7.若x 的相反数是3,│y │=5,则x +y 的值为( )
A .-8
B .2
C .8或-2
D .-8或2
8. 如图,数轴上A 、B 两点所表示的两数的( )
A. 和为正数
B. 和为负数
C. 积为正数
D. 积为负数 A B O -3。
