第13章 C++基础
2024—2025学年华东师大版数学八年级上册第13章《全等三角形》基础复习

第13章基础复习知识点1命题、定理与证明1.一般地,判断某一件事情的语句叫做命题.命题一般由条件和结构两部分组成,可以写成“如果……,那么……”的形式.2.基本事实是在继续学习过程中用来判断其他命题真假的原始依据.3.定理:有些命题可以从基本事实或其他真命题出发,用逻辑推理的方法判断它们是正确的,并且可以作为进一步判断其他命题真假的依据,这样的真命题叫做定理.4.根据条件、定义以及基本事实、定理等,经过演绎推理,来判断一个命题是否正确,这样的推理过程叫做证明.1.下列命题中,是真命题的是()A.无限小数是无理数B.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离C.平行于同一条直线的两条直线平行D.过一点有且只有一条直线与已知直线垂直2.判断命题“如果n<1,那么W−1<0”是假命题,只需举出一个反例.反例中的n可以为()A.-2u−12 C.0D123.把命题“对顶角相等”改写成“如果⋯⋯,那么⋯⋯”的形式:.4.填写下列证明过程中的推理根据:已知:如图所示,AC、BD相交于点O,DF平分∠CDO与AC相交于点F,BE平分∠ABO与AC相交于点E,∠A=∠C.求证:∠1=∠2.证明:∵∠A=∠C(),∴AB∥CD(),∴∠ABO=∠CDO(),又∵DF平分∠CDO,BE平分∠ABO,∴∠1=12∠Cs∠2=12∠B(),∴∠1=∠2().知识点2三角形全等的判定1.能够完全重合的两个三角形是全等三角形,相互重合的顶点是对应顶点,相互重合的边是对应边,相互重合的角是对应角,全等三角形的对应边相等,对应角相等.2.全等三角形的判定条件:①两边及其夹角分别相等的两个三角形全等.简写为S. A.S.(或边角边).②两角及其夹边分别相等的两个三角形全等.简写为A.S. A.(或角边角).③两角分别相等且其中一组等角的对边相等的两个三角形全等.简写为A. A.S.(或角角边).④三边分别相等的两个三角形全等.简写为S.S.S.(或边边边).⑤斜边和一条直角边分别相等的两个直角三角形全等.简写为H.L.(或“斜边直角边”).5.如图,AB=AD,CB=CD,∠B=32°,∠BAD=72°,则∠ACD的度数是()A.102°B.112°C.114°D.1226.如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是()A.∠A=∠DB.AC=DFC.AB=EDD.BF=EC7.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是()A.0.5B.1C.1.5D.28.图中的小正方形边长都相等,若△MNP≌△MFQ,则点Q可能是图中的()A.点DB.点CC.点BD.点A9.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC一定全等的是()A.甲和乙B.乙和丙C.甲和丙D.只有丙10.如图所示,在Rt△ACD和Rt△BCE中,若AD=BE,DC=EC,则不正确的结论是()A.Rt△ACD≌Rt△BCEB.OA=OBC.E是AC的中点D.AE=BD11.如图,点D在线段BC上,若BC=DE,AC=DC,AB=EC,且∠ACE=180°-∠ABC-2x°,则下列角中,大小为x°的角是()A.∠EFCB.∠ABCC.∠FDCD.∠DFC12.如图,在等腰△ABC中,AB=AC,AB>BC,点D在边BC上,且C B=14,点E、F在线段AD上,满足∠BED=∠CFD=∠BAC,若△B=20,则.△B+△C=()A.18B.15C.12D.913.如图,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有()A.1个B.2个C.3个D.4个14.如图,AC=DC,BC=EC,请你添加一个适当的条件:,使得△ABC≌△DEC.15.如图,∠1=∠2,∠3=∠4,,则全等三角形有对.16.如图,已知△ABC中,F是高AD和BE的交点,且AD=BD,CD=4,则线段DF的长度为.17.(南通中考)如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连结AC并延长到点D,使CD=CA.连结BC并延长到点E,使CE= CB.连结DE,那么量出DE的长就是A、B的距离.为什么?18.如图,在△ABC中,AC=5,中线AD=7,求边AB的取值范围.19.如图,点O是线段AB的中点,OD∥BC且OD=BC.(1)求证:△AOD≌△OBC.(2)若∠ADO=35°,求∠DOC的度数.20.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合.(1)求证:△ADC≌△CEB.(2)求两堵木墙之间的距离.21.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)求证:△ABC≌△ADE.(2)求∠FAE的度数.(3)求证:CD=2BF+DE.。
人教版物理九年级全册课件PPT第13章 第3节 比热容(第1课时)

返回目录
第十三章
内能
7.(2018·眉山改编)某同学从下表提供的信息中,得出以下几
个结论,其中错误的是(
)
物质 c/[J·(kg·℃)-1] 物质 c/[J·(kg·℃)-1]
水 4.2×103 干泥土 约 0.84×103
酒精 2.4×103
铜
0.39×103
冰 2.1×103
铝
0.88×103
返回目录
第十三章
内能
5.下列各种情况下比热容会发生变化的是( B )
A.一杯水倒去变成 45 ℃的水
返回目录
第十三章
内能
6.下列说法正确的是( C )
A.物体的温度越高,比热容越大 B.物体的质量越大,比热容越小 C.物质的比热容跟物体的质量、温度变化以及物体吸收热量 的多少都无关 D.物体吸收的热量越多,比热容越大
间接反映液体吸收热量的多少。
返回目录
第十三章
内能
3.某小组在“比较两种物质在太阳照射下升温快慢”的活动
中,经过讨论,同学们一致认为应控制两种物质的 质质量量 和初
温相等,确保这两种物质的受热面积相同且正对阳光,这样做是
为了让两种物质在相同的时间内 吸吸收收的的热热量量 相同。若采用正
确的方法进行探究,半小时后,甲物质的温度升高了 5℃,乙物质
知识点 1:比较不同物质吸热的情况 1.如图所示,用两个相同的电加热器,分别给盛在两个相同的烧杯中质量 和温度都相同的水和煤油同时通电加热。在这两个烧杯中各用一支温度计测量液
体的温度的变化,加热一段时间会看到插在煤油中的温度计示数上升得较快。若
要使水和煤油升高相同的温度,需要给 水水 加热的时间长;这说明升高相同的 温度, 水水 (选填“水”或“煤油”)吸收的热量较多。为了了解其他物质是否
《新编基础物理学》第13章习题解答和分析

第13章电磁场与麦克斯韦方程组13-1如题图13-1所示,两条平行长直导线和一个矩形导线框共面, 且导线框的一个边与长直导线平行,到两长直导线的距离分别为r ,,r 2。
已知两导线中电流都为 I l 0sin t ,其中I o 和 为常数,t 为时间。
导线框长为 a ,宽为b ,求导线框中的感应电动势。
分析:当导线中电流I 随时间变化时,穿过矩形线圈的磁通量也将随 时间发生变化,用法拉第电磁感应定律 jd ^m计算感应电动势,dt其中磁通量m B dS , B为两导线产生的磁场的叠加。
s解:无限长直电流激发的磁感应强度为B 一必。
取坐标Ox 垂直于直2 r导线,坐标原点取在矩形导线框的左边框上,坐标正方向为水平向右。
取回路的绕行正方向为顺时针。
由场强的叠加原理可得 x 处的磁感应强度大小12 (A x)方向垂直纸面向里。
通过微分面积dS adx 的磁通量为d m通过矩形线圈的磁诵量为v v BdS BdSIadx2 (r 2 x)2 (A x) bmIIadx 0aln$ b , r 2 b ,.丄In I 0S1 n t 02(r 1 x)2(r 2 x)2r 1 r 2 感生电动势d mar-i bbilnInI 0 cos tdt2r 1「2o a | ln(r 1b)(r 2 b)2恥为逆时针。
0时,回路中感应电动势的实际方向为顺时针;i0时,回路中感应电动势的实际方向cos t题图13-1解图13-113-2 如题图13-2所示,有一半径为r=10cm的多匝圆形线圈,匝数vN=100,置于均匀磁场B中(B=)。
圆形线圈可绕通过圆心的轴O1O2转动,转速n 600r min 1。
求圆线圈自图示的初始位置转过/2时,(1)线圈中的瞬时电流值(线圈的电阻为R=100 ,不计自感);(2)圆心处磁感应强度。
分析:应用法拉第电磁感应定律求解感应电动势。
应用载流圆环在其圆心处产生的磁场公式求出感应电流在圆心处产生的磁感应强度。
高中物理人教必修三第13章第1节磁感应强度磁通量 讲义

2 磁感应强度 磁通量1.理解磁感应强度的概念,知道磁感应强度是描述磁场强弱和方向的物理量.2.知道什么是匀强磁场,知道匀强磁场磁感线的特点.3.理解磁通量的概念,会计算磁通量的大小.一、磁感应强度1.定义:一段通电直导线垂直放在磁场中所受的力与导线中的电流和导线的长度的乘积的比值,叫磁感应强度.2.定义式:B =F Il. 3.单位:特斯拉,简称特,符号为T.4.B 反映了磁场的强弱.5.磁感应强度是矢量,小磁针的N 极在磁场中某点受力的方向,就是这点磁感应强度的方向.二、匀强磁场1.概念:各点磁感应强度大小相等、方向相同的磁场.2.磁感线特点:匀强磁场的磁感线是间隔相等的平行直线.三、磁通量1.定义:匀强磁场中磁感应强度和与磁场方向垂直的平面面积S 的乘积.即Φ=BS .2.拓展:磁场与平面不垂直时,这个面在垂直于磁场方向的投影面积S ′与磁感应强度的乘积表示磁通量.3.单位:国际单位是韦伯,简称韦,符号是Wb,1 Wb =1 T·m 2.4.引申:B =ΦS ,表示磁感应强度的大小等于穿过垂直磁场方向的单位面积的磁通量.一、磁感应强度1.物理意义:磁感应强度是表示磁场强弱和方向的物理量.2.大小:当导线方向与磁场方向垂直时B =F Il.3.方向:磁感应强度的方向就是小磁针北极在磁场中某点受力的方向,也就是该处的磁场方向.4.描述:磁感线的疏密程度表示磁感应强度的大小,磁感线的切线方向表示磁感应强度的方向.5.匀强磁场如果磁场中各处的磁感应强度大小和方向都相同,则该磁场为匀强磁场.二、磁通量1.磁通量的计算:(1)公式:Φ=BS.适用条件:①匀强磁场;①磁感线与平面垂直.(2)若磁感线与平面不垂直,则Φ=BS cos θ.其中S cos θ为面积S在垂直于磁感线方向上的投影面积S1,如图所示.2.磁通量的正负:磁通量是标量,但有正负,若磁感线从某一面穿入时,磁通量为正值,磁感线从此面穿出时则为负值.3.磁通量可用穿过某一平面的磁感线条数表示.若有磁感线沿相反方向穿过同一平面,则磁通量等于穿过该平面的磁感线的净条数(磁通量的代数和).三、磁感应强度矢量的叠加磁感应强度是矢量,当空间存在几个磁体(或电流)时,每一点的磁场等于各个磁体(或电流)在该点产生磁场的矢量和.磁感应强度叠加时遵循平行四边形定则.1.如图所示,矩形线框平面与匀强磁场方向垂直,穿过的磁通量为Φ,若线框绕某条边转过90°角,则磁通量变为()A.0B.12ΦC.ΦD.2Φ2.如图所示为某匀强磁场的磁感线分布,则磁场中各点的磁感应强度( )A .大小相等,方向相同B .大小不等,方向相同C .大小相等,方向不同D .大小不等,方向不同 3.下列物理量中属于矢量的是( )A .磁感应强度B .感应电动势C .电流D .磁通量4.如图所示,直角三角形abc 中,①abc =30°,将一电流为I 、方向垂直纸面向外的长直导线放置在顶点a 处,则顶点c 处的磁感应强度大小为B 0。
理论力学:第13章 虚位移原理及分析力学基础
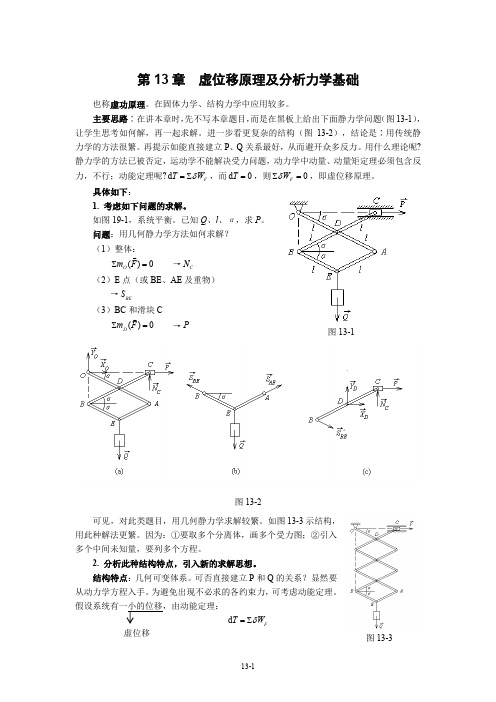
第13章 虚位移原理及分析力学基础也称虚功原理。
在固体力学、结构力学中应用较多。
主要思路∶在讲本章时,先不写本章题目,而是在黑板上给出下面静力学问题(图13-1),让学生思考如何解,再一起求解。
进一步看更复杂的结构(图13-2),结论是∶用传统静力学的方法很繁。
再提示如能直接建立P 、Q 关系最好,从而避开众多反力。
用什么理论呢?静力学的方法已被否定,运动学不能解决受力问题,动力学中动量、动量矩定理必须包含反力,不行;动能定理呢?d F T W δ=∑,而d 0T =,则0F W δ∑=,即虚位移原理。
具体如下:1. 考虑如下问题的求解。
如图19-1,系统平衡。
已知Q 、l 、α,求P 。
问题:用几何静力学方法如何求解? (1)整体:()0O m F ∑=→C N (2)E 点(或BE 、AE 及重物)→BE S(3)BC 和滑块C()0D m F ∑=→P图13-2可见,对此类题目,用几何静力学求解较繁。
如图13-3示结构,用此种解法更繁。
因为:①要取多个分离体,画多个受力图;②引入多个中间未知量,要列多个方程。
2. 分析此种结构特点,引入新的求解思想。
结构特点:几何可变体系。
可否直接建立P 和Q 的关系?显然要从动力学方程入手。
为避免出现不必求的各约束力,可考虑动能定理。
假设系统有一小的位移,由动能定理:d F T W δ=∑图13-1图13-3虚位移由于系统平衡,动能无变化,d 0T =,则0F W δ∑= → 虚功方程此方程中只包含P 和Q ,故建立了简单的方程,可求P 。
此便是虚位移原理的思想。
严格建立虚位移原理,需有诸多基本概念。
13.1 约束 约束的运动学分类静力学中讲的约束——约束的力的性质(约束的力的方面),用约束力表示,常指物体; 此处讲的约束——约束的运动的性质(约束的运动的方面),用约束方程表示,指限制条件。
一、 约束和约束方程自由质点系:运动不受任何限制。
非自由质点系:运动受到限制——约束。
人教版(2019)必修第三册《第13章_电磁感应与电磁波初步》2024年单元测试卷(2)+答案解析

人教版(2019)必修第三册《第13章电磁感应与电磁波初步》2024年单元测试卷(2)一、单选题:本大题共7小题,共24分。
1.关于对热辐射的认识,下列说法正确的是()A.温度高的物体向外辐射电磁波,温度低的物体只吸收电磁波B.爱因斯坦为解释黑体辐射的规律,提出了“能量子”C.黑体辐射电磁波的强度按波长的分布情况只与温度有关D.常温下我们看到物体是因为物体在不断辐射电磁波2.磁场中某区域的磁感线如图所示,则()A.B.C.a处没有磁感线,所以磁感应强度为零D.a、b两处磁感应强度的方向相同3.如图所示,条形磁铁以速度v向螺线管靠近。
下列说法正确的是()A.螺线管会产生感应电流B.螺线管不会产生感应电流C.只有磁铁速度足够大,螺线管才会产生感应电流D.只有磁铁磁性足够强,螺线管才会产生感应电流4.目前市面上流行一种手摇手机充电器。
当人摇动手柄给手机充电时,其内部线圈在匀强磁场中绕垂直于磁感线的轴匀速转动,如图所示。
下列说法正确的是()A.当线圈转到图示位置时,电流方向将发生改变B.当线圈转到图示位置时,穿过线圈磁通量的变化率最大C.若从图示位置开始计时,线圈中的电流瞬时值表达式为D.图示位置在中性面,穿过线圈磁通量为最大5.如图所示,一无限长直导线通有恒定电流,有一圆形线圈与其共面,则线圈在靠近直导线的过程中,通过线圈的磁通量将()A.增大B.减小C.不变D.由于条件不足,无法确定变化情况6.已知真空中的电磁波波速是在真空中波长是5m的无线电波,它的频率是()A. B. C. D.7.如图所示,五根垂直纸面放置的平行长直导线通过纸面内的a、b、c、d、e五个点,五个点恰好为正五边形的五个顶点,o点为正五边形的中心。
仅给其中一根直导线通大小为的电流时,o点的磁感应强度大小为。
若每根直导线通电时电流大小均为,则()A.仅给a处直导线通电时,o、b、e点的磁感应强度大小相同B.仅给a、b处直导线通同向电流时,o点的磁感应强度大小为C.仅给a、b、c处直导线通同方向电流时,o点的磁感应强度方向一定平行de连线D.给任意四根直导线通电时,o点的磁感应强度大小均为二、多选题:本大题共4小题,共16分。
《C语言程序设计》(第2版)苏小红-13章 12

2021/7/31
40/60
struct sample {
short i; char ch; float f; };
union sample {
short i; char ch; float f; };
2021/7/31
共用体
【例12.8】
printf("%d\n", sizeof(struct sample));
Before function call:1999/04/23 After function call:2000/05/22
指针作函数形参 实参必须为地址值
2021/7/31
33/60
struct date
{
int year; int month;
结构体变量
int day; };
作函数返回值
struct date Func(struct date p)
2021/7/31
【例12.3】利用 结构体数组计 算每个学生的 平均分
25/60
结构体指针的定义和初始化
如何定义指向结构体变量的指针?
pt STUDENT stu1; STUDENT *pt; pt = &stu1;
等价于
STUDENT *pt = &stu1;
stu1 成员1 成员2 成员3 成员4
i ch
f
8个字节
printf("%d\n", sizeof(union sample));
0x0037b00
cfih
4个字节 41/60
共用体
sizeof(union number)取决于占空间最多的那个成员 变量
同一内存单元在每一瞬时只能存放其中一种类型的成员 起作用的成员是最后一次存放的成员,不能作为函数参数 不能进行比较操作,只能对第一个成员初始化
人教版九年级全一册物理第13章基础达标检测题含答案

人教版九年级全一册物理第13章基础达标检测题含答案13.1第1节分子热运动一选择题1.下列说法中错误的是 ( )A.物质是由大量分子构成的 B.分子是很小的C.一滴水就是一个分子 D.分子是保持物质化学性质的最小微粒2.下列现象中,能说明分子在不停地做无规则运动的是( )A.冬天大雪纷飞 B.桂花香飘满园C.成群的蝴蝶翩翩起舞 D.美丽的烟花在空中绽放3.液体很难被压缩,主要是因为 ( )A.液体分子不停地运动 B.液体分子间存在引力C.液体分子间存在斥力 D.液体分子间没有间隙4.如图所示,两表面磨平的铅块紧密接触后可吊起台灯,这说明 ( )A.分子间存在斥力B.分子间存在引力C.分子间存在间隙D.分子在不停地做无规则运动5.下列现象中不能说明分子在不停地做无规则运动的是( )A.刮风时灰尘在空中飞舞B.酒精瓶盖打开可以嗅到酒精气味C.夏日的“荷城”贵港,荷花飘香D.在一杯热水中加盐,过一段时间整杯水都变咸了6.PM是指大气中直径小于或等于2.5μm的颗粒物,是造成雾霾天气的主要原因之一。
把它2.5和电子、原子核、分子等粒子一起按照空间尺度由大到小排序,以下排列正确的是( ) A.PM分子原子核电子2.5原子核电子B.分子PM2.5电子C.分子原子核PM2.5D.分子原子核电子PM2.57.关于分子动理论,下列说法正确的是 ( )A.打开香水瓶,不久就满屋子都能闻到香气,说明分子在永不停息地做无规则的运动B.打扫教室地面时,看到灰尘在空中飞舞,说明分子在永不停息地做无规则的运动C.酒精和水混合后体积减小的实验,说明分子间有引力D.堆在墙角的煤会使墙体内部变黑,说明分子间有引力8.“遥知不是雪,为有暗香来”,下列各句诗词中描述的现象产生的原因与“暗香来”不同的是 ( )A.移时风扬沙,人马俱失路——《出居庸关》(汪元量)B.水晶帘动微风起,满架蔷薇一院香——《山亭夏日》(高骈)C.花气袭人知骤暖,鹊声穿树喜新晴——《村居山喜》(陆游)D.幽兰生谷香生径,方竹满山绿满溪——《游武夷泛舟九曲》(郭沫若)9.科学家最新研究表明,壁虎脚掌没有吸盘,壁虎的每只脚底部长着数百万根极细的刚毛,而每根刚毛末端又有更多更细的分支,这种精细结构使得刚毛与物体表面分子间的距离非常近,由此可知壁虎在天花板上攀爬本质上靠的是 ( )A.分子引力B.大气压强C.地球引力D.板壁弹力二非选择题1.分子动理论的初步知识:常见的物质是由大量的_____、_____构成的;物质内的分子在不停地做________;分子之间存在____力和____力。
沪科版八年级数学上第13章三角形中的边角关系、命题与证明13

自主学习
基础夯实
整合运用
思维拓展
第2页
八年级 数学 上册 沪科版
典例导学 如图,在△ABC 中,∠ACB=90°,∠ACD=∠B.求证:△CDB 是直角
三角形.
【思路分析】要证△CDB 是直角三角形,可证∠B+∠DCB=90°,在△ABC
中,已知∠ACB=90°,易证△CDB 是直角三角形.
自主学习
A.85° B.90° C.95° D.100°
自主学习
基础夯实
整合运用
思维拓展
第 14 页
八年级 数学 上册 沪科版
9.如图,在△ABC 中,∠C=90°,则∠B 为 A.15° B.30° C.50° D.60°
(D)
自主学习
基础夯实
整合运用
思维拓展
第 15 页
八年级 数学 上册 沪科版
10.已知三角形 ABC 的三个内角满足关系∠B+∠C=3∠A,则此三角形 (D)
八年级 数学 上册 沪科版
第 3 课时 三角形内角和定理的证明及 推论
自主学习
基础夯实
整合运用
思维拓展
第1页
八年级 数学 上册 沪科版
要点感知 1.三角形内角和定理:三角形的内角和等于 18180°0°. 2.为了证明的需要,在原来图形上添画的线叫做辅辅助线助线. 3.直角三角形的两锐角互互余 余. 4.有两个角互余的三角形是直直角角三三角形角形.
1 ∴∠EGD=3×(180°-60°)=40°, ∴∠1=40°.
自主学习
基础夯实
整合运用
思维拓展
第 23 页
八年级 数学 上册 沪科版
(2)∠AEF+∠FGC=90°. 理由:∵AB∥CD, ∴∠AEG+∠CGE=180°, 即∠AEF+∠FEG+∠EGF+∠FGC=180°, 又∵∠FEG+∠EGF=90°, ∴∠AEF+∠FGC=90°.
物理13章知识点归纳总结

物理13章知识点归纳总结第一节:力和牛顿运动定律1. 力的概念:力是物体相互作用的结果,具有大小和方向。
2. 牛顿第一定律(惯性定律):物体静止或匀速直线运动时,受力和加速度为零。
3. 牛顿第二定律(动力学方程):物体受到的力与其加速度成正比,反比于物体质量。
4. 牛顿第三定律(作用-反作用定律):相互作用的两个物体对彼此施加的力大小相等、方向相反。
第二节:运动的描述和曲线运动1. 位移和位移矢量:物体从初始位置到终点位置的位移以及与距离的区别。
2. 平均速度和瞬时速度:描述物体运动的速度概念。
3. 加速度:速度随时间的变化率,可以是正值、负值或零。
4. 一维曲线运动:描述物体在一条直线上的运动,如匀速运动和变速运动。
5. 二维曲线运动:描述物体在平面上的运动,如圆周运动和抛体运动。
第三节:牛顿运动定律的应用1. 平面运动:应用牛顿运动定律解决平面上匀速直线运动和曲线运动问题。
2. 弹力和重力:弹力由弹性物体恢复形状产生,重力是地球对物体的吸引力。
3. 摩擦力:物体之间表面接触产生的阻碍运动力,可以分为静摩擦力和动摩擦力。
4. 斜面运动:分析物体在斜面上的运动情况,考虑斜面的倾角和摩擦力的影响。
5. 圆周运动:物体围绕固定轴的运动,通过角速度和圆周加速度等参数来描述。
第四节:功、动能和机械能守恒1. 功:力对物体做功的量度,与力的大小、物体的位移以及力和位移之间的夹角有关。
2. 动能:描述物体运动能量的概念,包括动能定理和动能守恒。
3. 功率:描述功在单位时间内所做的工作量。
4. 动量:物体运动的量度,由质量和速度的乘积得出。
5. 机械能守恒定律:在没有外力和摩擦力的情况下,一个系统的机械能保持不变。
第五节:弹性碰撞和静电场1. 弹性碰撞:两个物体发生碰撞后能量守恒,动量守恒,且碰撞前后的动能之和保持不变。
2. 静电场:电荷相互作用产生的力场,由带电物体周围的电荷引起。
3. 应用静电定律:静电力和电场强度的关系,通过库伦定律计算电荷之间的作用力。
Photoshop CS基础教程与上机指导第十三章

/webnew/
13.2 路径绘制工具
在介绍创建路径的基本操作以前, 在介绍创建路径的基本操作以前,首先来了解一下制作路径的相关 工具,主要包括3个部分:钢笔工具组、路径选择工具组和【路径】面板。 工具,主要包括3个部分:钢笔工具组、路径选择工具组和【路径】面板。
/webnew/
钢笔工具除了可以绘制直线路径以外,还可以绘制曲线, 钢笔工具除了可以绘制直线路径以外,还可以绘制曲线,绘制曲线 路径要比绘制直线路径复杂一些, 路径要比绘制直线路径复杂一些,用户可以通过沿曲线伸展的方向拖动 钢笔工具来创建曲线。方法如下: 钢笔工具来创建曲线。方法如下: 选择钢笔工具在图像编辑窗口单击定义第一个锚点, (1) 选择钢笔工具在图像编辑窗口单击定义第一个锚点,不要松开 鼠标并向任意方向拖动,指针将变成箭头状,如图 13.12所示 鼠标并向任意方向拖动,指针将变成箭头状, 13.12所示 (2) 松开鼠标,从第一个锚点处移开,定义下一个锚点,如图13.13 松开鼠标,从第一个锚点处移开,定义下一个锚点, 所示。 所示。向绘制曲线段的方向拖动指针 ,指针将引导其中一个 方向点的移动。如果按住Shift键 则可限制该工具沿着45 45° 方向点的移动。如果按住Shift键 ,则可限制该工具沿着45° Shift 的倍数方向移动。 的倍数方向移动。
/webnew/
图13.3
【路径】 路径】
/webnew/
13.3 建 立 路 径
13.3.1 使用【钢笔工具】建立路径 使用【钢笔工具】 使用【自由钢笔工具】 13.3.2 使用【自由钢笔工具】建立路径 13.3.3 增加和删除锚点
图13.1 钢笔工具组
/webnew/
3. 【路径】面板 路径】
选择【窗口】 路径】命令,可打开【路径】面板。 选择【窗口】|【路径】命令,可打开【路径】面板。在创建了 路径以后,该面板才会显示路径的相关信息,如图13.3所示。 路径以后,该面板才会显示路径的相.7
华东师大版八年级数学上册第13章全等三角形

03
全等三角形在几何图形 中的应用
利用全等三角形求线段长度
通过全等三角形的对应边相等 ,可以求出一些线段的长度。
在一些复杂的几何图形中,可 以通过构造全等三角形来简化 问题,进而求出所需线段的长 度。
利用全等三角形的性质,可以 通过已知条件推导出其他线段 的长度。
利用全等三角形求角度大小
通过全等三角形的对应角相等,可以求出一些角的大小。 在一些涉及到角度计算的几何问题中,可以通过构造全等三角形来简化计算过程。
过程中的细节和准确性避免出错。
06
章节小结与拓展延伸
知识点总结回顾
全等三角形的定义和性质
01
能够准确描述全等三角形的定义,理解全等三角形的对应边相
等、对应角相等的性质。
全等三角形的判定方法
02
掌握SSS、SAS、ASA、AAS和HL五种全等三角形的判定方法,
并能够灵活运用它们来解决实际问题。
全等三角形的应用
全等三角形的对应边上的中线 相等。
全等三角形的判定方法
ASA(角边角)
SAS(边角边)
两边和它们的夹角对应相等的两 个三角形全等。
两角和它们的夹边对应相等的两 个三角形全等。
AAS(角角边)
两角和其中一个角的对边对应相 等的两个三角形全等。
SSS(边边边)
三边对应相等的两个三角形全等 。
HL(斜边、直角边)
直角三角形全等的判定
判定方法一
判定方法二
斜边和一条直角边对应相等的两个直角三 角形全等(HL)。
两个锐角对应相等的两个直角三角形,若 斜边相等,则这两个直角三角形全等。
判定方法三
注意事项
两个锐角对应相等的两个直角三角形,若 一条直角边相等,则这两个直角三角形全 等。
七年级数学 第13章《平面图形的认识》复习基础知识

C
D
B
03 多边形的知识
03 多边形的知识
1.n边形从一个顶点出发的对角线的条数(n-3)条,这些对角线把多边形分为(n-2)个三角形 2.n边形总的对角线条数为 3.n边形内角和=(n-2)·180°,正多边形一个内角= 4.任何多边形外角和都等于360°,正多边形一个外角=
03 多边形的知识
1.下列图形①等边三角形②直角三角形③平行四边形④正方形,其中正多边形的个数有
( )个
A.1
B.2
C.3
D.4
2.一个凸多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发的对角线
的条数是( )
A.9
B.8
C.7
D.6
提醒:请按下“暂停键”,完成后继续
03 多边形的知识
1.下列图形①等边三角形②直角三角形③平行四边形④正方形,其中正多
提醒:请按下“暂停键”,完成后继续
04 圆的知识
2 .已知⊙O的周长为10π .
(1)若PO=5.5,则点P与圆的位置关系是什么? (2)若PO = 4,则点P与圆的位置关系是什么? (3)若PO = ,则点P在圆上.
知识点:点与圆的三种位置关系
Or
(1)点在圆上:点到圆心的距离等于半径
(2)点在圆内:点到圆心的距离小于半径
(3)点在圆外:点到圆心的距离大于半径 思路分析:要想求点与圆的位置关系必须先求出圆的半径再与点到圆心的线段长度进行比较
解:2πr=10π 2r=10 r=5
(1)因为5.5>5,所以点P在圆外 (2)以为4<5,所以点P在圆内, (3)当PO=5时,即PO=r,点P在圆上
感谢聆听
EP
解析:因为AD平分∠BAC,所以∠PAB= ½ ∠CAB, 又因为BE平分∠ABC,所以∠PBA= ½ ∠CBA 因为∠C= 90º,所以∠CAB+∠CBA = 90º,
人教版数学八年级上册 第13章 基础复习题含答案
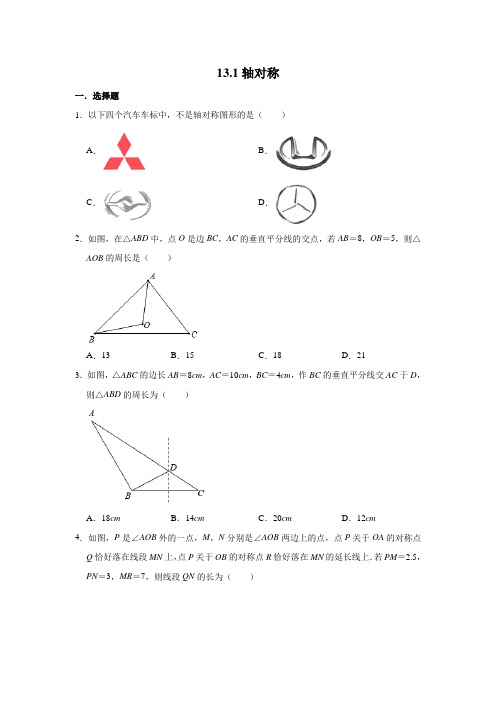
13.1轴对称一.选择题1.以下四个汽车车标中,不是轴对称图形的是()A.B.C.D.2.如图,在△ABD中,点O是边BC,AC的垂直平分线的交点,若AB=8,OB=5,则△AOB的周长是()A.13B.15C.18D.213.如图,△ABC的边长AB=8cm,AC=10cm,BC=4cm,作BC的垂直平分线交AC于D,则△ABD的周长为()A.18cm B.14cm C.20cm D.12cm4.如图,P是∠AOB外的一点,M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R恰好落在MN的延长线上.若PM=2.5,PN=3,MR=7,则线段QN的长为()A.1B.1.5C.2D.2.55.如图是台球桌面示意图,阴影部分表示四个入球孔,小明按图中方向击球(球可以多次反弹),则球最后落入的球袋是()A.1号袋B.2号袋C.3号袋D.4号袋6.如图,若△ABC与△A'B'C′关于直线MN对称,BB'交MN于点O.则下列说法中不一定正确的是()A.∠ABC=∠A'B'C′B.AA'⊥MNC.AB∥A′B′D.BO=B′O7.如图,有A、B、C三个居民小区,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在()A.∠A、∠B两内角的平分线的交点处B.AC、AB两边高线的交点处C.AC、AB两边中线的交点处D.AC、AB两边垂直平分线的交点处8.如图,△ABC和△AB'C'关于直线l对称,l交CC'于点D,若AB=4,B'C'=2,CD=0.5,则五边形ABCC′B'的周长为()A.14B.13C.12D.119.如图,在△ABC中,∠A=30°,∠C=110°,AB的垂直平分线交AB于点D,交边AC 于点E,则∠EBC的度数是()A.10°B.15°C.20°D.25°10.如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=35°,则∠A+∠C=()A.30°B.40°C.17.5°D.35°二.填空题11.如图,在△ABC中,DE是AC的垂直平分线,AE=3,△BCD的周长为13,则△ABC 的周长是.12.雨后,地上的积水犹如一块澄澈的平面镜,某路段监控摄像头在雨后拍摄,由于位置偏离,拍摄中心聚集在了水面上,摄像头侦测到一小轿车超速行驶,积水中倒映的车牌为“”,那么该小轿车的真实车牌号为.13.如图,△ABC与△DEF关于直线l对称,若∠A=65°,∠B=80°,则∠F=.14.如图,线段AB,BC的垂直平分线l1,l2交于点O.若∠B=35°,则∠AOC=°.15.已知:△ABC是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、O同时在不等边△ABC的内部时,那么∠BOC和∠BPC的数量关系是:∠BOC=.三.解答题16.如图,在ΔABC中,∠C=90°,DE是AB的垂直平分线.(1)若AC=5,BC=7,求ΔACD的周长;(2)若∠BAD:∠CAD=2:1,求∠B的度数.17.如图,在△ABE中,AD⊥BE于点D,C是BE上一点,BD=DC,且点C在AE的垂直平分线上,若△ABC的周长为18cm,求DE的长.18.如图所示,在△ABC中,AB,AC的垂直平分线分别交BC于D,E,垂足分别是M,N.(1)若△ADE的周长为6,求BC的长;(2)若∠BAC=100°,求∠DAE的度数.19.求证:到线段两端距离相等的点在线段的垂直平分线上.已知:;求证:.参考答案与试题解析一.选择题1.【解答】解:A、是轴对称图形,故此选项不合题意;B、是轴对称图形,故此选项不合题意;C、不是轴对称图形,故此选项符合题意;D、是轴对称图形,故此选项不合题意;故选:C.2.【解答】解:连接OC,∵点O是边BC,AC的垂直平分线的交点,∴OB=OC,OA=OC,∴OA=OB,∵OB=5,∴OA=OB=5,∵AB=8,∴△AOB的周长是AB+OA+OB=8+5+5=18,故选:C.3.【解答】解:∵BC的垂直平分线交AC于D,∴DB=DC,∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=8+10=18(cm),故选:A.4.【解答】解:∵点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R 落在MN的延长线上,∴PM=MQ,PN=NR,∵PM=2.5,PN=3,MR=7,∴RN=3,MN=MR﹣NR=7﹣3=4,MQ=MP=2.5,即NQ=MN﹣MQ=4﹣2.5=1.5,故选:B.5.【解答】解:如图所示,,球最后落入的球袋是2号袋,故选:B.6.【解答】解:∵△ABC与△A'B'C′关于直线MN对称,BB'交MN于点O,∴△ABC≌△A'B'C′,AA′⊥MN,OB=OB′∴∠ABC=∠A′B′C′,故A,B,D正确,故选:C.7.【解答】解:根据线段垂直平分线上的点到线段两个端点的距离相等,超市应建在AC、AB两边垂直平分线的交点处,故选:D.8.【解答】解:∵△ABC和△AB'C'关于直线l对称,l交CC'于点D,∴AB=AB′,BC=B′C′,DC=DC′,∵AB=4,B'C'=2,CD=0.5,∴AB′=4,BC=2,DC′=0.5,∴五边形ABCC′B'的周长为:4+2+0.5+0.5+2+4=13.故选:B.9.【解答】解:∵AB的垂直平分线交AB于点D,交边AC于点E,∴∠ABE=∠A=30°,∵∠A=30°,∠C=110°,∴∠ABC=180°﹣30°﹣110°=40°,∴∠EBC=40°﹣30°=10°,故选:A.10.【解答】解:连接OB,∵线段AB、BC的垂直平分线l1、l2相交于点O,∴AO=OB=OC,∴∠AOD=∠BOD,∠BOE=∠COE,∠A=∠ABO,∠C=∠CBO,∴∠A+∠C=∠ABC,∵∠DOE+∠1=180°,∠1=35°,∴∠DOE=145°,∴∠ABC=360°﹣∠DOE﹣∠BDO﹣∠BEO=35°;故选:D.二.填空题(共5小题)11.【解答】解:∵DE是AC的垂直平分线,AE=3,∴DA=DC,AC=2AE=6,∵△BCD的周长为13,∴BC+BD+CD=13,∴BC+BD+DA=BC+AB=13,∴△ABC的周长=BC+AB+AC=13+6=19,故答案为:19.12.【解答】解:利用轴对称的性质得出:该汽车牌照号码为:苏N2020N.故答案为:苏N2020N.13.【解答】解:∵∠A=65°,∠B=80°,∴∠C=180°﹣∠A﹣∠B=180°﹣65°﹣80°=35°,∵△ABC与△DEF关于直线l对称,∴∠C=∠F=35°,故答案为:35°.14.【解答】解:连接BO并延长,点D在BO的延长线上∵线段AB,BC的垂直平分线l1,l2交于点O,∴OA=OB,OC=OB,∴∠OAB=∠OBA,∠OCB=∠OBC,∴∠AOD=2∠ABO,∠COD=2∠CBO,∴∠AOC=∠AOD+∠COD=2(∠ABO+∠CBO)=70°,故答案为:70.15.【解答】解:∵BP平分∠ABC,CP平分∠ACB,∴∠PBC=∠ABC,∠PCB=∠ACB,∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(∠ABC+∠ACB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠BAC)=90°+∠BAC,即∠BAC=2∠BPC﹣180°;如图,连接AO.∵点O是这个三角形三边垂直平分线的交点,∴OA=OB=OC,∴∠OAB=∠OBA,∠OAC=∠OCA,∠OBC=∠OCB,∴∠AOB=180°﹣2∠OAB,∠AOC=180°﹣2∠OAC,∴∠BOC=360°﹣(∠AOB+∠AOC)=360°﹣(180°﹣2∠OAB+180°﹣2∠OAC),=2∠OAB+2∠OAC=2∠BAC=2(2∠BPC﹣180°)=4∠BPC﹣360°,故答案为:4∠BPC﹣360°.三.解答题(共4小题)16.【解答】解:(1)∵DE是AB的垂直平分线,∴DA=DB,∴ΔACD的周长=AC+CD+DA=AC+CD+DB+AC+CB=5+7=12;(2)∵DA=DB,∴∠BAD=∠B,设∠CAD=x,则∠BAD=∠B=2x,∵∠C=90°,∴∠CAB+∠B=90°,即x+2x+2x=90°,解得,x=18°,∴∠B=2x=36°.17.【解答】解:∵点C在AE的垂直平分线上,∴CA=CE,∵AD⊥BE,BD=DC,∴AB=AC,∵△ABC的周长为18,∴AB+BC+AC=18,∴2AC+2DC=18,∴AC+DC=9,∴DE=DC+CE=AC+CD=9(cm).18.【解答】解:(1)∵DM和EN分别垂直平分AB和AC,∴AD=BD,EA=EC,∵△ADE的周长为6,∴AD+DE+EA=6.∴BD+DE+EC=6,即BC=6;(2)∵DM和EN分别垂直平分AB和AC,∴AD=BD,EA=EC,∴∠B=∠BAD=∠ADE,∠C=∠EAC=∠AED.∵∠BAC=∠BAD+∠DAE+∠EAC=∠B+∠DAE+∠C=100°,∴∠B+∠C=100°﹣∠DAE,在△ADE中,∠DAE=180°﹣(∠ADE+∠AED)=180°﹣(2∠B+2∠C)∴∠DAE=180°﹣2(100°﹣∠DAE)∴∠DAE=20°.19.【解答】已知:如图,QA=QB,求证:点Q在线段AB的垂直平分线上.证明:当点Q在线段AB上时,∵QA=QB∴点Q为线段AB的中点,∴点Q在线段AB的垂直平分线上;当点Q在线段AB外时,过点Q作QM⊥AB,垂足为点M,如图,则∠QMA=∠QMB=90°,在Rt△QMA和Rt△QMB中,,∴Rt△QMA≌Rt△QMB(HL)13.2 画轴对称图形一.填空题1.在平面直角坐标系中,点A(a,﹣3)向左平移3个单位得点A′,若点A和A′关于y 轴对称,则a=.2.已知点P(﹣1,2),那么点P关于直线x=1的对称点Q的坐标是.3.如图,在平面直角坐标系中,已知点A的坐标为(4,4),若△ABC是关于直线y=1的轴对称图形,则点B的坐标为;若△ABC是关于直线y=a的轴对称图形,则点B的坐标为.4.若P关于x轴的对称点为(3,a),关于y轴对称的点为(b,2),则P点的坐标为.5.已知点A(a,2),B(﹣3,b)关于y轴对称,则ab=.6.若点P(3,﹣1)关于y轴的对称点Q的坐标是(a+b,1﹣b),则ab的值为.7.如果A(a﹣1,3),A′(4,b﹣2)关于x轴对称,则a=,b=.8.已知P1(a﹣1,5)和P2(2,b﹣1)关于x轴对称,则(a+b)2019的值为.9.如图,在平面直角坐标系中,一颗棋子从点P(0,﹣2)处开始依次关于点A(﹣1,﹣1),B(1,2),C(2,1)作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…,如此下去.则经过第2011次跳动之后,棋子落点的坐标为.10.已知P1点关于x轴的对称点P2(3﹣2a,2a﹣5)是第三象限内的整点(横、纵坐标都为整数的点,称为整点),则P1点的坐标是.二.解答题11.在平面直角坐标系xOy中,△ABC的位置如图所示.(1)顶点A关于x轴对称的点的坐标A'(,),顶点C先向右平移3个单位,再向下平移2个单位后的坐标C'(,);(2)将△ABC的纵坐标保持不变,横坐标分别乘﹣1得△DEF,请你直接画出图形;(3)在平面直角坐标系xOy中有一点P,使得△ABC与△PBC全等,这样的P点有个.(A点除外)12.在直角坐标系中,△ABC的顶点坐标如图所示,(1)请你在图中先作出△ABC关于直线m(直线m上点的横坐标均为﹣1)对称图形△A1B1C1,再作出△A1B1C1关于直线n(直线n上点的纵坐标均为2)对称图形△A2B2C2;(2)线段BC上有一点M(a,b),点M关于直线m的对称点为N,点N关于直线的n 的对称点为E,求N、E的坐标(用含a,b的代数式表示).13.如图,在棋盘中有A(﹣1,1)、O(0,0)、B(1,0)三个棋子,若再添加一个棋子A、O、B、P四个棋子成为一个轴对称图形,请在三个图中分别画出三种不同的对称轴分别写出棋子P的坐标.14.已知△ABC,A(﹣4,1)、B(﹣1,﹣1)、C(﹣3,2).(1)请在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;(2)请在同一平面直角坐标系中画出△A1B1C1关于直线m(直线m上各点的横坐标都是1)对称的△A2B2C2,并直接写出点A2,C2的坐标;(3)直接写出△ABC边上一点M(x,y),经过上述两次图形变换后得到△A2B2C2上的对应点M2的坐标.15.在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在如图给出的图中画出4个这样的△DEF.(每个3×3正方形格点图中限画一种,若两个图形中的对称轴是平行的,则视为一种)16.如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).(1)在图中画出△ABC关于x轴对称的△A'B'C'并在下面填写出点A',B',C'的坐标:A'(,);B'(,);C'(,).(2)求出△ABC的面积为(填出结果即可)17.如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);点A关于x轴对称的点坐标为点B关于y轴对称的点坐标为点C关于原点对称的点坐标为(2)若网格上的每个小正方形的边长为1,则△ABC的面积是.参考答案一.填空题1.1.5.2.(3,2).3.(4,﹣2),(4,2a﹣4).4.(3,2).5.6.6.﹣10.7.a=5,b=﹣1.8.﹣1.9.(﹣2,0).10.(﹣1,1).二.解答题11.解:(1)∵A(﹣4,3),C(﹣2,5),∴A′(﹣4,﹣3),C'(1,3);故答案为:﹣4,﹣3;1,3;(2)如图所示:即为所求;(3)△ABC与△PBC全等,这样的P点有3个.故答案为:3.12.解:(1)如图所示,△A1B1C1,△A2B2C2即为所求;(2)设点N的坐标为(x,y),点E的坐标为(p,q),∵点M与点N关于直线m对称,∴=﹣1,y=b,解得x=﹣2﹣a,y=b,∴点N的坐标为(﹣2﹣a,b),又∵点N与点E关于直线n对称,∴p=﹣2﹣a,=2,解得p=﹣2﹣a,q=4﹣b,∴点E的坐标为(﹣2﹣a,4﹣b).13.解:如图所示,棋子P的坐标分别为(﹣1,﹣1),(2,1),(0,﹣1),(﹣1,2).(答案不唯一)14.解:(1)如图所示,△A1B1C1即为所求;(2)如图所示,△A2B2C2即为所求,点A2,C2的坐标分别为(6,﹣1)和(5,﹣2);(3)点M(x,y)关于x轴对称的点M1的坐标为(x,﹣y),点M1关于直线m对称的点M2的坐标为(﹣x+2,﹣y).∴经过上述两次图形变换后得到△A2B2C2上的对应点M2的坐标为(﹣x+2,﹣y).15.解:如图,△DEF即为所求.(答案不唯一)16.解:(1)如图所示,△A'B'C'即为所求:由图可得:A'(2,﹣4);B'(﹣3,2);C'(3,﹣1).故答案为:2,﹣4;﹣3,2;3,﹣1.(2)△ABC的面积为:6×6﹣×1×3﹣×3×6﹣×5×6=36﹣﹣9﹣15=10.故答案为:10.17.解:(1)点A关于x轴对称的点坐标为(﹣1,﹣3);点B关于y轴对称的点坐标为:(﹣2,0);点C关于原点对称的点坐标为:(3,1);故答案为:(﹣1,﹣3),(﹣2,0),(3,1);(2)△ABC的面积是:4×5﹣×2×4﹣×3×3﹣×1×5=9.故答案为:9.13.3等腰三角形一.选择题1.等腰三角形的一边长为6,一边长为2,则该等腰三角形的周长为()A.8B.10C.14D.10或142.在△ABC中,∠B=∠C,∠A=20°,则∠B的大小为()A.20°B.70°C.80°D.160°3.如图,△ABC是等边三角形,D是AC边的中点,延长BC到点E,使CE=CD,连接DE,则下列结论错误是()A.CE=AB B.BD=ED C.∠BDE=∠DCE D.∠ADE=120°4.下列条件不能得到等边三角形的是()A.有一个内角是60°的锐角三角形B.有一个内角是60°的等腰三角形C.顶角和底角相等的等腰三角形D.腰和底边相等的等腰三角形5.已知一个等腰三角形的两边长分别为2cm和4cm,那么该等腰三角形的周长为()A.8cm B.10cm C.8cm或10cm D.不能确定6.三个等边三角形的摆放位置如图所示,若∠1+∠2=110°,则∠3的度数为()A.90°B.70°C.45°D.30°7.如图,点D在△ABC的边AC上,且AD=BD=CD,若∠A=40°,则∠C=()A.40°B.50°C.60°D.45°8.如图,已知OC=CD=DE,且∠BDE=72°,则∠CDE的度数是()A.63°B.65°C.75°D.84°9.如图,在△ABC中,∠BAC=90°,AB=6,AC=8,BC=10,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是()①△ABE的面积=△BCE的面积;②∠AFG=∠AGF;③∠F AG=2∠ACF;④AD=2.4.A.①②③④B.①②③C.①②④D.③④10.已知三个城镇中心A、B、C恰好位于等边三角形的三个顶点,在A、B、C之间铺设光缆连接,实线为所铺的路线,四种方案中光缆铺设路线最短的是()A.B.C.D.二.填空题11.如果一等腰三角形的顶角为钝角,过这个等腰三角形的一个顶点的直线将这个等腰三角形分成两个等腰三角形,那么这个等腰三角形的顶角的度数为.12.已知O为平面直角坐标系的坐标原点,等腰三角形△AOB中,A(2,4),点B是x轴上的点,则△AOB的面积为.13.等腰三角形的一个内角为130°,则这个等腰三角形顶角的度数为.14.在△ABC中,AD为∠BAC的角平分线,AB∥DE,AC=7,CD=3,则△CDE的周长为.15.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若AB=6,AC=8,则△AMN的周长为.三.解答题16.如图,已知AD平分∠EAC,且AD∥BC,求证AB=AC.17.如图,在△ABC中,线段AB、AC的垂直平分线分别交BC于点P、Q两点,且BP=PQ=QC.试证明△APQ为等边三角形.18.用一条长为20cm的细绳能围成有一边的长为4cm的等腰三角形吗?说明理由.19.在△ABC中,∠B=∠C,点D在BC上,点E在AC上,连接DE且∠ADE=∠AED.{计算发现}(1)若∠B=70°,∠ADE=80°,则∠BAD=,∠CDE=.{猜想验证}(2)当点D在BC(点B,C除外)边上运动时(如图1),且点E在AC边上,猜想∠BAD与∠CDE的数量关系式,并证明你的猜想.{拓展思考}(3)①当点D在BC(点B,C除外)边上运动时(如图2),且点E在AC边上,若∠BAD=25°,则∠CDE=.②当点D在BC(点B,C除外)边上运动时(如图2),且点E在AC边所在的直线上,若∠BAD=25°,则∠CDE=.参考答案与试题解析一.选择题1.【解答】解:①当2为底时,其它两边都为6,2、6、6可以构成三角形,则该等腰三角形的周长为14;②当2为腰时,其它两边为2和6,∵2+2<6,∴不能构成三角形,故舍去.∴这个等腰三角形的周长为14.故选:C.2.【解答】解:因为三角形的内角和是180°,∠A=20°,∠B=∠C,那么∠B=(180°﹣20°)=80°.故选:C.3.【解答】解:∵△ABC是等边三角形,D是AC边的中点,∴AB=AC,CD=AC,∴CD=AB,∵CE=CD,∴CE=AB,A选项结论正确,不符合题意;∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,∵D是AC边的中点,∴∠DBC=30°,∵CD=CE,∴∠E=∠EDC=∠ACB=30°,∴∠DBC=∠E,∴BD=ED,B选项结论正确,不符合题意;∵△ABC是等边三角形,D是AC边的中点,∴∠BDC=90°,∴∠BDE=120°,∵∠DCE=120°﹣∠ACB=120°,∴∠BDE=∠DCE,C选项结论正确,不符合题意;∠ADE=180°﹣30°=150°,D选项错误,符合题意;故选:D.4.【解答】解:因为有一个内角是60°的等腰三角形是等边三角形,所以A选项符合题意;所以B选项不符合题意;因为顶角和底角相等的等腰三角形是等边三角形,所以C不符合题意;因为腰和底边相等的等腰三角形是等边三角形,所以D选项不符合题意.故选:A.5.【解答】解:当4cm的边长为腰时,三角形的三边长为:4cm、4cm、2cm,满足三角形的三边关系,其周长为4+2+4=10(cm),当2cm的边长为腰时,三角形的三边长为:2cm、2cm、4cm,此时4=2+2,不满足三角形的三边关系,所以此时不存在三角形,故选:B.6.【解答】解:如图,∵∠3+∠6+60°=180°,∠2+∠4+60°=180°,∠1+∠5+60°=180°,∴∠1+∠2+∠3+∠4+∠5+∠6=540°﹣180°,∴∠3=180°﹣(∠1+∠2)=70°,故选:B.7.【解答】解:∵AD=BD=CD,∴∠ABD=∠A,∠C=∠DBC,∵∠A=40°,∴∠C=(180°﹣40°×2)÷2=50°.故选:B.8.【解答】解:∵OC=CD=DE,∴∠O=∠ODC,∠DCE=∠DEC,∴∠DCE=∠O+∠ODC=2∠ODC,∵∠O+∠OED=3∠ODC=∠BDE=72°,∴∠ODC=24°,∵∠CDE+∠ODC=180°﹣∠BDE=108°,∴∠CDE=108°﹣∠ODC=84°.故选:D.9.【解答】解:∵BE是中线,∴AE=CE,∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故①正确;∵CF是角平分线,∴∠ACF=∠BCF,∵AD为高,∴∠ADC=90°,∵∠BAC=90°,∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,∴∠ABC=∠CAD,∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,∴∠AFG=∠AGF,故②正确;∵AD为高,∴∠ADB=90°,∵∠BAC=90°,∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,∴∠ACB=∠BAD,∵CF是∠ACB的平分线,∴∠ACB=2∠ACF,∴∠BAD=2∠ACF,即∠F AG=2∠ACF,故③正确;∵∠BAC=90°,AD是高,=ABAC=ADBC,∴S△ABC∵AB=6,AC=8,BC=10,∴AD==4.8,故④错误,故选:B.10.【解答】解:设等边三角形ABC的边长为a,A、铺设的电缆长为a+a=2a;C、如图1:∵△ABC为等边三角形,AD⊥BC,∴D为BC的中点,∴BD=DC=BC=a,在Rt△ABD中,根据勾股定理得:AD===,则铺设的电缆长为a+a=a;B、由垂线段最短得:方案B中光缆比方案C中长;D、如图2所示,∵△ABC为等边三角形,且O为三角形三条高的交点,∴设DO=x,则BO=2x,BD=,故x2+()2=(2x)2,解得:x=a,则BO=a,则铺设的电缆长为AO+OB+OC=3×a=a,∵a<a<2a,∴方案D中光缆最短;故选:D.二.填空题(共5小题)11.【解答】解:①如图,∠ACB是钝角,直线CD将这个等腰三角形分成两个等腰三角形,AC=BC=BD,AD=CD,设∠B=x°,∵AC=BC,∴∠A=∠B=x°,∵AD=CD,∴∠ACD=∠A=x°,∴∠BDC=∠A+∠ACD=2x°,∵BC=BD,∴∠BCD=∠BDC=2x°,∴∠ACB=3x°,∴x+x+3x=180,解得x=36°,∴顶角是108°.②若过A或B作直线,则不能将这个等腰三角形分成两个等腰三角形.综上所述,这个等腰三角形的顶角的度数为108°.故答案为:108°.12.【解答】解:如图所示:过点A作AE⊥x轴于点E,∵点O(0,0),A(2,4),∴AE=4,OE=2,OA==2,=AE==8;当OA=AB时,B的坐标为(4,0),此时S△AOB当OA=OB时,B的坐标为(,0),此时S=AE=×4=4;△AOB=AE==10;当OB=AB时,B的坐标为(5,0),此时S△AOB∴△AOB的面积为:8或4或10.故答案为:8或4或10.13.【解答】解:∵若这个130°的内角是底角,则这两个底角的和就大于180°,∴等腰三角形的一个内角为130°,则这个等腰三角形顶角的度数为130°,故答案为130°.14.【解答】解:∵AD为∠BAC的角平分线,∴∠BAD=∠CAD,∵AB∥DE,∴∠BAD=∠ADE,∴∠DAE=∠ADE,∴AE=DE,∴△CDE的周长=CE+DE+CD=AE+CE+CD=AC+CD,∵AC=7,CD=3,∴△CDE的周长为7+3=10,故答案为:10.15.【解答】解:∵EB平分∠ABC,∴∠ABE=∠EBC,∵MN∥BC,∴∠EBC=∠BEM,∴∠ABE=∠BEM,∴BM=EM同理可得CN=EN,∴△AMN的周长=AM+ME+EN+AN=AM+BM+CN+AN=AB+AC,∵AB=6,AC=8,∴△AMN的周长=6+8=14,故答案为:14.三.解答题(共4小题)16.【解答】证明:∵AD平分∠EAC,∴∠1=∠2,∵AD∥BC,∴∠1=∠B,∠2=∠C,∴∠B=∠C,∴AB=AC.17.【解答】证明:∵线段AB、AC的垂直平分线分别交BC于点P、Q两点,∴BP=AP,QC=AQ,∵BP=PQ=QC,∴AP=AQ=PQ,∴△APQ是等边三角形.18.【解答】解:能围成有一边的长为4cm的等腰三角形.理由:若腰长为4cm,则底边长为20﹣2×4=12(cm),∵4+4+<12,∴不能围成腰长为4cm的等腰三角形;若底边长为4cm,则腰长为×(20﹣4)=8(cm),∵4+8>8,∴能围成底边长为4cm的等腰三角形,综上,可以围成底边是4cm的等腰三角形.19.【解答】解:(1)∵∠B=∠C,∠ADE=∠AED,∠B=70°,∠ADE=80°,∴∠C=70°,∠AED=80°,∴∠CDE=∠AED﹣∠C=10°,∠DAE=180°﹣∠ADE﹣∠AED=20°,∴∠BAD=180°﹣∠B﹣∠C﹣∠DAE=20°,故答案为:20°;10°;(2)∠BAD=2∠CDE.理由如下:设∠B=x,∠ADE=y,∵∠B=∠C,∴∠C=x,∵∠AED=∠ADE,∴∠AED=y,∴∠CDE=∠AED﹣∠C=y﹣x,∠DAE=180°﹣∠ADE﹣∠AED=180°﹣2y,∴∠BAD=180°﹣∠B﹣∠C﹣∠DAE=180°﹣x﹣x﹣(180°﹣2y)=2(y﹣x),∴∠BAD=2∠CDE;(3)①由(2)知,∠BAD=2∠CDE,∴∠CDE=∠BAD=,故答案为:12.5°;②当E点在AC的延长线上时,AD<AC<AE,此时∠ADE≠∠AED,故点E不可能在AC的延长线上,分两种情况:当点E在线段AC上时,与①相同,∠CDE=12.5°;当点E在CA的延长线上时,如图2,在AC边上截取AE′=AE,连接DE′,∵∠ADE =∠AED,∴AE=AD=AE′,∴∠ADE=∠AE′D,由①知,∠CDE′=12.5°,∴∠ADE+∠ADE′=∠AED+∠AE′D,∵∠ADE+∠ADE′+∠AED+∠AE′D=180°。
汽车机械基础课件 第13章 平面机构

第十三章 平面机构
• 13.1 • 13.2 • 13.3
平面机构运动分析 平面连杆机构 凸轮机构
2024/9/2
汽车机械基础
第十三章
平面机构
• 学习目标: • 1.了解机构及运动副的概念;知道平面机构运动简
图的绘制;
• 2.掌握平面机构自由度的计算; • 3.熟练掌握铰链四杆机构基本形式、演化及应用; • 4.掌握平面四杆机构的基本特性; • 5.熟悉凸轮机构的应用和分类; • 6.认识凸轮机构的工作过程及从动件的运动规律;
2024/9/2
汽车机械基础
13.1平面机构运动分析
• 13.1.1 机构的组成 • 13.1.2 运动副及分类 • 13.1.3 自由度及约束 • 13.1.4 机构运动简图及绘制 • 13.1.5 平面机构自由度的计算 • 13.1.6 平面机构具有确定运动的条件
2024/9/2
汽车机械基础
体,消除局部自由度,再去除掉移动副
E和 E′中的一个虚约束,C处复合铰链
含有二个转动副。则可得该机构的可动
件数n=7, PL=9(其中有2个移动副、 7 个转动副), PH=1。由公式(13—
1)可得该机构的自由度F为:
F=3n - 2PL - PH =3×7 -2×9 -1 =2
汽车机械基础
13.2平面连杆机构
活动构件数 n
构件总自由度 3×n
低副约束数 2 × PL
高副约束数 1 × Ph
计算公式: F=3n-(2PL +Ph )
• 由前述可知,曲轴4与齿轮4′、齿轮6′与凸轮6均都是固连
成一个构件,因此该机构共有6个构件,即N=6, n=6-1=5 。另外,机构中有2 个移动副、4个转动副和2个高副,则PL =6,PH=2,由公式可得该机构的自由度F为
基础护理学第13章考试题及答案

基础护理学第13章考试题及答案
一、填空题。
1、常用的晶体溶液有(葡萄糖溶液)、(等渗电解质溶液)、(碱性溶液)、(高渗溶液)。
2、常用的胶体溶液有(右旋糖酐溶液)、(代血浆)、(血液制品)。
3、输入溶液通常遵循(先晶后胶)、(先盐后糖)、(宁酸勿碱)的原则。
补钾应遵循“四不宜”原则:(不宜过浓)、(不宜过快)、(不宜过多)、(不宜过早)。
4、常见的输液反应有(发热反应)、(循环负荷过重反应)、(静脉炎)、(空气栓塞)。
5、库存血在(4℃)环境下可以保存(2~3周)。
6、常见的输血反应有(发热反应)、(过敏反应)、(溶血反应)、(与大量输血有关的反应)和其他。
7、静脉炎主要是长期输注(高浓度)、(刺激性较强)的药液,或静脉内放置刺激性较强的塑料导管时间过长,引起局部静脉壁发生(化学炎性反应)。
8、发现空气栓塞后应立即将患者置于(左侧卧位)卧位,并保持(头低脚高)位,该体位有助于气体浮向(右心室尖部),避免阻塞(肺动脉入口).
9、严重感染的患者应输入(新鲜血)以补充抗体和补体,切忌使用(库存血)。
10、血液自血库取出后,勿(剧烈震荡),以免红细胞破坏而引
起(溶血)。
二、名词解释。
1、静脉输液:是将大量无菌溶液或药物直接输入静脉的治疗方法。
2、全血:指采集的血液未经任何加工而全部保存备用的血液。
3、溶血反应:是受血者或供血者的红细胞发生异常破坏或溶解引起的一系列临床症状。
4、大量输血:一般是指在24小时内紧急输血量相当于或大于患者总血容量。
5、静脉输血:是将全血或成分血如血浆、红细胞、白细胞或血小板等通过静脉输入体内的方法。
第13章第3节 比热容(第2课时:热量的计算)习题PPT课件(人教版)

A.3∶8
B.8∶3
C.4∶3
D.3∶2
返回
物理
9.甲、乙两个物体的比热容之比为 2∶1,升温之比为 1∶3,
吸热之比为 2∶3,甲、乙的质量之比为( D )
A.1∶6
B.2∶1
C.1∶4
D.1∶1
返回
物理
10.对质量是 50 g 的水加热,使水温从 40 ℃升高到 80 ℃, 水吸收的热量是 8.4×103 J[c 水=4.2×103 J/(kg·℃)]. 11.有一根烧红的铁钉,质量是 2 g,放出 920 J 的热量后, 温度降低到 20 ℃,则铁钉的初温是 1 020 ℃. [铁的比热容是 0.46×103 J/(kg·℃)]
返回
物理 12.质量为 0.5 kg 的某金属块,当温度从 110 ℃降低到 80 ℃
时,放出了 5 850 J 热量.
物质 比热容 c[J/(kg·℃)]
铁
0.46×103
铜
0.39×103
汞
0.14×103
(1)该金属的比热容是多少?
(2)它可能是哪种金属?
返回
物理
解:(ቤተ መጻሕፍቲ ባይዱ)根据 Q 放=cmΔt=cm(t0-t)可得,金属的比热容:
返回
物理 (2)将煅烧后的刀具迅速取出放入 20 ℃的水中冷却,最后刀具 与水达到共同的温度,设为 t′, 则有:Q 水吸=Q 合放,即:c 水 m 水(t′-t0′)=c 合金钢 m 合金钢(t-t′), 代入数据:4.2×103 J/(kg·℃)×5 kg×(t′-20 ℃)=0.42×103 J/(kg·℃)×1 kg×(836 ℃-t′), 解得:t′=36 ℃. 答:(1)此刀具在火炉中吸收了 3.4272×105 J 的热量;(2)淬火 后水的温度为 36 ℃.
第十三章 国家重点区域发展规划与政策(new)第十三章 基础练习题综合练习与答案

第十三章国家重点区域发展规划与政策(new)第十三章基础练习题综合练习与答案一、单选题1、京津冀协同发展的空间布局是()A.一核.双城.三轴.四区.多节点B.一核.双轴.三城.四区.多节点C.一核.两区.三轴.四城.多节点D.一核.双城.三轴.四区.五节点【参考答案】:A【试题解析】:京津冀协同发展的空间布局是“一核、双城、三轴、四区、多节点”。
2、下列有关“西部大开发战略”到2020年总体指导思想的表述错误的是()。
A.进一步解放思想.开拓创新B.进一步加大投入.强化支持C.使“三基地.一枢纽”地位更加巩固D.更加注重优化区域布局,着力培育新的经济增长极【参考答案】:C【试题解析】:本题考查的是西部大开发战略。
选项C错误,使“三基地、一枢纽”地位更加巩固是促进中部地区崛起的战略目标。
参见教材P312。
3、在西部大开发总体规划的三个阶段中,增强部分率先发展地区的实力,普遍提高西部人民的生产.生活水平,全面缩小差距的阶段是()。
A.奠定基础阶段B.加速发展阶段C.冲刺发展阶段D.全面推进现代化阶段【参考答案】:D【试题解析】:本题考查的是西部大开发战略。
全面推进现代化阶段。
从2031年到2050年,在一部分率先发展地区增强实力,融入国内国际现代化经济体系自我发展的基础上,着力加快边远山区.落后农牧区开发,普遍提高西部人民的生产.生活水平,全面缩小差距。
参见教材P301。
4、关于西部大开发总体规划的阶段划分的说法,错误的是()。
A.思想准备阶段,从1991年到2000年B.奠定基础阶段,从2001年到2010年C.加速发展阶段,从2010年到2030年D.全面推进现代化阶段,从2031年到2050年【参考答案】:A【试题解析】:西部大开发总体规划可按50年划分为三个阶段:(1)奠定基础阶段。
从2001年到2010年。
(2)加速发展阶段。
从2010年到2030年。
(3)全面推进现代化阶段。
从2031年到2050年。
_新教材高中数学第13章立体几何初步2

3.垂直于梯形两腰的直线与梯形所在平面的位置关系是( ) A.垂直 B.相交但不垂直 C.平行 D.不确定
【解析】选 A.因为梯形两腰所在直线为两条相交直线,所以由线面垂直的判定定理 知,直线与平面垂直.
4.直线 l 与平面 α 内的无数条直线垂直,则直线 l 与平面 α 的关系是( ) A.l 和平面 α 相互平行 B.l 和平面 α 相互垂直 C.l 在平面 α 内 D.不能确定
【解析】由线面垂直的判定定理可知①③能判定,而②中线面可能平行、相交、还可 能线在平面内,④中由于正六边形的两边可能平行,所以也无法判定线面垂直. 答案:①③
四、解答题 10.如图所示,在三棱柱 ABC-A1B1C1 中,侧棱 AA1⊥底面 ABC,AB=AC=1,AA1 =2,∠B1A1C1=90°,D 为 BB1 的中点.求证:AD⊥平面 A1DC1.
【证明】(1)因为 PA⊥平面 ABCD,BC⊂平面 ABCD,所以 PA⊥BC.又 AB⊥BC,PA∩AB =A, 所以 BC⊥平面 PAB,因为 AE⊂平面 PAB,所以 AE⊥BC.又 AE⊥PB,PB∩BC=B, 所以 AE⊥平面 PBC,因为 PC⊂平面 PBC,所以 AE⊥PC.又因为 PC⊥AF,AE∩AF =A,所以 PC⊥平面 AEF. (2)由(1)知 PC⊥平面 AEF,所以 PC⊥AG,因为 CD⊥平面 PAD,AG⊂平面 PAD, 所以 CD⊥AG,PC∩CD=C,所以 AG⊥平面 PCD,PD⊂平面 PCD,所以 AG⊥PD.
对于④,由图形可以看出,B 到线段 EF 的距离与 A 到 EF 的距离不相等,故△ AEF 的面积与△ BEF 的面积不相等,故④错误. 答案:①②③
7.如图,PA⊥平面 ABCD,底面 ABCD 为矩形,AE⊥PB 于 E,AF⊥PC 于 F.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#include <iostream.h> int a=10; void main() { float a=3.14; cout<<”a=”<<::a<<endl; } 输出结果为a=10 C++通过作用域运算符“::” 来使用全局变量a
13.2.5 变量的引用
(1)引用的概念
引用是以别名的方式来使用另一变量或常量,其作用是为变 量取一个别名。 – 引用的声明格式: 类型标识符 &引用名; 其中&为引用声明符,不是取地址。 – 例如: int a; int &b=a; b是a的引用,亦即b是a的别名,对b的任何操作就是对a 的操作。a和b具有相同的存储单元,只是名称不同而 已,b就是a本身。
上一页 下一页
13.2.3 const常量定义与使用
• C语言中,用define宏定义来定义常量。但在编译预处 理时将符号常量用其后的常量作简单的替换,易出现 意想不到的问题。 – 例如: #define N 2 #define M N+1 #define NUM (M+1)*M/2 通常将NUM的值看成6:NUM=(3+1)*3/2=6 实际上编译预处理后其值:NUM=(2+1+1)*2+1/2=8 • C++常量定义格式为: const 类型标识符 常量标识符=常量表达式; const解决了上述问题,它定义的常量可以用指针操作
上一页 下一页
不带参数(定义在iostream.h中)与带参数的 格式控制操作符(定义在iomanip.h中):
① dec以十进制形式输入或输出整数; ② oct以八进制形式输入或输出整数; ③ hex以十六进制形式输入或输出整数; ④ ws用于输入时跳过开头的空白符; ⑤ endl用于输出时换行; ⑥ ends用于输出时插入空格字符; ⑦ setbase(int n)基数转换成n(n的取值为0,8,10或16),可用于 输入和输出; ⑧ setw(int n)设置域宽为n,可用于输入和输出; ⑨ setfill(int c)设置填充字符为c,可用于输出; ⑩ setprecision(int n)设置精度为n位,可用于输入和输出,但用于 输入时应多加一位。
上一页
下一页
例13.4 输入一个班学生的C语言成绩(最多40 人),求全班平均成绩。
#include <iostream.h> const int MaxN=40; // MaxN表示每班最多人数 void main( ) { float sum=0; // sum存放学生的总成绩 for (int n=1;n<=MaxN;n++) //使用前定义n { float score; cout<<“\n输入第“<< n <<“名学生分数:”; cin>>score; sum+=score; { cout<<“继续吗?”; char y_or_n; // C语言要求这种变量定义必须在块开始 cin>>y_or_n; if (y_or_n = =‟N‟|| y_or_n = =‟n‟) break;} } cout<<“\n学生人数为:”<<n<<endl<<“平均成绩为:"<<sum/n<<endl; } 上一页 下一页
上一页 下一页
13.2 C++对C语言的扩充
• C++的输入输出 • C++的行注释 • const常量定义与使用 • 局部变量的定义与全局变量的作用域运算符
• 变量的引用
• 函数重载 • 带缺省参数的函数 • 内联函数 • new和delete算符
上一页 下一页
13.2.1 C++的输入输出
• 在头文件iostream.h中, C++提供了标准流:
上一页 下一页
13.2.2 C++的行注释
• 注释界限符:/*和*/
“/*…*/”注释方式不能嵌套
• 单行注释符: //
注释自“//”开始至行尾,适合于不超过一行的注释。 main( ) 该注释方 { /*main( )函数 式不允许 /*嵌套注释。*/ */ … /* main( )函数 该注释方 式允许 //嵌套注释。 */ … }
下一页
class
delete
new reinterpre t_cast try
上一页
(2) 数据描述
• 在C++中,结构、联合和枚举类型名可直接作类 型名定义变量
如:struct STUDENT { char name[20]; /*学生姓名*/ char num[10]; /*学生学号*/ int score; /*成绩*/ }; – C++中类型变量定义形式: STUDENT lisi; – C语言中该类型变量定义形式: struct STUDENT lisi;
上一页 下一页
(2)用标准输入流cin进行输入
• 从键盘输入数据时,使用cin与提取运算符 >>从输入流中提取数据。
– 例如: int a; float x; cin>>a>>x; //相当于scanf(“%d%f ”, &a,&x); 连续输入多个量值时,各值以空格或回车分 隔。
上一页
下一页
例13.1 流cin与cout的使用
上一页 下一页
• 在使用引用时,应注意以下几个方面:
①创建一个引用时必须将其初始化成对某一具 体变量或常量的引用; ②程序中不能改变引用对象,即不能改变成对 另一变量或常量的引用;
③必须确保引用是和一个合法的存储单元相连;
④对常量的别名引用必须是const类型的引用。
上一页
下一页
(2)引用作为函数参数 • C语言中,函数的参数传递有两种:
例如:下面的操作都是错误的。 str=”Changsha”; str[2]=‟A‟;
上一页
下一页
13.2.4 局部变量的定义与全局变量作用域运算符
(1) 局部变量的定义
C++语言把局部变量的定义看成是执行语 句,只要在局部变量首次使用前已定义即 可。这样,可将变量定义置于使用该变量 的语句之前,便于阅读和修改。
– 但str没有定义为指向常量,其所指的值可以改 变。
例如:str[0]=‟S‟;是合法的。
上一页 下一页
(3)指向常量的常指针,指针和它所指的对象都 为常量
const 类型标识符 *const 变量名=常量;
例如:const char *const str=”China”;
指针str不能指向”China”以外的字符串,也不能 改变指针所指的对象
上一页 下一页
(2)指针为常量,称为指针常量,定义格式为: 类型标识符 * const 指针变量名=常量;
例如:
char *const str=”China”; 不能写为:char const *str=”China”;
– str是一个常量,不能修改str的值。
例:str=”Changsha”; 在C++中是非法的。
第 13 章
13.1 13.2 C++概述
C++基础
C++对C语言的扩充
13.3
C++面向对象程序设计
13.1 C++概述
(1) 保留字
(2) 数据描述 (3) C与C++亦有不同之处
上一页
下一页
• C++是从C语言的基础上发展而来的 • C语言编写的程序可以在C++下使用
– C语言源程序文件的扩展名为.C – C++源程序文件的扩展名一般为.cpp
上一页 下一页
• cout通过控制符setw来设置。 – 格式为:setw(n) 表明要为后续的一个输出项预留n列。如输出项长度 不够n,则数据右对齐;如超过n列,则按实际长度 输出。 – 例如: cout<<”a=”<<setw(4)<<a<<”b=”<<b <<endl <<”a+b=”<<a+b<<endl <<”x=”<<setw(3)<<x<<endl; 输出结果为: a=□□□5b=10 //□代表空格 a+b=15 x=3.14159
(2) 全局变量作用域运算符::
例13.5 变量作用域示例。 include <stdio.h> int a=10; main() { float a=3.14; printf(“a=%f\n”,a); } 输出结果为:3.140000 • C语言规定:局部变量与全局 变量同名时,在局部变量作 用域内,全局变量被屏蔽。
(1)用标准输出流cout 进行输出
– 格式: cout<<输出项; “<<”叫插入运算符,将输出项插入到输出流中 例如: cout<<” This is a C++ Program\n” ; 相当于语句: printf(” This is a C++ Program\n”);
上一页
下一页
• cout允许使用多个插入运算符“<<”将多个输出项插 入到输出流中。 • 插入运算符<<的结合方向是自左向右。 – 例如: int a=15,b=32; cout<<”a=”<<a<<‟\n‟<<”b=”<<b<<‟\n‟; 输出结果为: a=15 b=32 • 在iostream.h中,定义了一个与’\n‟相同的控制字符 endl。 cout<<”a=”<<a<<endl<<”b=”<<b<<endl ;
